安徽省淮南市2015届高三第一次模拟考试文科综合试题(扫描版)
2015届淮南市高三一模语文试卷

淮南市2015届高考第一次模拟考试语文试题第I卷(阅读题,共66分)一、(9分)阅读下面的文字,完成1 ~ 3题。
①现代德国哲学家斯播格耐在他的名著《西方之衰落》里面曾经阐明每一种独立的文化都有它的基本象征物,具体地表象它的基本精神。
在埃及是“路”,在希腊是“立体”,在近代欧洲文化是“无尽的空间”。
这三种基本象征都是取之于空间境界,而他们最具体的表现是在艺术里面。
埃及金字塔里的甬道,希腊的雕像,近代欧洲的最大油画家伦勃朗的风景,是我们领悟这三种文化的最深的灵魂之媒介。
②我们若用这个观点来考察中国艺术,尤其是画与诗中所表现的空间意识,再拿来同别种文化作比较,是一极有趣味的事。
③西洋十四世纪文艺复兴初期油画家梵埃格的画极注重写实,精细地描写人体,画面上表现屋宇内的空间,画家用科学及数学的眼光看世界。
于是透视法的知识被发挥出来,而用之于绘画。
④中国十八世纪雍正、乾隆时,名画家邹一桂对于西洋透视画法表示惊异而持不同情的态度,邹一桂认为西洋的透视的写实的画法“笔法全无,虽工亦匠”,只是一种技巧,与真正的绘画艺术没有关系,所以“不入画品”。
而能够入画品的画,即能“成画”的画,应是不采取西洋透视法的立场,而采沈括所说的“以大观小之法”。
⑤早在宋代一位博学家沈括在他名著《梦溪笔谈》里就曾讥评大画家李成采用透视立场“仰画飞檐”,而主张“以大观小之法”。
他说:“李成画山上亭馆及楼阁之类,皆仰画飞檐。
其说以谓‘自下望上,如人立平地望塔檐间,见其榱桷’。
此论非也。
”沈括以为画家画山水,并非如常人站在平地上在一个固定的地点,仰首看山;而是用心灵的眼,笼罩全景,从全体来看部分,“以大观小”。
把全部景界组织成一幅气韵生动、有节奏有和谐的艺术画面,不是机械的照相。
这画面上的空间组织,是受着画中全部节奏及表情所支配。
“其间折高折远,自有妙理”。
这就是说须服从艺术上的构图原理,而不是服从科学上算学的透视法原理。
他并且以为那种依据透视法的看法只能看见片面,看不到全面,所以不能成画。
安徽省淮南市高三下学期第一模拟考试文科综合能力测试政治试卷

安徽省淮南市高三下学期第一模拟考试文科综合能力测试政治试卷1.下图描述的是某品牌奶粉的需求曲线由D1左移到D2。
下列事件中能导致这种变动的是( )A.该奶粉生产商供给减少B.政府提高了商品消费税C.居民收入水平大幅上升D.该奶粉检测出有害物质2.清华大学国情研究院院长胡鞍钢认为,中国改革比较成功的是“靠两条腿走路”,一条腿是国有企业,它是通过改革,包括公司制改革、股份多元化改革、垄断行业改革,形成有效的市场竞争格局,使得国有企业做大做强做优;另一条腿就是发展非国有经济。
对这段话认识正确的是( )A.我国公有制经济和非公有制经济地位平等、公平竞争B.股份制改革是所有企业做大做强做优的必经之路C.我国应坚持公有制为主体、多种所有制经济共同发展的基本经济制度D.我国应毫不动摇地鼓励、支持和引导公有制经济发展,毫不动摇地巩固和发展非公有制经济3.读漫画《“分蛋糕”》。
要解决天价薪酬问题,应该( )①完全依靠市场对经济进行调节②加强和完善国家宏观调控③积极扩大居民消费需求④提高劳动报酬在初次分配中的比重A.①②B.①③C.②③D.②④4.随着互联网的快速发展,越来越多的公民通过网络参与政治生活,以网络为媒介的“政府—民间”互动模式已成为我国政治文明的重要元素。
“政府—民间”互动模式( )①方便了公民直接管理国家事务②保障了人民群众对政府的质询权③拓宽了公民参与民主监督的渠道④有利于政府了解民意和汇集民智A.①②B.②③C.①④D.③④5.从“问钱”“问粮”到“问医”“问房”,从“问食品安全”到“问环境治理”。
“专题询问”是对“询问”这种监督方式的进一步完善。
下列属于人大行使监督权的是( )A.人大常委会审议政府财政决算报告B.人大对社会生活中的重大事项作出决策C.人大代表依照法律规定的程序提出议案D.人大代表听取和反映人民群众的意见和要求6.中共中央政治局决定从2013年下半年开始,用一年左右时间,在全党自上而下分批开展党的群众路线教育实践活动。
安徽省淮南市2015届高三第一次模拟考试数学(文)试题(扫描版)

安徽省淮南市2015届高三第一次模拟考试数学(文科)试卷答案三、解答题16、解:(Ⅰ)21)62sin(22cos12sin 23)(++=++=πx xx x f ………………3分 由,226222πππππk x k +≤+≤+-得)(432434Z k k x k ∈+≤≤+-ππππ 所以单调递增区间为).](432,434[Z k k k ∈++-ππππ………………….6分 (Ⅱ)由 C B B C B A cos sin cos sin cos sin 2=-知 21cos ,sin )sin(cos sin 2==+=B A C B B A)32,0(,3),,0(πππ∈=∴∈A B B …………………………………9分21)62sin()(++=∴πA A f1)62sin(21,2626<+<<+<∴ππππA A )23,1()(∈∴A f …………………………………………..12分18、(Ⅰ)当CN AD N 中点时,有为∥平面AMP …………………1分 证明:∵中点分别为AD BC N M ,,∴为AMCN BM AN ∴//平行四边形 ∴CN ∥AM ………….4分 ∵AMP M CN AMP AM 面面⊄⊂,∴CN ∥平面AMP ……………6分(Ⅱ)证明:取 OP O CD 则中点,⊥CD ∵面ABCD PCD 面⊥CD ABCD PCD =⋂面面 PCD OP 面⊂∴为直角三角形从而面MPO APO ABCD OP ∆∆⊥,,……………………….9分∵的正三角形是边长为2PCD ∆ ∴3=OP 又∵为矩形,ABCD CD AB BC AD 2,22====∴6,6;32393===+==AM PM PA OA 同理:,……………11分∴222AM PM PA += ∴PM AM ⊥……………………………………….12分MPDC BAN19、(Ⅰ)()分得则设切点5......................1,101ln )(01)(,1)(),0(,0,00000''00==⎪⎩⎪⎨⎧=+-==-=-=>x k kx x x f k x x f k xx f x x(Ⅱ)1,0)(;10,0)(ln )1(ln 1)()0(1ln )(6 (1)ln 01ln )(''22'><<<>-=+-=>+=+≥⇔≤+-=x x g x x g x xx x x g x xx x g xx k kx x x f 令分∴)单减,)单增,(在(∞+11,0)(x g ………………………11分 ∴1)1()(==g x g m an ∴1≥k ………………………………… 12分20、(Ⅰ)解:∵n n a s 3161-=…………………1分 ∴n n n n n a a S S a 31312n 11-=-=≥--时,当∴141-=n n a a ……………………………………………………3分又∵81,3161111=∴-=a a S ……………………………………4分∴121214181+-⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛=n n n a ……………………………5分(Ⅱ)证明:12log 211+==-+n a C C n n n 由…………………….6分)(...)()(2123121--++-+-+=≥n n n C C C C C C C C n 时,则当)1)(1(1)12( (5302)-+=-=-++++=n n n n ……8分∴11...1411311211 (1112)222432-++-+-+-=++++n C C C C n 分12 (4)31112143111211211111...5131412131121<⎪⎭⎫ ⎝⎛++-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++-⎪⎭⎫ ⎝⎛+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=n n n n n n又∵3111...1112432=≥++++C C C C C n ………………………………………13分 ∴原式得证(Ⅲ)解:对于椭圆C 上的任意两点P 、Q,当错误!不能通过编辑域代码创建对象。
安徽省淮南市高考数学一模试卷 文(含解析)

2015年安徽省淮南市高考数学一模试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.复数的虚部为()A.﹣2 B.﹣2i C.2 D.2i2.集合A={1,2,3},集合B={﹣1,1,3},集合S=A∩B,则集合S的子集有()A.2个B.3 个 C.4 个 D.8个3.设A,B为两个不相等的集合,条件p:x∈A∩B,条件q:x∈A或x∈B,则p是q的()A.充分且必要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件4.若某算法框图如图所示,则输出的结果为()A.7 B.15 C.31 D.635.已知双曲线kx2﹣y2=1(k>0)的一条渐近线与直线2x+y﹣3=0垂直,则双曲线的离心率是()A.B.C.4 D.6.将函数y=cosx的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,所得函数图象的一条对称轴方程是()A.x=π B.C.D.7.在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是()A.众数 B.平均数C.中位数D.标准差8.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,m⊥α,则l⊥α;②若m∥l,m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则l∥m.其中正确命题的个数是()A.1 B.2 C.3 D.49.已知定义在R上的可导函数y=f(x)是偶函数,且满足xf′(x)<0, =0,则满足的x的范围为()A.(﹣∞,)∪(2,+∞)B.(,1)∪(1,2)C.(,1)∪(2,+∞)D.(0,)∪(2,+∞)10.已知直线x+y+a=0与圆x2+y2=1交于不同的两点A、B,O是坐标原点,且,那么实数a的取值范围是()A.B.C.D.二、填空题:(本大题共5小题,5每小题5分,共25分)11.已知角α终边上一点为P(﹣1,2),则值等于.12.已知实数x,y满足约束条,则z=的最小值为.13.已知数列{a n}满足a1=1,a2=2,a n+2=(1+cos2)a n+sin2,则该数列的前16项和为.14.已知点F是抛物线y2=4x的焦点,M,N是该抛物线上两点,|MF|+|NF|=6,M,N,F三点不共线,则△MNF的重心到准线距离为.15.下列命题:①函数y=sinx和y=tanx在第一象限都是增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,S n最大值为S5;④在△ABC中,A>B的充要条件是cos2A<cos2B;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强.其中正确命题的序号是(把所有正确命题的序号都写上).三.解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)16.已知函数f(x)=(Ⅰ)求函数f(x)单调递增区间;(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣c)cosB=bcosC,求f (A)的取值范围.17.某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100](Ⅰ)求图中x 的值,并估计该班期中考试数学成绩的众数;(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.18.如图,已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点(Ⅰ)试在棱AD上找一点N,使得CN∥平面AMP,并证明你的结论.(Ⅱ)证明:AM⊥PM.19.已知函数f(x)=lnx﹣kx+1(k∈R).(Ⅰ)若x轴是曲线f(x)=lnx﹣kx+1一条切线,求k的值;(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围.20.若数列{a n}的前n项和为S n,点(a n,S n)在y=x的图象上(n∈N*),(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若c1=0,且对任意正整数n都有,求证:对任意正整数n≥2,总有.21.已知椭圆C的中心在坐标原点O,长轴在x轴上,离心率为,且椭圆C上一点到两个焦点的距离之和为4.(Ⅰ)椭圆C的标准方程.(Ⅱ)已知P、Q是椭圆C上的两点,若OP⊥OQ,求证:为定值.(Ⅲ)当为(Ⅱ)所求定值时,试探究OP⊥OQ是否成立?并说明理由.2015年安徽省淮南市高考数学一模试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.复数的虚部为()A.﹣2 B.﹣2i C.2 D.2i【考点】复数代数形式的乘除运算;复数的基本概念.【专题】数系的扩充和复数.【分析】利用复数的运算法则、虚部的定义即可得出.【解答】解:复数===1+2i的虚部为2.故选;C.【点评】本题考查了复数的运算法则、虚部的定义,属于基础题.2.集合A={1,2,3},集合B={﹣1,1,3},集合S=A∩B,则集合S的子集有()A.2个B.3 个 C.4 个 D.8个【考点】交集及其运算.【专题】集合.【分析】根据集合的基本运算进行求解.【解答】解:∵集合A={1,2,3},集合B={﹣1,1,3},∴集合S=A∩B={1,3},则集合S的子集有22=4个,故选:C.【点评】本题主要考查集合的基本运算和集合子集个数的求解,要求熟练掌握集合的交并补运算,比较基础.3.设A,B为两个不相等的集合,条件p:x∈A∩B,条件q:x∈A或x∈B,则p是q的()A.充分且必要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【专题】集合;简易逻辑.【分析】根据充分条件和必要条件的定义进行判断即可.【解答】解:若x∈A∩B,则x∈A或x∈B成立,若x∈A,且x∉A∩B,满足x∈A或x∈B但x∈A∩B,不成立,故p是q的充分不必要条件,故选:B【点评】本题主要考查充分条件和必要条件的判断,根据集合关系是解决本题的关键.4.若某算法框图如图所示,则输出的结果为()A.7 B.15 C.31 D.63【考点】程序框图.【专题】图表型;算法和程序框图.【分析】模拟执行算法框图,依次写出每次循环得到的A,B的值,当A=6时,不满足条件A≤5,退出循环,输出B的值为63.【解答】解:模拟执行算法框图,可得A=1,B=1满足条件A≤5,B=3,A=2满足条件A≤5,B=7,A=3满足条件A≤5,B=15,A=4满足条件A≤5,B=31,A=5满足条件A≤5,B=63,A=6不满足条件A≤5,退出循环,输出B的值为63.故选:D.【点评】本题主要考查了程序框图和算法,正确得到每次循环A,B的值是解题的关键,属于基础题.5.已知双曲线kx2﹣y2=1(k>0)的一条渐近线与直线2x+y﹣3=0垂直,则双曲线的离心率是()A.B.C.4 D.【考点】双曲线的简单性质.【专题】计算题;圆锥曲线的定义、性质与方程.【分析】已知双曲线kx2﹣y2=1的一条渐近线与直线2x+y+1=0垂直,可求出渐近线的斜率,由此求出k的值,得到双曲线的方程,再求离心率.【解答】解:由题意双曲线kx2﹣y2=1的一条渐近线与直线2x+y+1=0垂直,可得渐近线的斜率为,又由于双曲线的渐近线方程为y=±x故=,∴k=,∴可得a=2,b=1,c=,由此得双曲线的离心率为,故选:A.【点评】本题考查直线与圆锥曲线的关系,解题的关键是理解一条渐近线与直线2x+y+1=0垂直,由此关系求k,熟练掌握双曲线的性质是求解本题的知识保证.6.将函数y=cosx的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,所得函数图象的一条对称轴方程是()A.x=π B.C.D.【考点】函数y=Asin(ωx+φ)的图象变换.【专题】三角函数的图像与性质.【分析】根据函数图象变换,求出函数解析式,结合三角函数的对称性即可得到结论.【解答】解:将函数y=cosx的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到y=cos x,再向右平移个单位得到y=cos[(x)],由(x)=kπ,得x=2kπ,即+2kπ,k∈Z,当k=0时,,即函数的一条对称轴为,故选:B【点评】本题主要考查三角函数的对称轴的求解,利用三角函数的图象关系求出函数的解析式是解决本题的关键.7.在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是()A.众数 B.平均数C.中位数D.标准差【考点】极差、方差与标准差;众数、中位数、平均数.【专题】概率与统计.【分析】利用众数、平均数、中位标准差的定义,分别求出,即可得出答案.【解答】解:A样本数据:82,84,84,86,86,86,88,88,88,88.B样本数据84,86,86,88,88,88,90,90,90,90众数分别为88,90,不相等,A错.平均数86,88不相等,B错.中位数分别为86,88,不相等,C错A样本方差S2= [(82﹣86)2+2×(84﹣86)2+3×(86﹣86)2+4×(88﹣86)2]=4,标准差S=2,B样本方差S2= [(84﹣88)2+2×(86﹣88)2+3×(88﹣88)2+4×(90﹣88)2]=4,标准差S=2,D正确故选D.【点评】本题考查众数、平均数、中位标准差的定义,属于基础题.8.设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,m⊥α,则l⊥α;②若m∥l,m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则l∥m.其中正确命题的个数是()A.1 B.2 C.3 D.4【考点】空间中直线与直线之间的位置关系.【专题】空间位置关系与距离.【分析】由直线与平面垂直的判定定理知命题①正确;在命题②的条件下,直线l可能在平面α内,故命题为假;在命题③的条件下,三条直线可以相交于一点,故命题为假;在命题④中,由α∩γ=n知,n?α且n?γ,由n?α及∥βα∩β=m,得n∥m,同理n∥l,故m∥l,命题④正确.【解答】解:∵①若m∥l,m⊥α,则由直线与平面垂直的判定定理,得l⊥α,故①正确;②若m∥l,m∥α,则l∥α或l⊂α,故②错误;③如图,在正方体ABCD﹣A1B1C1D1中,平面ABB1A1∩平面ABCD=AB,平面ABB1A1∩平面BCC1B1=BB1,平面ABCD∩平面BCC1B1=BC,由AB、BC、BB1两两相交,得:若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n不成立,故③是假命题;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则由α∩γ=n知,n⊂α且n⊂γ,由n⊂α及n∥β,α∩β=m,得n∥m,同理n∥l,故m∥l,故命题④正确.故选:B.【点评】本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.9.已知定义在R上的可导函数y=f(x)是偶函数,且满足xf′(x)<0, =0,则满足的x的范围为()A.(﹣∞,)∪(2,+∞)B.(,1)∪(1,2)C.(,1)∪(2,+∞)D.(0,)∪(2,+∞)【考点】指、对数不等式的解法;导数的运算.【专题】函数的性质及应用.【分析】根据函数的奇偶性以及函数单调性和导数之间的关系进行求解即可.【解答】解:当x>0时,由xf′(x)<0,得f′(x)<0,即此时函数单调递减,∵函数f(x)是偶函数,∴不等式等价为f(||)<,即||>,即>或<﹣,解得0<x<或x>2,故x的取值范围是(0,)∪(2,+∞)故选:D【点评】本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系是解决本题的关键.10.已知直线x+y+a=0与圆x2+y2=1交于不同的两点A、B,O是坐标原点,且,那么实数a的取值范围是()A.B.C.D.【考点】直线与圆的位置关系;向量在几何中的应用.【专题】计算题;直线与圆.【分析】设AB的中点为C,因为,所以|OC|≥|AC|,因为|OC|=,|AC|2=1﹣|OC|2,所以2()2≥1,可得a≤﹣1或a≥1,结合<1,即可求出实数a的取值范围【解答】解:设AB的中点为C,则因为,所以|OC|≥|AC|,因为|OC|=,|AC|2=1﹣|OC|2,所以2()2≥1,所以a≤﹣1或a≥1,因为<1,所以﹣<a<,所以实数a的取值范围是,故选:A.【点评】本题考查直线与圆的位置关系,考查点到直线的距离公式,考查学生的计算能力,属于中档题.二、填空题:(本大题共5小题,5每小题5分,共25分)11.已知角α终边上一点为P(﹣1,2),则值等于.【考点】任意角的三角函数的定义.【专题】三角函数的求值.【分析】利用任意角的三角函数的定义求出正切函数值,然后利用二倍角的正切函数求解即可.【解答】解:角α终边上一点为P(﹣1,2),所以tanα=﹣2.===﹣.故答案为:﹣.【点评】本题考查二倍角的正切函数,三角函数的定义的应用,考查计算能力.12.已知实数x,y满足约束条,则z=的最小值为.【考点】简单线性规划.【专题】不等式的解法及应用.【分析】由z==32x+y设t=2x+y,利用线性规划的知识先求出t的最小值即可得到结论.【解答】解:作出不等式组对应的平面区域如图:(阴影部分).由z==32x+y,设t=2x+y,则y=﹣2x+t,平移直线y=﹣2x+t,由图象可知当直线y=﹣2x+t经过点B时,直线y=﹣2x+t的截距最小,此时t最小.由,解得,即B(﹣3,3),代入t=2x+y得t=2×(﹣3)+3=﹣3.∴t最小为﹣3,z有最小值为z==3﹣3=.故答案为:.【点评】本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.13.已知数列{a n}满足a1=1,a2=2,a n+2=(1+cos2)a n+sin2,则该数列的前16项和为546 .【考点】数列的求和.【专题】等差数列与等比数列.【分析】当n=2k﹣1(k∈N*)时,a2k+1=a2k﹣1+1,数列{a2k﹣1}为等差数列,a2k﹣1=k;当n=2k(k∈N*)时,a2k+2=2a2k,数列{a2k}为等比数列,.分别利用等差数列与等比数列的前n和公式即可得出.【解答】解:当n=2k﹣1(k∈N*)时,a2k+1=a2k﹣1+1,数列{a2k﹣1}为等差数列,a2k﹣1=a1+k﹣1=k;当n=2k(k∈N*)时,a2k+2=2a2k,数列{a2k}为等比数列,.∴该数列的前16项和S16=(a1+a3+…+a15)+(a2+a4+…+a16)=(1+2+...+8)+(2+22+ (28)=+=36+29﹣2=546.故答案为:546.【点评】本题考查了等差数列与等比数列的通项公式及前n项和公式、“分类讨论方法”,考查了推理能力与计算能力,属于中档题.14.已知点F是抛物线y2=4x的焦点,M,N是该抛物线上两点,|MF|+|NF|=6,M,N,F三点不共线,则△MNF的重心到准线距离为.【考点】抛物线的简单性质.【专题】计算题;圆锥曲线的定义、性质与方程.【分析】根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标,进而求出△MNF的重心到准线距离.【解答】解:∵F是抛物线y2=4x的焦点,∴F(1,0),准线方程x=﹣1,设M(x1,y1),N(x2,y2),∴|MF|+|NF|=x1+1+x2+1=6,解得x1+x2=4,∴△MNF的重心的横坐标为,∴△MNF的重心到准线距离为.故答案为:.【点评】本题考查解决抛物线上的点到焦点的距离问题,利用抛物线的定义将到焦点的距离转化为到准线的距离.15.下列命题:①函数y=sinx和y=tanx在第一象限都是增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,S n最大值为S5;④在△ABC中,A>B的充要条件是cos2A<cos2B;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强.其中正确命题的序号是②③④⑤(把所有正确命题的序号都写上).【考点】命题的真假判断与应用.【专题】简易逻辑.【分析】①不正确,取x=,,即可判断出;②利用函数零点判定定理即可判断出;③由S10>0,S11<0,可得=5(a6+a5)>0, =11a6<0,可得a6<0,a5>0.即可得出S n最大值为S5;④在△ABC中,cos2A﹣cos2B=﹣2sin(A+B)sin(A﹣B)=2sin(A+B)sin(B﹣A)<0⇔A >B;⑤利用线性相关系数与线性相关性的关系即可判断出.【解答】解:①函数y=sinx和y=tanx在第一象限都是增函数,不正确,取x=,,但是,,因此不是单调递增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点,正确;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,∴ =5(a6+a5)>0, =11a6<0,∴a5+a6>0,a6<0,∴a5>0.因此S n最大值为S5,正确;④在△ABC中,cos2A﹣cos2B=﹣2sin(A+B)sin(A﹣B)=2sin(A+B)sin(B﹣A)<0⇔A >B,因此正确;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强,正确.其中正确命题的序号是②③④⑤.【点评】本题综合考查了三角函数的单调性、函数零点存在判定定理、等差数列的性质、两角和差化积公式、线性回归分析,考查了推理能力与计算能力,属于难题.三.解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)16.已知函数f(x)=(Ⅰ)求函数f(x)单调递增区间;(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣c)cosB=bcosC,求f (A)的取值范围.【考点】三角函数中的恒等变换应用;正弦定理.【专题】计算题;三角函数的图像与性质.【分析】(Ⅰ)由倍角公式化简可得f(x)=sin(+),由2k≤+≤2kπ,k∈Z可解得函数f(x)单调递增区间.(Ⅱ)利用正弦定理可得(2sinA﹣sinC)cosB=sinBcosC,化简可得cosB=,B=,0<A <从而得到+的范围,进而得到函数f(A)的取值范围.【解答】解:(Ⅰ)∵f(x)=sin cos+cos2=sin(+),∴由2k≤+≤2kπ,k∈Z可解得:4kπ﹣≤x≤4kπ,k∈Z,∴函数f(x)单调递增区间是:[4kπ﹣,4kπ],k∈Z.(Ⅱ)∵f(A)=sin(+),∵由条件及正弦定理得sinBcosC=(2sinA﹣sinC)cosB=2sinAcosB﹣sinCcosB,∴则sinBcosC+sinCcosB=2sinAcosB,∴sin(B+C)=2sinAcosB,又sin(B+C)=sinA≠0,∴cosB=,又0<B<π,∴B=.∴可得0<A<,∴<+<,∴sin(+)<1,故函数f(A)的取值范围是(1,).【点评】本题考查三角函数性质及简单的三角变换,要求学生能正确运用三角函数的概念和公式对已知的三角函数进行化简求值,属于中档题.17.某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100](Ⅰ)求图中x 的值,并估计该班期中考试数学成绩的众数;(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.【考点】列举法计算基本事件数及事件发生的概率;频率分布直方图.【专题】概率与统计.【分析】(Ⅰ)根据所有小矩形面积之和为1,可求出x的值,注意x是高度,再根据众数的定义求出即可;(Ⅱ)先分别求出成绩不低于90分的学生和成绩低于50分的学生人数,再利用古典概型知识求解.【解答】解:(Ⅰ)由(0.006×3+0.01+0.054+x)×10=1,解得x=0.018,前三组的人数分别为:(0.006×2+0.01+0.018)×10×50=20,第四组为0.054×10×50=27人,故数学成绩的众数落在第四组,故众数为75分.(Ⅱ)分数在[40,50)、[90,100]的人数分别是3人,共6人,∴这2人成绩均不低于90分的概率P==.【点评】本题考查频率分布直方图及古典概型的问题,前者要熟练掌握直方图的基本性质和如何利用直方图求众数;后者往往和计数原理结合起来考查.18.如图,已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点(Ⅰ)试在棱AD上找一点N,使得CN∥平面AMP,并证明你的结论.(Ⅱ)证明:AM⊥PM.【考点】直线与平面平行的判定;空间中直线与直线之间的位置关系.【专题】空间位置关系与距离.【分析】(Ⅰ)在棱AD上找中点N,连接CN,则CN∥平面AMP;利用线面平行的判定定理证明即可;(Ⅱ)过P作PE⊥CD,连接AE,ME,只要证明PE⊥AM,并且AM⊥ME,利用线面垂直的判定定理得到AM⊥平面PME,再利用线面垂直的性质可证.【解答】(Ⅰ)解:在棱AD上找中点N,连接CN,则CN∥平面AMP;证明:因为M为BC的中点,四边形ABCD是矩形,所以CM平行且相等于DN,所以四边形MCNA为矩形,所以CN∥AM,又CN⊄平面AMP,AM⊂平面AMP,所以CN∥平面AMP.(Ⅱ)证明:过P作PE⊥CD,连接AE,ME,因为边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点所以PE⊥平面ABCD,CM=,所以P E⊥AM,在△AME中,AE==3,ME==,AM==,所以AE2=AM2+ME2,所以AM⊥ME,所以AM⊥平面PME所以AM⊥PM.【点评】本题考查了线面平行的判定定理和线面垂直的判定定理的运用;正确利用已知条件得到线线关系是关键,体现了转化的思想.19.已知函数f(x)=lnx﹣kx+1(k∈R).(Ⅰ)若x轴是曲线f(x)=lnx﹣kx+1一条切线,求k的值;(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围.【考点】利用导数研究曲线上某点切线方程;利用导数求闭区间上函数的最值.【专题】综合题;导数的综合应用.【分析】(1)函数f(x)的定义域为(0,+∞),f′(x)=﹣k=0,可得切点的坐标,进而可求k的值;(2)确定函数的单调区间,k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1﹣k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(),由此能确定实数k 的取值范围.【解答】解:(1)函数f(x)的定义域为(0,+∞),f′(x)=﹣k=0,∴x=,由ln﹣1+1=0,可得k=1;(2)当k≤0时,f′(x)=﹣k>0,f(x)在(0,+∞)上是增函数;当k>0时,若x∈(0,)时,有f′(x)>0,若x∈(,+∞)时,有f′(x)<0,则f(x)在(0,)上是增函数,在(,+∞)上是减函数.k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1﹣k>0,f(x)≤0不成立,故k>0,∵f(x)的最大值为f(),要使f(x)≤0恒成立,则f()≤0即可,即﹣lnk≤0,得k≥1.【点评】本题考查导数的几何意义,考查函数单调区间的求法,确定实数的取值范围,渗透了分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.20.若数列{a n}的前n项和为S n,点(a n,S n)在y=x的图象上(n∈N*),(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若c1=0,且对任意正整数n都有,求证:对任意正整数n≥2,总有.【考点】数列的求和;数列递推式.【专题】等差数列与等比数列.【分析】(I)由点(a n,S n)在y=x的图象上(n∈N*),可得,利用递推式与等比数列的通项公式即可得出;(II)对任意正整数n都有=2n+1,利用“累加求和”可得c n=(c n﹣c n﹣1)+(c n﹣1﹣c n﹣2)+…+(c2﹣c1)+c1=(n+1)(n﹣1).当n≥2时, ==.再利用“裂项求和”即可得出.【解答】(I)解:∵点(a n,S n)在y=x的图象上(n∈N*),∴,当n≥2时,,∴,化为,当n=1时,,解得a1=.∴==.(2)证明:对任意正整数n都有=2n+1,∴c n=(c n﹣c n﹣1)+(c n﹣1﹣c n﹣2)+…+(c2﹣c1)+c1=(2n﹣1)+(2n﹣3)+…+3==(n+1)(n﹣1).∴当n≥2时, ==.∴=+…+=<=,又=.∴.【点评】本题考查了等比数列的通项公式与等差数列的前n项和公式、“累加求和”、“裂项求和”、对数的运算性质、“放缩法”、递推式,考查了推理能力与计算能力,属于中档题.21.已知椭圆C的中心在坐标原点O,长轴在x轴上,离心率为,且椭圆C上一点到两个焦点的距离之和为4.(Ⅰ)椭圆C的标准方程.(Ⅱ)已知P、Q是椭圆C上的两点,若OP⊥OQ,求证:为定值.(Ⅲ)当为(Ⅱ)所求定值时,试探究OP⊥OQ是否成立?并说明理由.【考点】直线与圆锥曲线的综合问题;椭圆的简单性质.【专题】圆锥曲线中的最值与范围问题.【分析】(I)由题意可设椭圆的坐标方程为(a>b>0).由题意可得,2a=4,及b2=a2﹣c2=3.即可得出.(II)当OP与OQ的斜率都存在时,设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=﹣x(k≠0),P(x,y).直线OP的方程y=kx与椭圆的方程联立可得,得到|OP|2=x2+y2=,同理可得|OQ|2=, =为定值.当直线OP或OQ的斜率一个为0而另一个不存在时,上式也成立.(III)当=定值时,试探究OP⊥OQ是否成立?并说明理由.OP⊥O Q不一定成立.下面给出分析:当直线OP或OQ的斜率一个为0而另一个不存在时,可得==,满足条件.当直线OP或OQ的斜率都存在时,设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=k′x(k≠k′,k′≠0),P(x,y).与椭圆的方程联立可得|OP|2=x2+y2=,|OQ|2=,利用=+=.解得kk′=±1.即可判断出.【解答】(I)解:由题意可设椭圆的坐标方程为(a>b>0).∵离心率为,且椭圆C上一点到两个焦点的距离之和为4.∴,2a=4,解得a=2,c=1.∴b2=a2﹣c2=3.∴椭圆C的标准方程为.(II)证明:当OP与OQ的斜率都存在时,设直线OP的方程为y=kx(k≠0),则直线OQ 的方程为y=﹣x(k≠0),P(x,y).联立,化为,∴|OP|2=x2+y2=,同理可得|OQ|2=,∴=+=为定值.当直线OP或OQ的斜率一个为0而另一个不存在时,上式也成立.因此=为定值.(III)当=定值时,试探究OP⊥OQ是否成立?并说明理由.OP⊥OQ不一定成立.下面给出证明.证明:当直线OP或OQ的斜率一个为0而另一个不存在时,则===,满足条件.当直线OP或OQ的斜率都存在时,设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=k′x(k≠k′,k′≠0),P(x,y).联立,化为,∴|OP|2=x2+y2=,同理可得|OQ|2=,∴=+=.化为(kk′)2=1,∴kk′=±1.∴OP⊥OQ或kk′=1.因此OP⊥OQ不一定成立.【点评】本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得交点坐标、相互垂直的直线斜率之间的关系,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.。
2015安徽一模 安徽省2015届高三第一次模拟考试文综试题(扫描版,word答案)

2015安徽省高三第一次高考模拟考试历史参考答案12.B 解析:材料的大意是汉武帝通过赏赐诸侯王并同意诸侯王将自己的食邑再次分封给兄弟、赐予列侯。
根据所学知识可知,汉武帝颁布“推恩令”。
A项属于表象,材料无法体现,只能说明汉武帝治国理政手段的高超,注重策略;C项中“阶级矛盾”不符合史实,料反映的是统治阶级内部的矛盾;D项是董仲舒为巩固政治上的统一而提出的建议,属于思想方面,题干材料不能体现,两项是对汉武帝同意诸侯王分封子弟的曲解。
“推恩令”的颁布,王国越分越小,无力对抗中央,从而起到加强中央集权的作用,故B项正确。
13.C 解析:表格中随着时间的后移,商税额度越来越大,说明了工商业经济规模的扩大, C 项符合题意。
材料没有体现对商业税收的程度,A项错误;国家税收来源于多种渠道,商业税是其中的一种,B项错误;商品经济的发展不等于农业经济受到排挤,D项错误。
14.D 解析:本题考查南京保卫战,材料新颖,视角独特。
由所学知识可知,1937年11月中旬,日军占领上海后,自太湖南北同时西进,威胁南京。
根据材料可知,蒋介石“决守城抗战,图挽战局”,若不战而退,有失体面,固守南京则表明政府抗战之决心和意志。
“如情势不能久持时,可相机撤退”,说明蒋介石对日军攻占南京有心理预期,对保卫南京摇摆不定,A、B两项错误,材料没有反映“军事策略”,C项错误。
从“国际形势必大变”、“内外形势必一大变”可知蒋介石在外交层面上有较多期望,故D项正确。
15.A 解析:图文信息显示:城乡居民家庭人均纯收入差距明显开始拉大开始于1990年以后。
城市居民家庭人均纯收入增速相对较快。
B项发生于1985年以后;C项中“开始”是在20世纪80年代初;D项中“已经”是21世纪初。
1984年以后,城市经济体制改革全面展开,1992年邓小平的“南方谈话”和党的十四大是改革开放和现代化建设进入新阶段的标志。
随着社会主义生产经济体制的逐步建立,城市经济活力被进一步激发,城市居民收入增长明显高于农村,故A项正确。
【语文】安徽省淮南市2015届高三第一次模拟考试

淮南市2015届高三第一次模拟考试语文试题注意事项:本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
全卷满分150分,考试时间150分钟。
【试卷综述】纵观2015届高三第一次模拟考试的整份试卷,无论是试卷题目材料的选择、能力考查点的设置,还是试卷结构、题型等,均在尽力地模拟2014年安徽省高考语文试卷,基本上体现了2014年安徽省《考试说明》的精神。
题目编制难易适度,没有偏、怪之类的题目,并且有一定的梯度。
如文学作品的小说阅读,选文阅读难度适中,题目考查点覆盖与安徽卷近几年的考查点基本一致,题目难易适中,并且对考生答题的规范性也有较好的导向性要求,等。
第一次模拟考试是在大部分学校以轮复习还没有完全结束的情况下进行的,它的主要目的是对一轮复习的做一个较为全面的检测,意在传达出师生通过测试和对试卷情况的分析,来总结一轮复习中还存在哪些值得注意的问题,也为后期复习明晰需要解决的问题。
第Ⅰ卷(阅读题,共66分)一、(9分)阅读下面的文字,完成1~3题。
①现代德国哲学家斯播格耐在他的名著《西方之衰落》里面曾经阐明每一种独立的文化都有它的基本象征物,具体地表象它的基本精神。
在埃及是“路”,在希腊是“立体”,在近代欧洲文化是“无尽的空间”。
这三种基本象征都是取之于空间境界,而他们最具体的表现是在艺术里面。
埃及金字塔里的甬道,希腊的雕像,近代欧洲的最大油画家伦勃朗的风景,是我们领悟这三种文化的最深的灵魂之媒介。
②我们若用这个观点来考察中国艺术,尤其是画与诗中所表现的空间意识,再拿来同别种文化作比较,是一极有趣味的事。
③西洋十四世纪文艺复兴初期油画家梵埃格的画极注重写实,精细地描写人体,画面上表现屋宇内的空间,画家用科学及数学的眼光看世界。
于是透视法的知识被发挥出来,而用之于绘画。
④中国十八世纪雍正、乾隆时,名画家邹一桂对于西洋透视画法表示惊异而持不同情的态度,邹一桂认为西洋的透视的写实的画法“笔法全无,虽工亦匠”,只是一种技巧,与真正的绘画艺术没有关系,所以“不入画品”。
2015年高考文综安徽卷及答案

文科综合能力测试试卷 第1页(共28页)文科综合能力测试试卷 第2页(共28页)绝密★启用前 2015年普通高等学校招生全国统一考试(安徽卷)文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷第1页至第8页,第Ⅱ卷第9页至第12页。
全卷满分300分,考试时间150分钟。
注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔记清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4. 考试结束,务必将试题卷和答题卡一并上交。
第Ⅰ卷(选择题 共132分)本卷共33小题,每小题4分,共132分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
1. 出境游作为一种大众消费,其需求量(Q )受出境游价格(P )、居民收入(M )等因素影响。
不考虑其他因素,图1中能正确反映P 与Q 、M 与Q 关系的图形有 ( )图1A. ①③B. ①④C. ②③D. ②④ 2. 2014年,我国实际使用外商直接投资1 196亿美元,居世界首位。
对外直接投资1 029亿美元,与利用外资并驾齐驱。
这表明我国( )①保持了进出口贸易平衡,不断提高开放型经济水平 ②可以主导国际金融市场,充分发挥经济的比较优势 ③实施“引进来”和“走出去”战略取得了重大成就 ④在经济发展中能够更好利用国际市场优化资源配置 A. ①②B. ①④C. ②③D. ③④3. 某国去年的商品价格总额为20万亿元,流通中所需要的货币量为4万亿元。
淮南市2015届高考模拟高三第一次模拟考试(整理精校版)

淮南市2015届高考模拟高三第一次模拟考试高考模拟试卷0525 19:42::淮南市2015届高考模拟高三第一次模拟考试语文试题详解及述评【试卷综述】2015届高考模拟高三的第一次模拟考试是在安徽高考考试说明还没有发布的情况下进行的,因此试题的命制以及试卷结构的编排是依据2015届高考模拟的安徽考试说明,在依据这个说明的前提下,题量、题型。
试卷结构、分值以及命题范围等都与上一年度的安徽高考语文卷基本相当,题目编制难易适度,没有偏、怪之类的题目,并且有一定的梯度。
所考查的知识点以及相关内容,整体上基本延续了上一年度安徽高考语文试卷的命题特征,比如古文的考查当中,出现了双音节词的题目;诗文默写中考查的是二选一的形式;大阅读考查的还是散文的内容;语言知识运用当中出现了补全对话的形式;如此等等。
不过在部分试题材料的选择、题目的设置方面也略有变动,体现了一定的灵活性。
比如,语用题方面出了图文转换等。
第一次模拟考试是在安徽高考考试说明还没有发布的情况下进行的,所以应该说模拟的还是2015届高考模拟高考,不具有预测的功能。
它的主要任务是对一轮复习的一个较为全面的检测,意在传达出师生通过试卷分析,总结一下一轮复习中还存在哪些值得注意的问题。
第I卷(阅读题,共66分)一、(9分)阅读下面的文字,完成1~3题。
车联网:解决交通问题的新思路车联网是物联网技术在交通系统领域的典型应用,近年来,这一概念备受关注。
一般认为,车联网是以车内网、车际网和车载移动互联网为基础,按照约定的通信协议和数据交互标准,在车—X(X:车、路、行人及互联网等)之间进行无线通讯和信息交换的大系统,是能实现智能交通管理、智能动态信息服务和车辆智能化控制的一体化网络。
其中,车是车联网的核心载体,信息化是车联网的核心,基于车辆信息化的应用是车联网的本质,安全、节能、环保、舒适、智能、高效(省时)是车联网的主要目的。
近日,由中国汽车工程学会承办的第31期“中国科技论坛——2015高考模拟车联网产业技术论坛”在京举行,来自汽车、通信、软件、交通等领域的众多专家学者,围绕车联网技术的应用和功能、车联网关键技术及趋势、如何促进车联网产业协调发展等话题,展开交流讨论。
2015年高考模拟试卷(新课标版)文综_模拟试
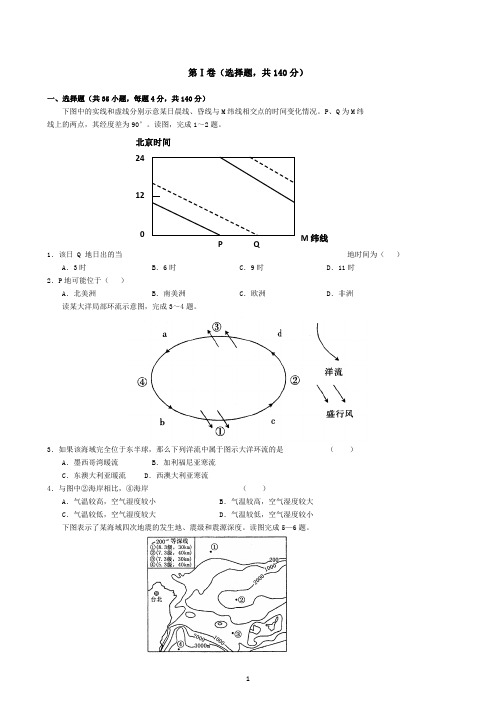
P Q M纬线北京时间24120 第Ⅰ卷(选择题,共140分)一、选择题(共35小题,每题4分,共140分)下图中的实线和虚线分别示意某日晨线、昏线与M纬线相交点的时间变化情况。
P、Q为M纬线上的两点,其经度差为90°。
读图,完成1~2题。
1.该日Q地日出的当地时间为()A.3时B.6时C.9时D.11时2.P地可能位于()A.北美洲B.南美洲C.欧洲D.非洲读某大洋局部环流示意图,完成3~4题。
3.如果该海域完全位于东半球,那么下列洋流中属于图示大洋环流的是()A.墨西哥湾暖流B.加利福尼亚寒流C.东澳大利亚暖流 D.西澳大利亚寒流4.与图中②海岸相比,④海岸()A.气温较高,空气湿度较小B.气温较高,空气湿度较大C.气温较低,空气湿度较大D.气温较低,空气湿度较小下图表示了某海域四次地震的发生地、震级和震源深度。
读图完成5—6题。
5.该海域地震频发的原因是( )A .板块碰撞B .板块张裂C .岩浆活动D .变质作用6.海啸是一种巨大的海浪。
一般当海底浅源大地震(震源深度小于50km ,震级大于里氏6.5级)造成大洋地壳局部隆起或陷落,并且带动震源上方的深层(水深不小于1000m )海水做大规模扰动时,就可能发生灾害性海啸。
若图中的四次地震都造成了地壳陷落,则四地中最可能发生灾害性海啸的是( ) A .①地B .②地C .③地D .④地下图中的甲、乙、丙、丁所示地区都是灌溉农业区。
完成7~9题。
7.图中所示地区为世界著名产棉区的是( ) A .甲与丙 B .甲与乙 C .丙与丁 D .乙与丁 8.图中所示地区不属于世界古代文明发祥地的是( )A .甲B .乙C .丙D .丁 9.图中所示地区共同面临的生态问题是( ) A .土地荒漠化 B .水土流失 C .气候变暖D .酸雨危害读“香港土地利用类型示意图”,完成10~11题。
10.图中最有可能成为中心商业区的是( ) A .a B .b C .c D .d11.制作香港土地利用类型分布图,优先采用的地理信息技术是( )①遥感(RS ) ②全球定位系统(GPS ) ③数字地球④地理信息系统(GIS )A .①②B .②③C.②④D .①④12.物联网是在互联网基础上进行信息交换和通信的一种网络,是物物相连的互联网。
2015年安徽文科综合高考真题打印

2015年安徽文科综合高考真题图4为25°N-32°N 之间某区域遥感影像。
完成23—24题。
图423、图示地区主要的陆地自然带是( ) A.荒漠带领 B.热带草原带 C.热带雨林带D.亚热带常绿阔叶林带 24、图示地区有世界重要的海上交通贸易通道。
该通道便捷地连接了( )A.北美东岸与西欧B.东亚与南亚C.北美东岸与西岸D.西欧与南亚[图5表示某市2003—2013年土地利用面积变化情况。
完成25---26题。
25、据图推测,2003—2013年该市A.退耕还林,林地面积持续增加B.围湖造田,水域面积不断减少C.水土流失,未利用地面积持续增加D.城市扩张,耕地面积不断减少 26、该市建设用地的变化可能导致A 、地表径流下渗量增加B 、居民平均通勤距离缩短C 、城市“热岛”效应增强D 、生物多样性增加图6为世界某区域略图,完成27—28题。
图627、图示区域西部沿海地区降水丰富,主要是由于A 、反气旋频繁过境B 、受沿岸寒流影响C 、东北季风受到地形抬升D 、西南季风带来丰沛水汽 28、甲地地貌形成的外力作用主是:A 、风力堆积B 、风力侵蚀C 、流水堆积D 、流水侵蚀 29、下列选项中,符合乙地农业地域类型特点的是A 、机械化水平高B 、水利工程量大C 、经营方式粗放D 、粮食单位面积总产量低企业总部是企业决策和控制中心。
表1表示2001年1月至2012年4月我国上市企业总部在四大区域间的迁移情况。
完成30—31题。
表130.2001年1月至2012年4月,我国上市企业总部在四大区域间的迁移表现为( )A 、东部地区上市企业总部主要向东北地区迁移B 、东部地区是上市企业总部迁移的主要目的地C 、中部地区上市企业总部的净迁出量最大D 、西部地区上市企业总部主要迁往中部 31.下列因素中,影响我国企业总部布局的主要是( ) ①原料 ②交通 ③劳动力 ④信息 ⑤政策A 、①②④B 、①③⑤C 、②④⑤D 、③④⑤图7表示一年中大气上界单位面积水平面上每日接收到的太阳辐射随纬度的变化为MJ /m2,图中阴影部分表示没有太阳辐射。
重点名校高考考前模拟——安徽省淮南一中等四校2015届高三5月联考文综试题(word版,含答案)

(在此卷上答题无效)绝密★启用前淮南一中 蒙城一中 颍上一中 怀远一中2015届高三“四校”联考文科综合能力测试命题学校:淮南一中 考试时间:2015年5月3日本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第7页,第Ⅱ卷第8页至第10页,全卷满分300分。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的班级、姓名和座位号。
2.答第Ⅰ卷时,每小题选出答案后,必须用0.5毫米黑色墨水签字笔在答题卷规定位置填写。
如需改动,用橡皮擦干净后重新填写。
3.答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
第Ⅰ卷(选择题 共132分)本卷共33小题,每小题4分,共132分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
1. 右图是2015年2月16日至2015年4月7日人民币汇率中间价变化图(人民 币元/1美元),在不考虑其他因素的情况 下,以下判断正确的是 ①从A 点到B 点,有利于美国对中 国的出口②从A 点到B 点,有利于中国引进美国资本 ③从C 点到D 点,有利于中国公民赴美国旅游④从C 点到D 点,有利于缓解中国出口企业就业压力A .①②B .①③C .②③D .③④ 2.《政府工作报告》指出,2015年继续实施积极的财政政策和稳健的货币政策。
下列属于积极财政政策的措施是A .提高存款准备金率B .结构性减税C .增加货币供应量D .减少财政支出3.城镇化是解决城乡差距的根本途径,也是最大的内需所在。
要坚持以人为核心,提升地级市、县城和中心镇产业和人口承载能力,方便农民就近城镇化,发挥好城镇化对现代化的支撑作用。
这说明①城镇化是我国扩大内需的最大潜力所在②要大力发展大、中城市,扩张城市规模③要迅速并大量推进农业转移人口市民化④城镇化有利于缩小城乡差距、统筹发展A.①③B.②③C.①④D.②④4.今年清明节期间,国家旅游局制定的《游客不文明行为记录管理暂行办法》(以下简称《办法》)开始施行。
2015安徽高考文综试卷

• ③抓住关键能够解决存在的各种问题 现整体的最优目标
• A.①② B.①③ C. ②④
④统筹全局可以实
D. ③④
38.(28分)阅读材料,回答下列问 题。
• 材料一 中国消费引领中国制造
• 近年来,伴随着收入水平提高,中国消费者有 了更多的选择。以往“你有,我有,人人有”的 跟风式消费观逐渐转变,国外的高品质产品越来 越多地受到消费者的青睐。消费水平的不断提高, 消费者话语权的愈益凸显,既对中国制造业提出 了挑战,也引领中国制造业加速转型升级,提质 增效。
• ①表明国家力量是国际关系的决定性因素
• ②离不开我国综合国力和国际地位的提升
• ③是由我国在联合国的地位和作用决定的
• ④说明国家合作事宜国家间共同利益为基础 • A.①② B.①③ C.②④ D.③④
• 7.中华民族精神传承了中华传统文化血脉,已经成为凝聚 人心的纽带。下列古语涵义与以爱国主义为核心的中华民 族精神疾病内涵对应恰当的是 • A 发愤忘食,乐以忘忧,不知老之将至(孔子) 不息 • B 穷则独善其身,达则兼善天下(孟子) 自强
A①③
B①④
C②③
D②④
• 2.2014年,我国实际使用外商直接投资1196亿美元,居 世界首位。对外直接投资1029亿美元,与利用外资并驾齐 驱。这表明 • ①保持了进出口贸易平衡,不断提高开放型经济水平
• ②可以主导国际金融市场,可以充分发挥经济的比较优势
• ③实施“引进来”和“走出去”战略取得了重大成就
• (1)根据材料一,分析其中体现的经济生活道理。 (8分)
• 材料二 工匠精神筑梦中国制造
• 自古以来,专注细节、精益求精一直是中国工 匠秉承的精神,这种精神铸就了传统制造业的辉 煌,也是助推现代制造业的重要动力。在大众创 业、万众创新的时代,要自觉弘扬工匠精神,主 动担当历史责任;要将工匠精神与现代高科技高 度融合,创造高品质产品,满足用户消费。中国 制造正在敞开一扇扇新的梦想之门。
安徽省淮南市2015届高三第一次模拟考试语文试卷及答案

淮南市2015届高三第一次模拟考试语文试题注意事项:本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。
全卷满分150分,考试时间150分钟。
第Ⅰ卷(阅读题,共66分)一、(9分)阅读下面的文字,完成1~3题。
①现代德国哲学家斯播格耐在他的名著《西方之衰落》里面曾经阐明每一种独立的文化都有它的基本象征物,具体地表象它的基本精神。
在埃及是“路”,在希腊是“立体”,在近代欧洲文化是“无尽的空间”。
这三种基本象征都是取之于空间境界,而他们最具体的表现是在艺术里面。
埃及金字塔里的甬道,希腊的雕像,近代欧洲的最大油画家伦勃朗的风景,是我们领悟这三种文化的最深的灵魂之媒介。
②我们若用这个观点来考察中国艺术,尤其是画与诗中所表现的空间意识,再拿来同别种文化作比较,是一极有趣味的事。
③西洋十四世纪文艺复兴初期油画家梵埃格的画极注重写实,精细地描写人体,画面上表现屋宇内的空间,画家用科学及数学的眼光看世界。
于是透视法的知识被发挥出来,而用之于绘画。
④中国十八世纪雍正、乾隆时,名画家邹一桂对于西洋透视画法表示惊异而持不同情的态度,邹一桂认为西洋的透视的写实的画法“笔法全无,虽工亦匠”,只是一种技巧,与真正的绘画艺术没有关系,所以“不入画品”。
而能够入画品的画,即能“成画”的画,应是不采取西洋透视法的立场,而采沈括所说的“以大观小之法”。
⑤早在宋代一位博学家沈括在他名著《梦溪笔谈》里就曾讥评大画家李成采用透视立场“仰画飞檐”,而主张“以大观小之法”。
他说:“李成画山上亭馆及楼阁之类,皆仰画飞檐。
其说以谓‘自下望上,如人立平地望塔檐间,见其榱桷’。
此论非也。
”沈括以为画家画山水,并非如常人站在平地上在一个固定的。
把全部景界组织成一幅地点,仰首看山;而是用心灵的眼,笼罩全景,从全体来看部分,“以大观小”气韵生动、有节奏有和谐的艺术画面,不是机械的照相。
这画面上的空间组织,是受着画中全部节奏及表情所支配。
“其间折高折远,自有妙理”。
2015年安徽省淮南市高考一模数学试卷(文科)【解析版】

2015年安徽省淮南市高考数学一模试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.(5分)复数的虚部为()A.﹣2B.﹣2i C.2D.2i2.(5分)集合A={1,2,3},集合B={﹣1,1,3},集合S=A∩B,则集合S的子集有()A.2个B.3 个C.4 个D.8个3.(5分)设A,B为两个不相等的集合,条件p:x∈A∩B,条件q:x∈A或x∈B,则p是q的()A.充分且必要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件4.(5分)若某算法框图如图所示,则输出的结果为()A.7B.15C.31D.635.(5分)已知双曲线kx2﹣y2=1(k>0)的一条渐近线与直线2x+y﹣3=0垂直,则双曲线的离心率是()A.B.C.4D.6.(5分)将函数y=cos x的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,所得函数图象的一条对称轴方程是()A.x=πB.C.D.7.(5分)在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B 两样本的下列数字特征对应相同的是()A.众数B.平均数C.中位数D.方差8.(5分)设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,m⊥α,则l⊥α;②若m∥l,m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则l∥m.其中正确命题的个数是()A.1B.2C.3D.49.(5分)已知定义在R上的可导函数y=f(x)是偶函数,且满足xf′(x)<0,=0,则满足的x的范围为()A.(﹣∞,)∪(2,+∞)B.(,1)∪(1,2)C.(,1)∪(2,+∞)D.(0,)∪(2,+∞)10.(5分)已知直线x+y+a=0与圆x2+y2=1交于不同的两点A、B,O是坐标原点,且,那么实数a的取值范围是()A.B.C.D.二、填空题:(本大题共5小题,5每小题5分,共25分)11.(5分)已知角α终边上一点为P(﹣1,2),则值等于.12.(5分)已知实数x,y满足约束条,则z=的最小值为.13.(5分)已知数列{a n}满足a1=1,a2=2,a n+2=(1+cos2)a n+sin2,则该数列的前16项和为.14.(5分)已知点F是抛物线y2=4x的焦点,M,N是该抛物线上两点,|MF|+|NF|=6,M,N,F三点不共线,则△MNF的重心到准线距离为.15.(5分)下列命题:①函数y=sin x和y=tan x在第一象限都是增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,S n最大值为S5;④在△ABC中,A>B的充要条件是cos2A<cos2B;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强.其中正确命题的序号是(把所有正确命题的序号都写上).三.解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)16.(12分)已知函数f(x)=(Ⅰ)求函数f(x)单调递增区间;(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣c)cos B =b cos C,求f(A)的取值范围.17.(12分)某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100](Ⅰ)求图中x 的值,并估计该班期中考试数学成绩的众数;(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.18.(12分)如图,已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点(Ⅰ)试在棱AD上找一点N,使得CN∥平面AMP,并证明你的结论.(Ⅱ)证明:AM⊥PM.19.(12分)已知函数f(x)=lnx﹣kx+1(k∈R).(Ⅰ)若x轴是曲线f(x)=lnx﹣kx+1一条切线,求k的值;(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围.20.(13分)若数列{a n}的前n项和为S n,点(a n,S n)在y=x的图象上(n∈N*),(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若c 1=0,且对任意正整数n都有,求证:对任意正整数n≥2,总有.21.(14分)已知椭圆C的中心在坐标原点O,长轴在x轴上,离心率为,且椭圆C上一点到两个焦点的距离之和为4.(Ⅰ)椭圆C的标准方程.(Ⅱ)已知P、Q是椭圆C上的两点,若OP⊥OQ,求证:为定值.(Ⅲ)当为(Ⅱ)所求定值时,试探究OP⊥OQ是否成立?并说明理由.2015年安徽省淮南市高考数学一模试卷(文科)参考答案与试题解析一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.(5分)复数的虚部为()A.﹣2B.﹣2i C.2D.2i【解答】解:复数===1+2i的虚部为2.故选:C.2.(5分)集合A={1,2,3},集合B={﹣1,1,3},集合S=A∩B,则集合S的子集有()A.2个B.3 个C.4 个D.8个【解答】解:∵集合A={1,2,3},集合B={﹣1,1,3},∴集合S=A∩B={1,3},则集合S的子集有22=4个,故选:C.3.(5分)设A,B为两个不相等的集合,条件p:x∈A∩B,条件q:x∈A或x∈B,则p是q的()A.充分且必要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【解答】解:若x∈A∩B,则x∈A或x∈B成立,若x∈A,且x∉A∩B,满足x∈A或x∈B但x∈A∩B,不成立,故p是q的充分不必要条件,故选:B.4.(5分)若某算法框图如图所示,则输出的结果为()A.7B.15C.31D.63【解答】解:模拟执行算法框图,可得A=1,B=1满足条件A≤5,B=3,A=2满足条件A≤5,B=7,A=3满足条件A≤5,B=15,A=4满足条件A≤5,B=31,A=5满足条件A≤5,B=63,A=6不满足条件A≤5,退出循环,输出B的值为63.故选:D.5.(5分)已知双曲线kx2﹣y2=1(k>0)的一条渐近线与直线2x+y﹣3=0垂直,则双曲线的离心率是()A.B.C.4D.【解答】解:由题意双曲线kx2﹣y2=1的一条渐近线与直线2x+y+1=0垂直,可得渐近线的斜率为,又由于双曲线的渐近线方程为y=±x故=,∴k=,∴可得a=2,b=1,c=,由此得双曲线的离心率为,故选:A.6.(5分)将函数y=cos x的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移个单位,所得函数图象的一条对称轴方程是()A.x=πB.C.D.【解答】解:将函数y=cos x的图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到y=cos x,再向右平移个单位得到y=cos[(x)],由(x)=kπ,得x=2kπ,即+2kπ,k∈Z,当k=0时,,即函数的一条对称轴为,故选:B.7.(5分)在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B 两样本的下列数字特征对应相同的是()A.众数B.平均数C.中位数D.方差【解答】解:A样本数据:82,84,84,86,86,86,88,88,88,88.B样本数据84,86,86,88,88,88,90,90,90,90众数分别为88,90,不相等,A错.平均数86,88不相等,B错.中位数分别为86,88,不相等,C错A样本方差S2=[(82﹣86)2+2×(84﹣86)2+3×(86﹣86)2+4×(88﹣86)2]=4,B样本方差S2=[(84﹣88)2+2×(86﹣88)2+3×(88﹣88)2+4×(90﹣88)2]=4,D正确故选:D.8.(5分)设l,m,n表示不同的直线,α,β,γ表示不同的平面,给出下列四个命题:①若m∥l,m⊥α,则l⊥α;②若m∥l,m∥α,则l∥α;③若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则l∥m.其中正确命题的个数是()A.1B.2C.3D.4【解答】解:∵①若m∥l,m⊥α,则由直线与平面垂直的判定定理,得l⊥α,故①正确;②若m∥l,m∥α,则l∥α或l⊂α,故②错误;③如图,在正方体ABCD﹣A1B1C1D1中,平面ABB1A1∩平面ABCD=AB,平面ABB1A1∩平面BCC1B1=BB1,平面ABCD∩平面BCC1B1=BC,由AB、BC、BB1两两相交,得:若α∩β=l,β∩γ=m,γ∩α=n,则l∥m∥n不成立,故③是假命题;④若α∩β=l,β∩γ=m,γ∩α=n,n∥β,则由α∩γ=n知,n⊂α且n⊂γ,由n⊂α及n∥β,α∩β=m,得n∥m,同理n∥l,故m∥l,故命题④正确.故选:B.9.(5分)已知定义在R上的可导函数y=f(x)是偶函数,且满足xf′(x)<0,=0,则满足的x的范围为()A.(﹣∞,)∪(2,+∞)B.(,1)∪(1,2)C.(,1)∪(2,+∞)D.(0,)∪(2,+∞)【解答】解:当x>0时,由xf′(x)<0,得f′(x)<0,即此时函数单调递减,∵函数f(x)是偶函数,∴不等式等价为f(||)<,即||>,即>或<﹣,解得0<x<或x>2,故x的取值范围是(0,)∪(2,+∞)故选:D.10.(5分)已知直线x+y+a=0与圆x2+y2=1交于不同的两点A、B,O是坐标原点,且,那么实数a的取值范围是()A.B.C.D.【解答】解:设AB的中点为C,则因为,所以|OC|≥|AC|,因为|OC|=,|AC|2=1﹣|OC|2,所以2()2≥1,所以a≤﹣1或a≥1,因为<1,所以﹣<a<,所以实数a的取值范围是,故选:A.二、填空题:(本大题共5小题,5每小题5分,共25分)11.(5分)已知角α终边上一点为P(﹣1,2),则值等于.【解答】解:角α终边上一点为P(﹣1,2),所以tanα=﹣2.===﹣.故答案为:﹣.12.(5分)已知实数x,y满足约束条,则z=的最小值为.【解答】解:作出不等式组对应的平面区域如图:(阴影部分).由z==32x+y,设t=2x+y,则y=﹣2x+t,平移直线y=﹣2x+t,由图象可知当直线y=﹣2x+t经过点B时,直线y=﹣2x+t的截距最小,此时t最小.由,解得,即B(﹣3,3),代入t=2x+y得t=2×(﹣3)+3=﹣3.∴t最小为﹣3,z有最小值为z==3﹣3=.故答案为:.13.(5分)已知数列{a n}满足a1=1,a2=2,a n+2=(1+cos2)a n+sin2,则该数列的前16项和为546.+1,数列{a2k﹣1}为等差数列,【解答】解:当n=2k﹣1(k∈N*)时,a2k+1=a2k﹣1a2k﹣1=a1+k﹣1=k;当n=2k(k∈N*)时,a2k+2=2a2k,数列{a2k}为等比数列,.∴该数列的前16项和S16=(a1+a3+…+a15)+(a2+a4+…+a16)=(1+2+...+8)+(2+22+ (28)=+=36+29﹣2=546.故答案为:546.14.(5分)已知点F是抛物线y2=4x的焦点,M,N是该抛物线上两点,|MF|+|NF|=6,M,N,F三点不共线,则△MNF的重心到准线距离为.【解答】解:∵F是抛物线y2=4x的焦点,∴F(1,0),准线方程x=﹣1,设M(x1,y1),N(x2,y2),∴|MF|+|NF|=x1+1+x2+1=6,解得x1+x2=4,∴△MNF的重心的横坐标为,∴△MNF的重心到准线距离为.故答案为:.15.(5分)下列命题:①函数y=sin x和y=tan x在第一象限都是增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,S n最大值为S5;④在△ABC中,A>B的充要条件是cos2A<cos2B;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强.其中正确命题的序号是②③④⑤(把所有正确命题的序号都写上).【解答】解:①函数y=sin x和y=tan x在第一象限都是增函数,不正确,取x =,,但是,,因此不是单调递增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点,正确;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,∴=5(a6+a5)>0,=11a6<0,∴a5+a6>0,a6<0,∴a5>0.因此S n最大值为S5,正确;④在△ABC中,cos2A﹣cos2B=﹣2sin(A+B)sin(A﹣B)=2sin(A+B)sin(B﹣A)<0⇔A>B,因此正确;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强,正确.其中正确命题的序号是②③④⑤.三.解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)16.(12分)已知函数f(x)=(Ⅰ)求函数f(x)单调递增区间;(Ⅱ)在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a﹣c)cos B =b cos C,求f(A)的取值范围.【解答】解:(Ⅰ)∵f(x)=sin cos+cos2=sin(+),∴由2k≤+≤2kπ,k∈Z可解得:4kπ﹣≤x≤4kπ,k∈Z,∴函数f(x)单调递增区间是:[4kπ﹣,4kπ],k∈Z.(Ⅱ)∵f(A)=sin(+),∵由条件及正弦定理得sin B cos C=(2sin A﹣sin C)cos B=2sin A cos B﹣sin C cos B,∴则sin B cos C+sin C cos B=2sin A cos B,∴sin(B+C)=2sin A cos B,又sin(B+C)=sin A≠0,∴cos B=,又0<B<π,∴B=.∴可得0<A<,∴<+<,∴sin(+)<1,故函数f(A)的取值范围是(1,).17.(12分)某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100](Ⅰ)求图中x 的值,并估计该班期中考试数学成绩的众数;(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.【解答】解:(Ⅰ)由(0.006×3+0.01+0.054+x)×10=1,解得x=0.018,前三组的人数分别为:(0.006×2+0.01+0.018)×10×50=20,第四组为0.054×10×50=27人,故数学成绩的众数落在第四组,故众数为75分.(Ⅱ)分数在[40,50)、[90,100]的人数分别是3人,共6人,∴这2人成绩均不低于90分的概率P==.18.(12分)如图,已知边长为2的等边△PCD所在的平面垂直于矩形ABCD 所在的平面,BC=2,M为BC的中点(Ⅰ)试在棱AD上找一点N,使得CN∥平面AMP,并证明你的结论.(Ⅱ)证明:AM⊥PM.【解答】(Ⅰ)解:在棱AD上找中点N,连接CN,则CN∥平面AMP;证明:因为M为BC的中点,四边形ABCD是矩形,所以CM平行且相等于DN,所以四边形MCNA为矩形,所以CN∥AM,又CN⊄平面AMP,AM⊂平面AMP,所以CN∥平面AMP.(Ⅱ)证明:过P作PE⊥CD,连接AE,ME,因为边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=2,M为BC的中点所以PE⊥平面ABCD,CM=,所以PE⊥AM,在△AME中,AE==3,ME==,AM==,所以AE2=AM2+ME2,所以AM⊥ME,所以AM⊥平面PME所以AM⊥PM.19.(12分)已知函数f(x)=lnx﹣kx+1(k∈R).(Ⅰ)若x轴是曲线f(x)=lnx﹣kx+1一条切线,求k的值;(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围.【解答】解:(1)函数f(x)的定义域为(0,+∞),f′(x)=﹣k=0,∴x=,由ln﹣1+1=0,可得k=1;(2)当k≤0时,f′(x)=﹣k>0,f(x)在(0,+∞)上是增函数;当k>0时,若x∈(0,)时,有f′(x)>0,若x∈(,+∞)时,有f′(x)<0,则f(x)在(0,)上是增函数,在(,+∞)上是减函数.k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1﹣k>0,f(x)≤0不成立,故k>0,∵f(x)的最大值为f(),要使f(x)≤0恒成立,则f()≤0即可,即﹣lnk≤0,得k≥1.20.(13分)若数列{a n}的前n项和为S n,点(a n,S n)在y=x的图象上(n∈N*),(Ⅰ)求数列{a n}的通项公式;(Ⅱ)若c 1=0,且对任意正整数n都有,求证:对任意正整数n≥2,总有.【解答】(I)解:∵点(a n,S n)在y=x的图象上(n∈N*),∴,当n≥2时,,∴,化为,当n=1时,,解得a1=.∴==.(2)证明:对任意正整数n都有=2n+1,∴c n=(c n﹣c n﹣1)+(c n﹣1﹣c n﹣2)+…+(c2﹣c1)+c1=(2n﹣1)+(2n﹣3)+…+3==(n+1)(n﹣1).∴当n≥2时,==.∴=+…+=<=,又=.∴.21.(14分)已知椭圆C的中心在坐标原点O,长轴在x轴上,离心率为,且椭圆C上一点到两个焦点的距离之和为4.(Ⅰ)椭圆C的标准方程.(Ⅱ)已知P、Q是椭圆C上的两点,若OP⊥OQ,求证:为定值.(Ⅲ)当为(Ⅱ)所求定值时,试探究OP⊥OQ是否成立?并说明理由.【解答】(I)解:由题意可设椭圆的坐标方程为(a>b>0).∵离心率为,且椭圆C上一点到两个焦点的距离之和为4.∴,2a=4,解得a=2,c=1.∴b2=a2﹣c2=3.∴椭圆C的标准方程为.(II)证明:当OP与OQ的斜率都存在时,设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=﹣x(k≠0),P(x,y).联立,化为,∴|OP|2=x2+y2=,同理可得|OQ|2=,∴=+=为定值.当直线OP或OQ的斜率一个为0而另一个不存在时,上式也成立.因此=为定值.(III)当=定值时,试探究OP⊥OQ是否成立?并说明理由.OP⊥OQ不一定成立.下面给出证明.证明:当直线OP或OQ的斜率一个为0而另一个不存在时,则===,满足条件.当直线OP或OQ的斜率都存在时,设直线OP的方程为y=kx(k≠0),则直线OQ的方程为y=k′x(k≠k′,k′≠0),P(x,y).联立,化为,∴|OP|2=x2+y2=,同理可得|OQ|2=,∴=+=.化为(kk′)2=1,∴kk′=±1.∴OP⊥OQ或kk′=1.因此OP⊥OQ不一定成立.。
安徽省淮南一中等四校2015届高三5月联考文综试卷

(在此卷上答题无效)绝密★启用前淮南一中蒙城一中颍上一中怀远一中2015届高三“四校”联考文科综合能力测试命题学校:淮南一中考试时间:2015年5月3日本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第7页,第Ⅱ卷第8页至第10页,全卷满分300分。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的班级、姓名和座位号。
2.答第Ⅰ卷时,每小题选出答案后,必须用0.5毫米黑色墨水签字笔在答题卷规定位置填写。
如需改动,用橡皮擦干净后重新填写。
3.答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
第Ⅰ卷(选择题共132分)本卷共33小题,每小题4分,共132分。
在每题给出的四个选项中,只有一项是最符1.右图是2015年2月16日至2015年4月7日人民币汇率中间价变化图(人民币元/1美元),在不考虑其他因素的情况下,以下判断正确的是①从A点到B点,有利于美国对中国的出口②从A点到B点,有利于中国引进美国资本③从C点到D点,有利于中国公民赴美国旅游④从C点到D点,有利于缓解中国出口企业就业压力A.①②B.①③C.②③D.③④2.《政府工作报告》指出,2015年继续实施积极的财政政策和稳健的货币政策。
下列属于积极财政政策的措施是A.提高存款准备金率B.结构性减税C.增加货币供应量D.减少财政支出3.城镇化是解决城乡差距的根本途径,也是最大的内需所在。
要坚持以人为核心,提升地级市、县城和中心镇产业和人口承载能力,方便农民就近城镇化,发挥好城镇化对现代化的支撑作用。
这说明①城镇化是我国扩大内需的最大潜力所在②要大力发展大、中城市,扩张城市规模③要迅速并大量推进农业转移人口市民化④城镇化有利于缩小城乡差距、统筹发展A.①③B.②③C.①④D.②④4.今年清明节期间,国家旅游局制定的《游客不文明行为记录管理暂行办法》(以下简称《办法》)开始施行。
安徽省淮南市高三文综(地理部分)一模考试试题(含解析)新人教版
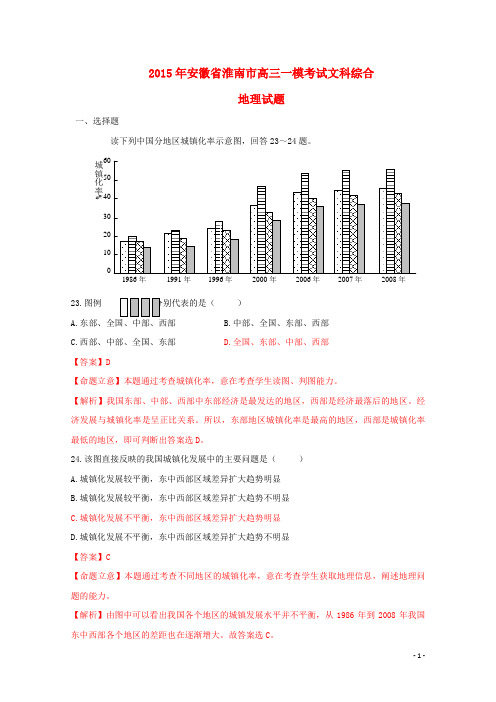
2015年安徽省淮南市高三一模考试文科综合地理试题一、选择题读下列中国分地区城镇化率示意图,回答23~24题。
城镇化率%23.图例)A.东部、全国、中部、西部B.中部、全国、东部、西部C.西部、中部、全国、东部D.全国、东部、中部、西部【答案】D【命题立意】本题通过考查城镇化率,意在考查学生读图、判图能力。
【解析】我国东部、中部、西部中东部经济是最发达的地区,西部是经济最落后的地区。
经济发展与城镇化率是呈正比关系。
所以,东部地区城镇化率是最高的地区,西部是城镇化率最低的地区,即可判断出答案选D。
24.该图直接反映的我国城镇化发展中的主要问题是()A.城镇化发展较平衡,东中西部区域差异扩大趋势明显B.城镇化发展较平衡,东中西部区域差异扩大趋势不明显C.城镇化发展不平衡,东中西部区域差异扩大趋势明显D.城镇化发展不平衡,东中西部区域差异扩大趋势不明显【答案】C【命题立意】本题通过考查不同地区的城镇化率,意在考查学生获取地理信息,阐述地理问题的能力。
【解析】由图中可以看出我国各个地区的城镇发展水平并不平衡,从1986年到2008年我国东中西部各个地区的差距也在逐渐增大。
故答案选C。
25.为了解决城市内涝频繁问题,我国打造海绵型城市(海绵型城市,是让城市像海绵一样,下大雨的时候吸水,干旱的时候把吸收的水再“吐”出来)。
下图中城市绿地建设,符合海绵型城市要求的是()图例道路绿地【答案】A【命题立意】本题通过道路的建设,意在考查学生读图、判图的能力,以及学生对地理事物的综合运用能力。
【解析】由题中材料可知,在下雨的时候地面由于吸水会上涨,在干旱的时候“吐”水,而能够吸水和“吐”水的是绿化用地而不是道路,所以在修建的时候绿化用地应低于路面,只有这样才不影响在雨天道路的使用。
若绿化用地高于道路,那么在雨天,会影响道路的形成安全及道路的整洁性。
故答案选A。
2014年12月,蒙(自)河(口)铁路正式开通运营。
下图为蒙河铁路及铁路线上的马英河大桥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三一模综政治答案
选择题
1.C
2.B
3. B
4. D
5.A
6.D
7.B
8.D
9.B 10.C 11.A
39.(1)①2014年第一季度,我省经济发展状况良好,全省固定资产投资增速最快,农村
居民可支配收入增速高于城市,但城乡差距仍较为明显。
②收入是消费的前提和基础,城乡
居民收入稳步增长,促进了社会消费品零售总额的快速增长。
③合理的收入分配格局的形成
有利于经济的发展,城乡居民收入差距逐渐缩小,会进一步促进我省经济发展。
④生产决定
消费,消费反作用生产,固定资产投资以及社会消费品零售总额的快速增长刺激我省经济,
拉动全省生产总值增加。
(每点2分,共8分)
(2)①社会存在决定社会意识,社会意识反作用社会存在,安徽省根据省情,简政放权,
充分激发市场和社会的活力。
(3分)改革是社会主义制度的自我完善和发展,通过改革转变
职能,进一步促进了我省发展。
(3分)人民群众是历史的创造者,安徽省政府就政策落实开
展相关工作,坚持群众观点群众路线。
(2分)
②政府积极履行职能,组织经济建设,最大限度发挥政策效应。
省政府简政放权,转变政府
职能,积极打造服务型政府。
政府坚持依法行政、审慎用权、自觉接受监督,提高政府威信。
我国政府是人民的政府,坚持为人民服务的宗旨和对人民负责的原则,维护人民群众利益。
(每点3分,共12分)
历史参考答案
题号12 13 14 15 16 17 18 19 20 21 22 答案 A B C C C D A D D B A
37.(1)调整:①向社会主义过渡方式上:从间接向社会主义过渡的路线到直接过渡;
②所有制结构上:从多种所有制并存到单一的公有制;
③经济管理体制上:从计划和市场调节并存到高度集中的计划经济体制。
④分配制度上:从按劳分配到绝对平均主义。
(任答三点即可)(6分)
(2)新模式:国家干预经济(或市场和政府的作用同时发挥)。
(2分)
措施:①整顿财政金融;②调整工业生产;③调节农业生产;④实行福利制度(加强救济工作;推行“以工代赈“);⑤进行社会立法。
(8分,任答四点即可)
(3)
等次论述
第一等认识全面,思路清晰。
史实准确,史论结合密切。
表达通顺。
第二等认识不够全面,有基本思路。
史实基本准确,史论结合不够密切。
表达较通顺。
第三等认识模糊,缺乏条理性。
未能结合史实。
表达欠通顺。
淮南市2015届高三一模文综地理试卷参考答案
选择题
23 24 25 26 27 28 29 30 31 32 33
D C A B C C B A D A D
34.(26分)
(1)空间分布不均;由东南向西北递减;山地降水多。
(6分)
降水季节分配不均;集中在夏秋季(6~9月)等。
(4分)
(2):原因:自然原因:04年以前,降水量减少。
人为原因:工程建设,如坡面防蚀工程;生物措施,如植树造林;产业结构调整,农业结构调整,如退耕还林等。
(8分)
影响:缓解水土流失;恢复提高土壤肥力;改善植被;降低河流含沙量;减轻水旱灾害等(8
分)。
