用EXCEL进行生产函数的多元线性回归分析

合集下载

Excel关于求解一元及多元线性回归方程图解详细

Excel求解一元线性回归方程步骤(图解详细)1．开始－程序－Microsoft Excel，启动Excel程序。

2．Excel程序启动后，屏幕显示一个空白工作簿。

3．选定单元格，在单元格内输入计算数据。

4．选中输入数据，点击“图表向导”按钮。

5．弹出图表向导对话窗，点击XY散点图，选择平滑线散点图，点击下一步。

6．选择系列产生在：列，点击下一步。

7．在图表标题中输入“硝基苯标准曲线”，数值（X）轴输入“硝基苯浓度”，数值（Y）轴输入“HPLC峰面积”。

此外还可以点击“坐标轴”，“网格线”，“图例”，“数据标志”下拉菜单，对其中选项进行选择。

8．点击完成后，即可得到硝基苯的标准曲线图。

9．将鼠标移至图表工作曲线上，单击鼠标右键，选择“添加趋势线”。

10．在“类型”选项中选择“线性”，“选项”中选择“显示公式”，“显示R平方值”，单击确定。

11．单击确定后即可得到附有回归方程的一元线性回归曲线。

12．至此，利用“图表向导”制作回归方程的操作步骤完毕。

利用Excel中“图表向导”制作标准曲线，使用者仅需按照向导说明填入相关信息即可完成图表的制作。

方法简单，适合对Excel了解不多的人员，如果你对Excel函数有一定的了解，那么你可以利Excel函数编制程序完成回归方程的计算。

4.4.2.2通过编制Excel程序计算一元线性回归方程1．打开一个新工作簿，以“一元线性回归方程”为文件名存盘。

2．单击插入，选择名称－定义。

3．在弹出的“定义名称”对话窗中“名称”栏输入“a”，“引用位置”栏输入“＝$E$4”，然后按“添加”按钮；再在“名称”栏输入“b”，“引用位置”栏输入“＝$E$3”，按“添加”按钮，依次输入下列内容，最后单击确定。

“名称”栏输入内容“引用位置”栏输入内容a =$E$4b =$E$3f =$G$4n =$G$3rf =$G$6rxy =$E$5x =$A$3:$A$888y =$B$3:$B$888aa=$G$2yi1 =$E$12yi2 =$E$134．完成命名后，在相关单元格内输入下列程序内容。

EXCEL在多元线性回归分析中的应用

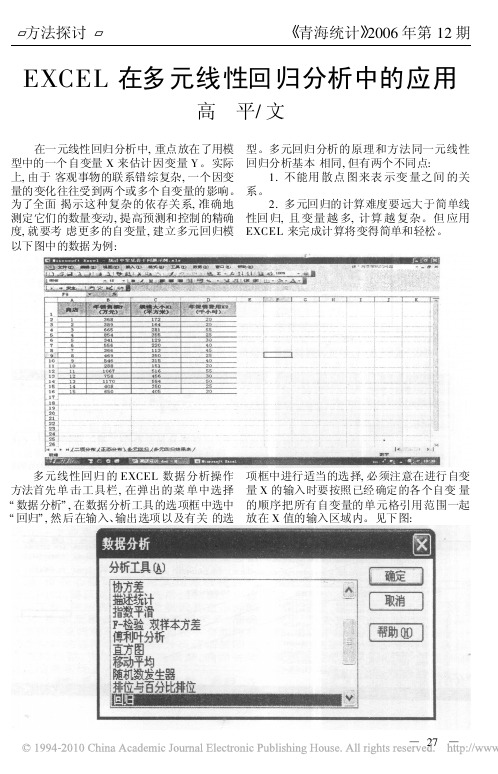
EXCEL 在多元线性回归分析中的应用高平/文在一元线性回归分析中,重点放在了用模型中的一个自变量X 来估计因变量Y 。

实际上,由于客观事物的联系错综复杂,一个因变量的变化往往受到两个或多个自变量的影响。

为了全面揭示这种复杂的依存关系,准确地测定它们的数量变动,提高预测和控制的精确度,就要考虑更多的自变量,建立多元回归模型。

多元回归分析的原理和方法同一元线性回归分析基本相同,但有两个不同点:1.不能用散点图来表示变量之间的关系。

2.多元回归的计算难度要远大于简单线性回归,且变量越多,计算越复杂。

但应用EXCEL 来完成计算将变得简单和轻松。

以下图中的数据为例: 多元线性回归的EXCEL 数据分析操作方法首先单击工具栏,在弹出的菜单中选择数据分析 ,在数据分析工具的选项框中选中回归 ,然后在输入、输出选项以及有关的选项框中进行适当的选择,必须注意在进行自变量X 的输入时要按照已经确定的各个自变量的顺序把所有自变量的单元格引用范围一起放在X 值的输入区域内。

见下图:!27!点击确定按钮,即可得到线性回归分析的结果。

见下图:!!28根据上图中的显示结果,可直接写出二元线性回归方程:Y i=b0+b1X1i+b2X2i=-51.3127+1. 4053x1i+6.3823x2ib1表示在促销费用固定时,商店的规模大小每增加1平方米,年销售额平均增加1.4053万元;b2表示在商店的规模大小固定时,促销费用每增加1万元,年销售额平均增加6.3823万元。

这里b1即商店的规模大小的回归系数比一元线性回归方程中的回归系数b= 1.6246小,是因为一元线性回归方程只考虑了商店的规模大小对年销售额的影响,忽略了促销费用这一很重要的因素,在商店的规模大小的影响中渗入了促销费用的影响。

这里的截距b0=-51.3127万元,与一元线性回归方程中的截距+99.01万元有很大的不同,因为X1=0和X2 =0都不在X1、X2的样本取值范围之内,因而对截距项的解释要非常谨慎。

用EXCEL做线性回归分析

用EXCEL做线性回归分析线性回归分析是一种常用的统计方法，用于研究两个变量之间的线性关系。

它可以帮助我们理解和预测两个变量之间的关系，并且可通过趋势线进行展示。

在Excel中，线性回归分析可以通过使用内置的回归工具函数来实现。

本文将介绍如何使用Excel进行线性回归分析。

首先，我们需要准备好要进行分析的数据。

在Excel中，我们可以将这些数据输入到一个工作表中的列中，每个变量占一列。

例如，我们有一组x变量和一组y变量的数据，可以将x变量输入到A列，y变量输入到B列。

确保每个数据点都位于一个单独的行。

接下来，我们将使用Excel的数据分析工具进行线性回归分析。

要启用数据分析工具，我们需要先打开Excel的选项菜单。

在选项菜单中，选择工具选项卡，然后点击加载项。

在加载项窗口中勾选"分析工具箱"，点击确定以启用该功能。

现在，我们可以使用数据分析工具进行线性回归分析了。

在Excel的数据选项卡上，点击数据分析按钮。

在弹出的对话框中，选择回归，然后点击确定。

Excel将生成回归分析的结果，并将其输出到一个新的工作表中。

在该工作表中，我们可以看到回归方程的系数、截距和相关系数等信息。

此外，Excel还会生成一个散点图，并绘制出回归线。

通过解读回归分析结果，我们可以得到一些关键的信息。

首先，回归方程的系数表示变量之间的关系。

系数越大，表明变量之间的关系越强。

此外，截距表示当自变量为0时，因变量的取值。

相关系数表示两个变量之间的相关性，相关系数值越接近于1或-1，相关性越强。

除了回归分析结果，我们还可以通过散点图来可视化数据。

在这个散点图中，我们可以看到每个数据点的位置以及回归线的趋势。

通过观察散点图，我们可以更好地理解变量之间的关系。

在实际应用中，线性回归分析可以帮助我们预测未来值，控制其他因素的影响，并评估因素对因变量的影响程度。

例如，我们可以利用线性回归分析来研究广告投入与销售业绩之间的关系，以了解广告对销售额的影响。

用EXCEL做线性回归的方法

用EXCEL做线性回归的方法在Excel中进行线性回归分析是一种常见的统计方法，可以用来建立和评估两个变量之间的线性关系。

以下是在Excel中进行线性回归的步骤：2. 打开Excel并导入数据：在Excel中创建一个新的工作簿并将数据导入其中。

确保每个变量处于独立的列中，并将列标题放在第一行。

3.绘制散点图：选择包含两个变量的数据范围，然后通过选择“插入”选项卡上的“散点图”图标绘制散点图。

确保选择一个表示线性趋势的散点图类型（例如，线性散点图）。

4.添加趋势线：右键单击散点图上的任何一个数据点，然后选择“添加趋势线”选项。

在弹出的对话框中，选择“线性”作为趋势线类型。

还可以选择“显示方程式”和“显示R方值”，以显示方程式和决定系数。

5. 进行线性回归分析：在Excel中进行线性回归分析有两种常见的方法。

一种是使用“利用工具”功能进行线性回归，另一种是使用“数据分析”工具。

-利用工具：选择工作表中的一个空单元格，然后选择“数据”选项卡上的“数据分析”功能。

在弹出的对话框中，选择“回归”然后点击“确定”。

在输入区域中选择两个变量的列，并勾选“置信区间”和“残差”，然后点击“确定”进行分析。

- 数据分析工具：如果Excel中没有“数据分析”选项，则需要先启用。

选择“文件”选项卡上的“选项”，然后选择“添加-加载项”。

在弹出的对话框中，选择“Excel加载项”，并勾选“数据分析工具”，然后点击“确定”。

在“数据”选项卡上就会出现“数据分析”选项，然后执行和利用工具方法相同的步骤。

6. 解读结果：分析完成后，Excel将在单元格区域中输出回归方程式和其他相关统计信息。

主要关注回归方程式中的系数，这些系数表示参与线性回归的变量之间的关系。

还可以评估决定系数（R²）的值以确定回归模型的拟合程度。

7.绘制拟合曲线：使用回归方程式中的系数，可以在散点图中绘制拟合曲线。

选择散点图上的一个空白区域，然后选择“插入”选项卡上的“散点图”功能。

如何使用Excel进行多元统计分析和回归模型

如何使用Excel进行多元统计分析和回归模型随着数据分析和统计学在各个领域的应用越发广泛，Excel作为一种常用的办公软件，也能提供一些强大的数据分析功能。

在本文中，我们将介绍如何使用Excel进行多元统计分析和回归模型。

一、多元统计分析多元统计分析是研究多个自变量对因变量的影响以及它们之间的关系的一种方法。

Excel提供了一些内置函数和工具，可以帮助我们进行多元统计分析。

1. 描述性统计分析描述性统计分析是将数据呈现为有意义的统计数字，包括平均值、中位数、方差等。

在Excel中，可以使用SUM、AVERAGE、MEDIAN等函数来计算这些统计数字。

2. 相关性分析相关性分析用于衡量两个或多个变量之间的关系强度。

Excel提供了CORREL函数，可以计算两个变量之间的相关系数。

相关系数的取值范围为-1到1，接近1表示正相关，接近-1表示负相关，接近0表示无相关。

3. 回归分析回归分析用于建立自变量与因变量之间的数学关系模型。

在Excel 中，可以使用内置的回归工具进行回归分析。

首先，选择需要分析的自变量和因变量的数据，然后打开“数据”选项卡，选择“数据分析”并选择“回归”。

填写相应的参数，并点击“确定”即可生成回归结果报告。

二、回归模型回归模型用于预测因变量在给定自变量的情况下的数值。

Excel提供了多种回归模型，包括线性回归、多项式回归、指数回归等。

1. 线性回归模型线性回归是最常用的回归模型，适用于自变量与因变量呈线性关系的情况。

在Excel中，可以使用内置的线性回归工具进行线性回归分析。

选择自变量和因变量的数据，打开“数据”选项卡，选择“数据分析”并选择“回归”。

在参数设置中选择线性回归，并点击“确定”生成回归结果报告。

2. 多项式回归模型多项式回归适用于自变量与因变量呈多项式关系的情况。

在Excel 中，可以使用数据分析工具中的“回归”选项进行多项式回归分析。

选择自变量和因变量的数据，打开“数据”选项卡，选择“数据分析”并选择“回归”。

利用Excel进行线性回归分析

利用Ｅxcel进行线性回归分析————————————————————————————————作者: ————————————————————————————————日期：ﻩ文档内容1.利用Excel进行一元线性回归分析２. 利用Ｅｘcｅｌ进行多元线性回归分析1．利用Excel进行一元线性回归分析第一步,录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。

录入结果见下图(图1)。

图1第二步,作散点图如图２所示，选中数据(包括自变量和因变量）,点击“图表向导”图标；或者在“插入”菜单中打开“图表(H)”。

图表向导的图标为。

选中数据后，数据变为蓝色(图２）。

图2点击“图表向导”以后，弹出如下对话框(图３）:图3在左边一栏中选中“XＹ散点图”，点击“完成”按钮,立即出现散点图的原始形式（图4)：灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图４第三步，回归观察散点图,判断点列分布是否具有线性趋势。

只有当数据具有线性分布特征时,才能采用线性回归分析方法。

从图中可以看出，本例数据具有线性分布趋势，可以进行线性回归。

回归的步骤如下:1. 首先，打开“工具”下拉菜单，可见数据分析选项（见图5）：图５用鼠标双击“数据分析”选项,弹出“数据分析”对话框（图6)：图62.然后，选择“回归”，确定，弹出如下选项表(图7)：图7进行如下选择：X 、Y 值的输入区域(B1：Ｂ11，C1:C11）,标志,置信度(95%),新工作表组，残差,线性拟合图(图８-１）。

或者:X 、Y 值的输入区域（B2:B11，C2:Ｃ11)，置信度(95%)，新工作表组,残差,线性拟合图（图8-2）。

注意：选中数据“标志”和不选“标志”,X 、Y 值的输入区域是不一样的：前者包括数据标志：最大积雪深度x （米) 灌溉面积y （千亩）后者不包括。

这一点务请注意(图8）。

图８－1包括数据“标志”图8-２不包括数据“标志”3.再后，确定,取得回归结果(图9）。

用Excel做线性回归分析

用Excel做线性回归分析第一步：收集数据首先需要准备一组数据，其中有一个自变量和一个因变量，通常将自变量列在左侧列，因变量列在右侧列。

例如：X（自变量）Y（因变量）2 4.24 7.46 8.98 11.610 15.3第二步：绘制散点图接下来需要绘制散点图，将自变量和因变量之间的关系可视化。

在Excel中，选择插入->散点图，可以选择带有线条或仅带有散点的散点图。

根据上面的数据，得到的散点图应该如下：（插入散点图）第三步：添加趋势线为了更直观地展示自变量和因变量之间的关系，需要添加趋势线。

在Excel中，右键单击散点图上的任意一个数据点，选择“添加趋势线”。

在“添加趋势线”对话框中，选择“线性”类型，勾选“显示方程式”选项，点击“确定”。

得到以下图表：第四步：计算线性回归方程Excel自带一个计算线性回归方程的函数：LINST。

在Excel中，可以直接在某个单元格中输入以下公式：=LINST(因变量的单元格范围, 自变量的单元格范围, TRUE, TRUE)例如：结果如下：（插入计算结果图表）其中，- 第一个TRUE表示需要截距项；- 第二个TRUE表示需要进行常规数组计算。

根据上面的结果，得到的线性回归方程为：y = 1.375x + 1.550第五步：预测结果在得到线性回归方程之后，可以使用该方程进行预测。

例如，如果自变量为12，则根据上述方程预测因变量的值应为：因此，当自变量为12时，因变量的预测值为18.7。

通过以上五个步骤，可以使用Excel进行简单的线性回归分析。

当然，Excel还提供了更多高级的统计分析功能，如多元线性回归、逻辑回归、二项式分布等。

excel多元回归求系数

excel多元回归求系数在Excel中进行多元回归分析，可以使用数据分析工具来求得回归系数。

按照以下步骤进行：假设自变量有多个（例如x1、x2、x3等），因变量是y。

1、首先，将数据按照以下格式整理：在Excel的数据表中，将自变量（x1、x2、x3等）放在不同的列，将因变量（y）放在一列。

2、确保已经启用了"数据分析"工具。

如果没有，按照以下步骤启用它：点击Excel的"文件" 菜单。

选择"选项"。

在Excel选项对话框中，选择"加载项" 选项卡。

在"管理" 列表中，选择"Excel加载项"，然后点击"转到" 按钮。

在"加载项" 对话框中，勾选"分析工具包"，然后点击"确定"。

3、现在，可以找到"数据分析" 工具了。

点击Excel的"数据" 标签，在"数据分析" 组中选择"数据分析"。

4、在弹出的"数据分析" 对话框中，选择"回归"，然后点击"确定"。

5、在"回归" 对话框中，填写以下信息：输入Y范围：选择因变量（y）所在的列。

输入X范围：选择所有自变量（x1、x2、x3等）所在的列。

勾选"标签"，以便在输出中包含变量名。

6、点击"确定"，Excel将进行回归分析，并在新的工作表中输出回归结果。

在输出结果中，将找到每个自变量的回归系数（Coefficients）。

这些系数表示对因变量的影响程度，正系数表示正向关系，负系数表示负向关系。

确保数据符合回归分析的前提条件，并注意回归模型的解释和适用性。

【免费下载】excel多元函数线性回归步骤

tiCj tiBj
-2 -3 -3 -2 -5 -1 -4 -5 -4
3.数据分析第一步：点击 excel2007 中工具栏的“数据”，然后点击“数据分析”，弹出数据分析的对话框，如图所示。
第二步：选中“回归”，点击确定，弹出对话框，如图所示。
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

用EXCEL进行生产函数的多元线性回归分析

用EXCEL进行生产函数的多元线性回归分析一、相关函数EXCEL电子制表系统中函数的语法分为函数名和参数两部分，参数用圆括号括起来，之间以逗号隔开。

参数可以为单元格区域、数组、函数、常数（逻辑型、数值型等）。

进行回归分析时，主要采用线性回归函数LINEST，辅以使用索引取值INDEX与四舍五入ROUND 函数。

1、线性回归函数LINEST。

使用最小二乘法对已知数据进行最佳直线拟合，并返回描述此直线的数组。

因为此函数返回数值数组，所以必须以数组公式的形式输入。

Excel中数组公式非常有用，它可建立产生多值或对一组值而不是单个值进行操作的公式。

要输入数组公式，首先必须选择用来存放结果的单元格区域，在编辑栏输入公式，然后按ctrl＋Shift＋Enter 组合键锁定数组公式，Excel将在公式两边自动加上括号“{}”。

不要自己键入花括号，否则，Excel认为输入的是一个正文标签。

要编辑或清除数组公式．需选择数组区域并且激活编辑栏，公式两边的括号将消失，然后编辑或清除公式，最后按Ctrl＋shift＋Enter键。

【实现目标】在Excel中巧编辑数组公式。

【操作方法】其具体操作如下：（1）选择用来存放结果的单元格区域，在编辑栏输入公式，然后按【Ctrl＋Shift＋Enter】键锁定数组公式，Excel将在公式两边自动加上括号“{}”。

（2）编辑或清除数组公式时，先选择数组区域并且激活编辑栏，然后编辑或清除公式，最后按【Ctrl＋Shift＋Enter】键即可。

该函数的功能为：运算结果返回一线性回归方程的参数，即当已知一组混合成本为Y因变量序列值、N组Xi有关自变量因素的数量序列值时，函数返回回归方程的系数bi（i=1，2…n单位变动成本）和常数a（固定成本或费用）。

多元回归方程模型则为：y=b1x1＋b2X2……＋bnXn＋a语法LINEST(known_y's,known_x's,const,stats)Known_y's 是关系表达式 y = mx + b 中已知的 y 值集合。

用Excel进行多元回归分析

用Excel进行多元回归分析Excel是一种使用方便的电子表格软件,它有强大的数据管理功能,能制作各种统计图表,具有丰富的医学统计函数。

利用Excel进行医学统计多元回归分析既简单又迅速,能够提高我们的工作效率。

标签：Excel 医学统计多元回归。

1数据分析在科学研究中,经常要对收集到的数据进行各种统计分析,大多使用较著名的统计分析软件包,如SAS,SPSS等。

这些统计分析软件包功能强大,不仅能做单变量分析,而且可做各种复杂的多变量分析。

然而,在对数据进行处理时,大多使用简单统计描述,绘制各种统计图表,或者进行回归分析、t 检验、方差分析等等。

作这些统计分析时,通常叫使用Windows下的Excel。

Excel是种使用极方便的电子表格软件,与SAS,SPSS等数据分析软件相比,它的优势在于[1]:(1)强大的数据与公式自动填充功能;(2)方便的数据编辑与透视分析功能;(3)灵活的单元格绝对引用与相对引用功能;(4)完美的图形绘制系统与丰富的内置函数功能。

Excel在“分析工具库”中,提供了组数据分析工具。

使用这些分析工具时,只需指出数据所在的单元格和提供必要的参数,该工具就会使用适宜的统计或工程函数,对数据做处理,给出相应的结果[2]。

有些工具在输出时还能产生图表。

单击“工具”菜单中的“数据分析”命令,浏览已有的分析工具。

如果在“工具”菜单上没有“数据分析”命令,则应在“工具”菜单上运行“加载宏”命令,并在“加载宏”对话框中选择“分析工具库”。

2多元回归分析在研究个应变量对多个自变量的线性依存关系时,可使用多元回归。

此工具通过对一组观察值使用“最小二乘法”直线拟合,进行线形回归分析[3]。

本工具可用来分析单个因变量是如何受一个或几个自变量影响的。

例如,观察某个运动员的运动成绩与一系列统计因素的关系,如年龄、身高和体重等。

在操作时,可以基于一组已知的体能统计数据,并辅以适当加权,对尚未进行过测试的运动员的表现作出预测。

用Excel做线性回归分析报告

用Excel做线性回归分析报告1. 引言1.1 主题背景介绍在当今数据分析日益普及的大背景下，Excel作为一款广泛使用的电子表格软件，凭借其强大的数据处理和计算能力，成为了众多行业和领域中不可或缺的工具。

线性回归作为统计学中最基础也是应用最广泛的预测模型之一，其在Excel中的实现和应用，极大地便利了各类研究和决策过程。

通过对Excel线性回归分析的深入研究，可以帮助我们更好地理解数据间的内在联系，为决策提供科学依据。

1.2 研究目的和意义本次研究的目的是通过Excel实现线性回归分析的全过程，探索其在实际数据中的应用效果。

研究意义主要体现在以下几个方面：1.提高数据处理效率：通过掌握Excel线性回归分析，可以快速处理大量数据，提高工作效率。

2.辅助决策制定：利用线性回归模型，可以为企业或个人提供更为准确的数据预测，辅助决策的制定。

3.普及统计知识：Excel线性回归分析的普及有助于提升公众对统计学基本概念的理解和认识。

1.3 研究方法概述本研究主要采用以下方法：•文献调研：收集和整理线性回归相关理论知识，以及Excel进行线性回归分析的实操步骤。

•数据实践：选取合适的数据集，使用Excel进行实际操作，包括数据清洗、模型建立、求解以及结果分析等。

•模型评估与优化：结合实际应用场景，对建立的模型进行评估和优化，确保分析结果的准确性和可靠性。

2. Excel线性回归分析基本概念2.1 线性回归的定义与原理线性回归是统计学中最基础也是应用最广泛的预测模型之一，它主要用于描述两个或两个以上变量之间的线性关系。

其基本原理是通过历史数据，寻找一个或多个自变量（解释变量）与因变量（响应变量）之间的最佳线性关系表达式。

简单线性回归涉及一个自变量和一个因变量，其模型可以表示为：[ Y = _0 + _1X + ]其中，( Y )代表因变量，( X )代表自变量，( _0 )是截距项，表示当( X = 0 )时( Y )的期望值，( _1 )是斜率，表示( X )每变化一个单位时( Y )的平均变化量，( )是误差项，表示模型未能解释的随机变异。

excel中关于线性回归计算运用

excel中关于线性回归计算运用
线性回归计算运用
目前，线性回归一般采用Origin和数学中常见的MATLAB、Excel等软件进行计算，下面以最大干密度和含石率（＞5mm含量）的一组数据为例进行说明。

最大干密度和含石率关系
最大干密度和含石率符合线性关系：
y=ax2+bx+c
式中：y------最大干密度，g/cm3
X------含石率，%
a，b，c------回归系数。

利用Excel软件拟合曲线，计算回归方程。

具体步骤如下：（1）打开Excel，将数据输入Excel中，如下图。

（2）点击菜单栏中“插入”菜单，并从下拉菜单中选择“图表”选项，如下图。

（3）在点击“图表”菜单后，进入“图表向导”中，点击类型为
“XY散点图”，选项如下图。

（4）进入如下图所示的界面，点击数据区域将含石率示值X、最大干密度Y产生在B1G2区域。

如下图。

（6）点击下一步，进入图表确认界面，如下图
（7）点击完成按钮，图表绘制完成如下图。

（8）用鼠标点在数据（点）上，点击右键出现图中的菜单，点添加“趋势线”，然后点击“选项”，选择“显示公式”、“显示R2值”，点击确定完成线性回归方程，如下图。

由图表中可以得知，该最大干密度和含石率线性回归方程为y=-0.00005x 2+0.0079x+2.1401，相关系数R 2=0.966。

利用Excel进行线性回归分析报告

文档内容1. 利用Excel进行一元线性回归分析2. 利用Excel进行多元线性回归分析1. 利用Excel进行一元线性回归分析第一步，录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。

录入结果见下图（图1）。

图1第二步，作散点图如图2所示，选中数据（包括自变量和因变量），点击“图表向导”图标；或者在“插入”菜单中打开“图表（H）”。

图表向导的图标为。

选中数据后，数据变为蓝色（图2）。

图2点击“图表向导”以后，弹出如下对话框（图3）：图3在左边一栏中选中“XY散点图”，点击“完成”按钮，立即出现散点图的原始形式（图4）：图4第三步，回归观察散点图，判断点列分布是否具有线性趋势。

只有当数据具有线性分布特征时，才能采用线性回归分析方法。

从图中可以看出，本例数据具有线性分布趋势，可以进行线性回归。

回归的步骤如下：1.首先，打开“工具”下拉菜单，可见数据分析选项（见图5）：图5用鼠标双击“数据分析”选项，弹出“数据分析”对话框（图6）：图62. 然后，选择“回归”，确定，弹出如下选项表（图7）：图7进行如下选择：X 、Y 值的输入区域（B1:B11，C1:C11），标志，置信度（95%），新工作表组，残差，线性拟合图（图8-1）。

或者：X 、Y 值的输入区域（B2:B11，C2:C11），置信度（95%），新工作表组，残差，线性拟合图（图8-2）。

注意：选中数据“标志”和不选“标志”，X 、Y 值的输入区域是不一样的：前者包括数据标志：最大积雪深度x(米) 灌溉面积y(千亩)后者不包括。

这一点务请注意（图8）。

图8-1包括数据“标志”图8-2不包括数据“标志”3.再后，确定，取得回归结果（图9）。

图9线性回归结果4. 最后，读取回归结果如下：截距：356.2=a ；斜率：813.1=b ；相关系数：989.0=R ；测定系数：979.02=R ；F 值：945.371=F ；t 值：286.19=t ；标准离差（标准误差）：419.1=s ；回归平方和：854.748SSr =；剩余平方和：107.16SSe =；y 的误差平方和即总平方和：961.764SSt =。

excel多元函数线性回归步骤

多元函数线性回归步骤
1.加载数据分析
第一步：打开2007excel，点击左上角的按钮，如图所示。

第二步：点击右下角的，如图所示。

第三步：点击左侧的加载项，如图所示。

第四步：点击最下面的“转到”，如图所示，然后选中“分析数据库”，点击“确定”。

2.数据的整理
已知和，和，和
，将其整理为
ln
C
ij B ij
P P ，C B
ij ij t t -和
C B
ij ij c c
-，见下表。

整理后的数据为：
3.数据分析
第一步：点击excel2007中工具栏的“数据”，然后点击“数据分析”，弹出数据分析的对话框，如图所示。

第二步：选中“回归”，点击确定，弹出对话框，如图所示。

第三步：“Y值输入区域”选择第一列，“X值输入区域”选择后两列，选择“置信度”，“新工作表组”，“残差”和“标准残差”。

如图所示，点击确定。

4.结果分析
结果如图所示。

只需找到如下表所示的内容，
Coefficients（系数）Intercept（截距）0.38980452（对应γ）X Variable 1 -0.079587874（对应α）
X Variable 2 -0.003868252（对应β）。

多元线性回归excel操作方法

多元线性回归excel操作方法
多元线性回归是指一种包含多个自变量的线性回归模型，Excel中可以通过“数据分析”工具进行多元线性回归分析。

以下是具体的操作步骤：
1.打开Excel，在Excel菜单栏中找到“数据”选项卡。

2.在“数据”选项卡中找到“数据分析”选项，如果没有，就需要先启用它。

方法是：点击“文件”->“选项”->“插入”->勾选“数据分析”，点击“确定”。

3.打开“数据分析”对话框，在“分析工具”列表中找到“回归”，然后点击“确定”。

4.在“回归”对话框中，设置输入数据范围。

在“输入X范围”中输入自变量的数据范围，在“输入Y范围”中输入因变量的数据范围。

5.在“回归”对话框中，勾选“标签”选项，然后在“输出选项”中选择“新工作表中”并指定输出位置。

6.在“回归”对话框中，勾选“加入常数项”选项，然后点击“确定”。

7.Excel会自动在输出位置生成一个新的工作表，其中包含了多元线性回归的结果，包括自变量系数、因变量截距、调整R方等。

以上就是Excel进行多元线性回归的具体操作方法。

使用Excel数据分析工具进行多元回归分析

使用Excel数据分析工具进行多元回归分析使用Excel数据分析工具进行多元回归分析与简单的回归估算分析方法基本相同。

但是由于有些电脑在安装办公软件时并未加载数据分析工具，所以从加载开始说起（以Excel2010版为例，其余版本都可以在相应界面找到）。

点击“文件”，如下图：在弹出的菜单中选择“选项”，如下图所示：在弹出的“选项”菜单中选择“加载项”，在“加载项”多行文本框中使用滚动条找到并选中“分析工具库”，然后点击最下方的“转到”，如下图所示：在弹出的“加载宏”菜单中选择“分析工具库”，然后点击“确定”，如下图所示：加载完毕，在“数据”工具栏中就出现“数据分析”工具库，如下图所示：给出原始数据，自变量的值在A2：I21单元格区间中，因变量的值在J2：J21中，如下图所示：假设回归估算表达式为：试使用Excel数据分析工具库中的回归分析工具对其回归系数进行估算并进行回归分析：点击“数据”工具栏中中的“数据分析”工具库，如下图所示：在弹出的“数据分析”-“分析工具”多行文本框中选择“回归”，然后点击“确定”，如下图所示：弹出“回归”对话框并作如下图的选择：上述选择的具体方法是：在“Y值输入区域”，点击右侧折叠按钮，选取函数Y数据所在单元格区域J2：J21，选完后再单击折叠按钮返回；这过程也可以直接在“Y值输入区域”文本框中输入J2：J21；在“X值输入区域”，点击右侧折叠按钮，选取自变量数据所在单元格区域A2：I21，选完后再单击折叠按钮返回；这过程也可以直接在“X值输入区域”文本框中输入A2：I21；置信度可选默认的95%。

在“输出区域”如选“新工作表”，就将统计分析结果输出到在新表内。

为了比较对照，我选本表内的空白区域，左上角起始单元格为K10.点击确定后，输出结果如下：第一张表是“回归统计表”(K12：L17):其中：Multiple R：（复相关系数R）R2的平方根，又称相关系数，用来衡量自变量x与y之间的相关程度的大小。

excel多元回归求系数

excel多元回归求系数
在Excel中进行多元回归并求取系数，可以使用数据分析工具包中的回归功能。

以下是进行多元回归求系数的一般步骤：
1.准备数据：将自变量和因变量的数据整理到Excel表格中，确保
它们在同一行或列中。

2.打开Excel并选择数据：确保包含自变量和因变量的数据区域处
于活动状态。

3.转至“数据”选项卡，找到“数据分析”工具：如果没有显示该
选项，可能需要先启用“数据分析”功能。

可以通过“文件”->“选项”->“加载项”->“Excel加载项”->“数据分析工具”的流程启用。

4.打开“数据分析”对话框：在“数据”选项卡下，找到“数据分
析”工具，然后选择“回归”。

5.填写对话框参数：在弹出的回归对话框中，选择自变量和因变量
的范围，确保选中“输出范围”选项，以获取回归结果。

6.点击“确定”开始回归分析：Excel将进行回归计算，并在指定
的输出范围中生成回归结果，包括系数、标准错误和显著性等信息。

根据回归结果，可以查找系数对应的列，通常标注为"Coef"、"Coefficient"、"Beta"或类似标签。

这些系数值表示每个自变量的影响程度。

进行多元回归时，要确保数据满足回归模型的假设，例如线性关系、
独立性、常数方差等。

此外，为了正确解释和应用回归结果，还需要考虑统计显著性和解释变量的实际意义。

用EXCEL进行生产函数的多元线性回归分析

Excel关于求解一元及多元线性回归方程 图解详细

EXCEL在多元线性回归分析中的应用

用EXCEL做线性回归分析

用EXCEL做线性回归的方法

如何使用Excel进行多元统计分析和回归模型

利用Excel进行线性回归分析

用Excel做线性回归分析

excel多元回归求系数

【免费下载】excel多元函数线性回归步骤

用EXCEL进行生产函数的多元线性回归分析

用Excel进行多元回归分析

用Excel做线性回归分析报告

excel中关于线性回归计算运用

利用Excel进行线性回归分析报告

excel多元函数线性回归步骤

多元线性回归excel操作方法

使用Excel数据分析工具进行多元回归分析

excel多元回归求系数

Excel关于求解一元及多元线性回归方程图解详细