固体物理作业答案
固体物理答案-第二章

N0=6.0221023,与N0对应的质量应为
M=23+35.5=58.5(g)
Na原子量
Cl原子量
阿伏加德罗常数
面心立方,最近邻原子有12个, 由N个惰性气体原子构成的分子晶体,其总互作用势能可表示为
(2)计及最近邻和次近邻,次近邻有6个。
2.14 KCl晶体的体积弹性模量为 相邻离子间距缩小0.5%,需要施加多大的压力。 ,若要使晶体中 解:根据体积弹性模量K的定义, 得 ,因而 设R为相邻离子间的距离。KCL具有NaCL结构,平均每体 才有一个离子,若晶体中共含N个离子,则晶体体积 积
式中,V为晶体体积,N为晶体包含的原子数,v为每个原子平 均占据的体积。若以
表示晶体包含的晶胞数,
中每个晶胞的体积,n表示晶胞中所含的粒子数,则(1)式完全 等效于
解:题给
表示晶体
(1)
于是得
(2)
R为离子间的最短距离。题给的各种晶格均为立方格子,如令
证明:
选取负离子O为参考离子,相邻两离子间的距离用R表示。
第j个离子与参考离子的距离可表示为
对于参考
离子O,它与其它离子的互作用势能为
马德隆常数
2.3 设两原子间的互作用能可由 表述。 式中第一项为吸引能,第二项为排斥能; 均为正的常数。证明,要使这两原子系统处于平衡状态,必须n>m。 且 即当 时, 证明:相互作用着的两原子系统要处于稳定平衡状态,相应 于平衡距离 处的能量应为能量的极小值,
为常数,试求
(1)平衡时原子间的最短距离;
(2)平衡时晶体体积;
(3)平衡时体积弹性模量;
(4)抗张强度。
解:
(1)
由
得
01
固体物理习题参考答案

固体物理第一次习题参考答案1.如果将等体积球分别排成下列结构,设x 表示刚球所占体积与总体积之比,证明结构 x简单立方 0.526x π=≈体心立方 30.688x π=≈ 面心立方 20.746x π=≈ 六角密排 20.746x π=≈ 金刚石 30.3416x π=≈解:设钢球半径为r ,立方晶系晶格常数为a ,六角密排晶格常数为a,c 钢球体积为V 1,总体积为V 2(1)简单立方单胞含一个原子,a r =2 52.06343321≈==ππa r V V(2)体心立方取惯用单胞,含两个原子,r a 43= 68.0833423321≈=⋅=ππar V V (3)面心立方取惯用单胞,含4个原子,r a =2 74.0623443321≈=⋅=ππar V V (4)六角密排与面心立方同为密堆积结构,可预期二者具有相同的空间占有率 取图示单胞,含两个原子,a r =2 单胞高度a c 38=(见第2题) 74.062233422321≈=⋅⋅=ππc a r V V (5)金刚石取惯用单胞,含8个原子,r a 2341= 34.01633483321≈=⋅=ππar V V2.试证六方密排密堆积结构中128() 1.6333c a =≈解: 六角密排,如图示,4个原子构成正四面体222)2332(2a a c =⋅+⎪⎭⎫⎝⎛ ⇒ a c 38=3.证明:体心立方晶格的倒格子是面心立方,面心立方的倒格子是体心立方。
证:体心立方基矢取为⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=++-=-+=)(2)(2)(2321k j i a a k j i a a k j i a a其中a 为晶格常数其倒格子基矢,按定义)(2)(21111114212)(223321j i b j i a kj ia a a a b+=+=--⋅=⨯Ω=πππ)(2)(2132k j b a a b +=⨯Ω=π)(2)(2213k i b a a b +=⨯Ω=π可见,体心立方的倒格子是晶格常数为a b π4=的面心立方。
固体物理第三章作业答案

dt
• 其中pt为电子的动量,τ为相邻两次碰撞之间的电
子自由运动时间(弛豫时间),f t为电子所受的
外力。请在线性响应的范围内,推导金属在频率
为ω的电磁波作用下的电导率。在此基础上,可
尝试导出金属的介电函数。
• 解:设频率为ω的电磁波中 E E0eit
B B0eit
• 金属在电磁波作用下的运动方程
• 电子热容系数 2.08mJ mol1 K 2
• 电子热质量
mt*h
m 观测值 自由电子气
m
2.08
2.08பைடு நூலகம்
2RkB 2 3 2n 2
3
m
2
3
2
2 a3
2
3
2RkB
2.08
1.05 1034
2
ai bj 2ij
则相应的倒格子基矢为:
基本无问题,少数同学没写 出基矢的表达式,没注意单 位化为cm-1
b1
2 a
i
108 i
cm1
b2
2 b
i
2
108 i
cm1
倒格子和第一布里渊区如图示:红色区域为第一布里渊区
b2
b1 108 cm1
dp t p t eE ev B
dt
• 忽略磁场项作用( eE ev B ),运动方程写为:
dp t p t
eE
dt
dv dt
v
e m
E0eit
固体物理作业及答案

固体物理作业2.1 光子的波长为20 nm ,求其相应的动量与能量。
答:由λhP =,υh E =得:动量12693410313.3102010626.6----⋅⋅⨯=⨯⋅⨯==m s J ms J hP λ 能量J ms m s J chh E 189183410932.9102010998.210626.6----⨯=⨯⋅⨯⨯⋅⨯===λυ2.2 作一维运动的某粒子的波函数可表达为:, 求归一化常数A? 粒子在何处的几率最大?答:再由2)()(x x ψω=得:222)()(x a x A x -=ω 其中 a x ≤≤0;322222462)(x A x aA x A a dx x d +-=ω 令0)(=dx x d ω得:2,21a x a x ==而a x =1时,0)(=x ω,显然不是最大; 故当22ax =时,粒子的几率最大。
3.1 晶体中原子间的排斥作用和吸引作用有何关系?在什么情况下排斥力和吸引力分别起主导作用? 答:在原子由分散无规的中性原子结合成规则排列的晶体过程中, 吸引力起到了主要作用. 在吸引力的作用下, 原子间的距离缩小到一定程度, 原子间才出现排斥力. 当排斥力与吸引力相等时, 晶体达到稳定结合状态. 可见, 晶体要达到稳定结合状态, 吸引力与排斥力缺一不可. 设此时相邻原子间的距离为0r , 当相邻原子间的距离0r r 时, 吸引力起主导作用;当相邻原子间的距离0r r 时, 排斥力起主导作用。
3.2已知某晶体中相邻两原子间的相互作用势能可表达为:(1) 求出平衡时两原子间的距离;(2) 平衡时的结合能;(3) 若取m=2, n=10,两原子间的平衡距离为3 Å,晶体的结合能为4 eV/atom 。
请计算出A 和B 的值。
答:设平衡时原子间的距离为0r 。
达到平衡时,相互作用势能应具有最小值,即)(r u 满足:0)(0=∂∂r rr u ,求得mn AmBn r -=10)(……(1) 将0r 代入,得平衡时的结合能mn mn m AmBn AmBn A r u --+-=n 0)(B )()( (2)当m=2,n=10时,由(1)式得5B=A 0r 8,再由0r =3Å,)(0r u -=4eV 代人(2)式可得: 109610001090.54)(m eV r r u B ⋅⨯=-=- 2192000100201050.4)(45)(m eV r r u r u r r A ⋅⨯=-=⎥⎥⎦⎤⎢⎢⎣⎡-=-B4.1 一定温度下,一个光学波的声子数目多,还是声学波的声子数目多? 答:频率为的格波的(平均) 声子数为:.因为光学波的频率比声学波的频率高, ()大于(), 所以在温度一定情况下, 一个光学波的声子数目少于一个声学波的声子数目.4.2 爱因斯坦模型和德拜模型的主要近似分别是什么?简述德拜温度及其物理意义。
固体物理答案第一章

bc
2π
b
c
2π
i
Ω
a bc a
同理
b
2π
j
b
c
2π
k
c
khkl
2π
h a
i
k b
j
l c
k
khkl
2π
h
2
k
2
l
2
a b c
d hkl
3π 16
32
a
图1.6 金刚石结构
1.7 证明:用半径不同的两种硬球构成下列稳定结构时小球半 径和大球半径之比值分别为
(1)体心立方(配位数为8):1 r / R 0.73 ; (2)简单立方(配位数为6):0.73 r / R 0.41 ; (3)正四面体结构(配位数为4):0.41 r / R 0.23 ; (4)层状结构(配位数为3):0.23 r / R 0.16 。
z
z
2 10
131
o
y
x
x
o
y
1.3 若基矢 a,b,c 构成简单正交系,试证明,晶面族(hkl)
的面间距为
dhkl
1 h 2 k 2 l 2 a b c
并说明面指数简单的晶面,其面密度比较大,容易解理。
证明:设
a,b,c
第一章 晶体结构和X射线衍射
1.1 指出立方晶格(111)面与(110)面的交线的晶向。
解: 立方晶格(111)面与(110)面的交线为AB,其等效
固体物理参考答案(前七章)

固体物理习题参考答案(部分)第一章 晶体结构1.氯化钠:复式格子,基元为Na +,Cl -金刚石:复式格子,基元为两个不等价的碳原子 氯化钠与金刚石的原胞基矢与晶胞基矢如下:原胞基矢)ˆˆ()ˆˆ()ˆˆ(213212211j i a a i k a a k j a a +=+=+= , 晶胞基矢 ka a j a a ia a ˆˆˆ321===2. 解:31A A O ':h:k;l;m==-11:211:11:111:1:-2:1 所以(1 1 2 1) 同样可得1331B B A A :(1 1 2 0); 5522A B B A :(1 1 0 0);654321A A A A A A :(0 0 0 1)3.简立方: 2r=a ,Z=1,()63434r 2r a r 3333πππ===F体心立方:()πππ833r4r 342a r 3422a 3r 4a r 4a 33333=⨯=⨯=∴===F Z ,,则面心立方:()πππ622r 4r 34434442r 4a r 4a 233ar 33=⨯=⨯=∴===F Z ,,则 六角密集:2r=a, 60sin 2c a V C = a c 362=,πππ622336234260sin 34223232=⨯⨯⨯=⨯=⎪⎭⎫ ⎝⎛a a c a r F a金刚石:()πππ163r 38r 348a r 3488Z r 8a 33333=⨯=⨯===F ,, 4. 解:'28109)31arccos(312323)ˆˆˆ()ˆˆˆ(cos )ˆˆˆ()ˆˆˆ(021*******12211=-=-=++-⋅+-=⋅=++-=+-=θθa a k j i a k j i a a a a a kj i a a kj i a a 5.解:对于(110)面:2a 2a a 2S =⋅=所包含的原子个数为2,所以面密度为22a2a22=对于(111)面:2a 2323a 22a 2S =⨯⨯= 所包含的原子个数为2,所以面密度为223a34a 232=8.证明:ABCD 是六角密堆积结构初基晶胞的菱形底面,AD=AB=a 。
固体物理习题带答案

第二章:原子的结合
1. 设原子间的互作用能表示为 u (r ) 态,则 n>m. 解:原子间的相互作用能为: u (r )
作用能处于极小值: 这时有
r
m
rn
。证明:要使两原子处于平衡状
r
m
rn
。若两原子处于平衡状态时,则其相互
du (r ) (m) m 1 (n) n 1 dr r r
子晶格的情形比较, 与 q 之间存在着两种不同的色散关系。一维复式晶体中可以存在两 种独立的格波。两种不同的格波的色散关系:
2 2
(m M ) 4mM {1 [1 sin 2 aq]1 / 2 } 2 mM (m M ) (m M ) 4mM {1 [1 sin 2 aq]1 / 2 } 2 mM (m M )
xn (t ) A cos(t 2 naq) 。试求格波的色散关系。
解:一维单原子链中,牛顿方程为:
n ( x n 1 xn 1 2 xn ) m x
若将其振动位移写成 xn (t )
A cos(t 2 naq) 代入牛顿方程,则有
2
2 [1 cos(2aq)] 因此其色散关系为 m
0 。 所 以 有
r0
m
r0
m 1
n
r0
n 1
。所以
m nm r0 。 n
0
r0
同
时
有
d 2u ( r ) (m)( m 1) m 2 (n)( n 1) n 2 2 dr r r
。
所
以
固体物理习题参考答案

其中 n = N /V 。因此系统总能量为 ∫
0
0 EF
4V π2
(
2m
2
)3/2
√ 3 0 E E dE = EF N. 5
(4) 电子出现在空间任意一点的几率为 |ψ (x, yky y ) sin2 (kz z ). V
(5) 电子 x 方向的平均动量为(y,z 方向类似) √ ∫ L ∫ L∫ L∫ L πnx x πnx x ∂ψ 2 nx π dxdy dz = sin cos dx = 0. < px >= ψ i ∂x L i L L 0 0 0 0 (6) 讨论 驻波解: 2
由于每个状态在 k 空间所占的体积为 ∆k = π 3 /V , 所以 k 空间状态密度为 V 1 = 3. ∆k π (2) 能量 E 到 E+dE 之间的状态数为 dN = 2 × 而
2
V 4πk 2 dk π3 ( m 2 2 )1/2 1 √ dE E
dE = 所以
2m
2k dk → dk = (
dN Am = = C2D . dE π 2 利用 Sommerfeld 积分,对于电子总数 ∫ E 0 Q(E ) = D(ε)dε = C2D E, Q (E ) = 0 → N = C2D EF , EF = EF . D(E ) =
4V dN = 2 π 能量空间状态密度为
2m
2
)3/2
√ E dE.
4V dN = 2 D (E ) = dE π (3) 状态密度积分得到电子总数 ∫
0
0 EF
(
2m
2
)3/2
√ E.
4V π2
(
2m
2
)3/2
固体物理习题解答参考答案晶体结构

r
( )
。由 R 所定义的也是一个点阵常数为
r
r r r ( i 2 的 SC 点阵,但相对于上面一个 SC 点阵位移了一个矢量 + j + k ) ,
这个点正好位于体心位置。 上面两个 SC 点阵穿套起来正好是一个 bcc 点阵,故 ni 或全为奇数,或全为偶数所定义的是一个 bcc 点阵。 (2)若
体心立方晶格原胞基矢 a1 = (−i + j + k ) a2 = (i − j + k ) a3 = (i + j − k ) 体心立方晶格原胞体积 倒格子基矢:
r
a 2
r
r
r r
ห้องสมุดไป่ตู้
a r 2
r
r r
a r 2
r
r
同理: 可见由 为基矢构成的格子为面心立方格子。
面心立方格子原胞基矢: 面心立方格子原胞体积: 倒格子基矢: 同理 可见由 为基矢构成的格子为体心立方格子。
(2) 体心立方(书P3,图1-3)
r 取 原 子 球 相 切 时 的 半 径 ( 体 对 角 线 的 1/4 ) , r= 3a / 4 ,n=2, V = a 3 所 以
ρ=
n 4π r 3 3 = 3π / 8 V
(3) 面心立方(书P4,图1-7)
r 取 原 子 球 相 切 时 的 半 径 ( 面 对 角 线 的 1/4 ) r= 2a / 4 ,n=4, V = a 3 , 所 以
则由 ε = AxT ε Ax 得
固体物理习题及答案

第一章1.凝聚态物质包括哪些?-液体、固体、介于其间的软物质(液晶、凝胶等)2.固体可分为哪些类型?-晶体、准晶体、非晶体3.什么是晶格?什么是晶体结构?晶体中原子的规则排列称为晶格;晶体中原子的具体排列形式称为晶体结构 。
4.常见的晶体结构有哪些?-简单立方晶体结构sc 、体心立方晶体结构bcc 、密堆晶体结构、金刚石晶体结构、NaCl 结构、CsCl 晶体结构、闪锌矿晶体结构、钙钛矿(ABO3)结构5.什么是配位数?-XX 晶体结构的配位数是多少?配位数:每个原子周围最近邻原子数;简单立方晶体结构(配位数6)、体心立方结构(8)、面心立方结构(12)、六角密堆结构(12)、金刚石晶体结构(4)6.试画出简单立方结构、体心立方结构、面心立方结构、六角密堆结构、金刚石结构等晶体结构图。
7.举例说明什么是简单晶格?什么是复式晶格?-简单晶格(布拉维格子):所有原子完全等价,作从一个原子到另一任意原子的平移,晶格完全复原,如sc 、fcc 、bcc 结构形成的晶格;复式格子:晶格结构中,存在两种或两种以上不等价的原子或离子,作从一个原子或离子到任意一个不等价的原子或离子的平移,晶格不能复原,如hcp 结构、金刚石结构、NaCl 结构8.什么是基元?简单晶格和复式晶格的基元各有什么特点?-一个最小的、完全等价的基本结构单元;简单晶格的基元只含一个原子,复式晶格的基元中含两个以上的原子或离子。
9.什么是结点?什么是点阵?点阵与晶体结构的逻辑关系是什么?-就晶格的平移对称性而言,忽略结构中基元内原子分布的细节,用来代表基元的几何点成为结点;点阵是反映晶格平移对称性的分位点的无限阵列;<点阵>+<基元>=<晶体结构>10.什么是点阵的基矢?什么是破缺的平移对称性?-对于一个给定的点阵,可以使矢量332211→→→→++=a l a l a l R l 的三个不共面的基本平移矢量a1、a2、a3;晶格并不对任意的平移不变,而只对一组离散平移矢量RL (L 为小写取整数)具有不变性的性质。
固体物理答案

固体物理答案1.“晶格振动”理论是半经典理论。
答:晶体中的格点表示原子的平衡位置,晶格振动便是指原子在格点附近的振动。
晶格振动的研究是从晶体热力学性质开始的杜隆-珀替定理总结了固体热容量在室温和更高的温度适合而在较低的温度下固体的热容量开始随温度的降低而不断降低,从而进一步发展出了量子热熔理论。
但是经典晶格振动理论知识局限于固体的热学性质,故是半经典理论。
首先只能求解牛顿方程,并引入了格波,而且每个格波的能量可用谐振子能量来表示。
之后进行了量子力学修正,量子力学修正体现在谐振子能量不用经典谐振子能量表示式,而用量子谐振子能量表示式。
2.声学波和光学波的区别。
长光学支格波与长声学支格波的本质差别。
格波支数的关系。
定性地讲,声学波描述了元胞质心的运动,光学波描述了元胞内原子的相对运动。
描述元胞内原子不同的运动状态是二支格波最重要的区别。
长光学支格波的特征是每个原胞内的不同原子做相对振动,振动频率较高,它包含了晶格振动频率最高的振动模式.长声学支格波的特征是原胞内的不同原子没有相对位移,原胞做整体运动,振动频率较低,它包含了晶格振动频率最低的振动模式,波速是一常数.任何晶体都存在声学支格波,但简单晶格(非复式格子)晶体不存在光学支格波.4.低温时,由德拜模型,V随温度下降而快速下降。
当温度趋于零时,V亦趋于零。
比热随温度的下降速度T3。
高温时,比热与温度的关系更加符合爱因斯坦模型。
比热与温度的一次方呈正比。
当温度T极大时4,对绝缘体费米能级Ef必处在导带、禁带、价带的哪一个?为什么?5,原子间的排斥作用和吸引作用有何关系各自起主导的范围是什么在原子由分散无规的中性原子结合成规则排列的晶体过程中,吸引力起了主要作用。
在吸引力的作用下,原子间的距离缩小到一定的程度,原子间才出现排斥力。
当排斥力与吸引力相等时,晶体达到稳定结合状态。
可见,晶体要达到稳定结合状态,吸引力与排斥力缺一不可。
设此时相邻原子间的距离为r0,当相邻原子间的距离r>r0时,吸引力起主导作用;当相邻原子间的距离r<r0时,排斥力起主导作用6,固体能带论的两个基本假设是什么7,你认为单原子分子的晶格存在强烈的红外吸收吗?离子晶体晶格又如何?说明理由。
固体物理学习题答案(朱建国版)

固体物理学习题答案(朱建国版) 第一章1.1有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以r和r代表面心立方和体心立方结构中最fb 近邻原子间的距离,试问r/r等于多少,fb答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a:2对于面心立方,处于面心的原子与顶角原子的距离为:r=af23对于体心立方,处于体心的原子与顶角原子的距离为:r=ab2 2a6rf那么,==3rb3a1.2晶面指数为(123)的晶面abc是离原点o最近的晶面,oa、ob和oc分别与基失a,1a和a重合,除o点外,oa,ob和oc上是否有格点,若abc面的指数为(234),情况又23如何,答:根据题意,由于oa、ob和oc分别与基失a,a和a重合,那么1231.3二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型:正方、矩形、六角、有心矩形和斜方。
分别如图所示:正方六方矩形带心矩形平行四边形a=ba=ba?ba=ba?ba^b=90?a^b=90?a^b=120?a^b=90?a^b?90?1.4在六方晶系中,晶面常用4个指数(hkil)来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120?的共平面轴a,a,a上的截距a/h,a/k,a/i,第四个指数123123表示该晶面的六重轴c上的截距c/l.证明:i=-(h+k)并将下列用(hkl)表示的晶面改用(hkil)表示:(001)(100)(010)(133)(110)(323)(213)答:证明设晶面族(hkil)的晶面间距为d,晶面法线方向的单位矢量为n?。
因为晶面族(hkil)中最靠近原点的晶面abc在a、a、a轴上的截距分别为a/h,a/k,a/i,因此123123oanhd,1oankd,………(1)2oanid,31由于a=–(a+a)312ooanaan,,,()313把(1)式的关系代入,即得idhdkd,,,()ihk,,,()根据上面的证明,可以转换晶面族为(001)?(0001),?,?,?,(100)?,33)1((1323)(110)(1100)(323)(3213)(1010)(010)?,?(0110)(213)(2 133)1.5如将等体积的硬球堆成下列结构,求证球可能占据的最大面积与总体积之比为(1)简立3,2,2,,方:(2)体心立方:(3)面心立方:(4)六方密堆积:(5)金刚石:68663,。
固体物理习题解答-完整版
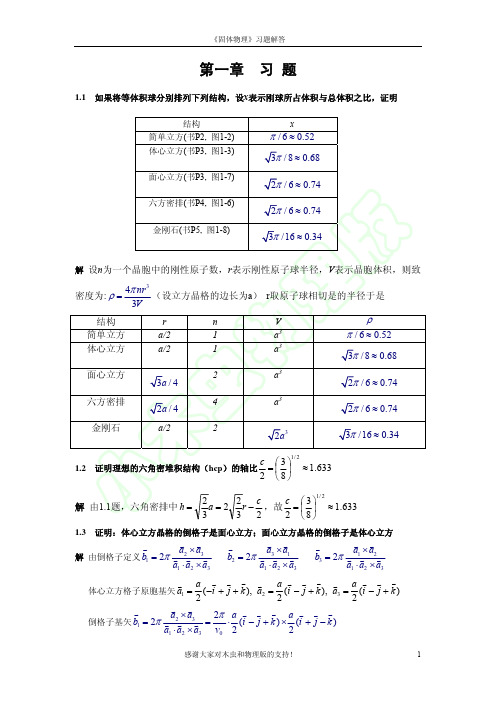
2.3
若一晶体的相互作用能可以表示为 u ( r ) = − 求 1 )平衡间距 r 0
α
r
m
+
β
rn
3 )体弹性模量 4 )若取
2 )结合能 W (单个原子的)
m = 2, n = 10, r0 = 0.3 nm, W = 4 eV ,计算 α , β 值。
解 1)晶体内能 U ( r ) =
N α β (− m + n ) 2 r r
⎛ ε 11 3ε 22 ⎜ + 4 4 0 ⎞ ⎜ ⎟ ⎜ 3ε 11 3ε 22 ε 23 ⎟ = ⎜ − + 4 4 ⎜ ε 33 ⎟ ⎠ ⎜ 3ε 23 − ⎜ 2 ⎝ − 3ε 11 3ε 22 + 4 4 3ε 11 ε 22 + 4 4 − − 3ε 23 ⎞ ⎟ 2 ⎟ ε ⎟ − 23 ⎟ 2 ⎟ ε 33 ⎟ ⎟ ⎠
h k l ( )2 + ( )2 + ( )2 a b c
说明面指数简单的晶面,其面密度较大,容易解理 证 简单正交系 a ⊥ b ⊥ c 倒格子基矢 b1 = 2π
a1 = ai , a2 = bj , a3 = ck b2 = 2π a3 × a1 a1 ⋅ a2 × a3 b3 = 2π a1 × a2 a1 ⋅ a2 × a3
⎛ ε 11 ε 12 ⎜ 假 设 六 角 晶 系 统 的 介 电 常 数 为 ε = ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
⎛ ε 11 ε 12 ⎜ ⎜ ε 21 ε 22 ⎜ε ⎝ 31 ε 32
ε 13 ⎞ ⎟ ε 23 ⎟ 则 由 ε = AT ε Ax 得 ε 33 ⎟ ⎠
x
ε 13 ⎞ ⎛ ε 11 − ε 12 − ε 13 ⎞ 0 ⎞ ⎛ ε 11 0 ⎟ ⎟ ⎜ ⎟ ⎜ ε 23 ⎟ = ⎜ − ε 21 ε 22 ε 23 ⎟ 可见 ε = ⎜ 0 ε 22 ε 23 ⎟ 将上式代入 ε = AzT ε Az ⎜ ⎜0 ε ε 33 ⎟ ε 33 ⎟ ε 33 ⎟ 32 ⎠ ⎠ ⎝ ⎠ ⎝ − ε 31 ε 32
固体物理作业答案

ω2 ω02
= dω
dq =
= dω
a ω02 − ω 2 dq 2
代入 ρ (ω )d ω= 2 ×
N Na dq = 2 × π 2π
ω02 − ω 2
2N
dω 1
一维单原子链的频率分布函数 ρ (ω ) =
π
ω −ω2
2 0
3.7.设三维晶格的光学振动在 q=0 附近的长波极限有 ω (q = ) ω0 − Aq 2
N α β (− m + n ) r 2 r N mα nβ 1 ( m +1 − n +1 ) = 2 r r 3 NAr 2
∂ 2U N ∂r ∂ mα nβ 1 = [( m +1 − n +1 ) ] 2 ∂V 2 ∂V ∂r r r 3 NAr 2 体弹性模量 = K ( ∂ 2U )V ⋅ V0 ∂V 2 0
1.3 证明:体心立方晶格的倒格子是面心立方;面心立方晶格的倒格子是体心立 方 。 a2 × a3 a3 × a1 a1 × a2 解 由倒格子定义 b1 = 2π b2 = 2π b3 = 2π a1 ⋅ a2 × a3 a1 ⋅ a2 × a3 a1 ⋅ a2 × a3
5
求证:频率分布函数为 f ( = ω)
V 1 1/ 2 ω − ω ) , ω < ω0 ; 2 3/ 2 ( 0 4π A
f (ω ) = 0 .
解
2
, ω > ω0
2
1 2 1 2
= 0, ω < 0 ⇒ ω0 − ω = Aq ⇒ q = A ( ω0 − ω ) ω > ω0时,ω − ω0= Aq > 0 f (ω )
固体物理基础(邵起越)所有作业答案汇总
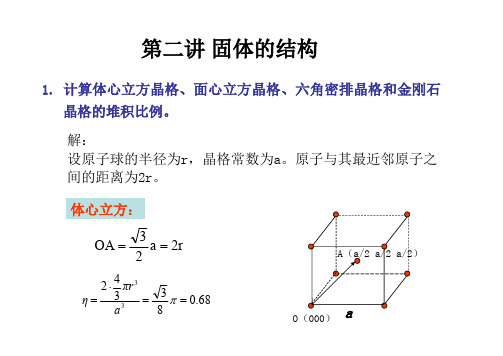
金刚石结构:OAO (0 0 0)A (a/4 a/4 a/4)2ra 43OA ==34.016334833==⋅=πa πrη3. 金刚石结构中,每个原子的四个最近邻正好对应一个正四面体的顶角位置。
求四面体角,即中心原子与四个最近邻原子连线的夹角。
OA B解:()()()()()o225.10931a43a 4316a AB AO AB AO cos 16aAB AO 4a- 4a 4a AB 4a- 4a - 4a -AO0 2a 2a B ,4a 4a 4a A ,0 0 0 O =-=⋅-=⋅⋅=-=⋅==θθ33. 证明:在NaCl 型离子晶体中晶面组(n 1 n 2 n 3)的衍射强度为:解: 晶胞内包括四个Na +离子和四个Cl -离子,原子位置:Na ✹f A ; Cl ✹f B其中f A ,f B 分别为正负离子的散射因子。
如何用此结果说明KCl 晶体中n 1、n 2、n 3均为奇数的衍射消失。
⎪⎪⎩⎪⎪⎨⎧-+∝其他情况为奇数当为偶数当 0n ,n ,n n ,n ,n 32123212321B A B A n n n f f f f I )21 0 0( ),0 21(0 0), 0 21( ),21 21 21( )210 21( ),21 21(0 0), 21 21( ),0 0 0( ::Cl Na -+∑++-=ii i i r z n y n x n i i G ef S )(2321π4. 讨论金刚石结构晶体的消光法则。
金刚石结构晶胞包含8个原子,分别处于:)43 43 41( ),43 4143( ),41 43 43( ),41 41 41( )210 21( ),21 21(0 0), 21 21( ),0 0 0( ∑++-=ii i i r z n y n x n i i G ef S )(2321π)33(2)33(2)33(2)n (2)()()(321321321321313221 n n n πi n n n πi n n n πi n n πi n n iπn n iπn n iπfefefefefefefef ++-++-++-++-+-+-+-+++++++=]1[]1[)()()()n (2)()()(313221321313221n n iπn n iπn n iπn n πi n n iπn n iπn n iπeeefee ee f +-+-+-++-+-+-+-+++++++=第三讲 固体的结合1. 石墨层中的C原子排布如图所示的六角网状结构。
固体物理习题答案

第四章 思考题
2、周期场是能带形成的必要条件吗? 答:周期场是由布洛赫函数描述的能带结构的必要条件。 布洛赫定理推导出周期场中单电子状态的一般属性(主要是能带 结构,参见图4.2-1 一维能带结构的表示图式),而晶格周期 势场是布洛赫定理的前提条件。 在晶体周期性结构(平移对称性)中,电子波函数 (k) 是布洛赫 函数,能量本征值和本征函数在 k 空间具有倒格矢反演和 周期性,电子波矢 k 是与平移对称性相联系的量子数 。 非晶态也具有相似的基本能带结构,即:导带、价带和禁带。 但非晶态的电子态与晶态比较有本质区别。非晶态不存在 周期性,因此 k 不再是具有类似特征的量子数。 非晶态能带中电子态分扩展态和局域态二类。扩展态的电子为 整个固体共有,可在整个固体内找到,在外场中运动类似 晶体中电子;局域态的电子基本局限在某一区域,状态波 函数只能在围绕某一不大的尺度内显著不为零,它们依靠 声子协助,进行跳跃式导电。
第一章 思考题
5、试画出体心立方和面心立方(100)、(110)、(111)面上格点的 分布图。 (100) (110) (111)
体心立方
面心立方
第一章 思考题
6、怎样判断一个体系对称性的高低?讨论对称性有何物理意义。 答: 一个物理体系对称性用其具有的对称操作集合来描述。一个体 系具有的对称操作越多,其对称性就越高。在数学上,基 本操作的集合构成 “群”,每个基本操作称为群的一个元 素。由于晶格周期性限制,描述晶体宏观对称性的“点群” 只有32种。描述晶体微观对称性的“空间群”只有230种。 一个物理体系,如知道其几何对称性,就可在一定程度上确定 它的某些物理性质。例如,若原子结构具有中心反演对称 性,则原子无固定偶极矩;若一个体系具有轴对称性,偶 极矩必在对称轴上;若有对称面,偶极矩必在对称面上。 由此可见,不必讨论体系结构细节,仅从体系的对称性,就可 对其物理性质作出某些判断。对称理论已成为定性和半定 量研究物理问题的重要方法。
固体物理作业答案

1.什么叫居里温度和奈耳温度?答:居里温度:是指材料可以在铁磁体和顺磁体之间改变的温度。
低于居里温度时该物质成为铁磁体,此时和材料有关的磁场很难改变。
当温度高于居里温度时,该物质成为顺磁体,磁体的磁场很容易随周围磁场的改变而改变。
这时的磁敏感度约为10的负6次方。
奈耳温度:奈耳温度(Néel temperature)指的是反铁磁性材料转变为顺磁性材料所需要达到的温度。
在这个温度的时候,晶体内部的原子内能会大到足以破坏材料内部宏观磁性排列,从而发生相变,由反铁磁性转变为顺磁性。
2.画出软磁、硬磁、矩磁材料的磁化曲线和磁滞回线?并说明其意义?答:3.什么叫自旋电子学?答:自旋电子学(Spintronics),是利用创新的方法,来操纵电子自旋自由度的科学,是一种新兴技术。
应用于自旋电子学的材料,需要具有较高的电子极化率,以及较长的电子自旋弛豫时间。
许多新材料,例如磁性半导体、半金属等,近年来被广泛的研究,以求能有符合自旋电子元件应用所需要的性质。
4.为什么磁性材料内部会形成磁畴和磁畴壁?答:在居里温度以下,铁磁或亚铁磁材料内部存在很多各自具有自发磁矩,且磁矩成对的小区域。
他们排列的方向紊乱,如不加磁场进行磁化,从整体上看,磁矩为零。
这些小区域即称为磁畴。
磁畴之间的界面称为磁畴壁(magnetic domain wall)。
当有外磁场作用时,磁畴内一些磁矩转向外磁场方向,使得与外磁场方向接近一致的总磁矩得到增加,这类磁畴得到成长,而其他磁畴变小,结果是磁化强度增高。
随着外磁场强度的进一步增高,磁化强度增大,但即使磁畴内的磁矩取向一致,成了单一磁畴区,其磁化方向与外磁场方向也不完全一致。
只有当外磁场强度增加到一定程度时,所有磁畴中磁矩的磁化方向才能全部与外磁场方向取向完全一致。
此时,铁磁体就达到磁饱和状态,即成饱和磁化。
一旦达到饱和磁化后,即使磁场减小到零,磁矩也不会回到零,残留下一些磁化效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)六方密堆积: 2 (5)6金刚石: 3
8
(3)面心立方:2
6
6
16
第二章
所以压缩因子
1/ K 9V0
mn UO
解:
Ur
N 2
rm
rn
dUr
由平衡条件
0 dr rr0
由题意得
ur
A r9
-
B r
1
1
r0
k
2 B
1.3810-23 J K-1
2.1510-8 K-2 T
n 6.021023 Zm 1022 ~ 1023 1
A
me 9.110-31kg 2.810-3
6.7103
前3 个指数表示晶面族中最靠近原点的晶面在互成 1200的共平面轴a1 , a2, a3上的截距a1 / h, a 2/ k , a3 / i ,第4 个指数表示该晶面的六重 轴c 上的截距为c / l 。证明:i = -(h+ k) 并将下列(hkl )表示的晶面改 用( hkil ) 表示(001)(-133)(1-10)(3-23)(100)(010)
对于面心立方,处于面心的原子与顶角原子的距离为: R f
2a 2
对于体心立方,处于体心的原子与顶角原子的距离为:Rb 那么
3a 2
Rf 2a 6
Rb
3a 3
1.2 晶面指数为(123)的晶面ABC是离原点O最近的晶面,OA、
OB和OC分别与基矢a1 ,a2 和a3 重合,除O点外,OA、OB和OC上是否 有格点?若ABC面的指数为(234)情况又如何?
2u r
r
2
r r0
1 9N r0
90A r011
-
2B r03
1.181010
答: CsCl为离子型晶体,n=11.5 马德隆常数 α=1.763
CsCl的势能为
ur
-
N 2
e2 4 0r
-
B rn
由
dur
n m
n-m
9A 9-1 1B
2.810 10 m
ur0
A r09
-
B r0
810 19
J
1
得
r0
n m
n-m
解得 A -1.05710-105 B -2.5210-28
晶体为体心立方
N
43 9
K
1 9N r0
(-2-13)。
答:
(1)证明:设晶面族的间距为d,晶面法向方向的单位矢量为n0。因为 晶面族(hkil)中最靠近原点的晶面ABC在a1 、a2、a3 轴上的截距分
别为a1 / h, a 2/ k , a3 / i ,因此
a1 ·n0=hd a2 ·n0=kd a3 ·n0 =id ….(1) 由于 a3=-( a1 + a2 ) a3 ·n0= -( a1 + a2 ) ·n0 把(1)式的关系代入,即得 id=-(hd+kd) i=-(h+k)(得证) 根据上面的证明,可以转换晶面族为:
答:晶面指数为(123)的晶面为ABC,其是离O点最近的晶面,
其截距为a1, a2, a3,故除O点外,OA上有一个格点(A点),OB,
OC上没有。若ABC的晶面指数为(234),其截距为 a a a
则除O点外,OA,OB,OC上均没有格点。
23 4
1.3在六方晶系中,晶面常用 4个指数(hkil) 来表示,如图所示,
0 dr rro
得
B
e2 4 0n
r0n-1
6.7 10-131
其中e=1.6 ×10-19 ε0=8.85 ×10-12
因此
ur
-
N 2
e2 4 0r0
-
B r0n
பைடு நூலகம்
5.610-19 N
第三章
第五章
答:
2kB2n T 3me
固体物理课后作业答案
第一章
1.1 有许多金属即可以形成体心立方结构,也可以形成面心立方结
构。 从一种结构转变为另一种结构时体积变化很小。设体积变化可 以忽略,并以 R f 和 R b代表面心立方和体心立方结构中最近邻原子间 的距离,试问 Rf 等于多少?
Rb
答:由题意已知,面心、体心立方结构同一棱边距离相等,都设为a:
(001) →(0001)(-133)→(-13-23)(1-10)→(1-100) (3-23)→(3-2-13)(100)→(10-10)(010)→(01-10) (-2-13)→(-2-133)
1.4如将等体积的硬球堆成下列结构,求证球可能占据的最大体积与总
体积之比为 :(1)简立方: (2)体心立方: 3
