反比例函数经典习题及答案
(完整版)反比例函数基础练习题及答案

反比例函数练习一一.选择题(共22小题)1.(2015春•泉州校级期中)下列函数中,y是x的反比例函数的为()A.y=2x+1 B.C.D.2y=x2.(2015春•兴化市校级期中)函数y=k是反比例函数,则k的值是()A.﹣1 B.2 C.±2 D.±3.(2015春•衡阳县期中)若y=(m﹣1)x|m|﹣2是反比例函数,则m的值为()A.m=2 B.m=﹣1 C.m=1 D.m=04.(2014•汕尾校级模拟)若y与x成反比例,x与z成反比例,则y是z的()A.正比例函数B.反比例函数C.一次函数D.不能确定5.(2014春•常州期末)反比例函数(m为常数)当x<0时,y随x的增大而增大,则m的取值范围是()A.m<0 B.C.D.m≥6.(2015•贺州)已知k1<0<k2,则函数y=和y=k2x﹣1的图象大致是()A.B. C.D.7.(2015•滦平县二模)在同一直角坐标系中,函数y=kx+k与y=(k≠0)的图象大致为()A.B.C.D.8.(2015•上海模拟)下列函数的图象中,与坐标轴没有公共点的是()A.B.y=2x+1 C.y=﹣x D.y=﹣x2+19.(2015•宝安区二模)若ab>0,则函数y=ax+b与函数在同一坐标系中的大致图象可能是()A.B.C.D.10.(2015•鱼峰区二模)若方程=x+1的解x0满足1<x0<2,则k可能是()A.1 B.2 C.3 D.611.(2012•颍泉区模拟)如图,有反比例函数y=,y=﹣的图象和一个圆,则图中阴影部分的面积是()第11题图第12题图A.πB.2πC.4πD.条件不足,无法求12.(2010•深圳)如图所示,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=B.y=C.y=D.y=13.(2014•随州)关于反比例函数y=的图象,下列说法正确的是()A.图象经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.当x<0时,y随x的增大而减小14.(2014•昆明)如图是反比例函数y=(k为常数,k≠0)的图象,则一次函数y=kx﹣k 的图象大致是()A.B.C.D.15.(2014•天水)已知函数y=的图象如图,以下结论:①m<0;②在每个分支上y随x的增大而增大;③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.其中正确的个数是()A.4个B.3个C.2个D.1个16.(2014•杭州)函数的自变量x满足≤x≤2时,函数值y满足≤y≤1,则这个函数可以是()A.y=B.y=C.y=D.y=17.(2014•阜新)反比例函数y=在每个象限内的函数值y随x的增大而增大,则m的取值范围是()A.m<0 B.m>0 C.m>﹣1 D.m<﹣118.(2015•凉山州)以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=经过点D,则正方形ABCD的面积是()第18题图第19题图A.10 B.11 C.12 D.1319.(2015•眉山)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D 点,垂足为C.若△ADO的面积为1,D为OB的中点,则k的值为()A.B.C.3 D.420.(2014•绥化)如图,过点O作直线与双曲线y=(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是()第20题图第21题图A.S1=S2B.2S1=S2C.3S1=S2D.4S1=S2 21.(2014•抚顺)如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小22.(2014•重庆)如图,反比例函数y=﹣在第二象限的图象上有两点A、B,它们的横坐标分别为﹣1,﹣3,直线AB与x轴交于点C,则△AOC的面积为()A.8 B.10 C.12 D.24二.填空题(共4小题)23.(2015•锦江区一模)已知y=(a﹣1)是反比例函数,则a=.24.(2014•江西模拟)已知反比例函数的解析式为y=,则最小整数k=.25.(2013•路北区二模)函数y=,当y≥﹣2时,x的取值范围是(可结合图象求解).26.(2014•贵阳)若反比例函数的图象在其每个象限内,y随x的增大而增大,则k的值可以是.(写出一个符合条件的值即可)三.解答题(共4小题)27.(2014春•东城区校级期中)已知反比例函数y=﹣(1)说出这个函数的比例系数;(2)求当x=﹣10时函数y的值;(3)求当y=6时自变量x的值.28.(2013春•汉阳区校级期中)已知函数y=(5m﹣3)x2﹣n+(n+m),(1)当m,n为何值时是一次函数?(2)当m,n为何值时,为正比例函数?(3)当m,n为何值时,为反比例函数?29.(2013•德宏州)如图,是反比例函数y=的图象的一支.根据给出的图象回答下列问题:(1)该函数的图象位于哪几个象限?请确定m的取值范围;(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?30.(2014•苏州)如图,已知函数y=(x>0)的图象经过点A、B,点A的坐标为(1,2),过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC、OD.(1)求△OCD的面积;(2)当BE=AC时,求CE的长.答案:一.选择题(共22小题)1.C 2.D 3.B 4.A 5.C 6.C 7.B 8.A 9.C 10.C 11.B 12.D 13.D 14.B 15.B 16.A 17.D 18.C 19.B20.B 21.C 22.C二.填空题(共4小题)23.-1 24.1 25.x≤-2或x>0 26.-1(答案不唯一)三.解答题(共4小题)27.28.29.30.。
反比例函数练习题及答案

一、选择题(每小题3分,共36分)1.(2022河口模拟)下列关系式中,y是x的反比例函数的是( C )A.x(y-1)=1B.y=1x+1C.y=13x D.y=1x32.对于反比例函数y=-5x,下列说法不正确的是( D )A.图象分布在第二、四象限B.当x<0时,y随x的增大而增大C.图象经过点(5,-1)D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y23.若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y=-3x的图象上,则y1,y2,y3的大小关系是( B )A.y1<y2<y3B.y2<y3<y1C.y3<y2<y1D.y2<y1<y34.若A(2,4)与B(-2,a)都是反比例函数y=kx(k≠0)图象上的点,则a 的值是( B )A.4B.-4C.2D.-25.在一个可以改变容积的密闭容器内,装有质量为m的某种气体,当改变容积V时,气体的密度ρ也随之改变,ρ与V在一定范围内满足,它的图象如图所示,则该气体的质量m为( C )ρ=mV第5题图A.1.4 kgB.5 kgC.7 kgD.6.4 kg6.正比例函数y=6x的图象与反比例函数y=6的图象的交点位于x( D )A.第一象限B.第二象限C.第三象限D.第一、三象限(k≠0)与一次函数y=kx+k(k≠0)在同一平面直角7.反比例函数y=kx坐标系内的图象可能是( D )A B C D的图象相交于点M(1,m),N(-2,n).8.如图所示,函数y1=x+1与函数y2=2x若y1>y2,则x的取值范围是( D )第8题图A.x<-2或0<x<1B.x<-2或x>1C.-2<x<0或0<x<1D.-2<x<0或x>19.如图所示,在平面直角坐标系中,点A是x轴负半轴上一个定点,点(x<0)图象上一个动点,PB⊥y轴于点B,当点P的横坐标P是函数y=-6x逐渐增大时,四边形OAPB的面积将会( D )第9题图A.先增后减B.先减后增C.逐渐减小D.逐渐增大10.如图所示的是某公园“水上滑梯”的侧面图,其中BC段可看成是双曲线的一段,建立如图所示的坐标系后,其中,矩形AOEB中有一向上攀爬的梯子,OA=5 m,进口AB∥OD,且AB=2 m,出口C点距水面的距离CD为1 m,则B,C之间的水平距离DE为( D )A.5 mB.6 mC.7 mD.8 m第10题图11.如图所示,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到△A′BC′.若反比例函数的图象恰好经过A′B的中点D,则k的值是( C )y=kx第11题图A.9B.12C.15D.18(x>0)的图象上,点C在反比例函12.如图所示,点B在反比例函数y=6x(x>0)的图象上,且BC∥y轴,AC⊥BC于点C,交y轴于点A,则数y=-2x△ABC的面积为( B )第12题图A.3B.4C.5D.6二、填空题(每小题3分,共18分)13.(2022栖霞模拟)一批零件有200个,一个工人每小时生产5个,则完成任务所需时间y(小时)与人数x之间的函数表达式为y=40.x与一次函数y=2x-1的图象的交点为(1,a),则14.已知反比例函数y=kxk的值为 1 .15.双曲线y=k+1在每个象限内,函数值y随x值的增大而增大,则k x的取值范围是k<-1 .16.王师傅用一根撬棒撬动一块大石头,已知阻力臂和阻力不变,分别为0.5 m和1 000 N,当动力臂l为2 m 时,撬动这块大石头需用的动力F为250 .17.如图所示,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=4x的图象交于A,B两点,则四边形MAOB的面积为10 .18.在平面直角坐标系xOy中,直线y=x与双曲线y=mx交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为0 .三、解答题(共46分)19.(6分)已知反比例函数y=kx(k为常数,k≠0)的图象经过点A(2,3).(1)求这个函数的表达式;(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;(3)当-2<x<-1时,求y的取值范围.解:(1)把A(2,3)代入y=kx ,得k=2×3=6,∴y=6x.(2)点B(-1,6)不在这个函数的图象上,点C(3,2)在这个函数的图象上.理由如下:当x=-1时,y=-6,∴点B(-1,6)不在这个函数的图象上.当x=3时,y=2,∴点C(3,2)在这个函数的图象上.(3)当x=-1时,y=-6;x=-2时,y=-3,∵k=6>0,∴当-2<x<-1时,y随x的增大而减小.∴当-2<x<-1时,y的取值范围为-6<y<-3.20.(8分)一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式t=kv ,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).(1)求k 和m 的值;(2)若行驶速度不得超过60 km/h,则汽车通过该路段最少需要多长 时间?解:(1)由题意,得函数图象经过点(40,1),(m,0.5),把(40,1)代入t=kv ,得k=40,故可得关系式为t=40v .再把(m,0.5)代入t=40v,得m=80.(2)把v=60代入t=40v,得t=23,故汽车通过该路段最少需要23h.21.(10分)某商场出售一批进价为2元的贺卡,在销售中发现此商品的日销售单价x(元)与日销售量y(张)之间有如下关系:(1)猜测并确定y 与x 的函数表达式.(2)当日销售单价为10元时,贺卡的日销售量是多少张?(3)设此贺卡的日销售利润为W 元,试求出W 与x 之间的函数表达式.若物价部门规定此贺卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大,并求出最大利润.解:(1)由题意设y=k(k为常数,且k≠0),x把(3,20)代入,得k=60,.∴y与x的函数表达式是y=60x=6,(2)当x=10时,y=6010∴当日销售单价为10元时,贺卡的日销售量是6张.,且2≤x≤10,(3)∵W=(x-2)y=60-120x=48(元).∴当x=10时,W最大,W最大=60-12010∴当日销售单价为10元时,每天获得的利润最大,最大利润为48元.22.(10分)如图所示,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数y=-12的图象交于A,B两点,且与x轴交于点C,与y轴交于x点D,A点的横坐标与B点的纵坐标都是3.(1)求一次函数的表达式;(2)求△AOB的面积;的解集.(3)写出不等式kx+b>-12x解:(1)∵一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数的图象交于A,B两点,y=-12x且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3,∴当y=3时,3=-12,解得x=-4;x当x=3时,y=-123=-4.故点B 的坐标为(-4,3),点A 的坐标为(3,-4), 把点A,B 的坐标代入y=kx+b,得 {-4k +b =3,3k +b =-4,解得{k =-1,b =-1, 故一次函数的表达式为y=-x-1. (2)y=-x-1,当y=0时,x=-1, 故点C 的坐标为(-1,0),∴S △AOB =S △BOC +S △AOC =12OC ·|y B |+12OC ·|y A |=12×1×3+12×1×4=72.∴△AOB 的面积为72.(3)由图象,知不等式kx+b>-12x 的解集为x<-4或0<x<3.23.(12分)(2022莱西模拟)如图所示,正比例函数y=12x 的图象与反比例函数y=kx(k ≠0)在第一象限的图象交于A 点,过A 点作x 轴的垂线,垂足为M,已知△OAM 的面积为1.(1)求反比例函数的表达式;(2)如果点B(a,b)为反比例函数在第一象限图象上的点,且b=2a,试探究在x 轴上是否存在点P,使△PAB 周长最小.若存在,求点P 的坐标;若不存在,请说明理由.解:(1)∵反比例函数y=kx (k ≠0)的图象在第一象限,∴k>0.∵△OAM 的面积为1,∴12k=1,解得k=2,故反比例函数的表达式为y=2x.(2)存在.∵点A 是正比例函数y=12x 与反比例函数y=2x图象的交点,且x>0,y>0,∴{y =12x ,y =2x ,解得{x =2,y =1,∴A(2,1). ∵B(a,b)为反比例函数在第一象限图象上的点,∴b=2a.又∵b=2a,∴a=1,b=2,∴B(1,2).∵AB 的距离为定值,∴若使△PAB 周长最小,则PA+PB 的值最小. 如图所示,作A 点关于x 轴的对称点C,并连接BC,交x 轴于点P,P 为所求点.设A 点关于x 轴的对称点为C,则C 点的坐标为(2,-1).设直线BC 的表达式为y=mx+n,将B,C 两点的坐标代入,得{2m +n =-1,m +n =2,解得{m =-3,n =5,故直线BC 的表达式为y=-3x+5.当y=0时,x=53,则点P 坐标为(53,0).。
完整版)反比例函数经典习题及答案

完整版)反比例函数经典习题及答案反比例函数练题1.下列函数中,经过点(1.-1)的反比例函数解析式是()A。
y = 1/xB。
y = -1/xC。
y = 2/xD。
y = -2/x2.反比例函数y = -(k/ x)(k为常数,k ≠ 0)的图象位于()A。
第一、二象限B。
第一、三象限C。
第二、四象限D。
第三、四象限3.已知反比例函数y = (k - 2)/x的图象位于第一、第三象限,则k的取值范围是()A。
k。
2B。
k ≥ 2C。
k ≤ 2D。
k < 24.反比例函数y = k/x的图象如图所示,点M是该函数图象上一点,MN垂直于x轴,垂足是点N,如果三角形MON 的面积是2,则k的值为()A。
2B。
-2C。
4D。
-45.对于反比例函数y = 2/x,下列说法不正确的是()A。
点(-2.-1)在它的图象上B。
它的图象在第一、三象限C。
当x。
0时,y随x的增大而增大D。
当x < 0时,y随x的增大而减小6.反比例函数y = (2m - 1)x/(m^2 - 2),当x。
0时,y随x 的增大而增大,则m的值是()A。
±1B。
小于1的实数C。
-1D。
1/27.如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形P1A1O、P2A2O、P3A3O,设它们的面积分别是S1、S2、S3,则()。
A。
S1 < S2 < S3B。
S2 < S1 < S3C。
S3 < S1 < S2D。
S1 = S2 = S38.在同一直角坐标系中,函数y = -2与y = 2x的图象的交点个数为()A。
3B。
2C。
1D。
09.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)与行驶速度v(km/h)的函数关系图象大致是()10.如图,直线y = mx与双曲线y = k/(x-2)交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若三角形ABM的面积为2,则k的值是()A。
反比例函数经典例题(有答案)

一、反比例函数的对称性1、直线y=ax (a>0)与双曲线y= 3/x 交于A (x i, y〔)、B (X2, y2)两点,贝U 4x i y2-3x2y i=2、如图1,直线y=kx (k>0)与双曲线y= 2/x交于A, B两点,若A B两点的坐标分别为A (x i, y i),B (x2, y2),贝U x i y2+x2y i 的值为( )A 、-8B 、4C 、-4D 、0解析:直线Y=KX和双曲线Y=2/X图象都关于原点对称因此两交点A、B也关于原点对称X2=-Xi, Y2=-Yi双曲线形式可变化为XY=2即双曲线上点的横纵坐标乘积为 2因此XiYi=2XiY2+X2Yi=Xi(-Yi) + (-Xi) Yi=-XiYi-XiYi=-4图i 图2 图3 图4二、反比例函数中“ K”的求法1、如图2,直线l是经过点(i, 0)且与y轴平行的直线.Rt△ ABC中直角边AC=4, BC=3将BC边在直线l上滑动,使A, B在函数y=k/x的图象上.那么k的值是( )A、3 B 、6 C 、i2 D 、i5/4解析:BC 在直线X=i 上,设B(i , M),贝U C(i, M-3), .••A(5, M-3), 又A B都在双曲线上,二i*M=5*(M-3) , M=i5/4 即K=i5/4 2、如图3,已知点A、B在双曲线y= k/x (x>0)上,Adx轴于点C, Bdy轴于点D, AC与BD交于点P, P是AC的中点,若△ ABP的面积为3,则k=解析:A(xi,k/xi),B(x2,k/x2)AC:x=xi BD:y=k/x2P(xi,k/x2)k/x2=k/2xi 2xi=x2BP=x2-xi=xiAP=k/xi-k/x2=k/2xiS=xi*k/(2xi)*i/2)=k/4=3 k=i23、如图4,双曲线y= k/x (k > 0)经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为3,则双曲线的解析式为( )A、y=i/xB、y=2/xC、y=3/xD、=6/解析:设E(x0,k/x0)E 是BC中点,二B(x0,2k/x0)B、D两点纵坐标相同,二D(x0/2,2k/x0)BD=x0/2,OC=x0,BC=2k/x0梯形面积=(BD+OC/ BC/2=3k/2=3•,- k=2 .•.双曲线的解析式为:y=2/x三、反比例函数“ K”与面积的关系1、如图5,已知双曲线y i=1/x(x >0) , y2=4/x(x >0),点P为双曲线y2=4/x上的一点,且PAlx 轴于点A, PBLy轴于点B, PA PB分别次双曲线y=/x于D C两点,则^ PCD的面积为( ) 图5 图6 图7解析:假设P的坐标为(a,b ),则C (a/4,b), D(a,b/4),PC=3/4*a PD=3/4*bS=1/2*3/4*a*3/4*b因为点P为双曲线y2=4/x上的一点所以a*b=4所以S=9/82、如图6,直线l和双曲线y=k/x(k >0)交于A B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为G D、E,连接OA OB 0P,设AAOC勺面积为S、△ BOD的面积为&、APOE的面积为S3,则( )A S I<S3B 、S I>S2>S3C 、S I=S2>&D 、S=S< S3解析:结合题意可得:AB者S在双曲线y=kx上,则有S1=S2而AB之间,直线在双曲线上方;故S1=SK S3.3、如图7,已知直线y=-x+3与坐标轴交于A、B两点,与双曲线y=k/x交于G D两点,且S3O C=&CO D=S\BOD 贝1J k=。
反比例函数练习题及答案6套

反比例函数练习(1)一、判断题 1.当x 与y 乘积一定时,y 就是x 的反比例函数,x 也是y 的反比例函数( ) 2.如果一个函数不是正比例函数,就是反比例函数 ( )3.y 与2x 成反比例时y 与x 并不成反比例( ) 二.填空题4.已知三角形的面积是定值S ,则三角形的高h 与底a 的函数关系式是h =__________,这时h 是a 的__________;5.如果y 与x 成反比例,z 与y 成正比例,则z 与x 成____ ___; 6.如果函数222-+=k kkx y 是反比例函数,那么k =________,此函数的解析式是____ ____;7. 有一面积为60的梯形,其上底长是下底长的31,若下底长为x ,高为y ,则y与x 的函数关系是______________ 三、选择题: 8.如果函数12-=m x y 为反比例函数,则m 的值是 ( )A1- B 0 C 21D 19.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。
在课堂上,李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图,同学们画出的示意图如下,你认为正确的是( )10、下列函数中,y 是x 反比例函数的是( )(A ) 12+=x y (B )22x y = (C )x y 51=(D )x y =2四.辨析题(1)兄弟二人分吃一碗饺子,每人吃饺子的个数如下表:①写出兄吃饺子数y 与弟吃饺子数x 之间的函数关系式(不要求写xy 的取值范围).②虽然当弟吃的饺子个数增多时,兄吃的饺子数(y )在减少,但y 与x 是成反例吗?(2)水池中有水若干吨,若单开一个出水口,水流速v 与全池水放光所用时t 如下表:①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系.②这是一个反比例函数吗? ③与(1)的结论相比,可见并非反比例函数有可能“函数值随自变量增大而减小”,反之,所有的反比例函数都是“函数值随自变量的增大而减小吗?这个问题,你可以提前探索、尝试,也可以预习下一课时”反比例函数的图象和性质,也可以等到下一节课我们共同解决.五.已知□ABCD 中,AB = 4,AD = 2,E 是AB 边上的一动点,设AE=x ,DE 延长线交CB 的延长线于F ,设CF =y ,求y 与x 之间的函数关系。
反比例函数试题及答案
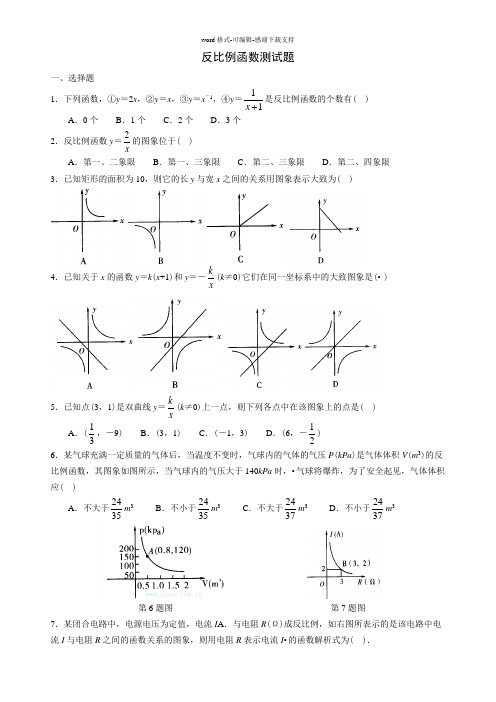
反比例函数测试题一、选择题1.下列函数,①y=2x,②y=x,③y=x-1,④y=11x是反比例函数的个数有()A.0个B.1个C.2个D.3个2.反比例函数y=2x的图象位于()A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象表示大致为()4.已知关于x的函数y=k(x+1)和y=-kx(k≠0)它们在同一坐标系中的大致图象是(• )5.已知点(3,1)是双曲线y=kx(k≠0)上一点,则下列各点中在该图象上的点是()A.(13,-9)B.(3,1)C.(-1,3)D.(6,-12)6.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,•气球将爆炸,为了安全起见,气体体积应()A.不大于2435m3B.不小于2435m3C.不大于2437m3D.不小于2437m3第6题图第7题图7.某闭合电路中,电源电压为定值,电流I A.与电阻R(Ω)成反比例,如右图所表示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I•的函数解析式为().A .I =6R B .I =-6R C .I =3R D .I =2R 8.函数y =1x与函数y =x 的图象在同一平面直角坐标系内的交点个数是( ).A .1个B .2个C .3个D .0个 9.若函数y =(m +2)|m |-3是反比例函数,则m 的值是( ).A .2B .-2C .±2D .×210.已知点A (-3,y 1),B (-2,y 2),C (3,y 3)都在反比例函数y =4x的图象上,则( ). A .y 1<y 2<y 3 B .y 3<y 2<y 1 C .y 3<y 1<y 2 D .y 2<y 1<y 3 二、填空题11.一个反比例函数y =kx(k ≠0)的图象经过点P (-2,-1),则该反比例函数的解析式是________. 12.已知关于x 的一次函数y =kx +1和反比例函数y =6x的图象都经过点(2,m ),则一次函数的解析式是________.13.一批零件300个,一个工人每小时做15个,用关系式表示人数x •与完成任务所需的时间y 之间的函数关系式为________.14.正比例函数y =x 与反比例函数y =1x的图象相交于A 、C 两点,AB ⊥x 轴于B ,CD •⊥x 轴于D ,如图所示,则四边形ABCD 的为_______.第14题图 第15题图 第19题图15.如图,P 是反比例函数图象在第二象限上的一点,且矩形PEOF 的面积为8,则反比例函数的表达式是_________. 16.反比例函数y =21039n n x--的图象每一象限内,y 随x 的增大而增大,则n =_______.17.已知一次函数y =3x +m 与反比例函数y =3m x-的图象有两个交点,当m =_____时,有一个交点的纵坐标为6.18.若一次函数y =x +b 与反比例函数y =kx图象,在第二象限内有两个交点,•则k ______0,b _______0,(用“>”、“<”、“=”填空)19.两个反比例函数y=3x,y=6x在第一象限内的图象如图所示,点P1,P2,P3……P2005,在反比例函数y=6x的图象上,它们的横坐标分别是x1,x2,x3,…x2005,纵坐标分别是1,3,•5•……,•共2005年连续奇数,过点P1,P2,P3,…,P2005分别作y轴的平行线与y=3x的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2005(x2005,y2005),则y2005=________.20.当>0时,两个函数值y,一个随x增大而增大,另一个随x的增大而减小的是( •).A.y=3x与y=1xB.y=-3x与y=1xC.y=-2x+6与y=1xD.y=3x-15与y=-1x21.在y=1x的图象中,阴影部分面积为1的有()22.如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B•两点,且与反比例函数y=mx(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,•若OA=OB=OD=1.(1)求点A、B、D的坐标;(2)求一次函数和反比例函数的解析式.第22题图23.如图,已知点A(4,m),B(-1,n)在反比例函数y=8x的图象上,直线AB•分别与x轴,y轴相交于C、D两点,(1)求直线AB的解析式.(2)C、D两点坐标.(3)S△AOC:S△BOD是多少?第23题图24.已知y=y1-y2,y1与x成正比例,y与x成反比例,且当x=1时,y=-14,x=4时,y=3.求(1)y与x之间的函数关系式.(2)自变量x的取值范围.(3)当x=14时,y的值.25.如图,一次函数y=kx+b的图象与反比例函数y=mx的图象交于A、B两点.(1)利用图中的条件,求反比例函数和一次函数的解析式.(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.第25题图26.如图,双曲线y=5x在第一象限的一支上有一点C(1,5),•过点C•的直线y=kx+b(k>0)与x轴交于点A(a,0).(1)求点A的横坐标a与k的函数关系式(不写自变量取值范围).(2)当该直线与双曲线在第一象限的另一个交点D的横坐标是9时,求△COA•的面积.第26题图反比例函数测试题(一)答案1.B.;2.D.;3.A.;4.A.;5.B.;6.B.;7.A.;8.B.;9.A.;10.D.;11.y=2x;12.y=x+1;13.y=20x;14.2;15.y=-8x;16.n=-3;17.m=5;18.<,>;19.2004.5;20.A.;B.;;21.A.;C.;D.;22.解:(1)∵OA=OB=OD=1,∴点A、B、D的坐标分别为A(-1,0),B(0,1),D(1,0).(2)∵点AB在一次函数y=kx+b(k≠0)的图象上,∴1k bb-+=⎧⎨=⎩解得11kb=⎧⎨=⎩∴一次函数的解析式为y =x +1,∵点C 在一次函数y =x +1的图象上,•且CD ⊥x 轴, ∴C 点的坐标为(1,2),又∵点C 在反比例函数y =mx(m ≠0)的图象上, ∴m =2,•∴反比例函数的解析式为y =2x.;23.(1)y =2x -6;(2)C (3,0),D (0,-6);(3)S △AOC :S △BOD =1:1.; 24.(1)y =216x 提示:设y =k-22k x,再代入求k 1,k 2的值. (2)自变量x 取值范围是x >0. (3)当x =14时,y =162=255.;25.解:(1)由图中条件可知,双曲线经过点A (2,1)∴1=2m ,∴m =2,∴反比例函数的解析式为y =2x. 又点B 也在双曲线上,∴n =21-=-2,∴点B 的坐标为(-1,-2).∵直线y =kx +b 经过点A 、B .∴122k b k b =+⎧⎨-=-+⎩ 解得11k b =⎧⎨=-⎩∴一次函数的解析式为y =x -1.(2)根据图象可知,一次函数的图象在反比例函数的图象的上方时,•一次函数的值大于反比例函数的值,即x >2或-1<x <0.;26.解:(1)∵点C (1,5)在直线y =-kx +b 上,∴5=-k +b , 又∵点A (a ,0)也在直线y =-kx +b 上,∴-ak +b =0,∴b =ak 将b =ak 代入5=-k +a 中得5=-k +ak ,∴a =5k+1. (2)由于D 点是反比例函数的图象与直线的交点∴599y y k ak⎧=⎪⎨⎪=-+⎩ ∵ak =5+k ,∴y =-8k +5 ③ 将①代入③得:59=-8k +5,∴k =59,a =10. ∴A (10,0),又知(1,5),∴S △COA =12×10×5=25.;。
反比例函数》测试题(含答案)

反比例函数》测试题(含答案)1、选择题(每小题5分,共50分)1、若点(x1.-1)、(x2.-2)、(x3.1)都在反比例函数y= k/x 上,则它们之间的大小关系是()A.x1<x3<x2B.x2<x1<x3C.x1<x2<x3D.x2<x3<x12、若反比例函数y=k/x的图象经过点(m,3m),其中m≠0,则此反比例函数的图象在()A.第一、二象限;B.第一、三象限;C.第二、四象限;D.第三、四象限3、在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=3/x上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小4、函数y=-kx与函数y=k/x的图象的交点个数是()A。
0B。
1C。
2D.不确定5、函数y=6-x与函数y=k/x的图象交于A、B两点,设点A的坐标为(x1,y1),则边长分别为x1、y1的矩形面积和周长分别为()A。
4,12B。
4,6C。
8,12D。
8,66、已知y1+y2=y,其中y1与x成反比例,且比例系数为k1,而y2与x2成正比例,且比例系数为k2,若x=-1时,y=0,则k1,k2的关系是( )A.k1+k2=0B.k1k2=1C.k1-k2=0D.k1k2=-17、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标系中的图象不可能是()18、如图,直线y=mx与双曲线y=k/(x-1)交与A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,则k的值是()A、2B、m-2C、mD、49、如图,点A在双曲线y=6/x上,且OA=4,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )A.47B.5C.27D.2210、如图,反比例函数y= k/x的图象经过点(1,2),则k=()。
二、填空题(每小题5分,共20分)11、若y=k/x是反比例函数,且x1y1=x2y2,则k=______。
反比例函数练习题(超经典含答案)

1.函数ky x=的图象经过点(23),,那么k 等于 A .6 B .16 C .23 D .322.已知反比例函数2k y x-=,其图象在第二、四象限内,则k 的值可为A .0B .2C .3D .53.已知反比例函数y =2x,则下列点中在这个反比例函数图象上的是 A .(1,2)B .(1,-2)C .(-2,-2)D .(-2,1)4.如果x 、y 之间的关系是10(0)ax y a -+=≠,那么y 是x 的 A .正比例函数 B .反比例函数 C .一次函数D .二次函数5.已知反比例函数y =-4x,则下列有关该函数的说法正确的是 A .该函数的图象经过点(2,2)B .该函数的图象位于第一、三象限C .当x >0时,y 的值随x 的增大而增大D .当x >-1时,y >46.如图,反比例函数ky x =(k >0)与一次函数12y x b =+的图象相交于两点A(1x ,1y ),B (2x ,2y ),线段AB 交y 轴与C ,当|1x -2x |=2且AC =2BC 时,k 、b 的值分别为A .k =12,b =2 B .k =49,b =1C.k=13,b=13D.k=49,b=137.如图,四边形QABC是矩形,ADEF是正方形,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=kx的图象上,OA=1,OC=6,则正方形ADEF的边长为A.2 B.3 C.4 D.58.如图,在平面直角坐标系中,梯形OACB的顶点O是坐标原点,OA边在y轴正半轴上,OB边在x轴正半轴上,且OA∥BC,双曲线y=kx(x>0)经过AC边的中点,若S梯形OACB=4,则双曲线y=kx的k值为A.5 B.4 C.3 D.29.如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=4x(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积是A.2 B.C.4 D.6 10.若y=(5+m)x2+n是反比例函数,则m、n的取值是__________.11.如果函数y=kx-2(k≠0)的图象不经过第一象限,那么函数kyx的图象一定在__________.12.反比例函数y =1k x与正比例函数y =k 2x 的图象的一个交点为(2,m ),则12k k =__________.13.如图,矩形OABC 的顶点A 、C 分别在x 轴、y 轴上,反比例函数y =kx(k ≠0,x >0)的图象经过矩形OABC 的对角线AC 的中点D .若矩形OABC 的面积为16,则k 的值为__________.14.已知函数2212mm y m m x --=+().(1)如果y 是x 的正比例函数,求m 的值;(2)如果y 是x 的反比例函数,求出m 的值,并写出此时y 与x 的函数关系式.15.已知121y y y y =+,与2x 在正比例关系,2y 与x 成反比例函数关系,且1x =时,31y x ==-,时,1y =.(1)求y 与x 的关系式; (2)求当2x =-时,y 的值.16.已知A(-4,2)、B(n,-4)两点是一次函数y=kx+b和反比例函数y=mx图象的两个交点.(1)求一次函数和反比例函数的解析式;(2)求△AOB的面积;(3)观察图象,直接写出不等式kx+b-mx>0的解集.17.如图,在平面直角坐标系中,四边形OABC为矩形,直线y=kx+b交BC于点E(1,m),交AB于点F(4,12),反比例函数y=nx(x>0)的图象经过点E,F.(1)求反比例函数及一次函数解析式;(2)点P是线段EF上一点,连接PO、PA,若△POA的面积等于△EBF的面积,求点P的坐标.18.如图,点A 、B 为直线y x =上的两点,过A 、B 两点分别作y 轴的平行线交双曲线1y x=(x >0)于点C 、D 两点.若2BD AC =,则224OC OD -的值为A .5B .6C .7D .819.如图,Rt OAB △的顶点与坐标原点重合,903AOB AO BO ∠=︒=,,当A 点在反比例函数9(0)y x x=>图象上移动时,B 点坐标满足的函数解析式是A .1(0)y x x =-< B .3(0)y x x =-< C .1(0)3y x x=-<D .1(0)9y x x=-<20.如图,点A 在反比例函数y =kx(k ≠0)的图象上,且点A 是线段OB 的中点,点D 为x 轴上一点,连接BD 交反比例函数图象于点C ,连接AC ,若BC ∶CD =2∶1,S △ADC =103.则k 的值为A .203 B .16 C .283D .1021.如图,直线y =x +m 与双曲线y =2x相交于A ,B 两点,BC ∥x 轴,AC ∥y 轴,则△ABC 面积的最小值为__________.22.如图,点A 的坐标是(2,0),△ABO 是等边三角形,点B 在第一象限,若反比例函数y =kx的图象经过点B ,则k 的值是__________.23.如图,在函数y 1=1k x (x <0)和y 2=2kx(x >0)的图象上,分别有A 、B 两点,若AB ∥x 轴,交y 轴于点C ,且OA ⊥OB ,S △AOC =12,S △BOC =92,则线段AB 的长度为__________.24.如图,矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上,点D 为对角线OB 的中点,点(4)E n ,在边AB 上,反比例函数(0)ky k x=≠在第一象限内的图象经过点D 、E ,且D 点的横坐标是它的纵坐标的2倍. (1)求边AB 的长;(2)求反比例函数的解析式和n 的值;(3)若反比例函数的图象与矩形的边BC 交于点F ,将矩形折叠,使点O 与点F 重合,折痕分别与x 、y 轴正半轴交于点H 、G ,求线段OG 的长.25.如图,直线2(0)y kx k =->与双曲线ky x=在第一象限内的交点为R ,与x 轴的交点为P ,与y 轴的交点为Q ,作RM x ⊥轴于点M ,若OPQ △与PRM △的面积是41∶,求k .26.(2018·辽宁本溪)反比例函数(0)ky k x=≠的图象经过点(-2,3),则该反比例函数图象在A .第一、三象限B .第二、四象限C .第二、三象限D .第一、二象限27.(2018·青海)若111()P x y ,,222()P x y ,是函数5y x=图象上的两点,当120x x >>时,下列结论正确的是 A .120y y <<B .210y y <<C .120y y <<D .210y y <<28.(2018·山东莱芜)在平面直角坐标系中,已知△ABC 为等腰直角三角形,CB =CA =5,点C (0,3),点B 在x 轴正半轴上,点A 在第三象限,且在反比例函数y =kx的图象上,则k = A .3B .4C .6D .1229.(2018·山东日照)已知反比例函数y =-8x,下列结论:①图象必经过(-2,4);②图象在二,四象限内;③y 随x 的增大而增大;④当x >-1时,则y >8.其中错误的结论有 A .3个B .2个C .1个D .0个30.(2018·甘肃天水)函数y 1=x 和y 2=1x的图象如图所示,则y 1>y 2时,x 的取值范围是A .x <-1或x >1B .x <-1或0<x <1C .-1<x <0或x >1D .-1<x <0或0<x <131.(2018·湖南益阳)若反比例函数2ky x-=的图象位于第二、四象限,则k 的取值范围是__________.32.(2018·江苏镇江)反比例函数y =kx(k ≠0)的图象经过点A (-2,4),则在每一个象限内,y 随x 的增大而__________.(填“增大”或“减小”) 33.(2018·广西壮族自治区)已知直线y =ax (a ≠0)与反比例函数y =kx(k ≠0)的图象一个交点坐标为(2,4),则它们另一个交点的坐标是__________. 34.(2018·山东济宁)如图,点A 是反比例函数y =4x(x >0)图象上一点,直线y =kx +b 过点A 并且与两坐标轴分别交于点B ,C ,过点A 作AD ⊥x 轴,垂足为D ,连接DC ,若△BOC 的面积是4,则△DOC 的面积是__________.35.(2018·甘肃兰州)如图,在平面直角坐标系中,一次函数1y ax b =+的图象与反比例函数2ky x=的图象交于点(12)A ,和(2)B m -,. (1)求一次函数和反比例函数的表达式; (2)请直接写出12y y >时,x 的取值范围;(3)过点B 作BE x ∥轴,AD BE ⊥于点D ,点C 是直线BE 上一点,若2AC CD =,求点C 的坐标.4.【答案】B【解析】∵1ax-+y=0,∴y=-1ax-.即y=-ax,∵a≠0,∴y是x的反比例函数.故选B.5.【答案】C【解析】∵当x=2时,y=-2,故不正确;∵-4<0,∴该函数的图象位于第二、四象限,故不正确;∵该函数的图象位于第二、四象限,∴当x>0时,y的值随x的增大而增大,故正确;∵当x>-1时,y<4,故不正确.故选C.6.【答案】D7.【答案】A【解析】∵OA=1,OC=6,∴B点坐标为(1,6),∴k=1×6=6,∴反比例函数解析式为y=6x,设AD =t ,则OD =1+t ,∴E 点坐标为(1+t ,t ),∴(1+t )·t =6,整理为t 2+t -6=0, 解得t 1=-3(舍去),t 2=2,∴正方形ADEF 的边长为2.故选A . 8.【答案】D【解析】过AC 的中点P 作DE x ∥轴交y 轴于D ,交BC 于E ,作PF x ⊥轴于F ,如图,在PAD △和PCE △中,APD CPE ADP PEC PA PC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴PAD PCE △≌△,∴PAD PCE S S =△△, ∴BODEAOBC S S =矩形梯形,∵12DOFP BODES S=矩形矩形,∴114222DOFP AOBC S S ==⨯=矩形梯形, ∴||2k =,而0k >,∴2k =.故选D . 9.【答案】C【解析】因为△OAB 与△ADC 均为正三角形,所以OB 与AD 平行,所以△OBP 与△OAB 的高相等,又因为有共同底边OB ,所以S △OBP =S △OAB .且顶点B 在双曲线y =4x(x >0)上,所以△OBP 的面积为4.故选C . 10.【答案】m ≠-5,n =-3【解析】∵y =(5+m )x 2+n是反比例函数,∴2150n m +=-⎧⎨+≠⎩,解得:m ≠-5,n =-3,故答案为:m ≠-5,n =-3.又因为矩形OABC 的面积为16,所以OA ⋅OC =ab =8,所以k =1644ab ==4,故答案为:4.14.【解析】(1)由221(2)mm y m m x --=+是正比例函数,得m 2-m -1=1且m 2+2m ≠0,解得m =2或m =-1. (2)由221(2)m m y m m x --=+是反比例函数,得m 2-m -1=-1且m 2+2m ≠0,解得m =1.故y 与x 的函数关系式y =3x -1.15.【解析】(1)∵1y 与2x 在正比例关系,2y 与x 成反比例函数关系,∴211y k x =,16.【解析】(1)把A (-4,2)代入my x=,得m =2×(-4)=-8, 所以反比例函数解析式为8y x=-, 把B (n ,-4)代入8y x=-,得-4n =-8,解得n =2, 把A (-4,2)和B (2,-4)代入y =kx +b ,得4224k b k b -+=⎧⎨+=-⎩ ,解得12k b =-⎧⎨=-⎩ ,所以一次函数的解析式为y =-x -2.(2)y =-x -2中,令y =0,则x =-2,即直线y =-x -2与x 轴交于点C (-2,0),∴S △AOB =S △AOC +S △BOC =12×2×2+12×2×4=6. (3)由图可得,不等式0mkx b x +->的解集为:x <-4或0<x <2.17.【解析】(1)∵反比例函数(0)n y x x =>经过点1(4)2F ,,∴n =2,反比例函数解析式为2y x=. ∵2y x=的图象经过点E (1,m ), ∴m =2,点E 坐标为(1,2).18.【答案】B【解析】如图,延长AC交x轴于E,延长BD交x轴于F.设A,B的横坐标分别是a,b,∵点A、B为直线y=x上的两点,∴A的坐标是(a,a),B的坐标是(b,b),则AE=OE=a,BF=OF=b.∵C、D两点在交双曲线y=1x(x>0)上,则CE=1a,DF=1b,∴BD=BF−DF=b−1b,AC=a−1a.又∵BD =2AC ,∴b −1b =2(a −1a ),两边平方得:b 2+21b −2=4(a 2+21a−2), 即b 2+21b =4(a 2+21a )−6.在直角△OCE 中,OC 2=OE 2+CE 2=a 2+21a,同理OD 2=b 2+21b ,∴4OC 2−0D 2=4(a 2+21a )−(b 2+21b)=6,故选B .19.【答案】A20.【答案】B【解析】如图,作AE ⊥OD 于E ,CF ⊥OD 于F .∵BC ∶CD =2∶1,S △ADC =103,∴S △ACB =203,∵OA=OB ,∴B (2m ,2n ),S △AOC =S △ACB =203,∵A、C在y=kx上,BC=2CD,∴C(32m,23n),∵S△AOC=S△AOE+S梯形AEFC-S△OCF=S梯形AEFC,∴12·(n+23n)×12m=203,∴mn=16,故选B.21.【答案】6【解析】设A(a,3a),B(b,3b),则C(a,3b).将y=x+m代入y=3x,得x+m=3x,整理,得x2+mx-3=0,则a+b=-m,ab=-3,∴(a-b)2=(a+b)2-4ab=m2+12.∵S△ABC=12AC·BC=1332ba-()(a-b)=12·3b aab-()·(a-b)=12(a-b)2=12(m2+12)=12m2+6,∴当m=0时,△ABC的面积有最小值6.故答案为:6.2223【解析】∵S△AOC=12,S△BOC=92,∴12|k1|=1122,|k2|=92,∴k1=-1,k2=9,∴两反比例解析式为y=-1x,y=9x,设B点坐标为(9t,t)(t>0),∵AB∥x轴,∴A点的纵坐标为t,把y =t 代入y =-1x 得x =-1t ,∴A 点坐标为(-1t,t ),∵OA ⊥OB ,∴∠AOC =∠OBC ,∴Rt △AOC ∽Rt △OBC ,∴OC ∶BC =AC ∶OC ,即t ∶91t t=∶t ,∴t ,∴A 点坐标为(B 点坐标为(AB 的长度(-..24.【解析】(1)如图,过D 作DM x ⊥轴,交x 轴于点M ,(3)由(12)F ,,得到1CF =, 由折叠得:OGH △≌FGH △, ∴OG FG =, ∵2OC AB ==,设OG FG x ==,得到2CG x =-,在Rt CFG △中,由勾股定理得:222FG CG CF =+,即22(2)1x x =-+, 整理得:45x =, 解得:54x =, 则54OG =. 25.【解析】设()R m n ,,则mn k =, 如图,连接OR ,26.【答案】B【解析】∵反比例函数y =kx(k ≠0)的图象经过点(−2,3),∴k =−2×3=−6,∴k <0,∴反比例函数y =kx(k ≠0)的图象在第二、四象限.故选B .27.【答案】A【解析】反比例函数5y x=中,k =5>0,图象位于一、三象限,在每一象限内,y 随着x 的增大而减小,∵111()P x y ,,222()P x y ,是函数5y x=图象上的两点,120x x >>,∴120y y <<,故选A . 28.【答案】A【解析】如图,作AH ⊥y 轴于H .∵CA =CB ,∠AHC =∠BOC ,∠ACH =∠CBO ,∴△ACH ≌△CBO ,∴AH =OC ,CH =OB ,∵C (0,3),BC =5,∴OC =3,OB ,∴CH =OB =4,AH =OC =3,∴OH =1, ∴A (-3,-1),∵点A 在y =kx上,∴k =3,故选A . 29.【答案】B30.【答案】C【解析】观察图象可知当-1<x <0或x >1时,直线在双曲线的上方,所以y 1>y 2的x 取值范围是-1<x <0或x >1,故选C . 31.【答案】k >2【解析】∵反比例函数y =2kx-的图象在第二、四象限,∴2-k <0,∴k >2.故答案为:k >2.32.【答案】增大【解析】把(-2,4)代入反比例函数y =k x ,得42k =-,∴k =-12, ∵k <0,∴在每一个象限内y 随x 的增大而增大,故答案为:增大.33.【答案】(-2,-4)【解析】∵正比例函数和反比例函数均关于原点对称,∴两函数的交点关于原点对称, ∵一个交点的坐标是(2,4),∴另一个交点的坐标是(-2,-4),故答案为:(-2,-4).34.【答案】2【解析】设A (a ,4a )(a >0),∴AD =4a,OD =a , ∵直线y =kx +b 过点A 并且与两坐标轴分别交于点B ,C ,∴C (0,b ),B (-bk,0), ∵△BOC 的面积是4,∴S △BOC =12OB ×OC =12×b k ×b =4,∴b 2=8k ,∴k =28b ,①∴AD ⊥x 轴,∴OC ∥AD ,∴△BOC ∽△BDA ,∴OB OC BD AD =,∴4bb kb a k a=+,∴a 2k +ab =4,②联立①②得,ab =-4-或ab-4,∴S △DOC =12OD ·OC =12ab2.故答案为:2.35.【解析】(1)∵点(12)A ,在反比例函数2ky x=的图象上,∴30DAC ∠=︒,由题意得,213AD =+=,在Rt ADC △中,tan CD DAC AD ∠=,即3CD =解得,CD =当点C 在点D 的左侧时,点C 的坐标为(11)-,当点C 在点D 的右侧时,点C 的坐标为11)-,,∴当点C 的坐标为(11)--或11)-,时,2AC CD =.。
反比例函数练习题及答案

反比例函数练习题一、填空题(每空3分,共42分) 1.已知反比例函数()0≠=k xky 的图象经过点(2,-3),则k 的值是_______,图象在__________象限,当x>0时,y 随x 的减小而__________.2.已知变量y 与x 成反比,当x =1时,y =-6,则当y = 3时,x=________。
3.若反比例函数y=(2m-1)22m x - 的图象在第一、三象限,则函数的解析式为___________.4.已知反比例函数xm y )23(1-=,当m 时,其图象的两个分支在第一、三象限内;当m 时,其图象在每个象限内y 随x 的增大而增大;5.在函数(为常数)的图象上有三个点(-2,),(-1,),(,),函数值,,的大小为 ; 6.已知111222(,),(,)P x y P x y 是反比例函数xky =(k≠0)图象上的两点,且12x x <<0时,12y y < ,则k________。
7.已知正比例函数y=kx(k≠0),y 随x 的增大而减小,那么反比例函数y=kx,当x< 0时,y 随x 的增大而_______.8.已知y 1与x 成正比例(比例系数为k 1),y 2与x 成反比例(比例系数为k 2),若函数y=y 1+y 2的图象经过点(1,2),(2,12),则8k 1+5k 2的值为________. 9. 若m <-1,则下列函数:①()0 x xmy =;② y =-mx+1; ③ y = mx; ④ y =(m + 1)x 中,y 随x 增大而增大的是___________。
10.当>0,<0时,反比例函数的图象在__________象限。
11.老师给出一个函数,甲、乙、丙、丁四人各指出这个函数的一个性质,甲:函数图象不经过第三象限;乙:函数图象经过第一象限;丙:y 随x 的增大而减小;丁:当2<x 时,0>y 。
(完整版)反比例函数练习题及答案

反比例函数综合一.选择题(共23小题)1.如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x 轴,且AC=BC,则AB等于()A.B.2C.4 D.3第1题第2题第3题第5题2.如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于()A.B.6 C.3 D.123.反比例函数y=的图象如图所示,点A是该函数图象上一点,AB垂直于x轴垂足是点B,如果S△AOB=1,则k的值为()A.1 B.﹣1 C.2 D.﹣24.在同一平面直角坐标系中,函数y=kx(k>0)与y=(k>0)的图象可能是()A.B.C.D.5.如图,在平面直角坐标系xOy中,反比例函数y=的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(,48)中,在该函数图象上的点有()A.4个B.3个C.2个D.1个6.已知反比例函数y=(k≠0)过点A(a,y1),B(a+1,y2),若y2>y1,则a的取值范围为()A.﹣1<a B.﹣1<a<0 C.a<1 D.0<a<17.如图,双曲线y=与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),点N的纵坐标为﹣1.根据图象信息可得关于x不等式<kx+b的解为()A.x<﹣3 B.﹣3<x<0 C.﹣3<x<1 D.﹣3<x<0 或x>1第7题第9题第11题第12题8.点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y3<y1C.y3<y2<y1D.y2<y1<y39.如图,A、B是双曲线y=(k>0)上的点,A、B两点的横坐标分别是a、3a,线段AB的延长=3.则k的值为()线交x轴于点C,若S△AOCA.2 B.1.5 C.4 D.610.已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=(k<0)的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y1<y3C.y3<y2<y1D.y3<y1<y211.如图,点A(m,1),B(2,n)在双曲线y=(k≠0),连接OA,OB.若S△ABO=8,则k的值是()A.﹣12 B.﹣8 C.﹣6 D.﹣412.如图,反比例函数与正比例函数的图象交于A、B两点,过点A作AC⊥x轴于点C.若△ABC 的面积是8,则这个反比例函数的解析式是()A.y=B.y=C.y=D.y=13.如图,在平面直角坐标系中,函数y=的图象与函数y=x的图象相交于A,B两点,点C是函数y=的图象右支上一点,连结AC,BC,若∠C=90°,则点C的坐标为()A.(2,4)B.(3,6)C.(4,2)D.(,)第13题第14题第15题第16题14.如图,直线y=x﹣3与x轴交于点A,与双曲线y=(k≠0)在第一象限内交于点B,过点A 作AC⊥x轴,交该双曲线于点C,若AB=AC,则k的值是()A.B.C.D.15.如图,在平面直角坐标系中,点A、B分别在第二象限和第一象限,AB与x轴平行,∠AOB=90°,OA=3,OB=4,函数y=(x<0)和y=(x>0)的图象分别经过点AB,则的值为()A.B.﹣C.D.﹣16.如图,在平面直角坐标系中,反比例函数y=(k≠0)经过▱ABCD的顶点B、D,点A的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),▱ABCD的面积是18,则点D的坐标是()A.(﹣2,2)B.(3,2)C.(﹣3,2)D.(﹣6,1)17.如图,点M是反比例函数y=(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为()A.1 B.2 C.4 D.不能确定第17题第18题18.如图,已知点A(0,4),B (1,4),点B在双曲线y=(k>0)上,在AB的延长线上取一点C,过C的直线交双曲线于点D,交x轴正半轴于点E,且CD=DE,则线段CE长度的取值范围是()A.4≤CE<4B.4≤CE<2C.2<CE<4 D.4<CE<219.如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为()A.5 B.6 C.4D.5第19题第20题第21题第23题20.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会()A.逐渐增大B.不变C.逐渐减小D.先增大后减小21.如图,一次函数y1=x+1的图象与反比例函数y2=的图象交于A、B两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是()A.点A和点B关于原点对称B.当x<1时,y1>y2C.S△AOC=S△BOD D.当x>0时,y1、y2都随x的增大而增大22.函数y=k(x﹣1)与y=﹣在同一直角坐标系内的图象大致是()A.B.C.D.23.如图,点A,C都在函数y=(x>0)的图象上,点B,D都在x轴上,且使得△OAB,△BCD 都是等边三角形,则点C的坐标是()A.(+1,﹣)B.(+1,﹣1)C.(+1,﹣)D.(+1,﹣)二.填空题(共9小题)24.如图,点M是函数图象上的一点,直线l:y=x,过点M分别作MA⊥y轴,MB⊥l,A,B为垂足,则MA•MB=.第24题第25题第30题第31题25.如图将直线向左平移m个单位,与双曲线交于点A,与x轴交于点B,则OB2﹣OA2+AB2=.26.如果反比例函数y=(m﹣3)的图象在第二、四象限,那么m=.27.已知双曲线y=(k≠0)上有一点P,PA⊥x轴于A,点O为坐标原点,且S△PAO=12,则此反比例函数的解析式为.28.反比例函数的图象同时过A(﹣2,a)、B(﹣3,b)、C(1,c)三点,则a、b、c 的大小关系是.29.函数y=(m2﹣m)x m2﹣3m+1是反比例函数,则m的值是,它的图象分布在象限,在每一个象限内,y随x的增大而.30.如图,A、B是反比例函数y=上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=OC,S四边形=14,则k=.ABDC31.如图,B为双曲线y=(x>0)上一点,直线AB平行于y轴交直线y=x于点A,若OB2﹣AB2=12,则k=.32.如图,正比例函数y=x与反比例函数y=的图象相交于A,C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为.三.解答题(共8小题)33.如图1,在平面直角坐标系中,四边形AOBC是矩形,点C的坐标为(4,3),反比例函数y=(k>0)的图象与矩形AOBC的边AC、BC分别相交于点E、F,将△CEF沿EF对折后,C点恰好落在OB上.(1)求证:△AOE与△BOF的面积相等;(2)求反比例函数的解析式;(3)如图2,P点坐标为(2,﹣3),在反比例函数y=的图象上是否存在点M、N(M在N的左侧),使得以O、P、M、N为顶点的四边形是平行四边形?若存在,求出点M、N的坐标;若不存在,请说明理由.34.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2),M、N分别是AB、BC的中点.(1)若反比例函数y=(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N 是否在该函数的图象上;(2)若反比例函数y=(x>0)的图象与△MNB(包括边界)有公共点,请直接写出m的取值范围.35.如图,反比例函数y=﹣与一次函数y=﹣x+2的图象交于A、B两点.(1)求A、B两点的坐标;(2)观察图象,直接写出x为何值时,一次函数值大于反比例函数?(3)求△AOB的面积.36.如图,反比例函数y1=的图象与一次函数y2=kx+b的图象交于A(m,3),B(﹣3,n)、两点.(1)求一次函数的解析式及△AOB的面积;(2)根据图象直接写出不等式的解集;(3)若点P是坐标轴上的一点,且满足△PAB面积等于△AOB的面积的2倍,直接写出点P的坐标.37.如图,若直线y=kx+b(k≠0)与x轴交于点,与双曲线在第二象限交于点B,且OA=OB,△OAB的面积为(1)求直线AB的解析式及双曲线的解析式;(2)求tan∠ABO的值.38.已知反比例函数y=和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.(1)求反比例函数的解析式?(2)已知A在第一象限,是两个函数的交点,求A点坐标?(3)利用②的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?39.如图,双曲线y=在第一象限的一支上有一点C(1,5),过点C的直线y=﹣kx+b(k>0)与x 轴交于点A(a,0).(1)求点A的横坐标a与k的函数关系式(不写自变量取值范围).(2)当该直线与双曲线在第一象限的另一个交点D的横坐标是9时,求△COA的面积.40.如图,一次函数y=ax+b的图象与反比例函数的图象交于M、N两点.(1)利用图中条件,求反比例函数和一次函数的解析式;(2)连接OM、ON,求三角形OMN的面积.(3)连接OM,在x轴的正半轴上是否存在点Q,使△MOQ是等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标,若不存在,说明理由.参考答案一.选择题(共23小题)1.如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x 轴,且AC=BC,则AB等于(B)A.B.2C.4 D.3设C(a,),则B(3a,),A(a,),∵AC=BC,∴﹣=3a﹣a,解得a=1,(负值已舍去)∴C(1,1),B(3,1),A(1,3),∴AC=BC=2,∴Rt△ABC中,AB=2,2.如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于(B)A.B.6 C.3 D.12解:如图,将C2及直线y=x绕点O逆时针旋转45°,则得到双曲线C3,直线l与y轴重合.双曲线C3,的解析式为y=﹣过点P作PB⊥y轴于点B∵PA=PB∴B为OA中点.∴S△PAB=S△POB=3∴△POA的面积是6由反比例函数比例系数k的性质,S△POB3.反比例函数y=的图象如图所示,点A是该函数图象上一点,AB垂直于x轴垂足是点B,如果S△AOB=1,则k的值为(D)A.1 B.﹣1 C.2 D.﹣24.在同一平面直角坐标系中,函数y=kx(k>0)与y=(k>0)的图象可能是(C)A.B.C.D.5.如图,在平面直角坐标系xOy中,反比例函数y=的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(,48)中,在该函数图象上的点有(C)A.4个B.3个C.2个D.1个第5题第7题第9题6.已知反比例函数y=(k≠0)过点A(a,y1),B(a+1,y2),若y2>y1,则a的取值范围为(B)A.﹣1<a B.﹣1<a<0 C.a<1 D.0<a<17.如图,双曲线y=与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),点N的纵坐标为﹣1.根据图象信息可得关于x不等式<kx+b的解为(D)A.x<﹣3 B.﹣3<x<0 C.﹣3<x<1 D.﹣3<x<0 或x>18.点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是(D)A.y1<y2<y3B.y2<y3<y1C.y3<y2<y1D.y2<y1<y39.如图,A、B是双曲线y=(k>0)上的点,A、B两点的横坐标分别是a、3a,线段AB的延长线交x轴于点C,若S△AOC=3.则k的值为(B)A.2 B.1.5 C.4 D.6解:如图,分别过点A、B作AF⊥y轴于点F,AD⊥x轴于点D,BG⊥y轴于点G,BE⊥x轴于点E,∵k>0,点A是反比例函数图象上的点,∴S△AOD =S△AOF=|k|,∵A、B两点的横坐标分别是a、3a,∴AD=3BE,∴点B是AC的三等分点,∴DE=2a,CE=a,∴S△AOC =S梯形ACOF﹣S△AOF=(OE+CE+AF)×OF﹣|k|=×5a×﹣|k|=3,解得k=1.5.10.已知点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=(k<0)的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是(D)A.y1<y2<y3B.y2<y1<y3C.y3<y2<y1D.y3<y1<y211.如图,点A(m,1),B(2,n)在双曲线y=(k≠0),连接OA,OB.若S△ABO=8,则k的值是(C)A.﹣12 B.﹣8 C.﹣6 D.﹣4第11题第12题解:过A作y轴的垂线,过B作x轴的垂线,交于点C,连接OC,设A(k,1),B(2,k),则AC=2﹣k,BC=1﹣k,∵S△ABO=8,∴S△ABC﹣S△ACO﹣S△BOC=8,即(2﹣k)(1﹣k)﹣(2﹣k)×1﹣(1﹣k)×2=8,解得k=±6,∵k<0,∴k=﹣6,12.如图,反比例函数与正比例函数的图象交于A、B两点,过点A作AC⊥x轴于点C.若△ABC 的面积是8,则这个反比例函数的解析式是(C)A.y=B.y=C.y=D.y=13.如图,在平面直角坐标系中,函数y=的图象与函数y=x的图象相交于A,B两点,点C是函数y=的图象右支上一点,连结AC,BC,若∠C=90°,则点C的坐标为(A)A.(2,4)B.(3,6)C.(4,2)D.(,)解:函数y=的图象与函数y=x的图象相交于A,B两点,解方程组,可得,,∴B(4,2),A(﹣4,﹣2),∴OB=AO=2,又∵∠ACB=90°,∴OC=AB=2,设C(a,),则OC==2,解得a=2,或a=4(舍去),∴C(2,4),14.如图,直线y=x﹣3与x轴交于点A,与双曲线y=(k≠0)在第一象限内交于点B,过点A 作AC⊥x轴,交该双曲线于点C,若AB=AC,则k的值是(D)A.B.C.D.解:如图,过B作BD⊥OA于D,则∠ADB=∠AOE=90°,由直线y=x﹣3,可得A(4,0),E(0,﹣3),∴AO=4,OE=3,AE=5,设点C的坐标为(4,),则AC=AB=,由△AOE∽△ADB,可得==,即==,∴AD=,BD=,∴B(4+,),∵双曲线y=(k≠0)经过点B,∴(4+)×k=k,解得k=,15.如图,在平面直角坐标系中,点A、B分别在第二象限和第一象限,AB与x轴平行,∠AOB=90°,OA=3,OB=4,函数y=(x<0)和y=(x>0)的图象分别经过点AB,则的值为(D)A.B.﹣C.D.﹣解:∵AB与x轴平行,∴AB⊥y轴,即∠AHO=∠OHB=90°,∵∠AOB=90°,∴∠AOH+∠BOH=∠AOH+∠OAH=90°,∴∠OAH=∠BOH,∴△AOH∽△OBH,∴=,即=,又∵k1<0,∴=﹣,16.如图,在平面直角坐标系中,反比例函数y=(k≠0)经过▱ABCD的顶点B、D,点A的坐标为(0,﹣1),AB∥x轴,CD经过点(0,2),▱ABCD的面积是18,则点D的坐标是(C)A.(﹣2,2)B.(3,2)C.(﹣3,2)D.(﹣6,1)解:如图,∵点A的坐标为(0,﹣1),AB∥x轴,反比例函数y=(k≠0)经过▱ABCD的顶点B,∴点B的坐标为(﹣k,﹣1),即AB=﹣k,又∵点E(0,2),∴AE=2+1=3,又∵平行四边形ABCD的面积是18,∴AB×AE=18,∴﹣k×3=18,∴k=﹣6,∴y=﹣,∵CD经过点(0,2),∴令y=2,可得x=﹣3,∴点D的坐标为(﹣3,2),17.如图,点M是反比例函数y=(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为(A)A.1 B.2 C.4 D.不能确定第17题第18题18.如图,已知点A(0,4),B (1,4),点B在双曲线y=(k>0)上,在AB的延长线上取一点C,过C的直线交双曲线于点D,交x轴正半轴于点E,且CD=DE,则线段CE长度的取值范围是(A)A.4≤CE<4B.4≤CE<2C.2<CE<4 D.4<CE<2解:如图1,过D作DF⊥OA于F,∵点A(0,4),B (1,4),∴AB⊥y轴,AB=1,OA=4,∵CD=DE,∴AF=OF=2,∵点B在双曲线y=(k>0)上,∴k=1×4=4,∴反比例函数的解析式为:y=,∵过点C的直线交双曲线于点D,∴D点的纵坐标为2,把y=2代入y=得,x=2,∴D(2,2),当O与E重合时,如图2,∵DF=2,∴AC=4,∵OA=4,∴CE=4,当CE⊥x轴时,CE=OA=4,∴4≤CE<4,19.如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为(D)A.5 B.6 C.4D.5第19题第20题第21题解:如图,过A作AD⊥y轴于D,将AB绕着点B顺时针旋转90°,得到A'B,过A'作A'H⊥y轴于H,由AB=BA',∠ADB=∠BHA'=90°,∠BAD=∠A'BH,可得△ABD≌△BA'H,∴BH=AD=2,又∵OB=2,∴点H与点O重合,点A'在x轴上,∴A'(1,0),又∵等腰Rt△ABA'中,∠BAA'=45°,而∠BAC=45°,∴点A'在AC上,由A(2,3),A'(1,0),可得直线AC的解析式为y=3x﹣3,解方程组,可得或,∴C(﹣1,﹣6),由点A(2,3)和点B(0,2),可得直线AB 的解析式为y=x+2,解方程组,可得或,∴M(﹣6,﹣1),∴CM==5,20.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线y=(x>0)上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会(C)A.逐渐增大B.不变C.逐渐减小D.先增大后减小21.如图,一次函数y1=x+1的图象与反比例函数y2=的图象交于A、B两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,连接AO、BO,下列说法正确的是(C)A.点A和点B关于原点对称B.当x<1时,y1>y2C.S△AOC=S△BOD D.当x>0时,y1、y2都随x的增大而增大解:A、,∵把①代入②得:x+1=,解得:x2+x﹣2=0,(x+2)(x﹣1)=0,x1=﹣2,x2=1,代入①得:y1=﹣1,y2=2,∴B(﹣2,﹣1),A(1,2),∴A、B不关于原点对称,故本选项错误;B、当﹣2<x<0或x>1时,y1>y2,故本选项错误;C、∵S△AOC=×1×2=1,S△BOD=×|﹣2|×|﹣1|=1,∴S△BOD=S△AOC,故本选项正确;D、当x>0时,y1随x的增大而增大,y2随x的增大而减小,故本选项错误;22.函数y=k(x﹣1)与y=﹣在同一直角坐标系内的图象大致是(A)A.B.C.D.23.如图,点A,C都在函数y=(x>0)的图象上,点B,D都在x轴上,且使得△OAB,△BCD都是等边三角形,则点C的坐标是(A)A.(+1,﹣)B.(+1,﹣1)C.(+1,﹣)D.(+1,﹣)第23题第24题解:如图,作AE⊥OB于E,CF⊥BD于F,∵△OAB,△BCD均为正三角形,A在反比例函数y=,∴A的横坐标是1,纵坐标是,∴OE=EB=1,OA=2OE=2,AE=,设BF=m,则C(2+m,m),代入y=,得:m2+2m﹣1=0,解得:m=﹣1±,∵m>0,∴m=﹣1+,∴点C的坐标为:(1+,).二.填空题(共9小题)24.如图,点M是函数图象上的一点,直线l:y=x,过点M分别作MA⊥y轴,MB⊥l,A,B为垂足,则MA•MB=.解:延长AM,交直线y=x于点D,设M(x,x+)则△AOD是等腰直角三角形,即∠ADO=45°,∴OA=AD=x+,AM=x,∴MD=AD﹣AM=,∵MB⊥l,∴MB=BD,∴△BDM是等腰直角三角形,∴MB2+BD2=MD2,∴MB=MD,∴MB=×=,∴MA•MB=x•=.25.如图将直线向左平移m个单位,与双曲线交于点A,与x轴交于点B,则OB2﹣OA2+AB2=.解:由题意知:平移后的直线解析式为:y=(x+m);设A(x,y),易知:B(﹣m,0),则有:OB2﹣OA2+AB2=m2﹣(x2+y2)+[(m+x)2+y2],联立y=(x+m),整理得:原式=﹣2x2﹣2mx;由于直线y=(x+m)与交于点A,联立两个函数解析式得:(x+m)=﹣,即x2+mx+2=0,得﹣x2﹣mx=2;故所求代数式=﹣2x2﹣2mx=4.故答案为:4.26.如果反比例函数y=(m﹣3)的图象在第二、四象限,那么m=1.【解答】解:根据题意m2﹣6m+4=﹣1,解得m=1或5,又m﹣3<0,m<3,所以m=1.故答案为:1.27.已知双曲线y=(k≠0)上有一点P,PA⊥x轴于A,点O为坐标原点,且S△PAO=12,则此反比例函数的解析式为y=﹣或y=.【解答】解:设点P的坐标为(x,y).∵P(x,y)在反比例函数y=kx(k≠0)的图象,∴k=xy,=12,∵S△PAO∴|xy|=12,∴|xy|=24,∴xy=±24,∴k=±24,∴y=﹣或y=.故答案为:y=﹣或y=.28.反比例函数的图象同时过A(﹣2,a)、B(﹣3,b)、C(1,c)三点,则a、b、c的大小关系是a>b>c.【解答】解:∵k<0,∴此函数的图象在二、四象限,∵﹣2<0,﹣3<0,1>0,∴A、B两点在第二象限,C点在第三象限,∴a>0,b>0,c<0,∵﹣2>﹣3,∴a>b>0,∴a>b>c.故答案为a>b>c.29.函数y=(m2﹣m)x m2﹣3m+1是反比例函数,则m的值是2,它的图象分布在第一、三象限,在每一个象限内,y随x的增大而减小.【解答】解:由题意得:m2﹣3m+1=﹣1,且m2﹣m≠0,解得:m=2,∵m2﹣m=4﹣2=2>0,∴图象分布在第一、三象限,在每一个象限内,y随x的增大而减小,故答案为:2;第一、三;减小.30.如图,A、B是反比例函数y=上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=OC,S四边形=14,则k=16.ABDC【解答】解:如图,分别延长CA,DB交于点E,根据AC⊥y轴于C,BD⊥x轴于D,AC=BD=OC,知△CED为直角三角形,且点A与点B的纵横坐标正好相反,设点A的坐标为(x A,y A),则点B的坐标为(y A,x A),点E的坐标为(y A,y A),四边形ACDB的面积为△CED的面积减去△AEB的面积.CE=ED=y A,AE=BE=y﹣y A,∴S ACDB=S△CED﹣S△AEB=[y A•y A﹣(y A﹣y A)(y A﹣y A)]=y A2=14,∵y A>0,∴y A=8,点A的坐标为(2,8),∴k=2×8=16.故答案为:16.31.如图,B为双曲线y=(x>0)上一点,直线AB平行于y轴交直线y=x于点A,若OB2﹣AB2=12,则k=6.【解答】解:如图,延长AB交x轴于点C,设点C的横坐标为a,则点B的纵坐标为,点A的纵坐标为a,所以,AB=a﹣,∵AB平行于y轴,∴AC⊥OC,在Rt△BOC中,OB2=OC2+BC2=a2+()2,∵OB2﹣AB2=12,∴a2+()2﹣(a﹣)2=12,整理得,2k=12,解得k=6.故答案为:6.32.如图,正比例函数y=x与反比例函数y=的图象相交于A,C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为2.【解答】解:根据反比例函数的对称性可知:OB=OD,AB=CD,∵四边形ABCD的面积等于S△ADB +S△BDC,∵A(1,1),B(1,0),C(﹣1,﹣1),D(﹣1,0)∴S△ADB=(DO+OB)×AB=×2×1=1,S△BDC=(DO+OB)×DC=×2×1=1,∴四边形ABCD的面积=2.故答案为:2.三.解答题(共8小题)33.如图1,在平面直角坐标系中,四边形AOBC是矩形,点C的坐标为(4,3),反比例函数y=(k>0)的图象与矩形AOBC的边AC、BC分别相交于点E、F,将△CEF沿EF对折后,C点恰好落在OB上.(1)求证:△AOE与△BOF的面积相等;(2)求反比例函数的解析式;(3)如图2,P点坐标为(2,﹣3),在反比例函数y=的图象上是否存在点M、N(M在N的左侧),使得以O、P、M、N为顶点的四边形是平行四边形?若存在,求出点M、N的坐标;若不存在,请说明理由.【解答】解:(1)∵点E、F均是反比例函数y=上的点,四边形AOBC是矩形,∴AE⊥y轴,BC⊥x轴,∴S△AOE =S△BOF=;(2)∵C坐标为(4,3),∴设E(,3),F(4,),如图1,将△CEF沿EF对折后,C点恰好落在OB边上的G点,作EH⊥OB,垂足为H,∵∠EGH+∠HEG=90°∠EGH+∠FGB=90°,∴∠HEG=∠FGB,又∵∠EHG=∠GBF=90°,∴△EGH∽△GFB,∴=,∴GB==,在Rt△GBF中,GF2=GB2+BF2,即(3﹣)2=()2+()2,解得k=,∴反比例函数的解析式为:y=;(3)存在.当OP是平行四边形的边时,如图2所示:平行四边形OPMN,可以看成线段PN沿PO的方向平移至OM处所得.设N(a,),∵P(2,﹣3)的对应点O(0,0),∴M(a﹣2,+3),代入反比例解析式得:(a﹣2)(+3)=,整理得4a2﹣8a﹣7=0,解得a=,当a=时,==,﹣2=,+3=,∴N(,),M(,)(舍去)或N(,),M(,).当OP为对角线时,如图3所示:设M(a,),N(b,),∵P(2,﹣3),∴,解得,,∴M(,),N(,)(舍去)或M(,),N(,),综上所述:M(,)N(,);或M(,),N(,).34.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(4,2),M、N分别是AB、BC的中点.(1)若反比例函数y=(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N 是否在该函数的图象上;(2)若反比例函数y=(x>0)的图象与△MNB(包括边界)有公共点,请直接写出m的取值范围.【解答】解:(1)∵顶点B的坐标为(4,2),M、N分别是AB、BC的中点,∴M点的坐标为(2,2),把M(2,2)代入反比例函数y=(m≠0)得,m=2×2=4,∴反比例函数的解析式为y=;∵M、N分别为矩形OABC的边AB、BC的中点,且M(2,2),B点坐标为(4,2),∴N点坐标为(4,1),∵4×1=4,∴点N在函数y=的图象上;(2)4≤m≤8.35.如图,反比例函数y=﹣与一次函数y=﹣x+2的图象交于A、B两点.(1)求A、B两点的坐标;(2)观察图象,直接写出x为何值时,一次函数值大于反比例函数?(3)求△AOB的面积.【解答】解:(1)联立两函数解析式得:,解得:或,即A(﹣2,4),B(4,﹣2);(2)根据图象得:当x<﹣2或0<x<4时,一次函数值大于反比例函数值.(3)令y=﹣x+2中x=0,得到y=2,即D(0,2),∴OD=2,∴S△AOB =S△AOC+S△BOC=×2×2+×2×4=6.36.如图,反比例函数y1=的图象与一次函数y2=kx+b的图象交于A(m,3),B(﹣3,n)、两点.(1)求一次函数的解析式及△AOB的面积;(2)根据图象直接写出不等式的解集;(3)若点P是坐标轴上的一点,且满足△PAB面积等于△AOB的面积的2倍,直接写出点P的坐标.【解答】解:(1)∵反比例函数y1=的图象与一次函数y2=kx+b的图象交于A(m,3),B(﹣3,n)、两点,将A与B坐标代入反比例解析式得:m=1,n=﹣1,∴A(1,3)、B(﹣3,﹣1),代入一次函数解析式得:,解得:k=1,b=2,∴一次函数的解析式为y=x+2,∵直线y=x+2与x轴、y轴的交点坐标为(﹣2,0)、(0,2),∴S△AOB=×2×(1+3)=4;(2)∵A(1,3),B(﹣3,﹣1),观察图象可知,当x<﹣3或0<x<1时,一次函数的图象在反比例函数图象的下方,∴不等式的解集是x<﹣3或0<x<1.(3)∵S△AOB=4,∴S△PAB =2S△AOB=8,设P1(p,0),即OP1=|p+2|,S△ABP1=S△AP1C+S△P1BC=|p+2|×3+|p+2|×1=8,解得:p=﹣6或p=2,则P1(﹣6,0)、P2(2,0),同理可得P3(0,6)、P4(0,﹣2).37.如图,若直线y=kx+b(k≠0)与x轴交于点,与双曲线在第二象限交于点B,且OA=OB,△OAB的面积为(1)求直线AB的解析式及双曲线的解析式;(2)求tan∠ABO的值.【解答】解:(1)∵直线y=kx+b(k≠0)与x轴交于点A,∴OA=,又∵OA=OB,∴OB=,过点B作BM⊥x轴于点M,∵△OAB的面积为,即OA•BM=,∴BM=2,在Rt△OBM中可求OM=1.5,∴B(﹣1.5,2),再根据待定系数法可得:,解得:k=﹣,b=,∴直线AB的解析式为:y=﹣x+;再将点B代入函数y=得:m=﹣3,∴双曲线的解析式为:y=﹣;(2)∵OA=OB,∴∠ABO=∠BAM,在Rt△ABM中,BM=2,∴MO=,AM=+=4,∴tan∠ABO=tan∠BAM==.38.已知反比例函数y=和一次函数y=2x﹣1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点.(1)求反比例函数的解析式?(2)已知A在第一象限,是两个函数的交点,求A点坐标?(3)利用②的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?【解答】解:(1)∵一次函数y=2x﹣1的图象经过(a,b),(a+k,b+k+2)两点,代入得:,解得:k=2,代入反比例函数的解析式得:y==,∴反比例函数的解析式是y=.(2)解方程组得:,,∴两函数的交点坐标是(﹣,﹣2),(1,1),∵交点A在第一象限,∴A(1,1).(3)在x轴上存在点P,使△AOP为等腰三角形,理由是:分为三种情况:①以O为圆心,以OA为半径作圆,交x轴于两点C、D,此时OA=0C=0D,∴当P于C或D重合时,△AOP是等腰三角形,此时P的坐标是(,0),(﹣,0);②以A为圆心,以OA为半径作圆,交x轴于点E,此时OA=AE,∴当P于E重合时,△AOP是等腰三角形,此时P的坐标是(2,0);③作OA的垂直平分线交x轴于F,此时AF=OF,∴当P于F重合时,△AOP是等腰三角形,此时P的坐标是(1,0);∴存在4个点P,使△AOP是等腰三角形.39.如图,双曲线y=在第一象限的一支上有一点C(1,5),过点C的直线y=﹣kx+b(k>0)与x 轴交于点A(a,0).(1)求点A的横坐标a与k的函数关系式(不写自变量取值范围).(2)当该直线与双曲线在第一象限的另一个交点D的横坐标是9时,求△COA的面积.【解答】解:(1)把C(1,5)代入直线y=﹣kx+b(k>0)得:﹣k+b=5,则b=5+k;把(a,0)代入直线y=﹣kx+b(k>0)得:﹣ak+b=0,把b=5+k代入﹣ak+b=0,得:﹣ak+5+k=0,解得:a=;(2)把x=9代入y=得:y=,则D的坐标是(9,),设直线AC的解析式是y=﹣kx+b,把C、D两点代入,得,解得:,则AC的解析式是:y=﹣x+.令y=0,解得:x=10.则OA=10,则△COA的面积=×10×5=25.40.如图,一次函数y=ax+b的图象与反比例函数的图象交于M、N两点.(1)利用图中条件,求反比例函数和一次函数的解析式;(2)连接OM、ON,求三角形OMN的面积.(3)连接OM,在x轴的正半轴上是否存在点Q,使△MOQ是等腰三角形,若存在,请直接写出所有符合条件的点Q的坐标,若不存在,说明理由.【解答】解:(1)把N(﹣1,﹣4)代入y=得:k=4,∴y=,把M(2,m)代入得:m=2,∴M(2,2),把N(﹣1,﹣4),M(2,2)代入y=ax+b得:,解得:a=2,b=﹣2,∴y=2x﹣2,答:反比例函数的解析式是y=,一次函数的解析式是y=2x﹣2.(2)设MN交x轴于C,y=2x﹣2,当y=0时,x=1,∴C(1,0),OC=1,∴△MON的面积是S=S△MOC +S△NOC=×1×2+×1×|﹣4|=3,答:三角形MON的面积是3.(3)当OM=OQ时,Q的坐标是(2,0);当OM=MQ时,Q的坐标是(4,0);当OQ=QM时,Q的坐标是(2,0);答:在x轴的正半轴上存在点Q,使△MOQ是等腰三角形,所有符合条件的点Q的坐标是(2,0)或(4,0)或(2,0).第31页(共31页)。
关于反比例函数的基础练习题

关于反比例函数的基础练习题1. 题目:设 y 是 x 的反比例函数,已知 y = 4 当 x = 2,则当 x = 5 时,y 的值是多少?解答:反比例函数的定义为 y = k/x,其中 k 是常数。
根据已知条件,代入 x = 2 和 y = 4,可以得出 k = 8。
现在需要找出当 x = 5 时 y 的值。
将 x = 5 和 k = 8 代入反比例函数公式,计算得 y = 8/5 = 1.6。
答案:当 x = 5 时,y 的值为 1.6。
2. 题目:设 y 是 x 的反比例函数,已知 y = 6 当 x = 3,则当 x = 4 时,y 的值是多少?解答:根据已知条件,代入 x = 3 和 y = 6,可以得出 k = 18。
现在需要找出当 x = 4 时 y 的值。
将 x = 4 和 k = 18 代入反比例函数公式,计算得 y = 18/4 = 4.5。
答案:当 x = 4 时,y 的值为 4.5。
3. 题目:已知 y 是 x 的反比例函数,当 x = 2 时,y = 10,求 x = 5 时 y 的值。
解答:根据已知条件,代入 x = 2 和 y = 10,可以得出 k = 20。
现在需要找出当 x = 5 时 y 的值。
将 x = 5 和 k = 20 代入反比例函数公式,计算得 y = 20/5 = 4。
答案:当 x = 5 时,y 的值为 4。
4. 题目:已知 y 是 x 的反比例函数,当 x = 6 时,y = 2,求 x = 9 时 y 的值。
解答:根据已知条件,代入 x = 6 和 y = 2,可以得出 k = 12。
现在需要找出当 x = 9 时 y 的值。
将 x = 9 和 k = 12 代入反比例函数公式,计算得 y = 12/9 = 4/3。
答案:当 x = 9 时,y 的值为 4/3。
反比例函数练习题及答案6套文库.doc

反比例函数练习(1)一、判断题1.当尤与y乘积一定时,v就是尤的反比例函数,尤也是),的反比例函数()2.如果一个函数不是正比回函数,就是反比例函数()3.),与疽成反比例时v与]并不成反比例()%1.填空题4.己知三角形的面积是定值S,则三角形的高与底。
的函数关系式是力=这时h是a的;5.如果),与尤成反比例,z与y成正比例,则z与尤成;6.如果函数y = kx2k2+k~2是反比例函数,那么如,此函数的解析式是—7.有一面积为60的梯形,其上底长是下底长的L,若下底长为x,高为y,则y 3与X的函数关系是三、选择题:8.如果函数y = r妇为反比例函数,则m的值是()A -1B 0 cl D 129.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。
在课堂上,李老师请学生画出自行车行进路程s千米与行进时间t的函数图像的示意图,同学们画出的示意图如下,你认为正确的是()10、下列函数中,y是x反比例函数的是()2 1(A))=M1 (B) y=—(C) y = —(D)2y=x•< 5x%1.辨析题(1)兄弟二人分吃一碗饺子,每人吃饺子的个数如下表:兄(y)29282726. . ♦ . .♦321 -……一逐渐凋沙弟(X)1234272829... —逐渐增多②这是一个反比例函数吗?③与(1)的结论相比,可见并非反比例函数有可能“函数值随自变量增大而减小”,反之,所有的反比例函数都是“函数值随自变量的增大而减小吗?这个问题,你可以提前探索、尝试,也可以预习下一课时”反比例函数的图象和性质,也可以等到下一节课我们共同解决.② 出兄吃饺子数y与弟吃饺子数x之间的函数关系式(不要求写X),的取值范围)②虽然当弟吃的饺子个数增多时,兄吃的饺子数()「)在减少,但y与尤是成反例吗?(2)水池中有水若干吨,若单开一个出水口,水流速v与全池水放光所用时t如下表:①写出放光池中水用时t(小时)与放水速度V(吨/小时)之间的函数关系.%1.已知y是邪勺反比例函数,当户2时,y=6.⑴写出),与尤的函数关系式;⑵求当x=4时y的值.%1.已知口48CD中,AB = 4, AD = 2, E是AB边上的一动点,设AE=X, DE延长线交CB的延长线于F,设CF = y,求)',与尤之间的函数关系。
反比例函数经典习题及标准答案

反比例函数练习题一、精心选一选!(30分)1.下列 函数中,图象经过点(11)-,的反比例函数解析式是( ) A .1y x=B .1y x-=C .2y x=D .2y x-=2. 反 比例函数2k y x=-(k 为常数,0k ≠)的图象位于( )A.第一、二象限 B.第一、三象限 C.第二、四角限 D.第三、四象限3.已知 反比例函数y =x2k -的图象位于第一、第三象限,则k 的取值范围是( ). (A )k >2 (B ) k ≥2 (C )k ≤2 (D ) k <24.反 比例函数xky =的图象如图所示,点M 是该函数图象上一点,MN 垂直于x 轴,垂足是点N ,如果S △MON =2,则k 的值为( ) (A)2 (B)-2 (C)4 (D)-4 5.对于反比 例函数2y x=,下列说法不正确...的是( ) A .点(21)--,在它的图象上B .它的图象在第一、三象限C .当0x >时,y 随x 的增大而增大D .当0x <时,y 随x 的增大而减小6.反比 例函数22)12(--=m xm y ,当x >0时,y 随x 的增大而增大,则m 的值时( )A 、±1B 、小于21的实数 C 、-1 D 、1 7.如 图,P 1、P 2、P 3是双曲线上的三点,过这三点分别作y 轴的垂线,得到三个三角形P 1A 1O 、P 2A 2O 、P 3A 3O ,设它们的面积分别是S 1、S 2、S 3,则( )。
A 、S 1<S 2<S 3B 、S 2<S 1<S 3C 、S 3<S 1<S 2D 、S 1=S 2=S 38.在同 一直角坐标系中,函数xy 2-=与x y 2=图象的交点个数为( ) A .3 B .2 C .1 D .0 9.已知 甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )10.如图,直线y=mx 与双曲线y=xk交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM,若ABM S ∆=2,则k 的值是( )A .2B 、m-2C 、mD 、4 OA 1 A 2 A 3 P 1 P 2 P 3xy11.在反比例函数xky =(k <0)的图象上有两点A (x 1,y 1),B (x 2,y 2),且1x >2x >0,则12y y -的值为( ) (A)正数 (B)负数 (C)非正数 (D)非负数 二、细心填一填!(30分)11.写出一个图象在第一、三象限的反比例函数的解析式 . 12.已知反比例函数8y x=-的图象经过点P (a+1,4),则a=_____. 13.反比例函数6y x=-图象上一个点的坐标是 . 14.一个函数具有下列性质:①它的图像经过点(-1,1);②它的图像在二、四象限内; ③在每个象限内,函数值y 随自变量x 的增大而增大.则这个函数的解析式可以为 .15.已知反比例函数的图象经过点(m ,2)和(-2,3)则m 的值为 .15.3-; 16.在ABC △的三个顶点(23)(45)(32)A B C ----,,,,,中,可能在反比例函数(0)ky k x=>的图象上的点是 . 17.在对物体做功一定的情况下,力F (牛)与此物体在力的方向上移动的距离s (米)成反比例函数关系,其图象如图所示,P (5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是 米. 18.已知点P 在函数2y x=(x >0)的图象上,PA⊥x 轴、PB⊥y 轴,垂足分别为A 、B ,则矩形OAPB 的面积为__________. 19.已知直线mx y =与双曲线xky =的一个交点A 的坐标为(-1,-2).则m =_____;k =____;它们的另一个交点坐标是______.20.如图,过原点的直线l 与反比例函数1y x=-的图象交于M ,N 两点,根据图象猜想线段MN 的长的最小值是___________. 三、用心解一解!(60分)21.在平面直角坐标系xOy 中,直线y x =-绕点O 顺时针旋转90得到直线l .直线l 与反比例函数ky x=的图象的一个交点为(3)A a ,,试确定反比例函数的解析式.(5分) 22.如图,点A 是反比例函数图象上的一点,自点A 向y 轴作垂线,垂足为T ,已知S △AOT=4,求此函数的表达式. (5分)23.已知点P (2,2)在反比例函数xky =(0≠k )的图象上, (Ⅰ)当3-=x 时,求y 的值;(Ⅱ)当31<<x 时,求y 的取值范围.(7分) 24.如图,已知双曲线ky x =(0x >)经过矩形OABC 的边AB BC ,的中点F E ,,且四边形OEBF 的面积为2,求k 的值.(7分)25.若一次函数y =2x -1和反比例函数y =2kx的图象都经过点(1,1).(1)求反比例函数的解析式;yFB ECOyMNl(2)已知点A 在第三象限,且同时在两个函数的图象上,求点A 的坐标;(8分) 26.已知点A (2,6)、B (3,4)在某个反比例函数的图象上. (1)求此反比例函数的解析式;(2)若直线mx y =与线段AB 相交,求m 的取值范围. (8分) 27.如图正方形OABC 的面积为4,点O 为坐标原点,点B 在函数ky x=(0,0)k x << 的图象上,点P(m ,n)是函数ky x=(0,0)k x <<的图象上异于B 的任意一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F . (1)设矩形OEPF 的面积为S l ,判断S l 与点P 的位置是否有关(不必说理由).(2)从矩形OEPF 的面积中减去其与正方形OABC 重合的面积,剩余面积记为S 2,写出S 2与m 的函数关系,并标明m 的取值范围.(8分)参考答案:一、1.B 2.C 3.A 4.D 5.C 6.C 7.D 8.D 9.C 10.A ;三、21.解:依题意得,直线l 的解析式为y x =.因为(3)A a ,在直线y x =上,则3a =. 即(33)A ,.又因为(33)A ,在k y x =的图象上,可求得9k =.所以反比例函数的解析式为9y x=. 22.解:设所求反比例函数的表达式为x ky =,因为S △AOT =k 21,所以k 21=4,即8±=k ,又因为图象在第二、四象限,因此8-=k ,故此函数的表达式为8y x =-;又反比例函数x y 4=在0>x 时y 值随x 值的增大而减小, ∴当31<<x 时,y 的取值范围为434<<y . 24.设B 点的坐标为(2a ,2b ),则E 点的坐标为(a ,2b ),F 点的坐标为(2a ,b ),所以k =2ab .因为4ab -21×2ab ×2=2,所以2ab =2. 25.(1) ∵反比例函数y =2k x 的图象经过点(1,1),∴1=2k解得k=2, ∴反比例函数的解析式为y=1x.∵点A 在第三象限,且同时在两个函数图象上, ∴A(12-,–2).26.解:(1)设所求的反比例函数为x k y =,依题意得: 6 =2k ,∴k=12. ∴反比例函数为xy 12=. AB CO y x(2) 设P (x ,y )是线段AB 上任一点,则有2≤x≤3,4≤y ≤6.∵m =xy, ∴34≤m ≤26.所以m 的取值范围是34≤m ≤3. 27.(1) 没有关系;(2) 当P 在B 点上方时,242(20)S m m =+-<<;当P 在B 点下方时,284(2)S m m=+<-。
反比例函数练习题及答案

反比例函数练习题及答案反比例函数练题一、填空题(每空3分,共42分)1.已知反比例函数 $y=\frac{k}{x}$,则 $k$ 的值是 $\pm6$,图象在第三象限,当 $x>0$ 时,$y$ 随 $x$ 的增大而减小。
2.已知变量 $y$ 与 $x$ 成反比,当 $x=1$ 时,$y=-6$,则当 $y=3$ 时,$x=-2$。
3.若反比例函数 $y=(2m-1)x$,则函数的解析式为$y=\frac{(2m-1)}{x}$。
4.已知反比例函数 $y=\frac{m^2-2}{(3m-2)x-k^2-21}$ 的图象在第一、三象限,则函数的解析式为 $y=\frac{m^2-2}{(3m-2)x-k^2-21}$。
5.在函数$y=\frac{k}{x^2}$ 的图象上有三个点$(-2,y_1)$,$(-1,y_2)$,$(1,y_3)$,函数值 $y_1$,$y_2$,$y_3$ 的大小为 $\frac{k}{4}$,$k$,$k$。
6.已知 $P_1(x_1,y_1)$,$P_2(x_2,y_2)$ 是反比例函数$y=\frac{k}{x}$($k\neq 0$)图象上的两点,且 $x_1y_2$,则 $k=\frac{x_1x_2(y_1-y_2)}{x_2-x_1}$。
7.已知正比例函数 $y=kx$($k\neq 0$),$y$ 随 $x$ 的增大而增大,那么反比例函数 $y=\frac{k}{x}$,当 $x<0$ 时,$y$ 随 $x$ 的增大而减小。
8.已知 $y_1$ 与 $x$ 成正比例(比例系数为 $k_1$),$y_2$ 与 $x$ 成反比例(比例系数为 $k_2$),若函数$y=y_1+y_2$ 的图象经过点 $(1,2)$,$(2,\frac{1}{k_2})$,则$8k_1+5k_2=0$。
9.若 $m<-1$,则下列函数:① $y=m\sqrt{x}$;② $y=-mx+1$;③ $y=mx$;④ $y=(m+1)x$ 中,$y$ 随 $x$ 增大而增大的是 $y=-mx+1$。
反比例函数练习题及答案全套

一、判断题1.当x 与y 乘积一定时,y 就是x 的反比例函数,x 也是y 的反比例函数( ) 2.假如一个函数不是正比例函数,就是反比例函数 ( )3.y 与2x 成反比例时y 与x 并不成反比例( ) 二.填空题4.已知三角形的面积是定值S ,则三角形的高h 与底a 的函数关系式是h =__________,这时h 是a 的__________;5.假如y 与x 成反比例,z 与y 成正比例,则z 与x 成____ ___;6.假如函数222-+=k k kxy 是反比例函数,那么k =________,此函数的解析式是____ ____; 7. 有一面积为60的梯形,其上底长是下底长的31,若下底长为x ,高为y ,则y 与x 的函数关系是______________ 三、选择题: 8.假如函数12-=m x y 为反比例函数,则m 的值是 ( )A 1-B 0 C21D 1 9.李老师骑自行车上班,最初以某一速度匀速行进,中途因为自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。
在课堂上,李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图,同学们画出的示意图如下,你认为准确的是( )10、以下函数中,y 是x 反比例函数的是( ) (A ) 12+=x y (B )22xy =(C )x y 51=(D )x y =2 四.辨析题(1)兄弟二人分吃一碗饺子,每人吃饺子的个数如下表:①写出兄吃饺子数y 与弟吃饺子数x 之间的函数关系式(不要求写xy 的取值范围). ②虽然当弟吃的饺子个数增多时,兄吃的饺子数(y )在减少,但y 与x 是成反例吗?(2)水池中有水若干吨,若单开一个出水口,水流速v 与全池水放光所用时t 如下表:①写出放光池中水用时t(小时)与放水速度v(吨/小时)之间的函数关系. ②这是一个反比例函数吗?③与(1)的结论相比,可见并非反比例函数有可能“函数值随自变量增大而减小”,反之,所有的反比例函数都是“函数值随自变量的增大而减小吗?这个问题,你能够提前探索、尝试,也能够预习下一课时”反比例函数的图象和性质,也能够等到下一节课我们共同解决.五.已知□ABCD 中,AB = 4,AD = 2,E 是AB 边上的一动点,设AE=x ,DE 延长线交CB 的延长线于F ,设CF =y ,求y 与x 之间的函数关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数练习题
一、精心选一选!
1.下列 函数中,图象经过点(1,-1)的反比例函数解析式是( ) A.1y x
=
B.1y x
-=
C.2y x
=
D.2y x
-=
2.反 比例函数2
k y x
=-(k 为常数,0k ≠)的图象位于( )
A.第一、二象限
B.第一、三象限
C.第二、四角限
D.第三、四象限
3.已知反比例函数x
k y 2
-=
的图象位于第一、第三象限,则k 的取值范围是( ). A.k >2 B. k ≥2 C.k ≤2 D. k <2 4.反 比例函数x
k
y =
的图象如图所示,点M 是该函数图象上一点,MN 垂直于x 轴,垂足是点N ,如果S △MON =2,则k 的值为( ).
A.2
B. -2
C.4
D. -4 5.对于反比 例函数x
y 2
=,下列说法不正确...的是( ). A.点(-2,-1)在它的图象上
B.它的图象在第一、三象限
C.当0x >时,y 随x 的增大而增大
D.当0x <时,y 随x 的增大而减小
6.反比 例函数2
2)12(--=m x
m y ,当x >0时,y 随x 的增大而增大,则m 的值时( ).
A.±1
B.小于
2
1
的实数 C.-1 D.1 7.如 图,P 1、P 2、P 3是双曲线上的三点,过这三点分别作y 轴的垂线,得到三个三角形P 1A 1O 、P 2A 2O 、P 3A 3O ,设它们的面积分别是S 1、S 2、S 3,则( ).
A .S 1<S 2<S 3
B .S 2<S 1<S 3
C .S 3<S 1<S 2
D .S 1=S 2=S 3
8.在同一直角坐标系中,函数x
y 2
-
=与x y 2=图象的交点个数为( D ). A.3 B.2 C.1 D .0
9.已知 甲、乙两地相距s (km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h)的函数关系图象大致是( ).
10.如图,直线mx y =与双曲线x
k
y =交于A 、B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM,若ABM S ∆=2,则k 的值是( ). A .2 B 、m-2 C 、m
D 、4
二、细心填一填!
O
A 1 A 2 A 3 P 1 P 2 P 3
x
y
11.写出一个图象在第一、三象限的反比例函数的解析式 . 12.已知反比例函数8
y x
=-的图象经过点P (a+1,4),则a=_____. 13.反比例函数6
y x
=-
图象上一个点的坐标是 . 14.一个函数具有下列性质:①它的图像经过点(-1,1);②它的图像在二、四象限内; ③在每个象限内,函数值y 随自变量x 的增大而增大.则这个函数的解析式可以为 .
15.已知反比例函数的图象经过点(m ,2)和(-2,3)则m 的值为 .15.3-; 16.在ABC △的三个顶点(23)(45)(32)A B C ----,,,,,中,可能在反比例函数
(0)k
y k x
=
>的图象上的点是 .
17.在对物体做功一定的情况下,力F (牛)与此物体在力的方向上移动的距离s (米)成反比例函
数关系,其图象如图所示,P (5,1)在图象上,则当力达到10牛时,物体在力的方向上移动的距离是 米.
18.已知点P 在函数2
y x
=
(x >0)的图象上,PA ⊥x 轴、PB ⊥y 轴,垂足分别为A 、B ,则矩形OAPB 的面积为__________. 19.已知直线mx y =与双曲线x
k
y =的一个交点A 的坐标为(-1,-2).则m =_____;k =____;
它们的另一个交点坐标是______. 三、用心解一解!
21.在平面直角坐标系xOy 中,直线y x =-绕点O 顺时针旋转90得到直线l .直线l 与反比例函数k
y x
=的图象的一个交点为(3)A a ,,试确定反比例函数的解析式.
24.如图,已知双曲线k
y x
=(X >0)经过矩形OABC 的边AB,BC 的中点F,E,且四边形OEBF 的面积为2,求k 的值.
参考答案:一、1.B 2.C 3.A 4.D 5.C 6.C 7.D 8.D 9.C 10.A ;
三、21.解:依题意
得,直线l 的解析式为y x =.因为(3)A a ,在直线y x =上,则3a =. 即(33)A ,.又因为(33)A ,在
k y x =
的图象上,可求得9k =.所以反比例函数的解析式为9
y x
=. y x
O
F
A
B E
C
22.解:设所求反比例函数的表达式为x k
y =
,因为S △AOT =k 21,所以k 2
1=4,即8±=k ,又因为图象在第二、四象限,因此8-=k ,故此函数的表达式为8
y x
=-;
又反比例函数x y 4=
在0>x 时y 值随x 值的增大而减小, ∴当31<<x 时,y 的取值范围为43
4
<<y . 24.设B 点的坐标为(2a ,2b ),则E 点的坐标为(a ,2b ),F 点的坐标为(2a ,b ),所以k =2ab .因为4ab -2
1
×2ab ×2=2,所以2ab =2. 25.(1) ∵反比例函数y =
2k x 的图象经过点(1,1),∴1=2
k
解得k=2, ∴反比例函数的解析式为y=
1
x
.
∵点A 在第三象限,且同时在两个函数图象上, ∴A(1
2-,–2).
26.解:(1)设所求的反比例函数为x k y =
,依题意得: 6 =2
k
,∴k=12. ∴反比例函数为x y 12=.
(2) 设P (x ,y )是线段AB 上任一点,则有2≤x ≤3,4≤y ≤6.∵m =x y , ∴34≤m ≤2
6
.
所以m 的取值范围是3
4
≤m ≤3.
27.(1) 没有关系;(2) 当P 在B 点上方时,242(20)S m m =+-<<;当P 在B 点下方时,28
4(2)S m m
=+<-。
