人教版八年级数学下册期末复习压轴题练习(1)

合集下载

专题01 二次根式选填题压轴训练(解析版)八年级数学下学期期末考试压轴题专练(人教版,尖子生专用)

专题01 二次根式选填题压轴训练（时间：60分钟总分：120）班级姓名得分选择题解题策略：（1）注意审题。

把题目多读几遍，弄清这道题目求什么，已知什么，求、知之间有什么关系，把题目搞清楚了再动手答题。

（2）答题顺序不一定按题号进行。

可先从自己熟悉的题目答起，从有把握的题目入手，使自己尽快进入到解题状态，产生解题的激情和欲望，再解答陌生或不太熟悉的题目。

若有时间，再去拼那些把握不大或无从下手的题目。

这样也许能超水平发挥。

（3）数学选择题大约有70%的题目都是直接法，要注意对符号、概念、公式、定理及性质等的理解和使用，例如函数的性质、数列的性质就是常见题目。

（4）挖掘隐含条件，注意易错、易混点。

（5）方法多样，不择手段。

中考试题凸显能力，小题要小做，注意巧解，善于使用数形结合、特值（含特殊值、特殊位置、特殊图形）、排除、验证、转化、分析、估算、极限等方法，一旦思路清晰，就迅速作答。

不要在一两道小题上纠缠，杜绝小题大做，如果确实没有思路，也要坚定信心，“题可以不会，但是要做对”，即使是“蒙”，也有25%的正确率。

（6）控制时间。

一般不要超过40分钟，最好是25分钟左右完成选择题，争取又快又准，为后面的解答题留下充裕的时间，防止“超时失分”。

填空题解题策略：由于填空题和选择题有相似之处，所以有些解题策略是可以共用的，在此不再多讲，只针对不同的特征给几条建议：一是填空题绝大多数是计算型（尤其是推理计算型）和概念（或性质）判断性的试题，应答时必须按规则进行切实的计算或合乎逻辑的推演和判断；二是作答的结果必须是数值准确，形式规范，例如集合形式的表示、函数表达式的完整等，结果稍有毛病便是零分；三是《考试说明》中对解答填空题提出的要求是“正确、合理、迅速”，因此，解答的基本策略是：快——运算要快，力戒小题大做；稳——变形要稳，防止操之过急；全——答案要全，避免对而不全；活——解题要活，不要生搬硬套；细——审题要细，不能粗心大意。

【勾股定理期末压轴题训练】2022-2023学年八年级数学下册(人教版)含解析

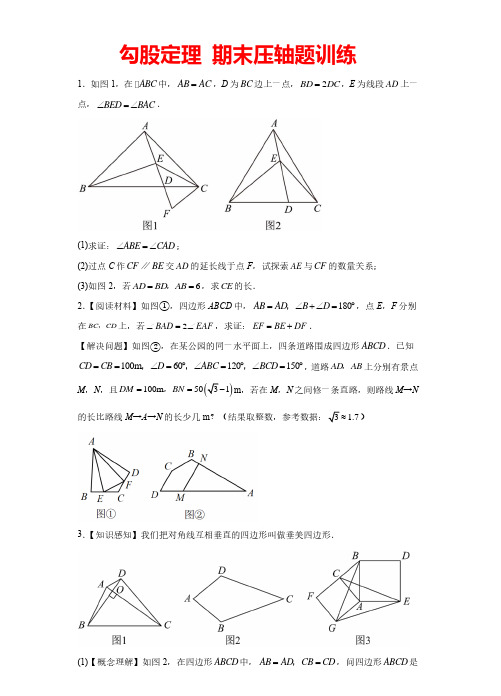
，在ABC 中，BAC ∠(1)求证：ABE CAD ∠=∠；(2)过点C 作CF BE ∥交AD 的延长线于点F ，试探索AE 与CF (3)如图2，若6AD BD AB ==，，求CE 的长．2．【阅读材料】如图①，四边形ABCD 中，AB AD B =∠+∠，3．【知识感知】我们把对角线互相垂直的四边形叫做垂美四边形．Rt ACB的直角边，，，BG GE，在ABC中，在整个运动过程中，当BCP是等腰三角形时，求，在平面直角坐标系中，点AQ CP交于点M，则在P、Q运动的过程中，(1)如图1，连接,（填“会”或“不会”）；(2)如图1，当PBQ是直角三角形时，求点P的坐标；在ABC中，．在等腰直角ABC中，，延长BC∠=∠；(1)求证：MQB PAC(2)若22，，求DQ DH==(3)用等式表示线段MB与CP．在ABC中，(2)如图2，若点D在线段AB上，取．在ABC 中，(1)如图1，当ABC 为锐角三角形时，①依题意补全图形，猜想BAE ∠与BCD ∠之间的数量关系并证明；②用等式表示线段AE ，CE ，DE 的数量关系，并证明．(2)如图2，当ABC ∠为钝角时，直接写出线段问题解决：(1)先考虑特殊情况：①如果点E刚好和点A重合，或者点B刚好和点F重合时，AE “>”，“<”或“=”）；形ABC和△⊥BC AD正方形的三个顶点，可得ABC ，则，在ABC 中，是BC ．如图，ABC 是等腰直角三角形，上一点．时，求DEF 的面．和CDE 中，AC 上，连接(1)如图1，若30EDC ∠=︒，6EF =，求AEF △的面积；(2)如图2，若BD AE =，求AF 、AE 、BC 之间的数量关系；(3)如图3，移动点D ，使得点F 是线段AB 的中点时，3DB =，4AB =别是线段AC ，BC 上的动点，且AP CQ =，连接DP ，FQ ，求DP FQ +(1)如图1，若45CBD ∠=︒①求BCG ∠的度数；②求证：CE DG =；(2)如图2，若60CBD ∠=︒，当6AC DE −=时，求CE 的值(2)如图2，ABC ∆中，2B C ∠=∠，线段AC 的垂直平分线交AC 于点E ，交BC 于点D ．求证：AD 是ABC ∆的一条双腰分割线；(3)如图3，已知ABC ∆中，AD 是三角形ABC 的双腰分割线，且AB AD =．①若64B ∠=︒，求C ∠的度数；②若3AB =，5AC =，求BC 的长．参考答案：1．(1)见解析(2)AE CF =【分析】（1）利用三角形外角的性质以及角的和差定义解决问题即可．（2）如图1中，在AF 上截取AJ ，使得AJ BE =．证明SAS ABE CAJ ≌（），推出AE CJ =，再证明CF CJ =即可解决问题．（3）如图2中，过点B 作BK AD ⊥于K ，作CF BE ∥交AD 的延长线于F ，过点C 作CQ DF⊥于Q ．首先证明BE BD =， CD DF =，再证明EK DK =，DQ FQ =，2DK DQ =，2BK CQ =，AE DE CD CF ===，利用参数构建方程解决问题即可．【解析】（1）证明：∵BED ABE BAE BAC BAE CAD ∠=∠+∠∠=∠+∠，，又∵BED BAC ∠=∠，∴ABE BAE BAE CAD ∠+∠=∠+∠，∴ABE CAD ∠=∠．（2）解：结论：AE CF =．理由：如图1中，在AF 上截取AJ ，使得AJ BE =．∵BA AC ABE CAJ BE AJ =∠=∠=，，，∴SAS ABE CAJ ≌（），∴AE CJ AEB AJC =∠=∠，，∴BED CJF ∠=∠，∵BE CF ∥，∴BEJ F ∠=∠，∴CJF F ∠=∠，∴CJ CF =，∴AE CF =．（3）如图2中，过点B 作BK AD ⊥于K ，作CF BE ∥交AD 的延长线于F ，过点C 作CQ DF ⊥于Q ．设ABE CAD x CBE y ∠=∠=∠=，，∵AB AC DB DA ==，，∴DBA DAB ACB x y ∠=∠=∠=+，∴22BED ABE DAB x y BDE ACB CAD x y ∠=∠+∠=+∠=∠+∠=+，，∴BED BDE ∠=∠，∴BE BD =，∵AB CA ABE CAD =∠=∠，，∴AAS ABE CAD ≌（），∴AE CD BE AD ==，，∵CF BE ∥，∴F BED ∠=∠，∴F CDF ∠=∠，∴CD CF =，∵BE BD BK DE CD CF CQ DF =⊥=⊥，，，，∴EK KD DQ QF ==，，∵CQ BK ∥，∴:::1:2DQ DK CD BD CQ BK ===，∴可以假设2DQ m DK m ==，，∵222BD BE AD CD CF AE =====，∴48AE DE m AD BD m ====，，∴BK ==，∴CQ =，在Rt ABK △中，∵222AB AK BK=+，∴()()22266m =+，∴m， ∴DQ =，CQ ，5EQ m ==，∵90CQE ∠=︒，∴CE =．【点评】本题属于三角形综合题，考查了等腰三角形的判定和性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．2．阅读材料：见解析；解决问题：少370m【分析】阅读材料：延长CB 到点M ，使BM DF =，连接AM ，如图，利用已知条件可得D ABM ∠=∠，进而可证明ABM ADF ≅，可得,AM AF MAB DAF =∠=∠，再证明AEM AEF ≅，可得=ME EF ，进而可得结论；解决问题：如图，作辅助线，构建阅读材料的图形，先根据四边形的内角和定理证明90G ∠=︒ ，分别计算,,,CG DG AD AG 的长，由线段的和与差可得,AM AN 的长，最后由阅读材料的结论可得MN 的长，计算AM AN MN +−可得答案．【解析】阅读材料：证明：延长CB 到点M ，使BM DF =，连接AM ，如图，∵180ABC D ∠+∠=︒，180ABC ABM ∠+∠=︒，∴D ABM ∠=∠，∵,,AB AD ABM D BM DF =∠=∠=，∴ABM ADF ≅，∴,AM AF MAB DAF =∠=∠，∵2BAD EAF ∠∠=，∴BAE DAF BAE BAM EAM EAF ∠+∠=∠+∠=∠=∠，又∵,AM AF AE AE ==，∴AEM AEF ≅，∴=ME EF ，∴EF MB BE BE DF =+=+；解决问题：解：如图，延长DC AB ，交于点G ，连接CN CM ，，∵60120150D ABC BCD ∠=︒∠=︒∠=︒，，，∴3606012015030A ∠=︒−︒−︒−︒=︒，∴90G ∠=︒，∴2AD DG =，在Rt CGB △中，18015030BCG ∠=︒−︒=︒，∴1502BG BC CG ===，∴100DG CD CG =+=+∴2200150AD DG AG ==+==+∵100DM =，∴200100100AM AD DM =−=+=+∵)50501BG BN ==，，∴)150********AN AG BG BN =−−=+−=+GN BG BN =+= ∵60CD DM D =∠=︒，，∴DCM △ 是等边三角形，∴60DCM ∠=︒，∵GC GN ==∴CGN 是等腰直角三角形，∴45GCN ∠=︒，∴453015BCN ∠=︒−︒=︒， ∴11506015752MCN BCD ∠=︒−︒−︒=︒=∠，由【阅读材料】的结论得：)10050150MN DM BN =+=+=+∵()10015050200370AM AN MN +−=++=+≈（m ）． ∴路线M→N 的长比路线M→A→N 的长少370m ．【点评】此题主要考查了含30︒的直角三角形的性质，勾股定理，等腰直角三角形的判定与性质、等边三角形的判定与性质、全等三角形的判定和性质，二次根式的混合运算等知识与方法，解题的关键是作出所需要的辅助线，构造含30︒的直角三角形，再利用线段的和与差进行计算．3．(1)是，见解析(2)2222AD BC AB CD ++＝，见解析【分析】（1）根据垂直平分线的判定定理证明即可；（2）根据垂直的定义和勾股定理解答即可；（3）根据垂美四边形的性质、勾股定理、结合（2）的结论计算．【解析】（1）如图2，四边形ABCD 是垂美四边形．证明：连接AC BD 、交于点E ，∵AB AD =，∴点A 在线段BD 的垂直平分线上，∵CB CD =，∴点C 在线段BD 的垂直平分线上，∴直线AC 是线段BD 的垂直平分线，∴AC BD ⊥，即四边形ABCD 是垂美四边形；（2）猜想结论2222AD BC AB CD ++＝．如图1，已知四边形ABCD 中，∵AC BD ⊥，∴90AOD AOB BOC COD ∠=∠=∠=∠=︒，由勾股定理得，222222AD BC AO DO BO CO +=+++，222222AB CD AO BO DO CO +=+++，∴2222AD BC AB CD ++＝；（3）如图3，连接CG BE 、，∵90CAG BAE ∠=∠=︒，∴CAG BAC BAE BAC ∠+∠=∠+∠，即GAB CAE ∠∠＝，在GA B 和CAE V 中，AG AC GAB CAEAB AE =⎧⎪∠=∠⎨⎪=⎩， ∴()SAS GAB CAE V V ≌， ∴ABG AEC ∠=∠，又90AEC AME ∠+∠=︒，∴90ABG BMN ∠+∠=︒，∴90BNC ∠=︒，即CE BG ⊥，∴四边形CGEB 是垂美四边形，由（2）得，2222CG BE CB GE +=+，∵810AC AB ==，，∴6BC CG ==，BE =∴((22222226292GE CG BE CB =+−=+−=，∴GE ==【点评】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用，正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键．4．(1)4,4t − (2)52t = (3)1或535或9.5或10【分析】（1）利用勾股定理求出AC ，利用CP AC AP =−，求出CP ；（2）过点P 作PD AB ⊥，交AB 于点D ，利用勾股定理列式求解即可；（3）分,,BC CP BP CP BC BP ===，三种情况进行讨论求解即可．【解析】（1）解：∵90,5,3ACB AB BC ∠=︒==，∴4AC =；∵点P 从点A 出发，以每秒1个单位长度的速度沿路线A C B A →→→运动，∴当点P 在AC 上时，AP t =，∴4CP AC AP t =−=−；故答案为：4,4t −；（2）解：点P 作PD AB ⊥，交AB 于点D ，则：90PDA PDB ∠=∠=︒，∵点P 在ABC ∠的角平分线上，90ACB ∠=︒，∴90ACB PDB ∠=∠=︒，PD PC =，又∵BP BP =，∴()HL PBD PBC ≌，∴3BD BC ==，∴2AD AB BD =−=，由（1）知,4AP t CP t ==−，∴4PD PC t ==−，在Rt ADP 中，222AP PD AD =+，即：()22242t t =−+，解得：52t =；（3）解：P 点运动的总时间为：()543112++÷=秒，当BCP 是等腰三角形时： ①当BC CP =，点P 在AC 上时：如图，此时：43t −=，解得：1t =；当BC CP =，点P 在AB 上时：如图，过点C 作CE AB ⊥，交AB 于点E ，则：72BP t AC BC t BE =−−=−=， ∵1122ABC S AC BC AB CE =⋅=⋅，即：435CE ⨯=， ∴125CE =，∴95BE ==， ∴1875BP t =−=， ∴535t =； ②当BP CP =时，如图：由①可知：912,7,55BE BP t CE ==−=， ∴97,75PE t CP t =−−=−，在Rt PEC 中，222CP PE CE =+，即：()2224412755t t ⎛⎫⎛⎫−=−+ ⎪ ⎪⎝⎭⎝⎭，解得：9.5t =；③当BC BP =时，如图：此时：73BP t =−=，解得10t =；综上：当BCP 是等腰三角形时，t 的值为：1或535或9.5或10．【点评】本题考查三角形上的动点问题．熟练掌握勾股定理，以及等腰三角形的定义是解题的关键．注意，分类讨论．5．(1)不会(2)当PBQ 是直角三角形时，点P的坐标为43⎛ ⎝⎭或23⎛ ⎝⎭(3)(1,P −，120CMQ ∠=︒【分析】(1)先利用SAS 证明ABQ CAP ≌，得BAQ ACP ∠=∠，利用外角的性质并进行等量代换可得60CMQ ACP CAM BAQ CAM BAC ∠=∠+∠=∠+∠=∠=︒(2)分90,90PQB BPQ ︒∠=︒∠=两种情况，利用直角三角形中30度角所对直角边等于斜边的一半列式求解（3）作PM x ⊥轴，先根据30度角的性质和勾股定理求出1MB =cm和MP =cm ，进而求出(1,P −，再根据SAS 证明ACQ CBP ≌，最后根据外角的性质并进行等量代换作答即可【解析】（1）解：在等边三角形ABC 中,60AB AC CBA CAP ︒=∠=∠=且点A 、点Q 同时出发，且它们的速度都为1cm/s AP =BQ ∴(SAS)ABQ CAP ∴≌BAQ ACP ∴∠=∠60CMQ ACP CAM BAQ CAM BAC ∴∠=∠+∠=∠+∠=∠=︒故答案为：不会（2）解：设运动时间为t 秒，则,4AP BQ t PB t ===−①当90PQB ∠=︒时60ABC ∠=︒30BPQ ∠=︒∴12BQ PB ∴=，即1(4)2t t =− 解得43t = 即48433BP =−= 60ABC ∠=︒∴43P ⎛ ⎝⎭ ②当90BPQ ∠=︒时60ABC ∠=︒30PQB ∴∠=︒12PB BQ ∴=，即142t t −= 解得83t = 即84433BP =−=60ABC ∠=︒∴23P ⎛ ⎝⎭ ∴当PBQ 是直角三角形时，点P的坐标为43⎛ ⎝⎭或23⎛ ⎝⎭ （3）∵12BP BC =∴2BP =cm作PM x ⊥轴∵60ABC ∠=︒∴60PBM ∠=︒∴60PBM ∠=︒∴30MPB ∠=︒∴1MB =cm由勾股定理得MP =cm∴(1,P −在等边三角形ABC 中,60BC AC ABC ACB ︒=∠=∠=∵点A 、点Q 同时出发，且它们的速度都为1cm/sBP CQ ∴=，120PBC ACQ ∠=∠=︒(SAS)ACQ CBP ∴≌CMQ APM PAM APM PAC CAQ AQB PAC CAQ ∴∠=∠+∠=∠+∠+∠=∠+∠+∠180AQB PAC CAQ ABC ∠+∠+∠+∠=︒，60ABC ∠=︒18060120CMQ ∴∠=︒−︒=︒【点评】本题考查了全等三角形的判定和性质，外角的性质，直角三角形30度角的性质，勾股定理，熟练掌握各知识点是解题的关键．6．(1)见解析(2)(1）是，证明见解析；(2）存在，66013CP =.【分析】（1）根据阅读材料给出的定义结合已经学过的三角形的知识点，推到即可得出结论；（2）根据已知条件利用相似三角形即可得出①中的作法是符合条件的；第②小题根据已知条件画出图形，再根据图形得出结论．【解析】（1）解：①∵BD 为△ABC 的角平分线，∠ABC ＝2∠C∴∠=∠DBC C∴BD CD =∴图中相等的线段有BD CD =∵A A ∠=∠，2ADB ABC C ∠=∠=∠∴ADB ABC ∽∴图中相似的三角形有：ADB 和ABC②∵AC 的中垂线交边BC 于点E∴AE EC =∴AEC △是等腰三角形∵2AEB C ∠=∠，2ABC C ∠∠＝∴AB AE =∴ABE 是等腰三角形（2）解：①符合要求，延长EF 交AD 于N ，则四边形ABEN 为矩形∴48AB EN ==，1662AN BE EC BC ====∵33EF =∴483315NF EN EF =−=−=∵PN BC ∥∴PFN CFE ∽ ∴PN NF PF EC EF FC == ∴153366PN = ∴1553311PF FC == ∴663036AP AN PN =−=−=∵90A ∠=︒∴60BP = ∴60513211BP FC == ∴BP PF BC FC = 作FK BP ⊥于K ∴BPF BCF SPF S FC =∴1212FK BP PF FCEF BC ⋅=⋅∴FK EF =∵FK BP ⊥，FE BC ⊥ ∴BF 平分PBC ∠∴1FBE PBC 2∠=∠∵F 在BC 的垂直平分线上∴FB FC =∴FBC FCB ∠=∠∴2PBC PCB ∠=∠∴符合要求②存在， 66013CP =.I.若P 在AD 上时，连接BD ，如图所示，∴PBC DBC ∠>∠，PCB DCB ∠<∠取BD 的中垂线交BC 与G ，作DH BC ⊥于H∴四边形ABHD 为矩形∴48HD AB ==，68BH AD ==，DG GB =，1326864CH BC BH =−=−=，∴80DC =，设GH x =，则68BG DG x ==−∵90DHG ∠=︒∴由勾股定理222GH DH DG +=∴()2226848x x −=+∴22136684811620x =−=⨯ ∴2906417x =<在CH 上取点M ，使29017HM GH ==，连接DM∴DMB DCB PCB ∠>∠>∠∵DG BG =∴DBC GDB ∠=∠∴22DGC GDB DBC DBC PBC ∠=∠+∠=∠<∠∴HM GH =，DH MG ⊥∴DG DM =∴DMB DGC ∠=∠∴2PBC PCB ∠>∠∴在AD 上所有点都满足2PBC PCB ∠>∠∴不存在；II. 若P 在AB 上时，如图所示，∵BP AB BC <<，∴45BCP ∠<︒，∴2PBC BCP ∠≠∠，∴在AB 上不存在其它满足要求的△BCP ；III. 若P 在AB 上时，如图所示，作BC 的垂直平分线交AD 于点L 、交BC 于点R ，作BCD ∠的平分线交RL 于点O ，连结BO 并延长交DC 于点P ，此时有22BCD BCO PBC ∠=∠=∠， ∴△BCP 是以BC 为底边的倍角三角形，作OU DC ⊥于点U ，连结OA 、OD ，∵CO 平分BCD ∠，OR BC ⊥，OU DC ⊥，∴OR OU =，设OR x =，则OU x =，48OL x =−，由AOB BOC COD AOD ABCD S S S S S =+++梯形得11111(68132)4848661328068(48)22222x x x ⨯+⨯=⨯⨯+⨯+⨯+⨯⨯−，解得：22x =在Rt BOR 中，OB =∴OC OB ==∵OCP OCB PBC ∠=∠=∠，2POC PBC OCB PBC PCB ∠=∠+∠=∠=∠，∴PBC PCO ~，∴CP BP BC OP CP OC ==∴OP =，BP =，由BP OP OB −=得= 解得，66013CP =【点评】本题考查了角的倍数关系，角平分线的性质，相似三角形的判定等相关知识，明确题意根据已知条件画出图形是解题的关键．7．(1)45，=(2)(3)【分析】（1）根据等腰直角三角形的三线合一即可得到90,ADC AD CD BD ∠=︒==，由此推出,45BC BA AD D C ⊥∠=︒=∠，证明ADE CDF △△≌，得到,DE DF ADE CDF =∠=∠，求出DEF 是等腰直角三角形，勾股定理得到EF =DE ；（2）证明(SAS)ADE CDF ≌V V ，得到DE DF =，ADE CDF ∠=∠，推出DE DF ⊥，再由勾股定理得到答案；（3）分两种情况，①当H 在线段AC 上时，②当H 在线段AC 的延长线上时，连接MC ，过点M 作MF AC ⊥于F ，由等腰三角形的性质及等腰直角三角形的性质可得出答案．【解析】（1）解：在ABC 中，90BAC ∠=︒，AB AC =，45B BCA ∠=∠=︒，D 是BC 的中点，∴,45BC BA AD D C ⊥∠=︒=∠，∴90,ADC AD CD BD ∠=︒==，∵AE CF =，∴ADE CDF △△≌（SAS ），∴,DE DF ADE CDF =∠=∠，∵90CDF ADF ADC ∠+∠=∠=︒，∴90ADE ADF ∠+∠=︒，∴DEF 是等腰直角三角形，∴EF ==，故答案为：45，=（2）解：∵AB AC =，90BAC ∠=︒，∴45B ACD ∠=∠=︒，∵AB AC =，点D 是BC 的中点，∴AD BC ⊥，45BAD CAD ∠=∠=︒∴AD CD =，90ADC ∠=︒，∴BAD ACD ∠=∠，∴180180BAD ACD ︒−∠=︒−∠，即EAD FCD ∠=∠，∵45ACD CAD ∠=∠=︒，∴AD CD =，在ADE V 和CDF 中，AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)ADE CDF ≌V V ，∴DE DF =，ADE CDF ∠=∠，∴90EDF CDF EDC ADE EDC ADC ∠=∠+∠=∠+∠=∠=︒，∴DE DF ⊥，在Rt EDF 中，DE DF =，4EF =，∴DE EF ==（3）解：①当H 在线段AC 上时，如图，连接MC ，过点M 作MF AC ⊥于F ，∵,AD BC BD CD ⊥=，∴AM 是线段BC 的中垂线，∴MB MC =，∴MBC MCB ∠=∠，∵AB AC =，∴A ABC CB =∠∠，∴ABM ACM ∠=∠，又∵90BAC BMH ∠=∠=︒，360BAH ABM BMH AHM ∠+∠+∠+∠=︒，∴180ABM AHM ∠+∠=︒，∵180AHM MHC ∠+∠=︒，∴ABM MHC ∠=∠，∴MCH MHC ∠=∠，∴MH MC =，∵2CH =， ∴112HF CF CH ===， ∵6AC =，∴615AF AC CF =−=−=，∵45DAC ∠=︒，∴5AF MF ==，∴AM =∵6AB AC ==，90BAC ∠=︒，D 是BC 的中点，∴12AD BC ==∴DM AM AD =−=②当H 在线段AC 的延长线上时，如图，连接MC ，过点M 作MF AC ⊥于F ，同理可得1CF HF ==，∴617AF AC CF =+=+=，∴AM =∴DM AM AD =−=综上，DM 的长为【点评】此题是三角形的综合题，主要考查了直角三角形的性质，等腰三角形的判定和性质，全等三角形的判定和性质及等腰直角三角形的判定和性质，根据已知得出ADE CDF V V ≌是解题的关键．8．(1)见解析(2)HM =(3)MB ，证明见解析【分析】（1）由直角三角形两个锐角互余即可得出90APC PAC ∠+∠=︒，90MQB APC ∠+∠=︒，从而得出MQB PAC ∠=∠；（2）连接AQ ，DP ．由题意易得出AC 为线段QP 的垂直平分线，即得出2DP DQ ==，QAC PAC ∠=∠，AP AQ =，从而由勾股定理可求出PH DH ．进而易证(AAS)DAH PQH ≌，得出2AH QH DQ DH ==+=，再根据勾股定理可求出2AQ ==．又易证QAM QMA ∠=∠，即得出2QM QA ==，从而由HM QM DH =−求解即可；（3）作ME QB ⊥于点E ，易证(AAS)APC QME ≌，即得出PC ME =．再根据MEB 是等腰直角三角形，即得出MB =，从而得出MB ．【解析】（1）∵90ACB ∠=︒，QH AP ⊥，∴90APC PAC ∠+∠=︒，90MQB APC ∠+∠=︒，∴MQB PAC ∠=∠；（2）如图，连接AQ ，DP ．∵CQ CP =，90ACB ∠=︒，∴AC 为线段QP 的垂直平分线，∴2DP DQ ==，QAC PAC ∠=∠，AP AQ =，∴PH DH =．又∵DAH PQH ∠=∠，90AHD QHP ∠=∠=︒，∴(AAS)DAH PQH ≌，∴2AH QH DQ DH ==+=∴2AQ ==．∵45QAM QAC CAB QAC ∠=∠+∠=∠+︒，45QMA MQB B BQM ∠=∠+∠=∠+︒， ∴QAM QMA ∠=∠，∴2QM QA ==，∴2(2HM QM DH =−=−=（3）MB ．证明如下，如图，作ME QB ⊥于点E ，由（2）可知AP AQ QM ==，又∵90MQE PAC ACP QEM ∠=∠∠=∠=︒，，∴(AAS)APC QME ≌，∴PC ME =．∵MEB 是等腰直角三角形，∴BE ME =．∵222BE ME MB +=，∴MB ，∴MB =．【点评】本题考查等腰三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理．正确作出辅助线是解题的关键．9．(1)见解析(2)①见解析；②2AE CF =；证明见解析【分析】（1）根据“SAS ”证明≌ACD BCE V V ，得出AD BE =，DAC CBE ∠=∠，证明ABE为直角三角形，根据勾股定理得出222AB BE AE +=，即可得出答案；（2）①根据题意补全图形即可；②延长CF ，截取FG CF =，连接BG ，证明CFD GFB ≌，得出CD BG =，GBF CDF ∠=∠，证明()SAS ACE CBG ≌即可得出结论．【解析】（1）证明：∵90ACB ∠=︒，AC BC =，∴190452CAB CBA ∠=∠=⨯︒=︒，∵90DCE ∠=︒，∴90DCA ACE ACE ECB ∠+∠=∠+∠=︒，∴DCA ECB ∠=∠，∵AC BC =，CE CD =，∴()SAS ACD BCE △≌△，∴AD BE =，DAC CBE ∠=∠，∵180135DAC CAB ∠=︒−∠=︒，∴135CBE ∠=︒，∴90ABE CBE CBA ∠=∠−∠=︒，∴ABE 为直角三角形，∴222AB BE AE +=，∴222AB AD AE +=．（2）解：①依题意补全图2如图所示：②2AE CF =；理由如下：如图，延长CF ，截取FG CF =，连接BG ，∵F 为BD 的中点，∴BF DF =，∵CFD GFB ∠=∠，CF FG =，∴()SAS CFD GFB ≌，∴CD BG =，GBF CDF ∠=∠，∵CD CE =，∴BG CE =，∵45CDF DCA CAD DCA ∠=∠+∠=∠+︒，∴45GBF CDF DCA ∠=∠=∠+︒，∴454590CBG FBG CBA DCA DCA ∠=∠+∠=∠+︒+︒=∠+︒，∵90ACE DCA DCE DCA ∠=∠+∠=∠+︒，∴ACE CBG ∠=∠，∵AC BC =，CE BG =，∴()SAS ACE CBG ≌，∴2AE CG CF FG CF ==+=．【点评】本题主要考查了三角形全等的判定和性质，勾股定理，等腰三角形的性质，三角形外角的性质，余角的性质，解题的关键是作出辅助线，构造全等三角形．10．(1)见解析(2)见解析(3)22AD =，20AB =【分析】（1）由“SAS ”可证AOB ≌COD △，可得OB OD =；（2）由AOB ≌COD △得OAB OCD ∠=∠，AOB COD ∠=∠，从而得出AOC BOD ∠=∠，AOC APC ∠=∠，根据180APC APD ∠+∠=︒和1902APD COB ∠=︒+∠进一步得出结论；（3）作BF OD ⊥于F ，作CG OA ⊥于G ，设2BD OE a ==，根据1122BOD S OD BF BD OE =⋅=⋅，BF =，从而45BF OB ，设4BF k =，5OD OB k ==，则3OF k =，根据B F O C G O ，表示各边，并求出OG 和CG ，根据AB CD =列出方程，从而求得k ，进一步求得结果．【解析】（1）证明：在AOB 和COD △中，OA OC BAO DCOAB CD =⎧⎪∠=∠⎨⎪=⎩，∴AOB ≌COD △，∴OB OD =；（2）证明：由（1）知：AOB ≌COD △，∴OAB OCD ∠=∠，AOB COD ∠=∠，∴AOB BOC COD BOC ∠−∠=∠−∠，即：AOC BOD ∠=∠.∵180A P C O C D C E P ∠=︒−∠−∠，180A O C B A O A E O ∠=︒−∠−∠，∴AOC APC ∠=∠.∵180APC APD ∠+∠=︒，∴180A O C A P D ∠+∠=︒. ∵1902APD COB ∠=︒+∠， ∴1(90)1802AOC COB ∠+︒+∠=︒，∴2180A O C B O C ∠+∠=︒，∴180A O C B O D B O C ∠+∠+∠=︒，∴A ，O ，D 三点共线；（3）解：如图，作BF OD ⊥于F ，作CG OA ⊥于G ，设2BD OE a ==，∵OB OD =，∴BE DE a ==.∵90BEO ∠=︒，∴OD OB ===. ∵1122BOD S OD BF BD OE =⋅=⋅，22BF a a ⋅=⋅，∴BF =，∴45BF OB=， ∴设4BF k =，5OD OB k ==，则3OF k =，∵AOC BOD ∠=∠，90B F O C G O ∠=∠=︒，∴B F O C G O ，∴::::3:4:5O G C G O C O F B F O B ==，设3OG x =，4CG x =，5OC x =，∴57x =，解得75x =， ∴2135OG x ==，2845CG x ==，在Rt CDG △和Rt AFB 中，由勾股定理得，222D C C G D G =+，222AB AF BF =+，且AB CD =， ∴22222821()(5)(37)(4)55k k k ++=++，解得3k =，∴412BF k ==，15OB OD ==，39OF k ==，33716A F =⨯+=，∴71522AD OA OD =+=+=.∵222221216400A B B F A F =+=+=，∴20AB =．【点评】本题主要考查了等腰三角形性质，勾股定理，全等三角形判定和性质等知识，解决问题的关键是作辅助线，根据面积法求得线段间关系．11．(1)①图形见解析；猜想：BAE BCD ∠=∠，理由见解析；②见解析；(2)线段AE ，CE ，DE 的数量关系：CE AE =．【分析】(1)①依题意补全图形，由直角三角形的性质得出90BAE B ∠+∠=︒，90BCD B ∠+∠=︒，即可得出BAE BCD ∠=∠；②在AE 上截取AF CE =，可证出ACD 是等腰直角三角形，得出AD CD =，可证明()ADF CDE SAS ≌△△，得出DF DE =，ADF CDE ∠=∠，可推出90CDE FDC EDF ∠︒+∠=∠=，证出EDF 是等腰直角三角形，即可得出结论CE AE =；(2) 在CE 上截取CF AE =，连接DF ，由CD AD ⊥，AE BC ⊥，可得EAD DCF ∠=∠，由45BAC ∠=︒可得AD CD =，可证()ADE CDF SAS △≌△，可得ED DF =，ADE CDF ∠=∠，可推出90EDF ∠=︒，可得EDF 是等腰直角三角形故EF ，即可得线段AE ，CE ，DE 的数量关系．【解析】（1）解：①依题意，补全图形，如图1所示．猜想：BAE BCD ∠=∠，理由如下：∵CD AB ⊥，AE BC ⊥，∴90BAE B ∠+∠=︒，90BCD B ∠+∠=︒，∴BAE BCD ∠=∠，②证明：如图2，在AE 上截取AF CE =，连接DF∵45BAC ∠=︒，CD AB ⊥，∴ACD 是等腰直角三角形，∴AD CD =，在ADF △和CDE 中，DA CD BAE BCDAF CE =⎧⎪∠=∠⎨⎪=⎩∴()ADF CDE SAS ≌△△，∴DF DE =，ADF CDE ∠=∠，∵AB CD ⊥，∴90ADF FDC ∠+∠=︒，∴90CDE FDC EDF ∠︒+∠=∠=，∴EDF 是等腰直角三角形，∴EF =，∵AF EF AE +=，∴CE AE =．（2）解：依题意补全图形，如图3所示，在CE 上截取CF AE =，连接DF ，∵CD AD ⊥，AE BC ⊥，∴90ADC AEC ∠=∠=︒，∴90EAB ABE ∠+∠=︒，90DBC DCF ∠+∠=︒，ABE CBD ∠=∠，∴EAD DCF ∠=∠，∵45BAC ∠=︒，∴45DCA ∠=︒，∴AD CD =，在ADE V 和CDF 中，AD CD EAD DCFCF AE =⎧⎪∠=∠⎨⎪=⎩∴()ADE CDF SAS △≌△，∴ED DF =，ADE CDF ∠=∠，∵90CDF ADF ∠+∠=︒，∴90ADE ADF ∠+∠=︒，∴90EDF ∠=︒，∴EDF 是等腰直角三角形，∴EF =，∵CE CF EF =+，∴CE AE =，∴线段AE ，CE ，DE 的数量关系：CE AE =．【点评】本题考查了全等三角形的判定与性质等腰直角三角形的判定与性质、直角三角形的性质等知，证明三角形全等是解题的关键．12．(1)①=，②＞(2)＞(3)【分析】（1）①连接BD ，先证明CDB △是等边三角形，即60ACB CBD BDC ∠=︒=∠=∠，当F 点与B 点重合时，即0BF =，根据“三线合一”可得AE EF =，即有AE BF EF +=，同理：如果点E 刚好和点A 重合，同样有AE BF EF +=；问题得解；②先证明DEF 是等边三角形，根据等腰三角形的性质可得AE EF =，再结合含30︒角的直角三角形的性质可以求出BF AC =，即问题得解；（2）将DF 绕D 点逆时针旋转120°至DM ，连接AM ME ，，先证明DEM DEF ≌V V ，再证明ADM BDF ≌△△，问题即可得解；（3）将DF 绕D 点逆时针旋转120︒至DN ，连接AN NE ，，根据（2）中的方法，同理可证明：DEN DEF ≌V V ，ADN BDF ≌V V ，再证明ANE 是直角三角形，90ANE ∠=︒，结合含30︒角的直角三角形的性质即可求解．【解析】（1）①如图，连接BD ，根据题意有90ABC ∠=︒，60ACB ∠=︒，即30CAB ∠=︒，∵点D 为AC 中点， ∴12AD DC BD AC ===，∴CDB △是等边三角形，（此结论也适用于第（2）和（3）问）∴60ACB CBD BDC ∠=︒=∠=∠，∵30CAB ∠=︒，∴在Rt ABC △中，12BC AC =，∴AB AC ，当F 点与B 点重合时，如上图左图，即0BF =，∵60EDF DBC ∠=︒=∠，∴DE BC ∥，∴90AED ABC ∠=∠=︒，∴DE AF ⊥，∵AD BD =，∴AE EF =，∵0BF =，∴AE BF EF +=，同理：如果点E 刚好和点A 重合，同样有AE BF EF +=，故答案为：=；②当30ADE ∠=︒时，如图，∵30ADE ∠=︒，30DAE ∠=︒，∴60DEF ∠=︒，AE DE =，∵60EDF ∠=︒，∴DEF 是等边三角形，90ADF Ð=°，∴DE EF =，∴AE EF =，∵90ADF Ð=°，30DAE ∠=︒，∴在Rt ADF 中，12DF AF =，∴AF AB =，∴AF AC =，∴BF AB AF AC AC AC =−==，∵AE EF =，BF AC ，∴AE BF EF +＞，故答案为：＞；（2）AE BF EF +＞，理由如下：将DF 绕D 点逆时针旋转120︒至DM ，连接AM ME ，，如图，根据旋转的性质有：120MDF ∠=︒，DF DM =，∵60FDE ∠=︒，∴60MDE ∠=︒，∵DE DE =，∴DEM DEF ≌V V ，∴EM EF =，∵60CDB ∠=︒，∴120ADB ∠=︒，即：ADB MDF ∠=∠，∵ADB ADF FDB ∠=∠+∠，MDF ADF ADM ∠=∠+∠，∴BDF ADM ∠=∠，∵AD BD =，MD DF =，∴ADM BDF ≌△△， ∴AM BF =，∴在AME △中，AM AE ME +＞，∴BF AE EF +＞，故答案为：＞；（3）将DF 绕D 点逆时针旋转120︒至DN ，连接AN NE ，，如图，根据（2）中的方法，同理可证明：DEN DEF ≌V V ，ADN BDF ≌V V ，∴AN BF =，NE EF =，DBF DAN ∠=∠，∵222BF EF AE +=，∴222AN NE AE +=，∴ANE 是直角三角形，90ANE ∠=︒，∵在（1）中已证明60CBD ∠=︒，∴30DAN DBF ∠=∠=︒，∴60NAE DAN CAB ∠=∠+∠=︒，∴30AEN ∠=︒， ∴12AN AE =，∴NE AE ，∴EF NE AE AE=．【点评】本题主要考查了全等三角形的判定与性质，含30︒角直角三角形的性质，等腰三角形的判定与性质，勾股定理及其逆定理等知识，合理构筑辅助线，证明三角形全等是解答本题的关键．13．(1)见解析(2) (3)94x =【分析】（1）表示出三个图形的面积进行加减计算可证222+=a b c ；（2）计算出ABC 的面积，再根据三角形的面积公式即可求得AB 边上的高；（3）运用勾股定理在Rt ABD 和Rt ADC 中求出2AD ，列出方程求解即可；【解析】（1）证明：∵2 12ABCD S c =四边形，() 12AEDC S b a b =+梯形，()12BED S a b a =−△， BED ABCD AEDC S S S =+△四边形梯形 ∴()()2111222c b a b a b a =++− ∴2221111122222c b ab a ab =++− ∴222+=a b c（2）111442424226222ABC S =⨯−⨯⨯−⨯⨯−⨯⨯=，AB =11622ABC S AB h =⨯=⨯=， 655h =即AB 边上的高是（3）解：在Rt △ABD 中，由勾股定理得222222416AD AB BD x x =-=-=-∵6BD CD BC +==，∴6CD BC BD x =−=−在Rt ACD △中，由勾股定理得()222222561112AD AC CD x x x =−=−−=−+−∴22161112x x x -=-+-， ∴94x =【点评】此题主要考查了梯形，证明勾股定理，勾股定理的应用，证明勾股定理常用的方法是利用面积证明，是解本题的关键．构造出直角三角形DEF 是解本题的难点．14．(1)见解析(2)(3)【分析】（1）证明ACE BCF △△≌，即可解决问题；（2）先由全等三角形的性质和三角形的外角性质，证出90ACD DFB ∠=∠=︒，再由勾股定理即可解决问题；（3）作FH BC ⊥于H ．先证明BCF △是底角为30°的等腰三角形，再求出CF FB FH ，，的长，然后根据DEF ECD CDF ECF S S S S =+−计算即可．【解析】（1）证明：∵ABC ECF ，都是等腰直角三角形，∴90CA CB CE CF ACB ECF ==∠=∠=︒，，，∴ACE BCF ∠=∠，∴()SAS ACE BCF ≌，∴CAE CBF ∠=∠；（2）解：∵90AC BC ACB ==∠=︒，∴AB ==由（1）得：CAD DBF ∠=∠，∵ADB CAD ACD DBF DFB ∠=∠+∠=∠+∠，∴90DFB ACD ∠=∠=︒，∴AF == （3）解：过点F 作FH BC ⊥于H ，如图3所示：∵ABC 是等腰直角三角形，90ACB AC BC ∠=︒=，，∴45BAC ABC ∠=∠=︒，∵15BAD ∠=︒，∴451530CAE ∠=︒−︒=︒，∴30ACE CAE ∠=∠=︒，∴==AE CE CF ，同（1）得：()SAS ACE BCF ≌，∴30BF AE ACE BCF =∠=∠=︒，，∴CF BF =，∴30BCF CBF ∠=∠=︒，∵FC FB FH BC =⊥，，∴12CH BH BC ===，32FH ==，23CF BF FH ===，∵60903060CED CAE ACE ECD ∠=∠+∠=︒∠=︒−︒=︒，，∴ECD 是等边三角形，∴3EC CF CD ===，∴DEF ECD CDF ECF S S S S =+−21313333222=+⨯⨯−⨯⨯=．【点评】本题属于三角形综合题，考查了等腰直角三角形的性质，等边三角形的判定和性质，含30°角的直角三角形的性质，全等三角形的判定和性质，等腰三角形的性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．15．(1)AEFS =；AC BD =+，证明见解析；(3)DP FQ +【分析】（1）过点F 作FG AC ^于点G ，在Rt EFG △中利用勾股定理求得GF 的长，在等腰直角三角形AFG 中即可求得AG 的长，从而可得答案；（2）过点E 作EH AC ⊥交AB 于点H ，过点H 作HM BC ⊥于点M ，通过证明HEF DBF ≌，利用全等三角形的性质与等腰直角三角形的性质即可得出结论；（3）过点F 作FM AC ⊥于点M ，延长FM 至F '使F M FM '=，则F '与F 关于AC 对称，过点F '作F N BC '⊥，交BC 的延长线于点N ，证明APF CQF ≌，利用轴对称解决路径最短问题即可求得结论．【解析】（1）解：过点F 作FG AC ^于点G ，如图，∵90,ACB AC BC ∠=︒=，∴45A ABC ∠=∠=︒，∵90,30ECD EDC ∠=︒∠=︒，∴60DEG ∠=︒．∵,6FG AC EF ⊥=， ∴132EG EF ==，∴FG ==∵,45FG AC A ⊥∠=︒，∴AG FG ==∴3AE AG EG =−=．∴)11322AEF S AE FG ==⨯=．（2）解：过点E 作EH AC ⊥交AB 于点H ，过点H 作HM BC ⊥于点M ，如图，∵,45EH AC A ⊥∠=︒，∴,AE EH AH ==．∵BD AE =，∴EH BD =．∵,EH AC DC AC ⊥⊥，∴HE CD ∥，∴HEF D ∠=∠．在HEF 和DBF 中，HEF D HFE BFD EH DB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()AAS HEF DBF ≌． ∴12HF BF BH ==．∵90HEC ACB HMC ∠=∠=∠=︒，则90EHM ∠=︒，∴HM AC ∥，而HE CD ∥，∴由平行线间的距离处处相等可得：,CM HE HM CE ==，∵,45HM BC ABC ⊥∠=︒，∴EC HM ==，∴12AF AH HF BH =++． ∴2AE BH =，即：AE AE CE AE AC =++=+． ∴AC BD =+．（3）解：∵AB = F 是线段AB 的中点，90ACB ∠=︒，∴4,45,AF FB FC AC BC A ABC CF AB =====∠=∠=︒⊥．∴45FCQ A ∠=∠=︒．在APF 和CQF △中，AP CQ A FCQ AF FC =⎧⎪∠=∠⎨⎪=⎩，∴APF CQF ≌．∴PF FQ =． ∴DP FQ DP PF +=+．过点F 作FN AC ⊥于点M ，延长FM 至F '使F M FM '=，则F '与F 关于AC 对称，连接DF '交AC 于点P ，如图，则此时DP FP DF '+=，取得最小值，过点F '作F N BC '⊥，交BC 的延长线于点N ，∵90,,45AFC FM AC A ∠=︒⊥∠=︒， ∴112,222AM MC AC FM AC =====． ∴2F M FM '==．。

人教版八年级下册数学期末压轴题专题训练(含答案)

人教版八年级下册数学期末压轴题专题训练1．如图，已知长方形的边AD ＝8，AB ＝4，动点M 从点A 出发，以每秒2个单位长度的速度沿A →D →A 的路径匀速运动，同时，动点N 从点C 出发，沿C →B 方向以每秒1个单位长度的速度匀速运动，当其中一个动点到达终点时，另一点也随之停止运动，设运动时间为t 秒．(1)如（图一），当运动时间为1秒时，求MN 的长度；(2)当0≤t ≤4时，直接写出AMN 为直角三角形时的运动时间t 的值； (3)如（图二），当4＜t ＜8时，判断AMN 的形状，并说明理由．2．（1）感知：如图①，在正方形ABCD 中，E 为边AB 上一点（点E 不与点AB 重合），连接DE ，过点A 作AF DE ⊥，交BC 于点F ，证明：DE AF =．（2）探究：如图②，在正方形ABCD 中，E ，F 分别为边AB ，CD 上的点（点E ，F 不与正方形的顶点重合），连接EF ，作EF 的垂线分别交边AD ，BC 于点G ，H ，垂足为O ．若E 为AB 中点，1DF =，4AB =，求GH 的长．（3）应用：如图③，在正方形ABCD 中，点E ，F 分别在BC ，CD 上，BE CF =，BF ，AE 相交于点G ．若3AB =，图中阴影部分的面积与正方形ABCD 的面积之比为2：3，则ABG 的面积为______，ABG 的周长为______．3．如图．菱形ABCD的对角线AC，BD交于点O．尺规作图：过点A作直线BC的垂线（不写作法和证明，保留作图痕迹）．该垂线与BC交于点E，F为AD边上一点，DF=AE，连接OF，若OD=2AO，请猜想CE与OF的数量关系，并证明你的猜想．4．图1、图2分别是65的网格，网格中每个小正方形的边长均为1，线段AB的端点在小正方形的顶点上，请在图1、图2中各画一个图形，分别满足以下要求：(1)在图1中画一个以线段AB为一边的菱形（非正方形），所画菱形各顶点必须在小正方形的顶点上．(2)在图2中画一个以线段AB为一边的等腰三角形，所画等腰三角形各顶点必须在小正方形的顶点上，且所画等腰三角形的面积为52．5．如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为OB，OD的中点，延长AE至G，使EG＝AE，连接CG．(1)求证：△ABE≌△CDF；(2)当AB与AC满足什么数量关系时，四边形EGCF是矩形？请说明理由．⊥，垂6．如图，在ABCD中，E，F分别为AD，BC的中点，AG BD⊥，CH BD足分别为G，H，连接EG，EH，FG，FH．(1)求证：四边形GEHF是平行四边形；BC=，当BD=______时，GEHF是矩形．(2)若2AB=，37．如图1，在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分线，DE⊥AB 于E．(1)发现：如图1，连接CE，则△BCE的形状是_______________，∠CDB=____________°；(2)探索：如图2，点P为线段AC上一个动点，当点P在CD之间运动时，连接BP，作∠BPQ=60°，PQ交射线DE于Q，连接BQ，即△BPQ是等边三角形；思路：在线段BD上截取点H，使DH=DP，得等边△DPH，由∠DPQ=∠HPB，PD=PH，∠QDP=∠BHP，易证△PDQ≌△PHB（ASA），得PQ=PB，即△BPQ是等边三角形．试判断线段DQ、DP、AD之间的关系，并说明理由；(3)类比：如图3，当点P在AD之间运动时连接BP，作∠BPQ=60°，PQ交射线DE于Q，连接BQ．①试判断△BPQ的形状，并说明理由；②若AD=2，设AP=x，DQ=y，请直接写出y与x之间的函数关系式．8．下面是小东设计的“作平行四边形ABCD，使∠B＝45°，AB＝2cm，BC＝3cm”的作图过程．作法：如图，①画∠B＝45°；②在∠B的两边上分别截取BA＝2cm，BC＝3cm．③以点A为圆心，BC长为半径画弧，以点C为圆心，AB长为半径画弧，两弧相交于点D；则四边形ABCD为所求的平行四边形．根据小东设计的作图过程：(1)使用直尺和圆规，补全图形；（保留作图痕迹）(2)完成下面的证明．证明：∵AB＝，CB＝，∴四边形ABCD为所求的平行四边形（）（填推理的依据）．9．如图，已知菱形ABCD中，分别以C、D为圆心，大于1CD的长为半径作弧，两弧2分别相交于M、N两点，直线MN交CD于点F，交对角线AC于点E，连接BE、DE．(1)求证：BE＝CE；(2)若∠ABC＝72°，求∠ABE的度数．10．如图，四边形ABCD是一个正方形，E、F分别在AD、DC边上，且DE=CF，AF、BE交于O点，请说出线段AF和BE的关系，并证明你的结论．11．如图，在由边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：(1)在网格中画出平行四边形ABCD；(2)线段AC的长为，CD的长为，AD的长为，△ACD为三角形，平行四边形ABCD的面积为．12．两个不全等的直角三角形ABC 和DEF 重叠在一起，其中∠A ＝60°，AC ＝1．固定△ABC 不动，将△DEF 进行如下操作：(1)如图（1），△DEF 沿线段AB 向右平移（D 点在线段AB 内移动），连接DC 、CF 、FB ，四边形CDBF 的形状在不断的变化，但它的面积不变化，请求出其面积；(2)如图（2），当D 点移到AB 的中点时，请你猜想四边形CDBF 的形状，并说明理由．13．如图，长方形ABCD 中，E 是AD 的中点，将ABE △沿BE 折叠后得到GBE ，且G 点在长方形ABCD 内部，延长BG 交DC 于点F ．(1)求证：GE DE =；(2)若9DC =，DF 2CF =，求AD 的长；(3)若DC n DF =⋅，求22AD AB 的值．14．在正方形ABCD 中，点E 是CD 边上任意一点．连接AE ，过点B 作BF ⊥AE 于F ．交AD 于H ．(1)如图1，过点D 作DG ⊥AE 于G ，求证：△AFB ≌△DGA ；(2)如图2，点E 为CD 的中点，连接DF ，求证：FH +FE ；(3)如图3，AB ＝1，连接EH ，点P 为EH 的中点，在点E 从点D 运动到点C 的过程中，点P 随之运动，请直接写出点P 运动的路径长．15．已知如图，四边形ABCD 是平行四边形．（1）尺规作图：作∠ABC 的角平分线交CD 的延长线于E ，交AD 于F （不写作法和证明，但要保留作图痕迹）．（2）请在（1）的情况下，求证：DE ＝DF ．16．如图，在Rt ABC ∆中，90ACB ∠=︒，CD 是斜边AB 上的中线，1AC CD ==，求直角边BC 的长．17．如图：正方形ABCD 中，点E 、F 分别在边BC 、CD 上，BE ＝CF ，连接AE ，BF 交于点O ，点M 为AB 中点，连接OM ，求证：12OM AB =．18．如图，在四边形ABCD 中，90ABD ACD ∠=∠=︒，E ，F 分别是BC 、AD 的中点．(1)若10AD =，求BF 的长； (2)求证：EF BC ⊥．19．如图，四边形ABDE 和四边形ACFG 都是正方形，CE 与BG 交于点M ，点M 在△ABC 的外部．(1)求证：BG ＝CE ； (2)求证：CE ⊥BG ； (3)求：∠AME 的度数．20．如图，△ABC中，D是AB边上任意一点，F是AC中点，过点C作CE//AB交DF 的延长线于点E，连接AE，CD．(1)求证：四边形ADCE是平行四边形；(2)若∠B＝30°，∠CAB＝45°，AC ，求AB的长．21．如图，△ABC中，∠C＝90°．(1)尺规作图：作边BC的垂直平分线，与边BC，AB分别交于点D和点E；（保留作图痕迹，不要求写作法）(2)若点E是边AB的中点，AC＝BE，求证：△ACE是等边三角形．22．已知：如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC 的平行线交BE的延长线于点F，且AF＝DC，连接CF．(1)求证：D是BC的中点；(2)如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．23．如图，四边形ABCD 是平行四边形．(1)尺规作图（不写作法，保留作图痕迹）；作出ABC ∠的角平分线BE ，交AD 于点E ；在线段BC 上截取BF BA =，连接EF ；(2)在（1）所作图中，请判断四边形ABFE 的形状，并说明理由．24．如图，矩形ABCD 中，E 、F 分别为边AD 和BC 上的点，BE ＝DF ，求证：DE ＝BF ．25．已知：在ABC 中，90BAC ∠=︒，AB AC =，点D 为直线BC 上一动点（点D 不与B 、C 重合）．以AD 为边作正方形ADEF ，连接CF ．(1)如图①，当点D 在线段BC 上时， ①求证：ABD △≌ACF ； ②ACF ∠的大小＝______°；③若8BC =，2CD =，则CF 的长＝______；(2)如图②，当点D 在线段BC 的延长线上时，其它条件不变，则CF 、BC 、CD 三条线段之间的关系是：CF =______；其它条件不变：①CF、BC、CD三条线段之间的关系是：CF ______；△的形状，并说明②若连接正方形的对角线AE、DF，交点为O，连接OC，探究AOC理由．26．已知：如图，▱ABCD中，延长BC至点E，使CE=BC，连接AE交CD于点O．(1)求证：CO=DO；(2)取AB中点F，连接CF，△COE满足什么条件时，四边形AFCO是正方形？请说明理由．参考答案：1．解：过点N作NR⊥AD于R．∵四边形ABCD是矩形，∴∠C=∠D=∠DRN=90°，∴四边形CDRN是矩形，∴RN=CD=4，CN=DR=1，∵AM=2，AD=8，∴RM=AD-AM-DR=8-2-1=5，∵∠MRN=90°，∴MN=(2)解：当0≤t≤4时，如果AM=BN，则△AMN是直角三角形，∴2t=8-t，∴t=83，当t=4时，点M与D重合，点N位于BC的中点，此时△AMN是等腰直角三角形，综上所述，当△AMN是直角三角形时，t的值为83或4．(3)解：∵当t=4时，△AMN是等腰直角三角形，∵点M的运动速度大于点N的运动速度，且M，N同时到达终点，即点M在点N的右侧，∴当4＜t＜8时，△AMN是锐角三角形．2．证明：∵四边形ABCD是正方形，∴AD AB =，90DAE ABF ∠=∠=︒，∵AF DE ⊥，∴90DAF BAF ∠+∠=︒，90DAF ADE ∠+∠=︒， ∴ADE BAF ∠=∠，在DAE △和ABF 中，ADE BAF AD AB DAE ABF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴DAE △≌ABF （ASA ），∴DE AF =．探究：解：分别过点A 、D 作AN GH ∥，DM EF ∥，分别交BC 、AB 于点N 、M ，如图②所示：∵四边形ABCD 是正方形，∴AB CD ∥，AB CD =，90DAB B ∠=∠=︒，∴四边形DMEF 是平行四边形，∴1ME DF ==，DM EF =， ∵AN GH ∥，GH EF ⊥，∴DM GH ⊥，同理，四边形AGHN 是平行四边形，∴GH AN =，∵DM EF ∥，GH EF ⊥，∴AN DM ⊥，∴90DAN ADM ∠+∠=︒，∵90DAN BAN ∠+∠=︒，∴ADM BAN ∠=∠，在ADM △和BAN 中，90ADM BAN AD AB DAM ABN ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩，∴ADM △≌BAN （ASA ），∴DM AN =，∴EF GH DM AN ===，∵E 为AB 中点，∴122AE AB ==， ∴211AM AE ME =-=-=，∴DM ==∴GH =应用：解：∵AB ＝3，∴S 正方形ABCD ＝3×3＝9，∵阴影部分的面积与正方形ABCD 的面积之比为2：3，∴阴影部分的面积为：23×9＝6， ∴空白部分的面积为：9﹣6＝3，在△ABE 和△BCF 中，90BECF ABE BCF AB BC ，∴△ABE ≌△BCF （SAS ），∴∠BEA ＝∠BFC ，S △ABG ＝S 四边形CEGF ，∴S △ABG ＝12×3＝32，∠FBC +∠BEA ＝90°， ∴∠BGE ＝90°，∴∠AGB ＝90°，设AG ＝a ，BG ＝b ，则12ab ＝32， ∴2ab ＝6，∵a 2+b 2＝AB 2＝32，∴a 2+2ab +b 2＝32+6＝15，即（a +b ）2＝15，而0,a b +>∴a +bBG +AG∴△ABG，故答案为：323． 3．解：所作图形如图所示：结论：CE =OF ．理由：∵四边形ABCD 是菱形，∴AC ⊥BD ，OA =OC ，AD ∥BC ，∵AE ⊥BC ，OF ⊥AD ，∴AE ⊥AD ，∴∠AEC =∠DAE =∠AOD =∠DFO =90°，∴∠EAC +∠DAO =90°，∠FDO +∠DAO =90°，∴∠CAE =∠ODF ，∵OD =2AO ，AC =2AO ，∴AC =OD ，在△AEC 和△DFO 中，AEC DFO CAE ODF AC DO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEC ≌△DFO （AAS ），∴CE =OF ．4．解：所画菱形如图所示；(答案不唯一)(2)解根据勾股定理，AB = 所画等腰三角形的面积为52， ∴作以线段AB 为直角边的等腰直角三角形即可，所画三角形如图所示．5．证明：∵四边形ABCD 是平行四边形，∴AB =CD ，AB CD ∥，OB =OD ，OA =OC ，∴∠ABE =∠CDF ，∵点E ，F 分别为OB ，OD 的中点， ∴12BE OB =，12DF OD =， ∴BE =DF ，在△ABE 和△CDF 中，AB CD ABE CDF BE DF =⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CDF(SAS).(2)解：当AC =2AB 时，可使四边形EGCF 为矩形；理由如下：∵△ABE ≌△CDF ，∴∠AEB =∠CFD ，∴∠AEO =∠CFO ，∴AE CF ∥，∵EA =EG ，OA =OC ，∴EO 是△AGC 的中位线，∴EO GC ∥，∴四边形EGCF 是平行四边形，∵AC =2AB ，AC =2AO ，∴AB =AO ，∵E 是OB 的中点，∴AE ⊥OB ，∴∠OEG =90°，∴平行四边形EGCF 是矩形．6．解：∵AG BD ⊥于G ，∴90AGD ∠=︒．∵在Rt AGD 中，E 为AD 的中点， ∴12EG ED AD ==，同理12HF BF BC ==． ∵在ABCD 中，AD BC =，∴EG FH =．∵在EGD 中，EG ED =，∴EDG EGD ∠=∠，同理在BFH △中，HBF FHB ∠=∠．∵在ABCD 中，AD BC ∥，∴EDG HBF ∠=∠．∴EGD FHB ∠=∠．∴EG FH ∥．又∵EG FH =，∴四边形GEHF 是平行四边形．(2)连接EF ，则EF =AB =CD =2，若四边形GEHF 是矩形，则EF =GH =2，在RtAGD 和Rt ΔCHB 中，41AGD CHB AD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ΔAGD ≅ΔCHB （AAS )，∴DG =BH ；∴DG -GH =BH -GH ，即BG =DH ，设BG =DH =x ，在Rt △ABG 中，AG 2=AB 2-BG 2=4-x 2，在Rt △AGD 中，AG 2=AD 2-DG 2=9-DG 2=9－（2+x ）2，∴4-x 2=9-(2+x )2，解得x =14， ∴BD =BG +GH +HD =14+2+1452= ． 7．解：如图1，∵在Rt △ABC 中，∠ACB =90°，∠A =30°，∴∠ABC =60°，∵BD 是△ABC 的角平分线，∴∠ABD =∠CBD =12∠ABC =30°，∴∠ABD =∠A ，∠CDB =90°－∠CBD =60°，∴AD =BD ，又DE ⊥AB ，∴AE =BE =12AB ，又∠ACB =90°，∴CE =12AB =BE ，又∠ABC =60°，∴△BCE 是等边三角形，故答案为：等边三角形，60；(2)解：AD =DQ +DP ，理由为：在线段BD 上截取点H ，使DH =DP ，如图2，∵∠CDB =60°，∴△DPH 为等边三角形，∴DP =PH ，∠DPH =∠DHP =60°，又∠BPQ =60°，∴∠DPQ +∠QPH =∠HPB +∠QPH =60°，∠BHP =120°，∴∠DPQ =∠HPB ，∵∠A =30°，DE ⊥AB ，∴∠QDP =∠A +∠AED =30°+90°=120°，∴∠QDP =∠BHP ，在△PDQ ≌△PHB 中， DPQ HPB PD PHQDP BHP ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△PDQ ≌△PHB （ASA ），∴DQ =BH ，PQ =PB ，∵AD =BD ，∠BPQ =60°，∴△BPQ 为等边三角形，AD =BD =BH +DH =DQ +DP ，即AD =DQ +DP ；(3)解：①△BPQ 为等边三角形，理由为：延长BD 至F ，使DF =DP ，连接PF ，设DQ 和BP 相交于O ，如图3， ∵∠PDF =∠CDB =60°，∴△PDF 为等边三角形，∴PF =DP ，∠F =∠PDF =∠DPF =60°，∵∠A =30°，DE ⊥AB ，∴∠PDQ =90°－∠A =60°，∴∠F =∠PDQ =60°，∵∠DPF +∠DPB =∠BPQ +∠DPB ，又∠BPQ =60°，∴∠BPF =∠QPD ，在△PBF 和△PQD 中，F PDQ PF DPBPF QPD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△PBF ≌△PQD （ASA ），∴PB =PQ ，BF =DQ ，又∠BPQ =60°，∴△BPQ 为等边三角形；②∵ DF =DP ，BF =DQ ，AD =BD ，∴DQ =BF =BD +DF =AD +DP ，∵AD =2， AP =x ，DQ =y ，∴y =2+2－x ，即y =－x +4．8．(1)补全图形如下，．(2)∵AB =CD ，CB =AD∴四边形ABCD 为所求的平行四边形（两组对边分别相等的四边形是平行四边形）．故答案为：CD ，AD ，两组对边分别相等的四边形是平行四边形．9．证明：∵四边形ABCD 是菱形，∴CB ＝CD ，∠ACB ＝∠ACD ，在△ECB 和△ECD 中，CE CE ECB ECD CB CD =⎧⎪∠=∠⎨⎪=⎩，∴△ECB ≌△ECD （SAS ），∴BE ＝DE ，由作图可知，MN 垂直平分线段CD ，∴EC ＝ED ，∴BE ＝CE ．(2)解：∵BA ＝BC ，∠ABC ＝72°，∴∠BAC ＝∠BCA ＝12（180°﹣72°）＝54°，∵EB ＝EC ，∴∠EBC ＝∠ECB ＝54°，∴∠ABE ＝∠ABC ﹣∠EBC ＝18°．10．解：AF⊥BE，AF=BE,证明如下：证明：∵正方形ABCD∴AB=AD=DC,∠D=∠BAD=90°∵CF=DE∴AE=AD-DE,DF=DC-CF∴AE=DF在△AEB和△AFD中AB=AD, ∠D=∠BAD, AE=DF∴△ABE≌△DAF（SAS）∴∠ABE=∠F AD，AF=BE∵∠BAD=90°∴∠ABE+∠AEB=90°∴∠F AD +∠AEB=90°∴∠AOE=90°，AF⊥BE．∴AF=BE，AF⊥BE．11．解：如图所示：平行四边形ABCD即为所求；(2)解：AC，CD =，5=AD ，∴222AC CD AD += ，∴△ACD 是直角三角形，∴平行四边形ABCD 的面积为122102ACD S=⨯ ． 12．解:过点C 作CG AE ⊥，垂足是点G ．由题可知，//CF AE ，CF AD BE ==，则四边形CDBF 是梯形．在直角ABC ∆中，90ACB ∠=︒，60A ∠=︒，1AC =，22AB AC ∴==，在直角ACG ∆中，90CGA ∠=︒，60A ∠=︒，1AC =，30ACG ∴∠=︒，1111222AG AC ==⨯=，CG ∴=．()()111122222CDBF S CE DB CG AD DB CG AB CG ∴=+⋅=+⋅=⋅=⨯=梯形； (2)证明：四边形CDBF 是菱形．理由如下：在直角ABC ∆中，D 是AB 的中点，AD DB CD ∴==，由（1）CF AD =，CF DB CD ∴==，又//CF AE ，∴四边形CDBF 是平行四边形．CD BD =，∴四边形CDBF 是菱形．13．证明∵GBE 是由ABE △折叠而成，∴△ABE ≌△GBE ，∴AE GE =，∵E 是AD 的中点，∴AE DE =，∴GE DE =；(2)解：连接EF ，∵DF 2CF =， ∴229633DF DC ==⨯=， ∴963CF DC DF =-=-=．∵四边形ABCD 是长方形，∴AD BC =，9AB DC ==，90A C D ∠=∠=∠=︒．∵△ABE ≌△GBE ，∴9BG AB ==，90A BGE FGE ∠=∠=∠=︒．在Rt EGF 和Rt EDF 中，∵GE DE =，EF EF =∴Rt △EGF ≌Rt △EDF (HL )，∴6GF DF ==．∴9615BF BG GF =+=+=，在Rt BCF 中，∵15BF =，3CF =，∴BC =．∴AD BC =＝(3)解：设DF a =，则AB DC n DF na ==⋅=，∴()1CF DC DF na a n a =-=-=-，又∵BG AB na ==，GF DF a ==，∴()1BF BG GF na a n a =+=+=+，在Rt BCF 中，∵()1BF n a =+，()1CF n a =-，∴ ()()22222222114BC BF CF n a n a na =-=+--=，∴ 2224AD BC na ==， ∴2222244AD na AB n a n==． 14．证明：∵四边形ABCD 是正方形，∴AB ＝AD ，∠BAD ＝90°∵DG ⊥AE ，BF ⊥AE∴∠AFB ＝∠DGA ＝90°∵∠F AB +∠DAG ＝90°，∠DAG +∠ADG ＝90°∴∠BAF ＝∠ADG在△AFB 和△DGA 中∵AFB DGABAF ADG AB AD∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFB≌△DGA（AAS）．(2)证明：如图2，过点D作DK⊥AE于K，DJ⊥BF交BF的延长线于J由题意知∠BAH＝∠ADE＝90°，AB＝AD＝CD∵BF⊥AE∴∠AFB＝90°∵∠DAE+∠EAB＝90°，∠EAB+∠ABH＝90°∴∠DAE＝∠ABH在△ABH和△DAE中∵BAH ADE AB ADABH DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABH≌△DAE（ASA）∴AH＝DE∵点E为CD的中点∴DE＝EC＝12CD∴AH＝DH∴DE＝DH∵DJ⊥BJ，DK⊥AE∴∠J＝∠DKE＝∠KFJ＝90°∴四边形DKFJ是矩形∴∠JDK ＝∠ADC ＝90°∴∠JDH ＝∠KDE在△DJH 和△DKE 中∵J DKE JDH KDE DH DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DJH ≌△DKE （AAS ）∴DJ ＝DK ，JH ＝EK∴四边形DKFJ 是正方形∴FK ＝FJ ＝DK ＝DJ∴DFFJ2FJ =∴FH +FE ＝FJ ﹣HJ +FK +KE ＝2FJDF ．(3)解：如图3，取AD 的中点Q ，连接PQ ，延长QP 交CD 于R ，过点P 作PT ⊥CD 于T ，PK ⊥AD 于K ，设PT ＝b由（2）得△ABH ≌△DAE （ASA ）∴AH ＝DE∵∠EDH ＝90°，点P 为EH 的中点∴PD ＝12EH ＝PH ＝PE∵PK ⊥DH ，PT ⊥DE∴∠PKD＝∠KDT＝∠PTD＝90°∴四边形PTDK是矩形∴PT＝DK＝b，PK＝DT∵PH＝PD＝PE，PK⊥DH，PT⊥DE ∴PT是△DEH的中位线∴DH＝2DK＝2b，DE＝2DT∴AH＝DE＝1﹣2b∴PK＝12DE＝12﹣b，QK＝DQ﹣DK＝12﹣b∴PK＝QK∵∠PKQ＝90°∴△PKQ是等腰直角三角形∴∠KQP＝45°∴点P在线段QR上运动，△DQR是等腰直角三角形∴QR DQ∴点P．15．解：（1）尺规作图如下：（2）四边形ABCD是平行四边形，,AB CE AD BC∴，,ABE E CBE DFE∴∠=∠∠=∠，BE平分ABC∠，ABE CBE∴∠=∠，E DFE ∴∠=∠，DE DF ∴=．16．解：在Rt △ABC 中，CD 是斜边AB 上的中线， ∴AB ＝2CD ＝2，由勾股定理得，BC ． 17．证明：∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABE ＝∠BCF ＝90°，又BE ＝CF ，∴△ABE ≌△BCF （SAS ）．∴∠BAE ＝∠CBF ．∵∠ABO +∠CBF ＝90°，∴∠ABO +∠BAO ＝90°，即∠AOB ＝90°．在Rt △ABO 中，M 点是斜边AB 中点， ∴12OM AB =． 18．(1) 解： 90ABD ∠=︒， F 为AD 的中点，10,AD = 1 5.2BFAD (2) 证明：如图，连接,CF90ABD ACD ∠=∠=︒， F 是AD 的中点，11,,22CF AD BF AD ,CF BF ∴=E 是BC 的中点，.EF BC19．解：证明：在正方形ABDE 和ACFG 中，AB AE =，AC AG =，90BAE CAG ∠=∠=︒， BAE BAC CAG BAC ∴∠+∠=∠+∠，即CAE BAG ∠=∠，在ABG ∆和AEC ∆中，{AB AECAE BAG AC AG=∠=∠=，()ABG AEC SAS ∴∆≅∆，BG CE ∴=；(2)解：证明：设BG 、CE 相交于点N ，ABG AEC ∆≅∆，ACE AGB ∴∠=∠，9090180NCF NGF ACF AGF ∠+∠=∠+∠=︒+︒=︒，360()360(18090)90CNG NCF NGF F ∴∠=︒-∠+∠+∠=︒-︒+︒=︒， BG CE ∴⊥；(3)解：过A 作BG，CE 的垂线段交于点P ，Q ，ABG AEC ∆≅∆，,ABP AEQ AB AE ∴∠=∠=，90APB AQE ∠=∠=︒，()ΔΔABP AEQ AAS ∴≅，∴=AP AQ ，AM ∴是角平分线，45AMC ∴∠=︒，135AME ．20．证明：∵AB //CE ，∴∠CAD ＝∠ACE ，∠ADE ＝∠CED ．∵F 是AC 中点，∴AF ＝CF ．在△AFD 与△CFE 中，CAD ACE ADE CED AF CF ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝， ∴△AFD ≌△CFE （AAS ），∴DF ＝EF ，∴四边形ADCE 是平行四边形；(2)解：过点C 作CG ⊥AB 于点G ，∵∠CAB ＝45°，∴AG CG =，在△ACG 中，∠AGC ＝90°，∴222AG CG AC +=，∵AC=∴CG＝AG＝1，∵∠B＝30°,∴12CG BC=,∴2BC=,在Rt△BCG中，BG==，∴1AB AG BG=+=．21．解：如图所示，直线DE即为所求；，(2)证明：∵∠ACB=90°，点E是边AB的中点，∴AE=BE=CE=12 AB，∵AC=BE，∴AC=AE=CE，∴△ACE是等边三角形．22．证明：E是AD的中点，AE DE∴=，//AF BC∴，FAE BDE∴∠=∠，AFE DBE∠=∠．在AFE∆和DBE∆中，FAE BDEAFE DBE AE DE∠=∠⎧⎪∠=∠⎨⎪=⎩，()AFE DBE AAS ∴∆≅∆，AF BD ∴=．AF DC =，BD DC ∴=．即：D 是BC 的中点．(2)解：四边形ADCF 是矩形；证明：AF DC =，//AF DC ，∴四边形ADCF 是平行四边形，AB AC =，BD DC =，AD BC ∴⊥即90ADC ∠=︒，∴平行四边形ADCF 是矩形．23．(1)如图所示，BE 就是所求的ABC ∠的角平分线．BF BA =，(2)四边形ABFE 为菱形．理由如下：∵BE 是ABC ∠的平分线，∴∠ABE =∠FBE∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠AEB =∠EBF ，∴∠ABE =∠AEB∴AB =AE∵BF BA =∴AE =BF∴四边形ABFE 为平行四边形，∵BF BA =，∴四边形ABFE 为菱形．24．证明：∵四边形ABCD 是矩形，∴AB ＝CD ，AD ＝BC ，∠A ＝∠D ＝90°，在Rt △ABE 和Rt △CDF 中，BE CF AB CD =⎧⎨=⎩， ∴Rt △ABE ≌Rt △CDF （HL ），∴AE ＝CF ，∴DE ＝BF ．25．（1）①证明：∵四边形ADEF 是正方形，∴AD AF =，90DAF ∠=︒，∵90BAC ∠=︒，∴BAD CAF ∠=∠，在ABD △和ACF 中，{AB ACBAD CAF AD AF=∠=∠=，∴ABD △≌ACF （SAS ）．②∵ABD △≌ACF ，∴ABD ACF ∠=∠，∵90BAC ∠=︒，AB AC =，∴45ABD ACB ∠=∠=︒，∴45ACF ∠=︒．故答案为：45．③∵ABD △≌ACF ，∴=CF BD ，∵826BD BC CD =-=-=．∴CF =6，故答案为：6．(2)（2）CF BC CD =+，由（1）同理可证ABD △≌ACF 得：CF BD BC CD ==+．故答案为：BC CD +．(3)（3）①由（1）同理可证ABD △≌ACF 得：CF BD CD BC ==-．故答案为：CD BC -．②AOC △为等腰三角形，理由如下：∵90BAC ∠=︒，AB AC =，∴18045135ABD ∠=︒-︒=︒，∵四边形ADEF 是正方形，∴AD AF =，90DAF ∠=︒，∴BAD CAF ∠=∠，同理可证BAD ≌CAF ，∴135ACF ABD ∠=∠=︒，∴90FCD ACF ACB ∠=∠-∠=︒，∴FCD 为直角三角形，∵正方形ADEF 中，O 为DF 的中点， ∴12OC DF =，12OA AE =，AE DF =， ∴OC OA =，∴AOC △是等腰三角形．26．证明：∵四边形ABCD 是平行四边形，∴AD=BC，AD//BC，∴∠DAE=∠E，∵CE=BC，∴CE=AD，又∵∠AOD=∠COE，∴△AOD≌△EOC（AAS），∴CO=DO；(2)解：当CO=EO，∠COE=90°时，四边形AOCF是正方形；理由如下：∵CO=DO，∴CO=1CD，2又∵F是AB的中点，∴AF=1AB，2∵四边形ABCD是平行四边形，∴AB=CD，AB//CD，∴AF=CO，AF//CO，∴四边形AFCO是平行四边形，∵△AOD≌△EOC，∴AO=EO，∵CO=EO，∴AO=CO，∴平行四边形AFCO是菱形，∵∠COE=90°，∴菱形AFCO是正方形．。

人教版八年级下册数学期末复习：动点问题压轴题

人教版八年级下册数学期末复习: 动点压轴题1. 如图, 在四边形ABCD中, ∠A=∠B=∠BCD=90°, AB=DC=3, AD=BC=7. 延长BC 到E, 使CE=4, 连接DE, 由直角三角形的性质可知DE=5. 动点P从点B出发, 以每秒2个单位的速度沿BC−CD−DA向终点A运动, 设点P运动的时间为t秒. (t>0)（1）当时, ______；（用含的代数式表示）（2）请用含t的代数式表示ABP△的面积S；（不包括点P与点A重合的情况）（3）当点在BC边上时, 直接写出点到四边形ABED任意相邻两边距离相等时的值.2. 如图, 在正方形ABCD中, E是边AB上的一动点（不与点A, B重合）, 连接DE, 点A关于直线DE的对称点为F, 连接EF并延长交BC于点G, 且∠CGD＝∠DGE, 连接DG, 过点E作EH⊥DE交DG的延长线于点H, 连接BH.(1)猜想: △DEH的形状, 并说明理由.(2)猜想BH与AE的数量关系, 并证明．3. 如图, 在中, , , AB＝8cm, 动点从点开始以的速度向点运动, 动点从点开始以的速度向点运动, 两点同时运动, 同时停止, 运动时间为.(1)当为何值时, 是等边三角形？(2)当为何值时, 是直角三角形？(3)过点作交于点, 连接, 求证：四边形是平行四边形．4. 已知正方形, 点F是射线上一动点（不与C, D重合）, 连接并延长交直线于点E, 交于点H, 连接, 过点C作交于点G.(1)若点F在边上, 如图1.①证明:⑤猜想线段CG与EF的数量关系并说明理由(2)取中点M, 连结, 若, 正方形边长为6, 求的长5. 已知: 如图, 在菱形ABCD中, ∠B=60°, 点E、F分别是AB.AD上的动点, 且BE=AF.(1)求证: △ECF是等边三角形(2)已知M为CD的中点, 仅用无刻度的直尺作出最短的EF（不写作法, 保留作图痕迹）6. 如图, 在矩形ABCD中, AB=9, 点E在边AB上, 且AE=5. 动点P从点A出发, 以每秒1个单位长度, 沿折线AD—DC运动, 到达点C后停止运动. 连接PE, 作点A关于直线PE的对称点F, 设点P的运动时间为t秒（t＞0）.(1)如图1, 在点P的运动过程中, 当F与点C重合时, 求BC的长；(2)如图2, 如果BC=4, 当点F落在矩形ABCD的边上时, 求t的值．7. 如图, 已知长方形的边AD＝8, AB＝4, 动点M从点A出发, 以每秒2个单位长度的速度沿A→D→A的路径匀速运动, 同时, 动点N从点C出发, 沿C→B方向以每秒1个单位长度的速度匀速运动, 当其中一个动点到达终点时, 另一点也随之停止运动, 设运动时间为t秒.(1)如（图一）, 当运动时间为1秒时, 求MN的长度；(2)当0≤t≤4时, 直接写出AMN为直角三角形时的运动时间t的值；(3)如（图二）, 当4＜t＜8时, 判断AMN的形状, 并说明理由．8. 如图1, 是正方形边上一点, 过点作, 交的延长线于点.(1)求证: ；(2)如图2, 若正方形边长为6, 线段上有一动点从点出发, 以1个单位长度每秒沿向运动. 同时线段上另一动点从点出发, 以2个单位长度每秒沿向运动, 当点到达点后点也停止运动. 连接, 点的运动时间为, 的面积为, 求关于的函数关系式；(3)如图3, 连接, 连接交于点, 连接并延长, 交于点, 已知, , 求的长．9. 在菱形中, , , 点E是边的中点, 点M是边上一动点（不与点A重合）, 连接并延长交射线于点N, 连接、,（1）求证: 四边形是平行四边形；（2）当_______时, 四边形是矩形；（3）四边形能否成为菱形？若能, 求出的值, 若不能, 请说明理由．10. 已知正方形ABCD, 点F是射线DC上一动点（不与C.D重合）, 连接AF并延长交直线BC于点E, 交BD于H, 连接CH, 过点C作CG⊥HC交AE于点G.（1）若点F在边CD上, 如图1．①证明: ∠DAH＝∠DCH；②猜想GFC的形状并说明理由.（2）取DF中点M, 连结MG．若MG＝5, 正方形边长为8, 求BE的长．11. 如图, 在△ABC中, ∠BAC＝90°, AB＝AC, 点D是直线BC上一动点（不与端点重合）, 以AD为边在AD右侧作正方形ADEF, 连接CF.（1）如图1, 当点D在线段BC上时, 求证: CF⊥BC；（2）如图2, 当点D在线段BC延长线上时, CF⊥BC还成立吗？如成立请证明, 如不成立请说明理由；（3）在图1、图2中, 选择一个图形证明：BD2＋CD2＝2AD2．12. 如图, 在直角梯形中, , , , , , 动点P从点A开始沿AD边向点D以速度运动, 动点Q从点C开始沿CB边向点B以的速度运动. 点P、Q分别从点A.C同时出发, 当其中一点到达端点时, 另一点随之停止运动. 设运动时间为t秒. 求:(1)t为何值时, 四边形PQCD为平行四边形？(2)t为何值时, 四边形ABQP为矩形？(3)是否存在, 使梯形ABQP的面积为？若存在请求出, 若不存在请说明理由．13. 在中, 为锐角, 点D为射线BC上一动点, 连接AD, 以AD为一边且在AD的右侧作正方形ADEF. 解答下列问题:(1)如果,①如图1, 当点D在线段BC上时（与点B不重合）, 线段CF、BD之间的位置关系为；数量关系为；②如图2, 当点D在线段BC的延长线上时, ①中的结论是否仍然成立, 并说明理由；(2)如图3, 如果, 点D在线段BC上运动（与点B不重合）．试探究：当时, （1）中的CF, BD之间的位置关系是否仍然成立, 并说明理由．14. 如图, 在平面直角坐标系中, 点O是坐标原点, 四边形OABC是平行四边形, 点A的坐标为（14, 0）, 点B的坐标为.(1)填空: 点C的坐标为；平行四边形OABC的对称中心的点的坐标为；(2)动点P从点O出发, 沿OA方向以每秒1个单位的速度向终点A匀速运动, 动点Q 从点A出发, 沿AB方向以每秒2个单位的速度向终点B匀速运动, 一点到达终点时, 另一点停止运动. 设点P运动的时间为t秒, 求当t为何值时, △PQC的面积是平行四边形OABC面积的一半？(3)当△PQC的面积是平行四边形OABC面积的一半时, 在平面直角坐标系中找到一点M, 使以M、P、Q、C为顶点的四边形是平行四边形, 请直接写出点M的坐标．15. 如图, 已知O是坐标原点, 点A的坐标是（5, 0）, 点B是y轴正半轴上一动点, 以OB, OA为边作矩形OBCA, 点E, H分别在边BC和边OA上, 将△BOE沿着OE对折, 使点B落在OC上的F点处, 将△ACH沿着CH对折, 使点A落在OC上的G点处.(1)求证: 四边形OECH是平行四边形；(2)当点B运动到使得点F, G重合时, 求点B的坐标, 并判断四边形OECH是什么四边形？说明理由；(3)当点B运动到使得点F, G将对角线OC三等分时, 直接写出点B的坐标．16. 如图, 把矩形OABC放入平面直角坐标系xOy中, 使分别落在x, y轴的正半轴上, 其中, 对角线AC所在直线解析式为, 将矩形OABC沿着BE折叠, 使点A落在边OC 上的D处.(1)求点B的坐标；(2)求EA的长度；(3)点P是y轴上一动点, 是否存在点P使得△PBE的周长最小, 若存在, 请求出点P的坐标, 如不存在, 请说明理由.17. 【情境】某校数学兴趣小组尝试自制数学学具进行自主合作探究. 图①是一块边长为的等边三角形学具, 是边上一个动点, 由点向点运动, 速度为, 是边延长线上一动点, 与点同时以相同的速度由点向延长线方向运动, 连接, 交于点, 设点运动的时间为.(1)【问题】填空: _____；(2)【问题】当时, 求的值；(3)【探究】如图②, 过点作, 垂足为, 在点, 点运动过程中, 线段的长度是否发生变化？若不变, 请求出的长度；若变化, 请说明理由．18. 在长方形ABCD中, AB＝4, BC＝8, 点P、Q为BC边上的两个动点（点P位于点Q的左侧, P、Q均不与顶点重合）, PQ＝2(1)如图①, 若点E为CD边上的中点, 当Q移动到BC边上的中点时, 求证: AP＝QE；(2)如图②, 若点E为CD边上的中点, 在PQ的移动过程中, 若四边形APQE的周长最小时, 求BP的长；(3)如图③, 若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合）, 当BP＝3, 且四边形PQNM的周长最小时, 求此时四边形PQNM的面积．19. 如图, 长方形ABCD中, AB＝4cm, BC＝6cm, 现有一动点P从A出发以2cm/秒的速度, 沿矩形的边A—B—C—D—A返回到点A停止, 点P的运动时间为t秒.（1）当t＝3秒时, BP＝cm；（2）当t为何值时, 连结CP, DP, △CDP为等腰三角形；（3）Q为AD边上的点, 且DQ＝5, 当t为何值时, 以长方形的两个顶点及点P为顶点的三角形与△DCQ全等．20. 在矩形ABCD中, AB=6, BC=8, 点E是射线BC上一个动点, 连接AE并延长交射线DC于点F, 将△ABE沿直线AE翻折到△AB'E, 延长AB'与直线CD交于点M.(1)求证: AM=MF；(2)当点E是边BC的中点时, 求CM的长；(3)当CF=4时, 求CM的长．参考答案:1. （1）2t−7；（2）S=；（3）点到四边形ABED任意相邻两边距离相等时的值为1.5秒或3秒.2. (1)等腰直角三角形,(2), 证明见解析3. (1)(2)4t=或8 5(3)见解析4. (1)①证明见解析；②结论,(2)BE的长为6+6-6. (1)BC的长为3；(2)t的值为6秒或12秒或14秒.7. (1)(2)83或4(3)⑤AMN是锐角三角形8. (2)(3)2.49. （2）1；（3）210. （1）②GFC是等腰三角形；（2）BE的长为14或2.11. （2）成立12. (1)6(2)13 2(3)不存在13. (1)①, ；②成立(2)成立14. (1), ；(2)当t为0或4时, △PQC的面积是平行四边形OABC面积的一半(3)或（10, -4）或或（18, 0）或或15. (2)B（0, ）；四边形OECH是菱形(3)点B的坐标是（0, ）或（0, ）16．(1)B（6, 10）(2)103 AE=(3)400,13 P⎛⎫ ⎪⎝⎭17. (1)24(2)4(3)线段DE的长度不改变, DE=618. (2)4(3)419. （1）2；（2）或或；（3）2.5或4.5或7.5或9.5 20．(2)8 3(3)215或21。

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1．（三角形翻折问题）如图，在Rt ABC △中，9086ABC AB BC ∠=︒==，，，分别在AB AC ，边上取点E F ，，将AEF △沿直线EF 翻折得到A EF '△，使得点A 的对应点A '恰好落在CB 延长线上，当60EA B '∠=︒时，AE 的长为，当A F AC '⊥时，AF 的长为．【答案】 32− 407【分析】由折叠的性质可得AE A E '=，先求出30A EB '∠=︒，从而可得1122A B A E AE ''==，再由勾股定理可得BE AE =，最后由AE BE AB +=，进行计算即可；令A F '交AB 于G ，连接CG ，由折叠的性质可得：A EA F '∠=∠，AFE A FE '∠=∠，AEF A EF '∠=∠，AF A F '=，由A F AC '⊥得出90A FA A FC ''∠=∠=︒，45AFE A FE '∠=∠=︒，证明()ASA A FC AFG '≌得到CF FG =，设CF FG x ==，则10AF x =−，AG ，根据1122ACG S AC FG AG BC =⋅=⋅建立方程，解方程即可得出CF 的长，即可求解．【详解】解：由折叠的性质可得：AE A E '=，90ABC ∠=︒，18090A BE ABC '∴∠=︒−∠=︒，60EA B '∠=︒，9030A EB EA B ''∴∠=︒−∠=︒，1122A B A E AE ''∴==，BE AE∴==，AE BE AB+=，8AE AE∴=，32AE∴=−如图，令A F'交AB于G，连接CG，A F AC'⊥，90A FA A FC''∴∠=∠=︒，由折叠的性质可得：A EA F'∠=∠，AFE A FE'∠=∠，AEF A EF'∠=∠，AF A F'=，90AFE A FE'∠+∠=︒，45AFE A FE'∴∠=∠=︒，设A EA Fα'∠=∠=，则45FEB AFEα∠=∠=+︒，180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠，()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−，902EA B A EBα''∴∠=︒−∠=，FA C EA B EA F Aα'''∴∠=∠−∠==∠，在A FC'和AFG中，CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩'，()ASAA FC AFG'∴≌，CF FG∴=，在Rt ABC△中，9086ABC AB BC∠=︒==，，，10AC∴，设CF FG x==，则10AF x=−，AG∴==1122ACGS AC FG AG BC=⋅=⋅，106x∴⋅=，整理得：271809000x x+−=，即29014400749x⎛⎫+=⎪⎝⎭，9012077x∴+=±，解得：307x=或30x=−（不符合题意，舍去），307CF∴=，30401077AF AC CF∴=−=−=，故答案为：32−407．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识，熟练掌握以上知识点，添加适当的辅助线是解此题的关键．例2．（坐标系中折叠问题）如图，在平面直角坐标系中，长方形ABCO的边OC OA、分别在x轴、y轴上，6AB=，点E在边BC上，将长方形ABCO沿AE折叠，若点B的对应点F 恰好是边OC的三等分点，则点E的坐标是．【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题，坐标与图形，由折叠的性质可得6AF AB==，BE EF=，90AFE B∠=∠=︒，再分当点F靠近点C时，24CF OF==，，当点F靠近点O 时，则42CF OF==，，两种情况利用勾股定理先求出OA的长，进而得到BC的长，设出CE 的长，进而得到EF的长，在Rt EFC△中，由勾股定理建立方程求解即可．【详解】解：在长方形ABCO 中，6CO AB ==，90BCO B AOC ∠=∠=∠=︒，由折叠的性质可得6AF AB ==，BE EF =，90AFE B ∠=∠=︒，F 恰好是边OC 的三等分点，∴当点F 靠近点C 时，24CF OF ==，，在Rt AFO V中，OA =，∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222EF CF CE =+，∴()2222xx =+，解得x =，∴点E的坐标是⎛− ⎝⎭；当点F 靠近点O 时，则42CF OF ==，，在Rt AFO V中，OA ==∴BC OA ==设CE x =，则BE EF x ==，在Rt EFC △中，由勾股定理得到222CF CE =+，∴()2224x x =+，解得x =∴点E的坐标是(−；综上所述，点E的坐标是⎛− ⎝⎭或(−，故答案为：⎛− ⎝⎭或(−．例3．（四边形折叠问题）如图，已知矩形ABCD ，4AB =，5BC =，点P 是射线BC 上的动点，连接AP ，AQP △是由ABP 沿AP 翻折所得到的图形．(1)当点Q 落在边AD 上时，QC = ；(2)当直线PQ 经过点D 时，求BP 的长；(3)如图2，点M 是DC 的中点，连接MP 、MQ ．①MQ 的最小值为；②当PMQ 是以PM 为腰的等腰三角形时，请直接写出BP 的长．【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】（1）根据折叠的性质和勾股定理进行求解即可；（2）分点P 在线段BC 上，点P 在线段BC 的延长线上，两种情况，进行讨论求解；（3）①连接AM ，勾股定理求出AM 的长，折叠求出AQ 的长，根据MQ AM AQ ≥−，求出最小值即可；②分PM MQ =和PM PQ =两种情况，再分点P 在线段BC 上，点P 在线段BC 的延长线上，进行讨论求解即可．【详解】（1）解：当点Q 落在边AD 上时，如图所示，∵矩形ABCD ，4AB =，5BC =，∴4,5CD AB AD BC ====，90BAD B BCD ADC ∠=∠=∠=∠=︒，∵翻折，∴4,90AQ AB AQP B ==∠=∠=︒，∴1DQ AD AQ =−=，在Rt CDQ △中，CQ ==（2）当直线PQ 经过点D 时，分两种情况：当点P 在线段BC 上时，如图：∵翻折，∴4AQ AB ==，90AQP B ∠=∠=︒，BP PQ =，∴90AQD ∠=︒，∴3DQ ==，设BP PQ x ==，则：5PC BC BP x =−=−，3DP DQ PQ x =+=+，在Rt PCD △中，222DP CP CD=+，即：()()222345x x +=+−，∴2x =；∴2BP =；②当P 在线段BC 的延长线上时：∵翻折，∴4,90AQ AB Q B ==∠=∠=︒，BP PQ =，∴3DQ ==，设BP PQ x ==，则：5PC BP BC x =−=−，3DP PQ DQ x =−=−，在Rt PCD △中，222DP CP CD =+，即：()()222345x x −=+−，∴8x =；∴8BP =；综上：2BP =或8BP =；（3）①连接AM ，∵M 是CD 的中点， ∴122DM CM CD ===，∴AM =∵翻折，∴4AQ AB ==，∵MQ AM AQ ≥−，∴当,,A Q M 三点共线时，MQ 的值最小，即：4MQ AM AQ =−=4；②当PM PQ =时，如图：∵翻折，∴BP PQ PM ==，设BP x =，则：,5PM x CP BC BP x ==−=−，在Rt PCM 中，222PM CM PC =+，即：()22225x x =+−，解得： 2.9x =，即： 2.9BP =；当PM QM =，点P 在线段BC 上时，如图：∵,QM PM DM CM ==，90D C ∠=∠=︒，∴()HL MDQ MCP ≌，∴CP DQ =，点Q 在AD 上，由（1）知：1DQ =，∴1CP DQ ==，∴4BP BC CP =−=；当点P 在BC 的延长线上时：如图：此时点M 在AP 上，连接BM ，∵翻折，∴BM MQ PM ==，∵MC BP ⊥，∴210BP BC ==；综上： 2.9BP =或4BP =或10BP =．质，综合性强，难度大，属于压轴题．利用数形结合和分类讨论的思想进行求解，是解题的关键．【模拟训练】1．如图，在长方形ABCD 中，点E 是AD 的中点，将ABE 沿BE 翻折得到FBE ，EF 交BC 于点H ，延长BF DC 、相交于点G ，若8DG =，10BC =，则DC = ．【答案】258【分析】本题考查了全等三角形的判定与性质，折叠的性质，勾股定理，连接EG ，根据点E 是AD 的中点得DE AE EF ==，根据四边形ABCD 是长方形得90D A ∠=∠=︒，根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒，利用HL 证明Rt Rt EFG EDG △≌△，得8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG V △中，根据勾股定理得，222CG BC BG +=，进行计算即可得．【详解】解：如图所示，连接EG ，∵点E 是AD 的中点，∴DE AE EF ==，∵四边形ABCD 是长方形，∴90D A ∠=∠=︒，∵将ABE 沿BE 翻折得到FBE ，∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中，EF ED EG EG =⎧⎨=⎩，∴()Rt Rt HL EFG EDG V V ≌，∴8FG DG ==，设DC x =，则8CG DG DC x =−=−，8BG BF FG AB FG DC FG x =+=+=+=+，在Rt BCG 中，根据勾股定理得，222CG BC BG +=，∴222(8)10(8)x x −+=+，解得258x =，故答案为：258．2．如图，在Rt ABC △中，90ACB ∠=︒，254AB =，154=AC ，点D 是AB 边上的一个动点，连接CD ，将BCD △沿CD 折叠，得到CDE ，当DE 与ABC 的直角边垂直时，AD 的长是．【答案】154或54【分析】本题考查了勾股定理，平行四边形的判定和性质，折叠的性质，全等三角形的判定和性质，分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案，根据题意，正确画出图形是解题的关键．【详解】解：如图，当DE BC ⊥时，延长ED 交BC 于点F ，CE 与AB 相交于点M ，∵EF BC ⊥，∴90EFC EFB ∠=∠=︒，∴90E ECF ∠+∠=︒，由折叠得，B E ∠=∠，CE CB =，MCD FCD ∠=∠，∴90B ECF ∠+∠=︒，∴90CMB ∠=︒，即C M A B ⊥，∵90ACB ∠=︒，254AB =，154=AC ，∴5BC ==， ∵1122ABC S AC BC AB CM ==△，∴11512552424CM ⨯⨯=⨯⨯，解得3CM =，∴4BM =，∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴()AAS CFD CMD ≌，∴3CF CM ==，DF DM =，∴532BF BC CF =−=−=，设DF DM x ==，则4BD x =−，在Rt BFD 中，222DF BF BD +=，∴()22224x x +=−，解得32x =， ∴35422BD =−=， ∴25515424AD AB BD =−=−=；当DE AB ⊥时，如图，设DE 与AC 相交于点M ，由折叠可得，BCD ECD ∠=∠，DE DB =，ED BD =，5EC BC ==，∵DE AB ⊥，90ACB ∠=︒，∴DE BC ∥，∴EDC BCD ∠=∠，∴EDC ECD ∠=∠，∴5ED EC ==，∴5BD ED ==， ∴255544AD AB BD =−=−=；综上，AD 的长是154或54，故答案为：154或54．3．如图，等边三角形ABC 中，16AB BD AC =⊥，于点D ，点E F 、分别是BC DC 、上的动点，沿EF 所在直线折叠CEF △，使点C 落在BD 上的点C '处，当BEC '△是直角三角形时，BE 的值为．【答案】24−或323【分析】本题考查了翻折变换，等边三角形的性质，折叠的性质，熟练运用折叠的性质是本题的关键．由等边三角形的性质可得30DBC ∠=︒，分9090BEC BC E ''∠=︒∠=︒，两种情况讨论，由直角三角形的性质即可求解．【详解】解：ABC 是等边三角形，BD AC ⊥，30,DBC ∴∠=︒ 由折叠的性质可得：,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323．4．如图，在ABC 中，120ACB ∠=︒，8AC =，4BC =，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，使点A 落在CD 的延长线上的点A '处，两条折痕与斜边AB 分别交于点E 、F ，则线段FA '的长为．【答案】【分析】本题考查了折叠的性质，勾股定理，直角三角形的性质，添加恰当辅助线构造直角三角形是本题的关键．过点A 作AH BC ⊥交BC 的延长线于H ，由直角三角形的性质可求142HC AC ==，AH =AB 的长，由面积法可求CE 的长，由折叠的性质可求90BEC DEC ∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，然后再求解即可．【详解】解：如图，过点A 作AH BC ⊥，交BC 的延长线于H ，120ACB ∠=︒，ACB H HAC ∠=∠+∠，30HAC ∴∠=︒，142HC AC ∴==，AH ==，448BH ∴=+=，AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯，4CE ∴=，CE ∴，将边BC 沿CE 翻折，使点B 落在AB 上的点D 处，再将边AC 沿CF 翻折，90BEC DEC ∴∠=∠=︒，BCE DCE ∠=∠，ACF DCF ∠=∠，1602ECF ACB ∴∠=∠=︒，30CFE ∴∠=︒，EF ∴，在Rt BCE中，BE ===，AF AB EF BE ∴=−−==FA AF '∴==故答案为：5．如图，点D 是ABC 的边AB 的中点，将BCD △沿直线CD 翻折能与ECD 重合，若4AB =，2CD =，1AE =，则点C 到直线AB 的距离为．【答案】【分析】连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质及中点性质可得AEB △为直角三角形，且G 为BE 中点，从而CG BE ⊥，由勾股定理可得BE的长，再根据2ABC BDC S S =△△，即11222AB CH CD BG ⋅=⨯⋅，从而可求得CH 的长．【详解】解：连接BE ，延长CD 交BE 于点G ，作CH AB ⊥于点H ，如图所示，由折叠的性质可得：BD ED =，CB CE =，∴CG 为BE 的中垂线， ∴12BG BE =，∵点D 是AB 的中点，4AB =，2CD =，1AE =， ∴122BD AD AB ===，CBD CAD S S =，AD DE =，∴DBE DEB ∠=∠，DEA DAE ∠=∠，∵180EDA DEA DAE ∠+∠+∠=︒，即22180DEB DEA ∠+∠=︒，∴90DEB DEA ∠+∠=︒，即90BEA ∠=︒，∴BE∴12BG BE ==， ∵2ABC BDCS S =△△， ∴11222AB CH CD BG ⋅=⨯⋅，∴422CH =⨯，∴CH ，∴点C 到直线AB 的距离为．故答案为：．【点睛】本题考查翻折变换，线段中垂线的判定，等腰三角形的性质，点到直线的距离，直角三角形的判定，勾股定理，利用面积相等求相应线段的长，解题的关键是得出CG 为BE 的中垂线，2ABC BDC S S =△△．6．如图，在ABC 中，90,A AB AC ∠=︒==D 为AC 边上一动点，将C ∠沿过点D 的直线折叠，使点C 的对应点C '落在射线CA 上，连接BC '，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为．【答案】或【分析】由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==时，分别根据勾股定理求出AC '的长，再求出CC '的长即可【详解】解：由翻折得，12CD CC '=，分三种情况：①当点C '在边AC 上，且12AC BC ''=（即2BC AC ''=）时，90,A AB AC ∠=︒==∴由勾股定理得，222BC AC AB ''−=，即222(2)AC AC ''−=，AC '∴=CC '∴CD ∴；②当点C '在CA 的延长线上，且12AC BC ''=（即2BC AC ''=）时，同理得AC 'CC '∴CD ∴；③当点C '在CA 的延长线上，且12AB BC '=（即2BC AB '==由勾股定理得，222AC BC AB ''=−，即22218AC '=−=，AC '∴=CC '∴CD ∴=，0>，CD AB ∴>，此时点D 不在边AC 上，不符合题意，舍去，综上，当Rt ABC '△的某一直角边等于斜边BC '长度的一半时，CD 的长度为或．故答案为：或．【点睛】本题主要考查图形的翻折变换（折叠问题），勾股定理，等腰直角三角形的性质等知识，灵活运用折叠的性质及勾股定理是解答本题的关键，同时要注意分类思想的运用．7．如图，在ABC 中，90ACB ∠=︒，3AC =，4BC =，P 为斜边AB 上的一动点（不包含A ，B 两端点），以CP 为对称轴将ACP △翻折得到A CP '，连结BA '．当A P AB '⊥时，BA '的长为．【答案】【分析】当A P AB '⊥时，过点C 作CD AB ⊥于D ，可知125CD =，95AD =，得出PDC △为等腰直角三角形，得到PD CD =，求出PA '和BP 的长，利用勾股定理即可求出BA '的长．【详解】过点C 作CD AB ⊥于D ，在Rt ADC 中，90ACB ∠=︒，3AC =，4BC =，∴5AB = ∵1122AC BC AB CD ⨯=⨯，125CD ∴=，在Rt ADC 中，3AC =∴95AD ==，当A P AB '⊥时，如图由折叠性质可知12∠=∠，PA PA '=，又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴，又2390∠+∠=︒，345∴∠=︒，23∴∠=∠，125PD CD ∴==，又PA PD AD =+，12921555PA ∴=+=，又PA PA '=，215PA '∴=，又BP AB PA =−，214555BP ∴=−=，在Rt BPA '△中，90BPA ∠='︒，222BP PA BA ∴='+，2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭，BA '∴=，故答案为：．【点睛】本题考查了勾股定理的应用，折叠问题，熟练掌握勾股定理是解题的关键．8．如图，在ABC 中，90ACB ∠=︒，AC BC =，D 为AB 上一点，连接DC ，将BDC 沿DC 翻折，得到EDC △，连接AE ，若AE CE =，4BC =，则D 到CE 的距离是．【答案】2【分析】本题考查等腰直角三角形中的折叠问题，涉及等边三角形判定与性质，勾股定理应用、面积法等知识．设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，根据将BDC 沿DC 翻折，得到EDC △，AC BC =，AE CE =，可得ACE △是等边三角形，即知60ACE ∠=︒，而90ACB ∠=︒，故150BCE ∠=︒，30ECF ∠=︒，可得75BCD ECD ∠=∠=︒，122EF CE ==，CF =BE =15CBE ∠=︒，可得90BGC ∠=︒，即CG BE ⊥，从而12BG BE GE ===，由勾股定理得CG ，在Rt BDG △中，DG ，即得CD DG CG =+，由面积法可得D 到CE 的距离是2．【详解】解：设BE 交CD 于G ，过E 作EF BC ⊥交BC 延长线于F ，如图：将BDC 沿DC 翻折，得到EDC △，4BC CE ∴==，BCD ECD ∠=∠，AC BC =，AE CE =，AC BC CE AE ∴===，ACE ∴是等边三角形，60ACE ∴∠=︒，90ACB ∠=︒，150BCE ∴∠=︒，30ECF ∠=︒，75BCD ECD ∴∠=∠=︒，122EF CE ==，CF =在Rt BEF △中，BE ==BCE 中，BC CE =，150BCE ∠=︒，15CBE ∴∠=︒，18090BGC BGC BCD ∴∠=︒−∠−∠=︒，即CG BE ⊥，12BG BE GE ∴==，CG ∴===，45ABC ∠=︒，15CBE ∠=︒，30DBG ∴∠=︒，在Rt BDG△中，DG =，CD DG CG ∴=+=，设D 到CE 的距离是h ，2DCE S CE h DC GE ∆=⋅=⋅，324DC GE h CE ⋅∴===，故答案为：2．9．在生活中、折纸是一种大家喜欢的活动、在数学中，我们可以通过折纸进行探究，探寻数学奥秘．【纸片规格】三角形纸片ABC ，120ACB ∠=︒，CA CB =，点D是底边AB 上一点．【换作探究】(1)如图1，若6AC =，AD =CD ，求CD 的长度；(2)如图2，若6AC =，连接CD ，将ACD 沿CD 所在直线翻折得到ECD ，点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直，求AD 的长；(3)如图3，将ACD 沿CD 所在直线翻折得到ECD ，边CE 与边AB 交于点F ，且DE BC ∥，再将DFE △沿DF 所在直线翻折得到DFG ，点E 的对应点为点G ，DG 与CE 、BC 分别交于H ，K ，若1KH =，请直接写出AC 边的长．【答案】(1)(2)3或(3)3【分析】（1）作CE AB ⊥于E ，求得30A B ==︒∠∠，从而得出132CE AC ==，AE AC =进而得出DE AE AD =−=（2）当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，依次得出45DAE DEA ∠=∠=︒，304575CAE CAD DAE ∠=∠+∠=︒+︒=︒，75CEA CAE ∠=∠=︒，30ACE ∠=︒，15ACD DCE ∠=∠=︒，45CDG CAB DAC ∠=∠+∠=︒，从而DG CG =，进一步得出结果；当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，可推出90AVC ∠=︒，60ACE ∠=︒，从而30ACD DCE ∠=∠=︒，进一步得出结果；当DE BC ⊥时，可推出180ACB BCE ∠+∠=︒，从而90ACD DCE ∠=∠=︒，进一步得出结果；（3）可推出CKH 和CDH △及CHK 是直角三角形，且30HCK ∠=︒，30HDF ∠=︒，45DCH ∠=︒，进一步得出结果．【详解】（1）解：如图1，作CE AB ⊥于E ，90AEC ∴∠=︒，CA CB =，120ACB ∠=︒，30A B ∴∠=∠=︒，132CE AC ∴==，AE =，DE AE AD ∴=−==CD ∴=；（2）解：如图2，当DE AB ⊥时，连接AE ，作CG AB ⊥于G ，由翻折得：AD DE =，CAD CED =∠∠，AC CE =，45DAE DEA ∠∠∴==︒，304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒，75CEA CAE ∴∠=∠=︒，30ACE ∴∠=︒，15ACD DCE ∴∠=∠=︒，45CDG CAB DAC ∴∠=∠+∠=︒，DG CG ∴=，由（1）知：3CG =，AG =3AD AG DG ∴=−=；如图3，当ED AC ⊥时，设ED 交AC 于点W CE ，交AB 于V ，90E ACE ∴∠+∠=︒，E A ∠=∠，90A ACE ∴∠+∠=︒，90AVC ∴∠=︒，60ACE∴∠=︒，30ACD DCE∴∠=∠=︒，ACD A∴∠=∠，AD CD∴=，3CV =，CD∴=，AD CD∴==如图4，当DE BC⊥时，30E A∠=∠=︒，60BCE∴∠=︒，180ACB BCE∴∠+∠=︒，90ACD DCE∴∠=∠=︒，AD∴=，综上所述：3AD=或（3）解：如图5，∵DE BC ∥，30B C ∠=∠=︒，30BCF E ∴∠=∠=︒，30EDF B ∠=∠=︒，120ACB ∠=︒，90ACE ∴∠=︒，1452ECD ACD ACE ∴∠=∠=∠=︒，将DFE △沿DF 所在直线翻折得到DFG ，30GDF EDF ∴∠=∠=︒，60EDG ∴∠=︒，90CHK EHD ∴∠=∠=︒，DH CH ∴=1FH ∴==，1CF CH FH ∴=+，3AC ∴==．【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质等知识，解决问题的关键是正确分类，画出图形．10．如图，在ABC 中，90BAC ∠=︒，AB AC =，点D 为线段BC 延长线上一点，以AD 为腰作等腰直角DAF △，使90DAF ∠=︒，连接CF ．(1)请判断CF 与BC 的位置关系，并说明理由；(2)若8BC =，4CD BC =，求线段AD 的长；(3)如图2，在（2）的条件下，将DAF △沿线段DF 翻折，使点A 与点E 重合，连接CE ，求线段CE 的长．【答案】(1)CF BC ⊥，理由见解析(2)(3)【分析】（1）证明()SAS ABD ACF △≌△，则ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，可得90FAO DCO ∠=∠=︒，进而可得CF BC ⊥；（2）如图2，过A 作AH BC ⊥于H ，则142BH CH AH BC ====，6DH =，由勾股定理得，AD =（3）由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，证明()AAS ADM DEN ≌，则46DN AM EN DM ====，，6CN =，由勾股定理得，CE =计算求解即可．【详解】（1）解：CF BC ⊥，理由如下：∵等腰直角DAF △，90DAF ∠=︒，∴AD AF =，又∵90BAC ∠=︒，∴BAC CAD DAF CAD ∠+∠=∠+∠，即BAD CAF ∠=∠，∵AB AC =，BAD CAF ∠=∠，AD AF =，∴()SAS ABD ACF △≌△，∴ADB AFC ∠=∠，如图1，记AD CF 、的交点为O ，∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠，AOF COD ∠=∠，∴90FAO DCO ∠=∠=︒，∴CF BC ⊥；（2）解：∵8BC =，4CD BC =，∴2CD =，如图2，过A 作AH BC ⊥于H ，∵ABC 是等腰直角三角形， ∴142BH CH AH BC ====，∴6DH =，由勾股定理得，AD =∴线段AD 的长为（3）解：由翻折的性质可知，DE AD =，45EDF ADF ∠=∠=︒，∴90ADE ∠=︒，如图3，过A 作AM BC ⊥于M ，过E 作EN BC ⊥于N ，∴90AMD DNE ∠=︒=∠，同理（2）可知，4AM =，6MD =，∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠，∴ADM DEN ∠=∠，∵90AMD DNE ∠=︒=∠，ADM DEN ∠=∠，AD DE =，∴()AAS ADM DEN ≌，∴46DN AM EN DM ====，，∴6CN =，由勾股定理得，CE =，∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质，三角形内角和定理，勾股定理，折叠的性质，等腰三角形的性质．熟练掌握全等三角形的判定与性质，折叠的性质是解题的关键．11．如图1，在Rt ABC △中，90C ∠=︒，5AC =，12BC =，点D 为BC 边上一动点，将ACD 沿直线AD 折叠，得到AFD △，请解决下列问题．(1)AB =______；当点F 恰好落在斜边AB 上时，CD =______；(2)连接CF ，当CBF V 是以CF 为底边的等腰三角形时，请在图2中画出相应的图形，并求出此时点F 到直线AC 的距离；(3)如图3，E 为边BC 上一点，且4，连接EF ，当DEF 为直角三角形时，CD = ．（请写出所有满足条件的CD 长）【答案】(1)13，103(2)画图见解析，600169(3)52或或5或10【分析】（1）根据勾股定理可得AB 的长，再利用等积法求出CD 即可；（2）过点F 作FG AC ^，交CA 的延长线于G ，首先由等积法求出CH 的长，再根据勾股定理求出AH 的长，再次利用等积法可得FG 的长；（3）分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形，从而解决问题．【详解】（1）解：在Rt ABC △中，由勾股定理得，13AB ，当点F 落在AB 上时，由折叠知，CD DF =， ∴111222AC CD AB DF AC BC ⋅+⋅=⋅，51360CD CD ∴+=，103CD ∴=，故答案为：13，103；（2）过点F 作FG AC ^，交CA 的延长线于G ，BC BF =，AC AF =，AB ∴垂直平分CF ，由等积法得6013AC BC CH AB ⋅==，在Rt ACH 中，由勾股定理得，2513AH ===， 1122ACF S AC FG CF AH =⋅=⋅△，6025260013135169CF AH FG AC ⨯⨯⋅∴===；（3）当90DEF ∠=︒时，当点D 在CE 上时，作FH AC ⊥于H ，则4HF CE ==，5AF AC ==，3AH ∴=，2CH EF AC AH ∴==−=，设CD x =，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)2x x =−+，解得52x =，52CD ∴=，当点D 在EB 上时，同理可得538CH AC AH =+=+=，设CD DF x ==，则4DE x =−，在Rt EDF 中，由勾股定理得，222(4)8x x −+=，解得10x =，10CD ∴=，当90DFE ∠=︒时，由勾股定理得AE设CD DF x ==，则520x +=，x ∴，CD ∴=；当90FDE ∠=︒时，则45ADC ADF ∠=∠=︒，5CD AC ∴==，综上：52CD =或或5或10，故答案为：52或或5或10．【点睛】本题是三角形综合题，主要考查了翻折的性质，直角三角形的性质，勾股定理，等腰直角三角形的判定与性质等知识，利用等积法求垂线段的长是解题的关键．。

人教版八年级下册压轴题训练（含答案）

人教版八年级下册压轴题训练（含答案）压轴题训练01一．解答题（共3小题）1．如图①，已知抛物线y＝ax2+bx+c的图象经过点A（0，3）、B（1，0），其对称轴为直线l：x＝2，过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P 是抛物线上的一个动点，设其横坐标为m．（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当m 为何值时，四边形AOPE 面积最大，并求出其最大值；（3）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．【分析】（1）利用对称性可得点D的坐标，利用交点式可得抛物线的解析式；（2）设P（m，m2﹣4m+3），根据OE的解析式表示点G的坐标，表示PG的长，根据面积和可得四边形AOPE的面积，利用配方法可得其最大值；（3）存在四种情况：如图3，作辅助线，构建全等三角形，证明△OMP≌△PNF，根据|OM|＝|PN|，列方程可得点P的坐标；同理可得其他图形中点P的坐标．【解答】解：（1）如图1，设抛物线与x轴的另一个交点为D，由对称性得：D（3，0），设抛物线的解析式为：y＝a（x﹣1）（x﹣3），把A（0，3）代入得：3＝3a，a＝1，∴抛物线的解析式；y＝x2﹣4x+3；（2）如图2，∵△AOE的面积是定值，所以当△OEP面积最大时，四边形AOPE面积最大，设P（m，m2﹣4m+3），∵OE平分∠AOB，∠AOB＝90°，∴∠AOE＝45°，∴△AOE是等腰直角三角形，∴AE＝OA＝3，∴E（3，3），易得OE的解析式为：y＝x，过P作PG∥y轴，交OE于点G，∴G（m，m），∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣3，∴S四边形AOPE＝S△AOE+S△POE，＝×3×3+PG?AE，＝+×3×（﹣m2+5m﹣3），＝﹣+，＝﹣（m﹣）2+，∵﹣＜0，∴当m＝时，S有最大值是；（3）分四种情况：①当P在对称轴的左边，且在x轴下方时，如图3，过P作MN⊥y 轴，交y轴于M，交l于N，∵△OPF是等腰直角三角形，且OP＝PF，易得△OMP≌△PNF，∴OM＝PN，∵P（m，m2﹣4m+3），则﹣m2+4m﹣3＝2﹣m，解得：m＝（舍）或，∴P的坐标为（，）；②当P在对称轴的左边，且在x轴上方时，如图3，同理得：2﹣m＝m2﹣4m+3，解得：m1＝（舍）或m2＝，③当P在对称轴的右边，且在x轴下方时，如图4，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP≌△PMF，∴PN＝FM，则﹣m2+4m﹣3＝m﹣2，解得：x＝或（舍）；P的坐标为（，）；④当P在对称轴的右边，且在x轴上方时，同理得m2﹣4m+3＝m﹣2，解得：m＝或（舍）P的坐标为：（，）；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．【点评】本题属于二次函数综合题，主要考查了二次函数的综合应用，相似三角形的判定与性质以及解一元二次方程的方法，解第（2）问时需要运用配方法，解第（3）问时需要运用分类讨论思想和方程的思想解决问题．压轴题训练04一．解答题（共1小题）1．如图，已知直线l的解析式为y＝x﹣1，抛物线y＝ax2+bx+2 经过点A（m，0），B（2，0），D（1，）三点．（1）求抛物线的解析式及A点的坐标，并在图示坐标系中画出抛物线的大致图象；（2）已知点P（x，y）为抛物线在第二象限部分上的一个动点，过点P作PE垂直x轴于点E，延长PE与直线l交于点F，请你将四边形P AFB的面积S表示为点P的横坐标x的函数，并求出S的最大值及S最大时点P的坐标；（3）将（2）中S最大时的点P与点B相连，求证：直线l上的任意一点关于x轴的对称点一定在PB所在直线上．压轴题训练02参考答案与试题解析一．解答题（共1小题）1．如图，已知直线l的解析式为y＝x﹣1，抛物线y＝ax2+bx+2经过点A（m，0），B（2，0），D（1，）三点．（1）求抛物线的解析式及A点的坐标，并在图示坐标系中画出抛物线的大致图象；（2）已知点P（x，y）为抛物线在第二象限部分上的一个动点，过点P作PE垂直x轴于点E，延长PE与直线l交于点F，请你将四边形P AFB的面积S表示为点P的横坐标x的函数，并求出S的最大值及S最大时点P的坐标；（3）将（2）中S最大时的点P与点B相连，求证：直线l上的任意一点关于x轴的对称点一定在PB所在直线上．【分析】（1）根据待定系数法可求抛物线的解析式，再根据A （m，0）在抛物线上，得到0＝﹣m2﹣m+2，解方程即可得到m的值，从而得到A点的坐标；（2）根据四边形P AFB的面积S＝AB?PF，可得S＝﹣（x+2）2+12，根据函数的最值可得S的最大值是12，进一步得到点P的坐标为；（3）根据待定系数法得到PB所在直线的解析式为y＝﹣x+1，设Q（a，a﹣1）是y ＝x﹣1上的一点，则Q点关于x轴的对称点为（a，1﹣a），将（a，1﹣a）代入y ＝﹣x+1显然成立，依此即可求解．【解答】解：（1）∵抛物线y＝ax2+bx+2经过点B（2，0），D（1，），∴，解得a＝﹣，b＝﹣，∴抛物线的解析式为y＝﹣x2﹣x+2，∵A（m，0）在抛物线上，∴0＝﹣m2﹣m+2，解得：m1＝﹣4，m2＝2（舍去），∴A点的坐标为（﹣4，0）．如图所示：（2）∵直线l的解析式为y＝x﹣1，∴S＝AB?PF＝×6?PF＝3（﹣x2﹣x+2+1﹣x）＝﹣x2﹣3x+9＝﹣（x+2）2+12，其中﹣4＜x＜0，∴S的最大值是12，此时点P的坐标为（﹣2，2）；（3）∵直线PB经过点P（﹣2，2），B（2，0），∴PB所在直线的解析式为y＝﹣x+1，设Q（a，a﹣1）是y＝x﹣1上的一点，则Q点关于x轴的对称点为（a，1﹣a），将（a，1﹣a）代入y＝﹣x+1显然成立，∴直线l上的任意一点关于x轴的对称点一定在PB所在直线上．【点评】本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求抛物线的解析式，待定系数法求直线的解析式，函数的最值问题，四边形的面积求法，以及关于x 轴的对称点的坐标特征．压轴题训练03姓名：班级；学号：一．解答题（共3小题）1．已知平面直角坐标系xOy（如图），双曲线y＝（k≠0）与直线y＝x+2都经过点A（2，m）．（1）求k与m的值；（2）此双曲线又经过点B（n，2），过点B的直线BC与直线y ＝x+2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）若（2）的条件下，设直线y＝x+2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．2．如图，在矩形OABC中，OA＝3，OC＝5，分别以OA、OC 所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y＝（k ＞0）的图象经过点D且与边BA交于点E，连接DE．（1）连接OE，若△EOA的面积为2，则k＝；（2）连接CA、DE与CA是否平行？请说明理由；（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．3．已知如图，二次函数图象经过点A（﹣6，0），B（0，6），对称轴为直线x＝﹣2，顶点为点C，点B关于直线x＝﹣2的对称点为点D．（1）求二次函数的解析式以及点C和点D的坐标；（2）联结AB、BC、CD、DA，点E在线段AB上，联结DE，若DE平分四边形ABCD 的面积，求线段AE的长；（3）在二次函数的图象上是否存在点P，能够使∠PCA＝∠BAC？如果存在，请求出点P的坐标；若不存在，请说明理由．参考答案与试题解析一．解答题（共3小题）1．已知平面直角坐标系xOy（如图），双曲线y＝（k≠0）与直线y＝x+2都经过点A（2，m）．（1）求k与m的值；（2）此双曲线又经过点B（n，2），过点B的直线BC与直线y ＝x+2平行交y轴于点C，联结AB、AC，求△ABC的面积；（3）若（2）的条件下，设直线y＝x+2与y轴交于点D，在射线CB上有一点E，如果以点A、C、E所组成的三角形与△ACD相似，且相似比不为1，求点E的坐标．【解答】解：（1）∵直线y＝x+2都经过点A（2，m），∴m＝2+2＝4，则A（2，4），∵双曲线y＝（k≠0）经过点A，∴k＝2×4＝8；（2）∵双曲线经过点B（n，2），∴2n＝8，解得n＝4，∴B（4，2），由题意可设直线BC解析式为y＝x+b，把B点坐标代入可得2＝4+b，解得b＝﹣2，∴直线BC解析式为y＝x﹣2，∴C（0，﹣2），∴AC＝＝＝2，BC＝＝＝4，AB＝＝＝2，∴BC2+AB2＝AC2，∴△ABC是以AC为斜边的直角三角形，∴S△ABC＝AB?BC＝×2×4＝8；（3）∵直线y＝x+2与y轴交于点D，∴D（0，2），∴AD＝＝2，且AC＝2如图所示，∵AD∥CE，∴∠DAC＝∠ACE，若∠ACD＝∠EAC，则AE∥CD，四边形AECD为平行四边形，此时△ADC≌△CEA，不满足条件，∴∠ACD＝∠AEC，∴△ACD∽△CAE，∴＝，即＝，解得CE＝10，∵E点在直线BC上，∴可设E（x，x﹣2）（x＞0），又∵C（0，﹣2），∴CE＝＝x，∴x＝10，解得x＝10，∴E点坐标为（10，8）．2．如图，在矩形OABC中，OA＝3，OC＝5，分别以OA、OC 所在直线为x轴、y轴，建立平面直角坐标系，D是边CB上的一个动点（不与C、B重合），反比例函数y＝（k ＞0）的图象经过点D且与边BA交于点E，连接DE．（1）连接OE，若△EOA的面积为2，则k＝4；（2）连接CA、DE与CA是否平行？请说明理由；（3）是否存在点D，使得点B关于DE的对称点在OC上？若存在，求出点D的坐标；若不存在，请说明理由．【解答】解：（1）连接OE，如，图1，∵Rt△AOE的面积为2，∴k＝2×2＝4．（2）连接AC，如图1，设D（x，5），E（3，），则BD＝3﹣x，BE＝5﹣，＝，∴，又∵∠B＝∠B，∴△BDE∽△BCA，∴∠BED＝∠BAC，∴DE∥AC．（3）假设存在点D满足条件．设D（x，5），E（3，），则CD ＝x，BD＝3﹣x，BE＝5﹣，AE＝．作EF⊥OC，垂足为F，如图2，易证△B′CD∽△EFB′，∴，即＝，∴B′F＝，∴OB′＝B′F+OF＝B′F+AE＝+＝，∴CB′＝OC﹣OB′＝5﹣，在Rt△B′CD中，CB′＝5﹣，CD＝x，B′D＝BD＝3﹣x，由勾股定理得，CB′2+CD2＝B′D2，（5﹣）2+x2＝（3﹣x）2，解这个方程得，x1＝1.5（舍去），x2＝0.96，∴满足条件的点D存在，D的坐标为D（0.96，5）．3．已知如图，二次函数图象经过点A（﹣6，0），B（0，6），对称轴为直线x＝﹣2，顶点为点C，点B关于直线x＝﹣2的对称点为点D．（1）求二次函数的解析式以及点C和点D的坐标；（2）联结AB、BC、CD、DA，点E在线段AB上，联结DE，若DE平分四边形ABCD 的面积，求线段AE的长；（3）在二次函数的图象上是否存在点P，能够使∠PCA＝∠BAC？如果存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵二次函数经过A（﹣6，0），B（0，6），对称轴为直线x＝2，∴二次函数图象经过（2，0），设二次函数解析式为y＝a（x+6）（x﹣2），把B（0，6）代入得：6＝﹣12a，即a＝﹣，∴二次函数解析式为y＝﹣（x+6）（x﹣2）＝﹣x2﹣2x+6＝﹣（x+2）2+8，则C（﹣2，8），D（﹣4，6）；（2）如图1所示，由题意得：AB＝6，BC＝CD＝2，BD＝4，∵BD2＝CD2+BC2，∴∠DCB＝90°，∵直线AB的解析式为y＝x+6，直线DC解析式为y＝x+10，∴DC∥AB，∴四边形ABCD为直角梯形，若S梯形ABCD＝2S△ADE，即×2×（2+6）＝2××2×AE，解得：AE＝4；（3）如图2，在二次函数的图象上存在点P，使∠PCA＝∠BAC，直线CP与AB交于点G，可得GA＝GC，∵A（﹣6，0），C（﹣2，8），直线AB解析式为y＝x+6，设G （x，x+6），∴＝，两边平方得：2x2+24x+72＝2x2+8，移项合并得：24x＝﹣64，解得：x＝﹣，经检验是原方程的根且符合题意，∴G（﹣，），设直线CG解析式为y＝kx+b，把C与G坐标代入得：，解得：，∴直线CG解析式为y＝7x+22，联立得：，解得：或（经检验不合题意，舍去），∴P坐标为（﹣16，﹣90）；由（2）得到四边形ABCD为直角梯形，AB∥CD，∴∠DCA＝∠BAC，此时P与D重合，即P（﹣4，6），综上，满足题意P的坐标为（﹣16，﹣90）或（﹣4，6）．。

2024八年级下册期末压轴题集训(原卷版)

2024八年级下册期末压轴题集训一（原卷版）1、我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微”．请你利用“数形结合”的思想解决以下问题．如图1，边长为a的正方形中有一个边长为b的小正方形，图2是由图1中阴影部分拼成的一个长方形，设图1中阴影部分面积为S1，图2中阴影部分面积为S2．（1）请直接用含a和b的代数式表示S1＝，S2＝；写出利用图形的面积关系所得到的公式：（用式子表达）；（2）请依据（1）得到的公式计算：（2+1）（22+1）（24+1）（28+1）+1；（3）请用（1）中的公式证明任意两个相邻奇数的平方差必是8的倍数．2、如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AC，AB上，AD＝AE，连接DE，BD，点F，P，G别为DE，BD，BC的中点．（1）线段PF与PG的数量关系是，位置关系是；（2）把△ADE绕点A顺时针方向旋转到图2的位置，连接PF，PG，FG，判断△FPG的形状，并说明理由；（3）若AD＝3，AB＝7，△ADE绕点A在平面内旋转过程中，请直接写出△FPG的面积取得最大值时BD的长．3、经调研发现，目前市场上有A，B两种类型的笔记本比较畅销．某超市计划最多投入6900元购进A，B两种类型的笔记本共500本，其中B型笔记本的进货单价比A型笔记本的进货单价多3元；用2400元购进A型笔记本与用3000元购进B型笔记本的数量相同．（1）求A，B两种类型笔记本的进货单价；（2）若A型笔记本每本的售价定为16元，B型笔记本每本的售价定为20元，该超市计划购进A型笔记本m本，两种类型的笔记本全部销售后可获利润为y元．①请直接写出y与m之间的函数关系式为：；②该超市如何进货才能获得最大利润？最大利润是多少元？4、在等边△ABC中，AB＝6，点D是射线CB上一点，连接AD．（1）如图1，当点D在线段CB上时，在线段AC上取一点E，使得CE＝BD，求证：AD＝BE；（2）如图2，当点D在CB延长线上时，将线段AD绕点A逆时针旋转角度θ（0°＜θ＜180°）得到线段AF，连接BF，CF．①当AF位于∠BAC内部，且∠DAF恰好被AB平分时，若BD＝2，求CF的长度；②如图3，当θ＝120°时，记线段BF与线段AC的交点为G，猜想DC与AG的数量关系，并说明理由．5、如图，已知函数y1＝﹣x+b，y2＝mx﹣1，其中y1的图象经过点（3，0）．（1）当y1＞0时，x的取值范围是；（2）当x＞2时，对于x的每一个值，都有y1＜y2，求m的取值范围；（3）若m＝1，，求A、B的值．6、如图，△ABC是等边三角形，，点F是∠BAC的平分线上一动点，将线段AF绕点A顺时针方向旋转60°得到AE，连接CF、EF．（1）尺规作图：在AF的上方找点D，使得DE⊥AF且DE＝AC；（2）在（1）的条件下，连接CD、DF．①求证：AE+CD＞AC；②求证：△CDF是等边三角形；③当△DEF是等腰三角形时，求AF的长度？7、【探索发现】“旋转”是一种重要的图形变换，图形旋转过程中蕴含着众多数学规律，以图形旋转为依托构建的解题方法是解决几何问题的常用方法．如图1，在正方形ABCD中，点E在AD上，点F在CD上，∠EBF＝45°．某同学进行如下探索：第一步：将△ABE绕点B顺时针旋转90°，得到△CBG，且F、C、G三点共线；第二步：证明△BEF≌△BGF；第三步：得到∠AEB和∠FEB的大小关系，以及AE、CF、EF之间的数量关系；请完成第二步的证明，并写出第三步的结论．【问题解决】如图2，在正方形ABCD中，点P在AD上，且不与A、D重合，将△ABP绕点B顺时针旋转，旋转角度小于90°，得到△A'BP'，当P、A′、P′三点共线时，这三点所在直线与CD交于点Q，要求使用无刻度的直尺与圆规找到Q点位置，某同学做法如下：连接AC，与BP交于点O，以O为圆心，OB为半径画圆弧，与CD相交于一点，该点即为所求的点Q．请证明该同学的做法．（前面【探索发现】中的结论可直接使用，无需再次证明）【拓展运用】如图3，在边长为2的正方形ABCD中，点P在AD上，BP与AC交于点O，过点O作BP的垂线，交AB于点M，交CD于点N，设AP+AB＝x（2≤x≤4），AM＝y，直接写出y关于x的函数表达式．8、如图1，四边形ABCD为正方形，E为对角线AC上一点，连接DE，BE．（1）求证：BE＝DE；（2）如图2，过点E作EF⊥DE，交边BC于点F，以DE，EF为邻边作矩形DEFG，连接CG．①求证：矩形DEFG是正方形；②若正方形ABCD的边长为9，CG＝3，求正方形DEFG的边长．9、【探究发现】如图①，已知矩形ABCD的对角线AC的垂直平分线与边AD，BC分别交于点E，F．求证：四边形AFCE是菱形；（2）【类比应用】如图②，直线EF分别交矩形ABCD的边AD，BC于点E，F，将矩形ABCD沿EF翻折，使点C的对称点与点A重合，点D的对称点为D'，若AB＝3，BC＝4，求四边形ABFE的周长；（3）【拓展延伸】如图③，直线EF分别交平行四边形ABCD的边AD，BC于点E，F，将平行四边形ABCD沿EF翻折，使点C的对称点与点A重合，点D的对称点为D'，若，BC＝4，∠C＝45°，求EF的长．10、阅读材料：在数轴上，x＝2表示一个点；在平面直角坐标系中，x＝2表示一条直线；以二元一次方程x+y＝2的所有解为坐标的点组成的图形就是一次函数y＝﹣x+2的图象，它也是一条直线．如图1，在平面直角坐标系中，不等式x≤2表示一个平面区域，即直线x＝2及其左侧的部分；如图2，不等式y≤﹣x+2也表示一个平面区域，即直线y＝﹣x+2及其下方的部分．请根据以上材料回答问题：（1）图3阴影部分（含边界）表示的是（填写不等式）表示的平面区域；（2）如图4，请求出表示阴影部分平面区域（含边界）的不等式组；（3）如图5，点A在x轴上，点B的坐标为（0，1），且∠ABO＝60°，点P为△ABO内部一点（含边界），过点P分别作PC⊥OA，PD⊥AB，PE⊥BO，垂足分别为C，D，E，若PC≤PE≤PD，则所有点P组成的平面区域的面积为．11、【课本重现】已知：如图1，D，E分别是等边△ABC的两边AB，AC上的点，且AD＝CE．若BE，CD交于点F，则∠EFD＝°；【迁移拓展】如图2，已知点D是等边△ABC的AB边上一点，点E是AC延长线上一点，若AD＝CE，连接ED，EB．求证：ED＝EB；【拓展延伸】如图3，若点D，E分别是等边三角形ABC的边BA，AC延长线上一点，且连接DE，以DE为边向右侧作等边△DEF，连接AF，求△ADF的面积．12、【综合与实践】生活中，我们所见到的地面、墙面、服装面料等，上面的图案常常是由一种或几种形状相同的图形拼接而成的．用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌．（1）如图1，在▱ABCD中，AB＝2，AD＝3，∠BAD＝60°，图2右侧的阴影部分可以看成是左侧阴影部分沿射线AD方向平移而成，其中，平移的距离是.同理，再进行一次切割平移，可得图3，即图4可以看成由平行四边形经过两次切割平移而成．我们可以用若干个如图4所示的图形，平面镶嵌成如图5的图形，则图5的面积是．（2）小明家浴室装修，在墙中央留下了如图6所示的空白，经测量可以按图7所示，全部用边长为1的正三角形瓷砖镶嵌．小明调查后发现：一块边长为1的正三角形瓷砖比一块边长为1的正六边形瓷砖便宜40元；用500元购买正三角形瓷砖与用2500元购买正六边形瓷砖的数量相等．①请问两种瓷砖每块各多少元？②小明对比两种瓷砖的价格后发现：用若干块边长为1的正三角形瓷砖和边长为1的正六边形瓷砖一起镶嵌总费用会更少，按小明的想法，将空白处全部镶嵌完，购买瓷砖最少需要元．13、在等腰Rt△ABC中，∠ABC＝90°，点D是射线AB上的动点，AE垂直于直线CD于点E，交直线BC于点F．（1）【探索发现】如图①，若点D在AB的延长线上，点E在线段CD上时，请猜想CF，BD，AB之间的数量关系为；（2）【拓展提升】如图②，若点D在线段AB上（不与点A，B重合），试猜想CF，BD，AB之间的数量关系，并说明理由；（3）【灵活应用】当AB＝3，时，直接写出线段BD的长为．14、如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点均在格点上，在建立平面直角坐标系后，点C的坐标为（﹣2，﹣1）．（1）将△ABC向上平移6个单位得到△A1B1C1，画出△A1B1C1；（2）以（0，﹣1）为对称中心，画出△ABC关于该点对称的△A2B2C2；（3）经探究发现，△A1B1C1和△A2B2C2成中心对称，则对称中心坐标为；（4）已知点P为x轴上不同于O、D的动点，当P A+PC＝时，∠OPC＝∠DP A．15、问题情境：在学习《图形的平移和旋转》时，数学兴趣小组遇到这样一个问题：如图1，点D为等边△ABC的边BC上一点，将线段AD绕点A逆时针旋转60°得到线段AE，连接CE．（1）【猜想证明】试猜想BD与CE的数量关系，并加以证明；（2）【探究应用】如图2，点D为等边△ABC内一点，将线段AD绕点A逆时针旋转60°得到线段AE，连接CE，若B、D、E三点共线，求证：EB平分∠AEC；（3）【拓展提升】如图3，若△ABC是边长为2的等边三角形，点D是线段BC上的动点，将线段AD绕点D顺时针旋转60°得到线段DE，连接CE．点D在运动过程中，△DEC的周长最小值＝（直接写答案）．。

人教版八年级数学下册经典压轴题考点及例题解析

人教版八年级数学下册经典压轴题考点及例题解析例题1古希腊数学家把数 1 ， 3 ， 6 ， 10 ，15 ， 21 ，...... 叫做三角形数，它有一定的规律性。

若把第一个三角形数记为 a1 ，第二个三角形数记为 a2 ，......，第 n 个三角形数记为 an ，则 an + a(n+1) = ?答案：（n + 1）^2 。

例题2在平面直角坐标系中，对于平面内任意一点 P（a , b）若规定以下三种变换：① f（a , b）= （-a , b），如 f（2 , 5）= （-2 , 5）；② g（a , b） = （b , a）, 如 g（2 , 5）= （5 , 2）；③ h（a , b）= （-a , -b），如 h（2 , 5）= （-2 , -5）。

根据以上变换，那么 f（h（5 ， -3））等于多少？答案：（5,3）。

例题3如图，已知等腰直角△ABC 的直角边长为 1 ，以 Rt△ABC 的斜边 AC 为直角边，画第二个等腰 Rt△ACD ，在以 Rt△ACD 的斜边 AD 为直角边，画第三个等腰 Rt△ADE ， ... ，依次类推到第五个等腰 Rt△AFG ，则由这五个等腰直角三角形所构成的图形的面积是多少？答案：31/2 。

例题4如图所示，直线 OP 经过点 P（4,4√3），过 x 轴上的点 1、3、5、7、9、11 ......分别作 x 轴的垂线，与直线 OP 相交得到一组梯形，其阴影部分梯形的面积从左至右依次记为 S1 , S2 , S3 , ... , Sn , 则 Sn 关于 n 的函数关系式是？答案：Sn = 4√3 （2n - 1）。

例题5现将 1、√2、√3、√6 四个数按下列方式排列。

若规定（m , n）表示第 m 排从左到右第 n 个数，则（5 ， 4）与（15 ， 7）表示的两数之积是多少？答案：2√3 。

例题6现将一块直角三角形的花圃进行改造，已知两直角边长分别为 6 m 、8 m 。

2020-2021学年人教版八年级数学下册期末复习(一次函数压轴题)

人教版2020-2021年八年级下册期末复习（一次函数压轴题）一．解答题（共15小题）1．在平面直角坐标系中，A （0，8），点B 是直线y ＝x ﹣8与x 轴的交点．（1）写出点B 的坐标（，）；（2）点C 是x 轴正半轴上一动点，且不与点B 重合，∠ACD ＝90°，且CD 交直线y ＝x ﹣8于D 点，求证：AC ＝CD ；（3）在第（2）问的条件下，连接AD ，点E 是AD 的中点，当点C 在x 轴正半轴上运动时，点E 随之而运动，点E 到BD 的距离是否为定值？若为定值，求出这个值，若不是定值，请说明理由．2．已知，如图：在正方形OABC 中，A （0，1），B （1，1），C （1，0），D 为OB 延长线上的一动点，以AD 为一边在直线AD 下方作正方形ADEF ，AF 交OC 于点G ．（1）若S △AOD ＝1，求D 点的坐标；（2）①求证：点E 始终落在x 轴上；②若S 四边形ABCG ＝a •S △ABE ，1＜a ＜2，利用a 表示此时直线AF 的解析式．3．如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A （0，4）、B （﹣2，0）、C （23，0），点D 是边AC 上的一点，DE ⊥BC 于点E ．点F 在边AB 上，且D ，F 两点关于y 轴上的某点成中心对称．连接DF ，EF ．设点D 的横坐标为m ，EF 2为l ，请解决下列问题：（1）若一次函数的图象经过A 、C 两点，则此一次函数的表达式为；（2）若以EF 为边长的正方形面积为S ，请你求出S 关于m 的函数表达式及自变量的取值范围，并求出线段EF 长度的最小值；（3）△BEF 能否成为直角三角形．若能，求出m 的值；若不能，说明理由．4．如图，在平面直角坐标系中，一次函数12x 512-y +=的图象交x 轴、y 轴于A 、B 两点，以AB 为边在直线右侧作正方形ABCD ，连接BD ，过点C 作CF ⊥x 轴于点F ，交BD 于点E ，连接AE ．（1）求线段AB 的长；（2）求点C 的坐标（3）求证：AD 平分∠EAF ；（4）求△AEF 的周长5．如图1，已知直线y ＝kx +1交x 轴于点A 、交y 轴于点B ，且OA ：OB ＝4：3．（1）求直线AB 的解析式（2）如图2，直线y ＝31x +2与x 轴、y 轴分别交于点C 、D ，与直线AB 交于点P ． ①若点E 在线段P A 上且满足S △CDE ＝S △CDO ，求点E 的坐标；②若点M是位于点B上方的y轴上一点，点Q在直线AB上，点N为第一象限内直线CD上一动点，是否存在点N，使得以点B、M、N、Q为顶点的四边形是菱形？若存在，求出点N坐标；若不存在，请说明理由．6．如图，直线y＝﹣x+1与y轴、x轴分别交于A、B两点，点C在线段AB上从A向B运动，另一动点P从B出发，沿直线x＝1运动，记AC的长为t，P的坐标为（1，b），分析此图后，对下列问题作出探究：（1）当t＝且b＝时，△AOC≌△BCP；（2）当OC与CP垂直时，①判断线段OC和CP的数量关系？并证明你得到的结论；②试写出b关于t的函数关系式和变量t的取值范围．③求出当△PBC为等腰三角形时点P的坐标．7．如图，在平面直角坐标系中，点O为坐标原点，直线y＝kx+6分别交x轴，y轴于点A，B，已知点A的坐标为（6，0）．（1）求k的值；（2）点C是线段OA上一点（不与点O，A重合），点D是OB的延长线上一点，连接CD交AB于点E，且CE＝DE，设OC的长为t，BD的长为d，求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，过点E 作EF ⊥CD 交y 轴于点F ，点G 在线段DE 上，且EG ＝EF ，连接BG 并延长交FE 的延长线于点H ，若BF ＝d 43-29，求点E 的坐标．8．平面直角坐标系中，O 为坐标原点，直线b x 3y +=交y 轴于A ，x 轴于B ，S △AOB ＝83．（1）求b 的值；（2）点C 为射线BA 上一动点，连接OC ，以C 为边作等边△OCD ，点D 在OC 的右侧，求点D 的纵坐标；（3）在（2）的条件下，连接AD 、BD ，△BOC 的面积是△ACD 的面积的2倍，M 是x 轴上一点，连接DM ，若∠DMB ﹣∠DBM ＝90°，求点M 坐标．9．如图1，在矩形ABCD 中，动点P 沿着边AB 从点A 运动到点B ，同时动点Q 沿着边BC ，CD 从点B 运动到点D ，它们同时到达终点，若点Q 的运动路程x 与线段BP 的长y 满足y ＝8x 74-+，BD 与PQ 交于点E ．（1）求AB ，BC 的长．（2）如图2，当点Q 在CD 上时，求DE BE ．（3）将矩形沿着PQ 折叠，点B 的对应点为点F ，连接EF ，当EF 所在直线与△BCD的一边垂直时，求BP的长．10．平面直角坐标系中，设一次函数y＝（2a﹣1）x+3﹣b的图象是直线l1．（1）如果把l1向下平移2个单位后得到直线y＝3x+1，求a，b的值；（2）当直线l1过点（m，6﹣b）和点（m+3，4a﹣7）时，且﹣3＜b＜12，求a的取值范围；（3）点P（﹣2n+3，3n﹣1）在直线l2上运动，直线l2与直线l1无交点，求a、b所需满足的条件．11．如图，在平面直角坐标系中，直线y＝kx+b与x轴，y轴分别相交于点A（4，0），点B（0，3），点C是线段OB的中点，动点P从点B开始以每秒1个单位长度的速度沿路线B→A向终点A匀速运动，设运动的时间为t秒，连接CP．（1）求直线AB的函数解析式；（2）请直接写出点P的坐标；（用含t的代数式表示）（3）①当S△BCP：S四边形AOCP＝1：4时，求t的值；②将△BCP沿CP翻折，使点B落在点B′处，当PB′平行于坐标轴时，请直接写出t的值．12．如图1，在平面直角坐标系xOy中，直线l：y＝mx+m（m＞1）与x轴、y轴分别交于A、B两点，点Q为x轴上一动点．（1）若OB＝2OA，求直线l的解析式；（2）在（1）的条件下，若∠QBA ＝45°，求满足条件的点Q 的坐标；（3）如图2，在x 轴的负半轴上是否存在点Q ，使得以BQ 为边作正方形BQMN 时，点M 恰好落在直线l 上，且正方形BQMN 的面积被x 轴分成了1：2的两部分？若存在，请求出点Q 的坐标，若不存在，请说明理由．13．如图，在平面直角坐标系xOy 中，一次函数y ＝kx +b （k ≠0）经过点A （6，0）和点B （0，9），其图象与直线y ＝x 43交于点C ．（1）求一次函数y ＝kx +b （k ≠0）的表达式；（2）点P 是线段OA 上的一个动点（点P 不与点O ，A 重合），过点P 作平行于y 轴的直线l ，分别交直线AB ，OC 于点M ，N ，设点P 的横坐标为m ．①线段PM 的长为；（用含m 的代数式表示）②当点P ，M ，N 三点中有一个点是另两个点构成线段的中点时，请直接写出m 的值； ③直线l 上有一点Q ，当∠PQA 与∠AOC 互余，且△PQA 的周长为227时，请直接写出点Q 的坐标．14．如图1，已知直线y ＝﹣2x +2与y 轴、x 轴分别交于A 、B 两点，以B 为直角顶点在第一象限内作等腰Rt △ABC ．（1）A （）；B （）；（2）求BC 所在直线的函数关系式；（3）如图2，直线BC 交y 轴于点D ，在直线BC 上取一点E ，使AE ＝AC ，AE 与x 轴相交于点F ．①求证：BD ＝ED ；②在直线AE 上是否存在一点P ，使△ABP 的面积等于△ABD 的面积？若存在，直接写出点P 的坐标；若不存在，说明理由．15．在平面直角坐标系中，直线y ＝32x ﹣6与x 轴交于点A ，与y 轴交于点B ，点D 在直线AB 上，点D 的横坐标为3，点C （﹣6，0），动点F 从C 出发，沿x 轴正方向运动，速度为每秒1个单位长度，到达终点A 停止运动，设运动时间为t （t ＞0）．（1）如图1①求点A 、B 的坐标；②当t ＝3时，求证DF ＝DA ．（2）过点B 作BE ∥OA ，当BE ＝ED 时，连接ED 并延长交x 轴于点Q①点Q 的坐标为；②当∠FDE ＝3∠QFD 时，t 的值为．。

人教版八年级下册数学期末复习：动点问题压轴题

人教版八年级下册数学期末复习：动点问题压轴题1．如图，已知O是坐标原点，点A的坐标是（5，0），点B是y轴正半轴上一动点，以OB，OA为边作矩形OBCA，点E，H分别在边BC和边OA上，将△BOE沿着OE 对折，使点B落在OC上的F点处，将△ACH沿着CH对折，使点A落在OC上的G 点处．(1)求证：四边形OECH是平行四边形；(2)当点B运动到使得点F，G重合时，求点B的坐标，并判断四边形OECH是什么四边形？说明理由；(3)当点B运动到使得点F，G将对角线OC三等分时，直接．．写出点B的坐标．2．如图1，正方形ABCD边长为4，点P是直线BC上的一动点，连接DP，以DP为边在直线DP右侧作等边三角形DPE．(1)请直接写出正方形ABCD的面积；(2)当BP为何值时，点C落在DPE的边上；(3)如图2，若点P在线段BC上从B向C运动，当BP为何值时，线段CE的长度最小？请求出CE的最小值，并直接写出点E所经过的路径的长度．3．如图，已知ABC 为等腰直角三角形，且面积为4．点D 是BC 的中点，点F 是直线AB 上一动点，连结DF ．(1)求线段BC 的长；(2)当点E 在射线BC 上，且2CE BC =时，连结FE ，若3AF AB =，试判断DEF 是否为等腰三角形，并说明理由；(3)直线AB 上是否存在点F （F 不与AB 重合），使ACF 的其中两边之比为存在，求出BF 的长；若不存在，请说明理由．4．如图1，在平面直角坐标系中，点A 的坐标为（5，0），点B 在第一象限内，且AB ＝4，OB ＝3．(1)试判断△AOB 的形状，并说明理由．(2)点P 是线段OA 上一点，且PB －P A ＝1，求点P 的坐标；(3)如图2，点C 、点D 分别为线段OB 、BA 上的动点，且OC ＝BD ，求AC ＋OD 的最小值．5．如图，在平面直角坐标系中，直线AB为y＝﹣34x＋b交y轴于点A（0，3），交x轴于点B，直线x＝1交AB于点D，交x轴于点E，P是直线x＝1上一动点，且在点D的上方，设P（1，n）．(1)求点B的坐标及点O到直线AB的距离；(2)求△ABP的面积（用含n的代数式表示）；(3)当S△ABP＝72时，在第一象限找点C，使△PBC为等腰直角三角形，直接写出点C的坐标．6．如图，直线y kx b=+经过点75,04A⎛⎫⎪⎝⎭，点()0,25B，与直线34y x=交于点C，点D为直线AB上一动点，过D点作x轴的垂线交直线OC于点E．（1）求点C的坐标；（2）当23DE OA=时，求△CDE的面积；（3）当OAD△沿着OD折叠，当点A落在直线OC上时，直接写出点D的坐标．7．点P为等边ABC的边AB延长线上的动点，点B关于直线PC的对称点为D，连接AD．（1）如图1，若2BP AB ==，依题意补全图形，并直接写出线段AD 的长度；（2）如图2，线段AD 交PC 于点E ， △设BCP α∠=，求AEC ∠的度数； △求证：AE CE DE =+．8．如图，在平面直角坐标系中，直线l 1：y ＝﹣x ＋5与y 轴交于点A ，直线l 2与x 轴、y 轴分别交于点B (﹣4，0)和点C ，且与直线l 1交于点D (2，m )．（1）求直线l 2的解析式；（2）若点E 为线段BC 上一个动点，过点E 作EF △x 轴，垂足为F ，且与直线l 1交于点G ，当EG ＝6时，求点G 的坐标；（3）若在平面上存在点H ，使得以点A ，C ，D ，H 为顶点的四边形是平行四边形，请直接写出点H 的坐标．9．如图1，直线AB ：y x b =-+分别与x ，y 轴交于()6,0A ，B 两点，过点B 的直线交x 轴负半轴于C ，且:3:1OB OC =．()1求直线BC的函数表达式；()2在x轴是否存在一点M，使得BCM是一个等腰三角形，若存在请求出点M的坐标，若不存在请说明理由；()3如图2，P为x轴上A点右侧的一动点，以P为直角顶点，BP为一腰在第一象限内作等腰直角三角形BPQ，连接QA并延长交y轴于点K．当P点运动时，K点的位置是否发生变化？如果不变请求出它的坐标；如果变化，请说明理由．10．如图，直线1与直线m交于点Q89,55⎛⎫⎪⎝⎭，直线m与坐标轴分别交于A、B两点，直线l与y轴交与点C，已知B、C两点关于x轴对称且BC＝6．（1）求直线l和直线m的解析式；（2）若P为直线l上一动点，S△P AB＝32S△OAB，求点P的坐标；（3）M为直线l上一动点，N为平面内一点，直接写出所有使得以A、B、M、N为顶点的四边形为菱形的点N的坐标，并把求其中一个点N的坐标的过程写出来．11．如图，在四边形ABCD 中，AD △BC ，△B ＝90°，△C ＝60°，AD ＝24cm ，CD ＝8cm ．点P 从点D 出发，以1cm /s 的速度向点A 运动；点Q 从点B 同时出发，以3cm /s 的速度向点C 运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点Q 的运动时间为x （s ）．（1）BC ＝ cm ，AB ＝ cm ；（2）当PQ ＝CD 时，x ＝；（3）当四边形ABQP 为矩形时，求x 的值．12．如图，正比例函数34y x =与一次函数7y ax =+的图像相交于点()4,P n ，过点(),0A t 作x 轴的垂线l ，且04t <<，交一次函数的图像于点B ，交正比例函数的图像于点C ，连接OB ．（1）求a 值；（2）设OBP 的面积为s ，求s 与t 之间的函数关系式；（3）当2t =时，在正比例函数34y x =与一次函数7y ax =+的图像上分别有一动点M 、N ，是否存在点M 、N ，使CMN △是等腰直角三角形，且90CNM ∠=︒，若存在，请直接写出点M 、N 的坐标；若不存在，请说明理由．13．如图1，在Rt△ABC中，△ACB＝90°，AC＝BC，将点C绕点B顺时针旋转105°得到点D，连接BD，过点D作DE△BC交CB延长线于点E，点F为线段DE上的一点，且△DBF＝45°，作△BFD的角平分线FG交AB于点G．（1）求△BFD的度数；（2）求BF，DF，GF三条线段之间的等量关系式；（3）如图2，设H是直线DE上的一个动点，连接HG，HC，若AB，求线段HG+HC的最小值（结果保留根号）．14．如图所示，点A是平面直角坐标系内一点坐标为（1，AB是过点A的一条直线，B是直线与x轴的交点，以OA、OB为邻边作平行四边形AOBC．若OD是△AOB的平分线，且D是AC的中点．（1）求B、D两点的坐标；（2）求直线AB的解析式；S平行四边形AOBC，请直接写出满足条件（3）若P是直线AB上一动点，且S△POD 12的点P的坐标．15．如图，矩形OABC的顶点A、C分别在x轴、y轴的正半轴上，点B的坐标为（3，4），一次函数y＝23x b-+的图象与边OC，AB分别交于点D，E，并且满足OD＝BE，点M是线段DE上的一个动点．（1）求b的值；（2）当DM：ME＝1：2时，求点M的坐标；（3）设点N是x轴上方的平面内的一点，当以点O，M，D，N为顶点的四边形是菱形时，直接写出点N的坐标．16．在矩形ABCD中，BC，点E、F分别是边AD、BC上的动点，且AE＝CF，连接EF，将矩形ABCD沿EF折叠，点C落在点G处，点D落在点H处．（1）如图1，当EH与线段BC交于点P时，求证：PE＝PF；（2）如图2，当点P在线段CB的延长线上时，交AB于点M，求证：点M在线段EF 的垂直平分线上；（3）当AB＝5时，在点E由点A移动到AD中点的过程中，直接写出点G运动路线长．交△BCA的平分线于点E，交△BCA的外角平分线于点F．（1）探究OE与OF的数量关系并加以证明；（2）四边形BCFE会是菱形吗？若是，请加以证明；若不是，则说明理由；（3）当点O运动到什么位置时，四边形AECF是矩形？请说明理由；（4）在（3）问的基础上，△ABC满足什么条件时，四边形AECF是正方形？为什么？18．如图，在平面直角坐标系中，直线123y x=-+与x轴交于点C，与y轴交于点A．（1）求AOC△的面积；（2）点P是直线AC上的动点，过P作x轴，y轴的垂线，垂足分别为点F，E，若2PF PE=，请求出点P的坐标；（3）点117,39B⎛⎫⎪⎝⎭在直线AC上，坐标轴上存在动点M，使ABM是以AB为直角边的直角三角形，请直接写出点M的坐标．把△COB沿BC翻折，点O恰好落在AB边的点D处，BC为折痕．（1）求线段AB的长；（2）求直线BC的解析式；（3）若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P 为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．20．如图，在平面直角坐标系中，直线y＝12x+2与y轴、x轴分别交于点A，B，点M在线段AB上运动（不与点A，B重合），连接OM．（1）求线段OB的长；（2）设点M的横坐标为m，△BOM的面积为S，求S关于m的函数关系式（不必写出自变量m的取值范围）；（3）若点M为线段AB的中点，点P为射线BO上的动点，将△APM沿直线PM折叠得到△A1PM，若以点A1、B、P、M为顶点的四边形是平行四边形，直接写出点A1的横坐标．参考答案：1． (2)B （0）；四边形OECH 是菱形(3)点B 的坐标是（00， 2．(1)16(2)4或4343或4(3)4-；2；E 所经过的路线的长度是43．(1)线段BC 的长为4；(2)△DEF 是等腰三角形(3)存在，BF 的长为或或-2．4．(1)△AOB 是直角三角形，(2)P (4514，0)5．(1)B （4，0），125(2)922n -(3)（5，7）或（8，3）或（92，72） 6．（1）点C 的坐标为(12，9)；（2）△CDE 的面积为752；（3）点D 的坐标为(15，5)或(-15，45)． 7．（1）AD =（2）△60AEC ∠=︒；△证明见解析．8．（1）122y x =+；（2）(﹣2，7)；（3）(2，0)或(2，6)或(﹣2，4)．9．()136y x =+； ()2 存在，M 的坐标为()12M --，()22M -+，()38,0M ，()42,0M ； ()3不变化，()0,6K -．10．（1）直线l 的解析式为33y x =-，直线m 的解析式为334y x =-+；（2）P （25，95-）或P （145，275）；（3）N 1（2910，2710）或N 2（295+，35-N 3（295-，35-）或N 4（4-，0）或N 5（75-，395） 11．（1）28，（2）5或7；（3）6．12．（1）1a =-；（2）7142s t =-+；（3）存在，1133,28M ⎛⎫ ⎪⎝⎭，3973,1616N ⎛⎫ ⎪⎝⎭或2053M ⎛⎫ ⎪⎝⎭，，7311,1212N ⎛⎫ ⎪⎝⎭．13．（1）120°；（2）BF +DF ＝GF ；（314．（1）B 点的坐标是（4，0），D 点的坐标是（3．（2）y （3）（4，0）或（0． 15．（1）3；（2）M （1，73）；（3）N （3613，5413）或N （﹣94，32）． 16．（1）见解析；（2）见解析；（3）103π 17．（1）OE =OF ，证明见解析；（2）不是；（3）点O 运动到AC 的中点；（4）△ACB 为直角18．（1）6；（2）612,77P ⎛⎫ ⎪⎝⎭或612,55P ⎛⎫- ⎪⎝⎭；（3）点M 的坐标为2,03⎛⎫- ⎪⎝⎭或92,027⎛⎫ ⎪⎝⎭或920,9⎛⎫- ⎪⎝⎭ 19．（1）AB =10；（2）y =2x +6；（3）存在，满足条件的P 点的坐标为（3，2）或（-4，8）．20．（1）4；（2）S =m +4；（3）-1或-3。

2020-2021学年人教版数学八年级下册期末压轴题专项复习卷(含答案)

2021年人教版数学八年级下册期末《压轴题专项》复习卷1.如图，点A的坐标是(－2，0)，点B的坐标是(6，0)，点C在第一象限内且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD，垂足为E，交OC于点F.(1)求直线BD的函数表达式；(2)求线段OF的长；(3)连接BF，OE，试判断线段BF和OE的数量关系，并说明理由．2.阅读下面材料：我们知道一次函数y=kx+b(k≠0，k、b是常数)的图象是一条直线，到高中学习时，直线通常写成Ax+By+C=0(A≠0，A、B、C是常数)的形式，点P(x0，y0)到直线Ax+By+C=0的距离可用公式d=计算．例如：求点P(3，4)到直线y=﹣2x+5的距离．根据以上材料解答下列问题：(1)求点Q(﹣2，2)到直线3x﹣y+7=0的距离；(2)如图，直线y=﹣x沿y轴向上平移2个单位得到另一条直线，求这两条平行直线之间的距离．3.已知正方形ABCD，AB=8，点E、F分别从点A、D同时出发，以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动，设运动时间为t．（1）求证：OE=OF．（2）在点E、F的运动过程中，连结AF．设线段AE、OE、OF、AF所形成的图形面积为S．探究：①S的大小是否会随着运动时间为t的变化而变化？若会变化，试求出S与t的函数关系式；若不会变化，请说明理由．②连结EF，当运动时间为t为何值时，△OEF的面积恰好等于的S．4.如图，在平面直角坐标系中，一次函数y=kx+b的图象与x轴交于点A（-3，0），与y轴交于点B，且与正比例函数的图象交点为C（m，4）．求：（1）一次函数y=kx+b的解析式；（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，则点D的坐标为；（3）在x轴上求一点P使△POC为等腰三角形，请求出所有符合条件的点P的坐标．5.将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0)，MN平行于y轴，E是BC的中点，现将纸片折叠，使点C落在MN上，折痕为直线EF.(1)求点G的坐标；(2)求直线EF的解析式；(3)设点P为直线EF上一点，是否存在这样的点P，使以P, F, G的三角形是等腰三角形?若存在，直接写出P点的坐标;若不存在，请说明理由.6.如图,已知直线y=kx+1经过点A(3,-2)、点B(a,2)，交y轴于点M.（1）求a的值及AM的长（2）在x轴的负半轴上确定点P，使得△AMP成等腰三角形，请你直接写出点P的坐标.（3）将直线AB绕点A逆时针旋转45°得到直线AC，点D（-3，b）在AC上，连接BD，设BE是△ABD 的高，过点E的射线EF将△ABD的面积分成2：3两部分，交△ABD的另一边于点F，求点F的坐标.7.阅读理解：运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法．如图1，在等腰△ABC中，AB=AC，AC边上的高为h，点M为底边BC 上的任意一点，点M到腰AB、AC的距离分别为h1、h2，连接AM，利用S△ABC=S△ABM+S△ACM，可以得出结论：h=h1+h2．类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论．拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y=0.75x+3，l2：y=﹣3x+3，若l2上一点M到l1的距离是1，试运用“阅读理解”和“类比探究”中获得的结论，求出点M 的坐标．8.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x ﹣2与x轴、y轴分别交于点E、F．（1）求：①点D的坐标；②经过点D,且与直线FC平行的直线的函数表达式；（2）直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形？若存在,求出点P 的坐标；若不存在,请说明理由．（3）在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形，请直接写出点M的坐标．9.如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为（4,0）,点B的坐标为（0,1）,点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE．（1）线段OC的长为；（2）求证：△CBD≌△COE；（3）将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1，其中点O,B,D,E的对应点分别为点O1，B1，D1，E1，连接CD,CE,设点E的坐标为（a，0）,其中a≠2,△CD1E1的面积为S．①当1＜a＜2时,请直接写出S与a之间的函数表达式；②在平移过程中,当S=时,请直接写出a的值．10.如图，直线y=2x+m(m>0)与x轴交于点A(-2,0)直线y=-x+n(n>0)与x轴、y轴分别交于B、C 两点，并与直线y=2x+m(m>0)相交于点D，若AB=4．（1）求点D的坐标；（2）求出四边形AOCD的面积；（3）若E为x轴上一点，且△ACE为等腰三角形，直接写出点E的坐标．11.如图，直线l：交x、y轴分别为A、B两点，C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合)，满足∠BPQ=∠BAO.(1)点A坐标是， BC= .(2)当点P在什么位置时，△APQ≌△CBP，说明理由。

八年级下册数学期末压轴题专辑(含解析,)

八年级下册数学期末压轴题专辑（含解析）1.如图，ON 为∠AOB 中的一条射线，点P 在边OA 上，PH ⊥OB 于H ，交ON 于点Q ，PM ∥OB 交ON 于点M, MD ⊥OB 于点D ，QR ∥OB 交MD 于点R ，连结PR 交QM 于点S 。

（1）求证：四边形PQRM 为矩形；（2）若OP=12PR ，试探究∠AOB 与∠BON 的数量关系，并说明理由。

（1）证明：∵PH ⊥OB ，MD ⊥OB ，∴PH ∥MD ，∵PM ∥OB ，QR ∥OB ，∴PM ∥QR ，∴四边形PQRM 是平行四边形， ∵PH ⊥OB ，∴∠PHO=90°，∵PM ∥OB ，∴∠MPQ=∠PHO=90°，∴四边形PQRM 为矩形；（2）∠AOB=3∠BON ．理由如下： ∵四边形PQRM 为矩形，∴PS=SR=SQ=12PR ，∴∠SQR=∠SRQ ，又∵OP=12PR ，∴OP=PS ，∴∠POS=∠PSO ， ∵QR ∥OB ，∴∠SQR=∠BON ，在△SQR 中，∠PSO=∠SQR+∠SRQ=2∠SQR=2∠BON ，∴∠POS=2∠BON ， ∴∠AOB=∠POS+∠BON=2∠BON+∠BON=3∠BON ，即∠AOB=3∠BON ． 2.如图，矩形OABC 在平面直角坐标系内（O 为坐标原点），点A 在x 轴上，点C 在y 轴上，点B 的坐标分别为（，点E 是BC 的中点，点H 在OA 上，且AH=12，过点H 且平行于y 轴的HG 与EB 交于点G ，现将矩形折叠，使顶点C 落在HG 上，并与HG 上的点D 重合，折痕为EF ，点F 为折痕与y 轴的交点。

（1）求∠CEF 的度数和点D 的坐标；（2）求折痕EF 所在直线的函数表达式；（3）若点P 在直线EF 上，当△PFD 为等腰三角形时，试问满足条件的点P 有几个？请求出点P 的坐标，并写出解答过程。

八年级数学压轴题期末复习试卷测试卷(含答案解析)

八年级数学压轴题期末复习试卷测试卷（含答案解析）一、压轴题1．（1）探索发现：如图1，已知Rt △ABC 中，∠ACB ＝90°，AC ＝BC ，直线l 过点C ，过点A 作AD ⊥l ，过点B 作BE ⊥l ，垂足分别为D 、E ．求证：AD ＝CE ，CD ＝BE ．（2）迁移应用：如图2，将一块等腰直角的三角板MON 放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O 重合，另两个顶点均落在第一象限内，已知点M 的坐标为（1，3），求点N 的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线y ＝﹣3x+3与y 轴交于点P ，与x 轴交于点Q ，将直线PQ 绕P 点沿逆时针方向旋转45°后，所得的直线交x 轴于点R ．求点R 的坐标．2．在ABC 中，AB AC =，D 是直线BC 上一点（不与点B 、C 重合），以AD 为一边在AD 的右侧作ADE ，AD AE =，DAE BAC ∠=∠，连接CE .（1）如图，当 D 在线段BC 上时，求证：BD CE =.（2）如图，若点D 在线段CB 的延长线上，BCE α∠=，BAC β∠=.则α、β之间有怎样的数量关系？写出你的理由.（3）如图，当点D 在线段BC 上，90BAC ∠=︒，4BC =，求DCES 最大值.3．（1）在等边三角形ABC 中，①如图①，D ，E 分别是边AC ，AB 上的点且AE=CD ，BD 与EC 交于点F ，则∠BFE 的度数是度；②如图②，D ，E 分别是边AC ，BA 延长线上的点且AE=CD ，BD 与EC 的延长线交于点F ，此时∠BFE 的度数是度；（2）如图③，在△ABC 中，AC=BC ，∠ACB 是锐角，点O 是AC 边的垂直平分线与BC 的交点，点D ，E 分别在AC ，OA 的延长线上，AE=CD ，BD 与EC 的延长线交于点F ，若∠ACB=α，求∠BFE 的大小．（用含α的代数式表示）．4．如图，在平面直角坐标系中，直线y＝﹣34x+m分别与x轴、y轴交于点B、A．其中B点坐标为（12，0），直线y＝38x与直线AB相交于点C．（1）求点A的坐标．（2）求△BOC的面积．（3）点D为直线AB上的一个动点，过点D作y轴的平行线DE，DE与直线OC交于点E （点D与点E不重合）．设点D的横坐标为t，线段DE长度为d．①求d与t的函数解析式（写出自变量的取值范围）．②当动点D在线段AC上运动时，以DE为边在DE的左侧作正方形DEPQ，若以点H（12，t）、G（1，t）为端点的线段与正方形DEPQ的边只有一个交点时，请直接写出t的取值范围．5．某校七年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC中，∠ABC与∠ACB的平分线交于点P，∠A＝64°，则∠BPC＝；（2）如图2，△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E．其中∠A＝α，求∠BEC．（用α表示∠BEC）；（3）如图3，∠CBM、∠BCN为△ABC的外角，∠CBM、∠BCN的平分线交于点Q，请你写出∠BQC与∠A的数量关系，并说明理由；（4）如图4，△ABC外角∠CBM、∠BCN的平分线交于点Q，∠A=64°，∠CBQ，∠BCQ的平分线交于点P ，则∠BPC= ゜，延长BC 至点E ，∠ECQ 的平分线与BP 的延长线相交于点R ，则∠R= ゜．6．在平面直角坐标系中，点A 、B 在坐标轴上，其中()0,A a 、(),0B b 满足|21|280a b a b --++-=．（1）求A 、B 两点的坐标；（2）将线段AB 平移到CD ，点A 的对应点为()2,C t -，如图1所示，若三角形ABC 的面积为9，求点D 的坐标；（3）平移线段AB 到CD ，若点C 、D 也在坐标轴上，如图2所示．P 为线段AB 上的一动点（不与A 、B 重合），连接OP 、PE 平分OPB ∠，2BCE ECD ∠=∠．求证：3()BCD CEP OPE ∠=∠-∠．7．已知在△ABC 中，AB =AC ，∠BAC =α，直线l 经过点A （不经过点B 或点C ），点C 关于直线l 的对称点为点D ，连接BD ，CD ．（1）如图1，①求证：点B ，C ，D 在以点A 为圆心，AB 为半径的圆上； ②直接写出∠BDC 的度数（用含α的式子表示）为；（2）如图2，当α=60°时，过点D 作BD 的垂线与直线l 交于点E ，求证：AE =BD ；（3）如图3，当α=90°时，记直线l与CD的交点为F，连接BF．将直线l绕点A旋转的过程中，在什么情况下线段BF的长取得最大值？若AC=22a，试写出此时BF的值．8．如图1中的三种情况所示，对于平面内的点M，点N，点P，如果将线段PM绕点P顺时针旋转90°能得到线段PN，就称点N是点M关于点P的“正矩点”．（1）在如图2所示的平面直角坐标系xOy中，已知(3,1),(1,3),(1,3)S P Q---，(2,4)M-．①在点P，点Q中，___________是点S关于原点O的“正矩点”；②在S，P，Q，M这四点中选择合适的三点，使得这三点满足：点_________是点___________关于点___________的“正矩点”，写出一种情况即可；（2）在平面直角坐标系xOy中，直线3(0)y kx k=+<与x轴交于点A，与y轴交于点B，点A关于点B的“正矩点”记为点C，坐标为(,)C CC x y．①当点A在x轴的正半轴上且OA小于3时，求点C的横坐标Cx的值；②若点C的纵坐标C y满足12Cy-<≤，直接写出相应的k的取值范围．9．已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求ABFACFSS的值．10．如图，在边长为2的等边三角形ABC 中，D 点在边BC 上运动（不与B ，C 重合），点E 在边AB 的延长线上，点F 在边AC 的延长线上，AD DE DF ==．（1）若30AED ∠=︒，则ADB =∠______．（2）求证：BED CDF △≌△．（3）试说明点D 在BC 边上从点B 至点C 的运动过程中，BED 的周长l 是否发生变化？若不变，请求出l 的值，若变，请求出l 的取值范围．11．在ABC 中，AB AC =，D 是直线AB 上一点，E 在直线BC 上，且DE DC =．（1）如图1，当D 在AB 上，E 在CB 延长线上时，求证：EDB ACD ∠=∠；（2）如图2，当ABC 为等边三角形时，D 是BA 的延长线上一点，E 在BC 上时，作//EF AC ，求证：BE AD =；（3）在（2）的条件下，ABC ∠的平分线BF 交CD 于点F ，连AF ，过A 点作AH CD ⊥于点H ，当30EDC ∠=︒，6CF =时，求DH 的长度．12．直角三角形ABC 中，90ACB ∠=︒，直线l 过点C ．（1）当AC BC =时，如图1，分别过点A 和B 作AD ⊥直线l 于点D ，BE ⊥直线l 于点E ，ACD 与CBE △是否全等，并说明理由；（2）当8AC cm =，6BC cm =时，如图2，点B 与点F 关于直线l 对称，连接BF CF 、，点M 是AC 上一点，点N 是CF 上一点，分别过点M N 、作MD ⊥直线l 于点D ，NE ⊥直线l 于点E ，点M 从A 点出发，以每秒1cm 的速度沿A C →路径运动，终点为C ，点N 从点F 出发，以每秒3cm 的速度沿F C B C F →→→→路径运动，终点为F ，点,M N 同时开始运动，各自达到相应的终点时停止运动，设运动时间为t 秒，当CMN △为等腰直角三角形时，求t 的值．【参考答案】***试卷处理标记，请不要删除一、压轴题1．（1）见解析（2）（4，2）（3）（6，0）【解析】【分析】（1）先判断出∠ACB=∠ADC ，再判断出∠CAD=∠BCE ，进而判断出△ACD ≌△CBE ，即可得出结论；（2）先判断出MF=NG ，OF=MG ，进而得出MF=1，OF=3，即可求出FG=MF+MG=1+3=4，即可得出结论；（3）先求出OP=3，由y=0得x=1，进而得出Q （1，0），OQ=1，再判断出PQ=SQ ，即可判断出OH=4，SH=0Q=1，进而求出直线PR 的解析式，即可得出结论. 【详解】证明：∵∠ACB＝90°，AD⊥l∴∠ACB＝∠ADC∵∠ACE＝∠ADC+∠CAD，∠ACE＝∠ACB+∠BCE∴∠CAD＝∠BCE，∵∠ADC＝∠CEB＝90°，AC＝BC∴△ACD≌△CBE，∴AD＝CE，CD＝BE，（2）解：如图2，过点M作MF⊥y轴，垂足为F，过点N作NG⊥MF，交FM的延长线于G，由已知得OM＝ON，且∠OMN＝90°∴由（1）得MF＝NG，OF＝MG，∵M（1，3）∴MF＝1，OF＝3∴MG＝3，NG＝1∴FG＝MF+MG＝1+3＝4，∴OF﹣NG＝3﹣1＝2，∴点N的坐标为（4，2），（3）如图3，过点Q作QS⊥PQ，交PR于S，过点S作SH⊥x轴于H，对于直线y＝﹣3x+3，由x＝0得y＝3∴P（0，3），∴OP＝3由y＝0得x＝1，∴Q（1，0），OQ＝1，∵∠QPR＝45°∴∠PSQ＝45°＝∠QPS∴PQ＝SQ∴由（1）得SH＝OQ，QH＝OP∴OH＝OQ+QH＝OQ+OP＝3+1＝4，SH＝OQ＝1∴S （4，1），设直线PR 为y ＝kx+b ，则341b k b =⎧⎨+=⎩ ，解得1k 2b 3⎧=-⎪⎨⎪=⎩∴直线PR 为y ＝﹣12x+3 由y ＝0得，x ＝6 ∴R （6，0）．【点睛】本题是一次函数综合题，主要考查了待定系数法，全等三角形的判定和性质，构造出全等三角形是解本题的关键.2．（1）见解析；（2）αβ=，理由见解析；（3）2 【解析】【分析】（1）证明()ABD ACE SAS ≅△△，根据全等三角形的性质得到BD CE =；（2）同（1）先证明()ABD ACE SAS ≅△△，得到∠ACE=∠ABD ，结合等腰三角形的性质和外角和定理用不同的方法表示∠ACE ，得到α和β关系式；（3）同（1）先证明()ABD ACE SAS ≅△△，得到ABC ADCE S S ∆=四边形，那么DCE ADE ADCE S S S ∆∆=-四边形，当AD BC ⊥时，ADE S ∆最小，即DCE S ∆最大．【详解】解：（1）∵BAC DAE ∠=∠， ∴BAC DAC DAE DAC ∠-∠=∠-∠， ∴BAD CAE ∠=∠，在ABD △和ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩， ∴()ABD ACE SAS ≅△△， ∴BD CE =；（2）同（1）的方法得()ABD ACE SAS ≅△△， ∴∠ACE=∠ABD ，∠BCE=α， ∴∠ACE=∠ ACB+∠BCE=∠ACB+α，在ABC 中， ∵AB= AC ，∠BAC=β， ∴∠ACB=∠ABC =12(180°-β)= 90°-12β，∴∠ABD= 180°-∠ABC= 90°+12β， ∴∠ACE=∠ACB +α= 90°-12β+α， ∵∠ACE=∠ABD = 90°+12β， ∴90°-12β+α= 90°+12β， ∴α = β；（3）如图，过A 做AH BC ⊥于点H ， ∵AB AC =，90BAC ∠=︒， ∴45ABC ∠=︒，122BH AH BC ===，同（1）的方法得，()ABD ACE SAS ≅△△，AEC ABD S S ∆∆∴=,AEC ADC ABD ADC S S S S ∆∆∆∆+=+，即142ABC ADCE S S BC AH ∆==⋅=四边形， ∴DCE ADE ADCE S S S ∆∆=-四边形，当ADE S ∆最小时，DCE S ∆最大，∴当AD BC ⊥2AD =，时最小，2122ADE S AD ∆==， 422DCE S ∆∴=-=最大．【点睛】本题考查全等三角形的性质和判定，等腰三角形的性质，三角形的外角和定理，解题的关键是抓住第一问中的那组全等三角形，后面的问题都是在这个基础上进行证明的． 3．（1）①60°；②60°；（2）∠BFE =α．【解析】【分析】（1）①先证明△ACE ≌△CBD 得到∠ACE=∠CBD ，再由三角形外角和定理可得∠BFE=∠CBD+∠BCF ；②先证明△ACE ≌△CBD 得∠ACE=∠CBD=∠DCF ，再由三角形外角和定理可得∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA ；（2）证明△AEC ≌△CDB 得到∠E=∠D ，则∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【详解】（1）如图①中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD，∴∠BFE=∠CBD+∠BCF=∠ACE+∠BCF=∠BCA=60°．故答案为60．（2）如图②中，∵△ABC是等边三角形，∴AC=CB，∠A=∠BCD=60°，∴∠CAE=∠BCD=′120°∵AE=CD，∴△ACE≌△CBD，∴∠ACE=∠CBD=∠DCF，∴∠BFE=∠D+∠DCF=∠D+∠CBD=∠BCA=60°．故答案为60．（3）如图③中，∵点O是AC边的垂直平分线与BC的交点，∴OC=OA，∴∠EAC=∠DCB=α，∵AC=BC，AE=CD，∴△AEC≌△CDB，∴∠E=∠D，∴∠BFE=∠D+∠DCF=∠E+∠ECA=∠OAC=α．【点睛】本题综合考查了三角形全等以及三角形外角和定理.4．（1）点A坐标为（0，9）；（2）△BOC的面积＝18；（3）①当t＜8时，d＝﹣9 8t+9，当t＞8时，d＝98t﹣9；②12≤t≤1或7617≤t≤8017．【解析】【分析】（1）将点B坐标代入解析式可求直线AB解析式，即可求点A坐标；（2）联立方程组可求点C坐标，即可求解；（3）由题意列出不等式组，可求解．【详解】解：（1）∵直线y＝﹣34x+m与y轴交于点B（12，0），∴0＝﹣34×12+m，∴m＝9，∴直线AB的解析式为：y＝﹣34x+9，当x＝0时，y＝9，∴点A坐标为（0，9）；（2）由题意可得：38394y xy x⎧=⎪⎪⎨⎪=+⎪⎩，解得：83 xy=⎧⎨=⎩，∴点C（8，3），∴△BOC的面积＝12×12×3＝18；（3）①如图，∵点D的横坐标为t，∴点D（t，﹣34t+9），点E（t，38t），当t＜8时，d＝﹣34t+9﹣38t＝﹣98t+9，当t＞8时，d＝38t+34t﹣9＝98t﹣9；②∵以点H（12，t）、G（1，t）为端点的线段与正方形DEPQ的边只有一个交点，∴12≤t≤1或919829918t tt t⎧-+≤-⎪⎪⎨⎪-+≥-⎪⎩，∴12≤t≤1或7617≤t≤8017．【点睛】本题是一次函数综合题，考查了待定系数法求解析式，三角形的面积公式，不等式组的应用，灵活运用这些性质解决问题是本题的关键．5．（1） 122°；（2）12BECα∠=；（3）01902BQC A；（4）119，29 ；【解析】【分析】（1）根据三角形的内角和角平分线的定义；（2）根据三角形的一个外角等于与它不相邻的两个内角的和，用A ∠与1∠表示出2∠，再利用E ∠与1∠表示出2∠，于是得到结论；（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出EBC ∠与ECB ∠，然后再根据三角形的内角和定理列式整理即可得解；（4）根据（1），（3）的结论可以得出∠BPC 的度数；根据（2）的结论可以得到∠R 的度数．【详解】解：（1）BP 、CP 分别平分ABC ∠和ACB ∠，12PBC ABC ∴∠=∠，12PCB ACB ∠=∠， 180()BPC PBC PCB ∴∠=︒-∠+∠11180()22ABC ACB =︒-∠+∠， 1180()2ABC ACB =︒-∠+∠， 1(180180)2A =︒-︒-∠， 1180902A =-︒+︒∠， 9032122，故答案为：122︒；（2）如图2示，CE 和BE 分别是ACB ∠和ABD ∠的角平分线，112ACB ∴∠=∠，122ABD ∠=∠，又ABD ∠是ABC ∆的一外角，ABD A ACB ∴∠=∠+∠，112()122A ABC A ∴∠=∠+∠=∠+∠， 2∠是BEC ∆的一外角，112111222BEC A A α∴∠=∠-∠=∠+∠-∠=∠=；（3）1()2QBC A ACB ∠=∠+∠，1()2QCB A ABC ∠=∠+∠， 180BQC QBC QCB ∠=︒-∠-∠，11180()()22A ACB A ABC =︒-∠+∠-∠+∠， 11180()22A A ABC ACB =︒-∠-∠+∠+∠，结论1902BQC A ∠=︒-∠．（4）由（3）可知，119090645822BQCA ，再根据（1），可得180()BPCPBC PCB 1118022QBC QCB 1180902Q 118090582119；由（2）可得：11582922R Q ;故答案为：119，29．【点睛】本题考查了三角形的外角性质与内角和定理，熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键．6．（1）A ，B 两点的坐标分别为()0,2，()3,0；（2）点D 的坐标是141,3⎛⎫-⎪⎝⎭；（3）证明见解析【解析】【分析】（1）根据非负数的性质得出二元一次方程组，求解即可；（2）过点B 作y 轴的平行线分别与过点A ，C 作x 轴的平行线交于点N ，点M ，过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ，根据三角形ABC 的面积=长方形CMNT 的面积-（三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积）列出方程，求解得出点C 的坐标，由平移的规律可得点D 的坐标；（3）过点E 作//EF CD ，交y 轴于点F ，过点O 作//OG AB ，交PE 于点G ，根据两直线平行，内错角相等与已知条件得出3BCD CEF ∠=∠，同样可证OGP OPE ∠=∠，由平移的性质与平行公理的推论可得FEP OGP ∠=∠，最后根据CEP CEF FEP ∠=∠+∠，通过等量代换进行证明．【详解】解：（1）210a b --=，又∵|21|0a b --≥0， |21|0a b ∴--=0=，即210280a b a b --=⎧⎨+-=⎩，解方程组2128a b a b -=⎧⎨+=⎩得23a b =⎧⎨=⎩， A ∴，B 两点的坐标分别为()0,2，()3,0；（2）如图，过点B 作y 轴的平行线分别与过点A ，C 作x 轴的平行线交于点N ，点M ，过点C 作y 轴的平行线与过点A 作x 轴的平行线交于点T ，∴三角形ABC 的面积=长方形CMNT 的面积-（三角形ANB 的面积+三角形ATC 的面积+三角形CMB 的面积），根据题意得，11195(2||)232(2||)5||222t t t ⎡⎤=⨯+-⨯⨯+⨯⨯++⨯⨯⎢⎥⎣⎦，化简，得3||42t =，解得，83t =±，依题意得，0t <， 83t ∴=-，即点C 的坐标为82,3⎛⎫-- ⎪⎝⎭， ∴依题意可知，点C 的坐标是由点A 的坐标先向左平移2个单位长度，再向下平移143个单位长度得到的，从而可知，点D 的坐标是由点B 的坐标先向左平移2个单位长度，再向下平移143个单位长度得到的， ∴点D 的坐标是141,3⎛⎫- ⎪⎝⎭；（3）证明：过点E作//EF CD，交y轴于点F，如图所示，则ECD CEF∠=∠，2BCE ECD∠=∠，33BCD ECD CEF∴∠=∠=∠，过点O作//OG AB，交PE于点G，如图所示，则OGP BPE∠=∠，PE平分OPB∠，OPE BPE∴∠=∠，OGP OPE∴∠=∠，由平移得//CD AB，//OG FE∴，FEP OGP∴∠=∠，FEP OPE∴∠=∠，CEP CEF FEP∠=∠+∠，CEP CEF OPE∴∠=∠+∠，CEF CEP OPE∴∠=∠-∠，3()BCD CEP OPE∴∠=∠-∠．【点睛】本题综合性较强，考查非负数的性质，解二元一次方程组，平行线的性质，平移的性质，坐标与图形的性质，第（3）题巧作辅助线构造平行线是解题的关键．7．（1）①详见解析；②12α；（2）详见解析；（3）当B、O、F三点共线时BF最长，102a 【解析】【分析】（1）①由线段垂直平分线的性质可得AD=AC=AB ，即可证点B ，C ，D 在以点A 为圆心，AB 为半径的圆上；②由等腰三角形的性质可得∠BAC=2∠BDC ，可求∠BDC 的度数；（2）连接CE ，由题意可证△ABC ，△DCE 是等边三角形，可得AC=BC ，∠DCE=60°=∠ACB ，CD=CE ，根据“SAS”可证△BCD ≌△ACE ，可得AE=BD ；（3）取AC 的中点O ，连接OB ，OF ，BF ，由三角形的三边关系可得，当点O ，点B ，点F 三点共线时，BF 最长，根据等腰直角三角形的性质和勾股定理可求10BO a =，2OF OC a ==，即可求得BF【详解】（1）①连接AD ，如图1．∵点C 与点D 关于直线l 对称，∴AC = AD ．∵AB = AC ，∴AB = AC = AD ．∴点B ，C ，D 在以A 为圆心，AB 为半径的圆上．②∵AD=AB=AC ，∴∠ADB=∠ABD ，∠ADC=∠ACD ，∵∠BAM=∠ADB+∠ABD ，∠MAC=∠ADC+∠ACD ，∴∠BAM=2∠ADB ，∠MAC=2∠ADC ，∴∠BAC=∠BAM+∠MAC=2∠ADB+2∠ADC=2∠BDC=α∴∠BDC=12α故答案为：12α．（2连接CE ，如图2．∵∠BAC=60°，AB=AC ，∴△ABC 是等边三角形，∴BC=AC ，∠ACB=60°，∵∠BDC=12α， ∴∠BDC=30°，∵BD ⊥DE ，∴∠CDE=60°， ∵点C 关于直线l 的对称点为点D ， ∴DE=CE ，且∠CDE=60°∴△CDE 是等边三角形，∴CD=CE=DE ，∠DCE=60°=∠ACB ，∴∠BCD=∠ACE ，且AC=BC ，CD=CE ，∴△BCD ≌△ACE （SAS ）∴BD=AE ，（3）如图3，取AC 的中点O ，连接OB ，OF ，BF ，，F 是以AC 为直径的圆上一点，设AC 中点为O ，∵在△BOF 中，BO+OF≥BF ，当B 、O 、F 三点共线时BF 最长；如图，过点O 作OH ⊥BC ，∵∠BAC=90°，2a ，∴24BC AC a ==，∠ACB=45°，且OH ⊥BC ，∴∠COH=∠HCO=45°，∴OH=HC ，∴2OC HC =， ∵点O 是AC 中点，AC 2a ， ∴2OC a =，∴OH HC a ==，∴BH=3a ，∴10BO a =，∵点C 关于直线l 的对称点为点D ，∴∠AFC=90°，∵点O 是AC 中点， ∴OF OC ==，∴BF a =， ∴当B 、O 、F 三点共线时BF 最长；最大值为)a ．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理，三角形的三边关系，灵活运用相关的性质定理、综合运用知识是解题的关键．8．（1）①点P ；②见解析；（2）①点C 的横坐标C x 的值为-3；②334k -≤<-【解析】【分析】（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ；②利用新定义得点S 是点P 关于点M 的“正矩点”（答案不唯一）；（2）①利用新定义结合题意画出符合题意的图形，利用新定义的性质证明△BCF ≌△AOB ，则FC=OB 求得点C 的横坐标；②用含k 的代数式表示点C 纵坐标，代入不等式求解即可．【详解】解：（1）①在点P ，点Q 中，点OS 绕点O 顺时针旋转90°能得到线段OP ，故S 关于点O 的“正矩点”为点P ，故答案为点P ；②因为MP 绕M 点顺时针旋转90︒得MS ，所以点S 是点P 关于点M 的“正矩点”，同理还可以得点Q 是点P 关于点S 的“正矩点”．（任写一种情况就可以）（2）①符合题意的图形如图1所示，作CE ⊥x 轴于点E ，CF ⊥y 轴于点F ，可得 ∠BFC=∠AOB=90°．∵直线3(0)y kx k =+<与x 轴交于点A ，与y 轴交于点B ，∴点B 的坐标为3(0,3),(,0)B A k-在x 轴的正半轴上， ∵点A 关于点B 的“正矩点”为点(,)C C C x y ，∴∠ABC=90°，BC=BA ，∴∠1＋∠2=90°，∵∠AOB=90°，∴∠2＋∠3=90°，∴∠1=∠3．∴△BFC ≌△AOB ，∴3FC OB ==，可得OE ＝3．∵点A 在x 轴的正半轴上且3OA <，0C x ∴<，∴点C 的横坐标C x 的值为－3．②因为△BFC ≌△AOB ，3(,0)A k-，A 在x 轴正半轴上，所以BF ＝OA ，所以OF ＝OB-OF ＝33k +点3(3,3)C k -+，如图2， -1＜C y ≤2，即：-1＜33k+ ≤2，则334k -≤<-．【点睛】本题考查的是一次函数综合运用，涉及到三角形全等、解不等式，新定义等，此类新定义题目，通常按照题设的顺序，逐次求解．9．（1）①见解析；②见解析；（2）2【解析】【分析】（1）①只要证明∠2+∠BAF ＝∠1+∠BAF ＝60°即可解决问题；②只要证明△BFC ≌△ADB ，即可推出∠BFC ＝∠ADB ＝90°；（2）在BF 上截取BK ＝AF ，连接AK ．只要证明△ABK ≌CAF ，可得S △ABK ＝S △AFC ，再证明AF ＝FK ＝BK ，可得S △ABK ＝S △AFK ，即可解决问题；【详解】（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB ＝∠2+∠4+∠BAC ，∵∠BFE ＝∠BAC ＝2∠EFC ，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB ＝AC ，∴△ABK ≌CAF ，∴∠3＝∠4，S △ABK ＝S △AFC ，∵∠1+∠3＝∠2+∠3＝∠CFE ＝∠AKB ，∠BAC ＝2∠CEF ，∴∠KAF ＝∠1+∠3＝∠AKF ，∴AF ＝FK ＝BK ，∴S △ABK ＝S △AFK ， ∴ABF AFCS 2S ∆∆=．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的判定和性质、直角三角形30度角性质等知识，解题的关键是能够正确添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．10．（1）90°；（2）证明见解析；（3）变化，24l +≤<．【解析】【分析】（1）由等边三角形的性质可得∠ABC=∠ACB=60°，由等腰三角形的性质可求DAE=∠DEA=30°，由三角形内角和定理可求解；（2）根据等腰三角形的性质，可证得∠CDF=∠DEA 和∠EDB=∠DFA ，由此可利用“ASA”证明全等；（3）根据全等三角形的性质可得l =2+AD ，根据AD 的取值范围即可得出l 的取值范围．【详解】解：（1）∵△ABC 是等边三角形，∴AB=AC=BC=2，∠ABC=∠ACB=60°，∵AD=DE∴∠DAE=∠DEA=30°，∴∠ADB=180°-∠BAD-∠ABD=90°，故答案为：90°；（2）∵AD=DE=DF ，∴∠DAE=∠DEA ，∠DAF=∠DFA ，∵∠DAE+∠DAF=∠BAC=60°，∴∠DEA+∠DFA=60°，∵∠ABC=∠DEA+∠EDB=60°，∴∠EDB=∠DFA ，∵∠ACB=∠DFA+∠CDF=60°，∴∠CDF=∠DEA ，在△BDE 和△CFD 中∵CDF DEA DE DF EDB DFA ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BDE ≌△CFD （ASA ）（3）∵△BDE ≌△CFD ，∴BE=CD ，∴l =BD+BE+DE=BD+CD+AD=BC+AD=2+AD ，当D 点在C 或B 点时，AD=AC=AB=2,此时B 、D 、E 三点在同一条直线上不构成三角形，2+AD=4；当D 点在BC 的中点时，∵AB=AC ，∴BD=112BC =，AD ==此时22l AD =+=综上可知24l +≤<．【点睛】本题考查全等三角形的性质和判定，勾股定理，等边三角形的性质，等腰三角形的性质，三角形内角和定理．（1）掌握等腰三角形等边对等角是解决此问的关键；（2）中注意角之间的转换；（3）中注意临界点是否可取．11．（1）见解析；（2）见解析；（3）3【解析】【分析】（1）根据等腰三角形的性质和外角的性质即可得到结论；（2）过E 作EF ∥AC 交AB 于F ，根据已知条件得到△ABC 是等边三角形，推出△BEF 是等边三角形，得到BE=EF ，∠BFE=60°，根据全等三角形的性质即可得到结论；（3）连接AF ，证明△ABF ≌△CBF ，得AF=CF ，再证明DH=AH=12CF=3．【详解】解：（1）∵AB=AC ，∴∠ABC=∠ACB ，∵DE=DC ，∴∠E=∠DCE ，∴∠ABC-∠E=∠ACB-∠DCB ，即∠EDB=∠ACD ；（2）∵△ABC 是等边三角形，∴∠B=60°，∴△BEF是等边三角形，∴BE=EF，∠BFE=60°，∴∠DFE=120°，∴∠DFE=∠CAD，在△DEF与△CAD中，EDF DCADFE CADDE CD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEF≌△CAD（AAS），∴EF=AD，∴AD=BE；（3）连接AF，如图3所示：∵DE=DC，∠EDC=30°，∴∠DEC=∠DCE=75°，∴∠ACF=75°-60°=15°，∵BF平分∠ABC，∴∠ABF=∠CBF，在△ABF和△CBF中，AB BCABF CBFBF BF=⎧⎪∠=∠⎨⎪=⎩，△ABF≌△CBF（SAS），∴AF=CF，∴∠FAC=∠ACF=15°，∴∠AFH=15°+15°=30°，∵AH⊥CD，∴AH=12AF=12CF=3，∵∠DEC=∠ABC+∠BDE，∴∠BDE=75°-60°=15°，∴∠ADH=15°+30°=45°，∴∠DAH=∠ADH=45°，∴DH=AH=3．【点睛】本题考查了全等三角形的判定与性质，等腰三角形和直角三角形的性质，三角形的外角的性质，等边三角形的判定和性质，证明三角形全等是解决问题的关键．12．（1）全等，理由见解析；（2）t=3.5秒或5秒【解析】【分析】（1）根据垂直的定义得到∠DAC=∠ECB，利用AAS定理证明△ACD≌△CBE；（2）分点F沿C→B路径运动和点F沿B→C路径运动两种情况，根据等腰三角形的定义列出算式，计算即可；【详解】解：（1）△ACD与△CBE全等．理由如下：∵AD⊥直线l，∴∠DAC+∠ACD=90°，∵∠ACB=90°，∴∠BCE+∠ACD=90°，∴∠DAC=∠ECB，在△ACD和△CBE中，ADC CEBDAC ECBCA CB∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△CBE（AAS）；（2）由题意得，AM=t，FN=3t，则CM=8-t，由折叠的性质可知，CF=CB=6，∴CN=6-3t，点N在BC上时，△CMN为等腰直角三角形，当点N沿C→B路径运动时，由题意得，8-t=3t-6，解得，t=3.5，当点N沿B→C路径运动时，由题意得，8-t=18-3t，解得，t=5，综上所述，当t=3.5秒或5秒时，△CMN为等腰直角三角形；【点睛】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理，灵活运用分情况讨论思想是解题的关键．。

八年级下册数学期末压轴题(含答案)

八年级数学下册期末压轴题练习（含答案）一、填空题：1.如图，在矩形ABCD中，AD=6，AE⊥BD，垂足为E，ED=3BE，点P、Q分别在BD，AD上，则AP+PQ 的最小值为 .2.如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为．3.如图，已知正方形ABCD边长为3，点E在AB边上且BE=1，点P，Q分别是边BC，CD的动点（均不与顶点重合），当四边形AE PQ的周长取最小值时，四边形AEPQ 的面积是．4.如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点(不与点A．点D重合)将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH.现给出以下四个命题（1）∠APB=∠BPH;（2）当点P在边AD上移动时，△PDH的周长不发生变化; （3）∠PBH=450 ; （4）BP=BH.其中正确的命题是．5.如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是．二、综合题：6. (1)如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE.求证：CE=CF；(2)如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用(1)的结论证明：GE=BE+GD.(3)运用(1)(2)解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC(BC＞AD)，∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积.7.如图，已知等腰Rt△ABC和△CDE，AC=BC,CD=CE，连接BE、AD，P为BD中点，M为AB中点、N为DE中点，连接PM、PN、MN.（1）试判断△PMN的形状，并证明你的结论；（2）若CD=5，AC=12，求△PMN的周长.8.已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．（1）①当E点旋转到DA的延长线上时（如图1），△ABE与△ADG的面积关系是：．②当E点旋转到CB的延长线上时（如图2），△ABE与△ADG的面积关系是：（2）当正方形AEFG旋转任意一个角度时（如图3），（1）中的结论是否仍然成立？若成立请证明，若不成立请说明理由．（3）已知△ABC，AB=5cm，BC=3cm，分别以AB、BC、CA为边向外作正方形（如图4），则图中阴影部分的面积和的最大值是 cm2．9.一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=a．（1）如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为，周长为；（2）将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为，周长为；（3）如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．10.在正方形ABCD中，点E，F分别在边BC，CD上，且∠EAF=∠CEF=45°．（1）将△ADF绕着点A顺时针旋转90°，得到△ABG（如图①），求证：△AEG≌△AEF；（2）若直线EF与AB，AD的延长线分别交于点M，N（如图②），求证：EF2=ME2+NF2；（3）将正方形改为长与宽不相等的矩形，若其余条件不变（如图③），请你直接写出线段EF，BE，DF之间的数量关系．参考答案1.答案为：3.3.答案为：4.5．2.答案为：7；解法一：如图1所示，过O作OF⊥BC，过A作AM⊥OF，∵四边形ABDE为正方形，∴∠AOB=90°，OA=OB，∴∠AOM+∠BOF=90°，又∠AMO=90°，∴∠AOM+∠OAM=90°，∴∠BOF=∠OAM，在△AOM和△BOF 中，，∴△AOM≌△BOF（AAS），∴AM=OF，OM=FB，又∠ACB=∠AMF=∠CFM=90°，∴四边形ACFM为矩形，∴AM=CF，AC=MF=5，∴OF=CF，∴△OCF为等腰直角三角形，∵OC=6，∴根据勾股定理得：CF2+OF2=OC2，解得：CF=OF=6，∴FB=OM=OF﹣FM=6﹣5=1，则BC=CF+BF=6+1=7．故答案为：7．解法二：如图2所示，过点O作OM⊥CA，交CA的延长线于点M；过点O作ON⊥BC于点N．易证△OMA≌△ONB，∴OM=ON，MA=NB．∴O点在∠ACB的平分线上，∴△OCM为等腰直角三角形．∵OC=6，∴CM=ON=6．∴MA=CM﹣AC=6﹣5=1，∴BC=CN+NB=6+1=7．故答案为：7．4.答案为：（1）（2）（3）．5.答案为：2；解：作D 关于AE 的对称点D′，再过D′作D′P′⊥AD于P′，∵DD′⊥AE，∴∠AFD=∠AFD′，∵AF=AF，∠DAE=∠CAE，∴△DAF≌△D′AF，∴D′是D关于AE的对称点，AD′=AD=4，∴D′P′即为DQ+PQ的最小值，∵四边形ABCD是正方形，∴∠DAD′=45°，∴AP′=P′D′，∴在Rt△AP′D′中，P′D′2+AP′2=AD′2，AD′2=16，∵AP′=P′D'，2P′D′2=AD′2，即2P′D′2=16，∴P′D′=2，即DQ+PQ的最小值为2，6. (1)证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠CDF=90°，∵∠ADC=90°，∴∠FDC=90°.∴∠B=∠FDC，∵BE=DF，∴△CBE≌△CDF(SAS).∴CE=CF.(2)证明：如图2，延长AD至F，使DF=BE，连接CF.由(1)知△CBE≌△CDF，∴∠BCE=∠DCF.∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，∴∠GCF=∠GCE=45°.∵CE=CF，GC=GC，∴△ECG≌△FCG.∴GE=GF，∴GE=GF=DF+GD=BE+GD.(3)解：如图3，过C作CG⊥AD，交AD延长线于G.在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∵∠CGA=90°，AB=BC，∴四边形ABCG为正方形.∴AG=BC.…∵∠DCE=45°，根据(1)(2)可知，ED=BE+DG.…∴10=4+DG，即DG=6.设AB=x，则AE=x﹣4，AD=x﹣6，在Rt△AED中，∵DE2=AD2+AE2，即102=(x﹣6)2+(x﹣4)2.解这个方程，得：x=12或x=﹣2(舍去).…∴AB=12.∴S梯形ABCD=0.5(AD+BC)•AB=0.5×(6+12)×12=108.即梯形ABCD的面积为108.…7.解：（1）①∵正方形ABCD和正方形AEFG有公顶点A，将正方形AEFG绕点A旋转，E 点旋转到DA的延长线上，∴AE=AG，AB=AD，∠EAB=∠GAD，∴△ABE≌△ADG（SAS），∴△ABE的面积=△ADG的面积；②作GH⊥DA交DA的延长线于H，如图2，∴∠AHG=90°，∵E点旋转到CB的延长线上，∴∠ABE=90°，∠HAB=90°，∴∠GAH=∠EAB，在△AHG和△AEB中，∴△AHG≌△AEB，∴GH=BE，∵△ABE的面积=0.5EB•AB，△ADG的面积=0.5GH•AD，∴△ABE的面积=△ADG的面积；（2）结论仍然成立．理由如下：作GH⊥DA交DA的延长线于H，EP⊥BA交BA的延长线于P，如图3，∵∠PAD=90°，∠EAG=90°，∴∠PAE=∠GAH，在△AHG和△AEP中，∴△AHG≌△AEP（AAS），∴GH=BP，∵△ABP的面积=0.5EP•AB，△ADG的面积=0.5GH•AD，∴△ABP的面积=△ADG的面积；（3）∵AB=5cm，BC=3cm，∴AC==4cm，∴△ABC的面积=0.5×3×4=6（cm2）；根据（2）中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2．故答案为相等；相等；18．8.解：（1）∵AM=MC=AC=a，则∴重叠部分的面积是△ACB的面积的一半为0.25a2，周长为（1+）a．（2）∵重叠部分是正方形∴边长为0.5a，面积为0.25a2，周长为2a．（3）猜想：重叠部分的面积为0.25a2．理由如下：过点M分别作AC、BC的垂线MH、MG，垂足为H、G 设MN与AC的交点为E，MK与BC的交点为F∵M是△ABC斜边AB的中点，AC=BC=a∴MH=MG=0.5a又∵∠HME+∠HMF=∠GMF+∠HMF，∴∠HME=∠GMF，∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG•MH=0.5a×0.5a =0.25a2,∴阴影部分的面积是0.25a2．9.（1）证明：∵△ADF绕着点A顺时针旋转90°,得到△ABG,∴AF=AG,∠FAG=90°，∵∠EAF=45°,∴∠GAE=45°，在△AGE与△AFE中，，∴△AGE≌△AFE（SAS）；（2）证明：设正方形ABCD的边长为a.将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM．则△ADF≌△ABG，DF=BG．由（1）知△AEG≌△AEF，∴EG=EF．∵∠CEF=45°，∴△BME、△DNF、△CEF均为等腰直角三角形，∴CE=CF，BE=BM，NF=DF，∴a﹣BE=a﹣DF，∴BE=DF，∴BE=BM=DF=BG，∴∠BMG=45°，∴∠GME=45°+45°=90°，∴EG2=ME2+MG2，∵EG=EF，MG=BM=DF=NF，∴EF2=ME2+NF2；（3）解：EF2=2BE2+2DF2．如图所示，延长EF交AB延长线于M点，交AD延长线于N点，将△ADF绕着点A顺时针旋转90°，得到△AGH，连结HM，HE．由（1）知△AEH≌△AEF，则由勾股定理有（GH+BE）2+BG2=EH2，即（GH+BE）2+（BM﹣GM）2=EH2又∴EF=HE，DF=GH=GM，BE=BM，所以有（GH+BE）2+（BE﹣GH）2=EF2，即2（DF2+BE2）=EF2。

人教版八年级下册数学期末动点压轴题训练(带答案)

人教版八年级下册数学期末动点压轴题训练（带答案）1．如图，平面直角坐标系xOy 中，直线334y x =-+交x 轴于点A ，交y 轴于点B ，点P 是线段OA 上一动点（不与点A 重合），过点P 作PC AB ⊥于点C ．(1)当点P 是OA 中点时，求APC △的面积；(2)连接BP ，若BP 平分ABO ∠，求此时点P 的坐标；(3)BP 平分ABO ∠，在x 轴上有一动点H ，H 横坐标为a ，过点H 作直线l x ⊥轴，l 与线段PC 有交点，求a 的取值范围；(4)BP 平分ABO ∠，M 为x 轴上动点，CPM △为等腰三角形，求M 坐标．2．如图，直线l 1：y ＝kx +b 与y 轴交于点B （0，3），直线l 2：y ＝﹣2x ﹣1交y 轴于点A ，交直线l 1于点P （﹣1，t ）．(1)求k 、b 和t 的值； (2)求△ABP 的面积；(3)过动点D（a，0）作x轴的垂线与直线l1、l2，分别交于M、N两点，且MN＜4．①求a的取值范围；①当△AMP的面积是△AMB的面积的1时，求MN的长度．23．在平面直角坐标系中，坐标轴上的三个点A(a，0)，B(0，b)，C(c，0)(a＜0，b＞0)满足|c﹣1|+(a+b)2＝0，F为射线BC上的一个动点．(1)c的值为，①ABO的度数为．(2)如图（a），若AF①BC，且交OB于点E，求证：OE＝OC．(3)如图（b），若点F运动到BC的延长线上，且①FBO＝2①F AO，O在AF的垂直平分线上，求①ABF的面积．4．已知，长方形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A 的坐标为（10，0），点B的坐标为（10，8）．(1)直接写出点C的坐标为：C（，）；(2)已知Q（5，n）在直线AC；求n的值；(3)若动点P 从A 点出发，沿折线AO →OC 的路径以每秒2个单位长度的速度运动，到达C 处停止．求①OPQ 的面积S 与点P 的运动时间t （秒）的函数关系式．5．在①ABC 中，90ACB ∠=︒，60ABC ∠=︒，点D 是直线AB 上一动点，以CD 为边，在它右侧作等边①CDE ．(1)如图1，当E 在边AC 上时，直接判断线段DE ，EA 的数量关系______； (2)如图2，在点D 运动的同时，过点A 作AF CE ∥，过点C 作CF AE ∥，两线交于点F ，判断四边形AECF 形状，并说明理由；(3)若BC =AECF 为正方形时，直接写出AD 的值．6．已知在平面直角坐标系中，点()0,2A ，动点P 在x 轴正半轴上，作矩形OABP ，点C 为PB 中点，①ABC 沿AC 折叠后得到①ADC ，直线CD 与矩形OABP 一边交于点E ．(1)如图，当点E 与原点O 重合时， ①求证：OCP ADO ≌△△． ①求OP 长．(2)当5EC ED =，求点P 坐标．7．如图（1），在平面直角坐标系中点(),A x y ，()2,0B x 满足0x ，点C 为线段OB 上一个动点，以CA 为腰作等腰直角ACD △，且AC AD =．(1)求点A 、B 的坐标及AOB 的面积；(2)试判断CD 、OC 、BC 间的数量关系，并说明理由；(3)如图（2），若点C 为线段OB 延长线上一个动点，则（2）中的结论是否成立，并说明理由．8．如图，在平面直角坐标系中，直线4y x =+交y 轴于A 点，与直线BC 相交于点B (－2，m )，直线BC 与y 轴交于点C (0，－2)，与x 轴交于点D ；(1)求①ABC 的面积；(2)过点A 作BC 的平行线交x 轴于点E ，求点E 的坐标；(3)在（2）的条件下，点P 是直线AB 上一动点且在x 轴的上方，Q 为直角坐标平面内一点，如果以点D 、E 、P 、Q 为顶点的平行四边形的面积等于①ABC 面积，请求出点P 的坐标，并直接写出点Q 的坐标．9．如图，已知①ABC中，①B = 90°，AB = 8cm，BC = 6cm，P、Q是①ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．(1)出发2秒后，求PQ的长；(2)从出发几秒钟后，①PQB第一次能形成等腰三角形？(3)当点Q运动到CA上时，求能使①BCQ是等腰三角形时点Q的运动时间．10．如图1，四边形形ABCD是一个边长为2的正方形，点E是AB边上的一个动点（点E与点A，B不重合），连接CE，过点B作BF①CE于点G，交AD于点F．(1)求证：①ABF①①BCE；(2)如图2，当点E运动到AB中点时，①求BG的长；①连接DG，求证：DC＝DG．11．如图，在平面直角坐标系中，点O 为坐标原点，点A 、B 、C 的坐标分别为（0，6）、（-8，0）、（-3，0），10AB =，将ABC 沿着射线AC 翻折，点B 落到y 轴上点D 处．(1)求点D 的坐标；(2)动点P 以每秒1个单位长度的速度从点B 出发沿着线段BO 向终点O 运动，运动时间为t 秒，请用含有t 的式子表示PCA 的面积，并直接写出t 的取值范围； (3)在（2）的条件下，动点M 以每秒2个单位长度的速度从点A 出发沿着线段AO 向终点O 运动，动点N 以每秒a 个单位长度的速度从点O 出发沿着x 轴正方向运动，点P 、M 、N 同时出发，点M 停止时，点P 、N 也停止运动，当DOP MON △△≌时，求a 的值．12．如图，在平面直角坐标系中，一次函数21y x =--的图象分别交x 轴、y 轴于点A 和B ，已知点C 的坐标为（－3，0）．若点P 是x 轴上的一个动点．(1)求直线BC 的函数解析式；(2)过点P 作y 轴的平行线交AB 于点M ，交BC 于点N ，当点P 恰好是MN 的中点时，求出P 点坐标．(3)若以点B 、P 、C 为顶点的①BPC 为等腰三角形时，请直接写出所有符合条件的P 点坐标．13．如图所示，菱形ABCD 的顶点A B ，在x 轴上，点A 在点B 的左侧，点D 在y 轴的正半轴上．点C 的坐标为(4．动点P 从点A 出发，以每秒1个单位长度的速度，按照A D C B A →→→→的顺序在菱形的边上匀速运动一周，设运动时间为t 秒．(1)①点B 的坐标； ①求菱形ABCD 的面积；(2)当3t =时，问线段AC 上是否存在点E ，使得PE DE +最小，如果存在，求出PE DE +最小值；如果不存在，请说明理由．14．如图，①ABC 中，①C ＝90°，AC ＝8cm ，BC ＝6cm ，若动点P 从点C 开始，按C →A →B →C 的路径运动，且速度为每秒1cm ，设运动的时间为t 秒．(1)当t ＝秒时，CP 把①ABC 的面积分成相等的两部分，此时CP ＝ cm ；(2)当t 为何值时，①ABP 为等腰三角形．(3)若点P 在线段AC 上运动，点Q 是线段AB 上的动点，求PB +PQ 的最小值．15．已知等边①ABC 中，AB ＝8，点D 为边BC 上一动点，以AD 为边作等边①ADE ，且点E 与点D 在直线AC 的两侧，过点E 作EF //BC ，EF 与AB 、AC 分别相交于点F 、G ．(1)求证：四边形BCEF 是平行四边形；(2)设BD ＝x ，FG ＝y ，求y 关于x 的函数解析式，并写出定义域； (3)当AD 的长为7时，求线段FG 的长．16．如图，在平面直角坐标系中，点D 的横坐标为4，直线1l ：2y x =+经过点D ，与x 轴、y 轴分别交于A 、B 两点，直线2l ：y kx b =+经过点()1,0C 、点D 两点．(1)求直线2l 的函数表达式； (2)求ACD △的面积；(3)点P 为线段AD 上一动点，连接CP ． ①求CP 的最小值；①当ACP△为等腰三角形时，直接写出点P的坐标．17．如图，在矩形ABCD中，E是BC上一动点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G，AB＝3，AD＝4．(1)如图1，当①DAG＝30°时，求BE的长；(2)如图2，当点E是BC的中点时，求线段GC的长；(3)如图3，点E在运动过程中，当△CFE的周长最小时，直接写出BE的长．18．如图1，点A在y轴上，点B，点C在x轴上，点D在第一象限，且△ABC与△ADC均为等边三角形，点B坐标为（﹣3，0），点E为线段BC上一动点，点F为直线DC上一动点，且∠EAF＝60°，连接EF．(1)填空：写出点A、点D的坐标，点A；点D；(2)试判断△AEF的形状，并给予证明；(3)直接写出EF长度的最小值以及此时点F的坐标；(4)将条件改为“点E为CB延长线上一点”，其他条件不变，△AEF的形状是否发生变化？在图2中画全图形（不必证明），直接写出当点E坐标为（﹣5，0）时，EF的长度以及此时点F的坐标．19．如图，在平面直角坐标系中，直线y＝kx过点B（m，6），过点B分别作x轴和y轴的垂线，垂足分别为点A，C，①AOB＝30°．动点P从点O出发，以每秒2个单位C运长度的速度向点B运动，动点Q从点B动．点P，Q同时开始运动，当点P到达点B时，点P，Q同时停止运动，设运动时间为t秒．(1)求m与k的值；(2)设①PQB的面积为S，求S与t的关系式；(3)若以点P，Q，B为顶点的三角形是等腰三角形，请求出t的值．（温擎提示：在直角三角形中，30°的角所对的直角边等于斜边的一半）20．如图，在平面直角坐标系中，OA=OB=6，OD=1，点C为线段AB的中点．(1)直接写出点C的坐标为；(2)点P是x轴上的动点，当PB+PC的值最小时，求此时点P的坐标；(3)在平面内是否存在点F，使得以A、C、D、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．参考答案：1．(1)解：如图，连接BP ，直线334y x =-+交x 轴于点A ，交y 轴于点B ，∴点()4,0A ，点()0,3B ， 4AO ∴=，3OB =，5AB ∴，点P 是OA 中点，2AP OP ∴==，1122ABP S AP OB AB CP =⨯⨯=⨯⨯， 65CP ∴=，85AC ∴==， 124225APC S AC PC ∴=⨯⨯=； (2)如图，连接BP ，BP 平分ABO ∠，OBP CBP ∴∠=∠，又BP BP =，90BOP BCP ∠=∠=︒，BOP ∴①()BCP AAS ，3BO BC ∴==，OP CP =，532AC AB BC ∴=-=-=，222AP PC AC =+，22(4)4OP OP ∴-=+，32OP ∴=， 3,02P ⎛⎫∴ ⎪⎝⎭； (3)过点C 作⊥CH x 轴于点H ．由()2得，OP CP =＝32，2AC =， 4AP ∴=－32＝52， ①65AC CP CH AP ⋅==,AH ∴85， OH OA AH ∴=-＝125， a ∴的取值范围31225a ≤≤； (4)设点(),0M x ，过点C 作⊥CH x 轴于点H ，则22222126()()55MC HM CH x =+=-+，同理可得：2239()24CP ==，223()2MP x =-，当MC CP =时，即221269()()554x -+=，解得3310x =或3(2舍去)；当MC MP =时，同理可得392x =；当CP MP =时，同理可得0x =或3，故点M 的坐标为33,010⎛⎫ ⎪⎝⎭或39,02⎛⎫ ⎪⎝⎭或()0,0或()3,0． 2．解：①点P （﹣1，t ）在直线直线l 2上，①t ＝﹣2×（﹣1）﹣1＝1，即P （﹣1，1），把B 、P 的坐标代入可得13k b b -+=⎧⎨=⎩，解得 23k b =⎧⎨=⎩， ①t ＝1，k ＝2，b ＝3；(2)解：①直线y ＝﹣2x ﹣1交y 轴于点A ，①A （0，﹣1），①P （﹣1，1），B （0，3）， ①1114222PAB SAB =⨯=⨯=； (3)解：①①MN ①y 轴，①M、N的横坐标为a，设M、N的纵坐标分别为ym和yn，由（1）可知直线l1的函数表达式为y＝2x+3，①ym＝2a+3，yn＝﹣2a﹣1，当MN在点P左侧时，此时a＜﹣1，则有MN＝yn﹣ym＝﹣2a﹣1﹣（2a+3）＝﹣4a﹣4，①MN＜4，①﹣4a﹣4＜4，解得a＞﹣2，①此时﹣2＜a＜﹣1；当MN在点P的右侧时，此时a＞﹣1，则有MN＝ym﹣yn＝2a+3﹣（﹣2a﹣1）＝4a+4，①MN＜4，①4a+4＜4，解得a＜0，①此时﹣1＜a＜0；当a＝﹣1时，也符合题意，综上可知当﹣2＜a＜0时，MN＜4；①由（2）可知S△APB＝2，由题意可知点M只能在y轴的左侧，当点M在线段BP上时，过点M作MC①y轴于点C，如图1①S△APM＝12S△AMB，①S△ABM＝23S△APB＝43，①12AB•MC＝43，即2MC＝43，解得MC＝23，①点M的横坐标为﹣23，即a＝﹣23，①MN＝4a+4＝﹣83+4＝43；当点M在线段BP的延长线上时，过点M作MD①y轴于点D，如图2，①S△APM＝12AMB S，①S△ABM＝2S△APB＝4，①12AB•MD＝4，即2MD＝4，解得MD＝2，①点M的横坐标为﹣2，①MN＝﹣4a﹣4＝8﹣4＝4（不合题意舍去），综上可知MN的长度为43．3．解：①|c﹣1|+(a+b)2＝0，①c＝1，a＝﹣b，①OA＝OB，①①ABO＝45°，故答案为：1，45°．(2)证明：①AF ①BC ，①①AOE ＝①BFE ＝90°，①①AEO ＝①BEF ，①①OBC ＝①OAE ，在①AOE 和①BOC 中，===OAE OBC AOE BOC OA OB ∠∠⎧⎪∠∠⎨⎪⎩， ①①AOE ①①BOC (AAS )，①OE ＝OC ；(3)解：连结OF ，过点F 作FG ①x 轴，垂足为点G ，设①F AO ＝x ，则①FBO ＝2①F AO ＝2x ，①O 在AF 的垂直平分线上，①AO ＝OF ，①①OAF ＝①OF A ＝x ，①①GOF ＝①OAF +①OF A ＝2x ，①①FBO ＝2①F AO ＝2x ，OB ＝OA ＝OF ，①①OFC ＝①OBF ＝2x ，①①BCO ＝①COF +①OFB ＝4x ，①①OBC +①OCB ＝90°，①6x ＝90°，解得x ＝15°，①①OBC ＝①GOF ＝2x ＝30°，①C (1，0)，①OC ＝1，①①BOC ＝90°，①OBC ＝30°，①BC ＝2OC ＝2，OB ，①OA ＝OF ＝OB，同理可得：FG = ，①=+AC AO OC ，①S △ABF ＝S △ACB +S △ACF ＝12×AC ×FG +12×AC ×OB ＝12＝94 4．(1)①四边形ABCO 是矩形①AB =OC ，AO =BC①A （10，0），B （10，8）①OC =OB =8①点C 的坐标为（0，8）故答案为：0，8(2)设直线AC 的解析式为y kx b =+把点A （10，0），B （0，8）代入y kx b =+得，1008k b b +=⎧⎨=⎩ 解得，458k b ⎧=-⎪⎨⎪=⎩ ①直线AC 的解析式为485y x =-+ 把点Q （5，n ）代入485y x =-+得， 45845n =-⨯+=； (3)①当05t ≤≤时，102OP OA AP t =-=-过点Q 作QD ①OA 于点D ，如图，①Q （5，4）①QD =4 ①1(102)42042S t t =-⨯=-； ①当59<≤t 时，OP = AP -AO =2t -10过点Q 作QE ①OC 于点E ，如图，①Q （5，4）①QE =5 ①1(210)55252S t t =-⨯=- 综上，204(05)=525(59)t t S t t -≤≤⎧⎨-<≤⎩5(1)①90ACB ∠=︒，60ABC ∠=︒①30A ∠=︒①CDE △为等边三角形①60DEC ∠=︒①DEC ∠是ADE 外角①DEC A ADE ∠=∠+∠①30ADE A ∠=︒=∠①DE EA =故答案为相等．(2)取AB 中点O ，连接OC 、OE①AF CE ∥, CF AE ∥①四边形AECF 是平行四边形①90ACB ∠=︒①OC OB OA ==①60ABC ∠=︒①①BCO 为等边三角形①①CDE 是等边三角形①60DCB OCE DCO ∠=∠=︒-∠①OC BC = CD CE =①BCD OCE ≌△△①60EOC B ∠=∠=︒①60EOA ∠=︒又①OE OE =，OA OC =①()OCE OAE SAS ≌△△①CE EA =①平行四边形AECF 是菱形(3)当点D 在AB 延长线上时，作CH AD ⊥于H ，当四边形AECF 为正方形时，45ACE BCE ∠=∠=︒，90AEC ∠=︒ ①60DCE ∠=︒①15DCB ∠=︒①60ABC ∠=︒①45CDH ∠=︒①BC =①AC ==①12CH AC =①AH ==①CDE △为等边三角形 ①CH DH ==①AD =当点D 在AB 上时作CH AB ⊥于H ，同理可得CDH △是等腰直角三角形，则AD AH DH =-=综上AD =6．解：①矩形OABP 中，()02A ，， AB OP ∴=，2BP OA ==，90AOP OAB ABC OPB ∠=∠=∠=∠=︒ ． ABC 沿AC 折叠后得到ADC ，90ADC ABC ∴∠=∠=︒，AD AB =，AD OP ∴=，当点E 与原点O 重合时，18090ADO ADC ∠=︒-∠=︒，90AOD COP AOP ∠+∠=∠=︒，90AOD OAD ∴∠+∠=︒，COP OAD ∴∠=∠．在OCP △和AOD △中，90OPC ADO COP OAD OP AD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩()OCP AOD AAS ∴≌；①①点C 为PB 的中点，112CP BC PB ∴===，由①知：OCP AOD ≌，2OC AO ∴==，在Rt COP 中，由勾股定理得OP ，即OP(2)解：当5EC DE =，则4CD DE =．ABC 沿AC 折叠后得到ADC ，1CD BC ∴==，90ADC ABC ∠=∠=︒，AD AB =，1144DE CD ∴==，90ADE ∠=︒，AD OP =， 554CE ED ∴==，设OP p =，则AD AB OP p ===，若点E 在OP 上，连接AE ，如下图，在Rt CPE △中，1CP =，34EP ∴=， 34OE OP PE p ∴=-=-，在Rt AOE 中，22222324AE OA OE p ⎛⎫=+=+- ⎪⎝⎭，在Rt ADE △中， 222221=4AE DE AD p ⎛⎫=++ ⎪⎝⎭， 222213+244p p ⎛⎫⎛⎫∴=+- ⎪ ⎪⎝⎭⎝⎭，即22139+416216p p p =+-+，解得3p =，此时，点P 的坐标为()30，；若点E 在OA 上，点D 在第一象限，过点E 作EF BC ⊥于F 点，如下图，则90EFP EFC ∠=∠=︒，90EOP OPF EFP ∴∠=∠=∠=︒，①四边形EFPO 是矩形，90CEF ECF ∠+∠=︒，EF OP ∴=，90OEF ∠=︒，AD EF ∴=，90CEF AED AEF ∠+∠=∠=︒，AED ECF ∴∠=∠．在AED 和ECF △中，AED ECF ADE EFC AD EF ∠=∠∠=∠=⎧⎪⎨⎪⎩，()AED ECF AAS ∴≌，54AE EC =∴=．在Rt ADE △中，AD ==OP AD ∴== 此时，点P的坐标为0⎫⎪⎪⎝⎭．若点E 在OA 上，点D 在第二象限时，过点C 作CF OA ⊥于F 点，如下图，则90AFC ∠=︒．①①F AB =①B =①AFC =90°，①四边形AFCB 是矩形，①AB =CF ，1AF BC ==ABC 沿AC 折叠后得到ADC ，①90ADC ABC ADE ∠=∠=∠=︒，AD AB OP CF ===，90ADE EFC ∴∠=∠=︒．在AED 和CEF △中，AED CEF ADE EFC AD CF ∠⎪∠⎧=∠∠=⎪⎨⎩=，()AED CEF AAS ∴≌，AE CE ∴=，DE EF =．5EC ED =，1AF AE EF BC =+==，15CE EF CE DE DE DE ∴+==+=+，16DE EF ∴==，556CE DE ==，在Rt EFC 中，CF =即OP ， ∴点P的坐标为⎫⎪⎪⎝⎭．综上所述，点P 坐标()30，或0⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭． 7．(1)①0x =，①(0x ≥0≥，①x y ==①A ，()B ，132AOB S =⨯=△． (2)结论：222CD OC BC =+．理由：连接，①OA AB ==OB =①222OA OB OB +=，①90OAB ∠=︒，45AOB ABO ∠=∠=︒，①OAB CAD ∠=∠，①OAC BAD ∠=∠，①AO AB ∠=，AC AD =，①OAC BAD △△≌，①OC BD =，45AOC ABD ∠=∠=︒，①90CBD ∠=︒，①222CD BC BD =+．①222CD OC BC =+．(3)（2）中的结论仍然成立理由：连接，①90OAB ∠=︒，45AOB ABO ∠=∠=︒，①OAB CAD ∠=∠，①OAC BAD ∠=∠，①AO AB =，AC AD =，①OAC BAD △△≌，①OC BD =，45AOC ABD ∠=∠=︒，①90OBD DBC ∠=∠=︒，①222CD BC BD =+，①222CD OC BC =+．8．(1)解：将点2()B m -，，代入4y x =+得24m ，解得2m =，①()22B -，，当0x =时，4y =，①()0,4A ， ①12662ABC S ∆=⨯⨯=． (2)解：设直线BC 的解析式为()20y kx k =-≠，将B 点坐标代入得222k --=，解得2k =-，①直线BC 的解析式为22y x =--，故设过点A 且平行于BC 的直线解析式为2y x b =-+，将A 点坐标代入得4b =，①过点A 且平行于BC 的直线解析式为24y x =-+，当0y =时，2x =，①()2,0E ．(3)解：由（2）可得()1,0D -，以点D 、E 、P 、Q 为顶点的平行四边形分两种情况求解： ①当DE 是平行四边形的边长时，则点Q 在x 轴上方，设(),4P m m +，①62DEPQ ABC DEP SS S ===， ①()1432DEP S DE m =⨯+=，解得2m =-，①()2,2P -，①PQ DE ∥，PQ DE =，①()5,2Q -；同理62DEQP ABC DEP S S S ===，①()2,2P -，①()1,2Q ；①当DE 是平行四边形的对角线时，则点Q 在x 轴下方，设(),4P m m +，同理62DQEP ABC DEP S S S ===，①()2,2P -，①D E 、的中点坐标为102，⎛⎫ ⎪⎝⎭， ①P Q 、的中点坐标为102，⎛⎫ ⎪⎝⎭， ①()3,2Q -；综上所述，P 点坐标为()2,2-，Q 的点坐标为()5,2- 或()1,2 或()3,2-．9．如图所示：BQ=2×2=4cm，BP=AB-AP=8- 2×1=6cm，①①B= 90°①PQ==；(2)当△PQB第一次形成等腰三角形时，BQ =BP，①BQ = 2t，BP= 8-t，①2t= 8-t，解得：t=83；(3)①①B = 90°，AB = 8cm，BC = 6cm，①AC10=cm，①当CQ= BQ时，如图则①C=①CBQ，①①ABC= 90°，①①CBQ +①ABQ = 90°，①①A+①C= 90°，①①A=①ABQ，①BQ= AQ，①CQ=AQ=5cm，①BC+ CQ = 11cm，①t= 11 ÷2= 5.5秒；①当CQ= BC时，如图2，则BC+CQ=12cm，①t= 12÷2= 6秒；①当BC = BQ时，如图3，过B点作BE①AC于点E，则BE=·6824105AB BCAC⨯==cm，①CE185=cm，①CQ= 2CE = 7.2cm，①BC+ CQ = 13.2cm，①t= 13.2÷2= 6.6秒；综上可知，当t为5.5秒或6秒或6.6秒时，△BCQ为等腰三角形．10．(1)证明：①BF ①CE ，①①CGB ＝90°，①①GCB +①CBG ＝90°，①四边形ABCD 是正方形， ①①CBE ＝90°＝①A ，BC ＝AB ， ①①FBA +①CBG ＝90°，①①GCB ＝①FBA ，在①ABF 和①BCE 中，A CBE AB BCABF BCF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ①①ABF ①①BCE （ASA ）；(2)解:①由题意可知AB ＝CD ＝BC ＝2， ①点E 是AB 的中点，①EA ＝EB ＝12AB ＝1，①CE在Rt①CEB 中，12BG •CE ＝12CB •EB ， ①BG ＝CB EB CE⋅①证明：如图，过点D 作DH ①CE 于H ，由①可得CG = ①①DCE +①BCE ＝90°，①CBF +①BCE ＝90°，①①DCE ＝①CBF ，①CD ＝BC ，①CHD ＝①CGB ＝90°，①①CHD ①①BGC （AAS ），①CH ＝BG①GH ＝CG ﹣CH ＝CH ， ①CH ＝GH ，DH ①CE ，①DC ＝DG ；11．(1)解：①AD 是由AB 折叠得到，①10AD AB ==，①()0,4D -；(2)BP t =，当05t ≤<时，①()8,0B -，()3,0C -，①8OB =，3OC =， ①1163922ACO S OA OC =⋅=⨯⨯=△，8OP OB BP t =-=-， ①()116824322APO S OA OP t t =⋅=⨯-=-△，①2439153PCA APO ACO S S S t t =-=--=-△△△，当58t <≤时，()9243315PCA ACO APO S S S t t =-=--=-△△△，综上所述，PCA 的面积是153S t =-，（05t ≤<），或315S t =-，（58t <≤）．(3)①DOP MON △△≌，①OP ON =，OM OD =，由题意可知：BP t =，2AM t =，ON at =，4OD =①8OP OB BP t =-=-，62OM AO AM t =-=-，①624t -=，解得1t =，8t at -=，解得7a =，①a 的值是7．12．(1)解：①一次函数21y x =--的图象分别交x 轴，y 轴于点A 和B ，①点A （－12，0），点B （0，－1），设直线BC 的解析式y kx b =+代入B （0，－1），C （－3，0）．解得13k =-，1b =- ①直线BC 的函数解析式113y x =--． (2)①设点P （m ，0），则点M （m ，21m --），点N （m ，113m --）依题意可得PM ＝PN ①1210013m m ⎛⎫---=--- ⎪⎝⎭解得：67m =- ①点P （－67，0） (3)设(),0,P x 而0,1,3,0,B C22222223,1,3110,PC x PB x BC 当PC PB =时，2231,x x 解得：4,3x4,0.3P 当,PB BC2110,x解得：3,x =±当3x =-时，不合题意舍去，3,0.P当PC BC =时，2310,x 12310,310,x x 310,0P 或310,0.P综上：点P （3，03，0）或（3，0）或4,03⎛⎫- ⎪⎝⎭． 13．(1)①①(490C AOD ∠=︒，，①4DC AD DO ===，①2OA ==，①四边形ABCD 是菱形，①42AB AD OB AB OA ===-=，，①点B 的坐标(2)0，，故答案为：(2)0，①①在菱形ABCD 中，4DC AB OD ===，①菱形ABCD 的面积•4AB OD ==⨯(2)如图所示：当3t =时，3AP =,在菱形ABCD 中，点P 关于AC 的对称点为3P AP ''=，，连接DP '交AC 于点E ，连接PE ，①PE DE P E ED P D ''+=+=．①2OA OD ==，①1OP '=，在Rt DOP '中，①222DO P O P D ''+=，①P D'①PE DE+14．(1)解：在直角三角形ACB中，由勾股定理得AB10，①CP把△ABC的面积分成相等的两部分，①P为AB的中点，CP＝152AB=．①运动的路径长为AC＋AP＝8＋5＝13．运动的时间为13÷1＝13（秒）所以t＝13；CP＝5．(2)解：①ABP为等腰三角形，点P只能在AC上且P A＝PB，设CP＝t，则AP＝BP＝8﹣t，在Rt①BCP中，BC2＋CP2＝BP2，即62＋t2＝（8﹣t）2，解得，t＝74，①当t＝74时，①ABP为等腰三角形；(3)作点B关于AC的对称点B′，过点B′作AB的垂线段，交AC于点P，交AB于点Q，连接AB′，则垂线段B′Q即为所求的PB＋PQ的最小值，①S△ABB′＝12×BB′×AC＝12×12×8＝48，S△ABB′＝12×AB×B′Q，①B′Q＝485，即PB＋PQ最小值为485．15．(1)①①ABC 是等边三角形① AB ＝AC①60,BAC ABC ACB ∠=∠=∠=︒①①ADE 是等边三角形①AD ＝AE①60,DAE ∠=︒BAC DAC DAE DAC∠-∠=∠-∠ 即BAD CAE∠=∠ ①ABD ACE ∆≅∆ （SAS ）① BD ＝EC①60ACE B ∠=∠=︒①120,BCE ACB ACE ∠=∠+∠=︒①180,B BCE ∠+∠=︒①AB //EC①EF //BC①四边形BCEF 是平行四边形(2)①EF //BC①60CGE ACB ∠=∠=︒①60CGE ACE ∠=∠=︒①GE ＝EC①GE ＝EC ＝BD ＝x①FG FE GE =-①8(08)y x x =-<<(3)作AH ①BC ，垂足为H在Rt AHB ∆中，90,AHD ∠=︒222AH BH AB +=①22248AH +=①AH =在Rt ADH ∆中，90,AHD ∠=︒①222AH DH AD +=即(222(4)7x +-=，解得5x =或3x =； ① 8FG x =-①FG 的长为3或516．(1)将4x =代入2y x =+得：6y =①点D 的坐标为()4,6．将()1,0C ，()4,6D 代入y kx b =+得046k b k b +=⎧⎨+=⎩解得22k b =⎧⎨=-⎩ ①直线2l 的表达式为22y x =-．(2)过点D 作DE x ⊥轴于点E ，①()4,6D ，①6DE =将0y =代入2y x =+得2x =①()2,0A -，①3AC = ①192ACD S AC DE =⋅=△． (3)①由题可知：当CP AB ⊥时，CP 的值最小，由（2）可知6DE =，①点E 坐标为()4,0，①246AE AO OE =+=+=在Rt ADE △中，90AED ∠=︒．①AD ==①192ACD S AD CP =⋅=△①29CP AD ⨯=== ①①点P 在直线y =x +2上，①设点P （x ，x +2）,①A (-2，0)，C (1，0)①22[1(2)]9AC =--=，222(2)PA x =+，222(1)(2)PC x x =-++ （a ）当AP AC =时，即22AP AC =，则：22(2)=9x +解得，x =当x =y =x =时，y =①点P （b ）当AC PC =时，即22AC PC =，则：22(1)(2)9x x -++=解得，x =1或x =-2（舍去）当1x =时，3y =；①点P 的坐标为（13，）（c ）当AP PC =时，即22AP PC =，则：22()2x +22(1)(2)x x =-++ 解得，12x =- ①32y = ①点P 的坐标为（12-，32）综上，点P 的坐标为：13，）或（12-，32） 17(1)解：①四边形ABCD 是矩形，①①BAD ＝90°，①①DAG ＝30°，①①BAG ＝60°由折叠知，①BAE ＝12①BAG ＝30°，在Rt △BAE 中，①BAE ＝30°，AB ＝3，①BE(2)解：如图4，连接GE ，①E 是BC 的中点，①BE ＝EC ，①①ABE 沿AE 折叠后得到△AFE ，①BE ＝EF ，①EF ＝EC ，①在矩形ABCD 中，①①C ＝90°，①①EFG ＝90°，①在Rt △GFE 和Rt △GCE 中，EG EG EF EC =⎧⎨=⎩①Rt △GFE ①Rt △GCE （HL ），①GF ＝GC ；设GC ＝x ，则AG ＝3+x ，DG ＝3﹣x ，在Rt △ADG 中，42+（3﹣x ）2＝（3+x ）2，解得x ＝43． (3)解：如图1，由折叠知，①AFE ＝①B ＝90°，EF ＝BE ， ①EF +CE ＝BE +CE ＝BC ＝AD ＝4，①当CF 最小时，△CEF 的周长最小，①CF≥AC-AF ，①当点A ，F ，C 在同一条直线上时，CF 最小，由折叠知，AF ＝AB ＝3，在Rt △ABC 中，AB ＝3，BC ＝AD ＝4，①AC＝5，①CF＝AC﹣AF＝2，在Rt△CEF中，EF2+CF2＝CE2，①BE2+CF2＝（4﹣BE）2，①BE2+22＝（4﹣BE）2，①BE＝32．18．解：（1）∵△ABC是等边三角形，AO⊥BC，∴OB＝OC，∠BAO＝∠CAO＝30°，∵点B坐标为（﹣3，0），∴OB＝OC＝3，∴AB＝6，∴OA∴A（0，，∵△ABC和△ADC都是等边三角形，∴AD＝AC＝AB＝6，∠ACB＝∠ACD＝∠D＝60°，∴∠D+∠BCD＝180°，∴AD∥BC，∴D（6，，故答案为：（0，，（6，；（2）△AEF是等边三角形．证明：∵△ABC和△ADC都是等边三角形，∴AB＝AC，∠B＝∠ACD＝∠BAC＝60°，∵∠EAF＝60°，∴∠BAE＝∠CAF，∴△ABE≌△ACF（ASA），∴AE＝AF，∴△AEF是等边三角形．（3）由（2）知AE＝EF＝AF，当AE⊥BC时，AE取得最小值，∴AE＝OA＝过点F作FM⊥x轴于点M，∵∠FOM＝30°，OF＝∴FM=∴OM92 =，∴F（92，即EF的最小值为F（92；（4）由（2）可知△ABE≌△ACF（ASA），∵E（﹣5，0），OB＝3，∴BE＝2，∴BE＝CF＝2，CE＝8，∵∠ACD＝∠ACB＝60°，∴∠ECF＝60°，过点F作FN⊥BC于点N，如图3，∴CN 12=CF ＝1，∴NF∴EF∵OC ＝3，∴ON ＝OC ﹣CN ＝3﹣1＝2，∴F （2，．19．(1)解：BA OA ⊥，90BAO ∴∠=︒，30AOB ∠=︒，6(),B m ，OA m ∴=，6AB =，212OB AB ∴==，OA =m ∴=B 6)，直线y kx =过点B 6)，k ∴= (2)如图1，过点P 作PF BC ⊥于点F ，BQ ∴，2OP t =，则122PB t =-，30OBC ∠=︒，∴在Rt PFB ∆中，6PF t =-，()2162S t ∴=⨯-=+； (3)分三种情况：①当BQ BP =122t =-，解得24t =-①当PQ PB =时，如图2，过点P 作PM BQ ⊥于点M ，BM ∴，2)t -，解得4t =；①当OB QP =时，如图3，过点Q 作ON BP ⊥于点N ，则6BN t =-，6t ∴-=，解得125t =；综上所述，当PQB ∆为等腰三角形时，t 的值为24-4或125． 20．(1)解：过点C 作CN OA ⊥于点N ，过点C 作CM OB ⊥于点N ．①CN OA ⊥①//CN OB又①点C 为线段AB 的中点，OA = 6 ①132ON OA == 同理132OM OB == ①C (3,3)(2)作点B关于x轴的对称点B'，连接CB'交x轴于点P，此时PB+PC的值最小，由已知得，点B的坐标为（0，6），①点B关于x轴的对称点B'（0，﹣6），由（1）知，C（3，3），可设直线CB'的解析式为y=kx+b，①633bk b-=⎧⎨=+⎩解得36kb=⎧⎨=-⎩① 直线CB'的解析式为y=3x﹣6，令y=0，则3x﹣6=0，解得：x=2，① P（2，0）；(3)存在点F，使以A、C、D、F为顶点的四边形为平行四边形，设点F的坐标为（m，n）．分三种情况考虑，如图所示：当AC为对角线时，①A（6，0），C（3，3），D（1，0），①1632200322mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：83mn=⎧⎨=⎩，①点F1的坐标为（8，3）；①当AD为对角线时，①A（6，0），C（3，3），D（1，0），①3162230022mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：43 mn=⎧⎨=-⎩，①点F2的坐标为（4，-3）；①当CD为对角线时，①A（6，0），C（3，3），D（1，0），①6312203022mn++⎧=⎪⎪⎨++⎪=⎪⎩，解得：23mn=-⎧⎨=⎩，①点F3的坐标为（-2，3）．综上所述，点F的坐标是（8，3），（4，-3）或（-2，3）．。

人教版八年级下册数学期末一次函数压轴题训练

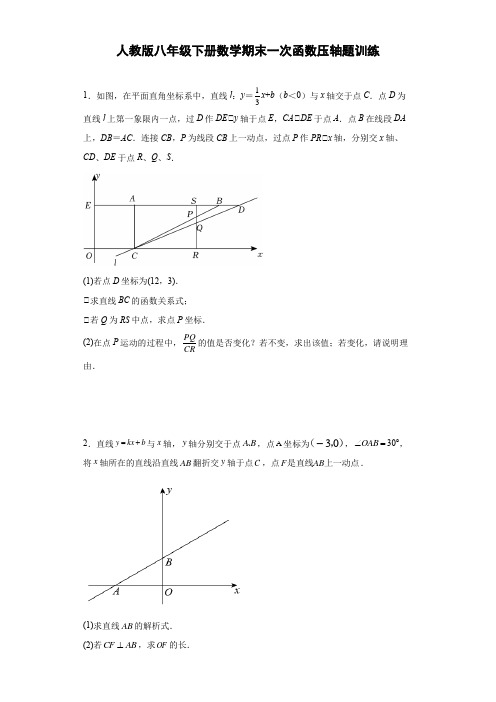
人教版八年级下册数学期末一次函数压轴题训练1．如图，在平面直角坐标系中，直线l ：y ＝13x +b （b ＜0）与x 轴交于点C ．点D 为直线l 上第一象限内一点，过D 作DE ⊥y 轴于点E ，CA ⊥DE 于点A ．点B 在线段DA 上，DB ＝AC ．连接CB ，P 为线段CB 上一动点，过点P 作PR ⊥x 轴，分别交x 轴、CD 、DE 于点R 、Q 、S ．(1)若点D 坐标为(12，3)． ⊥求直线BC 的函数关系式； ⊥若Q 为RS 中点，求点P 坐标． (2)在点P 运动的过程中，PQCR的值是否变化？若不变，求出该值；若变化，请说明理由．2．直线y kx b =+与x 轴，y 轴分别交于点A B 、，点A 坐标为30-（，），OAB ∠=30°，将x 轴所在的直线沿直线AB 翻折交y 轴于点C ，点F AB 是直线上一动点．(1)求直线AB 的解析式． (2)若CF AB ⊥，求OF 的长．(3)若AOF是等腰三角形，直接写出点F的坐标．3．在平面直角坐标系xOy中，点A、B分别在y轴和x轴上，已知点A（0，4）．以AB为直角边在AB左侧作等腰直角△ABC，⊥CAB＝90°．(1)当点B在x轴正半轴上，且AB＝8时⊥求AB解析式；⊥求C点坐标；(2)当点B在x轴上运动时，连接OC，求AC+OC的最小值及此时B点坐标．4．已知，如图1，直线AB分别交平面直角坐标系中x轴和y轴于A，B两点，点A坐标为（﹣3，0），点B坐标为（0，6），点C在直线AB上，且点C坐标为（﹣a，a），(1)求直线AB的表示式和点C的坐标：(2)点D是x轴上的一动点，当S△AOB＝S△ACD时，求点D坐标；(3)如图2，点E 坐标为（0，﹣1），连接CE ，点P 为直线AB 上一点，且⊥CEP ＝45°，求点P 坐标．5．如图，在平面直角坐标系中，函数28y x =-+的图象分别交x 轴，y 轴于A 、B 两点过点A 的直线交y 轴正半轴于点M ，且点M 为线段OB 的中点．(1)求直线AM 的解析式．(2)试在直线AM 上找一点P ，使得=ABP AOB S S △△，请求出点P 的坐标．(3)若点H 为坐标平面内任意一点，在坐标平面内是否存在这样的点H ，使以A 、B 、M 、H 为顶点的四边形是直角梯形？若存在，请直接写出点H 的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，直线AB 和直线BC 相交于点()2,2-，直线AB 与y 轴相交于点A ()0,4，直线BC 与x 轴、y 轴分别交于点()1,0D -，点C ．(1)求直线AB 的解析式．(2)过点A 作BC 的平行线交x 轴于点E ，求点E 的坐标．(3)在（2）的条件下，点P是直线AB上一个动点，且点P在x轴的上方，如果以点D、E、P、Q为顶点的平行四边形的面积等于三角形ABC的面积．⊥求出点P的坐标．⊥画出所有情况并直接写出点Q的坐标．7．已知：如图，一次函数334y x=-的图像分别与x轴、y轴相交于点A、B，且与经过x轴负半轴上的点C的一次函数y＝kx＋b的图像相交于点D，直线CD与y轴相交于点E，E与B关于x轴对称，OA＝3OC．(1)直线CD的函数表达式为______；点D的坐标______；（直接写出结果）(2)点P为线段DE上的一个动点，连接BP．⊥若直线BP将⊥ACD的面积分为79∶两部分，试求点P的坐标；⊥点P是否存在某个位置，将⊥BPD沿着直线BP翻折，使得点D恰好落在直线AB上方的坐标轴上？若存在，求点P的坐标；若不存在，请说明理由．8．如图，在平面直角坐标系xOy 中，直线AP 交x 轴于点P （p ，0），与y 轴交于点A（0，a ），且a 、p +（p ﹣1）2＝0．(1)求直线AP 的解析式；(2)如图1，直线x ＝﹣2与x 轴交于点N ，点M 在x 轴上方且在直线x ＝﹣2上，若⊥MAP 的面积等于6，请求出点M 的坐标；(3)如图2，已知点C （﹣2，4），若点B 为射线AP 上一动点，连接BC ，在坐标轴上是否存在点Q ，使⊥BCQ 是以BC 为底边的等腰直角三角形，直角顶点为Q ，若存在，请求出点Q 坐标；若不存在，请说明理由．9．如图1，直线AB 分别与x 轴、y 轴交于A 、B 两点，已知A （m ，0），B （0，n ），且m 、n 满足281620n n n m -++-=．(1)求A 、B 两点的坐标；(2)如图2，若点C 在第一象限，⊥ACB =90°，AC =BC ，点D 为边AB 中点，以点D 为顶点的直角⊥EDF 两边分别交边BC 于E ，交边AC 于F ，求四边形EDFC 的面积； (3)如图3，若点C 在y 轴的正半轴上，H 是第一象限内的一点，且H 点的横、纵坐标始终相等，点P （x ，24x -+）为直线AB 上一点，⊥HCP =90°，HC =CP ，当点P 在x 轴下方时，求出点P 的坐标．10．如图所示，在平面直角坐标系中，直线y ＝x ＋1与y ＝－34x ＋3分别交x 轴于点B和点C ，点D 是直线y ＝－34x ＋3与y 轴的交点．(1)直接写出点B 、C 、D 的坐标；(2)设M (x ，y )是直线y ＝x ＋1在x 轴上方图像上一点，⊥BCM 的面积为S ，请写出S 与x 的函数关系式；并探究当点M 运动到什么位置时(求出M 点坐标即可)，⊥BCM 的面积为10，并说明理由；(3)线段CD 上是否存在点P ，使⊥CBP 为等腰三角形，如果存在，直接写出P 点的坐标；如果不存在，请说明理由．11．若直线122y x =+分别交x 轴、y 轴于A 、C 两点，点P 是该直线上在第一象限内的一点，PB ⊥x 轴，B 为垂足，且S △ABC = 6(1)求点B 和P 的坐标；(2)点D 是直线AP 上一点，△ABD 是直角三角形，求点D 坐标；(3)请问坐标平面是否存在点Q，使得以Q、C、P、B为顶点四边形是平行四边形，若存在请直接写出点Q的坐标；若不存在，请说明理由．12．如图，在平面直角坐标系中，直线AB为y＝﹣34x＋b交y轴于点A（0，3），交x轴于点B，直线x＝1交AB于点D，交x轴于点E，P是直线x＝1上一动点，且在点D的上方，设P（1，n）．(1)求点B的坐标及点O到直线AB的距离；(2)求⊥ABP的面积（用含n的代数式表示）；(3)当S△ABP＝72时，在第一象限找点C，使⊥PBC为等腰直角三角形，直接写出点C的坐标．13．如图，在直角坐标系内，把y＝12x的图象向下平移1个单位得到直线AB，直线AB分别交x轴于点A，交y轴于点B，C为线段AB的中点，过点C作AB的垂线，交y轴于点D．(1)求A ，B 两点的坐标； (2)求BD 的长；(3)直接写出所有满足条件的点E ；点E 在坐标轴上且⊥ABE 为等腰三角形．14．已知：如图1，一次函数y ＝mx ＋5m 的图像与x 轴、y 轴分别交于点A 、B ，与函数y ＝－23x 的图像交于点C ，点C 的横坐标为－3．（1）求点B 的坐标；（2）若点Q 为直线OC 上一点，且S △QAC ＝2S △AOC ，求点Q 的坐标；（3）如图2，点D 为线段OA 上一点，⊥ACD ＝⊥AOC ．点P 为x 轴负半轴上一点，且点P 到直线CD 和直线CO 的距离相等．⊥ 在图2中，只利用圆规．．．．．作图找到点P 的位置； (保留作图痕迹，不得在图2中作无关元素．) ⊥ 求点P 的坐标．15．如图1，直线AB 的解析式为6y kx =+，D 点坐标为()8,0，O 点关于直线AB 的对称点C 点在直线AD 上．（1）求直线AB 的解析式；（2）如图2，在x 轴上是否存在点F ，使ABC 与ABF 的面积相等，若存在求出F 点坐标，若不存在，请说明理由；（3）如图3，过点()5,2G 的直线:l y mx b =+．当它与直线AB 夹角等于45°时，求出相应m 的值．16．如图，在平面直角坐标系中，点O 是坐标原点，直线y ＝﹣34x +6与x 轴交于点A ，与y 轴交于点B ，与直线y ＝34x 交于点C ．（1）求点C 的坐标；（2）点P 是线段OA 上的一个动点（点P 不与点O ，A 重合），过点P 作平行于y 轴的直线l ，分别交直线AB ，OC 于点D ，点E ，设点P 的横坐标为m ． ⊥求线段PD 的长（用含m 的代数式表示）；⊥当点P ，D ，E 三点中有一个点是另两个点构成线段的中点时，请直接写出的值；（3）过点C 作CF ⊥y 轴于点F ，点M 在线段CF 上且不与点C 重合，点N 在线段OC 上，CM ＝ON ，连接BM ，BN ，BM +BN 是否存在最小值？如果存在，请直接写出最小值；如果不存在，请说明理由．17．如图，在平面直角坐标系中，O为坐标原点，一次函数y＝1x+4与x轴，y轴分2别交于点B，点A，点C的坐标为C（5，0），点P是射线BO上一动点．（1）点A的坐标是；点B的坐标是；（2）连接AP，若⊥ABP的面积为10，求点P的坐标；（3）当点P在射线BO上运动时，若⊥APC是等腰三角形，请直接写出点P的坐标．18．把正方形纸片放在直角坐标系中，如图所示，正方形纸片ABCD的边长为3，点E、F分别在BC、CD上，将AB、AD分别沿AE、AF折叠，点B、D恰好都落在点G 处，已知3BE＝BC．（1）请直接写出D、E两点的坐标，并求出直线EF的解析式；（2）在直线EF上是否存在点M，使得⊥AFM的面积是⊥AEF的面积的一半，若存在，请求出点M的坐标，若不存在，请说明理由．（3）若点P、Q分别是线段AG、AF上的动点，则EP＋PQ的最小值是多少？并求出此时点Q的坐标．19．如图，已知菱形ABCD，AD∥x轴，点A的坐标为(4，﹣1)，点B的坐标为(1，3)．（1）请求出C、D两点的坐标．（2）若点P在CD上，点P关于坐标轴对称的点Q落在直线l：y＝12x+12上，求点P的坐标．（3）若点M在y轴上，点N在直线l上，如果以A、B、M、N为顶点的四边形是平行四边形，请直接写出点N的坐标．20．已知一次函数y=34x+6的图象与x轴、y轴分别交于点A、B，与直线y=54x相交于点C，过B作x轴的平行线l，点P是直线l上的一个动点．（1）直接写出点A、B的坐标：A______、B______；（2）若S△AOC=S△BCP，求点P的坐标；（3）若点E是平面内的一个动点，当⊥ABE是AB为直角边的等腰直角三角形，则点E的坐标为________ ．参考答案：1．(1)⊥1322y x =-；⊥15(2P ，9)4 (2)结论：16PQ CR =2．(1)y x =； (2)3；(3)（32-32 3，32）或（3- ，32-）3．(1)⊥4y x =+；⊥C (4,4--(2)(2,0)B4．(1)26y x =+，(2,2)C -(2)(6.0)或(12,0)- (3)7(3，32)3或35(11-，4)11- 5．(1)4y x =-+(2)()14,8P -，()212,8P -(3)存在，()6,2H ，()4,8，124,55⎛⎫- ⎪⎝⎭，836,55⎛⎫- ⎪⎝⎭ 6．(1)y =x +4(2)（2，0）(3)⊥P （-2，2），Q 1（1，2），Q 2（-5，2），Q 3（3，-2）7．(1)934y x =+，（-4，-6） (2)⊥P 点坐标为5334⎛⎫-- ⎪⎝⎭，或918⎛⎫- ⎪⎝⎭，；⊥存在，P 点坐标为2421,1111⎛⎫-- ⎪⎝⎭或833⎛⎫-- ⎪⎝⎭， 8．(1)y =3x -3；(2)（-2，3）；(3)Q 的坐标为（-72，0）或（0，74）或（0，132） 9．(1)A （2，0），B （0，4） (2)52(3)P （4，4-）10．(1)(1,0)B -，(4,0)C ，(0,3)D(2)55(1)22y x x =+>-，点M 运动到(3,4)时，BCM ∆的面积为10 (3)存在点P ，P 点的坐标是(0,3)或3(2，15)811．(1)B （2，0），P （2，3）(2)（2，3）或（45，125） (3)（0，5）或（0，-1）或（4，1）12．(1)B （4，0），125(2)922n - (3)（5，7）或（8，3）或（92，72） 13．(1)(2,0)A ，(0,1)B - (2)52BD =(3)(2+，(2，(2,0)-，3(,0)4，(0,1)，(0,1-+，(0,1-，3(0,)2 14．（1）B （0，5）；（2）点Q 的坐标为（-9，6）或（3，-2）；（3）⊥点P 的坐标为（-5-20）或（，0）． 15．（1）直线AB 的解析式为26y x =-+；（2）()6,0F ；（3）13m =-或3m =． 16．（1）C (4，3) （2）⊥PD =|364m -+|，⊥m =163或m =83；（3）存在最小值，最小值是17．（1）（0，4），（﹣8，0）；（2）P （﹣3，0）；（3）（﹣5，0）或()5或()5或9010⎛⎫ ⎪⎝⎭，． 18．（1）D 点坐标为（3，3），E 点坐标为（1，0），直线EF 的解析式为33y x 44=-；（2）当M 的坐标为（2，34）或（4，94）时，使得⊥AFM 的面积是⊥AEF 的面积的一半；（3）（2，2）19．（1）C (﹣4，3)，D (﹣1，﹣1)；（2）(﹣115，35)或(﹣175，115)；（3）(5，3)或(3，2)或(﹣3，﹣1)20．（1）（8，0）、（0，6）；（2）（403，6）或（-403，6）；（3）点E 的坐标为（6，14）或（-6，-2）或（14，8）或（2，-8）．。

人教版八年级下册数学压轴题及答案

人教版八年级下册数学压轴题及答案本页仅作为文档页封面，使用时可以删除八年级下数学压轴题1．已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：；（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）2．如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．（1）若点D是BC边的中点（如图①），求证：EF=CD；（2）在（1）的条件下直接写出△AEF和△ABC的面积比；（3）若点D是BC边上的任意一点（除B、C外如图②），那么（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．3．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．4．如图，正方形ABCD中，E为AB边上一点，过点D作DF⊥DE，与BC延长线交于点F．连接EF，与CD边交于点G，与对角线BD交于点H．（1）若BF=BD=，求BE的长；（2）若∠ADE=2∠BFE，求证：FH=HE+HD．5．如图，将一三角板放在边长为1的正方形ABCD上，并使它的直角顶点P 在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于Q．探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与PB之间有怎样的数量关系？试证明你的猜想；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数关系，并写出函数自变量x的取值范围；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置．并求出相应的x值，如果不可能，试说明理由．6．Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起，CB与DE重合．（1）求证：四边形ABFC为平行四边形；（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△A′B′C′位置，直线B'C'与AB、CF分别相交于P、Q两点，猜想OQ、OP长度的大小关系，并证明你的猜想；（3）在（2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形（不要求证明）7．如图，在正方形ABCD中，点F在CD边上，射线AF交BD于点E，交BC 的延长线于点G．（1）求证：△ADE≌△CDE；（2）过点C作CH⊥CE，交FG于点H，求证：FH=GH；（3）设AD=1，DF=x，试问是否存在x的值，使△ECG为等腰三角形？若存在，请求出x的值；若不存在，请说明理由．8．在平行四边形ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．（1）在图1中证明CE=CF；（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．9．如图，已知▱ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD．（1）求证：△ADG≌△FDM．（2）猜想AB与DG+CE之间有何数量关系，并证明你的猜想．10．如图，在正方形ABCD中，E、F分别为BC、AB上两点，且BE=BF，过点B作AE的垂线交AC于点G，过点G作CF的垂线交BC于点H延长线段AE、GH交于点M．（1）求证：∠BFC=∠BEA；（2）求证：AM=BG+GM．11．如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4，（1）求AC所在直线的解析式；（2）将纸片OABC折叠，使点A与点C重合（折痕为EF），求折叠后纸片重叠部分的面积．（3）求EF所在的直线的函数解析式．12．已知一次函数的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．（2）求直线AE的表达式；（3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．（4）若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F．设OE=x，BF=y，试求y与x之间的函数关系式，并写出函数的定义域．13．如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求点D的坐标；（2）求直线l2的解析表达式；（3）求△ADC的面积；（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．14．如图1，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A、B分别在x轴与y轴上，已知OA=6，OB=10．点D为y轴上一点，其坐标为（0，2），点P从点A出发以每秒2个单位的速度沿线段AC﹣CB 的方向运动，当点P与点B重合时停止运动，运动时间为t秒．（1）当点P经过点C时，求直线DP的函数解析式；（2）①求△OPD的面积S关于t的函数解析式；②如图②，把长方形沿着OP折叠，点B的对应点B′恰好落在AC边上，求点P的坐标．（3）点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．15．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣5，1），B（﹣2，4），C（5，4），点D在第一象限．（1）写出D点的坐标；（2）求经过B、D两点的直线的解析式，并求线段BD的长；（3）将平行四边形ABCD先向右平移1个单位长度，再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边A 1B1C1D1重叠部分的面积．16．如图，一次函数的图象与x轴、y轴交于点A、B，以线段AB 为边在第一象限内作等边△ABC，（1）求△ABC的面积；（2）如果在第二象限内有一点P（a，）；试用含有a的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值；（3）在x轴上，是否存在点M，使△MAB为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．2018年06月17日梧桐听雨的初中数学组卷参考答案与试题解析一．解答题（共16小题）1．已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N，AH⊥MN于点H．（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：AH=AB ；（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB 的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，求AH的长．（可利用（2）得到的结论）【解答】解：（1）如图①AH=AB．（2）数量关系成立．如图②，延长CB至E，使BE=DN．∵ABCD是正方形，∴AB=AD，∠D=∠ABE=90°，在Rt△AEB和Rt△AND中，，∴Rt△AEB≌Rt△AND，∴AE=AN，∠EAB=∠NAD，∵∠DAN+∠BAN=45°，∴∠EAB+∠BAN=45°，∴∠EAN=45°，在△AEM和△ANM中，，∴△AEM≌△ANM．∴S△AEM =S△ANM，EM=MN，∵AB、AH是△AEM和△ANM对应边上的高，∴AB=AH．（3）如图③分别沿AM、AN翻折△AMH和△ANH，得到△ABM和△AND，∴BM=2，DN=3，∠B=∠D=∠BAD=90°．分别延长BM和DN交于点C，得正方形ABCD，由（2）可知，AH=AB=BC=CD=AD．设AH=x，则MC=x﹣2，NC=x﹣3，在Rt△MCN中，由勾股定理，得MN2=MC2+NC2∴52=（x﹣2）2+（x﹣3）2（6分）解得x1=6，x2=﹣1．（不符合题意，舍去）∴AH=6．2．如图，△ABC是等边三角形，点D是边BC上的一点，以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．（1）若点D是BC边的中点（如图①），求证：EF=CD；（2）在（1）的条件下直接写出△AEF和△ABC的面积比；（3）若点D是BC边上的任意一点（除B、C外如图②），那么（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．【解答】（1）证明：∵△ABC是等边三角形，D是BC的中点，∴AD⊥BC，且∠BAD=∠BAC=30°，∵△AED是等边三角形，∴AD=AE，∠ADE=60°，∴∠EDB=90°﹣∠ADE=90°﹣60°=30°，∵ED∥CF，∴∠FCB=∠EDB=30°，∵∠ACB=60°，∴∠ACF=∠ACB﹣∠FCB=30°，∴∠ACF=∠BAD=30°，在△ABD和△CAF中，，∴△ABD≌△CAF（ASA），∴AD=CF，∵AD=ED，∴ED=CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF=CD．（2）解：△AEF和△ABC的面积比为：1：4；（易知AF=BF，延长EF交AD于H，△AEF的面积=•EF•AH=•CB•AD=••BC•AD，由此即可证明）（3）解：成立．理由如下：∵ED∥FC，∴∠EDB=∠FCB，∵∠AFC=∠B+∠BCF=60°+∠BCF，∠BDA=∠ADE+∠EDB=60°+∠EDB∴∠AFC=∠BDA，在△ABD和△CAF中，∴△ABD≌△CAF（AAS），∴AD=FC，∵AD=ED，∴ED=CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF=DC．3．（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．【解答】（1）证明：∵四边形ABCD是正方形，∴BC=CD，∠B=∠CDF=90°，∵∠ADC=90°，∴∠FDC=90°．∴∠B=∠FDC，∵BE=DF，∴△CBE≌△CDF（SAS）．∴CE=CF．（2）证明：如图2，延长AD至F，使DF=BE，连接CF．由（1）知△CBE≌△CDF，∴∠BCE=∠DCF．∴∠BCE+∠ECD=∠DCF+∠ECD，即∠ECF=∠BCD=90°，又∠GCE=45°，∴∠GCF=∠GCE=45°．∵CE=CF，GC=GC，∴△ECG≌△FCG．∴GE=GF，∴GE=GF=DF+GD=BE+GD．（3）解：如图3，过C作CG⊥AD，交AD延长线于G．在直角梯形ABCD中，∵AD∥BC，∴∠A=∠B=90°，又∵∠CGA=90°，AB=BC，∴四边形ABCG为正方形．∴AG=BC．…（7分）∵∠DCE=45°，根据（1）（2）可知，ED=BE+DG．…（8分）∴10=4+DG，即DG=6．设AB=x，则AE=x﹣4，AD=x﹣6，在Rt△AED中，∵DE2=AD2+AE2，即102=（x﹣6）2+（x﹣4）2．解这个方程，得：x=12或x=﹣2（舍去）．…（9分）∴AB=12．=（AD+BC）•AB=×（6+12）×12=108．∴S梯形ABCD即梯形ABCD的面积为108．…（10分）4．如图，正方形ABCD中，E为AB边上一点，过点D作DF⊥DE，与BC延长线交于点F．连接EF，与CD边交于点G，与对角线BD交于点H．（1）若BF=BD=，求BE的长；（2）若∠ADE=2∠BFE，求证：FH=HE+HD．【解答】（1）解：∵四边形ABCD正方形，∴∠BCD=90°，BC=CD，∴Rt△BCD中，BC2+CD2=BD2，即BC2=（）2﹣（BC）2，∴BC=AB=1，∵DF⊥DE，∴∠ADE+∠EDC=90°=∠EDC+∠CDF，∴∠ADE=∠CDF，在△ADE和△CDF中，∵，∴△ADE≌△CDF（ASA），∴AE=CF=BF﹣BC=﹣1，∴BE=AB﹣AE=1﹣（﹣1）=2﹣；（2）证明：在FE上截取一段FI，使得FI=EH，∵△ADE≌△CDF，∴DE=DF，∴△DEF为等腰直角三角形，∴∠DEF=∠DFE=45°=∠DBC，∵∠DHE=∠BHF，∴∠EDH=∠BFH（三角形的内角和定理），在△DEH和△DFI中，∵，∴△DEH≌△DFI（SAS），∴DH=DI，又∵∠HDE=∠BFE，∠ADE=2∠BFE，∴∠HDE=∠BFE=∠ADE，∵∠HDE+∠ADE=45°，∴∠HDE=15°，∴∠DHI=∠DEH+∠HDE=60°，即△DHI为等边三角形，∴DH=HI，∴FH=FI+HI=HE+HD．5．如图，将一三角板放在边长为1的正方形ABCD上，并使它的直角顶点P 在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于Q．探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与PB之间有怎样的数量关系？试证明你的猜想；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数关系，并写出函数自变量x的取值范围；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置．并求出相应的x 值，如果不可能，试说明理由．【解答】解：（1）PQ=PB，（1分）过P点作MN∥BC分别交AB、DC于点M、N，在正方形ABCD中，AC为对角线，∴AM=PM，又∵AB=MN，∴MB=PN，∵∠BPQ=90°，∴∠BPM+∠NPQ=90°；又∵∠MBP+∠BPM=90°，∴∠MBP=∠NPQ，在Rt△MBP≌Rt△NPQ中，∵∴Rt△MBP≌Rt△NPQ，（2分）∴PB=PQ．（2）∵S四边形PBCQ =S△PBC+S△PCQ，∵AP=x，∴AM=x，∴CQ=CD﹣2NQ=1﹣x，又∵S△PBC=BC•BM=•1•（1﹣x）=﹣x，S△PCQ=CQ•PN=（1﹣x）•（1﹣x），=﹣+，∴S=﹣x+1．（0≤x≤）．（4分）四边形PBCQ（3）△PCQ可能成为等腰三角形．①当点P与点A重合时，点Q与点D重合，PQ=QC，此时，x=0．（5分）②当点Q在DC的延长线上，且CP=CQ时，（6分）有：QN=AM=PM=x，CP=﹣x，CN=CP=1﹣x，CQ=QN﹣CN=x﹣（1﹣x）=x﹣1，∴当﹣x=x﹣1时，x=1．（7分）．6．Rt△ABC与Rt△FED是两块全等的含30°、60°角的三角板，按如图（一）所示拼在一起，CB与DE重合．（1）求证：四边形ABFC为平行四边形；（2）取BC中点O，将△ABC绕点O顺时钟方向旋转到如图（二）中△A′B′C′位置，直线B'C'与AB、CF分别相交于P、Q两点，猜想OQ、OP 长度的大小关系，并证明你的猜想；（3）在（2）的条件下，指出当旋转角至少为多少度时，四边形PCQB为菱形（不要求证明）【解答】（1）证明：∵△ABC≌△FCB，∴AB=CF，AC=BF．∴四边形ABFC为平行四边形．（2）解：OP=OQ，理由如下：∵OC=OB，∠COQ=∠BOP，∠OCQ=∠PBO，∴△COQ≌△BOP．∴OQ=OP．（3）解：90°．理由：∵OP=OQ，OC=OB，∴四边形PCQB为平行四边形，∵BC⊥PQ，∴四边形PCQB为菱形．7．如图，在正方形ABCD中，点F在CD边上，射线AF交BD于点E，交BC 的延长线于点G．（1）求证：△ADE≌△CDE；（2）过点C作CH⊥CE，交FG于点H，求证：FH=GH；（3）设AD=1，DF=x，试问是否存在x的值，使△ECG为等腰三角形？若存在，请求出x的值；若不存在，请说明理由．【解答】（1）证明：∵四边形ABCD是正方形，∴DA=DC，∠1=∠2=45°，DE=DE，∴△ADE≌△CDE．（2）证明：∵△ADE≌△CDE，∴∠3=∠4，∵CH⊥CE，∴∠4+∠5=90°，又∵∠6+∠5=90°，∴∠4=∠6=∠3，∵AD∥BG，∴∠G=∠3，∴∠G=∠6，∴CH=GH，又∵∠4+∠5=∠G+∠7=90°，∴∠5=∠7，∴CH=FH，∴FH=GH．（3）解：存在符合条件的x值此时，∵∠ECG＞90°，要使△ECG为等腰三角形，必须CE=CG，∴∠G=∠8，又∵∠G=∠4，∴∠8=∠4，∴∠9=2∠4=2∠3，∴∠9+∠3=2∠3+∠3=90°，∴∠3=30°，∴x=DF=1×tan30°=．8．在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．（1）在图1中证明CE=CF；（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．【解答】（1）证明：如图1，∵AF平分∠BAD，∴∠BAF=∠DAF，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAF=∠CEF，∠BAF=∠F，∴∠CEF=∠F．∴CE=CF．（2）解：连接GC、BG，∵四边形ABCD为平行四边形，∠ABC=90°，∴四边形ABCD为矩形，∵AF平分∠BAD，∴∠DAF=∠BAF=45°，∵∠DCB=90°，DF∥AB，∴∠DFA=45°，∠ECF=90°∴△ECF为等腰直角三角形，∵G为EF中点，∴EG=CG=FG，CG⊥EF，∵△ABE为等腰直角三角形，AB=DC，∴BE=DC，∵∠CEF=∠GCF=45°，∴∠BEG=∠DCG=135°在△BEG与△DCG中，∵，∴△BEG≌△DCG，∴BG=DG，∵CG⊥EF，∴∠DGC+∠DGA=90°，又∵∠DGC=∠BGA，∴∠BGA+∠DGA=90°，∴△DGB为等腰直角三角形，∴∠BDG=45°．（3）解：延长AB、FG交于H，连接HD．∵AD∥GF，AB∥DF，∴四边形AHFD为平行四边形∵∠ABC=120°，AF平分∠BAD∴∠DAF=30°，∠ADC=120°，∠DFA=30°∴△DAF为等腰三角形∴AD=DF，∴CE=CF，∴平行四边形AHFD为菱形∴△ADH，△DHF为全等的等边三角形∴DH=DF，∠BHD=∠GFD=60°∵FG=CE，CE=CF，CF=BH，∴BH=GF在△BHD与△GFD中，∵，∴△BHD≌△GFD，∴∠BDH=∠GDF∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°9．如图，已知▱ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD．（1）求证：△ADG≌△FDM．（2）猜想AB与DG+CE之间有何数量关系，并证明你的猜想．【解答】证明：（1）∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∴∠BAF=∠DFA，∵AF平分∠BAD，∴∠DAF=∠DFA，∴AD=FD，∵DE⊥BC，DH⊥AB，∴∠ADG=∠FDM=90°，在△ADG和△FDM中，，∴△ADG≌△FDM（ASA）．（2）AB=DG+EC．证明：延长GD至点N，使DN=CE，连接AN，∵DE⊥BC，AD∥BC，∴∠ADN=∠DEC=90°，在△ADN和△DEC中，，∴△ADN≌△DEC（SAS），∴∠NAD=∠CDE，AN=DC，∵∠NAG=∠NAD+∠DAG，∠NGA=∠CDE+∠DFA，∴∠NAG=∠NGA，∴AN=GN=DG+CE=DC，∵四边形ABCD是平行四边形，∴AB=CD，∴AB=DG+EC．10．如图，在正方形ABCD中，E、F分别为BC、AB上两点，且BE=BF，过点B作AE的垂线交AC于点G，过点G作CF的垂线交BC于点H延长线段AE、GH交于点M．（1）求证：∠BFC=∠BEA；（2）求证：AM=BG+GM．【解答】证明：（1）在正方形ABCD中，AB=BC，∠ABC=90°，在△ABE和△CBF中，，∴△ABE≌△CBF（SAS），∴∠BFC=∠BEA；（2）连接DG，在△ABG和△ADG中，，∴△ABG≌△ADG（SAS），∴BG=DG，∠2=∠3，∵BG⊥AE，∴∠BAE+∠2=90°，∵∠BAD=∠BAE+∠4=90°，∴∠2=∠3=∠4，∵GM⊥CF，∴∠BCF+∠1=90°，又∠BCF+∠BFC=90°，∴∠1=∠BFC=∠2，∴∠1=∠3，在△ADG中，∠DGC=∠3+45°，∴∠DGC也是△CGH的外角，∴D、G、M三点共线，∵∠3=∠4（已证），∴AM=DM，∵DM=DG+GM=BG+GM，∴AM=BG+GM．11．如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4，（1）求AC所在直线的解析式；（2）将纸片OABC折叠，使点A与点C重合（折痕为EF），求折叠后纸片重叠部分的面积．（3）求EF所在的直线的函数解析式．【解答】解：（1）∵=，∴可设OC=x，则OA=2x，在Rt△AOC中，由勾股定理可得OC2+OA2=AC2，∴x2+（2x）2=（4）2，解得x=4（x=﹣4舍去），∴OC=4，OA=8，∴A（8，0），C（0，4），设直线AC解析式为y=kx+b，∴，解得，∴直线AC解析式为y=﹣x+4；（2）由折叠的性质可知AE=CE，设AE=CE=y，则OE=8﹣y，在Rt△OCE中，由勾股定理可得OE2+OC2=CE2，∴（8﹣y）2+42=y2，解得y=5，∴AE=CE=5，∵∠AEF=∠CEF，∠CFE=∠AEF，∴∠CFE=∠CEF，∴CE=CF=5，∴S=CF•OC=×5×4=10，△CEF即重叠部分的面积为10；（3）由（2）可知OE=3，CF=5，∴E（3，0），F（5，4），设直线EF的解析式为y=k′x+b′，∴，解得，∴直线EF的解析式为y=2x﹣6．12．已知一次函数的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．（1）求点B的坐标；（2）求直线AE的表达式；（3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．（4）若将已知条件“AE平分∠BAO，交x轴于点E”改变为“点E是线段OB上的一个动点（点E不与点O、B重合）”，过点B作BF⊥AE，垂足为F．设OE=x，BF=y，试求y与x之间的函数关系式，并写出函数的定义域．【解答】解：（1）对于y=﹣x+6，当x=0时，y=6；当y=0时，x=8，∴OA=6，OB=8，在Rt△AOB中，根据勾股定理得：AB=10，则A（0，6），B（8，0）；（2）过点E作EG⊥AB，垂足为G（如图1所示），∵AE平分∠BAO，EO⊥AO，EG⊥AG，∴EG=OE，在Rt△AOE和Rt△AGE中，，∴Rt△AOE≌Rt△AGE（HL），∴AG=AO，设OE=EG=x，则有BE=8﹣x，BG=AB﹣AG=10﹣6=4，在Rt△BEG中，EG=x，BG=4，BE=8﹣x，根据勾股定理得：x2+42=（8﹣x）2，解得：x=3，∴E（3，0），设直线AE的表达式为y=kx+b（k≠0），将A（0，6），E（3，0）代入y=kx+b得：，解得：，则直线AE的表达式为y=﹣2x+6；（3）延长BF交y轴于点K（如图2所示），∵AE平分∠BAO，∴∠KAF=∠BAF，又BF⊥AE，∴∠AFK=∠AFB=90°，在△AFK和△AFB中，∵，∴△AFK≌△AFB，∴FK=FB，即F为KB的中点，又∵△BOK为直角三角形，∴OF=BK=BF，∴△OFB为等腰三角形，过点F作FH⊥OB，垂足为H（如图2所示），∵OF=BF，FH⊥OB，∴OH=BH=4，∴F点的横坐标为4，设F（4，y），将F（4，y）代入y=﹣2x+6，得：y=﹣2，∴FH=|﹣2|=2，=OB•FH=×8×2=8；则S△OBF（4）在Rt△AOE中，OE=x，OA=6，根据勾股定理得：AE==，=AE•BF=BE•AO（等积法），又BE=OB﹣OE=8﹣x，S△ABE∴BF==（0＜x＜8），又BF=y，则y=（0＜x＜8）．13．如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．（1）求点D的坐标；（2）求直线l2的解析表达式；（3）求△ADC的面积；（4）在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．【解答】解：（1）由y=﹣3x+3，令y=0，得﹣3x+3=0，∴x=1，∴D（1，0）；（2）设直线l2的解析表达式为y=kx+b，由图象知：x=4，y=0；x=3，，代入表达式y=kx+b，∴，∴，∴直线l2的解析表达式为；（3）由，解得，∴C（2，﹣3），∵AD=3，∴S△ADC=×3×|﹣3|=；（4）△ADP与△ADC底边都是AD，面积相等所以高相等，△ADC高就是点C 到直线AD的距离，即C纵坐标的绝对值=|﹣3|=3，则P到AD距离=3，∴P纵坐标的绝对值=3，点P不是点C，∴点P纵坐标是3，∵y=﹣6，y=3，∴﹣6=3x=6，所以P（6，3）．14．如图1，在平面直角坐标系中，O是坐标原点，长方形OACB的顶点A、B分别在x轴与y轴上，已知OA=6，OB=10．点D为y轴上一点，其坐标为（0，2），点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动，当点P与点B重合时停止运动，运动时间为t秒．（1）当点P经过点C时，求直线DP的函数解析式；（2）①求△OPD的面积S关于t的函数解析式；②如图②，把长方形沿着OP折叠，点B的对应点B′恰好落在AC边上，求点P的坐标．（3）点P在运动过程中是否存在使△BDP为等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）∵OA=6，OB=10，四边形OACB为长方形，∴C（6，10）．设此时直线DP解析式为y=kx+b，把（0，2），C（6，10）分别代入，得，解得则此时直线DP解析式为y=x+2；（2）①当点P在线段AC上时，OD=2，高为6，S=6；当点P在线段BC上时，OD=2，高为6+10﹣2t=16﹣2t，S=×2×（16﹣2t）=﹣2t+16；②设P（m，10），则PB=PB′=m，如图2，∵OB′=OB=10，OA=6，∴AB′==8，∴B′C=10﹣8=2，∵PC=6﹣m，∴m2=22+（6﹣m）2，解得m=则此时点P的坐标是（，10）；（3）存在，理由为：若△BDP为等腰三角形，分三种情况考虑：如图3，①当BD=BP1=OB﹣OD=10﹣2=8，在Rt△BCP1中，BP1=8，BC=6，根据勾股定理得：CP1==2，∴AP1=10﹣2，即P1（6，10﹣2）；②当BP2=DP2时，此时P2（6，6）；③当DB=DP3=8时，在Rt△DEP3中，DE=6，根据勾股定理得：P3E==2，∴AP3=AE+EP3=2+2，即P3（6，2+2），综上，满足题意的P坐标为（6，6）或（6，2+2）或（6，10﹣2）．15．如图，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、B、C的坐标分别是A（﹣5，1），B（﹣2，4），C（5，4），点D 在第一象限．（1）写出D点的坐标；（2）求经过B、D两点的直线的解析式，并求线段BD的长；（3）将平行四边形ABCD先向右平移1个单位长度，再向下平移1个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少？并求出平行四边形ABCD与四边形A1B1C1D1重叠部分的面积．【解答】解：（1）∵B（﹣2，4），C（5，4），∴BC=5﹣（﹣2）=5+2=7，∵A（﹣5，1），∴点D的横坐标为﹣5+7=2，∴点D的坐标为（2，1）；（2）设直线BD的解析式为y=kx+b，将B（﹣2，4）、D（2，1）代入得：，解得，∴经过B、D两点的直线的解析式为y=﹣x+，过B点作AD的垂线，垂足为E，则BE=4﹣1=3，DE=2﹣（﹣2）=2+2=4，在Rt△BDE中，BD===5；（3）∵▱ABCD向右平移1个单位长度，再向下平移1个单位长度，∴A1（﹣4，0），B1（﹣1，3），C1（6，3）D1（3，0），∴重叠部分的底边长7﹣1=6，高为3﹣1=2，∴重叠部分的面积S=6×2=12．16．如图，一次函数的图象与x轴、y轴交于点A、B，以线段AB 为边在第一象限内作等边△ABC，（1）求△ABC的面积；（2）如果在第二象限内有一点P（a，）；试用含有a的代数式表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值；（3）在x轴上，是否存在点M，使△MAB为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．【解答】解：（1）分别令y=0和x=0，得一次函数y=x+1的图象与x 轴．y轴的交点坐标分别是A（，0），B（0，1），即OA=，OB=1，∴AB==2∵△ABC为等边三角形，∴S△ABC=；（2）如图1，S△AOB =，S△AOP=，S△BOP=|a|•OB=﹣．∴S四边形ABPO =S△AOB+S△BOP=，而S△ABP =S四边形ABPO﹣S△APO，∴当S△ABP =S△ABC时，=，解得a=﹣；（3）如图2，满足条件的点M有4个：M1（﹣，0），M2（﹣2，0），M3（，0），M4（+2，0）．。

人教版八年级数学下册期末复习压轴题练习(1)

专题01 二次根式选填题压轴训练(解析版)八年级数学下学期期末考试压轴题专练(人教版,尖子生专用)

【勾股定理 期末压轴题训练】2022-2023学年八年级数学下册(人教版)含解析

人教版八年级下册数学期末压轴题专题训练(含答案)

最新2019-2020年人教版八年级数学下册期末压轴题练习卷(有答案)

人教版八年级下册数学期末复习：动点问题压轴题

期末考试勾股定理与几何翻折压轴题专项训练—2023-2024学年八年级数学下学期(人教版)(解析版)

人教版八年级下册压轴题训练（含答案）

2024八年级下册期末压轴题集训(原卷版)

人教版八年级数学下册经典压轴题考点及例题解析

2020-2021学年人教版八年级数学下册期末复习(一次函数压轴题)

人教版八年级下册数学期末复习：动点问题压轴题

2020-2021学年人教版数学八年级下册期末压轴题专项复习卷(含答案)

八年级下册数学期末压轴题专辑(含解析,)

八年级数学压轴题 期末复习试卷测试卷(含答案解析)

八年级下册数学期末压轴题(含答案)

人教版八年级下册数学期末动点压轴题训练(带答案)

人教版八年级下册数学期末一次函数压轴题训练

人教版八年级下册数学压轴题及答案

【勾股定理期末压轴题训练】2022-2023学年八年级数学下册(人教版)含解析

八年级数学压轴题期末复习试卷测试卷(含答案解析)