置换流水车间调度问题的MATLAB求解
求解置换流水车间调度问题的memetic算法

求解置换流水车间调度问题的memetic算法
Memetic算法是一种基于遗传算法和局部搜索算法结合的混合
算法,在求解置换流水车间调度问题时,可以通过将遗传算法和局部搜索算法结合,以提高求解效率。
步骤一:初始化参数
首先,需要初始化算法的参数,包括种群规模、变异率、交叉率、迭代次数等。
步骤二:初始化种群
然后,初始化种群,即产生一组初始解,用于进行后续的搜索。
步骤三:进行遗传算法迭代
接着,进行遗传算法的迭代,即对当前种群进行变异、交叉、选择等操作,以获得新的种群,并计算当前种群的适应度。
步骤四:进行局部搜索
然后,对当前种群中的某个解进行局部搜索,以求得更优的解。
步骤五:更新种群
最后,将局部搜索得到的更优解替换原有解,更新当前种群,并重复以上步骤,直至达到迭代次数为止。
matlab车辆调度优化算法

车辆调度优化算法在现代物流和运输领域中扮演着重要的角色。
随着城市化进程的加快和人们对快速高效货运的需求不断增加,车辆调度优化算法的研究和应用变得尤为重要。
其中,matlab作为一种强大的计算工具,被广泛应用于车辆调度优化算法的研究和实践中。
本文将从以下几个方面对matlab车辆调度优化算法进行探讨。
一、matlab在车辆调度优化算法中的应用概述1. Matlab在数学建模方面的优势Matlab作为一种强大的数学软件工具,拥有丰富的数学函数库和强大的矩阵运算能力,能够快速高效地进行数学建模和优化计算。
在车辆调度优化算法中,这种优势使得Matlab成为一种理想的工具。
2. Matlab在算法研究和实现中的应用Matlab提供了丰富的算法工具箱,包括遗传算法、模拟退火算法、粒子裙优化算法等常用的优化算法,这些算法的灵活性和易用性使得Matlab成为车辆调度优化算法研究和实现的理想选择。
二、matlab在车辆路径规划中的应用1. 车辆路径规划的基本问题和挑战车辆路径规划是车辆调度优化算法中的重要问题之一,它涉及到如何合理安排车辆的行驶路线,以最大限度地减少行驶距离和时间。
这是一个 NP 难题,需要运用各种优化算法来求解。
2. Matlab在车辆路径规划中的具体应用Matlab提供了丰富的优化算法工具箱,可以很方便地用来解决车辆路径规划中的优化问题。
可以利用遗传算法来对车辆路径进行优化,或者利用模拟退火算法来寻找最优路径。
三、matlab在车辆调度问题中的应用实例1. 基于Matlab的车辆调度优化算法研究以某物流公司的货物配送路线为例,通过Matlab对车辆调度优化算法进行研究和实现,能够有效降低运输成本,提高运输效率。
2. 基于Matlab的算法实现与性能评测通过实际案例,可以用Matlab对车辆调度优化算法进行实现,并进行性能评测,评估算法的优劣,为实际应用提供参考。
matlab在车辆调度优化算法中具有重要的应用价值,并且在实际的研究和实践中得到了广泛的应用。
matlab生产调度问题及其优化算法

生产调度问题及其优化算法(采用遗传算法与MATLAB编程)信息014 孙卓明二零零三年八月十四日生产调度问题及其优化算法背景及摘要这是一个典型的Job-Shop动态排序问题。
目前调度问题的理论研究成果主要集中在以Job-Shop问题为代表的基于最小化完工时间的调度问题上。
一个复杂的制造系统不仅可能涉及到成千上万道车间调度工序,而且工序的变更又可能导致相当大的调度规模。
解空间容量巨大,N个工件、M台机器的问题包含M(N)!种排列。
由于问题的连环嵌套性,使得用图解方法也变得不切实际。
传统的运筹学方法,即便在单目标优化的静态调度问题中也难以有效应用。
本文给出三个模型。
首先通过贪婪法手工求得本问题最优解,既而通过编解码程序随机模拟优化方案得出最优解。
最后采用现代进化算法中有代表性发展优势的遗传算法。
文章有针对性地选取遗传算法关键环节的适宜方法,采用MATLAB 软件实现算法模拟,得出优化方案,并与计算机随机模拟结果加以比较显示出遗传算法之优化效果。
对车间调度系列问题的有效解决具有一定参考和借鉴价值。
一.问题重述某重型机械厂产品都是单件性的,其中有一车间共有A,B,C,D四种不同设备,现接受6件产品的加工任务,每件产品接受的程序在指定的设备上加工,条件:1、每件产品必须按规定的工序加工,不得颠倒;2、每台设备在同一时间只能担任一项任务。
(每件产品的每个工序为一个任务)问题:做出生产安排,希望在尽可能短的时间里,完成所接受的全部任务。
要求:给出每台设备承担任务的时间表。
注:在上面,机器 A,B,C,D 即为机器 1,2,3,4,程序中以数字1,2,3,4表示,说明时则用A,B,C,D二.模型假设1.每一时刻,每台机器只能加工一个工件,且每个工件只能被一台机器所加工 ,同时加工过程为不间断; 2.所有机器均同时开工,且工件从机器I 到机器J 的转移过程时间损耗不计; 3.各工件必须按工艺路线以指定的次序在机器上加工多次; 4.操作允许等待,即前一操作未完成,则后面的操作需要等待,可用资源有限。
matlab鸟群算法求解车间调度问题详解及实现源码
matlab鸟群算法求解车间调度问题详解及实现源码⽬录⼀、车间调度简介1 车间调度定义2 传统作业车间调度3 柔性作业车间调度⼆、蝴蝶优化算法(MBO)简介1 介绍2 ⾹味3 具体算法三、部分源代码五、matlab版本及参考⽂献⼀、车间调度简介1 车间调度定义车间调度是指根据产品制造的合理需求分配加⼯车间顺序,从⽽达到合理利⽤产品制造资源、提⾼企业经济效益的⽬的。
车间调度问题从数学上可以描述为有n个待加⼯的零件要在m台机器上加⼯。
问题需要满⾜的条件包括每个零件的各道⼯序使⽤每台机器不多于1次,每个零件都按照⼀定的顺序进⾏加⼯。
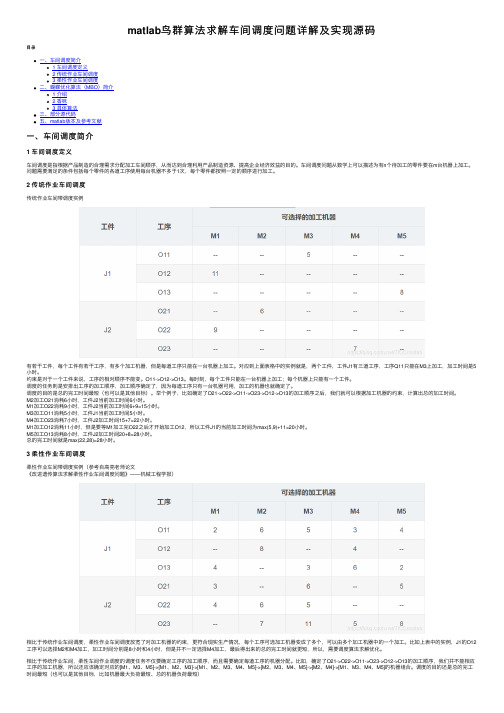
2 传统作业车间调度传统作业车间带调度实例有若⼲⼯件,每个⼯件有若⼲⼯序,有多个加⼯机器,但是每道⼯序只能在⼀台机器上加⼯。
对应到上⾯表格中的实例就是,两个⼯件,⼯件J1有三道⼯序,⼯序Q11只能在M3上加⼯,加⼯时间是5⼩时。
约束是对于⼀个⼯件来说,⼯序的相对顺序不能变。
O11->O12->O13。
每时刻,每个⼯件只能在⼀台机器上加⼯;每个机器上只能有⼀个⼯件。
调度的任务则是安排出⼯序的加⼯顺序,加⼯顺序确定了,因为每道⼯序只有⼀台机器可⽤,加⼯的机器也就确定了。
调度的⽬的是总的完⼯时间最短(也可以是其他⽬标)。
举个例⼦,⽐如确定了O21->O22->O11->O23->O12->O13的加⼯顺序之后,我们就可以根据加⼯机器的约束,计算出总的加⼯时间。
M2加⼯O21消耗6⼩时,⼯件J2当前加⼯时间6⼩时。
M1加⼯O22消耗9⼩时,⼯件J2当前加⼯时间6+9=15⼩时。
M3加⼯O11消耗5⼩时,⼯件J1当前加⼯时间5⼩时。
M4加⼯O23消耗7⼩时,⼯件J2加⼯时间15+7=22⼩时。
M1加⼯O12消耗11⼩时,但是要等M1加⼯完O22之后才开始加⼯O12,所以⼯件J1的当前加⼯时间为max(5,9)+11=20⼩时。
M5加⼯O13消耗8⼩时,⼯件J2加⼯时间20+8=28⼩时。
MATLAB粒子群算法工具箱求解水电站优化调度问题

文章编号:1007 2284(2009)01 0114 03MATLAB 粒子群算法工具箱求解水电站优化调度问题芮 钧1,2,陈守伦1(1.河海大学水利水电学院,江苏南京210098; 2.国网南京自动化研究院,江苏南京210003)摘 要:粒子群算法因其原理简单、易于编程、适于并行计算等优点而得到了广泛的应用。
本文探讨和分析了M at lab 粒子群算法工具箱,并提出了基于该工具箱来实现水电站优化调度计算的方法。
计算实例表明,M atlab 粒子群算法工具箱可以很好地用于解决水电站优化调度问题,可获得比动态规划算法更好的精度。
关键词:M atlab;粒子群算法;水电站;优化调度 中图分类号:T V697.1 文献标识码:AOptimal Dispatch of Hydropower Stations by Using Matlab Particle S warm Algorithm ToolboxesRUI Jun 1,2,C HEN Shou lun 1(1.Colleg e o f Water Co nser vancy and H ydro po wer Eng ineering,H ohai U niver sity ,N anjing 210098,China;2.N anjing A utomation Resea rch I nstit ute,Nanjing 210003,China)Abstract:Because of its simplicity ,generality and parallelism,PSO (P article Sw arm Optimization)is w idely used.T he M atlab par ti cle sw ar m alg or ithm too lbox is ana lyzed,and a metho d based o n it is also pr oposed to solve the pr oblem of optimal dispatch o f hy dr o pow er stations.Pr actical application indicates that t he M atlab par ticle swar m algo rithm too lbox can solve pr oblems mo re precisely than dynamic prog ramming.Key words:M atlab;hy dr opow er statio n;optimal reg ulatio n;pa rticle sw arm o pt imizatio n algo rit hm收稿日期:2008 03 01作者简介:芮 钧,(1978 ),男,工程师、博士研究生,主要从事梯级水电站群优化调度及自动发电控制研究。
解决多目标置换流水车间问题的改进MDPSO算法

解决多目标置换流水车间问题的改进MDPSO算法摘要:置换流水车间调度问题(flow-shop scheduling problem)是生产调度问题的一个子问题,是NP-hard组合优化离散问题之一,具有很强的实际研究意义。
在现代的生产制造过程中,单一的目标优化已经满足不了日益发展的工业需求,所以对多目标流水车间调度问题的研究显得尤为重要,已在实际生产中得到广泛应用。
本文在多目标进化算法粒子群算法PSO的基础上设计了一种多目标进化算法离散多目标粒子群优化算法MDPSO以求解该问题,用 MATLAB 编程实现该算法并对几个标准多目标flowshop 算例进行仿真测试。
实验结果表明,提出的算法比已有的NSGA_II算法具有更好的优化性能。
关键词:多目标flowshop问题;MDPSO算法;NSGA-II;Improved MDPSO method for Multi-objective flow-shop scheduling problemWu Ye, Li Xiaoyu, Yao Jun(Shanghai zhengfan technology co. Ltd , School of Mechatronics and Automation, Shanghai University, Shanghai, China)AbstractMulti-objective flow-shop scheduling problem is a sub problem of production scheduling problem. It is one of the discrete problems of NP-hard optimization and has strong theoretical and actual purpose.In the modern production and manufacturing process, single-objective optimization can’t meet the growing industrial demand, sothe research on the scheduling problem of multi-objective flow-shop is particularly important. This paper designs a Multi-objective evolutionary algorithm based on the PSO to solve this problem. It was implemented by MATLAB and simulation on a kind of benchmark functions. The experimental results show that the proposed algorithm hasa better optimization performance than the NSGA – II.Keywords: Multi-objective flow-shop scheduling problem; MDPSO; NSGA-II1 引言在现实生活中,许多问题都需要寻找一个最优决策或者是最佳解决方案,这类问题被统称为优化问题,仅有一个目标函数的最优化问题称为单目标优化问题,目标函数超过一个的最优化问题称为多目标优化问题(Multi-objective Optimization Problems,MOP)[1]。
置换流水车间调度问题的MATLAB求解

置换流⽔车间调度问题的MATLAB求解物流运筹实务课程设计题⽬:置换流⽔车间调度问题的MATLAB求解置换流⽔车间调度问题的MATLAB求解⽬录⼀、前⾔ (5)⼆、问题描述 (6)三、算法设计 (7)四、实验结果 (15)摘要⾃从Johnson 1954年发表第⼀篇关于流⽔车间调度问题的⽂章以来.流⽔车间调度问题引起了许多学者的关注。
安排合理有效的⽣产调度是⽣产活动能井然有序开展,⽣产资源得到最佳配置,运作过程简明流畅的有⼒保证。
流⽔车间调度问题是许多实际流⽔线⽣产调度问题的简化模型。
它⽆论是在离散制造⼯业还是在流程⼯业中都具有⼴泛的应⽤。
因此,对进⾏研究具有重要的理论意义和⼯程价值。
流⽔线调度问题中⼀个⾮常典型的问题,⽽置换流⽔线调度问题作为FSP 问题的⼦问题,是⼀个著名的组合优化问题。
该问题是⼀个典型的NP难问题,也是⽣产管理的核⼼内容。
随着⽣产规模的扩⼤,流⽔线调度问题的优化对提⾼资源利⽤率的作⽤越来越⼤,因此对其研究具有重要的理论和现实意义。
关键字:流⽔车间,单件⼩批量⽣产,jsp模型,Matlab前⾔企业资源的合理配置和优化利⽤很⼤程度上体现在车间⼀层的⽣产活动中,所以加强车间层的⽣产计划与控制⼀直在企业⽣产经营活动中占有⼗分重要的地位。
车间⽣产计划与控制的核⼼理论是调度理论。
车间调度问题是⼀类重要的组合优化问题。
为适应订货式、多品种、⼩批量⽣产的需要,引进了置换流⽔车间调度概念。
在置换流⽔车间调度优化后,可以避免或⼤⼤减少流程⼯作时间、提⾼⽣产效率。
因此,研究成组技术下车间调度问题是很有必要的。
⽣产调度,即对⽣产过程进⾏作业计划,是整个个先进⽣产制造系统实现管理技术、优化技术、⽩动化与计算机技术发展的核⼼。
置换流⽔车间调度问题是许多实际⽣产调度问题的简化模型。
⽣产计划与调度直接关系着企业的产出效率和⽣产成本,有效的计划与调度算法能最⼤限度地提⾼企业的效益。
调度问题是组合优化问题,属于NP问题,难以⽤常规⼒⼀法求解。
粒子群算法解决置换流水车间调度问题方法综述

lsfrsaceso ov i ego igaddvl igop rceSO not i i grh .eet o erhr tsle t t rwn ee pn a i WI i z o a oi mR cn— to e w hh n o f tl T p m a nl t t - l, eea t m to s n e f rhs rbe .o rm t te ut r v l m n p r c w r y t r r ul eh d di a o ip olmT o oe h f r e eo e tf at l s am h e oo f a ds t p h d e p o ie ot i i loim n ov emuao f wso ceuigpolm dpoi e rne o e piz o a rh adsl p r tin o hpshdl m a n g t t e t l n rbe sa rv er eec fr — n d f d s nn e e g rh smm r e em to dpe fr ahs pi li epo ut nsh d l g i i b t r oi m, g g t a t l u ai st h d a o t o c e s vn t rd ci e ui z he s d e t no gh o c n
机 械 设 计 与 制 造
8 4
文章 编 号 :0 1 39 (0 2 0 — 0 4 0 10 — 9 7 2 1 )8 0 8 — 3
改进的蚁群算法求解置换流水车间调度问题

改进的蚁群算法求解置换流水车间调度问题张丽萍【摘要】In order to avoid the shortcomings of ant algorithm for solving permutation flow shop scheduling problem that easily fall into local best situation and long calculation time, in this paper, an improved Max-MinAnt System (MMAS)algorithm which apply Nawaz-Enscore-Ham ( NEH ) heuristic algorithm to enhance the quality of the initial solutions and further improve the search capabil-ities through regulation of adaptive strategies is proposed . Finally we use the proposed algorithm to solve Taillard benchmarks set . Compared with other approaches , the experimental results show the effectiveness of the proposed algorithm .%针对蚂蚁算法在求解置换流水车间调度问题时易陷入局部最优以及计算时间较长的缺点,对最大最小蚂蚁系统( MMAS )进行了改进。
在该算法中,采用 NEH 启发式算法提高初始解质量,并通过自适应的调节策略进一步提高蚁群算法的搜索能力。
运用提出的混合算法求解 Taillard 基准测试集,并将测试结果与其他算法进行比较,验证了该调度算法的有效性。
一种多目标置换流水车间调度问题的优化算法①

一种多目标置换流水车间调度问题的优化算法①何启巍;张国军;朱海平;刘敏【摘要】针对最大完工时间最小和总流经时间最小的多目标置换流水车间调度问题(permutation flow shop scheduling problem, PFSP),提出一种粒子群优化算法与变邻域搜索算法结合的混合粒子群优化(hybrid particle swarm optimization algorithm, HPSO)算法,并使算法在集中搜索和分散搜索之间达到合理的平衡。
在该混合算法中,采用 NEH 启发式算法进行种群初始化,以提高初始解质量;运用随机键表示法设计基于升序排列规则(ranked-order-value, ROV),将连续PSO算法应用于置换流水车间调度问题;引入外部档案集存贮Pareto解,并采用强支配关系和聚集距离相结合的混合策略保证解集的分布性;采用 Sigma 法和基于聚集距离的轮盘赌法进行全局最优解的选择;提出变邻域搜索算法,对外部集中的 Pareto 解作进一步地局部搜索。
最后,运用提出的混合算法求解Taillard 基准测试集,并将测试结果与SPEA2算法进行比较,验证该调度算法的有效性。
%This paper proposes a hybrid particle swarm optimization algorithm for the minimization of makespan and total flowtime in permutation flow shop scheduling problems, which combines particle swarm optimization algorithm with variable neighborhood search algorithm. The initial population is generated by the NEH constructive heuristic to enhance the quality of the initial solutions. A heuristic rule called the ranked order value (ROV) borrowed from the random key representation is developed, which apply the continuous particle swarm optimization algorithm to all classes of sequencing problems. The strategy of constructing external data set based on combining strong predominance ranking and crowding distanceranking was introduced. The global best solution was updated based on the strategy of combining Sigma method and roulette method. VNS was applied to enhance the local search for the pareto solutions. Finally, the proposed algorithm is tested on a set of standard instances taken from the literature provided by Taillard and compared with SPEA2. The computation results validate the effectiveness of the proposed algorithm.【期刊名称】《计算机系统应用》【年(卷),期】2013(000)009【总页数】9页(P111-118,110)【关键词】粒子群优化算法;变邻域搜索;多目标;置换流水车间调度【作者】何启巍;张国军;朱海平;刘敏【作者单位】华中科技大学机械科学与工程学院,武汉,430074;华中科技大学机械科学与工程学院,武汉,430074;华中科技大学机械科学与工程学院,武汉,430074;华中科技大学机械科学与工程学院,武汉,430074【正文语种】中文1 引言置换流水车间调度问题是目前研究最广泛的一类典型调度问题, 对该问题的研究具有很重要的意义.国内外学者过去几十年里在这方面做了大量研究, 其中绝大多数的研究都是集中在求解单目标的置换流水车间调度问题. 然而, 在实际生产制造的过程中, 往往面临多目标决策的问题, 因此对于求解多目标置换流水车间调度问题算法的研究具有重要的理论意义和工程实用价值.近年来, 基于智能算法的多目标调度研究逐渐得到了学术界和工程界的广泛重视, 特别是《欧洲运筹学》等著名国际期刊相继推出相应的专刊, 更是推动了多目标智能算法在车间调度问题上的应用.Ishibuchi和 Murata[1]将遗传算法和局部搜索策略相结合, 采用基于随机加权的适配值函数进行解的评价和指导遗传操作, 提出了一种多目标遗传局部搜索(multi-objective genetic local search, MOGLS)算法. 类似地, Jaszkiewicz[2]采用基于随机权的适配值函数, 选择父代个体和指导局部搜索, 进而给出了一种多目标混合遗传算法. 另外, Loukil等[3]提出了一类多目标模拟退火算法, 通过产生一定数量的随机权向量来构造评价函数集合, 进而基于每个评价函数在模拟退火策略的指导下进行局部搜索.区别于上述方法, Arroyo 和 Armentano[4]采用Pareto支配的概念对当前种群进行层级划分, 并基于此对种群中的个体赋予合适的适配值, 同时对种群实施并行的多目标局部搜索, 以加强对目标空间中解密度较低地区的搜索能力. Li和Wang最近提出了一种基于量子计算的混合遗传算法, 同样采用了快速排序和适配值赋值的评价方法, 同时算法引入了两种消除种群个体冗余性的环节.粒子群优化(Particle Swarm Optimization, PSO)算法作为一种新型的基于群体的优化算法, 最早由Kennedy和Eberhart[5]于1995年提出. PSO算法是通过种群内粒子之间的合作与竞争产生的群体智能优化算法. 与遗传算法比较, PSO算法保留了基于种群的全局搜索策略, 搜索模型简单, 还有收敛速度快和鲁棒性高等特点. PSO算法早期用于无约束连续函数的优化, 并在很多问题上都取得了成功的应用, 例如, 电压控制、神经网络训练. Tasgetiren等[6]又成功将PSO算法用于求解单目标的置换流水车间调度问题, 推动了PSO算法在离散组合优化问题上的应用. 然而, 当前粒子群优化算法在多目标调度问题上的研究还是寥寥无几, 代表性的工作是 Arroyo 和Armentano[7]最近提出的一种多目标PSO算法, 作者通过对平均完成时间和加权平均拖后时间进行加权来处理评价环节.本文在已有研究基础上, 结合粒子群优化算法和变邻域搜索算法各自的优点, 设计了一种混合粒子群优化算法, 并求解双目标置换流水车间调度问题. 该混合算法采用基于升序排列规则(ROV)的连续PSO算法进行全局搜索, 应用基于关键路径的变邻域搜索算法对全局优化的粒子进行局部搜索, 使算法在分散搜索和集中搜索达到合理的平衡. 并基于 Pareto支配的概念, 设计了一种有效的非劣解集的更新策略. 对Taillard提出的基准测试集进行仿真实验, 与其他多目标算法比较, 证实算法的有效性.2 问题描述2.1 多目标优化问题的描述多目标优化问题(multi-objective optimization problem), MOP问题可以描述为[8]: 寻找一组既满足约束条件又使总目标函数最优化的决策变量的取值, 总目标函数的元素是子目标函数. 若MOP问题的目标函数为:其中, f1, f2, …, fN为N个目标函数, x表示决策解,X表示解空间考虑两个解x1和x2, 若满足则称解x1支配解x2, 记作 x 1 ≻ x 2.给定一个解x* , 若在解空间X中不存在支配x*的解, 则称 x*为 Pareto最优解, 或非支配解集(non-dominated solution). 所有费支配解的集合构成多目标意义下的最优解集, 这些解在目标空间中构成问题的Pareto前沿(Pareto Front).2.2 置换流水车间调度问题描述置换流水车间调度可以描述为[9]: n个工件要在m台机器上进行加工, 每个工件的加工顺序相同, 每台机器加工的工件顺序也相同, 各工件在各机器上的加工时间已知, 要求得到一个加工方案使得某一调度目标最优. 调度目标一般有: 使工件最大延期量最小;使工件的总流经时间(total flow time, TFT)最短; 使所有工件最大完工时间(Makespan)最短; 工件的平均等待时间最短等. 本文选取最大完工时间最短和总流经时间最短为双目标, 对该问题通常做如下的假设:1)一个工件在同一时刻只能在一台机器上加工;2)一台机器在同一时刻只能加工一个工件;3)工件一旦在某台机器上进行加工就不能停止;4)每台机器上工件的加工顺序相同.置换流水车间调度问题的数学描述如下. 令 tij为工件i在机器j上的加工时间, 不计同一机器上加工完工件i后马上加工工件j所需的准备时间, C(πi, j)为工件πi的在机器j加工完毕时间, 不失一般性, 假设各工件按机器1至m的顺序进行加工, 令π={π1, π2, …, πn}为所有工件的一个排序式(4)和式(5)分别为最大完工时间和总流经时间的计算公式.3 求解多目标置换流水车间调度问题的混合粒子群优化算法3.1 标准粒子群优化算法(PSO)基本粒子群算法采用速度-位置模型进行搜索, 待优化问题的每个候选解称为一个“粒子”, 每个粒子都有自己的位置和速度, 还有一个由被优化函数决定的适应值.各个粒子记忆、追随当前的最优粒子, 在解空间中搜索.每次迭代的过程不是完全随机的, 如果找到较好解, 将会以此为依据来寻找下一个解. 令PSO算法初始化为一群随机粒子, 在每一次迭代中, 粒子通过跟踪两个“极值”来更新自己: 第一个就是粒子本身所找到的最好解,叫做个体极值点(用pbest表示其位置), 全局版PSO中的另一个极值点是整个种群目前找到的最好解, 称为全局极值点(用 gbest表示其位置), 而局部版 PSO 不用整个种群而是用其中一部分作为粒子的邻居, 所有邻居中的最好解就是局部极值点(用 lbest表示其位置). 在找到这两个最好解后, 粒子根据如下的式(6)和式(7)来更新自己的速度和位置. 粒子i的信息可以用n维向量表示, 位置表示为Xi= [xi1, xi2,…, xin], 速度为Vi=[vi1, vi2, …, vin], 其他向量类似. 则速度和位置更新方程为:其中: wt=wt-1×β是惯性系数, β为线性递减因子,其主要作用是产生扰动, 以防止算法的早熟收敛; c1和c2为学习因子, 分别调节向个体最好粒子和全局最好粒子方向飞行的最大步长, 若太小, 则粒子可能远离目标区域, 若太大则会导致突然向目标区域飞去,或飞过目标区域, 合适的c1和c2可在加快收敛速度的同时还能不易陷入局部最优, 通常令c1=c2=2; r1和r2是[0, 1]之间均匀产生的随机数.3.2 求解PFSP的粒子群优化算法3.2.1 解的表示和ROV规则对于 PFSP问题, 文献中最常用的编码方式就是直接采用工件的排序. 由于连续PSO算法中微粒的位置为连续值矢量, 为了实现微粒位置矢量到工件排序的映射关系, 借用随机键编码, 王凌等[10]提出了ROV规则, 将粒子的连续位置矢量Xi= [ xi1, xi2, …, xin]转换为离散的加工排序π={π1, π2, …, πn}, 即机器上各工件的加工顺序.ROV规则具体描述如下. 对于一个微粒的位置矢量, 首先将值最小的分量位置赋予ROV值为1, 其次将值第二小的分量位置赋予 ROV值为 2, 依次类推,直到将所有的分量位置都赋予一个唯一的ROV值, 从而基于ROV值则可构造出一个工件排序. 表1中用一个简单的例子来表示了ROV规则的构造过程. 考虑 7个工件的置换流水车间调度, 粒子的位置矢量则为6维, 设位置矢量Xi= [0.49, 2.90, 1.58,0.82, 2.81, 0.35, 1.28], 比较可知xi6为最小, 所以将xi6对应的分量位置ROV值赋为1,接下来将xi1对应的分量位置ROV值赋为2, 依次类推分别赋予xi4、xi7、xi3、xi5和xi2对应的分量位置ROV值为3、4、5、6和7, 从而得到工件的加工次序, 即π={2, 7, 5, 3, 6, 1, 4}.表1 粒子位置矢量对应的ROV值分量位置 1 2 3 4 5 6 7位置分量值0.49 2.90 1.58 0.82 2.81 0.35 1.28 ROV值 2 7 5 3 6 1 43.2.2 种群初始化初始种群应该具有一定的分布性, 能够以较大的概率覆盖整个解空间. 此外为了提高种群的搜索效率,避免盲目搜索, 初始种群中也应该包括部分质量较高的解. 因此初始解的产生方式基本上可分为两种, 一是在一连续区间内随机产生; 二是用构造性启发式方法产生. 在这里我们选用性能最好的NEH启发式算法,NEH启发式算法[11]是由Nawaz, Enscore和Ham共同提出的算法步骤如下:步骤1: 按工件在机器上的总加工时间递减的顺序排列n个工件.步骤2: 取前两个工件调度, 使部分总完工时间达到最小.步骤3: 从k=3, …, n, 把第k个工件插入到k个可能的位置, 求得最小的部分总完工时间.NEH启发式方式产生的解是工件序列, 必须转换为一定区间内的位置矢量, 在此, 按如下方式实现转换.其中,为粒子在第j维的位置值,是通过NEH方法得到解的第j维工件序号和分别为连续空间上粒子位置矢量的上界值和下界值, r3代表0至1间的均匀产生的随机数. 随机产生的方式为, x0=x +(x -x)×r1 ,ijminmax minv0=v +(v -v )×r 2, 其中位置矢量值在连续区ijminmax min间[xm in,xm ax]间变化, 速度矢量值在连续区间[vm in,xm ax]变化, r1和r2均为0至1之间均匀产生的随机数.3.3 多目标进化策略多目标进化算法需保证 Pareto前沿的收敛性和多样性特征, 关键是设置合理的Pareto集多样性维持策略和粒子群全局最优值更新操作. 本文采用基于Pareto关系的快速排序法来构造非支配集, 用外部集合(external set, ES)存贮, 引入强支配关系和聚集距离相结合的存档策略, 以使Pareto前沿具有良好的分布性. 在全局最优解的选择上, 也采取两阶段领导策略, 前期采用收敛速度极快的Sigma方法领导, 后期采用基于聚集距离的轮盘赌方法领导以进行更深入的搜索.3.3.1 外部集合ES的生成初始种群产生后, 计算各粒子的目标值, 利用快速排序法, 根据目标函数值对粒子进行支配关系排序,将非支配解存入外部集合ES中.快速排序的思想是每一次循环都从种群中选择一个个体x(通常选择第一个个体), 种群中其它个体依次与 x进行比较. 通过一趟比较将种群分割成两部分:种群的后半部分是被x支配的个体, 前半部分是支配x或者与x不相关的个体. 若x不被其它任何一个个体支配, 则将 x并入到非支配集, 接着再对前半部分重复上述过程直到前半部分为空.快速排序的伪代码如图1所示:图1 快速排序的伪代码在每一代粒子更新完成后, 计算单个粒子在各个目标上的适应度值, 更新外部集合ES. 如图 2所示,其更新原则为: (1)若该粒子支配外部集合ES中的某些粒子, 则删除被支配的粒子, 将该粒子加入外部集合ES; (2)若外部集合 ES中有粒子支配该粒子, 则忽略;(3)若该粒子与外部集合 ES中的各个粒子互不支配,则将该粒子加入外部集合ES中.图2 外部集合更新原则3.3.2 外部集合ES的维护对于复杂的多目标优化问题, 若保留进化过程中出现的所有的 Pareto最优解, 会导致外部集合中出现大量的相似解, 不仅影响解的分布性能, 同时也会增加求解的内存开销和时间复杂性. 为保持外部集合的分布性, 本文采用强支配关系和聚集距离相结合的存档策略对外部集合进行维护.引入强支配关系可使各个粒子保持一定距离, 有效控制粒子的聚合程度,有助于保持粒子群的多样性.强支配关系的定义为: 1)如果粒子 A ≻ B , 则认为A≻强B ; 2)对于A~B, ∀目标函数m, 如果有(m=1, 2, …, k)为正常数, 则随机选择A或B; 如果A 被选中, 则认为A≻强B, 反之亦然.如果εm取的过小, 则强支配关系的作用就会变小,当εm=0时, 强支配关系就退化为支配关系; 如果取值过大, 强支配关系变强, 会使粒子变得过于稀疏. 可见εm的取值十分重要. 本文利用经验公式取值.对于只有两个目标的情况:其中C为强支配系数, C >80.聚集距离是由 Deb等[12]在 2002年提出并用于NSGA-II保持种群多样性的算子, 可以用来表示解的疏密程度. 聚集密度小的个体其聚集距离反而大, 一个个体的聚集距离可以通过与其相邻的两个个体在每个子目标上的距离差之和来求取. 计算聚集距离的伪代码如下:图3 计算聚集距离的伪代码3.3.3 全局最优值的选取由于全局最优解对粒子的导向作用非常明显, 因此如何选取较好的全局最优解gbest来引导粒子的飞行, 对算法具有非常重要的作用, 关系到算法的收敛速度、解的多样性等. 采取两阶段领导策略, 前期采用收敛速度极快的 Sigma方法领导, 后期采用基于聚集距离的轮盘赌方法领导以进行更深入的搜索.Mostaghim等[13]提出了基于Sigma值的领导选择方法, 其基本思想是: 赋予群和外部档案中每个粒子一个Sigma值, 可定义粒子的Sigma值. 两目标情况下的Sigma(δ表示)的计算公式为:其中f1, f2分别为粒子的两个目标的函数值.为防止由于目标函数值相差大而造成δ的值总是接近于1或-1的情况, 对目标函数进行归一化处理, 即其中分别为粒子在两个目标上的最大值和最小值. 从而得到新的δ的计算公式:Sigma方法求解全局极值的步骤如下:1)分别求解种群中每个粒子的δ值、外部集 ES中各非支配解集的δ值;2)找出距离种群第i个粒子δ值最近的外部集中的粒子j;3)将外部集合中第j个粒子的解作为种群第i个粒子的gbest(i).在算法的前期采用Sigma方法从外部集合中寻找粒子 i的全局极值点, 这样能够促使算法很快收敛到全局非劣最优面. 当算法运行到一定代数时, 作为全局极值的粒子己经在非劣最优面上, 这时需要考虑选择处于 Pareto前沿中分散区域的个体, 引导粒子群向分散区域进化. 因此, 在进化后期用以下策略对全局最优个体进行更新: 1)若Pareto中所有个体的拥挤距离都为无穷大, 即仅包括数量较少的边界个体,则随机选择一个作为gbest.2)若 Pareto中含有拥挤距离不为无穷大的个体,则使用轮盘法选择,即以较大概率选择拥挤距离较大的个体为Gbest. 计算公式为其中P(i)为外部集合中第i个个体被选中的概率,为第i个个体的聚集距离, psize为当前外部集合的粒子个数. 需要注意的是, 个体聚集距离含有无穷大会造成轮盘法选择失效, 因此公式中的psize不计边界点.3.4 变邻域搜索Mladenovic和Hansen[14]提出了一种变邻域搜索算法, 其在很多问题中取得了很好的应用. Zobolas[15]将遗传算法与变邻域搜索算法结合, Bassem[16]将分布评估算法与变邻域搜索算法结合. 变邻域搜索算法的应用大大加强了这些算法的集中搜索能力, 因此对Pareto解采用变邻域搜索算法进行有效的邻域搜索.变邻域搜索算法的执行流程如图4所示:图4 变邻域搜索算法流程3.5 算法流程本文采用一种多目标粒子群优化算法对 PFSP进行分散搜索, 提出了其Pareto解集的构成和维护策略,并提出了一种两阶段的全局最优解的选择机制, 有效地领导粒子向非支配解前沿收敛. 提出结合变邻域搜索算法, 对多目标粒子群算法求的的非支配解进行集中地邻域搜索, 以搜索到更多的 Pareto解. 混合算法的具体算法流程如下.1)初始化算法参数: 进化种群大小popsize, 外部集合ES大小psize, 惯性系数w、认知系数c1和社会系数c2, 强支配系数C.2)初始化粒子种群:① 利用NEH生成10%个工件加工序列, 计算调度目标, 并据公式(5)转换为一个粒子的位置矢量;② 随机产生余下的 90%个粒子的位置矢量, 根据ROV规则得出其对应的工件加工序列, 根据加工序列计算各粒子的两个调度目标;③ 随机初始化种群中所有粒子的速度矢量;④ 令各粒子的局部最优为当前位置, 并对初始化种群执行快速排序, 将非支配解加入外部集合ES中;⑤ 根据3.3.3更新全体极值.3)循环步骤4)—6)直到满足停止条件.4)对所有粒子执行下列操作:① 采用式(6)和(7)更新所有粒子的速度和位置;② 根据 ROV规则, 确定各粒子位置矢量所对应的工件加工序列, 并计算各粒子两个调度目标;③ 根据3.3.1和3.3.2更新外部集合ES, 并更新各粒子的个体极值.5)对ES外部集合中的Pareto解执行变邻域搜索算法, 更新外部集合ES.6)根据3.3.3更新全体极值.7)输出外部集合ES.混合粒子群算法的具体算法流程如图5所示.图5 混合粒子群优化算法具体流程4 实例仿真与结果分析为了测试提出的混合粒子群优化算法, 本文数据基于Taillard[17]在1993年提出的120个基准测试问题, 用本文提出的多目标混合离子群优化算法进行求解, 并在同样的硬件条件下用著名的强支配进化算法(SPEA2)进行求解, 将两种算法求得的结果进行比较. 算法运用Visual C++ 6.0编程实现, 计算机CPU是Intel Celeron M 520, 主频为 1. 6G, 物理内存 512MB, 操作系统Windows XP. 首先, 对强支配进化算法作简单介绍.4.1 强支配进化算法Zitzler和Thiele[18]于1999年提出了基于Pareto解的强支配进化算法(strong pareto evolutionary algorithm,SPEA), 2001年针对其存在的不足, 对SPEA做了改进,提出了 SPEA2[19]. 在SPEA2算法中, 种群和精英集合中每一个粒子都被赋予一个强度值, 强度值包括了支配关系信息和密度信息. 基于强度值, 每一个粒子的排序值就由支配当前这个粒子的个体的强度值之和来确定. 同时, 算法采用小生境策略确定每一个粒子的密度信息. 最终的适应度值就为粒子的排序值和密度值之和. 最后, 采用竞标赛策略来保证精英集合的规模.4.2 评判指标1)非支配解的数目(number of pareto solution,NPS)比较不同算法所能找到非支配解的个数, 并可以与完整的Pareto前沿进行较.2)均匀性指标(spacing metric, SM)通过计算解集中每个个体与邻居个体的距离变化来评价解集在目标空间的分布情况, 其评价函数定义如下:其中,为解集中个体的数目;d为所有 di的平均值; S的值越小说明解集分布越均匀.3)多样性指标(diversification metric, DM)这个指标用来测试解集的延展性, 它通过个体与其它个体的最大欧式距离来评价. 其评价函数定义如下:其中为非支配解xi和yi之间的欧式距离.4)相对增长比指标(relative percentage increase,RPI)这个指标用来评判解集中的解相对理想点的目标值相对增长比例, 将算法中以单一目标最优值组成的解为理想点, RPI则为解集中每一个解相对理想点目标值增长比例的平均值. 设理想解的 makespan值为min(MS), TFT值为min(TFT). 第i个Pareto的makespan值表示为MS(S(i)), TFT值表示为TFT(S(i)); 则相对增长比指标的函数定义如下:其中N为Pareto解集中解的个数.4.3 实验参数设置本文算法实验参数设置如下: c1=c2=2.0, 惯性系数w初始值设为0.9, β=0.975, 最小不能小于0.4,粒子的最小位置值 x m in=0, 粒子的最大位置值xm ax=4.0, 粒子的最小速度值 v m in =-4.0, 粒子的最大速度值 v m ax=4.0, 最大迭代次数设为500, 种群规模设为40, 外部集合规模设为60, 强支配系数C为90每个实例独立连续运行10次.SPEA算法实验参数设置如下: 初始化方法如本文算法一样, 采用NEH和随机初始化结合, 采用竞标赛选择策略, 交叉算子采用 OX交叉, 变异方式为互换变异,交叉概率设为 0.8, 变异概率设为0.8, 递减系数0.9, 最小不小于0.4. 种群规模设为40, 最大迭代次数为500.4.4 实验结果比较与分析本文选取TA测试集问题中的20个工件系列的30个问题进行了测试和比较实例的数据通过 Taillard网站http://mistic.heig-vd.ch/taillard/获得. 本文的混合多目标粒子群算法用MPSO-VNS表示, 以NPS, SM, DM,RPI四个指标对两种算法进行比较, 实验比较结果如表2所示.由实验比较结果可得, 本文提出的多目标混合粒子群优化算法相比SPEA2算法在大多数实例上的实验结果在各指标上都好一些, 能够获得更多的非支配解的数目, 具有良好的分布性和延展性, 相对增长比例指标也有一定程度上的改进, 因而证实了算法的有效性.两种算法求解ta021问题所产生的Pareto解集的比较如图6所示, 可以看出MPSO-VNS获得的Pareto解集具有相当好的分布性和收敛性.图6 两种算法求解ta021问题的结果比较表2 实验比较结果?5 结语本文针对多目标 PFSP问题提出了一种结合粒子群优化算法和变邻域搜索算法的多目标混合优化算法.算法采用NEH启发式算法初始化种群, 大大提高了初始解的质量; 基于ROV规则, 运用连续PSO算法进行有效的全局搜索; 引入外部集合管理非支配解, 采用强支配关系和聚集距离结合的策略对外部集合进行有效的维护; 采用两阶段全局最优解的选择机制, 合理引导了种群的收敛; 采用变邻域搜索算法对外部集合中的 Pareto解集进行集中搜索, 加强了算法的集中搜索能力. 算法将PSO 算法的全局搜索能力和变邻域搜索算法的局部搜索能力相结合, 并使分散搜索和集中搜索达到有效的平衡, 大大增加了算法的搜索能力.运用混合算法求解Taillard基准问题, 并将测试结果与SPEA2算法比较, 本文算法都取得了很好的效果, 验证了该算法的有效性.参考文献【相关文献】1 Ishibuchi H, Murata T. A multi-objective genetic local search algorithm and its application to flowshop scheduling. IEEE Trans Syst Man Cybern,1998,28(2):392-403.2 Ishibuchi H, Yoshida T, Murata T. Balance between genetic search and local search in memetic algorithms for multiobjective permutation flowshop scheduling.IEEE Trans Evol Comput,2003,7(2):204-223.3 Jaszkiewicz A. Genetic local search for multi-objective combinatorial optimization. Eur.J.Oper.Res.,2002,137(1):50-71.4 Loukil T, Teghem J, Tuyttens D. Solving multi-objective production scheduling problems using metaheuristics. Eur.J.Oper. Res.,2005,161(1):42-61.5 Arroyo JEC, Armentano VA. Genetic local search for multiobjective flowshop scheduling problems. Eur.J.Oper.Res.,2005,167(3):717-738.6 Li BB, Wang L. A hybrid quantum-inspired genetic algorithm for multi-objective flow shop scheduling. IEEE Trans.Syst.,Man,Cybern.,2007,37(3):576-591.7 Rahim-Vahed AR, Mirghorbani SM. A multi-objective particle swarm for a flow shop scheduling problem. b.Optim.,2007,13(1):79-102.8 郑金华.多目标进化算法及其应用.北京:科学出版社,2007.9 王凌.车间调度及其遗传算法.北京:清华大学出版社,2003.。
02流水线车间生产调度的遗传算法MATLAB源代码

流水线车间生产调度的遗传算法MATLAB源代码n个任务在流水线上进行m个阶段的加工,每一阶段至少有一台机器且至少有一个阶段存在多台机器,并且同一阶段上各机器的处理性能相同,在每一阶段各任务均要完成一道工序,各任务的每道工序可以在相应阶段上的任意一台机器上加工,已知任务各道工序的处理时间,要求确定所有任务的排序以及每一阶段上机器的分配情况,使得调度指标(一般求Makespan)最小。
function [Zp,Y1p,Y2p,Y3p,Xp,LC1,LC2]=JSPGA(M,N,Pm,T,P)%--------------------------------------------------------------------------% JSPGA.m% 流水线型车间作业调度遗传算法% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensim%--------------------------------------------------------------------------% 输入参数列表% M 遗传进化迭代次数% N 种群规模(取偶数)% Pm 变异概率% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻,可根据它绘出甘特图% Y2p 最优方案中,各工件各工序的结束时刻,可根据它绘出甘特图% Y3p 最优方案中,各工件各工序使用的机器编号% Xp 最优决策变量的值,决策变量是一个实数编码的m×n矩阵% LC1 收敛曲线1,各代最优个体适应值的记录% LC2 收敛曲线2,各代群体平均适应值的记录% 最后,程序还将绘出三副图片:两条收敛曲线图和甘特图(各工件的调度时序图)%第一步:变量初始化[m,n]=size(T);%m是总工件数,n是总工序数Xp=zeros(m,n);%最优决策变量LC1=zeros(1,M);%收敛曲线1LC2=zeros(1,N);%收敛曲线2%第二步:随机产生初始种群farm=cell(1,N);%采用细胞结构存储种群for k=1:NX=zeros(m,n);for j=1:nfor i=1:mX(i,j)=1+(P(j)-eps)*rand;endfarm{k}=X;endcounter=0;%设置迭代计数器while counter<M%停止条件为达到最大迭代次数%第三步:交叉newfarm=cell(1,N);%交叉产生的新种群存在其中Ser=randperm(N);for i=1:2:(N-1)A=farm{Ser(i)};%父代个体Manner=unidrnd(2);%随机选择交叉方式if Manner==1cp=unidrnd(m-1);%随机选择交叉点%双亲双子单点交叉a=[A(1:cp,:);B((cp+1):m,:)];%子代个体b=[B(1:cp,:);A((cp+1):m,:)];elsecp=unidrnd(n-1);%随机选择交叉点b=[B(:,1:cp),A(:,(cp+1):n)];endnewfarm{i}=a;%交叉后的子代存入newfarmnewfarm{i+1}=b;end%新旧种群合并FARM=[farm,newfarm];%第四步:选择复制FITNESS=zeros(1,2*N);fitness=zeros(1,N);plotif=0;for i=1:(2*N)X=FARM{i};Z=COST(X,T,P,plotif);%调用计算费用的子函数FITNESS(i)=Z;end%选择复制采取两两随机配对竞争的方式,具有保留最优个体的能力 Ser=randperm(2*N);for i=1:Nf2=FITNESS(Ser(2*i));if f1<=f2farm{i}=FARM{Ser(2*i-1)};fitness(i)=FITNESS(Ser(2*i-1));elsefarm{i}=FARM{Ser(2*i)};end%记录最佳个体和收敛曲线minfitness=min(fitness)meanfitness=mean(fitness)LC1(counter+1)=minfitness;%收敛曲线1,各代最优个体适应值的记录 LC2(counter+1)=meanfitness;%收敛曲线2,各代群体平均适应值的记录 pos=find(fitness==minfitness);Xp=farm{pos(1)};%第五步:变异for i=1:Nif Pm>rand;%变异概率为PmX=farm{i};I=unidrnd(m);J=unidrnd(n);X(I,J)=1+(P(J)-eps)*rand;farm{i}=X;endendfarm{pos(1)}=Xp;counter=counter+1end%输出结果并绘图figure(1);plotif=1;X=Xp;[Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif);figure(2);plot(LC1);figure(3);plot(LC2);function [Zp,Y1p,Y2p,Y3p]=COST(X,T,P,plotif)% JSPGA的内联子函数,用于求调度方案的Makespan值% 输入参数列表% X 调度方案的编码矩阵,是一个实数编码的m×n矩阵% T m×n的矩阵,存储m个工件n个工序的加工时间% P 1×n的向量,n个工序中,每一个工序所具有的机床数目% plotif 是否绘甘特图的控制参数% 输出参数列表% Zp 最优的Makespan值% Y1p 最优方案中,各工件各工序的开始时刻% Y2p 最优方案中,各工件各工序的结束时刻% Y3p 最优方案中,各工件各工序使用的机器编号%第一步:变量初始化[m,n]=size(X);Y1p=zeros(m,n);Y2p=zeros(m,n);Y3p=zeros(m,n);%第二步:计算第一道工序的安排Q1=zeros(m,1);Q2=zeros(m,1);R=X(:,1);%取出第一道工序Q3=floor(R);%向下取整即得到各工件在第一道工序使用的机器的编号%下面计算各工件第一道工序的开始时刻和结束时刻for i=1:P(1)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1Q1(pos(1))=0;if lenpos>=2for j=2:lenposQ1(pos(j))=Q2(pos(j-1));Q2(pos(j))=Q2(pos(j-1))+T(pos(j),1);endendendendY1p(:,1)=Q1;Y3p(:,1)=Q3;%第三步:计算剩余工序的安排for k=2:nR=X(:,k);%取出第k道工序Q3=floor(R);%向下取整即得到各工件在第k道工序使用的机器的编号%下面计算各工件第k道工序的开始时刻和结束时刻for i=1:P(k)%取出机器编号pos=find(Q3==i);%取出使用编号为i的机器为其加工的工件的编号lenpos=length(pos);if lenpos>=1EndTime=Y2p(pos,k-1);%取出这些机器在上一个工序中的结束时刻POS=zeros(1,lenpos);%上一个工序完成时间由早到晚的排序for jj=1:lenposPOS(jj)=ppp(1);EndTime(ppp(1))=Inf;end%根据上一个工序完成时刻的早晚,计算各工件第k道工序的开始时刻和结束时刻Q1(pos(POS(1)))=Y2p(pos(POS(1)),k-1);Q2(pos(POS(1)))=Q1(pos(POS(1)))+T(pos(POS(1)),k);%前一个工件的结束时刻if lenpos>=2for j=2:lenposQ1(pos(POS(j)))=Y2p(pos(POS(j)),k-1);%预定的开始时刻为上一个工序的结束时刻if Q1(pos(POS(j)))<Q2(pos(POS(j-1)))%如果比前面的工件的结束时刻还早Q1(pos(POS(j)))=Q2(pos(POS(j-1)));endendendendendY1p(:,k)=Q1;Y2p(:,k)=Q2;Y3p(:,k)=Q3;end%第四步:计算最优的Makespan值Y2m=Y2p(:,n);Zp=max(Y2m);%第五步:绘甘特图if plotiffor i=1:mfor j=1:nmPoint1=Y1p(i,j);mPoint2=Y2p(i,j);mText=m+1-i;PlotRec(mPoint1,mPoint2,mText);Word=num2str(Y3p(i,j));%text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word);hold onx1=mPoint1;y1=mText-1;x2=mPoint2;y2=mText-1;x4=mPoint1;y4=mText;%fill([x1,x2,x3,x4],[y1,y2,y3,y4],'r');fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,0.5,1]);text(0.5*mPoint1+0.5*mPoint2,mText-0.5,Word);endendendfunction PlotRec(mPoint1,mPoint2,mText)% 此函数画出小矩形% 输入:% mPoint1 输入点1,较小,横坐标% mPoint2 输入点2,较大,横坐标% mText 输入的文本,序号,纵坐标vPoint = zeros(4,2) ;vPoint(1,:) = [mPoint1,mText-1];vPoint(2,:) = [mPoint2,mText-1];vPoint(3,:) = [mPoint1,mText];vPoint(4,:) = [mPoint2,mText];plot([vPoint(1,1),vPoint(2,1)],[vPoint(1,2),vPoint(2,2)]); hold on ;plot([vPoint(1,1),vPoint(3,1)],[vPoint(1,2),vPoint(3,2)]); plot([vPoint(2,1),vPoint(4,1)],[vPoint(2,2),vPoint(4,2)]); plot([vPoint(3,1),vPoint(4,1)],[vPoint(3,2),vPoint(4,2)]);。
求解置换流水车间调度问题的一种混合算法

求解置换流水车间调度问题的一种混合算法0. 前言置换流水车间调度问题(PFSP是对经典的流水车间调度问题进行简化后得到的一类子问题,最早在石化工业中得到应用,随后扩展到制造系统、生产线组装和信息设备服务上[1] 。
该问题一般可以描述为,n个待加工工件需要在m台机器上进行加工。
问题的目标是求出这n 个工件在每台机器上的加工顺序,从而使得某个调度指标达到最优,最常用的指标为工件的总完工时间(makespar)最短。
PFSP最早由Johnson于1954年进行研究[2],具有NP难性质[3] 。
求解方法主要有数学规划,启发式方法和基于人工智能的元启发式算法[4] 。
数学规划等适用于小规模问题,启发式方法计算便捷,却又无法保证解的质量。
随着计算智能的发展,基于人工智能的元启发式优化算法成为研究的重点。
遗传算法(GA是研究与应用得最为广泛的智能优化算法,利用遗传算法求解PFSP问题的研究也有很多。
遗传算法具有操作简单、容易实现的优点,且求解时不受约束条件限制。
然而,遗传算法通常存在着过早收敛,容易陷入局部最优的现象。
导致这一现象的原因在于遗传算法的交叉、变异操作具有一定的随机性,在求解PFSP问题的过程中往往会破坏构造块,产生所谓的连锁问题。
为了克服遗传算法的缺陷,研究人员提出了一种不进行遗传操作的分布估计算法[5] (EDA。
EDA是一种运用统计学习的新型优化算法。
相比GA EDA在全局搜索上有较大的优势,而局部搜索能力不足,同样会导致局部最优[6][7] 。
以混合优化为思路,本文将设计一种EDA与GA吉合的混合算法来求解PFSP 问题,混合算法通过EDA的概率模型和GA的交叉变异操作两种方式来生成个体,并引入模糊控制理论[8] 来自适应调节两种算法生成个体的比例。
1. 置换流水车间调度问题PFSP问题通常假设:(1)n台工件在m台机器上加工。
(2)每个工件以相同的顺序在m台机器上加工。
(3)每个工件在每台机器上的加工时间是预先确定的。
置换流水线车间调度问题的研究

LI U Yi g n ’ 。 GU We n - x i a n g 2 ' 。 LI Xi a n g - t a o 。 ( C o l l e g e o f Hu ma n i t i e s& S c i e n c e s o f No r t h e a s t No r ma l Un i v e r s i t y , C h a ge n h u n 1 3 0 1 1 7 , C h i n a ) 1
计
算
机
科
学
Vo 1 .3
Co mp u t e r S c i e n c e
置 换 流 水 线 车 间调 度 问题 的研 究
刘 莹L 。 谷 文祥 。 李 向涛。
( 东北 师 范大学人 文 学院 长 春 1 3 0 1 1 7 ) ( 长 春建 筑 学院基 础教 学部 长 春 1 3 O 6 O 7 ) 。 ( 东北 师 范大 学计算 机科 学 与信 息技术 学 院 长 春 1 3 0 1 1 7 ) 。
c o mp r e h e n s i v e u n d e r s t a n d i g. n
Ab s t r a c t As t h e s c i e n c e a n d t e c h n o l o g y d e v e l o p a n d t h e p r o d u c t i o n s c a l e e x p a n d s c o n s t a n t l y , t h e r e s e a r c h o n p e r mu t a -
求解改进布谷鸟算法的置换流水车间调度问题

BING Xiaofeng,TAO Yifei,DONG Yuanyuan,SUN Sihan (Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology,
调度⑴研究的内容是将稀缺资源分配给在一定时
间内的不同任务[2]%它一
程,其目的 :
化一
目标。
调的 对于企
业及相关 人员都有着重要的
和理论价
值。置换流水车间调度问题[3] ( Permutation Flow Shop
Scheduling Problem, PFSP )是对流水车间调度问题⑷
(Flow Shop Scheduling Problxm, FSP)的扩展,是一类典
鸟算法(Cuckoo Search,CS)是近年提出的一种新颖的 化算法,是模拟自然中布谷鸟寄生孵育雏鸟的
为发展而来的一种群
化。该 的优化
思想基 拟布谷鸟的孵育寄 为和鸟类的莱维飞
行行为,对解 整体更新评价策略从 现全局优
化,
、调参数少、收敛速度快的优点。
目前国内已有文献大多将布谷鸟
解项目
管理中资源调度[13]、函数优化[14]、整数规划[15]问题
、壬a巧區2019年第32卷第10期
Electenie Sci. & Tech. /Oct. 15,2019
求解改进布谷鸟算法的置换流水车间调度问题
丙『孝锋,陶翼飞,董圆圆,孙思汉
置换流水车间调度问题的中心引力优化算法求解

置换流水车间调度问题的中心引力优化算法求解刘勇;马良【摘要】目前求解置换流水车间调度问题的智能优化算法都是随机型优化方法,存在的一个问题是解的稳定性较差.针对该问题,本文给出一种确定型智能优化算法——中心引力优化算法的求解方法.为处理基本中心引力优化算法对初始解选择要求高的问题,利用低偏差序列生成初始解,提高初始解质量;利用加速度和位置迭代方程更新解的状态;利用两位置交换排序法进行局部搜索,提高算法的优化性能.采用置换流水车间调度问题标准测试算例进行数值实验,并和基本中心引力优化算法、NEH 启发式算法、微粒群优化算法和萤火虫算法进行比较.结果表明该算法不仅具有更好的解的稳定性,而且具有更高的计算精度,为置换流水车间调度问题的求解提供了一种可行有效的方法.%The existing intelligent optimization algorithms for permutation flow-shop scheduling problem are all stochastic optimization methods.One problem with these approaches is that they have poor solution stability.In this paper,a method based on central force optimization algorithm which is a deterministic intelligent optimization algorithm is proposed to resolve this problem.The basic algorithm depends upon the choice of the initial solutions.To deal with this problem,low-discrepancy sequences are used to generate initial solutions to improve the quality of initial solutions.The acceleration and position equations are employed to update the solutions.A sorting method to swap two positions in a solution is used to conduct local searches,to enhance the performance of the algorithm.The benchmarks are used to perform numerical experiments.The presented algorithm is compared with basiccentral force optimization algorithm,NEH heuristic algorithm,particle swarm optimization algorithm,and firefly algorithm.The results demonstrate that the proposed method not only has better solution stability but also higher accuracy.The presented approach provides a feasible and effective way to solve the permutation flowshop scheduling problem.【期刊名称】《运筹与管理》【年(卷),期】2017(026)009【总页数】6页(P46-51)【关键词】置换流水车间调度;最大完工时间;中心引力优化算法;确定性【作者】刘勇;马良【作者单位】上海理工大学管理学院,上海200093;上海理工大学管理学院,上海200093【正文语种】中文【中图分类】O221.3置换流水车间调度问题(Permutation Flow-Shop Scheduling Problem,PFSP)是一种典型的生产调度问题,有着广泛的工程应用背景,大概10%的产品制造系统、装配线系统和信息服务设施都可以转换为PFSP模型[1]。
置换流水车间调度问题的两阶段分布估计算法

置换流水车间调度问题的两阶段分布估计算法孙良旭;曲殿利;刘国莉【摘要】Aiming to solve the permutation flow shop scheduling problem, minimizing the total flow time as the objective function, it proposes a novel two-stage estimation of distribution algorithm. In the first stage, it firstly uses NEH (Nawaz-Enscore-Ham, NEH)heuristic to construct a relatively optimal initial individual, and then generates initial popu-lation randomly. To keep the diversities of the population, it puts forward a preferred mechanism to select individuals and establish the probability model, and at the same time, uses elite mechanism to keep the optimal individual in the contem-porary populations. Finally it uses probability model to sample and generate the next generation of population. In the second stage, it uses the insert and interchange operator to do neighborhood search around the optimal individual which is got in the first stage in order to improve the global search ability of estimation of distribution algorithm and prevent it from entrapping the local optimal. Through sufficient experiments, contrast and analysis for outcome of the examples, it proves the feasibility and effectiveness of the proposed algorithm.%针对置换流水车间调度问题,以最小化总流水时间为目标,提出了一种新颖的两阶段分布估计算法。
置换流水车间调度问题的离散粒子群优化算法

置换流水车间调度问题的离散粒子群优化算法第13卷第2期集美大学学报(自然科学版)Vol .13 No .2 2008年4月Journal of J i m ei University (Natural Science )Ap r .2008[收稿日期]2007-08-28 [修回日期]2008-03-05[基金项目]福建省自然科学基金资助项目(2006J0018);福建省青年人才科技创新基金(2006F3013)[作者简介]宁正元(1957—),男,教授,从事计算智能、算法设计与分析等方向的研究.[文章编号]1007-7405(2008)02-0097-05置换流水车间调度问题的离散粒子群优化算法宁正元,林大辉,李丽珊,钟一文(福建农林大学计算机与信息学院,福建福州350002)[摘要]提出了一种求解置换流水车间调度问题的离散粒子群优化算法.在该算法中,定义粒子的位置为作业的置换,粒子的速度为置换中作业的交换,根据离散量运算的特点,对粒子的运动规则进行了重新定义.采用变邻域搜索算子和逆序算子来保持粒子群的多样性和提高算法的局部求精能力,使算法在空间探索和局部求精间取得了较好的平衡.在Taillard 测试问题集上对算法性能进行了仿真实验,结果表明,离散粒子群优化算法具有良好的性能.[关键词]离散粒子群优化;置换流水车间调度问题;变邻域搜索;逆序算子[中图分类号]TP 301[文献标志码]A0 引言置换流水车间调度问题PFSP (Per mutati on Fl owshop Scheduling Pr oble m )是一类经典的加工调度问题,该问题可描述为:n 个作业以相同的顺序依次在m 台机器上流水加工,约定每一时刻每台机器最多只能加工一个作业,并且每一作业只能在一台机器上加工,已知各作业在各机器上的加工时间,要求确定所有作业的加工顺序,使得某项指标最小.若指标为最终加工完成时间,即makes pan,则此问题通常记为n /m /P /c max .PFSP 的求解方法通常可分为精确方法、构造型方法及基于计算智能的方法等[1].由于问题本身是NP -困难的,精确方法(如列举法、分支定界、动态规划等)计算量和存储量大,仅适合于小规模问题.构造型方法通过一定的规则来构造问题的解,如NEH 法[2]等,这类算法能快速构造解,但通常解的质量和算法通用性较差.基于计算智能的算法,特别是基于混合策略的算法,通常能产生较好的结果,比如文献[3]提出的结合遗传算法G A (Genetic A lgorithm )和模拟退火算法的G AS A 算法、文献[4]提出的结合蚁群优化ACO (Ant Col ony Op ti m izati on )算法和局部搜索算法的AM 算法及文献[5]提出的结合经典粒子群优化PS O (Particle S war m Op ti m izati on )算法和变邻域搜索VNS (Variable Neighborhood Search )算法[6] 的PS O VN S 算法.PS O 算法最早是由Kennedy 和Eberhart[7-8]提出的,它的基本原理源于对鸟群捕食行为的仿真.与ACO 算法类似,PS O 算法是一种基于群智能方法的优化技术,同时还与G A 类似,是一种基于进化的优化工具.目前,PS O 算法在解决组合优化问题中的应用主要有两条途径:一是利用经典的连续PS O 算法,比如,文献[9]使用PS O 算法去解决单一机器调度问题,它采用随机键表示法去表示粒子的位置,通过根据粒子在每一维的值对作业进行排序,就可以把粒子的位置映射为一个合法的调度,文献[5,10]也用相同的方式把连续PS O 算法应用到PFSP 及单一机器带权总拖期调度问题的求解中.显然,这些方法并没有充分考虑到离散型组合优化的特点,不可避免地存在表示冗余大、搜索效率低等缺点.另一种方式最早由Clerc [11]提出,它根据组合优化的特点,定义相应的离散粒子群优化DPS O (D iscrete Particle S war m Op ti m izati on )算法,采用这种思想,文献[12-13]分别提出了集美大学学报(自然科学版)第13卷求解旅行商问题和二次分配问题的DPS O 算法,都具有良好的性能.与文献[12-13]类似,本文提出了一种求解PFSP 的DPS O 算法,与文献[5]使用连续PS O 算法去处理PFSP 不同,DPS O 算法根据PFSP 及离散量运算的特点,定义粒子的位置为作业的置换,粒子的速度为置换中的作业的交换,并对粒子的运动规则进行了重新定义,与文献[5]类似,采用VNS 算法来平衡算法的空间勘探与局部求精能力,但VNS 算法的具体实现与文献[5]不同,同时,还使用了逆序算子来进一步提高粒子群的多样性.在Taillard 测试问题集上对DPS O 算法的性能进行了测试,结果表明它具有良好的性能.1 粒子群优化算法根据粒子对粒子群中的其它粒子的感知程度,可以把PS O 算法分为全局PS O 算法和局部PS O 算法,全局PS O 算法中的每个粒子能知道粒子群中所有粒子中的历史最好解,而局部PS O 算法中的粒子只知道某种近邻结构中的最好解.PS O 算法通常采用随机化的方式去为粒子产生初始位置和速度(随机初始解),在此之后,在每一次迭代中,粒子通过跟踪两个“极值”来更新自己:第一个就是粒子本身所找到的最好解,叫做个体极值点(用p best 表示其位置),全局版PS O 算法中的另一个极值点是整个种群目前找到的最好解,称为全局极值点(用g best 表示其位置),而局部版PS O 算法不用整个种群而是用其中一部分作为粒子的邻居,所有邻居中的最好解就是局部极值点(用l best 表示其位置).粒子的信息可以用N 维向量表示,把粒子的位置表示为X =(x 1,x 2,…,x n ),而把粒子的速度表示为V =(v 1,v 2,…,v n ),其他向量类似.式(1)和式(2)是粒子速度和位置的更新方程(对局部PS O 算法,用l best 替换式(1)中的g best ):v t+1j=w v t j +c 1r 1(p best t j-x t j )+c 2r 2(g best t j -x tj ),(1)x t+1j=x t j +v t+1j .(2)其中:w 是惯性系数,其主要作用是产生扰动,以防止算法的早熟收敛;c 1和c 2是加速系数(或称学习因子),分别调节向个体最好粒子和全局最好粒子方向飞行的最大步长,若太小,则粒子可能远离目标区域,若太大则会导致突然向目标区域飞去,或飞过目标区域,合适的c 1和c 2可在加快收敛速度的同时还能不易陷入局部最优,通常令c 1=c 2=2;r 1和r 2是[0,1]之间的随机数.2 求解PFSP 的离散粒子群优化算法与PS O 算法类似,DPS O 算法的关键就是要根据问题领域定义粒子的位置和速度的表示,同时,根据离散量的运算特点,定义这些量的运算规律和粒子的运动方程,下面对求解PFSP 的DPS O 算法的基本量及其运算法则进行描述.211 粒子的位置粒子的位置X 是一个N 维向量(它是n 个作业的一个置换,直接表示一种调度方案),在X 中,维表示调度顺序,每一维的数据表示作业,粒子的位置X 可表示为:X =(x 1,x 2,…,x i ,…,x N ),1≤i ≤N ,1≤x i ≤N ,N 是作业数.212 粒子的速度速度V 的作用是改变粒子的位置,与粒子的位置X 的定义类似,速度V 是一个N 维向量,表示为:V =(v 1,v 2,…,v i ,…,v N ),1≤i ≤N ,1≤v i ≤N .速度V 的每一维上的数据有二种含义,如果v i 等于0,表示空操作,即如果用该分速度作用某一个位置,它将不影响位置上相应维的数据,而如果不等于0,表示把此位置的相应维上的数据修改为v i ,它实际上是一种交换操作,即交换X 中的作业v i 和x i ,由于速度的作用只是交换X 中的作业,这样就保证了X 在任意V 的作用下依然是n 个作业的一个置换,亦即保证了解的可行性.89?第2期宁正元,等:置换流水车间调度问题的离散粒子群优化算法213 位置与速度的加法运算位置与速度的加法运算实现了粒子位置的移动,使粒子进入了一个新的位置,表示为:X =X +V .新位置的每一维的数据依次由式(3)的操作确定:if v i =0,s wap (x i ,v i )else,(3)式中s wap (x i ,v i )表示交换X 中的作业x i 和v i .214 位置的减法两个位置X 2和X 1相减的结果是一个速度V ,表示V =X 2-X 1,它表示如果把V 作用在X 1上将得到位置X 2,可以通过下述过程来计算:比较X 1和X 2在每一维i 上的值,如果相同,则使v i 等于0,如果不同,则使v i 等于x 2,i ,即V 中的任意一个元素可表示为:v i =if x 1,i =x 2,i ,x 2,ielse .(4)215 速度的数乘速度的数乘具有概率意义,它可以表示为:V 2=c ?V 1,c ∈[0,1].式中c 是一个常数,它具有概率的意义,在实际计算V 2时,对V 1中的每一维的速度v 1,i ,生成一个0到1之间的随机数rand,如果rand 小于c,则使v 2,i 等于v 1,i ,否则,v 2,i 等于0,即V 2中的任意一个元素可表示为: v 2,i =v 1,iif rand ≥c,0else .216 速度的加法两个速度相加,得到的新速度表示为:V =V 1+V 2,其中每一个速度分量v i 定义为:v i =v 1,i if (v 1,i ≠0and v 2,i =0)or (v 1,i ≠0and v 2,i ≠0and rand <0.5),v 2,i ,式中rand 是一个0到1之间的随机数.217 粒子的运动方程由于离散量运算的特殊性,对粒子的运动方程作了修改,取消了原有的惯性项,即式(1)中右边的第一项,因为速度的定义使位置的运动是一步到位的,所以它已经意义不大,粒子的运动方程具体描述如下:V =c 1(X p best -X )+c 2(X g best -X ),X =X +V .(5)由于惯性的主要作用是产生扰动,维持粒子群的多样性,没有它的作用,DPS O 算法将迅速陷入早熟,本文把VNS 算子作用到每个粒子上,它既能提高粒子个体的适应性,又能提高群体的多样性,为了进一步提高群体的多样性,当发现粒子个体极值停滞时,采用逆序(inversi on )算子来进一步提高群体的多样性.3 变邻域搜索算子VNS 算法是近年来新涌现的一种计算智能方法,它通过系统性地改变邻域搜索中的邻域结构,使算法获取全局最优解的可能性比用单个邻域结构的搜索算法高[6].本文所使用的VNS 算子采用了两种邻域结构,即交换邻域和插入邻域,位置X 的交换领域是交换X 中任意2个作业所产生的集合,而插入领域是将X 中的任意一个作业插入到任意一个其他位置所产生的集合,在此基础上定义了交换邻域搜索算子S wap (X )和插入邻域搜索算子Insert (X ),它们都采用首次改进的策略,为了增加随机性,邻域搜索的顺序用随机的方式产生,在此基础上,采用I nsert 为第一邻域,S wap 为第二邻域,定义VNS 算子的伪代码为:99?集美大学学报(自然科学版)第13卷重复下述操作:重复下述操作: insertI m p r oved =I nsert (X );直到insertI m p r oved 等于false;s wap I m p r oved =S wap (X );直到s wap I m p r oved 等于false .4 仿真实验及结果采用全局版PS O 实现了DPS O 算法,在根据式(5)修改了粒子的位置后,把VNS 算子作用到每个粒子上,以提高粒子的适应值.在Taillard 标准测试问题集上进行了仿真实验,与文献[4]相同,选用其中从20×5到100×20的9个不同维数的测试问题,每一种维数有10个不同的问题实例.对DPS O 算法在带VNS 算子(表示为DPS O VN S )和不带VNS 算子(表示为DPS O )的情况下的性能进行了对比实验,DPS O VN S 算法由于使用了VNS 算子和逆序算子,它可以有效地保持粒子群的多样性,所以粒子群可以比较小,仿真表明,取粒子数为10就能产生满意的结果.为了选择确定参数c 1和c 2的值,在20×10和50×10测试集上进行了仿真,结果表明c 1和c 2的鲁棒性较强,比如,在0101到0150之间,其结果都比AM 算法的结果好,在后面的仿真中,c 1和c 2都设置为0110;对DPS O 算法,由于比较容易陷入早熟收敛,所以要求粒子群足够大,实验中取粒子数为2×n ×m .表1是在Taillard 测试问题集上的性能比较.其中AM 的数据来源于文献[4],是4种不同策略的最佳解,其中蚁群的大小为10;PS O VNS 的数据来源于文献[5],粒子群的大小为2倍的作业数,迭代次数为100,每个测试用例运行5次,取平均值.DPS O VN S 算法和DPS O 算法在每个测试用例运行20次,取平均值.表1中最后一列是DPS O VN S 算法的迭代次数,在所有问题集上,DPS O VN S 算法的迭代次数与粒子群数的乘积都小于PS O VNS 所使用的值,为公平比较,使DPS O 算法与DPS O VNS 算法的运行时间相当.表1中所给出的计算结果均表示为相对于标准测试库中给出的最好结果的平均百分比偏差.表1 在Taillard 测试问题集上与其它算法的性能比较Tab 11 S i m u l a ti o n re su lts com p a ri ng w ith o the r a l go rithm s o n T a ill a rd p r o b l em se tn ×mNEH AM PS O VNS DPS O DPS O VNS 迭代次数20×53.6630.0410.280.8850.04110020×104.6010.2270.702.2920.091 10020×203.7310.1810.562.0710.08010050×50.7270.0080.180.59 20.00520050×105.0731.1811.043.1070.92220050×205.9711.932 1.714.6841.583200100×50.5270.0080.110.4670.004200100×102. 2150.3700.671.7680.364200100×204.2751.8781.283.6281.064200从表1中可以看出,在所有的测试问题上,DPS O VNS 、A M 和PS O VNS 都远远好于NEH 算法,与PS O VNS 相比,DPS O VNS 算法在所有问题上都具有更好的性能,与A M 相比,DPS O VNS 算法只是在20×5问题上相同,在其它问题上都优于A M 的结果,而DPS O 算法尽管比NEH 好,但和使用了邻域搜索算法的DPS O VNS 、A M 和PS O VNS 算法相比有明显的差距,充分说明了VNS 算子能有效地提高DPS O 算法的性能.5 结论以求解PFSP 为例,提出了一个DPS O 算法的具体实现,算法中使用VNS 算子和逆序算子来保持粒子群的多样性和提高算法的局部求精能力,使算法在粒子群比较小的情况下依然能在空间探索和局001?第2期宁正元,等:置换流水车间调度问题的离散粒子群优化算法部求精间取得较好的平衡,仿真实验表明DPS O 算法具有良好的性能,说明如果能够针对问题的特点,重新定义DPS O 算法的位置、速度等量及其运算规则,DPS O 算法能够很好地应用到NP -困难的组合优化问题的求解中.[参考文献][1]王凌.智能优化算法及其应用[M ].北京:清华大学出版社,施普林格出版社,2001:1702174.[2]韦有双,杨湘龙,冯允成.一种新的求解Fl ow -shop 问题的启发式方法[J ].系统工程理论与实践,2000,20(9):41247.[3]王凌,郑大钟.求解同顺序加工调度问题的一种改进遗传算法[J ].系统工程理论与实践,2002,22(6):74279.[4]王笑蓉,吴铁军.Fl owshop 问题的蚁群优化调度方法[J ].系统工程理论与实践,2003,23(5):65271.[5]T ASGETI RE N M F,SE VK L IM ,L I A NG Y C,et al .Particle S war m Op ti m izati on A lgorith m for Per mutati on Fl owshopSequencing Pr oble m [C ]//Ant Col ony Op ti m izati on and S war m I ntelligence:the 4th I nternati onal Workshop.Berlin: Sp ringer 2Verlag,2004:3822390.[6]MLADE NOV I C ’N,HANSE N P .Variable neighborhood search [J ].Computers and Operati ons and Research,1997,24:102721100.[7]KE NNE DY J,E BERHART R.Particle S war m Op ti m izati on [C ]//I EEE I ntl Conf on Neural Net w orks .New Jersey:I EEE Service Center,1995:194221948.[8]E BERHART R,KE NNE DY J.A Ne w Op ti m izer U singParticle S war m Theory [C ]//Pr oc of the Sixth I nternati onal Sy m 2posiu m on M icr o Machine and Hu man Science .Ne w Jersey:I EEE Service Center,1995:39243.[9]C AG N I N A L,ES QU I V E L l S,G ALLARD R.Particle S war m Op ti m izati on f or Sequencing Pr oble m s:A Case Study [C ]// Pr oceeding of the 2004Congress on Ev oluti onary Co mputati on .O reg on:I EEE Press,2004:5362541.[10]T ASGETI RE N M F,SE VK L IM ,L I A NG Y C,et al .Particle S war m Op ti m izati on A lgorith m f or Single Machine T otalW eighted Tardiness Pr oble m [C ]//Pr oceedings of the 2004Congress on Evoluti onary Computati on .O regon:I EEEPress,2004:141221419.[11]CLERC M.D iscrete particle s war m op ti m izati on [M ].Berlin:Sp ringer 2Verlag,2004:2192240.[12]钟一文,杨建刚,宁正元.求解TSP 问题的离散粒子群优化算法[J ].系统工程理论与实践,2006,26(6):88294.[13]钟一文,蔡荣英.求解二次分配问题的离散粒子群优化算法[J ].自动化学报,2007,33(8):8712874.D iscrete Parti cle Swar m O pti m i za ti on A lgor ith m forPer m ut a ti on Flowshop Scheduli n g ProblemN ING Zheng 2yuan,L IN Da 2hui,L IL i 2shan,Z HONG Yi 2wen (College of Computer and I nf or mati on Science,Fujian Agriculture and Forestry University,Fuzhou 350002,China ) Abstract:A discrete particle s war m op ti m izati on algorithm was designed t o tackle the per mutati on fl ow 2shop scheduling p r oble m (PFSP ).It defined the per mutati on of j obs as the positi on of the particle,and it defined the s wap of j obs in permutati on as the vel ocity of the particle .Based on the characteristics of the oper 2ati ons of discrete variables,it redefined the move ment rules of the particle .A variable neighborhood search operat or and an inversi on operat or were used t o keep the diversity of s war m and i m p r ove the algorith m πs inten 2sificati on ability .U sing those operat ors,the p r oposed algorithm could get a good balance bet w een exp l orati on and exp l oitati on .I n order t o observe its perf or mance,si m ulati on experi m ents were carried on Taillard πs benchmark p r oble m s .The results show that it can p r oduce good results .Key words:discrete particle s war m op ti m izati on;per mutati on fl owshop scheduling p r oble m;variable neighborhood search;inversi on operat or(责任编辑陈敏)101?。
Matlab与Visual C++混合编程求解车间调度问题

0 引 言
制 造 车 间 作 为 先 进 制 造 系 统 的 核 心 , 其 构 建 高 为 效 的调 度 方 案 与 优 化 技 术 已成 为 提 高 先 进 制 造 系 统 性 能 的主导 因素 , 间调 度 问题 应 运 而 生 。 随着 制 造 业 车
的快速 发 展 , 规模 定制 生产 、 球 化制 造 等思 想 的提 大 全
维普资讯
2 6 第2 0 年 期 0
文章 编号 :O 1— 2 5 20 )2— 0 1— 3 l0 26 (0 6 0 0 3 0
・ 设计与研 究 ・
M tb与 Vsa C +混合编程求解车 间调度 问题 aa l i l + u
常建娥 , 燕 何
p o igt e p o a s g s o e a d a p i t n V U S rv n h r g ms u i c p p l a i a e . r n n c o l
Ke o d : t b v u +;o b e rga n ;o c eue Gat y w r s mal ; i a C+ c m i p o mmigjbsh l; n t a sl n d r d
srcin o c e uef n s u cin r be , s a h w c e ued a clGa t pi u e h si tit sJ b S h o d l i e sfn t sp o lms a o C s o sh t o l n d l yn mia n t c rst u m- t
Co i e o r mmi g Mal b a d Vi a ++ t ov o c e u ePr b e mb n d Pr g a n ta n s lC u o S l eJ b S h d l o lms
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
物流运筹实务课程设计题目:置换流水车间调度问题的MATLAB求解置换流水车间调度问题的MATLAB求解目录一、前言 (5)二、问题描述 (6)三、算法设计 (7)四、实验结果 (15)摘要自从Johnson 1954年发表第一篇关于流水车间调度问题的文章以来.流水车间调度问题引起了许多学者的关注。
安排合理有效的生产调度是生产活动能井然有序开展,生产资源得到最佳配置,运作过程简明流畅的有力保证。
流水车间调度问题是许多实际流水线生产调度问题的简化模型。
它无论是在离散制造工业还是在流程工业中都具有广泛的应用。
因此,对进行研究具有重要的理论意义和工程价值。
流水线调度问题中一个非常典型的问题,而置换流水线调度问题作为FSP问题的子问题,是一个著名的组合优化问题。
该问题是一个典型的NP难问题,也是生产管理的核心内容。
随着生产规模的扩大,流水线调度问题的优化对提高资源利用率的作用越来越大,因此对其研究具有重要的理论和现实意义。
关键字:流水车间,单件小批量生产,jsp模型,Matlab前言企业资源的合理配置和优化利用很大程度上体现在车间一层的生产活动中,所以加强车间层的生产计划与控制一直在企业生产经营活动中占有十分重要的地位。
车间生产计划与控制的核心理论是调度理论。
车间调度问题是一类重要的组合优化问题。
为适应订货式、多品种、小批量生产的需要,引进了置换流水车间调度概念。
在置换流水车间调度优化后,可以避免或大大减少流程工作时间、提高生产效率。
因此,研究成组技术下车间调度问题是很有必要的。
生产调度,即对生产过程进行作业计划,是整个个先进生产制造系统实现管理技术、优化技术、白动化与计算机技术发展的核心。
置换流水车间调度问题是许多实际生产调度问题的简化模型。
生产计划与调度直接关系着企业的产出效率和生产成本,有效的计划与调度算法能最大限度地提高企业的效益。
调度问题是组合优化问题,属于NP问题,难以用常规力一法求解。
随着制造业的快速发展,大规模定制生产、全球化制造等思想的提出,使车间调度问题呈现出以下的新特点:约束条件多,时间复杂度高,空问复杂度高。
这将导致在许多情况下,求解所建立的数学模型的快速性无法满足,如果采用适度线形化处理之后求解,将会因简化太多而使结果严承失真。
所以需选择功能强大的数值计算工具来实现这一问题的求解。
MATLAB恰好提供了这样的平台。
MATLAB是一个高度集成的系统,集科学计算、图像处理、声音处理于一体,具有极高的编程效率。
典型JSP模型分析与Matlab的应用结合使流水车间调度问题迎刃而解。
最大完工时间是生产调度中最常用的性能度量指标之一,最大完工时间越短,则说明产品总的生产周期越短,生产能力越大;此类调度问题的优化研究有助于提高企业的生产效率与资源利用率。
一、问题描述n m流水车间调度问题通常可以描述为个工件要在台机器上加工,m每个工件有道工序,每道工序都要在不同的机器上加工,所有工件的加工顺序都相同,问题的目标是确定每台机器上工件的加工顺序及开工时间,使得特定的性能指标最优。
置换流水车间调度问题PFSP是对流水车间调度问题的进一步约束,即约定每台机器上所有工件的加工顺序相同,其解空间的规模为,远远小于流水车间调度问题的规模!n。
n(!)m本次课程实验主要研究PFSP中的最小化最大完工时间问题,利用F prmu C三元组表示法()求解Carlier (1978)提出的8个算例、以及maxReeves (1995)提出的21个算。
由于三台机器以上的调度问题被证明是NP 难问题,对于大规模的调度,至今仍未出现求解最优的方法,常常采用启发式算法来求解近优解。
本案例主要采用instance car2进行求解。
案例:某产品,需要经过4道工序对13个工件进行加工,这13个工件的生产流程是一样的。
加工时间表见下:表4-3 某产品加工时间表12345678910111213tj178963021457321865821420778569653212457tj293021425789653214254786532112412345678tj321475320124752147532145763214257854123tj4320142753214528653514527536214528888999计算步骤如下:首先确定n/m/F/C max 的最大完工时间为:1,11)1,(c j t j = k=2,...,m k j t k j c i j c 1)1,(),(11+-=i=2,...,n111)1,(c )1,(c i j i t j j +=- kj i i i i t k j c k j k j +-=-)}1,();,(c max{),(c 1工加则 C max =),(c nm j 二、算法设计(一)假设工件在机器上的加工顺序是相同的,同时假定各工件准备就绪,机器一开动就投入生产,开工时间为0,则最大完工时间等于最大流程时间。
同时3台机器以上的流水车间调度是NP 难问题,所以本文只考虑了2台、3台机器的情况,解决3台机器以上的问题方法也可运用人工智能算法,解的质量更高,但因该类算法需良好的软件编程能力,故本文不加探究。
n 个工件在m 台机器上的加工顺序相同。
工件在机器上的加工时间是给定的。
问题的目标是求n 个工件在每合机器上的最大完工时间等于最大流程时间。
这种流水线调度问题要在满足以下两个约束条件的前提下,使得加工完所有的工件所花的时间尽可能地少:1、工件约束每个工件在每台机器上恰好加工一次,每个工件在各机器上加工顺序相同。
不失一般性,假设各工件按机器1至m 的顺序进行加工。
各工件在各机器上的加工时间已知。
2、机器约束每台机器在任何时刻至多加工一个工件,每台机器加工的各工件的顺序相同。
置换流水线调度问题实质是如何调整加工工件的序列,提高机器的利用率的问题,即在同一时刻正在加工的机攫数越多,机器利用率越大口根据该原则,我们根据下面规则安排工件的加工顺序:(l)在前面机器加工时间较短、后面机器加工时间较长的工件,安排在序列前。
这样可以使得后面的机器尽快参加工作,并且后面的机器不需要作空等待,(2)机器加工时间较为平均且加工时间较长的工件,安排在序列的中部。
这样可以使得各个机器在中期的时候都能得到运作。
(3〕前面加工时间较长,后面加一〔时间较短的上件女排在序列尾部。
这样使得前面的机器能“延迟”完工,后面的机器尽快完工。
(二)利用Matlab软件对上面的案例进行求解,编程如下:软件输出相应的结果,如下:clc; clear all;temp=[ 0 456 1 856 2 963 3 6960 789 1 930 2 21 3 3200 630 1 214 2 475 3 1420 214 1 257 2 320 3 7530 573 1 896 2 124 3 2140 218 1 532 2 752 3 5280 653 1 142 2 147 3 6530 214 1 547 2 532 3 2140 204 1 865 2 145 3 5270 785 1 321 2 763 3 5360 696 1 124 2 214 3 2140 532 1 12 2 257 3 5280 12 1 345 2 854 3 8880 457 1 678 2 123 3 999];T=temp(:,2:2:end);[n,m]=size(T); %n为工件数,m为机器数txm=[]; %所有m-1个两台虚拟机器问题的加工时间矩阵Cmax=[]; %所有m-1个两台虚拟机器问题的总完工时间TXY=[]; %存放m-1个加工顺序ticfor i=1:m-1for j=1:ntx(j,1)=sum(T(j,1:i)); %第一台虚拟机器上的加工时间tx(j,2)=sum(T(j,m+1-i:m)); %第二台虚拟机器上的加工时间end[cmax,xy]=johnson(tx,T,n,m); %调用Johnson 算法函数Cmax =[ Cmax,cmax];txm=[txm,tx];TXY=[TXY,xy];endtxm, Cmax, TXYoptim=min(Cmax) %近似最优总完工时间ind=find(Cmax ==optim);optim_seq=TXY(:,ind)' %近似最优加工顺序rumTime=tocMatlab运行:txm =456 696 1312 1659 2275 2515789 320 1719 341 1740 1271630 142 844 617 1319 831214 753 471 1073 791 1330573 214 1469 338 1593 1234218 528 750 1280 1502 1812653 653 795 800 942 942214 214 761 746 1293 1293204 527 1069 6721214 1537785 536 1106 1299 1869 1620696 214 820 428 1034 552532 528 544 785 801 79712 888 357 1742 1211 2087457 999 1135 1122 1258 1800Cmax =8679 8423 8667TXY =13 13 49 4 74 12 138 6 96 7 141 10 814 1 67 14 110 8 1012 9 22 3 55 11 311 2 123 5 11optim =8423optim_seq =13 4 12 6 7 10 1 14 8 9 3 11 2 5(三)绘制甘特图编程如下:% 已知nbjobs, nbmachines, P% 通过computeCmax计算完工时间矩阵,然后画甘特图temp=[ 0 456 1 856 2 963 3 6960 789 1 930 2 21 3 3200 630 1 214 2 475 3 1420 214 1 257 2 320 3 7530 573 1 896 2 124 3 2140 218 1 532 2 752 3 5280 653 1 142 2 147 3 6530 214 1 547 2 532 3 2140 204 1 865 2 145 3 5270 785 1 321 2 763 3 5360 696 1 124 2 214 3 2140 532 1 12 2 257 3 5280 12 1 345 2 854 3 8880 457 1 678 2 123 3 999];P=temp(:,2:2:end);nbjobs=14;nbmachines=4;% 给定工件的加工顺序,计算完工时间,进而求makespanjobOrder=[ 13 4 12 6 7 10 1 14 8 9 3 11 2 5];C=zeros(nbjobs,nbmachines); % 完工时间矩阵%% 第一道工序,工件的完工时间C(jobOrder(1),1)=P(jobOrder(1),1); % 第一个工件的完工时间for i=2:nbjobs % 在加工顺序里面的位置% 第一道工序上,上一个工件加工完下一个工件才可以加工C(jobOrder(i),1)=C(jobOrder(i-1),1)+P(jobOrder(i),1);end%% 其余工序,工件的完工时间for j=2:nbmachinesC(jobOrder(1),j)=C(jobOrder(1),j-1)+P(jobOrder(1),j);for i=2:nbjobs% 在上道工序加工完,且前一个工件加工完,才可以加工C(jobOrder(i),j)=max(C(jobOrder(i),j-1),C(jobOrder(i-1),j))+P(jobOr der(i),j);endendCmax=max(C(:,nbmachines)); % Cmaxfigure_handle=figure;hold on;% Create titletitle(['置换流水车间调度甘特图(Cmax= ',num2str(Cmax),')'],...'FontWeight','bold','FontSize',12);xlabel('时间');ymax=nbmachines+1;xmax=Cmax;axis([0 xmax 0 ymax]);%--------------------------------------------------------------------------YLabel=cell(ymax,1);y=ymax;for j=1:nbmachinesYLabel{y}=['M' int2str(j)];y=y-1;endset(gca,'Ygrid','on','YTickLabel',YLabel,'YTick',0:ymax);%%hi=0.7;nb=1; % machineyi=ymax-1;for j=1:nbmachinesfor i=1:nbjobsxi=C(jobOrder(i), j)-P(jobOrder(i),j);wi=P(jobOrder(i), j);rectangle('Position',[xi,yi,wi,hi]);text(xi+0.5*wi,yi+0.5*hi,int2str(jobOrder(i)),'HorizontalAlignment',...'center');endyi=yi-1;nb=nb+1;endyi=yi-1;hold off;三、实验结果1、根据上面matlab的求解得到以下实验结果:最优排序为13 4 12 6 7 10 1 14 8 9 3 11 25min(Cmax)= 84232、甘特图如下所示:四、流水线型车间作业调度问题遗传算法MATLAB源码流水线型车间作业调度问题可以描述如下:n个任务在流水线上进行m个阶段的加工,每一阶段至少有一台机器且至少有一个阶段存在多台机器,并且同一阶段上各机器的处理性能相同,在每一阶段各任务均要完成一道工序,各任务的每道工序可以在相应阶段上的任意一台机器上加工,已知任务各道工序的处理时间,要求确定所有任务的排序以及每一阶段上机器的分配情况,使得调度指标(一般求Makespan)最小。
