直线内插法计算公式精编版

直线内插法计算公式

直线内插法计算公式附件二直线插值法计算收费基价公式（收费基价）（账单金额）注：1） X1和X2为《建设工程监理及相关服务收费标准》附表二收费金额的截面值；Y1和Y2是对应于X1和X2的基本电荷；X是节之间的插入值；Y是通过插入法计算的与x相对应的基价。

2）计费额小于500万元的，以计费额乘以3.3％的收费率计算收费基价；3）计费额大于1，000，000万元的，以计费额乘以1.039％的收费率计算收费基价。

y2-y1y=y1+(x-x1)x2-x1【例】若计算得计费额为600万，计算其收费基价。

根据《建设工程监理及相关服务收费标准：建设工程监理服务基准价格表》附表二，如果收费金额在500万（基准价格为16.5万）至1000万（基准价格为30.1万）之间，则相当于600万的基准价格30.1-16.5y=16.5+×（600-500）=1922001000-500１附件三否、责令改正违法违规行为的处罚标准，没收违法所得，可以依照《中华人民共和国价格法》第三十九条的规定处罚；《中华人民共和国价格法》第四十五条价格违法行为行政处罚；1、发包人、监理人不执行政府指导价的，处以5倍以下罚款；没有违法所得的，可以处二万元以上二十万元以下的罚款；情节严重的，责令停业整顿。

地方各级人民政府可以责令改正，可以通报批评；各级人民政府有关部门负责人和其他直接责任人员不执行政府指导价，三不客观公正履行职责的，依法给予政治处分。

建立评标专家库的政府部门或招标代理机构也应处以1万元以下的罚款。

有关行政监察部门应当给予警告；情节严重的，按照《评标专家和评标专家库管理办法》第十五条、第五十三条的规定，取消评标专家资格，并予以公告。

2.。

内插法的计算公式

内插法的计算公式在数学和金融等领域，内插法是一种常用的计算方法，它能够帮助我们在已知的数据点之间估算未知的值。

内插法的应用范围广泛，从科学研究到金融分析，都能看到它的身影。

那什么是内插法呢？简单来说，就是在已知的两个点之间，根据一定的规律和假设，推测出中间未知点的值。

为了实现这个目的，我们需要用到内插法的计算公式。

内插法的基本原理基于线性关系。

假设我们有两个已知点（x₁, y₁) 和（x₂, y₂)，现在要估算一个位于 x₁和 x₂之间的 x 所对应的 y 值。

内插法的计算公式为：y ＝ y₁＋（y₂ y₁) ／（x₂ x₁) ×（xx₁)我们来逐步拆解这个公式，以便更好地理解。

首先，（y₂ y₁) ／（x₂ x₁) 这个部分表示的是两个已知点之间的斜率。

斜率反映了数据的变化趋势。

然后，（x x₁) 表示我们要估算的点与已知点x₁之间的水平距离。

最后，将这两个部分相乘，就得到了在这个斜率下，水平距离所对应的垂直变化量。

再加上 y₁，就得到了估算的 y 值。

为了更直观地理解内插法的计算公式，我们来看一个实际的例子。

假设某商品的价格与销售量之间存在一定的关系。

已知当价格为 10 元时，销售量为 500 件；当价格为 15 元时，销售量为 300 件。

现在我们想知道当价格为 12 元时，销售量大概是多少。

首先，x₁＝ 10，y₁＝ 500，x₂＝ 15，y₂＝ 300。

斜率＝（300 500) ／（15 10) ＝－40然后，x ＝ 12，x₁＝ 10垂直变化量＝－40 ×（12 10) ＝－80最后，y ＝ 500 ＋（－80) ＝ 420所以，当价格为 12 元时，估计销售量为 420 件。

内插法不仅在简单的线性关系中有用，在一些稍微复杂的情况中，比如曲线关系，也可以通过分段线性化等方法来应用内插法。

再比如，在金融领域，计算债券的到期收益率时，可能会用到内插法。

已知两个不同利率下债券的价格，要估算某个特定价格对应的利率，就可以借助内插法。

直线内插法(设计费)

附件：
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+
=
说明： 1、X1、Y1为《工程设计收费标准》附表一中计费额的区段值；Y1、Y2为对应于X1、X2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而得的收费基价。

2、计费额＞2000000万元的，以计费额乘以1.6%的收费率计算收费基价。

；
【例】若计算得计费额为270万元，计算其设计收费基价。

根据《工程设计收费标准》附表一：工程设计收费基价表，计费额处于区段值200万元（收费基价为9万元）与500万元（收费基价为20.9万元）之间，则对应于270万元计费额的收费基价：
万元）(78.11)200270(200
50099.209=-⨯--+
=Y
Y （收费基价） Y 2 Y Y 1 0
12 X （计费额）
工程设计收费按照下列公式计算
1 工程设计收费＝工程设计收费基准价×（1±浮动幅度值）
2 工程设计收费基准价＝基本设计收费＋其他设计收费
3 基本设计收费＝工程设计收费基价×专业调整系数×工程复杂程度调整系。

直线内插法计算公式

直线内插法计算公式(总2页)
--本页仅作为文档封面，使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
２
附件二
收费基价直线内插法计算公式
y=y 1+ (x-x 1)
注：
1）x 1、x 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；y 1、y 2为对应于x 1、x 2的收费基价；x 为某区段间的插入值；y 为对应于x 由插入法计算而得的收费基价。

2）计费额小于500万元的，以计费额乘以％的收费率计算收费基价； 3）计费额大于1，000，000万元的，以计费额乘以％的收费率计算收费基价。

【例】若计算得计费额为600万，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万（收费基价为万）与1000万（收费基价为万）之间，则对应于600万计费额的收费基价
y=+ ×(600-500)＝（万）
（计费额）
（收费基价）
y 2-y 1
x 2-x 1
1000-500
附件三
3
建设工程监理与相关服务价格违法违规行为处罚标准和处罚依据
4。

内插法计算方式

附件：
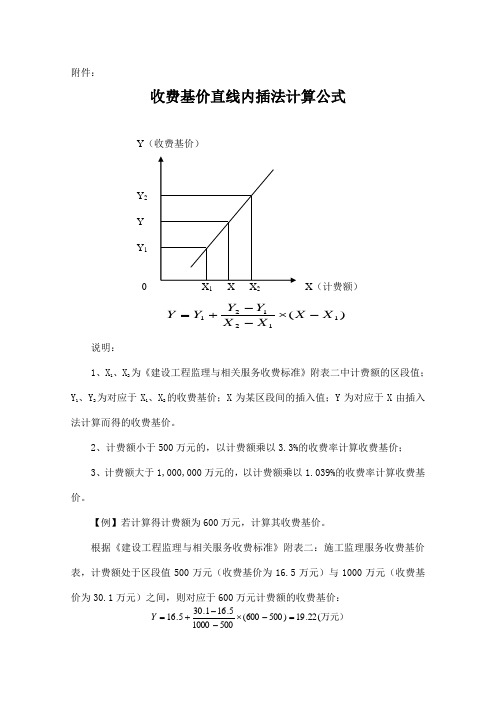
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+
=
说明： 1、X 1、X 2为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；
Y 1、Y 2为对应于X 1、X 2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入
法计算而得的收费基价。

2、计费额小于500万元的，以计费额乘以3.3%的收费率计算收费基价；
3、计费额大于1,000,000万元的，以计费额乘以1.039%的收费率计算收费基价。

【例】若计算得计费额为600万元，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万元（收费基价为16.5万元）与1000万元（收费基价为30.1万元）之间，则对应于600万元计费额的收费基价：
万元）(22.19)500600(500
10005.161.305.16=-⨯--+=Y
Y （收费基价） Y 2 Y Y 1 0
12 X （计费额）。

线性内插法

线性内插法具体怎么计算？内插法：就是在给定的二组数据为直线关系，在其区域之间的值，位于此直线上从而求出，在其区域之间的某一数据。

就是二者之间对应的情况下，按内插入法来求出另个数值，如二组数据：Y1，Y2 X1，X2已知：(X1，X2)一组上的某点值，求另一组（Y1，Y2）上的某点对应值。

现在要求已知：(X1，X2) )一组上的奌X，求：另一组（Y1，Y2）上的Y点对应值。

公式：Y＝Y1＋﹙Y2－Y1﹚÷﹙X2－X1﹚×﹙X－X1﹚式中：Y——所要求某区间的内插值；Y1、Y2——分别为所要求某区间之间的低值和高值；X1、X2——分别为所要求某区间之间对应的低值和高值。

图集11G101—1第53页中：锚固区的保护层厚度3d时受拉钢筋搭接长度修正系数ζa＝0.8：5d时受拉钢筋搭接长度修正系数ζa＝0.7。

【例1】假设，锚固区的保护层厚度为3.2d。

求受拉钢筋搭接长度修正系数ζa？公式：Y＝Y1＋﹙Y2－Y1﹚÷﹙X2－X1﹚×﹙X－X1﹚式中：Y——受拉钢筋锚固长度修正系数内插ζa取值；Y1、Y2——分别受拉钢筋锚固长度修正系数表中的低值ζa＝0.7和高值ζa＝0.8；X1、X2——锚固区的保护层厚度表中的低值3d和高值5d；解：Y＝Y1＋﹙Y2－Y1﹚÷﹙X2－X1﹚×﹙X－X1﹚＝0.7＋﹙0.8－0.7﹚÷﹙5d －3d﹚×﹙3.2d－3d﹚＝0.7＋0.05×0.2＝0.71。

答：锚固区的保护层厚度为3.2d。

受拉钢筋锚固长度修正系数ζa＝0.71。

【例2】假设，锚固区的保护层厚度为3.4d。

求受拉钢筋锚固长度修正系数ζa？解：Y＝Y1＋﹙Y2－Y1﹚÷﹙X2－X1﹚×﹙X－X1﹚＝0.7＋﹙0.8－0.7﹚÷﹙5d －3d﹚×﹙3.4d－3d﹚＝0.7＋0.05×0.4＝0.72。

直线内插法计算公式举例

直线内插法计算公式举例
《直线内插法计算公式举例》
直线内插法是一种用于拟合数据的统计学方法，它可以用来求出没有给定的数据点之间的函数值。

它的计算公式为：y=ax+b，其中a是斜率，b是截距。

举例来说，假设有两个给定的数据点（2，3）和（4，5），则可以用直线内插法来求出它们之间的函数值。

首先，用两个数据点求出斜率，即a=(y2-y1)/(x2-x1)=(5-3)/(4-2)=1。

然后，用一个数据点求出截距，即b=y1-ax1=3-2*2=−1。

最后，将斜率和截距代入计算公式，得到y=ax+b=x−1，即在两个数据点之间的函数值为y=x−1。

由此可见，直线内插法是一种简单而有效的统计学方法，可以用来求出没有给定的数据点之间的函数值。

它的计算公式为y=ax+b，其中a是斜率，b是截距，可以通过求斜率和截
距来计算出函数值。

直线内插法计算公式-直线内差法计算

直线内插法计算公式-直线内差法计算直线内插法计算公式直线内差法计算在数学和统计学领域，直线内插法（也称为直线内差法）是一种常用的数值计算方法。

它主要用于根据已知的两个数据点来估算位于这两个点之间的未知数据点的值。

直线内插法的基本原理是基于线性关系假设，即认为两个已知数据点之间的数值变化是呈直线趋势的。

让我们先来看一个简单的例子，以便更好地理解直线内插法的概念。

假设我们知道在温度为 10 摄氏度时，某种物质的电阻为 20 欧姆；在温度为 20 摄氏度时，电阻为 30 欧姆。

现在我们想知道当温度为 15 摄氏度时，该物质的电阻是多少。

在这个例子中，我们可以将温度看作自变量（x），电阻看作因变量（y）。

已知的两个数据点分别是（10, 20）和（20, 30）。

直线内插法的计算公式可以表示为：＼y ＝ y_1 ＋＼frac{（y_2 y_1)｝｛（x_2 x_1)｝＼times （x x_1)＼其中，＼（y\）是我们要求的未知值，＼（y_1\）和\（y_2\）分别是已知的两个因变量的值，＼（x_1\）和\（x_2\）分别是对应的自变量的值，＼（x\）是我们要估算的自变量的未知值。

回到刚才的电阻例子，＼（x_1 ＝ 10\），＼（y_1 ＝ 20\），＼（x_2 ＝ 20\），＼（y_2 ＝ 30\），＼（x ＝ 15\）。

首先计算斜率：＼（＼frac{（y_2 y_1)｝｛（x_2 x_1)｝＝＼frac{（30 20)｝｛（20 10)｝＝ 1\）然后代入公式计算：＼y ＝ 20 ＋ 1 ＼times （15 10) ＝ 20 ＋ 5 ＝ 25\所以，当温度为 15 摄氏度时，该物质的电阻估计为 25 欧姆。

直线内插法在实际应用中非常广泛。

比如在实验数据处理中，如果我们只测量了有限的几个数据点，但需要了解中间未测量点的值，就可以使用直线内插法进行估算。

在金融领域，预测股票价格的走势、计算债券的收益率等也可能会用到直线内插法。

收费基价直线内插法计算公式

【例】若计算得计费额为600万元，计算其收费基价。
根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万元（收费基价为16.5万元）与1000万元（收费基价为30.1万元）之间，则对应于600万元计费额的收费基价：
附ቤተ መጻሕፍቲ ባይዱ：
收费基价直线内插法计算公式
说明：
1、X1、Y1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；Y1、Y2为对应于X1、X2的收费基价；X为某区段间的插入值；Y为对应于X由插入法计算而得的收费基价。
2、计费额小于500万元的，以计费额乘以3.3%的收费率计算收费基价；
3、计费额大于1,000,000万元的，以计费额乘以1.039%的收费率计算收费基价。

内插法计算公式

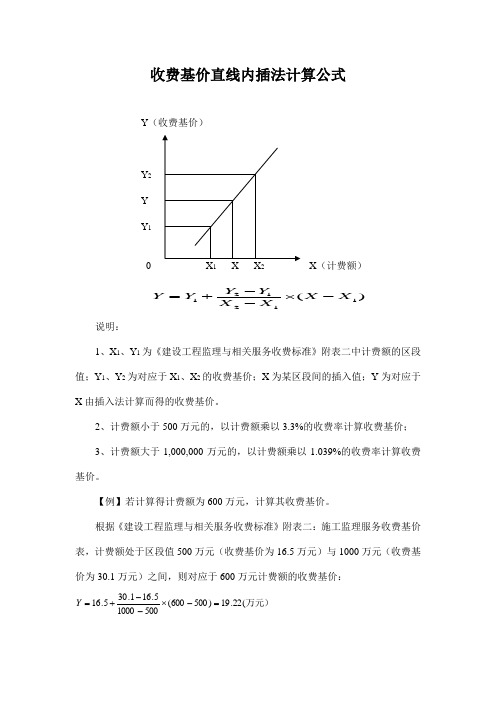
收费基价直线内插法计算公式
)(112121X X X X Y Y Y Y -⨯--+=
说明：
1、X 1、Y 1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；Y 1、Y 2为对应于X 1、X 2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而得的收费基价。

2、计费额小于500万元的，以计费额乘以3.3%的收费率计算收费基价；
3、计费额大于1,000,000万元的，以计费额乘以1.039%的收费率计算收费基价。

【例】若计算得计费额为600万元，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万元（收费基价为16.5万元）与1000万元（收费基价为30.1万元）之间，则对应于600万元计费额的收费基价：万元）(22.19)500600(50010005.161.305.16=-⨯--+=Y Y （收费基价） Y 2 Y Y 1 0
12 X （计费额）。

内插法的计算公式

内插法的计算公式在数学和金融等领域，内插法是一种常用的数值计算方法。

它可以帮助我们在已知的一些数据点之间，估算出其他未知点的值。

接下来，让我们深入了解一下内插法的计算公式及其应用。

内插法的基本思想是假设在两个已知数据点之间的函数关系是线性的。

也就是说，我们可以用一条直线来连接这两个点，然后根据这条直线来估算中间未知点的值。

假设我们有两个已知的数据点$（x_1, y_1)＄和$（x_2, y_2)＄，现在要估算某个$x$值对应的$y$值，其中$x_1 ＜ x ＜ x_2$。

内插法的计算公式为：＼y ＝ y_1 ＋＼frac{（x x_1)（y_2 y_1)｝｛x_2 x_1}＼为了更好地理解这个公式，我们可以把它分成几个部分来看。

首先，＄（y_2 y_1)／（x_2 x_1)＄表示的是这两个已知点之间的斜率。

斜率反映了函数在这一段区间内的变化率。

然后，＄（x x_1)＄表示我们要求的未知点$x$与已知点$x_1$之间的距离。

最后，将这两个部分相乘，就得到了在这个斜率下，由于距离变化所引起的$y$值的变化量。

再加上$y_1$，就得到了在$x$点处的估计值$y$。

让我们通过一个简单的例子来看看内插法是如何工作的。

假设我们知道当$x ＝ 1$时，＄y ＝ 5$；当$x ＝ 3$时，＄y ＝ 9$。

现在要估算当$x ＝ 2$时$y$的值。

首先，计算斜率：＄（9 5)／（3 1) ＝ 2$然后，计算变化量：＄（2 1)×2 ＝ 2$最后，估算$y$的值：＄5 ＋ 2 ＝ 7$所以，当$x ＝ 2$时，估计$y$的值为$7$。

内插法在实际中有很多应用。

在金融领域，比如计算债券的到期收益率、估计股票的价格等。

在科学研究中，当实验数据不是连续的，但需要估算中间值时，内插法也能发挥作用。

例如，在债券市场中，投资者购买了一种债券，已知在利率为 5%时，债券价格为 100 元；在利率为 6%时，债券价格为 95 元。

直线内插法(设计费)之欧阳地创编

附件：
收费基价直线内插法计算公式
说明： 1、X1、Y1为《工程设计收费标准》附表一中计费额的区段值；Y1
、Y2为对应于X1、X2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而得的收费
基价。

2、计费额＞2000000万元的，以计费额乘以1.6%的收费率计算收费基价。

；
【例】若计算得计费额为270万元，计算其设计收费基价。

根据《工程设计收费标准》附表一：工程设计收费基价表，计费额处于区段值200万元（收费基价为9万元）与500万元（收费基价为20.9万元）之间，则对应于270万元计费额的收费基价：
工程设计收费按照下列公式计算
1 工程设计收费＝工程设计收费基准价×（1±浮动幅度值）
2 工程设计收费基准价＝基本设计收费＋其他设计收费
Y （收费基价）
Y 2
Y Y 1
0 X 1 X X 2 X （计费额）
3 基本设计收费＝工程设计收费基价×专业调整系数×工程复杂程度调整系。

直线内插法计算公式-直线内差法计算

直线内插法计算公式-直线内差法计算直线内插法计算公式直线内差法计算在数学和统计学中，直线内插法（也称为直线内差法）是一种常用的数值计算方法，用于根据已知的数据点来估算位于这些点之间的未知值。

这种方法基于线性关系的假设，在一定范围内能够提供较为合理和准确的估计。

直线内插法的基本原理是假设在两个已知数据点之间的数值变化是线性的。

也就是说，如果我们知道两个点的坐标（x1, y1) 和（x2, y2)，那么对于位于 x1 和 x2 之间的某个 x 值，对应的 y 值可以通过线性关系计算得出。

假设我们有两个已知点 A(x1, y1) 和 B(x2, y2)，要估算位于 x 处（其中 x1 ＜ x ＜ x2）的 y 值。

首先，计算出两点之间的斜率 k：k ＝（y2 y1) ／（x2 x1)然后，通过点斜式方程可以得到直线方程：y y1 ＝ k （x x1)将其变形可得：y ＝ y1 ＋ k （x x1)这就是直线内插法的计算公式。

为了更好地理解直线内插法，让我们来看一个实际的例子。

假设我们知道在温度为 10°C 时，某种物质的溶解度为 20 克，在温度为 20°C 时，溶解度为 30 克。

现在我们想知道在温度为 15°C 时，该物质的溶解度大约是多少。

首先，确定已知点：A(10, 20) 和 B(20, 30)。

计算斜率 k：k ＝（30 20) ／（20 10) ＝ 1然后，使用直线内插法计算公式：y ＝ 20 ＋ 1 （15 10) ＝ 20 ＋ 5 ＝ 25所以，我们估计在温度为 15°C 时，该物质的溶解度约为 25 克。

直线内插法在许多领域都有广泛的应用。

在科学实验中，如果我们只测量了有限的几个数据点，但需要了解中间值的情况，就可以使用直线内插法进行估算。

在金融领域，例如计算利率、股价的中间值等，也常常会用到这种方法。

在工程领域，对于一些无法直接测量但可以通过已知数据进行推测的值，直线内插法也是一种有效的工具。

直线内插法计算公式0

直线内插法计算公式0
直线内插法是一种用于计算两个已知数据点之间未知数据点的方法。

假设我们有两个已知数据点A和B，其中A的横坐标为x1，纵坐标为y1，B的横坐标为x2，纵坐标为y2、我们要计算在A和B之间一些横坐标为x
的数据点的纵坐标。

y=y1+(x-x1)*(y2-y1)/(x2-x1)
其中，y表示未知数据点的纵坐标，x表示未知数据点的横坐标。

这个公式的推导过程如下：
根据直线的斜率的定义，斜率k等于两个点的纵坐标之差除以横坐标
之差：
k=(y2-y1)/(x2-x1)
假设我们要计算的未知数据点与已知数据点A的横坐标之差为
Δx=x-x1，则未知数据点与已知数据点A的纵坐标之差为Δy=k*Δx：Δy=k*Δx=(y2-y1)/(x2-x1)*(x-x1)
将已知数据点A的纵坐标y1加上Δy，得到未知数据点的纵坐标y：y=y1+Δy=y1+(x-x1)*(y2-y1)/(x2-x1)
使用直线内插法可以通过已知数据点之间的线性关系推算出未知数据
点的近似值，但是需要注意的是，这种方法只适用于数据点之间的关系是
线性的情况。

如果数据点之间的关系是非线性的，直线内插法将产生较大
的误差。

在实际应用中，我们需要根据数据点之间的关系选择合适的计算
方法。

直线内插法(设计费)之欧阳学创编

附件：
收费基价直线内插法计算公式
说明： 1、X1、Y1为《工程设计收费标准》附表一中计费额的区段值；Y1
、Y2为对应于X1、X2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而得的收
费基价。

2、计费额＞2000000万元的，以计费额乘以1.6%的收费率计算收费基价。

；
【例】若计算得计费额为270万元，计算其设计收费基价。

根据《工程设计收费标准》附表一：工程设计收费基价表，计费额处于区段值200万元（收费基价为9万元）与500万元（收费基价为20.9万元）之间，则对应于270万元计费额的收费基价：
工程设计收费按照下列公式计算
1 工程设计收费＝工程设计收费基准价×（1±浮动幅度值）
2 工程设计收费基准价＝基本设计收费＋其他设计收费
Y （收费基价）
Y 2
Y Y 1
0 X 1 X X 2 X （计费额）
3 基本设计收费＝工程设计收费基价×专业调整系数×工程复杂程度调整系。

内插法计算公式-内插法公式之欧阳语创编

欧阳语创编
欧阳语创编附件1：
收费基价直线内插法计算公式
说明： 1、X 1、Y 1为《建设工程监理与相关服务收费标准》附表二中计费额的区段值；Y 1、Y 2为对应于X 1、X 2的收费基
价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而
得的收费基价。

2、计费额小于500万元的，以计费额乘以3.3%的收费率计算收费基价；
3、计费额大于1,000,000万元的，以计费额乘以1.039%的收费率计算收费基价。

【例】若计算得计费额为600万元，计算其收费基价。

根据《建设工程监理与相关服务收费标准》附表二：施工监理服务收费基价表，计费额处于区段值500万元（收费基价为16.5万元）与1000万元（收费基价为30.1万元）之间，则对应于600
万元计费额的收费基价：
Y （收费基价）
Y 2
Y Y 1
0 X 1 X X 2 X （计费额）。

直线内插法(设计费)之欧阳道创编

附件：
收费基价直线内插法计算公式
说明： 1、X1、Y1为《工程设计收费标准》附表一中计费额的区段值；
Y1、Y2为对应于X1、X2的收费基价；X 为某区段间的插入值；Y 为对应于X 由插入法计算而
得的收费基价。

2、计费额＞2000000万元的，以计费额乘以1.6%的收费率计算收费基价。

；
【例】若计算得计费额为270万元，计算其设计收费基价。

根据《工程设计收费标准》附表一：工程设计收费基价表，计费额处于区段值200万元（收费基价为9万元）与500万元（收费基价为20.9万元）之间，则对应于270万元计费额的收费基价：
工程设计收费按照下列公式计算
1 工程设计收费＝工程设计收费基准价×（1±浮动幅度值）
2 工程设计收费基准价＝基本设计收费＋其他设计收费
3 基本设计收费＝工程设计收费基价×专业调整系数×
Y （收费基价）
Y 2
Y
Y 1
0 X 1 X X 2 X （计费额）
工程复杂程度调整系。