2017高考试题分类汇编-函数导数
【K12高考数学】2017年高考真题分类汇编(理数):专题2导数(解析版)

2017年高考真题分类汇编(理数):专题2导数一、单选题(共3题;共6分)1、(2017•浙江)函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是()A、B、C、D、2、(2017•新课标Ⅱ)若x=﹣2是函数f(x)=(x2+ax﹣1)e x﹣1的极值点,则f(x)的极小值为()A、﹣1B、﹣2e﹣3C、5e﹣3D、13、(2017•新课标Ⅲ)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A、﹣B、C、D、1二、解答题(共8题;共50分)4、(2017•浙江)已知函数f(x)=(x﹣)e﹣x(x≥).(Ⅰ)求f(x)的导函数;(Ⅱ)求f(x)在区间[,+∞)上的取值范围.5、(2017•山东)已知函数f(x)=x2+2cosx,g(x)=e x(cosx﹣sinx+2x﹣2),其中e≈2.17828…是自然对数的底数.(13分)(Ⅰ)求曲线y=f(x)在点(π,f(π))处的切线方程;(Ⅱ)令h(x)=g(x)﹣af(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.6、(2017•北京卷)已知函数f(x)=e x cosx﹣x.(13分)(1)求曲线y=f(x)在点(0,f(0))处的切线方程;(2)求函数f(x)在区间[0,]上的最大值和最小值.7、(2017·天津)设a∈Z,已知定义在R上的函数f(x)=2x4+3x3﹣3x2﹣6x+a在区间(1,2)内有一个零点x0,g(x)为f(x)的导函数.(Ⅰ)求g(x)的单调区间;(Ⅱ)设m∈[1,x0)∪(x0,2],函数h(x)=g(x)(m﹣x0)﹣f(m),求证:h(m)h(x0)<0;(Ⅲ)求证:存在大于0的常数A,使得对于任意的正整数p,q,且∈[1,x0)∪(x0,2],满足|﹣x0|≥.8、(2017•江苏)已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)(Ⅰ)求b关于a的函数关系式,并写出定义域;(Ⅱ)证明:b2>3a;(Ⅲ)若f(x),f′(x)这两个函数的所有极值之和不小于﹣,求a的取值范围.9、(2017•新课标Ⅰ卷)已知函数f(x)=ae2x+(a﹣2)e x﹣x.(12分)(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.10、(2017•新课标Ⅱ)已知函数f(x)=ax2﹣ax﹣xlnx,且f(x)≥0.(Ⅰ)求a;(Ⅱ)证明:f(x)存在唯一的极大值点x0,且e﹣2<f(x0)<2﹣2.11、(2017•新课标Ⅲ)已知函数f(x)=x﹣1﹣alnx.(Ⅰ)若f(x)≥0,求a的值;(Ⅱ)设m为整数,且对于任意正整数n,(1+)(1+)…(1+)<m,求m的最小值.答案解析部分一、单选题1、【答案】D【考点】函数的图象,函数的单调性与导数的关系【解析】【解答】解:由当f′(x)<0时,函数f(x)单调递减,当f′(x)>0时,函数f(x)单调递增,则由导函数y=f′(x)的图象可知:f(x)先单调递减,再单调递增,然后单调递减,最后单调递增,排除A,C,且第二个拐点(即函数的极大值点)在x轴上的右侧,排除B,故选D【分析】根据导数与函数单调性的关系,当f′(x)<0时,函数f(x)单调递减,当f′(x)>0时,函数f(x)单调递增,根据函数图象,即可判断函数的单调性,然后根据函数极值的判断,即可判断函数极值的位置,即可求得函数y=f(x)的图象可能2、【答案】A【考点】导数的运算,利用导数研究函数的单调性,利用导数研究函数的极值【解析】【解答】解:函数f(x)=(x2+ax﹣1)e x﹣1,可得f′(x)=(2x+a)e x﹣1+(x2+ax﹣1)e x﹣1,x=﹣2是函数f(x)=(x2+ax﹣1)e x﹣1的极值点,可得:﹣4+a+(3﹣2a)=0.解得a=﹣1.可得f′(x)=(2x﹣1)e x﹣1+(x2﹣x﹣1)e x﹣1,=(x2+x﹣2)e x﹣1,函数的极值点为:x=﹣2,x=1,当x<﹣2或x>1时,f′(x)>0函数是增函数,x∈(﹣2,1)时,函数是减函数,x=1时,函数取得极小值:f(1)=(12﹣1﹣1)e1﹣1=﹣1.故选:A.【分析】求出函数的导数,利用极值点,求出a,然后判断函数的单调性,求解函数的极小值即可.3、【答案】C【考点】利用导数研究函数的单调性,导数在最大值、最小值问题中的应用,函数的零点与方程根的关系,函数的零点【解析】【解答】解:因为f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)=﹣1+(x﹣1)2+a(e x﹣1+)=0,所以函数f(x)有唯一零点等价于方程1﹣(x﹣1)2=a(e x﹣1+)有唯一解,等价于函数y=1﹣(x﹣1)2的图象与y=a(e x﹣1+)的图象只有一个交点.①当a=0时,f(x)=x2﹣2x≥﹣1,此时有两个零点,矛盾;②当a<0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,且y=a(e x﹣1+)在(﹣∞,1)上递增、在(1,+∞)上递减,所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(e x﹣1+)的图象的最高点为B(1,2a),由于2a<0<1,此时函数y=1﹣(x﹣1)2的图象与y=a(e x﹣1+)的图象有两个交点,矛盾;③当a>0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,且y=a(e x﹣1+)在(﹣∞,1)上递减、在(1,+∞)上递增,所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(e x﹣1+)的图象的最低点为B(1,2a),由题可知点A与点B重合时满足条件,即2a=1,即a=,符合条件;综上所述,a=,故选:C.【分析】通过转化可知问题等价于函数y=1﹣(x﹣1)2的图象与y=a(e x﹣1+)的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.二、解答题4、【答案】解:(Ⅰ)函数f(x)=(x﹣)e﹣x(x≥),导数f′(x)=(1﹣••2)e﹣x﹣(x﹣)e﹣x=(1﹣x+)e﹣x=(1﹣x)(1﹣)e﹣x;(Ⅱ)由f(x)的导数f′(x)=(1﹣x)(1﹣)e﹣x,可得f′(x)=0时,x=1或,当<x<1时,f′(x)<0,f(x)递减;当1<x<时,f′(x)>0,f(x)递增;当x>时,f′(x)<0,f(x)递减,且x≥⇔x2≥2x﹣1⇔(x﹣1)2≥0,则f(x)≥0.由f()=e,f(1)=0,f()=e,即有f(x)的最大值为e,最小值为f(1)=0.则f(x)在区间[,+∞)上的取值范围是[0,e].【考点】简单复合函数的导数,利用导数研究函数的单调性,导数在最大值、最小值问题中的应用【解析】【分析】(Ⅰ)求出f(x)的导数,注意运用复合函数的求导法则,即可得到所求;(Ⅱ)求出f(x)的导数,求得极值点,讨论当<x<1时,当1<x<时,当x>时,f(x)的单调性,判断f(x)≥0,计算f(),f(1),f(),即可得到所求取值范围.5、【答案】解:(Ⅰ)f(π)=π2﹣2.f′(x)=2x﹣2sinx,∴f′(π)=2π.∴曲线y=f(x)在点(π,f(π))处的切线方程为:y﹣(π2﹣2)=2π(x﹣π).化为:2πx﹣y﹣π2﹣2=0.(Ⅱ)h(x)=g(x)﹣af(x)=e x(cosx﹣sinx+2x﹣2)﹣a(x2+2cosx)h′(x)=e x(cosx﹣sinx+2x﹣2)+e x(﹣sinx﹣cosx+2)﹣a(2x﹣2sinx)=2(x﹣sinx)(e x﹣a)=2(x﹣sinx)(e x﹣e lna).令u(x)=x﹣sinx,则u′(x)=1﹣cosx≥0,∴函数u(x)在R上单调递增.∵u(0)=0,∴x>0时,u(x)>0;x<0时,u(x)<0.(i)a≤0时,e x﹣a>0,∴x>0时,h′(x)>0,函数h(x)在(0,+∞)单调递增;x<0时,h′(x)<0,函数h(x)在(﹣∞,0)单调递减.∴x=0时,函数h(x)取得极小值,h(0)=﹣1﹣2a.(ii)a>0时,令h′(x)=2(x﹣sinx)(e x﹣e lna)=0.解得x1=lna,x2=0.①0<a<1时,x∈(﹣∞,lna)时,e x﹣e lna<0,h′(x)>0,函数h(x)单调递增;x∈(lna,0)时,e x﹣e lna>0,h′(x)<0,函数h(x)单调递减;x∈(0,+∞)时,e x﹣e lna>0,h′(x)>0,函数h(x)单调递增.∴当x=0时,函数h(x)取得极小值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极大值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].②当a=1时,lna=0,x∈R时,h′(x)≥0,∴函数h(x)在R上单调递增.③1<a时,lna>0,x∈(﹣∞,0)时,e x﹣e lna<0,h′(x)>0,函数h(x)单调递增;x∈(0,lna)时,e x﹣e lna<0,h′(x)<0,函数h(x)单调递减;x∈(lna,+∞)时,e x﹣e lna>0,h′(x)>0,函数h(x)单调递增.∴当x=0时,函数h(x)取得极大值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极小值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].综上所述:a≤0时,函数h(x)在(0,+∞)单调递增;x<0时,函数h(x)在(﹣∞,0)单调递减.x=0时,函数h(x)取得极小值,h(0)=﹣1﹣2a.0<a<1时,函数h(x)在x∈(﹣∞,lna)是单调递增;函数h(x)在x∈(lna,0)上单调递减.当x=0时,函数h(x)取得极小值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极大值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].当a=1时,lna=0,函数h(x)在R上单调递增.a>1时,函数h(x)在(﹣∞,0),(lna,+∞)上单调递增;函数h(x)在(0,lna)上单调递减.当x=0时,函数h(x)取得极大值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极小值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].【考点】导数的加法与减法法则,导数的乘法与除法法则,函数的单调性与导数的关系,利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程【解析】【分析】(Ⅰ)f(π)=π2﹣2.f′(x)=2x﹣2sinx,可得f′(π)=2π即为切线的斜率,利用点斜式即可得出切线方程.(Ⅱ)h(x)=g(x)﹣af(x)=e x(cosx﹣sinx+2x﹣2)﹣a(x2+2cosx),可得h′(x)=2(x﹣sinx)(e x﹣a)=2(x﹣sinx)(e x﹣e lna).令u(x)=x﹣sinx,则u′(x)=1﹣cosx≥0,可得函数u(x)在R上单调递增.由u(0)=0,可得x>0时,u(x)>0;x<0时,u(x)<0.对a分类讨论:a≤0时,0<a<1时,当a=1时,a>1时,利用导数研究函数的单调性极值即可得出.6、【答案】(1)解:函数f(x)=e x cosx﹣x的导数为f′(x)=e x(cosx﹣sinx)﹣1,可得曲线y=f(x)在点(0,f(0))处的切线斜率为k=e0(cos0﹣sin0)﹣1=0,切点为(0,e0cos0﹣0),即为(0,1),曲线y=f(x)在点(0,f(0))处的切线方程为y=1;(2)解:函数f(x)=e x cosx﹣x的导数为f′(x)=e x(cosx﹣sinx)﹣1,令g(x)=e x(cosx﹣sinx)﹣1,则g(x)的导数为g′(x)=e x(cosx﹣sinx﹣sinx﹣cosx)=﹣2e x•sinx,当x∈[0,],可得g′(x)=﹣2e x•sinx≤0,即有g(x)在[0,]递减,可得g(x)≤g(0)=0,则f(x)在[0,]递减,即有函数f(x)在区间[0,]上的最大值为f(0)=e0cos0﹣0=1;最小值为f()=e cos﹣=﹣.【考点】利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程【解析】【分析】(1.)求出f(x)的导数,可得切线的斜率和切点,由点斜式方程即可得到所求方程;(2.)求出f(x)的导数,再令g(x)=f′(x),求出g(x)的导数,可得g(x)在区间[0,]的单调性,即可得到f(x)的单调性,进而得到f(x)的最值.7、【答案】(Ⅰ)解:由f(x)=2x4+3x3﹣3x2﹣6x+a,可得g(x)=f′(x)=8x3+9x2﹣6x﹣6,进而可得g′(x)=24x2+18x﹣6.令g′(x)=0,解得x=﹣1,或x=.当x变化时,g′(x),g(x)的变化情况如下表:x(﹣∞,﹣1)(﹣1,)(,+∞)g′(x)+﹣+g(x)↗↘↗所以,g(x)的单调递增区间是(﹣∞,﹣1),(,+∞),单调递减区间是(﹣1,).(Ⅱ)证明:由h(x)=g(x)(m﹣x0)﹣f(m),得h(m)=g(m)(m﹣x0)﹣f(m),h(x0)=g(x0)(m﹣x0)﹣f(m).令函数H1(x)=g(x)(x﹣x0)﹣f(x),则H′1(x)=g′(x)(x﹣x0).由(Ⅰ)知,当x∈[1,2]时,g′(x)>0,故当x∈[1,x0)时,H′1(x)<0,H1(x)单调递减;当x∈(x0,2]时,H′1(x)>0,H1(x)单调递增.因此,当x∈[1,x0)∪(x0,2]时,H1(x)>H1(x0)=﹣f(x0)=0,可得H1(m)>0即h(m)>0,令函数H2(x)=g(x0)(x﹣x0)﹣f(x),则H′2(x)=g′(x0)﹣g(x).由(Ⅰ)知,g(x)在[1,2]上单调递增,故当x∈[1,x0)时,H′2(x)>0,H2(x)单调递增;当x∈(x0,2]时,H′2(x)<0,H2(x)单调递减.因此,当x∈[1,x0)∪(x0,2]时,H2(x)>H2(x0)=0,可得得H2(m)<0即h(x0)<0,.所以,h(m)h(x0)<0.(Ⅲ)对于任意的正整数p,q,且,令m=,函数h(x)=g(x)(m﹣x0)﹣f(m).由(Ⅱ)知,当m∈[1,x0)时,h(x)在区间(m,x0)内有零点;当m∈(x0,2]时,h(x)在区间(x0,m)内有零点.所以h(x)在(1,2)内至少有一个零点,不妨设为x1,则h(x1)=g(x1)(﹣x0)﹣f()=0.由(Ⅰ)知g(x)在[1,2]上单调递增,故0<g(1)<g(x1)<g(2),于是|﹣x0|=≥=.因为当x∈[1,2]时,g(x)>0,故f(x)在[1,2]上单调递增,所以f(x)在区间[1,2]上除x0外没有其他的零点,而≠x0,故f()≠0.又因为p,q,a均为整数,所以|2p4+3p3q﹣3p2q2﹣6pq3+aq4|是正整数,从而|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1.所以|﹣x0|≥.所以,只要取A=g(2),就有|﹣x0|≥.【考点】利用导数研究函数的单调性,利用导数研究函数的极值,不等式的证明,函数的零点【解析】【分析】(Ⅰ)求出函数的导函数g(x)=f′(x)=8x3+9x2﹣6x﹣6,求出极值点,通过列表判断函数的单调性求出单调区间即可.(Ⅱ)由h(x)=g(x)(m﹣x0)﹣f(m),推出h(m)=g(m)(m﹣x0)﹣f(m),令函数H1(x)=g(x)(x﹣x0)﹣f(x),求出导函数H′1(x)利用(Ⅰ)知,推出h(m)h(x0)<0.(Ⅲ)对于任意的正整数p,q,且,令m=,函数h(x)=g(x)(m﹣x0)﹣f(m).由(Ⅱ)知,当m∈[1,x0)时,当m∈(x0,2]时,通过h(x)的零点.转化推出|﹣x0|=≥=.推出|2p4+3p3q﹣3p2q2﹣6pq3+aq4|≥1.然后推出结果.8、【答案】(Ⅰ)解:因为f(x)=x3+ax2+bx+1,所以g(x)=f′(x)=3x2+2ax+b,g′(x)=6x+2a,令g′(x)=0,解得x=﹣.由于当x>﹣时g′(x)>0,g(x)=f′(x)单调递增;当x<﹣时g′(x)<0,g(x)=f′(x)单调递减;所以f′(x)的极小值点为x=﹣,由于导函数f′(x)的极值点是原函数f(x)的零点,所以f(﹣)=0,即﹣+﹣+1=0,所以b=+(a>0).因为f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,所以f′(x)=3x2+2ax+b=0有两个不等的实根,所以4a2﹣12b>0,即a2﹣+>0,解得a>3,所以b=+(a>3).(Ⅱ)证明:由(1)可知h(a)=b2﹣3a=﹣+=(4a3﹣27)(a3﹣27),由于a>3,所以h(a)>0,即b2>3a;(Ⅲ)解:由(1)可知f′(x)的极小值为f′(﹣)=b﹣,设x1,x2是y=f(x)的两个极值点,则x1+x2=,x1x2=,所以f(x1)+f(x2)=++a(+)+b(x1+x2)+2=(x1+x2)[(x1+x2)2﹣3x1x2]+a[(x1+x2)2﹣2x1x2]+b(x1+x2)+2=﹣+2,又因为f(x),f′(x)这两个函数的所有极值之和不小于﹣,所以b﹣+﹣+2=﹣≥﹣,因为a>3,所以2a3﹣63a﹣54≤0,所以2a(a2﹣36)+9(a﹣6)≤0,所以(a﹣6)(2a2+12a+9)≤0,由于a>3时2a2+12a+9>0,所以a﹣6≤0,解得a≤6,所以a的取值范围是(3,6].【考点】导数的运算,利用导数研究函数的单调性,利用导数研究函数的极值,导数在最大值、最小值问题中的应用【解析】【分析】(Ⅰ)通过对f(x)=x3+ax2+bx+1求导可知g(x)=f′(x)=3x2+2ax+b,进而再求导可知g′(x)=6x+2a,通过令g′(x)=0进而可知f′(x)的极小值点为x=﹣,从而f(﹣)=0,整理可知b=+(a>0),结合f(x)=x3+ax2+bx+1(a >0,b∈R)有极值可知f′(x)=0有两个不等的实根,进而可知a>3.(Ⅱ)通过(1)构造函数h(a)=b2﹣3a=﹣+=(4a3﹣27)(a3﹣27),结合a>3可知h(a)>0,从而可得结论;(Ⅲ)通过(1)可知f′(x)的极小值为f′(﹣)=b﹣,利用韦达定理及完全平方关系可知y=f(x)的两个极值之和为﹣+2,进而问题转化为解不等式b﹣+﹣+2=﹣≥﹣,因式分解即得结论.9、【答案】(1)解:由f(x)=ae2x+(a﹣2)e x﹣x,求导f′(x)=2ae2x+(a﹣2)e x ﹣1,当a=0时,f′(x)=2e x﹣1<0,∴当x∈R,f(x)单调递减,当a>0时,f′(x)=(2e x+1)(ae x﹣1)=2a(e x+)(e x﹣),令f′(x)=0,解得:x=ln,当f′(x)>0,解得:x>ln,当f′(x)<0,解得:x<ln,∴x∈(﹣∞,ln)时,f(x)单调递减,x∈(ln,+∞)单调递增;当a<0时,f′(x)=2a(e x+)(e x﹣)<0,恒成立,∴当x∈R,f(x)单调递减,综上可知:当a≤0时,f(x)在R单调减函数,当a>0时,f(x)在(﹣∞,ln)是减函数,在(ln,+∞)是增函数;(2)由f(x)=ae2x+(a﹣2)e x﹣x=0,有两个零点,由(1)可知:当a>0时,f(x)=0,有两个零点,则f(x)min=a+(a﹣2)﹣ln,=a()+(a﹣2)×﹣ln,=1﹣﹣ln,由f(x)min<0,则1﹣﹣ln<0,整理得:a﹣1+alna<0,设g(a)=alna+a﹣1,a>0,g′(a)=lna+1+1=lna+2,令g′(a)=0,解得:a=e﹣2,当a∈(0,e﹣2),g′(a)<0,g(a)单调递减,当a∈(e﹣2,+∞),g′(a)>0,g(a)单调递增,g(a)min=g(e﹣2)=e﹣2lne﹣2+e﹣2﹣1=﹣﹣1,由g(1)=1﹣1﹣ln1=0,∴0<a<1,a的取值范围(0,1).【考点】导数的运算,利用导数研究函数的单调性,利用导数求闭区间上函数的最值,函数零点的判定定理【解析】【分析】(1.)求导,根据导数与函数单调性的关系,分类讨论,即可求得f (x)单调性;(2.)由(1)可知:当a>0时才有个零点,根据函数的单调性求得f(x)最小值,由f(x)min<0,g(a)=alna+a﹣1,a>0,求导,由g(a)min=g(e﹣2)=e﹣2lne﹣2+e﹣2﹣1=﹣﹣1,g(1)=0,即可求得a的取值范围.10、【答案】(Ⅰ)解:因为f(x)=ax2﹣ax﹣xlnx=x(ax﹣a﹣lnx)(x>0),则f(x)≥0等价于h(x)=ax﹣a﹣lnx≥0,因为h′(x)=a﹣,且当0<x<时h′(x)<0、当x>时h′(x)>0,所以h(x)min=h(),又因为h(1)=a﹣a﹣ln1=0,所以=1,解得a=1;(Ⅱ)证明:由(1)可知f(x)=x2﹣x﹣xlnx,f′(x)=2x﹣2﹣lnx,令f′(x)=0,可得2x﹣2﹣lnx=0,记t(x)=2x﹣2﹣lnx,则t′(x)=2﹣,令t′(x)=0,解得:x=,所以t(x)在区间(0,)上单调递减,在(,+∞)上单调递增,所以t(x)min=t()=ln2﹣1<0,从而t(x)=0有解,即f′(x)=0存在两根x0,x2,且不妨设f′(x)在(0,x0)上为正、在(x0,x2)上为负、在(x2,+∞)上为正,所以f(x)必存在唯一极大值点x0,且2x0﹣2﹣lnx0=0,所以f(x0)=﹣x0﹣x0lnx0=﹣x0+2x0﹣2=x0﹣,由x0<可知f(x0)<(x0﹣)max=﹣+=;由f′()<0可知x0<<,所以f(x)在(0,x0)上单调递增,在(x0,)上单调递减,所以f(x0)>f()=﹣+=>;综上所述,f(x)存在唯一的极大值点x0,且e﹣2<f(x0)<2﹣2.【考点】导数的运算,利用导数研究函数的极值,利用导数求闭区间上函数的最值,导数在最大值、最小值问题中的应用,不等式的综合【解析】【分析】(Ⅰ)通过分析可知f(x)≥0等价于h(x)=ax﹣a﹣lnx≥0,进而利用h′(x)=a﹣可得h(x)min=h(),从而可得结论;(Ⅱ)通过(Ⅰ)可知f(x)=x2﹣x﹣xlnx,记t(x)=f′(x)=2x﹣2﹣lnx,解不等式可知t(x)min=t()=ln2﹣1<0,从而可知f′(x)=0存在两根x0,x2,利用f(x)必存在唯一极大值点x0及x0<可知f(x0)<,另一方面可知f(x0)>f()=﹣+=>.11、【答案】解:(Ⅰ)因为函数f(x)=x﹣1﹣alnx,x>0,所以f′(x)=1﹣=,且f(1)=0.所以当a≤0时f′(x)>0恒成立,此时y=f(x)在(0,+∞)上单调递增,所以在(0,1)上f(x)<0,这与f(x)≥0矛盾;当a>0时令f′(x)=0,解得x=a,所以y=f(x)在(0,a)上单调递减,在(a,+∞)上单调递增,即f(x)min=f(a),又因为f(x)min=f(a)≥0,所以a=1;(Ⅱ)由(Ⅰ)可知当a=1时f(x)=x﹣1﹣lnx≥0,即lnx≤x﹣1,所以ln(x+1)≤x当且仅当x=0时取等号,所以ln(1+)<,k∈N*,所以,k∈N*.一方面,因为++…+=1﹣<1,所以,(1+)(1+)…(1+)<e;另一方面,(1+)(1+)…(1+)>(1+)(1+)(1+)=>2,同时当n≥3时,(1+)(1+)…(1+)∈(2,e).因为m为整数,且对于任意正整数n(1+)(1+)…(1+)<m,所以m的最小值为3.【考点】函数的单调性与导数的关系,利用导数研究函数的单调性,等比数列的前n项和,反证法与放缩法【解析】【分析】(Ⅰ)通过对函数f(x)=x﹣1﹣alnx(x>0)求导,分a≤0、a>0两种情况考虑导函数f′(x)与0的大小关系可得结论;(Ⅱ)通过(Ⅰ)可知lnx≤x﹣1,进而取特殊值可知ln(1+)<,k∈N*.一方面利用等比数列的求和公式放缩可知(1+)(1+)…(1+)<e;另一方面可知(1+)(1+)…(1+)>2,且当n≥3时,(1+)(1+)…(1+)∈(2,e).。
2017年高考数学理试题分类汇编:导数及其应用

2017年高考数学理试题分类汇编:导数及其应用sin2 x(2017年新课标I 文)&函数y的部分图像大致为1 cosx【答案】A令f (x)0,解得x 2或x 1,所以f(x)在(,2),(1,)单调递增,在(2,1)单调递减所以f (x)极小值 f(1) (1 11)e 1 11,故选A 。
3.(2017年新课标I 文)9 •已知函数f (x) lnx ln(2 x),贝y (C)A • f(x)在(0,2)单调递增B • f (x)在(0,2)单调递减C • y= f(x)的图像关于直线x=1对称D • y= f (x)的图像关于点(1,0)对称4.(2017年浙江卷)函数y=f(x )的导函数y f (x)的图像如图所示,则函数y=f(x)的图像可能是【答案】D【解析】原函数先减再增,再减再增,因此选 D.2x 1x 15.(2017年新课标川卷理)11 •已知函数f(x) x 2x a(e e )有唯一零点,则 a=(C )1.2. (2017年新课标n 卷理A.)11.若x 2是函数f (x)(x 2ax x 1'1)e 的极值点,则f (x)的极小值为()B. 2e 3C. 5e 3D.1【解析】由题可得 f (x) (2x a)e x 1 (x 2x 12ax 1)e[x(a 2)x a 1]e x 1因为f ( 2)0,所以af(x) (x 2x 1)e x 1,故 f (x) (x 2x 1x 2)e111A.-B. -C . —D . 12 3 2【答案】C【解析】£ -2 “ -a {訂十严J ,谡g M =訐+童创,『(© =尸-产 J 戶-二r 二 j当現0 = 0咋r=l,函数里调递矶当11巧 /(x)>0, MM 调递增.当*1时,團数职得最小值胃⑴二2,设/i(x) = x 2-2x f 当*1时、函数取得最小1S-1J 若-GA O,函数矗(£ ,和口冒(兀)浚有交点,当一口 vO 时,一口雷(1)二方⑴日寸「止匕时函数工|和昭(尤)有一个交点,即 p K 2 二 一1 二 a =—、故选 C 1设g x = ax - a - l nx ,贝y f x = xg x , f x 0 等价于 g x 0 因为 g 1 =0, g x 1 0,故g' 1 =0,而g' x a, g' 1 =a 1,得a 1x若 a=1,则 g' x =11 •当0 v x v 1时,g' x <0, g x 单调递减;当 x > 1时,g' x > 0, g x 单调递增•所以x=1x是g x 的极小值点,故 g x g 1 =0 综上,a=1(2)由 11)知 f ( JT : = x 2 - jr * jr In jr T f ' (r) = 2x - 2 - In A当兀三卫;时.^T (x) <0 i 当才=二十力时,/rUD , 调递增1 1 1又he 2 >0,h $ v 0,h 1 0,所以h x 在0,2有唯一零点x 。
2017年北京市各区高三理科数学分类汇编----函数与导数

1 (, ) ( D) 4
(2017 年丰台二模 ) 2. 下列函数中,既是偶函数又是
( A) y
x3
(0, + ) 上的增函数的是
x
(B) y 2
1
( C) y x2
(D) y log 3 ( x)
填空题:
( 2017 东城期末) ( 14)关于 x 的方程 g( x) t (t R) 的实根个数记为 f (t ) .若 g( x) ln x ,则 f (t ) =____1___;
(2017 年海淀一模 ) 13. 已知函数 f ( x)
(2017 年东城一模 ) ( 14)已知函数 f ( x)
1 1, 0 x ,
2 1, 1 x 1, 和 g(x)
2 0, x 0或x 1
1, 0 x 1, 0, x 0或x 1,
则 g (2 x) ____ g(x)
1, 0 x 1 ,
2
__ ;
1 0, x 0或 x .
2
若 m, n Z ,且 m g(n x) g( x) f ( x) ,则 m n __ 4 ___ .
若 g ( x)
x, x 0,
x2
2ax
a, x
(a 0,
R ) ,存在 t 使得 f (t 2)
f (t ) 成立,则 a 的取值范围是 ____
(1, ) _____.
( 2017海淀期末) 14. 已知函数 f ( x) e |x| cos πx ,给出下列命题:
① f (x) 的最大值为 2;
( C) y = x
(D) y e |x|
(2017 年海淀二模 ) 6. 已知 f ( x) 是 R 上的奇函数,则“ x1 x2 0 ”是“ f ( x1 ) f ( x2 ) 0 ”的( A )
(完整word版)高考数学真题导数专题及答案(2)

2017 年高考真题导数专题一.解答 (共12 小 )1.已知函数 f ( x )=ae 2x +(a 2)e xx .( 1) f (x )的 性;( 2)若 f (x )有两个零点,求 a 的取 范 .2.已知函数 f ( x )=ax 2ax xlnx ,且 f (x )≥ 0.( 1)求 a ;( 2) 明: f (x )存在独一的极大 点 x 0,且 e ﹣2<f (x 0)< 2﹣2.3.已知函数 f ( x )=x1 alnx .( 1)若 f (x )≥ 0,求 a 的 ;( 2) m 整数,且 于随意正整数 n ,(1+)( 1+ )⋯(1+ )< m ,求m 的最小 .4.已知函数 f ( x ) =x 3+ax 2+bx+1(a >0,b ∈R )有极 ,且 函数f ′(x )的极点是 f (x )的零点.(极 点是指函数取极 的自 量的 )( 1)求 b 对于 a 的函数关系式,并写出定 域;( 2) 明: b 2>3a ;( 3)若 f ( x ),f (′x ) 两个函数的全部极 之和不小于 ,求 a 的取 范 .5. 函数 f (x )=(1 x 2)e x .( 1) f (x )的 性;( 2)当 x ≥0 , f (x )≤ ax+1,求 a 的取 范 .( ) (﹣ x6.已知函数 f )e(x ≥ ).x = x( 1)求 f (x )的 函数;( 2)求 f (x )在区 [ , +∞)上的取 范 .7.已知函数 f (x )=x 2+2cosx ,g (x )=e x (cosxsinx+2x 2),此中 e ≈2.17828 ⋯是自然 数的底数.( Ⅰ)求曲 y=f (x )在点( π,f (π)) 的切 方程;( Ⅱ)令 h (x )=g (x ) a f ( x )(a ∈R ), h ( x )的 性并判断有无极值,有极值时求出极值.8.已知函数 f ( x )=e x cosx ﹣ x .( 1)求曲线 y=f (x )在点( 0, f (0))处的切线方程;( 2)求函数 f ( x )在区间 [ 0,] 上的最大值和最小值.∈ ,已知定义在 R 上的函数4+3x 3﹣3x 2﹣6x+a 在区间( 1,2) 9.设 a Z f (x )=2x内有一个零点 x 0, ( )为f ( x )的导函数.g x( Ⅰ)求 g ( x )的单一区间;( Ⅱ)设 m ∈[ 1,x 0 )∪( 0, 2] ,函数 ( ) ( )( m ﹣ 0)﹣ ( m ),求证:x h x =g x x fh (m ) h ( x 0)< 0;( Ⅲ)求证:存在大于 0 的常数 A ,使得对于随意的正整数 p ,q ,且 ∈[ 1,x 0)∪( x 0,2] ,知足 | ﹣ x 0| ≥.10.已知函数 f (x )= x 3﹣ ax 2,a ∈R ,( 1)当 a=2 时,求曲线 y=f (x )在点( 3, f (3))处的切线方程;( 2)设函数 g ( x )=f (x ) +( x ﹣ a ) cosx ﹣sinx ,议论 g (x )的单一性并判断有无极值,有极值时求出极值.11.设 a ,b ∈R ,| a| ≤ 1.已知函数 f ( x )=x 3﹣6x 2﹣3a (a ﹣4)x+b ,g ( x )=e x f( x ).( Ⅰ)求 f ( x )的单一区间;( Ⅱ)已知函数 y=g (x )和 y=e x 的图象在公共点( x 0, y 0)处有同样的切线, ( i )求证: f (x )在 x=x 0 处的导数等于 0;( ii )若对于 x 的不等式 g (x )≤ e x 在区间 [ x 0﹣ 1, x 0 +1] 上恒建立,求 b 的取值范围.12.已知函数 f ( x )=e x (e x ﹣ a )﹣ a 2x .( 1)议论 f ( x )的单一性;( 2)若 f (x )≥ 0,求 a 的取值范围.2017 年高考真题导数专题参照答案与试题分析一.解答题(共12 小题)1.(2017?新课标Ⅰ)已知函数 f (x)=ae2x+( a﹣ 2) e x﹣x.(1)议论 f(x)的单一性;(2)若 f (x)有两个零点,求 a 的取值范围.【解答】解:( 1)由 f(x)=ae2x+( a﹣2)e x﹣ x,求导 f (′ x)=2ae2x+( a﹣ 2) e x ﹣1,当a=0 时, f ′(x) =﹣ 2e x﹣ 1< 0,∴当 x∈R,f (x)单一递减,当a>0 时, f ′( x)=(2e x+1)(ae x﹣1)=2a( e x+ )(e x﹣),令f ′(x) =0,解得: x=ln ,当f ′(x)> 0,解得: x>ln ,当f ′(x)< 0,解得: x<ln ,∴ x∈(﹣∞, ln)时,f(x)单一递减,x∈(ln,+∞)单一递加;当 a<0 时, f ′( x)=2a( e x+ )(e x﹣)<0,恒建立,∴当 x∈R,f (x)单一递减,综上可知:当 a≤0 时, f( x)在 R 单一减函数,当 a>0 时, f (x)在(﹣∞, ln)是减函数,在(ln,+∞)是增函数;(2)①若 a≤0 时,由( 1)可知: f(x)最多有一个零点,当 a>0 时, f (x)=ae2x+(a﹣ 2) e x﹣x,当x→﹣∞时, e2x→0, e x→0,∴当x→﹣∞时, f (x)→+∞,当x→∞,e2x→+∞,且远远大于e x和x,∴当 x→∞, f(x)→+∞,∴函数有两个零点, f( x)的最小值小于0 即可,由f( x)在(﹣∞, ln )是减函数,在( ln ,+∞)是增函数,∴f(x)min =f(ln )=a×()+(a﹣2)×﹣ln <0,∴ 1﹣﹣ln <0,即 ln + ﹣1>0,设 t= ,则 g(t) =lnt+t ﹣1,( t> 0),求导 g′(t )= +1,由 g(1)=0,∴t= >1,解得: 0<a<1,∴a 的取值范围( 0,1).方法二:(1)由 f(x)=ae2x+(a﹣2)e x﹣x,求导 f ′(x)=2ae2x+(a﹣2)e x﹣1,当a=0 时, f ′(x) =2e x﹣1<0,∴当 x∈R,f (x)单一递减,当a>0 时, f ′( x)=(2e x+1)(ae x﹣1)=2a( e x+ )(e x﹣),令f ′(x) =0,解得: x=﹣lna,当 f ′(x)> 0,解得: x>﹣ lna,当 f ′(x)< 0,解得: x<﹣ lna,∴x∈(﹣∞,﹣ lna)时, f(x)单一递减, x∈(﹣ lna,+∞)单一递加;当 a<0 时, f ′( x)=2a( e x+ )(e x﹣)< 0,恒建立,∴当 x∈R,f (x)单一递减,综上可知:当 a≤0 时, f( x)在 R 单一减函数,当a>0 时, f (x)在(﹣∞,﹣ lna)是减函数,在(﹣ lna,+∞)是增函数;( 2)①若 a≤0 时,由( 1)可知: f(x)最多有一个零点,②当 a>0 时,由( 1)可知:当 x=﹣lna 时, f(x)获得最小值, f(x)min=f(﹣lna)=1﹣﹣ln,当a=1,时, f(﹣ lna) =0,故 f( x)只有一个零点,当a∈( 1,+∞)时,由 1﹣﹣ln >0,即 f(﹣ lna)> 0,故f( x)没有零点,当 a∈( 0,1)时, 1﹣﹣ln<0,f(﹣lna)<0,由f(﹣ 2)=ae﹣4+(a﹣2)e﹣2+2>﹣ 2e﹣2+2> 0,故 f( x)在(﹣∞,﹣ lna)有一个零点,假定存在正整数n0,知足n0>ln(﹣1),则f(n0)=(a+a﹣2)﹣ n0>﹣n0>﹣n0>0,由ln(﹣ 1)>﹣ lna,所以在(﹣ lna, +∞)有一个零点.∴ a 的取值范围( 0,1).2.(2017?新课标Ⅱ)已知函数 f (x)=ax2﹣ ax﹣xlnx,且 f( x)≥ 0.(1)求 a;(2)证明: f(x)存在独一的极大值点 x0,且 e﹣2<f (x0)< 2﹣2.【解答】(1)解:因为f(x)=ax2﹣ax﹣xlnx=x(ax﹣a﹣lnx)(x>0),则 f( x)≥ 0 等价于 h(x)=ax﹣a﹣lnx≥0,求导可知 h′( x) =a﹣.则当 a≤0 时 h′(x)< 0,即 y=h(x)在( 0, +∞)上单一递减,所以当 x0>1 时, h(x0)< h(1)=0,矛盾,故 a>0.因为当 0<x<时 h′(x)< 0、当 x>时 h′(x)> 0,所以 h(x)min=h(),又因为 h( 1) =a﹣a﹣ln1=0,所以=1,解得 a=1;(2)证明:由( 1)可知 f( x) =x2﹣ x﹣xlnx,f ′(x) =2x﹣2﹣lnx,令 f ′(x) =0,可得 2x﹣2﹣lnx=0,记 t(x)=2x﹣ 2﹣ lnx,则 t ′(x)=2﹣,令 t ′(x)=0,解得: x=,所以 t (x)在区间( 0,)上单一递减,在(,+∞)上单一递加,所以 t (x)min=t ()﹣<,从而t()=0有解,即f(′ )=0存在两根=ln2 1 0x xx0, x2,且不如 f ′(x)在( 0, x0)上正、在( x0,x2)上、在( x2, +∞)上正,所以 f (x)必存在独一极大点x0,且00 ,2x2lnx =0所以 f (x0)=x0 x0lnx0=x0+2x0 2=x0,由 x0<可知f ( 0)<( 0) max+=;x x=由 f ′()< 0 可知 x0<<,所以 f (x)在( 0,x0)上增,在(0)上减,x ,所以 f (x0)> f()=;上所述, f( x)存在独一的极大点x0,且 e﹣2< f(x0)< 2﹣2.3.(2017?新Ⅲ)已知函数 f (x)=x 1 alnx.( 1)若 f(x)≥ 0,求 a 的;( 2) m 整数,且于随意正整数 n,(1+)(1+)⋯(1+)<m,求m的最小.【解答】解:(1)因函数 f (x)=x 1 alnx,x>0,所以 f ′(x)=1 = ,且 f( 1)=0.所以当 a≤ 0 f ′(x)> 0 恒建立,此 y=f( x)在( 0,+∞)上增,与 f( x)≥ 0 矛盾;当 a>0 令 f ′( x) =0,解得 x=a,所以 y=f(x)在( 0, a)上减,在( a,+∞)上增,即 f(x)min=f( a),又因 f(x)min =f(a)≥ 0,所以 a=1;(2)由( 1)可知当 a=1 f (x)=x 1 lnx≥0,即 lnx≤ x 1,所以 ln( x+1)≤ x 当且当 x=0 取等号,所以 ln( 1+)<,k∈N*.一方面, ln(1+)+ln(1+)+⋯+ln(1+)<+ +⋯+ =1<1,即( 1+ )(1+)⋯(1+)<e;另一方面,( 1+)(1+)⋯(1+)>(1+)(1+)(1+)=>2;从而当 n≥ 3 ,(1+)(1+)⋯(1+)∈(2,e),因 m 整数,且于随意正整数n,(1+)(1+)⋯(1+)<m建立,所以 m 的最小 3.4.(2017?江)已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极,且函数f (′x)的极点是 f(x)的零点.(极点是指函数取极的自量的)(1)求 b 对于 a 的函数关系式,并写出定域;(2)明: b2>3a;( 3)若 f( x),f (′x)两个函数的全部极之和不小于,求a的取范.【解答】(1)解:因 f(x)=x3+ax2+bx+1,所以 g(x)=f ′( x) =3x2 +2ax+b,g′(x)=6x+2a,令 g′(x)=0,解得 x= .因为当 x>g′( x)> 0, g( x) =f (′x)增;当 x<g′(x)<0,g(x)=f (′x)减;所以 f ′(x)的极小点x=,因为函数 f ′(x)的极点是原函数f( x)的零点,所以 f ()=0,即++1=0,所以 b=+(a>0).因 f (x) =x3+ax2 +bx+1(a>0,b∈R)有极,所以 f ′(x)=3x2+2ax+b=0 的根,所以 4a212b≥ 0,即 a2+≥0,解得a≥3,所以 b=+(a≥3).( 2)证明:由( 1)可知 h( a) =b2﹣ 3a=﹣+ =(4a3﹣27)( a3﹣ 27),因为 a>3,所以 h(a)> 0,即 b2>3a;( 3)解:由( 1)可知 f ′( x)的极小值为 f ′(﹣)=b﹣,设 x1, 2 是y=f ()的两个极值点,则 1 2, 1 2,x x x +x =x x =所以 f (x1)+f( x2)=++a(+)+b(x1+x2)+2=(x1+x2)[ (x1+x2)2﹣3x1x2]+ a[ ( x1 +x2)2﹣2x1 x2]+ b(x1+x2)+2=﹣+2,又因为 f(x), f ′(x)这两个函数的全部极值之和不小于﹣,所以 b﹣+﹣+2=﹣≥﹣,因为 a>3,所以 2a3﹣63a﹣54≤0,所以 2a(a2﹣36)+9( a﹣6)≤ 0,所以( a﹣6)( 2a2+12a+9)≤ 0,因为 a>3 时 2a2+12a+9>0,所以 a﹣6≤0,解得 a≤6,所以 a 的取值范围是( 3,6] .5.(2017?新课标Ⅱ)设函数 f( x) =( 1﹣ x2)e x.(1)议论 f(x)的单一性;(2)当 x≥0 时, f(x)≤ ax+1,求 a 的取值范围.【解答】解:(1)因为 f(x)=(1﹣x2) e x,x∈ R,所以 f ′(x)=(1﹣2x﹣ x2)e x,令 f ′(x) =0 可知 x=﹣1±,当 x<﹣ 1﹣或x>﹣1+时f′(x)<0,当﹣1﹣<x<﹣1+时f′(x)>0,所以 f(x)在(﹣∞,﹣ 1﹣),(﹣1+,+∞)上第 8页(共 17页)﹣ 1+ )上单一递加;( 2)由题可知 f (x ) =( 1﹣ x )(1+x )e x .下边对 a 的范围进行议论:①当 a ≥1 时,设函数 h (x )=(1﹣x ) e x ,则 h ′(x )=﹣xe x < 0( x > 0),所以 h (x )在 [ 0,+∞)上单一递减,又因为 h ( 0) =1,所以 h (x )≤ 1,所以 f (x ) =( 1﹣x ) h ( x )≤ x+1≤ax+1;②当 0<a <1 时,设函数 g (x )=e x ﹣ x ﹣ 1,则 g ′( x )=e x ﹣1>0(x >0),所以 g (x )在 [ 0,+∞)上单一递加,又 g (0)=1﹣0﹣1=0, 所以 e x ≥ x+1.因为当 0< x <1 时 f ( x )>( 1﹣x )( 1+x )2,所以( 1﹣x )( 1+x )2﹣ ax ﹣1=x (1﹣a ﹣x ﹣x 2), 取 x 0 ∈( , ),则( ﹣ 0)( 1+x0)2﹣ax 0﹣,=0 1 1 x1=0所以 f (x 0)> ax 0+1,矛盾;③当 a ≤0 时,取 x 0 ∈( , ),则 ( 0 )>( ﹣ 0 )( 0)2 ≥ 0 ,= 0 1 f x 1 x 1+x =1 ax +1矛盾;综上所述, a 的取值范围是 [ 1,+∞).6.(2017?浙江)已知函数 f ( ) ( ﹣﹣x (x ≥).x = x)e( 1)求 f (x )的导函数;( 2)求 f (x )在区间 [ , +∞)上的取值范围.【解答】 解:(1)函数 f (x )=(x ﹣ )e ﹣x (x ≥ ),导数 f ′(x )=(1﹣ ??2)e ﹣x﹣( x ﹣)e﹣x=(1﹣x+) e ﹣ x =(1﹣x )( 1﹣) e ﹣x ;( 2)由 f (x )的导数 f ′(x )=(1﹣x )(1﹣ ﹣ x) e ,可得 f ′(x )=0 时, x=1 或 ,当<x<1,f(′x)<0,f(x)减;当1<x<, f (′x)> 0, f(x)增;当x>, f ′( x)< 0, f(x)减,且x≥? x2≥2x 1? (x 1)2≥0,f( x)≥ 0.由 f()=e,f(1)=0,f()=e,即有 f (x)的最大e,最小f(1)=0.f( x)在区 [,+∞)上的取范是[ 0,e] .7.(2017?山)已知函数 f( x)=x2+2cosx,g(x)=e x(cosx sinx+2x 2),此中 e≈2.17828 ⋯是自然数的底数.(Ⅰ)求曲 y=f(x)在点(π,f (π))的切方程;(Ⅱ)令 h(x)=g (x) a f( x)(a∈R), h( x)的性并判断有无极,有极求出极.【解答】解:(I)f (π)=π22.f ′(x)=2x2sinx,∴ f ′(π) =2π.2∴曲 y=f( x)在点(π,f (π))的切方程: y(π 2)=2π(xπ).化: 2πx yπ22=0.(II) h( x)=g ( x) a f(x)=e x(cosx sinx+2x 2) a(x2 +2cosx)h′( x)=e x(cosx sinx+2x 2)+e x( sinx cosx+2) a(2x 2sinx)=2(x sinx)(e x a)=2( x sinx)( e x e lna).令 u(x) =x sinx, u′( x) =1 cosx≥ 0,∴函数 u(x)在 R 上增.∵ u( 0) =0,∴ x>0 , u(x)> 0;x<0 , u( x)< 0.(1) a≤0 , e x a>0,∴ x> 0 , h′(x)> 0,函数 h( x)在( 0,+∞)增;x<0 , h′(x)< 0,函数 h(x)在(∞, 0)减.∴x=0 时,函数h(x)获得极小值,h(0)=﹣1﹣2a.( 2) a>0 时,令 h′(x)=2( x﹣sinx)(e x﹣ e lna)=0.解得 x1=lna,x2=0.① 0< a<1 时,x∈(﹣∞, lna)时, e x﹣e lna<0,h′(x)>0,函数 h(x)单一递加;x∈( lna,0)时, e x﹣e lna>0,h′( x)< 0,函数 h( x)单一递减;x∈( 0,+∞)时, e x﹣ e lna> 0, h′(x)> 0,函数 h(x)单一递加.∴当 x=0 时,函数 h(x)获得极小值, h( 0) =﹣ 2a﹣1.当x=lna 时,函数 h(x)获得极大值, h(lna)=﹣a[ ln2a﹣ 2lna+sin(lna)+cos (lna) +2] .②当 a=1 时, lna=0,x∈R 时, h′(x)≥ 0,∴函数 h( x)在 R 上单一递加.③ 1< a 时, lna>0,x∈(﹣∞, 0)时, e x﹣e lna<0,h′( x)> 0,函数 h( x)单一递加;x∈( 0,lna)时, e x﹣e lna<0,h′( x)< 0,函数 h( x)单一递减;x∈( lna,+∞)时, e x﹣ e lna> 0, h′(x)> 0,函数 h(x)单一递加.∴当 x=0 时,函数 h(x)获得极大值, h( 0) =﹣ 2a﹣1.当x=lna 时,函数 h(x)获得极小值, h(lna)=﹣a[ ln2a﹣ 2lna+sin(lna)+cos (lna) +2] .综上所述: a≤ 0 时,函数 h(x)在( 0,+∞)单一递加; x< 0 时,函数 h(x)在(﹣∞, 0)单一递减.x=0 时,函数 h(x)获得极小值, h( 0) =﹣ 1﹣ 2a.0<a<1 时,函数 h(x)在 x∈(﹣∞, lna)是单一递加;函数 h(x)在 x∈(lna,0)上单一递减.当 x=0 时,函数 h(x)获得极小值, h( 0)=﹣ 2a﹣1.当 x=lna时,函数 h( x)获得极大值, h(lna)=﹣ a[ ln2a﹣2lna+sin(lna)+cos(lna)+2] .当 a=1 时, lna=0,函数 h(x)在 R 上单一递加.a>1 时,函数 h( x)在(﹣∞, 0),( lna,+∞)上单一递加;函数h(x)在(0,lna)上单一递减.当 x=0 时,函数 h( x)获得极大值, h(0)=﹣ 2a﹣1.当 x=lna时,函数 h( x)获得极小值, h(lna)=﹣ a[ ln2a﹣2lna+sin(lna)+cos(lna)+2] .第11页(共 17页)8.(2017?北京)已知函数 f(x)=e x cosx﹣ x.( 1)求曲线 y=f(x)在点( 0, f(0))处的切线方程;( 2)求函数 f( x)在区间 [ 0,] 上的最大值和最小值.【解答】解:(1)函数 f(x)=e x﹣的导数为f ′()x(cosx﹣ sinx)﹣ 1,cosx x x=e可得曲线y=f(x)在点(0,f(0))处的切线斜率为k=e0(cos0﹣sin0)﹣1=0,切点为( 0, e0cos0﹣0),即为( 0,1),曲线 y=f(x)在点( 0,f( 0))处的切线方程为y=1;(2)函数 f(x)=e x cosx﹣x 的导数为 f (′x) =e x( cosx﹣sinx)﹣1,令 g(x) =e x( cosx﹣sinx)﹣ 1,则 g(x)的导数为 g′( x)=e x(cosx﹣sinx﹣sinx﹣ cosx)=﹣2e x?sinx,当 x∈[ 0, ] ,可得 g′(x)=﹣2e x?sinx≤0,即有 g(x)在 [ 0,] 递减,可得 g(x)≤ g(0)=0,则 f( x)在 [ 0,] 递减,即有函数 f( x)在区间 [ 0,] 上的最大值为f(0)=e0cos0﹣ 0=1;最小值为 f()=e cos﹣=﹣.9.(2017?天津)设 a∈ Z,已知定义在 R 上的函数 f( x)=2x4+3x3﹣3x2﹣6x+a在区间( 1,2)内有一个零点 x0, g( x)为 f( x)的导函数.(Ⅰ)求 g( x)的单一区间;(Ⅱ)设 m∈[ 1,x0)∪(x0,2] ,函数 h(x)=g(x)(m﹣x0)﹣ f(m ),求证:h(m) h( x0)< 0;(Ⅲ)求证:存在大于 0 的常数 A,使得对于随意的正整数p,q,且∈[ 1,x0)∪( x0,2],知足|﹣ 0≥.x |【解答】(Ⅰ )解:由 f(x) =2x4+3x3﹣ 3x2﹣ 6x+a,可得 g( x)=f ′(x)=8x3+9x2﹣6x﹣6,从而可得 g′(x)=24x2+18x﹣6.令 g′( x)=0,解得 x=﹣ 1,或 x=.当 x 变化时, g′(x), g( x)的变化状况以下表:x(﹣∞,﹣ 1)(﹣1,)(,+∞)g′( x)+﹣+g( x)↗↘↗所以, g(x)的单一递加区间是(﹣∞,﹣1),(,+∞),单一递减区间是(﹣1,).(Ⅱ)证明:由 h(x) =g(x)(m﹣x0)﹣ f(m ),得 h(m)=g(m)(m﹣x0)﹣ f(m),h(x0) =g(x0)(m﹣ x0)﹣ f(m).令函数 H1(x)=g( x)(x﹣x0)﹣ f(x),则 H′1(x)=g′(x)( x﹣ x0).由(Ⅰ)知,当 x∈ [ 1,2] 时, g′(x)> 0,故当 x∈[ 1,x0)时, H′1(x)< 0, H1(x)单一递减;当 x∈( x0,2] 时, H′1(x)> 0,H1(x)单一递加.所以,当x∈[ 1, x0)∪( x0,2] 时, H1(x)> H1(x0) =﹣f (x0) =0,可得 H1( m)> 0 即 h(m)> 0,令函数 H2(x)=g(x0)(x﹣x0)﹣ f( x),则 H′2( x)=g′(x0)﹣ g( x).由(Ⅰ)知, g( x)在 [ 1,2] 上单一递加,故当 x∈[ 1,x0)时, H′2(x)> 0,H2(x)单一递加;当 x∈( x0, 2] 时, H′2(x)< 0, H2(x)单一递减.所以,当 x∈[ 1,x0)∪( x0, 2] 时,H2(x)> H2(x0)=0,可得得 H2( m)< 0 即 h(x0)< 0,.所以, h(m) h( x0)<.(Ⅲ)对于随意的正整数 p,q,且,令 m= ,函数 h(x)=g(x)(m﹣x0)﹣ f( m).由(Ⅱ)知,当m∈[ 1,x0)时,h(x)在区间(m,x0)内有零点;当 m∈( x0,2] 时, h(x)在区间( x0,m)内有零点.所以 h(x)在( 1, 2)内起码有一个零点,不如设为x1,则 h( x1)=g( x1)(﹣ x0)﹣ f ()=0.由(Ⅰ)知 g(x)在 [ 1,2] 上单一递加,故0< g( 1)< g(x1)< g(2),于是 | ﹣x0≥=.| =因为当 x∈[ 1,2] 时, g(x)> 0,故 f(x)在 [ 1,2] 上单一递加,所以 f (x)在区间 [ 1,2] 上除 x0外没有其余的零点,而≠0,故f ()≠ .x0又因为 p, q, a 均为整数,所以 | 2p4+3p3﹣ 2 2﹣6pq3+aq4| 是正整数,q 3p q从而 | 2p4+3p3q﹣3p2q2﹣6pq3+aq4| ≥1.所以 | ﹣x0≥.所以,只需取(),就有|﹣0≥.|A=g 2x |10.( 2017?山东)已知函数f(x)= x3﹣a x2,a∈R,(1)当 a=2 时,求曲线 y=f(x)在点( 3, f(3))处的切线方程;(2)设函数 g( x)=f(x) +( x﹣ a) cosx﹣sinx,议论 g(x)的单一性并判断有无极值,有极值时求出极值.【解答】解:(1)当 a=2 时, f (x)= x3﹣x2,∴f ′( x)=x2﹣2x,∴k=f ′(3) =9﹣ 6=3, f(3)= ×27﹣9=0,∴曲线 y=f( x)在点( 3,f(3))处的切线方程y=3(x﹣3),即 3x﹣ y﹣ 9=0(2)函数 g(x)=f( x) +( x﹣a)cosx﹣sinx= x3﹣ ax2+( x﹣ a) cosx﹣sinx,∴g′(x) =( x﹣ a)(x﹣sinx),令g′(x)=0,解得 x=a,或 x=0,①若 a>0 时,当 x<0 时, g′(x)> 0 恒建立,故 g(x)在(﹣∞, 0)上单一递加,当x>a 时, g′( x)> 0 恒建立,故 g( x)在( a,+∞)上单一递加,当0<x< a 时, g′( x)< 0 恒建立,故 g( x)在( 0,a)上单一递减,∴当 x=a 时,函数有极小值,极小值为 g( a) =﹣ a3﹣sina当 x=0 时,有极大值,极大值为g( 0)=﹣ a,②若 a<0 时,当 x>0 时, g′(x)> 0 恒建立,故 g(x)在(﹣∞, 0)上单一递加,当x<a 时, g′( x)> 0 恒建立,故 g( x)在(﹣∞, a)上单一递加,当a<x< 0 时, g′( x)< 0 恒建立,故 g( x)在( a,0)上单一递减,∴当 x=a 时,函数有极大值,极大值为 g( a) =﹣ a3﹣sina当x=0 时,有极小值,极小值为 g( 0)=﹣ a③当 a=0 时, g′(x)=x( x+sinx),当x>0 时, g′( x)> 0 恒建立,故 g( x)在( 0,+∞)上单一递加,当x<0 时, g′( x)> 0 恒建立,故 g( x)在(﹣∞, 0)上单一递加,∴ g( x)在 R 上单一递加,无极值.11.( 2017?天津)设 a, b∈ R, | a| ≤1.已知函数 f(x)=x3﹣6x2﹣3a( a﹣4)x+b, g(x)=e x f( x).(Ⅰ)求 f( x)的单一区间;(Ⅱ)已知函数 y=g(x)和 y=e x的图象在公共点( x0, y0)处有同样的切线,(i)求证: f(x)在 x=x0处的导数等于 0;(ii)若对于 x 的不等式 g(x)≤ e x在区间 [ x0﹣ 1, x0 +1] 上恒建立,求 b 的取值范围.【解答】(Ⅰ )解:由 f( x) =x3﹣6x2﹣3a( a﹣ 4) x+b,可得 f'( x)=3x2﹣ 12x﹣ 3a(a﹣4)=3( x﹣ a)(x﹣( 4﹣a)),令f' (x) =0,解得 x=a,或 x=4﹣a.由 | a| ≤1,得 a<4﹣a.当 x 变化时, f' (x), f(x)的变化状况以下表:x(﹣∞,)(,﹣)(﹣,∞)a a 4 a 4 a +f'(x)+﹣+f(x)↗↘↗∴ f( x)的单一递加区间为(﹣∞,a),(4﹣a,+∞),单一递减区间为(a, 4﹣ a);(Ⅱ)(i)证明:∵ g'(x)=e x(f( x)+f' (x)),由题意知,∴,解得.∴ f(x)在 x=x0处的导数等于0;(ii)解:∵ g(x)≤ e x,x∈ [ x0﹣ 1, x0+1] ,由 e x>0,可得 f( x)≤ 1.又∵ f( x0)=1, f'( x0)=0,故 x0为 f( x)的极大值点,由( I)知x0=a.另一方面,因为 | a| ≤ 1,故 a+1< 4﹣a,由(Ⅰ)知 f (x)在( a﹣1,a)内单一递加,在( a, a+1)内单一递减,故当 x0=a 时,f (x)≤ f(a)=1 在 [ a﹣1,a+1] 上恒建立,从而 g(x)≤ e x在[ x0﹣ 1, x0 +1] 上恒建立.由f( a) =a3﹣ 6a2﹣ 3a(a﹣4)a+b=1,得 b=2a3﹣ 6a2+1,﹣1≤a≤1.令 t( x) =2x3﹣6x2+1, x∈[ ﹣1,1] ,∴ t'( x)=6x2﹣12x,令 t' (x)=0,解得 x=2(舍去),或 x=0.∵t(﹣ 1) =﹣ 7, t(1)=﹣3,t (0)=1,故 t (x)的值域为 [ ﹣7,1] .∴ b 的取值范围是 [ ﹣7,1] .12.( 2017?新课标Ⅰ)已知函数f(x)=e x(e x﹣a)﹣ a2x.(1)议论 f( x)的单一性;(2)若 f (x)≥ 0,求 a 的取值范围.【解答】解:(1)f(x)=e x(e x﹣ a)﹣ a2x=e2x﹣e x a﹣a2x,∴f (′ x)=2e2x﹣ ae x﹣ a2=( 2e x+a)( e x﹣a),①当 a=0 时, f ′(x)>0 恒建立,∴f(x)在 R 上单一递加,②当 a>0 时, 2e x+a>0,令 f ′( x) =0,解得 x=lna,第16页(共 17页)当 x>lna 时, f ′(x)> 0,函数 f(x)单一递加,③当 a<0 时, e x﹣a>0,令 f (′ x) =0,解得 x=ln(﹣),当x<ln(﹣)时, f ′(x)< 0,函数 f(x)单一递减,当x>ln(﹣)时, f ′(x)> 0,函数 f(x)单一递加,综上所述,当 a=0 时, f (x)在 R 上单一递加,当a>0 时, f (x)在(﹣∞, lna)上单一递减,在( lna,+∞)上单一递加,当a<0 时, f(x)在(﹣∞, ln(﹣))上单一递减,在( ln(﹣),+∞)上单一递加,( 2)①当 a=0 时, f(x)=e2x>0 恒建立,②当 a>0 时,由( 1)可得 f(x)min=f( lna) =﹣ a2lna≥ 0,∴lna≤ 0,∴0< a≤1,③当 a<0 时,由( 1)可得 f(x)min=f( ln(﹣))=﹣a2ln(﹣)≥ 0,∴ ln(﹣)≤,∴﹣ 2 ≤ a< 0,综上所述 a 的取值范围为 [ ﹣ 2,1]。
2017-2018年高考数学汇编专题函数与导数的应用及答案详解

2017-2018年高考数学分类汇编函数一.选择题1、(2017课标1,理5)函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是A .[2,2]-B .[1,1]-C .[0,4]D .[1,3](答案)D(解析)因为()f x 为奇函数且在(,)-∞+∞单调递减,要使1()1f x -≤≤,则x 满足11x -≤≤,从而由211-x -≤≤得13x ≤≤,即满足21()1x f --≤≤成立的x 的取值范围是[1,3] 考点:函数的奇偶性、单调性2.(2017课标1,理11)设x 、y 、z 为正数,且235x y z ==,则A .2x <3y <5zB .5z <2x <3yC .3y <5z <2xD .3y <2x <5z(答案)D(解析)试题分析:令235(1)x y z k k ===>,则2log x k =,3log y k =,5log z k = ∴22lg lg 3lg 913lg 23lg lg8x k y k =⋅=>,则23x y >, 22lg lg5lg 2515lg 25lg lg32x k z k =⋅=<,则25x z <,故选D. 考点:指、对数运算性质3.(2017天津,理4)设θ∈R ,则“ππ||1212θ-<”是“1sin 2θ<”的 (A )充分而不必要条件 (B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件 (答案)A (解析)πππ||012126θθ-<⇔<< 1sin 2θ⇒< ,但10,sin 2θθ=<,不满足 ππ||1212θ-<,所以是充分不必要条件,选A. 考点: 充要条件4.(2017北京,理5)已知函数1()3()3xx f x =-,则()f x(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数(C )是奇函数,且在R 上是减函数 (D )是偶函数,且在R 上是减函数(答案)A 考点:函数的性质5.(2017山东,理1)设函数x 2y=4-的定义域A ,函数y=ln(1-x)的定义域为B ,则A B ⋂= (A )(1,2) (B )⎤⎦(1,2 (C )(-2,1) (D )[-2,1) (答案)D(解析)试题分析:由240x -≥得22x -≤≤,由10x ->得1x <,故A B={|22}{|1}{|21}x x x x x x -≤≤⋂<=-≤<,选D.考点:1.集合的运算2.函数的定义域3.简单不等式的解法.6.(2017山东,理3)已知命题p:()x x ∀+>0,ln 1>0;命题q :若a >b ,则a b 22>,下列命题为真命题的是(A ) ∧p q (B )⌝∧p q (C ) ⌝∧p q (D )⌝⌝∧p q (答案)B考点:1.简易逻辑联结词.2.全称命题.7.(2017山东,理10)已知当[]0,1x ∈时,函数()21y mx =-的图象与y x m =+的图象有且只有一个交点,则正实数m 的取值范围是(A )(])0,123,⎡+∞⎣ (B )(][)0,13,+∞ (C )()0,223,⎤⎡+∞⎦⎣ (D )([)0,23,⎤+∞⎦(答案)B(解析)试题分析:当01m <≤时,11m ≥ ,2(1)y mx =- 单调递减,且22(1)[(1),1]y mx m =-∈-,y x m =+单调递增,且[,1]y x m m m =+∈+ ,此时有且仅有一个交点;当1m >时,101m << ,2(1)y mx =-在1[,1]m上单调递增,所以要有且仅有一个交点,需2(1)13m m m -≥+⇒≥ 选B.考点:函数的图象、函数与方程及函数性质的综合应用.8.(2017天津,理6)已知奇函数()f x 在R 上是增函数,()()g x xf x =.若2(log 5.1)a g =-,0.8(2)b g =,(3)c g =,则a ,b ,c 的大小关系为(A )a b c << (B )c b a << (C )b a c <<(D )b c a <<(答案)C(解析)因为()f x 是奇函数且在R 上是增函数,所以在0x >时,()0f x >, 从而()()g x xf x =是R 上的偶函数,且在[0,)+∞上是增函数,22(log 5.1)(log 5.1)a g g =-=,0.822<,又4 5.18<<,则22log 5.13<<,所以即0.8202log 5.13<<<,0.82(2)(log 5.1)(3)g g g <<,所以b a c <<,故选C .考点: 指数、对数、函数的单调性9、(2018年高考全国卷1理科2)(5分)已知集合A={x|x 2﹣x ﹣2>0},则∁R A=( ) A .{x|﹣1<x <2} B .{x|﹣1≤x ≤2} C .{x|x <﹣1}∪{x|x >2} D .{x|x ≤﹣1}∪{x|x ≥2}(解答)解:集合A={x|x 2﹣x ﹣2>0}, 可得A={x|x <﹣1或x >2}, 则:∁R A={x|﹣1≤x ≤2}. 故选:B .10、(2018年高考全国卷1理科5)(5分)设函数f (x )=x 3+(a ﹣1)x 2+ax .若f (x )为奇函数,则曲线y=f (x )在点(0,0)处的切线方程为( ) A .y=﹣2x B .y=﹣x C .y=2xD .y=x(解答)解:函数f (x )=x 3+(a ﹣1)x 2+ax ,若f (x )为奇函数, 可得a=1,所以函数f (x )=x 3+x ,可得f′(x )=3x 2+1, 曲线y=f (x )在点(0,0)处的切线的斜率为:1, 则曲线y=f (x )在点(0,0)处的切线方程为:y=x . 故选:D .11、(2018年高考全国卷1理科9)(5分)已知函数f (x )=,g (x )=f (x )+x+a .若g (x )存在2个零点,则a 的取值范围是( ) A .[﹣1,0) B .[0,+∞) C .[﹣1,+∞) D .[1,+∞)(解答)解:由g (x )=0得f (x )=﹣x ﹣a , 作出函数f (x )和y=﹣x ﹣a 的图象如图:当直线y=﹣x﹣a的截距﹣a≤1,即a≥﹣1时,两个函数的图象都有2个交点,即函数g(x)存在2个零点,故实数a的取值范围是[﹣1,+∞),故选:C.12、(2018年高考全国卷2理科3)(5分)函数f(x)=的图象大致为()A.B. C. D.(解答)解:函数f(﹣x)==﹣=﹣f(x),则函数f(x)为奇函数,图象关于原点对称,排除A,当x=1时,f(1)=e﹣>0,排除D.当x→+∞时,f(x)→+∞,排除C,故选:B.13.(2018年高考全国卷2理科11)(5分)已知f(x)是定义域为(﹣∞,+∞)的奇函数,满足f(1﹣x)=f(1+x),若f(1)=2,则f(1)+f(2)+f(3)+…+f(50)=()A.﹣50 B.0 C.2 D.50(解答)解:∵f(x)是奇函数,且f(1﹣x)=f(1+x),∴f(1﹣x)=f(1+x)=﹣f(x﹣1),f(0)=0,则f(x+2)=﹣f(x),则f(x+4)=﹣f(x+2)=f(x),即函数f(x)是周期为4的周期函数,∵f(1)=2,∴f(2)=f(0)=0,f(3)=f(1﹣2)=f(﹣1)=﹣f(1)=﹣2,f(4)=f(0)=0,则f(1)+f(2)+f(3)+f(4)=2+0﹣2+0=0,则f(1)+f(2)+f(3)+…+f(50)=12[f(1)+f(2)+f(3)+f(4)]+f(49)+f(50)=f (1)+f (2)=2+0=2, 故选:C .14、(2018年高考全国卷3理科7)(5分)函数y=﹣x 4+x 2+2的图象大致为( )A .B .C .D .(解答)解:函数过定点(0,2),排除A ,B . 函数的导数f′(x )=﹣4x 3+2x=﹣2x (2x 2﹣1), 由f′(x )>0得2x (2x 2﹣1)<0, 得x <﹣或0<x <,此时函数单调递增,排除C ,故选:D .15.(2018年高考全国卷3理科12)(5分)设a=log 0.20.3,b=log 20.3,则( ) A .a+b <ab <0 B .ab <a+b <0 C .a+b <0<ab D .ab <0<a+b (解答)解:∵a=log 0.20.3=,b=log 20.3=,∴=,,∵,,∴ab <a+b <0. 故选:B .16.(2018年北京市高考数学试卷理科8)(5分)设集合A={(x ,y )|x ﹣y ≥1,ax+y >4,x ﹣ay ≤2},则( )A .对任意实数a ,(2,1)∈AB .对任意实数a ,(2,1)∉AC .当且仅当a <0时,(2,1)∉AD .当且仅当a ≤时,(2,1)∉A(解答)解:当a=﹣1时,集合A={(x ,y )|x ﹣y ≥1,ax+y >4,x ﹣ay ≤2}={(x ,y )|x ﹣y ≥1,﹣x+y >4,x+y ≤2},显然(2,1)不满足,﹣x+y >4,x+y ≤2,所以A ,C 不正确;当a=4,集合A={(x,y)|x﹣y≥1,ax+y>4,x﹣ay≤2}={(x,y)|x﹣y≥1,4x+y>4,x ﹣4y≤2},显然(2,1)在可行域内,满足不等式,所以B不正确;故选:D.17.(2018年上海市高考数学试卷16)(5分)设D是含数1的有限实数集,f(x)是定义在D上的函数,若f(x)的图象绕原点逆时针旋转后与原图象重合,则在以下各项中,f(1)的可能取值只能是()A.B. C. D.0(解答)解:设D是含数1的有限实数集,f(x)是定义在D上的函数,若f(x)的图象绕原点逆时针旋转后与原图象重合,故f(1)=cos=,故选:B.18.(2018年浙江省高考数学试卷5)(4分)函数y=2|x|sin2x的图象可能是()A. B. C. D.(解答)解:根据函数的解析式y=2|x|sin2x,得到:函数的图象为奇函数,故排除A和B.当x=时,函数的值也为0,故排除C.故选:D.19、(2018年天津市高考数学试卷文科3)(5分)设x∈R,则“x3>8”是“|x|>2”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件(解答)解:由x3>8,得x>2,则|x|>2,反之,由|x|>2,得x<﹣2或x>2,则x3<﹣8或x3>8.即“x3>8”是“|x|>2”的充分不必要条件.故选:A.20、(2018年天津市高考数学试卷文科5)(5分)已知a=log3,b=(),c=log,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b(解答)解:∵a=log3,c=log=log35,且5,∴,则b=()<,∴c>a>b.故选:D.21、(2018年天津市高考数学试卷理科5)(5分)已知a=log2e,b=ln2,c=log,则a,b,c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b(解答)解:a=log2e>1,0<b=ln2<1,c=log=log23>log2e=a,则a,b,c的大小关系c>a>b,故选:D.二.填空题1、(2017课标3,理15)设函数10()20xx xf xx+≤⎧=⎨>⎩,,,,则满足1()()12f x f x+->的x的取值范围是_________.(答案)1,4⎛⎫-+∞ ⎪⎝⎭写成分段函数的形式:()())132,021112,0222112,2x x x x g x f x f x x x x -⎧+≤⎪⎪⎪⎛⎫=+-=++<≤⎨ ⎪⎝⎭⎪⎪>⎪⎩,函数()g x 在区间(]11,0,0,,,22⎛⎤⎛⎫-∞+∞ ⎪⎥⎝⎦⎝⎭ 三段区间内均单调递增,且:)001111,201,12142g -⎛⎫-=++>⨯> ⎪⎝⎭,据此x 的取值范围是:1,4⎛⎫-+∞ ⎪⎝⎭.考点: 分段函数;分类讨论的思想2、(2017北京,理13)能够说明“设a ,b ,c 是任意实数.若a >b >c ,则a +b >c ”是假命题的一组整数a ,b ,c 的值依次为______________________________.(答案)-1,-2,-3(答案不唯一) 考点:不等式的性质3、(2017山东,理15)若函数()x e f x ( 2.71828e =是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为 .①()2x f x -=②()3x f x -=③()3f x x =④()22f x x =+(答案)①④(解析)试题分析:①()22xx x x e e f x e -⎛⎫=⋅= ⎪⎝⎭在R 上单调递增,故()2x f x -=具有M 性质;②()33xxxxe ef x e -⎛⎫=⋅= ⎪⎝⎭在R 上单调递减,故()3x f x -=不具有M 性质;③()3x x e f x e x =⋅,令()3x g x e x =⋅,则()()32232x x x g x e x e x x e x '=⋅+⋅=+,∴当2x >-时,()0g x '>,当2x <-时,()0g x '<,∴()3x x e f x e x =⋅在(),2-∞-上单调递减,在()2,-+∞上单调递增,故()3f x x =不具有M 性质;④()()22x x e f x e x =+,令()()22x g x e x =+,则()()()2222110x x x g x e x e x e x ⎡⎤'=++⋅=++>⎣⎦,∴()()22x x e f x e x =+在R 上单调递增,故()22f x x =+具有M 性质.考点:1.新定义问题.2.利用导数研究函数的单调性.4、(2017北京,理14)三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点A i 的横、纵坐标分别为第i 名工人上午的工作时间和加工的学科&网零件数,点B i 的横、纵坐标分别为第i 名工人下午的工作时间和加工的零件数,i =1,2,3.①记Q 1为第i 名工人在这一天中加工的零件总数,则Q 1,Q 2,Q 3中最大的是_________. ②记p i 为第i 名工人在这一天中平均每小时加工的零件数,则p 1,p 2,p 3中最大的是_________. (答案)1Q ;2.p考点:1.图象的应用;2.实际应用.5、(2017北京,理8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是(参考数据:lg3≈0.48)(A )1033 (B )1053 (C )1073 (D )1093 (答案)D (解析)试题分析:设36180310M x N == ,两边取对数,36136180803lg lg lg3lg10361lg38093.2810x ==-=⨯-=,所以93.2810x =,即MN最接近9310,故选D. 考点:对数运算6、(2017浙江,17)已知α∈R ,函数a a xx x f +-+=|4|)(在区间[1,4]上的最大值是5,则a 的取值范围是___________.(答案)9(,]2-∞考点:基本不等式、函数最值7.(2017江苏,1)已知集合{1,2}A =,2{,3}B a a =+,若{1}A B =则实数a 的值为 ▲ . (答案)1(解析)由题意1B ∈,显然233a +≥,所以1a =,此时234a +=,满足题意,故答案为1.考点:元素的互异性8、(2017江苏,11)已知函数31()2e e x xf x x x =-+-, 其中e 是自然对数的底数. 若2(1)(2)0f a f a -+≤,则实数a 的取值范围是 ▲ .(答案)1[1,]2-考点:利用函数性质解不等式9、(2017江苏,14)设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩其中集合1,*n D x x n n -⎧⎫==∈⎨⎬⎩⎭N ,则方程()lg 0f x x -=的解的个数是 ▲ . (答案)8(解析)由于()[0,1)f x ∈ ,则需考虑110x ≤< 的情况 在此范围内,x Q ∈ 且x ∈Z 时,设*,,,2qx p q p p=∈≥N ,且,p q 互质 若lg x Q ∈ ,则由lg (0,1)x ∈ ,可设*lg ,,,2nx m n m m=∈≥N ,且,m n 互质 因此10n mq p =,则10()n m qp= ,此时左边为整数,右边非整数,矛盾,因此lg x Q ∉ 因此lg x 不可能与每个周期内x D ∈ 对应的部分相等, 只需考虑lg x 与每个周期x D ∉ 的部分的交点,考点:函数与方程10、(2018年高考全国卷I 文科13)(5分)已知函数f (x )=log 2(x 2+a ),若f (3)=1,则a= .(解答)解:函数f (x )=log 2(x 2+a ),若f (3)=1, 可得:log 2(9+a )=1,可得a=﹣7. 故答案为:﹣7.11、(2018年高考全国卷2理科13)(5分)曲线y=2ln (x+1)在点(0,0)处的切线方程为 . (解答)解:∵y=2ln (x+1), ∴y′=,当x=0时,y′=2,∴曲线y=2ln(x+1)在点(0,0)处的切线方程为y=2x.故答案为:y=2x.17、(2018年高考全国卷3文科16)(5分)已知函数f(x)=ln(﹣x)+1,f(a)=4,则f(﹣a)= .(解答)解:函数g(x)=ln(﹣x)满足g(﹣x)=ln(+x)==﹣ln(﹣x)=﹣g(x),所以g(x)是奇函数.函数f(x)=ln(﹣x)+1,f(a)=4,可得f(a)=4=ln(﹣a)+1,可得ln(﹣a)=3,则f(﹣a)=﹣ln(﹣a)+1=﹣3+1=﹣2.故答案为:﹣2.18、(2018年高考全国卷3理科14)(5分)曲线y=(ax+1)e x在点(0,1)处的切线的斜率为﹣2,则a= .(解答)解:曲线y=(ax+1)e x,可得y′=ae x+(ax+1)e x,曲线y=(ax+1)e x在点(0,1)处的切线的斜率为﹣2,可得:a+1=﹣2,解得a=﹣3.故答案为:﹣3.19、(2018年北京市高考数学试卷理科13)(5分)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是.(解答)解:例如f(x)=sinx,尽管f(x)>f(0)对任意的x∈(0,2]都成立,当x∈[0,)上为增函数,在(,2]为减函数,故答案为:f(x)=sinx.20、(2018年江苏省高考数学试卷5)(5分)函数f(x)=的定义域为.(解答)解:由题意得:≥1,解得:x≥2,∴函数f (x )的定义域是[2,+∞). 故答案为:[2,+∞).21、(2018年江苏省高考数学试卷9)(5分)函数f (x )满足f (x+4)=f (x )(x ∈R ),且在区间(﹣2,2]上,f (x )=,则f (f (15))的值为 .(解答)解:由f (x+4)=f (x )得函数是周期为4的周期函数, 则f (15)=f (16﹣1)=f (﹣1)=|﹣1+|=, f ()=cos ()=cos =,即f (f (15))=,故答案为:22、(2018年江苏省高考数学试卷11)(5分)若函数f (x )=2x 3﹣ax 2+1(a ∈R )在(0,+∞)内有且只有一个零点,则f (x )在[﹣1,1]上的最大值与最小值的和为 . (解答)解:∵函数f (x )=2x 3﹣ax 2+1(a ∈R )在(0,+∞)内有且只有一个零点, ∴f′(x )=2x (3x ﹣a ),x ∈(0,+∞), ①当a ≤0时,f′(x )=2x (3x ﹣a )>0,函数f (x )在(0,+∞)上单调递增,f (0)=1,f (x )在(0,+∞)上没有零点,舍去; ②当a >0时,f′(x )=2x (3x ﹣a )>0的解为x >, ∴f (x )在(0,)上递减,在(,+∞)递增, 又f (x )只有一个零点, ∴f ()=﹣+1=0,解得a=3,f (x )=2x 3﹣3x 2+1,f′(x )=6x (x ﹣1),x ∈[﹣1,1], f′(x )>0的解集为(﹣1,0),f (x )在(﹣1,0)上递增,在(0,1)上递减, f (﹣1)=﹣4,f (0)=1,f (1)=0,∴f (x )min =f (﹣1)=﹣4,f (x )max =f (0)=1, ∴f (x )在[﹣1,1]上的最大值与最小值的和为: f (x )max +f (x )min =﹣4+1=﹣3.23、(2018年上海市高考数学试卷4)(4分)设常数a∈R,函数f(x)=1og(x+a).若f(x)2的反函数的图象经过点(3,1),则a= .(解答)解:∵常数a∈R,函数f(x)=1og(x+a).2f(x)的反函数的图象经过点(3,1),∴函数f(x)=1og(x+a)的图象经过点(1,3),2(1+a)=3,∴log2解得a=7.故答案为:7.24、(2018年上海市高考数学试卷7)(5分)已知α∈{﹣2,﹣1,﹣,1,2,3},若幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,则α=.(解答)解:∵α∈{﹣2,﹣1,,1,2,3},幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,∴a是奇数,且a<0,∴a=﹣1.故答案为:﹣1.25、(2018年上海市高考数学试卷11)(5分)已知常数a>0,函数f(x)=的图象经过点P(p,),Q(q,).若2p+q=36pq,则a= .(解答)解:函数f(x)=的图象经过点P(p,),Q(q,).则:,整理得:=1,解得:2p+q=a2pq,由于:2p+q=36pq,所以:a2=36,由于a>0,故:a=6.故答案为:626、(2018年上海市高考数学试卷12)(5分)已知实数x1、x2、y1、y2满足:x12+y12=1,x22+y22=1,x 1x2+y1y2=,则+的最大值为.(解答)解:设A(x1,y1),B(x2,y2),=(x1,y1),=(x2,y2),由x12+y12=1,x22+y22=1,x1x2+y1y2=,可得A,B两点在圆x2+y2=1上,且•=1×1×cos∠AOB=,即有∠AOB=60°,即三角形OAB为等边三角形,AB=1,+的几何意义为点A,B两点到直线x+y﹣1=0的距离d1与d2之和,显然d1+d2≤AB=1,即+的最大值为1,故答案为:1.27、(2018年天津市高考数学试卷文科10)(5分)已知函数f(x)=e x lnx,f′(x)为f(x)的导函数,则f′(1)的值为.(解答)解:函数f(x)=e x lnx,则f′(x)=e x lnx+•e x;∴f′(1)=e•ln1+1•e=e.故答案为:e.28、(2018年天津市高考数学试卷文科13)(5分)已知a,b∈R,且a﹣3b+6=0,则2a+的最小值为.(解答)解:a,b∈R,且a﹣3b+6=0,可得:3b=a+6,则2a+==≥2=,当且仅当2a=.即a=﹣3时取等号.函数的最小值为:.故答案为:.(2018年天津市高考数学试卷文科14)(5分)己知a∈R,函数f(x)=.若29、对任意x∈[﹣3,+∞),f(x)≤|x|恒成立,则a的取值范围是.(解答)解:当x≤0时,函数f(x)=x2+2x+a﹣2的对称轴为x=﹣1,抛物线开口向上,要使x≤0时,对任意x∈[﹣3,+∞),f(x)≤|x|恒成立,则只需要f(﹣3)≤|﹣3|=3,即9﹣6+a﹣2≤3,得a≤2,当x>0时,要使f(x)≤|x|恒成立,即f(x)=﹣x2+2x﹣2a,则直线y=x的下方或在y=x 上,由﹣x2+2x﹣2a=x,即x2﹣x+2a=0,由判别式△=1﹣8a≤0,得a≥,综上≤a≤2,故答案为:[,2].30、(2018年天津市高考数学试卷理科13)(5分)已知a,b∈R,且a﹣3b+6=0,则2a+的最小值为.(解答)解:a,b∈R,且a﹣3b+6=0,可得:3b=a+6,则2a+==≥2=,当且仅当2a=.即a=﹣3时取等号.函数的最小值为:.故答案为:.31、(2018年天津市高考数学试卷理科14)(5分)已知a>0,函数f(x)=.若关于x的方程f(x)=ax恰有2个互异的实数解,则a的取值范围是.(解答)解:当x≤0时,由f(x)=ax得x2+2ax+a=ax,得x2+ax+a=0,得a(x+1)=﹣x2,得a=﹣,设g(x)=﹣,则g′(x)=﹣=﹣,由g(x)>0得﹣2<x<﹣1或﹣1<x<0,此时递增,由g(x)<0得x<﹣2,此时递减,即当x=﹣2时,g(x)取得极小值为g(﹣2)=4,当x>0时,由f(x)=ax得﹣x2+2ax﹣2a=ax,得x2﹣ax+2a=0,得a(x﹣2)=x2,当x=2时,方程不成立,当x≠2时,a=设h(x)=,则h′(x)==,由h(x)>0得x>4,此时递增,由h(x)<0得0<x<2或2<x<4,此时递减,即当x=4时,h(x)取得极小值为h(4)=8,要使f(x)=ax恰有2个互异的实数解,则由图象知4<a<8,故答案为:(4,8)32、(2018年浙江省高考数学试卷15)(6分)已知λ∈R,函数f(x)=,当λ=2时,不等式f(x)<0的解集是.若函数f(x)恰有2个零点,则λ的取值范围是.(解答)解:当λ=2时函数f (x )=,显然x ≥2时,不等式x ﹣4<0的解集:{x|2≤x <4};x <2时,不等式f (x )<0化为:x 2﹣4x+3<0,解得1<x <2,综上,不等式的解集为:{x|1<x <4}. 函数f (x )恰有2个零点, 函数f (x )=的草图如图:函数f (x )恰有2个零点,则λ∈(1,3]. 故答案为:{x|1<x <4};(1,3]. 三、解答题1、(2017课标1,理21)已知函数2()(2)x x f x ae a e x =+--. (1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围.试题分析:(1)讨论()f x 单调性,首先进行求导,发现式子特点后要及时进行因式分解,在对a 按0a ≤,0a >进行讨论,写出单调区间;(2)根据第(1)题,若0a ≤,()f x 至多有一个零点.若0a >,当ln x a =-时,()f x 取得最小值,求出最小值1(ln )1ln f a a a-=-+,根据1a =,(1,)a ∈+∞,(0,1)a ∈进行讨论,可知当(0,1)a ∈有2个零点,设正整数0n 满足03ln(1)n a>-,则00000000()e (e 2)e 20n n n n f n a a n n n =+-->->->.由于3ln(1)ln a a ->-,因此()f x 在(ln ,)a -+∞有一个零点.所以a 的取值范围为(0,1).考点:含参函数的单调性,利用函数零点求参数取值范围.2、(2017课标II ,理)已知函数()2ln f x ax ax x x =--,且()0f x ≥。
2017全国一卷数学导数题

2017全国一卷数学导数题天上的星星真多啊!数也数不清。
有的星星喜欢穿着一身黑色的衣服,那是因为它们害怕被太阳公公看到自己穿着的白衣服。
可我发现了一颗明亮的星星,它的身体呈黄色,它那乌黑的眼睛里闪烁着神奇的光芒,像是在对我说:“请问你需要什么帮助吗?”你猜我想对它说什么呢?(注意:写完后再仔细读一遍)(5分)一、下面两个命题,哪个与原命题等价?(4分)(1)小数的性质命题A: 1/ x=1/(x+y)=1/ x+y(2)正数的性质命题B: 1/ x=1/(x+y)=x(2分)1、1。
(4分)命题A:假设,并证明。
结论:假设:小数点右移两位,将得到假设命题:若y大于0,则x可以省略。
由假设知x>0,并且x是整数。
证明:∵ x^2+(y-1)(x-y)=0,∴(x^2+(y-1)(x-y))+((x-y)^2+(x^2+(y-1)(x-y)))=0,∴(x^2+(y-1)(x-y))+((x-y)^2+(x^2+(y-1)(x-y)))=0,∴x=y-1,∵x=y-1,∴x+y=y-1,综上,∴x>y-1,∴(x^2+(y-1)(x-y))+((x-y)^2+(x^2+(y-1)(x-y)))>0,即x>y-1。
二、比较,选择(6分) 1。
(6分)小数的性质和正数的性质。
命题A与原命题无关。
命题B与原命题有关。
证明:原命题为假设与结论均为整数,由小数的性质有小数点右移两位将得到小数,并且小数点左移两位将得到原小数的近似值,根据近似值的特点和定义可知,原命题为真,从而得到命题B为真。
3。
(4分)正数的性质与小数的性质。
命题A与原命题无关。
命题B与原命题有关。
17年高考真题—文科数学2:导数

2017高考真题分类汇编:导数1.【2017浙江 7】函数()y f x =的导函数()y f x '=的图像如图所示,则函数()y f x =的图像可能是( )2.【2017天津 10】已知a R ∈,设函数()ln f x ax x =-的图象在点()()1,1f 处的切线为l ,则l 在y 轴上的截距为__________。
3.【2017课标I 14】曲线21y x x=+在点()1,2处的切线方程为__________________。
4.【2017天津 19】设,a b R ∈,||1a ≤。
已知函数()()32634f x x x a a x b =---+,()()xg x e f x =。
⑴求()f x 的单调区间;⑵已知函数()y g x =和x y e =的图象在公共点()00,x y 处有相同的切线,①求证:()f x 在0x x =处的导数等于0;②若关于x 的不等式()x g x e ≤在区间[]001,1x x -+上恒成立,求b 的取值范围。
5.【2017北京 20】已知函数()cos xf x e x x =-。
⑴求曲线()y f x =在点()()0,0f 处的切线方程;⑵求函数()f x 在区间[]0,2π上的最大值和最小值。
6.【2017江苏 20】已知函数()()3210,f x x ax bx a b R =+++>∈有极值,且导函数()f x '的极值点是()f x 的零点(极值点是指函数取极值时对应的自变量的值)。
⑴求b 关于a 的函数关系式,并写出定义域;⑵证明:23b a >;⑶若()(),f x f x '这两个函数的所有极值之和不小于72-,求a 的取值范围。
7.【2017山东 20】已知函数()()321132f x x ax a R =-∈。
⑴当2a =时,求曲线()y f x =在点()()3,3f 处的切线方程;⑵设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值。
2017年全国2卷数学导数

2017年全国2卷数学导数
导数是数学中的重要概念,可以用于研究函数的性质,例如单调性、极值和最值等。
全国卷数学在考察导数时,一般会涉及以下几个方面的知识点:
1. 导数的定义和几何意义:导数描述的是函数在某一点的切线斜率,即函数在该点的变化率。
2. 导数的计算:包括基本初等函数的导数、复合函数的导数、幂函数的导数等。
3. 导数的应用:包括利用导数研究函数的单调性、极值和最值,以及利用导数解决实际问题等。
4. 导数的综合应用:包括导数与其他知识点的综合,例如导数与不等式、导数与数列等。
具体到2017年全国2卷数学导数部分,可能涉及的题目类型包括选择题、填空题和解答题。
题目难度通常为中等或较难,需要学生熟练掌握导数的相关知识和解题技巧。
2017年高考数学理试题分类汇编:导数及其应用
2017年高考数学理试题分类汇编:导数及其应用1. (2017年新课标Ⅰ文) 8.函数sin21cos xy x=-的部分图像大致为 (C )2. ( 2017年新课标Ⅱ卷理) 11。
若2x =-是函数21`()(1)x f x x ax e-=+-的极值点,则()f x 的极小值为( )A.1- B 。
32e -- C.35e - D 。
1 【答案】A【解析】由题可得12121()(2)(1)[(2)1]x x x f x x a ex ax e x a x a e ---'=+++-=+++-因为(2)0f '-=,所以1a =-,21()(1)x f x x x e-=--,故21()(2)x f x x x e -'=+-令()0f x '>,解得2x <-或1x >,所以()f x 在(,2),(1,)-∞-+∞单调递增,在(2,1)-单调递减 所以()f x 极小值(1)f =11(111)1e-=--=-,故选A 。
3. (2017年新课标Ⅰ文) 9.已知函数()ln ln(2)f x x x =+-,则 (C ) A .()f x 在(0,2)单调递增B .()f x 在(0,2)单调递减C .y =()f x 的图像关于直线x =1对称D .y =()f x 的图像关于点(1,0)对称4. (2017年浙江卷)函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是【答案】D【解析】原函数先减再增,再减再增,因此选D.5. (2017年新课标Ⅲ卷理) 11.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12- B .13C .12D .1【答案】C6. ( 2017年新课标Ⅱ卷理)21.已知函数()2ln f x ax ax x x =--,且()0f x ≥。
高考数学真题导数专题及答案

高考数学真题导数专题及答案2017年高考真题:导数专题一、解答题(共12小题)1.已知函数f(x) = ae^(2x) + (a-2)e^x - x。
1) 讨论f(x)的单调性;2) 若f(x)有两个零点,求a的取值范围。
2.已知函数f(x) = ax^2 - ax - xlnx,且f(x) ≥ 0.1) 求a;2) 证明:f(x)存在唯一的极大值点x,且e^-2 < f(x) < 2^-2.3.已知函数f(x) = x^-1 - alnx。
1) 若f(x) ≥ 0,求a的值;2) 设m为整数,且对于任意正整数n,(1+1/n)^m 的最小值。
4.已知函数f(x) = x^3 + ax^2 + bx + 1 (a。
0,b∈R)有极值,且导函数f'(x)的极值点是f(x)的零点。
1) 求b关于a的函数关系式,并写出定义域;2) 证明:b^2.3a;3) 若f(x)和f'(x)这两个函数的所有极值之和不小于 -1,求a的取值范围。
5.设函数f(x) = (1-x^2)e^x。
1) 讨论f(x)的单调性;2) 当x≥1时,f(x) ≤ ax+1,求a的取值范围。
6.已知函数f(x) = (x-1)/(x+1)。
1) 求f(x)的导函数;2) 求f(x)在区间(-1.+∞)上的取值范围。
7.已知函数f(x) = x^2 + 2cosx,g(x) = e^x(cosx-sinx+2x^-2),其中e≈2.…是自然对数的底数。
I) 求曲线y=f(x)在点(π。
f(π))处的切线方程;II) 令h(x) = g(x) - af(x) (a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值。
8.已知函数f(x) = e^x*cosx - x。
1) 求曲线y=f(x)在点(0.f(0))处的切线方程;2) 求函数f(x)在区间[0.π]上的最大值和最小值。
9.设a∈Z,已知定义在R上的函数f(x) = 2x^4 + 3x^3 -3x^2 - 6x + a在区间(1.2)内有一个零点x,g(x)为f(x)的导函数。
2017高考试题解析分类汇编-函数导数

函数导数1(2017北京文)已知函数,则(A )是偶函数,且在R 上是增函数 (B )是奇函数,且在R 上是增函数 (C )是偶函数,且在R 上是减函数 (D )是奇函数,且在R 上是增函数 【答案】B2(2017北京文)(本小题13分)已知函数.(Ⅰ)求曲线在点处的切线方程;(Ⅱ)求函数在区间上的最大值和最小值.【答案】(Ⅰ);(Ⅱ)最大值1;最小值.(Ⅱ)设,则.1()3()3x xf x =-()fx ()e cos xf x x x =-()y f x =(0,(0))f ()f x π[0,]21y =2π-()e (cos sin )1x h x x x =--()e (cos sin sin cos )2e sin x x h x x x x x x '=---=-当时,,所以在区间上单调递减.所以对任意有,即.所以函数在区间上单调递减.因此在区间上的最大值为,最小值为. 3(2017新课标Ⅱ理)(12分)已知函数2()ln f ax a x x x x =--,且()0f x ≥. (1)求a ;(2)证明:()f x 存在唯一的极大值点0x ,且220e()2f x --<<.π(0,)2x ∈()0h x '<()h x π[0,]2π(0,]2x ∈()(0)0h x h <=()0f x '<()f x π[0,]2()f x π[0,]2(0)1f =ππ()22f =-所以()220e2f x --<<.4(2017天津理)(本小题满分14分)设a ∈Z ,已知定义在R 上的函数432()2336f x x x x x a =+--+在区间(1,2)内有一个零点0x ,()g x 为()f x 的导函数. (Ⅰ)求()g x 的单调区间;(Ⅱ)设00[1,)(,2]m x x ∈U ,函数0()()()()h x g x m x f m =--,求证:0()()0h m h x <; (Ⅲ)求证:存在大于0的常数A ,使得对于任意的正整数,p q ,且00[1,)(,2],px x q∈U 满足041||p x q Aq-≥. 【答案】(1)增区间是(,1)-∞-,1(,)4+∞,减区间是1(1,)4-.(2)(3)证明见解析 【解析】(Ⅰ)由432()2336f x x x x x a =+--+,可得32()()8966g x f x x x x '==+--, 进而可得2()24186g x x x '=+-.令()0g x '=,解得1x =-,或14x =. 当x 变化时,(),()g x g x '的变化情况如下表:所以,()g x 的单调递增区间是(,1)-∞-,(,)4+∞,单调递减区间是(1,)4-. (Ⅰ)证明:由0()()()()h x g x m x f m =--,得0()()()()h m g m m x f m =--,000()()()()h x g x m x f m =--.(III )证明:对于任意的正整数 p ,q ,且00[1)(,],2px x q∈U ,令pm q=,函数0()()()()h g m x x x m f =--. 由(II )知,当0[1),m x ∈时,()h x 在区间0(,)m x 内有零点; 当0(,2]m x ∈时,()h x 在区间0(),x m 内有零点.所以041|2|()p x q g q -≥.所以,只要取()2A g =,就有041||p x q Aq-≥. 5(2017新课标Ⅲ理数)(12分)已知函数()f x =x ﹣1﹣a ln x . (1)若()0f x ≥ ,求a 的值;(2)设m 为整数,且对于任意正整数n ,21111++1+)222n K ()(1)(﹤m ,求m 的最小值.解:(1)()f x 的定义域为()0,+∞.2211111111++1+++1+<+++=1-<12222222n n n ln ln ln ⎛⎫⎛⎫⎛⎫⋅⋅⋅⋅⋅⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故21111+1+1+<222n e ⎛⎫⎛⎫⎛⎫⋅⋅⋅ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭而231111+1+1+>2222⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭,所以m 的最小值为3. 6(2017山东理)(本小题满分13分)已知函数()22cos f x x x =+,()()cos sin 22x g x e x x x =-+-,其中 2.71828e =L 是自然对数的底数.(Ⅰ)求曲线()y f x =在点()(),f x π处的切线方程;(Ⅱ)令()()()()h x g x af x a R =-∈,讨论()h x 的单调性并判断有无极值,有极值时求出极值.【答案】(Ⅰ)222y x ππ=--.(Ⅱ)综上所述:当0a ≤时,()h x 在(),0-∞上单调递减,在()0,+∞上单调递增,函数()h x 有极小值,极小值是()021h a =--;当01a <<时,函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增,在()ln ,0a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--;当1a =时,函数()h x 在(),-∞+∞上单调递增,无极值;当1a >时,函数()h x 在(),0-∞和()ln ,a +∞上单调递增,在()0,ln a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()021h a =--;极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.【解析】解:(Ⅰ)由题意()22f ππ=-又()22sin f x x x '=-,所以()2f ππ'=,因此 曲线()y f x =在点()(),f ππ处的切线方程为()()222y x πππ--=-,即 222y x ππ=--.(Ⅱ)由题意得 ()()()22cos sin 222cos h x e x x x a x x =-+--+,因为()()()()cos sin 22sin cos 222sin x x h x e x x x e x x a x x '=-+-+--+--()()2sin 2sin x e x x a x x =---()()2sin x e a x x =--,令()sin m x x x =-则()1cos 0m x x '=-≥所以()m x 在R 上单调递增.所以 当0x >时,()m x 单调递减,当0x >时,()0m x <(2)当0a >时,()()()ln 2sin x ah x e e x x '=--由 ()0h x '=得 1ln x a =,2=0x①当01a <<时,ln 0a <,当(),ln x a ∈-∞时,()ln 0,0x a e e h x '-<>,()h x 单调递增;当()ln ,0x a ∈时,()ln 0,0x a e e h x '-><,()h x 单调递减;当()0,x ∈+∞时,()ln 0,0x a e e h x '->>,()h x 单调递增.所以 当ln x a =时()h x 取得极大值.极大值为()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦,当0x =时()h x 取到极小值,极小值是 ()021h a =--;②当1a =时,ln 0a =,所以 当(),x ∈-∞+∞时,()0h x '≥,函数()h x 在(),-∞+∞上单调递增,无极值;极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.综上所述:当0a ≤时,()h x 在(),0-∞上单调递减,在()0,+∞上单调递增,函数()h x 有极小值,极小值是()021h a =--;当01a <<时,函数()h x 在(),ln a -∞和()0,ln a 和()0,+∞上单调递增,在()ln ,0a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦极小值是()021h a =--;当1a =时,函数()h x 在(),-∞+∞上单调递增,无极值;当1a >时,函数()h x 在(),0-∞和()ln ,a +∞上单调递增,在()0,ln a 上单调递减,函数()h x 有极大值,也有极小值,极大值是()021h a =--;极小值是()()()2ln ln 2ln sin ln cos ln 2h a a a a a a ⎡⎤=--+++⎣⎦.7(2017天津文)(本小题满分14分)设,a b ∈R ,||1a ≤.已知函数32()63(4)f x x x a a x b =---+,()e ()x g x f x =. (Ⅰ)求()f x 的单调区间;(Ⅱ)已知函数()y g x =和e x y =的图象在公共点(x 0,y 0)处有相同的切线, (i )求证:()f x 在0x x =处的导数等于0;(ii )若关于x 的不等式()e x g x ≤在区间00[1,1]x x -+上恒成立,求b 的取值范围. 【答案】(1)递增区间为(,)a -∞,(4,)a -+∞,递减区间为(),4a a -.(2)(ⅰ)()f x 在0x x =处的导数等于0.(ⅱ)b 的取值范围是[7],1-.【解析】(I )由324()63()f x x a x x a b =--+-,可得(ii )因为()e xg x ≤,00[11],x x x ∈-+,由e 0x >,可得()1f x ≤. 又因为0()1f x =,0()0f 'x =,故0x 为()f x 的极大值点,由(I )知0x a =. 另一方面,由于||1a ≤,故14a a +<-,由(I )知()f x 在(,)1a a -内单调递增,在(),1a a +内单调递减,故当0x a =时,()()1f f x a ≤=在[1,1]a a -+上恒成立,从而()e xg x ≤在00,[11]x x -+上恒成立.由32()63()14a a f a a a a b =---+=,得32261b a a =-+,11a -≤≤。
2017年高考数学试题分项版—函数、导数应用(原卷版)

2017年高考数学试题分项版—函数、导数应用(原卷版)一、选择题1.(2017·全国Ⅰ文,8)函数y =sin 2x1-cos x的部分图象大致为( )2.(2017·全国Ⅰ文,9)已知函数f (x )=ln x +ln(2-x ),则( ) A .f (x )在(0,2)上单调递增 B .f (x )在(0,2)上单调递减C .y =f (x )的图象关于直线x =1对称D .y =f (x )的图象关于点(1,0)对称3.(2017·全国Ⅱ文,8)函数f (x )=ln(x 2-2x -8)的单调递增区间是( ) A .(-∞,-2) B .(-∞,1) C .(1,+∞)D .(4,+∞)4.(2017·全国Ⅲ文,7)函数y =1+x +sin x x2的部分图象大致为( )5.(2017·全国Ⅲ文,12)已知函数f (x )=x 2-2x +a (e x -1+e-x +1)有唯一零点,则a 等于( )A .-12B .13C .12D .16.(2017·北京文,5)已知函数f (x )=3x -⎝⎛⎭⎫13x,则f (x )( ) A .是偶函数,且在R 上是增函数B .是奇函数,且在R 上是增函数C .是偶函数,且在R 上是减函数D .是奇函数,且在R 上是减函数7.(2017·北京文,8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是( )(参考数据:lg 3≈0.48)A .1033B .1053C .1073D .10938.(2017·天津文,6)已知奇函数f (x )在R 上是增函数.若a =-f ⎝⎛⎭⎫log 215,b =f ()log 24.1,c =f (20.8),则a ,b ,c 的大小关系为( ) A .a <b <c B .b <a <c C .c <b <aD .c <a <b9.(2017·天津文,8)已知函数f (x )=⎩⎪⎨⎪⎧|x |+2,x <1,x +2x ,x ≥1.设a ∈R ,若关于x 的不等式f (x )≥⎪⎪⎪⎪x2+a 在R 上恒成立,则a 的取值范围是( ) A .[-2,2] B .[-23,2] C .[-2,23]D .[-23,23]10.(2017·山东文,9)设f (x )=⎩⎨⎧x ,0<x <1,2 x -1 ,x ≥1,若f (a )=f (a +1),则f ⎝⎛⎭⎫1a 等于( ) A .2 B .4 C .6 D .811.(2017·山东文,10)若函数e x f (x )(e =2.718 28…是自然对数的底数)在f (x )的定义域上单调递增,则称函数f (x )具有M 性质,下列函数中具有M 性质的是( ) A .f (x )=2-xB .f (x )=x 2C .f (x )=3-xD .f (x )=cos x12.(2017·浙江,5)若函数f (x )=x 2+ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M -m ( )A .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关13.(2017·浙江,7)函数y =f (x )的导函数y =f ′(x )的图象如图所示,则函数y =f (x )的图象可能是( )14.(2017·全国Ⅰ理,5)已知函数f (x )在(-∞,+∞)上单调递减,且为奇函数.若f (1)=-1,则满足-1≤f (x -2)≤1的x 的取值范围是( ) A .[-2,2] B .[-1,1] C .[0,4] D .[1,3]15.(2017·全国Ⅰ理,11)设x ,y ,z 为正数,且2x =3y =5z ,则( ) A .2x <3y <5z B .5z <2x <3y C .3y <5z <2xD .3y <2x <5z16.(2017·全国Ⅱ理,11)若x =-2是函数f (x )=(x 2+ax -1)e x -1的极值点,则f (x )的极小值为( ) A .-1 B .-2e -3C .5e -3D .117.(2017·全国Ⅲ理,11)已知函数f (x )=x 2-2x +a (e x -1+e-x +1)有唯一零点,则a 等于( )A .-12B .13C .12D .118.(2017·北京理,5)已知函数f (x )=3x -⎝⎛⎭⎫13x,则f (x )( ) A .是奇函数,且在R 上是增函数 B .是偶函数,且在R 上是增函数 C .是奇函数,且在R 上是减函数 D .是偶函数,且在R 上是减函数19.(2017·北京理,8)根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是( )(参考数据:lg 3≈0.48) A .1033 B .1053 C .1073D .109320.(2017·天津理,6)已知奇函数f (x )在R 上是增函数,g (x )=xf (x ).若a =g (-log 25.1),b =g (20.8),c =g (3),则a ,b ,c 的大小关系为( )A .a <b <cB .c <b <aC .b <a <cD .b <c <a21.(2017·天津理,8)已知函数f (x )=⎩⎪⎨⎪⎧x 2-x +3,x ≤1,x +2x ,x >1.设a ∈R ,若关于x 的不等式f (x )≥⎪⎪⎪⎪x2+a 在R 上恒成立,则a 的取值范围是( ) A.⎣⎡⎦⎤-4716,2 B.⎣⎡⎦⎤-4716,3916 C.[]-23,2D.⎣⎡⎦⎤-23,3916 22.(2017·山东理,10)已知当x ∈[0,1]时,函数y =(mx -1)2的图象与y =x +m 的图象有且只有一个交点,则正实数m 的取值范围是( ) A .(0,1]∪[23,+∞) B .(0,1]∪[3,+∞) C .(0,2]∪[23,+∞) D .(0,2]∪[3,+∞)二、填空题1.(2017·全国Ⅰ文,14)曲线y =x 2+1x在点(1,2)处的切线方程为________.2.(2017·全国Ⅱ文,14)已知函数f (x )是定义在R 上的奇函数,当x ∈(-∞,0)时,f (x )=2x 3+x 2,则f (2)=________.3.(2017·全国Ⅲ文,16)设函数f (x )=⎩⎪⎨⎪⎧x +1,x ≤0,2x ,x >0,则满足f (x )+f ⎝⎛⎭⎫x -12>1的x 的取值范围是________.4.(2017·天津文,10)已知a ∈R ,设函数f (x )=ax -ln x 的图象在点(1,f (1))处的切线为l ,则l 在y 轴上的截距为________.5.(2017·山东文,14)已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当x ∈[-3,0]时,f (x )=6-x ,则f (919)=________.6.(2017·浙江,17)已知a ∈R ,函数f (x )=|x +4x -a |+a 在区间[1,4]上的最大值是5,则a 的取值范围是________.7.(2017·江苏,11)已知函数f (x )=x 3-2x +e x -1e x ,其中e 是自然对数的底数,若f (a -1)+f (2a 2)≤0,则实数a 的取值范围是________.8.(2017·江苏,14)设f (x )是定义在R 上且周期为1的函数,在区间[0,1)上,f (x )=⎩⎪⎨⎪⎧x 2,x ∈D ,x ,x ∉D ,其中集合D =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x =n -1n ,n ∈N *,则方程f (x )-lg x =0的解的个数是________.9.(2017·全国Ⅲ理,15)设函数f (x )=⎩⎪⎨⎪⎧x +1,x ≤0,2x ,x >0,则满足f (x )+f ⎝⎛⎭⎫x -12>1的x 的取值范围是________.10.(2017·山东理,15)若函数e x f (x )(e =2.718 28…是自然对数的底数)在f (x )的定义域上单调递增,则称函数f (x )具有M 性质,下列函数中所有具有M 性质的函数的序号为________. ①f (x )=2-x ;②f (x )=3-x ;③f (x )=x 3;④f (x )=x 2+2.三、解答题1.(2017·全国Ⅰ文,21)已知函数f (x )=e x (e x -a )-a 2x . (1)讨论f (x )的单调性;(2)若f (x )≥0,求a 的取值范围.2.(2017·全国Ⅱ文,21)设函数f (x )=(1-x 2)e x . (1)讨论f (x )的单调性;(2)当x ≥0时,f (x )≤ax +1,求a 的取值范围.3.(2017·全国Ⅲ文,21)已知函数f (x )=ln x +ax 2+(2a +1)x . (1)讨论f (x )的单调性;(2)当a <0时,证明f (x )≤-34a -2.4.(2017·北京文,20)已知函数f (x )=e x cos x -x . (1)求曲线y =f (x )在点(0,f (0))处的切线方程; (2)求函数f (x )在区间⎣⎡⎦⎤0,π2上的最大值和最小值.5.(2017·天津文,19)设a ,b ∈R ,|a |≤1.已知函数f (x )=x 3-6x 2-3a (a -4)x +b ,g (x )=e x f (x ). (1)求f (x )的单调区间;(2)已知函数y =g (x )和y =e x 的图象在公共点(x 0,y 0)处有相同的切线. ①求证:f (x )在x =x 0处的导数等于0;②若关于x 的不等式g (x )≤e x 在区间[x 0-1,x 0+1]上恒成立,求b 的取值范围.6.(2017·山东文,20)已知函数f (x )=13x 3-12ax 2,a ∈R .(1)当a =2时,求曲线y =f (x )在点(3,f (3))处的切线方程;(2)设函数g (x )=f (x )+(x -a )cos x -sin x ,讨论g (x )的单调性并判断有无极值,有极值时求出极值.7.(2017·浙江,20)已知函数f (x )=(x -2x -1)e -x ⎝⎛⎭⎫x ≥12. (1)求f (x )的导函数;(2)求f (x )在区间⎣⎡⎭⎫12,+∞上的取值范围.8.(2017·江苏,20)已知函数f (x )=x 3+ax 2+bx +1(a >0,b ∈R )有极值,且导函数f ′(x )的极值点是f (x )的零点.(极值点是指函数取极值时对应的自变量的值) (1)求b 关于a 的函数关系式,并写出定义域; (2)证明:b 2>3a ;(3)若f (x ),f ′(x )这两个函数的所有极值之和不小于-72,求a 的取值范围.9.(2017·全国Ⅰ理,21)已知函数f (x )=a e 2x +(a -2)e x -x . (1)讨论f (x )的单调性;(2)若f (x )有两个零点,求a 的取值范围.10.(2017·全国Ⅱ理,21)已知函数f (x )=ax 2-ax -x ln x ,且f (x )≥0. (1)求a ;(2)证明:f (x )存在唯一的极大值点x 0,且e -2<f (x 0)<2-2.11.(2017·全国Ⅲ理,21)已知函数f (x )=x -1-a ln x . (1)若f (x )≥0,求a 的值;(2)设m 为整数,且对于任意正整数n ,⎝⎛⎭⎫1+12⎝⎛⎭⎫1+122·…·⎝⎛⎭⎫1+12n <m ,求m 的最小值.12.(2017·北京理,19)已知函数f (x )=e x cos x -x . (1)求曲线y =f (x )在点(0,f (0))处的切线方程; (2)求函数f (x )在区间⎣⎡⎦⎤0,π2上的最大值和最小值.13.(2017·天津理,20)设a ∈Z ,已知定义在R 上的函数f (x )=2x 4+3x 3-3x 2-6x +a 在区间(1,2)内有一个零点x 0,g (x )为f (x )的导函数. (1)求g (x )的单调区间;(2)设m ∈[1,x 0)∪(x 0,2],函数h (x )=g (x )(m -x 0)-f (m ),求证:h (m )h (x 0)<0;(3)求证:存在大于0的常数A ,使得对于任意的正整数p ,q ,且p q ∈[1,x 0)∪(x 0,2],满足⎪⎪⎪⎪p q -x 0≥1Aq 4.14.(2017·山东理,20)已知函数f (x )=x 2+2cos x ,g (x )=e x (cos x -sin x +2x -2),其中e = 2.718 28…是自然对数的底数.(1)求曲线y =f (x )在点(π,f (π))处的切线方程;(2)令h (x )=g (x )-af (x )(a ∈R ),讨论h (x )的单调性并判断有无极值,有极值时求出极值.。
2017年高考真题分类汇编(理数)导数

2017年高考真题分类汇编(理数):专题2 导数一、单选题(共3题;共6分)1、(2017•浙江)函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )A、B、C、D、2、(2017•新课标Ⅱ)若x=﹣2是函数f(x)=(x2+ax﹣1)e x﹣1的极值点,则f(x)的极小值为()A、﹣1B、﹣2e﹣3C、5e﹣3D、13、(2017•新课标Ⅲ)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A、﹣B、C、D、1二、解答题(共8题;共50分)4、(2017•浙江)已知函数f(x)=(x﹣)e﹣x(x≥ ).(Ⅰ)求f(x)的导函数;(Ⅱ)求f(x)在区间[ ,+∞)上的取值范围.5、(2017•山东)已知函数f(x)=x2+2cosx,g(x)=e x(cosx﹣sinx+2x﹣2),其中e≈2.17828…是自然对数的底数.(13分)(Ⅰ)求曲线y=f(x)在点(π,f(π))处的切线方程;(Ⅱ)令h(x)=g (x)﹣a f(x)(a∈R),讨论h(x)的单调性并判断有无极值,有极值时求出极值.6、(2017•北京卷)已知函数f(x)=e x cosx﹣x.(13分)(1)求曲线y=f(x)在点(0,f(0))处的切线方程;(2)求函数f(x)在区间[0, ]上的最大值和最小值.7、(2017·天津)设a∈Z,已知定义在R上的函数f(x)=2x4+3x3﹣3x2﹣6x+a在区间(1,2)内有一个零点x0,g(x)为f(x)的导函数.(Ⅰ)求g(x)的单调区间;(Ⅱ)设m∈[1,x0)∪(x0,2],函数h(x)=g(x)(m﹣x0)﹣f(m),求证:h(m)h(x0)<0;(Ⅲ)求证:存在大于0的常数A,使得对于任意的正整数p,q,且∈[1,x0)∪(x0,2],满足|﹣x0|≥ .8、(2017•江苏)已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值,且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)(Ⅰ)求b关于a的函数关系式,并写出定义域;(Ⅱ)证明:b2>3a;(Ⅲ)若f(x),f′(x)这两个函数的所有极值之和不小于﹣,求a的取值范围.9、(2017•新课标Ⅰ卷)已知函数f(x)=ae2x+(a﹣2)e x﹣x.(12分)(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.10、(2017•新课标Ⅱ)已知函数f(x)=ax2﹣ax﹣xlnx,且f(x)≥0.(Ⅰ)求a;(Ⅱ)证明:f(x)存在唯一的极大值点x0, 且e﹣2<f(x0)<2﹣2.11、(2017•新课标Ⅲ)已知函数f(x)=x﹣1﹣alnx.(Ⅰ)若f(x)≥0,求a的值;(Ⅱ)设m为整数,且对于任意正整数n,(1+ )(1+ )…(1+ )<m,求m的最小值.答案解析部分一、单选题1、【答案】D【考点】函数的图象,函数的单调性与导数的关系【解析】【解答】解:由当f′(x)<0时,函数f(x)单调递减,当f′(x)>0时,函数f(x)单调递增,则由导函数y=f′(x)的图象可知:f(x)先单调递减,再单调递增,然后单调递减,最后单调递增,排除A,C,且第二个拐点(即函数的极大值点)在x轴上的右侧,排除B,故选D【分析】根据导数与函数单调性的关系,当f′(x)<0时,函数f(x)单调递减,当f′(x)>0时,函数f(x)单调递增,根据函数图象,即可判断函数的单调性,然后根据函数极值的判断,即可判断函数极值的位置,即可求得函数y=f(x)的图象可能2、【答案】A【考点】导数的运算,利用导数研究函数的单调性,利用导数研究函数的极值【解析】【解答】解:函数f(x)=(x2+ax﹣1)e x﹣1,可得f′(x)=(2x+a)e x﹣1+(x2+ax﹣1)e x﹣1,x=﹣2是函数f(x)=(x2+ax﹣1)e x﹣1的极值点,可得:﹣4+a+(3﹣2a)=0.解得a=﹣1.可得f′(x)=(2x﹣1)e x﹣1+(x2﹣x﹣1)e x﹣1,=(x2+x﹣2)e x﹣1,函数的极值点为:x=﹣2,x=1,当x<﹣2或x>1时,f′(x)>0函数是增函数,x∈(﹣2,1)时,函数是减函数,x=1时,函数取得极小值:f(1)=(12﹣1﹣1)e1﹣1=﹣1.故选:A.【分析】求出函数的导数,利用极值点,求出a,然后判断函数的单调性,求解函数的极小值即可.3、【答案】C【考点】利用导数研究函数的单调性,导数在最大值、最小值问题中的应用,函数的零点与方程根的关系,函数的零点【解析】【解答】解:因为f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)=﹣1+(x﹣1)2+a(e x﹣1+ )=0,所以函数f(x)有唯一零点等价于方程1﹣(x﹣1)2=a(e x﹣1+ )有唯一解,等价于函数y=1﹣(x﹣1)2的图象与y=a(e x﹣1+ )的图象只有一个交点.①当a=0时,f(x)=x2﹣2x≥﹣1,此时有两个零点,矛盾;②当a<0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,且y=a(e x﹣1+ )在(﹣∞,1)上递增、在(1,+∞)上递减,所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(e x﹣1+ )的图象的最高点为B(1,2a),由于2a<0<1,此时函数y=1﹣(x﹣1)2的图象与y=a(e x﹣1+ )的图象有两个交点,矛盾;③当a>0时,由于y=1﹣(x﹣1)2在(﹣∞,1)上递增、在(1,+∞)上递减,且y=a(e x﹣1+ )在(﹣∞,1)上递减、在(1,+∞)上递增,所以函数y=1﹣(x﹣1)2的图象的最高点为A(1,1),y=a(e x﹣1+ )的图象的最低点为B(1,2a),由题可知点A与点B重合时满足条件,即2a=1,即a= ,符合条件;综上所述,a= ,故选:C.【分析】通过转化可知问题等价于函数y=1﹣(x﹣1)2的图象与y=a(e x﹣1+ )的图象只有一个交点求a的值.分a=0、a<0、a>0三种情况,结合函数的单调性分析可得结论.二、解答题4、【答案】解:(Ⅰ)函数f(x)=(x﹣)e﹣x(x≥ ),导数f′(x)=(1﹣••2)e﹣x﹣(x﹣)e﹣x=(1﹣x+ )e﹣x=(1﹣x)(1﹣)e﹣x;(Ⅱ)由f(x)的导数f′(x)=(1﹣x)(1﹣)e﹣x,可得f′(x)=0时,x=1或,当<x<1时,f′(x)<0,f(x)递减;当1<x<时,f′(x)>0,f(x)递增;当x>时,f′(x)<0,f(x)递减,且x≥ ⇔x2≥2x﹣1⇔(x﹣1)2≥0,则f(x)≥0.由f()= e ,f(1)=0,f( )= e ,即有f(x)的最大值为 e ,最小值为f(1)=0.则f(x)在区间[,+∞)上的取值范围是[0, e ].【考点】简单复合函数的导数,利用导数研究函数的单调性,导数在最大值、最小值问题中的应用【解析】【分析】(Ⅰ)求出f(x)的导数,注意运用复合函数的求导法则,即可得到所求;(Ⅱ)求出f(x)的导数,求得极值点,讨论当<x<1时,当1<x<时,当x>时,f(x)的单调性,判断f(x)≥0,计算f(),f(1),f(),即可得到所求取值范围.5、【答案】解:(Ⅰ)f(π)=π2﹣2.f′(x)=2x﹣2sinx,∴f′(π)=2π.∴曲线y=f(x)在点(π,f(π))处的切线方程为:y﹣(π2﹣2)=2π(x﹣π).化为:2πx﹣y﹣π2﹣2=0.(Ⅱ)h(x)=g (x)﹣a f(x)=e x(cosx﹣sinx+2x﹣2)﹣a(x2+2cosx)h′(x)=e x(cosx﹣sinx+2x﹣2)+e x(﹣sinx﹣cosx+2)﹣a(2x﹣2sinx)=2(x﹣sinx)(e x﹣a)=2(x﹣sinx)(e x﹣e lna).令u(x)=x﹣sinx,则u′(x)=1﹣cosx≥0,∴函数u(x)在R上单调递增.∵u(0)=0,∴x>0时,u(x)>0;x<0时,u(x)<0.(i)a≤0时,e x﹣a>0,∴x>0时,h′(x)>0,函数h(x)在(0,+∞)单调递增;x<0时,h′(x)<0,函数h(x)在(﹣∞,0)单调递减.∴x=0时,函数h(x)取得极小值,h(0)=﹣1﹣2a.(ii)a>0时,令h′(x)=2(x﹣sinx)(e x﹣e lna)=0.解得x1=lna,x2=0.①0<a<1时,x∈(﹣∞,lna)时,e x﹣e lna<0,h′(x)>0,函数h(x)单调递增;x∈(lna,0)时,e x﹣e lna>0,h′(x)<0,函数h(x)单调递减;x∈(0,+∞)时,e x﹣e lna>0,h′(x)>0,函数h(x)单调递增.∴当x=0时,函数h(x)取得极小值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极大值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].②当a=1时,lna=0,x∈R时,h′(x)≥0,∴函数h(x)在R上单调递增.③1<a时,lna>0,x∈(﹣∞,0)时,e x﹣e lna<0,h′(x)>0,函数h(x)单调递增;x∈(0,lna)时,e x﹣e lna<0,h′(x)<0,函数h(x)单调递减;x∈(lna,+∞)时,e x﹣e lna>0,h′(x)>0,函数h(x)单调递增.∴当x=0时,函数h(x)取得极大值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极小值,h(lna)=﹣a[ln2a﹣2lna+sin(lna)+cos(lna)+2].综上所述:a≤0时,函数h(x)在(0,+∞)单调递增;x<0时,函数h(x)在(﹣∞,0)单调递减.x=0时,函数h(x)取得极小值,h(0)=﹣1﹣2a.0<a<1时,函数h(x)在x∈(﹣∞,lna)是单调递增;函数h(x)在x∈(lna,0)上单调递减.当x=0时,函数h(x)取得极小值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极大值,h(lna)=﹣a[ln2a﹣2lna+sin (lna)+cos(lna)+2].当a=1时,lna=0,函数h(x)在R上单调递增.a>1时,函数h(x)在(﹣∞,0),(lna,+∞)上单调递增;函数h(x)在(0,lna)上单调递减.当x=0时,函数h(x)取得极大值,h(0)=﹣2a﹣1.当x=lna时,函数h(x)取得极小值,h(lna)=﹣a[ln2a ﹣2lna+sin(lna)+cos(lna)+2].【考点】导数的加法与减法法则,导数的乘法与除法法则,函数的单调性与导数的关系,利用导数研究函数的单调性,利用导数研究函数的极值,利用导数研究曲线上某点切线方程【解析】【分析】(Ⅰ)f(π)=π2﹣2.f′(x)=2x﹣2sinx,可得f′(π)=2π即为切线的斜率,利用点斜式即可得出切线方程.(Ⅱ)h(x)=g (x)﹣a f(x)=e x(cosx﹣sinx+2x﹣2)﹣a(x2+2cosx),可得h′(x)=2(x﹣sinx)(e x ﹣a)=2(x﹣sinx)(e x﹣e lna).令u(x)=x﹣sinx,则u′(x)=1﹣cosx≥0,可得函数u(x)在R上单调递增.由u(0)=0,可得x>0时,u(x)>0;x<0时,u(x)<0.对a分类讨论:a≤0时,0<a<1时,当a=1时,a>1时,利用导数研究函数的单调性极值即可得出.6、【答案】(1)解:函数f(x)=e x cosx﹣x的导数为f′(x)=e x(cosx﹣sinx)﹣1,可得曲线y=f(x)在点(0,f(0))处的切线斜率为k=e0(cos0﹣sin0)﹣1=0,切点为(0,e0cos0﹣0),即为(0,1),曲线y=f(x)在点(0,f(0))处的切线方程为y=1;(2)解:函数f(x)=e x cosx﹣x的导数为f′(x)=e x(cosx﹣sinx)﹣1,令g(x)=e x(cosx﹣sinx)﹣1,则g(x)的导数为g′(x)=e x(cosx﹣sinx﹣sinx﹣cosx)=﹣2e x•sinx,当x∈[0,],可得g′(x)=﹣2e x•sinx≤0,即有g(x)在[0, ]递减,可得g(x)≤g(0)=0,则f(x)在[0, ]递减,即有函数f(x)在区间[0, ]上的最大值为f(0)=e0cos0﹣0=1;最小值为f()=e cos ﹣=﹣.【考点】利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程【解析】【分析】(1.)求出f(x)的导数,可得切线的斜率和切点,由点斜式方程即可得到所求方程;(2。
2017函数导数专题(文)(2017高考真题分专题复习)
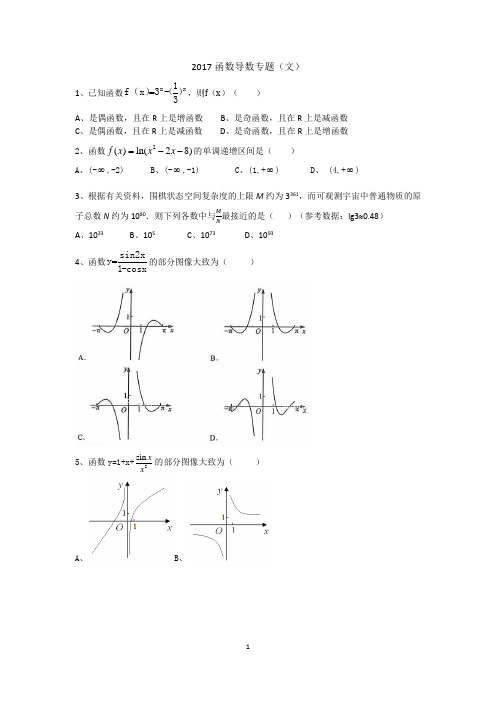
2017函数导数专题(文)1、已知函数xx )31(-3)x (f =,则f (x )( ) A 、是偶函数,且在R 上是增函数 B 、是奇函数,且在R 上是减函数C 、是偶函数,且在R 上是减函数D 、是奇函数,且在R 上是增函数2、函数2()ln(28)f x x x =--的单调递增区间是( )A 、(-∞,-2)B 、(-∞,-1)C 、(1,+∞)D 、 (4,+∞)3、根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N 最接近的是( )(参考数据:lg3≈0.48) A 、1033 B 、105 C 、1073 D 、10934、函数cosx-1sin2x y =的部分图像大致为( )A 、B 、C 、D 、 6、已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a=( ) 7、已知函数f (x )=lnx +ln(2−x ),则( )A 、f (x )在(0,2)单调递增B 、f (x )在(0,2)单调递减C 、y =f (x )的图像关于直线x =1对称D 、y =f (x )的图像关于点(1,0)对称8、设())021<<1,1=-≥⎪⎩x f x x x ,若f (a )=f (a +1),则1=⎛⎫ ⎪⎝⎭f a ( ) A 、2 B 、4 C 、6 D 、89、已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==,则,,a b c 的大小关系为( )A 、a b c <<B 、b a c <<C 、c b a <<D 、c a b <<10、若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – m ( )A 、与a 有关,且与b 有关B 、与a 有关,但与b 无关C 、与a 无关,且与b 无关D 、与a 无关,但与b 有关11、若函数()x e fx (e=2.71828……是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质,下列函数中具有M 性质的是() A 、()2-x f x = B 、()2f x =x C 、()3-xf x = D 、()cos f x =x12、已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ,若关于x 的不等式()||2x f x a ≥+在R 上恒成立,则a 的取值范围是( )A 、[2,2]-B 、[2]-C 、[2,-D 、[-13、已知a ∈R ,设函数()ln f x ax x =-的图象在点(1,(1)f )处的切线为l ,则l 在y 轴上的截距为 .14、已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当[3,0]x ∈-时,()6xf x -=,则f (919)= .1516、曲线在点(1,2)处的切线方程为_________________________.17、已知函数()f x 是定义在R 上的奇函数,当x ()-,0∈∞时,()322=+f x x x ,则()2=f18、已知函数()e cos x f x x x =-. (1)求曲线()y f x =在点(0,(0))f 处的切线方程;(2)求函数f (x )在区间[0,,π2]上的最大值和最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数导数1(2017北京文)已知函数,则(A )是偶函数,且在R 上是增函数 (B )是奇函数,且在R 上是增函数 (C )是偶函数,且在R 上是减函数 (D )是奇函数,且在R 上是增函数 2(2017北京文)(本小题13分)已知函数.(Ⅰ)求曲线在点处的切线方程; (Ⅱ)求函数在区间上的最大值和最小值. 3(2017新课标Ⅱ理)(12分)已知函数2()ln f ax a x x x x =--,且()0f x ≥.(1)求a ;(2)证明:()f x 存在唯一的极大值点0x ,且220e ()2f x --<<. 4(2017天津理)(本小题满分14分)设a ∈Z ,已知定义在R 上的函数432()2336f x x x x x a =+--+在区间(1,2)内有一个零点0x ,()g x 为()f x 的导函数. (Ⅰ)求()g x 的单调区间;(Ⅱ)设00[1,)(,2]m x x ∈ ,函数0()()()()h x g x m x f m =--,求证:0()()0h m h x <; (Ⅲ)求证:存在大于0的常数A ,使得对于任意的正整数,p q ,且00[1,)(,2],px x q∈ 满足041||p x q Aq-≥. 1()3()3x xf x =-()f x ()e cos x f x x x =-()y f x =(0,(0))f ()f x π[0,]25(2017新课标Ⅲ理数)(12分)已知函数()f x =x ﹣1﹣a ln x . (1)若()0f x ≥ ,求a 的值;(2)设m 为整数,且对于任意正整数n ,21111++1+)222n ()(1)(﹤m ,求m 的最小值.6(2017山东理)(本小题满分13分)已知函数()22cos f x x x =+,()()cos sin 22x g x e x x x =-+-,其中 2.71828e = 是自然对数的底数.(Ⅰ)求曲线()y f x =在点()(),f x π处的切线方程;(Ⅱ)令()()()()h x g x af x a R =-∈,讨论()h x 的单调性并判断有无极值,有极值时求出极值.7(2017天津文)(本小题满分14分)设,a b ∈R ,||1a ≤.已知函数32()63(4)f x x x a a x b =---+,()e ()x g x f x =.(Ⅰ)求()f x 的单调区间;(Ⅱ)已知函数()y g x =和e x y =的图象在公共点(x 0,y 0)处有相同的切线, (i )求证:()f x 在0x x =处的导数等于0;(ii )若关于x 的不等式()e x g x ≤在区间00[1,1]x x -+上恒成立,求b 的取值范围.8(2017新课标Ⅰ理数)(12分) 已知函数2()(2)x x f x ae a e x =+--. (1)讨论()f x 的单调性;(2)若()f x 有两个零点,求a 的取值范围. 9(2017江苏)(本小题满分16分)已知函数有极值,且导函数的极值点是的零点.(极值点是指函数取极值时对应的自变量的值)32()1(0,)f x x ax bx a b =+++>∈R ()f x '()f x(1)求关于的函数关系式,并写出定义域; (2)证明:;(3)若,这两个函数的所有极值之和不小于,求的取值范围.10(2017新课标Ⅱ文)(12分) 设函数2()(1)e x f x x =-. (1)讨论()f x 的单调性;(2)当0x ≥时,()1f x ax ≤+,求a 的取值范围.11(2017北京理)(本小题13分)已知函数f (x )=e x cos x −x .(Ⅰ)求曲线y = f (x )在点(0,f (0))处的切线方程; (Ⅱ)求函数f (x )在区间[0,]上的最大值和最小值.12(2017浙江)(本题满分15分)已知函数f (x )=(x(). (Ⅰ)求f (x )的导函数;(Ⅱ)求f (x )在区间上的取值范围. 13(2017新课标Ⅲ文数)(12分)已知函数()f x =ln x +ax 2+(2a +1)x . (1)讨论()f x 的单调性; (2)当a ﹤0时,证明3()24f x a≤--.14(2017新课标Ⅰ文数)(12分)已知函数()f x =e x (e x ﹣a )﹣a 2x .(1)讨论()f x 的单调性;(2)若()0f x ≥,求a 的取值范围.b a 23b a >()f x ()f x '72-a π2e x -12x ≥1[+)2∞,15(2017山东文)(本小题满分13分)已知函数()3211,32f x x ax a =-∈R . (Ⅰ)当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程;(Ⅱ)设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.16(2017浙江)若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – m A .与a 有关,且与b 有关 B .与a 有关,但与b 无关 C .与a 无关,且与b 无关D .与a 无关,但与b 有关17(2017浙江)函数y=f (x )的导函数的图象如图所示,则函数y=f (x )的图象可能是(第7题图)18(2017新课标Ⅲ文数)函数y =1+x +2sin xx 的部分图像大致为( )A BD .()y f x '=C D19(2017新课标Ⅲ文数)已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =( )A .12- B .13C .12D .120(2017新课标Ⅲ文数)设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________.21(2017新课标Ⅲ理数)已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12- B .13C .12D .122(2017新课标Ⅲ理数)设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是_________。
23(2017新课标Ⅱ文)函数2()ln(28)f x x x =--的单调递增区间是 A .(,2)-∞- B . (,1)-∞ C . (1,)+∞ D . (4,)+∞24(2017新课标Ⅱ文)已知函数()f x 是定义在R 上的奇函数,当(,0)x ∈-∞时,32()2f x x x =+,则(2)f =.25(2017新课标Ⅱ理)若2x =-是函数21()(1)ex f x x ax -=+-的极值点,则()f x 的极小值为 A .1-B .32e --C .35e -D .126(2017新课标Ⅰ文数)函数sin21cos xy x=-的部分图像大致为27(2017新课标Ⅰ文数)已知函数()ln ln(2)f x x x =+-,则 A .()f x 在(0,2)单调递增B .()f x 在(0,2)单调递减C .y =()f x 的图像关于直线x =1对称D .y =()f x 的图像关于点(1,0)对称28(2017新课标Ⅰ文数)曲线21y x x=+在点(1,2)处的切线方程为_________________________.29(2017新课标Ⅰ理数)函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是 A .[2,2]-B .[1,1]-C .[0,4]D .[1,3](6)(2017天津文)已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==,则,,a b c 的大小关系为(A )a b c <<(B )b a c <<(C )c b a <<(D )c a b <<30(2017天津文)已知函数||2,1,()2, 1.x xf x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ,若关于x 的不等式()||2xf x a ≥+在R 上恒成立,则a 的取值范围是 (A )[2,2]-(B)[-(C)[-(D)[-zx xk31(2017天津文)已知a ∈R ,设函数()ln f x ax x =-的图象在点(1,(1)f )处的切线为l,则l 在y 轴上的截距为 .32(2017天津理)已知奇函数()f x 在R 上是增函数,()()g x xf x =.若2(log 5.1)a g =-,0.8(2)b g =,(3)c g =,则a ,b ,c 的大小关系为(A )a b c << (B )c b a << (C )b a c <<(D )b c a <<33(2017天津理)已知函数23,1,()2, 1.x x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩设a ∈R ,若关于x 的不等式()||2xf x a ≥+在R 上恒成立,则a 的取值范围是 (A )47[,2]16- (B )4739[,]1616-(C)[- (D)39[]16-34(2017山东文)设()()121,1x f x x x <<=-≥⎪⎩,若()()1f a f a =+,则1f a ⎛⎫= ⎪⎝⎭(A )2 (B )4 (C )6 (D )8(10)(2017山东文)若函数()e xf x (e=2.71828 是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质.下列函数中具有M 性质的是 (A )()2xf x -=(B )()2f x x =(C )()3xf x -=(D )()cos f x x =35(2017山东文)已知f (x )是定义在R 上的偶函数,且f (x +4)=f (x -2).若当[3,0]x ∈-时,()6x f x -=,则f (919)= .36(2017山东理)已知当[]0,1x ∈时,函数()21y mx =-的图象与y m 的图象有且只有一个交点,则正实数m 的取值范围是 (A )(])0,1⎡+∞⎣(B )(][)0,13,+∞(C)()⎡+∞⎣(D)([)3,+∞37(2017山东理)若函数()x e f x ( 2.71828e = 是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为.①()2x f x -= ②()3x f x -=③()3f x x = ④()22f x x =+38(2017江苏)已知函数,其中e 是自然对数的底数.若,则实数的取值范围是 ▲ .39(2017江苏).设是定义在上且周期为1的函数,在区间上,其中集合,,则方程的解的个数是 ▲ . 40(2017北京理)已知函数,则(A )是奇函数,且在R 上是增函数 (B )是偶函数,且在R 上是增函数 (C )是奇函数,且在R 上是减函数(D )是偶函数,且在R 上是减函数31()2e e xxf x x x =-+-2(1)(2)0f a f a -+≤a ()f x R [0,1)2,,(),,x x D f x x x D ⎧∈⎪=⎨∉⎪⎩1{n D x x n-==*}n ∈N ()lg 0f x x -=1()3()3x xf x =-()f x。
