从零开始3D maxwell磁场仿真之边界条件
从零开始3D maxwell磁场仿真之建模

从零开始学习3D MAXWELL之建模1,教程概要2,MAXWELL软件建模3,外部设计导入4,注意事项一,教程概要1,为什么是maxwell?ansoft maxwell(ansoft maxwell EM)是一种工业应用中的电磁软件,是电磁场分析软件,ANSOFT制作发行于2003年。
工业应用中的电磁元件,如传感器,调节器,电动机,变压器都可以利用maxwell仿真电磁场方面的问题,自带的电机仿真模块更是行业的标杆。
2,为什么是maxwell 3D?Maxwell 3D有向导式的用户界面、精度驱动的自适应剖分技术和强大的后处理能力使Maxwell 3D成为业界最佳的高性能三维电磁设计软件。
Maxwell 3D可以分析涡流、位移电流、集肤效应和邻近效应等具有不可忽视作用的影响,可以得到电机、母线、变压器、线圈等电磁部件的整体特性。
而且功率损耗、线圈损耗、某一频率下的阻抗(R和L)、力、转矩、电感、储能等参数可以自动计算,同时也可以给出整个相位的磁力线、B和H分布图、能量密度、温度分布等图形结果。
并且3D结构更具有直观性,可以清晰的向其他人分享自己的设计,能够更加生动的向人展示整个使用过程中的电磁变化。
3,使用maxwell自带的命令还是外部导入?对于结构简单的器件,建议直接使用maxwell自带的命令建立模型,这样得到的模型会减少剖分和处理的时间,提高仿真的效率。
但是对于结构复杂的器件,自带的命令很难/或是需要耗费很多的时间来建立模型,这样可以使用solidworks或是proe等三位软件直接建立模型后转成maxwell可以接受的模型并导入设计。
这样可以节省时间。
但是如果模型中有很多圆弧倒角和小尺寸的细节部分,会导致仿真时间的增加。
二,maxwell软件建模1,画线命令‐‐‐画直线命令:直线/曲线/圆弧/公式曲线。
这些操作都是所见即所得,很简单,只有公式曲线输入稍有困难。
‐‐‐画面命令:矩形/多边形/椭圆/公式曲面‐‐‐画体命令:圆柱/长方体/多面体/圆锥体/球体/弹簧/螺旋备注:弹簧和螺旋命令很有用,需要额外学习下。
【精品】第八讲:麦克斯韦方程组、电磁场的边界条件
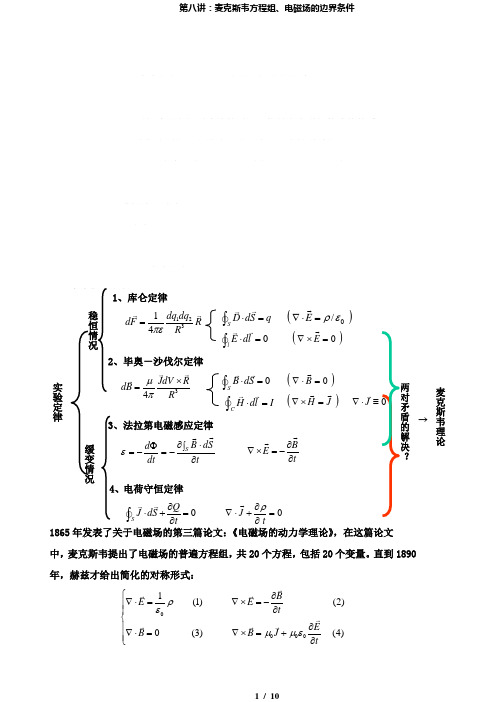
第八讲:麦克斯韦方程组、电磁场的边界条件2.6麦克斯韦方程组2.7电磁场的边值关系1、了解麦克斯韦方程组的建立过程,掌握它的基本性质;2、了解边界上场不连续的原因,能导出电磁场的边值关系;3、掌握电磁场方程微分形式和边界形式的联系与区别。
重点:1)麦克斯韦方程组的基本性质;2)电磁场的边值关系 难点:电磁场切向边值关系的推导 讲授法、讨论 2学时2.6麦克斯韦方程组(Maxwell ’sEquations )一、麦克斯韦方程1865年发表了关于电磁场的第三篇论文:《电磁场的动力学理论》,在这篇论文中,麦克斯韦提出了电磁场的普遍方程组,共20个方程,包括20个变量。
直到1890 年,赫兹才给出简化的对称形式:00001(1)(2)0(3)(4)BE E tE B B J tρεμμε⎧∂∇⋅=∇⨯=-⎪∂⎪⎨∂⎪∇⋅=∇⨯=+⎪∂⎩实验定律3、法拉第电磁感应定律4、电荷守恒定律12314dq dq dF RR πε=S D dS q ⋅=⎰0l E dl ⋅=⎰34JdV R dB R μπ⨯=0SB dS ⋅=⎰()0=⋅∇B CH dl I ⋅=⎰()JH =⨯∇tB E ∂∂-=⨯∇ 0=∂∂+⋅∇tJ ρ 0J ∇⋅≡对矛盾的解决麦克斯韦理论稳恒况缓变情况2、毕奥-沙伐尔定律1、库仑定律()/ερ=⋅∇E()=⨯∇E t S d B dt d S ∂⎰⋅∂-=Φ-= ε0S QJ dS t ∂⋅+=∂⎰→上式即为真空中的麦克斯韦方程组,其中(2)(4)含有对时间的偏导数,对应 运动方程,(1)(3)为约束方程。
二、麦克斯韦方程组的基本性质 1、线性性麦克斯韦方程组是一组线性方程,表明场服从迭加原理。
2、自洽性方程组各个方程彼此协调,且与电荷守恒定律协调。
如(2)式和(3)式一致:由(2)式有:()0=∂⋅∂∇-=⨯∇⋅∇tBE⇒C B =⋅∇ ,考虑到静磁时0=⋅∇B,所以取0=C 。
第二章边界条件

第二章:边界条件这一章主要介绍使用边界条件的基本知识。
边界条件能够使你能够控制物体之间平面、表面或交界面处的特性。
边界条件对理解麦克斯韦方程是非常重要的同时也是求解麦克斯韦方程的基础。
§2.1 为什么边界条件很重要用Ansoft HFSS求解的波动方程是由微分形式的麦克斯韦方程推导出来的。
在这些场矢量和它们的导数是都单值、有界而且沿空间连续分布的假设下,这些表达式才可以使用。
在边界和场源处,场是不连续的,场的导数变得没有意义。
因此,边界条件确定了跨越不连续边界处场的性质。
作为一个 Ansoft HSS 用户你必须时刻都意识到由边界条件确定场的假设。
由于边界条件对场有制约作用的假设,我们可以确定对仿真哪些边界条件是合适的。
对边界条件的不恰当使用将导致矛盾的结果。
当边界条件被正确使用时,边界条件能够成功地用于简化模型的复杂性。
事实上,Ansoft HSS 能够自动地使用边界条件来简化模型的复杂性。
对于无源RF 器件来说,Ansoft HSS 可以被认为是一个虚拟的原型世界。
与边界为无限空间的真实世界不同,虚拟原型世界被做成有限的。
为了获得这个有限空间, Ansoft HSS使用了背景或包围几何模型的外部边界条件。
模型的复杂性通常直接与求解问题所需的时间和计算机硬件资源直接联系。
在任何可以提高计算机的硬件资源性能的时候,提高计算机资源的性能对计算都是有利的。
§2.2 一般边界条件有三种类型的边界条件。
第一种边界条件的头两个是多数使用者有责任确定的边界或确保它们被正确的定义。
材料边界条件对用户是非常明确的。
1、激励源波端口(外部)集中端口(内部)2、表面近似对称面理想电或磁表面辐射表面背景或外部表面3、材料特性两种介质之间的边界具有有限电导的导体§2.3 背景如何影响结构所谓背景是指几何模型周围没有被任何物体占据的空间。
任何和背景有关联的物体表面将被自动地定义为理想的电边界(Perfect E)并且命名为外部(outer)边界条件。
maxwell的边界条件

maxwell的边界条件Maxwell的边界条件是电磁场理论中的重要概念,它描述了电磁波在两种介质之间传播时的行为。
这些边界条件起着关键作用,帮助我们理解和解决各种电磁问题。
本文将详细介绍Maxwell的边界条件,并讨论它们在实际应用中的意义和影响。
我们来了解一下Maxwell的边界条件是什么。
在电磁场理论中,Maxwell方程组描述了电场和磁场的演化和相互作用。
当电磁波在两种介质之间传播时,它们必须满足一定的条件,这些条件被称为Maxwell的边界条件。
这些条件是在介质界面上成立的,用于描述电磁场的连续性和边界行为。
我们来看一下Maxwell的第一边界条件,即电场的切向分量在界面上连续。
这意味着当电磁波从一种介质传播到另一种介质时,电场的方向和大小在界面上保持不变。
这个条件的物理意义是介质界面上没有电荷堆积或电流流失,从而保证了电场的连续性。
接下来,我们来讨论Maxwell的第二边界条件,即磁场的切向分量在界面上连续。
这意味着当电磁波从一种介质传播到另一种介质时,磁场的方向和大小在界面上保持不变。
这个条件的物理意义是介质界面上没有磁荷堆积或磁流失,从而保证了磁场的连续性。
除了以上两个边界条件,Maxwell的第三边界条件是电场和磁场的法向分量在界面上满足一定的关系。
具体来说,电场和磁场的法向分量的叉乘等于界面上的表面电流密度。
这个条件的物理意义是介质界面上的电荷和电流会影响电磁场的分布和传播。
我们来讨论Maxwell的第四边界条件,即介质界面上的法向分量的叉乘等于零。
这意味着在介质界面上没有自由电荷产生的电流。
这个条件的物理意义是介质界面上的电荷和电流的分布不会产生额外的电场和磁场。
Maxwell的边界条件在电磁场理论和应用中起着重要的作用。
它们帮助我们理解电磁波在不同介质中的传播和反射现象。
通过将Maxwell的边界条件应用到具体问题中,我们可以计算电磁场的分布和传播特性,解决各种电磁问题。
Maxwell的一些操作操作技巧

Maxwell的⼀些操作操作技巧Maxwell的⼀些操作操作技巧我很早前发的⼀个帖⼦从simwe上复制粘贴过来希望对⼤家有⽤PS:为了节约⼤家的银⼦,就没有发word版本的附件了这个写的是maxwell 10.0版本时候的现在⼤家可能都⽤11.0了,11.0跟10.0相⽐变化还是很⼤的,到11.0时候我就没有⽤过了在此抛砖引⽟,希望有⼈来个11.0的介绍⽼早就说把Maxwell后处理的⼀些操作给整理⼀下,可是⼀直⽐较忙。
昨天写了⼤半天,可是越写越发现⾃⼰知道的东西好少,⽽且我以前⼀直都没有发现关于后处理的帮助,但还是尽我所知写了些东西。
希望对⼤家有所帮助。
我主要是把关于后处理器的⼀些操作的功能写出来了。
其实后处理对理论要求还是很⾼的,因为求解得出的只有⼀些基本的量,⽐如BHJ,其他你想得到的就要⽤各种公式得到了。
我还把前处理⼀些我以前⾛了点弯路的地⽅也写出来了。
也希望由我开个头,⼤家把⾃⼰知道的觉得对⼤家有⽤的东西都整理⼀下,贴出来,让别⼈少⾛点弯路。
其实有些东西你会了可能觉得很简单,但是初学者可能要摸索很久。
⼀、模型建⽴Draw模块中各个选项介绍。
File就不⽤多说了。
EditAttribute ⽤来改变已经建⽴模型的属性。
主要有名称、颜⾊。
Visibility ⽤来改变模型是否显⽰出来。
Viewsetup grid ⽤来设置坐标系,⼯作平⾯的⼤⼩,以及⼯作平⾯中⿏标可选择的最⼩距离。
这对有时候直接⽤⿏标建图形⽐较有⽤。
Coordinates 设置坐标系,可以将坐标系原点移到到当前选取的点的位置。
还可以旋转坐标系。
在取截⾯或者局部由⾯旋转成体的时候⽐较有⽤Lines ⽣成线。
如果⽣成的线闭合,则Covered选项可选,选择后⽣成以闭合线为边界的⾯。
Surface ⽤来⽣成⾯。
Cover Lines 由闭合的线⽣成⾯Uncover Face 由⾯得到外边界的线。
Detach Face 将⼀部分⾯由整个⾯中分离出来。
MAXWELL2D,3D使用说明

MAXWELL2D,3D使⽤说明Ansoft Maxwell 2D/3D 使⽤说明⽬录第1章Ansoft 主界⾯控制⾯板简介第2章⼆维(2D)模型计算的操作步骤2、1 创建新⼯程 (2)2、2 选择求解问题的类型 (3)2、3 创建模型(Define Model) (4)2、4 设定模型材料属性(Setup Materials) (6)2、5 设定边界条件与激励源(Setup Boundaries/Sources) (8)2、6 设定求解参数(Setup Executive Parameters) (9)2、7 设定求解选项(Setup Solution Options) (10)2、8 求解(Solve) (10)2、9 后处理(Post Process) (11)2、10 ⼯程应⽤实例 (12)第3章三维(3D)模型计算的操作步骤3、1 建模 (14)3、2 定义材料属性 (17)3、3 加载激励与边界条件 (18)3、4 设置求解选项与求解 (18)3、5 后处理 (18)3、6 补充说明 (18)3、7 例 1 两电极电场计算 (18)3、8 例 2 电压互感器下半部分电场计算 (22)第4章有限元⽅法简介4、1 有限元法基本原理 (28)4、2 有限元⽹格⾃适应剖分⽅法 (29)第1章Ansoft 主界⾯控制⾯板简介在Windows下安装好Ansoft软件的电磁场计算模块Maxwell之后,点击Windows 的“开始”、“程序”项中的Ansoft、Maxwell Control Panel,可出现主界⾯控制⾯板(如下图所⽰),各选项的功能介绍如下。
1、1 ANSOFT介绍Ansoft公司的联系⽅式,产品列表与发⾏商。
1、2 PROJECTS创建⼀个新的⼯程或调出已存在的⼯程。
要计算⼀个新问题或调出过去计算过的问题应点击此项。
点击后出现⼯程控制⾯板,可以实现以下操作:●新建⼯程。
●运⾏已存在⼯程。
从零开始3Dmaxwell磁场仿真之边界条件

从零开始3Dmaxwell磁场仿真之边界条件从零开始学习3D MAXWELL之边界条件MAXWELL仿真电磁场的本质还是计算麦克斯维尔⽅程,所以要定义仿真的边界条件,这样才能得到⽅程的解。
3D仿真⼀共有六种求解类型,为静磁场/涡流/瞬态磁场/静电场/传导/瞬态电场。
每⼀种求解类型都有边界条件。
1,静磁场求解器边界条件默认边界条件⽰意图如下:(默认边界条件普遍存在于Maxwell 3D仿真的各种求解器中。
正确应⽤默认边界条件,求解域的设置⾮常关键。
尼曼边界条件将磁场限定在边界之内。
当磁场较封闭或求解域⾜够⼤时,应⽤尼曼边界条件才会得到相对正确的分析结果。
)磁场边界条件:磁场边界条件指定在求解域表⾯:1)定义切向⽅向磁场强度为零的边界条件:选择要添加边界条件的⾯--增加切线⽅向磁场强度为零的磁场;2)定义正切磁场边界条件:选择要添加边界条件的⾯--增加正切磁场--增加X/Y⽅向的磁场分量值--在坐标系统中定义X/Y⽮量或是使⽤默认值;(正切⽅向为零,磁场⽅向与表⾯垂直)(磁场边界条件,磁场的切向分量被指定为预定义的值,但如果该分量的值被指定为0,则其效果与Zero Tangential H Field相同,磁场与该边界垂直,适⽤于施加外部磁场,如地磁仿真。
)绝缘边界条件,除电流⽆法穿过边界以外,其他特性与Neumann边界相同,适⽤于2个接触导体之间完美绝缘的薄⽚。
(未添加绝缘边界条件)(添加绝缘边界条件后)对称边界条件:对称边界条件适合⼏何对称或是磁场对称的结构。
对称边界条件,奇对称(磁⼒线正切),磁场与边界正切,磁场法向分量为0;偶对称(磁⼒线垂直),磁场与边界垂直,磁场切向分量为0。
对称边界条件主要⽤来减少仿真时间,增加计算效率。
匹配边界条件,有主边界(Master)和从边界(Slave)两种,需要配合使⽤。
偶对称时,Slave边界的磁场被定义为匹配Master边界的幅值和⽅向。
奇对称时,Slave边界的磁场与Master边界的幅值相同,⽅向相反。
maxwell方程组及边界条件

CQU
将电荷守恒定律 J c t
D 0 t
带入上式
D C
时变场中不考虑恒定量,令 C =0
D
磁通连续性原理
B ( B) ( E ) 0 t t
B 0
CQU
0 (静态场) 当 t
D H J t
B E t B 0 D
恒定场是时变电磁场的特殊形式
H J
E 0 B 0 D
s
高斯定律
s
D dS q
麦克斯韦第一、二方程是独立方程,后面两个方程可以从 中推得,由第1方程推导高斯定律。
D H J c v 对第一方程 两边取散度 t D H J c t D 左边为零,右边整理后得 J c D t t
cqu53电磁场基本方程组分界面上的衔接条件531电磁场基本方程组1865年maxwell总结了电磁场基本方程组maxwell方程为全电流定律磁通连续性原理高斯定律全电流定律麦克斯韦第一方程表明传导电流和时变的电场都能产生磁场
5.3
5.3.1
电磁场基本பைடு நூலகம்程组 • 分界面上的衔接条件
CQU
电磁场基本方程组
积分形式
D 全电流定律 l H dl s J c dS s t dS s v dS B dS 电磁感应定律 l E dl S t 磁通连续性原理 B dS 0
en B2 B1 0
微波仿真论坛_Maxwell软件使用技巧

一、模型建立Draw模块中各个选项介绍。
File就不用多说了。
EditAttribute 用来改变已经建立模型的属性。
主要有名称、颜色。
Visibility 用来改变模型是否显示出来。
Viewsetup grid 用来设置坐标系,工作平面的大小,以及工作平面中鼠标可选择的最小距离。
这对有时候直接用鼠标建图形比较有用。
Coordinates 设置坐标系,可以将坐标系原点移到到当前选取的点的位置。
还可以旋转坐标系。
在取截面或者局部由面旋转成体的时候比较有用Lines 生成线。
如果生成的线闭合,则Covered选项可选,选择后生成以闭合线为边界的面。
Surface 用来生成面。
Cover Lines 由闭合的线生成面Uncover Face 由面得到外边界的线。
Detach Face 将一部分面由整个面中分离出来。
Move Face 将面沿法线方向或者沿一个矢量方向移动。
Section 对一个体或者面取截面,用xy、yz或者xy截面去切体或者面,得到一个闭合的曲线Connect 得到以所选两条曲线为两端的一个柱面(长方体的侧面或者其他不规则的面)。
Sitch 将两个面粘合成一个面如果操作过程中提示你操作会失去原来的面或者线的时候,不妨把面或者线先copy,操作了之后再paste就好。
Solid 用来生成体。
第一栏用来直接生成一些规则的体。
Sweep是通过旋转、拉伸面模型得到体。
第二栏是对体进行一些布尔操作,如加减等。
Split是将一个体沿一个面(xy、yz、xz)劈开成两部分,可以选择要保留的部分。
在减操作时,如有必要,还是先copy一下被减模型。
第三栏cover surface是通过闭合的曲面生成体。
Arrange 选取模型组件后,对模型组件进行移动、旋转、镜像(不保存原模型)、缩放等操作。
Options 用来进行一些基本的设置。
单位的转换,检查两个体是否有重叠(保存的时候会自动检查)、设置background大小、定义公式以及设置颜色。
第2章1-2 Maxwell方程组与边界条件 [兼容模式]
![第2章1-2 Maxwell方程组与边界条件 [兼容模式]](https://img.taocdn.com/s3/m/c86945e19e3143323968932a.png)
矢量恒等式: A (A) 2A 理想介质内部无自由电荷的条件: E(x,y,z) = 0
2E(x,y,z) + 2 E(x,y,z) 0 2H(x,y,z) + 2 H(x,y,z) 0
(2-6a) (2-6b)
理想介质中电磁场的波动方程(两个一元二次偏微 分方程,有对称性)
2016/2/26 8
第二章 电磁波传输系统理论
——麦克斯韦方程组和边界条件
辅助方程(物质方程):
,, 是表征媒质电磁性质的三个参量,它们都有量纲,一
般说来可能与 x,y,z,t 有关。 有关
—— 电容率(法拉/米), —— 磁导率 率 (亨利/米), —— 电导率 (西门子/米 1/欧姆米)。
r和r 是相对于真空而言的相对值,是无量纲的数值。
2016/2/26
Байду номын сангаас
11
第二章 电磁波传输系统理论
——麦克斯韦方程组和边界条件
求解一个任意截面、无限长、均匀传输系统内的电磁场。 麦克斯韦方程组是一个矢量偏微分方程组
分别求解矢量各分量所满足的偏微分方程
分离变量
(试探解)
2016/2/26
将偏微分方程分解为若干常微分方程
2016/2/26 10
第二章 电磁波传输系统理论
——麦克斯韦方程组和边界条件 方
真空中的介电常数和磁导率为: 0 8.854 真空中的介电常数和磁导率为 8 8541012 (法拉/米), 0 1.2566106 (亨利/米),都有量纲,但与 x,y,z,t 无关。
对于均匀(与坐标、时间无关)、线性(与场强无关,不产生新的频 率分量,可应用线性叠加原理)、各向同性 (与方向无关,标量) 的媒质,定义相对介电常数r 和相对磁导率r : r 0 (2-3a) r 0 (2 3b) (2-3b)
磁场边界条件磁屏蔽磁能
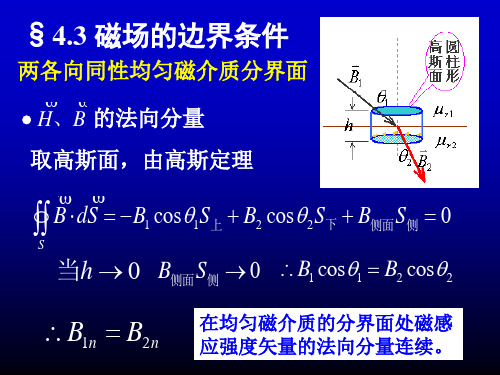
当电场和磁场共存时, 当电场和磁场共存时,由
1v v we = D⋅ E 2
1 v v wm = B⋅ H 2
得空间某点能量密度为
1v v 1 v v we = D⋅ E + B⋅ H 2 2
B1t
=
B2t
B1n = B2n
铁磁质µ很大, 铁磁质 很大,有铁磁质包围 很大 的空腔, 的空腔,外界 B线进入铁磁质 线进入铁磁质 后变为几乎与界面平行, 后变为几乎与界面平行,很少 有外磁场进入腔内
v B
磁场的能量与能量密度
按照近距作用观点, 按照近距作用观点,磁能是 定域在磁场中的
µ0
µr
长度为l的一段 的一段同轴传输线之磁能 例: 求长度为 的一段同轴传输线之磁能
I µr µ0I H= B =µr µ0H = 2πr 2π r 1 µrµ0I 2 wm = BH = 2 2 2 8π r
dV = 2π rldr
Wm = ∫ wm dV =
R 1 R2
µr µ0I 2l
4π
∫
R2
R 1
dr r
=
µrµ0I l
2
4π
R2 ln R 1
这段同轴电缆的自感为
2Wm µr µ0l R2 Ll = 2 = ln I 2π R1
也可采用下面的方法求自感 同轴电缆内的总磁通量 µ0µr Il R2 R2 µ0µr I l ln Φ = ∫ dΦ = ∫R dr = 2π R 1 2πr 1
Φ µr µ0l R2 L= = ln I 2π R1
定义磁能密度
Wm 1 wm = = BH V 2
可以证明: 可以证明:在普遍情况下有 1 v v wm = B⋅ H 2 总磁能
maxwell中boundaries and excitations

maxwell中boundaries and excitations Maxwell方程组是电磁学中的基本方程组,描述了电场和磁场如何相互作用和运动。
当这些方程被应用于特定情境时,会引出一些边界条件和激发现象的考虑。
本文将详细说明Maxwell方程组的边界条件和激发现象。
一、边界条件Maxwell方程组描述了电磁场的起源和演化,但在特定问题中,电磁场必须满足某些边界条件才能符合实际情况。
下面是Maxwell方程组的边界条件:1. 电场和磁场的法向分量(即与边界垂直的分量)在界面上是连续的。
2. 电场和磁场的切向分量(即与边界平行的分量)在界面上满足以下关系式:(a)电场的切向分量在界面上是连续的。
(b)磁场的切向分量在界面上是连续的。
3. 对于导体表面,电场切向分量为零。
这些边界条件反映了电场和磁场在边界上的行为。
根据这些条件,可以在给定问题中解出满足边界条件的电磁场的分布。
二、激发现象在一些特定情况下,电磁场可以由激励源引起。
这些激励源可以是电流、电荷、变化的磁场等等。
根据Maxwell方程组,可以推导出在激发源存在的情况下电磁场的行为。
1. 静电场的激发:在没有变化的电流或磁场情况下,电磁场方程简化为静电场方程,即库仑定律。
在这种情况下,只有电场分量存在,并且由电荷分布引起。
2. 静磁场的激发:在没有变化的电流或电场情况下,电磁场方程简化为静磁场方程,即安培定律。
在这种情况下,只有磁场分量存在,并且由电流分布引起。
3. 变化的电场的激发:当电流变化时,电磁场会产生变化,根据法拉第电磁感应定律,变化的电场会引起旋转的磁场。
这种激发现象被称为电磁感应。
4. 变化的磁场的激发:同样地,当电场的变化率发生变化时,根据法拉第电磁感应定律,变化的磁场会引起旋转的电场。
这种激发现象被称为电磁感应。
这些激发现象在电磁学中起着重要的作用,它们描述了电磁场是如何与其它物质和场相互作用和演化的。
三、应用举例边界条件和激发现象在许多现实应用中发挥着关键作用。
MAXWELL2D,3D使用说明

Ansoft Maxwell 2D/3D 使用说明目录第1章Ansoft 主界面控制面板简介第2章二维(2D)模型计算的操作步骤2.1 创建新工程 (2)2.2 选择求解问题的类型 (3)2.3 创建模型(Define Model) (4)2.4 设定模型材料属性(Setup Materials) (6)2.5 设定边界条件和激励源(Setup Boundaries/Sources) (8)2.6 设定求解参数(Setup Executive Parameters) (9)2.7 设定求解选项(Setup Solution Options) (10)2.8 求解(Solve) (10)2.9 后处理(Post Process) (11)2.10 工程应用实例 (12)第3章三维(3D)模型计算的操作步骤3.1 建模 (14)3.2 定义材料属性 (17)3.3 加载激励和边界条件 (18)3.4 设置求解选项和求解 (18)3.5 后处理 (18)3.6 补充说明 (18)3.7 例 1 两电极电场计算 (18)3.8 例 2 电压互感器下半部分电场计算 (22)第4章有限元方法简介4.1 有限元法基本原理 (28)4.2 有限元网格自适应剖分方法 (29)第1章Ansoft 主界面控制面板简介在Windows下安装好Ansoft软件的电磁场计算模块Maxwell之后,点击Windows 的“开始”、“程序”项中的Ansoft、Maxwell Control Panel,可出现主界面控制面板(如下图所示),各选项的功能介绍如下。
1.1 ANSOFT介绍Ansoft公司的联系方式,产品列表和发行商。
1.2 PROJECTS创建一个新的工程或调出已存在的工程。
要计算一个新问题或调出过去计算过的问题应点击此项。
点击后出现工程控制面板,可以实现以下操作:●新建工程。
●运行已存在工程。
●移动,复制,删除,压缩,重命名,恢复工程。
maxwell边界条件问题
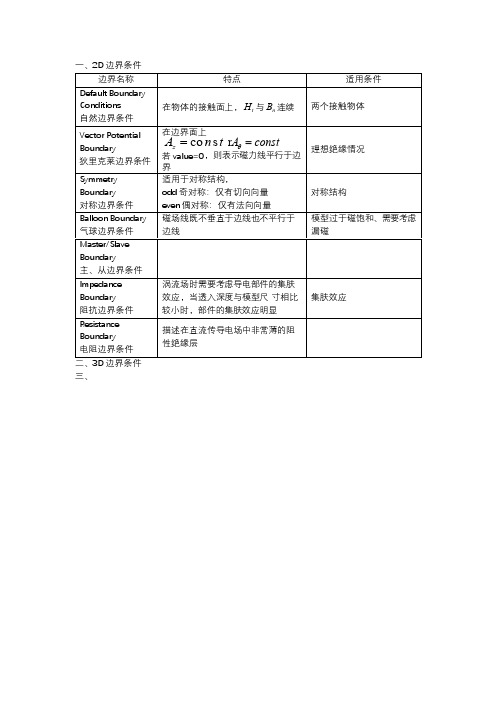
一、2D边界条件
边界名称特点适用条件Default Boundary
Conditions 自然边界条件在物体的接触面上,
t
H与
n
B连续两个接触物体
Vector Potential Boundary
狄里克莱边界条件在边界面上
co s
z
A n t
=r A const
θ
=
若value=0,则表示磁力线平行于边
界
理想绝缘情况
Symmetry Boundary
对称边界条件适用于对称结构,
odd奇对称:仅有切向向量
even偶对称:仅有法向向量
对称结构
Balloon Boundary 气球边界条件磁场线既不垂直于边线也不平行于
边线
模型过于磁饱和、需要考虑
漏磁
Master/Slave Boundary
主、从边界条件
Impedance Boundary
阻抗边界条件涡流场时需要考虑导电部件的集肤
效应,当透入深度与模型尺寸相比
较小时,部件的集肤效应明显
集肤效应
Resistance Boundary
电阻边界条件描述在直流传导电场中非常薄的阻性绝缘层
二、3D边界条件三、。
2.9 电磁场的边界条件

2.9 电磁场的边界条件自强●弘毅●求是●拓新实际电磁场问题都是在一定的空间和时间范围内发 生的,它有起始状态(静态电磁场例外)和边界状 态。
即使是无界空间中的电磁场问题,该无界空间也可 能是由多种不同介质组成的,不同介质的交界面和 无穷远界面上电磁场构成了边界条件。
边界条件: 即电磁场在不同介质的边界面上服从的条件,也可 以理解为界面两侧相邻点在无限趋近时所要满足的 约束条件。
边界条件是完整的表示需要导出界面两 侧相邻点电磁场矢量所满足的约束关系。
由于在分界面两侧介质的特性参数发生突变,场在界 面两侧也发生突变。
所以Maxwell方程组的微分形式 在分界面两侧失去意义(因为微分方程要求场量连续 可微)。
而积分方程则不要求电磁场量连续,从积分 形式的麦克斯韦方程组出发,导出电磁场的边界条件把积分Maxwell方程组应用到图所表示的两媒质交界 面的扁平圆盘。
根据Gauss定理,让h→0,场在扁平 圆盘壁上的通量为零,得到: n ˆ ˆ D ds D ( n ) S D ( n S ) D 1 2 S 2 ( D2 n D1n )S s Sˆ s (D2 D1 ) n ˆ 0 (B 2 B1 ) nhr2D1 r1在介质分界面两侧,选取如图所示的积环路,应用安培环路积 分公式: D H dl H l H ( l ) ( H H ) t l ( J ) ds 1 2 1 2 l S t t N n ( H 2 H1 ) t ( H 2 H1 ) ( N n ) ˆ J N ˆ ˆ (H H ) N n2 1 sˆ ( H 2 H1 ) J s nˆ ( E 2 E1 ) 0 nD 0 E P, B 0 H Mn ( P 2 P1 ) f n (M 2 M 1 ) J mˆ s (D 2 D1 ) nn ( H 2 H1 ) J s n (B 2 B1 ) 0 ( J f J m )n ( E2 E1 ) ( f p ) / 0①任何分界面上E的切向分量是连续的 ②在分界面上有面电荷(在理想导体表面上)时,D的法向分量不 连续,其差等于面电荷密度;否则,D的法向分量是连续的 ③在分界面上若存在面电流(仅在理想导体表面上存在),H的切 向分量 不连续 ,其差等于面电流密度;否则,H的切向分量是 连续的 ④任何分界面上B的法向分量是连续的理想介质理想介质是指 0,即无欧姆损耗的简单媒质。
磁场边界条件

在实际工程中,往往要遇到由不同的媒质组成的电磁系统。
在不同媒质分界面上,由于媒质的特性发生了突变,相应的场量一般也将发生突变。
在这一节中,我们将研究电磁场在两种媒质分界面上的变化规律。
决定分界面两侧电磁场变化关系的方程称为边界条件。
研究边界条件的出发点,仍然是麦克斯韦方程组。
但在不同媒质的交界面处,由于媒质不均匀,媒质的性质发生了突变,因此,微分形式的方程不再适用,只能从麦克斯韦方程组的积分形式出发,推导边界条件。
3.5.1 电场法向分量的边界条件如图 3.9所示的两种媒质的分界面,第一种媒质的介电常数、磁导率和电导率分别为,和,第二种媒质的介电常数、磁导率和电导率分别为,和。
在这两种媒质分界面上取一个小的柱形闭合面,如图3.9所示,其高为无限小量,上下底面与分界面平行,并分别在分界面两侧,且底面积非常小,可以认为在上的电位移矢量和面电荷密度是均匀的。
,分别为上下底面的外法线单位矢量,在柱形闭合面上应用电场的高斯定律故(3.48a)若规定为从媒质Ⅱ指向媒质Ⅰ为正方向,则,,式(3.48a)可写为(3.48b)或(3.48c)式(3.48)称为电场法向分量的边界条件。
因为,所以式(3.48)可以用的法向分量表示(3.49a)或(3.49b)若两种媒质均为理想介质时,除非特意放置,一般在分界面上不存在自由面电荷,即,所以电场法向分量的边界条件变为(3.50a)或(3.50b)若媒质Ⅰ为理想介质,媒质Ⅱ为理想导体时,导体内部电场为零,即,,在导体表面存在自由面电荷密度,则式(3.48)变为(3.51a)或(3.51b) 3.5.2 电场切向分量的边界条件在两种媒质分界面上取一小的矩形闭合回路abcd,如图3.10所示,该回路短边为无限小量,其两个长边为,且平行于分界面,并分别在分界面两侧。
在此回路上应用法拉第电磁感应定律因为和故(3.52a)若为从媒质Ⅱ指向媒质Ⅰ为正方向,式(3.52a)可写为(3.52b)式(3.52)称为电场切向分量的边界条件。
maxwell2d控制方程,计算区域大小,激励源,边界条件

Maxwell2D是一个二维电磁场仿真软件,其控制方程基于麦克斯韦方程组,包括电场和磁场的波动方程、以及电荷和电流的连续性方程。
在Maxwell2D中,可以通过指定不同的边界条件来模拟各种不同的情况。
常见的边界条件包括:完美电导体(PEC)、完美磁导体(PMC)、理想电绝缘体(IE)、理想磁绝缘体(IM)等。
在计算区域大小时,需要考虑所研究的电磁系统的规模和复杂性。
一般来说,计算区域应该足够大,以保证电磁波在边界外能够充分衰减,从而避免产生反射和干扰。
同时,计算区域的大小也需要根据具体的问题和场景来进行调整和优化。
激励源是用来产生电磁波的源,可以是电流、电压、电荷等。
在Maxwell2D中,可以通过定义不同的激励源来模拟各种不同的电磁波源,如天线、微波源等。
在设置激励源时,需要考虑其频率、幅度和相位等因素,以确保模拟结果的准确性和可靠性。
总之,Maxwell2D是一个强大的电磁场仿真工具,通过合理的设置控制方程、计算区域大小、激励源和边界条件,可以模拟各种不同的电磁波传播和散射现象,为电磁系统的设计和优化提供重要的支持。
maxwell中boundaries and excitations -回复

maxwell中boundaries and excitations -回复题目:Maxwell中的边界与激发导言:Maxwell方程组是描述电磁现象的基本物理定律,它们由詹姆斯·克拉克·麦克斯韦在19世纪提出。
其中,边界条件与激发是研究电磁波传播和电磁场变化的关键问题。
本文将以Maxwell方程组中的边界条件和激发为主题,一步一步回答这两个问题。
一、边界条件(Boundaries):边界条件是指电磁波传播或电磁场变化在介质界面上的行为。
根据Maxwell方程组,边界条件可以被量化为电场与磁场的连续性和法向分量的跃进关系。
1. 电场的连续性:在介质界面上,电场的切向分量可以不连续,但电场的法向分量必须连续。
这意味着,介质界面上的电场在跨越界面时会有突变。
2. 磁场的连续性:与电场类似,介质界面上的磁场的切向分量可以不连续,但磁场的法向分量必须连续。
这意味着,介质界面上的磁场在跨越界面时会有突变。
3. 法向分量的跃进关系:介质界面上的电场与磁场的法向分量之间存在一个跃进关系。
具体而言,电场法向分量的跃进值等于自由电荷面密度与介质内部电流密度之和与自由电流面密度之比。
而磁场法向分量的跃进值则等于介质内部电荷密度与自由电流面密度之和与介质内部电流密度之比。
通过以上三个条件,我们可以描述介质界面上电场和磁场的行为。
这些边界条件在求解电磁波方程时是非常重要的。
二、激发(Excitations):激发是指在Maxwell方程组中引入新的电流或电荷项,导致电磁场的时空变化。
有两种常见的激发方式:电流激发和电荷激发。
1. 电流激发:电流激发是指通过引入电流分布来改变电磁场的时空变化。
具体而言,我们可以通过在给定区域内施加电流源来激发电磁场的变化。
这可以通过引入电源的电流密度项来完成。
2. 电荷激发:电荷激发是指通过引入电荷分布来改变电磁场的时空变化。
类似于电流激发,我们可以通过在给定区域内引入电荷源来激发电磁场的变化。
电磁场的边界条件一

2. 全电流定理
•电流概念的推广
凡是能产生磁场的物理量均称电流
1)传导电流 载流子定向运动
I0 Id
2)位移电流 变化的电场
•全电流 •全电流定理
I I0 Id
H dl I全
L i
12
•全电流 •全电流定理
I 0 J 0 dS
S
I I0 Id
四电磁场的边界条件物质分界面上电场磁场电流电场在分界面上的边界条件介质1介质2介质1一侧紧邻界面p点的p1点的场量介质2一侧紧邻界面p点的p2点的场量分界面上一点p的情况?法线分量的关系在界面两侧p2作底面平行界面的扁圆柱面介质2处底面积记作s介质1处记作s介质1介质2因为所以由介质方程有介质1介质2在界面两侧过p1介质介质介质1介质2因为所以由介质方程有介质1介质2磁场在物质分界面上的边界条件界面某点p两侧的磁场场量的关系由介质方程有介质1介质2有了场量边界关系可为解题带来方便过场点作狭长矩形回路由于由介质方程有介质1介质2例如
H dl Ii内
L i
S2
S1
L
i
i
H dl i
L
•若取以L为边界的曲面S1
I
i
i内
i得•若取以L为边界的源自面S2Iii内
0
得
H dl 0
L
6
•若取以L为边界的曲面S1 得 I i内 i
i
H dl i
J0 0
0 0
情况下
E
H
满足的微分 方程形式是 波动方程
对沿 x 方向传播的电磁场(波) 有
Ey
2
x
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从零开始学习3D MAXWELL之边界条件
MAXWELL仿真电磁场的本质还是计算麦克斯维尔方程,所以要定义仿真的边界条件,这样才能得到方程的解。
3D仿真一共有六种求解类型,为静磁场/涡流/瞬态磁场/静电场/传导/瞬态电场。
每一种求解类型都有边界条件。
1,静磁场求解器边界条件
默认边界条件示意图如下:(默认边界条件普遍存在于Maxwell 3D仿真的各种求解器中。
正确应用默认边界条件,求解域的设置非常关键。
尼曼边界条件将磁场限定在边界之内。
当磁场较封闭或求解域足够大时,应用尼曼边界条件才会得到相对正确的分析结果。
)
磁场边界条件:磁场边界条件指定在求解域表面:1)定义切向方向磁场强度为零的边界条件:选择要添加边界条件的面--增加切线方向磁场强度为零的磁场;2)定义正切磁场边界条件:选择要添加边界条件的面--增加正切磁场--增加X/Y方向的磁场分量值--在坐标系统中定义X/Y矢量或是使用默认值;(正切方向为零,磁场方向与表面垂直)(磁场边界条件,磁场的切向分量被指定为预定义的值,但如果该分量的值被指定为0,则其效果与Zero Tangential H Field相同,磁场与该边界垂直,适用于施加外部磁场,如地磁仿真。
)
绝缘边界条件,除电流无法穿过边界以外,其他特性与Neumann边界相同,适用于2个接触导体之间完美绝缘的薄片。
(未添加绝缘边界条件)
(添加绝缘边界条件后)
对称边界条件:对称边界条件适合几何对称或是磁场对称的结构。
对称边界条件,奇对称(磁力线正切),磁场与边界正切,磁场法向分量为0;偶对称(磁力线垂直),磁场与边界垂直,磁场切向分量为0。
对称边界条件主要用来减少仿真时间,增加计算效率。
匹配边界条件,有主边界(Master)和从边界(Slave)两种,需要配合使用。
偶对称时,Slave边界的磁场被定义为匹配Master边界的幅值和方向。
奇对称时,Slave边界的磁场与Master边界的幅值相同,方向相反。
(适用于电机类结构,场每隔一定角度会重复,可以使用最小循环周期进行计算)
边界条件磁场状态使用场合
默认边界条件(自然边界条件和尼曼边界条
件) 自然边界条件—磁场连续的穿过表
面
尼曼边界条件—磁场方向与表面正
切,无磁通穿过
物体表面是自然边界条件;
求解域表面和排除物体的表
面是尼曼边界条件
零正切分量磁场边界
条件如果添加零正切分量磁场边界条件,
磁通是垂直的
外部交变磁场
正切磁场边界条件磁场的正切分量设为初始值
绝缘边界条件电流无法穿过表面
相接触的两个导体之间完美
的绝缘薄片
对称边界条件奇对称(磁通正切) —磁场与边界相
切; 法向分量为零
偶对称(法向方向磁通) —磁场与边
界垂直; 正切方向的分量为零
几何面和磁场对称
匹配边界条件(主从边界条件) 从边界上的磁场方向要服从主边界上
的磁场大小和方向(或是相反的方向)
周期性对称平面,磁场方向与
边界呈角度
辐射边界条件磁场无限定限制无界限涡流
阻抗边界条件包括超出边界表面的激磁电流效
应
有很小的集肤尺寸的导体
零正切分量磁场边界条件:磁场H的切向分量被设置为0,磁力线垂直于该边界条件,适用于施加外部磁场,如地磁场的垂直面。
辐射边界条件,对磁场表现无限制
阻抗边界条件,阻抗边界条件,应用于涡流场,当透入深度较小时,磁场不能进入到实心导体的内部。
此时如果计算导体内的真实磁场分布时,由于集肤区域的存在,计算量会非常大。
如果不关心其内部的场分布,可以采用阻抗边界条件。
