初中数学平面几何知识定理
初中数学竞赛重要定理公式(平面几何篇)

初中数学竞赛重要定理公式(平面几何篇)初中数学竞赛中,平面几何是一个重要的考点。
以下是一些重要的定理、公式和结论。
三角形面积公式(包括海伦公式):三角形的面积S可以用以下公式计算:$S=\sqrt{p(p-a)(p-b)(p-c)}$,其中$p=\frac{1}{2}(a+b+c)$,$a$,$b$,$c$分别为三角形的三条边长。
另外,三角形的面积也可以用以下公式计算:$S=\frac{1}{2}ab\sin C$,其中$a$,$b$为两边,$C$为两边之间的夹角。
还有一个海伦公式:$S=\frac{1}{2}ah_a$,其中$h_a$为三角形顶点$A$到边$BC$的垂线长度,$a$为边$BC$的长度。
XXX定理:对于三角形$\triangle ABC$及其底边上的一点$D$,有$AB^2\cdot DC+AC^2\cdot BD-AD^2\cdotBC=BC\cdot DC\cdot BD$。
XXX定理:对于一个内接四边形,其对角线之积等于两组对边乘积之和,即$AC\cdot BD=AB\cdot CD+AD\cdot BC$。
逆命题也成立。
同时还有广义托勒密定理:$AB\cdotCD+AD\cdot BC\geq AC\cdot BD$。
蝴蝶定理:如果$AB$是圆$O$的弦,$M$是$AB$的中点,弦$CD$,$EF$经过点$M$,$CF$,$DE$交$AB$于$P$,$Q$,则$MP=QM$。
勾股定理(毕达哥拉斯定理):对于一个直角三角形,锐角对边的平方等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍;钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍。
同时还有广义勾股定理。
中线定理(巴布斯定理):对于一个三角形$\triangleABC$,如果$BC$的中点为$P$,则有$AB^2+AC^2=2(AP^2+BP^2)$。
同时,中线的长度可以用以下公式计算:$m_a=\frac{1}{2}\sqrt{2b^2+2c^2-a^2}$。
初中数学几何知识点整理

初中数学几何知识点整理
一、平面几何基本概念
1.点、线、面、角的定义和性质
2.相交线、平行线、垂直线的关系
3.线段的长度、角的度量和角的分类
4.三角形的分类和性质
5.四边形的分类和性质
6.正多边形和圆的性质
二、平面图形的性质和计算
1.三角形内角和定理
2.三角形外角和定理
3.三角形的相似性质
4.三角形的全等性质
5.直角三角形的勾股定理
6.三角形的中线、高线、角平分线等的性质
7.四边形的对角线、角平分线等的性质
8.圆的圆心角、弧、弦等的性质
9.弧长、扇形面积、圆周角等的计算
三、空间几何基本概念
1.空间的基本概念和几何图形的投影
2.空间几何体的表达和展开图
3.空间的点、线、面、体的关系
4.空间角、棱、面、顶点等的定义和性质
5.空间直角坐标系和向量的性质和运算
6.空间几何体的视图、投影和尺寸关系
四、平面图形的位置关系和计算
1.直线和平面的位置关系
2.点和直线的距离、点和平面的距离
3.直线和平面的夹角和包含关系
4.直线与直线、直线与平面的位置关系
5.各种图形之间的位置关系和投影关系
6.平面图形的面积、周长和体积的计算
五、解题方法与应用
1.图形分析法
2.推理证明法
3.运动解法
4.化归为已知
5.整体几何法
6.利用几何工具求解
7.几何建模
以上是初中数学几何知识点的整理,对于学生来说,掌握这些知识有助于提高解决几何问题的能力,同时也为将来进一步学习更高级数学打下坚实的基础。
希望同学们认真学习,勤加练习,掌握好这些知识点,提高自己的数学水平。
初中平面几何重要定理汇总

初中平面几何重要定理汇总平面几何是初中数学中的重要内容之一,在几何学中有很多重要的定理被广泛应用。
本文将对初中平面几何中的一些重要定理进行汇总和介绍。
一、等腰三角形的性质等腰三角形是指两边的边长相等的三角形。
等腰三角形具有以下性质:1. 等腰三角形的底角(夹在两边上的角)相等。
2. 等腰三角形的顶角(夹在两边之间的角)是一个锐角。
3. 等腰三角形的两条底边平行。
二、全等三角形的条件全等三角形是指具有相同大小和形状的三角形。
判断两个三角形全等的条件有以下几种:1. 三边对应相等:若两个三角形的边分别对应相等,则这两个三角形全等。
2. 两边一夹角对应相等:若两个三角形两边和夹角分别对应相等,则这两个三角形全等。
3. 两角一边对应相等:若两个三角形两角和一边分别对应相等,则这两个三角形全等。
三、直角三角形的性质直角三角形是指其中一个角为90度的三角形。
直角三角形具有以下性质:1. 勾股定理:直角三角形的斜边的平方等于两个直角边的平方和。
2. 斜边较长:在一个直角三角形中,斜边是其他两条边中最长的。
3. 垂直关系:直角三角形的两个直角边互相垂直。
四、平行线的性质平行线是指在同一个平面上永远不会相交的直线。
平行线具有以下性质:1. 对顶角相等:当一组平行线被一条横截线(不与平行线平行的线)截断时,对顶角相等。
2. 内错角互补:当一组平行线被两条截断线(交叉形成的两对内角)截断时,内错角互补(角的度数和为180度)。
3. 鍊夹角相等:当一组平行线被两条截断线截断时,同位角相等(同位角指位于两条平行线之间、位于同一边的两个角)。
五、相似三角形的性质相似三角形是指具有相似形状但不一定相等大小的三角形。
相似三角形具有以下性质:1. 相似三角形的对应角相等。
2. 相似三角形的对应边成比例。
六、圆的性质圆是一个由一组等距离的点组成的集合,具有以下性质:1. 圆的半径是从圆心到圆上任意一点的距离。
2. 圆的直径是通过圆心的一条线段,两端点在圆上。
初中几何证明的所有公理和定理

初中几何证明的所有公理和定理几何学是数学的一个分支,研究平面和空间中的图形、形状、大小以及它们之间的关系。
在几何学中,有一些基本的公理和定理被广泛应用于证明其他几何结论。
以下是初中几何中常用的公理和定理。
一、公理1.尺规公理:任意两点可以用直尺连接,任意一点可以用剪刀间距来复原。
2.同位角公理:同位角互等。
3.平行公理:通过点外一条直线的直线,与这条直线平行的直线只有唯一一条。
4.直线偏转公理:过直线和不在直线上的一点,有且只有一条直线与该直线相交。
二、定理1.垂直平分线定理:平分一条线段的直线必垂直于该线段。
2.三角形内角和定理:三角形内角的和为180°。
3.直角三角形定理:在直角三角形中,两个直角三角形的边长和斜边相等。
4.点到直线的距离定理:点到直线的距离等于点到该直线上垂线的距离。
5.等腰三角形定理:等腰三角形的底边中点到顶点的距离等于底边的一半。
6.等边三角形定理:等边三角形的三条边相等。
7.三角形外角定理:三角形外角等于其对应内角的和。
8.直角三角形的勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方。
9.海伦公式:已知三角形的三边长,可以通过海伦公式求解其面积。
10.等周定理:等周的两角相等,反之亦成立。
11.三角形中位线定理:三角形两边中点连线中位线,且平分第三边。
12.周长定理:四边形周长等于各边长的和。
13.三角形周长定理:三角形的周长等于三边长的和。
14.三角形中线定理:三角形中线等分中位线,且平分第三边。
15.三角形终边定理:一个角的终边上的点,到另一个角所在的直线的距离永远相等。
16.五边形内角和定理:五边形的内角和是540°。
17.钝角三角形的边长关系:钝角三角形两边长的平方和小于斜边长的平方。
18.三角形的相似性定理:对应角等价、对应边成比例的两个三角形为相似三角形。
19.平行线的性质定理:平行条边分别过枚角且长度成正比,则连线为平行线。
20.重叠三角形定理:如果两个角和一个边分别相等,则两个三角形相等。
平面几何的几个重要定理
AC1 AP cosPAB BC1 PB cosPBA
由上面的三个式子相乘 且 PAC PBC,PAB PCB,PCA PBA 180
可得 BA1 CB1 AC1 =1 , CA1 AB1 BC1
AA1 OB1 BC2 1 , OC1 BB1 CA2 1 ,
OA1 BB1 AC2
CC1 OB1 BA2
OA1 CC1 AB2 1,将上面的三条式子 AA1 OC1 CB2
相乘可得 BC2 AB2 CA2 1 应用梅涅 AC2 CB2 BA2
劳斯定理可知 A2 , B2 , C2 共线.
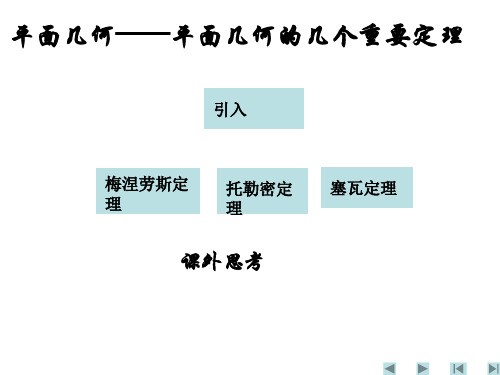
平面几何──平面几何的几个重要定理
引入
梅涅劳斯定 理
托勒密定 理
塞瓦定理
课外思考
平面几何──平面几何的几个重要定理
平面几何是培养严密推理能力的很好数学分支,且因其证 法多种多样:除了几何证法外,还有三角函数法、解析法、复 数法、向量法等许多证法,这方面的问题受到各种竞赛的青睐, 现在每一届的联赛的第二试都有一道几何题.
ACI BAC DAC ACJ
ACI ACJ IAC JAC GAC EAC
; 亚博 亚博足彩 ;
寂状态. 随时随地! 白重炙差点震惊の下巴都掉下来了! 这灵魂静寂状态の逆天之处在于,进入这状态,灵魂会飞速の飙升!神力也会随着不断の上涨,并且在这灵魂静寂状态之内——法则修炼の速度飙升! 梦幻宫为何成为神帝之下第一神器?因为在梦幻宫修炼速度是外面の几倍,法则 感悟速度也是外面の双倍,还有强者自己の对战!有这神器在手,将会培养出无数の神王强者出来.所以才名动神界,让无数强者势力为之眼红,为之垂涎不已,更有无数强者,用无数财富
初中平面几何定理全套

直线、角、平行、垂直(直线公理)经过两点有一条直线,并且只有一条直线。
注:简称“两点确定一条直线”。
(距离公理)在所有联结两点的线中,线段最短。
注:简称“两点之间线段最短”。
两条直线相交,只有一个交点。
同角(或等角)的余角相等。
同角(或等角)的补角相等。
对顶角相等。
经过一点有一条而且只有一条直线垂直于已知直线。
直线外一点与直线上各点联结的所有线段中,垂线段最短。
平行公理经过直线外一点,有一条而且只有一条直线和这条直线平行。
如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
(平行线判定)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
注:简称“同位角相等,两直线平行”。
课本作为公理。
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
注:简称“内错角相等,两直线平行”。
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
注:简称“同旁内角互补,两直线平行”。
(平行线性质)两条平行线被第三条直线所截,同位角相等。
注:简称“两直线平行,同位角相等”。
两条平行线被第三条直线所截,内错角相等。
注:简称“两直线平行,内错角相等”。
两条平行线被第三条直线所截,同旁内角互补。
注:简称“两直线平行,同旁内角互补”。
如果一个角的两边分别平行于另一个角的两边,则那么这两个角相等或互补。
定理如果两条直线都和第三条直线垂直,那么这两条直线平行。
定理如果一条直线和两条平行线中的一条垂直,那么,这条直线也和另一条垂直。
三角形定理(三角形不等式)三角形任何两边的和大于第三边。
推论三角形任何两边的差小于第三边。
三角形内角和定理三角形三个内角的和等于180°。
推论1 三角形的一个外角等于和它不相邻的两个内角的和。
注:有书上称之“外角定理”。
推论2 三角形的一个外角大于任何一个和它不相邻的内角。
推论三角形的三个外角的和等于360°。
(三角形全等判定法则)边角边公理有两边和它们的夹角对应相等的两个三角形全等。
初中平面几何四个重要定理

初中平⾯⼏何四个重要定理初中数学知识重点整理-平⾯⼏何四个重要定理四个重要定理:梅涅劳斯(Menelaus)定理(梅⽒线)△ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充要条件是。
塞⽡(Ceva)定理(塞⽡点)△ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点的充要条件是。
托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对⾓线乘积的充要条件是该四边形内接于⼀圆。
西姆松(Simson)定理(西姆松线)从⼀点向三⾓形的三边所引垂线的垂⾜共线的充要条件是该点落在三⾓形的外接圆上。
例题:1.设AD是△ABC的边BC上的中线,直线CF交AD于F。
求证:。
【分析】CEF截△ABD→(梅⽒定理)【评注】也可以添加辅助线证明:过A、B、D之⼀作CF的平⾏线。
2.过△ABC的重⼼G的直线分别交AB、AC于E、F,交CB于D。
求证:。
【分析】连结并延长AG交BC于M,则M为BC的中点。
DEG截△ABM→(梅⽒定理)DGF截△ACM→(梅⽒定理)∴===1【评注】梅⽒定理3. D、E、F分别在△ABC的BC、CA、AB边上,,AD、BE、CF交成△LMN。
求S△LMN。
【分析】【评注】梅⽒定理4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。
求证:AE、BF、CG相交于⼀点。
【分析】【评注】塞⽡定理5.已知△ABC中,∠B=2∠C。
求证:AC2=AB2+AB·BC。
【分析】过A作BC的平⾏线交△ABC的外接圆于D,连结BD。
则CD=DA=AB,AC=BD。
由托勒密定理,AC·BD=AD·BC+CD·AB。
【评注】托勒密定理6.已知正七边形A 1A2A3A4A5A6A7。
求证:。
(第21届全苏数学竞赛)【分析】【评注】托勒密定理7.△ABC的BC边上的⾼AD的延长线交外接圆于P,作PE⊥AB于E,延长ED交AC延长线于F。
初中数学平面几何常见定理补充

1.角平分线定理方法4(正弦定理)作三角形的外接圆,AM交圆于D,由正弦定理,得,证明4图AB/sin∠BMA=BM/sin∠BAM,AC/sin∠CMA=CM/sin∠CAM又∠BAM=∠CAM,∠BMA+∠AMC=180sin∠BAM=sin∠CAM,sin∠BMA=sin∠AMC,所以AB/AC=MB/MC2.梅涅劳斯定理(简称梅氏定理)证明一:过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1 证明二:过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=13.塞瓦定理在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1证法简介(Ⅰ)本题可利用梅涅劳斯定理证明:∵△ADC被直线BOE所截,∴ (CB/BD)*(DO/OA)*(AE/EC)=1 ①而由△ABD被直线COF所截,∴ (BC/CD)*(DO/OA)*(AF/FB)=1②②÷①:即得:(BD/DC)*(CE/EA)*(AF/FB)=1(Ⅱ)也可以利用面积关系证明∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③同理CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤③×④×⑤得BD/DC*CE/EA*AF/FB=14.广勾股定理:在任一三角形中,(1)锐角对边的平方,等于两夹边之平方和,减去某夹边和另一夹边在此边上的投影乘积的两倍.(2)钝角对边的平方,等于两夹边的平方和,加上某夹边与另一夹边在此边延长上的投影乘积的两倍.证明:设△ABC中,BC是锐角A的对边(图2-4).作CH⊥AB于H,根据勾股定理:BC^2 = BH^2 + CH^2而BH = AB-AH , CH^2 = AC^2 - AH^2带入后有:BC^2 = (AB-AH)^2 + AC^2 - AH^2简化后:BC^2 = AB^2 +AC^2 -2AB·AH 式(1)同理:BC^2 = AB^2+AC^2 -2AC·AH5.四边形的余弦定理设四边形ABCD的边长为AB=a,BC=b,CD=c,DA=d,对角线为m,n。
平面几何基本定理总结

平面几何基本定理总结平面几何是研究二维图形、点、线和角度之间的关系和性质的数学分支。
它是数学中的基础学科,对于建立几何推理和解决实际问题具有重要意义。
在平面几何中,存在一些基本定理,它们为我们理解和运用几何知识提供了重要的依据。
本文将对平面几何的基本定理进行总结和概述。
一、点、线和角度1. 点:- 点是平面几何中最基本的概念,它没有长度、宽度和高度,只有位置。
- 点可以用大写字母表示,如A、B、C等。
2. 线:- 线是由一系列无限延伸的点组成的,它没有宽度。
- 线可以用小写字母表示,如AB、CD等。
3. 角度:- 角度是由两条射线共享一个端点而形成的图形,常用来表示两条线的夹角大小。
- 角度可以用小字母表示,如∠ABC、∠DEF等。
二、平面几何基本定理1. 直线的性质:- 直线上的任意两点可以确定一条直线。
- 一条直线上的所有点在同一条直线上。
2. 线段的性质:- 线段是由两个端点和它们之间的所有点组成的有限部分。
- 线段的长度可以通过两个端点的坐标计算得出。
3. 角度的性质:- 角度大小可以用度数或弧度来表示。
- 两条直线垂直时,它们所形成的角度为直角,即90度或π/2弧度。
- 两条直线平行时,它们所形成的角度为零度或零弧度。
4. 三角形的性质:- 三角形是由三条线段组成的图形。
- 三角形的内角和为180度或π弧度。
- 直角三角形中,直角的对边和斜边之间满足勾股定理:c² = a² +b²,其中c为斜边,a、b为直角边的长度。
5. 四边形的性质:- 四边形是由四条线段组成的图形。
- 平行四边形的对边互相平行且相等。
- 矩形是一种特殊的平行四边形,它的内角均为直角。
6. 圆的性质:- 圆是由等距离于圆心的所有点组成的图形。
- 圆心到圆上任意一点的距离称为半径。
- 圆的周长可以通过半径和圆周率π的乘积计算得出:周长= 2πr。
三、应用及实例平面几何的基本定理在各个领域都有广泛的应用,例如建筑、工程、地理测量等。
初中数学平面几何基本定理

1. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:222222a c b m a -+=2. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例.如△ABC 中,AD 平分∠BAC ,则ACAB DC BD =;(外角平分线定理) 3. 正弦定理:R Cc B b A a 2sin sin sin ===,(其中R 为三角形外接圆半径) 4. 余弦定理:C ab b a c cos 2222-+=5. 布拉美古塔(Brahmagupta )定理: 在圆内接四边形ABCD 中,AC ⊥BD ,自对角线的交点P 向一边作垂线,其延长线必平分对边6. 托勒密(Ptolemy )定理:圆内接四边形对角线之积等于两组对边乘积之和,即AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD7. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,则有:MP =QM .8. 欧拉(Euler )公式:设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr .重心性质:①设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,则1:2:=GD AG ; ②设G 为△ABC 的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31③设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===ABKH CA FP BC DE AB KH CA FP BC DE ④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;⑤三角形内到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).11. 垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;(4)设O ,H 分别为△ABC 的外心和垂心, HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,12. 内心:三角形的三条角分线的交点—内接圆圆心,即内心到三角形各边距离相等内心性质:(1)设I 为△ABC 的内心,则I 到△ABC 三边的距离相等,反之亦然(2)设I 为△ABC 的内心,则C AIB B AIC A BIC ∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,219013. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;外心性质:(1)外心到三角形各顶点距离相等(2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360(3)∆=S abcR 4;(4)锐角三角形的外心到三边的距离之和等于其内切圆与外接圆半径之和14.其中a h 表示BC 边上的高,R 为外接圆半径,r 为内切圆半径,)(21c b a p ++= 1920·两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+①121212||,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.21·点到直线的距离d =(点00(,)P x y ,直线l :0Ax By C ++=).。
初中数学公式定理大全

初中数学公式定理大全1.代数公式- 两个数的乘积等于它们的积:ab = ba- 两个数乘积的倒数等于它们的倒数的乘积:(ab)^-1 = a^-1 * b^-1- 两个数的平方和等于它们的平方和的两倍加上它们的积:(a + b)^2 = a^2 + 2ab + b^2- 两个数的平方差等于它们的平方差的两倍减去它们的积:(a -b)^2 = a^2 - 2ab + b^22.平面几何定理- 锐角三角形的三条边的平方之和等于两倍的三个角的余弦值之和:a^2 + b^2 + c^2 = 2(abcosC + bccosA + cacosB)-三角形内角和定理:三角形的三个内角的和等于180度:A+B+C=180度-等腰三角形底角定理:等腰三角形的底角等于顶角的一半:A=B/2 -相似三角形的对应边成比例:a/b=c/d3.空间几何定理-空间直角三角形的斜边的平方等于两个直角边的平方的和:c^2=a^2+b^2-空间三角形内角和定理:空间三角形的三个内角的和等于180度:A+B+C=180度-垂直平分线定理:平面内相交的两条直线的垂直平分线互相垂直4.数列与数学归纳法-等差数列的通项公式:an = a1 + (n - 1)d-等差数列的前n项和公式:Sn = (n/2)(a1 + an)-等比数列的通项公式:an = a1 * r^(n - 1)-等比数列的前n项和公式(当r不等于1时):Sn=a1*(1-r^n)/(1-r) -数学归纳法:若数学命题在数的一部分上成立且下一部分数的成立是依赖于上一部分数的成立,则该数学命题在全体正整数上成立5.概率-事件的概率:P(A)=n(A)/n(S),其中n(A)表示事件A中的有利结果数,n(S)表示样本空间中的总结果数-互斥事件的概率和:P(A+B)=P(A)+P(B),其中A和B是互斥事件- 事件的相对频率概率:P(A) = lim(n(A) / n),其中n表示试验次数6.函数- 一次函数的解析式:y = kx + b,其中k表示斜率,b表示截距- 二次函数的解析式:y = ax^2 + bx + c,其中a表示二次项系数,b表示一次项系数,c表示常数项这只是初中数学常用的一些公式和定理的简要介绍,数学含有广泛且深奥的知识。
平面几何的26个定理

高一数学竞赛班二试讲义第1讲 平面几何中的26个定理班级 姓名一、知识点金1. 梅涅劳斯定理:若直线l 不经过ABC ∆的顶点,并且与ABC ∆的三边,,BC CA AB 或它们的延长线分别交于,,P Q R ,则1BP CQ AR PC QA RB⋅⋅= 注:梅涅劳斯定理的逆定理也成立(用同一法证明)2. 塞瓦定理: 设,,P Q R 分别是ABC ∆的三边,,BC CA AB 或它们的延长线上的点,若,,AP BQ CR 三线共点,则1BP CQ AR PC QA RB⋅⋅= 注:塞瓦定理的逆定理也成立3. 托勒密定理:在四边形ABCD 中,有AB CD BC AD AC BD ⋅+⋅≥⋅,并且当且仅当四边形ABCD 内接于圆时,等式成立。
AB AE AC ADBC ED AC AD==⇒又4. 西姆松定理:若从ABC ∆外接圆上一点P 作,,BC AB CA 的垂线,垂足分别为,,D E F ,则,,D E F 三点共线。
西姆松定理的逆定理:从一点P 作,,BC AB CA 的垂线,垂足分别为,,D E F 。
若,,D E F 三点共线,则点P 在ABC ∆的外接圆上。
5. 蝴蝶定理:圆O 中的弦PQ 的中点M ,过点M 任作两弦AB ,CD ,弦AD 与BC 分别交PQ 于X ,Y ,则M 为XY 之中点。
证明:过圆心O 作AD 与BC 的垂线,垂足为S 、T ,,OY ,OM ,SM ,MT 。
∴AM/CM=AD/BC∵AS=1/2AD,BT=1/2BC ∴AM/CM=AS/CT又∵∠A=∠C ∴△AMS∽△CMT∴∠MSX=∠MTY∴∠OMX+∠OSX=180°∴O,S ,X ,M同理,O ,T ,∴∠MTY=∠MOY,∠MSX=∠MOX∴∠MOX=∠MOY , ∵OM⊥PQ ∴XM=YM注:把圆换成椭圆、抛物线、双曲线蝴蝶定理也成立6. 坎迪定理:设AB 是已知圆的弦,M 是AB 上一点,弦,CD EF 过点M ,连结,CF ED ,分别交AB 于,L N ,则1111LM MN AM MB-=-。
中考数学之平面几何最全总结+经典习题

平面几何知识要点(一)【线段、角、直线】1.过两点有且只有一条直线.2.两点之间线段最短。
3.过一点有且只有一条直线和已知直线垂直。
4.直线外一点与直线上各点连接的所有线段中,垂直线段最短。
垂直平分线,简称“中垂线”。
定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)。
线段的垂直平分线可看作和线段两端点距离相等的所有点的集合。
中垂线性质:垂直平分线垂直且平分其所在线段。
垂直平分线定理:垂直平分线上任意一点,到线段两端点的距离相等。
逆定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等。
角1.同角或等角的余角相等。
2.同角或等角的补角相等.3.对顶角相等。
角的平分线性质角的平分线是到角的两边距离相等的所有点的集合定理1:角的平分线上的点到这个角的两边的距离相等.定理2:到一个角的两边距离相等的点,在这个角的平分线上.三角形各内角平分线的交点,该点叫内心,它到三角形三边距离相等。
【平行线】平行线性质1:两直线平行,同位角相等。
平行线性质2:两直线平行,内错角相等。
平行线性质3:两直线平行,同旁内角互补。
平行线判定1:同位角相等,两直线平行。
平行线判定2:内错角相等,两直线平行。
平行线判定3:同旁内角互补,两直线平行。
平行线判定4:如果两条直线都和第三条直线平行,这两条直线也互相平行.平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
平面几何知识要点(二)【三角形】面积公式:1. 已知三角形底a ,高h ,12S ah =2. 正三角形面积 S=24(a 为边长正三角形)3.已知三角形三边a ,b,c ,则S =(海伦公式) 其中:()2a b c p ++= (周长的一半) 4.已知三角形两边a ,b 及这两边夹角C ,则1sin 2S ab C =. 5.设三角形三边分别为a 、b 、c,内切圆半径为r ,则()2a b c r S ++= 6.设三角形三边分别为a 、b 、c,外接圆半径为R ,则4abc S R =记住★:已知正三角形边长为a ,其外接圆半径为R ,内切圆半径为r ,则有:R = ,r = , 2R r = 内角和定理:三角形三个内角的和等于180°推论1 :直角三角形的两个锐角互余推论2 :三角形的一个外角等于和它不相邻的两个内角的和推论3 :三角形的一个外角大于任何一个和它不相邻的内角全等三角形性质:如果两三角形全等,那么其对应边,对应角相等.其中对应边除了三角形的边长外,还包括对应高,对应中线,对角平分线.全等三角形判定定理:边边边公理:有三边对应相等的两个三角形全等.(SSS )边角边公理:有两边和它们的夹角对应相等的两个三角形全等。
初一数学平面几何基本定理总结

初一数学平面几何基本定理总结数学是一门研究数量、结构、变化以及空间和形式等概念的学科,而平面几何则是研究平面上的形状和尺寸关系的一部分数学内容。
在初一数学学习中,平面几何基本定理是学习平面几何的基础和起点。
下面将对初一数学中常见的平面几何基本定理进行总结。
1. 垂直平分线定理:垂直平分线定理是指如果一条直线同时是一条线段的垂直平分线,那么它将把这条线段分成两个相等的部分。
这个定理在平面几何中非常常见,经常用于解决线段的问题。
2. 直角三角形定理:直角三角形定理是指在一个直角三角形中,两条边的平方和等于斜边的平方。
这个定理在解决直角三角形相关问题时非常有用,可以通过已知两边求第三边的长度。
3. 同位角定理:同位角定理是指当一条直线被两个平行线相交时,同位角是相等的。
这个定理在解决平行线问题、角的计算问题等方面非常常用。
4. 垂直角定理:垂直角定理是指垂直的两条直线所形成的两对相邻角是相等的。
利用这个定理可以在已知一个角的情况下求解另一个角的大小。
5. 顶角定理:当一条直线穿过两条平行线时,位于平行线之间的对应角是相等的。
这个定理在解决平行线问题、角的计算等方面常常被使用。
6. 外角定理:外角定理是指一个三角形的外角等于与其不相邻的两个内角的和。
这个定理可以用于求解三角形内角的大小,还可以用于证明一些性质。
7. 同旁内角定理:同旁内角定理是指两条平行线被一条横切线切割后,同旁内角互补。
这个定理在解决平行线图形的内角问题时特别有用。
8. 直角平分线定理:直角平分线定理是指在一个直角三角形中,从直角的顶点到斜边上某一点引一条直线,将直角平分成两个相等的角。
这个定理在证明几何命题时常常被使用。
以上是初一数学中常见的平面几何基本定理的总结。
掌握这些基本定理,可以帮助我们解决平面几何的问题,进一步提高数学运算和推理的能力。
当然,这些定理只是平面几何中的一小部分,随着学习的深入,我们还会接触到更多的定理和推论。
中考数学平面几何的重要定理与证明方法

中考数学平面几何的重要定理与证明方法数学中的平面几何是中考数学中的一个重要部分,其中涉及了许多重要的定理和证明方法。
了解这些定理和方法对于应对中考数学题目至关重要。
本文将介绍中考数学平面几何的一些重要定理,并阐述其证明方法。
一、直角三角形的勾股定理直角三角形的勾股定理是平面几何中最常用的定理之一。
它表明,在直角三角形中,直角边的平方等于两个其他边平方的和。
定理表述如下:在直角三角形ABC中,假设∠C为直角。
设AB=c,BC=a,AC=b,则有a²+b²=c²。
勾股定理的证明方法多种多样,下面我们介绍其中一种思路。
证明思路:我们以直角边AC为边,构造正方形ACDE。
连接BD。
由正方形的性质可知,∠ADC是直角,且AD=DC=AC=b。
根据正方形对角线的性质可知,AC²+AD²=CD²。
此外,根据余弦定理可知,∠CBD的余弦值为:cos∠CBD=(AC²+BC²-BD²)/(2×AC×BC)。
由于∠ACB=90°,所以cos∠ACB=0,即AC和BC垂直。
因此,cos∠CBD=0,即AC²+BC²=BD²。
由于BD²=CD²,所以AC²+BC²=CD²,即a²+b²=c²。
证毕。
二、全等三角形的判定方法全等三角形的判定方法是平面几何中另一个重要的定理。
掌握了全等三角形的判定方法,可以快速解决一些与全等三角形相关的题目。
定理表述如下:两个三角形的对应边长度相等,且对应角相等,则这两个三角形全等。
全等三角形的判定方法主要有以下几种:1. SSS判定法(边边边):若两个三角形的三条边分别相等,则这两个三角形全等。
2. SAS判定法(边角边):若两个三角形的两边分别相等,且夹角也相等,则这两个三角形全等。
初中数学几何公式

初中数学几何公式数学几何是初中数学教学的重要内容之一,它主要研究空间中的点、线、面以及它们之间的位置关系和几何图形的性质等。
在初中数学中,几何公式是学生必须掌握的基础知识,接下来我将详细介绍一些常见的初中数学几何公式。
一、平面图形的面积公式1.矩形的面积公式:矩形的面积等于矩形的长乘以宽,即S=l*w。
2.正方形的面积公式:正方形的面积等于边长的平方,即S=a^23.三角形的面积公式:三角形的面积等于底边乘以高并除以2,即S=1/2*b*h。
4.梯形的面积公式:梯形的面积等于上底加下底乘以高再除以2,即S=1/2*(a+b)*h。
二、立体图形的表面积和体积公式1.正方体的表面积公式:正方体的表面积等于边长的平方乘以6,即S=6*a^22.正方体的体积公式:正方体的体积等于边长的立方,即V=a^33. 直方体的表面积公式:直方体的表面积等于底面积乘以2再加上侧面积,即S = 2lw + 2lh + 2wh。
4. 直方体的体积公式:直方体的体积等于底面积乘以高,即V = lwh。
5. 圆柱体的表面积公式:圆柱体的表面积等于底面积加上侧面积,即S = 2πr^2 + 2πrh。
6.圆柱体的体积公式:圆柱体的体积等于底面积乘以高,即V=πr^2h。
7.圆锥体的表面积公式:圆锥体的表面积等于底面积加上母线的周长乘以半个展开图的弧长,即S=πr^2+πr1+πr28.圆锥体的体积公式:圆锥体的体积等于底面积乘以高再除以3,即V=1/3*πr^2h。
三、平面几何常用的定理和公式1.同位角定理:同位角相等。
2.对顶角定理:对顶角相等。
3.垂直角定理:垂直角相等。
4.同位角、对顶角和垂直角之间的关系:同位角、对顶角和垂直角之间是互相等于180°的关系。
5.三角形内角和定理:三角形的三个内角之和等于180°。
6.三角形外角和定理:三角形的外角之和等于360°。
7.相似三角形的性质:相似三角形对应角相等,对应边成比例。
平面几何基础学习平面几何的基本概念和定理

平面几何基础学习平面几何的基本概念和定理在数学领域中,平面几何是研究平面上的图形、形状、大小、位置关系以及性质的一门学科。
通过学习平面几何的基本概念和定理,我们可以深入理解和掌握几何学的基础知识,为后续进一步的学习打下坚实的基础。
一、点、线、面的基本概念点、线、面是平面几何中最基本的概念。
点是没有大小和形状的,用字母表示,如A、B、C等;线是由一连串的点连在一起形成的,用两个点的字母表示,如AB、CD等;面是由一连串的线围成的平面,用大写字母表示,如面ABC。
二、线段、直线、射线的定义线段是由两个端点和两个端点之间的点组成,用字母表示,如AB;直线是一条没有端点的无限延伸的线段,在字母上加一个横杠表示,如AB;射线是由一个端点和这个端点向一个方向无限延伸的线段,用字母表示,如→AB。
三、平行线与垂直线的性质平行线指在同一个平面内永不相交的直线,用符号“∥”表示;垂直线指两条线段、直线或射线相交时,所成的角度为90度,用符号“⊥”表示。
平行线具有性质:1.平行关系具有传递性,即若AB∥CD,CD∥EF,则AB∥EF;2.任意一条直线与平行线横切时,所成的对应角相等。
四、三角形的性质三角形是由三条线段组成的多边形。
根据边的关系和角的关系,我们可以得出三角形的一些基本性质:1.三角形的内角和等于180度;2.等边三角形的三个边相等,三个角都是60度;3.等腰三角形的两条边相等,两个底角也相等;4.直角三角形的一个角是90度。
五、平面图形的面积计算矩形、正方形、三角形和梯形是我们常见的平面图形,根据其特点我们可以计算出它们的面积。
矩形的面积等于长乘以宽,正方形的面积等于边长的平方,三角形的面积等于底乘以高的一半,梯形的面积等于上底加下底乘以高的一半。
六、三角形的重心、外心、内心和垂心三角形有四个特殊的点,分别是重心、外心、内心和垂心。
重心是三条中线的交点,中线是由一个顶点与对应边的中点组成;外心是三角形外接圆的圆心,外接圆通过三个顶点;内心是三角形内切圆的圆心,内切圆与三条边都相切;垂心是三角形的三条高线的交点,高线是由一个顶点与对边垂直相交的线段组成。
初二数学平面几何中的重要定理归纳与运用

初二数学平面几何中的重要定理归纳与运用数学是一门严谨而又广泛应用的学科,而数学中的平面几何部分特别重要。
在初二的数学学习中,学生们会接触到许多平面几何的重要定理。
这些定理不仅具有理论意义,而且在实际问题中也有着广泛的应用。
本文将对初二数学平面几何中的一些重要定理进行归纳和运用。
1. 直线的性质和定理直线是平面几何中最基本的要素之一,我们首先来看一些与直线相关的性质和定理。
a. 直线垂直平分线给定一条直线段,若有一条直线同时与该线段垂直且平分该线段,那么这条直线就被称为垂直平分线。
垂直平分线的一个重要性质是,它通过线段的中点,并与该线段垂直。
b. 平行线的定理平行线具有许多重要的性质和定理。
其中一个重要的定理是“平行线上的对应角相等”。
根据这个定理,我们可以在解决多个平行线相关的问题时,运用角度的相等性,更方便地求解。
c. 垂直线的定理垂直线也有一些重要的定理。
例如,“两条互相垂直的直线,其斜率的乘积等于-1”。
这个定理的应用范围很广,可以用于求解垂直线的方程以及判断两条线是否垂直等。
2. 三角形的定理和性质三角形是平面几何中常见的形状,其定理和性质的应用也非常广泛。
a. 三角形的角平分线定理三角形的角平分线定理指出,如果一条直线将一个角平分,那么它将把对边分成一条比另一条长的线段。
这个定理的应用可以帮助我们求解三角形内部的角度,以及判断某个点是否在三角形内部等。
b. 三角形的中位线定理三角形的中位线定理是指,如果一条线段连接一个三角形的两边中点,那么这条线段被称为三角形的中位线,并且它的长度等于另外两条边长度之和的一半。
这个定理的应用范围广泛,可以用于求解三角形的面积、判断三角形是否为等边三角形等。
c. 三角形的外角定理三角形的外角定理指出,三角形的一个外角等于其余两个内角的和。
根据这个定理,我们可以利用外角的性质来解决一些三角形成立的问题,例如判断三角形是否可以构成等边三角形等。
3. 圆的性质和定理圆是平面几何中一个重要的概念,它具有许多独特的性质和定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学平面几何知识定理
1 过两点有且只有一条直线
2 两点之间线段最短
3 同角或等角的补角相等
4 同角或等角的余角相等
5 过一点有且只有一条直线和已知直线垂直
6 直线外一点与直线上各点连接的所有线段中,垂线段最短
7 平行公理经过直线外一点,有且只有一条直线与这条直线平行
8 如果两条直线都和第三条直线平行,这两条直线也互相平行
9 同位角相等,两直线平行
10 内错角相等,两直线平行
11 同旁内角互补,两直线平行
12两直线平行,同位角相等
13 两直线平行,内错角相等
14 两直线平行,同旁内角互补
15 定理三角形两边的和大于第三边
16 推论三角形两边的差小于第三边
17 三角形内角和定理三角形三个内角的和等于180°
18 推论1 直角三角形的两个锐角互余
19 推论2 三角形的一个外角等于和它不相邻的两个内角的和
20 推论3 三角形的一个外角大于任何一个和它不相邻的内角
21 全等三角形的对应边、对应角相等
22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等
23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等
24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等
25 边边边公理(SSS) 有三边对应相等的两个三角形全等
26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等
27 定理1 在角的平分线上的点到这个角的两边的距离相等
28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上
29 角的平分线是到角的两边距离相等的所有点的集合
30 等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角)
31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边
32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
33 推论3 等边三角形的各角都相等,并且每一个角都等于60°
34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
35 推论1 三个角都相等的三角形是等边三角形
36 推论2 有一个角等于60°的等腰三角形是等边三角形
37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半
38 直角三角形斜边上的中线等于斜边上的一半
39 定理线段垂直平分线上的点和这条线段两个端点的距离相等
40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
42 定理1 关于某条直线对称的两个图形是全等形
43 定理2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线
44 定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上
45 逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称
46 勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^2
47 勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形
48 定理四边形的内角和等于360°
49 四边形的外角和等于360°
50 多边形内角和定理n边形的内角的和等于(n-2)×180°
51 推论任意多边的外角和等于360°
52 平行四边形性质定理1 平行四边形的对角相等
53 平行四边形性质定理2 平行四边形的对边相等
54 推论夹在两条平行线间的平行线段相等
55 平行四边形性质定理3 平行四边形的对角线互相平分
56 平行四边形判定定理1 两组对角分别相等的四边形是平行四边形
57 平行四边形判定定理2 两组对边分别相等的四边形是平行四边形
58 平行四边形判定定理3 对角线互相平分的四边形是平行四边形
59 平行四边形判定定理4 一组对边平行相等的四边形是平行四边形
60 矩形性质定理1 矩形的四个角都是直角
61 矩形性质定理2 矩形的对角线相等
62 矩形判定定理1 有三个角是直角的四边形是矩形
63 矩形判定定理2 对角线相等的平行四边形是矩形
64 菱形性质定理1 菱形的四条边都相等
65 菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角
66 菱形面积=对角线乘积的一半,即S=(a×b)÷2
67 菱形判定定理1 四边都相等的四边形是菱形
68 菱形判定定理2 对角线互相垂直的平行四边形是菱形
69 正方形性质定理1 正方形的四个角都是直角,四条边都相等
70 正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
71 定理1 关于中心对称的两个图形是全等的
72 定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分
73 逆定理如果两个图形的对应点连线都经过某一点,并且被这一
点平分,那么这两个图形关于这一点对称
74 等腰梯形性质定理等腰梯形在同一底上的两个角相等
75 等腰梯形的两条对角线相等。
