锐角三角函数应用题
锐角的三角函数随堂练习3

欲与天公试比高。
须晴日,看红装素裹,分外妖娆。
江山如此多娇,引无数英雄竞折腰。
惜秦皇汉武,略输文采;
唐宗宋祖,稍逊风骚。
一代天骄,成吉思汗,
只识弯弓射大雕。
俱往矣,数风流人物,还看今朝。
薄雾浓云愁永昼,瑞脑消金兽。佳节又重阳,玉枕纱厨,半夜凉初透。
东篱把酒黄昏后,有暗香盈袖。莫道不消魂,帘卷西风,人比黄花瘦。
锐角的三角函数练习
1.如图,在△ABC中,∠C=90°,BC=5,AC=12,则cosA等于().
A. B. C. D.
2.如图,一个钢球沿坡角31°的斜坡向上滚动了5m,此时钢球距地面的高度是(单位:m)().
A.5cos31°B.5sin31°
C. D.5tan31°
3.AE,CF是锐角△ABC的两条高,如果AE∶CF=3∶2,则sinA∶sinC等于().
参考答案
1解析:AB= =13,
所以cosA= .
答案:D
2答案:B
3解析:如图,sinA= ,sinC= ,
∴sinA∶sinC= ∶ =CF∶AE=2∶3.
答案:B
4答案:D
5解析:AB= =10,AD=DB=5,△AED∽△ABC.
∴ .∴ .
∴AE= .∴CE= .
∴tan∠CBE= .
5答案:C
A. B. C. D.
6. 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠DCA= ,BC=10,则AB的值是().
A.9B.8C.6D.3
7.在平面直角坐标系中,有一点P(2,5),连接OP,且OP与x轴正半轴的夹角为α,则sinα=________,cosα=________,tanα=________.
锐角三角函数实际应用

2021年九年级数学中考分类训练:锐角三角函数实际应用必刷题1.如图1是一个手机的支架,由底座、连杆和托架组成,如图2是它的平面示意图,底座AD,连杆AB和托架BC始终在一个平面内.连杆AB可以绕着点A在5°﹣120°范围内旋转,托架BC可以绕着点B在5°﹣90°范围内旋转,连杆BA的长度为18厘米,托架CB的长度为8厘米.当连杆AB和托架BC旋转至图3位置,∠DAB=∠ABC =60°,请你计算此时点C到底座AD的距离CM的长.(结果保留根号)2.如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.(参考数据:tan31°≈0.6,tan50°≈1.2)(1)求B,C两点间的距离(结果精确到1m);(2)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.3.小强洗漱时的侧面示意图如图所示,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时身体前倾,下半身与地面的夹角∠FGK=80°,上半身与下半身所成夹角∠EFG=125°,脚与洗漱台距离GC=15cm,点D,C,G,K在同一直线上.(1)求此时小强腰部点F到墙AD的距离.(2)此时小强头部点E是否恰好在洗漱盆AB的中点O的正上方?若是,请说明理由;若不是,则他应向前还是向后移动多少厘米,使头部点E恰好在洗漱盆AB的中点O的正上方?(计算过程及结果的长度均精确到1cm.参考数据;sin80°≈0.98,cos80°≈0.17,≈1.41)4.如图①,在我国古建筑的大门上常常悬挂着巨大的匾额,图②中的线段BC就是悬挂在墙壁AM上的某块匾额的截面示意图.已知BC=1米,∠MBC=37°.从水平地面点D处看点C的仰角∠ADC=45°,从点E处看点B的仰角∠AEB=53°,且DE=2.4米.(1)求点C到墙壁AM的距离;(2)求匾额悬挂的高度AB的长.(参考数据:sin37°≈,cos37°≈,tan37°≈)5.某学习小组,为了测量旗杆AB的高度,他们在大楼MN第10层D点测得旗杆底端B 的俯角是32°,又上到第35层,在C点测得旗杆顶端A的俯角是60°,每层楼高度是2.8米,请你根据以上数据计算旗杆AB的高度.(精确到0.1米,已知:sin32°≈0.37,cos32°≈0.93,tan32°≈0.62,≈1.73)6.如图是某堤坝经过改造后的横断面梯形ABCD,高DH=10米,斜坡CD的坡度是1:1,此处,堤坝的正上方有高压线通过,点P,D,H在一条直线上,点P是高压线上离堤面AD最近的点,测得∠PCD=26°.(1)求斜坡CD的坡角α.(2)电力部门要求此处高压线离堤面AD的安全距离不低于18米,此次改造是否达到了安全要求?(参考数据:sin26°≈0.44,tan26°≈0.49,sin71°≈0.95,tan71°≈2.90)7.如图,已知在Rt△ABC中,∠C=90°,sin∠ABC=,点D在边BC上,BD=4,联结AD,tan∠DAC=.(1)求边AC的长;(2)求cot∠BAD的值.8.如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处(点A、B、C在同一直线上).某测量员从悬崖底C点出发沿水平方向前行60米到D点,再沿斜坡DE方向前行65米到E点(点A、B、C、D、E在同一平面内),在点E处测得5G 信号塔顶端A的仰角为37°,悬崖BC的高为92米,斜坡DE的坡度i=1:2.4.(1)求斜坡DE的高EH的长;(2)求信号塔AB的高度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)9.为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC 是梯形).(1)求限速道路AB的长(精确到1米);(2)如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)10.吴兴区某中学开展研学实践活动,来到了“两山”理论发源地﹣﹣安吉余村,看到了“两山”纪念碑.如图,想测量纪念碑AB的高度,小明在纪念碑前D处用测角仪测得顶端A的仰角为60°,底端B的俯角为45°;小明又在同一水平线上的E处用测角仪测得顶端A的仰角为30°,已知DE=8m,求该纪念碑AB的高度.(≈1.7,结果精确到0.1m)11.某校为检测师生体温,在校门安装了某型号的测温门,如图为该“测温门”截面示意图.身高1.6米的小聪做了如下实验:当他在地面M处时“测温门”开始显示额头温度,此时在额头B处测得A的仰角为30°;当他在地面N处时,“测温门”停止显示额头温度,此时在额头C处测得A的仰角为53°.如果测得小聪的有效测温区间MN的长度是0.98米,求测温门顶部A处距地面的高度约为多少米?(注:额头到地面的距离以身高计,sin53°≈0.8,cos53°=0.6,cot53°≈0.75,≈1.73.)12.为了监控大桥下坡路段车辆行驶速度,通常会在下引桥处设置电子眼进行区间测速.如图,电子眼位于点P处,离地面的铅锤高度PQ为9米,区间测速的起点为下引桥坡面点A处,此时电子眼的俯角为30°;区间测速的终点为下引桥坡脚点B处,此时电子眼的俯角为60°(A、B、P、Q四点在同一平面).(1)求路段BQ的长(结果保留根号);(2)当下引桥坡度i=1:2时,求电子眼区间测速路段AB的长(结果保留根号).13.如图,是小明家房屋的纵截面图,其中线段AB为屋内地面,线段AE、BC为房屋两侧的墙,线段CD、DE为屋顶的斜坡.已知AB=6米,AE=BC=3.2米,斜坡CD、DE的坡比均为1:2.(1)求屋顶点D到地面AB的距离;(2)已知在墙AE距离地面1.1米处装有窗ST,如果阳光与地面的夹角∠MNP=β=53°,为了防止阳光通过窗ST照射到屋内,所以小明请门窗公司在墙AE端点E处安装一个旋转式遮阳棚(如图中线段EF),公司设计的遮阳棚可作90°旋转,即0°<∠FET=α≤90°,长度为1.4米,即EF=1.4米.试问:公司设计的遮阳棚是否能达到小明的要求?说说你的理由.(参考数据:≈1.41,≈1.73,≈2.24,≈3.16,sin53°=0.8,cos53°=0.6,tan53°=).14.如图,海中有一个小岛A,它的周围25海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西60°的B处,往东航行20海里后到达该岛南偏西45°的C处后,货船继续向东航行,你认为货船在航行途中有没有触礁的危险.15.如图,为了测量河宽,在河的一边沿岸选取B、C两点,对岸岸边有一块石头A,在△ABC中,测得∠B=64°,∠C=45°,BC=50米,求河宽(即点A到边BC的距离)(结果精确到0.1米).(参考数据:≈1.41,sin64°=0.90,cos64°=0.44,tan64°=2.05)。
锐角三角函数练习题及答案
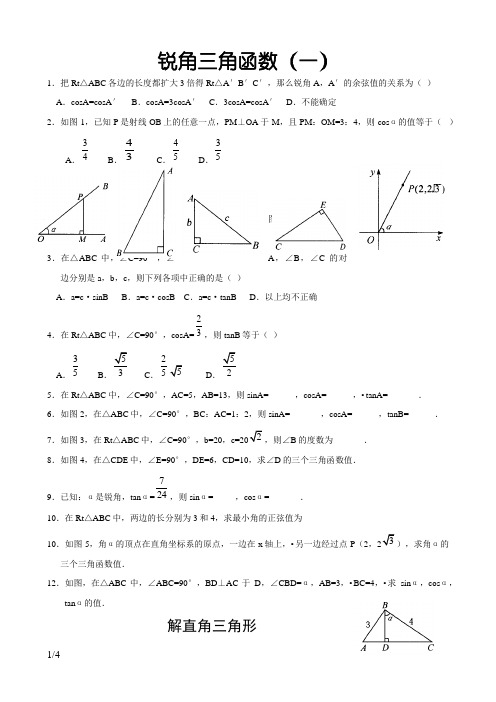
锐角三角函数(一)1.把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A,A′的余弦值的关系为()A.cosA=cosA′ B.cosA=3cosA′ C.3cosA=cosA′ D.不能确定2.如图1,已知P是射线OB上的任意一点,PM⊥OA于M,且PM:OM=3:4,则cosα的值等于()A.34 B.43 C.45 D .35图 1 图 2 图3 图4图53.在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,则下列各项中正确的是()A.a=c·sinB B.a=c·cosB C.a=c·tanB D.以上均不正确4.在Rt△ABC中,∠C=90°,cosA=23,则tanB等于()A.35 B.53 C.255 D.525.在Rt△ABC中,∠C=90°,AC=5,AB=13,则sinA=______,cosA=______,•tanA=_______.6.如图2,在△ABC中,∠C=90°,BC:AC=1:2,则sinA=_______,cosA=______,tanB=______.7.如图3,在Rt△ABC中,∠C=90°,b=20,c=202,则∠B的度数为_______.8.如图4,在△CDE中,∠E=90°,DE=6,CD=10,求∠D的三个三角函数值.9.已知:α是锐角,tanα=724,则sinα=_____,cosα=_______.10.在Rt△ABC中,两边的长分别为3和4,求最小角的正弦值为10.如图5,角α的顶点在直角坐标系的原点,一边在x轴上,•另一边经过点P(2,23),求角α的三个三角函数值.12.如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3,•BC=4,•求sinα,cosα,tanα的值.解直角三角形一、填空题1. 已知cosA=23,且∠B=900-∠A ,则sinB=__________.2. 在Rt △ABC 中,∠C 为直角,cot(900-A)=1.524,则tan(900-B)=_________.3. ∠A 为锐角,已知sinA=135,那么cos (900-A)=___________.4. 已知sinA=21(∠A 为锐角),则∠A=_________,cosA_______,tanA=__________.5. 用不等号连结右面的式子:cos400_______cos200,sin370_______sin420.6. 若cot α=0.3027,cot β=0.3206,则锐角α、β的大小关系是______________. 7. 计算: 2sin450-3tan600=____________. 8. 计算: (sin300+tan450)·cos600=______________.9. 计算: tan450·sin450-4sin300·cos450+6cot600=__________.10. 计算: tan 2300+2sin600-tan450·sin900-tan600+cos 2300=____________. 二、选择题:1. 在Rt △ABC 中,∠C 为直角,AC=4,BC=3,则sinA=( )A . 43;B . 34;C .53;D . 54.2. 在Rt △ABC 中,∠C 为直角,sinA=22,则cosB 的值是( )A .21;B .23;C .1;D .223. 在Rt △ABC 中,∠C 为直角,∠A=300,则sinA+sinB=( )A .1;B .231+;C .221+;D .414. 当锐角A>450时,sinA 的值( )A .小于22; B .大于22; C .小于23; D .大于235. 若∠A 是锐角,且sinA=43,则( )A .00<∠A<300; B .300<∠A<450;C .450<∠A<600;D . 600<∠A<9006. 当∠A 为锐角,且tanA 的值大于33时, ∠A( )A .小于300; B .大于300; C .小于600; D .大于6007. 如图,在Rt △ABC 中,∠C 为直角,CD ⊥AB 于D ,已知AC=3,AB=5,则tan ∠BCD 等于( )A .43;B .34;C .53;D .548. Rt △ABC 中,∠C 为直角,AC=5,BC=12,那么下列∠A 的四个三角函数中正确的是( )A . sinA=135; B .cosA=1312; C . tanA=1213;D . cotA=1259. 已知α为锐角,且21<cos α<22,则α的取值范围是( )A .00<α<300;B .600<α<900;C .450<α<600;D .300<α<450.三、解答题1、 在△ABC 中,∠C 为直角,已知AB=23,BC=3,求∠B 和AC .2、在△ABC 中,∠C 为直角,直角边a=3cm ,b=4cm ,求sinA+sinB+sinC 的值.3、在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知b=3, c=14. 求∠A 的四个三角函数.4、在△ABC 中,∠C 为直角,不查表解下列问题: (1)已知a=5,∠B=600.求b ; (2)已知a=52,b=56,求∠A .5、在△ABC 中,∠C 为直角, ∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,已知a=25,b=215,求c 、∠A 、∠B .6、在Rt △ABC 中,∠C =90°,由下列条件解直角三角形: (1) 已知a =156, b =56,求c; (2) 已知a =20, c =220,求∠B ; (3) 已知c =30, ∠A =60°,求a ;(4) 已知b =15, ∠A =30°,求a .7、已知:如图,在ΔABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,若∠B =30°,CD =6,求AB 的长.8、已知:如图,在山脚的C 处测得山顶A 的仰角为︒45,沿着坡度为︒30︒=∠30DCB ,400=CD 米),测得A 的仰角为︒60,求山的高度DCAB9、会堂里竖直挂一条幅AB,如图5,小刚从与B成水平的C点观察,视角∠C=30°,当他沿CB方向前进2米到达到D时,视角∠ADB=45°,求条幅AB的长度。
锐角三角函数解直角三角形例题

主题:锐角三角函数解直角三角形例题【序言】直角三角形是我们初中数学学习中的一个重要内容,而锐角三角函数作为直角三角形中的一个重要概念,在解题中也扮演着重要的角色。
下面我们将通过一些例题来详细讲解锐角三角函数在直角三角形中的应用。
【例一】已知直角三角形中的一角为30°,对边长为3cm,求斜边长。
求sin30°、cos30°、tan30°的值。
1. 根据三角函数的定义,sin30°=对边/斜边=3/斜边,而cos30°=邻边/斜边,tan30°=对边/邻边2. 根据30-60-90三角形的性质,可知对边为3cm,邻边为3*sqrt(3)cm,斜边为2*3cm=6cm3. 所以sin30°=1/2,cos30°=sqrt(3)/2,tan30°=1/sqrt(3)【例二】已知直角三角形中的一角为45°,斜边长为5cm,求对边和邻边的长度。
求sin45°、cos45°、tan45°的值。
1. 根据三角函数的定义,sin45°=对边/斜边,cos45°=邻边/斜边,tan45°=对边/邻边2. 根据45-45-90三角形的性质,可知对边和邻边的长度相等,且均为斜边的1/sqrt(2)倍3. 所以对边和邻边的长度均为5/sqrt(2)cm,sin45°=1/sqrt(2),cos45°=1/sqrt(2),tan45°=1【例三】已知直角三角形中的一角为60°,对边长为4cm,求斜边和邻边的长度。
求sin60°、cos60°、tan60°的值。
1. 根据三角函数的定义,sin60°=对边/斜边,cos60°=邻边/斜边,tan60°=对边/邻边2. 根据30-60-90三角形的性质,可知对边为4cm,邻边为2*4cm=8cm,斜边为4*sqrt(3)cm3. 所以sin60°=sqrt(3)/2,cos60°=1/2,tan60°=sqrt(3)【总结】通过以上三个例题的讲解,我们可以得出在直角三角形中,根据已知角度和已知边长来求解斜边长、对边长、邻边长以及三角函数值的具体方法。
锐角三角函数及应用经典例题

锐角三角函数及应用经典例题锐角三角函数是指在单位圆上,从原点出发,与 x 轴正半轴之间的夹角小于90° 的角的三角函数。
其中包括正弦函数sinα、余弦函数cosα、正切函数tanα,以及它们的倒数函数cscα、secα、cotα。
锐角三角函数在数学中有广泛的应用,尤其在几何、物理以及工程学中涉及到角度测量、距离计算等方面经常用到。
下面我们来看一些经典的例题,以加深对锐角三角函数的理解:例题1:已知在锐角 ABC 中,边长 BC = 5, AC = 13、求角 A 的正弦值 sinA、余弦值 cosA 和正切值 tanA。
解答:由于边长BC=5,AC=13,我们可以根据勾股定理求得边长AB=√(AC^2-BC^2)=12角 A 的正弦值 sinA = BC / AC = 5 / 13,余弦值 cosA = AB / AC = 12 / 13,正切值 tanA = BC / AB = 5 / 12例题2:已知在锐角 ABC 中,角B = 35°,边长 BC = 8、求角 A 的正弦值 sinA、余弦值 cosA 和正切值 tanA。
解答:由于已知角B = 35°,边长 BC = 8,我们可以根据正弦函数的定义求得角 A 的正弦值为 sinA = BC / AC。
由于 sinA = BC / AC,我们可以得到 AC = BC / sinA = 8 /sin(180° - A - B)。
根据余弦定理,可以计算出边长AC = √(AB^2 + BC^2 - 2 * AB * BC * cosB)。
代入已知的B = 55° 和 BC = 8,我们可以求得AC = √(AB^2 +8^2 - 2 * AB * 8 * cos35°)。
我们可以进一步根据余弦函数的定义计算 AB 的值,即 cosA = AB / AC,所以 AB = AC * cosA。
7.6锐角三角函数的简单应用(2)

O
仰角 俯角 视线
水平线
1、当从低处观测高处的目标时,视线与水平线 所成的锐角称为仰角. 2、当从高处观测低处的目标时,视线与水平线 所成的锐角称为俯角.
问题1:如图,AB和CD是同一地面上的两座相距 36米的楼房,在楼AB的楼顶A点测得楼CD的楼 顶C的仰角为45°,楼底D的俯角为30°.求楼 CD的高。 C
练习:为改善楼梯的安全性能,准备将楼梯的 倾斜角由60°调整为45 °.已知调整后的楼 梯比原来多占地4米,求楼梯的高度. D
Aபைடு நூலகம்
B
C
请你试一试: 升国旗时,某同学站在离旗杆底部24m处行 注目礼,当国旗升至旗杆顶端时,该同学视线的 仰角恰为30°,若双眼离地面1.5m,求旗杆的高 度.
B
A
C
A
45° 30°
36
B D
问题2:如图,飞机在距地面9km高空上飞行,先 在A处测得正前方某小岛C的俯角为30°,飞行 一段距离后,在B处测得该小岛的俯角为 60°.求飞机的飞行距离。
变一变:如图,飞机在一定高度上飞行,先在A 处测得正前方某小岛C的俯角为30°,航行 10km后,在B处测得该小岛的俯角为60°.求飞 机的高度。 D A B
C
数学活动室
怎样测量停留在空中的气球高度呢?
仪器:卷尺,测角仪
明明设计了这样一个方案: 先站在地面上某点处观测气球,测得仰角为27°, 然后他向气球方向前进了50m,此时观测气球,测 得仰角为40°.若明明的眼睛离地面1.6m, 如何 计算气球的高度呢?
C
A
B
D
sin 27°≈ 0.45,cos 27° 0.89, tan 27° 0.51 ≈ ≈ sin 40°≈ 0.64,cos 40° 0.77, tan 40° 0.84 ≈ ≈
锐角三角函数应用举例
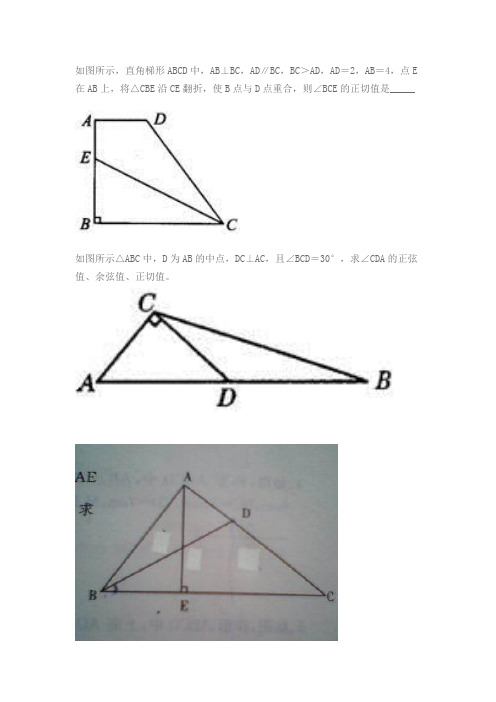
如图所示,直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E 在AB上,将△CBE沿CE翻折,使B点与D点重合,则∠BCE的正切值是_____如图所示△ABC中,D为AB的中点,DC⊥AC,且∠BCD=30°,求∠CDA的正弦值、余弦值、正切值。
如图,在平面直角坐标系中,Rt△PBD的斜边PB落在y轴上,tan∠BPD=.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.(1)求点C的坐标;(2)若点D在反比例函数y=(k>0)的图象上,求反比例函数的解析式.13一副直角三角板如图放置,点C 在FD 的延长线上,AB ∥CF ,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD 的长。
4.盐城电视塔是我市标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测电视塔的高度AB.小明在D处用高1.5m的测角仪CD,测得电视塔顶端A的仰角为30°,然后向电视塔前进224m 到达E处,又测得电视塔顶端A的仰角为60°.求电视塔的高度AB.(取1.73,结果精确到0.1m)如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是450,然后:沿平行于AB的方向水平飞行1.99×104米到达点D处,在D处测得正前方另一海岛顶端B的俯角是600,求两海岛间的距离AB.如图,海中有一灯塔P,它的周围8海里内有暗礁.海伦以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50方向上,在救助船B的西北方向上,船B在船A正东方向140海里处。
2020中考数学 九年级下册锐角三角函数在实际问题中的应用(含答案)
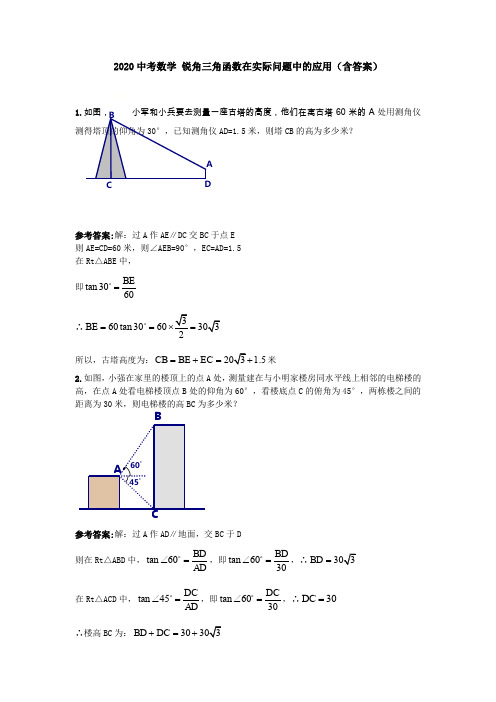
2020中考数学 锐角三角函数在实际问题中的应用(含答案)1.如图,小军和小兵要去测量一座古塔的高度,他们在离古塔60米的A 处用测角仪测得塔顶的仰角为30°,已知测角仪AD=1.5米,则塔CB 的高为多少米?参考答案:解:过A 作AE ∥DC 交BC 于点E 则AE=CD=60米,则∠AEB=90°,EC=AD=1.5 在Rt △ABE 中, 即tan 3060BE=∴60tan 3060BE === 所以,古塔高度为: 1.5CB BE EC =+=米2.如图,小强在家里的楼顶上的点A 处,测量建在与小明家楼房同水平线上相邻的电梯楼的高,在点A 处看电梯楼顶点B 处的仰角为60°,看楼底点C 的俯角为45°,两栋楼之间的距离为30米,则电梯楼的高BC 为多少米?参考答案:解:过A 作AD ∥地面,交BC 于D 则在Rt △ABD 中,tan 60BD AD ∠=,即tan 6030BD∠=,∴BD =在Rt △ACD 中,tan 45DC AD ∠=,即tan 6030DC ∠=,∴30DC = ∴楼高BC 为:30BD DC +=+AD BC3.小明在热气球A 上看到正前方横跨河流两岸的大桥BC ,并测得B ,C 两点的俯角分别为45°,35°。
已知大桥BC 与地面在同一水平面上,其长度为100米,请求出热气球离地面的高度。
(结果保留整数,参考数据:7sin 3512≈,5cos356≈,7tan 3510≈)参考答案:解:过A 作AD ⊥BC 于点D则AD 即为热气球的高度,且∠1=∠2=45∴可设AD=BD=x 则CD=x+100 在Rt △ADC 中tan AD C DC =,即tan 35100xx =+得:7003x =即热气球的高度为7003AD =米 4.如图,某建筑物BC 顶部有一旗杆AB ,且点A ,B ,C 在同一直线上.小红在D 处观测旗杆顶部A 的仰角为47°,观测旗杆底部B 的仰角为42°.已知点D 到地面的距离DE 为1.56m ,EC=21m ,求旗杆AB 的高度和建筑物BC 的高度(结果保留小数点后一位,参考数据:tan47°≈1.07,tan42°≈0.90).参考答案:解:根据题意,DE=1.56,EC=21,∠ACE=90°,∠DEC=90°.过点D 作DF ⊥AC,垂足为F .则∠DFC=90°,∠ADF=47°,∠BFD=42°.1.41≈ 1.73≈)参考答案:解:过C 作CD ⊥AB 于点D , 则∠DBC=45°=∠BCD ∴可设BD=CD=x在Rt △ACD 中可得:tan DCDAC AD∠=即:tan 302x x =+得1 2.73x =≈即,点C 与探测面的 距离大约为2.73米。
锐角三角函数帮你解决生活中的问题

锐角三角函数帮你解决生活中的问题锐角三角函数是学好三角学及本章内容的关键和基础. 锐角三角函数, 既是本章的重点,也是难点. 此内容又是数形结合的典范. 这涉及数学各个分支,又在工程,测量,军事,工业,农业,航海,航空等诸领域都有应用. 因而,对本单元的学习必须引起足够的重视,特别是在日常生活中的应用更加广泛,下面举几例与同学们共赏一、车厢离地面多少米?问题1:如图,自卸车厢的一个侧面是矩形ABCD ,AB =3米,BC =0.5米,车厢底部离地面1.2米,卸货时,车厢倾斜的角度060=θ,问此时车厢的最高点A 离地面多少米?(精确到1米)【思路解析:】此题只需求出点A 到CE 的距离,于是过A 、D 分别作AG ⊥CE ,DF ⊥CE ,构造直角三角形,解Rt △AHD 和Rt △CDF 即可求解.过点A 、D 分别作CE 的垂线AG 、DF ,垂足分别为G 、F ,过D 作DH ⊥AG 于H ,则有:23323360sin 0=⨯=⋅=CD DF 41215.060cos 0=⨯=⋅=AD AH 于是A 点离地面的高度为42.141233≈++(米). 所以,车厢的最高点A 离地面约为4米.点评:本题只要将实际问题转化为解直角三角形的问题,然后,运用三角函数的有关知识即可解决.二、如何将角橱搬进房间?问题2:如图1所示是某立式家具(角书橱)的横断面,请你设计一个方案(角书橱高2米,房间高2.6米,所以不从高度方面考虑方案的设计),按此方案可以使该家具通过如图2中的长廊搬入房间,在图2中把你的设计方案画成草图,并说明按此方案可把家问题一图HG FDCB A具搬入房间的理由(注:搬动过程中不准拆卸家具,不准损坏墙壁).问题二图1问题二图2【思路解析:】如说理图所示,作直线AB ,延长DC 交AB 于E ,由题意可知,△ACE 是等腰直角三角形,所以CE =0.5,DE =DC +CE =2,作DH ⊥AB 于H ,则245sin 2sin 0==∠⋅=HED DE DH ,∵5.12<,∴可按此方案设计图将家具从长廊搬入房间. 答案:设计方案草图如图所示.设计方案图设计方案说理图.点评:本题是一道比较贴近生活的实际问题,学生看到题目感到比较亲切、自然,但本题重点考查学生综合运用所学知识解决实际问题的探究和创新能力.本题还反映了生活中常见的实际情况,很有创意,并充分体现了学数学用数学的价值,角书橱过长廊进入房间,必须要放倒倾斜搬进,不能正面直入,方案的设计也多种多样.三、是否有进入危险区域的可能?问题3:一艘渔船正以30海里/小时的速度由西向东追赶鱼群,在A 处看见小岛C 在船的北偏东600方向,40分钟后,渔船行至B 处,此时看见小岛C 在船的北偏东300方向,已知以小岛C 为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向东追赶鱼群,是否有进入危险区域的可能?【思路解析】此题是一个重要题型——航海问题,解这类题要弄清方位角、方向角的概念,正确地画出示意图,然后根据条件解题.此题可先求出小岛C 与航向(直线AB )的距离,再与10海里进行比较得出结论.解:过C 作AB 的垂线CD 交AB 的延长线于点D ∵CD AD =30cot ,CDBC =060cot , ∴030cot ⋅=CD AD ,60cot ⋅=CD BD ,∴20)60cot 30(cot 0=-=-CD BD AD ∴31033320=-=CD , ∵310>10.∴这艘渔船继续向东追赶鱼群不会进入危险区域.点评:正确解答这类问题,第一步,根据材料提供的生活背景,画出几何图形,并把实际问题数学化,分析出作为一个数学问题的已知条件和问题。
锐角三角函数的实际应用

锐角三角函数的实际应用一、仰角、俯角问题例1. 某数学课外活动小组利用课余时间,测量了安装在一幢楼房顶部的公益广告牌的高度.如图,矩形CDEF 为公益广告牌,CD为公益广告牌的高,DM为楼房的高,且C、D、M三点共线.在楼房的侧面A处,测得点C与点D的仰角分别为45°和37.3°,BM=15米.根据以上测得的相关数据,求这个广告牌的高(CD的长).(结果精确到0.1米,参考数据:sin37.3°≈0.6060,cos37.3°≈0.7955,tan37.3°≈0.7618)例2.如图,在电线杆上的C处引拉线CE,CF固定电线杆,拉线CE和地面成57.5°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处的仰角为30°.已知测角仪AB的高为1.5米,求拉线CE的长.(结果精确到0.01米,参考数据:sin57.5°≈0.843,cos57.5°≈0.537,tan57.5°≈1.570,3≈1.732,2≈1.414)二、坡度、坡角问题例3. 如图,水坝的横断面是梯形,背水坡AB的坡角∠BAE=45°,坝高BE=20米.汛期来临,为加大水坝的防洪强度,将坝底从A处向后水平延伸到F处,使新的背水坡BF的坡角∠F=30°,求AF的长度.(结果精确到1米,参考数据:2≈1.414,3≈1.732)例4. 如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB,BC表示连接缆车站的钢缆,已知A,B,C 三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米,310米,710米,钢缆AB的坡度i1=1∶2,钢缆BC的坡度i2=1∶1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)三、测量问题例5、为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥.建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°.请你根据以上测量数据求出河的宽度.(参考数据:2≈1.41,3≈1.73;结果保留整数)例6、如图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4米,AB=6米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于A B的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)四、方向角问题例7:某海域有A、B两个港口,B港口在A港口北偏西30°的方向上,距A港口60海里.有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处.求该船与B港口之间的距离即CB的长(结果保留根号).例8:如图,在海面上生产了一股强台风,台风中心(记为点M)位于海滨城市(记作点A)的南偏西15°,距离为612千米,且位于临海市(记作点B)正西方向603千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?巩固练习:1、如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.(参考数据:sin37°≈35,tan37°≈34,sin48°≈710,tan48°≈1110)2. 张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度.(结果精确到0.1米,参考数据:3≈1.732)3.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)4、如图,斜坡AC的坡度(坡比)为1:3,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.5、如图,某军港有一雷达站,军舰停泊在雷达站的南偏东方向36海里处,另一艘军舰位于军舰的正西方向,与雷达站相距海里.求:(1)军舰在雷达站的什么方向?(2)两军舰的距离.(结果保留根号)6、(某中学九年级学生在学习“直角三角形的边角关系”一章时,开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度.如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进60米到达点D,又测得点A的仰角为45°。
锐角三角函数应用举例

A c = 2 、 / 了, 求t a n B 的值.
2 . 已知 直 角 三 角 形 的 一 个 锐 角A满 足 条 件 : 0 。 < A< 4 5 。 且s i nAC O S A=
3 x / -  ̄ -
—
AD: ̄ v / — AB2 AD2
_
—
:
何
:
: 3 ,
1 ,
A
A 02 DC :  ̄ V / AC — 2
_
:
所 以B C = 3 + 1 = 4 ,
或B C = 3 — 1 = 2 .
嚣
/ \
C 占
—
所 以B C = 4 或2 .
ห้องสมุดไป่ตู้
例4 如 图所 示 ,建筑 物A B 高 为2 0 0 米 ,从 定 点A观 察 到另 一建 筑物
磨
牙 吉林 宋 凤英
如 图, 在R t AAB C d ? , LC = 9 0 。 , LA, B, C 的对 边分 别为n , 6 , c - 则
( 3
例 l 已知 AAB C r  ̄/ _ AC B = 9 0 。 , LAB C = 1 5 0 7 B C = 1 , 拟 C 的长. 解: 如 图, 作 LB A D= 1 5 o , 交B C 于D,
2
.
.
4
3 . 由于 A: LB : C = 1 : 2 : 3 , 所 以 B : 2 LA, C = 3 6 LA= 1 8 0 。 , 得 , A+ LB + C = 1 8 0 o .
= 3 0 o , LB = 6 0 o , C = 9 0 。 ,
3.锐角三角函数的实际应用(10道)

锐角三角函数的实际应用1. 如图为放置在水平桌面上的台灯的平面示意图,灯臂AO 长为40 cm ,与水平面所形成的夹角∠OAM 为75°,由光源O 射出的边缘光线OC 、OB 与水平面所形成的夹角∠OCA 、∠OBA 分别为90°和30°,求该台灯照亮水平面的宽度BC .(结果精确到 1 cm ,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,3≈1.73).第1题图解:∵tan ∠OBC =tan30°=3OC BC ∴OC 3BC , ∵sin ∠OAC =sin75°=OC OA≈0.97, ∴3340BC ≈0.97, ∴BC ≈67(cm).答:该台灯照亮水平面的宽度BC 约为67 cm.2. 某种三角形台历放置在水平桌面上,其左视图如图②所示,点O是台历支架OA,OB的交点,同时又是台历顶端连接日历的螺旋线圈所在圆的圆心,现测得OA=OB=14 cm,CA =CB=4 cm,∠ACB=120°,台历顶端螺旋连接线圈所在圆的半径为0.6 cm.求点O到直线AB的距离.(结果保留根号)第2题图解:如解图,连接AB、OC,并延长OC交AB于点D,第2题解图∵OA=OB,AC=BC,∴OC垂直平分AB,即AD=BD,∠CDA=90°,又∠ACB=120°,∠ACD=60°,∴在Rt △ACD 中,sin ∠ACD =AD AC , ∴AD =AC ·sin60°=4×32=23cm ,∵在Rt △AOD 中,AD =2 3 cm ,AO =14 cm ,∴OD =AO 2-AD 2=142-(23)2=246 cm ,∴点O 到直线AB 的距离为246 cm.3. 如图①是一台仰卧起坐健身器,它主要由支架、坐垫、靠背和档位调节器组成,靠背的角度α可以用档位调节器调节,将图①仰卧起坐板的主体部分抽象成图②,已知OA =OD =81 cm ,OC =43 cm ,∠C =90°,∠A =20°.求BC 的长和点O 到地面的距离.(结果保留整数)(参考数据:sin20°≈0.3420,cos20°≈0.9397,tan20°≈0.3640;sin80°≈0.9848,cos80°≈0.1736,tan80°≈5.6713)第3题图解:根据题意可知AC =OA +OC =81+43=124 (cm),在Rt △ABC 中,tan A =BC AC ,∴BC =AC ·tan A ≈124×0.3640≈45(cm),如解图,过点O 作OE ⊥AB 于点E ,在Rt △AOE 中,sin A =OE OA ,∴OE =OA ·sin A ≈81×0.3420≈28(cm),第3题解图答:BC 的长和点O 到地面的距离分别约为45 cm 和28 cm.4. 为了给人们的出行带来方便,某市准备在部分城区实施公共自行车免费服务,如图①是公共自行车的实物图,如图②是公共自行车的车架示意图,点A ,D ,C ,E 在同一条直线上,点F 在AM 上,FD ⊥AC 于点D ,AF =30 cm ,DF =24 cm ,CD =35 cm ,∠EAB =71°.若∠B =49°,求AB 的长.(结果保留整数,参考数据:sin71°≈0.9,cos71°≈0.3,tan71°≈2.9,sin49°≈0.8,cos49°≈0.7,tan49°≈1.2,3≈1.7)第4题图解:如解图,过点A 作AG ⊥BC 于点G ,第4题解图∵∠CAB =71°,∠B =49°,∴∠ACB =60°,∵FD ⊥AC ,AF =30 cm ,DF =24 cm ,∴AD =18 cm.在Rt △AGC 中,sin ∠ACG =AG AC ,cos ∠ACG =CG AC ,∴sin60°=AG 18+35,∴AG=53×32=5332cm.在Rt△ABG中,AB=AGsin49°≈53320.8≈56 cm,答:AB的长约为56 cm.5. “高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90 cm.低杠上点C 到直线AB的距离CE的长为155 cm,高杠上点D到直线AB 的距离DF的长为234 cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF 为80.3°,求高、低杠间的水平距离CH的长.(结果精确到1 cm.参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.986,cos80.3°≈0.168,tan80.3°≈5.850)第5题图解:在Rt△CAE中,AE=CEtan∠CAE=155tan82.4°≈1557.500≈20.7,在Rt△DBF中,BF=DFtan∠DBF=234tan80.3°≈2345.850=40,∴EF=AE+AB+BF≈20.7+90+40=150.7≈151.∵四边形CEFH为矩形,∴CH=EF≈151.即高、低杠间的水平距离CH的长约为151 cm.6. 图①是一商场的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转37°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图②,求此时B 与C 之间的距离(结果保留一位小数).(参考数据:sin37°≈0.6,cos37°≈0.8,2≈1.4)第6题图解:如解图,连接BC ,过点B 作BE ⊥AD 于点E ,作CF ⊥AD 于点F ,过点C 作CG ⊥BE ,交BE 的延长线于点G ,在Rt △ABE 中,∵AB =12AD =1米,∠A =37°,∴BE =AB ·sin37°≈0.6米,AE =AB ·cos37°≈0.8米,第6题解图在Rt △CDF 中,CD =12AD =1米,∠D =45°,∴CF =AB ·sin45°=22≈0.7米,DF =CD ·cos45°≈0.7米,∴EG =CF ≈0.7米,GC =EF =AD -AE -DF ≈2-0.8-0.7=0.5米,∴BC =BG 2+CG 2=(0.6+0.7)2+0.52≈1.4米.答:B 、C 之间的距离约为1.4米.7. 西成高铁自2017年12月6日正式开通运营,标志着华北地区至西南地区又增加一条大能力、高密度的旅客运输主通道.如图,西成高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支架底端与桌面顶端的距离AO =75 cm ,展开小桌板使桌面保持水平时,有CB ⊥AO ,∠AOB =∠ACB =37°,且支架长OB 与桌面宽BC 的长度之和等于OA 的长度.求小桌板桌面的宽度BC (结果精确到 1 cm).(参考数据sin37°≈35,cos37°≈45,tan37°≈34)第7题图解:如解图,延长CB 交OA 于点E ,延长OB 交AC 于点F . 设BC =x ,则OB =OA -BC =75-x ,第7题解图∵∠AOB =∠ACB ,∠OBE =∠CBF ,∠AOB +∠OBE =90°, ∴∠ACB +∠CBF =90°,∴∠BFC =90°.在Rt △BFC 中,∵sin37°=BF BC ,∴BF =BC ·sin37°=sin37°·x ,在Rt △OAF 中,cos37°=OF AO ,即cos37°=75-x +sin37°·x 75, ∴x =75(1-cos37°)1-sin37°≈75×(1-45)1-35=37.5≈38(cm), ∴小桌板桌面的宽度BC 约为38 cm.8. 为促进农业发展,加快农村建设,某地政府计划扶持兴建一批新型钢管装配式大棚,如图①.线段AB,BD分别表示大棚的墙高和跨度,AC表示保温板的长.已知墙高AB为2米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C 点的仰角分别为9°,15.6°,如图②.求保温板AC的长是多少米.(精确到0.1米)(参考数据:32≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)图①图②第8题图解:如解图,过点C作CE⊥BA交BA的延长线于点E,过点C作CF⊥BD于点F,第8题解图∵∠BAC=150°,∴在Rt△ACE中,∠EAC=30°,设EC=x,则AE=3x,AC=2x,∵EC⊥AB,BD⊥AB,CF⊥BD,∴四边形ECFB是矩形,∴CF=AB+AE=2+3x(米),在Rt△ABD中,AB=2,∠ADB=9°,∴BD=ABtan9°≈20.16=252(米),∴DF=BD-CE=12.5-x(米),在Rt△CDF中,CF=2+3x(米),DF=12.5-x(米),∴tan∠CDF=CFDF=2+3x12.5-x≈0.28,解得x=0.75米,∴AC=2x=1.5米.答:保温板AC的长约为1.5米.9. 某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC 的夹角∠BCD 恰好等于56°,若主杆最高点A 到调节旋钮B 的距离为40 cm ,支架CD 的长度为30 cm ,旋转钮D 是脚架BE 的中点,求支架最高点A 到地面的距离.(结果精确到0.1 cm.参考数据:sin56°≈0.83,cos56°≈0.56,tan56°≈1.48,2≈1.41)第9题图解:如解图,过点D 作DG ⊥BC 于点G ,延长AC 交MN 于点H ,则AH ⊥MN,第9题解图在Rt △DCG 中,根据sin ∠GCD =DG DC ,得DG =CD ·sin ∠GCD =30×sin56°≈30×0.83=24.9 (cm),在Rt △BDG 中,根据sin ∠GBD =DG BD ,得BD =DG sin ∠GBD =24.922≈24.91.412≈35.3 (cm). ∵D 为BE 的中点,∴BE =2BD =70.6 cm ,在Rt △BHE 中,根据cos ∠HBE =BH BE ,得BH =BE ·cos ∠HBE =70.6×22≈70.6×1.412≈49.8 (cm),∴AH =AB +BH =40+49.8=89.8 (cm).答:支架最高点A 到地面的距离约为89.8 cm.10. 某款折叠床其配套的折叠床板的实物图如图①所示,图②为其抽象的几何图形.将床板折叠到如图②所示位置,点A 、B 、C 在同一条直线上,AG =BG =BD =CD ,CD ∥BG ,BD ∥AG ,∠DCB =70°,BC =0.34米,四边形CDEF 为矩形.(1)求床板完全展开后的总长度;(2)若∠DCB =80°时,该床板折叠后具有最好的稳定性,当折叠该床板使其最稳定时,顶点D 在垂直方向上有何变化,请说明理由.(结果精确到0.01米,参考数据:sin70°≈0.94, cos70°≈0.34, tan70°≈2.75,sin80°≈0.98, cos80°≈0.17, tan80°≈5.67)第10题图解:(1)如解图,过点D 作DH ⊥BC 于点H ,由题意可知,△BCD 为等腰三角形,∠DCB =70°,BC =0.34米,第10题解图∴CH =BC 2=0.17米,DC =HC cos70°≈0.170.34=0.50米,∴床板完全展开后的总长度约为0.50×4=2.00米;(2)顶点D 会在垂直方向上升约0.02米.理由;当∠DCB=70°时,DH=0.5×sin70°≈0.47米,当∠DCB=80°时,DH=0.5×sin80°≈0.49米,∴0.49-0.47=0.02米,∴当折叠该床板使其最稳定时,顶点D会在垂直方向上升约0.02米.。
锐角三角函数应用题专项习题一

锐角三角函数应用题专项习题一1、数学活动小组来到校园内一盏路灯下测量路灯高度,测角仪AB高度为1.5米,测得仰角α为30°,点B到电灯杆底端N距离BN为10米,求路灯高度MN是多少米?(=1.414,=1.732,结果保留两位小数)2、某中学九年级学生开展测量物体高度活动,他们要测量学校教学楼高度.如图他们先在点C测得教学楼AB顶点A仰角为30°,然后向教学楼前进60米到达点D,又测得点A仰角为45度.求出这幢教学楼高度.3、东方山主峰海拔约为600米,主峰AB上建有一座电信信号发射架BC,现在山脚P处测得峰顶仰角为α,发射架顶端仰角为β,其中tanα=tanβ=求发射架高BC.4、如图,小芸在自家楼房窗户A处,测量楼前一棵树CD的高.现测得树顶C处俯角为45°,树底D处俯角为60°,楼底到大树距离BD为20米.请计算树高度(精确到0.1米).5、数学活动小组去测量太子灵踪塔高度,小华先在塔前平地上选择一点A,用测角仪测出看塔顶(M)仰角α=35°,在A点和塔之间选择一点B,测出看塔顶(M)仰角β=45°,然后用皮尺量出A、B两点距离为18.6m,自身高度为1.6m.请计算出塔高度?(tan35°≈0.7,结果保留整数)6、同学们去测量一座古塔CD高度.他们首先从A处安置测倾器,测得塔顶C仰角∠CFE=21°,然后往塔方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD高度.(参考数据:sin37°≈ ,tan37°≈ ,sin21°≈ ,tan21°≈ )7、某旅游区有一个望天洞,D点是洞入口,游人从入口进洞游览后,可经山洞到达山顶出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下B处.在同一平面内,若测得斜坡BD长为100米,坡角∠DBC=10°,在B处测得A仰角∠ABC=40°,在D处测得A仰角∠ADF=85°,过D点作地面BE垂线,垂足为C.(1)求∠ADB度数;(2)求索道AB长.(结果保留根号)8、如图斜坡AC坡度(坡比)为1:3,AC=10米.坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC高度.9、如图∠MON=25°,矩形ABCD对角线AC⊥ON,边BC在OM上,当AC=3时,AD长是多少?(结果精确到0.01)10、同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=30m,BC=70m,∠CAB=120°,请计算A,B两个凉亭之间的距离.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数应用
1.(2015青岛)小明在热气球A 上看到正前方横跨河流两岸的大桥BC ,并测得B ,C 两点的俯角分别为45°和35°,已知大桥BC 与地面在同一水平面上,其长度为100m 。
请求出热气球离地面的高度。
(结果保留整数,参考数据:12
735sin ≈︒, 6535cos ≈︒,10735tan ≈︒
2.
3.(2014东营)热气球的探测器显示,从热气球底部A处看一栋高楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球A处与高楼的水平距离为120m,这栋高楼有多高(≈1.732,结果保留小数点后一位)
4.(2014•枣庄)如图,一扇窗户垂直打开,即OM⊥OP,AC是长度不变的滑动支架,其中一端固定在窗户的点A处,另一端在OP上滑动,将窗户OM按图示方向想内旋转35°到达ON位置,此时,点A、C的对应位置分别是点B、D.测量出∠ODB为25°,点D到点O的距离为30cm.
(1)求B点到OP的距离;
(2)求滑动支架的长.
(结果精确到1cm.参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
5.(2015济宁)在一个三角形中,各边和它所对角的正弦的比相等.即
sin sin sin a b c A B C
==.利用上述结论可以求解如下题目.如: 在ABC ∆中,若45A ∠=,30B ∠=,6a =,求b .
解:在ABC ∆中,sin sin a b A B =
16sin 6sin 30sin sin 45a B b A ⨯∴==== 问题解决:
如图,甲船以每小时海里的速度向正北方航行,当甲船位于1A 处时,乙船位于甲船的北偏西105方向的1B 处,且乙船从1B 处按北偏东
15方向匀速直线航行,当甲船航行20分钟到达2A 处时,乙船航行到
甲船的北偏西120
方向的2B 处,此时两船相距.
(1) 判断122A A B ∆的形状,并给出证明
. (2) 乙船每小时航行多少海里?。
