建筑结构抗震设计第三章--有图(1)--2
重大社2023《建筑结构抗震设计(第3版)》教学课件2

地球介质 (含场地)
工程结构
地震 地面运动
结构 地震响应
Acc.(m/s2)
400 300 200 100
0 -100 -200 -300
0
5
10
15
20
25
30
35
40
t(sec.)
(1)描述地震动的物理量有加速度、速度和位移。
汶川地震什邡八角站记录的NS方向加速度时程
(2)地震动包括两个水平分量和一个竖向分量。
a (t ) (m/s2)
10.0 5.0 0.0 -5.0 -10.0
0 10.0 5.0
10.0 东西分量
5.0
南北分量
a (t ) (m/s2)
地震动是一个具有随机性的不规则0.0 时间历程 -5.0
-10.0
20
40
60
80 t (s) 100
120
140
160
0
20
40
60
80 t (s) 100
与临界阻尼比ζ=1相应的阻尼系数 为cr=2wm,称为临界阻尼系数
一般工程结构均为欠阻尼, (ζ=0.01~0.1)
2023年9月6日
2.4.1 单自由度弹性体系的地震反应分析
确定系数c1、c2
x(t) (c1 cos't c2 sin 't)et
考虑初始条件: x0 x(0), x0 x(0)
xg
•
质点所受冲击力为:P
m 0
xg
0 dt dt
dt
•
质点在0~dt时间内的加速度为:
抗震设计中如何把握地震动的 特性?如何保证所考虑地震动 的合理性?
2.2 地震动特性
建筑结构抗震设计(第三版)习题解答1-5章

第一章的习题答案1. 震级是衡量一次地震强弱程度(即所释放能量的大小)的指标。
地震烈度是衡量一次地震时某地区地面震动强弱程度的尺度。
震级大时,烈度就高;但某地区地震烈度同时还受震中距和地质条件的影响。
2. 参见教材第10面。
3. 大烈度地震是小概率事件,小烈度地震发生概率较高,可根据地震烈度的超越概率确定小、中、大烈度地震;由统计关系:小震烈度=基本烈度-1.55度;大震烈度=基本烈度+1.00度。
4. 概念设计为结构抗震设计提出应注意的基本原则,具有指导性的意义;抗震计算为结构或构件达到抗震目的提供具体数据和要求;构造措施从结构的整体性、锚固连接等方面保证抗震计算结果的有效性以及弥补部分情况无法进行正确、简洁计算的缺陷。
5. 结构延性好意味可容许结构产生一定的弹塑性变形,通过结构一定程度的弹塑性变形耗散地震能量,从而减小截面尺寸,降低造价;同时可避免产生结构的倒塌。
第二章的习题答案1. 地震波中与土层固有周期相一致或相近的波传至地面时,其振幅被放大;与土层固有周期相差较大的波传至地面时,其振幅被衰减甚至完全过滤掉了。
因此土层固有周期与地震动的卓越周期相近,2. 考虑材料的动力下的承载力大于静力下的承载力;材料在地震下地基承载力的安全储备可低于一般情况下的安全储备,因此地基的抗震承载力高于静力承载力。
3. 土层的地质年代;土体中的粘粒含量;地下水位;上覆非液化土层厚度;地震的烈度和作用时间。
4. a 中软场地上的建筑物抗震性能比中硬场地上的建筑物抗震性能要差(建筑物条件均同)。
b. 粉土中粘粒含量百分率愈大,则愈容易液化. c .液化指数越小,地震时地面喷水冒砂现象越轻微。
d .地基的抗震承载力为承受竖向荷载的能力。
5. s m v m 5.2444208.32602.82008.51802.220=+++=因m v 小于s m 250,场地为中软场地。
6. 设计地震分组为第二组,烈度为7度,取80=N砂土的临界标贯值:[])(1.09.00w s cr d d N N -+=,其中m d w 5.1=土层厚度:第i 实测标贯点所代表的土层厚度的上界取上部非液化土层的底面或第1-i 实测标贯点所代表土层的底面;其下界取下部非液化土层的顶面或相邻实测标贯点的深度的均值。
抗震作业第三章

第三章 结构地震反应分析与抗震极限状态计算 思考题3.1 什么是地震动反应谱和抗震设计反应谱反应谱的影响因素和特点是什么答:根据给定的地面运动加速度记录和体系的阻尼比,计算出质点的最大绝对加速度S a ,与体系的自振周期T ,绘制成一条曲线-地震加速度反应谱,不同的阻尼比可以绘制出不同曲线。
规范根据同一类场地在各级烈度地震作用下地面运动的 ,分别计算出的反应谱曲线,再进行统计分析,求出最有代表性的平均反应谱曲线作为设计依据;通常称之为抗震设计反应谱。
反应谱影响因素:受地震动特性即峰值、频谱、持续时间的影响。
特点是随机性。
3.2 什么是地震影响系数其谱曲线的形状参数有何特点答:单自由度体系绝对加速度反应)(T Sa 与重力加速度g 之比。
3.3 什么是地震作用怎样确定单自由度弹性体系的地震作用答:地震作用:地面振动过程中作用在结构上的惯性力就是地震荷载,可理解为能反映地震影响的等效荷载,实际上,地震荷载是由于地面运动引起的动态作用,属于间接作用,应称为“地震作用”,而不应称为“地震荷载”。
确定单自由度弹性体系的地震作用: 水平方向:E Ek G T F )(α= 竖直方向:E v Evk G F max ,α=3.4 抗震设计中的重力荷载代表值是什么其中可变组合值系数的物理含义如何答:重力荷载代表值是指地震作用下计算有关效应标准值时,永久性结构构配件、非结构构件和固定设备等自重标准值加上可变动荷载组合值。
变组合值系数的物理含义:是根据可变重力荷载与地震的遇合概率确定的。
3.5 多自由度集中质量体系地震下的运动方程如何说明方程中各参数的含义。
答:)(}]{[)}(]{[)}(]{[)}(]{[t x R M t x K t x C t x M g •••••-=++3.6 写出振型质量、振型参与质量、振型参与系数的表达式。
答:振型质量:{}[]{}j Tj j x M x M =振型参与质量:{}[]{}j Rpj x M R M =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n m m m m 0...0][21⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n c c c c c c c c c c .....................][212222111211⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=nn n n n n k k k k k k k k k k .....................][212222111211)(t x 0&&振型参与系数:jpj j M M V =3.7 简述多自由度体系地震反应的振型分解法与振型分解反应谱法的原理和步骤。
《建筑抗震设计规范》

《建筑抗震设计规范》(GB50011-2001)强制性条文内容《建筑抗震设计规范》GB50011-2001,自2002年1月1日起施行,原《建筑抗震设计规范》GBJ11-89以及《工程建设国家标准局部修订公告》(第1号)于2002年12月31日废止。
《建筑抗震设计规范》GB50011-2001,其中有52条为强制性条文,必须严格执行。
现将该52条强制性条文摘录如下:一.第一章“总则”部分第 1.0.2 条:抗震设防烈度为6度及以上地区的建筑,必须进行抗震设计。
第 1.0.4条:抗震设防烈度必须按国家规定的权限审批、颁发的文件(图件)确定。
二.第三章“抗震设计的基本要求”部分第3.1.1条:建筑应根据其使用功能的重要性分为甲类、乙类、丙类、丁类四个抗震设防类别。
甲类建筑应属于重大建筑工程和地震时可能发生次生灾害的建筑;乙类建筑应属于地震时使用功能不能中断或需尽快恢复的建筑;丙类建筑应属于除甲类、乙类、丁类以外的一般建筑;丁类建筑应属于抗震次要建筑。
第3.1.3条:各抗震设防类别建筑的抗震设防标准,应符合下列要求:1:甲类建筑,地震作用应高于本地区抗震设防烈度的要求,其值应按批准的地震安全性评价结果确定;抗震措施,当抗震设防烈度为6~8度时,应符合本地区抗震设防烈度提高一度的要求,当抗震设防烈度为9度时,应符合比9度抗震设防更高的要求。
2:乙类建筑,地震作用应符合本地区抗震设防烈度的要求;抗震措施,一般情况下,当抗震设防烈度为6~8度时,应符合本地区抗震设防烈度提高一度的要求,当抗震设防烈度为9度时,应符合比9度抗震设防更高的要求;地基基础的抗震措施,应符合有关规定。
另外,对较小的乙类建筑,当其结构改用抗震性能较好的结构类型时,应允许仍按本地区抗震设防烈度的要求采取抗震措施。
3:丙类建筑,地震作用和抗震措施均应符合本地区抗震设防烈度的要求。
4:丁类建筑,一般情况下,地震作用仍应符合本地区抗震设防烈度的要求;抗震措施,应允许比本地区抗震设防烈度的要求适当降低,但当抗震设防烈度为6度时不应降低。
建筑结构抗震设计第三章单自由度弹性体系的水平地震作用

2
max
1
Tg
2021/3/7
结构抗震设计
16
设计特征周期
规范规定,根据建筑工程的实际情况,将地震动反应
谱特征周期Tg,取名为“设计特征周期”。
设计特征周期的值应根据建筑物所在地区的地震环境 确定。(所谓地震环境,是指建筑物所在地区及周围 可能发生地震的震源机制、震级大小、震中距远近以 及建筑物所在地区的场地条件等。)
式中 k11——使质点1产生单位位移而质点2保持不动时,
在质点1处所需施加的水平力; k12——使质点2产生单位位移而质点1保持不动时,
在质点1处引起的弹性反力; c11——质点1产生单位速度而质点2保持不动时,
在质点1处产生的阻尼力; c12——质点2产生单位速度而质点1保持不动时,
在质点1处产生的阻尼力;
在进行建筑结构地震反应分析时, 除了少数质量比较集中的结构 可以简化为单质点体系外,大 量的多层和高层工业与民用建 筑、多跨不等高单层工业厂房 等,质量比较分散,则应简化 为多质点体系来分析,这样才 能得出比较符合实际的结果。
一般,对多质点体系,若 只考虑其作单向振动时,则体 系的自由度与质点个数相同。
1、两自由度运动方程的建立 2、两自由度弹性体系的运动微分方程组 3、两自由度弹性体系的自由振动 三、多自由度弹性体系的自由振动 1、n自由度体系运动微分方程组 2、n自由度弹性体系的自由振动 四、振型分解法 1、两自由度体系振型分解法 2、n自由度体系振型分解法
2021/3/7
结构抗震设计
21
一、多质点和多自由度体系
15
多层砌体结构抗震设计

7.不应在房屋转角处设置转角窗。 8.横墙较少、跨度较大的房屋,宜采用现浇钢筋混凝土楼、屋盖。
3.2.2 房屋的总高度和层数
●为什么限制? ●砌体房屋的震害与其总高度和层数有密切关系,随层数增加,震害随之加重,特别是房屋的 倒塌率与房屋的层数成正比率增加 ●对砌体房屋的总高度及层数要予以限制,这也是一种最经济的抗震措施。 ●《抗震规范》对砌体房屋的限值如表3.1所示
2.纵横墙应对称、均匀布置,沿平面应对齐、贯通,同一轴线上墙体宜等宽匀
称,沿竖向宜上下连续。
3.对8度、9度区且有下列情况之一时宜设防震缝 ⑴立面高差在6m以上 ⑵房屋有错层,且楼板高差大于层高的1/4; ⑶部分结构的刚度、质量截然不同 4. 楼梯间不宜设置在房屋的尽端和转角处 5. 烟道、风道、垃圾道等不应削弱墙体,当墙体被削弱时,应对墙体采取加强措施;
1923年日本关东大地震,东京约有砖石结构房屋7000栋,几乎全部遭到不同程度的破坏。 1948年原苏联阿什哈巴德地震,砖石结构房屋的破坏和倒塌率达到7080%。 1976年唐山地震,对烈度为10度、11度区的123栋2-8层砖混结构房屋调查,倒塌率为
63.2%,严重破坏为23.6%,尚能修复使用的4.2%,实际破坏率达95.8%。
楼层地震剪力的分配 横向的地震剪力由横向墙体承担。 纵向的地震剪力由纵向墙体承担。
楼层地震剪力的分配与墙体的刚度和楼盖的刚度有关。
3.3.1 加强结构的连接 1. 纵横墙的连接 当未设构造柱时,应沿墙高每隔0.5m配置 2Q6 拉结钢筋
沿墙高每500 放2φ6
图 纵横墙的连接
沿墙高每500 放2φ6
震害及其分析
第三章2 工程结构地震反应分析与抗震验算.ppt

h 1 ---直线下降段的斜率调整系数;按下式确定
h1 = 0.02 + (0.05 - z ) / 8 当h1 < 0时,取h1 = 0
h2 - -阻尼调整系数,h2 < 0.55时,取h2 = 0.55
h2
=1+
0.05 - z 0.06 +1.7z
Tg : 特征周期,见表3.2
max:水平地震系数的最大值 α max = kβ max ,β max= 2.25
结构在地震持续过程中经受的最大地震作用为
F
=
F (t ) max
= m &x&(t) + &x&g (t) max
= mSa
= mg Sa
&x&g (t) max = Gk = G
&x&g (t) max
g
G ---集中于质点处的重力荷载代表值;
g ---重力加速度
= Sa
&x&g (t) max
地震特征周期分组的特征周期值(s)
场地类别
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一组 0.25
0.35
0.45 0.65
查表确定 Tg Tg = 0.3
第二组 0.30
0.40
第三组 0.35
0.45
0.55 0.75 0.65 0.90
例:单层单跨框架。屋盖刚度为无穷大,质量集中于屋 盖处。已知设防烈度为8度,设计地震分组为二组,Ⅰ类 场地;屋盖处的重力荷载代表值G=700kN,框架柱线刚 度 ic = EIc / h = 2.6104 kN m ,阻尼比为0.05。试求该结构多 遇地震时的水平地震作用。
建筑抗震设计规范

back
场地和地基
项目
评价 选 地段 择 不利 场 地段 地 危险
地段
甲类
结构型式时可不提高
原设防烈度 原设防烈度
丙类
GBJ11-89 甲、乙、丁类以外的一般
GB50011
建筑
原设防烈度
原设防烈度
丁类 GBJ11-89 GB50011
抗震次要的建筑 抗震次要的建筑
降低一度(6度不降) 适当降低(6度不降)
原设防烈度 原设防烈度
back
地震影响
项目
GBJ11-89
GB50011-2001
两阶段设计
地震影 50年超越 地震重现期
响
概率
小震 63.2%
50年
中震 10%
475年
大震 2-3% 1642-2475年
• 一般关系
– 烈度:Im=I0-1.55, Is<=I0+1 – 加速度:PGAm=PGA0*1/3
PGAs=PGAm*(4-6)
阶段 目 标 烈度 地震作用性质 受力状态
作用效应组合
条文对比及介绍
• 概述 • 总则 • 术语和符号 • 抗震设计的基本要求 • 场地、地基和基础 • 地震作用和结构抗震验算 • 多层和高层钢筋混凝土结构 • 多层砌体、底部框架、内框架 • 多层和高层钢结构 • 单层工业厂房 • 单层空旷房屋、土木石结构 • 隔震和消能减震设计 • 非结构构件
back
混凝土建筑结构第三章作业答案

第三章思考题3.1 房屋结构设计时应考虑那些荷载或作用?P52,P56答:主要考虑竖向荷载(自重、楼屋面活荷载等)和水平作用(风荷载和地震作用等)。
3.2 房屋建筑结构的竖向荷载如何取值?进行竖向荷载作用下的内力计算时,是否要考虑活荷载的不利布置?P52答:对永久荷载,采用标准值作为代表值;对可变荷载应根据设计要求采用标准值、组合值、频遇值或准永久值作为代表值;对偶然和在应按建筑结构使用的特点确定其代表值。
一般情况下可不考虑活荷载的最不利布置,但如果楼面活荷载大于4kN/2m 时,其不利分布对梁弯矩的影响会比较明显,应予考虑。
3.3 结构承受的风荷载与哪些因素有关?P56答:由k z s z 0=w βμμω,可知结构承受的风荷载与基本风压、风荷载体型系数、风压高度变化系数和高度z 处的风振系数有关。
其中,基本风压与地区有关;风压高度系数与高度有关、也与地貌及周围环境有关;风荷载体形系数与建筑物的体型与尺寸有关、也与周围环境和地面粗糙度有关;风振系数与地面类别、结构阻尼比和地面尺寸有关。
3.4 房屋结构风荷载计算时,基本风压、结构体型系数和高度变化系数应分别如何取值?(P56)答:基本风压系以当地比较空旷平坦地面上离地10m 高统计所得的50年一遇10min 平均最大风速0v (m/s )为标准,按200/1600w v =确定的风压值。
按《荷规》附录E 中附表E.5给出的50年重现期的风压采用,但不得小于0.3kN/2m 。
结构体形系数取值如下: 1) 圆形平面建筑取0.8.2)0.8 1.2/s μ=+3) 高宽比H/B 不大于4的矩形、方形、十字形平面建筑取1.3. 4) 下列建筑取1.4:(A ) V 型、Y 型、弧形、双十字形、井字形平面建筑; (B ) L 型、槽型和高宽比H/B 大于4的十字形平面建筑;(C ) 高宽比H/B 大于4,长宽比L/B 不大于1.5的矩形、鼓型平面建筑 5) 在需要更细致进行风荷载计算的情况下,风荷载体形系数可按《高规》附录B 采用,或由风洞试验确定。
建筑结构抗震设计复习资料(完美篇)..

《建筑结构抗震设计》总复习(武汉理工配套)考试的具体题型和形式可能会有变化,但知识点应该均在以下内容中。
复习不要死记硬背,而应侧重理解.第一章:绪论1.什么是地震动和近场地震动?P3由地震波传播所引发的地面振动,叫地震动。
其中,在震中区附近的地震动称为近场地震动.2。
什么是地震动的三要素?P3地震动的峰值(振幅)、频谱和持续时间称作地震动的三要素。
3. 地震按其成因分为哪几类?其中影响最大的是那一类?答:地震按其成因可分为构造地震、火山地震、陷落地震和诱发地震等几类,其中影响最大的是构造地震。
4。
什么是构造地震、震源、震中、震中距、震源深度?P1 答:由于地壳构造运动使深部岩石的应变超过容许值,岩层发生断裂、错动而引起的地面震动,这种地震称为构造地震,一般简称地震.地壳深处发生岩层断裂、错动的地方称为震源。
震源至地面的距离称为震源深度。
一般震源深度小于60km的地震称为浅源地震;60~300km的称为中源地震;大于300km的称为深源地震;我国绝大部分发生的地震属于浅源地震,一般深度为5~40km。
震源正上方的地面称为震中,震中邻近地区称为震中区,地面上某点至震中的距离称为震中距。
5。
地震波分哪几类?各引起地面什么方向的振动?P1—3 答:地震波按其在地壳传播的位置不同可分为体波和面波。
在地球内部传播的波称为体波,体波又分为纵波(P波)和横波(S波)。
纵波引起地面垂直方向的震动,横波引起地面水平方向震动。
在地球表面传播的波称为面波.地震曲线图中,纵波首先到达,横波次之,面波最后到达.分析纵波和横波到达的时间差,可以确定震源的深度。
6。
什么是震级和地震烈度?几级以上是破坏性地震?我国地震烈度表分多少度?P4答:震级:指一次地震释放能量大小的等级,是地震本身大小的尺度。
(1)m=2~4的地震为有感地震.(2)m〉5的地震,对建筑物有不同程度的破坏。
(3)m>7的地震,称为强烈地震或大地震。
地震烈度:是指某一区域内的地表和各类建筑物遭受一次地震影响的平均强弱程度。
建筑结构抗震ppt课件

第一章 绪论
建筑结构抗震设计
烈度表
分为1-12度(不同的国家的分度方法不同)
中国地震烈度表
分项:人的感觉,大多数房屋震害程度,其他现象, 加速度(水平向)厘米/秒² ,速度(水平向)厘米/秒
I度:为无感觉,损坏一个别砖瓦掉落墙体微细裂缝; 河岸和松软土上出现裂缝。
第一章 绪论
建筑结构抗震设计
VI (6)度:惊慌失措,仓惶逃出;饱和砂层出现喷砂冒 水。地面上有的砖烟囱轻度裂缝、掉头;加 速度63厘米/秒² 。
第一章 绪论
建筑结构抗震设计
(多遇烈度)
.55度
(设防烈度)
度左右
(罕遇烈度)
第一章 绪论
设计地震分组
6度近震
设计地震分组是新规范新提 出的概念,用以代替旧规范设计 近震、设计远震的概念。 6度远震
在宏观烈度大体相同 条件下,处于大震级远离 震中的高耸建筑物的震害 比中小级震级近震中距的 情况严重的多。
第一章 绪论
建筑结构抗震设计
板块说:
大陆漂移假说:它是德国气象学家魏格纳(Wegener) (1880~1930年)在讲课中提出来的。
这一假说在约10年时间内没有受到地质界的重视。在 1922年2月16日有一篇评述魏格纳的书的一无人署名的短文, 发表于著名的科学杂志《自然》上,说“该书直接应用了物 理学原理,但遭到许多地质学家的强烈反对”。
建筑结构抗震设计
震级是一次地震强弱的等级。
现国际上的通用震级表示为
里氏震级。(Richter)
查尔斯·里 克特(1900~
用标准的地震仪在距震中100km19处85年记) 录 最大水平位移A(以µm=10-6 m计)。
震级M=logA
抗震作业第三章

第三章 结构地震反应分析与抗震极限状态计算 思考题3.1 什么是地震动反应谱和抗震设计反应谱反应谱的影响因素和特点是什么答:根据给定的地面运动加速度记录和体系的阻尼比,计算出质点的最大绝对加速度S a ,与体系的自振周期T ,绘制成一条曲线-地震加速度反应谱,不同的阻尼比可以绘制出不同曲线。
规范根据同一类场地在各级烈度地震作用下地面运动的 ,分别计算出的反应谱曲线,再进行统计分析,求出最有代表性的平均反应谱曲线作为设计依据;通常称之为抗震设计反应谱。
反应谱影响因素:受地震动特性即峰值、频谱、持续时间的影响。
特点是随机性。
3.2 什么是地震影响系数其谱曲线的形状参数有何特点答:单自由度体系绝对加速度反应)(T Sa 与重力加速度g 之比。
3.3 什么是地震作用怎样确定单自由度弹性体系的地震作用答:地震作用:地面振动过程中作用在结构上的惯性力就是地震荷载,可理解为能反映地震影响的等效荷载,实际上,地震荷载是由于地面运动引起的动态作用,属于间接作用,应称为“地震作用”,而不应称为“地震荷载”。
确定单自由度弹性体系的地震作用:水平方向:E Ek G T F )(α= 竖直方向:E v Evk G F max ,α= 3.4 抗震设计中的重力荷载代表值是什么其中可变组合值系数的物理含义如何答:重力荷载代表值是指地震作用下计算有关效应标准值时,永久性结构构配件、非结构构件和固定设备等自重标准值加上可变动荷载组合值。
变组合值系数的物理含义:是根据可变重力荷载与地震的遇合概率确定的。
3.5 多自由度集中质量体系地震下的运动方程如何说明方程中各参数的含义。
)(t x答:)(}]{[)}(]{[)}(]{[)}(]{[t x R M t x K t x C t x M g •••••-=++3.6 写出振型质量、振型参与质量、振型参与系数的表达式。
答:振型质量:{}[]{}j Tj j x M x M =振型参与质量:{}[]{}j Rpj x M R M =振型参与系数:jpj j M M V =3.7 简述多自由度体系地震反应的振型分解法与振型分解反应谱法的原理和步骤。
清华大学出版社抗震结构与抗震设计第一章

板块构造学说认为,地壳和上地漫顶部厚约70—
100km的岩石组成了全球岩石圈。全球岩石圈可以 划分为若干大小的板块。根据板块构造学说,全球 岩石圈被分为六大板块,即欧亚板块、太平洋板块、 美洲板块、非洲板块、印澳板块和南极板块。各大 板块之内还可以划分为较小的板块。板块之间的接 合部类型主要有:海岭、海沟、转换断层及缝合线。
国内外大量震害表明,采用合理的抗震设防标准,抗
震设计方法和构造措施,是当前减轻地震灾害的最有效 措施。
近年来全球8级及8级以上地震一览表
1995 1996 1997 1998 1999 2000 2001 2002 2003
2次 1次 0次 1次 0次 1次 1次
0次 2003
2004 2次
2005 1次
1.2.2 地震类型和成因
地震
天然地震 ---天然地震包括构造地震、火山地震、陷落地震 人工地震
构造地震
92%的地震发生在 地壳中, 其余的发 生在地幔上部
破坏性地震主要属于构造地震。据统计,构造地震约 占世界地震总数的90%以上。
地震成因
在1887年G.Hartwig曾写道:“地震的原因仍
然隐藏在蒙昧之中,而且可能永远如此,因为这 种剧烈的震动起源于地球深部,远远处于人类所 能进行观察的范围之下。”
然而今天,地震学中变形介质的方程已把地震中多半
属于定性揣测的领域与定量分析的领域分离开来了。 地震学在许多方面已经发展成为最严谨的学科之一。
地震成因
地基和基础的抗震设计

上一页 下一页 返回
第一节建筑场地
• (2)当地面5 m以下存在剪切波速大于其上部各土层剪切波速 2. 5倍 的土层,且该层及其下卧各层岩土的剪切波速均不小于400 m/s时, 可按地面至该土层顶面的距离确定。
• (2)地震是有限次数不等幅的随机荷载,其等效循环荷载不超过十几 次到几十次,而多数土在有限次数的动载下强度较静载下稍高。基于 这两方面原因,新规范延续采用抗震承载力与静力承载力的比值作为 地基土承载力调整系数,其值也可通过动静强度之比求得。
• 《抗震规范》中地基抗震承载力设计值,可采用在地基静力承载力 设计值基础上乘以调整系数若。来计算。调整系数若。是综合考虑了 土在动荷载下强度的提高和可靠度指标的降低两个因素而确定的。地 基抗震承载力按下式确定:
第三章地基和基础的抗震设计
• 第一节建筑场地 • 第二节地基和基础的抗震设计 • 第三节可液化地基和抗液化措施
返回
第一节建筑场地
• 地震对建筑物的破坏作用是通过场地、地基和基础传递给上部结构 的;同时,场地与地基在地震时又支撑着上部结构,因此,建筑场地 具有双重作用。任何一个建筑物,都坐落和嵌固在建设场地的地基上。 研究工程在地震作用的震害形态、破坏机理,以及抗震设计等问题, 都离不开对场地土和地基的研究;而研究场地和地基在地震作用下的 反应及其对上部结构的影响,正是场地抗震评价的重要任务。通过对 地震地质、工程地质、地形地貌以及岩土工程环境等场地条件的分析, 研究场地条件对基础和上部结构震害的影响,从而合理地选择有利建 筑场地和地基,避免和减轻地震对建筑物或工程设施的破坏。
上一页 下一页 返回
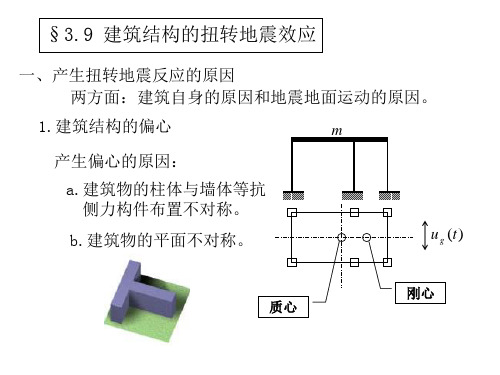
第三章 建筑结构的扭转地震效应(第12节课讲义)
由结构动力学,可建立结构的运动方程为
M D CD K D 0
式中 M ---质量矩阵 D ---位移矩阵
m
M
m
J
J ——转动惯量
m1
m
J1
J
m2
mn
J2
J
n
C ---阻尼矩阵
影响系数;
Ftji x
ri Ji / Mi ---i层转动半径;
Fy ji
j振型i层质心处地震作用
考虑扭转地震效应时水平地震作用标准值
的计算公式:
Fxji j tj x jiGi
y 质心
Fyji j tj y jiGi
Fx ji
Ftji x
Ftji j tj ri2 jiGi
tj ---考虑扭转的j振型参与系数;
静力法
——取结构或构件重力的某个百分数作为其竖向地震作用
水平地震作用折减法
——取结构或构件水平地震作用的某个百分数作为其竖向 地震作用;
竖向地震反应谱法
——与水平地震反应谱法相同
时程分析法
规范采用的是:基于竖向地震反应谱法的拟静力法
一、竖向地震反应谱
竖向地震反应谱与水平地震反应谱的比较: 形状相差不大; 加速度峰值约为水平的1/2至2/3。 因此,可利用水平地震反应谱进行分析。
ny
K X K X s Y s
s 1
y1s
Y s
y2s
s yis
yns
y
r
x
第i层 xir
yis ——第i层第s榀x方向的y轴座标;
nx
KY KY r X rr1x1r X r
建筑抗震课件(第三章 地震作用和结构抗震验算)

筑 震作用(即结构地震惯性力)是间接作用,而不称为荷载,但 为了应用方便,将地震作用等效为某种形式的荷载作用,
抗 这就是等效地震荷载。
震
3.1 概述
第 3.1.2 质点体系及其自由度
三
实际结构在地震作用下摇晃的现象十分复杂。在计 算地震作用时,为了将实际问题的主要矛盾突出来,
三 质点自振周期变化的曲线为地震反应谱。 由于地震的随机性,即使在同一地点、同一烈度,每次地震的地面加速
章 度记录也很不一致,因此需要根据大量的强震记录计算出对应于每一条 强震记录的反应谱曲线,然后统计求出最有代表性的平均曲线作为设计 依据,这种曲线称为标准反应谱曲线。
建 筑 抗 震 各种因素对反应谱的影响
章 运用理论公式进行计算设计,需将复杂的建筑结构
简化为动力计算简图。
单质点弹性体系
建 筑 多质点弹性体系 抗 震
3.1 概述
第 单质点弹性体系 三 章
常常将水箱及其支 架的一部分质量集 中在顶部,以质点 m来表示
建
筑
抗
震
水塔
支承水箱的支架 则简化为无质量 而有弹性的杆件, 其高度等于水箱
的重心高
3.1 概述
建 去的微量,故:
筑
m[x(t) xg (t)] kx(t)
抗
震
3.3单质点弹性体系的水平地震作用计算
第
这样,在地震作用下,质点在任一时刻的相对位移
三 将与该时刻的瞬时惯性力成正比。因此,可认为这一相
章 对位移是在惯性力的作用下引起的,虽然惯性力并不是
真实作用于质点上的力,但惯性力对结构体系的作用和
工程结构抗震设计教学大纲

《工程结构抗震设计》课程教学大纲1.课程概况第一章地震工程基本知识1.教学要求(1)了解地震的主要类型及其成因;(2)了解世界及我国地震活动性以及地震成灾机制;(3)掌握地震波的运动规律和震级、地震烈度等地震强度度量指标;(4)掌握建筑抗震设防分类、抗震设防目标和抗震设计方法;(5)理解工程结构抗震概念设计基本要求;(6)了解地震预警与救援的原则与意义。
2.教学重点地震基础知识,地震活动与地震分布,地震特征描述,工程结构抗震设防,工程结构抗震概念设计。
3.教学难点里氏震级和矩震级的定义和区别,设计基本地震加速度、设计特征周期、设计地震分组运用,工程结构概念设计的把握与理解。
第二章场地、地基与基础抗震1.教学要求(1)理解工程地质条件对结构震害的影响,(2)掌握场地与场地土的概念,场地与场地土的分类以及场地条件对工程结构抗震的影响;(3)掌握天然地基、基础的抗震验算方法;(4)掌握场地土液化的概念及其影响因素;(5)了解场地土液化的判别方法、可液化地基与软弱地基的抗震处理措施。
2.教学重点场地与场地土的概念及分类,天然地基、基础的抗震验算方法,砂土液化的概念与判别方法等。
3.教学难点场地土与场地的分类及区别,天然地基、基础的抗震验算方法中地基抗震承载力提高的原因。
第三章地震作用与结构抗震验算1.教学要求(1)掌握结构的动力地震反应的特性。
(2)掌握反应谱的概念,地震系数、动力系数、地震影响系数、重力荷载代表值的概念。
(3)掌握振型分解反应谱法计算多自由度弹性体系地震反应的方法。
(4)掌握用底部剪力法计算水平地震作用(5)理解结构竖向地震作用的计算方法。
(6)了解结构的扭转效应的概念。
(7)了解结构时程分析法的概念。
(8)理解和掌握结构构件抗震承载力验算、多遇地震下结构抗震变形验算及罕遇地震下结构抗震变形验算的概念与方法。
2.教学重点地震影响系数和反应谱的概念与表达式,振型分解的概念,振型分解反应谱法,底部剪力法,结构构件抗震承载力验算及变形验算等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构抗震设计
7
2、两自由度弹性体系的运动微分方程组
根据达朗贝尔原理,I1+R1+S1=0,经整理得下列运 1 t) ( x ( c11 x c12 x ( k11 x ( k12 x ( m1 x ( 1 t) 2 t) 1 t) 2 t) g t) 动方程 m1 ( ( x ( c21x c22 x k21x ( k22 x ( m2 x ( 2 t) 1 t) 2 t) 1 t) 2 t) g t) 同理对于质点2: m2 上二式就是两自由度弹性体系在水平地震作用下的运 动微分方程组。 上述列动力平衡方程求解的方法常称为刚度法。运动 方程中的系数kij反映了结构刚度的大小,称为刚度系 数。
x( X 12 sin (1t 1) X 22 sin ( 2t 2) 2 t)
其中X11、X12、X21、X22、φ1、φ2由初始条件确定。 由上式可见,在一般初始条件下,任一质点的振动都 是由各主振型的简谐振动叠加而成的复合振动。
2015/11/19
结构抗震设计
13
4)、质点复合振动振型曲线和惯性力
2015/11/19 结构抗震设计 4
一、多质点和多自由度体系
在进行建筑结构地震反应分析时, 除了少数质量比较集中的结构 可以简化为单质点体系外,大 量的多层和高层工业与民用建 筑、多跨不等高单层工业厂房 等,质量比较分散,则应简化 为多质点体系来分析,这样才 能得出比较符合实际的结果。 一般,对多质点体系,若 只考虑其作单向振动时,则体 系的自由度与质点个数相同。
2015/11/19
结构抗震设计
2
第三章重点、难点和基本要求
重点和难点: 1、重要术语、概念、定义 2、单(多)自由度体系地震反应和地震作用计算 3、底部剪力法 4、结构抗震验算 基本要求: 掌握结构抗震验算基本方法
2015/11/19
结构抗震设计
3
§3-4多自由度弹性体系的地震反应
一、多质点和多自由度体系 二、两自由度弹性体系的自由振动 1、两自由度运动方程的建立 2、两自由度弹性体系的运动微分方程组 3、两自由度弹性体系的自由振动 三、多自由度弹性体系的自由振动 1、n自由度体系运动微分方程组 2、n自由度弹性体系的自由振动 四、振型分解法 1、两自由度体系振型分解法 2、n自由度体系振型分解法
2
由此可求得 ω的两个正实根,它们就是体系的两个自振圆频率。其 中较小的一个用ωl表示,称为第一频率或基本频率,较大的一个ω2 称为第二频率。 利用式 T 2 / 可由ωl和ω2求得体系的两个自振周期,即 T1=2π/ω1 和 T2=2π/ω2,且 T1 > T2 ,T1 称为第一周期或基本周期, T2称为第二周期。
2 ( 2) (
k12 0 2 k 22 m2
展开行列式,可得ω2的二次方程 : 上式称为频率方程,解之得:
2
k11 k 22 k k k k ) 2 11 22 12 21 0 m1 m2 m1 m2
1 k k k k11 k 22 k12 k 21 1 k ( 11 22 ) ( 11 22 ) 2 m1 m2 2 m m m1m2 1 2
两自由度弹性体系分别按频率ω1和ω2作简谐振动时,两个振型的 变形曲线及两质点上相应的惯性力如图所示。 ji mi 2 j x ji ,其中i为质点编号,j为振型 x 惯性力可表示为 mi 序号,而且主振型变形曲线可视为体系上相应的惯性力引起的静 力变形曲线,因为由 可知,结构在任一瞬时的位移就是 F (t ) kx(t ) 等于惯性力所产生的静力位移。 在一般初始条件下,任一质点的振动都是由各主振型的简谐振动 叠加而成的复合振动。
2 2 12 12 1 1 11 22 22 1 2 11 11 11 12 21 21 12
2015/11/19
结构抗震设计
12
3)、自由振动方程的通解
两自由度弹性体系自由振动方程式的通解为其特解即 分别对应两个自振圆频率的质点位移的线性组合,也 即:x ( X 11 sin (1t 1) X 21 sin ( 2t 2) 1 t)
第三章 地震作用和结构抗震验算
一、课程内容 二、重点、难点和基本要求
2015/11/19
结构抗震设计
1
第三章 课程内容
§3-1 概述 §3-2 单自由度弹性体系的地震反应 §3-3 单自由度弹性体系的水平地震作用——地震反应谱法 §3-4 多自由度弹性体系的地震反应 §3-5 多自由度弹性体系的水平地震作用——振型分解反应谱法 §3-6 底部剪力法和时程分析法 §3-7 水平地震作用下的扭转效应 §3-8 结构的竖向地震作用 §3-9 结构自振周期的近似计算 §3-10 地震作用计算的一般规定 §3-11 结构抗震验算
2015/11/19
结构抗震设计
8
3、两自由度弹性体系的自由振动
以两自由度体系为例,令方程组等号右边荷载项为零, 由于阻尼对体系自振周期影响很小,故略去阻尼,即 1 t) 得该体系无阻尼自由振动方程组: m1 x ( k11 x ( k12 x( 0 1 t) 2 t)
m2 x ( k 21 x ( k 22 x( 0 2 t) 1 t) 2 t)
m1 X 11 X 21 m2 X 12 X 22 0 由于ω1≠ω2,所以: 上式所表示的关系,称为主振型的正交性,它反映了主 振型的一种特性,即体系各质点的质量与其在两个不同 振型上的位移振幅的连乘积的代数和为零。 物理意义是:某一振型在振动过程中所引起的惯性力不 在其它振型的位移上作功。这说明某一振型的动能不会 转移到其它振型上去,也就是体系按某一振型作自由振 动时不会激起该体系其它振型的振动。
设两个质点作同频率、同相位的简谐振动,则上列微 ( X 1 sin (t ) 分方程组的解为: x 1 t)
x( X 2 sin (t ) 2 t)
式中 X1和X2——分别为质点1和质点2的位移振幅; ω——振动频率; φ——初相位。 (k11 m1 2)X 1 k12 X 2 0 经整理后得下列振幅方程 :
2015/11/19
结构抗震设计
14
5)、主振型的正交性
根据功的互等定理,第一主振型上的惯性力在第二主振 型的位移上所做的功等于第二主振型上的惯性力在第一 主振型的位移上所做的功,这样可得到:
2 2 (m112 X 11)X 21 (m112 X 12)X 22 (m1 2 X 21)X 11 (m2 2 X 22)X 12 2 (12 2 )(m1 X 11 X 21 m2 X 12 X 22) 0 整理后得到:
式中Cij——质点j产生单位速度,而其它质点保持不动时, 在质点i处产生的阻尼力; kij——质点j产生单位位移,而其它质点保持不动时, 在质点i处引起的弹性反力; mi——集中在质点i的质量。 求解上述运动方程组,一般采用振型分解法。该法需要 利用多自由度弹性体系的振型,它们是由分析体系的自 由振动得来的。为此,须先讨论多自由度体系的自由振 动问题。
在质点1处所需施加的水平力; k12——使质点2产生单位位移而质点1保持不动时, 在质点1处引起的弹性反力; c11——质点1产生单位速度而质点2保持不动时, 在质点1处产生的阻尼力; c12——质点2产生单位速度而质点1保持不动时, 在质点1处产生的阻尼力; m1——集中在质点1上的质量。
2015/11/19
2015/11/19 结构抗震设计 10
2)、主振型
由于线性齐次方程组的系数行列式等于零,所以两个频 率方程并不是独立的,振幅方程的解只能是两质点位移 振幅的比值,如:X 2 m1 2 k11 或 X 2 k21
X1 k12
X1
m2 2 k22
当 1 ,振幅比值为: X m k 当 2 ,振幅比值为: X k 式中: X ji ——体系按频率ωj (频率序号j=1,2)自由振 动时,质点i (质点编号i=1,2)的位移振幅。 (t) X 12 sin (1t 1) x11 (t) X 11 sin (1t 1)和 x12 当 1 ,质点位移: (t) X 22 sin ( 2 t 2) x21 (t) X 21 sin ( 2 t 2) 当 2 ,质点位移: 和 x22 式中 x ji ——体系按频率ωj(频率序号j=1,2)自由振动 时,质点i (质点编号i=1,2)的位移
2015/11/19 结构抗震设计 17
j 1 j 1
2、n自由度弹性体系的自由振动
对于n自由度体系,由上式可得其自由振动方程组: n (i=1,2,…,n) i t) mi x ( k ij x( ) 0 j t
k21 X 1 (k22 m2 2)X 2 0
2015/11/19
结构抗震设计
9
1)、自振频率和自振周期
上式为 Xl和 X2 的线性齐次方程组;体系在自由振动时, X1和X2不能同时为零,否则体系就不可能产生振动。 为使上式有非零解,其系数行列式必须等于零,即:
k11 m1 2 k 21
2015/11/19
结构抗震设计
5
二、两自由度弹性体系的自由振动
左图为一两自由度弹性体系在 水平地震作用下,在时刻t的变 形情况。Xg(t)为地震时地面运 动的水平位移,质点1和质点2 沿地面运动方向产生的相对于 地面的水平位移分别为x1(t)和 ( x2(t),而相对速度则为 x 1 t) ( 1 t) x ( 和 x ,相对加速度为 2 t) x ( x ( 2 t) 和 ,绝对加速度分别为 g t) 1 t) x ( x ( + 和 + 。 x ( 2 t) g t)
2015/11/19
结构抗震设计
