六年级数学下册圆柱与圆锥知识点(最新整理)
北师大版六年级数学下册第1单元 圆柱与圆锥 知识点汇总
一 圆柱与圆锥一、面的旋转 1.点动成线....,.线动成面....,.面动成体。
.....2.将一个长方形以长(宽)为轴,快速旋转后可以形成一个圆柱。
3.将一个直角三角形沿一条直角边快速旋转,会形成一个圆锥。
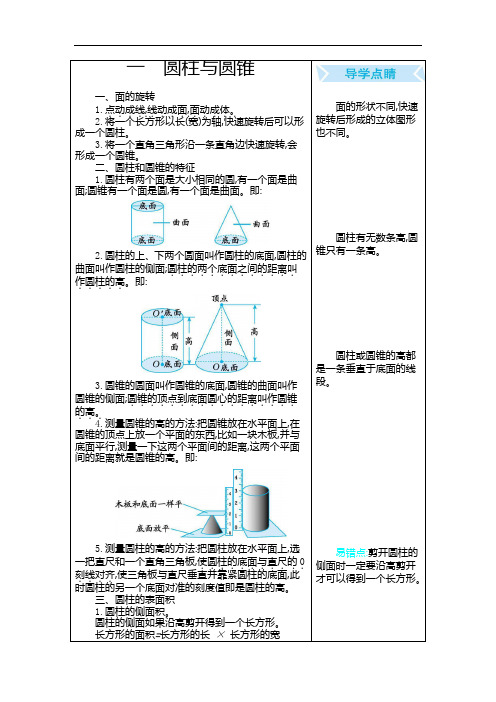
二、圆柱和圆锥的特征1.圆柱有两个面是大小相同的圆,有一个面是曲面;圆锥有一个面是圆,有一个面是曲面。
即:2.圆柱的上、下两个圆面叫作圆柱的底面,圆柱的曲面叫作圆柱的侧面;圆柱的两个底面之间的距离叫.............作圆柱的高.....。
即:3.圆锥的圆面叫作圆锥的底面,圆锥的曲面叫作圆锥的侧面;圆锥的顶点到底面圆心的距离叫作圆锥.................的高。
...4.测量圆锥的高的方法:把圆锥放在水平面上,在圆锥的顶点上放一个平面的东西,比如一块木板,并与底面平行,测量一下这两个平面间的距离,这两个平面间的距离就是圆锥的高。
即:5.测量圆柱的高的方法:把圆柱放在水平面上,选一把直尺和一个直角三角板,使圆柱的底面与直尺的..........0.刻线对齐....,使三角板与直尺垂直并靠紧圆柱的底面,此时圆柱的另一个底面对准的刻度值即是圆柱的高。
三、圆柱的表面积1.圆柱的侧面积。
圆柱的侧面如果沿高剪开得到一个长方形。
长方形的面积=长方形的长 × 长方形的宽面的形状不同,快速旋转后形成的立体图形也不同。
圆柱有无数条高,圆锥只有一条高。
圆柱或圆锥的高都是一条垂直于底面的线段。
易错点:剪开圆柱的侧面时一定要沿高剪开才可以得到一个长方形。
↓ ↓ ↓ 圆柱的侧面积=圆柱的底面周长×圆柱的高 用字母表示:S 侧=Ch 或S 侧=πdh 或S 侧=2πrh2.圆柱的表面积。
圆柱的表面积......=.侧面积...+.两个底面积.....不同的圆柱形实物,它们的表面积也不相同。
比如圆柱形烟囱的表面积等于烟囱的侧面积,圆柱形水桶的表面积就是水桶的侧面积加上一个底面积。
四、圆柱的体积1.意义:圆柱形物体所占空间的大小叫作圆柱的体积。
人教版六年级下册数学 圆柱与圆锥整理和复习

40
(单位:厘米)
增加两个长方形的面, 长等于圆柱的高,宽等 于底面直径。
滚、刷、切、削、熔……
切割前后的表面积 增加了,体积不变
。
滚、刷、切、削、熔……
把圆柱削成最大的圆锥,需要削去多少?
50
问题1:怎么削才算是最大的圆锥?
问题2:削成的圆锥与圆柱有什么关系?
2
3.14×(40÷2)2×50×
选择 一个有盖的圆柱形铁桶。 1、求这个铁桶的占地面积,是求( A. 容积 B. 底面积 C. 表面积
B) D. 体积
2、做这样一个铁桶用多少铁皮,是求( C ) A. 容积 B. 底面积 C. 表面积 D. 体积
3、这个铁桶能装多少水,是求( A ) A. 容积 B. 底面积 C. 表面积 D. 体积
0.5m 1m 4.5m ——
314dm3 2.198m3 6280cm3 10.048dm3 1.1775m3
3.妈妈给小雨的塑料壶做了一个布套(如图)小雨每天上学带一壶水。 (1)至少用了多少布料? (2)小雨在学校一天喝1.5L的水,这壶水够喝吗?(水壶的厚度忽略不 计。)
分析:求所用布料就是求水壶的表面积,求能装多少水 即求水壶的体积。
答:旋转一周后围成的立体图形的体积是301.44cm3。
3.一个圆柱形鱼缸,底面直径是40cm,高是25cm,里面盛了一 些水,把一个底面半径为10cm的圆锥放入鱼缸中(圆锥全部浸 入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
水面升高的那部分圆柱的体积就是
放入水中的圆锥的体积。
2cm
V 锥 = V 柱=3.14×(40÷2)2×2 =3.14×800 =2512(cm3)
3.一个圆柱形鱼缸,底面直径是40cm,高是25cm,里面盛了一 些水,把一个底面半径为10cm的圆锥放入鱼缸中(圆锥全部浸 入水中),鱼缸中的水面升高了2cm。这个圆锥的高是多少?
六年级下学期 圆柱与圆锥 详细知识点总结+重难点题型训练+详细答案 很全面

圆柱与圆锥【考点要求】1、认知圆柱与圆锥,掌握它们的各部分特征2、理解并掌握圆柱的侧面积和表面积的计算方法,并会正确计算3、理解并掌握圆柱与圆锥的体积的计算方法,会运用公式计算体积、容积,解决有关的简单的实际问题。
【基础知识回顾】考点一、圆柱的各部分名称,展开图一、圆柱的各部分名称,展开图1、底面、侧面、高:(1)圆柱的两个圆面叫做底面,圆柱的两个底面都是圆,并且大小一样;(2)周围的面叫做侧面,圆柱的侧面是曲面;(3)两个底面之间的距离叫做高,圆柱的高有无数条;拿一张长反省的硬纸,贴在木棒上,快速转动,转动起来的形状就是个一个圆柱。
2、圆柱的侧面展开图:圆柱的侧面展开图是一个长方形,长方形的长相当于圆柱的底面周长,长方形的宽相当于圆柱的高。
【练习一】1、点的运动可以形成(),线的运动可以形成一个(),面的运动可以形成()。
长方形绕一条边旋转一周可以形成()2、圆柱由()个面组成,分别是()()()组成,上下底面都是(),侧面的展开是一个()。
3、圆柱的侧面展开是一个长方形,长方形的长等于圆柱的(),长方形的宽等于圆柱的()4、如右图,以长方形的长为轴,旋转一周,得到的立体图形是(),那么,得到的这个立体图形的高是()厘米,底面周长是()厘米。
3厘米6厘米5、判断(1)长方体中最多有4个面可能是正方形()(2)一个圆柱,如果底面直径和高相等,则圆柱的侧面展开是正方形()(3)如果一个物体上、下底面是面积相等的两个圆,那么这个物体一定是圆柱()。
考点二、圆柱的表面积π+2πrh=2πr(r+h)二、圆柱的表面积=2个圆的面积+1个侧面积=2r21、圆柱的侧面积=底面周长×高=πdh=2πrh因为圆柱的侧面展开是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,所以长方形的面积就是圆柱的侧面积=底面周长×高π×22、圆柱的2个底面积:S=r2π+2πrh=2πr(r+h)3、圆柱的表面积:2个底面积+1个侧面积=2r2注意:有时题目计算表面积时,并不是三个面的面积都要计算,要结合具体题目具体分析,比如,通风管就只用计算侧面积即可,无盖的水桶就只用计算侧面积和1个底面积4、圆柱的截断与拼接:(1)把一个圆柱截成两个圆柱,增加的表面积是两个底面积;(2)把两个同样粗细的圆柱拼成一个圆柱,减少的表面积是两个底面积。
六年级数学圆柱和圆锥知识点

六年级数学圆柱和圆锥知识点本课内容是九年制义务教育课程标准实验教材(苏教版)六年级下册第18-20页《圆柱和圆锥的认识》。
学生已经在一年级的时候初次认识了圆柱,已经会辨别;圆锥这一立体图形没有见识过,从未接触;这里给大家分享一些六年级数学圆柱和圆锥知识点,欢迎阅读!六年级数学圆柱和圆锥教案一、说教材。
《圆柱和圆锥是小学阶段几何知识的最后一部分新课内容,内容包括:面的旋转、圆柱的表面积、圆柱的体积及圆锥的体积四小节,本节复习课旨在通过回顾梳理,交流互补,使学生将零散的知识在头脑中串成线,联成片,形成完整的知识网络,加深各个图形之间的内在联系,综合运用有关知识解决实际问题。
《课程标准》中对本学段的教学要求是:认识并掌握圆柱体、圆锥体的特征,明白表面积和体积的意义,通过操作、实验、转化、类比、推理等逻辑方法得到表面积和体积的计算方法,掌握常用的体积(容积)单位,会计算一些形体的表面积和体积(容器的容积),并能应用所学知识解决简单的实际问题。
二、根据此要求以及学生的特点,我确定了如下的教学目标:1、通过复习、交流,我会说出圆柱和圆锥的特征和相关的计算公式。
2、通过练习、展示,我会运用公式正确解决有关圆柱的表面积和体积及圆锥体积的实际问题。
三、教学重点:运用所学知识解决实际问题。
四、教学难点:综合运用所学知识解决问题。
五、说教法学法。
本节课我采取“练习法”,让学生在回顾整理、交流互补、巩固练习、展示自我等一系列活动中掌握知识、发展智力、锻炼能力。
六、说教学过程“复习课”作为数学课的一种基本类型,它不同于新授课的探索发现,也有别于练习课的巩固应用,它的一个重要功能就是引导学生对所学的知识进行整理,把分散的知识综合成一个整体,使之形成一个较为完整的知识体系,提高学生对知识的掌握水平。
承载着“回顾与整理,沟通与生成”的独特功能。
本节课我设计了以下几个环节:第一环节:谈话导入,明确目标。
本学期,我们结识了小学阶段几何形体中的最后两位朋友,他们是——(圆柱和圆锥)。
六年级数学下册圆柱与圆锥知识点总结(全面)

圆柱与圆锥一.圆柱1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的;圆柱也可以由长方形卷曲而得到。
2、圆柱各部分的名称:圆柱的的两个圆面叫做底面(又分上底和下底);周围的面叫做侧面;两个底面之间的距离叫做高(高有无数条他们的数值是相等的)。
3、圆柱的侧面展开图:A、沿着高展开,展开图形是长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高,当底面周长和高相等时(h=2πR),侧面沿高展开后是一个正方形,展开图形为正方形。
B、不沿着高展开,展开图形是平行四边形或不规则图形。
C、无论如何展开都得不到梯形.侧面积=底面周长×高S侧=Ch=πd×h=2πr×h4、圆柱的表面积:圆柱表面的面积,叫做这个圆柱的表面积。
圆柱的表面积=2×底面积+侧面积,即S表=S侧+S底×2=2πr×h+2×πr2(实际中,使用的材料都要比计算的结果多一些,因此,要保留数的时候,都要用进一法)圆柱的体积:圆柱所占空间的大小,叫做这个圆柱的体积。
圆柱切拼成近似的长方体,分的份数越多,拼成的图形越接近长方体。
长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
长方体的体积=底面积×高圆柱体积=底面积×高V柱=S h=πr2hh=V柱÷S=V柱÷(πr2)S=V柱÷h5、圆柱的切割:A.横切:切面是圆,表面积增加2倍底面积,即S增=2πr2B.竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh考试常见题型:A.已知圆柱的底面积和高,求圆柱的侧面积,表面积,体积,底面周长B.已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积C.已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积D.已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积E.已知圆柱的侧面积和高,求圆柱的底面半径,表面积,体积,底面积以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算。
(苏教版)六年级数学下册课件_圆柱和圆锥的整理与复习

3.已知两个体积不同的圆柱, 高相等,它们的底面半径的比 是1:2,那么它们的体积的比是 ( 1:4 )
半 径 底面积 高 体 积
圆柱体1 圆柱体2
1
1 1
2
4 1
1
4
4.如下图,有三块不同的硬纸 片,让它们分别绕PQ边旋转一 周,它们所掠边的空间是圆锥 体的是( B )。
P
A
Q
B
P Q
P
C
Q
5.甲乙两人分别利用一张长20厘米, 宽15厘米的纸用两种不同的方法围成 一个圆柱体(接头处不重叠),那么 围成的圆柱( B )。 A高一定相等 B侧面积一定相等 C侧面积和高都相等D侧面积和高都不 A y 相等
1 圆柱表面积 = 1个侧面积 + 2个底面积 圆锥的体积:V= --Sh
圆柱体积 = 底面积 ×高(V=Sh)
3
1.冬天护林工人给圆 柱形的树干的下端涂 防蛀涂料,那么粉刷 树干的面积是指( B )。 A.底面积 C.表面积 B.侧面积 D.体积
2.一个圆锥的体积是a立 方米,和它等底等高的圆 柱体的体积是( C )立 方米。 A. a÷3 1 C. 3a B. 2a D. a的立方
30
15
8
20
请同学们自己将圆柱和圆锥 的内容整理一遍。
2 2 2
2×3.14×2
10.一个近似圆锥形的 沙堆,底面直径和高 相等,已知底面周长 是15.7米,每立方米沙 重2吨。这堆沙重多少 吨?
1号题
如图,想想办法,你能 否求它的体积?( 单位: 厘米)
4
2 6
2号 一个酒瓶里面深30厘米,底面直 题 径是8厘米,瓶里有酒深15厘米,
把酒瓶塞紧后倒置(瓶口向下), 这时酒深20厘米,你能算出酒瓶 的容积是多少毫升来吗?
(完整版)六年级数学下册圆柱与圆锥知识点

六年级数学下册《圆柱与圆锥》知识点六年级数学下册《圆柱与圆锥》知识点知识点1。
圆柱是由两个底面和一个侧面三部分组成的。
2.(1)圆柱的两个圆面叫做底面。
(2)底面各部分的名称:圆柱的底面圆的圆心、半径、直径和周长分别叫做圆柱的底面圆心、底面半径、底面直径和底面周长。
(3)底面的特征:圆柱底面是完全相同的两个圆.3。
(1)圆柱周围的面叫做侧面。
(2)特征:圆柱的侧面是曲面。
4.(1)圆柱两个底面之间的距离叫做圆柱的高。
(2)一个圆柱有无数条高。
5。
把圆柱平行于底面进行切割,切面是和底面大小相同的两个圆;把圆柱沿底面直径垂直于底面进行切割,切面是两个完全相同的长方形。
6。
圆柱的侧面展开图是一个长方形,这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
7.在圆柱的上下底面周长上任取一点分别为A、B,连接AB(使AB不是圆柱的高),沿着AB将圆柱的侧面剪开,圆柱展开后是一个平行四边形.8。
温馨提示:圆柱的底面是圆形,面不是椭圆。
9.温馨提示:沿高剪开时,圆柱的侧面展开图是一个长方形。
10。
从圆柱的上下两个底面观察会得到圆;从圆柱的正面或侧面观察会得到长方形(或正方形).11。
如果圆柱的侧面展开图是个长方形,那么该圆柱的底面周长大约是其底面直径长度的3倍。
如果圆柱的侧面展开图是个正方形,那么该圆柱的高大约是其底面直径长度的3倍。
12。
圆柱的侧面积=底面周长×高.如果用字母S表示圆柱的侧面积,用C表示底面周长,用h表示高,则圆柱的侧面积的计算公式是S=Ch13。
(1)已知圆柱的底面直径和高,可以根据公式:S=πdh直接求出圆柱的侧面积。
(2)已知圆柱的底面半径和高,可以根据公式:S=2πrh直接求出圆柱的侧面积。
14。
圆柱的表面积是指圆柱的侧面积和两个底面的面积之和。
15.圆柱的表面积=圆柱的侧面积+底面积×2,用字母表示为S表=S侧+2S底。
16.(1)已知圆柱的底面半径和高,可以根据公式:S表=2πrh+2πr2直接求出圆柱的表面积。
北师大版六年级数学下册知识点归纳总结

(北师大版)六年级数学下册知识点归纳总结第一单元圆柱和圆锥1、“点、线、面、体”之间的关系是:点的运动形成线;线的运动形成面;面的旋转形成体。
2、圆柱的特征:(1)圆柱的两个底面是半径相等的两个圆,侧面是曲面。
(2)两个底面间的距离叫做圆柱的高。
(3)圆柱有无数条高,且高的长度都相等。
(4)圆柱是由长方形绕长或宽旋转360度得到的立方体,所以沿高线切割后的切面是长方形。
3、圆锥的特征:(1)圆锥的底面是一个圆,和底面相对的位置有一个顶点。
(2)圆锥的侧面是一个曲面。
(3)圆锥只有一条高。
(4)圆锥是由直角三角形绕一条直角边旋转360度得到的立方体,所以沿高线切割后的切面是等腰三角形。
4、沿圆柱的高剪开,圆柱的侧面展开图是一个长方形(或正方形)(如果不是沿高剪开,有可能还会是平行四边形)。
圆柱的侧面积=底面周长×高用字母表示为:S侧=Ch。
圆柱的侧面积公式的应用:(1)已知底面周长和高,求侧面积,可运用公式:S侧=ch;(2)已知底面直径和高,求侧面积,可运用公式:S侧=πdh;(3)已知底面半径和高,求侧面积,可运用公式:S侧=2πrh。
圆柱表面积的计算方法:如果用S侧表示一个圆柱的侧面积,S底表示底面积,d表示底面直径,r表示底面半径,h表示高,那么这个圆柱的表面积为:S表=S侧+2S底或S表=πdh+πd2/2 或S表=2πrh+2πr2圆柱表面积的计算方法的特殊应用:(1)圆柱的表面积只包括侧面积和一个底面积的,例如无盖水桶等圆柱形物体。
(2)圆柱的表面积只包括侧面积的,例如烟囱、油管等圆柱形物体。
5、圆柱的体积:一个圆柱所占空间的大小。
6、圆柱体积公式的推导:复习六年级上册圆的面积公式的推导:把圆等分的份数越多,拼成的图形就越接近平行四边形或长方形。
拼成的平行四边形的底相当于圆周长的一半,高相当于圆的半径;拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。
所以:圆的面积=π×半径×半径=π×半径²。
小学六年级数学小升初珍藏版复习资料第18讲 圆柱和圆锥的认识、表面积与体积(解析)

2022-2023学年小升初数学精讲精练专题汇编讲义第18讲圆柱和圆锥的认识、表面积与体积知识点一:圆柱与圆锥的认识1.圆柱的定义:以长方形的一条边所在的直线为轴旋转一周,得到的几何体叫作圆柱。
2.圆锥的定义:以直角三角形的一条直角边所在的直线为轴旋转一周,得到的几何体叫作圆锥。
3.圆柱和圆锥的特征:名称图形展开图特征圆柱(1)上下两个底面是两个相等的圆;两个底面之间的距离叫作高(h);圆柱有无数条高。
(2)侧面展开图是长方形(或正方形),长方形的长相当于圆柱的底面周长,宽相当于圆柱的高圆锥(1)底面是圆,顶点到底面圆心(O)的距离叫作高(h),圆锥只有 1 条高。
(2)圆锥的侧面展开图是一个扇形知识点二:圆柱与圆锥的测量1.圆柱的侧面积、表面积。
(1)圆柱的侧面积=底面周长×高,用字母表示为:S侧=πdh(或2πrh)(2)圆柱的表面积=底面积×2+侧面积,用字母表示为:S= 2πr2+2πrh 2.圆柱的体积=底面积×高,用字母表示为:V=πr2h 。
知识精讲3.圆锥的体积=13×底面积×高,用字母表示为:V=13πr2h知识点三:用排水法计算不规则物体的体积1.体积小的物体可以直接放入有水的长方体或圆柱等规则的容器里,观察水面所处的刻度的变化体积差就是物体的体积。
2.体积大的物体,可以放入装满水的长方体或圆柱等规则的容器里,排出水的体积就是物体的体积。
一.选择题(共5小题,满分10分,每小题2分)1.(2分)(2022•东昌府区)一个圆柱和一个圆锥等底等高,它们的体积之和是48立方分米,圆锥的体积是()立方分米。
A.12 B.16 C.36【思路点拨】底等高的圆柱的体积是圆锥体积的3倍,那么等底等高的圆柱与圆柱的体积和相当于圆锥体积的(3+1)倍,根据已知一个数的几倍是多少,求这个数,用除法解答。
【规范解答】解:48÷(3+1)=48÷4=12(平方分米)答:圆锥的体积是12立方分米。
【精品原创】人教版六年级下册数学期末复习专题讲义(知识点归纳 典例讲解 同步测试)-3.圆柱和圆锥

人教版六年级下册数学期末复习专题讲义-3.圆柱和圆锥【知识点归纳】一、圆柱1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得的。
圆柱也可以由长方形卷曲而得到。
两种方式:(1)以长方形的长为底面周长,宽为高;(2)以长方形的宽为底面周长,长为高。
其中,第一种方式得到的圆柱体体积较大。
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的3、圆柱的特征:(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征:圆柱有无数条高4、圆柱的切割:①横切:切面是圆,表面积增加2倍底面积,即S增=2πr²②竖切(过直径):切面是长方形(如果2r,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果2πr,则展开图形为正方形②不沿着高展开,展开图形是平行四边形或不规则图形③无论怎么展开都得不到梯形6、圆柱的相关计算公式:底面积:S底=πr²底面周长:C底=2πr 侧面积:S侧=2πrh表面积:S表=2S底+S侧=2πr²+2πrh 体积:V柱=πr²h考试常见题型:①已知圆柱的底面积和高,求圆柱的侧面积,表面积,体积,底面周长②已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积③已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积④已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积⑤已知圆柱的侧面积和高,求圆柱的底面半径,表面积,体积,底面积以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算无盖水桶的表面积=侧面积+一个底面积油桶的表面积=侧面积+两个底面积4、圆柱与圆锥等底等高 ,体积相差32 四、温馨提示: (1)已知圆锥的底面半径和高,可以直接利用公式:πr 2h ÷3来求圆锥的体积;(2)已知圆锥的底面直径和高,可以直接利用公式:π(d ÷2)2h ÷3求圆锥的V;(3)已知圆锥的底面周长和高,可以直接利用公式:π(C ÷2÷π)2h ÷3求出圆锥的体积。
最新北师大版小学六年级数学下册《圆柱与圆锥》重难点题型

六年级下册数学圆柱与圆锥的重难点题型一、高的变化引起表面积的变化底面积不变,圆柱高的变化引起表面积的变化,由于底面积没有变,所以实际上发生变化的是侧面积,由此可以求出底面周长,进而求出表面积。
【例题】一个圆柱被截去10厘米后(如下图),圆柱的表面积减少了628平方厘米,原来圆柱的表面积是多少平方厘米?(π取3.14)2、一个圆柱,如果把它的高截短3m,它的表面积就会减少94.2m²,那么这个圆柱的体积减少多少立方米?【练习】1、一个圆柱体,高减少2厘米,表面积就减少了50.24平方厘米,圆柱的底面积是多少平方厘米?2、一个圆柱的底面直径为4厘米,如果高增加1厘米,表面积增加多少平方厘米。
一个圆柱的底面周长和高相等,如果高缩短了2厘米,表面积就减少12.56平方厘米,求这个圆柱体原来的表面积?二:圆柱竖切引起的表面积变化垂直于底面切(竖切):多出的两个面是长方形,即以底面圆的直径为长,以圆柱的高为宽的长方形。
【例题】工人把一根高是1米的圆柱形木料,沿底面直径平均分成两部分,这时两部分的表面积之和比原来增加了0.8平方米。
求这根木料原来的表面积。
【练习】1、一个底面半径4cm,高5cm的圆柱,如果沿底面直径把它平均切成两半,它的表面积增加了多少平方厘米?2、把一个半径2分米、长1米的圆木平均截成3段,表面积共增加多少平方分米?3、把一个底面半径是40cm,长是12分米的圆柱形木头锯成长短不同的4小段圆柱形木头,表面积增加了多少平方分米?4、把一根长为1.2米的圆柱形钢材截成3段,表面积增加了6.28平方分米,原来这根钢材的体积是多少?5、底面直径是20厘米的圆钢,将其截成两段同样的圆钢,两段表面积的和为7536平方厘米,原来圆钢的体积是多少立方厘米?【例题】把一个底面半径是6cm的圆柱切拼成一个近似的长方体后(如图),表面积增加了180cm²,原来圆柱的体积是多少立方厘米?【练习】1、把一个高为1米的圆柱体切成底面是许多相等的扇形,再拼成一个近似的长方体,已知拼成后长方体表面积比原来圆柱表面积增加了40平方分米,原来圆柱体的体积是多少立方分米?2、把高5厘米的圆柱底面分成若干等份,把圆柱切开拼成一个近似的长方体,长方体表面积比圆柱增加20平方厘米。
小学数学六年级下册圆柱和圆锥锥(基础知识点提高)

小学数学六年级下册圆柱和圆锥锥(基础知识点提高)圆柱和圆锥第一部分基础部分一、圆柱和圆锥的认识1、图形的形成圆柱是以长方形的一边为轴旋转而得到的,也可以由长方形(或正方形)卷曲而得到;圆锥是以直角三角形的一直角边为轴旋转而得到的,圆锥也可以由扇形卷曲而得到。
2、高的条数:圆柱有无数条高;圆锥只有一条高3、侧面展开图圆柱:沿着高展开,展开图形是长方形,长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高,当底面周长和高相等时(h=2πR),侧面沿高展开后是一个正方形,展开图形为正方形。
圆锥:侧面展开得到一个扇形4、图形的形成:(1)圆柱:卷曲:也可以由长方形(或正方形)卷曲而得到;旋转:圆柱是以长方形的一边为轴旋转而得到的2)圆锥:卷曲:也可以由扇形卷曲而得到;旋转:以直角三角形的一条直角边为轴旋转得到【例1】:下面()图形是圆柱的展开图。
(单位:cm)易错题】一个圆柱的侧面沿高展开是一个长12.56CM,宽6.28CM的长方形,求这个圆柱的底面半径。
例2】在下图中,以直线为轴旋转,可以得出圆柱体的是()【易错题】1、把长为5cm.宽为3cm的长方形旋转成一个圆柱,则这个圆柱的表面积是多少平方厘米?2、把两条直角边分别是5cm和3cm的直角三角形旋转成一个圆锥,这个圆锥的体积是多少立方厘米?练:】一、选择1、圆柱侧面积的大小是由()决定的。
A圆柱的底面周长B底面直径和高C圆柱的高。
2、下面的材料中,()能做成圆柱。
12cm6.28cmA.1号、2号和3号B.1号、4号和5号C.1号、2号和4号2cm2cm4cm4cm1号2号3号4号5号2、解答题一个长为8m,宽为6m的长方形扭转成一个圆柱,它的侧面积是几何平方米?2、圆柱表面积的计较方法①公式:圆柱的表面积=+S表=S侧+S底×2=2πrh + 2πr2②圆柱表面积计较公式的应用应用1:圆柱的底面半径和高,求圆柱的表面积;应用2:圆柱的底面直径和高,求圆柱的表面积;运用3:已知圆柱的底面周长和高求圆柱的表面积。
人教版六年级数学下册第三单元《圆柱与圆锥》第一讲讲义-含解析(知识精讲+典型例题+同步练习+进门考)
人教版六年级数学下册第三单元《圆柱与圆锥上》知识点1圆柱的表面积猫小咪和猫小喵发现了一大瓶鱼罐头,他们在密谋着如何解决掉这瓶罐头。
提问鱼罐头的包装盒属于哪种立体图形?认识圆柱总结:1.圆柱的上下两个底面面积相等。
2.周围的面(除底面外)叫做侧面。
思考:将圆柱沿侧面展开后得到什么图形?思考1.圆柱的侧面积=底面周长×高。
S侧=2πrh。
2.圆柱的表面积=圆柱的侧面积+两个底面圆的面积。
S表=2πrh+2πr²思考:一个圆柱体底面半径是1厘米,高是5厘米,那么它的侧面积和表面积分别是多少?(π取3.14)步骤:圆柱的表面积分为几个部分?三部分:两个底面积和一个侧面积。
两个底面积是多少?S底=3.14×1²×2=6.28平方厘米。
侧面积是多少?侧面积=底面周长×高。
S侧=3.14×1×2×5=31.4平方厘米。
圆柱体的表面积是多少?6.28+31.4=37.68平方厘米。
思考:如果把圆柱横着切一刀,它的表面积有什么变化?总结:切一刀表面积增加两个圆的面积。
思考:把一根长1米的圆柱分成3段,表面积增加了48平方厘米,原来圆柱的表面积是多少平方厘米?(π取3)步骤:分成三段增加几个面?(3-1)×2=4个。
圆柱的底面半径是多少厘米?48÷4=12平方厘米。
12÷3=4 4=2×2。
所以半径是2厘米。
原来圆柱的表面积是多少?1米=100厘米2×3×2×100=1200平方厘米1200+12×2=1224平方厘米思考:把一张长方形铁皮按图剪开,正好能制成一个圆柱形水桶(有盖),那么这个水桶的表面积是多少平方厘米?(π取3.14,接头处忽略不计)步骤:水桶的表面积包含哪几部分?两个底面圆的面积和侧面积。
圆柱的底面周长等于右侧小长方形的长还是宽?等于小长方形的长。
冀教版数学六年级下学期第四单元《圆柱和圆锥》单元知识点归纳与教案

四圆柱和圆锥一、认识圆柱、圆柱的组成部分1.圆柱的形成:圆柱是以长方形的一条边为轴旋转得到的;也可以由长方形卷起来得到。
2.生活中常见的圆柱:3.圆柱各部分的名称及其特征:(1)圆柱的上、下两个面都是圆形的,大小相同,叫做底面。
(2)圆柱周围的面是曲面,我们叫它侧面。
(3)圆柱两底之间的距离叫做高,一个圆柱有无数条高,它们都相等。
二、圆柱的侧面以及侧面积的求法1.圆柱的侧面展开图及其形状:(1)沿着高展开,展开图是长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;当底面周长和高相等时(h=2πr),侧面展开图为正方形。
(2)如果不沿着高展开,展开图形是平行四边形或不规则图形。
(3)无论如何展开都得不到梯形。
2.圆柱的侧面展开后各个部分与圆柱的关系:展开后长方形的长等于圆柱的底面周长,宽等于圆柱的高。
3.圆柱的侧面积=底面的周长×高,即S侧=Ch=πd×h=2πr×h。
三、圆柱的表面积的计算1.圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
巧记小圆柱直挺挺,上、下底面都相同,可以看作是由长方形旋转而成的,还可以看作是由平面卷曲而成的。
易错点:1.圆柱的侧面是曲面,高有无数条,不是1条。
2.高指圆柱两底面之间的距离。
易错点:1.如果底面周长和高相等,展开图为正方形。
2.底面直径和高相等,侧面展开图不是正方形。
巧记规律沿高剪,圆柱侧面展开是长方形,侧面积是底面周长和高的积。
2.圆柱的表面积=2×底面积+侧面积,即S表=S侧+S底×2=2πr×h+2πr2。
3.圆柱的切割引起表面积的变化:(1)横切:切面是圆,表面积增加2个底面积,即S增=2πr2。
(2)竖切(过直径):切面是长方形(如果h=2r,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh。
四、圆柱表面积的计算在实际生活中的应用在实际生活中,有时需要计算圆柱的表面积,如制作水桶时,不要上底面;制作圆柱形通风管时,不需要两个底面,这时需要计算圆柱的侧面积。
六年级数学下册第三单元(圆柱与圆锥)知识点

六年级数学下册第三单元(圆柱与圆锥)知识点六年级数学下册第三单元(圆柱与圆锥)知识点【圆柱】圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的;圆柱也可以由长方形卷曲而得到。
一、圆柱:圆柱由3个面围成。
(1)底面:圆柱的上、下两个面;(2)侧面:圆柱周围的面(上下底面除外);(3)高度:圆柱体两个底面之间的距离。
二、圆柱的特征:(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱体的侧面是曲面。
(3)高度的特性:一个圆柱体的高度有无数种。
圆柱的侧面展开图:沿着高展开,展开图形是长方形。
长方形的长等于圆柱底面的周长,长方形的宽等于圆柱的高,长方形的面积等于(圆柱的侧面积),因为长方形面积=长×宽,所以圆柱的侧面积=底面周长×高圆柱的侧面积:圆柱的侧面积=底面的周长×高,用字母表示为:S侧=Ch h=S侧÷CC= S侧÷hS侧=∏dh=2∏rh注:(1)当底面周长和高相等时,沿高展开图是正方形;(2)不沿高度铺展,铺展图案为平行四边形或不规则图案。
(3)无论如何展开都得不到梯形.四、圆柱的表面积:圆柱的表面积=侧面积+底面积×2。
即S表= S侧+ S底×2=2∏rh+∏r²×2【解题方法】一.圆柱的切割:1.横切:切面是圆,表面积增加2倍底面积,即S增=2πr22.竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh二、常见的圆柱解决问题:侧面积+两个底面积:油桶、米桶、罐桶类侧面积+一个底面积:玻璃杯、水桶、笔筒、帽子、游泳池只求侧面积:烟囱、灯罩、排水管、漆柱、通风管、压路机、卫生纸中轴、薯片盒包装底面周长:压路机压过路面长度五、圆柱的体积:圆柱所占空间的大小,叫做这个圆柱体的体积。
将圆柱体切割成近似的长方体,分割的份数越多,图形越接近长方体。
六年级下册第二章圆和圆锥的知识点

六年级下册第二章圆和圆锥的知识点六年级下册第二章圆和圆锥的知识点导语:活在别人的掌声中,是禁不起考验的人。
下面是小编为大家整理的,数学知识。
想要知更多的资讯,请多留意CNFLA学习网!知识点梳理:知识点一:圆柱、圆锥的认识相关概念:①圆柱由一个上底面、一个下底面和一个侧面组成。
上下底面是两个完全相同的圆形;侧面是一个曲面。
②圆柱的高:上下底面之间的距离。
圆柱有无数条高,每条高相等。
③圆锥由一个底面和一个侧面组成。
底面是一个圆形;侧面是一个曲面。
④圆柱的高:圆锥的定点到底面圆心的距离。
圆锥只有一条高。
知识点二:圆柱侧面积的计算方法理解掌握:圆柱的侧面展开图:有可能是长方形,也有可能是正方形。
①假如是长方形,那么长方形的'长a,就是圆柱底面的周长C,宽b就是圆柱的高h。
长方形的面积S=a×b=C×h=2πr×h=2πrh,就是圆柱的侧面积。
②假如是正方形,那么正方形的边长a既等于圆柱底面的周长C,也等于圆柱的高h,也就是说底面周长和高相等。
正方形的面积S=a×a=C×h=2πr×h=2πrh,就是圆柱的侧面积。
所以圆柱的侧面积公式=Ch或者=2πrh或者=πdh知识点三:圆柱表面积的计算方法理解掌握:圆柱的表面积由一个侧面加上两个底面组成,计算方法是S表=S侧+2S底,因为S侧=Ch,S底=πr2,所以S表=Ch+2πr2=2πrh+2πr2 用乘法分配率得圆柱的表面积公式=2π(rh+r2) 知识点四:圆柱体积的计算方法理解掌握:利用我们以前学过的长方体的体积公式V长方体=S底×h,可以得到圆柱的体积公式V圆柱= S底×h,长方体的底面积是长方形或正方形,而圆柱的底面积是圆。
相关公式:①已知半径和高,V圆柱=πr2h ②已知直径和高,V 圆柱=π(d÷2)2h③已知周长和高,V圆柱=π(C÷2π)2h难点解析:把圆柱的底面平均分成n份,切开后平成一个近似的长方体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级数学下册《圆柱与圆锥》知识点
六年级数学下册《圆柱与圆锥》知识点
知识点
1.圆柱是由两个底面和一个侧面三部分组成的。
2.(1)圆柱的两个圆面叫做底面。
(2)底面各部分的名称:圆柱的底面圆的圆心、半径、直径和周长分别叫做圆柱的底面圆心、底面半径、底面直径和底面周长。
(3)底面的特征:圆柱底面是完全相同的两个圆。
3.(1)圆柱周围的面叫做侧面。
(2)特征:圆柱的侧面是曲面。
4.(1)圆柱两个底面之间的距离叫做圆柱的高。
(2)一个圆柱有无数条高。
5.把圆柱平行于底面进行切割,切面是和底面大小相同的两个圆;把圆柱沿底面直径垂直于底面进行切割,切面是两个完全相同的长方形。
6.圆柱的侧面展开图是一个长方形,这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
7.在圆柱的上下底面周长上任取一点分别为A、B,连接AB(使AB不是圆柱的高),沿着AB将圆柱的侧面剪开,圆柱展开后是一个平行四边形。
8.温馨提示:圆柱的底面是圆形,面不是椭圆。
9.温馨提示:沿高剪开时,圆柱的侧面展开图是一个长方形。
10.从圆柱的上下两个底面观察会得到圆;从圆柱的正面或侧面观察会得到长方形(或正方形)。
11.如果圆柱的侧面展开图是个长方形,那么该圆柱的底面周长大约是其底面直径长度的3倍。
如果圆柱的侧面展开图是个正方形,那么该圆柱的高大约是其底面直径长度的3倍。
12.圆柱的侧面积=底面周长×高。
如果用字母S表示圆柱的侧面积,用C表示底面周长,用h表示高,则圆柱的侧面积的计算公式是
S=Ch
13.(1)已知圆柱的底面直径和高,可以根据公式:S=πdh直接求出
圆柱的侧面积。
(2)已知圆柱的底面半径和高,可以根据公式:S=2πrh直接求出圆柱的侧面积。
14.圆柱的表面积是指圆柱的侧面积和两个底面的面积之和。
15.圆柱的表面积=圆柱的侧面积+底面积×2,用字母表示为S表=S 侧+2S底。
16.(1)已知圆柱的底面半径和高,可以根据公式:S表
=2πrh+2πr2直接求出圆柱的表面积。
(2)已知圆柱的底面直径和高,求圆柱的表面积时,可以根据公式:S表=πdh+π(d÷2)2直接求出圆柱的表面积。
(3)已知圆柱的底面周长和高,求圆柱的表面积,可以根据公式:
S表=Ch+π(C/2π)2=Ch+C2/4π求出圆柱的表面积。
17.温馨提示:求通风管、烟囱、油管等圆柱形物体的表面积其实就是求它们的侧面积。
18.温馨提示:把一个圆柱截成n段后,其表面积增加了2(n-1)个底面积。
19.一个圆柱占空间的大小,叫做这个圆柱的体积。
20.圆柱的体积=底面积×高,字母公式:V=Sh或V=πr^2h
21.温馨提示:容积的计算方法和体积的计算方法相同,只是计算容积的数据要从里面测量。
22.在计算过程中,如果已知圆柱的底面半径、直径或周长,那么要先求出底面积,再求体积。
计算公式是:V=πr^2h,V=π(d÷2)
^2h,V=π[C÷(2π)]^2h
23.温馨提示:圆柱的高不变,底面半径、直径或周长扩大到原来的n倍,则体积扩大到原来的n^2倍,若底面半径、直径或周长缩小到原来的1/n,则体积缩小到原来的1/(n^2)。
24.温馨提示:在圆柱的立体图形中,两个底面圆心之间的距离是圆柱的高,但在圆柱的平面展开图中,长方形的宽(或正方形的边长)才是圆柱的高。
25.两个圆柱的半径比是1:a(a>0),高的比是a:1,则它们的体积之比是1:a。
26.圆锥是由一个底面和一个侧面两部分组成。
(1)底面:圆锥的圆面就是它的底面,它有一个底面。
圆锥底面的圆心、半径、直径和周长分别叫做圆锥的底面圆心、底面半径、底面
直径和底面周长,分别用字母O、r、d和C表示。
(2)侧面:圆锥周围的曲面就是它的侧面。
(3)高:从圆锥的顶点到底面圆心的距离是圆锥的高。
高用字母h表示。
(4)圆锥只有一条高。
(5)转动直角三角形可以形成圆锥。
27.温馨提示:
(1)从圆锥的顶点到底面圆周上任意一点的线段是圆锥的母线,圆锥母线的长度大于圆锥的高。
(2)任意画一条母线,把圆锥的侧面展开,得到一个扇形,因此圆锥的侧面展开图是一个扇形。
(3)把圆锥平行于底面切割,切面是两个完全相同的圆,该圆要比圆锥的底面圆小;把圆锥沿高垂直于底面进行切割,切面则是两个完全相同的等腰三角形。
28.温馨提示:半圆能围成圆锥,但整圆不能围成圆锥。
29.圆锥的体积=底面积×高÷3,用字母表示:V圆锥=V圆柱
÷3=Sh÷3
30.圆柱和圆锥的关系:
(1)等底等高的圆柱和圆锥:圆柱的体积比圆锥的体积多2倍;圆锥
的体积比圆柱的体积少2/3。
(2)等底等高的圆柱和圆锥:圆锥的高是圆柱的高的3倍,或者说圆锥的高比圆柱的高多2倍;圆柱的高是圆锥的高的1/3,或者说圆柱
的高比圆锥的高少2/3。
(3)等高等体积的圆柱和圆锥:圆锥的底面积是圆柱的底面积的3倍,或者说圆锥的底面积比圆柱的底面积多2倍;圆柱的底面积是圆锥的底面积的1/3,或者说圆柱的底面积比圆锥的底面积少2/3。
31.温馨提示:
(1)已知圆锥的底面半径和高,可以直接利用公式:V=πr^2h÷3来
求圆锥的体积。
(2)已知圆锥的底面直径和高,可以直接利用公式:V=π(d÷2)
^2h÷3来求圆锥的体积。
(3)已知圆锥的底面周长和高,可以直接利用公式:V=π(C÷2÷π) ^2h÷3求出圆锥的体积。
32.利用V=Sh÷3计算圆锥的体积时不要忘记除以3或乘1/3。
33.温馨提示:圆柱体积是圆锥体积的3倍或者说圆锥体积是圆柱体积的1/3,必须以“圆柱和圆锥等底等高”为前提。
34.在以直角三角形的直角边为轴旋转而成的两个圆锥中,以较短直角边为轴旋转而成的圆锥的体积比较大。
“”
“”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
