第七次函数 实验报告(答案已做望大家多多指教)
函数实验报告总结

函数实验报告总结
在本次实验中,我们对不同类型的函数进行了研究和分析,以便更好地理解它们的特性和用途。
通过实验,我们深入探讨了线性函数、二次函数、指数函数和对数函数等不同类型的函数。
我们学习了线性函数,它的图像是一条直线,具有恒定的斜率。
我们了解到线性函数的特点是通过两个点就可以确定一条直线,而且它的增长速度是恒定的。
在实际应用中,线性函数常常用来描述两个变量之间的简单关系,比如成本和产量之间的关系。
我们研究了二次函数,它的图像是一个抛物线。
二次函数的特点是有一个最高点或最低点,这取决于二次项系数的正负。
我们了解到二次函数在现实生活中有许多应用,比如抛物线运动、天文学中的行星轨道等。
接着,我们探讨了指数函数,它的图像是一个逐渐增长或逐渐减小的曲线。
指数函数的特点是底数不为1时,函数值随自变量的增加而迅速增长或迅速减小。
指数函数在经济学和生物学等领域有着广泛的应用,比如人口增长模型和利息计算等。
我们研究了对数函数,它是指数函数的反函数。
对数函数的图像是一条直线,它的特点是随着自变量的增加,函数值增长速度逐渐减慢。
对数函数在信息论和物理学中有重要的应用,比如信噪比计算和半衰期计算等。
通过本次实验,我们对不同类型的函数有了更深入的理解,更加熟练地掌握了函数的性质和用法。
我们将继续努力学习和实践,以便更好地运用函数知识解决实际问题,提高自己的数学能力和分析能力。
希望通过这次实验总结,能够对读者有所启发和帮助,让大家更好地理解和应用函数知识。
函数实训报告

一、实训目的通过本次函数实训,使学生掌握函数的定义、性质、图像及其应用,培养学生的逻辑思维能力和实际操作能力。
同时,通过实训,提高学生对数学知识的应用能力,为后续学习打下坚实基础。
二、实训内容1. 函数的基本概念(1)函数的定义:给定两个非空数集D和C,如果按照某种对应关系f,对于D中的任意一个数x,在C中都有唯一确定的数y与之对应,则称f是D到C的一个函数,记作y=f(x),x∈D,y∈C。
(2)函数的性质:奇偶性、单调性、周期性、有界性等。
2. 函数的图像(1)一次函数:y=kx+b(k≠0)的图像是一条直线,斜率k表示直线的倾斜程度,截距b表示直线与y轴的交点。
(2)二次函数:y=ax²+bx+c(a≠0)的图像是一条抛物线,开口方向由a的正负决定,顶点坐标为(-b/2a, c-b²/4a)。
(3)指数函数:y=a^x(a>0且a≠1)的图像是一条不断上升的曲线,当a>1时,图像在y轴右侧不断上升;当0<a<1时,图像在y轴右侧不断下降。
(4)对数函数:y=log_a(x)(a>0且a≠1)的图像是一条不断上升的曲线,当a>1时,图像在x轴右侧不断上升;当0<a<1时,图像在x轴右侧不断下降。
3. 函数的应用(1)经济领域:函数可以用来描述供需关系、成本收益、利润等。
(2)工程技术:函数可以用来描述物理现象、工程问题等。
(3)社会问题:函数可以用来描述人口、资源、环境等问题。
三、实训过程1. 函数定义及性质的学习:通过阅读教材、上网查询资料等方式,了解函数的基本概念、性质,并进行总结归纳。
2. 函数图像的学习:通过绘制函数图像,观察函数的图像特点,加深对函数性质的理解。
3. 函数应用的学习:结合实际生活,分析函数在经济、工程、社会等领域的应用,提高解决实际问题的能力。
4. 实训报告撰写:根据所学内容,撰写实训报告,总结实训过程中的收获和体会。
函数(二)实验报告

函数(二)实验报告
《函数(二)实验报告》
实验目的:通过本次实验,掌握函数的概念、性质和应用,加深对函数的理解,提高数学分析和解决问题的能力。
实验内容:
1. 函数的概念和性质:通过观察和分析不同函数的图像,探讨函数的定义域、
值域、单调性、奇偶性等性质。
2. 函数的应用:结合实际问题,利用函数的概念和性质进行建模和求解,探讨
函数在生活中的应用。
实验步骤:
1. 确定实验的函数范围和内容,选择适当的函数进行实验。
2. 绘制函数的图像,观察函数的变化规律,分析函数的性质。
3. 结合实际问题,利用函数建立数学模型,并求解相关问题。
实验结果:
1. 通过实验,我们深入理解了函数的定义和性质,掌握了函数的图像和变化规律。
2. 在实际问题中,我们成功利用函数的概念和性质建立了数学模型,并求解了
相关问题,验证了函数在生活中的应用价值。
实验结论:
通过本次实验,我们加深了对函数的理解,提高了数学分析和解决问题的能力。
函数是数学中的重要概念,具有广泛的应用价值,我们将继续深入学习和探索
函数的相关知识,不断提高自己的数学素养和解决问题的能力。
实验总结:
本次实验不仅加深了对函数的理解,还提高了我们的数学分析和解决问题的能力。
在今后的学习和工作中,我们将继续加强对函数的学习和应用,不断提升自己的数学素养和解决问题的能力。
特殊函数与图像实验报告

hold on
subplot(2,2,2)
[a,b]=meshgrid(-8:.3:8);%先生成一个网格
c=sqrt(a.^2+b.^2)+eps;
z=sin(c)./c;
mesh(a,b,z)
i=find(a.^2+b.^2>=64);
z1=z;z1(i)=NaN;
mesh(a,b,z1);
7、子图的绘制:subplot(m,n,p)
8、图像的修饰与其它函数:grid on 添加网格grid off 取消网格
holdon 保持图像窗口的图形
实验过程记录(含基本步骤、主要程序清单及异常情况记录等):
基本步骤:
第一步:在E盘上或其他盘上建立存储M文件的文件夹,命名为matlab
第二步:重设搜索路径,使其路径为第一步所建的文件夹
c=sqrt(a.^2+b.^2)+eps;
z=(sin(c)-c)./c;
mesh(a,b,z)
i=find(a.^2+b.^2>=121);
z1=z;z1(i)=NaN;
mesh(a,b,z1);
axis square
hold on
3、图三的球面,椭球面,单叶双曲面,双叶双曲面的的图像程序是:
subplot(2,2,1)
axis auto
4、图四的田螺线的图像程序是:
t=0:.1:30;
x=5*t.*cos(t);
y=5*t.*sin(t);
z=t.^2;
plot3(x,y,-z)
axis equal
5、图五马鞍面(颜色为灰色,有一个标题“马鞍面”)的图像程序是:
数值分析上机实验报告

数值分析上机实验报告导言:本次上机实验主要是针对数值分析课程中的一些基本算法进行实验验证。
实验内容包括迭代法、插值法、数值积分和常微分方程的数值解等。
在实验过程中,我们将会使用MATLAB进行算法的实现,并对结果进行分析。
一、迭代法迭代法是解决函数零点、方程解等问题的常用方法。
我们将选择几个常见的函数进行迭代求根的实验。
(1)二分法二分法是一种简单而有效的迭代求根法。
通过函数在区间两个端点处的函数值异号来确定函数在区间内存在零点,并通过不断缩小区间来逼近零点。
(2)牛顿法牛顿法利用函数的一阶导数和二阶导数的信息来逼近零点。
通过不断迭代更新逼近值,可以较快地求得零点。
实验结果表明,对于简单的函数,这两种迭代法都具有很好的收敛性和稳定性。
但对于一些复杂的函数,可能会出现迭代失效或者收敛速度很慢的情况。
二、插值法插值法是在给定一些离散数据点的情况下,通过构造一个插值函数来逼近未知函数的值。
本实验我们将使用拉格朗日插值和牛顿插值两种方法进行实验。
(1)拉格朗日插值拉格朗日插值通过构造一个多项式函数来逼近未知函数的值。
该多项式经过离散数据点,并且是唯一的。
该方法简单易懂,但插值点越多,多项式次数越高,插值函数的精度也就越高。
(2)牛顿插值牛顿插值利用差商的概念,通过构造一个插值多项式来逼近未知函数的值。
与拉格朗日插值相比,牛顿插值的计算过程更加高效。
但同样要求插值点的选择要合理,否则可能出现插值函数不收敛的情况。
实验结果表明,这两种插值方法都能够很好地逼近未知函数的值。
插值点的选择对插值结果有很大的影响,过多或者过少的插值点都可能导致插值结果偏离真实函数的值。
三、数值积分数值积分是一种将定积分问题转化为数值求和的方法。
本实验我们将使用复合梯形求积法和复合辛普森求积法进行实验。
(1)复合梯形求积法复合梯形求积法将定积分区间等分为若干小区间,然后使用梯形公式对每个小区间进行近似求积,最后将结果相加得到整个定积分的近似值。
高考数学第七次仿真模拟试题理PDF

卜人入州八九几市潮王学校2021届昆一中高三联考卷第七期联考理科数学参考答案及评分HY一、选择题1.解析:{}{}210A x x x ==-=-,,{}{}2111B x x x x =--<=>-,所以{}0AB =.选B.2.解析:因为()()()()1i 1i 11i z a a a =-+=++-在复平面内对应的点位于虚轴上,所以10a +=,所以1a =-.选A.3.解析:该正三棱柱的左视图是边长分别为2C .4.解析:由得:tan 3α=,因为cos sin 1tan 2cos sin 1tan αααααα++==---,选A .5.解析:412340123444444111111C C C C C x x x x x ⎛⎫⎫⎫⎫⎫=++++ ⎪⎪⎪⎪⎪⎝⎭⎭⎭⎭⎭对31x ⎫⎪⎭,常数项为13C ,对11x ⎫⎪⎭,21x ⎫⎪⎭,41x ⎫⎪⎭展开式中无常数项,所以41x ⎛⎫ ⎪⎝⎭的展开式中常数项为03144313C C C +=,选D.6.解析:最短的弦为过点(1,1)且与圆心(0,0)和点(1,1)连线垂直的弦,此时弦长为最长的弦为直径,选D .7.解析:函数()()e esin xxf x x -=-⋅为偶函数,排除B 、C ,当2x π=时,()0f x >,选D. 8.解析:5(1)9P ξ≥=⇒1222225(1)29C p p C p p p -+=-=⇒13p =,选B .9.解析:sin sin 2sin B C A +=,22248=b c a b c b c +==⇒+≥,当且仅当,取得等号,设D 是BC边上的中点,那么22222211142cos 232222b c AD AB AC c b bc A c b bc bc+-=+=++=++ C.10.解析:因为=2AB ,=23AC =60ABC ︒∠,所以△ABC 是直角三角形,1223232S =⨯⨯=,设h 为三棱锥顶点O 到底面的高,461233V h ==⨯,=22h ,4823R +=球的体积为34=3233R ππ,选D. 11.解析:由题意知,如图AO AB ⊥,那么,OB b OA a ==,因为5,可设5c k=,2a k b k ==,,0)k >(那么21tan 2AOF ∠=,24tan tan 23AOB AOF ∠=∠=,2OA k =,83k AB =,所以△OAB 的面积为18162233k k ⨯⨯=,所以2k =,那么双曲线的焦距为225=210c k = B.12.解析:构造函数()()()1ln F x g x f x ax b x a =-=++--,min ()0F x ≥,易知0a >,11()ax F x a x x -'=-=,可推出min 1()11ln 0ln 2F b a a b a a a=+++-≥⇒≥--,ln 21b a a a +≥-,构造函数ln 2()1a x aϕ+=-,min ()1e x ϕ=-,选B. 二、填空题13.解析:设()a x y =,,那么()12a c x y -=--,,由a ∥b ,得3x y =,由()a a c ⊥-得()()120x x y y -+-=,解方程组得:32x =,12y =,所以3122a ⎛⎫= ⎪⎝⎭,. 14.解析:直线20x y +=的斜率为12-,故曲线()f x 在点()1,0处的切线斜率2k =,()1ln f x a x a x'=++,由导数的几何意义知()11k f a '==+,故1a =. 15.解析:由2()sin 0f x x x ==得:0x =或者2sin 0x =,所以2x k π=(k ∈Z ),而[0,3]x ∈,所以012k =,,,一共有3个零点.16.解析:△2PEF 的周长为2222++22PE PF EF PE a PF EF a +=-+≥,当且仅当P,E,F 1三点一共线,P 在射线1F E 与椭圆的交点时,△2PEF 的周长最小值为2a ,所以2=6a b ,所以22e = 三、解答题〔一〕必考题17.解析:〔1〕设{}n a 的公比为q ,由6542a a a -=得5431112a q a q a q -=,即220q q --=,因为0q >,解得2q =,又223a =,得113a =,所以1123n n a -=⋅.………6分 〔2〕1211111(2)(2)2339n n n n n n b a a --+==⋅⋅⋅=⋅ 13212111112(14)1222(22)99991427n n n n S -+-=⋅+⋅+⋅⋅⋅+⋅=⋅=--.………12分18.解:〔1〕由图中表格可得22⨯列联表如下:将22⨯列联表中的数据代入公式计算得()()()()()()22210045153010 3.03 3.84125755545n ad bc K a b c d a c b d -⨯-⨯==≈<++++⨯⨯⨯,所以在犯错误概率不超过0.05的前提下,不能认为是否喜欢骑行一共享单车与性别有关.………6分〔2〕视频率为概率,在我“骑行达人〞中,随机抽取1名用户,该用户为男“骑行达人〞的概率为35,女“骑行达人〞的概率为25.记抽出的女“骑行达人〞人数为Y ,那么500X Y =. 由题意得2~4,5Y B ⎛⎫ ⎪⎝⎭,所以()442355iii P Y i C -⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭〔0,1,2,3,4i =〕,所以Y 的分布列为所以X 的分布列为所以()28455E Y =⨯=, 所以X 的数学期望()()500800E X E Y ==元.………12分19.〔1〕证明:因为菱形ABCD 的对角线AC 与BD 交于点O ,所以AO BD ⊥, 因为OF ⊥平面ABCD ,所以OF AO ⊥, 又因为OFBD O =,所以AO ⊥平面BDF ;因为H 为线段BF 上一点,所以AO OH ⊥,因为四边形AOFE 为平行四边形,所以AO ∥EF , 所以EF OH ⊥;………5分〔2〕解:设点H 到平面ABCD 的间隔为h ,那么113H ABCABCV V S h -==⋅⋅=, 213EFCA D V S O ⋅==⋅四边形,因为213V V =,所以12h OF =,故H为线段BF 中点; 连接OM ,因为OF ⊥平面ABCD ,所以OF BC ⊥, 又因为FM BC ⊥,且FMOF F =,所以BC ⊥平面FOM ,所以BC OM ⊥,由得4OB =, 所以cos602BM OB ==,作MN OB ⊥,交OB 于N ,那么1BN =,MN =3ON =;如图建立直角坐标系,那么()0,0,6F ,()M ,()0,A -,()C ,()4,0,0B ,所以()2,0,3H,()AC =,()AH =,所以()3,6FM =-,设平面HAC 的法向量为(),,n x y z =,由00AC A n n H ⎧⋅=⎪⎨⋅=⎪⎩即0230x z ⎧=⎪⎨++=⎪⎩,取()3,0,2n =-, 设直线FM 与平面AHC 所成角为θ,那么739sin cos ,FM n FM n FM nθ⋅===⋅, 即直线FM 与平面AHC 所成角的正弦值为………12分 20.解:(1)由条件可得,1c =,1AB k =-;设11(,)A x y ,22(,)B x y ,那么22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩,两式相减得 121212122211()()()()0x x x x y y y y a b-++-+=, 12122242()()33x x y y a b -=--,12222212()422233()33y y k a b x x b b -=-=-=-, 所以222a b =,又222c a b =-,21b =,22a =,所以椭圆22:12x E y +=.………6分(2)设33(,)M x y ,44(,)N x y ,当直线MN 斜率不存在时,343412OM ONy y k k x x ==-,34x x =,34y y =-,所以232312OM ON y k k x =-=-,又223312x y +=,解得223311,2x y ==,CDMN S =.………7分 当直线MN 斜率存在时,设直线方程为:l y kx m =+,联立2212y kx m x y =+⎧⎪⎨+=⎪⎩得222(12)4220k x kmx m +++-=,所以34223424122212km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩,………8分 由343412OM ONy y k k x x ==-得22222211222212m k k m k-+=--+,即22221m k =+,…………10分原点到直线MN 的间隔为d =所以312OMN S MN d x ∆=-====,所以4CDMN OMN S S ∆==………12分21.解:〔1〕当0a =时,()()222e 2xf x x x =-⋅+-,()()21e xf x x '=⋅-,假设0x ≤,那么1e 0x-≥,那么()0f x '≤,那么()f x 在(],0-∞单调递减;假设0x >,那么1e 0x-<,那么()0f x '<,那么()f x 在()0,+∞单调递减;故()f x 在R 上单调递减,又()00f =,故当0x <时,()0f x >;当0x >时,()0f x <.………4分 〔2〕假设0a ≤,当0x >时,因为e 10x ->,所以()2e 10xax-≤,由〔1〕可知,当0x >时,()222e 20xx x -⋅+-<, 那么()()()22e 122e 20xxf x axx x=-+-⋅+-<,与0x =是()f x 的极小值点矛盾.假设0a >,()()()2(22)e 21(22)e 21x xf x a x ax a x a ax a x '⎡⎤⎡⎤=-+⋅+-⋅=-+⋅+-⋅⎣⎦⎣⎦设函数()()(22)e 21xg x a ax a =-+⋅+-,那么()()32e xg x a ax '=-+⋅,设函数()32h x a ax =-+,令()00h x =,解得023x a=-,因为()h x 在R 上单调递增, 故当2,3x a ⎛⎫∈-∞- ⎪⎝⎭时,()0h x <,那么()0g x '<,那么()g x 在2,3a ⎛⎫-∞- ⎪⎝⎭单调递减;当23,x a ⎛⎫∈-+∞ ⎪⎝⎭时,()0h x >,那么()0g x '>,那么()g x 在23,a ⎛⎫-+∞ ⎪⎝⎭单调递增;假设23a =,那么()()00g x g ≥=,故当(),0x ∈-∞时,()0f x '<,那么()f x 在(),0-∞单调递减;当()0,x ∈+∞时,()0f x '>,那么()f x 在()0,+∞单调递增,此时0x =是()f x 的极小值点.假设203a <<,那么230a ->,因为()g x 在20,3a ⎛⎫- ⎪⎝⎭单调递减,故当20,3x a ⎛⎫∈- ⎪⎝⎭时,()0g x <,那么()0f x '<,故()f x 在20,3a ⎛⎫- ⎪⎝⎭单调递减,与0x =是()f x 的极小值点矛盾. 假设23a >,那么230a -<,因为()g x 在23,0a ⎛⎫- ⎪⎝⎭单调递增,故当23,0x a ⎛⎫∈- ⎪⎝⎭时,()0g x <,那么()0f x '>,故()f x 在23,0a ⎛⎫- ⎪⎝⎭单调递增,与0x =是()f x 的极小值点矛盾. 综上,当23a =.………12分 〔二〕选考题:第22、23题中任选一题做答。
函数实验报告

函数实验报告函数实验报告引言:函数是数学中一个重要的概念,它描述了一种特定的关系,将一个或多个输入值映射到一个输出值。
在数学和计算机科学中,函数被广泛应用于各种问题的建模和解决。
本实验旨在通过实际案例和数据分析,探索函数的特性和应用。
一、函数的定义和特性1.1 函数的定义函数是一种映射关系,它将一个或多个输入值映射到一个唯一的输出值。
函数通常用符号表示,如f(x)、g(x)等。
1.2 函数的特性函数具有以下特性:- 唯一性:对于每一个输入值,函数只能有一个输出值。
- 定义域:函数的输入值的集合称为定义域,它决定了函数的有效输入范围。
- 值域:函数的输出值的集合称为值域,它决定了函数的有效输出范围。
- 可逆性:如果一个函数的每一个输出值都可以通过逆映射找到唯一的输入值,则该函数是可逆的。
二、函数的应用案例2.1 函数在物理学中的应用函数在物理学中有广泛的应用,例如描述运动的函数、描述力的函数等。
通过建立合适的函数模型,可以对物理系统进行分析和预测。
2.2 函数在经济学中的应用函数在经济学中也有重要的应用,例如成本函数、收益函数等。
通过对经济系统中的各种变量建立函数关系,可以进行经济政策的制定和分析。
2.3 函数在计算机科学中的应用函数在计算机科学中是一种基本的概念,它被广泛应用于算法设计、软件开发等领域。
例如,计算机程序可以看作是由一系列函数构成的。
三、函数实验设计与数据分析3.1 实验设计本次实验设计了一个函数实验,通过收集和分析数据来验证函数的特性和应用。
实验对象是一组学生的身高和体重数据。
3.2 数据收集在实验中,我们随机选择了100名学生,并测量了他们的身高和体重。
通过这些数据,我们可以建立身高和体重之间的函数关系。
3.3 数据分析通过对身高和体重数据的分析,我们可以得出以下结论:- 身高和体重之间存在正相关关系,即身高增加时,体重也会增加。
- 身高和体重之间的函数关系可以用线性函数来描述,即体重 = a * 身高 + b。
第七次实验
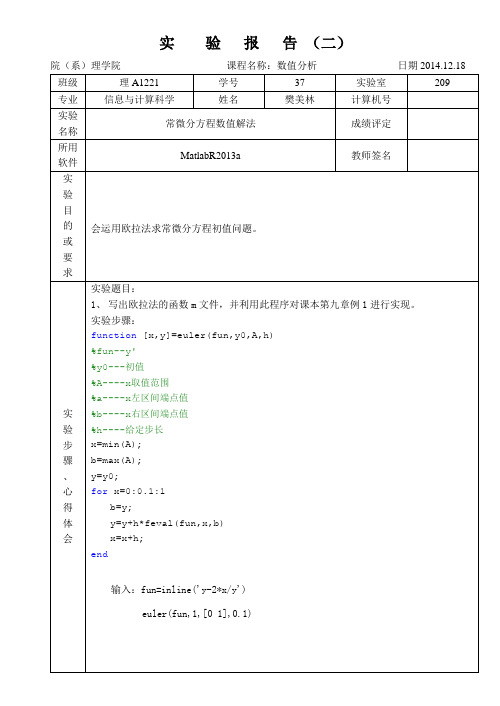
function[x,y]=euler(fun,y0,A,h)
%fun--y'
%y0---初值
%A----x取值范围
%a----x左区间端点值
%b----x右区间端点值
%h----给定步长
x=min(A);
b=max(A);
y=y+h*feval(fun,x,b)
x=x+h;
end
输入:fun=inline('y-2*x/y')
euler(fun,1,[01],0.1)
得到:
x =0.1000y =1.1000
x =0.2000 y =1.1918
x =0.3000 y =1.2774
x =0.4000 y =1.3582
x =0.5000 y =1.4351
实验报告(二)
院(系)理学院课程名称:数值分析日期2014.12.18
班级
理A1221
学号
37
实验室
209
专业
信息与计算科学
姓名
樊美林
计算机号
实验
名称
常微分方程数值解法
成绩评定
所用
软件
MatlabR2013a
教师签名
实
验
目
的
或
要
求
会运用欧拉法求常微分方程初值问题。
实
验
步
骤
、
心
得
体
会
实验题目:
1、写出欧拉法的函数m文件,并利用此程序对课本第九章例1进行实现。
x =0.6000 y =1.5090
x =0.7000 y =1.5803
x =0.8000 y =1.6498
