高频电子线路 第二章 习题解答
(完整版)高频电子线路张肃文第五版_第2章习题答案

高频电子线路(用于学习之间交流,不得用于出版等商业用途!)第2章习题答案2-1已知某一并联谐振回路的谐振频率f 0=1MHz,要求对990kHz 的干扰信号有足够的衰减,问该并联回路应如何设计?解 为了有效滤除990kHz 的干扰信号,应使它位于通频带之外。
若取BW 0.7=20kHz ,则由通频带与回路Q 值之间的关系有502010007.00===BW f Q因此应设计Q >50的并联谐振回路.2-2试定性分析题图2—2所示的电路在什么情况下呈现串联谐振或并联谐振状态.解 题图2-2(a )中L 1C 1或L 2C 2之一呈并联谐振状态,则整个电路即为并联谐振状态。
若L 1C 1与L 2C 2呈现为容抗,则整个电路可能成为串联谐振。
题图2-2(b)只可能呈现串联谐振,不可能呈现并联谐振状态.题图2-2(c)只可能呈现并联谐振,不可能呈现串联谐振状态。
2—3有一并联回路,其电感、电容支路中的电阻均为R 。
当C L R =时(L 和C 分别为电感和电容支路的电感值和电容值),试证明回路阻抗Z 与频率无关。
解 ()()()⎪⎭⎫ ⎝⎛-++⎪⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+=⎪⎭⎫⎝⎛-++⎪⎭⎫ ⎝⎛-+=C L j R R C R LR j C L R R C j R L j R C j R L j R Z abωωωωωωωω11121112212121 要想使Z ab 在任何频率下,都呈现纯阻性,就必须使分子与分母的相角相等,亦即必须有2121121R R C L CL R R C R LR +-==-ωωωω 上式化简得C R C L LR C L 2122222-=⎪⎪⎭⎫ ⎝⎛-ω 要使上式在任何频率下都成立,必有0222=-LR C L 或 C L R =2 0212=-C R C L 或 CL R =1 因此最后得CL R R ==212-4有一并联回路在某频段内工作,频段最低频率为535kHz ,最高频率为1605kHz 。
《高频电子线路》(周选昌)习题解答完整答案

1 LC ∑
。
1-9 画出图 P1-9 所示的四个无耗的电抗~频率特性曲线,并写出关键点的频率值。
L C (a)
L
C
L1
L2 C
C1
L C2
(b) 图 P1-9
(c)
(d)
解:其电抗~频率特性曲线及关键点的频率如下图所示。
X f
X fp 0 f
0
fs
(a) f S = X
1 2p LC
(b ) X f
f0 f0 6.5 × 10 6 = → Q0 = = = 26 Q0 BW0.7 250 × 10 3
→L=
f0 =
1 2π LC
(2πf 0 )2 C
1
= 11.76 µH
Q0 =
RT
ρ
→ RT = ρQ0 = ω 0 LQ0 = 12.49 KΩ
若希望回路的通频带宽展宽一倍,则要求品质因素 Q 降低一倍,即谐振电阻减少一倍,则 应在回路两端并一个与谐振电阻 RT 一样的电阻,即 R x = RT = 12.49 KΩ 。
fp =
1 2p LC
fp
0
fp
fs
0
fs
f
(c)
(d)
1 , fp = fS = 2p L2C 2p
' = RS
1 1 ' ' ' ,回路总电容: = 2 RL 。 此 时 有 谐 振 阻 抗 : RT = R0 // RS RS , R L // RL 2 PL PC
RT
C ∑ = C1 // C 2 ,有载品质因素: Qe =
ρ
= RT ω 0 C ∑ ,其中 ω 0 =
1 LC ∑
高频电子线路答案+完整

第二章 高频电路基础2-1对于收音机的中频放大器,其中心频率f 0=465 kHz .B 0.707=8kHz ,回路电容C=200pF ,试计算回路电感和 Q L 值。
若电感线圈的 Q O =100,问在回路上应并联多大的电阻才能满足要求。
解2-1:答:回路电感为0.586mH,有载品质因数为58.125,这时需要并联236.66k Ω的电阻。
2-5 一个5kHz 的基频石英晶体谐振器, C q =2.4X10-2pF C 0=6pF ,,r o =15Ω。
求此谐振器的Q 值和串、并联谐振频率。
解2-5:答:该晶体的串联和并联频率近似相等,为5kHz ,Q 值为88464260。
2-7 求如图所示并联电路的等效噪声带宽和输出均方噪声电压值。
设电阻R=10k Ω,C=200 pF ,T=290 K 。
解:答:电路的等效噪声带宽为125kHz ,和输出均方噪声电压值为19.865μV2.2-10 接收机等效噪声带宽近似为信号带宽,约 10kHz ,输出信噪比为 12 dB ,要求接收机的灵敏度为 1PW ,问接收机的噪声系数应为多大? 解2-10:根据已知条件答:接收机的噪音系数应为32dB 。
第三章 高频谐振放大器3-4 三级单调谐中频放大器,中心频率f 0=465 kHz ,若要求总的带宽B0.7=8 kHZ ,求每一级回路的 3 dB 带宽和回路有载品质因数Q L 值。
解3-4: 设每级带宽为B 1,则:答:每级带宽为15.7kHz,有载品质因数为29.6。
3-5 若采用三级临界耦合双回路谐振放大器作中频放大器(三个双回路),中心频率为f o =465 kHz ,当要求 3 dB 带宽为 8 kHz 时,每级放大器的3 dB 带宽有多大?当偏离中心频率 10 kHZ 时,电压放大倍数与中心频率时相比,下降了多少分贝? 解3-5 设每级带宽为B 1,则:0226120611244651020010100.5864465200f L f C mHπππ-==⨯⨯⨯⨯=≈⨯⨯2由()03034651058.125810LL 0.707f Q f Q B =⨯===⨯0.707由B 得:900312000000000010010171.222465102001024652158.1251171.22237.6610058.125L LLL L L L Q R k C C C Q Q R g g g R Q Q R R R k Q Q Q ΩωππωωΩ∑-===≈⨯⨯⨯⨯⨯⨯===++=-==⨯≈--因为:所以:()0q q0q 00q0q 093120q C C 60.024C 0.024pF C C C 60.024f f f 0.998f 4.99kHz C 11122C 1110Q 884642602f Cr 25100.0241015 3.6-⨯==≈=++==≈=⎛⎫++ ⎪⎝⎭====ππ⨯⨯⨯⨯⨯π总电容串联频率品质因数20220002064121),11|()|11()11arctan(2)1(2)211101254410200108RH R j CR j C R H j df df H CR df fCR fCR CR kHz CR ωωωωωπππ∞∞∞∞-===++=+==+====⨯⨯⨯⎰⎰⎰0n 网络传输函数为H(j 则等效噪音带宽为B =22202343214444 1.3710290101251019.865()n n n n kTGB H kTB R kTRB R V μ-====⨯⨯⨯⨯⨯⨯=输出噪音电压均方值为U 121212234061015.85101015.8515.85 1.3710290101015883215.85 1.3729o i i F o S N S N kTB N S N dB---=====⨯⨯⨯⨯=≈≈⨯⨯。
(完整版)高频电子线路(胡宴如耿苏燕主编)习题答案

高频电子线路(胡宴如 耿苏燕 主编)习题解答目 录第2章 小信号选频放大器 1 第3章 谐振功率放大器 4 第4章 正弦波振荡器10 第5章 振幅调制、振幅解调与混频电路 22 第6章 角度调制与解调电路 38 第7章 反馈控制电路49第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻?[解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.7 2.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L =12=/10,n N N =L 1k R =Ω。
第2章《高频电子线路》_(曾兴雯)_版高等教育出版社课后答案

2.2 高频电路中的基本电路
1、简单振荡回路 (1)并联谐振回路 (2)串联谐振回路
17
第2章 高频电路基础
(1)并联谐振回路 谐振特性:
振荡回路的阻抗在某一特定频率上具 有最大或最小值的特性称为谐振特性。
1 jC Zp 1 r jL j C (当 L r 时) L C 1 r j (L ) 谐振条件: C 当回路总电抗 X=0 时,回路呈谐振状态
Q0
L
r
品质因数 Q
Q 定义:高频电感器的感抗与其串联损耗电阻之比。
Q 值越高,表明该电感器的储能作用越强,损耗越小。
8
第2章 高频电路基础
2.1 高频电路中的元器件
二、高频电路中的有源器件 主要是:
二极管 晶体管
集成电路
完成信号的放大、非线性变换等功能。
9
第2章 高频电路基础
2.1 高频电路中的元器件
第2章 高频电路基础
第2章 高频电路基础
2.1 高频电路中的元器件 2.2 高频电路中的基本电路 2.3 电子噪声及其特性 2.4 噪声系数和噪声温度
1
第2章 高频电路基础
2.1 高频电路中的元器件
一、高频电路中的元件 高频电路中使用的元器件与在低频电路中使 用的元器件基本相同,但要注意它们在高频使用 时的高频特性。
号中心频率fs=10 MHz,回路电容C=50 pF,
试计算所需的线圈电感值。
(1) 若线圈品质因数为Q=100,试计算回路谐振电阻
及回路带宽。 (2) 若放大器所需的带宽B0.7=0.5 MHz,则应在回路 上并联多大电阻才能满足放大器所需带宽要求?
36
第2章 高频电路基础
(2)串联谐振回路 串联谐振回路是与并联谐振回路对偶的电路, 其基本特性与并联谐振回路呈对偶关系,通频带、 矩形系数与并联谐振回路相同。 电路组成: 电抗特性:
高频电子线路课后答案

说明所有习题都是我们上课布置的作业题,所有解答都是本人自己完成,其中难免有错误之处,还望大家海涵。
第2章 小信号选频放大器已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=并联谐振回路如图所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200kΩ=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω并联回路如图所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L = 12=/10,n N N =L 1k R =Ω。
高频电子线路最新版课后习题解答第二章 选频网络与阻抗变换习题解答

第二章 选频网络与阻抗变换网络思考题与习题2.1选频网络的通频带指归一化频率特性由1下降到 0.707 时的两边界频率之间的宽度。
理想选频网络矩形系数1.0k = 1 。
2.2 所谓谐振是指LC串联回路或并联回路的固有频率0f 等于 信号源的工作频率f 。
当工作频率f <0f 时,并联回路呈 感 性;当工作频率f >0f 并联回路呈 容 性;当工作频率f =0f 时,并联谐振回路的阻抗呈 纯阻 性且最 大 。
2.3 若0f 为串联回路的固有频率。
当信号源的工作频率f<0f 时,串联回路呈 容 性;当工作频率f >0f 串联回路呈 感 性;当工作频率f =0f 时,串联谐振回路的阻抗呈 纯阻 性且最 小 。
2.4 串、并联谐振回路的Q值定义为2π谐振时回路总储能谐振时回路一周内的耗能。
Q值越大,意味着回路损耗小 ,谐振曲线越 陡 ,通频带宽越 窄 。
当考虑LC谐振回路的内阻和负载后,回路品质因数 下降 。
2.5 设r 为LC 并联谐振回路中电感L 的损耗电阻,则该谐振回路谐振电阻为reo L R C =,品质因数为ro o L Q ω= ,谐振频率为o ω谐振时流过电感或电容支路的电流为信号源电流的o Q 倍。
2.6 设r 为LC串联谐振回路中电感L的损耗电阻,则回路的品质因数为ro o L Q ω=,谐振频率为o ω=o Q 倍。
2.7 已知LC 串联谐振回路的C =100pF ,0f =1.5MHz ,谐振时的电阻5r =Ω,试求:L 和0Q 。
解:由0f =得22025330253301.5100L f C ==⨯112.6H μ=66002 1.510112.6105LQ r ωπ-⨯⨯⨯⨯==212≈2.8 在图2.T.1所示电路中,信号源频率f 0=1MHz ,信号源电压振幅s V =0.1mV ,回路空载Q值为100,r 是回路损耗电阻。
将1、2两端短路,电容C 调至100pF 时回路谐振。
廖惜春 高频电子线路课后答案

第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解]900.035610H z 35.6M H z f ===⨯=3640.722.4k 22.361022.36k 35.610H z35.610H z 356kH z100p R Q f BW Q ρρ===Ω=⨯Ω=Ω⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解]0465kHz f ≈==.70114k Ω////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω/465kH z/37=12.6kH zp e s p Lee e R Q R R R R R Q BWf Q ρρ===========2.3 已知并联谐振回路的00.710M H z ,C =50p F ,150k H z ,f B W ==求回路的L 和Q 以及600k H z f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH(2π)(2π1010)5010L H f C--===⨯=⨯⨯⨯⨯6030.7101066.715010f Q BW ⨯===⨯8.1poUU ∙∙=== 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f Cρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L =12=/10,n N N =L 1k R =Ω。
高频电子线路 邹传云 第二章作业解答

N
N1 is Rs C
N2 RL
图题1.3 解:本电路可将部分接入电路(图(a))等效成电路图(b)。
1
3
2 1
is
Rs C
4
RL
5
P1is
P12 gs
3
C Rp
L
1
P22 gL
图(a)
图(b)
图中, Rp 为谐振电阻,部分接入系数 P1 = N1 N = 40 160 = 1 4 ,
P2 = N2 N = 10 160 = 1 16 。 根据谐振频率有:
Auo 和通频带 B 。
2
EC
C
34
2
15 VT1
VT2
图题1.9
解:其交流通路如图 1.9(a)所示,相应的 Y 参数微变等效电路如图 1.9(b)所示。
C
14
C
14
2
2
+
35 VT1
VT2
ui
yreuce y feui
gie Cie
goe Coe
35
gie Cie
-
图1.9(a)
图1.9(b)
由BW0.7
=
f0 Qe
得:
Qe
=
f0 BW0.7
=
465 ×103 8 ×103
= 58.125
则:
R总 =
Qe ω0C
=
58.125 1.86 ×π ×10-4
=99.5kΩ
而:
1 R总
=
1 Rp
+
1 R并
⇒
R并 =237.5kΩ
答:回路电感为 0.586mH,有载品质因数为 58.125,这时需要并联 237.5kΩ的电阻。 2.4 在图题 1.3 所示电路中,已知回路谐振频率 f0 = 465kHz , Q0 = 100 , N = 160 匝, N1 = 40 匝, N2 = 10 匝, C = 200pF , Rs = 16kΩ , RL = 1kΩ 。试求回路电感 L 、有载 Q 值 和通频带 BW0.7 。
高频电子线路_阳昌汉_习题与解答
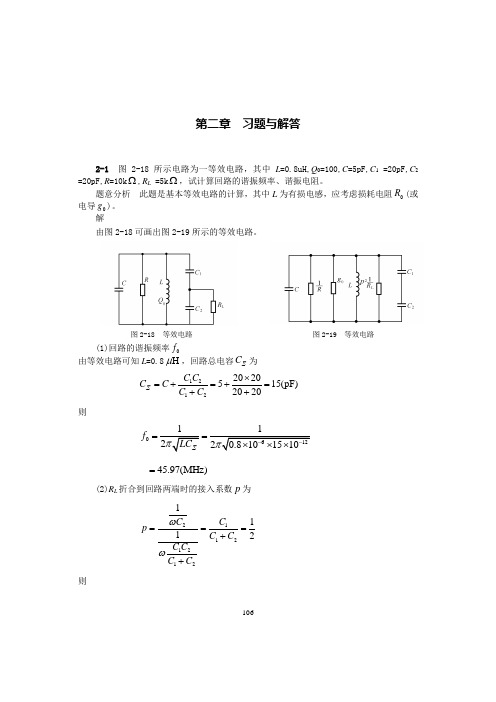
106第二章 习题与解答2-1 图2-18所示电路为一等效电路,其中L =0.8uH,Q 0=100,C =5pF,C 1 =20pF,C 2 =20pF,R =10k Ω,R L =5k Ω,试计算回路的谐振频率、谐振电阻。
题意分析 此题是基本等效电路的计算,其中L 为有损电感,应考虑损耗电阻0R (或电导0g )。
解由图2-18可画出图2-19所示的等效电路。
图2-18 等效电路 图2-19 等效电路(1)回路的谐振频率0f由等效电路可知L =0.8H μ,回路总电容C ∑为12122020515(pF)2020C C C C C C ∑⨯=+=+=++则0f ==45.97(MHz)=(2)R L 折合到回路两端时的接入系数p 为211212121112C C p C C C C C C ωω===++则107()2233110.50.0510s 510L P R -=⨯=⨯⨯ 电感L 的损耗电导0g 为0660011245.97100.810100g LQ ωπ-==⨯⨯⨯⨯⨯ ()643.3010s -=⨯总电导 23-3031110.0433100.05101010L g g P R R ∑-=++=+⨯+⨯⨯ ()30.193310s -=⨯谐振电阻 ()P 1 5.17k R g ∑==Ω2-2 有一个RLC 并联谐振电路如图2-20所示,已知谐振频率f 0=10MHz,L =4μH ,Q 0=100,R =4k Ω。
试求(1)通频带20.7f ∆;(2)若要增大通频带为原来的2倍,还应并联一个多大电阻?题意分析 此题是一个RLC 并联谐振电路的基本计算,了解通频带的变化与回路电阻的关系。
解 (1)计算通频带电感L 的损耗电导0g 为 图2-20 RLC 并联谐振回路066001121010410100g LQ ωπ-==⨯⨯⨯⨯⨯()639.810s -=⨯回路总电导6031139.810410g g R ∑-=+=+⨯⨯ ()6289.810s -=⨯108回路的有载品质因数L Q 为666011g 21010410289.810L Q L ∑ωπ--==⨯⨯⨯⨯⨯⨯13.74=回路通频带()()6600.7101020.72810Hz 0.728MHz 13.74L f f Q ∆⨯===⨯= (2)若通带增大一倍,即20.71.456MHz f ∆=,计算应再并多大电阻R '根据题意要求通频带增大一倍,则回路的有载品质因数应减小一倍,即16.872LL Q Q '== 对应的'g ∑应该增大一倍,即 ()6'2579.610s g g ∑∑-==⨯ 因为0'11g g R R∑=++' 所以0''11g g g g R R ∑∑∑⎛⎫=-+=- ⎪'⎝⎭()6289.810s -=⨯则 3.45k R '=Ω图2-21 单调谐放大电路1092-3 单调谐放大器如图2-21所示。
高频电路第二章习题答案

解: 设放大电路的选频电路由简单LC 并联回路构成.则LC 回路谐振频率465kHz,为满足带宽要求,回路的品质因数应为5810810465337.0≈⨯⨯==BW f Q o L 此回路谐振电阻为5.922==C f Q R o Lπ (k Ω) 改为1992L o Q R f Cπ== (k Ω)回路未接电阻时固有谐振电阻为1592≈=Cf Q R o oo π (k Ω)改为3422oo o Q R f Cπ=≈ (k Ω)因此需并联电阻为221=-=RR RR R o oL (k Ω)改为476oL o RR R R R==- (k Ω)2.4解:为计算简化,这里1R 与电容2C 的容抗之比π221=C X R 较大,可采用部分接入法公式 )(1002121pF C C C C C =+=∑电感 )(253.0)2(12mH C f L o ≈=∑π接入系数 P=5.0212=+C C C1R 在两端等效为)(2021Ω==k P R R T 电感固有品质因数50,对应的固有谐振电阻)(58.792Ω≈=∑k C f Q R o oo π端等效电阻为)(16Ω≈+k R R R R oT oT有载品质因数10101623=⨯⨯=∑C f Q o L π习题3.1 高频功率放大器的主要作用是什么?应对它提出哪些主要要求?答:高频功率放大器的主要作用是放大高频信号或高频已调波信号,将直流电能转换成交流输出功率。
要求具有高效率和高功率输出。
3.2 为什么丙类谐振功率放大器要采用谐振回路作负载?若回路失谐将产生什么结果?若采用纯电阻负载又将产生什么结果?答:因为丙类谐振功率放大器的集电极电流i c为电流脉冲,负载必须具有滤波功能,否则不能获得正弦波输出。
若回路失谐集电极管耗增大,功率管有损坏的危险。
若采用纯电阻负载则没有连续的正弦波输出。
3.3 高频功放的欠压、临界和过压状态是如何区分的?各有什么特点?答:根据集电极是否进入饱和区来区分,当集电极最大点电流在临界线右方时高频功放工作于欠压状态,在临界线上时高频功放工作临界状态,在临界线左方时高频功放工作于过压状态。
(完整版)高频电子线路课后答案(胡宴如_狄苏燕)

说明所有习题都是我们上课布置的作业题,所有解答都是本人自己完成,其中难免有错误之处,还望大家海涵。
第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L = 12=/10,n N N =L 1k R =Ω。
高频电子线路2章答案

6.如图7.10所示并联谐振回路,信号源与负载都是部分接入的。
已知R s、R,并已知回路参数L1、L2、C1、C2和空载品质因数Q0,试求谐振频率f0与带宽LBW。
0.7解:1.求谐振频率f0回路总电感(不考虑互感)L=L1+L2回路总电容谐振频率2.求带宽BW0.7设信号源对回路的接入系数为P1,负载R L对回路的接入系数为P2,则把g s=1/R s和g L=1/R L折合到回路两端,变为,它与、并联,构成总的回路电回路的自身损耗电导导,即因此,有载品质因数Q e和带宽BW0.7分别为BW0.7=9.图7.2所示的单调谐放大器中,若谐振频率f0=10.7MH Z,CΣ= 50pF,BW0.7=150kHZ,求回路的电感L和Q e。
如将通频带展宽为300kH Z,应在回路两端并接一个多大的电阻?解:(1)求L和Q e(H)= 4.43μH(2)电阻并联前回路的总电导为47.1(μS)电阻并联后的总电导为94.2(μS)因故并接的电阻为10.一单调谐振放大器,集电极负载为并联谐振回路,其固有谐振频率f 0=6.5MHZ,回路总电容C= 56pF,回路通频带BW0.7=150kH Z。
(1)求回路调谐电感、品质因数;(2)求回路频偏Δf=600kH Z时,对干扰信号的抑制比d。
解:(1)已知f0=6.5MH Z, C= 56pF, BW0.7=150kH Z,则(H)= 10.7μH(2)根据定义,抑制比,故(dB)11.调谐在中心频率为f0=10.7MH Z的三级相同的单调谐放大器,要求BW0.7≥100kHZ ,失谐±250kHZ时的衰减大于或等于20dB。
试确定每个谐振回路的有载品质因数Q e值。
解:由带宽要求得由选择性指标得(dB)即=50故取Q(dB)单调谐放大器和临界耦合的双调谐放大器,若Q e 13.中心频率都是6.5MHZ均为30,试问两个放大器的通频带各为多少?解:单调谐放大器的通频带为kHZ临界耦合的双调谐放大器的通频带为kHZ14.在小信号谐振放大器中,三极管与回路之间常采用部分接入,回路与负载之间也采用部分接入,这是为什么?解:这是因为外接负载阻抗会使回路的等效电阻减小,品质因数下降,导致增益下降,带宽展宽,谐振频率变化等,因此,采用部分接入,可以减小它们的接入对回路Q值和谐振频率的影响,从而提高了电路的稳定性,且使前后级的阻抗匹配。
(完整版)高频电子线路第2章习题答案

第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW . [解] 90-612110.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 011465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω42k Ω371.14k Ω390μH/300 PF /465kHz/37=12.6kHzp e s p Le e e R Q R R R R R Q BWf Q ρρ=========== 2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯ 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2。
(完整版)高频电子线路(胡宴如耿苏燕主编)习题答案

高频电子线路(胡宴如 耿苏燕 主编)习题解答目 录第2章 小信号选频放大器 1 第3章 谐振功率放大器 4 第4章 正弦波振荡器10 第5章 振幅调制、振幅解调与混频电路 22 第6章 角度调制与解调电路 38 第7章 反馈控制电路49第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390μH/300 PF/465kHz/37=12.6kHzp e s p Lee e R Q R R R R R Q BWf Q ρρ===========2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻?[解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯g而471266.7 2.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯g由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L =12=/10,n N N =L 1k R =Ω。
高频电子线路习题及答案

第2章 选频网络1.有一并联回路在某频段内工作,频段最低频率为535kHz ,最高频率为1605kHz 。
现有两个可变电容器,一个电容器的最小电容量为12pF ,最大电容量为100pF ;另一个电容器的最小电容量为15pF ,最大电容量为450pF 。
试问:1)应采用哪一个可变电容器,为什么?2)回路电感应等于多少?3)绘出实际的并联电路图。
(答案:1)选15450pF pF 的电容;2)180H μ)2.给定串联谐振回路的001.5,100,f MHz C pF ==谐振时电阻Ω=5R 。
试求0Q 和0L 。
又若信号源电压振幅1sm V mV =,求谐振时回路中的电流0I 以及回路元件上的电压0L m V 和0C m V 。
(答案:0212.2Q =;0112.6L H μ=;00.2I mA =; 00212.2L m C m V V mV ==)3.串联回路如图1所示。
信号源频率01f MHz =,电压振幅0.1sm V V =。
将11端短接,电容C 调到100pF 时谐振。
此时,电容C 两端的电压为10V 。
如11端开路再串接一阻抗X Z (电阻与电容串联),则回路失谐,C 调到200pF时重新谐振,总电容两端电压变为 2.5sm V V =。
试求线圈的电感量L 、回路品质因数0Q 值以及未知阻抗X Z 。
(答案:253L H μ=;0100Q =;47.7X R =Ω;200X C pF =) 图14.给定并联谐振回路的MHz f 50=,pF C 50=,通频带kHz f 15027.0=∆。
试求电感L 、品质因数0Q 以及对信号源频率为MHz 5.5时的失调。
又若把7.02f ∆加宽至kHz 300,应在回路两端再并联上一个阻值多大的电阻?(答案:20L H μ=;033.3Q =;6.36ξ=;21L R k =Ω)5.并联谐振回路如图2所示。
已知通频带7.02f ∆,电容C 。
廖惜春-高频电子线路课后答案

第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 90-6120.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p HR Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示,已知:300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390μH 300PFf LC≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390μH/300 PF /465kHz/37=12.6kHzp e s p Le e e R Q R R R R R Q BWf Q ρρ=========== 2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ,应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯ 6030.7101066.715010f Q BW ⨯===⨯2236022*********.78.11010p oU f Q f U ••⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯由于,p e pRR R R R=+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4 并联回路如图P2.4所示,已知:360pF,C =1280μH,L ==100,Q 250μH,L = 12=/10,n N N =L 1k R =Ω。
高频电子线路习题答案杨霓清第二章_高频小信号放大器daan

第二章 思考题与习题2.1 试用矩形系数说明选择性与通频带的关系。
2.2 证明式(2.2.21)。
2.3 在工作点合理的情况下,图(2.2.6)(b )中的三极管能否用不含结电容的小信号等效电路等效?为什么? 2.4 说明图(2.2.6)(b )中,接入系数、对小信号谐振放大器的性能指标有何影响? 1n 2n 2.5 如若放大器的选频特性是理想的矩形,能否认为放大器能够滤除全部噪声,为什么? 2.6 高频谐振放大器中,造成工作不稳定的主要因素是什么?它有哪些不良影响?为使放大器稳定工作应采取哪些措施? 2. 7 单级小信号调谐放大器的交流电路如图2. T.1所示。
要求谐振频率0f =10.7 MHz ,500kHz ,100。
晶体管参数为 0.7BW =0||A υ=ie y =(2+j0.5)ms ;re y =0;fe y =(20-j5)ms ; oe y =(20+j40)ms如果回路空载品质因数100,试计算谐振回路的、C 、0Q =L R 。
图2. T.1 题2.8图解:根据电路图可画出放大器的高频等效电路如下图所示。
其中20oe g s μ=,6640100.59210.710oe C pF π-⨯==⨯⨯,20.6fe y ms == 根据题设要求0100fe y A g υ∑==则320.6100.206100fe oy g m A υ-∑⨯===s因为0.7ef BW Q =所以00.710.721.40.5e f Q BW === 因为01e Q Lg ω∑=所以63011210.7100.2061021.4e L g Q ωπ-∑==⨯⨯⨯⨯⨯=63.3710 3.37s s μ-⨯=由等效电路可知262601165.65pF (2)(210.710) 3.3710C f L ππ∑-===⨯⨯⨯⨯66001144.142210.710 3.3710100eo g s f LQ μππ-===⨯⨯⨯⨯⨯ 则65.650.5965.06oe C C C pF ∑=-=-=666117.0520610201044.1410oe eo R k g g g ---∑===--⨯-⨯-⨯Ω 2.8 在图2. T.2中,晶体管3DG39的直流工作点是=+8V ,CEQ V EQ I =2 mA ;工作频率0f =10.7MHz ;调谐回路采用中频变压器,=4μH ,=100,其抽头为3~1L 0Q =23N 5匝,20匝, 5匝。
高频电子线路第二章课后习题答案

2-3 图示为一电容抽头的并联振荡回路。谐振频率f0=1MHz, C1=400 pf,C2=100 pF 求回路电感L。若 Q0=100, RL=2kΩ,求回路有载 QL值。 解2-3
C C 1C 2 40000 80 pF , C1 C 2 500
Psmi 得噪音系数为 N F Psmo
Rs R1 R2 R3 R0 Rs R1 R1 Rs R3 R R3 )( Rs R1 ) Rs R1 R3 1 R s R0 R1 Rs R2 Rs R1 R2 R 1
2 n 2 0
答:电路的等效噪声带宽为125kHz,和输出均方噪声电压值 为19.865μV2.
2-8 如图所示噪声产生电路,已知直流电压 E=10 V, R=20 kΩ,C=100 pF,求等效噪声带宽B和输出噪声电 压均方值(图中二极管V为硅管)。
解2-8: 此题中主要噪音来自二极管的散粒噪音,因此
2
(2)采用开路电压法
U
2 no
4kTB R0 R R 3 1 4kTB Rs R1R s R1 Rs R R 2 3 R R 1 s R R 0 1 4kTB Rs R1R s R1 Rs R 2 R R 1 s R1 4kT B R sR 0 R1R s R 2R1 R 2R s
1 由 f0 得 : 2 LC 1 1 L 2 2 ( 2 f0) C 4 4652 106 2001012
106 2 0.586mH 2 4 465 200 f0 由B0.707 得: QL
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 为什么谐振功率放大器能工作于丙类,而电阻性负载功率放大器不能工作于丙类? 解:因为谐振功放的输出负载为并联谐振回路,该回路具有选频特性,可从输出的余弦脉冲电流中选出基波分量,并在并联谐振回路上形成不失真的基波余弦电压,而电阻性输出负载不具备上述功能
2-2 放大器工作于丙类比工作于甲、乙类有何优点?为什么?丙类工作的放大器适宜于放大哪些信号?
解:(1)丙类工作,管子导通时间短,瞬时功耗小,效率高。
(2) 丙类工作的放大器输出负载为并联谐振回路,具有选频滤波特性,保证了输出信号的不失真。
为此,丙类放大器只适宜于放大载波信号和高频窄带信号。
2-4 试证如图所示丁类谐振功率放大器的输出功率2)sat (CE CC L 2o )2(π2
V V R P -=,集电极
效率CC
)
sat (CE CC C 2V V V -=
η。
已知V CC = 18 V ,V CE(sat) = 0.5 V ,R L = 50 Ω,试求放大器的P D 、
P o 和ηC 值。
解:(1) v A 为方波,按傅里叶级数展开,其中基波分量电压振幅。
)2(π
2
)sat (CE CC cm V V V -=通过每管的电流为半个余弦波,余弦波幅度,)2(π2
)sat (CE CC L
L cm cm V V R R V I -== 其中平均分量电流平均值
cm C0π
1I I =
所以 2)sat (CE CC L
2cm cm o )2(π2
21V V R I V P -==
)2(π2
)sat (CE CC CC L
2C0CC D V V V R I V P -==
CC
)
sat (CE CC D o C 2/V V V P P -=
=η
(2) W 24.1)2(π2
)sat (CE CC CC L
2D =-=
V V V R P W 17.1)2(π22)sat (CE CC L
2o =-=V V R P
%36.94/D o C ==P P η
2-5 谐振功率放大器原理电路和功率管输出特性曲线如图所示,已知V CC = 12 V ,V BB = 0.5 V ,V cm = 11 V ,V bm = 0.24 V 。
试在特性曲线上画出动态线。
若由集电极电流i C 求得I C0 = 32 mA ,I cIm = 54 mA ,试求P D 、P o 、ηC 及所需的R e 。
解:
(1) ⎩⎨⎧+=+=-=-=V )cos 24.05.0(cos V
)cos 1112(cos bm BB BE
cm CC CE t t V V v t t V V v ωωωω
(2)
mW 384C0CC D ==I V P
mW 2972
1
cm cm o ==I V P
%34.77/D o C ==P P η
R e = V cm /I c1m = 204 Ω
2-8 谐振功率放大器工作在欠压区,要求输出功率P o = 5 W 。
己知V CC = 24 V ,V BB =V BE(on),R e = 53 Ω,设集电极电流为余弦脉冲,即
i C = ⎩
⎨⎧≤>000cos b b Cmax v v t i ω
试求电源供给功率P D 、集电极效率ηC 。
解:因为V BB = V BE(on),放大器工作在甲乙类,近似作乙类,
mA 434221e
o c1m e 2
cm o ===R P I R I P
因为,Cmax 2π
2πC C0
π1d π21i t i I ==⎰-ω ,Cmax 2π
2πC c1m 2
1
d cos π1i t t i I ==⎰-ωτωτ 所以 mA 3.2762c1m C0==I I
则 ,W 63.6C0CC D ==I V P %42.75/D o C ==P P η
2-12 设两个谐振功率放大器具有相同的回路元件参数,它们的输出功率P o 分别为1 W 和0.6 W 。
现若增大两放大器的V CC ,发现其中P o = 1 W 放大器的输出功率增加不明显,而P o = 0.6 W 放大器的输出功率增加明显,试分析其原因。
若要增大P o = 1 W 放大器的输出功率,试问还应同时采取什么措施(不考虑功率管的安全工作问题)?
解:P o = 1 W 的放大器处于临界或欠压状态,增大V CC 时,放大器更趋于欠压状态,I c1m
略有增大。
因此P o 增大不明显。
(若 P o ↑ 需 V CC ↑ 同时R e ↑ 或V BB ↑)
P o = 0.6 W 的放大器处于过压状态,V CC 增大,发大器趋于临界,I c1m 迅速增大,所以P o 迅速增大。
