格利森弧形锥齿轮计算
弧齿锥齿轮几何参数设计分解

弧齿锥齿轮⼏何参数设计分解弧齿锥齿轮⼏何参数设计分解————————————————————————————————作者:————————————————————————————————⽇期:第14章弧齿锥齿轮的轮坯设计14.1弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,⼀般采⽤锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所⽰,与直齿锥齿轮相⽐,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥⼀样,相当于⼀对相切圆锥⾯作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切⾯成为齿轮副的节平⾯。
齿轮轴线与节平⾯的夹⾓,即节锥的半锥⾓称为锥齿轮的节锥⾓δ1或δ2。
两齿轮轴线之间的夹⾓称为锥齿轮副的轴交⾓∑。
节锥任意⼀点到节锥顶点O 的距离称为该点的锥距Ri ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则 21δδ+=∑⼤⼩轮的齿数之⽐称为锥齿轮的传动⽐1212z z i =(14-1)⼩轮和⼤轮的节点半径r1、r 2分别为11sin δR r = 22sin δR r =(14-2)它们与锥齿轮的齿数成正⽐,即121212sin sin z z r r ==δδ (14-3)传动⽐与轴交⾓已知,则节锥可惟⼀的确定,⼤、⼩轮节锥⾓计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑=(14-4)当090=∑时,即正交锥齿轮副,122i tg =δ14.1.2弧齿锥齿轮的旋向与螺旋⾓图14-2 锥齿轮的图14-1 弧齿锥1.旋向弧齿锥齿轮的轮齿对母线的倾斜⽅向称为旋向,有左旋和右旋两种(图14-3)。
⾯对轮齿观察,由⼩端到⼤端顺时针倾斜者为右旋齿轮(图14-3b),逆时针倾斜者则为左旋齿(图14-3a )。
⼤⼩轮的旋向相反时,才能啮合。
⼀般情况下,⼯作⾯为顺时针旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋⽅向为左旋,被动轮为右旋(图14-1);⼯作⾯为逆时针旋转的,情况相反。
弧齿锥齿轮铣齿计算

弧齿锥齿轮铣齿计算弧齿锥齿轮是传动行业中常用的一种齿轮,其结构相对复杂,铣齿计算难度较大。
本文将围绕弧齿锥齿轮铣齿计算进行分步骤的阐述。
第一步:确定齿轮参数在进行弧齿锥齿轮铣齿计算之前,需要确定齿轮参数,包括轴距、锥距、锥度、压力角等参数。
这些参数需要在设计时给出,或者由实际应用中的传递比、轴功率等参数推算得出。
第二步:计算齿数弧齿锥齿轮铣齿计算的第一步是计算齿数。
通常情况下,弧齿锥齿轮的齿数较小,一般不超过20个。
计算齿数需要使用弧齿锥齿轮铣刀的几何参数,以及齿面曲线的基本方程。
每个齿面曲线可以看做一条螺旋线,其截面积呈三角形状。
根据这些参数计算得出的齿数,不一定是整数,需要舍入到最接近的整数。
第三步:计算铣刀参数在确定齿数之后,就可以开始计算铣刀参数了。
铣刀的参数包括齿宽、齿高、齿间隙等。
齿宽可以由齿数和啮合角度计算得出;齿高可以由矢高、压力角等参数计算得出;齿间隙可以采用经验数据或理论计算得出。
第四步:计算加工参数铣齿前需要确定加工参数,包括进给量、转速等。
这些参数需要根据加工机床和工件材质等具体情况进行选取,以获得最佳的加工效果。
进给量的选择要尽量保证加工效率和质量,而转速的选择则要考虑切削油,刀具材料等方面的因素。
第五步:检验加工精度最后一步是检验加工精度。
通过测量齿轮的齿高、齿宽、轴向距离、齿距等参数,可以判断齿轮加工的精度是否符合要求。
如果齿轮加工精度不足,则需要对铣刀的加工参数进行调整,并重新进行铣齿计算。
综上所述,弧齿锥齿轮铣齿计算需要经过齿轮参数计算、齿数计算、铣刀参数计算、加工参数选择和加工精度检验等多个步骤,这些步骤需要根据具体的工件、机床和材料等因素进行调整。
只有经过认真的计算和精细的加工,才能获得符合要求的弧齿锥齿轮。
全工序法弧齿锥齿轮加工参数计算方法

全工序法弧齿锥齿轮加工参数计算方法
全工序法是一种用于弧齿锥齿轮加工的常用方法,它通过一系列工序来逐步完成锥齿轮的加工。
以下是全工序法中常用的弧齿锥齿轮加工参数计算方法:
1.齿轮模数:齿轮模数是弧齿锥齿轮加工的基本参数,表示
齿轮齿数与有效齿轮直径的比值,用M表示。
根据具体
应用需求和设计要求,选择合适的齿轮模数。
2.压力角:压力角是指斜齿轮齿廓与法线之间的夹角,常用
标准值为20度。
选择合适的压力角,以确保齿轮的传动
效果和强度。
3.齿数:根据需要计算齿数。
在弧齿锥齿轮加工中,通常齿
数是通过参考传动比和齿轮齿数之间的关系来计算的。
4.锥度:锥度是指齿轮齿条与齿轮轴的夹角,常用度数表示。
计算锥度的方法包括参考标准值、设计要求和实际使用情
况。
5.齿轮齿宽:齿轮齿宽是指齿轮齿条的宽度,一般由设计要
求和传动功率等因素决定。
6.齿根圆直径:计算齿根圆直径以确定弧齿锥齿轮的基准尺
寸。
齿根圆直径是齿轮齿廓最低点的圆形位置。
7.齿顶圆直径:计算齿顶圆直径以确定弧齿锥齿轮的基准尺
寸。
齿顶圆直径是齿轮齿廓最高点的圆形位置。
8.齿廓修形参数:根据特定设计要求和加工方法,确定齿廓
修形参数,如修形系数和修形位移。
以上仅是全工序法中一些常用的弧齿锥齿轮加工参数计算方法的概述。
在实际应用中,还需结合具体工件的设计要求、加工设备和工艺流程等因素来确定适当的参数值。
弧齿、零度弧齿锥齿轮计算-任意轴交角

14 齿宽中点螺旋角 15 中点模数 16 中点法向模数 17 中点锥距 18 小端锥距 19 切向变位系数 20 径向变位系数 21 齿顶高 22 齿根高 23 顶隙 24 全齿高 25 工作齿高 26 27 28 齿顶角(不等顶隙) 齿顶角(等顶隙) 齿根角
m em m nm Rm Ri xt x ha hf C
K ψ mn S mn
h am d0
β β
e i
533.4 39.87016633 30.84621438 48.69468613 29.79729163 22.24976736 18.51003688 18.8973945 14.27481083 8.179908056
Pe
se s ne h ne
ht h
θ
a
θ δ δ
f
2.165679711 27.27235224 21.0329108 265.7804032 184.6753387
29 顶锥角(等顶隙) 30 根锥角 31 大端齿顶圆直径 32 小端齿顶圆直径
a
f
d ae d ai
33 冠顶距 34 中点法向齿厚 35 中点法向齿厚半角 36 中点齿厚角系数 37 中点分度圆弦齿厚 38 中点分度圆弦齿高 39 铣刀盘名义直径 40 大端螺旋角 41 小端螺旋角 42 齿距 43 大端分度圆理论弧齿厚 44 大端理论弦齿厚 45 大端理论弦齿高 46 当量齿数 47 48 49 50 51 端面重合度 52 纵向重合度 53 总重合度 54 不根切的许用最大齿根角 55 不产生根切的最少齿数
Zv
at
α
vat
α β
29.69023654 161.6468434 23.95680324 0.418125095 36.92510996 0.644464745 25.43970428 0.4440066
弧齿锥齿轮主要参数的测绘计算

弧齿锥齿轮主要参数的测绘计作者: 日期:弧齿锥齿轮主要参数的测绘计算零部件加工部麻俊方弧齿锥齿轮具有承载能力高、运转平稳、噪音低等特点,在汽车行业中得到了广泛的应用。
通常由一对弧齿锥齿轮组成汽车驱动桥主减速器的主要传动机构。
弧齿锥齿轮的设计与测绘计算均比较复杂,下面仅介绍几种主要参数的测绘计算方法。
1.轴交角一对弧齿锥齿轮副的住从动齿轮中心轴线交于一点。
轴线间的交角刀可成任意角度,但在绝大多数汽车驱动桥上,主减速齿轮副都采用90°相交的布置。
2.齿制渐开线锥齿轮的齿制很多,多达40多种,我国常用的齿制有Gleason(格利森)制、Oerlikon(奥利康)制、Kingelnberg(克林贝格)制三种。
其中应用最广泛也是最常见到的是Gleaso n(格利森)制弧齿锥齿轮。
不同的齿制,对应不同的参数计算方法与计算公式,在测量齿轮时一定要注意区分。
3•模数弧齿锥齿轮模数是一个变值,由大端向小端与锥距成比例缩小,通常以大端面模数叫来计算。
GB12368-9C规定了锥齿轮大端端面模数,其中以》1为例,有1、1.125、1.375、1.5、1.75、2等等。
但是所测量的齿轮模数不一定为整数,也不一定符合标准模数系列。
对于模数的测绘与计算,有以下方式:1. 由测量的锥距R,可初步估算锥齿轮的大端模数 叫h(用深度尺来测量)加以复核。
对于等顶隙收缩齿(格里森制),齿顶高系数ha = 0.85,顶隙系*数C *=0.188则齿高 h=(2 ha +C *)m 。
*由此得出模数m=h(2ha +C *),进而复核模数m s 。
tm s—2.测量出锥齿轮的周节t ,根据公式 来进行计算,这种方法要求测量数据准 确无误,且被测绘齿轮无磨损现象。
3. 由齿顶圆直径反求模数。
首先测绘出齿顶圆的直径尺寸,利用齿顶圆计算公式,然 后反求模数。
所使用的反求公式为4. 由刀顶距的数值计算模数。
弧齿锥齿轮铣刀盘的刀顶距W 叫席2式中ms—大端模数的估算数值;1 0.5— L e ;R因为2 Z2 ^ 、、, ,于是便可确定锥齿轮大端模数m 2R人『云。
弧齿锥齿轮副参数计算(格里森制等顶隙收缩齿)

名 称 齿数 旋向 大端端面模数 齿形角 齿顶高系数 顶隙系数 轴交角 齿宽中点螺旋角 大端螺旋角 齿数比 变位系数 切向变为系数 分锥角 分度圆直径 分度圆锥距 齿宽系数 齿宽 铣刀盘名义直径 齿顶高 全齿高 符号 Z1 Z2 主动轮 从动轮 m α ha* c* ∑ β m β μ x1 x2 xt δ δ
备
注
单位° 单位° 单位° 单位° 单位° 单位° 单位° 单位°
δ a1 δ a2 δ f1 δ f2 Ak1 Ak2 A1 A2 H1 H2 Rm s1 s2 Zv1 Zv2
按结构确定,一般凑成整数
A1-Ak1 A2-Ak2 19.27414012 2.395974063 1.923715762 28.10354121 42.19802237
f1 f2 a1 a2
数值 1.182150 1.672350 21.81275382 27.63823083 2.971416149 4.199805087 4.199805087 2.971416149 29.20045046 37.97077078 22.02922922 30.79954954 20.04273869 18.12585546
1 2
数值 14 19 左旋 右旋 1.375 20 0.85 0.188 60 35 40.92242589 1.357143 0.18 -0.18 0.00 25.00064537 34.99935463 19.25 26.125 22.77414012 R/3.5~R/3 7 38.1 1.413850 0.923650 2.596000
ε α 端面重合度 1.222798812 对于α =20°可查表 注:只要填写黄色区域,其余将自动生成
弧齿锥齿轮的几何尺寸计算表
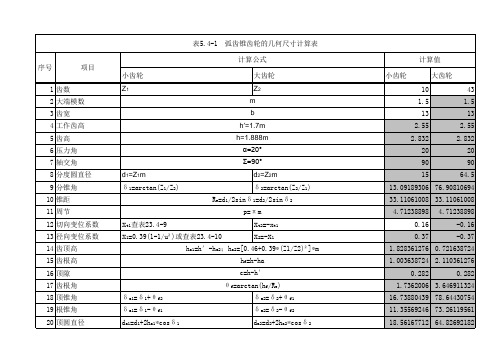
13.09189306 76.90810694 33.11061008 33.11061008 4.71238898 0.16 0.37 4.71238898 -0.16 -0.37
xt1查表23.4-9 x1=0.39(1-1/u²)或查表23.4-10
xt2=-xt1 x2=-x1
hf=h-ha c=h-h′ θ f=arctan(பைடு நூலகம்f/Re) δ δ
s2=p/2-(ha1-ha2)tanα /cosβ m-xt1m
Smn1=(0.5πcosβm+2x1tanα+xt1)mm ψmn=Smn*cosδ*cos²βm/(mmZ) Kψ mn=1-ψ mn²/6 S′mn=SmnKψmn h′am1=ha1-0.5b*tanθf2+0.25Smn1ψmn1 查表23.4-11 N0=(θ
f1+θf2)sinβm/20
Smn2=πmmcosβm-Smn1
h′am2=ha2-0.5b*tanθf1+0.25Smn2ψmn2
1.472078944 0.525395815 9.262878463 9.262878463
设定值 传动比 4.3 齿顶高系数 顶隙系数 0.85 0.188
da1=d1+2ha1*cosδ
da2=d2+2ha2*cosδ
21 锥点至轮冠距离 22 理论弧齿厚 23 侧隙 24 中点螺旋角 25 齿宽系数 26 中点模数 27 中点法向模数 28 中点法向齿厚 29 中点法向齿厚半角 30 中点齿厚角系数 31 中点分度圆弦齿厚 32 中点分度圆弦齿高 33 刀盘直径 34 刀号
表5.4-1 序号 1 齿数 2 大端模数 3 齿宽 4 工作齿高 5 齿高 6 压力角 7 轴交角 8 分度圆直径 9 分锥角 10 锥距 11 周节 12 切向变位系数 13 径向变位系数 14 齿顶高 15 齿根高 16 顶隙 17 齿根角 18 顶锥角 19 根锥角 20 顶圆直径 δ δ
弧齿锥齿轮的加工调整计算

第二章弧齿锥齿轮的加工调整计算第一节弧齿锥齿轮切齿原理、方法概述弧齿锥齿轮的切齿就是按照“假想齿轮”的原理进行的,而采用的切齿方法要根据具体情况而定。
一、弧齿锥齿轮的切齿原理YS2250(Y225)和Y2280等机床是按所谓“假想平顶齿轮”原理考虑的。
就是在切齿的过程中,假想有一个平顶齿轮与机床摇台同心,它通过机床摇台的转动而与被切齿轮做无隙的啮合。
这个假想平顶齿轮的轮齿表面,是由安装在机床摇台上的铣刀盘刀片切削刃的相对于摇台运动的轨迹表面所代替,如图2-1中所示。
在这个运动过程中,代表假想平顶齿轮轮齿的刀片切削刃就在被切齿轮的轮坯上逐渐地切出齿形。
图2-1图2-2在调整切齿机床的时候,必须使被切齿轮的节锥面与假想平顶齿轮的节锥面相切并做纯滚动,而刀顶旋转平面则需和被切齿轮的根锥相切,如图2-2所示。
所以铣刀盘轴线与被切齿轮的节锥面倾斜一个大小等于被切齿轮齿根角的角度,这样就产生了刀号修正问题,从而导致被切齿轮的加工调整较为复杂,刀片的规格比较多。
在加工渐缩齿圆弧齿锥齿轮时,都是采用这种切齿原理的。
二、弧齿锥齿轮的切齿方法弧齿锥齿轮的切齿方法分为成形法和展成法两大类。
1.成形法用成形法加工的大齿轮齿形与刀具切削刃的形状一样。
渐开线齿形的曲率和它的基圆大小有关,基圆越大、齿形曲率就越小,渐开线就直些;当基圆足够大时,渐开线就接近于直线。
而齿轮的基圆大小是由模数m、齿数z和压力角的余弦大小来决定的。
模数和压力角一定时,齿数愈多,基圆直径就越大,相应的齿形曲率越小,也就是齿形越接近于直线。
对于螺旋锥齿轮,传动比也是影响因素之一,当传动比大一些时,大轮的齿形就更直一些。
)一定时,传动比越大,大轮齿数也就越多,这时大轮的当量圆柱小轮齿数(z1齿轮的基圆直径也越大,其齿形接近于直线形,采用成形加工比较方便.当锥齿轮传动比大于2.5,时,大轮就可采用成形加工。
同时,为了保证其正确啮合,相配小轮的齿形应加以相应的修正,用展成法加工,这种切齿方法叫半滚切法或成形法。
格里森弧齿锥齿轮校核_V0.1
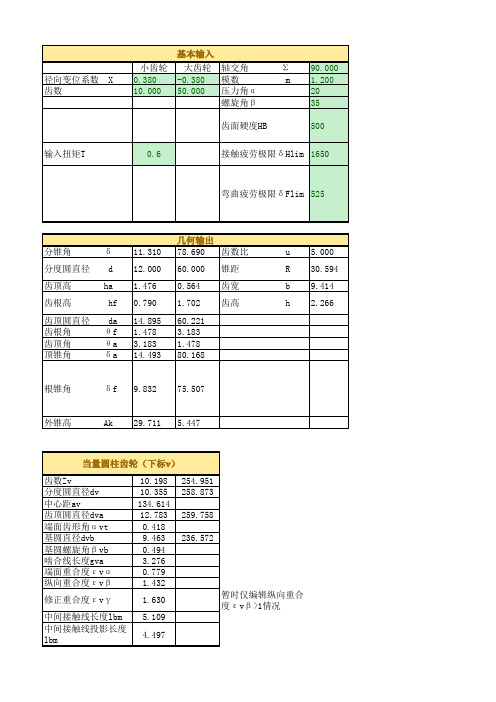
hf
齿顶圆直径 da
齿根角
θf
齿顶角
θa
顶锥角
δa
11.310
12.000
1.476
0.790
14.895 1.478 3.183 14.493
几何输出 78.690 齿数比
60.000 锥距
0.564 齿宽
1.702 齿高
60.221 3.183 1.478 80.168
根锥角
δf 9.832 75.507
润滑油膜影响系数 Zlvr
工作硬化系数 Zw
尺寸系数Zx 最小安全系数S 齿形系数Yfa 应力修正系数Ysa
1 0.905 0.8
0.95
1
0.982
1 1.25 2.7 2.05
重合度系数Yε
0.625
锥齿轮系数Yk 载荷分担系数Yls 应力修正系数 Yst
寿命系数Ynt
齿根圆角敏感系数 Yδr 齿根表面状况系数 Yrr 尺寸系数Yx 最小安全系数S
计算根据GB10062-2003(正交情况)
切向力Fmt 齿轮计算接触应力 许用接触应力 小齿轮计算齿根应力
100 363.46319 1231.8706 66.271104
小齿轮许用齿根应力
712.5
作用力——主动轮:右旋左转
小齿轮径向力
57.301911
大齿轮径向力
59.947056
小齿轮轴向力
10.198 10.355 134.614 12.783 0.418 9.463 0.494 3.276 0.779 1.432
1.630
5.109
4.497
254.951 258.873 259.758 236.572
弧齿锥齿轮设计计算

小轮齿数 16 小轮螺旋角 54 大轮齿数 41 工作齿高系数 4.000 输入齿轮基本参数 大轮齿面宽 偏置距 29.2 38.6 锥度系数 压力角和 0.788532 38 大轮节径 刀盘半径 190.5 95.25 大轮齿顶高系数 齿侧间隙 0.325 0.20--0.30 计算刀盘半径 95.24998171 旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250
19 下38.6 107.52 2.7719 6.668 8.5281 9.440 -3.543 15.51547 -4.812 23.86825 -1.819 89.93 50.973 60.46 25.63205 62.3573 29.79222 64.44521 23.63867 58.02087 54.49766 30.86347 0 右旋 190.5 0.20--0.30 190.5 120.7404 193.0721
名
准双曲面齿轮计算结果 称 小轮 16
大轮 41 4.646
ห้องสมุดไป่ตู้
齿数 模数 压力角 小轮偏置 外锥距 齿顶高 齿根高 工作齿高 全齿高 节锥定点到交错点的距离 面锥顶点到交错点的距离 根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径 侧隙 刀具直径 外径
圆弧齿锥齿轮传动设计几何计算过程

中点分度圆法向齿厚smn
smn=(0.5πcosβm+2xtanα+xt)mm
smn1=7.962mm,smn2=5.851mm
18
中点法向齿厚半角ψmn
ψmn=smnsinδcos2βm/dm
ψmn1=1.803°,
ψmn2=.147°
19
中点分圆法向弦齿厚smn
smn=smn(1-ψmn2/6)
Ak1=d2/2-ha1sinδ1,=d1/2-ha2sinδ2
Ak1=267.73,Ak2=87.14mm
15
齿宽中点分度圆直径dm
dm1=d1-bsinδ1,dm2=d2-bsinδ2
dm1=161.026mm,dm2=483.079mm
16
齿宽中点模数mm
mm=dm1/z1=dm2/z2
mm=5.368mm
8
顶隙c
c=c*m
c=1.13mm
9
齿根角θf
θf1=arctg(hf1/R),θf2=arctg(hf2/R)
θf1=.835°,θf2=1.672°
10
齿顶角θa
θa1=θf2,θa2=θf1(等顶隙收缩齿)
θa1=1.672°,θa2=.835°
11
顶锥角δa
δa1=δ1+θf2,δa2=δ2+θf1
+Z2(tanαvat2-tanαt)/cosδ2]/2π
其中:tanαt=(tanα/cosβm)
cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]
εα=1.317
23
齿线重合度εβ
εβ=btanβmπ/mm
εβ=2.491
圆弧齿锥齿轮计算公式演示教学

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分。
通常的已知条件是由水平线除2组成的大边和以垂直线组成的小边。
弧齿锥齿轮主要参数的测绘计算

弧齿锥齿轮测绘计算
弧齿锥齿轮是传动装置中常用的机械零部件,其主要参数的测绘计算
对于产品的质量至关重要。
测绘计算通常包含三个步骤:测量齿距、
测量基本圆的参数、计算副圆和半螺距参数。
第一步,测量齿距。
齿距是指齿轮相邻齿节圆心距离,它是齿轮的核
心参数,影响到齿轮的齿廓特性及传动整体特性,因此必须准确测量,在测量之前,要仔细检查齿轮和齿轮毂的形状和尺寸,确保使用正确
的测量工具,避免测量误差。
第二步,测量基本圆参数。
齿轮的基本尺寸参数是圆的相应参数,要
准确地测量每一个参数,如节圆的半径、圆弧的中径、角等,以保证
基本尺寸的准确性,否则可能会产生传动特性的差异。
第三步,计算副圆和半螺距参数。
副圆和半螺距是齿轮传动中互动作
用重要因素,左右面齿轮必须正确配准,因此需要准确计算副圆和半
螺距参数,确保互动特性和传动效率达到设计要求。
综上,正确测绘计算弧齿锥齿轮的参数有助于保障齿轮产品质量,使
弧齿锥齿轮传动均能达到设计要求,以实现传动效果。
弧齿锥齿轮的加工调整计算

第15章 弧齿锥齿轮的加工调整计算弧齿锥齿轮的切齿是按照“假想齿轮”的原理进行的,而采用的切齿方法要根据具体情况而定。
15.1 弧齿锥齿轮的切齿原理与刀号对于收缩齿弧齿锥齿轮的加工,通常采用平顶齿轮原理进行加工。
就是在切齿的过程中,假想有一个平顶齿轮与机床摇台同心,它通过机床摇台的转动而与被切齿轮做无隙的啮合。
这个假想平顶齿轮的轮齿表面,是由安装在机床摇台上的铣刀盘刀片切削刃的相对于摇台运动的轨迹表面所代替,如图15-1中所示。
在这个运动过程中,代表假想平顶齿轮轮齿的刀片切削刃就在被切齿轮的轮坯上逐渐地切出齿形。
YS2250(Y225)和Y2280等机床就是按“假想平顶齿轮”原理设计的。
在调整切齿机床的时候,必须使被切齿轮的节锥面与假想平顶齿轮的节锥面相切并做纯滚动。
而切齿时刀顶旋转平面则需和被切齿轮的根锥相切,也就是说,刀盘轴线与根锥母线垂直,而非与节锥母线垂直,如图15-2所示。
所以铣刀盘轴线与被切齿轮的节锥面倾斜了一个大小等于被切齿轮齿根角θf 的角度,使被切齿轮两则齿面的压力角出现了误差,这样就产生了刀号修正问题。
如图15-2,用螺旋角接近900时的情况予以说明刀号与压力角的关系。
由于在切齿时采用了“平顶产形轮”原理,工件是按照根锥角进行安装的,铣刀盘轴线垂直于根锥母线,因而和节锥母线倾斜一个齿根角θf 。
这样,当外切刀片与内切刀片使用相同的压力角时,切出来的齿轮凹面与凸面在节锥上的压力角是不相等的(α”≠α’)。
如果要使轮齿中点处的两侧压力角相等,就需要对刀具的两个侧刃的压力角进行修图15-1弧齿锥齿轮的切齿原理摇台刀盘 被加工齿轮正。
修正时,外侧刃齿形角减少α∆,内侧刃增加α∆。
α∆的确定可按以下公式计算βθαsin f ≈∆ (15-1)其中β代表螺旋角。
由于大轮与小轮具有不同齿根角θf ,所以从严格意义上来讲,在加工大轮与小轮时,相应的切齿刀盘的刀刃修正量α∆也应不同。
按照现有的刀号制度,将α∆的单位设置为分,并规定10分为一号,则刀号的计算公式为小轮理论刀盘刀号βθβθαsin 610sin 6010c 111*1f f ==∆= (15-2a)大轮理论刀盘刀号βθβθαsin 610sin 6010c 222*2f f ==∆=(15-2b) 所以,在用双面法分别加工大轮与小轮时,应该用不同刀号的刀盘。
圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分。
通常的已知条件是由水平线除2组成的大边和以垂直线组成的小边。
圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1—θf1,δf2=δ2—θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2—ha1sinδ1,=d1/2—ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1—ψmn2/6)20中点分圆法向弦齿高hamham=ha—btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1—tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分. 通常的已知条件是由水平线除2组成的大边和以垂直线组成的小边. 如图:这类制作,在各种场合都时有所见。
格利森弧齿锥齿轮啮合传动节线的数学原理

2. 1 节线关系的定性分析 用范成法加工锥齿轮 , 相当于一对啮合的锥齿
轮传动 ,但是为了使刀具易于制造及机床结构易于 实现 ,加工锥齿轮的过程并不是一对普通锥齿轮啮 合过程的再现 ,而是将其中的一个锥齿轮转化成平 面齿轮.
在图 5 中锥齿轮 1 和锥齿轮 2 分别同一个相同 的平面齿轮相啮合 , 则这 2 个锥齿轮也能彼此相啮 合. 弧齿锥齿轮的切齿就是按这一个基本原理实现
θ( t)
= arctan
y x
( t) ( t)
.
点为 P1 ,容易求得 P1 在 X O Y 面上的极坐标为 :
ρ1 ( t)
φ1 ( t)
= θ2π1ρ( t) = θ2π1θ( t)
, ,
P P1 =
[ρ( t) ]2 - [ρ1 ( t) ]2 =ρ( t)
1-
θ1 2π
2
.
所以 , P 点的空间坐标 ( 曲线在空间的参数方
θ2π1 arctan
ssin β+ sco sβ+
rsi n rco s
t t
,
Y
=
θ1 2π
( sco sβ+ rco s t) 2 + ( ssin β+ rsin t) 2 sin
θ2π1 arctan
ssin β+ sco sβ+
rsi n rco s
t t
,
Z=
( sco sβ+ rco s t) 2 + ( ssin β+ rsin t) 2
1-
θ1 2π
2
.
(1)
11 2 圆锥面上特定曲线方程推导
圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=ar ctg(hf2/R)10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)11顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm22端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1 +Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=23齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分。
