music 方位估计 实验报告三 MATLAB 代码
三维music算法三维doa估计matlab程序

三维music算法三维doa估计matlab程序以下是一个使用MATLAB实现三维DOA估计的示例程序: ```matlab% 生成三维音频信号fs = 44100; % 采样率t = 0:1/fs:1; % 时间向量f1 = 200; % 音频1频率f2 = 500; % 音频2频率s1 = sin(2*pi*f1*t); % 音频1信号s2 = sin(2*pi*f2*t); % 音频2信号s = [s1; s2]; % 两个音频信号% 设置麦克风阵列参数M = 4; % 麦克风数量d = 0.1; % 麦克风间距% 计算信号到达时间差(TDOA)theta_x = 30; % X轴方向DOA角度theta_y = 45; % Y轴方向DOA角度theta_z = 60; % Z轴方向DOA角度c = 343; % 声速tau_x = d*sin(theta_x*pi/180)/c; % X轴方向TDOA tau_y = d*sin(theta_y*pi/180)/c; % Y轴方向TDOA tau_z = d*sin(theta_z*pi/180)/c; % Z轴方向TDOAtau = [tau_x; tau_y; tau_z]; % 三维TDOA% 添加信号延迟s_delayed = zeros(M, length(s1));for i = 1:Ms_delayed(i, :) = circshift(s(i, :), round(tau(i)*fs)); end% 添加噪声noise = randn(M, length(s1));s_noisy = s_delayed + 0.1*noise;% 使用MUSIC算法进行DOA估计R = s_noisy*s_noisy" / length(s1); % 信号协方差矩阵[V, D] = eig(R); % 计算协方差矩阵的特征向量和特征值[~, ind] = sort(diag(D), "descend"); % 对特征值进行降序排序V_music = V(:, ind(M+1:end)); % MUSIC算法估计的信号子空间theta_range = -90:0.1:90; % DOA角度范围P_music = zeros(size(theta_range));for i = 1:length(theta_range)a = exp(1j*2*pi*d/c*[sin(theta_range(i)*pi/180);sin(theta_range(i)*pi/180);sin(theta_range(i)*pi/180)]*(0:M-1)");P_music(i) = 1/abs(a"*V_music*V_music"*a);end% 绘制DOA估计结果figure;plot(theta_range, P_music);xlabel("DOA (degrees)");ylabel("MUSIC Spectrum");title("3D DOA Estimation using MUSIC Algorithm");```这个程序生成了两个不同频率的音频信号,并模拟了一个四麦克风阵列。
music仿真报告

基于MUSIC 方法功率谱估计的matlab 仿真1. 实验理论:当空间存在多个信号时,常常要对这些信号进行分离,一边跟踪或者检测我们感兴趣的空间信号,抑制那些被认为是干扰的信号。
Music 方法就是进行此项工作的方法之一。
若等间距直线型天线由m 个阵元组成,则信号si(t)到达各个阵元的相位差所组成的方向向量()()[]T m j j i ii e e a ωωθ1,...,,1---= (1) 如果总共有p 个远场信号(p 不大于m ),则在第k 个阵元上的接收信号为()()()()n e n s a n x k p i i i k k +=∑=1ω (2)其中k=1,2,…,m,最后一项为加在此信号上的噪声。
将m 个阵元上的观测数据组成一个数据向量()()()[]T m n x n x n x ,...,1= (3)进行N 次快拍,得出下边的矩阵()()n x n x NR H N i xx ∑==11 (4) 对xx R 进行特征值分解并存储特征向量s1,…,sp,组成信号子空间s=[s1,…,sp]。
最后利用下面的公式进行功率谱估计()()()()ωωωa SS I a P H H -=1 (5) 其中()()()[]p a a a ωωω,..,1= 在实际应用中,通常将ω划分为数百个等间距单位,得到f i ∆=πω2 (6)然后将每个i ω带入(5)式求出所有对应的ω 值。
2. 算法步骤:1) 根据原信号求解其自相关函数。
2) 对其自相关函数进行奇异值分解确定信号特征向量和噪声特征向量。
3) 将求得的特征向量代入公式(5)即得功率谱,最后将w 划分若干等间距单位并画出功率谱。
3. 算法实现:仿真内容:设阵列为均匀直线阵,阵元个数m=30,快拍次数N=80,对正弦信号π进行谐波恢复的计算机仿真。
nw)n(nn=π+x+20sin(.0213)(2sin(22.0))2仿真程序:对应的m文件为music.mclearN=80; %设定快拍次数n=1:128;M=30; %设定阵元个数x(n)=sqrt(20)*sin(2*pi*0.2*n)+sqrt(2)*sin(2*pi*0.213*n)+randn(size(n) );for i=1:Nfor k=1:MX(i,k)=x(i+k-1); %对全零矩阵各元素重新赋值生成X信号矩阵endendRxx=zeros(M,M);for i=1:N;Rxx=Rxx+(X(i,:))'*X(i,:)*1/N; %按照公式(4)求自相关函数生成Rxx矩阵end[U,A,V]=svd(Rxx); %奇异值分解方法G=U(:,5:M); %生成噪声特征向量S=U(:,1:4); %生成信号特征向量syms w Pw %创建多个符号对象aw=exp(-j.*(0:M-1).*(2*pi*w)); %方向向量Pw=1/(aw*(eye(M)-S*S')*aw'); %按照公式(5)求功率Pw=20*log10(abs(Pw));w=0:2*pi*0.0001:0.5; %按照公式(6)求w值从而确定波达方向plot(w,subs(Pw));grid on;仿真图如下:4.结果分析:从上面实验图谱可以看出,MUSIC算法实现谐波恢复的有效性和科学性。
基于MUSIC算法波达方向估计的仿真实现

基于MUSIC算法波达方向估计的仿真实现史萌萌【摘要】波达估计技术对感兴趣的空域信号进行各种处理、计算,实现对信号到达方向等参数的准确估计.它的本质要求在于研究估计精度高、角度分辨率高、运算速度快和易于工程实现的算法.通过对中心对称性阵列结构的数学分析,研究基于噪声子空间的MUSIC工程实现算法,在不减少估计精度和角度分辨率的前提下,减少了算法的实现复杂度.利用各阵元通道正交下变频并滤波后的数据构造实对称协方差矩阵,然后对其进行实特征分解,并通过极值搜索得到来波估计值.最后,对算法具体工程实现思路进行MATLAB仿真,验证了该算法实现路线的正确性和可行性.【期刊名称】《通信技术》【年(卷),期】2018(051)011【总页数】5页(P2570-2574)【关键词】波达估计技术;MUSIC中心对称性;协方差矩阵;工程实现;MATLAB仿真【作者】史萌萌【作者单位】陕西烽火通信集团有限公司,陕西宝鸡 721006【正文语种】中文【中图分类】TN9110 引言在无线电通信、导航、雷达、声纳、电子侦察等领域,获得信号的来波方向极其重要。
在军事领域,获得高分辨率的波达方向和精确的速度距离等参数,不仅有助于我方目标的导航、跟踪,还可以进行准确定位和打击敌方目标。
在民用无线通信领域,准确的来波方向估计有益于提升系统容量和减少多址干扰等。
波达方向估计又称到达角估计或谱估计。
有很多算法定义空间谱,如波束形成、天线阵相关矩阵、特征分析、线性预测、最小方差、最大似然、最小范数等[1]。
在各种空间谱估计算法中,多重信号分类(MUltiple Signal Classification,MUSIC)算法是一种基于子空间分解的算法,特点为测向误差小、精度高、分辨率高、灵敏度高,可以对入射信号数目、到达角及波形的强度做出无偏估计。
因此,研究MUSIC算法对促进更广泛的应用有着十分重要的意义。
1 MUSIC基本原理MUSIC算法的基本原理是把阵列输出数据的协方差矩阵进行特征分解,得到与信号分量相对应的信号子空间和与信号分量正交的噪声子空间,然后利用两个子空间的正交性实现信号的入射方向估计。
MUSIC算法仿真实验

MUSIC 算法仿真实验一、数学模型与MUSIC 算法多重信号分类(MUSIC )算法的基本思想是将任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间,然后利用这两个子空间的正交性来估计信号的参数。
考虑N 个远场信号入射到空间某阵列上,其中天线由M 个阵元组成。
当信号源是窄带的假设下,信号可用如下的复包络形式表示:00(()()()()()j t t i i j ii s t u t e s t s t e ωϕ)ωττ+−⎧=⎨−=⎩ (1) 第l 个阵元接收信号为1()()(),1,2,,Nl li i li l i x t g s t n t l τ==−+=∑"M (2)式中是第l 个阵元对第i 个信号的增益,表示第l 个阵元在t 时刻的噪声,li g ()l n t li τ表示第个信号到达第个阵元时相对于参考阵元的时延。
写为矩阵形式:i l()()()X t AS t N t =+ (3)[]12()()()()TM X t x t x t x t ="为1M ×维快拍数据矢量,[]12()()()()TM N t n t n t n t ="为1M ×维快拍噪声数据矢量,为12()[()()()]TN S t s t s t s t ="1N ×维空间信号矢量,为011012010210220201020111212122212NNM M MN 维流型矩阵(导向矢量阵),且 j j j N j j j N j j j M M MN g e g e g e g e g e g e A g e g e g e ωτωτωτωτωτωτωτωτωτ−−−−−−−−−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦""##%#"M N ×10200[()()()]N A a a a ωω="ωN =" (4)假设阵列中各阵元是各向同性的且不存在通道不一致或互相耦合等因素的影响,则,此时导向矢量1,(,)({1,2,,},{1,2,,})ij g i j M N =∈""(5)010200()[],1,2,,ii Mi j j j T i a e e e i ωτωτωτω−−−="注意到通常τ与信号到达方向有关,因此问题可表述为:如何根据式(3)由接收到的数据()X t 去估计信号的参数,包括信号源数目,信号方向(与()S t N τ有关)等。
波束成形music算法matlab程序 -回复

波束成形music算法matlab程序-回复什么是波束成形音乐算法?波束成形音乐算法是一种利用数字信号处理技术,对音频信号进行处理,以实现增强声音传播方向性和扩大声音覆盖范围的技术。
波束成形音乐算法常用于会议系统、音乐演出、广播等领域,旨在提升听众的听音体验。
此算法可以改变音频信号的辐射特性,将音频信号进行加权处理,并使其主要方向上的声压级变大,从而在特定区域内形成一个虚拟的声学“波束”。
这个“波束”具有比周围环境更高的声音强度,可用于增强目标区域内的听音效果,并减少噪音干扰。
波束成形音乐算法的基本原理是基于声学波动理论和数字信号处理技术相结合,其主要步骤包括:1. 信号采集:首先需要用麦克风阵列或其他声音传感器采集到音频信号。
2. 时延补偿:根据麦克风阵列的位置和信号采集时间,对每个麦克风的信号进行时延补偿,以保证在后续处理中信号的同步性。
3. 空间滤波器设计:通过设计适当的空间滤波器来增强目标方向上的声音,并抑制其他方向上的噪音。
常用的空间滤波器设计方法有传统的最小均方误差准则和实时自适应滤波器算法。
4. 权重计算:根据声源位置和阵列结构,计算每个麦克风的权重系数。
这些权重系数用于对每个麦克风的信号进行加权处理,以增强目标方向上的声音。
5. 信号合成:对加权后的麦克风信号进行合成,得到波束成形后的音频信号。
6. 输出处理:进一步对波束成形后的音频信号进行降噪、均衡等处理,以提升音质和听音效果。
7. 实时控制:根据实际需求和环境条件,对空间滤波器和权重系数进行动态调整和优化,以适应不同的声音场景和目标要求。
使用MATLAB进行波束成形音乐算法的实现有很多优势。
MATLAB提供了丰富的数字信号处理工具箱和声学信号处理函数,可以方便地进行信号处理、算法设计和数据分析。
同时,MATLAB还支持图形界面设计和仿真平台的开发,使得算法的实时调试和性能评估变得更加简单和直观。
综上所述,波束成形音乐算法是一种利用数字信号处理技术,通过采集、处理和合成音频信号,实现对声音传播方向性和范围的控制。
二维music算法matlab程序

二维music算法matlab程序音乐是一种非常丰富的艺术形式,而数字信号处理技术的发展带来了许多新的应用。
在音乐领域,二维music算法是一种非常常见的用于音频处理和分析的算法,Matlab则是一种常用的工具,本文将围绕着如何编写二维music算法的Matlab程序来进行详细的阐述。
第一步,准备数据。
在编写二维music算法的Matlab程序之前,我们需要准备一些音频数据。
可以使用MATLAB自带的音频数据,也可以使用外部音频数据。
我们将数据载入到Matlab中,然后进行预处理,使其适合二维music算法。
第二步,实现二维music算法。
二维music算法的主要目的是确定信号的子空间,通常用于估计信号的DOA(方向性),以及其他分析任务。
在Matlab中,实现二维music算法需要编写一些函数。
可以使用现有的函数库,也可以自己编写函数。
需要注意的是,在编写二维music算法时,要对算法的每个步骤进行详细的解释,以便理解并调试程序。
第三步,测试程序。
在完成二维music算法的Matlab程序之后,我们需要进行测试以确保程序的正确性。
我们可以使用MATLAB自带的测试工具箱,也可以使用自己编写的测试脚本。
测试应该考虑多种情况,包括不同的输入数据、不同的参数和不同的场景等。
第四步,调整程序。
在进行测试之后,我们可能需要对程序进行一些调整以满足特定的应用场景。
这可能包括更改算法的参数、使用不同的输入数据、修改算法的实现等。
需要注意的是,在进行调整之前,我们应该对调整进行仔细的分析,以便避免出现错误。
最后,我们需要进行程序的文档化和发布。
这是确保程序的可复用性和可维护性的重要步骤。
我们应该对程序进行详细的文档,包括说明程序的使用方法、输入和输出的格式、算法的实现等等。
然后,我们可以将程序发布到工具箱或其他适合的地方,使其可以被其他用户使用和下载。
总之,在实现二维music算法的Matlab程序时,我们需要遵循严谨的编程规范和文档化要求。
matlab基于music算法的二维方向的空间普估计

matlab基于music算法的二维方向的空间普估计一、引言空间普估计是信号处理领域中重要的一个研究方向,其主要目的是估计传感器阵列中信号源的方向和功率。
在音频处理方面,空间普估计也有着广泛的应用,包括环绕声、语音识别等方面。
本文将介绍一种matlab基于music算法的二维方向的空间普估计方法。
二、matlab中的music算法music算法是一种高分辨率的方向估计算法,其基本思想是通过计算信号的子空间噪声功率谱,估计信号的空间频率。
在matlab中,可以通过使用music函数实现该算法。
具体步骤如下:1.设置传感器阵列的位置和方位;2.获取某一时刻的信号数据;3.使用music函数指定传感器阵列和信号数据,计算噪声功率谱;4.使用噪声功率谱计算信号的协方差矩阵;5.对协方差矩阵进行谱分解,并计算信号的子空间;6.使用子空间计算信号的空间频率和方向。
三、二维方向的空间普估计在二维空间中,信号源的方向可以由两个角度表示。
因此,在进行二维方向的空间普估计时,需要计算两个频率分量。
这可以通过使用matlab中的estimatespectrum函数实现。
具体步骤如下:1.设置传感器阵列的位置和方位;2.获取某一时刻的信号数据;3.使用estimatespectrum函数指定传感器阵列和信号数据,计算谱估计;4.使用谱估计计算信号的角频率;5.使用角频率计算信号在平面直角坐标系中的方向。
四、总结matlab基于music算法的二维方向的空间普估计方法是一种简单、高效的信号处理方法,可以广泛应用于音频处理领域。
通过计算信号的子空间噪声功率谱和谱估计,可以估计信号源的方向和功率。
本文介绍的方法具有较高的信号处理精度和实用价值,有着广阔的应用前景。
Music 算法仿真实验报告

Music 算法仿真实验报告一,实验原理取第一个阵元为参考点,设参考点接收的入射波信号为:x1(t)=s(t)e jwt其中s(t)为信号的复振幅,w为信号的角频率阵元m接收到的信号为:x m(t)=s[t−τ(θ)]e jw[t−τm(θ)]τ(θ)为阵元m接收到的入射波相对于参考点入射波的延时,θ为入射角。
对于窄带信号,相对于τ(θ)时间延迟的信号复包络变化可以忽略,则:s[t−τ(θ)]≈s(t)所以阵元m接收到的信号可简化为:x m(t)=s(t)e jw(t−τm)=x1(t)e−jwτm将M个阵元接收到的信号表示成矢量的形式,可以得到阵列接收信号矢量X为:X=[x1(t)⋮x M(t)]=x1(t)[1⋮e−jwτM(θ)]=x1(t)a(θ)a(θ)=[1,…,e−jwτM(θ)]为阵列导向矢量。
如果入射到天线阵列的信号为D个远场信号,并且入射信号的入射角分别为(θ1,θ2,…θD),此时阵列接收信号矢量表示式为:X(t)=∑s i(t)a(θi)=AS(t)Di=1其中,A=[a(θ1),a(θ2),…a(θD)]为阵列对信号的导向矢量矩阵。
S(t)=[s1(t),s2(t),⋯,s M(t)]T,为信号矢量。
考虑到各个振元存在噪声,阵列接收矢量可表示为:X(t)=AS(t)+N(t)N(t)为阵列接收的噪声矢量,表示为:N(t)=[n1(t),n2(t),⋯n M(t)]T而且n i(t)为零均值,方差为σ2的相互独立的白噪声采样对阵列输出X作相关处理,得到其协方差矩阵R xR x=E[XX H]假设信号与噪声互不相关,且噪声为零均值白噪声,因此可以得到:R X=E[(AS+N)(AS+N)H]=AE[SS H]A H+E[NN H]=AR S A H+R NR N=σ2IR N是噪声的相关矩阵,σ2是噪声功率,I是单位矩阵当所有信号互不相关是,有E[s i(t)s i∗(t)]={0, i≠jP i, i=j其中,P i为第i个信号源的功率。
用Music算法估计非相干信号的仿真
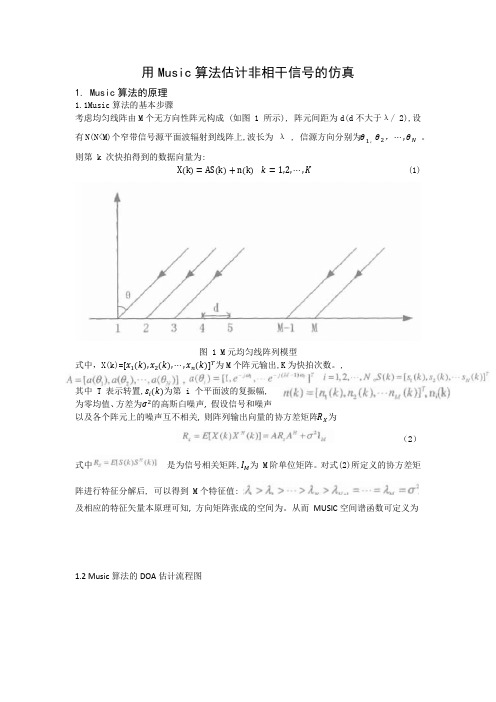
1. Music 算法的原理
1.1Music 算法的基本步骤 考虑均匀线阵由 M 个无方向性阵元构成 (如图 1 所示), 阵元间距为 d(d 不大于λ / 2),设 有 N(N<M)个窄带信号源平面波辐射到线阵上,波长为 λ 则第 k 次快拍得到的数据向量为: X k = AS k + n k , 信源方向分别为������1, ������2 , ⋯ , ������������ 。 (1)
第一题: 由题干信息可知:每个接收机接收到的信号为:
H0 : xi (t) Bisin(0 t i ) ni (t),0 t T H1 : xi (t) Ai sin(1 t i ) ni (t),0 t T {n i (t)} 是均值为 0,功率谱密度为 N0/2 的高斯白噪声,且统计相互独立。Ai,Bi 都统计相
因此 Pe
1 2 Es / N
2 N0 a T 2 1[x(t)] exp( l1 ),l1 0 2 2 N0 a T N0 (N0 a T )
2 式中,参数 a T 是信号的平均能量。
2 2 2 2 l 0 xR xR 0 xI 0 , l1 1 xI 1 ,其中 X R 0
H1
最小平均错误概率为: P e P(H0 ) P(H1 | H0 ) P(H1 ) P(H0 | H1 ) 。
P(H0 | H1 )
同理, P(H1 | H0 )
N0 1 2 2 N0 a T 2 E s / N0
N0 1 2 , Es a T 为信号的平均能量。 2 2 N0 a T 2 E s / N0
(g)dt
Music 算法仿真实验报告

Music 算法仿真实验报告一,实验原理取第一个阵元为参考点,设参考点接收的入射波信号为:x1(t)=s(t)e jwt其中s(t)为信号的复振幅,w为信号的角频率阵元m接收到的信号为:x m(t)=s[t−τ(θ)]e jw[t−τm(θ)]τ(θ)为阵元m接收到的入射波相对于参考点入射波的延时,θ为入射角。
对于窄带信号,相对于τ(θ)时间延迟的信号复包络变化可以忽略,则:s[t−τ(θ)]≈s(t)所以阵元m接收到的信号可简化为:x m(t)=s(t)e jw(t−τm)=x1(t)e−jwτm将M个阵元接收到的信号表示成矢量的形式,可以得到阵列接收信号矢量X为:X=[x1(t)⋮x M(t)]=x1(t)[1⋮e−jwτM(θ)]=x1(t)a(θ)a(θ)=[1,…,e−jwτM(θ)]为阵列导向矢量。
如果入射到天线阵列的信号为D个远场信号,并且入射信号的入射角分别为(θ1,θ2,…θD),此时阵列接收信号矢量表示式为:X(t)=∑s i(t)a(θi)=AS(t)Di=1其中,A=[a(θ1),a(θ2),…a(θD)]为阵列对信号的导向矢量矩阵。
S(t)=[s1(t),s2(t),⋯,s M(t)]T,为信号矢量。
考虑到各个振元存在噪声,阵列接收矢量可表示为:X(t)=AS(t)+N(t)N(t)为阵列接收的噪声矢量,表示为:N(t)=[n1(t),n2(t),⋯n M(t)]T而且n i(t)为零均值,方差为σ2的相互独立的白噪声采样对阵列输出X作相关处理,得到其协方差矩阵R xR x=E[XX H]假设信号与噪声互不相关,且噪声为零均值白噪声,因此可以得到:R X=E[(AS+N)(AS+N)H]=AE[SS H]A H+E[NN H]=AR S A H+R NR N=σ2IR N是噪声的相关矩阵,σ2是噪声功率,I是单位矩阵当所有信号互不相关是,有E[s i(t)s i∗(t)]={0, i≠jP i, i=j其中,P i为第i个信号源的功率。
波束成形music算法matlab程序

波束成形music算法matlab程序一、程序概述本程序实现了一种基于Music算法的波束成形算法,可用于信号处理领域中的方向性信号处理。
Music算法是一种基于信号统计特性的自适应算法,能够根据信号的方向信息自动调整波束方向,从而实现信号的高灵敏度和低噪声接收。
二、程序代码```matlab%参数初始化fs=1000;%采样频率time=-1:1/fs:1;%时间向量theta=0;%信号方向N=length(time);%样本数d=10;%接收器间距theta_max=atan2(sin(theta),cos(theta));%最大信号方向mu=0.05;%最大信号功率因子lambda=0.3;%自适应步长因子theta_ini=theta-pi/2;%初始搜索范围R=sqrt(d^2+theta_ini^2);%距离矩阵U=zeros(N,N);%方向矩阵p=zeros(N,1);%接收器位置向量%Music算法主程序fork=1:Np(k)=R(k,round(rand()*N));%随机选择一个接收器位置endU(:,k)=exp(-1i*pi*R(:,k)'*p(:)/p(:).^2);%方向矩阵初始化forn=1:100%自适应迭代次数fork=theta_ini:pi:pi/lambda%搜索范围ifabs(U(:,k).^2)>mu%如果当前方向上信号功率大于最大信号功率因子,则更新方向矩阵U(:,k)=exp(-1i*pi*R(:,k)'*p(:)/p(:).^2)*U(:,k);%更新方向矩阵元素endendendU=U/sum(U);%归一化方向矩阵%波束成形输出S=U*signal;%将信号乘以方向矩阵得到输出信号```三、程序说明程序首先初始化了一些参数,包括采样频率、时间向量、信号方向、接收器间距、最大信号方向、最大信号功率因子、自适应步长因子等。
(完整word版)基于经典MUSIC的DOA估计Matlab仿真

信息与通信工程学院阵列信号处理实验报告(基于经典MUSIC的DOA估计Matlab仿真)学号:XXXXXX专业:XXXXXX学生姓名:XXX任课教师:XXX2015年X月题目:基于经典MUSIC 的DOA 估计Matlab 仿真1. 算法简述:基于天线阵列协方差矩阵的特征分解类DOA 估计算法中,多重信号分类(MUSIC )算法具有普遍适用性,只要已知天线阵的分布形式,无论直线阵还是圆阵,不管阵元是否等间隔分布,都可以得到高分辨率的估计结果。
阵列协方差矩阵R 可以划分为两个空间,即H Hs s s N N N =+R U ΣU U ΣU 。
因导向矩阵的各矢量与噪声子空间正交,可得到阵列空间谱函数MUSIC H H 1()()()N N θθθ=P a U U a 使θ变化,按照MUSIC ()θP 来搜索峰值来达到波达方向的估计值。
2. 实验内容与结果:实验使用8阵元均匀线阵,阵元间距为信号波长的一半,输入信号为1个BPSK 信号,1个非相干的单频干扰,设置载波频率10MHz 、采样频率30MHz 、快拍数30、信干比0dB 、信号方位角0、干扰方位角5,分析信噪比从1到20dB 估计均方误差。
实验结果见下图。
-100-80-60-40-20020406080100-40-2020406080入射角/degree空间谱/d B经典MUSIC 估计图1信噪比 15dB 情况下的波束图24681012141618200.51-3SNR(dB)0°角测量均方误差24681012141618200.51-3SNR(dB)5°角测量均方误差图2不同信噪比测得的均方误差3. 仿真分析由仿真结果可知,在实验前提条件下,经典music 算法的DOA 估计可有效估计出信号的来向。
当信噪比较小时,估计得均方误差较大;随着信噪比的提高,估计均方误差逐渐减小;当信噪比大于10dB 以后,角度估计成功率100%。
music 方位估计 实验报告三 MATLAB 代码

实验报告三实验目的:实现常规波束形成及基于MUSIC 方法的方位估计。
实验内容:1)若干阵元的接收阵,信号频率为10KHz ,波束主轴12度,仿真给出常规波束形成的波束图。
2)16个阵元的均匀线列阵,信号频率为10KHz ,信号方位为12度,用MUSIC 方法完成目标定向,信噪比-5dB ,0dB ,5dB 。
i) 波束形成时的阵型设计为两种,一种是均匀线列阵,阵元16个;一种是均匀圆阵,阵元数为16个,比较这两种阵型的波束图。
ii )比较不同信噪比下MUSIC 方法估计的性能(统计100次)。
实验原理:i)常规波束形成:如图所示,基阵的输出),(θt v 。
∑∑=*=*==Mm i i M m i iw t x t x w t v 11)()()()(),(θθθ采用向量符号则有,)()()()(),(H H θθθw x x w t t t v ==式中,x(t)和w(q )分别为观测数据向量和加权系数向量,),(θt v 图 1 波束形成器基本原理图T M 21])()()([)(t x t x t x t =x T M 21])()()([)(θθθθw w w =w基阵输出端的空间功率谱表示为:)()( )()]()([)( )]()()()([ )],(),([ ]),([)(H H H H H *2θθθθθθθθθθRw w w x x w w x x w =====t t E t t E t v t v E t v E P式中,R 为观测数据的协方差矩阵。
ii )基于MUSIC 方法的方位估计:)()()()(1t n t s a t x i di +=∑=θT M 21])()()([)(t x t x t x t =x)()()()(t n t s A t x +=θ假设:(1 ) 信号源的数目d 是已知的, 且d < M ;(2 ) 各信号的方向矢量是相互独立的, 即)(θA 是一个列满秩矩阵;(3 ) 噪声)(t n 是空间平稳随机过程, 为具有各态历经性的均值为零、方差为σ2n 的高斯过程;(4 ) 噪声各取样间是统计独立的。
MUSIC算法仿真实验

MUSIC 算法仿真实验一、数学模型与MUSIC 算法多重信号分类(MUSIC )算法的基本思想是将任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间,然后利用这两个子空间的正交性来估计信号的参数。
考虑N 个远场信号入射到空间某阵列上,其中天线由M 个阵元组成。
当信号源是窄带的假设下,信号可用如下的复包络形式表示:00(()()()()()j t t i i j ii s t u t e s t s t e ωϕ)ωττ+−⎧=⎨−=⎩ (1) 第l 个阵元接收信号为1()()(),1,2,,Nl li i li l i x t g s t n t l τ==−+=∑"M (2)式中是第l 个阵元对第i 个信号的增益,表示第l 个阵元在t 时刻的噪声,li g ()l n t li τ表示第个信号到达第个阵元时相对于参考阵元的时延。
写为矩阵形式:i l()()()X t AS t N t =+ (3)[]12()()()()TM X t x t x t x t ="为1M ×维快拍数据矢量,[]12()()()()TM N t n t n t n t ="为1M ×维快拍噪声数据矢量,为12()[()()()]TN S t s t s t s t ="1N ×维空间信号矢量,为011012010210220201020111212122212NNM M MN 维流型矩阵(导向矢量阵),且 j j j N j j j N j j j M M MN g e g e g e g e g e g e A g e g e g e ωτωτωτωτωτωτωτωτωτ−−−−−−−−−⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦""##%#"M N ×10200[()()()]N A a a a ωω="ωN =" (4)假设阵列中各阵元是各向同性的且不存在通道不一致或互相耦合等因素的影响,则,此时导向矢量1,(,)({1,2,,},{1,2,,})ij g i j M N =∈""(5)010200()[],1,2,,ii Mi j j j T i a e e e i ωτωτωτω−−−="注意到通常τ与信号到达方向有关,因此问题可表述为:如何根据式(3)由接收到的数据()X t 去估计信号的参数,包括信号源数目,信号方向(与()S t N τ有关)等。
波束成形music算法matlab程序 -回复

波束成形music算法matlab程序-回复如何在MATLAB中编写波束成形音乐算法。
波束成形音乐算法是一种利用波束成形技术来调整音频信号的方法,以提高音频信号的质量和方向性。
在本文中,我将提供一步一步的指导,向您展示如何在MATLAB中编写波束成形音乐算法。
第一步是准备工作。
首先,确保您已经安装了MATLAB软件,并具备基本的MATLAB编程知识。
另外,您需要了解波束成形的基本概念和原理。
波束成形是一种声学信号处理技术,通过调整传感器阵列中的信号加权来改变声波传播的方向性。
了解这些基本知识将有助于更好地理解算法的实现过程。
在第二步中,我们需要创建一个声音文件以供后续处理。
您可以使用MATLAB的音频处理工具箱来生成和加载音频文件。
将所需的音频数据加载到MATLAB变量中,以便进行后续处理。
第三步是对音频数据进行预处理。
在波束成形音乐算法中,我们需要对音频信号进行滤波和降噪处理,以减少噪声对波束成形效果的影响。
通过应用合适的数字滤波器和噪声抑制算法,我们可以改善音频信号的质量。
MATLAB提供了许多用于音频信号处理的函数和工具,如滤波器设计工具箱和信号处理工具箱,可以帮助我们完成这些处理步骤。
接下来,我们需要计算波束权重。
波束成形的关键部分是通过调整传感器阵列中的信号加权来改变声波传播的方向性。
在波束成形音乐算法中,我们需要根据所需的方向性目标来计算每个传感器的加权系数。
根据传感器的位置和所需的波束成形方向,可以使用波束成形算法计算出每个传感器的权重。
MATLAB提供了许多用于计算和优化算法的数值计算函数和工具,如优化工具箱和数学工具箱。
然后,我们需要应用波束成形权重到音频数据上。
在这一步中,我们通过将波束权重应用到原始音频数据上,实现对音频信号的调整和增强。
根据计算得到的权重系数和原始音频数据,可以使用MATLAB的向量和矩阵运算函数对音频数据进行加权处理。
最后一步是播放和保存结果。
根据波束成形的算法结果,我们可以播放和保存经过波束成形处理后的音频数据。
基于MUSIC算法的DOA估计

……θP。在第 n 次采样时刻, 得 到 的 数 据 向 量
为:
+
( 1)
式 中 : X( n) =[x1(n),x2(n),…xM(n)]T 为 M 个 阵 元的输出。
,
,
, T 表示转置; , 表示第 i 个
平面波的复振幅; ( 2)
Ni(n)为 均 值 为 0, 方 差 为 σ2 的 高 斯 白 噪 声, 且信号源不相关, N 为采样数。
度矢量和位移矢量。
有的同学认为课本上通常所画的平抛物
体的运动轨迹就是平抛运动的 s- t 图象, 这也
是一种错误, 轨迹图是物体实际运动路线的形
象描绘, 而 s- t 图象是数学 函 数 的 抽 象 概 括 , 它
们 的 结 构 、涵 义 各 不 相 同 。
那么平抛运动 能 否 用 s- t 图 象 和 v- t 图 象
( 9) 令 Y(n)=JMX!(n), 其中X!(n)为的复共轭, 则的 相关矩阵为:
由于 JMJM=IM, 我们可以定义:
( 10)
这 样 做 就 使 成 为 Hermite 的 Toeplitz 矩 阵 [4]。Toeplitz 矩阵是关于东—西南对角线对称的, 由于数据是有限的, Rxxx 的 协 方 差 矩 阵 的 统 计 估 值 R! 一 般 情 况 下 只 是 Hermite 矩 阵 , 不 是 Toeplitz 矩 阵 , 对 R 进 行 修 改 , 得 到 Toeplitz 的 协 方 差 矩 阵 的 估 计 值 Rxx=R+JMR! JM, 显 然 是 Hermite 的 Toeplitz 矩阵, 由此可知, Rxx 是 R 的 无偏估计。再对进行奇异值分解, 在分解所得到 的对角矩阵中令最小的 p 个特征值置零, 然后 再重 新 组 合 成 RxxRxxR!xx, 对R!xx 再 进 行 分 解 , 得到噪声子空间。把由 R 得到的噪声子空间和 由得到的噪声子空间进行求平均作为我们处理 后的新的噪声子空间, 并依此为依据带入空间 谱函数进行 DOA 估计。
声源定位matlab程序

声源定位matlab程序在MATLAB中进行声源定位的程序通常涉及到信号处理和声学定位技术。
声源定位的目标是确定声音的方向,通常使用麦克风阵列来实现。
以下是一个简单的MATLAB程序示例,用于声源定位:matlab.% 定义麦克风阵列参数。
numMics = 4; % 麦克风数量。
micSpacing = 0.1; % 麦克风间距(以米为单位)。
% 模拟接收到的声音信号。
fs = 44100; % 采样率。
t = (0:1/fs:1-1/fs)'; % 时间向量。
f1 = 1000; % 第一个声源的频率。
f2 = 2000; % 第二个声源的频率。
signal1 = sin(2pif1t); % 第一个声源的信号。
signal2 = sin(2pif2t); % 第二个声源的信号。
% 模拟麦克风接收到的声音。
micSignals = zeros(length(t), numMics);for i = 1:numMics.distance = (i-1) micSpacing; % 麦克风到声源的距离。
delay = distance/340; % 延迟(声音传播速度为340m/s)。
micSignals(:,i) = [zeros(round(delayfs),1);signal1(1:end-round(delayfs))] + [zeros(round(delayfs),1); signal2(1:end-round(delayfs))];end.% 声源定位。
[azimuth,elevation] =locateSource(micSignals,fs,micSpacing);% 显示结果。
disp(['声源方位角: ', num2str(azimuth), '°']);disp(['声源俯仰角: ', num2str(elevation), '°']);需要注意的是,以上代码中的`locateSource`函数是一个虚构的函数,实际上需要根据具体的声源定位算法来实现。
采用的论文 基于MUSIC算法方位角估计的对比性仿真研究

基于 MUSIC 算法方位角估计的对比性 仿真研究
[黄娇 袁正午]
摘要
方位角估计是估计空间目标的空间位置的一项重要工作。文中利用基本 MUSIC算法和ROOT-MUSIC算法进行方位角估计的对比研究。针对不同信噪比 情况下,用这两种算法估计方位角的估计效果进行对比研究;对算法估计同一 个方位角时的估计均方误差进行MATLAB仿真分析。通过对比研究,验证了基于 MUSIC算法的方位角估计在信噪比较小时,估计性能差,以至于难以分辨多个信 号的方位角。
式(8)
3
MUSIC算法
在众多高分辨 DOA 估计算法中,最经典的算法是基 于特征分解的多重信号分类算法,由Schmidt在1979年提 出。该算法是以空间划分来进行参数估计的,原理是根据 信号子空间和噪声子空间的正交性划分空间。
1 ˆ arcsin[ arg( zi )] (i 1, 2,..., N ) = θ = 2π d
各种算法在方位角估计方面的优势,以便更广泛的应用。
就需要先知道目标反射回波信号的方位角(DOA,Direction of Arrival)。方位角估计[1]技术是阵列信号处理技术的主要 组成部分,包括常规方法、参数模型方法、子空间类方 法、解卷积方法以及其他方法。传统的关于阵列信号参数 估计的研究主要集中于空间目标的波达方向[2](Direction-ofArrival,DOA)估计方法及其统计性能、相应的估计性能下 界(CRB)问题。对空间目标的DOA估计一般称为空间谱估 计。本文是利用MUSIC类方法中的算法估计方位角。 本文通过信噪比对基本MUSIC算法和ROOT-MUSIC算 法估计方位角的性能进行对比仿真,再对比分析这算法估 计方位角时的均方误差进行仿真分析,据得到的结果验证
MUSIC算法matlab程序

clear allclose allderad = pi/180; % deg -> radradeg = 180/pi;twpi = 2*pi;kelm = 8; % 阵列数量dd = 0.5; % spaced=0:dd:(kelm-1)*dd; %iwave = 4; % number of DOAtheta = [-60 -30 30 60]; % 角度snr = 10; % input SNR (dB)n = 500; %A=exp(-j*twpi*d.'*sin(theta*derad));%%%% direction matrixS=randn(iwave,n);X=A*S;X1=awgn(X,snr,'measured');%在信号X中加入高斯白噪声,信噪比SNR,'measured'函数在加入噪声前测定信号强度Rxx=X1*X1'/n;InvS=inv(Rxx); %%%%[EV,D]=eig(Rxx);%%%% [V,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量。
EVA=diag(D)';%返回矩阵D的主对角线上的元素[EVA,I]=sort(EVA);%其中I是一个大小等于size(EVA)的数组,其每一列是EVAA中列向量的元素相对应的置换位置记号。
EVA=fliplr(EVA);%将矩阵A的列绕垂直轴进行左右翻转,如果A是一个行向量,fliplr(A)将A 中元素的顺序进行翻转。
如果A是一个列向量,fliplr(A)还等于A。
EV=fliplr(EV(:,I));% MUSICfor iang = 1:361angle(iang)=(iang-181)/2;phim=derad*angle(iang);a=exp(-j*twpi*d*sin(phim)).';L=iwave;En=EV(:,L+1:kelm);SP(iang)=(a'*a)/(a'*En*En'*a);end%画图SP=abs(SP);SPmax=max(SP);SP=10*log10(SP/SPmax);h=plot(angle,SP);set(h,'Linewidth',2)xlabel('angle (degree)')ylabel('magnitude (dB)')axis([-90 90 -60 0])set(gca, 'XTick',[-90:30:90])grid on(注:文档可能无法思考全面,请浏览后下载,供参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告三实验目的:实现常规波束形成及基于MUSIC 方法的方位估计。
实验内容:1)若干阵元的接收阵,信号频率为10KHz ,波束主轴12度,仿真给出常规波束形成的波束图。
2)16个阵元的均匀线列阵,信号频率为10KHz ,信号方位为12度,用MUSIC 方法完成目标定向,信噪比-5dB ,0dB ,5dB 。
i) 波束形成时的阵型设计为两种,一种是均匀线列阵,阵元16个;一种是均匀圆阵,阵元数为16个,比较这两种阵型的波束图。
ii )比较不同信噪比下MUSIC 方法估计的性能(统计100次)。
实验原理:i)常规波束形成:如图所示,基阵的输出),(θt v 。
∑∑=*=*==Mm i i M m i iw t x t x w t v 11)()()()(),(θθθ采用向量符号则有,)()()()(),(H H θθθw x x w t t t v ==式中,x(t)和w(q )分别为观测数据向量和加权系数向量,),(θt v 图 1 波束形成器基本原理图T M 21])()()([)(t x t x t x t =x T M 21])()()([)(θθθθw w w =w基阵输出端的空间功率谱表示为:)()( )()]()([)( )]()()()([ )],(),([ ]),([)(H H H H H *2θθθθθθθθθθRw w w x x w w x x w =====t t E t t E t v t v E t v E P式中,R 为观测数据的协方差矩阵。
ii )基于MUSIC 方法的方位估计:)()()()(1t n t s a t x i di +=∑=θT M 21])()()([)(t x t x t x t =x)()()()(t n t s A t x +=θ假设:(1 ) 信号源的数目d 是已知的, 且d < M ;(2 ) 各信号的方向矢量是相互独立的, 即)(θA 是一个列满秩矩阵;(3 ) 噪声)(t n 是空间平稳随机过程, 为具有各态历经性的均值为零、方差为σ2n 的高斯过程;(4 ) 噪声各取样间是统计独立的。
在上述假设条件下, 基阵输出的协方差矩阵可表示为:I A AR t x t x E R H s H 2])()([α+==其中, R s 为信号的协方差矩阵;I 为单位矩阵。
对R 进行特征分解, 并以特征值降值排列可得Hmm Md m m Hm m dm m ee e e R ∑∑+==+=11λλ信号子空间与噪声子空间正交。
若噪声子空间记为E N , 即∑+==Md m Hmm N eeE 1则有:0)(=i N a E θ因此,对矩阵R 进行特征分解后, 取噪声特征矢量, 就可得到信号源的到达角。
定义多重信号分类法的空间谱函数为:)()(1θθa E E a P H NN HMUSIC =实验过程及结论:1.常规波束形成,阵列为均匀线列阵:-100-80-60-40-20020*********-70-60-50-40-30-20-10均匀线列阵 12度主轴方位角/度归一化功率/d B2.常规波束形成,阵列为均匀圆阵:-200-150-100-50050100150200-80-70-60-50-40-30-20-100均匀圆阵 12度主轴方位角/度归一化功率/d B结论:由上面两个仿真结果可以看出,采用均匀线列阵和均匀圆阵都可以完成波束形成,都可以获得阵处理增益。
3.MUSIC算法方位估计:-100-80-60-40-20020406080100-60-50-40-30-20-10方位角 / 度归一化功率 / d B结论:从上图得出,信噪比越高,MUSIC方位估计越准确。
附录:MATLAB仿真程序代码1.常规波束形成%%clear all;close all;clc%%%%%%常规波束形成%信号参数f0=10e3;fs=10*f0;T=2e-3;t=1:1/fs:T-1/fs;%均匀线列阵阵列参数c=1500;lamda=c/f0;d=lamda/2;M=16;direct=12;%波束指向%阵列流行theta=-90:90;for i_theta=1:length(theta)fai=2*pi*d*sin(theta(i_theta)*pi/180)/lamda;for i_M=1:MA(i_M,i_theta)=exp(-sqrt(-1)*(i_M-1)*fai);endend%加权向量wfai_direct=2*pi*f0*d*sin(direct*pi/180)/c;for i_M=1:Mw(i_M)=exp(sqrt(-1)*(i_M-1)*fai_direct);endw=w';%无噪声输出P=w'*A;P=20*log10(abs(P)/max(abs(P)));figure(1)plot(theta,P);title('均匀线列阵 12度主轴');xlabel('方位角/度');ylabel('归一化功率/dB'); gridhold onclear all;clc%%%%%%常规波束形成%信号参数f0=10e3;fs=10*f0;T=2e-3;t=1:1/fs:T-1/fs;%元阵阵列参数c=1500;lamda=c/f0;d=lamda/2;M=16;i_M=0:M-1;fai=2*pi/M.*i_M;B=[d*cos(fai);d*sin(fai);d*zeros(1,M)];direct=12;%波束指向%阵列流行theta=-180:180;theta=theta*pi/180;for i_theta=1:length(theta)e=[cos(theta(i_theta));sin(theta(i_theta));0];tao=-e.'*B./c;for i_M=1:MA(i_M,i_theta)=exp(sqrt(-1)*2*pi*f0*tao(i_M));endend%加权向量wfai_direct=2*pi*f0*d*sin(direct*pi*180)/c;for i_M=1:Mw(i_M)=exp(sprt(-1)*2*pi*f0*d*cos(fai(i_M)-direct/180*pi)/c); endw=w';%无噪声输出P=w'*A;P=20*log10(abs(P)/max(abs(P)));figure(2)plot(theta./pi*180,P);title('均匀圆阵 12度主轴');xlabel('方位角/度');ylabel('归一化功率/dB'); grid2.MUSIC方位估计%%clc; clear; close all;M=16;c=1500;f0=10e3;lamda=c/f0;d=lamda/2;fs=10*f0;T=2;t=[0:1/fs:T];N=fs*T;signalnum=1;%%%信噪比SNR=-5;theta1=12;num=100;theta1=theta1*pi/180;tau0=d*sin(theta1)/c;for i_M=1:MS(i_M,:)=exp(sqrt(-1)*2*pi*f0*t)*exp(-sqrt(-1)*2*pi*f0*(i_M-1)*tau0); endP=zeros(1,181); %length(theta)for i=1:numX=awgn(S,SNR);R=X*X'/N; %协方差矩阵[V,I]=eig(R);[Order Index]=sort(diag(I),'descend'); %特征值降值排列VS=[]; %向量子空间P_music=[];for i_M=1:MVS=[VS,V(:,Index(i_M))]; %排序后的特征向量endE=VS(:,signalnum+1:M); %后M-signalnum向量构成向量子空间En=E*E'; %噪声子空间theta=-90:1:90;fai=2*pi*f0*d*sin(theta*pi/180)/c;for i_theta=1:length(theta)for i_M=1:Mw(i_theta,i_M)=exp(sqrt(-1)*(i_M-1)*fai(i_theta));%方向矢量endP_music(i,i_theta)=1./(w(i_theta,:)*En*En'*w(i_theta,:)');endendP=abs(P)/num;P=P+P_music(i,:);figure(3)plot(theta,10*log10(P/max(P)),'r');xlabel('方位角 / 度');ylabel('归一化功率 / dB');gridtitle('不同信噪比下MUSIC方法估计的性能(统计100次)')hold on%%%信噪比SNR=0;theta1=12;num=100;theta1=theta1*pi/180;tau0=d*sin(theta1)/c;for i_M=1:MS(i_M,:)=exp(sqrt(-1)*2*pi*f0*t)*exp(-sqrt(-1)*2*pi*f0*(i_M-1)*tau0); endP=zeros(1,181); %length(theta)for i=1:numX=awgn(S,SNR);R=X*X'/N; %协方差矩阵[V,I]=eig(R);[Order Index]=sort(diag(I),'descend'); %特征值降值排列VS=[]; %向量子空间P_music=[];for i_M=1:MVS=[VS,V(:,Index(i_M))]; %排序后的特征向量endE=VS(:,signalnum+1:M); %后M-signalnum向量构成向量子空间En=E*E'; %噪声子空间theta=-90:1:90;fai=2*pi*f0*d*sin(theta*pi/180)/c;for i_theta=1:length(theta)for i_M=1:Mw(i_theta,i_M)=exp(sqrt(-1)*(i_M-1)*fai(i_theta));%方向矢量endP_music(i,i_theta)=1./(w(i_theta,:)*En*En'*w(i_theta,:)');endendP=abs(P)/num;P=P+P_music(i,:);figure(3)plot(theta,10*log10(P/max(P)),'*');xlabel('方位角 / 度');ylabel('归一化功率 / dB');gridtitle('不同信噪比下MUSIC方法估计的性能(统计100次)')hold on%%%信噪比SNR=5;theta1=12;num=100;theta1=theta1*pi/180;tau0=d*sin(theta1)/c;for i_M=1:MS(i_M,:)=exp(sqrt(-1)*2*pi*f0*t)*exp(-sqrt(-1)*2*pi*f0*(i_M-1)*tau0); endP=zeros(1,181); %length(theta)for i=1:numX=awgn(S,SNR);R=X*X'/N; %协方差矩阵[V,I]=eig(R);[Order Index]=sort(diag(I),'descend'); %特征值降值排列VS=[]; %向量子空间P_music=[];for i_M=1:MVS=[VS,V(:,Index(i_M))]; %排序后的特征向量endE=VS(:,signalnum+1:M); %后M-signalnum向量构成向量子空间En=E*E'; %噪声子空间theta=-90:1:90;fai=2*pi*f0*d*sin(theta*pi/180)/c;for i_theta=1:length(theta)for i_M=1:Mw(i_theta,i_M)=exp(sqrt(-1)*(i_M-1)*fai(i_theta));%方向矢量endP_music(i,i_theta)=1./(w(i_theta,:)*En*En'*w(i_theta,:)');endendP=abs(P)/num;P=P+P_music(i,:);figure(3)plot(theta,10*log10(P/max(P)),'.');xlabel('方位角 / 度');ylabel('归一化功率 / dB');gridtitle('不同信噪比下MUSIC方法估计的性能(统计100次)') hold onlegend('-5dB','0dB','5dB');。
