综合训练解答-1
人教版六年级上册第五单元圆综合训练(一)(含答案)

人教版六上第五单元圆综合训练(一)一、选择题(满分16分)1.下面几种说法中正确的是()A.圆周率表示圆的周长B.圆周率表示圆的周长与它直径的比的比值C.圆周率表示π保留两位小数的近似值2.大圆周长和直径的比()小圆周长和直径的比.A.大于B.小于C.等于D.不确定3.一个长方形的长是4厘米,宽是2厘米,在长方形内画一个最大的圆,圆的直径长是()厘米.A.4 B.1.25 C.2.5 D.24.以下四个图形中阴影部分面积最大的一个是()A.B.C.D.5.利用半径为5厘米的圆形纸片剪一个面积最大的正方形,此正方形的面积为()A..60平方厘米B.、55平方厘米C..50平方厘米6.在一个边长是8厘米的正方形里面画一个最大的圆,这个圆的半径是()厘米.A.4 B.8 C.167.在正方形内画一个最大的圆,若此圆周长是12.56厘米,则正方形面积是()A.16平方厘米B.16π平方厘米C.4平方厘米D.4π平方厘米8.如图中圆的直径是6厘米,则正方形的面积是()A.9.42cm2B.18cm2C.25cm2D.28.26cm2二、填空题(满分16分)9.一条线段长4cm,以它的中点为圆心画出的圆的周长是(______)cm,面积是(______)cm2。
10.一个圆形花坛的直径是3米,它的周长是(________)米,面积是(________)平方米。
11.用一条长20m的绳子绕一根圆柱形柱子6圈还余下1.16m这根圆柱形柱子底面的周长是(________)m,直径是(________)m。
12.推导圆的面积公式时,把圆剪成若干等份后拼成一个近似长方形,长方形的长是18.84分米,这个圆的半径是(________)分米,面积是(________)平方分米。
13.用一张正方形纸片剪成一个最大的圆,若正方形的周长是40cm。
剪成的圆的面积是(________)cm2。
14.如图长方形的长为12厘米,长方形的宽是(________)cm,两个等圆的半径是(________)cm。
四年级下册数学试题-思维训练专题:综合训练(1)(解析版)全国通用

备课说明:1、本讲课内部分内容(小数的组成、凑整、加减运算、计算体育比赛中的场次)较简单,可由学生自行完成。
整体难度不大,可让学生先做一部分然后教师再讲评。
填空4为格点面积计算,回顾格点面积公式;5为最值问题中考虑最不利情况求最值;7、8行程问题中涉及了和差问题、植树问题;9利用分割的方法求图形的面积;10利用枚举法解题,一些学生可能容易漏项。
简答题2应用包含与排除求阴影部分的面积;3为竞赛真题,是一道盈亏、行程综合题;4为2010年春蕾杯决赛题,关键在于通过错误的钟计算出正确的用时,学生意思到位即可。
由7个0.1和8个0.01组成的小数是 ,它的计数单位是 。
把它改写成三位小数是 。
解:0.78 ,百分位,0.780。
太平洋的面积约是179679000平方千米,改写成用“万”为单位的数是 平方千米,改写成用“亿”为单位的数是 平方千米。
(保留一位小数)解:17967.9万,1.8亿。
某小学进行乒乓球比赛,一共有18个队参加。
把18个队分成2组,进行单循环赛,每组要进行 场比赛。
解:一组 9218=÷(队)每组比赛场次 36289=÷⨯(场)有一个数,在它的末尾添上一个数字6,所得的数比原来大600000,这个数是 。
解:66666下图网格中的小正方形的边长是1,那么阴影部分的面积是 。
解:5.1318213=-+÷一个布袋里有大小相同、颜色不同的一些小球,其中红的10个,白的9个,黄的8个,蓝的2个,一次至少取 个球,才能保证有4个相同颜色的球。
解:12。
考虑最不利情况:蓝球2个,其它三色各3个,之后再取一个球即可保证有4个相同颜色的球,所以一次至少取121332=+⨯+(个)两地间的水路长252千米,一只船从甲地开往乙地顺流9小时到达;从乙地逆流返回甲地14小时到达。
船在静水中的速度是_____千米/时,水流的速度是_____千米/时。
(新知杯,第一届1试)解:顺水速度为 289252=÷(千米/时),逆水速度为 1814252=÷(千米/时)船速为 232)1828(=÷+(千米/时),水速为 52)1828(=÷-(千米/时) 一列火车长400米,铁路沿线的电杆间隔都是40米,这列火车从车头到达第一根电线杆到车尾离开第51根电线杆用了2分钟。
【2019年中考复习指南】2018-2019学年中考语文复习第二部分综合训练一积累与应用专题三病句的辨识与修改

【2019年中考复习指南】2018-2019学年中考语文复习第二部分综合训练一积累与应用专题三病句的辨识与修改一、单选题1. 下列句子中没有语病的一项是()A.在保留现有水源的基础上,杭州将逐步形成以千岛湖为主,钱塘江、东苕溪为辅的多水源供水,从而提高居民的用水品质。
B.如何在加快发展经济的同时,减少人口增长速度,保持人类与生态环境的平衡,这是摆在一些国家面前的重大课题。
C.我们欣赏古代诗词,应该全面了解作者的生平以及他所处的时代和环境,真正走进作品,去获得独特的审美体验。
D.当灵感迸发、文思泉涌时,美妙的文辞会源源不断地流泻到笔下,这都源于写作者平时注重知识和生活的积累为基础。
2. 下面句子没有语病的一项是()A.由于安倍政府对历史的严重歪曲,使日本和东亚各国的关系不断恶化。
B.只要你悉心品读汉字,认读汉字,就会发现它的神奇之处。
C.柳宗元的山水游记在中国文学史上具有独特的地位。
D.心理学家认为,让孩子讲故事有助于培养孩子的语言表达水平。
3. 下列句子没有语病的一项是()A.只有走好人生的每一步,我们才能真正拥有一个灿烂的明天。
B.由于母亲对我的悉心培育,使我从小就养成了勇敢的性格。
C.综艺节目深受欢迎的主要原因是其形式多样造成的。
D.谁能否认李时珍没有对中国的医学事业做出过巨大贡献呢?4. 下列各句中,没有语病的一项是()A.作为一档新兴的电视节目,《中国好声音》目前最重要的当务之急就是扬长避短,带给观众更为持久的音乐享受和情感感受。
B.当前,青少年深受网络语言的影响,忽视了汉语的规范化,这应引起教育工作者的高度重视。
C.“光盘”行动是一家民间组织发起的公益活动,意在发扬人人节约粮食的良好习惯。
D.语文课堂其实就是微缩的社会言语交际场,学生在这里学习将来步入广阔社会所需要的言语交际本领与素养。
5. 下列句子没有语病的一项是()A.今年中考期间,呼市市政府将严格整治辖区内的噪音污染,为考生营造安静的考试环境。
原电池综合训练习题(1)答案
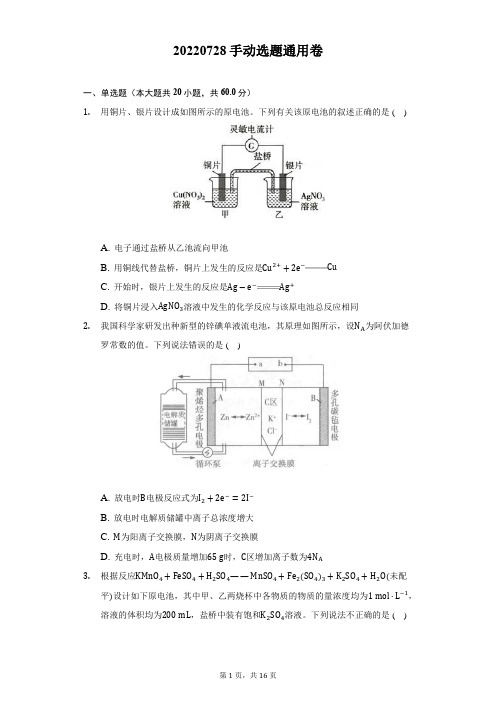
20220728手动选题通用卷一、单选题(本大题共20小题,共60.0分)1.用铜片、银片设计成如图所示的原电池。
下列有关该原电池的叙述正确的是( )A. 电子通过盐桥从乙池流向甲池B. 用铜线代替盐桥,铜片上发生的反应是Cu2++2e−CuC. 开始时,银片上发生的反应是Ag−e−Ag+D. 将铜片浸入AgNO3溶液中发生的化学反应与该原电池总反应相同2.我国科学家研发出种新型的锌碘单液流电池,其原理如图所示,设N A为阿伏加德罗常数的值。
下列说法错误的是( )A. 放电时B电极反应式为I2+2e−=2I−B. 放电时电解质储罐中离子总浓度增大C. M为阳离子交换膜,N为阴离子交换膜D. 充电时,A电极质量增加65g时,C区增加离子数为4N A3.根据反应KMnO4+FeSO4+H2SO4——MnSO4+Fe2(SO4)3+K2SO4+H2O(未配平)设计如下原电池,其中甲、乙两烧杯中各物质的物质的量浓度均为1mol·L−1,溶液的体积均为200mL,盐桥中装有饱和K2SO4溶液。
下列说法不正确的是( )A. 石墨b是原电池的负极,发生氧化反应B. 忽略溶液体积变化,Fe2(SO4)3浓度变为1.5mol·L−1,则反应中转移的电子为0.1molC. 甲烧杯中的电极反应为MnO4−+5e−+8H+Mn2++4H2OD. 电池工作时,盐桥中的K+向甲烧杯中移动4.一种以NaBH4和H2O2为原料的新型电池的工作原理如图所示。
下列说法错误的是( )A. 电池的负极反应为BH4−−8e−+8OH−BO2−+6H2OB. 电池放电时Na+从b极区移向a极区C. 电子从电极a经外电路流向电极bD. 放电一段时间后,正负两极生成的OH−和消耗的OH−的量相等5.利用小粒径零价铁(ZVI)的电化学腐蚀处理三氯乙烯进行水体修复,修复过程如图所示。
H+、O2、NO3−等共存物的存在会影响水体修复效果。
九年级数学竞赛综合训练题(1)(含解答)-

九年级数学竞赛综合训练题(1)(满分120分,考试时间120分)学校 班级 姓名一、选择题:(每小题5分,共30分)1.过点P (-1,3)作直线,使它与两坐标轴围成的三角形面积为5,这样的直线可以作( )条 (A )4 (B )3 (C )2 (D )1 2.方程13++x x -y=0的整数解有( )组 (A )1 (B )2 (C )3 (D )4 3.如图,若将图(a )的正方形剪成四块,恰能拼成图(b)的矩形,设a=1,则这个正方形的面积为( )(A )2537+ (B )253+(C )251+ (D )21(+)24.关于x 的不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有5个整数解,则a 的取值范围是( )(A )-6<a <-211 (B )-6≤a <-211 (C )-6<a ≤-211 (D )-6≤a ≤-2115.已知四边形ABCD ,从下列条件:(1)AB ∥CD (2)BC ∥AD (3)AB =CD (4)BC =AD (5)∠A =∠C (6)∠B =∠D中任取其中两个,可以得出“四边形ABCD 是平行四边形”这一结论的情况有( )种(A )4 (B )9 (C )13 (D )15 6.已知x 、y 、z 都是实数,且x 2+y 2+z 2=1,则m=xy+yz+zx ( )(A)只有最大值 (B )只有最小值 (C )既有最大值又有最小值 (D )既无最大值又无最小值 二、填空题:(每小题5分,共30分)jab a b ⅠⅡⅢⅣⅣⅢⅡⅠ(b)(a)ba7.已知x=1313+-,y=1313-+, 则x 4+y 4等于 .8.甲、乙两商店某种铅笔标价都是1元,一天,让学生小王欲购这种铅笔,发现甲、乙两商店都让利优惠:甲店实行每买5枝送1枝(不足5枝不送);乙店实行买4枝或4枝以上打8.5折,小王买了13枝这种铅笔,最少需要花 元.9.若1≤p ≤20, 1≤q ≤10,且方程4x 2-px+q=0的两根均为奇数,则此方程的根为 . 10.在1、2、……,2003中有些正整数n ,使得x 2+x -n 能分解为两个整系数一次式的乘积,则这样的n 共有 个.11.已知如图所示,∠MON=40°,P 为∠MON 内一点,A 为OM 上一点,B 为ON 上一点,则当△PAB 的周长取最小值时,∠APB 的度数为 .12.若关于x 的方程rx 2-(2r+7)x+r+7=0的根是正整数,则整数r 的值可以是 .三、解答题:(每小题15分,共60分)13.已知a 、b 、c满足方程组2848a b ab c +=⎧⎪⎨-+=⎪⎩, 试求方程bx 2+cx-a=0的根.PNMBOA14.已知两个二次函数y1 和y2,当x=a(a>0)时,y1取得最大值5,且y2=25. 又y2的最小值为-2,y1+y2=x2+16x+13. 求a的值及二次函数y1、y2的解析式.15.如图所示,正方形ABCD的边长为1,点M、N分别在BC、CD上,使得△CMN的周长为2.求:(1)∠MAN的大小;(2)△MAN面积的最小值.ND CMAB16.如图所示,四边形ABCD 是矩形,甲、乙两人分别从A 、B 同时出发,沿矩形按逆时针方向前进,即按A →B →C →D →……顺序前进,已知甲的速度为每分钟65米,乙的速度为每分钟74米,问乙至少在跑第几圈时才有可能第一次追上甲?又乙至多在跑第几圈时一定能追上甲?请说明理由。
2020-2021部编版七年级上册语文综合实践练习题含答案(1)

部编版七年级上册语文综合实践训练试题一、综合实践题1.综合运用。
某班拟开展以“漫步古诗苑”为主题的系列活动,请你参加并完成下列任务。
[古诗分类](1)班委会准备将教材中出现过的诗句分类编辑,下列诗句不宜放在“思乡”主题类的一项是③(只填序号)①仍怜故乡水,万里送行舟。
②浊酒一杯家万里,燕然未勒归无计。
③深林人不知,明月来相照。
④共看明月应垂泪,一夜乡心五处同。
⑤因思杜陵梦,凫雁满回塘。
[诗人竞猜](2)班委会举行“诗人竞猜”的猜谜活动,请仿照示例,在横线上填上适当的语句。
示例:(谜面)最恨凡尘世,一生独爱菊。
﹣﹣(谜底)陶渊明(谜面)生梦铁马冰河,死悲九州未同。
﹣﹣(谜底)陆游【分析】(1)本题考查诗句欣赏。
①②④⑤.正确;③.有误,“深林人不知,明月来相照”意思是说,自己僻居深林之中,也并不为此感到孤独,因为那一轮皎洁的月亮还在时时照耀自己。
这里使用了拟人化的手法,把倾洒着银辉的一轮明月当成心心相印的知己朋友,显示出诗人新颖而独到的想象力。
全诗的格调幽静闲远,仿佛诗人的心境与自然的景致全部融为一体了。
可见其中并无思乡情绪。
故选:③(2)本题考查古诗积累。
陆游是我国著名的爱国诗人,根据他所写的“死去元知万事空,但悲不见九州同”和“铁马冰河入梦来”可拟写谜面为:生梦铁马冰河,死悲九州未同。
不要求统一答案,意近即可。
【解答】答案:(1)③(2)示例:生梦铁马冰河,死悲九州未同。
【点评】综合读写就是灵活地联系生活,联系社会实际,考查学生在一个具体情境中综合运用语文的能力,看学生是否可以发现问题,是否可以简洁、流畅地表达自己的见解。
2.综合性学习。
学习了《雨的四季》,同学们一定熟悉了那灵动的声音、奇异的形体和清透的心灵,那么,请完成下列题目,让大家都能读懂雨的心曲。
【活动一:收集雨的词汇】自古以来,雨因为常见,所以在文字中均能见到它的身影。
请摘录含“雨”的两个成语和一个俗语写在下面。
成语:风调雨顺俗语:雷声大,雨点小【活动二:说说雨的功过】同学们针对雨的利与弊展开辩论,你赞成哪一方观点?请写出理由。
【整合】部编版七年级上册语文综合实践练习题及答案(1)

2.“一年之计在于春”,让我们走进春天,去寻觅春的芳踪。 (1)【描春】请联系全诗,仿照画线的诗句,将下面这首小诗补充完整。 春天的色彩 东风吹开了河面的薄冰 多彩的春姑娘便亮相了 洁白的头巾上 闪烁着纯真与无邪 湛蓝的眼眸里 透露出憧憬和希望
翠绿的衣裙间 展现出青春与美丽 (2)【赏春】春天到了,小明同学去踏春,欣赏春天的美景,并拍摄了两张照片,想各用 一个成语给照片取名字,请你帮他从下列成语中选择恰当的成语,将序号填入C.春回大地
(3)【护春】因为人类对自然的破坏,如今,朱自清笔下的春已失去了昔日的美丽。为了 让人类重新拥有美丽的春天,请你拟写一则环保公益广告。 【分析】(1)本题考查句子的仿写。根据前面给出的句子,可见此句应描写的是“春姑 娘”的美丽外貌,然后根据前两个句子的结构仿写即可。如:细嫩的面庞上,洋溢着青春 的气息。 (2)本题考查成语的理解。观察图画内容,再根据成语的理解,即可作出正确的选择。第 一幅图中是出土的嫩芽,应是“春回大地”合适;第二幅图中是盛开的花,选择“春暖花 开”。 (3)本题考查拟写广告语。为某个活动拟写广告语,所拟写的广告语一定要主题突出,语 意简洁明了,有号召性和鼓动性,一般多采用比喻和对偶的修辞。据此可拟写为:树木拥 有绿色,地球才有脉搏。 【解答】答案: (1)示例:翠绿的衣裙间 展现出青春与美丽 (2)C A (3)示例:树木拥有绿色,地球才有脉搏。 【点评】仿写要注意的几个问题: 1.仿句与被仿句不能雷同。二者的内容要做到:“花开两朵,各表一枝”。要有创新。
部编版七年级上册语文综合实践训练试题
一、综合实践题
1.学完课文《济南的冬天》后,班级开展了以“感悟冬天”为主题的综合性学习活动,请 你完成下面的任务。 (1)【补填诗句】请结合你的知识积累,将下面描写冬天的诗句补充完整。(任选两句) ①日暮苍山远, 天寒白屋贫 。 ② 燕山雪花大如席 ,纷纷吹落轩辕台。 ③千山鸟飞绝, 万径人踪灭 。 ④墙角数枝梅, 凌寒独自开 。 (2)【提取信息】“冬至”是二十四节气之一,请仔细阅读下面两段文字,从中提取关于 “冬至”的三条信息。
【专项】部编版七年级上册语文综合实践练习题及答案(1)

部编版七年级上册语文综合实践训练试题一、综合实践题1.冬天是一个洁白而美丽的季节。
冬天,虽然百花凋谢,寒气逼人,却带给人一种独特的情趣。
班级开展以“冬天的魅力”为主题的综合性学习活动,请你积极参与,完成下面的小题。
(1)请为这次活动设计一个主题词。
(2)班内两位文学爱好者在闲暇之余歌颂了“冬之美”,请根据你的理解,仿照例句,在空白处补写恰当的句子。
同学甲:冬之美,在于色彩之美。
夕阳的余辉洒在枯黄的落叶上,反射出淡黄色的光泽,照得大地熠熠生辉。
同学乙:冬之美,在于意境之美。
【分析】第一题考查拟写主题语。
第二题考查仿写。
【解答】(1)为某个活动拟写主题语,可以理解为拟写宣传语。
为某个活动拟写宣传语,所拟写的宣传语一定要主题突出,语意简洁明了,有号召性和鼓动性,一般多采用对偶的修辞。
可拟写为:走进冬天,领略美景。
(2)作答仿写类题目,需认真观察例句,分析例句的格式和语义,仿句要与例句格式相同,语义相关。
本题可仿写为:天地万物的枯荣如同人生的起起伏伏,枯萎中暗含着勃勃生机。
答案:(1)示例:走进冬天,领略美景。
(2)天地万物的枯荣如同人生的起起伏伏,枯萎中暗含着勃勃生机。
【点评】仿写句的类型有三种:以内容格式为主的仿写、从句式词性角度去仿写、以修辞为主的仿写。
仿写语句时要注意:一是仿写的句式和修辞手法的运用要与例句一致;二是所仿写的句子的内容与提示的内容要构成一个整体,语意连贯,合理顺畅。
2.班级组织了以“我为济南添色彩”为主题的语文实践活动,请你参与。
(1)【搜集古诗词】老舍先生非常喜欢济南的冬天,对济南情有独钟。
你能分别写出两句描写冬天和描写济南的诗句吗(2)【设计导游词】假如你是一位导游,冬季带领游客来济南观光,请追随老舍的足迹,设计一段导(3)【拟写宣传语】假定济南“泉水节”将于2018年10月下句开幕,请你为“泉水节”拟写一则宣传标语【分析】(1)本题考查古诗词句句的积累。
根据平时的积累,写出描写冬天的古诗句不难,比如:“墙角数枝梅,凌寒独自开”等,不要出现错别字即可。
人教版三年级数学下册第2单元综合训练 附答案 (1)
人教版三年级数学下册第2单元综合训练训练时间:80分钟满分:100分书写(3分)分)一、填空题。
(每空1分,共24分)1.从248里连续减4,减( )次后结果是0。
2.632÷3的商是( )位数,商的最高位在( )位上;426÷7的商是( )位数,商的最高位在( )位上。
3.△÷9=68……,余数最大是( ),此时被除数是( )。
4.估算570÷8时,可以把570看成( )来估算,结果大约是( )。
5. 305的4倍是( ),525是( )的5倍。
6.在里填上“>”“<”或“=”。
352÷4352÷6 480÷3960÷6320÷5420÷5 402÷3804÷47.( )里最大能填几?7×( )<285 ( )×5<358546>9×( ) 326>( )×88.把117辆玩具汽车装在7个箱子里,平均每个箱子装( )辆,还剩( )辆。
9. 68÷6,要使商中间有0且没有余数,里可以填( );52÷4,要使商的末尾有0,里最大填( )。
10.小马虎在计算一道除法算式时,错把除数6看成了9,得到的商是48,正确的商应该是( )。
二、判断题。
(对的画“√”,错的画“×”)(5分)1. 0除以任何数都得0。
( )2. 508÷3的商的中间有0。
( )3.一个数的7倍是861,这个数是123。
( )4.验算有余数的除法时,用“被除数=商×除数+余数”来验算。
( ) 5.在笔算除法时,除到哪一位不够商1,要商0占位。
( )三、选择题。
(将正确答案的序号填在括号里)(5分)1.下面算式中,商最接近60的是( )。
A.369÷6 B.336÷5 C.218÷42.有46支铅笔,每个小朋友分2支,可以分给多少个小朋友?才才用竖式计算出了结果,下面竖式中箭头所指的“4”表示( )。
第三章 勾股定理 实际应用综合训练(一)2021-2022学年苏科版八年级数学上册

第三章《勾股定理》实际应用综合训练(一)1.为了积极响应国家新农村建设的号召,遂宁市某镇政府采用了移动宣讲的形式进行广播宣传.如图,笔直的公路MN的一侧点A处有一村庄,村庄到公路MN的距离为600m,假使宣讲车P周围1000m以内能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶.(1)村庄能否听到广播宣传?请说明理由.(2)已知宣讲车的速度是200m/min,如果村庄能听到广播宣传,那么总共能听多长时间?2.如图,将长为2.5米的梯子AB斜靠在墙AO上,BO长0.7米.如果将梯子的顶端A沿墙下滑0.4米,即AM等于0.4米,则梯脚B外移(即BN长)多少米?3.图,A,B两个村庄分别在两条公路MN和EF的边上,且MN∥EF,某施工队在A,B,C三个村之间修了三条笔直的路.若∠MAB=65°,∠CBE=25°,AB=160km,BC=120km,求A,C两村之间的距离.4.某初中“数学兴趣小组”开展实践活动,在校园里测量一块四边形场地ABCD(如图所示)的周长,其中边CD上有水池和建筑物遮挡,没有办法直接测量其长度.经测量得知AB=AD=60米,∠A=60°,BC=80米,∠ABC=150°.如果你是数学兴趣小组的成员,请根据测量数据求出CD的长度.5.如图,小磊将一个梯子斜靠在墙上,梯子顶端距离地面的垂直距离记作MA,测得MA=a,梯子的底端P保持不动,将梯子的顶端靠在对面墙上,此时∠MPN=90°,梯子的顶端距离地面的垂直距离记作NB,测得NB=b,求A、B之间的距离.6.绿地广场有一块三角形空地将进行绿化,如图,在△ABC中,AB=AC,E是AC上的一点,CE=5,BC=13,BE=12.(1)判断△ABE的形状,并说明理由;(2)求线段AB的长.7.如图,已知某学校A与直线公路BD相距3000米,且与该公路上一个车站D相距5000米,现要在公路边建一个超市C,使之与学校A及车站D的距离相等,那么该超市与车站D的距离是多少米?8.交通安全是社会关注的热点问题,安全隐患主要是超速和超载.某中学八年级数学活动小组的同学进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点P,在公路l上确定点O、B,使得PO⊥l,PO=100米,∠PBO=45°.这时,一辆轿车在公路l上由B向A匀速驶来,测得此车从B处行驶到A处所用的时间为3秒,并测得∠APO=60°.此路段限速每小时80千米,试判断此车是否超速?请说明理由9.如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.(1)此时梯子顶端离地面多少米?(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?10.学校校内有一块如图所示的三角形空地ABC,计划将这块空地建成一个花园,以美化校园环境,预计花园每平方米造价为30元,学校修建这个花园需要投资多少元?11.如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.(1)A城是否受到这次台风的影响?为什么?(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?12.如图,笔直的公路上A、B两点相距25km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?13.如图,在树上距地面10m的D处有两只猴子,它们同时发现地面上C处有一筐水果,一只猴子从D 处向上爬到树顶A处,然后利用拉在A处的滑绳AC滑到C处,另一只猴子从D处先滑到地面B,再由B跑到C,已知两猴子所经过的路程都是15m,求树高AB.14.“引葭赴岸”是《九章算术》中的一道题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B'(如图).问水深和芦苇长各多少?(画出几何图形并解答)15.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)16.如图所示,公路MN和公路PQ在点P处交汇,点A处有一所中学,AP=160m,点A到公路MN 的距离为80m.假设拖拉机行驶时,周围100m以内会受到噪声影响,那么拖拉机在公路MN上沿PN 方向行驶时,学校是否会受到影响?请说明影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?17.甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源,为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为13.5km,如图,早上8:00甲先出发,他以6km/h的速度向东行走,1小时后乙出发,他以5km/h的速度向北行走,上午10:00,甲步行到A,乙步行到B.(1)求甲、乙二人相距多远?(2)甲、乙二人是否能保持联系并说明理由?18.郑州市CBD如意湖的两岸有A,B两棵景观树,数学兴趣小组设计实验测量两棵景观树之间的距离,他们在与AB垂直的BC方向上取点C,测得BC=30米,AC=50米.求:(1)两棵景观树之间的距离;(2)点B到直线AC的距离.19.我国古代的数学名著《九章算术》中记载“今有竹高一丈,末折抵地,去本三尺.问:折者高几何?”译文:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好着地,着地处离原竹子根部3尺远.问:原处还有多高的竹子?(1丈=10尺)20.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.(1)海港C受台风影响吗?为什么?(2)若台风的速度为25km/h,台风影响该海港持续的时间有多长?。
鲁教版2020七年级数学上册期中综合复习能力达标训练题1(附答案详解) (1)

33.已知△ABC在平面直角坐标系中的位置如图所示:
(1)画出△ABC关于y轴对称的△AB1C1;并写出B点的对应点B1的坐标;
(2)在y轴上找一点P,使得△PBC的周长最短;
34.如图,在四边形ABCD中,AB=4,BC=3,CD=12,AD=13,∠B=90°,连接AC.求四边形ABCD的面积.
21.如图,将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上,如果∠2=50°,那么∠1的度数为__.
22.已知点A(6a+3,4)与点B(2﹣a,b)关于y轴对称,则ab=_____.
23.如图,在△ABC中,AC=BC=9,∠C=120°,D为AC边上一点,且AD=6,E是AB边上一动点,连接DE,将线段DE绕点D逆时针旋转30°得到DF,若F恰好在BC边上,则AE的长为_____.
29.如图所示,A、D、E三点在同一直线上, , , 于点D, 于点E.
(1)求证:△BAD≌△ACE.
(2)判断BD、DE、CE之间的数量关系,并证明你的结论.
30.(1)如图, , 平分 ,若 , ,求 的度数;
(2)如图, , , 平分 ,若 的2倍与 的补角的和为 ,求 的度数.
(3)如图, 为(2)中射线 上一点, 是 上任一点, 平分 , , 平分 ,求 的度数.
35.在 中, , , 是 的角平分线,过点 作 于点 ,将 绕点 旋转,使 的两边交直线 于点 ,交直线 于点 ,请解答下列问题:
31.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
2020-2021人教部编版七年级上册语文综合实践练习题及答案(1)

部编版七年级上册语文综合实践训练试题一、综合实践题1.对联的基本要求。
①必须是两句,而且这两句字数一样多。
②头一句与第二句所用短语的结构与词性应当相同或相似,即是说必须形成对偶的修辞格。
如:国家富强,人民幸福。
这两句就可以称作对联:“国家富强”是主谓短语,“人民幸福”也是主谓短语:“国家”与“人民”都是名词,“富强”与“幸福”都是形容词。
③两句的内容必须有必然的联系,如果内容没有联系,即使符合前两点要求,也不能叫做对联。
④上联最后一个字应为仄声,下联最后一个字应为平声。
请根据对联要求,解答下面的问题。
你认为下面三个选项中,哪一个选项的内容不可以作为对联,请具体说出两个理由。
A.发奋识遍天下字,立志读尽人间书B.百花迎春满地香,幸福临门多喜气C.东风化雨山山翠,政策归心处处春【分析】本题考查对联常识。
认真阅读题干,了解对联一些常识。
然后分析选项,做出正确选择。
【解答】答案:AC可以作为对联。
B.项两句中,“满地香”与“多喜气”不构成对偶(或短语结构与词性不同)。
上联最后一个字应为仄声,而“香”是平声;下联最后一个字应为平声,而“气”是仄声。
B项不可以作为对联。
故选:B。
【点评】对联常识需要多加学习,长期坚持阅读就会增强悟性。
2.综合性学习。
阅读下面表格,按要求答题。
下面是一份“学生课外阅读种类统计表”,请认真研读后回答问题。
政治历史类文学艺术类科普类体育军事类其它高中生18%47%20%9%6%初中生9%68%15%3%5%小学生2%82%10%2%4%(1)随着年级的升高,学生的课外阅读呈现出怎样的特点?(2)你们学校要举行“读书节”,请你为你们班想几个读书活动。
【分析】(1)本题考查学生对表格内容的分析能力。
这一份表格的信息说明了年级越高学生的阅读面越广。
(2)本题考查设计活动板块的能力,结合题目中给的提示,再结合活动主题来组织答案即可。
例如:互相交换自己的好书,阅读,开展读书报告会等。
【解答】答案:(1)随着年级的升高,学生的课外阅读面越来越广,尽管仍以文艺类为主,但政治历史类、体育军事类和科普类等都有了很大的增长。
08第1、2章综合训练(1)-苏科版七年级数学上册同步训练
训练8:第1、2章综合训练(1)一、选择题1.一张纸片,第一次把它撕成两张小纸片,以后每次将其中的一张小纸片撕成更小的两张纸片,则第2019次后共有纸片( )A.2019张B.2020张C.4032张D.20160张2.观察图中正方形四个顶点所标的数字规律,可知数2019应标在( )A.第504个正方形的左下角B.第504个正方形的右下角C.第505个正方形的左上角D.第505个正方形的右下角3.如图,在数轴上,点A 表示1,现将点A 沿着数轴作如下移动,第一次将点A 向左移动3个单位长度到达点A 1,第2次将A 1点向右移动6个单位长度到达点A 2,第3次将点A 2向左移动9个单位长度到达点A 3,按照这种移动规律移动下去,第n 次移动到点n A ,如果n A 与原点的距离不小于20,那么n 的最小值是( )A.13B. 14C.15D. 164.设c b a ,,是从1到9的互不相同的整数,则abcc b a ++的最大值为( ) A.78 B. 1 C.87 D.924 5.观察下列一组数:1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6...其中每个数n 都连续出现n 次,那么这一组数的第119个数是( )A.14B.15C.16D.176.小学时候大家喜欢玩的“幻方”游戏,老师稍加创新改成了“幻圆”游戏,现在将-1,2,-3,4,-5,6,-7,8分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中b a +的值为( )A.-6或-3B. -8或1C.-1或-4D.1或-1二、填空题7.已知c b a ,,为有理数,若0,0<>bc ab ,则cc b b a a ||||||++的值为 . 8.设[x )表示大于x 的最小整数,如[3)=4,[-1.2)=-1,则下列结论:①[0)=0;②[x )-x 的最小值是0;③[x )-x 的最大值是1;④存在实数x ,使[x )-x =0.5成立.其中正确的有 .(填序号)三、解答题:9.计算:(1));361()1276521(-÷-+ (2)).3(]2)3(12[22-÷⨯--+-10.(1)观察一列数:,,81,27,934321⋅⋅⋅====a a a a ,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果)(为正整数n a n 表示这个数列的第n 项,那么=6a ,=n a .(可用幂的形式表示)(2)如果想要求103222221+⋅⋅⋅++++的值,可令①,10321022221+⋅⋅⋅++++=S 将①式两边同时乘2,得 ②,②-①,得10S = .(3)若(1)中的数列共有20项,设,20203...812793+++++=S 请利用上述规律和方法计算20S .(列式计算)11.埃及同中国一样,也是世界著名的文明古国,古代埃及人处理分数与众不同,他们一般只使用分子为1的分数,例如用15131+来表示52,用2817141++来表示73等。
小升初数学试题解答应用题训练综合练习带答案解析(1)1

小升初数学试题解答应用题训练综合练习带答案解析(1)1一、人教六年级下册数学应用题1.为了测量一个空瓶子的容积,一个学习小组进行了如下实验。
①测量出整个瓶子的高度是22厘米;②测量出瓶子圆柱形部分的内直径是6厘米;③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是5厘米;④把瓶盖拧紧,将瓶子倒置放平,无水部分是圆柱形,测量出无水部分圆柱的高度是12厘米。
(1)要求这个瓶子的容积,上面记录中的哪些信息是必须有的?________(填实验序号)(2)请根据选出的信息,求出这个瓶子的容积。
2.水果店里西瓜个数与哈密瓜个数的比为7:5,如果每天卖哈密瓜40个,西瓜50个,若干天后,哈密瓜正好卖完,西瓜还剩36个。
水果店里原来有西瓜多少个?3.以小强家为观测点,量一量,填一填,画一画。
(1)新城大桥在小强家________方向上________m处。
(2)火车站在小强家________偏________(________)°方向上________m处。
(3)电影院在小强家正南方向上1500m处。
请在图中标出电影院的位置。
(4)商店在小强家北偏西45°方向上2000m处。
请在图中标出商店的位置。
4.民航部门规定:乘坐飞机的旅客,携带行李超过20千克的部分,每千克要按飞机票原价的1.5%另行支付行李逾重费。
李青青从上海乘飞机,购买了七折机票,付钱707元,他携带了30千克的行李,应付行李逾重费多少元?5.某商店按15%的利润定价,然后又按定价打九折出售,结果每件还赚70元,这一商品的成本价是多少元?6.一个底面半径是6cm的圆柱形玻璃器皿里装有一部分水,水中浸没着一个高9cm的圆锥形铅锥,当铅锥从水中取出后,水面下降了0.5cm,这个圆锥的底面积是多少平方厘米?7.一堆圆锥形小麦,量得它的底面周长是12.56米,高是1.2米,如果每立方米小麦重0.6吨,这堆小麦重多少吨?(用“四舍五入”法保留一位小数)8.爸爸想在网上买一个小家电,A店打八五折销售,B店每满200元减30元。
[2020-2021]部编版七年级上册语文综合实践练习题含答案(1)
![[2020-2021]部编版七年级上册语文综合实践练习题含答案(1)](https://img.taocdn.com/s3/m/c9459f9827284b73f3425057.png)
部编版七年级上册语文综合实践训练试题一、综合实践题1.综合实践活动。
如今正是北雁南飞、瓜果飘香,大地丰收的季节,班上准备进行一次“感受自然,享受秋天”的秋游活动请你参与。
(1)请你为这次活动拟写一条标语,号召同学们积极参加吧!(2)在这次感受自然的综合性活动中,除了秋游活动,还可以开展哪些活动?请你再设计两个活动形式。
(3)假如你与大自然展开心灵对话,想试着结交几个自然界的朋友,你会选择哪个朋友,并说说你的理由。
(4)出发之前,老师和同学们推荐你给同学们讲几句话,请把你要讲的话写在下面。
【分析】(1)本题考查拟写宣传标语。
为某个活动拟写宣传语,所拟写的宣传语一定要主题突出,语意简洁明了,有号召性和鼓动性,一般多采用对偶的修辞。
据此可拟写为:走进自然,陶冶情操。
(2)本题考查设计活动。
为某个主题设计活动,活动的内容要与主题密切相关,要有可行性。
活动的名称要易于识记。
如:举行以“秋韵”为主题的摄影(摄像)比赛等。
(3)本题考查语言表达。
解答此题,首先要弄清讲话设定的情景及要求,了解对话的原因、对象、及讲话人身份,选择得体的语言表达。
首先选择自然界的朋友,然后说明为什么和它做朋友。
(4)本题考查语言表达。
解答此题,首先要弄清讲话的目的,语言要流畅得体。
【解答】答案:(1)示例:走进自然,陶冶情操;品味秋天的绚丽,体验丰收的快;拥抱秋天,放飞梦想。
(2)①举行以“秋韵”为主题的摄影(摄像)比赛②办一期以“秋天,我想对你说”为主题的手抄报(3)我选择秋水做我的朋友,因为秋水潺潺,像和万物依依低语,那若有若无的音符弹跳在心间,洗涤着心扉,叫人心旷神怡。
或:我选择大山做我的朋友,因为我敬佩它的不卑不亢,朴实坚强,隐忍厚重。
(4)示例:今天我们和秋天约会。
踏着轻快的脚步,哮着欢快的歌曲,我们去送足秋游!走进大自然、拥抱大自然,不仅能让我们领略秋天的美丽,感受生活的欢快,也会让我们学会思考,学会生活。
让我们付用心灵去审视大自然,审视人类,审视自己,善待周围的植物、动物,做大自然的好朋友。
浙江语文题型攻略文档:第二章 实用类、论述类文本阅读 综合训练1 含答案

综合训练1阅读下面的文字,完成文后题目.魏晋南北朝之时,侠客的书写开始出现在诗歌中。
魏晋诗歌中的男侠大多是边塞的少年侠客.他们的特质,总是自恋、爱美、高傲、挥霍无度、重友情而轻金钱和死生,甚至可以为友人或知遇者牺牲生命,然而魏晋南北朝的边塞诗歌大多是诗人的想象之作。
到了唐朝,这种书写传统有了很大的改变,促成了侠客诗风的发展高峰。
唐朝诗歌的侠客传统,主要出现在边塞诗中。
唐朝边塞诗所描写的侠客,大多是胸怀大志的少年侠客,也有些是住在西北边境、生活浪荡、喜欢逞凶斗狠的游侠儿,还有些则是在长安、洛阳犯案之后逃到边塞的侠客。
然而,当他们眼见西北外族入侵而国家危难之时,他们体内的另一种侠客情怀--爱国之情随之兴起,因而毅然从军报国.唐朝边塞诗中,就有许多作品是描写侠客的从军报国。
然而对于许多诗人侠客而言,从军只是纯粹的爱国表现。
许多诗人与侠客甚至是反战的。
从汉末到唐初,长期以来一直是战争频发的乱世。
到了盛唐,又因拓展疆域的政策而长年征战。
到了中晚唐,更因为“安史之乱”与藩镇割据,内战不断。
侠客与诗人,甚至是平民百姓,早已厌倦而害怕战争.在唐朝边塞诗中,许多作品深刻反映了诗人与侠客的厌战与反战的心态。
特别是晚唐,除了内战之外,还有外族入侵。
由于藩镇割据与长期的内战消耗,士兵与百姓,不管是在实质的体力还是精神上,都已经无法抵抗外族的入侵,因此有许多作品不仅主张反战,甚至大胆直言以投降的方式来争取和平。
报恩与报仇是侠客最显著的特质.报恩,尤其是报知遇之恩,从《史记》的《刺客列传》就已是侠客特质的标签.而这个特质,对诗人侠客也不例外。
高适报答哥舒翰即是典型的例子。
侠客复仇,不管是为知遇者、友人、国家、正义或是为自己复仇,一直是古典文学所称颂的侠客精神。
侠客复仇,并不是文学所虚构出来的。
从史料得知,从春秋战国、汉魏六朝,甚至到了唐朝,复仇风气在社会上一直都非常盛行。
虽然复仇是侠客用来展现侠义精神的重要行为,但男性侠客与女性侠客在复仇上,有着相当大的差别.男侠客可以为知遇者、为朋友、为弱小、为国家、为正义、为自己复仇,但从来没有为家人复仇的,而诗歌中的女侠客,只为家人复仇。
排列 组合综合训练(一)

排列组合综合训练(一)1. 从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有A .240种B .280种C .96种D .180种2. 5个人排成一排,甲和乙不相邻,甲和丙也不相邻的不同排法种数为A .24B .36C .48D .603. 将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中.若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有A .12种B .18种C .36种D .54种4. 五位同学参加某作家的签字售书活动,则甲、乙都排在丙前面的方法有A .20种B .24种C .40种D .56种5. 将红、黑、黄、蓝4个不同的小球放入3个不同的盒子,每个盒子至少放一个球,且红球和蓝球不能放到同一个盒子,则不同放法的种数为A .18B .24C .30D .366. 现有男、女学生共7人,从男生中选1人,从女生中选2人分别参加数学、物理、化学三科竞赛,共有108种不同方案,那么男、女生人数分别是A .男生4人,女生3人B .男生3人,女生4人C .男生2人,女生5人D .男生5人,女生2人.7. 西大附中数学组有实习老师共5名,现将他们分配到高二年级的1、2、3三个班实习,每班至少1名,最多2名,则不同的分配方案有A .30种B .90种C .180种D .270种8. 设m ∈N *,且m <25,则(25-m )(26-m )…(30-m )等于A .625m A -B .2530m m A --C .630m A -D .530m A -9. 将A 、B 、C 、D 、E 五种不同的文件放入编号依次为1,2,3,4,5,6的六个抽屉内,每个抽屉至多放一种文件,若文件A 、B 必须放入相邻的抽屉内,文件C 、D 也必须放入相邻的抽屉内,则文件放入抽屉内的满足条件的所有不同的方法有 种A .24B .48C .96D .19210. 式子(1)(2)(100)100!n n n n ++⋅⋅⋅+可表示为 A .100100n A +B .100100nC + C .101100100n C +D .101101100n C + 11. 5男生,2个女生排成一排,若女生不能排在两端但又必须相邻,则不同的排法有A .480B .960C .720D .144012. 有五名同学站成一排照毕业纪念照,其中甲不排在乙的左边,又不与乙相邻,则不同的站法共有A .66种B .60种C .36种D .24种13. 从0,1,2,…,9这10个数字中,任取两个不同数字作为平面直角坐标系中点的坐标,能够确定不在x 轴上的点的个数是A .100B .90C .81D .7214. 方程),,(100N z y x z y x ∈=++的解的组数为A .299CB .2100C C .2101CD .2102C15. 某班学生参加植树节活动,苗圃中有甲、乙、丙3种不同的树苗,每种树苗足够多,从中取出5棵分别种植在排成一排的5个树坑内,同种树苗不能相邻,且第一个树坑和第5个树坑只能种甲种树苗的种法共有A .15种B .12种C .9种D .6种16. 5名同学去听同时进行的4个课外知识讲座,每名同学可自由选择听其中的1个讲座,不同选法的种数是A .45B .54C .2345⨯⨯⨯D .!42345⨯⨯⨯ 17. 6人站成一排,甲、乙、丙3个人不能都站在一起的排法种数为____________.18. 从1到9的九个数字中,取三个偶数四个奇数,组成没有重复数字的7位数,其中任意两个偶数不相邻的七位数有___________个(结果用数字作答)19. 5本不同的书,分给三名同学,每人至少一本,则不同的分配方法种数为 .20. 从甲、乙、丙、丁四名同学中选出三名同学,分别参加三个不同科目的竞赛,其中甲同学必须参赛,则不同的参赛方案共有________.21. 7名学生按要求排成一排,分别有多少种排法?(1)甲乙二人不站在两端;(2)甲、乙、丙必须相邻;(3)7名学生中有4男3女,4名男生站在一起,3名女生要站在一起。
人教版三年级数学下册第4单元综合训练 附答案 (1)

人教版三年级数学下册第4单元综合训练训练时间:80分钟满分:100分书写(3分)分)一、填空题。
(每空1分,共27分)1.已知17×9=153,那么170×9=( ),17×900=( )。
2.计算45×22,可以先口算45×20=( ),再口算( ),最后把两次算得的积加起来,即( )。
3.4.求31个45相加的和是多少,列简便算式是( ),结果是( )。
5.估算52×29时,可以把52看作( ),把29看作( ),估算结果是( )。
6.78与最小的两位数的积是( ),最大的两位数与28的积是( )。
7.在里填上“>”“<”或“=”。
80×807×900 13×1514×1414×300140×308.6×16,要使积是三位数,里最大填( );要使积是四位数,里最小填( )。
9.张老师去文具店买了32支相同的钢笔,付给营业员600元。
A种钢笔每支25元,B种钢笔每支16元,C种钢笔每支10元。
他买的是( )种钢笔,一共用去( )元,应找回( )元。
10.在庆“六一”合唱比赛中,有35支合唱队参赛,每支合唱队站2排,每排18人。
参加这次合唱比赛的一共有( )人。
二、判断题。
(对的画“√”,错的画“×”)(5分)1.两位数乘两位数,乘数的末尾一共有几个0,积的末尾一定也有几个0。
( )2.两个数的积一定大于这两个数的和。
( )3. 48×21的积与84×12的积相等。
( )4. 69×38的计算结果小于2800。
( )5.一本书有400页,元元如果每天读28页,两周就能全部读完。
( )三、选择题。
(将正确答案的序号填在括号里)(5分)1. 39×51的积与算式( )的积最接近。
A.30×50 B.40×60 C.40×502.下面表述正确的是( )。
平行线综合训练(难题)-附答案

绝密★启用前平行线第I 卷(选择题)一、单选题1.(2021·四川宜宾市·七年级期末)将一副三角板中的两块直角三角尺的直角顶点C 按如图方式叠放在一起(其中,∠A =60°,∠D =30°;∠E =∠B =45°)将三角尺ACD 固定,三角尺BCE 的CE 边与CA 边重合,绕点C 顺时针方向旋转,当0°<∠ACE <180°且点E 在直线AC 的上方时,下列结论中:∠若∠DCE =35°,∠ACB =145°;∠∠ACB +∠DCE =180°;∠当三角尺BCE 的边与AD 平行时∠ACE =30°或120°;∠当三角尺BCE 的边与AD 垂直时∠ACE=30°或75°或120°,正确个数有( )A .4个B .3个C .2个D .1个2.(2020·甘肃天水市·七年级期末)如图的四个图中,∠1与∠2是同位角的有( )A .②③B .①②③C .①D .①②④第II 卷(非选择题)二、填空题3.(2020·黑龙江哈尔滨市·七年级期末)如图,AB ,CD 相交于点E ,ACE AEC ∠=∠,BDE BED ∠=∠,过A 作AF BD ⊥,垂足为F .求证:AC AF ⊥.证明:∵ACE AEC ∠=∠,BDE BED ∠=∠ 又AEC BED ∠=∠(________________) ∴ACE BDE ∠=∠∴//AC DB (________________________) ∴CAF AFD ∠=∠(________________________) ∵AF DB ⊥∴90AFD ∠=︒(________________________) ∴90CAF =︒∠ ∴AC AF ⊥4.(2020·宁波市惠贞书院七年级期中)如图,//AB EF ,设90C ∠=︒,那么x ,y ,z 的关系式______.5.(2020·宁波市惠贞书院七年级期中)如图,//EF AD ,//AD BC ,CE 平分BCF ∠,120DAC ∠=︒,20ACF ∠=︒,FEC ∠为______°.三、解答题6.(2020·浙江金华市·七年级期中)如图,已知直线a ⊥直线b ,垂足为点O .将直角三角形纸板ABC 的直角边AC 放置在直线a 上,线段AB (或射线AB )与直线b 交于点D ,直线//CE AB 交直线b 于点E ,AF 平分DAO ∠,EF 平分DEC ∠,设BAC x ∠=度,ABC y ∠=度,且:1:2x y =. (1)求x ,y 的值及ADO ∠的度数:(2)如图,当A 、C 两点在点O 的两侧时,求AFE ∠的度数;7.(2020·浙江金华市·七年级期中)如图(1)所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”.(1)如图(2)所示,已知//AB CD ,请问B ,D ∠,E ∠有何关系并说明理由; (2)如图(3)所示,已知//AB CD ,请问B ,E ∠,D ∠又有何关系并说明理由;(3)如图(4)所示,已知//AB CD ,请问E G +∠∠与B F D ++∠∠∠有何关系并说明理由.8.(2020·长汀县第四中学七年级月考)如图,已知AB ∥CD ,BE 平分∠ABC ,DE 平分∠ADC ,∠BAD =80°,试求: (1)∠EDC 的度数.(2)若∠BCD =n °,试求∠BED 的度数.(用含n 的式子表示)(3)类比探究:已知AB ∥CD ,BE 、DE 分别是∠ABC 、∠ADC 的n 等分线,ABE ∠=1ABC n ∠,1CDE ADC n∠=∠,∠BAD =α,∠BCD =β,请猜想∠BED = .9.(2021·重庆万州区·七年级期末)已知AB ∥CD ,CF 平分∠ECD . (1)如图1,若∠DCF =25°,∠E =20°,求∠ABE 的度数.(2)如图2,若∠EBF =2∠ABF ,∠CFB 的2倍与∠CEB 的补角的和为190°,求∠ABE 的度数.10.(2020·四川资阳市·七年级期末)如图,直线AB 和直线BC 相交于点B ,连接AC ,点,,D E H 分别在AB 、AC 、BC 上,连接DE 、DH ,F 是DH 上一点,已知13180︒∠+∠=(1)求证:CEF EAD ∠=∠;(2)若DH 平分BDE ∠,2α∠=∠,求3∠的度数.(用α表示)11.(2021·北京通州区·九年级期末)如图,将正方形ABCD 绕点B 顺时针旋转()090θθ︒<<︒,得到正方形BEFG .连接AG ,与正方形交于点H ,K ,连接EC ,DF .(1)求BAG ∠的值(用θ表示); (2)求证://AG EC ;(3)写出线段AG ,EC ,DF 之间的数量关系,并证明.12.(2020·吉林长春市·七年级期末)(感知)如图①,//AB CD ,130PAB ∠=︒ ,120PCD ∠=︒.求APC ∠的度数.(提示:过点P 作直线//PQ AB )(探究)如图②,//AD BC ,点P 在射线OM 上运动,ADP a ∠=∠ ,BCP β∠=∠.(1)当点P 在线段AB 上运动时,CPD ∠,α∠,β∠之间的数量关系为_______________.(2)当点P 在A ,B 两点外侧运动时(点P 与点A ,B ,O 三点不重合),直接写出CPD ∠,a ∠,β∠ 之间的数量关系为____________________________________________________________.13.(2020·黑龙江哈尔滨市·七年级期末)三角形ABC 中,D 是AB 上一点,//DE BC 交AC 于点E ,点F 是线段DE 延长线上一点,连接FC ,180BCF ADE ∠+∠=︒.(1)如图1,求证://CF AB ;(2)如图2,连接BE ,若40ABE ∠=︒,60ACF ∠=︒,求BEC ∠的度数; (3)如图3,在(2)的条件下,点G 是线段FC 延长线上一点,若:7:13EBC ECB ∠∠=,BE 平分ABG ∠,求CBG ∠的度数.14.(2020·黑龙江哈尔滨市·七年级期末)如图1是长方形纸带将长方形ABCD 沿EF 折叠成图2,使点C 、D 分别落在点1C 、1D 处,再沿BF 折叠成图3,使点1C 、1D 分别落在点2C 、2D 处.(1)若20DEF ∠=︒,求图1中CFE ∠的度数; (2)在(1)的条件下,求图2中1C FC ∠的度数;(3)在图3中写出2C FE ∠、EGF ∠与DEF ∠的数量关系,并说明理由.15.(2020·重庆沙坪坝区·七年级期末)如图1,AB ∥CD ,直线AE 分别交AB 、CD 于点A 、E .点F 是直线AE 上一点,连结BF ,BP 平分∠ABF ,EP 平分∠AEC ,BP 与EP 交于点P .(1)若点F 是线段AE 上一点,且BF ⊥AE ,求∠P 的度数;(2)若点F 是直线AE 上一动点(点F 与点A 不重合),请直接写出∠P 与∠AFB 之间的数量关系.16.(2020·河南新乡市·七年级期末)把一块含60°角的直角三角尺()0090,60EFG EFG EGF ∠=∠=放在两条平行线,AB CD 之间.(1)如图1,若三角形的60°角的顶点G 放在CD 上,且221∠=∠,求1∠的度数;(2)如图2,若把三角尺的两个锐角的顶点,E G 分别放在AB 和CD 上,请你探索并说明AEF ∠与FGC ∠间的数量关系;(3)如图3,若把三角尺的直角顶点F 放在CD 上,30°角的顶点E 落在AB 上,请直接写出AEG ∠与CFG ∠的数量关系.17.(2020·山东省青岛第五十九中学八年级期末)如图,已知BC AE ⊥,DE AE ⊥,23180∠+∠=︒.(1)请你判断1∠与ABD ∠的数量关系,并说明理由; (2)若170∠=︒,BC 平分ABD ∠,试求ACF ∠的度数.18.(2020·忠县乌杨初级中学校七年级月考)如图,已知直线l 1//l 2,l 3、和l 1、l 2分别交于点A 、B 、C 、D ,点P 在直线l 3或上且不与点A 、B 、C 、D 重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P 在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P 在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系; (3)若点P 在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明; (4)若点P 在线段DC 延长线上运动时,请直接写出∠1、∠2、∠3之间的关系.19.(2020·福建福州市·七年级期末)已知两条直线l 1,l 2,l 1∥l 2,点A ,B 在直线l 1上,点A 在点B 的左边,点C ,D 在直线l 2上,且满足115ADC ABC ∠=∠=o .(1)如图①,求证:AD ∥BC ;(2)点M ,N 在线段CD 上,点M 在点N 的左边且满足MAC BAC ∠=∠,且AN 平分∠CAD ;(Ⅰ)如图②,当30ACD ∠=o 时,求∠DAM 的度数; (Ⅱ)如图③,当8CAD MAN ∠=∠时,求∠ACD 的度数.20.(2020·四川省成都市玉林中学七年级期中)如图1,已知//AB CD ,直线MN 分别与直线AB 、CD 相交于点N M 、,点E 在直线上AB ,连接CE 交直线MN 于点H .(1) 求证:EHM AEH CMH ∠=∠+∠.(2)如图2,连接DN ,交CE 于点K ,过点C 作CG DN ⊥交DN 的延长线于点G ,交AB 于点F ,且2BND ECD MND ∠=∠=∠,当CE 平分DCG ∠时,求EHM ∠的大小.(3)在(2)的条件下,将EHN ∆绕着点N 以每秒10︒的速度按顺时针方向旋转,设旋转时间为t 秒)018t ≤≤(当EHN ∆的边HE 与GNF ∆的某一边平行时,请直接写出此时t 的值.参考答案1.B【详解】解:∵∠ECB=90°,∠DCE=35°,∴∠DCB=90°-35°=55°,∴∠ACB=∠ACD+∠DCB=90°+55°=145°,故∠正确;∵∠ACD+∠BCE=∠ACD+∠BCD+∠DCE =180°,∴∠ACB+∠DCE=180°,故∠正确;当AD//BC时,如图所示:∵AD//BC,∠∠DCB=∠D=30°,∵∠ACE+∠ECD=∠ECD+∠BCD=90°,∠∠ACE=∠DCB=30°;当AD//CE时,如图所示:∠AD//CE;∴∠DCE=∠D=30°,∴∠ACE=∠ACD+∠DCE=120°,当BE//AD时,延长AC交BE于F,如图所示:∠BE//AD,∠∠CFB=∠A=60°,∠∠CFE=120°,∠∠E=45°,∠∠ECF=180°-∠E-∠CFE=15°,∠∠ACE=165°,综上,当三角尺BCE的边与AD平行时,∠ACE=30°或120°或165°,故∠错误;当CE⊥AD时,如下图∵CE⊥AD,∴∠A+∠ACE=90°,∵∠A=60°,∴∠ACE=30°,当EB⊥CD时,如下图,∵EB⊥CD,∴∠E+∠EFD=90°,∵∠E=45°,∴∠AFC=∠EFD=∠E=45°,∴∠ACE=180°-∠A-∠AFC=75°, 当BC ⊥AD 时,如下图,∠BC∠AD ,BC ⊥CE , ∠AD//CE ,∴∠DCE=∠ADC=30°, ∴∠ACE=∠ACD+∠DCE=120°. 综上所述当三角尺BCE 的边与AD 垂直时∠ACE=30°或75°或120°,④正确. 故正确的有3个, 2.D 【详解】解:①∠1和∠2是同位角; ②∠1和∠2是同位角;③∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共,∠1和∠2不是同位角;④∠1和∠2是同位角.∴∠1与∠2是同位角的有①②④. 故选:D .3.对顶角相等;内错角相等,两直线平行;两直线平行,内错角相等;垂直定义4.90x y z +-=︒ 【详解】如图,过C 作//CN AB ,过D 作//DM AB ,∴//////AB CN DM EF ,∴1x =∠,23∠∠=,4z ∠=, ∵90BCD ∠=︒, ∴1290∠+∠=︒, ∴390x +∠=︒,∴3490x z +∠+∠=︒+, ∴90x y z +=︒+,∴90x y z +-=︒. 故答案为:90x y z +-=︒.5.20 【详解】 ∵//AD BC ,∴180DAC ACB ∠+∠=︒. ∵120DAC ∠=︒, ∴180********ACB DAC ∠=︒-∠=︒-︒=︒.∵60BCF ACF ACB ∠+∠=∠=︒. 又∵20ACF ∠=︒, ∴602040BCF ACB ACF ∠=∠-∠=︒-︒=︒.∵CE 平分BCF ∠, ∴∠BCE =∠ECF =12∠BCF =20° ∵//EF BC ,∴20FEC BCE ∠=∠=︒, ∴20FEC ∠=︒. 故答案为:20.6.(1)30x =︒,60y =︒,60ADO ∠=︒;(2)45︒;【详解】解:(1)∵ABC 是直角三角形, ∴90BAC ABC ∠+∠=︒,即90x y +=︒,∵:1:2x y =, ∴30x =︒,60y =︒, ∵a b ⊥,∴90DOA BCA ∠=︒=∠, ∴//DO BC ,∴60ADO ABC ∠=∠=︒; (2)如图,连接AE ,∵//AB CE ,∴30BAC OCE ∠=∠=︒, ∴9060CEO OCE ∠=︒-∠=︒, ∵AF 平分BAC ∠,∴1152FAO BAC ∠=∠=︒, 同理1302FEO CEO ∠=∠=︒,∵90AOE ∠=︒,∴90OAE OEA ∠+∠=︒, ∴159030FAO OAE OEA FEO ∠+∠+∠+∠=︒+︒+︒,∴135FAE FEA ∠+∠=︒, ∴()18045AFE FAE FEA ∠=︒-∠+∠=︒;7.(1)E B D ∠=∠+∠,理由见解析;(2)360B D E ∠+∠+∠=︒,理由见解析;(3)B F D E G ∠+∠+∠=∠+∠,【详解】(1)E B D ∠=∠+∠,理由如下: 如图所示,过点E 作直线a ,使得////a AB CD ,则1B ∠=∠,D 2∠=∠,(两直线平行,内错角相等),∴12BED B D ∠=∠+∠=∠+∠, 即:E B D ∠=∠+∠;(2)360B D E ∠+∠+∠=︒,理由如下:如图所示,过点E 作直线b ,使得////b AB CD ,则3180B ∠+∠=︒,4180D ∠+∠=︒,(两直线平行,同旁内角互补), ∴34360B D ∠+∠+∠+∠=︒, ∵34BED ∠=∠+∠,∴360B D BED ∠+∠+∠=︒, 即:360B D E ∠+∠+∠=︒;(3)B F D E G ∠+∠+∠=∠+∠,理由如下:如图所示,过点E ,F ,G 作直线c ,d ,e ,使得////////c d e AB CD , 则5B ∠=∠,67∠=∠,89∠=∠,10D ∠=∠,(两直线平行,内错角相等),∵65BEF BEF B ∠=∠-∠=∠-∠,910FGD FGD D ∠=∠-∠=∠-∠,∴7869EFG BEF B FGD D∠=∠+∠=∠+∠=∠-∠+∠-∠, ∴EFG B D BEF FGD∠+∠+∠=∠+∠,即:B F D E G ∠+∠+∠=∠+∠.8.(1)40︒;(2)1402BED n ∠=︒+︒;(3)1()αβ+n【详解】解:(1)∵AB ∥CD , ∴∠ADC =∠BAD =80°, 又∵DE 平分∠ADC ,∴1402EDC ADC ∠=∠=︒;(2)如图,过点E 作EF ∥AB ,则EF ∥AB ∥CD ,∵AB ∥CD ,∴∠ABC =∠BCD =n °, 又∵BE 平分∠ABC , ∴12ABE n ∠=︒, ∵EF ∥AB , ∴12BEF ABE n ∠=∠=︒, ∵EF ∥CD ,∴∠FED =∠EDC =40°,∴1402BED n ∠=︒+︒.(3)1()αβ+n. 如图,过点E 作EF ∥AB ,则EF ∥AB ∥CD ,∵AB ∥CD , ∴∠ABC =∠BCD =β,∠ADC =∠BAD =α, ∴1ABE nβ∠=,111FED CDE ADC BAD n n nα∠=∠=∠=∠=,∵EF ∥AB ,∴1 BEF ABEnβ∠=∠=,∴1() BEDnαβ∠=+.故答案为:1()αβ+n.9.(1)∠ABE=30°;(2)∠ABE=30°【详解】解:(1)假设CE与AB相交于点G,如图所示:∵CF平分∠DCE,∠DCF=25°,∴∠DCE=50°,∵AB∥DC,∴∠DCE+∠AGC=180°,∴∠AGC=130°,∴∠EGB=∠AGC=130°,∵∠E=20°,∴∠ABE=30°;(2)假设CE与AB、BF相交于点M、N,如图所示:设∠ABF=x,∠DCF=y,∵∠EBF=2∠ABF,CF平分∠DCE,∴∠EBF=2x,∠ABE=3x,∠FCE=y,∠DCE=2y,∵AB∥DC,∴∠DCE+∠AMC=180°,∴∠EMB=∠AMC=180°-2y,∵∠E+∠EMB+∠ABE=180°,∴∠E=2y-3x,∵∠E+∠ENB+∠FBE=180°,∴∠ENB=180°+x-2y,∵∠CFB+∠CNF+∠FCE=180°,∴∠CFB=y-x,∵∠CFB的2倍与∠CEB的补角的和为190°,∴2∠CFB-∠CEB=10°,∴()()22310y x y x---=︒,解得:10x=︒,∴∠ABE=30°.10.(1)见解析(2)90°+12α【详解】解:(1)∵∠3+∠DFE=180°,∠1+∠3=180°∴∠DFE=∠1,∴AB∥EF,∴∠CEF=∠EAD;(2)∵AB∥EF,∴∠2+∠BDE=180°又∵∠2=α∴∠BDE=180°−α又∵DH平分∠BDE∴∠1=12∠BDE=12(180°−α)∴∠3=180°− 12(180°−α)=90°+12α.11.(1)452BAGθ︒=-∠;(2)见解析;(3)AG DF EC=+,见解析【详解】(1)由旋转得090EBG =∠,AB BG =∴000180(90)4522BAG θθ-+==-∠(2)∵BE BC =,090EBC θ-∠=∴()0180-90-=2245CEB θθ︒︒+∠=又∵00452245EHA θθθ-+=+∠=∴∠CEB=∠EHA ∴ AG EC ∥.(3)如图延长FD 到I 使DI EC =,联结EI ,AI∵BE CB = ∴BEC BCE ∠=∠ ∴12∠=∠ ∴EJ JC = ∵CD EF = ∴DJ JF = ∴34∠=∠ ∵EJC DJF ∠=∠ ∴23∠∠= ∵DF EC ∥即DI EC ∥ 又∵DI EC =∴四边形DIEC 为平行四边形 ∴DC IE =,DC IE ∥ ∵DC AB =,DC AB ∥∴IE AB =,IE AB ∥ ∴四边形IABE 为平行四边形 ∴IA EB =,IA EB ∥ ∵FG EB =,FGEB∴FG IA =,FG IA ∥ ∴四边形IAGF 为平行四边形 ∴AG IF =∴AG DF EC =+.12.【感知】110︒;【探究】(1)CPD αβ∠=∠+∠;(2)CPD αβ∠=∠-∠或CPD βα∠=∠-∠.【详解】解:过点P 作直线//PQ AB , ∠//AB CD ,∠//PQ CD .∠180PAB APQ ∠+∠=︒,180QPC PCD ∠+∠=︒,∠130PAB ∠=︒,120PCD ∠=︒, ∠50APQ ∠=︒,60CPQ ∠=︒, ∠5060110APC ∠=︒+︒=︒. ∠APC ∠的度数为110︒. 探究(1)CPD αβ∠=∠+∠. 如图∠:作//PQ BC , ∠//AD BC ,∠////PQ BC AD ,∠∠DPQ=∠α,∠CPQ=∠β , ∠DP C Q PD CPQ αβ∠+∠=∠=∠+∠;(2)CPD αβ∠=∠-∠或CPD βα∠=∠-∠.如图∠:当P 在AM 上时,作//PQ BC ,∠//AD BC , ∠////PQ BC AD ,∠∠DPQ=∠α,∠CPQ=∠β , ∠CP C Q PD DPQ βα∠-∠=∠=∠-∠;当P 在OB 上时,同理:CPD αβ∠=∠-∠.综上所述,CPD βα∠=∠-∠或CPD αβ∠=∠-∠.13.(1)证明见解析;(2)100°;(3)12°. 【详解】(1)证明:∵DE ∥BC , ∴ADE B ∠=∠,又∵∠BCF +∠ADE =180°, ∴180BCF B ∠+∠=︒, ∴//CF AB ,(2)解:过E 作//EK AB ,∵//CF AB , ∴//CF EK ,∵//EK AB ,40ABE ∠=︒, ∴40BEK ABE ∠=∠=︒, ∵//CF EK ,60ACF ∠=︒, ∴60CEK ACF ∠=∠=︒, 又∵BEC BEK CEK ∠=∠+∠, ∴4060100BEC ∠=︒+︒=︒, 答:BEC ∠的度数是100°,(3)解:∵BE 平分ABG ∠,40ABE ∠=︒,∴40EBG ABE ∠=∠=︒, ∴:7:13EBC ECB ∠∠=,∴设7EBC x ∠=︒,则13ECB x ∠=︒, ∵DE ∥BC ,∴7DEB EBC x ∠=∠=︒,13AED ECB x ∠=∠=︒,∵180AED DEB BEC ∠+∠+∠=︒,∴137100180x x ++=, ∴4x =,∴728EBC x ∠=︒=︒, 又∵EBG EBC CBG ∠=∠+∠, ∴CBG EBG EBC ∠=∠-∠, ∴402812CBG ∠=-=︒, 答:CBG ∠的度数是12°.14.(1)160°;(2)40°;(3)2C FE DEF EGF ∠+∠=∠,理由见解析 【详解】解:(1)∵长方形ABCD , ∴//AD BC ,∴180DEF CFE ∠+∠=︒ ∵20DEF ∠=︒, ∵180********CFE DEF ∠=︒-∠=︒-︒=︒(2)∵四边形EDCF 折叠得到四边形11ED C F ,∴120D EF DEF ∠=∠=︒, ∴1202040DEG DEF D EF ∠=∠+∠=︒+︒=︒,∵长方形ABCD , ∴//AD BC ,∴140CGD DEG ∠=∠=︒ ∵11//FC ED ,∴1140C FC CGD ∠=∠=︒(3)答:2C FE DEF EGF ∠+∠=∠ 理由如下:∵长方形ABCD , ∴//,AD BC ∴EFB DEF ∠=∠,180DEF CFE ∠+∠=︒,180DEG EGF ∠+∠=︒设DEF x ∠=︒ ∴EFB x ∠=︒,180180CFE DEF x ∠=︒-∠=︒-︒∵四边形EDCF 折叠得到四边形11ED C F ,∴1D EF DEF x ∠=∠=︒, ∴12DEG DEF D EF x ∠=∠+∠=︒ ∴1801802EGF DEG x ∠=︒-∠=︒-︒ ∵11//FC ED ,∴11802C FG EGF x ∠=∠=︒-︒ ∵四边形11GD C F 折叠得到四边形22GD C F ,∴211802C FG C FG x ∠=∠=︒-︒,//,AD BC,EFB DEF x ∴∠=∠=︒2218021803C FE C FG EFB x x x ∠=∠-∠=︒-︒-︒=︒-︒∴218031802C FE DEF x x x EGF ∠+∠=︒-︒+︒=︒-︒=∠15.(1)45°;(2)当E点在A点上方时,∠BPE=12∠AFB,当E点在A点下方时,∠BPE=90°﹣12∠AFB【详解】解:(1)过点P作PQ∥AB,过点F作FH∥AB,∵AB∥CD,∴AB∥CD∥PQ∥FH,∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,∴∠ABP+∠CEP=∠BPQ+∠EPQ=∠BPE,∠ABF+∠CEF=∠BFH+∠EFH =∠BFE,∵BF⊥AE,∴∠ABF+∠CEF=∠BFE=90°,∵BP平分∠ABF,EP平分∠AEC,∴∠ABP+∠CEP=1 2(∠ABF+∠CEF)=45°,∴∠BPE=45°;(2)①当点F在EA的延长线上时,∠BPE=12∠AFB,理由如下:如备用图1,过点P作PQ∥AB,过点F作FH∥AB,∵AB∥CD,∴AB∥CD∥PQ∥FH,∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,∴∠CEP﹣∠ABP=∠EPQ﹣∠BPQ=∠BPE,∠CEF﹣∠ABF=∠EFH﹣∠BFH=∠BFE,∵BP平分∠ABF,EP平分∠AEC,∴∠CEP﹣∠ABP=12(∠CEF﹣∠ABF)=12∠BFE=∠AFB,∴∠BPE=12∠AFB;②当点F在线段AE上(不与A点重合)时,∠BPE=90°﹣12∠AFB;理由如下:如备用图2,过点P作PQ∥AB,过点F作FH∥AB,∵AB∥CD,∴AB∥CD∥PQ∥FH,∴∠ABP=∠BPQ,∠CEP=∠EPQ,∠ABF=∠BFH,∠CEF=∠EFH,∴∠ABP+∠CEP=∠BPQ+∠EPQ=∠BPE,∠ABF+∠CEF=∠BFH+∠EFH=∠BFE,∵BP平分∠ABF,EP平分∠AEC,∴∠ABP+∠CEP=1 2(∠ABF+∠CEF),∴∠BPE=12∠BFE∴∠BFE=180°﹣∠AFB,∴∠BPE=90°﹣12∠AFB;③当点F在AE的延长线上时,∠BPE=90°﹣12∠AFB,理由如下:如备用图3,过点P作PQ∥AB,过点F作FH∥AB,∵AB∥CD,∴AB∥CD∥PQ∥FH,∴∠ABP=∠BPQ,∠CEP=∠EPQ,180°﹣∠ABF=∠BFH,∠AEC=∠EFH,∴∠CEP+∠ABP=∠EPQ+∠BPQ=∠BPE,∠BFH﹣∠EFH=180°﹣∠ABF ﹣∠AEC=∠AFB,∵BP平分∠ABF,EP平分∠AEC,∴∠CEP+∠ABP=1 2(∠AEC+∠ABF)=12(180°﹣∠AFB),∴∠BPE=90°﹣12∠AFB;综上,当E点在A点上方时,∠BPE=12∠AFB,当E点在A点下方时,∠BPE=90°﹣12∠AFB.16.(1)40°;(2)∠AEF+∠FGC=90°;(3)AEG∠+CFG∠=300°【详解】(1)∵AB∥CD,∴∠1=∠EGD,∵∠2+∠FGE+∠EGD=180°,∠2=2∠1,∴2∠1+60°+∠1=180°,解得∠1=40°;(2)如图,过点F作FP∥AB,∵CD∥AB,∴FP∥AB∥CD,∴∠AEF=∠EFP,∠FGC=∠GFP.∴∠AEF+∠FGC=∠EFP+∠GFP=∠EFG,∵∠EFG=90°,∴∠AEF+∠FGC=90°;(3) AEG∠+CFG∠=300°,理由如下:∵AB∥CD,∴∠AEF+∠CFE=180°,即AEG∠−30°+CFG∠−90°=180°,整理得:AEG∠+CFG∠=300°.17.(1)∠1=∠ABD,证明见解析;(2)∠ACF=55°.【详解】解:(1)∠1=∠ABD,理由:∵BC⊥AE,DE⊥AE,∴BC∥DE,∴∠3+∠CBD=180°,又∵∠2+∠3=180°,∴∠2=∠CBD,∴CF∥DB,∴∠1=∠ABD.(2)∵∠1=70°,CF∥DB,∴∠ABD=70°,又∵BC平分∠ABD,∴1352DBC ABD︒∠=∠=,∴∠2=∠DBC=35°,又∵BC⊥AG,∴∠ACF=90°-∠2=90°-35°=55°.18.(1)证明见详解;(2)∠3=∠2﹣∠1;(3)∠3=360°﹣∠1﹣∠2,证明见详解;(4)∠3=360°﹣∠1﹣∠2.【详解】解:(1)如图(1)证明:过P作PQ∥l1∥l2,由两直线平行,内错角相等,可得:∠1=∠QPE、∠2=∠QPF;∵∠EPF=∠QPE+∠QPF,∴∠EPF=∠1+∠2.(2)∠3=∠2﹣∠1;证明:如图2,过P作直线PQ∥l1∥l2,则:∠1=∠QPE、∠2=∠QPF;∵∠EPF=∠QPF﹣∠QPE,∴∠EPF=∠2﹣∠1.(3)∠3=360°﹣∠1﹣∠2.证明:如图(3),过P作PQ∥l1∥l2;∴∠EPQ+∠1=180°,∠FPQ+∠2=180°,∵∠EPF=∠EPQ+∠FPQ;∴∠EPQ +∠FPQ +∠1+∠2=360°,即∠EPF=360°﹣∠1﹣∠2;(4)点P在线段DC延长线上运动时,∠3=∠1﹣∠2.证明:如图(4),过P作PQ∥l1∥l2;∴∠1=∠QPE、∠2=∠QPF;∵∠QPE﹣∠QPF=∠EPF;∴∠3=∠1﹣∠2.19.(1)证明见解析;(2)(∠)5DAM∠=︒;(∠)25ACD∠=︒.【详解】 (1)12//,115l l ADC ∠=︒,18065BAD ADC ∴∠=︒-∠=︒,又115ABC ∠=︒,180BAD ABC ∴∠+∠=︒, //AD BC ∴;(2)(∠)12//,30l l ACD ∠=︒,30BAC ACD ∴∠=∠=︒, MAC BAC ∠=∠, 30MAC ∴∠=︒,由(1)已得:65BAD ∠=︒,35DAC BAD BAC ∴∠=∠-∠=︒,35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒;(∠)设MAN x ∠=,则8CAD x ∠=, AN 平分CAD ∠, 142CAN CAD x ∴∠=∠=, 5MAC CAN MAN x ∴∠=∠+∠=, MAC BAC ∠=∠, 5BAC x ∴∠=,由(1)已得:65BAD ∠=︒,65CAD BAC BAD ∴∠+∠=∠=︒,即8565x x +=︒,解得5x =︒,525BAC x ∴∠==︒,又12//l l ,25ACD BAC ∴∠=∠=︒.20.(1)证明见解析;(2)75︒;(3)3t =或6t =或15t =.【详解】()1过H 点作AB 的平行线QP ,如图://QP AB ,AEH EHP ∴∠=∠,又//AB CD ,//QP CD ∴,CMH MHP ∴∠=∠,CMH AEH EHP PHM∴∠+∠=∠+∠,即:EHM AEH CMH ∠=∠+∠.()2设MND α∠=,如图:则2BND ECD α∠=∠=,CE 平分DCG ∠, 2GCE ECD α∴∠=∠=,又//AB CD ,2CDG BND α∴∠=∠=,3BNM CMN α∠=∠=, 90GCD GDC ∠+∠=︒, 4290αα∴+=︒,15α=︒,又5EHM ECM NMC α∠=∠+∠=, 75EHM ∴∠=︒.() 3①旋转后点E 、H 分别对应点E '、H ',若//H E FN '',如图所示:两种情况:其一,当E '、H '位于直线AB 下方时,//H E AB '',在第二小题条件下,30NEH ∠=︒,则30H E N ''∠=︒, =30E NB H E N ''∴∠'∠=︒(两直线平行,内错角相等),1030t ︒⨯=︒,13t =;其二,若//FN H E '''',当E ''、H ''位于直线AB 上方时,//E E AB '''',在第二小题条件下,30NEH ∠=︒,则30H E N ''''∴∠=︒, 30E NA H E N ''''''∴∠=∠=︒,∴30180210E NB ''∠=︒+︒=︒,10210t ︒⨯=︒,221t =(舍去);②旋转后点E 、H 分别对应点E '、H ',若//H E GN '',如图://H E GN '',,在第二小题条件下,30NE H NEH ''∠=∠=︒, 30E ND H E N '''∴∠=∠=︒(两直线平行,内错角相等),303060E NB E ND BND ''∴∠=∠+∠=︒+︒=︒,31060t ︒⨯=︒,36t =;③旋转后点E 、H 分别对应点E '、H ',若//H E GF '',E H ''交AB 于点T ,如图://H E FG '',∴E TN CFN '∠=∠(两直线平行同位角相等), ∵9030=120CFN G GNF ∠=∠+∠=︒+︒︒,∴120E TN '∠=︒, 在E TN '中,1801203030TNE '∠=︒-︒-︒=︒∴180********E NB TNE ''∠=︒-∠=︒-︒=︒,410150t ︒⨯=︒,415t =.综上可得:3t =或6t =或15t =.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Packet Tracer 综合技能练习解答-致用户:或许您无需借助打印说明也可以完成本练习,不过我们仍在启动此练习的页面上为您提供了PDF 版说明(位于页面的左侧)。
地址表学习目标•配置静态路由和默认路由•添加并连接BRANCH 路由器•添加并连接交换机•添加并连接PC•执行基本设备配置•配置OSPF 路由•配置STP•配置VTP•配置VLAN•检验端到端连通性简介本练习覆盖了您在前三门Exploration 课程中所学的许多技能。
这些技能包括构建网络,应用编址方案,配置路由、VLAN、STP 和VTP 以及测试连通性。
在继续学习之前您应先检查这些技能的掌握程度。
此外,借此练习机会,您还可以复习有关Packet Tracer 程序的基本知识。
本课程各章都提供Packet Tracer。
您必须知道如何浏览Packet Tracer 环境才能完成本课程的学习。
如果您需要复习Packet Tracer 的基本知识,请阅读Packet Tracer Help(帮助)菜单中提供的相关教程。
注:本练习包含150 多道考题。
因此,每次输入命令后显示的完成比例不一定会上升。
用户执行口令是cisco,特权执行口令是class。
任务1:配置静态路由和默认路由步骤 1. 配置从ISP 到CENTRAL 的静态路由使用拓扑图为ISP 配置到所有网络的静态路由。
每个网络都可以从ISP 通过S0/0/1 到达。
使用送出接口参数配置到下列网络的静态路由:•10.1.1.0/30•172.17.1.0/24•172.17.10.0/24•172.17.20.0/24•172.17.30.0/24•172.17.99.0/24ISP配置命令configure terminalip route 10.1.1.0 255.255.255.252 s0/0/1ip route 172.17.1.0 255.255.255.0 s0/0/1ip route 172.17.10.0 255.255.255.0 s0/0/1ip route 172.17.20.0 255.255.255.0 s0/0/1ip route 172.17.30.0 255.255.255.0 s0/0/1ip route 172.17.99.0 255.255.255.0 s0/0/1endcopy running-config startup-config步骤 2. 配置从CENTRAL 到ISP 的默认路由。
在CENTRAL 上使用送出接口参数配置默认路由,将所有默认流量发送到ISP。
CENTRAL配置命令configure terminalip route 0.0.0.0 0.0.0.0 s0/0/1end步骤 3. 测试与Web Server 的连通性。
CENTRAL 现在应能成功ping 通Web Server (209.165.201.2)。
步骤 4. 检查结果。
完成比例应为4%。
如果并非如此,请单击Check Results(检查结果)查看尚未完成哪些必要部分。
任务2:添加并连接BRANCH 路由器步骤 1. 添加BRANCH 路由器。
单击Custom Made Devices(定制设备),然后将一台1841 路由器添加到拓扑中。
使用Config(配置)选项卡,将Display Name(显示名称)和Hostname(主机名)都改为BRANCH。
Display Name(显示名称)区分大小写。
目前不要配置路由器。
步骤 2. 将BRANCH 连接到CENTRAL。
•将BRANCH 连接到CENTRAL。
•配置BRANCH 和CENTRAL 之间的链路。
•时钟频率用64000 bpsBRANCH配置命令configure terminalinterface s0/0/0ip address 10.1.1.1 255.255.255.252clock rate 64000no shutdownend步骤 3. 检查结果。
完成比例应为8%。
如果并非如此,请单击Check Results(检查结果)查看尚未完成哪些必要部分。
任务3:添加并连接交换机位置、交换机名称和接口请参照拓扑图。
步骤 1. 使用2960 型添加S1、S2 和S3 交换机。
步骤 2. 将S1 连接到BRANCH。
步骤 3. 将S1 连接到S2。
步骤 4. 将S1 连接到S3。
步骤 5. 将S2 连接到S3。
步骤 6. 检查结果。
完成比例应为27%。
如果并非如此,请单击Check Results(检查结果)查看尚未完成哪些必要部分。
任务4:添加并连接PC请使用拓扑图和地址表中指定的接口。
步骤 1. 添加PC1、PC2 和PC3。
步骤 2. 将PC1、PC2 和PC3 连接到S2。
步骤 3. 配置PC。
步骤 4. 检查结果。
完成比例应为41%。
如果并非如此,请单击Check Results(检查结果)查看尚未完成哪些必要部分。
任务5:执行基本设备配置步骤 1. 在BRANCH、S1、S2 和S3 上配置基本命令。
基本配置命令应包括主机名、执行模式口令、标语、控制台和vty 线路。
BRANCH配置命令configure terminalbanner motd #AUTHORIZED ACCESS ONLY#hostname BRANCHenable secret classline console 0password ciscologinexitline vty 0 4password ciscologinendS1配置命令configure terminalbanner motd # AUTHORIZED ACCESS ONLY# hostname S1enable secret classline console 0password ciscologinexitline vty 0 4password ciscologinendS2配置命令configure terminalbanner motd # AUTHORIZED ACCESS ONLY# hostname S2enable secret classline console 0password ciscologinexitline vty 0 4password ciscologinendS3配置命令configure terminalbanner motd #AUTHORIZED ACCESS ONLY#hostname S3enable secret classline console 0password ciscologinexitling vty 0 4password ciscologinend步骤 2. 在BRANCH 上配置快速以太网子接口。
不要忘记为每个子接口配置802.1q 封装和VLAN 设置。
每个子接口地址的第三组二进制八位数与VLAN 编号对应。
例如,子接口Fa0/0.30 应使用IP 地址172.17.30.1,属于VLAN 30。
VLAN 99 为本征VLAN。
BRANCH配置命令configure terminalinterface f0/0no shutdownendconfigure terminalinterface f0/0.1encapsulation dot1q 1ip address 172.17.1.1 255.255.255.0 no shutdownexitinterface f0/0.10encapsulation dot1q 10ip address 172.17.10.1 255.255.255.0 no shutdownexitinterface f0/0.20encapsulation dot1q 20ip address 172.17.20.1 255.255.255.0 no shutdownexitinterface f0/0.30encapsulation dot1q 30ip address 172.17.30.1 255.255.255.0 no shutdownexitinterface f0/0.99encapsulation dot1q 99 nativeip address 172.17.99.1 255.255.255.0no shutdownend步骤 3. 配置交换机。
•配置VLAN 99 接口。
•配置默认网关。
S1配置命令configure terminalinterface vlan 99ip add 172.17.99.11 255.255.255.0 no shutdownexitip default-gateway 172.17.99.1 endS2配置命令configure terminalinterface vlan 99ip add 172.17.99.12 255.255.255.0 no shutdownexitip default-gateway 172.17.99.1 endS3配置命令configure terminalinterface vlan 99ip add 172.17.99.13 255.255.255.0no shutdownexitip default-gateway 172.17.99.1end步骤 4. 检查结果。
完成比例应为59%。
如果并非如此,请单击Check Results(检查结果)查看尚未完成哪些必要部分。
任务6:配置OSPF 路由步骤 1. 在CENTRAL 上配置OSPF 并传播默认路由。
•使用进程ID 1 配置OSPF。
•使用OSPF 区域0。
•仅添加与BRANCH 共享的网络。
•向OSPF 相邻设备传播默认路由。
步骤 2. 在BRANCH 上配置OSPF。
•使用进程ID 1 配置OSPF。
•使用OSPF 区域0。
•添加通过BRANCH 路由的所有网络。
CENTRAL配置命令configure terminalrouter ospf 1network 10.1.1.0 0.0.0.3 area 0default-information originateendBRANCH配置命令configure terminalrouter ospf 1network 10.1.1.0 0.0.0.3 area 0network 172.17.1.0 0.0.0.255 area 0network 172.17.10.0 0.0.0.255 area 0network 172.17.20.0 0.0.0.255 area 0network 172.17.30.0 0.0.0.255 area 0network 172.17.99.0 0.0.0.255 area 0end步骤 3. 在CENTRAL 和BRANCH 的适当接口上禁用OSPF 更新。
