物理PPT课件:振动和波动
大学普通物理课件 第21章 - 波动

§21-1 机械波 行波
Mechanical Wave and Travelling Wave
1. 机械波的产生和传播 机械波——机械振动的传播。
机械波产生和传播的条件:
波源 弹性介质
波源——引起介质振动,即产生形变和位移的振(扰)动 系统。锣鼓 琴弦 声带 扬声器纸膜 抖绳的手
O点的振动状态向右传播到 x 点需要时间:t x / u x处的质元开始振动的时刻比原点晚 x / u ,所以 x 处的质元在 时刻 t 的位移应该等于原点在 (t x / u) 的位移,即
y A cos[ (t x u) 0 ]
y A cos[ (t x u) 0 ]
2. 均匀细棒中纵波波动方程的推导
设细棒密度为,截面积为S,沿细棒取x坐标,设波沿x
正向传播。考察媒质中 x x +x 段质元:
y (x)
y ( x x)
S
F (x)
F ( x x)
x x x x
x
t 时刻两端面的位移如图,则x处微小质元的线应变可表
结论:波形曲线也是余弦函数曲线;
波的传播表现为波形曲线的平移. 波形曲线以波速u向传播方向平移。x ut
[例1] 设波源位于 x 轴的原点处, y (cm) 波源的振动曲线如图所示,已知波速为 2 u = 5 m/s ,波向 x 正向传播。 O 6 t (s) 2 4 (1)画出距波源 15 m处质元的振 2 动曲线; (2)画出 t = 3 s 时的波形曲线。(3)写出 20m 处质元的速度表达式。 解:由图可知
1 G 2 ( SD ) 2 材料发生切变时,单位体积内的弹性势能为:
10612_大学物理振动波动优秀ppt课件

01
02
03
声波传播速度
声波在介质中的传播速度 与介质的密度和弹性模量 有关。
2024/1/25
声波衰减
声波在传播过程中会因介 质的吸收和散射而逐渐衰 减。
声波反射和折射
声波在遇到不同介质界面 时会发生反射和折射现象 。
29
案例分析:医学超声诊断技术应用
超声成像原理
利用超声波在人体组织中的反射和折 射特性,将回声信号转换为图像,从 而实现对人体内部结构的可视化。
04
2024/1/25
05
阻尼振动的能量逐渐转化为 热能或其他形式的能量。
9
受迫振动产生条件及规律
受迫振动的定义:物 体在周期性外力作用 下产生的振动。
存在周期性外力作用 。
2024/1/25
受迫振动的产生条件
10
受迫振动产生条件及规律
外力频率与物体固有频率 不同。
2024/1/25
受迫振动的频率等于驱动 力频率,与物体固有频率 无关。
大学物理振动波 动优秀ppt课件
2024/1/25
1
目录
• 振动基本概念与简谐振动 • 阻尼振动、受迫振动与共振 • 波动基本概念与波动方程 • 干涉、衍射与偏振现象 • 多普勒效应与声波传播特性 • 非线性振动与混沌现象初步探讨
2024/1/25
2
01
振动基本概念与简谐振动
2024/1/25
3
受迫振动的规律
当驱动力频率接近物体固 有频率时,振幅显著增大 ,产生共振现象。
11
共振现象及其危害防范
2024/1/25
12
共振现象及其危害防范
对机器、设备等造成损坏 。
对建筑物、桥梁等结构造 成破坏。
大连理工大学《大学物理-力学、振动与波动》课件-第5章

§5惠更斯原理波的衍射波的反射与折射一、惠更斯原理OS 1S 2u ∆tu ∆tS 1S 2在均匀的自由空间波传播时,任一波面上的每一点都可以看作发射子波的点波源,以后任意时刻,这些子波的包迹就是该时刻的波面。
——波沿直线传播t+∆t 时波面t 时波面t+∆t 时波面S1i 2三、波的反射与折射介质1MN反射波与入射波在同一介质中传播tu MD AN ∆==i容易算出i i '=(n 1)(n 2)A B C DMNi 1i1tu MD ∆1=tu AN ∆2=21u u AN MD =2sin i AD AN =1sin i AD MD =11u c n =22u c n =2211sin sin i n i n =介质2A B C D1122sin sin i u i u =21n =介质2相对于介质1的折射率折射波与入射波在不同介质中传播介质相对于空气的折射率声波—机械纵波一、声压媒质中有声波传播时的压力与无声波传播时的静压力之差纵波—疏密波稀疏区域:实际压力小于静压力,声压为负值稠密区域:实际压力大于静压力,声压为正值§7声波与声强级次声波可闻声超声波声压是仪器所测得的物理量定义声压:p = p -p 0对某声波媒质无声波——静压力p 0 、密度ρ0有声波——压力p 、密度ρ)(Hz ν2020000p+pV+∆V ∆V。
05137_大学物理学振动与波动

2024/1/26
11
波速、波长和频率关系
波速(v)
单位时间内波动传播的距离,单位是m/s。波速 与介质性质有关。
频率(f)
单位时间内质点振动的次数,单位是Hz。频率 与波源性质有关。
ABCD
2024/1/26
波长(λ)
波动中相邻两个同相位点之间的距离,单位是m 。波长与波动形式和介质性质有关。
波速、波长和频率之间的关系为
物理意义解释
解释波动方程中各项的物理意义,如 波的传播方向、波的叠加原理等。
05
2024/1/26
04
求解波动方程
通过求解波动方程,得到波动中各点 的位移、速度、加速度等物理量与时 间和空间的关系。
16
振动图像和波动图像分析
振动图像分析
通过振动图像可以直观地了解振动的周期、振幅、相位等特 征。同时,可以通过比较不同振动图像的异同点,分析不同 振动系统的特性。
v = λf。这个公式表示在给定介质中,波速与波 长和频率的乘积成正比。
12
波动在生活中的应用
01
声学
声音是一种典型的波动现象, 人们利用声音进行通信、音乐 演奏等。此外,在建筑设计中 ,需要考虑声音的传播和隔音
效果。
2024/1/26
02
光学
光也是一种波动现象,人们利 用光的波动性质发明了各种光 学仪器,如显微镜、望远镜等 。同时,在通信领域,光纤通 信利用光的全反射原理实现高
利用超声波在介质中的传 播、反射、折射等特性, 进行无损检测、医学成像 、清洗等应用。
25
光学领域中振动和波动应用
2024/1/26
光的干涉
01
光波在叠加区域产生加强或减弱的现象,应用于光学测量、表
大学物理知识点总结(振动及波动)省公开课获奖课件市赛课比赛一等奖课件

相位、相位差和初相位旳求法: 解析法和旋转矢量法。
1、由已知旳初条件求初相位:
①已知初位置旳大小、正负以及初速度旳正负。
[例1]已知某质点振动旳初位置
y0
A 2
且v0
0
。
y A cos(t ) y Acos(t )
3
3
2
1
2
r2 r1
干涉加强: 2k (k 0,1,2,...)
若1 2 r2 r1 k
干涉减弱: (2k 1) (k 0,1,2,...)
若1 2
(2k 1)
2
3)驻波(干涉特例) 能量不传播
波节:振幅为零旳点 波腹:振幅最大旳点
多普勒效应: (以媒质为参照系)
所以y
2cos(πt 2
π3 );
(2)u
T
1,y
2cos[π(t 2
-
x)π3 ]
t(s)
[例2] 一平面简谐波在 t = 0 时刻旳波形图,设此简谐波旳频率
为250Hz,且此时质点P 旳运动方向向下 , 200m 。
求:1)该波旳波动方程;
2)在距O点为100m处质点旳振动方程与振动速度体现式。
动能势能相互转化
简谐振动旳描述
一、描述简谐振动旳物理量
① 振幅A:
A
x02
v02
2
② 角频率 : k
ห้องสมุดไป่ตู้
2
m
T
③ 相位( t + ) 和 初相 :
tg v0 x0
旳拟定!!
④相位差 : (2t 2 ) (1t 1 )
⑤周期 T 和频率 ν : T 2
第七章 振动和波动(2)

y
u
x
x = u t
O
t
t + t
x
y
O
u t + t
x y A cos[ ( t ) ] u
x
★ 波函数的物理意义
t
— 波函数既描述了波线上各质点振动状态及相位差异, 又描述了随着时间的推移,波形以波速 u 沿传播方向传播的
情况,具有完整的波动意义。
★ 简谐波具有空间和时间周期性:
2
①
t x y 1.0 cos[ 2 ( ) ] 2.0 4.0 2
(2) 将 t = 1.0 s 代入 ①式得出此时刻波形方程:
1.0 x y 1.0 cos[2 ( ) ] 1.0 cos( x ) 2.0 4.0 2 2 2 y /m u ② y 1.0 sin x 1.0 2 由②式可画出 t = 1.0 s 的波形图:
2、横波和纵波
1) 横波: 振动方向⊥传播方向的波。 2)纵波: 振动方向∥传播方向的波。
固体中的波源可以产生横波和纵波。 液体和气体中的波源只能产生纵波。 水面波既不是纵波,也不是横波。
任一波(如水波、地表波)都能分解为横波与纵波进行研究。
3、波的几何描述
1) 波面 — 振动相位相同的各点连成的面(同相面)。
空间上每隔λ的距离出现振动状态相同的点; 时间上每隔 T 的时间波形重复一次。
★ 平面简谐波的波函数既适用于横波,也适用于纵波。
3.波沿着x轴负方向传播
y A cos [ t 2
4.波函数的复数表示
波函数
x
]
]
y A cos [ t 2
振动图象和波动图象的区别

振动图象和波动图象的区别
振动图象波动图象
研究对象一个振动质点各个质点
研究内容位移随时间变化规律某时刻所有质点空间分布
图象
x
O T t y
λx/m
物理意义同一质点在不同时刻位移不同质点在同一时刻的位移
图象变化随时间不变随时间推移,图象沿传播方向平移振动图像与波的图
一、振动图象和波的图象
振动是一个质点随时间的推移而呈现的现象,波动是全部质点联合起来共同呈现的现象.简谐运动和其引起的简谐波的振幅、频率相同,二者的图象有相同的正弦(余弦)曲线形状,但二图象是有本质区别的.见表:。
高中物理机械振动和机械波PPT课件
练习2:
有两个简谐运动:
x1
3a sin(4bt
4
)和x2
9a sin(8bt
)
2
它们的振幅之比是多少?它们的周期各是
多少 ?t =0时它们的相位差是多少?
五、简谐运动的几何描述—参考圆
匀速圆周运动在x轴上的投影为简谐运动。
五、简谐运动的几何描述—参考圆
用旋转矢量图画简谐运动的 x t 图
t 1 t 2 1 2
同相:频率相同、初相相同(即相差为0) 的两个振子振动步调完全相同。
反相:频率相同、相差为π 的两个振子 振动步调完全相反。
练习1:
下图是甲乙两弹簧振子的 x – t 图象,两
振动振幅之比为_2__∶___1,频率之比为_1_∶___1 ,
甲和乙的相差为_____ 。
实验器材
带有铁夹的铁架台、中心有小孔的金属小球,不易伸长的细线(约 1 米)、秒表、毫米刻度尺和游标卡尺.
实验步骤
(1)用细线和金属小一个球制作单摆。 (2)把单摆固定悬挂在铁架台上,让摆球自然下垂,在单摆平衡位 置处作上标记。 (3)用毫米刻度尺量出摆线长度 l′,用游标卡尺测出摆球的直径, 即得出金属小球半径 r,计算出摆长 l=l′+r. (4)把单摆从平衡位置处拉开一个很小的角度(不超过 5°),然后放 开金属小球,让金属小球摆动,待摆动平稳后测出单摆完成 30~ 50 次全振动所用的时间 t,计算出金属小球完成一次全振动所用时 间,这个时间就是单摆的振动周期,即 T=Nt (N 为全振动的次数).
解析 作一条过原点的与 AB 线平行的直线,所作的直线就是准确测
量摆长时所对应的图线.过横轴上某一点作一条平行纵轴的直线,则 和两条图线的交点不同,与准确测量摆长时的图线的交点对应的摆长
振动图像和波动图像PPT课件

0
t/s 1 2 3 4 5 图乙
图甲
解: λ=4m T=4s v=λ/ T =1m/s 由图乙得: x=2m处质点在t = 3s 时的位移为0, 振动 方向为+y方向, 如甲图蓝线所示, 所以该横波的传播方向为-x方向。
054.08年北京市海淀区一模试卷17 17. 一列横波在x轴上传播,图(甲)为t=1.0s时的波 动图像,图(乙)为介质中质点P的振动图像。对该 波的传播方向和传播波速度的说法正确的是 ( B ) A.沿+x方向传播,波速为4.0m/s B.沿- x方向传播, 波速为4.0m/s C.沿+ x方向传播,波速为2.5m/s D.沿- x方向传播,波速为2.5 m/s y/cm y/cm 0.2 0.2 P 0 0 1 2 3 4 0.5 1.0 t/s x/m -0.2 -0.2 图 (甲 ) 图 (乙 ) 解: 由图乙, t=1.0s时P的振动方向向下, 所以波沿- x方向传播.
振动图像和波动图像
振动图象和波的图象 振动图象和波的图象从图形上看好象没有什么区别 , 但实际上它们有本质的区别。 ⑴物理意义不同:振动图象表示同一质点在不同时刻 的位移;波的图象表示介质中的各个质点在同一时刻 的位移。
⑵图象的横坐标的单位不同:振动图象的横坐标表 示时间;波的图象的横坐标表示距离。
y/cm 15 x/cm 0 -15 10 20 30 40 50 0 -15 5 10 15 20 25 15 t/10-3 s y/cm
图2 图1 【解析】本小题考查对振动图像和波动图像的理解 和对波动规律的数学表达能力,考查理解能力。
006.江苏南通08届第一次基础调研测试12B (1) 12. B.(1) (模块3-4试题) (1)一列简谐横波沿x轴传播,图甲是t = 3s时的 波形图,图乙是波上x=2m处质点的振动图线.则该 横波的速度为 1 m/s,传播方向为 -x方向 . y/cm y/cm 0 x/ 1 2 3 4 5m
大学物理学完整10PPT课件

上式还可写为: 2π
上式表明,ω是频率的2π倍,表示物体在2π秒内完成的全 振动次数,故ω称为角频率或圆频率。
周期、频率和角频率都是描述物体振动快慢的物理量。在
国际单位制中,周期的单位为秒(s);频率的单位为赫兹(Hz );角频率的单位为弧度每秒(rad/s)。
对弹簧振子,由于
k m
故有:
T 2π m k
第4篇 振动与波动
第10章 机械振动
.
1
本章学习要点
简谐振动 简谐振动的合成 阻尼振动、受迫振动与共振 本章小结
.2ຫໍສະໝຸດ 10.1 简谐振动物体运动时,如果离开平衡位置的位移(或角位移)按余 弦函数或正弦函数的规律随时间变化,则这种运动称为简谐振 动。在忽略阻力的情况下,弹簧振子的振动及单摆的小角度摆 动等都可视为简谐振动。
当t=0时,相位ωt+φ=φ,φ称为初相位,简称初相,它是 决定初始时刻振动物体运动状态的物理量。在国际单位制中, 相位的单位为弧度(rad)。
.
12
用相位描述物体的运动状态,还能充分体现出振动的周期 性。例如:
ωt+φ=0时,物体位于正位移最大处,且v=0; ωt+φ=π/2时,物体位于平衡位置,且向x轴负方向运动 ,v=ωA; ωt+φ=π时,物体位于负位移最大处,且v=0; ωt+φ=3π/2时,物体位于平衡位置,且向x轴正方向运动 ,v=ωA; ωt+φ=2π时,物体位于正位移最大处,且v=0。
【解】以OO′为平衡位置,设逆时针转向为θ 角正向,棒在任意时刻的角位移都可用棒与OO′ 的夹角θ表示。根据题意,棒所受的重力矩为:
M1mgslin
2
.
7
当摆角θ很小时,sinθ≈θ,故
M 1mgl
振动图象和波动图象的区别

振动图象和波动图象的区别
振动图象波动图象
研究对象一个振动质点各个质点
研究内容位移随时间变化规律某时刻所有质点空间分布
图象
x
O T t y
λx/m
物理意义同一质点在不同时刻位移不同质点在同一时刻的位移
图象变化随时间不变随时间推移,图象沿传播方向平移振动图像与波的图
一、振动图象和波的图象
振动是一个质点随时间的推移而呈现的现象,波动是全部质点联合起来共同呈现的现象.简谐运动和其引起的简谐波的振幅、频率相同,二者的图象有相同的正弦(余弦)曲线形状,但二图象是有本质区别的.见表:
振动图象波动图象
研究对象一振动质点沿波传播方向所有质点
研究内容一质点的位移随时间的变化规律某时刻所有质点的空间分布规律
图线
物理意义表示一质点在各时刻的位移表示某时刻各质点的位移
图线变化随时间推移图延续,但已有形状
不变
随时间推移,图象沿传播方向平
移
一完整曲线占横坐
标距离
表示一个周期表示一个波长。
大学物理振动和波动ppt课件(2024)

2024/1/28
1
目录
2024/1/28
• 振动基本概念与分类 • 波动基本概念与传播特性 • 振动与波动相互作用原理 • 光学中振动和波动现象解析 • 声学中振动和波动现象解析 • 总结与展望
2
01 振动基本概念与分类
2024/1/28
3
振动的定义及特点
振动的定义
振幅
声源振动的幅度用振幅表示,振幅越大,声音的 响度越大。
3
相位
声波在传播过程中,各质点的振动状态用相位描 述。相位差反映了声波在空间中的传播情况。
2024/1/28
25
室内声学环境评价指标体系
响度
音调
人耳对声音强弱的主观感受称为响度,与 声源的振幅和频率有关。
人耳对声音高低的主观感受称为音调,与 声源的频率有关。
物体在平衡位置附近所做的往复运动。
振动的特点
周期性、重复性、等时性。
2024/1/28
4
简谐振动与阻尼振动
2024/1/28
简谐振动
物体在回复力作用下,离开平衡位置 后所做的往复运动,其回复力与位移 成正比,方向相反。
阻尼振动
在振动过程中,由于摩擦、空气阻力 等因素,振幅逐渐减小的振动。
5
受迫振动与共振现象
传播途径控制
在噪声传播途径中采取措施,阻断或减弱噪声的传播。例如设置声屏 障、采用吸音材料等。
接收者防护
对受噪声影响的人员采取防护措施,如佩戴耳塞、耳罩等个人防护用 品。
案例分析
以某工厂噪声控制为例,通过采取上述综合措施,使工厂噪声降低到 国家标准以内,改善了工人的工作环境和周边居民的生活环境。
27
物理振动和波动

( 20 10 )
2
y o x
x
x2 y 2 2 1 2 A1 A2
所以是在X轴半轴长为 A1 , Y轴半轴长为 A2 的椭圆方程,且顺时针旋转。
讨论4
2
3 ( 20 10 ) 2
2
y
x y 2 1 2 A1 A2
o
x
所以是在X轴半轴长为 A1 , Y轴半轴长为 A2 的椭圆方程,且逆时针旋转。 讨论5
500 v (Hz)
北京大钟寺内的巨钟的频谱图
⒈在平衡位置附近来回做往复运动的现象 叫做机械振动,简称振动。
⒉机械振动的主要特征是:
“空间运动”的往复性和“时间”上的周 期性。
产生机械振动的基本条件:
1.
物体受到回复力的作用(指向平衡位置);
2.
回复力和物体惯性交替作用,维持机械振动。
二、简谐振动
这两类波本质不同,但有许多共同特征,如能 产生折射、反射、衍射和干涉等现象,且都伴随 着能量的传播。
第一节
振动的传播过程称为波动。 机械振动在媒质中的传播过程称为机械波。 产生机械波的必要条件:
波源 媒质 作机械振动的物体; 能够传播机械振动的弹性媒质。
波源带动弹性媒质中与其相邻的质点发生振动,振动相继 传播到后面各相邻质点,其振动时间和相位依次落后。 波动现象是媒质中各质点运动状态的集体表现,各质点仍 在其各自平衡位置附近作振动。
补充:简谐振动的速 度和加速度 位移: x
1.简谐振动的各阶导数也 都作简谐振动 2. x,a,v相位依次相差/2
t A cos t
dx A sin t 速度: v dt A cos t
《普通物理学》课件-第七章 振动
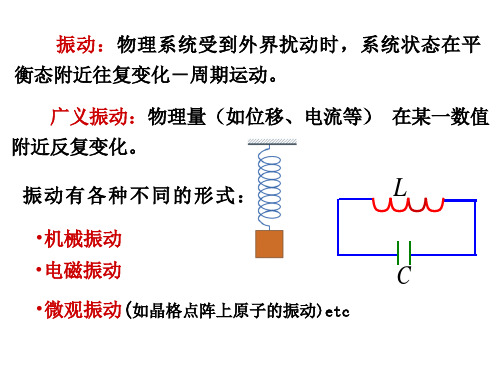
5g
等效劲度系数 (ke) f ke x
f: 恢复力 x: 偏离平衡位置的位移
0
ke m
弹簧的串联和并联
• 串联公式: 1/k = 1/k1 +1/k2
• 并联公式: k = k1 + k2
k1
k2
k1
k2
例:一劲度系数为 k 的弹簧均分为二,试求 均分后两弹簧并联的等效劲度系数 k'。
解:串联公式:
sinθ≈θ (θ<5o 0.3 rad)
O
l
T
当振幅很小时,单摆的振动为简谐振动。
mg
Quasi 1-D restoring force
f = -mgsinθ≈-mgθ= -mgx/l
k = mg/l, ω02 = k/m = g/l ω0 = √g/l
T 2 l
g
单摆实验 可以测g
复摆(物理摆)
A
ωt+
0
xx
旋 转 矢量 A的
x 端点在
轴上的投
影点的运
动为简谐
运动.
x Acos(t )
x Acos(t )
•复数表示:
将xy平面看作一个复平面
矢量端点对应于一个复数 (包含模和辐角)
xt Acost 0
x t Aeit0辐角
eit0 cost 0 i sin t 0
设B的质量为m, A的质量便是γm
A
v0
B
B
第一阶段是弹性碰撞
第二阶段:A做匀速直线运动;B,B '的质心做匀速直线运动,
B,B '相对质心作简谐振动。
弹性碰撞
mvA
mvB
(0)
大学物理课件-第7章 波动(wave)66页PPT

2 0.1 2 3
0.3(m)
鞍山科技大学 姜丽娜
17
例2:已知一平面简谐波沿X轴负向传播,波速u=9m/s ,距原点
1m处的A点振动方程为
yA0.02 co3s t(1 4)yO 1m A
X
求:波函数。
例2 解: 3,2 3, u6(m )
y0 .0c 2o 3 ts (12 x 1 )
yq=Acos(ω(t+△t -(xp +u△t )/u)+φ) =Acos(ω(t-xp /u)+φ) =yp
Y
q
O
p
X
鞍山科技大学 姜丽娜
15
Y
q
O
p
X
上式说明:t时刻p点的运动状态经△t时间传到了q点,所以 波函数表示波形的传播过程。当t连续变化时,波形连续不断前 进,故波动过程可以表示为波形随时间不断向前移动的过程,波 形不断前进的波称行波。
。
鞍山科技大学 姜丽娜
21
解 : u / 1/0 5 0 0 2 (m )
波 1 t 0 源 时 ,y 0 振 : y A 2 0, v 0 2 动 0 c 4 o 1 方 s 2 3 0 t( 0 3 2 程 )m ( )m
⑵波函数: y2c 4o 1s0 (t 03 22 x)m ( )m
第7章 波 动(wave)
§7.1 行波
§7.6 惠更斯原理
§7.2 简谐波
§7.7 波的叠加 驻波
§7.3 物体的弹性形变 §7.8 声波
§7.4 弹性介质中的波速§7.9 多普勒效应
§7.5 波的能量
鞍山科技大学 姜丽娜
1
第7章 波 动(wave)
第三章波动方程 ppt课件

第二组解:当 VVs / 时,
u0
i
v A2 exp[ V ( x Vst )]
i
w A3 exp[ V ( x Vs t )]
其位移方向与波的传播方向垂直,所以称为平面横波,也称为剪
切波,通常简称为S波。S波有两个质点振动方向:沿Z轴振动的S波分
量为垂直偏振剪切波,称为SV波,沿Y轴振动的S波为水平偏振剪切波,
▪ 该式是齐次方程的解,只反映了波的传播特点。当力位 函数不为零时,需求非齐次方程的解,即达朗贝尔解。
2 t2V p 2 2 2 t2V p 2divg r(a t)d
▪ 将点震源用半径r=a的小球代替,小球体积为W。对上式 求体积分,并令r->0,其极限情况就是点震源的达朗贝 尔解。
lr i0m W2 t2 dW Vp2lr i0m Wdivgd raW dlr i0m W(t)dW
r
lim
r0
S
r
dS
1 Vp2
1
(
t
)
再将特解带入左端项, 则有:
19
lim
r0
S
r
dS lim r0
S
C1 r2
C
' 1
dS
rV p
lim r0
1 r2
(
C1
r Vp
C
' 1
)
S
dS
lim
r0
4 ( C1
r V
C
' 1
)
4C1
带回原式,则得:
r
1
r
C1( t
Vp
换句话说,目前的勘探方法主要还是纵波勘探。
25
3.3 地震波的动力学特点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F mg Vg
2x
d
2
g
2
1 d 2g x kx
2
是简谐振动
返回
二 简谐振动的方程
方程的建立
k
m
o
m
k
F
k
mo
F
o
平衡位置 x 0
x
F 0
x 弹簧伸长 x 0 F 0
x x0 弹簧压缩 F 0
公式的推导
F kx
F
ma
m
d2x dt 2
d2x m dt2 kx
E
1 2
kA2
sin
2
(t
0
)
1 2
kA2
cos2
(t
0
)
1 k A2 2
系统的动能Ek随时间周期性变化
系统的势能Ep随时间周期性变化
系统的总机械能与时间变化无关,即简谐振动的总能量守恒
2
ω表示在2π秒内完成整振动的次数-------角频率(圆频率),
ω的大小由弹簧振子的固有性质决定。单位弧度/秒
2 k k
m
m
2 1 k 2 m
1 T 2 m
T
k
固有角频率 固有频率 固有周期
0的物理意义:
我们称 t为相0位。则 表示初0 始时刻的相位----初 相位,的0 大小由弹簧振子的初始状态决定。单位rad. 取0
2
第一节 简谐振动
• 简谐振动的基本特征 • 简谐振动的方程 • 简谐振动的矢量图解法 • 简谐振动的能量
2020/8/17
3
一 简谐振动的基本特征
2:24
运动的形式: x A cos(t 0 )
受力的形式:弹性力(回复力)
F kx
(注:k称为劲度系数或倔强系数)
例一
直径d的U形管,装有质量为m的液体,若液体一个小的初始 位移,液体在管中作微振动,这种振动是否是简谐振动.
解:用矢量图解法 平衡位置有两个
x
a x0 0 v0 0
b x0 0 v0 0
X=+12cm 位置有两个 c X=+12cm v>0 d X=+12cm v<0
有两个时间
ac bc
其中最短时间为
bc
tm in
sin
t m in
12 15
0.8
tmin 0.927 tmin 0.037 s
d2x dt 2
k m
x
0
令 2 k (为微分常数)
m
得到简谐振动的微分方程: d 2 x 2 x 0
dt 2
其解为:
重要结论
位移 x A cos(t 0 )
利用速度和加速度的数学定义,可得:
速度
v
dx dt
Asin(t
0
)
加速度
a
d2x dt 2
2 Acos(t
0)
A与
为积分常数
s cos(
g s
t
0
)
将初始条件代入上式: t 0 , x0 s , v0 0
s s cos0 0
x s cos( g t )
s
返回
三 简谐振动的矢量图解法
简谐振动可以用一个旋转矢量描绘
A 矢量的长度代表振幅 A
A矢量逆时针旋转的角速度代表角频率
A矢量在初始时刻与x轴的角度代表初相位 0
值范围 0
求方0 法:
①已知
x0 , v0 ,
x0 A cos0 v0 Asin 0
tan 0
v0
x0
②已知 A, x0 , v0的符号
x0 Acos0
0
arccosx0 A
v0 Asin0
v0 v0
0则sin 0 0则sin 0
0 0
0 0 0 0
例二
已知某简谐振动的振动曲线如图所示,试写出该振动的简谐 振动方程。
L
mg kx ks
mg kx mg
S
kx
是简谐振动。
(2)求 A, ,
L
解 t 0时 , x0 s
且 静止放手 v0 0 代入 A
x0 2
( v0
)2
S
A x0 s
F
x
x
k
m
mg k s
g s
mg
1 g
2 2 s
(3)若以放手时开始计时,求简谐振动方程
解 x Acos(t 0 )
0
aV
x
0
t
简谐振动的位移、速度和加速度的函数曲线
振动方程中参数的物理意义
A的物理意义:
A xmax
A是物体离开平衡位置的最大幅度-----振幅,A的大小由弹 簧振子的初始状态决定。单位m
x0 Acos0 A v0 Asin 0
x0 2
( v0
)2
ω的物理意义,分三步分析
(1)T 的引入 t 0 x0 A cos0
振动和波动
▪振动(Vibration):任一物理量在某一定值附近随 时间作往复变化。其中物体位置随时间的变更 称为机械振动。
▪波动(Wave):振动的传播
2020/8/17
1
内容提要
第一节 简谐振动 第二节 两个简谐振动的合成 第三节 平面简谐波动 第四节 两个平面简谐波动的合成
2020/8/17
解: 从图中可以看出,
A 4cm , x0 2cm , v0 0 x1 0 , v1 0
求振动方程需分三步:
(1)求A 从图中可以看出
A 4cm
x 4 cos( t 0 )
(2)求 0
(3)求
2
4 cos0
0
3
v0 0
0
3
x 4 cos( t )
3
0 4 cos( )
返回
四 简谐振动的能量
总能量=振子的动能+弹簧的弹性势能
E Ek E p
其中
Ek
1 2
mv2
1 2
m A s in(t
0 )2
1 2
m
2
A2
s in 2
(t
0)
1 2
k A2
s in 2
(t
0 )
Ep
1 2
k x2
1 2
kA
cos(t
0
)2
1 2
k A2
c os2
(t
0
)
(注: 2 k )
m
A矢量在任一时刻与x轴的角度代表相位 t 0
矢量在x轴投影
t=t
A
x0 Acos0
A
t=0
x Acos(t 0 )
t
0
o
xx0Biblioteka x例四一物体作简谐振动,振幅为15cm,频率为4Hz,求物体从平衡位 置运动到 x=+12cm (且向x轴正向运动)处,所需的最短时间。
a
d
o 12cm
c b
3
3
2
v1 0
32
5
6
x 4 cos(5 t )
63
例三
如图,一长为L的弹簧上端固定,下端挂一重物后长度变为
(L+S),并仍在弹性限度之内。若将重物向上托起,使弹簧缩 回原来的长度,然后放手,重物将作上下运动。
(1)证明重物的运动是简谐振动。
解: F mg k(x s)
t 2
x
A cos (
2
0)
A cos 0
x0
T 2T/表示完成一次完整振动所需要的时间-----周
期,T 的大小由弹簧振子的固有性质决定。单位s
(2) υ的引入 1
T
υ表示在单位时间内完成整振动的次数------频率, υ 的大小由弹簧振子的固有性质决定。单位Hz
(3) ω的引入
T 2
