七下数学期末专题训练(二)画图题
北师大版七下期末复习数学试卷(二)

一七下期末复习数学试卷(二) 班级 姓名 座号 一. 选择题:(每题2分,共22分)1、下列说法中正确的是( )A 、 43a 不是整式B 、 43a 是单项式 C 、 2+a 是单项式 D 、 是多项式2、下列各式中,正确的是 ( ) A 、 633x x x =+;B 、 m m x x x 55=⋅; C 、 222)(y x y x +=+;D 、 32)()(x x x -=-⋅-3、如图,1∠与2∠是对顶角的是 ( )A 、B 、C 、D 、4、如果一个事件发生的可能性是99%,那么这个事件 ( )A 、 很可能发生B 、 很可能不发生C 、一定发生D 、一定不发生5、如图, 1∠和2∠是同位角的是 ( )A 、B 、C 、D 、6如图,已知1∠=2∠,那么 ( )A 、AB//CD,根据内错角相等,两直线平行、B 、AD//BC,根据内错角相等,两直线平行、C 、AB//CD,根据两直线平行,内错角相等、D 、AD//BC,根据两直线平行,内错角相等、7、下列说法正确的是 ( )A 、近似数4.3万精确到千位B 、 近似数0.010只有一个有效数字C 、近似数2.8与2.80表示的意义相同;D 、近似数43.0精确到个位8、盒子中装有2个红球和4个绿球,每个球除颜色外都相同,从盒子中任意摸出一个球,是绿球的概率是( )A 、 41 B 、 31 C 、 32 D 、 219、200520048125.0⨯的值为 ( )A 、 8 B 、 81 C 、 4 D 、 41二10、如图,一飞镖游戏板,其中每个小正方形的大小相等,则随意投掷一个飞镖,击中黑色区域的概率是( )A 、 21 B 、 83 C 、 41 D 、 31 11、观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,……根据其规律可知810的末位数是( )A 、2B 、4C 、6D 、8二、填空题(每空1分,其中22题2分,共22分)11、单项式102xy π-是系数是 ,次数是 ,多项式142332-+-x xy y x是 次 项式12、=⋅55x x ; =-232)3(bc a ; ⋅-3)(b 5b -=。
人教版2022-2023学年七年级下册数学期末复习专题:二元一次方程组的应用(方案问题) (2)

人教版2022-2023学年七年级下册数学期末复习专题二元一次方程组的应用(方案问题)原计划两班都以班为单位分别购票,则一共应付1106元.请回答下列问题:(1)初一(2)班有多少人?(2)你作为组织者如何购票最省钱?比原计划省多少钱?4.某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200吨,如用新工艺,则废水排量比环保限制的最大量少100吨,新、旧工艺的废水量之比为2:5,两种工艺的废水量各是多少?5.列二元一次方程组解应用题:学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元,购买5个A奖品和4个B奖品共需210元.求A B,两种奖品的单价.6.某同学在A,B两家网店发现他看中的随身听的单价相同,书包单价也相同.随身听和书包单价之和是492元,且随身听的单价比书包单价的3倍少108元.(1)求该同学看中的随身听和书包的单价各是多少元.(2)某一天恰好赶上商家促销,网店A所有商品打八折销售,网店B全场每购满100元减25元销售,怎样购买更省钱?写出必要的理由过程.7.已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有36吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.根据以上信息,解答下列问题:(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)请你帮该物流公司设计租车方案.8.抗击新冠肺炎疫情期间,全国上下万众一心为武汉捐赠物资.某物流公司运送捐赠物资,已知用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.(1)求1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)该物流公司现有31吨货物需要运送,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.若A型车每辆需租金100元/次,B型车每辆需租金120元/次,请你设计出所有租车方案并选出最省钱的租车方案,求出此时最少租车费.9.随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A 型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元(1)求A B、两种型号的汽车每辆进价分别为多少万元?(2)若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案;(3)若该汽车销售公司销售1辆A型汽车可获利8000元,销售1辆B型汽车可获利5000元,在(2)中的购买方案中,假如这些新能源汽车全部售出,哪种方案获利最大?最大利润是多少元?10.某运输公司有A、B两种货车,3辆A货车与2辆B货车一次可以运货90吨,5辆A货车与4辆B货车一次可以运货160吨.(1)请问1辆A货车和1辆B货车一次可以分别运货多少吨?(2)目前有190吨货物需要运输,该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货车均满载),其中每辆A货车一次运货花费500元,每辆B货车一次运货花费400元.请你列出所有运输方案并指出哪种运输方案费用最少.11.某汽车制造厂开发了一款新式电动汽车计划一年生产安装240辆,由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)如果工厂抽调熟练工m名,再招聘()<<名新工人,使得招聘的新工人和n n010抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案? 12.我校组织一批学生开展社会实践活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元.(1)这批学生的人数是多少?原计划租用45座客车多少辆?(2)若租用同一种客车,要使每位学生都有座位,应该怎样租用合算?13.小志从甲、乙两超市分别购买了10瓶和6瓶cc饮料,共花费51元;小云从甲、乙两超市分别购买了8瓶和12瓶cc饮料,且小云在乙超市比在甲超市多花18元,在小志和小云购买cc饮料时,甲、乙两超市cc饮料价格不一样,若只考虑价格因素,到哪家超市购买这种cc饮料便宜?请说明理由.14.有大、小两种货车,2辆大车与3辆小车一次可以运货15.5吨;5辆大车与6辆小车一次可以运货35吨.求3辆大车与5辆小车一次可以运货多少吨?15.某学校现有若干间学生宿舍,准备安排给若干名学生住宿.原计划每间住8人,则有10间宿舍无人居住.由于疫情防控需要,每间宿舍只能住5人,则有10人无法入住.问该校现有多少间学生宿舍?16.鹏程中学拟组织七年级部分师生赴滁州市琅琊山进行文学采风活动.下面是活动负责人李老师和小芳同学、小明同学有关租车问题的对话:李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”(1)全部物资一次性运送可用甲型车8辆,乙型车5辆,丙型车辆.(2)若全部物资仅用甲、乙两种车型一次性运完,需运费9600元,求甲、乙两种车型各需多少辆?(3)若该公司打算用甲、乙、丙三种车型同时参与运送,已知车辆总数为14辆,(1)甲、乙两种货车每辆可装多少吨货物?(2)若某货主共有20吨货物,计划租用该公司的货车,正好(每辆货车都满载)把这批货物运完,则该货主有________种租车方案?(3)王先生要租用该公可的甲、乙两种货车送一批货,如果租用甲种货车数量比乙种货车数量多1辆,而乙种货车每辆的运费是甲种货车的1.4倍,结果甲种货车共付运费800元,乙种货车共付运费980元,试求此次甲、乙两种货车每辆各需运费多少元?答案1.(1)每辆甲种货车能装货4吨,每辆乙种货车能装货3吨(2)方案1:租用3辆甲种货车、11辆乙种货车;方案2:租用6辆甲种货车、7辆乙种货车;方案3:租用9辆甲种货车、3辆乙种货车2.(1)A种产品4件,B种产品3件;(2)利润是12万元.3.(1)初一(2)班共有53人或59人;(2)两个一起买票更省钱,比原计划节省298元或290元4.新、旧工艺的废水排量分别为200吨和500吨5.A奖品单价30元,B奖品单价15元.6.(1)随身听单价为342元,书包单价为150元(2)在A购买书包,在B购买随身听更省钱,费用为387元7.(1)1辆A型车和1辆B型车都装满货物一次可分别运货3吨,4吨;(2)故共有四种租车方案,分别为:①A型车0辆,B型车9辆;②A型车4辆,B 型车6辆;③A型车8辆,B型车3辆;④A型车12辆,B型车0辆.8.(1)1辆A型车装满货物一次可运3吨,1辆B型车装满货物一次可运4吨;(2)共有3种租车方案:方案一,A型车9辆,B型车1辆;方案二,A型车5辆,B型车4辆;方案三,A型车1辆,B型车7辆,最省钱的租车方案是A型车1辆,B型车7辆,最少租车费为940元9.(1)A型汽车每辆的进价为25万元,B型汽车每辆的进价为10万元;(2)方案一:购进A型车6辆,B型车5辆;方案二:购进A型车4辆,B型车10辆;方案三:购进A型车2辆,B型车15辆;(3)购进A型车2辆,B型车15辆获利最大,最大利润是91000元10.(1)1辆A货车和1辆B货车一次可以分别运货20吨和15吨;(2)共有3种租车方案,方案1:租用A型车8辆,B型车2辆;方案2:租用A型车5辆,B型车6辆;方案3:租用A型车2辆,B型车10辆;租用A型车8辆,B 型车2辆最少.11.(1)每名熟练工每月可以安装4辆电动汽车,新工人每月分别安装2辆电动汽车;(2)12.(1)240人,原计划租用45座客车5辆;(2)租4辆60座客车划算.13.到甲超市购买这种cc饮料便宜.14.24.5吨15.该校现有30间学生宿舍16.(1)平安客运公司60座和45座的客车每辆每天的租金分别是1000元,800元.(2)按小明提出的租车方案,七年级师生到该公司租车一天,共需租金6000元.(3)租用5辆60座和1辆45座的客车,此时租车费为5800元.17.(1)建设一个A类美丽村庄需120万元,建设一个B类美丽村庄需180万元;(2)共需资金1080万元.18.(1)4;(2)甲种车型需8辆,乙种车型需10辆;(3)甲车2辆,乙车5辆,丙车7辆,此时的总运费为8800元.19.(1)1辆A型车满载时一次可运柑橘3吨,1辆B型车满载时一次可运柑橘2吨;(2)①共有4种租车方案,方案1:租用1辆A型车,9辆B型车;方案2:租用3辆A型车,6辆B型车;方案3:租用5辆A型车,3辆B型车;方案4:租用7辆A型车;②最省钱的租车方案是租用7辆A型车,最少租车费是840元20.(1)甲种货车每辆可装2吨货物,乙种货车每辆可装3吨货物;(2)4种租车方案;(3)甲种货车每辆需运费100元,乙种货车每辆需运费140元。
初一下数学期末专题复习3--画图题

1初一下数学期末专题复习3---动手操作题 班姓名1朝.如图,在平面直角坐标系xOy 中,三角形ABC 三个顶点的坐标分别是A (4,2),B (1,0),C (5,-3),三角形ABC 中任意一点P (x 0,y 0),经平移后对应点为P ′(x 0-6,y 0+2),将三角形ABC 作同样的平移得到三角形A′B′C′,点A ,B ,C 的对应点分别为A′,B′,C′.(1)点A′的坐标为____ __,点B′的坐标为__ ____; (2)①画出三角形A′B′C′;②写出三角形A′B′C′的面积 ;(3)过点A′作A′D ∥y 轴,交B′C′于点D ,则点D 的坐标为___ ___.2东. 下面是小红设计的“过直线外一点作这条直线的平行线”的作图过程.已知:点C 在直线AB 上,点D 在直线AB 外,且∠DCB =60°. 求作:直线DE , 使得DE ∥AB . 作法:如图,①在线段CD 的延线上任取一点 M ;②以D 为顶点,DM 为一边,通过量角器度量,在DM 右侧作∠MDE =60°;③将射线DE 反向延长; 直线DE 就是所求作的直线.根据小红的作图过程, (1)补全图形,完成证明过程;证明:∵∠MDE =60°,∠DCB =60°, ∴∠MDE =∠DCB .∴DE ∥AB (______________________________________)(填推理的依据).(2)在(1)的条件下,过点C 作CD 的垂线,交直线DE 于点F .求∠CFE 的度数.3海. 如图,点A 在直线l 外,点B 在直线l 上,连接AB . 选择适当的工具作图. (1)在直线l 上作点C ,使90ACB ∠=︒,连接AC ; (2)在BC 的延长线上任取一点D ,连接AD ;(3)在AB ,AC ,AD 中,最短的线段是 , 依据是 .4丰. 在平面直角坐标系xOy 中,如图,已知点A (4,1),点B (1,-2),过点B 作轴于点C .(1)画出线段BC ,并写出点C 的坐标 ;(2)连接AB ,AC ,得到三角形ABC .平移三角形ABC ,使得点A 与点O 重合,点B ,C 的对应点分别是1B ,1C ,画出三角形11OB C ; (3)直接写出三角形11OB C 的面积 .25房. 按要求画图,并解答问题: 已知:如图,OC 平分AOB ∠.(1)在射线OA 上取一点D ,过点D 作直线DE ∥OB ,交OC 于点E ; (2)若70AOB ∠=︒,求DEC ∠的度数.6密.如图,在平面直角坐标系x O y 中,A (4,3),B (3,1),C (1,2).将三角形ABC 向左平移4个单位长度,再向上平移1个单位长度,可以得到三角形A 1B 1C 1,其中点A 1、B 1、C 1分别与点A 、B 、C 对应. (1)画出平移后的三角形A 1B 1C 1;(2)直接写出A 1、B 1、C 1三个点的坐标 ; (3)已知点P 在y 轴上,以A 1、B 1、P 为顶点的三角形面积为2,求点P 的坐标.7密.如图,直线AB ∥CD ,E 为直线CD 上一点,射线EH 交直线AB 于点F . (1)按要求画图:① 利用量角器及直尺,画∠FED 的角平分线EM ,交直线AB 于点N ; ② 过点N 作NP ⊥CD ,垂足为P . (2)完成下列填空:比较线段NE 和NP 的大小,可以得到NE NP ;(填“>”、“=” 或“<”) 理由是 .8平.如图,点B 是射线CA 上一点,点D 是射线CE 上一点, .21,//∠=∠AC DF(1) 试判断CE FB //吗?请说明理由.(2) 用量角器作FDC ∠的角平分线DG 交FB 的延长线于点G ,过点D 作DG DM ⊥交射线CA 的反向延长线于点M . ①补全图形;②若α=∠DMC ,用α表示FGD ∠为_______________. (1)结论: 证明:C。
七下数学期末专题训练(二)画图题

七下数学期末专题训练(二)画图题1、如图,在正方形网格中,点A 、B 、C 、M 、N 都在格点上都在格点上. . (1)作△)作△ABC ABC 关于直线MN 对称的图形;对称的图形;(2)若网格中最小正方形的边长为1,求△,求△ABC ABC 的面积的面积. .2、如图,在正方形网格中,点A 、B 、C 、O 都在格点上,直线l 过点C 、O 两点.两点.(1)作ABC D 关于直线l 成轴对称的111A B C D ; (2)作ABC D 关于点O 中心对称的222A B C D .3、如图,在方格纸中每个小正方形的边长均为1个单位, △ABC 的三个顶点都在小方格的顶点上.(1)在图中作出将△在图中作出将△ABC ABC 向右平移5个单位后的图形△个单位后的图形△A A 1B 1C 1; (2)在图中作出△)在图中作出△ABC ABC 以C 为旋转中心,沿顺时针方向旋转9090°后的图形△°后的图形△°后的图形△A A 2B 2C .4、如图方格图的小方格都是边长为1的正方形,的正方形,△ABC 的顶点和O 点都是格点.点都是格点.(1)以点O 为对称中心,在方格图中作出△ABC 的中心对称图形△A′B′C′;(2)将△A′B′C′绕点B′顺时针旋转90°,在方格图,在方格图 中画出旋转后得到的△A″B′C″.5、如图,在边长为1个单位长度的小正方形组成的网格中,△ABC 的三个顶点都在格点上,请按要求完成下列各题. (1)画出△ABC 向左平移6个单位长度得到的图形△A 1B 1C 1;(2)将△ABC 绕点O 按逆时针方向旋转180°得到△A 2B 2C 2,请画出△A 2B 2C 2.6、如图,在正方形网格中,ABC D 的三个顶点都在格点上,点O 也在格点上也在格点上. .⑴画C B A ¢¢¢D ,使C B A ¢¢¢D 与ABC D 关于关于 直线OP 成轴对称,点A 的对应点是A ¢; ⑵画C B A ¢¢¢¢¢¢D ,使C B A ¢¢¢¢¢¢D 与C B A ¢¢¢D 关于关于 点O 成中心对称,点A ¢的对应点是A ¢¢. 7、如图,△、如图,△ABC ABC 的三个顶点和点O 都在正方形网格的格点上,每个小正方形的边长都为1. (1)将△)将△ABC ABC 先向右平移4个单位,再向上平移2个单位得到△个单位得到△A A 1B 1C 1,请画出△,请画出△A A 1B 1C 1; (2)请画出△)请画出△A A 2B 2C 2,使△,使△A A 2B 2C 2和△和△ABC ABC 关于点O 成中心对称;成中心对称;(3)在)在(1)(1)(1)、、(2)(2)中所得到的△中所得到的△中所得到的△A A 1B 1C 1与△与△A A 2B 2C 2成轴对称吗?若成轴对称,请画出对称轴;若不成轴对称,请说明理由若不成轴对称,请说明理由. .·ACBOACB PO; 10、如图,在所给网格图(每小格均为边长是、如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(顶点均在格点上)关于直线DE 对称的1B A D ,使PCPB +1最小;最小;,使QC QA +最小.最小. AB CDEFO现已有两种不同的分法:⑴分别作两条对角线(如图中的图⑴)14、某居民小区要在一块长方形的空地上建花坛,现征集设计方案.要求设计的图案由圆和AB C A B C A B C A B C A B C。
北师大七年级数学下作图
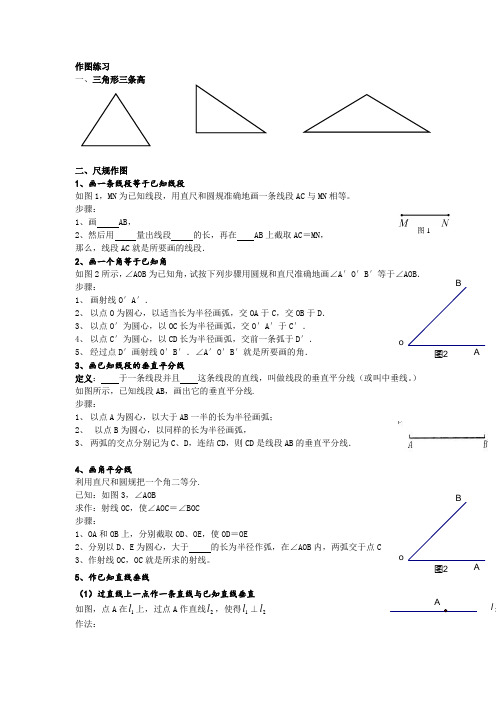
图 1作图练习一、三角形三条高二、尺规作图1、画一条线段等于已知线段如图1,MN 为已知线段,用直尺和圆规准确地画一条线段AC 与MN 相等。
步骤:1、画 AB ,2、然后用 量出线段 的长,再在 AB 上截取AC =MN , 那么,线段AC 就是所要画的线段. 2、画一个角等于已知角 如图2所示,∠AOB 为已知角,试按下列步骤用圆规和直尺准确地画∠A ′O ′B ′等于∠AOB . 步骤:1、 画射线O ′A ′.2、 以点O 为圆心,以适当长为半径画弧,交OA 于C ,交OB 于D .3、 以点O ′为圆心,以OC 长为半径画弧,交O ′A ′于C ′.4、 以点C ′为圆心,以CD 长为半径画弧,交前一条弧于D ′.5、 经过点D ′画射线O ′B ′.∠A ′O ′B ′就是所要画的角. 3、画已知线段的垂直平分线定义: 于一条线段并且 这条线段的直线,叫做线段的垂直平分线(或叫中垂线。
) 如图所示,已知线段AB ,画出它的垂直平分线. 步骤:1、 以点A 为圆心,以大于AB 一半的长为半径画弧;2、 以点B 为圆心,以同样的长为半径画弧,3、 两弧的交点分别记为C 、D ,连结CD ,则CD 是线段AB 的垂直平分线.4、画角平分线利用直尺和圆规把一个角二等分. 已知:如图3,∠AOB求作:射线OC ,使∠AOC =∠BOC 步骤:1、OA 和OB 上,分别截取OD 、OE ,使OD =OE2、分别以D 、E 为圆心,大于 的长为半径作弧,在∠AOB 内,两弧交于点C3、作射线OC ,OC 就是所求的射线。
5、作已知直线垂线(1)过直线上一点作一条直线与已知直线垂直 如图,点A 在1l 上,过点A 作直线2l ,使得1l ⊥2l 作法:o BA图2Al 1o BA图21、以点A 为圆心,以为适当长为半径画弧交1l 于B 、C2、分别以点B 、C 为圆心,以大于21BC 为半径,在1l 一侧作弧,交点为D 3、连接AD那么,AD 就是所求的直线直线2l(2)过直线上一点作一条直线与已知直线垂直1、以点A 为圆心,以大于点A 到1l 的距离的长度为半径画弧交1l 于B 、C2、分别以点B 、C 为圆心,以大于21BC 为半径,在另一侧作弧,交点为D 3、连接AD那么,AD 就是所求的直线直线2l 练习一1、已知线段AB 和CD ,如下图,求作一线段,使它的长度等于AB +2CD.2、如图,已知∠A 、∠B ,求作一个角,使它等于∠A-∠B.5、如图,已知∠AOB 及M 、N 两点,求作:点P ,使点P 到∠AOB 的两边距离相等,且到M 、N 的两点也距离相等。
人教版七年级数学下册期末专题五 作图专题

5.如图,点A表示小明家,点B表示小明外婆家.若小 明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路程 最短?请画出行走路径,并说明理由.
解:两点之间,线段最短,所以去外 婆家走直线.点到直线上一点最短为 垂线,因此应沿垂直河岸的路线 走.行走路径如图所示.
6.在平面直角坐标系内,描出A(-1,0)、B(1,0)、 C(1,2)、D(-1,2)四点,顺次连接A,B,C,D四点, 写出四边形的形状.
(3)PE<PO<FO. 依据是:∵PE是点P到DE的垂线 ,∴PE<PO ∵OP是点O到PF的垂线,∴OP<FO,∴PE<PO<FO.
11.如图,已知△ABC向上平移3个单位长度,再向右平移2 个单位长度,得到△A′B′C′. (1)在图中画出△A′B′C′;(2)写出点A′,B′的坐标; (3)在y轴上是否存在一点P,使得△BCP与△ABC面积相等? 若存在,写出点P的坐标;若不存在,说明理由.
8.如图,给出A的坐标(-1,-1),B的坐标为(1,2). (1)画出对应的平面直角坐标系; (2)将线段AB向右平移2个单位,得到对应的线段为A′B′, 求四边形AA′B′B的面积. 解:(1)如图. (2)如图,平行四边形AA′B′B的高为2-(-1) =3,底为2, ∴S四边形AA′B′B=2×3=6.
解:(1)如图
(2)如图 (3)如图
3.作图: (1)如图①,平面内两条直线AB,CD交于点O,过点P作 直线PM∥AB,PN∥CD; (2)如图②,过C点画CE∥AD,交BA的延长线于E对 应点,试画出线段AB;
(2)如图,三角形ABC和三角形ABC外的一点A′,把三角 形ABC平移,使A与A′重合.
解:如图,四边形 ABCD是正方形.
7.如图,(1)过BC上任意一点P(不与B,C重合)画AB的平 行线交AC于T; (2)过点C画MN∥AB; (3)直线PT,MN具有何种位置关系?试说明理由.
人教版七年级下册数学几何作图(习题及答案)

几何作图(习题)例题示范例 1:在直线l 上任取一点A,截取AB=20cm,再截取BC=50cm,则AB 的中点D 与AC 的中点E 之间的距离为,并作图说明.思路分析首先,理解题意,找关键词,其中l 为直线,AB,BC 为l 上的两条线段.其次,设计作图方案,作图.作直线l,任取一点作为A,取适当长作为AB;此时点B 位置固定,但点C 可在点B 左侧或右侧,位置不定,故分两种情况.①点C 在点B 左侧,如图,50lC A B20接着取AB 的中点D,AC 的中点E.50lC E 设计算法:AD B20DE =AD +AE=1AB +1AC 2 2=1 BC 2= 25②点C 在点B 右侧,如图,20 50lA B C接着取AB 的中点D,AC 的中点E.20 50lA DB E C设计算法:DE = AE - AD= 1 AC - 1 AB2 2= 1 BC2= 25综上,DE 的长度为 25cm .巩固练习1. 如图 1,点 C ,D 是直线 AB 外两点,按下列要求作图:(1); (2). 得到的图形如图 2,请在横线填上作法. DDCAB 图1图2 2. 如图,已知线段 AB ,按要求作图:①分别以点 A 和点 B 为圆心、以 AB 的长为半径作弧,两弧相交于点 C 和点 D ;②作直线 CD ,交线段 AB 于点 E ;③请通过测量猜想线段 AB 和直线 CD 的位置关系,线段 AE 与线段 BE 的数量关系.A BC A E F B3.作图:已知线段a,b(a>b),作一条线段,使它等于a -b .(保留作图痕迹,不必写作法)ab4.已知线段AB=15cm,点C 在直线AB 上,且BC=2AB,则线段A C 的长为,并作图说明.5.已知点C 在直线A B 上,若A C=4cm,BC=6cm,E,F 分别为线段AC,BC 的中点,则E F 的长为,并作图说明.6.已知线段AB=24,点C 在直线AB 上,BC=3AC,M,N 分别为线段AB,AC 的中点,则M N 的长为,并作图说明.7.已知从点O 出发的三条射线OA,OB,OC,若∠AOB=60°,∠AOC 1∠AOB ,则∠BOC 的度数为,3并作图说明.8.已知∠AOB 为直角,∠BOC=40°,OM 平分∠AOB,ON 平分∠BOC,则∠MON 的度数为,并作图说明.9.已知∠AOB=120°,∠AOC=4∠BOC,OD 平分∠AOB,OE 平分∠AOC,则∠EOD 的度数为,并作图说明.思考小结1. 我们学过的需要分类讨论的情况:第一类:由定义本身引起的.比如:已知x + 2 = 3 ,y = 3 ,求xy的值.思路分析由绝对值的定义,得x= ,y=然后借助进行分类讨论,求解可得xy= .第二类:位置不确定引起的.比如:习题中的第9题.思路分析首先可画出∠AOB,然后根据题意画出射线OC,但射线OC 的位置不确定,所以要分情况讨论:①射线OC在∠AOB的内部;②射线OC在∠AOB的.AO B【参考答案】巩固练习1.(1)作射线DC 交AB 于点E(2)过点C 作CF⊥DE 于点C,交AB 于点F2.作图略,AB⊥CD,AE=BE3.作图略4.15cm 或45cm,作图说明略5.1cm 或5cm,作图说明略6.9 或 18,作图说明略7.40°或80°,作图说明略 8.25°或65°,作图说明略 9.12°或20°,作图说明略思考小结1. -5 或1,±3,树状图,±3 或±15.外部,图略。
苏科版初中数学七年级下册第七章《平面图形的认识(二)》专题训练试题(含答案)
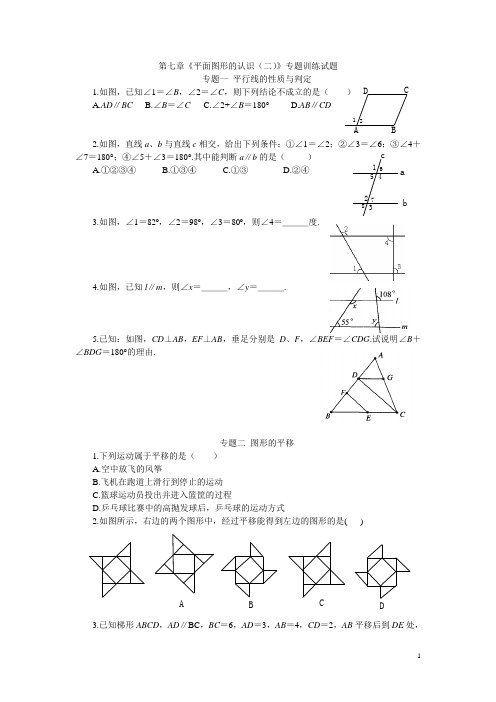
第七章《平面图形的认识(二)》专题训练试题专题一 平行线的性质与判定1.如图,已知∠1=∠B ,∠2=∠C ,则下列结论不成立的是( ) A.AD ∥BC B.∠B =∠C C.∠2+∠B =180° D.AB ∥CD2.如图,直线a 、b 与直线c 相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠3=180°.其中能判断a ∥b 的是( )A.①②③④B.①③④C.①③D.②④3.如图,∠1=82º,∠2=98º,∠3=80º,则∠4=___度.4.如图,已知l ∥m ,则∠x =___,∠y =___.5.已知:如图,CD ⊥AB ,EF ⊥AB ,垂足分别是D 、F ,∠BEF =∠CDG .试说明∠B +∠BDG =180°的理由.专题二 图形的平移1.下列运动属于平移的是( )A.空中放飞的风筝B.飞机在跑道上滑行到停止的运动C.篮球运动员投出并进入篮筐的过程D.乒乓球比赛中的高抛发球后,乒乓球的运动方式2.如图所示,右边的两个图形中,经过平移能得到左边的图形的是( )3.已知梯形ABCD ,AD ∥BC ,BC =6,AD =3,AB =4,CD =2,AB 平移后到DE 处,12DCBA 876c b a 54321D CB A则ΔCDE 的周长是___.4.如果△ABC 经过平移后得到△DEF ,若∠A =41°,∠C =32°,EF =3cm ,则∠E =__,BC =__cm.5.已知:如图,是两个重叠的直角三角形,将其中的一个直角三角形沿着BC 方向平移BE 的长得到此图形,若其中AB =8,BE =5,DH =3.求四边形DHCF 的面积.专题三 与三角形有关的计算1.一个三角形的两个内角分别是55°和65°,这个三角形的外角不可能是( )A.115°B.120°C.125°D.130°2.若三角形三边的长分别为整数,周长为13,且一边长为4,则这个三角形的最大边长为( )A.7B.6C.5D.43.如图所示,在锐角△ABC 中,BE 分别是AB ,AC 边上的高,且CD ,BE 交于一点P ,若∠A =50°,则∠BPC 的度数是___.4.明明家有一块三角形ABC 空地,他要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价230元,AC =12m ,AC 边上的高BD =15m ,则购买这种草皮至少需要___元.5.(1)如图1,有一块直角三角板XYZ 放置在△ABC 上,恰好三角板XYZ 的两条直角边XY 、XZ 分别经过点B 、C .△ABC 中,∠A =30°,则∠ABC +∠ACB =______,∠XBC +∠XCB =______.(2)如图,改变直角三角板XYZ 的位置,使三角板XYZ 的两条直角边XY 、XZ•仍然分别经过B 、C ,那么∠ABX +∠ACX 的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX +∠ACX 的大小.图 2图1专题四 与多边形有关的计算1.如果一个正多边形的内角和是900°,则这个正多边形是正______边形.A.五边形B.六边形C.七边形D.八边形2.如果多边形的内角和是外角和的k 倍,那么这个多边形的边数是( )A.kB.2k +1C.2k +2D.2k -23.现提供下列几个角的度数:①270°;②540°;③630°;④1800°;⑤2430°.其中是某一个多边形内角和的有___.4.如图,小亮从A 点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…照这样走下去,他第一次回到出发地A 点时,一共走了___米.5.有两个多边形,如果它们都是各边相等,各内角相等的多边形,且这两个多边形的边数之比为1∶2,内角之比是3∶4,则这两个多边形的边数各是多少?专题五 综合创新应用1.在正方形ABCD 所在的平面内找点P ,使△P AB ,△PBC ,△PCD ,△P AD 均为等腰三角形,这样的点P 有( )A.1个B.4个C.5个D.9个2.如图,△ABC 内有三个点D 、E 、F ,现分别以A 、B 、C 、D 、E 、F 这六个点为顶点构建三角形,使得任意点不落在另一个三角形内部,那么这些三角形的所有内角之和为( )A.360°B.900°C.1260°D.1440°3.如果等腰三角形周长为20,则腰长x 的取值范围是___,底边长y 的取值范围是___.4.用黑白两种颜色的正六边形地面砖按如图所示的规律,拼成若干个图案.则第4个图案中有白色地面砖___块;第n 个图案中有白色地面砖___块.5.小明在进行多边形内角和计算时,求得一多边形的内角和为1125°.重新检查时,发现少加了一个内角.问这个内角是多少度?小明求的是几边形的内角和?6.如图所示是一个广场地面的一部分,地面的中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖拼成,从里往外共12层(不包括中央的正六边形地砖),每一层30° 30° 30° A (7)B F AC ED 第1个 第2个 第3个的外界都围成一个多边形.若中央正六边形地砖的边长是0.5米,则第12层的外边界所围成的多边形的周长是多少?专题一:1,B ;2,B.3,80º;4,125°、72°.5,∵CD ⊥AB ,EF ⊥AB ,∴∠BFE =90°,∠BDC =90°,∴CD ∥EF (同位角相等,两直线平行),∴∠BEF =∠BCD (两直线平行,同位角相等),又因为∠BEF =∠CDG ,∴∠BCD =∠CDG ,∴BC ∥DG (内错角相等,两直线平行),∴∠B +∠BDG =180°(两直线平行,同旁内角互补).专题二:1,B ;2,C.3,9;4,117°,3.5,要求四边形DHCF 的面积,依题意,本来两个直角三角形是重合的,即两个直角三角形的面积相等,再由平移的知识可以知道四边形DHCF 的面积等于直角梯形ABEH 的面积,而此时DE =AB ,所以EH =8-3=5,所以直角梯形ABEH 的面积=12(EH +AB )×BE =12(5+8)×5=32.5.所以四边形DHCF 的面积是13.5平方单位.专题三:1,C ;2,C.3,②④;4,120.5,设其中一个多边形的边数为n ,则另一个多边形的边数为2n ,于是,根据题意,得()2180n n -⨯o∶()221802n n -⨯o=3∶4,解得n =5.所以2n =10.即这两个多边形的边数分别是5和10.专题四:1,D ;2,B.3,130°;4,41400.5,(1)150°;90°.(2)不变化.∵∠A=30°,∴∠ABC+∠ACB=150°,∵∠X=•90°,∴∠XBC+∠XCB =90°,∴∠ABX+∠ACX =(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.点拨:此题注意运用整体法计算.专题五:1,D.提示:形内有5个,形外有4个;2,D. 提示:图形共有8个三角形.3,5<x<10、0<y<10.提示:依题意,得x+x>20-x-x,且x-x<20-x-x,即x >5,且x<10,所以5<x<10.同理0<y<10;4,4n+2.提示:第1个图案需要白色地面砖6=4×1+2,第2个图案需要白色地面砖10=4×2+2,第3个图案需要白色地面砖14=4×3+2,第4个图案需要白色地面砖18=4×4+2,…第n个图案需要白色地面砖10=4×n +2=4n+2.5,设这个内角的度数为x,这个多边形为n边形.则根据题意,得1125°+x=(n-2)·180°.由于1 125°+x是180°的倍数,而1 125°=180°×6+45°,所以x+45°=180°,解得x=135°,进而解得n=9.所以这个内角的度数为135°,这个多边形为九边形.6,36米. 提示:第一层即正六边形有6×1=6个边长,第二层有6×2=12个边长,第三层6×3=18个边长,…第12层有6×12=72个边长,而一个边长是0.5米,所以第12层的外边界所围成的多边形的周长是36米.。
2020-2021人教版数学七年级下册 专项测试卷(二)新定义数学问题

人教版数学七年级下册 专项测试卷(二)新定义数学问题一、按要求做题1.用“※”定义一种新运算:对于任意有理数a 和b .规定a ※b =ab ²+2ab+a ,如1※2=1x2²+2x1x2+1=9.(1)求(-4)※3;(2)若21+a ※3=-16,求a 的值.2.定义新运算:对于任意实数a 、b 都有a ▲b=ab -a -b+1,等式右边是通常的加法、减法及乘法运算,例如:2▲4= 2x4-2-4+1=3.试根据上述知识解决下列问题.(1)若3▲x =6,求x 的值;(2)若▲x 5的值不大于9,求x 的取值范围.3.对于实数a ,我们规定:用符号[a ]表示不大于a 的最大整数,称为a 的根整数,例如:[9]=3,[10]_3.(1)仿照以上方法计算:[4]=____,[37]=____.(2)若[x ]=1,写出满足题意的x 的整数值:____;如果我们对a 连续求根整数,直到结果为1.例如:对10连续求根整数2次,[10]=3→[3]=1,这时的结果为1.(3)对120连续求根整数,____次之后结果为1;(4)只需进行3次连续求根整数运算,最后结果为1的所有正整数中,最大的是____.4.对于实数a 、b ,定义两种新运算“※”和“*”:a ※b=a+kb ,a*b=ka+b(其中k 为常数,且k ≠0).若对于平面直角坐标系xOy 中的点P(a ,b),有点P'(a ※b ,a*b)与之对应,则称点P 的“k 衍生点”为点P',例如:P(1,3)的“2衍生点”为P'(1+2x3,2x1+3),即P'(7,5).(1)点P( -1,5)的“3衍生点”的坐标为____;(2)若点P 的“5衍生点”的坐标为(9,-3),求点P 的坐标;(3)若点P 的“k 衍生点”为点P',且直线PP'平行于y 轴,线段PP'的长度为线段OP 长度的3倍,求k 的值.5.在平面直角坐标系xOy 中,对于任意两点P ₁(x ₁,y ₁)与P ₂(x ₂,y ₂)的“识别距离”,给出如下定义: 若y y x x 2121-≥-,则点P ₁(x ₁,y ₁)与点P ₂(x ₂,y ₂)的“识别距离”为x x 21-;若y y x x 2121--<,则点P ₁(x ₁,y ₁)与点P ₂(x ₂,y ₂)的“识别距离”为y y 21-.(1)已知点A(-1,0),点B 为y 轴上的动点.①若点A 与点B 的“识别距离”为2,则写出满足条件的点B 的坐标为____;②直接写出点A 与点B 的“识别距离”的最小值为____;(2)已知点C 的坐标为⎪⎭⎫ ⎝⎛+343m m ,点D 的坐标为(0,1),求点C 与点D 的“识别距离”的最小值及相应的点C 的坐标.6.在平面直角坐标系xOy 中,对于任意三点A 、B 、C 的“矩面积”,给出如下定义,“水平底”a :任意两点横坐标差的最大值,“铅垂高”h :任意两点纵坐标差的最大值,则“矩面积”S=ah.例如:三点坐标分别为A(1,2)、B(-3,1)、C(2,-2),则“水平底”a=5,“铅垂高”h=4,“矩面积”D=ah=20.根据所给定义解决下列问题:(1)已知点D(1,2)、E(-2,1)、F(0,6),则这三点的“矩面积”S=____;(2)若D(1,2)、E(-2,1)、F(0,t)三点的“矩面积”S 为18,求点F 的坐标.7.[阅读材料,获取新知]在航空、航海等领域我们经常用距离和角度来确定点的位置,规定如下:在平面内取一个定点O .叫做极点,引一条射线O x ,叫做极轴,再选定单位长度和角度的正方向(通常取逆时针方向).对于平面内任意一点M ,用p 表示线段OM 的长度(有时也用r 表示),p 表示从O x 到OM 的角度,p 叫做点M 的极径,ρ叫做点M 的极角,有序数对(p ,θ)就叫做点M 的极坐标,这样建立的坐标系叫做极坐标系.通常情况下,M 的极径坐标单位为1(长度单位),极角坐标单位为rad(或°).例如:如图①所示,点M 到点O 的距离为5个单位长度,OM 与O x 的夹角为70°(O x 的逆时针方向).则点M 的极坐标为(5,70°);点N 到点O 的距离为3个单位长度,ON 与O x 的夹角为50°(O x 的顺时针方向),则点N 的极坐标为(3,-500).[利用新知,解答问题]如图②所示,已知过点O 的所有射线等分圆周且相邻两射线的夹角为15°,且极径坐标单位为1.(1)点A 的极坐标是____,点D 的极坐标是____.(2)请在图②中标出点B(5,45°),点E(2,-90°);(3)怎样从点B 运动到点C?小明设计的一条路线为点B →(4,45°)→(3,45°)→(3,30°)→点C .请你设计一条与小明不同的路线,也可以从点B 运动到点C .8.定义:可化为其中一个未知数的系数都为1,另一个未知数的系数互为倒数,并且常数项互为相反数的二元一次方程组,称为“相关线性方程组”,如所示,其中k 、b 称为该方程组的“相关系数”.(1)若关于x 、y 的方程组可化为“相关线性方程组”,则该方程组的解为____,(2)若某“相关线性方程组”有无数组解,求该方程组的两个“相关系数”之和.9.阅读下列材料:我们给出如下定义:数轴上给定不重合的两点A 、B ,若数轴上存在一点M ,使得点M 到点A 的距离等于点M 到点B 的距离,则称点M 为点A 与点B 的“平衡点”.解答下列问题:(1)若点A 表示的数为-3。
2020年秋人教版数学七年级期末复习专题 :找规律之解答题专项(二)

如果别人思考数学的真理像我一样深入持久,他也会找到我的发现。
——高斯2020年秋人教版数学七年级期末复习专题:找规律之解答题专项(二)1.如图所示,有一个形如六边形的点阵,它的中心是一个点,第二层每边有两个点,第三层每边有三个点,依此类推(1)填写下表:层次 1 2 3 4 5 6 该层对应的点数所有层的总点数(2)写出第n层(n≥2)所对应的点数;(3)写出六边形的点阵共有n层(n≥2)时的总点数;(4)如果六边形的点阵共有n层(n≥2)时的总点数为397,你知道共有多少层吗?2.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有n张桌子时,两种摆放方式各能坐多少人?(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌为什么?3.图①是一个三角形,分别连接这个三角形三边的中点得到图②,再分别连接图②中间小三角形三边的中点,得到图③.(1)图②有个三角形;图③有个三角形;(2)按上面的方法继续下去,第n个图形中有个三角形(用n的代数式表示).(3)是否存在正整数n,使得第n个图形中存在2018个三角形?如果存在,请求出n 的值;如果不存在,请说明理由.4.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面.请观察下列图形并解答有关问题:(1)在第n个图中,每一横行共有块瓷砖,每一竖列共有块瓷砖(均用含n的代数式表示);(2)设铺设地面所用瓷砖的总块数为y,用(1)中的n表示y;(3)当n=20时,求此时y的值;(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元钱购买瓷砖?5.如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.尝试(1)求前4个台阶上数的和是多少?(2)求第5个台阶上的数x是多少?应用求从下到上前31个台阶上数的和.发现试用含k(k为正整数)的式子表示出数“1”所在的台阶数.6.如图,图1中小黑点的个数记为a1=4,图2中小黑点的个数记为a2=8,图3中小黑点的个数记为a3=13,…根据以上图中的规律完成下列问题:(1)图4中小黑点的个数记为a4,则a4=;(2)图n中小黑点的个数记为a n,则a n=(用含n的式子表示);(3)第几个图形中的小黑点的个数为43个?7.用黑白两种颜色的正六边形地砖按如图所示的方式,拼成若干个图案:(1)当黑色地砖有1块时,白色地砖有块,当黑色地砖有2块时,白色地砖有块;(2)第n(n为正整数)个图案中,白色地砖有块;(3)第几个图案中有2018块白色地砖?请说明理由.8.找规律.一张长方形桌子可坐6人,按如图方式把桌子拼在一起.(1)2张桌子拼在一起可坐人;3张桌子拼在一起可坐人;n张桌子拼在一起可坐人.(2)一家餐厅有45张这样的长方形桌子,按照如图方式每5张桌子拼成一张大桌子,请问45张长方形桌子这样摆放一共可坐多少人.9.如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A,B,C,D把原正方形分割成一些三角形(互相不重叠).(1)填写下表:正方形ABCD内点的个数 1 2 3 4 …n分割成的三角形的个数 4 6 …(2)如果原正方形被分割成2018个三角形,此时正方形ABCD内部有多少个点?(3)上述条件下,正方形又能否被分割成2019个三角形?若能,此时正方形ABCD 内部有多少个点?若不能,请说明理由.(4)综上所述,你有什么发现?(写出一条即可)10.为了庆祝元旦,某商场在门前的空地上用花盆排列出了如图所示的图案,第1图案中10个花盆,第2个图案中有19个花盆,……,按此规律排列下去.(1)第3个图案中有个花盆,第4个图案中有个花盆;(2)根据上述规律,求出第n个图案中花盆的个数(用含n的代数式表示).(3)是否存在恰好由2018个花盆排列出的具有上述规律的图案?若存在,说明它是第几个图案?若不存在,请说明理由.参考答案1.解:第一层上的点数为1;第二层上的点数为6=1×6;第三层上的点数为6+6=2×6;第四层上的点数为6+6+6=3×6;…第n层上的点数为(n﹣1)×6.所以n层六边形点阵的总点数为1+1×6+2×6+3×6+…+(n﹣1)×6=1+6[1+2+3+4+…+(n﹣1)]=1+6[(1+2+3+…+n﹣1)+(n﹣1+n﹣2+…+3+2+1)]÷2=1+6×=1+3n(n﹣1)(1)填表如下:层次 1 2 3 4 5 6 该层对应的点数 1 6 12 18 24 30所有层的总点数 1 7 19 37 61 91 (2)根据分析可得第n层的点数之和为6(n﹣1)(n≥2)3)根据分析可得共有n层时的点数之和为1+3n(n﹣1);(4)根据题意得:1+3n(n﹣1)=397.n(n﹣1)=132;(n﹣12)(n+11)=0n=12或﹣11.故n=12,答:共有12层.2.解:(1)第一种中,只有一张桌子是6人,后边多一张桌子多4人.即有n张桌子时是6+4(n﹣1)=4n+2.第二种中,有一张桌子是6人,后边多一张桌子多2人,即6+2(n﹣1)=2n+4.(2)中,分别求出两种对应的n的值,或分别求出n=25时,两种不同的摆放方式对应的人数,即可作出判断.打算用第一种摆放方式来摆放餐桌.因为,当n=25时,4×25+2=102>98当n=25时,2×25+4=54<98所以,选用第一种摆放方式.3.解:(1)图②中有5个三角形,图③中有9个三角形.故答案为:5,9;(2)依题意得:n=1时,有1个三角形;n=2时,有5个三角形;n=3时,有9个三角形;…∴当n=n时,有(4n﹣3)个三角形.故答案为:4n﹣3;(3)假设存在正整数n,使得第n个图形中有2018个三角形,根据题意得:4n﹣3=2018,解得:n=,不是整数,故不存在正整数n,使得第n个图形中有2018个三角形.4.解:(1)第n个图形的瓷砖的每行有(n+3)个,每列有n+2个;(2)y=(n+2)(n+3);(3)当n=20时,y=(n+2)(n+3)=(20+2)(20+3)=506;(4)当n=20时,有白瓷砖420块,黑瓷砖86块,共需花费86×4+420×3=1604(元).5.解:尝试:(1)由题意得前4个台阶上数的和是﹣5﹣2+1+9=3;(2)由题意得﹣2+1+9+x=3,解得:x=﹣5,则第5个台阶上的数x是﹣5;应用:由题意知台阶上的数字是每4个一循环,∵31÷4=7…3,∴7×3+1﹣2﹣5=15,即从下到上前31个台阶上数的和为15;发现:数“1”所在的台阶数为4k﹣1.6.解:(1)根据题意知a4=1+2+3+4+5+4=19,故答案为:19;(2)a n=1+2+3+…+n+n+1+n=+2n+1=n2+n+1,故答案为:n2+n+1;(3)当n2+n+1=43时,解得:n=7或﹣12(负值舍去),所以第7个图形中的小黑点的个数为43个.7.解:(1)当黑色地砖有1块时,白色地砖有2+4=6块,当黑色地砖有2块时,白色地砖有2+4×2=10块,故答案为:6、10;(2)根据题意知第n(n为正整数)个图案中,白色地砖有2+4n(块),故答案为:4n+2.(3)令4n+2=2018,解得:n=504,所以,第504个图案中有2018块白色地砖.8.解:(1)由图可知,2张桌子拼在一起可坐8人,3张桌子拼在一起可坐10人,…依此类推,每多一张桌子可多坐2人,所以,n张桌子拼在一起可坐2n+4;故答案为:8,10,2n+4;(2)当n=5时,2n+4=2×5+4=14(人),可拼成的大桌子数,45÷5=9,14×9=126(人);9.解:(1)有1个点时,内部分割成4个三角形;有2个点时,内部分割成4+2=6个三角形;有3个点时,内部分割成4+2×2=8个三角形;有4个点时,内部分割成4+2×3=10个三角形;…以此类推,有n个点时,内部分割成4+2×(n﹣1)=(2n+2)个三角形,补全表格如下:正方形ABCD内点的个数 1 2 3 4 …n 分割成的三角形的个数 4 6 8 10 …2n+2 (2)能,由(1)知2n+2=2018,解得:n=1008,即此时正方形ABCD内部有1008个点;(3)不能,理由如下:由(1)知2n+2=2019,解得n=1008,不是整数,所以不能分割成2019个三角形.初中数学**精品文档**(4)由题意知分割成的三角形个数是其内部点的个数的2倍与2的和.10.解:(1)第1个图案中有10个花盆,第2个图案中有2×10﹣1=19个花盆,第3个图案中有3×10﹣2=28个花盆,第4个图案中有4×10﹣3=37个花盆;(2)第n个图案中有10n﹣(n﹣1)=9n+1个花盆;(3)假设存在恰好由2018个花盆排列出的具有上述规律的图案,则有9n+1=2018,解得:n=,不是整数,所以不存在由2018个花盆排列出的具有上述规律的图案;故答案为:28;37经过大海的一番磨砺,卵石才变得更加美丽光滑。
2013-2014七年级数学下期末复习专题训练二----作图题

北师大数学七年级下期末复习专题训练二----作图题
姓名
1、(1)尺规作图:用尺规过点B 作一条平行线BE 使BE//AD
(2)已知△ABC ,用尺规作图过一点A 作一条直线使它与BC 平行
2、已知b AC a BC ABC c b a ==∆,;,,,使得求作三条线段分别为,c AB =。
(只保留作图痕迹,不写作法)
3、已知:∠α、∠β,线段a , 求作:△ABC ,使∠B=∠α,∠C=∠β,BC= a 。
(保留作图痕迹,不写作法)
4、已知:线段a 、c 和∠β(如图),利用尺规作ΔABC ,使BC=a ,
AB=c ,∠ABC=∠β。
(不写作法,保留作图痕迹)。
5、已知ΔABC ,作关于这条直线的对称图形ΔDEF
a
b
c
D
C A B
6、平原上,有三个村庄A,B,C,为解决当地的吃水问题,三村联合出资修建一个蓄水池,请你确定一个建池点位置,使他到个村庄的距离相等。
村庄布局如图:
A . . C
B .
7、如下图,两个班的学生分别在M、N处参加植树劳动。
现要在道路AB、AC的交叉区域内设一个茶水供应P点,使P到两条道路的距离相等,且使PM=PN,请在下图中,用尺规作出这个供应点的位置。
8、某汽车探险队要从A城穿越沙漠去B城,途中需要到河流L边为汽车加水,汽车在河边
哪一点加水,才能使行驶的总路程最短?请你在图上画出这一点.。
北师大版七下数学试题(图形版)

七下数学试题复习(图形版)1,如图所示,已知O是∠APB内的一点,点M,N分别是O点关于PA,PB的对称点,MN与PA,PB分别相交于点E,F,已知MN=5cm,则△OEF的周长______cm.2,如图,△ABC中,∠ACB=90°,沿CD边折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,则∠BDC等于______°.3,在一个暗箱里放有a个除颜色外完全相同的球,这a个球中红球只有3个.每次将球搅拌均匀后,任意摸出一个球,记下颜色后,再放回暗箱,通过大量的重复试验后发现,摸到红球的频率稳定在25%.那么估计a大约有______个.4,如图所示是一条线段,AB的长为10厘米,MN的长为2厘米,假设可以随意在这条线段上取一个点,那么这个点取在线段MN上的概率为______.5,如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于50,则BC= 。
(第5题图)(第6题图)(第7题图)6,如图,在△ABC中,∠A=50°,AB=AC,AB的垂直平分线DE交AC于D,则∠DBC的度数是7,如图,在△ABC中,BC边的中垂线交BC于D,交AB于E.若CE平分∠ACB,∠B=40°,则∠A=______度.8,如图,在ΔABC中,AC=DC=DB,∠ACD=100°,则∠B等于9,如图,锐角三角形ABC中,直线L为BC的中垂线,直线M为∠ABC的角平分线,L与M 相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为(第9题图)(第10题图)(第12题图)10,用直尺和圆规作一个角的角平分线示意图如图所示,则说明∠AOC=∠BOC的依据是______.11如果三角形内一点P到三角形各边的距离相等的点是三角形的交点,如果三角形内一点P到三角形各顶点的距离相等的点是三角形的交点.(填:中线、高线、角平分线、中垂线)12,如图,已知OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点.若PA=2,则PQ的最小值为______,理论根据为______.13,如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B= .14,如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,∠1=20°,则∠2等于15,如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP 并延长交BC于点D,则下列正确的是(1)AD是∠BAC的平分线(2)∠ADC=60(3)点D在AB的中垂线上(第15题图)(第16题图)(第17题图)16,如图所示,△A B C的三边A B、B C、C A的长分别为12、10、6,其三条角平分线的交点为O,则S△A B O∶S△B C O∶S△C A O=________.17,如图,AB∥CD,点E在BC上,且CD=CE,∠D=78°,则∠B的度数为18,如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为19,如图,已知△ABC是等边三角形,点B、C,D、E在同一直线上,且CG=CD,DF=DE,则∠E=20,如图所示,已知等边三角形ABC的周长是2a,BM是AC边上的高,N为BC延长线上的一点,且CN=CM,则BN=21,如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.(1)求证:CE=BF;(2)求∠BPC的度数.22,如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶90千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的关系.请根据图象填空:(1)摩托车的速度为______千米/小时;汽车的速度为______千米/小时;(2)汽车比摩托车早______小时到达B地.(3)在汽车出发后几小时,汽车和摩托车相遇?说明理由.23,如图,AD、BC相交于O,OA=OC,∠OBD=∠ODB. 求证:AB=CD.24,如图,已知:Rt△ABC中,∠C=90°,AC=BC=2,将一块三角尺的直角顶点与斜边AB的中点M重合,当三角尺绕着点M旋转时,两直角边始终保持分别与边BC、AC交于D,E两点(D、E不与B、A重合).(1)试说明:MD=ME;(2)求四边形MDCE的面积.(3)若只将原题目中的“AC=BC=2”改为“BC=a,AC=b,(a≠b)”其它都不变,请你探究:MD 和ME还相等吗?如果相等,请证说明;如果不相等,请求出MD∶ME的值.。
2020春北师大版七年级下册数学习题课件:期末复习综合题(二) (共17张PPT) (2)

6.计算:
-
������ ������
-������
×10-1-
-
������ ������
������
=
-������������
.
7.如图,直线 AB,CD 相交于点 E,DF∥AB.若∠AEC=100°,
则∠D= 80° .
8.如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径 作弧,交AC于点D,连接BD,则∠ABD= 36 °.
当 a=������������,b=-2 时, 原式=6×������������×(-2)-4×4=-6-16=-22.
13.如图,已知∠1=∠2,∠B=∠C,可推出AB∥CD.理由如下: 因为∠1=∠2(已知),且∠1=∠4( 对顶角相等 ), 所以∠2=∠4(等量代换), 所以CE∥BF( 同位角相等,两直线平行 ), 所以∠ C =∠3(两直线平行,同位角相等 ). 又因为∠B=∠C(已知), 所以∠3=∠B(等量代换), 所以AB∥CD( 内错角相等,两直线平行 ).
解:(1)国内拨打时间与电话费之间的关系,打电话时间是自变 量,电话费是因变量. (2)由题意可得y=0.36x.
(3)当x=25时,y=0.36×25=9(元),即如果打电话超出25分钟,需
付186+9=195(元)的电话费. (4)当 y=54 时,x=���������.���������������������=150(分钟). 答:小明的爸爸打电话超出 150 分钟.
3.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC= 70°,则∠BOD的度数等于( B )
A.30° B.35°
C.20° D.40°
4.A,B,C,D四名选手参加50米决赛,赛场共设1,2,3,4四条跑道,
柳沟中学七年级下册数学作图题汇总练习

柳沟中学七年级下册数学作图题汇总练习 1、过直线外一点作已知直线的平行线。
.P作图方法:一重二靠三移四画。
唯一性:过直线外一点有且只有一条直线与已知直线平行。
n2、(1)过直线外一点作已知直线的垂线。
如图① .P 作图方法:一重二移三画。
(2)过直线上一点作已知直线的垂线。
如图② .唯一性:过直线外(或直线上)一点有且只有 图① 图②一条直线与已知直线平行。
垂线段性质:连接直线外一点与已知直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短。
3、作平移图形。
如下图:将四边形ABCD 进行平移后,使点A 的对应点为点1A ,请你画出平移后所得的四边形1111A B C D . 方法一:作图依据: 连接各组对应点的线段平行且相等。
作图过程:(1)连接A 1A , (2)过点B 、C 、D 作直线A 1A 的平行线,(3)BB 1、CC 1、DD 1的长等于A 1A 。
方法二:作图依据:平移前后两个图形的对应边平行且相等。
4、平面直角坐标系中的作图。
(1)、在图所示的平面直角坐标系中表示下面各点:A (0,3),B (1,-3),C (-3,-5)。
①A 点到原点O 的距离是__ __个单位长。
②计算△ABC 的面积。
③将△ABC 先向左平移3个单位,再向上 平移4个单位,作出平移后的△A ′B ′C ′。
写出点A ′、B ′、C ′的坐标。
④作出点C 关于x 轴对称的点D, 作出点C关于y 轴对称的点E ,并写出点D 、点E 的坐标。
⑤点D 到x 、y 轴的距离分别是多少?. (2)、如图,已知A (-4,-1),B (-5,-4),C (-1,-3),△ABC 经过平移得到△A ′B ′C ′,△ABC 中任意一点P (x 1,y 1)平移后的对应点为p ′(x 1+6,y 1+4)①请在图中作出△A ′B ′C ′; ②写出点A ′、B ′、C ′的坐标。
(7分)(3)如图,这是某市部分简图,为了确定各建筑物的位置: ①请你以火车站为原点建立平面直角坐标系.②写出市场、超市的坐标.③请将体育场、宾馆和火车站看作三点用线段连起来,得△ABC ,然后将此三角形向下平移4个单位长度,再画出平移后的△A /B /C /,然后求出其面积5、作三角形的高、中线、角平分线。
七年级数学下册综合算式专项练习题函数像的绘制

七年级数学下册综合算式专项练习题函数像的绘制在数学学习中,函数是一个非常重要的概念,它在解决各种实际问题中起着至关重要的作用。
而在学习函数的过程中,绘制函数图像是一个非常重要的环节,它可以帮助我们更好地理解函数的性质和特点。
本文将通过综合算式专项练习题的方式,介绍如何绘制函数的图像。
假设我们有以下综合算式专项练习题:例题1: 绘制函数y = 2x + 1的图像。
例题2: 绘制函数y = x^2的图像。
例题3: 绘制函数y = 3/x的图像。
下面我们逐个解答这些练习题,并给出相应的图像。
例题1: 绘制函数y = 2x + 1的图像。
这是一个一次函数,即斜率为2,截距为1的直线函数。
我们可以选择几个不同的x值来计算对应的y值,然后将这些点连接成直线,就可以得到函数的图像。
取x = 0时,y = 2*0 + 1 = 1,得到点(0, 1);取x = 1时,y = 2*1 + 1 = 3,得到点(1, 3);取x = 2时,y = 2*2 + 1 = 5,得到点(2, 5);取x = -1时,y = 2*(-1) + 1 = -1,得到点(-1, -1)。
将这些点连接起来,就可以得到函数y = 2x + 1的图像,如下图所示:[图像1]例题2: 绘制函数y = x^2的图像。
这是一个二次函数,即抛物线函数。
我们可以选择几个不同的x值来计算对应的y值,然后将这些点连接起来,就可以得到函数的图像。
取x = -2时,y = (-2)^2 = 4,得到点(-2, 4);取x = -1时,y = (-1)^2 = 1,得到点(-1, 1);取x = 0时,y = 0^2 = 0,得到点(0, 0);取x = 1时,y = 1^2 = 1,得到点(1, 1);取x = 2时,y = 2^2 = 4,得到点(2, 4)。
将这些点连接起来,就可以得到函数y = x^2的图像,如下图所示:[图像2]例题3: 绘制函数y = 3/x的图像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七下数学期末专题训练(二)画图题
1、如图,在正方形网格中,点A 、B 、C 、M 、N 都在格点上.
(1)作△ABC 关于直线MN 对称的图形;
(2)若网格中最小正方形的边长为1,求△ABC 的面积.
2、如图,在正方形网格中,点A 、B 、C 、O 都在格点上,直线l 过点C 、O 两点.
(1)作ABC ∆关于直线l 成轴对称的111A B C ∆; (2)作ABC ∆关于点O 中心对称的222A B C ∆.
3、如图,在方格纸中每个小正方形的边长均为1个单位, △ABC 的三个顶点都在小方格的顶点上.
(1)在图中作出将△ABC 向右平移5个单位后的图形△A 1B 1C 1; (2)在图中作出△ABC 以C 为旋转中心,沿顺时针方向旋转90°后的图形△A 2B 2C .
4、如图方格图的小方格都是边长为1的正方形,
△ABC 的顶点和O 点都是格点.
(1)以点O 为对称中心,在方格图中作出△ABC
的中心对称图形△A′B′C′;
(2)将△A′B′C′绕点B′顺时针旋转90°,在方格图
中画出旋转后得到的△A″B′C″.
5、如图,在边长为1个单位长度的小正方形组成的网格中,△ABC 的三个顶点都在格点上,请按要求完成下列各题.
(1)画出△ABC 向左平移6个单位长度得到的图形△A 1B 1C 1;
(2)将△ABC 绕点O 按逆时针方向旋转180°得到△A 2B 2C 2,请画出△A 2B 2C 2.
6、如图,在正方形网格中,ABC ∆的三个顶点都在格点上,点O 也在格点上.
⑴画C B A '''∆,使C B A '''∆与ABC ∆关于 直线OP 成轴对称,点A 的对应点是A '; ⑵画C B A ''''''∆,使C B A ''''''∆与C B A '''∆关于 点O 成中心对称,点A '的对应点是A ''.
7、如图,△ABC 的三个顶点和点O 都在正方形网格的格点上,每个小正方形的边长都为1. (1)将△ABC 先向右平移4个单位,再向上平移2个单位得到△A 1B 1C 1,请画出△A 1B 1C 1; (2)请画出△A 2B 2C 2,使△A 2B 2C 2和△ABC 关于点O 成中心对称;
(3)在(1)、(2)中所得到的△A 1B 1C 1与△A 2B 2C 2成轴对称吗?若成轴对称,请画出对称轴;
若不成轴对称,请说明理由.
·
A
C
B
O
8、如图8,在正方形网格中,每个小正方形的边长 都是1个单位长度,△ABC 和△DEF 的三个顶点都在 格点上.
⑴画出ABC ∆沿水平方向向左平移1个单位长度得到 的111C B A ∆;
⑵画出111C B A ∆绕点O 逆时针旋转180°后得到的222C B A ∆
⑶判断DEF ∆与222C B A
∆
属于哪种对称?若是中心对称, 试画出对称中心点Q ;若是轴对称,试画出对称轴l (用粗线表示).
9、如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC 的三个顶点都在格点上.
(1)在网格中画出△ABC 向下平移3个单位得到的△A 1B 1C 1; (2)在网格中画出△ABC 关于直线m 对称的△A 2B 2C 2; (3)在直线m 上画一点P ,使得||2PC PA -的值最大.
10、如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:(用直尺画图) (1)画出格点ABC ∆(顶点均在格点上)关于直线DE 对称的111C B A ∆; (2)在DE 上画出点P ,使PC PB +1最小; (3)在DE 上画出点Q ,使QC QA +最小.
(图8)
11、现有如图①所示的两种瓷砖.请从这两种瓷砖中各选2块,拼成一个新的正方
形地板图案,使拼铺的图案成轴对称图形或中心对称图形(如示例图②).
(要求:分别在图③、图④中各设计一种与示例图不同的拼法,这两种拼法各不相同,且在
图③拼成的图案是轴对称图形,在图④拼成的图案既是轴对称图形,又是中心对称图形.)
12、在33⨯的正方形网格图中,ABC ∆和DEF ∆的顶点都在格点上,且ABC ∆和DEF ∆关于某直线成轴对称.请在备用图中至少画出三种.
13、为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:⑴分割后的整个图形必须是轴对称图形;⑵四块图形形状相同;⑶四块图形面积相等.
现已有两种不同的分法:⑴分别作两条对角线(如图中的图⑴);⑵过一条边的四等分点作这边的垂线段(图⑵)(图⑵中两个图形的分割看作同一方法).请你按照上述三个要求,分别在图⑶、图⑷两个正方形中画出另外两种不同的分割方法.............
(正确画图,不写画法)
14、某居民小区要在一块长方形的空地上建花坛,现征集设计方案.要求设计的图案由圆和
正方形组成(圆和正方形的个数不限).满足方案1的整个长方形花坛成轴对称图形且对称轴只有一条;满足方案2的整个长方形花坛成轴对称图形且对称轴只有两条.请你分别在下面两个方框内画出两种设计方案并画出其对称轴.
第24题图① 图② 图③ 图④ A
B C A B C A B C A B C A B C (方案1)
(方案2)。
