小专题训练(九) 圆中动点与最值问题.ppt
微专题12 与圆有关的定点、定值、最值、范围问题

微专题12与圆有关的定点、定值、最值、范围问题真题感悟(2019·全国Ⅰ卷)已知点A,B关于坐标原点O对称,AB=4,⊙M过点A,B且与直线x+2=0相切.(1)若A在直线x+y=0上,求⊙M的半径;(2)是否存在定点P,使得当A运动时,MA-MP为定值?并说明理由.解(1)因为⊙M过点A,B,所以圆心M在AB的垂直平分线上.由已知A在直线x+y=0上,且A,B关于坐标原点O对称,所以M在直线y=x上,故可设M(a,a).因为⊙M与直线x+2=0相切,所以⊙M的半径为r=|a+2|.连接MA,由已知得AO=2.又MO⊥AO,故可得2a2+4=(a+2)2,解得a=0或a=4.故⊙M的半径r=2或r=6.(2)存在定点P(1,0),使得MA-MP为定值.理由如下:设M(x,y),由已知得⊙M的半径为r=|x+2|,AO=2.由于MO⊥AO,故可得x2+y2+4=(x+2)2, 化简得M的轨迹方程为y2=4x.因为曲线C:y2=4x是以点P(1,0)为焦点,以直线x=-1为准线的抛物线,所以MP=x+1.因为MA-MP=r-MP=x+2-(x+1)=1,所以存在满足条件的定点P.考点整合1.最值与范围问题(1)研究与圆有关的最值问题时,可借助圆的性质,利用数形结合求解.(2)常见的最值问题有以下几种类型:①形如μ=y-bx-a的最值问题,可转化为动直线斜率的最值问题;②形如t=ax+by的最值问题,可转化为动直线截距的最值问题;③形如μ=(x -a )2+(y -b )2的最值问题,可转化为动点到定点的距离的平方的最值问题.(3)对于圆的方程也可以利用三角代换,转化为三角函数问题:对于圆(x -a )2+(y -b )2=r 2,可设x =a +r cos θ,y =b +r sin θ.2.定点问题的求解步骤(1)选参变量:需要证明过定点的动直线(曲线)往往随着某一个量的变化而变化,可以选择这个量为参变量.(2)求动直线(曲线)方程:求出含上述参变量的动直线(曲线)方程,通过消元或整体思想,使得方程只含有一个参量(当根据几何条件建立的等式中含有多个参量时,要注意区别对待,与动点、动直线、动圆有关的参量是主要参量,其他参量可看作系数).(3)定点:求出定点坐标.利用方程ax +b =0恒成立来处理定点问题.在处理时也可以用从特殊到一般的思想,先求出一个特殊点,再代入进行验证.3.定值问题的处理(1)可以直接求出相关等式,再论证该等式与参数无关,类似于三角化简求值.(2)也可以用从特殊到一般的思想,先让参数取特殊值来论证性质,再将性质推广至一般情形.热点一 最值与范围问题【例1】 已知圆M 的圆心M 在x 轴上,半径为1,直线l :y =43x -12被圆M 所截的弦长为3,且圆心M 在直线l 的下方.(1)求圆M 的方程;(2)设A (0,t ),B (0,t +6)(-5≤t ≤-2),若圆M 是△ABC 的内切圆,求△ABC 的面积S 的最大值和最小值.解 (1)设圆心M (a ,0),由已知得圆心M 到l :8x -6y -3=0的距离为12-⎝ ⎛⎭⎪⎫322=12,∴|8a -3|82+(-6)2=12,又∵M (a ,0)在l 的下方,∴8a -3>0,∴8a -3=5,a =1.故圆M 的方程为(x -1)2+y 2=1.(2)由已知可设AC 的斜率为k 1,BC 的斜率为k 2(k 1>k 2),则直线AC 的方程为y =k 1x +t ,直线BC 的方程为y =k 2x +t +6.由方程组⎩⎨⎧y =k 1x +t ,y =k 2x +t +6, 得C 点的横坐标为x 0=6k 1-k 2. ∵AB =t +6-t =6,∴S =12⎪⎪⎪⎪⎪⎪6k 1-k 2×6=18k 1-k 2. ∵圆M 与AC 相切,∴1=|k 1+t |1+k 21,∴k 1=1-t 22t , 同理,k 2=1-(t +6)22(t +6),∴k 1-k 2=3(t 2+6t +1)t 2+6t, ∴S =6(t 2+6t )t 2+6t +1=6⎝ ⎛⎭⎪⎫1-1t 2+6t +1. ∵-5≤t ≤-2,∴-2≤t +3≤1,∴-8≤t 2+6t +1≤-4,∴S max =6×⎝ ⎛⎭⎪⎫1+14=152,S min =6×⎝ ⎛⎭⎪⎫1+18=274, ∴△ABC 的面积S 的最大值为152,最小值为274.探究提高 直线与圆中的最值问题主要包含两个方面(1)参量的取值范围:由直线和圆的位置关系或几何特征,引起的参量如k ,b ,r 的值变化.此类问题主要是根据几何特征建立关于参量的不等式或函数.(2)长度和面积的最值:由于直线或圆的运动,引起的长度或面积的值变化.此类问题主要是建立关于与参数如k 或(x ,y )的函数,运用函数或基本不等式求最值.【训练1】 已知实数x ,y 满足方程x 2+y 2-4x +1=0.(1)求y -x 的最大值和最小值;(2)求x 2+y 2的最大值和最小值.解 由x 2+y 2-4x +1=0得(x -2)2+y 2=3,它表示以(2,0)为圆心,3为半径长的圆.(1)y -x 可看作是直线y =x +b 在y 轴上的截距,当直线y =x +b 与圆相切时,纵截距b 取得最大值或最小值,此时|2-0+b |2=3,解得b =-2±6. 所以y -x 的最大值为-2+6,最小值为-2- 6.(2)x 2+y 2表示圆上的点与原点距离的平方,由平面几何知识知,过原点和圆心的直线与圆有两个交点,在这两个交点处x 2+y 2取得最值.因为圆心到原点的距离为(2-0)2+(0-0)2=2, 所以x 2+y 2的最大值是(2+3)2=7+43,x 2+y 2的最小值是(2-3)2=7-4 3.热点二 与圆有关的定点问题【例2】 (2019·北京卷)已知抛物线C :x 2=-2py (p >0)经过点(2,-1).(1)求抛物线C 的方程及其准线方程;(2)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线y =-1分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.(1)解 由抛物线C :x 2=-2py 经过点(2,-1)得p =2.所以抛物线C 的方程为x 2=-4y ,其准线方程为y =1.(2)证明 抛物线C 的焦点为F (0,-1).设直线l 的方程为y =kx -1(k ≠0).由⎩⎨⎧y =kx -1,x 2=-4y ,得x 2+4kx -4=0. 设M (x 1,y 1),N (x 2,y 2),则解方程得 x 1,2=-2k ±2k 2+1,从而x 1x 2=-4.直线OM 的方程为y =y 1x 1x . 令y =-1,得点A 的横坐标x A =-x 1y 1, 同理得B 的横坐标x B =-x 2y 2.所以A ⎝ ⎛⎭⎪⎫-x 1y 1,-1,B ⎝ ⎛⎭⎪⎫-x 2y 2,-1. 设点D (0,n ),则DA →=⎝ ⎛⎭⎪⎫-x 1y 1,-1-n , DB →=⎝ ⎛⎭⎪⎫-x 2y 2,-1-n , DA →·DB →=x 1x 2y 1y 2+(n +1)2=x 1x 2⎝ ⎛⎭⎪⎫-x 214⎝ ⎛⎭⎪⎫-x 224+(n +1)2 =16x 1x 2+(n +1)2=-4+(n +1)2. 令DA →·DB→=0,即-4+(n +1)2=0,得n =1或n =-3. 故以AB 为直径的圆经过y 轴上的定点(0,1)和(0,-3).探究提高 圆锥曲线中的定值与定点问题是高考的常考题型,运算量较大,题目逻辑性较强.解决这类问题一般有两种方法:一是根据题意求出相关的表达式,再根据已知条件列出方程组,消去参数,求出定值或定点坐标;二是先利用特殊情况确定定值或定点坐标,再从一般情况进行验证.【训练2】 已知圆x 2+y 2=9的圆心为P ,点Q (a ,b )在圆P 外,以PQ 为直径作圆M 与圆P 相交于A ,B 两点.(1)试判断直线QA 与圆P 的位置关系;(2)若QA =QB =4,试问点Q 在什么曲线上运动?(3)若点Q 在直线x +y -9=0上运动,问:直线AB 是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.解 (1)因为以PQ 为直径的圆M 与圆P 相交于A ,B ,所以P A ⊥QA ,又AP 为圆P 的半径,所以AQ 为圆P 的切线,从而直线QA 与圆P 相切.(2)因为P A ⊥QA ,AP =3,AQ =4,所以PQ =32+42=5,故点Q 在以P 为圆心,5为半径的圆上运动.(3)因为点Q (a ,b )在直线x +y -9=0上,所以点Q (a ,9-a ),所以,以PQ 为直径的圆M 的方程为x 2+y 2-ax -(9-a )y =0,又AB 为圆P 与圆M 的公共弦,所以直线AB 的方程为ax +(9-a )y -9=0,即a(x-y)-9y-9=0,从而此直线过x-y=0与9y-9=0的交点,即过定点(1,1).热点三与圆有关的定值问题【例3】(2018·高邮调研)如图,已知圆O的方程为x2+y2=1,直线l的方程为x-y+22=0,点P是直线l上的动点,过点P作圆O的切线P A,PB,切点为A,B.(1)若∠APB=60°,试求点P的坐标;(2)在(1)的条件下,对于圆O上任意一点M,平面内是否存在一定点R,使MR MP为定值?如果存在,求出点R的坐标;如果不存在,请说明理由.解(1)连接OP,OA,OB,因为P A,PB为过点P的圆O的切线,切点为A,B,所以OA⊥P A,OB⊥PB.因为∠APB=60°,∠APO=30°,在Rt△APO中,OA=1,所以OP=2.设点P的坐标为(t,t+22),则t2+(t+22)2=4,t2+22t+2=0,即(t+2)2=0,解得t=-2,所以点P的坐标为(-2,2).(2)假设存在符合条件的定点R.设点M(x,y),R(x0,y0),MR2MP2=λ,则x2+y2=1,即(x-x0)2+(y-y0)2=λ[(x+2)2+(y-2)2],整理得-2x0x-2y0y+x20+y20+1=λ(22x-22y+5),上式对任意x,y∈R,且x2+y2=1恒成立,则⎩⎨⎧-2x 0=22λ,-2y 0=-22λ,x 20+y 20+1=5λ,解得⎩⎪⎨⎪⎧λ=14,x 0=-24,y 0=24或⎩⎨⎧λ=1,x 0=-2,(舍去)y 0=2.所以R 的坐标为⎝ ⎛⎭⎪⎫-24,24, 经检验,符合条件MR MP =12,所以对于圆O 上任意一点M ,平面内存在一定点R ,使MR MP 为定值,且R 的坐标为⎝ ⎛⎭⎪⎫-24,24. 探究提高 本题考查直线与圆相切问题以及定值问题.相切问题的基本处理方法是将切点与圆心连接,从而它与切线相互垂直,利用这一直角来进行转化研究问题;第(2)问是探索性问题,在研究探索性问题时,先假设存在是一般性的处理方法,其次将所要研究的问题转化为关于点M 的坐标为元的方程问题,利用该方程的解与点M 的坐标无关来研究问题.【训练3】 (2019·泰州中学检测)已知圆O :x 2+y 2=4与坐标轴交于点A 1,A 2,B 1,B 2(如图).(1)点Q 是圆O 上除A 1,A 2外的任意点(如图1),A 2Q ,A 1Q 与直线y +3=0交于不同的两点M ,N ,求MN 的最小值;(2)点P 是圆O 上除A 1,A 2,B 1,B 2外的任意点(如图2),直线B 2P 交x 轴于点F ,直线A 1B 2交A 2P 于点E .设A 2P 的斜率为k ,EF 的斜率为m ,求证:2m -k 为定值.(1)解 由题意可设直线A 2Q 的方程为y =k ′(x -2),直线A 1Q 的方程为y =-1k ′(x+2),k ′≠0.由⎩⎨⎧y =k ′(x -2),y +3=0,解得⎩⎪⎨⎪⎧x =2-3k ′,y =-3,由⎩⎪⎨⎪⎧y =-1k ′(x +2),y +3=0,解得⎩⎨⎧x =3k ′-2,y =-3. 所以直线A 2Q 与直线y +3=0的交点为M ⎝ ⎛⎭⎪⎫2-3k ′,-3, 直线A 1Q 与直线y +3=0的交点为N (3k ′-2,-3),所以MN =⎪⎪⎪⎪⎪⎪3k ′+3k ′-4. 当k ′>0时,MN =⎪⎪⎪⎪⎪⎪3k ′+3k ′-4≥6-4=2,当且仅当k ′=1时等号成立; 当k ′<0时,MN =⎪⎪⎪⎪⎪⎪3k ′+3k ′-4≥|4-(-6)|=10,当且仅当k ′=-1时等号成立. 故线段MN 长度的最小值是2.(2)证明 由题意可知点A 1(-2,0),A 2(2,0),B 1(0,-2),B 2(0,2),A 2P 的斜率为k ,所以直线A 2P 的方程为y =k (x -2),由⎩⎨⎧y =k (x -2),x 2+y 2=4,得P ⎝ ⎛⎭⎪⎫2k 2-2k 2+1,-4k k 2+1, 则直线B 2P 的方程为y =-k +1k -1x +2, 令y =0,则x =2(k -1)k +1,即F ⎝ ⎛⎭⎪⎫2(k -1)k +1,0. 因为直线A 1B 2的方程为x -y +2=0,由⎩⎨⎧x -y +2=0,y =k (x -2),解得⎩⎪⎨⎪⎧x =2k +2k -1,y =4k k -1,所以E ⎝ ⎛⎭⎪⎫2k +2k -1,4k k -1, 所以EF 的斜率m =4kk -12k +2k -1-2(k -1)k +1=k +12, 所以2m -k =2·k +12-k =1(定值).【新题感悟】 (2019·苏北七市高三一模)在平面直角坐标系xOy 中,圆O :x 2+y 2=1,圆C :(x -4)2+y 2=4.若存在过点P (m ,0)的直线l ,l 被两圆截得的弦长相等,则实数m 的取值范围是________.解析 直线l 的斜率k 不存在或为0时均不成立,设直线l 的方程为kx -y -km =0,则圆心O (0,0)到直线l 的距离d 1=|km |k 2+1,圆心C (4,0)到直线l 的距离d 2=|4k -km |k 2+1.因为l 被两圆截得的弦长相等,所以21-d 21=24-d 22,即d 22-d 21=3,所以16k 2+k 2m 2-8k 2m -k 2m 2k 2+1=3,化为:16k 2-8k 2m =3k 2+3,k 2=313-8m>0,得:m <138.又d 21=k 2m 2k 2+1=m 21+1k 2=m 21+13-8m 3=3m 216-8m <1,即3m 2+8m -16<0,解得:-4<m <43.综上,-4<m <43.答案 ⎝ ⎛⎭⎪⎫-4,43一、填空题1.(2015·江苏卷)在平面直角坐标系xOy 中,以点(1,0)为圆心且与直线mx -y -2m -1=0(m ∈R )相切的所有圆中,半径最大的圆的标准方程为________.解析直线mx-y-2m-1=0恒过定点(2,-1),由题意,得半径最大的圆的半径r=(1-2)2+(0+1)2= 2.故所求圆的标准方程为(x-1)2+y2=2.答案(x-1)2+y2=22.(2019·靖江调研)已知圆C:x2+y2-2x-2y+1=0,直线l:3x+4y-17=0.若在直线l上任取一点M作圆C的切线MA,MB,切点分别为A,B,则AB的长度取最小值时直线AB的方程为________.解析圆C的标准方程为(x-1)2+(y-1)2=1,当AB的长度最小时,圆心角∠ACB最小,设为2θ,则由cos θ=ACCM=1CM,知当θ最小时,cos θ最大,即CM最小,那么CM⊥l,所以k AB=k l=-34.设直线AB的方程为3x+4y=m.又由CM=|3+4-17|5=2,此时cos θ=12,则点C到直线AB的距离为AC cos θ=12,即1 2=|3+4-m|5,解得m=192或m=92,经检验m=192,则直线AB的方程为6x+8y-19=0.答案6x+8y-19=03.在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为________.解析由题意可知以线段AB为直径的圆C过原点O,要使圆C的面积最小(D 为切点),只需圆C的半径或直径最小,又圆C与直线2x+y-4=0相切,所以由平面几何知识,当OC所在直线与直线2x+y-4=0垂直时,OD最小(D为切点),即圆C的直径最小,此时OD=|2×0+0-4|5=45,所以圆的半径为25,圆C的面积的最小值为S=πr2=4 5π.答案4 5π4.(2018·全国Ⅲ卷改编)直线x+y+2=0分别与x轴、y轴交于A,B两点,点P 在圆(x-2)2+y2=2上,则△ABP面积的取值范围是________.解析由题意知圆心的坐标为(2,0),半径r=2,圆心到直线x+y+2=0的距离d=|2+2|1+1=22,所以圆上的点到直线的最大距离是d+r=32,最小距离是d-r= 2.易知A(-2,0),B(0,-2),所以AB=22,所以2≤S△ABP≤6. 答案[2,6]5.(2019·常州调研)在平面直角坐标系xOy中,若圆(x-2)2+(y-2)2=1上存在点M,使得点M关于x轴的对称点N在直线kx+y+3=0上,则实数k的最小值为________.解析圆(x-2)2+(y-2)2=1关于x轴的对称圆的方程为(x-2)2+(y+2)2=1,由题意得圆心(2,-2)到直线kx+y+3=0的距离d=|2k-2+3|k2+1≤1,解得-43≤k≤0,所以实数k的最小值为-4 3.答案-4 36.(2019·南京、盐城模拟)在平面直角坐标系xOy中,已知点P为函数y=2ln x的图象与圆M:(x-3)2+y2=r2的公共点,且它们在点P处有公切线,若二次函数y=f(x)的图象经过点O,P,M,则y=f(x)的最大值为________.解析设P(x0,2ln x0),x0>0,则函数y=2ln x在点P处的切线斜率为2x0,则2x0·2ln x0x0-3=-1,即4ln x0=-x0·(x0-3)①.由二次函数y=f(x)的图象经过点O和M可设f (x )=ax (x -3),代入点P (x 0,2ln x 0),x 0>0,得2ln x 0=ax 0(x 0-3) ②.由①②比较可得a =-12,则f (x )=-12x (x -3),则f (x )max =f ⎝ ⎛⎭⎪⎫32=-12×32×⎝ ⎛⎭⎪⎫-32=98.答案 987.直线2ax +by =1与圆x 2+y 2=1相交于A ,B 两点(其中a ,b 是实数),且△AOB 是直角三角形(O 是坐标原点),则点P (a ,b )与点(0,1)之间距离的最小值为________.解析 根据题意画出图形,如图所示,过点O 作OC ⊥AB 于C ,因为△AOB 为等腰直角三角形,所以C 为弦AB 的中点,又OA =OB =1,根据勾股定理得AB =2, ∴OC =12AB =22.∴圆心(0,0)到直线2ax +by =1的距离为12a 2+b 2=22,即2a 2+b 2=2,即a 2=-12b 2+1≥0.∴-2≤b ≤ 2.则点P (a ,b )与点(0,1)之间的距离d =(a -0)2+(b -1)2=a 2+b 2-2b +1=12b 2-2b +2.设f (b )=12b 2-2b +2=12(b -2)2,此函数图象为对称轴为b =2的开口向上的抛物线,∴当-2≤b ≤2<2时,函数为减函数.∴f (b )min =f (2)=12(2-2)2, ∴d 的最小值为12(2-2)2=(2-1)2=2-1.答案2-18.(2019·南京师大附中模拟)已知直线x -y +b =0与圆x 2+y 2=9交于不同的两点A ,B .若O 是坐标原点,且|OA →+OB →|≥22|AB →|,则实数b 的取值范围是________. 解析 设AB 的中点为D ,则OA→+OB →=2OD →,故|OD →|≥24|AB →|,即|OD →|2≥18|AB →|2.再由直线与圆的弦长公式可得,AB =2r 2-d 2(d 为圆心到直线的距离),又直线与圆相交,故d <r ,得|b |2<3,所以-32<b <32,根据|OD→|2≥18|AB →|2,|AB →|2=4(9-OD →2),得|OD →|2≥3.由点到直线的距离公式可得|OD →|2=b 22,即b 22≥3,所以b ≥6或b ≤- 6.综上可得,b 的取值范围是(-32,-6]∪[6,32). 答案 (-32,-6]∪[6,32) 二、解答题9.如果实数x ,y 满足(x +2)2+y 2=3. (1)求yx 的最大值; (2)求2x -y 的最小值.解 (1)问题可转化为求圆(x +2)2+y 2=3上任意一点到原点连线的斜率k =yx 的最大值,由图形性质可知,由原点向圆(x +2)2+y 2=3作切线,其中切线斜率的最大值即为yx 的最大值.设切线方程为y =kx ,即kx -y =0,由|-2k -0|k 2+1=3,解得k =3或k =-3,所以yx 的最大值为 3.(2)将2x -y 看作直线y =2x +b 在y 轴上的纵截距的相反数,当直线y =2x +b 与圆(x +2)2+y 2=3相切时,纵截距b 取得最大值或最小值.此时|-4+b |22+1=3,所以b =4±15,所以2x -y 的最小值为-4-15. 10.(2019·扬州模拟)已知圆O :x 2+y 2=4.(1)直线l 1:3x +y -23=0与圆O 相交于A ,B 两点,求弦AB 的长度; (2)如图,设M (x 1,y 1),P (x 2,y 2)是圆O 上的两个动点,点M关于原点的对称点为M 1,点M 关于x 轴的对称点为M 2,如果直线PM 1,PM 2与y 轴分别交于(0,m )和(0,n ),问mn 是否为定值?若是,求出该定值;若不是,请说明理由.解 (1)由于圆心(0,0)到直线l 1:3x +y -23=0的距离d =|-23|2= 3.圆的半径r =2,所以AB =2r 2-d 2=2.(2)由于M (x 1,y 1),点M 关于原点的对称点为M 1,点M 关于x 轴的对称点为M 2,可得M 1(-x 1,-y 1),M 2(x 1,-y 1), 由M (x 1,y 1),P (x 2,y 2)是圆O 上的两个动点,可得x 21+y 21=4,x 22+y 22=4.直线PM 1的方程为y +y 1y 2+y 1=x +x 1x 2+x 1,令x =0,求得y =m =x 1y 2-x 2y 1x 2+x 1.直线PM 2的方程为y +y 1y 2+y 1=x -x 1x 2-x 1,令x =0,求得y =n =-x 1y 2-x 2y 1x 2-x 1.所以mn =x 22y 21-x 21y 22x 22-x 21=x 22(4-x 21)-x 21(4-x 22)x 22-x 21=4. 故mn 为定值.11.如图所示,已知圆A 的圆心在直线y =-2x 上,且该圆上存在两点关于直线x +y -1=0对称,又圆A 与直线l 1:x +2y +7=0相切,过点B (-2,0)的动直线l 与圆A 相交于M ,N 两点,Q 是MN 的中点,直线l 与l 1相交于点P .(1)求圆A 的方程;(2)当MN =219时,求直线l 的方程;(3)(BM →+BN →)·BP→是否为定值?如果是,求出此定值;如果不是,请说明理由.解 (1)由圆上存在两点关于直线x +y -1=0对称知圆心A 在直线x +y -1=0上.由⎩⎨⎧y =-2x ,x +y -1=0,得A (-1,2). 设圆A 的半径为R ,∵圆A 与直线l 1:x +2y +7=0相切,∴R =|-1+4+7|5=25, ∴圆A 的方程为(x +1)2+(y -2)2=20.(2)当直线l 与x 轴垂直时,易知x =-2符合题意; 当直线l 与x 轴不垂直时, 设直线l 的方程为y =k (x +2),即kx -y +2k =0,连接AQ ,则AQ ⊥MN , ∵MN =219,∴AQ =20-19=1. 由AQ =|k -2|k 2+1=1,得k =34, ∴直线l 的方程为y =34(x +2),即3x -4y +6=0, ∴所求直线l 的方程为x =-2或3x -4y +6=0. (3)∵AQ ⊥BP ,∴AQ →·BP→=0,∴(BM →+BN →)·BP →=2BQ →·BP →=2(BA →+AQ →)·BP →=2BA →·BP →; 当直线l 与x 轴垂直时,得P ⎝ ⎛⎭⎪⎫-2,-52,则BP →=⎝ ⎛⎭⎪⎫0,-52,又BA →=(1,2), ∴(BM →+BN →)·BP →=2BA →·BP→=-10;当直线l 的斜率存在时,设直线l 的方程为y =k (x +2), 由⎩⎨⎧y =k (x +2),x +2y +7=0,解得P ⎝ ⎛⎭⎪⎫-4k -71+2k ,-5k 1+2k , ∴BP →=⎝⎛⎭⎪⎫-51+2k ,-5k 1+2k , ∴(BM →+BN →)·BP →=2BA →·BP→=2⎝ ⎛⎭⎪⎫-51+2k -10k 1+2k =-10. 综上所述,(BM →+BN →)·BP→为定值-10.。
初中数学圆中最值定值问题专题(推荐)

初中数学圆中最值定值问题专题(推荐)圆中最值域定值问题研究类型一:例1:在图中,AB是⊙O的直径,AB=10cm,M是半圆AB的一个三等分点,N是半圆AB的一个六等分点,P是直径AB上一动点,连接MP、NP。
求MP+NP的最小值。
例2:已知圆O的面积为3π,AB为直径,弧AC的度数为80度,弧BD的度数为20度,点P为直径AB上任一点。
求PC+CD的最小值。
例3:在菱形ABC中,∠A=60度,AB=3,圆A、圆B的半径为2和1,P、E、F分别是CD、圆A和圆B上的动点。
求PE+PF的最小值。
类型二:折叠隐圆基本原理】:点A为圆外一点,P为圆O上动点,连接AO并延长交圆于P1,则AP的最小值为AP2,最大值为AP1.例1:在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△XXX沿MN所在的直线翻折得到△A′MN,连接A′C,求A′B长度的最小值。
例2:已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(1,1),点B(5,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,则CB’的最小值为多少?例3:在四边形ABCD中,AD∥BC,∠A=90,AD=1,AB=2,BC=3,P是线段AD上一动点,将△ABP沿BP所在直线翻折得到△QBP,则△CQD的面积最小值为多少?类型三:随动位似隐圆例:在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=6,点D是边AC上一点且AD=23,将线段AD绕点A旋转得线段AD′,点F始终为BD′的中点,则将线段CF最大值为多少?分析]:易知D’轨迹为以A为圆心AD为半径的圆,则在运动过程中AD’为定值23,故取AB中点G,则FG为中位线,FG=3,故F点轨迹为以G为圆心,3为半径的圆。
问题实质为已知圆外一点C和圆G上一点F,求CF的最大值。
方法归纳:1.如图,点A和点O1为定点,圆O1半径为定值,P为圆O1上动点,M为AP中点。
专题九(动点型问题)

中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练
③如图②, 当EO=EF时, 过点E作EH⊥y轴 于点H ,在△AOE和△BEF中, ∵∠EAO=∠FBE, EO=EF, ∠AOE=∠BEF, ∴△AOE≌△BEF(AAS)。∴BE=AO=2。 ∵EH⊥OB ,∴∠EHB=90°。 ∴∠AOB=∠EHB。 ∴EH∥AO。 ∴∠BEH=∠BAO=45°。
4
全效学习中考学练测
中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练
中考典例剖析 (二)以双动点为载体,探求结论开放性问题 4 例轴8,.O如A为图y,轴在建矩立形平A面B直CD角中坐,标AO系=3,,设taDn、∠EA分CB别= 是3.线以段OA为C、坐O标C上原的点动,点OC,为它x 们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单 位的速度从点C向点O运动.设运动时间为t(秒) (1)求直线AC的解析式; (2)用含t的代数式表示点D的坐标; (3)在t为何值时,△ODE为直角三角形? (4)在什么条件下,以Rt△ODE的三个顶点能确定一条对称轴平行于y轴的 抛物线?并请选择一种情况,求出所确定的抛物线的解析式.
全效学习中考学练测
中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练 全效学习中考学练测
中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练 全效学习中考学练测
中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练 全效学习中考学练测
中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练 全效学习中考学练测
全效学习中考学练测
中考专题诠释 解题策略与解法精讲 中考典例剖析 中考真题演练
第二章 习题课 与圆有关的最值问题

习题课 与圆有关的最值问题学习目标 1.能用直线与圆的方程解决一些简单的最值问题.2.初步了解用代数方法处理几何问题的思想. 导语2017年7月我国首座海上风电平台4G 基站在黄海建成,信号覆盖范围达60公里. 一艘船由于机械故障在海上遇险,想要求救,却发现手机没有信号.已知基站在海面上的信号覆盖范围是以基站为圆心的一个圆及其内部区域,那么船到达信号区域的最短路程是多少呢?(引出课题:探究与圆有关的最值问题.) 一、与距离有关的最值问题1.圆外一点到圆上任意一点距离的最小值=d -r ,最大值=d +r .2.直线与圆相离,圆上任意一点到直线距离的最小值=d -r ,最大值=d +r .3.过圆内一定点的直线被圆截得的弦长的最小值=2r 2-d 2,最大值=2r .4.直线与圆相离,过直线上一点作圆的切线,切线长的最小值=d 2-r 2.例1 (1)当直线l :(2m +1)x +(m +1)y -7m -4=0(m ∈R )被圆C :(x -1)2+(y -2)2=25截得的弦最短时,m 的值为________. 答案 -34解析 直线l 的方程可化为(2x +y -7)m +x +y -4=0,所以直线l 会经过定点⎩⎪⎨⎪⎧2x +y -7=0,x +y -4=0, 解得定点坐标为M (3,1) ,圆心C 为(1,2),当直线l 与CM 垂直时,直线被圆截得的弦长最短,k CM =2-11-3=-12,k l =-2m +1m +1,所以k CM ×k l =⎝⎛⎭⎫-12×⎝ ⎛⎭⎪⎫-2m +1m +1=-1,解得m =-34. (2)已知圆C :x 2+y 2-2x +4y +1=0关于直线l :3ax +2by +4=0对称,则由点M (a ,b )向圆C 所作的切线中,切线长的最小值是( ) A .2 B. 5 C .3 D.13 答案 B解析 因为圆C :x 2+y 2-2x +4y +1=0,即圆C :(x -1)2+(y +2)2=4, 所以圆心为C (1,-2),半径R =2.因为圆C 关于直线l :3ax +2by +4=0对称,所以l :3a -4b +4=0,所以点M (a ,b )在直线l 1:3x -4y +4=0上, 所以|MC |的最小值为d =|3+8+4|5=3,切线长的最小值为d 2-R 2=9-4= 5.反思感悟 (1)形如(x -a )2+(y -b )2形式的最值问题,可转化为动点(x ,y )到定点(a ,b )的距离的平方的最值问题.(2)定点到圆上动点距离的最值可以先计算定点到圆心的距离,然后利用数形结合确定距离的最值.跟踪训练1 (1)从点P (1,-2)向圆x 2+y 2-2mx -2y +m 2=0作切线,当切线长最短时,m 的值为( )A .-1B .1C .2D .0 答案 B解析 x 2+y 2-2mx -2y +m 2=0可化为(x -m )2+(y -1)2=1,圆心C (m ,1),半径为1, 切线长最短时,|CP |最小,|CP |=(m -1)2+9,即当m =1时,|CP |最小,切线长最短.(2)过点(3,1)作圆(x -2)2+(y -2)2=4的弦,其中最短弦长为________. 答案 2 2解析 设点A (3,1),易知圆心C (2,2),半径r =2.当弦过点A (3,1)且与CA 垂直时为最短弦, |CA |=(2-3)2+(2-1)2= 2.∴半弦长=r 2-|CA |2=4-2= 2.∴最短弦长为2 2.二、与面积相关的最值问题例2 已知点O (0,0),A (0,2),点M 是圆(x -3)2+(y +1)2=4上的动点,则△OAM 面积的最小值为( )A .1B .2C .3D .4 答案 A解析 根据题意,得圆(x -3)2+(y +1)2=4的圆心为(3,-1),半径r =2,O (0,0),A (0,2),OA 所在的直线是y 轴,当M 到直线AO 的距离最小时,△OAM 的面积最小, 则M 到直线AO 的距离的最小值d =3-2=1, 则△OAM 的面积最小值S =12×|OA |×d =1.反思感悟 求圆的面积的最值问题,一般转化为寻求圆的半径相关的函数关系或者几何图形的关系,借助函数求最值的方法,如配方法、基本不等式法等求解,有时可以通过转化思想,利用数形结合思想求解.跟踪训练2 (1)直线y =kx +3与圆O :x 2+y 2=1相交于A ,B 两点,则△OAB 面积的最大值为( )A .1 B.12 C.24 D.34答案 B解析 设圆心到直线的距离为d (0<d <1), 则所截得的弦长l =21-d 2,所以S △ABO =12·21-d 2·d =(1-d 2)·d 2,由基本不等式,可得S △ABO =(1-d 2)·d 2≤1-d 2+d 22=12,当且仅当d =22时,等号成立. (2)已知点P (x ,y )是直线kx +y +4=0(k >0)上一动点,P A ,PB 是圆C :x 2+y 2-2y =0的两条切线,A ,B 是切点,若四边形P ACB 的最小面积是2,则k =________. 答案 2解析 圆C :x 2+y 2-2y =0的圆心为C (0,1),半径r =1,由圆的性质可知,四边形的面积S =2S △PBC ,又四边形P ACB 的最小面积是2,则S △PBC 的最小值为S =1=12r |PB |min =12|PB |min ,则|PB |min =2, 因为|PB |=|PC |2-r 2=|PC |2-1,所以当|PC |取最小值时,|PB |最小. 又点P (x ,y )是直线kx +y +4=0上的动点,当CP 垂直于直线kx +y +4=0时,|PC |最小,即为圆心C (0,1)到直线的距离, 所以|1+4|k 2+1=22+12=5,解得k =±2,因为k >0,所以k =2.三、利用数学式的几何意义解圆的最值问题例3 已知点P (x ,y )在圆C :x 2+y 2-6x -6y +14=0上. (1)求yx的最大值和最小值;(2)求x 2+y 2+2x +3的最大值与最小值; (3)求x +y 的最大值与最小值.解 方程x 2+y 2-6x -6y +14=0可化为(x -3)2+(y -3)2=4.(1)yx表示圆上的点P 与原点连线所在直线的斜率,如图(1)所示,显然PO (O 为坐标原点)与圆相切时,斜率最大或最小.设切线方程为y =kx (由题意知,斜率一定存在),即kx -y =0,由圆心C (3,3)到切线的距离等于半径2,可得|3k -3|k 2+1=2,解得k =9±2145,所以yx 的最大值为9+2145,最小值为9-2145. (2)x 2+y 2+2x +3=(x +1)2+y 2+2,它表示圆上的点P 到E (-1,0)的距离的平方再加2,所以当点P 与点E 的距离最大或最小时,所求式子取得最大值或最小值,如图(2)所示,显然点E 在圆C 的外部,所以点P 与点E 距离的最大值为|P 1E |=|CE |+2,点P 与点E 距离的最小值为|P 2E |=|CE |-2.又|CE |=(3+1)2+32=5,所以x 2+y 2+2x +3的最大值为(5+2)2+2=51,最小值为(5-2)2+2=11.(3)设x +y =b ,则b 表示动直线y =-x +b 在y 轴上的截距,如图(3)所示,显然当动直线y =-x +b 与圆(x -3)2+(y -3)2=4相切时,b 取得最大值或最小值,此时圆心C (3,3)到切线x +y =b 的距离等于圆的半径2,则|3+3-b |12+12=2,即|b -6|=22,解得b =6±22,所以x +y的最大值为6+22,最小值为6-2 2.反思感悟 (1)形如u =y -bx -a 形式的最值问题,可转化为过点(x ,y )和(a ,b )的动直线斜率的最值问题.(2)形如l =ax +by 形式的最值问题,可转化为动直线y =-a b x +lb 的截距的最值问题.跟踪训练3 (多选)已知实数x ,y 满足方程x 2+y 2-4x +1=0,则下列说法正确的是( ) A .y -x 的最大值为6-2 B .x 2+y 2的最大值为7+4 3 C.y x 的最大值为32D .x +y 的最大值为2+ 3 答案 AB解析 对于A ,设z =y -x ,则y =x +z ,z 表示直线y =x +z 的纵截距,当直线与圆(x -2)2+y 2=3有公共点时,|2+z |2≤3,解得-6-2≤z ≤6-2,所以y -x 的最大值为6-2,故A 说法正确;对于B ,x 2+y 2的几何意义是表示圆上的点到原点距离的平方,易知原点到圆心的距离为2,则原点到圆上的最大距离为2+3,所以x 2+y 2的最大值为(2+3)2=7+43,故B 说法正确;对于C ,设yx =k ,把y =kx 代入圆方程得(1+k 2)x 2-4x +1=0,则Δ=16-4(1+k 2)≥0,解得-3≤k ≤3,yx的最大值为3,故C 说法错误;对于D ,设m =x +y ,则y =-x +m ,m 表示直线y =-x +m 的纵截距,当直线与圆(x -2)2+y 2=3有公共点时,|-2+m |2≤3,解得-6+2≤m ≤6+2,所以x +y 的最大值为6+2,故D 说法错误.1.知识清单:(1)与距离、面积有关的最值问题(2)利用数学式的几何意义解圆的最值问题. 2.方法归纳:数形结合、转化思想. 3.常见误区:忽略隐含条件导致范围变大.1.圆x 2+y 2=4上的点到直线4x -3y +25=0的距离的取值范围是( ) A .[3,7] B .[1,9] C .[0,5] D .[0,3]答案 A解析 x 2+y 2=4,圆心(0,0),半径r =2, 圆心到直线4x -3y +25=0的距离d =|0-0+25|42+(-3)2=5,所以圆上的点到直线的距离的最小值为5-2=3,最大值为5+2=7,所以圆上的点到直线的距离的取值范围为[3,7].2.已知O 为坐标原点,点P 在单位圆上,过点P 作圆C :(x -4)2+(y -3)2=4的切线,切点为Q ,则|PQ |的最小值为( ) A. 3 B .2 3 C .2 D .4 答案 B解析 根据题意,圆C :(x -4)2+(y -3)2=4,其圆心C (4,3),半径r =2,过点P 作圆C :(x -4)2+(y -3)2=4的切线,切点为Q ,则|PQ |=|PC |2-4,当|PC |最小时,|PQ |最小,又由点P 在单位圆上,则|PC |的最小值为|OC |-1=9+16-1=4,则|PQ |的最小值为16-4=2 3.3.点M (x ,y )在圆x 2+(y -2)2=1上运动,则yx 的取值范围是( )A .[3,+∞) B. (-∞,-3]C. (-∞,-3]∪[3,+∞)D. [-3,3] 答案 C解析 将yx看作圆上动点(x ,y )与原点O (0,0)连线的斜率,如图,可得k ≥3或k ≤- 3.4.已知圆C 1:x 2+y 2+4x -4y =0,动点P 在圆C 2:x 2+y 2-4x -12=0上,则△PC 1C 2面积的最大值为_________. 答案 4 5解析 因为C 1(-2,2),r 1=22,C 2(2,0),r 2=4, 所以|C 1C 2|=(-2-2)2+22=25,当PC 2⊥C 1C 2时,△PC 1C 2的面积最大,其最大值为12×25×4=4 5.课时对点练1.已知过点(1,1)的直线l 与圆x 2+y 2-4x =0交于A ,B 两点,则|AB |的最小值为( ) A. 2 B .2 C .2 2 D .4 答案 C解析 将圆的方程x 2+y 2-4x =0化为标准方程为(x -2)2+y 2=4, 则圆心为(2,0),半径r =2,则圆心(2,0)到定点(1,1)的距离为2, |AB |的最小值为222-(2)2=2 2.2.已知点P 是直线3x +4y +5=0上的动点,点Q 为圆(x -2)2+(y -2)2=4上的动点,则|PQ |的最小值为( ) A.195 B.95 C.59 D.295 答案 B解析 圆(x -2)2+(y -2)2=4的圆心为(2,2),半径为2, 则圆心到直线3x +4y +5=0的距离为|6+8+5|5=195,所以|PQ |的最小值为195-2=95.3.已知实数x ,y 满足方程x 2+y 2-4x -1=0,则y -2x 的最小值和最大值分别为( ) A .-9,1 B .-10,1 C .-9,2 D .-10,2答案 A解析 y -2x 可看作是直线y =2x +b 在y 轴上的截距,如图所示,当直线y =2x +b 与圆x 2+y 2-4x -1=0相切时,b 取得最大值或最小值,此时|2×2+b |1+22=5,解得b=-9或1,所以y-2x的最大值为1,最小值为-9.4.已知直线l:x-y+4=0与圆C:(x-1)2+(y-1)2=2,则圆C上的点到直线l的距离的最小值为()A. 2B. 3 C.1 D.3答案 A解析由题意知,圆C上的点到直线l的距离的最小值等于圆心(1,1)到直线l的距离减去圆的半径,即|1-1+4|12+(-1)2-2= 2.5.在平面直角坐标系xOy中,已知(x1-2)2+y21=5,x2-2y2+4=0,则(x1-x2)2+(y1-y2)2的最小值为()A.55 B.15 C.1215 D.1155答案 B解析由已知得点(x1,y1)在圆(x-2)2+y2=5上,点(x2,y2)在直线x-2y+4=0上,故(x1-x2)2+(y1-y2)2表示(x-2)2+y2=5上的点和直线x-2y+4=0上点的距离的平方,而距离的最小值为|2+4|1+4-5=55,故(x1-x2)2+(y1-y2)2的最小值为15.6.已知点P是直线l:3x+4y-7=0上的动点,过点P引圆C:(x+1)2+y2=r2(r>0)的两条切线PM,PN,M,N为切点,则当PM的最小值为3时,r的值为()A.2 B. 3 C. 2 D.1答案 D解析如图,由题意得|PM|2=|PC|2-r2,当PC⊥l时,|PC|最小时,|PM|最小.由题意得|PC|min=d=|3×(-1)+4×0-7|32+42=2,所以(3)2=22-r2,∴r=1.7.在平面直角坐标系xOy 中,以点(1,0)为圆心且与直线mx -y -2m -1=0(m ∈R )相切的所有圆中,半径最大的圆的标准方程为________________. 答案 (x -1)2+y 2=2解析 ∵直线mx -y -2m -1=0恒过定点(2,-1), ∴圆心(1,0)到直线mx -y -2m -1=0的最大距离为d =(2-1)2+(-1)2=2,∴半径最大为2,∴半径最大的圆的标准方程为(x -1)2+y 2=2.8.已知圆C :(x -4)2+(y -3)2=4和两点A (-m ,0),B (m ,0)(m >0).若圆C 上存在点M ,使得AM ⊥MB ,则m 的最小值为________. 答案 3解析 根据题意,点A (-m ,0),B (m ,0)(m >0), 则AB 的中点为(0,0),|AB |=2m ,则以AB 的中点为圆心,半径r =12×|AB |的圆为x 2+y 2=m 2,设该圆为圆O ,若圆C 上存在点M ,使得AM ⊥MB ,则圆C 与圆O 有交点,必有|m -2|≤|OC |≤m +2,即⎩⎪⎨⎪⎧|m -2|≤5,m +2≥5,又由m >0, 解得3≤m ≤7, 即m 的最小值为3.9.已知M 为圆C :x 2+y 2-4x -14y +45=0上任意一点,且点Q (-2,3). (1)求|MQ |的最大值和最小值;(2)若M (m ,n ),求n -3m +2的最大值和最小值.解 (1)由圆C 的方程x 2+y 2-4x -14y +45=0化为标准方程得(x -2)2+(y -7)2=8,∴圆心C 的坐标为(2,7),半径r =22,又|QC |=(2+2)2+(7-3)2=42,∴|MQ |max =42+22=62,|MQ |min =42-22=2 2.(2)由题可知n -3m +2表示直线MQ 的斜率, 设直线MQ 的方程为y -3=k (x +2),即kx -y +2k +3=0,则n -3m +2=k . 由直线MQ 与圆C 有交点,得|2k -7+2k +3|1+k2≤22, 可得2-3≤k ≤2+3,∴n -3m +2的最大值为2+3,最小值为2- 3. 10.已知直线l :3x +4y +1=0,一个圆与x 轴正半轴、y 轴正半轴都相切,且圆心C 到直线l 的距离为3.(1)求圆的方程.(2)P 是直线l 上的动点,PE ,PF 是圆的两条切线,E ,F 分别为切点,求四边形PECF 的面积的最小值.解 (1)圆与x ,y 轴正半轴都相切,∴圆的方程可设为(x -a )2+(y -a )2=a 2(a >0),圆心C 到直线的距离为3,∴由点到直线的距离公式,得d =|3a +4a +1|32+42=3, 解得a =2,∴半径为2.∴圆的方程为(x -2)2+(y -2)2=4.(2)PE ,PF 是圆的两条切线,E ,F 分别为切点,∴△PCE≌△PCF,∴S四边形PECF=2S△PCE,PE是圆的切线,且E为切点,∴PE⊥CE,|CE|=2,|PE|2=|PC|2-|CE|2=|PC|2-4,∴当斜边PC取最小值时,PE也最小,即四边形PECF的面积最小.|PC|min即为C到l的距离,由(1)知|PC|min=3,∴|PE|2min=32-4=5,即|PE|min=5,∴S△PCE=12|EC|·|PE|=12×2×5=5,∴四边形PECF面积的最小值为2 5.11.设P是圆(x-3)2+(y+1)2=4上的动点,Q是直线x=-3上的动点,则|PQ|的最小值为()A.6 B.4 C.3 D.2答案 B解析如图,圆心M(3,-1)与定直线x=-3的最短距离为|MQ|=3-(-3)=6.又因为圆的半径为2,故所求最短距离为6-2=4.12.已知AC,BD为圆O:x2+y2=4的两条互相垂直的弦,且垂足为M(1,2),则四边形ABCD面积的最大值为()A.5 B.10 C.15 D.20答案 A解析如图,作OP⊥AC于P,OQ⊥BD于Q,则|OP|2+|OQ|2=|OM|2=3,∴|AC|2+|BD|2=4(4-|OP|2)+4(4-|OQ|2)=20.又|AC|2+|BD|2≥2|AC|·|BD|,则|AC|·|BD|≤10,∴S 四边形ABCD =12|AC |·|BD |≤12×10=5,当且仅当|AC |=|BD |=10时,等号成立,∴四边形ABCD 面积的最大值为5.13.已知圆C 的方程为(x -2)2+(y -1)2=5,点B 的坐标为(0,2),设P ,Q 分别是直线l :x +y +2=0和圆C 上的动点,则|PB |+|PQ |的最小值为________.答案 2 5解析 由于点B (0,2)关于直线l :x +y +2=0的对称点为B ′(-4,-2),则|PB |+|PQ |=|PB ′|+|PQ |≥|B ′Q |,又B ′到圆上点Q 的最短距离为|B ′C |-R =35-5=25,所以|PB |+|PQ |的最小值为2 5.14.已知实数x ,y 满足方程y =-x 2+4x -1,则y x的取值范围是________. 答案 [0,3]解析 方程y =-x 2+4x -1化为(x -2)2+y 2=3(y ≥0),表示的图形是一个半圆,令y x=k ,即y =kx ,如图所示,当直线与半圆相切时,k =3,所以y x的取值范围是[0,3].15.已知直线l :x -y =1与圆M :x 2+y 2-2x +2y -1=0相交于A ,C 两点,点B ,D 分别在圆M 上运动,且位于直线AC 两侧,则四边形ABCD 面积的最大值为________. 答案 30解析 把圆M :x 2+y 2-2x +2y -1=0化为标准方程为(x -1)2+(y +1)2=3,圆心M (1,-1),半径r = 3.直线l 与圆相交,由点到直线的距离公式得弦心距d =|1-(-1)-1|12+(-1)2=22,由勾股定理得半弦长=3-⎝⎛⎭⎫222=102,所以弦长|AC |=2×102=10. 又B ,D 两点在圆上,并且位于直线l 的两侧,四边形ABCD 的面积可以看成是△ABC 和△ACD 的面积之和,当B ,D 为如图所示位置,即BD 为弦AC 的垂直平分线时(即为直径),两三角形的面积之和最大,即四边形ABCD 的面积最大,最大面积为S =12|AC |×|BE |+12|AC |×|DE |=12|AC |×|BD |=12×10×23=30. 16.已知圆心在x 轴上的圆C 与直线l :4x +3y -6=0切于点M ⎝⎛⎭⎫35,65.(1)求圆C 的标准方程;(2)已知N (2,1),经过原点且斜率为正数的直线l 1与圆C 交于P (x 1,y 1),Q (x 2,y 2).①求证:1x 1+1x 2为定值; ②求|PN |2+|QN |2的最大值.(1)解 由圆心在x 轴上的圆C 与直线l :4x +3y -6=0切于点M ⎝⎛⎭⎫35,65,设C (a ,0),直线l :4x +3y -6=0的斜率为-43, 则k CM =6535-a , 所以6535-a ·⎝⎛⎭⎫-43=-1, 所以a =-1,所以C (-1,0),|CM |=⎝⎛⎭⎫-1-352+⎝⎛⎭⎫652=2, 即r =2,所以圆C 的标准方程为(x +1)2+y 2=4.(2)①证明 设直线l 1:y =kx (k >0),与圆联立方程组可得(1+k 2)x 2+2x -3=0,Δ=4+12(1+k 2)>0,x 1+x 2=-21+k 2,x 1x 2=-31+k 2, 则 1x 1+1x 2=x 1+x 2x 1x 2=23为定值.②解 |PN |2+|QN |2=(x 1-2)2+(y 1-1)2+(x 2-2)2+(y 2-1)2=(x 1-2)2+(kx 1-1)2+(x 2-2)2+(kx 2-1)2=(1+k 2)(x 1+x 2)2-2(1+k 2)x 1x 2-(4+2k )(x 1+x 2)+10=12+4k 1+k 2+16, 令t =3+k (t >3),则k =t -3,所以12+4k 1+k 2+16=4t 1+(t -3)2+16=4t +10t-6+16≤4210-6+16=210+22, 当且仅当t =10t,即t =10时,取等号,此时k =10-3, 所以|PN |2+|QN |2的最大值为210+22.。
2022年浙教版九年级数学中考二轮复习圆中最值问题专题突破训练

2022年春浙教版九年级数学中考二轮复习《圆中最值问题》专题突破训练(附答案)1.在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=6,EF=4,点M在以半径为2的⊙D上运动,则MF2+MG2的最大值为()A.104 B.116 C.120 D.1002.Rt△ABC中,AB⊥BC,AB=4,BC=3,P是△ABC内部的一个动点,满足∠P AB=∠PBC,则线段CP长的最小值为()A.B.1 C.D.3.如图,⊙O的半径为4,将劣弧沿弦AB翻折,恰好经过圆心O,点C为优弧AB上的一个动点,则△ABC面积的最大值是()A.B.C.D.4.如图,AB为半圆的直径,AB=8,点P为半圆的三等分点,点D为弧BP上一动点,作OM⊥PD,连接AD交OM于点N,则BN的最小值为.5.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC 交AD于点E,则OE的最小值是.6.如图,在Rt△ABC中,已知∠A=90°,AB=6,BC=10,D是线段BC上的一点,以C为圆心,CD为半径的半圆交AC边于点E,交BC的延长线于点F,射线BE交于点G,则BE•EG的最大值为.7.如图,已知⊙O的直径AB=4,弦CD⊥AB于点E,点E为OB的中点,点F 为圆O上的一个动点,过点A作AG⊥CF于点G,在点F的运动过程中,线段OG长度的最小值为.8.如图,∠CAB=60°,D为射线AB上一点,AD=2,E为射线AC上一动点,作∠DEF=30°,交射线AB于点F(F在D的右侧),则DF的最小值为.9.如图1,直线l1⊥l2于点M,以l1上的点O为圆心画圆,交l1于点A,B,交l2于点C,D,OM=4,CD=6,点E为AD上的动点,CE交AB于点F,AG ⊥CE于点G,连接DG,AC,AD.(1)求⊙O的半径长;(2)若∠CAD=40°,求劣弧的长;(3)如图2,连接DE,是否存在常数k,使CE﹣DE=k•EG成立?若存在,请求出k的值;若不存在,请说明理由;(4)若DG∥AB,则DG的长为;(5)当点G在AD的右侧时,请直接写出△ADG面积的最大值.10.【发现问题】爱好数学的小明在做作业时碰到这样一道题:如图1,圆O的半径为2,OA=4,动点B在圆O上,连接AB,作等边三角形ABC(A、B、C为顺时针顺序),求OC的最大值.【解决问题】小明经过多次的尝试和探索,终于得到解题思路:在图1中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE;(1)请你找出图中与OC相等的线段,并说明理由;(2)请直接写出线段OC的最大值;【迁移拓展】(3)如图2,BC=,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请求出AC的最值,并说明理由.11.在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以原点O为圆心,半径为3的⊙O上,连接OC,过点O作OD⊥OC,OD与⊙O 相交于点D(其中点C,O,D按逆时针方向排列),连接AB.(1)当OC∥AB时,∠BOC的度数为;(2)连接AC,BC,点C在⊙O上运动的过程中,当△ABC的面积最大时,请直接写出△ABC面积的最大值是.(3)连接AD,当OC∥AD,点C位于第二象限时,①求出点C的坐标;②直线BC是否为⊙O的切线?并说明理由.12.已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.(1)求⊙O的半径.(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.13.如图所示,点A为半圆O直径MN所在直线上一点,射线AB垂直于MN,垂足为A,半圆绕M点顺时针转动,转过的角度记作α;设半圆O的半径为R,AM的长度为m,回答下列问题:探究:(1)若R=2,m=1,如图1,当旋转30°时,圆心O′到射线AB的距离是;如图2,当α=°时,半圆O与射线AB相切;(2)如图3,在(1)的条件下,为了使得半圆O转动30°即能与射线AB 相切,在保持线段AM长度不变的条件下,调整半径R的大小,请你求出满足要求的R,并说明理由.(3)发现:(3)如图4,在0°<α<90°时,为了对任意旋转角都保证半圆O与射线AB能够相切,小明探究了cosα与R、m两个量的关系,请你帮助他直接写出这个关系;cosα=(用含有R、m的代数式表示)拓展:(4)如图5,若R=m,当半圆弧线与射线AB有两个交点时,α的取值范围是,并求出在这个变化过程中阴影部分(弓形)面积的最大值(用m表示)14.问题探究:(1)如图1,点A、B、C是⊙O上三点,∠ACB=35°,那么∠AOB=.(2)如图2,BD是边长为4的正方形ABCD的对角线,在正方形内部(不含边界)找一点O,使得∠AOB=2∠ADB,在图中画出满足条件的点O所形成的图形,并求出△AOB面积的最大值;问题解决:(3)如图3,将百姓家园小区平面图绘制在平面直角坐标系中,点A、B、C 分别是家园小区门房及两个停车场,其中OA=100m,AB=200m,OC=300m,为安全期间,在一点P安装监控使△APB面积最大,且∠APB=2∠ACB,是否存在满足条件的点P?若存在,请求出点P的坐标;若不存在,请说明理由.15.已知:如图,已知⊙O是△ABC的外接圆,AB为⊙O的直径,AC=6cm,BC=8cm.(1)求⊙O的半径;(2)请用尺规作图作出点P,使得点P在优弧CAB上时,△PBC的面积最大,请保留作图痕迹,并求出△PBC面积的最大值.16.已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.(1)求证:∠MBN=45°;的最大值.并求出此时AM的长度;(2)当E在弧上运动时,求出S△DMN(3)若BM,BN分别于对角线交于P,Q两点,设AM=x,PQ=y,求出y 关于x的函数解析式.17.如图,⊙O的半径为1,等腰直角三角形ABC的顶点B固定且坐标为(,0),顶点A在⊙O上运动,始终保持∠CAB=90°,AC=AB(1)当点A在x轴上时,求点C的坐标;(2)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;(3)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(4)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.18.数学课中,李老师提出了下面问题:已知正数x,y满足x2+y2=16,求xy 的最大值.(1)为了求xy的最大值,小王想到了直角三角形,把问题转化为已知直角三角形的斜边求面积最大值的问题,请你画出图形,写出转化后问题的“已知”和“求”;(2)一个直角三角形的斜边固定时,它的直角顶点是可以变化的,请画出问题(1)中直角三角形的直角顶点的所有可能位置所组成的图形,猜想(1)中问题的结论并证明结论;(3)拓展:根据上述思考,你能进一步求出x+y的最大值和最小值吗?19.在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.(1)当OC∥AB时,∠BOC的度数为;(2)连接AC,BC,在点C在⊙O运动过程中,△ABC的面积是否存在最大值?并求出△ABC的最大值;(3)直接写出在(2)的条件下D点的坐标.20.如图,在平面直角坐标系xOy中,点A从点O开始沿x轴的正方向移动,点B在∠xOy平分线上移动,移动中保持AB=2不变,以AB为一边,着AB 右侧作矩形ABCD,且BC=1.(1)当AB⊥OA时,请求出OC的长;(2)取AB的中点E,当O、E、C三点共线时,请求出OA、OC的长;(3)设△OAB的外接圆半径为R,请判断着移动过程中R的值是否发生变化,若不变,请求出R的值,若变化,请说明理由;(4)请直接写出线段OC的最大值.21.如图,已知⊙O的半径为2,弦AB的长为2,D是优弧上的任意一点(点D不与A,B重合).(1)连接OA,OB,求∠AOB的度数;(2)连接AD,BD.问:△ABD什么时候面积最大?并求出最大面积.22.如图1,Rt△ABC两直角边的边长为AC=3,BC=4.(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC 的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.23.如图1,Rt△AOB中OA=OB=6,以O为圆心作一半径为3的圆,点C为⊙O上一动点,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D,∠COD 绕圆心O旋转.(1)当OC∥AB时,∠BOC的度数为;(2)连接AD,当OC∥AD时,如图2,求证:直线BC为⊙O的切线;(3)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.24.⊙O的半径为1,等腰直角三角形ABC的顶点B的坐标为(,0),∠CAB =90°,AC=AB,顶点A在⊙O上运动.(1)当点A运动到x轴的负半轴上时,试判断直线BC与⊙O位置关系,并说明理由;(2)设点A的横坐标为x,△ABC的面积为S,求S与x之间的函数关系式,并求出S的最大值与最小值;(3)当直线AB与⊙O相切时,求AB所在直线对应的函数关系式.25.我们把三角形内部的一个点到这个三角形三边所在直线距离的最小值叫做这个点到这个三角形的距离.如图1,PD⊥BC于D,PE⊥AC于E,PF⊥AB 于F,如果PE≥PF≥PD,则称PD的长度为点P到△ABC的距离.如图2、图3,在平面直角坐标系中,已知A(6,0),B(0,8),连接AB.(1)若P在图2中的坐标为(2,4),则P到OA的距离为,P到OB的距离为,P到AB的距离为,所以P到△AOB的距离为;(2)若点Q是图2中△AOB的内切圆圆心,求点Q到△AOB距离的最大值;(3)若点R是图3中△AOB内一点,且点R到△AOB的距离为1,请画出所有满足条件的点R所形成的封闭图形,并求出这个封闭图形的周长.(画图工具不限)26.问题背景:如图,点C是半圆O上一动点(点C与A、B不重合),AB=2,连接AC、BC、OC,将△AOC沿直线AC翻折得△ADC,点、E、F、G、H 分别是DA、AO、OC、CD的中点.(1)猜想证明:猜想四边形AOCD以及四边形EFGH的形状,并证明你的结论;(2)拓展探究:探究点C在半圆弧上哪个位置时,四边形EFGH面积最大?求出这个最大值,判断此时四边形EFGH的形状,并说明理由.参考答案1.解:取GF的中点O,连接OM,OD,DM.∵四边形DEFG是矩形,∴∠DGO=90°,DG=EF=4,FG=DE=6,∵MG2+MF2=2GO2+2OM2,∵OG=OF=3,∴OM的值最大时,MG2+MF2的值最大,∵DM=2,OD===5,∴OM≤OD+DM=5+2=7,∴OM的最大值为7,∴MG2+MF2的最大值=2×32+2×72=116,故选:B.2.解:∵∠ABC=90°,∴∠ABP+∠PBC=90°,∵∠P AB=∠PBC∴∠BAP+∠ABP=90°,∴∠APB=90°,∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,在Rt△BCO中,∠OBC=90°,BC=3,OB=2,∴OC===,∴CP=OC﹣OP=﹣2.∴CP最小值为﹣2.故选:D.3.解:如图,过点C作CT⊥AB于点T,过点O作OH⊥AB于点H,交⊙O于点K,连接AO,AK.由题意AB垂直平分线段OK,∴AO=AK,∵OA=OK,∴OA=OK=AK,∴∠OAK=∠AOK=60°.∴AH=OA•sin60°=4×=2,∵OH⊥AB,∴AH=BH,∴AB=2AH=4,∵OC+OH≥CT,∴CT≤4+2=6,∴CT的最大值为6,∴△ABC的面积的最大值为××6=12,故选:A.4.解:如图,连接OP,PN.∵点P为半圆的三等分点,∴∠POD=60°,∠POA=120°,∴∠ADP=∠AOP=60°,∵OM⊥PD,∴PM=DM,∴NP=ND,∴∠NPD=∠NDP=60°,∴∠PNM=90°﹣60°=30°,∴∠PNO=180°﹣30°=150°,作△OPN是外接圆⊙K,在优弧AP上取一点J,连接JP,JO,KP,KO,过点K作KH⊥AB于H.则点N的运动轨迹是,∵∠J+∠PNO=180°,∴∠J=30°,∴∠PKO=2∠J=60°,∵KP=KO,∴△KPO是等边三角形,∴OK=OP=KP=4,∴点K在⊙O上,∴KN=KO=4,在Rt△OKH中,∠KOH=60°,∴∠OKH=30°,∴OH=OK=2,KH=OH=2,∴BH=OH+OB=6,∴BK====4,∵BN≥BK=KN=4﹣4,∴BN的最小值为4﹣4.故答案为:4﹣4.5.解:如图,作△AEC的外接圆⊙O′,延长BC交⊙O′于D2R,连接AR,则AR是直径,连接OO′,EO′.∵EC⊥CD,∴∠ECD=90°,∵AB是直径,∴∠ACB=90°,∴BC===4,∵∠D+∠DEC=90°,∠B+∠BAC=90°,∠B=∠D,∴∠DEC=∠BAC=定值,∴∠AEC是定值,∴点E的运动轨迹是,∵∠R+∠AEC=180°,∠AEC+∠DEC=180°,∴∠R=∠DEC=∠BAC,∴∠R+∠B=90°,∴∠BAR=90°,∵∠B=∠B,∠ACB=∠BAR=90°,∴△BCA∽△BAR,∴=,∴=,∴BR=,∴CR=BR﹣BC=,∴AR===,∴EO′=AR=,∵AO=OB,AO′=O′R,∴OO′=BR=,∵OE≥OO′﹣EO′=﹣=,∴OE的最小值为.故答案为:.6.解:如图,过点C作CH⊥EG于点H.∵CH⊥EG,∴EH=GH,∵∠A=∠CHE=90°,∠AEB=∠CEH,∴△ABE∽△HCE,∴=,∴BE•EH=AE•EC,∴BE•2EH=2•AE•EC,∴EB•EG=2AE•EC,设EC=x,在Rt△ABC中,AC===8,∴EB•EG=2x•(8﹣x)=﹣2(x﹣4)2+32,∵﹣2<0,∴x=4时,BE•EG的值最大,最大值为32,故答案为:32.7.解:如图,连接OC,CB,取AC的中点T,连接OT,TG.∵AB⊥CD,OE=EB,∴CO=CB,∵OC=OB,∴OC=OB=CB=2,∴∠B=60°,∵AB是直径,∴∠ACB=90°,∴AC=AB•sin60°=2,∵AT=CT,AO=OB,∴OT=BC=1,∵AG⊥CF,∴∠CGA=90°,∴TG=AC=,∵OG≥TG﹣OT=﹣1,∴OG的最小值为﹣1.故答案为:﹣1.8.解:如图,作△DEF的外接圆⊙O,连接OD,OF,OE,过点O作OT∥AB 交AC于点T,OM⊥AC于点M.∵∠DOF=2∠DEF,∠DEF=30°,∴∠DOF=60°,∵OD=FO,∴△DFO是等边三角形,∴∠ODF=60°,∵∠CAB=60°,∴∠CAB=∠ODF,∴OD∥AC,∵OT∥AD,∴四边形ADOT是平行四边形,∴AD=OT=2,∵∠OTM=∠CAB=60°,∴OM=OT•sin60°=2×=,∵DF=OD=OE≥OM=,∴DF的最小值为.故答案为:.9.解:(1)如图1中,连接OD.∵AB是直径,AB⊥CD,∴CM=MD=CD=3,在Rt△OMD中,OD===5,∴⊙O的半径为5;(2)如图1中,∵AB垂直平分线段CD,∴AC=AD,∴∠CAB=∠DAB=20°,∵OA=OD,∴∠OAD=∠ODA=20°,∴∠AOD=180°﹣20°﹣20°=140°,∴的长==π;(3)如图2中,连接AE,过点A作AT⊥DE交DE的延长线于点E.∵AG⊥CE,AT⊥DT,∴∠AGC=∠T=90°,∵∠ACG=∠ADT,AC=AD,∴△AGC≌△ATD(AAS),∴AG=AT,CG=DT,∵∠AGE=∠T=90°,AE=AE,∴Rt△AEG≌Rt△AET(HL),∴EG=ET,∴CE﹣DE=(CG+EG)﹣(DT﹣ET)=2EG,∵CE﹣DE=k•EG,∴k=2;(4)如图3中,∵DG∥AB,CM=DM,∴CF=FG,∴FM=DG,设FM=x,则DG=2x,∵∠AFG=∠CFM,∠AGF=∠FMC=90°,∴△AGF∽△CMF,∴=,∴=,解得x=3或,∴DG=6或3.故答案为:6或3;(4)如图4中,过点C作CR⊥AD于点R,∵AG⊥CE,∴∠AGC=90°,取AC的中点T,连接OG,过点T作TJ⊥AD于点J,交于点K,点G在以T为圆心,TG为半径的上运动,当点G与K重合时,△ADG的面积最大,∵•CD•AM=•AD•CR,AD==3,∴×6×9=×3×CR,∴CR=,∵TJ∥CR,AT=CT,∴AJ=JR,∴TJ=CR=,∵TK=TG=AC=,∴JK=JK﹣TJ=﹣=,的最大值=•AD•JK=×3×=9.∴S△AGD10.解:【解决问题】(1)如图1中,结论:OC=AE,理由:∵△ABC,△BOE都是等边三角形,∴BC=BA,BO=BE,∠CBA=∠OBE=60°,∴∠CBO=∠ABE,∴△CBO≌△ABE(SAS),∴OC=AE.(2)在△AOE中,AE≤OE+OA,∴当E、O、A共线,∴AE的最大值为6,∴OC的最大值为6.【迁移拓展】(3)如图2中,以BC为边作等边三角形△BCM,∵∠ABD=∠CBM=60°,∴∠ABC=∠DBM,∵AB=DB,BC=BM,∴△ABC≌△DBM(SAS),∴AC=MD,∴欲求AC的最大值,只要求出DM的最大值即可,∵BC=6定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,如图,由图可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=3+3,∴AC的最大值为3+3.当点A线段BD的右侧时,同法可得AC的最小值为3﹣3.综上,AC的最小值为3﹣3,AC最大值为3+3.11.解:(1)∵点A(6,0),点B(0,6),∴OA=OB=6,∴△OAB为等腰直角三角形,∴∠OBA=45°,∵OC∥AB,∴当C点在y轴左侧时,∠BOC=∠OBA=45°;当C点在y轴右侧时,∠BOC=90°+∠OBA=135°;综上所述,∠BOC的度数为45°或135°,故答案为:45°或135°;(2)∵△OAB为等腰直角三角形,∴AB=OA=6,∴当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,如图1:此时C点到AB的距离的最大值为CE的长,∴OE=AB=3,∴CE=OC+OE=3+3,∴△ABC的面积=CE•AB=×(3+3)×6=9+18;即当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9+18;故答案是:9+18;(3)①过C点作CF⊥x轴于F,如图2:∵OC∥AD,∴∠COF=∠DAO,又∵∠ADO=∠CFO=90°,∴△OCF∽Rt△AOD,∴=,即=,解得:CF=,在Rt△OCF中,OF===,∴C点坐标为(﹣,);②直线BC是⊙O的切线.理由如下:由①得:(﹣,),在Rt△OCF中,OC=3,CF=,∴CF=OC,∴∠COF=30°,∴∠OAD=30°,∴∠BOC=60°,∠AOD=60°,∵在△BOC和△AOD中,,∴△BOC≌△AOD(SAS),∴∠BCO=∠ADO=90°,∴OC⊥BC,∴直线BC为⊙O的切线.12.28.解:(1)∵AB为⊙O的直径,∴∠C=90°,在Rt△ABC中,∵AC=6cm,BC=8cm,∴AB==10(cm),∴⊙O的半径为5cm;(2)如图,作BC的垂直平分线交优弧CAB于P,交BC于D,则BD=CD=BC=4(cm),在Rt△OBD中,∵OD==3(cm),∴PD=3+5=8(cm),=PD•BC=×8×8=32(cm2).∴S△PBC13.解:(1)如图1中,作O′E⊥AB于E,MF⊥O′E于F.则四边形AMFE 是矩形,EF=AM=1.想办法求出O′E的长即可.在Rt△MFO′中,∵∠MO′F=30°,MO′=2,∴O′F=O′M•cos30°=,O′E=+1,∴点O′到AB的距离为+1.如图2中,设切点为F,连接O′F,作O′E⊥OA于E,则四边形O′EAF 是矩形,∴AE=O′F=2,∵AM=1,∴EM=1,在Rt△O′EM中,cosα==,∴α=60°故答案为+1,60°.(2)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.∵O′P=R,∴R=R+1,∴R=4+2.(3)设切点为P,连接O′P,作MQ⊥O′P,则四边形APQM是矩形.在Rt△O′QM中,O′Q=R•cosα,QP=m,∵O′P=R,∴R•cosα+m=R,∴cosα=.故答案为.(4)如图5中,当半圆与射线AB相切时,之后开始出现两个交点,此时α=90°;当N′落在AB上时,为半圆与AB有两个交点的最后时刻,此时∵MN′=2AM,所以∠AMN′=60°,所以,α=120°因此,当半圆弧线与射线AB有两个交点时,α的取值范围是:90°<α≤120°故答案为90°<α≤120°;当N′落在AB上时,阴影部分面积最大,所以S=﹣•m•m=﹣m2.14.解:(1)∵点A、B、C是⊙O上三点,∴∠AOB=2∠ACB=70°,故答案为:70°;(2)满足∠AOB=2∠ADB的点O在以AB为直径的半圆(不含A、B端点)图形上;∵BD是正方形ABCD的对角线,∴∠ADB=45°,则∠AOB=2∠ADB=90°,∵90°圆周角所对弦为直径,∴点O在以AB为直径的半圆(不含A、B端点)图形上;过点O作OH⊥AB于点H,则OH≤AB,∴S△AOB=AB•OH≤AB2,∵边长为4的正方形ABCD,∴AB=4,∴S△AOB ≤4,即S△AOB最大值为4;(3)存在满足条件的点P;作△ABC的外接圆⊙K,连接AC、BC、AK、BK,当△APB的面积最大,且∠APB=2∠ACB时,点P与点K重合,此时,点P为符合条件的点,连接PC,∵OB=OC=300,∴∠OBC=45°,∴∠CP A=2∠OBC=90°,在Rt△AOC中,由勾股定理得:AC2=OC2+OA2,在Rt△P AC中,由勾股定理得:AC2=AP2+PC2=2AP2,∴2AP2=OC2+OA2=3002+1002=100000,∴AP=100,∴点P在直线x=200上,设直线x=200交x轴于点H,则AH=BH,∵OB=OC=300,OA=100,∴AB=200,∴AH=100,在Rt△P AH中,由勾股定理得:PH==200,∴P(200,200),∴点P关于x轴的对称点P'(200,﹣200)也符合题意;∴存在符合条件的点P,坐标为(200,200)或(200,﹣200).15.解:(1)∵AB为⊙O的直径,∴∠C=90°,在Rt△ABC中,∵AC=6,BC=8,∴AB==10,∴⊙O的半径为5cm;(2)如图,作BC的垂直平分线交优弧CAB于P,交BC于D,则BD=CD=BC=4,在Rt△OBD中,OD==3,∴PD=3+5=8,S△PBC=PD•BC=×8×8=32(cm2).16.解:(1)如图1,连接BE,∵MN与⊙B相切,∴BE⊥MN,∴∠BEM=90°,∵四边形ABCD是正方形,∴∠BAD=90°,∴∠BAD=∠BEM=90°,∵AB=BE,BM=BM,∴Rt△ABM≌Rt△EBM(HL),∴∠ABM=∠EBM,同理得:∠EBN=∠CBN,∴∠EBM+∠EBN=∠ABM+∠CBN,即∠MBN=∠ABM+∠CBN=∠ABC=×90°=45°;(2)如图2,将△ABM绕点B顺时针旋转90°得到△CBM′,∴AM=CM′,BM=BM′,∵∠BAM=∠BCD=∠BCM′=90°,∴M′、C、D三点共线,易证明△BMN≌△BM′N,∴MN=NM′,由(1)得:AM=ME,CN=EN,∵S五边形MABCN =S△ABM+S△BMN+S△CBN=AB•AM+MN•BE+BC•CN=AB•2MN=×4×2MN=4MN,当4MN最小时,S△DMN最大,△DMN中,DM+DN+MN=DM+EM+EN+DN=AD+DC=8,设DM=a,DN=b,∴MN=,∵DM+DN+MN=8,∴a+b+=8,8=+=+≤+=(+1)=(+1)MN,∴MN≥=8(﹣1),当a=b时,MN有最小值是8(﹣1),此时S△DMN最大,△DMN是等腰直角三角形,此时,S△DMN =S正方形ABCD﹣S五边形MABCN=42﹣4MN=16﹣4×8(﹣1)=48﹣32;(3)如图1,∵AM∥BC,∴△AMP∽CBP,∴=,∴,∴PB=,同理得:PC=,∵AC==4,∴PC==,∵∠PBQ=∠PCB=45°,∠BPQ=∠CPB,∴△BPQ∽△CPB,∴PB2=PQ•PC,∴PQ=====;即y=.17.解:(1)当点A的坐标为(1,0)时,AB=AC=﹣1,点C的坐标为(1,﹣1)或(1,1﹣);当点A的坐标为(﹣1,0)时,AB=AC=+1,点C的坐标为(﹣1,+1)或(﹣1,﹣﹣1);(2)直线BC与⊙O相切.如图1,过点O作OM⊥BC于点M,∴∠OBM=∠BOM=45°,∴OM=OB•sin45°=1∴直线BC与⊙O相切;(3)过点A作AE⊥OB于点E,如图2,在Rt△OAE中,AE2=OA2﹣OE2=1﹣x2,在Rt△BAE中,AB2=AE2+BE2=(1﹣x2)+(﹣x)2=3﹣2x ∴S=AB•AC=AB2=(3﹣2x)=﹣x,其中﹣1≤x≤1,当x=﹣1时,S的最大值为+,当x=1时,S的最小值为﹣;(4)①当点A位于第一象限时(如右图3):连接OA,并过点A作AE⊥OB于点E,∵直线AB与⊙O相切,∴∠OAB=90°,又∵∠CAB=90°,∴∠CAB+∠OAB=180°,∴点O、A、C在同一条直线∵OA=1,OB=,∴AB==1,∴OA=AB,∴∠AOB=45°,∵∠C=45°,∴∠AOB=∠C=45°,在Rt△OAE中,OE=AE=,点A的坐标为(,)过A、B两点的直线为y=﹣x+;②当点A位于第四象限时(如图4),点A的坐标为(,﹣)∵B的坐标为(,0)∴过A、B两点的直线为y=x﹣.18.解:(1)已知:如图,Rt△ABC中,∠C=90°,斜边AB=4,求:△ABC 面积的2倍是最大值;(2)问题(1)中直角三角形的直角顶点的所有位置组成的图形是以AB为直径的圆(A,B两点除外),如图所示,过C作CE⊥AB,根据垂径定理,CD=CE,∵AB=4,∴当CD最大时,△ABC面积最大.又∵CE的最大值为直径的长4,∴CD的最大值是半径2,即当点D与圆心O重合,即x=y时,△ABC面积最大,最大值为4,∴当x=y=2时,xy有最大值8.(3)∵x+y=,而xy的最大值是8,∴x+y≤=4,∴x+y的最大值是4,没有最小值.19.解:(1)∵点A(6,0),点B(0,6),∴OA=OB=6,∴△OAB为等腰直角三角形,∴∠OBA=45°,∵OC∥AB,∴当C点在y轴左侧时,∠BOC=∠OBA=45°,当C点在y轴右侧时,∠BOC=180°﹣∠OBA=135°,∴∠OBA=45°或135°;故答案为:45°或135°;(2)∵△OAB为等腰直角三角形,∴AB=OA=6,∴当点C到AB的距离最大时,△ABC的面积最大,过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,如图:此时C点到AB的距离最大值为CE的长,∵△OAB为等腰直角三角形,∴OE=AB=3,∴CE=OC+OE=3+3,△ABC的面积=CE•AB=(3+3)×6=9+18,当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时,△ABC的面积最大,最大值为9+18.(3)过点D作DH⊥OB,DM⊥AO,由(2)可知点C在⊙O上运动到第三象限的角平分线与圆的交点位置,∴∠COM=45°,∵OD⊥OC,∴∠DOM=45°,∵OD=3,∴DM=,DH=,∴点D坐标是(﹣,).20.解:(1)当AB⊥OA时,∵∠BOA=45°,∴OA=AB=2,∵AD=BC=1,∴OD=OA+AD=3,由勾股定理可知:OC==,(2)当O、E、C三点共线时,如图所示,过点E作EF⊥OB于点F,过点C作CG⊥OB于点G,过点A作AH⊥OB于点H,设CG=x,BG=y,∵E是AB的中点,∴BE=BC=1,∵∠ABC=90°,∴∠FBE+∠CBG=∠CBG+∠BCG=90°,∴∠FBE=∠BCG,在△BFE与△BCG中,∴△BFE≌△BCG(AAS)∴EF=BG=y,BF=CG=x,∵E是AB的中点,EF∥AH,∴AH=2FE=2y,∵∠AOB=45°,∴OH=AH=2y,∵EF∥CG,∴△OEF∽△OCG,=,∴=,∴x2=3y2,在Rt△BEF中,由勾股定理可知:x2+y2=1,∴4y2=1,∴y=或y=﹣(舍)∴x=,∴OG=2x+3y=+,CG=,在Rt△BEC中,∴CE=,∵=,∴,∴OE=,∴OC=OE+CE=∵OA=OH=2y,∴OA=,(3)设△OAB的外接圆M,连接BM并延长交⊙M于N,连接AN,∵,∴∠BOA=∠BNA=45°,∵BN是⊙M的直径,∴∠BAN=90°,∴BN=AB=2,∴R=∴移动过程中R的值不会发生变化,(4)由题意可知:原点O在以AB为弦,半径为的圆O′上,如图所示,∴OC≤OO′+O′C,当O′在线段OC上时,此时OC有最大值,过点O′作O′E⊥AB,交CD于点F,∴由垂径定理与勾股定理可知:O′E=1,∵CF=1,∴由勾股定理可知:O′C==,∴OC的最大值为:+.21.解:(1)作OC⊥AB于C,则AC=BC=AB=,在Rt△AOC中,∵OA=2,AC=,∴cos∠OAC==,∴∠OAC=30°,∴∠AOB=180°﹣2∠OAB=120°;(2)∵∠OAC=30°,∴OC=OA=1,设D点到AB的距离为h,∴S=AB•h=h,△ABD∴当h最大时,S最大,∵当D、O、C在一条直线上时,h最大,∴h=OD+OC=2+1=3,∴S的最大值为3.22.解:(1)由∠B得角平分线、平角∠BXA的平分线、平角∠BYC的角平分线中的任意两条得交点即为所求圆的圆心O;(2)若⊙P与△ABC的BA、BC两条边相切,且面积最大,则点P为∠ABC 的角平分线与AC边的交点,作PH⊥AB于H,∵Rt△ABC两直角边的边长为AC=3,BC=4,∴AB=5,则BH=BC=4,∴AH=1,∵∠A=∠A,∠PHA=∠BCA,∴△APH∽△ABC,∴==,∴PH=AH,在Rt△APH中,PH=AH=,即R1=,同理,⊙P与△ABC的CA、AC两条边相切,R2=,若⊙P与△ABC的CA、BC两条边相切,R3=,故R3>R2>R1,符合要求⊙P的最大面积为:.23.(1)解:∵Rt△AOB中OA=OB=6,∴∠OBA=∠A=45°,当C点在OB左侧,AO上面时,当OC∥AB时,∠ABO=∠BOC,则∠BOC 的度数为45°,当C点在OB右侧,AO下面时,当OC∥AB时,∠BOC的度数为:90°+45°=135°,故答案为:45°或135°;(2)证明:如图2,∵OC∥AD,∠AOB=90°∴∠ADO=∠COD=∠AOB=90°,∴∠1+∠2=90°∠3+∠2=90°∴∠1=∠3在△BOC和△AOD中,,∴△BOC≌△AOD(SAS),∴∠BCO=∠ADC=90°,∴OC⊥BC,∴直线BC为⊙O的切线;(3)解:当点C在⊙O上运动到∠AOB的平分线OE的反向延长线与⊙O的交点位置C时,△ABC的面积最大,(如图3)过O点作OE⊥AB于E,OE的反向延长线交⊙O于C,此时C点到AB的距离的最大值为CE的长,∵△OAB为等腰直角三角形,∴AB=OA=6,∴OE=AB=3,OC=3∴CE=OC+CE=3+3,△ABC的面积=CE•AB=×(3+3)×6=9+18.∴△ABC的面积最大值为:9+18.24.解:(1)直线BC与⊙O相切,过点O作OM⊥BC于点M,∵AB=AC,∠CAB=90°,∴∠ABC=45°,当A在x轴的负半轴上时,∠OBM=∠BOM=45°,∵OB=∴OM=1,∴直线BC与⊙O相切;(2)过点A作AE⊥OB于点E在Rt△OAE中,AE2=OA2﹣OE2=1﹣x2,在Rt△BAE中,AB2=AE2+BE2=(1﹣x2)+(﹣x)2=3﹣2x ∴S=AB•AC=AB2=(3﹣2x)=其中﹣1≤x≤1,当x=﹣1时,S的最大值为,当x=1时,S的最小值为;(3)①当点A位于第一象限时(如右图):连接OA,并过点A作AE⊥OB于点E∵直线AB与⊙O相切,∴∠OAB=90°,又∵∠CAB=90°,∴∠CAB+∠OAB=180°,∴点O、A、C在同一条直线∴∠AOB=∠C=45°,即∠CBO=90°,在Rt△OAE中,OE=AE=,点A的坐标为(,)过A、B两点的直线为y=﹣x+;②当点A位于第四象限时(如右图):点A的坐标为(,﹣)∵B的坐标为(,0)∴过A、B两点的直线为y=x﹣.25.解:(1)如图2,∵P在图2中的坐标为(2,4),∴P到OA的距离为:4,P到OB的距离为:2,∵(6,0),B(0,8),∴OB=8,AO=6,则AB=10,设P到AB的距离为x,则×2×BO+×AO×4+×AB×x=×6×8,解得:x=0.8,故P到AB的距离为:0.8,所以P到△AOB的距离为:0.8;故答案为:4,2,0.8,0.8;(2)当点Q到△AOB三边距离相等即Q为△AOB的内心时,Q到△AOB的距离最大.设这个最大值为h,则×8×h+×6×h+×10×h=×6×8,解得:h=2.∴点Q到△AOB距离的最大值为2.(3)设点Q为△AOB的内心,如图3,连接QA,QB,QO,分别取QA,QB,QO的中点E,F,G,连接EF,FG,GE,则△EFG即为所要画的图形.(只要画图正确即可,不必书写画图过程),由画图可知,△EFG∽△ABO,由上题及已知条件可知,△EFG与△ABO的相似比为,因为△ABO的周长为24,所以△EFG的周长为12.26.解:(1)四边形AOCD是菱形;四边形EFGH是矩形.证明如下:由翻折可得AO=AD,CO=CD.∵OA=OC,∴AO=OC=CD=DA.∴四边形AOCD是菱形;∴AC⊥OD.又∵EF是△AOD的中位线,∴EF∥OD,且EF=OD,同理可得FG∥AC,且FG=AC,EH∥AC,且EH=AC,∴FG平行且等于EH,∴四边形EFGH是平行四边形,且FG⊥EF,∴四边形EFGH是矩形.(2)∵AB为半圆O的直径,∴∠ACB=90°.∴AC⊥BC.∵四边形AOCD 是菱形,∴DC 平行且等于OA ,又∵AO =OB ,∴DC 平行且等于OB ,∴四边形OBCD 是平行四边形,∴DO 平行且等于BC ,∴S 矩形EFGH =EF •EH =OD •AC =BC •AC =×S △ACB , ∴当点C 位于半圆弧中点时,AB 边上的高最大, 即S △ACB 的最大值为1.∴S 矩形EFGH 的最大值为.此时AC =BC ,∴AC =OD .∴EF =FG ,∴矩形EFGH 是正方形.。
2022年人教版九年级数学中考复习与圆有关的最值问题专题突破训练
2022年春人教版九年级数学中考复习《与圆有关的最值问题》专题突破训练(附答案)1.如图,AB是⊙O的弦,AB=10,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是BC、AB的中点,则MN长的最大值是()A.10 B.5C.10D.202.如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为()A.3 B.4 C.6 D.83.如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是()A.1.4 B.C.D.2.64.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为()A.B.2﹣2 C.2﹣2 D.45.如图,在平面直角坐标系中,C(0,4),A(3,0),⊙A半径为2,P为⊙A上任意一点,E是PC的中点,则OE的最小值是()A.1 B.C.2 D.6.如图,AB是半圆O的直径,点D在半圆O上,AB=2,AD=10,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H,连接BH,在点C移动的过程中,BH的最小值是()A.5 B.6 C.7 D.87.如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.(1)求证:△ABC是等边三角形;(2)填空:①PC、PB、PA之间的数量关系是;②四边形APBC的最大面积为.8.如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为.9.如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为.10.如图,已知△ABC,外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE,CD交于点P,则OP的最小值是.11.等腰直角△ABC中,∠C=90°,AC=BC=6,D为线段AC上一动点,连接BD,过点C作CH⊥BD于H,连接AH,则AH的最小值为.12.如图,在半径为4,圆心角为90°的扇形OAB的上有一动点P,过P作PH⊥OA于H.设△OPH的内心为I,当点P在上从点A运动到点B时,内心I所经过的路径长为.13.如图,正方形ABCD的边长为4,点E是AB边上一个动点,点F是CD边上一个动点,且AE=CF,过点B作BG⊥EF于点G,连接AG,则AG长的最小值是.14.如图,已知等腰三角形ABC,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,BP最大值为.15.如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,点D是半径为2的⊙A上一动点,点M是CD的中点,则BM的最大值是.16.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为.17.如图,在Rt△ABC中,∠ACB=90°,BC=5,AC=12,点D是边BC上的一动点,连接AD,作CE⊥AD 于点E,连接BE,则BE的最小值为.18.如图,在Rt△ABC中,∠ACB=90°,BC=4,AC=10,点D是AC上的一个动点,以CD为直径作圆O,连接BD交圆O于点E,则AE的最小值为.19.如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC 的内心为E,连接OE、CE.当点C从点B运动到点A时,内心E所经过的路径长为.20.如图,在正方形ABCD中,AB=4,E,F分别为BC,AD上的点,过点E,F的直线将正方形ABCD的面积分为相等的两部分,过点A作AG⊥EF于点G,连接DG,则线段DG的最小值为.参考答案1.解:∵点M,N分别是AB,BC的中点,∴MN=AC,∴当AC取得最大值时,MN就取得最大值,当AC是直径时,最大,如图,∵∠ACB=∠D=45°,AB=10,∴AD=20,∴MN=AD=10,故选:A.2.解:∵PA⊥PB,∴∠APB=90°,∵AO=BO,∴AB=2PO,若要使AB取得最小值,则PO需取得最小值,连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,过点M作MQ⊥x轴于点Q,则OQ=3、MQ=4,∴OM=5,又∵MP′=2,∴OP′=3,∴AB=2OP′=6,故选:C.3.解:如图,连接OP交⊙P于M′,连接OM,由勾股定理得:OP==5,∵OA=AB,CM=CB,∴AC=OM,∴当OM最小时,AC最小,∴当M运动到M′时,OM最小,此时AC的最小值=OM′=(OP﹣PM′)==,故选:B.4.解:如图∵AE⊥BE,∴点E在以AB为直径的半⊙O上,连接CO交⊙O于点E′,∴当点E位于点E′位置时,线段CE取得最小值,∵AB=4,∴OA=OB=OE′=2,∵BC=6,∴OC===2,则CE′=OC﹣OE′=2﹣2,故选:B.5.解:如图,连接AC,取AC的中点H,连接EH,OH.∵CE=EP,CH=AH,∴EH=PA=1,∴点E的运动轨迹是以H为圆心半径为1的圆,∵C(0,4),A(3,0),∴H(1.5,2),∴OH==2.5,∴OE的最小值=OH﹣EH=2.5﹣1=1.5,故选:B.6.解:如图,取AD的中点M,连接BD,HM,BM.∵DH⊥AC,∴∠AHD=90°,∴点H在以M为圆心,MD为半径的⊙M上,∴当M、H、B共线时,BH的值最小,∵AB是直径,∴∠ADB=90°,∴BD==12,BM===13,∴BH的最小值为BM﹣MH=13﹣5=8.故选:D.7.(1)在⊙O中,∠BAC与∠CPB是所对圆周角,∠ABC与∠APC是所对的圆周角,∴∠BAC=∠CPB,∠ABC=∠APC,∵∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC为等边三角形;故答案为:等边三角形;(2)①如图1,在PC上截取PD=AP,又∵∠APC=60°,∴△APD是等边三角形,∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.又∵∠APB=∠APC+∠BPC=120°,∴∠ADC=∠APB,在△APB和△ADC中,,∴△APB≌△ADC(AAS),∴BP=CD,又∵PD=AP,∴CP=BP+AP,故答案为:CP=BP+AP;②当点P为的中点时,四边形APBC的面积最大.理由如下,如图2,过点P作PE⊥AB,垂足为E.过点C作CF⊥AB,垂足为F.∵S△APB=AB•PE,S△ABC=AB•CF,∴S四边形APBC=AB•(PE+CF),当点P为的中点时,PE+CF=PC,PC为⊙O的直径∴此时四边形APBC的面积最大.又∵⊙O的半径为1,∴其内接正三角形的边长AB=,∴S四边形APBC=×2×=.,故答案为:.8.解:如图,∵AE⊥BE,∴点E在以AB为直径的半⊙O上,连接CO交⊙O于点E′,∴当点E位于点E′位置时,线段CE取得最小值,∵AB=4,∴OA=OB=OE′=2,∵BC=6,∴OC===2,则CE′=OC﹣OE′=2﹣2,故答案为:2﹣2.9.解:∵△ABC是等边三角形,∴∠ABC=∠BAC=60°,AC=AB=2,∵∠PAB=∠ACP,∴∠PAC+∠ACP=60°,∴∠APC=120°,∴点P的运动轨迹是,当O、P、B共线时,PB长度最小,设OB交AC于D,如图所示:此时PA=PC,OB⊥AC,则AD=CD=AC=1,∠PAC=∠ACP=30°,∠ABD=∠ABC=30°,∴PD=AD•tan30°=AD=,BD=AD=,∴PB=BD﹣PD=﹣=.故答案为:.10.解:如图,∵∠BAD=∠CAE=90°,∴∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∴∠PDB+∠PBD=90°,∴∠DPB=90°,∴点P在以BC为直径的圆上,∵外心为O,∠BAC=60°,∴∠BOC=120°,又BC=10,∴OH=,所以OP的最小值是5﹣.11.解:∵∠CHB=90°,BC是定值,∴H点是在以BC为直径的半圆上运动(不包括B点和C点),连接HO,则HO=BC=3.∵OA===3,当A、H、O三点共线时,AH最短,此时AH=AO﹣HO=3﹣3.故答案为3﹣3.12.解:如图,连接IP、IO、IA,∵I是△OPH的内心,∴∠IOP=∠IOA,∠IPO=∠IPH,∴∠PIO=180°﹣∠IPO﹣∠IOP,∵PH⊥OA,即∠PHO=90°,∴∠PIO=180°﹣(∠HOP+∠OPH)=180°﹣(180°﹣90°)=135°,∵在△POI和△AOI中,,∴△POI≌△AOI(SAS),∴∠AIO=∠PIO=135°,所以点I在以OA为弦,且所对的圆周角为135°的一段劣弧上;过点A、I、O三点作圆O′,如上图,连接O′O,O′A,在优弧OA取点P',连接P'A、P'O,∵∠AIO=135°,∴∠AP'O=180°﹣135°=45°,∴∠AO′O=90°,∵OA=4,∴O′O=OA=2,∴的长为:=π.,所以内心I所经过的路径长为π.故答案为π.13.解:设正方形的中心为O,可证EF经过O点.连接OB,取OB中点M,连接MA,MG,则MA,MG为定长,过点M作MH⊥AB于H.则MH=BH=1,AH=3,由勾股定理可得MA=,MG=OB=,∵AG≥AM﹣MG=﹣,当A,M,G三点共线时,AG最小=﹣,故答案为:﹣.14.解:∵∠ACB=120°,∠APB=60°,∴A、P、B、C四点共圆,∴当PB是圆的直径时最长,∴∠PAB=90°,∴∠ABP=30°.过点C作AB的垂线交PB于点O,则点O即为圆心,∵∠ACB=120°且AC=BC=4,∴∠BCO=60°,∠ACB=30°,∴∠OBC=60°,∴△OBC是等边三角形,∴OC=BC=4,∴PB=2OC=8.故答案为:8.15.解:如图,取AC的中点N,连接MN,BN.∵∠ABC=90°,AB=4,BC=3,∴AC==5,∵AN=NC,∴BN=AC=,∵AN=NC,DM=MC,∴MN=AD=1,∴BM≤BN+NM,∴BM≤1+,∴BM≤,∴BM的最大值为.16.解:∵∠ABC=90°,∴∠ABP+∠PBC=90°,∵∠PAB=∠PBC∴∠BAP+∠ABP=90°,∴∠APB=90°,∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,∴OC==5,∴PC=OC﹣OP=5﹣3=2.∴PC最小值为2.故答案为2.17.解:∵CE⊥AD,∴∠AEC=90°,∴点E在以AC为直径的圆上,取AC的中点O,以AC为直径作⊙O,当O、E、B共线时,BE的长最小,Rt△OCB中,OC=OE=6,BC=5,∴OB==,∴BE=OB﹣OE=﹣6,则BE的最小值为:﹣6,故答案为:﹣6.18.解:连接CE,取BC的中点F,作直径为BC的⊙F,连接EF,AF,∵BC=4,∴CF=2,∵∠ACB=90°,AC=10,∴AF=,∵CD是⊙O的直径,∴∠CED=∠CEB=90°,∴E点在⊙F上,∵在D的运动过程中,AE≥AF﹣EF,且A、E、F三点共线时等号成立,∴当A、E、F三点共线时,AE取最小值为AF﹣EF=2﹣2.故答案为:2﹣2.19.解:如图,连接BE,∵点E是△ODC的内心,∴∠EOC=∠COD,∠ECO=∠OCD,∴∠EOC+∠ECO=(∠COD+∠DCO),∵DC⊥OB,∴∠CDO=90°,∴∠COD+∠DCO=90°,∴∠EOC+∠ECO=(∠COD+∠DCO)=45°,∴∠OEC=180°﹣45°=135°,∵OE平分∠COD,∴∠COE=∠BOE,∵OB=OC,OE=OE,∴△COE≌△BOE(SAS),∴∠CEO=∠OEB=135°,∴当点C从点B运动到点A时,内心E所经过的路径长为图中的长度,设△BOE的外接圆为⊙M,在优弧BNO上任取一点N,连接BN,ON,则∠N=45°,∴∠M=90°,∴BM=OM=OB=2∴的长==π,故答案为:π.20.解:连接AC,BD交于O,∵过点E、F的直线将正方形ABCD的面积分为相等的两部分,∴EF过点O,∵AG⊥EF,∴∠AGO=90°,∴点G在以AO为直径的半圆弧上,设AO的中点为M,连接DM交半圆弧于G,则此时,DG最小,∵四边形ABCD是正方形,AB=4,∴AC=8,AC⊥BD,∴AO=OD=AC=4,∴AM=OM=AO=2,∴DM==2,∴DG=2﹣2.故答案为:2﹣2.。
与圆有关的最值问题ppt课件
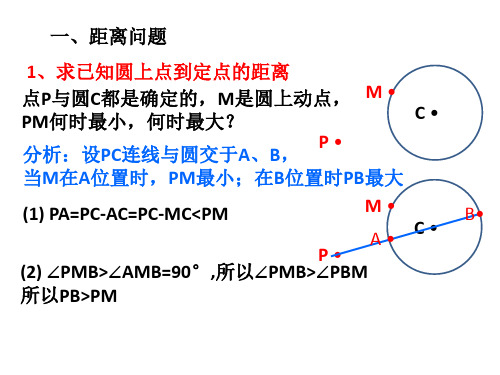
1、求已知圆上点到定点的距离
点P与圆C都是确定的,M是圆上动点, M •
PM何时最小,何时最大?
C•
分析:设PC连线与圆交于A、B, P •
当M在A位置时,PM最小;在B位• A• C•
B•
P•
(2) ∠PMB>∠AMB=90°,所以∠PMB>∠PBM
切线最短
-1 o C
x
所以PC⊥直线x=-1时,PC最短,从而切线最短, 此时m=0
3、其他举例
已知圆C内一定点P,过P的
P•
所有弦中,那一条最短
C•
上式中, r是定值, 所以d最大时,弦最短, 即P为弦的中点时
(3)求ΔCAB面积的最大值
所以PB>PM
y
o
x
2、圆上动点到定直线的距离
M是圆C上动点,什么时候M到L 距离最大或最小?
分析:过圆心作L的垂线交圆于A、B ,则M在A(B)位置时到L距离最小(大)
M到L的距离等于过M与L平行的 直线与L的距离
L
M• C•
L
M• A•
C• B•
y
o
x
y
因为r是定值。所以PC最小时, P•
初中数学圆中最值定值问题专题(推荐)

圆中最值域定值问题研究类型一、例1、如图,AB是⊙O的直径,AB=10cm,M是半圆AB的一个三等分点,N是半圆AB 的一个六等分点,P是直径AB上一动点,连接MP、NP,则MP+NP的最小值是_______1、已知圆O的面积为3 ,AB为直径,弧AC的度数为80度,弧BD的度数为20度,点P为直径AB上任一点,则PC+CD的最小值为______2、如图,菱形ABC中,∠A=60度,AB=3, 圆A、圆B的半径为2和1,P、E、F分别是CD,圆A和圆B上的动点,则PE+PF的最小值为_________类型二、折叠隐圆【基本原理】(一箭穿心)点A为圆外一点,P为圆O上动点,连接AO并延长交圆于P1、P2,则AP的最小值为AP2,,最大值为A P1例、如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′B长度的最小值.1、已知一个矩形纸片OACB,将该纸片放置在平面直角坐标洗中,点A(11,0),点B (0,6),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,则CB’的最小值为______2、四边形ABCD中,AD∥BC,∠A=90,AD=1,AB=2,BC=3,P是线段AD上一动点,将△ABP沿BP所在直线翻折得到△QBP,则△CQD的面积最小值为____类型三、随动位似隐圆例、在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=6.点D是边AC上一点D且AD=23,将线段AD绕点A旋转得线段AD′,点F始终为BD′的中点,则将线段CF最大值为_________[分析]:易知D’轨迹为以A为圆心AD为半径的圆,则在运动过程中AD’为定值23,故取AB中点G,则FG为中位线,FG=12AD'=3,故F点轨迹为以G为圆心,3为半径的圆。
人教版九年级数学上册期末圆动点最值问题压轴题

人教版九年级数学上册期末圆动点最值问题压轴题一、单选题1.如图,O的直径12AB=,弦CD垂直平分半径OA,动点M从点C出发在优弧CBD 上运动到点D停止,在点M整个运动过程中,线段AM的中点P的运动路径长为()A.3πB.4πC.5πD.6π2.如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最大值与最小值之差是()A.5 B.6 C.7 D.83.如图,线段AB=6,点C为线段AB外一动点,45∠=︒,连接BC,M,N分别ACB为AB,BC的中点,则线段MN的最大值为()A.3 B.4 C.2D.24.如图,已知⊙O半径OA=4,点B为圆上的一点,点C为劣弧AB上的一动点,CD⊥OA,CE⊥OB,连接DE,要使DE取得最大值,则∠AOB等于()A .60°B .90°C .120°D .135°5.如图,O 的半径为13,弦AB 的长为24,M 是弦AB 上的动点,则线段OM 长的最小值为( )A .8B .7C .6D .56.如图,在Rt AOB 中,OA =OB =42,⊙O 的半径为2, 点P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则线段PQ 长的最小值为( )A .23B .3C .1D .27.如图,AC 为半圆的直径,弦3AB =,30BAC ∠=︒,点E 、F 分别为AB 和AC 上的动点,则BF EF +的最小值为( )A 3B 33C .3D .3328.如图,AB 是⊙O 的弦,AB 长为8,P 是⊙O 上一个动点(不与A ,B 重合),过点O 作OC ⊥AP 于点C ,OD ⊥PB 于点D ,则CD 的长为( ).A .3B .23C .43D .4二、填空题 9.如图所示,AB 是O 的直径,20AB =,30CAB ∠=︒,点D 为弧BC 的中点,点P 是直径AB 上的一个动点,PC PD +的最小值为__________.10.如图,⊙O 的半径是2,AB 是⊙O 的弦,P 是弦AB 上的动点,且1≤OP ≤2,则弦AB 所对的圆心角的度数是__________.11.如图,AB 是O 的弦,5AB =,点C 是O 上的一个动点,且45ACB ∠=︒,若点M ,N 分别是AB ,AC 的中点,则MN 长的最大值是______.12.如图,在扇形ABD 中,60BAD ∠=︒,AC 平分BAD ∠交弧BD 于点C ,点P 为半径AB 上一动点,若4AB =,则阴影部分周长的最小值为___________.13.在ABC 中,90,2,3ABC AB BC ∠=︒==.点D 为平面上一个动点,45ADB ∠=︒,则线段CD 长度的最小值为_____.14.如图,在扇形AOB 中,45AOB ∠=︒,点C 是AB 的中点,点D ,E 分别为半径OA ,OB 上的动点.若2OB =,则CDE △周长的最小值为______.15.如图,矩形ABCD 中,AB =6,BC =9,M 是AB 的中点,P 是BC 边上的动点,连结PM ,以点P 为圆心,PM 长为半径作⊙P .当⊙P 与矩形ABCD 的边CD 相切时,则BP 的长为________.三、解答题16.如图,在正方形ABCD 中,动点E ,F 分别在边DC ,CB 上移动(不与顶点重合),且满足DE CF =.连接AE 和DF ,交于点P .(1)请你写出AE 与DF 的数量关系和位置关系,并说明理由;(2)由于点E ,F 的移动,使得点P 也随之运动.①请用文字描述并且在图中画出点P 的运动路径;②若10AD =,请求出线段CP 的最小值.17.如图,O为Rt ABC的外接圆,90,43,4∠=︒==,点D是O上的ACB BC AC、分别位于AB的两侧.动点,且点C D(1)求O的半径;∠的度数;(2)当42CD=时,求ACD(3)设AD的中点为M,在点D的运动过程中,线段CM是否存在最大值?若存在,求出CM的最大值;若不存在,请说明理由.18.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE的长为半径作半圆,交AO于点F.(1)求证:AC是⊙O的切线;(2)若点F是AO的中点,OE=3,求图中阴影部分的面积;(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,求出BP的长.19.如图,在平行四边行ABCD 中,AB =5,BC =8,BC 边上的高AH =3,点P 是边BC 上的动点,以CP 为半径的⊙C 与边AD 交于点E ,F (点E 在点F 的左侧). (1)当⊙C 经过点A 时,求CP 的长;(2)连接AP ,当AP ∥CE 时,求⊙C 的半径及弦EF 的长.20.如图,在Rt ABC 中,90ACB ∠=︒,10AB =,6AC =,点D 为BC 边上的一个动点,以CD 为直径的O 交AD 于点E ,过点C 作//CF AB ,交O 于点F ,连接CE 、EF .(1)当45CFE ∠=︒时,求CD 的长;(2)求证:BAC CEF ∠=∠;(3)是否存在点D ,使得CFE 是以CF 为底的等腰三角形,若存在,求出此时CD 的长;若不存在,试说明理由.参考答案1.B解:如图,连接OC,设CD交AB于点E.∵CD垂直平分线段OA,∴CA=CO,∵OC=OA,∴AC=OC=OA,∴△AOC是等边三角形,∴∠CAE=60°,当点M与C重合时,连接PE,OP,∵P A=PM,∴OP⊥AM,∴∠APO=90°,∵AE=EO,OA=3,∴EP=12∵PE=AE=3,∠P AE=60°,∴△P AE是等边三角形,∴∠AEP=60°;在点M整个运动过程中,如下图,∵点P 是AM 的中点,点E 是AO 的中点, ∴1122PE OM OA AE EO ====, ∴线段AM 的中点P 的运动轨迹是图中IOJ ,∵260120IEJ ∠=⨯︒=︒,∴IOJ 的圆心角360120240=︒-︒=︒,∴运动路径的长=24034180ππ•=. 故选:B .2.D解:如图,设⊙O 与AC 相切于点D ,连接OD ,过点O 作OP ⊥BC 垂足为P 交⊙O 于F ,此时垂线段OP 最短,PF 最小值为OP ﹣OF ,∵AC =12,BC =9,∴AB 22AC BC +22129+15,∵∠OPB =90°,∴OP ∥AC ,,OPB ACB ∴∽2,3OP OB AC AB ∴== ∵点O 是AB 的三等分点,∴21510,3OB =⨯=, ∴OP =8,∵⊙O 与AC 相切于点D ,∴OD ⊥AC ,∴OD ∥BC ,,AOD ABC ∴∽ ∴13OD OA BC AB ==, ∴OD =3,∴MN 最小值为OP ﹣OF =8﹣3=5,如图,当N 在AB 边上时,M 与B 重合时,MN 经过圆心,经过圆心的弦最长, MN 最大值=OB +OE =10+3=13,∴MN 长的最大值与最小值的差是13﹣5=8.故选:D .3.C解:由题知A 、B 、C 三点共圆,M ,N 分别为AB ,BC 的中点,12MN AC ∴=, ∴当AC 过圆心即AC 是直径时(如图所示),AC 取得最大值,此时MN 取的最大值, 45ACB =︒∠,90ABC ∠=︒∴此时ABC 是等腰直角三角形,BMN △是等腰直角三角形,132BM BN AB ∴===,MN ∴=故选C .4.B解:如图,延长CD交⊙O于P,延长CE交⊙O于T,连接PT.∵OA⊥PC,OB⊥CT,∴CD=DP,CE=TE,∴DE=12 PT,∴当PT是直径时,DE的长最大,连接OC,∵OP=OC=OT,OD⊥PC,OE⊥CT,∴∠COA=∠POA,∠COB=∠BOT,∴∠AOB=∠COA+∠COB=12∠POT=90°,故选:B.5.D解:过O作OM AB'⊥于M',此时线段OM'的长最短,连接OA,OM '过点O ,OM AB '⊥, 11241222AM AB '∴==⨯=, 在Rt AMO △中,由勾股定理得:221691445OM OA AM ''=-=-=. 故选:D .6.A解:连接OQ .∵PQ 是⊙O 的切线,∴OQ ⊥PQ ;根据勾股定理知PQ 2=OP 2-OQ 2,∴当PO ⊥AB 时,线段PQ 最短,∵在Rt △AOB 中,2∴2OA=8,∴OP=4OA OB AB•=, ∴2223OP OQ =-故选:A .7.B解:作B 点关于直径AC 的对称点B′,过B′点作B′E ⊥AB 于E ,交AC 于F ,如图,则FB=FB′,∴FB+FE=FB′+FE=B′E,此时FB+FE的值最小,∵∠BAC=30°,∴∠B′AC=30°,∴∠BAB′=60°,∵AB=AB′,∴△ABB′为等边三角形,∵B′E⊥AB,∴AE=BE=32,∴B′E333即BF+EF33故选:B.8.D∵过点O作OC⊥AP于点C,OD⊥PB于点D,∴AC=PC,BD=PD,∴CD∥AB,且CD=12AB,∵AB=8,∴CD=12AB=4.故选择:D.9.102解:作出D 关于AB 的对称点D ′,连接OC ,OD ′,CD ′.又∵点C 在⊙O 上,∠CAB =30°,D 为弧BC 的中点,即BD BD '=,∴∠BAD ′=12∠CAB =15°.∴∠CAD ′=45°.∴∠COD ′=90°.则△COD ′是等腰直角三角形.∵OC =OD ′=12AB =10,∴CD ′=2故答案为:10210.120︒解:作OD ⊥AB ,∵P 是弦AB 上的动点,且1≤OP ≤2,∴OD=1,∵⊙O 的半径是2,∴12OD OA , ∵OA=OB ,∴30OAB OBA ==︒∠∠,∴弦AB 所对的圆心角120AOB ∠=︒,故答案为:120︒ .11.522 解:∵点M ,N 分别是AB ,AC 的中点,∴MN =12BC , ∵当BC 最大时,线段MN 长的最大,当BC 为⊙O 的直径时,BC 的长度最大,此时,∠A =90°,∠ACB =45°,∴直径BC =2AB =52,则线段MN 长的最大值为522, 故答案为:522. 12.2423π+ 解:如图,作点C 关于AB 的对称点C ',连接C D '交OB 于点P ',连接P C '、OC ',此时P C P D ''+最小,即=P C P D C D '''+,由题意得,30DAC CAB BAC '∠=∠=∠=︒,∴90DAC '∠=︒, ∴22224442C D OC OD ''=+=+=,CD 的长3042==1803l ππ⨯, ∴阴影部分周长的最小值为242+3π, 故答案为:242+3π. 13.52-如图: 以12AB 为半径作圆,过圆心O 作,ON AB OM BC ⊥⊥, 以O 为圆心OB 为半径作圆,则点D 在圆O 上,45ADB ∠=︒90AOB ∠=︒∴2AB =1AN BN ==22112AO ∴=+=112ON OM AB ===,3BC = 221(31)5OC ∴=+-=52CO OD ∴-=线段CD 长度的最小值为52-. 52-14.2解:如图,作点C 关于,OA OB 的对称点,M N ,连接,,,,DM EN OM OC ON ,则,,,,,DM CD OM OC AOM AOC EN CE ON OC BON BOC ==∠=∠==∠=∠, CDE ∴的周长为CD DE CE DM DE EN ++=++,由两点之间线段最短得:当点,,,M D E N 共线时,CDE △周长最小,最小值为MN , ,AOM AOC BON BOC ∠=∠∠=∠,45AOC BOC AOB ∠+∠=∠=︒,2()90MON AOM AOC BON BOC AOC BOC ∴∠=∠+∠+∠+∠=∠+∠=︒,由同圆半径相等得:2OC OB ==,2OM ON ∴==,在Rt MON 中,2222MN OM ON +=即CDE △周长的最小值为22 故答案为:2215.4当⊙P 与直线CD 相切时,设PC =PM =x .则PB =9-x ,132BM AB == 在Rt △PBM 中,∵222PM BM PB =+,∴2223(9)x x =+-,∴x =5,∴PC =5,∴BP =BC ﹣PC =9﹣5=4.故答案为:4.16.解:(1)AE DF =,AE DF ⊥,理由是:∵四边形ABCD 是正方形,∴AD DC =,90ADE DCF ∠=∠=︒,∵DE CF =,在ADE 和DCF 中AD DC ADE DCF DE CF =⎧⎪∠=∠⎨⎪=⎩,∴ADE DCF ≅△△,∴AE DF =,DAE FDC ∠=∠∵90ADE ∠=︒,∴90ADP FDC ∠+∠=︒,∴90ADP DAE ∠+∠=︒,∴1809090APD ∠=︒-︒=︒,∴AE DF ⊥;(2)如图,①∵点P 在运动中保持90APD ∠=︒,设正方形ABCD 的中心为O , ∴得出点P 的运动路径是以AD 为直径的圆的圆弧DPO (去除端点D ,O ),②设AD 的中点(圆心)为G ,连接CG 交圆弧于点P ,此时线段CP 的长度最小. 在Rt CDG 中,222210555CG CD DG ++∴555=-=-CP CG GP即线段CP的最小值是555-.17.(1)4;(2)15°;(3)存在,232+解:(1)如图1中,∵AB是直径,∴∠ACB=90°,∵AC=4,BC=3∴AB2222++=8,4(43)AC BC∴⊙O的半径为4.(2)如图1中,连接OC,OD.∵CD=2,OC=OD=4,∴CD2=OC2+OD2,∴∠COD=90°,∴∠OCD=45°,∵AC=OC=OA,∴△AOC是等边三角形,∴∠ACO=60°,∴∠ACD=∠ACO﹣∠DCO=60°﹣45°=15°.(3)如图2中,连接OM,OC.∵AM=MD,∴OM⊥AD,∴点M的运动轨迹以AO为直径的⊙J,连接CJ,JM.∵△AOC是等边三角形,AJ=OJ,∴CJ⊥OA,∴CJ22=-=23,AC AJ∵CM≤CJ+JM=23+2,∴CM的最大值为23+2.18.【详解】(1)证明:如图,过O作AC的垂线OM,垂足为M.∵AB=AC,AO⊥BC,∴AO平分∠BAC,∵OE⊥AB,OM⊥AC,∴ OE =OM ,∵ OE 为⊙O 的半径,∴ OM 为⊙O 的半径,∴ AC 是⊙O 的切线.(2)解:∵OM =OE =OF =3.且F 是OA 的中点,∴ AO =6,在Rt ΔAEO 中,AE =33, ∴ AEO S =12OE AE =932. ∵ OE ⊥AB ,在Rt ΔAEO 中,∠OEA =90°,AO =6,AE =33,OE =3,∴ ∠EOF =60°,∴ OEF S 扇形=260333602ππ⋅=, ∴ S 阴影AEO OEF S S =-扇形△93322π=-. (3)解:如图,作点F 关于BC 的对称点G ,连接EG 交BC 于P ,∵ =PF PG ,∴ PE PF PE PG EG +=+=,此时EP +FP 最小,∵ OG =OF =OE ,∴ =G OEG ∠∠,而 =+=60AOE G OEG ︒∠∠∠,∴=30G︒∠,∴=G EAG∠∠,∴33EG EA==,即PE PF+最小值为33,在Rt OPG中,333OP OG==,在Rt ABO中,3362333OB OA==⨯=,∴=23-3=3BP,即当PE+PF取最小值时,BP的长为3.19.(1)CP=5;(2)⊙C的半径为258,EF=74.解:(1)连接AC,如图1所示:∵AH⊥BC,∴∠AHB=∠AHC=90°,∴BH=2222534AB AH-=-=,∴CH=BC﹣BH=4,∴CA=225AH CH+=,当⊙C经过点A时,CP=CA=5;(2)∵四边形ABCD是平行四边形,∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,∵CP=CE,∴四边形APCE是菱形,∴P A=CP,设P A=CP=x,则PH=4﹣x,在Rt△APH中,由勾股定理得:AH2+PH2=P A2,即32+(4﹣x )2=x 2,解得:x =258, 即⊙C 的半径为258, 作CM ⊥EF 于M ,如图2所示:则CM =AH =3,ME =MF =12EF ,在Rt △CEM 中,由勾股定理得:ME =2222257()388CE CM -=-=, ∴EF =2ME =74.20.解:(1)∵45CDE CFE ∠=∠=︒,90ACB ∠=︒∴45DAC CDA ∠=∠=︒∴6CD AC ==(2)∵//CF AB ,∴B FCB ∠=∠,∵FCB DEF ∠=∠,∴B DEF ∠=∠,①又90BAC B ∠+∠=︒②∵CD 是圆O 的直径,90CED ∠=︒,∴90DEF CEF ∠+∠=︒③由①②③可得BAC CEF ∠=∠(3)CFE 是CF 为底的等腰三角形,则EF CE =,则∠EFC =∠ECF . 连接FD ,并延长和AB 相交于G ,∵四边形CEDF为圆内接四边形,∴∠ADG=∠ECF,又∵∠CDE=∠CFE,∴∠ADG=∠CDE,∵CD为⊙O的直径,∴∠DFC=90°,∵FC∥AB,∴∠FGA=90°,∴∠FGA=∠ACD,∵AD=AD,∴△AGD≌△ACD(AAS),∴DG=CD,在Rt△BDG中,设CD=x,BG2+DG2=BD2,∴42+x2=(8-x)2,解得x=3,即CD=3。
中考热点:(一)圆中动点“PA+...

中考热点:圆中动点“PA+kPB”型最值问题一、问题导读在初中数学中,有一类几何动点“PA+kPB”型最值问题,学生普遍感到“害怕”。
普通方法求解可能就会失效!当k=1时,可以转化为“将军饮马”模型,我们可以利用对称变换来处理。
而如果k不等于1的话,我们必须利用转换思路,截取线段灵活转化线段值,转化为常见求解模式。
二、典例精析类型1 探究圆中“PA+kPB”型的最值问题例1.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0),(2,0),点M是AO中点,⊙A 的半径为2.(1)若△PAB是直角三角形,则点P的坐标为______.(直接写出结果)(2)若PM⊥AB,则BP与⊙A有怎样的位置关系?为什么?(3)若点E的坐标为(0,3),那么⊙A上是否存在一点P,使PE+1/2PB最小,如果存在,求出这个最小值,如果不存在,简要说明理由.【解析】(1)分两种情形:①∠PAB=90°,②∠APB=90°分别求解即可解决问题;答案为(﹣2,2)或(﹣2,﹣2)或(﹣1,√3)或(﹣1,﹣√3).(2)求出PA,PB的长,利用勾股定理的逆定理证明即可;(3)如图,连接EM.∵PA=4,AMAB=4,∴PA=AMAB,∴PA/AM=AB/PA,∵∠PAM=∠BAP,∴△PAM∽△BAP,∴PM/PB=PA/AB=1/2,∴PM=1/2PB,∴PE+1/2PB=PE+PM,∵PE+PM≥EM,∴PE+PM的最小值为线段EM的长,∵E(0,3),∴OE=3,∴由勾股定理可求得EM=√10,∴PE+1/2PB的最小值为√10.【点评】本题属于属于圆综合题,考查了勾股定理以及逆定理,相似三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会利用分类讨论的思想思考问题,学会构造相似三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.例2.如图,已知AB是圆O的直径,F是圆O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC 于点C,过点E作ED⊥AF,交AF的延长线于点D.(1)求证:DE是⊙O的切线;(2)若DE=3,CE=2,①求BC/AE的值;②若点G为AE上一点,求OG+1/2EG最小值.【解析】(1)根据切线的判定,连接过切点E的半径OE,利用等腰三角形和平行线性质即能证得OE⊥DE.(2)①观察DE所在的△ADE与CE所在的△BCE的关系,由等角的余角相等易证△ADE∽△BEC,即得BC/AE 的值.②先利用BC/AE的值和相似求出圆的直径,发现∠BAC=30°;利用30°所对直角边等于斜边一半,给EG构造以EG为斜边且有30°的直角三角形,把1/2EG转化到EP,再从P出发构造PQ=OG,最终得到三点成一直线时线段和最短的模型.解:①连接BE∵AB是⊙O直径∴∠AEB=90°∴∠BED=∠D=90°,∠BAE+∠ABE=90°∵BC是⊙O的切线,∴∠ABC=∠ABE+∠CBE=90°,∴∠BAE=∠CBE∵∠DAE=∠BAE,∴∠DAE=∠CBE,∴△ADE∽△BEC, ∴AE/BC=DE/CE,∵DE=3,CE=2,∴BC/AE=2/3②过点E作EH⊥AB于H,过点G作GP∥AB交EH于P,过点P作PQ∥OG交AB于Q,∴EP⊥PG,四边形OGPQ 是平行四边形,∴∠EPG=90°,PQ=OG∵BC/AE=2/3,∴设BC=2x,AE=3x,∴AC=AE+CE=3x+2∵∠BEC=∠ABC=90°,∠C=∠C,∴△BEC∽△ABC,∴BC/AC=CE/BC,∴BC =ACCE 即(2x)=2(3x+2),解得:x =2,x =﹣1/2(舍去)∴BC=4,AE=6,AC=8,∴sin∠BAC=BC/AC=1/2,∴∠BAC=30°∴∠EGP=∠BAC=30°,∴PE=1/2EG,∴OG+1/2EG=PQ+PE∴当E、P、Q在同一直线上(即H、Q重合)时,PQ+PE=EH最短∵EH=1/2AE=3,∴OG+1/2EG的最小值为3【点评】本题考查了等腰三角形和平行线性质,切线的判定和性质,相似的判定和性质,最短路径问题.第(1)题为常规题型较简单;第(2)①题关键是发现DE、CE所在三角形的相似关系;②是求出所有线段长后发现30°角,利用30°构造1/2EG,考查了转化思想.类型2 由已知含有PA+kPB型最值条件,探究圆的综合问题例3.如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且⊙O的直径AB在线段AE上.(1)试说明CE是⊙O的切线;(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)设点D是线段AC上任意一点(不含端点),连接OD,当1/2CD+OD的最小值为4√3时,求⊙O的直径AB的长.【解析】(1)连接OC,要证CE是⊙O的切线,只需证∠OCE=90°即可(2)过点C作CH⊥AB于H,连接OC,在Rt△OHC中运用三角函数即可求AB=4√3h/3AB;(3)作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,先证明四边形AOCF是菱形,根据对称性可得DF =DO,过点D作DH⊥OC于H,DH=1/2DC,1/2DC+OD=DH+FD,根据两点之间线段最短可得:当F、D、H三点共线时,DH+FD最小,然后在Rt△OHF中运用三角函数求得AB的长.解:作OF平分∠AOC,交⊙O于F,连接AF、CF、DF则∠AOF=∠COF=1/2∠AOC=1/2(180°﹣60°)=60°.∵OA=OF=OC,∴△AOF、△COF是等边三角形,∴AF=AO=OC=FC,∴四边形AOCF是菱形,∴根据对称性可得DF=DO.过点D作DM⊥OC于M,∵OA=OC,∴∠OCA=∠OAC=30°,∴DM=DCsin∠DCM=DCsin30°=1/2DC,∴1/2CD+OD=DM+FD.根据两点之间线段最短可得:当F、D、M三点共线时,DM+FD(即1/2 CD+OD)最小,此时FM=OFsin∠FOM=√3/2OF=4√3,则OF=8,AB=2OF=16.∴当 CD+OD的最小值为4√3时,⊙O的直径AB的长为16.三、总结提升“PA+kPB”型最值问题问题核心解题思想就是“折转直”,通过截取构造等值线段,利用相似三角形、解直角三角形等,将问题利用这类问题常用定理:①三角形的三边关系:两边之和大于第三边,两边之差小于第三边;②两点间线段最短;③垂线段最短,从而求解问题。
解题技巧专题:圆中的最值问题(含隐圆问题)

8.如图,已知⊙O的半径为m,点C为直径AB延 长线上一点,BC=m.过点C任作一直线l,若l上总 存在点P,使过P所作的⊙O的两切线互相垂直, 则∠ACP的最大值等于 45°.
解析:设PM、PN是过P所作的⊙O的两切线且互 相垂直,则∠MON=90°.∴四边形PMON是正方 形.根据勾股定理求得OP= 2m.∴P点在以O为圆 心,以 2m长为半径的大圆⊙O上.过C点作大 ⊙O的切线,切点即为P点,此时∠ACP有最大值, 如图所示.∵PC是大圆⊙O的切线, ∴OP⊥PC.∵OC=2m,OP= 2 m, ∴PC= OC2 OP2= 2m.∴OP=PC. ∴∠ACP=45°. ∴∠ACP的最大值等于45°.故答案为45°.
(2)解:∵OF⊥AC,∴AF=CF.
而OA=OB,
∴OF为△ACB的中位线. ∴OF= 1 BC=3.
2 ∴DF=OD-OF=5-3=2.
(3)若⊙O的半径为5,∠DOA=80°,点P是线段 AB上任意一点,试求出PC+PD的最小值. (3)解:作C点关于AB的对称点C′,连接C′D交AB于 P,连接OC,如图. ∵PC=PC′, ∴PD+PC=PD+PC′=DC′. ∴此时PC+PD的值最小. ∵ AD=CD,∴∠COD=∠AOD=80°.
9.如图,P是矩形ABCD内一点,AB=4,AD=2, AP⊥BP,则当线段DP最短时,CP= 2 3 .
解析:以AB为直径作半圆O,连接OD,与半圆O交 于==O2点BP2=,′,12∠当AAB点D=PO2与=.∵P∠′A重ADO合=D时2=,,∠∠DOBPDA最CD短==,4950则°°A.,∴O∴=DPOO′=DP′ OD-OP′=2 2-2.过P′作P′E⊥CD于点E,则易得 P′E=DE=2- 2.∴CE=CD- DE= 2+2.∴CP′= PE2 CE2 =2 3.故答案为2 3.
专题9二次函数与圆综合问题-挑战2022年中考数学压轴题之学霸秘笈大揭秘(原卷版)
专题9二次函数与圆综合问题解决函数与圆的综合问题的关键是找准函数与圆的结合点,弄清题目的本质,利用圆的基本性质和函数的性质、数形结合、方程思想、全等与相似,以便找到对应的解题途径.常见的考法有:1.直线与圆的位置关系:平面直角坐标系中的直线与圆的位置关系问题关键是圆心到直线的距离等于半径的大小,常用的方法有:(1)利用圆心到直线的距离等于半径的大小这一数量关系列出关系式解决问题(2)利用勾股定理解决问题(3)利用相似列出比例式解决问题2.函数与圆的新定义题目:利用已掌握的知识和方法理解新定义,化生为熟3.函数与圆的性质综合类问题:利用几何性质,结合图形,找到问题中的“不变”关键因素和“临界位置”.【例1】(2021•花都区三模)如图,抛物线y=ax2+bx+2经过A(﹣1,0),B(4,0)两点,与y轴交于点C.(1)求该抛物线的解析式;(2)在y轴上是否存在点P使得∠OBP+∠OBC=45°,若存在,求出点P的坐标,若不存在,请说明理由;(3)点M是BC为直径的圆上的动点,将点M绕原点O顺时针旋转90°得点N,连接NA,求NA的取值范围.【例2】(2020•遵义)如图,抛物线y=ax2+94x+c经过点A(﹣1,0)和点C(0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.(1)求该抛物线的解析式;(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.【例3】(2020•济宁)我们把方程(x﹣m)2+(y﹣n)2=r2称为圆心为(m,n)、半径长为r的圆的标准方程.例如,圆心为(1,﹣2)、半径长为3的圆的标准方程是(x﹣1)2+(y+2)2=9.在平面直角坐标系中,⊙C与x轴交于点A,B,且点B的坐标为(8,0),与y轴相切于点D(0,4),过点A,B,D的抛物线的顶点为E.(1)求⊙C的标准方程;(2)试判断直线AE与⊙C的位置关系,并说明理由.【例4】(2020•西藏)在平面直角坐标系中,二次函数y=12x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.(1)求二次函数的解析式;(2)如图甲,连接AC,P A,PC,若S△P AC=152,求点P的坐标;(3)如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D,交⊙M于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.【例5】(2020•宜宾)如图,已知二次函数的图象顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M、N两点.(1)求二次函数的表达式;(2)P为平面内一点,当△PMN是等边三角形时,求点P的坐标;(3)在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和点N,且与直线y=﹣1相切.若存在,求出点E的坐标,并求⊙E的半径;若不存在,说明理由.【例6】(2021•嘉兴二模)定义:平面直角坐标系xOy中,过二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.(1)已知点P(2,2),以P为圆心,为半径作圆.请判断⊙P是不是二次函数y=x2﹣4x+3的坐标圆,并说明理由;(2)已知二次函数y=x2﹣4x+4图象的顶点为A,坐标圆的圆心为P,如图1,求△POA 周长的最小值;(3)已知二次函数y=ax2﹣4x+4(0<a<1)图象交x轴于点A,B,交y轴于点C,与坐标圆的第四个交点为D,连结PC,PD,如图2.若∠CPD=120°,求a的值.【题组一】1.(2020•雨花区校级一模)如图1,已知抛物线y=ax2﹣12ax+32a(a>0)与x轴交于A,B两点(A在B的左侧),与y轴交于点C.(1)连接BC,若∠ABC=30°,求a的值.(2)如图2,已知M为△ABC的外心,试判断弦AB的弦心距d是否有最小值,若有,求出此时a的值,若没有,请说明理由;(3)如图3,已知动点P(t,t)在第一象限,t为常数.问:是否存在一点P,使得∠APB达到最大,若存在,求出此时∠APB的正弦值,若不存在,也请说明理由.2.(2020•汇川区三模)如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B(3,0)、C(0,3)三点,连接BC并延长.(1)求抛物线的解析式;(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.1°求线段MN的最大值;2°当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.3.(2020•望城区模拟)如图,在平面直角坐标系中,抛物线y=12x2﹣bx+c交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).(1)求此抛物线的解析式;(2)在抛物线上取点D ,若点D 的横坐标为5,求点D 的坐标及∠ADB 的度数;(3)在(2)的条件下,设抛物线对称轴l 交x 轴于点H ,△ABD 的外接圆圆心为M (如图1),①求点M 的坐标及⊙M 的半径;②过点B 作⊙M 的切线交于点P (如图2),设Q 为⊙M 上一动点,则在点运动过程中QH QP的值是否变化?若不变,求出其值;若变化,请说明理由.4.(2020•天桥区二模)如图,抛物线y =ax 2+bx +c (a ≠0),与x 轴交于A (4,0)、O 两点,点D (2,﹣2)为抛物线的顶点.(1)求该抛物线的解析式;(2)点E 为AO 的中点,以点E 为圆心、以1为半径作⊙E ,交x 轴于B 、C 两点,点M 为⊙E 上一点.①射线BM 交抛物线于点P ,设点P 的横坐标为m ,当tan ∠MBC =2时,求m 的值; ②如图2,连接OM ,取OM 的中点N ,连接DN ,则线段DN 的长度是否存在最大值或最小值?若存在,请求出DN 的最值;若不存在,请说明理由.【题组二】5.(2021•乐山模拟)如图,抛物线y =ax 2+bx +2与直线AB 相交于A (﹣1,0),B (3,2),与x 轴交于另一点C .(1)求抛物线的解析式;(2)在y 上是否存在一点E ,使四边形ABCE 为矩形,若存在,请求出点E 的坐标;若不存在,请说明理由;(3)以C 为圆心,1为半径作⊙O ,D 为⊙O 上一动点,求DA +DB 的最小值6.(2021•河北区二模)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+3的对称轴是直线x=2,与x轴相交于A,B两点(点A在点B的左侧),与y轴交于点C.(Ⅰ)求抛物线的解析式及顶点坐标;(Ⅱ)M为第一象限内抛物线上的一个点,过点M作MN⊥x轴于点N,交BC于点D,连接CM,当线段CM=CD时,求点M的坐标;(Ⅲ)以原点O为圆心,AO长为半径作⊙O,点P为⊙O上的一点,连接BP,CP,求2PC+3PB的最小值.7.(2021•长沙模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a>0)的顶点为M,经过C(1,1),且与x轴正半轴交于A,B两点.(1)如图1,连接OC,将线段OC绕点O顺时针旋转,使得C落在y轴的负半轴上,求点C的路径长;(2)如图2,延长线段OC至N,使得ON=,若∠OBN=∠ONA,且,求抛物线的解析式;(3)如图3,抛物线y=ax2+bx+c的对称轴为直线,与y轴交于(0,5),经过点C 的直线l:y=kx+m(k>0)与抛物线交于点C、D,若在x轴上存在P1、P2,使∠CP1D =∠CP2D=90°,求k的取值范围.8.(2020•东海县二模)如图,△AOB的三个顶点A、O、B分别落在抛物线C1:y=x2+ x上,点A的坐标为(﹣4,m),点B的坐标为(n,﹣2).(点A在点B的左侧)(1)则m=﹣4,n=﹣1.(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线C2:y=ax2+bx+4经过A'、B'两点,延长OB'交抛物线C2于点C,连接A'C.设△OA'C的外接圆为⊙M.①求圆心M的坐标;②试直接写出△OA'C的外接圆⊙M与抛物线C2的交点坐标(A'、C除外).【题组三】9.(2019•鄂尔多斯)如图,抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C,直线y=﹣x与该抛物线交于E,F两点.(1)求抛物线的解析式.(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.(3)以点C为圆心,1为半径作圆,⊙C上是否存在点M,使得△BCM是以CM为直角边的直角三角形?若存在,直接写出M点坐标;若不存在,说明理由.10.(2019•日照)如图1,在平面直角坐标系中,直线y=﹣5x+5与x轴,y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴的另一交点为B.(1)求抛物线解析式及B点坐标;(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;(3)如图2,若P点是半径为2的⊙B上一动点,连接PC、P A,当点P运动到某一位置时,PC+12P A的值最小,请求出这个最小值,并说明理由.11.(2018•宿迁)如图,在平面直角坐标系中,二次函数y=(x﹣a)(x﹣3)(0<a<3)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点D,过其顶点C作直线CP ⊥x轴,垂足为点P,连接AD、BC.(1)求点A、B、D的坐标;(2)若△AOD与△BPC相似,求a的值;(3)点D、O、C、B能否在同一个圆上?若能,求出a的值;若不能,请说明理由.12.(2018•福建)已知抛物线y=ax2+bx+c过点A(0,2).(1)若点(−√2,0)也在该抛物线上,求a,b满足的关系式;(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.①求抛物线的解析式;②若点P与点O关于点A对称,且O,M,N三点共线,求证:P A平分∠MPN.【题组四】13.(2018•长沙模拟)如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B 两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.(1)求顶点D的坐标(用含a的代数式表示);(2)若以AD为直径的圆经过点C.①求抛物线的函数关系式;②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.14.(2018•济宁)如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.15.(2018•遵义)在平面直角坐标系中,二次函数y=ax2+53x+c的图象经过点C(0,2)和点D(4,﹣2).点E是直线y=−13x+2与二次函数图象在第一象限内的交点.(1)求二次函数的解析式及点E的坐标.(2)如图①,若点M是二次函数图象上的点,且在直线CE的上方,连接MC,OE,ME.求四边形COEM面积的最大值及此时点M的坐标.(3)如图②,经过A、B、C三点的圆交y轴于点F,求点F的坐标.16.(2018•福建)已知抛物线y=ax2+bx+c过点A(0,2),且抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.(1)求抛物线的解析式;(2)若MN与直线y=﹣2√3x平行,且M,N位于直线BC的两侧,y1>y2,解决以下问题:①求证:BC平分∠MBN;②求△MBC外心的纵坐标的取值范围.【题组五】17.(2021•常州二模)如图1:抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y 轴交于点C.动点E(m,0)(0<m<3),过点E作直线l⊥x轴,交抛物线于点M.(1)求抛物线的解析式及C点坐标;(2)连接BM并延长交y轴于点N,连接AN,OM,若AN∥OM,求m的值.(3)如图2.当m=1时,P是直线l上的点,以P为圆心,PE为半径的圆交直线l于另一点F(点F在x轴上方),若线段AC上最多存在一个点Q使得∠FQE=90°,求点P纵坐标的取值范围.18.(2021•靖江市一模)如图,抛物线y=mx2﹣4mx+n(m>0)与x轴交于A,B两点,点B在点A的右侧,抛物线与y轴正半轴交于点C,连接CA、CB,已知tan∠CAO=3,sin ∠CBO=.(1)求抛物线的对称轴与抛物线的解析式;(2)设D为抛物线对称轴上一点,①当△BCD的外接圆的圆心在△BCD的边上时,求点D的坐标;②若△BCD是锐角三角形,直接写出点D纵坐标的取值范围.19.(2019秋•江都区期末)已知二次函数y=18x2+bx+c(b、c为常数)的图象经过点(0,﹣1)和点A(4,1).(1)求b、c的值;(2)如图1,点C(10,m)在抛物线上,点M是y轴上的一个动点,过点M平行于x 轴的直线l平分∠AMC,求点M的坐标;(3)如图2,在(2)的条件下,点P是抛物线上的一动点,以P为圆心、PM为半径的圆与x轴相交于E、F两点,若△PEF的面积为2√6,请直接写出点P的坐标.20.(2020•越秀区校级模拟)已知:二次函数y=ax2﹣2ax﹣3(a>0),当2≤x≤4时,函数有最大值5.(1)求此二次函数图象与坐标轴的交点;(2)将函数y=ax2﹣2ax﹣3(a>0)图象x轴下方部分沿x轴向上翻折,得到的新图象与直线y=n恒有四个交点,从左到右,四个交点依次记为A,B,C,D,当以BC为直径的圆与x轴相切时,求n的值.(3)若点P(x0,y0)是(2)中翻折得到的抛物线弧部分上任意一点,若关于m的一元二次方程m2﹣y0m+k﹣4+y0=0恒有实数根时,求实数k的最大值.【题组六】21.(2021•雨花区二模)如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E四点,B为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.22.(2021秋•西湖区校级期中)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,﹣3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.(1)求“蛋圆”抛物线部分的解析式及“蛋圆”的弦CD的长;(2)已知点E是“蛋圆”上的一点(不与点A,点B重合),点E关于x轴的对称点是点F,若点F也在“蛋圆”上,求点E坐标;(3)点P是“蛋圆”外一点,满足∠BPC=60°,当BP最大时,直接写出点P的坐标.23.(2021秋•上城区校级期中)如图,已知抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.若抛物线的顶点D的坐标为(1,4).(1)求抛物线的解析式,及A、B、C三点的坐标;(2)求⊙M的半径和圆心M的坐标;(3)如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请直接写出点坐标;若不存在,请说明理由.24.(2021•黔西南州)如图,直线l:y=2x+1与抛物线C:y=2x2+bx+c相交于点A(0,m),B(n,7).(1)填空:m=1,n=3,抛物线的解析式为y=2x2﹣4x+1.(2)将直线l向下移a(a>0)个单位长度后,直线l与抛物线C仍有公共点,求a的取值范围.(3)Q是抛物线上的一个动点,是否存在以AQ为直径的圆与x轴相切于点P?若存在,请求出点P的坐标;若不存在,请说明理由.。
专题09 几何中最小值计算压轴真题训练(解析版)--2023 年中考数学压轴真题汇编

挑战2023年中考数学选择、填空压轴真题汇编专题09几何中最小值计算压轴真题训练一.轴对称-最短路线问题1.(2022•眉山)如图,点P为矩形ABCD的对角线AC上一动点,点E为BC 的中点,连接PE,PB,若AB=4,BC=4,则PE+PB的最小值为.【答案】6【解答】解:如图,作点B关于AC的对称点B',交AC于点F,连接B′E 交AC于点P,则PE+PB的最小值为B′E的长度,∵四边形ABCD为矩形,∴AB=CD=4,∠ABC=90°,在Rt△ABC中,AB=4,BC=4,∴tan∠ACB==,∴∠ACB=30°,由对称的性质可知,B'B=2BF,B'B⊥AC,∴BF=BC=2,∠CBF=60°,∴B′B=2BF=4,∵BE=BF,∠CBF=60°,∴△BEF是等边三角形,∴BE=BF=B'F,∴△BEB'是直角三角形,∴B′E===6,∴PE+PB的最小值为6,故答案为:6.2.(2022•自贡)如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为.【答案】3【解答】解:解法一:如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,∵CH=EF=1,CH∥EF,∴四边形EFCH是平行四边形,∴EH=CF,∴G'H=EG'+EH=EG+CF,∵AB=4,BC=AD=2,G为边AD的中点,∴DG'=AD+AG'=2+1=3,DH=4﹣1=3,由勾股定理得:HG'==3,即GE+CF的最小值为3.解法二:∵AG=AD=1,设AE=x,则BF=AB﹣EF﹣AE=4﹣x﹣1=3﹣x,由勾股定理得:EG+CF=+,如图,矩形EFGH中,EH=3,GH=2,GQ=1,P为FG上一动点,设PG=x,则FP=3﹣x,∴EP+PQ=+,当E,P,Q三点共线时,EP+PQ最小,最小值是3,即EG+CF的最小值是3.故答案为:3.3.(2022•鄂州)如图,定直线MN∥PQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AE∥BC∥DF,AE=4,DF=8,AD =24,当线段BC在平移过程中,AB+CD的最小值为()A.24B.24C.12D.12【答案】C【解答】解:如图,作DL⊥PQ于L,过点A作PQ的垂线,过点D作PQ的平行线,它们交于点R,延长DF至T,使DT=BC=12,连接AT,AT交MN于B′,作B′C′∥BC,交PQ于C′,则当BC在B′C′时,AB+CD最小,最小值为AT的长,可得AK=AE•sin60°==2,DL==4,=6,∴AR=2+6+4=12,∵AD=24,∴sin∠ADR==,∴∠ADR=30°,∵∠PFD9=60°,∴∠ADT=90°,∴AT===12,故答案为:C.4.(2022•贺州)如图,在矩形ABCD中,AB=8,BC=6,E,F分别是AD,AB的中点,∠ADC的平分线交AB于点G,点P是线段DG上的一个动点,则△PEF的周长最小值为.【答案】5+【解答】解:如图,在DC上截取DT,使得DT=DE,连接FT,过点T作TH⊥AB于点H.∵四边形ABCD是矩形,∴∠A=∠ADT=90°,∵∠AHT=90°,∴四边形AHTD是矩形,∵AE=DE=AD=3.AF=FB=AB=4,∴AH=DT=3,HF=AF﹣AH=4﹣3=1,HT=AD=6,∴FT===,∵DG平分∠ADC,DE=DT,∴E、T关于DG对称,∴PE=PT,∴PE+PF=PF+PT≥FT=,∵EF===5,∴△EFP的周长的最小值为5+,故答案为:5+.5.(2022•滨州)如图,在矩形ABCD中,AB=5,AD=10.若点E是边AD 上的一个动点,过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F,则在点E移动的过程中,AF+FE+EC的最小值为.【答案】+【解答】解:如图,过点E作EH⊥BC于点H.∵四边形ABCD是矩形,∴∠B=∠BAD=∠BHE=90°,∴四边形ABHE是矩形,∴EH=AB=5,∵BC=AD=10,∴AC===5,∵EF⊥AC,∴∠COF=90°,∴∠EFH+∠ACB=90°,∵∠BAC+∠ACB=90°,∴∠EFH=∠BAC,∴△EHF∽△CBA,∴==,∴==,∴FH=,EF=,设BF=x,则DE=10﹣x﹣=﹣x,∵EF是定值,∴AF+CE的值最小时,AF+EF+CE的值最小,∵AF+CE=+,∴欲求AF+CE的最小值相当于在x轴上找一点P(x,0),使得P到A(0,5),B(,5)的距离和最小,如图1中,作点A关于x轴的对称点A′,连接BA′交xz轴于点P,连接AP,此时PA+PB 的值最小,最小值为线段A′B的长,∵A′(0,﹣5),B(,5),∴A′B==,∴AF+CE的最小值为,∴AF+EF+CE的最小值为+.解法二:过点C作CC′∥EF,使得CC′=EF,连接C′F.∵EF=CC′,EF∥CC′,∴四边形EFC′C是平行四边形,∴EC=FC′,∵EF⊥AC,∴AC⊥CC′,∴∠ACC=90°,∵AC′===,∴AF+EC=AF+FC′≥AC′=,∴AF+EF+CE的最小值为+.故答案为:+二.胡不归问题6.(2022•鄂尔多斯)如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为.【答案】4【解答】解:如图,在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,此时P A+2PB最小,∴∠AFB=90°∵AB=AC,AD⊥BC,∴∠CAD=∠BAD=,∴∠EAD=∠CAE+∠CAD=30°,∴PF=,∴P A+2PB=2()=2(PF+PB)=2BF,在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,∴BF=AB•sin45°=4×=2,∴(P A+2PB)=2BF=4,最小故答案为:4.三.旋转的性质7.(2022•黄石)如图,等边△ABC中,AB=10,点E为高AD上的一动点,以BE为边作等边△BEF,连接DF,CF,则∠BCF=,FB+FD的最小值为.【答案】30°5【解答】解:如图,∵△ABC是等边三角形,AD⊥CB,∴∠BAE=∠BAC=30°,∵△BEF是等边三角形,∴∠EBF=∠ABC=60°,BE=BF,∴∠ABE=∠CBF,在△BAE和△BCF中,,∴△BAE≌△BCF(SAS),∴∠BAE=∠BCF=30°,作点D关于CF的对称点G,连接CG,DG,BG,BG交CF的延长线于点F′,连接DF′,此时BF′+DF′的值最小,最小值=线段BG的长.∵∠DCF=∠FCG=30°,∴∠DCG=60°,∵CD=CG=5,∴△CDG是等边三角形,∴DB=DC=DG,∴∠CGB=90°,∴BG===5,∴BF+DF的最小值为5,故答案为:30°,5.8.(2022•柳州)如图,在正方形ABCD中,AB=4,G是BC的中点,点E是正方形内一个动点,且EG=2,连接DE,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,则线段CF长的最小值为.【答案】2﹣2【解答】解:连接DG,将DG绕点D逆时针旋转90°得DM,连接MG,CM,MF,作MH⊥CD于H,∵∠EDF=∠GDM,∴∠EDG=∠FDM,∵DE=DF,DG=DM,∴△EDG≌△MDF(SAS),∴MF=EG=2,∵∠GDC=∠DMH,∠DCG=∠DHM,DG=DM,∴△DGC≌△MDH(AAS),∴CG=DH=2,MH=CD=4,∴CM==2,∵CF≥CM﹣MF,∴CF的最小值为2﹣2,故答案为:2﹣2.9.(2022•广州)如图,在矩形ABCD中,BC=2AB,点P为边AD上的一个动点,线段BP绕点B顺时针旋转60°得到线段BP′,连接PP′,CP′.当点P′落在边BC上时,∠PP′C的度数为;当线段CP′的长度最小时,∠PP′C的度数为.【答案】120°,75°【解答】解:如图,以AB为边向右作等边△ABE,连接EP′.∵△BPP′是等边三角形,∴∠ABE=∠PBP′=60°,BP=BP′,BA=BE,∴∠ABP=∠EBP′,在△ABP和△EBP′中,,∴△ABP≌△EBP′(SAS),∴∠BAP=∠BEP′=90°,∴点P′在射线EP′上运动,如图1中,设EP′交BC于点O,当点P′落在BC上时,点P′与O重合,此时∠PP′C=180°﹣60°=120°,当CP′⊥EP′时,CP′的长最小,此时∠EBO=∠OCP′=30°,∴EO=OB,OP′=OC,∴EP′=EO+OP′=OB+OC=BC,∵BC=2AB,∴EP′=AB=EB,∴∠EBP′=∠EP′B=45°,∴∠BP′C=45°+90°=135°,∴∠PP′C=∠BP′C﹣∠BP′P=135°﹣60°=75°.故答案为:120°,75°.10.(2022•无锡)△ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC =20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.【答案】80,4﹣.【解答】解:∵△ACB,△DEC都是等边三角形,∴AC=CB,DC=EC,∠ACB=∠DCE=60°,∴∠BCD=∠ACE,在△BCD和△ACE中,,∴△BCD≌△ACE(SAS),∴∠DBC=∠EAC=20°,∵∠BAC=60°,∴∠BAF=∠BAC+∠CAE=80°.如图1中,设BF交AC于点T.同法可证△BCD≌△ACE,∴∠CBD=∠CAF,∵∠BTC=∠ATF,∴∠BCT=∠AFT=60°,∴点F在△ABC的外接圆上运动,当∠ABF最小时,AF的值最小,此时CD ⊥BD,∴BD===4,∴AE=BD=4,∠BDC=∠AEC=90°,∵CD=CE,CF=CF,∴Rt△CFD≌Rt△CFE(HL),∴∠DCF=∠ECF=30°,∴EF=CE•tan30°=,∴AF的最小值=AE﹣EF=4﹣,故答案为:80,4﹣.四.折叠有关最值问题11.(2022•青岛)如图,已知△ABC,AB=AC,BC=16,AD⊥BC,∠ABC的平分线交AD于点E,且DE=4.将∠C沿GM折叠使点C与点E恰好重合.下列结论正确的有:.(填写序号)①BD=8②点E到AC的距离为3③EM=④EM∥AC【答案】①④【解答】解:在△ABC中,AB=AC,BC=16,AD⊥BC,∴BD=DC=BC=8,故①正确;如图,过点E作EF⊥AB于点F,EH⊥AC于点H,∵AD⊥BC,AB=AC,∴AE平分∠BAC,∴EH=EF,∵BE是∠ABD的角平分线,∵ED⊥BC,EF⊥AB,∴EF=ED,∴EH=ED=4,故②错误;由折叠性质可得:EM=MC,DM+MC=DM+EM=CD=8,设DM=x,则EM=8﹣x,Rt△EDM中,EM2=DM2+DE2,∴(8﹣x)2=42+x2,解得:x=3,∴EM=MC=5,故③错误;设AE=a,则AD=AE+ED=4+a,BD=8,∴AB2=(4+a)2+82,∵=,∴,∴,∴AB=2a,∴(4+a)2+82=(2a)2,解得:a=或a=﹣4(舍去),∴tan C==,又∵tan∠EMD=,∴∠C=∠EMD,∴EM∥AC,故④正确,故答案为:①④.12.(2022•铜仁市)如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE 上的动点,过点N作NP∥EM交MC于点P,则MN+NP的最小值为.【答案】【解答】解:作点P关于CE的对称点P′,由折叠的性质知CE是∠DCM的平分线,∴点P′在CD上,过点M作MF⊥CD于F,交CE于点G,∵MN+NP=MN+NP′≥MF,∴MN+NP的最小值为MF的长,连接DG,DM,由折叠的性质知CE为线段DM的垂直平分线,∵AD=CD=2,DE=1,∴CE==,∵CE×DO=CD×DE,∴DO=,∴EO=,∵MF⊥CD,∠EDC=90°,∴DE∥MF,∴∠EDO=∠GMO,∵CE为线段DM的垂直平分线,∴DO=OM,∠DOE=∠MOG=90°,∴△DOE≌△MOG,∴DE=GM,∴四边形DEMG为平行四边形,∵∠MOG=90°,∴四边形DEMG为菱形,∴EG=2OE=,GM=DE=1,∴CG=,∵DE∥MF,即DE∥GF,∴△CFG∽△CDE,∴,即,∴FG=,∴MF=1+=,∴MN+NP的最小值为;方法二:同理方法一得出MN+NP的最小值为MF的长,DO=,∴OC==,DM=2DO=,=DM•OC=CD•MF,∵S△CDM即×=2×MF,∴MF=,∴MN+NP的最小值为;故答案为:.13.(2022•辽宁)如图,正方形ABCD的边长为10,点G是边CD的中点,点E是边AD上一动点,连接BE,将△ABE沿BE翻折得到△FBE,连接GF,当GF最小时,AE的长是.【答案】5﹣5【解答】解:∵将△ABE沿BE翻折得到△FBE,∴BF=BA=10,∴点F在以B为圆心,10为半径的圆上运动,∴当点G、F、B三点共线时,GF最小,连接EG,设AE=x,由勾股定理得,BG=5,=S△EDG+S△ABE+S△EBG,∵S梯形ABGD∴(5+10)×10=++,解得x=5﹣5,∴AE=5﹣5,故答案为:5﹣5.14.(2022•台州)如图,在菱形ABCD中,∠A=60°,AB=6.折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD交于点E,F.当点M 与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为.【答案】3,6﹣3.【解答】解:如图1中,∵四边形ABCD是菱形,∴AD=AB=BC=CD,∠A=∠C=60°,∴△ADB,△BDC都是等边三角形,当点M与B重合时,EF是等边△ADB的高,EF=AD•sin60°=6×=3.如图2中,连接AM交EF于点O,过点O作OK⊥AD于点K,交BC于点T,过点A作AG⊥CB交CB的延长线于点G,取AF的中点R,连接OR.∵AD∥CG,OK⊥AD,∴OK⊥CG,∴∠G=∠AKT=∠GTK=90°,∴四边形AGTK是矩形,∴AG=TK=AB•sin60°=3,∵OA=OM,∠AOK=∠MOT,∠AKO=∠MTO=90°,∴△AOK≌△MOT(AAS),∴OK=OT=,∵OK⊥AD,∴OR≥OK=,∵∠AOF=90°,AR=RF,∴AF=2OR≥3,∴AF的最小值为3,∴DF的最大值为6﹣3.解法二:如图,过点D作DT⊥CB于点T.∵DF=AD﹣AF,∴当AF最小时,DF的值最大,∵AF=FM≥DT=3,∴AF的最小值为3,∴DF的最大值为6﹣3.故答案为:3,6﹣3.五.与圆有关最值计算15.(2022•泸州)如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,半径为1的⊙O在Rt△ABC内平移(⊙O可以与该三角形的边相切),则点A 到⊙O上的点的距离的最大值为.【答案】2+1【解答】解:当⊙O与BC、BA都相切时,连接AO并延长交⊙O于点D,则AD为点A到⊙O上的点的距离的最大值,设⊙O与BC、BA的切点分别为E、F,连接OE、OF,则OE⊥BC,OF⊥AB,∵AC=6,BC=2,∴tan∠ABC==,AB==4,∴∠ABC=60°,∴∠OBF=30°,∴BF==,∴AF=AB﹣BF=3,∴OA==2,∴AD=2+1,故答案为:2+1.37.(2022•桂林)如图,某雕塑MN位于河段OA上,游客P在步道上由点O 出发沿OB方向行走.已知∠AOB=30°,MN=2OM=40m,当观景视角∠MPN最大时,游客P行走的距离OP是米.【答案】20【解答】解:如图,取MN的中点F,过点F作FE⊥OB于E,以直径MN作⊙F,∵MN=2OM=40m,点F是MN的中点,∴MF=FN=20m,OF=40m,∵∠AOB=30°,EF⊥OB,∴EF=20m,OE=EF=20m,∴EF=MF,又∵EF⊥OB,∴OB是⊙F的切线,切点为E,∴当点P与点E重合时,观景视角∠MPN最大,此时OP=20m,故答案为:20.。
圆中动点与最值问题集锦

第20题图第21题图第22题图
21.如图,Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC上的一点O为圆心OA为半径作⊙O,若⊙O与边BC始终有交点(包括B、C两点),则线段AO的取值范围是.
(1)求弦CD的长;(2)如果a+b=10,求ab的最大值,并求出此时a,b的值.
第15题图第16题图第17题图
16.如图,⊙O的半径为2,点P是⊙O内一点,且OP= ,过P作互相垂直的两条弦AC、BD,则四※边形ABCD面积的最大值为_________.
※17.如图,以O为圆心,1为半径的圆内有一定点A,过A引互相垂直的弦PQ,RS.求PQ+RS取值范围.
8.如图,已知AB是⊙O的弦,C是⊙O上的一个动点,连接AC、BC,∠C=60°,⊙O的半径为2,则△ABC面积的最大值是_________.
9.如图,已知直线MN经过⊙O上的点A,点B在MN上,连OB交⊙O于C点,且点C是OB的中点,AC= OB,若点P是⊙O上的一个动点,当AB= 时,△APC的面积的最大值为_________.
10.如图,若Rt△ABC的斜边AB=2,内切圆的半径为r,则r的最大值为_________.
第10题图第11题图第12题图
11.如图,在平面直角坐标系xOy中,直线AB经过点A(﹣4,0)、B(0,4),⊙O的半径为1(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为_________.
12.如图所示,在直角坐标系中,A点坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为_________.
初三专题 圆中的最值问题

初三专题圆中的最值问题一.选择题(共18小题)1.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为()A.4B.C.D.22.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.B.C.D.3.如图,▱ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为()A.+1B.+1C.D.+14.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为()A.B.C.2D.5.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为()A.2﹣2B.C.D.6.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D为AB上不与AB重合的一个动点,过点D分别作DE⊥AC于点E,DF⊥BC于点F,则线段EF的最小值为()A.3B.4C.D.7.在等腰直角三角形ABC中,∠BAC=90°,BC=6,点P是线段BC上的一个动点,过点P分别作AB、AC的垂线交AB、AC于点M、N,连接MN,则MN的最小值为()A.4B.3C.2D.18.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为()A.4B.C.D.9.如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是()A.2B.3C.4D.510.如图,△ABC内接于⊙O,AB是⊙O的直径,AB=10,AC=BC,点E,F 分别是边AC,BC的中点,点P是线段EF上的一个动点,连接AP、OP,则△AOP的周长的最小值为()A.5B.5+5C.10D.1511.如图,点D,E分别是⊙O的内接正三角形ABC的AB,AC边的中点,若DE=,则⊙O的半径为()A.B.C.1D.212.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是()A.4.75B.4.8C.5D.413.如图,已知∠AOB=60°,半径为2的⊙M与边OA、OB相切,若将⊙M 水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为()A.2B.2或6C.4或6D.1或5 14.已知⊙O的半径为1,圆心0到直线l的距离为2,过l上任一点A作⊙O 的切线,切点为B,则线段AB的最小值为()A.1B.C.D.215.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙O上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值为()A.2+B.2+C.1D.216.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是()A.3B.C.D.417.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为()A.2+B.3+C.3+D.4+18.如图∠BAC=60°,半径长1的⊙O与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为()A.3B.6C.D.二.填空题(共11小题)19.如图,已知线段AB=6,C为线段AB上的一个动点(不与A、B重合),将线段AC绕点A逆时针旋转120°得到AD,将线段BC绕点B顺时针旋转120°得到BE,⊙O外接于△CDE,则⊙O的半径最小值为.20.如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O是一动点且P在第一象限内,过P作⊙O切线与x轴相交于点A,与y 轴相交于点B.则线段AB的最小值是.21.如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为.22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P 是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ 的最小值为.23.如图,矩形ABCD中,AB=6,BC=5,以D为圆心,2为半径画⊙D,E是圆⊙D上一动点,P是BC上一动点,则PE+PA最小值是.24.如图,在矩形ABCD中,AB=3,AD=4,点E是边BC的中点,连接AE,与对角线BD交于点F.点M是AD边上的一个动点,连接MF、MC,则MF+MC的最小值为.25.如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是.26.如图,已知A、B两点的坐标分别为(﹣4,0)、(0,4),⊙C的圆心坐标为C(2,0),半径为2.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值是.27.如图,平面直角坐标系中,分别以点M(2,3)、N(3,﹣5)为圆心,以l、2为半径作⊙M、⊙N,A、B分别是⊙M、⊙N上的动点,P为y轴上的动点,则PA+PB的最小值等于.28.如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为.29.如图,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于.三.解答题(共1小题)30.问题情境:如图1,P是⊙O外的一点,直线PO分别交⊙O于点A、B,则PA是点P到⊙O上的点的最短距离.(1)探究:如图2,在⊙O上任取一点C(不为点A、B重合),连接PC、OC.试证明:PA <PC.(2)直接运用:如图3,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,则AP的最小值是.(3)构造运用:如图4,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′B长度的最小值.解:由折叠知A′M=AM,又M是AD的中点,可得MA=MA′=MD,故点A′在以AD为直径的圆上.(请继续完成解题过程)(4)综合应用:(下面两小题请选择其中一道完成)①如图5,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是.②如图6,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于.初三专题圆中的最值问题参考答案与试题解析一.选择题(共18小题)1.如图,线段AB=4,C为线段AB上的一个动点,以AC、BC为边作等边△ACD和等边△BCE,⊙O外接于△CDE,则⊙O半径的最小值为()A.4B.C.D.2【分析】分别作∠A与∠B角平分线,交点为P.由三线合一可知AP与BP为CD、CE垂直平分线;再由垂径定理可知圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点;连OC,若半径OC最短,则OC⊥AB,由△AOB为底边4,底角30°的等腰三角形,可求得OC=.【解答】解:如图,分别作∠A与∠B角平分线,交点为P.∵△ACD和△BCE都是等边三角形,∴AP与BP为CD、CE垂直平分线.又∵圆心O在CD、CE垂直平分线上,则交点P与圆心O重合,即圆心O是一个定点.连接OC.若半径OC最短,则OC⊥AB.又∵∠OAC=∠OBC=30°,AB=4,∴OA=OB,∴AC=BC=2,∴在直角△AOC中,OC=AC•tan∠OAC=2×tan30°=.故选:B.【点评】本题考查了圆的综合题.需要掌握等边三角形的“三线合一”的性质,三角形的外接圆圆心为三角形的垂心,点到直线的距离垂线段最短以及解直角三角形等知识点.难度不大,注意数形结合数学思想的应用.2.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为()A.B.C.D.【分析】连接AC,AG,由OG垂直于AB,利用垂径定理得到O为AB的中点,由G的坐标确定出OG的长,在直角三角形AOG中,由AG与OG的长,利用勾股定理求出AO的长,进而确定出AB的长,由CG+GO求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D 时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACO中,利用锐角三角函数定义求出∠ACO的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长.【解答】解:连接AC,AG,∵GO⊥AB,∴O为AB的中点,即AO=BO=AB,∵G(0,1),即OG=1,∴在Rt△AOG中,根据勾股定理得:AO==,∴AB=2AO=2,又CO=CG+GO=2+1=3,∴在Rt△AOC中,根据勾股定理得:AC==2,∵CF⊥AE,∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,当E位于点B时,CO⊥AE,此时F与O重合;当E位于D时,CA⊥AE,此时F与A重合,∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在Rt△ACO中,tan∠ACO==,∴∠ACO=30°,∴度数为60°,∵直径AC=2,∴的长为=π,则当点E从点B出发顺时针运动到点D时,点F所经过的路径长π.故选:B.【点评】此题属于圆综合题,涉及的知识有:坐标与图形性质,勾股定理,锐角三角函数定义,弧长公式,以及圆周角定理,其中根据题意得到点E从点B出发顺时针运动到点D时,点F所经过的路径长是解本题的关键.3.如图,▱ABCD的对角线AC,BD相交于点O,E是以A为圆心,以2为半径为圆上一动点,连接CE,点P为CE的中点,连接BP,若AC=a,BD=b,则BP的最大值为()A.+1B.+1C.D.+1【分析】连接OP,根据平行四边形对角线互相平分知AO=CO=AC=a、BO=DO=BD=b,由点P为CE中点得知随着点E的运点,点P的运动轨迹是以O为圆心、1为半径的圆,据此解答可得.【解答】解:如图,连接OP,∵四边形ABCD是平行四边形,∴AO=CO=AC=a,BO=DO=BD=b,∵点P为CE中点,∴OP∥AE,且OP=AE=1,∴随着点E的运点,点P的运动轨迹是以O为圆心、1为半径的圆,则当⊙O与OD交于点P时,BP最大,为BO+OP=+1,故选:B.【点评】本题主要考查圆的综合问题,掌握平行四边形的性质、中位线定理及点的运动轨迹问题是解题的关键.4.如图,在平面直角坐标系xOy中,A(﹣2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为()A.B.C.2D.【分析】当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM于N,由切线性质得OC⊥AC,在△AOC中判断∠OAC=30°,∠AOC=60°,再在Rt△AOD中利用含30度的直角三角形三边的关系得到OD=OA=,则在Rt△BDP中,由于∠BDP=∠ADO=60°,则可计算出DP=BD=1﹣,然后在Rt△DPN中计算出PN=DP=﹣,最后计算PN+MN,从而可得到P点纵坐标的最大值.【解答】解:当AC与⊙O相切于点C时,P点纵坐标的最大值,如图,直线AC交y轴于点D,连结OC,作CH⊥x轴于H,PM⊥x轴于M,DN⊥PM 于N,∵AC为切线,∴OC⊥AC,在△AOC中,∵OA=2,OC=1,∴∠OAC=30°,∠AOC=60°,在Rt△AOD中,∵∠DAO=30°,∴OD=OA=,在Rt△BDP中,∵∠BDP=∠ADO=60°,∴DP=BD=(2﹣)=1﹣,在Rt△DPN中,∵∠PDN=30°,∴PN=DP=﹣,而MN=OD=,∴PM=PN+MN=1﹣+=,即P点纵坐标的最大值为.故选:B.【点评】本题考查了圆的综合题:熟练掌握切线的性质和含30度的直角三角形三边的关系;理解坐标与图形性质,题目比较好,有一定的难度.5.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为()A.2﹣2B.C.D.【分析】连结AE,如图1,先根据等腰直角三角形的性质得到AB=AC=2,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E 在以AB为直径的⊙O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC=,从而得到CE的最小值为﹣1.【解答】解:连结AE,如图1,∵∠BAC=90°,AB=AC,BC=2,∴AB=AC=2,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的⊙O上,∵⊙O的半径为1,连接OE,OC,∴OE=AB=1在Rt△AOC中,∵OA=2,AC=4,∴OC==,由于OC=,OE=1是定值,点E在线段OC上时,CE最小,如图2,∴CE=OC﹣OE=﹣1,即线段CE长度的最小值为﹣1.故选:C.【点评】本题考查了圆的综合题:熟练掌握圆周角定理和等腰直角三角形的性质;会利用勾股定理计算线段的长.解决本题的关键是确定E点运动的规律,从而把问题转化为圆外一点到圆上一点的最短距离问题.6.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D为AB上不与AB重合的一个动点,过点D分别作DE⊥AC于点E,DF⊥BC于点F,则线段EF的最小值为()A.3B.4C.D.【分析】连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出方程求解即可.【解答】解:如图,连接CD.∵∠ACB=90°,AC=6,BC=8,∴AB==10,∵DE⊥AC,DF⊥BC,∠C=90°,∴四边形CFDE是矩形,∴EF=CD,由垂线段最短可得CD⊥AB时,线段CD的值最小,即线段EF的值最小,=BC•AC=AB•CD,此时,S△ABC即×8×6=×10•CD,解得CD=,∴EF=.故选:D.【点评】本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.7.在等腰直角三角形ABC中,∠BAC=90°,BC=6,点P是线段BC上的一个动点,过点P分别作AB、AC的垂线交AB、AC于点M、N,连接MN,则MN的最小值为()A.4B.3C.2D.1【分析】首先证明四边形PMAN是矩形,可得MN=PA,根据垂线段最短即可解决问题;【解答】解:∵PM⊥AB,PN⊥AC,∴∠PMA=∠PNA=∠A=90°,∴四边形PMAN是矩形,∴MN=PA,∴当PA⊥BC时,PA的值最小,此时∵AB=AC,PA⊥BC,∴PB=PC,∴PA=BC=3,∴MN的最小值为3,故选:B.【点评】本题考查等腰直角三角形的性质、矩形的判定和性质、垂线段最短等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.8.如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为()A.4B.C.D.【分析】当P点移动到平行于OA且与⊙D相切时,△AOP面积的最大,由于P 为切点,得出MP垂直与切线,进而得出PM⊥AC,根据勾股定理先求得AC 的长,进而求得OA的长,根据△ADM∽△ACD,求得DM的长,从而求得PM的长,最后根据三角形的面积公式即可求得;【解答】解:当P点移动到平行于OA且与⊙D相切时,△AOP面积的最大,如图,∵P是⊙D的切线,∴DP垂直与切线,延长PD交AC于M,则DM⊥AC,∵在矩形ABCD中,AB=3,BC=4,∴AC==5,∴OA=,∵∠AMD=∠ADC=90°,∠DAM=∠CAD,∴△ADM∽△ACD,∴=,∵AD=4,CD=3,AC=5,∴DM=,∴PM=PD+DM=1+=,∴△AOP的最大面积=OA•PM=××=,故选:D.【点评】本题考查了圆的切线的性质,矩形的性质,平行线的性质,勾股定理的应用以及三角形相似的判定和性质,本题的关键是判断出P处于什么位置时面积最大;9.如图,矩形ABCD中,AB=2,BC=3,分别以A、D为圆心,1为半径画圆,E、F分别是⊙A、⊙D上的一动点,P是BC上的一动点,则PE+PF的最小值是()A.2B.3C.4D.5【分析】以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆D′,连接AD′交BC于P,交⊙A、⊙D′于E、F′,连接PD,交⊙D于F,EF′就是PE+PF 最小值;根据勾股定理求得AD′的长,即可求得PE+PF最小值.【解答】解:如图,以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆A′,连接A′D交BC于P,则DE′就是PE+PD最小值;∵矩形ABCD中,AB=2,BC=3,圆A的半径为1,∴A′D′=BC=3,AA′=2AB=4,AE=D′F′=1,∴AD′=5,EF′=5﹣2=3∴PE+PF=PF′+PE=EF′=3,故选:B.【点评】本题考查了轴对称﹣最短路线问题,勾股定理的应用等,作出对称图形是本题的关键.10.如图,△ABC内接于⊙O,AB是⊙O的直径,AB=10,AC=BC,点E,F 分别是边AC,BC的中点,点P是线段EF上的一个动点,连接AP、OP,则△AOP的周长的最小值为()A.5B.5+5C.10D.15【分析】连接:OC,PC.先证明EF为OC的垂直平分线,从而可得到PC=OP,然后依据三角形的三边关系可知当点A、P、C在一条直线上时,AP+OP有最小值,然后由OA为定值可知当AP+OP最小时,△APO的周长最小.【解答】解:连接:OC,PC.∵AC=BC,AO=OB,OC=OC,∴△AOC≌△BOC,∴∠AOC=∠BOC=90°.∴OC⊥AB.∵点E,F分别是边AC,BC的中点,∴EF∥AB.∴OC⊥EF,且CG=OG.∴GP为CO的垂直平分线,∴CP=OP.∴AP+OP=AP+CP.∴当点A、P、C在一条直线上时(点P与点E重合时),AP+OP有最小值.又∵OA为定值,∴当AP+OP最小时,△APO的周长有最小值.∴△APO的周长最小值=AO+AC=AO+OA=5+5.故选:B.【点评】本题主要考查的是三角形的外接圆与外心、找出△APO周长取得最小值的条件是解题的关键.11.如图,点D,E分别是⊙O的内接正三角形ABC的AB,AC边的中点,若DE=,则⊙O的半径为()A.B.C.1D.2【分析】连接OB、OC,作OF⊥BC于F,根据三角形中位线定理求出BC,根据圆周角定理得到∠BOC=120°,利用余弦的概念计算即可.【解答】解:连接OB、OC,作OF⊥BC于F,则BF=CF=BC,∵点D,E分别AB,AC边的中点,∴BC=2DE=2,由圆周角定理得,∠BOC=2∠A=120°,∴∠OBF=30°,∴OB==2,故选:D.【点评】本题考查的是三角形的外接圆与外心,掌握三角形中位线定理、圆周角定理以及锐角三角函数的定义是解题的关键.12.如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA、CB分别相交于点P、Q,则线段PQ长度的最小值是()A.4.75B.4.8C.5D.4【分析】设QP的中点为F,圆F与AB的切点为D,连接FD,连接CF,CD,则有FD⊥AB;由勾股定理的逆定理知,△ABC是直角三角形,FC+FD=PQ,由三角形的三边关系知,FC+FD>CD;只有当点F在CD上时,FC+FD=PQ 有最小值,最小值为CD的长,即当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,由直角三角形的面积公式知,此时CD=BC•AC ÷AB=4.8.【解答】解:如图,设QP的中点为F,圆F与AB的切点为D,连接FD、CF、CD,则FD⊥AB.∵AB=10,AC=8,BC=6,∴∠ACB=90°,FC+FD=PQ,∴FC+FD>CD,∵当点F在直角三角形ABC的斜边AB的高CD上时,PQ=CD有最小值,∴CD=BC•AC÷AB=4.8.故选:B.【点评】本题利用了切线的性质,勾股定理的逆定理,三角形的三边关系,直角三角形的面积公式求解.13.如图,已知∠AOB=60°,半径为2的⊙M与边OA、OB相切,若将⊙M 水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为()A.2B.2或6C.4或6D.1或5【分析】讨论:当将⊙M水平向左平移,当点M运动到M′位置时,作MC⊥OA 于C点,M′H⊥OA于H,M′Q⊥MC于Q,连结M′E,根据切线的性质得MM′∥OB,MC=2,再根据垂径定理得EH=EF=3,在Rt△EHM′中利用勾股定理计算出HM′=,则CQ=M′H=,所以MQ=2﹣=,然后利用含30°的直角三角形三边的关系可得到MM′;当将⊙M水平向左平移,当点M运动到M″位置时,作MC⊥OA于C点,M″H ⊥OA于H,M″M交OA于D点,同理得到MC=2,M′H=,利用平行线的性质得∠MDC=∠M″DH=∠AOB=60°,则∠HM″D=30°,∠CMD=30°,根据含30°的直角三角形三边的关系可得到M″D和MD,则可得到MM″=6.【解答】解:当将⊙M水平向左平移,当点M运动到M′位置时,如图作MC⊥OA于C点,M′H⊥OA于H,M′Q⊥MC于Q,连结M′E,∵⊙M与边OB、OA相切,∴MM′∥OB,MC=2,∵M′H⊥OA,∴EH=FH=EF=×6=3,在Rt△EHM′中,EM′=2,∴HM′==,∵M′Q⊥MC,∴四边形M′QCH为矩形,∴CQ=M′H=,∴MQ=2﹣=,∵∠QMM′=∠AOB=60°,∴∠QM′M=30°,∴M′Q==1,∴MM′=2;当将⊙M水平向左平移,当点M运动到M″位置时,如图2,作MC⊥OA于C点,M″H⊥OA于H,M″M交OA于D点,易得MC=2,M′H=,∵∠MDC=∠M″DH=∠AOB=60°,∴∠HM″D=30°,∠CMD=30°,在Rt△HM″D中,M″D=,则DH==1,∴M″D=2DH=2,在Rt△CDM中,CM=2,则DC==2,∴DM=2DC=4,∴MM″=2+4=6,综上所述,当⊙M平移的距离为2或6.故选:B.【点评】本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了垂径定理以及含30°的直角三角形三边的关系.14.已知⊙O的半径为1,圆心0到直线l的距离为2,过l上任一点A作⊙O 的切线,切点为B,则线段AB的最小值为()A.1B.C.D.2【分析】先连接OB,易知△AOB是直角三角形,再利用勾股定理即可求出AB.【解答】解:如右图所示,OA⊥l,AB是切线,连接OB,∵OA⊥l,∴OA=2,又∵AB是切线,∴OB⊥AB,在Rt△AOB中,AB===.故选:C.【点评】本题考查了切线的性质、勾股定理.解题的关键是连接OB,构造直角三角形.15.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙O上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值为()A.2+B.2+C.1D.2【分析】由题意可得当AD和⊙C相切时,△ABE的面积最大,画出此时的图形,然后由已知条件和三角形的相似,可以求得此时的△ABE面积的最大值.【解答】解:由题意可得,当AD与⊙C相切时,△ABE的面积最大,此时点D 在D1的位置,如下图所示,连接CD1,则∠CD1A=90°,∴△CD1A∽△OE1A,∴∵OA=2,AC=3,CD1=1,∴,∴,∴=2+,故选:B.【点评】本题考查切线的性质、一次函数图象上点的坐标特征、三角形的相似、最值,解题的关键是明确题意画出相应的图形,求出相应的图形的面积.16.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是()A.3B.C.D.4【分析】当射线AD与⊙C相切时,△ABE面积的最大.设EF=x,由切割线定理表示出DE,可证明△CDE∽△AOE,根据相似三角形的性质可求得x,然后求得△ABE面积.【解答】解:当射线AD与⊙C相切时,△ABE面积的最大.连接AC,∵∠AOC=∠ADC=90°,AC=AC,OC=CD,∴Rt△AOC≌Rt△ADC,∴AD=AO=2,连接CD,设EF=x,∴DE2=EF•OE,∵CF=1,∴DE=,∴△CDE∽△AOE,∴=,即=,解得x=,S△ABE===.故选:B.【点评】本题是一个动点问题,考查了切线的性质和三角形面积的计算,解题的关键是确定当射线AD与⊙C相切时,△ABE面积的最大.17.如图,已知A、B两点的坐标分别为(﹣2,0)、(0,1),⊙C的圆心坐标为(0,﹣1),半径为1,E是⊙C上的一动点,则△ABE面积的最大值为()A.2+B.3+C.3+D.4+18.如图∠BAC=60°,半径长1的⊙O与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为()A.3B.6C.D.【分析】连接AO并延长,与圆O交于P点,当AF垂直于ED时,线段DE长最大,设圆O与AB相切于点M,连接OM,PD,由对称性得到AF为角平分线,得到∠FAD为30度,根据切线的性质得到OM垂直于AD,在直角三角形AOM中,利用30度角所对的直角边等于斜边的一半求出AO的长,由AO+OP求出AP的长,即为圆P的半径,由三角形AED为等边三角形,得到DP为角平分线,在直角三角形PFD中,利用30度所对的直角边等于斜边的一半求出PF的长,再利用勾股定理求出FD的长,由DE=2FD求出DE的长,即为DE的最大值.【解答】解:连接AO并延长,与ED交于F点,与圆O交于P点,此时线段ED最大,连接OM,PD,可得F为ED的中点,∵∠BAC=60°,AE=AD,∴△AED为等边三角形,∴AF为角平分线,即∠FAD=30°,在Rt△AOM中,OM=1,∠OAM=30°,∴OA=2,∴PD=PA=AO+OP=3,在Rt△PDF中,∠FDP=30°,PD=3,∴PF=,根据勾股定理得:FD==,则DE=2FD=3.故选:D.【点评】此题考查了切线的性质,等边三角形的判定与性质,勾股定理,含30度直角三角形的性质,熟练掌握切线的性质是解本题的关键.二.填空题(共11小题)19.如图,已知线段AB=6,C为线段AB上的一个动点(不与A、B重合),将线段AC绕点A逆时针旋转120°得到AD,将线段BC绕点B顺时针旋转120°得到BE,⊙O外接于△CDE,则⊙O的半径最小值为3.【分析】如图,连接OD、OA、OC、OB、OE.只要证明△AOB是等边三角形,即可推出当OC⊥AB时,OC的长最短,此时OC=OA•sin60°;【解答】解:如图,连接OD、OA、OC、OB、OE.∵OA=OA,OD=OC,AD=AC,∴△OAD≌△OAC,∴∠OAC=∠OAD=∠CAD=60°,同法可证:∠OBC=∠OBE=∠ABE=60°,∴△AOB是等边三角形,∴当OC⊥AB时,OC的长最短,此时OC=OA•sin60°=3,故答案为3.【点评】本题考查三角形的外心,全等三角形的判定和性质、等边三角形的判定和性质、垂线段最短等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.20.如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O是一动点且P在第一象限内,过P作⊙O切线与x轴相交于点A,与y 轴相交于点B.则线段AB的最小值是4..【分析】如图,设AB的中点为C,连接OP,由于AB是圆的切线,故△OPC 是直角三角形,有OP<OC,所以当OC与OP重合时,OC最短;【解答】解:(1)线段AB长度的最小值为4,理由如下:连接OP,∵AB切⊙O于P,∴OP⊥AB,取AB的中点C,∴AB=2OC;当OC=OP时,OC最短,即AB最短,此时AB=4.故答案为:4.【点评】本题利用了切线的性质,等腰直角三角形的性质求解,属于基础性题目.21.如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为2.【分析】因为PQ为切线,所以△OPQ是Rt△.又OQ为定值,所以当OP最小时,PQ最小.根据垂线段最短,知OP=3时PQ最小.根据勾股定理得出结论即可.【解答】解:∵PQ切⊙O于点Q,∴∠OQP=90°,∴PQ2=OP2﹣OQ2,而OQ=1,∴PQ2=OP2﹣1,即PQ=,当OP最小时,PQ最小,∵点O到直线l的距离为3,∴OP的最小值为3,∴PQ的最小值为=2.故答案为2.【点评】此题综合考查了切线的性质及垂线段最短等知识点,如何确定PQ最小时点P的位置是解题的关键,难度中等偏上.22.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P 是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为.【分析】当PC⊥AB时,线段PQ最短;连接CP、CQ,根据勾股定理知PQ2=CP2﹣CQ2,先求出CP的长,然后由勾股定理即可求得答案.【解答】解:连接CP、CQ;如图所示:∵PQ是⊙C的切线,∴CQ⊥PQ,∠CQP=90°,根据勾股定理得:PQ2=CP2﹣CQ2,∴当PC⊥AB时,线段PQ最短,∵在Rt△ACB中,∠A=30°,BC=2,∴AB=2BC=4,AC=2,∴CP===,∴PQ==,∴PQ的最小值是;故答案为:.【点评】本题考查了切线的性质以及勾股定理的运用;注意掌握辅助线的作法,注意当PC⊥AB时,线段PQ最短是关键.23.如图,矩形ABCD中,AB=6,BC=5,以D为圆心,2为半径画⊙D,E是圆⊙D上一动点,P是BC上一动点,则PE+PA最小值是11.【分析】以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆D′,连接AD'交BC于P,交⊙D'于E,则AE′就是PE+PD最小值;根据勾股定理求得AD'的长,即可求得PE+PA最小值.【解答】解:如图,以BC为轴作矩形ABCD的对称图形A′BCD′以及对称圆D′,连接AD'交BC于P,交⊙D'于E,则AE′就是PE+PA最小值,∵矩形ABCD中,AB=6,BC=5,圆D的半径为2,∴AD=BC=5,DD′=2DC=12,∴由勾股定理得:AD'===13,∵D'E'=2,∴AE′=13﹣2=11,∴PE+PA=PE′+PA=AE′=11,故答案为11.【点评】本题考查了轴对称﹣最短路线问题,勾股定理的应用等,作出对称图形,确定点P的位置是本题的关键.24.如图,在矩形ABCD中,AB=3,AD=4,点E是边BC的中点,连接AE,与对角线BD交于点F.点M是AD边上的一个动点,连接MF、MC,则MF+MC的最小值为.【分析】作点C关于AD的对称点C',连接C'F,利用相似三角形的性质和勾股定理解答即可.【解答】解:作点C关于AD的对称点C',连接C'F,过F作FP⊥CD于P,∵矩形ABCD,∴BE∥AD,∴△BEF∽△ADF,∴,∴△BFE的高:△ADF的高=1:2,∴,∴DP=2,∵,∴FP=,在Rt△C'FP中,C'F=,即MF+MC的最小值为,故答案为:【点评】此题主要考查轴对称、矩形的性质、相似三角形的性质,考查知识点比较多,综合性比较强,另外要注意辅助线的作法.25.如图,已知A,B两点的坐标分别为(2,0),(0,2),⊙C的圆心坐标为(﹣1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是2﹣.26.如图,已知A、B两点的坐标分别为(﹣4,0)、(0,4),⊙C的圆心坐标为C(2,0),半径为2.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值是2+8.【分析】由于OA的长为定值,若△ABE的面积最大,则BE的长最长,此时AD与⊙相切且位于x轴的下方;可连接CD,在Rt△ADC中,由勾股定理求得AD的长,即可得到△ADC的面积;易证得△AEO∽△ACD,可以求出OE的长,进而可得出△AOB和△AOE的面积和,由此得解.【解答】解:若△ABE的面积最大,则AD与⊙C相切,连接CD,则CD⊥AD;∴△AEO∽△ACD∴∵A(﹣4,0)、B(0,4)、C(2,0),∴AC=6,AO=4,CD=2,∴AD=4,∴,∴OE=,∴△ABE的最大面积为:×4×+×4×4=2+8,故答案为:2+8【点评】本题考查了直线与圆的位置关系,坐标与图形的性质,三角形的面积公式的运用.27.如图,平面直角坐标系中,分别以点M(2,3)、N(3,﹣5)为圆心,以l、2为半径作⊙M、⊙N,A、B分别是⊙M、⊙N上的动点,P为y轴上的动点,则PA+PB的最小值等于﹣3.【分析】作⊙M关于y轴的对称⊙M′,连接NM′分别交⊙M′和⊙N于A、B,交y轴于P,如图,根据两点之间线段最短得到此时PA+PB最小,再利用对称确定M′的坐标,接着利用两点间的距离公式计算出M′N的长,然后用M′N 的长减去两个圆的半径即可得到AB的长,即得到PA+PB的最小值.【解答】解:作⊙M关于y轴的对称⊙M′,连接NM′分别交⊙M′和⊙N于A、B,交y轴于P,如图,则此时PA+PB最小,。
直线与圆的最值问题归纳(推荐)

直线与圆的最值专题一、动点的最值问题1.若动点P 在直线l 1:2x -y -2=0上,动点Q 在直线圆(x -2)2+(y -1)2=1上,线段PQ 的最小值是________.2.若动点P 在直线l 1:x -y -2=0上,动点Q 在直线l 2:x -y -6=0上,设线段PQ 的中点为M(x 0,y 0),且(x 0-2)2+(y 0+2)2≤8,则x 20+y 20的取值范围是________.3.已知圆C 1:(x -2)2+(y -3)2=1,圆C 2:(x -3)2+(y -4)2=9,M ,N 分别是圆C 1,C 2上的动点,P 为x 轴上的动点,则PM +PN 的最小值为________.4.在平面直角坐标系xOy 中,设点P 为圆C :22(1)4x y -+=上的任意一点,点Q (2a ,3a -)(a ∈R ),则线段PQ 长度的最小值为______.5.直线2ax +by =1与圆x 2+y 2=1相交于A ,B 两点(其中a ,b 是实数),且△AOB 是直角三角形(O 是坐标原点),则点P(a ,b)与点(0,1)之间的距离的最大值为________.6.直线l 过点(0,-4),从直线l 上的一点P 作圆C :x 2+y 2-2y =0的切线PA ,PB (A ,B 为切点),若四边形PACB 面积的最小值为2,则直线l 的斜率k 为________.7.C :(x -a )2+(y -1)2=1在不等式x +y +1≥0所表示的平面区域内,则a 的最小值为________二、定直线与定圆的最值问题8.已知x ,y 满足x +2y -5=0,则(x -1)2+(y -1)2的最小值为________.9.已知点P (x ,y )是圆(x +2)2+y 2=1上任意一点.(1)求点P 到直线3x +4y +12=0的距离的最大值和最小值;(2)求y -2x -1的最大值和最小值. 10.若曲线x 2+y 2+2x -4y +1=0上的任意一点关于直线2ax -by +2=0(a ,b ∈R +)的对称点仍在该曲线上,则1a +1b的最小值是________. 三、动直线与的动圆的最值问题11.过点(2,0)引直线l 与曲线y =1-x 2相交于A 、B 两点,O 为坐标原点,当△AOB 的面积取最大值时,直线l 的斜率为________.12.过点(2,0)引直线l 与曲线y =1-x 2相交于A 、B 两点,O 为坐标原点,当△AOB 的面积取最大值时,直线l 的斜率为________.13.在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2-8x +15=0,若直线y =kx -2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是________.14.若圆x 2+y 2=r 2(r >0)上有且只有两个点到直线x -y -2=0的距离为1,则实数r 的取值范围是________15.若对于给定的正实数k ,函数()k f x x=的图像上总存在点C ,使得以C 为圆心,1为半径的圆上有两个不同的点到原点O 的距离为2,则k 的取值范围是_________.四、弦长的最值问题16.已知圆:C 22(2)4x y ++=,相互垂直的两条直线1l 、2l 都过点(,0)A a .(Ⅰ)当2a =时,若圆心为(1,)M m 的圆和圆C 外切且与直线1l 、2l 都相切,求圆M 的方程;(Ⅱ)当1a =-时,求1l 、2l 被圆C 所截得弦长之和的最大值,并求此时直线1l 的方程.17.1y kx =+与圆C ()2214x y +-=相交于,A B 两点,则AB 的最小值是多少?18.已知圆C :(x -1)2+(y -2)2=25,直线l :(2m +1)x +(m +1)y -7m -4=0(m ∈R).(1)求证不论m 取什么实数,直线l 与圆恒交于两点;(2)求直线被圆C 截得的弦长最小时的l 的方程. 五、切线的最值问题19.与直线x -y -4=0和圆A :x 2+y 2+2x -2y =0都相切的半径最小的圆C 的方程是20.由直线y =x +2上的点P 向圆C :(x -4)2+(y +2)2=1引切线PT (T 为切点),当PT 最小的时候P 的坐标?21.点P 是直线2x +y +10=0上的动点,PA ,PB 与圆x 2+y 2=4分别相切于A ,B 两点,则四边形PAOB 面积的最小值为________.六、面积的最值问题22.过点P(1,1)的直线,将圆形区域{(x ,y)|x 2+y 2≤4}分为两部分,使得这两部分的面积之差最大,则该直线的方程为23.已知圆M 过两点C(1,-1),D(-1,1),且圆心M 在x +y -2=0上.。
