哈工大机械原理大作业2-凸轮27
机械原理大作业二-凸轮机构设计..

机械原理大作业二课程名称:机械原理设计题目:凸轮机构设计院系:机械设计制造及其自动化班级:1208104完成者:郑鹏伟学号:**********指导教师:林琳刘福利设计时间:2014年6月4日哈尔滨工业大学一、 设计题目:凸轮的机构运动简图如下图所示:序 号 升程 (mm ) 升程运动角(°) 升程运 动规律 升程 许用压力角(°)回程运动角 (°) 回程运动规律回程许用压力角(°) 远休止角(°) 近休止角(°) 14 90120余弦 加速 度3590等减等加速657575二、 凸轮推杆升程、回程运动方程及推杆位移,速度加速度线图:(1)凸轮推杆升程运动方程: 根据题意知:00120759075s s Φ=Φ='Φ='Φ=(1)从动件升程运动方程(设为1rad sω=)122212s [1cos()]2sin()2cos()2h h h a πϕπωπυϕπωπϕ=-Φ=ΦΦ=ΦΦ(2)从动件远休止运动方程在远休止s Φ段,即213312πϕπ≤≤时,90,0,0s h mm a υ====。
(3)从动件回程运动方程升程段采用等减等加运动规律,运动方程为:①当回程0002s s ϕ'ΦΦ+Φ≤≤Φ+Φ+134()123πϕπ≤≤时: 20s 201022122[-+]4[()]4s hs h h h a ϕωυϕω=-ΦΦ'Φ=--Φ+Φ'Φ=-'Φ()②当回程0002s s ϕ'Φ'Φ+Φ+≤≤Φ+Φ+Φ419()312πϕπ≤≤时:20020100202122[)]4[)]4s s h s h h a ϕωυϕω'=Φ+Φ+Φ-'Φ'=-Φ+Φ+Φ-'Φ='Φ(((4)从动件近休止运动方程在近休止s 'Φ段,即19212πϕπ≤≤时,s 0,0,0a υ===。
哈工大机械设计大作业二

哈工大机械设计大作业二————————————————————————————————作者:————————————————————————————————日期:大作业计算说明书题目:盘形凸轮轮廓的图解法设计学院:英才学院班号:班学号:6121820510姓名:林海奇日期:2014年9月27日哈尔滨工业大学大作业任务书题目:盘形凸轮轮廓的图解法设计设计原始数据:用图解法设计偏置滚子直动从动盘形凸轮轮廓。
原始数据如表格1(推杆的偏置方向及推杆推程和回程运动规律代号见表下方的注)。
表格错误!不能识别的开关参数。
设计原始数据凸轮角速度ω方向基圆半径r(mm)偏距e(mm)滚子半径rr(mm)推杆运动规律推程回程升程h(mm)推程角φ远休止角sφ回程角'φ近休止角'sφ逆时针50 12 12错误!错误!4513°50°130°50°注:(1)推杆的偏置方向应使机构推程压力角较小。
(2)推杆的运动规律(推程、回程)①——等速运动规律;②——等加速度等减速运动规律;③——余弦加速度运动规律;——正弦加速度运动规律。
设计要求:1. 用A3图纸,按1:1比例绘图。
2. 凸轮理论轮廓线用点划线,实际轮廓线用粗实线。
3. 用虚线画出机架和从动件。
4. 作图过程中用到的线用细实线画。
5. 不校验压力角。
目录1. 设计过程…………………………………………………………………………………1 (1)取比例尺并作基圆(2)作反转运动,量取''00s s φφφφ、、、 ,并等分'00φφ、(3)计算推杆的预期位移 (4)确定理论轮廓线上的点 (5)绘制理论轮廓线 (6)绘制实际轮廓线2. 参考文献 (2)1.设计过程(1)取比例尺并作基圆,比例尺选为1:1,实际基圆半径为基圆半径0r 与滚子半径r r 之和,即62mm 如图1所示。
(2)作反转运动,量取''00s s φφφφ、、、 ,并等分'00φφ、。
哈工大、机械原理大作业、凸轮机构设计20题

Harbin Institute of Technology机械原理大作业二课程名称:机械原理设计题目:凸轮机构设计院系:能源科学与工程学院班级:1102301设计者:刘平成学号:1110200724指导教师:唐德威设计时间:2013年6月7日凸轮机构设计1.设计题目(1) 凸轮机构运动简图:(2)凸轮机构的原始参数表2-1.凸轮机构原始参数 序号 升程(mm )升程运动角 升程运动规律升程许用压力角20 110 120° 正弦加速度35°回程运动角回程运动规律 回程许用压力角 远休止角近休止角 90°正弦加速度 65°90°60°(二)凸轮运动方程及相关图像、程序凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图: ○1 凸轮推杆升程、回程方程 πϕπϕϕs)650(πϕ≤≤140)(2=ϕs 511()69πφπ≤≤pi))*5708)/(23.2289)/1.-(sin(2+57083.2289)/1.-(-140(1)(3ϕπϕϕ=s1116()99πφπ≤≤)2914(πϕπ≤≤ 0)(4=ϕs ○2速度方程/2.0944;/2.09440))cos(2-140(1)(1πϕϕ=v 16(2)9πφπ≤≤ 0)(2=ϕv 511()69πφπ≤≤ 708;5708))/1.53.2289)/1.-(cos(2-140(1)(3ϕπϕ=v 1116()99πφπ≤≤ 0)(4=ϕv 16(2)9πφπ≤≤○3加速度方程 .0944^2;/2.0944)/2sin(2280)(1πϕπϕ=a )650(πϕ≤≤0)(2=ϕa 511()69πφπ≤≤08^25708)/1.573.2289)/1.-(sin(2280)(3ϕππϕ=a 1116()99πφπ≤≤ 0)(4=ϕa 16(2)9πφπ≤≤推杆位移、速度、加速度线图matlab编程clear,clcpu=0*pi/180:0.0001:120*pi/180; %升程运动角范围pf=120*pi/180:0.0001:210*pi/180; %远休止角范围pd=210*pi/180:0.0001:300*pi/180; %回程运动角范围pn=300*pi/180:0.0001:2*pi; %近休止角范围h=110e-3; %升程w=10; %凸轮角速度p0=120*pi/180; %升程运动角p01=90*pi/180; %回程运动角ps=90*pi/180; %远休止角%----------推程-----------------------------------------su=h.*(pu./p0-sin(2.*pi.*pu./p0)/(2*pi)); %推杆位移vu=h*w/p0*(1-cos(2*pi*pu./p0)); %推程速度au=2*pi*h*w^2/p0^2*sin(2*pi*pu./p0); %推程加速度%------------远休止----------------------------nf=size(pf);sf=h*ones(nf); %推杆位移vf=zeros(nf); %推程速度af=zeros(nf); %推程加速度%---------------回程------------------------------T=pd-(p0+ps);sd=h/2*(1+cos(pi/p01*T)); %回程位移vd=-pi*h*w/(2*p01)*sin(pi/p01*T); %回程速度ad=-pi^2*h*w^2/(2*p01^2)*cos(pi/p01*T); %回程加速度%--------------------近休止---------------------------------nn=size(pn);sn=zeros(nn); %推杆位移vn=zeros(nn); %推程速度an=zeros(nn); % 推程加速度%------画出推杆位移、速度、加速度线图---------------p=[pu,pf,pd,pn];s=[su,sf,sd,sn];subplot(2,3,1),hold onplot(p,s*1e3,'linewidth',2),xlabel('\phi/rad'),ylabel('s/mm'),grid on,title('推杆位移'),axis([0,2*pi,1.1*min(s)*1e3,1.1*max(s)*1e3]) subplot(2,3,2) v=[vu,vf,vd,vn];plot(p,v,'linewidth',2),xlabel('\phi/rad'),ylabel('v/m/s'),grid on,title('推杆速度'),axis([0,2*pi,1.1*min(v),1.1*max(v)]) subplot(2,3,3) a=[au,af,ad,an];plot(p,a,'linewidth',2),xlabel('\phi/rad'),ylabel('a/m/s^2'),grid on,title('推杆加速度'),axis([0,2*pi,1.1*min(a),1.1*max(a)]) hold off(三)凸轮机构s d ds-ϕ图像及程序代码 %--------------------求ds/d_phi-------------------subplot(2,3,4),plot(v/w*1e3,s*1e3,'linewidth',2),xlabel('ds/d\phi/mm'),ylabel('s/mm'),axis equal,grid on,title('ds/d\phi —s')%---------------------凸轮轴心许用区域--------------------------- alpha_up=35*pi/180; %升程许用压力角 alpha_down=65*pi/180; %回程许用压力角 p1=pi/2-alpha_up; %推程斜率角 p2=alpha_down-pi/2; %回程斜率角 ku=tan(p1); %推程切线斜率 kd=tan(p2); %回程切线斜率 R2=[cos(-p2),-sin(-p2);sin(-p2),cos(-p2)];%推程旋转矩阵 R1=[cos(-p1),-sin(-p1);sin(-p1),cos(-p1)];%推程旋转矩阵 nu=size(pu); for i=1:nu(2)Temp=R1*[vu(i)/w;su(i)];vut(i)=Temp(1); %旋转推程ds/dp-s 曲线 sut(i)=Temp(2); endnd=size(pd); for i=1:nd(2)Temp=R2*[vd(i)/w;sd(i)];vdt(i)=Temp(1); %旋转回程ds/dp-s 曲线 sdt(i)=Temp(2); endfor j=1:nu(2)if sut(j)==min(sut)temu=j; %旋转推程ds/dp-s 曲线后求最低点 end endfor j=1:nd(2)if sdt(j)==min(sdt)temd=j; %旋转回程ds/dp-s曲线后求最低点endendt1=1.2*min(vd/w):0.01:1.2*max(vu/w); %切线定义域t2=min(vd/w)/6:0.01:1.2*max(vu/w);t3=0:0.01:1.2*max(vu/w);s1=ku*(t2-vu(temu)/w)+su(temu); %推程切线s2=kd*(t1-vd(temd)/w)+sd(temd); %回程切线s3=tan(-p1)*t3; %推程起点压力角限制线subplot(2,3,5) %画图hold on,axis equal,grid onplot(v/w*1e3,s*1e3,'linewidth',2)plot(t2*1e3,s1*1e3,'linewidth',1,'color','r')plot(t1*1e3,s2*1e3,'linewidth',1,'color','r')plot(t3*1e3,s3*1e3,'linewidth',1,'color','r')xlabel('ds/d\phi/mm'),ylabel('s/mm'),hold off,title('ds/d\phi—s,轴向许用范围')(四)确定凸轮的基圆半径和偏距、绘制凸轮机圆、偏距圆、理论轮廓曲线---------------画理论廓线图-------------------------e=36e-3;s0=52e-3;r0=sqrt(s0^2+e^2);x=(s0+s).*cos(p)-e.*sin(p);y=(s0+s).*sin(p)+e.*cos(p);x1=r0*cos(p);y1=r0*sin(p);subplot(2,3,6)plot(x*1e3,y*1e3,'linewidth',1),axis equal,grid on,hold on,title('廓线图')plot(x1*1e3,y1*1e3,'linewidth',1,'color','r')%-------------求最小曲率半径-----------------------nx=size(x);nx1=nx(2)-2;dydp=diff(y)./diff(p);%求微分dxdp=diff(x)./diff(p);d2ydp2=diff(dydp)./diff(p(1:nx1+1));d2xdp2=diff(dxdp)./diff(p(1:nx1+1));rho=(dxdp(1:nx1).^2+dydp(1:nx1).^2).^1.5./abs((dxdp(1:nx1).*d2ydp2(1:nx1)-dydp(1:nx1).*d2x dp2(1:nx1)));%理论廓线曲率半径rhomin=min(rho);%最小曲率半径rr=rhomin-3e-3;%----------------实际廓线图----------------X=x(1:nx(2)-1)-rr*dydp./(dxdp.^2+dydp.^2).^0.5;%求实际廓线坐标Y=y(1:nx(2)-1)+rr*dxdp./(dxdp.^2+dydp.^2).^0.5;plot(X*1e3,Y*1e3,'linewidth',2,'color','k')%画实际廓线图Legend('理论廓线','基圆','实际廓线'),axis([1.1*min(x)*1e3,1.1*max(x)*1e3,1.1*min(y)*1e3,1.1*max(y)*1e3])得到基圆半径311mm、偏距36mm。
机械原理大作业——凸轮

大作业(二)凸轮机构设计题号: 6班级:姓名:学号:同组者:成绩:完成时间:目录一凸轮机构题目要求 (1)二摆杆的运动规律及凸轮轮廓线方程 (2)三计算程序 (3)四运算结果及凸轮机构图 (9)4.1 第一组(A组)机构图及计算结果 (9)4.2 第二组(B组)机构图及计算结果 (14)4.3 第三组(C组)机构图及计算结果 (19)五心得体会 (24)第一组(A组) (24)第二组(B组) (24)第三组(C组) (24)六参考资料 (25)附录程序框图 (26)一凸轮机构题目要求(摆动滚子推杆盘形凸轮机构)题目要求:试用计算机辅助设计完成下列偏置直动滚子推杆盘形凸轮机构或摆动滚子推杆盘形凸轮机构的设计,已知数据如下各表所示。
凸轮沿逆时针方向作匀速转动。
表一摆动滚子推杆盘形凸轮机构的已知参数题号初选的基圆半径R0/mm机架长度Loa/mm摆杆长度Lab/mm滚子半径Rr/mm推杆摆角φ许用压力角许用最小曲率半径[ρamin][α1] [α2]A 15 60 55 10 24°35°70°0.3RrB 20 70 65 14 26°40°70°0.3RrC 22 72 68 18 28°45°65°0.35Rr 要求:1)凸轮理论轮廓和实际轮廓的坐标值2)推程和回程的最大压力角,及凸轮对应的转角3)凸轮实际轮廓曲线的最小曲率4)半径及相应凸轮转角5)基圆半径6)绘制凸轮理论廓线和实际廓线7)计算点数:N:72~120推杆运动规律:1)推程运动规律:等加速等减速运动2)回程运动规律:余弦加速度运动二摆杆的运动规律及凸轮轮廓线方程1)推程:1,运动规律:等加速等减速运动;2,轮廓线方程:A:等加速推程段设定推程加速段边界条件为: 在始点处 δ=0,s=0,v=0。
在终点处 h /2 s ,2/==δοδ。
整理得:⎪⎩⎪⎨⎧===^2^2/*h *4a ^2/**h *4v ^2^2/*h *2s δοωδοδωδοδ( 注意:δ的变化范围为0~δ0/2。
机械原理大作业——凸轮.docx

大作业(二)凸轮机构设计题号:6班级:姓名:学号:同组者:成绩:完成时间:目录一凸轮机构题目要求 (1)二摆杆的运动规律及凸轮轮廓线方程 (2)三计算程序 (3)四运算结果及凸轮机构图 (9)4.1 第一组(A组)机构图及计算结果 (9)4.2 第二组(B组)机构图及计算结果 (14)4.3 第三组(C组)机构图及计算结果 (19)五心得体会 (24)第一组(A组) (24)第二组(B组) (24)第三组(C组) (24)六参考资料 (25)附录程序框图 (26)一凸轮机构题目要求(摆动滚子推杆盘形凸轮机构)题目要求:试用计算机辅助设计完成下列偏置直动滚子推杆盘形凸轮机构或摆动滚子推杆盘形凸轮机构的设计,已知数据如下各表所示。
凸轮沿逆时针方向作匀速转动。
表一摆动滚子推杆盘形凸轮机构的已知参数题号初选的基圆半径R0/mm机架长度Loa/mm摆杆长度Lab/mm滚子半径Rr/mm推杆摆角φ许用压力角许用最小曲率半径[ρamin][α1] [α2]A 15 60 55 10 24°35°70°0.3RrB 20 70 65 14 26°40°70°0.3RrC 22 72 68 18 28°45°65°0.35Rr 要求:1)凸轮理论轮廓和实际轮廓的坐标值2)推程和回程的最大压力角,及凸轮对应的转角3)凸轮实际轮廓曲线的最小曲率4)半径及相应凸轮转角5)基圆半径6)绘制凸轮理论廓线和实际廓线7)计算点数:N:72~120推杆运动规律:1)推程运动规律:等加速等减速运动2)回程运动规律:余弦加速度运动二摆杆的运动规律及凸轮轮廓线方程1)推程:1,运动规律:等加速等减速运动;2,轮廓线方程:A:等加速推程段设定推程加速段边界条件为:在始点处δ=0,s=0,v=0。
在终点处。
整理得:(注意:δ的变化范围为0~δ0/2。
哈工大机械原理大作业凸轮机构设计第题

哈工大机械原理大作业-凸轮机构设计(第题)————————————————————————————————作者:————————————————————————————————日期:机械原理大作业二课程名称:机械原理设计题目:凸轮机构设计院系:机电学院班级:1208103完成者:xxxxxxx学号:11208103xx指导教师:林琳设计时间:2014.5.2哈尔滨工业大学凸轮机构设计一、设计题目如图所示直动从动件盘形凸轮机构,其原始参数见表,据此设计该凸轮机构。
序号 升程(mm ) 升程运动角(°) 升程运动规律 升程许用压力角(°) 回程运动角(°) 回程运动规律 回程许用压力角(°)远休止角(°) 近休止角(°)3 50 150 正弦加速度 30 100 余弦加速度60 30 80二、凸轮推杆升程、回程运动方程及其线图1 、凸轮推杆升程运动方程(650πϕ≤≤) 升程采用正弦加速度运动规律,故将已知条件mm h 50=,650π=Φ带入正弦加速度运动规律的升程段方程式中得:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=512sin 215650ϕππϕS ; ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=512cos 1601ππωv ; ω⎪⎭⎫ ⎝⎛=512sin 14421ϕπωa ; 2、凸轮推杆推程远休止角运动方程(πϕπ≤≤65) mm h s 50==;0==a v ;3、凸轮推杆回程运动方程(914πϕπ≤≤) 回程采用余弦加速度运动规律,故将已知条件mm h 50=,95'0π=Φ,6s π=Φ带入余弦加速度运动规律的回程段方程式中得:⎥⎦⎤⎢⎣⎡-+=)(59cos 125πϕs ; ()πϕω--=59sin451v ; ()πϕω-=59cos 81-a 21;4、凸轮推杆回程近休止角运动方程(πϕπ2914≤≤) 0===a v s ;5、凸轮推杆位移、速度、加速度线图根据以上所列的运动方程,利用matlab 绘制出位移、速度、加速度线图。
哈工大机械原理大作业直动从动件盘形凸轮机构满分完美版哈尔滨工业大学

end
%曲率半径
dx=diff(x);
dx(36001)=0;
dy=diff(y);
dy(36001)=0;
dydx=dy./dx;
ddy=diff(dydx);
ddy(36001)=0;
ddy=ddy./dx;
~7~
xlabel('凸轮转角φ/°');
ylabel('从动件加速度 a/(mm/s^2)');
title('加速度');
subplot(2,3,4);
plot(dsdPhi,s);
axis equal
axis([-30 50 -50 30]);
hold on
plot(x1,f1,'r');
hold on
axis equal
hold on
plot(x,y,'k')
legend('理论廓线',-1);
hold on
%轮廓图
%实际廓线
%理论廓线
~8~
哈尔滨工业大学
直动从动件盘型凸轮机构设计说明书
plot(x0,y0,':')
hold on
%基圆
plot(xe,ye,'k:')
%偏距圆
legend('实际廓线','理论廓线','基圆','偏距圆',-1);
subplot(2,3,1);
plot(Phi,s);
grid on
axis([0 360 0 27]);
机械原理大作业2-凸轮机构设计

Harbin Institute of Technology机械原理大作业二课程名称:机械原理设计题目:凸轮机构设计院系:机电工程学院姓名:学号:班级:指导教师:1.设计题目设计直动从动件盘形凸轮机构,其原始参数见表1 表一:凸轮机构原始参数升程(mm ) 升程运动角(º)升程运动规律升程许用压力角(º)回程运动角(º)回程运动规律回程许用压力角(º)远休止角(º)近休止角(º)30 70 等加等减速30 170 正弦加速度60 100 1202.凸轮推杆运动规律(1)推程运动规律(等加速等减速运动)推程035≤ϕ0≤推程0070≤ϕ35≤(2)回程运动规律(正弦加速度)回程00240≤ϕ170≤开始输入初始参数运行各部分程序输出1 输出2 输出3 输出4 结束从动件位移、速度、加速度曲线ds/dψ-s曲线,确定基圆半径和偏距理论轮廓线上的压力角和曲率半径图绘制理论轮廓线和实际轮廓线3.运动线图及凸轮s d ds -φ线图采用Matlab 编程,其所有源程序见附页:令可得运动规律图如下:1.凸轮的基圆半径和偏距以ds/dfψ-s图为基础,可分别作出三条限制线(推程许用压力角的切界限D t d t,回程许用压力角的限制线D t'd t',起始点压力角许用线B0d''),以这三条线可确定最小基圆半径及所对应的偏距e,在其下方选择一合适点,即可满足压力角的限制条件。
得图如下:得最小基圆对应的坐标位置大约为(20,-35)经计算取偏距e=20mm,r0=40.3mm.2.绘制理论轮廓线上的压力角曲线和曲率半径曲线针对凸轮转向及推杆偏置,令N1=1凸轮逆时针转;N2=1偏距为正。
压力角数学模型:曲率半径数学模型:)/)(/()/)(/(])/()/[(22222/322ϕϕϕϕϕϕρd x d d dy d y d d dx d dy d dx -+= 其中:)sin(])/[()cos(])/(2[/102212122ϕϕϕϕϕN s s d s d N e N N d ds d x d --+-=)cos(])/[()(sin ])/(2[/202212122ϕϕϕϕϕN s s d s d N e N N d ds d y d --+--=3.凸轮理论廓线和实际廓线理论廓线数学模型:ϕϕϕϕsin cos )(cos sin )(00e s s y e s s x -+=++=凸轮实际廓线坐标方程式:22'22')/()/()/()/()/()/(ϕϕϕϕϕϕd dy d dx d dy r y y d dy d dx d dx r x x tt+-=++=其中rt 为确定的滚子半径。
哈工大机械原理大作业2凸轮机构设计

机械原理大作业(二)作业名称:凸轮机构设计设计题目:23题院系:班级:设计者:学号:指导教师:设计时刻:哈尔滨工业大学机械设计1.运动分析题目:设计直动从动件盘形凸轮机构,其原始参数见下表2.确信凸轮机构推杆升程、回程运动方程(设定角速度为ω=10 rad/s)升程:0°< Φ < 120°由公式可得:s=60-60*cos(3*Φ/2);v=90*ω*sin(3*Φ/2);a=135*ω2 *cos(3*Φ/2);远停止:120°< Φ < 200°由公式可得:s=120;v=0;a=0;回程:200°< Φ < 290°由公式可得:s=h[1-(10T23-15T24+6T25)]v=(-30hω1/Φ0')T22(1–2T2+T22)a=(-60hω12/Φ0'2)T2(1–3T2+2T22)式中:T2=(Φ-Φ0-Φs)/ Φ0'近停止: 290°< Φ < 360°由公式可得:s=0;v=0;a=0;3.绘制推杆位移、速度、加速度线图(设ω=10rad/s)1) 推拉位移曲线代码:%推杆位移曲线;x=0:(pi/1000):(2*pi/3);s1=60-60*cos(1.5*x);y=(2*pi/3):(pi/1000):(10*pi/9);s2=120;z=(10*pi/9):(pi/1000):(29*pi/18);T2=(z-10*pi/9)*2/pi;s3=120*(1-(10*T2.^3-15*T2.^4+6*T2.^5));m=(29*pi/18):(pi/1000):(2*pi);s4=0;plot(x,s1,'b',y,s2,'b',z,s3,'b',m,s4,'b'); xlabel('角度(rad)');ylabel('行程(mm)');title('推杆位移曲线');grid;2)推杆速度曲线代码:%推杆速度曲线;w=10;x=0:(pi/1000):(2*pi/3);v1=90*w*sin(1.5*x);y=(2*pi/3):(pi/1000):(10*pi/9);v2=0;z=(10*pi/9):(pi/1000):(29*pi/18);T2=(z-10*pi/9)*2/pi;v3=(-30*120*w/(pi/2))*T2.^2.*(1-2*T2.^2+T2.^2); % v3=-120*w*sin(2*z-20*pi/9);m=(29*pi/18):(pi/1000):(2*pi);v4=0;plot(x,v1,'r',y,v2,'r',z,v3,'r',m,v4,'r'); xlabel('角度(rad)');ylabel('速度(mm/s)');title('推杆速度曲线(w=10rad/s)');grid;3)凸轮推杆加速度曲线代码:%凸轮推杆加速度曲线;w=10;x=0:(pi/1000):(2*pi/3);a1=135*w^2*cos(3*x/2);y=(2*pi/3):(pi/1000):(10*pi/9);a2=0;z=(10*pi/9):(pi/1000):(29*pi/18);T2=(z-10*pi/9)*2/pi;a3=(-60*120*w^2/(pi/2)^2)*T2.*(1-3*T2.^2+2*T2.^2); m=(29*pi/18):(pi/1000):(2*pi);a4=0;plot(x,a1,'m',y,a2,'m',z,a3,'m',m,a4,'m');xlabel('角度(rad)');ylabel('加速度(mm/s^2)');title('凸轮推杆加速度曲线(w=10rad/s)');grid;4)绘制凸轮机构的dd/dd−d线图,并依次确信凸轮的基圆半径和偏距代码:%dd/dd−d线图,确信e,s0;x=0:(pi/1000):(2*pi/3);s1=60-60*cos(1.5*x);ns1=90*sin(1.5*x);y=(2*pi/3):(pi/1000):(10*pi/9);s2=120;ns2=0;z=(10*pi/9):(pi/1000):(29*pi/18);T2=(z-10*pi/9)*2/pi;s3n=120*(1-(10*T2.^3-15*T2.^4+6*T2.^5));ns3=-120*10*3*T2.^2+120*15*4*T2.^3-120*6*5*T2.^4 ;m=(29*pi/18):(pi/1000):(2*pi);s4=0;ns4=0;x1=0:pi/36000:pi/2;s1n=60-60*cos(1.5*x1);v1=90*sin(1.5*x1);m1=diff(s1n);%求切线1n1=diff(v1);z=m1./n1;for i=1:length(z);if abs(z(i)+tan(-55*pi/180))<0.001;breakendendb11=s1n(i)-z(i)*v1(i);x1=-300:200;y01=z(i)*x1+b11;%切线1k1=z(i);plot(x1,y01)x3=10*pi/9:pi/36000:14*pi/9;%求切线2s3n=120*(1-(10*T2.^3-15*T2.^4+6*T2.^5));v3=-120*10*3*T2.^2+120*15*4*T2.^3-120*6*5*T2.^4 ;m3=diff(s3n);n3=diff(v3);p=m3./n3;for o=1:length(p);if abs(p(o)-tan(-25*pi/180))<0.01;breakendendo;b33=s3n(o)-p(o)*v3(o);x3=-300:700;y03=p(o)*x3+b33;%切线2plot(x3,y03);sym uv[u,v]=solve('u= 1.4281*v-81.7665','u=-0.4663*v-59.6715');%v=11.66332347972972972972972972973 x%u=-65.110107738597972972972972972973 yplot(ns1,s1,'m',ns2,s2,'b',ns3,s3n,'b',ns4,s4,'b',x1,y01,'g',x3,y03,'g',v,u,'*'); xlabel('ds/d¦µ');ylabel('S');axis([-300,200,-300,300]);title('s0,e 的确信');grid;确信凸轮基圆半径与偏距:偏距e=90mm,d020mm;基圆半径为d0=150mm。
哈工大机械原理大作业二凸轮机构

void main()
{
float fi=0,fi0=90,h=100,S=0,v=0,a=0,fis=110,fi01=80,fis1=80,T2=0,w1=10,A=0,B=0,v0=0,v01=0,v02=0,f11=30,f31=70,A11=0,A12=0,B11=0,B12=0,A21=0,A22=0,B21=0,C11=0,C21=0,W=0;
{
W=fi*2*PI/360.0;
if(fi<=90)
{
S=h*(W/fi0-(1/(2*PI))*sin((2*PI/fi0)*W));
v=(h*w1/fi0)*(1-cos((2*PI/fi0)*W));
a=(2*PI*h*w1*w1/(fi0*fi0))*sin(2*PI*W/fi0);
}
elseif(fi>=90&&fi<200)
{
A=90;
A=A*2*PI/360.0;
S=h*(A/fi0-(1/(2*PI))*sin((2*PI/fi0)*A));
v=(h*w1/fi0)*(1-cos((2*PI/fi0)*A));
a=(2*PI*h*w1*w1/(fi0*fi0))*sin(2*PI*A/fi0);
}
elseif(fi>=200&&fi<=280)
}
printf("%f\n",a);
}
}
此程序计算推杆位移,速度,加速度线图。
程序二:
#include "stdio.h"
#include "math.h"
哈工大机械原理大作业凸轮 - 黄建青

H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业二课程名称:机械原理设计题目:凸轮机构设计院系:能源学院班级: 1302402 设计者:黄建青学号: 1130240222 指导教师:焦映厚陈照波设计时间: 2015年06月23日凸轮机构设计说明书1. 设计题目设计直动从动件盘形凸轮机构,机构运动简图如图1,机构的原始参数如表1所示。
图1 机构运动简图表1 凸轮机构原始参数序号升程升程运动角升程运动规律升程许用压力角回程运动角回程运动规律回程许用压力角远休止角近休止角13 45mm 50°余弦加速度35°90°抛-直-抛70°100°120°计算流程框图:2. 凸轮推杆升程,回程运动方程及推杆位移、速度、加速度线图2.1 确定凸轮机构推杆升程、回程运动方程 设定角速度为ω=1 rad/s(1) 升程:0°<φ<50°由公式可得 )]cos(1[20ϕπΦh s -=计算推程、回程的推杆s 、v 、a运动线图及凸轮dss d ϕ-线图 确定凸轮机构基圆半径和偏距计算曲率半径和压力角,确定滚子半径确定凸轮的理论廓线和实际廓线)s i n (2001ϕπωπΦΦh v =)cos(2020212ϕπωπΦΦh a =(2) 远休止:50°<φ<150° 由公式可得s = 45 v = 0a = 0(3) 回程:150°<φ<240° 由公式得:()()2200002000000022000000,2(1)(1)1,12(1)(1),2(1)s s s s s s s s s Φhn s h ΦΦΦΦΦΦn Φn ΦΦn h n s h ΦΦΦΦΦΦn Φn n ΦΦΦn hn s ΦΦΦΦΦn Φn ϕϕϕϕϕϕ'⎧=---+<≤++⎪'-⎪⎪⎡⎤''-⎪=----++<≤++⎨⎢⎥'-⎣⎦⎪⎪'---⎪'=-++<≤++'-⎪⎩2010000001000200100000n (),(1)(1)n ,(1)(1)n (1),(1)s s s s s s s s Φh v ΦΦΦΦΦΦn Φn ΦΦn h v ΦΦΦΦn Φn n ΦΦΦn h v ΦΦΦΦΦn ΦΦn ωϕϕωϕϕωϕ⎧'=---+<≤++⎪'-⎪⎪''-⎪=-++<≤++⎨'-⎪⎪'---'⎪=--++<≤++''-⎪⎩220100200000220100020n ,(1)(1)0,(1)n ,(1)s s s s s s Φh a ΦΦΦΦn Φn ΦΦn a ΦΦΦΦn n Φn h a ΦΦΦΦΦn Φn ωϕϕωϕ'⎧=-+<≤++⎪'-⎪⎪''-=++<≤++⎨⎪⎪'-'=-++<≤++⎪'-⎩式中 Φ0——推程运动角; Φs ——远休止角;Φ0‘——回程运动角。
(完整word版)哈工大机械原理大作业凸轮DOC

H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业二课程名称:机械原理设计题目: 凸轮机构设计院系:班级:设计者:学号:指导教师:哈尔滨工业大学一、设计题目如右图所示直动从动件盘形凸轮机构,选择一组凸轮机构的原始参数,据此设计该凸轮机构。
凸轮机构原始参数序号升程(mm)升程运动角升程运动规律升程许用压力角27130150正弦加速度30°回程运动角回程运动规律回程许用压力角远休止角近休止角100°余弦加速度60°30°80°二. 凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图凸轮推杆升程运动方程:)]512sin(2156[130s ϕππϕ-= )512sin(4.374)]512cos(1[156v 211ϕπϕπωω=-=a% t 表示转角,s 表示位移t=0:0.01:5*pi/6;%升程阶段s= [(6*t)/(5*pi )- 1/(2*pi )*sin(12*t/5)]*130; hold on plot(t ,s ); t= 5*pi/6:0。
01:pi; %远休止阶段s=130; hold on plot(t,s );t=pi :0.01:14*pi/9;%回程阶段s=65*[1+cos(9*(t-pi )/5)]; hold on plot(t ,s );t=14*pi/9:0.01:2*pi ;s=0;hold onplot(t,s);grid onhold off%t表示转角,令ω1=1t=0:0。
01:5*pi/6;%升程阶段v=156*1*[1-cos(12*t/5)]/pi hold onplot(t,v);t= 5*pi/6:0。
01:pi;v=0hold onplot(t,v);t=pi:0.01:14*pi/9;%回程阶段v=—117*1*sin(9*(t—pi)/5) hold onplot(t,v);t=14*pi/9:0。
机械原理大作业凸轮结构设计

机械原理大作业(二) 作业名称:机械原理设计题目:凸轮机构设计院系: 机电工程学院班级:设计者:学号:指导教师:丁刚陈明设计时间:哈尔滨工业大学机械设计1、设计题目如图所示直动从动件盘形凸轮机构,根据其原始参数设计该凸轮。
表一:凸轮机构原始参数序号升程(mm) 升程运动角(º)升程运动规律升程许用压力角(º)回程运动角(º)回程运动规律回程许用压力角(º)远休止角(º)近休止角(º)12 80 150正弦加速度30 100 正弦加速度60 60 502、凸轮推杆运动规律(1)推杆升程运动方程S=h[φ/Φ0-sin(2πφ/Φ0)]V=hω1/Φ0[1-cos(2πφ/Φ0)]a=2πhω12sin(2πφ/Φ0)/Φ02式中:h=150,Φ0=5π/6,0<=φ<=Φ0,ω1=1(为方便计算)(2)推杆回程运动方程S=h[1-T/Φ1+sin(2πT/Φ1)/2π]V= -hω1/Φ1[1-cos(2πT/Φ1)]a=-2πhω12sin(2πT/Φ1)/Φ12式中:h=150,Φ1=5π/9,7π/6<=φ<=31π/18,T=φ-7π/63、运动线图及凸轮线图运动线图:用Matlab编程所得源程序如下:t=0:pi/500:2*pi;w1=1;h=150;leng=length(t);for m=1:leng;if t(m)<=5*pi/6S(m) = h*(t(m)/(5*pi/6)-sin(2*pi*t(m)/(5*pi/6))/(2*pi));v(m)=h*w1*(1-cos(2*pi*t(m)/(5*pi/6)))/(5*pi/6);a(m)=2*h*w1*w1*sin(2*pi*t(m)/(5*pi/6))/((5*pi/6)*(5*pi/6));% 求退程位移,速度,加速度elseift(m)<=7*pi/6S(m)=h;v(m)=0;a(m)=0;% 求远休止位移,速度,加速度elseif t(m)<=31*pi/18T(m)=t(m)-21*pi/18;S(m)=h*(1-T(m)/(5*pi/9)+sin(2*pi*T(m)/(5*pi/9))/(2*pi));v(m)=-h/(5*pi/9)*(1-cos(2*pi*T(m)/(5*pi/9)));a(m)=-2*pi*h/(5*pi/9)^2*sin(2*pi*T(m)/(5*pi/9));%求回程位移,速度,加速度elseS(m)=0;v(m)=0;a(m)=0;% 求近休止位移,速度,加速度endend推杆位移图推杆速度图推杆加速度图4、确定凸轮基圆半径与偏距在凸轮机构得ds/dφ-s线图里再作斜直线Dt dt与升程得[ds/dφ-s(φ)]曲线相切并使与纵坐标夹角为升程许用压力角[α],则D t d t线得右下方为选择凸轮轴心得许用区。
哈工程机械原理凸轮机构

哈工程机械原理凸轮机构1. 引言凸轮机构是机械工程中广泛应用的一种机构,包括了凸轮、滑块、连杆等部件。
在哈工程机械中,凸轮机构常用于控制机械运动的节奏和轨迹。
本文将介绍哈工程机械原理凸轮机构的工作原理以及在机械设计中的应用。
2. 凸轮机构的工作原理凸轮机构是一种基于凸轮运动的机械机构,可以将轴向转动运动转化为连杆运动或滑块运动。
凸轮通过主动轴驱动,使得凸轮轴随着转动,而凸轮则由于轴上的凸状物而在转动过程中产生周期性的起伏变化。
在哈工程机械中,凸轮机构常用于控制机器的工作节奏,例如控制挖掘机的铲斗起升。
通过控制凸轮的形状和凸轮轴的转速,可以实现不同速度和轨迹的运动。
凸轮机构的工作原理可以简要概括为以下几个步骤:1.凸轮轴的转动:凸轮机构的主动轴通过电机或其它动力装置驱动,使得凸轮轴开始转动。
2.凸轮的曲线轮廓:凸轮的轮廓可以根据具体的要求设计和加工,常见的形状包括圆形、椭圆形等。
不同的轮廓形状可以实现不同的动作轨迹。
3.滑块或连杆的运动:凸轮的曲线轮廓通过接触滑块或连杆,将轴向转动运动转化为连杆运动或滑块运动。
滑块或连杆的运动速度和轨迹由凸轮的形状和凸轮轴的转速决定。
4.控制机器的运动:滑块或连杆的运动可以用于控制机器的工作,例如挖掘机的铲斗起升运动。
通过调整凸轮的形状和凸轮轴的转速,可以调节机器的运动速度和轨迹。
3. 哈工程机械原理凸轮机构的设计与应用哈工程机械原理凸轮机构在机械设计中具有广泛的应用。
在以下几个方面,哈工程机械原理凸轮机构发挥了重要的作用:3.1 挖掘机挖掘机构挖掘机是哈工程机械中常见的设备之一,它的挖掘机构是由凸轮机构控制的。
凸轮机构通过控制铲斗的起升和倾斜,实现了挖掘机的挖掘和卸料功能。
凸轮的形状和凸轮轴的转速可以调节铲斗的升降速度和倾斜角度,使挖掘机能够适应不同的工作条件。
3.2 压路机振动机构哈工程机械中的压路机常常采用凸轮机构实现振动功能。
凸轮的曲线轮廓可以使滑块产生上下振动运动,从而使压路机产生振动力。
02-机械原理大作业-凸轮机构

序号
升程 (mm) 100
升程运 动规律 正弦加速度
18
升程 许用 压力角 ( ) 40
回程运 动规律 等减等加速
2.确定凸轮推杆升程、回程运动方程
(1)推杆升程运功方程(0 < φ ≤ Φ0 = 150°) 推程为正弦加速度运动规律,因此,运动方程为: ������ 1 2������ s = h[ − sin ( ������)] Φ0 2������ Φ0 v= ℎ������ 2������ ( ������)] [1 − cos Φ0 Φ0 2������ℎ������2 Φ0
如图 2-1 所示直动从动件盘形凸轮机构,其原始参数见表 2-1。从表 2-1 中选择一组凸 轮机构的原始参数,据此设计该凸轮机构。
图 2-1 表 2-1 升程运 动角 ( ) 150 凸轮机构原始参数 回程运 动角 ( ) 100 回程 许用 压力角 ( ) 60 远休 止角 ( ) 70 近休 止角 ( ) 40
′2
Φ0 2
′
′
= 270°时
[������ − (Φ0 + Φ������ )]2
v=−
4ℎ������ Φ0
′2
[������ − (Φ0 + Φ������ )]
a=−
4ℎ������2 Φ0
′2
其中 h=100mm,Φ0 = 150°,Φ������ = 70°,Φ0 = 100°,������ = 10rad/s。 b)在270° = Φ0 + Φ������ +
3
凸轮机构设计 VB 编程
Call S2 Picture2.PSet (i, v), RGB(255, 0, 0) Next i For i = 270 To 320 Step 0.01 φ = i * pa Call S3 Picture2.PSet (i, v), RGB(255, 0, 0) Next i For i = 320 To 360 Step 0.01 φ = i * pa v = 0 Picture2.PSet (i, v), RGB(255, 0, 0) Next i End Sub Private Sub Command3_Click() '加速度 a 曲线 Picture3.Scale (-50, 15000)-(380, -15000) '定义坐标系 Picture3.Line (0, 0)-(380, 0) '画 x 轴 Picture3.Line (0, 15000)-(0, -15000) '画 y 轴 For i = 0 To 360 Step 30 '竖直网格线 Picture3.DrawStyle = 2 Picture3.Line (i, 15000)-(i, -15000) Picture3.CurrentX = i - 14: Picture3.CurrentY = -2 Picture3.Print i Picture3.CurrentX = 365: Picture3.CurrentY = 1800 Picture3.Print "φ" Next i For i = -14000 To 14000 Step 2000 '水平网格线 Picture3.DrawStyle = 2 Picture3.Line (0, i)-(370, i) Picture3.CurrentX = -50: Picture3.CurrentY = i + 500 Picture3.Print i Picture3.CurrentX = 10: Picture3.CurrentY = 15700 Picture3.Print "a" Next i Picture3.DrawWidth = 2 For i = 0 To 150 Step 0.01 φ = i * pa Call S1 Picture3.PSet (i, a), RGB(255, 0, 0) Next i
机械原理大作业凸轮..

Harbin Institute of Technology机械原理大作业二课程名称:机械原理设计题目:凸轮结构设计院系:机电工程学院班级:1308108设计者:仲星光学号:1130810816指导教师:林琳设计时间:2015年6月7日一、设计题目如图所示直动从动件盘形凸轮机构,其原始参数见表,据此设计该凸轮机构。
行程(mm)升程运动角(°)升程运动规律升程许用压力角(°)回程运动角(°)回程运动规律回程许用压力角(°)远休止角(°)近休止角(°)6080余弦加速度30 60 摆抛摆60 100 120二.数学计算方法(设计书中所给出的回程运动方程有误)1.理论轮廓和工作轮廓廓线方程正偏置平面凸轮,反转法,小滚子中心在反转运动中的轨迹即为凸轮的理论轮廓,推杆所在直线一直与偏心圆相切,由几何关系可得盘形凸轮理论轮廓线方程为:滚子从动件盘形凸轮的实际轮廓线是以理论轮廓上各点为圆心,以小滚子半径为半径的圆族的包络线,理论廓线B点相对应的实际廓线B'点的方程为:2.压力角3.凸轮轮廓曲率半径由数学分析知,凸轮理论轮廓曲线上任一点的曲率半径的计算公式为:(以上方程来自《基于MatLab语言的机构设计与分析》上海科学技术出版社)三.MatLab程序程序设计流程1.主程序:推杆位clc;clear;h=60;%行程phi01=80;%推程运动角phis1=100;%远休止角phi02=60;%回程运动角phis2=120;%近休止角alpha1=pi/6;%升程许用压力角alpha2=pi/3;%回程许用压力角omiga=1;%凸轮角速度设为1%计算凸轮转角、从动件位移,速度和加速度%绘制从动件位移、速度、加速度线图[psi,s,v,a]=CanShuJiSuan(h,phi01,phis1,phi02,phis2,... omiga,alpha1,alpha2);e=22;r0=57;%由ds/dpsi-s图像确定基圆半径和偏距%计算凸轮轮廓线曲率半径及压力角%绘制凸轮理论轮廓线上的压力角线图和曲率半径图[ang,rou,DxDpsi,DyDpsi]=YaLiJiao_QuLvBanJin( r0,psi,s, v,a,e,omiga );Rr=9;%由曲率半径最小值确定小滚子半径%计算凸轮轮廓曲线%绘制理论和实际轮廓曲线LunKuoXian( r0,psi,s,e,Rr,DxDpsi,DyDpsi );2.余弦加速运动规律子函数function [ s1,v1,a1,psi1 ] = Yuxian( phi01,h,omiga )%计算余弦加速度运动规律psi1=linspace(0,phi01,round(phi01));s1=(h/2).*[1 - cos(pi.*psi1./phi01)];v1=(pi*h*omiga./(2.*(phi01*pi/180))) .*sin(pi.*psi1./phi01);a1=pi^2*h*omiga^2/(2*(phi01*pi/180)^2)*cos(pi.*psi1./p hi01)end3.远休止程子函数function [ s2,v2,a2,psi2 ] = YuanXiu( phi01,phis1,h ) psi2=linspace(phi01+1,phi01+phis1,round(phis1));s2=h*psi2./psi2;v2=0*psi2;a2=0*psi2;end4.摆抛摆子函数function [ s3,v3,a3,psi3 ] =BaiPaoBai( phi01,phis1,phi02,h,omiga )%计算回程摆线-抛物线-摆线运动规律%计算当phi01+phis1<psi<=phi01+phis1+phi02/8时,从动件的位移、速度、加速度psi3_1=linspace(phi01+phis1+phi02/8/100,phi01+phis1+ph i02/8,100);s3_1=h-h*(2*(psi3_1-phi01-phis1)/phi02-sin(4*pi*(psi3_ 1-phi01-phis1)/...phi02)/(2*pi))/(2+pi);v3_1=-2*h*omiga*(1-cos(4*pi*(psi3_1-phi01-phis1)/phi02 ))/((2+pi)*...phi02*pi/180);a3_1=-8*h*pi*omiga^2*sin(4*pi*(psi3_1-phi01-phis1)/phi 02)/((2+pi)*...(phi02*pi/180)^2);%计算当phi01+phis1<psi<=phi01+phis1+3*phi02/8时,从动件的位移、速度、加速度psi3_2=linspace(phi01+phis1+phi02/8+phi02/4/100,phi01+ phis1+3*phi02/8,100);s3_2=h-h*(4*pi*((psi3_2-phi01-phis1).^2)/(phi02^2)-(pi -2)*(psi3_2-phi01...-phis1)/phi02+pi/16-1/(2*pi))/(2+pi);v3_2=-h*omiga*(8*pi*(psi3_2-phi01-phis1)/phi02-pi+2)/( (2+pi)*phi02*pi/180);a3_2=-8*h*pi*omiga^2/((2+pi)*(phi02*pi/180)^2)*psi3_2. /psi3_2;%计算当phi01+phis1<psi<=phi01+phis1+5*phi02/8时,从动件的位移、速度、加速度psi3_3=linspace(phi01+phis1+3*phi02/8+phi02/4/100,phi0 1+phis1+5*phi02/8,100);s3_3=h-h*(2*(pi+1)*(psi3_3-phi01-phis1)/phi02-pi/2-sin (4*pi*(psi3_3-phi01...-phis1)/phi02-pi)/(2*pi))/(2+pi);v3_3=-2*h*omiga*(pi+1-cos(4*pi*(psi3_3-phi01-phis1)/ph i02-pi))/((2+pi)...*phi02*pi/180);a3_3=-8*h*pi*omiga^2*sin(4*pi*(psi3_3-phi01-phis1)/phi 02-pi)/((2+pi)*...(phi02*pi/180)^2);%计算当phi01+phis1<psi<=phi01+phis1+7*phi02/8时,从动件的位移、速度、加速度psi3_4=linspace(phi01+phis1+5*phi02/8+phi02/4/100,phi0 1+phis1+7*phi02/8,100);s3_4=h-h*(-4*pi*((psi3_4-phi01-phis1).^2)/(phi02^2)+(7 *pi+2)*(psi3_4-...phi01-phis1)/phi02-33*pi/16+1/(2*pi))/(2+pi);v3_4=-h*omiga*(-8*pi*(psi3_4-phi01-phis1)/phi02+7*pi+2 )/((2+pi)*phi02*pi/180);a3_4=8*h*pi*omiga^2/((2+pi)*(phi02*pi/180)^2)*psi3_4./ psi3_4;%计算当phi01+phis1<psi<=phi01+phis1+phi02时,从动件的位移、速度、加速度psi3_5=linspace(phi01+phis1+7*phi02/8+phi02/8/100,phi0 1+phis1+phi02,100);s3_5=h-h*(2*(psi3_5-phi01-phis1)/phi02+pi-sin(4*pi*(ps i3_5-phi01-phis1).../phi02-2*pi)/(2*pi))/(2+pi);v3_5=-2*h*omiga*(1-cos(4*pi*(psi3_5-phi01-phis1)/phi02 -2*pi))/((2+pi)...*phi02*pi/180);a3_5=-8*h*pi*omiga^2*sin(4*pi*(psi3_5-phi01-phis1)/phi 02-2*pi)/((2+pi)...*(phi02*pi/180)^2);%输出回程阶段凸轮的转角、从动件的位移速度加速度的数组s3=[s3_1,s3_2,s3_3,s3_4,s3_5];v3=[v3_1,v3_2,v3_3,v3_4,v3_5];a3=[a3_1,a3_2,a3_3,a3_4,a3_5];psi3=[psi3_1,psi3_2,psi3_3,psi3_4,psi3_5];end5.近休止程子函数function [ s4,v4,a4,psi4 ] =JinXiu( phi01,phis1,phi02,phis2 )psi4=linspace(phi01+phis1+phi02+1,phi01+phis1+phis2+ph i02,round(phis2));s4=0*psi4;v4=0*psi4;a4=0*psi4;End6.参数计算及图像绘制[s1,v1,a1,psi1]=YuXian(phi01,h,omiga);%推程[s2,v2,a2,psi2]=YuanXiu(phi01,phis1,h);%远休程[s3,v3,a3,psi3]=BaiPaoBai(phi01,phis1,phi02,h,omiga);%回程[s4,v4,a4,psi4]=JinXiu(phi01,phis1,phi02,phis2);%近休程psi=[psi1,psi2,psi3,psi4];%凸轮转角s=[s1,s2,s3,s4];%从动件位移v=[v1,v2,v3,v4];%从动件速度a=[a1,a2,a3,a4];%从动件加速度%绘制从动件位移、速度、加速度线图figure(1)subplot(3,1,1)plot(psi,s);grid onxlabel('凸轮转角(度)');ylabel('位移(mm)');subplot(3,1,2);plot(psi,v);grid onxlabel('凸轮转角(度)');ylabel('速度(mm/s)');subplot(3,1,3)plot(psi,a);grid onxlabel('凸轮转角(度)');ylabel('加速度(mm/s^2)');%绘制ds/dphi-s线图,并确定凸轮基圆半径和偏距DsDphi=v/omiga;figure(2)plot(DsDphi,s);hold onx1=-150:100;y1=tan(pi/2-alpha1)*(x1-65.26)+22.33; plot(x1,y1);hold ony2=tan(pi/2+alpha2)*(x1+107.6)+22.36; plot(x1,y2);7.轮廓线绘制if Rr==0x=x0;y=y0;elseA=sqrt(DxDpsi.^2+DyDpsi.^2);x=x0+Rr*DyDpsi./A;y=y0-Rr*DxDpsi./A;endfigure(4)plot(r0.*cos(psi.*pi/180),r0.*sin(psi.*pi/180),'-.',.. .x0,y0,'--',x,y,e*cos(psi.*pi/180),e*sin(psi.*pi/180)); grid on;legend('基圆','凸轮理论轮廓','凸轮实际轮廓','偏距圆');axis equalend8.压力角曲线及曲率半径function[ang,rou,DxDpsi,DyDpsi]=YaLiJiao_QuLvBanJin( r0,psi,s, v,a,e,omiga )s0=sqrt(r0.^2-e.^2);rs1=s0+s;ang=abs(atan((v/omiga-e)./rs1))*180/pi;DxDpsi=(v./omiga-e).*sin(psi.*pi/180)+...(s0+s).*cos(psi.*pi/180);DyDpsi=(v./omiga-e).*cos(psi.*pi/180)-...(s0+s).*sin(psi.*pi/180);DDxDpsi=(a./(omiga^2)-(s0+s)).*sin(psi.*pi/180)... +(2*v./omiga-e).*cos(psi.*pi/180);DDyDpsi=(a./(omiga^2)-(s0+s)).*cos(psi.*pi/180)... +(2*v./omiga-e).*sin(psi.*pi/180);A=(DxDpsi.^2+DyDpsi.^2).^1.5;B=abs(DxDpsi.*(DDyDpsi)-DyDpsi.*(DDxDpsi));rou=A./B;%凸轮理论轮廓曲率半径%绘图figure(3)axis onplotyy(psi,rou,psi,ang);%绘制曲率半径图[AX]=plotyy(psi,rou,psi,ang);set(AX(1),'yTick',[0:20:200]);set(AX(2),'yTick',[0:10:100]);end四.程序运行结果与生成图像。
哈工大机械原理大作业2号凸轮
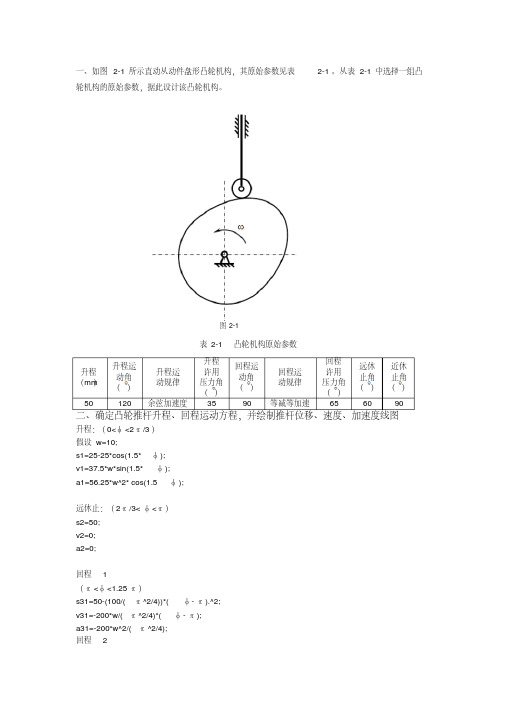
一、如图2-1所示直动从动件盘形凸轮机构,其原始参数见表2-1。
从表2-1中选择一组凸轮机构的原始参数,据此设计该凸轮机构。
表2-1 凸轮机构原始参数升程(mm)升程运动角()升程运动规律升程许用压力角()回程运动角()回程运动规律回程许用压力角()远休止角()近休止角()50 120 余弦加速度35 90 等减等加速65 60 90二、确定凸轮推杆升程、回程运动方程,并绘制推杆位移、速度、加速度线图升程:(0<φ<2π/3)假设w=10;s1=25-25*cos(1.5*φ);v1=37.5*w*sin(1.5*φ);a1=56.25*w^2* cos(1.5φ);远休止:(2π/3<φ<π)s2=50;v2=0;a2=0;回程・1(π<φ<1.25π)s31=50-(100/(π^2/4))*( φ-π).^2;v31=-200*w/(π^2/4)*( φ-π);a31=-200*w^2/(π^2/4);回程・2图2-1(1.25π<φ<1.5π)s32=100/(π^2/4)*(3*π/2-φ).^2; v32=-200*w/(π^2/4)*( 3*π/2-φ); a32=200*w^2/(π^2/4);近休止(1.5π<φ<2π)s4=0;v4=0;a4=0;三、求ds/dφ与s的关系:x=0:(pi/1000):(2*pi/3);s1=25-25*cos(1.5*x);ns1=37.5*sin(1.5*x);y=(2*pi/3):(pi/1000):(pi);s2=50;ns2=0;z1=(pi):(pi/1000):(1.25*pi);s31=50-(100/(pi^2/4))*(z1-(pi)).^2;ns31=-(100/(pi^2/4))*(2*z1-2*pi)z2=(1.25*pi):(pi/1000):(1.5*pi);s32=100/(pi^2/4)*(3*pi/2-z2).^2;ns32=100/(pi^2/4)*(-3*pi+2*z2)m=(1.5*pi):(pi/1000):(2*pi);s4=0;ns4=0;plot(ns1,s1,'b',ns2,s2,'b',ns31,s31,'b',ns32,s32,'b',ns4,s4,'b')凸轮机构的s s dd 线图-80-60-40-200204005101520253035404550凸轮中心应该取在公共区下方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H a r b i n I n s t i t u t e o f T e c h n o l o g y机械原理大作业说明书课程名称:机械原理设计题目:凸轮机构设计院系:能源科学与工程班级:1302403设计者:闫昭琦学号:1130240312指导教师:陈照波焦映厚设计时间:2015年6月哈尔滨工业大学一、设计题目 如右图所示直动从动件盘形凸轮机构,选择一组凸轮机构的原始参数,据此设计该凸轮机构。
二. 凸轮推杆升程、回程运动方程及推杆位移、速度、加速度线图凸轮推杆升程运动方程:)]512sin(2156[130s ϕππϕ-= )512sin(4.374)]512cos(1[156v 211ϕπϕπωω=-=aclear;clc;hu=pi/180; %输入题目要求的参数 h=130; %从动件最大线位移 w1=10; %假设的凸轮 fi0=150*hu; %推程运动角 fis=100*hu; %远休止角 fi02=70*hu; %回程运动角 fis2=40*hu; %近休止角 %开始计算 %推程计算xfi1=0:0.01:fi0; %凸轮转角 T1=xfi1/fi0;s1=h*(10*T1.^3-15*T1.^4+6*T1.^5);v1=30*h*w1*T1.^2.*(1-2*T1+T1.^2)/fi0;a1=60*h*w1^2*T1.*(1-3*T1+2*T1.^2)/fi0^2; xfi2=(fi0+fis):0.01:(fi0+fis+fi02);%远休程计算xfi3=fi0:0.01:(fi0+fis);s3=h*ones(1,length(xfi3));v3=zeros(1,length(xfi3));a3=zeros(1,length(xfi3));%回程计算T=xfi2-fi0-fis;s2=h*(1-T/fi02+1/(2*pi)*sin(2*pi*T/fi02)); v2=-h*w1*(1-cos(2*pi*T/fi02))/fi02;a2=-2^pi*h*w1^2*sin(2*pi*T/fi02)/fi02^2;%近休程计算xfi4=(2*pi-fis2):0.01:2*pi;s4=zeros(1,length(xfi4));v4=zeros(1,length(xfi4));a4=zeros(1,length(xfi4));% t表示转角,令ω1=1t=0:0.01:5*pi/6;%升程阶段v=156*1*[1-cos(12*t/5)]/pi hold onplot(t,v);t= 5*pi/6:0.01:pi;%远休止阶段v=0hold onplot(t,v);t=pi:0.01:14*pi/9;%回程阶段v=-117*1*sin(9*(t-pi)/5) hold onplot(t,v);t=14*pi/9:0.01:2*pi;%近休止阶段v=0hold ont=0:0.001:5*pi/6;a=374.4*sin(12*t/5)/pi;hold onplot(t,a);t=5*pi/6:0.01:pi;a=0;hold onplot(t,a);t=pi:0.001:14*pi/9;a=-210.6*cos(9*(t-pi)/5); hold onplot(t,a);t=14*pi/9:0.001:2*pi;a=0;hold on三. 绘制凸轮机构的sdds-ϕ线图% t表示转角,x(横坐标)表示速度ds/dφ,y(纵坐标)表示位移s t=0:0.001:5*pi/6;% 升程阶段x= 156*1*(1-cos(12*t/5))/pi;y= 130*((6*t)/(5*pi)-1/(2*pi)*sin(12*t/5));hold onplot(x,y,'-r');t= 5*pi/6:0.01:pi;%远休止阶段x=0;y=130;hold onplot(x,y,'-r');t=pi:0.001:14*pi/9;% 回程阶段x=-117*1*sin(9*(t-pi)/5); y=65*(1+cos(9*(t-pi)/5)); hold onplot(x,y,'-r');t=14*pi/9:0.01:2*pi;%近休止阶段x=0;y=0;hold onplot(x,y,'-r');grid onhold off四.按许用压力角确定凸轮基圆半径和偏距1. 求切点转角(1)在图-4中,右侧曲线为升程阶段的类速度-位移图,作直线D t d t与其相切,且位移轴正方向呈夹角[α1]=300,则切点处的斜率与直线D t d t的斜率相等,因为k Dtdt=tan300,右侧曲线斜率可以表示为错误!未找到引用源。
,所以,错误!未找到引用源。
,通过编程求其角度。
编码:求得转角t =1.1123进而求的切点坐标(x,y)=(93.8817, 45.8243)(2)在图-4中,左侧曲线为回程阶段的类速度-位移图,作直线D’t d’t与其相切,且位移轴正方向呈夹角[α1]=600,则切点处的斜率与直线D’t d’t的斜率相等,因为k Dtdt=tan300同理求得切点坐标(x,y)=( -110.0654, 42.3144)2. 确定直线方程直线D t d t:y =tan(pi/3)(x-93.8817)=45.8243;直线D t’d t’: y =-tan(pi/3)(x+84.3144)+110.0654;3. 绘图确定基圆半径和偏距% 直线Dtdtx=-125:1:150;y= tan(pi/3)*(x-93.8798)+45.8243;hold onplot(x,y);% 直线Dt’dt’x=-125:1:150;y=-tan(pi/6)*(x+110.0654)+34.3144;hold onplot(x,y);%直线Ddx=0:1:150;y=tan(2*pi/3)*x;hold onplot(x,y);t=0:0.001:5*pi/6;% 升程阶段x= 156*1*[1-cos(12*t/5)]/pi;y= 130*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)]; hold onplot(x,y,'-r');t= 5*pi/6:0.01:pi;%远休止阶段x=0;y=130;hold onplot(x,y,'-r');t=pi:0.001:14*pi/9;% 回程阶段x=-117*1*sin(9*(t-pi)/5);y=65*[1+cos(9*(t-pi)/5)];hold onplot(x,y,'-r');t=14*pi/9:0.01:2*pi;%近休止阶段x=0;y=0;hold onplot(x,y,'-r');grid onhold off如图,在这三条直线所围成的公共许用区域,只要在公共许用区域内选定凸轮轴心O的位置,凸轮基圆半径r0和偏距e就可以确定了。
现取轴心位置为x=20,y=-125,则可得偏距e=20,基圆半径=127五.绘制凸轮理论轮廓线编码:%凸轮的理论轮廓,t表示转角,x表示横坐标,y表示纵坐标t=0:0.0001:5*pi/6;x=(125+130*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)]).*cos(t)-20*sin(t);y=(125+130*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)]).*sin(t)+20*cos(t);hold onplot(x,y);t= 5*pi/6:0.0001:pi;x=(125+130).*cos(t)- 20*sin(t);y=(125+130).*sin(t)+ 20*cos(t);hold onplot(x,y);t=pi:0.0001:14*pi/9;x=(125+65*[1+cos(9*(t-pi)/5)]).*cos(t)- 20*sin(t);y=(125+65*[1+cos(9*(t-pi)/5)]).*sin(t)+ 20*cos(t);hold onplot(x,y);t= 14*pi/9:0.0001:2*pi;x=(125).*cos(t)- 20*sin(t);y=(125).*sin(t)+ 20*cos(t);hold onplot(x,y);%基圆t=0:0.001:2*pi;x=20.1074*cos(t);y=20.1074*sin(t);hold onplot(x,y);% 偏心圆t=0:0.001:2*pi;x=13.3509*cos(t);y=13.3509*sin(t);hold onplot(x,y);grid onhold off六、在理论廓线上分别绘出基圆与偏距圆:编码:%凸轮的理论轮廓,t表示转角,x表示横坐标,y表示纵坐标t=0:0.0001:5*pi/6;x=(125+130*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)]).*cos(t)-20*sin(t);y=(125+130*[(6*t)/(5*pi)-1/(2*pi)*sin(12*t/5)]).*sin(t)+20*cos(t);hold onplot(x,y);t= 5*pi/6:0.0001:pi;x=(125+130).*cos(t)- 20*sin(t);y=(125+130).*sin(t)+ 20*cos(t);hold onplot(x,y);t=pi:0.0001:14*pi/9;x=(125+65*[1+cos(9*(t-pi)/5)]).*cos(t)- 20*sin(t); y=(125+65*[1+cos(9*(t-pi)/5)]).*sin(t)+ 20*cos(t); hold onplot(x,y);t= 14*pi/9:0.0001:2*pi;x=(125).*cos(t)- 20*sin(t);y=(125).*sin(t)+ 20*cos(t);hold onplot(x,y);%基圆t=0:0.001:2*pi;x=127*cos(t);y=127*sin(t);hold onplot(x,y);% 偏心圆t=0:0.001:2*pi;x=20*cos(t);y=20*sin(t);hold onplot(x,y);grid onhold off七.确定滚子半径1. 绘制曲率半径图% 凸轮理论轮廓半径,t表示转角,p表示曲率半径,%dxi表示dx/dφ, dyi表示dy/dφ,i=1,2,3,4h=130; %升程t0=pi*5/6; % 升程角t01=pi*5/9; % 回程角ts=pi/6; %远休止角ts1=pi*4/9; %近休止角e=20; %偏距s0=125;% 升程阶段t=linspace(0,pi*5/6,1000);s=h*(t/t0-sin(2*pi*t/t0)/(2*pi));dx1 =(h/t0-h*cos(2*pi*t/t0)).*cos(t)-(s0+s).*sin(t)- e*cos(t); dy1=(h/t0-h*cos(2*pi*t/t0)).*sin(t)+(s0+s).*cos(t)- e*sin(t); p=sqrt(dx1.^2+dy1.^2);hold onplot(t,p);% 远休止阶段t=linspace(pi*5/6,pi,1000);s=h;dx2 =- sin(t).*(s + s0) - e*cos(t);dy2 =cos(t).*(s + s0) - e*sin(t);p=sqrt(dx2.^2+dy2.^2);hold onplot(t,p);% 回程阶段t=linspace(pi,pi*14/9,1000);s=0.5*h*(1+cos(pi*(t-(t0+ts))/t01));dx3 =-0.5*h*pi/(2*t01)*sin((pi/t01)*(t-(t0+ts))).*cos(t)- sin(t).*(s + s0) - e*cos(t); dy3 =-0.5*h*pi/(2*t01)*sin((pi/t01)*(t-(t0+ts))).*sin(t)+ cos(t).*(s + s0) - e*sin(t); p=sqrt(dx3.^2+dy3.^2);hold onplot(t,p);%近休止阶段t=linspace(pi*14/9,pi*2,1000);s=0;dx4 =- sin(t).*(s + s0) - e*cos(t);dy4 =cos(t).*(s + s0) - e*sin(t);p=sqrt(dx4.^2+dy4.^2);hold onplot(t,p);hold offtitle('曲率半径ρ','FontSize',20);grid on八. 绘制实际轮廓线% 凸轮理论轮廓半径,t表示转角,p表示曲率半径,%dxi表示dx/dφ, dyi表示dy/dφ,i=1,2,3,4h=130; %升程t0=pi*5/6; % 升程角t01=pi*5/9; % 回程角ts=pi/6; %远休止角ts1=pi*4/9; %近休止角e=20; %偏距s0=125;rr=10; %滚子半径% 升程阶段t=linspace(0,pi*5/6,1000);s=h*(t/t0-sin(2*pi*t/t0)/(2*pi));x1=(s0+s).*cos(t)-e*sin(t);y1=(s0+s).*sin(t)+e*cos(t);dx1 =(h/t0-h*cos(2*pi*t/t0)).*cos(t)-(s0+s).*sin(t)- e*cos(t); dy1=(h/t0-h*cos(2*pi*t/t0)).*sin(t)+(s0+s).*cos(t)- e*sin(t);X1=x1-rr*dy1./(sqrt(dx1.^2+dy1.^2));Y1=y1+rr*dx1./(sqrt(dx1.^2+dy1.^2));hold onplot(x1,y1);plot(X1,Y1);% 远休止阶段t=linspace(pi*5/6,pi,1000);s=h;x2=(s+s0).*cos(t)-e*sin(t);y2=(s+s0).*sin(t)+e*cos(t);dx2 =- sin(t).*(s + s0) - e*cos(t);dy2 =cos(t).*(s + s0) - e*sin(t);X2=x2-rr*dy2./(sqrt(dx2.^2+dy2.^2));Y2=y2+rr*dx2./(sqrt(dx2.^2+dy2.^2));hold onplot(x2,y2);plot(X2,Y2);% 回程阶段t=linspace(pi,pi*14/9,1000);s=0.5*h*(1+cos(pi*(t-(t0+ts))/t01));x3=(s+s0).*cos(t)-e*sin(t);y3=(s+s0).*sin(t)+e*cos(t);dx3 =-0.5*h*pi/(2*t01)*sin((pi/t01)*(t-(t0+ts))).*cos(t)- sin(t).*(s + s0) - e*cos(t); dy3 =-0.5*h*pi/(2*t01)*sin((pi/t01)*(t-(t0+ts))).*sin(t)+ cos(t).*(s + s0) - e*sin(t);X3=x3-rr*dy3./(sqrt(dx3.^2+dy3.^2));Y3=y3+rr*dx3./(sqrt(dx3.^2+dy3.^2));hold onplot(x3,y3);plot(X3,Y3);%近休止阶段t=linspace(pi*14/9,pi*2,1000);s=0;x4=(s+s0).*cos(t)-e*sin(t);y4=(s+s0).*sin(t)+e*cos(t);dx4 =- sin(t).*(s + s0) - e*cos(t);dy4 =cos(t).*(s + s0) - e*sin(t);X4=x4-rr*dy4./(sqrt(dx4.^2+dy4.^2));Y4=y4+rr*dx4./(sqrt(dx4.^2+dy4.^2));hold onplot(x4,y4);plot(X4,Y4);hold offgrid ontitle('凸轮实际轮廓线','FontSize',20);。
