2020年版挑战中考数学压轴题详解(115页)

合集下载

2020年中考数学压轴题十大题型(含详细答案)

2020年中考数学压轴题十大题型(含详细答案)函数型综合题：是给定直角坐标系和几何图形，先求函数的解析式，再进行图形的研究，求点的坐标或研究图形的某些性质。

求已知函数的解析式主要方法是待定系数法，关键是求点的坐标，而求点的坐标基本方法是几何法（图形法）和代数法（解析法）。

几何型综合题：是先给定几何图形，根据已知条件进行计算，然后有动点（或动线段）运动，对应产生线段、面积等的变化，求对应的（未知）函数的解析式，求函数的自变量的取值范围，最后根据所求的函数关系进行探索研究。

一般有：在什么条件下图形是等腰三角形、直角三角形，四边形是平行四边形、菱形、梯形等，或探索两个三角形满足什么条件相似等，或探究线段之间的数量、位置关系等，或探索面积之间满足一定关系时求x的值等，或直线（圆）与圆的相切时求自变量的值等。

求未知函数解析式的关键是列出包含自变量和因变量之间的等量关系（即列出含有x、y的方程），变形写成y＝f（x）的形式。

找等量关系的途径在初中主要有利用勾股定理、平行线截得比例线段、三角形相似、面积相等方法。

求函数的自变量的取值范围主要是寻找图形的特殊位置（极端位置）和根据解析式求解。

而最后的探索问题千变万化，但少不了对图形的分析和研究，用几何和代数的方法求出x的值。

解中考压轴题技能：中考压轴题大多是以坐标系为桥梁，运用数形结合思想，通过树立点与数即坐标之间的对应干系，一方面可用代数方法研究几何图形的性子，另一方面又可借助几何直观，得到某些代数问题的解答。

关键是把握几种常用的数学思想方法。

一是运用函数与方程思想。

以直线或抛物线知识为载体，列（解）方程或方程组求其解析式、研究其性质。

二是运用分类讨论的思想。

对问题的条件或结论的多变性进行考察和探究。

三是运用转化的数学的思想。

由已知向未知，由复杂向简单的转换。

中考压轴题它是对考生综合能力的一个全面考察，所涉及的知识面广，所使用的数学思想方法也较全面。

因此，可把压轴题分离为相对独立而又单一的知识或方法组块去思考和探究。

2020-2021备战中考数学——初中数学旋转的综合压轴题专题复习附答案解析

2020-2021备战中考数学——初中数学旋转的综合压轴题专题复习附答案解析一、旋转1．操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．（1）连接AE，求证：△AEF是等腰三角形；猜想与发现：（2）在（1）的条件下，请判断MD、MN的数量关系和位置关系，得出结论．结论1：DM、MN的数量关系是；结论2：DM、MN的位置关系是；拓展与探究：（3）如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．【答案】（1）证明参见解析；（2）相等，垂直；（3）成立，理由参见解析.【解析】试题分析：（1）根据正方形的性质以及等腰直角三角形的知识证明出CE=CF，继而证明出△ABE≌△ADF，得到AE=AF，从而证明出△AEF是等腰三角形；（2）DM、MN的数量关系是相等，利用直角三角形斜边中线等于斜边一半和三角形中位线定理即可得出结论.位置关系是垂直，利用三角形外角性质和等腰三角形两个底角相等性质，及全等三角形对应角相等即可得出结论；（3）成立，连接AE，交MD于点G，标记出各个角，首先证明出MN∥AE，MN=AE，利用三角形全等证出AE=AF，而DM=AF，从而得到DM，MN数量相等的结论，再利用三角形外角性质和三角形全等，等腰三角形性质以及角角之间的数量关系得到∠DMN=∠DGE=90°．从而得到DM、MN的位置关系是垂直.试题解析：（1）∵四边形ABCD是正方形，∴AB=AD=BC=CD，∠B=∠ADF=90°，∵△CEF 是等腰直角三角形，∠C=90°，∴CE=CF，∴BC﹣CE=CD﹣CF，即BE=DF，∴△ABE≌△ADF，∴AE=AF，∴△AEF是等腰三角形；（2）DM、MN的数量关系是相等，DM、MN的位置关系是垂直；∵在Rt△ADF中DM是斜边AF的中线，∴AF=2DM，∵MN 是△AEF的中位线，∴AE=2MN，∵AE=AF，∴DM=MN；∵∠DMF=∠DAF+∠ADM，AM=MD，∵∠FMN=∠FAE，∠DAF=∠BAE，∴∠ADM=∠DAF=∠BAE，∴∠DMN=∠FMN+∠DMF=∠DAF+∠BAE+∠FAE=∠BAD=90°，∴DM⊥MN；（3）（2）中的两个结论还成立，连接AE，交MD于点G，∵点M为AF的中点，点N为EF的中点，∴MN∥AE，MN=AE，由已知得，AB=AD=BC=CD，∠B=∠ADF，CE=CF，又∵BC+CE=CD+CF，即BE=DF，∴△ABE≌△ADF，∴AE=AF，在Rt△ADF中，∵点M为AF的中点，∴DM=AF，∴DM=MN，∵△ABE≌△ADF，∴∠1=∠2，∵AB∥DF，∴∠1=∠3，同理可证：∠2=∠4，∴∠3=∠4，∵DM=AM，∴∠MAD=∠5，∴∠DGE=∠5+∠4=∠MAD+∠3=90°，∵MN∥AE，∴∠DMN=∠DGE=90°，∴DM⊥MN．所以（2）中的两个结论还成立.考点：1.正方形的性质；2.全等三角形的判定与性质；3.三角形中位线定理；4.旋转的性质．2．已知正方形ABCD的边长为4，一个以点A为顶点的45°角绕点A旋转，角的两边分别与BC、DC的延长线交于点E、F，连接EF，设CE＝a，CF＝b．（1）如图1，当a＝42时，求b的值；（2）当a＝4时，在图2中画出相应的图形并求出b的值；（3）如图3，请直接写出∠EAF绕点A旋转的过程中a、b满足的关系式．【答案】（1）422）b＝8；（3）ab＝32．【解析】试题分析：（1）由正方形ABCD的边长为4，可得AC＝2，∠ACB＝45°．再CE＝a＝2∠CAE＝∠AEC，从而可得∠CAF的度数，既而可得 b=AC；（2）通过证明△ACF∽△ECA，即可得；（3）通过证明△ACF∽△ECA，即可得.试题解析：（1）∵正方形ABCD的边长为4，∴AC＝42，∠ACB＝45°．∵CE＝a＝42，∴∠CAE＝∠AEC＝452︒＝22.5°，∴∠CAF＝∠EAF－∠CAE＝22.5°，∴∠AFC＝∠ACD－∠CAF＝22.5°，∴∠CAF＝∠AFC，∴b=AC＝CF＝42；（2）∵∠FAE＝45°，∠ACB＝45°，∴∠FAC＋∠CAE＝45°，∠CAE＋∠AEC＝45°，∴∠FAC ＝∠AEC．又∵∠ACF＝∠ECA＝135°，∴△ACF∽△ECA，∴AC CFEC CA=，∴42442=，∴CF＝8，即b＝8．（3）ab＝32．提示：由（2）知可证△ACF∽△ECA，∴∴AC CFEC CA=，∴4242a=，∴ab＝32．3．已知正方形ABCD 中，E 为对角线BD 上一点，过E 点作EF⊥BD 交BC 于F，连接DF，G 为DF 中点，连接EG，CG.(1) 求证：EG=CG；(2) 将图①中△BEF 绕B 点逆时针旋转 45∘,如图②所示,取DF 中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立，请给出证明；若不成立，请说明理由；(3) 将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).【答案】解：（1）CG=EG（2）（1）中结论没有发生变化，即EG=CG．证明：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．在△DAG与△DCG中，∵ AD=CD，∠ADG=∠CDG，DG=DG，∴△DAG≌△DCG．∴ AG=CG．在△DMG与△FNG中，∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG．∴ MG=NG在矩形AENM中，AM=EN．在Rt△AMG 与Rt△ENG中，∵ AM=EN， MG=NG，∴△AMG≌△ENG．∴ AG=EG∴ EG=CG．（3）（1）中的结论仍然成立．【解析】试题分析：（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG=EG．（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG=CG；再证出△DMG≌△FNG，得到MG=NG；再证明△AMG≌△ENG，得出AG=EG；最后证出CG=EG．（3）结论依然成立．还知道EG⊥CG;试题解析：解：（1）证明：在Rt△FCD中，∵G为DF的中点，∴，同理，在Rt△DEF中，，∴CG=EG；（2）（1）中结论仍然成立，即EG=CG；连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点，如图所示：在△DAG与△DCG中，∵AD=CD，∠ADG=∠CDG，DC=DC，∴△DAG≌△DCG，∴AG=CG，在△DMG与△FNG中，∵∠DGM=∠FGN，DG=FG，∠MDG=∠NFG，∴△DMG≌△FNG，∴MG=NG，在矩形AENM中，AM=EN.，在Rt△AMG与Rt△ENG中，∵AM=EN，MG=NG，∴△AMG≌△ENG，∴AG=EG，∴EG=CG，（3）（1）中的结论仍然成立，即EG=CG且EG⊥CG。

2020年中考数学压轴题-专题10 动点产生的面积关系(解析版)

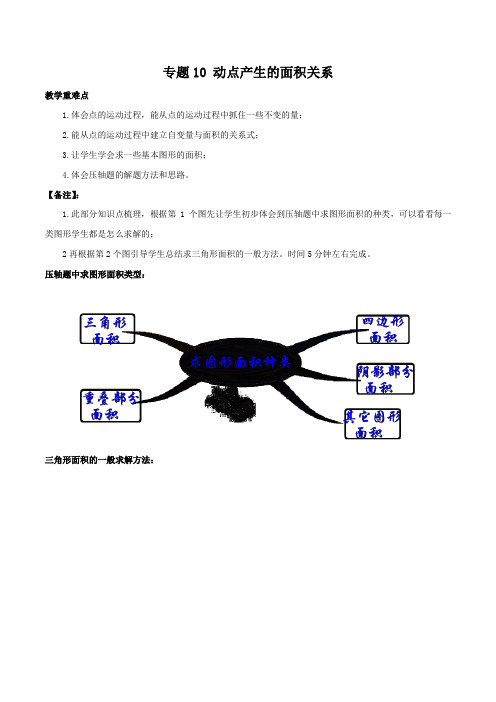
专题10 动点产生的面积关系教学重难点1.体会点的运动过程，能从点的运动过程中抓住一些不变的量；2.能从点的运动过程中建立自变量与面积的关系式；3.让学生学会求一些基本图形的面积；4.体会压轴题的解题方法和思路。

【备注】：1.此部分知识点梳理，根据第1个图先让学生初步体会到压轴题中求图形面积的种类，可以看看每一类图形学生都是怎么求解的；2再根据第2个图引导学生总结求三角形面积的一般方法。

时间5分钟左右完成。

压轴题中求图形面积类型：三角形面积的一般求解方法：【备注】：1.以下每题教法建议，请老师根据学生实际情况参考；2.在讲解时：不宜采用灌输的方法，应采用启发、诱导的策略，并在读题时引导学生发现一些题目中的条件（相等的量、不变的量、隐藏的量等等），使学生在复杂的背景下自己发现、领悟题目的意思；3.可以根据各题的“参考教法”引导学生逐步解题，并采用讲练结合；注意边讲解边让学生计算，加强师生之间的互动性，让学生参与到例题的分析中来；4.例题讲解，可以根据“参考教法”中的问题引导学生分析题目，边讲边让学生书写，每个问题后面有答案提示；5.引导的技巧：直接提醒，问题式引导，类比式引导等等；6.部分例题可以先让学生自己试一试，之后再结合学生做的情况讲评；7.每个题目的讲解时间根据实际情况处理，建议每题7分钟，选讲例题在时间足够的情况下讲解。

例1（2020静安区建承中学一模）在平面直角坐标系xOy 中（如图），已知二次函数2y ax bx c =++（其中a 、b 、c 是常数，且a ≠0）的图像经过点A （0，-3）、B （1，0）、C （3，0），联结AB 、AC ．（1）求这个二次函数的解析式；（2）点D 是线段AC 上的一点，联结BD ，如果:3:2ABD BCD S S ∆∆=，求tan∠DBC 的值；（3）如果点E 在该二次函数图像的对称轴上，当AC 平分∠BAE 时，求点E 的坐标．【整体分析】（1）直接利用待定系数法，把A 、B 、C 三点代入解析式，即可得到答案；（2）过点D 作DH ∠BC 于H ，在∠ABC 中，设AC 边上的高为h ，利用面积的比得到32AD DC =，然后求出DH 和BH ，即可得到答案；（3）延长AE 至x 轴，与x 轴交于点F ，先证明△OAB∠∠OFA ，求出点F 的坐标，然后求出直线AF 的方程，即可求出点E 的坐标. 【详解】解：（1）将A （0，-3）、B （1，0）、C （3，0）代入20y ax bx c a =++≠（）得，03,0934,300a b a b c =+-⎧⎪=+-⎨⎪-=++⎩解得143a b c =-⎧⎪=⎨⎪=-⎩，∴此抛物线的表达式是：243y x x =-+-．（2）过点D 作DH ⊥BC 于H ，在∠ABC中，设AC边上的高为h，则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==，又∠DH//y轴，∴25 CH DC DHOC AC OA===．∵OA=OC=3，则∠ACO=45°，∴△CDH为等腰直角三角形，∴26355 CH DH==⨯=．∴64255 BH BC CH=-=-=．∴tan∠DBC=32 DHBH=.（3）延长AE至x轴，与x轴交于点F，∠OA=OC=3，∴∠OAC=∠OCA=45°，∠∠OAB=∠OAC-∠BAC=45°-∠BAC，∠OFA=∠OCA-∠FAC=45°-∠FAC，∠∠BAC=∠FAC，∴∠OAB=∠OFA ． ∴△OAB∠∠OFA ， ∴13OB OA OA OF ==． ∴OF=9，即F （9，0）；设直线AF 的解析式为y=kx+b （k≠0），可得093k b b =+⎧⎨-=⎩ ，解得133k b ⎧=⎪⎨⎪=-⎩，∴直线AF 的解析式为：133y x =-，将x=2代入直线AF 的解析式得：73y =-，∴E （2，73-）. 【点睛】本题考查了相似三角形的判定和性质，二次函数的性质，求二次函数的解析式，等腰直角三角形的判定和性质，求一次函数的解析式，解题的关键是掌握二次函数的图像和性质，以及正确作出辅助线构造相似三角形.例2..已知9023ABC AB BC AD BC P ∠===°，，，∥，为线段BD 上的动点，点Q 在射线AB 上，且满足PQ AD PC AB =（如图所示）。

圆与射影定理结合型压轴题专题—2024年挑战中考数学压轴题(全国通用)(解析版)

圆与射影定理结合型压轴题专题射影定理模型：射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。

射影定理是数学图形计算的重要定理，在初三各名校的数学和各地中考试题中都多次考查了这一模型的应用。

1.（长沙中考）如图，点P 在以MN 为直径的半圆上运动（点P 不与M ，N 重合），PQ ⊥MN ，NE 平分∠MNP ，交PM 于点E ，交PQ 于点F ．（1）+＝．（2）若PN 2＝PM •MN ，则＝．【解答】解：（1）∵MN 为⊙O的直径，∴∠MPN ＝90°，∵PQ ⊥MN ，∴∠PQN ＝∠MPN ＝90°， ∵NE 平分∠PNM ，∴∠MNE ＝∠PNE ，∴△PEN ∽△QFN ，∴，即①，∵∠PNQ +∠NPQ ＝∠PNQ +∠PMQ ＝90°，∴∠NPQ ＝∠PMQ ，∵∠PQN ＝∠PQM ＝90°， ∴△NPQ ∽△PMQ ，∴②，∴①×②得，∵QF ＝PQ ﹣PF ，∴＝1﹣，∴+＝1，故答案为：1；（2）∵∠PNQ ＝∠MNP ，∠NQP ＝∠NPM ，∴由射影定理得：PN 2＝QN •MN ，∵PN 2＝PM •MN ，∴PM ＝QN ，∴，∵，∴，∴，∴NQ 2＝MQ 2+MQ •NQ ，即，设，则x 2+x ﹣1＝0，解得，x ＝，或x ＝﹣＜0（舍去）．2．（北雅）如图，点P 在以MN 为直径的半圆上运动（不与M 、N 重合），PH MN ⊥于H 点，过N 点作NQ 与PH 平行交MP 的延长线于Q 点．（1）求QPN ∠的度数；（2）求证：QN 与O 相切；（3）若2PN PM MN =⋅，求MHNH的值．【解答】（1）解：MN 是直径，90MPN ∴∠=︒，90QPN ∴∠=︒；（2）证明：PH MN ⊥，90PHM ∴∠=︒，//QN PH ，90QNM PHM ∴∠=∠=︒，ON QN ∴⊥，ON 是半径，QN ∴与O 相切；（3）解：90MNP PNQ ∠+∠=︒，90PNQ Q ∠+∠=︒，MNP Q ∴∠=∠，MPN QPN ∠=∠， NPM QPN ∴∆∆∽，∴PN PMQP PN=，2PN PM QP ∴=⋅，2PN PM MN =⋅，QP MN ∴=，//PH QN ，∴MH MP HN PQ =，∴MH MP HN MN =，同理得，MHP MPN ∆∆∽，∴MP MHMN MP =，HN MP ∴=，设PQ MN a ==，MP b =，∴MH MP HN PQ =，∴a b bb a −=，a ∴（舍)或a =∴MH a b HN b −==． 3．（长沙中考）如图，点A ，B ，C 在O 上运动，满足222AB BC AC =+，延长AC 至点D ，使得DBC CAB ∠=∠，点E 是弦AC 上一动点（不与点A ，C 重合），过点E 作弦AB 的垂线，交AB 于点F ，交BC 的延长线于点N ，交O 于点M （点M 在劣弧AC 上）．（1）BD 是O 的切线吗？请作出你的判断并给出证明；（2）记BDC ∆，ABC ∆，ADB ∆的面积分别为1S ，2S ，S ，若212()S S S ⋅=，求2(tan )D 的值；（3）若O 的半径为1，设FM x =，FE FN y ⋅=，试求y 关于x 的函数解析式，并写出自变量x 的取值范围．【解答】解：（1）BD 是O 的切线．证明：如图，在ABC ∆中，222AB BC AC =+，90ACB ∴∠=︒．又点A ，B ，C 在O 上，AB ∴是O 的直径．90ACB ∠=︒，90CAB ABC ∴∠+∠=︒．又DBC CAB ∠=∠，90DBC ABC ∴∠+∠=︒．90ABD ∴∠=︒．BD ∴是O 的切线．（2）由题意得，112S BC CD =⋅，212S BC AC =⋅，12S AD BC =⋅．212()S S S ⋅=，∴2111()222BC CD AD BC BC AC ⋅⋅⋅=⋅．2CD AD AC ∴⋅=．2()CD CD AC AC ∴+=．又90D DBC ∠+∠=︒，90ABC A ∠+∠=︒，DBC A ∠=∠，D ABC ∴∠=∠．tan tan BC AC D ABC CD BC ∴∠==∠=．2BC CD AC ∴=．又2()CD CD AC AC +=，∴4222BC BC AC AC +=．4224BC AC BC AC ∴+⋅=．241()()AC AC BC BC ∴+=．由题意，设2(tan )D m ∠=，2()AC m BC ∴=．21m m ∴+=．m ∴=0m >，m ∴．2(tan )D ∴∠=（3）设A α∠=，90A ABC ABC DBC ABC N ∠+∠=∠+∠=∠+∠=︒，A DBC N α∴∠=∠=∠=．如图，连接OM ．∴在Rt OFM ∆中，OF ．1BF BO OF ∴=+=1AF OA OF =−=∴在Rt AFE ∆中，tan (1tan EF AF αα=⋅=⋅，cos AF AE α==．在Rt ABC ∆中，sin 2sin BC AB αα=⋅=．(1r =，2AB ∴=．)cos 2cos AC AB αα=⋅=．在Rt BFN ∆中，sin BF BN α=tan BF FN α==y FE FN ∴=⋅2x =2x =2x =21x x =⋅x =．即y x =．FM AB ⊥，FM ∴最大值为F 与O 重合时，即为1．01x ∴<…．综上，y x =，01x <…．4.（长沙中考）如图，四边形ABCD 内接于⊙O ，对角线AC 为⊙O 的直径，过点C 作AC 的垂线交AD 的延长线于点E ，点F 为CE 的中点，连接DB ，DC ，DF ．（1）求∠CDE 的度数；（2）求证：DF 是⊙O 的切线；（3）若AC=2DE ，求tan ∠ABD 的值．解：（1）∵对角线AC 为⊙O 的直径，∴∠ADC ＝90°，∴∠EDC ＝90°；（2）证明：连接DO ，∵∠EDC ＝90°，F 是EC 的中点，∴DF ＝FC ，∴∠FDC ＝∠FCD ，∵OD ＝OC ，∴∠OCD ＝∠ODC ，∵∠OCF ＝90°，∴∠ODF ＝∠ODC+∠FDC ＝∠OCD+∠DCF ＝90°，∴DF 是⊙O 的切线；(3)设DE ＝1，则AC ＝2，由射影定理得：AC 2＝AD ×AE,∴20＝AD （AD +1），∴AD ＝4或﹣5（舍去），∵DC 2＝AC 2﹣AD 2，∴DC ＝2，∴tan ∠ABD ＝tan ∠ACD ＝＝2；5.（青竹湖三模）如图，在Rt △ABC 中，∠ABC ＝90°，D 是AC 的中点，⊙O 经过A 、B 、D 三点， CB 的延长线交⊙O 于点E ．（1）求证：AE ＝CE ；（2）EF 与⊙O 相切于点E ，交AC 的延长线于点F ，若CD ＝CF ＝2cm ，求⊙O 的直径；（3）在（2）的条件下，若CF:CD=n （n ＞0），求sin ∠CAB ．解：（1）证明：连接DE ，∵∠ABC ＝90°∴∠ABE ＝90°∴AE 是⊙O 直径， ∴∠ADE ＝90°∴DE ⊥AC 又∵D 是AC 的中点∴DE 是AC 的垂直平分线∴AE ＝CE ；（2）解：在△ADE 和△EF A 中，∵∠ADE ＝∠AEF ＝90°，由射影定理得：AE 2＝AD ×AF ,∴AE 2＝2×6,∴AE ＝2cm ；（3）解：∵AE 是⊙O 直径，EF 是⊙O 的切线，∵CF:CD=n,令CD=1，则CF=n ，∵∠ADE ＝∠AEF ＝90°，由射影定理得：AE 2＝AD ×AF ，∴AE 2＝1×(n+2)，∴AE ＝=CE ，∵∠CAB ＝∠DEC,∴sin ∠CAB ＝sin ∠DEC ＝＝＝．6.（长郡）如图，AB 为⊙O 的直径，弦CD 与AB 相交于E ，DE ＝EC ，过点B 的切线与AD 的延长线交于F ，过E 作EG ⊥BC 于G ，延长GE 交AD 于H ．（1）求证：AH ＝HD ；（2）若BFBD＝，DF ＝9，求⊙O 的半径．【解答】（1）证明：∵AB 为⊙O 的直径，DE ＝EC ，∴AB ⊥CD ，∴∠C +∠CBE ＝90°，∵EG ⊥BC ， ∴∠C +∠CEG ＝90°，∴∠CBE ＝∠CEG ，∵∠CBE ＝∠CDA ，∠CEG ＝∠DEH ，∴∠CDA ＝∠DEH ， ∴HD ＝EH ，∵∠A +∠ADC ＝90°，∠AEH +∠DEH ＝90°，∴AH ＝EH ，∴AH ＝HD ；（2）解：∵∠BDF ＝90°，BFBD ＝，令BD=4x ，BF=5x ，则222)5(94x x =+）（，∴2=x ，BD=12, 由射影定理得：BD 2＝DF •DA ，∴144＝9×DA ，∴DA=16，又由射影定理得：AB 2＝AF •DA ，∴AB 2＝25×16，∴AB=20,即半径为10.7.如图，AB 是O 的直径，点C 是O 上一点，AD 与过点C 的切线垂直，垂足为D ，直线DC 与AB 的延长线交于点P ，弦CE 平分ACB ∠，交AB 于点F ，连接BE，BE =（1）求证：AC 平分DAB ∠；（2）若5BC =，求阴影部分的面积；（3）若3CD =，求PC 的长度（射影定理）.【解答】（1）证明：连接OC ．∵OA ＝OC ，∴∠OAC ＝∠OCA ．∵PC 是⊙O 的切线，AD ⊥CD ， ∴∠OCP ＝∠D ＝90°，∴OC ∥AD ．∴∠CAD ＝∠OCA ＝∠OAC ．即AC 平分∠DAB ．（2）解：连接AE ．∵∠ACE ＝∠BCE ，∴，∴AE ＝BE ．又∵AB 是直径，∴∠AEB ＝90°．∴AB ＝BE ＝×5＝10，∵OB ＝5，∴BC ＝OB ＝OC ＝5，即△OBC 是等边三角形，∴∠BOC ＝60°，∴OH ＝＝，CH ＝OH ＝，∴S △BOC ＝×5×＝，S 扇形BOC ＝×π×52＝π，∴阴影部分的面积为π﹣；（3）解：过点C 作CH ⊥AB H ，如图：由（2）得：OC ＝OB ＝5，（2）∵AC 平分∠DAB ，CH ⊥AB ，CD ⊥AD ，∴CH ＝CD ＝3，∵∠ACB ＝∠BHC ＝90°，由射影定理得： CH 2＝BH •AH ，设BH ＝x ，AH ＝10-x ，∴32＝x （10﹣x ），解得：x ＝1或9(舍)，又由射影定理得： CH 2＝O H •HP ，∴32＝4HP ，解得：HP ＝．8.（雅礼）如图，已知BC ⊥AC ，圆心O 在AC 上，点M 与点C 分别是AC 与⊙O 的交点，点D 是MB 与⊙O 的交点，点P 是AD 延长线与BC 的交点，且AD •AO ＝AM •AP ．（1）连接OP ，证明：△ADM ∽△APO ；（2）证明：PD 是⊙O 的切线；（3）若AD ＝24，AM ＝MC ，求的值．PA解：（1）证明：连接OD、OP、CD．∵AD•AO＝AM•AP，∴＝，∠A＝∠A，∴△ADM∽△APO．（2）∵△ADM∽△APO，∴∠ADM＝∠APO，∴MD∥PO，∴∠1＝∠4，∠2＝∠3，∵OD＝OM，∴∠3＝∠4，∴∠1＝∠2，∵OP＝OP，OD＝OC，∴△ODP≌△OCP，∴∠ODP＝∠OCP，∵BC⊥AC，∴∠OCP＝90°，∴OD⊥AP，∴PD是⊙O的切线．（2）连接CD．由（1）可知：PC＝PD，∵AM＝MC，∴AM＝2MO＝2R，在Rt△AOD中，OD2+AD2＝OA2，∴R2+242＝9R2，∴R＝6，∴OD＝6，MC＝12，∵＝＝，∴DP＝12，∵O是MC的中点，∴＝＝，∴点P是BC的中点，∴BP＝CP＝DP＝12，∵MC是⊙O的直径，∴∠BDC＝∠CDM＝90°，在Rt△BCM中，∵BC＝2DP＝24，MC＝12，∴BM＝12，由射影定理得：MC2＝MD×MB,∴122＝12×MD，∴MD＝4，∴＝．9.（广益）如图，已知PB与⊙O相切于点B，A是⊙O上的一点，满足P A=PB，连接PO，交AB于E，交⊙O于C，D两点，E在线段OD上，连接AD，OB。

挑战2024年中考数学压轴题之学霸秘笈大揭秘(全国通用)专题02解方程与解不等式篇(原卷版+解析)

专题02 解方程与解不等式1. 解一元一次方程的步骤：①去分母——等式左右两边同时乘分母的最小公倍数。

②去括号。

注意括号前的符号，是否需要变号。

③移项——含有未知数的项移到等号左边，常数移到等号右边。

移动的项一定要变符号。

④合并——利用合并同类项的方法合并。

⑤系数化为1——等式左右两边同时除以系数（或乘上系数的倒数）。

2. 解二元一次方程组的方法：①代入消元法：将其中一个方程的其中一个未知数用另一个未知数表示出来代入另一个方程中，实现消元，进而求出方程组的解的方法叫做代入消元法。

（通常适用于有未知数的系数是±1的方程组） ②加减消元法：当方程组中的两个方程的同一个未知数的系数相同或相反时，则可以利用将两个方程相减或相加的方法消掉这个未知数的方法叫做加减消元法。

3. 解分式方程的步骤：①去分母——分式方程的两边同时乘上分母的最简公分母。

把分式方程化成整式方程。

②解整式方程。

③检验——把解出来的未知数的值带入公分母中检验公分母是否为0。

若公分母不为0，则未知数的值即是原分式方程的解。

若公分母为0，则未知数的值是原分式方程的曾根，原分式方程无解。

4. 解一元二次方程的方法：（1）直接开方法：适用形式：p x =2或()p a x =+2或()p b ax =+2（p 均大于等于0） ①p x =2时，方程的解为：p x p x -==21，。

②()p a x =+2时，方程的解为：a p x a p x --=-=21，。

③()p b ax =+2时，方程的解为：a b p x a b p x --=-=21，。

（2）配方法的具体步骤：①化简——将方程化为一般形式并把二次项系数化为1。

②移项——把常数项移到等号右边。

③配方——两边均加上一次项系数一半的平方得到完全平方式。

④开方——整理式子，利用完全平方式开方降次得到两个一元一次方程。

⑤解一元一次方程即得到一元二次方程的根。

（3）公式法：根的判别式：ac b 42-=∆；求根公式：a ac b b x 242-±-=。

2020年中考数学压轴题(含答案)

2020年中考数学压轴题一、选择题1．如图，平行于x轴的直线与函数y=（k1＞0，x＞0），y=（k2＞0，x＞0）的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点，若△ABC的面积为4，则k1﹣k2的值为（）A．8 B．﹣8 C．4 D．﹣4第1题第2题2．如图，在平面直角坐标系中，已知点A坐标（0,3），点B坐标（4,0），将点O沿直线34y x b=-+对折，点O恰好落在∠OAB的平分线上的O’处，则b的值为（）A.12B.65C.98D.1516二、填空题3．如图，在Rt△ABC中BC＝AC＝4，D是斜边AB上的一个动点，把△ACD沿直线CD折叠，点A落在同一平面内的A′处，当A′D垂直于Rt△ABC的直角边时，AD的长为．第3题第4题4.如图，在正方形ABCD中，AB=4，以B为圆心，BA长为半径画弧，点M为弧上一点，MN ⊥CD 于N ，连接CM ，则CM －MN 的最大值为．三、解答题5.如图，四边形ABCD 是⊙O 的内接四边形，AC 为直径， ⌒ BD ＝ ⌒AD ，DE ⊥BC ，垂足为E ．（1）求证：CD 平分∠ACE ；（2）判断直线ED 与⊙O 的位置关系，并说明理由；（3）若CE =2，AC ＝8，阴影部分的面积为．6．如图，抛物线y ＝ax 2+bx +c （a ＜0，a 、b 、c 为常数）与x 轴交于A 、C 两点，与y 轴交于B 点，A （﹣6，0），C （1，0），B （0，）．（1）求该抛物线的函数关系式与直线AB 的函数关系式；（2）已知点M （m ，0）是线段OA 上的一个动点，过点M 作x 轴的垂线l ，分别与直线AB 和抛物线交于D 、E 两点，当m 为何值时，△BDE 恰好是以DE 为底边的等腰三角形？（3）在（2）问条件下，当△BDE 恰妤是以DE 为底边的等腰三角形时，动点M 相应位置记为点M ′，将OM ′绕原点O 顺时针旋转得到ON （旋转角在0°到90°之间）；i ：探究：线段OB 上是否存在定点P （P 不与O 、B 重合），无论ON 如何旋转，始终保持不变，若存在，试求出P 点坐标：若不存在，请说明理由；ii ：试求出此旋转过程中，（NA +NB ）的最小值．EO CBA【答案与解析】一、选择题1．A2．D二、填空题3．【分析】由等腰直角三角形的性质和勾股定理得出AB＝4，∠B＝∠A′CB＝45°，①如图1，当A′D∥BC，设AD＝x，根据折叠的性质得到∠A′＝∠A＝∠A′CB＝45°，A′D＝AD ＝x，推出A′C⊥AB，求得BH＝BC＝2，DH＝A′D＝x，然后列方程即可得到结果，②如图2，当A′D∥AC，根据折叠的性质得到AD＝A′D，AC＝A′C，∠ACD ＝∠A′CD，根据平行线的性质得到∠A′DC＝∠ACD，于是得到∠A′DC＝∠A′CD，推出A′D＝A′C，于是得到AD＝AC＝2．【解答】解：Rt△ABC中，BC＝AC＝4，∴AB＝4，∠B＝∠A′CB＝45°，①如图1，当A′D∥BC，设AD＝x，∵把△ACD沿直线CD折叠，点A落在同一平面内的A′处，∴∠A′＝∠A＝∠A′CB＝45°，A′D＝AD＝x，∵∠B ＝45°， ∴A ′C ⊥AB ， ∴BH ＝BC ＝2，DH ＝A ′D ＝x ，∴x +x +2＝4，∴x ＝4﹣4， ∴AD ＝4﹣4；②如图2，当A ′D ∥AC ，∵把△ACD 沿直线CD 折叠，点A 落在同一平面内的A ′处， ∴AD ＝A ′D ，AC ＝A ′C ，∠ACD ＝∠A ′CD ， ∵∠A ′DC ＝∠ACD ， ∴∠A ′DC ＝∠A ′CD ， ∴A ′D ＝A ′C ， ∴AD ＝AC ＝4，综上所述：AD 的长为：4﹣4或4．4. 2 三、解答题 5、（1）,BD AD BAD ACD =∴=∠∠°+180ABCD O BAD BCD ∴=四边形内接于圆，∠∠°+180BCD DCE =又∠∠,DCE BAD ∴=∠∠ACD DCE ∴=∠∠即CD 平分∠ACE（2）直线ED 与⊙O 相切。

2020年中考数学压轴题(含答案) (2)

2020年中考数学压轴题一、选择题1．如图，在△ABC中，点D、E、F分别在AB、AC、BC边上，DE∥BC，EF∥AB，则下列比例式中错误的是（）A．B．C．D．第1题第2题2．如图，在平面直角坐标系xOy中，A（﹣3，0），B（3，0），若在直线y＝﹣x+m上存在点P满足∠APB＝60°，则m的取值范围是（）A．≤m≤B．﹣﹣5≤m≤+5C．﹣2≤m≤+2D．﹣﹣2≤m≤+2二、填空题18．如图，点G是矩形ABCD的对角线BD上一点，过点G作EF∥AB交AD于E，交BC 于F，若EG＝5，BF＝2，则图中阴影部分的面积为．第3题第4题24．如图为二次函数y＝ax2+bx+c图象，直线y＝t（t＞0）与抛物线交于A，B两点，A，B 两点横坐标分别为m，n．根据函数图象信息有下列结论：①abc＞0；②若对于t＞0的任意值都有m＜﹣1，则a≥1；③m+n＝1；④m＜﹣1；⑤当t为定值时，若a变大，则线段AB变长．其中，正确的结论有（写出所有正确结论的序号）三、解答题5．如图，已知点A（1，0），B（0，3），将△AOB绕点O逆时针旋转90°，得到△COD，设E为AD的中点．（1）若F为CD上一动点，求出当△DEF与△COD相似时点F的坐标；（2）过E作x轴的垂线l，在直线l上是否存在一点Q，使∠CQO＝∠CDO？若存在，求出Q点的坐标；若不存在，请说明理由．6．如图1，在平面直角坐标系中，直线y＝x+4与抛物线y＝﹣x2+bx+c（b，c是常数）交于A、B两点，点A在x轴上，点B在y轴上．设抛物线与x轴的另一个交点为点C．（1）求该抛物线的解析式；（2）P是抛物线上一动点（不与点A、B重合），①如图2，若点P在直线AB上方，连接OP交AB于点D，求的最大值；②如图3，若点P在x轴的上方，连接PC，以PC为边作正方形CPEF，随着点P的运动，正方形的大小、位置也随之改变．当顶点E或F恰好落在y轴上，直接写出对应的点P的坐标．【答案与解析】一、选择题1．【分析】根据平行线分线段成比例定理列出比例式，再分别对每一项进行判断即可．【解答】A．∵EF∥AB，∴＝，故本选项正确，B．∵DE∥BC，∴＝，∵EF∥AB，∴DE＝BF，∴＝，∴＝，故本选项正确，C．∵EF∥AB，∴＝，∵CF≠DE，∴≠，故本选项错误，D．∵EF∥AB，∴＝，∴＝，故本选项正确，故选：C．2．【分析】作等边三角形ABE，然后作外接圆，求得直线y＝﹣x+m与外接圆相切时的m的值，即可求得m的取值范围．【解答】解：如图，作等边三角形ABE，∵A（﹣3，0），B（3，0），∴OA＝OB＝3，∴E在y轴上，当E在AB上方时，作等边三角形ABE的外接圆⊙Q，设直线y＝﹣x+m与⊙Q相切，切点为P，当P与P1重合时m的值最大，当P与P1重合时，连接QP1，则QP1⊥直线y＝﹣x+m，∵OA＝3，∴OE＝3，设⊙Q的半径为x，则x2＝32+（3﹣x）2，解得x＝2，∴EQ＝AQ＝PQ＝2，∴OQ＝，由直线y＝﹣x+m可知OD＝OC＝m，∴DQ＝m﹣，CD＝m，∵∠ODC＝∠P1DQ，∠COD＝∠QP1D，∴△QP1D∽△COD，∴＝，即＝，解得m＝+2，当E在AB下方时，作等边三角形ABE的外接圆⊙Q，设直线y＝﹣x+m与⊙Q相切，切点为P，当P与P2重合时m的值最小，当P与P2重合时，同理证得m＝﹣﹣2，∴m的取值范围是﹣﹣2≤m≤+2，故选：D．二、填空题3．【分析】由矩形的性质可证明S矩形AEGM＝S矩形CFGN＝2×5＝10，即可求解．【解答】解：作GM⊥AB于M，延长MG交CD于N．则有四边形AEGM，四边形DEGN，四边形CFGN，四边形BMGF都是矩形，∴AE＝BF＝2，S△ADB＝S△DBC，S△BGM＝S△BGF，S△DEG＝S△DNG，∴S矩形AEGM＝S矩形CFGN＝2×5＝10，∴S阴＝S矩形CFGN＝5，故答案为：5．4．【分析】由图象分别求出a＞0，c＝﹣2，b＝﹣a＜0，则函数解析式为y＝ax2﹣ax﹣2，则对称轴x＝，由开口向上的函数的图象开口与a的关系可得：当a变大，函数y＝ax2﹣ax﹣2的开口变小，依据这个性质判断m的取值情况．【解答】解：由图象可知，a＞0，c＝﹣2，∵对称轴x＝﹣＝，∴b＝﹣a＜0，∴abc＞0；∴①正确；A、B两点关于x＝对称，∴m+n＝1，∴③正确；a＞0时，当a变大，函数y＝ax2﹣ax﹣2的开口变小，则AB的距离变小，∴⑤不正确；若m＜﹣1，n＞2，由图象可知n＞1，∴④不正确；当a＝1时，对于t＞0的任意值都有m＜﹣1，当a＞1时，函数开口变小，则有m＞﹣1的时候，∴②不正确；故答案①③．三、解答题5．【分析】（1）当△DEF∽△COD时，＝，DF＝DE cos∠CDO＝，据此求出EF的长度和点F的坐标即可；（2）首先以CD为直径作圆，设其圆心为P，交直线a于点Q、Q′，连接PQ，P Q′，由圆周角定理，可得∠CQO＝∠CQ′O＝∠CDO，在Rt△CDO中，由勾股定理可得CD＝，则PQ＝CD＝；然后求出点P的坐标是多少；设Q（﹣1，a），则（）2+（a﹣）2＝，据此求出a的值是多少，进而求出Q点坐标是多少即可．【解答】解：（1）∵A（1，0），B（0，3），∴OA＝1，OB＝3，∵将△AOB绕点O逆时针旋转90°，得到△COD，∴OC＝1，OD＝3，∴C（0，1），D（﹣3，0），如图1，当△DEF∽△COD时，＝∴EF＝，∴F（﹣1，）；当△DEF∽△COD时，DF＝DE cos∠CDO＝，作FK⊥OD于K，则FK＝DF sin∠CDO＝，DK＝DF cos∠CDO＝，∴F（﹣，）；（2）如图2，以CD为直径作圆，设其圆心为P，交直线a于点Q、Q′，连接PQ，P Q′，由圆周角定理，可得∠CQO＝∠CQ′O＝∠CDO，在Rt△CDO中，由勾股定理可得CD＝，则PQ＝CD＝，又∵P为CD中点，P（﹣，），设Q（﹣1，a），则（）2+（a﹣）2＝，解得a＝2或﹣1，∴Q（﹣1，2）或（﹣1，﹣1）．6．【分析】（1）利用直线解析式求出点A、B的坐标，再利用待定系数法求二次函数解析式解答；（2）作PF∥BO交AB于点F，证△PFD∽△OBD，得比例线段，则PF取最大值时，求得的最大值；（3）（i）点F在y轴上时，P在第一象限或第二象限，如图2，3，过点P作PH⊥x轴于H，根据正方形的性质可证明△CPH≌△FCO，根据全等三角形对应边相等可得PH＝CO＝2，然后利用二次函数解析式求解即可；（ii）点E在y轴上时，过点PK⊥x轴于K，作PS⊥y轴于S，同理可证得△EPS≌△CPK，可得PS＝PK，则P点的横纵坐标互为相反数，可求出P点坐标；点E在y轴上时，过点PM⊥x轴于M，作PN⊥y轴于N，同理可证得△PEN≌△PCM，可得PN＝PM，则P点的横纵坐标相等，可求出P点坐标．由此即可解决问题．【解答】解：（1）直线y＝x+4与坐标轴交于A、B两点，当x＝0时，y＝4，x＝﹣4时，y＝0，∴A（﹣4，0），B（0，4），把A，B两点的坐标代入解析式得，，解得，，∴抛物线的解析式为；（2）如图1，作PF∥BO交AB于点F，∴△PFD∽△OBD，∴，∵OB为定值，∴当PF取最大值时，有最大值，设P（x，），其中﹣4＜x＜0，则F（x，x+4），∴PF＝＝，∵且对称轴是直线x＝﹣2，∴当x＝﹣2时，PF有最大值，此时PF＝2，；（3）∵点C（2，0），∴CO＝2，（i）如图2，点F在y轴上时，若P在第二象限，过点P作PH⊥x轴于H，在正方形CPEF中，CP＝CF，∠PCF＝90°，∵∠PCH+∠OCF＝90°，∠PCH+∠HPC＝90°，∴∠HPC＝∠OCF，在△CPH和△FCO中，，∴△CPH≌△FCO（AAS），∴PH＝CO＝2，∴点P的纵坐标为2，∴，解得，，x＝﹣1+（舍去）．∴，如图3，点F在y轴上时，若P在第一象限，同理可得点P的纵坐标为2，此时P2点坐标为（﹣1+，2）（ii）如图4，点E在y轴上时，过点PK⊥x轴于K，作PS⊥y轴于S，同理可证得△EPS≌△CPK，∴PS＝PK，∴P点的横纵坐标互为相反数，∴，解得x＝2（舍去），x＝﹣2，∴，如图5，点E在y轴上时，过点PM⊥x轴于M，作PN⊥y轴于N，同理可证得△PEN≌△PCM，∴PN＝PM，∴P点的横纵坐标相等，∴，解得，（舍去），∴，综合以上可得P点坐标为，，．。

2020年中考数学压轴题十大题型(含详细答案)

求已知函数的解析式主要方法是待定系数法，关键是求点的坐标，而求点的坐标基本方法是几何法（图形法）和代数法（解析法）。

求未知函数解析式的关键是列出包含自变量和因变量之间的等量关系（即列出含有x、y的方程），变形写成y＝f（x）的形式。

找等量关系的途径在初中主要有利用勾股定理、平行线截得比例线段、三角形相似、面积相等方法。

求函数的自变量的取值范围主要是寻找图形的特殊位置（极端位置）和根据解析式求解。

而最后的探索问题千变万化，但少不了对图形的分析和研究，用几何和代数的方法求出x的值。

解中考压轴题技能：中考压轴题大多是以坐标系为桥梁，运用数形结合思想，通过建立点与数即坐标之间的对应关系，一方面可用代数方法研究几何图形的性质，另一方面又可借助几何直观，得到某些代数问题的解答。

关键是掌握几种常用的数学思想方法。

一是运用函数与方程思想。

以直线或抛物线知识为载体，列（解）方程或方程组求其解析式、研究其性质。

二是运用分类讨论的思想。

对问题的条件或结论的多变性进行考察和探究。

三是运用转化的数学的思想。

由已知向未知，由复杂向简单的转换。

中考压轴题它是对考生综合能力的一个全面考察，所涉及的知识面广，所使用的数学思想方法也较全面。

因此，可把压轴题分离为相对独立而又单一的知识或方法组块去思考和探究。

2020年九年级数学备战中考—中考真题计算压轴题(图形题)含解析

2020年九年级备战中考——中考题型计算压轴题（图形题）1.如图1，在Rt△ABC中，∠ACB=90°，∠B=30°，点M是AB的中点，连接MC，点P是线段BC延长线上一点，且PC<BC，连接MP交AC于点H.将射线MP绕点M逆时针旋转60°交线段CA的延长线于点D.（1）找出与∠AMP相等的角，并说明理由.（2）如图2，CP=12BC，求ADBC的值.（3）在（2）的条件下，若MD=√133，求线段AB的长.2.如图，四边形ABCD是菱形，∠BAD＝120°，点E在射线AC上（不包括点A和点C），过点E的直线GH 交直线AD于点G，交直线BC于点H，且GH∥DC，点F在BC的延长线上，CF＝AG，连接ED，EF，DF.（1）如图1，当点E在线段AC上时，①判断△AEG的形状，并说明理由.②求证：△DEF是等边三角形.（2）如图2，当点E在AC的延长线上时，△DEF是等边三角形吗？如果是，请证明你的结论；如果不是，请说明理由.3.已知，在Rt△ABC中，∠ACB＝90°，D是BC边上一点，连接AD，分别以CD和AD为直角边作Rt△CDE 和Rt△ADF，使∠DCE＝∠ADF＝90°，点E，F在BC下方，连接EF.（1）如图1，当BC＝AC，CE＝CD，DF＝AD时，求证：①∠CAD＝∠CDF，②BD＝EF；（2）如图2，当BC＝2AC，CE＝2CD，DF＝2AD时，猜想BD和EF之间的数量关系？并说明理由. 4.如图，△ABC是等腰直角三角形，∠ACB＝90°，D是射线CB上一点（点D不与点B重合），以AD为斜边作等腰直角三角形ADE（点E和点C在AB的同侧），连接CE.（1）如图①，当点D与点C重合时，直接写出CE与AB的位置关系；（2）如图②，当点D与点C不重合时，（1）的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当∠EAC＝15°时，请直接写出CEAB 的值.5.如图，是具有公共边AB的两个直角三角形，其中，AC=BC，∠ACB=∠ADB=90°.（1）如图1，若延长DA到点E，使AE=BD，连接CD，CE.①求证：CD=CE，CD⊥CE；②求证：AD+BD= √2 CD；（2）若△ABC与△ABD位置如图2所示，请直接写出线段AD，BD，CD的数量关系.6.如图，点E，F分别在正方形ABCD的边CD，BC上，且DE=CF，点P在射线BC上（点P不与点F重合）.将线段EP绕点E顺时针旋转90°得到线段EG，过点E作GD 的垂线QH，垂足为点H，交射线BC于点Q .（1）如图1，若点E是CD的中点，点P在线段BF上，线段BP，QC，EC的数量关系为________.（2）如图2，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立.若成立，请写出证明过程；若不成立，请说明理由.（3）正方形ABCD的边长为6，AB=3DE，QC=1，请直接写出线段BP的长.7.如图，四边形ABCD是正方形，连接AC，将△ABC绕点A逆时针旋转α得△AEF，连接CF，O为CF的中点，连接OE，OD.（1）如图1，当α=45°时，请直接写出OE与OD的关系（不用证明）.（2）如图2，当45°<α<90°时，（1）中的结论是否成立？请说明理由.（3）当α=360°时，若AB=4√2，请直接写出点O经过的路径长.8.如图，在四边形ABCD中，AB//CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE .（1）求证：AE=BC；（2）若AB＝3，CD＝1，求四边形ABCE的面积.9.在Rt△ABC中，∠ACB＝90°，D是△ABC内一点，连接AD，BD.在BD左侧作Rt△BDE，使∠BDE＝90°，以AD和DE为邻边作▱ADEF，连接CD，DF.（1）若AC＝BC，BD＝DE.①如图1，当B，D，F三点共线时，CD与DF之间的数量关系为________.②如图2，当B，D，F三点不共线时，①中的结论是否仍然成立？请说明理由.________（2）若BC＝2AC，BD＝2DE，CDAC =45，且E，C，F三点共线，求AFCE的值.10.已知：在△ABC外分别以AB，AC为边作△AEB与△AFC.（1）如图1，△AEB与△AFC分别是以AB，AC为斜边的等腰直角三角形，连接EF.以EF为直角边构造Rt△EFG，且EF＝FG，连接BG，CG，EC.求证：①△AEF≌△CGF；②四边形BGCE是平行四边形.（2）小明受到图1的启发做了进一步探究：如图2，在△ABC外分别以AB，AC为斜边作Rt△AEB与Rt△AFC，并使∠FAC＝∠EAB＝30°，取BC的中点D，连接DE，EF后发现，两者间存在一定的数量关系且夹角度数一定，请你帮助小明求出EDEF 的值及∠DEF的度数.（3）小颖受到启发也做了探究：如图3，在△ABC外分别以AB，AC为底边作等腰三角形AEB和等腰三角形AFC，并使∠CAF+∠EAB＝90°，取BC的中点D，连接DE，EF后发现，当给定∠EAB＝α时，两者间也存在一定的数量关系且夹角度数一定，若AE＝m，AB＝n，请你帮助小颖用含m，n的代数式直接写出EDEF 的值，并用含α的代数式直接表示∠DEF的度数.11.如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G.（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB＝25，∠CBG＝45°，BC＝4 √2，则▱ABCD的面积是________.12.如图1，ΔABC（12AC<BC<AC）绕点C顺时针旋转得ΔDEC，射线AB交射线DE于点F .（1）∠AFD与∠BCE的关系是________；（2）如图2，当旋转角为60°时，点D，点B与线段AC的中点O恰好在同一直线上，延长DO 至点G，使OG=OD，连接GC .①写出∠AFD与∠GCD的关系，请说明理由；②如图3，连接AE,BE，若∠ACB=45∘，CE=4，求线段AE的长度.13.阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图1，ΔABC中，∠BAC=90∘，点D,E在BC上，AD=AB，AB=kBD（其中√22<k<1）∠ABC=∠ACB+∠BAE，∠EAC的平分线与BC相交于点F，BG⊥AF垂足为G，探究线段BG与AC的数量关系，并证明.同学们经过思考后，交流了自已的想法：小明：“通过观察和度量，发现∠BAE与∠DAC相等.”小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系.”……老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出AH的值.”HC（1）求证：∠BAE=∠DAC；（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；的值（用含k的代数式表示）.（3）直接写出AHHC答案解析部分1.【答案】（1）解： ∠D =∠AMP . 理由如下：∵ ∠ACB =90° ， ∠B =30° ， ∴ ∠BAC =60° . ∴ ∠D +∠DMA =60° .由旋转的性质知， ∠DMA +∠AMP =60° . ∴ ∠D =∠AMP（2）解：如图，过点C 作 CG ∥BA 交MP 于点G.∴ ∠GCP =∠B =30° ， ∠BCG =150° .∵ ∠ACB =90° ，点M 是AB 的中点， ∴ CM =12AB =BM =AM . ∴ ∠MCB =∠B =30° . ∴ ∠MCG =120° .∵ ∠MAD =180°−60°=120° . ∴ ∠MAD =∠MCG .∵ ∠DMG −∠AMG =∠AMC −∠AMG ， ∴ ∠DMA =∠GMC . 在 △MDA 与 △MGC 中， {∠MAD =∠M CGAM =CM∠DMA =∠GMC∴ △MDA ≌△MGC(ASA) . ∴ AD =CG . ∵ CP =12BC . ∴ CP =13BP . ∵ CG ∥BM ，∴ △CGP ∽△BMP . ∴CG BM=CP BP =13 .设 CG =AD =t ，则 BM =3t ， AB =6t . 在 Rt △ABC 中， cos B =BC AB=√32.∴ BC =3√3t .∴AD BC=3√3t=√39（3）解：如图，由（2）知 △CGP ∽△BMP .则 MD =MG =√133.∵ CG ∥MA .∴ ∠CGH =∠AMH . ∵ ∠GHC =∠MHA ， ∴ △GHC ∽△MHA . ∴HG HH=CH AH =CG AM =13 .∴ HG =14MG =14×√133=√1312.∴ MH =√133−√1312=√134 .由（2）知， CG =AD =t ，则 BM =AM =CA =3t . ∴ CH =34t ， AH =94t .∵ ∠MHA =∠DHM ， ∠HMA =∠D . ∴ △MHA ∽△DMH . ∴MH DH=AHMH .∴ MH 2=AH ⋅DH ，即 (√134)2=94t ⋅134t . 解得 t 1=13， t 2=−13（舍去）.∴ AB ＝6t ＝2 .2.【答案】（1）解：①解：△AEG是等边三角形；理由如下： ∵四边形ABCD 是菱形，∠BAD＝120°，∴AD∥BC，AB ＝BC ＝CD ＝AD ，AB∥CD，∠CAD＝ 12∠BAD＝60°， ∴∠BAD+∠ADC＝180°， ∴∠ADC＝60°， ∵GH∥DC，∴∠AGE＝∠ADC＝60°，∴∠AGE＝∠EAG＝∠AEG＝60°， ∴△AEG是等边三角形；②证明：∵△AEG是等边三角形， ∴AG＝AE ， ∵CF＝AG ， ∴AE＝CF ，∵四边形ABCD 是菱形， ∴∠BCD＝∠BAD＝120°， ∴∠DCF＝60°＝∠CAD，在△AED和△CFD中， {AD =CD ∠EAD =∠FCD AE =CF，∴△AED≌△CFD（SAS ） ∴DE＝DF ，∠ADE＝∠CDF， ∵∠ADC＝∠ADE+∠CDE＝60°， ∴∠CDF+∠CDE＝60°，即∠EDF＝60°，∴△DEF是等边三角形（2）解：△DEF是等边三角形；理由如下：同（1）①得：△AEG是等边三角形，∴AG＝AE，∵CF＝AG，∴AE＝CF，∵四边形ABCD是菱形，∴∠BCD＝∠BAD＝120°，∠CAD＝12∠BAD＝60°，∴∠FCD＝60°＝∠CAD，在△AED和△CFD中，{AD=CD∠EAD=∠FCDAE=CF，∴△AED≌△CFD（SAS），∴DE＝DF，∠ADE＝∠CDF，∵∠ADC＝∠ADE﹣∠CDE＝60°，∴∠CDF﹣∠CDE＝60°，即∠EDF＝60°，∴△DEF是等边三角形.3.【答案】（1）证明：①∵∠ACB＝90°，∴∠CAD+∠ADC＝90°，∵∠CDF+∠ADC＝90°，∴∠CAD＝∠CDF；②作FH⊥BC交BC的延长线于H，则四边形FECH为矩形，∴CH＝EF，在△ACD和△DHF中，{∠CAD=∠HDF∠ACD=∠DHF=90°AD=DF ，∴ΔACD≅ΔDHF(AAS)∴DH=AC，∵AC=CB，∴DH=CB，∴DH−CD=CB−CD，即HG=BD，∴BD=EF（2）解：BD=EF，理由如下：作FG⊥BC交BC的延长线于G，则四边形FECG为矩形，∴CG=EF，∵∠CAD=∠GDF，∠ACD=∠DGF=90°，∴ΔACD∽ΔDGF，∴DGAC =DFAD=2，即DG=2AC，GF＝2CD，∵BC＝2AC，CE＝2CD，∴BC＝DG，GF＝CE，∴BD＝CG，∵GF∥CE，GF＝CE，∠G＝90°，∴四边形FECG为矩形，∴CG＝EF，∴BD＝EF.4.【答案】（1）解：当点D与点C重合时，CE∥AB，理由如下：∵△ABC是等腰直角三角形，∴∠CAB＝45°，∵△ADE是等腰直角三角形，∴∠ADE＝45°，∴∠CAB＝∠ADE，∴CE∥AB（2）解：当点D与点C不重合时，（1）的结论仍然成立，理由如下：在AC上截取AF＝CD，连接EF，∵∠AED＝∠ACB＝90°，∴∠EAF＝∠EDC，在△EAF和△EDC中，{AE=ED∠EAF=∠EDC AF=DC ，∴△EAF≌△EDC（SAS），∴EF＝EC，∠AEF＝∠DEC，∵∠AED＝90°，∴∠FEC＝90°，∴∠ECA＝45°，∴∠ECA＝∠CAB，∴CE∥AB；（3）解：如图②，∠EAC＝15°，∴∠CAD＝30°，∴AD＝2CD，AC＝√3CD，∴ FC＝（√3﹣1）CD，∵△CEF为等腰直角三角形，∴ EC＝√22FC＝√6−√22CD，∵△ABC是等腰直角三角形，∴ AB＝√2AC＝√6CD，∴ CEAB √6−√22√63−√36，如图③，∠EAC＝15°，由（2）得，∠EDC＝∠EAC＝15°，∴∠ADC＝30°，∴ CD＝√3AC，AB＝√2AC，延长AC至G，使AG＝CD，∴CG＝AG﹣AC＝DC﹣AC＝√3 AC﹣AC，在△EAG和△EDC中，{AG=DC∠EAG=∠EDC AC=DE ，∴△EAG≌△EDC（SAS），∴EG＝EC，∠AEG＝∠DEC，∴∠CEG＝90°，∴△CEG为等腰直角三角形，∴ EC＝√22CG＝√6−√22AC，∴ CEAB √3−12，综上所述，当∠EAC＝15°时，CEAB 的值为3−√36或√3−12.5.【答案】（1）证明：①在四边形ADBC中，∠DAC+∠DBC+∠ADB+∠ACB=360°，∵∠ADB+∠ACB=180°，∴∠DAC+∠DBC=180°，∵∠EAC+∠DAC=180°，∴∠DBC=∠EAC，∵BD=AE，BC=AC，∴△BCD≌△ACE(SAS)，∴CD=CE，∠BCD=∠ACE，∵∠BCD+∠DCA=90°，∴∠ACE+∠DCA=90°，∴∠DCE=90°，∴CD⊥CE；②∵CD=CE，CD⊥CE，∴△CDE是等腰直角三角形，∴DE= √2 CD，∵DE=AD+AE，AE=BD，∴DE=AD+BD，∴AD+BD= √2 CD（2）解：AD-BD= √2 CD；理由：如图2，在AD上截取AE=BD，连接CE，∵AC=BC，∠ACB=90°，∴∠BAC=∠ABC=45°，∵∠ADB=90°，∴∠CBD=90°-∠BAD-∠ABC=90°-∠BAD-45°=45°-∠BAD，∵∠CAE=∠BAC-∠BAD=45°-∠BAD，∴∠CBD=∠CAE，∵BD=AE，BC=AC，∴△CBD≌△CAE(SAS)，∴CD=CE，∠BCD=∠ACE，∵∠ACE+∠BCE=∠ACB=90°，∴∠BCD+∠BCE=90°，即∠DCE=90°，∴DE= √CD2+CE2 = √2CD2 = √2 CD，∵DE=AD-AE=AD-BD，∴AD-BD= √2 CD.6.【答案】（1）BP+QC=EC（2）解：（1）中的结论仍然成立，理由如下：由题意得：∠PEG=90°，EG=EP，∴∠PEQ +∠GEH =90° ，∵QH ⊥GD ，∴∠H =90° ， ∠G +∠GEH =90° ，∴∠PEQ =∠G ，∵ 四边形 ABCD 是正方形，∴∠DCB =90° ， BC =DC ，∴∠EPQ +∠PEC =90° ，∵∠PEC +∠GED =90° ，∴∠GED =∠EPQ ，在 ΔPEQ 和 ΔEGD 中， {∠EPQ =∠GEDEP =EG ∠PEQ =∠G，∴ΔPEQ ≅ΔEGD(ASA) ，∴PQ =ED ，∴BP +QC =BC −PQ =CD −ED =EC ，即 BP +QC =EC（3）解：分两种情况：①当点 P 在线段 BF 上时，点 Q 在线段 BC 上，由（2）可知： BP =EC −QC ，∵AB =3DE =6 ，∴DE =2 ， EC =4 ，∴BP =4−1=3 ；②当点 P 在射线 FC 上时，点 Q 在线段 BC 的延长线上，如图3所示：同（2）可得： ΔPEQ ≅ΔEGD(AAS) ，∴PQ =ED ，∵BC =DC ， DC =EC +DE ，∴BP =BC +PC =DC +PC =EC +DE +PC =EC +PQ +PC =EC +QC ，∴BP =QC +EC =1+4=5 ；综上所述，线段 BP 的长为3或5.7.【答案】（1）解： OE =OD ， OE ⊥OD ；理由如下：由旋转的性质得： AF =AC ， ∠AFE =∠ACB ，∵四边形ABCD 是正方形，∴ ∠ACB =∠ACD =∠FAC =45° ，∴ ∠ACF =∠AFC =12(180°−45°)=67.5° ，∴ ∠DCF =∠EFC =22.5° ，∵ ∠FEC =90° ，O 为CF 的中点，∴ OE =12CF =OC =OF ，同理： OD =12CF ，∴ OE =OD =OC =OF ，∴ ∠EOC =2∠EFO =45° ， ∠DOF =2∠DCO =45° ，∴ ∠DOE =180°−45°−45°=90° ，∴ OE ⊥OD（2）解：当 45°<α<90° 时，（1）中的结论成立，理由如下：延长EO 到点M ，使 OM =EO ，连接DM 、CM 、DE ，如图2所示：∵O为CF 的中点，∴ OC =OF ，在 △COM 和 △FOE 中， {OM =OE∠COM =∠FOE OC =OF，∴ △COM ≌ △FOE （SAS ），∴ ∠MCF =∠EFC ， CM =EF .∵四边形ABCD 是正方形，∴ AB =BC =CD ， ∠BAC =∠BCA =45° ，∵ ΔABC 绕点A 逆时针旋转α得 ΔAEF ，∴ AB =AE =EF =CD ， AC =AF ，∴ CD =CM ， ∠ACF =∠AFC ，∵ ∠ACF =∠ACD +∠FCD ， ∠AFC =∠AFE +∠CFE ， ∠ACD =∠AFE =45° ，∴ ∠FCD =∠CFE =∠MCF ，∵ ∠EAC +∠DAE =45° ， ∠FAD +∠DAE =45° ，∴ ∠EAC =∠FAD ，在 △ACF 中，∵ ∠ACF +∠AFC +∠CAF =180° ，∴ ∠DAE +2∠FAD +∠DCM +90°=180° ，∵ ∠FAD +∠DAE =45° ，∴ ∠FAD +∠DCM =45° ，∴ ∠DAE =∠DCM ，在 △ADE 和 △CDM 中， {AE =CM∠DAE =∠DCM AD =CD ，∴ △ADE ≌ △CDM （SAS ），∴ DE =DM ，∵ OE =OM ，∴ OE ⊥OD ，在 △COM 和 △COD 中， {CM =CD∠MCF =∠FCD OC =OC ，∴ △COM ≌ △COD （SAS ），∴ OM =OD .∴ OE =OD ，∴ OE =OD ， OE ⊥OD（3）解：连接AO ，如图3所示：∵ AC=AF，CO=OF，∴ AO⊥CF，∴ ∠AOC=90°，∴点O在以AC为直径的圆上运动，∵ α=360°，∴点O经过的路径长等于以AC为直径的圆的周长，∵ AC=√2AB=√2×4√2=8，∴点O经过的路径长为：πd=8π .8.【答案】（1）证明：∵AB//CD，∠B＝45°∴∠C+∠B＝180°∴∠C＝135°∵DE＝DA，AD⊥CD∴∠E＝45°∵∠E+∠C＝180°∴AE//BC，且AB//CD∴四边形ABCE是平行四边形∴AE＝BC（2）解：∵四边形ABCE是平行四边形∴AB＝CE＝3∴AD＝DE＝AB−CD＝2∴四边形ABCE的面积＝3×2＝69.【答案】（1）DF＝√2 CD.；结论仍然成立.理由：如图2中，连接CF.延长BD交AF的延长线于H，设AC交BH于G.∵四边形AFED是平行四边形，∴AF＝DE，DE∥AF，∵BD＝DE，∴AF＝BD，∵∠BDE＝90°，∴∠DEH＝∠DHA＝90°＝∠BCG，∵∠CGB＝∠AGH，∴∠CBD＝∠CAF，∵BC＝AC，∴△BCD≌△ACF（SAS），∴∠BCD＝∠ACF，CD＝CF，∴∠BCA＝∠DCF＝90°，∴△CDF是等腰直角三角形，∴DF＝√2 CD（2）解：如图3中，延长BD交AF于H.设BH交AC于G.∵四边形AFED是平行四边形，∴AF＝DE，DE∥AF，∵∠BDE＝90°，∴∠DEH＝∠DHA＝90°＝∠BCG，∵∠CGB＝∠AGH，∴∠CBD＝∠CAF，∵ BDDE =BCAC=2，∴ BDAF =BCAC，∴△CBD∽△CAF，∴ CDCF =BCAC=2，∠BCD＝∠ACF，∴∠BCA＝∠DCF＝90°，∵AD∥EF，∴∠ADC+∠DCF＝180°，∴∠ADC＝90°，∵CD：AC＝4：5，设CD＝4k，AC＝5k，则AD＝EF＝3k，∴CF＝12CD＝2k，∴EC＝EF﹣CF＝k，∴DE＝AF＝√CD2+EC2=√(4k)2+k2=√17k，∴ AFCE =√17kk=√17 .10.【答案】（1）解：证明：①如图1中，∵△EFC与△AFC都是等腰直角三角形，∴FA＝FC，FE＝FG，∠AFC＝∠EFG＝90°，∴∠AFE＝∠CFG，∴△AFE≌△CFG（SAS）.②∵△AFE≌△CFG，∴AE＝CG，∠AEF＝∠CGF，∵△AEB是等腰直角三角形，∴AE＝BE，∠BEA＝90°，∴CG＝BE，∵△EFG是等腰直角三角形，∴∠FEG＝∠FGE＝45°，∴∠AEF+∠BEG＝45°，∵∠CGE+∠CGF＝45°，∴∠BEG＝∠CGE，∴BE∥CG，∴四边形BECG是平行四边形（2）解：如图2中，延长ED到G，使得DG＝ED，连接CG，FG.∵点D是BC的中点，∴BD＝CD，∵∠EDB＝∠GDC，∴EB＝GC，∠EBD＝∠GCD，在Rt△AEB与Rt△AFC中，∵∠EAB＝∠FAC＝30°，∴ EBAE =√33，FCAF=√33，∴ CGAE =FCAF，∵∠EBD＝∠2+60°，∴∠DCG＝∠2+60°，∴∠GCF＝360°﹣60°﹣（∠2+60°）﹣∠3＝360°﹣120°﹣（∠2+∠3）＝360°﹣120°﹣（180°﹣∠1）＝60°+∠1，∵∠EAF＝30°+∠1+30°＝60°+∠1，∴∠GCF＝∠EAF，∴△CGF∽△AEF，∴ FG FE =FC FA =√33 ，∠CFG＝∠AFE，∴∠EFG＝∠CFG+∠EFC＝∠AFE+∠EFC＝90°，∴tan∠DEF＝ FG FE =√33 ，∴∠DEF＝30°，∴FG＝ 12 EG ，∵ED＝ 12 EG ，∴ED＝FG ，∴ ED EF =√33（3）解：如图3中，延长ED 到G ，使得DG ＝ED ，连接CG ，FG.作EH⊥AB于H ，连接FD.∵BD＝DC ，∠BDE＝∠CDG，DE ＝DG ，∴△CDG≌△BDE（SAS ），∴CG＝BE ＝AE ，∠DCG＝∠DBE＝α+∠ABC，∵∠GCF＝360°﹣∠DCG﹣∠ACB﹣∠ACF＝360°﹣（α+∠ABC）﹣∠ACB﹣（90°﹣α）＝270°﹣（∠ABC+∠ACB）＝270°﹣（180°﹣∠BAC）＝90°+∠BAC＝∠EAF，∴△EAF≌△GCF（SAS ），∴EF＝GF ，∠AFE＝∠CFG，∴∠AFC＝∠EFC，∴∠DEF＝∠CAF＝90°﹣α，∵∠AEH＝90°﹣α，∴∠AEH＝∠DEF，∵AE＝m ，AH ＝ 12 AB ＝ 12 n ，∴EH＝ √AE 2−AH 2=√m 2−14n 2=√4m 2−n 22 ，∵D E ＝DG ，EF ＝GF ，∴DF⊥EG，cos∠DEF=cos∠AEH=EHAE =√4m2−n22m=√4m2−n22m.11.【答案】（1）证明：∵AE＝CF，∴AE+EF＝CF+EF，即AF＝CE，∵DF∥BE，∴∠DFA＝∠BEC，∵DF＝BE，∴△ADF≌△CBE（SAS），∴AD＝CB，∠DAF＝∠BCE，∴AD∥CB，∴四边形ABCD是平行四边形；（2）24.12.【答案】（1）∠AFD=∠BCE（2）解：① ∠AFD=12∠GCD或∠AFD+∠GCD=180°，理由：如图2，连接AD，由旋转知，∠CAB=∠CDE，CA=CD，∠ACD=60°，∴ ΔACD是等边三角形，∴ AD=CD，∵ ∠AMC=∠DMF，∴ ΔACM∽ ΔDFM，∴ ∠ACD=∠AFD，∵ O是AC的中点，∴ AO=CO，∵ OD=OG，∠AOD=∠COG，∴ ΔAOD≌ ΔCOG（SAS），∴ AD=CG，∴ CG=CD，∴ ∠GCD=2∠ACD=120°，∴ ∠AFD=12∠GCD或∠AFD+∠GCD=180°，故答案为：∠AFD=12∠GCD或∠AFD+∠GCD=180°；②由①知，∠GCD=120°，∠ACD=∠BCE=60°，∴ ∠GCA=∠GCD−∠ACD=60°，∴ ∠GCB=∠BCE，∵ ∠GCB=∠GCA+∠ACB，∠ACE=∠BCE+∠ACB，∴ ∠GCB=∠ACE，由①知，CG=CD,CD=CA，∴ CG=CA，∵ BC=EC=4，∴ △GCB≅△ACE(SAS)，∴ BC=CE=4，∴ GB=AE，∵ CG=CD,OG=OD，∴ CO⊥GD，∴ ∠COG=∠COB=90°在RtΔBOC中，BO=BC⋅sin∠ACB=2√2，CO=BC⋅cos∠ACB=2√2，在RtΔGOC中，GO=CO•tan∠GCA=2√6，∴ GB=CO+BO=2√6+2√2，∴ AE=2√6+2√2 .13.【答案】（1）证明：∵ AB=AD∴ ∠ABD=∠ADB∵ ∠ADB=∠ACB+∠DAC , ∠ABD=∠ABC=∠ACB+∠BAE∴ ∠BAE=∠DAC（2）解：设∠DAC=α=∠BAE，∠C=β∴ ∠ABC=∠ADB=α+β∵ ∠ABC+∠C=α+β+β=α+2β=90∘，∠BAE+∠EAC=90∘=α+∠EAC ∴ ∠EAC=2β∵ AF平分∠EAC∴ ∠FAC=∠EAF=β∴ ∠FAC=∠C，∠ABE=∠BAF=α+β∴ ∠ABE=∠BAF=α+β∴ AF=12BC=BF∵ ∠ABE=∠BAF，∠BGA=∠BAC=90∘∴ ΔABG∽ ΔBCA∴ BGAC =ABBC∵ ∠ABE=∠BAF，∠ABE=∠AFB ∴ ΔAFB∽ ΔBAD∴ ABBD =BFAB，且AB=kBD，AF=12BC=BF∴ k=BC2AB ，即ABBC=12k∴ BGAC =12k（3）解：∵ ∠ABE=∠BAF，∠BAC=∠AGB=90∘∴ ∠ABH=∠C，且∠BAC=∠BAC∴ ΔABH∽ ΔACB∴ ABAC =AHAB∴ AB2=AC×AH设BD=m,AB=km，∵ ABBC =12k∴ BC=2k2m∴ AC=√BC2−AB2=km√4k2−1∴ AB2=AC×AH(km)2=km√4k2−1×AH∴ AH=√4k2−1∴ HC=AC−AH=km√4k2−1√4k2−1=2√4k2−1∴ AHCH =14k2−2。

2020年中考数学压轴题限时专训2(含解析)

2020年中考数学压轴题限时专训2一、选择题（共6题）1．已知函数y＝ax2+bx+c的图象的一部分如图所示，则a+b+c取值范围是（）A．﹣2＜a+b+c＜0 B．﹣2＜a+b+c＜2 C．0＜a+b+c＜2 D．a+b+c＜22．如图所示，矩形OABC中，OA＝2OC，D是对角线OB上的一点，OD＝OB，E是边AB上的一点．AE＝AB，反比例函数y＝（x＞0）的图象经过D，E两点，交BC于点F，AC与OB交于点M．EF与OB交于点G，且四边形BFDE的面积为．下列结论：①EF∥AC；②k＝2；③矩形OABC的面积为；④点F的坐标为（，）正确结论的个数为（）A．1个B．2个C．3个D．4个3．如图，平面直角坐标系中，A（﹣8，0），B（﹣8，4），C（0，4），反比例函数y＝的图象分别与线段AB，BC交于点D，E，连接DE．若点B关于DE的对称点恰好在OA 上，则k＝（）A．﹣20 B．﹣16 C．﹣12 D．﹣84．如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E．将△BDE沿直线DE折叠，得到△B′DE，若B′D，B′E分别交AC于点F，G，连接OF，OG，则下列判断错误的是（）A．△ADF≌△CGEB．△B′FG的周长是一个定值C．四边形FOEC的面积是一个定值D．四边形OGB'F的面积是一个定值5．如图，△ABC中，AB＝AC＝2，∠B＝30°，△ABC绕点A逆时针旋转α（0°＜α＜120°）得到△AB′C′，B′C′与BC，AC分别交于点D，E．设CD+DE＝x，△AEC′的面积为y，则y与x的函数图象大致（）A．B．C．D．6．如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2＝8．若将⊙O1绕点P按顺时针方向旋转360°，在旋转过程中，⊙O1与正方形ABCD的边只有一个公共点的情况一共出现（）A．3次B．5次C．6次D．7次二、填空题（共6题）1．如图，二次函数y＝（x+2）2+m的图象与y轴交于点C，与x轴的一个交点为A（﹣1，0），点B在抛物线上，且与点C关于抛物线的对称轴对称．已知一次函数y＝kx+b的图象经过A，B两点，根据图象，则满足不等式（x+2）2+m≤kx+b的x的取值范围是．2．如图，AE=4，以AE为直径作⊙O，点B是直径AE上的一动点，以AB为边在AE的上方作正方形ABCD，取CD的中点M，将△ADM沿直线AM对折，当点D的对应点D´落在⊙O上时，BE的长为.3．如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A 旋转，当∠ABF最大时，S△ADE＝．第3题第4题4．如图，△ABC中，∠C＝90°，AC＝3，AB＝5，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为．5．如图所示，菱形ABCD的对角线AC、BD相交于点O．若AC＝6，BD＝8，AE⊥BC，垂足为E，则AE的长为．第5题第6题6．如图，AB是⊙O的直径，弦BC＝2cm，∠ABC＝60°．若动点P以2cm/s的速度从BEAO BD CMD´点出发沿着B→A的方向运动，点Q以1cm/s的速度从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t（s），当△APQ是直角三角形时，t的值为．三、解答题（共6题）1．在平面直角坐标系xOy中，有不重合的两个点Q（x1，y1）与P（x2，y2）．若Q，P为某个直角三角形的两个锐角顶点，且该直角三角形的直角边均与x轴或y轴平行（或重合），则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“折距”，记做D PQ．特别地，当PQ与某条坐标轴平行（或重合）时，线段PQ的长即点Q与点P 之间的“折距”．例如，在图1中，点P（1，﹣1），点Q（3，﹣2），此时点Q与点P之间的“折距”D PQ＝3．（1）①已知O为坐标原点，点A（3，﹣2），B（﹣1，0），则D AO＝，D BO＝．②点C在直线y＝﹣x+4上，请你求出D CO的最小值．（2）点E是以原点O为圆心，1为半径的圆上的一个动点，点F是直线y＝3x+6上以动点．请你直接写出点E与点F之间“折距”D EF的最小值．2．如图1，在矩形ABCD中，AB＝4，BC＝5，点E在AD上，ED＝3．动点P从点B出发沿BC方向以每秒3个单位的速度向点C运动，过点P作PF∥CE，与边BA交于点F，过点F作FG∥BC，与CE交于点G，当点F与点A重合时，点P停止运动，设点P运动的时间为t秒．（1）用含t的代数式分别表示线段BF和PF的长度，则有BF＝，PF＝．（2）如图2，作点D关于CE的对称点D′，当FG恰好过点D′时，求t的值．（3）如图3，作△FGP的外接圆⊙O，当点P在运动过程中．①当外接圆⊙O与四边形ABCE的边BC或CE相切时，请求出符合要求的t的值；②当外接圆⊙O的圆心O落在△FGP的内部（不包括边上）时，直接写出t的取值范围．3．如图，矩形ABCD，AB＝2，BC＝10，点E为AD上一点，且AE＝AB，点F从点E出发，向终点D运动，速度为1cm/s，以BF为斜边在BF上方作等腰直角△BFG，以BG，BF为邻边作▱BFHG，连接AG．设点F的运动时间为t秒．（1）试说明：△ABG∽△EBF；（2）当点H落在直线CD上时，求t的值；（3）点F从E运动到D的过程中，直接写出HC的最小值．4．已知，如图，二次函数y＝ax2+2ax﹣3a（a＞0）图象的顶点为C与x轴交于A、B两点（点A在点B左侧），点C、B关于过点A的直线l：y＝kx﹣对称．（1）求A、B两点坐标及直线l的解析式；（2）求二次函数解析式；（3）如图2，过点B作直线BD∥AC交直线l于D点，M、N分别为直线AC和直线l 上的两动点，连接CN，NM、MD，求D的坐标并直接写出CN+NM+MD的最小值．5．如图1，已知在平面直角坐标系xOy中，四边形OABC是矩形，点A，C分别在x轴和y 轴的正半轴上，连结AC，OA＝3，∠OAC＝30°，点D是BC的中点，（1）OC＝：点D的坐标为（2）若点E在线段0A上，直线DE把矩形OABC面积分成为2：1，求点E坐标；（3）如图2，点P为线段AB上一动点（与A、B重合），连接DP；①将△DBP沿DP所在的直线翻折，若点B恰好落在AC上，求此时BP的长；②以线段DP为边，在DP所在直线的右上方作等边△DPQ，当动点P从点B运动到点A 时，点Q也随之运动，请直接写出点Q运动路径的长．6．如图，抛物线y＝ax2+bx+4交x轴于A（﹣1，0）、B（3，0）两点，交y轴于点C，连接BC．（1）求抛物线的解析式；（2）点P是抛物线上一点，设P点的横坐标为m．①当点P在第一象限时，过点P作PD⊥x轴，交BC于点D，过点D作DE⊥y轴，垂足为E，连接PE，当△PDE和△BOC相似时，求点P的坐标；②请直接写出使∠PBA＝∠ABC的点P的坐标．【答案与解析】一、选择题1．【分析】函数y＝ax2+bx+c的图象开口向下可知a小于0，由于抛物线顶点在第一象限即抛物线对称轴在y轴右侧，当x＝1时，抛物线的值必大于0由此可求出a的取值范围，将a+b+c用a表示出即可得出答案．【解答】解：由图象可知：a＜0，图象过点（0，1），所以c＝1，图象过点（﹣1，0），则a﹣b+1＝0，当x＝1时，应有y＞0，则a+b+1＞0，将a﹣b+1＝0代入，可得a+（a+1）+1＞0，解得a＞﹣1，所以，实数a的取值范围为﹣1＜a＜0．又a+b+c＝2a+2，∴0＜a+b+c＜2．故选：C．2．【分析】设E（a，b），F（m，n），则a＝OA＝BC，b＝AE，CF＝m，n＝CO＝AB，证明＝即可判断①；表示出D和E的坐标，根据系数k的几何意义求得k的值即可判断②；求得B的坐标，求得矩形OABC的面积即可判断③；求得F的坐标即可判断④．【解答】解：设E（a，b），F（m，n），则a＝OA＝BC，b＝AE，CF＝m，n＝CO＝AB，∴B（a，n），∵E，F在反比例函数y＝上，∴ab＝mn，∴BC•AE＝CF•AB，∴＝，∴EF∥AC，故①正确；∵OD＝OB，AE＝AB，∴D（a，n），E（a，n），∵OA＝2OC，∴a＝2n，∴B（2n，n），D（n，n），E（2n，n），∵反比例函数y＝经过点F，E，∴k＝mn＝2n•n，∴m＝n，∴F（n，n），∴BF＝2n﹣n＝n，BE＝n，∵四边形BFDE的面积＝S△BDF+S△BDE＝，∴×n×（n﹣n）+×n×（2n﹣n）＝，解得n＝，∴E（3，），F（，）∴k＝3×＝2，故②④正确；∵B（3，），∴矩形OABC的面积为，故③正确；故选：A．3．【分析】根据A（﹣8，0），B（﹣8，4），C（0，4），可得矩形的长和宽，易知点D的横坐标，E的纵坐标，由反比例函数的关系式，可用含有k的代数式表示出点D的纵坐标和点E的横坐标，由三角形相似和对称，可求出AF的长，然后把问题转化到三角形ADF 中，由勾股定理建立方程求出k的值．【解答】解：过点E作EG⊥OA，垂足为G，设点B关于DE的对称点为F，连接DF、EF、BF，如图所示：则△BDE≌△FDE，∴BD＝FD，BE＝FE，∠DFE＝∠DBE＝90°易证△ADF∽△GFE∴，∴AF：EG＝BD：BE，∵A（﹣8，0），B（﹣8，4），C（0，4），∴AB＝OC＝EG＝4，OA＝BC＝8，∵D、E在反比例函数y＝的图象上，∴E（，4）、D（﹣8，）∴OG＝EC＝，AD＝﹣，∴BD＝4+，BE＝8+∴，∴AF＝，在Rt△ADF中，由勾股定理：AD2+AF2＝DF2即：（﹣）2+22＝（4+）2解得：k＝﹣12故选：C．4．【分析】A、根据等边三角形ABC的内心的性质可知：AO平分∠BAC，根据角平分线的定理和逆定理得：FO平分∠DFG，由外角的性质可证明∠DOF＝60°，同理可得∠EOG ＝60°，∠FOG＝60°＝∠DOF＝∠EOG，可证明△DOF≌△GOF≌△GOE，△OAD≌△OCG，△OAF≌△OCE，可得AD＝CG，AF＝CE，从而得△ADF≌△CGE；B、根据△DOF≌△GOF≌△GOE，得DF＝GF＝GE，所以△ADF≌△B'GF≌△CGE，可得结论；C、根据S四边形FOEC＝S△OCF+S△OCE，依次换成面积相等的三角形，可得结论为：S△AOC＝（定值），可作判断；D、方法同C，将S四边形OGB'F＝S△OAC﹣S△OFG，根据S△OFG＝•FG•OH，FG变化，故△OFG的面积变化，从而四边形OGB'F的面积也变化，可作判断．【解答】解：A、连接OA、OC，∵点O是等边三角形ABC的内心，∴AO平分∠BAC，∴点O到AB、AC的距离相等，由折叠得：DO平分∠BDB'，∴点O到AB、DB'的距离相等，∴点O到DB'、AC的距离相等，∴FO平分∠DFG，∠DFO＝∠OFG＝（∠F AD+∠ADF），由折叠得：∠BDE＝∠ODF＝（∠DAF+∠AFD），∴∠OFD+∠ODF＝（∠F AD+∠ADF+∠DAF+∠AFD）＝120°，∴∠DOF＝60°，同理可得∠EOG＝60°，∴∠FOG＝60°＝∠DOF＝∠EOG，∴△DOF≌△GOF≌△GOE，∴OD＝OG，OE＝OF，∠OGF＝∠ODF＝∠ODB，∠OFG＝∠OEG＝∠OEB，∴△OAD≌△OCG，△OAF≌△OCE，∴AD＝CG，AF＝CE，∴△ADF≌△CGE，故选项A正确；B、∵△DOF≌△GOF≌△GOE，∴DF＝GF＝GE，∴△ADF≌△B'GF≌△CGE，∴B'G＝AD，∴△B'FG的周长＝FG+B'F+B'G＝FG+AF+CG＝AC（定值），故选项B正确；C、S四边形FOEC＝S△OCF+S△OCE＝S△OCF+S△OAF＝S△AOC＝（定值），故选项C正确；D、S四边形OGB'F＝S△OFG+S△B'GF＝S△OFD+S△ADF＝S四边形OF AD＝S△OAD+S△OAF＝S△OCG+S△OAF＝S△OAC﹣S△OFG，过O作OH⊥AC于H，∴S△OFG＝•FG•OH，由于OH是定值，FG变化，故△OFG的面积变化，从而四边形OGB'F的面积也变化，故选项D不一定正确；故选：D．5．【分析】可证△ABF≌△AC′E（AAS）、△CDE≌△B′DF（AAS），则B′D+DE＝CD+ED ＝x，y＝EC′×△AEC′的EC′边上的高，即可求解．【解答】解：∵△ABC绕点A逆时针旋转α，设AB′与BC交于点F，则∠BAB′＝∠CAC′＝α，∠B＝∠C′＝30°，AB＝AC＝AC′，∴△ABF≌△AC′E（AAS），∴BF＝C′E，AE＝AF，同理△CDE≌△B′DF（AAS），∴B′D＝CD，∴B′D+DE＝CD+ED＝x，AB＝AC＝2，∠B＝30°，则△ABC的高为1，等于△AEC′的高，BC＝2＝B′C′，y＝EC′×△AEC′的EC′边上的高＝（2）＝﹣x+，故选：B．6．【分析】根据⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，设O1O2交圆O于M，求出PM＝4，得出圆O1与以P为圆心，以4为半径的圆相外切，即可得到答案．【解答】解：∵⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，设O1O2交圆O于M，∴PM＝8﹣3﹣1＝4，圆O1与以P为圆心，以4为半径的圆相外切，∴根据图形得出有5次．故选：B．二、填空题1．【分析】将点A代入抛物线中可求m＝﹣1，则可求抛物线的解析式为y＝x2+4x+3，对称轴为x＝﹣2，则满足（x+2）2+m≤kx+b的x的取值范围为﹣4≤x≤﹣1．【解答】解：抛物线y＝（x+2）2+m经过点A（﹣1，0），∴m＝﹣1，∴抛物线解析式为y＝x2+4x+3，∴点C坐标（0，3），∴对称轴为x＝﹣2，∵B与C关于对称轴对称，点B坐标（﹣4，3），∴满足（x+2）2+m≤kx+b的x的取值范围为﹣4≤x≤﹣1，故答案为﹣4≤x≤﹣1．2.3．【分析】作DH⊥AE于H，如图，由于AF＝4，则△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，当BF为此圆的切线时，∠ABF最大，即BF⊥AF，利用勾股定理计算出BF＝3，接着证明△ADH≌△ABF得到DH＝BF＝3，然后根据三角形面积公式求解．【解答】解：作DH⊥AE于H，如图，∵AF＝4，当△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，∴当BF为此圆的切线时，∠ABF最大，即BF⊥AF，在Rt△ABF中，BF＝＝3，∵∠EAF＝90°，∴∠BAF+∠BAH＝90°，∵∠DAH+∠BAH＝90°，∴∠DAH＝∠BAF，在△ADH和△ABF中，∴△ADH≌△ABF（AAS），∴DH＝BF＝3，∴S△ADE＝AE•DH＝×3×4＝6．故答案为6．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．4．【分析】过点O作OE⊥AB于点E，OF⊥BC于点F．根据切线的性质，知OE、OF是⊙O 的半径；然后由三角形的面积间的关系（S△ABO+S△BOD＝S△ABD＝S△ACD）列出关于圆的半径的等式，求得圆的半径即可．【解答】解：过点O作OE⊥AB于点E，OF⊥BC于点F．∵AB、BC是⊙O的切线，∴点E、F是切点，∴OE、OF是⊙O的半径；∴OE＝OF；在△ABC中，∠C＝90°，AC＝3，AB＝5，∴由勾股定理，得BC＝4；又∵D是BC边的中点，∴S△ABD＝S△ACD，又∵S△ABD＝S△ABO+S△BOD，∴AB•OE+BD•OF＝CD•AC，即5×OE+2×OE＝2×3，解得OE＝，∴⊙O的半径是．故答案为：．5．【分析】利用菱形的面积公式：•AC•BD＝BC•AE，即可解决问题；【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，OA＝OC＝3，OB＝OD＝4，∴AB＝BC＝5，∵•AC•BD＝BC•AE，∴AE＝，故答案为：，6．【分析】应分两种情况进行讨论：①当PQ⊥AC时，△APQ为直角三角形，根据△APQ ∽△ABC，可将时间t求出；②当PQ⊥AB时，△APQ为直角三角形，根据△APQ∽△ACB，可将时间t求出．【解答】解：∵AB是直径，∴∠C＝90°，又∵BC＝2cm，∠ABC＝60°，∴AB＝2BC＝4，AC＝2，则AP＝（4﹣2t）cm，AQ＝t，∵当点P到达点A时，点Q也随之停止运动，∴0＜t≤2，①如图1，当PQ⊥AC时，PQ∥BC，则△APQ∽△ABC，∴，∴，解得t＝3﹣，②如图2，当PQ⊥AB时，△APQ∽△ACB，则，故，解得t＝，故答案为：3﹣，．三、解答题1．【分析】（1）①D AO＝|3﹣0|+|﹣2﹣0|＝5，即可求解；②设点C（m，4﹣m），则D CO＝|m|+|m﹣4|，当0≤m≤4时，D CO最小，即可求解；（2）EF1是“折距”D EF的最小值，即求EF1的最小值即可，当点E在y轴左侧于平行于直线y＝﹣x+4的直线相切时，EF1最小，即可求解．【解答】解：（1）①D AO＝|3﹣0|+|﹣2﹣0|＝5，同理D BO＝1，故答案为：5，1；②设点C（m，4﹣m），则D CO＝|m|+|m﹣4|，当0≤m≤4时，D CO最小，最小值为4；（2）如图2，过点E分别作x、y轴的平行线交直线y＝﹣x+4于F1、F2，则EF1是“折距”D EF的最小值，即求EF1的最小值即可，当点E在y轴左侧于平行于直线y＝﹣x+4的直线相切时，EF1最小，如图3，将直线y＝﹣x+4向右平移与圆相切于点E，平移后的直线与x轴交于点G，连接OE，设原直线与x、y轴交于点M、N，则点M、N的坐标分别为（﹣2，0）、点N（0，6），则MN＝2，则△MON∽△GEO，则，即，则GO＝，EF1＝MG＝2﹣＝．2．【分析】（1）由△PFB∽△ECD，得＝＝，由此即可解决问题．（2）如图2中，由△D′MG∽△CDE，得＝，求出MG，根据PF＝CG＝CM﹣MG，列出方程即可解决问题．（3）①存在．如图4中，当⊙O与BC相切时，连接OP延长PO交FG于M，连接OF、OG，由PB＝MF＝MG＝FG＝PC，得到3t＝（5﹣3t），即可解决问题．如图5中，当⊙O与BC相切时，连接GO，延长GO交PF于M，连接OF、OP，由△FGM∽△PFB，得＝，列出方程即可解决问题．②求出两种特殊位置t的值即可判断．【解答】解：（1）如图1中，∵四边形ABCD是矩形，∴AB＝CD＝4，BC＝AD＝5，∠B＝∠D＝90°，AD∥BC，在Rt△ECD中，∵∠D＝90°，ED＝3．CD＝4，∴EC＝＝5，∵PF∥CE，FG∥BC，∴四边形PFGC是平行四边形，∴∠FPB＝∠ECB＝∠DEC，∴△PFB∽△ECD，∴＝＝，∴＝＝，∴BF＝4t，PF＝5t，故答案为4t，5t．（2）如图2中，∴D、D′关于CE对称，∴DD′⊥CE，DM＝MD′，∵•DE•DC＝•EC•DM，∴DM＝D′M＝，CM＝＝，由△D′MG∽△CDE，得＝，∴＝，∴MG＝，∴PF＝CG＝CM﹣MG，∴5t＝﹣，∴t＝．∴t＝时，D′落在FG上．（3）存在．①如图4中，当⊙O与BC相切时，连接OP延长PO交FG于M，连接OF、OG．∵OP⊥BC，BC∥FG，∴PO⊥FG，∴FM＝MG由PB＝MF＝MG＝FG＝PC，得到3t＝（5﹣3t），解得t＝．如图5中，当⊙O与EC相切时，连接GO，延长GO交PF于M，连接OF、OP．∵OG⊥EC，BF∥EC，∴GO⊥PF，∴MF＝MP＝t，∵△FGM∽△PFB，∴＝，∴＝，解得t＝．综上所述t＝或时，⊙O与四边形ABCE的一边（AE边除外）相切．②如图6中，当∠FPG＝90°时，由cos∠PCG＝cos∠CED，∴＝，∴t＝，如图7中，当∠FGP＝90°时，∴＝，∴t＝，观察图象可知：当＜t＜时，外接圆⊙O的圆心O落在△FGP的内部．3．【分析】（1）根据两边成比例夹角相等即可证明两三角形相似；（2）如图构建如图平面直角坐标系，作HM⊥AD于M，GN⊥AD于N．设AM交BG于K．首先证明△GFN≌△FHM，想办法求出点H的坐标，构建方程即可解决问题；（3）由（2）可知H（2+t，4+t），令x＝2+t，y＝4+t，消去t得到y＝x+．推出点H在直线y＝x+上运动，根据垂线段最短即可解决问题；【解答】（1）证明：如图1中，∵△ABE，△BGF都是等腰直角三角形，∴＝＝，∵∠ABE＝∠GBF＝45°，∴∠ABG＝∠EBF，∴△ABG∽△EBF．（2）解：如图构建如图平面直角坐标系，作HM⊥AD于M，GN⊥AD于N．设AM交BG于K．∵△GFH是等腰直角三角形，∴FG＝FH，∠GNF＝∠GFH＝∠HMF＝90°，∴∠GFN+∠HFM＝90°，∠HFM+∠FHM＝90°，∴∠GFN＝∠FHM，∴△GFN≌△FHM，∴GN＝FM，FN＝HM，∵△ABG∽△EBF，∴＝＝，∠AGB＝∠EFB，∵∠AKG＝∠BKF，∴∠GAN＝∠KBF＝45°，∵EF＝t，∴AG＝t，∴AN＝GN＝FM＝t，∴AM＝2+t，HM＝FN＝2+t，∴H（2+t，4+t），当点H在直线CD上时，2+t＝10，解得t＝．（3）由（2）可知H（2+t，4+t），令x＝2+t，y＝4+t，消去t得到y＝x+．∴点H在直线y＝x+上运动，如图，作CH垂直直线y＝x+垂足为H．根据垂线段最短可知，此时CH的长最小，易知直线CH的解析式为y＝﹣3x+30，由，解得，∴H（8，6），∵C（10，0），∴CH＝＝2，∴HC最小值是2．4．【分析】（1）令二次函数解析式y＝0，解方程即求得点A、B坐标；把点A坐标代入直线l解析式即求得直线l．（2）把二次函数解析式配方得顶点C（﹣1，﹣4a），由B、C关于直线l对称可知AB＝AC，用a表示AC的长即能列得关于的方程．求得a有两个互为相反数的解，由二次函数图象开口向上可知a＞0，舍去负值．（3）①用待定系数法求直线AC解析式，由BD∥AC可知直线BD解析式的k与AC的k相同，再代入点B坐标即求得直线BD解析式．把直线l与直线BD解析式联立方程组，求得的解即为点D坐标．②由点B、C关于直线l对称，连接BN即有B、N、M在同一直线上时，CN+MN＝BN+MN＝BM最小；作点D关于直线AC的对称点Q，连接DQ交直线AC于点E，可证B、M、Q在同一直线上时，BM+MD＝BM+MQ＝BQ最小，CN+NM+MD最小值＝BM+MD最小值＝BQ．由直线AC垂直平分DQ且AC∥BD可得BD⊥DQ，即∠BDQ＝90°．由B、D坐标易求BD的长；由B、C关于直线l对称可得l平分∠BAC，作DF⊥x轴于F则有DF＝DE，所以DQ＝2DE＝2DF＝4；利用勾股定理即求得BQ的长．【解答】解：（1）当y＝0时，ax2+2ax﹣3a＝0解得：x1＝﹣3，x2＝1∴点A坐标为（﹣3，0），点B坐标为（1，0）∵直线l：y＝kx﹣经过点A∴﹣3k﹣＝0 解得：k＝﹣∴直线l的解析式为y＝﹣x﹣（2）∵y＝ax2+2ax﹣3a＝a（x+1）2﹣4a∴点C坐标为（﹣1，﹣4a）∵C、B关于直线l对称，A在直线l上∴AC＝AB，即AC2＝AB2∴（﹣1+3）2+（﹣4a）2＝（1+3）2解得：a＝±（舍去负值），即a＝∴二次函数解析式为：y＝x2+x﹣（3）∵A（﹣3，0），C（﹣1，﹣2），设直线AC解析式为y＝kx+b∴解得：∴直线AC解析式为y＝﹣x﹣3∵BD∥AC∴设直线BD解析式为y＝﹣x+c把点B（1，0）代入得：﹣+c＝0 解得：c＝∴直线BD解析式为y＝﹣x+∵解得：∴点D坐标为（3，﹣2）如图，连接BN，过点D作DF⊥x轴于点F，作D关于直线AC的对称点点Q，连接DQ 交AC于点E，连接BQ，MQ．∵点B、C关于直线l对称，点N在直线l上∴BN＝CN∴当B、N、M在同一直线上时，CN+MN＝BN+MN＝BM，即CN+MN的最小值为BM ∵点D、Q关于直线AC对称，点M在直线AC上∴MQ＝MD，DQ⊥AC，DE＝QE∴当B、M、Q在同一直线上时，BM+MD＝BM+MQ＝BQ，即BM+MD的最小值为BQ ∴此时，CN+NM+MD＝BM+MD＝BQ，即CN+NM+MD的最小值为BQ∵点B、C关于直线l对称∴AD平分∠BAC∵DF⊥AB，DE⊥AC∴DE＝DF＝|y D|＝2∴DQ＝2DE＝4∵B（1，0），D（3，﹣2）∴BD2＝（3﹣1）2+（﹣2）2＝16∵BD∥AC∴∠BDQ＝∠AEQ＝90°∴BQ＝∴CN+NM+MD的最小值为8．5．【分析】（1）在Rt△AOC中，解直角三角形求出OC即可解决问题．（2）设E（m，0）．由题意，分两种情形：S四边形OEDC＝•（CD+OE）•OC＝•S矩形OABC或S四边形OEDC＝•（CD+OE）•OC＝•S矩形OABC，分别构建方程即可解决问题．（3）①如图1﹣1中，在Rt△DPB中，解直角三角形求出PB即可．②如图2中，以BD为边向上作等边三角形DBQ′，连接QQ′．证明△Q′DQ≌△BDP（SAS），推出QQ′＝PB，∠DQ′Q＝∠DBP＝90°，推出点Q的运动轨迹是线段QQ′，即可解决问题．【解答】解：（1）如图1中，∵四边形OABC是矩形，∴∠AOC＝90°，∵OA＝3，∠OAC＝30°，∴OC＝OA•tan30°＝，故答案为，（，）．（2）设E（m，0）．由题意，S四边形OEDC＝•（CD+OE）•OC＝•S矩形OABC或S四边形OEDC ＝•（CD+OE）•OC＝•S矩形OABC，∴•（CD+OE）•OC＝×3×或•（CD+OE）•OC＝×3×，∴•（+m）•＝×3×或•（+m）•OC＝×3×，解得，m＝4﹣或2﹣．（3）①如图1﹣1中，∵tan∠OAC＝，∴∠OAC＝30°，∴∠ACB＝∠OAC＝30°，设将△DBP沿DP所在的直线翻折后，点B恰好落在AC上的B'处，则DB'＝DB＝DC，∠BDF＝∠B'DF，∴∠DB'C＝∠ACB＝30°∴∠BDB'＝60°，∴∠BDP＝∠B'DF＝30°，∵∠B＝90°，∴BP＝BD•tan30°＝，②如图2中，以BD为边向上作等边三角形DBQ′，连接QQ′．∵∠Q′DB＝∠QDP＝60°，∴∠Q′DQ＝∠BDP，∵Q′D＝BD，QD＝PD，∴△Q′DQ≌△BDP（SAS），∴QQ′＝PB，∠DQ′Q＝∠DBP＝90°，∴点Q的运动轨迹是线段QQ′，当动点P从点B运动到点A时，QQ′＝AB＝，∴点Q运动路径的长为．6．【分析】（1）用待定系数法进行解答便可；（2）①设出P点的横坐标为m，用m的代数式表示PD和DE，根据相似三角形的两种情况，由两直角边对应成比例，列出m的方程便可；②过B作BP平分∠ABC，交抛物线于点P，交OC于点M，过M作MN⊥BC于点N，设OM＝x，根据勾股定理求出x值，求得M点坐标，进而求出直线BM与抛物线的交点坐标便可得出其中一个满足条件的P点坐标；再取M关于x轴的对称点K的坐标，进而求得BK与抛物线的交点坐标，便可得另一个满足条件的P点坐标．【解答】解：（1）∵抛物线y＝ax2+bx+4交x轴于A（﹣1，0）、B（3，0）两点，∴，解得，，∴抛物线的解析式为：；（2）令x＝0，得＝4，∴C（0，4），∴OC＝4，∵B（3，0），∴OB＝3，设直线BC的解析式为y＝kx+n（k≠0），则，解得，∴直线BC的解析式为：y＝，设P（m，），则D（m，），∴DP＝，DE＝m，∴，∵∠BOC＝∠PDE＝90°，∴当△PDE和△BOC相似时，有两种情况：当△PDE∽△BOC时，则，即＝，解得，m＝，∴P（，）；当△PDE∽△COB时，则，即＝，解得，m＝2，∴P（2，4）．综上，当△PDE和△BOC相似时，点P的坐标（，）或（2，4）；②过B作BP平分∠ABC，交抛物线于点P，交OC于点M，过M作MN⊥BC于点N，如图1，则∠PBA＝∠ABC，OM＝MN，在Rt△BOM和Rt△BNM中，，∴Rt△BOM≌Rt△BNM（HL），∴BN＝BO＝3，设OM＝t，则MN＝MO＝t，CM＝4﹣t，CN＝BC﹣BN＝﹣3＝2，∵MN2+CN2＝MC2，∴t2+22＝（4﹣t）2，∴t＝，∴M（0，），设BM的解析式为：y＝mx+（m≠0），代入B（3，0）得，m＝，∴直线BM的解析式为：y＝﹣，解方程组得，，，∴p（，），取M（0，）关于x轴的对称点，K（0，﹣），连接BK，延长BK，交抛物线于点P'，如图2所示，则∠ABP＝∠ABC，设直线BK的解析式为y＝px（p≠0），代入B（3，0）得，p＝，∴直线BK的解析式为：y﹣，解方程组得，，∴P'（，），综上，使∠PBA＝∠ABC的点P的坐标为（，）或（，）．。

2020年全国中考数学压轴题全析全解(2)

2020年全国中考数学压轴题全解全析11、（河北卷）如图，在Rt △ABC 中，∠C ＝90°，AC ＝12，BC ＝16，动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动，动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动．P ，Q 分别从点A ，C 同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ 关于直线PQ 对称的图形是△PDQ ．设运动时间为t （秒）．（1）设四边形PCQD 的面积为y ，求y 与t 的函数关系式；（2）t 为何值时，四边形PQBA 是梯形？（3）是否存在时刻t ，使得PD ∥AB ？若存在，求出t 的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t ，使得PD ⊥AB ？若存在，请估计t 的值在括号中的哪个时间段内（0≤t ≤1；1＜t ≤2；2＜t ≤3；3＜t ≤4）；若不存在，请简要说明理由． [解] （1）由题意知 CQ ＝4t ，PC ＝12－3t ，∴S △PCQ =t t CQ PC 246212+-=⋅． ∵△PCQ 与△PDQ 关于直线PQ 对称，∴y=2S △PCQ t t 48122+-=．（2）当CQCP CA CB=时，有PQ ∥AB ，而AP 与BQ 不平行，这时四边形PQBA 是梯形， ∵CA =12，CB =16，CQ ＝4t ， CP ＝12－3t ，∴16412312tt =-，解得t ＝2． ∴当t ＝2秒时，四边形PQBA 是梯形．（3）设存在时刻t ，使得PD ∥AB ，延长PD 交BC 于点M ，如图2，若PD ∥AB ，则∠QMD =∠B ，又∵∠QDM =∠C =90°，∴Rt △QMD ∽Rt △ABC ，从而ACQD AB QM =， ∵QD =CQ =4t ，AC ＝12，AB=20，∴QM =203t ．若PD ∥AB ，则CP CMCA CB=，得20412331216t t t +-=，解得t ＝1211． ∴当t ＝1211秒时，PD ∥AB ．（4）存在时刻t ，使得PD ⊥AB ．P图2图7D 时间段为：2＜t ≤3．[点评]这是一道非常典型的动态几何问题，考查相似形、图形变换等知识，难度比起2005年河北非课改区的那道压轴题略有降低，但仍保留了足够的区分度，在解第3小题时应当先假设结论存在，再根据已知求解，若出现矛盾，则说明结论不存在，第4小题应该通过画图来判断时间段。

决战2020年中考数学压轴题综合提升训练《三角形》(含解析)

《三角形》1．已知，△ABC是等边三角形，过点C作CD∥AB，且CD＝AB，连接BD交AC于点O．（1）如图1，求证：AC垂直平分BD；（2）如图2，点M在BC的延长线上，点N在线段CO上，且ND＝NM，连接BN．求证：NB ＝NM．（1）证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠CAB＝60°，∵CD∥AB，且CD＝AB，∴CD＝CA＝BC，∠ACD＝∠ACB＝60°，∴BO＝DO，CO⊥BD，∴AC垂直平分BD；（2）由（1）知AC垂直平分BD，∴NB＝ND，∵ND＝NM，∴NB＝NM．2．等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F．（1）求证：△ADG≌△CDE．（2）若点H恰好为CE的中点，求证：∠CGF＝∠CFG．证明：（1）在等腰Rt△ABC中，∵点D为斜边AB上的中点，∴CD＝AB，CD⊥AB，∵AD＝AB，∴AD＝CD，∵CD⊥AB，∴∠ADG＝∠CDE＝90°，∵AH⊥CE，∴∠CGH+∠GCH＝90°，∵∠AGD+∠GAD＝90°，又∵∠AGD＝∠CGH，∴∠GAD＝∠GCH，在△△ADG和△CDE中∵∠ADG＝∠CDE＝90°，AD＝CD，∠GAD＝∠GCH∴△ADG≌△CDE（ASA），（2）∵AH⊥CE，点H为CE的中点，∴AC＝AE，∴∠CAH＝∠EAH，∵∠CAH+∠AFC＝90°，∠EAH+∠AGD＝90°，∴∠AFC＝∠AGD，∵∠AGD＝∠CGH，∴∠AFC＝∠CGH，即∠CGF＝∠CFG．3．如图，在△ABC中，AD⊥BC且BD＝DE，EF垂直平分AC，交AC于点F，交BC于点E．（1）若∠BAE＝32°，求∠C的度数；（2）若AC＝6cm，DC＝5cm，求△ABC的周长．解：（1）∵AD⊥BC，BD＝DE，EF垂直平分AC∴AB＝AE＝EC∴∠C＝∠CAE，∵∠BAE＝32°∴∠AED＝（180°﹣32°）＝74°；∴∠C＝∠AED＝37°；（2）由（1）知：AE＝EC＝AB，∵BD＝DE，∴AB+BD＝EC+DE＝DC，∴△ABC的周长＝AB+BC+AC，＝AB+BD+DC+AC，＝2DC+AC＝2×5+6＝16（cm）．4．如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D．（1）求证：∠AOB＝90°+∠C；（2）求证：AE+BF＝EF；（3）若OD＝a，CE+CF＝2b，请用含a，b的代数式表示△CEF的面积，S△CEF＝ab（直接写出结果）．证明：（1）∵OA，OB平分∠BAC和∠ABC，∴，，∴∠AOB＝180°﹣∠OAB﹣∠OBA＝＝＝＝（2）∵EF∥AB，∴∠OAB＝∠AOE，∠ABO＝∠BOF又∠OAB＝∠EAO，∠OBA＝∠OBF，∴∠AOE＝∠EAO，∠BOF＝∠OBF，∴AE＝OE，BF＝OF，∴EF＝OE+OF＝AE+BF；（3）∵点O在∠ACB的平分线上，∴点O到AC的距离等于OD，∴S△CEF＝（CE+CF）•OD＝•2b•a＝ab，故答案为：ab．5．如图，在△ABC中，AB＝AC，AD为BC边上的中线，DE⊥AB于点E．（1）求证：BD•AD＝DE•AC．（2）若AB＝13，BC＝10，求线段DE的长．（3）在（2）的条件下，求cos∠BDE的值．证明：（1）∵AB＝AC，BD＝CD，∴AD⊥BC，∠B＝∠C，∵DE⊥AB，∴∠DEB＝∠ADC，∴△BDE∽△CAD．∴，∴BA•AD＝DE•CA；（2）∵AB＝AC，BD＝CD，∴AD⊥BC，在Rt△ADB中，AD＝＝＝12，∵•AD•BD＝•AB•DE，∴DE＝．（3）∵∠ADB＝∠AED＝90°，∴∠BDE＝∠BAD，∴cos∠BDE＝cos∠BAD＝．6．如图，在△ABC中，AB＝AC，以AB为直径作半圆O，交BC于点D，交AC于点E．（1）求证：BD＝CD．（2）若弧DE＝50°，求∠C的度数．（3）过点D作DF⊥AB于点F，若BC＝8，AF＝3BF，求弧BD的长．（1）证明：如图，连接AD．∵AB是圆O的直径，∴AD⊥BD．又∵AB＝AC，∴BD＝CD．（2）解：∵弧DE＝50°，∴∠EOD＝50°．∴∠DAE＝∠DOE＝25°．∵由（1）知，AD⊥BD，则∠ADB＝90°，∴∠ABD＝90°﹣25°＝65°．∵AB＝AC，∴∠C＝∠ABD＝65°．（3）∵BC＝8，BD＝CD，∴BD＝4．设半径OD＝x．则AB＝2x．由AF＝3BF可得AF＝AB＝x，BF＝AB＝x，∵AD⊥BD，DF⊥AB，∴BD2＝BF•AB，即42＝x•2x．解得x＝4．∴OB＝OD＝BD＝4，∴△OBD是等边三角形，∴∠BOD＝60°．∴弧BD的长是：＝．7．阅读下面材料：数学课上，老师给出了如下问题：如图，AD为△ABC中线，点E在AC上，BE交AD于点F，AE＝EF．求证：AC＝BF．经过讨论，同学们得到以下两种思路：思路一如图①，添加辅助线后依据SAS可证得△ADC≌△GDB，再利用AE＝EF可以进一步证得∠G＝∠FAE＝∠AFE＝∠BFG，从而证明结论．思路二如图②，添加辅助线后并利用AE＝EF可证得∠G＝∠BFG＝∠AFE＝∠FAE，再依据AAS可以进一步证得△ADC≌△GDB，从而证明结论．完成下面问题：（1）①思路一的辅助线的作法是：延长AD至点G，使DG＝AD，连接BG；②思路二的辅助线的作法是：作BG＝BF交AD的延长线于点G．（2）请你给出一种不同于以上两种思路的证明方法（要求：只写出辅助线的作法，并画出相应的图形，不需要写出证明过程）．解：（1）①延长AD至点G，使DG＝AD，连接BG，如图①，理由如下：∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，，∴△ADC≌△GDB（SAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EFA，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．故答案为：延长AD至点G，使DG＝AD，连接BG；②作BG＝BF交AD的延长线于点G，如图②．理由如下：∵BG＝BF，∴∠G＝∠BFG，∵AE＝EF，∴∠EAF＝∠EFA，∵∠EFA＝∠BFG，∴∠G＝∠EAF，在△ADC和△GDB中，，∴△A DC≌△GDB（AAS），∴AC＝BG，∴AC＝BF；故答案为：作BG＝BF交AD的延长线于点G；（2）作BG∥AC交AD的延长线于G，如图③所示：则∠G＝∠CAD，∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，，∴△ADC≌△GDB（AAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EFA，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．8．如图1，直线AB分别与x轴、y轴交于A、B两点，OC平分∠AOB交AB于点C，点D为线段AB上一点，过点D作DE∥OC交y轴于点E，已知AO＝m，BO＝n，且m、n满足n2﹣8n+16+|n﹣2m|＝0．（1）求A、B两点的坐标；（2）若点D为AB中点，求OE的长；（3）如图2，若点P（x，﹣2x+4）为直线AB在x轴下方的一点，点E是y轴的正半轴上一动点，以E为直角顶点作等腰直角△PEF，使点F在第一象限，且F点的横、纵坐标始终相等，求点P的坐标．解：（1）∵n2﹣8n+16+|n﹣2m|＝0，∴（n﹣4）2+|n﹣2m|＝0，∵（n﹣4）2≥0，|n﹣2m|≥0，∴（n﹣4）2＝0，|n﹣2m|＝0，∴m＝2，n＝4，∴点A为（2，0），点B为（0，4）；（2）延长DE交x轴于点F，延长FD到点G，使得DG＝DF，连接BG，设OE＝x，∵OC平分∠AOB，∴∠BOC＝∠AOC＝45°，∵DE∥OC，∴∠EFO＝∠FEO＝∠BEG＝∠BOC＝∠AOC＝45°，∴OE＝OF＝x，在△ADF和△BDG中，，∴△ADF≌△BDG（SAS），∴BG＝AF＝2+x，∠G＝∠AFE＝45°，∴∠G＝∠BEG＝45°，∴BG＝BE＝4﹣x，∴4﹣x＝2+x，解得：x＝1，∴OE＝1；（3）如图2，分别过点F、P作FM⊥y轴于点M，PN⊥y轴于点N，设点E为（0，m），∵点P的坐标为（x，﹣2x+4），∴PN＝x，EN＝m+2x﹣4，∵∠PEF＝90°，∴∠PEN+∠FEM＝90°，∵FM⊥y轴，∴∠MFE+∠FEM＝90°，∴∠PEN＝∠MFE，在△EFM和△PEN中，，∴△EFM≌△PEN（AAS），∴ME＝NP＝x，FM＝EN＝m+2x﹣4，∴点F为（m+2x﹣4，m+x），∵F点的横坐标与纵坐标相等，∴m+2x﹣4＝m+x，解得：x＝4，∴点P为（4，﹣4）．9．在等边△ABC中，线段AM为BC边上的中线．动点D在直线AM上时，以CD为一边在CD 的下方作等边△CDE，连结BE．（1）若点D在线段AM上时（如图1），则AD＝BE（填“＞”、“＜”或“＝”），∠CAM ＝30 度；（2）设直线BE与直线AM的交点为O．①当动点D在线段AM的延长线上时（如图2），试判断AD与BE的数量关系，并说明理由；②当动点D在直线AM上时，试判断∠AOB是否为定值？若是，请直接写出∠AOB的度数；若不是，请说明理由．解：（1））∵△ABC与△DEC都是等边三角形∴AC＝BC，CD＝CE，∠ACB＝∠DC E＝60°∴∠ACD+∠DCB＝∠DCB+∠BCE∴∠ACD＝∠BCE．在△ADC和△BEC中，∴△ACD≌△BCE（SAS），∴AD＝BE；∵△ABC是等边三角形，∴∠BAC＝60°．∵线段AM为BC边上的中线∴∠CAM＝∠BAC，∴∠CAM＝30°．故答案为：＝，30；（2）①AD＝BE，理由如下：∵△ABC和△CDE都是等边三角形∴AB＝BC，DC＝EC，∠ACB＝∠DCE＝60°，∵∠ACD＝∠ACB﹣∠DCB，∠BCE＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，∴△ACD≌△BCE（SAS）∴AD＝BE．②∠AOB是定值，∠AOB＝60°，理由如下：当点D在线段AM上时，如图1，由①知△ACD≌△BCE，则∠CBE＝∠CAD＝30°，又∠ABC＝60°，∴∠CBE+∠ABC＝60°+30°＝90°，∵△ABC是等边三角形，线段AM为BC边上的中线∴AM平分∠BAC，即，∴∠BOA＝90°﹣30°＝60°．当点D在线段AM的延长线上时，如图2，∵△ABC与△DEC都是等边三角形∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°∴∠ACB+∠DCB＝∠DCB+∠DCE∴∠ACD＝∠BCE在△ACD和△BCE中，∴△ACD≌△BCE（SAS）∴∠CBE＝∠CAD＝30°，同理可得：∠BAM＝30°，∴∠BOA＝90°﹣30°＝60°．10．数学课上，王老师出示了如下框中的题目．小明与同桌小聪讨论后，进行了如下解答：（1）特殊情况•探索结论：在等边三角形ABC中，当点E为AB的中点时，点D在CB点延长线上，且ED＝EC；如图1，确定线段AE与DB的大小关系．请你直接写出结论AE ＝DB；（2）特例启发，解答题目王老师给出的题目中，AE与DB的大小关系是：AE＝DB．理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）（3）拓展结论，设计新题在△ABC中，AB＝BC＝AC＝1；点E在AB的延长线上，AE＝2；点D在CB的延长线上，ED ＝EC，如图3，请直接写CD的长1或3 ．解：（1）如图1，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠AFE＝∠ACB＝∠ABC＝60°，△AEF为等边三角形，∴∠EFC＝∠EBD＝120°，EF＝AE，∵ED＝EC，∴∠EDB＝∠ECB，∠ECB＝∠FEC，∴∠EDB＝∠FEC，在△BDE和△FEC中，，∴△BDE≌△FEC（AAS），∴BD＝EF，∴AE＝BD，故答案为：＝；（2）解答过程如下：如图2，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠AFE＝∠ACB＝∠ABC＝60°，△AEF为等边三角形，∴∠EFC＝∠EBD＝120°，EF＝AE，∵ED＝EC，∴∠EDB＝∠ECB，∠ECB＝∠FEC，∴∠EDB＝∠FEC，在△BDE和△FEC中，∴△BDE≌△FEC（AAS），∴BD＝EF，∴AE＝BD．故答案为：AE＝DB．（3）解：分为四种情况：如图3，∵AB＝AC＝1，AE＝2，∴B是AE的中点，∵△ABC是等边三角形，∴AB＝AC＝BC＝1，△ACE是直角三角形（根据直角三角形斜边的中线等于斜边的一半），∴∠ACE＝90°，∠AEC＝30°，∴∠D＝∠ECB＝∠BEC＝30°，∠DBE＝∠ABC＝60°，∴∠DEB＝180°﹣30°﹣60°＝90°，即△DEB是直角三角形．∴BD＝2BE＝2（30°所对的直角边等于斜边的一半），即CD＝1+2＝3．如图4，过A作AN⊥BC于N，过E作EM⊥CD于M，∵等边三角形ABC，EC＝ED，∴BN＝CN＝BC＝，CM＝MD＝CD，AN∥EM，∴△BAN∽△BEM，∴，∵△ABC边长是1，AE＝2，∴，∴MN＝1，∴CM＝MN﹣CN＝1﹣＝，∴CD＝2CM＝1；如图5，∵∠ECD＞∠EBC（∠EBC＝120°），而∠ECD不能大于120°，否则△EDC不符合三角形内角和定理，∴此时不存在EC＝ED；如图6，∵∠EDC＜∠ABC，∠ECB＞∠ACB，又∵∠ABC＝∠ACB＝60°，∴∠ECD＞∠EDC，即此时ED≠EC，∴此时情况不存在，答：CD的长是3或1．故答案为：1或3．11．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．（1）如图1，△ABC中，AB＝AC，∠A＝36°，求证：△ABC是倍角三角形；（2）若△ABC是倍角三角形，∠A＞∠B＞∠C，∠B＝30°，AC＝，求△ABC面积；（3）如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE＝AB，若AB+AC＝BD，请你找出图中的倍角三角形，并进行证明．（1）证明：∵AB＝AC，∴∠B＝∠C，∵∠A+∠B+∠C＝180°，∠A＝36°，∴∠B＝∠C＝72°，∴∠A＝2∠C，即△ABC是倍角三角形，（2）解：∵∠A＞∠B＞∠C，∠B＝30°，①当∠B＝2∠C，得∠C＝15°，过C作CH⊥直线AB，垂足为H，可得∠CAH＝45°，∴AH＝CH＝AC＝4．∴BH＝，∴AB＝BH﹣AH＝﹣4，∴S＝．②当∠A＝2∠B或∠A＝2∠C时，与∠A＞∠B＞∠C矛盾，故不存在．综上所述，△ABC面积为．（3）∵AD平分∠BAE，∴∠BAD＝∠EAD，∵AB＝AE，AD＝AD，∴△ABD≌△AED（SAS），∴∠ADE＝∠ADB，BD＝DE．又∵AB+AC＝BD，∴AE+AC＝BD，即CE＝BD．∴CE＝DE．∴∠C＝∠BDE＝2∠ADC．∴△ADC是倍角三角形．12．如图，在平面直角坐标系中，OA＝OB，AC＝CD，已知两点A（4，0），C（0，7），点D 在第一象限内，∠DCA＝90°，点B在线段OC上，AB的延长线与DC的延长线交于点M，AC与BD交于点N．（1）点B的坐标为：（0，4）；（2）求点D的坐标；（3）求证：CM＝CN．解：（1）∵A（4，0），∴OA＝OB＝4，∴B（0，4），故答案为：（0，4）．（2）∵C（0，7），∴OC＝7，过点D作DE⊥y轴，垂足为E，∴∠DEC＝∠AOC＝90°，∵∠DCA＝90°，∴∠ECD+∠BCA＝∠ECD+∠EDC＝90°∴∠BCA＝∠EDC，∴△DEC≌△COA（AAS），∴DE＝OC＝7，EC＝OA＝4，∴OE＝OC+EC＝11，∴D（7，11）；（3）证明：∵BE＝OE﹣OB＝11﹣4＝7 ∴BE＝DE，∴△DBE是等腰直角三角形，∴∠DBE＝45°，∵OA＝OB，∴∠OBA＝45°，∴∠DBA＝90°，∴∠BAN+∠ANB＝90°，∵∠DCA＝90°，∴∠CDN+∠DNC＝90°，∵∠DNC＝∠ANB，∴∠CDN＝∠BAN，∵∠DCA＝90°，∴∠ACM＝∠DCN＝90°，∴△DCN≌△ACM（ASA），∴CM＝CN．13．如图，在△ABC中，BD⊥AC，垂足为C，且∠A＜∠C，点E是一动点，其在BC上移动，连接DE，并过点E作EF⊥DE，点F在AB的延长线上，连接DF交BC于点G．（1）请同学们根据以上提示，在上图基础上补全示意图．（2）当△ABD与△FDE全等，且AD＝FE，∠A＝30°，∠AFD＝40°，求∠C的度数．解：（1）补全示意图如图所示，（2）∵DE⊥EF，BD⊥AC，∴∠DEF＝∠ADB＝90°．∵△ABD与△DEF全等，∴AB＝DF，又∵AD＝FE，∴∠ABD＝∠FDE，∴BD＝DE．在Rt△ABD中，∠ABD＝90°﹣∠A＝60°．∴∠FDE＝60°．∵∠ABD＝∠BDF+∠AFD，∵∠AFD＝40°，∴∠BDF＝20°．∴∠BDE＝∠BDF+∠FDE＝20°+60°＝80°．∵BD＝DE，∴∠DBE＝∠BED＝（180°﹣∠BDE）＝50°．在Rt△BDC中，∠C＝90°﹣∠DBE＝90°﹣50°＝40°．14．如图．CP是等边△ABC的外角∠ACE的平分线，点D在边BC上，以D为顶点，DA为一条边作∠ADF＝60°，另一边交射线CP于F．（1）求证．AD＝FD；（2）若AB＝2，BD＝x，DF＝y，求y关于x的函数解析式；（3）联结AF，当△ADF的面积为时，求BD的长．证明：（1）如图1，连接AF，∵∠ACB＝60°，∴∠ACE＝120°，∵CP平分∠ACE，∴∠ACP＝∠PCE＝60°，∴∠ADF＝∠ACP＝60°，∴A、D、C、F四点共圆，∴∠AFD＝∠ACB＝60°，∴∠ADF＝∠AFD＝60°，∴∠DAF＝60°，∴△ADF是等边三角形，∴AD＝FD；（2）如图2，过点A作AH⊥BC，∵△ABC是等边三角形，AH⊥BC，AB＝2，∴BH＝1，AH＝BH＝，∴HD＝BD﹣BH＝x﹣1，∵DF＝＝，∴y＝（3）∵△ADF是等边三角形，且△ADF的面积为，∴DF2＝，∴DF2＝＝x2﹣2x+4∴x＝∴BD＝或15．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN ＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．解：（1）结论BM+CN＝BD成立，理由如下：如图②，过点D作DE∥AC交AB于E，∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∵DE∥AC，∴∠BED＝∠A＝60°，∠BDE＝∠C＝60°，∴∠B＝∠BED＝∠BDE＝60°，∴△BDE是等边三角形，∠EDC＝120°，∴BD＝BE＝DE，∠EDN+∠CDN＝120°，∵∠EDM+∠EDN＝∠MDN＝120°，∴∠CDN＝∠EDM，∵D是BC边的中点，∴DE＝BD＝CD，在△CDN和△EDM中，，∴△CDN≌△EDM（ASA），∴CN＝EM，∴BD＝BE＝BM+EM＝BM+CN；（2）上述结论不成立，BM，CN，BD之间的数量关系为：BM﹣CN＝BD；理由如下：如图③，过点D作DE∥AC交AB于E，∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∴∠NCD＝120°，∵DE∥AC，∴∠BED＝∠A＝60°，∠BDE＝∠C＝60°，∴∠B＝∠BED＝∠BDE＝60°，∴△BDE是等边三角形，∠MED＝∠EDC＝120°，∴BD＝BE＝DE，∠NCD＝∠MED，∠EDM+∠CDM＝120°，∵∠CDN+∠CDM＝∠MDN＝120°，∴∠CDN＝∠EDM，∵D是BC边的中点，∴DE＝BD＝CD，在△CDN和△EDM中，，∴△CDN≌△EDM（ASA），∴CN＝EM，∴BD＝BE＝BM﹣EM＝BM﹣CN，∴BM﹣CN＝BD．。

决胜2020年中考数学压轴题专题15 动点综合问题(含答案)

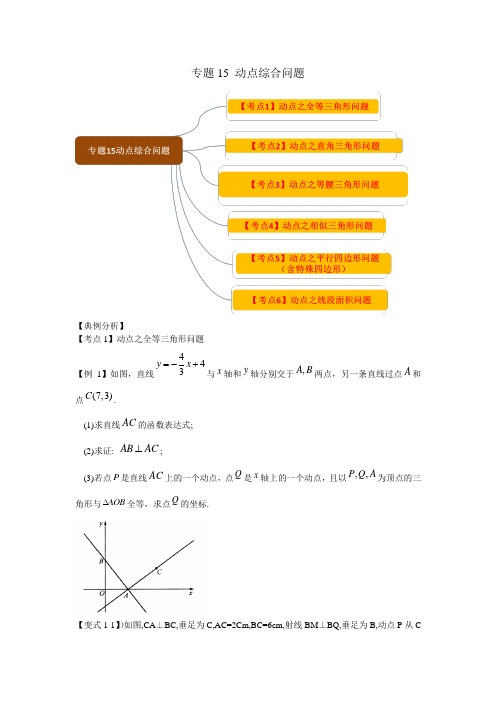
专题15 动点综合问题【典例分析】【考点1】动点之全等三角形问题【例1】如图，直线443y x=-+与x轴和y轴分别交于,A B两点，另一条直线过点A和点(7,3) C.(1)求直线AC的函数表达式;(2)求证: AB AC⊥;(3)若点P是直线AC上的一个动点，点Q是x轴上的一个动点，且以,,P Q A为顶点的三角形与AOB∆全等，求点Q的坐标.【变式1-1】）如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ 运动,点N 为射线BM 上一动点,满足PN=AB,随着P 点运动而运动,当点P 运动_______秒时，△BCA 与点P 、N 、B 为顶点的三角形全等.(2个全等三角形不重合)【考点2】动点之直角三角形问题【例2】（模型建立）（1）如图1，等腰直角三角形ABC 中，90ACB ∠=o，CB CA =，直线ED 经过点C ，过A 作AD ED ⊥于点D ，过B 作BE ED ⊥于点E .求证：BEC CDA ∆≅∆；（模型应用）（2）已知直线1l：443y x =+与坐标轴交于点A 、B ，将直线1l 绕点A 逆时针旋转45o 至直线2l，如图2，求直线2l的函数表达式；（3）如图3，长方形ABCO ，O 为坐标原点，点B 的坐标为()8,6-，点A 、C 分别在坐标轴上，点P 是线段BC 上的动点，点D 是直线26y x =-+上的动点且在第四象限.若APD ∆是以点D 为直角顶点的等腰直角三角形，请直接写出点D 的坐标.【变式2-1】（2019·辽宁中考模拟）如图，已知二次函数y ＝ax2+bx+4的图象与x 轴交于点A(4，0)和点D(﹣1，0)，与y 轴交于点C ，过点C 作BC 平行于x 轴交抛物线于点B ，连接AC(1)求这个二次函数的表达式；(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动；点N 从点B 同时出发，以每秒1个单位长度的速度向点C 运动，其中一个动点到达终点时，另一个动点也随之停动，过点N 作NQ 垂直于BC 交AC 于点Q ，连结MQ.①求△AQM的面积S与运动时间t之间的函数关系式，写出自变量的取值范围；当t为何值时，S有最大值，并求出S的最大值；②是否存在点M，使得△AQM为直角三角形？若存在，求出点M的坐标；若不存在，说明理由．【变式2-2】如图，四边形ABCD是正方形，以DC为边向外作等边△DCE，连接AE交BD 于点F，交CD于点G，点P是线段AE上一动点，连接DP、BP．（1）求∠AFB的度数；（2）在点P从A到E的运动过程中，若DP平分∠CDE，求证：AG•DP＝DG•BD；（3）已知AD＝6，在点P从A到E的运动过程中，若△DBP是直角三角形，请求DP的长．【考点3】动点之等腰三角形问题【例3】（2019·湖南中考真题）如图一，在射线DE的一侧以AD为一条边作矩形ABCD，53AD=5CD=，点M是线段AC上一动点（不与点A重合），连结BM，过点M作BM的垂线交射线DE于点N，连接BN．（1）求CAD ∠的大小；（2）问题探究：动点M 在运动的过程中，①是否能使AMN ∆为等腰三角形，如果能，求出线段MC 的长度；如果不能，请说明理由． ②MBN ∠的大小是否改变？若不改变，请求出MBN ∠的大小；若改变，请说明理由．（3）问题解决：如图二，当动点M 运动到AC 的中点时，AM 与BN 的交点为F ，MN 的中点为H ，求线段FH 的长度．【变式3-1】如图①，已知正方形ABCD 边长为2，点P 是AD 边上的一个动点，点A 关于直线BP 的对称点是点Q ，连结PQ 、DQ 、CQ 、BQ .设AP=x.（1）当1x =时，求BP 长；（2）如图②，若PQ 的延长线交CD 边于E ，并且90CQD ∠=o，求证：CEQ ∆为等腰三角形；（3）若点P 是射线AD 上的一个动点，则当CDQ ∆为等腰三角形时，求x 的值.【变式3-2】（2019·河南中考模拟）如图，抛物线y=ax2+bx+3交y 轴于点A ，交x 轴于点B （-3，0）和点C （1，0），顶点为点M ．（1）求抛物线的解析式；（2）如图，点E 为x 轴上一动点，若△AME 的周长最小，请求出点E 的坐标；（3）点F 为直线AB 上一个动点，点P 为抛物线上一个动点，若△BFP 为等腰直角三角形，请直接写出点P 的坐标．【变式3-3】（2019·广西中考真题）已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -，点O 为坐标原点，点P 为抛物线上的动点，直线y x b =-+与x 轴、y 轴分别交于AB 、两点．（1）求m b 、的值；（2）当PAM ∆是以AM 为底边的等腰三角形时，求点P 的坐标；（3）满足（2）的条件时，求sin BOP ∠的值．【考点4】动点之相似三角形问题【例4】在边长为4的正方形ABCD 中，动点E 以每秒1个单位长度的速度从点A 开始沿边AB 向点B 运动,动点F 以每秒2个单位长度的速度从点B 开始沿边BC 向点C 运动，动点E 比动点F 先出发1秒,其中一个动点到达终点时，另一个动点也随之停止运动，设点F 的运动时间为t 秒.()1如图1，连接DE ,AF ，若DE AF ⊥，求t 的值 ()2如图2，连接,EF DF ，当t 为何值时，?EBF DCF V :V【变式4-1】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝34AC（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D 的坐标；（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．【变式4-2】如图，已知抛物线2y ax bx c =++经过A（－3，0）、B（8，0）、C（0，4）三点，点D是抛物线上的动点，连结AD与y轴相交于点E，连结AC，CD．（1）求抛物线所对应的函数表达式；（2）当AD平分∠CAB时．①求直线AD所对应的函数表达式；②设P是x轴上的一个动点，若△PAD与△CAD相似，求点P的坐标．【考点5】动点之平行四边形问题（含特殊四边形）【例5】（2019·广东中考模拟）如图，点O是平面直角坐标系的原点，点A33），AC⊥OA 与x轴的交点为C．动点M3A向点O运动．同时，动点N以每秒3个单位长度由点O向点C运动，当一动点先到终点时，另一动点立即停止运动．（1）写出∠AOC的值；（2）用t表示出四边形AMNC的面积；（3）求点P的坐标，使得以O、N、M、P为顶点的四边形是特殊的平行四边形？【变式5-1】（2019·江西中考真题）在图1，2，3中，已知，，点为线段上的动点，连接，以为边向上作菱形，且．（1）如图1，当点与点重合时，________°；（2）如图2，连接．①填空：_________（填“>”，“<”，“=”）；②求证：点在的平分线上；（3）如图3，连接，，并延长交的延长线于点，当四边形是平行四边形时，求的值．【变式5-2】（2019·湖南中考真题）如图，二次函数213y x bx c=-++的图象过原点，与x轴的另一个交点为() 8,0【变式5-3】．如图，在平面直角坐标系中，AOB ∆的顶点O 是坐标原点，点A 坐标为()1,3，A 、B 两点关于直线y x =对称，反比例函数()0ky x x =>图象经过点A ，点P 是直线y x=上一动点.（1）B 点的坐标为______；（2）若点C 是反比例函数图象上一点，是否存在这样的点C ，使得以A 、B 、C 、P 四点为顶点的四边形是平行四边形？若存在，求出点C 坐标；若不存在，请说明理由；（3）若点Q 是线段OP 上一点（O 不与O 、P 重合），当四边形AOBP 为菱形时，过点Q 分别作直线OA 和直线AP 的垂线，垂足分别为E 、F ，当QE QF QB ++的值最小时，求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图已知平面内有一动点A ，x 轴上有一定点B （4，0），连接AB ，且将线段AB 绕B 点逆时针旋转90°得到线段BC ．①当A 点坐标为（1，1）时，求C 点坐标；②当A 点在直线x=1上滑动时，求在此运动过程中△BOC 的面积是否发生变化，若不变，请求出面积，若变化，请说明理由；③若总条件中的动点A 改为直线y=x 上的动点A ，其余条件都不变，请直接写出当A 点在直线y=x 上滑动时，点D （0，-2）到C 点的最短距离．【变式6-1】（2019·山东中考模拟）如图，抛物线2y x bx c =-++交x 轴于点()30A -,和点B ，交y 轴于点()0,3C .（1）求抛物线的函数表达式；（2）若点P 在抛物线上，且4AOP BOCS S ∆∆=，求点P 的坐标；（3）如图，设点Q 是线段AC 上的一动点，作DQ x ⊥轴，交抛物线于点D ，求线段DQ 长度的最大值，并求出DAC ∆面积的最大值.【变式6-2】如图，矩形ABCD 中，3,4AD AB ==，点P 是对角线AC 上一动点（不与A C 、重合），连接PB ，过点P 作PE PB ⊥，交射线DC 于点E ，以线段,PE PB 为邻边作矩形BPEF ，过点P 作GH CD ⊥。

挑战2023年中考数学压轴题专题11 二次函数与单线段最值问题(含答案解析)

专题11二次函数与单线段最值问题【例1】（2022•襄阳）在平面直角坐标系中,直线y＝mx﹣2m与x轴,y轴分别交于A,B两点,顶点为D的抛物线y＝﹣x2+2mx﹣m2+2与y轴交于点C．（1）如图,当m＝2时,点P是抛物线CD段上的一个动点．①求A,B,C,D四点的坐标；②当△P AB面积最大时,求点P的坐标；（2）在y轴上有一点M（0,m）,当点C在线段MB上时,①求m的取值范围；②求线段BC长度的最大值．【例2】（2022•湖州）如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C 分别在x轴的正半轴和y轴的正半轴上．抛物线y＝﹣x2+bx+c经过A,C两点,与x轴交于另一个点D．（1）①求点A,B,C的坐标；②求b,c的值．（2）若点P是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M（如图2所示）．当点P在BC 上运动时,点M也随之运动．设BP＝m,CM＝n,试用含m的代数式表示n,并求出n的最大值．【例3】（2021•青海）如图,在平面直角坐标系中,直线y＝x+2与坐标轴交于A,B两点,点A在x轴上,点B在y轴上,C点的坐标为（1,0）,抛物线y＝ax2+bx+c经过点A,B,C．（1）求抛物线的解析式；（2）根据图象写出不等式ax2+（b﹣1 ）x+c＞2的解集；（3）点P是抛物线上的一动点,过点P作直线AB的垂线段,垂足为Q点．当PQ＝时,求P点的坐标．【例4】（2022•雅安）已知二次函数y＝ax2+bx+c的图象过点A（﹣1,0）,B（3,0）,且与y轴交于点C（0,﹣3）．（1）求此二次函数的表达式及图象顶点D的坐标；（2）在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由；（3）在平面直角坐标系中,存在点P,满足P A⊥PD,求线段PB的最小值．1．（2020•河北模拟）已知抛物线C：y＝ax2+bx+c（a＞0,c＜0）的对称轴为x＝4,C为顶点,且A（2,0）,C（4,﹣2）【问题背景】求出抛物线C的解析式．【尝试探索】如图2,作点C关于x轴的对称点C′,连接BC′,作直线x＝k交BC′于点M,交抛物线C于点N．①连接ND,若四边形MNDC′是平行四边形,求出k的值．②当线段MN在抛物线C与直线BC′围成的封闭图形内部或边界上时,请直接写出线段MN的长度的最大值．【拓展延伸】如图4,作矩形HGOE,且E（﹣3,0）,H（﹣3,4）,现将其沿x轴以1个单位每秒的速度向右平移,设运动时间为t,得到矩形H′G′O′E′,连接AC′,若矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分,请求出t的取值范围．2．（2018秋•宁城县期末）已知,如图,抛物线与x轴交点坐标为A（1,0）,C（﹣3,0）,（1）如图1,已知顶点坐标D为（﹣1,4）或B点（0,3）,选择适当方法求抛物线的解析式；（2）如图2,在抛物线的对称轴DH上求作一点M,使△ABM的周长最小,并求出点M的坐标；（3）如图3,将图2中的对称轴向左移动,交x轴于点P（m,0）（﹣3＜m＜﹣1）,与抛物线,线段BC的交点分别为点E、F,用含m的代数式表示线段EF的长度,并求出当m为何值时,线段EF最长．3．（2021•桥西区模拟）如图1,抛物线y＝ax2+bx+3与x轴交于A（﹣1,0）,B两点,与y轴交于点C,且CO＝BO,连接BC．（1）求抛物线的解析式；（2）如图2,抛物线的顶点为D,其对称轴与线段BC交于点E,求线段DE的长度；（3）如图3,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,连接CP,CD,抛物线上是否存在点P,使△CDE∽△PCF,如果存在,求出点P的坐标,如果不存在,请说明理由．4．（2022•和平区二模）如图,在平面直角坐标系中,已知抛物线顶点A的坐标为（﹣2,4）,且经过坐标原点,与x轴负半轴交于点B．（1）求抛物线的函数表达式并直接写出点B的坐标；（2）过点A作AC⊥x轴于点C,若点D是y轴左侧的抛物线上一个动点（点D与点A不重合）,过点D作DE⊥x轴于点E,连接AO,DO,当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,求点D的坐标；（3）在（2）的条件下,当点D在第二象限时,在平面内存在一条直线,这条直线与抛物线在第二象限交于点F,在第三象限交于点G,且点A,点B,点D,到直线FG的距离都相等,请直接写出线段FG的长．5．（2022•鹿城区校级二模）如图,抛物线y＝x2+bx+c与x轴交于点A（﹣1,0）,B（5,0）,与y轴交于点C．（1）求抛物线的解析式和顶点D的坐标．（2）连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F（F在E的右侧）,过点F作FG ∥x轴交ED于点H,交AD于点G,求HF的长．6．（2021•南岗区模拟）如图,抛物线y＝ax2+bx﹣4交x轴于点A（﹣3,0）,B（4,0）,交y轴于点C．（1）求抛物线的解析式；（2）点P为第一象限抛物线上一点,过点P作x轴的平行线,与抛物线的另一个交点为点G,连接CG交x轴于点N,设点P的横坐标为t,ON的长为d,求d与t之间的函数解析式（不要求写出自变量t的取值范围）；（3）在（2）的条件下,连接PB,将线段PB绕着点P顺时针旋转90°得到线段PD,点D恰好落在y轴上,点E在线段OB上,连接PE,点Q在EB的延长线上,且EQ＝PE,连接DQ交PE于点F,若PE＝3PF,求QN的长．7．（2021•凉山州模拟）如图1,在平面直角坐标系中,已知B点坐标为（1,0）,且OA＝OC＝3OB,抛物线y＝ax2+bx+c（a≠0）图象经过A,B,C三点,其中D点是该抛物线的顶点．（1）求抛物线的解析式；（2）判断△ADC的形状并且求△ADC的面积；（3）如图2,点P是该抛物线第三象限部分上的一个动点,过P点作PE⊥AC于E点,当PE的值最大时,求此时P点的坐标及PE的最大值．8．（2022•无锡二模）已知抛物线y＝mx2﹣2mx+3（m＜0）与x轴交于A、B两点（点A在点B的左侧）,与y轴交于点C,且OB＝3OA．（1）求抛物线的函数表达式；（2）若M、N是第一象限的抛物线上不同的两点,且△BCN的面积总小于△BCM的面积,求点M的坐标；（3）若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP、DP,分别交y轴于点E、F,若EF＝OC,求点P的坐标．9．（2021•乳源县三模）如图,在平面直角坐标系中,已知抛物线y＝ax2+bx+c与x轴交于A（5,0）,B（﹣1,0）两点,与y轴交于点C（0,）．（1）求抛物线的解析式；（2）若点M是抛物线的顶点,连接AM,CM,求△AMC的面积；（3）若点P是抛物线上的一个动点,过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为点F,连接EF,当线段EF的长度最短时,求出点P的坐标．10．（2021•河池）在平面直角坐标系中,抛物线y＝﹣（x﹣1）2+4与x轴交于A,B两点（A在B的右侧）,与y轴交于点C．（1）求直线CA的解析式；（2）如图,直线x＝m与抛物线在第一象限交于点D,交CA于点E,交x轴于点F,DG⊥CA于点G,若E为GA 的中点,求m的值．（3）直线y＝nx+n与抛物线交于M（x1,y1）,N（x2,y2）两点,其中x1＜x2．若x2﹣x1＞3且y2﹣y1＞0,结合函数图象,探究n的取值范围．11．（2021•桂林）如图,已知抛物线y＝a（x﹣3）（x+6）过点A（﹣1,5）和点B（﹣5,m）,与x轴的正半轴交于点C．（1）求a,m的值和点C的坐标；（2）若点P是x轴上的点,连接PB,P A,当＝时,求点P的坐标；（3）在抛物线上是否存在点M,使A,B两点到直线MC的距离相等？若存在,求出满足条件的点M的横坐标；若不存在,请说明理由．12．（2021•吉林）如图,在平面直角坐标系中,二次函数y＝x2+bx+c的图象经过点A（0,﹣）,点B（1,）．（1）求此二次函数的解析式；（2）当﹣2≤x≤2时,求二次函数y＝x2+bx+c的最大值和最小值；（3）点P为此函数图象上任意一点,其横坐标为m,过点P作PQ∥x轴,点Q的横坐标为﹣2m+1．已知点P 与点Q不重合,且线段PQ的长度随m的增大而减小．①求m的取值范围；②当PQ≤7时,直接写出线段PQ与二次函数y＝x2+bx+c（﹣2≤x＜）的图象交点个数及对应的m的取值范围．13．（2020•武汉模拟）已知：在平面直角坐标系中,抛物线y＝ax2﹣2ax﹣3a交x轴于A、B两点（点A在点B的左边）,交y轴负半轴于点C．（1）则点A的坐标为,点B的坐标为．（2）如图1,过点A的直线y＝ax+a交y轴正半轴于点F,交抛物线于点D,过点B作BE∥y轴交AD于E,求证：AF＝DE．（3）如图2,直线DE：y＝kx+b与抛物线只有一个交点D,与对称轴交于点E,对称轴上存在点F,满足DF＝FE．若a＝1,求点F坐标．14．（2020•哈尔滨模拟）如图,抛物线y＝ax2+bx+5经过坐标轴上A、B和C三点,连接AC,tan C＝,5OA＝3OB．（1）求抛物线的解析式；（2）点Q在第四象限的抛物线上且横坐标为t,连接BQ交y轴于点E,连接CQ、CB,△BCQ的面积为S,求S 与t的函数解析式；（3）已知点D是抛物线的顶点,连接CQ,DH所在直线是抛物线的对称轴,连接QH,若∠BQC＝45°,HR∥x 轴交抛物线于点R,HQ＝HR,求点R的坐标．15．（2019•衡阳）如图,二次函数y＝x2+bx+c的图象与x轴交于点A（﹣1,0）和点B（3,0）,与y轴交于点N,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接CP,过点P作CP的垂线与y轴交于点E．（1）求该抛物线的函数关系表达式；（2）当点P在线段OB（点P不与O、B重合）上运动至何处时,线段OE的长有最大值？并求出这个最大值；（3）在第四象限的抛物线上任取一点M,连接MN、MB．请问：△MBN的面积是否存在最大值？若存在,求出此时点M的坐标；若不存在,请说明理由．16．（2020•天津）已知点A（1,0）是抛物线y＝ax2+bx+m（a,b,m为常数,a≠0,m＜0）与x轴的一个交点．（Ⅰ）当a＝1,m＝﹣3时,求该抛物线的顶点坐标；（Ⅱ）若抛物线与x轴的另一个交点为M（m,0）,与y轴的交点为C,过点C作直线l平行于x轴,E是直线l 上的动点,F是y轴上的动点,EF＝2．①当点E落在抛物线上（不与点C重合）,且AE＝EF时,求点F的坐标；②取EF的中点N,当m为何值时,MN的最小值是？17．（2020•凉山州）如图,二次函数y＝ax2+bx+c的图象过O（0,0）、A（1,0）、B（,）三点．（1）求二次函数的解析式；（2）若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD 的解析式；（3）在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标．18．（2020•滨州）如图,抛物线的顶点为A（h,﹣1）,与y轴交于点B（0,﹣）,点F（2,1）为其对称轴上的一个定点．（1）求这条抛物线的函数解析式；（2）已知直线l是过点C（0,﹣3）且垂直于y轴的定直线,若抛物线上的任意一点P（m,n）到直线l的距离为d,求证：PF＝d；（3）已知坐标平面内的点D（4,3）,请在抛物线上找一点Q,使△DFQ的周长最小,并求此时△DFQ周长的最小值及点Q的坐标．19．（2016•巴彦淖尔）如图所示,抛物线y＝ax2﹣x+c经过原点O与点A（6,0）两点,过点A作AC⊥x轴,交直线y＝2x﹣2于点C,且直线y＝2x﹣2与x轴交于点D．（1）求抛物线的解析式,并求出点C和点D的坐标；（2）求点A关于直线y＝2x﹣2的对称点A′的坐标,并判断点A′是否在抛物线上,并说明理由；（3）点P（x,y）是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点Q,设线段PQ的长为l,求l与x的函数关系式及l的最大值．20．（2018•葫芦岛）如图,抛物线y＝ax2+4x+c（a≠0）经过点A（﹣1,0）,点E（4,5）,与y轴交于点B,连接AB．（1）求该抛物线的解析式；（2）将△ABO绕点O旋转,点B的对应点为点F．①当点F落在直线AE上时,求点F的坐标和△ABF的面积；②当点F到直线AE的距离为时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标．【例1】（2022•襄阳）在平面直角坐标系中,直线y＝mx﹣2m与x轴,y轴分别交于A,B两点,顶点为D的抛物线y＝﹣x2+2mx﹣m2+2与y轴交于点C．（1）如图,当m＝2时,点P是抛物线CD段上的一个动点．①求A,B,C,D四点的坐标；②当△P AB面积最大时,求点P的坐标；（2）在y轴上有一点M（0,m）,当点C在线段MB上时,①求m的取值范围；②求线段BC长度的最大值．【分析】（1）根据函数上点的坐标特点可分别得出A,B,C,D的坐标；①当m＝2时,代入上述坐标即可得出结论；②过点P作PE∥y轴交直线AB于点E,设点P的横坐标为t,所以P（t,﹣t2+4t﹣2）,E（t,2t﹣4）．根据三角形的面积公式可得△P AB的面积,再利用二次函数的性质可得出结论；（2）由（1）可知,B（0,﹣2m）,C（0,﹣m2+2）,①y轴上有一点M（0,m）,点C在线段MB上,需要分两种情况：当点M的坐标大于点B的坐标时；当点M的坐标小于点B的坐标时,分别得出m 的取值范围即可；②根据①中的条件可知,分两种情况,分别得出BC的长度,利用二次函数的性质可得出结论．【解答】解：（1）∵直线y＝mx﹣2m与x轴,y轴分别交于A,B两点,∴A（2,0）,B（0,﹣2m）；∵y＝﹣（x﹣m）2+2,∴抛物线的顶点为D（m,2）,令x＝0,则y＝﹣m2+2,∴C（0,﹣m2+2）．①当m＝2时,﹣2m＝﹣4,﹣m2+2＝﹣2,∴B（0,﹣4）,C（0,﹣2）,D（2,2）．②由上可知,直线AB的解析式为：y＝2x﹣4,抛物线的解析式为：y＝﹣x2+4x﹣2．如图,过点P作PE∥y轴交直线AB于点E,设点P的横坐标为t,∴P（t,﹣t2+4t﹣2）,E（t,2t﹣4）．∴PE＝﹣t2+4t﹣2﹣（2t﹣4）＝﹣t2+2t+2,∴△P AB的面积为：×（2﹣0）×（﹣t2+2t+2）＝﹣（t﹣1）2+3,∵﹣1＜0,∴当t＝1时,△P AB的面积的最大值为3．此时P（1,1）．（2）由（1）可知,B（0,﹣2m）,C（0,﹣m2+2）,①∵y轴上有一点M（0,m）,点C在线段MB上,∴需要分两种情况：当m≥﹣m2+2≥﹣2m时,可得≤m≤1+,当m≤﹣m2+2≤﹣2m时,可得﹣3≤m≤1﹣,∴m的取值范围为：≤m≤1+或﹣3≤m≤1﹣．②当≤m≤1+时,∵BC＝﹣m2+2﹣（﹣2m）＝﹣m2+2m+2＝﹣（m﹣1）2+3,∴当m＝1时,BC的最大值为3；当m≤﹣m2+2≤﹣2m时,即﹣3≤m≤1﹣,∴BC＝﹣2m﹣（﹣m2+2）＝m2﹣2m﹣2＝（m﹣1）2﹣3,当m＝﹣3时,点M与点C重合,BC的最大值为13．∴当m＝1时,BC的最大值为3；当m＝﹣3时,BC的最大值为13．【例2】（2022•湖州）如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上．抛物线y＝﹣x2+bx+c经过A,C两点,与x轴交于另一个点D．（1）①求点A,B,C的坐标；②求b,c的值．（2）若点P是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M（如图2所示）．当点P在BC上运动时,点M也随之运动．设BP＝m,CM＝n,试用含m的代数式表示n,并求出n的最大值．【分析】（1）①根据正方形的性质得出点A,B,C的坐标；②利用待定系数法求函数解析式解答；（2）根据两角相等证明△MCP∽△PBA,列比例式可得n与m的关系式,配方后可得结论．【解答】解：（1）①四边形OABC是边长为3的正方形,∴A（3,0）,B（3,3）,C（0,3）；②把A（3,0）,C（0,3）代入抛物线y＝﹣x2+bx+c中得：,解得：；（2）∵AP⊥PM,∴∠APM＝90°,∴∠APB+∠CPM＝90°,∵∠B＝∠APB+∠BAP＝90°,∴∠BAP＝∠CPM,∵∠B＝∠PCM＝90°,∴△MCP∽△PBA,∴＝,即＝,∴3n＝m（3﹣m）,∴n＝﹣m2+m＝﹣（m﹣）2+（0≤m≤3）,∵﹣＜0,∴当m＝时,n的值最大,最大值是．【例3】（2021•青海）如图,在平面直角坐标系中,直线y＝x+2与坐标轴交于A,B两点,点A在x轴上,点B在y轴上,C点的坐标为（1,0）,抛物线y＝ax2+bx+c经过点A,B,C．（1）求抛物线的解析式；（2）根据图象写出不等式ax2+（b﹣1 ）x+c＞2的解集；（3）点P是抛物线上的一动点,过点P作直线AB的垂线段,垂足为Q点．当PQ＝时,求P点的坐标．【分析】（1）根据题意得出A、B点的坐标,然后利用待定系数法求出二次函数的解析式；（2）根据（1）的解析式由图象判断即可；（3）作PE⊥x轴于点E,交AB于点D,根据函数图象点P的位置分三种情况分别计算出P点的坐标即可．【解答】解：（1）当x＝0,y＝0+2＝2,当y＝0时,x+2＝0,解得x＝﹣2,∴A（﹣2,0）,B（0,2）,把A（﹣2,0）,C（1,0）,B（0,2）代入抛物线解析式,得,解得,∴该抛物线的解析式为：y＝﹣x2﹣x+2；（2）方法一：ax2+（b﹣1 ）x+c＞2,即﹣x2﹣2x+2＞2,当函数y＝﹣x2﹣2x+2＝2时,解得x＝0或x＝﹣2,由图象知,当﹣2＜x＜0时函数值大于2,∴不等式ax2+（b﹣1 ）x+c＞2的解集为：﹣2＜x＜0；方法二：ax2+（b﹣1 ）x+c＞2,即﹣x2﹣x+2＞x+2,观察函数图象可知当﹣2＜x＜0时y＝﹣x2﹣x+2的函数值大于y＝x+2的函数值,∴不等式ax2+（b﹣1 ）x+c＞2的解集为：﹣2＜x＜0；（3）作PE⊥x轴于点E,交AB于点D,作PQ⊥AB于Q,①如图1,当P在AB上方时,在Rt△OAB中,∵OA＝OB＝2,∴∠OAB＝45°,∴∠PDQ＝∠ADE＝45°,在Rt△PDQ中,∠DPQ＝∠PDQ＝45°,∴PQ＝DQ＝,∴PD＝＝1,设点P（x,﹣x2﹣x+2）,则点D（x,x+2）,∴PD＝﹣x2﹣x+2﹣（x+2）＝﹣x2﹣2x,即﹣x2﹣2x＝1,解得x＝﹣1,∴此时P点的坐标为（﹣1,2）,②如图2,当P点在A点左侧时,同理①可得PD＝1,设点P（x,﹣x2﹣x+2）,则点D（x,x+2）,∴PD＝（x+2）﹣（﹣x2﹣x+2）＝x2+2x,即x2+2x＝1,解得x＝±﹣1,由图象知此时P点在第三象限,∴x＝﹣﹣1,∴此时P点的坐标为（﹣﹣1,﹣）,③如图3,当P点在B点右侧时,在Rt△OAB中,∵OA＝OB＝2,∴∠OAB＝45°,∴∠PDQ＝∠DPQ＝45°,在Rt△PDQ中,∠DPQ＝∠PDQ＝45°,∴PQ＝DQ＝,∴PD＝＝1,设点P（x,﹣x2﹣x+2）,则点D（x,x+2）,∴PD＝（x+2）﹣（﹣x2﹣x+2）＝x2+2x,即x2+2x＝1,解得x＝±﹣1,由图象知此时P点在第一象限,∴x＝﹣1,∴此时P点的坐标为（﹣1,）,综上,P点的坐标为（﹣1,2）或（﹣﹣1,﹣）或（﹣1,）．【例4】（2022•雅安）已知二次函数y＝ax2+bx+c的图象过点A（﹣1,0）,B（3,0）,且与y轴交于点C（0,﹣3）．（1）求此二次函数的表达式及图象顶点D的坐标；（2）在此抛物线的对称轴上是否存在点E,使△ACE为Rt△,若存在,试求点E的坐标,若不存在,请说明理由；（3）在平面直角坐标系中,存在点P,满足P A⊥PD,求线段PB的最小值．【分析】（1）设二次函数的表达式为交点式,将点C坐标代入,进而求得结果；（2）先把AC,CE,AE的平方求出或表示出来,然后分为∠CAE＝90°,∠ACE＝90°及∠AEC＝90°,然后根据勾股定理逆定理列出方程,解方程,进而求得结果；（3）根据∠APD＝90°确定点P在以AD的中点为圆心,为半径的圆上,进一步求得结果．【解答】解：（1）由题意设二次函数表达式为：y＝a（x+1）•（x﹣3）,∴a•（﹣3）＝﹣3,∴a＝1,∴y＝（x+1）•（x﹣3）＝x2﹣2x﹣3＝（x﹣1）2﹣4,∴D（1,﹣4）；（2）存在点E,使△ACE是直角三角形,过程如下：设点E（1,m）,∵A（﹣1,0）,C（0,﹣3）,∴AC2＝10,AE2＝4+m2,CE2＝1+（m+3）2,当∠EAC＝90°时,AE2+AC2＝CE2,∴14+m2＝1+（m+3）2,∴m＝,∴E1（1,）,当∠ACE＝90°时,AC2+CE2＝AE2,∴11+（m+3）2＝4+m2,∴m＝﹣,∴E2（1,﹣）,当∠AEC＝90°时,AE2+CE2＝AC2,∴5+m2+（m+3）2＝10,∴m＝﹣1或﹣2,∴E3（1,﹣1）,E4（1,﹣2）,综上所述：点E（1,）或（1,﹣）或（1,﹣1）或（1,﹣2）；（3）设AD的中点为I,∵A（﹣1,0）,D（1,﹣4）,∴AD＝＝2,I（0,﹣2）,∴P A⊥PD,∴∠ADP＝90°,∴点P在以AD的中点I为圆心,为半径的圆上,∵BI＝＝,∴PB最小＝﹣．1．（2020•河北模拟）已知抛物线C：y＝ax2+bx+c（a＞0,c＜0）的对称轴为x＝4,C为顶点,且A（2,0）,C （4,﹣2）【问题背景】求出抛物线C的解析式．【尝试探索】如图2,作点C关于x轴的对称点C′,连接BC′,作直线x＝k交BC′于点M,交抛物线C于点N．①连接ND,若四边形MNDC′是平行四边形,求出k的值．②当线段MN在抛物线C与直线BC′围成的封闭图形内部或边界上时,请直接写出线段MN的长度的最大值．【拓展延伸】如图4,作矩形HGOE,且E（﹣3,0）,H（﹣3,4）,现将其沿x轴以1个单位每秒的速度向右平移,设运动时间为t,得到矩形H′G′O′E′,连接AC′,若矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分,请求出t的取值范围．【分析】【问题背景】A（2,0）,对称轴为x＝4,则点B（6,0）,则抛物线的表达式为：y＝a（x﹣2）（x ﹣6）,将点C的坐标代入上式即可求解；【尝试探索】①四边形MNDC′是平行四边形,则MN＝DC′＝2,即|k2﹣4k+6﹣（﹣k+6）|＝2,解得：k＝3或3,②MN＝（﹣k+6）﹣（k2﹣4k+6）＝﹣k2+3k,即可求解；【拓展延伸】（Ⅰ）当t＝2时,矩形过点A,此时矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分；（Ⅱ）当H′E′与对称轴右侧抛物线有交点时,此时y＝H′E′＝4,即x2﹣4x+6＝4,解得：x＝4（舍去4﹣2）,即可求解．【解答】解：【问题背景】A（2,0）,对称轴为x＝4,则点B（6,0）,则抛物线的表达式为：y＝a（x﹣2）（x﹣6）,将点C的坐标代入上式得：﹣2＝a（4﹣2）•（4﹣6）,解得：a＝,故抛物线的表达式为：…①；【尝试探索】①点C′（4,2）,由点B、C′的坐标可得,直线BC′的表达式为：y＝﹣x+6…②,四边形MNDC′是平行四边形,则MN＝DC′＝2,设点N的坐标为：（x,k2﹣4k+6）,则点M（k,﹣k+6）,即|k2﹣4k+6﹣（﹣k+6）|＝2,解得：k＝3或3,故k的值为：；②联立①②并解得：x＝0或6,故抛物线C与直线BC′围成的封闭图形对应的k值取值范围为：0≤k≤6,MN＝（﹣k+6）﹣（k2﹣4k+6）＝﹣k2+3k,∵0,故MN有最大值,最大值为；【拓展延伸】由点A、C′的坐标得,直线AC′表达式为：y＝x﹣2…③,联立①③并解得：x＝2或8,即封闭区间对应的x取值范围为：2≤x≤8,（Ⅰ）当t＝2时,矩形过点A,此时矩形H′G′O′E′与直线AC′和抛物线C围成的封闭图形有公共部分,（Ⅱ）当H′E′与对称轴右侧抛物线有交点时,此时y＝H′E′＝4,即x2﹣4x+6＝4,解得：x＝4（舍去4﹣2）,即x＝4+2,则t＝3+4+2＝7+2,故t的取值范围为：2≤t≤．2．（2018秋•宁城县期末）已知,如图,抛物线与x轴交点坐标为A（1,0）,C（﹣3,0）,（1）如图1,已知顶点坐标D为（﹣1,4）或B点（0,3）,选择适当方法求抛物线的解析式；（2）如图2,在抛物线的对称轴DH上求作一点M,使△ABM的周长最小,并求出点M的坐标；（3）如图3,将图2中的对称轴向左移动,交x轴于点P（m,0）（﹣3＜m＜﹣1）,与抛物线,线段BC 的交点分别为点E、F,用含m的代数式表示线段EF的长度,并求出当m为何值时,线段EF最长．【分析】（1）根据顶点D坐标设其顶点式,再将点C（2）连接BC,交DH于点M,使△ABM周长最小,即AM+BM最小,先求出BC直线解析式,再令x＝﹣1,求得M（﹣1,2）；（3）由题意得出E（m,﹣m2﹣2m+3）,F（m,m+3）,据此可知EF＝EP﹣FP＝﹣m2﹣2m+3﹣（m+3）,再根据二次函数的性质可得答案．【解答】解：（1）由抛物线的顶点D的坐标（﹣1,4）可设其解析式为y＝a（x+1）2+4,将点C（﹣3,0）代入,得：4a+4＝0,解得a＝﹣1,则抛物线解析式为y＝﹣（x+1）2+4＝﹣x2﹣2x+3；（2）连接BC,交DH于点M,此时△ABM的周长最小,当y＝0时,﹣（x+1）2+4＝0,解得x＝﹣3或x＝1,则A（1,0）,C（﹣3,0）,当x＝0时,y＝3,则B（0,3）,设直线BC的解析式为y＝kx+b,将B（0,3）,C（﹣3,0）代入得,解得：,∴直线BC解析式为y＝x+3,当x＝﹣1时,y＝﹣1+3＝2,所以点M坐标为（﹣1,2）；（3）由题意知E（m,﹣m2﹣2m+3）,F（m,m+3）,则EF＝EP﹣FP＝﹣m2﹣2m+3﹣（m+3）＝﹣m2﹣3m＝﹣（m+）2+,∴当m＝﹣时,线段EF最长．3．（2021•桥西区模拟）如图1,抛物线y＝ax2+bx+3与x轴交于A（﹣1,0）,B两点,与y轴交于点C,且CO＝BO,连接BC．（1）求抛物线的解析式；（2）如图2,抛物线的顶点为D,其对称轴与线段BC交于点E,求线段DE的长度；（3）如图3,垂直于x轴的动直线l分别交抛物线和线段BC于点P和点F,连接CP,CD,抛物线上是否存在点P,使△CDE∽△PCF,如果存在,求出点P的坐标,如果不存在,请说明理由．【分析】（1）根据题意可求得点C,B的坐标,将A,B坐标代入抛物线解析式求出a,b的值,即可得到抛物线解析式；（2）设直线BC的解析式为y＝kx+b,将点C,B的坐标代入求得k,b的值,即可求得直线BC的解析式,再求DE即可；（3）根据△CDE∽△PCF,DE∥PF,可得：＝,设点P坐标为（t,﹣t2+2t+3）,点F坐标为（t,﹣t+3）,建立关于t的方程求解即可．【解答】解：（1）在抛物线y＝ax2+bx+3中,令x＝0,得y＝3,∴C（0,3）,∴CO＝3,∵CO＝BO,∴BO＝3,∴B（3,0）,∵A（﹣1,0）,∴,解得：,∴抛物线的解析式为：y＝﹣x2+2x+3；（2）设直线BC的解析式为y＝kx+b,∵B（3,0）,C（0,3）,∴,解得：,∴直线BC的解析式为y＝﹣x+3,∵抛物线y＝﹣x2+2x+3的顶点D坐标为（1,4）,∴当x＝1时,y＝﹣1+3＝2,∴E（1,2）,∴DE＝2；（3）∵PF∥DE,∴∠CED＝∠CFP,当＝时,△PCF∽△CDE,由D（1,4）,C（0,3）,E（1,2）,利用勾股定理,可得CE＝＝,DE＝4﹣2＝2,设点P坐标为（t,﹣t2+2t+3）,点F坐标为（t,﹣t+3）,∴PF＝﹣t2+2t+3﹣（﹣t+3）＝﹣t2+3t,CF＝＝t,∴＝,∵t≠0,∴t＝2,当t＝2时,﹣t2+2t+3＝﹣22+2×2+3＝3,∴点P坐标为（2,3）．4．（2022•和平区二模）如图,在平面直角坐标系中,已知抛物线顶点A的坐标为（﹣2,4）,且经过坐标原点,与x轴负半轴交于点B．（1）求抛物线的函数表达式并直接写出点B的坐标；（2）过点A作AC⊥x轴于点C,若点D是y轴左侧的抛物线上一个动点（点D与点A不重合）,过点D作DE⊥x轴于点E,连接AO,DO,当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,求点D的坐标；（3）在（2）的条件下,当点D在第二象限时,在平面内存在一条直线,这条直线与抛物线在第二象限交于点F,在第三象限交于点G,且点A,点B,点D,到直线FG的距离都相等,请直接写出线段FG的长．【分析】（1）设该抛物线解析式为y＝a（x+2）2+4（a≠0）,把点（0,0）代入,即可求解；（2）根据题意得OC＝2,AC＝4,设点D（x,﹣x2﹣4x）,则DE＝|﹣x2﹣4x|,OE＝﹣x,根据∠ACO＝∠DEO＝90°,可得当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,∠AOC＝∠ODE或∠AOC＝∠DOE,分两种讨论,即可求解；（3）求出直线BD的解析式y＝x+14,直线BD与y轴交于（0,14）,可得过点A平行于BD的直线AM的解析式为y＝x+11,交y轴于（0,11）,可得直线FG的的解析式为y＝x+,联立方程组,得到点F．G的坐标,即可求解．【解答】解：（1）∵抛物线顶点的坐标为（﹣2,4）,∴设抛物线解析式为y＝a（x+2）2+4（a≠0）,把点（0,0）代入得：0＝a（x+2）2+4．解得：a＝﹣1,∴抛物线解析式为y＝﹣（x+2）2+4＝﹣x2﹣4x．令y﹣0,则﹣x2﹣4x＝0,解得：x1＝﹣4,x2＝0,∴点B（﹣4,0）,∴抛物线解析式为y＝﹣x2﹣4x．点B（﹣4,0）；（2）∵AC⊥x轴,点A（﹣2,4）,∴点C（﹣2,0）,∴OC＝2,AC＝4,∵∠ACO＝∠DEO＝90°,∴当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,∠AOC＝∠ODE或∠AOC＝∠DOE,设D（x,﹣x2﹣4x）,①当∠AOC＝∠ODE时,△AOC∽△ODE,如图：∵∠AOC＝∠ODE,∴tan∠AOC＝tan∠ODE,∴＝＝2,∴＝2,∴﹣x＝2（x2+4x）或﹣x＝﹣2（x2+4x）,∴x1＝0（舍去）,x2＝﹣或x3＝0（舍去）,x4＝﹣,∴点D的坐标为（﹣,﹣）或（﹣,）；②当∠AOC＝∠DOE时,△AOC∽△DOE,如图：∵∠AOC＝∠DOE,∴tan∠AOC＝tan∠DOE,∴＝＝2,∴＝2,∴﹣2x＝x2+4x或2x＝x2+4x,∴x1＝0（舍去）,x2＝﹣6或x3＝0（舍去）,x4＝﹣2（舍去）,∴点D的坐标为（﹣6,﹣12）；点D（﹣6,﹣12）；综上所述,当以A,O,C为顶点的三角形与以D,O,E为顶点的三角形相似时,点D的坐标为（﹣6,﹣12）或（﹣,﹣）或（﹣,）；（3）∵在（2）的条件下,点D在第二象限,∴点D的坐标为（﹣,）,直线BD的解析式y＝kx+m,∴,解得,∴直线BD的解析式y＝x+14,直线BD与y轴交于（0,14）,∴过点A平行于BD的直线AM的解析式为y＝x+11,交y轴于（0,11）,∵点A,点B,点D,到直线FG的距离都相等,∴直线FG的的解析式为y＝x+,联立得,解得,,∴F（﹣,）,G（﹣5,﹣5）,∴FG＝＝．5．（2022•鹿城区校级二模）如图,抛物线y＝x2+bx+c与x轴交于点A（﹣1,0）,B（5,0）,与y轴交于点C．（1）求抛物线的解析式和顶点D的坐标．（2）连结AD,点E是对称轴与x轴的交点,过E作EF∥AD交抛物线于点F（F在E的右侧）,过点F作FG∥x轴交ED于点H,交AD于点G,求HF的长．【分析】（1）把点A（﹣1,0）,B（5,0）代入抛物线解析式即可求解；（2）延长FG交y轴于点I,根据A,E,D坐标求出AE＝3,DE＝9,在Rt△EAD中,tan∠EAD＝3,再根据四边形AGFE是平行四边形,得出tan∠EFH＝tan∠EAD＝3,设HF＝m,EH＝3m,易证四边形OIHE是矩形,把点F（m+2,﹣3m）代入y＝x2﹣4x﹣5,求出m即可．【解答】解：（1）把点A（﹣1,0）,B（5,0）代入抛物线解析式,得：,解得：,∴y＝x2﹣4x﹣5＝（x﹣2）2﹣9,∴抛物线解析式为y＝x2﹣4x﹣5,顶点D坐标为（2,﹣9）；（2）延长FG交y轴于点I,∵A（﹣1,0）,E（2,0）,D（2,﹣9）,∴AE＝3,DE＝9,∴在Rt△EAD中,,∵EF∥AD,FG∥x轴,∴四边形AGFE是平行四边形,∴tan∠EFH＝tan∠EAD＝3,∴在Rt△EHF中,EH＝3HF,设HF＝m,EH＝3m,易证四边形OIHE是矩形,把点F（m+2,﹣3m）代入y＝x2﹣4x﹣5,得,﹣3m＝（m+2）2﹣4（m+2）﹣5,解得：或m＝（舍去）,∴．6．（2021•南岗区模拟）如图,抛物线y＝ax2+bx﹣4交x轴于点A（﹣3,0）,B（4,0）,交y轴于点C．（1）求抛物线的解析式；（2）点P为第一象限抛物线上一点,过点P作x轴的平行线,与抛物线的另一个交点为点G,连接CG 交x轴于点N,设点P的横坐标为t,ON的长为d,求d与t之间的函数解析式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下,连接PB,将线段PB绕着点P顺时针旋转90°得到线段PD,点D恰好落在y 轴上,点E在线段OB上,连接PE,点Q在EB的延长线上,且EQ＝PE,连接DQ交PE于点F,若PE＝3PF,求QN的长．【分析】（1）运用待定系数法即可得出答案；（2）设P（t,t2﹣t﹣4）,则G（1﹣t,t2﹣t﹣4）,利用tan∠GCH＝＝,求出CN,即可得出答案；（3）过点P作PT⊥x轴于点T,可证得△PDH≌△PBT（AAS）,过点F作x轴的垂线,垂足为K,过点D作KF的垂线,垂足为R,KR与PH交于点M,再证得△DRF≌△QKF（ASA）,过点Q作QW∥PD,可证得△DPF≌△QWF（AAS）,过点Q作QZ⊥PE于点Z,再证明△EQZ≌△EPT（AAS）,再利用HL证明Rt△QWZ≌Rt△PBT,设EB＝m,运用勾股定理建立方程求解即可．【解答】解：（1）∵抛物线y＝ax2+bx﹣4交x轴于点A（﹣3,0）,B（4,0）,∴,解得：,∴抛物线的解析式为；（2）如图1,设P（t,t2﹣t﹣4）,∵抛物线的对称轴为直线,PG∥x轴,∴点G与点P是抛物线上的一对对称点,∴G（1﹣t,t2﹣t﹣4）,设PG与y轴交于点H,则H（0,t2﹣t﹣4）,在抛物线中,令x＝0,得y＝﹣4,∴C（0,﹣4）,∴OC＝4,又CH＝t2﹣t﹣4﹣（﹣4）＝t2﹣t,GH＝t﹣1,∵tan∠GCH＝＝,∴,解得：,∴d与t之间的函数解析式为d＝；（3）如图2,过点P作PT⊥x轴于点T,∵∠DPB＝∠PHO＝∠HOB＝∠PTO＝∠PHD＝90°,∴四边形PHOT为矩形,∴∠HPT＝90°,∴∠DPH＝∠BPT,∵PD＝PB,∴△PDH≌△PBT（AAS）,∴DH＝BT,PH＝PT,∴,解得：t1＝6,t2＝﹣2（舍）,∴P（6,6）,∴DH＝BT＝2,ON＝d＝2,过点F作x轴的垂线,垂足为K,过点D作KF的垂线,垂足为R,KR与PH交于点M,∵PE＝3PF,∴EF＝2PF,∵cos∠PFM＝cos∠EFK,∴,∴FK＝2FM,∵∠MPT＝∠PTK＝∠TKM＝90°,∴四边形PMKT为矩形,∴MK＝PT＝6,∴FM＝2,FK＝4,同理四边形DHMR为矩形,∴DH＝RM＝2,RF＝FK＝4,∠R＝∠FKQ＝90°,∵∠DFR＝∠KFQ,∴△DRF≌△QKF（ASA）,∴DF＝QF,过点Q作QW∥PD,∴∠DPF＝∠QWF∵∠DFP＝∠WFQ,DF＝FQ,∴△DPF≌△QWF（AAS）,∴DP＝QW＝PB,PF＝WF,∴,过点Q作QZ⊥PE于点Z,∴∠EZQ＝∠PTE＝90°,∵∠PET＝∠QEZ,EP＝EQ,∴△EQZ≌△EPT（AAS）,∴PT＝QZ,EZ＝ET,∵QW＝PB,∴Rt△QWZ≌Rt△PBT（HL）,∴EW＝EB．设EB＝m,则EW＝WF＝FP＝m,∴EP＝3m,∵BT＝2,∴ET＝m+2,PT＝6,在Rt△EPT中,∵PE2＝ET2+PT2,∴（3m）2＝（m+2）2+62,解得：,m2＝﹣2（舍）,∴,∴BQ＝2BE＝5,∵OB＝4,∴OQ＝9,∵ON＝2,∴QN＝OQ+ON＝11．7．（2021•凉山州模拟）如图1,在平面直角坐标系中,已知B点坐标为（1,0）,且OA＝OC＝3OB,抛物线y＝ax2+bx+c（a≠0）图象经过A,B,C三点,其中D点是该抛物线的顶点．（1）求抛物线的解析式；（2）判断△ADC的形状并且求△ADC的面积；（3）如图2,点P是该抛物线第三象限部分上的一个动点,过P点作PE⊥AC于E点,当PE的值最大时,求此时P点的坐标及PE的最大值．【分析】（1）根据B点坐标为（1,0）,且OA＝OC＝3OB,得出B,C点的坐标,用待定系数法求解析式即可；（2）根据坐标求出三角形各边的长,利用勾股定理判断其为直角三角形,再用三角形面积公式求面积即可；（3）求出直线AC的解析式,过点P作PH∥y轴交AC于H,设出P点和H点坐标,用含x的代数式求出PE的值,根据二次函数性质求最值即可．【解答】解：（1）∵B点坐标为（1,0）,∴OB＝1,又∵OA＝OC＝3OB,∴OA＝OC＝3,∴A（﹣3,0）,C（0,﹣3）,将A,B,C三点代入解析式得,,解得,∴抛物线的解析式为：y＝x2+2x﹣3；（2）由（1）知抛物线的解析式为y＝x2+2x﹣3,∴对称轴为直线x＝﹣＝﹣1,当x＝﹣1时,y＝（﹣1）2+2×（﹣1）﹣3＝﹣4,∴D点的坐标为（﹣1,﹣4）,∴|AD|＝＝2,|AC|＝＝3,|CD|＝＝,∵|AD|2＝|AC|2+|CD|2,∴△ACD是直角三角形,S△ABC＝|AC|•|CD|＝×＝3；（3）设直线AC的解析式为y＝sx+t,代入A,C点坐标,得,解得,∴直线AC的解析式为y＝﹣x﹣3,如右图,过点P作y轴的平行线交AC于点H,∵OA＝OC,∴∠OAC＝∠OCA＝45°,∵PH∥y轴,∴∠PHE＝∠OCA＝45°,设点P（x,x2+2x﹣3）,则点H（x,﹣x﹣3）,∴PH＝﹣x﹣3﹣（x2+2x﹣3）＝﹣x2﹣3x,∴PE＝PH•sin∠PHE＝（﹣x2﹣3x）×＝﹣（x+）2+,∴当x＝﹣时,PE有最大值为,此时P点的坐标为（﹣,﹣）．8．（2022•无锡二模）已知抛物线y＝mx2﹣2mx+3（m＜0）与x轴交于A、B两点（点A在点B的左侧）,与y轴交于点C,且OB＝3OA．（1）求抛物线的函数表达式；（2）若M、N是第一象限的抛物线上不同的两点,且△BCN的面积总小于△BCM的面积,求点M的坐标；（3）若D为抛物线的顶点,P为第二象限的抛物线上的一点,连接BP、DP,分别交y轴于点E、F,若EF＝OC,求点P的坐标．【分析】（1）设A（x1,0）,B（x2,0）,因为OB＝3OA,所以x2＝﹣3x1,又由于x1,x2是方程mx2﹣2mx+3＝0的两根,所以x1+x2＝2,从而求出x1的值,得到A点坐标,代入到解析式中,求出m,即可解决问题；（2）由题意可得,只要求得第一象限内M点,使△BCM面积最大,过M作y轴平行线交BC于G点,设M（a,﹣a2+2a+3）,先求出直线BC的解析式,可以得到G（a,﹣a+3）,从而得的MG＝﹣a2+3a,利用S△MBC＝S△MGC+S△MGB,得到S△MBC＝,当a＝时,△MBC面积最大,从而求得M点坐标；（3）由EF＝得EF＝1,过D作DQ∥y轴交BP于Q点,设出P点坐标,求出D点坐标和直线BP解析式,从而表示出DQ的长度,由△PEF∽△PQD,利用相似三角形对应边上的高的比等于相似比,。

2020年九年级中考数学压轴试题(附答案)

那么∠BAF 的大小为（）
A.40°
B.45°
C.50°
D.10°
第 4 题图
第 5 题图
第 6 题图
5.如图，在△ ABC 中，AB＝AC，∠A＝30°，AB 的垂直平分线 l 交 AC 于点 D，则∠CBD 的
度数为（）
A.30°
B.45°
C.50°
D.75°
6.甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路
九年级数学中考压轴试题第 7 页
∴FC＝4cos30°＝2 3（cm）．
故答案为：2 3． 14.解：∵y＝ax2＋（a2﹣1）x﹣a＝（ax﹣1）（x＋a）， ∴当 y＝0 时，x1＝1a，x2＝﹣a， ∴抛物线与 x 轴的交点为（1a，0）和（﹣a，0）． ∵抛物线与 x 轴的一个交点的坐标为（m，0）且 2＜m＜3， ∴当 a＞0 时，2＜1a＜3，解得：13＜a＜12；当 a＜0 时，2＜﹣a＜3，解得﹣3＜a＜﹣2．故答案为：13＜a＜12或﹣3＜a＜﹣2．【少填给 1 分，填错或不填不给分】
程后，乙开始出发，当乙超出甲 150 米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速
度跑向体育馆．如图是甲、乙两人在跑步的全过程中经过的路程 y（米）与甲出发的时间 x（秒）
的函数图象，则乙在途中等候甲用了（）秒
A.200
B.150
C.100
D.80
二、填空题（本大题共 8 小题，每小题 3 分，共 24 分）
21.（8 分）AB 为⊙O 直径，BC 为⊙O 切线，切点为 B，CO 平行于弦 AD，作直线 DC．（1）求证：DC 为⊙O 切线；（2）若 AD•OC＝8，求⊙O 半径 r．

2020年江苏中考数学压轴题精选精练5(解析版)

2020年中考数学压轴题精选精练5一、选择题1．若0＜m＜2，则关于x的一元二次方程﹣（x+m）（x+3m）＝3mx+37根的情况是（）A．无实数根B．有两个正根C．有两个根，且都大于﹣3mD．有两个根，其中一根大于﹣m2．如图，正方形ABCD内接于⊙O，点P在劣弧AB上，连接DP，交AC于点Q．若QP ＝QO，则的值为（）A．B．C．D．3．如图，D是△ABC内一点，BD⊥CD，AD＝7，BD＝4，CD＝3，E、F、G、H分别是AB、BD、CD、AC的中点，则四边形EFGH的周长为（）A．12 B．14 C．24 D．214．如图，AB是半圆O的直径，且AB＝12，点C为半圆上的一点．将此半圆沿BC所在的直线折叠，若圆弧BC恰好过圆心O，则图中阴影部分的面积是（）A．4πB．5πC．6πD．8π5．如图，△ABC和△DCE都是边长为8的等边三角形，点B，C，E在同一条直线上接BD，AE，则四边形FGCH的面积为（）A．B．C．D．6．如图，△ABC内接于⊙O，∠A＝60°，BC＝4，当点P在上由B点运动到C点时，弦AP的中点E运动的路径长为（）A．πB．πC．πD．2二、填空题1．如图，四边形ABCD中，已知AB＝AD，∠BAD＝60°，∠BCD＝120°，若四边形ABCD 的面积为4，则AC＝．第1题第2题2．如图，AB为⊙O的直径，AB＝4，C为半圆AB的中点，P为上一动点，延长BP至点Q，使BP•BQ＝AB2．若点P由A运动到C，则点Q运动的路径长为．3．如图，边长为5的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN 长度的最小值是．第3题第4题4．如图，AB为⊙O的直径，点C、D分别是半圆AB的三等分点，AB＝4，点P自A点出发，沿弧ABC向C点运动，T为△P AC的内心．当点P运动到使BT最短时就停止运动，点T运动的路径长为5．如图，在四边形ABCD中，∠ADC＝90°，∠BAD＝60°，对角线AC平分∠BAD，且AB＝AC＝4，点E、F分别是AC、BC的中点，连接DE、EF、DF，则DF的长为．第3题第4题6．如图，AB为半圆O的直径，点C在半圆O上，AB＝8，∠CAB＝60°，P是弧上的一个点，连接AP，过点C作CD⊥AP于点D，连接BD，在点P移动过程中，BD长的最小值为．三、解答题1．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN ＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．2．如图，抛物线23(0)y ax ax c a =-+≠与x 轴交于A ，B 两点，交y 轴于点C ，其中A （－1，0），C （0，3）. (1) 求抛物线的解析式(2) 点P 是线段BC 上方抛物线上一动点（不与B ，C 重合），过点P 作PD ⊥x 轴，垂足为D ，交BC 于点E ，作PF ⊥直线BC 于点F ，设点P 的横坐标为x ，△PEF 的周长记为l ,求l 关于x 的函数关系式，并求出l 的最大值及此时点P 的坐标(3) 点H 是直线AC 上一点，该抛物线的对称轴上一动点G ，连接OG ，GH ，则两线段OG ，GH 的长度之和的最小值等于______,此时点G 的坐标为_____（直接写出答案。

2020年江苏省九年级中考数学压轴题选择、填空、解答题精选精练(含解析)

2020年中考数学压轴题考前冲刺练习6一、选择题1．如图，是半径为1的圆弧，△AOC为等边三角形，D是上的一动点，则四边形AODC 的面积s的取值范围是（）A．≤s≤B．＜s≤C．≤s≤D．＜s＜2．如图，分别以Rt△ABC的斜边AB，直角边AC为边向外作等边△ABD和等边△ACE，F 为AB的中点，DE，AB相交于点G，若∠BAC＝30，下列结论：①EF⊥AC；②AD＝AE；③AD＝4AG；④记△ABC的面积为S1，四边形FBCE的面积为S2，则S1：S2＝2：3．其中正确的结论的序号是（）A．①③B．②④C．①③④D．①②③④3．如图，小桥用黑白棋子组成的一组图案，第1个图案由1个黑子组成，第2个图案由1个黑子和6个白子组成，第3个图案由13个黑子和6个白子组成，按照这样的规律排列下去，则第9个图案中共有（）和黑子．A．37 B．42 C．73 D．1214．如图，已知A，B是反比例函数y＝（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于t的函数图象大致为（）A．B．C．D．5．若整数a使关于x的不等式组无解，且使关于x的分式方程﹣＝﹣3有正整数解，则满足条件的a的值之积为（）A．28 B．﹣4 C．4 D．﹣26．如图，等边三角形ABC的边长为4，点O是△ABC的中心，∠FOG＝120°，绕点O旋转∠FOG，分别交线段AB、BC于D、E两点，连接DE，给出下列四个结论：①OD＝OE；②S△ODE＝S△BDE；③四边形ODBE的面积始终等于；④△BDE周长的最小值为6．上述结论中正确的个数是（）A．1 B．2 C．3 D．4二、填空题1．如图，⊙O是△ABC的外接圆，其中AB是⊙O的直径，将△ABC沿AB翻折后得到△ABD，点E在AD延长线上，BE与⊙O相切于点B，分别延长线段AE、CB相交于点F，若BD＝3，AE＝10，则线段EF的长为．2．已知关于x的方程x2﹣4x+t﹣2＝0（t为实数）两非负实数根a，b，则（a2﹣1）（b2﹣1）的最小值是．3．如图，长方形纸片ABCD中，AB＝4，将纸片折叠，折痕的一个端点F在边AD上，另一个端点G在边BC上，若顶点B的对应点E落在长方形内部，E到AD的距离为1，BG＝5，则AF的长为．第3题第4题4．如图，射线OP过Rt△ABC的边AC、AB的中点M、N，AC＝4cm，BC＝4cm，OM ＝3cm．射线OP上有一动点Q从点O出发，沿射线OP以每秒1cm的速度向右移动，以Q为圆心，QM为半径的圆，经过t秒与BC、AB中的一边所在的直线相切，请写出t 的所有可能值（单位：秒）5．如图，点P是⊙O的直径AB的延长线上一点，过点P作直线交⊙O于C、D两点．若AB＝6，BP＝2，则tan∠P AC•tan∠P AD＝．第5题第6题6．如图，在△ABC中，∠C＝90°，AC＝BC＝4，D是AB的中点，点E，F分别在AC，BC边上运动（点E不与点A，C重合），且保持ED⊥FD，连接DE，DF，EF，在此运动变化的过程中，有下列结论：①AE＝CF；②EF最大值为2；③四边形CEDF的面积不随点E位置的改变而发生变化；④点C到线段EF的最大距离为．其中结论正确的有（把所有正确答案的序号都填写在横线上）三、解答题1．如图，已知AC为正方形ABCD的对角线，点P是平面内不与点A，B重合的任意一点，连接AP，将线段AP绕点P顺时针旋转90°得到线段PE，连接AE，BP，CE．（1）求证：△APE∽△ABC；（2）当线段BP与CE相交时，设交点为M，求的值以及∠BMC的度数；（3）若正方形ABCD的边长为3，AP＝1，当点P，C，E在同一直线上时，求线段BP 的长．2．如图，在平面直角坐标系xOy中，抛物线y＝ax2+x+c与x轴交于A，B两点（点A 在点B的左侧），交y轴于点C，经过B，C两点的直线为y＝．（1）求抛物线的函数表达式；（2）点P为抛物线上的动点，过点P作x轴的垂线，交直线BC于点M，连接PC，若△PCM为直角三角形，求点P的坐标；（3）当P满足（2）的条件，且点P在直线BC上方的抛物线上时，如图2，将抛物线沿射线BC方向平移，平移后B，P两点的对应点分别为B′，P′，取AB的中点E，连接EB′，EP′，试探究EB'+EP'是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．3．△ABC内接⊙O，AD⊥BC与D，连接OA．（1）如图1，求证：∠BAO＝∠CAD；（2）如图2，作BE⊥AC交CA延长线于E交⊙O于F，延长AD交⊙O于G，连接AF，求证：AD+AF＝DG；（3）在第（2）问的条件下，如图3，OA交BC于点T，CA＝CT，AD＝2AF，AB＝4，求DT长．4．如图1，在平面直角坐标系xOy中，三角形ABC如图放置，点C（0，4），点A，B 在x轴上，且OB＝4OA，tan∠CBO＝．（1）求过点A、C直线解析式；（2）如图2，点M为线段BC上任意一点，点D在OC上，且CD＝DM，设M的横坐标为t，△CDM的面积为S，求S与t之间的函数关系式，直接写出t的取值范围；（3）在（2）的条件下，如图3，在OB上取点N，过N作NF⊥DM，垂足为点F，连接CF，AF，∠DCF+∠AFN＝60°，NF＝BO时，求点D的坐标．5．阅读下列材料，解答下列问题材料一：一个三位以上的自然数，如果该自然数的末三位表示的数与末三位之前的数字表示的数之差是11的倍数，我们称满足此特征的数叫“网红数”，如：65362，362﹣65＝297＝11×27，称65362是“网红数”．材料二：对任的自然数p均可分解为P＝100x+10y+z（x≥0，0≤y≤9，0≤z≤9且x、y，z均为整数）如：5278＝52×100+10×7+8，规定：G（P）＝．（1）求证：任两个“网红数”之和一定能被11整除；（2）已知：S＝300+10b+a，t＝1000b+100a+1142（1≤a≤7，0≤b≤5，其a、b均为整数），当s+t为“网红数”时，求G（t）的最大值．6．如图已知：直线y＝﹣x+3交x轴于点A，交y轴于点B，抛物线y＝ax2+bx+c经过A、B、C（1，0）三点．（1）求抛物线的解析式；（2）若点D的坐标为（﹣1，0），在直线y＝﹣x+3上有一点P，使△ABO与△ADP相似，求出点P的坐标；（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．【答案与解析】一、选择题1．【分析】根据题意，得四边形AODC的最小面积即是三角形AOC的面积，最大面积即是当OD⊥OC时四边形的面积．要求三角形AOC的面积，作CD⊥AO于D．根据等边三角形的性质以及直角三角形的性质，求得CD＝，得其面积是；要求最大面积，只需再进一步求得三角形DOC的面积，即是，则最大面积是．【解答】解：根据题意，得四边形AODC的面积最小即是三角形AOC的面积，最大面积即是当OD⊥OC时四边形的面积．作CH⊥AO于H，∵△AOC为等边三角形∴CH＝∴S△AOC＝；当OD⊥OC时面积最大，∴S△OCD＝，则最大面积是+＝∴四边形AODC的面积s的取值范围是＜s≤．故选：B．2．【分析】根据直角三角形的性质和线段垂直平分线的性质，可得①正确；根据等边三角形的性质和直角三角形的斜边与直角边不相等，可得②不正确；根据等边三角形的性质、全等三角形的判定和性质、平行四边形的判定和性质，可得③正确；根据直角三角形的性质、三角形面积、梯形面积公式，可得④正确．【解答】证明：如图，分别以Rt△ABC的斜边AB，直角边AC为边向外作等边△ABD 和等边△ACE，F为AB的中点，DE，AB相交于点G，若∠BAC＝30，下列结论：①EF⊥AC；②AD＝AE；③AD＝4AG；④记△ABC的面积为S1，四边形FBCE的面积为S2，则S1：S2＝2：3．其中正确的结论的序号是（①③④）①连接CF，∵F是Rt△ABC的斜边AB的中点，∴AF＝CF＝AB，又∵△ACE是等边三角形，∴AE＝CE∴EF是线段AC的垂直平分线，∴EF⊥AC故①正确；②∵△ABD和△ACE是等边三角形，∴AD＝AB，AC＝AE，在Rt△ABC中，AB≠AC，∴AD≠AE，故②不正确；③∵△ABD是等边三角形，F是AB中点，∴DF⊥AB，又∵∠BAC＝30，△ACE是等边三角形，∴∠EAC＝60，∴∠BAE＝90，∴BA⊥AE，∴DF∥AE，又∠DBA＝∠ABC＝60，∠BFD＝∠BCA＝90，BD＝AB，∴△FBD≌△CBA，∴DF＝AE，∴四边形DFEA是平行四边形，∴AG＝GF＝AF，又AF＝AB，AG＝AB，又AB＝AD，∴AD＝4AG．故③正确；④在Rt△ABC中，AC＝BC，CH＝AC，∴EH＝CH＝•CB＝CB，FH＝BC，∴FE＝FH+HE＝2BC，∵BC⊥AC，EF⊥AC，∴EF∥BC，又FB与CE不平行，∴四边形FBCE是梯形，∴S2＝（BC+FE）•CH＝BC•CH，S1＝BC•AC＝BC•CH，∴S1：S2＝2：3．∴故④正确，故选：C．3．【分析】观察图象得到第1、2图案中黑子有1个，第3、4图案中黑子有1+2×6＝13个，第5、6图案中黑子有1+2×6+4×6＝37个，…，据此规律可得．【解答】解：第1、2图案中黑子有1个，第3、4图案中黑子有1+2×6＝13个，第5、6图案中黑子有1+2×6+4×6＝37个，第7、8图案中黑子有1+2×6+4×6+6×6＝73个，第9、10图案中黑子有1+2×6+4×6+6×6+8×6＝121个，故选：D．4．【分析】结合点P的运动，将点P的运动路线分成O→A、A→B、B→C三段位置来进行分析三角形OMP面积的计算方式，通过图形的特点分析出面积变化的趋势，从而得到答案．【解答】解：设∠AOM＝α，点P运动的速度为a，当点P从点O运动到点A的过程中，S＝＝a2•cosα•sinα•t2，由于α及a均为常量，从而可知图象本段应为抛物线，且S随着t的增大而增大；当点P从A运动到B时，由反比例函数性质可知△OPM的面积为k，保持不变，故本段图象应为与横轴平行的线段；当点P从B运动到C过程中，OM的长在减少，△OPM的高与在B点时相同，故本段图象应该为一段下降的线段；故选：A．5．【分析】表示出不等式组的解集，由不等式组无解确定出a的范围，分式方程去分母转化为整式方程，表示出分式方程的解，由分式方程有正整数解确定出a的值，即可求出所求．【解答】解：不等式组整理得：，由不等式组无解，得到3a﹣2≤a+2，解得：a≤2，分式方程去分母得：ax+5＝﹣3x+15，即（a+3）x＝10，由分式方程有正整数解，得到x＝，即a+3＝1，2，10，解得：a＝﹣2，2，7，综上，满足条件a的为﹣2，2，之积为﹣4，故选：B．6．【分析】连接OB、OC，如图，利用等边三角形的性质得∠ABO＝∠OBC＝∠OCB＝30°，再证明∠BOD＝∠COE，于是可判断△BOD≌△COE，所以BD＝CE，OD＝OE，则可对①进行判断；利用S△BOD＝S△COE得到四边形ODBE的面积＝S△ABC＝，则可对③进行判断；作OH⊥DE，如图，则DH＝EH，计算出S△ODE＝OE2，利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断；由于△BDE的周长＝BC+DE＝4+DE＝4+OE，根据垂线段最短，当OE⊥BC时，OE最小，△BDE的周长最小，计算出此时OE的长则可对④进行判断．【解答】解：连接OB、OC，如图，∵△ABC为等边三角形，∴∠ABC＝∠ACB＝60°，∵点O是△ABC的中心，∴OB＝OC，OB、OC分别平分∠ABC和∠ACB，∴∠ABO＝∠OBC＝∠OCB＝30°∴∠BOC＝120°，即∠BOE+∠COE＝120°，而∠DOE＝120°，即∠BOE+∠BOD＝120°，∴∠BOD＝∠COE，在△BOD和△COE中，∴△BOD≌△COE，∴BD＝CE，OD＝OE，所以①正确；∴S△BOD＝S△COE，∴四边形ODBE的面积＝S△OBC＝S△ABC＝××42＝，所以③正确；作OH⊥DE，如图，则DH＝EH，∵∠DOE＝120°，∴∠ODE＝∠OEH＝30°，∴OH＝OE，HE＝OH＝OE，∴DE＝OE，∴S△ODE＝•OE•OE＝OE2，即S△ODE随OE的变化而变化，而四边形ODBE的面积为定值，∴S△ODE≠S△BDE；所以②错误；∵BD＝CE，∴△BDE的周长＝BD+BE+DE＝CE+BE+DE＝BC+DE＝4+DE＝4+OE，当OE⊥BC时，OE最小，△BDE的周长最小，此时OE＝，∴△BDE周长的最小值＝4+2＝6，所以④正确．故选：C．二、填空题1．【分析】证明△ABD∽△BED，得出＝，求出AD＝9，DE＝1，由勾股定理得出BE＝＝，AB＝＝3，再证△FBE∽△F AB得出比例式，得出BF＝3EF，在Rt△ACF中根据AF2＝AC2+CF2可得关于EF的一元二次方程，解之可得．【解答】解：∵AB为⊙O的直径，∴∠C＝90°，∵将△ABC沿AB翻折后得到△ABD，∴△ABC≌△ABD，∴∠ADB＝∠C＝90°，AC＝AD，BC＝BD＝3，∵BE与⊙O相切于点B，∴∠ABE＝90°，∠DBE＝∠BAD，∴△ABD∽△BED，∴＝，∴AD×DE＝BD2＝9，∴AD（AE﹣AD）＝9，∴AD（10﹣AD）＝9，解得：AD＝9或AD＝1（舍去），∴AD＝9，DE＝1，∴BE＝＝，AB＝＝3，∵四边形ACBD内接于⊙O，∴∠FBD＝∠F AC，即∠FBE+∠DBE＝∠BAE+∠BAC，又∵∠DBE+∠ABD＝∠BAE+∠ABD＝90°，∴∠DBE＝∠BAE，∴∠FBE＝∠BAC，又∠BAC＝∠BAD，∴∠FBE＝∠BAD，∴△FBE∽△F AB，∴＝＝＝，∴BF＝3EF，在Rt△ACF中，∵AF2＝AC2+CF2，∴（10+EF）2＝92+（3+3EF）2，整理得：4EF2﹣EF﹣5＝0，解得：EF＝，或EF＝﹣1（舍），∴EF＝；故答案为：．2．【分析】a，b是关于x的一元二次方程x2﹣4x+t﹣2＝0的两个非负实根，根据根与系数的关系，化简（a2﹣1）（b2﹣1）即可求解．【解答】解：∵a，b是关于x的一元二次方程x2﹣4x+t﹣2＝0的两个非负实根，∴可得a+b＝4，ab＝t﹣2≥0，△＝16﹣4（t﹣2）≥0．解得：2≤t≤6（a2﹣1）（b2﹣1）＝（ab）2﹣（a2+b2）+1＝（ab）2﹣（a+b）2+2ab+1，∴（a2﹣1）（b2﹣1），＝（t﹣2）2﹣16+2（t﹣2）+1，＝（t﹣1）2﹣16，∵2≤t≤6，∴当t＝2时，（t﹣1）2取最小值，最小值为1，∴代数式（a2﹣1）（b2﹣1）的最小值是1﹣16＝﹣15，故答案为：﹣15．3．【分析】设EH与AD相交于点K，过点E作MN∥CD分别交AD、BC于M、N，然后求出EM、EN，在Rt△ENG中，利用勾股定理列式求出GN，再根据△GEN和△EKM相似，利用相似三角形对应边成比例列式求出EK、KM，再求出KH，然后根据△FKH和△EKM 相似，利用相似三角形对应边成比例列式求解即可．【解答】解：设EH与AD相交于点K，过点E作MN∥CD分别交AD、BC于M、N，∵E到AD的距离为1，∴EM＝1，EN＝4﹣1＝3，在Rt△ENG中，GN＝＝＝4，∵∠GEN+∠KEM＝180°﹣∠GEH＝180°﹣90°＝90°，∠GEN+∠NGE＝180°﹣90°＝90°，∴∠KEM＝∠NGE，又∵∠ENG＝∠KME＝90°，∴△GEN∽△EKM，∴＝＝，即＝＝，解得EK＝，KM＝，∴KH＝EH﹣EK＝4﹣＝，∵∠FKH＝∠EKM，∠H＝∠EMK＝90°，∴△FKH∽△EKM，∴＝，即＝，解得FH＝，∴AF＝FH＝．故答案为．4．【分析】如图，作OG⊥AB于G，由题意OG＝ON＝＞3，所以⊙Q在AC的左边不可能与AB相切．接下来分三种情形讨论求解即可．【解答】解：如图，作OG⊥AB于G，由题意OG＝ON＝＞3，所以⊙Q在AC 的左边不可能与AB相切．相切有三种可能：当⊙Q与BC相切时，MQ＝2，∴|t﹣3|＝2，∴t＝1或5．当⊙Q与AB相切时，设切点为H，连接QH．易知QN＝2QH，∴2﹣（t﹣3）＝2（t﹣3），解得t＝，综上所述，t＝1s或5s或（）s时，⊙Q与BC/AB相切．故答案为1s或5s或（）s5．【分析】连接BC、BD．因为AB是直径，推出∠ACB＝∠ADB＝90°，可得tan∠P AC•tan ∠P AD＝•＝•，利用相似三角形的性质转化即可解决问题；【解答】解：连接BC、BD．∵AB是直径，∴∠ACB＝∠ADB＝90°，∴tan∠P AC•tan∠P AD＝•＝•，∵△PCB∽△P AD，∴＝，∵△PBD∽△PCA，∴＝，∴tan∠P AC•tan∠P AD＝•＝＝，故答案为．6．【分析】①作常规辅助线连接CD，由SAS定理可证△CDF和△ADE全等，即可证得AE ＝CF；②根据AE＝CF，设CE＝x，用含x的式子表示出CF的长，根据勾股定理，即可表示出EF的长，根据二次函数的增减性，表示出EF的最小值；③由割补法可知四边形CEDF的面积保持不变；④由①可知，DE＝EF，可得△DEF是等腰直角三角形，当DF与BC垂直，即DF最小时，FE取最小值2，此时点C到线段EF的最大距离．【解答】解：如图，连接CD．∵在△ABC中，AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵D是AB的中点，∴CD＝AD＝BD，∠ADC＝90°，∠ACD＝∠BCD＝45°，∴∠1+∠2＝90°，∵ED⊥FD，∴∠2+∠3＝90°，∴∠1＝∠3，在△ADE和△CDF中，，∴△ADE≌△CDF（ASA），∴AE＝CF；故①正确；（2）设CE＝x，则CF＝AE＝4﹣x，在Rt△CEF中，，∵2（x﹣2）2+8有最小值，最小值为8，∴EF有最小值，最小值为．故②错误；③由①知，△ADE≌△CDF，∴S四边形EDFC＝S△EDC+S△FDC＝S△EDC+S△ADE＝S△ADC，∴四边形CEDF的面积不随点E位置的改变而发生变化．故③正确；④由①可知，△ADE≌△CDF，∴DE＝DF，∴△DEF是等腰直角三角形，∴，当EF∥AB时，∵AE＝CF，∴E，F分别是AC，BC的中点，故EF是△ABC的中位线，∴EF取最小值＝，∵CE＝CF＝2，∴此时点C到线段EF的最大距离为．故④正确．故答案为：①③④．三、解答题1．【分析】（1）先求出∠APE＝∠ABC＝90°，∠P AE＝∠PEA＝∠ABC＝45°，即可得出结论；（2）由（1）知，△APE∽△ABC，得出，再判断出∠P AB＝∠EAC，进而判断出△P AB∽△EAC，即可得出结论；（3）先画出图形，利用勾股定理求出CP'，再分两种情况，求出CE和CE'，借助（2）的结论，即可得出结论．【解答】解：（1）∵AC是正方形ABCD的对角线，∴∠ABC＝90°，∠BAC＝∠BCA＝45°，由旋转知，P A＝PE，∠APE＝90°＝∠ABC，∴∠P AE＝∠PEA＝45°＝∠BAC，∴△APE∽△ABC；（2）在Rt△ABC中，AB＝CB，∴AC＝AB，由（1）知，△APE∽△ABC，∴，∵∠BAC＝∠P AE＝45°，∴∠P AB＝∠EAC，∴△P AB∽△EAC，∴＝＝，∵△P AB∽△EAC，∴∠ABP＝∠ACE，∴∠BCE+∠CBM＝∠BCE+∠ABP+∠ABC＝∠BCE+∠ACE+∠ABC＝∠ACB+∠ABC＝45°+90°＝135°，∴∠BMC＝180°﹣（∠BCE+∠CBM）＝45°；（3）如图，在Rt△ABC中，AB＝BC＝3，∴AC＝3，∵点P，C，E在同一条线上，且∠APE＝90°，∴CP＝＝，∴CE＝CP﹣PE＝﹣1或CE'＝CP'+P'E＝+1，由（2）知，＝，∴BP＝CE＝（﹣1）＝或BP'＝CE'＝；即：BP的长为或．2．【分析】（1）y＝，过点B，C，则点B、C的坐标分别为：（3，0）、（0，），则c＝，将点B的坐标代入抛物线表达式，即可求解；（2）分∠PCM＝90°、∠CPM＝90°两种情况，分别求解即可；（3）作点E关于P′B′的对称点E′，将点E′沿P′B′方向平移2个单位得到点E″，连接E、E″交P′B′所在的直线于点B′，点B′沿P′B′方向平移2个单位得到点P′，则点P′、B′为所求，即可求解．【解答】解：（1）y＝，过点B，C，则点B、C的坐标分别为：（3，0）、（0，），则c＝，将点B的坐标代入抛物线表达式并解得：a＝﹣，故抛物线的表达式为：y＝﹣x2+x+；（2）①当∠PCM＝90°时，由点A、B、C的坐标知，△ABC为直角三角形，故AC⊥BC，当△PCM为直角三角形时，点P与点A重合，∴点P（﹣1，0）；②当∠CPM＝90°时，则点C、P关于函数对称轴对称，此时点P（2，），故点P的坐标为（﹣1，0）或（2，）；（3）存在，理由：点P（2，），设图象沿BC方向向左平移3m个单位，则向上平移m个单位，则平移后点B′、P′的坐标分别为：（3﹣3m，m）、（2﹣3m，m+），点E（1，0），分别过点A、E作直线BC的平行线n、m，过点B′作直线m的对称点B″，则EB′＝EB″，当B″、E、P′三点共线时，EB'+EP'＝EB″+EP′＝B″P′最小；点E是AB的中点，则直线m与直线n、直线m与直线AC等距离，则点B″在直线n 上，直线BC的倾斜角为30°，则直线B′B″的倾斜角为60°，则设直线B′B″的表达式为：y＝x+b，将点B′的坐标代入上式并解得：直线B′B″表达式为：y＝x+（4m﹣3）…①，设过点A的直线n的表达式为：y＝﹣x+b′，将点A的坐标代入上式并解得：直线n的表达式为：y＝﹣（x+1）…②，联立①②并解得：x＝2﹣3m，故点B″（2﹣3m，m﹣），而P′（2﹣3m，m+），故EB'+EP'的最小值B″P′＝2．3．△ABC内接⊙O，AD⊥BC与D，连接OA．（1）如图1，求证：∠BAO＝∠CAD；（2）如图2，作BE⊥AC交CA延长线于E交⊙O于F，延长AD交⊙O于G，连接AF，求证：AD+AF＝DG；（3）在第（2）问的条件下，如图3，OA交BC于点T，CA＝CT，AD＝2AF，AB＝4，求DT长．【分析】（1）延长AO交圆于点M，连结BM，由∠M+∠BAM＝90°，∠C+∠CAD＝90°，结论可得证；（2）分别延长DA、BE交于点H，连结BG，可证得△AFM和△BGM是等腰三角形，由等腰三角形的性质可证出结论；（3）连GO并延长GO交AB于点N，连BG，由CA＝CT可得∠TAC＝∠ATC，证得AG ＝BG，得出AN长，证出△BAD∽△GAN，由比例线段可求出AD长，BD长，再证明△ADT∽△BDA，得AD2＝DT•BD，则DT长可求．【解答】（1）证明：如图1，延长AO交圆于点M，连结BM，∵AM是圆的直径，∴∠ABM＝90°，∴∠M+∠BAM＝90°，∵AD⊥BC，∴∠C+∠CAD＝90°，∵∠M＝∠C，∴∠BAO＝∠CAD；（2）证明：如图2，分别延长DA、BE交于点H，连结BG，∵AE⊥BE，AD⊥DC，∴∠EAH+∠H＝90°，∠DAC+∠C＝90°，∵∠DAC＝∠EAH，∴∠H＝∠C，∵四边形AFBC是圆内接四边形，∴∠EF A＝∠C，∴∠EF A＝∠H，∴AF＝AH，又∵∠C＝∠BGH，∴∠H＝∠BGH，∵BD⊥GH，∴DG＝DM＝AD+AH＝AD+AF；（3）解：如图3，连GO并延长GO交AB于点N，连BG，∵CT＝AC，∴∠TAC＝∠ATC，∵∠TAC＝∠TAD+∠DAC，∠ATC＝∠TBA+∠BAT，∠DAC＝∠BAT，∴∠TAD＝∠TBA，又∵∠GBC＝∠DAC＝∠BAO，∴AG＝BG，由轴对称性质可知NG⊥AB，∴∠GNA＝∠BDA＝90°，AN＝BN＝2，∵∠NAG＝∠BAD∴△BAD∽△GAN，∴，∵AD+AF＝DG，AD＝2AF，∴，∴，设AD＝x，则AG＝，∴，解得：x＝4，即AD＝4，∴＝＝8，在△ADT和△BDA中，∠TAD＝∠DBA，∠TDA＝∠BDA＝90°，∴△ADT∽△BDA，∴，∴，∴DT＝2．4．【分析】（1）由锐角三角函数可求点A坐标，由待定系数法可求解析式；（2）过点M作MH⊥OC于H，由锐角三角函数可求∴∠BCO＝30°，由直角三角形的性质可求CD的长，由三角形面积公式可求解；（3）作FE⊥OB于E，CP⊥EF于P，FK⊥OC于K．则四边形CPEO是矩形，设PC＝OE＝m．只要证明△PCF∽△EF A，可得，由此构建方程求出m即可解决问题．【解答】解：（1）∵点C（0，4），∴OC＝4，∵tan∠CBO＝＝，∴OB＝4，∵OB＝4OA，∴OA＝1，∴点A（﹣1，0）设过点A、C直线解析式为：y＝kx+4，∴0＝﹣k+4，∴k＝4，∴过点A、C直线解析式为：y＝4x+4；（2）如图2，过点M作MH⊥OC于H，∵M的横坐标为t，∴MH＝t，∵tan∠BCO＝＝＝，∴∠BCO＝30°，∵CD＝DM，∴∠DCM＝∠CMD＝30°，∴∠MDH＝60°，且MH⊥OC，∴DH＝t，DM＝2DH＝t＝CD，∴△CDM的面积为S＝×t×t＝t2，（0＜t≤4）（3）作FE⊥OB于E，CP⊥EF于P，FK⊥OC于K．则四边形CPEO是矩形，∴CP＝OE，CO＝PE＝4，设PC＝OE＝m．∵∠DON+∠DFN+∠ODF+∠ONF＝360°，∴∠FNO＝120°，∴∠FNE＝60°，且EF⊥BO，FN＝OB＝4，∴EF＝2，∴PF＝2∵∠DCF+∠AFN＝60°，∠DCF+∠DFC＝60°，∴∠DFC＝∠AFN，∴∠CF A＝∠DFN＝90°，∴∠FCP+∠PFC＝90°，∠PFC+∠AFE＝90°，∴∠PCF＝∠AFE，且∠P＝∠AEF＝90°，∴△PCF∽△EF A，∴，∴∴m＝3或﹣4（舍弃），∴F（3，2），在Rt△DEK中，∵∠DFK＝30°，FK＝3，∴DK＝，∴OD＝3，∴D（0，3）．5．【分析】（1）设两个“网红数”为，，（n、b表示末三位表示的数，m、a表示末三位之前的数字），则n﹣m＝11k，b﹣a＝11h，所以+＝1001m+1001a+11（k+h）＝11（91m+91n+h+k），即可证明；（2）s＝3×100+10b+a，t＝1000（b+1）+100（a+1）+4×10+2，所以s+t＝1000（b+1）+100（a+4）+10（b+4）+a+2；①当1≤a≤5时，s+t＝，则﹣（b+1）能被11整除，即101a+9b+441＝11×9a+2a+11b﹣2b+40×11+1能被11整除，由已知可得﹣7≤2a﹣2b+1≤11，求出a＝5，b＝0；②当6≤a≤7时，s+t＝，则﹣（b+2）能被11整除，所以101a+9b﹣560＝11×9a+2a+11b﹣2b﹣51×11+1能被11整除，可得3≤2a﹣2b+1≤15，求出a＝6，b＝1或a＝7，b＝2，分别求出相应的G（t）值即可．【解答】解：（1）设两个“网红数”为，，（n、b表示末三位表示的数，m、a表示末三位之前的数字），∴n﹣m＝11k，b﹣a＝11h，∵+＝1001m+1001a+11（k+h）＝11（91m+91n+h+k），∴m、a、k、h都是整数，∴91m+91n+h+k为整数，∴任两个“网红数”之和一定能被11整除；（2）s＝3×100+10b+a，t＝1000（b+1）+100（a+1）+4×10+2，∴s+t＝1000（b+1）+100（a+4）+10（b+4）+a+2，①当1≤a≤5时，s+t＝，则﹣（b+1）能被11整除，∴101a+9b+441＝11×9a+2a+11b﹣2b+40×11+1能被11整除，∴2a﹣2b+1能被11整除，∵1≤a≤5，0≤b≤5，∴﹣7≤2a﹣2b+1≤11，∴2a﹣2b+1＝0或11，∴a＝5，b＝0，∴t＝1642，G（1642）＝17.25；②当6≤a≤7时，s+t＝，则﹣（b+2）能被11整除，∴101a+9b﹣560＝11×9a+2a+11b﹣2b﹣51×11+1能被11整除，∴2a﹣2b+1能被11整除，∵6≤a≤7，0≤b≤5，∴3≤2a﹣2b+1≤15，∴2a﹣2b+1＝11，∴a＝6，b＝1或a＝7，b＝2，∴t＝2742或3842，∴G（2742）＝28或G（3842）＝39，∴G（t）的最大值39．6．【分析】（1）首先确定A、B、C三点的坐标，然后利用待定系数法求抛物线的解析式；（2）△ABO为等腰直角三角形，若△ADP与之相似，则有两种情形，如答图1所示．利用相似三角形的性质分别求解，避免遗漏；（3）如答图2所示，分别计算△ADE的面积与四边形APCE的面积，得到面积的表达式．利用面积的相等关系得到一元二次方程，将点E是否存在的问题转化为一元二次方程是否有实数根的问题，从而解决问题．需要注意根据（2）中P点的不同位置分别进行计算，在这两种情况下，一元二次方程的判别式均小于0，即所求的E点均不存在．【解答】解：（1）由题意得，A（3，0），B（0，3）∵抛物线经过A、B、C三点，∴把A（3，0），B（0，3），C（1，0）三点分别代入y＝ax2+bx+c，得方程组解得：∴抛物线的解析式为y＝x2﹣4x+3（2）由题意可得：△ABO为等腰三角形，如答图1所示，若△ABO∽△AP1D，则∴DP1＝AD＝4，∴P1（﹣1，4）若△ABO∽△ADP2 ，过点P2作P2 M⊥x轴于M，AD＝4，∵△ABO为等腰三角形，∴△ADP2是等腰三角形，由三线合一可得：DM＝AM＝2＝P2M，即点M与点C重合，∴P2（1，2）综上所述，点P的坐标为P1（﹣1，4），P2（1，2）；（3）不存在．理由：如答图2，设点E（x，y），则S△ADE＝①当P1（﹣1，4）时，S四边形AP1CE＝S△ACP1+S△ACE＝＝4+|y|∴2|y|＝4+|y|，∴|y|＝4∵点E在x轴下方，∴y＝﹣4，代入得：x2﹣4x+3＝﹣4，即x2﹣4x+7＝0，∵△＝（﹣4）2﹣4×7＝﹣12＜0∴此方程无解②当P2（1，2）时，S四边形AP2CE＝S△ACP2+S△ACE＝＝2+|y|，∴2|y|＝2+|y|，∴|y|＝2∵点E在x轴下方，∴y＝﹣2，代入得：x2﹣4x+3＝﹣2，即x2﹣4x+5＝0，∵△＝（﹣4）2﹣4×5＝﹣4＜0∴此方程无解综上所述，在x轴下方的抛物线上不存在这样的点E．。

2020年中考数学压轴题专题讲解：四边形综合题(含答案)

备战2020年中考数学压轴题专题讲解：四边形综合题1．如图，四边形ABCD是菱形，120BAD∠=︒，点E在射线AC上（不包括点A和点)C，过点E的直线GH交直线AD于点G，交直线BC于点H，且//GH DC，点F在BC的延长线上，CF AG=，连接ED，EF，DF．（1）如图1，当点E在线段AC上时，①判断AEG∆的形状，并说明理由．②求证：DEF∆是等边三角形．（2）如图2，当点E在AC的延长线上时，DEF∆是等边三角形吗？如果是，请证明你的结论；如果不是，请说明理由．2．（1）如图1，在四边形ABCD中，AB AD=，180B D∠+∠=︒，E，F分别是边BC，CD上的点，且12EAF BAD∠=∠，则BE，EF，DF之间的数量关系是EF BE DF=+．（2）如图2，若E，F分别是边BC，CD延长线上的点，其他条件不变，则BE，EF，DF 之间的数量关系是什么？请说明理由．（3）如图3，在某次军事演习中，舰艇甲在指挥中心(O处）北偏西30︒的A处，舰艇乙在指挥中心南偏东70︒的B处，并且两舰艇到指挥中心的距离相等，接到行动命令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50︒的方向以80海里/小时的速度前进，1.5小时后，指挥中心观察到舰艇甲、乙分别到达E，F处，且两舰艇与指挥中心O 连线的夹角70EOF∠=︒，试求此时两舰艇之间的距离．3．将一个等边三角形纸片AOB 放置在平面直角坐标系中，点(0,0)O ，点(6,0)B ．点C 、D 分别在OB 、AB 边上，//DC OA ，23CB =．()I 如图①，将DCB ∆沿射线CB 方向平移，得到△D C B '''．当点C 平移到OB 的中点时，求点D '的坐标；()II 如图②，若边D C ''与AB 的交点为M ，边D B ''与ABB ∠'的角平分线交于点N ，当BB '多大时，四边形MBND '为菱形？并说明理由．()III 若将DCB ∆绕点B 顺时针旋转，得到△D C B ''，连接AD '，边D C ''的中点为P ，连接AP ，当AP 最大时，求点P 的坐标及AD '的值．（直接写出结果即可）．4．如图（1），在ABC ∆中，AB AC =，90BAC ∠=︒，AD BC ⊥于点D ，20BC cm =，10AD cm =．点P 从点B 出发，在线段BC 上以每秒2cm 的速度向点C 匀速运动，与此同时，垂直于AD 的直线t 从点A 沿AD 出发，以每秒1cm 的速度沿AD 方向匀速平移，分别交AB 、AC 、AD 于M 、N 、E ．当点P 到达点C 时，点P 与直线l 同时停止运动，设运动时间为t 秒(0)t >．（1）在运动过程中（点P 不与B 、C 重合），连接PN ，求证：四边形MBPN 为平行四边形；（2）如图（2），以MN 为边向下作正方形MFGN ，FG 交AD 于点H ，连结PF 、PG ，当1003t <<时，求PFG ∆的面积最大值；（3）在整个运动过程中，观察图（2）、（3），是否存在某一时刻t ，使PFG ∆为等腰三角形？若存在，直接写出t 的值；若不存在，请说明理由．5．如图①，在矩形ABCD 中，动点P 从点A 出发，以1/cm s 的速度沿AD 向终点D 移动，设移动时间为()t s ，连接PC ，以PC 为一边作正方形PCEF ，连接DE 、DF ，设PCD ∆的面积为2()y cm ，y 与t 之间的函数关系如图②所示．（1）AB = cm ，AD = cm ；（2）当t 为何值时，DEF ∆的面积最小？请求出这个最小值；（3）当t 为何值时，DEF ∆为等腰三角形？请简要说明理由．6．如图，在平行四边形ABCD 中，AC BC ⊥，10AB =．6AC =．动点P 在线段BC 上从点B 出发沿BC 方向以每秒1个单位长的速度匀速运动；动点Q 在线段DC 上从点D 出发沿DC 的力向以每秒1个单位长的速度匀速运动，过点P 作PE BC ⊥．交线段AB 于点E ．若P 、Q 两点同时出发，当其中一点到达终点时整个运动随之停止，设运动时间为t 秒．（1）当t 为何值时，//QE BC ？（2）设PQE ∆的面积为S ，求出S 与t 的函数关系式：（3）是否存在某一时刻t ，使得PQE ∆的面积S 最大？若存在，求出此时t 的值；若不存在，请说明理由．（4）是否存在某一时刻t ，使得点Q 在线段EP 的垂直平分线上？若存在，求出此时t 的值；若不存在，请说明理由．7．如图一，在射线DE的一侧以AD为一条边作矩形ABCD，53AD=，5CD=，点M是线段AC上一动点（不与点A重合），连结BM，过点M作BM的垂线交射线DE于点N，连接BN．（1）求CAD∠的大小；（2）问题探究：动点M在运动的过程中，①是否能使AMN∆为等腰三角形，如果能，求出线段MC的长度；如果不能，请说明理由．②MBN∠的大小是否改变？若不改变，请求出MBN∠的大小；若改变，请说明理由．（3）问题解决：如图二，当动点M运动到AC的中点时，AM与BN的交点为F，MN的中点为H，求线段FH的长度．8．如图，点E，F分别在正方形ABCD的边CD，BC上，且DE CF=，点P在射线BC上（点P不与点F重合）．将线段EP绕点E顺时针旋转90︒得到线段EG，过点E作GD的垂线QH，垂足为点H，交射线BC于点Q．（1）如图1，若点E是CD的中点，点P在线段BF上，线段BP，QC，EC的数量关系为+=．BP QC EC（2）如图2，若点E不是CD的中点，点P在线段BF上，判断（1）中的结论是否仍然成立．若成立，请写出证明过程；若不成立，请说明理由．（3）正方形ABCD的边长为6，3QC=，请直接写出线段BP的长．=，1AB DE9．小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在ABC ∆中，AD BC ⊥于点D ，正方形PQMN 的边QM 在BC 上，顶点P ，N 分别在AB ，AC 上，若BC a =，AD h =，求正方形PQMN 的边长（用a ，h 表示）．（2）操作：如何画出这个正方形PQMN 呢？如图2，小波画出了图1的ABC ∆，然后按数学家波利亚在《怎样解题》中的方法进行操作：先在AB 上任取一点P '，画正方形P Q M N ''''，使点Q '，M '在BC 边上，点N '在ABC ∆内，然后连结BN '，并延长交AC 于点N ，画NM BC ⊥于点M ，NP NM ⊥交AB 于点P ，PQ BC ⊥于点Q ，得到四边形PQMN ．（3）推理：证明图2中的四边形PQMN 是正方形．（4）拓展：小波把图2中的线段BN 称为“波利亚线”，在该线上截取NE NM =，连结EQ ，EM （如图3)，当90QEM ∠=︒时，求“波利亚线” BN 的长（用a ，h 表示）．请帮助小波解决“温故”、“推理”、“拓展”中的问题．10．性质探究如图①，在等腰三角形ABC 中，120ACB ∠=︒，则底边AB 与腰AC 的长度之比为 3 ．理解运用（1）若顶角为120︒的等腰三角形的周长为843+，则它的面积为；（2）如图②，在四边形EFGH中，EF EG EH==．①求证：EFG EHG FGH∠+∠=∠；②在边FG，GH上分别取中点M，N，连接MN．若120EF=，直接写出FGH∠=︒，10线段MN的长．类比拓展顶角为2α的等腰三角形的底边与一腰的长度之比为（用含α的式子表示）．11．如图1，在矩形ABCD中，3BC=，动点P从B出发，以每秒1个单位的速度，沿射线t s．BC方向移动，作PAB∆关于直线PA的对称PAB∆'，设点P的运动时间为()（1）若23AB=．①如图2，当点B'落在AC上时，显然PAB∆'是直角三角形，求此时t的值；②是否存在异于图2的时刻，使得PCB∆'是直角三角形？若存在，请直接写出所有符合题意的t的值？若不存在，请说明理由．（2）当P点不与C点重合时，若直线PB'与直线CD相交于点M，且当3t<时存在某一时刻有结论45PAMt>的任意时刻，结论“45∠=︒”是否总是PAM∠=︒成立，试探究：对于3成立？请说明理由．12．如图，在以点O为中心的正方形ABCD中，4AD=，连接AC，动点E从点O出发沿∆的外→以每秒1个单位长度的速度匀速运动，到达点C停止．在运动过程中，ADEO C接圆交AB于点F，连接DF交AC于点G，连接EF，将EFG∆．∆沿EF翻折，得到EFH （1）求证：DEF∆是等腰直角三角形；（2）当点H 恰好落在线段BC 上时，求EH 的长；（3）设点E 运动的时间为t 秒，EFG ∆的面积为S ，求S 关于时间t 的关系式．13．操作体验：如图，在矩形ABCD 中，点E 、F 分别在边AD 、BC 上，将矩形ABCD 沿直线EF 折叠，使点D 恰好与点B 重合，点C 落在点C '处．点P 为直线EF 上一动点（不与E 、F 重合），过点P 分别作直线BE 、BF 的垂线，垂足分别为点M 和N ，以PM 、PN为邻边构造平行四边形PMQN ．（1）如图1，求证：BE BF =；（2）特例感知：如图2，若5DE =，2CF =，当点P 在线段EF 上运动时，求平行四边形PMQN 的周长；（3）类比探究：若DE a =，CF b =．①如图3，当点P 在线段EF 的延长线上运动时，试用含a 、b 的式子表示QM 与QN 之间的数量关系，并证明；②如图4，当点P 在线段FE 的延长线上运动时，请直接用含a 、b 的式子表示QM 与QN 之间的数量关系．（不要求写证明过程）14．在矩形ABCD 中，连结AC ，点E 从点B 出发，以每秒1个单位的速度沿着B A C →→的路径运动，运动时间为t （秒）．过点E 作EF BC ⊥于点F ，在矩形ABCD 的内部作正方形EFGH ．（1）如图，当8AB BC ==时，①若点H 在ABC ∆的内部，连结AH 、CH ，求证：AH CH =；②当08t <时，设正方形EFGH 与ABC ∆的重叠部分面积为S ，求S 与t 的函数关系式；（2）当6AB=，8BC=时，若直线AH将矩形ABCD的面积分成1:3两部分，求t的值．15．如图，在平面直角坐标系xOy中，矩形ABCD的边4AB=，6BC=．若不改变矩形ABCD 的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y 轴的正半轴上随之上下移动．（1）当30OAD∠=︒时，求点C的坐标；（2）设AD的中点为M，连接OM、MC，当四边形OMCD的面积为212时，求OA的长；（3）当点A移动到某一位置时，点C到点O的距离有最大值，请直接写出最大值，并求此时cos OAD∠的值．参考答案1、【解答】（1）①解：AEG ∆是等边三角形；理由如下：四边形ABCD 是菱形，120BAD ∠=︒，//AD BC ∴，AB BC CD AD ===，//AB CD ，1602CAD BAD ∠=∠=︒， 180BAD ADC ∴∠+∠=︒， 60ADC ∴∠=︒， //GH DC ，60AGE ADC ∴∠=∠=︒， 60AGE EAG AEG ∴∠=∠=∠=︒， AEG ∴∆是等边三角形；②证明：AEG ∆是等边三角形， AG AE ∴=， CF AG =， AE CF ∴=，四边形ABCD 是菱形， 120BCD BAD ∴∠=∠=︒， 60DCF CAD ∴∠=︒=∠，在AED ∆和CFD ∆中，AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩，()AED CFD SAS ∴∆≅∆DE DF ∴=，ADE CDF ∠=∠，60ADC ADE CDE ∠=∠+∠=︒， 60CDF CDE ∴∠+∠=︒，即60EDF ∠=︒， DEF ∴∆是等边三角形；（2）解：DEF ∆是等边三角形；理由如下：同（1）①得：AEG ∆是等边三角形， AG AE ∴=，CF AG =， AE CF ∴=，四边形ABCD 是菱形， 120BCD BAD ∴∠=∠=︒，1602CAD BAD ∠=∠=︒， 60FCD CAD ∴∠=︒=∠，在AED ∆和CFD ∆中，AD CD EAD FCD AE CF =⎧⎪∠=∠⎨⎪=⎩，()AED CFD SAS ∴∆≅∆， DE DF ∴=，ADE CDF ∠=∠，60ADC ADE CDE ∠=∠-∠=︒， 60CDF CDE ∴∠-∠=︒，即60EDF ∠=︒， DEF ∴∆是等边三角形．2、【解答】解：（1）延长FD 到点G ，使DG BE =，连结AG ，如图1所示：在ABE ∆和ADG ∆中，90BE DG B ADG AB AD =⎧⎪∠=∠=︒⎨⎪=⎩，()ABE ADG SAS ∴∆≅∆， AE AG ∴=，BAE DAG ∠=∠，12EAF BAD ∠=∠， GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠，在AEF ∆和GAF ∆中，AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩，()AEF AGF SAS ∴∆≅∆， EF FG ∴=，FG DG DF BE DF =+=+， EF BE DF ∴=+，故答案为：EF BE DF =+；（2）BE ，EF ，DF 之间的数量关系是：EF BE DF =-；理由如下：在CB 上截取BM DF =，连接AM ，如图2所示：180B D ∠+∠=︒，180ADC ADF ∠+∠=︒，B ADF ∴∠=∠，在ABM ∆和ADF ∆中，AB ADB ADF BM DF=⎧⎪∠=∠⎨⎪=⎩，()ABM ADF SAS ∴∆≅∆，AF AM ∴=，DAF BAM ∠=∠，BAD MAF ∴∠=∠，2BAD EAF ∠=∠，2MAF EAF ∴∠=∠，MAE EAF ∴∠=∠，在FAE ∆和MAE ∆中，AE AEFAE MAE AF AM=⎧⎪∠=∠⎨⎪=⎩，()FAE MAE SAS ∴∆≅∆，EF EM BE BM BE DF ∴==-=-，即EF BE DF =-；（3）连接EF ，延长AE 、BF 相交于点C ，如图3所示：3090(9070)140AOB ∠=︒+︒+︒-︒=︒，70EOF ∠=︒，12EOF AOB ∴∠=∠，OA OB =，(9030)(7050)180OAC OBC ∠+∠=︒-︒+︒+︒=︒，∴符合（1）中的条件，即结论EF AE BF =+成立，1.5(6080)210EF ∴=⨯+=（海里）．答：此时两舰艇之间的距离是210海里．3、【解答】解：（Ⅰ）如图①中，作DH BC ⊥于H ．AOB ∆是等边三角形，//DC OA ，60DCB AOB ∴∠=∠=︒，60CDB A ∠=∠=︒，CDB ∴∆是等边三角形， 23CB =DH CB ⊥，3CH HB ∴==3DH =，(63D ∴，3)，3C B '=，233CC ∴'=-，233DD CC ∴'='=-，(33D ∴'+3)．（Ⅱ）当3BB '=时，四边形MBND '是菱形．理由：如图②中，ABC ∆是等边三角形，60ABO ∴∠=︒，180120ABB ABO '∴∠=︒-∠=︒， BN 是ACC '∠的角平分线， 1602NBB ABB D C B ''∴∠'=∠=︒=∠''，//D C BN ''∴，//AB B D ''∴四边形MBND '是平行四边形，60ME C MCE '''∠=∠=︒，60NCC NC C ''∠=∠=︒，∴△MC B ''和NBB '∆是等边三角形，MC CE '∴=，NC CC '=，23B C ''=，四边形MBND '是菱形，BN BM ∴=，132BB B C '''∴==；（Ⅲ）如图连接BP ，在ABP ∆中，由三角形三边关系得，AP AB BP <+，∴当点A ，B ，P 三点共线时，AP 最大，如图③中，在△D BC ''中，由P 为D C ''的中点，得AP D C ''⊥，3PD '=，3CP ∴=，639AP ∴=+=，在Rt APD '∆中，由勾股定理得，AD '==此时15(2P ，．4、【解答】（1）证明：l AD ⊥，BC AD ⊥，//l BC ∴， ∴AM ANAB AC =，AB AC =，AM AN ∴=，90BAC ∠=︒，ME NE ∴=，22MN AE t ∴==，2BP t =，MN BP ∴=，∴四边形MBPN 为平行四边形；（2）解：四边形MFGN 是正方形，22FG MN MF AE t ∴====，2EH MF t ==，103DH AD AH t ∴=-=-，2115252(103)3()2233PFG S FG DH t t t ∆∴==⨯⨯-=--+，30a =-<，1003t <<，∴当53t =时，PFG S ∆最大253=；（3）解：存在，当t =5t =或10t =时，PFG ∆为等腰三角形；理由如下：利用勾股定理得：222(103)PF t =-，222(103)(10)PG t t =-+-，又22(2)FG t =，当PF FG =时，则222(103)(2)t t -=，解得：t =，当PF PG =时，2222(103)(103)(10)t t t -=-+-，解得：5t =，或0t =（舍去）；当FG PG =时，222(2)(103)(10)t t t =-+-，解得：10t =，或103t =（舍去）；综上所述，t =5t =或10t =时，PFG ∆为等腰三角形．5、【解答】解：（1）由图②知：5AD =，当0t =时，P 与A 重合，152y AD CD =⨯⨯=，1552CD ⨯⨯=，2CD cm =，四边形ABCD 是矩形，2AB CD cm ∴==，故答案为：2，5；（2）由题意得：AP t =，5PD t =-，112(5)522y CD PD t t ∴==-=-，四边形EFPC 是正方形，12DEF PDC EFPC S S S ∆∆∴+=正方形，222PC PD CD =+，22222(5)1029PC t t t ∴=+-=-+，222111913(1029)(5)4(4)22222DEF S t t t t t t ∆∴=-+--=-+=-+，当t 为4时，DEF ∆的面积最小，且最小值为32；（3）当DEF ∆为等腰三角形时，分四种情况：①当FD FE =时，如下图所示，过F 作FG AD ⊥于G ，四边形EFPC 是正方形，PF EF PC ∴==，90FPC ∠=︒，PF FD ∴=，FG PD ⊥， 12PG DG PD ∴==， 90FPG CPD CPD DCP ∠+∠=∠+∠=︒，FPG DCP ∴∠=∠，90FGP PDC ∠=∠=︒，()FPG PDC AAS ∴∆≅∆，2PG DC ∴==，4PD ∴=，541AP ∴=-=，即1t =；②当DE DF =时，如下图所示，E 在AD 的延长线上，此时正方形EFPC 是正方形，2PD CD ==，523AP t ∴==-=；③当DE EF =时，如下图所示，过E 作EG CD ⊥于G ，FE DE EC ==，112CG DG CD ∴===，同理得：()PDC CGE AAS ∆≅∆，1PD CG ∴==，514AP t ∴==-=，④当DF EF =时，如下所示，2PC EF PF ===，且PC BC ⊥，此时P 与D 重合，5t =，综上，当1t s =或3s 或4s 或5s 时，DEF ∆为等腰三角形．6、【解答】解：（1）如图1，记EQ 与AC 的交点为G ，AC BC ⊥，90ACB ∴∠=︒，在Rt ABC ∆中，10AB =，6AC =，根据勾股定理得，8BC =，3tan 4AC B BC ==，四边形ABCD 是平行四边形，10CD AB ∴==，8AD BC ==，由运动知，BP t =，DQ t =，8PC t ∴=-，10CQ t =-，PE BC ⊥，90BPE ∴∠=︒，在Rt BPE ∆中，3sin 5B =，4cos 5B =，3tan 4PE PE B BP t ===， 34PE t ∴=， //EQ BC ，90PEQ BPE ∴∠=∠=︒，∴四边形CPEG 是矩形，34CG PE t ∴==， //EQ BC ，CGQ CAD ∴∆∆∽， ∴CG CQ AC CD=， ∴3104610t t -=． 409t ∴=；（2）如图2，过点Q 作QH BC ⊥交BC 的延长线于H ，四边形ABCD 是平行四边形，//AB CD ∴，DCH B ∴∠=∠，在Rt CHQ ∆中，3sin 105QH QH QCH CQ t ∠===-， 3(10)5QH t ∴=-，4cos 105CH CH HCQ CQ t ∠===-， 4(10)5CH t ∴=-， 498(10)1655PH PC CH t t t ∴=+=-+-=-， ()()2133919327404010161610()25452554093QPH QHPE S S S t t t t t t ∆⎡⎤⎛⎫⎛⎫∴=-=-+⨯--⨯-⨯-=--+ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭梯形，点E 在线段AB 上，∴点P 在线段BC 上，08t ∴<，点Q 在CD 上，010t ∴<<，08t ∴<，即：2274040()(08)4093S t t =--+<；（3）由（2）知，2274040()(08)4093S t t =--+<；409t ∴=时，403S =最大；（4）如图3，过点Q 作QM PE ⊥于M ，交AC 于N ，点Q 在线段EP 的垂直平分线上，1328PM PE t ∴==，同（2）的方法得，3(10)5CN t =-，易知，四边形PCNM 是矩形，PM CN ∴=，∴33(10)85t t =-，8013t ∴=．7、【解答】解：（1）如图一（1）中，四边形ABCD 是矩形，90ADC ∴∠=︒，53tan 353DC DAC AD ∠===，30DAC ∴∠=︒．（2）①如图一（1）中，当AN NM =时，90BAN BMN ∠=∠=︒，BN BN =，AN NM =， Rt BNA Rt BNM(HL)∴∆≅∆，BA BM ∴=，在Rt ABC ∆中，30ACB DAC ∠=∠=︒，5AB CD ==， 210AC AB ∴==，60BAM ∠=︒，BA BM =，ABM ∴∆是等边三角形，5AM AB ∴==，5CM AC AM ∴=-=．如图一（2）中，当AN AM =时，易证15AMN ANM ∠=∠=︒，90BMN ∠=︒，75CMB ∴∠=︒，30MCB ∠=︒，180753075CBM ∴∠=︒-︒-︒=︒，CMB CBM ∴∠=∠，3CM CB ∴==，综上所述，满足条件的CM 的值为5或53②结论：30MBN ∠=︒大小不变．理由：如图一（1）中，180BAN BMN ∠+∠=︒，A ∴，B ，M ，N 四点共圆，30MBN MAN ∴∠=∠=︒．如图一（2）中，90BMN BAN ∠=∠=︒，A ∴，N ，B ，M 四点共圆，180MBN MAN ∴∠+∠=︒，180DAC MAN ∠+∠=︒，30MBN DAC ∴∠=∠=︒，综上所述，30MBN ∠=︒．（3）如图二中，AM MC =，BM AM CM ∴==，2AC AB ∴=，AB BM AM ∴==，ABM ∴∆是等边三角形，60BAM BMA ∴∠=∠=︒，90BAN BMN ∠=∠=︒，30NAM NMA ∴∠=∠=︒，NA NM ∴=，BA BM =，BN ∴垂直平分线段AM ，52FM ∴=，53cos303FM NM ∴==︒，90NFM ∠=︒，NH HM =，12FH MN ∴==8、【解答】解：（1）BP QC EC +=；理由如下：四边形ABCD 是正方形，BC CD ∴=，90BCD ∠=︒，由旋转的性质得：90PEG ∠=︒，EG EP =，90PEQ GEH ∴∠+∠=︒，QH GD ⊥，90H ∴∠=︒，90G GEH ∠+∠=︒，PEQ G ∴∠=∠，又90EPQ PEC ∠+∠=︒，90PEC GED ∠+∠=︒， EPQ GED ∴∠=∠，在PEQ ∆和EGD ∆中，EPQ GEDEP EG PEQ G∠=∠⎧⎪=⎨⎪∠=∠⎩，()PEQ EGD ASA ∴∆≅∆，PQ ED ∴=，BP QC BC PQ CD ED EC ∴+=-=-=，即BP QC EC +=；故答案为：BP QC EC +=；（2）（1）中的结论仍然成立，理由如下：由题意得：90PEG ∠=︒，EG EP =，90PEQ GEH ∴∠+∠=︒，QH GD ⊥，90H ∴∠=︒，90G GEH ∠+∠=︒，PEQ G ∴∠=∠，四边形ABCD 是正方形，90DCB ∴∠=︒，BC DC =，90EPQ PEC ∴∠+∠=︒，90PEC GED ∠+∠=︒，GED EPQ ∴∠=∠，在PEQ ∆和EGD ∆中，EPQ GEDEP EG PEQ G∠=∠⎧⎪=⎨⎪∠=∠⎩，()PEQ EGD ASA ∴∆≅∆，PQ ED ∴=，BP QC BC PQ CD ED EC ∴+=-=-=，即BP QC EC +=；（3）分两种情况：①当点P 在线段BC 上时，点Q 在线段BC 上，由（2）可知：BP EC QC =-，36AB DE ==，2DE ∴=，4EC =，413BP ∴=-=；②当点P 在线段BC 上时，点Q 在线段BC 的延长线上，如图3所示：同（2）可得：()PEQ EGD AAS ∆≅∆，2PQ DE ∴==，1QC =，1PC PQ QC ∴=-=，615BP BC PC ∴=-=-=；综上所述，线段BP 的长为3或5．9、【解答】（1）解：如图1中，//PN BC，APN ABC∴∆∆∽，∴PN AEBC AD=，即PN h PNa h-=，解得ah PNa h=+（2）能画出这样的正方形，如图2中，正方形PNMQ即为所求．（3）证明：如图2中，由画图可知：90QMN PQM NPQ BM N∠=∠=∠=∠''=︒，∴四边形PNMQ是矩形，//MN M N''，∴△BN M BNM''∆∽，∴M N BN MN BN'''=，同理可得：P N BN PN BN '''=∴M N P N MN PN''''=，M N P N''=''，MN PN∴=，∴四边形PQMN是正方形（4）如图，过点N作ND ME⊥于点D图3MN EN =，ND ME ⊥，NEM MNE ∴∠=∠，ED DM =90BMN QEM ∠=∠=︒90EQM EMQ ∴∠+∠=︒，90EMQ EMN ∠+∠=︒EMN EQM ∴∠=∠，且MN QN =，90QEM NDM ∠=∠=︒()QEM MDN AAS ∴∆≅∆12EQ DM EM ∴==，90BMN QEM ∠=∠=︒90BEQ NEM ∴∠+∠=︒，90BME NME ∠+∠=︒BEQ BME ∴∠=∠，且MBE MBE ∠=∠BEQ BME ∴∆∆∽ ∴12BQ BE EQ BE BM EM ===，2BM BE ∴=，2BE BQ =4BM BQ ∴=3QM BQ MN ∴==，5BN BQ = ∴3355MN BQ BN BQ ==55()33ahBN MN a h ∴==+10、【解答】性质探究解：作CD AB ⊥于D ，如图①所示：则90ADC BDC ∠=∠=︒，AC BC =，120ACB ∠=︒，AD BD ∴=，30A B ∠=∠=︒，2AC CD ∴=，AD =，2AB AD ∴==，∴AB AC =；理解运用（1）解：如图①所示：同上得：2AC CD =，AD =，8AC BC AB ++=+，48CD ∴+=+解得：2CD =，AB ∴=，ABC ∴∆的面积11222AB CD =⨯=⨯=故答案为：（2）①证明：EF EG EH ==，EFG EGF ∴∠=∠，EGH EHG ∠=∠，EFG EHG EGF EGH FGH ∴∠+∠=∠+∠=∠； ②解：连接FH ，作EP FH ⊥于P ，如图②所示：则PF PH =，由①得：120EFG EHG FGH ∠+∠=∠=︒，360120120120FEH ∴∠=︒-︒-︒=︒，EF EH =，30EFH ∴∠=︒，152PE EF ∴==，PF ∴==，2FH PF ∴==，点M 、N 分别是FG 、GH 的中点，MN ∴是FGH ∆的中位线， 1532MN FH ∴==；类比拓展解：如图③所示：作AD BC ⊥于D ，AB AC =，BD CD ∴=，12BAD BAC α∠=∠=，sin BDAB α=，sin BD AB α∴=⨯，22sin BC BD AB α∴==⨯，∴2sin 2sin BC AB AB AB αα==；故答案为：2sin α．11、【解答】解：（1）①如图1中，四边形ABCD 是矩形，90ABC ∴∠=︒，2221AC AB BC ∴=+=PCB ACB ∠'=∠，90PB C ABC ∠'=∠=︒， PCB ACB ∴∆'∆∽，∴CB PB CB AB ''=，∴2123323PB -'=，274PB ∴'=-．274t PB ∴==-． ②如图21-中，当PCB ∠’ 90=︒时，四边形ABCD 是矩形，90D ∴∠=︒，23AB CD ==，3AD BC ==，22(23)33DB ∴'=-=，3CB CD DB ∴'=-'=，在Rt PCB ∆'中，222B P PC B C '=+'，222(3)(3)t t ∴=+-，2t ∴=．如图22-中，当PCB ∠’ 90=︒时，在Rt ADB ∆'中，223DB AB AD '='-=， 33CB ∴'=在Rt PCB ∆’中则有：222(33)(3)t t +-=，解得6t =．如图23-中，当CPB ∠’ 90=︒时，易证四边形ABP ’为正方形，易知23t =．综上所述，满足条件的t 的值为2s 或6s 或23s ．（2）如图31-中，45PAM ∠=︒2345∴∠+∠=︒，1445∠+∠=︒又翻折，12∴∠=∠，34∠=∠，又ADM AB ∠=∠’ M ，AM AM =， ()AMD AMB AAS ∴∆≅∆'，AD AB ∴=’ AB =，即四边形ABCD 是正方形，如图，设APB x ∠=．90PAB x ∴∠=︒-，DAP x ∴∠=，易证MDA ∆≅△B ’ ()AM HL ， BAM DAM ∴∠=∠，翻折，PAB PAB ∴∠=∠’ 90x =︒-， DAB ∴∠’ PAB =∠’ 902DAP x -∠=︒-， 12DAM DAB ∴∠=∠’ 45x =︒-，45MAP DAM PAD ∴∠=∠+∠=︒．12、【解答】（1）证明：四边形ABCD 是正方形， 45DAC CAB ∴∠=∠=︒，FDE CAB ∴∠=∠，DFE DAC ∠=∠， 45FDE DFE ∴∠=∠=︒， 90DEF ∴∠=︒，DEF ∴∆是等腰直角三角形；（2）设OE t =，连接OD ， 90DOE DAF ∴∠=∠=︒， OED DFA ∠=∠，DOE DAF ∴∆∆∽，∴22OEODAF AD ==，∴2AF t =，又AEF ADG ∠=∠，EAF DAG ∠=∠，AEF ADG ∴∆∆∽， ∴AE AFAD AG =， ∴42AG AE AD AF t ==，又AE OA OE t =+=+，∴AG =，EG AE AG ∴=-=当点H 恰好落在线段BC 上454590DFH DFE HFE ∠=∠+∠=︒+︒=︒， ADF BFH ∴∆∆∽，∴FH FB FD AD ==， //AF CD ，∴FG AF DG CD ==∴FG DF =∴=，解得：1t =-，2t =（舍去），EG EH ∴====-；（3）过点F 作FK AC ⊥于点K ，由（2）得EG =，DE EF =，90DEF ∠=︒，DEO EFK ∴∠=∠，()DOE EKF AAS ∴∆≅∆，FK OE t ∴==， 31242EFG t S EG FK ∆+∴==13、【解答】（1）证明：如图1中，四边形ABCD 是矩形，//AD BC ∴，DEF EFB ∴∠=∠，由翻折可知：DEF BEF ∠=∠，BEF EFB ∴∠=∠，BE BF ∴=．（2）解：如图2中，连接BP ，作EH BC ⊥于H ，则四边形ABHE 是矩形，EH AB =．5DE EB BF ===，2CF =，7AD BC ∴==，2AE =，在Rt ABE ∆中，90A ∠=︒，5BE =，2AE =，225221AB ∴=-=，BEF PBE PBF S S S ∆∆∆=+，PM BE ⊥，PN BF ⊥， ∴111222BF EH BE PM BF PN =+， BE BF =，21PM PN EH ∴+==，四边形PMQN 是平行四边形，∴四边形PMQN 的周长2()221PM PN =+=（3）①证明：如图3中，连接BP ，作EH BC ⊥于H ．ED EB BF a ===，CF b =，AD BC a b ∴==+，AE AD DE b ∴=-=， 22EH AB a b ∴==-，EBP BFP EBF S S S ∆∆∆-=，∴111222BE PM BF PN BF EH -=， BE BF =，22PM PN EH a b ∴-==-，四边形PMQN 是平行四边形，22()QN QM PM PN a b ∴-=-=-．②如图4，当点P 在线段FE 的延长线上运动时，同法可证：22QM QN PN PM a b -=-=-．14、【解答】解：（1）①如图1中，四边形EFGH 是正方形，AB BC =，BE BG ∴=，AE CG =，90BEH BGH ∠=∠=︒，90AEH CGH ∴∠=∠=︒，EH HG =，()AEH CGH SAS ∴∆≅∆，AH CH ∴=．②如图1中，当04t <时，重叠部分是正方形EFGH ，2S t =．如图2中，当48t <时，重叠部分是五边形EFGMN ，2211882(8)163222ABC AEN CGM S S S S t t t ∆∆∆=--=⨯⨯-⨯-=-+-．综上所述，22(04)1632(48)t t S t t t ⎧<=⎨-+-<⎩．（2）如图31-中，设直线AH 交BC 于M ，当4BM CM ==时，直线AH 将矩形ABCD 的面积分成1:3两部分．//EH BM ，∴AE EH AB BM =， ∴664t t -=， 125t ∴=．如图32-中，设直线长AH 交CD 于M 交BC 的延长线于K ，当3CM DM ==时，直线AH 将矩形ABCD 的面积分成1:3两部分，易证8AD CK ==，//EH BK ，∴AE EH AB BK=，∴6616t t -=， 4811t ∴=．如图33-中，当点E 在线段AC 上时，设直线AH 交CD 于M ，交BC 的延长线于N ．当CM DM =时，直线AH 将矩形ABCD 的面积分成1:3两部分，易证8AD CN ==．在Rt ABC ∆中，226810AC =+=，//EF AB ，∴CE EFCA AB =，∴16106tEF-=，3(16)5EF t ∴=-，//EH CN ，∴EH AECN AC =，∴3(16)65810t t --=，解得727t =．当正方形EFGH 在AC 的左边时，由EH AE CN AC =，可得3(16)65410t t --=，解得12t =．综上所述，满足条件的t 的值为125或4811或727或12．15、【解答】解：（1）如图1，过点C 作CE y ⊥轴于点E ，矩形ABCD 中，CD AD ⊥，90CDE ADO ∴∠+∠=︒，又90OAD ADO ∠+∠=︒，30CDE OAD ∴∠=∠=︒，∴在Rt CED ∆中，122CE CD ==，2223DE CD CE =-=在Rt OAD ∆中，30OAD ∠=︒，132OD AD ∴==，∴点C 的坐标为(2,33)+（2）M 为AD 的中点，3DM ∴=，6DCM S ∆=，又212OMCD S =四边形，92ODM S ∆∴=，9OAD S ∆∴=，设OA x =、OD y =，则2236x y +=，192xy =，222x y xy ∴+=，即x y =，将x y =代入2236x y +=得218x =，解得32x =（负值舍去），32OA ∴=（3）OC 的最大值为8，如图2，M 为AD 的中点，3OM ∴=，225CM CD DM =+=，8OC OM CM ∴+=，当O 、M 、C 三点在同一直线时，OC 有最大值8，连接OC ，则此时OC 与AD 的交点为M ，过点O 作ON AD ⊥，垂足为N ， 90CDM ONM ∠=∠=︒，CMD OMN ∠=∠，CMD OMN ∴∆∆∽， ∴CDDMCMON MN OM ==，即4353ON MN ==，解得95MN =，125ON =，65AN AM MN ∴=-=，在Rt OAN ∆中，22655OA ON AN =+=，5cos 5ANOAD OA ∴∠==．。

2020年中考数学压轴题(含答案解析)

2020年中考数学压轴题一、选择题1．在平面直角坐标系xOy中，将一块含有45°角的直角三角板如图放置，直角顶点C的坐标为（1，0），顶点A的坐标（0，2），顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为（）A．（，0）B．（2，0）C．（，0）D．（3，0）2．如图，在等腰直角三角形ABC中，∠ACB＝90°，BC＝2，D是BC边上一动点，将AD绕点A逆时针旋转45°得AE，连接CE，则线段CE长的最小值为（）A．B．C．﹣1 D．2﹣二、填空题3．如图，在矩形ABCD中，AB＝5，BC＝4，以CD为直径作⊙O．将矩形ABCD绕点C旋转，使所得矩形A′B′CD′的边A′B′与⊙O相切，切点为E，边CD′与⊙O相交于点F，则CF的长为．第3题第4题4．问题背景：如图1，将△ABC绕点A逆时针旋转60°得到△ADE，DE与BC交于点P，可推出结论：PA+PC ＝PE．问题解决：如图2，在△MNG中，MN＝6，∠M＝75°，MG＝．点O是△MNG内一点，则点O 到△MNG三个顶点的距离和的最小值是．三、解答题5．如图（1），在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，动点P在线段AC上以5cm/s的速度从点A运动到点C，过点P作PD⊥AB于点D，将△APD绕PD的中点旋转180°得到△A′DP，设点P的运动时间为x（s）．（1）当点A′落在边BC上时，求x的值；（2）在动点P从点A运动到点C过程中，当x为何值时，△A′BC是以A′B为腰的等腰三角形；（3）如图（2），另有一动点Q与点P同时出发，在线段BC上以5cm/s的速度从点B运动到点C，过点Q作QE⊥AB于点E，将△BQE绕QE的中点旋转180°得到△B′EQ，连结A′B′，当直线A′B′与△ABC的一边垂直时，求线段A′B′的长．6．在△AOB中，∠ABO＝90°，AB＝3，BO＝4，点C在OB上，且BC＝1，（1）如图1，以O为圆心，OC长为半径作半圆，点P为半圆上的动点，连接PB，作DB⊥PB，使点D落在直线OB的上方，且满足DB：PB＝3：4，连接AD①请说明△ADB∽△OPB；②如图2，当点P所在的位置使得AD∥OB时，连接OD，求OD的长；③点P在运动过程中，OD的长是否有最大值？若有，求出OD长的最大值：若没有，请说明理由．（2）如图3，若点P在以O为圆心，OC长为半径的圆上运动．连接PA，点P在运动过程中，PA﹣是否有最大值？若有，直接写出最大值；若没有，请说明理由．【答案与解析】一、选择题1．【分析】过点B作BD⊥x轴于点D，易证△ACO≌△BCD（AAS），从而可求出B的坐标，进而可求出反比例函数的解析式，根据解析式与A的坐标即可得知平移的单位长度，从而求出C的对应点．【解答】解：过点B作BD⊥x轴于点D，∵∠ACO+∠BCD＝90°，∠OAC+∠ACO＝90°，∴∠OAC＝∠BCD，在△ACO与△BCD中，∴△ACO≌△BCD（AAS）∴OC＝BD，OA＝CD，∵A（0，2），C（1，0）∴OD＝3，BD＝1，∴B（3，1），∴设反比例函数的解析式为y＝，将B（3，1）代入y＝，∴k＝3，∴y＝，∴把y＝2代入，∴x＝，当顶点A恰好落在该双曲线上时，此时点A移动了个单位长度，∴C也移动了个单位长度，此时点C的对应点C′的坐标为（，0）故选：A．2．【分析】在AB上截取AF＝AC＝2，由旋转的性质可得AD＝AE，由勾股定理可求AB＝2，可得BF ＝2﹣2，由“SAS”可证△ACE≌△AFD，可得CE＝DF，则当DF⊥BC时，DF值最小，即CE的值最小，由直角三角形的性质可求线段CE长的最小值．【解答】解：如图，在AB上截取AF＝AC＝2，∵旋转∴AD＝AE∵AC＝BC＝2，∠ACB＝90°∴AB＝2，∠B＝∠BAC＝45°，∴BF＝2﹣2∵∠DAE＝45°＝∠BAC∴∠DAF＝∠CAE，且AD＝AE，AC＝AF∴△ACE≌△AFD（SAS）∴CE＝DF，当DF⊥BC时，DF值最小，即CE的值最小，∴DF最小值为＝2﹣故选：D．二、填空题3．【分析】连接OE，延长EO交CD于点G，作OH⊥B′C，由旋转性质知∠B′＝∠B′CD′＝90°、AB＝CD ＝5、BC＝B′C＝4，从而得出四边形OEB′H和四边形EB′CG都是矩形且OE＝OD＝OC＝2.5，继而求得CG＝B′E＝OH＝＝＝2，根据垂径定理可得CF的长．【解答】解：连接OE，延长EO交CD于点G，作OH⊥B′C于点H，则∠OEB′＝∠OHB′＝90°，∵矩形ABCD绕点C旋转所得矩形为A′B′C′D′，∴∠B′＝∠B′CD′＝90°，AB＝CD＝5、BC＝B′C＝4，∴四边形OEB′H和四边形EB′CG都是矩形，OE＝OD＝OC＝2.5，∴B′H＝OE＝2.5，∴CH＝B′C﹣B′H＝1.5，∴CG＝B′E＝OH＝＝＝2，∵四边形EB′CG是矩形，∴∠OGC＝90°，即OG⊥CD′，∴CF＝2CG＝4，故答案为：4．4．【分析】（1）在BC上截取BG＝PD，通过三角形全等证得AG＝AP，BG＝DP，得出△AGP是等边三角形，得出AP＝GP，则PA+PC＝GP+PC＝GC＝PE，即可证得结论；（2）以MG为边作等边三角形△MGD，以OM为边作等边△OME．连接ND，可证△GMO≌△DME，可得GO＝DE，则MO+NO+GO＝NO+OE+DE，即当D、E、O、N四点共线时，MO+NO+GO值最小，最小值为ND的长度，根据勾股定理先求得MF、DF，然后求ND的长度，即可求MO+NO+GO 的最小值．【解答】（1）证明：如图1，在BC上截取BG＝PD，在△ABG和△ADP中，∴△ABG≌△ADP（SAS），∴AG＝AP，BG＝DP，∴GC＝PE，∵∠GAP＝∠BAD＝60°，∴△AGP是等边三角形，∴AP＝GP，∴PA+PC＝GP+PC＝GC＝PE∴PA+PC＝PE；（2）解：如图2：以MG为边作等边三角形△MGD，以OM为边作等边△OME．连接ND，作DF⊥NM，交NM的延长线于F．∵△MGD和△OME是等边三角形∴OE＝OM＝ME，∠DMG＝∠OME＝60°，MG＝MD，∴∠GMO＝∠DME在△GMO和△DME中∴△GMO≌△DME（SAS），∴OG＝DE∴NO+GO+MO＝DE+OE+NO∴当D、E、O、M四点共线时，NO+GO+MO值最小，∵∠NMG＝75°，∠GMD＝60°，∴∠NMD＝135°，∴∠DMF＝45°，∵MG＝．∴MF＝DF＝4，∴NF＝MN+MF＝6+4＝10，∴ND＝＝＝2，∴MO+NO+GO最小值为2，故答案为2，三、解答题5．【分析】（1）根据勾股定理求出AC，证明△APD∽△ABC，△A′PC∽△ABC，根据相似三角形的性质计算；（2）分A′B＝BC、A′B＝A′C两种情况，根据等腰三角形的性质解答；（3）根据题意画出图形，根据锐角三角函数的概念计算．【解答】解：（1）如图1，∵在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，∴AC＝＝4cm，当点A′落在边BC上时，由题意得，四边形APA′D为平行四边形，∵PD⊥AB，∴∠ADP＝∠C＝90°，∵∠A＝∠A，∴△APD∽△ABC，∵AP＝5x，∴A′P＝AD＝4x，PC＝4﹣5x，∵∠A′PD＝∠ADP，∴A′P∥AB，∴△A′PC∽△ABC，∴，即＝，解得：x＝，∴当点A′落在边BC上时，x＝；（2）当A′B＝BC时，（5﹣8x）2+（3x）2＝32，解得：．∵x≤，∴；当A′B＝A′C时，x＝．（3）Ⅰ、当A′B′⊥AB时，如图6，∴DH＝PA'＝AD，HE＝B′Q＝EB，∵AB＝2AD+2EB＝2×4x+2×3x＝5，∴x＝，∴A′B′＝QE﹣PD＝x＝；Ⅱ、当A′B′⊥BC时，如图7，∴B′E＝5x，DE＝5﹣7x，∴cos B＝，∴x＝，∴A′B′＝B′D﹣A′D＝；Ⅲ、当A′B′⊥AC时，如图8，由（1）有，x＝，∴A′B′＝PA′sin A＝；当A′B′⊥AB时，x＝，A′B′＝；当A′B′⊥BC时，x＝，A′B′＝；当A′B′⊥AC时，x＝，A′B′＝．6．【分析】（1）①由∠ABO＝90°和DB⊥PB可得∠DBA＝∠PBO，结合边长关系由两边对应成比例及其夹角相等的三角形相似即可证明结论．②过D点作DH⊥BO交OB延长线于H点，由AD∥OB平行可得∠DAB＝90°，而△ADB∽△OPB可知∠POB＝90°，由已知可求出AD．由Rt△DHO即可计算OD的长，③由△ADB∽△OPB可知，可求AD＝，由此可知D在以A为圆心AD为半径的圆上运动，所以OD的最大值为OD过A点时最大．求出OA即可得到答案．（2）在OC上取点B′，使OB′＝OP＝，构造△BOP～△POB′，可得＝PA﹣PB′≤AB'，求出AB’即可求出最大值．【解答】解：（1）①∵DB⊥PB，∠ABO＝90°，∴∠ADB＝∠CDP，又∵AB＝3，BO＝4，DB：PB＝3：4，即：，∴△ADB∽△OPB；②如解图（2），过D点作DH⊥BO交OB延长线于H点，∵AD∥OB，∠ABD＝90°，∴∠DAB＝90°，又∵△ADB∽△OPB，∴，∴AD＝，∵四边形ADHB为矩形，∴HD＝AB＝3，HB＝AD＝，∴OH＝OB+HB＝在Rt△DHO中，OD＝＝＝．③在△AOB中，∠ABO＝90°，AB＝3，BO＝4，∴OA＝5．由②得AD＝，∴D在以A为圆心AD为半径的圆上运动，∴OD的最大值为OD过A点时最大，即OD的最大值为＝OA+AD＝5+＝．（2）如解图（4），在OC上取点B′，使OB′＝OP＝，∵∠BOP＝∠POB′，＝，∴△BOP～△POB′，∴，∴＝PA﹣PB′≤AB'，∴∴有最大值为AB′，在Rt△ABB′中，AB＝3，BB′＝＝，∴AB′＝＝＝，即：点P在运动过程中，PA﹣有最大值为，2020年中考数学压轴题一、选择题1．如图，在五边形ABCDE中，∠BAE＝120°，∠B＝∠E＝90°，AB＝BC，AE＝DE，在BC、DE上分别找一点M、N，使得△AMN的周长最小时，则∠AMN+∠ANM的度数为（）A．90°B．100°C．110°D．120°2．如图，P是半圆O上一点，Q是半径OA延长线上一点，AQ＝OA＝1，以PQ为斜边作等腰直角三角形PQR，连接OR．则线段OR的最大值为（）A．B．3 C．D．1二、填空题3．如图，E、F，G、H分别为矩形ABCD的边AB、BC、CD、DA的中点，连接AC、HE、EC，GA，GF．已知AG⊥GF，AC＝，则AB的长为．第3题第4题4．如图，AB为半圆O的直径，点C在半圆O上，AB＝8，∠CAB＝60°，P是弧上的一个点，连接AP，过点C作CD⊥AP于点D，连接BD，在点P移动过程中，BD长的最小值为．三、解答题5．如图，⊙O是四边形ABCD的外接圆．AC、BD是四边形ABCD的对角线，BD经过圆心O，点E在BD的延长线上，BA与CD的延长线交于点F，DF平分∠ADE．（1）求证：AC＝BC；（2）若AB＝AF，求∠F的度数；（3）若，⊙O半径为5，求DF的长．6．如图，△ABC是边长为2的等边三角形，点D与点B分别位于直线AC的两侧，且AD＝AC，联结BD、CD，BD交直线AC于点E．（1）当∠CAD＝90°时，求线段AE的长．（2）过点A作AH⊥CD，垂足为点H，直线AH交BD于点F，①当∠CAD＜120°时，设AE＝x，y＝（其中S△BCE表示△BCE的面积，S△AEF表示△AEF的面积），求y关于x的函数关系式，并写出x的取值范围；②当＝7时，请直接写出线段AE的长．【答案与解析】一、选择题1．【分析】根据要使△AMN的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A关于BC和ED的对称点A′，A″，即可得出∠AA′M+∠A″＝∠HAA′＝60°，进而得出∠AMN+∠ANM＝2（∠AA′M+∠A″）即可得出答案．【解答】解：作A关于BC和ED的对称点A′，A″，连接A′A″，交BC于M，交ED于N，则A′A″即为△AMN的周长最小值．作EA延长线AH，∵∠BAE＝120°，∴∠HAA′＝60°，∴∠A′+∠A″＝∠HAA′＝60°，∵∠A′＝∠MAA′，∠NAE＝∠A″，且∠A′+∠MAA′＝∠AMN，∠NAE+∠A″＝∠ANM，∴∠AMN+∠ANM＝∠A′+∠MAA′+∠NAE+∠A″＝2（∠A′+∠A″）＝2×60°＝120°，故选：D．2．【分析】将△RQO绕点R顺时针旋转90°，可得△RPE，可得ER＝RO，∠ERO＝90°，PE＝OQ＝2，由直角三角形的性质可得EO＝RO，由三角形三边关系可得EO≤PO+EP＝3，即可求解．【解答】解：将△RQO绕点R顺时针旋转90°，可得△RPE，∴ER＝RO，∠ERO＝90°，PE＝OQ＝2∴EO＝RO，∵EO≤PO+EP＝3∴RO≤3∴OR的最大值＝故选：A．二、填空题3．【分析】如图，连接BD．由△ADG∽△GCF，设CF＝BF＝a，CG＝DG＝b，可得＝，推出＝，可得b＝a，在Rt△GCF中，利用勾股定理求出b，即可解决问题；【解答】解：如图，连接BD．∵四边形ABCD是矩形，∴∠ADC＝∠DCB＝90°，AC＝BD＝，∵CG＝DG，CF＝FB，∴GF＝BD＝，∵AG⊥FG，∴∠AGF＝90°，∴∠DAG+∠AGD＝90°，∠AGD+∠CGF＝90°，∴∠DAG＝∠CGF，∴△ADG∽△GCF，设CF＝BF＝a，CG＝DG＝b，∴＝，∴＝，∴b2＝2a2，∵a＞0．b＞0，∴b＝a，在Rt△GCF中，3a2＝，∴a＝，∴AB＝2b＝2．故答案为2．4．【分析】以AC为直径作圆O′，连接BO′、BC．在点P移动的过程中，点D在以AC为直径的圆上运动，当O′、D、B共线时，BD的值最小，最小值为O′B﹣O′D，利用勾股定理求出BO′即可解决问题．【解答】解：如图，以AC为直径作圆O′，连接BO′、BC，O'D，∵CD⊥AP，∴∠ADC＝90°，∴在点P移动的过程中，点D在以AC为直径的圆上运动，∵AB是直径，∴∠ACB＝90°，在Rt△ABC中，∵AB＝8，∠CAB＝60°，∴BC＝AB•sin60°＝4，AC＝AB•cos60°＝4，∴AO'＝CO'＝2，∴BO'＝＝＝2，∵O′D+BD≥O′B，∴当O′、D、B共线时，BD的值最小，最小值为O′B﹣O′D＝2﹣2，故答案为2﹣2．三、解答题5．【分析】（1）根据角平分线的定义得到∠EDF＝∠ADF，根据圆内接四边形的性质和圆周角定理结论得到结论；（2）根据圆周角定理得到AD⊥BF，推出△ACB是等边三角形，得到∠ADB＝∠ACB＝60°，根据等腰三角形的性质得到结论；（3）设CD＝k，BC＝2k，根据勾股定理得到BD＝＝k＝10，求得＝2，BC＝AC＝4，根据相似三角形的性质即可得到结论【解答】（1）证明：∵DF平分∠ADE，∴∠EDF＝∠ADF，∵∠EDF＝∠ABC，∠BAC∠BDC，∠EDF＝∠BDC，∴∠BAC＝∠ABC，∴AC＝BC；（2）解：∵BD是⊙O的直径，∴AD⊥BF，∵AF＝AB，∴DF＝DB，∴∠FDA＝∠BDA，∴∠ADB＝∠CAB＝∠ACB，∴△ACB是等边三角形，∴∠ADB＝∠ACB＝60°，∴∠ABD＝90°﹣60°＝30°，∴∠F＝∠ABD＝30°；（3）解：∵，∴＝，设CD＝k，BC＝2k，∴BD＝＝k＝10，∴k＝2，∴CD＝2，BC＝AC＝4，∵∠ADF＝∠BAC，∴∠FAC＝∠ADC，∵∠ACF＝∠DCA，∴△ACF∽△DCA，∴＝，∴CF＝8，∴DF＝CF﹣CD＝6．6．【分析】（1）过点E作EG⊥BC，垂足为点G．AE＝x，则EC＝2﹣x．根据BG＝EG构建方程求出x 即可解决问题．（2）①证明△AEF∽△BEC，可得，由此构建关系式即可解决问题．②分两种情形：当∠CAD＜120°时，当120°＜∠CAD＜180°时，分别求解即可解决问题．【解答】解：（1）∵△ABC是等边三角形，∴AB＝BC﹣AC＝2，∠BAC＝∠ABC＝∠ACB＝60°．∵AD＝AC，∴AD＝AB，∴∠ABD＝∠ADB，∵∠ABD+∠ADB+∠BAC+∠CAD＝180°，∠CAD＝90°，∠ABD＝15°，∴∠EBC＝45°．过点E作EG⊥BC，垂足为点G．设AE＝x，则EC＝2﹣x．在Rt△CGE中，∠ACB＝60°，∴，，∴BG＝2﹣CG＝1+x，在Rt△BGE中，∠EBC＝45°，∴，解得．所以线段AE的长是．（2）①设∠ABD＝α，则∠BDA＝α，∠DAC＝∠BAD﹣∠BAC＝120°﹣2α．∵AD＝AC，AH⊥CD，∴，又∵∠AEF＝60°+α，∴∠AFE＝60°，∴∠AFE＝∠ACB，又∵∠AEF＝∠BEC，∴△AEF∽△BEC，∴，由（1）得在Rt△CGE中，，，∴BE2＝BG2+EG2＝x2﹣2x+4，∴（0＜x＜2）．②当∠CAD＜120°时，y＝7，则有7＝，整理得3x2+x﹣2＝0，解得x＝或﹣1（舍弃），．当120°＜∠CAD＜180°时，同法可得y＝当y＝7时，7＝，整理得3x2﹣x﹣2＝0，解得x＝﹣（舍弃）或1，∴AE＝1．2020年中考数学压轴题一、选择题1．已知函数y ＝ax 2+bx +c 的图象的一部分如图所示，则a +b +c 取值范围是（）A ．﹣2＜a +b +c ＜0B ．﹣2＜a +b +c ＜2C ．0＜a +b +c ＜2D ．a +b +c ＜22．如图所示，矩形OABC 中，OA ＝2OC ，D 是对角线OB 上的一点，OD ＝OB ，E 是边AB 上的一点．AE ＝AB ，反比例函数y ＝（x ＞0）的图象经过D ，E 两点，交BC 于点F ，AC 与OB 交于点M ．EF与OB 交于点G ，且四边形BFDE 的面积为．下列结论：①EF ∥AC ；②k ＝2；③矩形OABC 的面积为；④点F 的坐标为（，）正确结论的个数为（）A ．1个B ．2个C ．3个D ．4个二、填空题 3．如图，二次函数y ＝（x +2）2+m 的图象与y 轴交于点C ，与x 轴的一个交点为A （﹣1，0），点B 在抛物线上，且与点C 关于抛物线的对称轴对称．已知一次函数y ＝kx +b 的图象经过A ，B 两点，根据图象，则满足不等式（x +2）2+m ≤kx +b 的x 的取值范围是．4．如图，AE=4，以AE 为直径作⊙O ，点B 是直径AE 上的一动点，以AB 为边在AE 的上方作正方形ABCD ，取CD 的中点M ，将△ADM 沿直线AM 对折，当点D 的对应点D ´落在⊙O 上时，BE 的长为 .三、解答题5．在平面直角坐标系xOy 中，有不重合的两个点Q （x 1，y 1）与P （x 2，y 2）．若Q ，P 为某个直角三角形的两个锐角顶点，且该直角三角形的直角边均与x 轴或y 轴平行（或重合），则我们将该直角三角形的两条直角边的边长之和称为点Q 与点P 之间的“折距”，记做D PQ ．特别地，当PQ 与某条坐标轴平EA OB D CM D´行（或重合）时，线段PQ的长即点Q与点P之间的“折距”．例如，在图1中，点P（1，﹣1），点Q（3，﹣2），此时点Q与点P之间的“折距”D PQ＝3．（1）①已知O为坐标原点，点A（3，﹣2），B（﹣1，0），则D AO＝，D BO＝．②点C在直线y＝﹣x+4上，请你求出D CO的最小值．（2）点E是以原点O为圆心，1为半径的圆上的一个动点，点F是直线y＝3x+6上以动点．请你直接写出点E与点F之间“折距”D EF的最小值．6．如图1，在矩形ABCD中，AB＝4，BC＝5，点E在AD上，ED＝3．动点P从点B出发沿BC方向以每秒3个单位的速度向点C运动，过点P作PF∥CE，与边BA交于点F，过点F作FG∥BC，与CE交于点G，当点F与点A重合时，点P停止运动，设点P运动的时间为t秒．（1）用含t的代数式分别表示线段BF和PF的长度，则有BF＝，PF＝．（2）如图2，作点D关于CE的对称点D′，当FG恰好过点D′时，求t的值．（3）如图3，作△FGP的外接圆⊙O，当点P在运动过程中．①当外接圆⊙O与四边形ABCE的边BC或CE相切时，请求出符合要求的t的值；②当外接圆⊙O的圆心O落在△FGP的内部（不包括边上）时，直接写出t的取值范围．【答案与解析】一、选择题1．【分析】函数y＝ax2+bx+c的图象开口向下可知a小于0，由于抛物线顶点在第一象限即抛物线对称轴在y轴右侧，当x＝1时，抛物线的值必大于0由此可求出a的取值范围，将a+b+c用a表示出即可得出答案．【解答】解：由图象可知：a＜0，图象过点（0，1），所以c＝1，图象过点（﹣1，0），则a﹣b+1＝0，当x＝1时，应有y＞0，则a+b+1＞0，将a﹣b+1＝0代入，可得a+（a+1）+1＞0，解得a＞﹣1，所以，实数a的取值范围为﹣1＜a＜0．又a+b+c＝2a+2，∴0＜a+b+c＜2．故选：C．2．【分析】设E（a，b），F（m，n），则a＝OA＝BC，b＝AE，CF＝m，n＝CO＝AB，证明＝即可判断①；表示出D和E的坐标，根据系数k的几何意义求得k的值即可判断②；求得B的坐标，求得矩形OABC的面积即可判断③；求得F的坐标即可判断④．【解答】解：设E（a，b），F（m，n），则a＝OA＝BC，b＝AE，CF＝m，n＝CO＝AB，∴B（a，n），∵E，F在反比例函数y＝上，∴ab＝mn，∴BC•AE＝CF•AB，∴＝，∴EF∥AC，故①正确；∵OD＝OB，AE＝AB，∴D（a，n），E（a，n），∵OA＝2OC，∴a＝2n，∴B（2n，n），D（n，n），E（2n，n），∵反比例函数y＝经过点F，E，∴k＝mn＝2n•n，∴m＝n，∴F（n，n），∴BF＝2n﹣n＝n，BE＝n，∵四边形BFDE的面积＝S△BDF+S△BDE＝，∴×n×（n﹣n）+×n×（2n﹣n）＝，解得n＝，∴E（3，），F（，）∴k＝3×＝2，故②④正确；∵B（3，），∴矩形OABC的面积为，故③正确；故选：A．二、填空题3．【分析】将点A代入抛物线中可求m＝﹣1，则可求抛物线的解析式为y＝x2+4x+3，对称轴为x＝﹣2，则满足（x+2）2+m≤kx+b的x的取值范围为﹣4≤x≤﹣1．【解答】解：抛物线y＝（x+2）2+m经过点A（﹣1，0），∴m＝﹣1，∴抛物线解析式为y＝x2+4x+3，∴点C坐标（0，3），∴对称轴为x＝﹣2，∵B与C关于对称轴对称，点B坐标（﹣4，3），∴满足（x+2）2+m≤kx+b的x的取值范围为﹣4≤x≤﹣1，故答案为﹣4≤x≤﹣1．4.三、解答题5．【分析】（1）①D AO＝|3﹣0|+|﹣2﹣0|＝5，即可求解；②设点C（m，4﹣m），则D CO＝|m|+|m﹣4|，当0≤m≤4时，D CO最小，即可求解；（2）EF1是“折距”D EF的最小值，即求EF1的最小值即可，当点E在y轴左侧于平行于直线y＝﹣x+4的直线相切时，EF1最小，即可求解．【解答】解：（1）①D AO＝|3﹣0|+|﹣2﹣0|＝5，同理D BO＝1，故答案为：5，1；②设点C（m，4﹣m），则D CO＝|m|+|m﹣4|，当0≤m≤4时，D CO最小，最小值为4；（2）如图2，过点E分别作x、y轴的平行线交直线y＝﹣x+4于F1、F2，则EF1是“折距”D EF的最小值，即求EF1的最小值即可，当点E在y轴左侧于平行于直线y＝﹣x+4的直线相切时，EF1最小，如图3，将直线y＝﹣x+4向右平移与圆相切于点E，平移后的直线与x轴交于点G，连接OE，设原直线与x、y轴交于点M、N，则点M、N的坐标分别为（﹣2，0）、点N（0，6），则MN＝2，则△MON∽△GEO，则，即，则GO＝，EF1＝MG＝2﹣＝．6．【分析】（1）由△PFB∽△ECD，得＝＝，由此即可解决问题．（2）如图2中，由△D′MG∽△CDE，得＝，求出MG，根据PF＝CG＝CM﹣MG，列出方程即可解决问题．（3）①存在．如图4中，当⊙O与BC相切时，连接OP延长PO交FG于M，连接OF、OG，由PB＝MF＝MG＝FG＝PC，得到3t＝（5﹣3t），即可解决问题．如图5中，当⊙O与BC相切时，连接GO，延长GO交PF于M，连接OF、OP，由△FGM∽△PFB，得＝，列出方程即可解决问题．②求出两种特殊位置t的值即可判断．【解答】解：（1）如图1中，∵四边形ABCD是矩形，∴AB＝CD＝4，BC＝AD＝5，∠B＝∠D＝90°，AD∥BC，在Rt△ECD中，∵∠D＝90°，ED＝3．CD＝4，∴EC＝＝5，∵PF∥CE，FG∥BC，∴四边形PFGC是平行四边形，∴∠FPB＝∠ECB＝∠DEC，∴△PFB∽△ECD，∴＝＝，∴＝＝，∴BF＝4t，PF＝5t，故答案为4t，5t．（2）如图2中，∴D、D′关于CE对称，∴DD′⊥CE，DM＝MD′，∵•DE•DC＝•EC•DM，∴DM＝D′M＝，CM＝＝，由△D′MG∽△CDE，得＝，∴＝，∴MG＝，∴PF＝CG＝CM﹣MG，∴5t＝﹣，∴t＝．∴t＝时，D′落在FG上．（3）存在．①如图4中，当⊙O与BC相切时，连接OP延长PO交FG于M，连接OF、OG．∵OP⊥BC，BC∥FG，∴PO⊥FG，∴FM＝MG由PB＝MF＝MG＝FG＝PC，得到3t＝（5﹣3t），解得t＝．如图5中，当⊙O与EC相切时，连接GO，延长GO交PF于M，连接OF、OP．∵OG⊥EC，BF∥EC，∴GO⊥PF，∴MF＝MP＝t，∵△FGM∽△PFB，∴＝，∴＝，解得t＝．综上所述t＝或时，⊙O与四边形ABCE的一边（AE边除外）相切．②如图6中，当∠FPG＝90°时，由cos∠PCG＝cos∠CED，∴＝，∴t＝，如图7中，当∠FGP＝90°时，∴＝，∴t＝，观察图象可知：当＜t＜时，外接圆⊙O的圆心O落在△FGP的内部．2020年中考数学压轴题一、选择题1．如图，平面直角坐标系中，A（﹣8，0），B（﹣8，4），C（0，4），反比例函数y＝的图象分别与线段AB，BC交于点D，E，连接DE．若点B关于DE的对称点恰好在OA上，则k＝（）A．﹣20 B．﹣16 C．﹣12 D．﹣82．如图，等边三角形ABC边长是定值，点O是它的外心，过点O任意作一条直线分别交AB，BC于点D，E．将△BDE沿直线DE折叠，得到△B′DE，若B′D，B′E分别交AC于点F，G，连接OF，OG，则下列判断错误的是（）A．△ADF≌△CGEB．△B′FG的周长是一个定值C．四边形FOEC的面积是一个定值D．四边形OGB'F的面积是一个定值二、填空题3．如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF 最大时，S△ADE＝．第3题第4题4．如图，△ABC中，∠C＝90°，AC＝3，AB＝5，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为．三、解答题5．如图，矩形ABCD，AB＝2，BC＝10，点E为AD上一点，且AE＝AB，点F从点E出发，向终点D 运动，速度为1cm/s，以BF为斜边在BF上方作等腰直角△BFG，以BG，BF为邻边作▱BFHG，连接AG．设点F的运动时间为t秒．（1）试说明：△ABG∽△EBF；（2）当点H落在直线CD上时，求t的值；（3）点F从E运动到D的过程中，直接写出HC的最小值．6．已知，如图，二次函数y＝ax2+2ax﹣3a（a＞0）图象的顶点为C与x轴交于A、B两点（点A在点B 左侧），点C、B关于过点A的直线l：y＝kx﹣对称．（1）求A、B两点坐标及直线l的解析式；（2）求二次函数解析式；（3）如图2，过点B作直线BD∥AC交直线l于D点，M、N分别为直线AC和直线l上的两动点，连接CN，NM、MD，求D的坐标并直接写出CN+NM+MD的最小值．【答案与解析】一、选择题1．【分析】根据A（﹣8，0），B（﹣8，4），C（0，4），可得矩形的长和宽，易知点D的横坐标，E的纵坐标，由反比例函数的关系式，可用含有k的代数式表示出点D的纵坐标和点E的横坐标，由三角形相似和对称，可求出AF的长，然后把问题转化到三角形ADF中，由勾股定理建立方程求出k的值．【解答】解：过点E作EG⊥OA，垂足为G，设点B关于DE的对称点为F，连接DF、EF、BF，如图所示：则△BDE≌△FDE，∴BD＝FD，BE＝FE，∠DFE＝∠DBE＝90°易证△ADF∽△GFE∴，∴AF：EG＝BD：BE，∵A（﹣8，0），B（﹣8，4），C（0，4），∴AB＝OC＝EG＝4，OA＝BC＝8，∵D、E在反比例函数y＝的图象上，∴E（，4）、D（﹣8，）∴OG＝EC＝，AD＝﹣，∴BD＝4+，BE＝8+∴，∴AF＝，在Rt△ADF中，由勾股定理：AD2+AF2＝DF2即：（﹣）2+22＝（4+）2解得：k＝﹣12故选：C．2．【分析】A、根据等边三角形ABC的内心的性质可知：AO平分∠BAC，根据角平分线的定理和逆定理得：FO平分∠DFG，由外角的性质可证明∠DOF＝60°，同理可得∠EOG＝60°，∠FOG＝60°＝∠DOF ＝∠EOG，可证明△DOF≌△GOF≌△GOE，△OAD≌△OCG，△OAF≌△OCE，可得AD＝CG，AF＝CE，从而得△ADF≌△CGE；B、根据△DOF≌△GOF≌△GOE，得DF＝GF＝GE，所以△ADF≌△B'GF≌△CGE，可得结论；C、根据S四边形FOEC＝S△OCF+S△OCE，依次换成面积相等的三角形，可得结论为：S△AOC＝（定值），可作判断；D、方法同C，将S四边形OGB'F＝S△OAC﹣S△OFG，根据S△OFG＝•FG•OH，FG变化，故△OFG的面积变化，从而四边形OGB'F的面积也变化，可作判断．【解答】解：A、连接OA、OC，∵点O是等边三角形ABC的内心，∴AO平分∠BAC，∴点O到AB、AC的距离相等，由折叠得：DO平分∠BDB'，∴点O到AB、DB'的距离相等，∴点O到DB'、AC的距离相等，∴FO平分∠DFG，∠DFO＝∠OFG＝（∠FAD+∠ADF），由折叠得：∠BDE＝∠ODF＝（∠DAF+∠AFD），∴∠OFD+∠ODF＝（∠FAD+∠ADF+∠DAF+∠AFD）＝120°，∴∠DOF＝60°，同理可得∠EOG＝60°，∴∠FOG＝60°＝∠DOF＝∠EOG，∴△DOF≌△GOF≌△GOE，∴OD＝OG，OE＝OF，∠OGF＝∠ODF＝∠ODB，∠OFG＝∠OEG＝∠OEB，∴△OAD≌△OCG，△OAF≌△OCE，∴AD＝CG，AF＝CE，∴△ADF≌△CGE，故选项A正确；B、∵△DOF≌△GOF≌△GOE，∴DF＝GF＝GE，∴△ADF≌△B'GF≌△CGE，∴B'G＝AD，∴△B'FG的周长＝FG+B'F+B'G＝FG+AF+CG＝AC（定值），故选项B正确；C、S四边形FOEC＝S△OCF+S△OCE＝S△OCF+S△OAF＝S△AOC＝（定值），故选项C正确；D、S四边形OGB'F＝S△OFG+S△B'GF＝S△OFD+S△ADF＝S四边形OFAD＝S△OAD+S△OAF＝S△OCG+S△OAF＝S△OAC﹣S△OFG，过O作OH⊥AC于H，∴S△OFG＝•FG•OH，由于OH是定值，FG变化，故△OFG的面积变化，从而四边形OGB'F的面积也变化，故选项D不一定正确；故选：D．二、填空题3．【分析】作DH⊥AE于H，如图，由于AF＝4，则△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，当BF为此圆的切线时，∠ABF最大，即BF⊥AF，利用勾股定理计算出BF＝3，接着证明△ADH ≌△ABF得到DH＝BF＝3，然后根据三角形面积公式求解．【解答】解：作DH⊥AE于H，如图，∵AF＝4，当△AEF绕点A旋转时，点F在以A为圆心，4为半径的圆上，∴当BF为此圆的切线时，∠ABF最大，即BF⊥AF，在Rt△ABF中，BF＝＝3，∵∠EAF＝90°，∴∠BAF+∠BAH＝90°，∵∠DAH+∠BAH＝90°，∴∠DAH＝∠BAF，在△ADH和△ABF中，∴△ADH≌△ABF（AAS），∴DH＝BF＝3，∴S△ADE＝AE•DH＝×3×4＝6．故答案为6．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了正方形的性质．4．【分析】过点O作OE⊥AB于点E，OF⊥BC于点F．根据切线的性质，知OE、OF是⊙O的半径；然后由三角形的面积间的关系（S△ABO+S△BOD＝S△ABD＝S△ACD）列出关于圆的半径的等式，求得圆的半径即可．【解答】解：过点O作OE⊥AB于点E，OF⊥BC于点F．∵AB、BC是⊙O的切线，∴点E、F是切点，∴OE、OF是⊙O的半径；∴OE＝OF；在△ABC中，∠C＝90°，AC＝3，AB＝5，∴由勾股定理，得BC＝4；又∵D是BC边的中点，∴S△ABD＝S△ACD，又∵S△ABD＝S△ABO+S△BOD，∴AB•OE+BD•OF＝CD•AC，即5×OE+2×OE＝2×3，解得OE＝，∴⊙O的半径是．故答案为：．三、解答题5．【分析】（1）根据两边成比例夹角相等即可证明两三角形相似；（2）如图构建如图平面直角坐标系，作HM⊥AD于M，GN⊥AD于N．设AM交BG于K．首先证明△GFN≌△FHM，想办法求出点H的坐标，构建方程即可解决问题；（3）由（2）可知H（2+t，4+t），令x＝2+t，y＝4+t，消去t得到y＝x+．推出点H在直线y＝x+上运动，根据垂线段最短即可解决问题；【解答】（1）证明：如图1中，∵△ABE，△BGF都是等腰直角三角形，∴＝＝，∵∠ABE＝∠GBF＝45°，∴∠ABG＝∠EBF，∴△ABG∽△EBF．（2）解：如图构建如图平面直角坐标系，作HM⊥AD于M，GN⊥AD于N．设AM交BG于K．∵△GFH是等腰直角三角形，∴FG＝FH，∠GNF＝∠GFH＝∠HMF＝90°，∴∠GFN+∠HFM＝90°，∠HFM+∠FHM＝90°，∴∠GFN＝∠FHM，∴△GFN≌△FHM，∴GN＝FM，FN＝HM，∵△ABG∽△EBF，∴＝＝，∠AGB＝∠EFB，∵∠AKG＝∠BKF，∴∠GAN＝∠KBF＝45°，∵EF＝t，∴AG＝t，∴AN＝GN＝FM＝t，∴AM＝2+t，HM＝FN＝2+t，∴H（2+t，4+t），当点H在直线CD上时，2+t＝10，解得t＝．（3）由（2）可知H（2+t，4+t），令x＝2+t，y＝4+t，消去t得到y＝x+．∴点H在直线y＝x+上运动，如图，作CH垂直直线y＝x+垂足为H．根据垂线段最短可知，此时CH的长最小，易知直线CH的解析式为y＝﹣3x+30，由，解得，∴H（8，6），∵C（10，0），∴CH＝＝2，∴HC最小值是2．6．【分析】（1）令二次函数解析式y＝0，解方程即求得点A、B坐标；把点A坐标代入直线l解析式即求得直线l．（2）把二次函数解析式配方得顶点C（﹣1，﹣4a），由B、C关于直线l对称可知AB＝AC，用a表示AC的长即能列得关于的方程．求得a有两个互为相反数的解，由二次函数图象开口向上可知a＞0，舍去负值．（3）①用待定系数法求直线AC解析式，由BD∥AC可知直线BD解析式的k与AC的k相同，再代入点B坐标即求得直线BD解析式．把直线l与直线BD解析式联立方程组，求得的解即为点D坐标．②由点B、C关于直线l对称，连接BN即有B、N、M在同一直线上时，CN+MN＝BN+MN＝BM最小；作点D关于直线AC的对称点Q，连接DQ交直线AC于点E，可证B、M、Q在同一直线上时，BM+MD＝BM+MQ＝BQ最小，CN+NM+MD最小值＝BM+MD最小值＝BQ．由直线AC垂直平分DQ且AC∥BD可得BD⊥DQ，即∠BDQ＝90°．由B、D坐标易求BD的长；由B、C关于直线l 对称可得l平分∠BAC，作DF⊥x轴于F则有DF＝DE，所以DQ＝2DE＝2DF＝4；利用勾股定理即求得BQ的长．【解答】解：（1）当y＝0时，ax2+2ax﹣3a＝0解得：x1＝﹣3，x2＝1∴点A坐标为（﹣3，0），点B坐标为（1，0）∵直线l：y＝kx﹣经过点A∴﹣3k﹣＝0 解得：k＝﹣∴直线l的解析式为y＝﹣x﹣（2）∵y＝ax2+2ax﹣3a＝a（x+1）2﹣4a∴点C坐标为（﹣1，﹣4a）∵C、B关于直线l对称，A在直线l上∴AC＝AB，即AC2＝AB2∴（﹣1+3）2+（﹣4a）2＝（1+3）2解得：a＝±（舍去负值），即a＝∴二次函数解析式为：y＝x2+x﹣（3）∵A（﹣3，0），C（﹣1，﹣2），设直线AC解析式为y＝kx+b∴解得：∴直线AC解析式为y＝﹣x﹣3∵BD∥AC∴设直线BD解析式为y＝﹣x+c把点B（1，0）代入得：﹣+c＝0 解得：c＝∴直线BD解析式为y＝﹣x+∵解得：∴点D坐标为（3，﹣2）如图，连接BN，过点D作DF⊥x轴于点F，作D关于直线AC的对称点点Q，连接DQ交AC于点E，连接BQ，MQ．∵点B、C关于直线l对称，点N在直线l上∴BN＝CN∴当B、N、M在同一直线上时，CN+MN＝BN+MN＝BM，即CN+MN的最小值为BM∵点D、Q关于直线AC对称，点M在直线AC上∴MQ＝MD，DQ⊥AC，DE＝QE∴当B、M、Q在同一直线上时，BM+MD＝BM+MQ＝BQ，即BM+MD的最小值为BQ∴此时，CN+NM+MD＝BM+MD＝BQ，即CN+NM+MD的最小值为BQ∵点B、C关于直线l对称∴AD平分∠BAC∵DF⊥AB，DE⊥AC∴DE＝DF＝|y D|＝2∴DQ＝2DE＝4∵B（1，0），D（3，﹣2）∴BD2＝（3﹣1）2+（﹣2）2＝16∵BD∥AC∴∠BDQ＝∠AEQ＝90°∴BQ＝∴CN+NM+MD的最小值为8．2020年中考数学压轴题一、选择题1．如图，在等腰△ABC中，AB＝AC，把△ABC沿EF折叠，点C的对应点为O，连接AO，使AO平分∠BAC，若∠BAC＝∠CFE＝50°，则点O是（）A．△ABC的内心B．△ABC的外心C．△ABF的内心D．△ABF的外心2．已知正方形ABCD的边长为5，E在BC边上运动，DE的中点G，EG绕E顺时针旋转90°得EF，问CE为多少时A、C、F在一条直线上（）A．B．C．D．二、填空题3．如图，现将四根木条钉成的矩形框ABCD变形为平行四边形木框A'BCD′，且A′D′与CD相交于CD边的中点E，若AB＝4，则△ECD′的面积是．4．如图，已知点A是第一象限内横坐标为的一个定点，AC⊥x轴于点M，交直线y＝﹣x于点N．若点P是线段ON上的一个动点，∠APB＝30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动．求当点P从点O运动到点N时，点B运动的路径长是．三、解答题5．如图，把矩形ABCD沿AC折叠，使点D与点E重合，AE交BC于点F，过点E作EG∥CD交AC于点G，交CF于点H，连接DG．（1）求证：四边形ECDG是菱形；（2）若DG＝6，AG＝，求EH的值．6．如图，已知△BAC为圆O内接三角形，AB＝AC，D为⊙O上一点，连接CD、BD，BD与AC交于点E，且BC2＝AC•CE①求证：∠CDB＝∠CBD；②若∠D＝30°，且⊙O的半径为3+，I为△BCD内心，求OI的长．【答案与解析】一、选择题1．【分析】连接OB、OC，根据AB＝AC，AO平分∠BAC，∠BAC＝50°，可得AO是BC的垂直平分线，∠BAO＝∠CAO＝25°，得OB＝OC，根据折叠可证明∠OAC＝∠OCA＝25°，得OA＝OC，进而OA＝OB＝OC，可得点O是三角形ABC的外心．【解答】解：如图，连接OB、OC，∵AB＝AC，AO平分∠BAC，∴AO是BC的垂直平分线，∴OB＝OC，∵∠BAC＝50°，AO平分∠BAC，∴∠BAO＝∠CAO＝25°，根据折叠可知：CF＝OF，∠OFE＝∠CFE＝50°，∴∠OFC＝100°，∴∠FCO＝（180°﹣100°）＝40°，∵AB＝AC，∠BAC＝50°，∴∠ACB＝（180°﹣50°）＝65°，∴∠OCA＝∠ACB﹣∠FCO＝65°﹣40°＝25°，∴∠OAC＝∠OCA＝25°，∴OA＝OC，∴OA＝OB＝OC，∴O是△ABC的外心．故选：B．2．【分析】过F作FN⊥BC，交BC延长线于N点，连接AC，构造直角△EFN，利用三角形相似的判定，得出Rt△FNE∽Rt△ECD，根据相似三角形的对应边成比例，求得NE＝CD＝，运用正方形性质，可得出△CNF是等腰直角三角形，从而求出CE．【解答】解：如图，过F作FN⊥BC，交BC延长线于N点，连接AC．∵DE的中点为G，EG绕E顺时针旋转90°得EF，∴DE：EF＝2：1．∵∠DCE＝∠ENF＝90°，∠DEC+∠NEF＝90°，∠NEF+∠EFN＝90°，∴∠DEC＝∠EFN，∴Rt△FNE∽Rt△ECD，∴CE：FN＝DE：EF＝DC：NE＝2：1，∴CE＝2NF，NE＝CD＝．∵∠ACB＝45°，∴当∠NCF＝45°时，A、C、F在一条直线上．则△CNF是等腰直角三角形，∴CN＝NF，∴CE＝NE＝×＝，∴CE＝时，A、C、F在一条直线上．故选：D．二、填空题3．【分析】作A'F⊥BC于F，则∠A'FB＝90°，根据题意得：平行四边形A′BCD′的面积＝BC•A'F＝BC•AB，A'F＝AB＝2，得出∠D'＝∠A'BC＝30°，得出BF＝A'F＝2，由矩形和平行四边形的性质得出BC＝AD＝A'D'，A'D'∥AD∥BC，CD⊥BC，得出CD⊥A'D'，得出A'F∥CD，证出四边形A'ECF 是矩形，得出CE＝A'F＝2，A'E＝CF，证出DE＝BF＝2，即可得出答案．【解答】解：作A'F⊥BC于F，如图所示：则∠A'FB＝90°，根据题意得：平行四边形A′BCD′的面积＝BC•A'F＝BC•AB，∴A'F＝AB＝2，∴∠D'＝∠A'BC＝30°，∴BF＝A'F＝2，∵四边形ABCD是矩形，四边形A′BCD′是平行四边形，∴BC＝AD＝A'D'，A'D'∥AD∥BC，CD⊥BC，∴CD⊥A'D'，∴A'F∥CD，∴四边形A'ECF是矩形，∴CE＝A'F＝2，A'E＝CF，∴DE＝BF＝2，∴△ECD的面积＝DE×CE＝×2×2＝2；4．【分析】首先，需要证明线段B1B2就是点B运动的路径（或轨迹），如图1所示．利用相似三角形可以证明；其次，证明△APN∽△AB1B2，列比例式可得B1B2的长．【解答】解：如图1所示，当点P运动至ON上的任一点时，设其对应的点B为B i，连接AP，AB i，BB i，∵AO⊥AB1，AP⊥AB i，∴∠OAP＝∠B1AB i，又∵AB1＝AO•tan30°，AB i＝AP•tan30°，∴AB1：AO＝AB i：AP，∴△AB1B i∽△AOP，∴∠B1B i＝∠AOP．同理得△AB1B2∽△AON，∴∠AB1B2＝∠AOP，∴∠AB1B i＝∠AB1B2，∴点B i在线段B1B2上，即线段B1B2就是点B运动的路径（或轨迹）．由图形2可知：Rt△APB1中，∠APB1＝30°，∴，Rt△AB2N中，∠ANB2＝30°，∴＝，∴，∵∠PAB1＝∠NAB2＝90°，∴∠PAN＝∠B1AB2，∴△APN∽△AB1B2，∴＝＝，∵ON：y＝﹣x，∴△OMN是等腰直角三角形，∴OM＝MN＝，∴PN＝，∴B1B2＝，综上所述，点B运动的路径（或轨迹）是线段B1B2，其长度为．故答案为：．。

2020挑战压轴题中考数学强化训练第二部分_一、图形的平移

第二部分填空题、选择题中的动态图形训练题一、图形的平移1、在平面直角坐标系中，点A向右平移4个单位得到点B，点B向下平移3个单位得到点C·那么△ABC 的面积为2、直线y=2x-1向上平移3个单位后得到的直线不经过第象限3、抛物线y=-x2+2x+1向下平移4个单位后得到的抛物线的解析式是4、将抛物线y=x2-4x-4向左平移3个单位，再向上平移5个单位，得到新抛物线的表达式为5、平面直角坐标系中，已知平行四边形ABCD的三个顶点坐标分别是A（m,n）、B（2，-1）、C（-m，-n），则点D的坐标是（）6、如图，△ABC中，BC=5cm，将△ABC沿BC方向平移至△A'B‘C'的位置时，A'B恰好经过AC的中点O，则△ABC平移的距离为7、如图，把三角板的斜边紧靠直尺平移，如果一个顶点从刻度“5”平移到刻度“10”，则顶点C平移的距离CC’=8、如图，正六边形ABCDEF内接于半径为4的圆，则B、E两点间的距离为9、如图，△ABC中，AB=AC,BC=12cm，点D在AC上，DC=4m，将线段DC沿CB方向平移7cm得到线段EF，点E、F分别落在边AB、BC上，则△BF的周长为10、如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标分别为（1,0）、（4,0），将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段BC扫过的面积为11、小军同学在网格纸上将某些图形进行平移操作，他发现平移前后的两个图形所组成的图形可以是轴对称图形如图所示，现在他将正方形ABCD从当前位置开始进行一次平移操作，平移后的正方形的顶点也在格点上，则使平移前后的两个正方形组成轴对称图形的平移方向有（）A、3个（B）4个（C）5个（D）无数12、如图，在平面直角坐标系中，点A、C在x轴上，点C的坐标为（-1,0），AC=2.将Rt△ABC先绕点C 顺时针旋转90°，再向右平移3个单位长度，则变换后点A的对应点的坐标是（）（A）（2,2）（B）（1,2）（C）（-1,2）（D）（2，-1）13、在平面直角坐标系中，将点A（-1，-2）向右平移3个单位得到点B，则点B关于x轴的对称点B的坐标为（）（A）（-3，-2）（B）（2,2）C（-2,2）D（2，-2）14、已知抛物线y=x2+2x-3与x轴交于A、B两点（点A在点B的左侧），将这条抛物线向右平移m（m>0）个单位，平移后的抛物线与x轴交于C、D两点（点C在点D的左侧），若B、C是线段AD的三等分点，则m的值为15、将直线y=2x-3向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为16、如图所示，在平面直角坐标系中，已知点A2），B（1,1）。

2020年版挑战中考数学压轴题详解(115页)

2020年中考数学压轴题十大题型(含详细答案)

2020-2021备战中考数学——初中数学 旋转的综合压轴题专题复习附答案解析

2020年中考数学压轴题-专题10 动点产生的面积关系(解析版)

圆与射影定理结合型压轴题专题—2024年挑战中考数学压轴题(全国通用)(解析版)

挑战2024年中考数学压轴题之学霸秘笈大揭秘(全国通用)专题02解方程与解不等式篇(原卷版+解析)

2020年中考数学压轴题(含答案)

2020年中考数学压轴题(含答案) (2)

2020年中考数学压轴题十大题型(含详细答案)

2020年九年级数学备战中考—中考真题计算压轴题(图形题)含解析

2020年中考数学压轴题限时专训2(含解析)

2020年全国中考数学压轴题全析全解(2)

决战2020年中考数学压轴题综合提升训练《三角形》(含解析)

决胜2020年中考数学压轴题专题15 动点综合问题(含答案)

挑战2023年中考数学压轴题专题11 二次函数与单线段最值问题(含答案解析)

2020年九年级中考数学压轴试题(附答案)

2020年江苏中考数学压轴题精选精练5(解析版)

2020年江苏省九年级中考数学压轴题选择、填空、解答题精选精练(含解析)

2020年中考数学压轴题专题讲解：四边形综合题(含答案)

2020年中考数学压轴题(含答案解析)

2020挑战压轴题中考数学强化训练第二部分_一、图形的平移

2020-2021备战中考数学——初中数学旋转的综合压轴题专题复习附答案解析