最新-天津市和平区七年级数学上期末试卷
2023-2024学年天津市部分区七年级(上)期末数学试卷+答案解析

2023-2024学年天津市部分区七年级(上)期末数学试卷一、选择题:本题共12小题,每小题3分,共36分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列四个数中,是负整数的是()A.0B.C.D.2.袁隆平院士被誉为“杂交水稻之父”,经过他带领的团队多年努力,目前我国杂交水稻种植面积约为亿亩.将250000000用科学记数法表示应为()A. B. C. D.3.如图所示的几何体,从上往下看的视图是()A. B. C. D.4.中国是最早采用正负数表示相反意义的量,并进行负数运算的国家.若把气温为零上记作,则表示气温为()A.零上B.零下C.零上D.零下5.下面的计算正确的是()A. B.C. D.6.如果是关于x的方程的解,那么a的值为()A. B.4 C.6 D.107.若多项式为常数化简后的结果不含字母y,则a的值为()A. B.0 C.2或 D.68.如图,某海域有三个小岛A,B,O,在小岛O处观测到小岛A在它的北偏东的方向上,观测到小岛B在它的南偏西的方向上,则的度数是()A.B.C.D.9.实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是()A. B. C. D.10.A,B,C三点在同一直线上,线段,,那么A,C两点的距离是()A.1cmB.9cmC.1cm或9cmD.以上答案都不对11.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:现有几个人共买一件物品,每人出8钱,多出3钱;每人出7钱,还差4钱.设人数为x,则可列方程为()A. B. C. D.12.观察如图“蜂窝图”,按照这样的规律,第2024个图案中的“”的个数是()A.6074B.6072C.6073D.6068二、填空题:本题共6小题,每小题3分,共18分。
13.已知一个角是,则它的余角是______.14.按括号内的要求,用四舍五入法求近似数:精确到______.15.如图所示,在我国“西气东输”的工程中,从A城市往B城市架设管道,有三条路可供选择,在不考虑其他因素的情况下,架设管道的最短路线是______,依据是______.16.若,则______,______.17.如图,,OC平分,OD平分,则的大小为______度18.已知数轴上A,B两点所对应的数分别是1和3,P为数轴上任意一点,对应的数为,B两点之间的距离为______;式子的最小值为______.三、计算题:本大题共1小题,共8分。
天津市和平区七年级(上)期末数学试卷
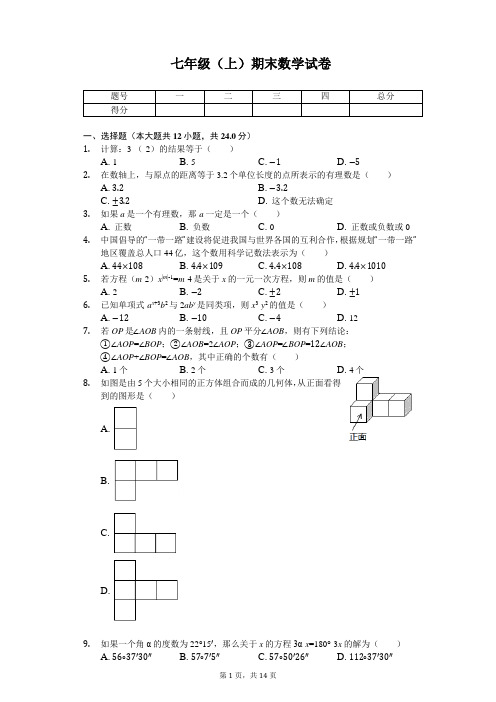
七年级(上)期末数学试卷题号一二三四总分得分一、选择题(本大题共12小题,共24.0分)1.计算:3-(-2)的结果等于()A. 1B. 5C. −1D. −52.在数轴上,与原点的距离等于3.2个单位长度的点所表示的有理数是()A. 3.2B. −3.2C. ±3.2D. 这个数无法确定3.如果a是一个有理数,那-a一定是一个()A. 正数B. 负数C. 0D. 正数或负数或04.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为()A. 44×108B. 4.4×109C. 4.4×108D. 4.4×10105.若方程(m-2)x|m|-1=m-4是关于x的一元一次方程,则m的值是()A. 2B. −2C. ±2D. ±16.已知单项式-a x+3b2与2ab y是同类项,则x3-y2的值是()A. −12B. −10C. −4D. 127.若OP是∠AOB内的一条射线,且OP平分∠AOB,则有下列结论:①∠AOP=∠BOP;②∠AOB=2∠AOP;③∠AOP=∠BOP=12∠AOB;④∠AOP+∠BOP=∠AOB,其中正确的个数有()A. 1个B. 2个C. 3个D. 4个8.如图是由5个大小相同的正方体组合而成的几何体,从正面看得到的图形是()A.B.C.D.10.一轮船A观测灯塔B在其北偏东40°,灯塔C在其南偏东60°,则此时∠BAC的度数是()A. 40∘B. 60∘C. 80∘D. 100∘11.如图,点C是线段AB上一点,D为BC的中点,且AB=12cm,BD=5cm.若点E在直线AB上,且AE=3cm,则DE的长为()A. 4cmB. 15cmC. 3cm或15cmD. 4cm段10cm12.若∠A与∠B互补,且∠A>∠B,则∠B的余角是()A. 12(∠A−∠B)B. 12(∠A+∠B)C. 12∠B−∠AD. ∠A−12∠B二、填空题(本大题共6小题,共18.0分)13.已知-a=5,则-[+(-a)]=______.14.建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后在两个木桩之间拉一条线,建筑工人沿着拉紧的这条直线砌墙,这样砌的砖整齐,这个事实说明的原理是______.15.方程x-x−12=2-x+25的解是______.16.若要使图中的平面展开图折叠成正方体后,相对面上的两个数之和为6,则x+y+z的值为______.17.如图,∠BOC-∠AOB=39°,∠BOC:∠COD:∠DOA=4:5:6,则∠AOB的度数为______.18.如图,线段AB=10.C,D,E分别为线段AB(端点A,B除外)上顺次三个不同的点,图中所有的线段和等于52,则CE=______.三、计算题(本大题共3小题,共26.0分)19.计算:(1)(-114)×25×(-6)-9÷(-32)220.已知A=a2-2b2+2ab-3,B=2a2-b2-25ab-15.(1)求2(A+B)-3(2A-B)的值(结果用化简后的a、b的式子表示);(2)当|a+12|与b2互为相反数时,求(1)中式子的值.21.列一元一次方程解应用题某超市计划购进甲、乙两种型号的台灯1000台,这两种型号台灯的进价、售价如下表:进价(元/台)售价(元/台)甲种4555乙种6080(1)如果超市的进货款为54000元,那么可计划购进甲、乙两种型号的台灯各多少台?(2)为确保乙种型号的台灯销售更快,超市决定对乙种型号的台灯打折销售,且保证乙种型号台灯的利润率为20%,问乙种型号台灯需打几折?四、解答题(本大题共4小题,共32.0分)22.已知关于x的一元一次方程x3+m=mx−36.(1)当m=-1时,求方程的解;(2)当m为何值时,方程的解为x=21.23.如图,∠2是∠1的4倍,∠2的补角比∠1的余角大45°.(2)若∠AOD=90°,试问OC平分∠AOB吗?为什么?24.已知C为线段AB上一点,关于x的两个方程12(x+1)=m与23(x+m)=m的解分别为线段AC,BC的长,(1)当m=2时,求线段AB的长;(2)若C为线段AB的三等分点,求m的值.25.如图,点O在直线AB上,射线OM,ON在直线AB上方,设∠MON=α,设射线OP1,OP2为∠AOM的三等分线,射线OQ1,OQ2为∠BON的三等分线.(1)若α=45°,求∠AOP1+∠BOQ1的度数;(2)用含α的式子表示∠P1OQ1和∠P2OQ2,并直接写出∠P1OQ1与∠P2OQ2所满足的数量关系.答案和解析1.【答案】B【解析】解:原式=3+2=5,故选:B.原式利用减法法则变形,计算即可求出值.此题考查了有理数的减法,熟练掌握运算法则是解本题的关键.2.【答案】C【解析】解:数轴上与原点O的距离等于3.2个单位长度的点表示的有理数是:-3.2和3.2,故选:C.由绝对值的几何意义可得出结论.本题考查数轴、有理数,解答本题的关键是明确数轴的特点,写出相应的有理数.3.【答案】D【解析】解:如果a是一个有理数,那-a可能是正数或负数或0,故选:D.根据有理数包括正数、0、负数进行判断即可.本题考查了对正数,负数,有理数等知识点的理解和运用,注意:0不是正数也不是负数,有理数包括正数、0、负数.4.【答案】B【解析】解:44亿=4.4×109.故选:B.用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|5.【答案】B【解析】解:∵方程(m-2)x|m|-1=m-4是关于x的一元一次方程,∴|m|-1=1,m-2≠0,解得:m=-2.故选:B.直接利用一元一次方程的定义进而分析得出答案.此题主要考查了一元一次方程的定义,正确把握定义是解题关键.6.【答案】A【解析】解:由题意可知:x+3=1,y=2,∴x=-2,y=2,∴原式=-8-4=-12,故选:A.根据同类项的定义即可求出答案.本题考查同类项,解题的关键是熟练运用同类项的定义,本题属于基础题型.7.【答案】D【解析】解:∵OP平分∠AOB,∴①∠AOP=∠BOP;②∠AOB=2∠AOP;③∠AOP=∠BOP=∠AOB;④∠AOP+∠BOP=∠AOB,故正确的个数有4个,故选:D.根据角平分线的定义解答即可.本题考查了角平分线的定义,熟记角平分线的定义是解题的关键.8.【答案】C【解析】解:从正面看,如图所示,,根据从正面看得到的图形是主视图,可得答案.本题考查了简单组合体的三视图,从正面看得到的图形是主视图.9.【答案】A【解析】解:把α=22°15′代入方程得:66°45′-x=180°-3x,解得:x=56°37′30″.故选:A.把α代入方程计算即可求出x的值.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.10.【答案】C【解析】解:如图∠BAC=180°-60°-40°=80°,故选:C.根据方向角的定义作出示意图,根据图形即可解答.本题考查了方向角的定义,理解定义作出示意图是关键.11.【答案】D【解析】解:∵D为BC的中点,BD=5cm,∴BC=10cm,CD=BD=5cm,∵AB=12cm,∴AC=2cm,如图1,∵AE=3cm,∴CE=1cm,∴DE=4cm,如图2,∵AE=3cm,∴DE=AE+AC+CD=3+2+5=10cm,故DE的长为4cm或10cm,根据线段中点的定义得到BC=10cm,CD=BD=5cm,求得AC=2cm,如图1,如图2,根据线段的和差即可得到结论.本题考查了两点间的距离,分类讨论是解题关键.12.【答案】A【解析】解:∵∠A与∠B互补,∴∠A+∠B=180°,∵∠A>∠B,∴∠B=180°-∠A,∴∠B的余角为:90°-(180°-∠A)=∠A-90°=∠A-(∠A+∠B)=∠A-∠B=(∠A-∠B),故选:A.首先根据∠A与∠B互补可得∠A+∠B=180°,再表示出∠B的余角90°-(180°-∠A),然后再把等式变形即可.此题主要考查了余角和补角,关键是掌握余角和补角的定义.如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.13.【答案】5【解析】解:∵-a=5,∴a=-5,-[+(-a)]=-(-a)=a=5,故答案为:5.先去括号,再代入数值,即可解答.本题考查了去括号,解决本题的关键是先去括号.14.【答案】两点确定一条直线【解析】解:建筑工人砌墙时,经常在两个墙角的位置分别插一根木桩,然后在两个木桩之间拉一条线,建筑工人沿着拉紧的这条直线砌墙,这样砌的砖整齐,这个实例体现的数学知识是两点确定一条直线.故答案为:两点确定一条直线.根据直线的性质:两点确定一条直线进行解答即可.此题主要考查了直线的性质,关键是掌握两点确定一条直线.15.【答案】x=117【解析】解:去分母得:10x-5x+5=20-2x-4,移项合并得:7x=11,解得:x=.故答案为:x=方程去分母,去括号,移项合并,把x系数化为1,即可求出解.此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.16.【答案】4【解析】解:这是一个正方体的平面展开图,共有六个面,其中面“z”与面“4”相对,面“y”与面“-2”相对,“x”与面“12”相对.则z+4=6,y+(-2)=6,x+12=6,解得z=2,y=8,x=-6.故x+y+z=4.故答案为:4.利用正方体及其表面展开图的特点,根据相对面上的两个数之和为6,列出方程求出x、y、z的值,从而得到x+y+z的值.本题考查了正方体相对两个面.注意正方体的空间图形,从相对面入手,分析及解答问题.17.【答案】45°【解析】解:∵∠BOC:∠COD:∠DOA=4:5:6,∴∠BOC=4x°,∠COD=5x°,∠DOA=6x°,∵∠BOC-∠AOB=39°,∴4x°+4x°-39°+6x°+5x°=360°,解得x=21,∴∠BOC=84°,∴∠AOB=84°-39°=45°.故答案为:45°设∠BOC=4x°,∠COD=5x°,∠DOA=6x°,可得∠AOB=4x°-39°,依据周角为360°得出方程,求出x即可.本题主要考查了角的有关计算的应用,理清题意,根据题意得出方程是解答本题的关键.18.【答案】6【解析】解:由已知得:AC+AD+AE+AB+CD+CE+CB+DE+DB+EB=52,即(AC+CB)+(AD+DB)+(AE+EB)+AB+(CD+DE)+CE=AB+AB+AB+AB+CE+CE=4AB+2CE=52,已知AB=10,∴4×10+2CE=52,∴CE=6,故答案为:6.此题可把所有线段相加,根据已知AB=10,图中所有线段的和等于52,于是得到结论.此题考查的知识点是两点间的距离,关键是表示出图中所有线段的和,根据线段间的关系求出.19.【答案】解:(1)(-114)×25×(-6)-9÷(-32)2=(-54)×25×(-6)-9÷94=54×25×6−9×49=3-4=-1;(2)313-22÷{[(-12)3-(0.75-13)]×24}=313-4÷{[(-18)-34+13]×24}=313-4÷[(-78+13)×24]=313-4÷(-21+8)=313-4÷(-13)=313+4×113=31339+1239=32539.【解析】(1)根据有理数的乘除法和减法可以解答本题;(2)根据有理数的乘除法和加减法可以解答本题.本题考查有理数的混合运算,解答本题的关键是明确有理数混合运算的计算方法.20.【答案】解:(1)2(A+B)-3(2A-B)=2A+2B-6A+3B=-4A+5B=-4(a2-2b2+2ab-3)+5(2a2-b2-25ab-15)=-4a2+8b2-8ab+12+10a2-5b2-2ab-1=6a2+3b2-10ab+11;(2)∵|a+12|与b2互为相反数,∴|a+12|+b2=0,则a=-12,b=0,6a2+3b2-10ab+11=6×14+11=252.【解析】(1)根据整式的混合运算法则计算;(2)根据非负数的性质求出a、b,代入计算.本题考查的是整式的混合运算、非负数的性质,掌握整式的混合运算法则是解题的关键.21.【答案】解:(1)设商场购进甲型号台灯x台,则购进乙型号台灯(1000-x)台,由题意,得45x+60(1000-x)=54000,解得:x=400,购进乙型台灯1000-x=1000-400=600(台).答:购进甲型台灯400台,购进乙型台灯600台进货款恰好为54000元.(2)设乙型节能灯需打a折,0.1×80a-60=60×20%,解得a=9,答:乙种型号台灯需打9折.【解析】(1)设商场购进甲型号台灯x台,则购进乙型号台灯(1000-x)台,根据甲乙两种灯的总进价为54000元列出一元一次方程,解方程即可;(2)设乙种型号台灯需打a折,根据利润=售价-进价列出a的一元一次方程,求出a的值即可.此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,设出未知数,列出方程.22.【答案】解:(1)当m=-1时,原方程变为:x3-1=−x−36,2x-6=-x-3,3x=3,解得:x=1;(2)将x=21代入方程,得213+m=21m−36,化简得:7+m=7m−1214+2m=7m-1,解得:m=3.【解析】(1)直接把m的之代入方程进而求出x的值;(2)把x=21代入方程即可求出m的值.此题主要考查了一元一次方程的解,正确解一元一次方程是解题关键.23.【答案】解:(1)∵∠2是∠1的4倍,∴∠2=4∠1,∠1的余角=90°-∠1,∠2的补角=180°-∠2=180°-4∠1,由题意得,(180°-4∠1)-(90°-∠1)=45°,解得∠1=15°,所以,∠2=4×15°=60°;(2)OC平分∠AOB.理由如下:∵∠AOD=90°,∠2=60°,∴∠AOB=90°-60°=30°,∵∠1=15°,∴∠BOC=30°-15°=15°,∴∠AOC=∠BOC,∴OC平分∠AOB.【解析】(1)根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°表示出∠1的余角和∠2的补角,然后列出方程求解即可;(2)先求出∠AOB,再求出∠BOC,然后根据角平分线的定义解答.本题考查了余角和补角,角平分线的定义,熟记余角和补角的概念并列出方程是解题的关键.24.【答案】解:(1)当m=2时,有12(x+1)=2与23(x+2)=2,由方程12(x+1)=2,解得:x=3,即AC=3,由方程23(x+2)=2,解得:x=1,即BC=1,∵C为线段AB上一点,∴AB=AC+BC=4;(2)解方程12(x+1)=m得,x=2m-1,即AC=2m-1,解方程23(x+m)=m得,x=12m,即BC=12m,①当C为靠近点A的三等分点时,则BC=2AC,即12m=2(2m-1),解得:m=47,②当C为靠近点B的三等分点时,则AC=2BC,即2m-1=2×12m,解得:m=1,综上所述,m=47或1.【解析】(1)解方程得到AC=3,BC=1,根据线段的和差即可得到结论;(2)解方程得到AC=2m-1,BC=m,①当C为靠近点A的三等分点时,②当C为靠近点B的三等分点时,列方程即可得到结论.本题考查了一元一次方程的解,两点间的距离,正确的理解题意是解题的关键.25.【答案】解:(1)因为α=45°,即∠MON=45°,所以∠AOM+∠BON=180°-45°=135°,因为射线OP1,OP2为∠AOM的三等分线,所以∠AOP1=13∠AOM,因为射线OQ1,OQ2为∠BON的三等分线,所以∠BOQ1=13∠BON,所以∠AOP1+∠BOQ2=13(∠AOM+∠BON)=13×135°=45°;(2)因为射线OP1,OP2为∠AOM的三等分线,所以∠MOP1=23∠AOM,∠MOP2=13∠AOM,又因为射线OQ1,OQ2为∠BON的三等分线,所以∠NOQ1=23∠BON,∠NOQ2=13∠BON,因为∠AOM+∠BON=180°-α,所以∠P1OQ1=∠MOP1+∠MON+∠NOQ1=23(∠AOM+∠BON)+α=23(180°−α)+α=120°+α3,∠P2OQ2=∠MOP2+∠MON+∠NOQ2=13(∠AOM+∠BON)+α,所以2∠P1OQ1-∠P2OQ2=180°.【解析】(1)先根据角的和差关系求出∠AOM+∠BON=180°-45°=135°,再根据射线OP1,OP2为∠AOM的三等分线得出,根据射线OQ1,OQ2为∠BON的三等分线,得出,然后把两角相加即可解答;(2)根据已知可得,,,,又∠AOM+∠BON=180°-α,然后根据角的和差关系解答即可.本题考查角平分线的定义、角的和差定义等知识,解题的关键是熟练掌握这些知识解决问题.。
2023-2024学年天津市和平区 七年级(上)期末数学试卷(含解析)

2023-2024学年天津市和平区七年级(上)期末数学试卷一、选择题:本题共12小题,每小题2分,共24分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.计算−3−2的值为( )A. −5B. −1C. 5D. 12.南京长江四桥线路全长约29000米,将29000用科学记数法表示为( )A. 0.29×105B. 2.9×103C. 2.9×104D. 29×1033.下列说法正确的是( )A. 单项式−3xy的系数是−3B. 单项式2πa3的次数是4C. 多项式x2y2−2x2+3是二次三项式D. 多项式x2−2x+6的项分别是x2、2x、34.如图所示,几何体由6个大小相同的立方体组成,其俯视图是( )A.B.C.D.5.如图,把矩形ABCD沿EF对折后使两部分重合,若∠1=50°,则∠BFE=( )A. 70°B. 65°C. 60°D. 50°6.如图,在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )A. 159°B. 141°C. 111°D. 69°7.下列等式变形错误的是( )A. 若a=b,则a1+x2=b1+x2B. 若a=b,则3a=3bC. 若a=b,则ax=bxD. 若a=b,则am =bm8.若(m−2)x|2m−3|=6是一元一次方程,则m等于.( )A. 1B. 2C. 1或2D. 任何数9.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?译文为:现有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人?这个物品的价格是多少?设共有x人,则可列方程为( )A. 8x+3=7x−4B. 8x−3=7x+4C. x−38=x+47D. x+38=x−4710.将一副三角板按如图所示的位置摆放,其中∠α与∠β一定互余的是( )A. B.C. D.11.已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN 的长度是( )A. 3cmB. 5cmC. 7cmD. 7cm或3cm12.现定义运算“∗”,对于任意有理数a,b满足a∗b={2a−b,a≥ba−2b,a<b.如5∗3=2×5−3=7,1 2∗1=12−2×1=−32,若x∗3=5,则有理数x的值为( )A. 4B. 11C. 4或11D. 1或11二、填空题:本题共6小题,每小题3分,共18分。
天津市七年级(上)期末数学试卷-(含答案)

. .2021-2021学年XX市和平区七年级〔上〕期末数学试卷副标题题号一二三四总分得分一、选择题〔本大题共7小题,共14.0分〕1.如下列图,学校、书店、体育馆在平面图上的位置分别是A、B、C,书店在学校的正向,体育馆在学校的南偏西35°方向,那么平面图上的∠CAB等于〔〕A. B. C. D.2.如图,以下说法错误的选项是〔〕A. 直线AC与射线BD相交于点AB. BC是线段C. 直线AC经过点A D. 点D在直线AB上3.〔a-1〕x2y a+1是关于x、y的五次单项式,那么这个单项式的系数是〔〕A. 1B. 2C. 3D. 04.假设a的相反数是2,那么a的值为〔〕A. 2B.C.D.5.关于x的方程a-3〔x-5〕=b〔x+2〕是一元一次方程,那么b的取值情况是〔〕A. B. C. D. b为任意数6.以下各数中,正确的角度互化是〔〕A. B. C. D.7.设一个锐角与这个角的补角的差的绝对值为α,那么〔〕A. 或B.C.D.二、填空题〔本大题共6小题,共18.0分〕8.假设3x=-,那么4x=______.9.以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,假设∠AOB=17°,∠AOP的度数为______.10.假设点M是线段AB的中点,N是线段AM的中点,假设图中所有线段的和是20cm,那么AN的长是______cm.11.有理数a在数轴上的位置如图,那么a+|a-1|=______.12.线段MN=16cm,点P为任意一点,那么线段MP与NP和的最小值是______cm.13.假设x=y+3,那么〔x-y〕2-2.3〔x-y〕+0.75〔x-y〕2+〔x-y〕+7等于______.三、计算题〔本大题共3小题,共27.0分〕14.列一元一次方程解应用题.有一批共享单车需要维修,维修后继续投放骑用,现有甲、乙两人做维修,甲每天维修16辆,乙每天维修的车辆比甲多8辆,甲单独维修完成这批共享单车比乙单独维修完多用20天,公司每天付甲80元维修费,付乙120元维修费.〔1〕问需要维修的这批共享单车共有多少辆.〔2〕在维修过程中,公司要派一名人员进展质量监视,公司负担他每天10元补助费,现有三种维修方案:①由甲单独维修;②由乙单独维修;③甲、乙合作同时维修,你认为哪种方案最省钱,为什么.15.计算:〔1〕25×-〔-25〕×+25÷〔-〕;〔2〕2-23÷[〔〕2-〔-3+0.75〕]×5.16.∠AOB=α,过点O作∠BOC=90°.〔1〕假设α=30,那么∠AOC的度数;〔2〕射线OE平分∠AOC,射线OF平分∠BOC.①假设α=50°,求∠EOF的度数;②假设90°<α<180°,那么∠EOF的度数为______〔直接填写用含α的式子表示的结果〕.四、解答题〔本大题共4小题,共31.0分〕. .17.解以下方程:〔1〕x+=6-;〔2〕-=.18.关于m的方程〔m-14〕=-2的解也是关于x的方程2〔x-〕-n=11的解.〔1〕求m、n的值;〔2〕假设线段AB=m,在直线AB上取一点P,恰好使=n,点Q是PB的中点,求线段AQ的长.19.如图,直线AB与CD相交于点O,∠BOE=∠DOF=90°.〔1〕写出图中与∠COE互补的所有的角〔不用说明理由〕.〔2〕问:∠COE与∠AOF相等吗.请说明理由;〔3〕如果∠AOC=∠EOF,求∠AOC的度数.20.,.化简:;与的同类项,求的值.答案和解析1.【答案】B【解析】解:从图中发现平面图上的∠CAB=∠1+∠2=90°+35°=125°.应选:B.根据方位角的概念,正确画出方位图表示出方位角,即可求解.此题考察了方向角的知识,解答此类题需要从运动的角度,正确画出方位角,找准中心是做这类题的关键.2.【答案】D【解析】解:A、直线AC与射线BD相交于点A,说确,故本选项错误;B、B、C是两个端点,那么BC是线段,说确,故本选项错误;C、直线AC经过点A,说确,故本选项错误;D、如下列图,点D在射线BD上,说法错误,故本选项正确.应选:D.根据射线、直线与线段的定义,结合图形解答.此题考察了直线、射线、线段,注意:直线没有端点.3.【答案】A【解析】解:由题意得:a+1+2=5,解得:a=2,那么这个单项式的系数是a-1=1,应选:A.根据一个单项式中所有字母的指数的和叫做单项式的次数可得a的值,然后根据单项式中的数字因数叫做单项式的系数可得答案.此题主要考察了单项式,关键是掌握单项式相关定义.4.【答案】B【解析】解:由a的相反数是2,得a=-2,应选:B.根据相反数的意义求解即可.此题考察了相反数的意义,一个数的相反数就是在这个数前面添上"-〞号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.5.【答案】A【解析】解:a-3〔x-5〕=b〔x+2〕,a-3x+15-bx-2b=0,〔3+b〕x=a-2b+15,∴b+3≠0,b≠-3,应选:A.先把方程整理为一元一次方程的一般形式,再根据一元一次方程的定义求出b的值即可.此题考察的是一元一次方程的定义,熟知只. .含有一个未知数〔元〕,且未知数的次数是1,这样的方程叫一元一次方程是解答此题的关键.6.【答案】D【解析】解:A、63.5°=63°30′≠63°50′,故A不符合题意;B、23.48°=23°28′48″≠23°12′36″,故B不符合题意;C、18.33°=18°19′48″≠18°18′18″,故C不符合题意;D、22.25°=22°15′,故D正确,应选:D.根据大单位化小单位乘以进率,小单位化单位除以进率,可得答案.此题考察了度分秒的换算,利用大单位化小单位乘以进率,小单位化单位除以进率是解题关键.7.【答案】B【解析】解:设这个角的为x且0<x<90°,根据题意可知180°-x-x=α,∴α=180°-2x,∴180°-2×90°<α<180°-2×0°,0°<α<180°.应选:B.根据补角的定义来求α的围即可.此题考察了余角和补角的概念.互为余角的两角的和为90°,互为补角的两角之和为180°.解此题的关键是能准确的从题意中找出这两个角之间的数量关系,从而判断出两角之间的关系.8.【答案】-【解析】解:系数化为1,得x=-,4x=-×4=-,故答案为:-.根据系数化为1,可得答案.此题考察了解一元一次方程,利用系数化为1是解题关键.9.【答案】10.2°或51°【解析】解:如图1,当射线OP在∠AOB的部时,设∠AOP=3x,那么∠BOP=2x,∵∠AOB=∠AOP+∠BOP=5x=17°,解得:x=3.4°,那么∠AOP=10.2°,如图2,当射线OP在∠AOB的外部时,设∠AOP=3x,那么∠BOP=2x,∵∠AOP=∠AOB+∠BOP,又∵∠AOB=17°,∴3x=17°+2x,解得:x=17°,那么∠AOP=51°.故∠AOP的度数为10.2°或51°.故答案为:10.2°或51°.分射线OP在∠AOB的部和外部两种情况进展讨论求解即可.此题考察了角的计算,关键是分两种情况进展讨论.10.【答案】【解析】解:如图,∵点M是线段AB的中点,N是线段AM的中点,∴AN=NM=AM=BM=BN=AB,∴AM=BM=2AN,BN=3AN,AB=4AN,又∵图中所有线段的和是20cm,∴AN+MN+BM+AM+BN+AB=20,∴AN+AN+2AN+2AN+3AN+4AN=20,解得AN=cm故答案为:.依据点M是线段AB的中点,N是线段AM的中点,可得AN=NM=AM=BM=BN=AB,再根据图中所有线段的和是20cm,即可得到AN+MN+BM+AM+BN+AB=20,进而得出AN的长.此题主要考察了两点间的距离,平面上任意两点间都有一定距离,它指的是连接这两点的线段的长度.11.【答案】1【解析】. .解:由数轴上a点的位置可知,a<0,∴a-1<0,∴原式=a+1-a=1.故答案为:1.先根据a在数轴上的位置确定出a的符号,再根据绝对值的性质把原式进展化简即可.此题考察的是数轴的特点及绝对值的性质,比较简单.12.【答案】16【解析】解:如下列图:所以线段MP与NP和的最小值是16cm,故答案为;16根据线段的性质解答即可.此题考察线段的性质,关键是根据两点之间线段最短解答.13.【答案】3.7【解析】解:∵x=y+3,∴x-y=3,那么原式=×32-2.3×3+0.75×3-×3+7=2.25-6.9+2.25-0.9+7=3.7,故答案为:3.7.由x=y+3得x-y=3,整体代入原式计算可得.此题考察了整式的加减-化简求值,熟练掌握整体代入思想的运用是解此题的关键.14.【答案】解:〔1〕设乙单独做需要x天完成,那么甲单独做需要〔x+20〕天,由题意可得:16〔x+20〕=24x,解得:x=40,总数:24×40=960〔套〕,答:乙单独做需要40天完成,甲单独做需要60天,一共有960辆共享单车;〔2〕方案一:甲单独完成:60×80+60×10=5400〔元〕,方案二:乙单独完成:40×120+40×10=5200〔元〕,方案三:甲、乙合作完成:960÷〔16+24〕=24〔天〕,那么一共需要:24×〔120+80〕+24×10=5040〔元〕,应选择方案三合算.【解析】〔1〕通过理解题意可知此题的等量关系,即甲乙单独修完共享单车的数量一样,列方程求解即可;〔2〕分别计算,通过比较选择最省钱的方案.此题主要考察了一元一次方程的应用,正确得出等量关系是解题关键.15.【答案】解:〔1〕25×-〔-25〕×+25÷〔-〕=25×+25×+25×〔-4〕=25×〔〕=25×〔-〕=-;〔2〕2-23÷[〔〕2-〔-3+0.75〕]×5=====-13.【解析】〔1〕根据有理数的乘除法和乘法分配律可以解答此题;〔2〕根据有理数的乘除法和加减法可以解答此题.此题考察有理数的混合运算,解答此题的关键是明确有理数混合运算的计算方法.16.【答案】α或180°-α【解析】. .解:〔1〕如图1中,∠AOC=∠AOB+∠BOC=120°,如图2中,∠AOC=∠BOC-∠AOB=60°.〔2〕①如图1-1中,∵∠AOC=∠AOB+∠BOC=140°,∴∠EOC=∠AOC=70°,∵∠FOC=∠BOC=45°,∴∠EOF=∠EOC-∠FOC=25°,如图2-1中,∵∠AOC=∠BOC-∠AOB=40°,∴∠EOC=∠AOC=20°,∵∠FOC=∠BOC=45°,∴∠EOF=∠FOC-∠EOC=25°.②如图1-2中,∵∠AOC=∠AOB-∠BOC=α-90°,∴∠EOC=∠AOC=〔α-90°〕,∵∠FOC=∠BOC=45°,∴∠EOF=∠EOC+∠FOC=α,如图2-2中,∵∠AOC=360°-∠AOB-∠BOC=270°-α∴∠EOC=∠AOC=〔270-α〕,∵∠FOC=∠BOC=45°,∴∠EOF=∠EOC+∠FOC=180°-α,故答案为α或180°-α.〔1〕分两种情形画出图形求解即可;〔2〕①分两种情形画出图形分别求解即可;③分两种情形分别画出图形分别求解即可;此题考察角的计算、角平分线的定义等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想解决问题,属于中考常考题型.17.【答案】解:〔1〕去分母,可得:6x+4〔x-3〕=36-x+7,去括号,可得:6x+4x-12=43-x,移项,合并同类项,可得:11x=55,解得x=5.〔2〕去分母,可得:6〔4x-1.5〕-150〔0.5x-0.3〕=2,去括号,可得:24x-9-75x+45=2,移项,合并同类项,可得:51x=34,解得x=.【解析】解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,据此求解即可.此题主要考察了解一元一次方程的方法,要熟练掌握,解答此题的关键是要明确解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.18.【答案】解:〔1〕〔m-14〕=-2,m-14=-6m=8,∵关于m的方程〔m-14〕=-2的解也是关于x的方程2〔x-〕-n=11的解.. .∴x=8,将x=8,代入方程2〔x -〕-n=11得:解得:n=4,故m=8,n=4;〔2〕由〔1〕知:AB=8,=4,①当点P在线段AB 上时,如下列图:∵AB=8,=4,∴AP =,BP =,∵点Q为PB的中点,∴PQ=BQ =BP =,∴AQ=AP+PQ =+=;②当点P在线段AB 的延长线上时,如下列图:∵AB=8,=4,∴PB =,∵点Q为PB的中点,∴PQ=BQ =,∴AQ=AB+BQ =8+=.故AQ =或.【解析】〔1〕先求出方程〔m-14〕=-2的解,然后把m的值代入方程2〔x-〕-n=11,求出n的值;〔2〕分两种情况:①点P在线段AB上,②点P在线段AB的. v .延长线上,画出图形,根据线段的和差定义计算即可;此题考察了一元一次方程的解,以及两点间的距离,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考常考题型.19.【答案】解:〔1〕∵直线AB与CD相交于点O,∴∠COE+∠DOE=180°,又∵∠BOE=∠DOF=90°,∴∠DOE=∠BOF,∴与∠COE互补的所有的角为∠DOE,∠BOF;〔2〕∠COE与∠AOF相等,理由:∵∠BOE=∠DOF=90°,∴∠AOE=∠COF,∴∠AOE-∠AOC=∠COF-∠AOC,∴∠COE=∠AOF;〔3〕设∠AOC=x,那么∠EOF=5x,∵∠COE=∠AOF,∴∠COE=∠AOF =〔5x-x〕=2x,∵∠AOE=90°,∴x+2x=90°,∴x=30°,∴∠AOC=30°.【解析】〔1〕依据直线AB与CD相交于点O,可得∠COE+∠DOE=180°,依据∠BOE=∠DOF=90°,可得∠DOE=∠BOF,即可得出与∠COE互补的所有的角;〔2〕依据∠AOE=∠COF,可得∠AOE-∠AOC=∠COF-∠AOC,进而得到∠COE=∠AOF;〔3〕设∠AOC=x,那么∠EOF=5x,依据∠AOE=90°,可得x+2x=90°,进而得出∠AOC的度数.此题考察了对顶角、邻补角,余角和补角计算的应用,常常与等式的性质、等量代换相关联.20.【答案】解:〔1〕2B-A=2〔2xy-3y2+4x2〕-〔3x2+3y2-5xy〕=4xy-6y2+8x2-3x2-3y2+5xy=9xy-9y2+5x2;〔2〕∵与的同类项,第12页,共13页. .∴=1,y=2,那么x=1或3,y=2,当x=1,y=2时,2B-A=18-36+5=-13,当x=3,y=2时,2B-A=54-36+45=63.【解析】此题考察的是整式的加减混合运算,掌握整式的加减混合运算法那么是解题的关键.〔1〕根据整式的加减混合运算法那么计算;〔2〕根据同类项的定义分别求出x、y,代入计算即可.. v .。
2023-2024学年天津市和平区七年级上学期期末数学模拟试题(含答案)

2023-2024学年天津市和平区七年级上学期期末数学模拟试题一、单选题(本题共10题,每小题3分,共30分)1.(3分)下列说法不正确的有( )①0是绝对值最小的数②3a﹣2的相反数是﹣3a﹣2 ③5πR2的系数是5 ④一个有理数不是整数就是分数⑤34x3是7次单项式.A.1个B.2个C.3个D.4个2.(3分)为在2020年实现全面建成小康社会的目标任务,自2016年以来,广东已向西部四省拨付财政资金105.8亿元援助脱贫攻坚项目.数据105.8亿用科学记数法表示为( )A.105.8×108B.10.58×109C.1.058×1010D.1.058×10113.(3分)已知2a2﹣3b+5=0,则9b﹣6a2+3的值为( )A.18B.15C.﹣12D.164.(3分)一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“祝你考试顺利”,把它折成正方体后,与“考”相对的字是( )A.祝B.你C.顺D.利5.(3分)下列等式变形中,结果正确的是( )A.如果a=b,那么a﹣m=b+mB.由﹣3x=2得x=﹣C.如果|a|=|b|,那么a=bD.如果=,那么a=b6.(3分)某车间28名工人生产螺栓和螺母,每人每天平均生产螺栓12个或螺母18个,一个螺栓需要两个螺母与之配套,如何安排生产螺栓才能让螺栓和螺母正好配套?设有x名工人生产螺栓,其余人生产螺母,依题意列方程应为( )A.12x=18(28﹣x)B.2×12x=18(28﹣x)C.12×18x=18(28﹣x)D.12x=2×18(28﹣x)7.(3分)某商店换季促销,将一件标价为240元的T恤打8折售出,获利20%,则这件T恤的成本为( )A.144元B.160元C.192元D.200元8.(3分)如图,AB是一段高铁行驶路线图,图中字母表示的5个点表示5个车站.在这段路线上往返行车,需印制( )种车票.A.20B.11C.12D.139.(3分)如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( )A.5对B.6对C.7对D.8对10.(3分)如图所示第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么第8个图案中有白色六边形地面砖( )块.A.33B.34C.35D.36二、填空题(本试题共8题,每题3分,共24分)11.(3分)若4a+9与3a+5互为相反数,则a的值为 .12.(3分)若单项式2x3y n+1与﹣5x m﹣2y2是同类项,则m﹣n= .13.(3分)钟表上2点15分时,时针与分针的夹角为 度.14.(3分)54.12°= 度 分 秒.15.(3分)如果关于x的方程2x+1=3和方程2﹣=1的解相同,那么a的值为 .16.(3分)如图,OA表示北偏东42°方向,OB表示南偏东53°方向,则∠AOB= .17.(3分)已知线段AB=10cm,直线AB上有一点C,且BC=2cm,点M是线段AB的中点,点N是线段BC的中点,则MN= cm.18.(3分)如图,C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各学习小组经过讨论后得到以下结论:①∠ACF与∠DCH互余;②∠HCG=60°;③∠ECF与∠BCH互补;④∠ACF﹣∠BCG=45°.请写出正确结论的序号 .三、解答题(本题共6道题,共46分)19.(6分)先化简,再求值2(x2﹣2x2y)﹣[3(x2﹣xy2)﹣(x2y﹣2xy2+x2)],其中x=﹣,y=﹣2.20.(8分)解下列方程:(1)1﹣2(2x+3)=﹣3(2x+1);(2).21.(6分)如图,线段AC上依次有D、B、E三点,,E是BC的中点,.(1)求线段AB的长;(2)求线段DE的长.22.(8分)已知直线AB与射线OC相交于点O.(1)如图1,∠AOC=90°,射线OD平分∠AOC,求∠BOD的度数;(2)如图2,∠AOC=130°,射线OD在∠AOC的内部,射线OE在∠BOC的内部,且∠BOD=5∠BOE,∠COD=3∠COE.求出∠DOE的度数.23.(8分)为促进节约用水,某地按月实行阶梯水价,价目如下表(m3表示立方米):阶梯月用水量(m3)单价(元/m3)第一阶梯不超过22的部分3第二阶梯超过22但不超过30的部分5第三阶梯超过30的部分7(1)若A居民家4月份共用水25m3,则应交水费为 元;(2)设月用水量为x m3,当月应交水费为y元.当x>30时,y= (用含有x 的式子表示);请利用上式计算:若B居民家5月份共交水费120元,则用水量为 m3;(3)若C居民家5、6月用水量共50m3(5月份用水量小于6月份用水量),这两个月共交水费174元,则C居民家5、6月用水量分别为多少立方米?24.(10分)如图,在数轴上点A表示的数为﹣6,点B表示的数为10,点M、N分别从原点O、点B同时出发,都向左运动,点M的速度是每秒1个单位长度,点N的速度是每秒3个单位长度,运动时间为t秒.(1)求点M、点N分别所对应的数(用含t的式子表示);(2)若点M、点N均位于点A右侧,且AN=2AM,求运动时间t;(3)若点P为线段AM的中点,点Q为线段BN的中点,点M、N在整个运动过程中,当PQ+AM=17时,求运动时间t.答案一、单选题(本题共10题,每小题3分,共30分)1.C ;2.C ;3.A ;4.D ;5.D ;6.B ;7.B ;8.A ;9.D ;10.B ;二、填空题(本试题共8题,每题3分,共24分)11.﹣2;12.4;13.22.5;14.54;7;12;15.4;16.85°;17.4或6;18.①③④;三、解答题(本题共6道题,共46分)19. ;32 20.(1)x =1;(2)x =﹣9.;21.(1)6;(2)6.;22.(1)135°;(2)100°.;23.81;7x ﹣104;32;24.(1)﹣t ,10﹣3t ;(2)4;(3)18或1.。
2021-2022学年天津市和平区耀华中学七年级(上)期末数学试卷(解析版)

2021-2022学年天津市和平区耀华中学七年级第一学期期末数学试卷一、选择题(共本大题共12小题,在每小题给出的四个选项中,只有一项符合要求.)1.计算3﹣(﹣2)的结果是()A.﹣5B.﹣1C.1D.52.2022年冬奥运即将在北京举行,北京也即将成为迄今为止唯一个既举办过夏季奥运会,又举办过冬季奥运会的城市,据了解北京冬奥会的预算规模为15.6亿美元,政府补贴6%(9400万美元).其中1 560 000 000用科学记数法表示为()A.1.56×109B.1.56×108C.15.6×108D.0.156×1010 3.如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是()A.两点之间,线段最短B.两点确定一条直线C.两直线相交只有一个交点D.经过一点有无数条直线4.下列四个几何体中,从正面看是三角形的是()A.B.C.D.5.下列说法中,不正确的是()A.是多项式B.6x2﹣3x+1的项是6x2,﹣3x,1C.多项式4a3﹣3a4b+2的次数是4D.x2﹣4x+1的一次项系数是﹣46.一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为()A.事故船在搜救船的北偏东60°方向B.事故船在搜救船的北偏东30°方向C.事故船在搜救船的北偏西60°方向D.事故船在搜救船的南偏东30°方向7.如图是一个正方体展开图,将其围成一个正方体后,与“罩”字相对的是()A.勤B.洗C.手D.戴8.下列判断错误的是()A.若a=b,则a﹣3=b﹣3B.若,则a=bC.若x=2,则x2=2x D.若ac2=bc2,则a=b9.如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是()A.AB=2AC B.AC+CD+DB=ABC.CD=AD﹣AB D.AD=(CD+AB)10.如图,OM平分∠AOB,∠MON=2∠BON,∠AON﹣∠BON=72°,则∠AOB=()A.96°B.108°C.120°D.144°11.下列说法中,正确的有()①射线AB和射线BA是同一条射线;②若AB=BC,则点B为线段AC的中点;③连接A、B两点,使线段AB过点C;④两点的所有连线中,线段最短.A.0个B.1个C.2个D.3个12.一列火车匀速行驶,经过一条长400米的隧道需要30秒的时间,隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒,则火车的长为()米.A.B.133C.200D.400二、填空题(本大题共6小题)13.﹣1的倒数是;绝对值等于3的数是.14.98°30'18″=度,90°﹣35°27'=°′.15.长方形纸片ABCD,点E、F分别在边AB、AD上,连接EF,将∠AEF沿EF翻折,得到∠A1EF,连接CE,将∠BEC翻折,得到∠B1EC,点B1恰好落在线段A1E上,若∠AEF =29°,则∠B1EC=°.16.已知线段AB=6,延长AB至点C,使BC=AB,反向延长AC至点D,使AD=AC,则CD的长为.17.已知a2+2ab=﹣5,ab﹣2b2=﹣3,则代数式3a2+ab+b2的值为.18.如图,点Q在线段AP上,其中PQ=10,第一次分别取线段AP和AQ的中点P1,Q1,得到线段P1Q1,则线段P1Q1=;再分别取线段AP1和AQ1的中点P2,Q2,得到线段P2Q2;第三次分别取线段AP2和AQ2的中点P3,Q3,得到线段P3Q3;连续这样操作2021次,则每次的两个中点所形成的所有线段之和P1Q1+P2Q2+P3Q3+…+P2021Q2021=.三、解答题(共7小题,解答题应写出解答过程.)19.计算:(1)﹣66×4﹣(﹣2.5)÷(﹣0.1);(2)﹣22÷×(﹣)2+[9﹣(﹣+)×36].20.解下列方程:(1)7x+2(3x﹣3)=20;(2)+=2﹣.21.老师布置了一道化简求值题,如下:求■x﹣2(x﹣y2)+(﹣x+y2)的值,其中x =﹣2,y=.(1)小海准备完成时发现第一项的系数被同学涂了一下模糊不清了,同桌说他记得系数是.请你按同桌的提示,帮小海化简求值;(2)科代表发现系数被涂后,很快把正确的系数写了上去.同学们计算后发现,老师给出的“x=﹣2”这个条件是多余的,请你算一算科代表补上的系数是多少?22.如图,O为直线AB上一点,∠AOC与∠AOD互补,OM,ON分别是∠AOC,∠AOD 的平分线.(1)根据题意,补全下列说理过程:∵∠AOC与∠AOD互补,∴∠AOC+∠AOD=180°.又∵∠AOC+∠=180°,∴∠=∠.(2)若∠MOC=68°,求∠AON的度数.(3)若∠MOC=α,则∠AON=(用α表示).23.工业园区某机械厂的一个车间主要负责生产螺丝和螺母,该车间有工人44人,其中女生人数比男生人数的2倍少10人,每个工人平均每天可以生产螺丝50个或者螺母120个.(1)该车间有男生、女生各多少人?(2)已知一个螺丝与两个螺母配套,为了使每天生产的螺丝螺母恰好配套,应该分配多少工人负责生产螺丝,多少工人负责生产螺母?24.已知∠AOD=160°,OB为∠AOD内部的一条射线(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠MON的度数为;(2)如图2,∠BOC在∠AOD内部(∠AOC>∠AOB),且∠BOC=20°,OF平分∠AOC,OG平分∠BOD(射线OG在射线OC左侧),求∠FOG的度数;(3)在(2)的条件下,∠BOC绕点O运动过程中,若∠BOF=8°,求∠GOC的度数.25.规定:A,B,C是数轴上的三个点,当CA=3CB时我们称C为[A,B]的“三倍距点”,当CB=3CA时,我们称C为[B,A]的“三倍距点”.点A所表示的数为a,点B所表示的数为b且a,b满足(a+3)2+|b﹣5|=0.(1)a=,b=;(2)若点C在线段AB上,且为[A,B]的“三倍距点”,则点C所表示的数为;(3)点M从点A出发,同时点N从点B出发,沿数轴分别以每秒3个单位长度和每秒1个单位长度的速度向右运动,设运动时间为t秒.当点B为M,N两点的“三倍距点”时,求t的值.参考答案一、选择题(共本大题共12小题,在每小题给出的四个选项中,只有一项符合要求.)1.计算3﹣(﹣2)的结果是()A.﹣5B.﹣1C.1D.5【分析】根据有理数的减法运算法则进行计算即可得解.解:3﹣(﹣2)=3+2=5.故选:D.2.2022年冬奥运即将在北京举行,北京也即将成为迄今为止唯一个既举办过夏季奥运会,又举办过冬季奥运会的城市,据了解北京冬奥会的预算规模为15.6亿美元,政府补贴6%(9400万美元).其中1 560 000 000用科学记数法表示为()A.1.56×109B.1.56×108C.15.6×108D.0.156×1010【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.解:1 560 000 000用科学记数法表示为1.56×109.故选:A.3.如图1,A、B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小.如图2,连接AB,与l交于点C,则C点即为所求的码头的位置,这样做的理由是()A.两点之间,线段最短B.两点确定一条直线C.两直线相交只有一个交点D.经过一点有无数条直线【分析】利用线段的性质解答即可.解:A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B 两个村庄的距离之和最小,图2中所示的C点即为所求的码头的位置,那么这样做的理由是两点之间,线段最短,故选:A.4.下列四个几何体中,从正面看是三角形的是()A.B.C.D.【分析】找到从正面看所得到的图形为三角形即可.解:A.主视图为长方形,不符合题意;B.主视图为三角形,符合题意;C.主视图为长方形,不符合题意;D.主视图为长方形,不符合题意.故选:B.5.下列说法中,不正确的是()A.是多项式B.6x2﹣3x+1的项是6x2,﹣3x,1C.多项式4a3﹣3a4b+2的次数是4D.x2﹣4x+1的一次项系数是﹣4【分析】根据多项式的概念即可求出答案.解:A、是多项式,故A不符合题意.B、6x2﹣3x+1的项是6x2,﹣3x,1,故B不符合题意.C、多项式4a3﹣3a4b+2的次数是5,故C符合题意.D、x2﹣4x+1的一次项系数是﹣4,故D不符合题意.故选:C.6.一艘海上搜救船借助雷达探测仪寻找到事故船的位置,雷达示意图如图所示,搜救船位于图中圆心O处,事故船位于距O点40海里的A处,雷达操作员要用方向角把事故船相对于搜救船的位置汇报给船长,以便调整航向,下列四种表述方式中正确的为()A.事故船在搜救船的北偏东60°方向B.事故船在搜救船的北偏东30°方向C.事故船在搜救船的北偏西60°方向D.事故船在搜救船的南偏东30°方向【分析】根据点的位置确定应该有方向以及距离,进而利用图象得出即可.解:如图所示:事故船A在搜救船北偏东30°方向,故选:B.7.如图是一个正方体展开图,将其围成一个正方体后,与“罩”字相对的是()A.勤B.洗C.手D.戴【分析】根据正方体的表面展开图找相对面的方法,“Z”字两端是对面判断即可.解:与“罩”字相对的是:手,故选:C.8.下列判断错误的是()A.若a=b,则a﹣3=b﹣3B.若,则a=bC.若x=2,则x2=2x D.若ac2=bc2,则a=b【分析】根据等式的性质逐个判断即可.解:A.∵a=b,∴a﹣3=b﹣3,故本选项不符合题意;B.∵=,∴等式的两边乘c得:a=b,故本选项不符合题意;C.∵x=2,∴x2=2x,故本选项不符合题意;D.当c=0时,由ac2=bc2不能推出a=b,故本选项符合题意;故选:D.9.如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是()A.AB=2AC B.AC+CD+DB=ABC.CD=AD﹣AB D.AD=(CD+AB)【分析】根据线段中点的定义对A进行判断;根据图形直接对B进行判断;根据AC=AB,则CD=AD﹣AC=AD﹣AB可对C进行判断;根据AD=AC+CD=AB+CD可对D进行判断.解:A、由点C是线段AB的中点,则AB=2AC,正确,不符合题意;B、AC+CD+DB=AB,正确,不符合题意;C、由点C是线段AB的中点,则AC=AB,CD=AD﹣AC=AD﹣AB,正确,不符合题意;D、AD=AC+CD=AB+CD,不正确,符合题意.故选:D.10.如图,OM平分∠AOB,∠MON=2∠BON,∠AON﹣∠BON=72°,则∠AOB=()A.96°B.108°C.120°D.144°【分析】根据已知设∠BON=x,则∠MON=2x,然后利用角平分线的定义表示出∠AON 和∠BON,列出关于x的方程进行计算即可解答.解:∵∠MON=2∠BON,∴设∠BON=x,则∠MON=2x,∴∠MOB=∠MON+∠BON=3x,∵OM平分∠AOB,∴∠AOM=∠MOB=3x,∴∠AON=∠AOM+∠MON=5x,∵∠AON﹣∠BON=72°,∴5x﹣x=72°,∴x=18°,∴∠AOB=6×18°=108°,故选:B.11.下列说法中,正确的有()①射线AB和射线BA是同一条射线;②若AB=BC,则点B为线段AC的中点;③连接A、B两点,使线段AB过点C;④两点的所有连线中,线段最短.A.0个B.1个C.2个D.3个【分析】根据射线的定义判断①;根据线段中点的定义判断②;根据语句画出图形判断③;根据线段的性质判断④.解:①射线AB和射线BA不是同一条射线,故错误;②若AB=BC,则点B为不一定线段AC的中点,故错误;③A、B、C三点不一定共线,故错误;④两点之间,线段最短,故正确.故选:B.12.一列火车匀速行驶,经过一条长400米的隧道需要30秒的时间,隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒,则火车的长为()米.A.B.133C.200D.400【分析】设火车的长为x米,根据经过一条长400米的隧道需要30秒的时间,灯光照在火车上的时间是10秒和火车的速度不变,列出方程求解即可.解:设火车的长为x米,由题意得:=,解得:x=200.答:这列火车的长度是200米.故选:C.二、填空题(本大题共6小题)13.﹣1的倒数是﹣;绝对值等于3的数是±3.【分析】根据倒数的定义和绝对值的性质解答即可.解:的倒数是﹣,绝对值等于3的数是±3.故答案为:﹣,±3.14.98°30'18″=98.505度,90°﹣35°27'=54°33′.【分析】根据度分秒的进制进行计算即可.解:∵1°=60′,1′=60″,∴18″=0.3′,∴30.3′=0.505°,∴98°30'18″=98.505度,90°﹣35°27'=89°60′﹣35°27′=54°33′,故答案为:98.505,54,33.15.长方形纸片ABCD,点E、F分别在边AB、AD上,连接EF,将∠AEF沿EF翻折,得到∠A1EF,连接CE,将∠BEC翻折,得到∠B1EC,点B1恰好落在线段A1E上,若∠AEF =29°,则∠B1EC=61°.【分析】由折叠可得∠AEF=∠A1EF,∠BEC=∠B1EC,则∠AEF=∠A1EF=29°,所以∠A1EB=180°﹣29°﹣29°=122°,从而推出∠BEC=∠B1EC==61°.解:由折叠可得∠AEF=∠A1EF,∠BEC=∠B1EC,∵∠AEF=29°,∴∠A1EF=29°,∴∠A1EB=180°﹣29°﹣29°=122°,∴∠BEC=∠B1EC==61°,故答案为61.16.已知线段AB=6,延长AB至点C,使BC=AB,反向延长AC至点D,使AD=AC,则CD的长为12.【分析】根据题意,画出图形,根据BC=AB,AD=AC,计算出线段AD和AC的长,即可得到答案.解:如图:;∵BC=AB,AB=6,∴BC=2,∴AC=AB+BC=6+2=8,∵AD=AC=4,∴CD=AD+AC=4+8=12.故答案为:12.17.已知a2+2ab=﹣5,ab﹣2b2=﹣3,则代数式3a2+ab+b2的值为﹣.【分析】根据整式的加减运算法则以及整体思想即可求出答案.解:当a2+2ab=﹣5,ab﹣2b2=﹣3,∴原式=3(a2+2ab)﹣(ab﹣2b2)=3×(﹣5)﹣×(﹣3)=﹣15+=﹣,故答案为:﹣.18.如图,点Q在线段AP上,其中PQ=10,第一次分别取线段AP和AQ的中点P1,Q1,得到线段P1Q1,则线段P1Q1=5;再分别取线段AP1和AQ1的中点P2,Q2,得到线段P2Q2;第三次分别取线段AP2和AQ2的中点P3,Q3,得到线段P3Q3;连续这样操作2021次,则每次的两个中点所形成的所有线段之和P1Q1+P2Q2+P3Q3+…+P2021Q2021=10﹣.【分析】根据线段中点的定义可得P1Q1=PQ,P2Q2=P1Q1,P3Q3=P2Q2,根据规律可得答案.解:∵线段AP和AQ的中点是P1,Q1,∴P1Q1=AP1﹣AQ1=AP﹣AQ=PQ=5,∵线段AP1和AQ1的中点P2,Q2,∴P2Q2=AP2﹣AQ2=AP1﹣AQ1=P1Q1=PQ=PQ,∵线段AP2和AQ2的中点P3,Q3,∴P3Q3=AP3﹣AQ3=AP2﹣AQ2=P2Q2=PQ=PQ,…,∴P1Q1+P2Q2+P3Q3+…+P2021Q2021=PQ+PQ+PQ+…+PQ=(+++…+)PQ=(1﹣)PQ=10﹣.故答案为:5,10﹣.三、解答题(共7小题,解答题应写出解答过程.)19.计算:(1)﹣66×4﹣(﹣2.5)÷(﹣0.1);(2)﹣22÷×(﹣)2+[9﹣(﹣+)×36].【分析】(1)先算乘除,再算加减即可;(2)先算乘方、括号里用乘法分配律,再算乘除,最后算加减.解:(1)原式=﹣264﹣25=﹣289;(2)原式=﹣4÷×+(9﹣×36+×36﹣×36)=﹣4××+9﹣28+33﹣6=﹣+9﹣28+33﹣6=﹣.20.解下列方程:(1)7x+2(3x﹣3)=20;(2)+=2﹣.【分析】(1)方程去括号,移项,合并同类项,把x系数化为1,即可求出解;(2)方程整理后,去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.解:(1)去括号得:7x+6x﹣6=20,移项得:7x+6x=20+6,合并得:13x=26,系数化为1,得:x=2;(2)方程整理得:+=2﹣,去分母得:4(5x+4)+3(x﹣1)=24﹣(5x﹣5),去括号得:20x+16+3x﹣3=24﹣5x+5,移项得:20x+3x+5x=24+5﹣16+3,合并得:28x=16,系数化为1,得:x=.21.老师布置了一道化简求值题,如下:求■x﹣2(x﹣y2)+(﹣x+y2)的值,其中x =﹣2,y=.(1)小海准备完成时发现第一项的系数被同学涂了一下模糊不清了,同桌说他记得系数是.请你按同桌的提示,帮小海化简求值;(2)科代表发现系数被涂后,很快把正确的系数写了上去.同学们计算后发现,老师给出的“x=﹣2”这个条件是多余的,请你算一算科代表补上的系数是多少?【分析】(1)将代入原多项式,先去括号,再合并同类项,最后把x和y的值代入即可;(2)设第一项的系数为a,再去括号,合并同类项,由于结果与x无关,则x的系数为0,由此可得出第一项的系数.解:(1)x﹣2(x﹣y2)+(﹣x+y2)=x﹣2x+y2﹣x+y2=﹣3x+y2∵x=﹣2,y=,∴﹣3x+y2=﹣3×(﹣2)+()2=6+=.(2)设第一项的系数为a,∴ax﹣2(x﹣y2)+(﹣x+y2)=ax﹣2x+y2﹣x+y2=(a﹣)x+y2由题意可得,结果与x无关,即x的系数为0,∴a﹣=0,即a=.22.如图,O为直线AB上一点,∠AOC与∠AOD互补,OM,ON分别是∠AOC,∠AOD 的平分线.(1)根据题意,补全下列说理过程:∵∠AOC与∠AOD互补,∴∠AOC+∠AOD=180°.又∵∠AOC+∠BOC=180°,∴∠AOD=∠BOC.(2)若∠MOC=68°,求∠AON的度数.(3)若∠MOC=α,则∠AON=90°﹣α(用α表示).【分析】(1)根据所给的过程进行分析即可;(2)由角平分线的定义可得∠AOC=2∠MOC=136°,利用补角的定义可求∠BOC=44°,从而得∠AOD=44°,再利用角平分线的定义可求得∠AON=22°;(3)结合(2)的过程进行求解即可.解:(1)∵∠AOC与∠AOD互补,∴∠AOC+∠AOD=180°.又∵∠AOC+∠BOC=180°,∴∠AOD=∠BOC.故答案为:BOC,AOD,BOC;(2)∵OM平分∠AOC,∠MOC=68°,∴∠AOC=2∠MOC=136°,∴∠BOC=180°﹣∠AOC=44°,∵∠AOD=∠BOC,∴∠AOD=44°,∵ON平分∠AOD,∴∠AON=∠AOD=22°;(3)∵OM平分∠AOC,∠MOC=α,∴∠AOC=2∠MOC=2α,∴∠BOC=180°﹣∠AOC=180°﹣2α,∵∠AOD=∠BOC,∴∠AOD=180°﹣2α,∵ON平分∠AOD,∴∠AON=∠AOD=90°﹣α;故答案为:90°﹣α.23.工业园区某机械厂的一个车间主要负责生产螺丝和螺母,该车间有工人44人,其中女生人数比男生人数的2倍少10人,每个工人平均每天可以生产螺丝50个或者螺母120个.(1)该车间有男生、女生各多少人?(2)已知一个螺丝与两个螺母配套,为了使每天生产的螺丝螺母恰好配套,应该分配多少工人负责生产螺丝,多少工人负责生产螺母?【分析】(1)设该车间有男生x人,则女生人数是(2x﹣10)人,根据“男生人数+女生人数=44”列出方程并解答;(2)首先设应分配y名工人生产螺丝,(44﹣y)名工人生产螺母,根据题意可得等量关系:螺丝数量×2=螺母数量,根据等量关系列出方程,再解即可.解:(1)设该车间有男生x人,则女生人数是(2x﹣10)人,则x+(2x﹣10)=44.解得x=18则2x﹣10=26.答:该车间有男生18人,则女生人数是26人.(2)设应分配y名工人生产螺丝,(44﹣y)名工人生产螺母,由题意得:120(44﹣y)=50y×2解得:y=24,44﹣y=20答:分配24名工人生产螺丝,20名工人生产螺母.24.已知∠AOD=160°,OB为∠AOD内部的一条射线(1)如图1,若OM平分∠AOB,ON平分∠BOD,∠MON的度数为80°;(2)如图2,∠BOC在∠AOD内部(∠AOC>∠AOB),且∠BOC=20°,OF平分∠AOC,OG平分∠BOD(射线OG在射线OC左侧),求∠FOG的度数;(3)在(2)的条件下,∠BOC绕点O运动过程中,若∠BOF=8°,求∠GOC的度数.【分析】(1)根据角平分线的意义以及角的和差关系得出∠MON=∠AOD即可;(2)根据角平分线的意义以及角的和差关系得到∠FOG=(∠AOD﹣∠BOC)即可;(3)分两种情况进行解答,即OF在OB的右侧、左侧时,分别画出相应的图形,利用角平分线的意义以及角的和差关系进行解答即可.解:(1)如图1,∵OM平分∠AOB,ON平分∠BOD,∴∠BON=∠BOD,∠BOM=∠AOB,∴∠MON=∠BOM+∠BON=∠BOD+∠AOB=(∠BOD+∠AOB)=∠AOD=×160°=80°;故答案为:80°;(2)∵OF平分∠AOC,OG平分∠BOD,∴∠FOC=AOC,∠BOG=∠BOD,∴∠FOG=∠FOC+∠BOG﹣∠BOC=∠AOC+∠BOD﹣∠BOC=(∠AOC+∠BOD)﹣∠BOC=(∠AOD+∠BOC)﹣∠BOC=(∠AOD﹣∠BOC)=(160°﹣20°)=70°;(3)当OF在OB的右侧时,如图2,设∠COG=x°,则∠BOG=(x+20°),∵OF平分∠AOC,OG平分∠BOD,∴∠AOF=∠FOC=20°+8°=28°,∠BOD=2(x+20°),∴∠AOD=∠AOB+∠BOD,即∠AOD=∠AOF+∠BOF+∠BOD,∴160°=28°+8°+2(x+20°),解得x=42°,即∠COG=42°,当OF在OB的左侧时,如图3,设∠COG=x°,则∠BOG=(x+20°),∵OF平分∠AOC,OG平分∠BOD,∴∠AOF=∠FOC=20°﹣8°=12°,∠BOD=2(x+20°),∵∠AOD=∠AOB+∠BOD,∴160°=2(x+20°)+12°﹣8°,解得x=58°,答:∠GOC的度数为42°或58°.25.规定:A,B,C是数轴上的三个点,当CA=3CB时我们称C为[A,B]的“三倍距点”,当CB=3CA时,我们称C为[B,A]的“三倍距点”.点A所表示的数为a,点B所表示的数为b且a,b满足(a+3)2+|b﹣5|=0.(1)a=﹣3,b=5;(2)若点C在线段AB上,且为[A,B]的“三倍距点”,则点C所表示的数为3;(3)点M从点A出发,同时点N从点B出发,沿数轴分别以每秒3个单位长度和每秒1个单位长度的速度向右运动,设运动时间为t秒.当点B为M,N两点的“三倍距点”时,求t的值.【分析】(1)根据非负性的性质.即可求得a,b的值;(2)根据“三倍距点”的定义即可求解;(3)分点B为[M,N]的“三倍距点”和点B为[N,M]的“三倍距点”两种情况讨论即可.解:(1)∵(a+3)2+|b﹣5|=0,∴a+3=0,b﹣5=0,∴a=﹣3,b=5,故答案为:﹣3;5;(2)∵点A所表示的数为﹣3,点B所表示的数为5,∴AB=5﹣(﹣3)=8,∵点C为[A,B]的“三倍距点”,点C在线段AB上,∴CA=3CB,CA+CB=AB=8,∴CB=2,∴点C所表示的数为5﹣2=3,故答案为:3;(3)根据题意可知:点M所表示的数为3t﹣3,点N所表示的数为t+5,∴BM=|5﹣(3t﹣3)|=|8﹣3t|,BN=|t+5﹣5|=t,(t>0),当点B为[M,N]的“三倍距点”时,即BM=3BN,∴|8﹣3t|=3t,∴8﹣3t=3t或8﹣3t=﹣3t,解8﹣3t=3t,得:t=,而方程8﹣3t=﹣3t,无解,当点B为[N,M]的“三倍距点”时,即3BM=BN,∴3|8﹣3t|=t,∴24﹣9t=t或24﹣9t=﹣t,解得:t=或t=3,综上所述,当t=或t=3或t=时,点B为M,N的“三倍距点”.。
2022-2023学年天津市和平区七年级(上)期末数学试题及答案解析

2022-2023学年天津市和平区七年级(上)期末数学试卷一、选择题(本大题共8小题,共24.0分。
在每小题列出的选项中,选出符合题目的一项)1. 计算−8+2的结果是( )A. −6B. 6C. −10D. 102. 节约是一种美德,节约是一种智慧。
据不完全统计,全国每年浪费食物总量折合粮食可养活约3亿5千万人。
350 000 000用科学记数法表示为( )A. 3.5×107B. 3.5×108C. 3.5×109D. 3.5×10103. 如图的几何体是由一些小正方体组合而成的,则这个几何体的左视图是( )A.B.C.D.4. 下列变形不一定正确的是( )A. 若a=b,m≠0,则am =bmB. 若a=b,则a2=b2C. 若a=b,则a+2c=b+2cD. 若ac=bc,则a=b5. 在灯塔O处观测到轮船A位于北偏西54°的方向,同时轮船B在南偏东15°的方向,则∠AOB 的大小为( )A. 69°B. 111°C. 159°D. 141°6. 若单项式13a m+1b3与−2a3b n的和仍是单项式,则方程x−7n−1+xm=1的解为( )A. x=−23B. x=23C. x=−29D. x=297. 下列说法正确的有( )①角的大小与所画边的长短无关;②如图,∠ABD也可用∠B表示;③如果∠AOC=12∠AOB,那么OC是∠AOB的平分线;④连接两点的线段叫做这两点之间的距离;⑤两点之间线段最短;⑥点E在线段CD上,若DE=12CD,则点E是线段CD的中点.A. 1个B. 2个C. 3个D. 4个8. 如图,O为直线AB上一点,∠DOC为直角,OE平分∠AOC,OG平分∠BOC,OF平分∠BOD,下列结论:①∠AOE与∠BOG互余;②∠EOF与∠GOF互补;③∠DOE与∠DOG互补;④∠AOC−∠BOD=90°,其中正确的有个( )A. 4B. 3C. 2D. 1二、填空题(本大题共6小题,共18.0分)9. 如图几何体中属于棱柱的有______ (填序号).10. 若a,b互为相反数,且ab≠0,c、d互为倒数,m是数轴上到原点的距离为2的点表示的数,则(a+b)2+(ba)3−3cd+m2的值为______.11. 若x =1时,代数式ax 3+bx +7的值为3,则当x =−1时,ax 3+bx +7的值为__ ____ .12. 某正方体的每个面上都有一个汉字,如图是它的一个展开图,则在原正方体中,与“我”字所在面相对的面上的汉字是______ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年天津市和平区七年级(上)期末数学试卷一、选择题:本大题共12小题,每小题2分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算5+(﹣5)=()A.1 B.0 C.10 D.﹣102.(﹣2)3表示()A.﹣2×3 B.(﹣2)+(﹣2)+(﹣2)C.﹣2×2×2D.(﹣2)×(﹣2)×(﹣2)3.下列说法正确的是()A.表示﹣x的平方的式子是﹣x2B.表示x、y2、3的积的式子是3xy2C.x、y两数差的平方表示为(x﹣y)2D.x2+y2的意义是x与y和的平方4.如图所示,小明家在A处,体育馆在B处,星期六小明由家去体育馆打篮球,他想尽快到达体育馆,请你帮助他选择一条最近的路线,应是()A.A→C→E→B B.A→C→D→B C.A→C→G→B D.A→C→F→E→B 5.如图,点P位于点O的()A.南偏西32°B.北偏东32°C.南偏东58°D.北偏西58°6.下面给出的三个平面图形,是从前面、左面、上面看一个立体图形得到的,那么这个立体图形应是()A.B.C.D.7.如图,四个图形都是由6个大小相同的正方形组成,其中是正方体展开图的是()A.①②④B.①②③C.②④D.②③④8.如图所示,点A、B、C在直线l上,则下列说法正确的是()A.图中有2条线段B.图中有6条射线C.点C在直线AB的延长线上D.A、B两点之间的距离是线段AB9.下列方程中,解为x=﹣2的方程是()A.2x+5=1﹣x B.3﹣2(x﹣1)=7﹣x C.x﹣2=﹣2﹣xD.1﹣x=x10.如图,下列关系式中与图不符的是()A.AD﹣CD=AC B.AB+BC=AC C.BD﹣BC=AB+BC D.AD﹣BD=AC﹣BC 11.若∠α与∠β互余,且∠α:∠β=3:2,那么∠α与∠β的度数分别是()A.36°,54°B.60°,40°C.54°,36°D.72°,108°12.如图,∠MON为锐角.下列说法:①∠MOP=∠MON;②∠MOP=∠NOP=∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有()A.1个B.2个C.3个D.4个二、填空题:笨蛋那天共6小题,每小题3分,共18分.13.56.28°=°′″.14.若单项式ax2y n+1与﹣ax m y4的差仍是单项式,则m﹣2n=.15.线段AB=4cm,点C在AB的延长线上,点D在AB的方向延长线上,且点B为AC 的中点,AD为BC的2倍,则线段CD=.16.已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC=度.17.若一个角的补角加上10°后,等于这个角的余角的3倍,则这个角的补角为度.18.如图,点A、B在数轴上,其对应的数分别是﹣14和10,若点C也在这个数轴上,且AC:BC=2:5,则点C对应的数是.三、解答题:本大题共7小题,共58分,解答应写出演算步骤或简单推理过程.19.计算:(1)÷(﹣2)﹣(﹣)×(﹣)+;(2){1+[﹣(﹣)2]×(﹣2)3}÷(﹣1+0.5).20.解下列方程:(1)3(2x﹣)﹣2(x+1)=2;(2)2y﹣=+3.21.已知A=3b2﹣2a2+5ab,B=4ab﹣2b2﹣a2.(1)化简:3A﹣4B;(2)已知a、b满足(a﹣1)2+|b+1|=0,求3A﹣4B的值.22.如图,已知∠AOB=155°,∠AOC=∠BOD=90°.(1)写出与∠COD互余的角;(2)求∠COD的度数;(3)图中是否有互补的角?若有,请写出来.23.列一元一次方程解应用题.某租赁公司拥有100辆轿车,当每辆轿车的月租金为3000元时,可全部租出,当每辆轿车的月租金每增加50元时,未租出的轿车将会增加一辆,租出的轿车每辆每月公司需要保养费150元,未租出的轿车每辆每月公司需要保养费50元.(1)已知10月份每辆轿车的月租金为3600元时,能租出多少辆轿车?(2)已知11月份的保养费开支为12900元,问该月租出了多少辆轿车?(3)比较10、11两月的月收益,哪个月的月收益多?多多少?24.如图,O为直线AB上一点,∠BOC=α.(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;(2)若∠AOD=∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)若∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),如图(c)所示,请用α和n 表示∠AOE的度数(直接写出结果).25.已知a、b均为有理数,且关于x的方程为=+1.(1)当a=4,b=﹣时,求x的值;(2)若关于x的方程有无数个解.①求a、b的值;②设线段AB=a,CD=b,线段CD在直线AB上(A在B的左侧,C在D的左侧),且M、N分别是线段AC、BD的中点,若BC=4,求MN的值.2016-2017学年天津市和平区七年级(上)期末数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题2分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.计算5+(﹣5)=()A.1 B.0 C.10 D.﹣10【考点】有理数的加法.【分析】根据有理数的加法法则可得.【解答】解:5+(﹣5)=0,故选:B.2.(﹣2)3表示()A.﹣2×3 B.(﹣2)+(﹣2)+(﹣2)C.﹣2×2×2D.(﹣2)×(﹣2)×(﹣2)【考点】有理数的混合运算.【分析】原式利用乘方的意义计算变形即可.【解答】解:(﹣2)3表示(﹣2)×(﹣2)×(﹣2),故选D3.下列说法正确的是()A.表示﹣x的平方的式子是﹣x2B.表示x、y2、3的积的式子是3xy2C.x、y两数差的平方表示为(x﹣y)2D.x2+y2的意义是x与y和的平方【考点】列代数式.【分析】根据有理数的乘方和乘法对各选项分析判断后利用排除法求解.【解答】解:A、错误.表示﹣x的平方的式子是(﹣x)2.B、错误.表示x、y2、3的积的式子是xy2.C、正确.x、y两数差的平方表示为(x﹣y)2.D、错误.x2+y2的意义是x与y的平方和.故选C.4.如图所示,小明家在A处,体育馆在B处,星期六小明由家去体育馆打篮球,他想尽快到达体育馆,请你帮助他选择一条最近的路线,应是()A.A→C→E→B B.A→C→D→B C.A→C→G→B D.A→C→F→E→B 【考点】线段的性质:两点之间线段最短.【分析】根据两点之间,线段最短进行解答即可.【解答】解:最近的路线,应是A→C→E→B,故选:A.5.如图,点P位于点O的()A.南偏西32°B.北偏东32°C.南偏东58°D.北偏西58°【考点】方向角.【分析】先确定OP和正北方向的夹角是58度,即可判断点P的方位.【解答】解:∵OP和正北方向的夹角是58度∴点P位于点O的北偏西58°的方向上.故选D6.下面给出的三个平面图形,是从前面、左面、上面看一个立体图形得到的,那么这个立体图形应是()A.B.C.D.【考点】由三视图判断几何体.【分析】由主视图和左视图可得此几何体为锥体,根据俯视图是四边形可判断出此几何体为四棱锥.【解答】解:∵主视图和左视图都是三角形,∴此几何体为椎体,∵俯视图是一个长方形,∴此几何体为四棱锥.故选:D.7.如图,四个图形都是由6个大小相同的正方形组成,其中是正方体展开图的是()A.①②④B.①②③C.②④D.②③④【考点】几何体的展开图.【分析】由平面图形的折叠及正方体的展开图解题.【解答】解:由四棱柱四个侧面和上下两个底面的特征可知,①,②,④选项可以拼成一个正方体,而③选项,上底面不可能有两个,故不是正方体的展开图.故选:A.8.如图所示,点A、B、C在直线l上,则下列说法正确的是()A.图中有2条线段B.图中有6条射线C.点C在直线AB的延长线上D.A、B两点之间的距离是线段AB【考点】两点间的距离;直线、射线、线段.【分析】根据两点间的距离的含义和求法,以及直线、射线和线段的认识,逐项判断即可.【解答】解:∵图中有3条线段,∴选项A不正确;∵图中有6条射线,∴选项B正确;∵点C在线段AB的延长线上,∴选项C不正确;∵A、B两点之间的距离是线段AB的长度,∴选项D不正确.故选:B.9.下列方程中,解为x=﹣2的方程是()A.2x+5=1﹣x B.3﹣2(x﹣1)=7﹣x C.x﹣2=﹣2﹣xD.1﹣x=x【考点】方程的解.【分析】将x=﹣2代入各选项中,若等式左右两边相等,则是该方程的解.【解答】解:将x=﹣2代入3﹣2(x﹣1)=7﹣x,∴左边=3﹣2×(﹣2﹣1)=3+6=9,右边=7﹣(﹣2)=9左边=右边,故选(B)10.如图,下列关系式中与图不符的是()A.AD﹣CD=AC B.AB+BC=AC C.BD﹣BC=AB+BC D.AD﹣BD=AC﹣BC 【考点】两点间的距离.【分析】结合图形根据线段的和差运算逐一判断即可.【解答】解:A、AD﹣CD=AC,正确;B、AB+BC=AC,正确;C、由BD﹣BC=CD、AB+BC=AC知BD﹣BC=AB+BC错误;D、由AD﹣BD=AB、AC﹣BC=AB知AD﹣BD=AC﹣BC,正确;故选:C.11.若∠α与∠β互余,且∠α:∠β=3:2,那么∠α与∠β的度数分别是()A.36°,54°B.60°,40°C.54°,36°D.72°,108°【考点】余角和补角.【分析】设∠α,∠β的度数分别为3x°,2x°,再根据余角的性质即可求得两角的度数.【解答】解:设∠α,∠β的度数分别为3x°,2x°,则3x+2x=90,∴x=18.∴∠α=3x°=54°,∠β=2x°=36°,故选C.12.如图,∠MON为锐角.下列说法:①∠MOP=∠MON;②∠MOP=∠NOP=∠MON;③∠MOP=∠NOP;④∠MON=∠MOP+∠NOP.其中,能说明射线OP一定为∠MON的平分线的有()A.1个B.2个C.3个D.4个【考点】角平分线的定义.【分析】根据角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线,判断各选项即可得出答案.【解答】解:根据角平分线的定义,结合各选项得:①如果P点不在∠MON夹角内,则OP不是∠MON的平分线;②正确;③如果P点在∠MON外面,则OP不是∠MON的平分线;④如果∠MOP≠∠NOP,则OP不是∠MON的平分线;故选A.二、填空题:笨蛋那天共6小题,每小题3分,共18分.13.56.28°=56°16′48″.【考点】度分秒的换算.【分析】根据度分秒是60进制,把小数部分乘以60依次计算即可得解.【解答】解:∵0.28×60=16.8,0.8×60=48,∴56.28°=56°26′48″.故答案为:56,16,48.14.若单项式ax2y n+1与﹣ax m y4的差仍是单项式,则m﹣2n=﹣4.【考点】合并同类项.【分析】根据差是单项式,可得它们是同类项,在根据同类项,可得m、n的值,根据有理数的减法,可得答案.【解答】解:∵单项式与的差仍是单项式,∴单项式与是同类项,m=2,n+1=4,n=3,m﹣2n=2﹣2×3=﹣4,故答案为:﹣4.15.线段AB=4cm,点C在AB的延长线上,点D在AB的方向延长线上,且点B为AC 的中点,AD为BC的2倍,则线段CD=16cm.【考点】两点间的距离.【分析】先根据题意画出图形,求出BC、AD,即可求出答案.【解答】解:∵AB=4cm,B为AC的中点,∴BC=AB=4cm,∵AD为BC的2倍,∴AD=8cm,∴CD=AD+AB+BC=16cm,故答案为:16cm.16.已知∠AOB=3∠BOC,若∠BOC=30°,则∠AOC=60或120度.【考点】角的计算.【分析】此题需要分类讨论,共两种情况.先作图后计算.【解答】解:∵∠BOC=30°,∠AOB=3∠BOC,∴∠AOB=3×30°=90°(1)当OC在∠AOB的外侧时,∠AOC=∠AOB+∠BOC=90°+30°=120度;(2)当OC在∠AOB的内侧时,∠AOC=∠AOB﹣∠BOC=90°﹣30°=60度.故填60或120.17.若一个角的补角加上10°后,等于这个角的余角的3倍,则这个角的补角为140度.【考点】余角和补角.【分析】设这个角的度数为x度,根据题意,列出方程,解答即可.【解答】解:设这个角的度数为x°,根据题意,得:180﹣x+10=3(90﹣x),解得:x=40,∴这个角的补角为:180°﹣40°=140°,故答案为:140.18.如图,点A、B在数轴上,其对应的数分别是﹣14和10,若点C也在这个数轴上,且AC:BC=2:5,则点C对应的数是﹣10或﹣.【考点】数轴.【分析】设点C表示的数为x,分点C在A、B之间和点C在点A的左边两种情况,利用两点间的距离公式列方程求解可得.【解答】解:设点C表示的数为x,当点C在A、B之间时,=,解得:x=﹣10;当点C在点A的左边时,=,解得:x=﹣,故答案为:﹣10或﹣.三、解答题:本大题共7小题,共58分,解答应写出演算步骤或简单推理过程.19.计算:(1)÷(﹣2)﹣(﹣)×(﹣)+;(2){1+[﹣(﹣)2]×(﹣2)3}÷(﹣1+0.5).【考点】有理数的混合运算.【分析】(1)原式先计算乘除运算,再计算加减运算即可得到结果;(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【解答】解:(1)原式=﹣×﹣+=﹣;(2)原式=(1﹣+)×(﹣)=﹣+﹣=﹣5.20.解下列方程:(1)3(2x﹣)﹣2(x+1)=2;(2)2y﹣=+3.【考点】解一元一次方程.【分析】(1)去括号,移项,合并同类项,系数化成1即可;(2)去分母,去括号,移项,合并同类项,系数化成1即可.【解答】解:(1)去括号得:6x﹣4﹣2x﹣2=26x﹣2x=2+4+2,4x=8,x=2;(2)去分母得:12y﹣3(y﹣3)=y+21,12y﹣3y+9=y+21,12y﹣3y﹣y=21﹣9,8y=12,y=1.5.21.已知A=3b2﹣2a2+5ab,B=4ab﹣2b2﹣a2.(1)化简:3A﹣4B;(2)已知a、b满足(a﹣1)2+|b+1|=0,求3A﹣4B的值.【考点】整式的加减—化简求值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】先将3A﹣4B的化简,然后求出a与b的值后代入求值即可.【解答】解:(1)3A﹣4B=3(3b2﹣2a2+5ab)﹣4(4ab﹣2b2﹣a2)=9b2﹣6a2+15ab)﹣16ab+8b2+4a2=2a2﹣ab+17b2(2)由题意可知:a﹣1=0,b+1=0,∴a=1,b=﹣1∴3A﹣4B=2×1﹣1×(﹣1)+17×1=﹣2+1+17=1622.如图,已知∠AOB=155°,∠AOC=∠BOD=90°.(1)写出与∠COD互余的角;(2)求∠COD的度数;(3)图中是否有互补的角?若有,请写出来.【考点】余角和补角.【分析】根据余角和补角的概念进行计算即可.【解答】解:(1)∵∠AOC=∠BOD=90°,∴∠COD+∠AOD=90°,∠COD+∠BOC=90°,∴与∠COD互余的角是∠AOD和∠BOC;(2)∠BOC=∠AOB﹣∠AOC=65°,∴∠COD=∠BOD﹣∠BOC=25°;(3)∠COD与∠AOB、∠AOC与∠BOD互补.23.列一元一次方程解应用题.某租赁公司拥有100辆轿车,当每辆轿车的月租金为3000元时,可全部租出,当每辆轿车的月租金每增加50元时,未租出的轿车将会增加一辆,租出的轿车每辆每月公司需要保养费150元,未租出的轿车每辆每月公司需要保养费50元.(1)已知10月份每辆轿车的月租金为3600元时,能租出多少辆轿车?(2)已知11月份的保养费开支为12900元,问该月租出了多少辆轿车?(3)比较10、11两月的月收益,哪个月的月收益多?多多少?【考点】一元一次方程的应用.【分析】(1)设10月份未租出x辆轿车,根据“当每辆车的月租金为3000元时,可全部租出;当每辆车的月租金每增加50元时,未租出的车将会增加一辆”可列出未租出车的代数式,再求租出的车辆数即可.(2)可以设出租了y辆,则未租出去的有100﹣x辆,据租出的车每辆每月公司需要维护费150元,未租出的车每辆每月公司需要维护费50元及总的维护费为12900元,即可列出方程,求解即可.(3)根据(1)(2)求得的出租出的车辆数,可分别计算出两月的收益,比较大小即可.【解答】解:(1)设10月份未租出x辆轿车,依题意得,50x=3600﹣300,解得x=12.所以,租出的轿车为100﹣12=88(辆).答:10月份能租出88辆轿车;(2)设11月份租出y辆轿车,依题意得:150y+50=12900解得y=79.答:11月份租出79辆轿车;(3)10月份收益:×88﹣50×12=303000(元).11月份收益:[3000+50]×79﹣12900=307050(元).因为307050﹣303000=4050(元),所以11月份收益多,多4050元.24.如图,O为直线AB上一点,∠BOC=α.(1)若α=40°,OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数;(2)若∠AOD=∠AOC,∠DOE=60°,如图(b)所示,请用α表示∠AOE的度数;(3)若∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),如图(c)所示,请用α和n 表示∠AOE的度数(直接写出结果).【考点】角的计算;角平分线的定义.【分析】(1)利用角平分线的性质得出∠AOD=∠DOC=70°,进而得出∠AOE的度数;(2)利用设∠AOD=x,则∠DOC=2x,∠BOC=180﹣3x=α,得出x的值,进而用α表示∠AOE的度数;(3)利用(2)中作法,得出x与α的关系,进而得出答案.【解答】解:(1)∵∠BOC=40°,OD平分∠AOC,∴∠AOD=∠DOC=70°,∵∠DOE=90°,则∠AOE=90°﹣70°=20°;故答案为:20°;(2)设∠AOD=x,则∠DOC=2x,∠BOC=180﹣3x=α,解得:x=,∴∠AOE=60﹣x=60﹣=α;(3)设∠AOD=x,则∠DOC=(n﹣1)x,∠BOC=180﹣nx=α,解得:x=,∴∠AOE==.25.已知a、b均为有理数,且关于x的方程为=+1.(1)当a=4,b=﹣时,求x的值;(2)若关于x的方程有无数个解.①求a、b的值;②设线段AB=a,CD=b,线段CD在直线AB上(A在B的左侧,C在D的左侧),且M、N分别是线段AC、BD的中点,若BC=4,求MN的值.【考点】两点间的距离;一元一次方程的解.【分析】(1)把a=4,b=﹣代入得到关于x的方程,解方程即可求得x;(2)①由=+1可得(a﹣8)x=﹣8|b|﹣ab+96,根据关于x的方程有无数个解,可得a﹣8=0,﹣8|b|﹣ab+96=0,解方程即可求解;②分三种情况:点C、D都在点A的左侧,点C在点A的左侧且点D在点A的右侧时,线段CD在线段AB上时;点C在点B的左侧,点D在点B的右侧时;点C、D都在点B的右侧时;进行讨论可求MN的值.【解答】解:(1)当a=4,b=﹣时,方程变为=+1,化简,得=+1,去分母,得2x﹣1=4x﹣2+48,﹣2x=47,x=﹣;(2)①去分母,得ax+ab=8x﹣8|b|+96,(a﹣8)x=﹣8|b|﹣ab+96,∵关于x的方程有无数个解,∴a﹣8=0,﹣8|b|﹣ab+96=0,解得a=8,则﹣8|b|﹣8b+96=0,当b≥0时,得﹣16b+96=0,解得b=6,当b<0时,得8b﹣8b+96=0,无解.综上可知,a=8,b=6.②依题意有AB=8,CD=6,当点C、D都在点A的左侧,点C在点A的左侧且点D在点A的右侧时,线段CD在线段AB上时,这三种情况均有BC>CD,不合题意;当点C在点B的左侧,点D在点B的右侧时,如图所示:,有BC<CD,符合题意;∵BC=4,CD=6,∴BD=2,∵N是线段BD的中点,∴BN=1,∴CN=CB+BN=4+1=5,∵AB=8,∴CM=AC=2,∴MN=CM+CN=2+5=7;当点C、D都在点B的右侧时,符合题意,如图所示:;则AC=AB+BC=8+4=12,BD=BC+CD=4+6=10,∵M、N分别是线段AC、BD的中点,∴CM=AC=6,BN=BD=5,∴MN=CM+BN﹣BC=6+5﹣4=7.综上所述,MN的值为7.。
