NOIP2015普及组复赛解题报告
noip2015初赛普及组答案分析

单项选择题1.A。
计算机内部的用来传送、存贮、加工处理的数据或指令都是以二进制形式进行的。
2.A。
写这题我用的是排除法,B选项显然不对,内存在断电后数据会丢失,C选项也是,屏幕的分辨率是可以手动调整的,D选项,当年我们都用宽带连接Internet的。
3.A。
二进制小数转化为十六进制小数时,每四位二进制数转化为以为十六进制数,故0.10002可以转化为0.816。
4.D。
我的做法是将每个数都化为二进制形式,因为十六进制数和八进制数转化为二进制数很容易,最后求得答案是D。
5.D。
在链表中,每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域,结点与结点之间是用指针连接的,故地址不必连续。
6.B。
模拟一下进栈出栈的过程就行了,共有6次操作:进栈,进栈,出栈,进栈,进栈,出栈,每次操作后栈内元素分别为”a”,”ab”,”a”,”a b c”,”a b c d”,”a b c”,故最后栈顶元素是c。
7.B。
前序遍历的顺序是”根->左->右”,后序遍历的顺序是”左->右->根”,对照四个答案,只有B能满足题目要求。
8.B。
我们知道树高为n的满二叉树的结点个数为2n−1,当树高为5时结点个数为31,当树高为6时结点个数为63,故答案是B。
9.B。
画一张图的事情,就不说了。
10.D。
由递推公式可得T(n)=1+(1+2+…+n)=n2+n2+1,故算法时间的复杂度为O(n2)。
11.D。
用vector存边,由一个顶点的边引到另一个顶点,再不断引出别的顶点,过程中每个顶点和每条边都只用到一遍,故复杂度为O(n+e)。
12.A。
哈夫曼算法用来求哈夫曼树,此树的特点就是引出的路程最短,求的过程运用到贪心思想,具体的请参考一下别的文章。
13.D。
llink和rlink分别指向前驱和后继,不妨设p的前驱为o,在未插入前p->llink就是o,o->rlink就是p,插入时,先将o->rlink赋为q,再将q->rlink赋为p,然后将q->llink赋为o,最后将p->llink赋为q。
NOIP普及组历届试题分析

对于100%的数据,3 ≤ n ≤ 100 测验题给出的正整数大小不超过10,000。
试题分析
题意大意:给你n个数,在这n个数中,找 到满足A+B=C的C的个数,注意不是这个 等式的个数。
样例中,1,2,3,4有1+2=3,1+3=4两个。
由于本题数据规模n<=100,我们可以直接
枚举C, A, B,三层循环解决问题。
扫雷游戏 (noip2015普及组第二题)
输入样例 1 33 *?? ??? ?*? 输入样例 2 23 ?*? *??
输出样例 1 mine.out *10 221 1*1 输出样例 2 mine.out 2*1 *21
对于 100%的数据,1≤n≤100,1≤m≤100
问题分析:
本题也是简单的枚举类试题。 我们从雷区的第一行第一列(1,1)开始,判断它周围 有多少个地雷。 由于本题读入的是字符,读入时需要注意: readln(n,m); for i=1 to n do begin for j=1 to m do read(a[i][j]); readln; end;
比例简化 (noip2014普及组第二题)
在社交媒体上,经常会看到针对某一个观点同意与 否的民意调查以及结果。例如,对某 一观点表示 支持的有 1498 人,反对的有 902 人,那么赞同与 反对的比例可以简单的记为1498:902。 不过,如果把调查结果就以这种方式呈现出来,大 多数人肯定不会满意。因为这个比例的数值太大, 难以一眼看出它们的关系。对于上面这个例子,如 果把比例记为 5:3,虽然与 真实结果有一定的误差, 但依然能够较为准确地反映调查结果,同时也显得 比较直观。 现给出支持人数 A,反对人数 B,以及一个上限 L, 请你将 A 比 B 化简为 A’比 B’,要求在 A’和 B’均 不大于 L 且 A’和 B’互质(两个整数的最大公约数 是 1)的前提下,A’/B’ ≥ A/B 且 A’/B’ - A/B 的值 尽可能小。
NOIP2015复赛普及组试题.docx
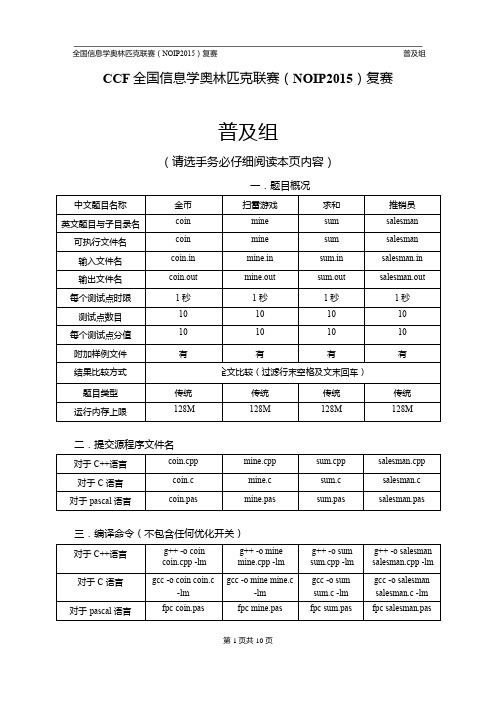
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)【问题描述】注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币(coin.cpp/c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为coin.in。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为coin.out。
输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【问题描述】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(mine.cpp/c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
noip2015普及组复赛试题

noip2015普及组复赛试题题目一:矩阵运算给定一个n阶方阵A(1 ≤ n ≤ 100),求A的所有指定行指定列删除后得到的新矩阵的行列式。
输入格式:输入第一行包含一个整数n,表示方阵的阶数。
接下来n行,每行包含n个整数,表示方阵A的元素。
接下来一行包含两个整数,表示要删除的行和列的序号。
输出格式:输出一个整数,表示新矩阵的行列式的值。
题目要求:首先,我们需要编写一个能够计算矩阵行列式的函数,然后根据题意进行修改,使其能够处理删除指定行列后的新矩阵,并返回新矩阵的行列式的值。
算法思路:我们可以使用拉普拉斯展开定理来计算矩阵行列式的值。
首先定义一个变量result,初始化为0。
然后遍历矩阵的第一行元素,对于第i 个元素,根据其正负性,计算其余元素组成的(n-1)阶子矩阵的行列式的值,并递归调用自身。
最后将每个元素计算得到的行列式值乘以其对应的元素,累加到result上。
然后根据题目要求,在计算每个元素对应的子矩阵时,判断是否需要删除指定的行列。
如果需要删除,则直接跳过该行列,否则继续计算。
代码如下:```pythondef determinant(matrix):n = len(matrix)if n == 1:return matrix[0][0]result = 0for i in range(n):if n > 2:sub_matrix = [row[:i] + row[i+1:] for row in matrix[1:]]else:sub_matrix = matrix[1:]det = determinant(sub_matrix)result += (-1) ** i * matrix[0][i] * detreturn resultn = int(input())matrix = []for _ in range(n):row = list(map(int, input().split()))matrix.append(row)row, col = map(int, input().split())matrix = [matrix[i][:col] + matrix[i][col+1:] for i in range(row)] # 删除指定列matrix = matrix[:row] + matrix[row+1:] # 删除指定行result = determinant(matrix)print(result)```题目二:水果分配小明和他的朋友们买了n个水果,其中有x个苹果和y个香蕉。
NOIP2015复赛普及组试题
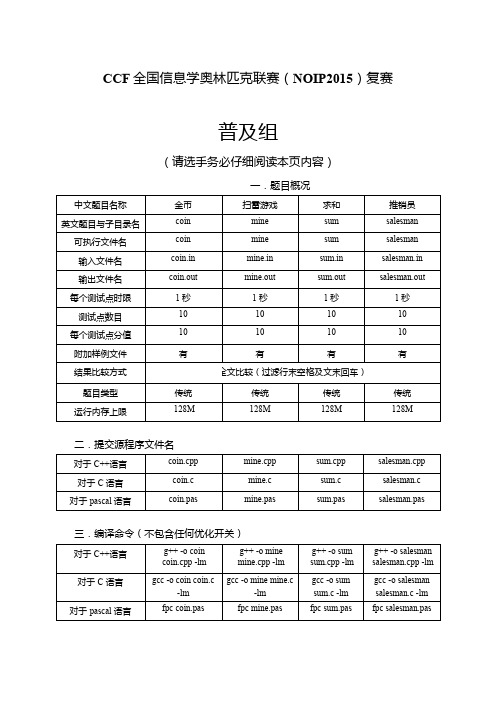
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛
普及组
(请选手务必仔细阅读本页内容)
一.题目概况
二.提交源程序文件名
三.编译命令(不包含任何优化开关)
注意事项:
1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,
内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币
(coin.cpp/c/pas)
国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】
输入文件名为coin.in。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】
输出文件名为coin.out。
输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】。
NOIP2015复赛普及组测试试题

NOIP2015复赛普及组试题————————————————————————————————作者:————————————————————————————————日期:CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况金币扫雷游戏求和推销员中文题目名称coin mine sum salesman 英文题目与子目录名coin mine sum salesman 可执行文件名coin.in mine.in sum.in salesman.in 输入文件名coin.out mine.out sum.out s alesman.out 输出文件名每个测试1 秒 1 秒 1 秒 1 秒点时限第3 页共14 页【问题描述】 第 4 页共 14 页测试点数目 10 10 10 10每个测试点分值 10 10 10 10附加样例文件 有有 有 有结果比较方式全文比较(过滤行末空格及文末回车)题目类型 传统 传统 传统 传统 运行内存上限128M128M128M128M二.提交源程序文件名对于 C++语言coin.cpp mine.cpp sum.cpp salesman.cpp【问题描述】 第 5 页共 14 页对于 C 语言 coin.c mine.c sum.c salesman.c对于 pascal 语言coin.pas mine.pas sum.pas salesman.pas三.编译命令(不包含任何优化开关)对于 C++语言 g++ -o coin coin.cpp -lm g++ -o mine mine.cpp -lm g++ -o sum sum.cpp -lm g++ -o salesmansalesman.cpp-lm对于 C 语言gcc -o coin coin.c -lm gcc -omine mine.c -lm gcc -o sum sum.c -lm gcc -o salesmansalesman.c -lm 对于pascal 语言fpc coin.pas fpc mine.pas fpc sum.pas fpc salesman.pas【问题描述】注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
NOIP2015提高组day1第二题解题报告

NOIP2015提高组day1第二题解题报告NOIP2015提高组复赛Day1第二题解题报告By 某蒟蒻zrw1.题目大概描述(因为写的时候题目还没放出来)几个小盆友们在传递自己的信息(生日),并且每个小盆友只会把自己知道的信息传给唯一的一个人【但是自己可以收到很多信息,并会在收到信息的下一轮把这些信息传给那个唯一的人】(单相思233333),问多少轮后自己会收到自己一开始传递出去的自己的信息。
输入:第一行一个整数n,表示有n个人接下来n行,每行一个数j,设这是除第一行外的第i行,那么j 表示第i个人只会把信息传给第j个人。
输出:一个整数,表示最少几轮后自己的信息会回到自己手中。
样例输入:52 4 23 1样例输出:3数据规模:100% n<=200000 60% n<=2500 30% 记不住了……2.大概需要什么样的算法根据数据规模,我们可以大概判断需要多少效率的算法,甚至有的时候可以猜出这题用的是什么算法。
对于本题来说,60%大概就是O(n^2)的算法了,一般是裸的暴力回溯或者是暴力广搜,也有用floyd的(我是从NOIP吧上看到的)。
如果要AC的话,算法效率至少要在O(nlogn)以下(log在这里是以2为底不是以10为底)。
然而,本题是有O(n)算法的,下面会讲。
3.我们还是画个图吧(图可能比较难看,但能看就行)画画图,就会知道这是在做一件什么事情了。
以样例数据为例:我们很容易发现,2,3,4,形成了一个环,而1和5,并没有什么卵用……所以在环234中,由于每一轮可以把在上一轮知道的信息传给唯一的下一个人,在234环中,就需要3轮,信息才能传到多画几个图(由于本人很懒,就只画一张特殊情况比较多的小图):(有木有一种贵圈真乱的感觉)我们可以看出来,1,5,6,成了一个环,而2,3,4,8,也成了一个环,7,9,是来打酱油的。
那么对于这两个环来说,因为每一轮可以传递上一轮信息给下一个人,所以显然是1,5,6这个环比较早传完,3轮。
NOIP2015复赛普及组精彩试题

CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数 main()的返回值类型必须是 int,程序正常结束时的返回值必须是 0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存 4G,上述时限以此配置为准。
4、只提供 Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币(coin.cpp/c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续 N 天每天收到 N 枚金币后,骑士会在之后的连续 N+1天里,每天收到 N+1 枚金币。
请计算在前 K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为 coin.in。
输入文件只有 1 行,包含一个正整数 K,表示发放金币的天数。
【输出格式】输出文件名为 coin.out。
输出文件只有 1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例 1】【输入输出样例 1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到 1+2+2+3+3+3=14 枚金币。
【输入输出样例 2】【数据说明】对于 100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(mine.cpp/c/pas)扫雷游戏是一款十分经典的单机小游戏。
在 n 行 m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
2015年NOIP信息学奥林匹克初赛试题和答案(普及组C++语言)

第二十一届全国青少年信息学奥林匹克联赛初赛普及组C++语言试题竞赛时间:2015 年10 月11 日14:30-16:30一、单项选择题(共20 题,每题1.5 分,共计30 分;每题有且仅有一个正确选项)⒈1MB 等于( )。
A.10000 字节B.1024 字节C.1000×1000 字节D.1024×1024 字节⒉在PC 机中,PENTIUM(奔腾)、酷睿、赛扬等是指()。
A.生产厂家名称 B.硬盘的型号 C.CPU 的型号 D.显示器的型号⒊操作系统的作用是()。
A.把源程序译成目标程序B.便于进行数据管理C.控制和管理系统资源D.实现硬件之间的连接⒋在计算机内部用来传送、存贮、加工处理的数据或指令都是以()形式进行的。
A.二进制码B.八进制码C.十进制码D.智能拼音码⒌下列说法正确的是()。
A.CPU 的主要任务是执行数据运算和程序控制B.存储器具有记忆能力,其中信息任何时候都不会丢失C.两个显示器屏幕尺寸相同,则它们的分辨率必定相同D.个人用户只能使用Wifi 的方式连接到Internet⒍二进制数00100100 和00010100 的和是( )。
A.00101000B.01100111C.01000100D.00111000⒎与二进制小数0.1 相等的十六进制数是()。
A.0.8B.0.4C.0.2D.0.1⒏所谓的“中断”是指()。
A.操作系统随意停止一个程序的运行B.当出现需要时,CPU 暂时停止当前程序的执行转而执行处理新情况的过程C.因停机而停止一个程序的运行D.电脑死机⒐计算机病毒是()。
A.通过计算机传播的危害人体健康的一种病毒B.人为制造的能够侵入计算机系统并给计算机带来故障的程序或指令集合C.一种由于计算机元器件老化而产生的对生态环境有害的物质D.利用计算机的海量高速运算能力而研制出来的用于疾病预防的新型病毒⒑FTP 可以用于( )。
A.远程传输文件B.发送电子邮件C.浏览网页D.网上聊天⒒下面哪种软件不属于即时通信软件()。
NOIP2015复赛普及组试题
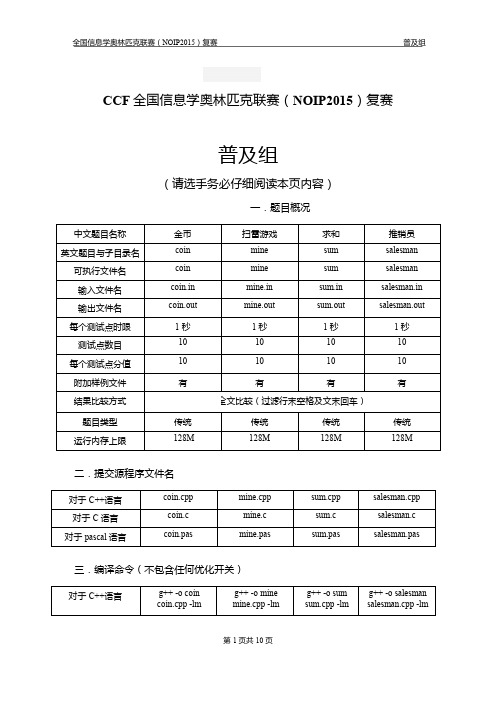
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)【问题描述】注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币(coin.cpp/c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为coin.in。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为coin.out。
【问题描述】输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(mine.cpp/c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷【问题描述】(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
NOIP2015复赛普及组试题
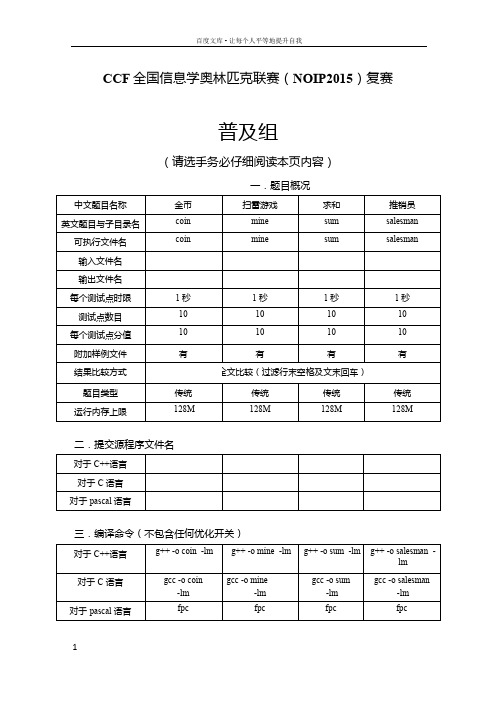
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为。
输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
玩家翻开一个非地雷格时,该格将会出现一个数字——提示周围格子中有多少个是地雷格。
NOIP2015复赛普及组试题
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为。
输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
玩家翻开一个非地雷格时,该格将会出现一个数字——提示周围格子中有多少个是地雷格。
NOIP2015普及组复赛解题报告

NOIP2015普及组解题报告南京师范大学附属中学树人学校CT1. 金币(coin.cpp/c/pas)【问题描述】国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N天每天收到N枚金币后,骑士会在之后的连续N+1天里,每天收到N+1枚金币。
请计算在前K天里,骑士一共获得了多少金币。
【输入格式】输入文件名为coin.in。
输入文件只有1行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为coin.out。
输出文件只有1行,包含一个正整数,即骑士收到的金币数。
【数据说明】对于100%的数据,1 ≤K ≤10,000。
【思路】模拟【时空复杂度】O(k),O(1)2、扫雷游戏(mine.cpp/c/pas)【问题描述】扫雷游戏是一款十分经典的单机小游戏。
在n行m列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
玩家翻开一个非地雷格时,该格将会出现一个数字——提示周围格子中有多少个是地雷格。
游戏的目标是在不翻出任何地雷格的条件下,找出所有的非地雷格。
现在给出n行m列的雷区中的地雷分布,要求计算出每个非地雷格周围的地雷格数。
注:一个格子的周围格子包括其上、下、左、右、左上、右上、左下、右下八个方向上与之直接相邻的格子。
【输入格式】输入文件名为mine.in。
输入文件第一行是用一个空格隔开的两个整数n和m,分别表示雷区的行数和列数。
接下来n行,每行m个字符,描述了雷区中的地雷分布情况。
字符’*’表示相应格子是地雷格,字符’?’表示相应格子是非地雷格。
相邻字符之间无分隔符。
【输出格式】输出文件名为mine.out。
输出文件包含n行,每行m个字符,描述整个雷区。
用’*’表示地雷格,用周围的地雷个数表示非地雷格。
NOIP2015复赛普及组试题
CCF 全国信息学奥林匹克联赛(NOIP2015)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 金币(coin.cpp/c/pas)国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续N 天每天收到N 枚金币后,骑士会在之后的连续N+1 天里,每天收到N+1 枚金币。
请计算在前K 天里,骑士一共获得了多少金币。
【输入格式】输入文件名为coin.in。
输入文件只有1 行,包含一个正整数K,表示发放金币的天数。
【输出格式】输出文件名为coin.out。
输出文件只有1 行,包含一个正整数,即骑士收到的金币数。
【输入输出样例1】【输入输出样例1 说明】骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。
因此一共收到1+2+2+3+3+3=14 枚金币。
【输入输出样例2】见选手目录下的coin/coin2.in 和coin/coin2.ans。
【数据说明】对于100%的数据,1 ≤ K ≤ 10,000。
2.扫雷游戏(mine.cpp/c/pas)扫雷游戏是一款十分经典的单机小游戏。
在n 行m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
noip复赛总结归纳c

noip复赛总结归纳(2010至2015年c++普及组复赛试题)一、【题目】1.数字统计(two.pas/c/cpp)【问题描述】请统计某个给定范围[L, R]的所有整数中,数字2 出现的次数。
比如给定范围[2, 22],数字2 在数2 中出现了1 次,在数12 中出现1 次,在数20 中出现1 次,在数21 中出现1 次,在数22 中出现2 次,所以数字2 在该范围内一共出现了6次。
【输入】输入文件名为two.in。
输入共1 行,为两个正整数L 和R,之间用一个空格隔开。
【输出】输出文件名为two.out。
输出共1 行,表示数字2 出现的次数。
【输入输出样例1】two.in two.out2 22 6【输入输出样例2】two.in two.out2 100 20【数据范围】1 ≤ L ≤ R≤ 10000。
【算法】把每一位分出来,一一判断【代码】#include<cstdio>using namespace std;int main(){int r,l,ans=0;scanf("%d%d",&r,&l);for(int i=r;i<=l;i++)//一一判断{int num=i;while(num>0)//把每一位分离{if(num%10==2)ans++;num/=10;}}printf("%d",ans);return 0;}【年份】2010二、【题目】2.接水问题(water.pas/c/cpp)【问题描述】学校里有一个水房,水房里一共装有m 个龙头可供同学们打开水,每个龙头每秒钟的供水量相等,均为1。
现在有n 名同学准备接水,他们的初始接水顺序已经确定。
将这些同学按接水顺序从1到n 编号,i 号同学的接水量为wi。
接水开始时,1 到m 号同学各占一个水龙头,并同时打开水龙头接水。
当其中某名同学j 完成其接水量要求wj 后,下一名排队等候接水的同学k马上接替j 同学的位置开始接水。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精心整理NOIP2015普及组解题报告南京师范大学附属中学树人学校CT1.金币(coin.cpp/c/pas)【问题描述】国王将金币作为工资,发放给忠诚的骑士。
第一天,骑士收到一枚金币;之后两天(第二天和第三天)放模式会一直这样延续下去:当连续N续N+1天里,每天收到N+1枚金币。
请计算在前K【输入格式】输入文件名为coin.in。
输入文件只有1【数据说明】对于100%的数据,1≤K≤10,000。
【思路】模拟【时空复杂度】O(k),O(1)2、扫雷游戏(mine.cpp/c/pas)【问题描述】扫雷游戏是一款十分经典的单机小游戏。
在n行m列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。
玩家翻开一个非地雷格时,该格将会出现一个数字——提示周围格子中有多少个是地雷格。
游戏的目标是在不翻出任何地雷格的条件下,找出所有的非地雷格。
现在给出n行m向上与之直接相邻的格子。
【输入格式】输入文件名为mine.in。
接下来n行,每行m雷个数表示非地雷格。
相邻字符之间无分隔符。
【数据说明】对于100%的数据,1≤n≤100,1≤m≤100。
【思路】模拟【技巧】可将数组多开一圈,省去边界条件的判断。
【时空复杂度】O(mn),O(mn)3.求和(sum.cpp/c/pas)【问题描述】一条狭长的纸带被均匀划分出了n个格子,格子编号从1到n。
每个格子上都染了一种颜色color i(用[1,m]当中的一个整数表示),并且写了一个数字number i。
定义一种特殊的三元组:(x,y,z),其中x,y,z都代表纸带上格子的编号,这里的三元组要求满足以下两个条件:1.x,y,z都是整数,x<y<z,y?x=z?y2.color x=color z满足上述条件的三元组的分数规定为带的分数除以10,007所得的余数即可。
【输入格式】输入文件名为sum.in。
m,n代表纸带上格子的个数,m代表纸第二行有n第i个数字number i代表纸带上编号为i的格子第三行有m个用空格隔开的正整数,第i个数字color i代表纸带上编号为i的格子染的颜色。
【输出格式】输出文件名为sum.out。
共一行,一个整数,表示所求的纸带分数除以10,007所得的余数。
【数据说明】对于第1组至第2组数据,1≤n≤100,1≤m≤5;对于第3组至第4组数据,1≤n≤3000,1≤m≤100;对于第5组至第6组数据,1≤n≤100000,1≤m≤100000,且不存在出现次数超过20的颜色;对于全部10组数据,1≤n≤100000,1≤m≤100000,1≤color i≤m,1≤number i≤100000。
【思路】件的三元组“找”出来。
至少需要枚举三元组(x,y,z)不要选y,因为y对分数没什么用)。
1、因为x<y<z2、因为y-x=z-y,所以y无关,只需枚举z和x。
3、因为colour x=colour z之前同奇偶且同色的x。
),能得40分。
如何快速枚举x呢?(x+z)·(number x+number z)显然我们不方便处理多项式乘法,那就把它拆开(事实上很多人到这步都放弃了,其实试一试立刻就明白了)=x·number x+x·number z+z·number x+z·number z那么对于z的所有合法决策x1,x2, (x)根据乘法分配率,分数=Σ(xi*number xi)+Σ(xi)*number z+Σ(number xi)*z+Σ(z*number z)(1<=i<=k)由于z是枚举的,所以只需快速得到Σ(x·number x),Σx,Σnumber x和k(注意最后一项被算了k次,要乘k)这样我们就可以开4个累加器,分别记录这四个量。
而对于不同奇偶性、不同颜色的z有不同的决策x,所以要开一个s[2][m][4]的累加器。
【时空复杂度】O(n),O(n+m)【样例程序】#include<cstdio>constintmaxn=100000;constintmaxm=100000;constintp=10007;intn,m,ans;ints[2][maxm+1][4];voidinit(){}voidsolve(){for(inti=1;i<=n;i++){intz=i%p,numz=number[i]%p,c=colour[i],t=i%2;intcount=s[t][c][0]%=p,x=s[t][c][1]%=p,numx=s[t][c][2]%=p,x_numx=s[t][c][3]%=p;ans=(ans+((count*z)%p*numz)%p)%p;ans=(ans+x_numx)%p;ans=(ans+x*numz)%p;ans=(ans+z*numx)%p;s[t][c][0]++;s[t][c][1]+=z;s[t][c][2]+=numz;s[t][c][3]+=z*numz;}}voidoutput(){printf("%d\n",ans);fclose(stdin);fclose(stdout);}intmain(){init();solve();output();return0;}4.推销员(salesman.cpp/c/pas)【问题描述】阿明是一名推销员,他奉命到螺丝街推销他们公司的产品。
螺丝街是一条死胡同,出口与入口是同一个,街道的一侧是围墙,另一侧是住户。
螺丝街一共有N家住户,第i家住户到入口的距离为S i米。
由于同一栋房子里可以有多家住户,所以可能有多家住户与入口的距离相等。
阿明会从入口进入,依次向螺丝街的X家住户推销产品,然后再原路走出去。
阿明每走1米就会积累1点疲劳值,向第i是工作狂,他想知道,对于不同的X少点疲劳值。
【输入格式】输入文件名为salesman.in。
第一行有一个正整数N接下来的一行有N S i表示第i家住户到入口的距离。
数据保证S1≤S2i个整数A i表示向第i户住户推销产品会积累的【输出格式】输出文件名为salesman.out。
输出N行,每行一个正整数,第i行整数表示当X=i时,阿明最多积累的疲劳值。
【数据说明】对于20%的数据,1≤N≤20;对于40%的数据,1≤N≤100;对于60%的数据,1≤N≤1000;对于100%的数据,1≤N≤100000。
【思路】题目要求每一个X的情况,显然不能每个X专门推一遍,要充分利用已知的X的情况,那么很可能会是DP。
定义f[i]为X=i时的最大疲劳值。
的决策应该会包含f[i]证明:设f[i]的决策为k1,k2,……,k i(k1<k2<……<k k s换成j并增加了一个决策k i+1,f[i+1]的决策kf[i]=2*s[k i]+Σa[k tf[i+1]=2*s[maxk]+Σa[k t t](s+1<=t<=i)+a[j]+a[k i+1]∵2*s[maxk]+Σa[k t是X=i时的一种决策的k s-1,k s+1,……k i,k j时)∴Σa[k t](s+1<=t<=i)+a[j]<=f[i]∴Σa[k t](s+1<=t<=i)+a[j]+a[k i+1] <=f[i]+a[k i+1](即决策为k1,k2,……,k s,……,k i,k i+1时的疲劳值)若小于,说明保留k s更优;若等于,对于两个目前疲劳值相等的决策序列k,max{k}越小越好(就是说目前走的路程越短越好),因为在max{k}左边的决策l只能增加a[l]的疲劳值,而对于max{k}右边的决策r则可以增加2*(s[r]-s[max{k}])+a[r],对于左边,max{k}没有影响,而对于右边,max{k}越小,后面的f[]增加疲劳值的空间越大。
根据以上原则,虽然决策k1,k2,……,k s,……,k i与决策k1,k2,……k s-1,k s+1,……k i,k j疲劳值相等,但f[i]选择了前者,说明前者更优。
综上,无论小于或等于,决策k1,k2,……,k s,……,k i都比决策k1,k2,……k s-1,k s+1,……k i,k j更优。
∴f[i+1]的最优决策一定包含了f[i]的最优决策,证毕.也就是说,对于f[i],只需在f[i-1]的基础上加一个最优决策就可以了。
易得出状态转移方程:其中k决策。
解释一下:因为maxi左边的决策k;而maxi右边的决策k2,也就是增加了枚举k的话时间复杂度是O(n分。
maxi的左边,我们需要动态求区间a[k]最值,无论是log2n级别的;而对于maxi右边,由于所,所以我们只要求区间2*s[k]+a[k]的最值,而且可用决策必然是不断减少的,可以预处理排个递减序,每次找第一个合法决策。
当然,左边的方法对于右边同样适用。
同时,如果选择了右边的决策k,还需要将maxi到k之间的决策加入到左边的待选决策中。
(因为它们的身份已经从右边的点变成了左边的点)。
由于每个决策最多从右边出一次,从左边进一次、出一次,均摊时间复杂度是O(nlog2n),能得100分。
(可惜考试时多写了一个“]”,编译错误,400变成了300)【时空复杂度】O(nlog2n),O(n)(取决于使用的数据结构)【样例程序】heap:#include<cstdio>#include<algorithm>usingnamespacestd;constintmaxn=100000;intn;ints[maxn+1],a[maxn+1],f[maxn+1];intleft[maxn+1],right[maxn+1],l,r=1,maxi; boolcmpl(constinti,constintj){if(a[i]!=a[j])returna[i]<a[j];elsereturni>j;}boolcmpr(constinti,constintj){elsereturni<j;}voidinit(){scanf("%d",&s[i]);for(inti=1;i<=n;i++){scanf("%d",&a[i]);right[i]=i;}sort(right+1,right+n+1,cmpr);}voidchoose_left(constinti){f[i]=f[i-1]+a[left[1]];pop_heap(left+1,left+l--+1,cmpl);}voidchoose_right(constinti){f[i]=f[i-1]+2*(s[right[r]]-s[maxi])+a[right[r]]; for(inti=maxi+1;i<right[r];i++){left[++l]=i;push_heap(left+1,left+l+1,cmpl);}maxi=right[r++];while(r<=n&&right[r]<=maxi)r++;}voidsolve(){for(inti=1;i<=n;i++)if(l==0)choose_right(i);elseif(r>n)choose_left(i);choose_left(i);elsechoose_right(i);}voidoutput(){}intmain(){init();solve();output();return0;}set:#include<cstdio>#include<algorithm>usingnamespacestd;constintmaxn=100000;intn;ints[maxn+1],a[maxn+1],f[maxn+1];intleft[maxn+1],right[maxn+1],l,r=1,maxi;boolcmpl(constinti,constintj){if(a[i]!=a[j])returna[i]<a[j];elsereturni>j;}boolcmpr(constinti,constintj){if(2*s[i]+a[i]!=2*s[j]+a[j])return2*s[i]+a[i]>2*s[j]+a[j];elsereturni<j;}voidinit(){freopen("salesman.in","r",stdin);freopen("salesman.out","w",stdout);scanf("%d",&n);for(inti=1;i<=n;i++)scanf("%d",&s[i]);for(inti=1;i<=n;i++){scanf("%d",&a[i]);right[i]=i;}}{}voidchoose_right(constinti){f[i]=f[i-1]+2*(s[right[r]]-s[maxi])+a[right[r]]; for(inti=maxi+1;i<right[r];i++){left[++l]=i;push_heap(left+1,left+l+1,cmpl);}maxi=right[r++];while(r<=n&&right[r]<=maxi)r++;}voidsolve(){for(inti=1;i<=n;i++)if(l==0)choose_right(i);elseif(r>n)choose_left(i);elseif(a[left[l]]>=2*(s[right[r]]-s[maxi])+a[right[r]]) choose_left(i);elsechoose_right(i);}voidoutput(){for(inti=1;i<=n;i++)printf("%d\n",f[i]);fclose(stdin);fclose(stdout);}intmain(){init();solve();output();return0;}intn;ints[maxn+1],a[maxn+1],f[maxn+1],maxi;classcmpl{public:booloperator()(constinti,constintj){returna[i]<a[j];}};classcmpr{booloperator()(constinti,constintj){if(2*s[i]+a[i]!=2*s[j]+a[j])return2*s[i]+a[i]<2*s[j]+a[j];elsereturni>j;}};priority_queue<int,vector<int>,cmpl>left; priority_queue<int,vector<int>,cmpr>right; voidinit(){freopen("salesman.in","r",stdin);freopen("salesman.out","w",stdout);scanf("%d",&n);for(inti=1;i<=n;i++)scanf("%d",&s[i]);for(inti=1;i<=n;i++){scanf("%d",&a[i]);right.push(i);}}voidchoose_left(constinti){f[i]=f[i-1]+a[left.top()];left.pop();}{maxi=r;while(!right.empty()&&right.top()<=maxi) right.pop();}voidsolve(){for(inti=1;i<=n;i++)if(left.empty())choose_right(i);elseif(right.empty())choose_left(i);{intl=left.top(),r=right.top();if(l>=2*(s[r]-s[maxi])+a[r])choose_left(i);elsechoose_right(i);}}voidoutput(){for(inti=1;i<=n;i++)printf("%d\n",f[i]);fclose(stdin);fclose(stdout);}intmain(){init();solve();output();return0;}鉴于set和priority_queue heap 低一些。
