NOIP2017普及组复赛-解题报告
NOIP2017复赛普及组试题
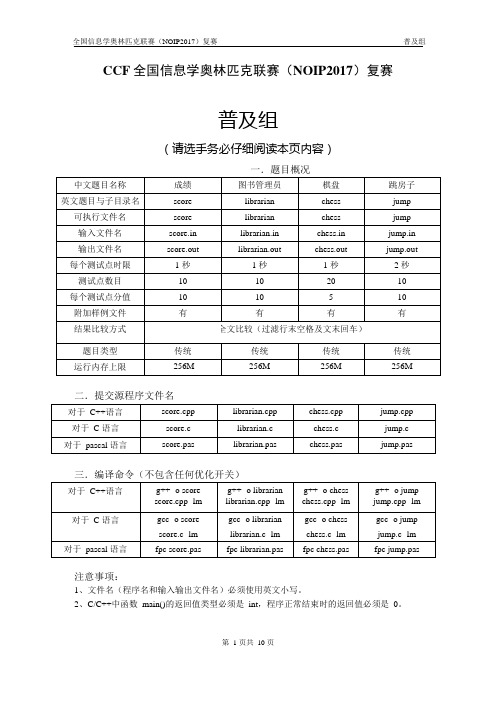
CCF全国信息学奥林匹克联赛(NOIP2017)复赛普及组(请选手务必仔细阅读本页内容)二.提交源程序文件名三.编译命令(不包含任何优化开关)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、提交的程序代码文件的放置位置请参照各省的具体要求。
6、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 成绩(score.cpp/c/pas)【问题描述】牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%牛牛想知道,这门课程自己最终能得到多少分。
【输入格式】输入文件名为score.in。
输入文件只有1 行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。
相邻两个数之间用一个空格隔开,三项成绩满分都是100 分。
【输出格式】输出文件名为score.out。
输出文件只有1 行,包含一个整数,即牛牛这门课程的总成绩,满分也是100 分。
【输入输出样例1】【输入输出样例1 说明】牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
【输入输出样例2】【输入输出样例2 说明】牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
noip2017提高组复赛解题报告

noip2017提高组复赛解题报告定期推送帐号信息学新闻,竞赛自主招生,信息学专业知识,信息学疑难解答,融科教育信息学竞赛培训等诸多优质内容的微信平台,欢迎分享文章给你的朋友或者朋友圈!以下解题思路及代码未经官方评测,仅供参考,复赛成绩以官方(CCF)评测结果为准。
Day11.小凯的疑惑(math.cpp/c/pas)【问题描述】小凯手中有两种面值的金币,两种面值均为正整数且彼此互素。
每种金币小凯都有无数个。
在不找零的情况下,仅凭这两种金币,有些物品他是无法准确支付的。
现在小凯想知道在无法准确支付的物品中,最贵的价值是多少金币?注意:输入数据保证存在小凯无法准确支付的商品。
【输入格式】输入文件名为math.in。
输入数据仅一行,包含两个正整数a 和b,它们之间用一个空格隔开,表示小凯手中金币的面值。
【输出格式】输出文件名为math.out。
输出文件仅一行,一个正整数N,表示不找零的情况下,小凯用手中的金币不能准确支付的最贵的物品的价值。
【输入输出样例1】math.in3 7 math.out11【数据规模与约定】对于30%的数据: 1 ≤a,b ≤50。
对于60%的数据: 1 ≤a,b ≤10,000。
对于100%的数据:1 ≤a,b ≤1,000,000,000。
数学太差只找规律吧。
设:其中一个数为2则:2、3=>1;2、5=>3;2、7=>5;2、11=>9得:2、n=>n-2设:其中一个数为3则:3、5=>7;3、7=>11;3、11=>19;3、13=>23得:3、n=>2n-3设:其中一个数为5则:5、7=>23;5、11=>39;5、13=>47;5、17=>63得:5、n=>4n-5所以:m、n=>(m-1)n-m #includeusing namespace std;int main(){ long long a,m,n;scanf('%lld %lld',&m,&n); a=(m-1)*n-m;printf('%lld',a); return 0;} 2.时间复杂度(complexity.cpp/c/pas)【问题描述】小明正在学习一种新的编程语言A++,刚学会循环语句的他激动地写了好多程序并给出了他自己算出的时间复杂度,可他的编程老师实在不想一个一个检查小明的程序,于是你的机会来啦!下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。
NOIP2017 解题报告 ZYH

NOIP2017解题报告一、成绩(score)这是一道送分题。
题目明确规定A、B、C都是10的正数倍。
所以我们可以将读入进来的a、b、c都先整除10,再分别将a*2,b*3,c*5,然后相加,就是最后的答案。
且结果可以保存在longint类型中。
代码如下:vara,b,c,sum:longint;beginassign(input,'score.in');reset(input);assign(output,'score.out');rewrite(output);readln(a,b,c);sum:=a div10*2+b div10*3+c div10*5;writeln(sum);close(input);close(output);end.但倘若题目没有说明A、B、C都是10的正数倍,那么我们就将a*0.2,b*0.3,c*0.5,然后相加。
但这一次结果需存在实型中。
二、图书管理员(librarian)这是一道简单题。
其实吧,本套试卷我们要认真阅读数据规模,总能发现一些微妙的细节。
例如本题,所有的图书编码和需求码均不超过10,000,000完全可以用longint存的(那不就很棒棒了~~)对于读入的每一个需求码,我们都去循环一遍,先判断当前的这本书符不符合需求,但怎么判断呢?数据会告诉我们需求码的长度k,也就是说我们要判断当前书码的后k位是否等于需求码。
哈哈哈,没错,只要用书码mod(10的k次方)即可。
如果相等,那么进行判断取小(因为题目君说要最小的啦~~)。
所以这里如果使用了快排从小到大,那么当你找到第一个满足要求的书码就是答案。
当然不用也可以,时间复杂度为O(nq),1000,000不会炸。
话不多说,代码如下:varn,m,i,j,x,y,sum,min:longint;a:array[0..1000]of longint;procedure f(l,r:longint);varx,y,mid,t:longint;beginx:=l;y:=r;mid:=a[(l+r)div2];repeatwhile a[x]<mid do inc(x);while a[y]>mid do dec(y);if x<=y thenbegint:=a[x];a[x]:=a[y];a[y]:=t;inc(x);dec(y);end;until x>y;if l<y then f(l,y);if x<r then f(x,r);end;beginassign(input,'librarian.in');reset(input);assign(output,'librarian.out');rewrite(output);readln(n,m);for i:=1to n do readln(a[i]);f(1,n);for i:=1to m dobeginreadln(x,y);sum:=1;for j:=1to x do sum:=sum*10;min:=maxlongint;for j:=1to n doif a[j]mod sum=y then begin min:=a[j];break;end;if min=maxlongint then writeln(-1)else writeln(min);end;close(input);close(output);end.但倘若我们的需求码和编码是一些很大很大的数(longint无法承受)时,最最高大上的字符串就闪亮登场了(蹬蹬蹬,天空一声巨响,字符串闪亮登场)。
noip2017普及组复赛解题报告

解法 2 最短路 Dijstra 数据太弱所以用了 dij,数据再强一点的话就需要用邻接表和 spfa 了 (毕竟普及组题难不到哪里去 写的看起来代码看起来很多, 但原理不难 把所有有颜色的点拿出来当做一张新图的结点 初始情况下这些点之间边的长度可以这样判断: 情况 1:如果两点在棋盘上位置相邻,那么同色距离为 0,异色距离为 1(对 应 tryStright 方法) 情况 2 :如果两点在棋盘上位置不相邻但有一个共同相邻的空白点可以做跳 板,使用魔法后同色距离为 2,异色距离为 3(对应 tryIndirect 方法) 然后对这张新图做最短路,求出点(1,1)到其他所有有颜色点的最短路 最后如果(m,m)有颜色, (1,1)到(m,m)之间的距离就是最短路 否则需要借助跳板(m,m-1)或(m-1,m)用魔法到(m,m).
tryIndirectPre(x[i],y[i],x[i]-1,y[i],x[i]-1,y[i]-1); //上上 下下 左左 右右 这些可能通过魔法通过跳板两步到达的点,且跳板唯一 //如原-上-上 情况 2 tryIndirectPre(x[i],y[i],x[i],y[i]+1,x[i],y[i]+2); tryIndirectPre(x[i],y[i],x[i],y[i]-1,x[i],y[i]-2); tryIndirectPre(x[i],y[i],x[i]+1,y[i],x[i]+2,y[i]); tryIndirectPre(x[i],y[i],x[i]-1,y[i],x[i]-2,y[i]); } //直接复制的自己以前写的最短路 dij 模板 //找到点(1,1)到其他所有有颜色的点的最短路 bool hasbeen[1001]; for (i=1;i<=n;i++) hasbeen[i]=false; int pos = abs(chess[1][1]); //棋盘上点(1,1)在新图 path 里是对应的第 pos 个点 for (i=1;i<=n;i++) if (i!=pos) { minPath=10000000; k=1; for ( j=1;j<=n;j++) if ( j!=pos) { if ((hasbeen[ j]==false)&&(path[pos][ j]!=-1)&&(path[pos][ j]<minPath)) { k=j; minPath=path[pos][ j]; } } hasbeen[k]=true; for ( j=1;j<=n;j++) if ( j!=pos) if((path[pos][k]!=-1)&&(path[k][ j]!=-1)) if ((path[pos][ j]>path[pos][k]+path[k][ j])||(path[pos][ j]==-1)) path[pos][ j]=path[pos][k]+path[k][ j]; }
noip普及组复赛入门测试(答案+测试数据)

一、新龟兔赛跑(文件名xgtsp.pas)新龟兔赛跑比赛即将举行,此次龟兔赛跑比赛的规则与以往有所不同,不再考察兔子和乌龟谁在最短的时间内跑完规定的路程,而是考察谁在规定时间内跑的路程更长,且兔子和乌龟跑步都是匀速的。
由于兔子的坏习惯,它总喜欢把比赛的总时间T小时中的K小时拿来睡觉。
现在给你比赛的总时间T、兔子的睡觉时间K、兔子的速度U、乌龟的速度V,需要你求出该次比赛谁最后获胜。
输入第一行为一个整数X,表示有X组输入数据。
每组数据只有一行,包括4个数T、K、U、V (1 ≤ T≤ 300,0 ≤ K ≤ T,1 ≤ U ≤ 100,1 ≤ V ≤ 100)。
对于每组数据,输出只有一个数,如果兔子获胜则输出-1,如果乌龟获胜则输出1,如果同时到达则输出0。
允许输入一组数后立即输出对应的结果。
样例输入:21 12 16 2 6 3样例输出:1-1varv,u,t,k,n,i:integer;beginreadln(n);for i:=1 to n do beginreadln(t,k,u,v);if v*t>U*(t-k) then writeln(1);if v*t<U*(t-k) then writeln(-1);if v*t=U*(t-k) then writeln(0);end;end.1、输入:26 2 6 28 6 8 2输出:-12、输入:2300 280 60 20120 0 12 13输出:113、输入:3100 20 50 30100 50 45 25100 80 27 17输出:-1114、输入:3150 77 29 23127 11 22 13139 22 13 7输出:1-1-1二、小球路程(文件名:XQLC.PAS )已知小球从100米高度自由下落,落地后反弹起,又落地,又弹起,……。
每次弹起的高度都是上一次高度的一半。
求小球第N次反弹起的高度和球在整个过程所经过的路程(包括下落和反弹),用键盘输入N,输出反弹高度和经过路程,结果保留两位小数。
NOIp2017普及组解题报告与参赛总结

5
10 2
时间复杂度 ������(1) 空间复杂度 ������(1)
NOIp2017 普及组解题报告&参赛总结
By 浙江省诸暨市浣江教育集团浣江初中 孟煜皓 3 / 28
NOIp2017 普及组解题报告&参赛总结 By 浙江省诸暨市浣江教育集团浣江初中 孟煜皓
代码_算法一(Pascal)
1 var
29
ans := a[j];
30
if ans = '666666666' then writeln(-1) else writeln(ans);
31 end;
32 close(input);
33 close(output);
34 end.
NOIp2017 普及组解题报告&参赛总结
By 浙江省诸暨市浣江教育集团浣江初中 孟煜皓 7 / 28
算法一(100pts)
因为题目较为简单,所以直接将正解吧。 先读入元素集合和 ������ 个询问,对于每个询问 ������������, ������������,因为已经给定位数,且位 数不多,直接枚举(暴力)求出 ������������������1≤������≤������ ������������ (������������ ������������������ 10������������ = ������������) 即可。 时间复杂度 ������(������������) 空间复杂度 ������(1)
20
ans := a[j];
21
if ans = maxlongint then writeln(-1) else writeln(ans);
22 end;
【NOIP2017普及组】棋盘

【NOIP2017普及组】棋盘题目描述有一个m×m的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。
你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的),你只能向上、下、左、右四个方向前进。
当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 1个金币。
另外,你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。
但这个魔法不能连续使用,而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法;只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?输入格式第一行包含两个正整数m,n以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的n行,每行三个正整数x,y,c分别表示坐标为(x,y)的格子有颜色c。
其中c=1代表黄色,c=0代表红色。
相邻两个数之间用一个空格隔开。
棋盘左上角的坐标为(1,1),右下角的坐标为(m,m)。
棋盘上其余的格子都是无色。
保证棋盘的左上角,也就是(1,1)一定是有颜色的。
输出格式一个整数,表示花费的金币的最小值,如果无法到达,输出−1。
数据范围对于 30%的数据, 1≤m≤5,1≤n≤10。
对于 60%的数据, 1≤m≤20,1≤n≤200。
对于 100%的数据, 1≤m≤100,1≤n≤1,000。
题解这道题写起来还是挺有意思的。
我们根据题目不难得出要用一个二维数组来记录棋盘的状态。
我们更习惯于用0来表示没有或空,而不是用0表示红色,这只需要在输入的时候略处理一下即可(把0变成2)。
很明显是要从左上角做到右下角,花费尽可能少。
noip2017年度提高组复赛解题报告

noip2017提高组复赛解题报告定期推送帐号信息学新闻,竞赛自主招生,信息学专业知识,信息学疑难解答,融科教育信息学竞赛培训等诸多优质内容的微信平台,欢迎分享文章给你的朋友或者朋友圈!以下解题思路及代码未经官方评测,仅供参考,复赛成绩以官方(CCF)评测结果为准。
Day11.小凯的疑惑(math.cpp/c/pas)【问题描述】小凯手中有两种面值的金币,两种面值均为正整数且彼此互素。
每种金币小凯都有无数个。
在不找零的情况下,仅凭这两种金币,有些物品他是无法准确支付的。
现在小凯想知道在无法准确支付的物品中,最贵的价值是多少金币?注意:输入数据保证存在小凯无法准确支付的商品。
【输入格式】输入文件名为math.in。
输入数据仅一行,包含两个正整数a 和b,它们之间用一个空格隔开,表示小凯手中金币的面值。
【输出格式】输出文件名为math.out。
输出文件仅一行,一个正整数N,表示不找零的情况下,小凯用手中的金币不能准确支付的最贵的物品的价值。
【输入输出样例1】math.in3 7 math.out11【数据规模与约定】对于30%的数据: 1 ≤a,b ≤50。
对于60%的数据: 1 ≤a,b ≤10,000。
对于100%的数据:1 ≤a,b ≤1,000,000,000。
数学太差只找规律吧。
设:其中一个数为2则:2、3=>1;2、5=>3;2、7=>5;2、11=>9得:2、n=>n-2设:其中一个数为3则:3、5=>7;3、7=>11;3、11=>19;3、13=>23得:3、n=>2n-3设:其中一个数为5则:5、7=>23;5、11=>39;5、13=>47;5、17=>63得:5、n=>4n-5所以:m、n=>(m-1)n-m #includeusing namespace std;int main(){ long long a,m,n;scanf('%lld %lld',&m,&n); a=(m-1)*n-m;printf('%lld',a); return 0;} 2.时间复杂度(complexity.cpp/c/pas)【问题描述】小明正在学习一种新的编程语言A++,刚学会循环语句的他激动地写了好多程序并给出了他自己算出的时间复杂度,可他的编程老师实在不想一个一个检查小明的程序,于是你的机会来啦!下面请你编写程序来判断小明对他的每个程序给出的时间复杂度是否正确。
NOIP普及组解题分析报告

NOIP普及组解题报告————————————————————————————————作者:————————————————————————————————日期:NOIP2014普及组复赛解题报告本人是潍坊一中的wyw,69级,今年高一,现在马上就要NOIP了,打算把历年的NOIP普及、提高组题目都做一下,然后写写解题报告∵这个报告主要是给初中同学看的,所以我会写的详细一点Prolem 1 珠心算测试(count)这道题其实很简单,意思就是说给你一些数a1,a2,a3,a4...a n,然后让你回答有多少个A+B=C(A ≠ B ≠ C)满足(回答C的数量,而不是等式的数量)方法一那么有一种很明显的做法就是三层循环枚举C、A、B,注意:C是在最外层,若找到了一个A和一个B,满足上述等式,则C是一个符合要求的解,这时ans++,并且退出当前枚举,枚举下一个C,这种算法的时间复杂度是O(N3)而我当时没想到这个算法,因为有更好用而且简单更不容易出错的解法,方法二两重循环,分别枚举i=1...n,j=i+1...n,如果ai+aj这个数在集合中存在,那么you[a i+a j]←true,然后再从a1到a n做一次扫描,只要you[a i],ans++这个算法的好处在于它很好写,不用退出什么的,也不用注意循环的顺序,而且时间复杂度是O(N2)代码(方法2):#include<cstdio>using namespace std;int n, a[101], i, j, count;bool you[20001]={false};int main(){freopen("count.in","r",stdin);freopen("count.out","w",stdout);scanf("%d",&n);for(i=1;i<=n;i++)scanf("%d",&a[i]);for(i=1;i<n;i++)for(j=i+1;j<=n;j++)you[ a[i]+a[j] ]=true;count=0;for(i=1;i<=n;i++)count += you[ a[i] ];printf("%d\n",count);return 0;}在此征求一下大神的意见,如有更快的做法,敬请奉上小结:这道题很简单,但很多人没有做对的原因就是没有好好理解题意,但是根本原因其实还在于心态太骄傲了,认为是第一题就可以轻视,这样是不好的,水题我们更要做好啊,你想想同样是100分,这100分多么好拿,所以是水题、越该放平心态,细心地做。
NOIP2017复赛(普及组)解题报告!

NOIP2017复赛(普及组)解题报告!定期推送帐号信息学新闻,竞赛自主招生,信息学专业知识,信息学疑难解答,融科教育信息学竞赛培训等诸多优质内容的微信平台,欢迎分享文章给你的朋友或者朋友圈!1.成绩(score.cpp/c/pas)【问题描述】牛牛最近学习了 C++入门课程,这门课程的总成绩计算方法是:总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%牛牛想知道,这门课程自己最终能得到多少分。
【输入格式】输入文件名为 score.in。
输入文件只有 1 行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。
相邻两个数之间用一个空格隔开,三项成绩满分都是 100 分。
【输出格式】输出文件名为 score.out。
输出文件只有 1 行,包含一个整数,即牛牛这门课程的总成绩,满分也是 100 分。
【输入输出样例 1】score.in100100 80score.out90【输入输出样例 2】score.in60 90 80score.out79【数据说明】对于 30% 的数据,A=B=0。
对于另外 30% 的数据,A = B = 100。
对于 100% 的数据,0 ≤ A、B、C ≤ 100且 A、B、C 都是 10 的整数倍。
#includeusing namespace std;int a,b,c;int main(){cin>>a>>b>>c;a/=5;b=b*3/10;c/=2;cout<><>return 0;}2. 图书管理员 (librarian.cpp/c/pas)【问题描述】图书馆中每本书都有一个图书编码,可以用于快速检索图书,这个图书编码是一个正整数。
每位借书的读者手中有一个需求码,这个需求码也是一个正整数。
如果一本书的图书编码恰好以读者的需求码结尾,那么这本书就是这位读者所需要的。
牛客NOIP暑期七天营-普及组1解题报告

⽜客NOIP暑期七天营-普及组1解题报告A对于\(100\%\),直接开个桶统计即可。
⼊门题⽬。
B对于\(100\%\),直接按题⽬模拟就好。
每次两个指针扫⼀下就是\(O(n)\)的了。
整个加起来是\(O(\max(n,len)\times m)\)的复杂度。
可以结合代码理解。
C对于\(10\%\)直接copy代码然后完善⼀下头⽂件什么的就⾏了。
考虑这个\(dp\)是在⼲什么,其实就是求对于每个位置往前的前\(k\)⼤的数的和。
那么对于\(40\%\),直接删掉第三重循环(考虑如果不选这个数,可以直接直接从\(f[i-1][j]\)转移,所以第三重循环完全多余)对于\(100\%\),⽤⼀个数据结构动态维护前\(k\)⼤即可。
(这⾥⽤\(set\)或者⼩根堆,都⾏)复杂度\(O(n\log n)\)D对于\(10\%\),很明显是个\(O(n^6 )\)的算法..那么直接暴⼒枚举两个端点,然后暴⼒统计和取\(\max\)即可。
对于\(30\%\),注意到这个矩阵的⽣成⽅式有点特别,把它写出来,就会发现⼀个矩阵的和是⼀段\(a_i\)乘上⼀段\(b_j\),那么便可以省去统计两重循环,复杂度\(O(n^4)\)对于\(50\%\),考虑优化\(30\)分的做法,30分的统计就是⼀个前缀和相乘的形式,那么要让它最⼤⽆⾮3种情况,正数最⼤\(\times\)正数最⼤,负数最⼩\(\times\)负数最⼩,正数最⼩\(\times\)负数最⼤,第三种⼜可以分为正数最⼩在\(A\)中,正数最⼩在\(B\)中两种情况,于是维护前缀\(\max\)和前缀\(\min\),分类讨论⼀下,就可以\(O(n^2)\)解决了。
对于\(100\%\),既然是⼀段\(a_i\)乘上⼀段\(b_j\),那么分别统计最⼤⼦段和和最⼩⼦段和即可。
最后根据\(50\%\)的做法分四类情况讨论⼀下就好。
这部分其实就是把\(30\)和\(50\)分做法综合起来⽽已。
NOIP2017第二十三届全国青少年信息学奥林匹克联赛初赛普及组答案

三、阅读程序写结果(共4题,每题8分,共计32分)
1.
z
2.
8
3.
11
4.
输出1:1 3
(3分)
输出2:2017 1
(5分)
四、完善程序(共计28分,以下各程序填空可能还有一些等价的写法,由各省赛区组织本省专家审定及上机验证,可以不上报CCF NOI科学委员会复核)
Pascal语言
C++语言
C语言
count+=len[i]
(2)
count<m或m>count
2.5
(3)
lbound<ubound或ubound>lbound
3
(lbound+ubound+1) div 2或
(lbound+ubound+1)/2或
(4)
(lbound+ubound+1) shr 1或
(lbound+ubound+1)>>1或
3
(lbound+ubound) div 2 + 1
(lbound+ubound)/2+1
(5)
count:=count + len[i] div mid或
count=count+len[i]/mid或
3
inc(count, len[i] div mid)
count+=len[i]/mid
分值
1.
(1)
1
2
(2)
p>0或p<>0
p>0或p!=0或p
3
(3)
result * x mod m
NOIP2017复赛普与组试题(卷)
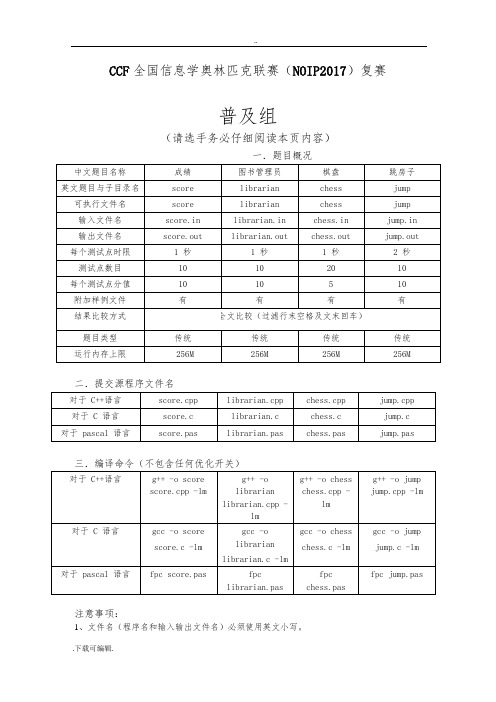
CCF全国信息学奥林匹克联赛(NOIP2017)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数 main()的返回值类型必须是 int,程序正常结束时的返回值必须是 0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存 4G,上述时限以此配置为准。
4、只提供 Linux 格式附加样例文件。
5、提交的程序代码文件的放置位置请参照各省的具体要求。
6、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 成绩(score.cpp/c/pas)【问题描述】牛牛最近学习了 C++入门课程,这门课程的总成绩计算方法是:总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%牛牛想知道,这门课程自己最终能得到多少分。
【输入格式】输入文件名为 score.in。
输入文件只有 1 行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。
相邻两个数之间用一个空格隔开,三项成绩满分都是 100 分。
【输出格式】输出文件名为 score.out。
输出文件只有 1 行,包含一个整数,即牛牛这门课程的总成绩,满分也是 100 分。
【输入输出样例 1】【输入输出样例 1 说明】牛牛的作业成绩是 100 分,小测成绩是 100 分,期末考试成绩是 80 分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
【输入输出样例 2】【输入输出样例 2 说明】牛牛的作业成绩是 60 分,小测成绩是 90 分,期末考试成绩是 80 分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
NOIP2017复赛普及组试题

CCF全国信息学奥林匹克联赛(NOIP2017)复赛普及组(请选手务必仔细阅读本页内容)一.题目概况二.提交源程序文件名三.编译命令(不包含任何优化开关)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux 格式附加样例文件。
5、提交的程序代码文件的放置位置请参照各省的具体要求。
6、特别提醒:评测在当前最新公布的NOI Linux 下进行,各语言的编译器版本以其为准。
1. 成绩(score.cpp/c/pas)【问题描述】牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%牛牛想知道,这门课程自己最终能得到多少分。
【输入格式】输入文件名为score.in。
输入文件只有1 行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。
相邻两个数之间用一个空格隔开,三项成绩满分都是100 分。
【输出格式】输出文件名为score.out。
输出文件只有1 行,包含一个整数,即牛牛这门课程的总成绩,满分也是100 分。
【输入输出样例1】【输入输出样例1 说明】牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
【输入输出样例2】【输入输出样例2 说明】牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
NOIP2017普及组复赛-解题报告

NOIP2017普及组复赛-解题报告衢州市兴华中学By 冯明浩给出三个整十数A,B,C ,求A*20%+B*30%+C*50%的值模拟直接粗暴地输出A*0.2+B*0.3+C*0.5时间复杂度:O(1) 期望得分:100由于分数均为整十数,先将分数各除以10,再直接输A*2+B*3+C*5。
这样就避免了精度问题时间复杂度:O(1) 期望得分:100给出N 个数Ai ,再进行Q 次询问,找后缀为给定数Bi 的最小的Ai模拟将Ai 及Bi 都转化成字符串。
每次询问都对N 个数进行后缀比较,挑出个最小的时间复杂度:O(N*Q*len) 期望得分:80 对算法一的比较进行优化——构造出n 10,对于Ai ,直接Ai Mod 10len ,判断是否相等。
这样每次比较的时间复杂度优至O(1)同时先将Ai 排序,再每次从小到大查询,一旦找到就停时间复杂度:小于O(N*Q)(一般情况) 期望得分:100读入Ai 时进行处理,构造ans[x]数组,记录询问X 的最小值。
对于每个Ai ,依次取出其后1、2、3……len 位,修正其的最小值。
这样每次查询,就可以O (1)出结果了时间复杂度:O(N*len) 空间复杂度:O(max(Bi)) 期望得分:100给出一个N*N 的矩阵,其中部分格有颜色每次可以从一个格向上下左右四个方向移动一格(不能越出矩阵且满足条件),根据两个格子的颜色有不同的代价求从左上角走至右下角的最小代价最短路(动态规划)直接暴力地按照题意进行DFS时间复杂度:O(n n *2) 期望得分:30以左上角为起点,右下角为终点,刷四个方向的SPFA(也可预先对相邻格建好边,刷最短路SPFA 或DIJ 或进行记忆化DFS )时间复杂度:O(k*n*n) 期望得分:100给出N 个格子的位置Xi 与价值Pi ,从起点0往右跳跃,初始跳跃的距离只能为d同时可以花费金币来调整其跳跃距离,花了t 个金币时可跳跃的距离为max(1,d-t)~(d+k)每遍历一个格子就会获得其代价Pi ,求要获得总价值为K 所需最少的金币数二分、动态规划、单调序列(堆)从小到大枚举所需金币数,用O(N*N)的DP 进行check ,一旦发现可行就为答案时间复杂度:O(max(Ai)*N*N) 期望得分:20分析发现,枚举的金币数越多,跳跃范围越大,总价值一定越多——满足二分答案的单调性,于是将算法一的枚举答案变为二分枚举时间复杂度:O()max(2log Xi *N*N) 期望得分:50 分析一下DP 的转移方程:F[i]=max(F[j])+P[i](max(1,d-t)≤a[i]-a[j]≤d+k)就会发现DP 的j 这次循环是为了找F[1~i-1]中的最大值,自然而然就想到了用堆优化——堆中存放F[1~i-1],若堆顶距当前X[i]大于d+k ,就丢掉该元素(再也没用)否则若堆顶距当前X[i]小于max(1,d-t),就暂存在临时数组中,最后在当前解更新好后记得塞回去则F[i]=F[heap[1]]+P[i]时间复杂度:O()max(2log Xi *N*k*N 2log ) 期望得分:80 继续优化算法三的DP :那些离当前X[i]太近的实际上完全没有必要塞入堆中,那么再另开一个变量j 记录当前往堆中塞入的最后一个元素。
历年noip普及组复赛试题

历年noip普及组复赛试题
NOIP(全国青少年信息学奥林匹克竞赛)是中国的一项信息学竞赛活动,包括普及组和提高组两个组别。
普及组主要面向初中生和高中生,复赛试题是选拔普及组的参赛选手的关键环节。
以下是历年NOIP普及组复赛试题的一些例子:
1. 2019年NOIP普及组复赛试题:
题目1,给定一个长度为N的字符串S,求出它的最长回文子串的长度。
题目2,给定一个N×M的迷宫,起点为(1, 1),终点为(N, M),求从起点到终点的最短路径长度。
2. 2018年NOIP普及组复赛试题:
题目1,给定一个长度为N的整数序列A,求出其中的最长上升子序列的长度。
题目2,给定一个N×N的矩阵,求出从左上角到右下角的
最短路径长度,每次只能向右或向下移动。
3. 2017年NOIP普及组复赛试题:
题目1,给定一个长度为N的整数序列A,求出其中的最长
连续递增子序列的长度。
题目2,给定一个N×M的棋盘,每个格子上有一个非负整数,求从左上角到右下角的路径,使得路径上的数字之和最小。
4. 2016年NOIP普及组复赛试题:
题目1,给定一个长度为N的整数序列A,求出其中的最长
连续递减子序列的长度。
题目2,给定一个N×M的迷宫,起点为(1, 1),终点为(N, M),求从起点到终点的路径数。
以上只是一些例子,每年的试题都会涉及不同的知识点和算法,题目难度也会有所不同。
参赛选手需要具备扎实的编程基础和算法
思维,才能在复赛中取得好成绩。
希望以上内容能对你有所帮助。
NOIP2017_普及组复赛试题

CCF全国信息学奥林匹克联赛(NOIP2017)复赛普及组(请选手务必仔细阅读本页内容)注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU AMD Athlon(tm) II x2 240 processor,2.8GHz,内存4G,上述时限以此配置为准。
4、只提供Linux格式附加样例文件。
5、提交的程序代码文件的放置位置请参照各省的具体要求。
6、特别提醒:评测在当前最新公布的NOI Linux下进行,各语言的编译器版本以其为准。
1. 成绩(score.cpp/c/pas)【问题描述】牛牛最近学习了C++入门课程,这门课程的总成绩计算方法是:总成绩=作业成绩×20%+小测成绩×30%+期末考试成绩×50%牛牛想知道,这门课程自己最终能得到多少分。
【输入格式】输入文件名为score.in。
输入文件只有1行,包含三个非负整数A、B、C,分别表示牛牛的作业成绩、小测成绩和期末考试成绩。
相邻两个数之间用一个空格隔开,三项成绩满分都是100分。
【输出格式】输出文件名为score.out。
输出文件只有1行,包含一个整数,即牛牛这门课程的总成绩,满分也是100分。
见选手目录下的score/score1.in和score/score1.ans。
【输入输出样例1说明】牛牛的作业成绩是100分,小测成绩是100分,期末考试成绩是80分,总成绩是100×20%+100×30%+80×50%=20+30+40=90。
【输入输出样例2说明】牛牛的作业成绩是60分,小测成绩是90分,期末考试成绩是80分,总成绩是60×20%+90×30%+80×50%=12+27+40=79。
【数据说明】对于30%的数据,A=B=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP2017普及组复赛-解题报告
衢州市兴华中学
By 冯明浩
给出三个整十数A,B,C ,求A*20%+B*30%+C*50%的值
模拟
直接粗暴地输出A*0.2+B*0.3+C*0.5
时间复杂度:O(1) 期望得分:100
由于分数均为整十数,先将分数各除以10,再直接输A*2+B*3+C*5。
这样就避免了精度问题
时间复杂度:O(1) 期望得分:100
给出N 个数Ai ,再进行Q 次询问,找后缀为给定数Bi 的最小的Ai
模拟
将Ai 及Bi 都转化成字符串。
每次询问都对N 个数进行后缀比较,挑出个最小的
时间复杂度:O(N*Q*len) 期望得分:80 对算法一的比较进行优化——构造出n 10,对于Ai ,直接Ai Mod 10len ,判断是否
相等。
这样每次比较的时间复杂度优至O(1)
同时先将Ai 排序,再每次从小到大查询,一旦找到就停
时间复杂度:小于O(N*Q)(一般情况) 期望得分:100
读入Ai 时进行处理,构造ans[x]数组,记录询问X 的最小值。
对于每个Ai ,依次
取出其后1、2、3……len 位,修正其的最小值。
这样每次查询,就可以O (1)出结
果了
时间复杂度:O(N*len) 空间复杂度:O(max(Bi)) 期望得分:100
给出一个N*N 的矩阵,其中部分格有颜色
每次可以从一个格向上下左右四个方向移动一格(不能越出矩阵且满足条件),根据
两个格子的颜色有不同的代价
求从左上角走至右下角的最小代价
最短路(动态规划)
直接暴力地按照题意进行DFS
时间复杂度:O(n n *2) 期望得分:30
以左上角为起点,右下角为终点,刷四个方向的SPFA
(也可预先对相邻格建好边,刷最短路SPFA 或DIJ 或进行记忆化DFS )
时间复杂度:O(k*n*n) 期望得分:100
给出N 个格子的位置Xi 与价值Pi ,从起点0往右跳跃,初始跳跃的距离只能为d
同时可以花费金币来调整其跳跃距离,花了t 个金币时可跳跃的距离为
max(1,d-t)~(d+k)
每遍历一个格子就会获得其代价Pi ,求要获得总价值为K 所需最少的金币数
二分、动态规划、单调序列(堆)
从小到大枚举所需金币数,用O(N*N)的DP 进行check ,一旦发现可行就为答案
时间复杂度:O(max(Ai)*N*N) 期望得分:20
分析发现,枚举的金币数越多,跳跃范围越大,总价值一定越多——
满足二分答案的单调性,于是将算法一的枚举答案变为二分枚举
时间复杂度:O()max(2log Xi *N*N) 期望得分:50 分析一下DP 的转移方程:
F[i]=max(F[j])+P[i](max(1,d-t)≤a[i]-a[j]≤d+k)
就会发现DP 的j 这次循环是为了找F[1~i-1]中的最大值,自然而然就想到了用堆
优化——
堆中存放F[1~i-1],若堆顶距当前X[i]大于d+k ,就丢掉该元素(再也没用)
否则若堆顶距当前X[i]小于max(1,d-t),就暂存在临时数组中,最后在当前解更
新好后记得塞回去
则F[i]=F[heap[1]]+P[i]
时间复杂度:O()max(2log Xi *N*k*N 2log ) 期望得分:80 继续优化算法三的DP :
那些离当前X[i]太近的实际上完全没有必要塞入堆中,那么再另开一个变量j 记录
当前往堆中塞入的最后一个元素。
每次将与当前X[i]的距离大于等于max(1,d-t)
的塞入堆中,只要检查一下堆顶是否太远即可,就保证了每个节点当且仅当入堆一次,
时间复杂度中k 就消去了
时间复杂度:O()max(2log Xi *N*N 2log ) 期望得分:100 在算法四的基础上再思考一下,其实也没有必要用堆了。
因为X[i]是在不断增大,
那么对于F[x]=F[y],显然距离起点远的更有用,即一旦F[y]进堆,F[x]就没有
存在的意义了(X[x]<X[y]);若远的更大,则更不必说;小的话,就要暂留着,以
备做前后的“中转站”。
这样的话,维护一个单调下降的单调序列来代替堆,每次将序列前面距离太远的干掉,
后面再如上进行维护,每次抓序列的头就是前面的最优解:
F[i]=F[que[hed]]+P[i]
于是连堆的N
2log 也成功去掉了
时间复杂度:O()max(2log Xi *N) 期望得分:100
另:除了上面的算法外,不排除还有其他更优的解法。
