卫星测控模型
卫星严格成像模型ppt课件

y
立体 像对
4.852 X
8.294 4.292 物方精度 Y
3.620 Z
0.648 X
0.622 0.316 物方精度 Y
1.556 Z
01 & 02 33.62 24.43 19.49 3.932 4.789 2.119
02 & 03 14.25 57.03 102.1 4.265 6.093 5.691
SPOT5严格成像模型:
M=(X,Y,Z)为地面上的一点, 则M点可表示为:
O TMP(t)u3
X
Y
XP YP
u3
X
u3 Y
Z ZP u3 Z
卫星位置、CCD像元视线及地面点间的几何关系
二、卫星影像的严格成像模型
SPOT5严格成像模型:
c x ,0
c x ,1 t
YS
t
Y
o S
b
s
t
c y,0
c y ,1
t
ZS
t
Z
o S
bs
t
c z ,0
c z ,1
t
r o ll t r o ll obs t e r ,0 e r ,1 t
p
itch
t
pitch obs t e p,0
令
(X2)X (Y2)X (Z2)X
R1 u1 '
u2 '
(X2)Y (X2)Z
(Y2)Y (Y2)Z
(Z2)Y•Mp•M r•My (Z2)Z
卫星测控

卫星和飞船的跟踪测控模型摘要:本文研究的是在不同条件下建立最少的卫星或飞船的跟踪测控站,以达到对卫星或飞船实施全程跟踪测控的目的。
问题一中不考虑地球的自转,卫星或飞船的飞行轨迹就是一个固定的圆周。
依据得到的图形运用三角函数相关知识建立数学模型一,先计算一个测控站测控范围,再求出测控整个飞行轨迹所需最少的测控站的数目。
并计算得出卫星或飞船在即将脱离地球引力的情况下对其测控所需的测控站的数目至少为3,最后又以神舟七号飞船为例检验了该模型,所得此种情况下要想对其全程测控需要12个测控站。
问题二中考虑到地球自转,此时卫星或飞船在运行过程中相继两圈的经度有一些差异,并且卫星或飞船的运行轨道与地球赤道平面有固定的夹角,因而卫星或飞船轨道构成一个环形区域。
然后,用圆的最大内接正方形来代替圆对环形区域进行覆盖,得到一个合理的所需测控站个数的一般表达式,并带入神七相关数据得到全程测控神七时所需的测控站的个数为37个。
问题三,用与问题二中类似的方法求出测控站的测控范围在环行区域投影圆的内接正方形的边长,再依据每一个纬度或经度在地球表面的实际跨度长求出测控站所测卫星或飞船在其环绕球面上纬度和经度范围,并用上述在地面上的投影描述测控站的实测范围。
本文中,巧妙之处在于采用易操作的圆内接正方形来代替圆覆盖环形区域,此方法有一定的借鉴和推广意义。
关键词:测控站环形区域投影测控范围一问题的重述和分析1.1问题的重述卫星和飞船在国民经济和国防建设中有着重要的作用,对它们的发射和运行过程进行测控是航天系统的一个重要组成部分。
航天测控的理想状况是对卫星和飞船(特别是载人飞船)进行全程跟踪测控。
测控设备只能观测到所在点切平面以上的空域,实际上每个测控站的测控范围只考虑与地平面夹角3度以上的空域。
在一个卫星或飞船的发射与运行过程中,往往有多个测控站联合完成测控任务。
请利用模型分析卫星或飞船的测控情况,具体问题如下:问题1:在所有测控站都与卫星或飞船的运行轨道共面的情况下至少应该建立多少个测控站才能对其进行全程跟踪测控?问题2:如果一个卫星或飞船的运行轨道与地球赤道平面有固定的夹角,且在离地面高度为H的球面S上运行。
全程跟踪卫星或飞船的测控站数量模型

A bs r c : od tr n en mb r f nmo i rn n o to tt n f t c igstl ts r p c s isi t a t T eemiet u e nt iga dc nr l ai s r kn aele a ehp ,n h oo o s o o a i os
全程跟 踪 卫 星或 飞船 的测控 站数 量模 型
王 积 建 王 晓 红 ,
( 江工 贸职业技 术学院 a 基础部 ;b 图书馆 ,浙江 温州 3 5 0 ) 浙 . . 2 0 3
[ 摘 要] 为 了 定全程跟踪 卫星或 飞船的测控站数量 ,在不考虑地球 自 确 转影响和考虑地球 自 转影响 的情 况
b t a eo ir g r i ga dr g d n lu n eo er tto ft ee rh. u n i tv d l ft ef we t o h t c s fd s e a d n n e a i g t i he r he nf e c ft o ai no at aq a t a i emo e e s h h t o h o o t rn nd c n r t to f r c i g s t lie rs c s i y g o e rc m eho si sa ih d. n n m nio i g a o tolsa i nso ta k n a e lt so pa e h psb e m ti t d se tbls e I a d t ,n v e o Sh nz o I”m a e p c s i , h e s o i rn n o to t t nsn e e sp e e td d ii on i iw f” e h uV I nn d s a e h p t ef we t m n t i ga dc n r lsa i e d di r s n e o o
卫星和飞船跟踪测控的数学模型

K e o ds y w r :mo io i g; lc s e s iti u in n t rn o u  ̄b td srb to
对 于 问题 二 , 地 球 自转 的 影 响 下 , 星运 行 过 程 中星 下 点 轨迹 在 地 球 表 面 形 成 一 些 “ ” 型 的轨 在 卫 8字
迹 , 称地 分 布 在 赤道 两边 . 虑到 卫 星 星 下点 轨 迹 的 密集 程 度 问题 , 于 星下 点 轨迹 圈数 较 少 的卫 星 , 对 考 对
1 问题 分析
本文讨论 的问题是2 0 年 “ 0 9 高教社” 杯全 国大学生数学建模 比赛c . 题 卫 星按 运 行 状 况 可 分 为 同 步卫 星 与 非 同步 卫 星 , 同步 卫 星 又 分 为 同 步静 止卫 星 、倾 斜 轨 道 卫 星 而
和极 地 轨 道 同步卫 星 . 于 问题 一 , 让 测 控 站 所在 平 面 与 卫 星轨 道 共 面 , 卫 星只 能 在赤 道 上 空 运行 , 对 要 且 只有 同步 轨道 静止 卫 星符合 条 件 . 如果 该 卫 星为 非 同 步卫 星 , 该卫 星距 离地 球 表 面 的高 度 处 于 一个 范 那 围值 , 即在 围绕 地 球运 行 的 最 小 高度 与 最 大高 度 之 间 .
Th ntrn f t e b cme jr p r f t e srn ui s s m . T i tei a ay e h e mo i ig o h m eo s a mao at o h ato a t y t o c e hs h s n lsd te s lcso vn bet ao n h at o u fmo ig o jcs ru d t ee r h,a d etbi e i l i i r uin mo e o ntr g n s lh d a s a s mpie ds i t d l fmo i i fd tb o on
卫星和飞船的跟踪测控大学生数学建模大赛C题优秀论文

卫星和飞船的跟踪测控摘要卫星和飞船在国民经济和国防建设中有着重要的作用,本文通过对卫星或飞船运行过程中测控站需要的数目进行求解,从而实现能够对卫星或飞船进行全程跟踪测控的目标。
对于问题一,由于测控站都与卫星运行轨道共面,且测控站的测控范围只考虑与地平面夹角3度以上的空域,所以,我们首先考虑将卫星或者飞船的运行轨道理想化成圆形,建立其与地球共心的圆形轨道模型,此时,运用几何知识和正弦定理计算出至少应建立12个测控站。
但是,在现实中卫星或飞船的轨道为椭圆形状,接着我们又给出了质点运行轨道为椭圆时的数学模型计算得出需要建立测控站数目的区间为12至16个。
问题二,我们利用每个测控站测控的锥形区域与卫星或飞船轨道曲面相交的圆的内接多边形来覆盖整个卫星轨道曲面,就可以将需要这样内接多边形的个数近似的看作需要建立测控站的最少个数,这里我们只给出内接正四边形和正六边形两种数学模型,此时,计算出需要测控站的最少数目分别为60和67个。
问题三,通过网络查询得到神舟七号的观测站位置和数目,以及飞船运行的倾角和高度等相关数据。
通过线性拟合我们发现测控站的位置近似符合正弦曲线。
最后,我们给出了模型优缺点的分析和评价,并提出了模型的改进的方向。
关键字:卫星或飞船的跟踪测控;圆形轨道模型;圆锥测控模型;测控站点的数目1、问题重述1.1 背景资料现代航天工业中卫星和飞船的测控设备只能观测到所在点切平面以上的空域,且在与地平面夹角3度的范围内测控效果不好,实际上每个测控站的测控范围只考虑与地平面夹角3度以上的空域。
在一个卫星或飞船的发射与运行过程中,往往有多个测控站联合完成测控任务,因此需要分析卫星或飞船的测控情况。
1.2 需要解决的问题问题一:在所有测控站都与卫星或飞船的运行轨道共面的情况下至少应该建立多少个测控站才能对其进行全程跟踪测控。
问题二:如果一个卫星或飞船的运行轨道与地球赤道平面有固定的夹角,且在离地面高度为H的球面S上运行。
卫星和飞船跟踪测控站点的研究

1 提 出 问题
如果 一个 卫星 或 飞船 的运行 轨道 与地 球赤 道平
3 建 立模 型 与 求 解
当卫 星 或飞船 的运行轨 道都 与地 球 赤道平 面 有 固定夹 角 , 在 离 地 面 高 度 为 H 的球 面 S上 运 行 且 时, 根据 轨 道与地 面 夹 角 的 不 同可 分 两 种 情 况 来 讨
自转 使 星下点 在地 球表 面移 动 , 成一些 “ ” 形 8 字型 的 轨 迹 , 称地 分布 在赤 道两边 , 下点轨 迹 就像 正 对 星 ] 弦 曲线 _ 。此 种情 况 下 , 想 知道 至 少 建 立 多少 个 _ 5 ] 要
测 控站 点才 能对卫 星或 飞船 的可 能飞行 区域 进行 全
s lsa egv n i h e s e t ,a d o h sb sst ed r cin o h d l si p o e . u t r ie n t r ea p c s n n t i a i h ie to ft emo e m r v d i Ke r s mo io i g s b r c ywo d : nt rn u ta k;l w- r i o o bt
盖, 以达到 全程 跟踪 测控 的 目的 。 由于此 时 1 个 测 6 控 站 点完全 可 以覆 盖卫 星或 飞船 的飞行 区域 , 因此 , 无 论地 球 自转 与否 , 不 会 影 响测 控 站点 对 飞 行 区 都 域 的全 程跟 踪 测 控 。其 中地球 同 步 轨 道 卫 星[ 的 1 ] 星下 点 ( 造地 球卫 星在 地 面的投 影点 ) 迹是 一条 人 轨
2 问题 的假 设
1 发 射 地点 的降 水 、 面 风 速小 于 8m/ 、 平 ) 地 s水 能见 度 大于 2 m。 0k 2 发射 前 8h至发射 后 1h 场 区 3  ̄ 4 m 范 ) , 0 0k
卫星测控分系统设计

遥控技术
➢ 通过对遥测参数、姿态和轨道参数的 研究和分析,发现航天器的轨道、姿 态、某个工程分系统或有效载荷工作 状况异常或出现故障,判断出故障部 位和做出决策,向卫星发出有关命令 ,修正轨道和姿态,调整分系统和有 效载荷的运行参数,甚至切换备份或 部件。
2020/7/21
17
测控频段
短波 超短波
微
波
波段
高频HF 甚高频VHF 特高频UHF
L波段 S C X Ku K Ka
毫米波
频率
3~30MHz 30~300MHz 300~1000MHz
1~2GHz 2~4GHz 4~8GHz 8~12GHz 12~18GHz 18~27GHz 27~40GHz 40~300GHz
测控系统组成
遥控天线1 合
遥控天
成
线2
器
1 组成
扩频应答
输机A入来自多扩频应答工
机B
器 USB应答机
遥测天线1
遥测天线2
功 分路器
分
负载
测控 开关
器
输
出
测控固放1
多
测控固放2
工
器
测控固放3
6)遥测和遥控原理方框图
14
测控特性
卫星测控特点
多路传输
精确性和 可靠性
信息的多 样性和数 据处理的 复杂性
1 几个概念
跟踪测轨:地面站跟踪卫星并测出其飞行轨道 遥测:采集或获取卫星工况或工程参数,并通过无线信道传 输到地面,以便地面及时了解卫星的工作状况 遥控:将地面的控制信息或数据通过无线信道发送给卫星, 以实现地面对卫星的控制 上行:遥控指令+数据注入 下行:遥测(工况信息)、数传(载荷或科学数据) 测控(TT&C, Tracking, Telemetry and Command)包括三 部分:跟踪、遥测和命令。 数传、测控的区别 地面测控站、船,飞行控制中心(北京、西安 )
航天智能测运控系统体系架构与应用-航天工程论文-工程论文

航天智能测运控系统体系架构与应用-航天工程论文-工程论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——摘要:随着商业航天的快速发展,各类卫星星座项目的持续推进,航天器的商业应用日趋普及,在轨航天器呈现出数量多、平台多、种类多、用途广等趋势,重点依靠资源投入和人力增加的测控模式,已经难以适应未来多星、多任务、多用户的测控服务的发展需要。
近年来,人工智能技术不断取得突破,在多类单项测试中超越人类。
将人工智能的发展成果应用到测控系统中,在自主测控、自主故障诊断、任务规划、资源分配方面,采用智能化方法,促进测运控以平台载荷为核心的管理模式向以数据业务为核心的管理模式转变, 提高测控任务的完成效率和资源利用率。
关键词:测控; 智能化; 故障自主诊断; 自主测控; 数据挖掘; 机器学习;1 、商业航天智能测运控需求分析1.1 、航天器数量快速增加近年来,万物互联成为人类社会的基本要求,许多全球性或者全天候航天任务越来越复杂,卫星将在今后一个时期内迎来快速发展,航天器的在轨数量将会激增。
卫星星座在信息传输、定位导航、侦察观测等领域,具有全球覆盖、实时性好等先天优势,应用日益广泛。
星座中卫星的数量从数十颗,发展到数百颗,数千颗,Space X 公司布局的Starlink星座计划发射约42000颗卫星。
星座构型在卫星轨道基础上,通过合理的时空布局,适应各种应用功能的需要。
1.2 、测运控系统日益复杂在轨航天器数量将越来越多,规模越来越大,类型与应用模式越来越复杂,管控要求和难度大幅提升。
相对于数量激增的在轨航天器,地面测运控系统将面临着数量不足、设备短缺的问题。
小卫星需要大天线,但是小卫星的寿命通常比较短,而地面测运控设备投入又比较大,因此要求地面测运控资源必须能够组网重复使用。
在传统单颗卫星的测运控任务外,对多星的同时测运控支持、多星及星座在轨运行管理等,对地面测运控网络如何提供及时、有效、灵活的测运控服务提出了极高的要求,增加了航天测运控系统的负担和操作复杂性。
卫星和飞船的跟踪测控模型

盯一 0— aci 2 2r n s
。故所 需 的测 控 站个数 n , 为 : ( H)
r 笪 1
【 一r s“ eR0 ’ s cJ o . n
的一个 重要 组成 部分 , 想 的状况 是对 卫 星和 飞船 ( 理 特别 是载 人飞 船 ) 进行全 程 跟踪 测控 。 测 控设 备 只能 观测 到所 在点切 平 面 以上 的空域 , 且在 与地 平 面夹 角 3度 的范 围内测控 效 果不好 , 际上 实
每个测 控 站 的测 控 范 围只考 虑与地 平 面夹 角 3度 以上 的空 域 。在 一个 卫 星 或 飞船 的发 射 与运 行 过 测控 任务 , 神舟七 号 飞船 发射 和运 行过 程 中测控 站 的分 布 。 如
请 利用 模型 分析 卫 星或 飞船 的测控 情况 , 体 问题 如 下 : 具
() 1 在所 有测 控 站都 与卫 星或 飞船 的 运行 轨 道 共 面 的情 况 下 , 少 应该 建 立 多 少个 测 控 站 才 能对 其 进 至 行 全程 跟踪 测控 ? () 2 如果 一个卫 星 或飞船 的运行 轨道 与地 球赤 道平 面 有 固定 的夹 角 , 在 离地 面高 度 为 日 的球 面 S上 且
所 能测控 的范 围。
2 问题 分 析 和 模 型 假 设
问题 一 , 设卫 星测 控站 分布 在 与卫 星轨道 共 面的地 球表 面 , 假 且卫 星 的运行 轨 道为 圆 。利用几 何关 系 给 出全部 覆 盖需要 的测控 站点数 与卫 星 高度 的关 系 。当卫 星 的运 行 轨 道 为椭 圆 , 星运 行 轨 道 的一 个 焦 点在 卫
卫星通信的信道测量和建模

卫星通信信道的建模和测量一、通信卫星分类卫星可以分类的方式有很多种,这里只列出常见的分类。
1.1 轨位卫星可以根据轨道的高度分为以下几种。
其中,近地轨道卫星(Land mobile satellite-LMS)为当前研究的热点。
因为在高轨位上,卫星信道更加趋近于高斯信道。
而在低轨位工作的卫星,由于其运动性,会存在遮挡、时变、多径效应和多普勒效应。
1.LEO (low earth orbit): 160~2000km2.MEO (medium earth orbit): 2000~36000km3.HEO (high earth orbit):>36000km4.GEO (geostationary orbit):36000km1.2 频段按照卫星工作的频段,一般可以分为以下几类。
其中,在卫星信道测量上,要特别考虑高频段所带来的阴影衰落,以及天气状况。
工作在ka波段的卫星,雨衰严重。
1.L-band: 0.3~3G2.S-band: 2-4G3.C-band: 4~8G4.X-band: 8~12G5.Ku-band: 12~18G6.Ka-band: 27~40G1.3 服务区域根据卫星服务的区域不同,又可以把卫星分为以下几类。
如果卫星服务的区域在城区,则遮挡会更加严重。
而在空旷的郊区,则遮挡会相应变少。
另外,最近有些工作是测量热带区域的卫星信道,主要是因为热带区域天气多变,因此,有必要单独考虑。
1.Rural2.Suburban3.Urban4.Tropical area1.4 极化方式根据卫星的极化方式不同,又可以把卫星分为多极化和双极化卫星。
1.Single-polarized2.Dual-polarized目前,大部分信道建模或者测量都是选择其中的一个子集,作为研究对象。
比如,研究近地轨道卫星在Ka波段下城区的信道的测量和建模。
就调研的结果来看,现在大部分文献都集中在低轨卫星条件下,研究卫星信道的测量和建模。
SimuLink仿真卫星姿态控制
将 H 与 w 引入 CrossProduct 模块(叉乘模块) 。 右键 Subsystem 模块-“Create Mask”来修改模块的外貌。 (为模块起名 Cross Product, 为输入输出起名,以防止叉乘顺序出错)
3
建立叉乘模块: 在模块里面添加两个 in,一个 out。添加两个 Mux,三个 Fuc,模型如下。Mux 的 Input 设置为[3 3]和[1 1 1]。
建立四元数求解模块: 使用 Subsystem 模块建立 Quaternion Solve Model,并 create mask 如下:
8
四元数主部与矢部分开计算积分如下:
根据上式画模块图如下:
9
利用 Integrator、Mux、Gain、Add 模块建立初始模块如下,其中两个 Integrator 的初值 即为初始姿态四元数的初值的主部和矢部。
孙亚辉,易涛 哈尔滨工业大学卫星技术研究所
syhhit@
2014 年 4 月 2 日
目录
SimuLink 仿真卫星姿态控制 ................................................................................................... 1 1. 姿态控制模块的组成............................................................................................... 1 2. 动力学模块的建立................................................................................................... 2 3. 运动学模块的建立................................................................................................... 6 4. 角速度陀螺模块的建立......................................................................................... 12 5. 星敏感器模块的建立............................................................................................. 14 6. 控制目标模块的建立............................................................................................. 14 7. 控制模块的建立..................................................................................................... 15 8. 执行机构模块的建立............................................................................................. 16 9. 观测器 Scope 的添加 ............................................................................................. 16 10. M 文件的代码 .................................................................................................... 18
基于DoDAF的遥感卫星地面系统体系结构建模与仿真

基于DoDAF的遥感卫星地面系统体系结构建模与仿真梁桂林;周晓纪;王亚琼【摘要】结合我国遥感卫星地面系统的体系特点,借鉴DoDAF体系结构模型的设计方法,利用SA软件中的DoDAFABM方法,从全景、业务活动、系统、技术四个视角设计与开发我国遥感卫星地面系统的体系结构模型框架.基于CPN ML语言规则,将所设计的体系结构模型转化为可执行CPN模型,通过CPN Tool仿真软件对部分模型的语法和逻辑进行仿真验证,结果表明了体系结构模型的合理性.该体系结构模型的设计与研究对优化和指导遥感卫星地面系统运行管理体系具有一定的参考价值,同时对遥感卫星地面系统的顶层设计具有一定的推动意义.%According to the characteristics of China's ground system for remote sensing satellite (GSRSS),under the design method of Department of Defense Architecture Framework (DoDAF),this paper applies the DoDAF ABM method in System Architecture(SA) software to design the architecture model of GSRSS from the four views (All view,Operational view,Systems view and Technical Standards view).Based on the CPN ML and transformation rules,the syntax and logic structure of submodels are simulated and verified by CPN Tool.The simulation results show that the proposed architecture model is reasonable.This research makes contribution to optimal management and top-level design of ground system for remote sensing satellite.【期刊名称】《指挥控制与仿真》【年(卷),期】2017(039)002【总页数】9页(P105-112,117)【关键词】DoDAF;遥感卫星地面系统;体系结构【作者】梁桂林;周晓纪;王亚琼【作者单位】中国航天系统科学与工程研究院,北京 100048;中国航天系统科学与工程研究院,北京 100048;中国航天系统科学与工程研究院,北京 100048【正文语种】中文【中图分类】V57;E917遥感卫星地面系统是卫星工程的五大系统之一,是发挥空间系统应用效能所必需的基础设施,主要包括接收站网、数据中心、共性应用支撑平台及其他辅助系统,负责实现遥感卫星任务的管理与控制,数据的接收、传输,标准产品生产、存储及分发服务[1]。
卫星或飞船的跟踪测控模型设计

问题 1 在所有 测控 站都 与卫星 或飞 船 的运 行轨 : 道共面 的情况 下 至少应该 建立 多少 个测控 站 才能对 其 进行 全程跟 踪测 控?
问题 2 如果 一个 卫 星或 飞船 的运行轨 道 与地球 :
3 问题 的解 答
() 1 问题 1 的解答
在 此 问题 中 . 了简化计 算 . 为 我们认 为绕地 球运
作者 简 介 : 徐 昕 (9 2 )女 , 南 岳 阳 人 , 教 授 , 南 师 范 大 学在 读 博 士 研 究 生 , 究 方 向为 微分 方 程 。 杨 17 一 , 湖 副 湖 研
・
1 3・ 8
杨徐 昕 , 曾玉华 , 成夏 炎 : 星或 飞船 的跟 踪测控模 型设 计 卫
故 A0C= T ACD A 1一 一
h p / w . v n r 2 0 — 9 4c net l 8 2 t :w wg . /z 0 8 0 / /o t _ 4 8 . t / oc j ̄ 2 n 1 0
h 。 t m)
请 利 用模 型分 析 卫 星或 飞 船 的测 控 情况 . 具体
问题如 下 :
与地 球球 面交点 的经 度差 异的绝 对值 ; 一不 超 过 []
2 模 型 的假 设
为 了便 于建 立相关 模 型 , 我们 假设 : 地球是 一个 标 准 的几何球 体 ;忽 略影 响测控 站布置 的地理 因素
和其他 因素 : 不考 虑地球 公转 的影 响 ; 把卫 星或 飞船 看 成一 个质点 ; 星在太 空 中运行 速度大 小不 变 。 卫 符 号说 明 : 地 球 自转 的周 期 ; 一 卫 星或 飞 一 船 在 轨 道 运行 的周 期 : 一 卫 星 或 飞 船 离地 平 引 力 常数 , 小 等 于66  ̄ 0 G 大 . 1 7
卫星信道模型总结
0.7
,r 0 ,r 0
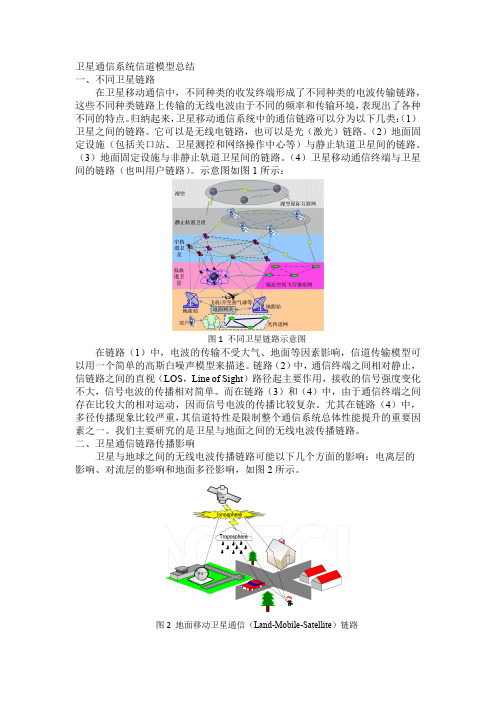
瑞利分布包络的概率密度曲线图
0.6
0.5
0.4
0.3 0.2 0.1 0 0
1
2
3
4 5 6 接收信号包络r
7
8
9
10
图 3 Rayleigh 模型的概率密度函数曲线图
15
图 5 Lognormal 分布的概率密度函数曲线
3.4 Nakagami 分布 Nakagami 分布是一种广义的 Rayleigh 分布,用于刻画无线传播环境中的 分簇散射现象。随着形状因子 m 的变化,Nakagami 分布涵盖了单边 Gaussian
分布、Rayleigh 分布和 Rician 分布,即:当 m=1/2 时,Nakagami 分布就变成了 单边高斯分布;当 m=1 时,Nakagami 分布就变成了 Rayleigh 分布;当 m>1 时,Nakagami 分布就和 Rician 分布很接近。 Nakagami 分布的概率密度函数为:
Corazza模 型 概 率 密 度 函 数 曲 线 图
0.5 0.45 0.4 0.35
概 率 密 度 函 数 pdf
0.3 0.25 0.2 0.15 0.1 0.05 0
0
1
2
3
4 5 6 接 收 信 号 包 络 r(v)
7
8
9
10
图 9 Corazza 模型信号包络概率密度函数曲线图
4.4 Abdi 模型 Abdi 模型认为阴影莱斯模型中直射分量的功率是伽玛随机过程,我们知道 伽玛随机变量的平方根服从 Nakagami 分布,也就是阴影莱斯模型中直射信号 包络服从 Nakagami 分布。Abdi 模型将接收信号表示为:
一种基于MBSE的小卫星测控分系统建模设计方法

MBSE随着航天技术的发展,小卫星已成为当前领域的热门研究方向。
而对小卫星进行测控是实现其稳定运行的重要保障,因此小卫星测控分系统建模设计方法的研究变得尤为重要。
本文将介绍一种基于MBSE 的小卫星测控分系统的建模设计方法。
一、MBSE 简介MBSE,即Model-Based Systems Engineering,指的是基于模型的系统工程方法。
该方法是个系统化的、基于模型的、集成的过程,用于在系统开发的整个生命周期中管理各种需求、设计、测试及文档等活动。
MBSE 的核心理念是“一切皆模型”(everything is a model),即在系统工程中,各种活动都可以交由模型来代表和管理。
二、小卫星测控分系统的建模1.需求分析在进行任何产品或系统的开发过程中,需求分析都是十分重要的一步。
小卫星测控分系统中,需求分析要考虑到各种控制台、通信、数据处理和信道控制等各方面的需求,以保证卫星的稳定运行。
这一阶段可以利用MBSE 中的系统工程工具,采用模型的形式对需求进行梳理与管理。
2.系统设计系统设计阶段是建立模型的关键之一,该阶段要考虑到各种软硬件和系统架构等因素。
利用MBSE 方法,可以将设计过程分解为一系列子模型,并对这些子模型进行自动化的集成和验证。
3.模型开发在建模的过程中,具体的物理组件和软件组件可以分别对应为建模中的属性和方法。
小卫星测控分系统的模型开发需要考虑到系统过程的多样化、可追溯性、层次结构和可修改性等特征,并对模型进行适当的验证。
4.模型管理小卫星测控分系统的模型开发比较复杂,需要进行动态管理。
MBSE 方法可以将系统工程的各个数据明确地存储在模型中,并利用模型解释并管理设计决策过程。
模型可以用于分析、设计和验证,从而最大限度地降低开发风险,确保模型的正确性和完整性。
三、小卫星测控分系统的建模案例分析基于MBSE 的小卫星测控分系统的建模方法为实现小卫星测控分系统建模提供了新的思路与方法。
卫星通信的信道测量和建模

卫星通信信道的建模和测量一、通信卫星分类卫星可以分类的方式有很多种,这里只列出常见的分类。
1.1 轨位卫星可以根据轨道的高度分为以下几种。
其中,近地轨道卫星(Land mobile satellite-LMS)为当前研究的热点。
因为在高轨位上,卫星信道更加趋近于高斯信道。
而在低轨位工作的卫星,由于其运动性,会存在遮挡、时变、多径效应和多普勒效应。
1.LEO (low earth orbit): 160~2000km2.MEO (medium earth orbit): 2000~36000km3.HEO (high earth orbit):>36000km4.GEO (geostationary orbit):36000km1.2 频段按照卫星工作的频段,一般可以分为以下几类。
其中,在卫星信道测量上,要特别考虑高频段所带来的阴影衰落,以及天气状况。
工作在ka波段的卫星,雨衰严重。
1.L-band: 0.3~3G2.S-band: 2-4G3.C-band: 4~8G4.X-band: 8~12G5.Ku-band: 12~18G6.Ka-band: 27~40G1.3 服务区域根据卫星服务的区域不同,又可以把卫星分为以下几类。
如果卫星服务的区域在城区,则遮挡会更加严重。
而在空旷的郊区,则遮挡会相应变少。
另外,最近有些工作是测量热带区域的卫星信道,主要是因为热带区域天气多变,因此,有必要单独考虑。
1.Rural2.Suburban3.Urban4.Tropical area1.4 极化方式根据卫星的极化方式不同,又可以把卫星分为多极化和双极化卫星。
1.Single-polarized2.Dual-polarized目前,大部分信道建模或者测量都是选择其中的一个子集,作为研究对象。
比如,研究近地轨道卫星在Ka波段下城区的信道的测量和建模。
就调研的结果来看,现在大部分文献都集中在低轨卫星条件下,研究卫星信道的测量和建模。
卫星和飞船的跟踪测控模型

度 值 , 一 经度 值 , 地 一地 球 自转 角速 度 , 一 卫
星 自转 角速 度 , 一 测控 站测控 时 问的一半 。 t
( )在所有 测控 站都 与卫 星或飞船 的运行 轨道 1 共 面 的情 况 下 至 少 应 该 建 立 多 少 个 测 控 站 才 能对
其进 行全 程跟 踪测控 ? ( )如果 一个卫 星或 飞船 的运行轨 道 与地球 赤 2 道平 面有 固定 的夹角 , 在离 地 面 高度 为 日 的球 面 且 S上 运行 。考虑 到地球 自转 时该 卫 星或 飞船 在 运 行
/C …c ( _ D s _ O i n
) 。
利用 三角 形 中三角 之和 等于 10 可 知 : 8。
0= 10 一 O D 一( 0 ) = 8。 C 9 。+
9 一c( 0 卢 s i n
3 0。 6 1 0。 R
第一作者简介 : 程红萍( 9 1 )女 , 17 一 , 陕西大荔人 , 讲师 , 硕士。研究
方 向: 高等数学 、 数学建模。E m i:hnhn p g2 0 @1 3cm。 - alce gogi _0 5 6 . o n
与地球 赤道平 面有 固定 的夹 角 , 在 离地 面 高 度 为 且 日 的球 面 s上 运 行 的情 况 下对 卫 星 测控 。方 案一 ,
夹 角 3度 以上 的空域 。
过程 中相 继两 圈 的经 度 有 一些 差 异 , 至少 应 该 建 问
立 多少个 测 控 站 才 能对 该 卫 星 或 飞船 可 能 飞 行 的
区域全 部覆盖 以达 到全 程跟踪 测控 的 目的? ( )收集 我 国一个 卫星或 飞船 的运行 资料 和发 3 射时测 控站点 的分 布 信 息 , 析这 些 测 控 站点 对 该 分
全球卫星移动通信星座天基星间链路测控方案

递测 控信 息 ,再 通过 G EO一 1卫星或 GE O一 2卫 星将 信 息传 回到我 国地 面测 控站 台网 。 方案 二 由于 星座卫 星数量较 少 ,可 以借 助 目前现有海 外站 协助测 控测控 问题 ,针 对上 述模 型设计测 控 系统 ,有 两种方 案 : 方案 一 GE O一 1 卫 星和 G E O一 2卫 星都 可以 由我 国地 面 测控 台 网 ( 东部 、西 部 ) 完 成测 控 任务 ,
GE O一 3卫星属 于远端 不可视 卫 星 ,需要 建立 它与 GE O一 1 卫 星 或 GE O一 2卫 星 的星 间链 路联 系来传
收 稿 日期 :2 0 1 2 - 1 0 — 1 0 。收 修 改 稿 日期 :2 0 1 2 — 1 2 — 2 8
主 垦奎 型堂垫 至 旦 在G E O 轨道 布置 3颗地球 静止 轨道卫 星 ,建 立 G E O 轨道 卫星与 L E O 星座卫 星之 间的星 间链 路来
G E O 轨 道卫 星与 L E O 星 座 卫 星之 间 的 星 间链 路 来 传 输 测 控 信 息 , 再 将 这 些 信 息 转 发 至 相 应 的 地 面 测 控 站 , 分 析 了测 控 链 路 的 传 输 指 标 , 评 估 了 星 间 测 控 链 路 的 双 向 传 输 性 能 , 最
传输各 种遥 控 、遥测与测 距信 号 ,再 将这 些信息 转发 至相应 的地面 测控站 。此外 ,需要 地面 测控站 或 同步轨道 节点 配备多条 独立 的上 、下行 信道 ,即提供 多址 能力 ,以实现对 多颗 星座卫 星 的同时跟 踪 和测控 ,可 以采用直 接序列 扩频 ( D S S S ) 的码 分 多址 ( C DMA) 测控 体 制 ,并 在 星 上采 用多 址 天线 技术来 有效 解决 测控多 目标 同时工作 以及 链路需 求量 大 的问题 。
太阳能卫星模型的测试和改进措施

太阳能卫星模型的测试和改进措施1.引言太阳能卫星作为未来能源领域的重要研究方向之一,其模型的测试和改进措施对于提高太阳能利用效率、解决能源短缺问题具有重要意义。
本文将从太阳能卫星模型的概念和原理入手,探讨其测试和改进的必要性,并提出相应的措施。
2.太阳能卫星模型的概念和原理太阳能卫星是指将太阳能转换成微波或激光束,从太空传输到地面,以实现长期、清洁、无限的能源供应。
其基本原理是通过太阳能电池板将太阳能转化为电能,进一步将电能转化为微波或激光能量,再通过天线等设备传输到地面接收站,最终转化为可用电能。
太阳能卫星模型的建立和改进对于提高能源利用效率、减缓地球资源枯竭具有重要意义。
3.太阳能卫星模型的测试及改进的必要性在太阳能卫星模型的发展过程中,不断进行测试和改进是非常必要的。
经过测试可以验证太阳能卫星模型的可行性和稳定性,同时检测其中存在的问题和不足;通过不断改进,可以提高太阳能卫星模型的效率和安全性,更好地适应各种复杂环境下的运行需求。
测试和改进是太阳能卫星模型发展不可或缺的重要环节。
4.太阳能卫星模型的测试及改进措施为了确保太阳能卫星模型的可靠性和稳定性,需要采取一系列的测试和改进措施:(1)模拟环境测试:通过模拟真实太空环境中的温度、辐射等因素对太阳能卫星模型进行全面测试,验证其在各种特殊环境下的运行情况。
(2)电磁兼容性测试:进行电磁兼容性测试,确保太阳能卫星模型在与其他卫星或设备进行通信时不会发生干扰或被干扰。
(3)飞行安全测试:对太阳能卫星的飞行安全性进行测试,以确保其在发射、定位、轨道调整等方面的安全可靠。
(4)系统效率改进:通过对太阳能电池、能量转换和传输等核心系统的改进,提高能源转化和传输的效率,以提高整个太阳能卫星系统的能量利用率。
5.总结太阳能卫星模型的测试和改进是保障其可靠性和稳定性的重要环节。
只有通过不断的测试和改进,太阳能卫星模型才能更好地适应各种复杂环境下的运行需求,实现长期、清洁、无限的能源供应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卫星或飞船测控模型摘要本文对通过测控站分布问题进行了简化,建立了数学模型。
我们对卫星或飞 船如何运行,如何使测控站合理分布,以及如何使测控站数最少等问题进行了分 析讨论,最终计算出最少的测控站数。
对于问题一,我们先得出每一个测控站的最大测控区域对应的圆心角与卫星 或飞船离地高度的关系式=2( 18093 arcsinR前93),因为所有测R \ H控站与运行轨道共面且是个圆周,则对卫星或飞船进行全程跟踪测控最少为N [36・]个测控站。
但是对于不同的轨道上的卫星或飞船,则有不同的情况。
为此我们分别对同步卫星、远距离的卫星或飞船、近地轨道的卫星或飞船进行分 类讨序号 出现的情况 所需要测控站个数1 离地36000km 同步卫星 12 远距离超过的卫星3 3近地轨道200km 的卫星或飞船16对于问题二,由于卫星或飞船的运行轨道与地球赤道平面有固定的夹角 : 所以卫星或飞船的运行轨道只在以球心为中心, 半径为R+H 的球面,去掉上下两 个高度为(H+R (1-sin )的球冠剩余的部分 。
方法一,首先,我们采用测控点测控区域重叠的方式, 以圆的内接正方形的 边为重叠部分的交线,所以得出重叠后能完全监控测控区域所对应的圆心角422arcta n( tan从而得出需要布控监控点的纬线数及纬度,最后得出总监控点数为12 cosi 11假设卫星或飞船沿固定的轨道运转 n 1后,卫星或飞船又回到了原来的出发点上,站数也减少了,其测控范围即为一条近似于正弦函数曲线图像。
再运用简化思想 把曲线拉直成为直线I 。
以测控站所对应的测控圆的直径 d 截取。
最后,得到最 方法二,我们经过公式推导,得出经度差的表达式:即满足n 1条件。
此时,测控站所要测控的范围, 并且所需要的测控少所需的测控站数为关键词:测控面,经度差, sin(87.Rsin93 arcs in排布2一.问题重述卫星或飞船和飞船在国民经济和国防建设中有着重要的作用,对它们的发射和运行过程进行测控是航天系统的一个重要组成部分,理想的状况是对卫星或飞船和飞船(特别是载人飞船)进行全程跟踪测控。
测控设备只能观测到所在点切平面以上的空域,且在与地平面夹角3度的范围内测控效果不好,实际上每个测控站的测控范围只考虑与地平面夹角3度以上的空域。
请利用模型分析卫星或飞船的测控情况,具体问题如下:1. 在所有测控站都与卫星或飞船的运行轨道共面的情况下至少应该建立多少个测控站才能对其进行全程跟踪测控?2. 如果一个卫星或飞船的运行轨道与地球赤道平面有固定的夹角,且在离地面高度为H的球面S上运行。
考虑到地球自转时该卫星或飞船在运行过程中相继两圈的经度有一些差异,问至少应该建立多少个测控站才能对该卫星或飞船可能飞行的区域全部覆盖以达到全程跟踪测控的目的?3. 收集我国一个卫星或飞船的运行资料和发射时测控站点的分布信息,分析这些测控站点对该卫星或飞船所能测控的范围。
二.问题分析对于问题一,因为所有测控站与卫星或飞船的运行轨道共面,所以卫星或飞船相对于地球的运行轨道是一个以地心为圆心,以地球半径R与卫星或飞船离地高度H的和为半径的圆;而每个测控站的测控范围是与地切平面夹角3度以上的空域,所以每个测控站的测控范围相对与卫星或飞船的运行轨道是一段弧,我们利用以上条件构造出一个三角形,利用正弦定理,得出测控弧所对应的圆心角,最后得出至少所需的测控站。
对于问题二:由于卫星或飞船的运行轨道与地球赤道平面有固定的夹角a,所以卫星或飞船的运行轨道只在北纬a南纬a之间,所以所有测控站的测控范围之和应等于北纬a南纬a之间的地区。
由于地球自转,所以卫星或飞船在运行过程中相继两圈有经度差△ A。
\ 三.模型假设1地球是一个球体2卫星或飞船做匀速圆周运动3不考虑卫星或飞船发射和降落的情况4不考虑其他天体对卫星万有引力的影响5不考虑空气对卫星或飞船的阻碍作用四.符号说明五.模型建立与求解建立问题一的模型5.1.1情形一:不考虑卫星或飞船发射的过程,假设卫星或飞船直接飞到同步卫星的轨道上,因为同步卫星运转的角速度与地球自转的角速度相同,所以相对于地球,同步卫星没有发生运动。
所以在同步卫星下设一个测控站就可以全程跟踪测控,\ 即N= 1 o5.1.2情形二:所有测控站都与卫星或飞船运行轨道共面的情况:因为卫星或飞船绕地球运行所需的向心力是由地球对卫星或飞船的万有引力所提供的,地球的卫星或飞船做圆周运动都是以地心为圆心,如下图1所示(为卫星或飞船飞行轨道的面),地心为0,在有测控点C,其测控范围与飞行轨道的交点为D,在三角形C0D 中,因为每个测控站的测控范围只考虑与地平面夹角3度以上的空域,由图1易得:/ 0C匡90 +3 = 93,0C为地球半径R, 0D为地球半径R与离地高度H的和,即:0D= H+R图1首先,在三角形OCD中,运用正弦定理,求出:…Rsin OCD(1)HCll VR因为三角形内角的和为180 度, 所以:2(180OCD )(2)由式(1)和(2)得高度H与测控弧所对的圆心角B的关系式:= 2(180 - OCD-arcsin 只攀°C D)Rsin 93 = 174 - 2 arcsin一R H(3)360度。
由此可得测控站数至少由模型分析可知,所以问题一的测控总角为为:(4)当H远大于R时,的近似值为Rsin 93lim arcs in 174H R HN 360域对应与地球南纬到北纬之间区域,所以只需要安排测控点使所有的测控点的测控范围覆盖该区域,并使测控点最少。
测控站测控的圆心角为360 2(93 arcsinR RT)因为每个测控点的测控区域为一个球冠表面,为了能测完整个卫星或飞船的飞行轨道,采用测控点测控区域部分重叠的方式,又因为圆内接四边形为正方形时面积最大,所以重叠部分的交线为圆内接正方形的边,如图2所示:那么,至少的测控站数为N5.1.3情形三:当卫星或飞船在近地轨道上运行时,由资料可知,卫星或飞船飞行的轨道的高度为H= 200km由上推导公式:0二口4° - 2 ar亡如空空可得:N=16建立问题二的模型5.2.1 模型二卫星或飞船的运行轨道与地球赤道平面有固定的夹角半径为(R+H)的球面去掉上、下两个高度为(R H)(1 sin )的球冠剩下的区域。
该区。
轨道的范围是:与地球同心i2 arcta n( — ta n )为能完全测控区域对应的圆心角。
我们采用在一条或多条同一纬2 2由i (i=…)可求出各条纬度线对应在卫星或飞船的飞行轨道球面上的圆的周长C i 2 (R H)cos i(i=-),根据弧长公式求出重叠后正方形对应的球冠的弧长为C il i (R H)。
所以,各条要布控的纬线上需要的测控点数为n i〒 (i=…)。
最后求出需要布控的总测控点数为N n 1 n 2 ... n j2 cos Ni 11以神舟七号为例,H=343km 42.25.2.2模型三由于模型二只是简单地考虑卫星可能飞行的区域, 没有从飞行原理上分析,因此我们对其进行改进,由于卫星或飞船的运行轨道与地球赤道平面有固定的夹 角,所以卫星或飞船的运行轨道。
如图 3所示:度线上布控测控点,由确定要布控测控点的纬度线的条数m 及度数i (i=1.2.3 …)。
求出31.24 , 1 22.37 , m=4, n 1 n 416 , n 2 n 3 14 , N 60。
当卫星或飞船转第一圈时:如图4所示,所设卫星或飞船从赤道与西经180 度的交点1出发,因为卫星或飞船相对于地球的速度由两部分合成(地球某一纬度的线速度和卫星或飞船的速度),而地球某一纬度的线速度是随纬度的升高而减少,即卫星或飞船从1到2时,水平速度不断减少,而垂直速度不变,从而得出卫星或飞船从1到2的路径大约下,同理,可以得出从2到3;从3到4的路径。
但由于地球处转的响影,会产经度差。
即如图4所示卫星或飞船转一圈从1 到4,而到不了东经180度,即1点。
当卫星或飞船转第二圈时:如图5所示,当卫星或飞船转完第一圈后,在4 点上,因为西经180度就是东经180度,所以4点可以是西经向西△ A度。
和第由上述可得:卫星或飞船每转一圈,其相对地球的的路径向西平移△A。
当卫星或飞船转第一圈后,第二圈的起点是第一圈的起点向西平移△Ao当卫星或飞船转第二圈后,第三圈的起点是第二圈的起点向西平移△Ao当卫星或飞船转第三圈后,第四圈的起点是第三圈的起点向西平移△Ao \当卫星或飞船转第n i圈后,每n i +1的起点是第n i圈的起点向西平移△ A由数学归纳法可得,当卫星或飞船转第n i圈后,每n i圈的起点是第一圈的起点向西平移n i A.假设当卫星或飞船绕地球转n i时,卫星或飞船回到了原起点。
如果卫星或飞船向西平移i圈重新回到了原出发点则:n i A 2 i如果卫星或飞船向西平移2圈重新回到了原出发点则:n i A 2 2如果卫星或飞船向西平移3圈重新回到了原出发点则:百度文库-让每个人平等地提升自我如果卫星或飞船向西平移4圈重新回到了原出发点则:n i由数学归纳法可得,若卫星或飞船绕地球转n2圈重新回到了原出发点则n i2n2(5)N, S)A522.2卫星或飞船可能出现的区域与测控站在J球面上的测控直径的讨论Step1 :假设卫星或飞船的运行轨道与地球赤道平面的夹角为,所以卫星或飞船到达的最高纬度为.因此卫星或飞船在北纬至肺纬之间运转,如图那么卫星或飞船可能出现在区域为(Step2:计算测控站在J球面上的测控直径R如图7所示在三角形ABO中运用正弦定理》sin.Rsin 93arcs in7得sin 93(6)在三角形ABO中,由一93 180得2-87 ( 7)2因为直角三角形0D沖得-si n— (R H) ( 8)2 2由式⑹(7)(8) 得d 2( R H )sin(87 arcsin Rsin 93 ) (9)R HStep3 :推导公式首先我们求出卫星或飞船的轨道周长\ l 2 (R H) (10)根据卫星或飞船的向心力等于地球对卫星或飞船的万有引力V2m(R H)位于赤道上的物体,其向心力由物体的重力提供,由2mR mg得(⑵图7G_^得(R H)2由式(10)(11)得卫星或飞船转一圈所用的时间t; 2®H)¥GM \由式(12)( 13)得飞船运行过程相继两圈的经度差最后由式(5)(16)可得:(R H);测控站在轨道运行球面的测控圆的直径为(13)根据物理黄金代换公式将式(15)带入式子(14)中得(R H). (R H)GMR (14)GM gR 2(15)(⑹n 1 n 2(17)由式(17),当山为正整数时, n 1越小,卫星或飞船回到原出发点的周期就 越短,其相对地球的路径就越简单, 小,所需的测控点就少比可能要测控的范围(北纬到南纬之间)由上述分析可得,这里以n 1 n 23R为目标函数,其模型如下R H目标函数: 3J Rmin n 1 n 2-------- V R Hs.t厲,n 2 N (自然数)H 0;当n 1 1时, 即卫星或飞船沿轨道转一圈时,回到了原出发点。
