算法设计与程序分析习题精选含答案(第四章)
算法设计与分析习题答案1-6章

习题11.图论诞生于七桥问题。
出生于瑞士的伟大数学家欧拉(Leonhard Euler ,1707—1783)提出并解决了该问题。
七桥问题是这样描述的:一个人是否能在一次步行中穿越哥尼斯堡(现在叫加里宁格勒,在波罗的海南岸)城中全部的七座桥后回到起点,且每座桥只经过一次,图1.7是这条河以及河上的两个岛和七座桥的草图。
请将该问题的数据模型抽象出来,并判断此问题是否有解。
七桥问题属于一笔画问题。
输入:一个起点 输出:相同的点 1, 一次步行2, 经过七座桥,且每次只经历过一次 3, 回到起点该问题无解:能一笔画的图形只有两类:一类是所有的点都是偶点。
另一类是只有二个奇点的图形。
2.在欧几里德提出的欧几里德算法中(即最初的欧几里德算法)用的不是除法而是减法。
请用伪代码描述这个版本的欧几里德算法 1.r=m-n2.循环直到r=0 2.1 m=n 2.2 n=r 2.3 r=m-n 3 输出m3.设计算法求数组中相差最小的两个元素(称为最接近数)的差。
要求分别给出伪代码和C ++描述。
//采用分治法//对数组先进行快速排序 //在依次比较相邻的差 #include <iostream> using namespace std;int partions(int b[],int low,int high) {图1.7 七桥问题int prvotkey=b[low];b[0]=b[low];while (low<high){while (low<high&&b[high]>=prvotkey)--high;b[low]=b[high];while (low<high&&b[low]<=prvotkey)++low;b[high]=b[low];}b[low]=b[0];return low;}void qsort(int l[],int low,int high){int prvotloc;if(low<high){prvotloc=partions(l,low,high); //将第一次排序的结果作为枢轴 qsort(l,low,prvotloc-1); //递归调用排序由low 到prvotloc-1qsort(l,prvotloc+1,high); //递归调用排序由 prvotloc+1到 high}}void quicksort(int l[],int n){qsort(l,1,n); //第一个作为枢轴,从第一个排到第n个}int main(){int a[11]={0,2,32,43,23,45,36,57,14,27,39};int value=0;//将最小差的值赋值给valuefor (int b=1;b<11;b++)cout<<a[b]<<' ';cout<<endl;quicksort(a,11);for(int i=0;i!=9;++i){if( (a[i+1]-a[i])<=(a[i+2]-a[i+1]) )value=a[i+1]-a[i];elsevalue=a[i+2]-a[i+1];}cout<<value<<endl;return 0;}4.设数组a[n]中的元素均不相等,设计算法找出a[n]中一个既不是最大也不是最小的元素,并说明最坏情况下的比较次数。
算法设计与程序分析习题精选含答案(第四章)

算法设计与程序分析习题精选含答案(第四章)作业四4.1.2 Alternating glassesa. There are 2n glasses standing next to each other in a row, the first n of them filled with a soda drink and the remaining n glasses empty. Make the glasses alternate in a filled-empty-filled-empty pattern in the minimum number of glass moves. [Gar78]b. Solve the same problem if 2n glasses—n with a drink and n empty—are initially in a random order答:图1 杯子分组a.两个为一组,在前n个杯子中判断偶数的杯子是否为空,不为空与同组的进行交换,共需要交换n/2次,考虑n为奇数对n/2进行向下取整即可。
b.由于最终偶数位置为空杯,奇数位置为满杯,从第一项开始遍历,如果在奇数位置出现空杯与后面偶数位置出现的第一个满杯进行交换,如果偶数位置出现满杯则与后面奇数出现的第一个空杯进行交换,每次交换使得两个位置满足条件,最坏情况是2n位置均为乱序,则需要交换n次,最好的情况为2n位置均满足条件,则交换次数为[0,n]4.1.7 Apply insertion sort to sort the list E, X, A, M, P, L, E in alphabetical order.4.2.1 Apply the DFS-based algorithm to solve the topological sorting problem for the following digraphs:答:(a) fe gb ca d从堆栈中弹出:efgbcad,反转输出为:dacbgfe(b) 由于存在回环b图不是无向回环图。
(整理)《计算机算法-设计与分析导论》课后习题答案.

4.1:在我们所了解的早期排序算法之中有一种叫做Maxsort 的算法。
它的工作流程如下:首先在未排序序列(初始时为整个序列)中选择其中最大的元素max ,然后将该元素同未排序序列中的最后一个元素交换。
这时,max 元素就包含在由每次的最大元素组成的已排序序列之中了,也就说这时的max 已经不在未排序序列之中了。
重复上述过程直到完成整个序列的排序。
(a) 写出Maxsort 算法。
其中待排序序列为E ,含有n 个元素,脚标为范围为0,,1n -。
void Maxsort(Element[] E) { int maxID = 0;for (int i=E.length; i>1; i--) { for (int j=0; j<i; j++) {if (E[j] > E[maxID]) maxID = k; }E[i] <--> E[maxID]; } }最坏情况同平均情况是相同的都是11(1)()2n i n n C n i -=-==∑。
几遍浏览序列实现。
排序策略是顺序比较相邻元素,如果这两个元素未排序则交换这两个元素的位置。
也就说,首先比较第一个元素和第二个元素,如果第一个元素大于第二个元素,这交换这两个元素的位置;然后比较第二个元素与第三个元素,按照需要交换两个元素的位起泡排序的最坏情况为逆序输入,比较次数为11(1)()2n i n n C n i -=-==∑。
(b) 最好情况为已排序,需要(n-1)次比较。
4.3: (a)归纳法:当n=1时显然成立,当n=2时经过一次起泡后,也显然最大元素位于末尾;现假设当n=k-1是,命题也成立,则当n=k 时,对前k-1个元素经过一次起泡后,根据假设显然第k-1个元素是前k-1个元素中最大的,现在根据起泡定义它要同第k 个元素进行比较,当k元素大于k-1元素时,它为k个元素中最大的,命题成立;当k元素小于k-1元素时,它要同k-1交换,这时处于队列末尾的显然时队列中最大的元素。
算法设计与分析第三版第四章课后习题答案

算法设计与分析第三版第四章课后习题答案4.1 线性时间选择问题习题4.1问题描述:给定一个长度为n的无序数组A和一个整数k,设计一个算法,找出数组A中第k小的元素。
算法思路:本题可以使用快速选择算法来解决。
快速选择算法是基于快速排序算法的思想,通过递归地划分数组来找到第k小的元素。
具体步骤如下: 1. 选择数组A的一个随机元素x作为枢纽元。
2. 使用x将数组划分为两个子数组A1和A2,其中A1中的元素小于等于x,A2中的元素大于x。
3. 如果k等于A1的长度,那么x就是第k小的元素,返回x。
4. 如果k小于A1的长度,那么第k小的元素在A1中,递归地在A1中寻找第k小的元素。
5. 如果k大于A1的长度,那么第k小的元素在A2中,递归地在A2中寻找第k-A1的长度小的元素。
6. 递归地重复上述步骤,直到找到第k小的元素。
算法实现:public class LinearTimeSelection {public static int select(int[] A, int k) { return selectHelper(A, 0, A.length - 1, k);}private static int selectHelper(int[] A, int left, int right, int k) {if (left == right) {return A[left];}int pivotIndex = partition(A, left, righ t);int length = pivotIndex - left + 1;if (k == length) {return A[pivotIndex];} else if (k < length) {return selectHelper(A, left, pivotInd ex - 1, k);} else {return selectHelper(A, pivotIndex + 1, right, k - length);}}private static int partition(int[] A, int lef t, int right) {int pivotIndex = left + (right - left) / 2;int pivotValue = A[pivotIndex];int i = left;int j = right;while (i <= j) {while (A[i] < pivotValue) {i++;}while (A[j] > pivotValue) {j--;}if (i <= j) {swap(A, i, j);i++;j--;}}return i - 1;}private static void swap(int[] A, int i, int j) {int temp = A[i];A[i] = A[j];A[j] = temp;}}算法分析:快速选择算法的平均复杂度为O(n),最坏情况下的复杂度为O(n^2)。
算法设计与分析考试题及答案-算法设计与优化答案

1.一个算法就是一个有穷规则的集合,其中之规则规定了解决某一特殊类型问题的一系列运算,此外,算法还应具有以下五个重要特性:_________,________,________,__________,__________。
2.算法的复杂性有_____________和___________之分,衡量一个算法好坏的标准是______________________。
3.某一问题可用动态规划算法求解的显著特征是____________________________________。
4.若序列X={B,C,A,D,B,C,D},Y={A,C,B,A,B,D,C,D},请给出序列X 和Y的一个最长公共子序列_____________________________。
5.用回溯法解问题时,应明确定义问题的解空间,问题的解空间至少应包含___________。
6.动态规划算法的基本思想是将待求解问题分解成若干____________,先求解___________,然后从这些____________的解得到原问题的解。
7.以深度优先方式系统搜索问题解的算法称为_____________。
8.0-1背包问题的回溯算法所需的计算时间为_____________,用动态规划算法所需的计算时间为____________。
9.动态规划算法的两个基本要素是___________和___________。
10.二分搜索算法是利用_______________实现的算法。
二、综合题(50分)1.写出设计动态规划算法的主要步骤。
2.流水作业调度问题的johnson算法的思想。
3.若n=4,在机器M1和M2上加工作业i所需的时间分别为a i和b i,且(a1,a2,a3,a4)=(4,5,12,10),(b1,b2,b3,b4)=(8,2,15,9)求4个作业的最优调度方案,并计算最优值。
4.使用回溯法解0/1背包问题:n=3,C=9,V={6,10,3},W={3,4,4},其解空间有长度为3的0-1向量组成,要求用一棵完全二叉树表示其解空间(从根出发,左1右0),并画出其解空间树,计算其最优值及最优解。
算法设计与分析智慧树知到课后章节答案2023年下山东交通学院

算法设计与分析智慧树知到课后章节答案2023年下山东交通学院山东交通学院第一章测试1.解决一个问题通常有多种方法。
若说一个算法“有效”是指( )A:这个算法能在一定的时间和空间资源限制内将问题解决B:这个算法能在人的反应时间内将问题解决C:这个算法比其他已知算法都更快地将问题解决D:(这个算法能在一定的时间和空间资源限制内将问题解决)和(这个算法比其他已知算法都更快地将问题解决)答案:(这个算法能在一定的时间和空间资源限制内将问题解决)和(这个算法比其他已知算法都更快地将问题解决)2.农夫带着狼、羊、白菜从河的左岸到河的右岸,农夫每次只能带一样东西过河,而且,没有农夫看管,狼会吃羊,羊会吃白菜。
请问农夫能不能过去?()A:不一定B:不能过去 C:能过去答案:能过去3.下述()不是是算法的描述方式。
A:自然语言 B:E-R图 C:程序设计语言 D:伪代码答案:E-R图4.有一个国家只有6元和7元两种纸币,如果你是央行行长,你会设置()为自动取款机的取款最低限额。
A:40 B:29 C:30 D:42答案:305.算法是一系列解决问题的明确指令。
()A:对 B:错答案:对6.程序=数据结构+算法()A:对 B:错答案:对7.同一个问题可以用不同的算法解决,同一个算法也可以解决不同的问题。
()A:错 B:对答案:对8.算法中的每一条指令不需有确切的含义,对于相同的输入不一定得到相同的输出。
( )A:错 B:对答案:错9.可以用同样的方法证明算法的正确性与错误性 ( )A:错 B:对答案:错10.求解2个数的最大公约数至少有3种方法。
( )A:对 B:错答案:错11.没有好的算法,就编不出好的程序。
()A:对 B:错答案:对12.算法与程序没有关系。
( )A:错 B:对答案:错13.我将来不进行软件开发,所以学习算法没什么用。
( )A:错 B:对答案:错14.gcd(m,n)=gcd(n,m m od n)并不是对每一对正整数(m,n)都成立。
算法设计与分析智慧树知到答案章节测试2023年山东科技大学

第一章测试1.程序运行结果往往与输入相关,所以程序可以不满足确定性()A:错B:对答案:A2.有关算法分析的事后统计法正确的是()。
A:结果是面向机器,面向程序员,面向语言的B:测试的结果与程序的编译和运行环境有关C:结果与测试的样本数据有关D:从理论上讲,在各种软硬件环境下进行算法测试,得到的资源耗费都是一样的。
答案:ABC3.下面哪些内容是算法设计之前要完成的内容? ( )A:使用何种计算机语言设计程序B:是求精确解还是近似解C:确定合适的数据结构D:证明算法的正确性。
答案:BC4.函数10logn3+5logn2的渐近表达式为():A:O(nlogn)B:O(logn3)C:O(logn)D:O(logn2)答案:C5.下列函数根据渐近阶从低到高顺序是()A:logn < n1/2 <2n <n3 <3n <n!B:n1/2 < logn <2n <n3 < n! < 3nC:n1/2 < logn <2n <n3 <3n <n!D:logn <n1/2<2n <n3 < n! < 3n答案:A6.研究NPC 问题的意义: 一旦某个NPC问题找到了多项式时间复杂性的算法,那么所有的NP问题都找到了多项式时间算法。
( )A:对B:错答案:A第二章测试1.直接或间接的调用自身的算法称为()。
A:递归算法B:迭代算法D:动态规划算法答案:A2.Hanoi塔问题如下图所示。
现要求将塔座A上的的所有圆盘移到塔座B上,并仍按同样顺序叠置。
移动圆盘时遵守Hanoi塔问题的移动规则。
由此设计出解Hanoi塔问题的递归算法正确的为:()A:B:C:D:答案:A3.分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题分别解决子问题最后将子问题的解组合起来形成原问题的解。
这要求原问题和子问题()。
A:问题规模相同,问题性质不同B:问题规模不同,问题性质不同C:问题规模相同,问题性质相同D:问题规模不同,问题性质相同答案:D4.利用二分搜索,最坏情况下的计算时间复杂性为()。
2020年算法分析设计习题答案

第3章 动态规划
2. 石子合并问题 问题描述: 在一个圆形操场的四周摆放着n堆石子. 现在要将石子有次序地合并 成一堆. 规定每次只能选相邻的2堆石子合并成一堆, 并将新的一堆石子数记为 该次合并的得分. 试设计一个算法, 计算出将n堆石子合并成一堆的最小得分和 最大得分. 算法设计: 对于给定n堆石子, 计算合并成一堆的最小得分和最大得分. 数据输入: 由文件input.txt提供输入数据. 文件的第1行是正整数n, 1n100, 表 示有n堆石子. 第2行有n个数, 分别表示n堆石子的个数. 结果输出: 将计算结果输出到文件output.txt, 文件第1行是最小得分, 第2行是最 大得分.
第五章 回溯
运动员最佳配对问题
问题描述: 羽毛球队有男女运动员各n人. 给定2个nn矩阵P和Q. P[i][j]是男运 动员i与女运动员j配混合双打的男运动员竞赛优势; Q[i][j]是女运动员i与男运 动员j配混合双打的女运动员竞赛优势. 由于技术配合和心理状态等各种因素 影响, P[i][j]不一定等于Q[j][i]. 男运动员i和女运动员j配对的竞赛优势是 P[i][j]*Q[j][i]. 设计一个算法, 计算男女运动员最佳配对法, 使得各组男女双方 竞赛优势的总和达到最大.
8.
若m[i,j]>t, 则m[i,j]=t; s[i,j]=k;
第3章 动态规划
再讨论圆周上的石子合并问题, 子结构[i:j]稍作修改 • 定义m[i][len]为合并第i堆到第i+len-1堆石子能得到的最少分数 • 当i+len-1>n时, 指跨过第n堆到第(i+len-1)%n堆,
仅sum函数需要修改
第2章 分治
2-8 设n个不同的整数排好序后存于T[1:n]中. 若存在一个下标i, 1 i n, 使得T[i]=i. 设计一个有效算法找到这个下标. 要求算 法在最坏情况下的计算时间O(log n).
算法分析与设计智慧树知到答案章节测试2023年黑龙江工程学院

第一章测试1.算法就是一组有穷的规则,它们规定了解决某一特定类型问题的一系列运算。
()A:对B:错答案:A2.计算机的资源最重要的是内存和运算资源。
因而,算法的复杂性有时间和空间之分。
()A:对B:错答案:A3.时间复杂度是指算法最坏情况下的运行时间。
()A:对B:错答案:B4.下面关于算法的说法中正确的是。
(1)求解某一问题的算法是唯一的。
(2)算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
(3)算法的每一条指令是清晰无歧义的。
(4)算法可以用某种程序设计语言具体实现,所以算法和程序是等价的。
()A:(2)(3)B:(1)(3)C:(1)(2)D:(2)(4)答案:A5.描述算法的基本方法有。
(1)自然语言(2)流程图(3)伪代码(4)程序设计语言()A:(1)(2)(3)B:(1)(3)(4)C:(1)(2)(3)(4)D:(2)(3)(4)答案:C6.算法分析是()A:将算法用某种程序设计语言恰当地表示出来B:证明算法对所有可能的合法出入都能算出正确的答案C:对算法需要多少计算时间和存储空间作定量分析D:在抽象数据数据集合上执行程序,以确定是否产生错误结果答案:C7.算法是由若干条指令组成的有穷序列,而且满足以下叙述中的性质。
(1)输入:有0个或多个输入(2)输出:至少有一个输出(3)确定性:指令清晰、无歧义(4)有限性:指令执行次数有限,而且执行时间有限()A:(1)(2)(3)B:(1)(2)(4)C:(1)(2)(3)(4)D:(1)(3)(4)答案:C8.下面函数中增长率最低的是()A:n2B:log2nC:nD:2n答案:B9.下面属于算法的特性有( )。
A:有限性:算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
B:输入:有0个或多个外部量作为算法的输入。
C:确定性:组成算法的每条指令是清晰,无歧义的。
D:输出:算法产生至少一个量作为输出。
答案:ABCD10.当m为24,n为60时,使用欧几里得算法求m和n的最大公约数,需要进行()次除法运算。
算法分析与设计(习题答案)

算法分析与设计教程习题解答第1章 算法引论1. 解:算法是一组有穷的规则,它规定了解决某一特定类型问题的一系列计算方法。
频率计数是指计算机执行程序中的某一条语句的执行次数。
多项式时间算法是指可用多项式函数对某算法进行计算时间限界的算法。
指数时间算法是指某算法的计算时间只能使用指数函数限界的算法。
2. 解:算法分析的目的是使算法设计者知道为完成一项任务所设计的算法的优劣,进而促使人们想方设法地设计出一些效率更高效的算法,以便达到少花钱、多办事、办好事的经济效果。
3. 解:事前分析是指求出某个算法的一个时间限界函数(它是一些有关参数的函数);事后测试指收集计算机对于某个算法的执行时间和占用空间的统计资料。
4. 解:评价一个算法应从事前分析和事后测试这两个阶段进行,事前分析主要应从时间复杂度和空间复杂度这两个维度进行分析;事后测试主要应对所评价的算法作时空性能分布图。
5. 解:①n=11; ②n=12; ③n=982; ④n=39。
第2章 递归算法与分治算法1. 解:递归算法是将归纳法的思想应用于算法设计之中,递归算法充分地利用了计算机系统内部机能,自动实现调用过程中对于相关且必要的信息的保存与恢复;分治算法是把一个问题划分为一个或多个子问题,每个子问题与原问题具有完全相同的解决思路,进而可以按照递归的思路进行求解。
2. 解:通过分治算法的一般设计步骤进行说明。
3. 解:int fibonacci(int n) {if(n<=1) return 1;return fibonacci(n-1)+fibonacci(n-2); }4. 解:void hanoi(int n,int a,int b,int c) {if(n>0) {hanoi(n-1,a,c,b); move(a,b);hanoi(n-1,c,b,a); } } 5. 解:①22*2)(−−=n n f n② )log *()(n n n f O =6. 解:算法略。
算法分析习题参考答案第四章

第四章作业 部分参考答案1. 设有n 个顾客同时等待一项服务。
顾客i 需要的服务时间为n i t i ≤≤1,。
应该如何安排n 个顾客的服务次序才能使总的等待时间达到最小?总的等待时间是各顾客等待服务的时间的总和。
试给出你的做法的理由(证明)。
策略:对 1i t i n ≤≤进行排序,,21n i i i t t t ≤≤≤ 然后按照递增顺序依次服务12,,...,ni i i 即可。
解析:设得到服务的顾客的顺序为12,,...,n j j j ,则总等待时间为,2)1(121n n j j j j t t t n nt T +++-+=- 则在总等待时间T 中1j t 的权重最大,jn t 的权重最小。
故让所需时间少的顾客先得到服务可以减少总等待时间。
证明:设,21n i i i t t t ≤≤≤ ,下证明当按照不减顺序依次服务时,为最优策略。
记按照n i i i 21次序服务时,等待时间为T ,下证明任意互换两者的次序,T都不减。
即假设互换j i ,)(j i <两位顾客的次序,互换后等待总时间为T ~,则有.~T T ≥由于,))(())(()2)(2()1)(1(21n j i i i i i i t j t j n i t i n t n t n T +--++--++--+--=,))(())(()2)(2()1)(1(~21n i j i i i i i t j t j n i t i n t n t n T +--++--++--+--=则有.0))((~≥--=-i j i i t t i j T T同理可证其它次序,都可以由n i i i 21经过有限次两两调换顺序后得到,而每次交换,总时间不减,从而n i i i 21为最优策略。
2. 字符h a ~出现的频率分布恰好是前8个Fibonacci 数,它们的Huffman 编码是什么?将结果推广到n 个字符的频率分布恰好是前n 个Fibonacci 数的情形。
算法设计与分析课后习题解答

C1*(g1+g2)<= t1(n)+t2(n) <=c2(g1+g2)—----(3)
不失一般性假设max(g1(n),g2(n))=g1(n)。
显然,g1(n)+g2(n)<2g1(n),即g1+g2〈2max(g1,g2)
又g2(n)〉0,g1(n)+g2(n)>g1(n),即g1+g2>max(g1,g2).
算法设计与分析基础课后练习答案
习题1.1
4。设计一个计算 的算法,n是任意正整数。除了赋值和比较运算,该算法只能用到基本的四则运算操作。
算法求
//输入:一个正整数n 2
//输出:。
step1:a=1;
step2:若a*a<n转step 3,否则输出a;
step3:a=a+1转step 2;
5. a.用欧几里德算法求gcd(31415,14142)。
b。该算法稳定吗?
c.该算法在位吗?
解:
a。该算法对列表”60,35,81,98,14,47”排序的过程如下所示:
b.该算法不稳定.比如对列表"2,2*”排序
c.该算法不在位.额外空间for S and Count[]
4.(古老的七桥问题)
第2章
习题2。1
7。对下列断言进行证明:(如果是错误的,请举例)
Else return A[n—1]
a.该算法计算的是什么?
b.建立该算法所做的基本操作次数的递推关系并求解
解:
a.计算的给定数组的最小值
b.
9。考虑用于解决第8题问题的另一个算法,该算法递归地将数组分成两半。我们将它称为Min2(A[0..n-1])
第04章的习题参考答案

2)穿好衣服、裤子及鞋子等;
3)下床;
4)洗漱(包括洗脸、刷牙等);
5)吃早餐(包括饭后洗碗等工作);
6)上课学习;
7)吃午餐;
8)午休;
程序结构应当怎样修改才能适应?
(2)又假定搬砖人的类别数也在变化时又如何处理?
(3)假定每人每次搬砖数已知,能否告知所需的最少人数及每类人的搬砖数?
(4)假定每个人每次允许搬砖的块数可以少于规定数,如何搬才能最省时间?
解:(1)有nMale个人和num块砖,在男、女和孩子每次搬砖的块数未知或可变的情
6)fac=1,然后转7);
7)输出n!的值(n非法时写‘非法’)
4-13 对例4-15,请绘制算法的PAD流程图和传统流程图。
PAD流程图:
传统流程图:
4-14 例4-15只解决了36个人搬36块砖的情形。请思考这样一些问题:
(1)假定nMale个人和num块砖,男、女和孩子每次搬砖的块数未知或可变,算法或
if(fa<fb) //如果fa<fb,将fb的值赋给中间变量temp,即temp=fb;
temp=fb;
else //否则,将fa的值赋给temp,即temp=fa;
temp=fa;
if(temp>fc) //如果中间变量temp>fc,则将temp的值赋给max,即max=temp;
4-6 试述算法的组成要素、算法的基本性质。
解:算法的实质是对问题求解方法和过程的描述,它由解决问题的基本操作及控制操作
过程次序的控制结构组成。其中基本操作包括算术、关系、逻辑等基本运算和输入输出以及
函数、位操作、文件操作等;控制结构主要是顺序、选择和循环三种基本的控制结构。
中科院计算机算法分析与设计_习题3-4_答案

1110
n2 n 3
1110
10
第n-1个字符:1个1 ,1个0, 第 n 个字符: 1个0 .
g的编码为: 10
h的编码为: 0
0
3. 设p1 p2,…,pn是准备存放到长为L的磁带上的n个程序,程序pi需要的带长为ai
设 ai L, 要求选取一个能放在带上的程序的最大子集合(即其中含有最多个
2.字符a~h出现的频率分布恰好是前8个Fibonacci数,它们的Huffman编码 是什么?将结果推广到n个字符的频率分布恰好是前n个个Fibonacci数的情 形。Fibonacci数的定义为 F0 1, F1 1, Fn Fn2 Fn1 if n 1 解:前8个数为a, b, c, d, e, f, g, h 1, 1, 2, 3, 5, 8,13, 21
pi Q
证明:不妨设 a1 a2 ... an ,若该贪心策略构造的子集合Q为 {a1, a2 ,, as } 则s必定满足 ai L 、 as as 1 L. 下证Q是最大子集。 i 1 i 1 ~ 即不存在多于s个的程序集合 Q {ai , ai ,, ai }, (k s) 使得 ai L. ~ p Q ~ 假设存在多于s个的程序集Q {ai , ai ,, ai }, (k s)使得 ai L, ~
as 1 代替 as , 子集合变为{a1 , a2 ,, ai 1 , ai 1} 并且其满足 ak ai 1 L
k 1 i 1
虽然程序个数不变仍为不变,但总长度更优的子集合。
t 则在总等待时间T中 t j1 的权重最大, jn 的权重最小。
对 ti 1 i n 进行排序ti ti ti , 按照递增顺序依次服务.
习题答案第四章算法设计与分析吕国英

习题答案第四章算法设计与分析吕国英习题答案第四章算法设计与分析吕国英main(void){ int buf[100]; int n; int i,j,k; scanf("%d",&n);for(i=0;i<n;i++)< bdsfid="66" p=""></n;i++)<>buf[i]=2; for(i=0;i<n-1;i++)< bdsfid="68" p=""></n-1;i++)<> { for(j=0;j<n-i-1;j++)< bdsfid="70" p=""></n-i-1;j++)<>{ buf[j]+=2; } } for(j=0;j<n;j++)< bdsfid="72" p=""></n;j++)<>{ if(buf[j]>=10){ buf[j+1]+=buf[j]/10; buf[j]=buf[j]%10; } } for(i=n-1;i>=0;i--)printf("%d",buf[i]); printf("\n"); return 0; }2、#includeint main(void){int n=2;inti;for(i=1;i<=9;i++){n=(n+2)*2;}printf("%d\n",n);return 0;}3、#includeint main(void){int a=54;int n;int m;printf("计算机先拿3张牌\n");a=a-3;while(a>=0){printf("还剩%d张牌\n",a);printf("你拿几张?请输入:");scanf("%d",&n);if(n>4||n<1||n>a){printf("错误!重新拿牌\n");continue;}a=a-n;printf("还剩%d张牌\n",a);if(a==0)break;m=5-n;printf("计算机拿%d\n",m);a=a-m;}return 0;}4、#includeint d;int a1,a2;intfun(int n);int main(void){intn;printf("n=?,d=?,a1=?,a2=?");scanf("%d%d%d%d\n",&n,&d ,&a 1,&a2);printf("%d\n",fun(n));return 0;}int fun(intn){if(n==1)return a1;if(n==2)return a2;return fun(n-2)-(fun(n-1)-d)*2;}5、#includechar chess[8][8];int is_safe(int row,int col);int queen(int row,int col,int n);int main(void){inti,j;for(i=0;i<8;i++)for(j=0;j<8;j++)chess[i][j]=X;queen(0 ,0,0);for(i=0;i<8;i++){for(j=0;j<8;j++)printf("%c",chess[i][j]);printf("\n");}return 0;}int is_safe(int row,int col){inti,j;for(i=0;i<8;i++){if(chess[row][i]==Q)return0;if(chess[i][col]==Q)return 0;}i=row;j=col;while(i!=-1&&j!=-1){if(chess[i--][j--]==Q)return0;}i=row;j=col;while(i!=-1&&j!=8){if(chess[i--][j++]==Q)return 0;}i=row;j=col;while(i!=8&&j!=-1){if(chess[i++][j--]==Q)return0;}i=row;j=col;while(i!=8&&j!=8){if(chess[i++][j++]==Q)re turn 0;}return1;}int queen(int row,int col,int n){inti,j;intresult=0;if(n==8)return1;elseif(is_safe(row,col)){chess[r ow][col]=Q;for(i=0;i<8;i++)for(j=0;j<8;j++){result+=queen (i,j,n+1);if(result>0)break;}if(result>0)return1;else{che ss[row][col]=X;return 0;}}elsereturn 0;}6、#includeint main(void){inti,j,k;for(i=1;i<=33;i++)for(j=1;j<=50;j++){k=100-i-j;if(k%2==0){if(3*i+2*j+k/2==100)printf("大马%d\n中马%d\n 小马%d\n\n\n",i,j,k);}}return 0;}7、#includeint main(void){inti;for(i=1;i<=10000;i++){if(i%2==1&&i%3==2&&i%5==4& &i%6==5 &&i%7==0)printf("%d\n",i);}return 0;}8、#includeint main(void){int i;int sum;inta1,a2,a3,a4;for(i=1000;i<=9999;i++){a1=i%10;a2=i/10%10;if (a1!=a2){a3=i/100%10;if(a1!=a3&&a2!=a3){a4=i/1000;if(a1!=a4&&a2!=a4&&a3!=a4){sum=(a1+a2+a3+a4)*(a1+a2+a3+a4);i f(i% sum==0)printf("%d\n",i);}}}}return 0;}9、#include #define N10 void max_min(int *a,int m,int n,int*min1,int *min2,int *max1,int *max2); int main(void) { inta[N]={2,3,4,5,34,7,9,6,43,21}; int min1,min2; int max1,max2; max_min(a,0,N-1,&min1,&min2,&max1,&max2);printf("min1=%d\nmin2=%d\nmax1=%d\nmax2=%d\n",min1, min2,m ax1,max2); return 0; } void max_min(int *a,int m,int n,int *min1,int *min2,int *max1,int *max2){ int lmin1,lmin2,lmax1,lmax2; intrmin1,rmin2,rmax1,rmax2; int mid; if(m==n){ *min1=*min2=*max1=*max2=a[m]; } else if(m==n-1){ if(a[m]<a[n])< bdsfid="114" p=""></a[n])<>{ *min1=a[m]; *min2=a[n]; *max1=a[n]; *max2=a[m]; } else { *min1=a[n]; *min2=a[m]; *max1=a[m]; *max2=a[n]; } } else { mid=(m+n)/2;max_min(a,m,mid,&lmin1,&lmin2,&lmax1,&lmax2);max_min(a,mid+1,n,&rmin1,&rmin2,&rmax1,&rmax2);if(lmin1<rmin1)< bdsfid="119" p=""></rmin1)<>{ if(lmin2<rmin1)< bdsfid="121" p=""></rmin1)<>{ *min1=lmin1; *min2=lmin2; } else { *min1=lmin1;*min2=rmin1; } } else if(rmin2<lmin1)< bdsfid="124" p=""></lmin1)<>{ *min1=rmin1; *min2=rmin2; } else { *min1=rmin1;*min2=lmin1; } if(lmax1>rmax1){ if(lmax2>rmax1){ *max1=lmax1; *max2=lmax2; } else { *max1=lmax1;*max2=rmax1; } } else if(rmax2>lmax1){ *max1=rmax1; *max2=rmax2; } else { *max1=rmax1;*max2=lmax1; } } }10、#include int add(int *a,int flag,int right); int main(void){ int a[10]={1,2,3,4,5,6,7,8,9,10}; intsum=add(a,0,9); printf("%d\n",sum); return 0; } intadd(int *a,int flag,int right){ int mid; if(flag==right){ return a[flag]; } else if(flag==right-1){ return a[flag]+a[right]; } else{ mid=(flag+right)/2; returnadd(a,flag,mid)+add(a,mid+1,right); } }11、#includeint main(void){int a[5][3]={{-50,17,-42},{-47,-19,-3},{36,-34,-43},{-30,-43,34},{-23,-8,-45}};int i,j;int max,n;int sum=0;for(i=0;i<5;i++){max=a[i][0];n=0;for(j=1;j<3;j++){i f(a[i][j]>max){max=a[i][j];n=j;}}sum+=max;printf("a[%d][%d]=%d\n",i,n,max);}printf("%d\n",sum);return 0;}12、/* * File: newmain、c* Author: nirnava** Created on全文结束》》年4月22日, 下午5:21*/#include#include#define N4void matrix_mul(int*mul1,int *mul2,int *mul3,int length);voidmatrix_add_sub(int * A,int * B,int * C,int m,charch);void update_half_value(int * A,int * B,int m);void get_half_value(int * A,int * B,int m);int main(void){int i,j;int mul1[N*N]={1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6};intmul2[N*N]={7,8,9,10,1,2,3,4,5,6,7,8,9,10,1,2};intmul3[N*N];matrix_mul(mul1,mul2,mul3,N);for(i=0;i<="" m,char="" matrix_add_sub(int="" p="" {printf("%5d",mul3[i]);if((i+1)%n='=0)printf("\n");}return'> i;for(i=0;i<="" bdsfid="156" p="" update_half_value(int=""> m){inti,j;for(i=0;i<="" p="">i,j;for(i=0;i<="" 2;i++){for(j="0;j<m/2;j++){A[i*m/2+j]=B[i*" bdsfid="161" m+j];}}}void="" matrix_mul(int="" p=""> m){if(m==2){int D,E,F,G,H,I,J;D=A[0]*(B[1]-B[3]);E=A[3]*(B[2]-B[0]);F=(A[2]+A[3])*B[0];G=(A[0]+A[1])*B[3];H=(A[2]-A[0])*(B[0]+B[1]);I=(A[1]-A[3])*(B[2]+B[3]);J=(A[0]+A[3])*(B[0]+B[3]);C[0]=E+I+J-G;C[1]=D+G;C[2]=E+F;C[3]=D+H+J-F;return ;}else{int A1[m*m/4],A2[m*m/4],A3[m*m/4],A4[m*m/4];intB1[m*m/4],B2[m*m/4],B3[m*m/4],B4[m*m/4];intC1[m*m/4],C2[m*m/4],C3[m*m/4],C4[m*m/4];intD[m*m/4],E[m*m/4],F[m*m/4],G[m*m/4],H[m*m/4],I[m*m/4 ],J[m*m/4];inttemp1[m*m/4],temp2[m*m/4];get_half_value(A1,&A[0],m);g et_half_value(A2,&A[m/2],m);get_half_value(A3,&A[m*m/2],m);get_half_value(A4,&A[m*m/2+m/2],m);get_half_value(B1,&B[0] , m);get_half_value(B2,&B[m/2],m);get_half_value(B3,&B[m*m/2],m);get_half_value(B4,&B[m*m/2+m/2],m);matrix_add_sub( B 2,B4,temp1,m/2,-);matrix_mul(A1,temp1,D,m/2);matrix_add_sub(B3,B1,temp1, m /2,-);matrix_mul(A4,temp1,E,m/2);matrix_add_sub(A3,A4,temp1, m /2,+);matrix_mul(temp1,B1,F,m/2);matrix_add_sub(A1,A2,tem p1,m/2,+);matrix_mul(temp1,B4,G,m/2);matrix_add_sub(A3,A1 ,t emp1,m/2,-);matrix_add_sub(B1,B2,temp2,m/2,+);matrix_mul(temp1,te mp 2,H,m/2);matrix_add_sub(A2,A4,temp1,m/2,-);matrix_add_sub(B3,B4,temp2,m/2,+);matrix_mul(temp1,te mp2,I,m/2);matrix_add_sub(A1,A4,temp1,m/2,+);matrix_add_sub (B1,B4,temp2,m/2,+);matrix_mul(temp1,temp2,J,m/2);matrix_ add_sub(E,I,temp1,m/2,+);matrix_add_sub(J,G,temp2,m/2,-);matr ix_add_sub(temp1,temp2,C1,m/2,+);matrix_add_sub(D,G ,C2,m/2,+);matrix_add_sub(E,F,C3,m/2,+);matrix_add_sub(D,H,temp1,m/2,+);matrix_add_sub(J,F,temp2,m/2,-);matrix_add_sub(temp1,temp2,C4,m/2,+);update_half_value ( C1,&C[0],m);update_half_value(C2,&C[m/2],m);update_half_v alue(C3,&C[m*m/2],m);update_half_value(C4,&C[m*m/2+m/2], m );return ;}}13、#includeint main(void){inta[6][7]={{16,4,3,12,6,0,3},{4,-5,6,7,0,0,2},{6,0,-1,-2,3,6,8},{5,3,4,0,0,-2,7},{-1,7,4,0,7,-5,6},{0,-1,3,4,12,4,2}};int b[6][7],c[6][7];int i,j,k;int max;int flag;inttemp;for(i=0;i<6;i++)for(j=0;j<7;j++){b[i][j]=a[i][j];c[i ][j]=-1;}for(i=1;i<5;i++){for(j=0;j<7;j++){max=0;for(k=j-2;k<=j+2;k++){if(k<0)continue;elseif(k>6)break;else{if(b[i][j]+b[i-1][k]>max){max=b[i][j]+b[i-1][k];flag=k;}}}b[i][j]=max;c[i][j]=flag;}}for(j=1;j<=5;j++){max=0;for(k=j-2;k<=j+2;k++){if(k<0)continue;elseif(k>6)break;else{if(b[i][j]+b[i-1][k]>max){max=b[i][j]+b[i-1][k];flag=k;}}}b[i][j]=max;c[i][j]=flag;}max=0;for(j=1;j<=5;j++){if(b[i][j]>max){max=b[i][j];flag=j;}}printf("%d\n",max);temp=c[i][flag];printf("%5d",a[i][temp]);for(j=i; j>0;j--){temp=c[j][temp];printf("%5d",a[j-1][temp]);}printf("\n");return 0;}14、#includeint main(void){intA[6]={0,3,7,9,12,13};int B[6]={0,5,10,11,11,11};intC[6]={0,4,6,11,12,12};int AB[6][6];int temp[6];intabc[6];int max;int flag;inti,j,k;for(i=0;i<=5;i++){max=0;for(j=0;j<=i;j++){AB[i][j]= A[i- j]+B[j];if(AB[i][j]>max)max=AB[i][j];}temp[i]=max;}max=0; for(i=0;i<=5;i++){abc[i]=temp[i]+C[5-i];if(abc[i]>max){max=abc[i];flag=i;}}printf("max=%d\n",m ax);printf("c=%d\n",5-flag);max=max-C[5-flag];for(i=0;i<=flag;i++){if(AB[flag][i]==max){printf("b =%d\n",i);printf("a=%d\n",flag-i);break;}}return 0;}16、#include#define N100int search(int*a,int left,int right);int sum_buf(int *a,int left,int right);int main(void){int a[N];int i;ints;for(i=0;i< bdsfid="203" p=""><>1);printf("%d\n",s);return 0;}int sum_buf(int *a,int left,int right){int i;intsum=0;for(i=left;i<=right;i++)sum+=a[i];return sum;}int search(int *a,int left,int right){intmid=(left+right)/2;if(left==right-1){if(a[left]<="">left;}if(mid*2!=(right+left-1)){if(sum_buf(a,left,mid-1)>sum_buf(a,mid+1,right)){return search(a,left,mid-1);}elseif(sum_buf(a,left,mid-1)<sum_buf(a,mid+1,right)){return< bdsfid="211" p=""></sum_buf(a,mid+1,right)){return<>search(a,mid+1,right);}elsereturnmid;}else{if(sum_buf(a,left,mid)>sum_buf(a,mid+1,right))r eturn search(a,left,mid);elsereturnsearch(a,mid+1,right);}}17、#includeintjob[6][2]={{3,8},{12,10},{5,9},{2,6},{9、3},{11,1}};int x[6],bestx[6],f1=0,bestf,f2[7]={0};void try(int i);void swap(int a,int b);int main(void){inti,j;bestf=32767;for(i=0;i<6;i++)x[i]=i;try(0);for(i=0;i<6 ;i++)p rintf("%d",bestx[i]);printf("\nbestf=%d\n",bestf);return 0;}void try(inti){intj;if(i==6){for(j=0;j<6;j++)bestx[j]=x[j];bestf=f2[i];}else{for(j=i;j<6;j++){f1=f1+job[x[j]][0];if(f2[i]>f1)f2[i+1]=f2[i]+job[x[j]][1];elsef2[i+1]=f1+job[x[j]][1];if(f2[i+1 ]< bdsfid="221" p=""><>job[x[j]][0];}}}void swap(int i,int j){inttemp;temp=x[i];x[i]=x[j];x[j]=temp;}18、#include#define N5 //N个数字#define M2 //M个加号char buf[N];int a[N];char b[M+1][N];intc[M+1];int try(int t);void swap(int t1,int t2);intadd();void output();int min=99999;int main(){inti;for(i=0;i<n;i++){scanf("%c",&buf[i]);}a[0]=0;for(i=1;i< 0;}int=""=m;i++){a[i]="1;}for(;i<N;i++){a[i]=0;}try(1);output();pri"bdsfid="229" i;int="" j;int="" ntf("%d\n",min);return="" sum;if(t="" t){int="" try(int="">=N){sum=add();if(sum<="" try(t+1);}}}void="" }else{for(j="t;j<N;j++){//if(a[t]!=a[j]"></n;i+ +){scanf("%c",&buf[i]);}a[0]=0;for(i=1;i<>t;t=a[t1];a[t1]=a[t2];a[t2]=t;}int add(){int sum=0;inti=0;int j;int k=0;inth=0;for(i=0;i\n",i,h,b[i][h]);h++;}else{b[i][h]=buf[j];//printf("%d %d %c \n",i,h,b[i][h]);//printf("%d",atoi(b[i]));h++;}}/*for(i=0;i< bdsfid="239" p=""><>[i]);}return sum;}void output(){inti;for(i=0;i< bdsfid="242" p=""><>tf("+");}printf("=");}19、#includeint main(void){int buf[100];int m,n;inti,j;buf[0]=1;buf[1]=1;scanf("%d%d",&n,&m);for(i=1;i<n;i++ < bdsfid="247" p=""></n;i++<>){buf[i+1]=buf[i];for(j=i;j>0;j--){buf[j]=buf[j]+buf[j-1];}}printf("%d\n",buf[m]);return 0;}20、#include int max_sum4(int *a,int n);int max_sub_sum(int *a,int left,int right); int main(void) { int a[6]={-2,11,-4,13,-5,-2};printf("%d\n",max_sum4(a,5)); return 0; } intmax_sum4(int *a,int n){ return max_sub_sum(a,0,n); } int max_sub_sum(int*a,int left,int right){ intcenter,i,max,left_sum,right_sum,s1,s2,s3,s4,lefts,rights, leftl,rightl; int buf[4]; if(left==right)return a[left]; else { center=(left+right)/2;left_sum=max_sub_sum(a,left,center);right_sum=max_sub_sum(a,center+1,right); s1=0; lefts=0;for(i=center;i>=left;i--){ lefts+=a[i]; if(lefts>s1)s1=lefts; } s2=0; rights=0;for(i=center+1;i<=right;i++){ rights+=a[i]; if(rights>s2)s2=rights; } s3=0; leftl=0; for(i=left;i<=center;i++) { leftl+=a[i]; if(leftl>s3)s3=leftl; } s4=0; rightl=0;for(i=right;i>=center+1;i--){ rightl+=a[i]; if(rightl>s4)s4=rightl; } buf[0]=s1+s2; buf[1]=s4+s3;buf[2]=left_sum; buf[3]=right_sum; max=0;for(i=0;i<=3;i++){ if(buf[i]>max)max=buf[i]; } return max; } }。
《算法设计与分析》考试题目及答案(DOC)

cg(n) }; B. O(g(n)) = { f(n) | 存在正常数 c 和 n0 使得对所有 n n0 有:0 cg(n)
f(n) }; C. O(g(n)) = { f(n) | 对于任何正常数 c>0,存在正数和 n0 >0 使得对所有
12. k 带图灵机的空间复杂性 S(n)是指(B) A. k 带图灵机处理所有长度为 n 的输入时,在某条带上所使用过的最大方格
数。 B. k 带图灵机处理所有长度为 n 的输入时,在 k 条带上所使用过的方格数的
总和。 C. k 带图灵机处理所有长度为 n 的输入时,在 k 条带上所使用过的平均方格
cg(n) }; B. O(g(n)) = { f(n) | 存在正常数 c 和 n0 使得对所有 n n0 有:0 cg(n)
f(n) };
C. (g(n)) = { f(n) | 对于任何正常数 c>0,存在正数和 n0 >0 使得对所有 n n0 有:0 f(n)<cg(n) };
n n0 有:0 f(n)<cg(n) }; D. O(g(n)) = { f(n) | 对于任何正常数 c>0,存在正数和 n0 >0 使得对所有
n n0 有:0 cg(n) < f(n) };
15. 记号 的定义正确的是(B)。 A. O(g(n)) = { f(n) | 存在正常数 c 和 n0 使得对所有 n n0 有:0 f(n)
return b;
}
11. 用回溯法解布线问题时,求最优解的主要程序段如下。如果布线区域划分 为 n m 的方格阵列,扩展每个结点需 O(1)的时间,L 为最短布线路径的长度, 则算法共耗时 ( O(mn) ),构造相应的最短距离需要(O(L))时间。
智慧树知到《算法分析与设计》章节测试答案

智慧树知到《算法分析与设计》章节测试答案第一章1、给定一个实例,如果一个算法能得到正确解答,称这个算法解答了该问题。
A:对B:错答案: 错2、一个问题的同一实例可以有不同的表示形式A:对B:错答案: 对3、同一数学模型使用不同的数据结构会有不同的算法,有效性有很大差别。
A:对B:错答案: 对4、问题的两个要素是输入和实例。
A:对B:错答案: 错5、算法与程序的区别是()A:输入B:输出C:确定性D:有穷性答案: 有穷性6、解决问题的基本步骤是()。
(1)算法设计(2)算法实现(3)数学建模(4)算法分析(5)正确性证明A:(3)(1)(4)(5)(2)B:(3)(4)(1)(5)(2)C:(3)(1)(5)(4)(2)D:(1)(2)(3)(4)(5)答案: (3)(1)(5)(4)(2)7、下面说法关于算法与问题的说法错误的是()。
A:如果一个算法能应用于问题的任意实例,并保证得到正确解答,称这个算法解答了该问题。
B:算法是一种计算方法,对问题的每个实例计算都能得到正确答案。
C:同一问题可能有几种不同的算法,解题思路和解题速度也会显著不同。
D:证明算法不正确,需要证明对任意实例算法都不能正确处理。
答案: 证明算法不正确,需要证明对任意实例算法都不能正确处理。
8、下面关于程序和算法的说法正确的是()。
A:算法的每一步骤必须要有确切的含义,必须是清楚的、无二义的。
B:程序是算法用某种程序设计语言的具体实现。
C:程序总是在有穷步的运算后终止。
D:算法是一个过程,计算机每次求解是针对问题的一个实例求解。
答案: 算法的每一步骤必须要有确切的含义,必须是清楚的、无二义的。
,程序是算法用某种程序设计语言的具体实现。
,算法是一个过程,计算机每次求解是针对问题的一个实例求解。
9、最大独立集问题和()问题等价。
A: 最大团B:最小顶点覆盖C:区间调度问题D:稳定匹配问题答案:最大团,最小顶点覆盖10、给定两张喜欢列表,稳定匹配问题的输出是()。
(陈慧南 第3版)算法设计与分析——第4章课后习题答案
点; 其余结点的任意一个孩子的 low 值都小于结点的 d 值,其余结点都不是
关节点。 综上所述,无向图 G1 中,有 1,3,7 三个关节点。 图 G1 的双连通分图如下图所示。
1
7
0
6
3
1 2
1
的一个孩子且low3d1因此结点1是关节的一个孩子且low2d3因此结点3是关节的一个孩子且low5d7因此结点7是关节其余结点的任意一个孩子的low值都小于结点的d值其余结点都不是关节点
第四章课后习题
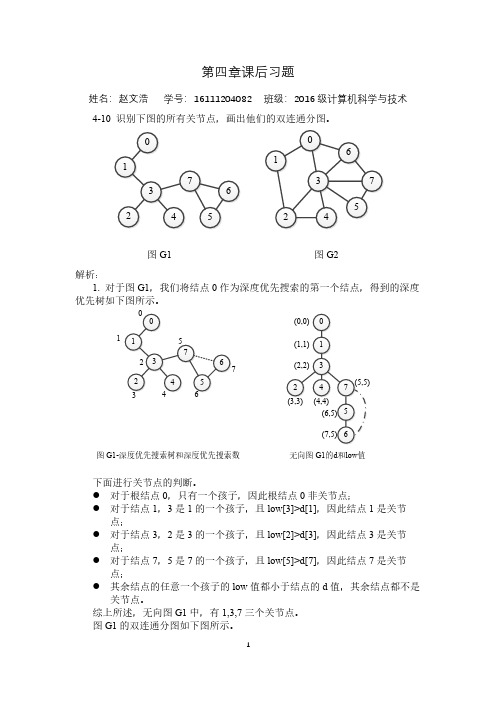
姓名:赵文浩 学号:16111204082 班级:2016 级计算机科学与技术 4-10 识别下图的所有关节点,画出他们的双连通分图。
3
5
7 3
3
4
图 G1的双连通分图
2. 对于图 G2,我们仍将结点 0 作为深度优先搜索的第一个结点,得到的深 度优先树如下图所示。
(0,0) 0
11
0 0
33
5 6
6 7
22
57 4 4
(1,0) 1
(2,0) 2
(3,0) 3
(4,2) 4
6 (5,0)
7 (6,3)
5 (7,3)
图 G2-深度优先搜索树和深度优先搜索数
无向图 G2的d和low值
下面进行关节点判断。 无向图 G2 的所有结点的任意一个孩子的 low 值都小于结点的 d 值,因此无 向图 G2 中不存在关节点。因此,该无向图的双连通图即为它本身,如下图所 示。
0 6
1
3
7
5
2
4
图 G2的双连通分图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业四
4.1.2 Alternating glasses
a. There are 2n glasses standing next to each other in a row, the first n of them filled with a soda drink and the remaining n glasses empty. Make the glasses alternate in a filled-empty-filled-empty pattern in the minimum number of glass moves. [Gar78]
b. Solve the same problem if 2n glasses—n with a drink and n empty—are initially in a random order
答:
图1 杯子分组
a.两个为一组,在前n个杯子中判断偶数的杯子是否为空,不为空与同组的进行交换,共需
要交换n/2次,考虑n为奇数对n/2进行向下取整即可。
b.由于最终偶数位置为空杯,奇数位置为满杯,从第一项开始遍历,如果在奇数位置出现空
杯与后面偶数位置出现的第一个满杯进行交换,如果偶数位置出现满杯则与后面奇数出现的第一个空杯进行交换,每次交换使得两个位置满足条件,最坏情况是2n位置均为乱序,则需要交换n次,最好的情况为2n位置均满足条件,则交换次数为[0,n]
4.1.7 Apply insertion sort to sort the list E, X, A, M, P, L, E in alphabetical order.
4.2.1 Apply the DFS-based algorithm to solve the topological sorting problem for the following digraphs:
答:
(a) f
e g
b c
a d
从堆栈中弹出:efgbcad,反转输出为:dacbgfe
(b) 由于存在回环b图不是无向回环图。
4.2.5 Apply the source-removal algorithm to the digraphs of Problem 1 above.
答:(a)得到的解为:dacbgfe
图2 源删除算法
图2 b的源删除算法
(b)无解
4.3.7 Write pseudocode for a recursive algorithm for generating all 2n bit strings of length n.
4.4.10 (a) Write pseudocode for the divide-into-three algorithm for the fake-coin problem. Make sure that your algorithm handles properly all values of n, not only those that are multiples of 3.
(b) Set up a recurrence relation for the number of weighings in the divide-intothree algorithm for the fake-coin problem and solve it for n = 3k.
(c) For large values of n, about how many times faster is this algorithm than the one based on dividing coins into two piles? Your answer should not depend on n.
答:
(a)①如果硬币为3K,则将硬币分为三堆K枚硬币;如果硬币为3K+1,则将硬币分为两堆K+1,一堆K-1;如果硬币为3K+2则将硬币分为两堆K+1,一堆K。
称重两堆个数一样的,②如果重量相同,则假币在第三堆中,对第三堆进行①操作再进行②操作,不断重复直至找出假币。
③如果有一堆轻(假设假币为轻的)则假币在这堆里,对该堆进行①操作再进行②操作。
(b)第n次分每堆为3k−n,最坏的情况为n为k时。
=log23
(c)log2n
log3n
4.5.2 Apply quickselect to find the median of the list of numbers 9, 12, 5, 17, 20, 30, 8.
答:
import random
# 快速选择排序
def quicksort(l):
if len(l)<2:
return l
else:
r = random.randint(0, len(l)-1)
base = l[r]
del l[r]
left =[i for i in l[:]if i <= base]
right =[i for i in l[:]if i > base]
return quicksort(left)+[base]+quicksort(right)
lists =list(eval(input("请输入列表,使用逗号隔开: ")))
lists =quicksort(lists)
L =len(lists)
if L %2==0:
print((lists[int(L /2)]+ lists[int((L /2)+1)])/2)
else:
print(lists[int((L -1)/2)])。
