初中数学知识结构图(可编辑修改word版)
初中数学知识点全总结(完美打印版)
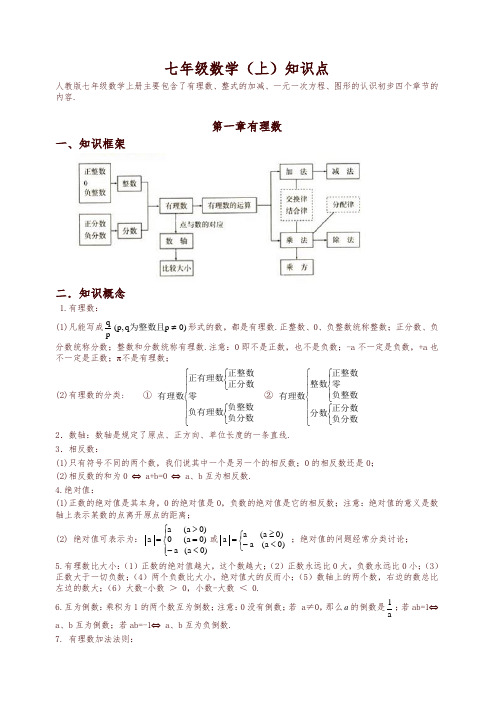
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线. 3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0. 6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数. 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc ); (3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则: (1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n=-a n或(a -b)n=-(b-a)n,当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n. 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学知识点全总结(完美打印版)

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线. 3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0. 6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数. 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc ); (3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则: (1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n=-a n或(a -b)n=-(b-a)n,当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n. 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
(完整word版)初中数学知识点全总结(完美打印版)
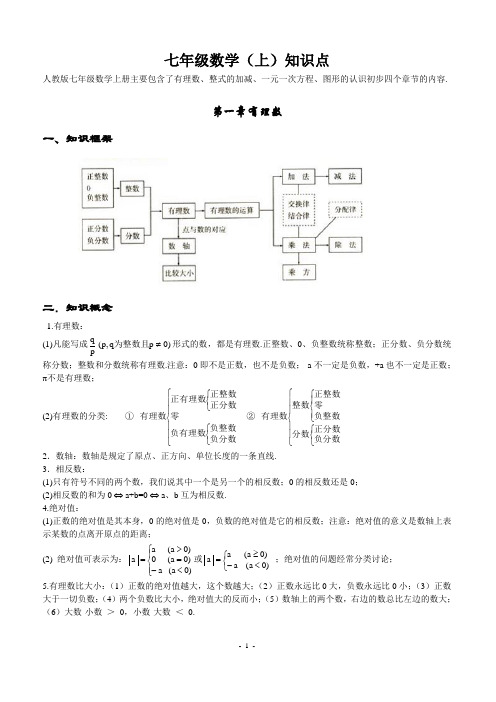
七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
(完整word版)初中数学知识点全总结(齐全)

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容。
第一章 有理数一、知识框架二.知识概念1。
有理数: (1)凡能写成)0p q ,p (pq≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;—a 不一定是负数,+a 也不一定是正数;不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线。
3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 a+b=0 a 、b 互为相反数。
4。
绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数—小数 > 0,小数—大数 < 0。
6。
互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1 a 、b 互为倒数;若ab=—1 a 、b 互为负倒数。
7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数。
初中数学八年级上册各章知识点梳理

八年级数学上册 各章知识点汇总第十一章 三角形一、知识结构图边与三角形有关的线段 高中线角平分线三角形的内角和 多边形的内角和三角形的外角和 多边形的外角和二、知识定义三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边。
高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性。
多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。
多边形的内角:多边形相邻两边组成的角叫做它的内角。
多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
正多边形:在平面内,各个角都相等,各条边都相等的多边形叫做正多边形。
三、公式与性质三角形的内角和:三角形的内角和为180°三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和。
性质2:三角形的一个外角大于任何一个和它不相邻的内角。
多边形对角线的条数:(1)从n 边形的一个顶点出发可以引(n-3)条对角线,把多边形分词(n-2)个三角形。
(2)n 边形共有23)-n(n 条对角线。
第十二章 全等三角形一、全等三角形角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)斜边、直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)4.证明两个三角形全等的基本思路:多边形的角和:多边形的外角和为360°。
多边形内角和公式: n 边形的内角和等于(n-2)·180°角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)边边边:三边对应相等的两个三角形全等(可简写成“SSS”)3.全等三角形的判定③全等三角形的对应边上的对应中线、角平分线、高线分别相等。
(最新版)北师大版初中数学各册章节知识点总结(K12教育文档)

(最新版)北师大版初中数学各册章节知识点总结(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((最新版)北师大版初中数学各册章节知识点总结(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(最新版)北师大版初中数学各册章节知识点总结(word版可编辑修改)的全部内容。
北师大版初中数学七年级(上册)各章知识点第一章丰富图形世界1、生活中常见的几何体:2、常见几何体的分类:3、平面图形折成立体图形应注意:4、圆柱的侧面展开图是一个长方形;表面全部展开是两个和一个 ;圆锥的表面全部展开图是一个和一个;正方体表面展开图是一个和两个;长方体的展开图是一个大和两个。
5、特殊立体图形的截面图形:(1)长方体、正方形的截面是:三角形、四边形(长方形、正方形、梯形、平行四边形)、五边形、六边形.(2)圆柱的截面是:长方形(正方形)、圆(3)圆锥的截面是:三角形、圆。
(4)球的截面是:圆。
6、我们经常把从正面看到的图形叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.7、常见立体图形的俯视图几何体长方体正方体圆锥圆柱球主视图长方形正方形三角形长方形圆俯视图长方形正方形圆(有一点)圆圆左视图长方形正方形三角形长方形圆8、点动成线,线动成面,面动成体。
第二章有理数1 、正数与负数在以前学过的0以外的数前面加上负号“—”的数叫负数。
与负数具有相反意义,即以前学过的0以外的数叫做正数(根据需要,有时在正数前面也加上“+”).2 、有理数(1)正整数、0、负整数统称,正分数和负分数统称。
整数和分数统称。
(完整版)初中数学知识点结构图
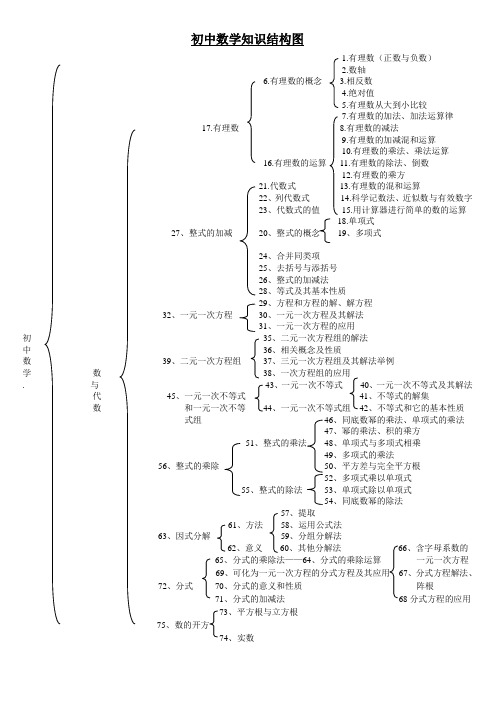
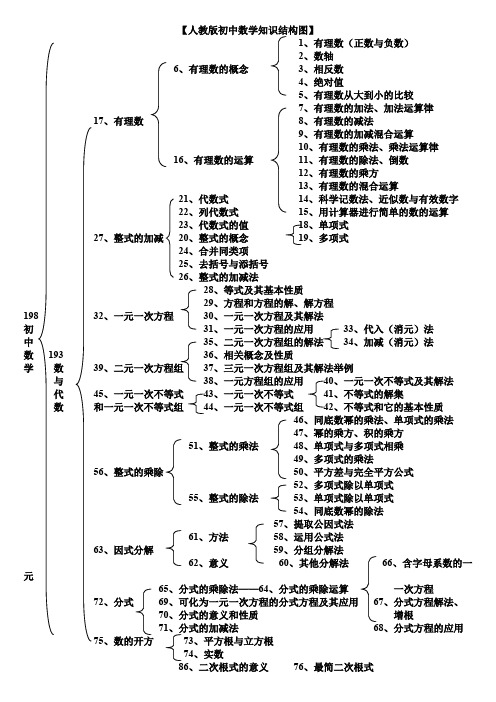
初中数学知识结构图1.有理数(正数与负数)2.数轴6.有理数的概念 3.相反数4.绝对值5.有理数从大到小比较7.有理数的加法、加法运算律17.有理数8.有理数的减法9.有理数的加减混和运算10.有理数的乘法、乘法运算16.有理数的运算11.有理数的除法、倒数12.有理数的乘方21.代数式13.有理数的混和运算22、列代数式14.科学记数法、近似数与有效数字23、代数式的值15.用计算器进行简单的数的运算18.单项式27、整式的加减20、整式的概念19、多项式24、合并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程32、一元一次方程30、一元一次方程及其解法31、一元一次方程的应用初35、二元一次方程组的解法中36、相关概念及性质数39、二元一次方程组37、三元一次方程组及其解法举例学数38、一次方程组的应用. 与43、一元一次不等式40、一元一次不等式及其解法代45、一元一次不等式41、不等式的解集数和一元一次不等44、一元一次不等式组42、不等式和它的基本性质式组46、同底数幂的乘法、单项式的乘法47、幂的乘法、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与完全平方根52、多项式乘以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法57、提取61、方法58、运用公式法63、因式分解59、分组分解法62、意义60、其他分解法66、含字母系数的65、分式的乘除法——64、分式的乘除运算一元一次方程69、可化为一元一次方程的分式方程及其应用67、分式方程解法、72、分式70、分式的意义和性质阵根71、分式的加减法68分式方程的应用73、平方根与立方根75、数的开方74、实数86、二次根式的意义76、最简二次根式79、二次根式的乘除法77、二次根式的除法87、二次根式78、二次根式的加减法82、二次根式的加减法80、二次根式的加减法81、同类二次根式85、二次根式的混合运算83、二次根式的混合运算84、有理化因式93、一元二次方程的解法98、一元二次方程的意义数100、二元二次方程组与102、一元二次方程99、一元二次方程组的根与系数的关系代94、分式方程的解法数97、可化为一元二次方程的分式方程式和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图像的图像和性质105、正比例函数的图像和性质108、二次函数——107二次函数的有关概念113、函数及其图像109、平面直角坐标系110、函数初111、函数的图像中112、反比例函数数114、线段学116、线段、角115、角117、相交线、对顶角、邻角、补角120、相交线118、垂线、点到直线的距离119、同位角、内错角、同旁内角126、相交、平行123、平行线121、平行线概念及性质122、平行线的判定124、空间直线、平面的位置关系空125、命题、公理、定理间129、与三角形有关的边与134、全等三角形图135、等腰三角形形138、三角形133、直角三角形——132、勾股定理131、与三角形有关的角——130、三角形的内角136、轴对称137、基本作图139、平行四边形的概念及其性质140、平行四边形的判定144、平行四边形141、矩形的概念、性质和判定149、多边形142、菱形的概念、性质和判定151、四边形150、中心对称143、正方形的概念、性质和判定145、梯形的相关概念148、梯形146、等腰梯形的概念、性质和判定147、三角形、梯形的中位线156、比例线段158、相似图形157、相似多边形152、相似三角形的相关概念155、相似三角形153、三角形相似的判定154、相似三角形的性质159、解直角三角形161、解直角三角形160、解直角三角形的应163、解直角三角形162、锐角三角形164、圆的有关概念及对称性165、点和圆的位置关系166、过不在同一直线上三点的圆空172、圆的有关性质167、三角形的外接圆间168、垂径定理及其逆定理与169、圆心角、弧、弦、弦心距初图170、圆周角定理中形171、圆内接四边形及其性质数173.直线和圆的位置关系学185、圆174.切线的判定和性质177.直线和圆的位置关系175.三角形的内切圆176. *切线长定理179.正多边形和圆——178.正多边形的有关计算180.圆周长、弧长183.弧长和扇形的面积181.圆、扇形、弓形的面积182.圆柱和圆锥的侧面展开图、侧面积184.圆和圆的位置关系186.几何体、几何图形187.平均数188.众数和中位数191.统计初步189.级差、方差、标准差195.统计与概率190.频数、频率、频率分布直方图192.概率初步——概率计算。
初中数学知识点及结构图

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a 1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a . 13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学知识结构图思维导图

公式 提公 法 因式 法
单项式除以单项式
同底数幂相除
除法
乘法公式
单项式与多项式 幂的乘法
乘法
运算
分母中 含字母、
分母 不为零
系数 相加 字母 不变
合并 同类项
加减 同类项
每个单项式 升降幂排列
项 次数
多项式
整式
最高项的次 数
意义
单项式
字母指数和
次数
系数
数字因 数
不改变 分式的值
公因式
通分化成同分 母
反比例函数
图象 性质
柱形储藏室轮船卸货 力学问题 电学问题
应用
一次函 数与反 比例函 数
解析式
形如y k x
(k为常数,k 0)
实际问题,图象在第 一象限
看图 象能 口述 性质
y
y
ox o
图象
1.开口方向 2.顶点坐标 3.对称轴 4.增减性 5.极值
性质
看式
子类
型能
口述
性质 ① yax2 ② yax2k
角平分线
条件
全等三角形
SSS
对应边、角、周长 面积、中线、高线、
角平分线相等
性质 表示方法
定义
两个三角形 用符号≌连接
完全重合 两个三角形
关系
位似变换
性质
两角对应 相等
相似三角形
判定
两边成比例 且夹角相等
全等 三角形 与 相似 三
角形
相似图形 形状相同
相似多边形
平行
比例线段
性质
ac bd
对应角相等, 周长的比=相似比 方
(3) a2 a
Y随 x的 增 大 而 增 大
(完整word版)人教版【初中数学】知识点总结-全面整理(超全)

人教版初中数学知识点总结目录七年级数学(上)知识点 (2)第一章有理数 (2)第二章整式的加减 (6)第三章一元一次方程 (7)第四章图形的认识初步 (8)七年级数学(下)知识点 (9)第五章相交线与平行线 (10)第六章平面直角坐标系 (12)第七章三角形 (13)第八章二元一次方程组 (17)第九章不等式与不等式组 (19)第十章数据的收集、整理与描述 (20)八年级数学(上)知识点 (21)第十一章全等三角形 (21)第十二章轴对称 (23)第十三章实数 (24)第十四章一次函数 (25)第十五章整式的乘除与分解因式 (26)八年级数学(下)知识点 (28)第十六章分式 (28)第十七章反比例函数 (30)第十八章勾股定理 (31)第十九章四边形 (32)第二十章数据的分析 (35)九年级数学(上)知识点 (36)第二十一章二次根式 (36)第二十二章一元二次根式 (37)第二十三章旋转 (39)第二十四章圆 (40)第二十五章概率 (42)九年级数学(下)知识点 (46)第二十六章二次函数 (46)第二十七章相似 (49)第二十八章锐角三角函数 (50)第二十九章投影与视图 (52)七年级数学(上)知识点 人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容。
第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0a+b=0 a 、b 互为相反数。
初三数学知识结构

初三数学知识结构
初三数学的知识结构主要包括以下两个部分:
一、数与代数
数与代数是数学学科的基础,主要包括整数与有理数、代数式与等式、方程与不等式等内容。
在初三数学学习中,学生需要掌握整数、有理数的性质和运算,理解代数式的含义,解决简单的一元一次方程与不等式等。
二、几何
几何主要包括平面几何和立体几何两部分。
平面几何包括点、线、面的性质、平面图形的性质等内容;立体几何则包括对立体图形的认识、立体图形的性质等。
学生需要通过几何的学习,培养空间思维能力和几何直观。
此外,还有一些重要的知识点,如数的分类及概念(包括非负数、倒数、相反数、数轴)、奇数、偶数、质数、合数的定义及表示等。
以上内容仅供参考,建议查询学校教材或咨询数学老师获取更全面的信息。
初中数学知识框架图
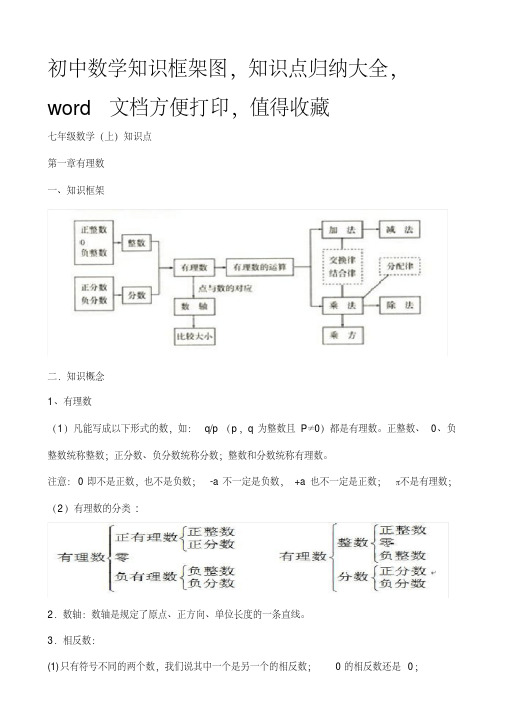
初中数学知识框架图,知识点归纳大全,word文档方便打印,值得收藏七年级数学(上)知识点第一章有理数一、知识框架二.知识概念1、有理数(1)凡能写成以下形式的数,如:q/p(p,q为整数且P≠0)都是有理数。
正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数。
注意:0即不是正数,也不是负数;-a不一定是负数,+a也不一定是正数;π不是有理数;(2)有理数的分类:2.数轴:数轴是规定了原点、正方向、单位长度的一条直线。
3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0,a+b=0 ,a、b互为相反数。
4、绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为或者:绝对值的问题经常讨论。
5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数>0,小数-大数<0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若a≠0,那么它的倒数是1/a;若ab=1,a、b互为倒数;若ab=-1,a、b互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b)+c=a+(b+c).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b).10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba;(2)乘法的结合律:(ab)c=a(bc);(3)乘法的分配律:a(b+c)=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,即a/0没有意义。
(完整版)人教版初中数学知识结构
【人教版初中数学知识结构图】1、有理数(正数与负数)2、数轴6、有理数的概念3、相反数4、绝对值5、有理数从大到小的比较7、有理数的加法、加法运算律17、有理数8、有理数的减法9、有理数的加减混合运算10、有理数的乘法、乘法运算律16、有理数的运算11、有理数的除法、倒数12、有理数的乘方13、有理数的混合运算21、代数式14、科学记数法、近似数与有效数字22、列代数式15、用计算器进行简单的数的运算23、代数式的值18、单项式27、整式的加减20、整式的概念19、多项式24、合并同类项25、去括号与添括号26、整式的加减法28、等式及其基本性质29、方程和方程的解、解方程198 32、一元一次方程30、一元一次方程及其解法初31、一元一次方程的应用33、代入(消元)法中35、二元一次方程组的解法34、加减(消元)法数193 36、相关概念及性质学数39、二元一次方程组37、三元一次方程组及其解法举例与38、一元方程组的应用40、一元一次不等式及其解法代45、一元一次不等式43、一元一次不等式41、不等式的解集数和一元一次不等式组44、一元一次不等式组42、不等式和它的基本性质46、同底数幂的乘法、单项式的乘法47、幂的乘方、积的乘方51、整式的乘法48、单项式与多项式相乘49、多项式的乘法56、整式的乘除50、平方差与完全平方公式52、多项式除以单项式55、整式的除法53、单项式除以单项式54、同底数幂的除法57、提取公因式法61、方法58、运用公式法63、因式分解59、分组分解法62、意义60、其他分解法66、含字母系数的一元65、分式的乘除法——64、分式的乘除运算一次方程72、分式69、可化为一元一次方程的分式方程及其应用67、分式方程解法、70、分式的意义和性质增根71、分式的加减法68、分式方程的应用75、数的开方73、平方根与立方根74、实数86、二次根式的意义76、最简二次根式79、二次根式的乘除法77、二次根式的除法78、二次根式的乘法87、二次根式82、二次根式的加减法80、二次根式的加减法81、同类二次根式85、二次根式的混合运算83、二次根式的混合运算84、有理化因式88、直接开平方法89、配方法193 93、一元一次方程的解法90、公式法198 数98、一元二次方程的意义91、因式分解法初与100、二元二次方程组92、一元二次方式根的判别法中代102、一元二次方程99、*一元二次方程的根与系数的关系数数94、分式方程的解法学97、可化为一元二次方程95、*无理方程的意义、解法的分式方程和无理方程96、分式方程、无理方程的应用101、一元二次方程的应用103、一次函数与一元一次不等式106、一次函数104、一次函数图象的图象和性质105、正比例函数的图象和性质108、二次函数——107、二次函数的有关概念113、函数及其图象109、平面直角坐标系110、函数111、函数的图象112、反比例函数116、线段、角114、线段115、角117、相交线、对顶角、邻角、补角120、相交线118、垂线、点到直线的距离119、同位角、内错角、同旁内角126、相交、平行123、平行线121、平行线概念及性质122、平行线的判定124、空间直线、平面的位置关系125、命题、公理、定理127、三角形三边关系129、与三角有关的边128、三角形的相关概念及分类、134、全等三角形角平分、中线、高135、等腰三角形133、直角三角形——132、勾股定理131、与三角形有关的角、130、三角形的内角136、轴对称139、平行四边形的概念及其性质138、三角形137、基本作图140、平行四边形的判定144、平行四边形141、矩形的概念、性质和判定149、多边形142、菱形的概念、性质和判定151、四边形150、中心对称143、正方形的概念、性质和判定145、梯形的相关概念148、梯形146、等腰梯形的概念、性质和判定194 147、三角形、梯形的中位线空156、比例线段间158、相似图形157、相似多边形152、相似三角形的相关概念198 与155、相似三角形153、三角形相似的判定初图154、相似三角形的性质中形161、解直角三角形159、解直角三角形数163、解直角三角形160、解直角三角形的应用公式学162、锐角三角形164、圆的有关概念及对称性165、点和圆的位置关系166、过不在同一直线上三点的圆172、圆的有关性质167、三角形的外接圆168、垂径定理及其逆定理169、圆心角、弧、弦、弦心距185、圆170、圆周角定理171、圆内接四边形及其性质173、直线和圆的位置关系177、直线和圆的位置关系174、切线的判定和性质175、三角形的内切圆176、切线长定理179、正多边形和圆——178、正多边形的有关计算180、圆周长、弧长183、弧长和扇形面积181、圆、扇形、弓形的面积182、圆柱和圆锥的侧面展开图、侧面积184、圆和圆的位置关系186、几何体、几何图形187、平均数191、统计初步188、众数和中位数195、统计与概率189、级差、方差、标准差190、频数、频率、频率分布直方图192、概率初步———概率计算196、中考复习197、总复习初中数学1.2.7 3.4.5.7 6.7.78...⎧⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩⎩有理数整式(上)一元一次方程图形认识初步相交线与平行线年级平面直角坐标系三角形(下)二元一次方程组9不等式与不等式组10数据的收集与整理11.12.813.14.15.816.17.818.19.20.⎧⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩⎨⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩全等三角形轴对称(上)实数一次函数整式的乘除与因式分解年级分式反比例函数(下)勾股定理四边形数据的分析21.22.923.24.25.926.27.928.29.⎧⎧⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎨⎩⎪⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩⎩二次根式一元二次方程(上)旋转圆概率初步年级二次函数相似(下)锐角三角形投影与视图高中数学1.1.2.1 2.23..4.1. 1.3 2.4 2.3.1. 1.5 2.1-1 2.3.3.1.1-2 2.3.⎧⎧⎪⎪⎪⎨⎨⎪⎪⎩⎪⎩⎧⎧⎪⎨⎨⎩⎪⎩⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩空间集合体集合与函数点,直线,平面之间的位置关系必修基本初等函数(1)必修直线与方程3函数的应用圆与方程算法初步三角函数必修统计必修平面向量概率解三角形常用逻辑语必修数列选修圆锥曲线与方程导数及其应用不等式统计案例选修推理证明数系的扩充 1.2-1 2.3.⎧⎧⎪⎪⎨⎨⎪⎪⎩⎩常用逻辑用语选修圆锥曲线与方程与复数的引入 空间向量与立体几何。
初中数学知识点及结构图(新人教版)

1 -七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一. 知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;(2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (a a ;绝对值的问题经常分类讨论; 5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;(3)一个数与0相加,仍得这个数.8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ).9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).2 -10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘;(2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.11 有理数乘法的运算律:(1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc );(3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n .14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
初中数学知识结构图

初中数学知识结构图(总11页)
--本页仅作为文档封面,使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
第一章有理数知识框架
第二章整式的加减知识框架
第三章一元一次方程知识框架
第四章图形的认识初步知识框架
第五章相交线与平行线知识框架
第六章平面直角坐标系知识框架
第七章三角形知识框架
第八章二元一次方程组知识结构图
第九章不等式与不等式组知识框架
第十章数据的收集、整理与描述知识框架
第十一章全等三角形知识框架
第十二章轴对称知识框架
第十三章实数知识框架:
有理数
实数
无理数
全面调查
抽样调查
收
集
数
据
描
述
数
据
整
理
数
据
分
析
数
据
得
出
结
论
第十四章 一次函数知识框架
第十五章 整式的乘除与分解因式知识框架
第十六章 分式知识框架
第十七章 反比例函数知识框架
整式乘法
整式除法
因式分解
乘法法则
第十八章勾股定理知识框架
第十九章四边形知识框架
第二十章数据的分析知识框架
第二十一章二次根式知识框架
第二十二章一元二次方程知识框架
第二十三章旋转知识框架
第二十四章圆知识框架
第二十五章概率
知识框架
第二十六章二次函数知识框架
第二十七章相似知识框架
第二十八章锐角三角函数知识框架
第二十九章投影与视图知识框架。
初一有理数的知识点总结 初一有理数知识结构图

初一有理数的知识点总结引言有理数是数学中的一个重要概念,也是初中数学的基础知识之一。
在初一学习有理数的过程中,我们需要掌握有理数的定义、有理数的大小比较、有理数的加减乘除运算等基本知识点。
本文将对初一有理数的知识点进行总结和归纳。
有理数的定义有理数是可以表示成两个整数的比值形式的数。
有理数包括整数和分数两种形式。
整数可以表示为正整数、负整数和 0,分数可以表示为有限小数或循环小数。
有理数可以用分数的形式表示为 a/b,其中 a 是整数,b 是非零整数。
例如,1/2、-3/4、5/8 都是有理数。
有理数的大小比较在初一学习有理数时,我们需要掌握有理数的大小比较。
有理数的大小比较可以通过以下几种方法进行判断: 1. 同号比大小:正数大于负数,负数小于正数。
2. 绝对值比大小:绝对值大的数较大,绝对值小的数较小。
3. 分数相等时比分子大小:如果两个分数的分母相等,分子较大的数较大。
4. 分数不等时通分比大小:将两个分数通分,然后比较分子的大小。
有理数的加减乘除运算加法运算有理数的加法运算是指两个有理数相加的操作。
有理数的加法运算规则如下: 1. 同号相加:两个正数相加,保留正号,数值相加;两个负数相加,保留负号,数值相加。
2. 异号相减:正数减去负数,保留正号,数值相加;负数减去正数,保留负号,数值相加。
3. 绝对值相等时:将同号数的绝对值相加,并使用原来的符号。
减法运算有理数的减法运算是指两个有理数相减的操作。
有理数的减法运算规则如下: 1. 减去一个数相当于加上这个数的相反数。
2. 两个数相减时,把减法变成加法,然后按照加法的规则进行计算。
乘法运算有理数的乘法运算是指两个有理数相乘的操作。
有理数的乘法运算规则如下: 1. 同号相乘为正,异号相乘为负。
2. 乘以零时结果为零。
3. 绝对值相等时,异号数相乘得负数。
除法运算有理数的除法运算是指两个有理数相除的操作。
有理数的除法运算规则如下: 1. 同号相除为正,异号相除为负。
(完整word版)初中数学知识点全总结(齐全)

七年级数学(上)知识点人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.第一章 有理数一、知识框架二.知识概念1.有理数:(1)凡能写成)0p q ,p (p q≠为整数且形式的数,都是有理数.正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.注意:0即不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数;π不是有理数;(2)有理数的分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 2.数轴:数轴是规定了原点、正方向、单位长度的一条直线.3.相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0; (2)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数. 4.绝对值:(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离;(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或⎩⎨⎧<-≥=)0a (a )0a (aa ;绝对值的问题经常分类讨论;5.有理数比大小:(1)正数的绝对值越大,这个数越大;(2)正数永远比0大,负数永远比0小;(3)正数大于一切负数;(4)两个负数比大小,绝对值大的反而小;(5)数轴上的两个数,右边的数总比左边的数大;(6)大数-小数 > 0,小数-大数 < 0.6.互为倒数:乘积为1的两个数互为倒数;注意:0没有倒数;若 a ≠0,那么a 的倒数是a1;若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数. 7. 有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值; (3)一个数与0相加,仍得这个数. 8.有理数加法的运算律:(1)加法的交换律:a+b=b+a ;(2)加法的结合律:(a+b )+c=a+(b+c ). 9.有理数减法法则:减去一个数,等于加上这个数的相反数;即a-b=a+(-b ). 10 有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定. 11 有理数乘法的运算律: (1)乘法的交换律:ab=ba ;(2)乘法的结合律:(ab )c=a (bc ); (3)乘法的分配律:a (b+c )=ab+ac .12.有理数除法法则:除以一个数等于乘以这个数的倒数;注意:零不能做除数,无意义即0a .13.有理数乘方的法则:(1)正数的任何次幂都是正数;(2)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或 (a-b)n =(b-a)n . 14.乘方的定义:(1)求相同因式积的运算,叫做乘方;(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂;15.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.16.近似数的精确位:一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.17.有效数字:从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字. 18.混合运算法则:先乘方,后乘除,最后加减.本章内容要求学生正确认识有理数的概念,在实际生活和学习数轴的基础上,理解正负数、相反数、绝对值的意义所在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
149、多边形
142、菱形的概念、性质和判定
151、四边形 150、中心对称
143、正方形的概念、性质和判定
148、梯形
145、梯形的相关概念 146、等腰梯形的概念、性质和判定 147、三角形、梯形的中位线
156、比例线段
158、相似图形 157、相似多边形 152、相似三角形的相关概念
155、相似三角形 153、三角形相似的判定
169、圆心角、弧、弦、弦心距
初
图
170、圆周角定理
中
形
171、圆内接四边形及其性质
数
173.直线和圆的位置关系
学
185、圆
174.切线的判定和性质
177.直线和圆的位置关系 175.三角形的内切圆
176. *切线长定理
179.正多边形和圆——178.正多边形的有关计算
180.圆周长、弧长
183.弧长和扇形的面积 181.圆、扇形、弓形的面积
字
198
初
中
数
193
学
数
.
与
法
代
数
法
初中数学知识结构图
17.有理数
6.有理数的概念
16.有理数的运算 21.代数式 22、列代数式
1.有理数(正数与负数) 2.数轴 3.相反数 4.绝对值 5.有理数从大到小比较 7.有理数的加法、加法运算律 8.有理数的减法 9.有理数的加减混和运算 10.有理数的乘法、乘法运算 11.有理数的除法、倒数 12.有理数的乘方 13.有理数的混和运算
82、二次根式的加减法 80、二次根式的加减法
81、同类二次根式
85、二次根式的混合运算 83、二次根式的混合运算
84、有理化因式
93、一元二次方程的解法
98、一元二次方程的意义
100、二元二次方程组
102、一元二次方程 99、*一元二次方程组的根与系数的关系
94、分式方程的解法
97、可化为一元二次方程
52、多项式乘以单项式
55、整式的除法 53、单项式除以单项式
54、同底数幂的除法
57、提取
61、方法 58、运用公式法
63、因式分解
59、分组分解法
62、意义 60、其他分解法
66、含字母系数的
65、分式的乘除法——64、分式的乘除运算
一元一次方程
69、可化为一元一次方程的分式方程及其应用 67、分式方程解法、
154、相似三角形的性质
159、解直角三角形
161、解直角三角形 160、解直角三角形的应
163、解直角三角形 162、锐角三角形
164、圆的有关概念及对称性
165、点和圆的位置关系
194.
166、过不在同一直线上三点的圆
空
172、圆的有关性质 167、三角形的外接圆
间
168、垂径定理及其逆定理
198. 与
43、一元一次不等式 40、一元一次不等式及其解
45、一元一次不等式 和一元一次不等 式组
41、不等式的解集 44、一元一次不等式组 42、不等式和它的基本性质
46、同底数幂的乘法、单项式的乘
47、幂的乘法、积的乘方
51、整式的乘法 48、单项式与多项式相乘
49、多项式的乘法
56、整式的乘除
50、平方差与完全平方根
95、*无理方程的意义、解法
的分式方程式和无理方程 96、分式方程、无理方程的应用
101、一元二次方程的应用
103、一次函数与一元一次不等式
106、一次函数 104、一次函数图像的图像和性质
105、正比例函数的图像和性质
108、二次函数——107 二次函数的有关概念
113、函数及其图像 109、平面直角坐标系
110、函数
111、函数的图像
112、反比例函数
114、线段
116、线段、角 115、角
117、相交线、对顶角、邻角、补角
120、相交线 118、垂线、点到直线的距离
119、同位角、内错角、同旁内角
126、相交、平行 123、平行线 121、平行线概念及性质
122、平行线的判定
124、空间直线、平面的位置关系
14.科学记数法、近似数与有效数
27、整式的加减 32、一元一次方程
39、二元一次方程组
23、代数式的值 15.用计算器进行简单的数的运算 18.单项式
20、整式的概念 19、多项式 24、合并同类项 25、去括号与添括号 26、整式的加减法 28、等式及其基本性质 29、方程和方程的解、解方程 30、一元一次方程及其解法 31、一元一次方程的应用 35、二元一次方程组的解法 36、相关概念及性质 37、三元一次方程组及其解法举例 38、一次方程组的应用
72、分式 70、分式的意义和性质 71、分式的加减法 73、平方根与立方根
75、数的开方 74、实数
阵根 68 分式方程的应用
193 数 与 代 数
198 初 中 数 学
194 空 间 与 图 形
86、二次根式的意义
76、最简二次根式
79、二次根式的乘除法 77、二次根式的除法
87、二次根式
78、二次根式的加减法
182.圆柱和圆锥的侧面展开图、侧面积
184.圆和圆的位置关系
186.几何体、几何图形
187.平均数
188.众数和中位数
191.统计初步 189.级差、方差、标准差
195.统计与概率
190.频数、频率、频率分布直方图
192.概率初步——概率计算
196.中考复习
197.总复习
125、命题、公理、定理
129、与三角形有关的边
134、全等三角形
1形——132、勾股定理
131、与三角形有关的角——130、三角形的内角
136、轴对称
139、平行四边形的概念及其性质
137、基本作图
140、平行四边形的判定
144、平行四边形 141、矩形的概念、性质和判定
