机器学习实验1-Fisher线性分类器设计
线性分类器设计fisher准则
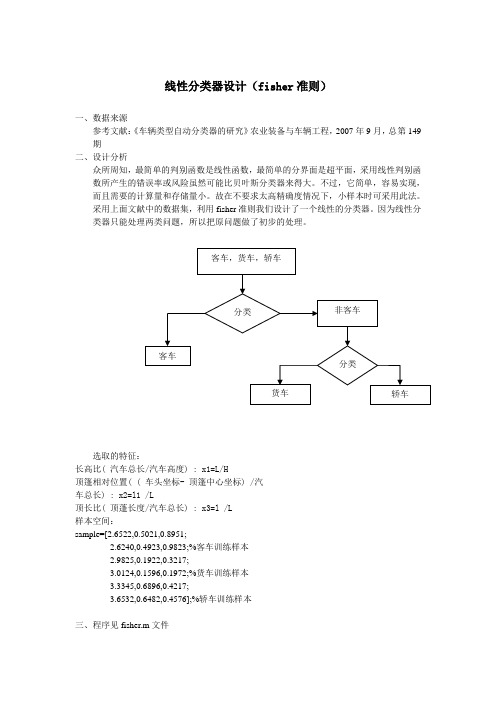
线性分类器设计(fisher准则)一、数据来源参考文献:《车辆类型自动分类器的研究》农业装备与车辆工程,2007年9月,总第149期二、设计分析众所周知,最简单的判别函数是线性函数,最简单的分界面是超平面,采用线性判别函数所产生的错误率或风险虽然可能比贝叶斯分类器来得大。
不过,它简单,容易实现,而且需要的计算量和存储量小。
故在不要求太高精确度情况下,小样本时可采用此法。
采用上面文献中的数据集,利用fisher准则我们设计了一个线性的分类器。
因为线性分类器只能处理两类问题,所以把原问题做了初步的处理。
选取的特征:长高比( 汽车总长/汽车高度) : x1=L/H顶篷相对位置( ( 车头坐标- 顶篷中心坐标) /汽车总长) : x2=l1 /L顶长比( 顶蓬长度/汽车总长) : x3=l /L样本空间:sample=[2.6522,0.5021,0.8951;2.6240,0.4923,0.9823;%客车训练样本2.9825,0.1922,0.3217;3.0124,0.1596,0.1972;%货车训练样本3.3345,0.6896,0.4217;3.6532,0.6482,0.4576];%轿车训练样本三、程序见fisher.m文件四、结果分析原文章中采用的的改进的BP神经网络算法,能很好的实现分类的效果。
而在这里我们挑了6个训练集样本和3个测试集样本,也很好的实现了分类效果。
但是,若对于大样本来说,贝叶斯分类器的效果更好。
下图就是采用线性分类器的效果图。
客车样本和非客车样本1 1.2 1.4 1.6 1.82 2.2 2.4 2.6 2.83客车样本和非客车样本1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92。
机器学习实验1-Fisher线性分类器设计

一、实验意义及目的掌握Fisher分类原理,能够利用Matlab编程实现Fisher线性分类器设计,熟悉基于Matlab算法处理函数,并能够利用算法解决简单问题。
二、算法原理Fisher准则基本原理:找到一个最合适的投影周,使两类样本在该轴上投影之间的距离尽可能远,而每一类样本的投影尽可能紧凑,从而使分类效果为最佳。
内容:(1)尝试编写matlab程序,用Fisher线性判别方法对三维数据求最优方向w的通用函数(2)对下面表1-1样本数据中的类别w1和w2计算最优方向w(3)画出最优方向w 的直线,并标记出投影后的点在直线上的位置(4)选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类三、实验内容(1)尝试编写matlab程序,用Fisher线性判别方法对三维数据求最优方向w的通用函数程序清单:clcclear all%10*3样本数据w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0.011;-0.35,.47,0.034;0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0.12,0.054,-0.063];w2=[0.83,1.6,-0.014;1.1,1.6,0.48;-0.44,-0.41,0.32;0.047,-0.45,1.4;0.28,0.35,3.1;-0.39,-0.48,0.11;0.34,-0.079,0.14;-0.3,-0.22,2.2;1.1,1.2,-0.46;0.18,-0.11,-0.49];W1=w1';%转置下方便后面求s1W2=w2';m1=mean(w1);%对w1每一列取平均值结果为1*3矩阵m2=mean(w2);%对w1每一列取平均值结果为1*3矩阵S1=zeros(3);%有三个特征所以大小为3S2=zeros(3);for i=1:10%1到样本数量ns1=(W1(:,i)-m1)*(W1(:,i)-m1)';s2=(W2(:,i)-m2)*(W2(:,i)-m2)';S1=S1+s1;S2=S2+s2;endsw=S1+S2;w_new=transpose(inv(sw)*(m1'-m2'));%这里m1m2是行要转置下3*3 X 3*1 =3*1 这里提前转置了下跟老师ppt解法公式其实一样%绘制拟合结果数据画图用y1=w_new*W1y2=w_new*W2;m1_new=w_new*m1';%求各样本均值也就是上面y1的均值m2_new=w_new*m2';w0=(m1_new+m2_new)/2%取阈值%分类判断x=[-0.7 0.0470.58 -0.40.089 1.04 ];m=0; n=0;result1=[]; result2=[];for i=1:2%对待观测数据进行投影计算y(i)=w_new*x(:,i);if y(i)>w0m=m+1;result1(:,m)=x(:,i);elsen=n+1;result2(:,n)=x(:,i);endend%结果显示display('属于第一类的点')result1display('属于第二类的点')result2figure(1)scatter3(w1(1,:),w1(2,:),w1(3,:),'+r'),hold onscatter3(w2(1,:),w2(2,:),w2(3,:),'sg'),hold onscatter3(result1(1,:),result1(2,:),result1(3,:),'k'),hold onscatter3(result2(1,:),result2(2,:),result2(3,:),'bd')title('样本点及实验点的空间分布图')legend('样本点w1','样本点w2','属于第一类的实验点','属于第二类的实验点')figure(2)title('样本拟合结果')scatter3(y1*w_new(1),y1*w_new(2),y1*w_new(3),'b'),hold onscatter3(y2*w_new(1),y2*w_new(2),y2*w_new(3),'sr')(2)对下面表1-1样本数据中的类别w1和w2计算最优方向w(3)画出最优方向w 的直线,并标记出投影后的点在直线上的位置最优方向w 的直线投影后的位置(4)选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类决策边界取法:分类结果:四、实验感想通过这次实验,我学会了fisher线性判别相关的分类方法,对数据分类有了初步的认识,尽管在过程中有不少中间量不会算,通过查阅网络知识以及模式识别专业课ppt等课件帮助,我最终完成了实验,为今后继续深入学习打下良好基础。
使用Fisher线性判别方法的提取分类器

文, 用 , … 分别表示 个个体分类器 , , … } 。
1 问题 形 式化 描述 及个 体分 类器 训练
对分 类问题而 言 , 问题 域为 类 对象 , 类别标 签分别为
,
, , 。每—个样本可以表示成一个 d 的权重特征向 J …, , 维
个体 分类器 训练指从 数据集 中训练 获得这 个分 类器 的过
p tr En iern n pia o s 2 1 4 ( 4 :3 - 3 . ue g e ig a d Ap l t n . 0 0。6 I ) 1 2 1 4 n ci
Ab t a t I r e o ei n t e aii ewe n n e ld ca s ir n mp o e f c n tb l y o o i e , n a p o c sr c : n od r t l mi ae rl t t b t e e s mb e ls i e a d i r v e e t a d sa i t f c mbn r a p r a h vy f s f i
e ta t ca sfes xr ci ng l si r ba e o Fih r i e r ic i n n a lss s o o e I c n e uc ca sfe s c wih ih i e in, i sd n s e ln a ds rmi a t nay i i pr p s d.t a r d e l s i r pa e i t hg dm nso
FISHER线性判别MATLAB实现

Fisher 线性判别上机实验报告班级: 学号: 姓名:一.算法描述Fisher 线性判别分析的基本思想:选择一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,同时变换后的一维数据满足每一类内部的样本尽可能聚集在一起,不同类的样本相隔尽可能地远。
Fisher 线性判别分析,就是通过给定的训练数据,确定投影方向W 和阈值w0, 即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
线性判别函数的一般形式可表示成0)(w X W X g T += 其中Fisher 选择投影方向W 的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求。
如下为具体步骤:(1)W 的确定w S 样本类间离散度矩阵b在投影后的一维空间中,各类样本均值Tiim '= Wm样本类内离散度和总类内离散度 T Ti i ww S ' = W S W S ' = W S W 样本类间离散度Tbb S ' = W S W Fisher 准则函数为 max 2221221~~)~~()(S S m m W J F +-=(2)阈值的确定w 0是个常数,称为阈值权,对于两类问题的线性分类器可以采用下属决策规则: 令)()()(21x x x g g g -=则:如果g(x)>0,则决策w x 1∈;如果g(x)<0,则决策w x 2∈;如果g(x)=0,则可将x 任意分到某一类,或拒绝。
(3)Fisher 线性判别的决策规则 Fisher 准则函数满足两个性质:1.投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
2.投影后,各类样本尽可能离得远,即样本类间离散度越大越好。
根据这个性质确定准则函数,根据使准则函数取得最大值,可求出W :-1w 12W = S (m - m ) 。
这就是Fisher 判别准则下的最优投影方向。
Fisher分类器(算法及程序)
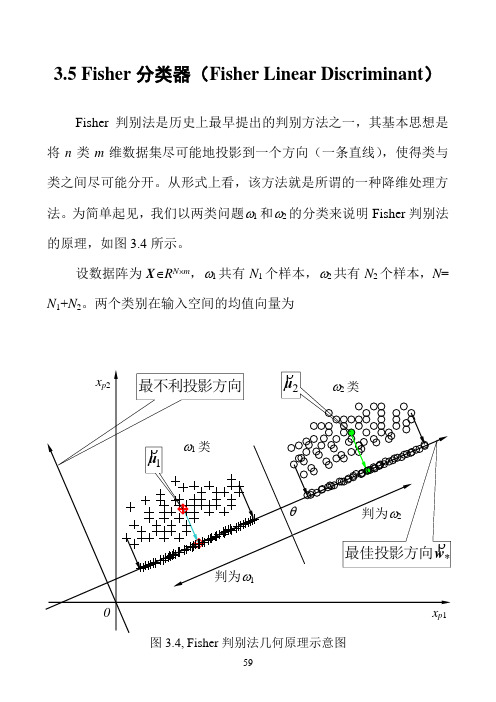
3.5 Fisher分类器(Fisher Linear Discriminant)Fisher判别法是历史上最早提出的判别方法之一,其基本思想是将n类m维数据集尽可能地投影到一个方向(一条直线),使得类与类之间尽可能分开。
从形式上看,该方法就是所谓的一种降维处理方法。
为简单起见,我们以两类问题ω1和ω2的分类来说明Fisher判别法的原理,如图3.4所示。
设数据阵为X∈R N⨯m,ω1共有N1个样本,ω2共有N2个样本,N= N1+N2。
两个类别在输入空间的均值向量为图3.4, Fisher判别法几何原理示意图)37.3(11212211⎪⎪⎩⎪⎪⎨⎧∈=∈=∑∑∈∈m pmp R N R N p pϖϖx x x μx μρρρρρρ设有一个投影方向()mT m R w w w ∈=,,,21Λρw ,这两个均值向量在该方向的投影为)38.3(1~1~1222111121⎪⎪⎩⎪⎪⎨⎧∈==∈==∑∑∈∈R N R N p p pT T p T T ϖϖx x x w μw μx w μw μρρρρρρρρρρρρ在w ρ方向,两均值之差为())39.3(~~2121μμw μμρρρρρ-=-=∇T类似地,样本总均值向量在该方向的投影为)40.3(1~11R NNp pT T ∈==∑=x w μw μρρρρρ定义类间散度(Between-class scatter)平方和SS B 为()()()()()()()()()[])41.3(~~~~~~222111222211221222211w S w w μμμμμμμμw μw μw μw μw μμμμμμρρρρρρρρρρρρρρρρρρρρρρρρρρB T T T T T T T T j j j B N N N N N N N SS =--+--=-+-=-=-+-=∑=其中()()()()()())42.3(21222111∑=--=--+--=j Tj j j TT B N N N μμμμμμμμμμμμS ρρρρρρρρρρρρ定义类ωj 的类内散度(Within-class scatter)平方和为()())43.3(~22∑∑∈∈-=-=jjNp jT p T N p jp T Wj x x SS μw w μw ρρρρρρρ两个类的总的类内散度误差平方和为()()())44.3(2121221wS w w μμw μw w ρρρρρρρρρρρρW T j Np T jp j p T j N p jT p T j wj W j jx x x SS SS =⎥⎥⎦⎤⎢⎢⎣⎡--=-==∑∑∑∑∑=∈=∈=其中,()())45.3(21∑∑=∈--=j N p Tjp j p W jx x μμS ρρρρ我们的目的是使类间散度平方和SS B 与类内散度平方和SS w 的比值为最大,即())46.3(max wS w w S w w ρρρρρW T B T WBSS SS J ==图3.5a, Fisher判别法—类间散度平方和(分子)的几何意义图3.5b, Fisher判别法—类内散度平方和(分母)的几何意义图3.5给出了类间散度平方和S B 与类内散度平方和S E 的几何意义。
《模式识别》课程实验 线性分类器设计实验

《模式识别》课程实验线性分类器设计实验一、实验目的:1、掌握Fisher 线性分类器设计方法;2、掌握感知准则函数分类器设计方法。
二、实验内容:1、对下列两种情况,求采用Fisher 判决准则时的投影向量和分类界面,并做图。
12{(2,0),(2,2),(2,4),(3,3)}{(0,3),(2,2),(1,1),(1,2),(3,1)}T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 12{(1,1),(2,0),(2,1),(0,2),(1,3)}{(1,2),(0,0),(1,0),(1,1),(0,2)}T T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 2、对下面的两类分类问题,采用感知准则函数,利用迭代修正求权向量的方法求两类的线性判决函数及线性识别界面,并画出识别界面将训练样本区分的结果图。
12{(1,1),(2,0),(2,1),(0,2),(1,3)}{(1,2),(0,0),(1,0),(1,1),(0,2)}T T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 三、实验原理:(1)Fisher 判决准则投影方向:*112()w w S μμ-=-(2)感知准则函数:()()kT p z Z J v v z ==-∑当k Z为空时,即()0J v ,*v即为所求p四、解题思路:1、fisher线性判决器:A.用mean函数求两类样本的均值B.求两类样本的均值的类内离散矩阵SiC.利用类内离散矩阵求总类内离散矩阵SwD.求最佳投影方向WoE.定义阈值,并求得分界面2、感知准则函数分类器:A.获得增广样本向量和初始增广权向量B.对样本进行规范化处理C.获得解区,并用权向量迭代修正错分样本集,得到最终解区五、实验结果:1、fisher线性判决分类器:条件:取pw1=pw2=0.5,阈值系数为0.5A.第一种情况B.第二种情况2、感知准则函数判决:条件:取步长row为1判决结果:六、结果分析:1、fisher线性判决器中,调整阈值系数时,分界面会随之平行上下移动,通过调整阈值系数的大小,就能比较合理的得到分界面。
Fisher线性

0810420209 沈旦Fisher线性分类器线性分类器(一定意义上,也可以叫做感知机) 是最简单也很有效的分类器形式。
感知机是集语音、文字、手语、人脸、表情、唇读、头势、体势等多通道为一体的,并对这些通道的信息进行编码、压缩、集成、融合的计算机智能接口系统。
面向中国手语识别与合成的多功能感知机是多功能感知机的初期阶段目标。
现阶段的研究重点包括:1、大词汇量实时中国手语的识别;2、PC版和掌上电脑版中国手语合成系统;3、人脸图像的监测与识别。
线性判别式分析(Linear Discriminant Analysis, LDA),也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD),是模式识别的经典算法,它是在1996年由Belhumeur引入模式识别和人工智能领域的。
性鉴别分析的基本思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证模式样本在新的子空间有最大的类间距离和最小的类内距离,即模式在该空间中有最佳的可分离性。
因此,它是一种有效的特征抽取方法。
使用这种方法能够使投影后模式样本的类间散布矩阵最大,并且同时类内散布矩阵最小。
就是说,它能够保证投影后模式样本在新的空间中有最小的类内距离和最大的类间距离,即模式在该空间中有最佳的可分离性。
线形判别分析(Linear Discriminant Analysis, LDA)方法是人脸识别领域十分流行的降维方法。
在经过LDA 降维后的子空间中,同一类的训练样本尽可能的靠近,且不同类的样本尽可能的分散(即降维后同一个人的训练图像尽可能的靠近,不同人的图像尽可能的分散)。
该方法自提出以来产生了很多改进算法,如正交LDA,基于零空间的LDA,核判别分析和模糊LDA 方法等。
其中模糊LDA 方法引入了模糊集理论来优化特征提取,利用隶属度来描述样本的分布信息,能得到一个较好的类中心位置估计。
非平衡数据集Fisher线性判别模型

文章编号:167320291(2006)0520015204非平衡数据集Fisher 线性判别模型谢纪刚,裘正定(北京交通大学计算机与信息技术学院,北京100044)摘 要:非平衡数据是指两类问题中正类样本与负类样本个数不相等,甚至相比悬殊.非平衡数据集会导致许多分类器的性能下降,这与分类器的构造原理有关.本文首先阐述了Fisher 线性判别的分类机制,指出当两类样本的协方差矩阵不同时,样本不平衡会导致Fisher 线性判别的性能下降.在此基础上,提出了一种加权Fisher 线性判别(WFLD ),以减小样本不平衡的影响.然后,从UCI 中选择了8个非平衡数据集,并采用ROC 曲线下面积作为评估指标进行比较,实验结果证明了WFLD 模型的有效性.关键词:非平衡数据集;Fisher 线性判别;ROC 曲线下面积(AUC )中图分类号:TP18 文献标识码:AFisher Linear Discriminant Model with Class ImbalanceX I E Ji-gang ,Q IU Zheng-di ng(School of Computer and Information Technology ,Beijing Jiaotong University ,Beijing 100044,China )Abstract :As the majority of classification methods previously designed usually assume that their train 2ing sets are well-balanced ,they have to be affected by class imbalance in which examples in training data belonging to one class heavily outnumber the examples in the other class.This paper demonstrates that ,when the two sample covariance matrices are not identical ,class imbalance has a negative effect on the performance of Fisher linear discriminant (FLD ).A weighted FLD (WFLD )is proposed for re 2ducing the negative effects of the class ing area under the ROC curve as performance measarement ,eight UCI imbalanced data sets are tested to show WFLD ’s effectiveness.K ey w ords :class imbalance ;Fisher linear discriminant (FLD );area under the ROC curve (AUC ) 非平衡数据通常是指两类问题中的负类样本个数远大于正类样本个数,并且,正类样本往往是分类问题的关注所在.现实中的例子如信用卡交易欺诈识别[1]、电信设备故障预测[2]、企业破产预测[3]和雷达图像监测海洋石油污染[4]等.然而,许多分类方法的设计是基于数据平衡分布假设的,如决策树、支持向量机和线性判别分析等.当把这些分类方法应用于非平衡数据时,就会导致训练出的分类器性能下降.因此,非平衡数据分类成为目前机器学习和数据挖掘的一个研究热点[529].已有研究指出[5-7],有两种方法可以有效地提高分类器在非平衡数据集上的泛化性能:一是随机抽样,即人为地减少负类样本个数(下抽样)或增加正类样本个数(上抽样),从而使两类样本个数趋于平衡;二是改进分类器的构造机制,使之适用于非平衡数据.然而,已有研究多针对于决策树、近邻法和支持向量机等分类方法[5-9],据作者所查阅文献,未见有关Fisher 线性判别(FLD )对非平衡数据分类的研究.FLD 具有计算简单、在一定条件下能够实现最优分类的性质,因此是一种实际应用非常广泛的收稿日期:2006201216基金项目:浙江省自然科学基金资助项目(Y104540);北京市重点实验室基金资助项目(TDXX0509)作者简介:谢纪刚(1973—),男,河北邢台人,博士生.em ail :xie-jigang @ 裘正定(1944—),男,浙江嵊县人,教授,博士生导师.第30卷第5期2006年10月 北 京 交 通 大 学 学 报JOURNAL OF BEI J IN G J IAO TON G UN IV ERSIT Y Vol.30No.5Oct.2006分类方法[10-11],研究它在非平衡数据集上的分类性能具有重要实际意义.本文作者首先讨论FLD 的分类机制,指出当两类样本的协方差矩阵不同时,样本不平衡会导致FLD 的性能下降.在此基础上,提出了一种加权Fisher 线性判别(Weighted Fisher Linear Discrimi 2nant ,WFLD )以减小样本不平衡的影响.然后,从本文作者UCI 中选择了8个非平衡数据集,并采用ROC 曲线和ROC 曲线下面积作为评估指标进行比较,实验结果表明WFLD 模型能有效地提高FLD 在非平衡数据集上的泛化性能.1 加权Fisher 线性判别1.1 Fisher 线性判别Fisher 线性判别(FLD )的基本原理如下,对于线性判别函数y (x )=a 0+a 1x 1+…+a d x d =a Tx +a 0(1)可以将d 维矢量a =(a 1,a 2,…,a d )T 视作特征空间X d 中的以a 1,a 2,…,a d 为分量的一个矢量,则a T x 表示矢量x 在以a 为方向的轴上投影的‖a ‖倍.我们希望所求的a 使投影后同类样本相距较近,即同类样本密集;不同类样本相距较远.FLD 就是求解,满足类间离散度和总类内离散度之比最大的投影方向,然后在一维空间中确定判决规则.FLD 数学推导如下[11]:设给定两类d 维训练样本X (i )={x i 1,x i 2,…,x iN i },i =1,2,各类样本均值矢量m i 和总的样本均值矢量m 分别为m i =∑Nij =1xijN i ,i =1,2(2)m =∑2i =1∑Nij =1xij∑2i=1Ni(3)各类类内离散度阵S i 和总的类内离散度阵S w 分别为S i =∑Nij =1(xij-m i )(x ij -m i )T ,i =1,2(4)S w =S 1+S 2(5)类间离散度阵S b 为S b =(m 1-m 2)(m 1-m 2)T(6) 将d 维矢量x 投影到以矢量a 为方向的轴上y (i )j =a T x (i )j (7)变换后在一维y 空间中各类样本的均值为珦m i =1N i∑jy (i )j =a T m i , i =1,2(8)类内离散度珘S 2i 和总的类内离散度珘S 2w 为珘S 2i =∑j(y (i )j -珦m i )2=a T S i a ,i =1,2(9)珘S 2w =珘S 21+珘S 22=a TS w a(10)类间离散度为珘S 2b =(珦m 1-珦m 2)2=a T S b a(11) 定义类间离散度与类内离散度之比为Fisher 准则函数J F (a )=(a T S b a )/(a TS w a )(12)并使其最大.将标量J F 对矢量a 求导并令其为零矢量,然后利用二次型关于矢量求导公式可得a 3=S -1w (m 1-m 2)(13)此时的a 3可使Fisher 准则函数取最大值,即确定了最佳投影方向.至此,解决了将d 维样本的分类转变为一维样本分类的问题.可以根据训练样本确定一个阈值y t ,并设i =1为正类,i =2为负类,于是FLD 分类器为:a 3T x =y ≥y t ;否则,判为负类.判决阈值y t 有多种选取方法[11],可选取两个类中心在投影轴a 3上的投影连线的中点,也可以选取总的样本均值矢量m 在a 3上的投影点珦m 作为阈值等.本文采用第一种阈值选取方法.1.2 加权模型当用ROC 曲线来评价FLD 分类器的性能时,判决阈值y t 的选取方法不会影响分类器性能,唯一影响分类器性能的是投影方向a 3.由式(13)可见,投影方向a 3由总类内离散度阵S w 和两类样本均值矢量之差共同决定.在独立同分布假设下,样本均值矢量与样本个数无关,即两类样本均值矢量差与样本不平衡无关.因此,投影方向a 3由类内离散度阵S w 唯一左右.设两类的样本协方差阵分别为Σ1和Σ2,则式(5)变为S w =S 1+S 2=N 1Σ1+N 2Σ2(14)可见,当Σ1=Σ2时,两类样本个数不平衡(N 1≠N 2)只改变S w 中的标量因子N 1+N 2,而不会影响投影方向a 3;当Σ1≠Σ2时,两类样本个数不平衡,尤其相比悬殊(N 1νN 2)时,N 2Σ2对S w 的贡献远远大于N 1Σ1对S w 的贡献,从而可能导致投影方向不利于分类.为消除样本个数不平衡的影响,对式(5)中的各类类内离散度阵S i 进行分别加权,使两类样本协方差阵对S w 的贡献平衡.S w =N 2S 1+N 1S 2=N 1N 2(Σ1+Σ2)(15)本文把这种改进的FLD 称作加权Fisher 线性判别(WFLD ).由式(15)可见,WFLD 实质上等价于一种特殊的上抽样方法:不但对正类样本进行N 2倍的上抽样,而且同时对负类样本进行N 1倍的上抽样.这相当于使原始非平衡数据集变成两类样本个61北 京 交 通 大 学 学 报 第30卷数为1∶1的平衡数据集.2 实验设计2.1 数据本文从公用机器学习数据库UCI[12]中选取了8个数据集,将每个数据集中的其中一类作为正类,其余各类都归为负类,从而构成具有不同非平衡程度的两类非平衡数据集(如表1所示).所有数据集都进行0均值、标准差1的规范化预处理.表1 实验数据集Tab.1 In experiments data sets数据集样本数类别标签(正,负)类别比例/%(正,负) Letter20000(a,其余)(3.95,96.05)G lass 214(Ve-win,其余)(7.94,92.06)Image 2310(Brickface,其余)(14.29,85.71)Vehicle 846(van,其余)(23.52,76.48)Wine 178(3,其余)(26.97,73.03)Iris 150(3,其余)(33.33,66.67) Waveform5000(1,其余)(33.33,66.67)Pima 768(1,0)(34.77,65.23) 2.2 评价标准已有研究表明[5-8],由于分类错误率只描述了特定判决阈值时的分类器性能,因此不适合非平衡数据集情况;而ROC(Receiver Operating Character2 istic)曲线全面地描述了分类器在不同判决阈值时的性能,所以成为数据不平衡时的分类器性能评价的主流方法.对于每一个测试样本,两类分类器有4种可能的判决结果:将本属于正类的样本判别为正类,将本属于负类的样本判别为负类,将本属于正类的样本判别为负类,将本属于负类的样本判别为正类.为便于说明,作一下假设.设测试集中的正类样本和负类样本总数分别为N1和N2,记为:a:分类器判别为正类的正类样本个数;b:分类器判别为正类的负类样本个数;c:分类器判别为负类的正类样本个数;d:分类器判别为负类的负类样本个数.显然有a+c=N1和b+d=N2.定义错误正比率FRB=b/N2,真实正比率TPR=a/N1,并将FPR 和TPR分别作为横、纵坐标.每一个阈值对应一个(FPR,TPR)点,改变阈值,将得到的所有(FPR, TPR)点连起来就是分类器在该测试集上的ROC曲线(图1是一个示意图).显然,ROC曲线越靠近左上角表示分类器性能越好.ROC曲线来描述分类器的分类性能虽然全面,但作为一种二维图形描述,ROC曲线不能给出分类器性能的定量评价.为此,人们常常采用ROC曲线下面积(AUC),来代替ROC曲线本身对分类器的性能进行评估[5-8,13-14].显然,AUC取值范围在0和1之间,并且AUC越大,分类器的性能就越好.本文采用AUC来评估分类器的泛化性能,并应用文献[14]中的算法3来计算AUC.图1 R OC曲线Fig.1 ROC curve2.3 实验步骤采用5重交叉验证技术进行实验比较.5重交叉验证描述如下:首先把数据集随机地分成5等份,并且保证每一等份中的两类样本个数比例与原数据集中两类样本个数比例一致.每重实验将其中一份作为测试集,其余4份作为训练集.最后将5重实验结果进行平均即为最后结果.用“非平衡FLD分类器”、“上抽样FLD分类器”和“下抽样FLD分类器”分别表示FLD从原始不平衡训练集、上抽样平衡训练集和下抽样平衡训练集学习得到的分类器,用“WFLD分类器”表示WFLD从原始不平衡训练集学习得到的分类器.其中,上抽样平衡训练集和下抽样平衡训练集分别由上抽样和下抽样得到.下抽样是从负类样本中随机地抽取出和正类样本个数一样多的样本,从而构成新的平衡训练集;上抽样采用数据“复制”的方法,即成倍地复制正类样本使之与负类样本个数相等或接近相等(上抽样不改变正类样本分布).本文用5重交叉验证技术比较这4种分类器在非平衡测试集上的泛化性能.3 实验结果及分析5重交叉验证得到的AUC见表2.表中用粗体标出了每一行的最大值.显然,WFLD分类器和上抽样FLD分类器的泛化性能优于其它两种分类器,并且WFLD分类器性能稍好于上抽样FLD分类器.下抽样FLD分类器在5个数据集上比非平衡FLD分类器性能好,在另外3个数据集上则相反.分析原因如下:对非平衡数据集进行上抽样或下抽样,实质上是增大或减小式(15)中的N1或N2,使之相等或接近相等.于是两类样本协方差阵Σ1和Σ2对求解投71第5期 谢纪刚等:非平衡数据集Fisher线性判别模型影方向的贡献将趋于相等.在上抽样方法中,由于负类样本与正类样本的个数比常常不是整数,所以由上抽样得到的平衡数据集中两类样本个数比常常不等于1(而是接近1).而WFLD等价于同时对正类和负类都进行上抽样,使两类样本个数比为1∶1.可见,WFLD比上抽样更有保证地使Σ1和Σ2对求解投影方向的贡献相等.因此,WFLD分类器的泛化性能稍好于上抽样FLD分类器.表2 5重交叉验证平均AUCTab.2 AUC of5-fold cross-validation数据集FLD非平衡下抽样上抽样WFLD Letter0.97640.98490.98520.9852G lass0.81600.82340.82140.8219 Image30.98900.99150.99420.9940 Vehicle0.98860.99160.99130.9916Wine0.99930.99790.99930.9993Iris0.97200.9800.98200.9820 Waveform0.94280.94220.94380.9438 Pima0.83510.83420.83600.8364 下抽样是从负类样本中随机地抽取出和正类样本个数一样多的样本,从而使训练集中的两类样本比例为1:1,但可能会漏掉有价值的数据信息,所以下抽样不能稳定地提高FLD对非平衡数据集的泛化性能.需要指出,在数据集Waveform和Pima上,性能最优的WFLD分类器的AUC只是略大于非平衡FLD分类器的AUC,而在数据集Wine上,两者相等.该结果说明这3个非平衡数据集的两类样本协方差阵相似或相等.4 结论本文作者首先阐述了Fisher线性判别的分类原理,指出当两类样本的协方差矩阵不同时,样本不平衡会导致Fisher线性判别的分类性能下降.在此基础上,本文作者提出了一种改进模型:加权Fisher线性判别(WFLD).WFLD本质上等价于一种特殊的上抽样方法,即同时对两类样本进行不同倍数的上抽样使两类样本个数之比为1∶1,从而消除样本不平衡对分类性能的影响.实验证明了WFLD能有效地提高Fisher线性判别在非平衡数据集上的泛化性能.参考文献:[1]Chan P K,Stolfo S J.Toward Scalable Learning with Non-Uniform Class and Cost Distributions:A Case Study inCredit Card Fraud Detection[C]∥In.Proc of the Fourth International Conference on Knowledge Discovery and Data Mining(K DD-98).New Y ork,1998:164-168.[2]Weiss G M,Hirsh H.Learning to Predict Rare Events inEvent Sequences[C]∥In.Proc of the Fourth Internation2 al Conference on Knowledge Discovery and Data Mining (K DD-98).New Y ork:1998:359-363.[3]Atiya A F.Bankruptcy Prediction for Credit Risk UsingNeural Network:a Survey and New Results[J].IEEE Trans.Neural Networks,2001,12(4):929-935.[4]Kubat M,Holte R C,Matwin S.Machine Learning forthe Detection of Oil Spills in Satellite Radar Images[J].Machine Learning,1998,30(2):195-215.[5]Chawla N V,Japkowicz N,K olcz A.Editorial:Special Is2sue on Learning from Imbalanced Data Sets[C]∥ACM SIGK DD Explorations,2004,6(1):1-6.[6]Weiss G M.Mining with Rarity-Problems and S olutions:A Unifying Framework[C]∥SIGK DD Explorations,2004,6(1):7-19.[7]Chawla N V,Japkowicz N.K olcz A(editors).ICML’2003Workshop on Learning from Imbalanced Data Sets [C/OL][2003].http:∥www.site.uottawa.ca/~nat/ Workshop2003/workshop2003.html[8]Japkowica N(editor).Proc of the AAAI’2000Workshopon Learning form Imbalanced Data Sets[R].AAAI Tech Report WS-00-05,AAAI,2000.[9]肖健华,吴今培.样本数目不对称时的SVM模型[J].计算机科学,2003,30(2):165-167.Xiao Jian-hua,Wu Jin-pei.SVM Model with Unequal Sample Number Between Classes[J].Computer Science, 2003,30(2):165-167.(in Chinese)[10]McLachlan GJ.Discriminant Analysis and Statistical Pat2tern Recognition[M].New Y ork:Wiley,1992.[11]边肇祺,张学工.模式识别[M].北京:清华大学出版社,2001.Bian Zhao-qi,Zhang Xue-gong.Pattern Recognition[M].Beijing:Qinghua University Press,2001.(in Chinese) [12]C L Blake,C J Merz.UCI Repository of Machine Learn2ing Database.1998,[R/OL].[2005].http://www.ics./~mlearn/ML Repository.html.[13]Bradley A e of the Area Under the ROC Curve inthe Evaluation of Machine Learning Algorithms[J].Pat2tern Recognition,1997,30(7):1145-1159.[14]Fawcett T.ROC Graphs:Notes and Practical Considera2tions for Researchers[R/OL].Tech.Report HPL-2003-4,2003.[2005]/N ET/tfawcett/papers/ROC101.pdf.81北 京 交 通 大 学 学 报 第30卷。
FISHER分类

Fisher 线性判别分类器成员姓名: 学号:莫文敏 201111921217 赵越 201111921229 顾瑞煌 201111921104一、实验目的1.实现基于FISHER 分类的算法程序;2.能够根据自己的设计加深对FISHER 分类的认识;3.掌握FISHER 分类的原理、特点。
二、实验设备1.手提电脑2.MATLAB三、FISHER 算法原理线性判别函数的一般形式可表示成0)(w X W X g T +=其中⎪⎪⎪⎭⎫ ⎝⎛=d x x X 1 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=d w w w W 21但是,在应用统计方法解决模式识别的问题时,经常会遇到“维数风暴”的问题,因此压缩特征空间的维数在此时十分重要,FISHER 方法实际上是涉及维数压缩的问题。
把多为特征空间的点投影到一条直线上,就能把特征空间压缩成一维,这在数学上是很容易做到的。
但是在高维空间里很容易一分开的样品,把它们投射到任意一条直线上,有可能不同类别的样品就混在一起,无法区分了,如图5-16(a )所示,投影1x 或2x 轴无法区分。
若把直线绕原点转动一下,就有可能找到一个方向,样品投射到这个方向的直线上,各类样品就能很好地分开,如图5-16(b )所示。
因此直线方向的选择是很重要的。
一般来说总能找到一个最好的方向,使样品投射到这个方向的直线上很容易分开。
如何找到这个最好的直线方向以及如何实现向最好方向投影的变换,这正是FISHER 算法要解决的基本问题,这个投影变换正是我们寻求的解向量*W 。
样品训练集以及待测样品的特征总数目为n ,为找到最佳投影方向,需要计算出各类样品的均值、样品类内离散度矩阵i S 和总类间矩阵w S 、样品类间离散度矩阵b S ,根据FISHER 准则找到最佳投影向量,将训练集内所有样品进行投影,投影到一维Y 空间,由于Y 空间是一维的,则需要求出Y 空间的划分边界点,找到边界点后,就可以对待测样品进行一维Y 空间的投影,判断它的投影点与分界点的关系将其归类。
fisher判别法

1 实验1 Fisher 线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题,在低维空间行得通的方法,在高维空间往往行不通。
因此,降低维数就成为解决实际问题的关键。
Fisher 的方法,实际上涉及维数压缩。
如果要把模式样本在高维的特征向量空间里投影到一条直线上,实际上就是把特征空间压缩到一维,这在数学上容易办到。
问题的关键是投影之后原来线性可分的样本可能变得混杂在一起而无法区分。
在一般情况下,总可以找到某个最好的方向,使样本投影到这个方向的直线上是最容易分得开的。
如何找到最好的直线方向,如何实现向最好方向投影的变换,是Fisher 法要解决的基本问题。
这个投影变换就是我们寻求的解向量*w本实验通过编制程序体会Fisher 线性判别的基本思路,理解线性判别的基本思想,掌握Fisher 线性判别问题的实质。
二、实验原理1.线性投影与Fisher 准则函数各类在d 维特征空间里的样本均值向量:∑∈=i k X x k i i x n M 1,2,1=i (4.5-2)通过变换w 映射到一维特征空间后,各类的平均值为:∑∈=i k Y y k i i y n m 1,2,1=i (4.5-3)映射后,各类样本“类内离散度”定义为:22()k i i k i y Y S y m ∈=-∑,2,1=i (4.5-4)显然,我们希望在映射之后,两类的平均值之间的距离越大越好,而各类的样本类内离散度越小越好。
因此,定义Fisher 准则函数:2122212||()F m m J w s s -=+ (4.5-5) 使F J 最大的解*w 就是最佳解向量,也就是Fisher 的线性判别式。
2.求解*w从)(w J F 的表达式可知,它并非w 的显函数,必须进一步变换。
2 已知:∑∈=i k Y y k ii y n m 1,2,1=i , 依次代入(4.5-1)和(4.5-2),有: i T X x k i T k X x T i i M w x n w x w n m i k i k ===∑∑∈∈)1(1,2,1=i (4.5-6) 所以:221221221||)(||||||||M M w M w M w m m T T T -=-=- w S w w M M M M w b T T T =--=))((2121 (4.5-7) 其中:T b M M M M S ))((2121--= (4.5-8) b S 是原d 维特征空间里的样本类内离散度矩阵,表示两类均值向量之间的离散度大小,因此,b S 越大越容易区分。
模式识别实验报告 实验一 BAYES分类器设计

P (i X )
P ( X i ) P (i )
P( X ) P( )
j 1 i i
c
j=1,…,x
(2)利用计算出的后验概率及决策表,按下面的公式计算出采取 ai ,i=1,…,a 的条件风 险
R (a i X ) (a i , j ) P ( j X ) ,i=1,2,…,a
1.2 1 0.8 0.6 0.4 0.2 0 -0.2 -5 正常细胞 异常细胞 后验概率分布曲线
后验概率
-4
-3
-2
-1 0 1 细胞的观察值
2
3
4
5
图 1 基于最小错误率的贝叶斯判决
最小风险贝叶斯决策 风险判决曲线如图 2 所示,其中带*的绿色曲线代表异常细胞的条件风险曲线;另一条
光滑的蓝色曲线为判为正常细胞的条件风险曲线。 根据贝叶斯最小风险判决准则, 判决结果 见曲线下方,其中“上三角”代表判决为正常细胞, “圆圈“代表异常细胞。 各细胞分类结果: 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 0 0 0 1 0 1 其中,0 为判成正常细胞,1 为判成异常细胞
实验一 Bayes 分类器设计
【实验目的】
对模式识别有一个初步的理解, 能够根据自己的设计对贝叶斯决策理论算法有一个深刻 地认识,理解二类分类器的设计原理。
【实验原理】
最小风险贝叶斯决策可按下列步骤进行: (1)在已知 P (i ) , P ( X i ) ,i=1,…,c 及给出待识别的 X 的情况下,根据贝叶斯公 式计算出后验概率:
4 0
请重新设计程序, 完成基于最小风险的贝叶斯分类器, 画出相应的条件风险的分布曲线和分 类结果,并比较两个结果。
实验三 线性分类器

线性分类器设计一、实验要求在本次实验中,将基于线性判别函数来设计线性分类器。
给出在两类情况下,基于几个常用的准则函数(准则函数包括Fisher准则,感知准则,最小平方误差即MSE准则)的线性分类器设计方法以及线性支持向量机分类,选择其中两种方法分别设计线性分类器并评价结果。
二、实验目的首先明确线性判别函数的基本概念和设计线性分类器的核心要求。
然后熟练掌握基于几个常用的准则函数和支持向量机进行线性分类器的设计,了解各个准则函数的相同和不同之处,各准则函数的特点。
最后要求掌握结果评价的方法。
三、实验结果1.基于Fisher准则函数来设计线性分类器。
Fisher线性判别的思想是:将所有的样本都投影到Fisher准则下的最佳投影方向,这样能保证投影后类间相隔远,而类内尽可能聚集。
然后在这个一维空间中确定一个分类的阈值,过这个阈值点且与投影方向垂直的超平面就是两类的分类面。
Fisher线性判别函数为:(1)两类样本线性可分由上图可以看出,当样本是线性可分的时候,Fisher准则函数能够较好的确定阈值、找出分类面。
(2)两类样本线性不可分当样本集线性不可分时,能找到最佳投影方向,投影后两类的样本还是混在一起,存在错分的现象2.基于感知准则函数来设计线性分类器。
感知器准则函数的思想是:找到一个解向量a,能够使规范化增广样本向量都满足,i=1,2,…,N。
为规范化增广样本向量感知器线性判别函数为:决策规则是:如果,则样本属于第一类,如果,则样本属于第二类。
为了使解向量更加靠近解区中间、更加可靠,可以适当的引入余量b,此时求解解向量的方程变为。
解向量可以用梯度下降方法来迭代求解,在求解解向量的过程中,采用不同的初始权向量、不同的步长、不同的余量求解得到的解向量会有所不同。
(1)两类样本线性可分(初始权向量[0;0;0],步长1,不考虑余量)(2)两类样本线性不可分(初始权向量[0;0;0],步长1,迭代次数 4800次)当用感知器来处理线性不可分的样本时,找不到一个解向量能够满足所有的样本,算法不收敛,上图为迭代4800次的结果。
线性判别函数-Fisher

任意x,在H上投影 xp X与xp距离r
多类的情况:
将c类问题转化为c个两类问题,有c个判别函数。
把ωi作为一类,其余作为一类,构建c个超平面
更复杂一些,用C(C-1)/2个线性判别函数进行判别。
判别函数和决策面:
超平面Hij的法向量 决策规则:对一切i ≠ j有gi(x)>gj(x),则把x归为ωi类。
线性判别函数的齐次简化
令x0=1则:
增广特征向量
增广权向量
一个三维增广特征空间y和增广权向量a(在原点)
这是广义线性判别函数的一个特例。y与x相比, 虽然增加了一维,但保持了样本间的欧式距离不变。
变换得到的y向量仍然都在d维的子空间中,即原X 空间中,方程aTy=0在Y空间确定了一个通过原点 的超平面H’,它对d维子空间的划分与原决策面 wTx+w0=0对原X空间的划分完全相同。
映射y把一条直线映射为三维空间中的一条抛物线01122123321xcyayyaacxyac????????????????????????????????????????????22gxccxcx令
线性判别函数
已知条件
贝叶斯决策
实际问题
条件未知
利用样本集直接设计分类器,即给定某个判别函 数类,然后利用样本集确定出判别函数中的未知 参数。
N个d维样本x , x ,...x ,
1
2
N
其中: X : N 个属于 的样本集
1
1
1
X : N 个属于 的样本集
2
2
2
对xn的分量作线性组合:
y wT x , n 1,2,..., N
n
基于线性判别分析的分类器设计研究

基于线性判别分析的分类器设计研究随着机器学习技术的不断发展,各种分类器也越来越多。
其中,基于线性判别分析的分类器(Linear Discriminant Analysis Classifier,LDA Classifier)在模式识别、人脸识别、图像分类等领域被广泛应用,并取得了不错的效果。
本文就设计基于线性判别分析的分类器进行研究并总结其中的相关内容。
一、线性判别分析简介线性判别分析也称为Fisher判别分析,是一种经典的线性分类方法,常用于数据降维和数据分类。
其主要目的就是将一组数据区分为两个或更多个类别,并确定识别边界。
线性判别分析认为,不同类别的数据在某个方向上的投影差异最大,而同一类别的数据在该方向上的投影差异最小。
二、基于线性判别分析的分类器设计基于线性判别分析的分类器是基于数据的线性辨别方向进行分类的,其设计流程如下:1. 数据预处理设计任何分类器之前,首先需要对原始数据进行预处理,包括数据清洗、特征提取、特征选择等。
对于线性判别分析,其输入数据应该是已经处理过的特征向量。
2. 计算类内离散度矩阵和类间离散度矩阵类内离散度矩阵描述了每个类别内部数据的分布情况,而类间离散度矩阵则描述了各个类别之间的分布情况。
通过计算这两个离散度矩阵,可以得到数据在各个方向上的投影差异大小。
3. 计算投影方向将类内离散度矩阵和类间离散度矩阵进行特征值分解,可以得到各个方向上的特征向量。
取特征值最大的前n个特征向量作为投影方向,即可使数据在该方向上的投影分布有最大的差异。
4. 计算阈值和决策边界在确定了投影方向后,需要计算阈值和决策边界,以将输入数据分类到不同的类别中。
阈值通常是基于训练数据中的类别分布情况确定的,而决策边界则是根据阈值及数据投影的分布情况确定的。
5. 模型训练和预测利用训练数据,可对分类器进行训练和优化。
而在实际应用中,需要将测试数据输入分类器,根据分类器预测结果判断其所属的类别。
三、优缺点及应用基于线性判别分析的分类器具有以下优点:1. 矩阵运算简单,计算复杂度低。
Fisher准则线性分类器设计

一 、基于F i s h e r 准则线性分类器设计1、 实验内容:已知有两类数据1ω和2ω二者的概率已知1)(ωp =0.6,2)(ωp =0.4。
1ω中数据点的坐标对应一一如下:数据:x =0.2331 1.5207 0.6499 0.7757 1.0524 1.1974 0.2908 0.2518 0.6682 0.5622 0.9023 0.1333 -0.5431 0.9407 -0.2126 0.0507 -0.0810 0.7315 0.3345 1.0650 -0.0247 0.1043 0.3122 0.6655 0.5838 1.1653 1.2653 0.8137 -0.3399 0.5152 0.7226 -0.2015 0.4070 -0.1717 -1.0573 -0.2099 y =2.3385 2.1946 1.6730 1.6365 1.7844 2.0155 2.0681 2.1213 2.4797 1.5118 1.9692 1.8340 1.8704 2.2948 1.7714 2.3939 1.5648 1.9329 2.2027 2.4568 1.7523 1.6991 2.4883 1.7259 2.0466 2.0226 2.3757 1.7987 2.0828 2.0798 1.9449 2.3801 2.2373 2.1614 1.9235 2.2604 z =0.5338 0.8514 1.0831 0.4164 1.1176 0.5536 0.6071 0.4439 0.4928 0.5901 1.0927 1.0756 1.0072 0.4272 0.4353 0.9869 0.4841 1.09921.02990.71271.01240.45760.85441.12750.77050.41291.00850.76760.84180.87840.97510.78400.41581.03150.75330.9548数据点的对应的三维坐标为2x2 =1.40101.23012.08141.16551.37401.18291.76321.97392.41522.58902.84721.95391.25001.28641.26142.00712.18311.79091.33221.14661.70871.59202.93531.46642.93131.83491.83402.50962.71982.31482.03532.60301.23272.14651.56732.9414 y2 =1.02980.96110.91541.49010.82000.93991.14051.06780.80501.28891.46011.43340.70911.29421.37440.93871.22661.18330.87980.55920.51500.99830.91200.71261.28331.10291.26800.71401.24461.33921.18080.55031.47081.14350.76791.1288 z2 =0.62101.36560.54980.67080.89321.43420.95080.73240.57841.49431.09150.76441.21591.30491.14080.93980.61970.66031.39281.40840.69090.84000.53811.37290.77310.73191.34390.81420.95860.73790.75480.73930.67390.86511.36991.1458数据的样本点分布如下图:1)请把数据作为样本,根据Fisher选择投影方向W的原则,使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求,求出评价投影方向W的函数,并在图形表示出来。
Fisher线性判别分析实验报告

Fisher线性判别分析实验报告Fisher 线性判别分析实验报告一、摘要Fisher 线性判别分析的基本思想:通过寻找一个投影方向(线性变换,线性组合),将高维问题降低到一维问题来解决,并且要求变换后的一维数据具有性质:同类样本尽可能聚集在一起,不同类样本尽可能地远。
Fisher 线性判别分析,就是通过给定的训练数据,确定投影方向w 和阈值y0,即确定线性判别函数,然后根据这个线性判别函数,对测试数据进行测试,得到测试数据的类别。
二、算法的基本原理及流程图1 基本原理(1) W 的确定各类样本均值向量 mi样本类内离散度矩阵iS 和总类内离散度矩阵w S12wS S S =+样本类间离散度矩阵b S在投影后的一维空间中,各类样本均值 T i i m '= W m样本类内离散度和总类内离散度 T T i i w w S ' = W S W S ' = W S W 样本类间离散度 T b b S ' = W S WFisher 准则函数满足两个性质:投影后,各类样本内部尽可能密集,即总类内离散度越小越好。
投影后,各类样本尽可能离得远,即样本类间离散度越大越好。
根据这个性质确定准则函数,根据使准则函数取得最大值,可求出wT x S (x m)(x m ), 1,2iiii X i ∈=--=∑T 1212S (m m )(m m )b =---1w12W = S(m - m)(2)阈值的确定实验中采取的方法:012y = (m' + m') / 2(3) Fisher线性判别的决策规则对于某一个未知类别的样本向量 x,如果y = W T x >y0, 则x∈w1否则x∈w22流程图方差标准化(归一化处理)一个样本集中,某一个特征的均值与方差为:归一化:三、实验结果分析1男女同学身高体重,训练数据和测试数据都是50当采用StudentData1作为训练数据,StudnetData2作为测试数据时男孩类的错误率女孩类的错误率总的错误率0.04 0.14 0.09当采用StudnetData2作为训练数据,StudentData2作为测试数据时男孩类的错误率女孩类的错误率总的错误率0.02 0.06 0.042IonoSphere数据G类错误率B类错误率总的类错误率第一组数据0.31 0.29 0.30第二组数据0.32 0.27 0.30第三组数据0.31 0.28 0.29第四组数据0.30 0.37 0.32第五组数据0.30 0.31 0.31第六组数据0.78 0.27 0.60第七组数据0.42 0.25 0.36第八组数据0.30 0.31 0.30第九组数据0.29 0.40 0.33第十组数据0.34 0.25 0.31考虑到第一组数据训练数据多,下面的实验以第一组数据的训练数据作为训练数据,分别用其他组的测试数据进行测试G类错误率B类错误率总的类错误率第一组数据0.31 0.29 0.30第二组数据0.31 0.26 0.29第三组数据0.32 0.26 0.30第四组数据0.31 0.26 0.29第五组数据0.31 0.26 0.29从实验结果看,Fisher线性判别用于两类的判别决策时,拥有不错的效果,并且当有足量的训练数据时,效果更好。
Fisher线性分类

Sw S1 S2
T
•
3.
样本类间离散度矩阵Sb:
Sb (m1 m2 )(m1 m2 )
离散矩阵在形式上与协方差矩阵很相似,但协方 差矩阵是一种期望值,而离散矩阵只是表示有限 个样本在空间分布的离散程度
一维Y空间样本分布的描述量
1. • 2. 各类样本均值
1 mi Ni
•
只要给出待分类的模式特征的数值, 看它在特征平面上落在判别函数的哪一 侧,就可以判别是男还是女了。
统计方法(判别分析)
判别分析—在已知研究对象分成若干类型, 并已取得各种类型的一批已知样品的观测数 据,在此基础上根据某些准则建立判别式, 然后对未知类型的样品进行判别分类。 距离判别法—首先根据已知分类的数据,分 别计算各类的重心,计算新个体到每类的距 离,确定最短的距离(欧氏距离、马氏距离) Fisher判别法—利用已知类别个体的指标构 造判别式(同类差别较小、不同类差别较 大),按照判别式的值判断新个体的类别.
的投影
中心
中心
Fisher准则的基本原理
找到一个最合适的投影轴,使两 类样本在该轴上投影之间的距离尽 可能远,而每一类样本的投影尽可 能紧凑,从而使两类分类效果为最 佳。
Fisher线性判别图例
x2 w
1
Fisher 判别
维空间样本分布的描述量fisherfisher判别判别离散矩阵在形式上与协方差矩阵很相似但协方差矩阵是一种期望值而离散矩阵只是表示有限个样本在空间分布的离散程度一维y空间样本分布的描述量fisherfisher判别判别以上定义描述d维空间样本点到一向量投影的分散情况因此也就是对某向量w的投影在w上的分布
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验意义及目的
掌握Fisher分类原理,能够利用Matlab编程实现Fisher线性分类器设计,
熟悉基于Matlab算法处理函数,并能够利用算法解决简单问题。
二、算法原理
Fisher准则基本原理:找到一个最合适的投影周,使两类样本在该轴上投影之间的距离尽可能远,而每一类样本的投影尽可能紧凑,从而使分类效果为最佳。
内容:
(1)尝试编写matlab程序,用Fisher线性判别方法对三维数据求最优方向w的通用函数(2)对下面表1-1样本数据中的类别w1和w2计算最优方向w
(3)画出最优方向w 的直线,并标记出投影后的点在直线上的位置
(4)选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类
三、实验内容
(1)尝试编写matlab程序,用Fisher线性判别方法对三维数据求最优方向w的通用函数程序清单:
clc
clear all
%10*3样本数据
w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0.011;-
0.35,.47,0.034;0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-
0.12,0.054,-0.063];
w2=[0.83,1.6,-0.014;1.1,1.6,0.48;-0.44,-0.41,0.32;0.047,-0.45,1.4;0.28,0.35,3.1;-
0.39,-0.48,0.11;0.34,-0.079,0.14;-0.3,-0.22,2.2;1.1,1.2,-0.46;0.18,-0.11,-0.49];
W1=w1';%转置下方便后面求s1
W2=w2';
m1=mean(w1);%对w1每一列取平均值结果为1*3矩阵
m2=mean(w2);%对w1每一列取平均值结果为1*3矩阵
S1=zeros(3);%有三个特征所以大小为3
S2=zeros(3);
for i=1:10%1到样本数量n
s1=(W1(:,i)-m1)*(W1(:,i)-m1)';
s2=(W2(:,i)-m2)*(W2(:,i)-m2)';
S1=S1+s1;
S2=S2+s2;
end
sw=S1+S2;
w_new=transpose(inv(sw)*(m1'-m2'));%这里m1m2是行要转置下3*3 X 3*1 =3*1 这里提前转置了下跟老师ppt解法公式其实一样
%绘制拟合结果数据画图用
y1=w_new*W1
y2=w_new*W2;
m1_new=w_new*m1';%求各样本均值也就是上面y1的均值
m2_new=w_new*m2';
w0=(m1_new+m2_new)/2%取阈值
%分类判断
x=[-0.7 0.047
0.58 -0.4
0.089 1.04 ];
m=0; n=0;
result1=[]; result2=[];
for i=1:2%对待观测数据进行投影计算
y(i)=w_new*x(:,i);
if y(i)>w0
m=m+1;
result1(:,m)=x(:,i);
else
n=n+1;
result2(:,n)=x(:,i);
end
end
%结果显示
display('属于第一类的点')
result1
display('属于第二类的点')
result2
figure(1)
scatter3(w1(1,:),w1(2,:),w1(3,:),'+r'),hold on
scatter3(w2(1,:),w2(2,:),w2(3,:),'sg'),hold on
scatter3(result1(1,:),result1(2,:),result1(3,:),'k'),hold on
scatter3(result2(1,:),result2(2,:),result2(3,:),'bd')
title('样本点及实验点的空间分布图')
legend('样本点w1','样本点w2','属于第一类的实验点','属于第二类的实验点')
figure(2)
title('样本拟合结果')
scatter3(y1*w_new(1),y1*w_new(2),y1*w_new(3),'b'),hold on
scatter3(y2*w_new(1),y2*w_new(2),y2*w_new(3),'sr')
(2)对下面表1-1样本数据中的类别w1和w2计算最优方向w
(3)画出最优方向w 的直线,并标记出投影后的点在直线上的位置
最优方向w 的直线
投影后的位置
(4)选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类
决策边界取法:
分类结果:
四、实验感想
通过这次实验,我学会了fisher线性判别相关的分类方法,对数据分类有了初步的认识,尽管在过程中有不少中间量不会算,通过查阅网络知识以及模式识别专业课ppt等课件帮助,我最终完成了实验,为今后继续深入学习打下良好基础。
