Fisher分类器设计
线性分类器设计fisher准则
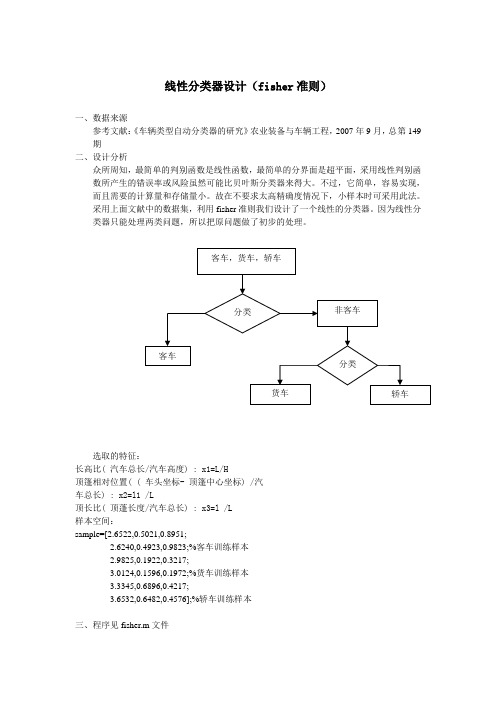
线性分类器设计(fisher准则)一、数据来源参考文献:《车辆类型自动分类器的研究》农业装备与车辆工程,2007年9月,总第149期二、设计分析众所周知,最简单的判别函数是线性函数,最简单的分界面是超平面,采用线性判别函数所产生的错误率或风险虽然可能比贝叶斯分类器来得大。
不过,它简单,容易实现,而且需要的计算量和存储量小。
故在不要求太高精确度情况下,小样本时可采用此法。
采用上面文献中的数据集,利用fisher准则我们设计了一个线性的分类器。
因为线性分类器只能处理两类问题,所以把原问题做了初步的处理。
选取的特征:长高比( 汽车总长/汽车高度) : x1=L/H顶篷相对位置( ( 车头坐标- 顶篷中心坐标) /汽车总长) : x2=l1 /L顶长比( 顶蓬长度/汽车总长) : x3=l /L样本空间:sample=[2.6522,0.5021,0.8951;2.6240,0.4923,0.9823;%客车训练样本2.9825,0.1922,0.3217;3.0124,0.1596,0.1972;%货车训练样本3.3345,0.6896,0.4217;3.6532,0.6482,0.4576];%轿车训练样本三、程序见fisher.m文件四、结果分析原文章中采用的的改进的BP神经网络算法,能很好的实现分类的效果。
而在这里我们挑了6个训练集样本和3个测试集样本,也很好的实现了分类效果。
但是,若对于大样本来说,贝叶斯分类器的效果更好。
下图就是采用线性分类器的效果图。
客车样本和非客车样本1 1.2 1.4 1.6 1.82 2.2 2.4 2.6 2.83客车样本和非客车样本1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.92。
机器学习实验1-Fisher线性分类器设计

一、实验意义及目的掌握Fisher分类原理,能够利用Matlab编程实现Fisher线性分类器设计,熟悉基于Matlab算法处理函数,并能够利用算法解决简单问题。
二、算法原理Fisher准则基本原理:找到一个最合适的投影周,使两类样本在该轴上投影之间的距离尽可能远,而每一类样本的投影尽可能紧凑,从而使分类效果为最佳。
内容:(1)尝试编写matlab程序,用Fisher线性判别方法对三维数据求最优方向w的通用函数(2)对下面表1-1样本数据中的类别w1和w2计算最优方向w(3)画出最优方向w 的直线,并标记出投影后的点在直线上的位置(4)选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类三、实验内容(1)尝试编写matlab程序,用Fisher线性判别方法对三维数据求最优方向w的通用函数程序清单:clcclear all%10*3样本数据w1=[-0.4,0.58,0.089;-0.31,0.27,-0.04;-0.38,0.055,-0.035;-0.15,0.53,0.011;-0.35,.47,0.034;0.17,0.69,0.1;-0.011,0.55,-0.18;-0.27,0.61,0.12;-0.065,0.49,0.0012;-0.12,0.054,-0.063];w2=[0.83,1.6,-0.014;1.1,1.6,0.48;-0.44,-0.41,0.32;0.047,-0.45,1.4;0.28,0.35,3.1;-0.39,-0.48,0.11;0.34,-0.079,0.14;-0.3,-0.22,2.2;1.1,1.2,-0.46;0.18,-0.11,-0.49];W1=w1';%转置下方便后面求s1W2=w2';m1=mean(w1);%对w1每一列取平均值结果为1*3矩阵m2=mean(w2);%对w1每一列取平均值结果为1*3矩阵S1=zeros(3);%有三个特征所以大小为3S2=zeros(3);for i=1:10%1到样本数量ns1=(W1(:,i)-m1)*(W1(:,i)-m1)';s2=(W2(:,i)-m2)*(W2(:,i)-m2)';S1=S1+s1;S2=S2+s2;endsw=S1+S2;w_new=transpose(inv(sw)*(m1'-m2'));%这里m1m2是行要转置下3*3 X 3*1 =3*1 这里提前转置了下跟老师ppt解法公式其实一样%绘制拟合结果数据画图用y1=w_new*W1y2=w_new*W2;m1_new=w_new*m1';%求各样本均值也就是上面y1的均值m2_new=w_new*m2';w0=(m1_new+m2_new)/2%取阈值%分类判断x=[-0.7 0.0470.58 -0.40.089 1.04 ];m=0; n=0;result1=[]; result2=[];for i=1:2%对待观测数据进行投影计算y(i)=w_new*x(:,i);if y(i)>w0m=m+1;result1(:,m)=x(:,i);elsen=n+1;result2(:,n)=x(:,i);endend%结果显示display('属于第一类的点')result1display('属于第二类的点')result2figure(1)scatter3(w1(1,:),w1(2,:),w1(3,:),'+r'),hold onscatter3(w2(1,:),w2(2,:),w2(3,:),'sg'),hold onscatter3(result1(1,:),result1(2,:),result1(3,:),'k'),hold onscatter3(result2(1,:),result2(2,:),result2(3,:),'bd')title('样本点及实验点的空间分布图')legend('样本点w1','样本点w2','属于第一类的实验点','属于第二类的实验点')figure(2)title('样本拟合结果')scatter3(y1*w_new(1),y1*w_new(2),y1*w_new(3),'b'),hold onscatter3(y2*w_new(1),y2*w_new(2),y2*w_new(3),'sr')(2)对下面表1-1样本数据中的类别w1和w2计算最优方向w(3)画出最优方向w 的直线,并标记出投影后的点在直线上的位置最优方向w 的直线投影后的位置(4)选择决策边界,实现新样本xx1=(-0.7,0.58,0.089),xx2=(0.047,-0.4,1.04)的分类决策边界取法:分类结果:四、实验感想通过这次实验,我学会了fisher线性判别相关的分类方法,对数据分类有了初步的认识,尽管在过程中有不少中间量不会算,通过查阅网络知识以及模式识别专业课ppt等课件帮助,我最终完成了实验,为今后继续深入学习打下良好基础。
Fisher分类器(算法及程序)

3.5 Fisher分类器(Fisher Linear Discriminant)Fisher 判别法是历史上最早提出的判别方法之一,其基本思想是将n 类m 维数据集尽可能地投影到一个方向(一条直线),使得类与类之间尽可能分开。
从形式上看,该方法就是所谓的一种降维处理方法。
为简单起见,我们以两类问题1和2的分类来说明Fisher 判别法的原理,如图3.4所示。
设数据阵为XR Nm,1共有N 1个样本,2共有N 2个样本,N = N 1+N 2。
两个类别在输入空间的均值向量为1类*w最佳投影方向2μ1μ2类判为判为最不利投影方向x p 1x p 2图3.4, Fisher 判别法几何原理示意图)37.3(11212211⎪⎪⎩⎪⎪⎨⎧∈=∈=∑∑∈∈m pmp R N R N p pϖϖx x x μx μ设有一个投影方向()mT m R w w w ∈=,,,21 w ,这两个均值向量在该方向的投影为)38.3(1~1~1222111121⎪⎪⎩⎪⎪⎨⎧∈==∈==∑∑∈∈R N R N p p pT T p T T ϖϖx x x w μw μx w μw μ在w方向,两均值之差为())39.3(~~2121μμw μμ -=-=∇T类似地,样本总均值向量在该方向的投影为)40.3(1~11R NNp pT T ∈==∑=x w μw μ定义类间散度(Between-class scatter)平方和SS B 为()()()()()()()()()[])41.3(~~~~~~222111222211221222211w S w w μμμμμμμμw μw μw μw μw μμμμμμ B T T T T T T T T j j j B N N N N N N N SS =--+--=-+-=-=-+-=∑=其中()()()()()())42.3(21222111∑=--=--+--=j Tj j j TT B N N N μμμμμμμμμμμμS定义类j 的类内散度(Within-class scatter)平方和为()())43.3(~22∑∑∈∈-=-=jjNp jT p T N p jp T Wj x x SS μw w μw两个类的总的类内散度误差平方和为()()())44.3(2121221wS w w μμw μw w W T j Np T jp j p T j N p jT p T j wj W j jx x x SS SS =⎥⎥⎦⎤⎢⎢⎣⎡--=-==∑∑∑∑∑=∈=∈=其中,()())45.3(21∑∑=∈--=j N p Tjp j p W jx x μμS我们的目的是使类间散度平方和SS B 与类内散度平方和SS w 的比值为最大,即())46.3(max wS w w S w wW T B T WB SS SS J ==2类1类图3.5a, Fisher判别法—类间散度平方和(分子)的几何意义2类1类图3.5b, Fisher判别法—类内散度平方和(分母)的几何意义图3.5给出了类间散度平方和S B 与类内散度平方和S E 的几何意义。
Fisher线性分类器通俗解释及MATLAB、Python实现

Fisher线性分类器通俗解释及MATLAB、Python实现⼀、通俗的解释:问题提出:还是以iris的数据为例,有A、B、C三种花,每⼀类的特征都⽤4维特征向量表⽰。
现在已知⼀个特征向量,要求对应的类别,⽽我们⼈可以直接通过眼睛看⽽作出分类的是在⼀维⼆维三维空间,⽽不适应这样的四维数据。
启⽰:假设有这样的⼀个⽅向向量,其与特征向量进⾏内积运算(即向⽅向向量的投影)后,结果为⼀个数值,若同类的特征向量投影后聚集在⼀起,不同类的特征投影后相对分散,那么,我们的⽬的就达到了。
⽬标:这样就有了⽅向,即要寻找⼀个独特的⽅向,使其达到我们的要求。
注:具体的推导过程,参看教科书,另外,在求解极值的时候,利⽤了矩阵论中的向量导数运算。
⼆、MATLAB程序:clearA=[5.1,3.5,1.4,0.24.9,3.0,1.4,0.24.7,3.2,1.3,0.24.6,3.1,1.5,0.25.0,3.6,1.4,0.25.4,3.9,1.7,0.44.6,3.4,1.4,0.35.0,3.4,1.5,0.24.4,2.9,1.4,0.24.9,3.1,1.5,0.15.4,3.7,1.5,0.24.8,3.4,1.6,0.24.8,3.0,1.4,0.14.3,3.0,1.1,0.15.8,4.0,1.2,0.25.7,4.4,1.5,0.45.4,3.9,1.3,0.45.1,3.5,1.4,0.35.7,3.8,1.7,0.35.1,3.8,1.5,0.35.4,3.4,1.7,0.25.2,4.1,1.5,0.15.5,4.2,1.4,0.24.9,3.1,1.5,0.15.0,3.2,1.2,0.25.5,3.5,1.3,0.24.4,3.2,1.3,0.25.0,3.5,1.6,0.6 5.1,3.8,1.9,0.44.8,3.0,1.4,0.35.1,3.8,1.6,0.24.6,3.2,1.4,0.25.3,3.7,1.5,0.2 5.0,3.3,1.4,0.2 7.0,3.2,4.7,1.4];B=[6.4,3.2,4.5,1.5 6.9,3.1,4.9,1.55.5,2.3,4.0,1.36.5,2.8,4.6,1.55.7,2.8,4.5,1.36.3,3.3,4.7,1.6 4.9,2.4,3.3,1.0 6.6,2.9,4.6,1.3 5.2,2.7,3.9,1.4 5.0,2.0,3.5,1.05.9,3.0,4.2,1.56.0,2.2,4.0,1.0 6.1,2.9,4.7,1.45.6,2.9,3.6,1.36.7,3.1,4.4,1.4 5.6,3.0,4.5,1.55.8,2.7,4.1,1.06.2,2.2,4.5,1.5 5.6,2.5,3.9,1.15.9,3.2,4.8,1.86.1,2.8,4.0,1.3 6.3,2.5,4.9,1.5 6.1,2.8,4.7,1.25.5,2.4,3.8,1.1 5.5,2.4,3.7,1.05.8,2.7,3.9,1.26.0,2.7,5.1,1.65.4,3.0,4.5,1.56.0,3.4,4.5,1.6 6.7,3.1,4.7,1.5 6.3,2.3,4.4,1.3 5.6,3.0,4.1,1.3 5.5,2.5,4.0,1.35.5,2.6,4.4,1.26.1,3.0,4.6,1.4 5.8,2.6,4.0,1.2 5.0,2.3,3.3,1.0 5.6,2.7,4.2,1.3 5.7,3.0,4.2,1.25.7,2.9,4.2,1.36.2,2.9,4.3,1.3 5.1,2.5,3.0,1.1 5.7,2.8,4.1,1.3];C=[6.3,3.3,6.0,2.5 5.8,2.7,5.1,1.9 7.1,3.0,5.9,2.1 6.3,2.9,5.6,1.86.5,3.0,5.8,2.27.6,3.0,6.6,2.1 4.9,2.5,4.5,1.7 7.3,2.9,6.3,1.86.7,2.5,5.8,1.87.2,3.6,6.1,2.5 6.5,3.2,5.1,2.0 6.4,2.7,5.3,1.97.7,2.6,6.9,2.36.0,2.2,5.0,1.56.9,3.2,5.7,2.35.6,2.8,4.9,2.07.7,2.8,6.7,2.06.3,3.4,5.6,2.46.4,3.1,5.5,1.86.0,3.0,4.8,1.86.9,3.1,5.4,2.16.7,3.1,5.6,2.46.9,3.1,5.1,2.35.8,2.7,5.1,1.96.8,3.2,5.9,2.36.7,3.3,5.7,2.56.7,3.0,5.2,2.36.3,2.5,5.0,1.96.5,3.0,5.2,2.06.2,3.4,5.4,2.35.9,3.0,5.1,1.8];%⽅法⼀:先将A作为⼀类,BC作为⼀类NA=size(A,1);NB=size(B,1);NC=size(C,1);A_train=A(1:floor(NA/2),:);%训练数据取1/2(或者1/3,3/4,1/4)B_train=B(1:floor(NB/2),:);C_train=C(1:floor(NC/2),:);A_test=A((floor(NA/2)+1):end,:);B_test=B((floor(NB/2)+1):end,:);C_test=C((floor(NC/2)+1):end,:);A_train=A_train;D_train=[B_train;C_train];A_test=A_test;D_test=[B_test;C_test];for i=1:size(A_train,1)S1=S1+(A_train(i,:)-u1)'*(A_train(i,:)-u1);endfor i=1:size(D_train,1)S2=S2+(D_train(i,:)-u2)'*(D_train(i,:)-u2);endSw=S1+S2;w1=(inv(Sw)*(u1-u2)')';w1=w1./norm(w1);y0=w1*(u1+u2)'/2;% a1=w*u1'% d1=w*u2'r1=0;for i=1:size(D_test,1)if w1*D_test(i,:)'<y0r1=r1+1;endendrate_D=r1/size(D_test,1)r2=0;for i=1:size(A_test,1)if w1*A_test(i,:)'>y0r2=r2+1;endendrate_A=r2/size(A_test,1)三、Python程序:from sklearn import discriminant_analysisfrom sklearn.model_selection import train_test_splitimport numpydata = numpy.genfromtxt('iris.csv', delimiter=',', usecols=(0,1,2,3)) target = numpy.genfromtxt('iris.csv', delimiter=',', usecols=(4), dtype=str) t = numpy.zeros(len(target))t[target == 'setosa'] = 1t[target == 'versicolor'] = 2t[target == 'virginica'] = 3#print(clf.predict([data[3]]))。
基于Fisher判决率加权的修正最近邻模糊分类器设计

weg tn i prpo e fr h p a g t e o n t n sn mu t—e t r s o h g r s l to r n e p o l ih i g s o s d o s i tr e r c g i o u i g i lif au e f i h e ou i n a g rf e i
决 率 加权 的修 正 最 近邻 模 糊 分 类 器 在 舰 船 目标 识 别 领 域 具有 很 好 的 实 际应 用 前 景 。
关 键 词 : 高 分 辨 距 离像 ; i e 判 决 率 ; 正 最 近 邻 模 糊 分 类 器 ;中 心 矩 Fs r h 修 中 图 分 类 号 : T 9 7 5 N 5. l 文献标 识码 : A
d s r m i a i htng ic i n ntwe g i
LI a — a U Xin k ng,LI ANG i g,REN i Jn Je,JANG a g q n I Gu n — i g
( o 7 1F c r o L N) B in 0 0 6 C ia N . 0 at y f A( , e ig 10 1 , hn ) o P j
文章 编号 : 1 7 7 4 ( 0 0 0 0 6 0 DoI1 . 4 4 ji n 17 6 2— 6 9 2 1 ) 2— 0 8— 5 :0 3 0 /.s . 6 2—7 4 . O 0 O . 1 s 692 1.206
FISHER分类

Fisher 线性判别分类器成员姓名: 学号:莫文敏 201111921217 赵越 201111921229 顾瑞煌 201111921104一、实验目的1.实现基于FISHER 分类的算法程序;2.能够根据自己的设计加深对FISHER 分类的认识;3.掌握FISHER 分类的原理、特点。
二、实验设备1.手提电脑2.MATLAB三、FISHER 算法原理线性判别函数的一般形式可表示成0)(w X W X g T +=其中⎪⎪⎪⎭⎫ ⎝⎛=d x x X 1 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=d w w w W 21但是,在应用统计方法解决模式识别的问题时,经常会遇到“维数风暴”的问题,因此压缩特征空间的维数在此时十分重要,FISHER 方法实际上是涉及维数压缩的问题。
把多为特征空间的点投影到一条直线上,就能把特征空间压缩成一维,这在数学上是很容易做到的。
但是在高维空间里很容易一分开的样品,把它们投射到任意一条直线上,有可能不同类别的样品就混在一起,无法区分了,如图5-16(a )所示,投影1x 或2x 轴无法区分。
若把直线绕原点转动一下,就有可能找到一个方向,样品投射到这个方向的直线上,各类样品就能很好地分开,如图5-16(b )所示。
因此直线方向的选择是很重要的。
一般来说总能找到一个最好的方向,使样品投射到这个方向的直线上很容易分开。
如何找到这个最好的直线方向以及如何实现向最好方向投影的变换,这正是FISHER 算法要解决的基本问题,这个投影变换正是我们寻求的解向量*W 。
样品训练集以及待测样品的特征总数目为n ,为找到最佳投影方向,需要计算出各类样品的均值、样品类内离散度矩阵i S 和总类间矩阵w S 、样品类间离散度矩阵b S ,根据FISHER 准则找到最佳投影向量,将训练集内所有样品进行投影,投影到一维Y 空间,由于Y 空间是一维的,则需要求出Y 空间的划分边界点,找到边界点后,就可以对待测样品进行一维Y 空间的投影,判断它的投影点与分界点的关系将其归类。
基于Fisher的分类器设计

7
8 9 10 11 12
2
3 4 1 3 3
2
3 4 1 3 3
13
14 15 16 17 18
1
2 4 2 4 3
1
2 4 2 4 2
19
20 21 22 23 24
4
2 2 3 3 1
4
2 3 3 3 1
25
26 27 28 29 30
1
4 1 3 3 3
1
4 1 3 3 3
结果分析:从表中可以看出有2个分类结果是错的,正确率为93.3%。
T
0 1
y y , x
0
2
算法实现
◆ 流程图
算法实现
◆ 样本均值
clear,close all; N=29; %N为训练样本总个数 X = [1495.18 1957.44 3498.02 %X为训练样本 1125.17 1594.39 2937.73 1269.07 1910.72 2701.97 …… ……] m1=mean(X(1:11,:)); %求得第一类样本均值 m2=mean(X(12:29,:)); %求得第二类样本均值
y0
Fisher投影原理
Fisher分类器设计
样本在d维特征空间的一些描述量 (1)各类样本均值 m 1 m i 1,2 x N (2)样本类内离散度矩阵 S 与总类内离散度矩阵 S
i
i X i i
i
w
S ( X m )( X m )
i X wi i i
T
基于Fisher的分类器设计
主 单 讲:周润景 教授 位:电子信息工程学院
Fisher分类器(算法及程序)
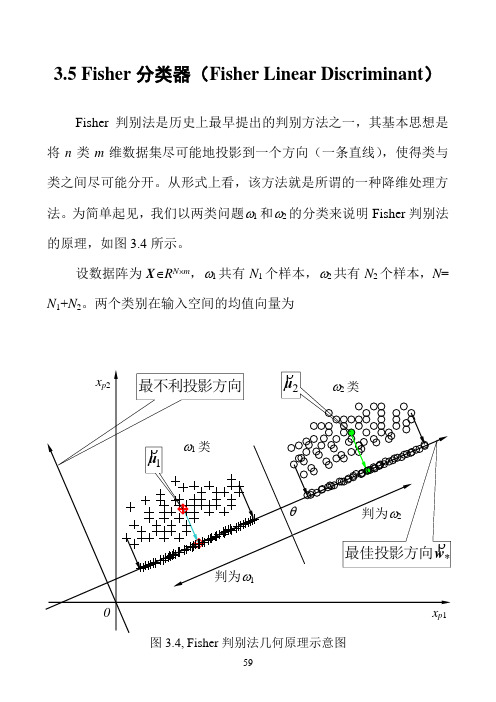
3.5 Fisher分类器(Fisher Linear Discriminant)Fisher判别法是历史上最早提出的判别方法之一,其基本思想是将n类m维数据集尽可能地投影到一个方向(一条直线),使得类与类之间尽可能分开。
从形式上看,该方法就是所谓的一种降维处理方法。
为简单起见,我们以两类问题ω1和ω2的分类来说明Fisher判别法的原理,如图3.4所示。
设数据阵为X∈R N⨯m,ω1共有N1个样本,ω2共有N2个样本,N= N1+N2。
两个类别在输入空间的均值向量为图3.4, Fisher判别法几何原理示意图)37.3(11212211⎪⎪⎩⎪⎪⎨⎧∈=∈=∑∑∈∈m pmp R N R N p pϖϖx x x μx μρρρρρρ设有一个投影方向()mT m R w w w ∈=,,,21Λρw ,这两个均值向量在该方向的投影为)38.3(1~1~1222111121⎪⎪⎩⎪⎪⎨⎧∈==∈==∑∑∈∈R N R N p p pT T p T T ϖϖx x x w μw μx w μw μρρρρρρρρρρρρ在w ρ方向,两均值之差为())39.3(~~2121μμw μμρρρρρ-=-=∇T类似地,样本总均值向量在该方向的投影为)40.3(1~11R NNp pT T ∈==∑=x w μw μρρρρρ定义类间散度(Between-class scatter)平方和SS B 为()()()()()()()()()[])41.3(~~~~~~222111222211221222211w S w w μμμμμμμμw μw μw μw μw μμμμμμρρρρρρρρρρρρρρρρρρρρρρρρρρB T T T T T T T T j j j B N N N N N N N SS =--+--=-+-=-=-+-=∑=其中()()()()()())42.3(21222111∑=--=--+--=j Tj j j TT B N N N μμμμμμμμμμμμS ρρρρρρρρρρρρ定义类ωj 的类内散度(Within-class scatter)平方和为()())43.3(~22∑∑∈∈-=-=jjNp jT p T N p jp T Wj x x SS μw w μw ρρρρρρρ两个类的总的类内散度误差平方和为()()())44.3(2121221wS w w μμw μw w ρρρρρρρρρρρρW T j Np T jp j p T j N p jT p T j wj W j jx x x SS SS =⎥⎥⎦⎤⎢⎢⎣⎡--=-==∑∑∑∑∑=∈=∈=其中,()())45.3(21∑∑=∈--=j N p Tjp j p W jx x μμS ρρρρ我们的目的是使类间散度平方和SS B 与类内散度平方和SS w 的比值为最大,即())46.3(max wS w w S w w ρρρρρW T B T WBSS SS J ==图3.5a, Fisher判别法—类间散度平方和(分子)的几何意义图3.5b, Fisher判别法—类内散度平方和(分母)的几何意义图3.5给出了类间散度平方和S B 与类内散度平方和S E 的几何意义。
Fisher分类器设计
Fisher分类器设计班级:自092 姓名:刘昌元学号:099064370 一、实验目的:1:根据fisher准则设计线性分类器2:由fisher分类器训练样本数据3:由fisher分类器测试样本观察出错率并与贝叶斯分类器的出错率比较判断两种分类器的性能优劣4:将测试数据和决策面画在一张图上直观显示是三、实验所用函数:类均值向量:∑=∈ixj j i x N M χ1类内离散度矩阵:Ti j i ixj j iM x M x S ))((--∑∈=χ总类内离散度矩阵:21S S S w +=类间离散度矩阵:T b M M M M S ))((2121--= 最有投影方向:)(211*M M S W w -=-决策函数:0)(w x w x G T +=阈值:)(21210M w M w w T T+-= 四、实验结果:1:得到参数:最有投影向量和阈值2:利用分类器输入身高和体重数据得到性别分类(实验结果如下)w=[ 0.0012; 0.0003] threshold =0.2318classify(165,56) 结果为“女” classify(178,70) 结果为“男”3:fisher准则分类器的出错率统计:测试test1:实际个数分类个数出错率男生84.0000 31.0000 0.6310女生40.0000 93.0000 1.3250测试test2:4:bayes分类器测试出错统计:测试test1:测试test2:结论:很显然bayes分类器比fisher分类器准确率高的多。
4:分类面决策图:五、程序:程序1:求最有投影方向和阈值%程序功能:应用fisher分类方法,使用训练数据获得阈值和最佳变换向量(投影方向)% function fisher(boys,girls) %调用男生和女生的训练样本数据%A=boys.';B=girls.';[k1,l1]=size(A);[k2,l2]=size(B);M1=sum(boys);M1=M1.';M1=M1/l1; %求男生身高与体重的均值%M2=sum(girls);M2=M2.';M2=M2/l2; %求女生身高与体重的均值%S1=zeros(k1,k1);S2=zeros(k2,k2);for i=1:l1S1=S1+(A(:,i)-M1)*((A(:,i)-M1).'); %求类内离散度矩阵S1%endfor i=1:l2S2=S2+(B(:,i)-M2)*((B(:,i)-M2).'); %求类内离散度矩阵S2%endfor i=1:2for j=1:2Sw(i,j)=S1(i,j)+S2(i,j); %求总类内离散度矩阵Sw%endendw=inv(Sw)*(M1-M2) %求最有投影方向%wT=w.';for i=1:l1Y1(i)=wT(1,1)*A(1,i)+wT(1,2)*A(2,i); %由分类函数g(x)=wT*x求男生身高和体重的阈值%endfor i=1:l2Y2(i)=wT(1,1)*B(1,i)+wT(1,2)*B(2,i); %由分类函数g(x)=wT*x求女生身高和体重的阈值%endm1=sum(Y1)/l1; %阈值平均%m2=sum(Y2)/l2; %阈值平均%threshold=(l1*m1+l2*m2)/(l1+l2) %求fisher决策面的阈值%程序2:构成fisher判别器%函数功能:应用Fisher准则构成的分类器判断一个身高体重二维数据的性别%函数使用方法:输入classify(hight,weight)其中hight和weight分别是身高和体重的数据function value=classify(hight,weight)w=[0.0012;0.0003];threshold=0.2318;tem=[hight;weight]; %将输入的身高和体重数据构成列向量%result=(w.')*tem; %根据fisher判别式求判别值%if result>threshold %判别值和决策面阈值比较%value=1;elsevalue=0;end程序3:%功能:调用Fisher分类器统计出错率%开发者:安徽工业大学自动化092班刘昌元function result=Error(file)[m,n]=size(file);Boy=0;Girl=0;boy=0;girl=0;for i=1:mif(file(i,3)==0)Girl=Girl+1;elseBoy=Boy+1;endA(i,1)=file(i,1);A(i,2)=file(i,2);endw=[0.0012;0.0003];threshold =0.2318;for i=1:mclassify(A(i,1),A(i,2));if(ans==0)girl=girl+1;elseboy=boy+1;endendtem1=abs(Boy-boy)/Boy;tem2=abs(Girl-girl)/Girl;result(1,1)=Boy;result(1,2)=boy;result(1,3)=tem1;result(2,1)=Girl;result(2,2)=girl;result(2,3)=tem2;程序4:%程序:画图%功能:将训练样本boy.txt和girl.txt中的数据和线性决策面以及贝叶斯决策面画到一幅图上function graphics(boys,girls)w=[0.0012;0.0003];threshold =0.2318;A=boys.';B=girls.';[m1,n1]=size(A);[m2,n2]=size(B);for i=1:n1x=A(1,i);y=A(2,i);plot(x,y,'R.');hold onendfor i=1:n2x=B(1,i);y=B(2,i);plot(x,y,'G.');hold onenda1=min(A(1,:));a2=max(A(1,:));b1=min(B(1,:));b2=max(B(1,:));a3=min(A(2,:));a4=max(A(2,:));b3=min(B(2,:));b4=max(B(2,:));if a1<b1a=a1;elsea=b1;endif a2>b2b=a2;elseb=b2;endif a3<b3c=a3;elsec=b3;endif a4>b4。
基于Fisher线性判别的基因分类器的设计

基于Fisher 线性判别的基因分类器的设计2000年6月人类基因组计划正式完成对人类分布在细胞核中的23条染色体的6万到10万个基因,大约30亿个碱基的测序工作,其中我国完成对3号染色体上的3000万个碱基的测序。
基因草图是由4个字符A 、T 、C 、G 按一定顺序排列组成的长约30亿的序列,其中没有断句,也没有标点。
除了知道这四个字符代表四种碱基之外,人类对基因知之甚少。
但众多的科研工作者发现,NDA 的序列中隐藏这重大的秘密,关系到人的生老病死,对基因的研究具有重大的意义。
本文对DNA 中的四种碱基:腺嘌呤(A ),鸟嘌呤(G ),胞嘧啶(C )和胸腺嘧啶(T )在基因链中出现的频率作为输入向量的四个特征成员,用Fisher 线性分类方法对已知类别的20个基因样本进行训练和测试,表明Fisher 线性分类方法能对这些已知类别的DNA 序列达到分类的目的。
本文采用的数据来自参考文献[1],数据表1所示:显然表1中的样本共分为两类,其中0P >的为一类,在神经网络中以输出为“1”表示;0P <的为另一类,在神经网络中以输出为“0”表示。
Fisher 线性判别:Fisher 线性判别的基本思想是将d 维空间中的样本投射到一维空间中的一条直线上,将维度由多维压缩到一维。
在一维的直线上找到一个阈值点,大于该阈值点的样本分为一类,小于该阈值点的样本分为另一类。
基于以上思想,假设集合ψ包含N 个d 维样本123,,,......N x x x x 其中1N 个属于1ψ的样本,2N 个属于2ψ的样本。
若对n x 的分量做线性组合,可得到标量,1,2,3,......T n n y x n N ω==这样便得到N 个一维样本n y 的集合,可分为两个子集12,y y 。
从几何上,如果||||1ω=,则每个n y 就是对应于n x 到方向为ω的直线的投影。
ω方向的不同,将使样本投影后的可分程度不同,从而直接影响识别的效果。
feisher线性判别分类器的设计实验报告()

实验二 Fisher 线性判别实验一、实验目的应用统计方法解决模式识别问题的困难之一是维数问题, 低维特征空间的分类问题一般比高维空间分类问题简单。
因此, 人们力图将特征空间进行降维, 降维的一个基本思路是将 d 维特征空间投影到一条直线上, 形成一维空间, 这在数学上比较容易实现。
问题的关键是投影之后原来线性可分的样本可能变为线性不可分。
一般对于线性可分的样本, 总能找到一个投影方向, 使得降维后样本仍然线性可分。
如何确定投影方向使得降维以后, 样本不但线性可分, 而且可分性更好(即不同类别的样本之间的距离尽可能远,同一类别的样本尽可能集中分布),就是 Fisher 线性判别所要解决的问题。
本实验通过编制程序让初学者能够体会 Fisher 线性判别的基本思路,理解线性判别的基本思想,掌握 Fisher 线性判别问题的实质。
二、实验原理Fisher 线性判别分类器(Fisher Linear Discriminant Analysis,FLDA ),此方法的基本思想是在Fisher 准则下,先求解最佳鉴别矢量,然后将高维的样本投影到最佳鉴别矢量张成的空间,使投影后的样本在低维空间有最大类间距离和最小类内距离,这样在低维空间中样本将有最佳的可分性,分类是一项非常基本和重要的任务,并有着极其广泛的应用。
分类是利用预定的已分类数据集构造出一个分类函数或分类模型(也称作分类器),并利用该模型把未分类数据映射到某一给定类别中的过程。
分类器的构造方法很多,主要包括规则归纳、决策树、贝叶斯、神经网络、粗糙集、以及支持向量机(SVM)等方法。
其中贝叶斯分类方法建立在贝叶斯统计学[v1和贝叶斯网络[s1基础上,能够有效地处理不完整数据,并且具有模型可解释、精度高等优点,而被认为是最优分类模型之一[9]。
尤其是最早的朴素贝叶斯分类器[l0l 虽然结构简单,但在很多情况下却具有相当高的分类精度,可以达到甚至超过其它成熟算法如c4.5[l ’]的分类精度,而且对噪声数据具有很强的抗干扰能力。
Fisher准则线性分类器设计

一 、基于F i s h e r 准则线性分类器设计1、 实验内容:已知有两类数据1ω和2ω二者的概率已知1)(ωp =0.6,2)(ωp =0.4。
1ω中数据点的坐标对应一一如下:数据:x =0.2331 1.5207 0.6499 0.7757 1.0524 1.1974 0.2908 0.2518 0.6682 0.5622 0.9023 0.1333 -0.5431 0.9407 -0.2126 0.0507 -0.0810 0.7315 0.3345 1.0650 -0.0247 0.1043 0.3122 0.6655 0.5838 1.1653 1.2653 0.8137 -0.3399 0.5152 0.7226 -0.2015 0.4070 -0.1717 -1.0573 -0.2099 y =2.3385 2.1946 1.6730 1.6365 1.7844 2.0155 2.0681 2.1213 2.4797 1.5118 1.9692 1.8340 1.8704 2.2948 1.7714 2.3939 1.5648 1.9329 2.2027 2.4568 1.7523 1.6991 2.4883 1.7259 2.0466 2.0226 2.3757 1.7987 2.0828 2.0798 1.9449 2.3801 2.2373 2.1614 1.9235 2.2604 z =0.5338 0.8514 1.0831 0.4164 1.1176 0.5536 0.6071 0.4439 0.4928 0.5901 1.0927 1.0756 1.0072 0.4272 0.4353 0.9869 0.4841 1.09921.02990.71271.01240.45760.85441.12750.77050.41291.00850.76760.84180.87840.97510.78400.41581.03150.75330.9548数据点的对应的三维坐标为2x2 =1.40101.23012.08141.16551.37401.18291.76321.97392.41522.58902.84721.95391.25001.28641.26142.00712.18311.79091.33221.14661.70871.59202.93531.46642.93131.83491.83402.50962.71982.31482.03532.60301.23272.14651.56732.9414 y2 =1.02980.96110.91541.49010.82000.93991.14051.06780.80501.28891.46011.43340.70911.29421.37440.93871.22661.18330.87980.55920.51500.99830.91200.71261.28331.10291.26800.71401.24461.33921.18080.55031.47081.14350.76791.1288 z2 =0.62101.36560.54980.67080.89321.43420.95080.73240.57841.49431.09150.76441.21591.30491.14080.93980.61970.66031.39281.40840.69090.84000.53811.37290.77310.73191.34390.81420.95860.73790.75480.73930.67390.86511.36991.1458数据的样本点分布如下图:1)请把数据作为样本,根据Fisher选择投影方向W的原则,使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求,求出评价投影方向W的函数,并在图形表示出来。
基于线性判别分析的分类器设计研究

基于线性判别分析的分类器设计研究随着机器学习技术的不断发展,各种分类器也越来越多。
其中,基于线性判别分析的分类器(Linear Discriminant Analysis Classifier,LDA Classifier)在模式识别、人脸识别、图像分类等领域被广泛应用,并取得了不错的效果。
本文就设计基于线性判别分析的分类器进行研究并总结其中的相关内容。
一、线性判别分析简介线性判别分析也称为Fisher判别分析,是一种经典的线性分类方法,常用于数据降维和数据分类。
其主要目的就是将一组数据区分为两个或更多个类别,并确定识别边界。
线性判别分析认为,不同类别的数据在某个方向上的投影差异最大,而同一类别的数据在该方向上的投影差异最小。
二、基于线性判别分析的分类器设计基于线性判别分析的分类器是基于数据的线性辨别方向进行分类的,其设计流程如下:1. 数据预处理设计任何分类器之前,首先需要对原始数据进行预处理,包括数据清洗、特征提取、特征选择等。
对于线性判别分析,其输入数据应该是已经处理过的特征向量。
2. 计算类内离散度矩阵和类间离散度矩阵类内离散度矩阵描述了每个类别内部数据的分布情况,而类间离散度矩阵则描述了各个类别之间的分布情况。
通过计算这两个离散度矩阵,可以得到数据在各个方向上的投影差异大小。
3. 计算投影方向将类内离散度矩阵和类间离散度矩阵进行特征值分解,可以得到各个方向上的特征向量。
取特征值最大的前n个特征向量作为投影方向,即可使数据在该方向上的投影分布有最大的差异。
4. 计算阈值和决策边界在确定了投影方向后,需要计算阈值和决策边界,以将输入数据分类到不同的类别中。
阈值通常是基于训练数据中的类别分布情况确定的,而决策边界则是根据阈值及数据投影的分布情况确定的。
5. 模型训练和预测利用训练数据,可对分类器进行训练和优化。
而在实际应用中,需要将测试数据输入分类器,根据分类器预测结果判断其所属的类别。
三、优缺点及应用基于线性判别分析的分类器具有以下优点:1. 矩阵运算简单,计算复杂度低。
Fisher线性分类器PPT课件

2021/1/20
-
21
-
10
Fisher’s Discriminant
Fisher’s Discriminant Function (FDF)
Fisher’s Principle
Maximize JF(w)
2021/1/20
-
11
Numerical Characters
Class Mean Vector Inter Divergence Matrix
Cluster
Given a unclassified sample X and the count of classes
cluster unconsidered in this report
2021/1/20
-
4
Linear Classifier
Find n linear function gi(x) i=1,…,n
Optimization problem
Mathematic solution
Lagrange Lemma of Maximization
2021/1/20
-
14
Lagrange method
Let wTSωw=c≠0 L(w,λ)= wTSbw –λwTSωw
=> Sbw* –λSωw*=0 => Sbw* =λSωw* => Sω-1Sbw* =λw*
Fisher’s Linear Classifier
2021/1/20
Machine Learning Seminar
-
1
基于Fisher准则的线性分类器设计

基于Fisher 准则的线性分类器设计一、 实验目的:1. 进一步了解分类器的设计概念,能够根据自己的设计对线性分类器有更深刻地认识;2. 理解Fisher 准则方法确定最佳线性分界面方法的原理,以及拉格朗日乘子求解的原理。
二、 实验条件:1. PC 微机一台和MATLAB 软件。
三、 实验原理:设有一个集合包含N 个d 维样本N x x x ,,,21 ,其中1N 个属于1ω类,2N 个属于2ω类。
线性判别函数的一般形式可表示成0)(w x W x g T +=,其中T d w w W ),,(1 =。
根据Fisher 选择投影方向W 的原则,即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开,类内样本投影尽可能密集的要求,用以评价投影方向W 的函数为:WS W WS W W J w T b T F =)(T W m m S W )(211*-=-其中:∑==i N j j i i x N m 11 2,1=i j x 为i N 类中的第j 个样本w S 为类内离散度,定义为:∑∑==--=2111))((i N j Ti j j w im x m x S b S 为类间离散度,定义为:T b m m m m S ))((2121--=上面的公式是使用Fisher 准则求最佳法线向量的解,我们称这种形式的运算为线性变换,其中)(21m m -是一个向量,1-W S 是W S 的逆矩阵,如)(21m m -是d 维,1-WS 和W S 都是d ×d 维,得到的*W 也是一个d 维的向量。
向量*W 就是使Fisher 准则函数)(W J F 达极大值的解,也就是按Fisher 准则将d 维X 空间投影到一维Y 空间的最佳投影方向,该向量*W 的各分量值是对原d 维特征向量求加权和的权值。
以上讨论了线性判别函数加权向量W 的确定方法,并讨论了使Fisher 准则函数极大的d 维向量*W 的计算方法,但是判别函数中的另一项0w 尚未确定,一般可采用以下几种方法确定0w 如2)(21*0m m W w T +-=或者212211*0)(N N m N m N W w T ++-=或当)(1ωP 与)(2ωP 已知时可用]2)](/)(ln[2)([212121*0-+-+-=N N P P m m W w T ωω当0w 确定之后,则可按以下规则分类,10*ω∈→->x w X W T20*ω∈→-<x w X W T四、 实验内容:(以下例为模板,自己输入实验数据)已知有两类数据1ω和2ω二者的概率已知)(1ωP =0.6,)(2ωP =0.4。
《模式识别》课程实验 线性分类器设计实验

《模式识别》课程实验线性分类器设计实验一、实验目的:1、掌握Fisher 线性分类器设计方法;2、掌握感知准则函数分类器设计方法。
二、实验内容:1、对下列两种情况,求采用Fisher 判决准则时的投影向量和分类界面,并做图。
12{(2,0),(2,2),(2,4),(3,3)}{(0,3),(2,2),(1,1),(1,2),(3,1)}T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 12{(1,1),(2,0),(2,1),(0,2),(1,3)}{(1,2),(0,0),(1,0),(1,1),(0,2)}T T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 2、对下面的两类分类问题,采用感知准则函数,利用迭代修正求权向量的方法求两类的线性判决函数及线性识别界面,并画出识别界面将训练样本区分的结果图。
12{(1,1),(2,0),(2,1),(0,2),(1,3)}{(1,2),(0,0),(1,0),(1,1),(0,2)}T T T T T T T T T T ωω⎧=⎪⎨=-----⎪⎩ 三、实验原理:(1)Fisher 判决准则投影方向:*112()w w S μμ-=-(2)感知准则函数:()()kT p z Z J v v z ==-∑当k Z为空时,即()0J v ,*v即为所求p四、解题思路:1、fisher线性判决器:A.用mean函数求两类样本的均值B.求两类样本的均值的类内离散矩阵SiC.利用类内离散矩阵求总类内离散矩阵SwD.求最佳投影方向WoE.定义阈值,并求得分界面2、感知准则函数分类器:A.获得增广样本向量和初始增广权向量B.对样本进行规范化处理C.获得解区,并用权向量迭代修正错分样本集,得到最终解区五、实验结果:1、fisher线性判决分类器:条件:取pw1=pw2=0.5,阈值系数为0.5A.第一种情况B.第二种情况2、感知准则函数判决:条件:取步长row为1判决结果:六、结果分析:1、fisher线性判决器中,调整阈值系数时,分界面会随之平行上下移动,通过调整阈值系数的大小,就能比较合理的得到分界面。
基于边际Fisher准则和迁移学习的小样本集分类器设计算法

基于边际Fisher准则和迁移学习的小样本集分类器设计算法舒醒;于慧敏;郑伟伟;谢奕;胡浩基;唐慧明【期刊名称】《自动化学报》【年(卷),期】2016(042)009【摘要】如何利用大量已有的同构标记数据(源域)设计小样本训练数据(目标域)的分类器是一个具有很强应用意义的研究问题。
由于不同域的数据特征分布有差异,直接使用源域数据对目标域样本进行分类的效果并不理想。
针对上述问题,本文提出了一种基于迁移学习的分类器设计算法。
首先,本文利用内积度量的边际Fisher 准则对源域进行特征映射,提高源域中类内紧凑性和类间区分性。
其次,为了筛选合理的训练样本对,本文提出一种去除边界奇异点的算法来选择源域密集区域样本点,与目标域中的标记样本点组成训练样本对。
在核化空间上,本文学习了目标域特征到源域特征的非线性转换,将目标域映射到源域。
最后,利用邻近算法(k-nearest neighbor, kNN)分类器对映射后的目标域样本进行分类。
本文不仅改进了边际Fisher准则方法,并且将基于自适应样本对筛选的迁移学习应用到小样本数据的分类器设计中,提高域间适应性。
在通用数据集上的实验结果表明,本文提出的方法能够有效提高小样本训练域的分类器性能。
%It has great practical significance to design a classifier on a small dataset (target domain) with the help of a large dataset (source domain). Since feature distribution varies on different datasets, the classifiers trained on the source domain cannot perform well on a target domain. To solve the problem, we propose a novel classifier-designing algorithm based on transfer learning theory. Firstly, to improve the compass of the same category and separateness of different categoriesin the source domain, this paper utilizes the extended margin Fisher criterion where the distance is measured by the inner product between data. Secondly, to select good sample pairs for transfer learning, this paper presents an algorithm to get rid of marginal singular points by selecting high-density samples in the source domain. The non-linear feature transformation mapping the target domain to the source domain is learned in the kernel space. Finally, k-nearest neighbor (kNN) classifiers are trained for classification. Compared with the existing works, this paper not only extends the margin Fisher criterion, but also applies the transfer learning theory based on the algorithm of selecting training sample pairs to design classifiers of a small dataset. We experimentally demonstrate the superiority of our method to effectively improve the performance of classifiers on the general datasets.【总页数】9页(P1313-1321)【作者】舒醒;于慧敏;郑伟伟;谢奕;胡浩基;唐慧明【作者单位】浙江大学信息与电子工程学院杭州 310027;浙江大学信息与电子工程学院杭州 310027; 浙江大学CAD&CG 国家重点实验室杭州 310027;浙江大学信息与电子工程学院杭州 310027;浙江大学信息与电子工程学院杭州 310027;浙江大学信息与电子工程学院杭州 310027;浙江大学信息与电子工程学院杭州310027【正文语种】中文【相关文献】1.基于元胞自动机的小样本集分类算法 [J], 刘应东;孙秉珍2.基于小样本集弱学习规则的KNN分类算法 [J], 冷明伟;陈晓云;谭国律3.基于K-均值聚类的小样本集KNN分类算法 [J], 刘应东;牛惠民4.迁移学习模型下的小样本人脸识别算法 [J], 黄振文;谢凯;文畅;盛冠群;文方青5.基于支持向量回归估计算法的小样本集回归分析 [J], 邱彤因版权原因,仅展示原文概要,查看原文内容请购买。
Fisher分类器(算法及程序)
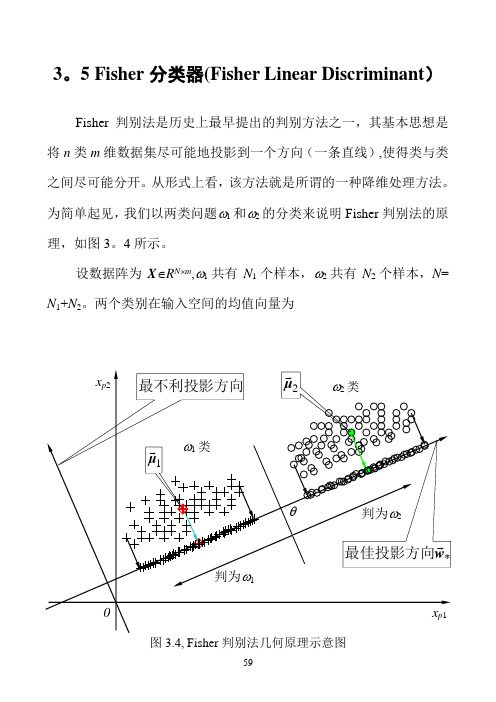
3。
5 Fisher分类器(Fisher Linear Discriminant)Fisher判别法是历史上最早提出的判别方法之一,其基本思想是将n类m维数据集尽可能地投影到一个方向(一条直线),使得类与类之间尽可能分开。
从形式上看,该方法就是所谓的一种降维处理方法。
为简单起见,我们以两类问题ω1和ω2的分类来说明Fisher判别法的原理,如图3。
4所示。
设数据阵为X∈R N⨯m,ω1共有N1个样本,ω2共有N2个样本,N= N1+N2。
两个类别在输入空间的均值向量为图3.4, Fisher判别法几何原理示意图)37.3(11212211⎪⎪⎩⎪⎪⎨⎧∈=∈=∑∑∈∈m pmp R N R N p pϖϖx x x μx μ设有一个投影方向()m Tm R w w w ∈=,,,21 w ,这两个均值向量在该方向的投影为)38.3(1~1~1222111121⎪⎪⎩⎪⎪⎨⎧∈==∈==∑∑∈∈R N R N p p pT T p T T ϖϖx x x w μw μx w μw μ在w方向,两均值之差为())39.3(~~2121μμw μμ -=-=∇T类似地,样本总均值向量在该方向的投影为)40.3(1~11R NNp pT T ∈==∑=x w μw μ定义类间散度(Between —class scatter )平方和SS B 为()()()()()()()()()[])41.3(~~~~~~222111222211221222211w S w w μμμμμμμμw μw μw μw μw μμμμμμ B T T T T T T T T j j j B N N N N N N N SS =--+--=-+-=-=-+-=∑=其中()()()()()())42.3(21222111∑=--=--+--=j Tj j j TT B N N N μμμμμμμμμμμμS定义类ωj 的类内散度(Within-class scatter )平方和为()())43.3(~22∑∑∈∈-=-=jjNp jT p T N p jp T Wj x x SS μw w μw两个类的总的类内散度误差平方和为()()())44.3(2121221wS w wμμw μw w W T j N p T j p j p T j N p jT p T j wj W j jx x x SS SS =⎥⎥⎦⎤⎢⎢⎣⎡--=-==∑∑∑∑∑=∈=∈=其中,()())45.3(21∑∑=∈--=j N p Tjp j p W jx x μμS我们的目的是使类间散度平方和SS B 与类内散度平方和SS w 的比值为最大,即())46.3(max wS w w S w wW T B T W B SS SS J ==图3.5a, Fisher判别法—类间散度平方和(分子)的几何意义图3.5b, Fisher判别法—类内散度平方和(分母)的几何意义图3.5给出了类间散度平方和S B 与类内散度平方和S E 的几何意义.根据图3.5a ,类间散度平方和S B 的另一种表示方式为()()()())47.3(~~2121221221ww w μμμμw μw μw μμ B T T T T T B S SS =--=-=-=这里()())48.3(2121TB μμμμS --=可以证明,(3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fisher分类器设计
班级:自092 姓名:刘昌元学号:099064370 一、实验目的:
1:根据fisher准则设计线性分类器
2:由fisher分类器训练样本数据
3:由fisher分类器测试样本观察出错率并与贝叶斯分类器的出错率比较判断两种分类器的性能优劣
4:将测试数据和决策面画在一张图上直观显示
是
三、实验所用函数:
类均值向量:∑=∈i
xj j i x N M χ1
类内离散度矩阵:T
i j i i
xj j i
M x M x S ))((--∑∈=χ
总类内离散度矩阵:21S S S w +=
类间离散度矩阵:T b M M M M S ))((2121--= 最有投影方向:)(211
*
M M S W w -=-
决策函数:0)
(w x w x G T +=
阈值:)(2
1210M w M w w T T
+-= 四、实验结果:
1:得到参数:最有投影向量和阈值
2:利用分类器输入身高和体重数据得到性别分类(实验结果如下)
w=[ 0.0012; 0.0003] threshold =0.2318
classify(165,56) 结果为“女” classify(178,70) 结果为“男”3:fisher准则分类器的出错率统计:
测试test1:
实际个数分类个数出错率
男生84.0000 31.0000 0.6310
女生40.0000 93.0000 1.3250
测试test2:
4:bayes分类器测试出错统计:
测试test1:
测试test2:
结论:很显然bayes分类器比fisher分类器准确率高的多。
4:分类面决策图:
五、程序:
程序1:求最有投影方向和阈值
%程序功能:应用fisher分类方法,使用训练数据获得阈值和最佳变换向量(投影方向)% function fisher(boys,girls) %调用男生和女生的训练样本数据%
A=boys.';
B=girls.';
[k1,l1]=size(A);
[k2,l2]=size(B);
M1=sum(boys);
M1=M1.';
M1=M1/l1; %求男生身高与体重的均值%
M2=sum(girls);
M2=M2.';
M2=M2/l2; %求女生身高与体重的均值%
S1=zeros(k1,k1);
S2=zeros(k2,k2);
for i=1:l1
S1=S1+(A(:,i)-M1)*((A(:,i)-M1).'); %求类内离散度矩阵S1%
end
for i=1:l2
S2=S2+(B(:,i)-M2)*((B(:,i)-M2).'); %求类内离散度矩阵S2%
end
for i=1:2
for j=1:2
Sw(i,j)=S1(i,j)+S2(i,j); %求总类内离散度矩阵Sw%
end
end
w=inv(Sw)*(M1-M2) %求最有投影方向%
wT=w.';
for i=1:l1
Y1(i)=wT(1,1)*A(1,i)+wT(1,2)*A(2,i); %由分类函数g(x)=wT*x求男生身高和体重的阈值%
end
for i=1:l2
Y2(i)=wT(1,1)*B(1,i)+wT(1,2)*B(2,i); %由分类函数g(x)=wT*x求女生身高和体重的阈值%
end
m1=sum(Y1)/l1; %阈值平均%
m2=sum(Y2)/l2; %阈值平均%
threshold=(l1*m1+l2*m2)/(l1+l2) %求fisher决策面的阈值%
程序2:构成fisher判别器
%函数功能:应用Fisher准则构成的分类器判断一个身高体重二维数据的性别
%函数使用方法:输入classify(hight,weight)其中hight和weight分别是身高和体重的数据
function value=classify(hight,weight)
w=[0.0012;0.0003];
threshold=0.2318;
tem=[hight;weight]; %将输入的身高和体重数据构成列向量%
result=(w.')*tem; %根据fisher判别式求判别值%
if result>threshold %判别值和决策面阈值比较%
value=1;
else
value=0;
end
程序3:
%功能:调用Fisher分类器统计出错率
%开发者:安徽工业大学自动化092班刘昌元function result=Error(file)
[m,n]=size(file);
Boy=0;
Girl=0;
boy=0;
girl=0;
for i=1:m
if(file(i,3)==0)
Girl=Girl+1;
else
Boy=Boy+1;
end
A(i,1)=file(i,1);
A(i,2)=file(i,2);
end
w=[0.0012;0.0003];
threshold =0.2318;
for i=1:m
classify(A(i,1),A(i,2));
if(ans==0)
girl=girl+1;
else
boy=boy+1;
end
end
tem1=abs(Boy-boy)/Boy;
tem2=abs(Girl-girl)/Girl;
result(1,1)=Boy;
result(1,2)=boy;
result(1,3)=tem1;
result(2,1)=Girl;
result(2,2)=girl;
result(2,3)=tem2;
程序4:
%程序:画图
%功能:将训练样本boy.txt和girl.txt中的数据和线性决策面以及贝叶斯决策面画到一幅图上function graphics(boys,girls)
w=[0.0012;0.0003];
threshold =0.2318;
A=boys.';
B=girls.';
[m1,n1]=size(A);
[m2,n2]=size(B);
for i=1:n1
x=A(1,i);
y=A(2,i);
plot(x,y,'R.');
hold on
end
for i=1:n2
x=B(1,i);
y=B(2,i);
plot(x,y,'G.');
hold on
end
a1=min(A(1,:));
a2=max(A(1,:));
b1=min(B(1,:));
b2=max(B(1,:));
a3=min(A(2,:));
a4=max(A(2,:));
b3=min(B(2,:));
b4=max(B(2,:));
if a1<b1
a=a1;
else
a=b1;
end
if a2>b2
b=a2;
else
b=b2;
end
if a3<b3
c=a3;
else
c=b3;
end
if a4>b4。
