计算机图形学 裁剪
chapt 6-1 裁剪——计算机图形学课件PPT

code1&code2≠0,对直线段可简弃之,转(7);当上述两条均 不满足时,进行步骤(4)。 (4)确编保码p。1在窗口外部:若p1在窗口内,则交换p1和p2的坐标值和 (5)按左、右、上、下的顺序求出直线段与窗口边界的交点,并 用分可以该为去交二掉点,p的并1s坐去。标掉转值p(21s)替。这换一p段1的。坐考标虑值到。p也1是即窗在口交外点的s一处点把线,段因一此 (6)用直线扫描转换算法画出当前的直线段p1p2。 (7)算法结束。
延长线与窗口矩形边界的交点
A
实交点
实交点 H
I 虚交点
G
F
窗口
虚交点 JD
实交点
E
B
虚交点
C
图6-25 实交点与虚交点
计算机图形学
1. Cohen-Sutherland算法
基本思想:对每条直线段p1(x1,y1)p2(x2,y2)分三种情况处理: (1) 直线段完全可见,“简取”之。 (2) 直线段完全不可见,“简弃”之。 (3) 直线段既不满足“简取”的条件,也不满足“简弃”
计算机图形学
5.2 二维裁剪
• 在二维观察中,需要在观察坐标系下对窗口进行裁剪,即只保留 窗口内的那部分图形,去掉窗口外的图形。
• 假设窗口是标准矩形,即边与坐标轴平行的矩形,由上 (y=wyt)、下(y=wyb)、左(x=wxl)、右( 1 点的裁剪 x=wxr)四条边描述。
• 5.2.1 点的裁剪
vxl
vxr X
(b)屏幕坐标系中的视区
计算机图形学 第5章 裁剪

3.直线裁剪实例 例5.1 用编码算法裁剪如图5-3(a)所示中的直线段 AB。
图5-3 AB线段的裁剪过程
例5.2 用编码算法裁剪如图5-4(a)所示中的直线段MN。
图5-4 MN线段的裁剪过程
5.1.2 中点分割算法 算法步骤:输入线段端点p1,p2;对于端点p2: (1) p2是否可见,若可见,则它为离p1最远的可见点, 处理结束。 (2) plp2是否全不可见,若是,没有输出,处理结束。 (3) 让pa = p1,pb = p2。
边 V1V2 V2V3 V3V4 V4V5 V5V1 n (1,1) (4,-3) (-1,-2) (-4,3) (0,1) f (2,0) (3,6) (3,6) (4,0) (2,0) w [-4,1] [-5,-5] [-5,-5] [-6,1] [-4,1] w· n -3 -5 15 27 1 D· n 11 30 -13 -30 2 -1/2 tL 3/11 1/6 15/13 9/10 tu
外裁剪有两个重要的应用。
(1) 应用于凹多边形裁剪窗口的线段裁剪。如图5-9 所示线段p1p2相对于凹多边形vlv2v3v4v5v1进行裁剪。 连接v2v4,v1v2v4v5v1为凸多边形,应用Cyrus-Beck算 法,先将p1p2对此凸多边形作内裁剪得到,再将对多 边形v2v3v4v2作外裁剪,最后得到窗口内部分为和。
(4) 沿vi+1p1将多边形一分为二,一个多边形由vi+1, vi+2,…, p1vi+1组成,另一个多边形由vip1及其余顶点组 成。 (5) 对分割的两个多边形递归地重复以上步骤,直到 所有新产生的多边形均为凸,算法结束。
5.1.7 Sutherland-Hodgman逐次多边形裁剪算法 多边形由顶点表p1, p2,…, pn所定义,于是边表为p1p2, p2p3,…, pn-1pn和pn p1。算法的基本思想是将原多边形和 每次裁剪所生成的多边形逐次对裁剪窗口的每一条边 界进行裁剪。考虑图5-12(a)原多边形被窗口左边界所 裁剪,如图5-12(b)所示;生成的多边形又被窗口顶边 所裁剪,如图5-12(c)所示;继续这一过程,生成的中 间多边形被窗口的右边界,如图5-12(d)所示,直至下 边界裁剪完,如图5-12(e)所示为止。
计算机图形学之裁剪算法

窗口特别小的场合。
2、中点裁剪法
中点分割裁剪法是将Cohen-Sutherland 算法中求线段与窗口边界的交点的过程用折 半查找(即求中点)的方法来代替。仍然采 用对线段端点进行编码的方式判断完全可见 和显然完全不可见的线段,对于与窗口有交 点的线段,该算法分别求离两个端点最近 (或最远)的可见点。这两个可见点之间的 线段即是原线段的可见部分。
计算P1P2的最近可见点Pma和 Pmb : (一)直线段P1P2的一个端点可见, P1 另一个端点不可见。 只需解算不可见端点的最近的 可见点。 1)设P1不可见,计算P1P2的中点Pm1。
P1
pm
P2
P2
判断中点Pm1如果落在(接近)窗口边上,则 确定该中点为最近可见点。裁剪结束。否则,
2)判断Pm1是否可见: 如果Pm1可见,以Pm1取代P2 ,返回到 1)计算 P1Pm1的中点Pm2,判断Pm2 如果Pm1不可见,以Pm1取代P1 ,返回到 1)计 算Pm1P2的中点Pm2,判断Pm2
关键: 根据多边形的边表,逐 次对每一段边与裁剪线 (窗口边直线)比较,判 别输入顶点的个数和坐 标,并联结成封闭多边 形。
不可见侧
2
多边形边与裁剪线相对位置的四种
情况与处理方法: (1) 位于可见一侧:输出终点作 为新多边形顶点 (2) 位于不可见一侧:不输出 (3) 由可见到不可见:输出与裁剪
P2
两种线段裁剪算法的比较
Cohen-Sutherland算法是最早的、使用最广泛的线
段裁剪算法之一。在裁剪窗口很大,大部分线段完全
可见,或裁剪窗口很小,大部分线段完全不可见的情 况下,该算法特别有效;在一般情况下,该算法有时 要做不必要的求交运算,因而效率不是太高.
计算机图形学 图形裁剪

一 当p<0时,参数r用于更新u0: u0=max u0,rk 二 当p>0时,参数r用于更新u一: u一=min u一,rk 三 如果更新了u0或u一后,使u0>u一,则舍弃该线段 四 当p=0且q<0时,因为线段平行于边界并且位于边界之外,则舍
弃该线段.
四、p、q的四个值经判断后,如果该线段未被舍弃,则裁
16
Cohen-Sutherland裁剪算法
求交
将两个端点的编码CtCbCrCl进行逻辑或操作, 根据其结果中一的位置来确定可能相交的窗口边 求交按照固定的顺序来进行 左右下上或上下右左 一条线段与窗口最多求交四次
A 一0一0 FD
E C B 0一0一
17
Cohen-Sutherland裁剪算法
1001
1000
1010
0001
0000
0010
utherland裁剪算法
先排除简单情形:
若某线段两个端点的四位二进制编码全为0000 线段位于窗口内,显示之
若对两端点的四位二进制编码进行逻辑与运算 & 结果
不为0 线段位于窗口外,直接舍弃
1001
不仅在于求出新的顶点,删去界外顶点,还在于形成 正确的顶点序列
36
多边形的描述方式
多边形可以描述为一组顶点按一定顺序连接而成的 有向点列
一般可将多边形的顶点按逆时针方向顺序形成有向 线段,进而连接成一个环来描述多边形的组成
数据结构上,可用链表结构来描述
2
1
3 4
37
多边形裁剪的特点
多边形的各条边是顺次连接 直线裁剪
10
Cohen-Sutherland裁剪算法
计算机图形学 第三章 二维图形的裁剪概述

3.2.3 梁友栋-Barsky裁剪算法
式中,Δx=x2-x1,Δy=y2-y1,参数u在0~1 之间取值,P(x,y)代表了该线段上的一个 点,其值由参数u确定,由公式可知,当u=0 时,该点为P1(x1,y1),当u=1时,该点 为P2(x2,y2)。如果点P(x,y)位于由 坐标(xwmin,ywmin)和(xwmax,ywmax)所 确定的窗口内,那么下式成立: xwmin≤x1+ u· Δx≤xwmax ywmin≤y1+ u· Δy≤ywmax(3-10)
3.2.1 Cohen-Sutherland算法
► Code(int ►{
x,int y,int *c)
*c=0; if(y>ymax) /*(xmin,ymin)和(xmax,ymax) 为窗口左下角、右上角坐标。*/ *c=*c|0x08; else if(y<ymin) *c=*c|0x04; if(x>xmax) *c=*c|0x02; else if(x<xmin) *c=*c|0x01; }
► 根据直线两点式方程:
►
2)
(3-
3.2 线段的裁剪
► 整理后得通用交点公式: ►
(3-3)
► ►
1、与上边界的求交公式: (3-4)
3.2 线段的裁剪
► ►
2、与下边界的求交公式:
(3-5)
►
► ►
3、与右边界的求交公式:
(3-6) 4、与左边界的求交公式:
►
(3-7)
3.2.1 Cohen-Sutherla2、判别 根据C1和C2的具体值,可以有三种情况: (1)C1=C2=0,表明两端点全在窗口内,因而 整个线段也在窗内,应予保留。 (2)C1&C2≠0(两端点代码按位作逻辑乘不为 0),即C1和C2至少有某一位同时为1,表明两端点 必定处于某一边界的同一外侧,因而整个线段全在 窗外,应予舍弃。 (3)不属于上面两种情况,均需要求交点。
计算机图形学的裁剪算法

计算机图形学的裁剪算法
计算机图形学的裁剪算法是图形学的一种重要算法,它的基本思想是将一个完整的几何图形(如线段、多边形、圆圈等)按照指定的裁剪窗口(矩形)进行裁剪,只保留在窗口内的部分,而把窗口外的部分抛弃掉。
由于裁剪算法的应用非常广泛,像图形显示系统、图形设备接口(GDI)和图形处理器(GPU)等都广泛使用裁剪算法。
计算机图形学的裁剪算法可以分为两种:2D裁剪算法和
3D裁剪算法。
2D裁剪算法是基于二维空间的,它将一个几何
图形投影到一个平面上,然后按照指定的窗口裁剪;而3D裁
剪算法是基于三维空间的,它将一个几何图形投影到一个三维空间,然后按照指定的窗口裁剪。
2D裁剪算法的基本步骤如下:首先,将要裁剪的几何图
形投影到平面上;其次,计算出投影后的几何图形以及裁剪窗口之间的交点;最后,将裁剪窗口内的部分保留,而把窗口外的部分抛弃掉。
3D裁剪算法的基本步骤如下:首先,将要裁剪的几何图
形投影到三维空间;其次,计算出投影后的几何图形以及裁剪窗口之间的交点;最后,将裁剪窗口内的部分保留,而把窗口外的部分抛弃掉。
计算机图形学的裁剪算法在图形处理中有着重要的作用,它不仅能够有效减少图形处理时间,而且还可以节约存储空间。
此外,它还可以有效提高图形处理效率,提高图形显示效果。
但是,它也存在着一定的局限性,比如,当几何图形的运动变得复杂时,它就会变得费时费力,这就对性能产生了一定的影响。
总之,计算机图形学的裁剪算法是图形学的重要算法,它的应用非常广泛,在图形处理中有着重要的作用。
虽然它也存在着一定的局限性,但是它仍然是一种有效的图形处理算法。
计算机图形学实验报告实验2裁剪算法实验

一、实验目的:直线段的裁剪:编码裁剪算法,中点分割裁剪算法。
二、实验内容://BasicGraph.cpp//请将下列裁剪程序补充完整,并用注释说明是何种裁剪算法void Encode (int x,int y,int *code,int XL,int XR,int YB,int YT) {//请将此程序补充完整int c=0;if(x<XL) c=c|LEFT;else if(x>XR) c=c|RIGHT;if(y<YB) c=c|BOTTOM;else if(y>YT) c=c|TOP;(*code)=c;}//编码裁剪算法:void C_S_Line(POINT &p1,POINT &p2,int XL,int XR,int YB,int YT) {//请将此程序补充完整int x1,x2,y1,y2,x,y,code1,code2,code;x1=p1.x; x2=p2.x; y1=p1.y; y2=p2.y;Encode(x1,y1,&code1,XL,XR,YB,YT);Encode(x2,y2,&code2,XL,XR,YB,YT);while(code1!=0||code2!=0){if((code1&code2)!=0) return;code=code1;if(code1==0) code=code2;if((LEFT&code)!=0){x=XL;y=y1+(y2-y1)*(XL-x1)/(x2-x1);}else if((RIGHT&code)!=0){x=XR;y=y1+(y2-y1)*(XR-x1)/(x2-x1);}if((BOTTOM&code)!=0){y=YB;x=x1+(x2-x1)*(YB-y1)/(y2-y1);}else if((TOP&code)!=0){y=YT;x=x1+(x2-x1)*(YT-y1)/(y2-y1);}if(code==code1){x1=x;y1=y;Encode(x,y,&code1,XL,XR,YB,YT);}else{x2=x;y2=y;Encode(x,y,&code2,XL,XR,YB,YT);}}p1.x=x1;p1.y=y1;p2.x=x2;p2.y=y2;}int IsInArea(POINT point,int XL,int XR,int YB,int YT){//请将此程序补充完整if(point.x>=XL && point.x<=XR && point.y>YB && point.y<YT) return 1;else return 0;}int NotIntersect(POINT begin,POINT end,int XL,int XR,int YB,int YT) {//请将此程序补充完整int maxx,maxy,minx,miny;maxx=(begin.x>end.x)?begin.x:end.x;minx=(begin.x<end.x)?begin.x:end.x;maxy=(begin.y>end.y)?begin.y:end.y;miny=(begin.y<end.y)?begin.y:end.y;if(maxx<XL|| minx>XR||maxy<YB||miny>YT) return 1;else return 0;}//中点裁剪算法:POINT ClipMid(POINT begin,POINT end,int XL,int XR,int YB,int YT){//请将此程序补充完整POINT mid,temp;if(IsInArea(begin,XL,XR,YB,YT)) temp=begin;else if(NotIntersect(begin,end,XL,XR,YB,YT)) temp=begin;else{mid.x=(begin.x+end.x)/2;mid.y=(begin.y+end.y)/2;if(abs(mid.x-end.x)<=1&& abs(mid.y-end.y)<=1) temp=mid;else{if(NotIntersect(begin,mid,XL,XR,YB,YT))temp=ClipMid(mid,end,XL,XR,YB,YT);elsetemp=ClipMid(begin,mid,XL,XR,YB,YT);}}return temp;}//Liang-Barsky直线裁剪算法:void ClipParameter(POINT &p1,POINT &p2,int XL,int XR,int YB,int YT) {float u1=0.0,u2=1.0;float dx=p2.x-p1.x,dy=p2.y-p1.y;if(clipTest(-dx,p1.x-XL,&u1,&u2))if(clipTest(dx,XR-p1.x,&u1,&u2))if(clipTest(-dy,p1.y-YB,&u1,&u2))if(clipTest(dy,YT-p1.y,&u1,&u2)){if(u2<1.0){p2.x=p1.x+u2*dx;p2.y=p1.y+u2*dy;}if(u1>0.0){p1.x=p1.x+u1*dx;p1.y=p1.y+u1*dy;}}}int clipTest(float p,float q,float *u1,float *u2){float r;int remainFlag=1;if(p<0.0){r=q/p;if(r>*u2) remainFlag=0;else if(r>*u1) *u1=r;}else if(p>0.0){r=q/p;if(r<*u1) remainFlag=0;else if(r<*u2) *u2=r;}else //*p=0if(q<0.0) remainFlag=0;return remainFlag;}//逐边裁剪算法://typedef struct tRes { int yes,isIn; POINT pout;} Res;Res TestIntersect(int edge,int type,POINT p1,POINT p2){//判断p2是否在所裁剪的窗边edge的内侧,是否与p1点分别在窗边edge的异侧float dx,dy,m;Res res;int isIn=0,yes=0;POINT pout;dy=p2.y-p1.y;dx=p2.x-p1.x;m=dy/dx;switch(type){case 1: /*right*/if(p2.x<=edge){isIn=1;if(p1.x>edge)yes=1;}else if(p1.x<=edge)yes=1;break;case 2: /*bottom*/if(p2.y>=edge){isIn=1;if(p1.y<edge)yes=1;}else if(p1.y>=edge)yes=1;break;case 3: /*left*/if(p2.x>=edge){isIn=1;if(p1.x<edge)yes=1;}else if(p1.x>=edge)yes=1;break;case 4: /*top*/if(p2.y<=edge){isIn=1;if(p1.y>edge)yes=1;}else if(p1.y<=edge)yes=1;default: break;}if(yes){if((type==1) || (type==3)){ pout.x=edge;pout.y=p1.y+m*(pout.x-p1.x);}if((type==2) || (type==4)){ pout.y=edge;pout.x=p1.x+(pout.y-p1.y)/m;}}res.isIn=isIn;res.yes=yes;res.pout=pout;return res;}int clipSingleEdge(int edge,int type,int nin,POINT pin[50],POINT pout[50])/*对多边形pin与窗边edge进行裁剪,返回裁剪后的多边形pout及点数*/ {int i,k=0;POINT p;Res res;p.x=pin[nin-1].x;p.y=pin[nin-1].y;for(i=0;i<nin;i++){res=TestIntersect(edge,type,p,pin[i]);if(res.yes){ pout[k].x=res.pout.x;pout[k].y=res.pout.y;k++;} if(res.isIn){ pout[k].x=pin[i].x;pout[k].y=pin[i].y;k++;}p.x=pin[i].x;p.y=pin[i].y;}return k;}void ClipEdgePolygon(POINT ps[50],int &n,int XL,int XR,int YB,int YT) { /*对多边形ps进行逐边裁剪*/int n1=0,n2=0;POINT pt[50];n1=clipSingleEdge(XR,1,n,ps,pt);n2=clipSingleEdge(YB,2,n1,pt,ps);n1=clipSingleEdge(XL,3,n2,ps,pt);n2=clipSingleEdge(YT,4,n1,pt,ps);n=n2;}//多边形编码裁剪算法:void ClipEncodePolygon(POINT ps[50],int &n,int XL,int XR,int YB,int YT) {POINT tp[50];int k=0,m;int code1,code2,code;int x,y;for(int i=0;i<n-1;i++){Encode(ps[i].x,ps[i].y,&code1,XL,XR,YB,YT);Encode(ps[i+1].x,ps[i+1].y,&code2,XL,XR,YB,YT);code=code1;m=i;for(int j=0;j<2;j++){if((code1 & code2)!=0) //线段两端都在窗口外的同一侧{switch(code){case 1:x=XL;y=ps[m].y;break;case 2:x=XR;y=ps[m].y;break;case 4:x=ps[m].x;y=YB;break;case 5:x=XL;y=YB;break;case 6:x=XR;y=YB;break;case 8:x=ps[m].x;y=YT;break;case 9:x=XL;y=YT;break;case 10:x=XR;y=YT;break;}tp[k].x=x;tp[k].y=y;k++;}else if((code1 & code2)==0) //线段两端不在窗口的同一侧{if(code==0){tp[k]=ps[m];k++;}else if ((LEFT & code) !=0) //线段与左边界相交 {x=XL;y=ps[i].y+(ps[i+1].y-ps[i].y)*(XL-ps[i].x)/(ps[i+1].x-ps[i].x);if(y>YB && y<YT){tp[k].x=x;tp[k].y=y;k++;}}else if((TOP & code)!=0) //线段与上边界相交{y=YT;x=ps[i].x+(ps[i+1].x-ps[i].x)*(YT-ps[i].y)/(ps[i+1].y-ps[i].y);if(x>XL && x<XR){tp[k].x=x;tp[k].y=y;k++;}}else if((RIGHT & code)!=0) //线段与右边界相交 {x=XR;y=ps[i].y+(ps[i+1].y-ps[i].y)*(XR-ps[i].x)/(ps[i+1].x-ps[i].x);if(y>YB && y<YT){tp[k].x=x;tp[k].y=y;k++;}}else if((BOTTOM & code) != 0) //线段与下边界相交 {y=YB;x=ps[i].x+(ps[i+1].x-ps[i].x)*(YB-ps[i].y)/(ps[i+1].y-ps[i].y);if(x>XL && x<XR){tp[k].x=x;tp[k].y=y;k++;}}}code=code2;m++;}//for(j)}//for(i)for(i=0;i<k;i++)ps[i]=tp[i];n=k;}//函数的调用,裁剪窗口的调整//DrawView.cpp文件//裁剪窗口的调整CDrawView::CDrawView(){/************请在此函数中将裁剪窗口大小调整为长度100单位像素,宽度50单位像素的矩形********/// TODO: add construction code here//m_pWidth=1;m_pStyle=PEN_STYLE_SOLID;m_pColor=RGB(0,0,0);m_FFlag=0;m_FColor=RGB(0,0,0);m_HFlag=0;CurrentDraw=DRAW_VCLINE;m_Num=0;m_Drag=0;m_HCursor=AfxGetApp()->LoadStandardCursor(IDC_CROSS);//DrawType=0;ClipFlag=0;ClipType=-1;XL=200;XR=300;YB=150;YT=200;//XL=200;XR=500;YB=150;YT=400;ClipWindowColor=RGB(192,192,50);}void CDrawView::OnDraw(CDC* pDC){CDrawDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereif(ClipFlag){CPen NewPen,*pOldPen;NewPen.CreatePen(PS_DASH,1,ClipWindowColor);pOldPen=pDC->SelectObject(&NewPen);pDC->MoveTo(XL,YB);pDC->LineTo(XR,YB);pDC->LineTo(XR,YT);pDC->LineTo(XL,YT);pDC->LineTo(XL,YB);}int index;index=pDoc->GetShapeNumber();for(int i=0;i<index;i++)pDoc->GetShape(i)->Drawing(pDC);}void CDrawView::OnInitialUpdate(){CSize sizeTotal;sizeTotal.cx = 640; sizeTotal.cy = 480;SetScrollSizes(MM_TEXT, sizeTotal);// TODO: Add your specialized code here and/or call the base class }void CDrawView::OnLButtonDown(UINT nFlags, CPoint point){// TODO: Add your message handler code here and/or call defaultCClientDC dc(this);OnPrepareDC(&dc);dc.DPtoLP(&point);m_pPrev=point;m_pOrigin=point; //点击鼠标左键作为拖动绘图的第一点m_Drag=1;SetCapture();RECT rect;GetClientRect(&rect);ClientToScreen(&rect);ClipCursor(&rect);CScrollView::OnLButtonDown(nFlags, point);}//函数调用处void CDrawView::OnLButtonUp(UINT nFlags, CPoint point){// TODO: Add your message handler code here and/or call defaultif(m_Drag){m_Drag=0;ReleaseCapture();ClipCursor(NULL);CDrawDoc *pDoc=GetDocument();CShape *pShape;POINT p1,p2;if(CurrentDraw==DRAW_VCLINE || CurrentDraw==DRAW_DDALINE ||CurrentDraw==DRAW_MIDLINE || CurrentDraw==DRAW_BSHLINE){if(ClipFlag){switch(ClipType){/****************编码裁剪函数调用处*************/case CLIP_ENCODE:C_S_Line(m_pOrigin,m_pPrev,XL,XR,YB,YT); break; /****************中点分割裁剪函数调用处************/case CLIP_MIDPOINT: ClipMid(m_pPrev,m_pOrigin,XL,XR,YB,YT);p1=ClipMid(m_pPrev,m_pOrigin,XL,XR,YB,YT);p2=ClipMid(m_pOrigin,m_pPrev,XL,XR,YB,YT);m_pOrigin=p1;m_pPrev=p2;break;case CLIP_PARAMETER:ClipParameter(m_pOrigin,m_pPrev,XL,XR,YB,YT);break;}}pShape=newCLine(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,DrawType);pDoc->AddShape(pShape);}if(CurrentDraw==DRAW_RECTANGLE){if(ClipType==CLIP_WINDOW){XL=m_pOrigin.x;XR=m_pPrev.x;YB=m_pOrigin.y;YT=m_pPrev.y;}else{pShape=newCRectangle(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,m_FFlag,m_FColor,m_HFlag,m_Hatch);pDoc->AddShape(pShape);}}if( CurrentDraw==DRAW_VCCIRCLE || CurrentDraw==DRAW_MIDCIRCLE || CurrentDraw==DRAW_BSHCIRCLE){pShape=newCCircle(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,m_FFlag,m_FColor,m_HFlag,m_Hatch,DrawType);pDoc->AddShape(pShape);}if(CurrentDraw==DRAW_VCELLIPSE || CurrentDraw==DRAW_MIDELLIPSE) {pShape=newCEllipse(m_pOrigin,m_pPrev,m_pWidth,m_pStyle,m_pColor,m_FFlag,m_FColor,m_HFlag,m_Hatch,DrawType);pDoc->AddShape(pShape);}pDoc->UpdateAllViews(NULL);}CScrollView::OnLButtonUp(nFlags, point);}三实验结果:四、实验总结通过这次试验使我了解到如何运用计算机程序对窗口进行剪裁,了解到编码剪裁算法直观方便,速度较快,中点分割剪裁算法不用进行乘除运算,剪裁效率高,Liang-Barsky直线裁剪算法更快。
计算机图形学裁剪

点之外的一段,再对另一段重复上述处理。
例题
(1)Code1=0001 Code2=1000 ,该 线段既非完全可见,也非完全不可见;
(2)与窗口左边求交点P3,舍去P1P3 (3)余下的P2P3不能简单判定,与窗
口右边求交点P4,
边和裁减窗口边之间的关系
(1) SP与窗口边 界的交点I与P均 被加入到输出顶 点表中
(2) P加入到输 出顶点表中
(3) SP与窗口边 界的交点I被加 入到输出顶点表 中
(4) 输出顶点表 中不增加任何顶 点
例题
退化情况
结论
凸多边形用此算法可以获得正确的裁剪结果, 而且可以推广到任意凸多边形窗口的情况。
(2)小窗口的场合,其中大部分线段为完全不 可见
但是求交计算较复杂
实验
利用Cohen-Sutherland算法实现直线的 裁剪
要求:裁剪窗口为矩形,可以对任意位 置直线进行裁剪。
中点分割法
中点分割算法的核心思想是通过 二分逼近来确定直线段与窗口的 交点。
是Sproul 和Sutherland为了便于 硬件实现而提出的。
舍去P5P4; (5)P3P4为完全可见线段。
舍去的这一段,应该是窗口外一端点到 交点之间这一段
如何减少求交次数?
验证两端点各位编码值,相异则求交。
该算法的特点
该算法用编码的方法实现了对完全可见 和不可见直线段的快速接受和拒绝,这 使得它在两类裁剪场合中非常高效:
(1)大窗口的场合,其中大部分线段为完全可 见;
第四章 二维图形裁剪
裁剪技术
所谓裁剪技术,就是按预先设置的窗口 参数,沿窗口边框线对图形进行裁剪, 保留窗口内部图形,裁剪掉窗口外图形 的方法。
计算机图形学-第三章-变换及裁剪

(x,y)点对应的齐次坐标为三维空间的一条 直线
xh hx
yh
hy
zh h
7
齐次坐标的作用
1. 将各种变换用阶数统一的矩阵来表示。提供了用矩阵 运算把二维、三维甚至高维空间上的一个点从一个坐 标系变换到另一坐标系的有效方法。
2. 便于表示无穷远点。
例如:(x h, y h, h),令h等于0
25
3 规格化设备坐标系 用于用户的图形是定义在用户坐标系里,
而图形的输出定义在设备坐标系里,它依赖于 基体的图形设备。由于不同的图形设备有不同 的设备坐标系,且不同设备间坐标范围也不尽 相同, 例如:分辨率为1024*768的显示器其屏幕坐标的 范围:x方向为0~1023,y方向为0~767,分辨 率为640*480的显示器,其屏幕坐标范围为:x 方向0~639,y方向0~479
y 1),则
1 0 0
P'x' y' 1 x y 1 0 1 0 x
Tx1
Ty1
1
y 1Tt1
经第二次平移变换后的坐标为P*(x* y* 1)
P * x *
y * 1 x'
y'
1
1 0
0 0 1 0
Tx
2
Ty 2
1
1 0 0 1 0 0
x y 1 0 1 0 0 1 0 x y 1 Tt1Tt2
44
关于透视投影
一点透视投影
两点透视投影
三点透视投影
45
内容
二维变换 三维变换 裁剪
二维线裁剪 二维多边形裁剪 文本裁剪 三维裁剪 关于三维变换与裁剪
46
三维变换流程图
计算机图形学--第五讲 裁剪的基本概念与直线裁剪

12直线生成算法圆与椭圆的绘制算法5图元的概念436区域填充算法裁剪反走样技术4.5 裁剪—4.5 裁剪—4.5 裁剪—4.5 裁剪—4.5 裁剪—4.5 裁剪—算法实现◆第一步◆第二步4.5 裁剪—编码实现(第一步)九个区域,每一个区域采用四位编码对于任一端点左),赋予一个◆左:若◆右:若◆下:若◆上:若4.5 裁剪—编码实现(第一步)对要被裁剪的线段的两个端点,如果其所在的区域的编码均是如果两个编码的见的,可简弃之;如果两个编码的少一个端点非在交点处把线段一分为二,其中必有一段完全在窗口外,可弃之。
再对另一段重复进行上述处理,直到该线段完全被舍弃或找到位于窗口内的一段线段为止。
4.5 裁剪—析出点。
求出其交点见的,因而只要对上述处理步骤。
y=裁剪结束。
算法步骤界坐标:code2(0100)之,转则交换段与窗口边界的交点除p算法的编码实现到另一端点间的线段重复上述过程直到接受或拒绝;计算线段if(LEFT&codeelse if(RIGHT&codeelse if(BOTTOM&code {y=YB;else if(TOP & code !=0) {y=YT;Cohen-SutherlandNicholl et al. An efficient new algorithm for 2-D line clipping: its4.5 裁剪—4.5 裁剪—4.5 裁剪—(((4.5 裁剪—)界L上;要条件A和该处内法向量P(t)4.5 裁剪—)。
4.5 裁剪—)终点组:N i ⋅(P 2-P 1)<0 起点组:N i ⋅(P 2-P 1)>0 特殊情况:N i ⋅(P 2-P 1)=0这时,,P 1P 2与对应边平行, 这时有两种情况:线段在区域外侧或内侧:前一种情况对应于N i ⋅(P 2-P 1)<0,可直接判断线段在多边形之外前一种情况对应于N i ⋅(P 2-P 1)>0,则不于考虑,继续处理其他边。
计算机图形学5.5裁剪算法

如何判定线段应该与窗口的哪条边求交呢?
编码中对应位为1的窗口边。
计算线段P1(x1,y1)P2(x2,y2)与窗口边界的交点 Code代表线段某个端点的编码。 if(LEFT&code !=0)
{ x=XL; y=y1+(y2-y1)*(XL-x1)/(x2-x1);} else if(RIGHT&code !=0) { x=XR; y=y1+(y2-y1)*(XR-x1)/(x2-x1);} else if(BOTTOM&code !=0) { y=YB; x=x1+(x2-x1)*(YB-y1)/(y2-y1);} else if(TOP & code !=0) { y=YT; x=x1+(x2-x1)*(YT-y1)/(y2-y1);}
P4 (1010)
上下右左 □□□□
P1 (1001)
Y=YT
P3: 0110 P4:& 1010
0010
X=XL
P1: 1001 P2:& 0010
0000
P2 (0010)
X=XR
Y=YB P3 (0110)
对于三维裁剪,需要6位编码。
一旦给定所有的线段端点的区域码,就可以快速 判断哪条直线完全在剪取窗口内,哪条直线完全在 窗口外。所以得到一个规律:
4.求交:假定直线的端点坐标为(x1, y1)和(x2, y2) (1)左、右边界交点的计算:y=y1+k(x-x1); (2)上、下边界交点的计算:x=x1+(y-y1)/k。
Cohen-Sutherland端点编码算法
优点:简单,易于实现。 特点:用编码方法可快速判断线段的完全可见和 显然不可见。
计算机图形学裁剪算法详解
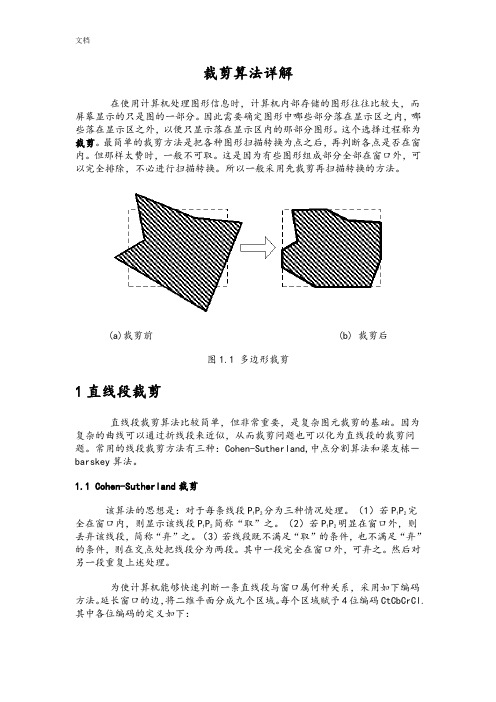
裁剪算法详解在使用计算机处理图形信息时,计算机内部存储的图形往往比较大,而屏幕显示的只是图的一部分。
因此需要确定图形中哪些部分落在显示区之内,哪些落在显示区之外,以便只显示落在显示区内的那部分图形。
这个选择过程称为裁剪。
最简单的裁剪方法是把各种图形扫描转换为点之后,再判断各点是否在窗内。
但那样太费时,一般不可取。
这是因为有些图形组成部分全部在窗口外,可以完全排除,不必进行扫描转换。
所以一般采用先裁剪再扫描转换的方法。
(a)裁剪前(b) 裁剪后图1.1 多边形裁剪1直线段裁剪直线段裁剪算法比较简单,但非常重要,是复杂图元裁剪的基础。
因为复杂的曲线可以通过折线段来近似,从而裁剪问题也可以化为直线段的裁剪问题。
常用的线段裁剪方法有三种:Cohen-Sutherland,中点分割算法和梁友栋-barskey算法。
1.1 Cohen-Sutherland裁剪该算法的思想是:对于每条线段P1P2分为三种情况处理。
(1)若P1P2完全在窗口内,则显示该线段P1P2简称“取”之。
(2)若P1P2明显在窗口外,则丢弃该线段,简称“弃”之。
(3)若线段既不满足“取”的条件,也不满足“弃”的条件,则在交点处把线段分为两段。
其中一段完全在窗口外,可弃之。
然后对另一段重复上述处理。
为使计算机能够快速判断一条直线段与窗口属何种关系,采用如下编码方法。
延长窗口的边,将二维平面分成九个区域。
每个区域赋予4位编码CtCbCrCl.其中各位编码的定义如下:图1.2 多边形裁剪区域编码图5.3线段裁剪裁剪一条线段时,先求出P1P2所在的区号code1,code2。
若code1=0,且code2=0,则线段P1P2在窗口内,应取之。
若按位与运算code1&code2≠0,则说明两个端点同在窗口的上方、下方、左方或右方。
可判断线段完全在窗口外,可弃之。
否则,按第三种情况处理。
求出线段与窗口某边的交点,在交点处把线段一分为二,其中必有一段在窗口外,可弃之。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0110
Cohen-Sutherland算法
裁剪一条线段时,先求出端点 p1 和 p2 的编码 code1 和 code2,然后: (1)若code1|code2=0,对直线段应“简取”之。 (2)若code1&code2≠0,对直线段可“简弃”之。
(3)若上述两条件均不成立。则需求出直线段与窗口边 界的交点。在交点处把线段一分为二,其中必有一段 完全在窗口外,可以弃之。再对另一段重复进行上述 处理,直到该线段完全被舍弃或者找到位于窗口内的 一段线段为止。
二维裁剪
直线段裁剪 • Cohen-Sutherland算法;
• • 中点算法 Nicholl-Lee-Nicholl算法
多边形裁剪
•
• Sutlerland_Hodgman算法 Weiler-Athenton算法
假设窗口是标准矩形,即边与坐标轴平行的矩 形,由上(y=yt)、下(y=yb)、左(x=xl)、 右(x=xr)四条边描述。
•如果线段平行于裁剪窗口的某两边界,则必有相应的 pk﹦0,如果还满足qk<0,则线段的端点位于窗口外部, 即线段在窗口外,应该舍弃。如果qk≥0,线段在窗口内。 •当 pk < 0 时,若直线与裁剪窗口第 k 条边界线相遇,则必 是从边界线外部延伸到内部。例如当p1 <0时,则x2>x1, 直线必然从裁剪窗口的左边界线的外部进入内部,如下图 中的线段P1P2。 •当 pk > 0 时,若直线与裁剪窗口第 k 条边界线相遇,则必 是从边界线的内部延伸到外部。例如p2 >0时,则x2>x1, 直线必然从裁剪窗口的右边界线的内部进入外部 ,如下图 中的线段P3P4。
当pk不等于零时,可以计算出线段与第k条裁剪窗 口边界线的交点参数:
qk rk pk
根据定义,对于每条线段,pk中必有两个小于零,而另 两个大于零。 •对于小于零的pk,直线同第k条裁剪窗口边线是从外到 内相遇的,此时如果线段同第k条裁剪窗口边界线有交 点的话,是参数 u 从 0 变大时遇到的,这时计算出相应 的rk值,取0和各个rk值之中的最大值记为u1。 •对于大于零的pk,计算出相应的rk值,取1和各个rk值 之中的最小值记为u2。两个参数u1和u2定义了在裁剪窗 口内的线段部分。如果u1>u2,则线段完全落在裁剪窗 口之外,应被舍弃。否则被裁剪线段可见部分的端点 由参数u1和u2计算出来。
– 可见一侧空间和不可见一侧空间 – 沿多边形依次处理顶点会遇到四种情况
当前裁剪边 可见一侧 Pi+1 Pi
窗口 当前裁剪边 当前裁剪边 当前裁剪边
可见一侧 Pi
可见一侧 Pi Pi+1
可见一侧
Pi+1 窗口
窗口 窗口
Pi+1
Pi
(a) 输出Pi+1
(a) 无输出
(a) 输出I
(a) 输出I和Pi+1
B
p1,p3小于0,决定u1(max),取0与r1和r3中的大者,u1=1/4 p2,p4大于0,决定u2,取1与r2和r4中的小者,u2=3/4 两交点由u1,u2决定: 1 x x1 u( x2 x1 ) x1 ux 计算:(1) x 1 4 4 2 y y1 u( y2 y1 ) y1 uy 1 1 y 2 1 2 4 4 (2) 3 x 1 4 4 4 3 3 y 2 1 2 4 4
x x1 u( x2 x1 ) x1 ux y y1 u( y2 y1 ) y1 uy
0≤u≤1
坐标(x,y)表示直线上两端点之间的任一点。当u=0时,得 点P1,当u=1时,得点P2。线段的裁剪条件可以由下面的不 等式表示: Wxl≤x1﹢uΔ x≤Wxr Wyb≤y1﹢uΔ y≤Wyt 这四个不等式可以表示为: upk≤qk k=1,2,3,4 Δx=x2-x1; Δy=y2-y1; 其中,参数p,q定义为: p1﹦-Δ x, q1﹦x1﹣Wxl p2﹦Δ x, q2﹦Wxr﹣x1 p3﹦-Δ y, q3﹦y1﹣Wyb p4﹦Δ y, q4﹦Wyt﹣y1 下标 k=1,2,3,4 分别对应裁剪窗口的左、右、下、上四条 边界线。
Cohen-SutherLand算法
对于那些非完全可见、又非显然不可见的线段,需要 求交求交前先测试与窗口哪条边所在直线有交?(按序判 断端点编码中各位的值D4D3D2D1)
1001 1000 0000 窗口 1010
• 求交测试顺序固定 • 最坏情形,线段求交四 次。
0001
0010
0101
0100
通常粱友栋-Barsky算法比Cohen-Sutherland算法 更有效,因为需要计算的交点数目减少了。一次计算 就可以确定出线段的可见性及可见部分。这两种线段 裁剪算法都可以扩展为三维线段裁剪算法。
多边形裁剪
• 用直线段裁剪算法,可以吗? • 新的问题:
A A B B
图1 因丢失顶点信息而去法确定裁剪区域
练习:试用 S-H 算法裁剪下图多边形,要求画出每 次裁剪对应的图形,并表明输入输出的顶点。
D(6,8)
y 6 E(1,5) 2
B(5,4)
0
A(4,1) 2 6
C(8,1) x
解:用左边界裁剪前后为:
D(6,8) y
6M(2,5.6) N(2,3.6) 2 0 A(4,1) 2 6 C(8,1) 0 x 2 C(8,1) 6 x D(6,8)
Cohen-Sutherland算法
基本思想:
对每条直线段p1(x1,y1)p2(x2,y2)分三步处理:
(1)判断点P1和P2是否完全在裁减窗口内,若是,直线段完全可见,“简取”之。
否则进入步骤(2)。 x1<xl and x1>xr x2<xl and x2>xr y1>yb and y1<yt
y 6 E(1,5) 2
B(5,4)
B(5,4)
A(4,1)
输入为:ABCDE
输出为:BCDMNA
2.如下图所示,裁减窗口为正方形,采用逐边裁件算法,依次按左、下、右、 上的顺序,用四条窗口边界裁减多边形ABCDE。试写出每条框口边界裁减 后输出的新的多边形的顶点序列。
答:左边界裁减后: ABCD12 下边界裁减后: 4B56D123 右边界裁减后: 4B7D123 上边界裁减后: 4B789123
• 消除C-S算法中多次求交的情况。 • 基本想法:对2D平面的更细的划分。
参数化线段裁剪算法
更快的线段裁剪算法基于线段的参数化方程的 分析,它是由粱友栋和Barsky提出的,也称为粱 友栋-Barsky线段裁剪算法。 设线段两端点坐标分别为 P1(x1,y1)和P2(x2,y2), 则其参数化直线方程可写成下列形式:
Cohen-Sutherland算法
特点: 对完全可见和不可见线段的快速判别。
编码方法:
由窗口四条边所在直线把二维平面分成 9个区域,每个区域赋予一个 4 位的二进制编码D4D3D2D1。编码规则如下: – 若x<xl,则D1=1,否则D1=0; – 若x>xr,则D2=1,否则D2=0; – 若y<yb,则D3=1, 否则D3=0; – 若y>yt,则D4=1,否则D4=0。
梁友栋线的裁剪算法例子 设:Wxl=2; Wxr=4; Wyb=2; Wyt=4 被裁剪线段的两端点:(1,2),(5,3) 计算:Δ x=5-1=4 Δ y=3-2=1 p1= -4,q1= -1 p2=4, q2=3 p3= -1,q3= 0 p4=1, q4=2
p1﹦-Δx, q1﹦x1﹣Wxl p2﹦Δx, q2﹦Wxr﹣x1 p3﹦-Δy, q3﹦y1﹣Wyb p4﹦Δy, q4﹦Wyt﹣y1 A
图2 原来封闭的多边形变成了孤立的线段
• 关键:
– 求出新的顶点,删去界外顶点 – 形成正确的顶点序列
Sutherland-Hodgman算法
• 分割处理策略:将多边形关于矩形窗口的裁剪分解为多边
形关于窗口四边所在直线的裁剪。
• 流水线过程(左上右下):左边的结果是右边的开始。
亦称逐边裁剪算法
Sutherland-Hodgman算法
y yt
yb
xl
xr
x
点的裁剪
对于任意一点P(x,y),若满足下列不等式
xl x xr , 且yb y yt
则点 P 在矩形窗口内;否则,点 P 在 矩形窗口外。
y yt P(x,y) yb
xl
xr
x
直线段的裁剪
• 直线段和剪裁窗口的可能关系:
(1) 完全落在窗口内
(2) 完全落在窗口外 为提高效率,算法设计时应考虑: (3) 与窗口边界相交 (一)快速判断情形(1)(2); (二) 设法减少情形(3)求交次数和每次求交时所需的计 算量。
中点分割算法 基本思想: 当对直线段不能简取也不能简弃时,简单地把线段等 分为二段,对两段重复上述测试处理,直至每条线段 完全在窗口内或完全在窗口外。
例
p1
×
p5
p1
p4ቤተ መጻሕፍቲ ባይዱ
p6
×
p7
p3
×
p2
p2
中点分割算法的核心思想是通过二分逼近来确定直线段与窗口的交点。
Nicholl-Lee-Nicholl算法
线段与当前裁剪边的位置关系
Sutherland-Hodgman算法
• 裁剪结果的顶点构成:裁剪边内侧的原顶点;多
边形的边与裁剪边 的交点。
• 顺序连接。
几点说明: 裁剪算法采用流水线方式, 适合硬件实现。 可推广到任意凸多边形裁剪 窗口
例子:对多边形ABCDEFGH进行裁剪
A
G B
