【全国市级联考word】东北三省四市教研联合体2018届高三第二次模拟考试文科数学试卷(原卷版)
东北三省四市教研联合体2018届高三第二次高考模拟语文试卷(有答案)

东北三省四市2018届高三第二次高考模拟2018年东北三省四市教研联合体高考模拟考试(二)
语文试卷
①形象地写出我们在日常生活的忙碌中遗忘了对贵贱的理解,令人警醒;②由哲理思考时的议论到日常生活的场景的描写,含蓄蕴籍,寓意深刻;③以富有诗意的画面结尾,给读者留下了想象空间。
①改革开放的深入和城镇化的推进,使电影市场空间不断扩大;②青年电影人才对人生和生活的探究,使中国电影与观众心灵共振更加强烈。
表过了作者卜邻时的渴慕与希冀之情。
暂时外出还要挑选陪伴之人,安居时更要选择邻居,表达了对友人的思慕与赞美;不只终身经常相见,甚至子孙也要长久为邻,表达了与元八世代结邻的美好愿望。
②首先可以用来确定方位
③不同节气日中时表影长短有变化评分参考:。
东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2018届高三第二次模拟考试语文试题

2018年三省三校二模考试语文参考答案1.B2.C3.C4.B5.①予人美感但不让人沉沦绝望的忧伤②富于气质的忧伤:或悲天悯人,或敬畏生命,或不断寻美③有疗救作用的忧伤:富于营养,给人(自己,他人)希望6.含义(1)生命的基础是深厚的,可以给生命以滋养(1分)(2)阿多尼斯和树的灵魂相通,彼此激励(1分)(3)他的忧伤是有节制的,有质量的(1分)作用(1)承上启下(1分),与上文川端康成和下文众多自杀的诗人的忧伤形成对比(1分)(2)说明阿多尼斯的忧伤有质量,突出主题(1分)7.D8.B9.⑴重视学习者的学习体验⑵回归教育原点,提高教育内容质量;⑶利用并强化前沿技术⑷注重价格优势、便捷优势和教育教学的效率效果(每点2分,第一点必须有,2.3.4点里任意答出2点即可)10.C11.D (存问,就是指慰问,没有“并进行请教”和“虚心纳谏”的意思)12.B(“这些都得到了皇帝的高度认可”错误,文中说“帝疑有侵冒,令罢归听勘”)13.(1)宗皋劝说皇帝推崇(崇尚)宽容敦厚,认真考察采纳忠诚的言论,不要只是把严明作为治理的标准。
(“惇崇”“察”“纳”“以……为”各1分,句意1分)(2)皇帝怀疑他有侵夺冒领之嫌,命令罢职回来听候调查。
不久事情真相得以查清楚。
(“侵冒” “勘”“ 白” 各1分,句意2分)参考译文:郭宗皋,字君弼,是福山人。
嘉靖八年的进士。
提拔为御史。
嘉靖十二年十月,星像下雨一般陨落。
没过多久,哀冲太子(明世宗朱厚熜皇太子朱载基,追封为哀冲太子)去世,大同军队发生动乱。
宗皋劝说皇帝推崇(崇尚)宽容敦厚,认真考察采纳忠诚的言论,不要只是把严明作为治理的标准。
皇帝大怒,下诏入狱,打四十大板释放了他。
历任苏州、松州、顺天府的巡按使。
恰逢朝廷推荐保定巡抚刘夔回来管理院中事务,宗皋评议刘夔曾经推荐大学士李时之子,奉承讨好没有品行,不讲作风纪律,(惹怒皇帝)被判罚剥夺两月俸禄。
二十三年十月,敌寇攻入万全右卫,抵达广昌,布列大营四十里。
东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2018届高三语文第二次模拟考试试题

东北三省三校(哈师大附中、东北师大附中、辽宁省实验中学)2018届高三语文第二次模拟考试试题一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
陆上和海上两条丝绸之路先后开通后,作为中国传统文化的代表——中国艺术厦其精神随之传至世界各地,并为世界艺术发展贡献着智慧。
《中国艺术如何影响世界》一书,主要将中国绘画艺术置于西方绘画艺术的坐标系中,从“末学西渐”的角度重点审视和探讨了中国艺术时世界艺术的影响和贡献。
本书认为西方一部分有重要影响的画家,之所以在创作中能取得辉煌的成就,都直接或间接地受到了中国绘画的深刻影响。
传统西方绘画用面表现物象,而中国绘画用线表现物象,空中的云、河中的水本来无线.但画家都用线条来表现。
至近现代,西方画家的作品凡有新意者,大多是改面为线而创作的,这是画家们借鉴中国绘画艺术得来的益处。
中国绘画艺术对世界艺术的影响,说到底是对中国之外的绘画创作者及其作品的影响。
本书中,作者以毕加索的画作为例展开论述。
毕加索早期的绘画以写实为主,但后来,他的画作以线条作为绘画的语言,笔法写意,绘画风格由具象转为抽象,实现了从画“形”到画“意”的转变。
这和他长期临摹中国画和倾心于中国绘画所倡导的价值追求颇有关系,毕加索曾赞许遭“谈到艺术,第一是你们中国人的艺术”。
而用线条造型,正是中国绘画艺术影响到和区别于其他风格绘画艺术的显著标志。
本书认为,西方绘画注重科学原理,中国绘画则更讲究哲学精神。
因此,西方绘画重在写形,强调视觉享受或冲击力:而中国绘画重在写心、畅神,强调人格的修炼、性情的抒发、思想的表达。
也就是说,在中国绘画理论视域中,绘画不过分强调描绘对象的真实与否,即不仅要画见到的“实”的东西,同时还要画见不到的和那些想象的“虚”的东西。
西方画家们仅在近一百年前,才领会其奥妙,而中国的画家们,一千多年前就已经在创作中自觉践行了这种理论。
笔者认为,深入挖掘中国艺术对世界艺术的影响和贡献迫在眉睫。
东北三省四市2018届高考第二次模拟数学试题(文)及答案

东北三省四市教研联合体2018届高三第二次模拟考试文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}(){}03,1 -==x x x B x x A ,则B A ( ) A .(-1,0) B .(0,1) C .(-1,3) D .(1,3) 2.若复数aiiz ++=11为纯虚数,则实数a 的值为( ) A .1 B .0 C .21-D .-1 3.中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”取意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算.算筹是将几寸长的小竹棍摆在下面上进行运算.算筹的摆放形式有纵横两种形式(如下图所示).表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列.但各位数码的筹式要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位数用横式表示.以此类推.例如3266用箅筇表示就是,则8771用算筹可表示为( )中国古代的算筹数码 A .B .C .D .4.右图所示的程序框图是为了求出满足2822n n -的最小偶数n ,那么在空白框内填入及最后输出的n 值分别是( )A .1+=n n 和6B .2+=n n 和6 C.1+=n n 和8 D .2+=n n 和85.函数xxx x f tan 1)(2++=的部分图像大致为( )A .B .C. D .6.等差数列{}n a 的公差不为零,首项11=a ,2a 是1a 和5a 的等比中项,则数列{}n a 的前9项之和是( ) A .9B .10C.81 D .907.某几何体的三视图如图所示(单位:cm ),其俯视图为等边三角形,则该几何体的体积(单位:3cm )是( )A .34B .3310 C.32 D .3388.已知首项与公比相等的等比数列{}n a 中,满足),(*242N n m a a a n m ∈=,则nm 12+的最小值为( ) A .1 B .23 C.2 D .29 9.已知过曲线x e y =上一点),(00y x P 做曲线的切线,若切线在y 轴上的截距小于0时,则0x 的取值范围是( )A .),0(+∞B .),1(+∞eC.),1(+∞ D .),2(+∞10.已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕,将ABC ∆折成直二面角C AD B --,则过D C B A ,,,四点的球的表面积为( )A .π3B .π4 C.π5 D .π6 11.将函数⎪⎭⎫⎝⎛+=32sin )(πx x f 的图像向右平移a 个单位得到函数()cos(2)4g x x π=+的图象,则a 的值可以为( ) A .512π B .712πC .924π1 D .4124π12.已知焦点在x 轴上的双曲线222211x y m m -=-的左右两个焦点分别为1F 和2F ,其右支上存在一点P 满足12PF PF ⊥,且12PF F ∆的面积为3,则该双曲线的离心率为( )A.2B .72C .2D .3第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设实数x ,y 满足约束条件0,40,5,y x y x y ≥⎧⎪-≥⎨⎪+≤⎩则25z x y =++的最大值为.14.为了了解居民天气转冷时期电量使用情况,某调查人员由下表统计数据计算出回归直线方程为2.1161.13y x =-+,现表中一个数据为污损,则被污损的数据为.(最后结果精确到整数位)15.已知函数()f x 满足(1)1()f x f x +=-,当(1)2f =时,)9()8(f f +的值为.16.已知菱形ABCD 的一条对角线BD 长为2,点E 满足ED AE 21=,点F 为CD 的的中点.若2-=⋅则AF CD ⋅=.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知ABC ∆的内角C B A ,,的对边分别为c b a ,,,若2=b ,且A c C a B b cos cos cos 2+=. (I )求B 的大小;(II )求ABC ∆面积的最大值.18.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占80%.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示.(I )求出a 的值;(II )求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);(III )现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.19.在如图所示的几何体中,四边形ABCD 是正方形,PA ⊥平面ABCD ,E ,F 分别是线段AD ,PB 的中点,1PA AB ==.(1)证明://EF 平面DCP ; (2)求平面EFC 与平面PDC 的距离.20.在平面直角坐标系中,椭圆C :22221(0)x y a b a b+=>>的离心率为12,点3(1,)2M 在椭圆C 上.(1)求椭圆C 的方程;(2)已知(2,0)P -与(2,0)Q 为平面内的两个定点,过(1,0)点的直线l 与椭圆C 交于A ,B 两点,求四边形APBQ 面积的最大值.21.已知函数)()(,ln )(R m m x x g x x f ∈+==.(I )若()f x )(x g ≤恒成立,求实数m 的取值范围;(II )已知21,x x 是函数)()()(x g x f x F -=的两个零点,且21x x ,求证:121 x x . 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线1C :cos 3ρθ=,曲线2C :4cos ρθ=(02πθ≤<).(I )求1C 与2C 交点的极坐标; (II )设点Q 在2C 上,23OQ QP =,求动点P 的极坐标方程. 23.选修4-5:不等式选讲已知函数()|2||23|f x x x m =+++,m R ∈. (I )当2m =-时,求不等式()3f x ≤的解集; (II )对于(,0)x ∀∈-∞都有2()f x x x≥+恒成立,求实数m 的取值范围.数学(文科)试题参考答案一、选择题1-5:CDCDD 6-10: CBACC 11、12:CB 二、填空题13.14 14.38 15.3716.-7 三、解答题 17.解: (1)由正弦定理CCB b A a sin sin sin ==可得 B AC C A B B sin cos sin cos sin cos sin 2=+=∵0sin B ,故21cos =B , ∵π B 0,∴3π=B(2)由3,2π==B b ,由余弦定理可得422-+=c a ac ,由基本不等式可得4,42422≤-≥-+=ac ac c a ac , 而且仅当2==c a 时B ac S ABC sin 21=∆取得最大值323421=⨯⨯, 故ABC ∆的面积的最大值为3.18.解:(1)由10(0.0100.0150.0300.010)1a ⨯++++=,得0.035a =, (2)平均数为200.1300.15400.35500.3600.141.5⨯+⨯+⨯+⨯+⨯=岁; 设中位数为x ,则100.010100.015(35)0.0350.5x ⨯+⨯+-⨯=,∴42.1x ≈岁.(3)第1,2组抽取的人数分别为20人,30人,从第1,2组中用分层抽样的方法抽取5人,则第1,2组抽取的人数分别为2人,3人,分别记为32121,,,,b b b a a .设从5人中随机抽取3人,为(121,,b a a ),(221,,b a a ),(321,,b a a ),(211,,b b a ),(311,,b b a ),(321,,b b a ),(212,,b b a ),(312,,b b a ),(322,,b b a ),(321,,b b b ),共10个基本事件,其中第2组恰好抽到2人包含(211,,b b a ),(311,,b b a ),(321,,b b a ),(212,,b b a ),(312,,b b a ),(322,,b b a )共6个基本事件从而第2组抽到2人的概率53106==19.解:(1)取PC 中点M ,连接DM ,MF , ∵M ,F 分别是PC ,PB 中点,∴//MF CB ,12MF CB =,∵E 为DA 中点,ABCD 为矩形,∴//DE CB ,12DE CB =, ∴//MF DE ,MF DE =,∴四边形DEFM 为平行四边形, ∴//EF DM ,∵EF ⊄平面PDC ,DM ⊂平面PDC , ∴//EF 平面PDC .(2)∵EF ∥平面PDC ,∴F 到平面PDC 的距离等于E 到平面PDC 的距离, ∵PA ⊥平面ABCD ,∴DA PA ⊥,∵1==AD PA ,在PAD Rt ∆中2=DP ,∵PA ⊥平面ABCD ,∴CB PA ⊥,∵A AB PA AB CB =⊥ ,,∴⊥CB 平面PAB ,∴⊥CB PB ,则3=PC ,∵222PC DC PD =+,∴PDC ∆为直角三角形,∴222121=⨯⨯=∆PDC S PD E C PD C E V V --=,设E 到平面PDC 的距离为h ,又∵A PA AD PA CD AD CD =⊥⊥ ,,,∴⊥CD 平面PAD 则2121131212131⋅⋅⋅⋅=⋅⋅⋅⋅h ∴42=h ∴F 到平面PDC 的距离为42 20.解:(1)∵12c a =,∴2a c =, 椭圆的方程为2222143x y c c+=,将3(1,)2代入得22191412c c+=,∴21c =, ∴椭圆的方程为22143x y +=. (2)设l 的方程为1x my =+,联立221,431,x y x my ⎧+=⎪⎨⎪=+⎩消去x ,得22(34)690m y my ++-=, 设点11(,)A x y ,22(,)B x y , 有122634m y y m -+=+,122934y y m -=+, 有2222212112(1)||13434m m AB m m m ++=+=++,点P (2,0)-到直线l 21m+点(2,0)Q 到直线l 21m+从而四边形APBQ 的面积2222112(1)2412341m m S m m++=⨯=++(或121||||2S PQ y y =-)令t =1t ≥, 有22431t S t =+2413t t =+,设函数1()3f t t t =+,21'()30f t t =->,所以()f t 在[1,)+∞上单调递增, 有134t t+≥,故2242461313t S t t t==≤++,所以当1t =,即0m =时,四边形APBQ 面积的最大值为6. 21.解:(1)令)0(ln )()()( x m x x x g x f x F --=-=,有xxx x F -=-='111)(, 当1 x 时,0)( x F ',当10 x 时,0)( x F ',所以)(x F 在(1,+∞)上单调递减,在(0,1)上单调递增,)(x F 在1=x 处取得最大值为m --1,若)()(x g x f ≤恒成立,则m --1≤0即1-≥m ,(2)由(1)可知,若函数)()()(x g x f x F -=有两个零点,则2110x x 要证121 x x ,只需证121x x,由于)(x F 在(1,+∞)上单调递减,从而只需证()⎪⎪⎭⎫ ⎝⎛121x F x F ,由于()()1121ln ,0x x m x F x F -===,即证0ln 11ln 11ln111111 x x x x m x x -+-=-- 令01221)(),10(ln 21)(222 x x x x x x x h x x x x x h +-=-+='-+-=, 有)(x h 在(0,1)上单调递增,0)1()(=h x h ,所以121 x x . 22.解:(1)联立cos 3,4cos ,ρθρθ=⎧⎨=⎩3cos 2θ=±, ∵02πθ≤<,6πθ=,23ρ=∴所求交点的极坐标3,)6π.(2)设(,)P ρθ,00(,)Q ρθ且004cos ρθ=,0[0,)2πθ∈,由已知23OQ QP =,得002,5,ρρθθ⎧=⎪⎨⎪=⎩∴24cos 5ρθ=,点P 的极坐标方程为10cos ρθ=,[0,)2πθ∈. 23.解:(1)当2m =-时,41,0,3()|2||23|21,0,2345,.2x x f x x x x x x ⎧⎪+≥⎪⎪=++-=-<<⎨⎪⎪--≤-⎪⎩当413,0,x x +≤⎧⎨≥⎩解得102x ≤≤;当302x -<<,13≤恒成立;当453,3,2x x --≤⎧⎪⎨≤-⎪⎩解得322x -≤≤-, 此不等式的解集为1|22x x ⎧⎫-≤≤⎨⎬⎩⎭. (2)令233,0,22()()2353,,2x m x x g x f x x x x m x x ⎧--++-≤<⎪⎪=--=⎨⎪--+-≤-⎪⎩当302x -≤<时,22'()1g x x=-+,当20x -<时,'()0g x ≥,所以()g x 在[2,0)-上单调递增,当322x -≤≤'()0g x ≤,所以()g x 在3[,2)2-上单调递减, 所以min ()(2)g x g =-2230m =+≥, 所以223m ≥-, 当32x ≤-时,22'()50g x x =-+<,所以()g x 在3(,]2-∞-上单调递减, 所以min 335()()026g x g m =-=+≥, 所以356m ≥-, 综上,223m ≥-.。
2018年东北三省四市联考模拟文数答案
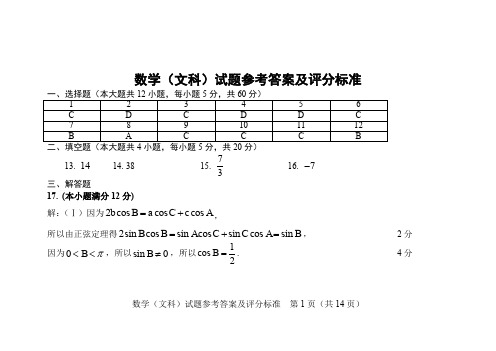
解: (Ⅰ)由 10 0.010 0.015 a 0.030 0.010 1 , 得 a 0.035 . ------------3 分 (Ⅱ)平均数为 20 0.1 30 0.15 40 0.35 50 0.3 60 0.1 41.5 岁; 数学(文科)试题参考答案及评分标准 第 3 页(共 14 页)
1 . 2
数学(文科)试题参考答案及评分标准 第 1 页(共 14 页)
因为 0 B ,所以 B (Ⅱ)因为 b 2, B
3
.
2 2
5分
3
,所以,由余弦定理可得 ac a c 4 ,
2 2
8分
因为由基本不等式可得 ac a c 4 2ac 4 , 所以 ac 4 ,当且仅当 a c 时,“等号”成立. (没有说明等号成立条件的扣除 1 分) 从而 SABC 10 分
所以 ac
16 8 8 1 sin A sin C cos A C cos A C cos A C , 3 3 3 2
9分
因为 0 A
2 2 2 2 ,所以 , ,0 C AC 3 3 3 3
PA AD 1,在 Rt△PAD 中, DP 2 , PA 平面 ABCD , PA CB ,
数学(文科)试题参考答案及评分标准 第 5 页(共 14 页)
CB AB , PA AB A , CB 平面 PAB ,CB PB ,
则 PC 3,
设中位数为 x ,则 10 0.010 10 0.015 x 35 0.035 0.5, ------------7 分 x 42.1 岁. (Ⅲ)第 1,2,3 组的人数分别为 20 人,30 人,从第 1,2 组中用分层抽样的方法抽取 5 人, 则第 1,2 组抽取的人数分别为 2 人,3 人,分别记为 a1 , a2 , b1 , b2 , b3 . 设从 5 人中随机抽取 3 人,为 (a1 , a2 , b1 ),(a1 , a2 , b2 ),(a1, a2 , b3 ),(a1, b1, b2 ), ,
东北三省四市教研联合体2018届高三第二次模拟考试文科数学含答案

东北三省四市教研联合体2018届高三第二次模拟考试文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}(){}03,1 -==x x x B x x A ,则B A ( ) A .(-1,0) B .(0,1) C .(-1,3) D .(1,3)2.若复数aiiz ++=11为纯虚数,则实数a 的值为( ) A .1 B .0 C .21- D .-13.中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”取意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算.算筹是将几寸长的小竹棍摆在下面上进行运算.算筹的摆放形式有纵横两种形式(如下图所示).表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列.但各位数码的筹式要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位数用横式表示.以此类推.例如3266用箅筇表示就是,则8771用算筹可表示为( )中国古代的算筹数码 A .B .C .D .4.右图所示的程序框图是为了求出满足2822 n n -的最小偶数n ,那么在空白框内填入及最后输出的n 值分别是( )A .1+=n n 和6B .2+=n n 和6 C.1+=n n 和8 D .2+=n n 和85.函数xxx x f tan 1)(2++=的部分图像大致为( )A .B .C. D .6.等差数列{}n a 的公差不为零,首项11=a ,2a 是1a 和5a 的等比中项,则数列{}n a 的前9项之和是( ) A .9B .10D .907.某几何体的三视图如图所示(单位:cm ),其俯视图为等边三角形,则该几何体的体积(单位:3cm )是( )A .34B .3310 C.32 D .3388.已知首项与公比相等的等比数列{}n a 中,满足),(*242N n m a a a n m ∈=,则nm 12+的最小值为( ) A .1 B .23 D .29 9.已知过曲线xe y =上一点),(00y x P 做曲线的切线,若切线在y 轴上的截距小于0时,则0x 的取值范围是( )A .),0(+∞B .),1(+∞eC.),1(+∞ D .),2(+∞10.已知边长为2的等边三角形ABC ,D 为BC 的中点,以AD 为折痕,将ABC ∆折成直二面角C AD B --,则过D C B A ,,,四点的球的表面积为( ) A .π3 B .π4 C.π5 D .π6 11.将函数⎪⎭⎫⎝⎛+=32sin )(πx x f 的图像向右平移a 个单位得到函数的图象,则的值可以为( ) A .B .C .D .12.已知焦点在轴上的双曲线的左右两个焦点分别为和,其右支上存在一点满足,且的面积为3,则该双曲线的离心率为( )ABC .D .()cos(2)4g x x π=+a 512π712π924π14124πx 222211x y m m -=-1F 2F P 12PF PF ⊥12PF F ∆23第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.设实数,满足约束条件则的最大值为 .14.为了了解居民天气转冷时期电量使用情况,某调查人员由下表统计数据计算出回归直线方程为,现表中一个数据为污损,则被污损的数据为 .(最后结果精确到整数位)15.已知函数满足,当时,)9()8(f f +的值为 .16.已知菱形ABCD 的一条对角线BD 长为2,点E 满足21=,点F 为CD 的的中点.若2-=⋅则⋅= .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知ABC ∆的内角C B A ,,的对边分别为c b a ,,,若2=b ,且A c C aB b cos cos cos 2+=.(I )求B 的大小;(II )求ABC ∆面积的最大值.18.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.x y 0,40,5,y x y x y ≥⎧⎪-≥⎨⎪+≤⎩25z x y =++2.1161.13y x =-+()f x 1()(1)1()f x f x f x ++=-(1)2f =80%[15,25)[25,35)[35,45)[45,55)[55,65)(I )求出a 的值;(II )求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);(III )现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.19.在如图所示的几何体中,四边形是正方形,平面,,分别是线段,的中点,.(1)证明:平面; (2)求平面与平面的距离.20.在平面直角坐标系中,椭圆:的离心率为,点在椭圆上.(1)求椭圆的方程;(2)已知与为平面内的两个定点,过点的直线与椭圆交于,两点,求四边形面积的最大值.21.已知函数)()(,ln )(R m m x x g x x f ∈+==. (I )若)(x g ≤恒成立,求实数m 的取值范围;ABCD PA ⊥ABCD E F AD PB 1PA AB ==//EF DCP EFC PDC C 22221(0)x y a b a b +=>>123(1,)2M C C (2,0)P -(2,0)Q (1,0)l C A B APBQ ()f x(II )已知21,x x 是函数)()()(x g x f x F -=的两个零点,且21x x ,求证:121 x x . 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程在直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线:,曲线:().(I )求与交点的极坐标; (II )设点在上,,求动点的极坐标方程. 23.选修4-5:不等式选讲已知函数,. (I )当时,求不等式的解集; (II )对于都有恒成立,求实数的取值范围.xOy x 1C cos 3ρθ=2C 4cos ρθ=02πθ≤<1C 2C Q 2C 23OQ QP =P ()|2||23|f x x x m =+++m R ∈2m =-()3f x ≤(,0)x ∀∈-∞2()f x x x≥+m数学(文科)试题参考答案一、选择题1-5: 6-10: CBACC 11、12:CB二、填空题15.37三、解答题17.解: (1)由正弦定理CCB b A a sin sin sin ==可得 B A C C A B B sin cos sin cos sin cos sin 2=+=∵0sin B ,故21cos =B , ∵π B 0,∴3π=B(2)由3,2π==B b ,由余弦定理可得422-+=c a ac ,由基本不等式可得4,42422≤-≥-+=ac ac c a ac ,而且仅当2==c a 时B ac S ABC sin 21=∆取得最大值323421=⨯⨯, 故ABC ∆的面积的最大值为3.18.解:(1)由,得, (2)平均数为岁; 设中位数为,则,∴岁. (3)第1,2组抽取的人数分别为20人,30人,从第1,2组中用分层抽样的方法抽取5人,则第1,2组抽取的人数分别为2人,3人,分别记为32121,,,,b b b a a .设从5人中随机抽取3人,为(121,,b a a ),(221,,b a a ),(321,,b a a ),(211,,b b a ),(311,,b b a ),(321,,b b a ),(212,,b b a ),(312,,b b a ),(322,,b b a ),(321,,b b b ),共10个基本事件, 其中第2组恰好抽到2人包含(211,,b b a ),(311,,b b a ),(321,,b b a ),(212,,b b a ),(312,,b b a ),(322,,b b a )共6个基本事件CDCDD 10(0.0100.0150.0300.010)1a ⨯++++=0.035a =200.1300.15400.35500.3600.141.5⨯+⨯+⨯+⨯+⨯=x 100.010100.015(35)0.0350.5x ⨯+⨯+-⨯=42.1x ≈从而第2组抽到2人的概率53106==19.解:(1)取中点,连接,,∵,分别是,中点,∴,, ∵为中点,为矩形,∴,,∴,,∴四边形为平行四边形, ∴,∵平面,平面, ∴平面.(2)∵EF ∥平面PDC ,∴F 到平面PDC 的距离等于E 到平面PDC 的距离, ∵PA ⊥平面ABCD ,∴DA PA ⊥,∵1==AD PA ,在PAD Rt ∆中2=DP ,∵PA ⊥平面ABCD ,∴CB PA ⊥,∵A AB PA AB CB =⊥ ,,∴⊥CB 平面PAB ,∴⊥CB PB ,则3=PC ,∵222PC DC PD =+,∴PDC ∆为直角三角形,∴222121=⨯⨯=∆PDC S PDE C PDC E V V --=,设E 到平面PDC 的距离为h ,又∵A PA AD PA CD AD CD =⊥⊥ ,,,∴⊥CD 平面PAD 则2121131212131⋅⋅⋅⋅=⋅⋅⋅⋅h ∴42=h ∴F 到平面PDC 的距离为42 20.解:(1)∵,∴, 椭圆的方程为,将代入得,∴, ∴椭圆的方程为. PC M DM MF M F PC PB //MF CB 12MF CB =E DA ABCD //DE CB 12DE CB =//MF DE MF DE =DEFM //EF DM EF ⊄PDC DM ⊂PDC //EF PDC 12c a =2a c =2222143x y c c+=3(1,)222191412c c+=21c =22143x y +=(2)设的方程为,联立 消去,得, 设点,, 有,, 有,点到直线点到直线从而四边形的面积(或) 令,, 有,设函数,,所以在上单调递增, 有,故, 所以当,即时,四边形面积的最大值为6. 21.解:(1)令)0(ln )()()( x m x x x g x f x F --=-=,有xxx x F -=-='111)(, 当1 x 时,0)( x F ',当10 x 时,0)( x F ',所以)(x F 在(1,+∞)上单调递减,在(0,1)上单调递增,)(x F 在1=x 处取得最大值为m --1,若)()(x g x f ≤恒成立,则m --1≤0即1-≥m ,l 1x my =+221,431,x y x my ⎧+=⎪⎨⎪=+⎩x 22(34)690m y my ++-=11(,)A x y 22(,)B x y 122634m y y m -+=+122934y y m -=+2212(1)||34m AB m +==+P (2,0)-l (2,0)Q l APBQ 222112(1)23434m S m m +=⨯=++121||||2S PQ y y =-t =1t ≥22431t S t =+2413t t =+1()3f t t t =+21'()30f t t =->()f t [1,)+∞134t t+≥2242461313t S t t t==≤++1t =0m =APBQ(2)由(1)可知,若函数)()()(x g x f x F -=有两个零点,则2110x x 要证121 x x ,只需证121x x,由于)(x F 在(1,+∞)上单调递减,从而只需证()⎪⎪⎭⎫⎝⎛121x F x F ,由于()()1121ln ,0x x m x F x F -===,即证0ln 11ln 11ln111111 x x x x m x x -+-=-- 令01221)(),10(ln 21)(222 xx x x x x x h x x x x x h +-=-+='-+-=, 有)(x h 在(0,1)上单调递增,0)1()(=h x h ,所以121 x x .22.解:(1)联立,∵,,,∴所求交点的极坐标.(2)设,且,,由已知,得∴,点的极坐标方程为,. 23.解:(1)当时,当解得;当,恒成立;cos 3,4cos ,ρθρθ=⎧⎨=⎩cos θ=02πθ≤<6πθ=ρ=)6π(,)P ρθ00(,)Q ρθ004cos ρθ=0[0,)2πθ∈23OQ QP =002,5,ρρθθ⎧=⎪⎨⎪=⎩24cos 5ρθ=P 10cos ρθ=[0,)2πθ∈2m =-41,0,3()|2||23|21,0,2345,.2x x f x x x x x x ⎧⎪+≥⎪⎪=++-=-<<⎨⎪⎪--≤-⎪⎩413,0,x x +≤⎧⎨≥⎩102x ≤≤302x -<<13≤11 当解得, 此不等式的解集为. (2)令 当时,,当时,,所以在上单调递增,当时,,所以在上单调递减, 所以,所以,当时,,所以在上单调递减, 所以, 所以, 综上,.453,3,2x x --≤⎧⎪⎨≤-⎪⎩322x -≤≤-1|22x x ⎧⎫-≤≤⎨⎬⎩⎭233,0,22()()2353,,2x m x x g x f x x x x m x x ⎧--++-≤<⎪⎪=--=⎨⎪--+-≤-⎪⎩302x -≤<22'()1g x x=-+0x ≤<'()0g x ≥()gx [0)32x -≤≤'()0g x ≤()gx 3[,2-min ()(g x g =30m =+≥3m ≥-32x ≤-22'()50g x x =-+<()g x 3(,]2-∞-min 335()()026g x g m =-=+≥356m ≥-3m ≥-。
东北三省三校(哈尔滨师大附中东北师大附中辽宁省实验中学)2018届高三第二次联合模拟考试语文试卷及答案

哈尔滨师大附中东北师大附中辽宁省实验中学2018年高三第二次联合模拟考试语文试卷一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
陆上和海上两条丝绸之路先后开通后,作为中国传统文化的代表——中国艺术及其精神随之传至世界各地,并为世界艺术发展贡献着智慧。
《中国艺术如何影响世界》一书,主要将中国绘画艺术置于西方绘画艺术的坐标系中,从“东学西渐"的角度重点审视和探讨了国艺术对世界艺术的影响和贡献。
本书认为西方一部分有重要影响的画家,之所以在创作中能取得辉煌的成就,都直接或间接地受到了中国绘画的深刻影响。
传统西方绘画用面表现物象,而中国绘画用线表现物象,空中的云、河中的水本来无线,但画家都用线条来表现。
至近现代,西方画家的作品凡有新意者,大多是改面为线而创作的,这是画家们借鉴中国绘画艺术得来的益处。
中国绘画艺术对世界艺术的影响,说到底是对中国之外的绘画创作者及其作品的影响。
本书中,作者以毕加索的画作为例展开论述。
毕加索早期的绘画以写实为主,但后来,他的画作以线条作为绘画的语言,笔法写意,绘画风格由具象转为抽象,实现了从画“形”到画“意”的转变。
这和他长期临摹中国画和倾心于中国绘画所倡导的价值追求颇有关系,毕加索曾赞许道“谈到艺术,第一是你们中国人的艺术”。
而用线条造型,正是中国绘画艺术影响到和区别于其他风格绘画艺术的显著标志。
本书认为,西方绘画注重科学原理,中国绘画则更讲究哲学精神。
因此,西方绘画重在写形,强调视觉享受或冲击力;一而中国绘画重在写心、畅神,强调人格的修炼、性情的抒发、思想的表达。
也就是说,在中国绘画理论视域中,绘画不过分强调描绘对象的真实与否,即不仅要画见到的“实”的东西,同时还要画见不到的和那些想象的“虚”的东西。
西方画家们仅在近一百年前,才领会其奥妙,而中国的画家们,一千多年前就已经在创作中自觉践行了这种理论。
笔者认为,深入挖掘中国艺术对世界艺术的影响和贡献迫在眉睫。
2018年东北三省四市教研联合体高考数学二模试卷(文科)

2018年东北三省四市教研联合体高考数学二模试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分。
在本小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合A={x|y=log2(1−x)},B={x|x>0},则A∩B=()A.⌀B.(0, 1)C.(0, +∞)D.(1, +∞)2. 设复数z=(1−i)(2−i),则它的共轭复数z的虚部为()A.3iB.−3iC.3D.−33. 向量a→,b→满足|a→|=1,|b→|=2,a→与b→的夹角为60∘,则|2a→−b→|=()A.2√3B.2√2C.4D.24. 如图是一个几何体的三视图,则这个几何体的表面积为()A.72B.66C.60D.305. 双曲线kx2+4y2=4k(k∈R)的离心率等于2,则k的值为()A.−3B.3C.−12D.126. 在可行区域内任取一点,其规则如流程图所示,则能输出数对(x, y)的概率是()A.π8B.π4C.π6D.π27. 已知α∈(π, 3π2),sinα=−√55,则tan(α+π4)的值为( )A.32B.−32C.3D.−38. 已知m ,n 是两条直线,α,β是两个平面.给出下列命题:①若m ⊥α,m ⊥n ,则n // α;②若m ⊥β,n ⊥β,则n // m ;③若m ⊥α,m ⊥β,则α // β;④若α // β,m ⊂α,n ⊂β,则n // m ;⑤α⊥β,m ⊂α,n ⊂β,则m ⊥n ,则命题正确的个数为( ) A.1 B.2 C.3 D.49. 已知过点M(−3, −3)的直线l 被圆x 2+y 2+12x +4y +15=0截得的弦长为8,则直线l 的方程为( )A.y =−3或4x −3y +3=0B.y =−3或4x +3y +21=0C.x =−3或4x −3y +3=0D.x =−3或4x +3y +21=010. 已知等差数列{a n }的前n 项和为S n ,a 21=10,S 3=144,则S n 取得最大值时,n 的为( ) A.25 B.27 C.25或26 D.26或2711. 已知椭圆E 的中心为坐标原点O ,过右焦点F(2, 0)且在y 轴上的截距为−2的直线l 与椭圆E 交于A ,B 两点,以OA 和OB 为邻边作平行四边形OBCA ,其中OC |OC →|=(2√55,−√55),则椭圆E 的方程为( ) A.x 212+y 28=1 B.x 25+y 2=1 C.x 26+y 22=1D.x 28+y 24=112. 函数f(x)=x +e x ln|x|的零点个数为( ) A.0 B.1 C.2 D.3二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东北三省四市教研联合体2018届高三第二次模拟考试
文科数学
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设集合,则()
A. (-1,0)
B. (0,1)
C. (-1,3)
D. (1,3)
2. 若复数为纯虚数,则实数的值为()
A. 1
B. 0
C.
D. -1
3. 中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”取意是指《孙子算经》中记载的算筹.古代是用算筹来进行计算.算筹是将几寸长的小竹棍摆在下面上进行运算.算筹的摆放形式有纵横两种形式(如下图所示).表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列.但各位数码的筹式要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位数用横式表示.以此类推.例如3266用箅筇表示就是,则8771用算筹可表示为()
中国古代的算筹数码
A. B. C. D.
4. 右图所示的程序框图是为了求出满足的最小偶数,那么在空白框内填入及最后输出的值分别是()
学,科,网...学,科,网...
A. 和6
B. 和6
C. 和8
D. 和8
5. 函数的部分图象大致为( )
A. B. C. D.
6. 等差数列的公差不为零,首项,是和的等比中项,则数列的前9项之和是()
A. 9
B. 10
C. 81
D. 90
7. 某几何体的三视图如图所示(单位:),其俯视图为等边三角形,则该几何体的体积(单位:)是()
A. B. C. D.
8. 已知首项与公比相等的等比数列中,满足,则的最小值为()
A. 1
B.
C. 2
D.
9. 已知过曲线上一点做曲线的切线,若切线在轴上的截距小于0时,则的取值范围是()
A. B. C. D.
10. 已知边长为2的等边三角形,为的中点,以为折痕,将折成直二面角,则过
四点的球的表面积为()
A. B. C. D.
11. 将函数的图像向右平移个单位得到函数的图象,则的值可以为()
A. B. C. D.
12. 已知焦点在轴上的双曲线的左右两个焦点分别为和,其右支上存在一点满足
,且的面积为3,则该双曲线的离心率为()
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13. 设实数,满足约束条件则的最大值为__________.
14. 为了了解居民天气转冷时期电量使用情况,某调查人员由下表统计数据计算出回归直线方程为
,现表中一个数据为污损,则被污损的数据为__________.(最后结果精确到整数位)
15. 已知函数满足,当时,的值为__________.
16. 已知菱形的一条对角线长为2,点满足,点为的的中点.若则
=__________.
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知的内角的对边分别为,若,且.
(I)求的大小;
(II)求面积的最大值.
18. 树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示.
(I)求出的值;
(II)求出这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(III)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
19. 在如图所示的几何体中,四边形是正方形,平面,,分别是线段,的中点,
.
(1)证明:平面;
(2)求平面与平面的距离.
20. 在平面直角坐标系中,椭圆:的离心率为,点在椭圆上.
(1)求椭圆的方程;
(2)已知与为平面内的两个定点,过点的直线与椭圆交于,两点,求四边形面积的最大值.
21. 已知函数.
(I)若恒成立,求实数的取值范围;
(II)已知是函数的两个零点,且,求证:.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22. 选修4-4:坐标系与参数方程
在直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线:,曲线:
().
(I)求与交点的极坐标;
(II)设点在上,,求动点的极坐标方程.
23. 选修4-5:不等式选讲
已知函数,.
(I)当时,求不等式的解集;
(II)对于都有恒成立,求实数的取值范围.。
