第四章 序列密码—trivium 7
【国家自然科学基金】_estream_基金支持热词逐年推荐_【万方软件创新助手】_20140801

推荐指数 1 1 1 1 1
2010年 序号
科研热词 1 流密码的设计准则 2 trivium 3 estream
推荐指数 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 非线性反馈移存器 非奇异性 相关密钥攻击 猜测决定攻击 状态刷新变换 流密码 序列密码 双射性 lex算法 grain算法 estream计划 aes算法
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1
科研热词 流密码 trivium 随机性检测 统计分析 线性近似 序列密码 差分故障分析 密钥流区分 密码学 密码分析 salsa20 estream
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
科研热词 流密码 密码分析 区分攻击 trivium 线性掩码 线性分析 立方攻击 猜测决定攻击 流密码算法 序列密码 密钥恢复 可滑动对 stream cipher sosemanuk算法 sosemanuk slid pair. sat问题 sat minisat hc-256 groebner基 grain estream计划 estream工程 estream
推荐指数 3 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
灰灰的密码学笔记

时间过的也真快,转眼我在密码吧已经混了一个月了,在此期间学到了不少东西,感谢各位高手的无私奉献。
不过也看到了很多不愉快的帖子,密码吧现在没有吧主,请大家多包容一点,不要老是吵架、制造垃圾帖子造成看贴不方便。
不多说了,我花了一个星期的时间把最近学到密码学知识整理成比较条理的笔记,现在拿出来与大家共享,愿能给密码的初学者带来方便,也欢迎高手来补充和指正。
另外我也把各种加密方法编写了网页程序的演示——密码机器 v1.0,现在正在调试中,先放张截图,过几天发上来,希望能够得到大家的支持哦,谢谢。
2楼目录:密码常识字母表顺序-数字进制转换密码Mod算法倒序间隔字母频率凯撒密码(Caesar Shifts, Simple Shift)凯撒移位(中文版)栅栏密码(The Rail-Fence Cipher)维吉尼亚密码(Vigenère Cipher)Polybius密码(Polybius Cipher)ADFGX/ADFGVX密码(ADFGX/ADFGVX Cipher)ADFGXADFGVX乘法密码(Multiplication Cipher)仿射密码(Affine Shift)希尔密码(Hill Cipher)加密解密Playfair密码(Playfair Cipher)摩斯电码置换密码(Transposition Cipher)替代密码(Monoalphabetic Substitution)字母表数字字母表代码反字母表随机乱序字母棋盘密码键盘密码键盘移位软键盘密码数字小键盘密码手机键盘密码数字谐音密码数字记忆编码百度/Google/网页字符百度字符(GB2312)Google字符(URI)网页编码(Unicode)Alt+数字小键盘MD52007-6-10 10:36 回复秋雨灰灰150位粉丝3楼【密码常识】字母表顺序-数字加密的时候,经常要把A~Z这26个字母转换成数字,最常见的一种方法就是取字母表中的数字序号。
【国家自然科学基金】_本原多项式_基金支持热词逐年推荐_【万方软件创新助手】_20140730

2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
2014年 科研热词 非周期长码直扩信号 解扰 自相关函数 线性递归序列 盲识别 盲解扩 波形设计 根式扩张 根式塔 本原序列 本原多项式 整数剩余类环 多输入多输出雷达 可解群 压缩映射 分裂域 分段相关 共轭根系 信道编码 信息码同步 代数方法 互相关函数 bch码 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9
科研热词 本原多项式 高阶统计 非合作通信 相关峰 盲估计 汉明码 对偶码字 tcf算法 m序列
推荐指数 2 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 高阶统计分析 高斯噪声 量子纠错码 矩阵斜消变换 流密码的设计准则 本原多项式 循环陪集 对偶码 trivium m序列 estream bch码
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
科研热词 本原多项式 有限域 陪集 逆元素 迹 生成幂等多项式 本原元 本原σ -lfsr序列 最小多项式 序列密码 对偶码 对偶基 块hankel矩阵 分位序列 三次剩余码
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1
密码学(范明钰)3.2-序列密码

K
K
安全信道
……
滚动密钥生成器
zi
xi
yi……滚动密钥生器ziyixi
同步序列密码
一次一密密码是加法序列密码的原型。事实上,如 果密钥使用滚动密钥流,则加法序列密码就退化成 一次一密密码。
实际使用中,密码设计者的最大愿望是设计出的滚 动密钥生成器,使得密钥经其扩展成的密钥流序列 具有如下性质:极大的周期、良好的统计特性、抗 线性分析、抗统计分析
基本概念
分组密码与序列密码的区别在于有无记忆性 序列密码的滚动密钥z0=f(k,σ0)由函数f、密钥k和指
定的初态σ0完全确定。此后,由于输入加密器的明文 可能影响加密器中内部记忆元件的存储状态,因而 σi(i>0)可能依赖于k,σ0,x0,x1,…,xi-1等参数。
同步序列密码
根据加密器中记忆元件的存储状态σi是否依赖 于输入的明(或密)文字符,序列密码可进一 步分成同步和自同步两种。
和σi产生的函数。
9
基本概念
序列密码将明文消息 M连续地分成字符
bit,并用密钥流来 加密每个字符bit
基本上,序列密码体
制只使用混乱技术,
而不使用散布技术。 这使得这种体制没有
错误扩散
基本情况
序列密码有广泛的理论基础,对于其各种设计原则已经 进行了详尽的分析。然而在公开的文献中详尽的序列密 码系统却相对较少 造成这种状况的部分原因是,在实际中使用的大部分序 列密码归私人所有或需要保密。相比之下,大量的分组 密码建议已经出版,其中的一些已经被标准化或公开
却希望它的输出(密钥序列k)对不知情的人来 说象是随机的。 到底该从哪些角度把握随机性等,才使所设计出 来的KG能够具有我们需要的安全程度?
序列密码 3.3 序列密码编码技术

lr
3.3
序列密码编码技术
初始乱源发生器:为前馈函数提供具有良好 统计特性的输入序列。 注:一般采用线性本原移存器。 源移存器初态通常由密钥决定。 抽头变换:控制前馈函数的输入,不同的输 入导致不同的输出,可变的抽头变换使输出序列 更加复杂。
3.3
序列密码编码技术
前馈函数:对初始乱源发生器提供的输入 序列进行非线性变换,提高输出序列的线性复 杂度。 破坏移存器序列固有的线性制约性,使由乱 数求初始密钥(或移存器初态、起点)是困难 的。 要求前馈函数不仅能将输入序列的优点 遗传下去,还要对输入序列的弱点进行有针 对性的改进。
实数和序列名称的由来 把N+1长序列a、b看成两个实数的二进制表示, 记 则有
AN ai 2 , BN bi 2 , Z N zi 2i
i i i 0 i 0 i 0 N N N
Z N ( AN BN ) mod 2 N 1
所得实数和的二进制表示就是输出序列。
…
LFSR2
…
… …
LFSRn
…
非线性变换 f (x)
…
3.3
序列密码编码技术
(二)有记忆变换模型
有记忆变换模型,使输出不仅与当前时刻的输 入因素有关,而且与以前时刻的输入和输出因素有 关,主要目的是实现输入信息的扩散。 1、累加器变换
a 输入为: {a1 , a2 , a3 } ;输出为:b {b1 , b2 , b3 }
序列密码就是利用少量的种子密钥产生密码学
性质好、抗还原能力强的伪随机序列,再将该伪随 机序列与明文以简单的方式相结合产生密文的一类 密码算法。 注:与明文结合的序列通常称为密钥流或乱数。
3.3
精品文档-密码学基础(范九伦)-第4章

第4章 Hash函数
实际应用中的Hash函数可分为简单的Hash函数和带密钥的 Hash函数。带密钥的Hash函数通常用来作为消息认证码(Message Authentication Code)。假定Alice和Bob有一个共享的密钥k, 通过该密钥可以产生一个Hash函数Hk。对于消息x,Alice和Bob 都能够计算出相应的消息摘要y=Hk(x)。Alice通过公共通信信道 将二元组(x,y)发送给Bob。当Bob接收到(x,y)后,它可以通过 检验y=Hk(x)是否成立来确定消息x的完整性。如果y=Hk(x)成立, 说明消息x和消息摘要y都没有被篡改。
第4章 Hash函数
下面给出带密钥的Hash函数族的定义。 定义4.1.4 一个带密钥的Hash函数族包括以下构成要素: (1) X:所有消息的集合(有限集或无限集); (2) Y:所有消息摘要构成的有限集合; (3) K:密钥空间,是所有密钥的有限集合; (4) 对任意的k∈K,都存在一个Hash函数Hk∈H,Hk: X→Y。 如果Hk(x)=y,则二元组(x,y)∈X×Y称为在密钥k下是有效 的。
第4章 Hash函数 生日攻击的思想来源于概率论中一个著名的问题——生日问
题。该问题是问一个班级中至少要有多少个学生才能够使得有两 个学生生日相同的概率大于1/2。该问题的答案是23。即只要班 级中学生的人数大于23人,则班上有两个人生日相同的概率就将 大于1/2。基于生日问题的生日攻击意味着要保证消息摘要对碰 撞问题是安全的,则安全消息摘要的长度就有一个下界。例如, 长度为40比特的消息摘要是非常不安全的,因为仅仅在220(大约 为一百万)个随机Hash函数值中就有50%的概率发现一个碰撞。所 以对于安全的消息摘要,现在通常建议可接受的最小长度为128 比特(此时生日攻击需要超过264个Hash函数值)。而实际使用的消 息摘要一般为160比特甚至更长。
【安全课件】第14讲—序列密码
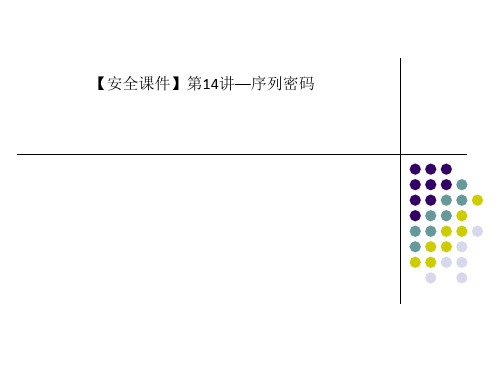
反馈多项式的含义
一个r级线性移存器的线性递推式表示为:
a n c 1 a n 1 c 2 a n 2 c r a n r( n r )
引进迟延算子D:D k a k 1 ,D ia k a k i,D 0 I 递推式可改写为:c 0 In a c 1 D n c 2 a D 2 a n c r D r a n 0 即:( c 0 c 1 D c 2 D 2 c r D r) a n 0c0 1
8
序列和周期
一般地,一个移存器序列表示为:aa0a1a2ai
• 对于序列 aa0a1a2,ai若存在整数p使得对任 意正整数k有ak akp 成立,称满足该式的最小 正整数p为序列的周期。
r级线性反馈移存器的最长周期: 2r 1 ,能达 到最长周期的线性移存器序列称为m序列。
• 在密码学中,我们希望参与变换的序列周期越 长越好,因此对线性反馈移存器我们更感兴趣 的是能达到最长周期的序列,即m序列。
特例:当q=2时,G(f)中任意两个序列之和仍然 属于G(f)。
5
(不)可约多项式
(不)可约多项式 定义:若存在g(x),h(x),使得f(x)=g(x)h(x),则
称f(x)是可约多项式;否则,称其为不可约多 项式。
6
定理2:若f(x)|h(x),则G(f) G(h).
例1:联结多项式为
将上式中的D用符号x代替,引入多项式:
f(x ) c rx r c r 1 x r 1 c 1 x 1
从而有:f(D )an0,(nr) 那么对于序列a, f (D)a0
18
14
二、m序列特性
(二)移加特性
L(t)(a)是左移变换,就是将序列 a 左移t位所得 到的序列。
crypt4-序列密码3
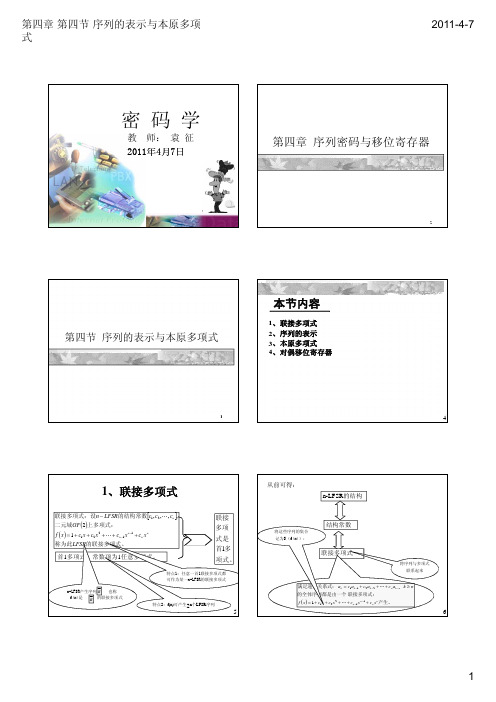
a 0 , a1 , a 2 , a 3 1,1, 0 ,1,求:序列
a的有理表示
9
10
有 理 表 示 2:设 GF 2 上 序 列 a的 周 期 为 p, 则 a的 有 理 表 示 有 a x a 0 a1 x a 2 x 2 a p 1 x p 1 1 x p
定理: 设 f x 是首1的 n次多项式,则 1 S f x S f x
总结: 序列有三种表示:
序列表示:
a a 0 a1a 2 a 3
2
非全零序列 a S f x 是 n级 m 序列的充分必要条件是 f x 是 n次本原多项式。
2011-4-7
2、序列的表示
序列表示: a a 0 a1a 2 a 3
定理:对于序列 a a 0 a1a 2 a 3 和首 1的 n 次多项式, f ( x ) c0 c1 x c 2 x 2 c n 1 x n 1 c n x n , c 0 1, a S ( f ( x ))的充要条件是: a的幂级表示为以下形式 : ( a x) g ( x )是次数小于 n 的多项式。 g ( x) 的展开式子 f ( x)
序列表示 :
a 1110011110 01
彻底解决了m-序 列的构造问题
构造出本原多项式,就构造出m-序列
11
12
2
第四章 第四节 序列的表示与本原多项 式
2011-4-7
常见的本原多项式: 1 x2 1 x x
3
1 x x2
4、对偶移位寄存器概述
为了便于计算机软件实现LFSR,我们引进了与 LFSR等价的移位寄存器——对偶移位寄存器。
序列密码(讲用)

此时反馈移位寄存器的输出序列 a0, a1, a2,…,at,…称为反馈移位寄存器序列 S0,S1,S2,…,St,…称为反馈移位寄存器的状态序列 其中S0=(a0,a1,…,an-1)为反馈移位寄存器的初始状态 例 设一个GF(2)上的3阶反馈移位寄存器如图所示,其反馈函 数为f(x1,x2,x3)=x1x2⊕x3, 其初始状态为 S0=(1,0,1),求输出序 列及其周期。 x3 x2 x1
20/32
定义 如果一个GF(2)上的n阶反馈移位寄存器的反馈函数形如 f (x1,x2,…,xn)=cnx1+cn-1x2+…+c1xn, 其中ci∈GF(2),1≤i≤n,则称其为线性反馈移位寄存器, 否则,称其为非线性反馈移位寄存器。 式中的c1,c2, ...... ,cn为反馈系数。对于二进制作用下, c1,......,cn的作用就相当于一个开关,用断开和闭合来表示0和1。 线性移位寄存器如图: 输出序列 …. an an-1 a2 a1 c1 + + c2 …. + cn-1 + cn
x3x2x1fx1x2x3x1x2x3一个gf2上的3阶非线性反馈移位寄存器输出在初始状态下即0时刻在第一个时钟到来时101fx1x2x3x1x2x3第1级第2级第3级s0101输出10fx1x2x3x1x2x3第1级第2级第3级s1011x11x20x311输出1a0由上面的结果可以看出这个反馈移位寄存器的状态序列和输出序列都是周期序列其周期为4
12/32
自同步序列密码
自同步序列密码的密钥流的产生和已经产生的固定数量 的密文字符有关,即是一种有记忆变换的序列密码。如图所 示。 密钥流 生成器 密 钥 流 ki 明文流mi 加密算法E 自同步序列密码模型
13/32
密钥流 生成器 密 钥 流 ki 密文流ci 解密算法D 明文流mi
达芬奇的密码重点攻略

《达芬奇密码》重点谜题详细攻略第一章卢浮宫(The Louvre)调查名片得号码454,洗手池附近得肥皂。
组合(Combine)肥皂和跟踪器后使用(USE),theMonalisa找到UV Light。
在蒙娜丽莎前用UV Light扫亮所有文字,下面对应字母的符号可以记录一下,后面的关卡还会用到。
Da vincipainted thosethat knewbetween bacchusand uriel liesthe clue调查岩间圣母左边的油画,得Priory Ring(修道院戒指)。
前往索尼埃办公室,调查所有物品,发现雕像被移动过,指向墙上地图。
调查地图,发现有酒精搽过的气味,使用UV Light,发现索尼埃标记的暗号。
帮助苏菲进入通风管道。
chitinase防止真菌及昆虫侵蚀dismutase基本氧化剂lactase分解乳糖catalase催化剂分解过氧化物为水和氧气urease可分解成二氧化痰和氨水依次注入chitinase dismutase catalase把鲜红色酶液体与抹布组合(Combine)在画布上使用,得胜利女神像。
经过蒙娜丽莎展厅来到胜利女神处,雕像左侧有女神之手,调查中使用Priory Ring(修道院戒指),得线索离开卢浮宫。
第二章圣叙尔比斯教堂(Saint Sulpice)调查修女尸体的右手,发现床下保险柜,(Clues→Chappe telegraph)把中间一行调成“SION”,得金属牌。
搜索二楼得钳子和油罐,教堂大厅,地板机关处摆成4月11日,得Station of the cross status。
搜索前厅得Ornate Key,返回楼上修女尸体房间,使用Ornate Key打开柜子,得Station of the cross status。
大厅前门附近使用钳子开锁上楼,钟表对成7:14,得cooper sild,第2块金属牌,教堂大厅把两尊塑像分别放在XIV Jesus is laid in the tomb;VII Jesus falls the second time,地板上秘密通道开启,地穴灯台前,调查后使用油罐把油灌入,把“JRU”金属板放在右侧灯里,把“AEM”金属板放在左侧灯里,分别用火柴点燃,JERUSALEM。
序列密码

∑
n −1 j=0
a( x) k (x) = * f ( x)
j
(∑ cn−l k j−l ) x
l=0
j
2011-3-29
20
特征多项式
* i l 证: k ( x ) f ( x ) = ( ∑ k i x )( ∑ c n − l x ) i=0 l =0 ∞ min( j , n ) l =0 ∞ n
。
• 同相自相关函数 的倍数, 时为, )=1 当j为p的倍数,即pj时为,R(j)=1; • 异相自相关函数 不是p的倍数时 当j不是 的倍数时 不是
2011-3-29 7
例 2- 2
二元序列111001011100101110010… 二元序列111001011100101110010… 周期p 周期p=7 同相自相关函数R )=1 同相自相关函数R(j)=1 异相自相关函数R )=- 异相自相关函数R(j)=-1/7。
2011-3-29
22
多项式的周期
• 多项式f(x)的周期p为使f(x)除尽xn-1的最小整数n的取 多项式f(x)的周期 为使f(x)除尽 的周期p 除尽x 的最小整数n 值。 • 序列的周期与生成序列特征多项式的周期密切相关。 序列的周期与生成序列特征多项式的周期密切相关。 引理3 引理3-2: 令f(x)为n次式,周期为p,令{ki}i≥0∈Ω(f),则{ki}i≥0的 次式,周期为p 周期p 周期p’p。
C3 决定了密码的强度 , 是序列密码理论的核心 。 它 决定了密码的强度,是序列密码理论的核心。 包含了序列密码要研究的许多主要问题, 包含了序列密码要研究的许多主要问题,如线性复杂度 相关免疫性、不可预测性等等。 、相关免疫性、不可预测性等等。
Trivium型级联反馈移存器的非奇异性判定

摘要: T r i v i u m 算 法是 e S T R E A M 工程 最终 胜 出的面 向硬件 实现 的 序 列 密码 算 法之 一 。对 以该
密码 算法 为特 例 的 T r i v i u m 型级联 反 馈移存 器 , 研 究 了其 非 奇异 性判定 , 给 出 了有 限域 上 T r i v i — a m 型 级联 反馈 移存 器 非奇 异 的充分 条件 和 二元域 上 T r i v i u m 型级联 反馈 移存 器 非奇异 的充 要
a n a l y z e s t h e n o n s i n g u l a r i t y o f Tr i v i um- l i k e c a s c a d e c o n n e c t i o n o f ̄ e d ba c k s h i t f r e g i s t e r s ,s h o ws t h e s u f ic f i e n t c o nd i t i o n f o r t he n o n s i n g u l a r i t y o f s u c h wo r d — o r i e n t e d f e e d ba c k s hi t f r e g i s t e r ,p r e s e n t s t h e n e c e s s a r y a n d s u f f i c i e n t c o n d i t i o n or f t h e n o n s i n g u l a r i t y o f s u c h b i t - o r i e n t e d f e e d ba c k s hi t f r e g i s t e r, a n d pr o v e s t h a t t h e s t a t e u pd a t e t r a n s f o r ma t i o n s o f T r i v i u m c i p he r i n i n i t i a l i z a t i o n p h a s e a n d k e y —
Trivium型级联反馈移存器的非奇异性判定

Trivium型级联反馈移存器的非奇异性判定
王秋艳;金晨辉
【期刊名称】《信息工程大学学报》
【年(卷),期】2013(014)005
【摘要】Trivium算法是eSTREAM工程最终胜出的面向硬件实现的序列密码算法之一.对以该密码算法为特例的Trivium型级联反馈移存器,研究了其非奇异性判定,给出了有限域上Trivium型级联反馈移存器非奇异的充分条件和二元域上Trivium型级联反馈移存器非奇异的充要条件,并证明了Trivium算法在初始化阶段和密钥流生成阶段的状态刷新变换都是双射.
【总页数】5页(P519-523)
【作者】王秋艳;金晨辉
【作者单位】信息工程大学,河南郑州450001;信息工程大学,河南郑州450001【正文语种】中文
【中图分类】TN918.1
【相关文献】
1.规则序列与奇异非线性移存器--求解快速自启动反馈函数 [J], 沈正元;何建萍
2.Grain型级联反馈移存器的非奇异性判定 [J], 王秋艳;金晨辉
3.序列密码非线性反馈移存器的可重构研究 [J], 徐光明;徐金甫;常忠祥;李伟
4.反馈移位寄存器非奇异性判定 [J], 李超;谢端强
5.一种级联H桥多电平变频器改进型载波移相PWM调制策略 [J], 赵慧;李海胜
因版权原因,仅展示原文概要,查看原文内容请购买。
非线性反馈移存器型序列密码的完全性通用算法

非线性反馈移存器型序列密码的完全性通用算法李俊志;关杰【摘要】非线性反馈移存器型序列密码被使用于智能卡、射频识别标签(RFID)和无线传感器等硬件资源受限设备的信息加密中,其典型代表为Trivium算法、Grain vl算法和Mickey算法,然而现有的完全性算法在应用于此类序列密码时存在分析轮数较少及对依赖关系区分不清楚等问题.本文提出了一种考察此类序列密码完全性的通用算法,将算法内部状态表示成线性集合和非线性集合,将序列密码每轮更新转化为集合的运算,通过迭代计算可给出算法达到非线性完全性所需轮数的下界,克服了现有完全性算法的不足.应用此通用算法给出Trivium算法更优的1比特差分区分器并完成对Trivium-B算法的实时攻击.本方法可为此类序列密码的设计提供一定的理论依据.【期刊名称】《电子学报》【年(卷),期】2018(046)009【总页数】6页(P2075-2080)【关键词】序列密码;非线性反馈移位寄存器;安全性指标;完全性;Trivium;区分攻击;分别征服攻击【作者】李俊志;关杰【作者单位】信息工程大学,河南郑州450000;信息工程大学,河南郑州450000【正文语种】中文【中图分类】TN918.11 引言非线性反馈移位寄存器型序列密码是将非线性反馈移位寄存器作为初始乱源的序列密码.由于其硬件实现的资源开销少,此类序列密码在资源极端受限的环境中得到广泛使用.在欧洲eSTREAM工程[1]等推动下非线性反馈移存器受到了人们的持续关注,Trivium算法[2]、Grain v1算法[3]及Mickey算法[4]都是典型的非线性反馈移位寄存器型序列密码.完全性是保证序列密码安全的重要指标之一,序列密码的完全性是指每个密钥流比特都包含所有密钥比特及IV比特的信息[5].目前研究完全性的方法有统计测试法[6],表达式判断法[7]和信息包含法[8]等.统计测试法的缺点在于只能以一定的概率否定完全性.表达式判断法是将一个密码系统看成是输出比特关于明文(IV)及密钥的布尔函数[6],该方法的缺点在于分析的轮数较少.信息包含法利用某一比特内部状态表达式中所包含的密钥和明文(IV)信息来判断算法是否达到完全,此方法的缺点在于考虑信息的包含时未区分输出比特与密钥和IV的线性依赖和非线性依赖关系.为了能够改善现有完全性算法的不足,本文提出了一种判断非线性反馈移位寄存器型序列密码是否达到非线性完全性的通用算法.该算法可以区分输出序列对于密钥和IV比特的线性依赖和非线性依赖,可以概率1否定完全性,能够从理论上给出算法非线性完全性轮数的下界.为了验证所提完全性通用算法的有效性,将其应用于Trivium系列算法[2,9],首次给出了Trivium系列算法的完全性质,据此对398轮Trivium算法进行了差分-区分攻击,攻击所需数据量为32,成功率为1-2-16,优于丁林等人在文献[10]中利用基于自动推导的差分分析技术构造的359轮Trivium算法的1比特差分区分器.此外,本文对满轮的Trivium-B算法进行了密钥分割攻击,攻击的时间复杂度为O(227),可以完成对该算法的实时攻击.2 完全性通用算法为了描述非线性完全性通用算法,首先给出非线性完全性的数学定义.令Pkij=Pr(Δzi=1|Δkj=1)(或Pvij=Pr(Δzi=1|Δvj=1)).则完全性的数学定义如下:若Pkij=0 (或Pvij=0),则称zi不依赖于kj(vj);若Pkij=1(或Pvij=1),则称zi线性依赖于kj(vj);若0<Pkij<1 (或0<Pvij<1),则称zi非线性依赖于kj(vj).当输出非线性依赖于所有密钥和IV时,称输出达到非线性完全性.因此要保证序列密码安全,输出密钥流至少达到非线性完全性.完全性通用算法的基本思想是从密钥和IV填充完毕开始,将内部状态分成线性部分和非线性部分两个集合,形式地按照算法更新函数和密钥流生成函数进行运算,得到输出密钥流中包含初始密钥和IV的信息.2.1 符号说明ki:密钥的第i比特;vi:IV的第i比特;密码算法的第i轮的第j比特内部状态;LF(X):多项式X的线性部分,LF(X)={x|变量x在多项式X的线性项中出现}∪{多项式X的常数项};NF(X):多项式X的非线性部分,NF(X)={x|变量x在多项式X的非线性项中出现}; 多项式Y的形式化描述,即PF(A):将集合A组成仿射多项式,即+:多项式的加法,指的是二元域上的加法;·:多项式的乘法,指的是二元域上的乘法;形式加法;形式乘法;⊙:集合乘法,运算过程如下:函数f的形式化描述,将其中的+和·换成和并将xi换成取形式化描述的线性部分,即LP((A,B))=A;取形式化描述的非线性部分,即NP((A,B))=B.2.2 形式加法和形式乘法下面定义通用算法中的形式加法与形式乘法:多项式f1,f2的形式化描述为:形式加法:NF(f1)∪NF(f2))(1)形式乘法:(2)其中B如下定义:B=NF[PF(LF(f1))·PF(LF(f2))] ∪(LF(f1) ⊙NF(f2))∪(LF(f2)⊙NF(f1)).(3)经验证,形式加法和形式乘法满足交换律,结合律及乘法对加法的分配律,这些运算法则在证明定理1及完全性通用算法的具体实现过程中将会用到.定理1给出了复合函数经过形式加法和形式乘法运算后的完全性描述,保证了形式运算后的结果与密码算法真实值相比不会损失信息.定理1 对多项式f(x1,…,xn),各xi是关于初始变量的表达式,则且NF(f(x1,…,xn))⊆证明设其中L(xn1,...,xns)为f函数的线性表达式,为f的非线性表达式,设x1, (x)均是关于y1,…,ym的多项式,其线性部分别为LF(xi),其中,1in,非线性部分别为NF(xi),其中,1in,则LF(f(x1,…,xn))只与LF(xi)有关,故根据形式加法和形式乘法的定义有:LF(f(x1,…,xn))=LF(L[PF(LF(xn1)),…,PF(LF(xns))]⊕考察NF(f(x1,…,xn)),设yj∈NF(f(x1,…,xn)),若yj∉由于yj∈NF(f(x1,…,xn)),必然存在使yj∈LF(xk1)且yj∈NF(PF(LF(xk1))·PF(LF(xk2)))⊆⊆否则,存在k3∈{1,…,n},使yj∈NF(xk3),由形式加法和形式乘法的定义,不管k3∈{n1,…,ns}或都有yj∈NF(xk3)⊆因此NF(f(x1,…,xn))⊆证毕.利用形式加法和形式乘法计算出来的达到完全性所需圈数是在假设运算过程的变量抵消不影响完全性时得出的,故此计算结果是达到完全性所需圈数的下界,并且当复合函数运算过程的变量抵消不影响完全性时,它就是所需的真实圈数.利用形式加法和形式乘法可以将原来基于内部状态比特的更新方程转化成现在基于内部状态线性和非线性部分的更新方程,并且保持所包含初始密钥及IV信息的完整性.这样克服了表达式判断法因计算量大而只能研究算法较少轮数的缺点,可以研究任意轮数算法的完全性,还能够区分输出序列对于密钥和IV比特的线性依赖和非线性依赖,而且可以概率1否定完全性和非线性完全性.2.3 通用算法描述输出密钥流(内部状态)非线性完全性所需轮数的定义:定义1 若小于t时刻时,输出密钥流(内部状态)关于初始密钥及IV的表达式非线性部分没有包含所有初始密钥及IV的信息,而第t时刻输出密钥流(内部状态)关于初始密钥及IV的表达式非线性部分包含了所有密钥及IV的信息,则称t为密钥流(内部状态)达到非线性完全性所需轮数,简称非线性完全性轮数.根据定义1给出基于非线性反馈移位寄存器序列密码非线性完全性轮数下界判断通用算法,即算法1.算法1 基于非线性反馈移位寄存器序列密码非线性完全性轮数下界判断通用算法---------------------------------------------------------- 输入:算法初始化轮数M 输出:内部状态达到非线性完全性的轮数rs及输出密钥流达到非线性完全性的轮数rz令flags=0,flagz=0;密钥及IV填充:将密钥及IV的填充过程转化为每个内部状态比特的线性部分和非线性部分,对内部状态比特进行初始化填充.初始化:Forj=1 toMIf 每个内部状态的非线性部分均包含所有密钥及IV且flags=0rs=j-1;flags=1;计算更新比特的线性部分和非线性部分,并按照初始化算法对内部状态比特进行移位和更新.计算输出比特的线性部分和非线性部分.If 输出比特的非线性部分均包含所有密钥及IV且flagz=0rz=j;flagz=1;If flags=0始化后内部状态不完全;If flagz=0初始化后密钥流不完全;由定理1可知如下结论:定理2 如果密码算法的第i轮的第j个内部状态包含初始密钥kt(或vt)的信息,则算法1得到的也一定包含kt(或vt)的信息,其中1iM,1jN,1tn.证明:由定理1可得,算法1得到的内部状态的线性部分组成的仿射函数表达式与密码算法实际内部状态的线性部分的表达式相同,的非线性部分包含算法实际内部状态表达式的非线性部分,定理得证.证毕.推论1 算法1得到的密钥流(内部状态)非线性完全性轮数r是真实算法非线性完全性轮数R的下界.证明:假设算法输出密钥流在第R轮达到非线性完全,即密钥流的非线性部分包含了所有的密钥及IV的信息,则由定理2,此时由算法1得到的密钥流输出的非线性部分也一定包含了所有的密钥及IV的信息.因此由算法1得到的算法非线性完全性轮数rR.证毕.推论1的逆否命题为:如果在某一轮,算法1得到密钥流(内部状态)还未达到非线性完全,则密码算法也一定未达到非线性完全.这个性质便于密码分析者构造区分攻击或密钥分割攻击.将具体的密码算法代入到算法1中,可得到密码算法密钥流(内部状态)非线性完全性轮数的下界,它可以为算法初始化设计提供一定的理论依据.3 Trivium算法及其修改版本的完全性研究3.1 Trivium算法完全性分析Trivium[2]的密钥和IV长度均为80比特.该算法初始化算法和密钥流生成算法两部分的内部状态更新方式相同,初始化算法共1152步,不输出密钥流,而后进入密钥流生成算法,每个时钟周期输出密钥流并更新寄存器.算法的伪代码描述如下:算法2 Trivium算法----------------------------------------------------------(s1,s2,...,s93)←(k1,k2,...,k80,0, 0(s94,s95,…,s177)←(v1,v2,…,v80,0,0,0,0)(s178,s179,…,s288)←(0,…,0,1,1,1)Fori=1 toNdozi←s66+s93+s162+s177+s243+s288t1←s66+s93+s91·s92+s171t2←s162+s177+s175·s176+s264t3←s243+s288+s286·s287+s69(s1,s2,…,s93)←(t3,s1,…,s92)(s94,s95,…,s177)←(t1,s94,…,s176)(s178,s179,…,s288)←(t2,s178,…,s287)将Trivium算法结构及参数代入到第2节的通用算法中,可得Trivium算法的完全性通用算法.为了验证算法的有效性,本文求得Trivium算法初始化第240轮的内部状态的表达式,并利用表达式判断法求出内部状态的完全性,与本文方法得到的第240轮的各状态完全性相对照,发现两者吻合,验证了完全性通用算法的有效性.同时,此实验也说明了变量抵消一般不影响完全性通用算法的计算结论.在考虑变量抵消时,算法1的计算结果往往与实际情况吻合或非常接近,所给出的完全性下界实用性强.而当初始化轮数再增大若干轮时,由于计算能力的限制,将很难获得内部状态的表达式,利用表达式判断法来研究完全性也变得不可行,这反映了表达式判断法的局限性,而本文提出的完全性通用算法依然有效.关于Trivium算法的完全性有以下结论:性质1 Trivium算法密钥流非线性完全性的下界为399.398轮的简化版Trivium算法输出密钥流的第1比特的非线性部分中没有包含v1的信息,但是线性部分却出现了v1.根据定理2,真实的初始化为398轮的简化版Trivium算法输出的第1比特的非线性部分中也一定没有出现v1,而其线性部分中一定出现v1.因此在密钥及IV的其它值不变的情况下改变v1的值,算法输出密钥流的第1比特一定改变.可以利用此性质构造差分区分器.算法3 对398轮的Trivium算法区分攻击----------------------------------------------------------输入:选择IV对数N输出:判断结果步骤1:选取N个(IV,IV′)对,每个(IV,IV′)对满足如下条件Δv1=1,其它Δvk=0,其中2k80.步骤2:对于一个固定的密钥K,将满足上述差分条件的(IV,IV′)对分别加载到初始化为398轮的Trivium算法中,检测算法输出密钥流第1比特的差分是否为1.步骤3:若这N对IV输出密钥流第1比特的差分均为1,判断此为Trivium算法输出,否则判断此为随机数.此攻击方案使用N对选择IV下产生的首个密钥流比特,计算量为2N次简化版Trivium算法,成功率为1-2-N.当N取16时,经过32次简化版Trivium算法,区分攻击成功率为1-2-16≈0.99998≈99.998%.与现有的差分区分攻击进行对比.文献[10]构造了359轮的Trivium算法的1比特差分区分器,区分攻击成功率77.9%,数据复杂度为O(266).本节对398轮Trivium 算法进行了差分-区分攻击,攻击所需数据量为32,成功率为1-2-16,在攻击轮数、复杂度和成功率方面都有很大改进.3.2 Trivium-B算法完全性分析文献[9]中作者给出了Trivium算法的4个修改版本,为了使内部状态的表达式的次数增长得更快,作者设计了Trivium-B算法,其密钥及IV填充过程及初始化轮数与Trivium相同,算法的伪代码描述如下:算法4 Trivium-B算法----------------------------------------------------------(s1,s2,...,s93)←(k1,k2,...,k80,0, 0(s94,s95,…,s177)←(v1,v2,…,v80,0,0,0,0)(s178,s179,…,s288)←(0,…,0,1,1,1)Fori=1 toNdozi←s36+s93+s126+s177+s213+s288t1←s36+s93+s66·s162+s147t2←s126+s177+s162·s243+s246t3←s213+s288+s243·s66+s63(s1,s2,…,s93)←(t3,s1,…,s92)(s94,s95,…,s177)←(t1,s94,…,s176)(s178,s179,…,s288)←(t2,s178,…,s287)将Trivium-B算法的结构代入算法1中,得到Trivium-B的非线性完全性算法.由该算法发现了Trivium-B算法的一个严重安全缺陷.无论Trivium-B算法初始化的轮数选取为多少,其输出密钥流均不完全,且有以下结论成立.性质2 对于Trivium-B算法有:(1)z3t-2只与k3i和v3i有关,其中t≥1,1i26;(2)z3t-1只与k3i-1和v3i-1有关,其中t≥1,1i27;(3)z3t只与k3i-2和v3i-2有关,其中t≥1,1i27.据此可以对Trivium-B算法进行密钥分割攻击.攻击的条件是已知IV及输出密钥流的前108比特Z=(z1,z2,…,z108)(4)攻击的准备工作是,先将密钥K分成三部分K(0)=(k1,k4,k7,…,k79)(5)K(1)=(k2,k5,k8,…,k77,k80)(6)K(2)=(k3,k6,…,k78)(7)相应地,IV也分成三部分V(0)=(v1,v4,v7, (v79)(8)V(1)=(v2,v5,v8,…,v77,v80)(9)V(2)=(v3,v6, (v78)(10)同样,由此密钥K和IV产生的密钥流也可分为三部分Z(0)=(z3,z6,…,z105,z108)(11)Z(1)=(z2,z4,z8, (107)(12)Z(2)=(z1,z4,z7,…,z106)(13)攻击的具体过程如下.算法5 针对Trivium-B算法的密钥分割攻击----------------------------------------------------------输入:IV及密钥流的前108比特Z输出:密钥K步骤1:令flag0=flag1=flag2=0;K0=K1=K2=0;步骤2:根据K(m)的取值和已知的V(m)计算Z′(m);步骤3:Form=0 to 2If flagm=0IfZ(m)=Z′(m)令此时的K(m)为候选密钥;令flagm=1;Else重新选取K(m);If flag0=flag1=flag2=1将得到的K作为正确密钥输出;Else返回步骤2计算Z′;此攻击需要的数据量为108比特密钥流,攻击的时间复杂度为O(227),攻击的成功率为⊗本文在个人电脑上进行了实验(计算环境为Intel Core i5-3470 CPU3.2GHz(4 CPUs),4GB内存),随机选取初始密钥及IV进行了1000组实验,平均45s 内可以求出所有初始密钥.4 小结完全性作为序列密码安全性的重要指标之一,对其进行深入研究是十分必要的,而现有的完全性算法存在着一些不足,针对这样的现状,本文提出了基于非线性反馈移位寄存器型序列密码完全性通用算法,可给出算法非线性完全性轮数的下界,为初始化算法的轮数选择及算法结构的设置提供有效指导.本文将通用算法应用于Trivium 系列算法中,首次给出了它们的完全性质并给出了新的分析结果.此外若对非线性完全性通用算法中的非线性部分的信息扩散进行更加细致的研究,例如具体给出非线性表达式中的二次项,将有望进一步提高通用算法的有效性.参考文献【相关文献】[1] Robshaw M.The eSTREAM project[A].Robshaw M.New Stream Cipher Designs:The eSTREAM Finalists[C].Berlin,Heidelberg:Springer Berlin Heidelberg,2008.1-6.[2] De Cannière C.Trivium:a stream cipher construction inspired by block cipher design principles[A].Katsikas S rmation Security:9th InternationalConference[C].Berlin,Heidelberg:Springer Berlin Heidelberg,2006.171-186.[3] Hell M,Johansson T,Meier W.Grain:a stream cipher for constrainedenvironments[J].International Journal of Wireless and Mobile Computing,2007,2(1):86-93.[4] Babbage S,Dodd M.The MICKEY stream ciphers[A].Robshaw M.New Stream Cipher Designs:The eSTREAM Finalists[C].Berlin,Heidelberg:Springer Berlin Heidelberg,2008.191-209.[5] 金晨辉,郑浩然,张少武,等.密码学[M].北京:高等教育出版社,2009.166-167.[6] Kölbl S,Leander G,Tiessen T.Obser vations on the SIMON block cipherfamily[A].Gennaro R.CRYPTO 2015:35th Annual CryptologyConference[C].Berlin,Heidelberg:Springer Berlin Heidelberg,2015.161-185.[7] Shannon C munication theory of secrecy systems[J].Bell System Technical Journal,1949,28(4):656-715.[8] Isobe T,Shibutani K.All subkeys recovery attack on block ciphers:extending meet-in-the-middle approach[A].Knudsen L R.Selected Areas in Cryptography:19th InternationalConference[C].Berlin,Heidelberg:Springer Berlin Heidelberg,2012.202-221.[9] Afzal M,Masood A.Modifications in the design of Trivium to increase its securitylevel[J].Proceedings of the Pakistan Academy of Sciences,2010,47(1):51-63.[10] 丁林,关杰.Trivium流密码的基于自动推导的差分分析[J].电子学报,2014,42(8):1647-1652. DING Lin,GUAN Jie.Differential cryptanalysis of Trivium stream cipher based on automatic deduction[J].Acta Electronica Sinica,2014,42(8):1647-1652.(in Chinese)。
Trivium算法在随机访问条件下的应用研究

Trivium算法在随机访问条件下的应用研究刘鹏焜;陈恭亮;李建华【期刊名称】《通信技术》【年(卷),期】2017(050)001【摘要】随机访问区别于循序访问,指的是同一时间内,访问序列中的任意一个元素。
随机访问效率是文件系统的重要指标。
对于文件系统的加密,所用的密码算法需能够实现随机访问,否则会严重降低访问效率。
J.Dj.GoliC'指出,基于密钥流生成器的流密码算法可以对随机访问的文件进行高效安全的加密,同时提出了支持随机访问的流密码算法设计原则。
Trivium 算法具有高速率、低硬件复杂度的特点,是欧洲eSTREAM 计划的获胜的7种算法之一。
基于Trivium 算法,运用分组加密的思想,提高了Trivium 的随机访问性能,使随机访问速率达到AES-CTR 的167%。
%Different from sequential access, random access means to access any element in the sequence at the same time. Random access efficiency is an important performance parameter of a file system, for which, the encryption algorithm in file system encryption must be able to support efficient random access, or otherwise could seriously reduce the access speed. It is pointed out by J.Dj.GoliC' that the stream ciphering algorithm based on keystream generator can implement efficient and safe encryption on random access file. Also, the design principles are proposed. The Trivium algorithm is one of the 7 winners in eSTREAM program with high efficiency and low hardware complexity. The random access performanceof Trivium is improved by using the idea of packet encryption, and the rate of random access reaches 167%of AES-CTR.【总页数】7页(P133-139)【作者】刘鹏焜;陈恭亮;李建华【作者单位】上海交通大学信息安全工程学院,上海200240;上海交通大学信息安全工程学院,上海200240;上海交通大学信息安全工程学院,上海200240【正文语种】中文【中图分类】TP309.7【相关文献】1.通讯访问约束条件下线性随机系统的状态可估计性 [J], 王丽娟;章辉2.随机多址访问协议中最优帧模式的混合遗传算法 [J], 薛亚茹;吕振肃3.非强凸和光滑条件下随机经典动量算法的收敛性 [J], 费经泰;查星星;王冬银4.通信访问约束条件下线性随机系统的可调节性研究 [J], 张索5.沉积微相约束条件下的随机地质建模方法及应用研究 [J], 王端平;杨耀忠;龚蔚青;柳世成;王延忠;于金标因版权原因,仅展示原文概要,查看原文内容请购买。
