四年级仁华思维导引解析第1-20讲
四年级-奥数与智能思维(下)【73页】-精品

第一讲组合与推理第一讲逻辑推理【一】桌上有排球、足球、篮球各1个。
排球在足球的右边,篮球在足球的左边。
请按从左到右的顺序排列出求的摆放情况。
练习1、甲、乙、丙比身高,甲说:“丙的身高没有乙高。
”乙说:“甲的身高没有丙高。
”丙说:“乙比甲矮。
”问:最高的是谁?2、A班学生中,如果:有红色铅笔的人没有绿色铅笔;没有红色铅笔的人又蓝色铅笔。
那么“有绿色铅笔的人就有蓝色铅笔”对吗?【二】何老师、邓老师和陈老师三人在语、数、英三门课中每人教一门。
已知:邓老师:我不教数学。
陈老师:我既不教语文,也不交数学。
请你说这三位老师分别教什么课?练习1、有4个球,编号为①、②、③、④,其中3个球一样重,有一个球比其他球轻1克。
为了找出这个轻球用天平称了两次,结果如下:第一次:①+②比③+④轻;第二次:①+③比②+④重。
那么,轻球的编号是几?2、华老师为表扬好人好事,要调查一件好事是谁做的。
他找来小红、小黄、小兰三人,进行询问。
小红说:“是小黄做的。
”小黄说:“不是我做的。
”小兰:“不是我做的。
”已知这三人中,只有一个说了实话。
问:这件好事是谁做的。
【三】有三个小朋友在谈论谁做的好事多。
风儿说:“云儿做的比雨儿多。
”云儿说:“风儿做的比雨儿多。
”雨儿说:“云儿做的比风儿少。
”这三位小朋友中谁做的好事最多?谁做的好事最少?练习1、小丁,小刚和小美一位是工程师,一位是医生,一位是飞行员。
现在知道:小丁和医生不同岁;医生比小刚年龄小;小美比飞行员年龄大。
请问,谁是工程师,谁是医生,谁是飞行员?2、张明、徐玲和秦汉是同学,大学毕业后分别当了教师、数学家和工程师。
秦汉比工程师年龄大;张明和数学家不同岁;数学家比徐玲年龄小想一想,谁是教师,谁是数学家,谁是工程师。
【四】有一个正方体,每个面分别写上汉字;数学奥林匹克。
三个人从不同角度观察的结果如下图所示。
问这个正方体每个汉字的对面各是什么字?练习1、下面三块正方体的六个面都是按相同的规律涂有红黄蓝绿白黑六种色。
四年级奥数教材

四年级奥数教材小学四年级奥数经典教材仁华思维导引解析,讲:整数与数列第 1 页共 136 页小学四年级奥数经典教材第 2 页共 136 页小学四年级奥数经典教材第 3 页共 136 页小学四年级奥数经典教材第 4 页共 136 页小学四年级奥数经典教材第 5 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:和差倍问题之三第 6 页共 136 页小学四年级奥数经典教材第 7 页共 136 页小学四年级奥数经典教材第 8 页共 136 页小学四年级奥数经典教材第 9 页共 136 页小学四年级奥数经典教材第 10 页共 136 页小学四年级奥数经典教材第 11 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:还原与年龄第 12 页共 136 页小学四年级奥数经典教材第 13 页共 136 页小学四年级奥数经典教材第 14 页共 136 页小学四年级奥数经典教材第 15 页共 136 页小学四年级奥数经典教材第 16 页共 136 页小学四年级奥数经典教材第 17 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:破译字母竖式第 18 页共 136 页小学四年级奥数经典教材第 19 页共 136 页小学四年级奥数经典教材第 20 页共 136 页小学四年级奥数经典教材第 21 页共 136 页小学四年级奥数经典教材第 22 页共 136 页小学四年级奥数经典教材第 23 页共 136 页小学四年级奥数经典教材第 24 页共 136 页小学四年级奥数经典教材第 25 页共 136 页小学四年级奥数经典教材第 26 页共 136 页小学四年级奥数经典教材小学四年级奥数经典教材第 28 页共 136 页小学四年级奥数经典教材第 29 页共 136 页小学四年级奥数经典教材第 30 页共 136 页小学四年级奥数经典教材第 31 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:直线形计算 第 32 页 共 136 页 小学四年级奥数经典教材第 33 页共 136 页小学四年级奥数经典教材第 34 页共 136 页小学四年级奥数经典教材第 35 页共 136 页小学四年级奥数经典教材第 36 页共 136 页小学四年级奥数经典教材第 37 页共 136 页小学四年级奥数经典教材第 38 页共 136 页小学四年级奥数经典教材第 39 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:几何图形剪拼第 40 页共 136 页小学四年级奥数经典教材第 41 页共 136 页小学四年级奥数经典教材第 42 页共 136 页小学四年级奥数经典教材第 43 页共 136 页小学四年级奥数经典教材第 44 页共 136 页小学四年级奥数经典教材第 45 页共 136 页小学四年级奥数经典教材第 46 页共 136 页小学四年级奥数经典教材第 47 页共 136 页小学四年级奥数经典教材第 48 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:加法原理与乘法原理第 49 页共 136 页小学四年级奥数经典教材第 50 页共 136 页小学四年级奥数经典教材第 51 页共 136 页小学四年级奥数经典教材第 52 页共 136 页小学四年级奥数经典教材第 53 页共 136 页小学四年级奥数经典教材第 54 页共 136 页小学四年级奥数经典教材第 55 页共 136 页小学四年级奥数经典教材仁华思维导引解析,讲:统筹与对策第 56 页共 136 页小学四年级奥数经典教材第 57 页共 136 页小学四年级奥数经典教材。
仁华思维导引解析8讲:几何图形认知

THSHtWWff. fSttfiae VHMll VM3mI«S^S> t*t»<l ☆ I.b & :cttJiati*nii tmut. e* A ・ LU AR . S9KM*/»cM»an*•■鼻《••4・ C4k» --■ . euyAVM ■细r«»<i ☆I ■・":•汁,AS«・GH ・《 n-tAftVMII. SBIKWItta■aswwtn”人«nai«・n2个o ••■■■SA[«々*■] ☆ ☆K ■・•】・ H3WMi*eT<XJW. UBS 初•・ WRM —tt*Pi It^tfwnMUt WnW- ■i ・MH ■汪 RH 吟費・"f FRi »ix ・i -ttArtfl. natTm. ■«£2r 正乃DST ・ AfleRii^tum. ■!我 £W»«4>O. IMdCWri. ・*・f ■ lllMl -iltftCTJB. 妞方*上敬十 14KI •兰叙•*, 卄代I It«*«»<• •£徘MM 巧2下■,QHt 柑E*••丽4*4x ・》«««/■■«,■ tfl»«£rftwr. MW ・r ・・4 ・2»eMR ・fiT ・.■«" £杠z 心IW 卜HI孔Kom ☆4.tfWMinffiAAO ®^0 ® △ FMM 小 N 4 4 ZHIRIH 心9l«»«l ☆ ☆弘・U・■ ■自■- S-ffiCfA-MIft ■»$><*- rt««e-^atw金一<MM*卜匸力dtmr- nelwr* ••VMIS* ■ ■ t* 2^ ETamAteft ft 2• 3■•n・i ifiUKKM. wm lyb ・・0^14- ■冲、■m&9S7・・ > B. X. HU只**«Mil «*<u a・ fi. 5?*we> mu^uxe^iiUK^*nu± >e*n*T^BUe<-S・・・GZA・B・t・a处*4輸1. 1 4. s. Mtft- WfltftIH-wHtnSl・Bs4 «*evhii«Bx?»»-w»««. fta»«n*ft±BmtCMVTkIX MM AfSii*tr< iaB4R2R< 十:.:WttAR, snium—i jtM—■丰*从A««*. «i>Tii- • A •只lUM%■•}«• H CS«PiSw->-4. ・gr—i7y Mmftan-..■•»,niM rawaaVKL "MlWKlvrim*、t«*<l ☆7- ab7nM4w«. *~f^*2muNnHr ■丄atc*M«*n.9i»«^vi nrcio. • d ®weuM-+iw». MTHj.4<tttMjivnt-ul4A*at ☆☆L EtiMx# "rXirSitayh 呎最■・机》・4 «IUT*«i£Q><l4^U«IHxtt-1xUtll -»a- <H1■T^HNEnV "VIlW2/V-«tHBWKUm *<¥74WIUT»4a ms 找射丄■衣粉WSm: .qiHHlkS依■*■(«-t«a£B -WMhM4^=iDWV4*Kn -Wir-WT® g:mr・>aix・c—丄岑•七・■«i^Mt*fM(MU74^l«9irr«SH 3te—”*fJMU?•卜•BHTVtfZ祢卑yRFUV+卯•fW>9*^:4ilA*・^BK+-V苹Tit■01 eiI””lH.glMKMW «M«a«n«■・ W < '佢lea丄•审*W4<ltf ・・fel44«*<H -MU -*«44avW:fW(T«tH«ai ■■ WWeVZH '•«•(!>■甘■■vilfi IK««IZQ A OI < I ♦ Is5*aW«M«W ■y. 'FW I W积WC fc.XF 击"Ffl. •♦|4A,・1 ☆☆n. «Et^«iB3tmimiE:m. XMtMta <.«.*. ii. M m£fr£r»«M«»«9b«卜DM.r1*1nafrbDr»・《■”卜EM7WW>"gpf,aRWl ■■“■wi”• I aiw.mfr-fl "P卄卄,■« + 3号nMUWBranMX ”"OmMOtMT^d亠亠〜2.・5・1儿》4・“+4・^・II. e»-»tM・nn・TT >>iuw0f ffioat-tiQwwuMti 2上匕kK・■WaAIMK・i ・W・ >i.AI(•■•■I fliTB. m«M4a金N*er ■益««•上annH'EWiWttincch i»mx0«M-上MiFbe «««*■• M■上■■C«*+S枷h(M-& ftV ■••MhMUetr卜ZA*九«*-o-(*<*<1 ☆☆☆M. 一•4**A 篌蓦vM—««I••匕■} snvm n>»・RffiR♦•丄fnaa lUVCliHac育W・-c-A-r-r*9-*-r- 4«K*7・, l*4*al ☆☆☆Ik «■< IB - £RMA>c・a❷.KC<0© BPtfACZHfcCe. - %iafi/dC'i«e.知liWw—Mimi■祈t ■ueas苔9t・»v,BZAMK as斤MMTWMM,HwmusffSMM,Ktwtl■上■ mwnww-fi dJM.AleiAwv] «ii«mu-ABi»eti*%u- KWUIHWK■二IIC>4U・ HBdMtUI FU・OKQBnW. MKItfOMIft. «X<A. mrinjvnixnfiinw. a 瓠■Pt・vr 抄恠■■mH. M—t«K.ft-f <4, z赛it・iaMflMc・rTgaDauBMu»r・ym”《> ea«.。
【机构秘籍思维导引】数学四年级第1讲整数计算综合(教师版+学生版,含详细解析)全国通用

第1讲整数计算综合内容概述熟练运用已学的各种方法解决复杂的整数四则运算问题;学会利用加减抵消、分组计算方法处理各种数列的计算问题。
学会处理“定义新运算”的问题,初步体会用字母表示数。
典型问题兴趣篇1.计算:(1) 121×32÷8;答案:484解析:原式=121×(32÷8)=121×4=484(2) 4×(250÷8)答案:125解析:原式=(4×250)÷8=1000÷8=125(3) 25×83×32×125答案:8300000解析:原式=(25×4)×(8×125)×83=100×1000×83=83000002.计算:(1) 56×22+56×33+56×44答案:5544解析:原式=56×(22+33+44)=56×99=56×(100-1)=56×100-56×1=5600-56=5544(2) 222×33+889×66.答案:66000解析:原式=111×66+889×66=66×(111+889)=66×1000=660003.计算:(1) 37×47+36×53答案:3647解析:原式=(36+1)×47+36×53=36×47+1×47+36×53=36×(47+53)+47=36×100+47=3600+47=3647(2) 123×76-124×75答案:48解析:原式=(124-1)×76-124×75=124×76-1×76-124×75=124×(76-75)-76=124-76=484.计算:100-99+98-97+96-95+…+12-11+10.答案:55解析:原式=(100-99)+(98-97)+(96-95)+…+(12-11)+10=1×45+10=555.计算:50+49-48-47+46+45-44-43+…-4-3+2+1.答案:51解析:原式=(50+49-48-47)+(46+45-44-43)+…+(6+5-4-3)+2+1=4×12+2+1=51 6.计算:(1+3+5+7+…+199+201) -(2+4+6+8+…+198+200).答案:101解析:原式=1+3+5+7+…+199+201-2-4-6-8-…-198-200=1+(3-2)+(5-4)+(7-6)+…+(199-198)+(201-200)=1+1×100=1017.计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.答案:2500解析:原式=(1+49)×49÷2×2+50=50×49+50=50×(49+1)=50×50=25008. 下面是一个叫做“七上八下”的数字游戏。
四年级仁华思维导引解析第1-20讲

四年级仁华思维导引解析
目录
四年级仁华思维导引解析第1讲:整数与数列
四年级仁华思维导引解析第2讲:和差倍问题之三
四年级仁华思维导引解析第3讲:还原与年龄
四年级仁华思维导引解析第4讲:破译字母竖式
四年级仁华思维导引解析第5讲:横式问题
四年级仁华思维导引解析第6讲:直线形计算
四年级仁华思维导引解析第7讲:几何图形剪拼
四年级仁华思维导引解析第8讲:加法原理与乘法原理
四年级仁华思维导引解析第9讲:统筹与对策
四年级仁华思维导引解析第10讲:构造与论证之一
四年级仁华思维导引解析第11讲:多位数与小数
四年级仁华思维导引解析第12讲:平均数问题
四年级仁华思维导引解析第13讲:行程问题之一
四年级仁华思维导引解析第14讲:行程问题之二
四年级仁华思维导引解析第15讲:复杂竖式
四年级仁华思维导引解析第16讲:幻方与数阵图扩展
四年级仁华思维导引解析第17讲:数表规律与数列综合
四年级仁华思维导引解析第18讲:排列与组合
四年级仁华思维导引解析第19讲:几何计数
四年级仁华思维导引解析第20讲:周期性问题
四年级仁华思维导引解析1讲:整数与数列
四年级仁华思维导引解析2讲:和差倍问题之三
四年级仁华思维导引解析3讲:还原与年龄
四年级仁华思维导引解析4讲:破译字母竖式
四年级仁华思维导引解析5讲:横式问题2008-06-05 11:00 来源:巨人学校作者:巨人奥数教研组
四年级仁华思维导引解析6讲:直线形计算2008-06-05 10:54 来源:巨人学校作者:巨人奥数教研组
四年级仁华思维导引解析7讲:几何图形剪拼2008-06-05 10:43 来源:巨人学校作者:巨人奥数教研组。
四年级导引解析-《华数思维训练导引》四年级上学期 还原与年龄

四年级导引解析->《华数思维训练导引》四年级上学期还原与年龄华数思维训练导引----还原与年龄四年级上学期第03讲应用题第08讲1. 某数加上6,乘以6,减去6,除以6,其结果等于6,则这个数是多少?解答:(6×6+6)÷6-6=1,这个数是1.2. 两个两位数相加,其中一个加数是73,另一个加数不知道,只知道另一个加数的十位数字增加5,个位数字增加1,那么求得的和的后两位数字是72,问另一个加数原来是多少?解答:和的后两位数字是72,说明另一个加数是99。
十位数字增加5,个位数字增加1,那么原来的加数是99-51=48。
3. 有砖26块,兄弟二人争着去挑。
弟弟抢在前面,刚摆好砖,哥哥赶到了。
哥哥看弟弟挑的太多,就抢过一半。
弟弟不肯,又从哥哥那儿抢走一半。
哥哥不服,弟弟只好给哥哥5块,这时哥哥比弟弟多挑2块。
问最初弟弟准备挑多少块?解答:先看最后兄弟俩各挑几块:哥哥比弟弟多挑2块,这是一个和差问题,哥哥挑的块数=(26+2)÷2=14块,弟弟=26-14=12块;然后再还原:哥哥还给弟弟5块:哥哥=14-5=9块,弟弟=12+5=17块;弟弟把抢走的一半还给哥哥:哥哥=9+9=18块,弟弟=17-9=8块;哥哥把抢走的一半还给弟弟:弟弟原来是8+8=16块。
4. 甲、乙、丙三人钱数各不相同,甲最多,他拿出一些钱给乙和丙,使乙和丙的钱数都比原来增加了两倍,结果乙的钱最多;接着乙拿出一些钱给甲和丙,使甲和丙的钱数都比原来增加了两倍,结果丙的钱最多;最后丙拿出一些钱给甲和乙,使甲和乙的钱数都比原来增加了两倍,结果三人钱数一样多了。
如果他们三人共有81元,那么三人原来的钱分别是多少元?解答:三人最后一样多,那么每人都是81÷3=27元;还原:甲和乙把钱还给丙:每人增加2倍,就是原来的3倍,那么甲和乙都是27/3=9元,丙是27+2*2*9=63元;甲和丙把钱还给乙:甲=9/3=3元,丙=63/3=21元,乙=9+2*3+2*21=57元;乙和丙把钱还给甲:乙=57/3=19元,丙=21/3=7元,甲=3+2*19+2*7==55元。
华数思维训练导引四年级上

华数思维训练导引四年级上华数思维训练导引——计算问题(三)整数与数列《思维训练导引》四年级第01讲计算问题第03讲整数与数列1、如图1-1所⽰的表中有55个数,那么它们的和加上多少才等于1994?1 7 13 19 25 31 37 43 49 55 612 8 14 20 26 32 38 44 50 56 623 9 15 21 27 33 39 45 51 57 634 10 16 22 28 34 40 46 52 58 645 11 17 23 29 35 41 47 53 59 65图1-1解:它们的和=3×5+9×5+15×5+21×5+27×5+33×5+39×5+45×5+51×5+57×5+63×5=(33×11)×5=1815[或者:它们的和=(31+32+33+34+35)×11=1815]1994-1815=179答:它们的和加上179才等于1994。
2、计算:1000+999-998-997+996+995-994-993+……+108+107-106-105+104+193-102-101。
解:1000+999-998-997+996+995-994-993+……+108+107-106-105+104+193-102-101=(1000+999-998-997)+(996+995-994-993)+……+(108+107-106-105)+(104+193-102-101)=4+4+……+4+4=[(1000-101)÷1+1]÷4×4=9003、计算:(1+3+5+……+1989)-(2+4+6+……+1988)。
解:(1+3+5+......+1989)-(2+4+6+ (1988)=1+(3-2)+(5-4)+……+(1989-1988)=1+1×(1989-1)÷2=1+994=9954、利⽤公式l×l+2×2+……+n×n=n×(n+1)×(2×n+1)÷6,计算:15×15+16×16+……+21×21。
华数知识点点击破(四年级新书推介)

华数知识点点击破(四年级分册)2016 年华数知识点点击破陈拓老师讲义作者简介陈拓,数学教育硕士,高级教师,94 年开始从事儿童超常思维开发教学研究,资深中小学教育专家,原人大附中仁华在线老师.多次担任暑期夏令营奥数教练,多年教授思维特训课程和竞赛辅导课程,为迎春杯、希望杯、IMC、华杯等杯赛辅导优秀教练,近百人在各级竞赛中获得不同奖项,每年都有多名学生升入人大附中、八中、四中、五分、清华附中等校实验班学习.IMC 命题委员会理事、主要命题人之一.陈老师教育方法灵活,知识讲解细腻,由浅入深,易于学生接受.教学中注重学生思维能力的培养,启发学生学习方法、解题思想的总结,激发学生学习的兴趣与自信,被家长称为京城思维启蒙名师.近期主要编写教材有:1、《儿童成长正能量课程》(思维、人格品质训练)2、《华数知识点点击破》(三年级)3、《华数知识点点击破》(四年级)4、《华数知识点点击破》(五年级)5、《小学思维训练数学知识宝典》6、《小升初重难点专题课程》(竞赛)7、《初中数学培优课程》(七年级)8、《初中数学培优课程》(八年级)9、《中考数学专题辅导课程》(九年级)10、《小学竞赛试题分类详解》11、《初中竞赛专题讲解》2 / 26华数知识点点击破陈拓老师讲义目录小学奥数问答 (4)1、四则混合运算的巧算 (7)2、整数的裂项 (11)3、填补不完整的算式 (14)4、和差倍问题 (20)5、平均数问题 (24)6、字母数字谜 (27)7、横式问题 (31)8、直线形面积 (34)9、图形剪拼 (37)10、相遇问题 (41)11、追及问题 (44)12、环形运动问题 (47)13、火车过桥问题 (50)14、加法原理 (53)15、乘法原理 (55)16、加法原理与乘法原理 (58)17、三角形的计数问题 (61)18、四边形的计数问题 (65)19、多位数与小数 (69)20、往返运动问题 (72)21、流水行船问题 (75)22、方程与方程组 (78)23、列方程(组)解应用题 (85)24、排列问题 (88)25、组合问题 (92)26、环形排列与相同对象排列 (95)27、质数与合数 (98)28、分解质因数 (101)29、约数与最大公约数 (104)30、倍数与最小公倍数 (107)31、约数的个数及约数和、积 (110)32、末位数字问题 (113)33、复杂的竖式 (116)34、数阵图综合 (121)35、数列数表综合 (126)36、阶乘的运用 (129)37、分数与循环小数 (132)38、综合练习一 (136)39、综合练习二 (139)40、综合练习三 (143)3 / 26华数知识点点击破陈拓老师讲义小学奥数问答奥数是现在小学家长热崇的一门学科.可是有些家长、甚至连学生自己都不明白为什么要学习奥数?学习奥数有什么意义?怎样才能学好奥数呢?并且现在社会出现了各种各样的奥数辅导班,又该如何选择辅导学习呢?带着这些问题,我想给大家提供了一些关于学习奥数的见解及建议.1、为什么要学习奥数,学习奥数有什么意义?现在学校所学的数学都是基础数学,面向的是大多数学生的水平,有一个最低的数学要求,而对上部封顶的过高要求没有一点具体的指点.这样就有些孩子对于学校所学的数学可能有简单的感觉,因此学习奥数是这个方面的有益补充,从而使得学生达到较高的教学要求起到一定的作用.另外孩子6~13 岁是大脑发育最快的时候,他接受的信息强,记忆力惊人.如果对大脑开发好,就是后天教育在遗传素质上的接力跑,通过学习奥数可以不仅拓宽了知识面,开阔了视野,丰富思想,提高速度,促进成绩的全面提高,而且培养了良好的思维能力,使学生获得心理上的优势,培养自信,是孩子一生当中最关键的几步中的第一步.同时可以启迪他们的智慧,有利于智力的开发,激发学习数学的兴趣,养成学习的好习惯,培养他们善于思考问题的习惯和方法,对于学生进入初中后学习物理、化学都非常有好处.学习奥数虽然有很多的益处,但是奥数教育是一种精英教育,不是大众教育,不是适合所有的人学习的,对于一个学习学校课本内容都很吃力的学生来讲,不顾现状的贪多求快,不仅学不好,可能反而因此带来负面的心理压力;如果明知不适合学习奥数而勉强为之,反而会因此使得丧失自信,最后甚至厌恶学习.因此家长在选择自己孩子是否学习奥数的时候一定要慎重.2、怎样才能好学奥数?适当学习,如果孩子确实有这方面的天份,或者想让孩子多见识点.我想学好奥数要注意几点:(1)好的培训机构.学习就要在学校班级的环境中学习,不能随便在家里做两道题就认为奥数就学好了,学生的思维就能开发出来了.其实奥数有一定的只是系统,只有知识系统建立起来,学生才能来运用这些知识和方法解题,培训机构毕竟在教学上都有一定的计划性.那些先讲?哪些后讲?哪些提高都有一定道理.(2)班级、时间不要,多要合理.找个专门的辅导机构,进行系统的学习,每周上课一次到两次,也可以是两个班各一次,每周做10~15 道相关试题就可以了.切记不能听说这个地方好,就到这个地方学,听说那个地方好就到那个地方学,结果每次都听的一知半解,挫伤孩子学习的积极性.(3)选个“懂教育”的老师.开始的时候要求老师讲解系统,有感染力,让孩子亲其师,来信其道.负责任的老师是很重要的.有些学生家长认为孩子小,随便找个学生或者是自己辅导一下就可以了,其实这恰恰忽视了学习的第一步.大家都知道“万事开头难”,良好的开端,是走向成功的一半.当然家长能有时间能和孩子一起学习是最好不过的,她能随时解决孩子学习过程中遇到的问题,能了解孩子学习的情况.好多家长放弃暂时的工作,与孩子一起听课,感慨说自己学到了很多大学都没有学到的东西,孩子学习几年下来,家长也成了奥数方面的专家啦.3、如何选择辅导班?选择课外辅导班应该是为孩子补充奥数这方面的不足,而不是让孩子提前学习.请想一想,在学校课本还没有学习的知识,在辅导班中却让孩子一接触就要掌握,并且马上会应用到解题中去,我们成人能达到这个水平吗?我的建议还是立足课本,适当提高.一、二年级不看任何系统学习数学的书籍,可以做一些数学游戏或趣题,以此来激发学生学习数学的兴趣.三、四年级不出现分数的计算.五、六年级不出现初中的负数、开方、绝对值等内容.现在孩子学习的机会很多,可是一定要选择一个管理规范,师资强大的培训学校.建议孩子不要报太多的辅导班,有些家长一星期给孩子报了5~6 个辅导班,孩子根本没有休息和玩乐的时间,却实是现在的学生比大人还累.可以报一、两个班级,同时买学习卡让孩子在网上学习,因为孩子喜欢这种形式的学习,时间也可以自己随便安排,并且有没有听懂的地方可以反复听,又有例题和习题,从这个方面比上辅导班还好,当然两者要互补,毕竟孩子自学能力不强,不能随时提问等缺陷.4 / 26华数知识点点击破陈拓老师讲义4、几年级学习奥数比较合适?如果孩子真有学习数学的天份,最好从三年级开始学习,或者二生三的暑假开始,进行思维训练.这时候孩子有一定的数学基础,可以适当提高,把有益的东西在他感觉好奇的时候“压”给他.因为三年级学生智力发育已经比较完善,对知识的认知已经比较明确,而且数学上的四则运算已经比较熟练,孩子正进入一个思维方式改造期,这个时候开始训练他们的思维方式,解题思路,效果是最好的.5、如果小学低年级想学奥数有什么好的建议吗?对于低年级的学生,主要还是重在语言的训练,对于奥数的学习,只能是寓教于乐,寓教于活动之中.0~6 岁孩子重点是语言的学习,对数有基本的认识,能把简单的事物计数是非常好的开发啦,但是不能拔苗助长.给孩子有个快乐的幼年,不建议对孩子有专门的学习奥数的安排,家长可以让孩子看一些立体的东西,搭建规则图形的积木,让孩子领略立体感,这个立体感是孩子今后学习中很重要的,有些女孩到高中学习立体几何不如男孩,就是因为小的时候男孩爱动,玩的多、见识多,在大脑中有储存,用的时候自然就能联系起来.7~8 岁的孩子,在上小学低年级,大脑还没有发育成熟,对由幼儿园的玩中学,一下子变成正轨的学习,有点不习惯,老师和家长要多鼓励,表扬孩子,发现闪光点,要大肆渲染,让孩子感受到成功的喜悦.家长可以出一点脑筋急转弯形式的数学题让学生学习,重点培养孩子对数的认识,对书面上数学符号的理解,和自己的思维对上号.即使外界信息与自己的大脑存取成功对接,也不易上什么辅导班之类的课程.可以多想想如何在孩子的游戏中,孩子的动画中进行思维的训练和知识的学习.我认为低年级一、二年级的学生只要把数认识清楚,能进行20 以内的加减法,能认识基本的立体和平面图形,会简单的计数,在数学游戏中多动手动脑就是超出目前学校的最高要求啦,孩子都是很优秀的啦.6、学习奥数的同时,也出现了各种数学竞赛,那么什么时间参加何种竞赛合适?现在小学竞赛很多,在北京参加竞赛的人数最多,组织比较好的有华杯赛、走进美妙的数学花园、希望杯、迎春杯、IMC、EMC 等,都是年后举行.建议学生在4、5 年级参加竞赛一显伸手,因为三年级以下,几乎小学不涉及竞赛,而六年级的学生忙于小升初,没有时间来准备竞赛的事情.同时六年级的竞赛结果有些是在每年的小升初结束后才出结果,对急于拿到证书为学生升学增加重量砝码,添加到简历中去有点晚.现在中学招生除了自己的分班考试以外,还比较注重孩子的平时参加的活动和获得的证书,所以最后在五年级就着手准备竞赛的事情.每年都有些家长到给孩子写简历的时候,感觉没有什么可以写的,而人家的孩子各种证书都有,就感觉很着急,认为是自己对孩子以前的学习没有太重视,但到用到的时候只能是于事无补.7、华数与奥数有什么区别呢?奥数与华数两者没有太大的区别.奥数是奥林匹克数学的简称,华数是华罗庚数学的简称,在我国,除北京外一般把小学生在课堂之外学习的竞赛数学或思维训练的数学都叫做奥数.只有北京人大附中有个超常儿童教育基地,创办了华罗庚数学学校,后来更名为仁华学校,目前停止招生状态.但人大附中现在从五年级中招收“小五班早培班”,这些学生要在五年级都要学完原来六年的奥数课程,更看中奥数成绩.甚至每年举办夏令营进行学生的筛选和考察,考察也是多方面的,如思维能力的测试(家长称为“神测”)、物理、化学、英语、语文、艺术特长等,当然华数是必须的,占相当大的比重.a1bc5d2 5 13 0。
四年级思维导引

四年级上学期第01讲,计算问题第03讲整数与数列【内容概述】等差数列的项和运算符号按某种规律排列所得算式的速算与巧算,这里有时要改变运算顺序,有时需通过裂项来实现求和。
按照给定的法则进行定义新运算。
较为复杂的整数四则运算问题。
【典型问题】2.计算:1000+999-998-997+996+995-994-993+…+108+107-106-105+104+193-102-101.=(1000+999-998-997)+(996+995-994-993)+…+(108+107-106-105)+(104+193-102-101)=4+4+…+4+4=[(1000-101)÷1+1]÷4×4=9004.利用公式l×l+2×2+…+n×n=n×(n+1)×(2×n+1)÷6,计算:15×15+16×16+…+21×21.=21×(21+1)×(2×21+1)÷6-14×(14+1)×(2×14+1)÷6=3311-1015=22966.计算:3333×5555+6×4444×2222.=3×1111×5×1111+6×1111×4×2×1111=15×1111×1111+2×3×1111×1111×4×2=1111×1111(15+48)=1111×1111×63=1111×1111×9×7=9999×7777=(1000-1)×7777=77770000-7777=777622238.两个十位数1111111111与9999999999的乘积中有几个数字是奇数?解1:1111111111×9999999999=1111111111×(10000000000-1)=11111111110000000000-1111111111=1111111118888888889有10个数为奇数。
奥数思维训练导引(4年级讲义)一

第1讲整数计算综合 (2)第2讲和差倍问题三 (10)第3讲还原问题与年龄问题 (19)第4讲数阵图初步 (26)第1讲整数计算综合内容概述熟练运用已学的各种方法解决复杂的整数四则运算问题;学会利用加减抵消、分组计算方法处理各种数列的计算问题。
学会处理“定义新运算”的问题,初步体会用字母表示数。
典型问题兴趣篇1. 计算:(1) 121×32÷8;(2) 4×(250÷8)(3) 25×83×32×1252. 计算:(1) 56×22+56×33+56×44(2) 222×33+889×66.3. 计算:(1) 37×47+36×53(2) 123×76-124×75。
4. 计算:100-99+98-97+96-95+…+12-11+10.5. 计算:50+49-48-47+46+45-44-43+…-4-3+2+1.6. 计算:(1+3+5+7+…+199+201) -(2+4+6+8+…+198+200).7. 计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8. 下面是一个叫做“七上八下”的数字游戏。
游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换。
口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大。
例如:给出的数是1995,口令是“8→7,”在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995。
如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?9. 规定运算“∇”为:a∇b= (a+1) ×(b-1), 请计算:(1)8∇10; (2) 10∇8.10. 规定运算“☺”为:a☺b=a×b-(a+b), 请计算:(1) 5☺8; (2) 8☺5; (3) (6☺5)4; (4)6☺ (54)拓展篇1. 计算:(1)72×27×88÷(9×11×12);(2) 31×121-88×125÷(1000÷121).2. 计算:(1) 555×445-556×444;(2) 42×137-80÷15+58×138-70÷15.3. 计算:20092009×2009-20092008×2008-20092008.4. 计算:1+2-3+4+5-6+7+8-9+……+97+98-99.5. 计算:100×99-99×98-98×97-97×96-96×95-95×94+…+4×3-3×2-2×1.6. 在不大于1000的自然数中,A为所有个位数字为8的数之和,B为所有个位数字为3的数之和. A与B的差是多少?7. 求图1-1中所有数的和.8. 已知平方差公式:22()()-=+⨯-,计算:a b a b a b22222222-+-+-++-201918171615219. 计算:951×949-52×48.10. 规定运算“Θ”为:aΘb=a+2b-2, 计算:(1) (8Θ7)Θ6; (2)8Θ(7Θ6)11. 规定运算“ ”为:a b=(a+1) ×(b-2). 如果6 ( 5)=91, 那么方格内应该填入什么数?12. 规定:符号“∆”为选择两数中较大的数的运算,“∇”为选择两数中较小的数的运算,例如:3∆5=5,3∇5=3请计算:1∆2∆3∇4∆5∆6∇7∆…∇100.(运算的顺序是从左至右)超越篇1. 观察下面算式的规律:2000+1991-1988-1982+1976+1970-1964-1958+1952+1946-1940-1934+……一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?2. 从1, 2, ……, 9, 10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?3. 计算:1-3+6-10+15-21+28- (4950)4. 已知平方差公式:22()()a b a b a b-=+⨯-, 计算:222222222222+--++--+++--1009998979695949343215. aΘb表示从a开始依次增加的b个连续自然数的和,例如:4Θ3=4+5+6=15, 5Θ4=5+6+7+8=26, 请计算:(1) 4Θ15 (2) 在算式( Θ7)Θ11=1056中,方框里的数应该是多少?6. 定义两种运算:aΩb=a-b+1, a∀b=a×b+1, 用“Ω”、“∀”和括号填入下面的式子,使得等式成立(不能用别的计算符号):7 3 4 5=27.现定义四种操作的规则如下:①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2. 例如从16可以得到8,从27可以得到14.②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉,例如从5304可以得到50,从408可以得到8. (不含数字3和4的自然数不能进行“丢三落四”操作)③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边。
高思奥数导引小学四年级含详解答案第20讲 幻方与数阵图扩展部分
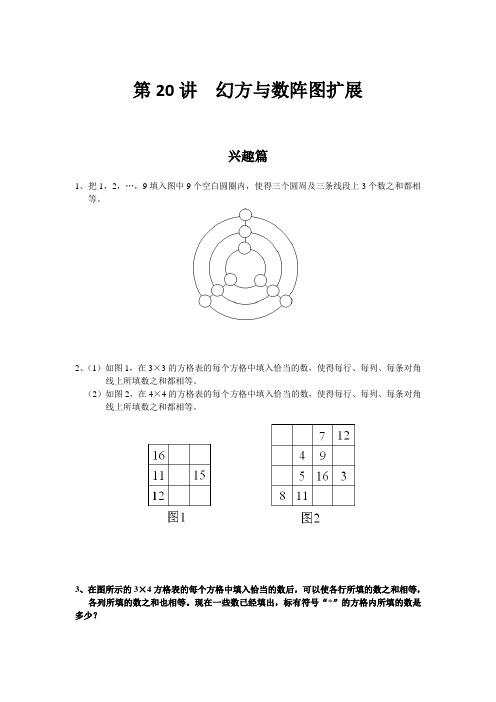
第20讲幻方与数阵图扩展兴趣篇1、把1,2,…,9填入图中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等。
2、(1)如图1,在3×3的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等。
(2)如图2,在4×4的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等。
3、在图所示的3×4方格表的每个方格中填入恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等。
现在一些数已经填出,标有符号“*”的方格内所填的数是多少?4、如图,请在空格中填入适当的数,组成一个三阶幻方。
5、请将图所示的5×5方格表补充完整,使得每个方格内都有一个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,1、2、3、4、5 恰好各出现一次。
请问:标有符号“△”,“▽”和“◯”的方格中所填的数分别是什么?6、请将1至9这9个数填入图中的方框内,使得所有不等号都成立。
所有满足要求的填法共有多少种?7、请在图所示的8个小圆圈内,分别填入1至8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好是1、2、3、4、5、6、7。
8、将1至5这5个数字填入图中的圆圈内,使得横线、竖线、大圆周上所填数之和都相等。
9、请在图中的六块区域内填入1、2、3、4、5、6,使得对每一个小圆圈来说,与它相邻的区域内的数之和都相等。
10、将0至9填入图的10块区域中(阴影区域除外),使得每个圆内的三个数之和都是相等的。
请问:这个和最小是多少?最大是多少?拓展篇1、将1,2,3,…,24,25分别填入图的各个方格中,使得每行、每列及两条对角线上的数的和相等。
现在已经填入了一些数,标有符号“*”的方格内所填的数是多少?2、请在图的每个空格内填入一个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等。
四年级上册数学思维训练讲义-第二十讲最优化问题人教版(含答案)

第二十讲最优化问题第一部分:趣味数学数字、符号家族之怪事数字、符号两大家族素有严谨认真的好名声,但今天却来了几个不速之客,搅得沸沸扬扬。
这不!您瞧:“110年=几百万年”“=”手牵着这两个八杆子也打不着的数字,得意得直眨眼。
“>”,“<</span>”立即吵了起来:“明明是100年<</span>几百万年嘛!”“是呀!是呀!”“=”你站错了,该让“<</span>”才对!大家一起责怪起“=”来。
“=”笑着拉起一旁“<</span>”的手说:“你别急,你瞧我前面的提示就知道了!”哦!原来前面还闪着“人口爆炸”四个字。
大家还有些不解。
“我明白了,这是说世界人口增长速度很快,照这样下去,100年内增长的人口比几百万内增长的人口还多。
这位子让给你了!”原来如此!大家恍然大悟!话音未落,“>”身披彩带牵上了这么一组式子:4>5,咦!咄咄怪事。
“>”见大家一头雾水的样子,笑着说:“这是数学家聪聪的至理名言:掌握正确的学习方法,4小时学习的效率比5小时还大!”大家听了这话,拍起巴掌,直称好!接着其他符号“≠”“……”……都纷纷登台,演出一幕幕令人吃惊的好戏,引得前来观看的知识老爷爷连连摸着胡子说:“好!好!哈,哈……”通过本节趣味数学的教学使学生学会解决等式加减法类型的题目,渗透解方程的一些方法。
第二部分:奥数小练在日常生活和生产中,我们经常会遇到下面的问题:完成一件事情,怎样合理安排才能做到用的时间最少,效果最佳。
这类问题在数学中称为统筹问题。
我们还会遇到“费用最省”、“面积最大”、“损耗最小”等等问题,这些问题往往可以从极端情况去探讨它的最大(小)值,这类问题在数学中称为极值问题。
以上的问题实际上都是“最优化问题”。
【例题1】用一只平底锅煎饼,每次只能放两个,剪一个饼需要2分钟(规定正反面各需要1分钟)。
问煎3个饼至少需要多少分钟?【思路导航】先将两个饼同时放入锅中一起煎,一分钟后两个饼都熟了一面,这时可将一个取出,另一个翻过去,再放入第三个。
四年级 奥数 讲义 566学子 教案库 仁华学校四升五考前集训一(学生版)

第一讲乘法原理一般地,如果完成一件事需要n个步骤,其中,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么,完成这件事一共有N=m1×m2×…×mn种不同的方法.这就是乘法原理.例1由数字0、1、2、3组成三位数,问:①可组成多少个不相等的三位数?②可组成多少个没有重复数字的三位数?例2由数字1、2、3、4、5、6共可组成多少个没有重复数字的四位奇数?习题一1.如右图,在三条平行线上分别有一个点,四个点,三个点(且不在同一条直线上的三个点不共线).在每条直线上各取一个点,可以画出一个三角形.问:一共可以画出多少个这样的三角形?2.由数字1、2、3、4、5、6、7、8可组成多少个①三位数?②三位偶数?③没有重复数字的三位偶数?④百位为8的没有重复数字的三位数?⑤百位为8的没有重复数字的三位偶数?第二讲加法原理一般地,如果完成一件事有k类方法,第一类方法中有m1种不同做法,第二类方法中有m2种不同做法,…,第k类方法中有mk种不同的做法,则完成这件事共有N=m1+m2+…+mk种不同的方法.这就是加法原理.例1从1到500的所有自然数中,不含有数字4的自然数有多少个?例2如下页左图,要从A点沿线段走到B,要求每一步都是向右、向上或者向斜上方.问有多少种不同的走法?第三讲排列一般地,从n个不同的元素中任取出m个(m≤n)元素,按照一定的顺序排成一列.叫做从n个不同元素中取出m个元素的一个排列.从n个不同元素中取出m个(m≤n)元素的所有排列的个数,叫做从例1用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数?习题三5.由数字1、2、3、4、5、6可以组成多少没有重复数字的①三位数?②个位是5的三位数?③百位是1的五位数?④六位数?第四讲组合从n个不同元素中取出m个元素(m≤n)的所有组合的个数,叫做从n个不同元素中取出m个不同元素的组合数.记作Cmn.一般地,求从n个不同元素中取出m个元素排成一列的排列数Pmn可以分两步求得:第一步:从n个不同元素中取出m个元素组成一组,共有Cmn种方法;第二步:将每一个组合中的m个元素进行全排列,共有Pmm种排法.故由乘法原理得到:Pmn=Cmn·Pmm因此这就是组合数公式.一般地,组合数有下面的重要性质:Cmn=C n-mn (m≤n)例1 在一个圆周上有10个点,以这些点为端点或顶点,可以画出多少不同的①直线段,②三角形,③四边形?例2 如下图,问:①下左图中,共有多少条线段?②下右图中,共有多少个角?例3 某校举行排球单循环赛,有12个队参加.问:共需要进行多少场比赛?例4 某班要在42名同学中选出3名同学去参加夏令营,问共有多少种选法?如果在42人中选3人站成一排,有多少种站法?习题四1.如右图,图上一共有六个点,且六个点中任意三个点不共线,问①从这六个点中任意选两点可以连成一条线段,这些点一共可以连成多少条线段?②从这六个点中任意选两点可以作一条射线,这些点一共可以作成多少条射线?(射线是一端固定,经另一点可以无限延长的.)第五讲排列组合例1在一个半圆周上共有12个点,如右图,以这些点为顶点,可以画出多少个①三角形?②四边形?例2 如下图,问①下左图中,有多少个长方形(包括正方形)?②下右图中,有多少个长方体(包括正方体)?习题五1.如下图,计算①下左图中有多少个梯形?②下右图中有多少个长方体?。
四年级上“创新思维数学讲义”

四年级上“创新思维数学讲义”——乘法数字谜热身场古希腊神话中有一位伟大的英雄阿吉里斯,他有着超乎普通人的神力和刀枪不入的身体,在激烈的特洛伊之战中无往不胜,取得了赫赫战功。
但就在阿吉里斯攻占特洛伊城奋勇作战之际,站在对手一边的太阳神阿波罗却悄悄一箭射中了伟大的阿吉里斯,在一声悲凉的哀叹中强大的阿吉里斯竟然倒下去了。
原来这支箭射中了阿吉里斯的脚后跟,这是他全身唯一的弱点。
在他还是婴儿的时候他的母亲就曾捏着他的右脚后跟,把他浸在神奇的斯堤克斯河中,被河水浸过的身体变得刀枪不入,近乎于神。
可那个被母亲捏着的脚后跟由于浸不到水,成了阿吉里斯全身唯一的弱点。
太阳神阿波罗就抓住阿吉里斯这唯一的弱点,以此为突破口,打败了伟大的英雄阿吉里斯。
我们今天要学习的数字谜,如在下面的方框中填上合适的数字。
4□ 2×□3□ 5 □它的特点也需要先找出突破口,根据提供的点滴信息,选择有特征的部分,把算式中缺少的数字补齐,使它成为一道完整的算式。
健身园〔例1〕在下面算是的□里填上适当的数字,不仅使等式成立,而且使等号两边的数字也对称。
12×46□=□64×21分析与思考:先考虑乘积相等,再考虑对称。
先找突破口——从积的个位入手,等式右边积的末位数字是4×1,那么左边末位数字也应该是4,46□的□只能填2或7,左边积的最高位是5,因此,右边也应是5,这样□就只能填2.〔练一练〕在下面算是的□里填上适当的数字,不仅使等式成立,而且使等号两边的数字也对称。
⑴□8×891=198×□⑵12×23□=□32×21例2〕在□中填入合适的数,使等式成立。
□□× 5 31 □ 83 3 □□□□□分析与思考:先从最低位找突破口,积1□8是3×□□得到的,因数□□的个位是什么?想一想?〔练一练〕⒈在□中填入合适的数,使等式成立。
□ 7×□□□ 8□□□□□□□⒉在□中填入合适的数,使等式成立。
四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(2021年整理)

四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为四年级数学思维训练导引(奥数)第15讲加法原理与乘法原理(word版可编辑修改)的全部内容。
第十五讲加法原理与乘法原理1.阿奇去吃午饭,发现附近的中餐厅有9个,西餐厅有3个,日式餐厅有2个.他准备找一家餐厅吃饭,一共有多少种不同的选择?2.阿奇进入一家中餐厅后,发现主食有3种,热菜有20种.他打算主食和热菜各买1种,一共有多少种不同的买法?3.老师要求冬冬在黑板上写出一个减法算式,而且被减数必须是两位数,减数必须是一位数,冬冬共有多少种不同的写法?4.传说地球上有7颗不同的龙珠,如果找齐这7颗龙珠,并且按照特定顺序排成一行就会有神龙出现.邪恶的沙鲁找到了这7颗龙珠,但是他不知道排列的特定顺序.请问:运气不好的沙鲁最坏要试几次才能遇见神龙?5.用红、黄、蓝三种颜色给图15-1的三个圆圈染色,一个圆圈只能染一种颜色,并且相连的两个圆圈不能同色,一共有多少种不同的染色方法?6.在图15-2中,从“北”字开始,每次向下移动到一个相邻的字可以读出“北京奥运会”,那么一共有多少种不同的读法?7.运动会中有四个跑步比赛项目,分别为50米、100米、200米、400米,规定每个参赛者只能参加其中的一项.甲、乙、丙、丁四名同学报名参加这四个项目,请问:(1)如果每名同学都可以任意报这四个项目,一共有多少种报名方法?(2)如果这四名同学所报的项目各不相同,一共有多少种报名方法?8.冬冬的书包里有5本不同的语文书、6本不同的数学书、3本不同的英语书,请问:(1)如果从中任取1本书,共有多少种不同的取法?(2)如果从中取出语文书、数学书、英语书各l本,共有多少种不同的取法?9.如图15-3,甲、乙两地之间有4条路,乙、丙两地之间有2条路,甲、丙两地之间有3条路,那么从甲地去丙地一共有多少条不同的路线?10.图15—4中有一个从A到曰的公路网络,一辆汽车从A行驶到曰,可以选择的最短路线一共有多少条?1.阿奇一家人外出旅游,可以乘火车,也可以乘汽车,还可以坐飞机,经过网上查询,出发的那一天中火车有4班,汽车有3班,飞机有2班,他们乘坐这些交通工具,一共可以有多少种不同的选择?2.“IMO”是“国际数学奥林匹克”的缩写,要求把这三个字母涂上三种不同的颜色,且每个字母只能涂一种颜色.现有五种不同颜色的笔,按上述要求能有多少种不同颜色搭配的“IMO”?3.书架上有三层书,第一层放了15本小说,第二层放了10本漫画,第三层放了5本科普书,并且这些书各不相同,请问:(1)如果从所有的书中任取1本,共有多少种不同的取法?(2)如果从每一层中各取1本,共有多少种不同的取法?(3)如果从中取出2本不同类别的书,共有多少种不同的取法?4.如图15-5,从甲地到乙地有3条路,从乙地到丙地有3条路,从甲地到丁地有2条路,从丁地到丙地有4条路.如果要求所走路线不能重复,那么从甲地到丙地共有多少条不同的路线?5.如图15-6,四张卡片上写有数字2、4、7、8.从中任取三张卡片,排成一行,就可以组成一个三位数.请问:一共可以组成多少个不同的三位数?其中有多少个不同的三位奇数?6.奥运场馆实行垃圾分类处理.每个地方放置五个垃圾桶,从左向右依次标明:电池、塑料、废纸、易拉罐、不可再造,如图15-7.现在准备把五个垃圾桶染成红、绿、蓝这3种颜色之一,要求相邻两个垃圾筒颜色不同,且回收废纸的垃圾桶不能染成红色,一共有多少种染色方法?7.如图15—8,把A、曰、C、D、E这五部分用4种不同的颜色染色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色,请问:这幅图共有多少种不同的染色方法?8.如图15—9,用红、蓝两种颜色来给图中的小圆圈染色,每个小圆圈只能染一种颜色.请问:(1)如果每个小圆圈可以随意染色,一共有多少种不同的染法?(2)如果要求关于中间那条竖线左右对称,一共有多少种不同的染法?9.甲、乙、丙、丁、戊五人要驾驶A、B、C、D、E这五辆不同型号的汽车.会驾驶汽车A的只有甲和乙,汽车E必须由甲、乙、丙三人中的某一人驾驶,则一共有多少种不同的安排方案?10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级仁华思维导引解析
目录
四年级仁华思维导引解析第1讲:整数与数列
四年级仁华思维导引解析第2讲:和差倍问题之三
四年级仁华思维导引解析第3讲:还原与年龄
四年级仁华思维导引解析第4讲:破译字母竖式
四年级仁华思维导引解析第5讲:横式问题
四年级仁华思维导引解析第6讲:直线形计算
四年级仁华思维导引解析第7讲:几何图形剪拼
四年级仁华思维导引解析第8讲:加法原理与乘法原理
四年级仁华思维导引解析第9讲:统筹与对策
四年级仁华思维导引解析第10讲:构造与论证之一
四年级仁华思维导引解析第11讲:多位数与小数
四年级仁华思维导引解析第12讲:平均数问题
四年级仁华思维导引解析第13讲:行程问题之一
四年级仁华思维导引解析第14讲:行程问题之二
四年级仁华思维导引解析第15讲:复杂竖式
四年级仁华思维导引解析第16讲:幻方与数阵图扩展
四年级仁华思维导引解析第17讲:数表规律与数列综合
四年级仁华思维导引解析第18讲:排列与组合
四年级仁华思维导引解析第19讲:几何计数
四年级仁华思维导引解析第20讲:周期性问题
四年级仁华思维导引解析1讲:整数与数列
四年级仁华思维导引解析2讲:和差倍问题之三
四年级仁华思维导引解析3讲:还原与年龄
四年级仁华思维导引解析4讲:破译字母竖式
四年级仁华思维导引解析5讲:横式问题2008-06-05 11:00 来源:巨人学校作者:巨人奥数教研组
四年级仁华思维导引解析6讲:直线形计算2008-06-05 10:54 来源:巨人学校作者:巨人奥数教研组
四年级仁华思维导引解析7讲:几何图形剪拼2008-06-05 10:43 来源:巨人学校作者:巨人奥数教研组。
