模糊自适应PID控制器及SIMULINK仿真实现

基于simulink的模糊PID控制例子

1模糊P1D用命令FUZZy翻开模糊控制工具箱。

AnfiSedit翻开自适应神经模糊控制器，它用给定的输入输出数据建个一个模糊推理系统，并用一个反向传播或者与最小二乘法结合的来完成隶属函数的调节。

SUrfVieW(newfis)可以翻开外表视图窗口8.1模糊PID串联型新建一个SimUIink模型同时拖入一个fuzzy1ogiccontro11er模块，双击输入已经保存的fis模糊控制器的名字。

由于这个控制模块只有一个输入端口，需要用到I I1UX模块。

模糊结合PID,当输出误差较大时，用模糊校正，当较小时，用PID校正。

8.2模糊自适应PID[1)PID参数模糊自整定的原那么PID调节器的控制规律为：u(k)=Kpe(k)+Ki∑e(i)+Kdec(k)其中：KP为比例系数；Ki为积分系数；Kd为微分系数；e(k)、ec(k)分别为偏差和偏差变化率.模糊自整定P1D参数的目的是使参数Kp、Ki、Kd随着e和ec的变化而自行调整,故应首先建立它们间的关系.根据实际经验,参数KP、Ki、Kd在不同的e和ec下的自调整要满足如下调整原那么：(1)当e较大时,为加快系统的响应速度，防止因开始时e的瞬间变大可能会引起的微分溢出,应取较大的Kp和较小的Kd,同时由于积分作用太强会使系统超调加大，因而要对积分作用加以限制,通常取较小的Ki值；(2)当e中等大小时,为减小系统的超调量，保证一定的响应速度，Kp应适当减小；同时Kd 和Ki的取值大小要适中；(3)当e较小时,为了减小稳态误差，Kp与Ki应取得大些,为了防止输出响应在设定值附近振荡，同时考虑系统的抗干扰性能,Kd值的选择根据IeC1值较大时，Kd取较小值，通常Kd为中等大小。

同时按照需要,将输入语言变量E和EC分为7个模糊子集,分别用语言值正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NM)、负大(NB)来表示,它们的隶属函数为高斯型(gaussmf),输出语言变量Kp/、Ki，、Ker用语言值小正大(PB)、正中(PM)、正小(PS)、零(Z)、负小(NS)、负中(NM)、负大(NB)来表示隶属函数为三角型(trimf),方法二：图-1模糊自适应Simu1ink模型根据各模糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计分数阶PID参数的模糊矩阵表，算出参数代入下式计算：Kp=KpO+(E,EOpjKi=KiO+(E,EC)I;Kd=KdO+(E,EC)d式中：KpO.KiO.KdO为P1D参数的初始设计值，由传统的PID控制器的参数整定方法设计。

自适应模糊PID控制器的设计与仿真

自适应模糊PID控制器的设计与仿真自适应模糊PID控制器是一种结合了模糊控制和PID控制的自适应控制器，它能够在系统的不同工况下根据实际需求对PID参数进行自适应调整，从而使得系统具有更好的动态性能和稳定性。

本文将介绍自适应模糊PID控制器的设计思路和仿真过程。

1.设计思路1.1系统建模首先需要对待控制的系统进行建模，得到系统的数学模型。

这可以通过实验数据或者理论分析来完成。

一般情况下，系统的数学模型可以表示为：$G(s)=\frac{Y(s)}{U(s)}=\frac{K}{s(Ts+1)}$其中，K是系统的增益，T是系统的时间常数。

1.2设计模糊控制器接下来需要设计模糊控制器，包括模糊规则、模糊集和模糊运算等。

模糊控制器的输入是系统的误差和误差的变化率，输出是PID参数的调整量。

1.3设计PID控制器在模糊控制器的基础上，设计PID控制器。

PID控制器的输入是模糊控制器的输出，输出是控制信号。

1.4设计自适应机制引入自适应机制，根据系统的性能指标对PID参数进行自适应调整。

一般可以采用Lyapunov函数进行系统性能的分析和优化。

2.仿真过程在仿真中，可以使用常见的控制系统仿真软件，如MATLAB/Simulink 等。

具体的仿真过程如下：2.1设置仿真模型根据系统的数学模型，在仿真软件中设置仿真模型。

包括系统的输入、输出、误差计算、控制信号计算等。

2.2设置模糊控制器根据设计思路中的模糊控制器设计，设置模糊控制器的输入和输出，并设置模糊规则、模糊集和模糊运算等参数。

2.3设置PID控制器在模糊控制器的基础上，设置PID控制器的输入和输出，并设置PID参数的初始值。

2.4设置自适应机制设置自适应机制，根据系统的性能指标进行PID参数的自适应调整。

2.5运行仿真运行仿真，观察系统的响应特性和PID参数的变化情况。

根据仿真结果可以对设计进行调整和优化。

3.结果分析根据仿真结果，可以分析系统的稳定性、动态性能和鲁棒性等指标，并对设计进行调整和改进。

模糊pid matlab(simulink)仿真详细步骤

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊控制实例及simulink仿真实验报告

模糊控制实例及simulink仿真实验报告
一、背景介绍
模糊控制是一种基于模糊逻辑的控制方法，其优点在于可以很好地处理复杂的非线性和不确定性系统，而且不需要精确的数学模型和计算，能够快速实现控制的优化。

二、实例介绍
本次实例采用一个双轮小车为对象，实现小车在平面上向指定位置运动的控制。

通过小车的速度和转向角两个输入变量，输出一个模糊控制信号，控制小车前进和转向。

三、实验过程
1. 建立模糊控制系统模型
打开Simulink软件，建立一个新模型，模型中包括输入变量、输出变量和控制器。

2. 设计输入变量和输出变量
（1）设计输入变量
本实例选择小车速度和转向角两个输入变量，每个变量包含三个模糊集合，速度变量分别为“慢速”、“中速”、“快速”，转向角变量分别为“左转”、“直行”、“右转”。

（2）设计输出变量
模糊控制信号输出变量选择小车的前进和转向，每个变量包含三个模糊集合，分别为“慢行”、“中行”、“快行”、“左转”、“直行”、“右转”。

3. 建立控制器
建立模糊控制器，包含输入变量和输出变量的关系，建立控制规则库和模糊关系。

4. 仿真实验
在Simulink下进行仿真实验，调整控制器参数，观察小车运动状态，对比试验。

四、实验结果
经过多次试验和调整，得到最优的小车模糊控制参数，可以实现小车的平滑运动
和准确转向。

五、实验结论
本实验通过建立一个小车的模糊控制系统，可以有效实现小车的平滑运动和准确转向，控制效果优于传统的PID控制方法。

模糊控制可以很好地处理非线性、不确定性和模糊性的系统，适合许多需要快速优化控制的场合。

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)2这个例子的程序百度文库里有很多版本，但我下了很多都有错误，运行不了。

以下程序我一字一字的敲出来的，已经成功运行，绝对无误。

仿真实例，被控对象为p G (s)=ss s 1047035.8752350023++ 采样时间为1ms ，采用模糊PID 控制进行阶跃响应，在第300个采样时间时控制器输出加1.0的干扰，相应的运行结果如图1~13所示。

仿真程序如下：将以下程序保存为fuzzypid.m 文件，即可得到仿真结果。

%fuzzy tunning PID controlclear all ;clear all ;a=newfis('fuzzpid');a=addvar(a,'input','e',[-3,3]); %parameter ea=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'input','ec',[-3,3]); %parameter eca=addmf(a,'input',2,'NB','zmf',[-3,-1]);a=addmf(a,'input',2,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',2,'Z','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);a=addmf(a,'input',2,'PM','trimf',[0,2,3]);a=addmf(a,'input',2,'PB','smf',[1,3]);a=addvar(a,'output','kp',[-0.3,0.3]); %parameter kpa=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);a=addmf(a,'output',1,'NM','trimf',[-0.3,-0.2,0]);a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);a=addmf(a,'output',1,'Z','trimf',[-0.2,0,0.2]);a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);a=addmf(a,'output',1,'PM','trimf',[0,0.2,0.3]);a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);a=addvar(a,'output','ki',[-0.06,0.06]); %parameter ki a=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);a=addmf(a,'output',2,'NM','trimf',[-0.06,-0.04,0]);a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]); a=addmf(a,'output',2,'Z','trimf',[-0.04,0,0.04]);a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);a=addmf(a,'output',2,'PM','trimf',[0,0.04,0.06]);a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);a=addvar(a,'output','kd',[-3,3]); %parameter kda=addmf(a,'output',3,'NB','zmf',[-3,-1]);a=addmf(a,'output',3,'NM','trimf',[-3,-2,0]);a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);a=addmf(a,'output',3,'Z','trimf',[-2,0,2]);a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);a=addmf(a,'output',3,'PM','trimf',[0,2,3]);a=addmf(a,'output',3,'PB','smf',[1,3]);rulelist=[1 1 7 1 5 1 1;1 2 7 1 3 1 1;1 3 62 1 1 1;1 4 62 1 1 1;1 5 5 3 1 1 1;1 6 4 42 1 1;1 7 4 4 5 1 1;2 1 7 1 5 1 1;2 2 7 13 1 1;2 3 6 2 1 1 1;2 4 53 2 1 1;2 5 53 2 1 1;2 6 4 43 1 1;2 734 4 1 1;3 1 6 14 1 1;3 2 6 2 3 1 1;3 3 6 3 2 1 1;3 4 5 3 2 1 1;3 54 4 3 1 1;3 6 3 5 3 1 1;3 7 3 54 1 1;4 1 6 2 4 1 1;4 2 6 2 3 1 1;4 35 3 3 1 1;4 4 4 4 3 1 1;4 5 3 5 3 1 1;4 6 2 6 3 1 1;4 7 2 6 4 1 1;35 1 5 2 4 1 1;5 2 5 3 4 1 1;5 3 4 4 4 1 1;5 4 3 5 4 1 1;5 5 3 5 4 1 1;5 6 2 6 4 1 1;5 7 2 7 4 1 1;6 1 5 47 1 1;6 2 4 4 5 1 1;6 3 3 5 5 1 1;6 4 2 5 5 1 1;6 5 2 6 5 1 1;6 6 27 5 1 1;6 7 1 7 7 1 1;7 1 4 4 7 1 1;7 2 4 4 6 1 1;7 3 2 5 6 1 1;7 4 2 6 6 1 1;7 5 2 6 5 1 1;7 6 1 7 5 1 1;7 7 1 7 7 1 1];a=addrule(a,rulelist);a=setfis(a,'DefuzzMethod','mom');writefis(a,'fuzzpid');a=readfis('fuzzpid');%PID controllerts=0.001;sys=tf(5.235e005,[1,87.35,1.047e004,0]); dsys=c2d(sys,ts,'tustin');[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0;y_1=0;y_2=0;y_3=0;x=[0,0,0]';4error_1=0;e_1=0.0;ec_1=0.0;kp0=0.40;kd0=1.0;ki0=0.0;for k=1:1:500time(k)=k*ts;rin(k)=1;%using fuzzy inference to tunning PIDk_pid=evalfis([e_1,ec_1],a);kp(k)=kp0+k_pid(1);ki(k)=ki0+k_pid(2);kd(k)=kd0+k_pid(3);u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);if k==300 %adding disturbance(1.0v at time 0.3s)u(k)=u(k)+1.0;endif u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endyout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;error(k)=rin(k)-yout(k);%%%%%%%%%%%%%%%%%%%%%%%%%return of pid parameters%%%%%%%%%%%%%%%%%%%%%%%% u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);5x(1)=error(k); %calculating Px(2)=error(k)-error_1; %calculating Dx(3)=x(3)+error(k); %calculating De_1=x(1);ec_1=x(2);error_2=error_1;error_1=error(k);endshowrule(a)figure(1);plot(time,rin,'b',time,yout,'r'); xlabel('time(s)');ylabel( 'rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel( 'error ');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel( 'u ');figure(4);plot(time,kp,'r');xlabel('time(s)');ylabel( 'kp ');figure(5);plot(time,ki,'r');xlabel('time(s)');ylabel( 'ki ');figure(6);plot(time,kd,'r');xlabel('time(s)');ylabel( 'kd ');figure(7);plotmf(a,'input',1);figure(8);plotmf(a,'input',2);figure(9);plotmf(a,'output',1);figure(10);plotmf(a,'output',2);figure(11);plotmf(a,'output',3);plotfis(a);fuzzy fuzzpid.fis6仿真运行结果：789。

实例：MATLABSimulink实现模糊PID控制

实例：MATLABSimulink实现模糊PID控制被控对象：Ts = 0.1;Plant = c2d(zpk([],[-1 -3 -5],1),Ts); %零极点模型，并离散化根据对象Plant，确定PID参数：C0 = pid(1,1,1,'Ts',Ts,'IF','B','DF','B'); % 定义PID结构C = pidtune(Plant,C0) %对PID参数进行优化[Kp, Ki, Kd] = piddata(C); % 输出参数得出PID结构及其参数值：接下来根据求出的PID参数确定GCE、GE 、GCU 和GU的取值：由模糊PID控制结构可得如下等式：Kp = GCU * GCE + GU * GEKi = GCU * GEKd = GU * GCE形式转换如下：GE = 10; %根据模糊控制的论语直接确定GCE = GE*(Kp-sqrt(Kp^2-4*Ki*Kd))/2/Ki=3.4285;GCU = Ki/GE=2.8631;GU = Kd/GCE=2.0138;模糊PID控制系统结构（连续模糊控制器）：图中的离散时间积分和微分块直接调用。

模糊控制器输入输出结构：模糊控制器输入输出隶属度函数：模糊控制器规则表：模糊控制器规则曲面图：连续模糊PID控制器，仿真结果：模糊PID控制系统结构（离散模糊控制器）：离散模糊控制器查询表：离散模糊PID控制器，仿真结果：主要代码如下：（1）、对象模型：Ts = 0.1;Plant = c2d(zpk([],[-1 -3 -5],1),Ts);（2）、PID参数优化：C0 = pid(1,1,1,'Ts',Ts,'IF','B','DF','B');C = pidtune(Plant,C0)[Kp, Ki, Kd] = piddata(C);（3）、比例因子确定：GE = 10;GCE = GE*(Kp-sqrt(Kp^2-4*Ki*Kd))/2/Ki;GCU = Ki/GE;GU = Kd/GCE;（4）、连续模糊PID控制建立：FIS = newfis('FIS','sugeno');%%% 定义输入E:FIS = addvar(FIS,'input','E',[-10 10]);FIS = addmf(FIS,'input',1,'Negative','gaussmf',[7 -10]); FIS = addmf(FIS,'input',1,'Positive','gaussmf',[7 10]); %%% 定义输入CE:FIS = addvar(FIS,'input','CE',[-10 10]);FIS = addmf(FIS,'input',2,'Negative','gaussmf',[7 -10]); FIS = addmf(FIS,'input',2,'Positive','gaussmf',[7 10]); %%% 定义输出u:FIS = addvar(FIS,'output','u',[-20 20]);FIS = addmf(FIS,'output',1,'Min','constant',-20);FIS = addmf(FIS,'output',1,'Zero','constant',0);FIS = addmf(FIS,'output',1,'Max','constant',20);% 定义规则:%% # If |E| is Negative and |CE| is Negative then |u| is -20 % # If |E| is Negative and |CE| is Positive then |u| is 0% # If |E| is Positive and |CE| is Negative then |u| is 0% # If |E| is Positive and |CE| is Positive then |u| is 20 ruleList = [1 1 1 1 1;... % Rule 11 2 2 1 1;... % Rule 22 1 2 1 1;... % Rule 32 23 1 1]; % Rule 4FIS = addrule(FIS,ruleList);gensurf(FIS) %生成模糊控制器（5）、离散模糊控制器查询表：Step = 2;E = -10:Step:10;CE = -10:Step:10;N = length(E);LookUpTableData = zeros(N);for i=1:Nfor j=1:N% compute output u for each combination of break points LookUpTableData(i,j) = evalfis([E(i) CE(j)],FIS);endend。

模糊pidmatlab(simulink)仿真详细步骤

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name中键入名称，在Type 中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊自适应PID控制器及Simulink仿真

模糊自适应PID控制器及Simulink仿真目录摘要 (1)ABSTRACT (1)第一章绪论 (1)1.1PID控制器的发展与应用 (1)1.2PID控制器参数设置中存在的问题 (2)1.3模糊自适应PID控制器发展研究现状 (2)1.4本文的主要工作 (4)第二章 PID控制原理简介 (4)2.1引言 (4)2.2PID控制原理 (5)2.3PID控制器系统概述 (5)2.3.1比例控制(P) (7)2.3.2 积分调节(I) (7)2.3.3微分调节(D) (9)第三章 PID控制器应用技术简介 (10)3.1数字PID控制算法原理 (11)3.2位置式PDI控制算法 (11)3.3控制规律的选择 (12)3.4PID控制器的参数整定 (13)第四章模糊PID控制器及系统仿真 (13)4.1模糊自适应PID控制系统 (13)4.2常规PID和模糊自适应PID控制系统的仿真比较 (14)4.3常规PID控制系统仿真 (14)4.4模糊自适应PID控制系统仿真 (16)4.5二者的比较 (18)第五章总结 (20)参考文献 (23)致谢 (24)*******大学2012届本科生毕业设计（论文）摘要随着工业生产的发展，于20世纪30年代，美国开始使用PID功调节器，它比直接作用式调节器具有更好的控制效果，因而很快得到了工业界的认可。

至今，在所有生产过程控制中，大部分的回路仍采用结构简单、鲁棒性强的PID控制或改进型PID控制策略。

PID控制作为一种经典的控制方法，几乎遍及了整个工业自动化领域，是实际工业生产过程正常运行的基本保证;控制器的性能直接关系到生产过程的平稳高效运行以及产品的最终质量，因此控制系统的设计主要体现在控制器参数的整定上。

随着计算机技术的飞跃发展和人工智能技术渗透到自动控制领域，近年来出现了各种实用的PID控制器参数整定方法。

PID控制算法作为最通用的控制方法，对它的参数整定有许多方法;对于不同的控制要求、不同的系统先验知识，考虑用不同的方法;这些算法既要考虑到收敛性、直观、简单易用，还要综合负载干扰、过程变化的影响，并能根据尽可能少的信息和计算量，给出较好的结果。

自整定模糊PID控制器的设计与Simulink仿真_龚齐斌

参考文献：
［ 1］王爽心， M］．北京：葛晓霞．汽轮机数字电液控制系统［ 2004．中国电力出版社，［ 2］胡晓冬， M］．北京：人董辰辉． MATLAB 从入门到精通［ 2010．民邮电出版社，［ 3］叶伟．基于 MATLAB 的模糊控制器设计与实现［ J］．机 2005 ，（ 10 ）： 126 ～ 128．床与液压，［ 4］张德丰． MATLAB / Simulink 建模与仿真［M］．北京：电 2009．子工业出版社，［ 5］李宜达．控制系统设计与仿真［M］．北京：清华大学出 2004．版社，
0Байду номын сангаас
引言
目前，绝大多数生产过程控制系统采用的控制
装置具有的控制规律大多都是比例、积分和微分规律，故称之为 PID 控制器。 PID 控制器是实际工业控制过程中应用最广泛的一种控制器。但是，为了取得很好地控制效果，常常需要对 PID 控制器的参这需要通过大量的实验和整定人员的数进行整定，本文将 PID 控制器与模糊控丰富实践经验。为此，制相结合，设计出了一种自整定模糊 PID 控制器。它既保留了 PID 控制器原有的控制算法，又通过模该糊控制在线整定 PID 控制器的参数。通过仿真，控制器的控制效果优于原有 PID 控制器。
参考文献：
［ 1］刘伟，许珉，杨宛辉．面向对象的电力系统图形程序设 J］．继电器， 2003 ，（ 11 ）．计方法［
The Application of GDI + in the MS． NETbased Vector Diagram in Power System
HU Runzi1 ， HU Pengfei2 （ 1． Dispatching and Control Center of Chongqing Electric Power Corporation， Chongqing 400014 ， China； 2． Maintenance Branch of Chongqing Electric Power Corporation 400039 ， China） Abstract： This essay introduces the application of GDI + （ Graphical Device Interface ） in the MS． NETbased vector analyzes its advantages， and points out its practical value in this field． diagram in power system， Key words： GDI + ； MS． NET； power system； vector diagram； ADO． NET （上接第 90 页）

模糊PID基本原理及matlab仿真实现(新手!新手!新手!)

模糊PID基本原理及matlab仿真实现（新⼿！新⼿！新⼿！）有关模糊pid的相关知识就把⾃⼰从刚接触到仿真出结果看到的⼤部分资料总结⼀下，以及⼀些⾃⼰的ps以下未说明的都为转载内容在讲解模糊PID前，我们先要了解PID控制器的原理（本⽂主要介绍模糊PID的运⽤,对PID控制器的原理不做详细介绍）。

PID控制器（⽐例-积分-微分控制器）是⼀个在⼯业控制应⽤中常见的反馈回路部件，由⽐例单元P、积分单元I和微分单元D组成。

PID控制的基础是⽐例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快⼤惯性系统响应速度以及减弱超调趋势。

1.1传统PID控制传统PID控制器⾃出现以来，凭借其结构简单、稳定性好、⼯作可靠、调整⽅便等优点成为⼯业控制主要技术。

当被控对象的结构和参数具有⼀定的不确定性，⽆法对其建⽴精确的模型时，采⽤PID控制技术尤为⽅便。

PID控制原理简单、易于实现，但是其参数整定异常⿇烦。

对于⼩车的速度控制系统⽽⾔，由于其为时变⾮线性系统不同时刻需要选⽤不同的PID参数，采⽤传统的PID控制器，很难使整个运⾏过程具有较好的运⾏效果。

1.2模糊PID控制模糊PID控制，即利⽤模糊逻辑并根据⼀定的模糊规则对PID的参数进⾏实时的优化，以克服传统PID参数⽆法实时调整PID参数的缺点。

模糊PID控制包括模糊化，确定模糊规则，解模糊等组成部分。

⼩车通过传感器采集赛道信息，确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec，根据给定的模糊规则进⾏模糊推理，最后对模糊参数进⾏解模糊，输出PID控制参数。

2.1模糊化模糊控制器主要由三个模块组成：模糊化，模糊推理，清晰化。

具体如下图所⽰。

⽽我们将⼀步步讲解如何将模糊PID算法运⽤到智能车上。

（最好⽤笔⼀步步⾃⼰写⼀遍）⾸先我们的智能车会采集到赛道的相关数据，例如摄像头车，其采集到的数据经过算法处理之后会得到与中线的偏差E，以及当前偏差和上次偏差的变化（差值）EC两个值（即此算法为2维输⼊，同理也可以是1维和3维，但2维更适合智能车）。

自适应pid控制simulink算法

自适应pid控制simulink算法自适应PID控制是一种根据系统响应动态调整PID参数的控制算法。

在Simulink中，可以使用两种方法实现自适应PID 控制算法。

方法一：使用Simulink自带的自适应PID控制器模块（Adaptive PID Controller block）。

这个模块可以根据系统的反馈信号和设定值信号，自动调整PID参数。

可以通过设置一些参数，如初始PID参数、自适应算法等，来控制自适应过程。

这个模块是较为简单方便的方法，适用于一般的自适应控制。

方法二：使用Matlab Function block来实现自适应PID控制算法。

Matlab Function block是一种可以在Simulink模型中使用自定义的Matlab代码块，可以用来实现更为个性化和复杂的算法。

可以在这个代码块中编写自适应PID控制算法的Matlab代码，并在Simulink模型中使用。

具体实现自适应PID控制算法的步骤如下：1. 在Simulink模型中添加控制系统组件，如输入信号、PID控制器、系统模型、反馈传感器等。

2. 使用上述的方法一或方法二，在Simulink模型中添加自适应PID控制算法的组件。

3. 针对具体的自适应PID算法，设置相关参数。

如果是使用自适应PID控制器模块，可以设置初始PID参数、自适应算法类型、自适应学习率等参数。

如果是使用Matlab Function block，可以在Matlab代码中设置相关参数。

4. 运行Simulink模型，观察系统响应，并根据实际情况调整参数。

5. 根据实际需要，对PID参数进行显示、记录或保存等操作，用于后续分析和调整。

以上是使用Simulink实现自适应PID控制算法的一般步骤，具体实现过程需要根据具体控制系统的需求和自适应算法的特点进行调整。

自适应模糊PID控制器的设计与仿真

毕业论文(设计) 题目自适应模糊PID控制器的设计与仿真学生姓名*******学号*******院系*******专业电气工程与自动化指导教师*******二Ｏ一一年五月二十五日目录1引言 (1)1.1 PID简介 (1)1.2 模糊控制简介 (2)1.3 本文研究的目的和意义 (2)1.4 本文的内容与安排 (3)2国内外现状 (3)3 MATLAB工具箱简介 (4)3.1 MATLAB 系统的应用 (4)3.2 Simlulink工具箱 (4)3.3 模糊逻辑工具箱 (5)3.4 MATLAB环境下的SIMULINK的应用 (5)3.4.1 MATLAB 环境中启动SIMULINK 的方法 (5)3.4.2打开SIMULINK 模型窗口的方法 (5)3.4.3 SIMULINK 仿真基本步骤 (5)4自适应模糊PID控制器的设计 (6)4.1 自适应模糊PID控制器的性能要求 (6)4.2 PID控制的理论基础 (6)4.3 模糊控制原理 (9)4.4 模糊PID控制系统结构及原理 (10)4.5 PID控制器参数自整定原则 (10)4.6 各变量隶属度函数的确定 (11)4.7 建立模糊规则表 (13)5 利用MATLAB对模糊PID控制系统进行仿真 (18)5.1建立系统结构仿真框图 (18)5.2 仿真结果分析 (19)6结论 (22)参考文献 (23)ABSTRACT (25)致谢 (26)附录 (27)自适应模糊PID控制器的设计与仿真摘要：本文在参数自适应模糊PID控制器的基础上，利用模糊推理的方法实现了对PID参数的在线自动整定，并且在MATLAB软件下将该控制器在某系统中的应用进行了研究，仿真结果表明，参数自适应模糊PID控制能使系统达到满意的控制效果，对进一步应用研究具有较大的参考价值。

关键词：自适应；PID控制器；模糊PID；MATLAB仿真1引言1.1 PID简介PID，（Proportional Integral Derivative）控制是目前工业上应用最广泛深入的控制方法。

Matlab模糊PID详细设计过程(包括程序和simulink工具箱两种方案)

2
其中k是量化因子，其值为：
b. 建立模糊集合：
k= 2��
�� −��
根据需要确定输入输出量的模糊集合个数，本次设计中输入输出都取了7个，NB（负大）、
NM（负中）、NS（负小）、ZE（零）、PS（正小）、PM（正中）、PB（正大），然后根
据主观看法在各个模糊集填入每个量化等级对应的隶属度值就得到了模糊集合。
55000 +90.5�� 2 +1000
��+7
（二）、模糊PID控制工作原理
• 自适应模糊PID控制器结构如下图所示，其以常规PID为基础，采用模糊推理的思想，将被控量的偏差e和偏差变化率ec作为二维模糊控制器的输入，PID的kp、ki、kd作为输出，利用模糊控制规律在线整定PID各个参数，其中模糊控制部分包括模糊化、模糊推理和解模糊化。
NB
NM
NS
NS
ZE
ZE
NS
NB
NM
NS
NS
ZE
PS
PS
ZE
NM
NM
NS
ZE
PS
PM
PM
PS
NM
NS
ZE
PS
PS
PM
PB
-0.06 -0.04 -0.02
0
0.02
0.04
0.06
kd
-3
-2
-1
0
1
2
3
量化等级 -3
-2
-1
0
1
2
3
状态变量
相关的隶属度函数
PB
0
0
0
0

Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真(word文档良心出品)

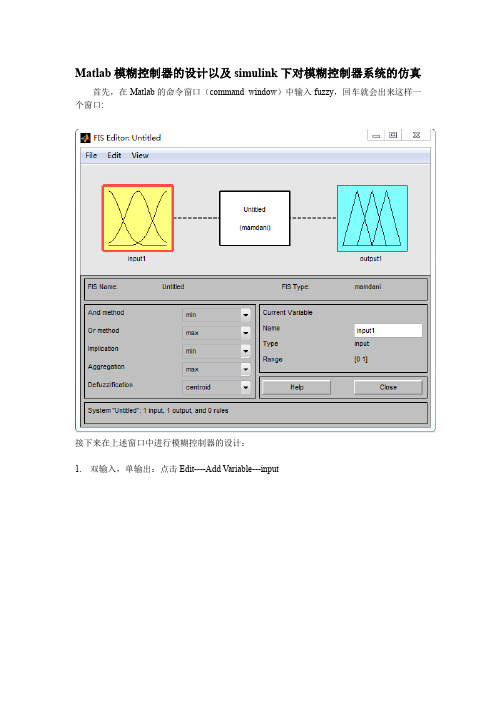
Matlab模糊控制器的设计以及simulink下对模糊控制器系统的仿真首先，在Matlab的命令窗口（command window）中输入fuzzy，回车就会出来这样一个窗口:接下来在上述窗口中进行模糊控制器的设计：1.双输入，单输出：点击Edit----Add Variable---input2.为E添加隶属度函数，E的论域为{-6，-5，-4，-3，-2，-1,0,1，2,3,4,5,6}，E的模糊集合为{NB,NM,NS,NZ,PZ,PS,PM,PB},Edit—Membership Function edit,如下图所示：3.为EB添加隶属度函数，EB的论域为{-6，-5，-4，-3，-2，-1,0,1，2,3,4,5,6}，EB的模糊集合为{NB,NM,NS,ZE,PS,PM,PB},Edit—Membership Function edit,如下图所示：4.为U添加隶属度函数，U的论域为{-6，-5，-4，-3，-2，-1,0,1，2,3,4,5,6}，U的模糊集合为{NB,NM,NS,ZE,PS,PM,PB},Edit—Membership Function edit,如下图所示：其中E,EB,U均为模糊量。

5.为模糊控制器设计模糊规则，由于E的语言变量有8个，EB的语言变量有7个，所以模糊控制器的模糊规则总共有8*7=56条，接下来为模糊控制器添加规则：双击untitled，则有下面的表格：制定完成后，会形成模糊规则矩阵，系统会根据模糊输入量E,EB，经过模糊控制规则[56条]，进而确定输出量U。

6.对输入量模糊化以及对输出量清晰化，我们采取最小最大重心法。

7.点击export—to file. ***#$.fis文件就是所设计的控制器。

8.下面对我们设计的模糊控制器进行检验，所构建的系统如下：系统分析：模糊控制器：双输入单输出，输入为误差以及误差的变化率的模糊量，输出为控制量的模糊量，模糊控制器中有56条规则。

模糊pid_matlab(simulink)仿真详细步骤

下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值围，本例中In_x和In_y的取值围均为[0 10], Out_x和Out_y的取值围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type 中选择形状，在Params中键入围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊PID的Simulink仿真设计及结果分析

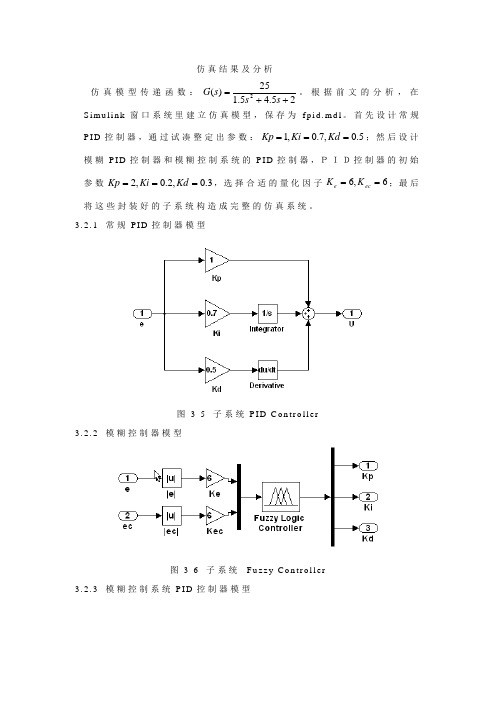
仿真结果及分析仿真模型传递函数：25.45.125)(2++=s s s G 。

根据前文的分析，在S i m u l i n k 窗口系统里建立仿真模型，保存为f p i d.m d l 。

首先设计常规P I D 控制器，通过试凑整定出参数：5.0,7.0,1===Kd Ki Kp ；然后设计模糊P I D 控制器和模糊控制系统的P I D 控制器，ＰＩＤ控制器的初始参数3.0,2.0,2===Kd Ki Kp ，选择合适的量化因子6,6==ec e K K ；最后将这些封装好的子系统构造成完整的仿真系统。

3.2.1 常规P I D 控制器模型图3-5 子系统P I D C o n t r o l l e r3.2.2 模糊控制器模型图3-6 子系统 F u z z y C o n t r o l l e r3.2.3 模糊控制系统P I D 控制器模型图3-7子系统P I D3.2.4模糊ＰＩＤ参数自整定模型图3-8模糊ＰＩＤ参数自整定控制系统3.2.5结果分析图3-9 仿真曲线图图3-9为常规P I D 控制和模糊P I D 自整定控制对阶跃响应曲线。

通过计算比较：常规P I D 的超调量%25.16%=σ，调节时间s t =5s ；模糊ＰＩＤ参数自整定控制的超调为０，调节时间为０.５ｓ。

实验结果表明，采用模糊P I D 参数自整定控制调节时间减小，系统的响应速度加快；系统的超调量减小，系统的动态特性和稳态特性均得到改善。

3.2.6 延迟二阶惯性系统模型分析仿真仿真模型：234.1)(23.0++=-s s e s G s。

仿真结果表明，对于延迟二阶系统模糊P I D 自整定控制阶跃响应曲线超动态特性较Z -N 整定P I D 控制阶跃响应有所改善，模糊控制对系统适应性更强。

模糊自整定PID控制器设计以及MATLAB仿真分析

收稿日期：2004-03-31第22卷第9期计算机仿真2005年9月文章编号：1006-9348（2005）09-0242-03模糊自整定PID 控制器设计以及MATLAB 仿真分析肖奇军1，李胜勇2（1.肇庆学院电子信息工程系，广东肇庆526061；2.上海交通大学微纳米科学技术研究院，上海200030）摘要：为了解决液压控制的关键技术，该文针对时变、非线性的电液伺服系统提出了模糊自整定PID 控制器设计的思路，结合Simuiink 和模糊工具箱并进行仿真分析，该仿真模型具有结构简单、界面直观、便于修改等特点，根据PID 参数变化需要提出了模糊控制规则选取方法，给出了系统软、硬件实现方法，该系统具有操作方便、人机界面风格良好等优点。

使用仿真和实验相结合的方法获取最佳控制参数，通过仿真和实验结果可以看出这种算法的实用性和有效性。

关键词：模糊自整定；仿真分析；应用分析；电液伺服系统中图分类号：TP391.9 文献标识码：B Design and Simulation Analysis of Fuzzy Self -adaptive PID ControlXIAO Oi -jun 1，LI Sheng -yong 2（1.Dept.of Eiectronics Information Engineering ，Zhaoging University ，Zhaoging Guangdong 526061，China ；2.Institute of Micronanometer Science and Technoiogy Shanghai Jiaotong Univ.，Shanghai 200030，China ）ABSTRACT ：The paper puts forward the idea of fuzzy seif -adaptive PID controiier design aimed at the time -chan-ging and non -iinear eiectro -hydrauiic servo and the simuiation anaiysis combined with Simuiink and fuzzy tooibox.The simuiation possesses the characteristic of simpie construction ，direct interface and easy modification etc and ob-tains the way for fuzzy controi ruie seiection according to the need of PID parameter changing.It aiso provides the way for software and hardware reaiization.The system possesses the merit of convenient operation and good interface.It ob-tains the best parameter through simuiation combined with experience and from the simuiation resuit we can see the practicaiity and vaiidity of this controi method and soive the key technoiogy of hydrauiic controi.KEYWORDS ：Fuzzy seif -adaptive ；Simuiation anaiysis ；Appiication anaiysis ；Eiectro -hydrauiic servo1 引言模糊控制一直是智能控制研究的热点，其应用水平代表着产品智能化水平，模糊控制以其控制简单、实现成本低廉、无需建立数学模型等独到的优点被广泛应用于家电等控制中，尤其是在时变、非线性的液压控制系统中得到广泛的应用。

基于simulink的模糊自适应pid三闭环控制设计及仿真

0 引言PID控制是目前应用于装备控制和自动化生产中一种比较成熟的控制方法,其具有算法相对简单、稳定性高和鲁棒性好的优点 [1]。

随着工业技术的发展对伺服电机的控制精度要求也在不断提高,单个PID控制器很难满足高精度的指标,目前常采用PID三闭环控制方法,即位置环、速度环、电流环组成的三环负反馈PID控制系统[2],PID 三闭环控制模型如图1所示。

其中内环是电流环,电流环为控制伺服电机输入电流大小的闭环回路,通过检测驱动器的输出电流值对设定电流进行调节,使得伺服电机的输入电流尽量接近设定电流;中间环是速度环,通过检测伺服电机编码器的速度反馈信号进行速度调节,速度环输出为电流环的设定,速度环的控制包含电流环控制;最外环为位置环,通过检测码盘位置信息进行位置控制,其输出为速度环的设定,在位置控制的同时进行速度和电流的控制[3-4]。

在使用PID三闭环控制方式控制伺服电机的过程中,需要对电流、速度、位置三环的PID参数依次进行调节,获得每个环中kp、ki、kd的最优值。

在实际调试中,由于三个PID控制器存在相互影响,需要调试人员具有较为丰富的经验,不断进行试验,以得到最优参数［5］。

当参数选择不合适时,系统容易发生超调现象,当一组最优PID参数选定后,负载变化或外部施加扰动时,伺服电机控制精度会迅速降低。

针对PID三闭环控制的缺点,本研究提出了基于模糊控制原理的模糊自适应PID三闭环控制方法。

1 模糊自适应PID三闭环控制方法设计模糊自适应PID控制以普通PID控制为基础,运用模糊数学的理论及方法,根据现有的工程经验,将相关运算规则用模糊集合表示,把模糊化后的控制规则作为先验知识储存于数据库中,然后根据系统输入信号的变化情况,计算机进行相应的模糊推理,实现对PID参数的自整定调整[6-8]。

在PID三闭环控制中,位置环反馈信号取自电机编码器或外部码盘,位置控制环输出为速度环的设定,在位置环控制模式下系统进行了电流、速度、位置三个环的运算,因此位置环PID控制器性能好坏很大程度上决定了PID三闭环控制的精度 [9]。

模糊自适应PID控制器及Simulink仿真实现_杨益兴

总第190期2010年第4期舰船电子工程Ship Elec tronic EngineeringV o l.30No.4127模糊自适应PID控制器及Simulink仿真实现＊杨益兴1)　崔大连2)　周爱军2)(海军驻武汉第七★一研究所军事代表室1)　武汉　430064)(海军大连舰艇学院装备系统与自动化系2)　大连　116018)摘　要　常规PID控制对非线性、时变系统的控制效果不是很理想,文章提出将模糊技术与P ID控制相结合的控制方式,即模糊自适应PID控制器,并结合实例在Simulink环境中实现了该模糊自适应PID控制器的仿真。

仿真结果表明,该模糊自适应PID控制具有控制灵活、响应快和适应性能强的优点。

关键词　模糊控制;P ID控制;Simulink中图分类号　T P273.2Self-adaptive Fuzzy PID Controllerand Re alizing the Control System in Simulink EnvironmentYang Yixing1)　Cui Dalian2)　Z hou Aijun2)(M ilitary A gent Roo m of701Resea rch Institute1),Wuhan　430064)(Dept.o f Equipment Sy stem and Automa tion,Da lian N aval Academy2),Dalian　116018)A bstract　T he conventio nal PID co nt roller is no t usua lly applicable to the ty pe o f time-var ying no nlinear systems.So a new se lf-ada ptive fuzzy P ID contro ller is presented using the fuzzy technology and PI D co ntrolle r,w hich realizing the self-a-daptive fuzzy PID contr ol sy stem in Simulink environment with a pa rticula r case.Simulatio n results sho w the self-adaptive fuzzy PID co ntrol has advantage s o f flex ibility co ntrol,fast r esponse and stro ng adaptio n.Key Words　fuzzy co ntrol,P ID contro l,SimulinkClass Nu mber　T P273.21　引言在复杂系统中,由于被控对象的时变性、非线性和不确定性,传统的PID控制难以取得很好的控制效果,将先进控制策略和传统PID控制相结合是解决上述问题的一种有效途径。