材料科学基础 第九章习题
材料科学基础习题与答案

第一章 原子排列与晶体结构1. fcc 结构的密排方向是 ,密排面是 ,密排面的堆垛顺序是 ,致密度为 ,配位数是 ,晶胞中原子数为 ,把原子视为刚性球时,原子的半径r 与点阵常数a 的关系是 ;bcc 结构的密排方向是 ,密排面是 ,致密度为 ,配位数是 ,晶胞中原子数为 ,原子的半径r 与点阵常数a 的关系是 ;hcp 结构的密排方向是 ,密排面是 ,密排面的堆垛顺序是 ,致密度为 ,配位数是 ,晶胞中原子数为 ,原子的半径r 与点阵常数a 的关系是 。
2. Al 的点阵常数为0.4049nm ,其结构原子体积是 ,每个晶胞中八面体间隙数为 ,四面体间隙数为 。
3. 纯铁冷却时在912ε 发生同素异晶转变是从 结构转变为 结构,配位数 ,致密度降低 ,晶体体积 ,原子半径发生 。
4. 在面心立方晶胞中画出)(211晶面和]211[晶向,指出﹤110﹥中位于(111)平面上的方向。
在hcp 晶胞的(0001)面上标出)(0121晶面和]0121[晶向。
5. 求]111[和]120[两晶向所决定的晶面。
6 在铅的(100)平面上,1mm 2有多少原子?已知铅为fcc 面心立方结构,其原子半径R=0.175×10-6mm 。
第二章 合金相结构一、 填空1) 随着溶质浓度的增大,单相固溶体合金的强度 ,塑性 ,导电性 ,形成间隙固溶体时,固溶体的点阵常数 。
2) 影响置换固溶体溶解度大小的主要因素是(1) ;(2) ;(3) ;(4) 和环境因素。
3) 置换式固溶体的不均匀性主要表现为 和 。
4) 按照溶质原子进入溶剂点阵的位置区分,固溶体可分为 和 。
5) 无序固溶体转变为有序固溶体时,合金性能变化的一般规律是强度和硬度 ,塑性 ,导电性 。
6)间隙固溶体是 ,间隙化合物是 。
二、 问答1、 分析氢,氮,碳,硼在α-Fe 和γ-Fe 中形成固溶体的类型,进入点阵中的位置和固溶度大小。
已知元素的原子半径如下:氢:0.046nm ,氮:0.071nm ,碳:0.077nm ,硼:0.091nm ,α-Fe :0.124nm ,γ-Fe :0.126nm 。
无机材料科学基础课后习题答案9

1.碳酸钙的加热分解:。
试用一般热力学方程求分解反应的及分解温度?答案:1123K提示:查表获得有关热力学数据,计算800-1400K间的,再作图,=0所对应的温度为即为分解温度。
解:由《硅酸盐热力学》查得下列数据H。
298=∑(△H。
生,298)产物-∑(△H。
生,298)反应物=-151.90×103-94.05×103+288.45×103=42.5×103卡/摩尔△G。
298=∑△G。
生,298)产物-∑△G。
生,298)反应物=-1.44.40×103-94.26×103+269.78×103=31.12×103卡/摩尔因为△a=11.67+10.55-24.98=-2.76△b=1.08×10-3+2.16×10-3-5.24×10-3=-2×10-3△c=-1.56×105-2.04×105+6.20×105=2.6×105△H.=△H.298-△a·298-1/2△b(298)2+△c(298)-=42500+2.76×298+1/2×2×10-3×(298)2+2.6×105×(298)-1=44283.76积分常数I=(△G..298-△H.)(298)-+△aln298+1/2△b·298+1/2△c(298)-2=-44.17-15.72-0.298+1.46=-58.73因为当△G。
〉0时,CaCO3不能自发分解,当△G。
〈0时,CaCO3自发分解,所以,△G。
=0的温度为CaCO3开始分解的温度由热力学方程△GT。
=△H。
-△aTlnT-1/2△bT2-1/2△CT-+IT令△G。
T=0 解得方程得T=1123K2.碳酸钙的加热分解:。
《材料科学基础》潘金生第九章课后答案

9-1 证明临界晶核的形核功与临界晶核体积的关系为:∆G=VV∗.∆GG VV2并证明非均匀形核有同样的关系。
均匀形核:∆G=−43ππrr3∆GG VV+4ππrr2γγSSSS其中,∆GG VV=∆GG VV SS−∆GG VV SS=SS VV.∆TT TT mm,∆TT=TT mm−TT,γγSSSS表示固-液相的界面能,LL VV表示单位体积的熔化潜热,数值为正利用dd∆GG ddrr=0求出临界形核半径rr∗=2γγSSSS∆GG VV所以,∆G∗=−43ππrr∗3∆GG VV+4ππrr∗2γγSSSS=−VV∗∆GG VV+VV∗.3rr∗.γγSSSS=−VV∗∆GG VV+VV∗.3.∆GG VV2γγSSSSγγSSSS=VV∗.∆GG VV2非均匀形核同理可得:∆G=VV∗.∆GG VV2ff(θθ)9-2 写出临界晶核中原子数目的表达式,假设为面心立方晶体。
→临界晶核中原子数目=晶胞数×4(每个面心立方晶胞有4个原思路:晶胞数=临界晶核体积单个晶胞体积子)解:单个晶胞的体积=a3,其中a表示晶格常数,其与原子半径的关系为:α=2√2rr所以,单个晶胞的体积=�2√2rr�3=16√2rr3=12√2VVππ(因为单个原子体积V=43ππrr3)临界晶核的体积=43ππrr∗3=43ππ(2γγ∆GG BB)3临界晶核中原子数目=晶胞数×4=临界晶核体积单个晶胞体积×4=43ππ�2γγ∆GG BB�3×ππ12√2VV×4=16√2γγ3ππ29VV∆GG BB39-3 设想液体在凝固时形成的临界核心是边长为a的立方体,(1)导出均匀形核时临界晶核边长和临界形核功。
(2)证明在同样过冷度下均匀形核时,球形晶核较立方晶核更易形成。
(1)∆G=−aa3∆GG VV+6aa2γγSSSS利用dd∆GG ddaa=0求出临界晶核边长,aa∗=4γγSSSS∆GG VV所以,∆G∗=−aa∗3∆GG VV+6aa∗2γγSSSS=32γγSSSS3∆GG VV2(2)因为∆GG VV=∆GG VV SS−∆GG VV SS=LL VV.∆TT TT mm所以在相同过冷度下,∆GG VV相同又因为对球形晶核有∆G∗==16ππγγSSSS33∆GG VV2所以,∆GG球∗<∆GG立∗,故在同样过冷度下均匀形核时,球形晶核较立方晶核更易形成。
武汉理工大学材料科学基础()课后习题和答案

第一章绪论1、仔细观察一下白炽灯泡,会发现有多少种不同的材料?每种材料需要何种热学、电学性质?2、为什么金属具有良好的导电性和导热性?3、为什么陶瓷、聚合物通常是绝缘体?4、铝原子的质量是多少?若铝的密度为2.7g/cm3,计算1mm3中有多少原子?5、为了防止碰撞造成纽折,汽车的挡板可有装甲制造,但实际应用中为何不如此设计?说出至少三种理由。
6、描述不同材料常用的加工方法。
7、叙述金属材料的类型及其分类依据。
8、试将下列材料按金属、陶瓷、聚合物或复合材料进行分类:黄铜钢筋混凝土橡胶氯化钠铅-锡焊料沥青环氧树脂镁合金碳化硅混凝土石墨玻璃钢9、Al2O3陶瓷既牢固又坚硬且耐磨,为什么不用Al2O3制造铁锤?第二章晶体结构1、解释下列概念晶系、晶胞、晶胞参数、空间点阵、米勒指数(晶面指数)、离子晶体的晶格能、原子半径与离子半径、配位数、离子极化、同质多晶与类质同晶、正尖晶石与反正尖晶石、反萤石结构、铁电效应、压电效应.2、(1)一晶面在x、y、z轴上的截距分别为2a、3b、6c,求出该晶面的米勒指数;(2)一晶面在x、y、z轴上的截距分别为a/3、b/2、c,求出该晶面的米勒指数。
3、在立方晶系的晶胞中画出下列米勒指数的晶面和晶向:(001)与[210],(111)与[112],(110)与[111],(322)与[236],(257)与[111],(123)与[121],(102),(112),(213),[110],[111],[120],[321]4、写出面心立方格子的单位平行六面体上所有结点的坐标。
5、已知Mg2+半径为0.072nm,O2-半径为0.140nm,计算MgO晶体结构的堆积系数与密度。
6、计算体心立方、面心立方、密排六方晶胞中的原子数、配位数、堆积系数。
7、从理论计算公式计算NaC1与MgO的晶格能。
MgO的熔点为2800℃,NaC1为80l℃, 请说明这种差别的原因。
8、根据最密堆积原理,空间利用率越高,结构越稳定,金钢石结构的空间利用率很低(只有34.01%),为什么它也很稳定?9、证明等径圆球面心立方最密堆积的空隙率为25.9%;10、金属镁原子作六方密堆积,测得它的密度为1.74克/厘米3,求它的晶胞体积。
材料科学基础课后习题及参考答案

绪论1、仔细观察一下白炽灯泡,会发现有多少种不同的材料每种材料需要何种热学、电学性质2、为什么金属具有良好的导电性和导热性3、为什么陶瓷、聚合物通常是绝缘体4、铝原子的质量是多少若铝的密度为cm3,计算1mm3中有多少原子5、为了防止碰撞造成纽折,汽车的挡板可有装甲制造,但实际应用中为何不如此设计说出至少三种理由。
6、描述不同材料常用的加工方法。
7、叙述金属材料的类型及其分类依据。
8、试将下列材料按金属、陶瓷、聚合物或复合材料进行分类:黄铜钢筋混凝土橡胶氯化钠铅-锡焊料沥青环氧树脂镁合金碳化硅混凝土石墨玻璃钢9、 Al2O3陶瓷既牢固又坚硬且耐磨,为什么不用Al2O3制造铁锤晶体结构1、解释下列概念晶系、晶胞、晶胞参数、空间点阵、米勒指数(晶面指数)、离子晶体的晶格能、原子半径与离子半径、配位数、离子极化、同质多晶与类质同晶、正尖晶石与反正尖晶石、反萤石结构、铁电效应、压电效应.2、(1)一晶面在x、y、z轴上的截距分别为2a、3b、6c,求出该晶面的米勒指数;(2)一晶面在x、y、z轴上的截距分别为a/3、b/2、c,求出该晶面的米勒指数。
3、在立方晶系的晶胞中画出下列米勒指数的晶面和晶向:(001)与[210],(111)与[112],(110)与[111],(322)与[236],(257)与[111],(123)与[121],(102),(112),(213),[110],[111],[120],[321]4、写出面心立方格子的单位平行六面体上所有结点的坐标。
5、已知Mg2+半径为,O2-半径为,计算MgO晶体结构的堆积系数与密度。
6、计算体心立方、面心立方、密排六方晶胞中的原子数、配位数、堆积系数。
7、从理论计算公式计算NaC1与MgO的晶格能。
MgO的熔点为2800℃,NaC1为80l℃, 请说明这种差别的原因。
8、根据最密堆积原理,空间利用率越高,结构越稳定,金钢石结构的空间利用率很低(只有%),为什么它也很稳定9、证明等径圆球面心立方最密堆积的空隙率为25.9%;10、金属镁原子作六方密堆积,测得它的密度为克/厘米3,求它的晶胞体积。
材料科学基础复习题

材料科学基础复习题第三章:晶体的范性形变(crystal plastic deformation)单晶体范性形变的两种基本⽅式:滑移(slip)和孪⽣(twinning)两者都为剪应变。
FCC的滑移⾯都是{111},滑移⽅向都是<110>,BCC的滑移⾯都有{110},滑移⽅向都是<111> 滑移⽅向都是最密排的⽅向,⽽滑移⾯则往往是密排⾯Schmid定律:当作⽤在滑移⾯上沿着滑移⽅向的分切应⼒达到某⼀临界值τc时,晶体便开始滑移。
P144.我们把只有⼀个滑移系统的滑移称为单滑移,具有两个或以上的滑移叫做双滑移或者多滑移。
晶粒和晶粒之间的过渡区域就称晶粒边界或称晶界。
晶粒越细,阻碍滑移的晶界便越多,屈服极限也就越⾼。
(细化晶粒不仅可以提⾼⾦属的强度,同时还可以提⾼其韧性)Hall 公式:拉伸应⼒变形(tensile stress deformation)晶体在外⼒作⽤下会发⽣形变,当外⼒较⼩时变形是弹性的,即卸载后变形也随之消失,这种可恢复的变形就称为,弹性变形(elastic deformation)当外⼒超过⼀定值后,应⼒和应变就不在成线性关系,卸载后变形也不能完全消失,⽽会留下⼀定的残余变形或者永久变形,这种不可恢复的变形就称为,塑性变形(plastic deformation)低碳钢的拉伸应⼒——应变曲线(图解计算题)延伸率(elongation):断裂前的最⼤相对伸长。
断⾯收缩率(reduction in cross-section):断裂前最⼤的相对⾯积缩减。
晶体的断裂(Crystal fracture)滑移系统(slip system):⼀个滑移⾯和位于该⾯上的⼀个滑移⽅向便组成了⼀个滑移系统。
孪⽣系统(twinning system):⼀个孪⽣⾯和该⾯上的⼀个孪⽣⽅向组成⼀个孪⽣系统。
加⼯硬化(work hardening):⾦属在冷加⼯过程中,要想不断地塑性变形,就需要不断增加外应⼒。
材料科学基础-习题

/jxtd/caike/这个网址有很多东西,例如教学录像,你可以上去看看,另外左下角有个“释疑解惑”,应该很有用第一章材料结构的基本知识习题1.原子中的电子按照什么规律排列?什么是泡利不相容原理?2.下述电子排列方式中,哪一个是惰性元素、卤族元素、碱族、碱土族元素及过渡金属?(1) 1s2 2s2 2p6 3s2 3p6 3d7 4s2(2) 1s2 2s2 2p6 3s2 3p6(3) 1s2 2s2 2p5(4) 1s2 2s2 2p6 3s2(5) 1s2 2s2 2p6 3s2 3p6 3d2 4s2(6) 1s2 2s2 2p6 3s2 3p6 4s13.稀土元素电子排列的特点是什么?为什么它们处于周期表的同一空格内?4.简述一次键与二次键的差异。
5.描述氢键的本质,什么情况下容易形成氢键?6.为什么金属键结合的固体材料的密度比离子键或共价键固体为高?7.应用式(1-2)~式(1-5)计算Mg2+O2-离子对的结合键能,以及每摩尔MgO晶体的结合键能。
假设离子半径为;;n=7。
8.计算下列晶体的离子键与共价键的相对比例(1) NaF(2) CaO9.什么是单相组织?什么是两相组织?以它们为例说明显微组织的含义以及显微组织对性能的影响。
10.说明结构转变的热力学条件与动力学条件的意义,说明稳态结构与亚稳态结构之间的关系。
11.归纳并比较原子结构、原子结合键、原子排列方式以及晶体的显微组织等四个结构层次对材料性能的影响。
第二章材料中的晶体结构习题第三章高分子材料的结构习题1.何谓单体、聚合物和链节?它们相互之间有什么关系?请写出以下高分子链节的结构式:①聚乙烯;②聚氯乙烯;③聚丙烯;④聚苯乙烯;⑤聚四氟乙烯。
2.加聚反应和缩聚反应有何不同?3.说明官能度与聚合物结构形态的关系。
要由线型聚合物得到网状聚合物,单体必须具有什么特征?4.聚合物的分子结构对主链的柔顺性有什么影响?5.在热塑性塑料中结晶度如何影响密度和强度,请解释之。
材料科学基础(武汉理工大学,张联盟版)课后习题及答案 第九章

第九章答案9-2什么叫相变?按照相变机理来划分,可分为哪些相变?解:相变是物质系统不同相之间的相互转变。
按相变机理来分,可以分为扩散型相变和非扩散型相变和半扩散型相变。
依靠原子或离子长距离扩散进行的相变叫扩散型相变。
非扩散型型相变指原子或离子发生移动,但相对位移不超过原子间距。
9-3分析发生固态相变时组分及过冷度变化相变驱动力的影响。
解:相变驱动力是在相变温度下新旧相的体自由能之差(),而且是新相形成的必要条件。
当两个组元混合形成固溶体时,混合后的体系的自由能会发生变化。
可以通过自由能-成分曲线来确定其相变驱动力的大小。
过冷度是相变临界温度与实际转变温度之差,相变形核的热力学条件是要有过冷度。
已知驱动力与过冷度之间的关系是:,这进一步说明了形核的热力学条件。
9-4马氏体相变具有什么特征?它和成核-生成相变有何差别?解:马氏体相变是替换原子经无扩散切变位移(均匀或不均匀)并由此产生形状改变和表面浮凸、曾不变平面应变特征的一级形核、长大的相变。
特征:具有剪切均匀整齐性、不发生原子扩散、相变速度快、相变有一定范围、有很大的切变型弹性应变能。
成核-生长过程中存在扩散相变,母相与晶相组成可相同可不同,转变速度较慢,无明显的开始和终了温度。
9-5试分析应变能及表面能对固态相变热力学、动力学及新相形状的影响。
解:物质的表面具有表面张力σ,在恒温恒压下可逆地增大表面积dA,则需功σdA,因为所需的功等于物系自由能的增加,且这一增加是由于物系的表面积增大所致,故称为表面自由能或表面能。
应变能和表面能可以影响相变驱动力的大小,和新相的形状。
9-6请分析温度对相变热力学及动力学的影响。
解:当温度降低,过冷度增大,成核势垒下降,成核速率增大,直至达到最大值;当温度继续下降,液相粘度增加,原子或分子扩散速率下降。
温度过高或过低对成核和生长速率均不利,只有在一定的温度下才有最大成核和生长速率。
9-7调幅分解与脱溶分解有何异同点?调幅分解所得到的显微结构与性能有何特点?解:调幅分解通过扩散偏聚由一种固溶体分解成与母相结构相同而成分不同的两种固溶体。
习题和思考题

《无机材料科学基础》习题和思考题第一章晶体1.球体按立方最紧密堆积方式堆积,取出立方晶胞,画出立方晶胞中的四面体空隙和八面体空隙的位置分布图。
2.用鲍林规则分析氧化镁晶体结构。
已知镁离子半径为0.65Å,氧离子半径为1.40Å。
(1)确定晶胞中质点的位置坐标;(2)计算每个晶胞中含氧化镁“分子”数,(3)已知晶胞常数a=4.20 Å,求氧化镁堆积系数和密度,(4)氧化镁晶体中最邻近的两个镁离子中心距为多少?次邻近的两个镁离子中心距为多少?最邻近和次邻近的两个氧离子中心距为多少?(5)画出氧化镁晶胞的(111)、(110)、(100)面的质点分布图并在图上标出氧离子的密排方向,求个面的面密度。
3.已知纤锌矿结构中存在两套硫离子和两套锌离子的六方底心格子,并已知锌离子填充在硫离子最紧密堆积体的四面体空隙中,现以一套硫离子的等同点为基准取六方晶胞,画出晶胞中的质点分布图,计算晶胞中所含式量分子数。
4.完成下表5. 六方最紧密堆积与四方最紧密堆积的堆积密度相同,为什么许多氧化物是以氧离子的立方最紧密堆积为基础,而较少以六方最紧密堆积为基础?6. 用鲍林规则分析镁橄榄石的结构:P48 图2-18(1)标记为50的Mg2+与哪几个氧离子配位形成[MgO6]八面体?写出O2+的标高;(2)标记为25的两个O2+与哪几个镁离子配位?写出Mg2+离子的标高;(3)标记为75的O2+离子与哪几个镁离子配位?写出Mg2+离子的标高;(4)标记为0和50的两个Mg2+的[MgO6] 八面体共用几个顶点?写出O2+的标高;(5)[SiO4] 和 [MgO6] 之间、[MgO6]和[MgO6] 八面体之间有那些连接方式?(6)镁橄榄石的晶胞是什么形状?计算晶胞中含有的式量分子数。
第二章晶体缺陷1.氧化镁为氯化钠型结构,氧化锂为反萤石型结构,在两种结构中氧离子都作立方最紧密堆积,为什么在氧化镁中主要的热缺陷是肖特基型,而在氧化锂中却是弗伦克尔型?萤石型结构的氧化物晶体中常见的热缺陷估计主要是什么类型?为什么?2.已知氯化钠晶体中肖特基缺陷形成焓为2.2ev,而氧化镁晶体中肖特基缺陷形成焓为6ev,试分别计算400℃时氯化纳晶体与氧化镁晶体中肖特基缺陷的浓度。
材料科学基础 第九章材料科学基础 第九章

第九章失效一、学习目的一个部件或结构的设计常常要求工程师使失效的可能性降到最小。
这样,理解各种失效模式的机制就很重要,即:断裂、疲劳和蠕变。
此外,熟悉所应用的合适的设计原理,以防止服役中失效二、本章主要教学内容学习本章后你可以做如下:1.描述韧性与脆性断裂的裂纹扩展机理。
2.解释脆性材料的强度比理论计算值低很多的原因。
以术语来定义断裂韧性(a)简单陈述(b)给出公式,说明公式中所有参数。
{4. 分辨应力集中系数、断裂韧性、平面应变断裂韧性。
}5. 简单解释为何相同陶瓷材料的同样试样的断裂强度通常会显著分散。
6. 简单描述陶器出现细微裂纹的现象。
7. 给出名称并描述两种冲击断裂实验技术。
8. 定义疲劳并特殊说明产生条件。
9. 从某种材料的疲劳图上确定:(a)疲劳寿命(在特定应力值下);(b)疲劳强度(在给定循环次数条件下)。
10. 定义蠕变,详细说明其产生条件。
11. 给出某种材料的蠕变图,判定(a)稳态蠕变率,(b)断裂寿命。
2.主要例题、习题的分析解答指导举例9.1较大块玻璃承受40 MPa拉力,如果其比表面能和弹性模量为0.3 J/m2和 69 GPa,求不产生断裂的最大表面裂纹长度。
解答:解此题必须用公式9.3,把a作为应变量重组表达式,已知:σ= 40 MPa, γs = 0.3 J/m2, E = 69 GPa ,代入得:设计举例9.1考虑半径为r厚度为t可以用作压力容器的薄壁球罐(图9.5)。
(a)设计球罐要求在由于形成临界尺寸裂纹并随后快速扩展之前球壁材料屈服,这样,球壁的塑性变形可以观察到,球罐内的压力可以在灾难性失效发生前释放掉。
显然,希望材料具有大的临界裂纹长度,以这一准则为基础,把金属合金按类别列表见附录B表B.5,临界裂纹尺寸从最长到最短。
(b)也常应用于压力容器的选择性设计术语为“破坏前泄露”。
利用断裂机制原理,在裂纹快速扩展发生之前,允许裂纹生长穿过整个容器壁厚度。
这样,裂纹将完全穿透容器壁,不会出现灾难性失效,允许通过带压液体泄露进行检测。
《材料科学基础》各章习题

图2-1 第一章 金属的晶体结构1. 试证明四方晶系中只有简单四方和体心四方两种点阵类型。
2. 为什么密排六方结构不能称作为一种空间点阵?3. 标出面心立方晶胞中(111)面上各点的坐标,并判断]101[是否位于(111)面上,然后计算]101[方向上的线密度。
4. 标出具有下列密勒指数的晶面和晶向:a) 立方晶系)421(,)231(,)130(,[]112,[]311;b) 六方晶系 )1112(,)0111(,)2123(,]1112[,]1321[。
5. 在立方晶系中画出{}111晶面族的所有晶面,并写出{123}晶面族和﹤221﹥晶向族中的全部等价晶面和晶向的密勒指数。
6. 在立方晶系中画出以]001[为晶带轴的所有晶面。
7. 试证明在立方晶系中,具有相同指数的晶向和晶面必定相互垂直。
8. 已知纯钛有两种同素异构体,低温稳定的密排六方结构Ti -α和高温稳定的体心立方结构Ti -β,其同素异构转变温度为882.5℃,计算纯钛在室温(20℃)和900℃时晶体中(112)和(001)的晶面间距(已知a a 20℃=0.2951nm, c a 20℃=0.4679nm, a β900℃=0.3307nm )。
9. 试计算面心立方晶体的(100),(110),(111)等晶面的面间距和面致密度,并指出面间距最大的面。
10. 平面A 在极射赤平面投影图中为通过NS 极和点0°N ,20°E 的大圆,平面B 的极点在30°N ,50°W处,a)求极射投影图上两极点A 、B 间的夹角;b)求出A绕B 顺时针转过40°的位置。
11. a)说明在fcc 的(001)标准极射赤面投影图的外圆上,赤道线上和0°经线上的极点的指数各有何特点?b)在上述极图上标出)101(、)011(、)112(极点。
12. 由标准的(001)极射赤面投影图指出在立方晶体中属于[110]晶带轴的晶带,除了已在图2-1中标出晶面外,在下列晶面中那些属于[110]晶带?)212(),231(),131(),210(),211(。
《无机材料科学基础》第九章复习题及答案

12.陶瓷的显微结构主要由哪些基本因子构成?
答:陶瓷是由晶体、玻璃体和气孔组成的多晶多相材料,其显 微结构包括晶体的种类和含量,晶粒尺寸和形状,玻璃相的含 量和分布情况,晶粒之间、晶粒与玻璃相之间的界面,气孔的 数量、尺寸、分布等。
13.氧化铝烧结到接近理论密度时,可使可见光几乎透过100%, 用它来装钠蒸气(在超过大气压的压力下)作为路灯。为通过 烧结实现这一点,请你列出研究方案。
2. 烧结的推动力和晶粒生长的推动力。并比较两者的大小?
解:烧结推动力是粉状物料的表面能(γsv)大于多晶烧结体 的晶界能(γgb),即γsv>γgb。 晶粒生长的推动力是晶界两侧物质的自由焓差,使界面向晶 界曲率半径小的晶粒中心推进。烧结的推动力较大,约为 4~20J/g。晶粒生长的推动力较小,约为0.4~2J/g,因而烧结推 动力比晶粒生长推动力约大十倍。
无机材料科学基础
第断题:(正确的打,错误的打)
1. 烧结中始终可以只有一相是固态。
(×)
2. 液相烧结与固相烧结的推动力都是表面能。
(√)
3. 二次再结晶对坯体致密化有利。
(×)
4. 扩散传质中压应力区空位浓度<无应力区空位浓度<张应力
区空位浓度。
(√)
5. 晶粒长大源于小晶体的相互粘结。
答:制备透明氧化铝陶瓷的主要技术措施是:(1)采用高纯 氧化铝原料,Al2O3>99.9%,无杂质和玻璃相;(2)添加 0.1~0.5%MgO,在晶粒表面生成镁铝尖晶石,降低晶界移动 速度,抑制晶粒生长;(3)在氢气或真空中烧结,促进气孔 扩散;(4)采用热压烧结,提高制品致密度。
6.试说明晶界能总是小于相邻二个晶粒表面能之和?
解:在恒温恒压条件下增加单位表面积时体系自由能的增量称 为表面能,而形成单位新界面所需要的能量称为界面能。表面 能和界面能的本质是处在表面或界面上的质点受到不对称力场 作用,与晶体内部质点相比具有较高的能量。晶粒的表面能指 晶粒与气相接触,界面能通常指两个晶粒相接触。显然,晶粒 与气相接触时,表面质点受到力场的不对称性远远大于两个晶 粒相接触时。因此,界面能总是小于相邻二个晶粒表面能之和。
材料科学基础相图习题
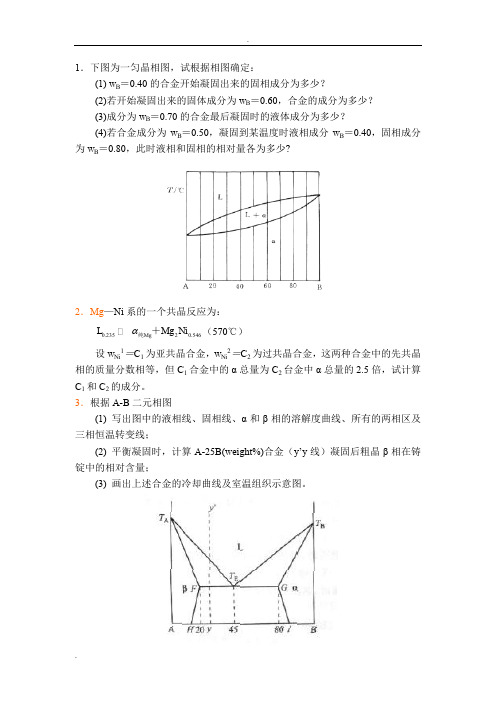
1.下图为一匀晶相图,试根据相图确定:(1) w B =0.40的合金开始凝固出来的固相成分为多少?(2)若开始凝固出来的固体成分为w B =0.60,合金的成分为多少?(3)成分为w B =0.70的合金最后凝固时的液体成分为多少?(4)若合金成分为w B =0.50,凝固到某温度时液相成分w B =0.40,固相成分为w B =0.80,此时液相和固相的相对量各为多少?2.Mg —Ni 系的一个共晶反应为:0.23520.546g g i M L M N 纯+(570℃)设w Ni 1=C 1为亚共晶合金,w Ni 2=C 2为过共晶合金,这两种合金中的先共晶相的质量分数相等,但C 1合金中的α总量为C 2台金中α总量的2.5倍,试计算C 1和C 2的成分。
3.根据A-B 二元相图(1) 写出图中的液相线、固相线、α和β相的溶解度曲线、所有的两相区及三相恒温转变线;(2) 平衡凝固时,计算A-25B(weight%)合金(y ’y 线)凝固后粗晶β相在铸锭中的相对含量;(3) 画出上述合金的冷却曲线及室温组织示意图。
4.根据如图所示的二元共晶相图(1)分析合金I,II的结晶过程,并画出冷却曲线;(2)说明室温下合金I,II的相和组织是什么,并计算出相和组织组成物的相对含量?(3)如果希望得到共晶组织加上5%的 初的合金,求该合金的成分。
(4)合金I,II在快冷不平衡状态下结晶,组织有何不同?5.指出下列相图中的错误:6.试述二组元固溶体相的吉布斯(Gibbs)自由能-成分曲线的特点?(a) (b)(c) (d)1.下图为一匀晶相图,试根据相图确定:(1) w B =0.40的合金开始凝固出来的固相成分为多少?(2)若开始凝固出来的固体成分为w B =0.60,合金的成分约为多少?(3)成分为w B =0.70的合金最后凝固时的液体成分约为多少?(4)若合金成分为w B =0.50,凝固到某温度时液相成分w B =0.40,固相成分为w B =0.80,此时液相和固相的相对量各为多少?第1题答案2.Mg —Ni 系的一个共晶反应为:0.23520.546g g i M L M N 纯+(570℃)设w Ni 1=C 1为亚共晶合金,w Ni 2=C 2为过共晶合金,这两种合金中的先共晶相的质量分数相等,但C 1合金中的α总量为C 2台金中α总量的2.5倍,试计算C 1和C 2的成分。
材料科学基础5---9章习题

第5章材料的形变和再结晶1. 有一70MPa应力作用在fcc晶体的[001]方向上,求作用在(111)和(111)滑移系上的分切应力。
答案:矢量数性积a×b=ïaï×ïbï Þ = a×bïaï×ïbï滑移系:(负号不影响切应力大小,故取正号)滑移系:2. Zn单晶在拉伸之前的滑移方向与拉伸轴的夹角为45°,拉伸后滑移方向与拉伸轴的夹角为30°,求拉伸后的延伸率。
答案 :如图所示,AC和A’C’分别为拉伸前后晶体中两相邻滑移面之间的距离。
因为拉伸前后滑移面间距不变,即AC=A’C’故3. 已知平均晶粒直径为1mm和0.0625mm的a-Fe的屈服强度分别为112.7MPa和196MPa,问平均晶粒直径为0.0196mm的纯铁的屈服强度为多少?答案:解得∴4. 铁的回复激活能为88.9 kJ/mol,如果经冷变形的铁在400℃进行回复处理,使其残留加工硬化为60%需160分钟,问在450℃回复处理至同样效果需要多少时间?答案:(分)5. 已知H70黄铜(30%Zn)在400℃的恒温下完成再结晶需要1小时,而在390℃完成再结晶需要2小时,试计算在420℃恒温下完成再结晶需要多少时间?答案:再结晶是一热激活过程,故再结晶速率:,而再结晶速率和产生某一体积分数所需时间t成反比,即∝∴在两个不同的恒定温度产生同样程度的再结晶时,两边取对数;同样故得。
代入相应数据,得到t3 = 0.26 h。
1.有一根长为5 m,直径为3mm的铝线,已知铝的弹性模量为70GPa,求在200N的拉力作用下,此线的总长度。
答案2.一Mg合金的屈服强度为180MPa,E为45GPa,a)求不至于使一块10mm⨯2mm的Mg板发生塑性变形的最大载荷;b)在此载荷作用下,该镁板每mm的伸长量为多少?答案3. 已知烧结Al2O3的孔隙度为5%,其E=370GPa。
《材料科学基础》练习题集02

厦门理工学院《材料科学基础》练习题集 02第9章材料的凝固一、名词解释:1、均匀形核:在一定条件下,从液态金属中直接产生,原子呈规则排列的结晶核心。
2、非均匀形核:是液态金属依附在一些未溶颗粒表面或固液界面所形成的晶核。
3、变质处理:在液态金属结晶前,特意加入某些难熔固态颗粒,造成大量可以成为非均匀形核晶核的固态质点,使结晶时的晶核数目大大增加,从而提高了形核率,细化晶粒,这种处理方法即为变质处理。
4、变质剂:在浇注前所加入的难熔杂质称为变质剂。
5、枝晶偏析:实际生产中,合金冷却速度快,原子扩散不充分,使得先结晶出来的固溶体合金含高熔点组元较多,后结晶含低熔点组元较多,这种在晶粒内化学成分不均匀的现象称为枝晶偏析。
6、比重偏析:比重偏析是由组成相与溶液之间的密度差别所引起的。
如果先共晶相与溶液之间的密度差别较大,则在缓慢冷却条件下凝固时,先共晶相便会在液体中上浮或下沉,从而导致结晶后铸件上下部分的化学成分不一致,产生比重偏析。
7、溶质再分配8、成分过冷二、判断题:1、液态金属的结构特点是近程有序,长程无序。
()2、晶粒尺寸和形核率N、线长大速度Vg之间的关系是N/Vg越大,晶粒尺寸越大。
()3、区域提纯技术的理论基础是凝固过程中的溶质再分配。
()4、液-固粗糙界面可描述为微观粗糙、宏观平整。
()5、在结晶过程中,晶核越多,生长速率越慢,则凝固后的晶粒越细小。
()6、在单相固溶体铸锭结晶时,成分过冷越大,越易形成枝晶。
()7、由凝固理论可知,细化晶粒的途径是提高形核率,降低长大速率。
()8、金属-非金属型共晶具有粗糙-光滑型界面,所以它多为树枝状,针状或螺旋状。
()三、选择题:1、纯金属结晶均匀形核,当过冷度 T很小时,形核率低,是因为。
A、原子可动性低,相变驱动力低;B、原子可动性高,相变驱动力低;C、原子可动性低,相变驱动力高;D、原子可动性高,相变驱动力高;2、合金凝固时,出现成分过冷的原因是。
《材料科学基础》习题及参考答案

形核功,还是可以成核的。
答案
(7)测定某纯金属铸件结晶时的最大过冷度,其实测
值与用公式ΔT=0.2Tm计算值基本一致。
答案
(8) 某些铸件结晶时,由于冷却较快,均匀形核率N1
提高,非均匀形核率N2也提高,故总的形核率为N=
N1 +N2。
答案
返回
53
(9) 若在过冷液体中,外加10 000颗形核剂,则结晶
❖ ②比较Cu-10% Sn合金铸件和Cu-30%合金铸件的铸造性能 及铸造组织,说明Cu-10% Sn合金铸件中有许多分散砂眼的 原因。
③ω(Sn}分别为2%,11%和15%的青铜合金,哪一种可进行 压力加工?哪种可利用铸造法来制造机件?
答案
返7回8
❖ 9.如下图所示,已知A,B,C三组元固态完全不互溶,质量 分数分别84%A,,10%B,10%C的O合金在冷却过程中将进 行二元共晶反应和三元共晶反应,在二元共晶反应开始时, 该合金液相成分(a点)为60%A,20%B,20%C,而三元共 晶反应开始时的液相成分(E点)为50%A,10%B,40%C。
答案
返回
6
❖ 6.位错受力后运动方向处处垂直于位错线,在运动
过程中是可变的,晶体作相对滑动的方向应是什么
方向?
答案
❖ 7.位错线上的割阶一般如何形成?
答案
❖ 8.界面能最低的界面是什么界面?
答案
❖ 9. “小角度晶界都是由刃型位错排成墙而构成的”这
种说法对吗?
答案
返回
7
三、综合题
❖ 1. 作图表示立方晶体的(123)(0 -1 -2) (421)晶面及[-102][-211][346]晶向。 答案
❖ 9. 在Fe中形成1mol 空位的能量为104. 67kJ,
《材料科学基础》课后习题及参考答案

绪论1、仔细观察一下白炽灯泡,会发现有多少种不同的材料?每种材料需要何种热学、电学性质?2、为什么金属具有良好的导电性和导热性?3、为什么陶瓷、聚合物通常是绝缘体?4、铝原子的质量是多少?若铝的密度为2.7g/cm3,计算1mm3中有多少原子?5、为了防止碰撞造成纽折,汽车的挡板可有装甲制造,但实际应用中为何不如此设计?说出至少三种理由。
6、描述不同材料常用的加工方法。
7、叙述金属材料的类型及其分类依据。
8、试将下列材料按金属、陶瓷、聚合物或复合材料进行分类:黄铜钢筋混凝土橡胶氯化钠铅-锡焊料沥青环氧树脂镁合金碳化硅混凝土石墨玻璃钢9、 Al2O3陶瓷既牢固又坚硬且耐磨,为什么不用Al2O3制造铁锤?晶体结构1、解释下列概念晶系、晶胞、晶胞参数、空间点阵、米勒指数(晶面指数)、离子晶体的晶格能、原子半径与离子半径、配位数、离子极化、同质多晶与类质同晶、正尖晶石与反正尖晶石、反萤石结构、铁电效应、压电效应.2、(1)一晶面在x、y、z轴上的截距分别为2a、3b、6c,求出该晶面的米勒指数;(2)一晶面在x、y、z轴上的截距分别为a/3、b/2、c,求出该晶面的米勒指数。
3、在立方晶系的晶胞中画出下列米勒指数的晶面和晶向:(001)与[210],(111)与[112],(110)与[111],(322)与[236],(257)与[111],(123)与[121],(102),(112),(213),[110],[111],[120],[321]4、写出面心立方格子的单位平行六面体上所有结点的坐标。
5、已知Mg2+半径为0.072nm,O2-半径为0.140nm,计算MgO晶体结构的堆积系数与密度。
6、计算体心立方、面心立方、密排六方晶胞中的原子数、配位数、堆积系数。
7、从理论计算公式计算NaC1与MgO的晶格能。
MgO的熔点为2800℃,NaC1为80l℃, 请说明这种差别的原因。
8、根据最密堆积原理,空间利用率越高,结构越稳定,金钢石结构的空间利用率很低(只有34.01%),为什么它也很稳定?9、证明等径圆球面心立方最密堆积的空隙率为25.9%;10、金属镁原子作六方密堆积,测得它的密度为1.74克/厘米3,求它的晶胞体积。
材料科学基础第九章答案

第九章答案9-2什么叫相变?按照相变机理来划分,可分为哪些相变?解:相变是物质系统不同相之间的相互转变。
按相变机理来分,可以分为扩散型相变和非扩散型相变和半扩散型相变。
依靠原子或离子长距离扩散进行的相变叫扩散型相变。
非扩散型型相变指原子或离子发生移动,但相对位移不超过原子间距。
9-3分析发生固态相变时组分及过冷度变化相变驱动力的影响。
解:相变驱动力是在相变温度下新旧相的体自由能之差(),而且是新相形成的必要条件。
当两个组元混合形成固溶体时,混合后的体系的自由能会发生变化。
可以通过自由能-成分曲线来确定其相变驱动力的大小。
过冷度是相变临界温度与实际转变温度之差,相变形核的热力学条件是要有过冷度。
已知驱动力与过冷度之间的关系是:,这进一步说明了形核的热力学条件。
9-4马氏体相变具有什么特征?它和成核-生成相变有何差别?解:马氏体相变是替换原子经无扩散切变位移(均匀或不均匀)并由此产生形状改变和表面浮凸、曾不变平面应变特征的一级形核、长大的相变。
特征:具有剪切均匀整齐性、不发生原子扩散、相变速度快、相变有一定范围、有很大的切变型弹性应变能。
成核-生长过程中存在扩散相变,母相与晶相组成可相同可不同,转变速度较慢,无明显的开始和终了温度。
9-5试分析应变能及表面能对固态相变热力学、动力学及新相形状的影响。
解:物质的表面具有表面张力σ,在恒温恒压下可逆地增大表面积dA,则需功σdA,因为所需的功等于物系自由能的增加,且这一增加是由于物系的表面积增大所致,故称为表面自由能或表面能。
应变能和表面能可以影响相变驱动力的大小,和新相的形状。
9-6请分析温度对相变热力学及动力学的影响。
解:当温度降低,过冷度增大,成核势垒下降,成核速率增大,直至达到最大值;当温度继续下降,液相粘度增加,原子或分子扩散速率下降。
温度过高或过低对成核和生长速率均不利,只有在一定的温度下才有最大成核和生长速率。
9-7调幅分解与脱溶分解有何异同点?调幅分解所得到的显微结构与性能有何特点?解:调幅分解通过扩散偏聚由一种固溶体分解成与母相结构相同而成分不同的两种固溶体。
《材料科学基础》课后习题(西工大版)

第一章1. 作图表示立方晶体的()()()421,210,123晶面及[][][]346,112,021晶向。
2. 在六方晶体中,绘出以下常见晶向[][][][][]0121,0211,0110,0112,0001等。
3. 写出立方晶体中晶面族{100},{110},{111},{112}等所包括的等价晶面。
4. 镁的原子堆积密度和所有hcp 金属一样,为0.74。
试求镁单位晶胞的体积。
已知Mg 的密度3Mg/m 74.1=m g ρ,相对原子质量为24.31,原子半径r=0.161nm 。
5. 当CN=6时+Na 离子半径为0.097nm ,试问:1) 当CN=4时,其半径为多少?2) 当CN=8时,其半径为多少?6. 试问:在铜(fcc,a=0.361nm )的<100>方向及铁(bcc,a=0.286nm)的<100>方向,原子的线密度为多少? 7. 镍为面心立方结构,其原子半径为nm 1246.0=Ni r 。
试确定在镍的(100),(110)及(111)平面上12mm 中各有多少个原子。
8. 石英()2SiO 的密度为2.653Mg/m 。
试问: 1) 13m 中有多少个硅原子(与氧原子)?2) 当硅与氧的半径分别为0.038nm 与0.114nm 时,其堆积密度为多少(假设原子是球形的)?9. 在800℃时1010个原子中有一个原子具有足够能量可在固体内移动,而在900℃时910个原子中则只有一个原子,试求其激活能(J/原子)。
10. 若将一块铁加热至850℃,然后快速冷却到20℃。
试计算处理前后空位数应增加多少倍(设铁中形成一摩尔空位所需要的能量为104600J )。
11. 设图1-18所示的立方晶体的滑移面ABCD 平行于晶体的上、下底面。
若该滑移面上有一正方形位错环,如果位错环的各段分别与滑移面各边平行,其柏氏矢量b ∥AB 。
1) 有人认为“此位错环运动移出晶体后,滑移面上产生的滑移台阶应为4个b ,试问这种看法是否正确?为什么?2) 指出位错环上各段位错线的类型,并画出位错运动出晶体后,滑移方向及滑移量。
材料科学基础课后习题答案9

Solutions for Chapter 91. FIND: What considerations are required for use of materialsin the named applications?SOLUTION: Heart valve - biocompatible, long life (fatigueendurance), ease of installation: Turbine blade - able towithstand high temperature and stress without creep, longlife (fatigue endurance): Leaf spring - low cost, stresswithout creep, long life (fatigue endurance): Coffee mug -not contaminate contents, able to withstand 0 - 100︒ cyclesand gradients: Golf club shaft: able to withstand, amplify,and transmit forces with little loss, long life (fatigueendurance), aesthetically and tactily attractive: Suture -biocompatible, long life (fatigue endurance)COMMENTS: There are many other requirements, and we couldbegin to specify materials' properties that are required tomeet the applications' needs.2. Find: Determine Young's Modulus.Data: Upper yield point stress of 207 MPa, Yield pointstrain of 0.001.Solution: Recall that Young's Modulus is the slope of thestress/strain curve in the elastic portion of thestress strain curve. That is: E=Stress/StrainSubstituting values into the above equation yields:E = 207/0.001 = 207,000 MPa = 207 GPa.3. FIND: Calculate the strain-to-fail of silicate glasses.GIVEN: The modulus is 107 psi and the strengths of threesamples are 5, 50, and 500 ksi.ASSUMPTIONS: The material behaves in a linear elastic manner up to failure.SKETCH: The beginnings of the three curves lie on top ofone another. The higher the strain-to-fail the longer thecurve extends to the upper right. The x's indicate thepoints of failure.tiSanrtSOLUTION: Hooke's law states:σ = Eε.Rearranging,ε = σ/E.Substitution for each of the samples:ε = 5000 psi / 107 psi = 0.05%ε = 50,000 psi / 107 psi = 0.5%ε = 500,000 psi / 107 psi = 5%.COMMENTS: The smallest value represents that of ordinary window glass. The largest value is characteristic of an optical fiber.4. Find: Determine if the stress is above or below theyield stress. If the stress is below the yield stresscompute Young's Modulus.Data: The yield stress for the mild steel is 207 MPa. A specimen has a diameter of 0.01m and a length of0.1m. It is loaded in tension to 1000N anddeflects 6.077 x 10-6m.Solution: To solve this problem, we must first determine the applied tensile stress. Recall that the tensilestress is given by the formula: Stress=Force(P)/Area Normal to force (A). The cross sectionalarea is: A= πD2/4 = 3.1416x(0.01)2/4 = 7.85x10-5The stress is: Stress = 1000/7.85x10-5 = 12.7MPaThe applied stress is much less than the yieldstress. To obtain the Modulus recall thedefinition: E=σ/ε. We must thus compute thestrain in order to determine the Modulus:ε=∆l/l o = 6.077x10-6/0.1 = 6.077x10-5Thus E=12.7/6.077x10-5 = 2.09x105 MPa.5. Find: Compute deflection of specimens.Data: E Al=70,460MPa, E Cu=122,500MPa, E W=388,080MPa,A=0.01m x 0.01m=10-4m2, Length(l o)=1m,Load(P)=5000N.Solution: Start with the relationship between stress andstrain for linear elastic behavior: σ=Eε (1)Note that: σ=P/A (2)ε=∆l/l o (3)Substitute (2) & (3) into (1): Thus P/A=E∆l/l o (4)Rearranging to solve for ∆l we have:∆l=Pl o/AE=5000 x 1/(10-4E)=5x107/E (5)Note that for ∆l to be in meters we require E tobe expressed in Pa. Using (5) and E in Pa we getthe following deflection values:Al=7.09x10-4m, Cu=4.08x10-4m, W=1.29x10-4m.6. Find: Deflection at 5000N.Data: E Nylon6/6=2.08GPa, Load(P)=5000N, l o=1m, A=10-4m2.Solution: Using the formula developed in the precedingproblem we have: ∆l o=Pl o/(AE).Thus: ∆l o=(5000 x 1)/(10-4x2.08x109)=2.4x10-2m.Comment: Note that the deflection is two orders ofmagnitude greater than for steels.7. FIND: Calculate the strength of a round textile fiber.GIVEN: The fiber diameter is 10 micrometers and the load-at-failure is 25 g.ASSUMPTIONS: The fiber need not be in the elastic region at failure.SOLUTION:σ = F/A = 002598510262../sec()kg mx m⨯-π= 3.1 GPa.8. Find: Determine the shear strain at yield.Data: For a particular steel: ν=0.295, E = 205,000MPa,σys=300MPa and τys = 1/2σys.Solution: Recall Hooke's Law in shear: τys= Gγys. Also, itis stated that τys = 1/2σys. Substitution yields:1/2σys = Gγys or γys= σys/2G. The problem now is todetermine G. Recall that G=E/(2(1+ν))=205,000/(2(1+0.295))=79,151 MPa. Substituting wehave: γys= 300/(2x79,151)=1.895x10-3.9. Find: Compute the 0.2% offset yield strength and thestrain at yield.Data: E Al=69x103 MPa and σ=295ε0.1.Solution: We require the intersection point of the twocurves shown below to solve the problems since the0.2% offset yield is defined as the point where aline whose slope is equal to the modulus, andwhich is displaced 0.002 on the strain axis,intersects the stress/strain curve. To find theintersection point we must first get the equationfor 0.2% offset yield. The general form of theequation is: σ=mε + b, where m=slope andb=intercept. We know that the point (0.002,0) ison the line thus: 0=69x103(0.002) + b, thereforeb= -1.38x102. The equation of the 0.2% offsetline is σ = 69x103ε - 1.38x102. The intersectionis obtained by rearranging and substituting theformer equation with the first equation: 295ε0.1 =69x103ε-1.38x102. This equation is best solved bytrial and error or by writing a short computerprogram to check for the equality of the right andleft hand sides of the equation for various valuesof ε. At a strain of 0.00448 the differencebetween the right and left-hand sides of theequation is negligible. Substituting this strainvalue into the equation for stress yields anestimate for the yield stress of 172 MPa.10. Find: (a) Poisson's ratio, (b) % volume change at σys/2and (c) % volume change at σys.Data: Aluminum specimen with the following properties:E=69x103 MPa loaded such that εl = 1.25x10-3 and εv= 4.17x10-4 .Solution: (a) Recall that Poisson's ratio is defined as ν = -εv/εl. Thus, ν = -(-4.17x10-4 /1.25x10-3)=0.333.(b) The volume change is given by ∆v/v o=εx+εy+εz.But εy = εl, εx,εz = εv and εv =-νεl. Thus, ∆v/v o=εx +νεl +νεl= εl(1-2ν). In the preceding problem it wasshown that the yield strain was 4.48x10-3. Athalf the yield the strain is 2.24x10-3. Then∆v/v o = (2.24x10-3)(1-0.666) = (7.48x10-4)x100=7.48x10-2.(c) At yield stress: ∆v/v o x 100=4.48x10-3 x 0.334x 100 = 1.50 x 10-1.11. Find: Predict the behavior of amorphous polymers.Solution: Steels have a definite yield point becausedislocations are pinned by carbon atoms thatreside in the interstitial positions. When stressrises to the point necessary for dislocations tobreak free from the carbon atoms, plasticdeformation occurs due to dislocation movement.Yield stress is the critical stress necessary forfreeing the dislocations from the carbon atoms.In Al and Cu, that have an FCC structure,dislocation mobility increases gradually as thestress is increased. Therefore, there is nosingle stress level at which the dislocationsbegin to move suddenly. In these materials,yielding occurs gradually, dislocations motion maybe impeded, but the dislocations are not pinned.In amorphous polymers, plastic deformation occursby sliding between adjacent molecular chains. Thesliding will commence at a definite stress level.Therefore, we expect a definite yield point tooccur in amorphous polymers.12. Find: Determine the ultimate tensile strength.Data: The stress-strain behavior is given by σ = Kεn.Solution: Let engineering stress be designated by S andengineering strain by e. The following equationsrelate engineering stress and strain to truestress and true strain:σ = S(1+e) (1)and ε = ln(1+e) (2)We are given σ = Kεn (3)Substituting (1) and (2) into (3), we get: S(1+e)= K[ln(1+e)]n. At the ultimate tensile stresspoint, dS/de = 0. Thus, dS/de = (d/de) [[(K/(1+e)](lu(1+e))n] = 0, or - (K/(1+e)2][(ln(1+e))n]+[Kn/(1+e)2][(ln(1+e))n-1] = 0or ln(1+e) = n (3a)If we designate e by e u at the ultimate tensilepoint, σu = K[ln(1+e u)]n (4)Substituting equation (4) into (3) we get σu =K[ln(1+e u)]n, or S u(1+e u) = Kn n. Solving for S uyields: S u = [K/(1+e u)] n n = Kn n-1 (4a)S u is the ultimate tensile strength.Comment: Equation (3a) is frequently used to estimate n ifa complete stress-strain curve is not available.Further, equation (4a) can be used to obtain thestrength coefficient, K.13. Find: 1) The physical basis for the observation and 2)show ν=0.5 during plastic deformation.Data: Volume of a crystalline material remains constantduring plastics deformation.Solution: 1) During purely plastic deformation interatomicdistance is not changing and the atoms eventuallyslide over one another. for this reason thevolume is constant during plastic deformation.2) Recall that ∆ν/νo = εx + εy + εz = ε(1-2ν) foruniaxial deformation. If ∆ν = 0 , then ν=1/2.14. Find: Compute the relative load bearing capacities of anAl alloy (σUTS = 400 MPa, ρ = 2.7 gm/cm3 ) and polypropylene(σUTS = 40 MPa, ρ=0.9 gm/cm3 ).Data: Relative load capacity for constant weight isproportional to the strength divided by thedensity.Solution:To have consistent units, convert density to kg/m3.ρAl= 2.7x103 kg/m3ρPP= 0.9x103 kg/m3σAl'= 400x106/2.7x103(Pa/kg/m3)=148x103(Pa m3/kg)Recall Pa=N/m2, therefore σAl'= 148x103 (N m/kg)and σpp'=40x106/0.9x103=44.4x103 (N-m/kg).16. Find: Plot the true strain to fracture, being sure toplace Cu and steel from the preceeding problem in the graph.Data: A range of %RA from 0 to 70%.Solution: Recall that the true strain may be computed fromthe %RA using the formula: f = ln(100/(100-%RA)).See graph for correlation of fracture strainand %RA.17. Find: Determine the engineering strain at which thedifference between the true strain and the engineeringstrain is ε = ln (1+e).Data: Equation relating engineering strain to truestrain.Solution: We can write a series expansion for the right hand side:ε = ln (1+e) = e-(e2/2!)+(e3/3!)-(e4/4!)+... Forsmall values of e, we need to consider only thefirst two terms in the expansion: ε = e-(e2/2!).For 5% difference ε =0.95e, therefore (0.95e)-e=-e2 or 0.05=e. Then, for a strain up to 5%, thedifference between the true and engineering strainwill be equal to or less that 5%.18. Find: Explain why we report different lengths fordifferent materials.Solution: Polymer specimens do not have a tendency to form a necked region like metals do. Instead, polymerspecimens deform uniformly through the gage length.Therefore, the final percent elongation inpolymer specimens is not dependent on the gagelength like it is for metals, and the informationon gage length then becomes redundant.19. Find: Compare the glass transition temperatures.Solution: Glass transition temperatures can be increased bycross-linking which also influences the elasticmodulus without changing its molecular weight.Therefore, the polymer with a higher glasstransition temperature will also have a higherelastic modulus.20. Find: Relaxation modulus, E r(t), of the polymer.Data: σ(t) = σo exp(-t/τ)σo = 2 MPa for a sudden strain of 0.2σ(t) = 0.5 MPa at t = 50 secondsSolution: It must be assumed that the strain remainsconstant during the relaxation process. σ(t) = 2MPa for t = 0, or σ0 = 2 MPa. Substituting σ(t) =0.5 MPa at t = 50 s into the given equation, weget 0.5 = 2 exp(-50/τ). Solving for τ,τ = -50/[ln(0.5/2)] = 36.07 s.E r(t) = (σ(t)/εo) = [2 exp(-t/36.07)]/0.2 = 10exp(-t/36.07) = 10 exp(-10/36.07) = 7.58 MPa21. FIND: Show with a sketch how the modulus changes with timein a creep test.GIVEN: The test sample is a polymer. The load history of a creep test is as follows:emTiASSUMPTIONS: The load is insufficient to break the polymer.SKETCH:meiTSOLUTION: The equation for the modulus is given in equation 9.2-7, which states that E(t) = σo / ε(t). Since the material creeps, its length increases with time. Since the denominator increases and the numerator is constant, the modulus decreases.COMMENTS: Shown is a sample that creeps only to a limit.Many polymers behave in this fashion.22. Find: (a) Explain why normal the tensile test isused (b) differences in three of four point bendspecimens and (c) some limitations on data.Solution: (a) Due to the brittle nature of ceramics,there is a very significant risk of failureoutside the gage section of the specimen duringgripping. Also, such specimens are difficult andexpensive to machine.(b)The three or four point bend specimens aresubjected to negative (or compressive) loads anddo not require grips for loading. Hence, there isno risk of premature failure.(c)The stress distribution in a 3-point or 4-pointbend specimen is non-uniform along the cross-section of the specimen. Hence, the strength isobtained by calculating the outer fiber stress inthe specimen at the time of the failure. Thestrength values obtained from these tests haveconsiderable scatter.23. Find: Determine the load, P, at fracture.Data: Modulus of rupture, σ, = 3000 MPa, diameter, d, of the cylindrical specimen = 5mm and separationbetween support points, L = 25 mm.Solution: σ = PLd/4I, where I (bending moment of inertia) = πd4/64. Hence, σ = (PLd)64/(4πd4) = 16PL/(πd3),or P=(σπd3)/16L=[(3000x106N)π(.005)3]/[16(0.025)]P = 2945 Newtons.24. Find: Compute the diameter of an indentation for aBrinell hardness test using a standard indenter of 10mmdiameter.Given: The tensile strength is 800 MPa.Solution: To solve the problem we must first determine thehardness corresponding to a strength of 800 MPa.Using the graph in the text the Brinell hardness(BHN) is approximately 241. We next note theformula relating BHN to indentation diameter:BHN = 2P/(πD(D-(D2-d2)1/2)) where P = load (kg), D= indenter diameter (mm), d = diameter ofindentation (mm). Substituting the appropriatevalues yields 241=(6000/(10π(10-(100-d2)1/2))=191/(10-(100-d2)1/2). We can rearrange theequation such that: (100-d2)1/2 = [10-(191/241)] =9.208, or 100-d2 = 9.2082, thus, d2 = 100-9.2082=1.521, therefore d=3.90 mm.25. Find: Calculate the Brinell hardness as a function ofload for 1/4 hard and 1/2 hard brass.Data: Indentation diameter vs load for 1/4 hard and 1/2 hard brass.Solution: The Brinell Hardness Number is obtained from thefollowing equation:BHN=Load/Indentation areaBHN=2P/(πD(D-(D2-d2)1/2)). For a 10mm diameterindenter the formula becomes: BHN=2P/(10π(10-(100-d2)1/2)). This equation is plotted below for thedata that was provided in the problem.Comment: The hardness values reach a plateau for the higher loads since the elastic springback as a percentageof the total deformation is smaller for the higherloads.26. Find: Using the average hardness values computed in theprevious problem, calculate the indentation diameter for aload of 1500 kg and a 5mm diameter ball.Data: The hardness of 1/4 hard brass is 80 kg/mm2 andfor 1/2 hard brass it is 87 kg/mm2.Solution: BHN=2P/(πD(D-(D2-d2)1/2))Solving for d we have:d={D2-[D-2P/(πD x BHN)]2}1/2d1/4={25-[5-3000/(π5 x 80)]2}1/2= 4.26mmd1/2={25-[5-3000/(π5 x 87)]2}1/2=4.14mm27. Find: Explain why BCC materials exhibit a definiteductile-to- brittle temperature and FCC do not.Solution: Ductile behavior is caused by the ability of thematerial to deform plastically to accommodatedeformation. Brittle behavior is caused by thematerial's lack of ability to deform plastically.In BCC materials, the number of operable slipsystems decreases considerably with decrease intemperature causing a transition to occur fromductile to brittle behavior. In FCC materials thetwelve primary slip systems continue to operateeven at low temperatures. Therefore, sharpdecreases in ductility does not occur.28. Find: (a) Plot impact energy v temperature (b) determineductile to brittle temperature and (c) determine whethersteel is appropriate for application.Data: Impact energy at various temperatures.Solution: (a)see attached(b) Ductile to brittle transition is the tempera-ture at which the impact energy is the mean of theenergy in the upper and lower shelves = 11o C.(c)Impact energy at -10o = 12J from the abovefigure. Hence, the design requirement has beenmet but the material is marginal.29. Find: Determine what factors promote brittle fractures.Solution: For materials in general, including thermoplasticpolymers, the following factors promote brittlefracture:• presence of cracks or sharp notches• increasing thickness• increasing loading rate• reduction in temperature• modification of structure, for example inpolymers structural changes which increasethe glass transition temperature30. FIND: Plot tan δ with temperature for a squash ball. GIVEN: The ball is not bouncy when cold, but becomessomewhat bouncy with increasing temperature. The ball is warmed by repeated hitting against the front wall.SKETCH:eTan δ SOLUTION: The ball converts kinetic energy into heat withevery impact with the wall and the racket strings. As the ball heats up, its bounce increases, indicating that tan δ decreases with increasing temperature.COMMENTS: A racquetball does not require hard hitting to improve its bounce.31. FIND: Describe how to process a polymer to give it a veryhigh modulus.GIVEN: You want to stress only primary bonds in deformation. Thus, you need to have the chains aligned with the test direction.SOLUTION: A fiber is a good geometry to work with. Itsuniaxial structure lends itself to aligning molecules along the fiber axis. You want to process the material to align molecules along the fiber length. This can be achieved in a number of ways. Most involve stretching the polymer along its axis during processing. The polymer may be stretched, or elongated, before solidification, after, or both.COMMENTS: This is how it is done commercially! There aremany variants.32. FIND: How can you determine the hardness of a series ofcrosslinked polymers?GIVEN: You suspect the hardness increases with crosslinkdensity.SOLUTION: Brinell hardness testing will probably not beuseful, since polymers are somewhat elastic and the indentor may not leave a permanent mark. One of the tests thatmeasures the penetration distance will probably provide more meaningful data.COMMENTS: The American Society for Testing Materials (ASTM) has developed standard test methods for polymer hardness. 33. FIND: Is brittle failure a problem with ceramics and oxideglasses?SOLUTION: Your experience with these materials shows thatbrittle failure is indeed the way ceramics and oxide glasses fail. The abrupt and catastrophic failure is the featurethat often limits their widespread use. The principlesdeveloped in the chapter apply to all brittle materials,regardless of the composition of the material.34. Find: Determine the difference between brittle andductile fracture.Solution: Brittle fracture refers to fracture that occurswith little absorption of energy. For metals thatfail in the brittle manner, this implies that onlya small amount of plastic deformation takes place.Ductile fracture generally refers to fracturethat takes place with considerable absorption ofenergy. In metals this implies considerableplastic deformation.35. Find: Explain why one would expect to have significantscatter in the fracture strength of ceramic materials.Solution: Fracture in brittle materials like ceramics occurs at the point where the largest flaw is present.Since the size of the largest flaw varies fromspecimen to specimen, the fracture strength alsovaries correspondingly. As we increase thespecimen size, the probability that a larger flawexists also increases. Therefore, fracture ismore likely to occur at a lower stress level.37. Find: Determine the maximum crack size that could existin each of these panels.Data: Fracture toughness of 7075-T6 Al (28MPa-m1/2), 300 Maraging Steel (66 MPa-m1/2) and Al2O3 (2.5 MPa-m1/2). Cracks are found in wide panels of thesematerials and the panels are subjected to a stressof 350 MPa.Solution: For the maximum crack size, the panel is just onthe verge of cracking. For crack length in apanel subjected to a uniform stress we have:K IC=σ(πa)1/2. Then a=(1/π)(K IC/σ)2, therefore 2a =crack length = (2/π)(K IC/σ)2.2a7075-T6 = 2/π(28/350)2 = 4.07x10-3 m2a300 Maraging=2/π(66/350)2 = 2.26x10-2 m2a Al2O3=2/π(2.5/350)2 = 3.25x10-5 mComment: Note that the toughest material, 300 Maragingsteel, can withstand the largest crack. Then apart made from this material would be safer to usesince it would be easier to detect defect cracksbefore fracture.38.Find: Compute fracture stresses for cracks that are 10cm long.Data: Fracture toughness of Kevlar 49 and F-155 epoxy is20 MPa m0.5. The fracture toughness of E-glasscloth in epoxy is 5 MPa m0.5.Solution: Recall that at fracture K=K IC. Thus K IC=σ(πa)1/2for center cracked panel. Recall also that thecrack length is 2a and not a and σ= K IC/√(πa).For Kevlar/epoxy: K IC= 20 MPa m0.5, a= 5cm=0.05m,then, σ= 20/(0.05π)1/2= 50.5 MPa. For E-glass/epoxy: K IC= 5 MPa m0.5, a= 0.05m, then σ=5/(0.05π)1/2= 12.6 MPa.Comment: Note that the fracture stresses for a given crack length is proportional to K IC. Thus we could havewritten σKev/σglass =K Kev/K glass =20/5=4.39.Find: Compute the crack length at failure.Data: Same materials as the preceding problem withapplied stress of 50 MPa.Solution: Recall that at fracture K IC=σ(πa)1/2, the cracklength at fracture is 2a=2/π (K IC/σ)2. Applyingthe latter equation to Kevlar and E-glass we have:2a Kevlar/Epoxy=2/π(20/50)2 = 0.102 m2a E-glass/Epoxy=2/π(5/50)2 =0.006 m.40.Find: Compute the fracture crack length and determine if such a crack length would be detectable.Data: Stabilized ZnO2 is loaded to its UTS.Solution: The crack length at fracture for a center cracked panel is given by: 2a=2/π (K IC/σ)2. The maximumstress is 140x103 MPa and K IC is 7.6 MPa-m1/2. Thus2a=2/π(7.6/140x103)2 = 1.88x10-9 m. Such a crackwould not be detectable by normal techniques.Since the "crack" length is on the order of a fewinteratomic spacings, it is not truly meaningfulto specify this as a crack.41.Find: Compute the maximum stress that could be appliedwithout failure.Data: The same material as in the preceding problemcontaining a crack of 1mm in a center crack panel.Solution:The maximum stress occurs when K is just below K IC: K IC=σ(πa)1/2 where a = 0.5mm=5x10-4m, K IC= 7.6MPa-m1/2.Therefore, σ= K IC/(πa)1/2=7.6/(5x10-4π)1/2=192MPa.Comment: Note that the maximum stress is only about 0.14%of the tensile strength! (i.e. (192/140x103)102=0.14)42.Find: Explain why certain requirements are necessary.Solution: These requirements insure that the followingconditions prevail at the time of fracture:1) The region of plastic deformation is small incomparison to the crack size, a, and the remainingligament size W-a, thus insuring that elasticconditions dominate the behavior of the specimen.2) By requiring that the thickness is also greaterthan or equal to 2.5(K Q/σys)2, plane strainconditions are ensured which also promote brittlefracture.43.Find: The fracture stress, σf, of alumina.Data: Maximum strength of alumina = 4000 MPa, fracturetoughness, K IC = 2.5 MPa√m, largest flaw size =100 μm.Solution: We assume that the largest flaw size can belocated at the surface of the specimen. Thestress intensity parameter at the flaw is given byK = 1.12σ√(πa), where, σ = stress, a = flaw size.At fracture, σ = σf and K = K IC. Therefore,σf = K IC/[1.12√(πa)] = 2.5/[1.12(πx100x10-10) =125.9 MPa.Comments: Notice that the presence of a small flaw canreduce the fracture strength from 4000 MPa to125.9 MPa.44.Find: Determine the minimum thickness, B, and theminimum width, W, to obtain valid K IC in PMMA,2024-T351 Al and 304 stainless steel.Data: Yield strength and K IC values for the abovematerialsSolution: In order to find the minimum thickness and width, we calculate the value of 2.5(K IC/σys)2 for eachmaterial. We further assume that a/W = 0.5. ForW-a ≥ 2.5(K IC/σys)2 it then is necessary that W ≥5(K IC/σys)2. The values of minimum B and W aregiven in the following table:Material 2.5(K IC/σys)2 (m) Min.B (mm) Min. W (mm)PMMA 0.051 51 1042024 Al 0.036 30.6 71.2304 SS 5.625 5625 11250Comments: Notice the big size specimen needed to measure the K IC of 304 stainless steel. The specimen isprohibitively large. Hence, the K IC of 304 SS isestimated using the principles of elastic-plasticfracture which are outside the scope of this text.45. Find: Determine an estimated value of K ICData: Surface energy, γs, = 1J/m2, strength, σf, = 100MPa, elastic modulus, E = 210,000 MPa.Solution: According to Griffith's equation, σf= (Eγs ½)/πa,where, a = flaw size. Solving for a yields: a =(2Eγs)/(πσf2) = (2x210,000x106x1)/(πx(100)2x1012) =13.37x10-6m = 0.01337 mm. K IC = σf√(πa) =100√(πx13.37x10-6) = 0.67 MPa√m. The implicitassumption in this calculation is that MgO doesnot deform plastically and the only energy neededfor fracture is that to overcome the energynecessary to create fresh surfaces.46. Find: Determine the basis for the Griffith's criterion.Solution: The original Griffith's criterion wasSolution:formulated on the assumption that theenergy required for fracture consists of only theenergy required to create new surfaces. Noallowance was made for energy needed for plasticdeformation. While this assumption was suitablefor the brittle glass, it was not suitable formetals that sustain plastic deformation prior to fracture.47. Find: Construct a graph of the critical crack length vs.crack size for this application and select a suitablematerial for this application if the minimum crack size that can be detected is 2mm.Data: A wide panel is required to operate at 50 MPa.Solution: Recall that for a center crack of length 2asubjected to a stress, the following equationapplies: K IC=σ(πa)1/2 or 2a=2/π (K IC/σ)2. For anapplied stress of 50 MPa, the latter equationbecomes 2a=2/π (K IC/50)2. This equation is plottedon the accompanying graph. From the graph we seethat the fracture toughness must be at least 28MPa-m1/2. From the Metals Handbook (Desk Edition,1985, pp. 6-47) we see that Al 7475-T7551 meetsall the requirements.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 试分析金属塑性变形行为对下列材料与零件的重要意义:
A 、冲压钢板;
B 、汽车板簧;
C 、铆钉;
D 、高压蒸汽管道法兰盘的紧固螺栓。
(2) 单滑移、复滑移及交滑移的滑移带形貌有什么特征?试结合图解说明。
(3) 若平均晶粒直径为1mm 和0.0625mm 的纯铁的屈服强度分别为112.7MPa 和196MPa ,则平均晶粒直径为0.0196mm 的纯铁的屈服强度为多少?
(4) 面心立方晶体的)111(和)111(面各有几个密排方向?共可组成几个滑移系?这些滑移系能否有数个共同发生作用的情况?若有,是复滑移还是交滑移?
(5) 通常强化金属材料的方法有哪些?试述它们强化金属的微观机理,并指出其共同点。
(6)
面心立方体沿[131]轴拉伸,确定如下滑移系的分切应力:(111) [01_
1]、(111) [101_]、(111) [11_
0]。
拉伸应力为6.9×105Pa 。
(7) 铝(层错能约为200mJ/m 2)和不锈钢(层错能约为10mJ/m 2),那一种材料的形变第III 阶段开始得更早?为什么
(8) 如图所示,1个单晶体经弯曲后,估计导致弯曲的同号刃位错的总柏氏矢量的大小。
求这些位错的位错密度。
(设单个位错柏氏矢量为b )
(9)
厚度为40mm 厚的铝板,轧制成一侧为20mm 另一侧仍保持为40mm 的楔形
板,经再结晶退火后,画出从20mm 的一侧到40mm 一侧的截面的组织示意图。
并说明。
(10)什么叫做二次在结晶,发生二次再结晶的条件是什么?
(11)动态回复与动态再结晶的真应力-真应变曲线有什么差异?试解释。
