(完整版)匀变速直线运动的推论及推理
匀变速直线运动公式 推论推导 及规律总结

匀变速直线运动公式推论推导及规律总结一、基本规律:1.基本公式:平均速度 v = s/t加速度 a = (v - v0)/t2.瞬时速度公式:瞬时速度 v = v0 + at初速度 v0 = 03.位移公式:s = vt + 1/2at^2二、匀变速直线运动的推论及推理掌握运用匀变速直线运动公式的推论是解决特殊问题的重要手段。
1.推论1:做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即 v = S/t2.推论2:做匀变速直线运动的物体在一段位移的中点的即时速度 v = (v0 + vt)/23.推论3:做匀变速直线运动的物体,在连续相等的时间间隔 t 内的位移分别为 S1、S2、S3……Sn,加速度为 a,则ΔS = S2 - S1 = S3 - S2 = ……= Sn - Sn-1 = at^2推论6:对于初速度为零的匀变速直线运动,从开始运动算起,物体经过连续相等的位移所用的时间之比为(a(2(n-1)S)^(1/2))]×(n-n+1)/2=a(n-n+1)/(2(n-1)S),代入可得推论7:对于初速度为零的匀加速直线运动,第一个s末、第二个s末、……第n个s末的速度之比为自由落体运动和竖直上抛运动的公式和推论如下:自由落体运动:平均速度v=gt/2瞬时速度vt=gt位移公式s=1/2gt^2重要推论2gs=vt^2竖直上抛运动:瞬时速度vt=v-gt位移公式s=vt-1/2gt^2重要推论-2gs=vt-v作为匀变速直线运动应用的竖直上抛运动,其处理方法有两种:其一是分段法。
将上升阶段看做末速度为零,加速度大小为g的匀减速直线运动;将下降阶段看做初速度为零,加速度大小为g的匀加速直线运动。
其二是通过将竖直上抛运动的轨迹分解为水平和竖直两个方向运动的合成,分别处理水平和竖直两个方向的运动。
(完整word版)匀变速直线运动的公式和推论

第一课时一、匀变速直线运动的规律 (一)匀变速直线运动的公式 1、匀变速直线运动常用公式有以下四个at v v t +=0 2021at t v s += as v v t 2202=- t v v s t 20+= 2、匀变速直线运动中几个常用的结论①Δs=aT 2,即任意相邻相等时间内的位移之差相等。
可以推广到s m —s n =(m-n)aT 2②tsv v v t t =+=202/,某段时间的中间时刻的即时速度等于该段时间内的平均速度. 22202/t s v v v +=,某段位移的中间位置的即时速度公式 (不等于该段位移内的平均速度)。
可以证明,无论匀加速还是匀减速,都有2/2/s t v v <。
说明:运用匀变速直线运动的平均速度公式tsv v v t t =+=202/解题,往往会使求解过程变得非常简捷,因此,要对该公式给与高度的关注.3.初速度为零(或末速度为零)的匀变速直线运动做匀变速直线运动的物体,如果初速度为零,或者末速度为零,那么公式都可简化为:at v = , 221at s = , as v 22= , t vs 2=以上各式都是单项式,因此可以方便地找到各物理量间的比例关系。
4.初速为零的匀变速直线运动①前1秒、前2秒、前3秒……内的位移之比为1∶4∶9∶…… ②第1秒、第2秒、第3秒……内的位移之比为1∶3∶5∶…… ③前1米、前2米、前3米……所用的时间之比为1∶2∶3∶…… ④第1米、第2米、第3米……所用的时间之比为1∶()12-∶(23-)∶……对末速为零的匀变速直线运动,可以相应的运用这些规律。
(二)常用的重要推论及其应用【例3】如图所示,物块以v 0=4m/s 的速度滑上光滑的斜面,途经A 、B 两点,已知在A 点时的速度是B 点时的速度的2倍,由B点再经0.5 s物块滑到斜面顶点C速度变为零,A、B相距0.75 m,求:(1)斜面的长度(2)物体由D运动到B的时间?【例4】两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知1234567A.在时刻t2以及时刻t5两木块速度相同B.在时刻t1两木块速度相同C.在时刻t3和时刻t4之间某瞬间两木块速度相同D.在时刻t4和时刻t5之间某瞬时两木块速度相同☆考点精炼2.一质点沿AD直线作匀加速运动,如图,测得它在AB、BC、CD三段的运动时间均为t,测得位移AC=L1,BD=L2,试求质点的加速度?第二课时(三)追及和相遇问题☆考点点拨1、讨论追及、相遇的问题,其实质就是分析讨论两物体在相同时间内能否到达相同的空间位置问题.(1)两个关系:即时间关系和位移关系(2)一个条件:即两者速度相等,它往往是物体间能否追上、追不上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
匀变速直线运动公式推论推导及规律总结

匀变速直线运动公式推论推导及规律总结v = v0 + at位移由速度的定义导出:s = v0t + 1/2at²在匀变速直线运动中,加速度是变化的,因此在不同的时间段内,可以得到不同的位移和速度的关系。
根据运动的规律,我们可以得到几个重要的推论:推论1:t=0时刻的速度为v0,t时刻的速度为v,则平均速度为(v0+v)/2根据速度的定义,可以得到:v = v0 + at从t=0到t时刻的时间段内,速度变化了v-v0,平均速度就是速度变化量的一半。
推论2:匀变速直线运动的位移与时间的关系可以由位移公式得出。
s = v0t + 1/2at²根据位移公式可以看出,位移与时间的平方成正比。
这说明,在匀变速直线运动中,物体的位移与时间的平方呈现出二次增长的规律。
推论3:匀变速直线运动的速度与时间的关系可以由加速度公式得出。
v = v0 + at在匀变速直线运动中,可以通过加速度的大小和方向的不同来改变速度的大小和方向。
加速度的大小和方向会影响速度的改变速率。
推论4:匀变速直线运动中,速度与位移的关系可以由速度公式和位移公式得出。
将速度公式和位移公式联立,并将速度v表示为位移s和时间t的函数,可以得到:v=(2/t)*(s-v0t)从上式中可以看出,速度与位移的关系呈现线性关系。
即速度与位移成正比,并且速度与时间的倒数成正比。
以上是对匀变速直线运动公式进行推论推导的过程,可以得出一些规律总结如下:1.在匀变速直线运动中,速度和位移与时间有关,速度与时间成一次函数关系,位移与时间成二次函数关系。
2.加速度的大小和方向会影响速度的改变速率,从而影响物体的运动轨迹和速度的变化。
3.速度与位移成正比,并且速度与时间的倒数成正比。
因此,在匀变速直线运动中,可以通过速度-时间图和位移-时间图来分析物体的运动情况。
4.在匀变速直线运动中,如果加速度为零,即物体的速度保持不变,则运动成为匀速直线运动;如果加速度为常数,即物体的速度随着时间的推移以恒定的速率加快或减慢,则运动成为等加速度运动。
匀变速直线运动6个推论推导过程

匀变速直线运动6个推论推导过程一、推论一:速度 - 位移公式v^2-v_0^2=2ax1. 推导依据。
- 匀变速直线运动的速度公式v = v_0+at,位移公式x=v_0t+(1)/(2)at^2。
2. 推导过程。
- 由v = v_0+at可得t=frac{v - v_0}{a}。
- 将t=frac{v - v_0}{a}代入位移公式x = v_0t+(1)/(2)at^2中,得到:- x=v_0frac{v - v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2。
- 展开式子:x=frac{v_0v - v_0^2}{a}+(1)/(2)frac{(v - v_0)^2}{a}。
- 进一步化简:ax=v_0v - v_0^2+(1)/(2)(v^2-2vv_0+v_0^2)。
- ax = v_0v - v_0^2+(1)/(2)v^2-vv_0+(1)/(2)v_0^2。
- 整理可得v^2-v_0^2=2ax。
二、推论二:平均速度公式¯v=frac{v_0+v}{2}(适用于匀变速直线运动)1. 推导依据。
- 位移公式x = v_0t+(1)/(2)at^2,速度公式v = v_0+at,平均速度定义¯v=(x)/(t)。
2. 推导过程。
- 由位移公式x = v_0t+(1)/(2)at^2。
- 又因为v = v_0+at,则t=frac{v - v_0}{a}。
- 将t=frac{v - v_0}{a}代入位移公式得x=v_0frac{v - v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2。
- 平均速度¯v=(x)/(t),t=frac{v - v_0}{a},则¯v=frac{v_0frac{v -v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2}{frac{v - v_0}{a}}。
匀变速直线运动的规律(推论

速度和物体的加速度。 则物体在斜面上和水平面上有位移之比?
突然发现正前方有一辆自行车以4 m/s的速度做同方向的匀速直线运动,汽车立即关闭油门,做加速度大小为 的匀减速直线运动,汽 车恰好不碰上自行车。
突然发现正前方有一辆自行车以4 m/s的速度做同方向的匀速直线运动,汽车立即关闭油门,做加速度大小为 的匀减速直线运动,汽
求: 车恰好不碰上自行车。
4 m m,求物体的加速度a和相邻各1s始末的瞬时速度v 1 、 v 2 、v 3 2、判断匀变速直线运动的方法:
(1)钢球运动的加速度; (1) v= v0+at 速度均匀变化或 (加速度不变)
(3)照片上D球离C 球的距离. 2、初速度为零的匀变速直线运动,第一个 T s,第二个 T s,第三个 T s内的位移之比
(1) v= v0+at 速度均匀变化或 (加速度不变) 4、中间时刻、中间位置的瞬时速度
v-t图像解题和追及相遇问题
例1、物体由静止开始做匀加速直线运动, 当速度达到10m/s时,立即改做匀减速直 到停下,物体共运动20s,则物体的位移 为多少?
车恰好不碰上自行车。
思考:如果上题改为自行车、汽车同一地点同向运动,其它条件不变,什么时候相遇?什么时候相距最远?为多少?
(1) v= v0+at 速度均匀变化或 (加速度不变)
例3、一质点做匀减速运动,走过36 m后 停止,若将这位移分为三段,而且通过 每段的时间相等,试求第一段的长度。
作业:(要求:至少两种以上
s放下一颗使之做匀加速直线运动,在连续放下 4、中间时刻、中间位置的瞬时速度
匀变速直线运动规律常见推论及推理过程

匀变速直线运动规律常见推论及推理过程本文对匀变速直线运动的常见推论、以及相关推理过程进行归纳总结,结合相关示意图将推理过程详细呈现给读者,适合高一学生学习参考。
匀变速直线运动基本公式如下: at v v +=02021at t v x +=()t v v x +=021ax v v 2202=-常用推论: 一.适用于任意匀变速直线运动的推论1. 某段匀变速直线运动中间时刻瞬时速度与该过程的平均速度相等,且都等于初、末速度和的一半,即:()v v t x v v t +===02212. 任意匀变速直线运动相邻相等时间间隔内的位移之差都相等,都等于2aT ,即:212312aT x x x x x x x n n =-==-=-=∆-拓展结论:x m −x n =(m −n)aT 23. 某段匀变速直线运动中间位置的瞬时速度:22202v v v x +=二. 仅适用于初速度为零的匀加速直线运动的推论1. 从开始运动起,前1个T 末、前2个T 末、前3个T 末……前n 个T 末的瞬时速度之比为:n v v v v n ::3:2:1::::321 =;2. 从开始运动起,前1个T 内、前2个T 内、前3个T 内……前n 个T 内的位移之比为:2222321::3:2:1::::n x x x x n =;3. 从开始运动起,第1个T 内、第2个T 内、第3个T 内……第n 个T 内的位移之比为:x Ⅰ:x Ⅱ:x Ⅲ: … :x N =1:3:5: … : (2n-1);4. 从开始运动起,前1个x 末、前2个x 末、前3个x 末……前n 个x 末的瞬时速度之比为:n v v v v n ::3:2:1::::321 =;5. 从开始运动起,第1个x 内、第2个x 内、第3个x 内……第n 个x 内所用时间之比为)1(::)23(:)12(:1::::321----=n n t t t t n 。
匀变速直线运动公式、推论推导、及规律总结
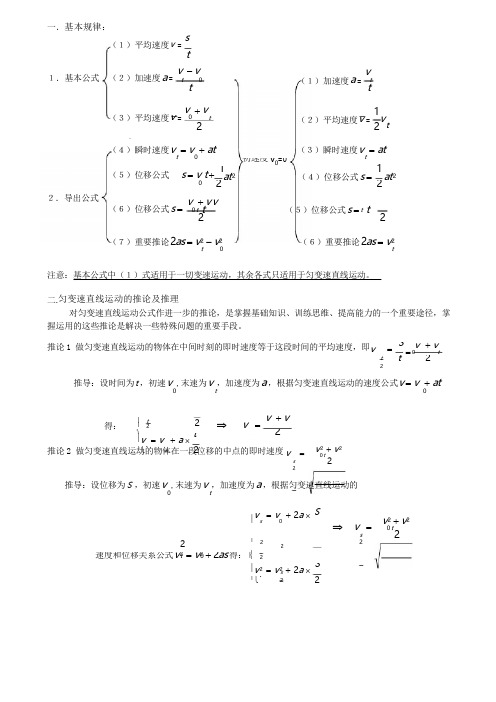
1.基本公式 (2)加速度 a = v - v初速度 v 0=0(5)位移公式 s = v t + 122推论 1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即v= St 2⇒ v = v + v ⎪ t 2 ⎪ 2 ⎨ 2 ⎪v = v + a ⨯ t ⎪⎩ t2 ⎧2速度和位移关系公式 v 2 = v 2 + 2as 得: ⎪ 2⎪v 2 = v 2+ 2 a ⨯ S⎪⎩ t 22一.基本规律:(1)平均速度 v =stvt 0(1)加速度 a = ttt(3)平均速度 v = v 0 +v2t1(2)平均速度 v = v2 t(4)瞬时速度 v = v + at(3)瞬时速度 v = attt1at 2(4)位移公式 s = at 22.导出公式(6)位移公式 s = v + v v0 t t (5)位移公式 s = t t2 2(7)重要推论 2as = v 2 - v 2t(6)重要推论 2as = v 2t注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
t v + v = 0t2推导:设时间为 t ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的速度公式 v = v + at0 t得:推论 2 做匀变速直线运动的物体在一段位移的中点的即时速度v=sv 2 + v 20 t22推导:设位移为 S ,初速 v ,末速为 v ,加速度为 a ,根据匀变速直线运动的0 t⎪vs = v 0+ 2 a ⨯2t 0 ⎨ s 2 S⇒ v =s2v 2 + v 20 t2经过第二个时间 t 后的速度为 v =2v +at ,这段时间内的位移为 S = v t + at 2 = v t + at 22 2 经过第三个时间 t 后的速度为 v =3v +at ,这段时间内的位移为 S = v t + at 2 = v t+ at 2 2 2 2 2 3 2 32 2 2 2t推论 3 做匀变速直线运动的物体,如果在连续相等的时间间隔 t 内的位移分别为 S 、 S 、 S …… S123n ,加速度为 a,则 ∆S =S 2- S 1 = S 3 - S 2= …… = S n - S推导:设开始的速度是 vn -1= at2经过第一个时间 t 后的速度为 v = v + a t ,这一段时间内的位移为 S = v t + 1 0 1 0 1 2 at 2,1 32 0 2 1 0 1 52 032…………………经过第 n 个时间 t 后的速度为 v =nv +at ,这段时间内的位移为 S =v t +1 a t 2 =v t + n 0 n n -1 02n -1 2at 2则 ∆S = S 2 - S 1 = S 3 - S 2 = …… = S n - Sn -1= at 2点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度 a 与时间 “有关的恒量”.这也提供了一种加速度的测量的方法: 即 a =∆S,只要测出相邻的相同时间内的位移之差 ∆S 和 t ,就容易测出加速度 a 。
匀变速直线运动规律推论

1.位移与时间的关系:匀变速直线运动的位移与时间之间的关系可以用以下公式表示:x = x0 + v0t + (1/2)at^2其中,x是物体的位移,x0是初始位置,v0是初始速度,a是加速度,t是时间。
这些推论适用于在匀变速直线运动下的物体。在这种情况下,物体在直线上的位置随时间的变化是二次函见的运动形式,在研究和实际应用中有着重要的意义。
2.速度与时间的关系:匀变速直线运动的速度与时间之间的关系可以用以下公式表示:v = v0 + at其中,v是物体的速度,v0是初始速度,a是加速度,t是时间。
3.位移与速度的关系:匀变速直线运动的位移与速度之间的关系可以用以下公式表示:v^2 = v0^2 + 2a(x - x0)其中,v是物体的速度,v0是初始速度,a是加速度,x是当前位置,x0是初始位置。
匀变速直线运动的推论整理
1 2 x2 a 2 2 1 2 x3 a 3 2
故 x1 : x2
: x3 : 1 : 4 : 9 :
(3)第一秒、第二秒、第三秒……位移之比
1 2 x = a 1 第一秒内位移 Ⅰ 2
(m)
1 1 3 2 2 第二秒内位移 xⅡ= a 2 a 1 a 2 2 2 1 1 5 2 2 第三秒内位移 xⅢ = a 3 a 2 = a 2 2 2
②为确定解题结果是否正确,用不同方法求 解是一有效措施。 ③一般应该先用字母代表物理量进行运算, 得出用已知量表达未知量的关系式,然后 再把数值代入。 这样做能够清楚地看出未知量与已知 量的关系,计算也比较简便。
四个比例式:初速为零的匀加速直线运动 的几个常用的比例式:
• • • • • • • (1)1秒末、2秒末、3秒末……瞬时速度 之比
位移公式:
速度位移公式:
v v 2ax
2 2 0
二、3个推论与一种方法
1. 2.
v
v0 v 2
vt
2
Vx
2
V02 V 2 2
2
3. x2 x1 x3 x2 aT 4.
逆向思维法
练习1:一物体做初速为零的匀加速直线运 动。求:
(1)1秒末、2秒末、3秒末……瞬时速度 之比 由速度公式
4.汽车刹车后做匀减速直线运动,经3 s后停止运动,那么,在这 连续的3个1 s内汽车通过的位移之比为( B ) A.1∶3∶5 C.1∶2∶3 B.5∶3∶1 D.3∶2∶1
解析:末速度为零的匀减速直线运动可以看作反向的初速度 为零的匀加速直线运动处理,初速度为零的匀加速直线运动 第1秒内、第2秒内、第3秒内……的位移之比为
匀变速直线运动的公式和推论

匀变速直线运动的公式和推论一、匀变速直线运动的公式1.位移公式在匀变速直线运动中,物体的位移等于初速度与末速度的平均速度乘以时间的的和,即s=(v0+v)*t/2其中,s为位移,v0为初速度,v为末速度,t为时间。
2.速度公式在匀变速直线运动中,物体的速度等于初速度加上速度变化率与时间的乘积,即v=v0+a*t其中,v为速度,v0为初速度,a为加速度,t为时间。
3.位移-时间公式如果初速度和末速度相等,同时加速度也恒定不变,那么我们可以将上述两个公式联立消去v,得到s=v0*t+0.5*a*t^24.速度-时间公式如果初速度和末速度相等,同时加速度也恒定不变,同样将上述两个公式联立消去s,得到v^2=v0^2+2*a*s二、匀变速直线运动的推论1.速度-时间图像在匀变速直线运动中,通过画速度-时间图像可以更加直观地看到速度的变化。
-当初速度和加速度都为正值时,速度-时间图像为从左下方斜向上的直线;-当初速度为正值,加速度为负值时,速度-时间图像为从左上方斜向下的直线;-当初速度为负值,加速度为正值时,速度-时间图像为从左下方斜向下的直线;-当初速度和加速度都为负值时,速度-时间图像为从左上方斜向上的直线。
2.位移-时间图像在匀变速直线运动中,通过画位移-时间图像可以更加直观地看到位移的变化。
-当速度为正值时,位移-时间图像为从左下方斜向上的二次函数曲线;-当速度为负值时,位移-时间图像为从左上方斜向下的二次函数曲线。
3.加速度的方向在匀变速直线运动中,加速度的方向与速度的方向并不一致,加速度的方向与速度变化的方向相同。
4.加速度与力的关系根据牛顿第二定律,物体的加速度与物体受到的合力成正比,即a=F/m其中,a为加速度,F为物体受到的合力,m为物体的质量。
综上所述,匀变速直线运动的公式和推论对于描述和解决匀变速直线运动问题具有重要的意义。
通过这些公式和推论,我们可以方便地计算位移、速度和加速度等运动参数,进而分析和描述物体在匀变速直线运动过程中的运动规律。
匀变速直线运动公式推论推导及规律总结
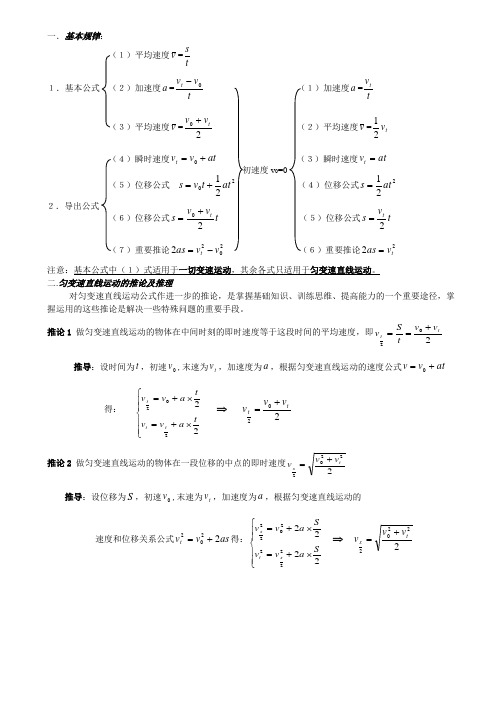
一.基本规律:v =ts 1.基本公式a =t v v t 0- a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s =t v v s t 20+= t vs t 2=2022v v as t -= 22t v as =注意:基本公式中(1)式适用于一切变速运动,其余各式只适用于匀变速直线运动。
二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即202t t v v t S v +==推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202ta v v t a v v t t t ⇒ 202t t v v v +=推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ,加速度为a ,则=-=-=∆2312S S S S S……21at S S n n =-=-推导:设开始的速度是0v经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为20121at t v S +=, 经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0,这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度a 与时间“有关的恒量”.这也提供了一种加速度的测量的方法:即2tSa ∆=,只要测出相邻的相同时间内的位移之差S ∆和t ,就容易测出加速度a 。
匀变速直线运动的三个推论

v +v v中 = 2
2 0
2 tLeabharlann 推论三: 推论三: 在任意相临相等的时间间隔 T 内所走的位移之 差是一个恒量: 差是一个恒量:
∆x = x2 − x1 = x3 − x2 = xn +1 − xn = aT
2
推广:x m − xn = (m − n)aT
2
例题1: 例题1: 一辆汽车做匀加速直线运动,通过A 一辆汽车做匀加速直线运动,通过A点 时的速度为V 通过B点时的速度为V 时的速度为V1,通过B点时的速度为V2,则 通过AB两点所用时间一半时的速度( AB两点所用时间一半时的速度 通过AB两点所用时间一半时的速度( ), 通过AB两点间的平均速度为( AB两点间的平均速度为 通过AB两点间的平均速度为( ), 通过AB中点的速度为( AB中点的速度为 通过AB中点的速度为( )。
例题5 纸带问题的处理(重点) 例题5:纸带问题的处理(重点)
例题2 例题2: 一物体从斜面顶端由静止开始匀加速下 经过斜面中点时速度为2m/s 2m/s, 滑,经过斜面中点时速度为2m/s,则物体 到达斜面底端时的速度为( 到达斜面底端时的速度为( )。
例题3: 例题3: 一个做匀加速直线运动的物体,在前4s 一个做匀加速直线运动的物体,在前4s 内经过的位移为24m 在第二个4s 24m, 4s内经过的 内经过的位移为24m,在第二个4s内经过的 位移是60m 60m, 位移是60m,求这个物体的加速度和初速度 各是多少? 各是多少?
匀变速直线运动的3 匀变速直线运动的3个推论
推论一: 在某段时间内的中间时刻的瞬时速度, 在某段时间内的中间时刻的瞬时速度,等于 这段时间的平均速度: 这段时间的平均速度:
vt 2
匀变速直线运动规律及推论(精选版)

v1=x/t1,v2=x/t2.
它们分别等于通过这两段位移所用的时间中点的瞬时速度, 由题意可知 这两个时间中点的间隔为: Δt=(t1+t2)/2.
根据加速度的定义式可知:
2 x(t1 t2 ) a v / t ( v 2 v1 ) / t . (t1 t2 )t1t2
1 1 解析 :由x at 2得 : xⅠ x1 at 2 , xⅡ x 2 x1 2 2 1 1 2 1 1 2 2 2 2 a 3t at 4at , x Ⅲ x 3 x 2 a 6t a 3t 2 2 2 2 27 2 at , 则xⅠ xⅡ x Ⅲ 1 8 27. ∶ ∶ ∶ ∶ 2
例:如图所示,两个光滑的斜面高度相同, 右边由两部分组成且AB+BC=AD,两小 球a、b分别从A点沿两侧斜面由静止滑下, 不计转折处的能量损失,哪一边的小球先 滑到斜面底端.
2 2
3.把物体做初速度为零的匀加速直线运动的总位移分成等 长的三段,按从开始到最后的顺序,经过这三段位移的平均 速度之比为(D )
A.1 3 5 ∶ ∶ C.1 2 3 ∶ ∶
B.1 4 9 ∶ ∶ D.1 ( 2 1) ( 3 2 ) ∶ ∶
解析 :由初速度为零的匀加速直线运动特点, 可知 x x x t∶t 2 t 3 1 ( 2 1) ( 3 2), 则v∶ 2 v3 ∶ ∶ , ∶ ∶ ∶ 1 v∶ 1 t1 t2 t3 即得答案D.
4、利用图像解决问题
• 常利用物体的位移-时间图像和速度-时间图 像,分析物体的运动过程并利用图像求解 问题,根据题意做出图像是关键。
1.做初速度为零的匀加速直线运动的物体,将其运动时间顺次 分成1∶2∶3三段,则每段时间内的位移之比为( C ) A.1∶3∶5 C.1∶8∶27 B.1∶4∶9 D.1∶16∶81
匀变速直线运动推论

推导一下
V t 和 V x 谁大谁小
2 2
可以证明:无论是匀加速直线运动还是匀减速直线运动, 都有唯一的结论,即:
V
t 2
< V
x 2
推论3、匀变速直线运动利用打点纸带求加速 推论3、匀变速直线运动利用打点纸带求加速 度公式
0
· x1 · x2 · x3
1
2
·
3
4
x4
·
x5
·
5
上图为物体运动时, 上图为物体运动时,打点计时器打出 的纸带。设相邻两测量点间的时间 间隔为T,打0 间隔为T,打0号测量点时瞬时速度 为 v0
(3)第一秒、第二秒、第三秒……位移之比 (3)第一秒、第二秒、第三秒……位移之比
第一秒内位移
1 2 xⅠ= a ⋅ 1 2
(m)
1 3 2 1 2 第二秒内位移 xⅡ= a × 2 − a ×1 = a 2 2 2
1 1 5 2 2 第三秒内位移 xⅢ= a × 3 − a × 2 = a 2 2 2
解法1:由匀变速直线运动的位移公式求解。 解法1:由匀变速直线运动的位移公式求解。 解法2 解法2:用平均速度公式求解。 解法3:用推论公式△x=aT 解法3:用推论公式△x=aT2求解。
例7:汽车刹车做匀减速直线运动,加速度大小为 :汽车刹车做匀减速直线运动, 求汽车停止前最后1s内的位移? 1m/s2。 求汽车停止前最后1s内的位移?
速度公式: 速度公式:
v = v 0 + at
1 2 x = v0t + at 2
位移公式: 位移公式:
速度位移公式: 速度位移公式:
v − v = 2ax
2 2 0
二、3个推论与一种方法 个推论与一种方法
匀变速直线运动的所有公式及推论

匀变速直线运动的所有公式及推论为了让你对匀变速直线运动的公式和推论有个清晰的了解,我们不妨先来聊聊这个话题。
你有没有发现,物理学这玩意儿就像那种千层饼,一层一层的,挺复杂但也有条理。
咱们就从最基础的开始,逐步深入,搞懂这些公式的来龙去脉吧。
1. 匀变速直线运动的基本概念首先,什么是匀变速直线运动呢?想象一下你骑车上坡,每踩一脚踏板,速度都会有所变化。
匀变速直线运动就是指物体在一段时间内加速或减速的过程中,速度的变化是均匀的,也就是说加速度保持不变。
就像你骑车时,每次加速的程度都是一样的,不是突然快起来然后慢下来。
1.1 速度与时间的关系在这个运动中,有两个基本的公式,咱们先说说速度和时间的关系。
假如你从静止开始加速,那么速度((v))等于初速度((v_0))加上加速度((a))乘以时间((t))。
也就是说,( v = v_0 + at )。
举个例子,你的自行车从静止开始,经过一段时间,你的速度就会变得越来越快。
这个公式就像是告诉你:“嘿,你的速度是如何一步一步增加的!”1.2 位移与时间的关系然后是位移((s))与时间的关系。
这个公式稍微复杂一点,不过不必担心,它其实也很简单。
位移等于初速度乘以时间,加上加速度乘以时间的平方再除以二。
也就是( s = v_0t + frac{1{2at^2 )。
这就像你骑车的时候,位移是你骑过的路程,不只是加速的速度,还有时间的影响。
2. 匀变速直线运动的常见推论一旦掌握了这两个基本公式,咱们可以进一步推导出其他有用的公式。
这些推论可以帮助我们更好地理解和解决实际问题。
2.1 速度与位移的关系一个常用的推论是速度和位移之间的关系。
你可能会想:“我怎么知道某一时刻的速度?”这时候,速度的平方等于初速度的平方加上两倍的加速度乘以位移。
公式是( v^2 = v_0^2 + 2as )。
这个公式特别适合当你知道了位移,想知道速度时用。
2.2 平均速度另一个实用的推论是计算平均速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
罗老师总结匀变速直线运动常用公式 (附匀变速直线运动的推论及推理过程)一、基本公式速度公式 at v v t +=0 当00=v 时,at v t = 位移公式 2021at t v s += 221at s = 二、几个常用的推论1.位移推导公式 2022v v as t -=, t v v s t20+=2.平均速度v 、中间时刻的瞬时速度2/t v 、中间位置的瞬时速度2/s v 为:0/22t t v v xv v t +===, 22202/t s v v v += 3.做匀变速直线运动的物体,在各个连续相等的时间T 内的位移分别是s 1、s 2、s 3…s n ,则Δs =s 2-s 1=s 3-s 2=…=s n -s n-1=aT 2.4.V 0=0的匀加速直线运动中的几个常用的比例公式(1)等分运动时间,以T 为单位时间.①1T 末,2T 末,3T 末…,n T 末的速度之比v 1:v 2:v 3:…:v n =1:2:3…:n②1T 内、2T 内、3T 内…n T 内通过的位移之比s 1:s 2:s 3:…:s n =1:4:9…:n 2③第1个T 内、第2个T 内、第3个T 内…、第n 个T 内通过的位移之比s Ⅰ:s Ⅱ:s Ⅲ:…:s N =1:3:5…:(2n —1)④第1个T 内、第2个T 内、第3个T 内…、第n 个T 内的平均速度之比v Ⅰ:v Ⅱ:v Ⅲ:…:v N =1:3:5…:(2n —1) (2)等分位移,以x 为位移单位. ①通过1x 、2x 、3x …、n x 所需时间之比t 1:t 2:t 3:…:t n =1:3:2…:n②通过第1个x 、第2个x 、第3个x 、…第n 个x 所需时间之比t Ⅰ:t Ⅱ:t Ⅲ:…:t N =1::23:12--…:1--n n③1x 末,2x 末,3x 末…,n x 末的速度之比v 1:v 2:v 3:…:v n =1:3:2…:n对匀变速直线运动公式作进一步的推论,是掌握基础知识、训练思维、提高能力的一个重要途径,掌握运用的这些推论是解决一些特殊问题的重要手段。
推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度,即202t t v v t S v +==推导:设时间为t ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度公式at v v +=0得: ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202t a v v t a v v t t t ⇒ 202t t v v v += 推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导:设位移为S ,初速0v ,末速为t v ,加速度为a ,根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得:⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒ 22202t s v v v += 推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ,加速度为a ,则=-=-=∆2312S S S S S ……21at S S n n =-=-推导:设开始的速度是0v经过第一个时间t 后的速度为at v v +=01,这一段时间内的位移为20121at t v S +=, 经过第二个时间t 后的速度为at v v +=022,这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023,这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0,这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨:只要是匀加速或匀减速运动,相邻的连续的相同的时间内的位移之差,是一个与加速度a 与时间“有关的恒量”.这也提供了一种加速度的测量的方法: 即2t Sa ∆=,只要测出相邻的相同时间内的位移之差S ∆和t ,就容易测出加速度a 。
推论4 初速度为零的匀变速直线运动的位移与所用时间的平方成正比,即t 秒内、2t秒内、3t 秒内……n t 秒内物体的位移之比1S :2S :3S :… :n S =1 :4 :9… :2n推导:已知初速度00=v ,设加速度为a ,根据位移的公式221at S =在t 秒内、2t 秒内、3t 秒内……n t 秒内物体的位移分别为: 2121at S =、22)2(21t a S =、23)3(21t a S = (2))(21nt a S n =则代入得 1S :2S :3S :... :n S =1 :4 :9 (2)推论5 初速度为零的匀变速直线运动,从开始运动算起,在连续相等的时间间隔内的位移之比是从1开始的连续奇数比,即1S :2S :3S :… :n S =1 :3 :5…… :(2n-1)推导:连续相同的时间间隔是指运动开始后第1个t 、第2个t 、第3个t ……第n 个t ,设对应的位移分别为、、、321S S S ……n S ,则根据位移公式得 第1个t 的位移为2121at S =第2个t 的位移为22222321)2(21at at t a S =-=第3个t 的位移为222325)2(21)3(21at t a t a S =-=……第n 个t 的位移为222212])1[(21)(21at n t n a nt a S n -=--=代入可得: )12(:5:3:1::::321-=n S S S S n ΛΛΛΛ推论6 初速度为零的匀变速直线运动,从开始运动算起,物体经过连续相等的位移所用的时间之比为1t :2t :3t …… :n t =1 :(12-) :(23-)…… :(1--n n )推导:通过连续相同的位移是指运动开始后,第一个位移S 、第二个S 、第三个S ……第n 个S ,设对应所有的时间分别为ΛΛ321t t t 、、n t , 根据公式221at S =第一段位移所用的时间为aSt 21=第二段位移所用的时间为运动了两段位移的时间减去第一段位移所用的时间aSa S a St 2)12(242-=-=同理可得:运动通过第三段位移所用的时间为 aSaSaSt 2)23(463-=-=以此类推得到aSn n a S n a nSt n 2)1()1(22--=--=代入可得)1(:)23(:)12(:1::321----=n n t t t t n ΛΛ从以上推导可知解决这些问题主要要理解:连续的时间内、连续相等的时间内、连续相等的位移的含义、要克服存在的思维障碍。
利用匀变速直线运动的推论解题,常可收到化难为易,简捷明快的效果。
讨论:在同一段匀变速直线运动中,对于加速或是减速,2tv 与2sv 有何关系?分析:若物体做匀加速直线运动,如图甲所示,物体由A 到B 历时t ,而经2t物体的位移不到一半,即经2t ,物体在中间位置O 的左侧,所以22st v v <。
若物体做匀减速直线运动,如图乙所示,物体由A 到B 历时t ,而经2t物体的位移已大于整个位移的一半,即达到O 点的右侧,由于是减速,所以22st v v <。
例1 运行着的汽车制动后做匀减速滑行,经3.5秒停止。
试问它在制动开始后的1秒内、2秒内、3秒内通过的位移之比为多少?解析:设汽车从Ο起制动,1秒末到A ,2秒末到B ,3秒末到C ,最后停在D 。
这个运动的逆过程可看初速为零的匀加速运动,加速度的大小不变。
将3.5秒分为7个0.5秒,那么,从D 逆过来在连续7个0.5秒的位移之比为1 :3 :5 :7 :9 :11 :13则S CB :S BA :S AO =8:16:24 所以得到汽车从Ο起在1秒内,2秒内,3秒内位移之比S O A :S O B :S O C = 24 :40 :48 = 3 :5 :6例2 火车从静止起动做匀加速直线运动,站在第1节车厢前端的人看到第2节车厢从他身边通过的时间是5秒,那么第6节车厢从他身边通过的时间是多少?解析:因为每节车厢的长度是相等的,利用从开始运动算起,经过连续相等位移所用的时间之比为1t :2t :3t …… :n t =1 :(12-) :(23-)…… :(1--n n )得:561262--=t t ⇒ )(58.2512566S t =⨯--=例3做匀变速度直线运动物体从A 点到B 点经过的时间t ,物体在A 、B 两点的速度分别为a v 和b v ,物体通过AB 中点的瞬时速度为1v ,物体在2t时刻的瞬时速度为2v ,则( )A. 若做匀加速运动,则1v >2vB. 若做匀减速运动,则1v >2vC. 不论匀加速运动还是匀减速运动,则1v >2vD. 不论匀加速运动还是匀减速运动,则2v >1v解析: 根据题意,1v 是时间中点的速度,所以21b a AB v v v v +==;而2v 是位移中点的速度,所以2222ba v v v +=22224)(2222222222222b a b b a a b b a a b a b a v v v v v v v v v v v v v v v +=++≥+++=+=+=1v = 因为b a v v ≠ 所以不论匀加速运动还是匀减速运动,则2v >1v 故选项D 正确。
【模拟试题】1、下列关于平均速度和即时速度的说法中正确的是A. 做变速运动的物体在相同时间间隔里的平均速度是相同的B. 即时速度就是运动的物体在一段较短的时间内的平均速度C. 平均速度就是初末时刻即时速度的平均值D. 某物体在某段时间里的即时速度都为零,则该物体在这段时间内静止2、下面关于加速度的描述中正确的有A. 加速度描述了物体速度变化的多少B. 加速度在数值上等于单位时间里速度的变化C. 当加速度与位移方向相反时,物体做减速运动D. 当加速度与速度方向相同且又减小时,物体做减速运动3、关于速度与加速度,下列说法中正确的是A. 速度越大,加速度一定越大B. 速度为零,加速度也一定为零C. 加速度为零,速度也一定为零D. 以上说法都不对4、做匀加速直线运动的物体,加速度是2米/秒2,它意味着A. 物体在任一秒末的速度是该秒初的两倍B. 物体在任一秒末的速度比该秒初的速度大2米/秒C. 物体在第一秒末的速度为2米/秒D. 物体任一秒的初速度比前一秒的末速度大2米/秒5、关于匀加速直线运动,下列说法中正确的是A. 速度与运动时间成正比B. 速度的增量与运动时间的平方成正比C. 位移与运动时间的平方成正比D. 在连续相同时间内的位移增量都相同6、对做匀减速运动的物体(无往返),下列说法中正确的是A. 速度和位移都随时间减小B. 速度和位移都随时间增大C. 速度随时间增大,位移随时间减小D. 速度随时间减小,位移随时间增大7、一个做初速度为零的匀加速直线运动的物体,下列说法中正确的是A. 第4秒内的平均速度大于4秒内的平均速度B. 第4秒内的平均速度大于第4秒末的即时速度C. 第4秒内的位移小于头4秒内的位移D. 第3秒末的速度等于第4秒初的速度8、甲、乙两物体沿一直线同向运动,其速度图象如图所示,在 t时刻,下列物理量中相等的是A. 运动时间B. 速度C. 位移D. 加速度9、四个质点做直线运动,它们的速度图象分别如下图所示,下列说法中正确的是A. 四个质点在2秒内速度变化快慢相同B. 在第2秒末,质点(2)离出发点最远C. 在第2秒内,质点(1)(3)做加速运动D. 在第2秒末,质点(2)(3)偏离出发点位移相同10、如果运动的物体的平均速度等于这段时间内初速度和末速度的算术平均值,则该运动一定不是A. 匀速直线运动B. 匀加速直线运动C. 匀减速直线运动D. 加速度减小的运动11、有一个物体开始时静止在O点,先使它向东做匀加速直线运动,经过5秒钟,使它的加速度方向立即改为向西,加速度的大小不改变,再经过5秒钟,又使它加速度方向改为向东,但加速度大小不改变,如此重复共历时20秒,则这段时间内:A. 物体运动方向时而向东时而向西B. 物体最后静止在O点C. 物体运动时快时慢,一直向东运动D. 物体速度一直在增大12、骑自行车的人沿着直线从静止开始运动,运动后,在第1、2、3、4秒内,通过的路程分别为1米、2米、3米、4米。
