2021-2022学年高三理科数学期末试题及答案
2021-2022学年上海市浦东新区高三(上)期末数学试卷(一模)

2021-2022学年上海市浦东新区高三(上)期末数学试卷(一模)试题数:21,总分:1501.(填空题,4分)已知复数z=1+2i (i 是虚数单位),则|z|=___ .2.(填空题,4分)函数f (x )= √x +1的反函数为f -1(x ),则f -1(3)=___ .3.(填空题,4分)已知cosθ=- 35 ,则cos2θ的值为 ___ .4.(填空题,4分)已知集合A={x|-1<x <1},B={x| x x−2 <0},则A∩B=___ .5.(填空题,4分)底面半径长为2,母线长为3的圆柱的体积为 ___ .6.(填空题,4分)三阶行列式 |125143356| 中,元素2的代数余子式的值为 ___ . 7.(填空题,5分)数列{a n }的通项公式为a n = {2n −1(1≤n ≤10)2−1n (n ≥11) ,则 n→∞a n =___ . 8.(填空题,5分)方程log 2(x+1)+log 2(x-1)=1的解为 ___ .9.(填空题,5分)已知函数f (x )=x 2+2x+3+m ,若f (x )≥0对任意的x∈[1,2]恒成立,则实数m 的取值范围是 ___ .10.(填空题,5分)某学校要从6名男生和4名女生中选出3人担任进博会志愿者,则所选3人中男女生都有的概率为 ___ .(用数字作答)11.(填空题,5分)已知A (-1,0)、B (1,0)、P (1, √3 ),点C 是圆x 2+y 2=1上的动点,则 PC ⃗⃗⃗⃗⃗ • PB ⃗⃗⃗⃗⃗ + PC⃗⃗⃗⃗⃗ • PA ⃗⃗⃗⃗⃗ 的取值范围是 ___ . 12.(填空题,5分)已知实数x 、y 满足 x|x|4+y|y|=1,则|x+2y-4|的取值范围是 ___ . 13.(单选题,5分)已知直线a 在平面β上,则“直线l⊥a”是“直线l⊥β”的( )条件.A.充分非必要B.必要非充分C.充要D.非充分非必要14.(单选题,5分)(x-1)10的二项展开式中第4项是( )A. C 103x 7B. C 104x 6C. −C 103x 7D. −C 104x 615.(单选题,5分)若方程4x2+ky2=4k表示双曲线,则此双曲线的虚轴长等于()A. 2√kB. 2√−kC. √kD. √−k(x∈[t,t+40])零点的个数不可能是()个16.(单选题,5分)函数f(x)=sinx- 12A.12B.13C.14D.1517.(问答题,14分)已知三棱锥P-ABC中,PA、BA、CA两两互相垂直,且长度均为1.(1)求三棱锥P-ABC的全面积;(2)若点D为BC的中点,求PD与平面PAC所成角的大小.(结果用反三角函数值表示)18.(问答题,14分)已知函数f(x)=x2+ax+1,a∈R.(1)判断函数f(x)的奇偶性,并说明理由;(x>0),写出函数g(x)的单调递增区间并用定义证明.(2)若函数g(x)= f(x)x19.(问答题,14分)某水产养殖户承包一片靠岸水域,如图,AO、OB为直线岸线,,该承包水域的水面边界是某圆的一段弧AB̂,过弧OA=1000米,OB=1500米,∠AOB= π3AB̂上一点P按线段PA和PB修建养殖网箱,已知∠APB= 2π.3(1)求岸线上点A与点B之间的直线距离;(2)如果线段PA上的网箱每米可获得40元的经济收益,线段PB上的网箱每米可获得30元的经济收益,记∠PAB=θ,则这两段网箱获得的经济总收益最高为多少?(精确到元)20.(问答题,16分)已知斜率为k的直线l经过抛物线C:y2=4x的焦点F,且与抛物线C 交于不同的两点A(x1,y1),B(x2,y2).和3,求|AB|;(1)若点A和B到抛物线准线的距离分别为32(2)若|AF|+|AB|=2|BF|,求k的值;(3)点M(t,0),t>0,对任意确定的实数k,若△AMB是以AB为斜边的直角三角形,判断符合条件的点M有几个,并说明理由.21.(问答题,18分)已知数列{a n},若存在A∈R使得数列{|a n-A|}是递减数列,则称数列{a n}是“A型数列”.是否为“A型数列”;(1)判断数列π、- √3、-1、12(2)若等比数列{a n}的通项公式为a n=q n(n∈N*),q>0,其前n项和为S n,且{S n}是“A型数列”,求A的值和q的取值范围;(3)已知k>0,数列{a n}满足a1=0,a n+1=k|a n|-1(n∈N*),若存在A∈R,使得{a n}是“A型数列”,求k的取值范围,并求出所有满足条件的A(用k表示).2021-2022学年上海市浦东新区高三(上)期末数学试卷(一模)参考答案与试题解析试题数:21,总分:1501.(填空题,4分)已知复数z=1+2i(i是虚数单位),则|z|=___ .【正确答案】:[1] √5【解析】:直接利用复数的模的求法公式,求解即可.【解答】:解:复数z=1+2i(i是虚数单位),则|z|= √12+22 = √5.故答案为:√5.【点评】:本题考查复数的模的求法,考查计算能力.2.(填空题,4分)函数f(x)= √x +1的反函数为f-1(x),则f-1(3)=___ .【正确答案】:[1]4【解析】:直接利用反函数的关系式的定义域和函数的值的对应关系求出结果.【解答】:解:∵已知函数y=f(x)存在反函数y=f-1(x),设f(x)=3,则√x +1=3,解得x=4,则f-1(3)的值是4.故答案为:4.【点评】:本题考查了反函数的性质的应用,利用原函数与反函数的定义域和值域恰相反,求出反函数的函数值.3.(填空题,4分)已知cosθ=- 3,则cos2θ的值为 ___ .5【正确答案】:[1]- 725【解析】:由题意利用二倍角的余弦公式,计算求得结果.【解答】:解:∵cosθ=- 35 ,则cos2θ=2cos 2θ-1=2× 925 -1=- 725 ,故答案为:- 725 .【点评】:本题主要考查二倍角的余弦公式的应用,属于基础题.4.(填空题,4分)已知集合A={x|-1<x <1},B={x| x x−2 <0},则A∩B=___ .【正确答案】:[1](0,1)【解析】:求出集合A ,B ,由此能求出A∩B .【解答】:解:∵集合A={x|-1<x <1},B={x| x x−2 <0}={x|0<x <2}, ∴A∩B={x|0<x <1}=(0,1).故答案为:(0,1).【点评】:本题考查集合的运算,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.5.(填空题,4分)底面半径长为2,母线长为3的圆柱的体积为 ___ .【正确答案】:[1]12π【解析】:利用圆柱体的体积公式求解即可.【解答】:解:因为底面半径长为2,母线长为3,所以圆柱的体积为V=Sh=π×22×3=12π.故选:12π.【点评】:本题考查了圆柱的体积公式的理解与应用,属于基础题.6.(填空题,4分)三阶行列式 |125143356| 中,元素2的代数余子式的值为 ___ . 【正确答案】:[1]3【解析】:根据已知条件,结合代数余子式的定义,即可求解.【解答】:解:在三阶行列式 |125143356| 中,元素2的代数余子式A 12=(-1)1+2 |1336| =-(1×6-3×3)=3.故答案为:3.【点评】:本题主要考查代数余子式的求解,考查计算能力,属于基础题.7.(填空题,5分)数列{a n }的通项公式为a n = {2n −1(1≤n ≤10)2−1n (n ≥11) ,则 n→∞a n =___ . 【正确答案】:[1]2【解析】:直接利用数列的极限的运算法则,化简求解即可.【解答】:解:数列{a n }的通项公式为a n = {2n −1(1≤n ≤10)2−1n(n ≥11) , 则 n→∞a n = lim n→∞ (2−1n) =2-0=2. 故答案为:2.【点评】:本题考查数列极限的运算法则的应用,是基础题.8.(填空题,5分)方程log 2(x+1)+log 2(x-1)=1的解为 ___ .【正确答案】:[1] √3【解析】:利用对数的性质及运算法则直接求解.【解答】:解:∵log 2(x+1)+log 2(x-1)=1,∴log 2(x+1)(x-1)=1=log 22,∴(x+1)(x-1)=2且x+1>0,x-1>0,故x= √3 ,故答案为: √3 .【点评】:本题考查对数方程的求法,是基础题,解题时要认真审题,注意对数的性质、运算法则的合理运用.9.(填空题,5分)已知函数f (x )=x 2+2x+3+m ,若f (x )≥0对任意的x∈[1,2]恒成立,则实数m 的取值范围是 ___ .【正确答案】:[1][-6,+∞)【解析】:将问题转化为x 2+2x+3≥-m 对任意的x∈[1,2]恒成立,构造g (x )=x 2+2x+3,利用二次函数的图象与性质,求解函数的最值,即可得到答案.【解答】:解:函数f (x )=x 2+2x+3+m ,且f (x )≥0对任意的x∈[1,2]恒成立, 则x 2+2x+3≥-m 对任意的x∈[1,2]恒成立,令g (x )=x 2+2x+3,函数g (x )在[1,2]上单调递增,所以g (x )min =g (1)=6,则6≥-m ,即m≥-6,所以实数m 的取值范围为[-6,+∞).故答案为:[-6,+∞).【点评】:本题考查了二次函数图象与性质的应用,利用函数单调性求解函数最值的应用,不等式恒成立问题,要掌握不等式恒成立问题的一般求解方法:参变量分离法、数形结合法、最值法等,属于中档题.10.(填空题,5分)某学校要从6名男生和4名女生中选出3人担任进博会志愿者,则所选3人中男女生都有的概率为 ___ .(用数字作答)【正确答案】:[1] 45【解析】:由排列组合的知识易得总数为120,不符合的有24,由古典概型概率公式求解即可.【解答】:解:从10人中任选3人有 C 103 =120种选法,这3人中只有女生的共有 C 43 =4种,这3人中只有男生的共有 C 63 =20种, ∴这3人中必须男女生都有的共96种,∴所求概率P= 96120 = 45 .故答案为: 45 .【点评】:本题考查古典概型及其概率公式,属基础题.11.(填空题,5分)已知A (-1,0)、B (1,0)、P (1, √3 ),点C 是圆x 2+y 2=1上的动点,则 PC ⃗⃗⃗⃗⃗ • PB ⃗⃗⃗⃗⃗ + PC⃗⃗⃗⃗⃗ • PA ⃗⃗⃗⃗⃗ 的取值范围是 ___ . 【正确答案】:[1][4,12]【解析】:设点C 坐标(c osθ,sinθ),将 PC ⃗⃗⃗⃗⃗ • PB ⃗⃗⃗⃗⃗ + PC⃗⃗⃗⃗⃗ • PA ⃗⃗⃗⃗⃗ 用θ函数表示,用正弦函数取值范围求解.【解答】:解:设C (cosθ,sinθ), PA ⃗⃗⃗⃗⃗ =(-2,- √3 ), PB ⃗⃗⃗⃗⃗ =(0,- √3 ), PC⃗⃗⃗⃗⃗ =(cosθ-1,sinθ- √3 ),PC ⃗⃗⃗⃗⃗ • PB ⃗⃗⃗⃗⃗ + PC ⃗⃗⃗⃗⃗ • PA ⃗⃗⃗⃗⃗ = PC ⃗⃗⃗⃗⃗ •( PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ )=(cosθ-1,sinθ- √3 )•(-2,-2 √3 )=-2(cosθ-1+ √3 sinθ-3)=8-4( √32 sinθ+ 12 cosθ)=8-4sin (θ+ π6 ),因为sin (θ+ π6 )∈[-1,1],所以 PC ⃗⃗⃗⃗⃗ • PB ⃗⃗⃗⃗⃗ + PC⃗⃗⃗⃗⃗ • PA ⃗⃗⃗⃗⃗ 的取值范围是[4,12], 故答案为:[4,12].【点评】:本题考查了平面向量数量积的性质及其运算,属于中档题.12.(填空题,5分)已知实数x 、y 满足x|x|4 +y|y|=1,则|x+2y-4|的取值范围是 ___ . 【正确答案】:[1][4-2 √2 ,4)【解析】:把 x|x|4 +y|y|=1等式变形,画出图形,利用线性规划知识求出x+2y-4的范围,取绝对值得答案即可.【解答】:解答】解:由 x|x|4+y|y|=1, 得 {x ≥0,y ≥0x 24+y 2=1 或 {x >0,y <0x 24−y 2=1 或 {x <0,y >0y 2−x 24=1 , 如图,令z=x+2y-4,得y=- 12 x+ 12 z+2,由图可知,当直线y=- 12 x+ 12 z+2与第一象限的椭圆相切时,直线在y 轴上的截距最大, 联立得 {y =−12x +12z +2x 24+y 2=1 ,即2x 2-(2z+8)x+z 2+8z+12=0,∵相切,∴Δ=(2z+8)2-4×2×(z 2+8z+12)=0,∴z 2+8z+8=0,∴z=-4±2 √2 ,∵椭圆的图象只在第一象限,∴z=-4 +2√2 ,根据双曲线的方程知,两条双曲线的渐近线方程都是y=- 12 x ,当直线y=- 12 x+ 12z+2无限靠近y=- 12x时,12z+2趋于0,即z趋于-4,∴-4<z≤-4 +2√2,∴|x+2y-4|的取值范围是[4-2 √2,4),故答案为:[4-2 √2,4).【点评】:本题考查简单的线性规划,考查直线与椭圆相切,双曲线的渐近线,考查数形结合思想,是中档题.13.(单选题,5分)已知直线a在平面β上,则“直线l⊥a”是“直线l⊥β”的()条件.A.充分非必要B.必要非充分C.充要D.非充分非必要【正确答案】:B【解析】:“直线l⊥a”成立时,“直线l⊥β”不一定成立;“直线l⊥β”⇒“直线l⊥a”,由此能求出结果.【解答】:解:直线a在平面β上,则“直线l⊥a”成立时,“直线l⊥β”不一定成立;“直线l⊥β”⇒“直线l⊥a”,∴直线a在平面β上,则“直线l⊥a”是“直线l⊥β”的必要非充分条件.故选:B.【点评】:本题考查充分条件、必要条件的判断,考查空间中线与面的位置关系等基础知识,考查空间立体感和推理论证能力,属于中档题.14.(单选题,5分)(x-1)10的二项展开式中第4项是()A. C103x7B. C104x6C. −C103x7D. −C104x6【正确答案】:C【解析】:写出(x-1)10的二项展开式的通项公式,令r=3,可得所求项.【解答】:解:(x-1)10的二项展开式的通项公式为T r+1= C10r x10-r(-1)r= C10r(-1)r x10-r,r=0,1,2, (10)令r=3,T4=- C103 x7,故选:C.【点评】:本题考查二项式定理的运用,考查运算能力,是一道基础题.15.(单选题,5分)若方程4x2+ky2=4k表示双曲线,则此双曲线的虚轴长等于()A. 2√kB. 2√−kC. √kD. √−k【正确答案】:B【解析】:根据双曲线标准方程直接求解.【解答】:解:方程4x2+ky2=4k,即为x2k +y24=1,由方程表示双曲线,可得y 24−x2−k=1,所以a=2,b=√−k,所以虚轴长为2b=2√−k.故选:B.【点评】:本题主要考查双曲线的几何性质,由双曲线方程求解虚轴的长度等知识,属于基础题.16.(单选题,5分)函数f(x)=sinx- 12(x∈[t,t+40])零点的个数不可能是()个A.12B.13C.14D.15【正确答案】:D【解析】:f(x)的零点个数,即为y=sinx的图象与直线y= 12的交点个数,在正弦函数的一个周期内,即在区间[t,t+2π)上总有两个交点,然后考虑,40减去个周期后,在区间[t,t+0.74π]中的交点个数,根据的不同取值可确定结论.的交点个数,【解答】:解:f(x)的零点个数,即为y=sinx的图象与直线y= 12≈6.37,易知在[t,t+2π)上它们有两个交点,而402π所以前6个周期共有交点12个,因此我们主要研究它们在区间[t,t+0.74π]中的交点个数,<t<-π时,它们在区间[t,t+0.74π]上无交点,当- 7π6<t<0时,它们在区间[t,t+0.74π]有1个交点,当- π3时,它们在区间[t,t+0.74π]上有2个交点,当0<t<π6因此交点个数可能为12,13,14,不可能是15.故选:D.【点评】:本题考查了函数的零点与方程的根的关系,属于中档题.17.(问答题,14分)已知三棱锥P-ABC中,PA、BA、CA两两互相垂直,且长度均为1.(1)求三棱锥P-ABC的全面积;(2)若点D为BC的中点,求PD与平面PAC所成角的大小.(结果用反三角函数值表示)【正确答案】:【解析】:(1)由已知易得△PAB≌△PAC≌△BAC且为直角三角形,则可得△PBC为边长为√2的等边三角形,进而可求全面积;(2)取AC的中点H,连接HD和HP,进而证明DH⊥平面PAC,可得∠DPH是PD与平面PAC所成角;在△PDH中求解即可.【解答】:解:(1)由题意知△PAB≌△PAC≌△BAC且为直角三角形,则可得△PBC为边长为√2的等边三角形,所以三棱锥P-ABC的全面积S= 12 ×1×1×3+ 12× √2 × √2 ×sin60°= 3+√32;(2)取AC的中点H,连接HD和HP,因为PA、BA、CA两两互相垂直,所以PA⊥平面ABC,DH在平面ABC内,所以PA⊥DH,又因为DH⊥AC,所以DH⊥平面PAC,所以∠DPH是PD与平面PAC所成角;因为DH= 12,PH= √52,所以tan∠DPH= √55,∠DPH=arctan √55,所以PD与平面PAC所成角的大小为arctan √55.【点评】:本题考查表面积的问题和线面角的求法,属中档题.18.(问答题,14分)已知函数f(x)=x2+ax+1,a∈R.(1)判断函数f(x)的奇偶性,并说明理由;(2)若函数g(x)= f(x)x(x>0),写出函数g(x)的单调递增区间并用定义证明.【正确答案】:【解析】:(1)分a=0和a≠0两种情况,分别利用奇函数与偶函数的定义分析判断即可;(2)利用函数单调性的定义判断并证明即可.【解答】:解:(1)当a=0时,函数f(x)为偶函数,证明如下:函数f(x)=x2+1,定义域为R,因为f(-x)=x2+1=f(x),所以当a=0时,函数f(x)为偶函数;当a≠0时,f(-1)=2-a,f(1)=2+a,则f(-1)≠f(1),f(-1)≠-f(1),函数f(x)为非奇非偶函数.(2)函数g(x)的单调递增区间为[1,+∞),证明如下:g(x)= f(x)x =x+1x+a,设1≤x1<x2,则g(x1)−g(x2)=x1+1x1+a−(x2+1x2+a) = (x1−x2)(1−1x1x2) = (x1−x2)(x1x2−1)x1x2,由于1≤x1<x2,则x1-x2<0,x1x2−1x1x2>0,所以f(x1)<f(x2),则函数g(x)的单调递增区间为[1,+∞).【点评】:本题考查了函数单调性和奇偶性的判断与证明,考查了函数奇偶性与单调性的定义,考查了逻辑推理能力与化简运算能力,属于基础题.19.(问答题,14分)某水产养殖户承包一片靠岸水域,如图,AO、OB为直线岸线,OA=1000米,OB=1500米,∠AOB= π3,该承包水域的水面边界是某圆的一段弧AB̂,过弧AB̂上一点P按线段PA和PB修建养殖网箱,已知∠APB= 2π3.(1)求岸线上点A与点B之间的直线距离;(2)如果线段PA上的网箱每米可获得40元的经济收益,线段PB上的网箱每米可获得30元的经济收益,记∠PAB=θ,则这两段网箱获得的经济总收益最高为多少?(精确到元)【正确答案】:【解析】:(1)根据已知条件,结合余弦定理,即可求解.(2)根据已知条件,结合正弦定义,以及三角函数的恒等变换,即可求解.【解答】:解:(1)∵OA=1000米,OB=1500米,∠AOB= π3,∴AB= √OA2+OB2−2×OA×OB×cosπ3 = √15002+10002−2×1500×1000×12=500√7,故岸线上点A与点B之间的直线距离为500√7米.(2)∵在△PAB中,500√7sin2π3=PAsin(π3−θ)=PBsinθ,∴ PA=√7√3(π3−θ),PB= √7√3(0<θ<π3),设两段网箱获得的经济总收益为y元,则y=40PA+30PB= √7√3(π3−θ) + √7√3= √7√3(π3−θ)+3sinθ]= √7√3√3cosθ+sinθ)=10000√91√3sin(θ+arctan2√3) ,当 θ+arctan2√3=π2,即 θ≈π2−arctan2√3 ∈(0, π3)时, y max =10000√91√3≈55076 (元),故两段网箱获得的经济总收益最高约为55076元.【点评】:本题主要考查函数的实际应用,掌握正弦定理,余弦定理是解本题的关键,属于中档题.20.(问答题,16分)已知斜率为k 的直线l 经过抛物线C :y 2=4x 的焦点F ,且与抛物线C 交于不同的两点A (x 1,y 1),B (x 2,y 2).(1)若点A 和B 到抛物线准线的距离分别为 32 和3,求|AB|; (2)若|AF|+|AB|=2|BF|,求k 的值;(3)点M (t ,0),t >0,对任意确定的实数k ,若△AMB 是以AB 为斜边的直角三角形,判断符合条件的点M 有几个,并说明理由.【正确答案】:【解析】:(1)根据抛物线的定义求得焦点弦长;(2)直线l 的方程为y=k (x-1),代入抛物线方程后应用韦达定理得x 1+x 2,x 1x 2,利用焦半径公式及已知|AF|+|AB|=2|BF|,得出x 1,x 2的关系,与韦达定理结合可求得k ;(3)把 MA⃗⃗⃗⃗⃗⃗ •MB ⃗⃗⃗⃗⃗⃗ =0 用坐标表示出来,代入韦达定理的结论,得出关于t 的方程,由一元二次方程根的分布可得t 的正数解的个数.【解答】:解:(1)根据抛物线定义,|AF|= 32 ,|BF|=3, ∴|AB|= 92;(2)设直线l 的方程为y=k (x-1), 由 {y =k (x −1)y 2=4x ,可得:k 2x 2-(2k 2+4)x+k 2=0,Δ=(2k 2+4)2-4k 4=16k 2+16>0, ∴x 1+x 2=2+ 4k 2 ,x 1x 2=1,|AF|=x 1+1,|BF|=x 2+1,|AB|=x 1+x 2+2, 又∵|AF|+|AB|=2|BF|,∴(x 1+1)+(x 1+x 2+2)=2(x 2+1), ∴x 2-2x 1=1, ∴x 1=k 2+43k 2 ,x 2= 5k 2+83k 2, 代入x 1x 2=1得: k 2+43k 2 • 5k 2+83k 2 =1, ∴k 4-7k 2-8=0,∴k 2=-1(舎)或k 2=8, ∴k= ±2√2 ;(3)∵△AMB 是以AB 为斜边的直角三角形, ∴MA⊥MB , MA⃗⃗⃗⃗⃗⃗ •MB ⃗⃗⃗⃗⃗⃗ =0 , 即(x 1-t ,y 1)(x 2-t ,y 2)=0, ∴(x 1-t )(x 2-t )+y 1y 2=0, 即x 1x 2-t (x 1+x 2)+t 2+y 1y 2=0,又因为y 1y 2=k 2(x 1-1)(x 2-1)=k 2(x 1x 2-x 1-x 2+1)=-4, ∴1-t (2+ 4k 2 )+t 2-4=0, 即t 2-(2+ 4k 2 )t-3=0, ∵ Δ=(2+4k 2)2+12>0 ,t 1t 2=-3<0,∴方程仅有一个正实数解, 存在一个满足条件的点M .【点评】:本题考查了直线和圆锥曲线(抛物线)的相关计算,属于综合性较强的题目,解决此类题的一个基本思路就是要联立直线方程和圆锥曲线方程,再用设而不解的方法来进行相关解答,属于中档题.21.(问答题,18分)已知数列{a n},若存在A∈R使得数列{|a n-A|}是递减数列,则称数列{a n}是“A型数列”.(1)判断数列π、- √3、-1、12是否为“A型数列”;(2)若等比数列{a n}的通项公式为a n=q n(n∈N*),q>0,其前n项和为S n,且{S n}是“A型数列”,求A的值和q的取值范围;(3)已知k>0,数列{a n}满足a1=0,a n+1=k|a n|-1(n∈N*),若存在A∈R,使得{a n}是“A型数列”,求k的取值范围,并求出所有满足条件的A(用k表示).【正确答案】:【解析】:(1)根据A型数列的新定义直接判断即可;(2)分q=1,q>1和0<q<1分别求出{a n}的前n项和为S n,再判断是否存在A满足|S n-A|递减即可求解;(3)分k≥1和0<k<1两种情况讨论,首先判断k≥1不符合题意,当0<k<1时,先证明a n≤0,进而可得a n以及符合题意的A的值,再证明A是唯一的即可.【解答】:解:(1)因为|π−0|>|−√3−0|>|−1−0|>|−12−0|,“A型数列“的定义可知该数列是“A型数列“.(2)若q=1,|S n-A|=|n-A|,不存在A∈R使得数列{|n-A|}是递减数列,此时{S n}不是“A型数列“;若q>1,S n=q(1−q n)1−q =q(q n−1)q−1,因为{S n}为递增数列,对于任意A,存在N,当n>N时,|S n-A|=S n-A,递增,因此不存在A,此时{S n}不是“A型数列“;若0<q<1,S n=−q1−q q n+q1−q,取A=q1−q,|S n−A|=q1−qq n,递减,此时符合题意;综上所述A=q1−q,q的取值范围{q|0<q<1}.(3)(i)若k≥1,则a1=0,a2=-1,a3=k-1.此时若存在A∈R使得{a n}是A型数列,则|A|>|A+1|>|k-1-A|,从而A<−12且k<1,矛盾;(ii)当0<k<1时,首先证明a n≤0(n∈N*).用反证法.由题意,此时a1=0,a2=-1,a3=k-1.因此,若存在n∈N*,使得a n>0,则n≥4.假设n=m为使得a n>0的最小正整数,则a m>0≥a m-1,故a m=−ka m−1−1>0⇒a m−1<−1k,而a m−1=−ka m−2−1<−1k ⇒a m−2>1−kk2>0,与m的最小性矛盾.故a n≤0(n∈N*),从而a n+1=-ka n-1对一切n∈N*成立.据此,可解得a n=(−k)n−1−1k+1.故当α=−1k+1时,|a n−α|=k n−1k+1,即:{|a n-α|}为递减数列.于是{a n}为α型数列.再证明α是唯一解.用反证法.假设存在A≠α使得{a n}是A型数列.若A>α,则由a2m−1=α+k2m−2k+1得,当m>log k2[(A−α)(k+1)]+1时,a2m-1<A.故|a2m−1−A|=A−α−k2m−2k+1<A−α−k2mk+1=|a2m+1−A|,{|a n-A|}不是递减数列,从而{a n}不是A型数列.同理可证A<α时,{a n}也不是A型数列,综上,k∈(0,1),相应的A=−1k+1.【点评】:本题主要考查数列中的新定义问题,数列知识的综合运用等知识,属于中等题.。
北京市海淀区2021-2022学年第一学期期末考试高三数学试题及答案

海淀区2021-2022学年第一学期期末练习高三数学 2022. 01本试卷共6页,共150分。
考试时长120分钟。
考生务必将答案答在答题纸上,在试卷上作答无效。
考试结束后,将本试卷和答题纸一并交回。
第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)已知集合{1,0,1,2},{|(2)0}A B x x x =−=−<,则AB =(A) ∅ (B) {0} (C) {1} (D) {01},(2)抛物线22x y =的准线方程为(A) 1x =− (B) 1y =− (C) 12x =− (D) 12y =−(3)复数52i+的虚部为 (A) 2− (B) 2 (C) 1− (D) 1(4)在421()x x−的展开式中,x 的系数为(A) 4− (B) 4 (C) 6− (D) 6 (5)已知角α的终边在第三象限,且tan 2=α,则sin cos −=αα(A) 1− (B) 1 (C) 5 (D)5(6)已知{}n a 是等差数列,n S 是其前n 项和. 则“43a a >”是“对于任意*N n ∈且3n ≠,3n S S >”的(A )充分而不必要条件 (B )必要而不充分条件(C )充要条件 (D )既不充分也不必要条件(7)若函数πsin(π)6y x =−在[0,]m 上单调递增,则m 的最大值为(A) 13(B) 12 (C) 23 (D) 1(8)已知圆C 过点(1,2),(1,0)A B −,则圆心C 到原点距离的最小值为(A) 12(B) 2 (C) 1 (D)(9)如图,,A B 是两个形状相同的杯子,且B 杯高度是A 杯高度的34,则B 杯容积与A 杯容积之比最接近的是 (A )1:3 (B )2:5 (C )3:5 (D )3:4(10)已知函数()2x f x =,()log a g x x =. 若对于()f x 图象上的任意一点P ,在()g x 的图象上总存在一点Q ,满足OP OQ ⊥,且||||OP OQ =,则实数a = (A)14 (B)12(C)2 (D)4第二部分(非选择题 共110分)二、填空题共5小题,每小题5分,共25分。
2021年全国乙卷理科数学试题及答案

绝密★启用前2021年全国乙卷理科数学试卷时间:120分钟满分:150分命卷人:审核人:一、选择题((每小题5分,共60分))1. 设,则( )A. B.C. D.2. 已知集合,,则( )A. B.C. D.3. 已知命题﹐;命题,则下列命题中为真命题的是( )A. B.C. D.4. 设函数,则下列函数中为奇函数的是( )A. B.C. D.5. 在正方体中,为的中点,则直线与所成的角为( )A. B.C. D.6. 将名北京冬奥会志愿者分配到花样滑冰,短道速滑、冰球和冰壶个项目进行培训,每名志愿者只分配到个项目,每个项目至少分配名志愿者,则不同的分配方案共有( )A. 种B. 种C. 种D. 种7. 把函数图像上所有点的横坐标缩短到原来的倍,纵坐标不变,再把所得曲线向右平移个单位长度,得到函数的图像,则( )A. B.C. D.8. 在区间与中各随机取个数,则两数之和大于的概率为( )A. B.C. D.9. 魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作.其中第一题是测量海岛的高.如图,点在水平线上,和是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,称为“表距”,和都称为“表目距”.与的差称为“表目距的差”,则海岛的高( )A.B.C.D.10. 设,若为函数的极大值点,则A. B.C. D.11. 设是椭圆:的上顶点,若上的任意一点都满足,则的离心率的取值范围是( )A. B.C. D.12. 设,,,则( )A. B.C. D.二、填空题((每小题5分,共20分))13. 已知双曲线:的一条渐近线为,则的焦距为__________.14. 已知向量,,若,则__________.15. 记的内角,,的对边分别为,,,面积为,,,则__________.16. 以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为__________(写出符合要求的一组答案即可).三、解答题((每小题12分,共60分))17. 某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了件产品,得到产品该项指标数据如下:旧设备和新设备生产产品的该项指标的样本平均数分别记为和, 样本方差分别记为和. (1)求,,,: (2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高 ( 如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高 , 否则不认为有显著提高 ) 。
2021年全国高考理科数学(全国一卷)试题及答案
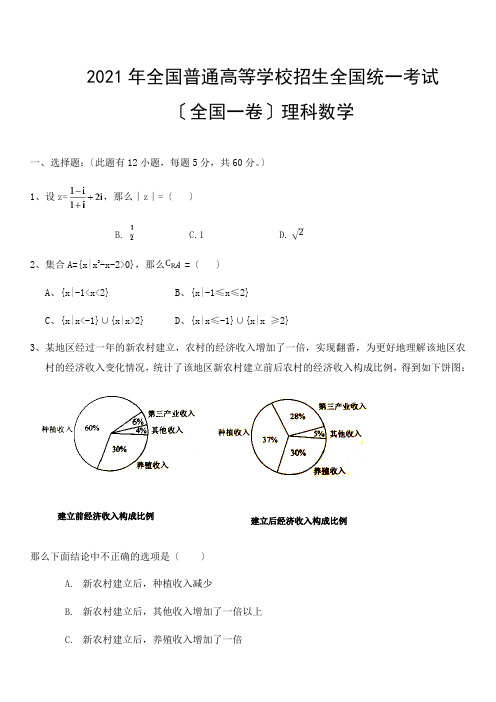
2021年全国普通高等学校招生全国统一考试〔全国一卷〕理科数学一、选择题:〔此题有12小题,每题5分,共60分。
〕 1、设z=,那么∣z ∣=〔 〕B. C.1 D.2、集合A={x|x 2-x-2>0},那么A =〔 〕A 、{x|-1<x<2}B 、{x|-1≤x ≤2}C 、{x|x<-1}∪{x|x>2}D 、{x|x ≤-1}∪{x|x ≥2}3、某地区经过一年的新农村建立,农村的经济收入增加了一倍,实现翻番,为更好地理解该地区农村的经济收入变化情况,统计了该地区新农村建立前后农村的经济收入构成比例,得到如下饼图:那么下面结论中不正确的选项是〔 〕A. 新农村建立后,种植收入减少B. 新农村建立后,其他收入增加了一倍以上 建立前经济收入构成比例建立后经济收入构成比例D.新农村建立后,养殖收入与第三产业收入的总和超过了经济收入的一半4、记Sn 为等差数列{an}的前n项和,假设3S3= S2+ S4,a1=2,那么a5=〔〕A、-12B、-10C、10D、125、设函数f〔x〕=x³+〔a-1〕x²+ax .假设f〔x〕为奇函数,那么曲线y= f〔x〕在点〔0,0〕处的切线方程为〔〕A.y= -2xB.y= -xC.y=2xD.y=x6、在∆ABC中,AD为BC边上的中线,E为AD的中点,那么=〔〕A. -B. -C. +D. +7、某圆柱的高为2,底面周长为16,其三视图如右图。
圆柱外表上的点M在正视图上的对应点为A,圆柱外表上的点N在左视图上的对应点为B,那么在此圆柱侧面上,从M到N的途径中,最短途径的长度为〔〕A. 2B. 2C. 3D. 28.设抛物线C:y²=4x的焦点为F,过点〔-2,0〕且斜率为的直线与C交于M,N两点,那么·=( )9.函数f〔x〕= g〔x〕=f〔x〕+x+a,假设g〔x〕存在2个零点,那么a的取值范围是( )A. [-1,0〕B. [0,+∞〕C. [-1,+∞〕D. [1,+∞〕10.下列图来自古希腊数学家希波克拉底所研究的几何图形。
2021-2022年高三下学期第六次模拟考试数学(理)试题含答案

2021年高三下学期第六次模拟考试数学(理)试题含答案一、选择题(本大题包括12小题,每小题5分,共60分,) 1.集合,,则( )A 、B 、C 、D 、 2.若复数,其中是虚数单位,则复数的模为 A . B .C .D .23.某学生在一门功课的22次考试中,所得分数如下茎叶图所示,则此学生该门功课考试分数的极差与中位数之和 为A .117B .118C .118.5D .119.5 4.已知,函数在上单调递减.则的取值范围是() A. B. C. D. 5.数列的前n 项和为,若,则( ) A. B. C.D.6.若程序框图如图所示,则该程序运行后输出的值是 A .B .C .D .7.设函数()log (01)a f x x a =<<的定义域为,值域为,若的最小值为,则实数a 的值为 A .B .或C .D .或8.设x ∈R ,向量a =(2,x ),b =(3,-2),且a ⊥b ,则|a -b |=A .5B .C .2D .6 9.二项式展开式中的系数是( )A .-14B .14C .-28D .28 10.在△ABC 中,若,,则b=( ) A .3 B .4 C.5 D .611.设函数11,(,2)()1(2),[2,)2x x f x f x x ⎧--∈-∞⎪=⎨-∈+∞⎪⎩,则函数的零点的个数为开始否 n =3n +1n 为偶数k =k +1 结束n =5,k =0 是 输出k n 否是A .4B .5C .6D .712.已知双曲线上一点,过双曲线中心的直线交双曲线于两点,记直线的斜率分别为,当最小时,双曲线离心率为( ) A . B . C D二、填空题(本大题包括4小题,每小题5分,共20分). 13.—个几何体的三视图如图所示(单位:m )则该几何体的体积为___.14.若整数..满足0700y x x y x -≥⎧⎪+-≤⎨⎪≥⎩,则的最大值为 . 15.向平面区域}10,20|),{(≤≤≤≤y x y x .内随机投入一点,则该点落在曲线⎪⎩⎪⎨⎧≤<-≤≤=)21(2)10(23x x x x y 下方的概率等于_______.16.若一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.已知一个正六棱锥的各个顶点都在半径为3的球面上,则该正六棱锥的体积的最大值为_____.三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤). 17.(本小题满分12分)已知二次函数的图像经过坐标原点,其导函数为,数列的前项和为,点均在函数的图像上. (Ⅰ)求数列的通项公式;(Ⅱ)设是数列的前项和, 求使得对所有都成立的最小正整数18.(本小题满分12分) A 、B 两个投资项目的利润率分别为随机变量X 1和X 2.根据市场分析,X 1和X 2的分布列分别为X 1 5% 10% P0.80.2X 2 2% 8% 12% P0.20.50.3(Ⅰ)在两个项目上各投资100万元,Y 1和Y 2分别表示投资项目A 和B 所获得的利润,求方差DY 1,DY 2;(Ⅱ)将万元投资A 项目,万元投资B 项目,表示投资A 项目所得利润的方差与投资B 项目所得利润的方差的和.求的最小值,并指C 1B 1A 1出x 为何值时,取到最小值.(注:)19.(本小题满分12分) 如图,在三棱柱中,侧面底面,, ,,为中点. (Ⅰ)证明:平面;(Ⅱ)求直线与平面所成角的正弦值;(Ⅲ)在上是否存在一点,使得平面?若存在,确定点的位置;若不存在,说明理由 20.(本小题满分12分)已知两定点,和定直线l :,动点在直线上的射影为,且. (Ⅰ)求动点的轨迹的方程并画草图;(Ⅱ)是否存在过点的直线,使得直线与曲线相交于, 两点,且△的面积等于?如果存在,请求出直线的方程;如果不存在,请说明理由 21.(本小题满分12分)已知函数,且.(Ⅰ)若曲线在点处的切线垂直于轴,求实数的值;(Ⅱ)当时,求函数的最小值;(Ⅲ)在(Ⅰ)的条件下,若与的图像存在三个交点,求的取值范围请考生在第22、23、24题中任选一...题.作答,如果多做,按所做第1题计分。
2021年全国高考理科数学试题及答案-全国

2021年普通高等学校招生全国统一考试理科数学〔必修+选修II 〕本试卷分第一卷〔选择题〕和第二卷〔非选择题〕两局部。
第一卷1至2页。
第二卷3至4页。
考试结束后,将本试卷和答题卡一并交回。
第一卷考前须知:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准条形码上的准考证号、姓名和科目。
2.每题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
.......... 3.第一卷共l2小题,每题5分,共60分。
在每题给出的四个选项中,只有一项为哪一项符合题目要求的。
一、选择题1.复数1z i =+,z 为z 的共轭复数,那么1zz z --=A .2i -B .i -C .iD .2i2.函数0)y x =≥的反函数为A .2()4x y x R =∈B .2(0)4x y x =≥C .24y x =()x R ∈ D .24(0)y x x =≥3.下面四个条件中,使a b >成立的充分而不必要的条件是A .1a b +>B .1a b ->C .22a b >D .33a b >4.设n S 为等差数列{}n a 的前n 项和,假设11a =,公差2d =,224k k S S +-=,那么k =A .8B .7C .6D .55.设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,那么ω的最小值等于A .13B .3C .6D .96.直二面角α− ι−β,点A ∈α,AC ⊥ι,C 为垂足,B ∈β,BD ⊥ι,D 为垂足.假设AB=2,AC=BD=1,那么D 到平面ABC 的距离等于A .3B C D .17.某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友每位朋友1本,那么不同的赠送方法共有A .4种B .10种C .18种D .20种8.曲线y=2xe -+1在点〔0,2〕处的切线与直线y=0和y=x 围成的三角形的面积为A .13 B .12C .23D .19.设()f x 是周期为2的奇函数,当0≤x≤1时,()f x =2(1)x x -,那么5()2f -=A .-12B .1 4-C .14D .1210.抛物线C :24y x =的焦点为F ,直线24y x =-与C 交于A ,B 两点.那么cos AFB ∠=A .45B .35C .35-D .45-11.平面α截一球面得圆M ,过圆心M 且与α成060二面角的平面β截该球面得圆N .假设该球面的半径为4,圆M 的面积为4π,那么圆N 的面积为A .7πB .9πC .11πD .13π12.设向量a ,b ,c 满足a =b =1,a b =12-,,a c b c --=060,那么c 的最大值等于A .2BCD .1第二卷考前须知:1.答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考 证号填写清楚,然后贴好条形码。
山西省太原市2022届高三上学期期末数学(理)试题(解析版)

,
令 ,则 ;令 ,则 .
是 的单调递增区间; 是 的单调递减区间.
【小问2详解】
在 恒成立,
即 在 恒成立,
即 在 恒成立,
令 ,
在 上单调递增且 ,
时, , 时, ,
在 上单调递减,在 上单调递增,
在 处取得最小值,即 ,
令 ,
令 , 在 单调递减,
因为 ,当 时, ;当 时, .
D选项, 内的任何直线都与 平行,则 ,D选项正确.
故选:D
4.等比数列 中, ,则 的通项公式为()
A. B.
C 或 D. 或
【答案】C
【解析】
【分析】由已知,结合等比数列的通项公式可得 求公比,进而写出 的通项公式.
【详解】令公比 ,由题设有 ,
所以 ,解得 或 ,经检验符合题设
所以 ,可得 或 .
可取 ,
则 ,
故平面PAB与平面BDM所成锐二面角的余弦值为 .
21.已知函数 .
(1)求函数 的单调区间;
(2)若 恒成立,求实数 的取值范围.
【答案】(1) 单调递增区间是 ,单调递减区间是
(2)
【解析】
【分析】(1)导数后解不等式即可求解;
(2)将问题转化为 在 恒成立,再分别研究 与 的最值,再比较即可.
从1到10这十个数中任取三个数所有的取法,这三个数的和为奇数的取法,由古典概型概率计算公式可得答案.
【详解】设“从1到10这十个数中任取三个,这三个数的和为奇数”为事件 ,
从1到10这十个数中任取三个数有 种取法,
要使这三个数的和为奇数,须取的三个数中有2个偶数一个奇数,或者三个数都为奇数两种情况;1到10这十个数分成偶数一组,奇数一组各有5个,所以
2021-2022学年青海省西宁市三县高三上学期期末数学试卷(理科)(含答案解析)

2021-2022学年青海省西宁市三县高三上学期期末数学试卷(理科)一、单选题(本大题共12小题,共60.0分)1.已知集合A={x|2x+3>9},B={x∈N|−x+1>−5},则A∩B=()A. (3,6)B. {3,4,5}C. {4,5}D. (4,5)2.已知复数z满足iz=3+i,则|z+1|=()A. √13B. 2√3C. √10D. 2√23.双曲线C:x2m −y24=1的离心率为3,则m=()A. 3B. 12C. 2D. 14.已知实数x,y满足{x+y+1≥02x−y−1≤0x−2y+4≥0,则目标函数z=3x−y的最大值为()A. −7B. 1C. 3D. 55.“m>6”是“方程x2+y2−mx+4y+m+7=0是圆的方程”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6.已知a=2−1.01,b=1.20.1,c=log43,则()A. b>a>cB. c>b>aC. a>b>cD. b>c>a7.一个几何体的三视图如图所示,其表面积为5π+√2π,则该几何体的体积为()A. 2πB. 7π3C. 11π3D. 17π68.若要得到函数f(x)=sin(2x+π6)的图象,只需将函数g(x)=cos(2x+π3)的图象()A. 向左平移π6个单位长度 B. 向右平移π6个单位长度C. 向左平移π3个单位长度 D. 向右平移π3个单位长度9. 已知e 是自然对数的底数,函数f(x)的定义域为(0,+∞),f′(x)是f(x)的导函数,且f(x)x+lnx ⋅f′(x)>0,则( )A. f(1e )+f(e)>0 B. f(1e )<0 C. f(e)<0D. f(1)=010. 2021年1月18号,国家航天局探月与航天工程中心表示,中国首辆火星车全球征名活动已经完成了初次评审.评审委员会遴选出弘毅、麒麟、哪吒、赤兔、祝融、求索、风火轮、追梦、天行、星火10个名称,将其作为中国首辆火星车的命名范围.某同学为了研究这些初选名称的涵义,计划从中选3个名称依次进行分析,其中有1个是祝融,其余2个从剩下的9个名称中随机选取,则祝融不是第3个被分析的情况有( )A. 144种B. 336种C. 672种D. 1008种11. 如图,P 是椭圆x 24+y 23=1第一象限上一点,A ,B ,C 是椭圆与坐标轴的交点,O 为坐标原点,过A 作AN 平行于直线BP 交y 轴于N ,直线CP 交x 轴于M ,直线BP 交x 轴于E.现有下列三个式子: ①|OE|⋅|ON|; ②|OE|⋅|OM|; ③|ON||OM|.其中为定值的所有编号是( )A. ①③B. ②③C. ①②D. ①②③12. 已知函数f(x)={lnx,x >0,−x 2−4x −3,x ≤0.若函数y =[f(x)]2+mf(x)+1有6个零点,则m 的取值范围是( )A. (−2,103)B. (−2,103]C. (2,103)D. (2,103]二、填空题(本大题共4小题,共20.0分)13. 在(x −2)5的展开式中,x 3的系数为______.(用数字作答)14. 已知向量a ⃗ ,b ⃗ 不共线,且(k a ⃗ −4b ⃗ )//(a ⃗ −k b ⃗ ),则k =______.15. 如图,在平面四边形ABCD 中,∠DAB =∠CBA =45°,AD =2,DC =√13,CB =1,则cos∠ADC =______.16. 在三棱锥P −ABC 中,PA ⊥底面ABC ,PA =AB =2,BC =3,AC =√7,则三棱锥P −ABC 外接球的表面积为______.三、解答题(本大题共7小题,共82.0分)17. 设等差数列{a n }的前n 项和为S n ,已知a 3+a 5=30,S 3=57. (1)求{a n }的通项公式; (2)求S n 的最大值.18. 如图,某市有南、北两条城市主干道,在出行高峰期,北干道有N 1,N 2,N 3,N 4四个交通易堵塞路段,它们被堵塞的概率都是13,南干道有S 1,S 2两个交通易堵塞路段,它们被堵塞的概率分别为12,23.某人在高峰期驾车从城西开往城东,假设以上各路段是否被堵塞互不影响.(1)求北干道的N 1,N 2,N 3,N 4四个易堵塞路段至少有一个被堵塞的概率; (2)若南干道被堵塞路段的个数为X ,求X 的分布列及数学期望E(X);(3)若按照“平均被堵塞路段少的路线是较好的高峰期出行路线”的标准,则从城西开往城东较好的高峰期出行路线是哪一条?请说明理由.19. 如图,在四棱锥P −ABCD 中,底面ABCD 为平行四边形,平面PCD ⊥底面ABCD ,且BC =2,AB =4,BD =2√5. (1)证明:BC ⊥PD ;(2)若PC =PD =√13,求二面角A −PB −C 的余弦值.20. 已知抛物线C :y 2=2px(p >0)与直线l :x +ky −1=0交于P ,Q 两点,O 为坐标原点,OP ⊥OQ . (1)求抛物线C 的方程;(2)若△POQ 的面积为√5,求直线l 的方程.21. 已知函数f(x)=(x −1)e x +x . (1)判断f(x)的单调性;(2)当x ∈[0,+∞)时,f(x)≥(x +1)ln(x +1)−ax 2−1恒成立,求实数a 的取值范围.22. 已知曲线C 1的参数方程为{x =cosϕy =1+sinϕ(φ为参数),曲线C 2的参数方程为{x =8−2t y =t (t 为参数),以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系. (1)求曲线C 1和曲线C 2的极坐标方程;(2)射线θ=π4(ρ>0)与曲线C 1和曲线C 2分别交于A ,B 零两点,已知点M(2,0),求△MAB 的面积.23. 已知函数f(x)=|2x +1|+x . (1)求不等式f(x)<1的解集;(2)已知a ∈[−1,2],证明:√a +1+√4−2a ≤2f(x)+4.参考答案及解析1.答案:C解析:∵集合A={x|2x+3>9}={x|x>3},B={x∈N|−x+1>−5}={x∈N|x<6}={0,1,2,3,4,5},∴A∩B={4,5}.故选:C.求出集合A,B,利用交集定义能求出A∩B.本题考查集合的运算,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.2.答案:A解析:∵iz=3+i⇒z=1+3i=1−3i,∴|z+1|=|2−3i|=√22+(−3)2=√13,故选:A.根据复数的基本运算法则进行化简即可.本题主要考查复数模长的计算,比较基础.3.答案:B解析:双曲线C:x2m −y24=1的离心率为3,可得√m+4√m =3,所以m=12.故选:B.利用双曲线的离心率,列出方程,求解即可.本题考查双曲线的简单性质的应用,是基础题.4.答案:C解析:画出可行域如下图所示,由图可知,当直线z=3x−y过点(2,3)时,z取得最大值3.故选:C.画出可行域,平移基准直线3x−y=0到可行域边界位置,由此求得z的最大值.本题考查线性规划,考查数形结合能力,属于中档题.5.答案:A解析:若方程x2+y2−mx+4y+m+7=0是圆的方程,则m2−4m−12>0,解得m>6或m<−2,故“m>6”是“方程x2+y2−mx+4y+m+7=0是圆的方程”的充分不必要条件.故选:A.根据已知条件,二元二次方程表示圆的条件,即可求解.本题主要考查二元二次方程表示圆的条件,属于基础题.6.答案:D,解析:a=2−1.01<2−1=12b=1.20.1>1.20=1,<c<1,∵log42<log43<log44,∴12∴b>c>a,故选:D.利用指数函数,对数函数的单调性,再借助中间量求解即可.本题考查了指数函数,对数函数的单调性,属于基础题.7.答案:B解析:根据几何体的三视图转换为直观图为:该几何体是由一个底面半径为r,高为r的圆锥和由一个底面半径为r,高为2r的圆柱组成的组合体;如图所示:所以S表=π⋅√2r⋅r+π⋅r2+2⋅πr⋅2r=√2πr2+5πr2=5π+√2π,解得r=1.故V体=13⋅π⋅12⋅1+π⋅12⋅2=7π3.故选:B.首先把三视图转换为几何体的直观图,进一步利用表面积公式求出r,进一步求出组合体的体积.本题考查的知识要点:三视图和几何体的直观图之间的转换,几何体的体积和表面积公式,主要考查学生的运算能力和数学思维能力,属于基础题.8.答案:D解析:函数f(x)=sin(2x+π6)=cos(π2−2x−π6)=cos(2x−π3)=cos[2(x−π3)+π3],所以只需将函数g(x)=cos(2x+π3)的图象向右平移π3个单位长度,即可得到函数f(x)=sin(2x+π6)的图象.故选:D.利用诱导公式化简三角函数为同名函数,然后判断函数图象平移的单位与方向.本题考查三角函数的图象的平移以及诱导公式的应用,是基本知识的考查.9.答案:A解析:令F(x)=lnxf(x),x∈(0,+∞),可得F′(x)=f(x)x+lnx⋅f′(x)>0,所以函数F(x)是增函数,F(1e)<F(e),即ln 1e f(1e )<lnef(e),可得f(1e )+f(e)>0.所以A 正确;f(1e ),f(e)不能判断符号,f(1)也不一定为0, 故选:A .构造函数,利用函数的导数,判断函数的单调性,然后判断选项即可. 本题考查函数的导数的应用,函数的单调性以及函数值的判断,是中档题.10.答案:A解析:其余2个从剩下的9个名称中随机选取,共有C 92=36种, 则祝融不是第3个被分析的情况有36×C 21A 22=144种,故选:A .其余2个从剩下的9个名称中随机选取,共有C 92=36种,然后再给祝融选择一个位置,其他再排列即可求解.本题考查了排列组合的简单计数问题,考查了学生的运算求解能力,属于基础题.11.答案:D解析:设P(x,y),由椭圆x 24+y 23=1知B(0,−√3),C(0,√3),所以k CP ⋅k BP =y−√3x ×y+√3x=y 2−3x 2所以k CP ⋅k BP =−34,则l BP :y =k BP x −√3,x E =√3k BP,l CP :y =k CP x +√3,x M =−√3k CP,l AN :y =k BP (x +2),y N =2k BP ,故|OE|⋅|ON|=2√3,∣OE ∣⋅∣OM ∣=∣∣∣√3k BP∣∣∣∣∣∣√3k CP∣∣∣=4,|ON||OM|=√334=√32. 故选:D .利用点P 在椭圆上得k CP ⋅k BP =−34,进而得直线方程,求得①②③均为定值. 本题考查椭圆的性质,属中档题.12.答案:D解析:设t =f(x),则y =g(t)=t 2+mt +1, 作出函数f(x)的大致图象,如图所示,。
江苏省泰州市2021-2022学年高三上学期期末考试数学试题

2021-2022学年度第一学期期末考试高三数学试题一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.请将答案填涂到答题卡相应区域.1.已知集合A ={x |x 2-2x -3<0},B ={x |2x >1},则A ∩(∁R B )=A .(-1,0)B .(0,3)C .(-1,0]D .(-1,3]2.已知复数z 满足|z |+z =8+4i ,则z =A .3+4iB .3-4iC .-3+4iD .-3-4i3.在平面直角坐标系xOy 中,已知角α的终边上有一点P (-3,4),则tan2α=A .724B .-724C .247D .-2474.在(x +2)(1x+8)8的展开式中,常数项为 A .27 B .28 C .29 D .305.在平面直角坐标系xOy 中,抛物线C :y 2=4x 的准线为l ,l 与x 轴交于点A ,过点A 作抛物线的一条切线,切点为B ,则△OAB 的面积为A .1B .2C .4D .86.“双十二”网购狂欢节是继“双十一”之后的又一次网络促销日.在这一天,许多网商还会进行促销活动,但促销力度不及“双十一”.已知今年“双十二”期间,某小区居民网上购物的消费金额(单位:元)近似服从正态分布N (6000,10000),则该小区800名居民中,网购金额超过800元的人数大约为(参考数据:P (|X -μ|<σ)=0.683,P (|X -μ|<2σ)=0.954,P (|X -μ|<3σ)=0.997)A .16B .18C .20D .257.已知定义在R 上的奇函数f (x )满足f (2-x )=f (x ).当0≤x ≤1时,f (x )=3x+a ,则f (2021)+f (2022)=A .-4B .-2C .2D .48.已知2a =3,5b =22,c =45,则a ,b ,c 的大小关系是 A .a >b >c B .c >b >a C .c >a >b D .a >c >b二、多选题:本大题共4小题,每小题5分,共计20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9.对于函数f (x )=sin x +cos x ,下列说法正确的有A .2π是一个周期B .关于(π2,0)对称 C .在[0,π2]的值域为[1,2] D .在[π4,π]上递增 10.在平行四边形ABCD 中,若→AE =12→AB ,→AF =12→AD ,则 A .→EF =12→BD B .→AD +→CD +→BE =0 C .→AC +2→DF +2→BE =0 D .若AC ⊥BF ,→AB ·→AD =→BC 2-2→CD 211.已知首项为正数的等比数列{a n }的公比为q ,曲线C n :a n x 2+a n +1y 2=1,则下列叙述正确的有A .q =1,C n 为圆B .q =-1,C n 离心率为2B .q >1,C n 离心率为1-1qD .q <0,C n 为共渐近线的双曲线 12.如图,两个底面为矩形的四棱锥S -ABCD ,S 1-ABCD 组合成一个新的多面体Γ,其中△SAD ,△S 1BC 为等边三角形,其余各面为全等的等腰直角三角形.平面α∥平面SAD ,平面α截多面体Γ所得截面多边形的周长为L ,则下列结论正确的有A .SB ⊥BC B .SC ⊥AB C .多面体Γ有外接球D .L 为定值三、填空题:本大题共4小题,每小题5分,共计20分.请将答案填写在答题卡相应的位置上.13.写出一个公差不为零,且满足a 1+a 2-a 3=1的等差数列{a n }的通项公式a n = .14.若直线x -ay +2a =0被圆x 2+y 2=4截得的弦长为2,则实数a 的值为 .15.若函数f (x )=cos2x +a cos x 在(0,π3)上是减函数,则实数a 的取值范围为 . 16.△ABC 的三条边分别为a ,b ,c ,若该三角形绕着三条边a ,b ,c 旋转一周所得几何体的体积分别为V a ,V b ,V c .若V a =14,V b =13,V c =12,则cos A 的值为 ;若∠BAC =π6,V b V c =1,则V b 2+V c 2-1V a 2的值为 .四、解答题:本大题共6小题,共计70分.解答时应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知a sin2B -3b sin A =0.(1)求角B 的大小;(2)给出三个条件:①b =3;②a +c =3+3;③c sin C =sin A ,试从中选出两个条件,求△ABC 的面积.18.(本小题满分12分)已知数列{a n }的前n 项和为S n ,a n >0,2S n =a n +1.(1)求数列{a n }的通项公式; (2)求数列{a n ·2a n }的前n 项和.19.(本小题满分12分)如图,在三棱锥P -ABC 中,AB =2,PB =BC =4,PA =PC =AC =23.(1)平面PAC ⊥平面ABC ;(2)点D 是棱BC 上一点,→BD =λ→BC ,且二面角B -PA -D 与二面角C -PA -D 的大小相等,求实数λ的值.20.(本小题镇分12分)一学校办公楼共有10层,安装了两部电梯I 和II .电梯运行方式如下:当某人在某层按键后,离他层距较小的电梯运行;当层距相同时,电梯I 先运行.设电梯在每一层运行时间为a .现王老师在第4层准备乘电梯,设等待电梯的时间为随机变量X .(1)求P (X =0);(2)为了响应国家节能减排号召,学校决定只运行一部电梯.求运行两部电梯比运行一部电梯,王老师在第4层乘电梯平均节省的时间.21.(本小题满分12分)在平面直角坐标系xOy 中,已知△ABC 的两个顶点坐标为B (-2,0),C (2,0),直线AB ,AC 的斜率乘积为14. (1)求顶点A 的轨迹Γ的方程;(2)过点P (1,0)的直线与曲线Γ交于点M ,N ,直线BM ,CN 相交于点Q ,求证:→OP ·→OQ 为定值.22.(本小题满分12分)已知函数f (x )=e x -ax 2-sin x ,e 为自然对数的底数.(1)求f (x )在x =0处的切线方程;(2)当x ≥0时,f (x )≥1-x -sin x ,求实数a 的最大值;(3)证明:当a <12时,f (x )在x =0处取极小值.数学参考答案。
2021-2022学年四川省普通高中高三上学期第三次联考数学试卷(理科)(含答案解析)

2021-2022学年四川省普通高中高三上学期第三次联考数学试卷(理科)一、单选题(本大题共12小题,共60.0分)1.设复数z=(2+i)(1−3i),则z的实部与虚部之和为()A. 0B. −10C. 5D. 102.已知集合A={x|m<x<m+5},B={x|−3<x<7},若A∪B={x|−3<x<8},则A∩B=()A. {x|2<x<7}B. {x|−3<x<2}C. {x|3<x<7}D. {x|−3<x<3}3.“tanα>0”是“α为锐角”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.截至2021年11月15日,《长津湖》的票房已超56亿,该片突出了革命先烈的牺牲精神,也更加显示出如今和平生活的来之不易,某影院记录了观看此片的70位观众的年龄,其中年龄位于区间[10,20)的有10位,位于区间[20,30)的有20位,位于区间[30,40)的有25位,位于区间[40,50]的有15位,则这70位观众年龄的中位数约为()A. 34B. 33C. 32D. 315.若曲线y=x3+ax在点(1,a+1)处的切线方程为y=7x+m,则m=()A. 3B. −3C. 2D.−26.执行如图所示的程序框图,若输出的S=8,则输入的k可能为()A. 9B. 5C. 4D. 37. 设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,△ABC 的面积S =(a 2+b 2−c 2)sin2C ,则cosC =( )A. ±√24B. √24C. ±14D. 148.函数f(x)=sin(2x −2−x )在[−π2,π2]上的图象大致为( )A.B.C.D.9.设数列{a n }的前n 项和为S n ,数列{S n +n}是公比为2的等比数列,且a 1=1,则a 8=( )A. 255B. 257C. 127D. 12910. 在矩形ABCD 中,AB =√3AD =3,DC⃗⃗⃗⃗⃗ =4MC ⃗⃗⃗⃗⃗⃗ ,BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ ,且AD ⃗⃗⃗⃗⃗⃗ ⋅AP ⃗⃗⃗⃗⃗ =2,则AM ⃗⃗⃗⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗ =( ) A. 234B. 5C. 194D. 411. 投壶是从先秦延续至清末的汉民族传统礼仪和宴饮游戏,在春秋战国时期较为盛行.如图为一幅唐朝的投壶图,假设甲、乙是唐朝的两位投壶游戏参与者,且甲、乙每次投壶投中的概率分别为12,13,每人每次投壸相互独立.若约定甲投壶2次,乙投壶3次,投中次数多者胜,则甲最后获胜的概率为( )A. 23B. 527C. 13D. 102712. 已知1.584<log 23<1.585,1.5843≈3.97,1.5853≈3.98.设a =log 2(log 34),b =log 3(log 42),c =log 4(log 23),则( )A. b <a <cB. b <c <aC. a <c <bD. c <b <a二、填空题(本大题共4小题,共20.0分) 13. (x 3−2x )4的展开式中的常数项等于______.14. 若x ,y 满足约束条件{y +2≥0x +y −3≤03x −2y +6≥0,则3x −y 的最小值为______.15. 已知函数f(x)=tan x2,现有下列四个命题: ①f(x)的最小正周期为2π; ②曲线y =f(x)关于点(π,0)对称; ③若f(α)=12,则tanα=−43;④若f(2α)=2,则sin(α−π4)=13sin(α+π4). 其中所有真命题的编号是______.16. 设直线x =t(0≤t ≤2)与函数y =x 3的图象交于点A ,与直线y =3x −4交于点B ,则|AB|的取值范围是______.三、解答题(本大题共7小题,共82.0分)17. 春见柑橘的学名是春见,俗称耙耙柑,2001年从中国柑橘研究所引进,广泛种植于四川、重庆、江西等地.四川省某个春见柑橘种植基地随机选取并记录了8棵春见柑橘树未使用新技术时的年产量(单位:千克)和使用了新技术后的年产量的数据的变化,得到如下表格: 未使用新技术时的8棵春见柑橘树的年产量使用了新技术后的8棵春见柑橘树的年产量已知该基地共有40亩地,每亩地有55棵春见柑橘树.(1)根据这8棵春见柑橘树年产量的平均值,估计该基地使用了新技术后,春见柑橘年总产量比未使用新技术时增加的百分比;(2)已知使用新技术后春见柑橘的成本价为每千克5元,市场销售价格为每千克10元.若该基地的所有春见柑橘有八成按照市场价售出,另外两成只能按照市场价的八折售出,试估计该基地使用新技术后春见柑橘的年总利润是多少万元.18. 如图,在四棱锥P −ABCD 中,PA ⊥平面ABCD ,底面为直角梯形,CD//AB ,AD ⊥AB ,且PA =AD ,E 为PD 的中点. (1)证明:AE ⊥平面PCD .(2)若AD =CD =12AB ,求二面角B −PC −D 的大小.19. 已知S n 为等差数列{a n }的前n 项和,从下面①②③中任意选择两个作为条件,证明另外个成立. ①a 3=9;②S n =n(a n −n +1); ③数列{1a n a n+1}的前n 项和为n10n+25.20. 已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的焦点恰为椭圆D :x 24+y 23=1长轴的端点,且C 的短轴长为2. (1)求C 的方程;(2)若直线l 与直线y =2x −1平行,且l 与C 交于A ,B 两点,M(1,0),求MA ⃗⃗⃗⃗⃗⃗ ⋅MB ⃗⃗⃗⃗⃗⃗ 的最小值.21. 已知函数f(x)=ax 2−(1+2a)x +lnx . (1)讨论f(x)的单调性; (2)当a =0时,证明:e x x>710−x 2−2f(x).22. 在极坐标系中,曲线C 的极坐标方程为ρ=−4cosθ,以极点O 为坐标原点,极轴为x 轴的正半轴,建立直角坐标系xOy .(1)写出曲线C的一个参数方程;(2)设P为曲线C上的一个动点,P到x轴,y轴的距离分别为d1,d2,求d1+d2的最大值.23. 已知函数f(x)=|x−3|.(1)求不等式f(x)<|3x−1|的解集.(2)若函数g(x)=f(2x)−2|x−6|的最大值为m,证明:(x2+y2+z4)(1x2+1y2+1z4)≥m.参考答案及解析1.答案:A解析:∵z=(2+i)(1−3i)=2+3−5i=5−5i,∴z的实部为5,虚部为−5,∴z的实部与虚部之和为0.故选:A.根据已知条件,结合复数的四则运算,即可求解.本题主要考查复数的四则运算,属于基础题.2.答案:C解析:集合A={x|m<x<m+5},B={x|−3<x<7},若A∪B={x|−3<x<8},则m+5=8,解答m=3,所以A={x|3<x<8},所以A∩B={x|3<x<7},故选:C.由并集运算可求得m的值,从而可得集合A,再利用交集运算求解即可.本题主要考查集合的交集和并集运算,考查运算求解能力,属于基础题.3.答案:B解析:若“α为锐角”,则“tanα>0”成立,反之,不一定成立.故选:B.直接利用三角函数的符号和充分条件和必要条件的应用求出结果.本题考查的知识要点:三角函数的值,充分条件和必要条件,主要考查学生的运算能力和数学思维能力,属于基础题.4.答案:C解析:根据中位数的定义,利用区间端点判断中位数在[30,40)内,×25=35,设中位数是x,则10+20+x−3010解得x=32,所以这70位观众年龄的中位数约为32.故选:C.根据中位数的定义,利用区间端点计算中位数即可. 本题考查了中位数的计算问题,是基础题.5.答案:D解析:由y =x 3+ax ,得y′=3x 2+a ,又曲线y =x 3+ax 在点(1,a +1)处的切线方程为y =7x +m , ∴{3+a =7a +1=7+m ,解得{a =4m =−2.∴m =−2. 故选:D .求出原函数的导函数,由题意可得关于a 与m 的方程组,求解得答案.本题考查利用导数研究过曲线上某点处的切线方程,关键是熟记基本初等函数的导函数,是基础题.6.答案:D解析:由S =k3=8,得k =24,则输入的k 的可能为12,6,3,⋅⋅⋅, ∴结合选项知:D 符合要求, 故选:D .根据输出结果可得输出时k =24,结合执行逻辑确定输入k 的可能值,即可知答案. 本题考查程序框图,考查学生分析问题的能力,属于容易题.7.答案:A解析:因为S =(a 2+b 2−c 2)sin2C , 所以12absinC =2abcosC ⋅2sinCcosC , 又sinC ≠0,所以cos 2C =18,解得cosC =±√24.故选:A .利用三角形的面积公式,余弦定理,二倍角的正弦公式化简已知等式即可求解cosC 的值. 本题主要考查了三角形的面积公式,余弦定理,二倍角的正弦公式在解三角形中的应用,考查了转化思想,属于基础题.8.答案:B解析:f(−x)=sin(2−x −2x )=−sin(2x −2−x )=−f(x) 所以f(x)为奇函数,图象关于原点对称,排除CD ;令t =2x −2−x 在(0,π2)递增,且x =0时,t =0, x =1时,t =2−12=32, f(1)=sin 32>0,所以y =sin(2x −2−x )在(0,π2)大于0, 排除A , 故选:B .根据函数图象的对称性判断函数的图象特点,以及函数值的单调性即可得到结论. 本题考查函数的图象分析,注意分析函数的奇偶性、单调性,属于基础题.9.答案:C解析:数列{a n }的前n 项和为S n ,数列{S n +n}是公比为2的等比数列,且a 1=1, ∴S 1+1=2,∴S n +n =2n ,∴S n =2n −n ,∴a 8=S 8−S 7=(28−8)−(27−7)=127. 故选:C .由数列{S n +n}是公比为2的等比数列,且a 1=1,得到S n +n =2n ,从而S n =2n −n ,再由a 8=S 8−S 7,能求出结果.本题考查等比数列的运算,考查等比数列的性质等基础知识,考查运算求解能力,是基础题.10.答案:A解析:解:建立如图所示的直角坐标系,则A(0,0),B(3,0),D(0,√3),C(3,√3), 因为DC ⃗⃗⃗⃗⃗ =4MC ⃗⃗⃗⃗⃗⃗ ,BP ⃗⃗⃗⃗⃗ =λBC ⃗⃗⃗⃗⃗ , 所以M(94,√3),P(3,√3λ),所以AM ⃗⃗⃗⃗⃗⃗ =(94,√3),DP ⃗⃗⃗⃗⃗ =(3,√3λ−√3), 又AD ⃗⃗⃗⃗⃗⃗ ⋅AP ⃗⃗⃗⃗⃗ =(0,√3)⋅(3,√3λ)=3λ=2, 所以λ=23则AM ⃗⃗⃗⃗⃗⃗⋅DP ⃗⃗⃗⃗⃗ =94×3+√3(√3λ−√3)=3λ+154=234. 故选:A .。
2021-2022学年高等数学期末考试卷(含答案)

2021-2022学年高等数学期末考试一、填空题(本题共5小题,每小题3分,共15分)1.极限(,)lim y x y →= 。
2.已知函数22ln(1)z x y =-+,则(1,2)|dz = 。
3.设:L 22(1)4x y -+=,则ds y x x L )2(22+-⎰= 。
4.判断级数21(1)1nn n +∞=-+∑ 。
(填绝对收敛,条件收敛,发散)5.点)3,1,2(-M 到平面 0332=+--z y x 的距离为 。
二、单项选择题(本题共5小题,每小题3分,共15分)6.函数(,)z f x y =在点),(00y x 处连续是它在该点偏导数存在的( )(A )必要而非充分条件; (B )充分而非必要条件;(C )充分必要条件; (D )非充分又非必要条件。
7.曲面2223z x y =+在点(1,2,14)处的切平面方程为( ) (A )41242x y z ++=; (B )12144121x y z ---==-; (C )41214x y z +-=; (D )12144121x y z ---==。
8.幂级数11(21)n n x n ∞=+∑的收敛域为( ) (A )(1,1)-; (B )[1,0)-; (C )(1,0]-; (D )[1,0]-。
9.直线 41112:1--==+z y x L 与 22221:2-=-+=z y x L 的夹角是( )。
(A )2π; (B )3π; (C )4π; (D )6π。
10.将函数()1f x x =+,[0,]x π∈展开为正弦级数1()sin n n f x b nx ∞==∑,则级数的系数4b =( )(A ) 12-; (B )13; (C )13-; (D )12。
三、计算题(本题8分)11. 直线l 过点M(1,2,3)且与两平面02=-+z y x 和6432=+-z y x 都平行,求直线l 的方程。
北京市朝阳区2021-2022学年高三上学期期末考试数学试卷(word版,含答案)

北京市朝阳区2021-2022学年高三上学期期末考试数学试卷数 学2022.1(考试时间120分钟 满分150分)本试卷分为选择题40分和非选择题110分第一部分(选择题 共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.2(1i)+= A.2-B.2C.2i -D.2i2.双曲线221169x y -=的渐近线方程为 A.34y x =±B. 43y x =±C. 35y x =±D. 916y x =±3. 在5道试题中有2道代数题和3道几何题,每次从中抽出1道题,抽出的题不再放回,则在第1次抽到代数题的条件下,第2次抽到几何题的概率为A .16B.310 C.12 D.344.已知抛物线24y x =上一点M 与焦点F 的距离为4,则点M 到x 轴的距离是 A.B.C.4D.125.设函数21,()l ,11()g ,2o .x x f x x x ⎧⎪=⎨⎪>⎩≤ 若()2f x ≤,则实数x 的取值范围是A .[)1,-+∞B .(0,4]C .[1,4]-D .(,4]-∞6. 在直角坐标平面xOy 内,O 为坐标原点,已知点A 1(,2-, 将向量OA 绕原点按逆时针方向旋转2π得到OA ',则OA '的坐标为A. 1()2B. 1)2-C. 1(,2D. 1(2-7. 某纯净水制造厂在净化水的过程中,每增加一次过滤可使水中杂质减少50%,若要使水中杂质减少到原来的10%以下,则至少需要过滤 (参考数据:lg20.3010≈) A.2次B.3次C.4次D.5次8.若函数x b x a x f cos sin )(+=的最大值为2,则下列结论不一定成立.....的是( )A.422=+b aB.2ab ≤C.2()8a b +≤D.()24a b -≤9.已知平面向量,a b 满足2,a a =与a b -的夹角为 120,记(1),()m a b t t t =+-∈R ,则m 的取值范围为_______ A.),3[+∞B.),2[+∞C.),1[+∞D.),21[+∞10.如图,将半径为1的球与棱长为1的正方体组合在一起,使正方体的一个顶点正好是球的球心,则这个组合体的体积为A.76π+1 B.7566π+ C.78π+1 D.1π+二、填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡上. 11.在51()x x+的展开式中,x 的系数为__________.12.已知圆222:C x y r +=()0r >,直线:2l y x =+,则使“圆C 上至少有3个点到直线l 距离都 是1”成立的一个充分条件是“r =_______”.13.如图,正方形ABCD 的边长为2,取正方形ABCD 各边的中点,,,E F G H ,作第2个正方形EFGH , 然后再取正方形EFGH 各边的中点,,,I J K L ,作第3个正方形IJKL ,依此方法一直继续下去.则第4个正方形的面积是_______;从正方形ABCD 开始,连续8个正方形面积之和是_______.14.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,PA ⊥底面ABCD ,==2PA AB ,E 为线段PB 的中点,F 为线段BC 上的动点,平面AEF 与平面PBC_______ (填“垂直”或“不垂直”);AEF △的面积的最大值为_______.15. 已知函数)2π0,)(sin()(<>+=ϕωϕωx x f 的部分图象如图所示,设()(),g x f x =给出以下四个结论:① 函数()g x 的最小正周期是π3;② 函数()g x 在区间7π5π(,)189上单调递增; ③ 函数()g x 的图象过点3(0,); ④ 直线1318x π=为函数()g x 的图象的一条对称轴. 其中所有正确结论的序号是_______._______._______E DB PF三、解答题:本大题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程. 16.(本小题满分13分)记ABC △的内角C B A ,,的对边分别为c b a ,,,已知14,4,12+==-=t c t b t a (1t >). (Ⅰ)当3=t 时,求cos B ;(Ⅱ)是否存在正整数t ,使得角C 为钝角?如果存在,求出t 的值,并求此时ABC △的面积;如果不存在,说明理由.17.(本小题满分13分)“双减”政策实施以来,各地纷纷推行课后服务“5+2”模式,即学校每周周一至周五5天都要面向所有学生提供课后服务,每天至少2小时.某学校的课后服务有学业辅导、体育锻炼、实践能力创新培养三大类别,为了解该校学生上个月参加课后服务的情况,该校从全校学生中随机抽取了100人作为样本,发现样本中未参加任何课后服务的有14人,样本中仅参加某一类课后服务的学生分布情况如下:(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月至少参加了两类课后服务活动的概率;(Ⅱ)从全校学生中随机抽取3人,以频率估计概率,以X 表示这3人中上个月仅参加学业辅导的人数,求X 的分布列和数学期望;(Ⅲ)若样本中上个月未参加任何课后服务的学生有(014)n n <≤人在本月选择仅参加学业辅导,样本中其他学生参加课后服务的情况在本月没有变化.从全校学生中随机抽取3人,以频率估计概率,以X 表示这3人中上个月仅参加学业辅导的人数,以Y 表示这3人中本月仅参加学业辅导的人数,试判断方差()D X ,()D Y 的大小关系(结论不要求证明).18.(本小题满分14分)刍甍(chú méng )是中国古代数学书中提到的一种几何体.《九章算术》中有记载“下有袤有广,而上有袤无广”,可翻译为:“底面有长有宽为矩形,顶部只有长没有宽为一条棱.”如图,在刍甍ABCDEF 中,四边形ABCD 是正方形,平面BAE 和平面CDE 交于EF . (Ⅰ)求证:CD 平面BAE ;(Ⅱ)若4AB =,=2EF ,ED FC =,AF =ABCDEF 存在,并求平面ADE 和平面BAE 夹角的余弦值.条件①:BF FC ⊥,AF FC ⊥; 条件②:平面CDE ⊥平面ABCD ; 条件③:平面CBF ⊥平面ABCD .19.(本小题满分15分)已知曲线W :221(,3x y m m m+=∈-R 0,m ≠且3m ≠).(Ⅰ)若曲线W 是焦点在x 轴上的椭圆,求m 的取值范围;(Ⅱ)当1m =时,过点(1,0)E 作斜率为k ()0k ≠的直线l 交曲线W 于点,A B (,A B 异于顶点),交直线2x =于P .过点P 作y 轴的垂线,垂足为Q ,直线AQ 交x 轴于C ,直线BQ 交x 轴于D ,求线段CD 中点M 的坐标.20.(本小题满分15分)已知函数()2ln ln f x x x a =--,0a >.(Ⅰ)求曲线()y f x =在(1,(1))f 处切线的斜率; (Ⅱ)求函数()f x 的极大值;(Ⅲ)设2()=e x g x a x -,当(1,e)a ∈时,求函数()g x 的零点个数,并说明理由.A(21)(本小题满分15分)对任意正整数n ,记集合1212{(,,,)|,,,n n n A a a a a a a =均为非负整数,且12}n a a a n +++=,集合1212{(,,,)|,,,n n n B b b b b b b =均为非负整数,且122}n b b b n +++=.设12(,,,)n n a a a A α=∈,12(,,,)n n b b b B β=∈,若对任意{1,2,,}i n ∈都有i i a b ≤,则记αβ.(Ⅰ)写出集合2A 和2B ;(Ⅱ)证明:对任意n A α∈,存在n B β∈,使得αβ;(Ⅲ)设集合{(,)|,,}n n n S A B αβαβαβ=∈∈,求证:n S 中的元素个数是完全平方数.北京市朝阳区2021-2022学年高三上学期期末考试数学试卷参考答案一、选择题:(本题满分40分)16.(本小题满分13分) 解:(Ⅰ) 3=t 时,5,12,13,a b c ===此时ABC △为直角三角形, 所以5cos 13a B c ==.............6分 (Ⅱ)由题意可得,2221,(21)(4)(41)cos 0.2(21)4t t t t C t t >⎧⎪-+-+⎨=<⎪-⋅⎩即24120,1.t t t ⎧-<⎨>⎩所以13,t <<t *∈N .则 2.t = 此时三边为3,8,9.a b c ===所以2223891cos .2386C +-==-⨯⨯所以sin C 所以11sin 3822ABC S ab C ==⨯⨯△............13分17.(本小题满分13分)解:(Ⅰ)由题意知,样本中仅参加学业辅导的学生有25人,仅参加体育锻炼的学生有18人,仅参加实践能力创新培养的学生有16人,未参加任何课后服务的学生有14人.故样本中至少参加了两类课后服务的学生有1002518161427----=人. 所以从全校学生中随机抽取1人,该学生上个月至少参加了两类课后服务的概率估计值为270.27100=.............4分 (Ⅱ)X 的所有可能值为0,1,2,3.从样本中随机抽取1人,该学生上个月仅参加学业辅导的概率为251=1004, 由此估计从全校学生中随机抽取1人,该学生上个月仅参加学业辅导的概率为14.0331127(0)()(1)4464P X C ==⨯⨯-=, 1231127(1)(1)4464P X C ==⨯⨯-=, 2213119(2)()(1)4464P X C ==⨯⨯-=, 33311(3)()464P X C ==⨯=. 所以X 的分布列为故X 的数学期望为()0123646464644E X =⨯+⨯+⨯+⨯=.............10分 (Ⅲ)()()D X D Y <.............13分 18.(本小题满分14分)解:(Ⅰ)证明:正方形ABCD 中,CD AB ,CD ⊄平面BAE ,AB ⊂平面BAE ,所以CD ∥平面BAE .............5分 (Ⅱ)条件②符合题意.过点F 作FO DC ⊥于点O ,过点O 作OH DC ⊥且交AB 于点H ,连接AO . 因为平面CDE ⊥平面ABCD ,且平面CDE 平面ABCD CD =,FO DC ⊥,所以FO ⊥平面ABCD .所以FO OH ⊥.以O 为坐标原点,分别以,,OD OH OF 所在直线为,,x yz 轴建立空间直角坐标系O xyz -. 因为CD平面BAE ,CD ⊂平面CDE ,平面BAE 平面CDE EF =, 所以CDEF .在四边形CDEF 中,ED FC =,=2EF ,4CD =,所以=1OC ,=3OD . 在正方形ABCD 中,4AB =,所以5AO =. 因为AO FO ⊥,且AF =FO .所以(0,4,0)H ,(3,0,0)D ,(3,4,0)A ,E ,F . 所以(0,4,0)DA =,(DE =-,(1,AE =--,(2,0,0)FE =.设平面ADE 的一个法向量为111(,,)x y z =n .由0,0,DA DE ⎧⋅=⎪⎨⋅=⎪⎩n n 得11140,0.y x =⎧⎪⎨-+=⎪⎩ 令11z =,所以n =.设平面BAE 的一个法向量为222(,,)x y z =m .AC由0,0,AE FE ⎧⋅=⎪⎨⋅=⎪⎩m m得222240,20.x y x ⎧--=⎪⎨=⎪⎩令21y =,所以m =.设平面ADE 与平面BAE 夹角为θ,则cos =cos <=||||n m n m n m ,θ⋅>=所以平面ADE 和平面BAE.............14分 19.(本小题满分15分)解:(Ⅰ)由题意可知30,0,3.m m m m ->⎧⎪>⎨⎪->⎩解得302m <<,所以m 的取值范围为3(0,)2.............4分(Ⅱ)当1m =时,曲线W 为椭圆221,2x y +=由题意,设直线l 的方程为(1)y k x =-()0k ≠.2212(1)x y y k x ⎧+=⎪⎨⎪=-⎩整理得2222(12)4220.k x k x k +-+-= 设直线l 交椭圆W 于点1122(,),(,)A x y B x y ,则 2122412k x x k +=+,21222212k x x k -=+. 由直线l 的方程(1)y k x =-,令2,x =解得y k =, 所以(2,)P k ,(0,)Q k . 所以直线AQ 的方程为11y ky x k x -=+,10x ≠. 令0,y =解得11kx x k y =-, 所以11(,0)kx C k y -. 直线BQ 的方程为22y ky x k x -=+,20x ≠. 令0,y =解得22kx x k y =-, 所以22(,0)kx D k y -. 11kx k y +-22kx k y -122112[()()]()()k x y k x y k y k y k --+-=--. 由于11(2)y k k x -=-,22(2)y k k x -=-.则11kx k y +-22kx k y - =]1221212[(2)(2)(2)(2)k x k x x k x k x x --+---1212122()2(2)(2)x x x x x x +-=--()121212122()224x x x x x x x x +-=-++=22222224222()1222841212k k k k k k k -++--+++ =2.所以线段CD 的中点M 的坐标为(1,0).............15分 20.(本小题满分15分) 解:(Ⅰ)()f x 定义域为(0,)+∞2()xf x x-'=, (1)1f '=,所以曲线()y f x =在()1,(1)f 处切线的斜率为1.............4分 (Ⅱ)()2ln ln f x x x a =--,则2()xf x x-'=. 令()0f x '=得2x =.当02x <<时,()0f x '>,()f x 单调递增;当2x >时,()0f x '<,()f x 单调递减.所以函数()f x 的极大值为(2)f =24lnea .............10分 (Ⅲ)()e 2(1e)x g x a x a '=-<<,当(],0x ∈-∞时,()0g x '>,所以函数()g x 在(],0x ∈-∞时单调递增.而(0)0g a =>,(1)10eag -=-<. 所以方程()0g x =在()1,0x ∈-时有且只有一个根,即方程()0g x =在(],0x ∈-∞时有且只有一个根. 当0x >时,讨论函数()g x 的零点个数即讨论方程2e x a x =根的个数,即研究方程ln 2ln a x x +=(1e >0)a x <<,的根的个数,即研究函数()f x =2ln ln x x a --(1e >0)a x <<,的零点个数. 当1e a <<时,22e e a >,2244(2)lnln 0e ef a =<<,则函数()f x 在(0,)+∞上无零点. 综上,当(1,e)a ∈时,函数()g x 有且仅有一个零点.............15分 21.(本小题满分15分)解:(Ⅰ)2{(0,2),(1,1),(2,0)}A =,2{(0,4),(1,3),(2,2),(3,1),(4,0)}B =......4分 (Ⅱ)对任意12(,,,)n n a a a A α=∈,设1(1,2,3,,)i i b a i n =+=,则12,,,n b b b 均为非负整数,且(1,2,3,,)i i a b i n =≤.令12(,,,)n b b b β=,则121212(1)(1)(1)()2,nn n b b b a a a a a a nn +++=++++++=++++=所以n B β∈,且αβ.............9分(Ⅲ)对任意12(,,,)n n a a a A α=∈,12(,,,)n n a a a A α''''=∈,记1122(,,,)n n a a a a a a αα'+=+'+'+',则1122,,,n n a a a a a a '''+++均为非负整数,且11221212(,)))(()(2()n n n n a a a a a a a a a a a n a n n +++++'''++'''=++=+++++=所以n B αα'+∈,且,αααααα'''++.设集合n A 中的元素个数为t ,设12{,,,}n t A ααα=.设集合{(,)|1,2,,,1,2,,}n i i j T i t j t ααα=+==.对任意i n A α∈(1,2,,i t =),都有12,,,i i i t n B αααααα+++∈,且,1,2,,ii j j t ααα+=.所以n n T S ⊆.若(,)n S αβ∈,其中12(,,,)n n a a a A α=∈,12(,,,)n n b b b B β=∈,设i i i c b a =-(1,2,,i n =),因为i i a b ≤,所以0i i i c b a =-≥,记12(,,,)n c c c α'=,则1211221212()()()()()2,nn n n n c c c b a b a b a b b b a a a n n n +++=-+-+-=+++-+++=-=所以n A α'∈,并且有βαα'=+,所以(,)n T αβ∈,所以n n S T ⊆. 所以n n S T =.因为集合n T 中的元素个数为2t ,所以n S 中的元素个数为2t ,是完全平方数.............15分。
2022年全国理科数学卷试题答案及解析

2022年全国理科数学卷试题答案及解析2022高考数学试题及答案已经出炉了,能给大家提前估分,下面小编给大家带来2022年全国理科数学卷试题答案及解析,欢迎大家阅读,希望大家喜欢!2022年全国理科数学卷试题答案及解析2022高考数学到底难不难今年高考数学因为太难冲上热搜榜第一,连平时数学120分,130分的学霸考完以后都沉默了。
很多人都说2022年的高考数学堪称史上的“最难高考数学”。
今年的高考数学实在太难了,有好多学生一出考场都哭了…本来今年高考语文作文题目都有点让人摸不着头脑。
如果审题不清楚的考生,很容易写跑题。
万万没想到,下一场的数学更是把很多学生都难哭了。
尤其是江苏、河南、山东、安徽这些人口大省,本来录取率都不高,结果今年的数学甚至超过2003年的高考数学。
说起今年的高考数学难,有一部分原因,就是今年的考试题目新一位考生一出考场就说:练了一年的很多题目,我觉得我们觉得已经是练了很多种了,然后也压了很多种。
但是它这个题型确实真的很新,跟以往练的也不一样。
今年的题目,我觉得思维可能会偏低一点,计算量确实都是逐渐增加的。
本来这届高中生经历了三年的疫情,在家上网课的时间比在校时间还长,但是今年的高考数学竟然还难出天际。
对于平时100分左右的考生打击最大,可能平时90多分的考生,如今只能考50-60分,所以很多人认为,今年的高考数学太不近人情。
很多家长也都有意见,认为孩子高中三年经历了前所未有的疫情,不应该出这么难的数学题。
我认为大可不必。
现在家长一定要明白,高考始终是最公平、最合理的考试,多开导孩子,要难大家一起难,不要让坏心情影响接下来的考试,高考不是终点,它只是人生的起点。
2022高考志愿填报方法及技巧高考志愿填报是一场没有硝烟的战争,在正式填报志愿之前,考生及家长一定明确相关问题并做好准备工作,才能让自己在这场几百万人的博弈中取得胜利。
(一)正确估分在所有科目考试结束后,大家可以去看参考答案。
2021年全国甲卷理科数学试题及答案
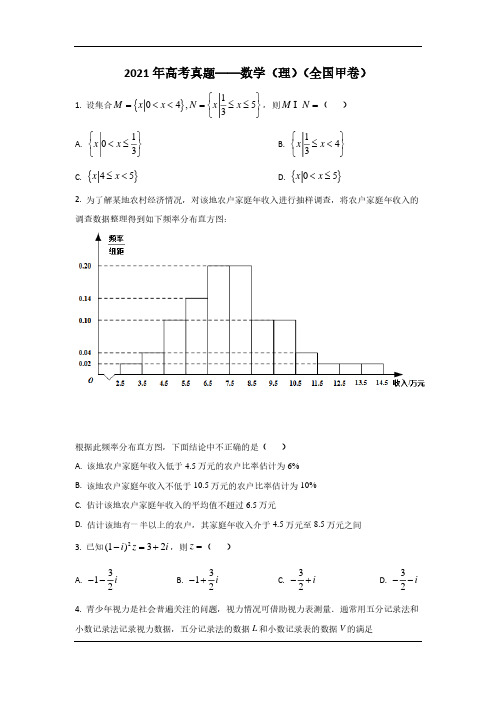
2021年高考真题——数学(理)(全国甲卷)1.设集合{}104,53M x x N xx ⎧⎫=<<=≤≤⎨⎬⎩⎭,则M N =I ( ) A. 103x x ⎧⎫<≤⎨⎬⎩⎭ B. 143x x ⎧⎫≤<⎨⎬⎩⎭C.{}45x x ≤< D.{}05x x <≤2.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:根据此频率分布直方图,下面结论中不正确的是( ) A.该地农户家庭年收入低于4.5万元的农户比率估计为6%B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%C.估计该地农户家庭年收入的平均值不超过6.5万元D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间3.已知2(1)32i z i −=+,则z =( ) A. 312i −−B. 312i −+C. 32i −+ D. 32i −−4.青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L 和小数记录表的数据V 的满足5lg L V =+.已知某同学视力的五分记录法的数据为4.9,则其视力的小数记录法的数据为( )(1010 1.259≈) A.1.5B.1.2C.0.8D.0.65. 已知12,F F 是双曲线C 的两个焦点,P 为C 上一点,且121260,3F PF PF PF ∠=︒=,则C 的离心率为()A.72 B.132C. 7D.136.在一个正方体中,过顶点A 的三条棱的中点分别为E ,F ,G .该正方体截去三棱锥A EFG −后,所得多面体的三视图中,正视图如图所示,则相应的侧视图是( )A. B. C. D.7.等比数列{}n a 的公比为q ,前n 项和为n S ,设甲:0q >,乙:{}n S 是递增数列,则( ) A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件8.2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8848.86(单位:m ),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A ,B ,C 三点,且A ,B ,C 在同一水平面上的投影,,A B C '''满足45A C B ∠'''=︒,60A B C ''∠'=︒.由C 点测得B 点的仰角为15︒,BB '与CC '的差为100;由B 点测得A点的仰角为45︒,则A ,C 两点到水平面A B C '''的高度差AA CC ''−约为(3 1.732≈)( )A.346B.373C.446D.4739.若cos 0,,tan 222sin παααα⎛⎫∈= ⎪−⎝⎭,则tan α=( ) A.15155C.53D.15310.将4个1和2个0随机排成一行,则2个0不相邻的概率为( ) A.13B.25C.23D.4511.已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC −的体积为( ) A.212B.3 C.24D.312.设函数()f x 的定义域为R ,()1f x +为奇函数,()2f x +为偶函数,当[]1,2x ∈时,2()f x ax b =+.若()()036f f +=,则92f ⎛⎫= ⎪⎝⎭( )A. 94−B. 32−C.74D.52二、填空题:本题共4小题,每小题5分,共20分.13.曲线212x y x −=+在点()1,3−−处的切线方程为__________.14.已知向量()()3,1,1,0,a b c a kb ===+r r r r r .若a c ⊥r r,则k =________.15.已知12,F F 为椭圆C :221164x y+=的两个焦点,P ,Q 为C 上关于坐标原点对称的两点,且12PQ F F =,则四边形12PFQF 的面积为________. 16.已知函数()2cos()f x x ωϕ=+的部分图像如图所示,则满足条件74()()043f x f f x f ππ⎛⎫⎛⎫⎛⎫⎛⎫−−−> ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭的最小正整数x 为________.三、解答题:共70分.解答应写出交字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表:一级品二级品 合计 甲机床150 50 200 乙机床120 80 200 合计270130400(1)甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)能否有99%的把握认为甲机床的产品质量与乙机床的产品质量有差异?附:22()()()()()n ad bc K a b c d a c b d −=++++()2P K k ≥0.050 0.0100.001k3.841 6.635 10.82818.已知数列{}n a 的各项均为正数,记n S 为{}n a 的前n 项和,从下面①②③中选取两个作为条件,证明另外一个成立. ①数列{}n a 是等差数列:②数列{}nS 是等差数列;③213aa =.注:若选择不同的组合分别解答,则按第一个解答计分.19.已知直三棱柱111ABC A B C −中,侧面11AA B B 为正方形,2AB BC ==,E ,F 分别为AC 和1CC 的中点,D 为棱11A B 上的点.11BF A B ⊥(1)证明:BF DE ⊥;(2)当1B D 为何值时,面11BB C C 与面DFE 所成的二面角的正弦值最小?20.抛物线C 的顶点为坐标原点O .焦点在x 轴上,直线l :1x =交C 于P ,Q 两点,且OP OQ ⊥.已知点()2,0M ,且M e 与l 相切.(1)求C ,M e 的方程;(2)设123,,A A A 是C 上的三个点,直线12A A ,13A A 均与M e 相切.判断直线23A A 与M e 的位置关系,并说明理由.21.已知0a >且1a ≠,函数()(0)ax x f x x a=>.(1)当2a =时,求()f x 的单调区间;(2)若曲线()y f x =与直线1y =有且仅有两个交点,求a 的取值范围.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](10分)22.在直角坐标系xOy 中,以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线C 的极坐标方程为22cos ρθ=.(1)将C 的极坐标方程化为直角坐标方程;(2)设点A 的直角坐标为()1,0,M 为C 上的动点,点P 满足2AP AM =u u u r u u u u r,写出Р的轨迹1C 的参数方程,并判断C 与1C 是否有公共点.[选修4-5:不等式选讲](10分)23. 已知函数()2,()2321f x x g x x x =−=+−−.(1)画出()y f x =和()y g x =的图像;(2)若()()f x a g x +≥,求a 的取值范围.2021年高考真题——数学(理)(全国甲卷) 答案解析1.B 解析:因为1{|04},{|5}3M x x N x x =<<=≤≤,所以1|43M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭,故选:B.2.C 解析:因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.该地农户家庭年收入低于4.5万元的农户的比率估计值为0.020.040.066%+==,故A 正确;该地农户家庭年收入不低于10.5万元的农户比率估计值为0.040.0230.1010%+⨯==,故B 正确;该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为0.100.140.2020.6464%50%++⨯==>,故D 正确;该地农户家庭年收入的平均值的估计值为30.0240.0450.1060.1470.2080.2090.10100.10110.04120.02130.02140.027.68⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=(万元),超过6.5万元,故C 错误. 综上,给出结论中不正确的是C. 故选:C.3.B 解析: 由已知得322iz i+=−,根据复数除法运算法则,即可求解. 2(1)232i z iz i −=−=+,32(32)23312222i i i i z i i i i ++⋅−+====−+−−⋅.故选B.4.C 解析:根据,L V 关系,当 4.9L =时,求出lg V ,再用指数表示V ,即可求解.由5lg L V =+,当 4.9L =时,lg 0.1V =−,则10.110101110100.81.25910V −−===≈≈. 故选C . 5.A 解析:根据双曲线的定义及条件,表示出12,PF PF ,结合余弦定理可得答案. 因为213PF PF =,由双曲线的定义可得12222PF PF PF a −==, 所以2PF a =,13PF a =;因为1260F PF ∠=︒,由余弦定理可得2224923cos60c a a a a =+−⨯⋅⋅︒,整理可得2247c a =,所以22274a c e ==,即72e =. 故选A 6.D 解析:根据题意及题目所给的正视图还原出几何体的直观图,结合直观图进行判断. 由题意及正视图可得几何体的直观图,如图所示,所以其侧视图为故选D 7.B 解析:当0q >时,通过举反例说明甲不是乙的充分条件;当{}n S 是递增数列时,必有0n a >成立即可说明0q >成立,则甲是乙的必要条件,即可选出答案. 由题,当数列为2,4,8,−−−L 时,满足0q >, 但是{}n S 不是递增数列,所以甲不是乙的充分条件.若{}n S 是递增数列,则必有0n a >成立,若0q >不成立,则会出现一正一负的情况,是矛盾的,则0q >成立,所以甲是乙的必要条件. 故选B . 8.B 解析:通过做辅助线,将已知所求量转化到一个三角形中,借助正弦定理,求得''A B ,进而得到答案.过C 作'CH BB ⊥,过B 作'BD AA ⊥,故()''''''100100AA CC AA BB BH AA BB AD −=−−=−+=+,由题,易知ADB △为等腰直角三角形,所以AD DB =. 所以''100''100AA CC DB A B −=+=+. 因为15BCH ∠=︒,所以100''tan15CH C B ==︒在'''A B C V 中,由正弦定理得:''''100100sin 45sin 75tan15cos15sin15A B C B ===︒︒︒︒︒,而sin15sin(4530)sin 45cos30cos 45sin 30︒=︒−︒=︒︒−︒︒=,所以1004''1)273A B ⨯==≈,所以''''100373AA CC A B −=+≈. 故选B . 9.A 解析:由二倍角公式可得2sin 22sin cos tan 2cos 212sin αααααα==−,再结合已知可求得1sin 4α=,利用同角三角函数的基本关系即可求解.cos tan 22sin ααα=−Q 2sin 22sin cos cos tan 2cos 212sin 2sin αααααααα∴===−−,0,2πα⎛⎫∈ ⎪⎝⎭Q ,cos 0α∴≠,22sin 112sin 2sin ααα∴=−−,解得1sin 4α=,cos 4α∴==,sin tan cos 15ααα∴==. 故选A. 10.C 解析:采用插空法,4个1产生5个空,分2个0相邻和2个0不相邻进行求解. 将4个1和2个0随机排成一行,可利用插空法,4个1产生5个空, 若2个0相邻,则有155C =种排法,若2个0不相邻,则有2510C =种排法,所以2个0不相邻的概率为1025103=+. 故选C. 11.A解析:由题可得ABC V 为等腰直角三角形,得出ABC V 外接圆的半径,则可求得O 到平面ABC 的距离,进而求得体积.,1AC BC AC BC ⊥==Q ,ABC ∴V 为等腰直角三角形,2AB ∴=,则ABC V 外接圆的半径为22,又球的半径为1, 设O 到平面ABC 的距离为d , 则,所以1112211332212O ABC ABC V S d −=⋅=⨯⨯⨯⨯=V . 故选A. 12.D 解析: 通过()1f x +是奇函数和()2f x +是偶函数条件,可以确定出函数解析式()222f x x =−+,进而利用定义或周期性结论,即可得到答案.因为()1f x +是奇函数,所以()()11f x f x −+=−+①;因为()2f x +是偶函数,所以()()22f x f x +=−+②.令1x =,由①得:()()()024f f a b =−=−+,由②得:()()31f f a b ==+, 因为()()036f f +=,所以()462a b a b a −+++=⇒=−,令0x =,由①得:()()()11102f f f b =−⇒=⇒=,所以()222f x x =−+.思路一:从定义入手.9551222222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=+=−+=− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1335112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫−=−+=−+=− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭511322=2222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫−=−+=−−+− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以935222f f ⎛⎫⎛⎫=−=⎪ ⎪⎝⎭⎝⎭. 思路二:从周期性入手由两个对称性可知,函数()f x 的周期4T =.所以91352222f f f ⎛⎫⎛⎫⎛⎫==−=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故选D .二、填空题:13.答案:520x y −+= 解析:先验证点在曲线上,再求导,代入切线方程公式即可. 由题,当1x =−时,3y =−,故点在曲线上. 求导得:()()()()222221522x x y x x +−−==++',所以1|5x y =−='.故切线方程为520x y −+=. 故答案为:520x y −+=. 14. 答案:103−. 解析:利用向量的坐标运算法则求得向量c r的坐标,利用向量的数量积为零求得k 的值()()()3,1,1,0,3,1a b c a kb k ==∴=+=+r r r r Q r,(),33110a c a c k ⊥∴⋅=++⨯=r r Q r r ,解得103k =−,故答案为:103−.15. 答案:8解析:根据已知可得12PF PF ⊥,设12||,||PF m PF n ==,利用勾股定理结合8m n +=,求出mn ,四边形12PFQF 面积等于mn ,即可求解.因为,P Q 为C 上关于坐标原点对称的两点, 且12||||PQ F F =,所以四边形12PFQF 为矩形,设12||,||PF m PF n ==,则228,48m n m n +=+=, 所以22264()2482m n m mn n mn =+=++=+,8mn =,即四边形12PFQF 面积等于8.故答案为8. 16. 答案:2 解析:先根据图象求出函数()f x 的解析式,再求出7(),()43f f π4π−的值,然后求解三角不等式可得最小正整数或验证数值可得. 由图可知313341234T πππ=−=,即2T ππω==,所以2ω=;由五点法可得232ππϕ⨯+=,即6πϕ=−;所以()2cos 26f x x π⎛⎫=− ⎪⎝⎭.因为7()2cos 143f π11π⎛⎫−=−= ⎪⎝⎭,()2cos 032f 4π5π⎛⎫== ⎪⎝⎭; 所以由74(()())(()())043f x f f x f ππ−−−>可得()1f x >或()0f x <;因为()12cos 22cos 1626f πππ⎛⎫⎛⎫=−<−= ⎪ ⎪⎝⎭⎝⎭,所以, 方法一:结合图形可知,最小正整数应该满足()0f x <,即cos 206x π⎛⎫−< ⎪⎝⎭, 解得,36k x k k π5ππ+<<π+∈Z ,令0k =,可得536x <<ππ,可得x 的最小正整数为2.方法二:结合图形可知,最小正整数应该满足()0f x <,又(2)2cos 406f π⎛⎫=−< ⎪⎝⎭,符合题意,可得x 的最小正整数为2. 故答案为:2.三、解答题: (一)必考题:17.答案:(1)75%;60%; (2)能. 解析:根据给出公式计算即可(1)甲机床生产的产品中的一级品的频率为15075%200=, 乙机床生产的产品中的一级品的频率为12060%200=. (2)()22400150801205040010 6.63527013020020039K ⨯−⨯==>>⨯⨯⨯, 故能有99%的把握认为甲机床的产品与乙机床的产品质量有差异. 18.答案:答案见解析 解析:,n n a S 的关系求出n a ,利用{}n a 是等差数列可证213a a =;,结合等差数列定义可证;an b =+,结合,n n a S 的关系求出n a ,根据213a a =可求b ,然后可证{}n a 是等差数列. 选①②作条件证明③:(0)an b a =+>,则()2n S an b =+, 当1n =时,()211a S a b ==+;当2n ≥时,()()221n n n a S S an b an a b −=−=+−−+()22a an a b =−+;因为{}n a 也是等差数列,所以()()222a b a a a b +=−+,解得0b =;所以()221n aa n =−,所以213a a =.选①③作条件证明②:因为213a a =,{}n a 是等差数列, 所以公差2112d a a a =−=,所以()21112n n n S na d n a −=+==,)1n =+=,所以是等差数列.选②③作条件证明①:(0)an b a =+>,则()2n S an b =+, 当1n =时,()211a S a b ==+;当2n ≥时,()()221n n n a S S an b an a b −=−=+−−+()22a an a b =−+;因为213a a =,所以()()2323a a b a b +=+,解得0b =或43a b =−;当0b =时,()221,21n a a a a n ==−,当2n ≥时,2-1-2n n a a a =满足等差数列的定义,此时{}n a 为等差数列; 当43a b =−时,4=3n S an b an a =+−,103a S =−<不合题意,舍去.综上可知{}n a 为等差数列. 19.答案:(1)见解析;(2)112B D =解析:通过已知条件,确定三条互相垂直的直线,建立合适的空间直角坐标系,借助空间向量证明线线垂直和求出二面角的平面角的余弦值最大,进而可以确定出答案. 因为三棱柱111ABC A B C −是直三棱柱,所以1BB ⊥底面ABC ,所以1BB AB ⊥因为11//A B AB ,11BF A B ⊥,所以BF AB ⊥, 又1BB BF B ⋂=,所以AB ⊥平面11BCC B . 所以1,,BA BC BB 两两垂直.以B 为坐标原点,分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系,如图.所以()()()()()()1110,0,0,2,0,0,0,2,0,0,0,2,2,0,2,0,2,2B A C B A C ,()()1,1,0,0,2,1E F .由题设(),0,2D a (02a ≤≤).(1)因为()()0,2,1,1,1,2BF DE a ==−−u u u v u u u v,所以()()0121120BF DE a ⋅=⨯−+⨯+⨯−=u u u v u u u v,所以BF DE ⊥.(2)设平面DFE 的法向量为(),,m x y z =u r,因为()()1,1,1,1,1,2EF DE a =−=−−u u u v u u u v,所以00m EF m DE ⎧⋅=⎨⋅=⎩u u u v v u u u v v ,即()0120x y z a x y z −++=⎧⎨−+−=⎩.令2z a =−,则()3,1,2m a a =+−v因为平面11BCC B 的法向量为()2,0,0BA =u u u r,设平面11BCC B 与平面DEF 的二面角的平面角为θ,则cos m BA m BA θ⋅===⋅u u u v v u u u v v当12a =时,2224a a −+取最小值为272,此时cos θ3=.所以()minsin 3θ==, 此时112B D =. 20.答案:(1)抛物线2:C y x =,M e 方程为22(2)1x y −+=;(2)相切,理由见解析解析:(1)根据已知抛物线与1x =相交,可得出抛物线开口向右,设出标准方程,再利用对称性设出,P Q 坐标,由OP OQ ⊥,即可求出p ;由圆M 与直线1x =相切,求出半径,即可得出结论;(2)先考虑12A A 斜率不存在,根据对称性,即可得出结论;若121323,,A A A A A A 斜率存在,由123,,A A A 三点在抛物线上,将直线121223,,A A A A A A 斜率分别用纵坐标表示,再由1212,A A A A 与圆M 相切,得出2323,y y y y +⋅与1y 的关系,最后求出M 点到直线23A A 的距离,即可得出结论.(1)依题意设抛物线200:2(0),(1,),(1,)C y px p P y Q y =>−,20,1120,21OP OQ OP OQ y p p ⊥∴⋅=−=−=∴=u u u r u u u r Q ,所以抛物线C 的方程为2y x =,(0,2),M M e 与1x =相切,所以半径为1,所以M e 的方程为22(2)1x y −+=; (2)设111222333(),(,),(,)A x y A x y A x y 若12A A 斜率不存在,则12A A 方程为1x =或3x =, 若12A A 方程为1x =,根据对称性不妨设1(1,1)A , 则过1A 与圆M 相切的另一条直线方程为1y =,此时该直线与抛物线只有一个交点,即不存在3A ,不合题意; 若12A A 方程为3x =,根据对称性不妨设12(3,A A 则过1A 与圆M 相切的直线13A A 为(3)3y x =−, 又131331313103A A y y k y x x y y −====∴=−+, 330,(0,0)x A =,此时直线1323,A A A A 关于x 轴对称,所以直线23A A 与圆M 相切; 若直线121323,,A A A A A A 斜率均存在, 则121323121323111,,A A A A A A k k k y y y y y y ===+++,所以直线12A A 方程为()11121y y x x y y −=−+,整理得1212()0x y y y y y −++=,同理直线13A A 的方程为1313()0x y y y y y −++=, 直线23A A 的方程为2323()0x y y y y y −++=,12A A Q 与圆M相切,1=整理得22212121(1)230y y y y y −++−=,13A A 与圆M 相切,同理22213131(1)230y y y y y −++−=所以23,y y 为方程222111(1)230y y y y y −++−=的两根,2112323221123,11y y y y y y y y −+=−⋅=−−,M 到直线23A A 的距离为:2123|2|y −+=22121111y y +===+,所以直线23A A 与圆M 相切;综上若直线1213,A A A A 与圆M 相切,则直线23A A 与圆M 相切. 21.答案:(1)20,ln2⎛⎤ ⎥⎝⎦上单调递增;2,ln2⎡⎫+∞⎪⎢⎣⎭上单调递减;(2)()()1,,e e ⋃+∞.解析:(1)求得函数的导函数,利用导函数的正负与函数的单调性的关系即可得到函数的单调性; (2)利用指数对数的运算法则,可以将曲线()y f x =与直线1y =有且仅有两个交点等价转化为方程ln ln x ax a =有两个不同的实数根,即曲线()y g x =与直线ln a y a=有两个交点,利用导函数研究()g x 的单调性,并结合()g x 的正负,零点和极限值分析()g x 的图象,进而得到ln 10a a e<<,发现这正好是()()0g a g e <<,然后根据()g x 的图象和单调性得到a 的取值范围.(1)当2a =时,()()()()22222ln 2222ln 2,242xx x x x x x x x x x f x f x ⋅−⋅−⋅===', 令()'0f x =得2ln 2x =,当20ln 2x <<时,()0f x '>,当2ln 2x >时,()0f x '<, ∴函数()f x 在20,ln2⎛⎤ ⎥⎝⎦上单调递增;2,ln2⎡⎫+∞⎪⎢⎣⎭上单调递减; (2)()ln ln 1ln ln a x a x x x af x a x x a a x a x a==⇔=⇔=⇔=,设函数()ln x g x x =, 则()21ln xg x x−'=,令()0g x '=,得x e =, 在()0,e 内()0g x '>,()g x 单调递增;在(),e +∞上()0g x '<,()g x 单调递减;()()1max g x g e e∴==,又()10g =,当x 趋近于+∞时,()g x 趋近于0,所以曲线()y f x =与直线1y =有且仅有两个交点,即曲线()y g x =与直线ln ay a=有两个交点的充分必要条件是ln 10a a e<<,这即是()()0g a g e <<, 所以a 的取值范围是()()1,,e e +∞U .(二)选考题:[选修4-4:坐标系与参数方程]22.答案:(1)(222x y −+=;(2)P 的轨迹1C的参数方程为32cos 2sin x y θθ⎧=+⎪⎨=⎪⎩(θ为参数),C 与1C 没有公共点.解析:(1)将曲线C 的极坐标方程化为2cos ρθ=,将cos ,sin x y ρθρθ==代入可得;(2)设(),P x y ,设)M θθ,根据向量关系即可求得P 的轨迹1C 的参数方程,求出两圆圆心距,和半径之差比较可得.(1)由曲线C 的极坐标方程ρθ=可得2cos ρθ=,将cos ,sin x y ρθρθ==代入可得22x y +=,即(222x y −+=,即曲线C 的直角坐标方程为(222x y +=;(2)设(),P x y ,设)M θθQAP =u u u r u u u r ,())()1,22cos 2sin x y θθθθ∴−=−=+−,则122cos 2sin x y θθ⎧−=+⎪⎨=⎪⎩32cos 2sin x y θθ⎧=−⎪⎨=⎪⎩,故P 的轨迹1C 的参数方程为32cos 2sin x y θθ⎧=−+⎪⎨=⎪⎩(θ为参数)Q曲线C 的圆心为),曲线1C 的圆心为()3,半径为2,则圆心距为3−,32−<Q ,∴两圆内含,故曲线C 与1C 没有公共点.[选修4-5:不等式选讲]23.答案:(1)图像见解析;(2)112a ≥解析:(1)分段去绝对值即可画出图像;(2)根据函数图像数形结和可得需将()y f x =向左平移可满足同角,求得()y f x a =+过1,42A ⎛⎫ ⎪⎝⎭时a 的值可求.(1)可得2,2()22,2x x f x x x x −<⎧=−=⎨−≥⎩,画出图像如下: 34,231()232142,2214,2x g x x x x x x ⎧−<−⎪⎪⎪=+−−=+−≤<⎨⎪⎪≥⎪⎩,画出函数图像如下: (2)()|2|f x a x a +=+−,如图,在同一个坐标系里画出()(),f x g x 图像,()y f x a =+是()y f x =平移了a 个单位得到,则要使()()f x a g x +≥,需将()y f x =向左平移,即0a >,当()y f x a =+过1,42A ⎛⎫ ⎪⎝⎭时,1|2|42a +−=,解得112a =或52−(舍去), 则数形结合可得需至少将()y f x =向左平移112个单位,112a ∴≥.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021 — 2022学年度第一学期期末试卷高三数学(理科)第Ⅰ卷(选择题 共40分)一、 选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合{|1}A x x =>,集合{2}B a =+,若A B =∅,则实数a 的取值范围是( )(A )(,1]-∞- (B )(,1]-∞(C )[1,)-+∞(D )[1,)+∞2. 下列函数中,值域为R 的偶函数是( )(A )21y x =+ (B )e e x x y -=- (C )lg ||y x = (D)y =3. 设命题p :“若1sin 2α=,则π6α=”,命题q :“若a b >,则11a b<”,则( ) (A )“p q ∧”为真命题 (B )“p q ∨”为假命题 (C )“q ⌝”为假命题 (D )以上都不对4. 在数列{}n a 中,“对任意的*n ∈N ,212n n n a a a ++=”是“数列{}n a 为等比数列”的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件 5. 一个几何体的三视图如图所示,那么这个 几何体的表面积是( ) (A)16+ (B)16+ (C)20+ (D)20+侧(左)视图正(主)视图俯视图6. 设x ,y 满足约束条件1,3,,x y y m y x +-⎧⎪⎨⎪⎩≤≤≥ 若3z x y =+的最大值与最小值的差为7,则实数m =( )(A )32 (B )32- (C )14(D )14-7.某市乘坐出租车的收费办法如下:相应系统收费的程序框图如图所示,其中x (单位:千米)为行驶里程,y (单位:元)为所收费用,用[x ]表示不大于x 的最大整数,则图中○1 (A )12[]42y x =-+(B )12[]52y x =-+(C )12[]42y x =++(D )12[]52y x =++8. 如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE AE =,2CF BF =.如果对于常数λ,在正方形ABCD 的四条边上,有且只有6个不同的点P 使得=PE PF λ⋅成立,那么λ的取值范围是( ) (A )(0,7) (B )(4,7) (C )(0,4) (D )(5,16)-FD P C B第Ⅱ卷(非选择题 共110分)二、填空题:本大题共6小题,每小题5分,共30分. 9. 已知复数z 满足(1i)24i z +=-,那么z =____.10.在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c . 若A B =,3a =,2c =,则cos C =____.11.双曲线C :221164x y -=的渐近线方程为_____;设12,F F 为双曲线C 的左、右焦点,P 为C 上一点,且1||4PF =,则2||PF =____.12.在ABC ∆中,90ABC ∠=,3AB =,4BC =,点O 为BC 的中点,以BC 为直径的半圆与AC ,AO 分别相交于点M ,N ,则AN =____;AMMC= ____.13. 现有5名教师要带3个兴趣小组外出学习考察,要求每个兴趣小组的带队教师至多2人,但其中甲教师和乙教师均不能单独带队,则不同的带队方案有____种.(用数字作答)14. 某食品的保鲜时间t (单位:小时)与储藏温度x (单位:C )满足函数关系60,264, , 0.kx x t x +⎧=⎨>⎩≤ 且该食品在4C 的保鲜时间是16小时.已知甲在某日上午10时购买了该食品,并将其遗放在室外,且此日的室外温度随时间变化如图所示. 给出以下四个结论: ○1 该食品在6C 的保鲜时间是8小时;○2 当[6,6]x ∈-时,该食品的保鲜时间t 随着x 增大而逐渐减少;○3 到了此日13时,甲所购买的食品还在保鲜时间内; ○4 到了此日14时,甲所购买的食品已然过了保鲜时间. 其中,所有正确结论的序号是____.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)已知函数()cos(sin)f x x x x=,x∈R.(Ⅰ)求()f x的最小正周期和单调递增区间;(Ⅱ)设0α>,若函数()()g x f xα=+为奇函数,求α的最小值.16.(本小题满分13分)甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分. 两人4局的得分情况如下:(Ⅰ)若从甲的4局比赛中,随机选取2局,求这2局的得分恰好相等的概率;(Ⅱ)如果7x y==,从甲、乙两人的4局比赛中随机各选取1局,记这2局的得分和为X,求X的分布列和数学期望;(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出x的所有可能取值.(结论不要求证明)17.(本小题满分14分)如图,在四棱锥P ABCD-中,底面ABCD是平行四边形,135BCD∠=,侧面PAB⊥底面ABCD,90BAP∠=,2AB AC PA===, ,E F分别为,BC AD的中点,点M在线段PD上.(Ⅰ)求证:EF⊥平面PAC;(Ⅱ)若M为PD的中点,求证://ME平面PAB;(Ⅲ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求PMPD的值.18.(本小题满分13分)已知函数2()1f x x=-,函数()2lng x t x=,其中1t≤.FCA DPMB E(Ⅰ)如果函数()f x 与()g x 在1x =处的切线均为l ,求切线l 的方程及t 的值; (Ⅱ)如果曲线()y f x =与()y g x =有且仅有一个公共点,求t 的取值范围.19.(本小题满分14分)已知椭圆C :)0(12222>>=+b a by a x 的离心率为23,点A 在椭圆C 上.(Ⅰ)求椭圆C 的方程;(Ⅱ)设动直线l 与椭圆C 有且仅有一个公共点,判断是否存在以原点O 为圆心的圆,满足此圆与l 相交两点1P ,2P (两点均不在坐标轴上),且使得直线1OP ,2OP 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.20.(本小题满分13分)在数字21,2,,()n n ≥的任意一个排列A :12,,,n a a a 中,如果对于,,i j i j *∈<N ,有i j a a >,那么就称(,)i j a a 为一个逆序对. 记排列A 中逆序对的个数为()S A .如=4n 时,在排列B :3, 2, 4, 1中,逆序对有(3,2),(3,1),(2,1),(4,1),则()4S B =.(Ⅰ)设排列 C : 3, 5, 6, 4, 1, 2,写出()S C 的值;(Ⅱ)对于数字1,2,,n 的一切排列A ,求所有()S A 的算术平均值;(Ⅲ)如果把排列A :12,,,n a a a 中两个数字,()i j a a i j <交换位置,而其余数字的位置保持不变,那么就得到一个新的排列A ':12,,,n b b b ,求证:()()S A S A '+为奇数.参考答案一、选择题:本大题共8小题,每小题5分,共40分.1.A 2.C 3.B 4.B 5.B 6.C 7.D 8.C 二、填空题:本大题共6小题,每小题5分,共30分. 9.13i -- 10.7911.12y x =±12 12. 2 91613.54 14.○1 ○4 注:第11,12题第一问2分,第二问3分.三、解答题:本大题共6小题,共80分. 其他正确解答过程,请参照评分标准给分. 15.(本小题满分13分)(Ⅰ)解:()cos (sin )f x x x x =+2sin cos 1)x x x =+-1sin 22x x=+ ………………4分πsin(2)3x =+,………………6分所以函数()f x 的最小正周期2π=π2T =. ………………7分由ππππ2π+23222x k k -+≤≤,k ∈Z ,得5ππππ+1212x k k -≤≤, 所以函数()f x 的单调递增区间为5ππππ+]1212[k k -,,k ∈Z . ………………9分 (注:或者写成单调递增区间为5ππππ+)1212(k k -,,k ∈Z . ) (Ⅱ)解:由题意,得π()()sin(22)3g x f x x αα=+=++,因为函数()g x 为奇函数,且x ∈R ,所以(0)0g =,即πsin(2)03α+=, ………………11分所以π2π3k α+=,k ∈Z ,解得ππ26k α=-,k ∈Z ,验证知其符合题意. 又因为0α>, 所以α的最小值为π3. ………………13分16.(本小题满分13分)(Ⅰ)解:记 “从甲的4局比赛中,随机选取2局,且这2局的得分恰好相等”为事件A , ………………1分 由题意,得2421()C 3P A ==, 所以从甲的4局比赛中,随机选取2局,且这2局得分恰好相等的概率为13. ……4分(Ⅱ)解:由题意,X 的所有可能取值为13,15,16,18, ………………5分且3(13)8P X ==,1(15)8P X ==,3(16)8P X ==,1(18)8P X ==,………………7分所以X 的分布列为:……………… 8分 所以3131()13151618158888E X =⨯+⨯+⨯+⨯=. ………………10分(Ⅲ)解:x 的可能取值为6,7,8. ………………13分17.(本小题满分14分)(Ⅰ)证明:在平行四边形ABCD 中,因为AB AC =,135BCD ∠=, 所以AB AC ⊥.由,E F 分别为,BC AD 的中点,得//EF AB ,所以EF AC ⊥. ………………1分 因为侧面PAB ⊥底面ABCD ,且90BAP ∠=,所以PA ⊥底面ABCD . ………………2分又因为EF ⊂底面ABCD ,所以PA EF ⊥. ………………3分又因为PA AC A =,PA ⊂平面PAC ,AC ⊂平面PAC ,所以EF ⊥平面PAC . ………………4分 (Ⅱ)证明:因为M 为PD 的中点,F 分别为AD 的中点, 所以//MF PA ,又因为MF ⊄平面PAB ,PA ⊂平面PAB , 所以//MF 平面PAB . ………………5分同理,得//EF 平面PAB . 又因为=MFEF F ,MF ⊂平面MEF ,EF ⊂平面 所以平面//MEF 平面PAB . ………………7分又因为ME ⊂平面MEF ,所以//ME 平面PAB . ………………9分(Ⅲ)解:因为PA ⊥底面ABCD ,AB AC ⊥,所以,,AP AB AC 两两垂直,故以,,AB AC AP 分别为x 轴、y 轴和z 轴,如上图建立空间直角坐标系,则(0,0,0),(2,0,0),(0,2,0),(0,0,2),(2,2,0),(1,1,0)A B C P D E -,所以(2,0,2)PB =-,(2,2,2)PD =--,(2,2,0)BC =-, ………………10分 设([0,1])PMPDλλ=∈,则(2,2,2)PM λλλ=--, 所以(2,2,22)M λλλ--,(12,12,22)ME λλλ=+--,易得平面ABCD 的法向量(0,0,1)=m . ………………11分 设平面PBC 的法向量为(,,)x y z =n , 由0BC ⋅=n ,0PB ⋅=n ,得220,220,x y x z -+=⎧⎨-=⎩ 令1x =, 得(1,1,1)=n . ………………12分因为直线ME 与平面PBC 所成的角和此直线与平面ABCD 所成的角相等,所以|cos ,||cos ,|ME ME <>=<>m n ,即||||||||||||ME ME ME ME ⋅⋅=⋅⋅m n m n , ………………13分所以 |22|λ-=, 解得λ=λ=. ………………14分 D18.(本小题满分13分)(Ⅰ)解:求导,得()2f x x '=,2()tg x x'=,(0)x >. ………………2分 由题意,得切线l 的斜率(1)(1)k f g ''==,即22k t ==,解得1t =. ……………3分 又切点坐标为(1,0),所以切线l 的方程为220x y --=. ………………4分 (Ⅱ)解:设函数2()()()12ln h x f x g x x t x =-=--,(0,)x ∈+∞. ………………5分 “曲线()y f x =与()y g x =有且仅有一个公共点”等价于“函数()y h x =有且仅有一 个零点”.求导,得2222()2t x th x x x x-'=-=. ………………6分① 当0t ≤时,由(0,)x ∈+∞,得()0h x '>,所以()h x 在(0,)+∞单调递增.又因为(1)0h =,所以()y h x =有且仅有一个零点1,符合题意. ………………8分② 当1t =时,当x 变化时,()h x '与()h x 的变化情况如下表所示:所以()h x 在(0,1)上单调递减,在(1,)+∞上单调递增,所以当1x =时,min()(1)0h x h ==,故()y h x =有且仅有一个零点1,符合题意. ………………10分③ 当01t <<时,令()0h x '=,解得x =.当x 变化时,()h x '与()h x 的变化情况如下表所示:所以()h x在上单调递减,在)+∞上单调递增,所以当x =时,min()h x h =. ………………11分因为(1)0h =1<,且()h x在)+∞上单调递增,所以(1)0h h <=.又因为存在12e (0,1)t -∈ ,111122()12ln 0t t t t h t ----=--=>e e e e ,所以存在0(0,1)x ∈使得0()0h x =,所以函数()y h x =存在两个零点0x ,1,与题意不符.综上,曲线()y f x =与()y g x =有且仅有一个公共点时,t 的范围是0{|t t ≤,或1}t =.………………13分19.(本小题满分14分)(Ⅰ)解:由题意,得c a =,222a b c =+, ………………2分又因为点A 在椭圆C 上,所以221314ab+=, ………………3分解得2a =,1b =,c ,所以椭圆C 的方程为1422=+y x . ………………5分(Ⅱ)结论:存在符合条件的圆,且此圆的方程为225x y +=. ………………6分 证明如下:假设存在符合条件的圆,并设此圆的方程为222(0)x y r r +=>.当直线l 的斜率存在时,设l 的方程为m kx y +=. ………………7分由方程组22,1,4y kx m x y =+⎧⎪⎨+=⎪⎩ 得0448)14(222=-+++m kmx x k , ………………8分 因为直线l 与椭圆C 有且仅有一个公共点,所以2221(8)4(41)(44)0km k m ∆=-+-=,即2241m k =+. ………………9分由方程组222,,y kx m x y r =+⎧⎨+=⎩ 得2222(1)20k x kmx m r +++-=, ………………10分则22222(2)4(1)()0km k m r ∆=-+->.设111(,)P x y ,222(,)P x y ,则12221km x x k -+=+,221221m r x x k -⋅=+, ………………11分 设直线1OP ,2OP的斜率分别为1k ,2k , 所以221212121212121212()()()y y kx m kx m k x x km x x m k k x x x x x x +++++=== 222222222222222111m r km k km m m r k k k m r m r k --⋅+⋅+-++==--+, ………………12分将2241m k =+代入上式,得221222(4)14(1)r k k k k r -+⋅=+-.要使得12k k 为定值,则224141r r-=-,即25r =,验证符合题意. 所以当圆的方程为225x y +=时,圆与l 的交点12,P P 满足12k k 为定值14-. ………………13分当直线l 的斜率不存在时,由题意知l 的方程为2x =±, 此时,圆225x y +=与l 的交点12,P P 也满足1214k k =-. 综上,当圆的方程为225x y +=时,圆与l 的交点12,P P 满足斜率之积12k k 为定值14-. ………………14分 20.(本小题满分13分)(Ⅰ)解:()10S C =; ………………2分 (Ⅱ)解:考察排列D :121,,,,n n d d d d -与排列1121,,,,n n D d d d d -:,因为数对(,)i j d d 与(,)j i d d 中必有一个为逆序对(其中1i j n <≤≤), 且排列D 中数对(,)i j d d 共有2(1)C 2n n n -=个, ………………3分 所以1(1)()()2n n S D S D -+=. ………………5分所以排列D 与1D 的逆序对的个数的算术平均值为(1)4n n -. ………………6分 而对于数字1,2,,n 的任意一个排列A :12,,,n a a a ,都可以构造排列A 1:121,,,,n n a a a a -,且这两个排列的逆序对的个数的算术平均值为(1)4n n -. 所以所有()S A 的算术平均值为(1)4n n -. ………………7分 (Ⅲ)证明:○1当1j i =+,即,i j a a 相邻时, 不妨设1i i a a +<,则排列A '为12112,,,,,,,,i i i i n a a a a a a a -++,此时排列A '与排列A :12,,,n a a a 相比,仅多了一个逆序对1(,)i i a a +,所以()()1S A S A '=+,所以()()2()1S A S A S A '+=+为奇数. ………………10分 ○2当1j i ≠+,即,i j a a 不相邻时,假设,i j a a 之间有m 个数字,记排列A :1212,,,,,,,,,,i m j n a a a k k k a a ,先将i a 向右移动一个位置,得到排列A 1:12112,,,,,,,,,,,,i i m j n a a a k a k k a a -,由○1,知1()S A 与()S A 的奇偶性不同, 再将i a 向右移动一个位置,得到排列A 2:121123,,,,,,,,,,,,i i m j n a a a k k a k k a a -,由○1,知2()S A 与1()S A 的奇偶性不同,以此类推,i a 共向右移动m 次,得到排列A m :1212,,,,,,,,,,m i j n a a k k k a a a ,再将j a 向左移动一个位置,得到排列A m +1:1211,,,,,,,,,,i m j i n a a a k k a a a -,以此类推,j a 共向左移动m +1次,得到排列A 2m +1:121,,,,,,,,,j m i n a a a k k a a ,即为排列A ',由○1,可知仅有相邻两数的位置发生变化时,排列的逆序对个数的奇偶性发生变化, 而排列A 经过21m +次的前后两数交换位置,可以得到排列A ', 所以排列A 与排列A '的逆序数的奇偶性不同, 所以()()S A S A '+为奇数.综上,得()()S A S A '+为奇数. ………………13分。
