ANSYS 有限元分析 平面薄板
Ansys机械工程应用精华60例第8例 平面问题的求解实例—厚壁圆筒问题

8.3.4
创建实体模型
拾 取 菜 单 Main Menu → Preprocessor → Modeling → Create → Areas → Circle → By Dimensions。弹出如图 8-8 所示的对话框,在“RAD1” 、 “RAD2” 、 “THETA2”文本框中分 别输入 0.1、0.05 和 90,单击“OK”按钮。 77
第8例
平面问题的求解实例——厚壁圆筒问题
“Item, Comp”两个列表中分别选“Stress” 、 “Y-direction SY” ,单击“OK”按钮。 注意:该路径上各节点 X、Y 方向上的应力即径向应力r 和切向应力t。
图 8-15
映射数据对话框
8.3.12
作路径图
拾取菜单 Main Menu→General Postproc→Path Operations→Plot Path Item→On Graph。弹 出如图 8-16 所示的对话框,在列表中选“SR” 、 “ST” ,单击“OK”按钮。
8.3.6
施加约束
拾取菜单 Main Menu→Solution→Define Loads→Apply→Structural→Displacement→On Lines。弹出拾取窗口,拾取面的水平直线边,单击“OK”按钮,弹出如图 8-11 所示的对话 框,在列表中选择“ UY ” ,单击“ Apply”按钮,再次弹出拾取窗口,拾取面的垂直直线 边,单击“OK”按钮,在图 8-11 所示对话框的列表中选择“UX” ,单击“OK”按钮。
76
第8例
平面问题的求解实例——厚壁圆筒问题
图 8-3 单元类型对话框
图 8-4
单元类型库对话框
图 8-5
板、壳问题的有限元分析

平面应变问题
y
一纵向 ( 即 Z 向 ) 很长,且沿横截 面不变的物体,受有平行于横截面 而且不沿长度变化的面力和体力, 如图1-11所示。 由于物体的纵向很长 ( 在力学上 可近似地作为无限长考虑 ),截面尺 寸与外力又不沿长度变化;当以任 一横截面为 xy 面,任一纵线为 Z 轴 时,则所有一切应力分量、应变分 量和位移分量都不沿Z方向变化,它 们都只是 x 和 y的函数。此外,在这 一情况下,由于对称(任一横截面都 可以看作对称面 ),所有各点都只会 有 x 和 y 方向的位移而不会有 Z 方向 的位移,即 w=0
第八章 ANSYS在结构分析中的应用
第二节 平面问题(平面应力、平面应 变、轴对称) 的有限元分析
y
平面 应力 问题
y t/2 t/2
0 x
¼ Í 1-10
z
厚度为 t 的很薄的均匀木板。只在边缘上受到平行于板面且不沿厚度变化 的面力,同时,体力也平行于板面且不沿厚度变化。 以薄板的中面为 xy面,以垂直于中面的任一直线为 Z轴。由于薄板两表面 上没有垂直和平行于板面的外力,所以板面上各点均有:
壳
对于两个曲面所限定的物体,如果曲面
之间的距离比物体的其它尺寸小很多,就
称之为壳体。并且这两个曲面称为壳面。
距两壳面等距的点形成的曲面成为中间曲
面,简称中面。
壳
表2是常用的壳单元类型和用途。
壳单元名称 SHELL28 SHELL41 SHELL43 SHELL51 SHELL61 SHELL63 SHELL91 SHELL93 SHELL99 SHELL143 SHELL150 SHELL181 说 明 二维剪切/扭转板单元,常用于框架结构中承担剪力载荷 薄模壳单元,用于只有面内刚度没有面外刚度 塑性大变形壳单元,用于线形、翘曲的中厚度壳结构 轴对称结构壳单元,用于轴对称壳结构 轴对称谐波结构壳单元 弹性壳单元,有弯曲和薄膜两种功能,是最常见的壳单元 非线性复合材料壳单元,用于多层结构壳模型或厚的夹层结构 八节点结构壳单元,适用于曲壳结构 线性多层复合材料壳单元,用于多层结构壳模型或厚的夹层结构 塑性壳单元,用于模拟非线性、平之或扭曲的、从薄壳到中厚度的壳结构系统 八节点结构壳P单元,适用于曲面壳体结构 有限应变壳单元,用于分析从薄到中等厚度的壳结构,适用于分析大应变特性 的应用问题
ansys关于薄板、厚板、壳单元的特性区别要点

一、板壳弯曲理论简介1. 板壳分类按板面内特征尺寸与厚度之比划分:当L/h < (5~8) 时为厚板,应采用实体单元。
当(5~8) < L/h < (80~100) 时为薄板,可选2D 实体或壳单元当L/h > (80~100) 时为薄膜,可采用薄膜单元。
壳类结构按曲率半径与壳厚度之比划分:当R/h >= 20 时为薄壳结构,可选择薄壳单元。
当6 < R/h < 20 时为中厚壳结构,选择中厚壳单元。
当R/h <= 6 时为厚壳结构。
上述各式中h 为板壳厚度,L 为平板面内特征尺度,R 为壳体中面的曲率半径。
2. 薄板理论的基本假定薄板所受外力有如下三种情况:①外力为作用于中面内的面内荷载。
弹性力学平面应力问题。
②外力为垂直于中面的侧向荷载。
薄板弯曲问题。
③面内荷载与侧向荷载共同作用。
所谓薄板理论即板的厚度远小于中面的最小尺寸,而挠度又远小于板厚的情况,也称为古典薄板理论。
薄板通常采用Kirchhoff-Love 基本假定:①平行于板中面的各层互不挤压,即σz = 0。
②直法线假定:该假定忽略了剪应力和所引起的剪切变形,且认为板弯曲时沿板厚方向各点的挠度相等。
③中面内各点都无平行于中面的位移。
薄板小挠度理论在板的边界附近、开孔板、复合材料板等情况中,其结果不够精确。
3. 中厚板理论的基本假定考虑横向剪切变形的板理论,一般称为中厚板理论或Reissner(瑞斯纳)理论。
该理论不再采用直法线假定,而是采用直线假定,同时板内各点的挠度不等于中面挠度。
自Reissner 提出考虑横向剪切变形的平板弯曲理论后,又出现了许多精化理论。
但大致分为两类,如Mindlin(明特林)等人的理论和Власов(符拉索夫)等人的理论。
厚板理论是平板弯曲的精确理论,即从3D 弹性力学出发研究弹性曲面的精确表达式。
4. 薄壳理论的基本假定也称为Kirchhoff-Love(克希霍夫-勒夫)假定:①薄壳变形前与中曲面垂直的直线,变形后仍然位于已变形中曲面的垂直线上,且其长度保持不变。
ansys关于薄板、厚板、壳单元的特性区别.

一、板壳弯曲理论简介1. 板壳分类按板面内特征尺寸与厚度之比划分:当L/h < (5~8) 时为厚板,应采用实体单元。
当(5~8) < L/h < (80~100) 时为薄板,可选2D 实体或壳单元当L/h > (80~100) 时为薄膜,可采用薄膜单元。
壳类结构按曲率半径与壳厚度之比划分:当R/h >= 20 时为薄壳结构,可选择薄壳单元。
当6 < R/h < 20 时为中厚壳结构,选择中厚壳单元。
当R/h <= 6 时为厚壳结构。
上述各式中h 为板壳厚度,L 为平板面内特征尺度,R 为壳体中面的曲率半径。
2. 薄板理论的基本假定薄板所受外力有如下三种情况:①外力为作用于中面内的面内荷载。
弹性力学平面应力问题。
②外力为垂直于中面的侧向荷载。
薄板弯曲问题。
③面内荷载与侧向荷载共同作用。
所谓薄板理论即板的厚度远小于中面的最小尺寸,而挠度又远小于板厚的情况,也称为古典薄板理论。
薄板通常采用Kirchhoff-Love 基本假定:①平行于板中面的各层互不挤压,即σz = 0。
②直法线假定:该假定忽略了剪应力和所引起的剪切变形,且认为板弯曲时沿板厚方向各点的挠度相等。
③中面内各点都无平行于中面的位移。
薄板小挠度理论在板的边界附近、开孔板、复合材料板等情况中,其结果不够精确。
3. 中厚板理论的基本假定考虑横向剪切变形的板理论,一般称为中厚板理论或Reissner(瑞斯纳)理论。
该理论不再采用直法线假定,而是采用直线假定,同时板内各点的挠度不等于中面挠度。
自Reissner 提出考虑横向剪切变形的平板弯曲理论后,又出现了许多精化理论。
但大致分为两类,如Mindlin(明特林)等人的理论和Власов(符拉索夫)等人的理论。
厚板理论是平板弯曲的精确理论,即从3D 弹性力学出发研究弹性曲面的精确表达式。
4. 薄壳理论的基本假定也称为Kirchhoff-Love(克希霍夫-勒夫)假定:①薄壳变形前与中曲面垂直的直线,变形后仍然位于已变形中曲面的垂直线上,且其长度保持不变。
ANSYS机械结构设计 第5节-二维薄板平面应力分析
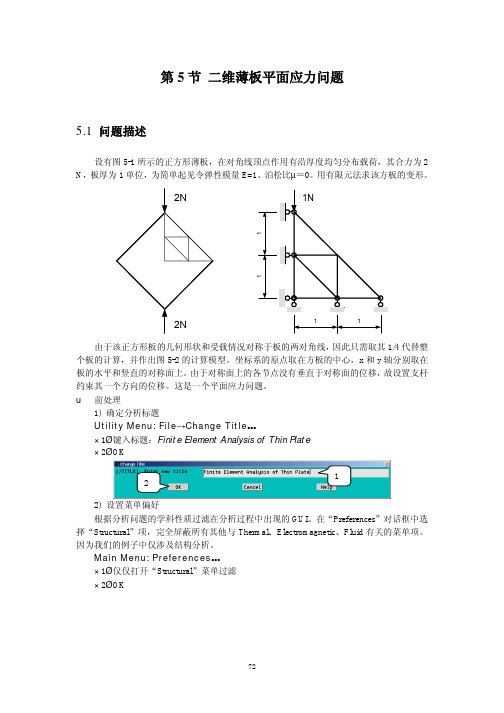
第5节 二维薄板平面应力问题5.1 问题描述设有图5-1所示的正方形薄板,在对角线顶点作用有沿厚度均匀分布载荷,其合力为2 N ,板厚为1单位,为简单起见令弹性模量E=1、泊松比µ=0。
用有限元法求该方板的变形。
由于该正方形板的几何形状和受载情况对称于板的两对角线,因此只需取其1/4代替整个板的计算,并作出图5-2的计算模型。
坐标系的原点取在方板的中心,x 和y 轴分别取在板的水平和竖直的对称面上。
由于对称面上的各节点没有垂直于对称面的位移,故设置支杆约束其一个方向的位移。
这是一个平面应力问题。
u 前处理1) 确定分析标题Utility Menu: File →Change Title …×1Ø键入标题:Finite Element Analysis of Thin Plate ×2ØOK2) 设置菜单偏好根据分析问题的学科性质过滤在分析过程中出现的GUI 。
在“Preferences ”对话框中选择“Structural ”项,完全屏蔽所有其他与Thermal 、Electromagnetic 、Fluid 有关的菜单项。
因为我们的例子中仅涉及结构分析。
Main Menu: Preferences … ×1Ø仅仅打开“Structural ”菜单过滤 ×2ØOK123) 定义单元类型:Main Menu: Preprocessor通过键盘命令直接添加单元类型,在ANSYS 窗口输入下面命令并按回车键。
ET, 1, PLANE42<回车>本例使用ANSYS 提供的PLANE42单元,该单元是ANSYS 早期开发的,已经逐步被淘汰。
如果直接通过图形用户界面(GUI)是不能找到该单元类型的。
执行了上面的命令后,我们可以通过GUI 可以检查其特性。
Main Menu: Preprocessor →Element type →Add/Edit/Delete 可以发现PLANE42单元类型已经存在。
ansys关于薄板、厚板、壳单元的特性区别

一、板壳弯曲理论简介1. 板壳分类按板面内特征尺寸与厚度之比划分:当L/h < (5~8) 时为厚板,应采用实体单元。
当(5~8) < L/h < (80~100) 时为薄板,可选2D 实体或壳单元当L/h > (80~100) 时为薄膜,可采用薄膜单元。
壳类结构按曲率半径与壳厚度之比划分:当R/h >= 20 时为薄壳结构,可选择薄壳单元。
当6 < R/h < 20 时为中厚壳结构,选择中厚壳单元。
当R/h <= 6 时为厚壳结构。
上述各式中h 为板壳厚度,L 为平板面内特征尺度,R 为壳体中面的曲率半径。
2. 薄板理论的基本假定薄板所受外力有如下三种情况:①外力为作用于中面内的面内荷载。
弹性力学平面应力问题。
②外力为垂直于中面的侧向荷载。
薄板弯曲问题。
③面内荷载与侧向荷载共同作用。
所谓薄板理论即板的厚度远小于中面的最小尺寸,而挠度又远小于板厚的情况,也称为古典薄板理论。
薄板通常采用Kirchhoff-Love 基本假定:①平行于板中面的各层互不挤压,即σz = 0。
②直法线假定:该假定忽略了剪应力和所引起的剪切变形,且认为板弯曲时沿板厚方向各点的挠度相等。
③中面内各点都无平行于中面的位移。
薄板小挠度理论在板的边界附近、开孔板、复合材料板等情况中,其结果不够精确。
3. 中厚板理论的基本假定考虑横向剪切变形的板理论,一般称为中厚板理论或Reissner(瑞斯纳)理论。
该理论不再采用直法线假定,而是采用直线假定,同时板内各点的挠度不等于中面挠度。
自Reissner 提出考虑横向剪切变形的平板弯曲理论后,又出现了许多精化理论。
但大致分为两类,如Mindlin(明特林)等人的理论和Власов(符拉索夫)等人的理论。
厚板理论是平板弯曲的精确理论,即从3D 弹性力学出发研究弹性曲面的精确表达式。
4. 薄壳理论的基本假定也称为Kirchhoff-Love(克希霍夫-勒夫)假定:①薄壳变形前与中曲面垂直的直线,变形后仍然位于已变形中曲面的垂直线上,且其长度保持不变。
基于ANSYS的平面板材中心受力分析

得分基于ANSYS的平面板材中心受力分析姓名:学号/序号:班级:基于ANSYS的平面板材中心受力分析摘要平面板材的中心受载荷作用的情况在日常生活和生产中很常见,平面板材在其中心受到载荷作用后,容易变形、损坏。
因此需要对平面板材主要受力及变形部位要给保护。
本文用PROE构建平面板材模型,并导入ANSYS进行形变及应力的分析,对平面板材在承受中心压力或拉力时各点的受力情况进行了研究。
得出了平面板材最大形变量和最大应力所在的点,以及应力、应变的变化规律,从而分析得出平面板材的加强筋应该设置为从中心向四周辐射的纵向,横向加强筋应该是内密外疏的蜘蛛网状才是最有效的。
同时本文还提出了本问题的进一步的研究方向。
关键词:平面板材中心载荷加强筋 PROE ANSYS一、平面板材相关数据本文为不失一般性,采用正十六边形的板材形状,对边的垂直距离为200毫米,厚度为2毫米,载荷作用于其中心直径2毫米的区域,四周的边界受约束。
载荷用1兆帕分析。
二、平面板材建模用PROE三维绘图软件建立平面板材模型,由于厚度方向的值比直径小很多,所以可以看做平面模型。
平面板材模型如图1所示。
图1:平面板材模型三、平面板材有限元模型将建立的平面板材模型导入ANSYS建立有限元模型,如图2所示。
图2:平面板材的有限元模型单元类型:SOLID45材料属性:45钢,EX=210E6MPA ,PRXY=0.3网格划分:自由划分,控制全局单元大小为5mm实体单元数目:40674四、载荷和约束加载平面板材受力一般是在其中心或者中心附近,而约束一般是在周围,本文在平面板材的边缘加约束,在中心加直径2毫米的区域内加载1兆帕,如图3所示。
图3:平面板材约束约束位置:平面板材的周围载荷位置:平面板材的中心直径2毫米区域载荷大小:1兆帕五、分析结果图4:平面板材中心受力的应变图图5:平面板材中心受力的应力图六、结论本文研究时赋予模型材料为45钢,其屈服强度为310MPA,抗拉强度为570MPA。
ansys关于薄板、厚板、壳单元的特性区别

一、板壳弯曲理论简介1. 板壳分类按板面内特征尺寸与厚度之比划分:当L/h < (5~8) 时为厚板,应采用实体单元。
当(5~8) < L/h < (80~100) 时为薄板,可选2D 实体或壳单元当L/h > (80~100) 时为薄膜,可采用薄膜单元。
壳类结构按曲率半径与壳厚度之比划分:当R/h >= 20 时为薄壳结构,可选择薄壳单元。
当6 < R/h < 20 时为中厚壳结构,选择中厚壳单元。
当R/h <= 6 时为厚壳结构。
上述各式中h 为板壳厚度,L 为平板面内特征尺度,R 为壳体中面的曲率半径。
2. 薄板理论的基本假定薄板所受外力有如下三种情况:①外力为作用于中面内的面内荷载。
弹性力学平面应力问题。
②外力为垂直于中面的侧向荷载。
薄板弯曲问题。
③面内荷载与侧向荷载共同作用。
所谓薄板理论即板的厚度远小于中面的最小尺寸,而挠度又远小于板厚的情况,也称为古典薄板理论。
薄板通常采用Kirchhoff-Love 基本假定:①平行于板中面的各层互不挤压,即σz = 0。
②直法线假定:该假定忽略了剪应力和所引起的剪切变形,且认为板弯曲时沿板厚方向各点的挠度相等。
③中面内各点都无平行于中面的位移。
薄板小挠度理论在板的边界附近、开孔板、复合材料板等情况中,其结果不够精确。
3. 中厚板理论的基本假定考虑横向剪切变形的板理论,一般称为中厚板理论或Reissner(瑞斯纳)理论。
该理论不再采用直法线假定,而是采用直线假定,同时板内各点的挠度不等于中面挠度。
自Reissner 提出考虑横向剪切变形的平板弯曲理论后,又出现了许多精化理论。
但大致分为两类,如Mindlin(明特林)等人的理论和Власов(符拉索夫)等人的理论。
厚板理论是平板弯曲的精确理论,即从3D 弹性力学出发研究弹性曲面的精确表达式。
4. 薄壳理论的基本假定也称为Kirchhoff-Love(克希霍夫-勒夫)假定:①薄壳变形前与中曲面垂直的直线,变形后仍然位于已变形中曲面的垂直线上,且其长度保持不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《有限元基础教程》作业二:平面薄板的有限元分析
班级:机自101202班 姓名:韩晓峰 学号:201012030210
一.问题描述:
P P h
1mm R1mm
10m m 10mm
条件:上图所示为一个承受拉伸的正方形板,长度和宽度均为10mm ,厚度为h 为1mm ,中心圆的半径R 为1mm 。
已知材料属性为弹性模量E=1MPa ,泊松比为0.3,拉伸的均布载荷q =
1N/mm 2。
根据平板结构的对称性,只需分析其中的二分之一即可,简化模型如上右图所示。
二.求解过程:
1 进入ANSYS
程序 →ANSYS 10.0→ANSYS Product Launcher →File management →input job name: ZY2→Run
2设置计算类型
ANSYS Main Menu: Preferences →select Structural → OK
3选择单元类型
ANSYS Main Menu: Preprocessor →Element Type →Add/Edit/Delete →Add →select Solid Quad 4node 42 →OK → Options… →select K3: Plane Strs w/thk →OK →Close 4定义材料参数
ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX: 1e6, PRXY:0.3 → OK
5定义实常数以及确定平面问题的厚度
ANSYS Main Menu: Preprocessor →Real Constants …→Add/Edit/Delete →Add →Type 1→OK →Real Constant Set No.1,THK:1→OK →Close
6生成几何模型
a 生成平面方板
ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Rectangle →By 2 Corners →WP X:0,WP Y:0,Width:5,Height:5→OK
b 生成圆孔平面
ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Circle →Solid Circle →WPX=0,WPY=0,RADIUS=1→OK
b 生成带孔板
ANSYS Main Menu: Preprocessor →Modeling →Operate →Booleans → Subtract →Areas →点击area1→OK →点击area2→OK
7 网格划分
ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool →(Size Controls) Global: Set →SIZE: 0.5 →OK →iMesh →Pick All → Close
8 模型施加约束
a 分别给左边施加x和y方向的约束
ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement →On lines →拾取左侧边→OK →select UX,UY→OK
b 给斜边施加x方向均布载荷
Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Lines →拾取右侧边;OK →V ALUE:-10→OK
9 分析计算
ANSYS Main Menu: Solution →Solve →Current LS →OK→Close
10 结果显示
ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape…→select Def + Undeformed →OK→Contour Plot →Nodal Solu…→select: DOF solution, Displacement vector sum, Def + Undeformed , Stress ,von Mises stress, Def + Undeformed→OK
11显示整体效果
Utility Menu→PlotCtrls→Style>Symmetry Expansion>Periodic/Cyclic Symmetry Expansion →1/4Dihedral Sym→OK
10 退出系统
ANSYS Utility Menu: File→Exit…→Save Everything→OK
三.结果分析:
图1 建模、网格划分、加载图图2 变形图
图3 整体应力。
