八下期末易错题练习
数学八年级下册数学期末试卷易错题(Word版含答案)

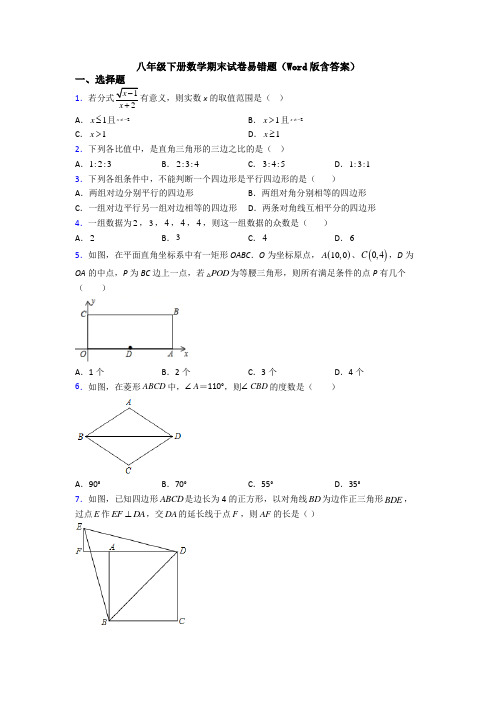
数学八年级下册数学期末试卷易错题(Word 版含答案) 一、选择题1.若分式12x x -+有意义,则实数x 的取值范围是( ) A .1x ≤且2x ≠-B .1x >且2x ≠-C .1x >D .1≥x 2.若ABC 的三边a 、b 、c 满足条件222()()0a b a b c -⋅+-=,则ABC 为( )A .等腰三角形B .直角三角形C .等腰三角形或直角三角形D .等腰直角三角形 3.如图,在△ABC 中,D ,E 分别是AB ,BC 的中点,点F 在DE 延长线上,添加一个条件使四边形ADFC 为平行四边形,则这个条件是( )A .∠B =∠F B .∠B =∠BCFC .AC =CFD .AD =CF 4.为了丰富校园文化,学校艺术节举行初中生书法大赛,设置了10个获奖名额.结果共有21名选手进入决赛,且决赛得分均不相同.若知道某位选手的决赛得分,要判断它是否获奖,只需知道学生决赛得分的( )A .平均数B .中位数C .众数D .方差5.如图,在平面直角坐标系中有一矩形OABC .O 为坐标原点,()10,0A 、()0,4C ,D 为OA 的中点,P 为BC 边上一点,若POD 为等腰三角形,则所有满足条件的点P 有几个( )A .1个B .2个C .3个D .4个6.如图,在三角形纸片ABC 中,∠A =60°,∠B =70°,将纸片的一角折叠,使点C 落在△ABC 外,若∠2=18°,则∠1的度数为( )A .50°B .118°C .100°D .90°7.如图,O 是矩形ABCD 的对角线AC 的中点,M 是AD 的中点,若AB =5,AD =12,则四边形ABOM 的周长为( )A.18 B.20 C.21 D.248.如图①,在矩形ABCD中,AB< AD,对角线AC、BD相交于点O,动点P从点A出发,沿A→B→C→D向点D运动.设点P的运动路程为x,ΔAOP的面积为y,y与x的函数关系图象如图②所示,则下列结论错误的是()A.四边形ABCD的面积为12 B.AD边的长为4C.当x=2.5时,△AOP是等边三角形D.ΔAOP的面积为3时,x的值为3或10二、填空题9.若2336=-+-+,则xy的平方根为________.y x x10.已知菱形ABCD的对角线AC,BD的长分别为6和8,则该菱形面积是_______.b=,则c=__________.11.直角三角形的三边长分别为a、b、c,若3a=,412.如图,在矩形ABCD中,点E在AD上,且EC平分BED∠,若1AB=,∠=︒,则DE的长为__________.EBC4513.已知一次函数y=kx﹣b,当自变量x的取值范围是1≤x≤3时,对应的因变量y的取值范围是5≤y≤10,那么k﹣b的值为_______.14.如图中,四边形ABCD是对角线互相垂直的四边形,且OB=OD,若使四边形ABCD为菱形,则需添加的条件是______.(只需添加一个条件即可)15.如图,在平面直角坐标系中,直线y =﹣x +2与x 轴交于点A ,与y 轴交于点B ,点P 是线段AB 的三等分点(AP >BP ),点C 是x 轴上的一个动点,连接BC ,以BC 为直角边,点B 为直角顶点作等腰直角△BCD ,连接DP .则DP 长度的最小值是___.16.如图,正方形ABCD 和正方形EFCG 的边长分别为3和1,点F 、G 分别在边,BC CD 上,P 为AE 的中点,连接PG ,则PG 的长为 _________ .三、解答题17.(123317(2)21148--- (2)1(615)3252 (3148312242 (4205112(31)(31)35+ 18.由于大风,山坡上的一颗甲树从A 点处被拦腰折断,其顶点恰好落在一棵树乙的底部C 处,如图所示,已知AB =4米,BC =13米,两棵树的水平距离是12米,求甲树原来的高度.19.如图,每个小正方形的边长都是1.A、B、C、D均在网格的格点上.(1)求边BC、BD的长度.(2)∠BCD是直角吗?请证明你的判断.(3)找到格点E,画出四边形ABED,使其面积与四边形ABCD面积相等(一个即可,且E与C不重合).20.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点M为AD的中点,过点M作//MN BD交CD延长线于点N.(1)求证:四边形MNDO是平行四边形;(2)请直接写出当四边形ABCD的边AB与BD满足什么关系时,四边形MNDO分别是菱形、矩形、正方形.21.先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性22232232121(2)212(12)+=+⨯⨯++⨯⨯+|12|=12解决问题:①146514235+=+⨯⨯_________________=________________=_________________②根据上述思路,试将下列各式化简:28103-3 12 +22.黄埔区某游泳馆推出以下两种收费方式.方式一:顾客不购买会员卡,每次游泳付费40元.方式二:顾客先购买会员卡,每张会员卡800元,仅限本人一年内使用,凭卡游泳,每次游泳再付费20元.设你在一年内来此游泳馆游泳的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y 2(元).(1)请分别写出y 1,y 2与x 之间的函数表达式;(2)如果你在一年内来此游泳馆游泳的次数超过60次,为省钱,你选择哪种方式? 23.如图,在▱ABCD 中,连接BD ,AB BD ⊥,且AB BD =,E 为线段BC 上一点,连接AE 交BD 于F .(1)如图1,若22AB =,BE =1,求AE 的长度;(2)如图2,过D 作DH ⊥AE 于H ,过H 作HG ⊥AD 交AD 于G ,交BD 于M ,过M 作MN ∥AD 交AE 于N ,连接BN ,证明:2NH BN =;(3)如图3,点E 在线段BC 上运动时,过D 作DH ⊥AE 于H ,延长DH 至Q ,使得12QH AH =,M 为AD 的中点,连接QM ,若42AD =,当QM 取最大值时,请直接写出△ADH 的面积.24.如图,在平面直角坐标系xOy 中,直线y =﹣2x +6交x 轴于点A ,交轴于点B ,过点B 的直线交x 轴负半轴于点C ,且AB =BC .(1)求点C 的坐标及直线BC 的函数表达式;(2)点D (a ,2)在直线AB 上,点E 为y 轴上一动点,连接DE .①若∠BDE =45°,求BDE 的面积;②在点E 的运动过程中,以DE 为边作正方形DEGF ,当点F 落在直线BC 上时,求满足条件的点E 的坐标.25.如图,已知平面直角坐标系中,1,0A 、()0,2C ,现将线段CA 绕A 点顺时针旋转90︒得到点B ,连接AB .(1)求出直线BC 的解析式;(2)若动点M 从点C 出发,沿线段CB 10,过M 作//MN AB 交y 轴于N ,连接AN .设运动时间为t 分钟,当四边形ABMN 为平行四边形时,求t 的值.(3)P 为直线BC 上一点,在坐标平面内是否存在一点Q ,使得以O 、B 、P 、Q 为顶点的四边形为菱形,若存在,求出此时Q 的坐标;若不存在,请说明理由.【参考答案】一、选择题1.D解析:D【分析】根据分式有意义,分母不为0,二次根式的被开方数是非负数列式解答即可.【详解】解:由题意得,10x -≥,且20x +≠,∴实数x 的取值范围是1≥x ,故选:D .【点睛】本题考查的是分式有意义和二次根式有意义的条件,掌握分式有意义,分母不为0,二次根式的被开方数是非负数是解题的关键.2.C解析:C【详解】解析:∵222()()0a b a b c -+-=,∴a b =或222+=a b c .当只有a b =成立时,是等腰三角形.当只有222+=a b c 成立时,是直角三角形.当a b =,222+=a b c 同时成立时,是等腰直角三角形.答案:C题型解法:此类题型首先根据题意化简式子,找出隐含条件,然后根据三边的关系判断三角形的形状.当三角形的三边满足勾股定理时,即可判断为直角三角形.3.B解析:B【解析】【分析】根据已知条件可以得到//AC DE ,对选项判断即可求出解.【详解】解:∵D ,E 分别是AB ,BC 的中点∴//AC DE ,12DE AC A :根据∠B =∠F 得不出四边形ADFC 为平行四边形,选项不符合题意;B :∠B =∠BCF ,∴CF//AD ,∴四边形ADFC 为平行四边形,选项符合题意; C :根据AC =CF 得不出四边形ADFC 为平行四边形,选项不符合题意;D :根据AD =CF 得不出四边形ADFC 为平行四边形,选项不符合题意;故答案为B .【点睛】此题考查了中位线的性质以及平行四边形的判定,熟练掌握有关性质即判定方法是解题的关键.4.B解析:B【解析】【分析】由于书法大赛设置了10个获奖名额,共有21名选手进入决赛,根据中位数的意义分析即可.【详解】解:将21名选手进入决赛不同的分数按从小到大排序后,中位数及中位数之后的共有11个数,故只要知道自己的分数和中位数就可以知道是否获奖了,故选B .【点睛】本题主要考查中位数,以及相关平均数、众数、方差的意义,熟练掌握相关知识是解题的关键.5.D解析:D【分析】由矩形的性质得出∠OCB =90°,OC =4,BC =OA =10,求出OD =AD =5,分情况讨论:①当PO =PD 时;②当OP =OD 时;③当DP =DO 时;根据线段垂直平分线的性质或勾股定理即可求出点P 的坐标.【详解】解:∵四边形OABC 是矩形,∴∠OCB =90°,OC =4,BC =OA =10,∵D 为OA 的中点,∴OD =AD =5,①当PO =PD 时,点P 在OD 得垂直平分线上,∴点P的坐标为:(2.5,4);②当OP=OD时,如图1所示:则OP=OD=5,2253PC=-∴点P的坐标为:(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,22DE=-=;543分两种情况:当E在D的左侧时,如图2所示:OE=5-3=2,∴点P的坐标为:(2,4);当E在D的右侧时,如图3所示:OE=5+3=8,∴点P的坐标为:(8,4);综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);故选:D【点睛】本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.6.B解析:B【解析】【分析】在△ABC中利用三角形内角和定理可求出∠C的度数,由折叠的性质,可知:∠CDE=∠C′DE,∠CED=∠C′ED,结合∠2的度数可求出∠CED的度数,在△CDE中利用三角形内角和定理可求出∠CDE 的度数,再由∠1=180°﹣∠CDE ﹣∠C ′DE 即可求出结论.【详解】解:在△ABC 中,∠A =60°,∠B =70°,∴∠C =180°﹣∠A ﹣∠B =50°.由折叠,可知:∠CDE =∠C′DE ,∠CED =∠C′ED ,∴∠CED =18022︒+∠=99°, ∴∠CDE =180°﹣∠CED ﹣∠C =31°,∴∠1=180°﹣∠CDE ﹣∠C′DE =180°﹣2∠CDE =118°.故选:B .【点睛】本题考查了三角形内角和定理以及折叠的性质,利用三角形内角和定理及折叠的性质求出∠CDE 的度数是解题的关键.7.B解析:B【解析】【分析】根据中位线的性质求得OM ,再根据直角三角形的性质求得OB ,即可求解.【详解】解:在矩形ABCD 中,5AB CD ==,90ABC ∠=︒由勾股定理得13AC∵O 是AC 的中点,M 是AD 的中点∴OM 为ACD △的中位线,162AM AD ==,11322BO AC == ∴1522OM CD == 四边形ABOM 的周长为135562022AB BO OM AM =+++=+++= 故选B【点睛】 此题考查矩形的性质,勾股定理,中位线的性质以及直角三角形的性质,熟练掌握相关基本性质是解题的关键.8.C解析:C【分析】过点P 作PE ⊥AC 于点E ,根据ΔAOP 的边OA 是一个定值,OA 边上的高PE 最大时是点P 分别与点B 和点D 重合,因此根据这个规律可以对各个选项作出判断.【详解】A 、过点P 作PE ⊥AC 于点E ,当点P 在AB 和BC 边上运动时,PE 逐渐增大,到点B 时最大,然后又逐渐减小,到点C时为0,而y=12OA PE中,OA为定值,所以y是先增大后减小,在B点时面积最大,在C点时面积最小;观察图②知,当点P与点B重合时,ΔAOP 的的面积为3,此时矩形的面积为:4×3=12,故选项A正确;B、观察图②知,当运动路程为7时,y的值为0,此时点P与点C重合,所以有AB+BC=7,又AB∙BC=12,解得:AB=3,BC=4,或AB=4,BC=3,但AB<BC,所以AB=3,BC=4,根据四边形ABCD为矩形,所以AD=4,故选项B正确;C、当x=2.5时,即x<3,点P在边AB上由勾股定理,矩形的对角线为5,则OA=2.5,所以OA=AP,△AOP是等腰三角形,但△ABC是三边分别为3,4,5的直角三角形,故∠BAC不可能为60°,从而△AOP不是等边三角形,故选项C错误;D、当点P在AB和BC边上运动时,点P与点B重合时最大面积为3,此时x的值为3;当点P在边CD和DA上运动时,PE逐渐增大,到点D时最大,然后又逐渐减小,到点A时为0,而y=12OA PE也是先增大再减小,在D点时面积最大,在A点时面积最小;所以当点P与点D重合时,最大面积为3,此时点P运动的路程为AB+BC+CD=10,即x=10,所以当x=3或10时,ΔAOP的面积为3,故选项D正确.故选:C.【点睛】本题是动点问题的函数图象,考查了函数的图象、图形的面积、矩形的性质、解方程等知识,关键是确定点P到AC的距离的变化规律,从而可确定y的变化规律,同时善于从函数图象中抓住有用的信息,获得问题的突破口.二、填空题9.2【解析】【分析】根据二次根式有意义的条件求出x,进而求出y,根据平方根的概念解答即可.【详解】3x 有意义,则x-3≥0,同理,3-x≥0,解得,x=3,则y=6,∴xy=18,∵18的平方根是∴xy的平方根为故答案为:【点睛】本题考查的是二次根式有意义的条件,掌握二次根式的被开方数是非负数是解题的关键.10.24【解析】【详解】解:根据菱形的面积等于菱形两条对角线乘积的一半可得菱形面积为16824 2⨯⨯=故答案为:24.115【解析】【分析】根据斜边分类讨论,然后利用勾股定理分别求出c的值即可.【详解】解:①若b是斜边长根据勾股定理可得:c==②若c是斜边长根据勾股定理可得:5c综上所述:c=55【点睛】此题考查的是勾股定理,掌握用勾股定理解直角三角形和分类讨论的数学思想是解决此题的关键.12.D1【分析】由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC,求得AE=AB=1,然后依据勾股定理可求得BC的长;【详解】解:∵四边形ABCD是矩形,∴AD∥BC,∴∠DEC=∠BCE,∵EC平分∠DEB,∴∠DEC=∠BEC,∴∠BEC=∠ECB,∴BE=BC,∵四边形ABCD是矩形,=∴∠A=90°,AD BC∵∠ABE=45°,∴∠ABE=∠AEB=45°,∴AB=AE=1,由勾股定理得:BE==,∴BC=AD=BE,∴=-,1DE AD AE1.【点睛】本题考查了矩形的性质,等腰三角形的性质与判定,勾股定理的应用;熟练掌握矩形的性质,证出BE=BC是解题的关键.13.5或10【分析】本题分情况讨论①k>0时,x=1时对应y=5;②k>0时,x=1时对应y=10.【详解】解:①k>0时,由题意得:x=1时,y=5,∴k-b=5;②k<0时,由题意得:x=1时,y=10,∴k-b=10;综上,k-b的值为5或10.故答案为:5或10.【点睛】本题考查了待定系数法求函数解析式,注意本题需分两种情况,不要漏解.14.A解析:OA OC=【分析】根据菱形的判定即可得出答案.【详解】=,∵四边形ABCD是对角线互相垂直的四边形,且OB=OD,OA OC∴四边形ABCD是菱形,=.故答案为:OA OC【点睛】本题主要考查菱形的判定,掌握菱形的判定方法是解题的关键.15.【分析】过点B作BM⊥轴于点B,使BM=OB,利用SAS证得△BOC△BMD,再证明M、D、A三点共线,推出四边形AMBO是正方形,当且仅当PD⊥AM时,线段DP的长度取得最小值,利用勾股定理即解析:43【分析】过点B 作BM ⊥y 轴于点B ,使BM =OB ,利用SAS 证得△BOC ≅△BMD ,再证明M 、D 、A 三点共线,推出四边形AMBO 是正方形,当且仅当PD ⊥AM 时,线段DP 的长度取得最小值,利用勾股定理即可求解.【详解】解:过点B 作BM ⊥y 轴于点B ,使BM =OB ,连接DM ,AD ,∵直线y =﹣x +2与x 轴交于点A ,与y 轴交于点B ,∴令0y =,则2x =;令0x =,则2y =;∴点A 的坐标为(2,0),点B 的坐标为(0,2),∴OA =OB =BM =2,∵BM ⊥y 轴,∴∠OBM =90°,∴点M 的坐标为(2,2),∵△BCD 是等腰直角三角形,∴BC =BD ,∠CBD =90°,∴∠CBD =∠OBM =90°,∴∠CBD -∠OBD =∠OBM -∠OBD ,∴∠CBO =∠DBM ,在△BOC 和△BMD ,BC BD CBO DBM OB MB =⎧⎪∠=∠⎨⎪=⎩, ∴△BOC ≅△BMD (SAS ),∴∠BOC =∠BMD =90°,∴BM ⊥DM ,∴DM ∥OB ,∵M 、D 、A 三点的横坐标相同,都为2,∴M 、D 、A 三点共线,∴四边形AMBO 是正方形,∴∠BAM=45°,∵AB=2222OB OA+=,点P是线段AB的三等分点(AP>BP),∴AP=23AB=423,当且当PD⊥AM时,线段DP的长度取得最小值,此时,△PAD为等腰直角三角形,∴PD=22AP=43,∴线段DP长度最小值为43,故答案为:43.【点睛】本题考查了一次函数的的图象与坐标轴的交点问题,正方形的判定和性质,等腰直角三角形的判定和性质,全等三角形的判定和性质等知识点,证得四边形AMBO是正方形,以及当PD⊥AM时,线段DP的长度取得最小值是解题的关键.16..【详解】试题分析:连接AC,根据正方形的性质可得A、E、C三点共线,连接FG交AC 于点M,因正方形和正方形的边长分别为3和1,根据勾股定理可求得EC=FG=,AC=3,即可得AE=2,因为的中解析:.【详解】试题分析:连接AC,根据正方形的性质可得A、E、C三点共线,连接FG交AC于点M,因正方形和正方形的边长分别为3和1,根据勾股定理可求得EC=FG=,AC=3,即可得AE=2,因为的中点,可得PE=AP=,再由正方形的性质可得GM=EM= ,FG垂直于AC,在Rt△PGM中,PM= ,由勾股定理即可求得PG=.三、解答题17.(1)1;(2);(3);(4).【分析】(1)直接利用二次根式的性质以及立方根的性质分别化简,再利用有理数的加减运算法则计算得出答案;(2)直接利用二次根式的乘法运算法则以及结合绝对值的性质解析:(1)1;(2)2-;(3)44)3.【分析】(1)直接利用二次根式的性质以及立方根的性质分别化简,再利用有理数的加减运算法则计算得出答案;(2)直接利用二次根式的乘法运算法则以及结合绝对值的性质化简,先算乘法,再化简二次根式,去绝对值,最后利用二次根式的加减运算法则计算得出答案;(3)直接利用二次根式的乘除运算法则化简,先算乘除,再利用二次根式的加减运算法则计算得出答案;(4)直接利用二次根式的乘法运算法则化简,先算乘除,再利用有理数的加减运算法则计算得出答案.【详解】解:(13=-21231=--+2122=1;(2)2=62=2=2-;(3==4=4(41)1205112313=÷+-⨯+- 21231=+-+-3=.【点睛】本题主要考查了二次根式的混合运算以及实数运算,正确化简二次根式是解题关键. 18.19米【分析】如图所示,过点C 作CD ⊥AB 交AB 延长线于D ,则根据题意可以得到CD=12米,根据勾股定理即可求出BD 的长,再利用勾股定理求出AC 的长即可得到AC+AB 的长.【详解】解:如图所解析:19米【分析】如图所示,过点C 作CD ⊥AB 交AB 延长线于D ,则根据题意可以得到CD =12米,根据勾股定理即可求出BD 的长,再利用勾股定理求出AC 的长即可得到AC +AB 的长.【详解】解:如图所示,过点C 作CD ⊥AB 交AB 延长线于D由题意得:CD =12,AB =4米,BC =13米在Rt △BCD 中222213125BD BC CD =-=-=米∴9AD AB BD =+=米在Rt △ACD 中222212915AC CD AD =+=+=米∴19AC AB +=米∴甲树原来的高度是19米.【点睛】本题主要考查了勾股定理的应用,解题的关键在于能够熟练掌握勾股定理.19.(1),;(2)不是直角,证明见解析;(3)见解析【解析】【分析】(1)利用勾股定理求解即可.(2)利用勾股定理的逆定理判断即可.(3)利用等高模型解决问题即可.【详解】解:(1)BC解析:(1)29,42;(2)不是直角,证明见解析;(3)见解析【解析】【分析】(1)利用勾股定理求解即可.(2)利用勾股定理的逆定理判断即可.(3)利用等高模型解决问题即可.【详解】解:(1)BC=2225+=29,BD=2244+=42.(2)结论:不是直角.理由:∵CD=5,BC=29,BD=42,∴BC2+CD2≠BD2,∴∠BCD≠90°.(3)如图,四边形ABED即为所求.【点睛】本题考查作图-应用与设计作图,勾股定理,勾股定理的逆定理,四边形的面积等知识,解题的关键是掌握勾股定理以及勾股定理的逆定理解决问题,属于中考常考题型.20.(1)见解析;(2)时,四边形MNDO是菱形;当时,四边形MNDO是矩形;当且时,四边形MNDO是正方形【分析】(1)利用平行四边形的性质及三角形中位线的性质,可得,再加已知条件,利用平行四边形解析:(1)见解析;(2)AB BD=时,四边形MNDO是菱形;当AB BD⊥时,四边形MNDO是矩形;当AB BD=且AB BD⊥时,四边形MNDO是正方形【分析】(1)利用平行四边形的性质及三角形中位线的性质,可得//OM CD,再加已知条件//MN BD,利用平行四边形的判定定理(有两组对边分别平行的四边形是平行四边形)即可证明;(2)①根据(1)中平行四边形的性质及三角形中位线的性质可得:12OM AB=,12MN BD =,当AB BD =时,OM MN =,利用菱形的判定定理(有一组邻边相等的平行四边形是菱形);②根据(1)中平行四边形的性质可得://OM AB ,//MN BD ,当AB BD ⊥时,OM MN ⊥,根据矩形的判定定理(有一个角是直角的平行四边形是矩形)即可证明; ③根据(1)中平行四边形的性质及三角形中位线的性质可得::12OM AB =,12MN BD =,且//OM AB ,//MN BD ,当AB BD =且AB BD ⊥时,OM MN =且OM MN ⊥,根据正方形的判定定理(一组邻边相等、有一个角是直角的平行四边形是正方形)即可证明.【详解】解:(1)证明:∵ABCD 对角线AC 、BD 交于点O ,∴OA OC =,又∵M 为AD 中点,∴//OM CD ,又∵//MN BD ,∴四边形MNDO 是平行四边形;(2)①当AB BD =时,四边形MNDO 是菱形,证明:根据(1)可得,四边形MNDO 是平行四边形,且12OM AB =,12MN BD =, 又∵AB BD =,∴OM MN =,∴四边形MNDO 是菱形;②当AB BD ⊥时,四边形MNDO 是矩形,证明:根据(1)可得,四边形MNDO 是平行四边形,且//OM AB ,//MN BD , 又∵AB BD ⊥,∴OM MN ⊥,∴四边形MNDO 是矩形;③当AB BD =且AB BD ⊥时,四边形MNDO 是正方形,证明:根据(1)可得,四边形MNDO 是平行四边形及三角形中位线的性质可得:12OM AB =,12MN BD =,且//OM AB ,//MN BD , 又∵AB BD =且AB BD ⊥,∴OM MN =且OM MN ⊥,∴四边形MNDO 是正方形.【点睛】题目主要考查平行四边形、菱形、矩形及正方形的判定定理,熟练运用特殊四边形的判定定理是解题关键.21.①,,3+;②(1)5-;(2) .【解析】【分析】①模仿阅读材料的方法将原式变形,计算即可得到结果;②仿照以上方法将各式化简即可.【详解】①===3+,故答案为,,3+;②(1)解析:3+②(1)5(2) 12 【解析】【分析】①模仿阅读材料的方法将原式变形,计算即可得到结果;②仿照以上方法将各式化简即可.【详解】3+3=5=12+=12. 【点睛】本题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.22.(1)y1=40x ,y2=20x+800;(2)在一年内来此游泳馆游泳的次数超过60次,为省钱,应选择方式二【分析】(1)根据题意可以写出y1,y2与x 之间的函数表达式;(2)将x=15代入(解析:(1)y 1=40x ,y 2=20x +800;(2)在一年内来此游泳馆游泳的次数超过60次,为省钱,应选择方式二【分析】(1)根据题意可以写出y 1,y 2与x 之间的函数表达式;(2)将x =15代入(1)中函数关系式,求出相应的函数值,然后比较大小即可解答本题.【详解】解:(1)当游泳次数为x 时,方式一费用为:y 1=40x ,方式二的费用为:y 2=20x +800;(2)若一年内来此游泳馆游泳的次数为60次,方式一的费用为:y 1=40×60=2400(元),方式二的费用为:y 2=20×60+800=2000(元),∵2400>2000,∴在一年内来此游泳馆游泳的次数超过60次,为省钱,应选择方式二.【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,求出y 1,y 2与x 之间的函数表达式,利用一次函数的性质解答.23.(1)见解析;(2)见解析;(3).【分析】(1)分别过点作,垂足分别为,勾股定理解即可;(2)连接,过点作于点,设,经过角度的变换得出,再证明,得出,,结合已知条件,继而证,得出,,进而得到解析:(1)见解析;(2)见解析;(3 【分析】(1)分别过点,B E 作,BS AD ER AD ⊥⊥,垂足分别为,S R ,勾股定理解Rt ARE △即可; (2)连接BH ,过点N 作NT AD ⊥于点T ,设BAN α∠=,经过角度的变换得出BAN HDB ∠=∠,再证明ATN △≌HGD △,得出,AN HD =,结合已知条件,继而证BAN ≌BDH △,得出ABN DBH ∠=∠,NB HB =,进而得到NBH △是等腰直角三角形,从而得证;(3)分别作,AD AQ 的中垂线,交于点O ,根据作图,先判断MQ 最大的时候的位置, 进而由12QH AH =,42AD =,构造直角三角形,勾股定理求得,AH HD ,从而求得△ADH 的面积 .【详解】(1)如图,分别过点,B E 作,BS AD ER AD ⊥⊥,垂足分别为,S RAB BD ⊥,AB BD =,22AB =ABD ∴是等腰直角三角形,ASB △是等腰直角三角形224AD AB BD ∴=+=∴122AS SD AD ===,2BS AS == 四边形ABCD 是平行四边形//AD BC ∴,BS AD ER AD ⊥⊥,1BE =∴四边形SBER 是矩形∴SR BE =1=,2RE SB ==3AR AS SR ∴=+=在Rt ARE △中22223213AE AR RE =+=+=(2)连接BH ,过点N 作NT AD ⊥于点T ,设BAN α∠=BAD 是等腰直角三角形45BAD BDA∴∠=∠=︒45 HAD BAD BANα∴∠=∠-∠=︒-DH AE⊥,9045ADH HADα∴∠=︒-∠=︒+4545HDB ADH ADBαα∴∠=∠-∠=︒+-︒= BAN HDB∴∠=∠NT AD⊥9090(45)45 ANT HADαα∴∠=︒-∠=︒-︒-=︒+,90ATN∠=︒ANT ADH HDG∴∠=∠=∠HG AD⊥90HGD∴∠=︒ATN HGD∴∠=∠又45BDA∠=︒9045DMG MDG∴∠=︒-∠=︒GD GM∴=//MN AD,HG AD⊥,NT AD⊥∴四边形TNMG是矩形GM TN∴=TN GD∴=在ATN△和HGD△中ANT HDGTN GDATN HGD∠=∠⎧⎪=⎨⎪∠=∠⎩∴ATN△≌HGD△(ASA)AN HD∴=在BAN和BDH△中AB BDBAN HDBAN HD=⎧⎪∠=∠⎨⎪=⎩∴BAN≌BDH△(SAS)ABN DBH∴∠=∠,NB HB=ABN NBD DBH NBD∠+∠=∠+∠即ABD NBH∠=∠AB BD⊥90ABD∴∠=︒90NBH∴∠=︒NBH∴△是等腰直角三角形∴NH=即NH=(3)分别作,AD AQ 的中垂线,交于点O ,由题意,当点E 在线段BC 上运动时,AQD ∠不变,AD 的长度不变,则,,A D Q 三点共圆,则点Q 在以O 为圆心OQ 为半径的圆上运动,DH AE ⊥,12QH AH =tan 2AH AQD QH∴∠== 在OMQ 中MQ MO OQ ≤+∴当,,M O Q 三点共线时,MQ 取得最大值,此时情形如图:,AB BD BM AD =⊥∴AM MD =,,M O Q 三点共线,∴点Q 在AB 的垂直平分线上QA QD ∴=DH AE ⊥,tan 2AH AQDQH∠== 设QH x =,则AH 2x =AQ ∴=QD =DH x ∴=-AD =222AH DH AD ∴+=即222(2))x x +-= 得:2x =△ADH 的面积12AH DH =⋅12)2x x =⨯⋅-21)x =1)=∴当QM 取最大值时,△ADH 【点睛】本题考查了平行四边形的性质,矩形的性质与判定,等腰三角形的性质,垂直平分线的性质,圆的性质,勾股定理,三角形三边关系,三角形全等的证明与性质,动点问题等,本题是一道综合性比较强的题,熟练平面几何的性质定理是解题的关键.24.(1)C(-3,0),y =2x+6;(2)①;②(0,7)或(0,-1)【解析】【分析】(1)利用等腰三角形的三线合一的性质求出点C 的坐标,再利用待定系数法求解即可. (2)①如图,取点Q(-解析:(1)C (-3,0),y =2x +6;(2)①103;②(0,7)或(0,-1) 【解析】【分析】(1)利用等腰三角形的三线合一的性质求出点C 的坐标,再利用待定系数法求解即可. (2)①如图,取点Q (-1,3),连接BQ ,DQ ,DQ 交AB 于E .证明△QDB 是等腰直角三角形,求出直线QD 的解析式即可解决问题.②分两种情形:点F 落在直线BC 上,点F′落在直线BC 上,分别求解即可.【详解】解:(1)∵直线y =﹣2x +6交x 轴于点A ,交轴于点B ,∴A (3,0),B (0,6),∴OA =3,OB =6,∵A B =BC ,OB ⊥AC ,∴OC =OA =3,∴C (-3,0),设直线BC 的解析式为y =kx +b ,则有630b k b =⎧⎨-+=⎩, 解得26k b =⎧⎨=⎩, ∴直线BC 的解析式为y =2x +6.(2)①如图,取点Q (-1,3),连接BQ ,DQ ,DQ 交AB 于E .∵D (a ,2)在直线y =﹣2x +6上,∴2=﹣2a+6,∴a =2,∴D (2,2),∵B (0,6), ∴221310QB +221310QD +,222425BD +=∴BD 2=QB 2+QD 2,QB =QD ,∴∠BQD =90°,∠BDQ =45°,∵直线DQ 的解析式为1833y x =-+, ∴E (0,83), ∴OE =83,BE =6﹣83=103, ∴110102233BDE S =⨯⨯=. ②如图,过点D 作DM ⊥OA 于M ,DN ⊥OB 于N .∵四边形DEGF是正方形,∴∠EDF=90°,ED=DF,∵∠EDF=∠MDN=90°,∴∠EDN=∠DFM,∵DE=DF,DN=DM,∴△DNE≌△DMF(SAS),∴∠DNE=∠DMF=90°,EN=FM,∴点F在x轴上,∴当点F与C重合时,FM=NE=5,此时E(0,7),同法可证,点F′在直线y=4上运动,当点F′落在BC上时,E(0,﹣1),综上所述,满足条件的点E的坐标为(0,7)或(0,﹣1).【点睛】本题属于一次函数综合题,考查了一次函数的性质,等腰三角形的性质,正方形的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于压轴题.25.(1);(2)t=s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:或或或.【分析】(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2解析:(1)123y x=-+;(2)t=23s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:618,55⎛⎫⎪⎝⎭或(3,1)-或(3,1)-或155,88⎛⎫-⎪⎝⎭.【分析】(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2,求出点B坐标,再利用待定系数法即可解决问题.(2)利用平行四边形的性质求出点N的坐标,再求出AN,BM,CM即可解决问题.(3)如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,分别求解即可解决问题.【详解】(1)如图1中,作BH ⊥x 轴于H .∵A (1,0)、C (0,2),∴OA=1,OC=2,∵∠COA=∠CAB=∠AHB=90°,∴∠ACO+∠OAC=90°,∠CAO+∠BAH=90°,∴∠ACO=∠BAH ,∵AC=AB ,∴△COA ≌△AHB (AAS ),∴BH=OA=1,AH=OC=2,∴OH=3,∴B (3,1),设直线BC 的解析式为y=kx+b ,则有231b k b =⎧⎨+=⎩, 解得:132k b ⎧=-⎪⎨⎪=⎩, ∴123y x =-+; (2)如图2中,∵四边形ABMN 是平行四边形,∴AN ∥BM ,∴直线AN 的解析式为:1133y x =-+, ∴10,3N ⎛⎫ ⎪⎝⎭,∴103BM AN ==, ∵B (3,1),C (0,2),∴BC=10,∴2103CM BC BM =-=, ∴21021033t =÷=, ∴t=23s 时,四边形ABMN 是平行四边形; (3)如图3中,如图3中,当OB 为菱形的边时,可得菱形OBQP ,菱形OBP 1Q 1.菱形OBP 3Q 3, 连接OQ 交BC 于E ,∵OE ⊥BC ,∴直线OE 的解析式为y=3x ,由3123y x y x =⎧⎪⎨=-+⎪⎩,解得:3595x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴E (35,95), ∵OE=OQ ,∴Q (65,185), ∵OQ 1∥BC ,∴直线OQ 1的解析式为y=-13x , ∵OQ 110,设Q 1(m ,-1m 3), ∴m 2+19m 2=10, ∴m=±3,可得Q1(3,-1),Q3(-3,1),当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,易知线段OB的垂直平分线的解析式为y=-3x+5,由3513y xy x=-+⎧⎪⎨=-⎪⎩,解得:15858xy⎧=⎪⎪⎨⎪=-⎪⎩,∴Q2(158,58-).综上所述,满足条件的点Q坐标为:618,55⎛⎫⎪⎝⎭或(3,1)-或(3,1)-或155,88⎛⎫-⎪⎝⎭.【点睛】本题属于一次函数综合题,考查了平行四边形的判定和性质,菱形的判定和性质,一次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.。
八年级下册数学期末试卷易错题(Word版含答案)
八年级下册数学期末试卷易错题(Word 版含答案) 一、选择题1.若分式12x x -+有意义,则实数x 的取值范围是( ) A .1x ≤且2x ≠-B .1x >且2x ≠-C .1x >D .1≥x 2.下列各比值中,是直角三角形的三边之比的是( ) A .1:2:3 B .2:3:4 C .3:4:5 D .1:3:1 3.下列各组条件中,不能判断一个四边形是平行四边形的是( )A .两组对边分别平行的四边形B .两组对角分别相等的四边形C .一组对边平行另一组对边相等的四边形D .两条对角线互相平分的四边形 4.一组数据为2,3,4,4,4,则这一组数据的众数是( )A .2B .3C .4D .6 5.如图,在平面直角坐标系中有一矩形OABC .O 为坐标原点,()10,0A 、()0,4C ,D 为OA 的中点,P 为BC 边上一点,若POD 为等腰三角形,则所有满足条件的点P 有几个( )A .1个B .2个C .3个D .4个6.如图,在菱形ABCD 中,∠A =110°,则∠CBD 的度数是( )A .90°B .70°C .55°D .35°7.如图,已知四边形ABCD 是边长为4的正方形,以对角线BD 为边作正三角形BDE ,过点E 作EF DA ⊥,交DA 的延长线于点F ,则AF 的长是( )A .232-B .222-C .31-D .438.两人在直线跑道上同起点、同终点、同方向匀速跑步400米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人之间的距离y (米)与乙出发的时间t (秒)之间的关系如图所示给出以下结论:①8a =;②72b =;③98c =.其中正确的是( )A .②③B .①②③C .①②D .①③二、填空题9.要使代数式1x x+有意义,则x 的取值范围是___________. 10.如图,菱形ABCD 中,DB 为对角线,5AB =,6DB =,点E 为边AB 上一点,则阴影部分的面积为______.11.一条直角边3,斜边长为5的直角三角的面积为_________.12.如图,矩形ABCD 的对角线AC ,BD 交于点O ,6AB =,8BC =,过点O 作OE AC ⊥,交AD 于点E ,过点E 作EF BD ⊥,垂足为F .则OE EF +的值为______.13.若直线y =kx +b (k ≠0)经过点A (0,3),且与直线y =mx ﹣m (m ≠0)始终交于同一点(1,0),则k 的值为________.14.如图,四边形ABCD 对角线AC ,BD 交于点O . AC BD ⊥,OB OD =,请你添加一个适当的条件 ______ ,使四边形ABCD 是菱形(只填一种情况即可).15.已知直线333y x =+与x 轴,y 轴分别交于点A ,B ,点C 是射线AB 上的动点,点D 在第一象限,四边形OACD 是平行四边形.若点D 关于直线OC 的对称点D 恰好落在y 轴上,则点C 的坐标为______.16.如图, ABCD 中,AB //x 轴,12AB =.点A 的坐标为()2,8-,点D 的坐标为()6,8-,点B 在第四象限,点G 是AD 与y 轴的交点,点P 是CD 边上不与点C ,D 重合的一个动点,过点P 作y 轴的平行线PM ,过点G 作x 轴的平行线GM ,它们相交于点M ,将△PGM 沿直线PG 翻折,当点M 的对应点落在坐标轴上时,点P 的坐标为______.三、解答题17.计算:(1)80205-+;(2)(53)(53)+-.18.一架云梯长25m ,如图所示斜靠在一而墙上,梯子底端C 离墙7m .(1)这个梯子的顶端A 距地面有多高?(2)如果梯子的顶端下滑了4 m ,那么梯子的底部在水平方向滑动了多少米? 19.如图,正方形网格中的△ABC ,若小方格边长为1(1)判断△ABC 是什么形状?并说明理由.(2)求AC 边上的高.20.如图,平行四边形ABCD 的对角线AC 、BD 相较于点O ,且AB AD =,//BE AC ,//CE DB .求证:四边形OBEC 是矩形.21.2m n ±a ,b ,使a b m +=,ab n =,即22(()a b m +=a b n =22()0)m n a b a b a b ±±=>>. 743+743+7212+这里7m =,12n =,由于437+=,4312⨯=, 所以22(4)(3)4312+== 27437212(43)23+=++=(14+23(213242-(3415-22.某超市以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到实惠,现决定降价销售,已知这种干果销售量y (千克)与每千克降价x (元)(0<x <20)之间满足一次函数关系,其图象如图所示.(1)求y 与x 之间的函数关系式;(2)当每千克干果降价3元时,超市获利多少元?23.已知在平行四边形ABCD中,,将ABC沿直线AC翻折,点B落在点尽处,AD与CE相交于点O,联结DE.AC DE;(1)如图1,求证://(2)如图2,如果,,,求的面积;(3)如果,,当是直角三角形时,求BC的长.24.如图所示,在平面直角坐标系中,点B的坐标为(4,8),过点B分别作BA⊥y轴,BC⊥x轴,得到一个长方形OABC,D为y轴上的一点,将长方形OABC沿着直线DM折叠,使得点A与点C重合,点B落在点F处,直线DM交BC于点E.(1)直接写出点D的坐标;(2)若点P为x轴上一点,是否存在点P使△PDE的周长最小?若存在,请求出△PDE 的最小周长;若不存在,请说明理由.(3)在(2)的条件下,若Q点是线段DE上一点(不含端点),连接PQ.有一动点H 从P点出发,沿线段PQ以每秒1个单位的速度运动到点Q,再沿着线段QE5单位长度的速度运动到点E后停止.请直接写出点H在整个运动过程中所用的最少时间t ,以及此时点Q 的坐标.25.在正方形AMFN 中,以AM 为BC 边上的高作等边三角形ABC ,将AB 绕点A 逆时针旋转90°至点D ,D 点恰好落在NF 上,连接BD ,AC 与BD 交于点E ,连接CD ,(1)如图1,求证:△AMC ≌△AND ;(2)如图1,若DF=3,求AE 的长;(3)如图2,将△CDF 绕点D 顺时针旋转α(090α<<),点C,F 的对应点分别为1C 、1F ,连接1AF 、1BC ,点G 是1BC 的中点,连接AG ,试探索1AG AF 是否为定值,若是定值,则求出该值;若不是,请说明理由.【参考答案】一、选择题1.D解析:D【分析】根据分式有意义,分母不为0,二次根式的被开方数是非负数列式解答即可.【详解】解:由题意得,10x -≥,且20x +≠,∴实数x 的取值范围是1≥x ,故选:D .【点睛】本题考查的是分式有意义和二次根式有意义的条件,掌握分式有意义,分母不为0,二次根式的被开方数是非负数是解题的关键.2.C解析:C【分析】先分别设三角形的三边,依据勾股定理的逆定理列式计算即可判断.【详解】解:A 、设三边分别为x 、2x 、3x ,∵222(2)(3)x x x +≠,∴三边比为1:2:3的三角形不是直角三角形;B、设三边分别为2x、3x、4x,∵222x x x+≠,(2)(3)(4)∴三边比为2:3:4的三角形不是直角三角形;C、设三边分别为3x、4x、5x,∵222x x x+=,(3)(4)(5)∴三边比为3:4:5的三角形是直角三角形;D、设三边分别为x、3x、x,∵222+≠,x x x(3)∴三边比为1:3:1的三角形不是直角三角形;故选:C.【点睛】此题考查应用勾股定理的逆定理判断三角形是否是直角三角形,熟记定理并应用解决问题是解题的关键.3.C解析:C【解析】【分析】根据平行四边形的判定方法逐一分析解题.【详解】解:A、B、D均可为判定四边形为平行四边形,故A、B、D不符合题意;C.一组对边平行另一组对边相等的四边形,不能判断它是平行四边形,如下图,是等腰梯形,故C符合题意,故选:C.【点睛】本题考查平行四边形的判定,是重要考点,难度较易,掌握相关知识是解题关键.4.C解析:C【解析】【分析】根据众数的定义求解即可,众数为一组数据中出现次数最多的数.【详解】解:这组数中4出现了3次,出现次数最多,众数为4故选C.【点睛】此题考查了众数的有关定义,熟练掌握众数的定义是解题的关键.5.D解析:D【分析】由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.【详解】解:∵四边形OABC是矩形,∴∠OCB=90°,OC=4,BC=OA=10,∵D为OA的中点,∴OD=AD=5,①当PO=PD时,点P在OD得垂直平分线上,∴点P的坐标为:(2.5,4);②当OP=OD时,如图1所示:则OP=OD=5,22PC=-53∴点P的坐标为:(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,22DE=-=;543分两种情况:当E在D的左侧时,如图2所示:OE=5-3=2,∴点P的坐标为:(2,4);当E在D的右侧时,如图3所示:OE=5+3=8,∴点P的坐标为:(8,4);综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);故选:D【点睛】本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.6.D解析:D【解析】【分析】根据菱形的性质得到∠ABD=∠CBD,AD∥BC,根据平行线的性质求出∠ABC的度数,可进而求出∠CBD的度数.【详解】解:∵四边形ABCD是菱形,∴∠ABD=∠CBD,AD∥BC,∠ABC,∴∠A+∠ABC=180°,∠CBD=12∵∠A=110°,∴∠ABC=180°﹣∠A=180°﹣110°=70°,∴∠CBD=1×70°=35°,2故选:D.【点睛】本题考查了菱形的性质、平行线的性质,解题的关键是熟练掌握菱形的对边互相平行,对角线平分一组对角.7.A解析:A【解析】【分析】连接EA并延长BD于点O,根据正方形和等边三角形的性质,可求出EA是BD垂直平分线,求出∠DEB,求出∠EDA,从而求出∠EAF=∠FEA=45°,可得到EF=AF,然后设AF=EF=x,则DF=x+4,在Rt△EFD中,由勾股定理得出方程求出即可.【详解】解:如图,连接EA并延长BD于点O,∵四边形ABCD 是正方形,∴∠ADB =45°,AB =AD ,∴A 在BD 垂直平分线上,∵三角形BDE 是等边三角形,∴∠BED =∠EDB =∠EBD =60°,ED =EB ,∴E 在BD 的垂直平分线上,∴AE 是BD 的垂直平分线,∴∠DEO =12 ∠DEB =30°,∵∠EDB =60°,∠ADB =45°,∴∠EDA =60°-45°=15°,∴∠EAF =15°+30°=45°,∵EF DA ⊥,∴∠EF A =90°,∴∠FEA =∠EAF =45°,∴EF =AF ,∵四边形ABCD 是正方形,∴AB =AD =4,∠BAD =90°,由勾股定理得:BD 2242AB AD +=ED =BD =2,设AF =EF =x ,则DF =x +4,在Rt △EFD 中,由勾股定理得:ED 2=EF 2+FD 2, ∴(()222424x x =++, 解得:12232,232x x ==- (是负数,不符合题意舍去),即AF =232 .故选:A .【点睛】本题考查了线段垂直平分线性质,等边三角形性质,等腰三角形性质,正方形性质,勾股定理的应用,熟练掌握相关知识是解题的关键.8.B解析:B【分析】易得乙出发时,两人相距8m ,除以时间2即为甲的速度;由于出现两人距离为0的情况,那么乙的速度较快.乙80s 跑完总路程400可得乙的速度,进而求得80s 时两人相距的距离可得b 的值,同法求得两人距离为0时,相应的时间,让两人相距的距离除以甲的速度,减2即为c 的值.【详解】由函数图象可知,甲的速度为824÷=(米/秒),乙的速度为400805÷=(米/秒),8(54)8∴÷-=(秒),8a ∴=,故①正确;5804(802)400328b =⨯-⨯+=-72=(米)故②正确;4004298c =÷-=(秒)故③正确;∴正确的是①②③.故选B .【点睛】本题考查了一次函数的应用,得到甲乙两人的速度是解决本题的突破点,得到相应行程的关系式是解决本题的关键.二、填空题9.x ≥﹣1且x ≠0【解析】【分析】根据二次根式和分式有意义的条件:被开方数大于等于0,分母不等于0,列不等式组求解.【详解】根据题意,得100x x +≥⎧⎨≠⎩, 解得x ≥﹣1且x ≠0.故答案为:x ≥﹣1且x ≠0.【点睛】本题考查的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.本题应注意在求得取值范围后,应排除不在取值范围内的值.理解分式与二次根式的意义是关键.10.A解析:12【解析】【分析】取对角线的交点为O ,根据菱形的性质及三角形面积的计算公式可知阴影部分的面积为Rt AOB 面积的两倍.【详解】解:取对角线的交点为O ,过点O 作AB 的垂线,交,AB DC 分别于点,N M ,如图所示:根据菱形的性质及三角形面积的计算知, 阴影部分的面积为122AOB AB MN S ⋅=,∠AOB =90°,5,6AB DB ==,3OB ∴=,224AO AB OB ∴=-,1134622AOB SAO OB ∴=⋅=⨯⨯=, 即1226122AOB AB MN S ⋅==⨯=,故阴影部分的面积为12,故答案是:12.【点睛】本题考查了菱形的性质、勾股定理、三角形面积求法,解题的关键是:利用转换的思想来解答.11.6【解析】【分析】根据勾股定理可以求得另一条直角边的长,然后即可求得此直角三角形的面积.【详解】解:∵直角三角形一直角边的长是3,斜边长是5,∴2253-,∴此直角三角形的面积为:342⨯=6, 故答案为:6.【点睛】本题考查勾股定理,解答本题的关键是明确题意,利用勾股定理和三角形的面积公式解答. 12.A 解析:245【分析】依据矩形的性质即可得到AOD ∆的面积为12,再根AOD AOE DOE SS S =+,即可到OE EF+的值.【详解】解:∵AB =6,BC =8,∴矩形ABCD 的面积为48,10AC == ,∴AO =DO =12AC =5, ∵对角线AC ,BD 交于点O , ∴1116812222∆==⨯⨯⨯=AOD ABC S S , ∵EO AO ⊥ ,EF DO ⊥, ∴AOD AOE DOE S S S=+ ,即12=1122⨯+⨯AO OE DO EF , ∴12115522=⨯⨯+⨯⨯OE EF , ∴()524+=OE EF , ∴245OE EF +=故答案:245. 【点睛】本题主要考查了矩形的性质,解题时注意:矩形的四个角都是直角,矩形的对角线相等且互相平分.13.A解析:-3【分析】根据题意直线y =kx +b (k ≠0)经过点A (0,3)和点(1,0),然后根据待定系数法即可求得k 的值.【详解】解:∵直线y =kx +b (k ≠0)经过点A (0,3)和点(1,0),∴30b k b =⎧⎨+=⎩, 解得k =﹣3,故答案为:-3.【点睛】本题考查了待定系数法求一次函数的解析式,熟练运用待定系数法是解题的关键. 14.OA OC =(答案不唯一)【分析】由条件AC BD ⊥,OB OD =,根据对角线互相垂直平分的四边形是菱形进行判定即可.【详解】解:添加OA OC =即可判断四边形ABCD 是菱形,∵AC BD ⊥,OB OD =,当OA OC =时,四边形ABCD 对角线AC ,BD 互相垂直平分,∴四边形ABCD 是菱形,故答案为:OA OC =(答案不唯一).【点睛】此题主要考查了菱形的判定,掌握一组对角线互相垂直平分的四边形是菱形是解题的关键.15.或.【分析】先根据题意求得,,,分点在第二象限和第一象限两种情况讨论,根据点关于直线的对称点恰好落在轴上,根据含30度角的直角三角形的性质,在第一象限时候,证明是等边三角形,在第二象限时候证明是解析:32⎛ ⎝⎭或32⎛- ⎝⎭. 【分析】先根据题意求得30BAO ∠=︒,60ABO ∠=︒,12OB AB =,分C 点在第二象限和第一象限两种情况讨论,根据点D 关于直线OC 的对称点D 恰好落在y 轴上,根据含30度角的直角三角形的性质,在第一象限时候,证明BCO 是等边三角形,在第二象限时候证明ODD '是等边三角形,利用等边三角形的性质,分别求得C 点的坐标.【详解】y =与x 轴,y 轴分别交于点A ,B , 令0y =,3x =-,∴(3,0)A -,令0x =,y =B ∴,3,OA OB ∴==90AOB ∠=︒,AB ∴=30BAO ∴∠=︒,60ABO ∠=︒,12OB AB ∴=, ①如图,当C 点在第二象限时,设DD '交x 轴于点E ,交AO 于点F ,CD 交y 轴于点G ,四边形OACD 是平行四边形,//AC OD ∴,//CD AO ,AC OD OD '==,30CAO ∠=︒,30DOE CAO ∴∠=∠=︒,30ODG DOE ∴∠=∠=︒,//CD AO ,AO OB ⊥,90DGD '∴∠=︒,9060DOG DOE ∴∠=︒-∠=︒,OD OD '=,30ODD OD D ''∴∠=∠=︒,点D 关于直线OC 的对称点为D 点,CO DD '∴⊥,60COB FOD '∴∠=∠=︒,60ABO ∠=︒,BCO ∴△是等边三角形,BO CO BC ∴==, 12BO AB =, 12BC AB =∴, C ∴点为AB 的中点,(3,0)A -,3)B ,33(2C ∴-, ②如图,当C 点在第二象限时,延长DC 交y 轴于点H ,则CH OD '⊥,点D 关于直线OC 的对称点为D 点,CD CD OD OD ''∴==,DOC D OC '∠=∠,60ABO BOD ∠=∠=︒,ODD '∴△是等边三角形,60DOD '∴∠=︒,30DOC D OC '∴∠=∠=︒,12CH OC ∴=, 30BAO ∠=︒,90AOB ∠=︒,3CO AO ∴==, ∴32CH =, 222233(2)3OH OC CH CH CH CH ∴=-=-=333()2C ∴. 综合①②可知C 的坐标为3332⎛ ⎝⎭或332⎛- ⎝⎭. 故答案为: 3332⎛ ⎝⎭或332⎛- ⎝⎭. 【点睛】本题考查了一次函数图像的性质,平行四边形的性质,等边三角形的性质,含30度角的直角三角形的性质,勾股定理,轴对称的性质,此题方法比较多,利用等边三角形的性质是解题的关键.16.,或,【分析】先求出直线的解析式为,则可求,设,则,可求,,分两种情况讨论:当在轴负半轴时,由折叠可知,在△中,由勾股定理可求,在△中,,,可求,所以,解得,则,;当在轴正半轴时,同理可得,,解 解析:85(5,8)或12(55-,8) 【分析】先求出直线AD 的解析式为24y x =--,则可求(0,4)G -,设(,8)P m ,则(,4)M m -,可求12PM =,8PN =,分两种情况讨论:当M '在x 轴负半轴时,由折叠可知12PM '=,在Rt △M NP '中,由勾股定理可求45M N '=,在Rt △M OG '中,M G x '=,4OG =,可求216M O x '=-,所以21645x x -+=,解得855x,则85(5P ,8);当M '在x 轴正半轴时,同理可得,21645x x -+-=,解得1255x =-,求得12(55P -,8). 【详解】解:设AD 的直线解析式为y kx b =+,将(2,8)A -,(6,8)D -代入可得,2868k b k b +=-⎧⎨-+=⎩, 解得24k b =-⎧⎨=-⎩, 24y x ∴=--,(0,4)G ∴-,点P 是CD 边上,//CD x 轴,设(,8)P m ,//GM y 轴,(,4)M m ∴-,12PM ∴=,8PN =,当M '在x 轴负半轴时,如图,由折叠可知GM GM '=,PM PM '=,12PM '∴=,在Rt △M NP '中,2245M N M P PN ''=-在Rt △M OG '中,M G x '=,4OG =, 216M O x '∴=-, ∴21645x x -+=, 解得855x, 85(5P ∴,8); 当M '在x 轴正半轴时,如图,同理可得,21645x x --解得1255x = 12(55P ∴8); 综上所述:P 点坐标为85(8)或12(558), 故答案为85(8)或12(558). 【点睛】 本题考查折叠的性质,熟练掌握平行四边形的性质、平面上点的坐标特点、并灵活应用勾股定理是解题的关键.三、解答题17.(1)3;(2)2【分析】(1)先把二次根式化为最简二次根式,然后合并即可;(2)利用平方差公式计算即可.【详解】解:(1)原式=(2)原式=5﹣3=2.【点睛】本题考查的是二次根式解析:(1)2)2【分析】(1)先把二次根式化为最简二次根式,然后合并即可;(2)利用平方差公式计算即可.【详解】解:(1)原式==(2)原式=5﹣3=2.【点睛】本题考查的是二次根式的加减运算,二次根式的混合运算,掌握利用平方差公式进行简便运算是解题的关键.18.(1)这个梯子的顶端距地面有高;(2)梯子的底部在水平方向滑动了.【分析】(1)根据勾股定理即可求解;(2)先求出BD ,再根据勾股定理即可求解.【详解】解:(1)由题意可知:,;,在中,解析:(1)这个梯子的顶端A 距地面有24m 高;(2)梯子的底部在水平方向滑动了8m .【分析】(1)根据勾股定理即可求解;(2)先求出BD ,再根据勾股定理即可求解.【详解】解:(1)由题意可知:90B ∠=︒,25m AC DE ==;7m BC =,在Rt ABC 中,由勾股定理得:222AB BC AC +=, ∴AB ==24=,因此,这个梯子的顶端A 距地面有24m 高.(2)由图可知:AD =4m ,24420BD AB AD =-=-=,在Rt DBE 中,由勾股定理得:222BE BD DE +=, ∴BE ==15=,∴1578CE BE BC =-=-=.答:梯子的底部在水平方向滑动了8m .【点睛】此题主要考查勾股定理的实际应用,解题的关键是根据题意在直角三角形中,利用勾股定理进行求解.19.(1)△ABC 是直角三角形.理由见解析;(2)【解析】【分析】(1)根据勾股定理和勾股定理的逆定理可直接判断;(2)根据三角形的面积公式可求解.【详解】解:(1)△ABC 是直角三角形.理解析:(1)△ABC 是直角三角形.理由见解析;(2【解析】【分析】(1)根据勾股定理和勾股定理的逆定理可直接判断;(2)根据三角形的面积公式可求解.【详解】解:(1)△ABC 是直角三角形.理由如下:由题意可得,AB BCAC =∴AB 2+BC 2=AC 2,∴∠B =90°,∴△ABC 是直角三角形;(2)设AC 边上的高为h .∵S △ABC =12AC •h =12AB •BC ,∴h =13AB BC AC == 【点睛】本题主要考查了勾股定理和勾股定理的逆定理,解题的关键在于能够熟练掌握相关知识进行求解.20.见解析【分析】先根据四边形是平行四边形且得到平行四边形是菱形,即可得到,再根据,,证明四边形是平行四边形,即可得到平行四边形是矩形.【详解】证明:∵四边形是平行四边形且 ∴平行四边形是菱形解析:见解析 【分析】先根据四边形ABCD 是平行四边形且AB AD =得到平行四边形ABCD 是菱形,即可得到90BOC ∠=,再根据//BE AC ,//CE DB ,证明四边形OBEC 是平行四边形,即可得到平行四边形OBEC 是矩形. 【详解】证明:∵四边形ABCD 是平行四边形且AB AD = ∴平行四边形ABCD 是菱形 ∴BD AC ⊥,即90BOC ∠= 又∵//BE AC ,//CE DB . ∴四边形OBEC 是平行四边形, ∴平行四边形OBEC 是矩形.【点睛】本题主要考查了平行四边形的判定,矩形的判定,菱形的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解.21.(1);(2);(3) 【解析】 【分析】根据题意把题目中的无理式转化成的形式,然后仿照题意化简即可. 【详解】 解:(1)∵, ∴,, ∵,, ∴,, ∴; (2)∵, ∴,, ∵,, ∴,,解析:(11;(23【解析】 【分析】【详解】解:(1)∵∴4m =,3n =, ∵314+=,313⨯=, ∴224+=∴1;(2)∵∴13m =,42n =, ∵7613+=,7642⨯=, ∴2213+==∴(3)∵ ∴8m =,15n =, ∵358+=,3515⨯=, ∴228+==∴==【点睛】本题考查了二次根式的化简,根据题中的范例把根号内的式子整理成完全平方的形式是解答此题的关键.22.(1)y=10x+100(0<x <20);(2)当每千克干果降价3元时,超市获利2210元 【分析】(1)由待定系数法即可得到函数的解析式;(2)根据(1)的解析式将x=3代入求出销售量,再根据解析:(1)y =10x +100(0<x <20);(2)当每千克干果降价3元时,超市获利2210元 【分析】(1)由待定系数法即可得到函数的解析式;(2)根据(1)的解析式将x =3代入求出销售量,再根据每千克利润×销售量=总利润列式求解即可.【详解】解:(1)设y与x之间的函数关系式为:y=kx+b,把(2,120)和(4,140)代入得,2120 4140k bk b+=⎧⎨+=⎩,解得:10100kb=⎧⎨=⎩,∴y与x之间的函数关系式为:y=10x+100(0<x<20);(2)根据题意得,销售量y=10×3+100=130,(60-3-40)×130=2210(元),答:当每千克干果降价3元时,超市获利2210元.【点睛】本题考查的是一次函数的应用,解题的关键是利用待定系数法求出y与x之间的函数关系式,此类题目主要考查学生分析、解决实际问题能力,又能较好的考查学生“用数学”的意识.23.(1)见解析;(2);(3)4或6【分析】(1)由折叠的性质得,,由平行四边形的性质得,.则,,得,证出,则,由等腰三角形的性质得,证出,即可得出结论;(2)证四边形是矩形,则,,,设,则,在解析:(1)见解析;(2);(3)4或6【分析】(1)由折叠的性质得,,由平行四边形的性质得,//AD BC.则,,得,证出OA OC=,则,由等腰三角形的性质得,证出,即可得出结论;(2)证四边形ABCD是矩形,则,,,设,则,在中,由勾股定理得出方程,求出,由三角形面积公式即可得出答案;(3)分两种情况:或,需要画出图形分类讨论,根据含30角的直角三角形的性质,即可得到BC的长.【详解】解:(1)证明:由折叠的性质得:△,,,四边形ABCD是平行四边形,,//AD BC.,,,,,,,,;(2)平行四边形ABCD中,,∴四边形ABCD是矩形,,,,=,由(1)得:OA OC设,则,在中,由勾股定理得:,解得:,,的面积;(3)分两种情况:①如图3,当时,延长交BC于G,,,,,,,,,,,是BC的中点,在中,,;②如图4,当时,,,由折叠的性质得:,,在和中,,,,,,,,,,,又,,A,E在同一直线上,,中,,,,;综上所述,当是直角三角形时,BC的长为4或6.【点睛】本题是四边形综合题目,考查了翻折变换的性质、平行四边形的性质、平行线的判定与性质、矩形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质、勾股定理、直角三角形的性质等知识;本题综合性强,熟练掌握翻折变换的性质和平行四边形的性质是解题的关键.24.(1)D(0,3);(2)存在,6;(3)5秒,Q(,)【解析】【分析】(1)设D(0,m),且m>0,运用矩形性质和折叠性质可得:OD=m,OA=8,CD=8﹣m,再利用勾股定理建立方程求解解析:(1)D(0,3);(2)存在,3)5秒,Q(32,154)【解析】【分析】(1)设D(0,m),且m>0,运用矩形性质和折叠性质可得:OD=m,OA=8,CD=8﹣m,再利用勾股定理建立方程求解即可;(2)如图1,作点D关于x轴的对称点D′,连接D′E,交x轴于点P,则点P即为所求,此时△PDE的周长最小,运用勾股定理可得CE=5,BE=3,作EG⊥OA,在Rt△DEG中,可得DE=Rt△D′EG中,可得'D E(3)运用待定系数法求得直线D′E的解析式为y=2x﹣3,进而求得P(32,0),过点E作EG⊥y轴于点G,过点Q、P分别作y轴的平行线,分别交EG于点H、H′,H′P交DE于点Q′,利用待定系数法可得直线DE的解析式为y=12x+3,设Q(t,12t+3),则H(t,5),再运用勾股定理即可求出答案.【详解】解:(1)设D(0,m),且m>0,∴OD=m,∵四边形OABC是矩形,∴OA=BC=8,AB=OC=4,∠AOC=90°,∵将长方形OABC沿着直线DM折叠,使得点A与点C重合,∴CD=AD=OA﹣OD=8﹣m,在Rt△CDO中,OD2+OC2=CD2,∴m2+42=(8﹣m)2,解得:m=3,∴点D的坐标为(0,3);(2)存在.如图1,作点D关于x轴的对称点D′,连接D′E,交x轴于点P,则点P即为所求,此时△PDE的周长最小,在Rt△CEF中,BE=EF=BC﹣CE,EF2+CF2=CE2,BC=8,CF=4,∴CE=5,BE=3,作EG⊥OA,∵OD=AG=BE=3,OA=8,∴DG=2,在Rt△DEG中,EG2+DG2=DE2,EG=4,∴DE=25在Rt△D′EG中,EG2+D′G2=D′E2,EG=4,D′G=8,∴D′E=45∴△PDE周长的最小值为DE+D′E=5(3)由(2)得,E(4,5),D′(0,﹣3),设直线D′E的解析式为y=kx+b,则453k bb+=⎧⎨=-⎩,解得:23kb=⎧⎨=-⎩,∴直线D′E的解析式为y=2x﹣3,令y=0,得2x﹣3=0,解得:x=32,∴P(32,0),过点E作EG⊥y轴于点G,过点Q、P分别作y轴的平行线,分别交EG于点H、H′,H′P 交DE于点Q′,设直线DE 的解析式为y =k ′x +b ′,则345b k b =⎧⎨+='''⎩,解得:123k b ⎧=⎪⎨⎪='⎩', ∴直线DE 的解析式为y =12x +3, 设Q (t ,12t +3),则H (t ,5), ∴QH =5﹣(12t +3)=2﹣12t ,EH =4﹣t ,由勾股定理得:DE 22221(2)(4)2QH EH t t +-+-52﹣12t 5,∴点H 在整个运动过程中所用时间=15PQ PQ +QH , 当P 、Q 、H 在一条直线上时,PQ +QH 最小,即为PH ′=5,点Q 坐标(32,154),故:点H 在整个运动过程中所用最少时间为5秒,此时点Q 的坐标(32,154).【点睛】本题考查了矩形的性质,折叠的性质,勾股定理,一次函数的性质,线段的动点问题,以及最短路径问题,解题的关键是熟练掌握所学的知识,正确的作出辅助线,从而进行分析.25.(1)见解析;(2)AE =;(3)(3),理由见解析. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明. (解析:(1)见解析;(2)AE =23;(3)(3)122AG AF =,理由见解析. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x ,则AE=2x GE=3x ,得到△GBE 是等腰直角三角形和∠DHF=30°,再结合直角三角形的性质,判定Rt △AMC ≌Rt △AND ,最后通过计算求得AE 的长;(3)延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM F G =,可得GMB ∆≌11GFC ∆,从而得到111BM FC DF == 1BMG GFN ∠=,可知BM ∥1F N , 再根据题意证明ABM ∆≌1ADF ∆,进一步说明1AMF ∆是等腰直角三角形,然后再使用勾股定理求解即可.【详解】(1)证明:∵四边形AMFN 是正方形, ∴AM=AN ∠AMC=∠N=90° ∴△AMC,△AND 是Rt △ ∵△ABC 是等边三角形 ∴AB=AC ∵旋转后AB=AD ∴AC=AD∴Rt △AMC ≌Rt △AND(HL)(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x 则AE=2x 3x易得△GBE 是等腰直角三角形 ∴BG=EG 3x ∴AB=BC=(31)x 易得∠DHF=30° ∴HD=2DF=23,HF=3 ∴BF=BH+HF=233 ∵Rt △AMC ≌Rt △AND(HL)∴易得CF=DF=3∴BC=BF-CF=233333+-=+ ∴(31)33x +=+ ∴3x = ∴AE =223x = (3)122AG AF =; 理由:如图2中,延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM F G =,则GMB ∆≌11GFC ∆,∴111BM FC DF == 1BMG GF N ∠=, ∴BM ∥1F N , ∴MBA N ∠=∠∵0190NAO OF D ∠=∠= 1AON DOF ∠=∠∴1N ADF ∠=∠ ∴1ABM ADF ∠=∠, ∵AB AD =∴ABM ∆≌1ADF ∆(SAS ) ∴1AM AF = 1MAB DAF ∠=∠∴0190MAF BAD ∠=∠=∴1AMF ∆是等腰直角三角形 ∴1AG MF ⊥ 1AG GF = ∴12AF AG = ∴12AG AF =【点睛】本题考查正方形的性质、三角形全等、以及勾股定理等知识点,综合性强,难度较大,但解答的关键是正确做出辅助线.。
八年级下册数学期末试卷易错题(Word版含答案)

八年级下册数学期末试卷易错题(Word版含答案)一、选择题1.要使式子﹣3x 有意义,则x的值可以为()A.﹣6 B.0 C.2 D.π2.下列各组数中,不能构成直角三角形的是()A.9、12、15 B.12、18、22 C.8、15、17 D.5、12、133.如图四边形ABCD的对角线AC,BD交于点O,则不能..判断四边形ABCD是平行四边形的是()A.AB∥CD,∠DAC=∠BCA B.AB=CD,∠ABO=∠CDOC.AC=2AO,BD=2BO D.AO=BO,CO=DO4.甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是()统计量甲乙丙丁平均数9.29.29.29.2方差0.600.620.500.44A.甲B.乙C.丙D.丁5.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.25B5C.35D.26.如图,在平面直角坐标系上,直线y=34x﹣3分别与x轴、y轴相交于A、B两点,将△AOB沿x轴翻折得到△AOC,使点B刚好落在y轴正半轴的点C处,过点C作CD⊥AB 交AB于D,则CD的长为()A .185B .245C .4D .57.如图,在Rt ABC △中,90ACB ∠=︒,D ,E ,F 分别是AC ,BC ,AB 的中点,连接DE ,CF .若1CF =,则DE 的长度为( )A .1B .2C .3D .48.如图,等腰直角三角形△OAB 的边OA 和矩形OCDE 的边OC 在x 轴上,OA =4,OC =1,OE =2.将矩形OCDE 沿x 轴正方向平移t (t >0)个单位,所得矩形与△OAB 公共部分的面积记为S (t ).将S (t )看作t 的函数,当自变量t 在下列哪个范围取值时,S (t )是t 的一次函数( )A .1<t <2B .2<t <3C .3<t <4D .1<t <2或4<t <5二、填空题9.若a ,b 都是实数,且338b a a --,则ab +1的平方根为 _____.10.已知菱形的周长等于8,一条对角线长为2,则此菱形的面积为___.11.在Rt ABC ∆中,90C ∠=︒,30A ∠=︒,2AC =,斜边AB 的长为__________. 12.如图,在矩形ABCD 中,6BC =,3CD =,将BCD ∆沿对角线BD 翻折,点C 落在点'C 处,'BC 交AD 于点E ,则线段DE 的长为____________.13.正比例函数(0)y kx k =≠经过点(1,3),则k =__________.14.在四边形ABCD 中,AB DC =,AD BC =.请再添加一个条件,使四边形ABCD 是菱形.你添加的条件是_______.(写出一种即可)15.如图1,在平面直角坐标系中,将平行四边形ABCD 放置在第一象限,且AB //x轴.直线y =﹣x 从原点出发沿x 轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l 与直线在x 轴上平移的距离m 的函数图象如图2,那么AB 的长为___.16.某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m (吨)与时间t (小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是________小时.三、解答题17.计算:(1)(520+|25(﹣1)2021;(26363147.18.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC 的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D 的位置,问船向岸边移动了多少米.(假设绳子是直的)19.如图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点.A ,B 两点均在格点上,在给定的网格中,按下列要求画图:(1)在图①中,画出以AB 为底边的等腰△ABC ,并且点C 为格点.(2)在图②中,画出以AB 为腰的等腰△ABD ,并且点D 为格点.(3)在图③中,画出以AB 为腰的等腰△ABE ,并且点E 为格点,所画的△ABE 与图②中所画的△ABD 不全等.20.请在横线上添加一个合适的条件,并写出证明过程:如图,平行四边形ABCD 对角线上有两点E ,F ,AE =CF , ,连接EB ,ED ,FB ,FD .求证:四边形EBFD 为菱形.21.21+21(21)(21)-+-221(2)1--21-21 (132+ ; (21n n ++= ; (321+32+43+10099+. 22.我国传统的计重工具﹣﹣秤的应用,方便了人们的生活,如图1,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量.称重时,若秤杆上秤砣到秤纽的水平距离为x (厘米)时,秤钩所挂物重为y (斤).如表中为若干次称重时所记录的一些数据. x (厘米) 1 2 4 8y(斤)0.75 1.00 1.50 2.5(1)在图2中将表x,y的数据通过描点的方法表示,观察判断x,y的函数关系,并求秤杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是多少斤?(2)已知秤砣到秤纽的最大水平距离为50厘米,这杆秤的可称物重范围是多少斤?23.如图,矩形ABCD中,AB=4,AD=3,∠A的角平分线交边CD于点E.点P从点A出发沿射线AE以每秒2个单位长度的速度运动,Q为AP的中点,过点Q作QH⊥AB于点H,在射线AE的下方作平行四边形PQHM(点M在点H的右侧),设P点运动时间为秒.(1)直接写出的面积(用含的代数式表示).(2)当点M落在BC边上时,求的值.(3)在运动过程中,整个图形中形成的三角形是否存在全等三角形?若存在,请写出所有全等三角形,并求出对应的的值;若不存在请说明理由(不能添加辅助线).24.如图1,在平面直角坐标系xOy中,直线AB交y轴于点A(0,3),交x轴于点B(﹣4,0).(1)求直线AB的函数表达式;(2)如图2,在线段OB上有一点C(点C不与点O、点B重合),将AOC沿AC折叠,使点O落在AB上,记作点D,在BD上方,以BD为斜边作等腰直角三角形BDF,求点F 的坐标;(3)在(2)的条件下,如图3,在平面内是否存在一点E,使得以点A,B,E为顶点的三角形与ABC全等(点E不与点C重合),若存在,请直接写出满足条件的所有点E的坐标,若不存在,请说明理由.25.如图,菱形纸片ABCD 的边长为2,60,BAC ∠=︒翻折,,B D ∠∠使点,B D 两点重合在对角线BD 上一点,,P EF GH 分别是折痕.设()02AE x x =<<.(1)证明:AG BE =;(2)当02x <<时,六边形AEFCHG 周长的值是否会发生改变,请说明理由; (3)当02x <<时,六边形AEFCHG 53吗?如果能,求此时x 的值;如果不能,请说明理由. 【参考答案】一、选择题1.D解析:D【分析】根据二次根式有意义的条件列出不等式,解不等式即可.【详解】解:由题意得:x ﹣3≥0,解得:x ≥3,各个选项中,π符合题意,故选:D .【点睛】此题主要考查二次根式有意义的条件,解题的关键是熟知二次根式的性质.2.B解析:B【分析】欲判断能否构成直角三角形,只需验证两小边的平方和是否等于最长边的平方.【详解】解:A 、92+122=152,能构成直角三角形;B 、122+182≠222,不能构成直角三角形;C 、82+152=172,能构成直角三角形;D 、52+122=132,能构成直角三角形.故选:B .【点睛】本题考查了利用勾股定理逆定理判定直角三角形的方法.在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.3.D解析:D【解析】【分析】A.证明//AD BC ,即可根据两组对边分别平行的四边形是平行四边形判断;B.证明AB ∥CD ,即可根据有一组对边平行且相等的四边形是平行四边形判断;C. 可根据对角线互相平分的四边形是平行四边形判断;D. 条件不足无法判断;【详解】∠DAC =∠BCA∴//AD BC ,∴四边形ABCD 是平行四边形,故A 选项正确,不符合题意;∠ABO =∠CDO//AB CD ∴ 又 AB =CD ,∴四边形ABCD 是平行四边形,故B 选项正确,不符合题意;AC =2AO ,BD =2BO,AO CO BO DO ∴==∴四边形ABCD 是平行四边形,故C 选项正确,不符合题意;D. 条件不足无法判断,符合题意;故选D【点睛】本题考查了平行四边形的判定,掌握平行四边形的判定方法是解题的关键.4.D解析:D【解析】【分析】根据方差的性质:方差越小,表示数据波动越小,也就是越稳定,据此进行判断即可.【详解】解:∵甲、乙、丙、丁的方差分别为0.60,0.62,0.50,0.44,又∵0.44<0.50<0.60<0.62,∴丁的方差最小即丁的成绩最稳定,故选D .【点睛】此题主要考查方差的应用,解题的关键是熟知方差的性质.5.B解析:B【分析】连接AC 、CF ,如图,根据正方形的性质得∠ACD =45°,∠FCG =45°,AC =2,CF =32,则∠ACF =90°,再利用勾股定理计算出AF =25,然后根据直角三角形斜边上的中线求CH 的长.【详解】连接AC 、CF ,如图,∵四边形ABCD 和四边形CEFG 都是正方形,∴∠ACD =45°,FCG =45°,AC =2BC =2,CF =2CE =32,∴∠ACF =45°+45°=90°,在Rt △ACF 中,AF =()()22232=25+, ∵H 是AF 的中点,∴CH =12AF =5 .故选B .【点睛】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.两条对角线将正方形分成四个全等的等腰直角三角形.也考查了直角三角形斜边上的中线性质及勾股定理.6.B解析:B【解析】【分析】利用一次函数图象上点的坐标特征可求出点A ,B 的坐标,在Rt △AOB 中,利用勾股定理可求出AB 的长,由折叠的性质可得出OC =OB ,进而可得出BC 的长,再利用面积法,即可求出CD 的长.【详解】解:当x =0时,y =34×0﹣3=﹣3, ∴点B 的坐标为(0,﹣3);当y =0时,34x ﹣3=0,解得:x =4, ∴点A 的坐标为(4,0).在Rt △AOB 中,∠AOB =90°,OA =4,OB =3, ∴5AB =由折叠可知:OC =OB =3,∴BC =OB +OC =6.∵S △ABC =12BC •OA =12AB •CD , ∴245BC OA CD AB == 故选B .【点睛】本题主要考查了一次函数与坐标轴的交点问题,折叠的性质,三角形的面积公式,勾股定理等等,解题的关键在于能够熟练掌握相关知识进行求解.7.A解析:A【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半,可得AB 的长,根据三角形中位线定理可得DE 的长.【详解】依题意,90ACB ∠=︒,D ,E ,F 分别是AC ,BC ,AB 的中点,1CF =, 22AB CF ∴==,112DE AB ==.故选A .【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,三角形中位线定理,掌握以上定理是解题的关键.8.D解析:D【分析】分12t <<,,24t <<,45t <<,5t >讨论即可得出结果.【详解】解:4=OA ,1OC =,2OE =,∴当矩形OCDE 在12t <<范围内移动时,()S t 由0变为2,()S t 随t 的增大而增大, 当矩形OCDE 在24t <<范围内移动时,()S t 为定值2,当矩形OCDE 在45t <<范围内移动时,()S t 由2变为0,()S t 随t 的增大而减小, 当矩形OCDE 在5t >时,()S t 为0,综上所述,矩形OCDE 在12t <<或45t <<范围内移动时,()S t 是t 的一次函数, 故选:D .【点睛】本题考查了图形的平移、一次函数的定义,抓住一次函数的定义分类讨论是解决本题的关键.二、填空题9.±5【解析】【分析】根据二次根式有意义的条件可得: 3030a a -≥⎧⎨-≥⎩,再解可得a 的值,然后可得b 的值,进而可得ab +1的平方根.【详解】解:由题意得:3030a a -≥⎧⎨-≥⎩, 解得:a =3,则b =8,∴ab +1=25,25的平方根为±5,故答案为:±5.【点睛】本题主要考查了二次根式的概念,平方根的运算,熟悉掌握二次根式的非负性是解题的关键.10.A解析:2.【解析】【分析】根据周长先求出边长,由菱形的对角线平分且垂直求出它的另一条对角线的长,再根据面积公式求得面积.【详解】解:如图:∵菱形ABCD 的周长等于8cm ,∴AB =8÷4=2cm ,AC ⊥BD ,AO =CO ,BO =DO ,∵AC=2,∴AO =1,∴BO 3∴菱形的面积为332. 故答案为:232.【点睛】本题考查了菱形的四条边相等的性质,以及对角线互相垂直平分的性质,还考查了菱形面积的计算,对角线乘积的一半.11.B 433【解析】【分析】由90C ∠=︒,30A ∠=︒得到2,AB BC = 利用勾股定理可得答案.【详解】解:设BC ,x =90C ∠=︒,30A ∠=︒, 2,AB x ∴=2AC =,222(2)2,x x ∴=+122323x x ∴==(舍去), 42 3.3AB x ∴==4 3.3【点睛】 本题考查的是含30角的直角三角形的性质与勾股定理的应用,掌握相关知识点是解题的关键.12.D 解析:154【分析】根据将BCD ∆沿对角线BD 翻折,点C 落在点'C 处,'BC 交AD 于点E ,可得到∠DBE =∠BDE ,在Rt ABE △ 中,利用勾股定理即可解答.【详解】∵在矩形ABCD 中,6BC =,3CD =,∴AB =CD =3,AD =BC =6,AD //CB ,∠BAD =90︒ ,∴∠EDB =∠DBC ,∵将BCD ∆沿对角线BD 翻折,点C 落在点'C 处,'BC 交AD 于点E ,∴∠EBD =∠DBC ,∴∠DBE =∠BDE ,∴BE =DE ,设DE =x ,则BE =x ,AE =6-x ,在Rt ABE △ 中,222AB AE BE += ,∴2223(6)x x +-= ,解得:154x =故答案为:154【点睛】本题主要考查了矩形的折叠问题,解题的关键是灵活运用矩形的折叠结合勾股定理解答问题. 13.3【分析】把(1,3)代入(0)y kx k =≠,利用待定系数法求解k 即可得到答案.【详解】解:把(1,3)代入(0)y kx k =≠,3,k ∴=故答案为:3.【点睛】本题考查的是利用待定系数法求解正比例函数的解析式,掌握待定系数法是解题的关键. 14.A解析:AB =BC 或BC =CD 或CD =AD 或AB =AD 或AC ⊥BD【分析】由在四边形ABCD 中,AB =DC ,AD =BC ,可判定四边形ABCD 是平行四边形,然后根据一组邻边相等的平行四边形是菱形与对角线互相垂直的平行四边形是菱形,即可判定四边形ABCD 是菱形,则可求得答案.【详解】解:∵在四边形ABCD 中,AB =DC ,AD =BC ,∴四边形ABCD 是平行四边形,∴当AB =BC 或BC =CD 或CD =AD 或AB =AD 时,四边形ABCD 是菱形;当AC ⊥BD 时,四边形ABCD 是菱形.故答案为:AB =BC 或BC =CD 或CD =AD 或AB =AD 或AC ⊥B D .【点睛】此题考查了菱形的判定定理.此题属于开放题,难度不大,注意掌握一组邻边相等的平行四边形是菱形与对角线互相垂直的平行四边形是菱形是解此题的关键.15.4【分析】由图1,当直线在DE 的左下方时,由图2可得AE 长度;由图1,当直线在DE 和BF 之间时,长度不变,由图2可得EB 的长度,从而AB=AE+EB ,即求得AB .【详解】如图1,当直线在DE解析:4【分析】由图1,当直线在DE 的左下方时,由图2可得AE 长度;由图1,当直线在DE 和BF 之间时,长度不变,由图2可得EB 的长度,从而AB =AE +EB ,即求得AB .【详解】如图1,当直线在DE 的左下方时,由图2得:AE =7-4=3;由图1,当直线在DE 和BF 之间时,由图2可得:EB=8-7=1,所以AB =AE +EB =3+1=4.故答案为:4.【点睛】本题考查一次函数的图象与图形的平移,平行四边形的性质,关键是明确题意,读懂函数图象,利用数形结合的思想.16.8【分析】通过分析题意和图象可以求出调进物资的速度,调出物资的速度,即可求出结果.【详解】解:调进物资的速度是:(吨/小时),当在第4个小时时,库存物资有60吨,在第8个小时时,库存物资是 解析:8【分析】通过分析题意和图象可以求出调进物资的速度,调出物资的速度,即可求出结果.【详解】解:调进物资的速度是:60415÷=(吨/小时),当在第4个小时时,库存物资有60吨,在第8个小时时,库存物资是20吨,∴调出速度是:()6020154425-+⨯÷=(吨/小时),∴剩余的20吨完全调出需要:20250.8÷=(小时),∴这批物资从开始调进到全部调出所需要的时间是:80.88.8+=(小时).故答案是:8.8.【点睛】本题考查一次函数图象的实际应用,解题的关键是将函数图象与实际意义相联系,分析出关键信息进行求解.三、解答题17.(1)﹣2;(2)3+.【分析】(1)先化简零指数幂,绝对值,有理数的乘方,然后再计算;(2)先利用平方差公式,二次根式的除法运算法则计算乘除,最后算加减.【详解】解:(1)原式=1+﹣2解析:(12;(2)【分析】(1)先化简零指数幂,绝对值,有理数的乘方,然后再计算;(2)先利用平方差公式,二次根式的除法运算法则计算乘除,最后算加减.【详解】解:(1)原式=2﹣12;(2)22=6﹣=【点睛】本题考查二次根式的混合运算,零指数幂,掌握二次根式混合运算的运算顺序和计算法则及平方差公式(a+b)(a﹣b)=a2﹣b2的结构是解题关键.18.船向岸边移动了9米.【分析】在Rt△ABC中,利用勾股定理计算出AB长,再根据题意可得CD长,然后再次利用勾股定理计算出AD长,再利用BD=AB-AD可得BD长.【详解】解:在Rt△ABC中解析:船向岸边移动了9米.【分析】在Rt△ABC中,利用勾股定理计算出AB长,再根据题意可得CD长,然后再次利用勾股定理计算出AD长,再利用BD=AB-AD可得BD长.【详解】解:在Rt△ABC中:∵∠CAB=90°,BC=17米,AC=8米,∴AB(米),∵此人以1米每秒的速度收绳,7秒后船移动到点D的位置,∴CD=17-1×7=10(米),∴AD(米),∴BD=AB-AD=15-6=9(米),答:船向岸边移动了9米.【点睛】本题主要考查了勾股定理的应用,关键是掌握从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.19.(1)见解析;(2)见解析;(3)见解析.【解析】【分析】(1)根据勾股定理AB=,以AB 为底等腰直角三角形,两直角边为x, 根据勾股定理求出,找横1竖2个格,或横2竖1个格画线即可;(2)解析:(1)见解析;(2)见解析;(3)见解析.【解析】【分析】(1)根据勾股定理AB =10,以AB 为底等腰直角三角形,两直角边为x , 根据勾股定理求出5x =,找横1竖2个格,或横2竖1个格画线即可;(2)以AB =10为腰的等腰△ABD ,AB =AD ,以点A 为起点找横1竖3个格,或横3竖1个格画线;如图△ABD ; AB =BD ,以点B 为起点找横1竖3个格,或横3竖1个格画线;如图△ABD .(3)以AB =10为腰的等腰△ABD ,AB =BE ,以点B 为起点找横1竖3个格,或横3竖1个格;如图△ABE .AB =AE ,以点A 为起点找横1竖3个格,或横3竖1个格;所画的△ABE 与图②中所画的△ABD 不同即可.【详解】解:(1)∵根据勾股定理AB =221310+=,以AB 为底等腰直角三角形,两直角边为x , 根据勾股定理()22210x x +=,解得5x =,横1竖2,或横2竖1个画线;如图△ABC ;(2)以AB =221310+=为腰的等腰△ABD ,AB =AD ,以点A 为起点找横1竖3个格,或横3竖1个格画线;如图△ABD ;AB =BD ,以点B 为起点找横1竖3个格画线,或横3竖1个格;如图△ABD ;(3)以AB=22+=为腰的等腰△ABD,AB=BE,以点B为起点找横1竖3个格,或1310横3竖1个格;如图△ABE.AB=AE,以点A为起点找横1竖3个格,或横3竖1个格;所画的△ABE与图②中所画的△ABD不全等.【点睛】本题考查网格作图,掌握网格作图方法与勾股定理,利用勾股定理确定腰长构造直角三角形是解题关键.20.,见解析【分析】根据题意和图形,可以在空格处填一个条件,注意填写的条件不唯一,只要可以证明结论成立即可,然后根据菱形的判定方法证明即可.【详解】补充条件:AB=BC,证明:连接BD交AC于=,见解析解析:AB BC【分析】根据题意和图形,可以在空格处填一个条件,注意填写的条件不唯一,只要可以证明结论成立即可,然后根据菱形的判定方法证明即可.【详解】补充条件:AB=BC,证明:连接BD交AC于点O,如图所示,∵四边形ABCD 是平行四边形,∴OB =OD ,OA =OC ,∵AE =CF ,∴OE =OF ,∴四边形EBFD 是平行四边形,∵AB =BC ,∴∠BAE =∠BCF ,在△BAE 和△BCF 中,BA BC BAE BCF AE CF =⎧⎪∠=∠⎨⎪=⎩, ∴△BAE ≌△BCF (SAS ),∴BE =BF ,∴平行四边形EBFD 是菱形,即四边形EBFD 为菱形.故答案为:AB =BC .【点睛】本题考查菱形的判定、平行四边形的性质、全等三角形的判定与性质,利用数形结合的思想解答是解答本题的关键.21.(1);(2)(3)9【解析】【详解】试题分析:(1)仔细阅读,发现规律:分母有理化,然后仿照规律计算即可求解;(2)根据规律直接写出结果;(3)根据规律写出结果,找出部分互为相反数的特点解析:(13221n n +3)9【解析】【详解】试题分析:(1)仔细阅读,发现规律:分母有理化,然后仿照规律计算即可求解; (2)根据规律直接写出结果;(3)根据规律写出结果,找出部分互为相反数的特点,然后计算即可.试题解析:(1)原式=32(32)(32)-+-=3232--=32-; (2)原式=1(1)(1)n n n n n n +-+++-=1n n +-; 故答案为1n n +-(3)由(2)可知:原式=2﹣1+32-+4﹣3+…+100﹣99=﹣1+100=9.22.(1)y =x+,杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤;(2)0≤y≤13【分析】(1)画出各点,根据图象判断是一次函数,利用待定系数法求解析式,代入数值计算即可;(2)解析:(1)y =14x +12,杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤;(2)0≤y ≤13【分析】(1)画出各点,根据图象判断是一次函数,利用待定系数法求解析式,代入数值计算即可;(2)把把x =50代入解析式,求出最大物重即可确定范围.【详解】解:(1)描点如图所示,这些点在一条直线上,故x ,y 的函数关系是一次函数,设x ,y 的函数关系式:y =kx +b ,∵当x =2时,y =1;x =4时,y =1.5;∴214 1.5k b k b +=⎧⎨+=⎩,解得k=14,b=12,∴x,y的函数关系式:y=14x+12,把x=16代入:y=14x+12,得y=4.5,∴杆上秤砣到秤纽的水平距离为16厘米时,秤钩所挂物重是4.5斤;(2)把x=50代入y=14x+12,得y=13,∴0≤y≤13,∴这杆秤的可称物重范围是0≤y≤13.【点睛】本题考查了一次函数的应用,掌握一次函数解析式的求法是解题关键.23.(1);(2);(3)存在,如图2(见解析),当时,;如图3(见解析),当时,;如图4(见解析),当时,.【分析】(1)先根据线段中点的定义可得,再根据矩形的性质、角平分线的定义可得,从而可得是解析:(1);(2);(3)存在,如图2(见解析),当时,;如图3(见解析),当时,;如图4(见解析),当时,.【分析】(1)先根据线段中点的定义可得,再根据矩形的性质、角平分线的定义可得,从而可得是等腰直角三角形,然后根据等腰直角三角形的性质可得AH的长,最后根据等腰直角三角形的面积公式即可得;(2)先根据平行四边形的性质可得,从而可得,再根据三角形中位线定理可得是的中位线,从而可得,然后与(1)所求的建立等式求解即可得;(3)分①当点H是AB的中点时,;②当点Q与点E重合时,;③当时,三种情况,分别求解即可得.【详解】(1)由题意得:,点Q为AP的中点,,四边形ABCD是矩形,,是BAD的角平分线,,,是等腰直角三角形,,则的面积为;(2)如图1,四边形PQHM是平行四边形,,点M在BC边上,,点Q为AP的中点,是的中位线,,由(1)知,,则,解得;(3)由题意,有以下三种情况:①如图2,当点H是AB的中点时,则,四边形PQHM是平行四边形,,,在和中,,,由(2)可知,此时;②如图3,当点Q与点E重合时,在和中,,,,则,解得;③如图4,当时,四边形ABCD是矩形,四边形PQHM是平行四边形,,,在和中,,,,,在中,,是等腰直角三角形,,,在中,,是等腰直角三角形,,则由得:,解得;综上,如图2,当时,;如图3,当时,;如图4,当时,.【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点,较难的是题(3),依据题意,正确分三种情况讨论并画出图形是解题关键.24.(1);(2);(3)或或【解析】【分析】(1)直接利用待定系数法,即可得出结论;(2)先求出AD =3,AB =5,进而求出点D 的坐标,再构造出△BMF ≌△FND ,得出BM =FN ,FM =DN ,解析:(1)334y x =+;(2)197(,)55F -;(3)5(,3)2E -或3312(,)105-或73(,)105- 【解析】 【分析】(1)直接利用待定系数法,即可得出结论;(2)先求出AD =3,AB =5,进而求出点D 的坐标,再构造出△BMF ≌△FND ,得出BM =FN ,FM =DN ,设F (m ,n ),进而建立方程组求解,即可得出结论;(3)分两种情况,①当ABC ABE '≌时,利用中点坐标公式求解,即可得出结论;②当ABC BAE ≌时,当点E 在AB 上方时,根据AE ∥BC ,AE BC =即可得出结论;③当点E在AB 下方时,过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴,过点E '作E P BP '⊥,证明QAE PBE '''△≌△,即可得出结论.【详解】(1)设直线AB 的函数表达式为y kx b =+,直线AB 交y 轴于点A (0,3),交x 轴于点B (﹣4,0),403k b b -+=⎧∴⎨=⎩ 343k b ⎧=⎪∴⎨⎪=⎩ ∴直线AB 的函数表达式为334y x =+;(2)如图,过点D 分别引,x y 轴的垂线,交,x y 轴于,G H 两点,∵点A (0,3),点B (-4,0),∴OA =3,OB =4, ∴AB=5, 由折叠知,AD =OA =3, 532DB ∴=-=设(,)D a b -(0,0)a b >>,DG b DH a ∴==,4,3BG a AH b =-=- 222222,AD DH AH DB BG DG =+=+∴()()2222223342a b a b ⎧+-=⎪⎨-+=⎪⎩ 解得:436a b -=D 在334y x =+上,334b a ∴=-+4363412a b a b -=⎧∴⎨+=⎩解得12565a b ⎧=⎪⎪⎨⎪=⎪⎩,126(,)55D ∴-, 过点F 作FM ⊥x 轴于M ,延长HD 交FM 于N , ∴∠BMF =∠FND =90°, ∴∠BFM +∠FBM =90°, ∵△BFD 是等腰直角三角形, ∴BF =DF ,∠BFD =90°, ∴∠BFM +∠DFN =90°, ∴∠FBM =∠DFN , ∴△BMF ≌△FND (AAS ), ∴BM =FN ,FM =DN , 设F (m ,n ), 则125645n m n m ⎧=--⎪⎪⎨⎪-=+⎪⎩19575m n ⎧=-⎪⎪∴⎨⎪=⎪⎩197(,)55F ∴-; (3)设OC =a ,则BC =4-a ,由折叠知,∠BDC =∠ADC =∠AOC =90°,CD =OC =a , 在Rt △BDC 中,222BC CD BD =+, ∴()2244a a -=+,∴a =32,335(,0),,222C OC BC ∴-==,∵点A ,B ,E 为顶点的三角形与△ABC 全等, ①当△ABC ≌△ABE '时, ∴BE '=BC ,∠ABC =∠ABE ', 连接CE '交AB 于D ,则CD =E 'D ,CD ⊥AB ,由(1)知, 126(,)55D - 设E '(b ,c ), ∴131216(),(0)22525b c -=-+= ∴3312,105b c =-=, ∴3312(,)105E '-; ②当△ABC ≌BAE 时,当点E 在AB 上方时, ∴AC =BE ,BC =AE ,EAB CBA =∠∠, ∴AE ∥BC ,∴5(,3)2E -;③当点E 在AB 下方时,AC =BE '',BC =AE '',ABC ABE '△≌△,∴BC BE '=,当ABC BAE ''△≌△时, ABE BAE '''∴△≌△,AE BE '''∴=,BAE ABE '''∠=∠,过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴,过点E '作E P BP '⊥,//PB AQ ∴,90P AQE ''∠=∠=︒,PBA QAB ∴∠=∠,PBA ABE QAB BAE '''∴∠-∠=∠-, 即PBE QAE '''∠=∠,90P AQE ''∠=∠=︒, QAE PBE '''∴△≌△,,PE QE AQ PE ''''∴==, 点3312(,)105E '-,(4,0)B -, ∴AQ PB ==125,PE QE '''==33741010-+=,123355OQ ∴=-=, ∴73(,)105E ''-, ∴满足条件的点E 的坐标为5(,3)2E -或3312(,)105-或73(,)105-. 【点睛】本题考查了待定系数法,折叠的性质,等腰直角三角形的性质,全等三角形的判定和性质,平移的性质,勾股定理,中点坐标公式,构造出全等三角形,分类讨论是解题的关键.25.(1)见解析;(2)不变,见解析;(3)能,或 【分析】(1)由折叠的性质得到BE=EP ,BF=PF ,得到BE=BF ,根据菱形的性质得到AB ∥CD ∥FG ,BC ∥EH ∥AD ,于是得到结论; (2)由解析:(1)见解析;(2)不变,见解析;(3)能,1x =1【分析】(1)由折叠的性质得到BE=EP ,BF=PF ,得到BE=BF ,根据菱形的性质得到AB ∥CD ∥FG ,BC ∥EH ∥AD ,于是得到结论;(2)由菱形的性质得到BE=BF ,AE=FC ,推出△ABC 是等边三角形,求得∠B=∠D=60°,得到∠B=∠D=60°,于是得到结论;(3)记AC 与BD 交于点O ,得到∠ABD=30°,解直角三角形得到AO=1,S 四边形ABCDAEFCHG 时,得到S △BEF +S △DGH GH 与BD 交于点M ,求得GM=12x ,根据三角形的面积列方程即可得到结论.【详解】解:()1折叠后B 落在BD 上, ,BE EP ∴=BF PF =BD 平分,ABC ∠BE BF ∴=,∴四边形BEPF 为菱形,同理四边形GDHP 为菱形,////,// //,AB CD FG BC EH AD ∴ ∴四边形AEPG 为平行四边形,AG EP BE ∴==.()2不变.理由如下:由()1得.AG BE = 四边形BEPF 为菱形, ,.BE BF AE FC ∴==60,BAC ABC ∠=︒为等边三角60B D ∴∠=∠=︒,,,EF BE GH DG ∴==36AEFCHG C AE EF FC CH GH AG AB ∴=+++++==六边形为定值.()3记AC 与BD 交于点O .2,60,AB BAC =∠= 30,ABD ∴∠=1,AO ∴=3,BO 12332ABCS∴=⨯23ABCD S ∴=四边形当六边形AEFCHG 53453233344DEFDGH SS +=由()1得BE AG =AE DG ∴= DG x =2BE x ∴=-记GH 与BD 交于点,M12GM x ∴=,3DM = 23DHGSx ∴= 同理)2233233BEFS x x =-= 223333334x x +化简得22410,x x -+= 解得121x =221x = ∴当21x =21AEPCHG 534 【点睛】此题是四边形的综合题,主要考查了菱形的性质,等边三角形的判定和性质,三角形的面积公式,菱形的面积公式,解本题的关键是用x 表示出相关的线段,是一道基础题目.。
八年级数学下册期末试卷易错题(Word版含答案)

八年级数学下册期末试卷易错题(Word版含答案)一、选择题1.下列式子中不一定是二次根式的是()A.3B.4C.a D.2a 2.下列条件中,满足ABC是直角三角形的是()A.∠A:∠B:∠C=3:4:5 B.a:b:c=1:3:1C.(a+b)2=c2+2ab D.111,,51213 a b c===3.下列说法中:①一组对边平行,另一组对边相等的四边形是平行四边形②对角线相等的四边形是矩形③有一组邻边相等的矩形是正方形④对角线互相垂直的四边形是菱形,正确的个数是().A.1个B.2个 C.3个D.4个4.小明和小兵两人参加了5次体育项目训练,其中小明5次训练测试的成绩分别为11、13、11、12、13;小兵5次训练测试成绩的平均分为12,方差为7.6.关于小明和小兵5次训练测试的成绩,则下列说法不正确的是()A.两人测试成绩的平均分相等B.小兵测试成绩的方差大C.小兵测试的成绩更稳定些D.小明测试的成绩更稳定些5.如图,将△ABC放在正方形网格中(图中每个小正方形边长均为1)点A,B,C恰好在网格图中的格点上,那么∠ABC的度数为()A.90°B.60°C.30°D.45°6.如图,在菱形ABCD中,CE AB⊥于点E,E点恰好为AB的中点,则菱形ABCD的较大内角度数为()A.100°B.120°C.135°D.150°7.如图,在长方形ABCD中,分别按图中方式放入同样大小的直角三角形纸片.如果按图①方式摆放,刚好放下4个;如果按图②方式摆放,刚好放下3个.若BC=4a,则按图③方式摆放时,剩余部分CF的长为()A.23aB.32aC.53aD.35a8.如图1,在矩形ABCD的边AD上取一点E,连接BE.点M,N同时以1cm/s的速度从点B出发,分别沿折线B-E-D-C和线段BC向点C匀速运动.连接MN,DN,设点M运动的时间为t s,△BMN的面积为S cm2,两点运动过程中,S与t的函数关系如图2所示,则当点M在线段ED上,且ND平分∠MNC时,t的值等于()A.2+25B.4+25C.14﹣25D.12﹣25二、填空题9.若121xx -+有意义,则x的取值范围为_______________.10.若菱形的两条对角线长分别是8cm和10cm,则该菱形的面积是________2cm.11.如图,每个方格都是边长为1的小正方形,则AB+BC=_____.12.如图,矩形ABCD的对角线相交于O,AB=2,∠AOB=60°,则对角线AC的长为___.13.经过点(2,0)且与坐标轴围成的三角形面积为2的直线解析式是__________________. 14.如图,矩形ABCD中,AB2,AD=2.点E是BC边上的一个动点,连接AE,过点D作DF⊥AE于点F.当△CDF是等腰三角形时,BE的长为_____.15.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y (米)与时间t (分)的关系图象,则小明回家的速度是每分钟步行____________米.16.小明从家步行到学校需走的路程为1800米.图中的折线OAB 反映了小明从家步行到学校所走的路程s (米)与时间t (分钟)的函数关系,根据图象提供的信息,当小明从家出发去学校步行15分钟时,到学校还需步行____米.三、解答题17.计算(1)321224843274⎛⎫÷+- ⎪ ⎪⎝⎭(2)()()()()0221123223431+-+++--- 18.如图,在甲村到乙村的公路一旁有一块山地正在开发.现A 处需要爆破,已知点A 与公路上的停靠站B ,C 的距离分别为400 m 和300 m ,且AC ⊥AB .为了安全起见,如果爆破点A 周围半径260 m 的区域内不能有车辆和行人,问在进行爆破时,公路BC 段是否需要暂时封闭?为什么19.已知,在边长为1的小正方形组成的48⨯网格中,ABC 的顶点均为格点.,请按要求分别作出ABC ,并解答问题.(1)在图1中作钝角ABC ,图2中作直角ABC ,图3中作锐角ABC ,都使5BC =; (2)在图4中作直角ABC ,AB 为斜边,两直角边长度为无理数,并直接写出ABC 的面积.20.如图,在平行四边形ABCD 中,对角线AC ,BD 相交于点O ,点M 为AD 的中点,过点M 作//MN BD 交CD 延长线于点N .(1)求证:四边形MNDO 是平行四边形;(2)请直接写出当四边形ABCD 的边AB 与BD 满足什么关系时,四边形MNDO 分别是菱形、矩形、正方形.21.阅读,并回答下列问题:公元3世纪,我国古代数学家刘徵就能利用近似公式22r a r a a +≈+得到2的近似值. (1)他的算法是:先将2看成211+,利用近似公式得到1321212≈+=⨯,再将2看成23124⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭,由近似公式得到2≈___________≈______________;依次算法,所得2的近似值会越来越精确.(2)按照上述取近似值的方法,当2取近似值577408时,求近似公式中的a 和r 的值. 22.某农科所为定点帮扶村免费提供一种优质番茄苗及大棚栽培技术.这种番茄苗早期在温室中生长,长到大约20cm 时,移至大棚内,沿插杆继续向上生长.研究表明,30天内,这种番茄苗生长的高度()cm y 与生长时间x (天)之间的关系大致如图所示.(1)求y 与x 之间的函数关系式;(2)当这种番茄苗长到大约65cm 时,开始开花,试求这种番茄苗移至大棚后.继续生长大约多少天,开始开花?23.问题发现:(1)如图1,点A 为线段BC 外一动点,且BC =a ,AB =b .填空:当点A 位于CB 延长线上时,线段AC 的长可取得最大值,则最大值为 (用含a ,b 的式子表示);尝试应用:(2)如图2所示,△ABC 和△ADE 均为等腰直角三角形,∠BAC =∠DAE =90°,M 、N 分别为AB 、AD 的中点,连接MN 、CE .AD =5,AC =3.①请写出MN 与CE 的数量关系,并说明理由.②直接写出MN 的最大值.(3)如图3所示,△ABC 为等边三角形,DA =6,DB =10,∠ADB =60°,M 、N 分别为BC 、BD 的中点,求MN 长.(4)若在第(3)中将“∠ADB =60°”这个条件删除,其他条件不变,请直接写出MN 的取值范围.24.如图,在平面直角坐标系中,直线24y x =+与x 轴交于点A ,与y 轴交于点B ,过点B 的直线交x 轴正半轴于C ,且ABC ∆面积为10.(1)求点C 的坐标及直线BC 的解析式;(2)如图,设点F 为线段AB 中点,点G 为y 轴上一动点,连接FG ,以FG 为边向FG 右侧作正方形FGQP ,在G 点的运动过程中,当顶点Q 落在直线BC 上时,求点G 的坐标; (3)如图2,若M 为线段BC 的中点,点E 为直线OM 上一动点,在x 轴上是否存在点D ,使以点D ,E ,B ,C 为顶点的四边形为平行四边形?若存在,请直接写出点D 的坐标;若不存在,请说明理由.25.定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径。
八年级数学下册期末试卷易错题(Word版含答案)

八年级数学下册期末试卷易错题(Word 版含答案) 一、选择题 1.()()1111a a a a +-=+⋅-成立的条件是( )A .﹣1≤a ≤1B .a ≤﹣1C .a ≥1D .﹣1<a <1 2.下列各比值中,是直角三角形的三边之比的是( ) A .1:2:3 B .2:3:4 C .3:4:5 D .1:3:1 3.在四边形ABCD 中,对角线AC 与BD 相交于点O ,下列条件不能判定这个四边形是平行四边形的是( )A .AB ∥DC ,AD ∥BCB .AD ∥BC ,AB =DC C .AB ∥DC ,∠DAB =∠DCBD .AO =CO ,BO =DO4.期间,红星中学门卫对周末提前返校的5名学生进行体温检测,记录如下:36.1℃,36.5℃,36.9℃,36.5℃,36.6℃,则这5名学生体温的众数是( )A .36.1℃B .36.6℃C .36.5℃D .36.9℃ 5.如图,在矩形纸片ABCD 中,AB =6,AD =8,折叠该纸片,使得AB 边落在对角线AC 上,点B 落在点F 处,折痕为AE ,则线段EF 的长为( )A .3B .4C .5D .66.如图,在菱形ABCD 中,8AB =,120BAD ∠=︒,点O 是对角线BD 的中点,OE CD ⊥于点E ,则OE 的长为( )A .23B .3C .4D .437.如图,在平行四边形ABCD 中,BD 为对角线,点O 是BD 的中点,且//AD EO ,//OF AB ,四边形BEOF 的周长为10,则平行四边形ABCD 的周长为( )A .10B .12C .15D .208.如图所示,已知点C (1,0),直线7y x =-+与两坐标轴分别交于A ,B 两点,D ,E 分别是线段AB ,OA 上的动点,则△CDE 的周长的最小值是( )A .42B .10C .424+D .12二、填空题 9.若式子1x x -在实数范围内有意义,则x 的取值范围是________. 10.若菱形的两条对角线长分别是8cm 和10cm ,则该菱形的面积是________2cm . 11.若一直角三角形的两直角边长为3,1,则斜边长为_____.12.如图,矩形ABCD 被两条对角线分成四个小三角形,如果四个小三角形的周长的和是40厘米,矩形的周长是22厘米,则对角线AC 的长为 ___厘米.13.在平面直角坐标系中,直线1y kx =-与直线3y x =-交于点(4,)A m ,则k =______. 14.如图,在正方形ABCD 中,点E 、F 分别在对角线BD 上,请你添加一个条件____________,使四边形AECF 是菱形.15.A ,B 两地相距60km ,甲、乙两人从两地出发相向而行,甲先出发,如图,l 1,l 2表示两人离A 地的距离:s (km )与时间t (h )的关系,则乙出发_____h 两人恰好相距5千米.16.“以自然之道,养自然之身”,生命在于运动,周末,小靓和小丽先后来到山脚,从山脚出发,沿着同一直线型登山步道进行锻炼,当小靓先匀速前行400米到达途中A 地观景台时,小丽开始从山脚匀速追赶,小靓继续以原速前行.追上后,小靓立即以原速的2倍率先到达山顶,然后立即以提高后的速度原路返回山脚.在上山过程中,小丽一直保持匀速登山,到达山顶后,立即以上山速度的1.5倍原路返回山脚.两人距A 地观景台的距离之和y (米)与小丽从山脚出发的时间t 分钟之间的部分函数关系如图所示,则两人第三次相遇时距A 地观景台________米.三、解答题17.计算:(1)02(52)()π++-;(2)3127683-+-. 18.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA 静止的时候,踏板离地高一尺(1AC =尺),将它往前推进两步(10EB =尺),此时踏板升高离地五尺(5BD =尺),求秋千绳索(OA 或OB )的长度.19.如图,每个小正方形的边长都为1.(1)求线段CD 与BC 的长;(2)求四边形ABCD 的面积与周长;(3)求证:90BCD ∠=︒.20.如图,在矩形ABCD 中,4AB =,8AD =,将矩形折叠,折痕为EF ,使点C 与点A 重合,点D 与点G 重合,连接CF .(1)判断四边形AECF 的形状,并说明理由;(2)求折痕EF 的长.21.[观察]请你观察下列式子的特点,并直接写出结果:221111111212++=+-= ; 221111112323++=+-= ; 221111113434++=+-= ; …… [发现]根据你的阅读回答下列问题:(1)请根据上面式子的规律填空: ()221111n n ++=+ (n 为正整数); (2)请证明(1) 中你所发现的规律.[应用]请直接写出下面式子的结果: ()222222221111111111111223341n n ++++++++++ .22.由于持续高温和连日无雨,某水库的蓄水量y (万立方米)与干旱时间t (天)之间的关系满足一次函数y kt b =+,(k ,b 为常数,且k ≠0),其图象如图所示.(1)由图象知k = ,其实际意义是 ;(2)若水库的蓄水量小于360万立方米时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?(3)在(2)的条件下,照这样干旱下去,预计再持续多少天,水库将干涸?23.(1)如图1,在平行四边形ABCD 中,对角线AC 、BD 相交于O 点,过点O 的直线l 与边AB 、CD 分别交于点E 、F ,绕点O 旋转直线l ,猜想直线l 旋转到什么位置时,四边形AECF 是菱形.证明你的猜想.(2)若将(1)中四边形ABCD 改成矩形ABCD ,使AB =4cm ,BC =3cm ,①如图2,绕点O 旋转直线l 与边AB 、CD 分别交于点E 、F ,将矩形ABCD 沿EF 折叠,使点A 与点C 重合,点D 的对应点为D′,连接DD′,求△DFD′的面积.②如图3,绕点O 继续旋转直线l ,直线l 与边BC 或BC 的延长线交于点E ,连接AE ,将矩形ABCD 沿AE 折叠,点B 的对应点为B′,当△CEB′为直角三角形时,求BE 的长度.请直接写出结果,不必写解答过程.24.如图,在平面直角坐标系中,直线24y x =+与x 轴交于点A ,与y 轴交于点B ,过点B 的直线交x 轴正半轴于C ,且ABC ∆面积为10.(1)求点C 的坐标及直线BC 的解析式;(2)如图,设点F 为线段AB 中点,点G 为y 轴上一动点,连接FG ,以FG 为边向FG 右侧作正方形FGQP ,在G 点的运动过程中,当顶点Q 落在直线BC 上时,求点G 的坐标; (3)如图2,若M 为线段BC 的中点,点E 为直线OM 上一动点,在x 轴上是否存在点D ,使以点D ,E ,B ,C 为顶点的四边形为平行四边形?若存在,请直接写出点D 的坐标;若不存在,请说明理由.25.在平面直角坐标中,四边形OCNM 为矩形,如图1,M 点坐标为(m ,0),C 点坐标为(0,n ),已知m ,n 满足550n m -+-=.(1)求m ,n 的值;(2)①如图1,P ,Q 分别为OM ,MN 上一点,若∠PCQ =45°,求证:PQ =OP+NQ ; ②如图2,S ,G ,R ,H 分别为OC ,OM ,MN ,NC 上一点,SR ,HG 交于点D .若∠SDG =135°,55HG =,则RS =______; (3)如图3,在矩形OABC 中,OA =5,OC =3,点F 在边BC 上且OF =OA ,连接AF ,动点P 在线段OF 是(动点P 与O ,F 不重合),动点Q 在线段OA 的延长线上,且AQ =FP ,连接PQ 交AF 于点N ,作PM ⊥AF 于M .试问:当P ,Q 在移动过程中,线段MN 的长度是否发生变化?若不变求出线段MN 的长度;若变化,请说明理由.【参考答案】一、选择题1.C解析:C【分析】直接利用二次根式有意义的条件、二次根式的乘法运算法则得出关于a 的不等式组,进而得出答案.【详解】解:由题意可得:1010a a +≥⎧⎨-≥⎩, 解得:a ≥1,故选:C .【点睛】本题考查二次根式有意义的条件,掌握二次根式有意义的条件是解题的关键.2.C解析:C【分析】先分别设三角形的三边,依据勾股定理的逆定理列式计算即可判断.【详解】解:A、设三边分别为x、2x、3x,∵222+≠,x x x(2)(3)∴三边比为1:2:3的三角形不是直角三角形;B、设三边分别为2x、3x、4x,∵222+≠,x x x(2)(3)(4)∴三边比为2:3:4的三角形不是直角三角形;C、设三边分别为3x、4x、5x,∵222+=,x x x(3)(4)(5)∴三边比为3:4:5的三角形是直角三角形;D、设三边分别为x、3x、x,∵222(3)+≠,x x x∴三边比为1:3:1的三角形不是直角三角形;故选:C.【点睛】此题考查应用勾股定理的逆定理判断三角形是否是直角三角形,熟记定理并应用解决问题是解题的关键.3.B解析:B【解析】【分析】依据平行四边形的定义和判定方法逐一判断即可得解;【详解】A、∵AB∥DC,AD∥BC,∴四边形ABCD是平行四边形,故选项A不符合题意;B、由AD∥BC,AB=DC,即一组对边平行,一组对边相等,无法判断四边形ABCD是平行四边形,举反例如等腰梯形,故选项B符合题意;C、∵AB∥DC,∴∠ABC+∠DCB=180°,∠DAB+∠ADC=180°,∵∠DAB=∠DCB,∴∠ABC=∠ADC,∴四边形ABCD是平行四边形,故选项C不符合题意;D、∵AO=CO,BO=DO,∴四边形ABCD是平行四边形,故选项D不符合题意;故选:B.【点睛】本题主要考查平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键,同时注意一组对边平行,一组对边相等得四边形不一定是平行四边形.4.C解析:C【解析】【分析】根据众数的定义:一组数据中出现次数最多的数据,进行求解即可.【详解】解:∵36.5℃出现了两次,出现的次数最多,∴这组数据的众数为36.5℃,故选C.【点睛】本题主要考查了众数的定义,解题的关键在于能够熟知众数的定义.5.A解析:A【分析】根据矩形的性质可得BC=AD,∠B=90°,利用勾股定理可求出AC的长,根据折叠的性质可得AF=AB,∠B=∠AFE=90°,BE=EF,在Rt△CEF中利用勾股定理列方程求出EF的长即可得答案.【详解】∵四边形ABCD是矩形,AD=8,∴∠B=90°,BC=AD=8,∴AC10,∵折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,∴BE=EF,AF=AB=6,∠AFE=∠B=90°,∴CF=AC-AF=10﹣6=4,在Rt△CEF中,由勾股定理得,EF2+CF2=CE2,∴EF2+CF2=(BC-EF)2,即EF2+42=(8-EF)2,解得:EF=3,故选:A.【点睛】本题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.6.A解析:A【解析】【分析】连接OA ,由菱形的性质得AD =AB =8、AO ⊥BD 、∠ADB =∠CDB =30°,然后由含30°角的直角三角形的性质求解即可.【详解】连接OA ,如图所示:∵四边形ABCD 为菱形,点O 是对角线BD 的中点,∴AD =AB =8,AO ⊥BD ,∠ADB =∠CDB∵120BAD ∠=︒∴∠ADB =∠CDB =30°,在Rt △AOD 中,142OA AD ==, ∴2243OD AD OA =-=∵OE ⊥CD ,∴∠DEO =90°,∴在Rt △DOE 中,1232OE OD == 故选:A .【点睛】本题考查了菱形的性质、含30°角的直角三角形的性质等知识;熟练掌握菱形的性质是解题的关键.7.D解析:D【解析】【分析】根据点O 是BD 的中点,且AD //EO ,OF //AB ,可得OE ,OF 分别是三角形ABD ,三角形BCD 的中位线,四边形OEBF 是平行四边形,则AD =2OE ,CD =2OF ,OE =BF ,OF =BE ,由此可以推出OE +OF =5,再由四边形ABCD 的周长=AB +BC +AD +CD =2(AD +CD )=4(OE +OF )进行求解即可.【详解】解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,∵点O 是BD 的中点,且AD //EO ,OF //AB ,∴OE ,OF 分别是三角形ABD ,三角形BCD 的中位线,BC //EO ,∴四边形OEBF 是平行四边形,AD =2OE ,CD =2OF ,OE =BF ,OF =BE ,∵四边形OEBF 的周长为10,∴OE+BE+BF+OF=10,∴OE+OF=5,∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∴四边形ABCD的周长=AB+BC+AD+CD=2(AD+CD)=4(OE+OF)=20,故选D.【点睛】本题主要考查了平行四边形的性质与判定,中位线定理,解题的关键在于能够熟练掌握相关知识进行求解.8.B解析:B【解析】【分析】点C关于OA的对称点C′(-1,0),点C关于直线AB的对称点C″(7,6),连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,可以证明这个最小值就是线段C′C″.【详解】解:如图,点C(1,0)关于y轴的对称点C′(-1,0),点C关于直线AB的对称点C″,∵直线AB的解析式为y=-x+7,∴直线CC″的解析式为y=x-1,由71 y xy x-+⎧⎨-⎩==解得43xy==⎧⎨⎩,∴直线AB与直线CC″的交点坐标为K(4,3),∵K是CC″中点,C(1,0),设C″坐标为(m,n),∴14232mn+⎧=⎪⎪⎨+⎪=⎪⎩,解得:76mn=⎧⎨=⎩∴C″(7,6).连接C′C″与AO交于点E,与AB交于点D,此时△DEC周长最小,△DEC的周长=DE+EC+CD=EC′+ED+DC″=C′C10故答案为10.【点睛】本题考查轴对称-最短问题、两点之间距离公式等知识,解题的关键是利用对称性在找到点D、点E位置,将三角形的周长转化为线段的长.二、填空题9.1x>【解析】【分析】利用分式和二次根式有意义的条件确定关于x的不等式,从而确定答案.【详解】解:根据题意得:10x-≥且10x-≠,∴10x->,解得:1x>,故答案为:1x>.【点睛】考查了二次根式及分式有意义的条件,属于基础题,比较简单.10.40【解析】【分析】根据菱形的面积公式计算即可.【详解】解:这个菱形的面积为:12×8×10=40cm2,故答案为:40【点睛】本题主要考查菱形的面积公式,熟知菱形的面积等于两条对角线乘积的一半是解题关键.11.2【解析】【分析】根据勾股定理计算,得到答案.【详解】2,故答案为2.【点睛】本题考查的是勾股定理,如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.12.A解析:5【分析】根据矩形性质得出OA=OB=OC=OD,AB=CD,AD=BC,求出8OA+2AB+2BC=40厘米和2AB+2BC=22厘米,求出OA,即可求出答案.【详解】解:∵四边形ABCD是矩形,∴AB=CD,AD=BC,AC=BD,AO=OC,OD=OB,∴AO=OC=OD=OB,∵矩形ABCD被两条对角线分成四个小三角形的周长的和是40厘米,∴OA+OD+AD+OD+OC+CD+OC+OB+BC+OA+OB+AB=40厘米,即8OA+2AB+2BC=40厘米,∵矩形ABCD的周长是22厘米,∴2AB+2BC=22厘米,∴8OA=18厘米,∴OA=2.25厘米,即AC=BD=2OA=4.5厘米.故答案为:4.5.【点睛】本题考查了矩形的性质的应用,注意:矩形的对边相等,矩形的对角线互相平分且相等.13.A解析:12【分析】利用y=x-3即可求得m的值,然后再把该点代入y=kx-1中可得k的值.【详解】解:把(4,m)代入y=x-3得:m=1,∴A(4,1),把(4,1)代入y=kx-1得1=4k-1,,解得k=12故答案为1.2【点睛】本题考查了两直线相交问题,首先会利用代入法求点的坐标,然后再根据待定系数法求k.14.B解析:BE=DF【分析】根据正方形的性质,可得正方形的四条边相等,对角线平分对角,根据 SAS,可得△ABF与△CBF与△CDE与△ADE的关系,根据三角形全等,可得对应边相等,再根据四条边相等的四边形,可得证明结果.【详解】添加的条件为:BE=DF,理由:正方形ABCD中,对角线BD,∴AB=BC=CD=DA,∠ABE=∠CBE=∠CDF=∠ADF=45°.∵BE=DF,∴△ABE≌△CBE≌△DCF≌△DAF(SAS).∴AE=CE=CF=AF,∴四边形AECF是菱形;故答案为:BE=DF.【点睛】本题考查了正方形的性质,菱形的判定,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.15.8或1【分析】分相遇前或相遇后两种情形分别列出方程即可解决问题.【详解】解:由题意可知,乙的函数图象是l2,甲的速度是=30(km/h),乙的速度是=20(km/h).设乙出发x小时两人解析:8或1【分析】分相遇前或相遇后两种情形分别列出方程即可解决问题.【详解】解:由题意可知,乙的函数图象是l2,甲的速度是602=30(km/h),乙的速度是603.50.5=20(km/h).设乙出发x小时两人恰好相距5km.由题意得:30(x+0.5)+20x+5=60或30(x+0.5)+20x﹣5=60,解得x=0.8或1,所以甲出发0.8小时或1小时两人恰好相距5km.故答案为:0.8或1.本题考查了一次函数的应用,解题的关键是读懂图象信息,灵活应用速度、路程、时间之间的关系解决问题.16.【分析】设小靓和小丽开始的速度分别为每分钟a 米和每分钟b 米,分析可知小丽出发第5分钟时,小丽追上了小靓,在这5分钟小丽比小靓多走400米;第11分钟时,小丽到达了山顶,此时y=3360;据此列方解析:【分析】设小靓和小丽开始的速度分别为每分钟a 米和每分钟b 米,分析可知小丽出发第5分钟时,小丽追上了小靓,在这5分钟小丽比小靓多走400米;第11分钟时,小丽到达了山顶,此时y=3360;据此列方程组求出a 和b ;然后求出小丽下山追上小靓的时间,即可求出两人第三次相遇时与A 地观景台的距离.【详解】解:设小靓和小丽开始的速度分别为每分钟a 米和每分钟b 米,函数关系图可知,小丽出发第5分钟时,小丽追上了小靓,在这5分钟小丽比小靓多走400米;第11分钟时,小丽到达了山顶,此时y=3360,此时小靓距离山顶(12a-6b)米,距A 地观景台(5a+6b) -(12a-6b)=(12b-7a)米,∴55400(56)(127)3360b a a b b a -=⎧⎨++-=⎩ ∴120200a b =⎧⎨=⎩∴A 地观景台距离山顶512062001800⨯+⨯=米,第11分钟时小靓距离山顶121206200240⨯-⨯=米,∴小丽下山追上小靓所需时间= 240(1.52002120)4÷⨯-⨯=(分钟)此时距离A 地观景台=1800 1.52004600-⨯⨯=,两人第三次相遇时距A 地观景台600米.故答案是:600.【点睛】本题考查了从函数图象获取信息的能力及二元一次方程组的应用,掌握数形结合思想是解题关键.三、解答题17.(1);(2)【分析】(1)根据二次根式乘法法则及零指数幂计算即可;(2)先把各二次根式化为最简二次根式,然后合并同类二次根式即可.【详解】解:(1)=+3;(2)=3-解析:(13;(22【分析】(1)根据二次根式乘法法则及零指数幂计算即可;(2)先把各二次根式化为最简二次根式,然后合并同类二次根式即可.【详解】解:(10()π+-2+13;(2=2,2.【点睛】此题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算;注意乘法运算公式的运用.18.秋千绳索的长度为尺.【分析】设OA=OB=x 尺,表示出OE 的长,在中,利用勾股定理列出关于x 的方程求解即可.【详解】解:设尺,由题可知:尺,尺,∴(尺),尺,在中,尺,尺,尺,由勾股解析:秋千绳索的长度为14.5尺.【分析】设OA =OB =x 尺,表示出OE 的长,在Rt OEB 中,利用勾股定理列出关于x 的方程求解即可.【详解】解:设OA OB x ==尺,由题可知:5EC BD ==尺,1AC =尺,∴514EA EC AC =-=-=(尺),()4OE OA AE x =-=-尺,在Rt OEB 中,()4OE x =-尺,OB x =尺,10EB =尺,由勾股定理得:()222410x x =-+,解得:14.5x =,则秋千绳索的长度为14.5尺.【点睛】本题考查了勾股定理的应用,熟练掌握勾股定理,学会利用方程解决问题是解题的关键. 19.(1),;(2)四边形的面积,的周长;(3)见解析【解析】【分析】(1)利用勾股定理直接计算即可得到答案;(2)利用四边形的周长公式计算四边形的周长即可,再利用割补法求解四边形的面积即可;解析:(1)BC =CD =2)四边形ABCD 的面积12.5=,ABCD 的周长5=;(3)见解析【解析】【分析】(1)利用勾股定理直接计算即可得到答案;(2)利用四边形的周长公式计算四边形的周长即可,再利用割补法求解四边形的面积即可;(3)利用勾股定理的逆定理证明即可.【详解】解:(1)BC =CD(2)5AB =,AD∴四边形ABCD 的周长55=,四边形ABCD 的面积111542124311222=⨯-⨯⨯-⨯⨯-⨯⨯- 2014 1.51=----12.5=(3)连接BD ,5BD =,222225BC CD +=+=,22525BD ==,222BC CD BD ∴+=,90BCD ∴∠=︒.【点睛】本题考查的是勾股定理与勾股定理的逆定理的应用,掌握利用勾股定理求解边长,利用勾股定理的逆定理判断直角三角形是解题的关键.20.(1)菱形,理由见解析;(2)【分析】(1)根据矩形的性质,可知,进而可得,根据折叠的性质可知,则,进而可得,又,根据四边相等的四边形是菱形即可判断;(2)连接,先根据折叠的性质,利用勾股定理解析:(1)菱形,理由见解析;(2)25【分析】(1)根据矩形的性质,可知//AD BC ,进而可得AFE AEF ∠=∠,根据折叠的性质可知CEF AEF ∠=∠,则AFE AEF ∠=∠,进而可得AF AE =,又,AF CF AE EC ==,根据四边相等的四边形是菱形即可判断;(2)连接AC ,先根据折叠的性质,利用勾股定理求得AF ,进而勾股定理求得AC ,根据菱形的面积12AF AB AC EF ⋅=⋅即可求得EF . 【详解】(1)四边形ABCD 是矩形,∴//AD BC ,∴AFE AEF ∠=∠, 根据折叠的性质,可知CEF AEF ∠=∠,,AF CF AE EC ==,∴AFE AEF ∠=∠,∴AF AE =,∴AF CF AE EC ===,∴四边形AECF 是菱形;(2)连接AC ,如图,四边形ABCD 是矩形,90B BCD ∴∠=∠=︒,4AB =,8AD =,2245AC AB BC ∴+=折叠,90G BCD ∴∠=∠=︒4,AG CD AB GF FG ====,设AF x =,则8GF FD AD AF x ==-=-,在Rt AGF △中,222AF AG FG =+,即222(8)4x x =-+,解得5x =,5AF ∴=,12AF AB AC EF ⋅=⋅, 22545AF AB EF AC ⋅∴===【点睛】本题考查了矩形的性质,折叠的性质,勾股定理,菱形的性质与判定,灵活晕用勾股定理是解题的关键.21.[观察],,;[发现](1)或;(2)证明见解析;[应用]或.【解析】【分析】(1)计算题目中结果,并根据计算过程和结果,总结得到一般规律,作出猜想,并对猜想进行计算,即可进行证明;(2)运解析:[观察]32,76,1312;[发现](1)1111n n +-+或221n n n n+++;(2)证明见解析;[应用]1n n n ++或221n n n ++. 【解析】【分析】(1)计算题目中结果,并根据计算过程和结果,总结得到一般规律,作出猜想,并对猜想进行计算,即可进行证明;(2)运用(1)中发现规律,进行计算即可.【详解】[观察]32,76,1312, [发现](1)1111n n +-+或221n n n n +++(2)左=====∵n 为正整数,∴()11111011n n n n +-=+>++ ∴左1111n n =+-=+右[应用11n +++111111111111223341n n =+-++-++-+++-+ (1111)n n =⨯+-+ 1n n n =++ 22=1n n n ++ ∴答案为:1n n n ++或221n n n ++. 【点睛】(1)此类规律探究问题一定要结合式子特点和数的规律进行探究,类比;(2)此类题目往往无法直接进行计算,一般要根据规律进行变形,往往会消去部分中间项,实现简化运算目的.22.(1);水库蓄水量每天减少30万立方米;(2)38;(3)12【分析】(1)根据图像运用待定系数法求得函数解析式即可得k 的值,解释k 的具体意义即可;(2)根据(1)中函数解析式,令万立方米时,解析:(1)30-;水库蓄水量每天减少30万立方米;(2)38;(3)12【分析】(1)根据图像运用待定系数法求得函数解析式即可得k 的值,解释k 的具体意义即可; (2)根据(1)中函数解析式,令360y =万立方米时,求出对应的干旱天数t 即可; (3)根据(1)中函数解析式,令0y =万立方米时,求出对应的干旱天数t ,减去(2)中的干旱天数即为所求.【详解】解:(1)一次函数y kt b =+,(k ,b 为常数,且k ≠0),根据图像可得:900=2030040k b k b+⎧⎨=+⎩, 解得:301500k b =-⎧⎨=⎩, 所以一次函数解析式为:301500y t =-+,k 的值代表每干旱一天水库蓄水量将减少30万立方米,故答案为:-30;水库蓄水量每天减少30万立方米;(2)由(1)知一次函数解析式为:301500y t =-+,令360y =,即360301500t =-+,解得:38t =,故38天后将发生严重干旱警报;(3)由(1)知一次函数解析式为:301500y t =-+,令0y =,即0301500t =-+,解得:50t =,503812-=(天),故预计再持续12天,水库将干涸.【点睛】此题考查了函数的图像问题,一次函数的实际应用,根据图像求出一次函数的解析式是解题的关键.23.(1)四边形AECF 是菱形,见解析;(2)① cm2;②BE 的长为cm 或cm 或4cm 或cm .【分析】(1)根据题意作图,先根据平行四边形得出∠FCO=∠EAO ,再证明△COF ≌△AOE ,结合题意解析:(1)四边形AECF 是菱形,见解析;(2)①147400 cm 2;②BE 的长为43cm 或16473-cm 或4cm 或16473+cm . 【分析】(1)根据题意作图,先根据平行四边形得出∠FCO =∠EAO ,再证明△COF ≌△AOE ,结合题意即可得出结论;(2)①根据四边形ABCD 是矩形,设DF =x cm ,则CF =(4﹣x )cm ,结合折叠和勾股定理得出CF ,过D′作D′H ⊥CF 于H ,由面积相等可得D′H =2125,进而得出所求面积; ②根据不同图示分情况设BE =x cm ,CE =(3﹣x )cm ,根据折叠并结合勾股定理得出x 即为所求.【详解】解:(1)猜想:当l ⊥AC 时,四边形AECF 是菱形,如图1:连接AF 、CE ,∵四边形ABCD 是平行四边形,∴OA =OC ,AB ∥CD ,∴∠FCO =∠EAO ,又∵∠FOC =∠EOA ,∴△COF ≌△AOE , ∴OE =OF ,∵AC ⊥EF ,∴四边形AECF 是菱形;(2)①∵四边形ABCD 是矩形,∴∠ADC =90°,CD =AB =4,AD =BC =3,设DF =x cm ,则CF =(4﹣x )cm ,由折叠性质可知:D′F =DF =x ,CD′=AD =3,∠CD′F =∠ADC =90°,由勾股定理得(4﹣x )2=32+x 2,解得x =78, ∴D′F =DF =78, ∴CF =4﹣78=258, 如图2,过D′作D′H ⊥CF 于H ,由面积相等可得,CF •D′H =D′F •CD′,∴D′H =2125, ∴S △DFD ′=12×78×2125=147400(cm 2); ②如图①,设BE =x cm ,CE =(3﹣x )cm ,∵AC =2234+=5cm ,∴B′C =5﹣4=1cm ,根据勾股定理可得B′C 2+B′E 2=CE 2,即:12+x 2=(3-x )2解得:x =43cm , 如图②,设BE =x cm ,则CE =(3﹣x )cm ,AB′=4cm ,B′E =x cm ,在R t △ADB′中,由勾股定理可得BD′22AB AD '-169-7,B′C =(47cm ,在R t △CB′E 中,B′C 2+CE 2=B′E 2,即16﹣7+7+9﹣6x +x 2=x 2,解得x 1647-cm , 如图③,当四边形ABEB′是正方形时,点B 和点B′关于直线AE 对称,△B′EC 是直角三角形, 此时CE =1cm ,BE =4cm ;如图④,BE =x cm ,AB′=4cm ,AD =3cm ,CE =(x ﹣3)cm ,在R t △ADB′中,B′D 22'AB AD -169-7,B′C 7,在R t △B′CE 中,7x 2﹣6x +9=x 2,解得x 1647+cm , 综上,BE 的长为43cm 1647-或4cm 1647+. 【点睛】此题属于四边形综合性试题,涉及到平行四边形,菱形,矩形,正方形的性质和勾股定理的应用,有一定难度,注意不同情况分别做图求解.24.(1),;(2)或;(3)存在,或或.【解析】【分析】(1)利用三角形的面积公式求出点坐标,再利用待定系数法即可解决问题.(2)设G (0,n )分两种情形:①当时,如图中,点落在上时,过作直线解析:(1)(3,0)C ,443y x =-+;(2)23(0,)7或(0,1)-;(3)存在,(0,0)或(6,0)-或(6,0).【解析】【分析】(1)利用三角形的面积公式求出点C 坐标,再利用待定系数法即可解决问题. (2)设G (0,n )分两种情形:①当2n >时,如图21-中,点Q 落在BC 上时,过G 作直线平行于x 轴,过点F ,Q 作该直线的垂线,垂足分别为M ,N .求出(2,1)Q n n --.②当2n <时,如图22-中,同法可得(2,1)Q n n -+,利用待定系数法即可解决问题.(3)由(0,4)B ,(3,0)C 得3(2M ,2),即得直线OM 为43y x =,设4(,)3E s s ,(,0)D t ,①以BC 、DE 为对角线,此时BC 、DE 中点重合,而BC 中点为03(2+,40)2+,DE 中点为(2s t +,403)2s +,即得0344003s t s +=+⎧⎪⎨+=+⎪⎩,解得(0,0)D ;②以BE 、CD 为对角线,同理可得:(6,0)D -;③以BD 、CE 为对角线,同理(6,0)D .【详解】解:(1)直线24y x =+与x 轴交于点A ,与y 轴交于点B ,(2,0)A ∴-,(0,4)B ,2OA ∴=,4OB =,1102ABC S AC OB ∆=⋅⋅=, 5AC ∴=,3OC ∴=,(3,0)C ∴,设直线BC 的解析式为y kx b =+,则有403bk b =⎧⎨=+⎩, 解得434k b ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为443y x =-+; (2)FA FB =,(2,0)A -,(0,4)B ,(1,2)F ∴-,设(0,)G n ,①当2n >时,如图21-中,点Q 落在BC 上时,过G 作直线平行于x 轴,过点F ,Q 作该直线的垂线,垂足分别为M ,N .四边形FGQP 是正方形,90FGQ ∴∠=︒,=FG QG ,90FGM NGQ GQN ∴∠=︒-∠=∠,而90FMG GNQ ∠=∠=︒,()FMG GNQ AAS ∴∆≅∆,1MG NQ ∴==,2FM GN n ==-,(2,1)Q n n ∴--,点Q 在直线443y x =-+上, 41(2)43n n ∴-=--+, 237n ∴=, 23(0,)7G ∴; ②当2n <时,如图22-中,同法可得(2,1)Q n n -+,点Q 在直线443y x =-+上, 41(2)43n n ∴+=--+, 1n ∴=-,(0,1)G ∴-.综上所述,满足条件的点G 坐标为23(0,)7或(0,1)-; (3)存在,理由如下: (0,4)B ,(3,0)C ,M 为线段BC 的中点,3(2M ∴,2), 设直线OM 为y mx =,则322m =, 解得43m =,∴直线OM 为43y x =, 设4(,)3E s s ,(,0)D t ,①以BC 、DE 为对角线,此时BC 、DE 中点重合,而BC 中点为03(2+,40)2+,DE 中点为(2s t +,403)2s +, ∴0344003s t s +=+⎧⎪⎨+=+⎪⎩,解得30s t =⎧⎨=⎩, (0,0)D ∴;②以BE 、CD 为对角线,同理可得: ∴0344003s t s +=+⎧⎪⎨+=+⎪⎩,解得36s t =-⎧⎨=-⎩, (6,0)D ∴-;③以BD 、CE 为对角线,同理可得: ∴0344003t s s +=+⎧⎪⎨+=+⎪⎩,解得36s t =⎧⎨=⎩, (6,0)D ∴;综上所述,D 的坐标为:(0,0)或(6,0)-或(6,0).【点睛】本题属于一次函数综合题,考查了待定系数法,三角形的面积,全等三角形的判定和性质,正方形的性质,平行四边形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题 25.(1)m =5,n=5;(2)①证明见解析;②;(3)MN 的长度不会发生变化,它的长度为.【分析】(1)利用非负数的性质即可解决问题.(2)①作辅助线,构建两个三角形全等,证明△COE ≌△CNQ解析:(1)m=5,n=5;(2)①证明见解析;②5103;(3)MN的长度不会发生变化,它的长度为102.【分析】(1)利用非负数的性质即可解决问题.(2)①作辅助线,构建两个三角形全等,证明△COE≌△CNQ和△ECP≌△QCP,由PE=PQ=OE+OP,得出结论;②作辅助线,构建平行四边形和全等三角形,可得▱CSRE和▱CFGH,则CE=SR,CF=GH,证明△CEN≌△CE′O和△E′CF≌△ECF,得EF=E′F,设EN=x,在Rt△MEF中,根据勾股定理列方程求出EN的长,再利用勾股定理求CE,则SR与CE相等,所以SR=5103;(3)在(1)的条件下,当P、Q在移动过程中线段MN的长度不会发生变化,求出MN 的长即可;如图4,过P作PD∥OQ,证明△PDF是等腰三角形,由三线合一得:DM=1 2FD,证明△PND≌△QNA,得DN=12AD,则MN=12AF,求出AF的长即可解决问题.【详解】解:(1)∵5|5|0n m-+-=,又∵5n-≥0,|5﹣m|≥0,∴n﹣5=0,5﹣m=0,∴m=5,n=5.(2)①如图1中,在PO的延长线上取一点E,使NQ=OE,∵CN=OM=OC=MN,∠COM=90°,∴四边形OMNC是正方形,∴CO=CN,∵∠EOC=∠N=90°,∴△COE≌△CNQ(SAS),∴CQ=CE,∠ECO=∠QCN,∵∠PCQ=45°,∴∠QCN+∠OCP=90°﹣45°=45°,∴∠ECP=∠ECO+∠OCP=45°,∴∠ECP=∠PCQ,∵CP=CP,∴△ECP≌△QCP(SAS),∴EP=PQ,∵EP=EO+OP=NQ+OP,∴PQ=OP+NQ.②如图2中,过C作CE∥SR,在x轴负半轴上取一点E′,使OE′=EN,得▱CSRE,且△CEN≌△CE′O,则CE=SR,过C作CF∥GH交OM于F,连接FE,得▱CFGH,则CF=GH=552,∵∠SDG=135°,∴∠SDH=180°﹣135°=45°,∴∠FCE=∠SDH=45°,∴∠NCE+∠OCF=45°,∵△CEN≌△CE′O,∴∠E′CO=∠ECN,CE=CE′,∴∠E′CF=∠E′CO+∠OCF=45°,∴∠E′CF=∠FCE,∵CF=CF,∴△E′CF≌△ECF(SAS),∴E′F=EF在Rt△COF中,OC=5,FC 55,由勾股定理得:OF225552⎛⎫-⎪⎪⎝⎭=52,∴FM=5﹣52=52,设EN=x,则EM=5﹣x,FE=E′F=x+52,则(x+52)2=(52)2+(5﹣x)2,解得:x=53,∴EN=53,由勾股定理得:CE2222553CN EN⎛⎫+=+ ⎪⎝⎭510∴SR=CE=5103.故答案为5103.(3)当P、Q在移动过程中线段MN的长度不会发生变化.理由:如图3中,过P作PD∥OQ,交AF于D.∵OF=OA,∴∠OFA=∠OAF=∠PDF,∴PF=PD,∵PF=AQ,∴PD=AQ,∵PM⊥AF,∴DM=12FD,∵PD∥OQ,∴∠DPN=∠PQA,∵∠PND=∠QNA,∴△PND≌△QNA(AAS),∴DN=AN,∴DN=12AD,∴MN=DM+DN=12DF+12AD=12AF,∵OF=OA=5,OC=3,∴CF2222534OF OC--=,∴BF=BC﹣CF=5﹣4=1,∴AF22221310BF AB++∴MN=12AF10∴当P、Q在移动过程中线段MN10【点睛】本题是四边形与动点问题的综合题,考查了矩形、正方形、全等三角形等图形的性质与判定,灵活运用所学知识是解答本题的关键.。
数学八年级下册数学期末试卷易错题(Word版含答案)

数学八年级下册数学期末试卷易错题(Word 版含答案)一、选择题1.已知二次根式21x +,则x 的最小值是( )A .0B .-1C .12D .12-2.要做一个直角三角形的木架,以下面各组木棒为三边,刚好能做成的是( ) A .5,6,7 B .10,4,8C .10,26,24D .9,15,173.下列说法中:①一组对边平行,另一组对边相等的四边形是平行四边形 ②对角线相等的四边形是矩形 ③有一组邻边相等的矩形是正方形④对角线互相垂直的四边形是菱形,正确的个数是( ).A .1个 B .2个 C .3个D .4个4.校篮球队所买10双运动鞋的尺码统计如表,则这10双运动鞋尺码的众数和中位数分别为( ) 尺码(cm ) 25 25.5 26 26.5 27 购买量(双)11242A .4 cm ,26 cmB .4 cm ,26.5 cmC .26.5 cm ,26.5 cmD .26.5 cm ,26 cm 5.在 △ABC 中, AC = 9 , BC = 12 , AB = 15 ,则 AB 边上的高是( ) A .365B .1225C .94D .3346.如图,在△ABC 中,AC =22,∠ABC =45°,∠BAC =15°,将△ABC 沿直线AC 翻折至△ABC 所在的平面内,得△ADC .过点A 作AE ,使∠EAD =∠DAC ,与CD 的延长线交于点E ,则线段ED 的长为( )A .36B .6﹣3C .62D .267.如图,在Rt ABC 中,90C ∠=︒,3AC =,4BC =,点P 为AB 边上任意一点过点P 分别作PE AC ⊥于点E ,PF BC ⊥于点F ,则线段EF 的最小值是( )A .2B .2.4C .3D .48.如图,在平面直角坐标系中,点A 的坐标是(4,0),点B 的坐标是(3,4),点P 是y 轴正半轴上的动点,连接AP 交线段OB 于点Q ,若△OPQ 是等腰三角形,则点P 的坐标是( )A .(0,53)B .(0,43)C .(0,43)或(0,163)D .(0,53)或(0,163)二、填空题9.△ABC 的三条边长a 、b 、c 满足8c =,460a b -+-=,则△ABC ____直角三角形(填“是”或“不是”)10.如图,在菱形ABCD 中对角线AC 、BD 相交于点O ,若AB =3,BD =4,则菱形ABCD 的面积为_____.11.如图,一名滑雪运动员沿着坡比为1:3i =的滑道,从A 滑行至B ,已知300AB =米,则这名滑雪运动员的高度下降了_______米.12.如图,点P 是矩形ABCD 的对角线AC 上一点,过点P 作EF ∥BC ,分别交AB ,CD 于点E 、F ,连接PB 、PD ,若AE =2,PF =9,则图中阴影面积为______;13.将一次函数24y x =-+的图象绕原点O 顺时针旋转90°,所得图象对应的函数解析式是______.14.如图,已知四边形ABCD 是一个平行四边形,则只须补充条件__________,就可以判定它是一个菱形.15.如图,在平面直角坐标系中,点()11,1A 在直线y x =图象上,过1A 点作y 轴平行线,交直线y x =-于点1B ,以线段11A B 为边在右侧作正方形1111D C B A ,11C D 所在的直线交y x =的图象于点2A ,交y x =-的图象于点2B ,再以线段22A B 为边在右侧作正方形2222A B C D 依此类推,按照图中反应的规律,第2020个正方形的边长是_______.16.已知如图,点()()()2,0,4,0,3,7A B D --,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A 出发,沿线段AF 以每秒1个单位的速度运动到F ,再沿线段FD 以2D 后停止,当点F 的坐标是____时,点M 在整个运动过程中用时最少。
人教版数学八年级下册数学期末试卷易错题(Word版含答案)

人教版数学八年级下册数学期末试卷易错题(Word 版含答案) 一、选择题 1.二次根式2x -中x 的值不能是( )A .0B .1C .2D .32.三条线段首尾相连,不能围成直角三角形的是( )A .1,2,3B .1,2,1C .3,4,5D .3,2,5 3.四边形BCDE 中,对角线BD 、CE 相交于点F ,下列条件不能判定四边形BCDE 是平行四边形的是( )A .BC ∥ED ,BE =CDB .BF =DF ,CF =EFC .BC ∥ED ,BE ∥CD D .BC =ED .BE =CD4.红河州博物馆拟招聘一名优秀讲解员,其中小华笔试、试讲、面试三轮测试得分分别为90分、94分、92分.综合成绩中笔试占30%、试讲占50%、面试占20%,那么小华的最后得分为( )A .92分B .92.4分C .90分D .94分 5.如图,在四边形ABCD 中,1AB BC ==, 22CD =,10AD =,AB BC ⊥,则四边形ABCD 的面积是( )A .2.5B .3C .3.5D .4 6.如图,在菱形ABCD 中,EF 、分别为边BC CD 、的中点,且AE BC ⊥于,E AF CD ⊥于,F 则EAF ∠的度数为( )A .30B .45C .60D .757.如图,在等腰Rt △ACD 中,∠ACD =90°,AC =DC ,且AD 2AD 、AC 、CD 为直径画半圆,其中所得两个月形图案AGCE 和DHCF (图中阴影部分)的面积之和等于( )A.8B.42C.4D.28.如图,点C、B分别在两条直线y=﹣3x和y=kx上,点A、D是x轴上两点,若四边形ABCD是正方形,则k的值为()A.3 B.2 C.23D.32二、填空题9.若232(2)x x-+--有意义,则x的取值范围是_______________.10.在菱形ABCD中,AB=m,AC+BD=n,则菱形ABCD的面积为_________.(用含m、n的代数式表示)11.在△ABC中,∠ACB=90°,若AC=5,AB=13,则BC=___.12.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E、F,连接PB、PD,若AE=2,PF=9,则图中阴影面积为______;13.直线y=kx+3经过点(1,2),则k=_____________.14.如图,在正方形ABCD中,点E、F分别在对角线BD上,请你添加一个条件____________,使四边形AECF是菱形.15.如图,将一块等腰直角三角板ABC放置在平面直角坐标系中,90,ACB AC BC∠=︒=,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,AC 所在直线的函数表达式是22y x =+,若保持AC 的长不变,当点A 在y 轴的正半轴滑动,点C 随之在x 轴的负半轴上滑动,则在滑动过程中,点B 与原点O 的最大距离是_______.16.如图,正方形OABC 的顶点A 、C 分别在坐标轴的正半轴上,点B 是第一象限内直线132y x =+上的一点,则点B 的坐标为______.三、解答题17.计算:(1)13823282+- (2)101()|33|(1)272π--+----. 18.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC 的长为17米,此人以1米每秒的速度收绳,7秒后船移动到点D 的位置,问船向岸边移动了多少米.(假设绳子是直的)19.如图,在4×3正方形网格中,每个小正方形的边长都是1,正方形顶点叫格点,连接两个网格格点的线段叫网格线段,点A 固定在格点上.(1)若a 是图中能用网格线段表示的最小无理数,b 是图中能用网格线段表示的最大无理数,则a = ,b = ;(2)请你画出顶点在格点上且边长为5的所有菱形ABCD ,你画出的菱形面积为 ; 20.如图,在正方形ABCD 中,点E ,F 在AC 上,且AF CE =.求证:(1)BE DE =.(2)四边形BEDF 是菱形.21.先观察下列等式,再回答问题:2211+2+()1=1+1=2; 2212+2+()212=2 12; 2213+2+()3=3+13=313;… (1)根据上面三个等式提供的信息,请猜想第四个等式;(2)请按照上面各等式规律,试写出用 n (n 为正整数)表示的等式,并用所学知识证明.22.暑期将至,某游泳馆面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次游泳费用按六折优惠;方案二:不购买学生暑期专享卡,每次游泳费用按八折优惠.设某学生暑期游泳x (次),按照方案一所需费用为y 1(元),且y 1=k 1x +b ;按照方案二所需费用为y 2(元),且y 2=k 2x .其函数图象如图所示.(1)求k 1和b 的值;(2)八年级学生小华计划暑期前往该游泳馆游泳8次,应选择哪种方案所需费用更少?请说明理由.23.已知如图1,四边形ABCD是正方形,.如图1,若点分别在边上,延长线段CB至G,使得,若求EF的长;如图2,若点分别在边延长线上时,求证:如图3,如果四边形ABCD不是正方形,但满足且,请你直接写出BE 的长.24.请你根据学习函数的经验,完成对函数y =|x |﹣1的图象与性质的探究.下表给出了y 与x 的几组对应值. x … ﹣3 ﹣2 ﹣1 01 2 3 … y … m 1 0 ﹣1 0 1 2 …【探究】(1)m = ;(2)在给出的平面直角坐标系中,描出表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;(3)根据函数图象,当y 随x 的增大而增大时,x 的取值范围是 ;【拓展】(4)函数y 1=﹣|x |+1的图象与函数y =|x |﹣1的图象交于两点,当y 1≥y 时,x 的取值范围是 ;(5)函数y 2=﹣|x |+b (b >0)的图象与函数y =|x |﹣1的图象围成的四边形的形状是 ,该四边形的面积为18时,则b 的值是 .25.(解决问题)如图1,在ABC ∆中,10AB AC ==,CG AB ⊥于点G .点P 是BC 边上任意一点,过点P 作PE AB ⊥,PF AC ⊥,垂足分别为点E ,点F .(1)若3PE =,5PF =,则ABP ∆的面积是______,CG =______.(2)猜想线段PE ,PF ,CG 的数量关系,并说明理由.(3)(变式探究)如图2,在ABC ∆中,若10AB AC BC ===,点P 是ABC ∆内任意一点,且PE BC ⊥,PF AC ⊥,PG AB ⊥,垂足分别为点E ,点F ,点G ,求PE PF PG ++的值.(4)(拓展延伸)如图3,将长方形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C '处,点P 为折痕EF 上的任意一点,过点P 作PG BE ⊥,PH BC ⊥,垂足分别为点G ,点H .若8AD =,3CF =,直接写出PG PH +的值.26.在正方形AMFN 中,以AM 为BC 边上的高作等边三角形ABC ,将AB 绕点A 逆时针旋转90°至点D ,D 点恰好落在NF 上,连接BD ,AC 与BD 交于点E ,连接CD ,(1)如图1,求证:△AMC ≌△AND ;(2)如图1,若DF=3,求AE 的长;(3)如图2,将△CDF 绕点D 顺时针旋转α(090α<<),点C,F 的对应点分别为1C 、1F ,连接1AF 、1BC ,点G 是1BC 的中点,连接AG ,试探索1AG AF 是否为定值,若是定值,则求出该值;若不是,请说明理由.【参考答案】一、选择题1.D解析:D【分析】根据二次根式有意义的条件即可得出答案.【详解】∴20x -≥,解得:2x ≤,故选项中符合条件的x 的值有0,12,, ∴x 不能为3,故选:D .【点睛】本题考查了二次根式有意义的条件,熟知根号下为非负数是解本题的关键.2.D解析:D【分析】根据勾股定理逆定理,验证两条较短边的平方和是否等于最长边的平方即可求解.【详解】解:A 、因为222142+== ,所以1,2意;B 、因为222112+== ,所以1,1能围成直角三角形,故本选项不符合题意;C 、因为22234255+== ,所以3,4,5能围成直角三角形,故本选项不符合题意;D 、因为222+2=7≠ 2意;故选:D .【点睛】本题主要考查了勾股定理逆定理,熟练掌握若一个三角形的两边的平方和等于第三边的平方,则这个三角形是直角三角形是解题的关键. 3.A解析:A【解析】【分析】根据平行四边形的判定定理分别进行分析即可.【详解】解:A 、不能判定四边形ABCD 是平行四边形,故此选项符合题意;B 、根据对角线互相平分的四边形是平行四边形,可判定四边形ABCD 为平行四边形,故此选项不合题意;C 、根据两组对边分别平行的四边形是平行四边形,可判定四边形ABCD 为平行四边形,故此选项不合题意;D 、根据两组对边分别相等的四边形是平行四边形,可判定四边形ABCD 为平行四边形,故此选项不合题意;故选;A .【点睛】本题考查平行四边形的判定定理,熟知平行四边形的判定条件是解题的关键. 4.B解析:B【解析】【分析】根据加权平均数的定义列式计算即可.【详解】解:小华的最后得分为90×30%+94×50%+92×20%=92.4(分),故选:B .【点睛】本题主要考查了加权平均数,解题的关键是掌握加权平均数的定义.5.A解析:A【分析】如下图,连接AC ,在Rt △ABC 中先求得AC 的长,从而可判断△ACD 是直角三角形,从而求得△ABC 和△ACD 的面积,进而得出四边形的面积.【详解】如下图,连接AC∵AB=BC=1,AB ⊥BC∴在Rt △ABC 中,2,111122ABC S=⨯⨯= ∵10,2又∵((2222210+= ∴三角形ADC 是直角三角形∴122ADC S == ∴四边形ABCD 的面积=12+2=52故选:A .【点睛】本题考查勾股定理的逆定理,遇到此类题型我们需要敏感一些,首先就猜测△ADC 是直角三角形,然后用勾股定理逆定理验证即可.6.C解析:C【解析】【分析】根据菱形的性质求出180C EAF ∠+∠=︒,又因为180B C ∠+∠=︒,得出EAF B ∠=∠,再由1122BE BC AB ==,可得60B ∠=︒最后可推出60EAF ∠=︒. 【详解】解:AE BC ⊥,AF CD ⊥,180AFC AEC ∴∠+=︒,180C EAF ∴∠+∠=︒.又180B C ∠+∠=︒,EAF B ∴∠=∠. 又12BE BC =,AB BC =,1BE AB 2∴=, 30BAE =∴∠︒,60B ∴∠=︒,60EAF ∴∠=︒.故选:C .【点睛】此题主要考查的知识点:(1)直角三角形中,30锐角所对的直角边等于斜边的一半的逆定理;(2)菱形的两个邻角互补;(3)同角的补角相等;(4)菱形的四边相等. 7.D解析:D【解析】【分析】由等腰三角形的性质及勾股定理可求解AC =CD =2,进而可求得S △ACD =2,再利用阴影部分的面积=以AC 为直径的圆的面积+△ACD 的面积-以AD 为直径的半圆的面积计算可求解.【详解】解:在等腰Rt △ACD 中,∠ACD =90°,AC =DC ,AD ,∴AC 2+DC 2=AD 2=8,∴AC =CD =2,∴S △ACD =12AC •DC =2, ∴221()()222ACD AC AD S S ππ∆=+-阴影 =π+2-π=2,故选:D .【点睛】 本题主要考查了等腰直角三角形,勾股定理,理清阴影部分的面积=以AC 为直径的圆的面积+△ACD 的面积-以AD 为直径的半圆的面积是解题的关键.8.D解析:D【分析】设点C 的横坐标为m ,则点C 的坐标为(m ,﹣3m ),点B 的坐标为(﹣3m k,﹣3m ),根据正方形的性质,即可得出关于k 的分式方程,解之经检验后即可得出结论.【详解】解:设点C 的横坐标为m ,∵点C 在直线y=-3x 上,∴点C 的坐标为(m ,﹣3m ),∵四边形ABCD 为正方形,∴BC ∥x 轴,BC=AB ,又点B 在直线y =kx 上,且点B 的纵坐标与点C 的纵坐标相等,∴点B 的坐标为(﹣3m k ,﹣3m ), ∴﹣3m k﹣m =﹣3m , 解得:k =32, 经检验,k =32是原方程的解,且符合题意. 故选:D .【点睛】本题考查正方形的性质,正比例函数的图象与性质以及解分式方程等知识点,灵活运用性质是解题的关键.二、填空题9.3x ≥-且2x ≠【解析】有意义可得30,x +≥ 由222x 有意义可得20,x -≠ 再解不等式组,从而可得答案.【详解】解: 22(2)x --有意义, 3020x x ①②由①得:3,x ≥-由②得:2,x ≠所以x 的取值范围是:3x ≥-且2,x ≠故答案为:3x ≥-且2x ≠【点睛】本题考查的是二次根式有意义的条件,负整数指数幂的含义,由二次根式有意义的条件,结合负整数指数幂的含义列出不等式组是解本题的关键.10.A 解析:2214n m - 【解析】【分析】根据菱形的性质及勾股定理计算即可;【详解】解:在菱形ABCD 中,AB =m ,AC +BD =n , ∴22221122AC BD AB m ⎛⎫⎛⎫+== ⎪ ⎪⎝⎭⎝⎭, ∴AC 2+BD 2=4m 2,∴菱形ABCD 的面积=()()22211222AC BD AC BD AC BD +-+=⨯, =221422n m -⨯, =2214n m -, 故答案为:2214n m -. 【点睛】本题主要考查了菱形的性质,勾股定理,准确计算是解题的关键.11.12【解析】【分析】根据勾股定理求解即可.由勾股定理得:222213512BC AB AC -=-==.故答案为:12.【点睛】本题主要考查了勾股定理的运用,熟练掌握相关概念是解题的关键.12.A解析:18【分析】作PM ⊥AD 于M ,交BC 于N ,根据矩形的性质可得S △PEB =S △PFD 即可求解.【详解】解:作PM ⊥AD 于M ,交BC 于N .则有四边形AEPM ,四边形DFPM ,四边形CFPN ,四边形BEPN 都是矩形,,,,,ADC ABC AMP AEP PBE PBN PFD PDM PFC PCN S S S S S S S S S S ∴=====,∴DFPM BEPN S S 矩矩=,12442DFP PBE S S ∴==⨯⨯=, ∴S 阴=9+9=18,故答案为:18.【点睛】本题考查矩形的性质、三角形的面积等知识,解题的关键是证明DFP PBE SS =.13.-1.【详解】试题分析:把(1,2)代入直线y=kx+3,即可得方程k+3=2,解得k=-1.考点:一次函数图象上点的坐标特征. 14.B解析:BE=DF【分析】根据正方形的性质,可得正方形的四条边相等,对角线平分对角,根据 SAS ,可得△ABF 与△CBF 与△CDE 与△ADE 的关系,根据三角形全等,可得对应边相等,再根据四条边相等的四边形,可得证明结果.【详解】添加的条件为:BE=DF ,理由:正方形ABCD 中,对角线BD ,∴AB=BC=CD=DA ,∠ABE=∠CBE=∠CDF=∠ADF=45°.∵BE=DF ,∴△ABE ≌△CBE ≌△DCF ≌△DAF (SAS ).∴AE=CE=CF=AF ,∴四边形AECF 是菱形;故答案为:BE=DF .【点睛】本题考查了正方形的性质,菱形的判定,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.15.【分析】根据自变量与函数值得对应关系,可得A ,C 点坐标,根据勾股定理,可得AC 的长度;根据全等三角形的判定与性质,可得CD ,BD 的长,可得B 点坐标;首先取AC 的中点E ,连接BE ,OE ,OB ,可求【分析】根据自变量与函数值得对应关系,可得A ,C 点坐标,根据勾股定理,可得AC 的长度;根据全等三角形的判定与性质,可得CD ,BD 的长,可得B 点坐标;首先取AC 的中点E ,连接BE ,OE ,OB ,可求得OE 与BE 的长,然后由三角形三边关系,求得点B 到原点的最大距离.【详解】解:当x =0时,y =2x +2=2,∴A (0,2);当y =2x +2=0时,x =-1,∴C (-1,0).∴OA =2,OC =1,∴AC如图所示,过点B 作BD ⊥x 轴于点D .∵∠ACO +∠ACB +∠BCD =180°,∠ACO +∠CAO =90°,∠ACB =90°,∴∠CAO =∠BC D .在△AOC 和△CDB 中,AOC CDB CAO BCD AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AOC ≌△CDB (AAS ),∴CD =AO =2,DB =OC =1,OD =OC +CD =3,∴点B 的坐标为(-3,1).如图所示.取AC 的中点E ,连接BE ,OE ,OB ,∵∠AOC =90°,AC =5, ∴OE =CE =12AC =5, ∵BC ⊥AC ,BC =5,∴BE =22BC CE +=52, 若点O ,E ,B 不在一条直线上,则OB <OE +BE =552, 若点O ,E ,B 在一条直线上,则OB =OE +BE =552, ∴当O ,E ,B 三点在一条直线上时,OB 取得最大值,最大值为55+, 故答案为:55+.【点睛】此题考查了一次函数综合题,利用自变量与函数值的对应关系是求AC 长度的关键,又利用了勾股定理;求点B 的坐标的关键是利用全等三角形的判定与性质得出CD ,BD 的长;求点B 与原点O 的最大距离的关键是直角三角形斜边上的中线的性质以及三角形三边关系.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.16.【分析】根据正方形的性质可得点B 的横纵坐标相等计算即可;【详解】由题可知:点B 在直线上且点B 是正方形ABCD 的一个顶点,设,∴,解得: ,∴,∴;故答案是.【点睛】本题主要考解析:()6,6【分析】根据正方形的性质可得点B 的横纵坐标相等计算即可;【详解】由题可知:点B 在直线132y x =+上且点B 是正方形ABCD 的一个顶点, 设1,32B x x ⎛⎫+ ⎪⎝⎭, ∴132x x =+,解得:6x = , ∴1362x +=, ∴()6,6B ;故答案是()6,6B .【点睛】本题主要考查了一次函数的性质、正方形的性质,准确计算是解题的关键.三、解答题17.(1);(2).【分析】(1)先进行二次根式的化简,再进行二次根式的加减即可求解;(2)根据负整数指数幂,绝对值,0指数幂,二次根式化简等知识进行整理,再进行二次根式加减即可求解.【详解】解析:(1)2)-【分析】(1)先进行二次根式的化简,再进行二次根式的加减即可求解;(2)根据负整数指数幂,绝对值,0指数幂,二次根式化简等知识进行整理,再进行二次根式加减即可求解.【详解】解:(1)==(2)101()3|(1)2π--+--231=-+-=- 【点睛】本题考查了二次根式的混合运算,负整数指数幂,0指数幂,绝对值等知识,熟知相关知识并正确进行化简是解题关键.18.船向岸边移动了9米.【分析】在Rt△ABC中,利用勾股定理计算出AB长,再根据题意可得CD长,然后再次利用勾股定理计算出AD长,再利用BD=AB-AD可得BD长.【详解】解:在Rt△ABC中解析:船向岸边移动了9米.【分析】在Rt△ABC中,利用勾股定理计算出AB长,再根据题意可得CD长,然后再次利用勾股定理计算出AD长,再利用BD=AB-AD可得BD长.【详解】解:在Rt△ABC中:∵∠CAB=90°,BC=17米,AC=8米,∴AB(米),∵此人以1米每秒的速度收绳,7秒后船移动到点D的位置,∴CD=17-1×7=10(米),∴AD(米),∴BD=AB-AD=15-6=9(米),答:船向岸边移动了9米.【点睛】本题主要考查了勾股定理的应用,关键是掌握从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.19.(1);(2)见解析,菱形面积为4或5.【解析】【分析】(1)根据题意,画出图形,即可求解;(2)先画出边长为的所有菱形ABCD,,然后求出面积即可.【详解】解:如图,(1)∵a是图解析:(12)见解析,菱形面积为4或5.【解析】【分析】(1)根据题意,画出图形,即可求解;(2ABCD,,然后求出面积即可.【详解】解:如图,(1)∵a是图中能用网格线段表示的最小无理数,∴22112a=+=,∵b是图中能用网格线段表示的最大无理数,224225b=+=;(2)∵22215+=,即可画出图形,如图,菱形ABC1D1和菱形ABC2D2即为所求;菱形ABC1D1的面积为12442⨯⨯=;菱形ABC2D2223110+=,故菱形ABC2D2的面积为1101052;5ABCD的面积为4或5.【点睛】本题主要考查了应用设计与作图以及勾股定理等知识,熟练掌握菱形的性质是解题关键.20.(1)见解析;(2)见解析【分析】(1)根据边角边证明全等即可得出结论;(2)同理可得,然后证明,即可得出,结论可得.【详解】解:(1)∵四边形是正方形,∴,,在和中,,∴,∴解析:(1)见解析;(2)见解析【分析】(1)根据边角边证明ABE ADE ≅△△全等即可得出结论;(2)同理可得BFC DFC ≅△△,然后证明()ABE CBF SAS ≅△△,即可得出BE BF DE DF ===,结论可得.【详解】解:(1)∵四边形ABCD 是正方形,∴AB AD CD BC ===,45DAE BAE BCF DCF ∠=∠=∠=∠=︒,在ABE △和ADE 中,AB AD BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩, ∴()ABE ADE SAS ≅△△,∴BE DE =.(2)同理可得BFC DFC ≅△△,可得BF DF =,∵AF CE =,∴AF EF CE EF -=-,即AE CF =,在ABE △和CBF 中,AB BC BAE BCF AE CF =⎧⎪∠=∠⎨⎪=⎩, ∴()ABE CBF SAS ≅△△,∴BE BF =,∴BE BF DE DF ===,∴四边形BEDF 是菱形.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,菱形的判定等知识点,熟练掌握全等三角形的判定定理是解本题的关键.21.(1);(2),证明见解析.【解析】【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,即可猜想出第四个等式为44;(2)根据等式的变化,找出变化规律“n解析:(1144+=144;(2211n n n n ++=,证明见解析.【解析】【分析】(1)根据“第一个等式内数字为1,第二个等式内数字为2,第三个等式内数字为3”,即=414+=414;(2)根据等式的变化,找出变化规律=n 211n n n ++=”,再利用222112n n n n++=+()()开方即可证出结论成立. 【详解】(1)∵1+1=2;=212+=212;=313+=313;里面的数字分别为1、2、3,∴ 144+= 144.(21+1=2,212+=212313+=313=414+=414,…,∴= 211n n n n ++=.证明:等式左边==n 211n n n++==右边.=n 211n n n ++=成立. 【点睛】本题考查了二次根式的性质与化简以及规律型中数的变化类,解题的关键是:(1)猜测出第四个等式中变化的数字为4;(2)找出变化规律n 211n n n ++=”.解决该题型题目时,根据数值的变化找出变化规律是关键.22.(1)y1=15x+30;(2)选择方案一所需费用更少,理由见解析【分析】(1)利用待定系数法求解即可;(2)求出y2与x 之间的函数关系式,将x=8分别代入y1、y2关于x 的函数解析式,比较即解析:(1)y 1=15x +30;(2)选择方案一所需费用更少,理由见解析【分析】(1)利用待定系数法求解即可;(2)求出y 2与x 之间的函数关系式,将x =8分别代入y 1、y 2关于x 的函数解析式,比较即可.【详解】解:(1)根据题意,得:138430k b b +=⎧⎨=⎩,解得:11830k b =⎧⎨=⎩, ∴方案一所需费用y 1与x 之间的函数关系式为y 1=18x +30,∴k 1=18,b =30;(2)∵打折前的每次游泳费用为18÷0.6=30(元),∴k 2=30×0.8=24;∴y 2=24x ,当游泳8次时,选择方案一所需费用:y 1=18×8+30=174(元),选择方案二所需费用:y 2=24×8=192(元),∵174<192,∴选择方案一所需费用更少.【点睛】本题考查了一次函数的应用,解题的关键是理解两种优惠活动方案,求出y 1、y 2关于x 的函数解析式.23.(1);(2)见解析;(3)【分析】(1)先用SAS 证ABG ≌ADF ,可得AG=AF ,∠BAG=∠DAF ,又可证∠EAG=∠EAF ,故可用SAS 证GAE ≌FAE ,EF=GE ,即EF 长度可求; (解析:(1);(2)见解析;(3) 【分析】(1)先用SAS 证ABG ≌ADF ,可得AG=AF ,∠BAG=∠DAF ,又可证∠EAG=∠EAF ,故可用SAS 证GAE ≌FAE ,EF=GE ,即EF 长度可求;(2)在DF 上取一点G,使得DG=BE, 连接AG ,先用SAS 证ABE ≌ADG ,可得AE=AG ,∠BAE=∠DAG ,又可证∠EAF=∠GAF ,故可用SAS 证AEF ≌AGF ,可得EF=GF ,且DG=BE ,故EF=DF-DG=DF-BE ; (3)在线段DF 上取BE=DG ,连接AG ,求证∠ABE=∠ADC ,即可用SAS 证ABE ≌ADG ,可得AE=AG ,∠BAE=∠DAG ,又可证∠EAF=∠GAF ,故可用SAS 证AEF ≌AGF ,可得EF=GF,设BE=x,则CE= 7+x,EF=18-x,根据勾股定理:,即可求得BE的长度.【详解】解:(1)证明:如图1所示,在正方形ABCD中,AB=AD,∠BAD=90°,在ABG和ADF中,∴ABG≌ADF(SAS),∴AG=AF,∠BAG=∠DAF,又∵∠DAF+∠FAB=∠FAB+∠BAG=90°,且∠EAF=45°,∴∠EAG=∠FAG-∠EAF=45°=∠EAF,在GAE和FAE中,∴GAE≌FAE(SAS),∴EF=GE=GB+BE=2+3=5;(2)如下图所示,在DF上取一点G,使得DG=BE, 连接AG,∵四边形ABCD是正方形,故AB=AD,∠ABE=∠ADG=90°,在ABE和ADG中,∴ABE≌ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠BAG+∠DAG=90°,故∠BAG+∠BAE=90°,∵∠EAF=45°,故∠GAF=45°,∠EAF=∠GAF=45°,在AEF和AGF中,∴AEF≌AGF(SAS),∴EF=GF,且DG=BE,∴EF=DF-DG=DF-BE;(3)BE=5,如下图所示,在线段DF上取BE=DG,连接AG,∵∠BAD=∠BCD=90°,故∠ABC+∠ADC=180°,且∠ABC+∠ABE=180°,∴∠ABE=∠ADC,在ABE和ADG中,∴ABE≌ADG(SAS),∴AE=AG,∠BAE=∠DAG,∵∠BAG+∠DAG=90°,故∠BAG+∠BAE=90°,∵∠EAF=45°,故∠GAF=45°,∠EAF=∠GAF=45°,在AEF和AGF中,∴AEF≌AGF(SAS),∴EF=GF,设BE=x,则CE=BC+BE =7+x,EF=GF=DC+CF-DG= DC+CF-BE=18-x,在直角三角形ECF中,根据勾股定理:,即:,解得x=5,∴BE=x=5.【点睛】本题主要考察了全等三角形的证明及性质、勾股定理,解题的关键在于添加辅助线,找出全等三角形,并用对应边/对应角相等的定理,解决该题.24.(1)2;(2)见解析;(3)x≥0;(4)﹣1≤x≤1;(5)正方形;5【解析】【分析】(1)把x=﹣3代入y=|x|﹣1,即可求出m;(2)描点连线画出该函数的图象即可求解;(3)根据解析:(1)2;(2)见解析;(3)x≥0;(4)﹣1≤x≤1;(5)正方形;5【解析】【分析】(1)把x=﹣3代入y=|x|﹣1,即可求出m;(2)描点连线画出该函数的图象即可求解;(3)根据图象即可解答;(4)画出函数y1=﹣|x|+1的图象,根据图象即可得当y1≥y时,x的取值范围;(5)取b=3,在同一平面直角坐标系中画出y2=﹣|x|+3的图象,结合y1=﹣|x|+1的图象可得围成的四边形的形状是正方形,根据正方形的面积公式即可求解.【详解】解:(1)①把x=﹣3代入y=|x|﹣1,得m=3﹣1=2,故答案为:2;(2)该函数的图象如图,(3)根据函数图象,当y随x的增大而增大时,x的取值范围是x≥0,故答案为:x≥0;(4)画出函数y1=﹣|x|+1的图象如图,由图象得:当y1≥y时,x的取值范围为﹣1≤x≤1,故答案为:﹣1≤x≤1;(5)取b=3,在同一平面直角坐标系中画出y2=﹣|x|+3的图象,如图:由图象得:y 1=﹣|x |+1的图象与函数y =|x |﹣1的图象围成的四边形的形状是正方形,y 2=﹣|x |+3的图象与函数y =|x |﹣1的图象围成的四边形的形状是正方形,∴函数y 2=﹣|x |+b (b >0)的图象与函数y =|x |﹣1的图象围成的四边形的形状是正方形,∵y =|x |﹣1,y 2=﹣|x |+b (b >0),∴y 与y 2的图象围成的正方形的对角线长为b +1,∵该四边形的面积为18, ∴12(b +1)2=18,解得:b =5(负值舍去),故答案为:正方形,5.【点睛】本题是一次函数综合题,考查了一次函数的图象与性质,一次函数图象上点的坐标特征,利用了数形结合思想.正确画出函数的图象是解题的关键.25.(1)15,8;(2),见解析;(3);(4)4【分析】解决问题(1)只需运用面积法:,即可解决问题;(2)解法同(1);(3)连接、、,作于,由等边三角形的性质得出,由勾股定理得出,得出的 解析:(1)15,8;(2)PE PF CG +=,见解析;(3)534)4【分析】解决问题(1)只需运用面积法:ABC ABP ACP S S S ∆∆∆=+,即可解决问题;(2)解法同(1);(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,由等边三角形的性质得出152BM BC ==,由勾股定理得出2253AM AB BM =-ABC ∆的面积12532BC AM =⨯=ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2532222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++= (4)过点E 作EQ BC ⊥,垂足为Q ,易证BE BF =,过点E 作EQ BF ⊥,垂足为Q ,由解决问题(1)可得PG PH EQ +=,易证EQ DC =,BF DF =,只需求出BF 即可.【详解】解:(1)∵PE AB ⊥,10AB =,3PE =,∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=, ∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =,∴358CG PE PF =+=+=.故答案为:15,8.(2)∵PE AB ⊥,PF AC ⊥,CG AB ⊥,且ABC ABP ACP S S S ∆∆∆=+,∴AB CG AB PE AC PF ⋅=⋅+⋅,∵AB AC =, ∴CG PE PF =+.(3)连接PA 、PB 、PC ,作AM BC ⊥于M ,如图2所示:∵10AB AC BC ===,∴ABC ∆是等边三角形,∵AM BC ⊥,∴152BM BC ==, ∴222210553AM AB BM =--=∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯= ∵PE BC ⊥,PF AC ⊥,PG AB ⊥,∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 253=∴22533PE PF PG ⨯++== (4)过点E 作EQ BC ⊥,垂足为Q ,如图3所示:∵四边形ABCD 是矩形,∴AD BC =,90C ADC ∠=∠=︒,∵8AD =,3CF =,∴5BF BC CF AD CF =-=-=,由折叠可得:5DF BF ==,BEF DEF ∠=∠,∵90C ∠=︒, ∴2222534DC DF FC =--,∵EQ BC ⊥,90C ADC ∠=∠=︒,∴90EQC C ADC ∠=︒=∠=∠,∴四边形EQCD 是矩形,∴4EQ DC ==,∵//AD BC ,∴DEF EFB ∠=∠,∵BEF DEF ∠=∠,∴BEF EFB ∠=∠,∴BE BF =,由解决问题(1)可得:PG PH EQ +=,∴4PG PH +=,即PG PH +的值为4.【点睛】本题是四边形综合题目,考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.26.(1)见解析;(2)AE =;(3)(3),理由见解析.【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(解析:(1)见解析;(2)AE =233)(3)12AG AF =. 【分析】(1)运用四边形AMFN 是正方形得到判断△AMC,△AND 是Rt △,进一步说明△ABC 是等边三角形,在结合旋转的性质,即可证明.(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x ,则AE=2x GE=3x ,得到△GBE 是等腰直角三角形和∠DHF=30°,再结合直角三角形的性质,判定Rt △AMC ≌Rt △AND ,最后通过计算求得AE 的长;(3)延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,可得GMB ∆≌11GFC ∆,从而得到111BM FC DF == 1BMG GFN ∠=,可知BM ∥1F N , 再根据题意证明ABM ∆≌1ADF ∆,进一步说明1AMF ∆是等腰直角三角形,然后再使用勾股定理求解即可.【详解】(1)证明:∵四边形AMFN 是正方形,∴AM=AN ∠AMC=∠N=90°∴△AMC,△AND 是Rt △∵△ABC 是等边三角形∴AB=AC∵旋转后AB=AD∴AC=AD∴Rt △AMC ≌Rt △AND(HL)(2)过E 作EG ⊥AB 于G,在BC 找一点H ,连接DH,使BH=HD ,设AG =x则AE=2x 3x易得△GBE 是等腰直角三角形∴BG=EG 3x∴AB=BC=(31)x易得∠DHF=30°∴HD=2DF=23,HF=3∴BF=BH+HF=233∵Rt △AMC ≌Rt △AND(HL)∴易得3∴BC=BF-CF=233333∴(31)33x +=+∴3x =∴AE =223x =(3)12AG AF =; 理由:如图2中,延长F 1G 到M,延长BA 交11F C 的延长线于N,使得1GM FG =,则GMB ∆≌11GFC ∆,∴111BM FC DF == 1BMG GFN ∠=, ∴BM ∥1F N ,∴MBA N ∠=∠∵0190NAO OF D ∠=∠= 1AON DOF ∠=∠∴1N ADF ∠=∠∴1ABM ADF ∠=∠,∵AB AD =∴ABM ∆≌1ADF ∆(SAS )∴1AM AF = 1MAB DAF ∠=∠∴0190MAF BAD ∠=∠=∴1AMF ∆是等腰直角三角形∴1AG MF ⊥ 1AG GF =∴12AF AG =∴12AG AF =【点睛】本题考查正方形的性质、三角形全等、以及勾股定理等知识点,综合性强,难度较大,但解答的关键是正确做出辅助线.。
八年级下册数学期末试卷易错题(Word版含答案)

八年级下册数学期末试卷易错题(Word 版含答案) 一、选择题 1.二次根式2x -中x 的值不能是( )A .0B .1C .2D .32.下列条件中,满足ABC 是直角三角形的是( )A .∠A :∠B :∠C =3:4:5B .a :b :c =1:3:1C .(a +b )2=c 2+2abD .111,,51213a b c === 3.下列命题:①对角线互相垂直且平分的四边形是菱形;②对角线相等的平行四边形是矩形;③有一组对边平行,另一组对边相等的四边形是平行四边形;④有一组对边相等且有一组对角相等的四边形是平行四边形.其中真命题的个数是( )A .1B .2C .3D .44.一次数学测试后,随机抽取八年级三班6名学生的成绩如下:80,85,86,88,88,95.关于这组数据的错误说法是( )A .极差是15B .中位数是86C .众数是88D .平均数是87 5.如图,在正方形ABCD 中,22CD =,若点P 为线段AD 上方一动点,且满足PD =2,∠BPD =90°,则点A 到直线BP 的距离为( )A .3B .3-C .31-D .31+ 6.如图,在菱形纸片ABCD 中,∠A=60°,点E 在BC 边上,将菱形纸片ABCD 沿DE 折叠,点C 落在AB 边的垂直平分线上的点C′处,则∠DEC 的大小为( )A .30°B .45°C .60°D .75°7.如图,在Rt ABC 中,90C ∠=︒,3AC =,4BC =,点P 为AB 边上任意一点过点P 分别作PE AC ⊥于点E ,PF BC ⊥于点F ,则线段EF 的最小值是( )A .2B .2.4C .3D .48.一个容器内有进水管和出水管,开始4min 内只进水不出水,在随后的8min 内既进水又出水,第12min 后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变,容器内水量y (单位:L )与时间x (单位:min )之间的关系如图所示.根据图象有下列说法:①进水管每分钟的进水量为5L ;②412x ≤≤时,5154y x =+;③当12x =时,30y =;④当15y =时,3x =,或17x =.其中正确说法的个数是( ) A .1个 B .2个 C .3个 D .4个二、填空题9.使式子32x x -+有意义的x 的取值范围是______. 10.一个菱形的边长是5cm ,一条对角线长6cm ,则此菱形的面积为______2cm . 11.若一个直角三角形的两边长分别是3和4,那么以斜边为边长的正方形的面积为______.12.如图,把矩形ABCD 沿EF 折叠,若140∠=︒,则∠=AEF ______°.13.正比例函数(0)y kx k =≠经过点(1,3),则k =__________.14.如图,已知四边形ABCD 是一个平行四边形,则只须补充条件__________,就可以判定它是一个菱形.15.某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y (千米)与货车行驶时间x (小时)之间的函数图象如图所示,现有以下4个结论:①快递车从甲地到乙地的速度为100千米/时;②甲、乙两地之间的距离为120千米; ③图中点B 的坐标为(334,75);④快递车从乙地返回时的速度为90千米/时.以上4个结论中正确的是 ___.16.如图,已知等腰△ABC 中,AB =AC =5,BC =8,E 是BC 上的一个动点,将△ABE 沿着AE 折叠到△ADE 处,再将边AC 折叠到与AD 重合,折痕为AF ,当△DEF 是等腰三角形时,BE 的长是___________.三、解答题17.计算(118232+ (2)13273 (3)(57)(57)2+(4)0214(37)8(12)2+ 18.如图,有一直立标杆,它的上部被风从B 处吹折,杆顶C 着地,离杆脚2m ,修好后又被风吹折,因新断处D 比前一次低0.5m ,故杆顶E 着地比前次远1m ,求原标杆的高度.19.如图,每个小正方形的边长都为1,AB的位置如图所示.(1)在图中确定点C,请你连接CA,CB,使CB⊥BA,AC=5;(2)在完成(1)后,在图中确定点D,请你连接DA,DC,DB,使CD=10,AD=17,直接写出BD的长.20.如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC 上,DE与AC相交于点O.(1)求证:△OEC为等腰三角形;(2)连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.21.先阅读下列材料,再解决问题:阅读材料:数学上有一种根号内又带根号的数,它们能通过完全平方公式及二次根式的性22232232121(2)212(12)+=+⨯⨯++⨯⨯+|12|=12解决问题:①146514235+=+⨯⨯_________________=________________=_________________②根据上述思路,试将下列各式化简:28103-3 12 +22.为了鼓励小强做家务,小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的.若设小强每月的家务劳动时间为x 小时,该月可得(即下月他可获得)的总费用为y 元,则y (元)和x (小时)之间的函数图象如图所示.(1)根据图象,请你写出小强每月的基本生活费;父母是如何奖励小强家务劳动的? (2)若小强2月份希望有300元费用,则小强1月份需做家务多少时间?23.已知四边形ABCD 是正方形,将线段CD 绕点C 逆时针旋转(),得到线段CE ,联结BE 、CE 、DE. 过点B 作BF ⊥DE 交线段DE 的延长线于F .(1)如图,当BE=CE 时,求旋转角的度数;(2)当旋转角的大小发生变化时,的度数是否发生变化?如果变化,请用含的代数式表示;如果不变,请求出的度数; (3)联结AF ,求证:.24.如图1,已知一次函数6y kx =+的图象分别交y 轴正半轴于点A ,x 轴正半轴于点B ,且AOB 的面积是24,P 是线段OB 上一动点.(1)求k 值;(2)如图1,将AOP 沿AP 翻折得到AO P '△,当点O '正好落在直线AB 上时, ①求点P 的坐标;②将直线AP 绕点P 顺时针旋转45︒得到直线A P ',求直线A P '的表达式;(3)如图2,上题②中的直线A P '与线段AB 相交于点M ,将PBM 沿着射线PA '向上平移,平移后对应的三角形为P B M '''△,当APB '是以AP 为直角边的直角三角形时,请直接写出点P '的坐标.25.已知E ,F 分别为正方形ABCD 的边BC ,CD 上的点,AF ,DE 相交于点G ,当E ,F 分别为边BC ,CD 的中点时,有:①AF=DE ;②AF ⊥DE 成立.试探究下列问题:(1)如图1,若点E 不是边BC 的中点,F 不是边CD 的中点,且CE=DF ,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)(2)如图2,若点E ,F 分别在CB 的延长线和DC 的延长线上,且CE=DF ,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;(3)如图3,在(2)的基础上,连接AE 和BF ,若点M ,N ,P ,Q 分别为AE ,EF ,FD ,AD 的中点,请判断四边形MNPQ 是“矩形、菱形、正方形”中的哪一种,并证明你的结论.【参考答案】一、选择题1.D解析:D【分析】根据二次根式有意义的条件即可得出答案.【详解】∴20x -≥,解得:2x ≤,故选项中符合条件的x 的值有0,12,, ∴x 不能为3,故选:D .【点睛】本题考查了二次根式有意义的条件,熟知根号下为非负数是解本题的关键.2.C解析:C【分析】由直角三角形的定义,只要验证最大角是否是90︒;由勾股定理的逆定理,只要验证两较短边的平方和是否等于最长边的平方即可.【详解】解:A 、∵::3:4:5A B C ∠∠=,518075345C ∴∠=⨯︒=︒++,故不能判定ABC 是直角三角形;B 、22211+≠,故不能判定ABC 是直角三角形;C 、由22()2a b c ab +=+,可得:222+=a b c ,故能判定ABC 是直角三角形;D 、222111()()()12135+≠,故不能判定ABC 是直角三角形;故选:C .【点睛】本题主要考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可,也考查了三角形的内角和定理的应用. 3.B解析:B【解析】【分析】根据菱形的判定、矩形的判定、平行四边形的判定进行判断即可.【详解】解:①对角线互相垂直且平分的四边形是菱形,是真命题;②对角线相等的平行四边形是矩形,是真命题;③有一组对边平行且相等的四边形是平行四边形,原命题是假命题;④有一组对边相等且有一组对角相等的四边形不一定是平行四边形,原命题是假命题;故选B.【点睛】本题主要考查了菱形的判定、矩形的判定、平行四边形的判定,解题的关键在于能够熟练掌握相关四边形的判定条件.4.B解析:B【解析】【分析】平均数只要求出数据之和再除以总个数即可;对于中位数,按从小到大的顺序排列,只要找出最中间的一个数(或最中间的两个数)即可,本题是最中间的两个数;对于众数是出现频数最大的数据.【详解】解:A、极差是95-80=15,故A正确;B、中位数是86882+=87,故B错误;C、88出现了2次,则众数是88,故C正确;D、平均数是8085868888956+++++=87,故D正确.故选:B.【点睛】本题重点考查平均数,中位数,众数及极差的概念及求法.5.C解析:C【分析】由题意可得点P在以D为圆心,2为半径的圆上,同时点P也在以BD为直径的圆上,即点P是两圆的交点,由勾股定理可求BP,AH的长,即可求点A到BP的距离.【详解】解:作正方形ABCD的外接圆,另外以点D为圆心,2为半径作圆,两圆在线段AD上方的交点即为点P,连接AC、BD、PD、PB、PA,作AH⊥BP,垂足为H,过点A作AE AP⊥,交BP于点E,如图,∵四边形ABCD 是正方形,∴∠ADB =45°, ∴2,90AB AD DC BC BAD ︒====∠=,∴BD =4,∵DP =2, ∴3BP =AE AP ⊥,90EAD DAP ∴∠+∠=,又90BAE EAD ∠+∠=,DAP BAE ∴∠=∠,,ADP ABE AD AB ∠=∠=,ADP ABE ∴∆≅∆,,BE DP AE AP ∴==, AEP 为等腰直角三角形,AH PE ⊥,2PE AH ∴=,2BP BE PE AH PD ∴=+=+, 即2322,AH +,31AH ∴=即点A 到BP 31.故选C .【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰三角形的判定和性质、勾股定理、圆等知识,解题的关键是灵活运用这些知识.6.D解析:D【解析】【分析】连接BD ,由菱形的性质及60A ∠=︒,得到ABD △为等边三角形,P 为AB 的中点,利用三线合一得到DP 为角平分线,得到30ADP ∠=︒,120ADC =∠︒,60C ∠=°,进而求出90PDC ∠=︒,由折叠的性质得到45CDE PDE ∠=∠=︒,利用三角形的内角和定理即可求出所求角的度数.【详解】解:连接BD ,如图所示:∵四边形ABCD 为菱形,∴AB AD =,∵60A ∠=︒,∴ABD △为等边三角形,120ADC =∠︒,60C ∠=°,∵P 为AB 的中点,∴DP 为ADB ∠的平分线,即30ADP BDP ∠=∠=︒,∴90PDC ∠=︒,∴由折叠的性质得到45CDE PDE ∠=∠=︒,在DEC 中,()18075DEC CDE C ∠=︒-∠+∠=︒.故选:D【点睛】此题考查了翻折变换(折叠问题),菱形的性质,等边三角形的性质,以及三角形内角和定理,熟练掌握折叠的性质是解本题的关键.7.B解析:B【解析】【分析】求出四边形PECF 是矩形,根据矩形的性质得出EF =CP ,根据垂线段最短得出C P ⊥AB 时,CP 最短,根据三角形的面积公式求出此时CP 值即可.【详解】解:连接CP ,∵PE ⊥AC ,PF ⊥BC ,∠ACB =90°,∴∠PEC =∠ACB =∠PFC =90°,∴四边形PECF 是矩形,∴EF =CP ,当CP ⊥AB 时,CP 最小,即EF 最小,在Rt △ABC 中,∠C =90°,AC =3,BC =4,由勾股定理得:AB =5,由三角形面积公式得:AC ×BC =AB ×C P ,CP =125,即EF 的最小值是125=2.4, 故选:B .【点睛】本题考查了勾股定理,三角形的面积,矩形的性质和判定,垂线段最短等知识点,能求出EF 最短时P 点的位置是解此题的关键.8.C解析:C【分析】根据图象可知进水的速度为5(L /min ),再根据第10分钟时容器内水量为27.5L 可得出水的速度,从而求出第12min 时容器内水量,利用待定系数法求出4≤x ≤12时,y 与x 之间的函数关系式,再对各个选项逐一判断即可.【详解】解:由图象可知,进水的速度为:20÷4=5(L /min ),故①说法正确;出水的速度为:5−(27.5−20)÷(10−4)=3.75(L /min ),第12min 时容器内水量为:20+(12−4)×(5−3.75)=30(L ),故③说法正确;15÷3=3(min ),12+(30−15)÷3.75=16(min ),故当y =15时,x =3或x =16,故说法④错误;设4≤x ≤12时,y 与x 之间的函数关系式为y =kx +b ,根据题意,得4201027.5k b k b +=⎧⎨+=⎩, 解得5415k b ⎧=⎪⎨⎪=⎩,所以4≤x ≤12时, y =54x +15,故说法②正确. 所以正确说法的个数是3个.故选:C .【点睛】此题考查了一次函数的应用,解题时首先正确理解题意,利用数形结合的方法即可解决问题.二、填空题9.3x ≤且2x ≠-【解析】【分析】根据分式的分母不能为0、二次根式的被开方数大于或等于0列出式子求解即可得.【详解】由题意得:2030x x +≠⎧⎨-≥⎩, 解得3x ≤且2x ≠-,故答案为:3x ≤且2x ≠-.【点睛】本题考查了分式和二次根式有意义的条件,熟练掌握分式和二次根式的定义是解题关键. 10.A解析:24【解析】【分析】首先根据菱形的性质和勾股定理求出另一条对角线的长度,然后利用菱形的面积公式求解即可.【详解】如图,5,6AB cm AC cm ==,∵四边形ABCD 是菱形, ∴113,,22AO AC cm OB BD AC BD ===⊥, 90AOB ∠=︒∴ ,224BO AB AO cm ∴-,28BD OB cm ∴==,211682422S AC BD cm ∴=⋅=⨯⨯=, 故答案为:24.【点睛】本题主要考查菱形的性质和面积,勾股定理,掌握菱形的性质和勾股定理是解题的关键. 11.25或16【解析】【分析】分两种情况考虑:若4为直角边,利用勾股定理求出斜边;若4为斜边,利用勾股定理求出第三边,分别求出斜边边长的正方形面积即可.【详解】解:分两种情况考虑:若4为直角边,根据勾股定理得:斜边为2234+=5,此时斜边为边长的正方形面积为25;若4为斜边,此时斜边为边长的正方形面积为16,综上,以斜边为边长的正方形的面积为为25或16.故答案为:25或16【点睛】本题考查勾股定理,分类讨论利用勾股定理算出第三边是解题关键.12.110【分析】根据折叠的性质及140∠=︒可求出2∠的度数, 再由平行线的性质即可解答.【详解】解:四边形EFGH 是四边形EFBA 折叠而成,23∴∠=∠,231180∠+∠+∠=︒,140∠=︒,1123(18040)1407022∴∠=∠=︒-︒=⨯︒=︒,又//AD BC ,180AEF EFB ∴∠+∠=︒,18070110AEF ∴∠=︒-︒=︒.故答案为:110︒【点睛】本题主要考查了平行线的性质和折叠的性质, 解题时注意: 折叠前后的图形全等,找出图中相等的角是解答此题的关键.13.3【分析】把(1,3)代入(0)y kx k =≠,利用待定系数法求解k 即可得到答案.【详解】解:把(1,3)代入(0)y kx k =≠,故答案为:3.【点睛】本题考查的是利用待定系数法求解正比例函数的解析式,掌握待定系数法是解题的关键.14.A解析:AB=BC(答案不唯一)【分析】根据有一组邻边相等的平行四边形是菱形添加即可.【详解】解:补充的条件是AB=BC,理由是:∵AB=BC,四边形ABCD是平行四边形,∴平行四边形ABCD是菱形,故答案为:AB=BC.【点睛】本题考查了平行四边形的性质和菱形的判定,注意:有一组邻边相等的平行四边形是菱形.此题是一道开放性的题目,答案不唯一.15.①③④【分析】根据两车速度之差×3小时=120,解方程可判断①,根据两车间的距离而且是同向可判断②,根据卸货与装货45分钟时间可求拐点B横坐标,利用货车行驶45分钟距离缩短求出B纵坐标可判断③,解析:①③④【分析】根据两车速度之差×3小时=120,解方程可判断①,根据两车间的距离而且是同向可判断②,根据卸货与装货45分钟时间可求拐点B横坐标,利用货车行驶45分钟距离缩短求出B纵坐标可判断③,根据返回快递车速与货车速度之和乘以返货到相遇时间=75,解方程可判断④.【详解】解:①设快递车从甲地到乙地的速度为x千米/时,则3(x﹣60)=120,x=100.故①正确;②因为120千米是快递车到达乙地后两车之间的距离,不是甲、乙两地之间的距离,故②错误;③因为快递车到达乙地后缷完物品再另装货物共用45分钟,所以图中点B的横坐标为3+34=334,点B纵坐标为120﹣60×34=75,故③正确;④设快递车从乙地返回时的速度为y千米/时,则(y+60)(134344-)=75,故④正确.故答案为①③④.【点睛】本题考查一次函数行程问题图像获取信息,利用速度,时间与路程关系解决问题,掌握一次函数行程问题图像获取信息,利用速度,时间与路程关系解决问题,一次函数的应用是解题关键.16.或或.【分析】分三种情况讨论:DE=DF ,DE=EF ,EF=DF .利用等腰三角形的性质和全等三角形解题.【详解】解:由折叠可知,BE=DE ,DF=CF ,AD=AB=AC=5,当DE=DF 时 解析:52或258或74. 【分析】分三种情况讨论:DE=DF ,DE=EF ,EF=DF .利用等腰三角形的性质和全等三角形解题.【详解】解:由折叠可知,BE=DE ,DF=CF ,AD=AB=AC=5,当DE=DF 时,如图1,此时DE=DF=BE=CF ,∵AB=AC ,∴∠B=∠C ,在△ABE 和△ACF 中,AB AC B C BE CF =⎧⎪=⎨⎪=⎩∠∠ ∴△ABE ≌△ACF ,∴AE=AF ,∴AD 垂直平分EF ,∴EH=FH ,142BH CH BC ===, ∴2222543AH AB BH =-=-=,∴532HD =-=,设BE DE x ==,则4EH x =-,则在直角△DHE 中,()22242x x -+=,解得52x =, 当DE=EF 时,如图2,作AH ⊥BC 于H ,连接BD ,延长AE 交BD 于N ,可知BE=DE=EF ,∵AH ⊥BC ,AB=AC ,BC=8∴BH=CH=4,∴2222543AH AB BH -=-,设EH m =,则4BE EF m ==-,∴()8242CF m m =--=,即2DF m = ∵AB=AD ,∠BAN=∠DAN ,∴AN ⊥BD ,BN=DN ,∴12EN DF m ==, ∴EN EH =在△AHE 和△BNE 中,90AHE BNE EH ENAEH BEN ==︒⎧⎪=⎨⎪=⎩∠∠∠∠ ∴△AHE ≌△BNE ,∴AE=BE ,设BE AE x ==,则4EH x =-,在直角△AEH 中,()22243x x -+=,解得258x =,当DF=EF时,如图3,过A作AH⊥BC于H,延长AF交DC于M,同理258 EF CF==∴252578884 BE=--=故答案为:52或258或74.【点睛】本题考查了折叠问题,全等三角形的判定和性质,等腰三角形的性质,注意分类讨论是解题的关键.三、解答题17.(1)1;(2);(3)0;(4).【分析】(1)先运用分母有理化化简,然后再计算即可;(2)先运用二次根式的性质化简,然后再计算即可;(3)先运用平方差公式计算,然后再化简即可;(4)先解析:(1)1;(2143;(3)0;(4)322+【分析】(1)先运用分母有理化化简,然后再计算即可;(2)先运用二次根式的性质化简,然后再计算即可;(3)先运用平方差公式计算,然后再化简即可;(4)先运用零次幂、二次根式的性质、完全平方公式化简,然后再计算即可.【详解】解:(118232+(1822322⨯=623 2+-=4-3=1;(2)=;(3)2+=5-7+2=0;(4)02(1+=41(12)⨯+-=423+-+=3+【点睛】本题主要考查了二次根式的运算,掌握分母有理化、二次根式的性质成为解答本题的关键.18.5米【分析】由题中条件,可设原标杆AB 的高为x ,进而再依据勾股定理建立方程,进而求解即可.【详解】解:依题意得AC =2,AE =3,设原标杆的高为x ,∵∠A =90°,∴由题中条件可得AB解析:5米【分析】由题中条件,可设原标杆AB 的高为x ,进而再依据勾股定理建立方程,进而求解即可.【详解】解:依题意得AC =2,AE =3,设原标杆的高为x ,∵∠A =90°,∴由题中条件可得AB 2+AC 2=BC 2,即AB 2+22=(x ﹣AB )2,整理,得x 2﹣2ABx =4,同理,得(AB ﹣0.5)2+32=(x ﹣AB +0.5)2,整理,得x2﹣2ABx+x=9,解得x=5.∴原来标杆的高度为5米.【点睛】本题主要考查了勾股定理的应用,解题的关键在于能够熟练掌握勾股定理. 19.(1)见解析;(2).【解析】【分析】(1)利用网格即可确定C点位置;(2)由勾股定理在Rt△DBG中,可求BD的长.【详解】解:(1)如图,∴∴BC⊥AB,在Rt△ACH中,A解析:(1)见解析;(2【解析】【分析】(1)利用网格即可确定C点位置;(2)由勾股定理在Rt△DBG中,可求BD的长.【详解】解:(1)如图,222===5,20,25,AB BC AC∴222+=AB BC AC∴BC⊥AB,在Rt△ACH中,AC=5;(2)∵CD AD D点位置如图,∴在Rt△DBG中,BD【点睛】本题考查勾股定理的应用,利用三角形内角和确定C点位置,由勾股定理确定D点的位置是解题的关键.20.(1)见解析;(2)当为的中点时,四边形是矩形,见解析【分析】(1)根据等腰三角形的性质得出∠B=∠ACB,根据平移得出AB∥DE,求出∠B=∠DEC,再求出∠ACB=∠DEC即可;(2)求出解析:(1)见解析;(2)当E为BC的中点时,四边形AECD是矩形,见解析【分析】(1)根据等腰三角形的性质得出∠B=∠ACB,根据平移得出AB∥DE,求出∠B=∠DEC,再求出∠ACB=∠DEC即可;(2)求出四边形AECD是平行四边形,再求出四边形AECD是矩形即可.【详解】(1)证明:∵AB=AC,∴∠B=∠ACB,∵△ABC平移得到△DEF,∴AB∥DE,∴∠B=∠DEC,∴∠ACB=∠DEC,∴OE=OC,即△OEC为等腰三角形;(2)解:当E为BC的中点时,四边形AECD是矩形,理由是:∵AB=AC,E为BC的中点,∴AE ⊥BC ,BE =EC ,∵△ABC 平移得到△DEF ,∴BE ∥AD ,BE =AD ,∴AD ∥EC ,AD =EC ,∴四边形AECD 是平行四边形,∵AE ⊥BC ,∴四边形AECD 是矩形.【点睛】本题考查了矩形的判定、平行四边形的判定、平移的性质、等腰三角形的性质和判定等知识点,能综合运用知识点进行推理是解此题的关键.21.①,,3+;②(1)5-;(2) .【解析】【分析】①模仿阅读材料的方法将原式变形,计算即可得到结果;②仿照以上方法将各式化简即可.【详解】①===3+,故答案为,,3+;②(1)解析:3+②(1)5(2) 12 【解析】【分析】①模仿阅读材料的方法将原式变形,计算即可得到结果;②仿照以上方法将各式化简即可.【详解】3+3=5=12+=12. 【点睛】本题考查了二次根式的性质与化简,熟练掌握运算法则是解本题的关键.22.(1)小强每月的基本生活费为元,当劳动时间不大于20小时,每小时劳动奖励为元,一个月内劳动时间超过小时,每小时劳动奖励为元;(2)小时【分析】(1)根据函数图象与轴的交点即可求得基本生活费,根据解析:(1)小强每月的基本生活费为150元,当劳动时间不大于20小时,每小时劳动奖励为2.5元,一个月内劳动时间超过20小时,每小时劳动奖励为4元;(2)45小时【分析】(1)根据函数图象与y 轴的交点即可求得基本生活费,根据函数图像是分段的,即可描述出父母是如何奖励小强做家务劳动的;(2)根据劳动时间超过30小时的部分的解析式即可求得1月份需做家务的时间【详解】解:(1)根据函数图象可知,当0x =时,150y =,∴小强每月的基本生活费为150元设劳动时间在20小时内的解析式为:1y ax b ()020x <≤将点()()0,150,20,200代入,得15020200b a b =⎧⎨+=⎩解得 2.5150a b =⎧⎨=⎩ ∴1 2.5150y x =+当20x >时,设2y mx n =+,将点()()20,200,30,240,代入得,2020030240m n m n +=⎧⎨+=⎩解得4120m n =⎧⎨=⎩ 则24120y x =+()20x >∴当020x <≤时,每小时劳动奖励为2.5元,一个月内劳动时间超过20小时,则每小时劳动奖励为4元(2)令2300y =,则3004120x =+解得45x =答:小强2月份希望有300元费用,则小强1月份需做家务45小时.【点睛】本题考查了一次函数的应用,理解题意,求得分段函数的解析式是解题的关键. 23.(1)30°;(2)不变;45°;(3)见解析【分析】(1)利用图形的旋转与正方形的性质得到△BEC 是等边三角形,从而求得=∠DCE=30°.(2)因为△CED 是等腰三角形,再利用三角形的内角解析:(1)30°;(2)不变;45°;(3)见解析【分析】(1)利用图形的旋转与正方形的性质得到△BEC 是等边三角形,从而求得=∠DCE=30°. (2)因为△CED 是等腰三角形,再利用三角形的内角和即可求∠BEF=.(3)过A 点与C 点添加平行线与垂线,作得四边形AGFH 是平行四边形,求得△ABG ≌△ADH.从而求得矩形AGFH 是正方形,根据正方形的性质证得△AHD ≌△DIC ,从而得出结论.【详解】(1)证明:在正方形ABCD 中, BC=CD.由旋转知,CE=CD,又∵BE=CE,∴BE=CE=BC,∴△BEC 是等边三角形,∴∠BCE=60°.又∵∠BCD=90°,∴=∠DCE=30°.(2)∠BEF 的度数不发生变化.在△CED 中,CE=CD,∴∠CED=∠CDE=,在△CEB 中,CE=CB,∠BCE=,∴∠CEB=∠CBE=,∴∠BEF=.(3)过点A作AG∥DF与BF的延长线交于点G,过点A作AH∥GF与DF交于点H,过点C作CI⊥DF于点I易知四边形AGFH是平行四边形,又∵BF⊥DF,∴平行四边形AGFH是矩形.∵∠BAD=∠BGF=90°,∠BPF=∠APD ,∴∠ABG=∠ADH.又∵∠AGB=∠AHD=90°,AB=AD,∴△ABG≌△ADH.∴AG=AH ,∴矩形AGFH是正方形.∴∠AFH=∠FAH=45°,∴AH=AF∵∠DAH+∠ADH=∠CDI+∠ADH=90°∴∠DAH=∠CDI又∵∠AHD=∠DIC=90°,AD=DC,∴△AHD≌△DIC∴AH=DI,∵DE=2DI,∴DE=2AH=AF【点晴】本题考查正方形的性质和判定、图形的旋转、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.(1);(2)①点(3,0),②,(3)点的坐标(7,12)或(4,3).【解析】【分析】(1)根据函数解析式可知OA长,再由即可求出OB长,将B点坐标代入解析式即可求出k 值;(2)①由折叠解析:(1)34k =-;(2)①点P (3,0),②39y x =-,(3)点P'的坐标(7,12)或(4,3).【解析】【分析】(1)根据函数解析式可知OA 长,再由1242AOB SOA OB ==即可求出OB 长,将B 点坐标代入解析式即可求出k 值;(2)①由折叠性质可求得'BO P 中'4BO =、'=90BO P ∠︒,用勾股定理列方程即可求解;②通过构造等腰直角三角形,利用K 字形模型全等求出直线A P '上点Q 坐标,再由A 、Q 点坐标用待定系数法求出解析式A P '即可,(3)根据平移性质可知'//BB A P ',先求出直线'BB 的解析式;再当APB '是以AP 为直角边的直角三角形时,分两种情况求出直线'BB 与过A 、P 点垂直于AP 直线的解析式,联立函数解析式得方程求出点'B 坐标,由此得出图形平移方式,由此求出点P '的坐标.【详解】解:(1)当x =0时,y =6,故点A 坐标为A (0,6),∵11=62422AOB S OA OB OB ==, ∴=8OB ,∴点B 坐标为(8,0),代入6y kx =+得860k +=,∴34k =-, (2)①如图2-1,由折叠性质可知:'AO AO =,'PO O P =;'=90AOP AO P ∠=∠︒,∵2210AB OA OB +,∴''1064BO AB AO =-=-=,设'=PO O P x =,则8PB x =-,由222''PB O P O B =+得222(8)4x x -=+,∴'=3PO O P =,即P 点坐标为(3,0)②如图,过点A 作AQ ⊥AP ,并在AQ 上取点Q 使AQ =AP ,过Q 点作HQ ⊥y 轴,∴90QAH PAO ∠+∠=︒,∵90APO PAO ∠+∠=︒,∴APO QAH ∠=∠,∴AOP QHA ≅(AAS )∴HQ =AO =6,AH =OP =3,∴点Q 坐标为(6,9),∵△APQ 是等腰直角三角形,∴将直线AP 绕点P 顺时针旋转45︒得到直线A P ',直线A P '与PQ 重合,设经过P (3,0),Q (6,9)的直线A P '解析式为y kx b =+得3069k b k b +=⎧⎨+=⎩ , 解得:39k b =⎧⎨=-⎩, 即直线A P '为39y x =-,(3)由平移性质可知:'//BB A P ',由(2)得直线A P '为39y x =-,∴设直线'BB 解析式为3y x m =+,当x =8时,y =0,即324=0m ⨯+,解得:=24m -,∴直线'BB 解析式为324y x =-,由(2)得A (0,6)、Q (6,9),则直线AQ 解析式为:162y x =+, I .当AP 为直角边,90B AP '∠=︒时,如图3-1联立直线'BB 和直线AQ 得:324162y x y x =-⎧⎪⎨=+⎪⎩, 解得:1212x y =⎧⎨=⎩, 即'B 坐标(12,12),故点B (8,0)向右移动4个单位,向上移动12个单位得到点'B ,∴故点P (3,0)向右移动4个单位,向上移动12个单位得到点P'(7,12), 即当AP 为直角边,90B AP '∠=︒时,点P'(7,12),II .当AP 为直角边,90B PA '∠=︒时,如图3-2,∴'//PB AQ ,设直线'PB 解析式为:12y x n =+, ∵P 点坐标为(3,0),∴1032n =⨯+, ∴32n =-∴直线'PB 解析式为1322y x =-, 联立直线'BB 和直线'PB 得:3241322y x y x =-⎧⎪⎨=-⎪⎩, 解得:93x y =⎧⎨=⎩, 即'B 坐标(9,3),故点B (8,0)向右移动1个单位,向上移动3个单位得到点'B , ∴故点P (3,0)向右移动1个单位,向上移动3个单位得到点P'(4,3),, 即当AP 为直角边,90B PA '∠=︒时,点P'(4,3).【点睛】本题综合考查了一次函数与几何综合,待定系数法求解析式是基础,解(2)关键是利用等腰直角三角形构建三垂直全等从而求出旋转45°直线的解析式;解(3)关键是利用平行直线的性质求出解析式.25.(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.【详解】试题分析:(1)因为四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE (SAS),即可得到AF=DE,∠DA解析:(1)成立;(2)成立,理由见试题解析;(3)正方形,证明见试题解析.【详解】试题分析:(1)因为四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠DAF=∠CDE,又因为∠ADG+∠EDC=90°,即有AF⊥DE;(2)∵四边形ABCD为正方形,CE=DF,可证△ADF≌△DCE(SAS),即可得到AF=DE,∠E=∠F,又因为∠ADG+∠EDC=90°,即有AF⊥DE;(3)设MQ,DE分别交AF于点G,O,PQ交DE于点H,因为点M,N,P,Q分别为AE,EF,FD,AD的中点,可得MQ=PN=12DE,PQ=MN=12AF,MQ∥DE,PQ∥AF,然后根据AF=DE,可得四边形MNPQ是菱形,又因为AF⊥DE即可证得四边形MNPQ是正方形.试题解析:(1)上述结论①,②仍然成立,理由是:∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠DAF=∠CDE,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;(2)上述结论①,②仍然成立,理由是:∵四边形ABCD为正方形,∴AD=DC,∠BCD=∠ADC=90°,在△ADF和△DCE中,∵DF=CE,∠ADC=∠BCD=90°,AD=CD,∴△ADF≌△DCE(SAS),∴AF=DE,∠E=∠F,∵∠ADG+∠EDC=90°,∴∠ADG+∠DAF=90°,∴∠AGD=90°,即AF⊥DE;(3)四边形MNPQ是正方形.理由是:如图,设MQ,DE分别交AF于点G,O,PQ交DE于点H,∵点M,N,P,Q分别为AE,EF,FD,AD的中点,∴MQ=PN=12DE,PQ=MN=12AF,MQ∥DE,PQ∥AF,∴四边形OHQG是平行四边形,∵AF=DE,∴MQ=PQ=PN=MN,∴四边形MNPQ是菱形,∵AF⊥DE,∴∠AOD=90°,∴∠HQG=∠AOD=90°,∴四边形MNPQ是正方形.考点:1.四边形综合题;2.综合题.。
初二下学期经典易错题含答案

初二下学期期末复习卷(经典易错题)1。
已知抛物线28y x x c =-+的顶点在x 轴上,则c 等于( )A 。
4 B. 8 C 。
-4 D 。
162。
若点(2,5),(4,5)是抛物线2y ax bx c =++上的两个点,那么抛物线的对称轴是( )A. 直线1x =B. 直线2x =C. 直线3x = D 。
直线4x =3。
已知实数1x ,2x 满足123x x +=,122x x =,则以1x ,2x 为根的一元二次方程是( )A 。
2320x x -+= B. 2320x x ++= C 。
2320x x +-= D. 2320x x --=4.若二次函数26y x x c =-+的图象过A ()11,y -,B ()22,y ,C ()35,y ,则1y ,2y ,3y 的大小关系是( ) A 。
123y y y >> B. 132y y y >> C. 213y y y >> D. 312y y y >>5。
如图,将矩形ABCD 绕点A 顺时针旋转到矩形///AB C D 的位置,旋转角为α(0°<α<90°)。
若∠1=112°,则∠α的大小是( )A. 68°B. 20°C. 28° D 。
22°6. O 是等边△ABC 内的一点,OB=1,OA=2,∠AOB=150°,则OC=( ) A. 3 B 。
5 C 。
7 D 。
37.一次函数y ax b =+()0a ≠与二次函数2y ax bx c =++()0a ≠在同一平面直角坐标系中的图象可能是( )8。
若1ab ≠,且有25201890a a ++=及29201850b b ++=,则a b的值为( ) A 。
95 B 。
59 C 。
20185- D 。
20189- 9。
【易错题】八年级数学下期末试卷(附答案)

【易错题】八年级数学下期末试卷(附答案)一、选择题1.一次函数y kx b =+的图象如图所示,点()3,4P 在函数的图象上.则关于x 的不等式4kx b +≤的解集是( )A .3x ≤B .3x ≥C .4x ≤D .4x ≥ 2.若等腰三角形的底边长为6,底边上的中线长为4,则它的腰长为( )A .7B .6C .5D .43.已知函数y =11x x +-,则自变量x 的取值范围是( ) A .﹣1<x <1 B .x ≥﹣1且x ≠1C .x ≥﹣1D .x ≠14.将一张长方形纸片按如图所示的方式折叠,,BC BD 为折痕,则CBD ∠的度数为( )A .60︒B .75︒C .90︒D .95︒5.小强所在学校离家距离为2千米,某天他放学后骑自行车回家,先骑了5分钟后,因故停留10分钟,再继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s (千米)与所用时间t (分)之间的关系( )A .B .C .D .6.若正比例函数的图象经过点(,2),则这个图象必经过点( ). A .(1,2)B .(,)C .(2,)D .(1,)7.如图1,四边形ABCD 中,AB ∥CD ,∠B =90°,AC =AD .动点P 从点B 出发沿折线B →A →D →C 方向以1单位/秒的速度运动,在整个运动过程中,△BCP 的面积S 与运动时间t (秒)的函数图象如图2所示,则AD 等于( )A .10B .89C .8D .418.二次根式()23-的值是( ) A .﹣3 B .3或﹣3C .9D .39.无论m 为任何实数,关于x 的一次函数y =x +2m 与y =-x +4的图象的交点一定不在( )A .第一象限B .第二象限C .第三象限D .第四象限 10.下列运算正确的是( ) A .235+= B .32﹣2=3 C .236⨯=D .632÷=11.如图,将四边形纸片ABCD 沿AE 向上折叠,使点B 落在DC 边上的点F 处.若AFD V 的周长为18,ECF V 的周长为6,四边形纸片ABCD 的周长为( )A .20B .24C .32D .4812.正比例函数()0y kx k =≠的函数值y 随x 的增大而增大,则y kx k =-的图象大致是( )A .B .C .D .二、填空题13.一艘轮船在小岛A 的北偏东60°方向距小岛80海里的B 处,沿正西方向航行3小时后到达小岛的北偏西45°的C 处,则该船行驶的速度为____________海里/时. 14.已知()()1,32,1A B -、,点P 在y 轴上,则当y 轴平分APB ∠时,点P 的坐标为______.15.在三角形ABC 中,点,,D E F 分别是,,BC AB AC 的中点,AH BC ⊥于点H ,若50DEF ∠=o ,则CFH ∠=________.16.如果将直线y=3x-1平移,使其经过点(0,2),那么平移后所得直线的表达式是______.17.已知一次函数y=kx+b 的图象如图,则关于x 的不等式kx+b >0的解集是______.18.一组数据:1、2、5、3、3、4、2、4,它们的平均数为_______,中位数为_______,方差是_______.19.如图,已如长方形纸片,ABCD O 是BC 边上一点,P 为CD 中点,沿AO 折叠使得顶点B 落在CD 边上的点P 处,则OAB ∠的度数是______.20.(多选)在同一条道路上,甲车从A 地到B 地,乙车从B 地到A 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离y (千米)与行驶时间x (小时)的函数关系,下列说法正确的是( )A .甲乙两车出发2小时后相遇B .甲车速度是40千米/小时C .相遇时乙车距离B 地100千米D .乙车到A 地比甲车到B 地早53小时 三、解答题21.2019年4月23日是第24个世界读书日.为迎接第24个世界读书日的到来,某校举办读书分享大赛活动:现有甲、乙两位同学的各项成绩如下表所示:若“推荐语”“读书心得”“读书讲座”的成绩按2:3:5确定综合成绩,则甲、乙二人谁能获胜?请通过计算说明理由 参赛者 推荐语 读书心得 读书讲座 甲 87 85 95 乙94888822.如图,在ABCD Y 中,E ,F 分别是边AD ,BC 上的点,且AE CF .求证:四边形BEDF 为平行四边形.23.如图,点B 、E 、C 、F 在一条直线上,AB =DF ,AC =DE ,BE =FC . (1)求证:△ABC ≌△DFE ;(2)连接AF 、BD ,求证:四边形ABDF 是平行四边形.24.已知:如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:∠EBF=∠EDF.25.我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;平均数(分)中位数(分)众数(分)初中部85高中部85100(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】 【分析】观察函数图象结合点P 的坐标,即可得出不等式的解集. 【详解】解:观察函数图象,可知:当3x ≤时,4kx b +≤. 故选:A . 【点睛】考查了一次函数与一元一次不等式以及一次函数的图象,观察函数图象,找出不等式4kx b +≤的解集是解题的关键. 2.C解析:C 【解析】 【分析】 【详解】∵等腰三角形ABC 中,AB =AC ,AD 是BC 上的中线, ∴BD =CD =12BC =3, AD 同时是BC 上的高线, ∴AB =22AD BD +=5.故它的腰长为5.故选C.3.B解析:B 【解析】 【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,就可以求解. 【详解】 解:根据题意得:1010x x +≥⎧⎨-≠⎩,解得:x≥-1且x≠1. 故选B .点睛:考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑: (1)当函数表达式是整式时,自变量可取全体实数; (2)当函数表达式是分式时,考虑分式的分母不能为0; (3)当函数表达式是二次根式时,被开方数为非负数.4.C解析:C 【解析】 【分析】根据图形,利用折叠的性质,折叠前后形成的图形全等,对应角相等,利用平角定义ABC ∠+A BC '∠+E BD '∠+EBD ∠=180°,再通过等量代换可以求出CBD ∠. 【详解】解:∵长方形纸片按如图所示的方式折叠,,BC BD 为折痕 ∴A BC ABC '∠=∠,E BD EBD '∠=∠∵ABC ∠+A BC '∠+E BD '∠+EBD ∠=180°(平角定义) ∴A BC '∠+A BC '∠+E BD '∠+E BD '∠=180°(等量代换)A BC '∠+E BD '∠=90° 即CBD ∠=90° 故选:C . 【点睛】本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.5.D解析:D 【解析】 【分析】根据描述,图像应分为三段,学校离家最远,故初始时刻s 最大,到家,s 为0,据此可判断. 【详解】因为小明家所在学校离家距离为2千米,某天他放学后骑自行车回家,行使了5分钟后,因故停留10分钟,继续骑了5分钟到家,所以图象应分为三段,根据最后离家的距离为0,由此可得只有选项DF 符合要求.故选D .【点睛】本题要求正确理解函数图象与实际问题的关系,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.6.D解析:D【解析】设正比例函数的解析式为y=kx(k≠0),因为正比例函数y=kx的图象经过点(-1,2),所以2=-k,解得:k=-2,所以y=-2x,把这四个选项中的点的坐标分别代入y=-2x中,等号成立的点就在正比例函数y=-2x的图象上,所以这个图象必经过点(1,-2).故选D.7.B解析:B【解析】【分析】当t=5时,点P到达A处,根据图象可知AB=5;当s=40时,点P到达点D处,根据三角形BCD的面积可求出BC的长,再利用勾股定理即可求解.【详解】解:当t=5时,点P到达A处,根据图象可知AB=5,过点A作AE⊥CD交CD于点E,则四边形ABCE为矩形,∵AC=AD,∴DE=CE=12 CD,当s=40时,点P到达点D处,则S=12CD•BC=12(2AB)•BC=5×BC=40,∴BC=8,∴AD=AC=故选B.【点睛】本题以动态的形式考查了函数、等腰三角形的性质、勾股定理等知识.准确分析图象,并结合三角形的面积求出BC的长是解题的关键.8.D解析:D【解析】【分析】本题考查二次根式的化简,(0)(0)a aa a⎧=⎨-<⎩….【详解】|3|3=-=.故选D.【点睛】本题考查了根据二次根式的意义化简.a≥0a;当a≤0a.9.C解析:C【解析】由于直线y=-x+4的图象不经过第三象限.因此无论m取何值,直线y=x+2m与y=-x+4的交点不可能在第三象限.故选C.10.C解析:C【解析】【分析】根据二次根式得加减法法则及乘除法法则逐一计算即可得答案.【详解】B.,故该选项计算错误,,故该选项计算正确,,故该选项计算错误.故选:C.【点睛】本题考查二次根式得运算,熟练掌握运算法则是解题关键.11.B解析:B【解析】【分析】根据折叠的性质易知矩形ABCD的周长等于△AFD和△CFE的周长的和.【详解】由折叠的性质知,AF=AB,EF=BE.所以矩形的周长等于△AFD和△CFE的周长的和为18+6=24cm.故矩形ABCD的周长为24cm.故答案为:B.【点睛】本题考查了折叠的性质,解题关键是折叠前后图形的形状和大小不变,对应边和对应角相等.12.B解析:B【解析】【分析】由于正比例函数y=kx(k≠0)函数值随x的增大而增大,可得k>0,-k<0,然后判断一次函数y=kx-k的图象经过的象限即可.【详解】解:∵正比例函数y=kx(k≠0)函数值随x的增大而增大,∴k>0,∴-k<0,∴一次函数y=kx-k的图象经过一、三、四象限;故选:B.【点睛】本题主要考查了一次函数的图象,一次函数y=kx+b(k≠0)中k,b的符号与图象所经过的象限如下:当k>0,b>0时,图象过一、二、三象限;当k>0,b<0时,图象过一、三、四象限;k<0,b>0时,图象过一、二、四象限;k<0,b<0时,图象过二、三、四象限.二、填空题13.【解析】【分析】设该船行驶的速度为x海里/时由已知可得BC=3xAQ⊥BC∠BAQ=60°∠CAQ=45°AB=80海里在直角三角形ABQ中求出AQBQ 再在直角三角形AQC中求出CQ得出BC=40+【解析】【分析】设该船行驶的速度为x海里/时,由已知可得BC=3x,AQ⊥BC,∠BAQ=60°,∠CAQ=45°,AB=80海里,在直角三角形ABQ中求出AQ、BQ,再在直角三角形AQC中求出CQ,得出BC=40+403=3x,解方程即可.【详解】如图所示:该船行驶的速度为x海里/时,3小时后到达小岛的北偏西45°的C处,由题意得:AB=80海里,BC=3x海里,在直角三角形ABQ中,∠BAQ=60°,∴∠B=90°−60°=30°,∴AQ=12AB=40,BQ3AQ=3在直角三角形AQC中,∠CAQ=45°,∴CQ=AQ=40,∴BC=40+33x,解得:x 40403+即该船行驶的速度为404033+海里/时;40403+【点睛】本题考查的是解直角三角形,熟练掌握方向角是解题的关键.14.【解析】【分析】作点A关于y轴对称的对称点求出点的坐标再求出直线的解析式将代入直线解析式中即可求出点P的坐标【详解】如图作点A关于y轴对称的对称点∵点A关于y轴对称的对称点∴设直线的解析式为将点和点解析:()0,5【解析】【分析】作点A关于y轴对称的对称点A',求出点A'的坐标,再求出直线BA'的解析式,将0x=代入直线解析式中,即可求出点P的坐标.【详解】如图,作点A 关于y 轴对称的对称点A ' ∵()1,3A ,点A 关于y 轴对称的对称点A ' ∴()1,3A '-设直线BA '的解析式为y kx b =+将点()1,3A '-和点()2,1B -代入直线解析式中312k bk b =-+⎧⎨=-+⎩解得2,5k b ==∴直线BA '的解析式为25y x =+ 将0x =代入25y x =+中 解得5y = ∴()0,5P 故答案为:()0,5.【点睛】本题考查了坐标点的问题,掌握角平分线的性质、轴对称的性质、一次函数的性质是解题的关键.15.80°【解析】【分析】先由中位线定理推出再由平行线的性质推出然后根据直角三角形斜边上的中线等于斜边的一半得到HF=CF 最后由三角形内角和定理求出【详解】∵点分别是的中点∴(中位线的性质)又∵∴(两直解析:80° 【解析】 【分析】先由中位线定理推出50EDB FCH ∠=∠=o ,再由平行线的性质推出CFH ∠,然后根据直角三角形斜边上的中线等于斜边的一半得到HF=CF ,最后由三角形内角和定理求出3AQ AP PQ =-=【详解】∵点,,D E F 分别是,,BC AB AC 的中点∴//,//EF BC DE AC (中位线的性质) 又∵//EF BC∴50DEF EDB o ∠=∠=(两直线平行,内错角相等) ∵//DE AC∴50EDB FCH ∠=∠=o (两直线平行,同位角相等) 又∵AH BC ⊥∴三角形AHC 是Rt 三角形 ∵HF 是斜边上的中线 ∴12HF AC FC == ∴50FHC FCH o ∠=∠=(等边对等角) ∴18050280CFH ∠=-⨯=o o o 【点睛】本题考查了中位线定理,平行线的性质,直角三角形斜边上的中线等于斜边的一半,和三角形内角和定理.熟记性质并准确识图是解题的关键.16.【解析】【分析】根据平移不改变k 的值可设平移后直线的解析式为y=3x+b 然后将点(02)代入即可得出直线的函数解析式【详解】解:设平移后直线的解析式为y=3x+b 把(02)代入直线解析式得2=b 解得 解析:32y x =+【解析】 【分析】根据平移不改变k 的值可设平移后直线的解析式为y=3x+b ,然后将点(0,2)代入即可得出直线的函数解析式. 【详解】解:设平移后直线的解析式为y=3x+b . 把(0,2)代入直线解析式得2=b , 解得 b=2.所以平移后直线的解析式为y=3x+2. 故答案为:y=3x+2. 【点睛】本题考查一次函数图象与几何变换,待定系数法求一次函数的解析式,掌握直线y=kx+b (k≠0)平移时k 的值不变是解题的关键.17.【解析】【分析】直接利用一次函数图象结合式kx+b >0时则y 的值>0时对应x 的取值范围进而得出答案【详解】如图所示:关于x 的不等式kx+b >0的解集是:x <2故答案为:x <2【点睛】此题主要考查了一 解析:2x <【解析】 【分析】直接利用一次函数图象,结合式kx+b >0时,则y 的值>0时对应x 的取值范围,进而得出答案. 【详解】 如图所示:关于x 的不等式kx+b >0的解集是:x <2. 故答案为:x <2. 【点睛】此题主要考查了一次函数与一元一次不等式,正确利用数形结合是解题关键.18.33【解析】【分析】根据平均数的公式即可求出答案将数据按照由小到大的顺序重新排列中间两个数的平均数即是中位数根据方差的公式计算即可得到这组数据的方差【详解】平均数=将数据重新排列是:12233445解析:3, 3, 32. 【解析】 【分析】根据平均数的公式即可求出答案,将数据按照由小到大的顺序重新排列,中间两个数的平均数即是中位数,根据方差的公式计算即可得到这组数据的方差. 【详解】平均数=1(12533424)38⨯+++++++=,将数据重新排列是:1、2、2、3、3、4、4、5,∴中位数是3332+=, 方差=222221(13)2(23)2(33)2(43)(53)8⎡⎤⨯-+⨯-+⨯-+⨯-+-⎣⎦=32, 故答案为:3,3,32. 【点睛】此题考查计算能力,计算平均数,中位数,方差,正确掌握各计算的公式是解题的关键.19.30°【解析】【分析】根据题意先通过△ADP 求出∠DAP 的因为△ABO ≌△APO即可求出∠OAB的度数【详解】解:∵P是CD的中点沿折叠使得顶点落在边上的点∴DP=PC=CD△ABO≌△APO∵四边解析:30°【解析】【分析】根据题意先通过△ADP求出∠DAP的,因为△ABO≌△APO,即可求出∠OAB的度数.【详解】解:∵ P是CD的中点,沿AO折叠使得顶点B落在CD边上的点P∴DP=PC=12CD, △ABO≌△APO∵四边形ABCD为长方形∴∠D=∠DAB=90°,AB=CD=AP=2DP ∴∠DAP=30°∵△ABO≌△APO∴∠PAO=∠OAP=12∠BAP∴∠OAP=12∠BAP=12(∠DAB-∠DAP)=12(90°-30°)=30°故答案为:30°【点睛】此题主要考查了全等三角形的性质和特殊直角三角形的性质,解题的关键是折叠前后图形全等.20.ABD【解析】【分析】根据图象的信息依次进行解答即可【详解】A出发2h 后其距离为零即两车相遇故正确;B甲的速度是千米/小时故正确;C相遇时甲行驶的路程为2×40=80km故乙车行驶路程为120千米故解析:ABD【解析】【分析】根据图象的信息依次进行解答即可.【详解】A、出发2h后,其距离为零,即两车相遇,故正确;B、甲的速度是200405=千米/小时,故正确;C、相遇时,甲行驶的路程为2×40=80km,故乙车行驶路程为120千米,故离B地80千米,故错误;D、乙车2小时行驶路程120千米,故乙的速度是120602=千米/小时,故乙车到达A地时间为20060=103小时,故乙车到A 地比甲车到B 地早5-103=53小时,D 正确; 故选:ABD. 【点睛】本题考查了行程问题的数量关系速度=路程÷时间的运用,速度和的运用,解答时正确理解函数图象的数据的意义是关键.三、解答题21.甲获胜;理由见解析. 【解析】 【分析】根据加权平均数的计算公式列出算式,进行计算即可. 【详解】 甲获胜;Q 甲的加权平均成绩为87285395590.4235⨯+⨯+⨯=++(分),乙的加权平均成绩为94288388589.2235⨯+⨯+⨯=++(分),∵90.489.2>, ∴甲获胜. 【点睛】此题考查了加权平均数的概念及应用,用到的知识点是加权平均数的计算公式,解题的关键是根据公式列出算式. 22.证明见解析. 【解析】 【分析】由平行四边形的性质,得到AD ∥BC ,AD=BC ,由AE CF =,得到ED BF =,即可得到结论. 【详解】证明:四边形ABCD 是平行四边形, ∴AD BC ∥,AD BC =. ∵AE CF =,∴AD AE BC CF -=-. ∴ED BF =,∵//ED BF ,ED BF =, ∴四边形BEDF 是平行四边形. 【点睛】本题考查了平行四边形的判定和性质,解题的关键是熟练掌握平行四边形的判定和性质进行证明.23.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)由SSS证明△ABC≌△DFE即可;(2)连接AF、BD,由全等三角形的性质得出∠ABC=∠DFE,证出AB∥DF,即可得出结论.【详解】详解:证明:,,在和中,,≌;解:如图所示:由知≌,,,,四边形ABDF是平行四边形.点睛:本题考查了平行四边形的判定、全等三角形的判定与性质、平行线的判定;熟练掌握平行四边形的判定方法,证明三角形全等是解决问题的关键.24.证明见解析.【解析】【分析】先连接BD,交AC于O,由于AB=CD,AD=CB,根据两组对边相等的四边形是平行四边形,可知四边形ABBCD是平行四边形,于是OA=OC,OB=OD,而AF=CF,根据等式性质易得OE=OF,再根据对角线互相平分的四边形是平行四边形可证四边形DEBF是平行四边形,于是∠EBF=∠FDE.【详解】解:连结BD,交AC于点O.∵四边形ABCD是平行四边形,∴OB=OD,OA=OC.∵AE=CF,∴OE=OF,∴四边形BFDE是平行四边形,∴∠EBF=∠EDF.25.(1)平均数(分)中位数(分)众数(分)初中部858585高中部8580100【解析】解:(1)填表如下:平均数(分)中位数(分)众数(分)初中部858585高中部8580100∵两个队的平均数都相同,初中部的中位数高, ∴在平均数相同的情况下中位数高的初中部成绩好些. (3)∵,222222S 7085100851008575858085160=-+-+-+-+-=高中队()()()()(),∴2S 初中队<2S 高中队,因此,初中代表队选手成绩较为稳定.(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答. (2)根据平均数和中位数的统计意义分析得出即可. (3)分别求出初中、高中部的方差比较即可.。
八年级数学下册期末试卷易错题(Word版含答案)

10.菱形 的对角线 与 相交于点O,若 ,则菱形 的面积是___________.
11.在 中, , , ,则线段AC的长为________.
12.如图,矩形 的对角线 , 相交于点 , 交 于点 ,连接 .若矩形 的周长为 ,则 的周长为__________ .
13.将直线 平移后经过原点,则平移后的解析式为___________.
14.在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,要使四边形EFGH为菱形,则四边形ABCD的对角线应满足的条件是__
15.正方形 , , ,…按如下图所示的方式放置.点 , , ,…和点 , , ,…分别在直线 和 轴上,已知正方形 的边长为 ,正方形 边长为 ,则 的坐标是______.
(3)在图3中,当 , , 时,求 之长.
【参考答案】
一、选择题
1.D
解析:D
【分析】
根据二次根式和分式有意义的条件列出不等式,求解不等式即可.
【详解】
根据题意得:x﹣3≥0且x﹣5≠0,
解得x≥3且x≠5.
∴自变量x的取值范围是x≥3且x≠5.
(2)请直接写出当四边形ABCD的边AB与BD满足什么关系时,四边形 分别是菱形、矩形、正方形.
21.阅读下列解题过程:
= = = =
= = =
请回答下列问题:
(1)观察上面的解题过程,请直接写出结果.
=.
(2)利用上面提供的信息请化简:
的值.
22.某网校规定:普通网上学习费用每小时4元.暑假为了促销,新推出两种优惠卡:
A. B. C. D.
6.如图,在△ABC中,点D为BC边的中点,点E为AC上一点.将∠C沿DE所在直线翻折,使点C落在AB上的点F处,若∠AEF=50°,则∠A的度数为()
八年级数学下册期末试卷易错题(Word版含答案)

八年级数学下册期末试卷易错题(Word 版含答案)一、选择题1.函数y =123x x -+-中自变量x 的取值范围是( ) A .x ≤2B .x =3C .x <2且x ≠3D .x ≤2且x ≠3 2.下列各组数中,能构成直角三角形的是( ) A .4,5,6 B .1,1,2 C .6,8,11 D .5,12,23 3.已知四边形ABCD 中,对角线AC 、BD 交于O ,则下列选项中不能证明四边形ABCD 为平行四边形的是( )A .AB ∥CD ,AB =CDB .AB =CD ,BC =AD C .AB ∥CD ,AC =BD D .OA =OC ,OB =OD4.在期末体育测试中,某校初二1班、2班、3班、4班四个班级学生成绩的平均分相等,方差分别为s 1班2=6.2,s 2班2=5.8,s 3班2=12.6,s 4班2=9.8,则这四个班级中学生体育成绩最整齐的是( )A .1班B .2班C .3班D .4班 5.ABC ∆的周长为60,三条边之比为13:12:5,则这个三角形的面积为( )A .30B .90C .60D .120 6.在菱形ABCD 中,80ABC ∠=︒,BA BE =,则DAE =∠( )A .20︒B .30C .40︒D .50︒7.勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要纽带.数学家欧几里得利用如图验证了勾股定理:以直角三角形ABC 的三条边为边长向外作正方形ACHI ,正方形ABED ,正方形BCGF ,连接BI ,CD ,过点C 作CJ ⊥DE 于点J ,交AB 于点K .设正方形ACHI 的面积为S 1,正方形BCGF 的面积为S 2,长方形AKJD 的面积为S 3,长方形KJEB 的面积为S 4,下列结论:①BI =CD ;②2S △ACD =S 1;③S 1+S 4=S 2+S 3;1S 2S 34S S + )A .1个B .2个C .3个D .4个8.如图,在平面直角坐标系中,四边形11112222333,,OA B C A A B C A A B C ,…都是菱形,点123,,A A A …都在x 轴上,点123,,C C C ,…都在直线3333y x =+上,且11212323160,1C OA C A A C A A OA ∠=∠=∠==︒=,则点n C 的横坐标是( )A .2321n -⨯-B .2321n -⨯+C .1321n -⨯-D .1321n -⨯+二、填空题9.若使163x-在实数范围内有意义,则x 的取值范围为______. 10.如图,菱形ABCD 的周长为45,对角线AC 和BD 相交于点O ,AC ∶BD=1∶2,则AO ∶BO=____,菱形ABCD 的面积S=____.11.若一个直角三角形的两边长分别是3和4,那么以斜边为边长的正方形的面积为______.12.如图,点P 是矩形ABCD 的对角线AC 上一点,过点P 作EF ∥BC ,分别交AB ,CD 于点E 、F ,连接PB 、PD ,若AE =2,PF =9,则图中阴影面积为______;13.一次函数2y x m =+的图象与y 轴的交点是()0,3,则m =______.14.如图中,四边形 ABCD 是对角线互相垂直的四边形,且 OB =OD ,若使四边形 ABCD 为菱形,则需添加的条件是______.(只需添加一个条件即可)15.将正方形111A B C O ,2221A B C C ,3332A B C C 按如图所示方式放置,点1A ,2A ,3A ,…和点1C ,2C ,3C ,…分别在直线1y x =+和x 轴上,则点4B 的坐标是______,2021B 的纵坐标是______.16.已知矩形ABCD ,点E 在AD 边上,DE AE >,连接BE ,将ABE △沿着BE 翻折得到BFE △,射线EF 交BC 于G ,若点G 为BC 的中点,1FG =,6DE =,则BE 长为________.三、解答题17.计算(118232+ (2)13273 (3)(57)(57)2+(4)0214(37)8(12)2+ 18.一艘轮船以30千米/时的速度离开港口,向东南方向航行,另一艘轮船同时离开港口,以40千米/时的速度航行,它们离开港口一个半小时后相距75千米,求第二艘船的航行方向.19.在所给的9×9方格中,每个小正方形的边长都是1,按要求画平行四边形,使它的四个顶点以及对角线交点都在方格的顶点上.(1)在图甲中画一个平行四边形,使它的周长是整数.(2)在图乙中画一个平行四边形,使它的周长是无理数.20.如图,在平行四边形ABCD 中,点E 是边AB 的中点,连接CE 并延长CE 交DA 的延长线于点F ,连接AC ,BF .(1)求证:四边形AFBC 是平行四边形(2)当AEC ∠的度数为______度时,四边形AFBC 是菱形;(3)若52D ∠=︒,则当AEC ∠的度数为______度时,四边形AFBC 是矩形. 21.先阅读下列的解答过程,然后再解答: 2m n ±a 、b ,使a +b =m ,ab =n ,使得22()()a b m +=a b n =22=()m n a b a b ±±=a >b ) 7+437+437+212m =7,n =12,由于4+3=7,4×3=12 即22(4)(3)7+=3412=∴7+43=27+212=(43)23+=+(1)填空:423-= ,9+45= ;(2)化简:19415-.22.为丰富同学们的课余活动,某校成立了篮球课外兴趣小组,计划购买一批篮球,需购买A 、B 两种不同型号的篮球共300个.已知购买3个A 型篮球和2个B 型篮球共需340元,购买2个A 型篮球和1个B 型篮球共需要210元.(1)求购买一个A 型篮球、一个B 型篮球各需多少元?(2)若该校计划投入资金W 元用于购买这两种篮球,设购进的A 型篮球为t 个,求W 关于t 的函数关系式;(3)学校在体育用品专卖店购买A 、B 两种型号篮球共300个,经协商,专卖店给出如下优惠:A 种球每个降价8元,B 种球打9折,计算下来,学校共付费16740元,学校购买A 、B 两种篮球各多少个?23.已知如图,在ABCD 中,点E 是AD 边上一点,连接BE 、CE ,BE CE =,BE CE ⊥,点F 是EC 上一动点,连接BF .(1)如图1,若点F 是EC 的中点,10BF =,求ABCD 的面积;(2)如图2,当BF AB ⊥时,连接DF ,求证:AB DF BF +=;(3)如图3,以BF 为直角边作等腰Rt FBG ,90FBG ∠=︒,连接GE ,若2DE =,5CD =,当点F 在运动过程中,请直接写出BEG 周长的最小值.24.如图所示,在平面直角坐标系中,点B 的坐标为(4,8),过点B 分别作BA ⊥y 轴,BC ⊥x 轴,得到一个长方形OABC ,D 为y 轴上的一点,将长方形OABC 沿着直线DM 折叠,使得点A 与点C 重合,点B 落在点F 处,直线DM 交BC 于点E .(1)直接写出点D 的坐标 ;(2)若点P 为x 轴上一点,是否存在点P 使△PDE 的周长最小?若存在,请求出△PDE的最小周长;若不存在,请说明理由.(3)在(2)的条件下,若Q 点是线段DE 上一点(不含端点),连接PQ .有一动点H 从P 点出发,沿线段PQ 以每秒1个单位的速度运动到点Q ,再沿着线段QE 以每秒5个单位长度的速度运动到点E 后停止.请直接写出点H 在整个运动过程中所用的最少时间t ,以及此时点Q 的坐标.25.如图,在平面直角坐标系中,点A 的坐标为(0,6),点B 在x 轴的正半轴上.若点P 、Q 在线段AB 上,且PQ 为某个一边与x 轴平行的矩形的对角线,则称这个矩形为点P 、Q 的“涵矩形”。
数学八年级下册数学期末试卷易错题(Word版含答案)
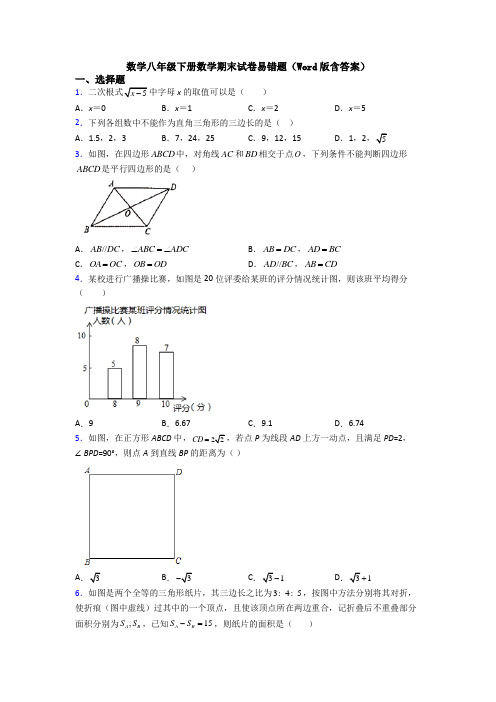
数学八年级下册数学期末试卷易错题(Word 版含答案) 一、选择题 1.二次根式5x -中字母x 的取值可以是( ) A .x =0B .x =1C .x =2D .x =5 2.下列各组数中不能作为直角三角形的三边长的是( ) A .1.5,2,3 B .7,24,25 C .9,12,15 D .1,2,5 3.如图,在四边形ABCD 中,对角线AC 和BD 相交于点O ,下列条件不能判断四边形ABCD 是平行四边形的是( )A .//AB DC ,ABC ADC ∠=∠B .AB DC =,AD BC = C .OA OC =,OB OD =D .//AD BC ,AB CD = 4.某校进行广播操比赛,如图是20位评委给某班的评分情况统计图,则该班平均得分( )A .9B .6.67C .9.1D .6.745.如图,在正方形ABCD 中,22CD =,若点P 为线段AD 上方一动点,且满足PD =2,∠BPD =90°,则点A 到直线BP 的距离为( )A 3B .3-C 31D 31 6.如图是两个全等的三角形纸片,其三边长之比为3: 4: 5,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为,A B S S ,已知15A B S S -=,则纸片的面积是( )A .102B .104C .106D .1087.如图,以Rt △ABC (AC ⊥BC )的三边为边,分别向外作正方形,它们的面积分别为S 1﹑S 2﹑S 3,若S 1+S 2+S 3=12,则S 1的值是( )A .4B .5C .6D .78.如图,菱形ABCD 的边长为4cm ,60ABC ∠=︒,且M 为BC 的中点,P 是对角线BD 上的一动点,则PM PC +的最小值为( )A .4cmB .3cmC .25cmD .23cm二、填空题9.若二次根式21x -在实数范围内有意义,则x 的取值范围是____.10.已知菱形的两条对角线长为6和8,菱形的周长是_______,面积是________. 11.如图,矩形ABCD 的对角线AC 与BD 相交于点O ,∠AOD =60°,AD =4,则AB =___.12.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,OE BD ⊥交AD 于点E ,连接BE .若矩形ABCD 的周长为8cm ,则ABE △的周长为__________cm .13.饮料每箱24瓶,售价48元,买饮料的总价y (元)与所买瓶数x 之间的函数________.14.如图,矩形ABCD 中,对角线AC 和BD 交于点O ,过O 的直线分别交AD 和BC 于点E 、F ,已知AD =4 cm ,图中阴影部分的面积总和为6 cm 2,则矩形的对角线AC 长为___cm.15.如图,在平面直角坐标系中,点A 1,A 2,A 3,…,都在x 轴正半轴上,点B 1,B 2,B 3,…,都在直线33y x =上,△A 1B 1A 2,△A 2B 2A 3,△A 3B 3A 4,…,都是等边三角形,且OA 1=1,则点B 6的纵坐标是______________.16.如图,Rt ,90,6,8ABC ACB AC BC ∠=︒==,将边AC 沿CE 翻折,使点A 落在AB 上的点D 处;再将BC 沿CF 翻折,使点B 落在CD 的延长线上的点B '处,两条折痕与斜边AB 分别交于点,E F ,则线段CE 的长等于_________,线段BF 的长等于_________.三、解答题17.计算:(11213127(2)(232318.由于大风,山坡上的一颗甲树从A 点处被拦腰折断,其顶点恰好落在一棵树乙的底部C 处,如图所示,已知AB =4米,BC =13米,两棵树的水平距离是12米,求甲树原来的高度.19.如图,在4×3正方形网格中,每个小正方形的边长都是1,正方形顶点叫格点,连接两个网格格点的线段叫网格线段,点A 固定在格点上.(1)若a 是图中能用网格线段表示的最小无理数,b 是图中能用网格线段表示的最大无理数,则a = ,b = ;(2)请你画出顶点在格点上且边长为5的所有菱形ABCD ,你画出的菱形面积为 ; 20.如图所示,在矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交BC ,AD 于点E ,F ,垂足为O ,连接AE ,CF .(1)求证:四边形AFCE 为菱形;(2)求AF 的长.21.[观察]请你观察下列式子的特点,并直接写出结果:221111111212++=+-= ; 221111112323++=+-= ; 221111113434++=+-= ; …… [发现]根据你的阅读回答下列问题:(1)请根据上面式子的规律填空:()221111n n ++=+ (n 为正整数); (2)请证明(1) 中你所发现的规律.[应用]请直接写出下面式子的结果:()222222221111111111111223341n n ++++++++++++=+ . 22.寒假将至,某健身俱乐部面向大中学生推出优惠活动,活动方案如下:方案一:购买一张学生寒假专享卡,每次健身费用按六折优惠;方案二:不购买学生寒假专享卡,每次健身费用按八折优惠.设某学生健身x (次),按照方案一所需费用为y 1(元),且y 1=k 1x +b ;按照方案二所需费用为y 2(元),且y 2=k 2x .在平面直角坐标系中的函数图象如图所示.(1)求k 1和b 的值,并说明它们的实际意义;(2)求k 2的值;(3)八年级学生小华计划寒假前往该俱乐部健身8次,应选择哪种方案所需费用更少?请说明理由.(4)小华的同学小琳也计划在该俱乐部健身,若她准备300元的健身费用,最多可以健身多少次?23.如图,在平面直角坐标系中,矩形ABCO 的顶点O 与坐标原点重合,顶点A 、C 在坐标轴上,B (8,4),将矩形沿EF 折叠,使点A 与点C 重合.(1)求点E 的坐标;(2)点P 从O 出发,沿折线O -A -E 方向以每秒2个单位的速度匀速运动,到达终点E 时停止运动,设点P 的运动时间为t ,△PCE 的面积为S ,求S 与t 的关系式,井直接写出t 的取值范围.(3)在(2)的条件下.当PA =PE 时,在平面直角坐标系中是否存在点Q .使得以点P 、E 、 G 、 Q 为顶点的四边形为平行四边形? 若不存在,请说明理出, 若存在,请求出点Q 的坐标.24.如图1,直线y=kx+b 经过第一象限内的定点P(3,4).(1)若b=7,则k=_______;(2)如图2,直线y=kx+b 与y 轴交于点C ,已知点A(6,t),过点A 作AB//y 轴交第一象限内的直线y=kx+b 于点B ,连接OB ,若BP 平分∠OBA .①证明OBC 是等腰三角形;②求k 的值;(3)如图3,点M 是x 轴正半轴上的一个动点,连接PM ,把线段PM 绕点M 顺时针旋转90°至线段NM (∠PMN=90°且PM=MN ),连接OP ,ON ,PN ,当OPN 周长最小时,求点N 的坐标;25.在平面直角坐标系xOy 中,对于点P 给出如下定义:点P 到图形1G 上各点的最短距离为1d ,点P 到图形2G 上各点的最短距离为2d ,若12d d =,就称点P 是图形1G 和图形2G 的一个“等距点”.已知点()6,0A ,()0,6B .(1)在点()6,0D -,()3,0E ,()0,3F 中,______是点A 和点O 的“等距点”;(2)在点()2,1G --,()2,2H ,()3,6I 中,______是线段OA 和OB 的“等距点”;(3)点(),0C m 为x 轴上一点,点P 既是点A 和点C 的“等距点”,又是线段OA 和OB 的“等距点”.①当8m =时,是否存在满足条件的点P ,如果存在请求出满足条件的点P 的坐标,如果不存在请说明理由;②若点P 在OAB 内,请直接写出满足条件的m 的取值范围.【参考答案】一、选择题1.D解析:D【分析】根据二次根式的被开方数是非负数得到50x -,求解即可.【详解】解:由题意,得50x -,解得5x ≥,故x 可以取5,故选:D .【点睛】0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.2.A解析:A【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.【详解】解:A 、1.52+22≠32,不符合勾股定理的逆定理,故本选项符合题意;B 、72+242=252,符合勾股定理的逆定理,故本选项不符合题意;C 、92+122=152,符合勾股定理的逆定理,故本选项不符合题意;D 、12+22=2,符合勾股定理的逆定理,故本选项不符合题意.故选:A .【点睛】本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.3.D解析:D【解析】【分析】根据平行四边形的判定定理逐项判断即可.【详解】A 、由//AB DC ,得180ABC ACD ∠+∠=︒,又ABC ADC ∠=∠,得180ADC ACD ∠+∠=︒,得//AD BC ,可得到四边形ABCD 是平行四边形,故A 选项不符合题意B 、由AB DC =,AD BC =,可得到四边形ABCD 是平行四边形,故B 选项不符合题意; C 、由OA OC =,OB OD =,可得到四边形ABCD 是平行四边形,故C 选项不符合题意; D 、由//AD BC ,AB CD =,不可得到四边形ABCD 是平行四边形,故D 选项符合题意. 故选:D .【点睛】本题主要考查了平行四边形的判定,解题的关键是理解并掌握平行四边形的判定定理,并会灵活运用.4.C解析:C【解析】【分析】根据加权平均数的定义列式计算即可.【详解】解:该班平均得分5889710587⨯+⨯+⨯++=9.1(分),故选:C.【点睛】本题主要考查了加权平均数,解题的关键是掌握加权平均数的定义.5.C解析:C【分析】由题意可得点P在以D为圆心,2为半径的圆上,同时点P也在以BD为直径的圆上,即点P是两圆的交点,由勾股定理可求BP,AH的长,即可求点A到BP的距离.【详解】解:作正方形ABCD的外接圆,另外以点D为圆心,2为半径作圆,两圆在线段AD上方的交点即为点P,连接AC、BD、PD、PB、PA,作AH⊥BP,垂足为H,过点A作AE AP⊥,交BP于点E,如图,∵四边形ABCD是正方形,∴∠ADB=45°,∴2,90AB AD DC BC BAD︒====∠=,∴BD=4,∵DP=2,∴3BP=AE AP⊥,90EAD DAP∴∠+∠=,又90BAE EAD∠+∠=,DAP BAE∴∠=∠,,ADP ABE AD AB∠=∠=,ADP ABE∴∆≅∆,,BE DP AE AP∴==,AEP为等腰直角三角形,AH PE⊥,2PE AH∴=,2BP BE PE AH PD∴=+=+,即2322,AH+,31AH ∴=- 即点A 到BP 的距离为31-.故选C .【点睛】本题考查四边形综合题、全等三角形的判定和性质、等腰三角形的判定和性质、勾股定理、圆等知识,解题的关键是灵活运用这些知识.6.D解析:D【解析】【分析】设3AC FH x ==,则4BC GH x ==,5AB GF x ==,根据勾股定理即可求得CD 的长,利用x 表示出A S ,同理表示出B S ,根据15A B S S -=,即可求得x 的值,进而求得三角形的面积.【详解】解:设3AC FH x ==,则4BC GH x ==,5AB GF x ==.设CD y =,则4BD x y =-,DE CD y ==,在直角BDE ∆中,532BE x x x =-=,根据勾股定理可得:2224(4)x y x y +=-,解得:32y x =, 则2113322222A S BE DE xx x ==⨯=, 同理可得:223B S x =,15A B S S -=, ∴22321523x x -=, 解得:32x =,∴纸片的面积是:213461082x x x ⨯==, 故选:D ..【点睛】本题主要考查了翻折变换(折叠问题),三角形面积的计算,根据勾股定理求得CD 的长是解题的关键.7.C解析:C【解析】【分析】根据正方形的面积公式结合勾股定理就可发现大正方形的面积是两个小正方形的面积和,即可得出答案.【详解】解:∵由勾股定理得:AC2+BC2=AB2,∴S3+S2=S1,∵S1+S2+S3=12,∴2S1=12,∴S1=6,故选:C.【点睛】题考查了勾股定理和正方形面积的应用,注意:分别以直角三角形的边作相同的图形,则两个小图形的面积等于大图形的面积.8.D解析:D【分析】根据菱形的性质,得知A、C关于BD对称,根据轴对称的性质,将PM+PC转化为AP+PM,再根据两点之间线段最短得知AM为PM+PC的最小值.【详解】∵四边形ABCD为菱形,∴A、C关于BD对称,∴连AM交BD于P,则PM+PC=PM+AP=AM,根据两点之间线段最短,AM的长即为PM+PC的最小值.连接AC,∵四边形ABCD是菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC为等边三角形,又∵BM=CM,∴AM⊥BC,∴AM=2222--,=42=23AB BM故选D.【点睛】本题考查了轴对称---最短路径问题,解答过程要利用菱形的性质及等腰三角形的性质,转化为两点之间线段最短的问题来解.二、填空题9.12x≥【解析】【分析】根据二次根式有意义的条件可直接进行求解.【详解】解:由二次根式21x-在实数范围内有意义可得:210x-≥,解得:12x≥;故答案为12x≥.【点睛】本题主要考查二次根式有意义的条件,熟练掌握二次根式有意义的条件是解题的关键.10.A解析:24【解析】【分析】首先根据题意画出图形,然后由菱形的两条对角线长分别是6和8,可求得OA=4,OB=3,再由勾股定理求得边长,继而求得此菱形的周长与面积.【详解】解:如图,菱形ABCD中,AC=8,BD=6,∴OA=12AC=4,OB=12BD=3,AC⊥BD,∴AB222243OA OB+=+=5,∴C菱形的周长=5×4=20,S菱形ABCD=12×6×8=24,故菱形的周长是20,面积是24.故答案为:20;24.【点睛】本题考查了菱形的周长和性质得求法,勾股定理,属于简单题,熟悉菱形的性质和菱形求面积的特殊方法是解题关键.11.B解析:【解析】【分析】由矩形对角线的性质得到AO DO =,结合题意证明ADO △是等边三角形,解得BD 的长,在Rt ABD △中,理由勾股定理解题即可.【详解】解:矩形ABCD 中,AC=BD 且AO=OC ,BO=DOAO DO ∴=ADO ∴△是等腰三角形∠AOD =60°ADO ∴△是等边三角形AD DO AO ∴==AD =44DO ∴=28BD DO ∴==Rt ABD △中AB ==故答案为:【点睛】本题考查矩形的性质、等边三角形的判定与性质、勾股定理等知识,是重要考点,掌握相关知识是解题关键.12.B解析:4【分析】由矩形的性质可得OB =OD ,AB =CD ,AD =BC ,可证OE 是线段BD 的中垂线,可得BE =DE ,即可求解.【详解】解:∵四边形ABCD 是矩形,∴OB =OD ,AB =CD ,AD =BC ,∵矩形ABCD 的周长为8cm ,∴AB +AD =4cm ,∵OE ⊥BD ,∴OE 是线段BD 的中垂线,∴BE =DE ,∴△ABE 的周长=AB +AE +BE =AB +AE +DE =AB +AD =4cm ,故答案为4.【点睛】本题考查了矩形的性质,线段的中垂线的性质以及三角形周长等知识,解答本题的关键是判断出OE是线段BD的中垂线.13.y=2x.【详解】试题解析:每瓶的售价是4824=2(元/瓶),则买的总价y(元)与所买瓶数x之间的函数关系式是:y=2x.考点:根据实际问题列一次函数关系式.14.A解析:5【解析】∵阴影部分的面积总和为6 cm 2,∴矩形面积为12 cm 2;∴AB×AD=12,∴AB=12÷4=3cm.22345AC cm∴=+=15.【分析】设△BnAnAn+1的边长为an,根据直线的解析式能的得出∠AnOBn=30°,再结合等边三角形的性质及外角的性质即可得出∠OBnAn=30°,从而得出AnBn=OAn,列出部分an的值解析:163【分析】设△B n A n A n+1的边长为a n,根据直线的解析式能的得出∠A n OB n=30°,再结合等边三角形的性质及外角的性质即可得出∠OB n A n=30°,从而得出A n B n=OA n,列出部分a n的值,发现规律 :a n+1=2a n,依此规律结合等边三角形的性质即可得出结论.【详解】设△B n A n A n+1的边长为a n,∵点B1,B2,B3,…是直线y= 33x上的第一象限内的点,过A1作A1N⊥x轴交直线OB1于N点,∵OA1=1,∴点N的横坐标为1,将x=1代入, 得到∴点N 的坐标为(1∴A 1在Rt △NOA 1tan ∠A1ON=11A NA O∴∠A 1OB 1 = 30°,又∵△B n A n A n+1为等边三角形,∴∠B n A n A n+1 = 60°,∴∠OB n A n = 30°,A nB n = OA n ,∵OA 1=1a 1 =1,a 2=1+1=2= 2a 1,a 3= 1++a 1 +a 2=4= 2a 2,a 4 = 1+a 1 +a 2十a 3 =8= 2a 3,a n+1 = 2a n ,a 5 =2a 4= 16, a 6 = 2a 5 = 32,a 7= 2a 6= 64,△A 6B 6A 7为等边三角形,点B 6的坐标为(a 7-12a 67- 12a 6)), ∴点B 6的坐标为(48,故答案为:【点睛】本题考查了一次函数的性质、等边三角形的性质以及三角形外角的性质,解题的关键是找出规律:a n+1=2a n 本题属于灵活题,难度较大,解决该题型题目时,根据等边三角形边的特征找出边的变化规律是关键.16.【分析】先依据勾股定理求得AB 的长,然后在△ABC 中,利用面积法可求得CE 的长,然后依据勾股定理定理可求得AE 的长,证明△ECF 为等腰直角三角形可求得EF 的长,依据FB=AB-A 解析:245 85【分析】先依据勾股定理求得AB 的长,然后在△ABC 中,利用面积法可求得CE 的长,然后依据勾股定理定理可求得AE 的长,证明△ECF 为等腰直角三角形可求得EF 的长,依据FB =AB -AF 求得FB 的长即可.【详解】解:在Rt △ABC 中,AB ,∵S △ABC =12AC •BC =12AB •CE ,∴CE =6824105⨯=, 在△AEC 中,依据勾股定理得:AE =185, 由翻折的性质可知∠ECD =12∠ACD ,∠DCF =12∠DCB ,CE ⊥AD ,∴∠ECF =45°.∵CE ⊥AD ,∴CE =EF =245, ∴FB =AB -AE -EF =10-185-245=85, 故答案为:245,85. 【点睛】 本题主要考查的是翻折的性质、勾股定理的应用,利用面积法求得CE 的长,然后再利用勾股定理和等腰三角形的性质求得AE 和EF 的长是解答问题的关键.三、解答题17.(1) ;(2)【分析】(1)先把每一个二次根式化为最简,然后再进行二次根式的加减运算即可; (2)先变形为原式= ,然后利用平方差公式计算;【详解】解:(1)﹣+,,;(2)(3解析:(1;(2)【分析】(1)先把每一个二次根式化为最简,然后再进行二次根式的加减运算即可;(2))11 ,然后利用平方差公式计算; 【详解】解:(1,=,=;(2)())11= , ()61=- ,=.【点睛】本题考查了平方差公式、二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.18.19米【分析】如图所示,过点C 作CD ⊥AB 交AB 延长线于D ,则根据题意可以得到CD=12米,根据勾股定理即可求出BD 的长,再利用勾股定理求出AC 的长即可得到AC+AB 的长.【详解】解:如图所解析:19米【分析】如图所示,过点C 作CD ⊥AB 交AB 延长线于D ,则根据题意可以得到CD =12米,根据勾股定理即可求出BD 的长,再利用勾股定理求出AC 的长即可得到AC +AB 的长.【详解】解:如图所示,过点C 作CD ⊥AB 交AB 延长线于D由题意得:CD =12,AB =4米,BC =13米在Rt △BCD 中5BD ==米∴9AD AB BD =+=米在Rt △ACD 中15AC ===米∴19AC AB +=米∴甲树原来的高度是19米.【点睛】本题主要考查了勾股定理的应用,解题的关键在于能够熟练掌握勾股定理. 19.(1);(2)见解析,菱形面积为4或5.【解析】【分析】(1)根据题意,画出图形,即可求解;(2)先画出边长为的所有菱形ABCD,,然后求出面积即可.【详解】解:如图,(1)∵a是图解析:(1)2,25;(2)见解析,菱形面积为4或5.【解析】【分析】(1)根据题意,画出图形,即可求解;(2)先画出边长为5的所有菱形ABCD,,然后求出面积即可.【详解】解:如图,(1)∵a是图中能用网格线段表示的最小无理数,∴22a=+=,112∵b是图中能用网格线段表示的最大无理数,22b=+=;425(2)∵22215+=,即可画出图形,如图,菱形ABC1D1和菱形ABC2D2即为所求;菱形ABC 1D 1的面积为12442⨯⨯= ; 菱形ABC 2D 2223110+=,故菱形ABC 2D 2的面积为1101052; 5ABCD 的面积为4或5.【点睛】本题主要考查了应用设计与作图以及勾股定理等知识,熟练掌握菱形的性质是解题关键. 20.(1)见解析;(2)AF=5【分析】(1)根据EF 是AC 的垂直平分线可以得到AF=CF ,AE=CE ,再只需证明△AFO ≌△CEO即可得到答案;(2)根据四边形AECF 是菱形可以得到AE=EC解析:(1)见解析;(2)AF =5【分析】(1)根据EF 是AC 的垂直平分线可以得到AF =CF ,AE =CE ,再只需证明△AFO ≌△CEO 即可得到答案;(2)根据四边形AECF 是菱形可以得到AE =EC =x ,则BE =8-x ,然后利用勾股定理求解即可.【详解】解:(1)∵EF 是AC 的垂直平分线,∴AF =CF ,AE =CE ,AO =CO∵四边形ABCD 是矩形,∴AF ∥EC∴∠FAO =∠ECO ,∠AFO =∠CEO ,在△AFO 和△CEO 中,AFO CEO AO COFAO ECO ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AFO ≌△CEO (AAS ),∴AF =EC ,∴AF =FC =AE =EC ,∴四边形AECF 是菱形;(2)由(1)得AE =CE =AF ,设AE =CE =AF =x ,则BE =8-x ,∵四边形ABCD 是矩形,∴∠B =90°,在直角三角形ABE 中222AB BE AE +=,∴()22248x x +-=, 解得x =5,∴AF =5,21.[观察],,;[发现](1)或;(2)证明见解析;[应用]或.【解析】【分析】(1)计算题目中结果,并根据计算过程和结果,总结得到一般规律,作出猜想,并对猜想进行计算,即可进行证明;(2)运解析:[观察]32,76,1312;[发现](1)1111n n +-+或221n n n n+++;(2)证明见解析;[应用]1n n n ++或221n n n ++. 【解析】【分析】(1)计算题目中结果,并根据计算过程和结果,总结得到一般规律,作出猜想,并对猜想进行计算,即可进行证明;(2)运用(1)中发现规律,进行计算即可.【详解】[观察]32,76,1312, [发现](1)1111n n +-+或221n n n n+++ (2)左()221111n n =+++()22221211n n n n n ++=-++()22121()1n n n n +=-++==∵n 为正整数, ∴()11111011n n n n +-=+>++ ∴左1111n n =+-=+右[应用11n +++111111111111223341n n =+-++-++-+++-+ (1111)n n =⨯+-+ 1n n n =++ 22=1n n n ++ ∴答案为:1n n n ++或221n n n ++. 【点睛】(1)此类规律探究问题一定要结合式子特点和数的规律进行探究,类比;(2)此类题目往往无法直接进行计算,一般要根据规律进行变形,往往会消去部分中间项,实现简化运算目的.22.(1),实际意义见解析;(2)20;(3)选择方案一所需费用更少,理由见解析;(4)小琳最多健身18次,理由见解析【分析】(1)把点(0,30),(10,180)代入y1=k1x+b ,得到关于k解析:(1)11530k b =⎧⎨=⎩,实际意义见解析;(2)20;(3)选择方案一所需费用更少,理由见解析;(4)小琳最多健身18次,理由见解析【分析】(1)把点(0,30),(10,180)代入y 1=k 1x +b ,得到关于k 1和b 的二元一次方程组,求解即可;(2)根据方案一每次健身费用按六折优惠,可得打折前的每次健身费用,再根据方案二每次健身费用按八折优惠,求出k 2的值;(3)将x =8分别代入y 1、y 2关于x 的函数解析式,比较即可.(4)分别求解小琳选择方案一,方案二的健身次数,再比较即可得到答案.【详解】解:(1)∵11y k x b =+过点(0,30),(10,180),∴13010180b k b =⎧⎨+=⎩,解得:11530k b =⎧⎨=⎩, 115k =表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元, b =30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),则k 2=25×0.8=20;(3)选择方案一所需费用更少.理由如下:由题意可知,y 1=15x +30,y 2=20x .当健身8次时, 选择方案一所需费用:y 1=15×8+30=150(元),选择方案二所需费用:y 2=20×8=160(元),∵150<160,∴选择方案一所需费用更少.(4)当1300y =时,1530300,x +=解得:18,x =即小琳选择方案一时,可以健身18次,当2300y =时,则20300,x =解得:15,x =即小琳选择方案二时,可以健身15次,1815,>所以小琳最多健身18次.【点睛】本题考查了一次函数的应用,最优化选择问题,解题的关键是理解两种优惠活动方案,求出y 1、y 2关于x 的函数解析式.23.(1);(2)或;(3)存在,点Q 坐标为:,,【分析】(1)设AE=x ,根据勾股定理列方程得:,解出可得结论;(2)分两种情况:P 在OA 或AE 上,分别根据三角形面积列式即可; (3)先根据分别解析:(1);(2)或;(3)存在,点Q 坐标为:,, 【分析】(1)设AE =x ,根据勾股定理列方程得:,解出可得结论; (2)分两种情况:P 在OA 或AE 上,分别根据三角形面积列式即可;(3)先根据分别计算PA 和PE 的长,分类讨论,当PE 为边时,如图4,过G 作GH⊥OC于H,设OF=y,根据勾股定理列方程可得y的值,利用面积法计算GH的长,得G 的坐标,根据平行四边形的性质和平移规律可得Q的坐标;当PE为对角线时,借助中点坐标法即可求得点Q的坐标,综上即可得出点Q所有可能性.【详解】解:(1)在矩形ABCO中,B(8,4),∴AB=8,BC=4,设AE=x,则EC=x,BE=8-x,Rt△EBC中,由勾股定理得:EB2+BC2=EC2,∴解得:x=5,即AE=5,∴E(5,4);(2)分两种情况:①当P在OA上时,0≤t≤2,如图2,由题意知:,,,,∴S=S矩形OABC-S△PAE-S△BEC-S△OPC,=8×4-12×5(4-2t)-12×3×4-12×8×2t,=-3t+16,②当P在AE上时,2<t≤4.5,如图3,由题意知:∴S=综上所述:(3)存在,由PA=PE可知:P在AE上当PE为边时,如图4所示,过G作GH⊥OC于H,∵AP+PE=5,∴AP=3,PE=2,设OF=y,则FG=y,FC=8-y,由折叠得:∠CGF=∠AOF=,OA=CG,由勾股定理得:FC2=FG2+CG2,∴(8-y)2=y2+42,解得:y=3,∴FG=3,FC=8-3=5,∴,∴12×5×GH=12×3×4,解得:GH=2.4,由勾股定理得:FH,∴OH=3+1.8=4.8,∴G(4.8,-2.4),∵点P、E、G、Q为顶点的四边形为平行四边形,且PE=2,∴Q(4.8,-2.4)或(6.8,-2.4).当PE为对角线时,如图5所示:过点G作交CF于点H由上述可知:,,,设由中点坐标法可得:解得:∴点综上所述:点Q的坐标为:,,【点睛】此题考查四边形综合题,矩形的性质、翻折变换、勾股定理、中点坐标法求解、平行四边形的判定和性质,解题的关键是学会用分类讨论的思想思考问题.24.(1)-1;(2)①证明见详解;②;(3)(,)【解析】【分析】(1)把P(3,4),b=7代入y=kx+b中,可得k=-1(2)①根据平行的性质:内错角相等,证明∠OCB=∠OBC,由等角解析:(1)-1;(2)①证明见详解;②34-;(3)(7715,2815-)【解析】【分析】(1)把P(3,4),b=7代入y=kx+b中,可得k=-1(2)①根据平行的性质:内错角相等,证明∠OCB=∠OBC,由等角对等边得到OBC是等腰三角形②根据坐标证明P是BC的中点,由等腰三角形三线合一性质得OP⊥BC,求出OP函数关系式中k的值,根据两个一次函数图像互相垂直时k的关系,求解出直线BC的表达式中的k=3 4 -(3)根据动点M的运动情况分析出N的轨迹函数,然后证明△OHG是等腰直角三角形,根据中点坐标公式求得直线O’P的表达式,联立方程求出N点坐标【详解】(1)把P(3,4),b=7代入y=kx+b中,可得4=3k+7解得k=-1故答案为-1(2)①∵AB∥y轴∴∠ABC=∠OCB∵BP平分∠OBA∴∠OBC=∠ABC∴∠OCB=∠OBC∴OBC是等腰三角形②如图4所示,连接OP∵AB//y轴,A(6,t)∴B点横坐标是6∵P横坐标是3∴P是BC的中点∴OP⊥BC设直线OP的表达式为y=kx将P(3,4)代入得4=3k解得k= 43,则设直线BC的表达式中的k=3 4 -.故答案为3 4 -.(3)①如图5-1,当点M与O重合时,作PE⊥y轴于点E,作NF⊥y轴于点F∵PM ⊥NM∴∠PMN=90°∴∠PME+∠NMF=90°∵∠FMN+∠FNM=90°∴∠PME=∠MNF在△PEM △MFN 中=PME MNF PEM MFN PM MN ∠=∠⎧⎪∠∠⎨⎪=⎩∴△PEO ≌△OFN (AAS )∴MF=PE=3,FN=ME=4则N 点的坐标为(4,-3)②如图5-2所示,,当PM ⊥x 轴时,N 点在x 轴上,则MN=PM=3,ON=OM+MN=7,∴N 的坐标为(7,0)综上所述得点N 在直线y=x-7的直线上运动设直线y=x-7与坐标轴分别交于点G 、H ,作O 关于直线HG 的对称点O`,连接O`P 交直线HG 于点N ,此时ON+PN 有最小值,最小值为线段O`P 的长度.如图5-3所示.当直线y=x-7可得H(0,-7),G(7,0),OG=OH,△OHG是等腰直角三角形,当OQ⊥HG时,Q是HG的中点,由中点坐标公式可得Q(72,-72),∵O`与O对称∴Q是OO`的中点由中点坐标公式可得O’(7,-7),∴可得直线O’P的表达式为1149y x44=-+联立方程1149447x xy x⎧=+⎪⎨⎪=-⎩﹣,解得77152815 xy⎧=⎪⎪⎨⎪=-⎪⎩∴N点坐标为(7715,2815-)∴当△OPN周长最小时,点N的坐标为(7715,2815-)故答案为(7715,2815-)【点睛】本题考查的是一次函数综合运用,涉及到三角形全等、角平分线的性质,平行的性质等,熟练掌握数形结合的解题方法是解决此题目的关键,综合性强,难度较大.25.(1)点E;(2)点H;(3)①存在,点P的坐标为(7,7);②【分析】(1)根据“等距点”的定义,即可求解;(2)根据“等距点”的定义,即可求解;(3)①根据点P是线段OA和OB的“等距点解析:(1)点E ;(2)点H ;(3)①存在,点P 的坐标为(7,7);②60m -<<【分析】(1)根据“等距点”的定义,即可求解;(2)根据“等距点”的定义,即可求解;(3)①根据点P 是线段OA 和OB 的“等距点”,可设点P (x ,x )且x >0,再由点P 是点A 和点C 的“等距点”,可得22AP CP = ,从而得到()()222286x x x x -+=-+ ,即可求解; ②根据点P 是线段OA 和OB 的“等距点”, 点P 在∠AOB 的角平分线上,可设点P (a ,a )且a >0,根据OA =OB ,可得OP 平分线段AB ,再由点P 在OAB 内,可得0<<3a ,根据点P 是点A 和点C 的“等距点”,可得22AP CP = ,从而得到()()22226a m a a a -+=-+,整理得到()()()2666m a m m -=+-,即可求解.【详解】解:(1)根据题意得:()6612AD =--= ,633AE =-= ,AF == ,6OD = ,3OE = ,3OF = ,∴AE OE = ,∴点()3,0E 是点A 和点O 的“等距点”;(2)根据题意得:线段OA 在x 轴上,线段OB 在y 轴上,∴点()2,1G --到线段OA 的距离为1,到线段OB 的距离为2,点()2,2H 到线段OA 的距离为2,到线段OB 的距离为2,点()3,6I 到线段OA 的距离为6,到线段OB 的距离为3,∴点()2,2H 到线段OA 的距离和到线段OB 的距离相等,∴点()2,2H 是线段OA 和OB 的“等距点”;(3)①存在,点P 的坐标为(7,7),理由如下:∵点P 是线段OA 和OB 的“等距点”,且线段OA 在x 轴上,线段OB 在y 轴上, ∴可设点P (x ,x )且x >0,∵点P 是点A 和点C 的“等距点”,∴22AP CP = ,∵点C (8,0),()6,0A ,∴()()222286x x x x -+=-+ , 解得:7x = ,∴点P 的坐标为(7,7);②如图,∵点P 是线段OA 和OB 的“等距点”,且线段OA 在x 轴上,线段OB 在y 轴上, ∴点P 在∠AOB 的角平分线上,可设点P (a ,a )且a >0,∵()6,0A ,()0,6B .∴OA =OB =6,∴OP 平分线段AB ,∵点P 在OAB 内,∴当点P 位于AB 上时, 此时点P 为AB 的中点,∴此时点P 的坐标为6060,22++⎛⎫ ⎪⎝⎭,即()3,3 , ∴0<<3a ,∵点P 是点A 和点C 的“等距点”,∴22AP CP = ,∵点(),0C m ,()6,0A ,∴()()22226a m a a a -+=-+, 整理得:()()()2666m a m m -=+- ,当6m = 时,点C (6,0),此时点C 、A 重合,则a =6(不合题意,舍去),当6m ≠时,62m a +=, ∴6032m +<<,解得:60m -<< , 即若点P 在OAB 内,满足条件的m 的取值范围为60m -<<.【点睛】本题主要考查了平面直角坐标系内两点间的距离,点到坐标轴的距离,等腰三角形的性质,角平分线的判定等知识,理解新定义,利用数形结合思想解答是解题的关键.。
人教版八年级下册数学期末试卷易错题(Word版含答案)

人教版八年级下册数学期末试卷易错题(Word 版含答案) 一、选择题 1.要使2100x 有意义,则x 的取值范围为( ) A .x ≠100 B .x >2 C .x ≥2 D .x ≤22.满足下列条件的三角形中,不是直角三角形的是( )A .三内角之比为1:2:3B .三边长分别为1、3、2C .三边长之比为3:4:5D .三内角之比为3:4:53.如图,在△ABC 中,D ,E 分别是AB ,BC 的中点,点F 在DE 延长线上,添加一个条件使四边形ADFC 为平行四边形,则这个条件是( )A .∠B =∠F B .∠B =∠BCFC .AC =CFD .AD =CF 4.某校有17名同学报名参加信息学竞赛,测试成绩各不相同,学校取前8名参加决赛,小童已经知道了自己的成绩,他想知道自己能否参加决赛,还需要知道这17名同学测试成绩的( )A .中位数B .平均数C .众数D .方差5.如图1,点F 从菱形ABCD 的顶点A 出发,沿A →D →B 以1cm/s 的速度匀速运动到点B ,图2是点F 运动时,△FBC 的面积y (cm 2)随时间x (s )变化的关系图象,则a 的值为( )A .2B .322C .32D .256.如图,在菱形ABCD 中MN 分别在AB 、CD 上且AM=CN ,MN 与AC 交于点O ,连接BO 若∠DAC=62°,则∠OBC 的度数为( )A .28°B .52°C .62°D .72° 7.如图,边长为22+的正方形,剪去四个角后成为一个正八边形,则这个正八边形的边长为( )A .0B .22C .1D .28.如图,在平面直角坐标系中,四边形11112222333,,OA B C A A B C A A B C ,…都是菱形,点123,,A A A …都在x 轴上,点123,,C C C ,…都在直线3333y x =+上,且11212323160,1C OA C A A C A A OA ∠=∠=∠==︒=,则点n C 的横坐标是( )A .2321n -⨯-B .2321n -⨯+C .1321n -⨯-D .1321n -⨯+二、填空题9.使式子32x x -+有意义的x 的取值范围是______. 10.已知菱形的两条对角线长分别为1和4,则菱形的面积为______.11.已知ABC 中,90C =∠,3AC =,5AB =,则BC =______.12.如图,DE 为ABC 的中位线,点F 在DE 上,且AFB ∠为直角.若3AB =,4BC =,则EF 的长为______.13.将直线23y x =-+平移后经过原点,则平移后的解析式为___________.14.如图,在矩形ABCD 中,AB=3,AD=4,点P 在AD 上,PE ⊥AC 于E ,PF ⊥BD 于F ,则PE+PF 等于_____.15.直线y =22x +3与两坐标轴围成的三角形面积是 __________________. 16.如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE ,延长 EF 交 CD 于 G ,接 CF ,AG .下列结论:① AE ∥FC ; ②∠EAG = 45°,且BE + DG = EG ;③ABCD 19CEF S S ∆=正方形;④ AD = 3DG ,正确是_______ (填序号).三、解答题17.计算(1)()()10202131351274π-⎛⎫---++-- ⎪⎝⎭ (2)148348542÷-⨯+ 18.如图,一根直立的旗杆高8米,一阵大风吹过,旗杆从点C 处折断,顶部(B )着地,离旗杆底部(A )4米,工人在修复的过程中,发现在折断点C 的下方1.25米D 处,有一明显裂痕,若下次大风将旗杆从D 处吹断,则距离旗杆底部周围多大范围内有被砸伤的危险?19.如图,每个小正方形的边长是1,①在图①5②在图②中画出一个面积是8的正方形.20.如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF .(1)求证:AF =DC ;(2)若AB ⊥AC ,AB =8,AC =6,求BF 的长.21.阅读材料:规定初中考试不能使用计算器后,小明是这样解决问题的:已知a 23+,求2281a a -+的值.他是这样分析与解的:∵a 23+2323(23)(23)-=+-, ∴23a -= ∴2(2)3,a -= 2443a a -+=∴241a a -=-, ∴2281a a -+=2(24)1a a -+=2(1)11⨯-+=-.请你根据小明的分析过程,解决如下问题:(1)若a 21-,直接写出2481a a -+的值是 . (21315375121119+++++ 22.某专用医疗仪器厂有两间仓库,其中A 仓库是传统人工仓库,B 仓库是进、出仓速度更大的智能无人值守仓库,且A 、B 仓库的最大库存量相同.某日,该厂要将仪器全部出仓,通过铁路货运送往外地.A 仓库上午7:00达到最大库存量,此时停止进仓、开始出仓,A 仓库库存量y (单位:件)随出仓时间t (单位:h )的变化情况如图所示;B 仓库上午7:00库存量为15000件,此时继续进仓,达到最大库存量后停止进仓、开始出仓,且进、出仓的速度相同,B 仓库的工作进度如表所示.仪器全部出仓后即关闭仓库. 时刻7:00 8:00 12:00 B 仓库工作进度 继续进仓 停止进仓开始出仓 出仓完毕(2)若上午7:48这两个仓库的库存量相同,则两个仓库在12:00前是否还会有库存量相同的时刻?若有,求出该时刻;若无,请说明理由;(3)在进、出仓的过程中,两个仓库库存量的差值也会发生变化,①你认为哪些时刻两个仓库库存量的差值可能达到最大?请直接写出这些时刻; ②根据①中你的结论,若在8:00到12:00这段时间,出现两个仓库库存量差值最大的情形,则A 仓库最迟能否在13:30完成出仓任务?请说明理由.23.(1)如图1,在平行四边形ABCD 中,对角线AC 、BD 相交于O 点,过点O 的直线l 与边AB 、CD 分别交于点E 、F ,绕点O 旋转直线l ,猜想直线l 旋转到什么位置时,四边形AECF 是菱形.证明你的猜想.(2)若将(1)中四边形ABCD 改成矩形ABCD ,使AB =4cm ,BC =3cm ,①如图2,绕点O 旋转直线l 与边AB 、CD 分别交于点E 、F ,将矩形ABCD 沿EF 折叠,使点A 与点C 重合,点D 的对应点为D′,连接DD′,求△DFD′的面积.②如图3,绕点O 继续旋转直线l ,直线l 与边BC 或BC 的延长线交于点E ,连接AE ,将矩形ABCD 沿AE 折叠,点B 的对应点为B′,当△CEB′为直角三角形时,求BE 的长度.请直接写出结果,不必写解答过程.24.已知:在平面直角坐标系中,点O 为坐标原点,直线y x b =-+交x 轴于点()8,0A ,交y 轴于点B .(1)如图1,求点B 的坐标;(2)如图2,点P 为线段AB 上一点,点Q 为x 轴负半轴上一点,连接BQ ,PQ ,且PQ BQ =,设点P 的横坐标为t ,AQ 的长为d ,求d 与t 之间的函数解析式(不要求写出自变量t 的取值范围);(3)如图3,在(2)的条件下,过点P 作BQ 的垂线,分别交x 轴,BQ 于点C ,D ,过点O 作OE CD ⊥于点E ,连接QE ,若QE 平分PQD △的周长,求d 的值.25.如图,四边形ABCD是边长为3的正方形,点E在边AD所在的直线上,连接CE,以CE为边,作正方形CEFG(点C、E、F、G按逆时针排列),连接BF.(1)如图1,当点E与点D重合时,BF的长为;(2)如图2,当点E在线段AD上时,若AE=1,求BF的长;(提示:过点F作BC的垂线,交BC的延长线于点M,交AD的延长线于点N.)(3)当点E在直线AD上时,若AE=4,请直接写出BF的长.26.如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。
八年级下册数学期末试卷易错题(Word版含答案)

八年级下册数学期末试卷易错题(Word 版含答案)一、选择题1.如果二次根式2x -有意义,那么x 的取值范围是( ) A .2x > B .2x ≥ C .2x ≠ D .2x ≤ 2.下面的每组数分别是一个三角形的三边长,其中能构成直角三角形的是( ) A .3,4,5 B .2,2,5C .32,42,52D .3,4,53.如图,四边形ABCD 的对角线交于点O ,下列不能判定四边形ABCD 为平行四边形的是( )A .AB =CD ,AD =BC B .∠ABC =∠ADC ,AB ∥CD C .OA =OC ,OB =ODD .AB ∥CD ,AD =BC4.班级准备推选一名同学参加学校演讲比赛,在五轮班级预选赛中,甲、乙、丙三名同学五轮预选赛成绩的平均数和方差如下表所示:甲 乙 丙 平均数/分 96 95 97 方差0.422丁同学五轮预选赛的成绩依次为:97分、96分、98分、97分、97分,根据表中数据,要从甲、乙、丙、丁四名同学中选择一名成绩好又发挥稳定的同学参赛应该选择( )A .甲B .乙C .丙D .丁5.如图,在四边形ABCD 中,AC =16,BD =12,且AC ⊥BD ,连接四边形ABCD 各边中点得到四边形EFGH ,下列说法错误的是( )A .四边形EFGH 是矩形B .四边形ABCD 的面积是92C .四边形EFGH 的面积是48D .四边形EFGH 的周长是286.如图,在菱形ABCD 中,8AB =,120BAD ∠=︒,点O 是对角线BD 的中点,OE CD ⊥于点E ,则OE 的长为( )A .23B .3C .4D .437.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形.如图所示,若AF =5,CE =12,则该三角形的面积为( )A .60B .65C .120D .1308.甲、乙两车分别从A ,B 两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为23︰,甲、乙两车离AB 中点C 的路程(y 千米)与甲车出发时间(t 时)的关系图象如图所示,则下列说法错误的是( )A .A ,B 两地之间的距离为180千米 B .乙车的速度为36千米/时C .a 的值为3.75D .当乙车到达终点时,甲车距离终点还有30千米二、填空题9.若函数y =5x -在实数范围内有意义,则自变量x 的取值范围是______. 10.已知菱形ABCD 的边长为4,∠A =60°,则菱形ABCD 的面积为_________.11.由四个全等的直角三角形组成如图所示的“赵爽弦图”,若直角三角形两直角边边长的和为3,面积为1,则图中阴影部分的面积为____________ .12.如图,在矩形ABCD 中,6BC =,3CD =,将BCD ∆沿对角线BD 翻折,点C 落在点'C 处,'BC 交AD 于点E ,则线段DE 的长为____________.13.写一个函数图象交y 轴于点()0,3-,且y 随x 的增大而增大的一次函数关系式_______.14.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,若∠AOD=120°, AB=2,则BC 的长为___________.15.如图1,在长方形ABCD 中,动点P 从点A 出发,沿A B C D →→→方向运动至D 点处停止,设点P 出发时的速度为每秒cm b ,a 秒后点P 改变速度,以每秒1cm 向点D 运动,直到停止.图2是APD △的面积()2cm S 与时间()s x的图像,则b 的值是_________.16.在Rt △ACB 中,∠ACB =90°,点D 在边AB 上,连接CD ,将△ADC 沿直线CD 翻折,点A 恰好落在BC 边上的点E 处,若AC =3,BE =1,则DE 的长是_____.三、解答题17.计算(1)(7+3)(7-3)(2)1 18322-+18.我国古代数学著作《九章算术》中“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,折断后竹子顶端落地,离竹子底端3尺处.折断处离地面的高度是多少?(1丈=10尺)19.如图,在4×4的正方形网格中,每个小格的顶点叫做格点,以格点为顶点按下列要求画图.(1)在图①中画一条线段AB,使AB=29,线段AB的端点在格点上;(2)在图②中画一个斜边长为34的等腰直角三角形DCE,其中∠DCE=90°,三角形的顶点在格点上.20.如图,MN∥PQ,直线l分别交MN、PQ于点A、C,同旁内角的平分线AB、CB相交于点B,AD、CD相交于点D.试证明四边形ABCD是矩形.21.阅读下列解题过程:54 +1(54)(54)(54)⨯-+-2254(5)(4)--545265 +1(65)(65)(65)⨯-+-2265(6)(5)--65请回答下列问题:(1)观察上面的解题过程,请直接写出结果.11n n ++= .(2)利用上面提供的信息请化简:1111 (21324320132014)++++++++的值. 22.甲乙两个批发店销售同一种苹果,批发店每千克苹果的价格为3元,乙批发店为了吸引顾客制定如下方案:当一次性购买不超过10千克时,每千克价格为4元,超过10千克时,超过部分每千克价格为2元.设小王在同一批发店一次性购买苹果的数量为x 千克(x >0).(1)若在甲批发店购买需花费y 1元,在乙批发店购买需花费y 2元,分别求y 1、y 2与x 的函数关系式;(2)请结合x 的范围,计算并说明在哪个批发店购买更省钱?23.如图,四边形ABCD 是边长为2的正方形,E 为线段BC 上一动点,EF AC ⊥,垂足为F .(1)如图1,连接DE 交AC 于点M ,若15DEF ∠=︒,求AM 的长;(2)如图2,点G 在BC 的延长线上,点E 在BC 上运动时,满足CG BE =, ①连接BF ,DG ,判断BF ,DG 的数量关系并说明理由;②如图3,若Q 为CG 的中点,直接写出2DE DQ +的最小值为 .24.[模型建立]如图等腰直角三角形ABC 中,∠ACB =90°,CB =CA ,直线ED 经过点C ,过A 作AD ⊥ED 于点D ,过B 作BE ⊥ED 于点E ,易证明△BEC ≌△CDA .(无需证明),我们将这个模型称为“K 形图”.接下来我们就利用这个模型来解决一些问题:[模型运用](1)如图1,若AD=2,BE=5,则△ABC的面积为;(2)如图2,在平面直角坐标系中,等腰Rt△ACB,∠ACB=90°,AC=BC,点C的坐标为(0,﹣2),A点的坐标为(4,0),求AB与y轴交点D的坐标;(3)如图3,在平面直角坐标系中,直线l函数关系式为:y=2x+1,点A(3,2),在其线l上是否存在点B,使直线AB与直线l的夹角为45°?若存在,求出点B的坐标;若不存在,请说明理由.[模型拓限](4)如图4,在平面直角坐标系中,已知点B(0,4),P是直线y=2x﹣5上一点,将线段BP延长至点Q,使BQ=2BP,将线段BQ绕点B顺时针旋转45°后得BA,直接写出OA的最小值为.(10≈3.2,结果精确到0.1)25.某数学活动小组在一次活动中,对一个数学问题作如下研究:(1)如图1,△ABC中分别以AB,AC为边向外作等腰△ABE和等腰△ACD使AE=AB,AD =AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.(2)如图2,△ABC中分别以AB,AC为边向外作等腰Rt△ABE和等腰Rt△ACD,∠EAB=∠CAD=90°,连接BD,CE,若AB=4,BC=2,∠ABC=45゜,求BD的长.(3)如图3,四边形ABCD中,连接AC,CD=BC,∠BCD=60°,∠BAD=30°,AB=15,AC=25,求AD的长.【参考答案】一、选择题1.B解析:B【分析】20x-≥,据此解题.【详解】20x-≥,2x∴≥,故选:B.【点睛】本题考查二次根式有意义的条件,是基础考点,掌握相关知识是解题关键.2.D解析:D【分析】由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.【详解】解:A2+2≠2,故不能构成直角三角形,故此选项不符合题意;B、22+22≠52,故不能构成直角三角形,故此选项不符合题意;C、因为32=9,42=16,52=25,92+162≠252,故不能构成直角三角形,故此选项不符合题意;D、32+42=52,故能构成直角三角形,故此选项符合题意.故选:D.【点睛】本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.3.D解析:D【解析】【分析】根据平行四边形的判定方法求解.【详解】解:A、∵AB=CD,AD=BC,∴四边形ABCD 是平行四边形,故选项A 不符合题意; B 、∵AB ∥CD ,∴∠BAD +∠ADC =∠ABC +∠BCD =180°, 又∵∠ABC =∠ADC , ∴∠BAD =∠BCD ,∴四边形ABCD 是平行四边形,故选项B 不符合题意; C 、∵OA =OC ,OB =OD ,∴四边形ABCD 是平行四边形,故选项C 不符合题意; D 、∵AB ∥CD ,AD =BC ,∴四边形ABCD 是等腰梯形或平行四边形,故选项D 符合题意; 故选:D . 【点睛】本题考查平行四边形的判定,熟练掌握平行四边形的判定方法是解题关键.4.D解析:D 【解析】 【分析】首先求出丁同学的平均分和方差,然后比较平均数,平均数相同时选择方差较小的的同学参赛. 【详解】 解:根据题意, 丁同学的平均分为:9796989797975++++=,方差为:222221[(9797)(9697)(9897)(9797)(9797)]0.45-+-+-+-+-=; ∴丙同学和丁同学的平均分都是97分,但是丁同学的方差比较小, ∴应该选择丁同学去参赛; 故选:D . 【点睛】本题考查了平均数和方差,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.5.B解析:B 【分析】利用三角形的中位线定理证得四边形EFGH 为平行四边形,然后利用有一个角是直角的平行四边形是矩形可判断选项A 是否正确;由AC =8,BD =6,且AC ⊥BD ,可求出四边形EFGH 和ABCD 的面积,由此可判断选项CD 是否正确;题目给出的数据求出四边形EFGH 的周长,所以选项B 不符合题意. 【详解】解:∵点E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点, ∴EF =12AC ,GH =12AC , ∴EF =GH ,同理EH =FG ∴四边形EFGH 是平行四边形; 又∵对角线AC 、BD 互相垂直, ∴EF 与FG 垂直.∴四边形EFGH 是矩形,故选项A 正确,不符合题意; ∵AC =16,BD =12,且AC ⊥BD ,∴四边形ABCD 的面积=12AC •BD =96,故选项B 错误,符合题意; ∵四边形EFGH 是矩形,且HG =12AC =8,HE =12BD =6, ∴四边形EFGH 的面积6×8=48,故选项C 正确,不符合题意; ∵EF =12AC =8,HE =12BD =6,∴四边形EFGH 的周长=2(6+8)=28,所以选项D 正确,不符合题意, 故选:B . 【点睛】本题考查了中点四边形的知识,解题的关键是灵活运用三角形的中位线定理,平行四边形的判断及矩形的判断进行证明,是一道综合题.6.A解析:A 【解析】 【分析】连接OA ,由菱形的性质得AD =AB =8、AO ⊥BD 、∠ADB =∠CDB =30°,然后由含30°角的直角三角形的性质求解即可. 【详解】连接OA ,如图所示:∵四边形ABCD 为菱形,点O 是对角线BD 的中点, ∴AD =AB =8,AO ⊥BD ,∠ADB =∠CDB ∵120BAD ∠=︒ ∴∠ADB =∠CDB =30°, 在Rt △AOD 中,142OA AD ==, ∴2243OD AD OA =-=∵OE ⊥CD , ∴∠DEO =90°,∴在Rt △DOE 中,1232OE OD ==,故选:A . 【点睛】本题考查了菱形的性质、含30°角的直角三角形的性质等知识;熟练掌握菱形的性质是解题的关键.7.A解析:A 【解析】 【分析】设小正方形的边长为x ,则AB =5+x ,BC =12+x ,由全等三角形的性质可求AC 得长,由勾股定理可求解小正方形的边长,进而可求解. 【详解】解:设小正方形的边长为x ,∵AF =5,CE =12, ∴AB =5+x ,BC =12+x ,∵△AFM ≌△ADM ,△CDM ≌△CEM , ∴AD =AF =5,CD =CE =12, ∴AC =AD +CD =5+12=17, 在Rt △ABC 中,AC 2=AB 2+BC 2, ∴172=(5+x )2+(12+x )2, 解得x =3(负值已舍), ∴AB =8,BC =15,∴△ABC 的面积为:12×8×15=60,故选:A . 【点睛】本题主要考查了勾股定理,解一元二次方程,利用勾股定理求解小正方形的边长是解题的关键.8.D解析:D 【分析】根据两车相遇时甲、乙所走路程的比为2:3及两车相遇所用时间,即可求出A 、B 两地之间的距离;根据乙车的速度=相遇时乙车行驶的路程÷两车相遇所用时间,进而求出乙车的速度;根据甲车的速度=相遇时甲车行驶的路程÷两车相遇所用时间即可求出甲车的速度,然后根据时间=两地之间路程的一半÷甲车的速度,进而求出a 值;根据时间=两地之间路程÷乙车的速度求出乙车到达终点所用时间,再求出该时间内甲车行驶的路程,用两地间的距离与甲车行驶的路程之差即可得出结论.【详解】解:A 、A 、B 两地之间的距离为18×2÷32()2323-++=180(千米),所以A 正确; B 、乙车的速度为180323⨯+÷3=36(千米/小时),所以B 正确; C 、甲车的速度为1802323⨯÷+=24(千米/小时), a 的值为180÷2÷24=3.75,所以C 正确;D 、乙车到达终点的时间为180÷36=5(小时),甲车行驶5小时的路程为24×5=120(千米),当乙车到达终点时,甲车距离终点距离为180﹣120=60(千米),所以D 错误. 故选:D【点睛】本题考查了一次函数的实际应用,结合函数的图象并逐一求出选项的内容判断正误是解题的关键二、填空题9.x ≤5【解析】【分析】利用二次根式有意义的条件得到5﹣x ≥0,然后解不等式即可.【详解】根据题意得5﹣x ≥0,所以x ≤5.故答案为x ≤5.【点睛】本题考查了函数自变量的取值范围,关键是掌握自变量的范围,二次根式有意义的范围:二次根式的被开方数是非负数.10.A解析:【解析】【分析】作出图形,利用30°直角三角形的性质求出高,利用菱形的面积公式可求解.【详解】如图所示,菱形ABCD 中,AB=AD=4,∠A=60°,过点D 作DE ⊥AB 于点E , 则3sin 60432DE AD =︒== ∴菱形ABCD 的面积为AB∙DE=4×2383故答案为:83【点睛】本题考查了菱形的性质,熟练运用30°直角三角形的性质以及菱形的面积公式是本题的关键.11.1【解析】【分析】设直角三角形的一条直角边长为x ,则另一条直角边长为3x -,由题意列方程()1312x x ⋅-⋅=,求出两直角边长,根据勾股定理求出斜边长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8B期末易错题一、单选题(本大题共30小题,共30.0分)1.Which of the following words CAN NOT add the suffix “er” to form a noun?A. speakB. playC. farmD. visit2.—Would you mind me taking the seat beside you, sir? — . The seat is empty.A. SureB. No, I wouldn’tC. Of course notD. You’d better not3.________ now people cut down many trees, ________ a lot of animals are losing their homes.A. Because; soB. So; becauseC. Because; /D. /; because4.— What happened?My mum’s room is empty.All her things are gone!—Oh,very sorry,sir.We thought she ________ the hotel this afternoon,so we took her bags downstairs.A. has leftB. will leaveC. is leavingD. was leaving5.An accident ______ on this road last week. And it caused three deaths.A. happenedB. was happenedC. is happenedD. has been happened6.---General Secretary Xi (习总书记)_______ us not to waste food while eating.---That’s a greatidea. China is not a rich country, after all.A. asksB. hopesC. suggestsD. leads7.Humans cut down too many trees, so some animals find ______ to live on now.A. nowhere newB. somewhere newC. something new8.— Tommy came late again and was punished by Mr. Morton. — ______. I told him yesterday toarrive earlyA. I’m sorry to hear thatB. That’s a piece of cakeC. So he didD. Serves him right9.---How can you do your homework _______the music is so loud? ---Well, I’ll turn it off.A. becauseB. whenC. forD. where10.Not only my parents but also my grandfather _____ driving after drinking wine isn’t allowed sincelast year.A. has gotB. have understoodC. has knownD. had learned11.—Would you mind my smoking here? —_______ It’s not allowed here.A. Of course not.B. Better not.C. Yes, please.12.The population of the world is over 7 _________. It has caused too many problems.A. billionB. billionsC. billions of13.We don’t allow ______in our office, but we allow people_______ in the smoking room.A. to smoke; to smokeB. smoking; smokingC. to smoke; smokingD. smoking; to smoke14.He turned off the lights and then_____ the classroom.A. leavesB. will leaveC. is leavingD. left15.—David, turn off your computer now! You _______ play on it too long. —I see, mum.A. couldn’tB. mustn’tC. wouldn’t16.-All the oil in the world will_____ some day. -What shall we use for power at that time?A. run outB. set outC. throw away17.Mona Lisa_______ as one of the world’s most famous oil paintings.A. was consideredB. is consideredC. considersD. considered18.--- Do you think teenagers should be allowed ______________ a car? --- No. They are not__________.A. to drive; enough seriousB. to drive; serious enoughC. driving; serious enoughD. driving; enough serious19.Turn off the water when you don’t use it . Don’t keep it ___ all the time.A. runB. to runC. ranD. running20.— How do you feel about life in the country, Mike?— Very nice. It’s quite different form ____ in the city.A. whichB. thatC. itD. those21.I go there by plane, but that depends.A. mustB. mightC. shouldD. would22.--- I think Lisa should be allowed to do some shopping alone. ---___________.She is old enough.A. I don’t think soB. Sorry, she can’tC. I agree with youD. No problem23._____ my grandparents _______ my parents allow me to play computer games too much. Theythink it is bad for my health.A. Neither; norB. Not only; but alsoC. Both; andD. Either; or24.—The rubbish is____ produced every day is becoming a serious problem in cities around theworld.— We should do everything _______to change the situation.A. that; we canB. which;what we canC. what; we can25._________energy, we should turn off the lights when we leave the room.A. To saveB. SavingC. SavesD. Saved26.Animals won’t lose their homes if people _____ cut down so many trees.A. won’tB. doesn’tC. don’tD. didn’t27.-----I think teenagers should be allowed to have part-time jobs.------ _______. They can learn more from practice.A. I think soB. I disagree with youC. Me eitherD. No problem28.—He has much trouble staying at school.—But be ________ caused any problems when he was a little boy.A. mostB. justC. seldomD. only29.Workers with rich are wanted in the factory.A. experienceB. experiencesC. experiencedD. inexperienced30.They are very ______ with the results of the survey.A. satisfyB. satisfiesC. satisfiedD. to satisfy二、单词拼写-单句(本大题共17小题,共17.0分)31.(1)Why don’t you spend your time and money more (明智地)?(2)Don’t worry. Tom is not b________(严重地)ill.(3)Yao Ming scored 41 points in a game a_________(对抗) the Atlanta Hawks in 2004.(4)My daughter is much t______(高的) now. The jeans she wore last year are already too short.(5)Everyone ,you need to have a dream. The future of China d________(依靠) on you.(6)He found a box f________(满的)with treasure in the ground.32.Nobody is in the room,it’s e ________.33.We’d better s_______ good ones from bad ones?34.________________ should be allowed to choose their clothes.(16岁的青少年们)35.The children were p for telling lies.36.Taking drugs is very h_____ to our health.37.(1)I (扔) a ball to her and she caught it.(2)Have you (准备) your Christmas presents?(3)Itˈs an unforgettable (经历).(4)All the workers get free (医疗的) care.(5)It is (有害的) to your health to drink too much.(6)A woman suddenly /ə5pɪəd/ at the door.(7)The /pə5lu:ʃn/ is out of hand and becomes very dangerous.(8)She kept on working /ɔ:lð[u/ she was tired.(9)We’re going on holiday soon, /prɔb[bli/ next month.(10)I can’t /ɪ5mædʒɪn/what has happened.38. (1)Works written by Mo Yan make you laugh and cry (同时) .妨碍) our studies.远离) the Internet?(4)---May I have two coffees, please? ---I’m sorry, we’ve (卖光) all of them.减少) air pollution, we should take the bus or subway instead of driving.39. 根据汉语或音标词提示填空。
