三角函数图像与性质
三角函数的图像与性质

三角函数的图像与性质三角函数的图像与性质在数学中,三角函数是一种基本的函数类型,其中的很多图像和性质对理解数学十分重要。
它们有助于理解各种模型的表示和应用,增强数学思维的能力和加深数学知识。
本文就三角函数的图像与性质做一些简单的介绍。
I、三角函数图像1、正弦曲线:正弦曲线是由参数从0到2π(2π是将一个周期跨越两次)形成的空间曲线。
它是圆的切线,有一定的规律性,并且把圆分为一个完整的一个周期,表现的曲线是一个“s”字形,形成有节奏的变化形式。
2、余弦曲线:余弦曲线是一条由参数从0到2π(2π是将一个周期跨越两次)形成的空间曲线,它也是圆的切线,有一定的规律性,但是它把圆分为两个半周期,比较起来更加缓和,表现的曲线是一个“v”字形,形成有节奏的变化形式。
3、正切曲线:正切曲线可以由参数0到π(π是将一个周期跨越一次)形成的曲线。
它也是一个椭圆的切线,有一定的规律性,把椭圆分为一完整周期,表现的曲线是一个“z”字形,形成有节奏的变化形式。
II、三角函数的性质1、周期性:三角函数的周期性就是说其值的变化是有如左图5000式的一个循环周期,在实际应用中可以利用该性质进行参数估计。
2、增减性:三角函数具有明显的增减性,具体表现为当参数逐渐增加时,函数值会自动增大,而当参数逐渐减小时,函数值则会自动减小。
3、几何性:三角函数有一个令人惊讶的性质,即在几何上其值就等于一定参数的弧度,而且参数的变化也不会影响该弧度。
4、极限性:参数π/2处的正切函数的值无穷大,表示非常接近的范围内函数的变化是接近无穷大的,而参数为0处的余弦函数为1,表示函数在某一点的取值趋势没有了变化,变成一个规定值。
总结来说,三角函数可以说是数学之中一个基本的概念,其图形和性质极其重要,可以帮助我们更深入的理解数学,增进数学的应用能力,因此,值得我们认真好好的学习。
高中数学三角函数专题:三角函数图像和性质

,
5
]
第一个单调区间和第二
22
22
个单调区间的间距: 3 ( ) 2 。 22
当 x [ 2k, 2k] ,其中 k Z 时:函数 f (x) sin x 单调递增。
2
2
②第一个单调递减区间 [
,
3
] ,第二个单调递减区间[5
,
7
]
第一个单调区间和第二
22
22
个单调区间的间距: 5 2 。 22
②第一个取得最小值 1的自变量为 ,第二个取得最小值 1的自变量为 3 第一个自 变量和第二个自变量的间距为 3 2 。 当 x 2k ,其中 k Z 时:函数 f (x) cos x 取得最小值 1。
性质三:对称性。
对称轴:对称轴是由最大值点和最小值点向 x 轴做的垂线。如下图所示:紫色直线为对称轴。
②第一个取得最小值 1的自变量为 ,第二个取得最小值 1的自变量为 3 第一个自
2
2
变量和第二个自变量的间距为 3 ( ) 2 。 22
当 x 2k ,其中 k Z 时:函数 f (x) sin x 取得最小值 1。 2
性质三:对称性。
对称轴:对称轴是由最大值点和最小值点向 x 轴做的垂线。如下图所示:紫色直线为对称轴。
高中数学三角函数专题:三角函数图像和性质
第一部分: f (x) sin x 的图像与性质
描点法:如下表所示:
x
0
3
2
2
2
f (x)
0
1
0
1
0
sin 0 sin( ) sin cos sin cos 0 。
sin
sin(
) sin cossi cos113
常见三角函数图像及其性质
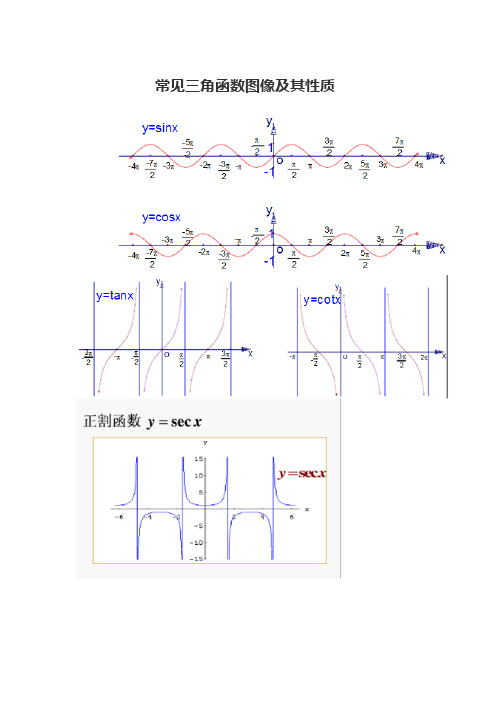
常见三角函数图像及其性质三角函数介绍正弦函数主词条:正弦函数格式:sin(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(θ)的倒数函数图像:波形曲线值域:[]1,1-余弦函数主词条:余弦函数格式:cos(θ)作用:在直角三角形中,将大小为(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(θ)的倒数函数图像:波形曲线值域:[]1,1-正切函数主词条:正切函数格式:tan(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(θ)的倒数。
函数图像:上图平面直角坐标系反映值域:()∞-∞,+余切函数主词条:余切函数格式:cot(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值,也是tan(θ)的倒数值域:()∞-∞,+正割函数主词条:正割函数格式:sec(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角邻边长度的比值求出,函数值为上述比的比值,也是cos(θ)的倒数函数图像:上图平面直角坐标系反映值域:(][)∞-1-,1∞,+余割函数主词条:余割函数格式:csc(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角对边长度的比值求出,函数值为上述比的比值,也是sin(θ)的倒数值域:(][)∞-1-∞,+,1。
三角函数的图象与性质 (共44张PPT)

(
)
3 3 A.-2,2 3 3 3 3 C. - , 2 2
解析: 当 故
π π 1 π π 5π x∈0,2 时, 2x- ∈- 6, 6 , sin2x-6 ∈-2,1, 6
上是减函数 - π , 0 C.在[0,π]上是增函数,在
)
π π π π D.在2,π和-π,-2上是增函数,在-2,2 上是减函数
3.(2015· 皖南八校模拟)函数 f(x)=cos 2x+2sin x 的最大值与最小值 的和是 A.-2 3 C.- 2
4.求函数 y=cos x+sin
2
π x|x|≤4 的最大值与最小值.
π 2 2 解:令 t=sin x,∵|x|≤ ,∴t∈- , . 4 2 2
∴y=-t
2
1 2 5 +t+1=-t-2 + , 4
1- 2 1 5 2 ∴当 t= 时,ymax= ,当 t=- 时,ymin= . 2 4 2 2 ∴函数 y=cos x+sin
sin 2x>0, 解析:由 2 9-x ≥0,
π kπ<x<kπ+ ,k∈Z, 2 得 -3≤x≤3.
π π ∴-3≤x<- 或 0<x< . 2 2 ∴函数 y=lg(sin 2x)+ 9-x
2
π π 的定义域为-3,2 ∪0,2 .
2
π 1- 5 x通法]
1.三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组),常借 助三角函数线或三角函数图象来求解.
2.三角函数值域的不同求法 (1)利用 sin x 和 cos x 的值域直接求;
三角函数的图象与性质
-
;
-1
y=cosx
2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
y
si-n6x的对称-5轴:x
k -4
2-,3对 称点-:2(k
,0);
-
y cosx的对称轴:x k , 对称点:(k ,0);
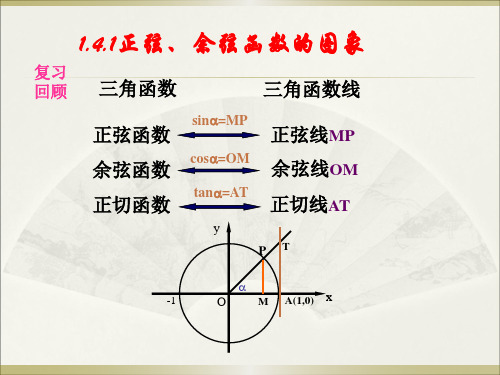
1.4.1正弦、余弦函数的图象
复习
回顾 三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦、余弦函数的图象
问题:如何作出正弦、余弦函数的图象?
途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
复习回顾
一.正弦余弦函数的作图: 几何描点法(利用三角函数线) 五点法作简图
二.周期性:
函数y Asin(x )和y Acos(x ),x R的周期T 2 | |
三.奇偶性:
y sin x为奇函数,图像关于原点对称; y cosx为偶函数图像关于y轴对称。
-6 -5
-4 -3
复习回顾 y y=sinx
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
y
五点画图法
1
(
2
,1)
三角函数的图像和性质

当0<A<1时,图像在y轴方向压缩。
02
周期变换
ω表示周期变换的系数,周期T=2π/|ω|。当ω>1时,周期减小,图像
在x轴方向压缩;当0<ω<1时,周期增大,图像在x轴方向拉伸。
03
相位变换
φ表示相位变换的角度,当φ>0时,图像左移;当φ<0时,图像右移。
正弦型曲线应用举例
振动问题
在物理学中,正弦函数常用来描述简谐振动,如弹簧振子 、单摆等。通过正弦函数的振幅、周期和相位等参数,可 以描述振动的幅度、频率和初始状态。
三角函数的图像和性 质
汇报人:XX 2024-01-28
contents
目录
• 三角函数基本概念 • 正弦函数图像与性质 • 余弦函数图像与性质 • 正切函数图像与性质 • 三角函数复合与变换 • 三角函数在解决实际问题中的应用
01
三角函数基本概念
角度与弧度制
角度制
01
将圆周分为360等份,每份称为1度,用度(°)作为单位来度量
角的大小。
弧度制
02
以弧长等于半径所对应的圆心角为1弧度,用符号rad表示,是
国际通用的角度度量单位。
角度与弧度的换算
03
1° = (π/180)rad,1rad = (180/π)°。
三角函数定义及关系
正弦函数
sinθ = y/r,表示单位圆上任意 一点P(x,y)与x轴正方向形成的 角θ的正弦值。
光学
在光的反射、折射等现象中,三角函数可以 帮助计算入射角、折射角等角度问题。
在工程问题中的应用
1 2
建筑设计
在建筑设计中,三角函数可以帮助计算建筑物的 角度、高度、距离等参数,确保设计的准确性和 安全性。
第五章 第四节 三角函数的图象与性质 课件(共63张PPT)

,解
得 ω=32 .
法二:由题意,得 f(x)max=fπ3
2.(必修 4P35 例 2 改编)若函数 y=2sin 2x-1 的最小正周期为 T,最大
值为 A,则( )
A.T=π,A=1
B.T=2π,A=1
C.T=π,A=2
D.T=2π,A=2
A [T=22π =π,A=2-1=1.]
3.(必修 4P40 练习 T4 改编)下列关于函数 y=4cos x,x∈[-π,π]的单 调性的叙述,正确的是( )
求三角函数单调区间的两种方法 (1)代换法:就是将比较复杂的三角函数含自变量的代数式整体当作一个 角 u(或 t),利用复合函数的单调性列不等式求解.(如本例(1)) (2)图象法:画出三角函数的正、余弦曲线,结合图象求它的单调区间. [注意] 要注意求函数 y=A sin (ωx+φ)的单调区间时 ω 的符号,若 ω<0, 那么一定先借助诱导公式将 ω 化为正数.同时切莫漏掉考虑函数自身的定义 域.
又当 x∈[0,π2
]时,f(x)∈[-
2 2
,1],所以π2
≤ω2π
-π4
≤5π4
,解得
3 2
≤ω≤3,故选 B.
π
π
π
优解:当 ω=2 时,f(x)=sin (2x- 4 ).因为 x∈[0,2 ],所以 2x- 4 ∈
π [- 4
,3π4
π ],所以 sin (2x- 4
)∈[-
2 2
,1],满足题意,故排除 A,C,
B.[kπ,kπ+π2 ](k∈Z)
C.[kπ+π6 ,kπ+23π ](k∈Z)
D.[kπ-π2 ,kπ](k∈Z)
(2)函数 y=tan x 在-π2,32π 上的单调减区间为__________.
§4.3 三角函数的图象与性质

于点( x0 ,0) 中心对称.
( ) 设 f( x) =
4cos
ωx-
π 6
sin ωx - cos ( 2ωx + π) , 其 中 ω
>0.
(1)求函数 y = f(x)的值域;
[ ] (2)若 f(x)在区间
- 32π,
π 2
上为增函数,求 ω 的最大值.
( ) 解析 (1)f(x)= 4
.
(2) (2019 成都七中 1 月月考,14) 如图为一弹簧振子作简 谐运动的图象,横轴表示振动的时间,纵轴表示振动的位移,则 这个振子振动的一个函数解析式是 .
解析
( 1) 由
T 4
=
11 12
π-
2 3
π=
π 4
,得
T
=
π,
∵
T=
2π ,∴
ω
ω = 2,∴
f( x) =
对称性
对称轴:x = kπ+
π 2
( k∈Z) ;
对称中心:( kπ,0) ( k∈Z)
周期
2π
单调性
单调增区间:
[ ] 2kπ-
π 2
,2kπ+
π 2
( k∈Z) ;
单调减区间:
[ ] 2kπ+
π 2
,2kπ+
3π 2
( k∈Z)
奇偶性
奇函数
[ -1,1]
对称轴:x = kπ( k∈Z) ;
( ) 对称中心:
换,设
z
=
ωx+φ,由
z
取
0,
π 2
3π ,π, ,2π
2
来求出相
应的
x,通过列
表、计算得出五点坐标,描点连线后得出图象.
2三角函数的图像及性质-拔高难度-讲义

三角函数的图像及性质知识讲解一、三角函数的图像和性质1.正弦函数图像和性质1)图像:2)定义域:R 3)值域:[11],- 4)单调性:[22]22x k k ππππ?++,(k Z Î)增函数3[22]22x k k ππππ?+,(k Z Î)减函数5)奇偶性:奇函数 6)最小正周期:2π7)对称性:对称轴2x k k Zππ=+?,;对称中心(0)k k Z πÎ,,. 2.余弦函数图像和性质1)图像2)定义域:R 3)值域:[11],- 4)单调性:[22]x k k πππ?+,(k Z Î)增函数 [22]x k k πππ?,(k Z Î)减函数5)奇偶性:偶函数 6)最小正周期:2π7)对称性:对称轴x k k Z π=?,;对称中心(0)2k k Zππ+?,,.3.正切函数图像和性质1)定义域:{|}2x x k k Z ππ??,2)值域:R3)单调性:在()22k k ππππ,-++(k Z Î)增函数.4)奇偶性:奇函数 5)最小正周期:π6)对称性:对称中心(0)2k k Z πÎ,,.二、三角函数的图像变换三角函数的几种变换:1)平移变换:函数sin()(0)y x ϕϕ=+?的图像可以看做将函数sin y x =的图像上的所有的点向左(当0ϕ>时)或向右(当0ϕ<时)平移ϕ个单位而得到.2)周期变换:函数sin()y x ωϕ=+(0ω>且1ω¹)的图像可以看做是把sin()y x ϕ=+的图像上所有的点的横坐标缩短为(当1ω>时)或伸长(当01ω<<时)到原来的1ω倍(纵坐标不变)而得到.3)振幅变换:函数sin()y A x ωϕ=+(0A >且1A ¹)的图像可以看做是将sin()y x ωϕ=+的图像上所有的点的纵坐标伸长(当1A >时)或缩短(当1A <时)到原来的A 倍(横坐标不变)而得到.经典例题一.填空题(共4小题)1.(2015春•建瓯市校级期末)函数f(x)=sin2x+2cos2x﹣,函数g(x)=mcos (2x﹣)﹣2m+3(m>0),若对所有的x2∈[0,]总存在x1∈[0,],使得f (x1)=g(x2)成立,则实数m的取值范围是[1,].【解答】解:∵f(x)=sin2x+(2cos2x﹣1)=sin2x+cos2x=2sin(2x+),当x∈[0,],2x+∈[,],∴sin(2x+)∈[1,2],∴f(x)∈[1,2].对于g(x)=mcos(2x﹣)﹣2m+3(m>0),2x﹣∈[﹣,],mcos(2x﹣)∈[,m],∴g(x)∈[﹣+3,3﹣m].由于对所有的x2∈[0,]总存在x1∈[0,],使得f(x1)=g(x2)成立,可得[﹣+3,3﹣m]⊆[1,2],故有3﹣m≤2,﹣+3≥1,解得实数m的取值范围是[1,].故答案为:,.2.(2013秋•滨江区校级期末)关于x的不等式(sinx+1)|sinx﹣m|+≥m对x ∈[0,]恒成立,则实数m的取值范围是(﹣∞,]∪[,+∞).【解答】解:∵x∈[0,],∴sinx∈[0,1],当m>1时,原不等式可化为:(sinx+1)(m﹣sinx)+≥m,整理得:msinx﹣sin2x﹣sinx+≥0恒成立;令sinx=t(0≤t≤1),g(t)=﹣t2+(m﹣1)t+,要使g(t)=﹣t2+(m﹣1)t+≥0(0≤t≤1)恒成立,必须,即,解得m≥;①当m<0时,原不等式可化为:(sinx+1)(sinx﹣m)+≥m,整理得:sin2x﹣(m﹣1)sinx﹣2m+≥0,令h(t)=t2﹣(m﹣1)t﹣2m+≥0(0≤t≤1),要使t2﹣(m﹣1)t﹣2m+≥0(0≤t≤1)恒成立,应有,解得:m≤,∴m<0;②当0≤m≤1时,(sinx+1)|sinx﹣m|+≥m对x∈[0,]恒成立⇔m≤(sinx+1)|sinx﹣m|+恒成立,令t(x)=(sinx+1)|sinx﹣m|+,m≤t(x)min,当sinx=m时,t(x)min=,∴m≤,又0≤m≤1,∴0≤m≤;③由①②③得:m≤或m≥,∴实数m的取值范围是:(﹣∞,]∪[,+∞).故答案为:(﹣∞,]∪[,+∞).3.已知x∈R,则函数f(x)=max,的最大值与最小值的和等于1﹣.【解答】解:,作出三个函数在一个周期内的图象如图:则f(x)对应的图象为三个图象中最上面的部分.则由图象可知当x=0时,函数f(x)取得最大值1,当x=时,函数f(x)取得最小值,故最大值和最小值之和为,故答案为:.4.(2011春•东港区校级期末)下列说法:①函数是最小正周期为π的偶函数;②函数可以改写为;③函数的图象关于直线对称;④函数y=tanx的图象的所有的对称中心为(kπ,0),k∈Z;⑤将函数y=sin2x的图象先向左平移个单位,然后纵坐标不变,横坐标伸长为原来的2倍,所得图象的函数解析式是;其中所有正确的命题的序号是②③.(请将正确的序号填在横线上)【解答】解:①函数=cos(﹣2x)=sin2x,∵ω=2,∴T==π,又正弦函数为奇函数,∴f(x)为奇函数,则f(x)为周期为π的奇函数,本选项错误;②函数=cos[﹣(+2x)]+1=sin(+2x)+1,本选项正确;③函数=cos[﹣(+2x)]=sin(+2x),令+2x=kπ,(k∈Z)解得x=﹣,∵k=4时,x=,则函数图象关于直线对称,本选项正确;④tan(﹣x)=﹣tanx,因此正切函数是奇函数,因而原点(0,0)是它的对称中心.又因为正切函数的周期是π,所以点(kπ,0)都是它的对称中心.平移坐标系,使原点(0,0)移到(,0)得到y=tan(x+)=﹣cotx,依旧是奇函数,所以在新坐标系中点(kπ,0)也是对称中心,返回原坐标系,这些点的原坐标是(kπ﹣,0)综合到一起就得到对称中心是(k +,0).(k是整数),本选项错误;⑤将函数y=sin2x的图象先向左平移个单位,得到y=sin2(x+),然后纵坐标不变,横坐标伸长为原来的2倍,所得图象的函数解析式为y=sin2(x+)=sin(x+)≠,本选项错误,则正确选项的序号为:②③.故答案为:②③二.解答题(共14小题)5.(2017秋•天津期末)已知函数.(Ⅰ)求f(x)的单调区间;(Ⅱ)求函数f(x)的对称轴和对称中心.【解答】解:(Ⅰ)函数中,令,得,∴f(x)的单调递增区间为:,,令,得,∴f(x)的单调递减区间为:,;(Ⅱ)令,得,∴f(x)的对称轴方程为:;令,得,∴f(x)的对称中心为:,.(注:单调区间写开区间不扣分;k∈Z不写扣1分)6.(2017秋•双流县校级月考)已知函数f(x)=sin(ωx+),其中ω>0(1)若对任意x∈R都有f(x)≤f(),求ω的最小值;(2)若函数y=f(x)在区间(,π)上单调递减,求ω的取值范围.【解答】解:(Ⅰ)由对任意x∈R都有f(x)≤f(),知f(x)在x=处取得最大值,∴ω+=+2kπ,k∈Z;解得ω=+k,k∈Z,又∵ω>0,∴当k=0时,ω的最小值为;(Ⅱ)设t=ωx+,x∈(,π),∴t∈(+,ωx+),由已知(+,ωπ+)⊆[+2kπ,+2kπ],k∈Z;∴,解得,又ω>0,,∴>解得﹣≤k≤,∴k=0,∴ω的取值范围是≤ω≤.7.(2016秋•金华期末)设函数f(x)=4sinx(cosx﹣sinx)+3(Ⅰ)当x∈(0,π)时,求f(x)的单调递减区间;(Ⅱ)若f(x)在[0,θ]上的值域为[0,2+1],求cos2θ的值.【解答】解:(Ⅰ)函数f(x)=4sinx(cosx﹣sinx)+3=4sinxcosx﹣4sin2x+3=2sin2x﹣4×+3=2sin2x+2cos2x+1=2sin(2x+)+1,令2kπ+≤2x+≤2kπ+,k∈Z,解得kπ+≤x≤kπ+,k∈Z,又x∈(0,π),所以f(x)的单调递减区间是[,];(Ⅱ)由f(x)=2sin(2x+)+1在[0,θ]上的值域为[0,2+1],令x=0,得f(0)=2sin+1=3;令f(x)=2+1,得sin(2x+)=1,解得x=,∴θ>;令f(x)=0,得sin(2x+)=﹣,∴2x+<,解得x<,即θ<;∴θ∈(,),∴2θ+∈(,);由2sin(2θ+)+1=0,得sin(2θ+)=﹣,所以cos(2θ+)=﹣=﹣,所以cos2θ=cos[(2θ+)﹣]=cos(2θ+)cos+sin(2θ+)sin=﹣×+(﹣)×=﹣.8.(2017春•长安区校级期中)设函数(1)求f(x)的最小正周期;(2)当,时,求f(x)的最大值和最小值.【解答】解:(1)函数=(cos2xcos﹣sin2xsin)+sin2x=(cos2x﹣sin2x)+=﹣sin2x+;∴f(x)的最小正周期为T==π;(2)当,时,2x∈[,],∴sin2x∈[,1],∴﹣sin2x+∈[0,],即f(x)的最大值为,最小值为0.9.(2018•上海二模)已知函数f(x)=2sin2x+sin(2x+).(1)求函数f(x)的最小正周期和值域;(2)设A,B,C为△ABC的三个内角,若cosB=,f(A)=2,求sinC的值.【解答】解:(1)∵f(x)=2sin2x+sin(2x+)=1﹣cos2x+sin2xcos+cos2xsin==.∴T=,∵﹣1,∴函数值域为[0,2];(2)∵A,B,C为△ABC的三个内角,∴由cosB=,得sinB=,又f(A)=2,即,则,∴2A=,得A=.∴sinC=sin(A+B)=sinAcosB+cosAsinB=.10.(2017•浙江二模)已知直线x=是函数f(x)=sin(3x+φ)(﹣π<φ<0)图象的一条对称轴.(1)求φ;(2)求函数y=f(x)+f(﹣x),x∈(0,)的值域.【解答】解:(1)∵直线x=是函数f(x)=sin(3x+φ)(﹣π<φ<0)图象的一条对称轴,∴3•+φ=kπ+,k∈Z,∴φ=﹣,f(x)=sin(3x﹣).(2)函数y=f(x)+f(﹣x)=sin(3x﹣)+sin[3(﹣x)﹣]=sin(3x﹣)+cos(3x+)=sin3x﹣cos3x+cos3x﹣sin3x=sin3x+cos3x=sin(3x+),∵x∈(0,),∴3x+∈(,),∴sin(3x+)∈(﹣,1],∴y∈[,).11.(2018•温州二模)如图,已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的图象与坐标轴交于点A,B,C(,),直线BC交f(x)的图象于另一点D,O是△ABD的重心.(Ⅰ)求φ;(Ⅱ)求△ACD的外接圆的半径.【解答】解:(Ⅰ)∵O是△ABD的重心,C(﹣,0),∴A(1,0),故函数f(x)的最小正周期为3,即=3,解得ω=,……………………(3分)f(﹣)=sin[×(﹣)+φ]=sin(﹣+φ)=0,∴φ=;……………………(6分)(Ⅱ)由(Ⅰ)知f(x)=sin(x+),∴B(0,)且C(﹣,0),∴∠BCO=60°;……………………(8分)∵C(﹣,0)是BD的中点,∴D(﹣1,﹣),……………………(10分)∴AD==;……………………(11分)∴2R===,∴外接圆半径R=.…………………………(14分)12.(2018春•吉林期中)已知定义在区间,上的函数y=f(x)的图象关于直线对称,当,时,函数>,>,<<,其图象如图所示.(1)求函数y=f(x)在,的表达式;(2)求方程解的集合;(3)求不等式的解集.【解答】解:(1)当,时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,<<),观察图象易得:A=1,ω=1,,则函数,由函数y=f(x)的图象关于直线对称得,,时,函数f(x)=﹣sinx,∴,,;(2)当,时,由,得或,解得x=0或;当,时,由得,或;∴方程的解集为,,,;(3)不等式,当x∈[﹣,]时,sin(x+)≥,∴≥x+≥,解得≥x≥﹣;当x∈[﹣π,﹣]时,﹣sinx≥,∴﹣≤x≤﹣;综上,不等式的解集为,,.13.(2018•奉贤区二模)某旅游区每年各个月份接待游客的人数近似地满足周期性规律,因而第n个月从事旅游服务工作的人数f(n)可近似地用函数f(n)=Acos(wn+θ)+k来刻画,其中正整数n表示月份且n∈[1,12],例如n=1表示1月份,A和k是正整数,w>0,θ∈(0,π).统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:①每年相同的月份,该地区从事旅游服务工作的人数基本相同;②该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差400人;③2月份该地区从事旅游服务工作的人数为100人,随后逐月递增直到8月份达到最多.(1)试根据已知信息,求f(n)的表达式;(2)一般地,当该地区从事旅游服务工作的人数在400或400以上时,该地区也进入了一年中的旅游“旺季”,那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.【解答】解:(1)根据题意知,T=12,∴ω==;又,解得,由×2+θ=﹣π+2kπ,k∈Z;解得θ=﹣+2kπ,k∈Z;又θ∈(0,π),∴θ=;∴函数f(n)=200cos(n+)+300;(2)令f(n)=200cos(n+)+300≥400,化简得cos(n+)≥,即﹣+2kπ≤n+≤+2kπ,k∈Z,解得n∈[12k﹣6,12k﹣2],k∈Z;又n∈[1,12],∴n∈[6,10],∴取n=6,7,8,9,10;即一年中6、7、8、9、10月是该地区的旅游“旺季”.14.(2018•徐汇区一模)如图是函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<)图象的一部分,M、N是它与x轴的两个交点,C、D分别为它的最高点和最低点,E(0,1)是线段MC的中点,(1)若点M的坐标为(﹣1,0),求点C、点N和点D的坐标(2)若点M的坐标为(﹣m,0)(m>0),=,试确定函数f (x)的解析式.【解答】解:(1)设点C(a,b),由中点坐标公式得,解得a=1,b=2,∴点C(1,2),∴点N(3,0),点D(5,﹣2);(2)同样由E(0,1)是线段MC的中点,得A=2,由M(﹣m,0),得C(m,2),D(5m,﹣2);∴•=2m•6m+2×(﹣2)=12m2﹣4,又•=﹣4,∴12m2=,解得m=;由T==8m=2π,解得ω=1,∴φ=;∴函数f(x)的解析式为f(x)=2sin(x+).15.(2018•江苏模拟)某海警基地码头O的正东方向40海里处有海礁界碑M,过点M且与OM成30°角(即北偏西60°)的直线l在此处的一段为领海与公海的分界线(如图所示),在码头O北偏东60°方向领海海面上的A处发现有一艘疑似走私船(可疑船)停留.基地指挥部决定在测定可疑船的行驶方向后,海警巡逻艇从O处即刻出发,按计算确定方向以可疑船速度的2倍航速前去拦截,假定巡逻艇和可疑船在拦截过程中均未改变航向航速,将在P处恰好截获可疑船.(1)如果O和A相距6海里,求可疑船倍截获的P点的轨迹;(2)若要确保在领海内捕获可疑船(即P不能在公海上),则O、A之间的最大距离是多少海里?【解答】解:(1)由题意知点A(6cos3°,6sin30°),即A(3,3);设走私船能被截获的点为P(x,y),则|OP|=2|AP|,即=2,整理得:(x﹣4)2+(y﹣4)2=16.∴走私船能被截获的点的轨迹是以(4,4)为圆心,以4为半径的圆;(2)由题意知,直线l的方程为y=﹣(x﹣40),即x+3y﹣40=0;设|OA|=t,则A(t,t)(t>0),设走私船能被截获的点为P(x,y),则|OP|=2|AP|,∴=2,整理得:(x﹣t)2+(y﹣t)2=t2,∴走私船能被截获的点的轨迹是以C(t,t)为圆心,以t为半径的圆.若保证在领海内捕获走私船,则圆心C到直线l的距离d≥r;即≥t,整理得t2﹣30t+450≥0,解得t≤15(﹣1)或t≥15(+1)(不合题意,舍去),∴O,A之间的最远距离是15(﹣1)海里.16.(2017秋•宜昌期末)如图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<,x∈R)的部分图象.(1)求函数解析式;(2)求函数f(x)的单调递增区间;(3)若方程f(x)=m在,上有两个不相等的实数根,则实数m的取值范围.【解答】解:(1)由题中的图象知,A=2,,即T=π,所以,根据五点作图法,令,,得到,,因为<,所以,解析式为.…(5分)(2)令,k∈Z,解得,k∈Z,所以f(x)的单调递增区间为[k,k],k∈Z.…(9分)(3)由在,上的图象如图知,当,上有两个不同的实根.…(12分)17.(2017春•新余期末)已知函数+cos2x+a(a ∈R,a为常数).(Ⅰ)求函数的最小正周期;(Ⅱ)求函数的单调递减区间;(Ⅲ)若,时,f(x)的最小值为﹣2,求a的值.【解答】解:(I)∴f(x)的最小正周期,T=(II)因为y=sinx的减区间为:,k∈Z所以即(k∈Z)时,函数f (x)单调递减,故所求区间为,(III),时,,时f(x)取得最小值∴2sin.18.(2017春•新余期末)设=,,=(4sinx,cosx﹣sinx),f(x)=•.(1)求函数f(x)的解析式;(2)已知常数ω>0,若y=f(ωx)在区间,是增函数,求ω的取值范围;(3)设集合A=,B={x||f(x)﹣m|<2},若A⊆B,求实数m 的取值范围.【解答】解:(1)f(x)=sin2•4sinx+(cosx+sinx)•(cosx﹣sinx)=4sinx•+cos2x=2sinx(1+sinx)+1﹣2sin2x=2sinx+1,∴f(x)=2sinx+1.(2)∵f(ωx)=2sinωx+1,ω>0.由2kπ﹣≤ωx≤2kπ+,得f(ωx)的增区间是,,k∈Z.∵f(ωx)在,上是增函数,∴, ⊆,.∴﹣≥﹣且≤,∴,.(3)由|f(x)﹣m|<2,得﹣2<f(x)﹣m<2,即f(x)﹣2<m<f(x)+2.∵A⊆B,∴当≤x≤时,不等式f(x)﹣2<m<f(x)+2恒成立,∴f(x)max﹣2<m<f(x)min+2,∵f(x)max=f()=3,f(x)min=f()=2,∴m∈(1,4).。
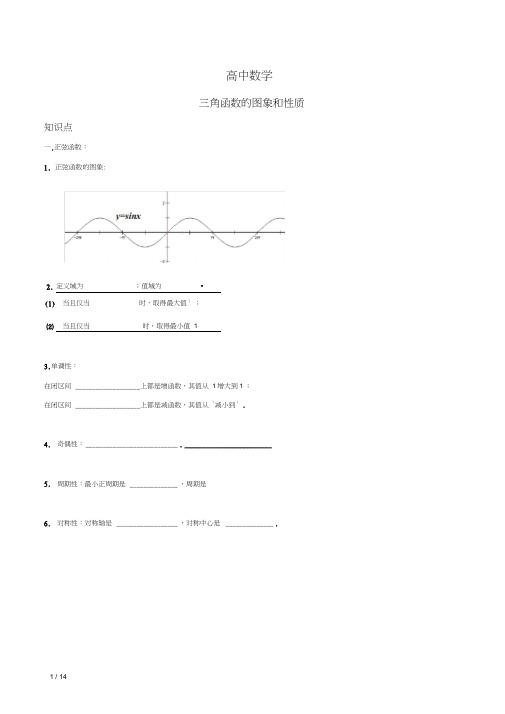
高中数学三角函数图像和性质
三角函数的图象和性质
知识点
一.正弦函数:
1.正弦函数的图象:
2.
定义域为
;值域为•
(1)
当且仅当
时,取得最大值1;
⑵
当且仅当
时,取得最小值1
3.单调性:
在闭区间上都是增函数,其值从1增大到1;
在闭区间上都是减函数,其值从1减小到1.
4.奇偶性:.
5.周期性:最小正周期是,周期是
6.对称性:对称轴是,对称中心是.
r
rK,
(1)将正切函数y tanx在区间(亍'上的图象向左、右扩展,就可以得到正切函y tanx,(x R, x-k , k Z)的图象,我们把它叫做正切曲线.正切曲线是由被互相平行的直线x
(k Z)所隔开的无数多支曲线组成的.这些平行直线x=(k Z)叫做正切曲线各支的
⑵结合正切曲线的特征,类比正弦、余弦函数的“五点法”作图,也可用三点两线作图法作出正切函数
6.对称性:对称轴是,对称中心是.
题型一 正弦,余弦函数的图象和性质
【例1】求函数y=g+sinx的定义域
函数y=2sin(4x+^)的对称轴方程为
3
【过关练习】
1•求函数y 3sin x2的值域以及取得最值时x的值
2.判断函数y=xsin( x)的奇偶性
3.求函数y1sinx的单调区间
二.余弦函数:
1.余弦函数的Βιβλιοθήκη 象:2.定义域为值域为
(1)当且仅当
时,取得最大值1;
(2)当且仅当
时,取得最小值1.
3.单调性:
在闭区间
上都是增函数,其值从
1增加到1;
在闭区间
上都是减函数,其值从
7.3三角函数的图像和性质课件高中数学苏教版必修第一册

当且仅当x=+2kπ(k∈Z)时,取 当且仅当x=2kπ(k∈Z)时,取得最
最值
得最大值1;当且仅当x=-+2kπ 大值1;当且仅当x=2kπ+π(k∈Z)
(k∈Z)时,取得最小值-1
时,取得最小值-1
奇偶性 奇函数
偶函数
对称轴 x=kπ+,k∈Z
x=kπ,k∈Z
对称
中心
(kπ,0),k∈Z
,k∈Z
3
π
π
kπ- ≤x≤kπ+ (k∈Z).
6
3
π
π
所以原函数的减区间是[kπ-6,kπ+3](k∈Z).
π
π
(2)y=2sin 4 - =-2sin - 4 .
π
令 z=x- ,则 y=-2sin z,求 y=-2sin z 的减区间,即求 2sin z 的增区间.
4
π
π
所以- +2kπ≤z≤ +2kπ,k∈Z,
(k∈Z)上都是增函数,其值由-1 (k∈Z)上都是增函数,其值由-1
单调性 增大到1;在每一个闭区间
增大到1;在每一个闭区间
[2kπ+,2kπ+] (k∈Z)上都是减函 [2kπ,2kπ+π] (k∈Z) 上都是减函
数,其值由1减小到-1
数,其值由1减小到-1
函数
正弦函数y=sin x
余弦函数 y=cos x
反思感悟与三角函数有关的函数的值域(或最值)的求解思路
1.求形如y=asin x+b的函数的最值或值域时,可利用正弦函数的有界性
(-1≤sin x≤1)求解.
2.对于形如y=Asin(ωx+φ)+k(Aω≠0)的函数,当定义域为R时,值域为
三角函数图像与性质

三角函数图像与性质三角函数的图像与性质一、正弦函数和余弦函数的图像:正弦函数y=sinx和余弦函数y=cosx的图像可以用五点法作图。
先取横坐标分别为-2π,-π,0,π,2π的五个点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图像。
二、正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的性质:1.定义域:都是R。
2.值域:1)都是[-1,1]。
2)正弦函数y=sinx,当x=2kπ+3π/2(k∈Z)时,y取最小值-1;当x=2kπ+π/2(k∈Z)时,y取最大值1.余弦函数y=cosx,当x=2kπ(k∈Z)时,y取最大值1;当x=2kπ+π(k∈Z)时,y取最小值-1.3.周期性:1)正弦函数y=sinx、余弦函数y=cosx的最小正周期都是2π。
2)函数f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)的最小正周期都是T=2π/|ω|。
4.奇偶性与对称性:1)正弦函数y=sinx是奇函数,对称中心是(2kπ,0)(k∈Z),对称轴是直线x=kπ+π/2(k∈Z)。
2)余弦函数y=cosx是偶函数,对称中心是(kπ,0)(k∈Z),对称轴是直线x=kπ(k∈Z)。
例:若函数y=a-bsin(3x+π/6)的最大值为1,最小值为-2,则a=1/2,b=1或b=-1.课堂练:1.函数y=sinx-sin2x的值域是[-1,1]。
2.已知f(x)的定义域为[0,1],求f(cosx)的定义域为[-1,1]。
3.下列函数中,最小正周期为π的是B.y=sin2x。
4.若f(x)=sin(πx/3),则f(1)+f(2)+f(3)+。
+f(2003)=0.答:1001/2)正弦型函数的对称轴为过最高点或最低点且垂直于x轴的直线,对称中心为图象与x轴的交点。
例如,函数y=sin(5π/2x)的奇偶性是偶函数。
已知函数f(x)=ax+bsin(3x)+1(a,b为常数),且f(5)=7,则f(-5)=-5.单调性方面,y=sinx在[2kπ-,2kπ+](k∈Z)上单调递增,在[2kπ+,2kπ+](k∈Z)上单调递减;y=cosx在[2kπ,2kπ+π](k∈Z)上单调递减,在[2kπ+π,2kπ+2π](k∈Z)上单调递增。
三角函数的图像与性质

2
y=sin2x图象由y=sinx图象(纵标不变), 1 横标缩短 而得。 2
y=si nx
y=si n2x
2π O x
横标伸长2倍而得。
1 y=sin 2 x图象由y=sinx图象(纵标不变),
返回目录
π 例2:如何由y=sinx 的图象得到y=3sin(2x+ 3
)
方法1:y=sinx
纵向伸长3倍
返回目录
2.求函数 y=sin4x+2 3 sinxcosx-cos4x 的最小正周期和最小值, 并写出该函数在 [0, ] 上的单调增区间. 解: ∵ y=sin4x+2 3 sinxcosx-cos4x =(sin2x-cos2x)(sin2x+cos2x)+ 3 sin2x = 3 sin2x-cos2x
2 2
(
2
k ,
2
k )( k z )
递增
递减
x 2k
2
y , k z 时, m ax 1
y , k z 时,m in 1
x 2 k , k z 时,y m a x 1
最值
奇偶性
x 2k
2
x 2k , k z
纵向伸长3倍
y=3sinx
y
方法2: y=sinx - O 6 纵向伸长3倍 y=3sinx 1 横向缩短 2 y=3sin2x π 左移 6 y=3sin(2x+π ) 3
π 3 π y=3sin(x+ 3 ) 1 横向缩短 2 π y=3sin(2x+ ) 3
左移
y=3sinx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合作探究(性质问题)规范解答
例题:设函数 f(x)=sin(2x+π)+ 3sin2x- 3cos2x.
33
3
(1)求 f(x)的最小正周期及其图象的对称轴方程;
(2)求
f(x)在区间
-π,π 63
上的值域.
[探究 1] 在本例条件下,讨论函数 f(x)在-π6,π3上
的单调性.
解 : 当 x [ , ]时 ,2 x [ , 5 ] ,
向上平移
3 6
个单位,得函数
h(x)的图象,若函数
y=
h(x) 在[0,b](b>0)上至少含有 10 个零点,求 b 的最小值.
解:函数 f(x)= 33sin
2x+π6
向右平移 π 个单位得 12
y=
33sin
2x,然后再向上平移
3个单位,得 6
h(x)=
33sin
2x+
63.
令 h(x)=0,则 x=kπ+71π2或 x=kπ+1112π(k∈Z).所以
解:(1)f(x)= 3sin ωx-1-cos ωx+1= 3sin ωx+
2
2
22
12cos
ωx=sin
ωx+π 6
,因为
f(x)最小正周期为π,
所以ω=2,于是 f(x)=sin 2x+π6 .
由 2kπ-π≤2x+π≤2kπ+π,k∈Z,
26
2
得 kπ-π≤x≤kπ+π,k∈Z.
3
6
所以 f(x)的单调递增区间为 kπ-π3,kπ+π6 ,k∈Z.
(2)因为
x∈
0,π 2
,所以
2x+π6∈
π,7π 66
,
则-12≤sin
2x+π 6
≤1.
所以 f(x)在 0,π2 上的取值范围是 -12,1 .
回顾总结
本节的学习,同学们要注意对以下思想方法的应用.
.数形结合的思想:函数的性质在图象上都有很好的体 现,因此图象是研究性质,解题的很好工具.
.化归转化的思想,研究类似于=(ω+φ)的性质时,通 过整体代换的方法,将其化归成=的形式.这样就可通 过=的性质来研究=(ω+φ)的性质.对于=(ω+φ)和= (ω+φ)用同样的方法来处理.
1、已知函数
f(x)=Asin(ωx+φ)+b
A>0,-π<φ<0,ω>0 2
的部分图象如图所示,则 f(x)=( ) A.3sin 2x+π3 -1
B.2sin
2x+π 3
-1
C.3sin 2x+π3 +1
D.2sin
2x-π 3
+1
2、将函数 f(x)=sin(ωx+φ)(ω>0,-π2≤φ<π2) 图象上每一点的横坐标缩短为原来的一半,
63
[探究 2] 若函数 f(x)的图象向左平移 θ(θ>0)个单
位,得到 F(x)的图象.若 y=F(x)的图象的一个对称中心
为71π2,0,则 θ 的最小值是多少?
解:f(x)=
33sin
2x+π 6
向左平移θ个单位得
y=
33sin
2
x+θ
+π 6
=
33sin
2x+2θ+π6
,
即 F(x)= 33sin 2x+2θ+π6 .
在[0,π]上恰有两个零点,若 y=g(x)在[0,b]上有 10 个零 点,则 b 不小于第 10 个零点的横坐标即可,即 b 的最小值 为 4π+11π=59π.
12 12
方法总结
研究三角函数的性质的两个步骤 第一步:先借助三角恒等变换及相应三角函数公式 把待求函数转化为 y=Asin(ωx+φ)+B 的形式; 第二步:把“ωx+φ”视为一个整体,借助复合函 数性质求 y=Asin(ωx+φ)+B 的单调性及奇偶性、最值、 对称性等问题.
三角函数的图像与性质
高考预测
.高考对三角函数图象的考查主要包括三个方面 :一是用五点法作图,二是图象变换,三是已知 图象求解析式或求解析式中的参数的值,以选择 题或填空题的形式考查.
.高考对三角函数性质的考查是重点,以解答题 为主,考查=(ω+φ)的周期性、单调性、对称性 以及最值等,常与平面向量、三角形结合进行综 合考查,试题难度属中低档.
目标检测 .已知函数( φ)(>)
2
在一个周期内的图象如图所示,
其中分别是这段图象的最高点
和最低点,,是图象与轴的交点,
且∠°,则的值为.
3
目标检测
2.已知函数 f(x)= 3sin ωx-sin2ωx+1(ω>0)的最小
2
22
正周期为π.
(1)求ω的值及函数 f(x)的单调递增区间;
(2)当 x∈ 0,π2 时,求函数 f(x)的取值范围.
因为函数 y=sin x 的对称中心为(kπ,0),k∈Z. 令 2x+2θ+π6=kπ,解得 x=k2π-1π2-θ.
又函数
y=F(x)的图象关于
7π,0 12
对称,
令kπ- π -θ=7π,解得θ=kπ-2π.
2 12 12
23
由θ>0 可知,当 k=2 时,θ取最小值π. 3
[探究 3] 若函数 f(x)的图象向右平移1π2个单位,再
纵坐标不变,再向右平移π个单位长度可得 6
π
2
y=sin x 的图象,则 f 6 =________. 2
方法总结
在利用图象求三角函数 y=Asin(ωx+φ)的有关 参数时,注意从图中观察振幅、周期,即可求出 A、 ω,然后根据图象过某一特殊点来求 φ,若是利用零 点值来求,则要注意是 ωx+φ=kπ(k∈Z),根据点在 单调区间上的关系来确定一个 k 的值,此时要利用数 形结合,否则易步入命题人所设置的陷阱.
,
0
)
y
ysixn,xR
o
π
2π x
起, .(关3π2 在键, 0 )确作定用余的( 2π弦五, 1函个) 数点=是在, [(,,0π,, ]1上) 的图(π象2 , 形0 ) 状时(,π, 1)
y ycox,sxR
2
o 2
3 2
x
ytanx,xk
2
y
3 3
2
指导自学(图像问题)
63
6
66
所 以 当 2 x ,即 x 时 ,
6
62
6
6
f ( x )单 调 递 增 ;
当 2 x 5 ,即 x 时 , f ( x)单 调 递 减 。
2
66
6
3
故 函 数 f ( x )在 [ , ]上 单 调 递 增 ;
66
在 [ , ]上 单 调 递 减 。
学习目标
.理解并熟记三角函数的图像与性质。 .会运用图像与性质解决相关问题。 .掌握数形结合与整体转化思想方法。
复习提问(根据图像说出性质)
在确定正弦函数=在[, 起关键作用的五个点是 , ( ,0 ,(.3π2 , 1 ) ( 2π, 0 )
π,,0]上) 的图(π象2 , 形1 ) 状时,(π
