信号与系统自测题(第1章 参考答案)
信号与系统试卷及参考答案

试卷及答案信号与系统试卷(1)(满分:100分,所有答案一律写在答题纸上)考试班级学号姓名成绩考试日期:年月日,阅卷教师:考试时间120分钟,试卷题共2页一一线性非时变离散系统,具有一初始状态x(0),当激励为时f(k),响应为y(k)=((1/2)k+1)u(k);若初始状态不变,当激励为-f(k)时,响应y(k)=((-1/2)k-1)u(k)为;试求当初始状态2x(0)为,激励为4f(k)时,系统的响应?(10分)二绘出下列函数的图形(1).已知一连续时间信号x(t)如图所示,试概略画出信号y(t)=x(2-t/3)的波形图。
(8分)t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。
(8分)三 计算下列函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt (4分) (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) (8分)(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) (8分) (4) 已知f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换 (8分) (5)y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? (8分) (6). y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? (8分)四 一线性非时变因果系统,当激励为u(t)时,响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ,求当激励f(t)=δ(t)时的响应)(t h 。
(10分)五 某一子系统,当输入f(t)=e -t u(t)时,零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时,总系统的冲激响应。
信号与系统第一章习题答案

t 0 > 0 函数式的信号的波形如图 1.2(b)所示. 。
3
cos ωt
1 … …
−
5π 2ω
−
3π 2ω
−
π 2ω
-1
π 2ω
(a)
3π 2ω
5π 2ω
t
cos ωtε (t )
1
ε (t )
1
…
π 2ω
3π 2ω
5π 2ω
t
t
(b)
-1 (c ) 图 1.1
cos ωtε (t − t 0 )
1
P = lim
E =∞
1 T → ∞ 2T
1 ∫ [ε (t )] dt = 2
T 2 −T
(2) ε (t ) − ε (t − 1) 是脉冲信号,其为能量信号,能量为:
E = lim
[ε (t ) − ε (t − 1)]2 dt = ∫0 [ε (t ) − ε (t − 1)]2 dt =1 T →∞ ∫−T
T
2
(4) 3 cos (ω 0t + θ ) 是功率信号,其平均功率为:
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
1 2T
2
∫
T
−T
9
cos 2(ω0 t + θ ) + 1 1 9 9 dt = lim ⋅ ⋅ 2T = T → ∞ 2 2T 2 2
T 2
2ω t 1 − cos 0 1 cos ω0 t + 1 9ω 0t ω t 5 dt = lim + sin − sin 0 + ∫ − T T →∞ 2T 2 20 20 2
信号与系统第一章习题及作业(1,2)

(2)(余弦序列是否为周期信号,取决于2л/Ω0是正整 (余弦序列是否为周期信号,取决于 Ω 有理数还是无理数。) 数、有理数还是无理数。) 因此, 因此, 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7; 所以基波周期为N=7; N=7
因为2л/Ω =16л 为无理数, (4) 因为 Ω0=16л,为无理数,则此信号不是周期 信号. 信号. (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统?为什么? 、判断是否为线性系统?为什么?
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的?非时变的?因果的? 试确定系统是否为线性的?非时变的?因果的?
解:积分系统是线性的,因此系统是线性系统。 积分系统是线性的,因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
《信号与系统》第一二章自测题及参考答案

第一、二章自测题1、判断题(1)若x (t )是一连续时间周期信号,则y (t )=x (2t )也是周期信号。
(2)两个周期信号之和一定是周期信号。
(3)所有非周期信号都是能量信号。
(4)两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。
(5)若)()()(t h t x t y *=,则)1()2()1(+*-=-t h t x t y 。
(6)一个系统的自由响应就等于它的零输入响应。
(7)一个系统的零状态响应就等于它的自由响应。
(8)零状态响应是指系统没有激励时的响应。
(9)系统的单位冲激响应是指系统在冲激信号作用下的全响应。
(10)两个功率信号之和必为功率信号。
2、判断下列信号是能量信号还是功率信号? (1)3cos(15)0()0t t f t t π≥⎧=⎨<⎩(2)50()0te tf t t -⎧≥=⎨<⎩ (3)()6sin 23cos3f t t t =+ (4)|2|()20sin 2t f t e t -=3、填空题(1)已知)()4()(2t t t f ε+=,则)(''t f =__________________。
(2)=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。
(3)=-⎰∞∞-dt t )(92δ_________________________ 。
(4)=-⎰∞∞-dt t t e t j )(0δω_________________________ 。
(5)信号cos(15)cos(30)t t -的周期为 。
4、试画出下列各函数的波形图 (1)100()(), 0f t u t t t =-> (2)2()cos3[()(4)]f t t u t u t π=-- (3)3()[sin ]f t u t π=5、已知f (t )的波形如图1.1所示,求f (2-t )与f (6-2t )的表达式,并画出波形图。
信号与系统(带答案)

第一套第1题,下列信号的分类方法不正确的是(A)A、数字信号和离散信号B、确定信号和随机信号C、周期信号和非周期信号:D、因果信号与反因果信号第2题,以下信号属于连续信号的是(B)A、e-nTB、e-at sin(ωt)C、cos(nπ)D、sin(nω0)第3题,下列说法正确的是(D)A、两个周期信号x(t),y(t)的和x(t)+y(t)一定是周期信号。
B、两个周期信号x(t),y(t)的周期分别为2和2开根号,其和信号x(t)+y(t)是周期信号。
C、两个周期信号x(t),y(t)的周期分别为2和Pi,其和信号x(t)+y(t)是周期信号。
D、两个周期信号x(t),y(t)的周期分别为2和3,其和信号x(t)+y(t)是周期信号。
第4题,将信号f(t)变换为( A ) 称为对信号f(t)的平移或移位。
A、f(t-t0)B、f( k -k0)C、f(at)D、f(-t)第五题,下列基本单元属于数乘器的是(A )A、B、C、D、第六题、下列傅里叶变换错误的是(D)А.1<-->2πδ(ω)B.ejω0t<-- > 2πδ(ω-ω0 )С.соѕ(ω0t) < -- > π[δ(ω-ω0 ) +δ (ω+ω0 )]D. ѕіn(ω0t)<-> jπ[δ(ω+ω0)+ δ(ω- ω0)]第7题、奇谐函数只含有基波和奇次谐波的正弦和余弦项,不会包含偶次谐波项。
(对)第8题、在奇函数的傅里叶级数中不会含有正弦项,只可能含有直流项和余弦项。
(错)第9题、满足均匀性和____条件的系统称为线性系统。
(叠加性)第10题.根据激励信号和内部状态的不同,系统响应可分为零输入响应和__响应(零状态)第二套1、当周期信号的周期增大时,频谱图中谱线的间隔( C)A:增大B:无法回答C:减小D:不变2、δ(t)的傅立叶变换为( A)。
A:1B: u(t)C: 0D:不存在3、已知f(t),为求f(3-2t)则下列运算正确的是(B)A:f(-2t)左移3/2B:f(-2t)右移3/2C:f(2t)左移3D:f(2t)右移3 ,4、下列说法不正确的是(D)。
信号与系统自测题(第1章 参考答案)

8
−∞
B B 1
) 。
C δ (t )
、
、
D sin t
、
∫
9
∞
−∞
、∫
sin(π t ) sin(π t ) δ (t )dt = t t
∞
t =0
=π
−∞
(t + sin t )δ ′(t − )dt = 6
π
(
B
cos(π t ) 1
B
t =0
=π
) 。
C 1+
、π + 6 注:
A
2 3
、 −1 −
3 2
、
3 2
D
、
3
∫
∞
−∞
(t + sin t )δ ′(t − )dt = −(t + sin t )′ 6
∞ −∞
π
t=
π
6
= −(1 + cos t )
t=
π
6
π 3 = −(1 + cos ) = −(1 + ) 6 2
、 ∫ f (t )δ (t )dt = ( A ) 。 A、f (0) B、f (t )
A
f (t )
1
−1
0
1
2 t
f (5 − 2t )
1
f (5 − 2t )
1 1
f (5 − 2t )
f (5 − 2t )
1
−0.5 0 A
0.5
1 t
−1 −0.5
0 0.5
t
B
0 C
11.5 2
3t
−2 −1
0 1 t D
信号与系统(应自炉)习题答案第1章 习题解重点

(222222j t k j t j t j k f t k e
e
e
e
f t π
π
π
πππ+++++==⨯==
∴原函数是周期函数,令1k =,则基波周期为2π。
1-2.
求信号( 14sin( 110cos(2--+=t t t f的基波周期。
解:cos(101 t +的基波周期为15
π,s i n (4
1-8.
用阶跃函数写出题图1-8所示各波形的函数表达式。
t
t
t
(a (
bc
题图1-8
解:(a)((((((3[31]2[11]f t t u t u t u t u t =++-+++-- (((3[13]t u t u t +-+---
(((((
(3 3(1 1(1 1(3 3f
t t u t t u t t u t t u t =+++--++-+-+--(b)([( (1]2[(1 (2]4(2 f t u t u t u t u t u t =--+---+-
1 t -的基波周期为
1
2
π二者的最小公倍数为π,故( 14sin( 110cos(2--+=t t t f的基波周期为π。
1-3.
设(3, 0<=tt f ,对以下每个信号确定其值一定为零的t值区间。
(1)(t f -1(2)((t f t f -+-21(3)((t f t f --21(4)(t f 3(5)(f
信号与系统(应自炉)习题答案第1章 习题解重点

(]
(sin[00t t a t t a --(6)](sin [t tu e dt d t -
解:
(1)(t u te t -(2)]2( 1([ 1(-----t u t u et
(3)]2( (][cos(1[--+t u t u t π(4)2( 1(2 (-+--t u t u t u
( (
(1 2(2
f t u t u t u t =+-+-。(c)( sin(
[( (]t
f t K u t u t T T
π=--
1-9.
绘出下列各信号的波形。
(1)(t u te t
-(2)]2( 1([
1(-----t u t u e t
(3)]2( (][cos(1[--+t u t u t π(4)2( 1(2 (-+--t u t u t u
(4)因为(3f t为(f t在时间轴上压缩3倍得到,故当(t<1时(30f t =。(5)因为3t f ⎛⎫
⎪⎝⎭为(f t在时间轴上拓展3倍得到,故当(t<9时03t f ⎛⎫= ⎪⎝⎭
。
1-4.
将下列信号的实部表示成(Φ+-t Ae at ωcos的形式,这里Φ, , , ωa A都是实数,且0
T
T P f t dt T
-→=⎰
,将((t tu t f =代入,20
1
lim
2T
T P t dt T
→∞=⎰
2
lim 6
T T →∞==∞,该式既不是功率信号也不是能量信号。1-6.
绘出下列各信号的波形。(1)[]4( ( sin(
u t u t T t T π--;(2)4[( 2( (2]sin( u t u t T u t T t T
(完整版)信号与系统第一章答案
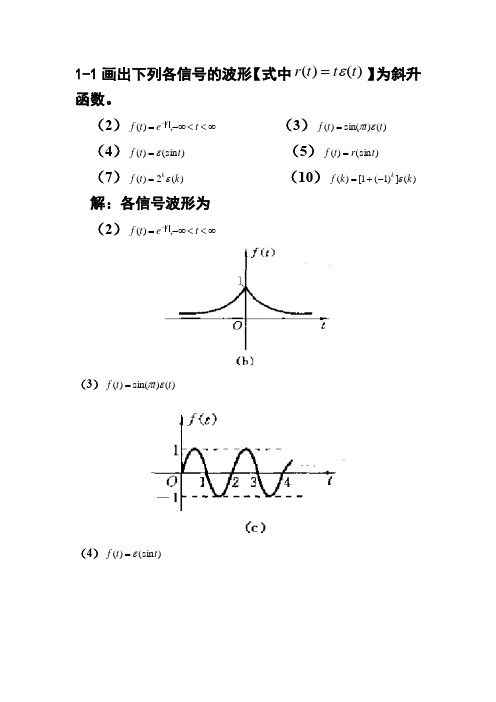
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与系统第一、二、三章自测题解答

第一章自测题答案1.已知)()4()(2t u t t f +=,则)(''t f =(t)4δ2u(t)'+ 2.2(2)1()t t d t t δ∞-∞+⋅+-=⎰3=-⋅+⎰∞∞-dt t t t )1()2(2δ。
3.=-⎰∞∞-dt t t e tj )(0δωoj ωet 。
4.试画出下列各函数式表示的信号图形: (1)0 ),()(001>-=t t t u t f(2))]4()([3cos )(2--=t u t u t t f π在0到4区间内的6个周期的余弦波,余弦波的周期为2/3。
(3)][sin )(3t u t f π=5.已知f (t )的波形如图1.1所示,求f (2-t )与f (6-2t )的表达式,并画出波形。
答:函数表达式:f(2-t) = [u(t)-u(t-1)]+2[u(t-1)-u(t-2)] f(6-2t)=[u(t-2)-u(t-2.5)]+2[u(t-2.5)-u(t-3)]6.信号f (5-3t )的波形如图1.2所示,试画出f (t )的波形。
答:f(5-3t)左移5/3得到f(-3t),然后再扩展3倍得到f(-t),最后反褶可得到f(t)7.对于下述的系统,输入为e (t ), 输出为r (t ),T [e (t )]表示系统对e (t )的响应,试判定下述系统是否为: (1) 线性系统;(2)非时变系统;(3)因果系统;(4)稳定系统:(a) r (t )=T [e (t )]=e (t -2)线性、非时变、因果、稳定系统 (b) r (t )=T [e (t )]=e (-t )线性、时变、非因果、稳定系统 (c) r (t )=T [e (t )]=e (t )cos t 线性、时变、因果、稳定系统 (d) r (t )=T [e (t )]=a e (t )非线性、时不变、因果、稳定系统9. 一线性非时变系统,当输入为单位阶跃信号u (t )时,输出r (t )为 )1()()(t u t u e t r t --+=-,试求该系统对图1.3所示输入e (t )的响应。
信号与系统课后习题答案

f 2 (−1) (t) =
δ (t − 2) − δ (t − 3)
*
t ε e(−t+1) (t + 1)dt
−∞
= [δ (t − 2) − δ (t − 3)]* (1 − e−(t+1) )ε (t + 1)
= (1 − e−(t−2+1) )ε (t − 2 + 1) − (1 − e−(t−3+1) )ε (t − 3 + 1)
) − iL (t) − uC (t) R1
R2
状态方程为:
⎪⎪⎧u&C (t) ⎨
=
f (t) R1C
−
uC (t) R1C
−
iL (t) C
⎪⎪⎩i&L
(t)
=
uC
(t)
− R2iL L
(t)
1.17 写出题图 1.8 系统的输入输出方程。
解: (b)系统框图等价为:
⎧x′′(t) = f (t) − 3x′(t) − 2 y(t)
x2(0-)=1 时,y2(t)=4e-t-2e-3t,t≥0 则 x1(0-)=5,x2(0-)=3 时,系统的零输入响应: yx(t)=y(t)=5y1(t)+3y2(t)=22e-t 十 9e-3t,t≥0
1.22 在题 1.21 的基础上,若还已知 f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,有 y(t)=2+e-t+2e-3t,t≥0 试求当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统响应 y(t)。 解: 记,f(t)=ε(t),x1(0-)=0,x2(0-)=0 时,系统响应 yf(t)=y(t)=2+e-t+2e-3t,t≥0 则当 f(t)=3ε(t),x1(0-)=2,x2(0-)=5 时的系统全响应 y(t)为: y(t)=3yf(t)+2y1(t)+5y2(t)
信号与系统考试题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
《信号与系统》第一章作业题答案

第一章 绪 论1.试判断系统()()r t e t =-是否是时不变系统?(给出检验步骤)解:由()()r t e t =-,得到输入为()e t 时,对应的输出为()r t :()()r t e t =-再由()()r t e t =-,得到输入为()e t τ-时,对应的输出为()e t τ--。
假设()()r t e t =-是一个时不变系统,则对应的()()r t e t ττ-=-+显然()()()r t e t e t τττ-=-+≠--假设不成立,这是一个时变系统。
2.已知信号1(/2)f t 和2()f t 的波形如图所示,画出11()(1)()y t f t u t =+-和22()(53)y t f t =-的波形。
图1解:根据一展二反三平移的步骤来做,对于第一个图,第一步将1(/2)f t 展成1()f t第二步将1()f t 平移成1(1)f t +第三步将1(1)f t +乘上()u t -得到11()(1)()y t f t u t =+-对于第二个图,先写出其表达式2()9(1)f t t δ=+则22()(53)9(531)y t f t t δ=-=-+9(63)9(36)3(2)t t t δδδ=-=-=-于是得到2()y t 的图形为3.系统如图2所示,画出1()f t ,2()f t 和3()f t 的图形,并注明坐标刻度。
图2解:由系统图可以得到1()()()f t t t T δδ=--它的图形为(设T>0)21()()[()()]ttf t f t dt t t T dt δδ-∞-∞==--⎰⎰它的图形为(设T>0)32()(2)()f t t T f t δ=-+它的图形为(设T>0)4.确定下列系统是因果还是非因果的,时变还是非时变的,并证明你的结论。
1()(5)cos ()y t t x t ⎛⎫=+ ⎪⎝⎭解:令0t =,则1(0)5cos (0)y x ⎛⎫= ⎪⎝⎭,故是因果系统。
信号与系统自测题套

信号与系统自测题(一)一、选择题 1.积分⎰+--00)()2(dt t t δ等于(??? )A.)(2t δ-????B.2-??C. )2(-t ε???D. )2(2-t δ 2.计算ε(3-t)ε(t)=( ) A .ε(t)- ε(t-3) B .ε(t) C .ε(t)- ε(3-t) D .ε(3-t)3.已知f (t ),为求f (t 0-at )则下列运算正确的是(其中t 0,a 为正数)( ) A .f (-at )左移t 0 B .f (-at )右移a t 0C .f (at )左移t 0D .f (at )右移at4.已知f (t )=δ′(t ),则其频谱F (j ω)=( ) A .ωj 1 B .)(1ωπδω+j C .ωjD .)(21ωπδω+j 5.信号f (t )的带宽为Δω,则信号f (2t -1)的带宽为( ) A .2Δω B .Δω-1 C .Δω/2D .(Δω-1)/26.已知周期电流i (t )=1+t t 2cos 22cos 22+,则该电流信号的平均功率P 为 ( ) A .17W B .9W C .4WD .10W7.如题7图所示的信号,其单边拉普拉斯变换分别为F 1(s ), F 2(s ), F 3(s ),则( ) A .F 1(s )= F 2(s )≠F 3(s ) B .F 1(s )≠F 2(s )≠F 3(s ) C .F 1(s )≠F 2(s )= F 3(s )D .F 1(s ) = F 2(s )= F 3(s )8.某系统的系统函数为H (s ),若同时存在频响函数H (j ω),则该系统必须满足条件( ) A .时不变系统 B .因果系统 C .稳定系统D .线性系统9.已知f (t )的拉普拉斯变换为F (s ),则dtt df )(的拉普拉斯变换为( ) A .sF (s )B .sF (s )-f (0-)C .sF (s )+f (0-)D .⎰-∞-+0)(1)(ττd f ss sF10.已知某离散序列,其它 ⎩⎨⎧=≤=n N n n f ,0||,1)(该序列还可以表述为( )A .)()()(N n N n n f --+=εεB .)()()(N n N n n f ---+-=εεC .)1()()(---+=N n N n n f εεD .)1()()(----+-=N n N n n f εε11.已知某离散系统的系统模拟框图如题11图所示,则该系统的差分方程为( ) A .)()1(31)(n f n y n y =-+ B .)()1(31)(n f n y n y =--C .)()(31)1(n f n y n y =-+ D .)()(31)1(n f n y n y =++ 12.若f (n )的z 变换为F (z ),则)(n f a n 的z 变换为( ) A .)(az F B .)(z aF C .)(1z F a D .⎪⎭⎫ ⎝⎛a z F二、填空题13.矩形脉冲信号ε(t)-ε(t-1)经过一线性时不变系统的零状态响应为g(t)-g(t-1),则该系统的单位冲激响应h(t)为________。
第一章自测题(含答案)

第一章补充习题一、判断题:1、现实世界中存在着多种多样的信息处理系统,图书馆就是一种以收藏、管理和检索信息为主要目的的信息处理系统。
2、信息在光纤中传输时,每隔一定距离需要加入中继器,将信号放大后再继续传输。
3、集成电路根据它所包含的晶体管数目可以分为小规模、中规模、大规模、超大规模和极大规模集成电路,现在PC机中使用的微处理器属于大规模集成电路。
4、集成电路的工作速度与芯片的尺寸有关。
芯片越大,其工作速度就越快。
5、在通信系统中,信道的带宽就是信道的容量。
6、信息在光纤中传输时,每隔一定距离需要加入中继器,将信号放大后再继续传输。
7、广播是一种特殊的、面向公众的单向通信,而通常所说的通信是指双向通信。
8、电信网主要由终端设备、传输设备、交换设备等组成,利用它可以实现远程通信。
9、CDMA是个人移动电话系统中采用的一种信道复用技术的简称。
10、在蜂窝移动通信系统中,每个移动台始终只能与一个固定的基站通过无线电传输信息。
11、所有的十进制数都可精确转换为二进制数。
二、单选题:1、下面关于个人移动通信的叙述中,错误的是。
A、第1代个人移动通信采用的是模拟通信技术。
B、目前广泛使用的GSM手机采用了数字通信技术,属于第2代移动通信系统。
C、移动通信系统中,移动电话交换中心直接接收手机(移动台)的无线信号,并负责向手机发送信号。
D、第3代移动通信系统将实现高质量的多媒体通信,包括语音通信、数据通信和高分辨率的图像通信等。
2、数据通信中数据传输速率是最重要的性能指标之一,它指单位时间内传送的二进制位数目,计量单位Gb/s的正确含义是。
A、每秒兆位B、每秒千兆位C、每秒百兆位D、每秒百万位3、下面关于比特的叙述中,错误的是。
A、比特是组成数字信息的最小单位B、比特只有0和1两个符号C、比特既可以表示数值和文字,也可以表示图像和声音D、比特“1”大于比特“0”4、使用存储器存储二进位信息时,存储容量是一项很重要的性能指标。
信号与系统第一章答案

w0 )*m, and m=3. w0 )*m=10
Because
w0 =3 /5, N=(2 /
m/3 ,
it’s not a rational number.
13/37
5 Exercises Answers
1.11 Solution
x[n ] 1 e e
j 4 n 7 j 4 n 7 j 2 n 5
Then,
y[n] 2 x[n 2] 5x[n 3] 2 x[n 4]
16/37
5 Exercises Answers
(b) No. For it’s linearity.
the relationship between
y1 [ n ]
and x 2 [n]
is the same in-out relationship with (a).
2
9/37
5 Exercises Answers
(e) x 2 [n] e
E
j(
) 2n 8 2 j( ) 2n 8
n
e
12
n -
N 1 1 1 P lim E lim 1 lim 2N+1 1 N 2N 1 N 2N 1 N 2N 1 n -N (f) x 2 [n ] cos( 4 n ) n 1 cos 2 E cos2 ( n ) 4 2 n n 1 cos n N 1 1 1 1 2 P lim E lim lim N N 2N 1 N 2N 1 N 2 2N 1 2 n N
<信号与系统学习指导>第一章自测题(参考答案)
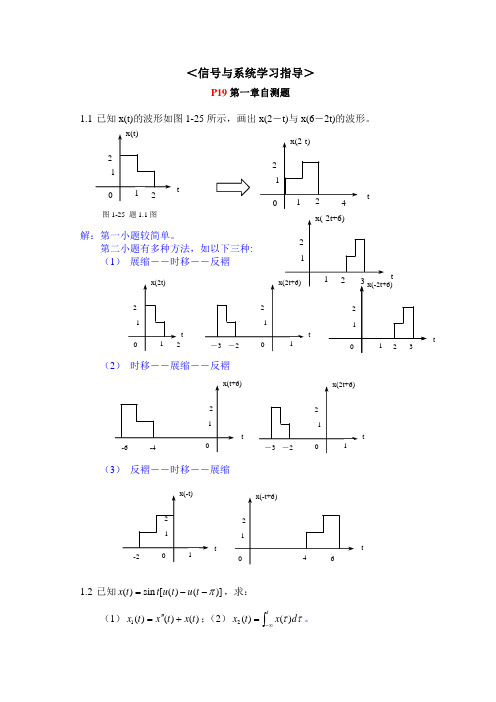
x2o(t)
-1 1/2 2
x2e(t)
-2 -1 1/2 2 1
t
-2
0
1
t
0
原信号的偶信号分量 x2e(t)
原信号的奇信号分量 x2o(t)
-1/2 图 1-26 题 1.4 图 (3)
图(3)
x3[n] 4 4
1
x3[-n] 4 n
2 0 4
-2
0
n
-2
-6 图 1-26 题 1.4 图 (3)
= − cost
t 0
⎧1− cost; 0 ≤ t ≤ π =⎨ ⎩ 2; π ≤ t
1.3 计算下列积分
(1) ∫ e −t δ (t + 2)dt ;
−∞ ∞
(2) ∫ e −t δ (t + 2)dt
−1
4
(3) ∫ x(t + 1)δ (t − 1)dt ;
−∞
∞
(5)
∫
∞
−∞
(t + sin t )δ (t −
x3[n] 4 4
1
x4[n] 2 1 n -3 -2 0 1 2 -1 2 3
-2
0
n
-6 图 1-26 题 1.4 图 (3)
图 1-26 题 1.4 图 (4)
解:因为一个信号可分解为偶信号与奇信号之和: x(t ) = xe (t ) + xo (t ) ;
1 其中: xe (t ) 为偶信号: xe (t ) = [ x(t ) + x(−t )] 2 1 xo (t ) 为奇信号: xo (t ) = [ x(t ) − x(−t )] 2 图(1) x1(t)
y (t ) = sin( 4t ) x(t ) = a1 sin( 4t ) x1 (t ) + a 2 sin( 4t ) x 2 (t ) = a1 y1 (t ) + a 2 y 2 (t ) , 是 线 性 系
宁夏大学物理电气信息学院信号与系统自测题填空题及答案(汤全武)

⎡ ẋ1(t)⎤ ⎡ 0 1 0 ⎤⎡ x1(t)⎤ ⎡0⎤
⎡ x1(t)⎤
方程分别是
⎢ ⎢
ẋ2
(t
)⎥⎥
=
⎢ ⎢
0
0
1
⎥ ⎥
⎢ ⎢
x2
(t
)⎥⎥
+
⎢⎢0⎥⎥
f
(t),
y(t)
=
[1
0
0]⎢⎢x2 (t)⎥⎥ + [0] f (t)
⎢⎣ẋ3(t)⎥⎦ ⎢⎣− 3 − 7 − 5⎥⎦⎢⎣x3(t)⎥⎦ ⎢⎣1⎥⎦
延时器 。
第 2 章 连续时间系统的的时域分析
一、填空题
1、冲激响应是指 系统在单位冲激信号 δ (t) 的激励下产生的零状态响应 。
2、阶跃响应是指系统在单位冲激信号 u(t) 的激励下产生的零状态响应 。
3、零状态响应是指 不考虑起始时刻系统储能的作用,仅由系统的外加激励信号产生的响 应。 4、零输入响应是指 没有外加激励信号的作用,仅由起始状态所产生的响应 。 5、系统的初始状态为零,仅由 系统的外加激励信号 引起的响应称为零状态响应。
10.某离散系统的状态方程
⎡ x1(n
⎢ ⎣
x2
(n
+ 1) ⎤ + 1)⎥⎦
=
⎡0 ⎢⎣− 6
1⎤ 5⎥⎦
⎡ x1(n)⎤
⎢ ⎣
x2
(n)⎥⎦
+
⎡0⎤ ⎢⎣1⎥⎦
f
(n)
,则该系统(是否)不
稳定?
⎡ 4 3⎤ 3.某连续系统的系统矩阵 A = ⎢⎣− 3 4⎥⎦ ,则系统的自然频率为 p1 = 4 + j3, p2 = 4 − j3
信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ;(3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+= 即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
大学科目《信号与系统》各章节习题答案
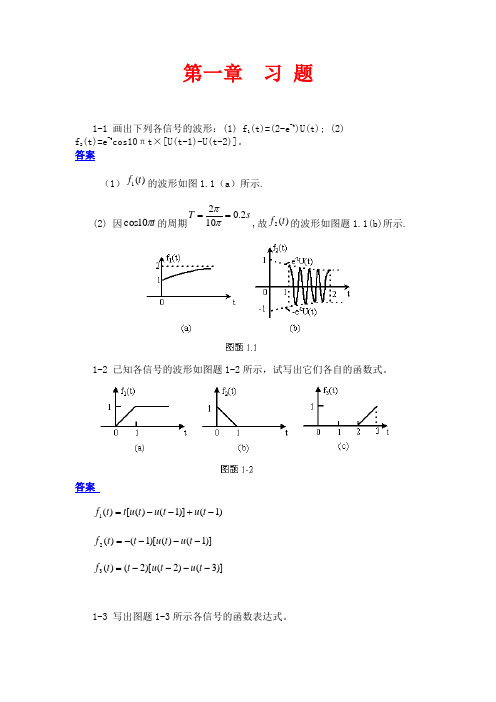
第一章 习 题1-1 画出下列各信号的波形:(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案(1))(1t f 的波形如图1.1(a )所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示,试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形:(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号,若是周期信号,求其周期T 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f (t )
0
0
2
28
、 、已知系统的激励 f (t ) 与响应 y(t ) 的关系为 y(t ) = e ∫ f (τ )e dτ ,则该系统为 ( A ) 。 A、线性时不变 B、线性时变系统 C、非线性时不变系统 D、非线性时变系统
−t
t
τ
−∞
f (t )
1
0
1
t
、 f (t ) = tu (t ) − tu(t − 1) B、 f (t ) = tu (t ) − (t − 1)u (t − 1) C、 f (t ) = (1 − t )u (t ) − (t − 1)u (t − 1) D、 f (t ) = (1 + t )u (t ) − (t + 1)u (t + 1) 注: f (t ) = (t − 1)[u (t ) − u(t − 1)] + u (t − 1) = tu (t ) − (t − 1)u (t − 1) 17、设两信号 f (t ) 和 f (t ) 如下图所示,则 f (t ) 与 f (t ) 间的变换关系为( C ) 。
−t
t =2
] = 2 + 2(4 + 6 + 2) = 26
d 、 dt [e u (t )] = ( C ) 。 −e u (t ) B、 δ (t ) C、 −e u (t ) + δ (t ) A、 d 注: dt [e u (t )] = (e )′u (t ) + e [u (t )]′ = −e u (t ) + e δ (t ) = −e 13、 ∫ δ ′(t )e dt = ( A ) 。 B、 2πδ (ω ) C、 2πδ (t ) A、 jω
18
2 2
D
、π 2
D
、8
注: π = 2π f 4
3 A
T=
1 =8 f
A C
2
、已知信号 y(t ) = cos(ωt ) ,该信号的功率为( 、1 2
B 1
) 。 、 +∞
=
1 2
D
、
、0
注: y(t ) = cos(ωt ) 的有效值为 12 ,平均功率为 ( 12 )
4
、下列各式中正确的是( B ) 。 1 A、 δ (2t ) = δ (t ) B、 δ (2t ) = δ (t ) C、 δ (2t ) = 2δ (t ) 2 B ) 。 5、下列等式成立的是( A、 δ ( at ) = aδ (t ) B、 δ ′( −t ) = −δ ′(t )
A
0 0 0 0 0 0
f (t )
t
、 f (t ) = tu(t ) B、 f (t ) = (t − 1)u (t − 1) C、 f (t ) = tu (t − 1) D、 f (t ) = 2(t − 1)u (t − 1) 注: 23、已知信号 f (t ) 的波形如下图所示,则 f (5 − 2t ) 的波形为( C ) 。
∞
8
−∞
B B 1
) 。
C δ (t )
、
、
D sin t
、
∫
9
∞
−∞
、∫
sin(π t ) sin(π t ) δ (t )dt = t t
∞
t =0
=π
−∞
(t + sin t )δ ′(t − )dt = 6
π
(
B
cos(π t ) 1
B
t =0
=π
) 。
C 1+
、π + 6 注:
A
2 3
、 −1 −
2 1 2 1 2 1 2 1 0 0
、 f (−at ) 左移 t B、 f ( at ) 右移 t t t C、 f ( at ) 左移 D、 f ( −at ) 右移 a a 注: f (t − at ) = f [−a(t − ta )] 20、 f ( −t + 2) 是下面哪一种运算的结果( B ) 。 B、 f ( −t ) 向右移 2 个单位 A、 f (t ) 向左移 2 个单位 C、 f ( −2t ) 向右移 1 个单位 D、 f (t ) 向右移 2 个单位 注: f (−t + 2) = f [−(t − 2)] 21、 f (2t ) 是下面哪一种运算的结果( C ) 。 A、 f (t ) 向左移 2 个单位 B、 f ( −t ) 向右移 2 个单位 C、 f (t ) 压缩 1 倍 D、 f (t ) 扩展 1 倍 22、已知信号的波形如下图所示,则 f (t ) 的表达式为( C ) 。
A
f (t )
1
−1
0
1
2 t
f (5 − 2t )
1
f (5 − 2t )
1 1
f (5 − 2t )
f (5 − 2t )
1
−0.5 0 A
0.5
1 t
−1 −0.5
0 0.5
t
B
0 C
11.5 2
3t
−2 −1
0 1 t D
注: f (5 − 2t ) = f [−2(t − 5 )] 2 24、对信号 y (t ) = tx(t ) 说法正确的是( B ) 。 A、线性、时不变 B、线性、时变 C、非线性、时不变 D、非线性、时变 25、已知 f (t ) 是激励, y (t ) 是系统响应,根据输入输出关系,下列系统中线性时不变系统 是( C ) 。 B、 y (t ) = f (t ) + f (t ) A、 y (t ) = kf (t ) + b ( k 、 b 为常数, b ≠ 0 ) C、 y (t ) = f ′′(t ) + f ′(t ) D、 y (t ) = e 注:原书答案为 A,显然不对;答案应当是 C。 26、下列系统中线性时不变系统是( D ) 。 df (t ) A、 y (t ) = 2 B、 y (t ) = f (t ) sin( n t ) ( n 为常数) dt D、 y (t ) = kf (t ) ( k 为常数) C、 y (t ) = x (t ) 27、已知 f (t ) 是已录制的声音磁带信号,则下列叙述错误的是( C ) 。 A、 f ( −t ) 表示将磁带倒转播放产生的信号 B、 f (2t ) 表示将磁带以二倍的速度加速播放 C、 f (2t ) 表示将磁带放音速度降低一半播放 D、 2 f (t ) 表示将磁带音量放大一倍播放
− jωt
t =0
)
t =0
= jω
t
−2τ
−∞
C
、 2u (t )
D
、 δ (t ) + u(t )
注: ∫
t
−∞
e −2τ δ (τ )dτ = ∫ e0δ (τ )dτ = u (t )
−∞
t
15 A
、已知信号 y(t ) = cos(ωt ) ,该信号的能量为(
C
) 。
、1 B、 1 C、 +∞ D、 0 2 注: y(t ) = cos(ωt ) 为周期信号,因此是功率信号,它的能量只能是无穷大。 16、如下图所示,信号 f (t ) 的数学表达式为( B ) 。
、对于一个自变量无穷但能量有限的信号,其平均功率为 0 。 6、对于下图示波形可用单位阶跃函数表示为 u (t ) + u (t − 1) + u (t − 2) − 3u (t − 3) 。
f (t )
3 2 1
1 2 3 t
、 ∫ (3t + 2t + 1)δ (1 − t )dt = 6 。 8、 ∫ (t − 3t + 2)δ (t − 1) dt = 0 。 9、 ∫ δ (t − t )u (t − 2t )dt = 0 (已知 t > 0 ) 。 τ 10、 ∫ δ ( )(τ − 2)dτ = -6 。 3 π 11、 ∫ sin( t )[δ (t − 1) + δ (t + 1)]dt = 1 。 2 π 12、 ∫ sin( t )δ (t − 1)dt = 1 。 2 13、系统的数学描述方法有 输入输出描述法 和 状态变量描述法 。 14、满足 齐次性 和 可加性或叠加性 条件的系统称为线性系统。 系统→ y (t ) ,应有 f (t − t ) 系统→ y (t − t ) 。 15、若某系统是时不变的,则当 f (t ) 16、系统对 f (t ) 的响应为 y (t ) ,若系统对 f (t − t ) 的响应为 y (t − t ) ,则该系统为 时不变 系统。 17、连续系统模拟中常用的理想运算器有 加法器 、 数乘器 、 乘法器 、 延时器 和 积分器 。
《信号与系统》 信号与系统》自测题
第 1 章 信号与系统的概念
一、填空题 1、描述信号的基本方法有 数学表达式 、 波形 。 2、 Sa (t ) 信号又称为 抽样信号或取样信号 du (t ) 3、 = δ (t ) 。 dt 4、 δ (−t ) = δ (t ) (用单位冲激函数表示) 。
5
。
A
1 2 1 2
1
f1 (t )
f 2 (t )
1 1 2 t 1 − 2 −3 −1.5
−1
A
0oLeabharlann t、 f (t ) = f ( 1 t + 3) B、 f (t ) = f (2t + 3) 2 1 C、 f (t ) = f (2t + 5) D、 f (t ) = f ( t + 5) 2 注:原书答案为 B。很显然正确答案为 C。 18、 f (6 − 3t ) 是下面哪一种运算的结果( D ) 。 A、 f ( −3t ) 左移 6 B、 f ( −3t ) 右移 6 C、 f ( −3t ) 左移 2 D、 f ( −3t ) 右移 2 注: f (−3t ) = f [−3(t − 2)] ,因此是 f (−3t ) 右移 2。 19 、已知 f (t ) ,为求 f (t − at ) 应按下列哪种运算求得正确结果(式中 t 、 a 都为正值) ( D ) 。
