《自动控制理论(第版)》邹伯敏课件第5章
合集下载
《自动控制理论(第3版)》第05章课件
频率特性 G(j) = j
= Im
（1）极坐标图
A() = () = 90
0 =0
Re
（2）波特图
L() = 20lgA() = 20lg () = 90
注意：由于微分环节与
L()/dB
20
0
1
20dB/dec
10
积分环节的传递函数互
为倒数， L()和 ()
仅相差一个符号。因此，
()/(°)
90°
Im
=
=0
Re
0
1
36
8 延迟环节
其频率特性为 ：G(j) = e jT 幅值为：A() = e jT = 1 相角为：() = T (rad) = 57.3T()
由于幅值总是1，相角随频率而变化，其极坐标图为一单位圆。
Im
L()/dB
0
0
=0
Re
()/(°)
0°
T大 T小
由于( )随频率的增长而线性滞后，将严重影响系统的稳定性 37
L ()2l0 g G (j) dB “分贝”
坐标特点 纵轴 (),(单位：度或者弧)度
⑴ 幅值相乘 = 对数相加，便于叠加作图；
特点 ⑵ 可在大范围内表示频率特性；
⑶ 利用实验数据容易确定 L(),进而确定G(s)。
17
频率特性 G(jw) 的表示方法
以 G(j) 1 为例。
Ts1sj
1. 幅相特性(Nyquist)
称为RC网络的幅频特性，后者称为相频特性。
⑤
1
jarc T tan 1
j 1 1 j T 1
e e 1 (T )2
1 j T
1 j T
完全地描述了网络在正弦输入电压作用下，稳态输
= Im
（1）极坐标图
A() = () = 90
0 =0
Re
（2）波特图
L() = 20lgA() = 20lg () = 90
注意：由于微分环节与
L()/dB
20
0
1
20dB/dec
10
积分环节的传递函数互
为倒数， L()和 ()
仅相差一个符号。因此，
()/(°)
90°
Im
=
=0
Re
0
1
36
8 延迟环节
其频率特性为 ：G(j) = e jT 幅值为：A() = e jT = 1 相角为：() = T (rad) = 57.3T()
由于幅值总是1，相角随频率而变化，其极坐标图为一单位圆。
Im
L()/dB
0
0
=0
Re
()/(°)
0°
T大 T小
由于( )随频率的增长而线性滞后，将严重影响系统的稳定性 37
L ()2l0 g G (j) dB “分贝”
坐标特点 纵轴 (),(单位：度或者弧)度
⑴ 幅值相乘 = 对数相加，便于叠加作图；
特点 ⑵ 可在大范围内表示频率特性；
⑶ 利用实验数据容易确定 L(),进而确定G(s)。
17
频率特性 G(jw) 的表示方法
以 G(j) 1 为例。
Ts1sj
1. 幅相特性(Nyquist)
称为RC网络的幅频特性，后者称为相频特性。
⑤
1
jarc T tan 1
j 1 1 j T 1
e e 1 (T )2
1 j T
1 j T
完全地描述了网络在正弦输入电压作用下，稳态输
经典自控第5章 频率特性.ppt
() ~ 为系统的相频特性。
A() 1 / 1 2T 2 , () arctgT
RC网络的幅频特性和相频特性
A() 1 / 1 2T 2 , () arctgT
G( j)
G(s)
s j
1
Tj 1
1
e j tan 1 (T )
(T )2 1
RC网络的幅相特性曲线
2、对数频率特性
1
j2
n
(o) 180
( )
arctg
1
2 (
/ n /n )
2
arctg
2 1 (
/ n / n )2
,
0
-180
非最小相位
0.1 1
10 ω/ωn
振荡环节的对数坐标图
L( ) 20lg (1 2 / n2 )2 4 2 ( / n )2
二阶微分环节
非最小相位二阶微分环节
G(s)
1、各典型环节频率特性图概览
（1）幅相曲线
j
j
· -k
0Байду номын сангаас
·k
比例环节K的幅相曲线
0 ω
积分环节的幅相曲线
23
j ω
0 ω=0
微分环节幅相曲线 j
T>0 ω
ω=0
0
1
T<0
一阶微分环节的幅相曲线
j
T<0
ω=∞
1
-45o 0
ω=0
T>0
ω=1/T
惯性环节的幅相曲线
24
0 -0.5
j
ζ=0.2—0.8
10 ω/ωn
,G( j ) 0 180o
二阶振荡、微分环节的渐近线
A() 1 / 1 2T 2 , () arctgT
RC网络的幅频特性和相频特性
A() 1 / 1 2T 2 , () arctgT
G( j)
G(s)
s j
1
Tj 1
1
e j tan 1 (T )
(T )2 1
RC网络的幅相特性曲线
2、对数频率特性
1
j2
n
(o) 180
( )
arctg
1
2 (
/ n /n )
2
arctg
2 1 (
/ n / n )2
,
0
-180
非最小相位
0.1 1
10 ω/ωn
振荡环节的对数坐标图
L( ) 20lg (1 2 / n2 )2 4 2 ( / n )2
二阶微分环节
非最小相位二阶微分环节
G(s)
1、各典型环节频率特性图概览
（1）幅相曲线
j
j
· -k
0Байду номын сангаас
·k
比例环节K的幅相曲线
0 ω
积分环节的幅相曲线
23
j ω
0 ω=0
微分环节幅相曲线 j
T>0 ω
ω=0
0
1
T<0
一阶微分环节的幅相曲线
j
T<0
ω=∞
1
-45o 0
ω=0
T>0
ω=1/T
惯性环节的幅相曲线
24
0 -0.5
j
ζ=0.2—0.8
10 ω/ωn
,G( j ) 0 180o
二阶振荡、微分环节的渐近线
浙江大学自动控制理论课第五章频率响应
2
10(S 1) j3)(S 2
j3)
试绘制系统的幅频和相频特性曲线。
解：令 S ， jq
G( j2)
10( j2 1)
( j2 2 j3)( j2 2 j3)
10 563.4 。
2968.2 5 26.6
1.857 21.8
图5-5
2020/6/16
课件
6
自动控制理论 图5-6
(1
2 n2
)2
4
2
2 n2
2
(
)
ar
c
tan 1
n 2
n2
limG( j) 10 0
limG( j) 0 180 0
2020/6/16
课件
28Leabharlann 自动控制理论根据不同的ζ值，作出的乃氏图如图5-23所示。
图5-23
2020/6/16
课件
29
自动控制理论
2)G( j) 1 2 j2
➢ 开环增益K在数值上等于低频渐近线（或延长线）与0dB线 相交点频率值的平方。
2020/6/16
课件
24
自动控制理论
第三节 极坐标图
G( j) p() jQ() p2 () Q2 ()e j() 式中() arctan Q()
p()
当输入信号的频率ω由0→∞变化时，向量G(j ω) 的端点在复平面上移动的轨迹叫极坐标图或称为乃氏图。
1
1
结论: Cs按顺时针方向围绕F(S)的一个零点,则其在F(S)平面上的
映射曲线CF亦按顺时针方向围绕F(S)平面的坐标原点旋转一周. 如果Cs按顺时针方向围绕F(S)的z个零点,则其在F(S)平台上的映射
自动控制理论第版邹伯敏 共53页
9
系统开环频率特性与系统性能指标密切相关，一般 可以将校正问题归纳为三类： 1、如果系统稳定且有较满意的暂态响应，但稳态
误差太大，这就必须增加低频段的增益来减小 稳态误差，同时保持中、高频特性不变； 2、如系统稳定且有较满意的误差，但其动态性能 较差，则应改变系统的中频段和高频段，以改 变系统的截止频率和相角裕度； 3、如果一个系统的稳态和动态性能均不能令人满 意，就必须增加低频增益，并改变中频段和高 频段。
自动控制理论
第六章
控制系统的校正
1
第一节 引 言
一、基本概念 1、系统校正
被控对象确定后，根据要求的控制目标，对
控制器的进行设计的过程叫作系统校正。
R
Gc
Y 对 象
2
2、控制目标——性能指标
时域调 超节 调时 量M间 pts% 性能指标 稳态误差 ess
频域谐 稳振 定峰 裕值 度 M，r,频 h，率幅带值宽 穿 b 越频率 c
40 30 20 10
m
m 增加不多。
m
tan1
2
1
0
10-2
10-1
ωm
100
101
14
三、超前校正环节的设计原理
频率法对系统进行校正的基本思路是：通过所 加校正装置，改变系统开环频率特性的形状，使校 正后系统的开环频率特性具有如下特点： 低频段：用以满足稳态精度的要求；
中频段：幅频特性的斜率为-20dB/dec,并具有较宽的 频带，这一要求是为了系统具有满意的动态性能；
0 10-2
10-1
ωm
1
G
c(s)
1 Ts 1 TsT s 1 1
s 2 1
系统开环频率特性与系统性能指标密切相关，一般 可以将校正问题归纳为三类： 1、如果系统稳定且有较满意的暂态响应，但稳态
误差太大，这就必须增加低频段的增益来减小 稳态误差，同时保持中、高频特性不变； 2、如系统稳定且有较满意的误差，但其动态性能 较差，则应改变系统的中频段和高频段，以改 变系统的截止频率和相角裕度； 3、如果一个系统的稳态和动态性能均不能令人满 意，就必须增加低频增益，并改变中频段和高 频段。
自动控制理论
第六章
控制系统的校正
1
第一节 引 言
一、基本概念 1、系统校正
被控对象确定后，根据要求的控制目标，对
控制器的进行设计的过程叫作系统校正。
R
Gc
Y 对 象
2
2、控制目标——性能指标
时域调 超节 调时 量M间 pts% 性能指标 稳态误差 ess
频域谐 稳振 定峰 裕值 度 M，r,频 h，率幅带值宽 穿 b 越频率 c
40 30 20 10
m
m 增加不多。
m
tan1
2
1
0
10-2
10-1
ωm
100
101
14
三、超前校正环节的设计原理
频率法对系统进行校正的基本思路是：通过所 加校正装置，改变系统开环频率特性的形状，使校 正后系统的开环频率特性具有如下特点： 低频段：用以满足稳态精度的要求；
中频段：幅频特性的斜率为-20dB/dec,并具有较宽的 频带，这一要求是为了系统具有满意的动态性能；
0 10-2
10-1
ωm
1
G
c(s)
1 Ts 1 TsT s 1 1
s 2 1
自动控制理论 ppt 详解
代数式 极坐标式 指数式
A( )
1
2T 2 1
∠G(jω)=－arctanTω
j
＝∞
0 ＝ 100 ＝5
＝0 1 ＝1
＝3 ＝2
2. 对数频率特性曲线（Bode 图）
由对数幅频曲线和对数相频曲线组成，是工程中广泛应用的一组曲线。
对数幅频曲线的横坐标采用对数分度lg(ω), 单位为弧度/秒（rad/s） 对数幅频曲线的纵坐标是对幅值 用 L()=20lgA(ω) 进行线性分度， 单位是分贝(dB) 。 对数相频特性图的纵坐标则对相 角进行线性分度，单位为度（o）, 仍用 ( )表示。
（红色线）
j 0
幅相曲线
L(ω)=-20lgω φ(ω)=-90o
L
20
0
1
两重积分 G( j ) ( j )2
（蓝色线）
1
0 0.1 -20
10 20 dB dec
0 -90
-180
40 dB dec
L 20 lg
1
G j 180
对于某一特定频率 ω下的G(jω)总可以用复平面上的一个向量与之对 应，该向量的长度为A(ω)，与正实轴的夹角为(ω)。
例：RC电路的幅相频率特性。
Uo ( j ) 1 1 G( j ) Ui ( j ) 1 RCj 1 Tj
ui
R C uo
G(jω)=R(ω)+jI(ω) =|G(jω)|∠G(jω) =A(ω)ejφ(ω)
§ 5.1 频率特性
§5.1.1 频率特性的基本概念
例：RC 电路如图所示，ui(t)=Asinωt, 求uo(t)=?
自动控制原理第五章3PPT课件
2. υ = 1
系统的伯德图：
L(ω)/dB
ω=1
20lgK
-20dB/dec
L(ω)=20lgK
ω0
0 1 ω1 ωc
ω
低频段的曲线与横
-40dB/dec
轴相交点的频率为ω0
因为
20lgK lgω0-lg1
=20
故
20lgK=20lgω0 K=ω0
第三节 用实验法确定系统传递函数
3. υ = 2
12
第三节 用实验法确定系统传递函数
例 已知采用积分控制液位系统的结构
和对数频率特性曲线,试求系统的传
递函数。
L(ω)/dB
20
1
4
0
-20dB/dec -20
φ(ω)
0
-90
-180
hr(t)
1
-S
K h(t) Ts+1
ω
-40dB/dec
ω
解: 将测得的对数 = 0.曲 近25线线S2+近: 11似.25成S+渐1)
φ(s)=
1 (S+1) (S/4+1)
2）若两个系统的幅频特性相同，则>0时，最小相
角系统的相角总小于非最小相角系统的相角。
3）对于最小相角系统，若其传递函数的分子和分母
的最高次数分别为m和n，则时，相频特性()
-(n-m)90°。非最小相角系统不满足此条件。
例：设两个传递函数分别为
1Ts
1Ts
G1(s) 1T1s , G2(s) 1T1s ,
一个稳定系统，若其传递函数在右半s平面无零 点，称为最小相角系统（最小相位系统）；否则， 称为非最小相角系统（非最小相位系统）。
《自动控制理论》课件
1.1 自动控制理论的定义1.2 自动控制系统的分类1.3 自动控制理论的应用领域二、数学基础2.1 线性代数基础2.2 微积分基础2.3 常微分方程2.4 拉普拉斯变换三、经典控制理论3.1 概述3.2 传递函数3.3 系统稳定性分析3.4 系统响应分析3.5 系统校正设计四、现代控制理论4.1 状态空间描述4.2 状态空间分析4.3 控制器设计4.4 观测器设计4.5 系统李雅普诺夫稳定性分析五、线性二次调节器5.2 性能指标5.3 调节器设计5.4 数字实现六、非线性控制系统6.1 非线性系统的特点6.2 非线性方程和方程组的求解6.3 非线性系统的分析和设计方法6.4 非线性控制系统的应用实例七、模糊控制系统7.1 模糊控制理论的基本概念7.2 模糊控制规则和推理方法7.3 模糊控制器的设计7.4 模糊控制系统的仿真和应用八、自适应控制系统8.1 自适应控制的基本概念8.2 自适应控制算法8.3 自适应控制系统的性能分析8.4 自适应控制的应用实例九、智能控制系统9.1 智能控制的基本概念9.2 人工神经网络在自动控制中的应用9.3 遗传算法在自动控制中的应用9.4 模糊神经网络在自动控制中的应用十、自动控制技术的应用10.1 工业自动化10.2 交通运输自动化10.3 生物医学工程自动化10.4 家居自动化六、非线性控制系统6.1 非线性系统的特点6.2 非线性方程和方程组的求解求解非线性方程和方程组通常需要使用数值方法，如牛顿法、弦截法和迭代法等。
6.3 非线性系统的分析和设计方法对于非线性系统，常用的分析方法有相平面分析、李雅普诺夫方法和描述函数法等。
设计方法包括反馈线性化和滑模控制等。
6.4 非线性控制系统的应用实例例如，臂的控制、电动汽车的稳定控制等。
七、模糊控制系统7.1 模糊控制理论的基本概念模糊控制是一种基于的控制方法，它通过模糊逻辑对系统的输入和输出进行处理，从而实现控制目的。
自动控制理论最新版精品课件第5章 频率法
5-1 频率特性的概念
一、频率特性的基本概念
➢频率响应：系统对正弦输入的稳态响应。
u1 U1 sint
在稳态情况下，输出电压 u2 U2 sinωt
1
•
U2
•
U1
jC
R 1
jC
1
1 j RC
1
1 jT
➢频率特性的定义：
该电路的频率特性
零初始条件的线性系统或环节，在正弦信号作用下， 稳态输出与输入的复数比。
➢与传递函数的关系：
G(j) G(s) s j
•
A() G(j)
U2
•
G( j )
A( )e j ( )
U1
1
1 (T )2
() G(j)
•
•
U 2 U1 arctan(T)
A(ω) 称幅频特性，φ(ω)称相频特性，G(jω) 称为幅相频率 特性。
二、频率特性的求取
➢已知系统的运动方程，输入正弦函数求其稳态解，取输出稳
特征点1: n 时
A,
An 1 2
n
2
特征点2: 令
dA d 0
1 0
0.3
0.5 0.707
r
n
谐振频率 r n 1 2 2 0.707
1
2
谐振峰值 Ar 2 1 2
0.5 0.3
0 0.707，出现谐振
0.707 阶跃响应既快又稳，比较理想（也称为“二阶最佳”）
G( j )
1
1
n
2 n2
2
2
2
n
2
j 1
2 n2
2 n
2 2
n
2
2019《自动控制理论教学课件》第五章 控制系统的频域分析.ppt
暂态分量
稳态分量
响应的稳态分量为： 1 uos U m sin t ( ) U m A( ) sin t ( ) 2 2 1 1 1 式中： A( ) 2 2 1 j 1
( ) arctan
1 s j 1 G (s ) G (j ) G (s ) s j e arctan 1 s 1 2 2 可见， A( )、 ( ) 分别为 G (j ) 的幅值 G (j )
和相角 G (j ) 。 设线性定常系统的传递函数为：
G (s ) C (s ) N (s ) N (s) R(s ) D(s ) (s p1 )(s p2 ) (s pn )
§5-8 根据闭环频率特性分析系统的时域响应
§5-1 频率特性及其与时域响应的关系
一、频率特性的基本概念
频率响应：在正弦输入信号的作用下，系统输出的稳态 分量。 频率特性：系统频率响应与正弦输入信号之间的关系。 频域分析法：应用频率特性研究线性系统的经典方法。其 特点是根据系统的开环频率特性去判断闭环系统的性能。
第五章
线性系统的频域分析法
§5-1 频率特性及其与时域响应的关系 §5-2 典型环节的频率特性 §5-3 系统开环频率特性的极坐标图
§5-4 系统开环对数频率特性的绘制 §5-5 乃奎斯特稳定判据和系统的相对稳定性 §5-6 控制系统对数坐标图与稳态误差及瞬态 响应的关系
*§5-7 系统的闭环频率特性
L( ) dB
( )
L( )
0 20
40
( )
0.01 0.1
1
0 30 60 90 10 100
1 ，1 用描点法绘制出 ( ) 曲线如图，图中令：
66自动控制原理第五章第12节PPT课件
A
B
相位差 2ar(c tT g )
2
它们都是ω和系统特征参数的函数。
15
结论 推广到一般，得出以下
：
1、对线性系统作用正弦信号，其稳态输出仍是一
正弦函数，频率不变，幅值和相位发生变化。
2、幅值比 B 和相位差ψ都是输入信号频率ω的函数，
A
其函数关系统称为频率特性。
B A
∽ ω 的关系称为幅频特性。
当输入 xA si n t时，
A X(s) s2 2
Y(s)G (s)X(s) K Ts1
A s2 2
TKs1(sjA)(sj)Tbs1sajsaj
b/T a
a
s1/T sj sj
12
b /T a a K A
Y (s) s 1 /Ts j
s j
T 1 s s22
经拉氏反变换，有：
二、频域分析法 1.什么是频域分析法 ➢系统对正弦输入信号的稳态响应称为频率响应；
➢系统的频率响应（正弦量）与正弦输入信号（正 弦量）在全范围内的比称为频率特性；
➢基于频率特性和频率响应对系统进行分析的方法 称为频域分析法。
7
2.频域分析法的特点：
1）频率特性是控制系统在频域中的一种数 学模型，是研究自动控制系统的另一种工 程方法；
Φ ∽ ω 的关系称为相频特性。
频率特性
3、频率特性与系统（环节）的动态特性有关，例
T、k。可以推论，尽管频率特性是从系统的稳
态响应中得到的，却反映出系统的动态特性，
3) 对工程中普遍存在的高频噪声干扰的研究无能为力。
5
2.根轨迹法
1）根轨迹法弥补了时域分析法中参数全局变化时特征不明显的 不足，在研究单一指定参数对整个系统的影响时很有用；
自动控制理论(邹伯敏第三版)第05章
普通高等教育“十一五”国家级规划教材
自动控制理论
第五章
频率响应
作者： 浙江大学
2015/12/11 第五章 频率响应
邹伯敏 教授
1
自动控制理论
第一节
一、频率特性的基本概念
频率特性
令
C (s) R(s)
G(s)
U (s) V (s)
A 已知 r (t ) A sint , R ( s ) 2 2 S
C (S )
U ( S ) A U (S ) A V (S ) S 2 2 (S P 1 )(S P 2 )(S P n ) ( S j )(S j )
n bj a a S j S j j 1 S p j
c(t ) ae jt a e jt b j e
1 T2 S 1 T2 j , Ga ( j ) 1 T1S 1 T1 j
Gb ( S )
这两个系统的幅频特性是相同的,即：
L( ) 20lg 1 (
1 T1
) 2 20lg 1 (
1 T2
)2
2015/12/11
第五章 频率响应
19
自动控制理论 相频特性却不同,分别为:
28
自动控制理论 根据不同的ζ值，作出的乃氏图如图5-24所示。
图5-24 0 式（5-43）的奈氏图
2015/12/11 第五章 频率响应 29
自动控制理论
2 2 2 2 2 j ( ) 2)G ( j ) 1 2 j 2 (1 2 ) 4 e 2 n n n n
第五章 频率响应
图5-14 由式（5-26）给出的对数幅 频曲线、渐近线和相频曲线
自动控制理论
第五章
频率响应
作者： 浙江大学
2015/12/11 第五章 频率响应
邹伯敏 教授
1
自动控制理论
第一节
一、频率特性的基本概念
频率特性
令
C (s) R(s)
G(s)
U (s) V (s)
A 已知 r (t ) A sint , R ( s ) 2 2 S
C (S )
U ( S ) A U (S ) A V (S ) S 2 2 (S P 1 )(S P 2 )(S P n ) ( S j )(S j )
n bj a a S j S j j 1 S p j
c(t ) ae jt a e jt b j e
1 T2 S 1 T2 j , Ga ( j ) 1 T1S 1 T1 j
Gb ( S )
这两个系统的幅频特性是相同的,即：
L( ) 20lg 1 (
1 T1
) 2 20lg 1 (
1 T2
)2
2015/12/11
第五章 频率响应
19
自动控制理论 相频特性却不同,分别为:
28
自动控制理论 根据不同的ζ值，作出的乃氏图如图5-24所示。
图5-24 0 式（5-43）的奈氏图
2015/12/11 第五章 频率响应 29
自动控制理论
2 2 2 2 2 j ( ) 2)G ( j ) 1 2 j 2 (1 2 ) 4 e 2 n n n n
第五章 频率响应
图5-14 由式（5-26）给出的对数幅 频曲线、渐近线和相频曲线
《自动控制原理教学课件》第5-1共41页文档
与微分方程及传递函数一样，频率特性也常 称为动态数学模型。
通信技术研究所
四、频率特性的三种图示法
1.极坐标图——Nyquist图（又叫幅相频率特性、
或奈奎斯特图简称奈氏图）
G(j)A()ej()
对于某一特定ω，总可以在复平面上找到一个 向量与G(jω)对应，该向量的长度为A(ω),与实轴 的夹角为φ( ω)。
频率特性 G(j)jej2
幅频特性 A()G(j)
相频特性 ()G(j)
2
对数幅频 L () 2 0 lg A () 2 0 lg
通信技术研究所
L()20lg
j
0
[G]
[20] 表示每10倍频程增加20dB 特征点： =1rad/s，L=0
通信技术研究所
四.惯性环节
传递函数
G(s) 1 Ts 1
频率特性 G(j) 1 =1ej(-2) j
幅频特性 A ( ) 1
相频特性 对数幅频
( )
2
L()20lg 120lg
7
通信技术研究所
L()20lg 120lg
j
0
[G]
[-20] 表示每10倍频程下降20dB 特征点： =1rad/s，L=0
通信技术研究所
三.微分环节
传递函数 G(s) s
3.相频宽 b ： () 2时 对 应 的 频 率
4.零频振幅比A（0）：ω＝0时输出输入振幅比
A( )
Am
A(0)
0.707 A(0)
b
0
b
2
通信技术研究所
3
三、频率特性说明 （1）适用于线性定常系统 （2）适用于稳定系统 （3）由表达式 ( j ) 可知，其包含了系统或元部 件的全部动态动态结构和参数。频率响应是一种 稳态响应，但动态过程的规律性必将寓于其中。
通信技术研究所
四、频率特性的三种图示法
1.极坐标图——Nyquist图（又叫幅相频率特性、
或奈奎斯特图简称奈氏图）
G(j)A()ej()
对于某一特定ω，总可以在复平面上找到一个 向量与G(jω)对应，该向量的长度为A(ω),与实轴 的夹角为φ( ω)。
频率特性 G(j)jej2
幅频特性 A()G(j)
相频特性 ()G(j)
2
对数幅频 L () 2 0 lg A () 2 0 lg
通信技术研究所
L()20lg
j
0
[G]
[20] 表示每10倍频程增加20dB 特征点： =1rad/s，L=0
通信技术研究所
四.惯性环节
传递函数
G(s) 1 Ts 1
频率特性 G(j) 1 =1ej(-2) j
幅频特性 A ( ) 1
相频特性 对数幅频
( )
2
L()20lg 120lg
7
通信技术研究所
L()20lg 120lg
j
0
[G]
[-20] 表示每10倍频程下降20dB 特征点： =1rad/s，L=0
通信技术研究所
三.微分环节
传递函数 G(s) s
3.相频宽 b ： () 2时 对 应 的 频 率
4.零频振幅比A（0）：ω＝0时输出输入振幅比
A( )
Am
A(0)
0.707 A(0)
b
0
b
2
通信技术研究所
3
三、频率特性说明 （1）适用于线性定常系统 （2）适用于稳定系统 （3）由表达式 ( j ) 可知，其包含了系统或元部 件的全部动态动态结构和参数。频率响应是一种 稳态响应，但动态过程的规律性必将寓于其中。
51-1 2 2 对数坐标图(典型环节) 对比极坐标
横轴
标定， 按 ω 标定，等距等比
L(ω ) = 20 lg G ( jω ) dB “分贝” 分贝”
纵轴 坐标特点
Pc Pc lg (贝尔 ) = 10 lg ( 分贝 ) Pr Pr
对数相加，便于叠加作图； ⑴ 幅值相乘 = 对数相加，便于叠加作图；
特点
可在大范围内表示频率特性； ⑵ 可在大范围内表示频率特性； ⑶ 利用实验数据容易确定 L(ω),进而确定 ω ,进而确定G(s)。 。
ω 的正弦信号
加到电路的输入端后，在稳态时，电路的输出与输入之比； 加到电路的输入端后，在稳态时，电路的输出与输入之比； 或者说输出与输入的幅值之比和相位之差。 或者说输出与输入的幅值之比和相位之差。
《自动控制理论》课件
§5.1 频率特性的基本概念（2）
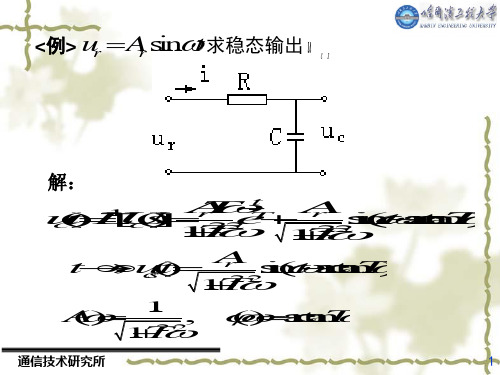
电路如图所示， 例1 RC 电路如图所示，ur(t)=Asinωt, 求uc(t)=? ω
5
2
4
1.5
3
1 0.5 0 -0.5 -1 -1.5 -2
2 1 0
线性系统
-1 -2 -3 -4 -5
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
2.5
3
图5-1
频率响应示意图
输出的振幅和相位一般均不同于输入量， 输出的振幅和相位一般均不同于输入量，且随着输入信 号频率的变化而变化。如上图5 号频率的变化而变化。如上图5-1。
《自动控制理论》课件
§5.2 对数坐标图 ( Bode)（3）
§5.2.1 典型环节的Bode图 典型环节的Bode图 Bode
⑴ 比例环节 G ( jω ) = K ⑵ 微分环节 G ( jω ) = jω ⑶ 积分环节 G ( jω ) =
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
普通高等教育“十一五”国家级规划教材
自动控制理论
第五章
频率响应
2020/5/4
作者： 浙江大学 邹伯敏 教授
第五章 频率响应
1
自动控制理论
第一节 频率特性
一、频率特性的基本概念
令
C(s)
U (s)
G(s)
R(s)
V (s)
已知
A r(t) A sin t, R(s) S 2 2
C(S) U (S) A
1 T
➢ 低频渐近线的斜率为-40dB/dec。
➢ 低频渐近线（或延长线）在ω=1处的坐标值为20lgK。
➢ 开环增益K在数值上等于低频渐近线（或延长线）与0dB线相交点频 率值的平方。
2020/5/4
第五章 频率响应
24
自动控制理论
第三节 极坐标图
G( j) p() jQ() p2 () Q2 ()e j() 式中() arctan Q()
20lg 1 jT 20lg 1 1 jT
arg(1 jT ) arg( 1 ) 1 jT
3. 积分、微分因子 ( j) 1
1)积分因子
1
j
L() 20lg
2020/5/4
图5-11 (1 j的T )伯1 德图
第五章 频率响应
10
自动控制理论
() 90
2)微分因子 j
() 20lg
() 90
U (S )
A
V (S ) S 2 2 (S P1)(S P2 ) (S Pn ) (S j)(S j)
a
a
n
bj
S j S j j1 S p j
n
c(t) ae jt ae jt b j e p jt
j 1
2020/5/4
第五章 频率响应
2
自动控制理论
当t→∞时,
c(t) ae jt ae jt
, 1
1 T
图5-8 比例因子的伯德图
2020/5/4
第五章 频率响应
8
自动控制理论
当 当
11时时,,略略去去1(,L1()2 ,)L(2)0lg201lg
1
0dB
图5-9 (1的jT对)1数幅频曲线、渐近线和相角曲线
2020/5/4
第五章 频率响应
9
自动控制理论
由于(1 jT )与(1 jT )1互为倒数,则有
(
)
arc
tan 1
n 2
n2
图5-24 式 0（5-44）的奈氏图
5、滞后因子 ej
G( j) ej 1
2020/5/4
第五章 频率响应
30
自动控制理论
ej
1 ej
1
j
1
1 ( j )2
2!
当
1时
e j
1
1
j
图5-27 e 的j奈氏图
e 图5-28 和j (1 的j奈T氏)图1
2020/5/4
例54
G( j)
10
10
e j ( )
( j)2 (1 j) 2 (1 2 )
() 180 arctan
2020/5/4
第五章 频率响应
图5-31 例5-4的奈氏图
36
自动控制理论
第四节 用频率法辩识线性定常系统的数学模型
一、由实验作出被测系统的博德图及对数幅频特性曲线的渐近线
1、在感兴趣的频率范围内，给被测系统输入不同频率的正弦信号。对 于大时间常数的系统，一般取的频率范围为0.01～10Hz；对于小时间常 数的系统，则应选择频率较高的正弦信号。在足够多的频率点上，测得 被测系统稳态输出信号与输入信号的幅值比和相位差。据此，作出该系 统的对数幅频特性和相频特性曲线。
2020/5/4
图5-23 (1 j和T )1 (因1 子j的T奈)氏1 图
第五章 频率响应
27
自动控制理论
4、二阶因子
1
1
j2
n
(
j n
)
2
1)G( j) 1 j2
1
(j
)2
n
n
1
e j ()
(1
2 n2
)2
4
2
2 n2
2
(
)
arc
tan 1
n 2
n2
limG( j) 10 0
limG( j) 0 180 0
2020/5/4
第五章 频率响应
28
自动控制理论 根据不同的ζ值，作出的乃氏图如图5-24所示。
图5-24 式 0（5-43）的奈氏图
2020/5/4
第五章 频率响应
29
自动控制理论
2)G(
j
)
1
2 n2
j2
n
(1
2 n2
)2
4
2
2 n2
e
j ( )
2
2020/5/4
第五章 频率响应
34
自动控制理论
图5-30 Ⅰ型二阶系统的奈氏图
3.Ⅱ型系统 m
K (1 i j)
G( j)
i 1 n2
,n m
( j)2 (1 l j)
l 1
2020/5/4
第五章 频率响应
35
自动控制理论
当 0时，G( j0 ) 180; 当 时，G( j) 0 90(n m)。
p()
当输入信号的频率ω由0→∞变化时，向量G( j ω)的端点在复平面上移动 的轨迹叫极坐标图或称为乃氏图。
一、典型因子的乃氏图
1、比例因子K
2020/5/4
第五章 频率响应
25
自动控制理论
G( j) K
() 0
参考图5-22(a)
图5-22 比例、积分和微分因子的奈氏图
2、积分和微分因子
G( j)
1
1
j
e2
j
j
G( j) j e 2
参考图5-22(b) 参考图5-22(c)
2020/5/4
第五章 频率响应
26
自动控制理论
3、一阶因子 (1 jT )1
1)G( j) 1
1e j ( )源自1 jT 1 T 2 2() arctanT
2)G( j) 1 jT 1T 22 e j() () arctanT
2020/5/4
第五章 频率响应
6
自动控制理论
图5-7 例5-1的频率响应曲线
2020/5/4
第五章 频率响应
7
自动控制理论
第二节 对数坐标图
一、典型因子的伯德图
1. 比例因子K
20lg K 20lg 1 K
2. 一阶因子 (1 jT ) 1
() arctan 1
L() 20lg 1 ( )2 1
2
10
特点：
1）低频段斜率为 20dB dec，在 1处，高度为20lg10 20dB。
2）为 2，斜率由 20dB dec 40dB dec；
3）为 10，斜率由 40dB dec 20dB dec。
（2）相频特性
() 90 arctan arctan
2
10
2020/5/4
K
3) j
L() 20 lg 20 lg K () 90
图5-12 对数幅频与相频曲线
2020/5/4
第五章 频图率响5-应13 K /的j对v 数幅频特性曲线
11
自动控制理论
4. 二阶因子 [1 2Tn j ( jTn )2 ] 1
1)G(
j)
1
2
2 n
1
j
n
L() 20lg
第五章 频率响应
14
自动控制理论
5. 滞后因子 ej
G( j) ej 1
()
2020/5/4
图5-17 滞后因子的相频特性
第五章 频率响应
15
自动控制理论
二、开环系统的伯德图
设开环传递函数
G(s) G1 (s)G2 (s) Gn (s)
L() 20lg G1( j) 20lg G2( j) 20lg Gn ( j)
() arg G1( j) arg G2 ( j) arg Gn ( j)
例5-2 G(s)H (s) 10(1 0.1s) 绘制Bode图。 s(1 0.5s)
解：（1）幅频特性
10(1 j )
G( j)
j (1
10
j)
2
2020/5/4
第五章 频率响应
16
自动控制理论
L() 20 lg10 20 lg 20 lg 1 ( )2 20 lg 1 ( )2
1 T
➢ 低频渐近线斜率为-20db/dec
➢ 低频渐近线（或延长线）在ω=1处的相交坐标值为20lgK。
➢ 开环增益K在数值上等于低频渐近线（或延长线）与0dB线相交点 的频率值。
2020/5/4
第五章 频率响应
23
自动控制理论
3、Ⅱ型系统
G( j)
K
( j)2 (1
j
)
1
T
L() 20 lg K 40 lg 20 lg 1 ( )2
第五章 频率响应
17
自动控制理论
图5-18 例5-2的博德图
2020/5/4
第五章 频率响应
18
自动控制理论
三、最小相位系统与非最小相位系统
设a和b两个系统的传递函数和频率特性分别为:
Ga (S )
1 T2S 1 T1S
, Ga
(
j)
1 T2 1 T1
自动控制理论
第五章
频率响应
2020/5/4
作者： 浙江大学 邹伯敏 教授
第五章 频率响应
1
自动控制理论
第一节 频率特性
一、频率特性的基本概念
令
C(s)
U (s)
G(s)
R(s)
V (s)
已知
A r(t) A sin t, R(s) S 2 2
C(S) U (S) A
1 T
➢ 低频渐近线的斜率为-40dB/dec。
➢ 低频渐近线（或延长线）在ω=1处的坐标值为20lgK。
➢ 开环增益K在数值上等于低频渐近线（或延长线）与0dB线相交点频 率值的平方。
2020/5/4
第五章 频率响应
24
自动控制理论
第三节 极坐标图
G( j) p() jQ() p2 () Q2 ()e j() 式中() arctan Q()
20lg 1 jT 20lg 1 1 jT
arg(1 jT ) arg( 1 ) 1 jT
3. 积分、微分因子 ( j) 1
1)积分因子
1
j
L() 20lg
2020/5/4
图5-11 (1 j的T )伯1 德图
第五章 频率响应
10
自动控制理论
() 90
2)微分因子 j
() 20lg
() 90
U (S )
A
V (S ) S 2 2 (S P1)(S P2 ) (S Pn ) (S j)(S j)
a
a
n
bj
S j S j j1 S p j
n
c(t) ae jt ae jt b j e p jt
j 1
2020/5/4
第五章 频率响应
2
自动控制理论
当t→∞时,
c(t) ae jt ae jt
, 1
1 T
图5-8 比例因子的伯德图
2020/5/4
第五章 频率响应
8
自动控制理论
当 当
11时时,,略略去去1(,L1()2 ,)L(2)0lg201lg
1
0dB
图5-9 (1的jT对)1数幅频曲线、渐近线和相角曲线
2020/5/4
第五章 频率响应
9
自动控制理论
由于(1 jT )与(1 jT )1互为倒数,则有
(
)
arc
tan 1
n 2
n2
图5-24 式 0（5-44）的奈氏图
5、滞后因子 ej
G( j) ej 1
2020/5/4
第五章 频率响应
30
自动控制理论
ej
1 ej
1
j
1
1 ( j )2
2!
当
1时
e j
1
1
j
图5-27 e 的j奈氏图
e 图5-28 和j (1 的j奈T氏)图1
2020/5/4
例54
G( j)
10
10
e j ( )
( j)2 (1 j) 2 (1 2 )
() 180 arctan
2020/5/4
第五章 频率响应
图5-31 例5-4的奈氏图
36
自动控制理论
第四节 用频率法辩识线性定常系统的数学模型
一、由实验作出被测系统的博德图及对数幅频特性曲线的渐近线
1、在感兴趣的频率范围内，给被测系统输入不同频率的正弦信号。对 于大时间常数的系统，一般取的频率范围为0.01～10Hz；对于小时间常 数的系统，则应选择频率较高的正弦信号。在足够多的频率点上，测得 被测系统稳态输出信号与输入信号的幅值比和相位差。据此，作出该系 统的对数幅频特性和相频特性曲线。
2020/5/4
图5-23 (1 j和T )1 (因1 子j的T奈)氏1 图
第五章 频率响应
27
自动控制理论
4、二阶因子
1
1
j2
n
(
j n
)
2
1)G( j) 1 j2
1
(j
)2
n
n
1
e j ()
(1
2 n2
)2
4
2
2 n2
2
(
)
arc
tan 1
n 2
n2
limG( j) 10 0
limG( j) 0 180 0
2020/5/4
第五章 频率响应
28
自动控制理论 根据不同的ζ值，作出的乃氏图如图5-24所示。
图5-24 式 0（5-43）的奈氏图
2020/5/4
第五章 频率响应
29
自动控制理论
2)G(
j
)
1
2 n2
j2
n
(1
2 n2
)2
4
2
2 n2
e
j ( )
2
2020/5/4
第五章 频率响应
34
自动控制理论
图5-30 Ⅰ型二阶系统的奈氏图
3.Ⅱ型系统 m
K (1 i j)
G( j)
i 1 n2
,n m
( j)2 (1 l j)
l 1
2020/5/4
第五章 频率响应
35
自动控制理论
当 0时，G( j0 ) 180; 当 时，G( j) 0 90(n m)。
p()
当输入信号的频率ω由0→∞变化时，向量G( j ω)的端点在复平面上移动 的轨迹叫极坐标图或称为乃氏图。
一、典型因子的乃氏图
1、比例因子K
2020/5/4
第五章 频率响应
25
自动控制理论
G( j) K
() 0
参考图5-22(a)
图5-22 比例、积分和微分因子的奈氏图
2、积分和微分因子
G( j)
1
1
j
e2
j
j
G( j) j e 2
参考图5-22(b) 参考图5-22(c)
2020/5/4
第五章 频率响应
26
自动控制理论
3、一阶因子 (1 jT )1
1)G( j) 1
1e j ( )源自1 jT 1 T 2 2() arctanT
2)G( j) 1 jT 1T 22 e j() () arctanT
2020/5/4
第五章 频率响应
6
自动控制理论
图5-7 例5-1的频率响应曲线
2020/5/4
第五章 频率响应
7
自动控制理论
第二节 对数坐标图
一、典型因子的伯德图
1. 比例因子K
20lg K 20lg 1 K
2. 一阶因子 (1 jT ) 1
() arctan 1
L() 20lg 1 ( )2 1
2
10
特点：
1）低频段斜率为 20dB dec，在 1处，高度为20lg10 20dB。
2）为 2，斜率由 20dB dec 40dB dec；
3）为 10，斜率由 40dB dec 20dB dec。
（2）相频特性
() 90 arctan arctan
2
10
2020/5/4
K
3) j
L() 20 lg 20 lg K () 90
图5-12 对数幅频与相频曲线
2020/5/4
第五章 频图率响5-应13 K /的j对v 数幅频特性曲线
11
自动控制理论
4. 二阶因子 [1 2Tn j ( jTn )2 ] 1
1)G(
j)
1
2
2 n
1
j
n
L() 20lg
第五章 频率响应
14
自动控制理论
5. 滞后因子 ej
G( j) ej 1
()
2020/5/4
图5-17 滞后因子的相频特性
第五章 频率响应
15
自动控制理论
二、开环系统的伯德图
设开环传递函数
G(s) G1 (s)G2 (s) Gn (s)
L() 20lg G1( j) 20lg G2( j) 20lg Gn ( j)
() arg G1( j) arg G2 ( j) arg Gn ( j)
例5-2 G(s)H (s) 10(1 0.1s) 绘制Bode图。 s(1 0.5s)
解：（1）幅频特性
10(1 j )
G( j)
j (1
10
j)
2
2020/5/4
第五章 频率响应
16
自动控制理论
L() 20 lg10 20 lg 20 lg 1 ( )2 20 lg 1 ( )2
1 T
➢ 低频渐近线斜率为-20db/dec
➢ 低频渐近线（或延长线）在ω=1处的相交坐标值为20lgK。
➢ 开环增益K在数值上等于低频渐近线（或延长线）与0dB线相交点 的频率值。
2020/5/4
第五章 频率响应
23
自动控制理论
3、Ⅱ型系统
G( j)
K
( j)2 (1
j
)
1
T
L() 20 lg K 40 lg 20 lg 1 ( )2
第五章 频率响应
17
自动控制理论
图5-18 例5-2的博德图
2020/5/4
第五章 频率响应
18
自动控制理论
三、最小相位系统与非最小相位系统
设a和b两个系统的传递函数和频率特性分别为:
Ga (S )
1 T2S 1 T1S
, Ga
(
j)
1 T2 1 T1