实验五-图操作实现
实验5活动图

实验五活动图
一、实验目的
1.熟悉动态建模的概念和内容。
2.熟悉活动图的基本功能和使用方法。
3. 掌握如何使用建模工具绘制活动图方法。
二、实验器材
1. 计算机一台;
2. Rational Rose 工具软件;
三、实验内容
根据图书馆管理需求分析、用例图、类图等,应针对每个用例进行业务分析,说明其具体的业务流程,完成系统活动图。
四、实验过程和结果
以“删除读者信息”用例为例,说明绘制活动图的步骤。
1.管理员在录入界面,输入待删除的读者名;
2.“业务逻辑”组件在数据库中,查找待删除的读者名;
3.如果不存在,则显示出错信息,返回步骤(1),如果存在则继续;
4.“业务逻辑”组件判断“待删除的读者”是否可以删除;
5.如果不可以,则显示出错信息,返回步骤(8),如果可以则继续;
6.在数据库中,删除相关信息;
7.显示删除成功信息;
8.结束。
以此为例,完成以下活动图:
1)借阅者的活动图
2)图书管理员的活动图
3)系统管理员的活动图
五、实验小结。
实验五-半桥型开关稳压电源

实验五-半桥型开关稳压电源概述实验五主要是通过实现半桥型开关稳压电源来深入理解开关电源的工作原理和实现方式。
半桥型开关稳压电源具有稳压性好、效率高等特点,是一种常用的开关稳压电源方案。
在本次实验中,我们将学习如何设计和实现半桥型开关稳压电源,包括电路原理、电路分析、元器件选型、电路布局等方面。
实验原理半桥型开关稳压电源通过半桥型开关电路来实现高效率、低数据损失的稳压电源。
半桥型开关电路是由电容、电感和开关管组成的,并且在电源稳压模式下,使用反馈电路来监测输出电压并控制开关管的导通和截止,以达到稳压的目的。
开关稳压电源的优点是效率高,经济性好,可靠性强,使用寿命长,并且适应性强,可以适应各种工作环境。
因此,开关稳压电源在电力系统、通讯设备、军事设备、机械工业等领域都有广泛的应用。
实验步骤元器件选型在设计半桥型开关稳压电源时,需要选择合适的元器件。
以下是一些常用的半桥型开关稳压电源的元器件:•电容:0.1uf 至 0.33uf,电容电压≥VDCmax•电感:至少选3.3uH的电感,电感电流≥2.5A•开关管:选用高亮度MOS管或IGBT管•反馈电路:可以选择非隔离型反馈电路或隔离型反馈电路电路设计根据实验要求,我们可以设计如下半桥型开关稳压电源电路:半桥型开关稳压电源电路图半桥型开关稳压电源电路图电路调试在实验电路得到组装和焊接之后,我们需要进行调试。
调试的主要步骤如下:1.打开电源并确认输出电压为0V。
2.调节偏置电压,使得MOS管和IGBT管的导通断开正常。
3.在调整偏压电源后,我们开始调整反馈电路以使输出电压稳定。
4.最后,检验电路的稳定性和输出电压的波动情况。
实验通过实验,我们可以掌握半桥型开关稳压电源的设计和实现方法,理解开关电源的工作原理、掌握元器件的选型、电路设计和调试等方面的知识。
在实际应用中,半桥型开关稳压电源具有效率高、稳压性好等优点,可以广泛应用于通信设备、医疗设备、机械工业等领域的电源供应。
mapgis实验(实例)教程实习五属性数据的操作
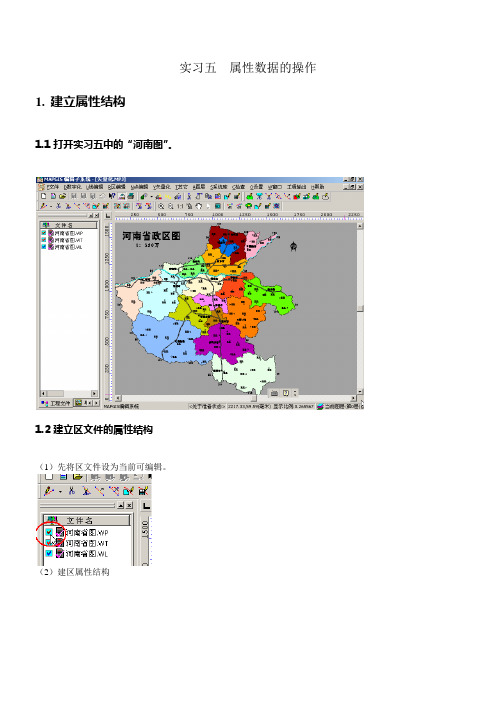
实习五属性数据的操作1.建立属性结构
1.1打开实习五中的“河南图”。
1.2建立区文件的属性结构
(1)先将区文件设为当前可编辑。
(2)建区属性结构
(图1)(图2)
图3
图4
图5
图1
(图2)
然后点击
(图3)
然后将所有的图斑统统输入属性。
(记住存盘)
3.1打开属性表
在实习五文件下双击excel表格文件。
浏览表格的内容
3.2将表格另存为*.DBF的数据格式。
(图1)
(图2)
(图3)
图4
然后关闭表格文件。
3.3联接属性
(1)启动“属性库管理”模块
图1
图2 (2)联接属性
(图1)
图2
分别通过单击上面的两个按钮,打开相应的文件。
图3
然后确定它们联接时选用的关键字,在此处为地市名称。
图4
3.4在输入编辑窗口中打开联接好的区文件,浏览联接的效果。
图1
图2
图3
在图上的某一图斑上单击,浏览其属性。
图4
4.输出属性
4.1在属性库管理模块中打开要转出属性的区文件。
图1
图2 4.2输出属性
图1
图2
图3
4.3将输出的属性表在excel中打开。
图1
图2
图3
图4
图5
思考:现在分析一下在2030年有哪些地市会出现粮食危及,并将分析的结果联接到图形的属性中。
操作系统原理实验5-实现一个简单的Shell

《操作系统原理》实验报告
实验序号:5 实验项目名称:实现一个简单的Shell
一、实验目的及要求
1. 加深对操作系统Shell的理解。
2. 理解进程控制的思想。
3. 深入掌握Linux操作系统下的进程控制编程。
二、实验设备(环境)及要求
1.虚拟机VMware Workstation、Ubuntu操作系统和C语言编程。
2.设计思路:Shell建立一个新的进程,然后在那个进程中运行一个程序(如完成ls操作)然后等待那个进程执行结束。
然后shell便可读取新的一行输入,建立一个新的进程,在这个进程中运行程序并等待这个进程结束。
所以要写一个shell,需要循环以下过程:
a. 获取命令行
b. 解析命令行
c. 建立一个子进程(fork)
d. 替换子进程(execvp)
e. 父进程等待子进程退出(wait)。
三、实验内容与步骤
主要代码
解析并执行指令
输出各进程的信息
四、实验结果与数据处理
五、分析与讨论
六、教师评语
成绩
签名:
日期:。
虚拟仪器上机实验五 图形与图表实验

上机实验五、图形与图表实验一、实验目的1、掌握波形图和波形图表控件的特点和使用方法;2、掌握公式节点的基本使用方法;3、学习XY图的使用方法。
二、实验仪器设备1、计算机;2、LabVIEW软件环境。
三、实验内容和实现分析(一)实验内容1、单曲线波形的显示设计一个VI,分别用波形图和波形图表控件显示y=x2+2x+1的图形,其中x取值为0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15。
观察显示过程。
2、多曲线波形的显示设计一个VI,分别用波形图和波形图表控件显示二函数:y=x2+2x+1,y1=50ln(x+1)的图形,其中x取值为0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15。
观察显示过程。
3、李萨茹图形的显示利用XY图控件显示李萨茹图形,输入信号为具有一定相位差的正弦波,改变相位差值,观察李萨茹图形的变化情况。
(二)实现分析1、单曲线波形的显示(1)前面板设计1)启动LabVIEW,在启动界面,点击选择“新建VI”选项。
新建一空白VI。
2)从打开的控件选板中选择“新式”→“图形”子选板,从中分别选取一个“波形图”控件和一个波形图表控件,放置在前面板上合适位置。
然后再创建一个一维数组控件,将数组元素初始值设置为0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15。
设置波形图控件和波形图表控件的外观颜色,例如一个为红色,一个为蓝色。
设置完成的前面板如下图所示。
(2)后面板设计切换到程序框图窗口,从函数选板中选择一个For循环图框,放置到后面板上,For循环结构位于函数选板的“编程”→“结构”子选板,然后在For循环图框内放入一个等待函数节点以及一个公式节点,等待函数的等待时间设置为1s。
在公式节点内建立公式,然后按照所需完成的功能进行连线。
设计完成的后面板见下图所示。
切换到前面板窗口,单击“运行”按钮,运行该VI。
观察波形显示过程。
实验五 视图的创建和使用

实验五视图的创建和使用5.1概述5.1.1任务一理解视图的概念视图是一个虚拟表,其内容由查询定义。
同真实的表一样,视图包含一系列带有名称的列和行数据。
但是,视图并不在数据库中以存储的数据集合形式存在。
行和列数据来自由定义视图的查询所引用的表,并且在引用视图时动态生成。
对其中所引用的基表来说,视图的作用类似于筛选。
定义视图的筛选可以来自当前或其他数据库的一个或多个表,或者其他视图。
视图被定义后便存放在数据库中,对视图中的数据的操作与对表的操作一样,可以对其进行查询、修改和删除,但对数据的操作要满足一定的条件。
当对视图所看到的数据进行修改时,相应的基表的数据也会发生变化,同时,若基表的数据发生变化,这种变化也会自动地反映到视图中。
5.1.2任务二理解视图的优点用户可以根据自己的实际需要创建视图,使用视图有很多优点,主要有以下几点:1、简单性视图可以屏蔽数据的复杂性,简化用户对数据库的操作。
使用视图,用户可以不必了解数据库的结构,就可以方便地使用和管理数据。
那些被经常使用的查询可以被定义为视图,从而使得用户不必为以后的操作每次指定全部的条件。
2、逻辑数据独立性视图可以使应用程序和数据库表在一定程度上独立。
如果没有视图,应用一定是建立在表上的。
有了视图之后,程序可以建立在视图之上,从而程序与数据库表被视图分割开来。
3、安全性通过视图用户只能查询和修改他们所能见到的数据。
数据库中的其他数据则既看不见也取不到。
5.2创建视图创建视图的方法有三种:在创建视图前请考虑如下原则:只能在当前数据库中创建视图.视图名称必须遵循标识符的规则,且对每个用户必须为唯一.此外,该名称不得与该用户拥有的任何表的名称相同.可在其他视图和引用视图的过程之上建立视图.SQLServer 2000允许嵌套多达32级视图若要创建视图,数据库所有者必须授予用户创建视图的权限,并且用户对视图定义中所引用的表或视图要有适当的权限5.2.1任务一使用企业管理器创建视图使用企业管理器创建视图的具体操作步骤如下:1、打开企业管理器窗口,打开“新建视图”对话框。
数据结构实验总结及心得体会

数据结构实验总结及心得体会引言数据结构作为计算机科学的基础课程,是理解和应用计算机编程的重要部分。
通过实验的形式,我们可以更加深入地理解不同数据结构的特点和应用场景。
本文将总结我在数据结构实验中的学习经验和心得体会。
实验一:线性表在线性表实验中,我学习了顺序表和链表两种基本的线性表结构。
顺序表使用数组来存储数据,具有随机访问的特点;链表使用指针来连接数据元素,具有插入和删除操作方便的特点。
通过这个实验,我深刻认识了线性表的存储结构和操作方法。
我遇到的难点是链表的插入和删除操作,因为涉及到指针的重新指向。
通过调试和分析代码,我逐渐理解了指针指向的含义和变化规律。
在实验结束后,我还进一步学习了循环链表和双向链表的特点和应用。
实验二:栈和队列栈和队列是两种常用的数据结构,可以用来解决很多实际问题。
在这个实验中,我学习了顺序栈、链式栈、顺序队列和链式队列四种基本实现方式。
实验中我遇到的最大困难是队列的循环队列实现,因为需要处理队列尾指针的位置变化。
我通过画图和调试发现了队列尾指针的变化规律,并在实验中成功实现了循环队列。
熟练掌握了栈和队列的操作方法后,我进一步学习了栈的应用场景,如表达式求值和括号匹配等。
队列的应用场景还有优先级队列和循环队列等。
实验三:串串是由零个或多个字符组成的有限序列,是实际应用中十分常见的数据类型。
在这个实验中,我学习了串的存储结构和常规操作。
实验中最具挑战性的部分是串的模式匹配。
模式匹配是在一个主串中查找一个子串的过程,可以使用暴力匹配、KMP 算法和BM算法等不同的匹配算法。
在实验中,我实现了KMP算法,并在实际应用中进行了测试。
从实验中我学到了使用前缀表和后缀表来提高模式匹配的效率。
同时,在应用中也了解到了串的搜索和替换等常见操作。
实验四:树和二叉树树是一种重要的非线性数据结构,应用广泛。
在这个实验中,我学习了树的基本概念、存储结构和遍历方式。
实验中最困难的部分是二叉树的遍历。
实验五图形化显示数据

LabVIEW的Graph子模板中有许多可供选用的控件
波形( Waveform ) XY 强度图( Intensity ) 数字图( Digital ) 三维曲面( 3D Surface ) 三维参变量( 3D Parametric ) 三维曲线 (3D Curve)
Chart *
*
Graph * * * * * * *
5.3 Graph图表——Waveform Graph
3、簇作为输入 • 簇作为输入时需要指定三个元素:起始位置x0、数据点 间隔dx和数组数据。
5.3 Graph图表——Waveform Gr aph
4、簇数组作为输入
• 一维簇数组也可以直接作为Graph的输入,此时相当 于x0为0,dx为1
5.3 Graph图表——Waveform Gr aph
1、一维数组作为输入
• 当输入数据为一维数组时,Waveform Graph直接将 一维数组画成一条曲线,纵坐标为数组元素的值,横 坐标为数组索引。
5.3 Graph图表——Waveform Gr aph
2、二维数组作为输入
• 当输入数组为二维数组时,缺省情况下每一行的数据 对应一条曲线,即曲线的数目和行数相同。
练习2 波形Graph数据显示
波形Graph数据显示的前面板
设定波形Graph的属性
在波形Graph上弹出快捷菜单,可以配置Graph的一些基本属 性。
• 栅格(Grid)和小栅格(Mini-grid); • 刻度图例(Scale Legend) • 游标(Cursor) • Graph模板(Graph Palette) • 曲线图例(Plot Legend)
5.3 Graph图表——Waveform Gr aph
实验 视图、索引与数据库关系图
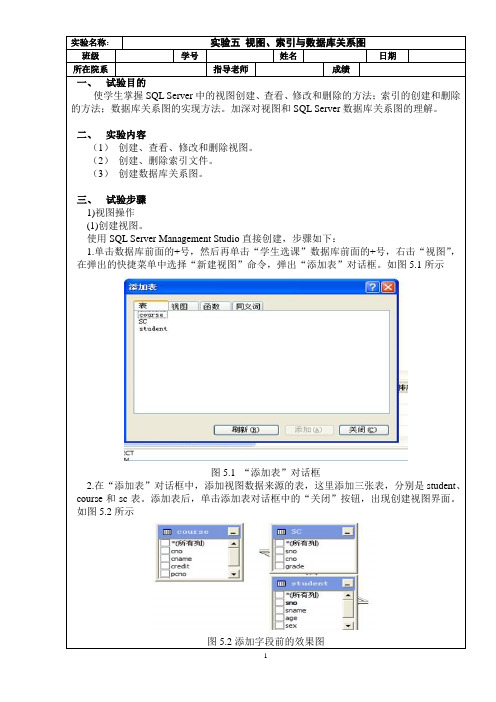
实验名称:实验五视图、索引与数据库关系图班级学号姓名日期所在院系指导老师成绩一、试验目的使学生掌握SQL Server中的视图创建、查看、修改和删除的方法;索引的创建和删除的方法;数据库关系图的实现方法。
加深对视图和SQL Server数据库关系图的理解。
二、实验内容(1)创建、查看、修改和删除视图。
(2)创建、删除索引文件。
(3)创建数据库关系图。
三、试验步骤1)视图操作(1)创建视图。
使用SQL Server Management Studio直接创建,步骤如下:1.单击数据库前面的+号,然后再单击“学生选课”数据库前面的+号,右击“视图”,在弹出的快捷菜单中选择“新建视图”命令,弹出“添加表”对话框。
如图5.1所示图5.1 “添加表”对话框2.在“添加表”对话框中,添加视图数据来源的表,这里添加三张表,分别是student、course和sc表。
添加表后,单击添加表对话框中的“关闭”按钮,出现创建视图界面。
如图5.2所示图5.2添加字段前的效果图3.如果要在视图中显示某些表的某个字段,只需单击其字段前的复选框即可,同时在中间列中会显示该字段,在代码区中会看到具体实现的代码。
4.如果要查看视图,单击常用工具栏中的“执行”按钮,就可以看到视图的数据显示,如由字段student.sno、sname、cname、grade生成的视图效果。
如图5.3所示图5.3 生成视图效果图5.在创建视图中还可以为字段添加列名、进行排序、添加多个筛选条件。
6.单击常用工具栏中的“保存”按钮,就可以弹出保存视图提示对话框,输入视图名字即可,为view_stu_grade。
(2)修改视图。
视图创建好后,就可以利用它进行查询信息了。
如果发现视图的结构不能很好的满足要求,还可以对它进行修改。
使用SQL Server Management Studio直接修改,步骤如下:1.在SQL Server Management Studio中,选择服务器、数据库、并使数据库展开,再单击“视图”前面的+,就可以看到已存在的视图了。
实验五-遥感图像的融合

实验五-遥感图像的融合实验五遥感图像的融合一、实验目的和要求1.理解遥感图像的融合处理方法和原理;2.掌握遥感图像的融合处理,即分辨率融合处理。
二、设备与数据设备:影像处理系统软件数据:TM SPOT 数据三、实验内容多光谱数据与高分辨率全色数据的融合。
分辨率融合是遥感信息复合的一个主要方法,它使得融合后的遥感图象既具有较好的空间分辨率,又具有多光谱特征,从而达到增强图象质量的目的。
注意:在调出了分辨率融合对话框后,关键是选择融合方法,定义重采样的方法。
四、方法与步骤融合方法有很多,典型的有 HSV、Brovey、PC、CN、SFIM、Gram-Schmidt 等。
ENVI 里除了 SFIM 以外,上面列举的都有。
HSV 可进行 RGB 图像到 HSV 色度空间的变换,用高分辨率的图像代替颜色亮度值波段,自动用最近邻、双线性或三次卷积技术将色度和饱和度重采样到高分辨率像元尺寸,然后再将图像变换回 RGB 色度空间。
输出的 RGB 图像的像元将与高分辨率数据的像元大小相同。
打开ENVI,在主菜单中打开数据文件LC81200362016120LGN00_MTL选择File>data manage,任意选择3个波段组合,查看效果打开分辨率为30和15的图像下图分别是分辨率为30、15的,可以看到图像清晰度明显发生改变,分辨率越高,图像越清晰选择如下图所示的三个波段选择分辨率高的为15的点击ok,Sensor选择landsat8_oil,Resampling选择三次方的Cubic Convolution,实现融合,选择输出路径为sssrong融合之后的图像如下图,可以发现图像清晰度提高,分辨率变高,图像质量变好五、实验心得多光谱数据与高分辨率全色数据的融合可以使遥感图象既具有较好的空间分辨率,又具有多光谱特征,继而达到增强图象质量的目的,可谓是一举两得。
这次实验虽然比较简单,但是一开始的时候还比较模模糊糊,甚至于连目的都不清楚。
数据结构实验课教案

数据结构实验课教案一、实验目的与要求1. 实验目的(1) 掌握数据结构的基本概念和算法。
(2) 培养实际操作能力,巩固课堂所学知识。
(3) 提高编程技能,为实际项目开发打下基础。
2. 实验要求(1) 严格按照实验指导书进行实验。
(2) 实验前认真预习,充分理解实验内容。
(3) 实验过程中积极思考,遇到问题及时解决。
(4) 按时完成实验,积极参与讨论与交流。
二、实验环境与工具1. 实验环境(1) 操作系统:Windows 7/8/10或Linux。
(2) 编程语言:C/C++、Java或Python。
(3) 开发工具:Visual Studio、Eclipse、IntelliJ IDEA或PyCharm。
2. 实验工具(1) 文本编辑器或集成开发环境(IDE)。
(2) 版本控制系统(如Git)。
(3) 在线编程平台(如LeetCode、牛客网)。
三、实验内容与安排1. 实验一:线性表的基本操作(1) 实现线性表的顺序存储结构。
(2) 实现线性表的插入、删除、查找等基本操作。
(3) 分析线性表的时间复杂度。
2. 实验二:栈与队列的基本操作(1) 实现栈的顺序存储结构。
(2) 实现队列的顺序存储结构。
(3) 实现栈与队列的进栈、出栈、入队、出队等基本操作。
(4) 分析栈与队列的时间复杂度。
3. 实验三:线性表的链式存储结构(1) 实现单链表的结构。
(2) 实现单链表的插入、删除、查找等基本操作。
(3) 分析单链表的时间复杂度。
4. 实验四:树与二叉树的基本操作(1) 实现二叉树的结构。
(2) 实现二叉树的遍历(前序、中序、后序)。
(3) 实现二叉搜索树的基本操作。
(4) 分析树与二叉树的时间复杂度。
5. 实验五:图的基本操作(1) 实现图的邻接矩阵存储结构。
(2) 实现图的邻接表存储结构。
(3) 实现图的深度优先搜索(DFS)和广度优先搜索(BFS)。
(4) 分析图的时间复杂度。
四、实验评价与成绩评定1. 实验评价(1) 代码质量:代码规范、注释清晰、易于维护。
实验五 完全互溶双液系相图

实验五 完全互溶双液系相图一 目的:1. 绘制常压下环乙烷—乙醇双液系的T —X 图2. 找出恒沸混合物的组成和最低恒沸点3. 掌握阿贝折射仪的使用方法二 原理:1. 双液系的沸点与外压,双液系的组成有关。
恒压下,采用回流冷凝的方法将完全互溶双液系蒸馏。
采用阿贝折射仪测定不同组分体系在不同温度时气相(馏出物),液相(蒸馏液)的折射率,间接获得组成来绘制相图,相图有三类如图(见书)2. 阿贝折射仪的原理:αββαn n =s i n s i n 000s i n 90sin sin ββββα⨯=⨯=n n n 光从光密介质进入光疏介质时 α<β光从光疏介质进入光密介质时 β<α光束从光密进入光疏时,β最大为090,此时的α为临界角,只有入射角小于临界角的光束才能进入光疏介质。
光束从光疏进入光密时,α=090时,折射角为0β,故任何方向的入射光都可进入光密介质,其0ββ≤三.仪器及试剂FDY 双液系沸点测定仪 阿贝折射仪恒温槽一套 移液管1m 2只环己烷(A.R) 无水乙醇(A.R)四.操作1.安装仪器设备,调节恒温槽温度比室温高05C 通恒温水于阿贝折射仪中2.测定折射率与组成的关系,绘制工作曲线。
按纯品的密度换算成质量百分比浓度,以折射率对浓度作图3.测定环己烷—乙醇体系的沸点与组成的关系① 先开冷凝水,再加热使液体沸腾。
②将袋状部的最初冷凝液体倾回蒸馏器,反复2-3次③溶液沸腾正常,温度恒定后,记录溶液沸点④分别取气,液相样品,测其折射率 g n ,L n右半支:取20mL 乙醇加入沸点仪中,依次加入环己烷0.5mL 1.0mL 1.5mL 2.0mL 4.0mL 14.0mL 测定左半支:取25mL 环己烷加入沸点仪中,依次加入乙醇0.1mL 0.2mL 0.3mL 0.4mL 1.0mL 5.0mL 测定五.注意事项1.阿贝折射仪的使用:恒温,硬物不能触及棱镜(滴管等),仪器平稳,光线充足,擦镜纸擦净2.加热时功率不可太大,液体沸腾即可。
实验五--1 顺序图和协作图

实验五—1 顺序图、协作图一、实验目的1.理解顺序图的基本概念。
2.理解协作图的基本概念。
3.掌握在Rational Rose 中绘制顺序图、协作图的操作方法。
二、实验器材1.计算机一台。
2.Rational Rose 工具软件。
三、实验内容通过对课堂学习和前面的实验,使我们完成了图书馆的管理系统的需求分析,并从业务对象中抽象出了类。
现在需要对前面所给出的用例进行实现,而用例的实现主要由顺序图来描述系统的动态特性,协作图与顺序图是同构的,Rose 可自动转换。
现指派你运用课堂所学的相关知识,完成如下任务:1.对图书管理功能中的借书用例、还书用例进行动态建模。
四、实验步骤4.1 分析阶段的动态建模1.分析:在分析阶段,绘制的顺序图中,所有消息可以使用便于理解的自然语言来描述,并且可以仅在实体类中识别对象职责,而不涉及边界类和控制类。
根据课堂讲授,参见教材P213 可完成借书用例和还书用例分析阶段的动态建模。
2.绘图步骤:(1)鼠标右击导航窗口“Logicl View”节点,选择“New——Package”,建立1 个子包:“Sequence Di ag ra m”(用于存放顺序图、协作图),完成后如图 3.1 所示。
(2)如图 3.2 所示,鼠标右击“Sequence Diagram”子包,选择快捷菜单项“New——Sequence Di ag ram”,创建一张新的顺序图,取名为“借出图书”(注意:为了好对应,顺序图名称最好与相应的用例名称相同)。
鼠标双击新建的顺序图,在右边绘图窗口中将其打开,如图 3.3 所示。
(3)设置支持嵌套消息的环境:选择主菜单项“Tools——O ptions”,打开Rose 环境设置的对话框,点击“D i a g r a m”选项卡,在如图3.4所示界面中,将“D i s p l a y”下的“Hierarchical Message”选中,点击“确定”即可。
图 3.1图 3.2图3.3图3.4(4)绘制类:从导航窗口中,将“Use Case View”节点下的参与者“图书管理员”拖到绘图窗口;将“Class Diagram”包下“BO”实体包中的相关类“Reader”、“ResourceItem”、“ResourceTitle”和“Loan”拖到绘图窗口中,如图3.5 所示。
数据库实验五:视图的应用

数据库实验五:视图的应用一、实验目的与要求:1.实验目的(1)理解视图的概念;(2)掌握视图的使用方法。
(3)理解视图和基本表的异同之处。
2.实验要求(1)参照实验五中完成的查询,按如下要求设计和建立视图:1)基于单个表按投影操作定义视图。
2)基于单个表按选择操作定义视图。
3)基于单个表按选择和投影操作定义视图。
4)基于多个表根据连接操作定义视图。
5)基于多个表根据嵌套操作定义视图。
6)定义含有虚字段的视图。
(2)分别在定义的视图设计一些查询(包括基于视图和基本表的连接或嵌套查询)。
(3)在定义的视图上进行插入、更新和删除操作,分情况讨论哪些操作可以成功完成,哪些操作不能完成,并分析原因。
(4)在实验报告中要给出具体的视图定义要求和操作要求,并针对各种情况做出具体的分析和讨论。
二、实验内容1、实验原理(1)视图是用SQL SELECT查询定义的,创建视图命令格式如下:CREATE VIEW <视图名> AS <SELECT-查询块>(2)删除视图的命令格式如下:DROP VIEW <视图名>2、实验步骤与结果(1)调出SQL Server2005软件的用户界面,进入SQL SERVER MANAGEMENT STUDIO。
(2)输入自己编好的程序。
(3)检查已输入的程序正确与否。
(4)运行程序,并分析运行结果是否合理和正确。
在运行时要注意当输入不同的数据时所得到的结果是否正确。
(5)输出程序清单和运行结果。
(1)参照实验五中完成的查询,按如下要求设计和建立视图:1)基于单个表按投影操作定义视图。
create view v asselect教师编号,姓名from教师create view v_order asselect*from教师where职称='教授'3)基于单个表按选择和投影操作定义视图。
create view v_cuss asselect教师编号,姓名,职称from教师where职称='教授'4)基于多个表根据连接操作定义视图。
实验五 顺序控制功能图编程实验

实验五顺序控制功能图编程实验一、实验目的通过一个钻床的PLC模拟控制编程,掌握顺序控制法的分析、画图和梯形图编程方法,强化用顺序控制法进行PLC编程的技能训练。
二、实验内容某专用钻床用来加工圆盘状零件上均匀分布的6个孔,如下图a和b所示。
开始自动运行时钻头在最上面的位置,即位开关I0.3和I0.5为ON。
操作人员放好I0.1为ON,Q0.1和Q0.3使两只钻头同时开始工作,钻到由限位开关I0.2和I0.4设定的深度时,Q0.2和Q0.4使两只钻头同时上行,升到由限位开关I0.3和I0.5设定的起始位置时停止上行。
设定值为3的计数器C0的当前值加1。
两个都上升到位后,工没有钻完3对孔,C0的常闭触点闭合,Q0.5使工件旋转120°,旋转到位时限位开关I0.6为ON,旋转结束后又开始钻第2对孔。
3对孔都钻完后,计数器的当前值等于设定值3,C0的常开触点闭合,Q0.6使工件松开,松开到位时,限位开关I0.7为ON,系统返回初始状态。
三、实验设备(1)S7-200 PLC一台(2)安装了编程软件的微型计算机一台(3)连接S7-200 PLC 和计算机的通信接口的PC/PPI编程电缆一根(4)紧锁导线若干四、实验要求分析系统的顺序步,画出顺序功能图和PLC控制系统的外部接线图,根据你画出的功能图分别用“起保停”方法、“以转换为中心”的方法和“使用SCR指令”的方法编制梯形图程序,并上机调试成功。
五、实验报告(1)画出PLC硬件连线图、顺序功能图。
(2)写出三种方法的梯形图程序。
(3)整理出运行和监控程序时出现的问题。
(4)根据你的理解,对比三种方法(“起保停”方法、“以转换为中心”的方法和使用SCR指令的方法)。
(5)实验心得。
六、本次实验考核评分表最后一页附在实验报告中上交。
实验5绘图操作

2)可以在等高线图中看出该丘陵地带的最高点是在x=200,y=200时,最
高点的高度z=712m 7. 已知矢量g= [68,83,61,70,75,82,57,5,76,85,62,71,96,78,76,68,72,75,83,93] 为某小组化学的期末考试成绩。 (1)用Matlab对数据进行分类,并画出条形图。 命令语句: g= [68,83,61,70,75,82,57,5,76,85,62,71,96,78,76,68,72,75,83,93]; s1=0; s2=0; s3=0; s4=0; for x=g if x>=90 s1=s1+1; elseif x>=80&x<=89 s2=s2+1; elseif x>=60&x<=79 s3=s3+1; else s4=s4+1; end end x=[s1,s2,s3,s4]; name = {'优秀', '良好', '及格', '不及格'}; bar(x,0.3,'group','g') set(gca, 'XTickLabel', name);%将横坐标设成不同的等级 set(gca,'ylim',[0,14])%只设置y坐标的数据范围 实验结果:
y3=sin(3*x); plot(x,y1,'r:',x,y2,'b-',x,y3,'g-.'); gtext('y_1=sinx'); gtext('y_2=sin2x'); gtext('y_3=sin3x') 运行结果:
实验五--8253方波实验

.STACK 100
.CODE
START: MOV DX,COM_ADDR
MOV AL,35H
OUT DX,AL ;计数器T0设置在模式2状态,BCD码计数
MOV DX,T0_ADDR
MOV AL,00H
OUT DX,AL
MOV AL,10H
OUT DX,AL ;CLK0/1000
MOV DX,COM_ADDR
MOV AL,77H
OUT DX,AL ;计数器T1为模式3状态,输出方波,BCD码计数
MOV DX,T1_ADDR
MOV AL,00H
OUT DX,AL
MOV AL,10H
OUT DX,AL ;CLK1/1000
JMP $ ;OUT1输出1S的方波
END START
六、实验结果
蜂鸣器间歇性蜂鸣,逻辑测试笔红绿灯交替亮灭。
七、实验总结
通过这次实验,我了解了8253的功能,即作为计时器可以输出各种不同的波形,实现
对电路的控制;了解了8253与8088的接口端,特别是片选端口及其对地址的选择;熟悉了8253的控制寄存器和初始化编程方法,熟悉了8253的6种工作模式,该实验中用的是模式
2和模式3,分别作为频率发生器和方波方波发生器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验五图操作实现实验日期:2017 年 4 月27 日实验目的及要求1. 熟练掌握图的邻接矩阵和邻接表的存储方式;2. 实现图的一些基本运算,特别是深度优先遍历和广度优先遍历;实验内容用邻接矩阵法建一个无向连通图(顶点信息为顺序字母A,B,C,D...,而非键盘输入),分别用dfs(深度优先搜索)和bfs(广度优先搜索)遍历,输出图中顶点信息并验证。
邻接矩阵图类型定义:#define MAX 40typedef char vexType; /*顶点类型*/typedef struct{vexType vex[MAX];int arcs[MAX][MAX];int vn,en;} MGraph;访问标记数组定义:int visited[MAX]; /*值为0时对应顶点未被访问,值为1时对应顶点已被访问*/顺序存储的循环队列类型定义:typedef int datatype; /*队列元素为图的顶点下标,int型*/typedef struct node{datatype data[MAX];int front, rear;} SeqQueue; /*顺序存储的循环队列类型*/任务1.自定义函数库文件,完成队列的相关操作。
2.创建一个程序文件,自定义相应函数完成以下操作:(1)void createGraph(MGraph *g) /*建邻接矩阵存储的无向图*/(2)void visit(MGraph *g,int v) /*访问v号顶点*/(3)void dfs(MGraph *g,int v) /*邻接矩阵存储的图的深度优先搜索*/(4)void bfs(MGraph *g,int v) /*邻接矩阵存储的图的广度优先搜索*/3.回答下列问题(1)现有定义:MGraph *g,并且g指针指向的无向图已创建完成,请写出该图遍历前需初始化visited数组的C程序语句。
for (i = 0; i < ; i++) { /*标记数组初始化*/visited[i] = 0;}(2)定义函数int count (MGraph *g)统计非连通图的连同分量个数。
(说明:借助遍历算法实现)int count (MGraph *g){ int i, m=0;for(i=0; i<g->vn; i++)if(visited[i]==0){ m++;dfs(g, i);}return m;}4.自定义函数库文件与源程序清单(含必要的注释):#include<>typedef int datatype; /*队列元素为图的顶点下标,int型*/ typedef struct node {datatype data[MAX];int front, rear;} SeqQueue; /*顺序存储的循环队列类型*/void InitQueue(SeqQueue *Q); /*初始化队列*/void EnQueue(SeqQueue *Q, int v); /*入队*/datatype DeQueue(SeqQueue *Q); /*出队*/int EmptyQueue(SeqQueue *Q); /*判队空*/int FullQueue(SeqQueue *Q); /*判队满*/void InitQueue(SeqQueue *Q) {Q->front = Q->rear = 0;}void EnQueue(SeqQueue *Q, int v) {if (FullQueue(Q)) {printf("队列已满!"); /*判队满*/return;}Q->rear = (Q->rear + 1) % MAX; /*入队*/Q->data[Q->rear] = v;}datatype DeQueue(SeqQueue *Q) {if (EmptyQueue(Q)) {printf("队列为空!"); /*判队空*/return -1;}Q->front = (Q->front + 1) % MAX; /*出队*/return Q->data[Q->front];}int EmptyQueue(SeqQueue *Q) {return Q->front == Q->rear;}int FullQueue(SeqQueue *Q) {return (Q->rear + 1) % MAX == Q->front;}:#define MAX 40#include""int visited[MAX]; /*值为0时对应顶点未被访问,值为1时对应顶点已被访问*/ typedef char vexType; /*顶点类型*/typedef struct {vexType vex[MAX];int arcs[MAX][MAX];int vn, en;} MGraph;void createGraph(MGraph *g); /*建邻接矩阵存储的无向图*/void visit(MGraph *g, int v); /*访问v号顶点*/void dfs(MGraph *g, int v); /*邻接矩阵存储的图的深度优先搜索*/ void bfs(MGraph *g, int v); /*邻接矩阵存储的图的广度优先搜索*/void createGraph(MGraph *g) {int i, j, v;char a = 'A';printf("输入顶点数:"); /*输入顶点数和边数*/scanf("%d", &g->vn);printf("输入边数:");scanf("%d", &g->en);for (i = 0; i < g->vn; i++) { /*二维数组初始化*/for (j = 0; j < g->vn; j++) {g->arcs[i][j] = 0;}}for (v = 0; v < g->vn; v++) { /*确定数据*/g->vex[v] = a;a++;}printf("输入结构:\n"); /*确定边*/for (v = 0; v < g->en; v++) {scanf("%d %d", &i, &j);g->arcs[i][j] = 1;g->arcs[j][i] = 1;}}void visit(MGraph *g, int v) {printf("%c", g->vex[v]);}void dfs(MGraph *g, int v) {int j;visit(g, v); /*输出数据*/visited[v] = 1; /*标记已访问*/for (j = 0; j < g->vn; j++) {if (g->arcs[v][j] == 1 && visited[j] == 0) {dfs(g, j); /*递归*/}}}void bfs(MGraph *g, int v) {int i, w;SeqQueue Q;InitQueue(&Q); /*队列初始化*/ EnQueue(&Q,v); /*入队*/visited[v] = 1; /*标记已访问*/while (!EmptyQueue(&Q)) {w = DeQueue(&Q); /*出队*/visit(g, w); /*输出数据*/for (i = 0; i < g->vn; i++) {if (g->arcs[w][i] == 1 && visited[i] == 0) {EnQueue(&Q, i); /*入队*/visited[i] = 1; /*标记已访问*/}}}}void main() {MGraph g;int i, v;createGraph(&g); /*建图*/for (i = 0; i < ; i++) { /*标记数组初始化*/visited[i] = 0;}printf("开始顶点:"); /*输入遍历开始顶点*/ scanf("%d", &v);printf("输出(dfs):"); /*DFS输出*/dfs(&g, v);printf("\n");for (i = 0; i < ; i++) { /*标记数组初始化*/visited[i] = 0;}printf("输出(bfs):"); /*BFS输出*/bfs(&g, v);printf("\n");}5.程序执行时屏幕上的输入输出内容A图结构: B C DE实验总结分析(本程序的重点与难点,调试中出现的问题及解决方法等)。
