2017年中考总复习—关于圆的经典题型汇总(含答案)
2017中考真题分类汇编—圆(解答题部分)(1)(含解析)

2017中考真题分类汇编—圆20.(10分)(2017?安徽)如图,在四边形ABCD 中,AD=BC ,∠B=∠D ,AD 不平行于BC ,过点C 作CE ∥AD 交△ABC 的外接圆O 于点E ,连接AE .(1)求证:四边形AECD 为平行四边形;(2)连接CO ,求证:CO 平分∠BCE .21世纪教育网2.(2017・福建)如图,四边形ABCD 内接于O e ,AB 是O e 的直径,点P 在CA 的延长线上,45CAD o .[w^m#~*][来@^源~:中国教育#出版网% ](Ⅰ)若4AB,求弧CD 的长;(Ⅱ)若弧BC 弧AD ,AD AP ,求证:PD 是O e 的切线.3. (2017・兰州)如图,ABC △内接于O ⊙,BC 是O ⊙的直径,弦AF 交BC 于点E ,延长BC 到点D ,连接OA ,AD ,使得FAC AOD =∠∠,D BAF =∠∠.(1)求证:AD 是O ⊙的切线; (2)若O ⊙的半径为5,2CE =,求EF 的长.4.(2017・天水)如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为6,BC=8,求弦BD的长.NB x轴,AB交M于点C.5.(2017・武威)如图,AN是M的直径,//A N ABN,求点B的坐标;(1)若点(0,6),(0,2),30(2)若D为线段NB的中点,求证:直线CD是M的切线.6.(2017・深圳)如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC(1)求CD的长;(2)求证:PC是⊙O的切线;(3)点G为的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交于点F (F与B、C不重合).问GE?GF是否为定值?如果是,求出该定值;如果不是,请说明理由.7.(2017・广东)如图,AB是⊙O的直径,AB=4,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;(2)求证:CF=CE;(3)当=时,求劣弧的长度(结果保留π)25. 如图,是的直径,,,连接.(1)求证:;(2)若直线为的切线,是切点,在直线上取一点,使,所在的直线与所在的直线相交于点,连接.①试探究与之间的数量关系,并证明你的结论;②是否为定值?若是,请求出这个定值;若不是,请说明理由.16. (2017・黄冈)已知:如图,MN为O的直径,ME是O的弦,MD垂直于过点的直线DE,垂足为点D,且ME平分DMN.[来#源:中国教~〈育出版&网@]求证:(1)DE是O的切线;(2)2ME MD MN.9. (2017・六盘水)如图,MN 是O ⊙的直径,4MN =,点A 在O ⊙上,30AMN =∠°,B 为AN 的中点,P 是直径MN 上一动点.(1)利用尺规作图,确定当PA PB +最小时P 点的位置(不写作法,但要保留作图痕迹).(2)求PA PB +的最小值.[来~源#:中国教育&出*版网%][来源%:^*中国~教育#出版10. (2017・河北)如图,16AB ,O 为AB 中点,点C 在线段OB 上(不与点O ,B 重合),将OC 绕点O 逆时针旋转270后得到扇形COD ,AP ,BQ 分别切优弧CD 于点P ,Q ,且点P ,Q 在AB 异侧,连接OP .(1)求证:APBQ ;(2)当43BQ 时,求QD 的长(结果保留);(3)若APO 的外心在扇形COD 的内部,求OC 的取值范围.11. (2017・菏泽)如图,AB 是⊙O 的直径,PB 与⊙O 相切于点B ,连接PA 交⊙O 于点C .连接BC .(1)求证:CBP BAC ;(2)求证:PA PC PB 2;(3)当3,6CP AC 时,求PAB sin 的值.12.(2017・怀化)如图,已知BC是⊙O的直径,点D为BC延长线上的一点,点A为圆上一点,且AB=AD,AC=CD.【来源:21・世纪・教育・网】(1)求证:△ACD∽△BAD;(2)求证:AD是⊙O的切线.13.(2017・随州)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).21.(2017・武汉)如图,ABC内接于O,,AB AC CO的延长线交AB于点D.[来源^:*&@中~教网][中国#教*&育出版^@网](1)求证AO平分BAC;(2)若36,sin5BC BAC,求AC和CD的长.14.(2017・张家界)在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.(1)求证:DF是⊙O的切线;(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.17. (2017・济宁)如图,已知⊙O的直径AB=12,弦AC=10,D是?BC的中点,过点D作DE⊥AC交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)求AE的长.18. (2017・江西)如图1,O的直径12,AB P是弦BC上一动点(与点,B C不重合),30ABC,过点P作PD OP交O于点D.(1)如图2,当//PD AB时,求PD的长;(2)如图3,当DC AC时,延长AB至点E,使12BE AB,连接DE.①求证:DE是O的切线;②求PC的长.19. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形.[ww~.(1)如图1,在半对角四边形ABCD 中,12B D =∠∠,12C A =∠∠,求B ∠与C ∠的度数之和;(2)如图2,锐角ABC △内接于O ⊙,若边AB 上存在一点D ,使得BD BO =,OBA ∠的平分线交OA 于点E ,连结DE 并延长交AC 于点F ,2AFE EAF =∠∠.求证:四边形DBCF 是半对角四边形;[w#w@w.zzstep.&%com*](3)如图3,在(2)的条件下,过点D 作DG OB ^于点H ,交BC 于点G ,当DH BG =时,求BGH △与ABC △的面积之比. 20.(2017・黔东南)如图,已知直线PT 与⊙O 相切于点T ,直线PO 与⊙O 相交于A ,B两点.(1)求证:PT 2=PA?PB ;(2)若PT=TB=,求图中阴影部分的面积.21. (2017・德州)如图,已知,90,Rt ABC C D 为BC 的中点.以AC 为直径的圆O交AB 于点E .(1)求证:DE 是圆O 的切线.(2)若:1:2,6AE EBBC ,求AE 的长.23.(10分)如图,在⊙O中,直径AB经过弦CD的中点E,点M在OD上,AM的延长线交⊙O于点G,交过D的直线于F,∠1=∠2,连结BD与CG交于点N.(1)求证:DF是⊙O的切线;(2)若点M是OD的中点,⊙O的半径为3,tan∠BOD=2,求BN的长.20.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.(1)求证:DH是圆O的切线;(2)若A为EH的中点,求的值;(3)若EA=EF=1,求圆O的半径.25.(10分)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.(1)求证:AF⊥EF;(2)若AC=6,CF=2,求⊙O的半径.22.(8分)如图,△ABC中,以BC为直径的⊙O交AB于点D,AE平分∠BAC交BC于点E,交CD于点F.且CE=CF.(1)求证:直线CA是⊙O的切线;(2)若BD=DC,求的值.24.(12分)如图,已知在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,点E是BC的中点,连接BD,DE.(1)若=,求sinC;(2)求证:DE是⊙O的切线.23.(9分)如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O 交于点F,设∠DAC,∠CEA的度数分别是α,β.(1)用含α的代数式表示β,并直接写出α的取值范围;(2)连接OF与AC交于点O′,当点O′是AC的中点时,求α,β的值.18. 如图,在ABC 中,AB AC ,以AB 为直径的⊙O 交AC 边于点D ,过点C 作//CF AB ,与过点B 的切线交于点F ,连接BD .(1)求证:BD BF ;(2)若10AB ,4CD ,求BC 的长.23.(2017四川省德阳市,第23题,11分)如图,已知AB 、CD 为⊙O的两条直线,DF 为切线,过AO 上一点N 作NM ⊥DF 于M ,连结DN 并延长交⊙O 于点E,连结CE .(1)求证:ΔDMN ≌ΔCED ;(2)设G 为点E关于AB 对称点,连结GD .GN ,如果∠DNO =45°,⊙O 的半径为3,求22DN GN 的值.22.如图,△ABC 中,以BC 为直径的⊙O 交AB 于点D ,AE 平分∠BAC 交BC 于点E ,交CD 于点F .且CE=CF .(1)求证:直线CA 是⊙O 的切线;(2)若BD=43DC ,求DFCF 的值.24.(2017四川省遂宁市,第24题,10分)如图,CD是⊙O的直径,点B在⊙O上,连接BC、BD,直线AB与CD的延长线相交于点A,2AB AD ACg,OE∥BD交直线AB 于点E,OE与BC相交于点F.(1)求证:直线AE是⊙O的切线;(2)若⊙O的半径为3,cosA=45,求OF的长.23.(本小题满分10分)如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.(1)求证:CE是⊙O的切线;(2)若BF=2,EF=13,求⊙O的半径长.21.(8分)(2017?黄石)如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.。
全国各地中考数学分类-圆综合题(解析版)

2017年圆中考分类(4)参考答案与试题解析一.解答题(共30小题)1.(2017?恩施州)如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB的延长线交于点P,连接BC.(1)求证:BC平分∠ABP;(2)求证:PC2=PB?PE;(3)若BE﹣BP=PC=4,求⊙O的半径.【考点】MC:切线的性质;KD:全等三角形的判定与性质;S9:相似三角形的判定与性质.【分析】(1)由BE∥CD知∠1=∠3,根据∠2=∠3即可得∠1=∠2;(2)连接EC、AC,由PC是⊙O的切线且BE∥DC,得∠1+∠4=90°,由∠A+∠2=90°且∠A=∠5知∠5+∠2=90°,根据∠1=∠2得∠4=∠5,从而证得△PBC∽△PCE即可;(3)由PC2=PB?PE、BE﹣BP=PC=4求得BP=2、BE=6,作EF⊥CD可得PC=FE=4、FC=PE=8,再Rt△DEF≌Rt△BCP得DF=BP=2,据此得出CD的长即可.【解答】解:(1)∵BE∥CD,∴∠1=∠3,又∵OB=OC,∴∠2=∠3,∴∠1=∠2,即BC平分∠ABP;(2)如图,连接EC、AC,∵PC是⊙O的切线,∴∠PCD=90°,又∵BE∥DC,∴∠P=90°,∴∠1+∠4=90°,∵AB为⊙O直径,∴∠A+∠2=90°,又∠A=∠5,∴∠5+∠2=90°,∵∠1=∠2,∴∠5=∠4,∵∠P=∠P,∴△PBC∽△PCE,∴=,即PC2=PB?PE;(3)∵BE﹣BP=PC=4,∴BE=4+BP,∵PC2=PB?PE=PB?(PB+BE),∴42=PB?(PB+4+PB),即PB2+2PB﹣8=0,解得:PB=2,则BE=4+PB=6,∴PE=PB+BE=8,作EF⊥CD于点F,∵∠P=∠PCF=90°,∴四边形PCFE为矩形,∴PC=FE=4,FC=PE=8,∠EFD=∠P=90°,∵BE∥CD,∴=,∴DE=BC,在Rt△DEF和Rt△BCP中,∵,∴Rt△DEF≌Rt△BCP(HL),∴DF=BP=2,则CD=DF+CF=10,∴⊙O的半径为5.【点评】本题主要考查切线的性质、相似三角形的判定与性质、全等三角形的判定与性质,熟练掌握平行线的性质、切线的性质、圆周角定理、相似三角形的判定与性质及全等三角形的判定与性质等知识点是解题的关键.2.(2017?常德)如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.(1)求证:BC是∠ABE的平分线;(2)若DC=8,⊙O的半径OA=6,求CE的长.【考点】MC:切线的性质.【分析】(1)由BE∥CO,推出∠OCB=∠CBE,由OC=OB,推出∠OCB=∠OBC,可得∠CBE=∠CBO;(2)在Rt△CDO中,求出OD,由OC∥BE,可得=,由此即可解决问题;【解答】(1)证明:∵DE是切线,∴OC⊥DE,∵BE∥CO,∴∠OCB=∠CBE,∵OC=OB,∴∠OCB=∠OBC,∴∠CBE=∠CBO,∴BC平分∠ABE.(2)在Rt△CDO中,∵DC=8,OC=0A=6,∴OD==10,∵OC∥BE,∴=,∴=,∴EC=4.8.【点评】本题考查切线的性质、平行线的性质、角平分线的定义、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.3.(2017?遵义)如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.(1)求证:四边形ACBP是菱形;(2)若⊙O半径为1,求菱形ACBP的面积.【考点】MC:切线的性质;LA:菱形的判定与性质.【分析】(1)连接AO,BO,根据PA、PB是⊙O的切线,得到∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=∠APB=30°,由三角形的内角和得到∠AOP=60°,根据三角形外角的性质得到∠ACO=30°,得到AC=AP,同理BC=PB,于是得到结论;(2)连接AB交PC于D,根据菱形的性质得到AD⊥PC,解直角三角形即可得到结论.【解答】解:(1)连接AO,BO,∵PA、PB是⊙O的切线,∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO=∠APB=30°,∴∠AOP=60°,∵OA=OC,∴∠OAC=∠OCA,∴∠AOP=∠CAO+∠ACO,∴∠ACO=30°,∴∠ACO=∠APO,∴AC=AP,同理BC=PB,∴AC=BC=BP=AP,∴四边形ACBP是菱形;(2)连接AB交PC于D,∴AD⊥PC,∴OA=1,∠AOP=60°,∴AD=OA=,∴PD=,∴PC=3,AB=,∴菱形ACBP的面积=AB?PC=.【点评】本题考查了切线的性质,菱形的判定和性质,解直角三角形,等腰三角形的判定,熟练掌握切线的性质是解题的关键.4.(2017?大连)如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.(1)求证:BD=BE;(2)若DE=2,BD=,求CE的长.【考点】MC:切线的性质;KQ:勾股定理;T7:解直角三角形.【分析】(1))设∠BAD=α,由于AD平分∠BAC,所以∠CAD=∠BAD=α,进而求出∠D=∠BED=90°﹣α,从而可知BD=BE;(2)设CE=x,由于AB是⊙O的直径,∠AFB=90°,又因为BD=BE,DE=2,FE=FD=1,由于BD=,所以tanα=,从而可求出AB==2,利用勾股定理列出方程即可求出x的值.【解答】解:(1)设∠BAD=α,∵AD平分∠BAC∴∠CAD=∠BAD=α,∵AB是⊙O的直径,∴∠ACB=90°,∴∠ABC=90°﹣2α,∵BD是⊙O的切线,∴BD⊥AB,∴∠DBE=2α,∠BED=∠BAD+∠ABC=90°﹣α,∴∠D=180°﹣∠DBE﹣∠BED=90°﹣α,∴∠D=∠BED,∴BD=BE(2)设AD交⊙O于点F,CE=x,连接BF,∵AB是⊙O的直径,∴∠AFB=90°,∵BD=BE,DE=2,∴FE=FD=1,∵BD=,∴tanα=,∴AC=2x∴AB==2在Rt△ABC中,由勾股定理可知:(2x)2+(x+)2=(2)2,∴解得:x=﹣或x=,∴CE=;【点评】本题考查圆的综合问题,涉及切线的性质,圆周角定理,勾股定理,解方程等知识,综合程度较高,属于中等题型.5.(2017?金华)如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.(1)求证:AC平分∠DAO.(2)若∠DAO=105°,∠E=30°①求∠OCE的度数;②若⊙O的半径为2,求线段EF的长.【考点】MC:切线的性质.【分析】(1)由切线性质知OC⊥CD,结合AD⊥CD得AD∥OC,即可知∠DAC=∠OCA=∠OAC,从而得证;(2)①由AD∥OC知∠EOC=∠DAO=105°,结合∠E=30°可得答案;②作OG⊥CE,根据垂径定理及等腰直角三角形性质知CG=FG=OG,由OC=2得出CG=FG=OG=2,在Rt△OGE中,由∠E=30°可得答案.【解答】解:(1)∵CD是⊙O的切线,∴OC⊥CD,∵AD⊥CD,∴AD∥OC,∴∠DAC=∠OCA,∵OC=OA,∴∠OCA=∠OAC,∴∠OAC=∠DAC,∴AC平分∠DAO;(2)①∵AD∥OC,∴∠EOC=∠DAO=105°,∵∠E=30°,∴∠OCE=45°;②作OG⊥CE于点G,则CG=FG=OG,∵OC=2,∠OCE=45°,∴CG=OG=2,∴FG=2,在Rt△OGE中,∠E=30°,∴GE=2,∴.【点评】本题主要考查圆的切线的性质、平行线的判定与性质、垂径定理及等腰直角三角形性质,熟练掌握切线的性质、平行线的判定与性质、垂径定理及等腰直角三角形性质是解题的关键.6.(2017?东营)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.(1)求证:DE⊥AC;(2)若DE+EA=8,⊙O的半径为10,求AF的长度.【考点】MC:切线的性质;KH:等腰三角形的性质;KQ:勾股定理;LD:矩形的判定与性质.【分析】(1)欲证明DE⊥AC,只需推知OD∥AC即可;(2)如图,过点O作OH⊥AF于点H,构建矩形ODEH,设AH=x.则由矩形的性质推知:AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.在Rt△AOH中,由勾股定理知:x2+(x﹣2)2=102,通过解方程得到AH的长度,结合OH⊥AF,得到AF=2AH=2×8=16.【解答】(1)证明:∵OB=OD,∴∠ABC=∠ODB,∵AB=AC,∴∠ABC=∠ACB,∴∠ODB=∠ACB,∴OD∥AC.∵DE是⊙O的切线,OD是半径,∴DE⊥OD,∴DE⊥AC;(2)如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,∴四边形ODEH是矩形,∴OD=EH,OH=DE.设AH=x.∵DE+AE=8,OD=10,∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,解得x1=8,x2=﹣6(不合题意,舍去).∴AH=8.∵OH⊥AF,∴AH=FH=AF,∴AF=2AH=2×8=16.【点评】本题考查了切线的性质,勾股定理,矩形的判定与性质.解题时,利用了方程思想,属于中档题.7.(2017?湖州)如图,O为Rt△ABC的直角边AC上一点,以OC为半径的⊙O与斜边AB 相切于点D,交OA于点E.已知BC=,AC=3.(1)求AD的长;(2)求图中阴影部分的面积.【考点】MC:切线的性质;MO:扇形面积的计算.【分析】(1)首先利用勾股定理求出AB的长,再证明BD=BC,进而由AD=AB﹣BD可求出;(2)利用特殊角的锐角三角函数可求出∠A的度数,则圆心角∠DOA的度数可求出,在直角三角形ODA中求出OD的长,最后利用扇形的面积公式即可求出阴影部分的面积.【解答】解:(1)在Rt△ABC中,∵BC=,AC=3.∴AB==2,∵BC⊥OC,∴BC是圆的切线,∵⊙O与斜边AB相切于点D,∴BD=BC,∴AD=AB﹣BD=2﹣=;(2)在Rt△ABC中,∵sinA===,∴∠A=30°,∵⊙O与斜边AB相切于点D,∴OD⊥AB,∴∠AOD=90°﹣∠A=60°,∵=tanA=tan30°,∴=,∴OD=1,∴S阴影==.【点评】本题考查了切线的性质定理、切线长定理以及勾股定理的运用,熟记和圆有关的各种性质定理是解题的关键.8.(2017?邵阳)如图所示,直线DP和圆O相切于点C,交直径AE的延长线于点P.过点C作AE的垂线,交AE于点F,交圆O于点B.作平行四边形ABCD,连接BE,DO,CO.(1)求证:DA=DC;(2)求∠P及∠AEB的大小.【考点】MC:切线的性质;L5:平行四边形的性质.【分析】(1)欲证明DA=DC,只要证明Rt△DAO≌△Rt△DCO即可;(2)想办法证明∠P=30°即可解决问题;【解答】(1)证明:在平行四边形ABCD中,AD∥BC,∵CB⊥AE,∴AD⊥AE,∴∠DAO=90°,∵DP与⊙O相切于点C,∴DC⊥OC,∴∠DCO=90°,在Rt△DAO和Rt△DCO中,,∴Rt△DAO≌△Rt△DCO,∴DA=DC.(2)∵CB⊥AE,AE是直径,∴CF=FB=BC,∵四边形ABCD是平行四边形,∴AD=BC,∴CF=AD,∵CF∥DA,∴△PCF∽△PDA,∴==,∴PC=PD,DC=PD,∵DA=DC,∴DA=PD,在Rt△DAP中,∠P=30°,∵DP∥AB,∴∠FAB=∠P=30°,∵AE是⊙O的直径,∴∠ABE=90°,∴∠AEB=60°.【点评】本题考查切线的性质、平行四边形的性质、相似三角形的判定和性质、直角三角形中30度角的判定、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,属于中考常考题型.9.(2017?温州)如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点 D(1)求证:四边形CDEF是平行四边形;(2)若BC=3,tan∠DEF=2,求BG的值.【考点】MC:切线的性质;L7:平行四边形的判定与性质;T7:解直角三角形.【分析】(1)连接CE,根据等腰直角三角形的性质得到∠B=45°,根据切线的性质得到∠FEO=90°,得到EF∥OD,于是得到结论;(2)过G作GN⊥BC于N,得到△GMB是等腰直角三角形,得到MB=GM,根据平行四边形的性质得到∠FCD=∠FED,根据余角的性质得到∠CGM=∠ACD,等量代换得到∠CGM=∠DEF,根据三角函数的定义得到CM=2GM,于是得到结论.【解答】解:(1)连接CE,∵在△ABC中,AC=BC,∠ACB=90°,∴∠B=45°,∴∠COE=2∠B=90°,∵EF是⊙O的切线,∴∠FEO=90°,∴EF∥OC,∵DE∥CF,∴四边形CDEF是平行四边形;(2)过G作GN⊥BC于N,∴△GMB是等腰直角三角形,∴MB=GM,∵四边形CDEF是平行四边形,∴∠FCD=∠FED,∵∠ACD+∠GCB=∠GCB+∠CGM=90°,∴∠CGM=∠ACD,∴∠CGM=∠DEF,∵tan∠DEF=2,∴tan∠CGM==2,∴CM=2GM,∴CM+BM=2GM+GM=3,∴GM=1,∴BG=GM=.【点评】本题考查了切线的性质,平行四边形的判定和性质,等腰直角三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.10.(2017?随州)如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O 与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).【考点】MC:切线的性质;KF:角平分线的性质;KW:等腰直角三角形;MO:扇形面积的计算.【分析】(1)连接DE,OD.利用弦切角定理,直径所对的圆周角是直角,等角的余角相等证明∠DAO=∠CAD,进而得出结论;(2)根据等腰三角形的性质得到∠B=∠BAC=45°,由BC相切⊙O于点D,得到∠ODB=90°,求得OD=BD,∠BOD=45°,设BD=x,则OD=OA=x,OB=x,根据勾股定理得到BD=OD=,于是得到结论.【解答】(1)证明:连接DE,OD.∵BC相切⊙O于点D,∴∠CDA=∠AED,∵AE为直径,∴∠ADE=90°,∵AC⊥BC,∴∠ACD=90°,∴∠DAO=∠CAD,∴AD平分∠BAC;(2)∵在Rt△ABC中,∠C=90°,AC=BC,∴∠B=∠BAC=45°,∵BC相切⊙O于点D,∴∠ODB=90°,∴OD=BD,∴∠BOD=45°,设BD=x,则OD=OA=x,OB=x,∴BC=AC=x+1,∵AC2+BC2=AB2,∴2(x+1)2=(x+x)2,∴x=,∴BD=OD=,∴图中阴影部分的面积=S△BOD﹣S扇形DOE=﹣=1﹣.【点评】本题主要考查了切线的性质,角平分线的定义,扇形面积的计算和勾股定理.熟练掌握切线的性质是解题的关键.11.(2017?河北)如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧于点P,Q,且点P,Q在AB异侧,连接OP.(1)求证:AP=BQ;(2)当BQ=4时,求的长(结果保留π);(3)若△APO的外心在扇形COD的内部,求OC的取值范围.【考点】MC:切线的性质;MN:弧长的计算;R2:旋转的性质.【分析】(1)连接OQ.只要证明Rt△APO≌Rt△BQO即可解决问题;(2)求出优弧DQ的圆心角以及半径即可解决问题;(3)由△APO的外心是OA的中点,OA=8,推出△APO的外心在扇形COD的内部时,OC 的取值范围为4<OC<8;【解答】(1)证明:连接OQ.∵AP、BQ是⊙O的切线,∴OP⊥AP,OQ⊥BQ,∴∠APO=∠BQO=90°,在Rt△APO和Rt△BQO中,,∴Rt△APO≌Rt△BQO,∴AP=BQ.(2)∵Rt△APO≌Rt△BQO,∴∠AOP=∠BOQ,∴P、O、Q三点共线,∵在Rt△BOQ中,cosB===,∴∠B=30°,∠BOQ=60°,∴OQ=OB=4,∵∠COD=90°,∴∠QOD=90°+60°=150°,∴优弧的长==π,(3)∵△APO的外心是OA的中点,OA=8,∴△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8.【点评】本题考查切线的性质、弧长公式、全等三角形的判定和性质、三角形的外心等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.12.(2017?天津)已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.(1)如图①,求∠T和∠CDB的大小;(2)如图②,当BE=BC时,求∠CDO的大小.【考点】MC:切线的性质.【分析】(1)根据切线的性质:圆的切线垂直于经过切点的半径,得∠TAB=90°,根据三角形内角和得∠T的度数,由直径所对的圆周角是直角和同弧所对的圆周角相等得∠CDB的度数;(2)如图②,连接AD,根据等边对等角得:∠BCE=∠BEC=65°,利用同圆的半径相等知:OA=OD,同理∠ODA=∠OAD=65°,由此可得结论.【解答】解:(1)如图①,连接AC,∵AT是⊙O切线,AB是⊙O的直径,∴AT⊥AB,即∠TAB=90°,∵∠ABT=50°,∴∠T=90°﹣∠ABT=40°,由AB是⊙O的直径,得∠ACB=90°,∴∠CAB=90°﹣∠ABC=40°,∴∠CDB=∠CAB=40°;(2)如图②,连接AD,在△BCE中,BE=BC,∠EBC=50°,∴∠BCE=∠BEC=65°,∴∠BAD=∠BCD=65°,∵OA=OD,∴∠ODA=∠OAD=65°,∵∠ADC=∠ABC=50°,∴∠CDO=∠ODA﹣∠ADC=65°﹣50°=15°.【点评】本题考查了圆的切线、圆周角定理、等腰三角形的性质、三角形的内角和,熟练掌握切线的性质是关键,注意运用同弧所对的圆周角相等.13.(2017?山西)如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.(1)若AC=4,BC=2,求OE的长.(2)试判断∠A与∠CDE的数量关系,并说明理由.【考点】MC:切线的性质;KQ:勾股定理;S9:相似三角形的判定与性质.【分析】(1)由圆周角定理得出∠ACB=90°,由勾股定理求出AB==2,得出OA=AB=,证明△AOE∽△ACB,得出对应边成比例即可得出答案;(2)连接OC,由等腰三角形的性质得出∠1=∠A,由切线的性质得出OC⊥CD,得出∠2+∠CDE=90°,证出∠3=∠CDE,再由三角形的外角性质即可得出结论.【解答】解:(1)∵AB为⊙O的直径,∴∠ACB=90°,在Rt△ABC中,由勾股定理得:AB===2,∴OA=AB=,∵OD⊥AB,∴∠AOE=∠ACB=90°,又∵∠A=∠A,∴△AOE∽△ACB,∴,即,解得:OE=;(2)∠CDE=2∠A,理由如下:连接OC,如图所示:∵OA=OC,∴∠1=∠A,∵CD是⊙O的切线,∴OC⊥CD,∴∠OCD=90°,∴∠2+∠CDE=90°,∵OD⊥AB,∴∠2+∠3=90°,∴∠3=∠CDE,∵∠3=∠A+∠1=2∠A,∴∠CDE=2∠A.【点评】本题考查了切线的性质、圆周角定理、勾股定理、相似三角形的判定与性质、等腰三角形的性质、直角三角形的性质、三角形的外角性质;熟练掌握圆周角定理和切线的性质是解决问题的关键.14.(2017?郴州)如图,AB是⊙O的弦,BC切⊙O于点B,AD⊥BC,垂足为D,OA是⊙O 的半径,且OA=3.(1)求证:AB平分∠OAD;(2)若点E是优弧上一点,且∠AEB=60°,求扇形OAB的面积.(计算结果保留π)【考点】MC:切线的性质;MO:扇形面积的计算.【分析】(1)连接OB,由切线的性质得出OB⊥BC,证出AD∥OB,由平行线的性质和等腰三角形的性质证出∠DAB=∠OAB,即可得出结论;(2)由圆周角定理得出∠AOB=120°,由扇形面积公式即可得出答案.【解答】(1)证明:连接OB,如图所示:∵BC切⊙O于点B,∴OB⊥BC,∵AD⊥BC,∴AD∥OB,∴∠DAB=∠OBA,∵OA=OB,∴∠OAB=∠OBA,∴∠DAB=∠OAB,∴AB平分∠OAD;(2)解:∵点E是优弧上一点,且∠AEB=60°,∴∠AOB=2∠AEB=120°,∴扇形OAB的面积==3π.【点评】本题考查了切线的性质、等腰三角形的性质、平行线的性质、圆周角定理、扇形面积公式等知识;熟练掌握切线的性质和圆周角定理是解决问题的关键.15.(2017?宜昌)已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.(1)求证:DE=OE;(2)若CD∥AB,求证:四边形ABCD是菱形.【考点】MC:切线的性质;L9:菱形的判定.【分析】(1)先判断出∠2+∠3=90°,再判断出∠1=∠2即可得出结论;(2)先判断出△ABO≌△CDE得出AB=CD,即可判断出四边形ABCD是平行四边形,最后判断出CD=AD即可.【解答】解:(1)如图,连接OD,∵CD是⊙O的切线,∴OD⊥CD,∴∠2+∠3=∠1+∠COD=90°,∵DE=EC,∴∠1=∠2,∴∠3=∠COD,∴DE=OE;(2)∵OD=OE,∴OD=DE=OE,∴∠3=∠COD=∠DEO=60°,∴∠2=∠1=30°,∵OA=OB=OE,OE=DE=EC,∴OA=OB=DE=EC,∵AB∥CD,∴∠4=∠1,∴∠1=∠2=∠4=∠OBA=30°,∴△ABO≌△CDE,∴AB=CD,∴四边形ABCD是平行四边形,∴∠DAE=∠DOE=30°,∴∠1=∠DAE,∴CD=AD,∴?ABCD是菱形.【点评】此题是切线的性质,主要考查了同角的余角相等,等腰三角形的性质,平行四边形的判定和性质,菱形的判定,判断出△ABO≌△CDE是解本题的关键.16.(2017?鄂州)如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.(1)求证:=;(2)若ED、EA的长是一元二次方程x2﹣5x+5=0的两根,求BE的长;(3)若MA=6,sin∠AMF=,求AB的长.【考点】MC:切线的性质;AB:根与系数的关系;T7:解直角三角形.【分析】(1)连接OA、OE交BC于T.想办法证明OE⊥BC即可;(2)由ED、EA的长是一元二次方程x2﹣5x+5=0的两根,可得ED?EA=5,由△BED∽△AEB,可得=,推出BE2=DE?EA=5,即可解决问题;(3)作AH⊥OM于H.求出AH、BH即可解决问题;【解答】(1)证明:连接OA、OE交BC于T.∵AM是切线,∴∠OAM=90°,∴∠PAD+∠OAE=90°,∵PA=PD,∴∠PAD=∠PDA=∠EDT,∵OA=OE,∴∠OAE=∠OEA,∴∠EDT+∠OEA=90°,∴∠DTE=90°,∴OE⊥BC,∴=.(2)∵ED、EA的长是一元二次方程x2﹣5x+5=0的两根,∴ED?EA=5,∵=,∴∠BAE=∠EBD,∵∠BED=∠AEB,∴△BED∽△AEB,∴=,∴BE2=DE?EA=5,∴BE=.(3)作AH⊥OM于H.在Rt△AMO中,∵AM=6,sin∠M==,设OA=m,OM=3m,∴9m2﹣m2=72,∴m=3,∴OA=3,OM=9,易知∠OAH=∠M,∴tan∠OAD==,∴OH=1,AH=2.BH=2,∴AB===2.【点评】本题考查切线的性质、解直角三角形、勾股定理、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考压轴题.17.(2017?贺州)如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.(1)求证:AF⊥EF;(2)若AC=6,CF=2,求⊙O的半径.【考点】MC:切线的性质;M5:圆周角定理.【分析】(1)连接OD,由切线的性质和已知条件可证得OD∥EF,则可证得结论;(2)过D作DG⊥AE于点G,连接CD,则可证得△ADF≌△ADG、△CDF≌△BDG,则可求得AB的长,可求得圆的半径.【解答】(1)证明:如图1,连接OD,∵EF是⊙O的切线,且点D在⊙O上,∴OD⊥EF,∵OA=OD,∴∠DAB=∠ADO,∵AD平分∠BAC,∴∠DAB=∠DAC,∴∠ADO=∠DAC,∴AF∥OD,∴AF⊥EF;(2)解:如图2,过D作DG⊥AE于点G,连接CD,∵∠BAD=∠DAF,AF⊥EF,DG⊥AE,∴BD=CD,DG=DF,在Rt△ADF和Rt△ADG中∴Rt△ADF≌Rt△ADG(HL),同理可得Rt△CDF≌Rt△BDG,∴BG=CF=2,AG=AF=AC+CF=6+2=8,∴AB=AG+BG=8+2=10,∴⊙O的半径OA=AB=5.【点评】本题主要考查切线的性质及圆周角定理,掌握过切点的半径与切线垂直是解题的关键,注意全等三角形的应用.18.(2017?威海)已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.(1)如图1,若DE∥AB,求证:CF=EF;(2)如图2,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.【考点】MC:切线的性质;KM:等边三角形的判定与性质.【分析】(1)如图1,连接OD、OE,证得△OAD、△ODE、△OEB、△CDE是等边三角形,进一步证得DF⊥CE即可证得结论;(2)根据切线的性质以及等腰三角形的性质即可证得结论.【解答】证明:如图1,连接OD、OE,∵AB=2,∴OA=OD=OE=OB=1,∵DE=1,∴OD=OE=DE,∴△ODE是等边三角形,∴∠ODE=∠OED=60°,∵DE∥AB,∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,∴△AOD和△BOE是等边三角形,∴∠OAD=∠OBE=60°,∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,∴△CDE是等边三角形,∵DF是⊙O的切线,∴OD⊥DF,∴∠EDF=90°﹣60°=30°,∴∠DFE=90°,∴DF⊥CE,∴CF=EF;(2)相等;如图2,点E运动至与点B重合时,BC是⊙O的切线,∵⊙O的切线DF交BC于点F,∴BF=DF,∴∠BDF=∠DBF,∵AB是直径,∴∠ADB=∠BDC=90°,∴∠FDC=∠C,∴DF=CF,∴BF=CF.【点评】本题考查了切线的性质、平行线的性质、等边三角形的判定、等腰三角形的判定和性质,作出辅助线构建等边三角形是解题的关键.19.(2017?南通)如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,求弦BE的长.【考点】MC:切线的性质;KQ:勾股定理.【分析】连接OD,首先证明四边形OFCD是矩形,从而得到BF的长,然后利用垂径定理求得BE的长即可.【解答】解:连接OD,作OF⊥BE于点F.∴BF=BE,∵AC是圆的切线,∴OD⊥AC,∴∠ODC=∠C=∠OFC=90°,∴四边形ODCF是矩形,∵OD=OB=FC=2,BC=3,∴BF=BC﹣FC=BC﹣OD=3﹣2=1,∴BE=2BF=2.【点评】本题考查了切线的性质、勾股定理及垂径定理的知识,解题的关键是能够利用切线的性质构造矩形形,难度不大.20.(2017?河南)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C 作CF∥AB,与过点B的切线交于点F,连接BD.(1)求证:BD=BF;(2)若AB=10,CD=4,求BC的长.【考点】MC:切线的性质;KH:等腰三角形的性质.【分析】(1)根据圆周角定理求出BD⊥AC,∠BDC=90°,根据切线的性质得出AB⊥BF,求出∠ACB=∠FCB,根据角平分线性质得出即可;(2)求出AC=10,AD=6,根据勾股定理求出BD,再根据勾股定理求出BC即可.【解答】(1)证明:∵AB是⊙O的直径,∴∠BDA=90°,∴BD⊥AC,∠BDC=90°,∵BF切⊙O于B,∴AB⊥BF,∵CF∥AB,∴CF⊥BF,∠FCB=∠ABC,∵AB=AC,∴∠ACB=∠ABC,∴∠ACB=∠FCB,∵BD⊥AC,BF⊥CF,∴BD=BF;(2)解:∵AB=10,AB=AC,∴AC=10,∵CD=4,∴AD=10﹣4=6,在Rt△ADB中,由勾股定理得:BD==8,在Rt△BDC中,由勾股定理得:BC==4.【点评】本题考查了切线的性质,勾股定理,角平分线性质,等腰三角形的判定等知识点,能综合运用定理进行推理是解此题的关键.21.(2017?北京)如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.(1)求证:DB=DE;(2)若AB=12,BD=5,求⊙O的半径.【考点】MC:切线的性质;KQ:勾股定理;M2:垂径定理.【分析】(1)欲证明DB=DE,只要证明∠DEB=∠DBE;(2)作DF⊥AB于F,连接OE.只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE==,由此求出AE即可解决问题.【解答】(1)证明:∵AO=OB,∴∠OAB=∠OBA,∵BD是切线,∴OB⊥BD,∴∠OBD=90°,∴∠OBE+∠EBD=90°,∵EC⊥OA,∴∠CAE+∠CEA=90°,∵∠CEA=∠DEB,∴∠EBD=∠BED,∴DB=DE.(2)作DF⊥AB于F,连接OE.∵DB=DE,AE=EB=6,∴EF=BE=3,OE⊥AB,在Rt△EDF中,DE=BD=5,EF=3,∴DF==4,∵∠AOE+∠A=90°,∠DEF+∠A=90°,∴∠AOE=∠DEF,∴sin∠DEF=sin∠AOE==,∵AE=6,∴AO=.∴⊙O的半径为.【点评】本题考查切线的性质、勾股定理、垂径定理、锐角三角函数、等腰三角形的性质等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.22.(2017?乌鲁木齐)如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.(1)求证:△ADC∽△CDB;(2)若AC=2,AB=CD,求⊙O半径.【考点】MC:切线的性质.【分析】(1)首先连接CO,根据CD与⊙O相切于点C,可得:∠OCD=90°;然后根据AB 是圆O的直径,可得:∠ACB=90°,据此判断出∠CAD=∠BCD,即可推得△ADC∽△CDB.(2)首先设CD为x,则AB=x,OC=OB=x,用x表示出OD、BD;然后根据△ADC∽△CDB,可得:=,据此求出CB的值是多少,即可求出⊙O半径是多少.【解答】(1)证明:如图,连接CO,,∵CD与⊙O相切于点C,∴∠OCD=90°,∵AB是圆O的直径,∴∠ACB=90°,∴∠ACO=∠BCD,∵∠ACO=∠CAD,∴∠CAD=∠BCD,在△ADC和△CDB中,∴△ADC∽△CDB.(2)解:设CD为x,则AB=x,OC=OB=x,∵∠OCD=90°,∴OD===x,∴BD=OD﹣OB=x﹣x=x,由(1)知,△ADC∽△CDB,∴=,即,解得CB=1,∴AB==,∴⊙O半径是.【点评】此题主要考查了切线的性质和应用,以及勾股定理的应用,要熟练掌握.23.(2017?白银)如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.【考点】MD:切线的判定;D5:坐标与图形性质.【分析】(1)在Rt△ABN中,求出AN、AB即可解决问题;(2)连接MC,NC.只要证明∠MCD=90°即可;【解答】解:(1)∵A的坐标为(0,6),N(0,2),∴AN=4,∵∠ABN=30°,∠ANB=90°,∴AB=2AN=8,∴由勾股定理可知:NB==,∴B(,2).(2)连接MC,NC∵AN是⊙M的直径,∴∠ACN=90°,∴∠NCB=90°,在Rt△NCB中,D为NB的中点,∴CD=NB=ND,∴∠CND=∠NCD,∵MC=MN,∴∠MCN=∠MNC,∵∠MNC+∠CND=90°,∴∠MCN+∠NCD=90°,即MC⊥CD.∴直线CD是⊙M的切线.【点评】本题考查圆的切线的判定、坐标与图形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.24.(2017?天水)如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为6,BC=8,求弦BD的长.【考点】MD:切线的判定.【分析】(1)连接OB,由垂径定理的推论得出BE=DE,OE⊥BD,=,由圆周角定理得出∠BOE=∠A,证出∠OBE+∠DBC=90°,得出∠OBC=90°即可;(2)由勾股定理求出OC,由△OBC的面积求出BE,即可得出弦BD的长.【解答】(1)证明:连接OB,如图所示:∵E是弦BD的中点,∴BE=DE,OE⊥BD,=,∴∠BOE=∠A,∠OBE+∠BOE=90°,∵∠DBC=∠A,∴∠BOE=∠DBC,∴∠OBE+∠DBC=90°,∴∠OBC=90°,即BC⊥OB,∴BC是⊙O的切线;(2)解:∵OB=6,BC=8,BC⊥OB,∴OC==10,∵△OBC的面积=OC?BE=OB?BC,∴BE===4.8,∴BD=2BE=9.6,即弦BD的长为9.6.【点评】本题考查了切线的判定、垂径定理的推论、圆周角定理、勾股定理、三角形面积的计算;熟练掌握垂径定理的推论和圆周角定理是解决问题的关键.25.(2017?福建)如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.(Ⅰ)若AB=4,求的长;(Ⅱ)若=,AD=AP,求证:PD是⊙O的切线.【考点】MD:切线的判定;M6:圆内接四边形的性质;MN:弧长的计算.【分析】(Ⅰ)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根据弧长公式即可得到结论;(Ⅱ)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD,求得∠ADP=CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.【解答】解:(Ⅰ)连接OC,OD,∵∠COD=2∠CAD,∠CAD=45°,∴∠COD=90°,∵AB=4,∴OC=AB=2,∴的长=×π×2=π;(Ⅱ)∵=,∴∠BOC=∠AOD,∵∠COD=90°,∴∠AOD=45°,∵OA=OD,∴∠ODA=∠OAD,∵∠AOD+∠ODA=∠OAD=180°,∴∠ODA=67.5°,∵AD=AP,∴∠ADP=∠APD,∵∠CAD=∠ADP+∠APD,∠CAD=45°,∴∠ADP=CAD=22.5°,∴∠ODP=∠ODA+∠ADP=90°,∴PD是⊙O的切线.【点评】本题考查了切线的判定,圆内接四边形的性质,弧长的计算,正确的作出辅助线是解题的关键.26.(2017?黄石二模)已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.(1)请说明DE是⊙O的切线;(2)若∠B=30°,AB=8,求DE的长.【考点】MD:切线的判定;T7:解直角三角形.【分析】(1)要想证DE是⊙O的切线,只要连接OD,求证∠ODE=90°即可.(2)利用直角三角形和等边三角形的特点来求DE的长.【解答】解:(1)连接OD,则OD=OB,∴∠B=∠ODB.(1分)∵AB=AC,∴∠B=∠C.(1分)∴∠ODB=∠C.∴OD∥AC.(2分)∴∠ODE=∠DEC=90°.(1分)∴DE是⊙O的切线.(1分)(2)连接AD,∵AB是⊙O的直径,∴∠ADB=90°.(1分)∴.(2分)又∵AB=AC,∴CD=BD=,∠C=∠B=30°.(2分)∴.(1分)【点评】本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.27.(2017?营口)如图,点E在以AB为直径的⊙O上,点C是的中点,过点C作CD垂直于AE,交AE的延长线于点D,连接BE交AC于点F.(1)求证:CD是⊙O的切线;(2)若cos∠CAD=,BF=15,求AC的长.【考点】ME:切线的判定与性质;T7:解直角三角形.【分析】(1)连接OC,由点C是的中点利用垂径定理可得出OC⊥BE,由AB是⊙O的直径可得出AD⊥BE,进而可得出AD∥OC,再根据AD⊥CD可得出OC⊥CD,由此即可证出CD 是⊙O的切线.(2)过点O作OM⊥AC于点M,由点C是的中点利用圆周角定理可得出∠BAC=∠CAE,根据角平分线的定理结合cos∠CAD=可求出AB的长度,在Rt△AOM中,通过解直角三角形可求出AM的长度,再根据垂径定理即可得出AC的长度.【解答】(1)证明:连接OC,如图1所示.∵点C是的中点,∴=,∴OC⊥BE.∵AB是⊙O的直径,∴AD⊥BE,∴AD∥OC.∵AD⊥CD,∴OC⊥CD,∴CD是⊙O的切线.(2)解:过点O作OM⊥AC于点M,如图2所示.∵点C是的中点,∴=,∠BAC=∠CAE,∴=.∵cos∠CAD=,∴=,∴AB=BF=20.在Rt△AOM中,∠AMO=90°,AO=AB=10,cos∠OAM=cos∠CAD=,∴AM=AO?cos∠OAM=8,∴AC=2AM=16.【点评】本题考查了切线的判定与性质、解直角三角形、平行线的性质、垂径定理、圆周角定理以及角平分线的性质,解题的关键是:(1)根据平行线的性质找出OC⊥CD;(2)根据角平分线的性质求出AB的长度.28.(2017?张家界)在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.(1)求证:DF是⊙O的切线;(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.【考点】ME:切线的判定与性质;KH:等腰三角形的性质;MO:扇形面积的计算.【分析】(1)连接OD,由等腰三角形的性质证出∠A=∠ODB,得出OD∥AC,证出DF⊥OD,即可得出结论;(2)证明△OBD是等边三角形,由等边三角形的性质得出∠BOD=60°,求出∠G=30°,由直角三角形的性质得出OG=2OD=2×6=12,由勾股定理得出DG=6,阴影部分的面积=△ODG 的面积﹣扇形OBD的面积,即可得出答案.【解答】(1)证明:连接OD,如图所示:∵AC=BC,OB=OD,∴∠ABC=∠A,∠ABC=∠ODB,∴∠A=∠ODB,∴OD∥AC,∵DF⊥AC,∴DF⊥OD,∵OD是⊙O的半径,∴DF是⊙O的切线;(2)解:∵AC=BC,∠A=60°,∴△ABC是等边三角形,∴ABC=60°,∵OD=OB,∴△OBD是等边三角形,∴∠BOD=60°,∵DF⊥OD,∴∠ODG=90°,∴∠G=30°,∴OG=2OD=2×6=12,∴DG=OD=6,∴阴影部分的面积=△ODG的面积﹣扇形OBD的面积=×6×6﹣=18﹣6π.【点评】本题考查了等腰三角形的性质,平行线的判定和性质,切线的判定,勾股定理、直角三角形的性质、等边三角形的判定与性质,是一道综合题,难度中等.29.(2017?济宁)如图,已知⊙O的直径AB=12,弦AC=10,D是的中点,过点D作DE⊥AC,交AC的延长线于点E.(1)求证:DE是⊙O的切线;(2)求AE的长.【考点】ME:切线的判定与性质;KQ:勾股定理;M2:垂径定理.【分析】(1)连接OD,由D为弧BC的中点,得到两条弧相等,进而得到两个同位角相等,确定出OD与AE平行,利用两直线平行同旁内角互补得到OD与DE垂直,即可得证;。
2017中考复习-圆综合题
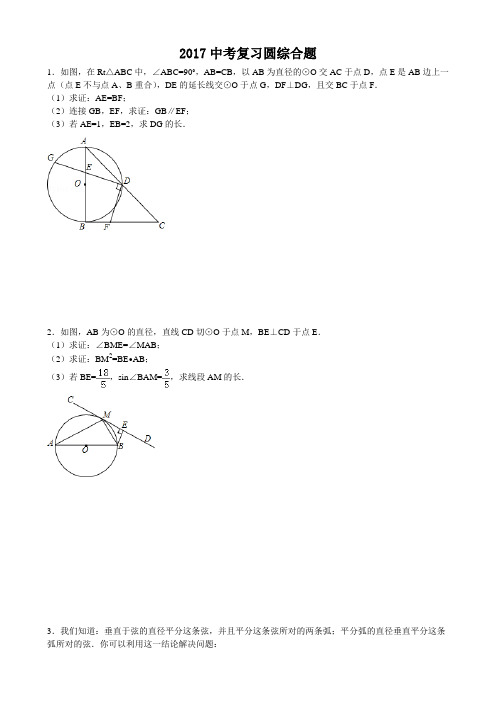
2017中考复习圆综合题1.如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.(1)求证:AE=BF;(2)连接GB,EF,求证:GB∥EF;(3)若AE=1,EB=2,求DG的长.2.如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;(2)求证:BM2=BE•AB;(3)若BE=,sin∠BAM=,求线段AM的长.3.我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.(1)比较与的大小;(2)若OH=2,求证:OP∥CD;(3)设直线MN、CD相交所成的锐角为α,试确定cosα=时,点P的位置.4.如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.(1)求证:BE是⊙O的切线;(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG=,DF=2BF,求AH 的值.5.如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.(1)求圆的半径及圆心P的坐标;(2)M为劣弧的中点,求证:AM是∠OAB的平分线;(3)连接BM并延长交y轴于点N,求N,M点的坐标.6.如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.(1)求证:DF是⊙O的切线;(2)求证:OC2=OE•OP;(3)求线段EG的长.7.如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.(1)求证:AB是⊙O的切线.(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=,求的值.(3)在(2)的条件下,设⊙O的半径为3,求AB的长.8.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.9.如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.(1)求证:MH为⊙O的切线.(2)若MH=,tan∠ABC=,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.10.已知:△ABC内接于⊙O,D是上一点,OD⊥BC,垂足为H.(1)如图1,当圆心O在AB边上时,求证:AC=2OH;(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=5,BN=3,tan∠ABC=,求BF的长.11.如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线.(2)当BC=8,AC=12时,求⊙O的半径.(3)在(2)的条件下,求线段BG的长.12.已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sinA=,求BH的长.13.已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.14.已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.(1)如图1,求证:EA•EC=EB•ED;(2)如图2,若=,AD是⊙O的直径,求证:AD•AC=2BD•BC;(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.15.如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.16.如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA 的延长线于点E,连接BC,交OD于点F.(1)求证:CD是⊙O的切线.(2)若,求∠E的度数.(3)连接AD,在(2)的条件下,若CD=,求AD的长.17.如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.(1)用关于x的代数式表示BQ,DF.(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.(3)在点P的整个运动过程中,①当AP为何值时,矩形DEGF是正方形?②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).18.如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O 于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.(1)求证:AC平分∠BAD;(2)探究线段PB,AB之间的数量关系,并说明理由;(3)若AD=3,求△ABC的面积.19.如图,AB是⊙O的直径,AB=6,过点O作OH⊥AB交圆于点H,点C是弧AH上异于A、H的动点,过点C作CD⊥OA,CE⊥OH,垂足分别为D、E,过点C的直线交OA的延长线于点G,且∠GCD=∠CED.(1)求证:GC是⊙O的切线;(2)求DE的长;(3)过点C作CF⊥DE于点F,若∠CED=30°,求CF的长.20.如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.(1)当B与O重合的时候,求三角板运动的时间;(2)如图2,当AC与半圆相切时,求AD;(3)如图3,当AB和DE重合时,求证:CF2=CG•CE.21.⊙O是△ABC的外接圆,AB是直径,过的中点P作⊙O的直径PG交弦BC于点D,连接AG、CP、PB.(1)如图1,若D是线段OP的中点,求∠BAC的度数;(2)如图2,在DG上取一点K,使DK=DP,连接CK,求证:四边形AGKC是平行四边形;(3)如图3,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:PH⊥AB.22.如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.(1)试说明CE是⊙O的切线;(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;(3)设点D是线段AC上任意一点(不含端点),连接OD,当CD+OD的最小值为6时,求⊙O的直径AB的长.23.AB,CD是⊙O的两条弦,直线AB,CD互相垂直,垂足为点E,连接AD,过点B作BF⊥AD,垂足为点F,直线BF交直线CD于点G.(1)如图1,当点E在⊙O外时,连接BC,求证:BE平分∠GBC;(2)如图2,当点E在⊙O内时,连接AC,AG,求证:AC=AG;(3)如图3,在(2)条件下,连接BO并延长交AD于点H,若BH平分∠ABF,AG=4,tan∠D=,求线段AH的长.24.已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.(1)求证:BD平分∠ABC;(2)延长AC到点P,使PF=PB,求证:PB是⊙O的切线;(3)如果AB=10,cos∠ABC=,求AD.25.如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.(1)求∠FDE的度数;(2)试判断四边形FACD的形状,并证明你的结论;(3)当G为线段DC的中点时,①求证:FD=FI;②设AC=2m,BD=2n,求⊙O的面积与菱形ABCD的面积之比.26.已知,如图,AB是半圆O的直径,弦CD∥AB,动点P,Q分别在线段OC,CD上,且DQ=OP,AP的延长线与射线OQ相交于点E,与弦CD相交于点F(点F与点C,D不重合),AB=20,cos∠AOC=,设OP=x,△CPF的面积为y.(1)求证:AP=OQ;(2)求y关于x的函数关系式,并写出它的定义域;(3)当△OPE是直角三角形时,求线段OP的长.27.已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.(1)图1的A、B、C、D、E五个点中,是否存在某两点间的距离等于线段CE的长?请说明理由;(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.①若CF=CD时,求sin∠CAB的值;②若CF=aCD(a>0)时,试猜想sin∠CAB的值.(用含a的代数式表示,直接写出结果)28.如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2.过点D作DF∥BC,交AB的延长线于点F.(1)求证:DF为⊙O的切线;(2)若∠BAC=60°,DE=,求图中阴影部分的面积;(3)若=,DF+BF=8,如图2,求BF的长.29.在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为上﹣点,且=连接DF,并延长DF交BA的延长线于点E.(1)判断DB与DA的数量关系,并说明理由;(2)求证:△BCD≌△AFD;(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.30.如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.(1)如图1,求⊙O的半径;(2)如图1,若点E是BC的中点,连接PE,求PE的长度;(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.答案1.(2016•包头)如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E 是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.(1)求证:AE=BF;(2)连接GB,EF,求证:GB∥EF;【分析】(1)连接BD,由三角形ABC为等腰直角三角形,求出∠A与∠C的度数,根据AB为圆的直径,利用圆周角定理得到∠ADB为直角,即BD垂直于AC,利用直角三角形斜边上的中线等于斜边的一半,得到AD=DC=BD=AC,进而确定出∠A=∠FBD,再利用同角的余角相等得到一对角相等,利用ASA得到三角形AED与三角形BFD全等,利用全等三角形对应边相等即可得证;(2)连接EF,BG,由三角形AED与三角形BFD全等,得到ED=FD,进而得到三角形DEF为等腰直角三角形,利用圆周角定理及等腰直角三角形性质得到一对同位角相等,利用同位角相等两直线平行即可得证;(3)由全等三角形对应边相等得到AE=BF=1,在直角三角形BEF中,利用勾股定理求出EF的长,利用锐角三角形函数定义求出DE的长,利用两对角相等的三角形相似得到三角形AED与三角形GEB相似,由相似得比例,求出GE的长,由GE+ED求出GD的长即可.【解答】(1)证明:连接BD,在Rt△ABC中,∠ABC=90°,AB=BC,∴∠A=∠C=45°,∵AB为圆O的直径,∴∠ADB=90°,即BD⊥AC,∴AD=DC=BD=AC,∠CBD=∠C=45°,∴∠A=∠FBD,∵DF⊥DG,∴∠FDG=90°,∴∠FDB+∠BDG=90°,∵∠EDA+∠BDG=90°,∴∠EDA=∠FDB,在△AED和△BFD中,,∴△AED≌△BFD(ASA),∴AE=BF;(2)证明:连接EF,BG,∵△AED≌△BFD,∴DE=DF,∵∠EDF=90°,∴△EDF是等腰直角三角形,∴∠DEF=45°,∵∠G=∠A=45°,∴∠G=∠DEF,(3)∵AE=BF,AE=1,∴BF=1,在Rt△EBF中,∠EBF=90°,∴根据勾股定理得:EF2=EB2+BF2,∵EB=2,BF=1,∴EF==,∵△DEF为等腰直角三角形,∠EDF=90°,∴cos∠DEF=,∵EF=,∴DE=×=,∵∠G=∠A,∠GEB=∠AED,∴△GEB∽△AED,∴=,即GE•ED=AE•EB,∴•GE=2,即GE=,则GD=GE+ED=.【点评】此题属于圆综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,勾股定理,圆周角定理,以及平行线的判定与性质,熟练掌握判定与性质是解本题的关键.2.(2016•青海)如图,AB为⊙O的直径,直线CD切⊙O于点M,BE⊥CD于点E.(1)求证:∠BME=∠MAB;(2)求证:BM2=BE•AB;(3)若BE=,sin∠BAM=,求线段AM的长.【分析】(1)由切线的性质得出∠BME+∠OMB=90°,再由直径得出∠AMB=90°,利用同角的余角相等判断出结论;(3)先在Rt△BEM中,用三角函数求出BM,再在Rt△ABM中,用三角函数和勾股定理计算即可.【解答】解:(1)如图,连接OM,∵直线CD切⊙O于点M,∴∠OMD=90°,∴∠BME+∠OMB=90°,∵AB为⊙O的直径,∴∠AMB=90°.∴∠AMO+∠OMB=90°,∴∠BME=∠AMO,∵OA=OM,∴∠MAB=∠AMO,∴∠BME=∠MAB;(2)由(1)有,∠BME=∠MAB,∵BE⊥CD,∴∠BEM=∠AMB=90°,∴△BME∽△BAM,∴,∴BM2=BE•AB;(3)由(1)有,∠BME=∠MAB,∵sin∠BAM=,∴sin∠BME=,在Rt△BEM中,BE=,∴sin∠BME==,∴BM=6,在Rt△ABM中,sin∠BAM=,∴sin∠BAM==,∴AB=BM=10,根据勾股定理得,AM=8.【点评】此题是圆的综合题,主要考查了切线的性质,直径所对的圆周角是直径,相似三角形的性质和判定,三角函数,解本题的关键是判断出,△BME∽△BAM.3.(2016•泉州)我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:如图,点P在以MN(南北方向)为直径的⊙O上,MN=8,PQ⊥MN交⊙O于点Q,垂足为H,PQ≠MN,弦PC、PD分别交MN于点E、F,且PE=PF.(1)比较与的大小;(2)若OH=2,求证:OP∥CD;(3)设直线MN、CD相交所成的锐角为α,试确定cosα=时,点P的位置.【分析】(1)根据等腰三角形的性质,由PE=PF,PH⊥EF可判断PH平分∠FPE,然后根据圆周角定理得到=;(2)连结CD、OP、OQ,OQ交CD于B,如图,先计算出PH=2,则可判断△OPH为等腰直角三角形得到∠OPQ=45°,再判断△OPQ为等腰直角三角形得到∠POQ=90°,然后根据垂径的推理由=得到OQ⊥CD,则根据平行线的判定方法得OP∥CD;(3)直线CD交MN于A,如图,由特殊角的三角函数值得∠α=30°,即直线MN、CD相交所成的锐角为30°,利用OB⊥CD得到∠AOB=60°,则∠POH=60°,然后在Rt△POH中利用正弦的定义计算出PH即可.【解答】(1)解:∵PE=PF,PH⊥EF,∴PH平分∠FPE,∴∠DPQ=∠CPQ,∴=;(2)证明:连结CD、OP、OQ,OQ交CD于B,如图,∵OH=2,OP=4,∴PH==2,∴△OPH为等腰直角三角形,∴∠OPQ=45°,而OP=OQ,∴△OPQ为等腰直角三角形,∴∠POQ=90°,∴OP⊥OQ,∵=,∴OQ⊥CD,(3)解:直线CD交MN于A,如图,∵cosα=,∴∠α=30°,即直线MN、CD相交所成的锐角为30°,而OB⊥CD,∴∠AOB=60°,∵OH⊥PQ,∴∠POH=60°,在Rt△POH中,∵sin∠POH=,∴PH=4sin60°=2,即点P到MN的距离为2.【点评】本题考查了圆的综合题:熟练掌握垂径定理及其推理、圆周角定理;能够灵活应用等腰直角三角形的性质和三角函数进行几何计算.4.(2016•泸州)如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.(1)求证:BE是⊙O的切线;(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG=,DF=2BF,求AH 的值.【分析】(1)欲证明BE是⊙O的切线,只要证明∠EBD=90°.(2)由△ABC∽△CBG,得=求出BC,再由△BFC∽△BCD,得BC2=BF•BD求出BF,CF,CG,GB,再通过计算发现CG=AG,进而可以证明CH=CB,求出AC即可解决问题.【解答】(1)证明:连接CD,∵BD是直径,∴∠BCD=90°,即∠D+∠CBD=90°,∵∠A=∠D,∠A=∠EBC,∴∠CBD+∠EBC=90°,∴BE是⊙O切线.(2)解:∵CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,∵∠CBG=∠ABC∴△ABC∽△CBG,∴=,即BC2=BG•BA=48,∴BC=4,∵CG∥EB,∴CF⊥BD,∴△BFC∽△BCD,∴BC2=BF•BD,∵DF=2BF,∴BF=4,在RT△BCF中,CF==4,∴CG=CF+FG=5,在RT△BFG中,BG==3,∵BG•BA=48,∴即AG=5,∴CG=AG,∴∠A=∠ACG=∠BCG,∠CFH=∠CFB=90°,∴∠CHF=∠CBF,∴CH=CB=4,∵△ABC∽△CBG,∴=,∴AC==,∴AH=AC﹣CH=.【点评】本题考查切线的判定、圆的有关知识、相似三角形的判定和性质、勾股定理.等腰三角形的判定和性质等知识,解题的关键是巧妙利用相似三角形的性质解决问题,属于中考压轴题.5.(2016•赤峰)如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.(1)求圆的半径及圆心P的坐标;(2)M为劣弧的中点,求证:AM是∠OAB的平分线;(3)连接BM并延长交y轴于点N,求N,M点的坐标.【分析】(1)先利用勾股定理计算出AB=10,再利用圆周角定理的推理可判断AB为⊙P的直径,则得到⊙P的半径是5,然后利用线段的中点坐标公式得到P点坐标;(2)根据圆周角定理由=,∠OAM=∠MAB,于是可判断AM为∠OAB的平分线;(3)连接PM交OB于点Q,如图,先利用垂径定理的推论得到PM⊥OB,BQ=OQ=OB=4,再利用勾股定理计算出PQ=3,则MQ=2,于是可写出M点坐标,接着证明MQ为△BON的中位线得到ON=2MQ=4,然后写出N点的坐标.【解答】解:(1)∵O(0,0),A(0,﹣6),B(8,0),∴OA=6,OB=8,∴AB==10,∵∠AOB=90°,∴AB为⊙P的直径,∴⊙P的半径是5∵点P为AB的中点,∴P(4,﹣3);(2)∵M点是劣弧OB的中点,∴=,∴∠OAM=∠MAB,∴AM为∠OAB的平分线;(3)连接PM交OB于点Q,如图,∵=,∴PM⊥OB,BQ=OQ=OB=4,在Rt△PBQ中,PQ===3,∴MQ=2,∴M点的坐标为(4,2);∵MQ∥ON,而OQ=BQ,∴MQ为△BON的中位线,∴ON=2MQ=4,∴N点的坐标为(0,4).【点评】本题考查了圆的综合题:熟练掌握垂径定理和圆周角定理;理解坐标与图形的性质,记住线段的中点坐标公式,会利用勾股定理计算线段的长.此类题目通常解由半径、弦心距和弦的一半所组成的直角三角形.6.(2016•恩施州)如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF 的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.(1)求证:DF是⊙O的切线;(2)求证:OC2=OE•OP;(3)求线段EG的长.【分析】(1)连接OD,由等腰三角形的性质得出∠DAB=∠ADO,再由已知条件得出∠ADO=∠DAF,证出OD∥AF,由已知DF⊥AF,得出DF⊥OD,即可得出结论;(2)由射影定理得出OD2=OE•OP,由OC=OD,即可得出OC2=OE•OP;(3)由垂径定理得出DE=CE=4,∠OEC=90°,由相交弦定理得出DE2=AE×BE,求出BE=2,得出直径CG=AB=AE+BE=10,半径OC=CG=5,由三角函数的定义得出cosC==,在△CEG中,由余弦定理求出EG2,即可得出EG的长.【解答】(1)证明:连接OD,如图所示:∵OA=OD,∴∠DAB=∠ADO,∵∠DAF=∠DAB,∴∠ADO=∠DAF,∴OD∥AF,又∵DF⊥AF,∴DF⊥OD,∴DF是⊙O的切线;(2)证明:由(1)得:DF⊥OD,∴∠ODF=90°,∵AB⊥CD,∴由射影定理得:OD2=OE•OP,∵OC=OD,∴OC2=OE•OP;(3)解:∵AB⊥CD,∴DE=CE=4,∠OEC=90°,由相交弦定理得:DE2=AE×BE,即42=8×BE,解得:BE=2,∴CG=AB=AE+BE=8+2=10,∴OC=CG=5,∴cosC==,在△CEG中,由余弦定理得:EG2=CG2+CE2﹣2×CG×CE×cosC=102+42﹣2×10×4×=52,∴EG==2.【点评】本题是圆的综合题目,考查了切线的判定、等腰三角形的性质、平行线的判定、射影定理、相交弦定理、余弦定理、三角函数等知识;本题综合性强,有一定难度,特别是(3)中,需要运用相交弦定理、三角函数和余弦定理采才能得出结果.7.(2016•鄂州)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.(1)求证:AB是⊙O的切线.(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=,求的值.(3)在(2)的条件下,设⊙O的半径为3,求AB的长.【分析】(1)由于题目没有说明直线AB与⊙O有交点,所以过点O作OF⊥AB于点F,然后证明OC=OF 即可;(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,所以,而tan∠D==;(3)由(2)可知,AC2=AE•AD,所以可求出AE和AC的长度,由(1)可知,△OFB∽△ABC,所以,然后利用勾股定理即可求得AB的长度.【解答】(1)如图,过点O作OF⊥AB于点F,∵AO平分∠CAB,OC⊥AC,OF⊥AB,∴OC=OF,∴AB是⊙O的切线;(2)如图,连接CE,∵ED是⊙O的直径,∴∠ECD=90°,∴∠ECO+∠OCD=90°,∵∠ACB=90°,∴∠ACE+∠ECO=90°,∴∠ACE=∠OCD,∵OC=OD,∴∠OCD=∠ODC,∴∠ACE=∠ODC,∵∠CAE=∠CAE,∴△ACE∽△ADC,∴,∵tan∠D=,∴=,∴=;(3)由(2)可知:=,∴设AE=x,AC=2x,∵△ACE∽△ADC,∴,∴AC2=AE•AD,∴(2x)2=x(x+6),解得:x=2或x=0(不合题意,舍去),∴AE=2,AC=4,由(1)可知:AC=AF=4,∠OFB=∠ACB=90°,∵∠B=∠B,∴△OFB∽△ACB,∴=,设BF=a,∴BC=,∴BO=BC﹣OC=﹣3,在Rt△BOF中,BO2=OF2+BF2,∴(﹣3)2=32+a2,∴解得:a=或a=0(不合题意,舍去),∴AB=AF+BF=.【点评】本题考查圆的综合问题,解题的关键是证明△ACE∽△ADC.本题涉及勾股定理,解方程,圆的切线判定知识,内容比较综合,需要学生构造辅助线才能解决问题,对学生综合能力要求较高.8.(2016•德州)如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E 做直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)在(2)的条件下,若DE=4,DF=3,求AF的长.【分析】(1)连接OE、OB、OC.由题意可证明,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF 的长.【解答】解:(1)直线l与⊙O相切.理由:如图1所示:连接OE、OB、OC.∵AE平分∠BAC,∴∠BAE=∠CAE.∴.∴∠BOE=∠COE.又∵OB=OC,∴OE⊥BC.∵l∥BC,∴OE⊥l.∴直线l与⊙O相切.(2)∵BF平分∠ABC,∴∠ABF=∠CBF.又∵∠CBE=∠CAE=∠BAE,∴∠CBE+∠CBF=∠BAE+∠ABF.又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB.∴BE=EF.(3)由(2)得BE=EF=DE+DF=7.∵∠DBE=∠BAE,∠DEB=∠BEA,∴△BED∽△AEB.∴,即,解得;AE=.∴AF=AE﹣EF=﹣7=.【点评】本题主要考查的是圆的性质、相似三角形的性质和判定、等腰三角形的性质、三角形外角的性质、切线的判定,证得∠EBF=∠EFB是解题的关键.9.(2016•大庆)如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC 的中点,连接MH.(1)求证:MH为⊙O的切线.(2)若MH=,tan∠ABC=,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.【分析】(1)连接OH、OM,易证OH是△ABC的中位线,利用中位线的性质可证明△COH≌△MOH,所以∠HCO=∠HMO=90°,从而可知MH是⊙O的切线;(2)由切线长定理可知:MH=HC,再由点M是AC的中点可知AC=3,由tan∠ABC=,所以BC=4,从而可知⊙O的半径为2;(3)连接CN,AO,CN与AO相交于I,由AC、AN是⊙O的切线可知AO⊥CN,利用等面积可求出可求得CI的长度,设CE为x,然后利用勾股定理可求得CE的长度,利用垂径定理即可求得NQ.【解答】解:(1)连接OH、OM,∵H是AC的中点,O是BC的中点,∴OH是△ABC的中位线,∴OH∥AB,∴∠COH=∠ABC,∠MOH=∠OMB,又∵OB=OM,∴∠OMB=∠MBO,∴∠COH=∠MOH,在△COH与△MOH中,,∴△COH≌△MOH(SAS),∴∠HCO=∠HMO=90°,∴MH是⊙O的切线;(2)∵MH、AC是⊙O的切线,∴HC=MH=,∴AC=2HC=3,∵tan∠ABC=,∴=,∴BC=4,∴⊙O的半径为2;(3)连接OA、CN、ON,OA与CN相交于点I,∵AC与AN都是⊙O的切线,∴AC=AN,AO平分∠CAD,∴AO⊥CN,∵AC=3,OC=2,∴由勾股定理可求得:AO=,∵AC•OC=AO•CI,∴CI=,∴由垂径定理可求得:CN=,设OE=x,由勾股定理可得:CN2﹣CE2=ON2﹣OE2,∴﹣(2+x)2=4﹣x2,∴x=,∴OE=,由勾股定理可求得:EN=,∴由垂径定理可知:NQ=2EN=.【点评】本题考查圆的综合问题,涉及垂径定理,勾股定理,全等三角形的判定与性质,切线的判定等知识内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.10.(2016•哈尔滨)已知:△ABC内接于⊙O,D是上一点,OD⊥BC,垂足为H.(1)如图1,当圆心O在AB边上时,求证:AC=2OH;(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=5,BN=3,tan∠ABC=,求BF的长.【分析】(1)OD⊥BC可知点H是BC的中点,又中位线的性质可得AC=2OH;(2)由垂径定理可知:,所以∠BAD=∠CAD,由因为∠ABC=∠ADC,所以∠ACD=∠APB;(3)由∠ACD﹣∠ABD=2∠BDN可知∠AND=90°,由tan∠ABC=可知NQ和BQ的长度,再由BF⊥OE和OD⊥BC可知∠GBN=∠ABC,所以BG=BQ,连接AO并延长交⊙O于点I,连接IC后利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=即可求得RG的长度,最后由垂径定理可求得BF的长度.【解答】解:(1)∵OD⊥BC,∴由垂径定理可知:点H是BC的中点,∵点O是AB的中点,∴OH是△ABC的中位线,∴AC=2OH;(2)∵OD⊥BC,∴由垂径定理可知:,∴∠BAD=∠CAD,∵,∴∠ABC=∠ADC,∴180°﹣∠BAD﹣∠ABC=180°﹣∠CAD﹣∠ADC,∴∠ACD=∠APB,(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,∵∠ACD﹣∠ABD=2∠BDN,∴∠ACD﹣∠BDN=∠ABD+∠BDN,∵∠ABD+∠BDN=∠AND,∴∠ACD﹣∠BDN=∠AND,∵∠ACD+∠ABD=180°,∴∠ABD+∠BDN=180°﹣∠AND,∴∠AND=180°﹣∠AND,∴∠AND=90°,∵tan∠ABC=,BN=3,∴NQ=,∴由勾股定理可求得:BQ=,∵∠BNQ=∠QHD=90°,∴∠ABC=∠QDH,∵OE=OD,∴∠OED=∠QDH,∵∠ERG=90°,∴∠OED=∠GBN,∴∠GBN=∠ABC,∵AB⊥ED,∴BG=BQ=,GN=NQ=,∵AI是⊙O直径,∴∠ACI=90°,∵tan∠AIC=tan∠ABC=,∴=,∴IC=10,∴由勾股定理可求得:AI=25,连接OB,设QH=x,∵tan∠ABC=tan∠ODE=,∴,∴HD=2x,∴OH=OD﹣HD=﹣2x,BH=BQ+QH=+x,由勾股定理可得:OB2=BH2+OH2,∴()2=(+x)2+(﹣2x)2,解得:x=或x=,当QH=时,∴QD=QH=,∴ND=QD+NQ=6,∴MN=3,MD=15∵MD>,∴QH=不符合题意,舍去,当QH=时,∴QD=QH=∴ND=NQ+QD=4,由垂径定理可求得:ED=10,∴GD=GN+ND=∴EG=ED﹣GD=,∵tan∠OED=,∴,∴EG=RG,∴RG=,∴BR=RG+BG=12∴由垂径定理可知:BF=2BR=24.【点评】本题考查圆的综合问题,涉及圆周角定理,中位线的性质,锐角三角函数,勾股定理等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.11.(2015•鄂州)如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.(1)求证:AE为⊙O的切线.(2)当BC=8,AC=12时,求⊙O的半径.(3)在(2)的条件下,求线段BG的长.【分析】(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是⊙O的切线;(2)设⊙O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到=,即可解得R=3,从而求得⊙O的半径为3;(3)过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.【解答】(1)证明:连接OM.∵AC=AB,AE平分∠BAC,∴AE⊥BC,CE=BE=BC=4,∵OB=OM,∴∠OBM=∠OMB,∵BM平分∠ABC,∴∠OBM=∠CBM,∴∠OMB=∠CBM,∴OM∥BC又∵AE⊥BC,∴AE⊥OM,∴AE是⊙O的切线;(2)设⊙O的半径为R,∵OM∥BE,∴△OMA∽△BEA,∴=即=,解得R=3,∴⊙O的半径为3;(3)过点O作OH⊥BG于点H,则BG=2BH,∵∠OME=∠MEH=∠EHO=90°,∴四边形OMEH是矩形,∴HE=OM=3,∴BH=1,∴BG=2BH=2.【点评】本题考查了圆的综合知识,题目中还运用到了切线的判定与性质、相似三角形的判定与性质,综合性较强,难度较大.12.(2015•荆门)已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sinA=,求BH的长.【分析】(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;(2)连接AC,由垂径定理得出,得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例,即可得出结论;(3)连接BE,由圆周角定理得出∠AEB=90°,由三角函数求出BE,再根据勾股定理求出EA,得出BE=CE=6,由(2)的结论求出EH,然后根据勾股定理求出BH即可.【解答】(1)证明:∵∠ODB=∠AEC,∠AEC=∠ABC,∴∠ODB=∠ABC,∵OF⊥BC,∴∠BFD=90°,∴∠ODB+∠DBF=90°,∴∠ABC+∠DBF=90°,即∠OBD=90°,∴BD⊥OB,∴BD是⊙O的切线;(2)证明:连接AC,如图1所示:∵OF⊥BC,∴,∴∠CAE=∠ECB,∵∠CEA=∠HEC,∴△CEH∽△AEC,∴,∴CE2=EH•EA;(3)解:连接BE,如图2所示:∵AB是⊙O的直径,∴∠AEB=90°,∵⊙O的半径为5,sin∠BAE=,∴AB=10,BE=AB•sin∠BAE=10×=6,∴EA===8,∵,∴BE=CE=6,∵CE2=EH•EA,∴EH==,在Rt△BEH中,BH===.【点评】本题是圆的综合题目,考查了切线的判定、圆周角定理、圆心角、弧、弦之间的关系定理、勾股定理、三角函数、相似三角形的判定与性质等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线证明三角形相似和运用三角函数、勾股定理才能得出结果.13.(2015•福建)已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.【分析】(1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度.(2)如图②,连接BC.利用三角形中位线的判定与性质得到BC∥OQ.根据圆周角定理推知BC⊥AC,所以,OQ⊥AC.(3)利用割线定理来求PQ的长度即可.【解答】解:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ===2,即PQ=2;(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC.(3)如图②,PC•PQ=PB•PA,即PQ2=2×6,解得PQ=2.【点评】本题考查了圆的综合题.掌握圆周角定理,三角形中位线定理,平行线的性质,熟练利用割线定理进行几何计算.14.(2015•宿迁)已知:⊙O上两个定点A,B和两个动点C,D,AC与BD交于点E.(1)如图1,求证:EA•EC=EB•ED;(2)如图2,若=,AD是⊙O的直径,求证:AD•AC=2BD•BC;(3)如图3,若AC⊥BD,点O到AD的距离为2,求BC的长.【分析】(1)根据同弧所对的圆周角相等得到角相等,从而证得三角形相似,于是得到结论;(2)如图2,连接CD,OB交AC于点F由B是弧AC的中点得到∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.证得△CBF∽△ABD.即可得到结论;(3)如图3,连接AO并延长交⊙O于F,连接DF得到AF为⊙O的直径于是得到∠ADF=90°,过O作OH⊥AD于H,根据三角形的中位线定理得到DF=2OH=4,通过△ABE∽△ADF,得到1=∠2,于是结论可得.【解答】(1)证明:∵∠EAD=∠EBC,∠BCE=∠ADE,∴△AED∽△BEC,∴,∴EA•EC=EB•ED;(2)证明:如图2,连接CD,OB交AC于点F∵B是弧AC的中点,∴∠BAC=∠ADB=∠ACB,且AF=CF=0.5AC.又∵AD为⊙O直径,∴∠ABD=90°,又∠CFB=90°.∴△CBF∽△ABD.∴,故CF•AD=BD•BC.∴AC•AD=2BD•BC;(3)解:如图3,连接AO并延长交⊙O于F,连接DF,∴AF为⊙O的直径,∴∠ADF=90°,过O作OH⊥AD于H,∴AH=DH,OH∥DF,∵AO=OF,∴DF=2OH=4,∵AC⊥BD,∴∠AEB=∠ADF=90°,∵∠ABD=∠F,∴△ABE∽△ADF,∴∠1=∠2,∴,∴BC=DF=4.【点评】本题考查了圆周角定理,垂径定理,相似三角形的判定和性质,三角形的中位线的性质,正确作出辅助线是解题的关键.15.(2015•长沙)如图,在直角坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找一点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.【分析】(1)由点A(,0)与点B(0,﹣),可求得线段AB的长,然后由∠AOB=90°,可得AB 是直径,继而求得⊙M的半径;(2)由圆周角定理可得:∠COD=∠ABC,又由∠COD=∠CBO,即可得BD平分∠ABO;(3)首先过点A作AE⊥AB,垂足为A,交BD的延长线于点E,过点E作EF⊥OA于点F,易得△AEC 是等边三角形,继而求得EF与AF的长,则可求得点E的坐标.【解答】解:(1)∵点A(,0)与点B(0,﹣),∴OA=,OB=,∴AB==2,。
2017年新疆中考分类复习《圆》(3年真题)练习题含答案.doc

新疆2017年中考分类复习圆(3年真题)练习题(含答案)一.选择题(共6小题) 1. (2016*乌鲁木齐)将圆心角为90。
,面积为4血0?的扇形围成一个圆锥的侧 而,则所围成的圆锥的底面半径为( )A. IcmB. 2cmC. 3cmD. 4cm2. (2015-乌鲁木齐)圆锥的侧面展开图是一个孤长为12兀的扇形,则这个圆锥 底面圆的半径是( )A. 24B. 12C. 6D. 33. (2015・新疆)如图,在矩形ABCD 中,CD=1, ZDBC=30°.若将BD 绕点 B 旋转后,点D 落在DC 延长线上的点E 处,点D 经过的路径瓦,则图中阴影 部分的面积是( )(3题图) (4题图) (5题图)4. (2014・乌鲁木齐)如图,半径为3的。
O 内有一点A, OA=后,点P 在。
O 上,当ZOPA 最大时,PA 的长等于( )A •如 B. & C. 3 D. 2如5. (2014*新疆内高班)如图,D 为OO 上一点,OA^BC, ZAOB=70°,则/ ADC 的度数是( )A. 110°B. 70°C. 35°D.不确定6. (2015*新疆内高改编)在 RtAABC 中,ZC=90°, AC=3, BC=4,将ZkABC 绕边AC 所在直线旋转一周得到圆锥,则该圆锥的侧面积是().A. 20兀・B. 107i.C. 30兀・D. 5兀.二.解答题(共9小题)7. (2016*新疆)如图,在。
O 中,半径OA_LOB,过点OA 的中点C 作FD 〃C. 兀1OB交。
O于D、F两点,且CD=姬,以O为圆心,OC为半径作血,交OB于E点•(1)求。
O的半径OA的长;(2)计算阴影部分的面积.8.(2016・新疆)如图,在ZkABC, AB=AC,以AB为直径的OO分别交AC、BC于点D、E,点F在AC的延长线上,且ZCBF=1ZCAB. 2(1)求证:直线BF是。
2017年中考数学试题分项版解析汇编(第01期)专题11 圆(含解析)

专题11 圆一、选择题1.(2017浙江衢州第10题)运用图形变化的方法研究下列问题:如图,AB 是⊙O 的直径,CD ,EF 是⊙O 的弦,且AB ∥CD ∥EF ,AB=10,CD=6,EF=8。
则图中阴影部分的面积是( )A. π225B. π10C. π424+D. π524+【答案】A.【解析】试题解析:作直径CG ,连接OD 、OE 、OF 、DG .∵CG 是圆的直径,∴∠CDG=90°,则2222106CG CD -=-=8,又∵EF=8,∴DG=EF ,∴DG EF =,∴S 扇形ODG =S 扇形OEF ,∵AB ∥CD ∥EF ,∴S △OCD =S △ACD ,S △OEF =S △AEF ,∴S 阴影=S 扇形OCD +S 扇形OEF =S 扇形OCD +S 扇形ODG =S 半圆=12π×52=252π.2考点:1.圆周角定理;2.扇形面积的计算.2.(2017浙江宁波第9题)如图,在Rt ABC △中,90A =∠°,22BC =以BC 的中点O 为圆心分别与AB ,AC 相切于D ,E 两点,则DE 的长为( )A.4pB.2pC.pD.2p 【答案】B.【解析】试题解析:如图,连接OD ,OE∵AC ,AB 是圆O 的切线∴OE ⊥AC ,OD ⊥AB∵O 是BC 的中点∴点E ,点D 分别是AC ,AB 的中点∴OE=12AB ,OD= 12AC∵OE=OD∴AC=AB∵2由勾股定理得AB=2∴OE=1DE 的弧长=901180π⨯⨯=2π.考点:1.三角形的中位线;2.弧长的计算.3.(2017重庆A 卷第9题)如图,矩形ABCD 的边AB=1,BE 平分∠ABC ,交AD 于点E ,若点E 是AD 的中点,以点B 为圆心,BE 为半径画弧,交BC 于点F ,则图中阴影部分的面积是( )A .24π- B .324π- C .28π- D .328π- 【答案】B.∴图中阴影部分的面积=S 矩形ABCD ﹣S △ABE ﹣S 扇形EBF=1×2﹣12×1×1﹣245360π⨯ =324π-. 故选B .考点:1.矩形的性质;2.扇形的面积计算.4.(2017广西贵港第9题)如图,,,,A B C D 是O 上的四个点,B 是AC 的中点,M 是半径OD 上任意一点,若40BDC ∠= ,则AMB ∠的度数不可能是( )A.45 B.60 C. 75 D.85【答案】D【解析】试题解析:∵B是AC的中点,∴∠AOB=2∠BDC=80°,又∵M是OD上一点,∴∠AMB≤∠AOB=80°.则不符合条件的只有85°.故选D.考点:圆周角定理;圆心角、弧、弦的关系.5.(2017贵州如故经9题)如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为()A.65B.85C.75D.35【答案】B4【解析】试题解析:连接BD.∵AB是直径,∴∠ADB=90°.∵OC∥AD,∴∠A=∠BOC,∴cos∠A=cos∠BOC.∵BC切⊙O于点B,∴OB⊥BC,∴cos∠BOC=25 OBOC,∴cos∠A=cos∠BOC=25.又∵cos∠A=ADAB,AB=4,∴AD=85.故选B.考点:解直角三角形;平行线的性质;圆周角定理.6.(2017湖北武汉第9题)已知一个三角形的三边长分别为5,7,8.则其内切圆的半径为()A.32C..【答案】C【解析】试题解析:如图,AB=7,BC=5,AC=8过A作AD⊥BC于D,设BD=x,则CD=5-x由勾腰定理得:72-x2=82-(5-x)2解得:x=1∴3设ΔABC的内切圆的半径为r,则有:1 2(5r+7r+8r)=12×5×3解得:3故选C.考点:三角形的内切圆.7.(2017江苏无锡第9题)如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于()A.5 B.6 C.D.6【答案】C.【解析】试题解析:如图作DH⊥AB于H,连接BD,延长AO交BD于E.∵菱形ABCD的边AB=20,面积为320,∴AB•DH=32O,∴DH=16,在Rt△ADH中,,∴HB=AB﹣AH=8,在Rt△BDH中,=设⊙O与AB相切于F,连接AF.∵AD=AB,OA平分∠DAB,∴AE⊥BD,∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,∴△AOF∽△DBH,∴OA OFBD BH=,108OF=,∴.故选C.考点:1.切线的性质;2.菱形的性质.8.(2017甘肃兰州第4题)如图,在O⊙中,AB BC=,点D在O⊙上,25CDB=∠°,则AOB=∠( )A.45°B.50°C.55°D.60°【答案】B考点:圆周角定理.9.(2017甘肃兰州第2题)如图,正方形ABCD内接于半径为2的O⊙,则图中阴影部分的面积为( ) A.1p+ B.2p+ C.1p- D.2p-【答案】D.【解析】试题解析:连接AO,DO,∵ABCD是正方形,∴∠AOD=90°,2222OA OD+=,圆内接正方形的边长为=14[4π﹣(2]=(π﹣2)cm2.故选D.8考点:1正多边形和圆;2.扇形面积的计算.10.(2017贵州黔东南州第5题)如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为()A.2 B.﹣1 C D.4【答案】A.【解析】试题解析:∵⊙O的直径AB垂直于弦CD,∴CE=DE,∠CEO=90°,∵∠A=15°,∴∠COE=30°,∵OC=2,∴CE=12OC=1,∴CD=2OE=2,故选A.考点:圆周角定理;勾股定理;垂径定理.11. (2017贵州黔东南州第8题)如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为()A.60° B.67.5°C.75° D.54°【答案】A.【解析】10 试题解析:如图,连接DF 、BF .∵FE ⊥AB ,AE=EB ,∴FA=FB ,∵AF=2AE ,∴AF=AB=FB ,∴△AFB 是等边三角形,∵AF=AD=AB ,∴点A 是△DBF 的外接圆的圆心,∴∠FDB=12∠FAB=30°, ∵四边形ABCD 是正方形,∴AD=BC ,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,∴∠FAD=∠FBC ,∴△FAD ≌△FBC ,∴∠ADF=∠FCB=15°,∴∠DOC=∠OBC+∠OCB=60°.故选A .考点:正方形的性质.12.(2017山东烟台第9题)如图,□ABCD 中,070=∠B ,6=BC ,以AD 为直径的⊙O 交CD 于点E ,则弧DE 的长为( )A .π31B .π32 C. π67 D .π34【答案】B .∴DE 的长=40321803ππ⨯=.故选:B .考点:弧长的计算;平行四边形的性质;圆周角定理.13.(2017四川泸州第6题)如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E .若AB=8,AE=1,则弦CD 的长是().6 D .8【答案】B .12考点:1.垂径定理;2.勾股定理.14.(2017四川自贡第10题)AB 是⊙O 的直径,PA 切⊙O 于点A ,PO 交⊙O 于点C ;连接BC ,若∠P=40°,则∠B 等于( )A .20°B .25°C .30°D .40°【答案】B.【解析】试题解析:∵PA 切⊙O 于点A ,∴∠PAB=90°,∵∠P=40°,∴∠POA=90°﹣40°=50°,∵OC=OB ,∴∠B=∠BCO=25°,故选B .考点:切线的性质.15.(2017新疆建设兵团第9题)如图,⊙O 的半径OD 垂直于弦AB ,垂足为点C ,连接AO 并延长交⊙O 于点E ,连接BE ,CE .若AB=8,CD=2,则△BCE 的面积为( )A .12B .15C .16D .18【答案】A.【解析】考点:圆周角定理;垂径定理.16.(2017江苏徐州第6题)如图,点,,A B C ,在⊙O 上,72AOB ∠=,则ACB ∠=()A .28B .54 C.18 D .36【答案】D .14【解析】试题解析:根据圆周角定理可知,∠AOB=2∠ACB=72°,即∠ACB=36°,故选D .考点:圆周角定理.二、填空题1.(2017浙江衢州第15题)如图,在直角坐标系中,⊙A 的圆心A 的坐标为(-1,0),半径为1,点P 为直线343+-=x y 上的动点,过点P 作⊙A 的切线,切点为Q ,则切线长PQ 的最小值是__________ 【答案】22【解析】试题解析:连接AP ,PQ ,当AP 最小时,PQ 最小,∴当AP ⊥直线y=﹣34x+3时,PQ 最小, ∵A 的坐标为(﹣1,0),y=﹣34x+3可化为3x+4y ﹣12=0,∴|3(1)4012|=3,∴.考点:1.切线的性质;2.一次函数的性质.2.(2017山东德州第17题)某景区修建一栋复古建筑,其窗户设计如图所示.圆O 的圆心与矩形ABCD 对角线的交点重合,且圆与矩形上下两边相切(E 为上切点),与左右两边相交(,F G 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m ,根据设计要求,若45EOF ∠= ,则此窗户的透光率(透光区域与矩形窗面的面枳的比值)为 .【解析】试题解析:如图,过F 作FG ⊥OF ,连接OG,OM,ON△OFH 是等腰直角三角形, ∴FH=OFsin45°=22,AB=2,BC=2OF=2 ∴矩形ABCD 面积=22∴S 空白=2S 扇形FOM+2S ΔAOG =290112+2113602π⨯⨯⨯⨯⨯⨯16 =+12π∴窗户的透光率=(+2)28π 考点:扇形的面积及概率3.(2017重庆A 卷第15题)如图,BC 是⊙O 的直径,点A 在圆上,连接AO ,AC ,∠AOB=64°,则∠ACB= .【答案】32°.【解析】试题解析:∵AO=OC ,∴∠ACB=∠OAC ,∵∠AOB=64°,∴∠ACB+∠OAC=64°,∴∠AC B=64°÷2=32°.考点:圆周角定理.4.(2017甘肃庆阳第14题)如图,△ABC 内接于⊙O ,若∠OAB=32°,则∠C= °.【答案】58°.【解析】试题解析:如图,连接OB ,∵OA=OB ,∴△AOB 是等腰三角形,∴∠OAB=∠OBA ,∵∠OAB=32°,∴∠OAB=∠OAB=32°,∴∠AOB=116°,∴∠C=58°.考点:圆周角定理.5. (2017甘肃庆阳第17题)如图,在△ABC 中,∠ACB=90°,AC=1,AB=2,以点A 为圆心、AC 的长为半径画弧,交AB 边于点D ,则弧CD 的长等于 .(结果保留π)【答案】3π. 【解析】考点:弧长的计算;含30度角的直角三角形.6.(2017广西贵港第17题)如图,在扇形OAB 中,C 是OA 的中点,,CD OA CD ⊥ 与AB 交于点D ,以O 为圆心,OC 的长为半径作CE 交OB 于点E ,若4,120OA AOB =∠=,则图中阴影部分的面积为 .(结果保留π)18【答案】4233π+ 【解析】试题解析:连接OD 、AD ,∵点C 为OA 的中点,∴∠CDO=30°,∠DOC=60°,∴△ADO 为等边三角形,∴S 扇形AOD =260483603ππ⨯=, ∴S 阴影=S 扇形AOB ﹣S 扇形COE ﹣(S 扇形AOD ﹣S △COD ) =221204120281(223)36036032πππ⨯⨯---⨯⨯ =164823333πππ--+=4233π+ 考点:扇形面积的计算;线段垂直平分线的性质.7.(2017湖南怀化第14题)如图,O ⊙的半径为2,点A ,B 在O ⊙上,90AOB =∠°,则阴影部分的面积为 .【答案】π﹣2.考点:扇形面积的计算.8. (2017湖南怀化第16题)如图,在菱形ABCD中,120∠°,10cmAB=,点P是这个菱形内部ABC=或边上的一点,若以,,P B C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为cm.【答案】10(cm).【解析】试题解析:连接BD,在菱形ABCD中,∵∠ABC=120°,AB=BC=AD=CD=10,∴∠A=∠C=60°,∴△ABD,△BCD都是等边三角形,①若以边BC为底,则BC垂直平分线上(在菱形的边及其内部)的点满足题意,此时就转化为了“直线外一点与直线上所有点连线的线段中垂线段最短”,即当点P与点D重合时,PA最小,最小值PA=10;②若以边PB为底,∠PCB为顶角时,以点C为圆心,BC长为半径作圆,与AC相交于一点,则弧BD(除点B外)上的所有点都满足△PBC是等腰三角形,当点P在AC上时,AP最小,最小值为10;③若以边PC为底,∠PBC为顶角,以点B为圆心,BC为半径作圆,则弧AC上的点A与点D均满足△PBC为等腰三角形,当点P与点A重合时,PA最小,显然不满足题意,故此种情况不存在;综上所述,PD的最小值为10(cm).2考点:菱形的性质;等腰三角形的性质.9.(2017江苏无锡第17题)如图,已知矩形ABCD 中,AB=3,AD=2,分别以边AD ,BC 为直径在矩形ABCD 的内部作半圆O 1和半圆O 2,一平行于AB 的直线EF 与这两个半圆分别交于点E 、点F ,且EF=2(EF 与AB 在圆心O 1和O 2的同侧),则由AE ,EF ,FB ,AB 所围成图形(图中阴影部分)的面积等于 .53﹣6π. 【解析】试题解析:连接O 1O 2,O 1E ,O 2F ,则四边形O 1O 2FE 是等腰梯形,过E 作EG ⊥O 1O 2,过F ⊥O 1O 2,∴四边形EGHF 是矩形,∴GH=EF=2,∴O 1G=12, ∵O 1E=1,∴3 ∴1112O G O E =;∴∠O 1EG=30°,∴∠AO 1E=30°,同理∠BO 2F=30°,∴阴影部分的面积=S 矩形ABO2O1﹣2S 扇形AO1E ﹣S 梯形EFO2O1=3×1﹣2×2301360π⨯⨯=12(2+3=36π. 考点:1.扇形面积的计算;2.矩形的性质.10.(2017江苏盐城第14题)如图,将⊙O 沿弦AB 折叠,点C 在AmB 上,点D 在AB 上,若∠ACB=70°,则∠ADB= °.【答案】110°【解析】试题解析:∵点C 在AmB 上,点D 在AB 上,若∠ACB=70°,∴∠ADB+∠ACB=180°,∴∠ADB=110°考点:圆周角定理.11.(2017山东烟台第18题)如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB .已知6=OA ,取OA 的中点C ,过点C 作OA CD ⊥交弧AB 于点D ,点F 是弧AB 上一点,若将扇形BOD 沿OD 翻折,点B 恰好与点F 重合.用剪刀沿着线段FA DF BD ,,依次剪下,则剪下的纸片(形状同阴影图形)面积之和为 .22【答案】36π﹣108【解析】试题解析:如图,∵CD ⊥OA ,∴∠DCO=∠AOB=90°,∵OA=OD=OB=6,OC=12OA=12OD , ∴∠ODC=∠BOD=30°,作DE ⊥OB 于点E ,则DE=12OD=3, ∴S 弓形BD =S 扇形BOD ﹣S △BOD =2306360π⨯﹣12×6×3=3π﹣9, 则剪下的纸片面积之和为12×(3π﹣9)=36π﹣108考点:扇形面积的计算12.(2017四川宜宾第15题)如图,⊙O 的内接正五边形ABCDE 的对角线AD 与BE 相交于点G ,AE=2,则EG 的长是 .1【解析】考点:正多边形和圆.13.(2017四川宜宾第17题)如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,,则AD= .如果CD=3【答案】4.【解析】试题解析:∵AB=AC,∴∠ABC=∠ACB=∠ADB=30°,∵BD是直径,∴∠BAD=90°,∠ABD=60°,∴∠CBD=∠ABD﹣∠ABC=30°,∴∠ABC=∠CBD,∴AC CD AB==,∴CB AD=,∴AD=CB,∵∠BCD=90°,433,∴AD=BC=4.考点:1.圆周角定理;2.等腰三角形的性质;3.含30°角的直角三角形.14.(2017江苏徐州第15题)正六边形的每个内角等于.【答案】120°.【解析】试题解析:六边形的内角和为:(6-2)×180°=720°,∴正六边形的每个内角为:7206︒=120°.考点:多边形的内角与外角.15. (2017江苏徐州第16题)如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为,2D AB BC==,则AOB∠=.【答案】60°.【解析】24考点:切线的性质.ABm=︒,16.(2017浙江嘉兴第13题)如图,小明自制一块乒乓球拍,正面是半径为8cm的O,90弓形ACB(阴影部分)粘贴胶皮,则胶皮面积为.【答案】(32+48π)cm2【解析】试题解析:连接OA、OB,∵AB=90°,∴∠AOB=90°,∴S△AOB=12×8×8=32,扇形ACB(阴影部分)=22036078π⨯⨯=48π,则弓形ACB胶皮面积为(32+48π)cm2考点:1.垂径定理的应用;2.扇形面积的计算.三、解答题1.(2017浙江衢州第19题)如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。
中考数学复习《圆》经典题型及测试题(含答案)
中考数学复习《圆》经典题型及测试题(含答案)【专题分析】圆在中考中的常见考点有圆的性质及定理,圆周角定理及其推论,圆心角、圆周角、弧、弦之间的“等推”关系;切线的判定,切线的性质,切线长定理,弧长及扇形面积的计算,求阴影部分的面积等.对圆的考查在中考中以客观题为主,考查题型多样,关于圆的基本性质一般以选择题或填空题的形式进行考查,切线的判定等综合性强的问题一般以解答题的形式进行考查;圆在中考中的比重约为10%~15%.【解题方法】解决圆的有关问题常用的数学思想就是转化思想,方程思想和数形结合思想;常用的数学方法有分类讨论法,设参数法等.【知识结构】【典例精选】如图,⊙O的半径是3,点P是弦AB延长线上的一点,连结OP,若OP =4,∠APO=30°,则弦AB的长为( )A.2 5 B. 5C.213 D. 13【思路点拨】先过点O作OC⊥AP,连结OB,根据OP=4,∠APO=30°,求出OC的值,在Rt△BCO中,根据勾股定理求出BC的值,进而得出AB的值.【解析】如图,过点O作OC⊥AP于点C,连结OB,∵OP=4,∠APO=30°,∴OC=4×sin 30°=2.∵OB=3,∴BC=OB2-OC2=32-22=5,∴AB=2 5.故选A.答案:A规律方法:利用垂径定理进行证明或计算,通常是在半径、圆心距和弦的一半所组成的直角三角形中,利用勾股定理构建方程求出未知线段的长.如图,从一块直径是8 m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )A.4 2 m B.5 m C. 30 m D.215 m【思路点拨】首先连结AO,求出AB,然后求出扇形的弧长BC,进而求出扇形围成的圆锥的底面半径,最后应用勾股定理求出圆锥的高即可.【解析】如图,连结AO,∵AB=AC,点O是BC的中点,∴AO⊥BC.又∵∠BAC=90°,∴∠ABO=∠ACO=45°,∴AB=2OB=2×(8÷2)=42(m).∴l BC=90π×42180=22π(m).∴将剪下的扇形围成的圆锥形的半径是22π÷2π=2(m).∴圆锥的高是422-22=30(m).故选C.答案:C规律方法:解决圆锥的相关问题,可以利用圆的周长等于扇形的弧长建立方程,利用方程解决问题.如图,在边长为6的正方形ABCD中,E是AB的中点,以E为圆心、ED 为半径作半圆,交A,B所在的直线于M,N两点,分别以MD,ND为直径作半圆,则阴影部分的面积为( )A.9 5 B.18 5 C.36 5 D.72 5【思路点拨】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN 的面积-大半圆的面积,MN为半圆的直径,从而可知∠MDN=90°,在Rt△MDN 中,由勾股定理可知MN2=MD2+DN2,从而可得到两个小半圆的面积=大半圆的面积,故此阴影部分的面积=△DMN的面积,在Rt△AED中,ED=AD2+AE2=62+32=35,所以MN=65,然后利用三角形的面积公式求解即可.【解析】根据图形可知阴影部分的面积=两个小的半圆的面积+△DMN的面积-大半圆的面积.∵MN为大半圆的直径,∴∠MDN=90°.在Rt△MDN中,MN2=MD2+DN2,∴两个小半圆的面积和=大半圆的面积.∴阴影部分的面积=△DMN 的面积.在Rt△AED中,ED=AD2+AE2=62+32=35,∴阴影部分的面积=△DMN的面积=12MN·AD=12×65×6=18 5.故选B.答案:B规律方法:求阴影部分的面积,一般是将所求阴影部分进行分割组合,转化为规则图形的和或差.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连结CD.(1)求证:∠A=∠BCD.(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.【思路点拨】(1)根据圆周角定理可得∠ADC=90°,根据直角三角形的性质可得∠A+∠ACD=90°,再由∠DCB+∠ACD=90°,可得∠A=∠BCD;(2)当点M是BC的中点时,直线DM与⊙O相切.连结DO,证明∠ODM =90°,进而证得直线DM与⊙O相切.【自主解答】(1)证明:∵AC为直径,∴∠ADC=90°,∴∠A+∠ACD=90°.∵∠ACB=90°,∴∠BCD+∠ACD=90°,∴∠A=∠BCD.(2)解:当点M是BC的中点时,直线DM与⊙O相切.理由如下:如图,连结DO,∵DO=CO,∴∠1=∠2.∵∠BDC=90°,点M是BC的中点,∴DM=CM,∴∠4=∠3.∵∠2+∠4=90°,∴∠1+∠3=90°,∴直线DM与⊙O相切.规律方法:在判定一条直线是圆的切线时,如果这条直线和圆有公共点,常作出经过公共点的半径,证明这条直线与经过公共点的半径垂直,概括为“连半径,证垂直,得切线”.【能力评估检测】一、选择题1.如图,AB是⊙O的直径,点C在⊙O上,AE是⊙O的切线,A为切点,连结BC并延长交AE于点D.若∠AOC=80°,则∠ADB的度数为( B )A.40° B.50° C.60° D.20°2.如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( C )A. 3 B.3 C.2 3 D.43.如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( A )A.25° B.50° C.60° D.30°4.如图,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD上移动.当∠APB的度数最大时,则∠ABP 的度数为( B )A.15° B.30° C.60° D.90°5.如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心、AB长为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( D )A.6 B.7 C.8 D.96.如图,已知AB为⊙O的直径,AD切⊙O于点A,EC=CB.则下列结论中不一定正确的是( D )A.BA⊥DA B.OC∥AEC.∠COE=2∠CAE D.OD⊥AC7.如图,菱形ABCD的对角线BD,AC分别为2,23,以B为圆心的弧与AD,DC相切,则阴影部分的面积是( D )A.23-33π B.43-33πC.43-π D.23-π8.如图,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间拉一条长为12 cm的无伸缩性细线,一端固定在点A,握住另一端点P拉直细线,把它全部紧紧缠绕在螺母上(缠绕时螺母不动),则点P运动的路径长为( B )A .13π cmB .14π cmC .15π cmD .16π cm9.如图,在矩形ABCD 中,AB =4,AD =5,AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,过点D 作⊙O 的切线交BC 于点M ,切点为N ,则DM 的长为( )A. 133B. 92C. 4313 D .2 5 解:如图,连接OE ,OF ,ON ,OG .∵AD ,AB ,BC 分别与⊙O 相切于E ,F ,G 三点,∴∠AEO =∠AFO =∠OFB =∠BGO =90°.∴四边形AFOE ,FBGO 都是正方形.∴AF =BF =AE =BG =2.∴DE =3.∵DM 是⊙O 的切线,∴DN =DE =3,MN =MG . ∴CM =5-2-MN =3-MN .在Rt △DMC 中,DM 2=CD 2+CM 2,∴(3+MN )2=(3-MN )2+42.∴NM =43.∴DM =3+43=133.故选A. 答案:A二、填空题10.在平面直角坐标系中,O 为坐标原点,则直线y =x +2与以O 点为圆心,1为半径的圆的位置关系为 相切.11.如图,圆内接四边形ABCD 两组对边的延长线分别相交于点E ,F ,且∠A =55°,∠E =30°,则∠F =40° .12.如图,正三角形ABC 的边长为2,点A ,B 在半径为2的圆上,点C 在圆内,将正三角形ABC 绕点A 逆时针旋转,当点C 第一次落在圆上时,点C 运动的路线长为 .【解析】设点C 落在圆上的点为C ′,连结OA ,OB ,OC ′,则OA =OB = 2.又∵AB =2,∴OA 2+OB 2=AB 2,∴∠AOB =90°,∴∠OAB =45°,同理∠OAC ′=45°,∴∠BAC ′=90°.∵△ABC 为等边三角形,∴∠CAB =60°,∴∠CAC ′=30°,∴点C 运动的路线长为30π×2180=π3.故答案为π3. 答案:π3 13.如图,在△ABC 中,∠BAC =90°,AB =5 cm ,AC =2 cm ,将△ABC 绕顶点C按顺时针方向旋转45°至△A 1B 1C 的位置,则线段AB 扫过区域(图中的阴影部分)的面积为 cm 2.【解析】在Rt△ABC 中,BC =AC 2+AB 2=29(cm),S 扇形BCB 1=45π×292360=29π8(cm 2),S △CB 1A 1=12×5×2=5(cm 2),S 扇形CAA 1=45π×22360=π2(cm 2),故S 阴影部分=S 扇形BCB 1+S △CB 1A 1-S △ABC -S 扇形CAA 1=29π8+5-5-π2=25π8(cm 2). 答案:25π8三、解答题14.如图,AB 是⊙O 的直径,BC 切⊙O于点B ,OC 平行于弦AD ,过点D 作DE ⊥AB 于点E ,连结AC ,与DE 交于点P .求证:(1)PE =PD ;(2)AC ·PD =AP ·BC .证明:(1)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴EP BC =AE AB .又∵AD ∥OC ,∴∠DAE =∠COB ,∴△AED ∽△OBC ,∴ED BC =AE OB =AE 12AB =2AE AB .∴ED =2EP ,∴PE =PD . (2)∵AB 是⊙O 的直径,BC 是切线,∴AB ⊥BC ,∵DE ⊥AB ,∴DE ∥BC ,∴△AEP ∽△ABC ,∴AP AC =PE BC .∵PE =PD ,∴AP AC =PD BC,∴AC ·PD =AP ·BC . 15.如图,在△OAB 中,OA =OB =10,∠AOB =80°,以点O 为圆心,6为半径的优弧MN 分别交OA ,OB 于点M ,N .(1)点P 在右半弧上(∠BOP 是锐角),将OP 绕点O 逆时针旋转80°得OP ′,求证:AP =BP ′;(2)点T 在左半弧上,若AT 与弧相切,求点T 到OA 的距离;(3)设点Q 在优弧MN 上,当△AOQ 的面积最大时,直接写出∠BOQ 的度数.(1)证明:如图,∵∠AOP=∠AOB+∠BOP=80°+∠BOP,∠BOP′=∠POP′+∠BOP=80°+∠BOP,∴∠AOP=∠BOP′.又∵OA=OB,OP=OP′,∴△AOP≌△BOP′.∴AP=BP′.(2)解:如图,连结OT,过点T作TH⊥OA于点H.∵AT与MN相切,∴∠ATO=90°.∴AT=OA2-OT2=102-62=8.∵12OA·TH=12AT·OT,即12×10×TH=12×8×6,∴TH=245,即点T到OA的距离为245.(3)10°,170°.16.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;(2)若AC=3,∠B=30°.①求⊙O的半径;②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).解:(1)直线BC与⊙O相切.理由如下:如图,连结OD,∵OA=OD,∴∠OAD=∠ODA,∵∠BAC的角平分线AD交BC边于点D,∴∠CAD=∠OAD,∴∠CAD=∠ODA,∴OD∥AC,∴∠ODB=∠C=90°,即OD⊥BC.∴直线BC与⊙O相切.(2)①设OA=OD=r,∵在Rt△BDO中,∠B=30°,∴OB=2r,∴在Rt△ACB中,∠B=30°,∴AB=2AC=6,∴3r=6,解得r=2.②∵在Rt△ODB中,∠B=30°,∴∠BOD=60°,∴S扇形ODE=60π×22360=23π,∴阴影部分面积为S△BOD-S扇形ODE=23-23π.11。
2017中考数学全国试题汇编------圆(含详细解析)

FhseFhee2017中考数学全国试题汇编-■■■■■圆24 (2017.北京)如图,AB是LI O的一条弦,LI O的切线交CE的延长线于点D .(1)求证:DB 二DE ;(2)若AB =12, BD =5,求LI O 的半径.【解析】E是AB的中点,过点E作EC_OA于点C ,过点B作试题分析:(1)由切线性质及等量代换推出/ 4=7 5,再利用等角对等边可得出结论;(2)由已知条件得出sin7 DEF和sin7 AOE的值,禾用对应角的三角函数值相等推出结论.试题解析:(1)证明:T DC 丄OA, A / 1 + 7 3=90°, v BD 为切线,二OB 丄BD, /-Z 2+7 5=90°, v OA=OB, •••7 1=7 2,v/ 3=7 4,A/ 4=7 5,在厶DEB中, 7 4=7 5,A DE=DB.⑵作DF丄AB 于F,连接OE, ・,.EF^-EE=3/在RTADEF中,EA3, DE=BD=5J EQ3 , J.f~nj jQ-F* 4Y彗一3 =斗——=-3「.在irrAAOE 中rDE5TAEh,二曲二二■ ■考点:圆的性质,切线定理,三角形相似,三角函数27 (2017甘肃白银)•如图,AN是L M的直径,NB//X轴, ~A OAB交L M于点C .(1)若点A 0,6 , N 0,2厂ABN =30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是L M的切线.解:(1)v A 的坐标为(0, 6), N (0, 2)••• AN=4, .............................................................................................................. 1 分vZ ABN=30°, / ANB=90°,••• AB=2AN=8, ...................................................................................................... 2分•••由勾股定理可知:NB=4..3 ,••• B ( 4 3 , 2) ....................................................... 3 分(2)连接MC , NC ........................................................................................... 4 分v AN是O M的直径,•••Z ACN=90°°•••Z NCB=90° ° ................................................................................................... 5 分在Rt A NCB中,D为NB的中点,1•CD= = N B=ND ,2•Z CND=Z NCD, .............................. 6 分v MC=MN ,•Z MCN=Z MNC.vZ MNC+Z CND=90°°• Z MCN+Z NCD=90° ° ...................... 7 分即MC I CD.•直线CD是。
2017年中考数学真题汇编:圆(带答案)

2017年浙江中考真题分类汇编(数学):专题11 圆一、单选题1、(2017·金华)如图,在半径为13的圆形铁片上切下一块高为8的弓形铁片,则弓形弦的长为()A、10B、16C、24D、262、(2017•宁波)如图,在△中,∠A=90°,=.以的中点O为圆心的圆分别与、相切于D、E两点,则的长为()A、B、C、D、3、(2017·丽水)如图,点C是以为直径的半圆O的三等分点,2,则图中阴影部分的面积是()A、B、C、D、4、(2017·衢州)运用图形变化的方法研究下列问题:如图,是⊙O的直径,,是⊙O的弦,且∥∥,10,6,8。
则图中阴影部分的面积是()A、B、C、D、二、填空题5、(2017•杭州)如图,切⊙O于点A,是⊙O的直径.若∠40°,则∠.6、(2017•湖州)如图,已知在中,.以为直径作半圆,交于点.若,则的度数是度.7、(2017·台州)如图,扇形纸扇完全打开后,外侧两竹条,的夹角为120°,长为30,则弧的长为(结果保留)8、(2017•绍兴)如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边,分别与⊙O交于点D,E.则∠的度数为.9、(2017·嘉兴)如图,小明自制一块乒乓球拍,正面是半径为的,,弓形(阴影部分)粘贴胶皮,则胶皮面积为.10、(2017•湖州)如图,已知,在射线上取点,以为圆心的圆与相切;在射线上取点,以为圆心,为半径的圆与相切;在射线上取点,以为圆心,为半径的圆与相切;;在射线上取点,以为圆心,为半径的圆与相切.若的半径为,则的半径长是.11、(2017·衢州)如图,在直角坐标系中,⊙A的圆心A的坐标为(-1,0),半径为1,点P为直线上的动点,过点P作⊙A的切线,切点为Q,则切线长的最小值是三、解答题12、(2017•湖州)如图,为的直角边上一点,以为半径的与斜边相切于点,交于点.已知,.(1)求的长;(2)求图中阴影部分的面积.13、(2017·台州)如图,已知等腰直角△,点P是斜边上一点(不与B,C重合),是△的外接圆⊙O的直径(1)求证:△是等腰直角三角形;(2)若⊙O的直径为2,求的值14、(2017·衢州)如图,为半圆O的直径,C为延长线上一点,切半圆O 于点D。
2017中考数学试卷汇编——圆(带答案)

•••CB 平分Z ABD ,圆的有关性质一、选择题1. ( 2016 •山东省滨州市•分)如图,AB 是O O 的直径,C , D 是O O 上的点,且OC //BD , AD 分别与BC , OC 相交于点E , F ,则下列结论:①AD 丄 BD ;②/AOC = /AEC ;③CB 平分Z ABD :④ AF =DF ;⑤ BD =2 OF ; ©△CEF ^z BED ,其中一定成立 的是( )A .②④⑤⑥B .①③⑤⑥C .②③④⑥D .①③④⑤【考点】圆的综合题.【分析】①由直径所对圆周角是直角,② 由于/AOC 是O O 的圆心角,/ AEC 是O O 的圆内部的角角,③ 由平行线得到/ OCB = Z DBC ,再由圆的性质得到结论判断出/ OBC = ZDBC ;④ 用半径垂直于不是直径的弦,必平分弦;⑤ 用三角形的中位线得到结论;⑥ 得不到厶CEF 和Z BED 中对应相等的边,所以不一定全等.【解答】解:①、••• AB 是O O 的直径,•••ZADB=90 ° ,•••AD 丄 BD ,② 、T /AOC 是O O 的圆心角,/ AEC 是O O 的圆内部的角角,•••ZAOC MZAEC ,③ 、T OC //BD ,•••/OCB = Z DBC ,••OC = OB ,•••ZOCB = Z OBC ,•••ZOBC = Z DBC,④、T AB是O O的直径,•••/ADB=9 0° ,•••AD 丄BD,••OC//BD,•••ZAFO=90 ° ,•••点O为圆心,•••AF= DF,⑤、由④有,AF= DF ,•••点O为AB中点,•••OF是△ABD的中位线,•••BD=2 OF,△:EF和A BED中,没有相等的边,• dCEF 与ABED 不全等,故选D【点评】此题是圆综合题,主要考查了圆的性质,平行线的性质,角平分线的性质,解本题的关键是熟练掌握圆的性质.2 .(2016 •山东省德州市•分)《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”()A. 3步B. 5步C. 6步D . 8步【考点】三角形的内切圆与内心.【专题】圆的有关概念及性质.【分析】根据勾股定理求出直角三角形的斜边,即可确定出内切圆半径.【解答】解:根据勾股定理得:斜边为膚1尹=17 ,8+15-17则该直角三角形能容纳的圆形(内切圆)半径r= -------------- ------- =3 (步),即直径为6步,故选C【点评】此题考查了三角形的内切圆与内心,Rt AABC ,三边长为a ,b , c (斜边),其内切圆半径r=一㊁一3 .(2016 •山东省济宁市•分)如图,在O O中,―AOB=40。
2017年中考总复习—关于圆的经典题型汇总(含答案)
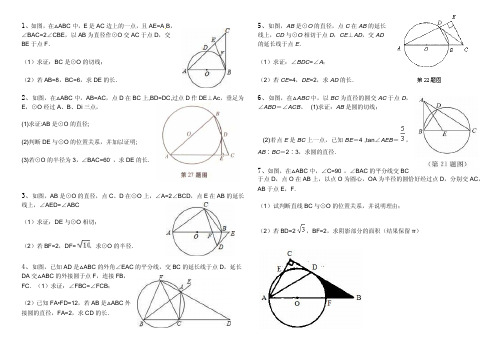
30、如图,AB 是⊙0 的直径,C 是⊙0 上的一点,直线 MN 经过点 C,过点 A 作直线
MN 的垂线,垂足为点 D,且∠BAC=∠DAC.
(1)猜想直线 MN 与⊙0 的位置关系,并 说明理由;
(2)如果⊙0 的半径为 5,sin∠ADE= ,求 BF 的长.
(1)求证:PA 是⊙O 的切线;
39、如图,点 D 是等边△ABC 中 BC 边的延长线上一点,且 AC=CD,以 AB 为直径
作⊙O,分别交边 AC、BC 于点 E、点 F
(1)求证:AD 是⊙O 的切线;
(2)连接 OC,交⊙O 于点 G,若
(2)若 = ,且 OC=4,求 PA 的长和 tanD 的值.
(3) 若 AC= DE,求 tan∠ABD 的值.
21、如图,在平面直角坐标系 xOy 中,以点 O 为圆心的
圆分别交 x 轴的正半轴于点 M,交 y 轴的正半轴于点 N.劣
弧 的长为 π,直线 y=﹣ x+4 与 x 轴、y 轴分别交于 点 A、B.
(1)求证:直线 AB 与⊙O 相切;
(2)求图中所示的阴影部分的面积(结果用 π 表示)
(2)已知 FA•FD=12,若 AB 是△ABC 外 接圆的直径,FA=2,求 CD 的长.
8、如图, AB 为⊙O 的直径,
C 是⊙O 上一点,过点 C 的直 线交 AB 的延长线于点 D, AE⊥DC,垂足为 E,F 是 AE 与⊙O 的交点,AC 平分∠BAE. (1)求证 :DE 是 ⊙O 的切线; (2)若 AE=6,∠D=30°,求图 中阴影部分的面积.
1、如图,在△ABC 中,E 是 AC 边上的一点,且 AE=A B,
中考数学专题11圆(第03期)-2017年中考数学试题分项版解析汇编(解析版)

一、选择题目1.(2017四川省南充市)如图,在Rt △ABC 中,AC =5cm ,BC =12cm ,∠ACB =90°,把Rt △ABC 所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( )A .60πcm 2B .65πcm 2C .120πcm 2D .130πcm 2 【答案】B .考点:1.圆锥的计算;2.点、线、面、体.2.(2017四川省广安市)如图,AB 是⊙O 的直径,且经过弦CD 的中点H ,已知cos ∠CDB =45,BD =5,则OH 的长度为( )A .32B .65C .1D .67【答案】D . 【解析】试题分析:连接OD ,如图所示:∵AB 是⊙O 的直径,且经过弦CD 的中点H ,∴AB ⊥CD ,∴∠OHD =∠BHD =90°,∵cos ∠CDB =DHBD=45,BD =5,∴DH =4,∴BH3,设OH =x ,则OD =OB =x +3,在Rt △ODH 中,由勾股定理得:x 2+42=(x +3)2,解得:x =67,∴OH =67;故选D .考点:1.圆周角定理;2.解直角三角形.3.(2017四川省眉山市)如图,在△ABC 中,∠A =66°,点I 是内心,则∠BIC 的大小为( )A .114°B .122°C .123°D .132° 【答案】C . 【解析】试题分析:∵∠A =66°,∴∠ABC +∠ACB =114°,∵点I 是内心,∴∠IBC =12∠ABC ,∠ICB =12∠ACB ,∴∠IBC +∠ICB =57°,∴∠BIC =180°﹣57°=123°,故选C .学*科网 考点:三角形的内切圆与内心.4.(2017四川省绵阳市)“赶陀螺”是一项深受人们喜爱的运动,如图所示是一个陀螺的立体结构图,已知底面圆的直径AB =8cm ,圆柱体部分的高BC =6cm ,圆锥体部分的高CD =3cm ,则这个陀螺的表面积是( )A .68πcm 2B .74πcm 2C .84πcm 2D .100πcm 2【答案】C.【解析】试题分析:∵底面圆的直径为8cm,高为3cm,∴母线长为5cm,∴其表面积=π×4×5+42π+8π×6=84πcm2,故选C.考点:1.圆锥的计算;2.几何体的表面积.5.(2017四川省达州市)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是()A B C.D【答案】A.考点:正多边形和圆.6.(2017山东省枣庄市)如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为()A.r << Br << C5r << D.5r <<【答案】B . 【解析】试题分析:给各点标上字母,如图所示. AB==,AC =AD==,AE==,AF==,AG =AM =AN5r <<A 为圆心,r 为半径画圆,选取的格点中除点A 外恰好有3个在圆内.故选B .考点:1.点与圆的位置关系;2.勾股定理;3.推理填空题目.7.(2017山东省济宁市)如图,在Rt △ABC 中,∠ACB =90°,AC =BC =1,将Rt △ABC 绕点A 逆时针旋转30°后得到Rt △ADE ,点B 经过的路径为,则图中阴影部分的面积是( )A . 6πB . 3πC .122π-D . 12【答案】A.【解析】试题分析:∵∠ACB=90°,AC=BC=1,∴AB,∴S扇形ABD=6π.又∵Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,∴Rt△ADE≌Rt△ACB,∴S阴影部分=S△ADE+S扇形ABD﹣S△ABC=S扇形ABD=6π.故选A.考点:1.扇形面积的计算;2.等腰直角三角形;3.旋转的性质.学科*网8.(2017广东省)如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为()A.130°B.100°C.65°D.50°【答案】C.考点:圆内接四边形的性质.9.(2017广西四市)如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于()A.2π3B.π3C.2√3π3D.√3π3【答案】A.【解析】试题分析:如图,连接OB 、OC ,∵∠BAC =30°,∴∠BOC =2∠BAC =60°,又OB =OC ,∴△OBC 是等边三角形,∴BC =OB =OC =2,∴劣弧BC 的长为:602180π⨯ =2π3.故选A .考点:1.弧长的计算;2.圆周角定理. 二、填空题目10.(2017四川省眉山市)如图,AB 是⊙O 的弦,半径OC ⊥AB 于点D ,且AB =8cm ,DC =2cm ,则OC = cm .【答案】5. 【解析】试题分析:连接OA ,∵OC ⊥AB ,∴AD =12AB =4cm ,设⊙O 的半径为R ,由勾股定理得,OA 2=AD 2+OD 2,∴R 2=42+(R ﹣2)2,解得R =5,∴OC =5cm .故答案为:5.考点:1.垂径定理;2.勾股定理.11.(2017四川省达州市)如图,矩形ABCD 中,E 是BC 上一点,连接AE ,将矩形沿AE 翻折,使点B 落在CD 边F 处,连接AF ,在AF 上取点O ,以O 为圆心,OF 长为半径作⊙O 与AD 相切于点P.若AB =6,BC=F 是CD 的中点;②⊙O 的半径是2;③AE =92CE;④S =阴影.其中正确结论的序号是 .【答案】. 【解析】试题分析:①∵AF 是AB 翻折而来,∴AF =AB =6,∵AD =BC=DF=3,∴F 是CD中点;∴①正确;②连接OP ,∵⊙O 与AD 相切于点P ,∴OP ⊥AD ,∵AD ⊥DC ,∴OP ∥CD ,∴AO OP AF DF =,设OP =OF =x ,则636x x -=,解得:x =2,∴②正确;③∵RT △ADF 中,AF =6,DF =3,∴∠DAF =30°,∠AFD =60°,∴∠EAF =∠EAB =30°,∴AE =2EF ; ∵∠AFE =90°,∴∠EFC =90°﹣∠AFD =30°,∴EF =2EC ,∴AE =4CE ,∴③错误;④连接OG ,作OH ⊥FG ,∵∠AFD =60°,OF =OG ,∴△OFG 为等边△;同理△OPG 为等边△;∴∠POG =∠FOG =60°,OHOG,S 扇形OPG =S 扇形OGF ,∴S 阴影=(S 矩形OPDH ﹣S 扇形OPG ﹣S △OGH )+(S 扇形OGF ﹣S △OFG )=S 矩形OPDH ﹣32S △OFG=312(222-⨯⨯.∴④正确;故答案为:①②④.考点:1.切线的性质;2.矩形的性质;3.扇形面积的计算;4.翻折变换(折叠问题);5.综合题.12.(2017山东省枣庄市)如图,在▱ABCD中,AB为⊙O的直径,⊙O与DC相切于点E,与AD相交于点F,已知AB=12,∠C=60°,则FE的长为.【答案】π.考点:1.切线的性质;2.平行四边形的性质;3.弧长的计算.学&科网13.(2017山东省济宁市)如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2,如此继续下去,则正六边形A4B4C4D4E4F4的面积是.考点:1.正多边形和圆;2.规律型;3.综合题.14.(2017四川省南充市)如图,在Rt △ABC 中,∠ACB =90°,以AC 为直径作⊙O 交AB 于点D ,E 为BC 的中点,连接DE 并延长交AC 的延长线于点F . (1)求证:DE 是⊙O 的切线;(2)若CF =2,DF =4,求⊙O 直径的长.【答案】(1)证明见解析;(2)6. 【解析】试题分析:(1)连接OD 、CD ,由AC 为⊙O 的直径知△BCD 是直角三角形,结合E 为BC的中点知∠CDE=∠DCE,由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案;(2)设⊙O的半径为r,由OD2+DF2=OF2,即r2+42=(r+2)2可得r=3,即可得出答案.试题解析:(1)如图,连接OD、CD.∵AC为⊙O的直径,∴△BCD是直角三角形,∵E为BC的中点,∴BE=CE=DE,∴∠CDE=∠DCE,∵OD=OC,∴∠ODC=∠OCD,∵∠ACB=90°,∴∠OCD+∠DCE=90°,∴∠ODC+∠CDE=90°,即OD⊥DE,∴DE是⊙O的切线;(2)设⊙O的半径为r,∵∠ODF=90°,∴OD2+DF2=OF2,即r2+42=(r+2)2,解得:r=3,∴⊙O的直径为6.考点:切线的判定与性质.15.(2017四川省广安市)如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D.(1)求证:直线AE是⊙O的切线.(2)若∠BAC=30°,BC=4,cos∠BAD=34,CF=103,求BF的长.【答案】(1)证明见解析;(2【解析】试题分析:(1)由直径所对的圆周角是直角得:∠ADB=90°,则∠ADC+∠CDB=90°,所以∠EAC+∠BAC=90°,则直线AE是⊙O的切线;(2)分别计算AC和BD的长,证明△DFB∽△AFC,列比例式得:BF BDFC AC,得出结论.试题解析:(1)连接BD,∵AB是⊙O的直径,∴∠ADB=90°,即∠ADC+∠CDB=90°,∵∠EAC=∠ADC,∠CDB=∠BAC,∴∠EAC+∠BAC=90°,即∠BAE=90°,∴直线AE是⊙O的切线;(2)∵AB是⊙O的直径,∴∠ACB=90°,Rt△ACB中,∠BAC=30°,∴AB=2BC=2×4=8,由勾股定理得:AC=,Rt△ADB中,cos∠BAD=34=ADAB,∴34=8AD,∴AD=6,∴BD=,∵∠BDC=∠BAC,∠DFB=∠AFC,∴△DFB∽△AFC,∴BF BDFC AC=,∴103BF=,∴BF=考点:1.切线的判定与性质;2.解直角三角形.16.(2017四川省绵阳市)如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.(1)求证:CA=CN;(2)连接DF,若cos∠DF A=45,AN=,求圆O的直径的长度.【答案】(1)证明见解析;(2)503.学&科网【解析】试题分析:(1)连接OF,根据切线的性质结合四边形内角和为360°,即可得出∠M+∠FOH=180°,由三角形外角结合平行线的性质即可得出∠M=∠C=2∠OAF,再通过互余利用角的计算即可得出∠CAN=90°﹣∠OAF=∠ANC,由此即可证出CA=CN;(2)连接OC,如图2所示.∵cos∠DF A=45,∠DF A=∠ACH,∴CHAC=45.设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN=a=,∴a=2,AH=3a=6,CH=4a=8.设圆的半径为r,则OH=r﹣6,在Rt△OCH中,OC=r,CH=8,OH=r﹣6,∴OC2=CH2+OH2,r2=82+(r﹣6)2,解得:r=253,∴圆O的直径的长度为2r=503.考点:1.切线的性质;2.勾股定理;3.圆周角定理;4.解直角三角形.17.(2017四川省达州市)如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD.(1)求证:PQ是⊙O的切线;(2)求证:BD2=AC•BQ;(3)若AC、BQ的长是关于x的方程4x mx+=的两实根,且tan∠PCD=13,求⊙O的半径.【答案】(1)证明见解析;(2)证明见解析;(3).【解析】试题分析:(1)根据平行线的性质和圆周角定理得到∠ABD=∠BDQ=∠ACD,连接OB,OD,交AB于E,根据圆周角定理得到∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,根据三角形的内角和得到2∠ODB+2∠O=180°,于是得到∠ODB+∠O=90°,根据切线的判定定理即可得到结论;(2)证明:连接AD,根据等腰三角形的判定得到AD=BD,根据相似三角形的性质即可得到结论;试题解析:(1)证明:∵PQ∥AB,∴∠ABD=∠BDQ=∠ACD,∵∠ACD=∠BCD,∴∠BDQ=∠ACD,如图1,连接OB,OD,交AB于E,则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,在△OBD中,∠OBD+∠ODB+∠O=180°,∴2∠ODB+2∠O=180°,∴∠ODB+∠O=90°,∴PQ是⊙O的切线;(2)证明:如图2,连接AD,由(1)知PQ是⊙O的切线,∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,∴AD=BD,∵∠DBQ=∠ACD,∴△BDQ∽△ACD,∴AD ACBQ BD=,∴BD2=AC•BQ;(3)解:方程4x mx+=可化为x2﹣mx+4=0,∵AC、BQ的长是关于x的方程4x mx+=的两实根,∴AC•BQ=4,由(2)得BD2=AC•BQ,∴BD2=4,∴BD=2,由(1)知PQ是⊙O的切线,∴OD⊥PQ,∵PQ∥AB,∴OD⊥AB,由(1)得∠PCD=∠ABD,∵tan∠PCD=13,∴tan∠ABD=13,∴BE=3DE,∴DE 2+(3DE )2=BD 2=4,∴DE=,∴BE=,设OB =OD =R ,∴OE =R﹣,∵OB 2=OE 2+BE 2,∴R 2=(R)2+2,解得:R=,∴⊙O的半径为.考点:1.相似三角形的判定与性质;2.分式方程的解;3.圆周角定理;4.切线的判定与性质;5.解直角三角形;6.压轴题.18.(2017山东省枣庄市)如图,在△ABC 中,∠C =90°,∠BAC 的平分线交BC 于点D ,点O 在AB 上,以点O 为圆心,OA 为半径的圆恰好经过点D ,分别交AC ,AB 于点E ,F . (1)试判断直线BC 与⊙O 的位置关系,并说明理由; (2)若BD=BF =2,求阴影部分的面积(结果保留π).【答案】(1)BC 与⊙O 相切;(2)23π.【解析】试题分析:(1)连接OD ,证明OD ∥AC ,即可证得∠ODB =90°,从而证得BC 是圆的切线;(2)设OF =OD =x ,则OB =OF +BF =x +2,由勾股定理得:OB 2=OD 2+BD 2,即(x +2)2=x 2+12,解得:x =2,即OD =OF =2,∴OB =2+2=4,∵Rt △ODB 中,OD =12OB ,∴∠B =30°,∴∠DOB =60°,∴S扇形AOB =604360π⨯ =23π,则阴影部分的面积为S △ODB ﹣S 扇形DOF =12×2×﹣23π=23π-.故阴影部分的面积为23π.考点:1.直线与圆的位置关系;2.扇形面积的计算;3.探究型.19.(2017山东省济宁市)如图,已知⊙O 的直径AB =12,弦AC =10,D 是BC 的中点,过点D 作DE ⊥AC ,交AC 的延长线于点E . (1)求证:DE 是⊙O 的切线; (2)求AE 的长.【答案】(1)证明见解析;(2)11. 【解析】试题分析:(1)连接OD ,由D 为弧BC 的中点,得到两条弧相等,进而得到两个同位角相等,确定出OD与AE 平行,利用两直线平行同旁内角互补得到OD 与DE 垂直,即可得证;(2)解:过点O 作OF ⊥AC ,∵AC =10,∴AF =CF=12AC =5,∵∠OFE =∠DEF =∠ODE =90°,∴四边形OFED 为矩形,∴FE =OD =12AB ,∵AB =12,∴FE =6,则AE =AF +FE =5+6=11.考点:1.切线的判定与性质;2.勾股定理;3.垂径定理.20.(2017广东省)如图,AB 是⊙O 的直径,AB =E 为线段OB 上一点(不与O ,B 重合),作CE ⊥OB ,交⊙O 于点C ,垂足为点E ,作直径CD ,过点C 的切线交DB 的延长线于点P ,AF ⊥PC 于点F ,连接CB .(1)求证:CB 是∠ECP 的平分线; (2)求证:CF =CE ;(3)当34CF CP =时,求劣弧BC 的长度(结果保留π)【答案】(1)证明见解析;(2)证明见解析;(3.【解析】试题分析:(1)根据等角的余角相等证明即可; (2)欲证明CF =CE ,只要证明△ACF ≌△ACE 即可;(3)作BM ⊥PF 于M .则CE =CM =CF ,设CE =CM =CF =4a ,PC =4a ,PM =a ,利用相似三角形的性质求出BM ,求出tan ∠BCM 的值即可解决问题;试题解析:(1)证明:∵OC =OB ,∴∠OCB =∠OBC ,∵PF 是⊙O 的切线,CE ⊥AB ,∴∠OCP =∠CEB =90°,∴∠PCB +∠OCB =90°,∠BCE +∠OBC =90°,∴∠BCE =∠BCP ,∴BC 平分∠PCE .(2)证明:连接AC .∵AB 是直径,∴∠ACB =90°,∴∠BCP +∠ACF =90°,∠ACE +∠BCE =90°,∵∠BCP =∠BCE ,∴∠ACF =∠ACE ,∵∠F =∠AEC =90°,AC =AC ,∴△ACF ≌△ACE ,∴CF =CE .(3)解:作BM ⊥PF 于M .则CE =CM =CF ,设CE =CM =CF =4a ,PC =4a ,PM =a ,∵△BMC ∽△PMB ,∴BM CMPM BM =,∴BM 2=CM •PM =3a 2,∴BM=a ,∴tan ∠BCM=BM CM =,∴∠BCM =30°,∴∠OCB =∠OBC =∠BOC =60°,∴BC 的长.考点:1.相似三角形的判定与性质;2.垂径定理;3.切线的性质;4.弧长的计算.21.(2017江苏省盐城市)如图,△ABC 是一块直角三角板,且∠C =90°,∠A =30°,现将圆心为点O 的圆形纸片放置在三角板内部.(1)如图①,当圆形纸片与两直角边AC 、BC 都相切时,试用直尺与圆规作出射线CO ;(不写作法与证明,保留作图痕迹)(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC =9,圆形纸片的半径为2,求圆心O 运动的路径长.【答案】(1)作图见解析;(2)15+ 【解析】试题分析:(1)作∠ACB 的平分线得出圆的一条弦,再作此弦的中垂线可得圆心O ,作射线CO 即可; (2)添加如图所示辅助线,圆心O 的运动路径长为12OO O C ∆,先求出△ABC 的三边长度,得出其周长,证四边形OEDO 1、四边形O 1O 2HG 、四边形OO 2IF 均为矩形、四边形OECF 为正方形,得出∠OO 1O 2=60°=∠ABC 、∠O 1OO 2=90°,从而知△OO 1O 2∽△CBA ,利用相似三角形的性质即可得出答案. 试题解析:(1)如图①所示,射线OC 即为所求;(2)如图2,圆心O 的运动路径长为12OO O C ∆,过点O 1作O 1D ⊥BC 、O 1F ⊥AC 、O 1G ⊥AB ,垂足分别为点D 、F 、G ,过点O 作OE ⊥BC ,垂足为点E ,连接O 2B ,过点O 2作O 2H ⊥AB ,O 2I ⊥AC ,垂足分别为点H 、I ,在Rt △ABC 中,∠ACB =90°、∠A =30°,∴AC =tan 30BC==,AB =2BC =18,∠ABC =60°,∴C △ABC =9++18=27+,∵O 1D ⊥BC 、O 1G ⊥AB ,∴D 、G 为切点,∴BD =BG ,在Rt △O 1BD 和Rt △O 1BG 中,∵BD =BG ,O 1B =O 1B ,∴△O 1BD ≌△O 1BG (HL ),∴∠O 1BG =∠O 1BD=30°,在Rt△O1BD中,∠O1DB=90°,∠O1BD=30°,∴BD=1tan 30O D==,∴OO1=9﹣2﹣=7﹣O1D=OE=2,O1D⊥BC,OE⊥BC,∴O1D∥OE,且O1D=OE,∴四边形OEDO1为平行四边形,∵∠OED=90°,∴四边形OEDO1为矩形,同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,又OE=OF,∴四边形OECF为正方形,∵∠O1GH=∠CDO1=90°,∠ABC=60°,∴∠GO1D=120°,又∵∠FO1D=∠O2O1G=90°,∴∠OO1O2=360°﹣90°﹣90°=60°=∠ABC,同理,∠O1OO2=90°,∴△OO1O2∽△CBA,∴1212OO OABCC O OC BC∆∆==,∴12OO OC∆=15+,即圆心O运动的路径长为15+考点:1.轨迹;2.切线的性质;3.作图—复杂作图;4.综合题.学科*网22.(2017江苏省连云港市)如图,在平面直角坐标系xOy中,过点A(﹣2,0)的直线交y轴正半轴于点B,将直线AB绕着点顺时针旋转90°后,分别与x轴、y轴交于点D.C.(1)若OB=4,求直线AB的函数关系式;(2)连接BD,若△ABD的面积是5,求点B的运动路径长.【答案】(1)y=2x+4;(21112.【解析】试题分析:(1)依题意求出点B坐标,然后用待定系数法求解析式;(2)设OB=m,则AD=m+2,根据三角形面积公式得到关于m的方程,解方程求得m的值,然后根据弧长公式即可求得.试题解析:(1)∵OB=4,∴B(0,4).∵A(﹣2,0),设直线AB的解析式为y=kx+b,则420bk b,解得24kb,∴直线AB的解析式为y=2x+4;(2)设OB=m,则AD=m+2,∵△ABD的面积是5,∴12AD•OB=5,∴12(m+2)•m=5,即22100m m+-=,解得111m 或111m(舍去),∵∠BOD=90°,∴点B 的运动路径长为:1111211142.考点:1.一次函数图象与几何变换;2.轨迹;3.弧长的计算.学#科网23.(2017河北省)如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O 逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧CD于点P,Q,且点P,Q在AB异侧,连接OP.(1)求证:AP=BQ;(2)当BQ=QD的长(结果保留π);(3)若△APO的外心在扇形COD的内部,求OC的取值范围.【答案】(1)见解析;(2)143π;(3)4<OC<8.(2)∵Rt △APO ≌Rt △BQO ,∴∠AOP =∠BOQ ,∴P 、O 、Q 三点共线,∵在Rt △BOQ 中,cos B =43382QB OB==,∴∠B =30°,∠BOQ =60°,∴OQ =12OB =4,∵∠COD =90°,∴∠QOD =90°+60°=150°,∴优弧QD 的长=2104180π⨯=143π;(3)∵△APO 的外心是OA 的中点,OA =8,∴△APO 的外心在扇形COD 的内部时,OC 的取值范围为4<OC <8.考点:1.切线的性质;2.弧长的计算;3.旋转的性质.24.(2017河北省)平面内,如图,在ABCD 中,AB =10,AD =15,tan A =43.点P 为AD 边上任意一点,连接PB ,将PB 绕点P 逆时针旋转90°得到线段PQ .(1)当∠DPQ =10°时,求∠APB 的大小;(2)当tan∠A tan A=3:2时,求点Q与点B间的距离(结果保留根号);(3)若点Q恰好落在ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积(结果保留π).【答案】(1)100°或80°;(2)(3)16π或20π或32π.【解析】试题分析:(1)根据点Q与点B和PD的位置关系分类讨论;(2)因为△PBQ是等腰直角三角形,所以求BQ的长,只需求PB,过点P作PH⊥AB于点H,确定BH,求得AH和BH,解直角△APH求PH,由勾股定理求PB;(2)如图2,过点P作PH⊥AB于点H,连接BQ.∵tan∠A tan A=:3:2PH PHHB AH=,∴HB=3:2.而AB=10,∴AH=6,HB=4.在Rt△PHA中,PH=AH·tan A=8,∴PQ=PB==Rt△PQB中,QBPB=(3)①点Q在AD上时,如图3,由tan A=43得,PB=AB·sin A=8,∴扇形面积为16π.②点A 在CD 上时,如图4,过点P 作PH ⊥AB 于点H ,交CD 延长线于点K ,由题意∠K =90°,∠KDP =∠A .设AH =x ,则PH =AH ·tan A =43x .∵∠BPH =∠KQP =90°-∠KPQ ,PB =QP ,∴Rt △HPB ≌Rt △KQP .∴KP =HB =10-x ,∴AP =53x,PD =()5104x -,AD =15=()551034x x +-,解得x =6.∵22280PB PH HB =+=,∴扇形的面积为20π.③点Q 在BC 延长线上时,如图5,过点B 作BM ⊥AD 于点M ,由①得BM =8.又∠MPB =∠PBQ =45°,∴PB =,∴扇形面积为32π. 所以扇形的面积为16π或20π或32π.考点:1.解直角三角形;2.勾股定理;3.扇形面积的计算;4.分类讨论;5.压轴题.25.(2017浙江省丽水市)如图,在Rt △ABC 中,∠C =Rt ∠,以BC 为直径的⊙O 交AB 于点D ,切线DE 交AC 于点E .(1)求证:∠A =∠ADE ;(2)若AD =16,DE =10,求BC 的长.【答案】(1)证明见解析;(2)15. 【解析】试题分析:(1)只要证明∠A +∠B =90°,∠ADE +∠B =90°即可解决问题;(2)连接CD .∵∠ADE =∠A ,∴AE =DE ,∵BC 是⊙O 的直径,∠ACB =90°,∴EC 是⊙O 的切线,∴ED =EC ,∴AE =EC ,∵DE =10,∴AC =2DE =20,在Rt △ADC 中,DC 12,设BD =x ,在Rt △BDC 中,BC 2=x 2+122,在Rt △ABC 中,BC 2=(x +16)2﹣202,∴x 2+122=(x +16)2﹣202,解得x =9,∴BC 15.考点:1.切线的性质;2.勾股定理.26.(2017浙江省台州市)如图,已知等腰直角三角形ABC ,点P 是斜边BC 上一点(不与B ,C 重合),PE 是△ABP 的外接圆⊙O 的直径. (1)求证:△APE 是等腰直角三角形; (2)若⊙O 的直径为2,求22PC PB +的值.【答案】(1)证明见解析;(2)4. 【解析】试题分析:(1)只要证明∠AEP =∠ABP =45°,∠P AB =90°即可解决问题;(2)作PM⊥AC于M,PN⊥AB于N,则四边形PMAN是矩形,∴PM=AN,∵△PCM,△PNB都是等腰直角三角形,∴PC=2PM,PB=2PN,∴22PC PB+=222()PM PN+ =222()AN PN+=22PA =2PE =22 =4.考点:1.三角形的外接圆与外心;2.等腰直角三角形.27.(2017湖北省襄阳市)如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;(2)若DE=1,BC=2,求劣弧BC的长l.【答案】(1)证明见解析;(2)23π.【解析】试题分析:(1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;(2)连接OD,DC,∵∠DAC=12∠DOC ,∠OAC=12∠BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=12DEDC=,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l=602180π⨯=23π.考点:1.切线的判定与性质;2.弧长的计算.祝你考试成功!祝你考试成功!。
2017年中考真题分类解析 与圆的有关计算

一、选择题1.(2017浙江丽水·9·3分)如图,点C是以AB为直径的半圆O的三等分点,AC=2,则图中阴影部分的面积是()A.433π-B.4233π-C.233π-D.2332π-答案:A.解析:连接OC,∵点C是半圆的三等分点,∴∠AOC=600,∴△AOC是等边三角形,∠BOC=1200,由三角形面积公式求得S△BOC=33221=⨯⨯,由扇形的面积公式求得S扇形BOC=2120243603ππ⋅⨯=∴S阴影=S扇形BOC-S△BOC=433π-,选A.2.(2017浙江衢州,10,3分)运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD、EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是()OFCE(第10题)ADBA.252πB.10πC.24+4πD.24+5π答案:A,解析:连接OA、OB、OC、OD,过O作OM⊥EF于M,反向延长线交CD于N.∵AB∥CD∥EF,易证阴影部分面积即为扇形COD与扇形EOF的和,由AB=10,CD=6,EF=8,MO⊥EF,ON⊥CD,易知OD=OF=5,FM=ON=4,OM=DN=3,故△OFM≌△DON,∴∠FOM+∠DON=90°,∴∠EOF+∠COD =180°,故阴影部分面积等于半圆面积.3. (2017山东济宁,9,3分)如图,在Rt △ABC 中,∠ACB =90°,AC =BC =1.将Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE ,点B 经过的路径为»BD,则图中阴影部分的面积是 A .6πB .3π C .122π-D .12答案:A ,解析:如图,阴影部分面积等于△ADE +扇形DAB -△ABC 的面积,由旋转可得△ADE 与△ABC 全等,由此可得面积也相等,阴影部分面积就是扇形DAB 的面积,根据扇形面积公式“2=360n r S π”计算答案为6π.4. (2017年四川绵阳,8,3分)“赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB=8cm ,圆柱部分的高BC=6cm ,圆锥体部分的高CD=3cm ,则这个陀螺的表面积是A .68πcm 2B .74πcm 2C .84πcm 2D .100πcm 2答案:C 解析:圆锥的表面积加上圆柱的侧面积即可求得其表面积.5. 2. (2017重庆,9,4分)如图,矩形ABCD 的边AB =1,BE 平分∠ABC ,交AD 于点E ,若点E 是AD 的中点,以点B 为圆心,BE 长为半径画弧,交BC 于点F ,则图中阴影部分的面积是( ) A .42π-B .423π-C . 82π-D .823π-答案:B 解析:∵四边形ABCD 是矩形,∴AD ∥BC ,AD =BC ,∠ABC =90゜,∵BE 平分∠ABC ,∴∠ABE =∠CBE =45゜,∵AD ∥BC ,∴∠AEB =∠CBE =45゜,∴AB =AE ,又∵AB =1,E 是AD 的中点,∴AE=1,AD =2,∴S矩形=1×2=2,S ∆ABE =21×1×1=21;在Rt ∆ABE 中,∠BAD =90゜,AB =AE =1,BE =21122=+,∴S 扇形=()24523604π︒⨯π⨯=︒,∴S 阴影= S 矩形-S ∆ABE -S 扇形=2-21-4π=324π-.7. (2017年四川南充,8,3分)如图5,在Rt △ABC 中,AC =5cm ,BC =12cm ,∠ACB =90°,把Rt △ABC 绕BC 所在的直线旋转一周得到一个几何体,则这个几何体的侧面积为( ) A .60πcm 2 B .65πcm 2 C .120πcm 2 D .130πcm 2答案:B 解析:AB =22BC AC +=22125+=13.这个几何体是圆锥,圆锥的底面半径AC =5,母线AB =13,圆锥的侧面积=πAC ·AB =π×5×13=65π(cm 2).故选B .8. (2017重庆B ,9,4分)如图,在矩形ABCD 中,AB =4,AD =2,分别以点A 、C 为圆心,AB 、CB 为半径画弧,交AB 于点E ,交CD 于点F ,则图中阴影部分的面积是ABC 图4FEDCBAA .π24-B .28-C .π28-D .π48-答案:C ,解析:矩形面积为8,两个全等扇形面积和为ππ22212=⨯⨯,∴阴影部分面积为π28-,故答案为C .9. (2017山东临沂,10,3分)如图,AB 是圆O 的直径,BT 是圆O 的切线,若∠ATB =45°,AB =2,则阴影部分的面积是( )OTABA .2B .3124π- C .1 D .1124π+答案:C解析:连接OD ,先由直径AB =2,TB 切⊙O 于B 得出∠ABT =90°,由∠ATB =45°得出△ABT 是等腰直角三角形,根据圆周角定理得出∠ADB =90°,根据S 阴影=S △DBT 进而可得出结论. 连接OD ,D O TAB∵直径AB =2,TB 切⊙O 于B ,∴OB =OA =1,∠ABT =90°,∠ADB =90°.∵∠ATB =45°,∴△ABT 是等腰直角三角形,∴∠A =45°,∴∠BOD =2∠A =90°,AT =22+22=22. ∴BD =12AT =DT =2.∴S 阴影=S △DBT =12BD ×DT =12×2×2=1.10. 7.(2017四川达州7,3分)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是()A.22B.32C. 2D.3答案:A,解析:如图1,∵OC=2,∴OD=2×sin30°=1;如图2,∵OB=2,∴OE=2×sin45°=2;如图3,∵OA=2,∴OD=2×cos30°=3,则该三角形的三边分别为:1,2,3,∵(1)2+(2)2=(3)2,∴该三角形是直角三角形,∴该三角形的面积是×1×2×=22,故选:A.11.(2017四川达州9,3分)如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90︒至图①位置,继续绕右下角的顶点按顺时针方向旋转90︒至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A 在整个旋转过程中所经过的路径总长为()A.2017πB.2034π C.3024πD.3026π答案:D,解析:转动一次A的路线长是:9042 180π⨯=π,转动第二次的路线长是:9055 1802π⨯=π,转动第三次的路线长是:9033 1802π⨯=π,转动第四次的路线长是:0,转动五次A的路线长是:9042 180π⨯=π,以此类推,每四次循环,故顶点A 转动四次经过的路线长为:532622π+π+π=π, ∵2017÷4=504 (1)∴这样连续旋转2016次后,顶点A 在整个旋转过程中所经过的路程之和是:6π×504+2π=3026π.故选:D .BA.B ,CA .5πcm 2B .10πcm 2C .15πcm 2D .20πcm 2答案:B ,解析:由“等底同高”可知:S △BOC =S △BOA ,S △DOA =S △DOC ,∴S 阴影=2S 扇形BOC =2×3605722⨯π=10π(cm 2).15. 7.(2017湖北咸宁,7,3分)如图,⊙O 的半径为3,四边形ABCD 内接于⊙O ,连接OB 、OD ,若∠BOD=∠BCD ,则»A .πB .π23C. π2 D .π3 答案:C 解析:∵∠BAD=12∠BOD=12∠BCD ,∠BAD+∠BCD=180°, ∴∠BOD=120°.又∵⊙O 的半径为3,∴»BD的长为1203=2180ππ⋅.故选C.16.(2017湖南邵阳,7,3分)如图(三)所示,边长为 a 的正方形中阴影部分的面积为( ) A .222⎪⎭⎫⎝⎛-a a πB .a 2-2a πC .a 2 – πaD .a 2 – 2πa答案:A ,解析:由图直观知,阴影部分的面积为正方形的面积减去半径为2a 的圆的面积,所以为222⎪⎭⎫⎝⎛-a a π,故选A .17. (2017湖北十堰,8,5分)如图,已知圆柱的底面直径BC =6π,高AB =3,小虫在圆柱表面爬行,从C 点爬到A 点,然后再沿另一面爬回C 点,则小虫爬行的最短路程为( )A.32B.35C.65D.62答案:D,解析:将已知圆柱展开得到如图所示矩形,小虫从C点爬到A点,然后再沿另一面爬回C点经过的路程为2AC,因为圆柱的底面直径BC=6π,所以此圆柱的底面周长为6,则展开图中AB的长为3,所以AC=32,所以小虫爬行的最短路程为62,故选D.18.(2017江苏宿迁,3分)若将半径为12cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是A.2cm B.3cm C.4cm D.6cm答案:D,解析:根据圆锥底面圆周长=扇形弧长,即l=C得12π=2πr,所以r=6.19. (2017甘肃天水.9.4分)如图所示,AB是圆O的直径,弦CD⊥AB.垂足为E,∠BCD=30°,CD=43则S阴影=()A.2πB.83πC.43πD.38π9题图OEDCA答案:B,解析:由AB是圆O的直径,弦CD⊥AB.有E为CD中点,DE=12CD=3∠BCD=30°,∴∠BOD =60°,OD =23÷cos 30°=4,OE =BE =12OD =2,∴△ODE ≌△BCE ,S 阴影=S 扇形DOB =2604360π⨯=83π,故选B .20. 7.(2017湖北天门,7,3分)一个扇形的弧长是10πcm ,面积是60πcm 2,则此扇形的圆心角的度数是A .300°B .150°C .120°D .75°答案:B ,解析:根据1=2S l r 弧长扇形 ,求的半径r =12,由弧长公式180n r l π= ,1210180n ππ⋅=,解得n =150°.21. 8.(2017宁夏,3分) 圆锥的底面半径r =3,高h =4,则圆锥的侧面积是A .12πB .15πC .24πD .30π答案:B ,解析:圆锥侧面积公式是S=p rl ,其中母线长l 可以根据勾股定理22l r h =+求得.22. .(2017浙江杭州,8,3分)如图,在Rt △ABC 中,∠ABC =90°,AB =2,BC =1.把△ABC 分别绕直线AB 和BC 旋转一周,所得几何体的底面圆的周长分别记作l 1,l 2,侧面积分别记作S 1,S 2,则( ) A .l 1:l 2=1:2,S 1:S 2=1:2 B .l 1:l 2=1:4,S 1:S 2=1:2 C .l 1:l 2=1:2,S 1:S 2=1:4 D .l 1:l 2=1:4,S 1:S 2=1:4CB A答案:A ,解析:△ABC 分别绕直线AB 旋转一周,所得几何体的底面圆的周长l 1=2π⋅BC =2π,侧面积分别记作S 1=2π⋅AC ,△ABC 分别绕直线BC 旋转一周,所得几何体的底面圆的周长l 2=2π⋅AB =4π,侧面积分别记作S 2=4π⋅AC ,故l 1:l 2=1:2,S 1:S 2=1:2.故选择A .23. 9.(2017浙江宁波,9,4分)如图,在Rt △ABC 中,90A =∠°,22BC =,以BC 的中点O 为圆心分别与AB ,AC 相切于D ,E 两点,则»DE的长为( ) A .4π B .2πC .πD .2π【答案】B【解析】连接OE,OD.AB,AC分别切⊙O于点D ,E,∴∠OED=∠ODA=90°,又∵∠A=90°,∴四边形OEAD为矩形.∵OD=OE,∴四边形OEAD为正方形.∴∠EOD=90°,OE∥AB,OD∥AC.∵O为BC的中点,∴OE、OD为△ABC的中位线,∴OE=21AB,OD=21AC,∵OD=OE,∴AB=AC.∴∠B=∠C=°.∴AB=BCsin45°=22×22=2,∴OE=OD=1.∴⌒DE 的长为:180190π=2π.故选B.12.(2017四川凉山,12,4分)如图,一个半径为1的1Oe经过一个半径为2的Oe的圆心,则图中阴影部分的面积为( ).1 B.12C.2D.22【答案】C【解析】如图,⊙O的半径为,⊙1O的半径为1,点O在⊙1O上,连OA,OB,OC,由OA=,1O A 1O O =1,则有,∴OA2=1O A2+1O O2,∴△O1O A为直角三角形,∴∠AO1O=45°,同理可得∠BO1O=45°,∴∠AOB=90°,∴AB为⊙1O的直径.∴S阴影部分=S半圆AB﹣S弓形AB=S半圆AB﹣(S扇形OAB △OAB半圆AB扇形OAB△OABO O125. (2017河南,10,3分)如图,将半径为2,圆心角为120゜的扇形OAB 绕点A 逆时针旋转60,点O ,B 的对应点分别为O',B',连接BB',则图中阴影部分的面积是( )A .32πB .332π-C .3232π-D .3234π-答案C ,解析:如图,连结OO ',O ′B 由旋转性质知:∠OAO'=60゜,∵OA =OO',∴∆AOO'是等边三角形,∴∠ AOO'=60゜,∵∠AOB =120゜,∴∠BOO'=60゜, ∵OB =OO',∴∆BOO'是等边三角形,∴∠BO'O =∠OBO'=60゜,∴OB =OO'=O'B= 2, ∵∠AO'B'=120゜,∴∠OO'B'=120゜+60゜=180゜,∴O 、O'、B'三点共线, ∵O'B'=O'B =OB ,∴∠O'BB'=∠O'B'B =30゜,∴∠OBB'=30゜+60゜=90゜,∴BB'=324222=+,∴S 阴影= 3232360*********ππ-=︒⨯⋅︒-⨯⨯.26. (2017黑龙江齐齐哈尔,9,3分)一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图的扇形的圆心角是( ) A. 120° B. 180° C. 240° D.300° 答案:A解析:设圆锥侧面展开图的扇形的圆心角的度数为x ,底面半径为r ,由题意得23r rl ππ=,∴l=3r , 又∵2223(3)360360x x r l r πππ==, ∴x=120°.27. (2017山东东营,8,3分)若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( ) A .60° B .90° C .120° D .180° 【答案】C【解析】利用圆锥的侧面积和圆面积公式计算即可。
2017年中考真题圆综合大题(可编辑修改word版)

2017 年圆综合大题8.(2011 年苏州市•第26 题8 分)如图,已知AB 是⊙O 的弦,OB=2,∠B=30°,C 是弦AB 上的任意一点(不与点A、B 重合),连接CO 并延长CO 交于⊙O 于点D,连接AD.(1)弦长AB 等于▲(结果保留根号);(2)当∠D=20°时,求∠BOD 的度数;(3)当AC 的长度为多少时,以A、C、D 为顶点的三角形与以B、C、O 为顶点的三角形相似?请写出解答过程.9.(2012 年苏州市第27 题满分8 分)如图,已知半径为2 的⊙O 与直线l 相切于点A,点P 是直径AB 左侧半圆上的动点,过点P 作直线l 的垂线,垂足为C,PC 与⊙O 交于点D,连接PA、PB,设PC 的长为x(2<x<4).5(1)当x=2时,求弦PA、PB 的长度;(2)当x 为何值时PD·CD 的值最大?最大值是多少?10.(2013 年苏州第27 题8 分)如图,Rt△ABC 中,∠ACB=90°,点D 是AB 边上一点,以BD 为直径的⊙O 与边AC 相切于点E,连接DE 并延长DE 交BC 的延长线于点F.(1)求证:BD=BF;(2)若CF=1,cosB= ,求⊙O 的半径.11.(2014•苏州第27 题8 分)如图,已知⊙O 上依次有A、B、C、D 四个点,=,连接AB、AD、BD,弦AB 不经过圆心O,延长AB 到E,使BE=AB,连接EC,F 是EC 的中点,连接BF.(1)若⊙O 的半径为3,∠DAB=120°,求劣弧的长;(2)求证:BF=BD;(3)设G 是BD 的中点,探索:在⊙O 上是否存在点P(不同于点B),使得PG=PF?并说明PB 与AE 的位置关系.江南汇教育网12.(2015 年苏州第26 题满分10 分)如图,已知AD 是△ABC 的角平分线,⊙O 经过A、B、D 三点,过点B 作BE∥AD,交⊙O 于点E,连接E D.(1)求证:ED∥AC;(2)若BD=2CD,设△EBD 的面积为S ,△ADC 的面积为S ,且S 2-16S + 4 = 0 ,1 2 1 2求△ABC 的面积.13.(2016 年苏州第26 题10 分)如图,AB 是⊙ O 的直径,D 、E 为⊙ O 上位于AB 异侧的两点,连接BD 并延长至点 C ,使得CD = BD ,连接AC 交⊙ O 于点 F ,连接AE 、DE 、DF .(1 )证明:∠ E =∠ C ;(2 )若∠ E = 55 °,求∠ BDF 的度数;(3 )设DE 交AB 于点G ,若DF =4,cos B= ,E 是的中点,求EG •E D 的值.14.(2017 年苏州市第27 题10 分)如图,已知△ABC 内接于⊙O,AB 是直径,点D 在⊙O 上,OD∥BC,过点D 作DE⊥AB,垂足为E,连接CD 交OE 边于点F.(1)求证:△DOE∽△ABC;(2)求证:∠ODF=∠BDE;(3)连接OC,设△DOE 的面积为S1,四边形BCOD的面积为S2,若= ,求sinA 的值.FADEG 模拟训练:1.(2017 年常熟市•本题满分 10 分)如图 1 , DE 是⊙ O 的直径,点 A 、C 是直径 DE 上方半圆上的两点,且 AO ⊥ CO .连接 AE , CD 相交于点 F .点 B 是直径 DE 下方半圆上的任意一点,连接 AB 交CD 于点G ,连接CB 交 AE 于点 H .(1) 求∠ABC 的度数;(2) 证明:∆CFH ∆CBG ;(3) 若弧 DB 为半圆的三分之一,把∠AOC 绕着点O 旋转,使点C 、O 、 B 在一直线上时,如图 2.①证明 FH : BG = 1: 2 ;②若⊙ O 的半径为 4,直接写出 FH 的长.2.(2018 年蔡老师预测•第 26 题 10 分)如图,在 Rt △ABC 中,∠A =90°,点 D 、E 分别在 AC 、BC 上,且 CD ·BC =AC ·CE ,以 E 为圆心,DE 长为半径作圆,⊙E 经过点 B , 与 AB 、BC 分别交于点 F 、G .(1)求证:AC 是⊙E 的切线;(2)若 AF =4,CG =5,①求⊙E 的半径;②若 Rt △ABC 的内切圆圆心为 I ,则 IE =.BC(第 26 题)3.( 2017 年张家港•26 题 10 分)如图,已知⊙ O 是V ABC 的外接圆, AD 是⊙ O 的直径, 且 BD = BC .延长 AD 到 E ,使得∠EBD = ∠CAB .(1) 如图 1,若 BD = 2,AC = 6 . 55 ①求证: BE 是⊙ O 的切线;②求 DE 的长;(2) 如图 2,连结CD ,交 AB 于点 F ,若 BD = 2,CF = 3 ,求⊙ O 的半径.4.(2017 年工业园区区•26 题 10 分) 如图,在△ABC 中,CD ⊥AB ,垂足为点 D .以 AB 为直径的半⊙O 分别与 AC 、CD 相交于点 E 、F ,连接 AF 、EF .(1) 求证:∠AFE=∠ACD ;(2) 若 CE=4,CB=4,tan ∠CAB= ,求 FD 的长.5.(2017 年吴江区••26 题 10 分) 如图,在∆ABC 中, ∠C = 90︒, D 、 F 是 AB 边上的两点,以 DF 为直径的⊙ O 与 BC 相交于点 E , 连接 EF , 过 F 作 FG ⊥ BC 于点 G , 其中∠OFE =1∠A .2(1)求证: BC 是⊙ O 的切线;(2) 若sin B = 3,⊙ O 的半径为 r ,求∆EHG 的面积5(用含 r 的代数式表示).EDCO6.(2017 年高新区•26 题10 分) 如图,在⊙O 的内接四边形ACDB 中,AB 为直径,AC:BC=1:2,点D 为»AB 的中点,BE⊥CD 垂足为E.(1)求∠BCE 的度数;(2)求证:D 为CE 的中点;(3)连接OE 交BC 于点F,若AB=A B,求OE 的长度.7.(2017 年吴中区•26 题10 分) 如图,AB 是⊙O 的直径,BC 是弦,过点O 作OE ⊥BC 于H 交⊙O 于E ,在OE 的延长线上取一点D ,使∠ODB =∠AEC ,AE 与BC 交于F 。
中考专题复习圆形(含答案)

中考专题复习圆形(含答案)本文档为中考数学专题复,主要涵盖了圆形的相关知识点及答案。
以下是题目及对应的答案:1. 求圆的面积题目:已知圆的半径为4cm,求圆的面积。
答案:圆的面积公式为$S = \pi \cdot r^2$,代入半径$r = 4$,得到$S = \pi \cdot 4^2 = 16\pi cm^2$。
2. 求圆的周长题目:已知圆的直径为6cm,求圆的周长。
答案:圆的周长公式为$C = \pi \cdot d$,代入直径$d = 6$,得到$C = \pi \cdot 6 = 6\pi cm$。
3. 求圆的直径题目:已知圆的周长为10π cm,求圆的直径。
答案:圆的周长公式为$C = \pi \cdot d$,代入周长$C = 10\pi$,解方程得到$d = \frac{C}{\pi} = \frac{10\pi}{\pi} = 10 cm$。
4. 求圆柱体的体积题目:已知圆柱体的底面积为9π $cm^2$,高度为5cm,求圆柱体的体积。
答案:圆柱体的体积公式为$V = \pi \cdot r^2 \cdot h$,代入底面积$S = 9\pi$,高度$h = 5$,得到$V = \pi \cdot 3^2 \cdot 5 = 45\pi cm^3$。
5. 求扇形的面积题目:已知扇形的半径为8cm,弧长为12cm,求扇形的面积。
答案:扇形的面积公式为$S = \frac{1}{2} \cdot r \cdot l$,代入半径$r = 8$,弧长$l = 12$,得到$S = \frac{1}{2} \cdot 8 \cdot 12 =48 cm^2$。
6. 求圆锥的体积题目:已知圆锥的底面积为16π $cm^2$,高度为6cm,求圆锥的体积。
答案:圆锥的体积公式为$V = \frac{1}{3} \cdot \pi \cdot r^2\cdot h$,代入底面积$S = 16\pi$,高度$h = 6$,得到$V =\frac{1}{3} \cdot \pi \cdot 4^2 \cdot 6 = 32\pi cm^3$。
2017中考数学全国试题汇编------圆(含详细解析)

2017中考数学全国试题汇编------圆24(2017.北京)如图,是的一条弦,是的中点,过点作于点,过点作的切线交的延长线于点.(1)求证:;(2)若,求的半径.【解析】试题分析:(1)由切线性质及等量代换推出∠4=∠5,再利用等角对等边可得出结论;(2)由已知条件得出sin ∠DEF 和sin ∠AOE 的值,利用对应角的三角函数值相等推出结论.试题解析:(1)证明:∵DC ⊥OA, ∴∠1+∠3=90°, ∵BD 为切线,∴OB ⊥BD, ∴∠2+∠5=90°, ∵OA=OB, ∴∠1=∠2,∵∠3=∠4,∴∠4=∠5,在△DEB 中, ∠4=∠5,∴DE=DB.考点:圆的性质,切线定理,三角形相似,三角函数27(2017甘肃白银).如图,AN 是M 的直径,//NB x 轴,AB 交M 于点C .(1)若点()()00,6,0,2,30A N ABN ∠=,求点B 的坐标; (2)若D 为线段NB 的中点,求证:直线CD 是M 的切线. 解:(1)∵A 的坐标为(0,6),N (0,2)AB O E AB E EC OA ⊥C B O CE D DB DE =12,5AB BD ==O∴AN =4, 1分 ∵∠ABN =30°,∠ANB =90°,∴AB =2AN =8, 2分 ∴由勾股定理可知:NB=∴B(2) 3分 (2)连接MC ,NC 4分 ∵AN 是⊙M 的直径, ∴∠ACN =90°,∴∠NCB =90°在Rt △NCB ∴CD =12NB =ND ,∴∠CND =∠NCD , 6分 ∵MC =MN , ∴∠MCN =∠MNC . ∵∠MNC +∠CND =90°,∴∠MCN +∠NCD =90°, 7分 即MC ⊥CD .∴直线CD 是⊙M 的切线. 8分25(2017广东广州).如图14,是的直径,,连接.(1)求证:;(2)若直线为的切线,是切点,在直线上取一点,使所在的直线与所在的直线相交于点,连接.AB O ,2AC BC AB ==AC 045CAB ∠=l O C l D ,BD AB BD =AC E AD①试探究与之间的数量关系,并证明你的结论; ②是否为定值?若是,请求出这个定值;若不是,请说明理由.【解析】试题分析:(1)直径所对的圆周角是圆心角的一半,等弧所对的圆周角是圆心角的一半;(2)①等角对等边;②(2)①如图所示,作 于F 由(1)可得, 为等腰直角三角形.是 的中点. 为等腰直角三角形. 又 是 的切线,四边形 为矩形②当 为钝角时,如图所示,同样,(3)当D 在C 左侧时,由(2)知,AE AD EBCDBF l ⊥ACB ∆O AB CO AO BO ∴==ACB ∴∆l O OC lBF l ∴⊥⊥∴OBEC 22AB BFBD BF ∴=∴=303075BDF DBA BDA BAD ∴∠=︒∴∠=︒∠=∠=︒,15901575CBE CEB DEA ∴∠=︒∠=︒-︒=︒=∠,,ADE AED AD AE ∴∠=∠∴=ABD ∠1,302BF BD BDC =∴∠=︒1801501509015152ABD AEB CBE ADB ︒-︒∴∠=︒∠=︒-∠=︒∠==︒,,AE AD ∴=CD AB ,30ACD BAE DAC EBA ∠=∠∠=∠=︒,在 中,当D 在C 右侧时,过E 作 于在 中, 考点:圆的相关知识的综合运用25(2017贵州六盘水).如图,MN 是O ⊙的直径,4MN =,点A 在O ⊙上,30AMN =∠°,B 为AN 的中点,P 是直径MN 上一动点.(1)利用尺规作图,确定当PA PB +最小时P 点的位置 (2)(不写作法,但要保留作图痕迹). (2)求PA PB +的最小值. 【考点】圆,最短路线问题.【分析】(1)画出A 点关于MN 的称点A ',连接A 'B ,就可以得到P 点(2)利用30AMN =∠°得∠AON =∠ON A '=60°,又B 为弧AN 的中点,∴∠BON =30°,所以∠A 'ON =90°,再求最小值22. 【解答】解:,AC CD CAD BAE AB AE ∴∆∆∴==,,15AE BA BD BAD BDA ∴==∠=∠=︒30IBE ∴∠=︒Rt IBE∆222BE EI AE CD ====2BECD∴=EI AB ⊥I Rt IBE∆222BE EI AE CD ====2BECD∴=20(2017湖北黄冈).已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.求证:(1)DE是⊙O的切线;(2)ME2=MD•MN.【考点】S9:相似三角形的判定与性质;ME:切线的判定与性质.【分析】(1)求出OE∥DM,求出OE⊥DE,根据切线的判定得出即可;(2)连接EN,求出∠MDE=∠MEN,求出△MDE∽△MEN,根据相似三角形的判定得出即可.【解答】证明:(1)∵ME平分∠DMN,∵OM=OE,∴∠OME=∠OEM,∴∠DME=∠OEM,∴OE ∥DM , ∵DM ⊥DE , ∴OE ⊥DE , ∵OE 过O , ∴DE 是⊙O 的切线; (2) 连接EN ,∵DM ⊥DE ,MN 为⊙O 的半径, ∴∠MDE=∠MEN=90°, ∵∠NME=∠DME , ∴△MDE ∽△MEN , ∴=,∴ME 2=MD •MN23. (2017湖北十堰)已知AB 为半⊙O 的直径,BC ⊥AB 于B ,且BC =AB ,D 为半⊙O 上的一点,连接BD 并延长交半⊙O 的切线AE 于E . (1) 如图1,若CD =CB ,求证:CD 是⊙O 的切线; (2) 如图2,若F 点在OB 上,且CD ⊥DF ,求AEAF的值.(1)证明:略;(此问简单) (2)连接AD . ∵DF ⊥DC ∴∠1+∠BDF =90° ∵AB 是⊙O 的直径CEC∵∠3+∠EAD =90°,∠E+∠EAD =90° ∴∠3=∠E又∵∠ADE=∠ADB=90° ∴△AD E ~△ABD∴AE ADAB BD =∴AE AF =∴∠2+∠BDF =90° ∴∠1=∠2又∵∠3+∠ABD =90°, ∠4+∠ABD =90° ∴∠3=∠4 ∴△ADF ~△BCDAF ADBC BD=21.(2017湖北武汉)如图,△ABC 内接于⊙O ,AB =AC ,CO 的延长线交AB 于点D (1) 求证:AO 平分∠BAC(2) 若BC =6,sin ∠BAC =53,求AC 和CD 的长【答案】(1)证明见解析;(2);.(2)过点C 作CE ⊥AB 于E∵sin ∠BAC =,设AC =5m ,则CE =3m ∴AE =4m ,BE =m在Rt ΔCBE 中,m 2+(3m )2=36 ∴m =, ∴AC =延长AO 交BC 于点H ,则AH ⊥BC ,且BH =CH =3,考点:1.全等三角形的判定与性质;2.解直角三角形;3.平行线分线段成比例.21. (2017湖北咸宁)如图,在ABC ∆中,AC AB =,以AB 为直径的⊙O 与边AC BC ,分别交于E D ,两点,过点D 作AC DF ⊥,垂足为点F . ⑴求证:DF 是⊙O 的切线;⑵若52cos ,4==A AE ,求DF 的长【考点】ME :切线的判定与性质;KH :等腰三角形的性质;T7:解直角三角形.【分析】(1)证明:如图,连接OD ,作OG ⊥AC 于点G ,推出∠ODB=∠C ;然后根据DF ⊥AC ,∠DFC=90°,推出∠ODF=∠DFC=90°,即可推出DF 是⊙O 的切线.(2)首先判断出:AG=AE=2,然后判断出四边形OGFD 为矩形,即可求出DF 的值是多少. 【解答】(1)证明:如图,连接OD ,作OG ⊥AC 于点G , ∵OB=OD ,∴∠ODB=∠B , 又∵AB=AC , ∴∠C=∠B , ∴∠ODB=∠C , ∵DF ⊥AC , ∴∠DFC=90°, ∴∠ODF=∠DFC=90°, ∴DF 是⊙O 的切线.(2)解:AG=AE=2, ∵cosA=, ∴OA===5,∴OG==,∵∠ODF=∠DFG=∠OGF=90°, ∴四边形OGFD 为矩形, ∴DF=OG=.23(2017湖北孝感). 如图,O 的直径10,AB =弦6,AC ACB=∠的平分线交O于,D过点D作DE AB交CA延长线于点E,连接,.AD BD(1)由AB,BD,AD围成的曲边三角形的面积是;(2)求证:DE是O的切线;(3)求线段DE的长.【分析】(1)连接OD,由AB是直径知∠ACB=90°,结合CD平分∠ACB知∠ABD=∠ACD=∠ACB=45°,从而知∠AOD=90°,根据曲边三角形的面积=S扇形AOD +S△BOD可得答案;(2)由∠AOD=90°,即OD⊥AB,根据DE∥AB可得OD⊥DE,即可得证;(3)勾股定理求得BC=8,作AF⊥DE知四边形AODF是正方形,即可得DF=5,由∠EAF=90°﹣∠CAB=∠ABC知tan∠EAF=tan∠CBA,即=,求得EF的长即可得.【解答】解:(1)如图,连接OD,∵AB是直径,且AB=10,∴∠ACB=90°,AO=BO=DO=5,∵CD平分∠ACB,∴∠ABD=∠ACD=∠ACB=45°,∴∠AOD=90°,则曲边三角形的面积是S扇形AOD +S△BOD=+×5×5=+,故答案为: +;(2)由(1)知∠AOD=90°,即OD⊥AB,∵DE∥AB,∴OD⊥DE,∴DE是⊙O的切线;(3)∵AB=10、AC=6,∴BC==8,过点A作AF⊥DE于点F,则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,∴tan∠EAF=tan∠CBA,∴=,即=,∴,∴DE=DF+EF=+5=.【点评】本题主要考查切线的判定、圆周角定理、正方形的判定与性质及正切函数的定义,熟练掌握圆周角定理、切线的判定及三角函数的定义是解题的关键.25(2017湖北荆州).如图在平面直角坐标系中,直线y=﹣x+3与x轴、y轴分别交于A、B两点,点P、Q同时从点A出发,运动时间为t秒.其中点P沿射线AB运动,速度为每秒4个单位长度,点Q沿射线AO运动,速度为每秒5个单位长度.以点Q为圆心,PQ长为半径作⊙Q.(1)求证:直线AB是⊙Q的切线;(2)过点A左侧x轴上的任意一点C(m,0),作直线AB的垂线CM,垂足为M.若CM与⊙Q相切于点D,求m与t的函数关系式(不需写出自变量的取值范围);(3)在(2)的条件下,是否存在点C,直线AB、CM、y轴与⊙Q同时相切?若存在,请直接写出此时点C的坐标;若不存在,请说明理由.【考点】FI:一次函数综合题.【分析】(1)只要证明△PAQ∽△BAO,即可推出∠APQ=∠AOB=90°,推出QP⊥AB,推出AB是⊙O的切线;(2)分两种情形求解即可:①如图2中,当直线CM在⊙O的左侧与⊙Q相切时,设切点为D,则四边形PQDM是正方形.②如图3中,当直线CM在⊙O的右侧与⊙Q相切时,设切点为D,则四边形PQDM 是正方形.分别列出方程即可解决问题.(3)分两种情形讨论即可,一共有四个点满足条件.【解答】(1)证明:如图1中,连接QP.在Rt△AOB中,OA=4,OB=3,∴AB==5,∵AP=4t,AQ=5t,∴==,∵∠PAQ=∠BAO,∴△PAQ∽△BAO,∴∠APQ=∠AOB=90°,∴QP⊥AB,∴AB是⊙O的切线.(2)解:①如图2中,当直线CM在⊙O的左侧与⊙Q相切时,设切点为D,则四边形PQDM是正方形.易知PQ=DQ=3t,CQ=•3t=,∵OC+CQ+AQ=4,∴m+t+5t=4,∴m=4﹣t.②如图3中,当直线CM在⊙O的右侧与⊙Q相切时,设切点为D,则四边形PQDM是正方形.∵OC+AQ﹣CQ=4,∴m+5t﹣t=4,∴m=4﹣t.(3)解:存在.理由如下:如图4中,当⊙Q 在y 则的右侧与y 轴相切时, 3t+5t=4,t=, 由(2)可知,m=﹣或.如图5中,当⊙Q 在y 则的左侧与y 轴相切时,5t ﹣3t=4,t=2,由(2)可知,m=﹣或.综上所述,满足条件的点C 的坐标为(﹣,0)或(,0)或(﹣,0)或(,0).22.(2017湖北鄂州)如图,已知BF 是⊙O 的直径,A 为 ⊙O 上(异于B 、F )一点. ⊙O 的切线MA与FB 的延长线交于点M ;P 为AM 上一点,PB 的延长线交⊙O 于点C ,D 为BC 上一点且PA =PD ,AD 的延长线交⊙O 于点E . (1)求证:BE = CE ;(2)若ED 、EA 的长是一元二次方程x 2-5x +5=0的两根,求BE 的长;(3)若MA ,1sin 3AMF ∠= , 求AB 的长.(1)∵PA =PD ∴∠PAD=∠PDA∴∠BAD+∠PAB=∠DBE+∠E ∵⊙O 的切线MA ∴∠PAB=∠DBE∴∠BAD=∠CBE ∴BE = CE(2)∵ED、EA的长是一元二次方程x2-5x+5=0的两根、∴ED·EA=5∵∠BAD=∠CBE,∠E=∠E∴△BDE∽△ABE∴BE2=ED·EA=5 ∴BE=521.(2017湖北黄石)如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.(1)求证:DB=DE;(2)求证:直线CF为⊙O的切线.【考点】MI:三角形的内切圆与内心;MD:切线的判定.【分析】(1)欲证明DB=DE,只要证明∠DBE=∠DEB;(2)欲证明直线CF为⊙O的切线,只要证明BC⊥CF即可;【解答】(1)证明:∵E是△ABC的内心,∴∠BAE=∠CAE,∠EBA=∠EBC,∵∠BED=∠BAE+∠EBA,∠DBE=∠EBC+∠DBC,∠DBC=∠EAC,∴∠DBE=∠DEB,∴DB=DE.(2)连接CD.∵DA平分∠BAC,∴∠DAB=∠DAC,∴=,∴BD=CD,∵BD=DF,∴CD=DB=DF,∴∠BCF=90°,∴BC⊥CF,∴CF是⊙O的切线.23(2017湖北恩施).如图,AB、CD是⊙O的直径,BE是⊙O的弦,且BE∥CD,过点C的切线与EB 的延长线交于点P,连接BC.(1)求证:BC平分∠ABP;(2)求证:PC2=PB•PE;(3)若BE﹣BP=PC=4,求⊙O的半径.【考点】MC:切线的性质;KD:全等三角形的判定与性质;S9:相似三角形的判定与性质.【分析】(1)由BE∥CD知∠1=∠3,根据∠2=∠3即可得∠1=∠2;(2)连接EC、AC,由PC是⊙O的切线且BE∥DC,得∠1+∠4=90°,由∠A+∠2=90°且∠A=∠5知∠5+∠2=90°,根据∠1=∠2得∠4=∠5,从而证得△PBC∽△PCE即可;(3)由PC2=PB•PE、BE﹣BP=PC=4求得BP=2、BE=6,作EF⊥CD可得PC=FE=4、FC=PE=8,再Rt△DEF ≌Rt△BCP得DF=BP=2,据此得出CD的长即可.【解答】解:(1)∵BE ∥CD , ∴∠1=∠3, 又∵OB=OC , ∴∠2=∠3,∴∠1=∠2,即BC 平分∠ABP ; (2)如图,连接EC 、AC , ∵PC 是⊙O 的切线, ∴∠PCD=90°, 又∵BE ∥DC , ∴∠P=90°, ∴∠1+∠4=90°,[ ∵AB 为⊙O 直径, ∴∠A+∠2=90°, 又∠A=∠5, ∴∠5+∠2=90°, ∵∠1=∠2, ∴∠5=∠4, ∵∠P=∠P , ∴△PBC ∽△PCE , 即PC 2=PB •PE ; (3)∵BE ﹣BP=PC=4, ∴BE=4+BP ,∵PC 2=PB •PE=PB •(PB+BE ),∴42=PB •(PB+4+PB ),即PB 2+2PB ﹣8=0, 解得:PB=2, 则BE=4+PB=6, ∴PE=PB+BE=8, 作EF ⊥CD 于点F , ∵∠P=∠PCF=90°, ∴四边形PCFE 为矩形,∴PC=FE=4,FC=PE=8,∠EFD=∠P=90°, ∵BE ∥CD , ∴DE=BC ,在Rt △DEF 和Rt △BCP 中, ∴Rt △DEF ≌Rt △BCP (HL ), ∴DF=BP=2, 则CD=DF+CF=10, ∴⊙O 的半径为5.22(2017湖北随州).如图,在Rt △ABC 中,∠C=90°,AC=BC ,点O 在AB 上,经过点A 的⊙O 与BC 相切于点D ,交AB 于点E . (1)求证:AD 平分∠BAC ;(2)若CD=1,求图中阴影部分的面积(结果保留π).【考点】MC :切线的性质;KF :角平分线的性质;KW :等腰直角三角形;MO :扇形面积的计算. 【分析】(1)连接DE ,OD .利用弦切角定理,直径所对的圆周角是直角,等角的余角相等证明∠DAO=∠CAD ,进而得出结论;(2)根据等腰三角形的性质得到∠B=∠BAC=45°,由BC 相切⊙O 于点D ,得到∠ODB=90°,求得OD=BD ,∠BOD=45°,设BD=x ,则OD=OA=x ,OB=x ,根据勾股定理得到BD=OD=,于是得到结论.【解答】(1)证明:连接DE ,OD . ∵BC 相切⊙O 于点D , ∴∠CDA=∠AED , ∵AE 为直径, ∴∠ADE=90°, ∵AC ⊥BC , ∴∠ACD=90°, ∴∠DAO=∠CAD , ∴AD 平分∠BAC ;(2)∵在Rt △ABC 中,∠C=90°,AC=BC , ∴∠B=∠BAC=45°,∵BC 相切⊙O 于点D , ∴∠ODB=90°,∴OD=BD ,∴∠BOD=45°, 设BD=x ,则OD=OA=x ,OB=x ,∴BC=AC=x+1, ∵AC 2+BC 2=AB 2, ∴2(x+1)2=(x+x )2,∴x=,∴BD=OD=,∴图中阴影部分的面积=S △BOD ﹣S 扇形DOE=﹣=1﹣.22(2017湖北襄阳).如图,AB 为⊙O 的直径,C 、D 为⊙O 上的两点,∠BAC=∠DAC ,过点C 做直线EF ⊥AD ,交AD 的延长线于点E ,连接BC .(1)求证:EF是⊙O的切线;(2)若DE=1,BC=2,求劣弧的长l.【考点】ME:切线的判定与性质;MN:弧长的计算.【分析】(1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;(2)连接OD,DC,根据角平分线的定义得到∠DAC=∠OAC,根据三角函数的定义得到∠ECD=30°,得到∠OCD=60°,得到∠BOC=∠COD=60°,OC=2,于是得到结论.【解答】(1)证明:连接OC,∵OA=OC,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∵∠AEC=90°,∴∠OCF=∠AEC=90°,∴EF是⊙O的切线;(2)连接OD,DC,∵∠DAC=DOC,∠OAC=BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l==π.21(2017湖北宜昌).已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.(1)求证:DE=OE;(2)若CD∥AB,求证:四边形ABCD是菱形.【考点】MC:切线的性质;L9:菱形的判定.【分析】(1)先判断出∠2+∠3=90°,再判断出∠1=∠2即可得出结论;(2)先判断出△ABO≌△CDE得出AB=CD,即可判断出四边形ABCD是平行四边形,最后判断出CD=AD 即可.【解答】解:(1)如图,连接OD,∵CD是⊙O的切线,∴OD⊥CD,∴∠2+∠3=∠1+∠COD=90°,∵DE=EC,∴∠1=∠2,∴∠3=∠COD,∴DE=OE;(2)∵OD=OE,∴OD=DE=OE,∴∠3=∠COD=∠DEO=60°,∴∠2=∠1=30°,∵OA=OB=OE,OE=DE=EC,∴OA=OB=DE=EC,∵AB∥CD,∴∠4=∠1,∴∠1=∠2=∠4=∠OBA=30°,∴△ABO≌△CDE,∴AB=CD,∴四边形A∴D是平行四边形,∴∠DAE=∠DOE=30°,∴∠1=∠DAE,∴CD=AD,∴▱ABCD是菱形.24(2017江苏南通).如图,Rt △ABC 中,∠C=90°,BC=3,点O 在AB 上,OB=2,以OB 为半径的⊙O 与AC 相切于点D ,交BC 于点E ,求弦BE 的长.【考点】MC :切线的性质;KQ :勾股定理.【分析】连接OD ,首先证明四边形OECD 是矩形,从而得到BE 的长,然后利用垂径定理求得BF 的长即可.【解答】解:连接OD ,作OE ⊥BF 于点E . ∴BE=BF , ∵AC 是圆的切线, ∴OD ⊥AC ,∴∠ODC=∠C=∠OFC=90°, ∴四边形ODCF 是矩形, ∵OD=OB=EC=2,BC=3, ∴BE=BC ﹣EC=BC ﹣OD=3﹣2=1, ∴BF=2BE=2.26(2017江苏镇江).如图,ACB Rt ∆中,090=∠C ,点D 在AC 上,A CBD ∠=∠,过D A ,两点的圆的圆心O 在AB 上.(1)利用直尺和圆规在图1中画出⊙O (不写作法,保留作图痕迹,并用黑色水笔把线条描清楚);(2)判断BD 所在直线与(1)中所作的⊙O 的位置关系,并证明你的结论;(3)设⊙O 交AB 于点E ,连接DE ,过点E 作BC EF ⊥,F 为垂足.若点D 是线段AC 的黄金分割点(即ACADAD DC =,)如图2,试说明四边形DEFC 是正方形.25(2017江苏扬州).如图,已知平行四边形OABC 的三个顶点A 、B 、C 在以O 为圆心的半圆上,过点C 作CD ⊥AB ,分别交AB 、AO 的延长线于点D 、E ,AE 交半圆O 于点F ,连接CF . (1)判断直线DE 与半圆O 的位置关系,并说明理由; (2)①求证:CF=OC ;②若半圆O 的半径为12,求阴影部分的周长.【考点】MB :直线与圆的位置关系;L5:平行四边形的性质;MN :弧长的计算.【分析】(1)结论:DE 是⊙O 的切线.首先证明△ABO ,△BCO 都是等边三角形,再证明四边形BDCG 是矩形,即可解决问题;(2)①只要证明△OCF 是等边三角形即可解决问题; ②求出EC 、EF 、弧长CF 即可解决问题. 【解答】解:(1)结论:DE 是⊙O 的切线. 理由:∵四边形OABC 是平行四边形, 又∵OA=OC ,∴四边形OABC 是菱形, ∴OA=OB=AB=OC=BC ,∴△ABO ,△BCO 都是等边三角形, ∴∠AOB=∠BOC=∠COF=60°, ∵OB=OF ,∴OG ⊥BF ,∵AF 是直径,CD ⊥AD ,∴∠ABF=∠DBG=∠D=∠BGC=90°, ∴四边形BDCG 是矩形, ∴∠OCD=90°, ∴DE 是⊙O 的切线.(2)①由(1)可知:∠COF=60°,OC=OF ,∴△OCF 是等边三角形, ∴CF=OC .②在Rt △OCE 中,∵OC=12,∠COE=60°,∠OCE=90°, ∴OE=2OC=24,EC=12,∵OF=12, ∴EF=12, ∴的长==4π,∴阴影部分的周长为4π+12+12.24(2017江苏盐城).如图,△ABC 是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O 的圆形纸片放置在三角板内部.(1) 如图①,当圆形纸片与两直角边AC 、BC 都相切时, (2) 试用直尺与圆规作出射线CO ; (3) (不写作法与证明,保留作图痕迹)(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周, 回到起点位置时停止,若BC=9,圆形纸片的半径为2, 求圆心O 运动的路径长.【考点】O4:轨迹;MC :切线的性质;N3:作图—复杂作图.【分析】(1)作∠ACB 的平分线得出圆的一条弦,再作此弦的中垂线可得圆心O ,作射线CO 即可; (2)添加如图所示辅助线,圆心O 的运动路径长为,先求出△ABC 的三边长度,得出其周长,证四边形OEDO 1、四边形O 1O 2HG 、四边形OO 2IF 均为矩形、四边形OECF 为正方形,得出∠OO 1O 2=60°=∠ABC 、∠O 1OO 2=90°,从而知△OO 1O 2∽△CBA ,利用相似三角形的性质即可得出答案. 【解答】解:(1)如图①所示,射线OC 即为所求;(2)如图,圆心O 的运动路径长为,过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB,垂足分别为点D、F、G,过点O作OE⊥BC,垂足为点E,连接O2B,过点O2作O2H⊥AB,O2I⊥AC,垂足分别为点H、I,在Rt△ABC中,∠ACB=90°、∠A=30°,∴AC===9,AB=2BC=18,∠ABC=60°,∴C△ABC=9+9+18=27+9,∵O1D⊥BC、O1G⊥AB,∴D、G为切点,∴BD=BG,在Rt△O1BD和Rt△O1BG中,∵,∴△O1BD≌△O1BG(HL),∴∠O1BG=∠O1BD=30°,在Rt△O1BD中,∠O1DB=90°,∠O1BD=30°,∴BD===2,∴OO1=9﹣2﹣2=7﹣2,∵O1D=OE=2,O1D⊥BC,OE⊥BC,∴O1D∥OE,且O1D=OE,∴四边形OEDO1为平行四边形,∵∠OED=90°,∴四边形OEDO1为矩形,同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形,又OE=OF,∴四边形OECF为正方形,∵∠O1GH=∠CDO1=90°,∠ABC=60°,∴∠GO1D=120°,又∵∠FO1D=∠O2O1G=90°,∴∠OO1O2=360°﹣90°﹣90°=60°=∠ABC,同理,∠O1OO2=90°,∴△OO1O2∽△CBA,∴=,即=,∴=15+,即圆心O运动的路径长为15+.25(2017江苏盐城).如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.(1)求证:BC是⊙F的切线;(2)若点A、D的坐标分别为A(0,﹣1),D(2,0),求⊙F的半径;试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.【考点】MR:圆的综合题.【分析】(1)连接EF,根据角平分线的定义、等腰三角形的性质得到∠FEA=∠EAC,得到FE∥AC,根据平行线的性质得到∠FEB=∠C=90°,证明结论;(2)连接FD,设⊙F的半径为r,根据勾股定理列出方程,解方程即可;(3)作FR⊥AD于R,得到四边形RCEF是矩形,得到EF=RC=RD+CD,根据垂径定理解答即可.【解答】(1)证明:连接EF,∵AE平分∠BAC,∴∠FAE=∠CAE,∵FA=FE,∴∠FAE=∠FEA,∴∠FEA=∠EAC,∴FE∥AC,∴∠FEB=∠C=90°,即BC是⊙F的切线;(2)解:连接FD,设⊙F的半径为r,则r2=(r﹣1)2+22,解得,r=,即⊙F的半径为;(3)解:AG=AD+2CD.证明:作FR⊥AD于R,则∠FRC=90°,又∠FEC=∠C=90°,∴四边形RCEF是矩形,∴EF=RC=RD+CD,∵FR⊥AD,∴AR=RD,∴EF=RD+CD=AD+CD,∴AG=2FE=AD+2CD.27、(2017•苏州)如图,已知内接于,是直径,点在上,,过点作,垂足为,连接交边于点.(1)求证:∽;(2)求证:;(3)连接,设的面积为,四边形的面积为,若,求的值.(1)证明:∵AB是圆O的直径,∴∠ACB=90°,∵DE⊥AB,∴∠DEO=90°,∴∠DEO=∠ACB,∵OD//BC,∴∠DOE=∠ABC,∴△DOE~△ABC,(2)证明:∵△DOE~△ABC,∴∠ODE=∠A,∵∠A和∠BDC是弧BC所对的圆周角,∴∠A=∠BDC,∴∠ODE=∠BDC,∴∠ODF=∠BDE。
2017全国中考数学真题 与圆的有关计算(选择题+填空题+解答题)解析版

15. 7.(2017 湖北咸宁,7,3 分)如图,⊙O 的半径为 3,四边形 ABCD 内接于⊙O,连接 OB、OD,若∠ BOD=∠ BCD,
则 BD 的长为( )
A.
B. 3 2
C. 2
D. 3
答案:C
解析:∵∠ BAD= 1 ∠ BOD= 1 ∠ BCD,∠ BAD+∠ BCD=180°,
转动五次 A 的路线长是:错误!未找到引用源。,
以此类推,每四次循环,
5
2017 全国中考数学真题(精品文档)
故顶点 A 转动四次经过的路线长为: 2 5 3 6 , 22
∵2017÷4=504……1
∴这样连续旋转 2016 次后,顶点 A 在整个旋转过程中所经过的路程之和是:6π×504+2π=3026π.故选:D.
18. (2017 江苏宿迁,3 分)若将半径为 12cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是
A.2cm
B.3cm
C.4cm
D.6cm
答案:D,解析:根据圆锥底面圆周长=扇形弧长,即 l=C 得 12π=2πr,所以 r=6.
19. (2017 甘肃天水.9.4 分)如图所示,AB 是圆 O 的直径,弦 CD⊥AB.垂足为 E,∠BCD=30°,CD=4 3 ,则
A.68πcm2
B.74πcm2
C.84πcm2
答案:C 解析:圆锥的表面积加上圆柱的侧面积即可求得其表面积.
D.100πcm2
5. 2. (2017 重庆,9,4 分)如图,矩形 ABCD 的边 AB=1,BE 平分∠ABC,交 AD 于点 E,若点 E 是 AD 的中点,
以点 B 为圆心,BE 长为半径画弧,交 BC 于点 F,则图中阴影部分的面积是(
初三关于圆的试题及答案

初三关于圆的试题及答案一、选择题(每题3分,共30分)1. 下列说法中,正确的是()A. 圆的直径是圆的半径的两倍B. 圆周率π是一个无限不循环小数C. 圆的周长与直径成正比例D. 圆的面积与半径的平方成正比例2. 圆的周长公式是()A. C = 2πrB. C = πdC. C = πrD. C = 2πd3. 圆的面积公式是()A. S = πr²B. S = 2πrC. S = πd²D. S = πd4. 一个圆的半径是5厘米,那么它的直径是()A. 10厘米B. 15厘米C. 20厘米D. 25厘米5. 如果一个圆的半径增加一倍,那么它的面积将增加()A. 1倍B. 2倍C. 4倍D. 8倍6. 一个圆的周长是62.8厘米,那么它的半径是()A. 10厘米B. 15厘米C. 20厘米D. 25厘米7. 圆内接四边形的对角线()A. 相等B. 垂直C. 互相平分D. 互相垂直8. 圆的直径是圆内最长的线段,这种说法()A. 正确B. 错误9. 圆的切线()A. 与半径垂直B. 与直径垂直C. 与圆心垂直D. 与圆周平行10. 圆的内切圆与外切圆的半径之和等于()A. 内切圆的半径B. 外切圆的半径C. 两圆半径之和D. 两圆半径之差二、填空题(每题3分,共30分)1. 圆的周长公式是______,面积公式是______。
2. 如果圆的半径是3厘米,那么它的周长是______厘米,面积是______平方厘米。
3. 圆的直径是半径的______倍。
4. 圆的周长与直径的比值是______。
5. 圆的面积与半径的平方的比值是______。
6. 圆的切线与半径的交点是______。
7. 圆内接四边形的对角线互相______。
8. 圆的内切圆与外切圆的半径之和等于______。
9. 圆的直径是圆内最长的线段,这种说法是______。
10. 圆的周长是圆的直径的______倍。
三、解答题(每题10分,共40分)1. 已知一个圆的半径是4厘米,求它的周长和面积。
江苏省中考数学真题《圆》专题汇编(选择、填空)(含解析)
2017年江苏省中考数学真题《圆》专题汇编(选择、填空)一、选择题1.(2017·南京第6题)过三点A (2,2),B (6,2),C (4,5)的圆的圆心坐标为( )A .(4,617) B .(4,3) C .(5,617) D .(5,3) 2.(2017·无锡第9题)如图,菱形ABCD 的边AB=20,面积为320,∠BAD <90°,⊙O 与边AB ,AD 都相切,AO=10,则⊙O 的半径长等于( ) A .5 B .6 C .52 D .23第2题图 第3题图 第4题图3.(2017·徐州第6题)如图,点A ,B ,C 在⊙O 上,∠AOB=72°,则∠ACB 等于( )A .28°B .54°C .18°D .36°4.(2017·苏州第9题)如图,在Rt △ABC 中,∠ACB=90°,∠A=56°.以BC 为直径的⊙O 交AB 于点D .E 是⊙O 上一点,且CE ⌒=CD⌒,连接OE .过点E 作EF ⊥OE ,交AC的延长线于点F ,则∠F 的度数为( )A .92°B .108°C .112°D .124°5.(2017·南通第6题)如图,圆锥的底面半径为2,母线长为6,则侧面积为( )A .4πB .6πC .12πD .16π第5题图 第6题图 第7题图6.(2017·南通第9题)已知∠AOB ,作图.步骤1:在OB 上任取一点M ,以点M 为圆心,MO 长为半径画半圆,分别交OA 、OB 于点P 、Q ;步骤2:过点M 作PQ 的垂线交PQ ⌒于点C ;步骤3:画射线OC .则下列判断:①PC ⌒=CQ⌒;②MC ∥OA ;③OP=PQ ;④OC 平分∠AOB ,其中正确的个数为( )A .1B .2C .3D .47.(2017·连云港第8题)如图所示,一动点从半径为2的⊙O 上的A 0点出发,沿着射线A 0O 方向运动到⊙O 上的点A 1处,再向左沿着与射线A 1O 夹角为60°的方向运动到⊙O 上的点A 2处;接着又从A 2点出发,沿着射线A 2O 方向运动到⊙O 上的点A 3处,再向左沿着与射线A 3O 夹角为60°的方向运动到⊙O 上的点A 4处;…按此规律运动到点A 2017处,则点A 2017与点A 0间的距离是( )A .4B .32C .2D .08.(2017·宿迁第6题)若将半径为12cm 的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径是( )A .2cmB .3cmC .4cmD .6cm二、填空题9.(2017·南京第15题)如图,四边形ABCD 是菱形,⊙O 经过点A 、C 、D ,与BC 相交于点E ,连接AC 、AE ,若78D ∠=︒,则EAC ∠= °.第9题图 第11题图 第12题图10.(2017·无锡第16题)若圆锥的底面半径为3cm ,母线长是5cm ,则它的侧面展开图的面积为 cm 2.11.(2017·无锡第17题)如图,已知矩形ABCD 中,AB=3,AD=2,分别以边AD ,BC 为直径在矩形ABCD 的内部作半圆O 1和半圆O 2,一平行于AB 的直线EF 与这两个半圆分别交于点E 、点F ,且EF=2(EF 与AB 在圆心O 1和O 2的同侧),则由AE ⌒,EF ,FB ⌒,AB 所围成图形(图中阴影部分)的面积等于 .12.(2017·徐州第17题)如图,AB 与⊙O 相切于点B ,线段OA 与弦BC 垂直,垂足为D ,AB=BC=2,则∠AOB= °.13.(2017·苏州第16题)如图,AB 是⊙O 的直径,AC 是弦,AC=3,∠BOC=2∠AOC .若用扇形OAC (图中阴影部分)围成一个圆锥的侧面,则这个圆锥底面圆的半径是 .第13题图 第15题图 第16题图14.(2017·南通第13题)四边形ABCD 内接于圆,若∠A=110°,则∠C= 度.15.(2017·连云港第14题)如图,线段AB 与⊙O 相切于点B ,线段AO 与⊙O 相交于点C ,AB=12,AC=8,则⊙O 的半径长为 .16.(2017·淮安第16题)如图,在圆内接四边形ABCD 中,若∠A ,∠B ,∠C 的度数之比为4:3:5,则∠D 的度数是 °.17.(2017·盐城第14题)如图,将⊙O 沿弦AB 折叠,点C 在AmB ⌒上,点D 在AB ⌒上,若∠ACB=70°,则∠ADB= °.第17题图 第18题图 第21题图18.(2017·扬州第15题)如图,已知⊙O 是△ABC 的外接圆,连接AO ,若∠B=40°,则∠OAC= °.19.(2017·泰州第12题)扇形的半径为3cm ,弧长为2πcm ,则该扇形的面积为 cm 2.20.(2017•常州第14题)已知圆锥的底面圆半径是1,母线是3,则圆锥的侧面积是 .21.(2017•常州第16题)如图,四边形ABCD 内接于⊙O ,AB 为⊙O 的直径,点C 为BD ⌒的中点,若∠DAB=40°,则∠ABC= °.22.(2017•镇江第6题)圆锥底面圆的半径为2,母线长为5,它的侧面积等于 (结果保留π).23.(2017•镇江第9题)如图,AB 是⊙O 的直径,AC 与⊙O 相切,CO 交⊙O 于点D ,若∠CAD=30°,则∠BOD= °.第23题图参考答案与解析1.【答案】A .【考点】坐标与图形性质.【分析】已知A (2,2),B (6,2),C (4,5),则过A 、B 、C 三点的圆的圆心,就是弦的垂直平分线的交点,故求得AB 的垂直平分线和BC 的垂直平分线的交点即可.【解答】解:已知A (2,2),B (6,2),C (4,5),∴AB 的垂直平分线是4262=+=x , 设直线BC 的解析式为)0(≠+=k b kx y ,把B (6,2),C (4,5)代入上式得:⎩⎨⎧=+=+5426b k b k ,解得⎪⎩⎪⎨⎧=-=1123b k ,1123+-=x y ,设BC 的垂直平分线为m x y +=32, 把线段BC 的中点坐标(5,27)代入得61=m ,∴BC 的垂直平分线是6132+=x y , 当4=x 时,617=y ,∴过A 、B 、C 三点的圆的圆心坐标为(4,617). 故选A .【点评】本题主要考查了待定系数法求一次函数的解析式,求两直线的交点,圆心是弦的垂直平分线的交点,理解圆心的作法是解决本题的关键.2.【答案】C .【考点】切线的性质;菱形的性质.【分析】如图作DH ⊥AB 于H ,连接BD ,延长AO 交BD 于E .利用菱形的面积公式求出DH ,再利用勾股定理求出AH ,BD ,由△AOF ∽△DBH ,可得:BHOF BD OA =,即可解决问题.【解答】解:如图作DH ⊥AB 于H ,连接BD ,延长AO 交BD 于E .∵菱形ABCD 的边AB=20,面积为320,∴AB •DH=320,∴DH=16,在Rt △ADH 中,1222=-=DH AD AH , ∴HB=AB-AH=8,在Rt △BDH 中,5822=+=BH DH BH ,设⊙O 与AB 相切于F ,连接OF .∵AD=AB ,OA 平分∠DAB ,∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,∴∠OAF=∠BDH ,∵∠AFO=∠DHB=90°,∴△AOF ∽△DBH , ∴BHOF BD OA =, ∴85810OF =, ∴52=OF .故选C .【点评】本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.3.【答案】D .【考点】圆周角定理.【分析】根据圆周角定理:同弧所对的圆周角等于同弧所对圆心角的一半即可求解.【解答】解:根据圆周角定理可知,∠AOB=2∠ACB=72°,即∠ACB=36°,故选D .【点评】本题主要考查了圆周角定理,正确认识∠ACB 与∠AOB 的位置关系是解题关键.4.【答案】C .【考点】圆心角、弧、弦的关系;多边形内角与外角.【分析】直接利用互余的性质再结合圆周角定理得出∠COE 的度数,再利用四边形内角和定理得出答案.【解答】解:∵∠ACB=90°,∠A=56°,∴∠ABC=34°,∵CE ⌒=CD⌒, ∴2∠ABC=∠COE=68°,又∵∠OCF=∠OEF=90°,∴∠F=360°-90°-90°-68°=112°.故选:C .【点评】此题主要考查了圆周角定理以及四边形内角和定理,正确得出∠OCE 的度数是解题关键.5.【答案】C .【考点】圆锥的计算.【分析】根据圆锥的底面半径为2,母线长为6,直接利用圆锥的侧面积公式求出它的侧面积.【解答】解:根据圆锥的侧面积公式:πrl=π×2×6=12π,故选C .【点评】本题主要考查了圆锥侧面积公式.熟练地应用圆锥侧面积公式求出是解决问题的关键.6.【答案】C .【考点】作图—复杂作图;圆周角定理.【分析】由OQ 为直径可得出OA ⊥PQ ,结合MC ⊥PQ 可得出OA ∥MC ,结论②正确;根据平行线的性质可得出∠PAO=∠CMQ ,结合圆周角定理可得出∠COQ=21∠POQ=∠BOQ ,进而可得出PC ⌒=CQ⌒,OC 平分∠AOB ,结论①④正确;由∠AOB 的度数未知,不能得出OP=PQ ,即结论③错误.综上即可得出结论.【解答】解:∵OQ 为直径,∴∠OPQ=90°,OA ⊥PQ .∵MC ⊥PQ ,∴OA ∥MC ,结论②正确;①∵OA ∥MC ,∴∠PAO=∠CMQ .∵∠CMQ=2∠COQ ,∴∠COQ=21∠POQ=∠BOQ , ∴PC ⌒=CQ⌒,OC 平分∠AOB ,结论①④正确; ∵∠AOB 的度数未知,∠POQ 和∠PQO 互余,∴∠POQ 不一定等于∠PQO ,∴OP 不一定等于PQ ,结论③错误.综上所述:正确的结论有①②④.故选C .【点评】本题考查了作图中的复杂作图、角平分线的定义、圆周角定理以及平行线的判定及性质,根据作图的过程逐一分析四条结论的正误是解题的关键.7.【答案】A .【考点】规律型:图形的变化类.【分析】根据题意求得A 0A 1=4,A 0A 2=32,A 0A 3=2,A 0A 4=32,A 0A 5=2,A 0A 6=0,A 0A 7=4,…于是得到A 2017与A 1重合,即可得到结论.【解答】解:如图,∵⊙O 的半径=2,由题意得,A 0A 1=4,A 0A 2=32,A 0A 3=2,A 0A 4=32,A 0A 5=2,A 0A 6=0,A 0A 7=4,…∵2017÷6=336…1,∴按此规律运动到点A 2017处,A 2017与A 1重合,∴A 0A 2017=2R=4.故选A .【点评】本题考查了图形的变化类,等边三角形的性质,解直角三角形,正确的作出图形是解题的关键.8.【答案】D .【考点】圆锥的计算.【分析】易得圆锥的母线长为12cm ,以及圆锥的侧面展开图的弧长,也就是圆锥的底面周长,除以2π即为圆锥的底面半径.【解答】解:圆锥的侧面展开图的弧长为2π×12÷2=12π(cm ),∴圆锥的底面半径为12π÷2π=6(cm ),故选:D .【点评】本题考查了圆锥的计算.用到的知识点为:圆锥的弧长等于底面周长.二、填空题9.【答案】27.【考点】圆周角定理;菱形的性质.【分析】根据菱形的性质得到∠ACB=21∠DCB=21(180°-∠D )=51°,根据圆内接四边形的性质得到∠AEB=∠D=78°,由三角形的外角的性质即可得到结论.【解答】解:∵四边形ABCD 是菱形,∠D=78°,∴∠ACB=21∠DCB=21(180°-∠D )=51°, ∵四边形AECD 是圆内接四边形,∴∠AEB=∠D=78°,∴∠EAC=∠AEB-∠ACE=27°,故答案为:27.【点评】本题考查了菱形的性质,三角形的外角的性质,圆内接四边形的性质,熟练掌握菱形的性质是解题的关键.10.【答案】15π.【考点】圆锥侧面积的计算.【分析】圆锥的侧面积=rl π.【解答】解:底面半径为3,母线为5,侧面面积=πππ1553=⨯⨯=rl【点评】本题利用圆锥侧面积公式求解.11.【答案】64353π--. 【考点】扇形面积的计算;矩形的性质.【分析】连接O 1O 2,O 1E ,O 2F ,过E 作EG ⊥O 1O 2,过F ⊥O 1O 2,得到四边形EGHF 是矩形,根据矩形的性质得到GH=EF=2,求得O 1G=21,得到∠O 1EG=30°,根据三角形、梯形、扇形的面积公式即可得到结果.【解答】解:连接O 1O 2,O 1E ,O 2F ,则四边形O 1O 2FE 是等腰梯形,过E 作EG ⊥O 1O 2,过FH ⊥O 1O 2,∴四边形EGHF 是矩形,∴GH=EF=2,∴O 1G=21, ∵O 1E=1, ∴GE=23, ∴2111=E O G O ; ∴∠O 1EG=30°,∴∠AO 1E=30°,同理∠BO 2F=30°,∴阴影部分的面积=S 矩形ABO 2O 1-2S 扇形AO 1E-S 梯形EFO 2O 1=3×1-2×3601302⨯⋅π-21(2+3)×23=3-435-6π. 故答案为:3-435-6π. 【点评】本题考查了扇形面积的计算,矩形的性质,梯形的性质,正确的作出辅助线是解题的关键.12.【答案】60.【考点】切线的性质.【分析】由垂径定理易得BD=1,通过解直角三角形ABD 得到∠A=30°,然后由切线的性质和直角三角形的两个锐角互余的性质可以求得∠AOB 的度数.【解答】解:∵OA ⊥BC ,BC=2,∴根据垂径定理得:BD=21BC=1. 在Rt △ABD 中,sin ∠A=AB BD =21. ∴∠A=30°.∵AB 与⊙O 相切于点B ,∴∠ABO=90°.∴∠AOB=60°.故答案是:60.【点评】本题主要考查的圆的切线性质,垂径定理和一些特殊三角函数值,有一定的综合性.13.【答案】21. 【考点】圆锥的计算.【分析】根据平角的定义得到∠AOC=60°,推出△AOC 是等边三角形,得到OA=3,根据弧长的规定得到AC ⌒的长度=ππ=⨯⋅180360,于是得到结论. 【解答】解:∵∠BOC=2∠AOC ,∠BOC+∠AOC=180°,∴∠AOC=60°,∵OA=OC ,∴△AOC 是等边三角形,∴OA=3,∴AC ⌒的长度=ππ=⨯⋅180360, ∴圆锥底面圆的半径=21, 故答案为:21. 【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.14.【答案】70.【考点】圆内接四边形的性质.【分析】根据圆内接四边形的性质计算即可.【解答】解:∵四边形ABCD 内接于⊙O ,∴∠A+∠C=180°,∵∠A=110°,∴∠C=70°,故答案为:70.【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.15.【答案】5.【考点】切线的性质.【分析】连接OB ,根据切线的性质求出∠ABO=90°,在△ABO 中,由勾股定理即可求出⊙O 的半径长.【解答】解:连接OB ,∵AB 切⊙O 于B ,∴OB ⊥AB ,∴∠ABO=90°,设⊙O 的半径长为r ,由勾股定理得:r 2+122=(8+r )2,解得r=5.故答案为:5.【点评】本题考查了切线的性质和勾股定理的应用,关键是得出直角三角形ABO ,主要培养了学生运用性质进行推理的能力.16.【答案】120.【考点】圆内接四边形的性质.【分析】设∠A=4x ,∠B=3x ,∠C=5x ,根据圆内接四边形的性质求出x 的值,进而可得出结论.【解答】解:∵∠A ,∠B ,∠C 的度数之比为4:3:5,∴设∠A=4x ,则∠B=3x ,∠C=5x .∵四边形ABCD 是圆内接四边形,∴∠A+∠C=180°,即4x +5x =180°,解得x =20°,∴∠B=3x =60°,∴∠D=180°-60°=120°.故答案为:120.【点评】本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.17.【答案】110.【考点】圆周角定理.【分析】根据折叠的性质和圆内接四边形的性质即可得到结论.【解答】解:∵点C 在AmB ⌒上,点D 在AB ⌒上,若∠ACB=70°,∴∠ADB+∠ACB=180°,∴∠ADB=110°,故答案为:110.【点评】本题考查了折叠的性质和圆内接四边形的性质,熟练掌握折叠的直线是解题的关键.18.【答案】50.【考点】圆周角定理.【分析】连接CO ,根据圆周角定理可得∠AOC=2∠B=80°,进而得出∠OAC 的度数.【解答】解:连接CO ,∵∠B=40°,∴∠AOC=2∠B=80°,∴∠OAC=(180°-80°)÷2=50°.故答案为:50.【点评】此题主要考查了圆周角定理,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.19.【答案】3π.【考点】扇形面积的计算;弧长的计算.【分析】先用弧长公式求出扇形的圆心角的度数,然后用扇形的面积公式求出扇形的面积.【解答】解:设扇形的圆心角为n ,则:18032⋅⋅=ππn ,得:n =120°. ∴S 扇形=36031202⋅⋅π=3π cm 2. 故答案为:3π.【点评】本题考查的是扇形面积的计算,根据题意先求出扇形的圆心角的度数,再计算扇形的面积.20.【答案】3π.【考点】圆锥侧面积的计算.【分析】圆锥的侧面积=rl π.【解答】解:底面半径为1,母线为3,侧面面积=πππ331=⨯⨯=rl【点评】本题利用圆锥侧面积公式求解.21.【答案】70.【考点】圆的内接四边形的性质、圆周角定理推论.【分析】连接BD ,根据AB 为直径,求出∠DBA=50°;再根据圆的内接四边形的性质可得:∠C=180°-40°=140°,又点C 为BD ⌒的中点,可得CD=BC ,求出∠CBD=20°,∠ABC=∠ABD+∠CBD=50°+20°=70°.【解答】解:连接BD ,∵AB 为直径,∴∠ADB=90°,又∵∠DAB=40°,∴∠DBA=50°,根据圆的内接四边形的性质可得:∠C=180°-40°=140°,又点C 为BD ⌒的中点, ∴CD=BC ,∴∠CDB=∠CBD=︒=︒-︒202140180, ∴∠ABC=∠ABD+∠CBD=50°+20°=70°【点评】本题利用圆的内接四边形的性质、圆周角定理推论求解.22.【答案】10π.【考点】圆锥侧面积的计算.【分析】圆锥的侧面积=rl π.【解答】解:底面半径为2,母线为5,侧面面积=πππ1052=⨯⨯=rl【点评】本题利用圆锥侧面积公式求解.23.【答案】120.【考点】切线的性质、等腰三角形的性质、外角定理.【分析】根据AC 是切线,可得:∠OAC=90°,结合∠CAD=30°,可得∠OAD=60°,根据等腰三角形的性质和外角定理即可得到结果.【解答】解:∵AC 是⊙O 的切线,∴∠OAC=90°,∵∠CAD=30°,∴∠OAD=60°.∵OA=OD ,∴∠ODA=∠OAD=60°.∴∠BOD=∠ODA+∠OAD =120°.【点评】本题利用切线的性质、等腰三角形的性质、外角定理求解.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图,在△ABC中,E是AC边上的一点,且AE=A B,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点
D,交BE 于点 F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
2、如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥Ac,垂足为
E,⊙O 经过 A、B、Di 三点,
(1)求证:AB 是⊙O 的直径;
(2)判断 DE 与⊙O 的位置关系,并加以证明;
(3)若⊙O 的半径为 3,∠BAC=60。
,求 DE 的长.
3、如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB 的延长线上,∠AED=∠ABC
(1)求证:DE与⊙O相切;
(2)若BF=2,DF= ,求⊙O的半径.
4、如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA 交△ABC 的外接圆于点 F,连接 FB,FC.(1)求证:∠FBC=∠FCB;
(2)已知FA•FD=12,若AB是△ABC外
接圆的直径,FA=2,求CD的长.5、如图,AB是⊙O的直径,点C在AB
的延长线上,CD与⊙O相切于点D,
CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.
6、如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB。
(1)求证:AB是圆的切
线;
(2)若点E是BC上一点,已知BE=4 ,tan∠AEB =,
AB∶BC=2∶3,求圆的直径.
7、如图,在△ABC中,∠C=90°,∠BAC的平分线交BC
于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB 于点 E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2,BF=2,求阴影部分的面积(结果保留π)
8、如图,AB为⊙O的直径,
C 是⊙O 上一点,过点 C 的直线
交AB的延长线于点D,
AE⊥DC,垂足为 E,F 是 AE
与⊙O的交点,AC平分
∠BAE.(1)求证:DE是⊙O
的切线;(2)若AE=6,
∠D=30°,求图中阴影部分的面
积.
9、如图,AB是⊙O的直径,C是⊙O上的一
点,直线MN经过点C,过点A作直线MN的
垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD= 30°,求⊙O的半径.
10、如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.(1)求证:BE是⊙O的切线;
(2)若BC= ,AC=5,求圆的直径AD及切线
BE 的长.
11、如图,在Rt△ABC中,∠ACB=90º,AO是△ABC
的角平分线。
以O为圆心,OC为半径作⊙O。
(1)求证:AB是⊙O的切线。
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD =,求的值。
(3)在(2)的条件下,设⊙O的半径为3,求AB的长。
12、如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结 BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
13、如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
14、如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.(1)求证:CE是⊙O的切线;
(2)若AC=4,BC=2,求BD和CE的长.
15、如图,点D在⊙O的直径AB的延长线上,点C在
⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
16、如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC 相交于点 E,连接 EF,过 F 作 FG⊥BC 于点 G,其中∠OFE= ∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB= ,⊙O的半径为r,求△EHG的面积
(用含r的代数式表示).17、如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点 F 为 OC 与⊙O 的交点,连接 AF.(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的
面积.
18、如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切
线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长.
19、如图,以△ABC的BC边上一点O为圆心,经过A, C 两点且与 BC 边交于点 E,点 D 为 CE 的下半圆弧的中点,连接 AD 交线段 EO 于点F,若 AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF= ,求⊙O的半径r及sinB.
20、如图,已知AB为半圆O的直径,C为半圆
O 上一点,连接 AC,BC,过点 O 作 OD⊥AC 于
点D,过点 A 作半圆 O 的切线交 OD 的延长线于
点E,连接 BD 并延长交 AE 于点 F.
(1)求证:AE•BC=AD•AB;
(2)若半圆O的直径为10,sin∠BAC= ,
求AF 的长.
21、如图,在平面直角坐标系xOy中,以点O为圆心的圆
分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣
弧的长为π,直线 y=﹣x+4 与 x 轴、y 轴分别交于
点A、B.
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
22、如图,在Rt ABC中,∠ACB=90°,∠BAC的角平分线交BC于点O,OC=1,以点O为圆心OC为半径作圆.
(1)求证:AB为⊙O的切线;
(2)如果tan∠CAO =,求cosB的值. 23、图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD 的延长线于点 E,点 F 为 CE 的中点,连接 DB、DC、DF
(1) 求∠CDE的度数;
(2) 求证:DF是⊙O的切线;
(3) 若AC=DE,求 tan∠ABD 的值.
24、如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC 的延长线相交于点 E.
(1)求证:AD是半圆O的切线;
(2)连结CD.求证:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求弧BD的长.
:
25、如图13,在中,,以边
为直径作⊙交边于点,过点作
于点,、的延长线交于点.
(1)求证:是⊙的切线;
(2)若,且,求⊙的半径与线段的长.
26、如图,点B、C、D 都在上,过点C 作交OB延长线于点A,连接CD ,且°,DB=cm.
(1)求证:AC 是的切线;
(2)求由弦CD、BD与弧BC所围成的阴
影部分的面积.(结果保留)27、如图,D为上一点,点C在直径BA的延长线上,且. (1)求证:;
(2)求证:是的切线;
(3)过点B 作的切线交CD的延长线于点E,
若BC=12,,求BE的长.
28、如图,BC是⊙O的直径,A是⊙O上一点,过点C作⊙O的切线,交BA 的延长线于点D,取CD的中点E,AE的延长线与BC的延长线交于点P.
(1)求证:AP是⊙O的切线;
(2)OC=CP,AB=6,求CD的长.。
