奥数 在变化中找规律
小学奥数-找规律题技巧-全

小学奥数找规律题技巧-全问题1:找出图中的变化规律,填出所缺少的图形。
问题1教学图分析:第一题,当然会是最简单的。
图形规律题最重要的是仔细观察,首先要看的是,有没有相同的图形。
有大发现是不是?问题1讲解图1问题1讲解图2问题1讲解图3橙色圈中的图形和黄色圈中的图形,每行都有,玫红色圈中的图形,第三行没有,所以缺少的就是玫红色圈中的图形。
做完之后可以检查一下,如果填玫红圈中图形,正好是每行都有这三种图形,只是依次往左移了一个位置,因此我们填的答案是正确的。
做这一题主要的麻烦在于,图形有点复杂,乍一看头很晕。
那就一个图形一个图形的看,单看一个,头一点都不会晕了吧,看完再比较,哪些图形是相同的。
麻烦的事情,要懂得分步来做。
问题2:问题2教学图你做出来了吗?分析:我要开始分析题目了,审题并不是把注意力平均分配,每个条件都注意,就等于一个都没注意,分析题目一定要抓住重点。
数学必须要做题,但是我不赞成题海战术。
题海真的是无边无际,一个知识点就可以编出无数道题来。
盲目的题海战术,迟早会被无穷的题目,折腾得筋疲力尽。
那应该怎么做呢?非常简单的题目做完就算了,这种题千万不要重复做,只是浪费时间。
有的家长买一堆资料,孩子只做简单题,难的全空着,那这一堆资料除了浪费钱、浪费时间,一点作用都起不到。
买一堆资料不如先只买一本,从头至尾每一题都让孩子认真做,这样才会简单、中等、极难的题都做全,考试也是什么难度的题都会出的。
如果做完还有时间,再去买第二本资料。
对于中等难度和极难的题,一定要做一题就要让它起到作用。
做完题只是一小步,思考总结才是最关键的,想一想:这一题我是怎么做出来的?为什么这种思路就能做出来呢?是因为哪个条件,还是哪个问题提示了我可以这样思考?以后遇到什么情况时,我可以用类似的方法做?了解清楚上面几个问题的答案,才真正把这一道题的思路理顺了,不仅知其然,而且知其所以然。
以后遇到类似的问题,就可以迅速的找到方法和思路了。
奥数图形找规律教师版

图形找规律找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一数量规律【例 1】请找出下面哪个图形与其他图形不一样.【解析】这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有〔4〕与其它不一样【例 2】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【稳固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【解析】〔方法一〕横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【稳固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】 〔方法一〕横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出 “?”处应是圆形.【例 3】 观察下面的图形,按规律在“?”处填上适当的图形.(5)(4)(3)(2)(1)?【解析】 此题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从〔2〕起,每一个格比前面一个格多两个黑三角形,所以,第〔4〕个方框中应填七个黑三角形.【例 4】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
小学奥数4-1-2 图形找规律.专项练习及答案解析(精品)

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化; ⑵图形形状的变化;⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例1】观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律 【难度】1星 【题型】填空【解析】 几个图形的边数依次增加,因此横线上应为一个七边形.【答案】七边形【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律 【难度】1星 【题型】填空 【解析】 这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样 【答案】(4)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律 【难度】2星 【题型】填空 【解析】 观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:例题精讲知识点拨4-1-2.图形找规律【答案】【例4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【考点】图形找规律【难度】2星【题型】填空【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律【难度】2星【题型】填空【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
二年级奥数第七讲-------找规律(二)
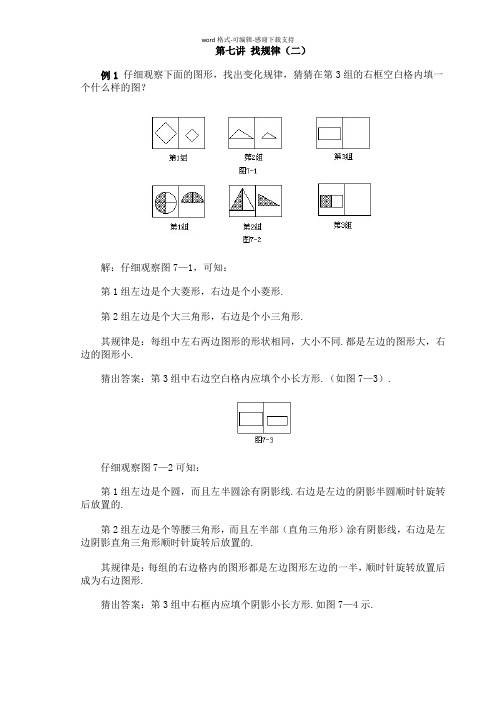
第七讲找规律(二)例1仔细观察下面的图形,找出变化规律,猜猜在第3组的右框空白格内填一个什么样的图?解:仔细观察图7—1,可知:第1组左边是个大菱形,右边是个小菱形.第2组左边是个大三角形,右边是个小三角形.其规律是:每组中左右两边图形的形状相同,大小不同.都是左边的图形大,右边的图形小.猜出答案:第3组中右边空白格内应填个小长方形.(如图7—3).仔细观察图7—2可知:第1组左边是个圆,而且左半圆涂有阴影线.右边是左边的阴影半圆顺时针旋转后放置的.第2组左边是个等腰三角形,而且左半部(直角三角形)涂有阴影线,右边是左边阴影直角三角形顺时针旋转后放置的.其规律是:每组的右边格内的图形都是左边图形左边的一半,顺时针旋转放置后成为右边图形.猜出答案:第3组中右框内应填个阴影小长方形.如图7—4示.例2按顺序仔细观察图7—5、7—6的形状,猜一猜第3组的“?”处应填什么图?解:图7—5的?处应填○▲.注意观察第1组和第2组,每组都是由三对小图形组成;而每对小图形都是由一个“空白”的和一个“黑色”的小图形组成;而且它俩的排列顺序都是“空白”的在左边,“黑色”的在右边.再按着第1、第2、第3组的顺序观察下去,可发现每对小图形在各组中的位置的变化规律:它们都在向左移动,当一对小图形移动到最左边后,下一步它就回到了最右边.按这个移动规律,可知图7—5中第3组“?”处应填:○▲.图7—6的?处应填□△0.仔细观察可发现第1组和第2组中间的部分都是由三个小图形构成的.构成的规律是:当你按照第1、第2、第3组的顺序观察时,6个小图形都在向左移动,而且移动的同时又在重新分组和组合,但排列顺序保持不变,当某一个小图形移动到了最左边时,下一步它就回到了最右边.按这个规律可知图7—6中第3组中间“?”处是:□△0.例3观察图7—7的变化,请先回答:在方框(4)中应画出怎样的图形?再答按(1)、(2)、(3)、……的顺序数下去,第(10)个方框中是怎样的图形?解:先按(1)、(2)、(3)、……的顺序仔细观察,可发现:方框中的箭头是按逆时针方向旋转的;方框中的其他小图形,如△、□和○也都是按逆时针方向旋转的.也就是说,方框连同内部的所有小图形作为一个整体在按逆时针方向旋转.因此,方框(4)中的小图形应画成图7—8状.再按已找到的规律,进一步可发现图形的变化是有“周期性”的,也就是说,每过4个方框后,同样的图形又重新出现一次.如,你可看到第(1)和第(5)是完全一样的;因此,你可以想像得到,第(2)和第(6)及第(10)个图形应当是完全一样的.即第(10)个方框中的图形应是图7—9所示的样子.例4观察图7—10的变化,请先回答:第(4)、(8)个图中,黑点在什么地方?第(10)、(18)个图中,黑点在什么地方?解:(1)按图7—10中(1)、(2)、(3)、……的顺序仔细观察,可发现黑点位置的变化规律:在(1)中,黑点在最上面第一条横线上;在(2)中,黑点下降了一格,在上面第二条横线上;在(3)中,黑点又下降了一格,在中间一条线上了.按黑点位置的这种变化可推测出:在(4)中,黑点又下降一格,它的位置应如图7—11所示.继续观察下去:在(5)中,黑点下降到最下面的一条横线上;在(6)中,黑点开始往上升一格;在(7)中,黑点再上升一格,按着黑点位置的这种变化可推测出:在(8)中,黑点又上升一格,它的位置应如图7—12所示.(2)进一步仔细观察图7—10(1)~(9),可发现黑点位置变化的“周期性”规律:也就是说,每隔8个小图,黑点又回到原来的位置.因为2+8=10,2+8+8=18.所以第(10)、(18)个小图中,黑点的位置应与第(2)个小图相同,见图7—13所示.习题七1.仔细观察图7—14,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?2.仔细观察图7—15,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?3.仔细观察图7—16,找找变化规律,猜猜在第3组的空白格内填一个什么样的图?4.按顺序仔细观察下列图形,猜一猜第3组的“?”处应填什么图?5.按顺序仔细观察下列图形,猜一猜第3组的“?”处应填什么图?6.按顺序仔细观察下列图形,猜一猜第3组的“?”应填什么图?7.按顺序仔细观察下列图形,猜一猜第3组的“?”应填什么图?8.仔细观察下列图形的变化,请先回答:①在方框(4)中应画出怎样的图形?②再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?9.仔细观察下列图形的变化,请先回答:①在方框(4)中应画出怎样的图形?②再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?习题七解答①先按(1)、(2)、(3)、……的顺序仔细观察,可以发现:在(1)中,*在左上角,在(2)中它在右上角,在(3)中它在右下角,……可见它在沿顺时针方向转动.其他三个小图形,即□、△、○,也和*一样都在沿着顺时针方向转动.发现规律:因方框中的每个小图形的位置的变化都是按顺时针方向旋转,可以说,方框连同内部的小图形及整体在按顺时针方向旋转.②进一步猜想,根据所发现的规律进一步推测可知,第(4)个方框中的图形的样子.③按(1)、(2)、(3)、……的顺序仔细观察,进一步还可发现,图形的变化是有“周期性”的,也就是说,每过4个方框后,完全同样的图形又重新出现,如第(1)、(5)、(9)个图形是完全一样的.因为2+4+4=10,所以第(10)个方框内的图形与第(2)完全相同.9.答:(见图7—31)。
四年级上册奥数第2讲 寻找规律(二)

第2讲:寻找规律(二)专题简析:对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考:1、对于几列数组成的一组数的变化规律的分析,需要我们灵活思考。
没有一成不变的方法,优势需要综合运用其他知识,如果一种方法不行,就要及时调整思路,换另一种方法再分析。
2、对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位置有关,这是我们解这类题的突破口。
3、对于找到的规律,应该适合这组数中的所有数或这组算式中的所有算式。
【例题1】根据下表中的排列规律,在空格里填上适当的数。
【习题一】找规律,在空格里填上适合的数。
【例题2】根据前面两个图形中数之间的关系,想一想第三个图形的括号里应填什么数?【习题二】根据前面两个图形中数之间的关系,想一想第三个图形的括号里应填什么数?12 18 68 15 74 89 16 716 21 54 98 17 510 11 912 164 11 96 247 35 30【例题3】先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几道题的得数。
12345679×9= 12345679×18=12345679×54= 12345679×81=【习题3】找规律,写得数。
(1)1+0×9= 2+1×9= 3+12×9= 4+123×9= 9+12345678×9=(2)1×1= 11×11= 111×111= 111…1×111…1=9个1 9个1(3) 19+9×9= 118+98×9= 1117+987×9=11116+9876×9= 111115+98765×9=【例题4】找规律,并计算。
(1)81-18=(8-1)×9=7×9=63(2)72-27=(7-2)×9=5×9=45(3)63-36=(□-□)×9=□×9=□【习题4】1、找规律,并计算。
四年级下册数学试题-奥数培优:在变化中找规律(含答案)全国通用

课题在变化中找规律教学内容事物的发展是有规律的,只有认真观察事物,找到事物发展变化的规律,才能深入地了解和掌握它,从而找到解决问题的方法和途径.在数学竞赛中,常常会出现一些数或者图形,它们的计算或者排列往往有一定的规律,我们要通过观察、思考去发现这些规律,也就是发现和总结数与数、图形与图形的内在联系和变化规律,然后就能分析和解决问题,根据下面四个算式,能否发现其中规律,然后在中,填人适当的数1×5+4 = 9-3×3,2×6+4=16=4×4;3×7+4=25=5×5;4×8+4=36-6×6;……10×+4= = ×;×+4= = ×102解四个算式中最重要的规律是被乘数与乘数相差4.10+4=14,就有10×14+4=144=12×12.又102×102= 10 404,10 404 - 4=10 400=100×104,于是得100×104+4=10404=102×102.请先计算下面一组算式的前三题,然后找出其中的规律,并根据规律直接写出后六题的得数1×8+1 =12×8+2 =123×8+3 =1234×8+4 =12 345×8+5 =123 456×8+6 =1234 567×8+7 =12 345 678×8+8 =123 456 789×8+9 =这组中的九个算式都是两个数的积加上一个数,数字的排列很有规律.通过计算,我们得出前三题的结果:1×8+1= 9,12×8+2=98:123×8+3 = 987.不难看出得数的变化规律:得数的位数与被乘数相同.最高位上的数是9.其余数位上的数依次是8,7,6,5,4,…解后六题的得数是:1234×8+4=9876:12 345×8+5 = 98 765;123 456×8+6 = 987 654;1234 567×8+7 = 9876 543,12 345 678×8+8 = 98 765 432;123 456 789×8+9 = 987 654 321.巩固练习1(1)找规律,在□里填上适当的数12 43 6 94 8 12 165 □□□□6 12 □□□□(2)找规律,填得数.12 345 679×9 = 111111111;12 345 679×18 =12 345 679×27 =12 345 679×36 =12 345 679×54 =12 345 679×45 =12 345 679×81=12 345 679×72 =12 345 679×63 =你做对了吗?答案:(1)10 15 20 25 18 24 30 36(2)222222222 333333333 444444444 666666666 555555555 999999999 888888888 777777777根据下列方框或等式中出现的数的规律,在括号内填上适当的数(1)(2) 22= 12+3;32= 22+5;42= 32+7;52= 42+9;…242=( ) 2+( ) 2(1)方框内上面两个数的差是3.且方框内下面第一个数是上面两个数的和,第二个数是方框内下面第二个数与下面第一个数的乘积,根据这一规律,括号内应填上:7,11和77.(2)从已给出的四个算式进行移项得到:22-12=3, 32-22=5,42-32=7,52- 42=9说明相邻自然数的平方相减的差等于这两个自然数的和,根据这一规律,括号内应该填上23和47.解(1)(2)242= (23) 2+(47).按规律填数(1){1,5,10},{2,10,20},{3,15,30}.{ }.(2)(1)观察已知三组数,发现:每组数中的第一个数是这个组的序号数,第二个数是第一个数的5倍,第三个数是第一个数的10倍(2) 前两组中,外围三个三角形内的三个数的乘积是中间三角形内的数的2倍,也就是中间三角形的数应是外围三个三角形内的=个数乘积的一半,解(1)第四组为{4,20,40},第五组为{5,25,50};(2)因为3×4×5÷2=30,所以应填30.巩固练习2(1)按规律填数,①2,3,5,8,13,21,( );②1,4,9,16,( ),( );③6,3,8,5,10,7,12,9,( ),( ).(2)找出规律后,直接填写出括号内的数.1999 998÷9 = 222 222;( )999 99( )÷9 = 333 333,( )999 99( )÷9= 444 444;( )999 99( )÷9 = 555 555;( )999 99( )÷9 = 666 666;( )999 99( )÷9 = 777 777;( )99999 ( )÷9= 888 888;( )999 99( )÷9 = 999 999.你做对了吗?答案:(1)○134 ○225 36 ○314 11(2)2,7 3,6 4,5 5,4 6,3 7,2 8,1如图5-l,一张黑白相间的方格纸,如果用记号(2,3)表示从上往下数第2行且从左往右数第3列的这一格,那么(18,7)这一格星黑色还是白色?解(1,1)是黑格,括号中一个数加1后就是白格,也就是两个数中,有一个数加l后,就改变一次颜色.(1,1)是(奇数,奇数),我们就知道(奇数,偶数)和(偶数,奇数)是白格;(奇数,奇数)和(偶数,偶数)是黑格.因此(18,7)是白色的格子想一想(99,102)和(200,198)这两格是黑色还是白色'如图5-2.在七色球下面,按照图示的规律,依次逐个写自然数.问:2012在什么颜色的球下面?解l到12算第一段,13到24算第二段,每12个数算一段,每段都是从赤色开始到紫色后再问到橙色结束,因此也可以看作是周期为12的循环,因为2012÷12=167……8.所以2012足在蓝色球的下面巩固练习3有249朵花,按照5朵红花、9朵黄花,13朵绿花的顺序循环排列,问:最后一朵花是什么颜色?这249朵花中,绿花有多少朵?你做对了吗?答案:最后一朵是黄色的,绿花有117朵“0”的故事小朋友,你们都知道,1,2,3,d,5.6,7,8,9,。
小学奥数 图形找规律 精选例题练习习题(含知识点拨)
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化; ⑵图形形状的变化; ⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律,在横线上画出适当的图形.【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
【例8】观察下面由点组成的图形(点群),请回答:(1)方框内的点群包含个点;(2)第(10)个点群中包含个点;(3)前十个点群中,所有点的总数是。
【例9】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形?(2)整个五层“宝塔”一共包含多少个小三角形?【例 10】 在纸上画5条直线,最多可有 个交点。
模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗? ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ ()()()()()()()()【例 12】 下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.(1)(2)(3)【例 13】 观察下图的变化规律,画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成,记为A ★B 、C ★D 、A ★D .请你画出表示A ★C 的图形.A★B C★D A★D【例15】(希望杯五年级一试第7题,6分)下列四个图形是由四个简单图形A、B、C、D(线段和正方形)组合(记为*)而成。
二年级奥数找规律.doc

一、图形找规律例1观察前几幅的变化规律,再接着画。
练习1、根据下面一串黑白珠子的排列规律,看应该把哪些珠子涂黑。
例2仔细观察下图,而第三组里缺少两个图,应该画什么?练习2、认真观察,找找变化规律,把第三幅图补充完整。
二、数字找规律例1、根据图中数字的规律,在最上边的空格中填上合适的数。
练习1、按规律填数30、25 、___ 、___3、6、9、___例2、观察数列的前面几项,找出规律,写出数列的第100项来。
12345,23451,34512,45123练习2、下面数列的每一项是由3个数组成的数组表示的,它们依次是(1,5,10),(2,10,20),(3,15,30),……,那么,第50个数组内的三个数分别是什么?三、趣味题判断他是否有罪某家商店的保险箱被开启了,发现了现金被盗案,经过公安部门的侦查,甲、乙、丙三人被认为有重大嫌疑,关于这三个人的调查结果是:(1)除此三人外,别无他人可疑;(2)若无甲同谋,即使有别人参与,丙也不会作案;(3)乙对于如何开启保险箱一无所知。
按这些线索分析,甲有罪吗?课后练习一1、请你根据前三幅图的规律接着画:2、仔细观察黑珠和白珠是怎样排列的?长方形应该画几个图形?几个折珠?3、在下面的五个图形中选一个画在空格处。
4、仔细观察下图,想一想第三幅图应该怎样画?5、找出前面几个数的排列规律,并填出括号里的数:(1)2,4,6,8,( ),12,( ),( )。
(2)1,5,9,13,( ),21,( ),( )。
6、按规律填数:(1)5,10,15,( ),( ),( )。
(2)35,( ),21,14,( ),( )。
7、按规律填数1,2,3,5,8,(),21,34,(),89。
8、找出规律,在()里填数。
1,50,2,45,3,40,(),()。
9、观察规律,按规律填出后面的数。
1,3,5,7,,,,;2,5,8,11,,,,;4,8,12,16,,,,;27,24,21,18,,,,。
小学奥数图形找规律四年级

找规律是解决数学问题的图形找规律一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化;⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一数量规律【例 1】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【例 2】观察下面的图形,按规律在“?”处填上适当的图形.【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【例 4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:板块二旋转、轮换型规律【例 5】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格,变成了下一排.(方法二)斜着看,每一斜列的图形是一样的.所以密码就是:□☆△○□☆△○【例 6】观察下图的变化规律,画出丙图.【总结】旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例 7】下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.【例 8】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【例 9】琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?【解析】从已摆好的第一行和第一列来看,无论横看或竖看,同一行中3只蝴蝶的翅膀形状各不相同,翅膀上的斑点的形状也各不相同.根据这个规律,剩下的3只蝴蝶图案的排列应该是:6号位置放图案C;8号位置放图案B;9号位置放图案A.【例 10】观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)【解析】(1)这四个图形的变化规律是:每一个图形都是由其前一个图形顺时针旋转90°而得到的.见下面左图;(2)甲乙丙丁四个图形变化规律也类似,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点.丁图处的图形应是下面右图:【例 11】请你认真仔细观察,按照下面图形的变化规律,在“?”处画出合适的图形。
小学奥数举一反三四年级 第2讲 找规律(二)

小学奥数【四年级】
2. 找规律,并计算。 (1) 62+26=(6+2)×11=8×11=88 (2) 87+78=(8+7)×11=15×11=165 (3) 54+45=(□+□)×11=□×11=□
第 2 讲 找 规 律 (二)
例 5 计算下面各题,你发现了什么规律?
(1)18×11=
(2)38×11=
(3)432×11=
练习 5:
用你发现的规律Hale Waihona Puke 算下面各题。(1)27×11=
(2)32×11=
(3)39×11=
(4)46×11=
(5)92×11=
(6)98×11=
(7)159×11=
(8)246×11=
想一想:这种算法的道理是什么?
小学奥数【四年级】
第 2讲
第 2 讲 找 规 律 (二)
找规律(二)
【专题简析】 对于较复杂的按规律填数的问题,我们可以从以下几个方面来思考: 1. 对于几列数组成的一组数变化规律的分析,需要我们灵活地思考,没有一成不变的方
法,有时需要综合运用其他知识,一种方法不行,就要及时调整思路,换一种方法再分析; 2. 对于那些分布在某些图中的数,它们之间的变化规律往往与这些数在图形中的特殊位
例 4 找规律,并计算。 (1) 81-18=(8-1)×9=7×9=63 (2) 72—27=(7-2)×9=5×9=45 (3) 63-36=(□-□)×9=□×9=□
练习 4: 1. 找规律,并计算。
(1)53-35= (4)61-16=
(2)82-28= (5)95-59=
(3)92-29=
练习 2: 根据前面图形中数之间的关系,想一想第三个图形的空白处应填什么数?
四年级奥数找规律填数的技巧与策略

四年级奥数找规律填数的技巧与策略随着数学水平的不断提高,越来越多的四年级学生开始接触奥数,而找规律填数是奥数常见的题型之一。
本文将为大家介绍一些四年级奥数找规律填数的技巧与策略,帮助大家提高解题能力。
一、寻找数字规律在找规律填数的问题中,我们首先需要观察一组数字的规律。
有时候规律可能是数字的变化规律,有时候则可能是数字之间的关系。
以下是一些常见的数字规律:1. 数字序列递增或递减:当数字序列出现递增或递减的规律时,我们可以通过观察数字之间的差异来填写下一个数字。
例如,序列1、3、5、7、9,下一个数字很有可能是11。
2. 数字间的运算规律:有时候数字之间可能存在一定的运算关系。
我们可以通过观察数字之间的运算规律来填写下一个数字。
例如,序列2、4、6、8,我们可以发现每个数字都是前一个数字加2得到的,下一个数字很有可能是10。
3. 数字之间的模式:有时候数字序列中存在一种模式,如乘法、幂运算等。
我们可以通过观察数字之间的模式来填写下一个数字。
例如,序列1、2、4、8,我们可以发现每个数字都是前一个数字的两倍,下一个数字很有可能是16。
二、尝试不同的策略当我们遇到找规律填数的问题时,可以尝试使用以下一些策略来解决问题:1. 递归法:如果我们找到了数字序列的规律,可以通过不断递归应用规律来填写下一个数字。
例如,序列2、4、8、16,我们可以发现每个数字都是前一个数字的两倍,我们可以继续递归应用这个规律,下一个数字很有可能是32。
2. 变化法:有时候可能存在多种规律,我们可以通过改变数字序列或者尝试不同的规律来填写下一个数字。
例如,序列2、6、18、54,我们可以发现每个数字都是前一个数字乘以3得到的,但是我们也可以发现每个数字都是前一个数字加2乘以3得到的。
3. 推理法:有时候我们需要根据已有的规律进行推理来填写下一个数字。
例如,序列5、10、20、40,我们可以发现每个数字都是前一个数字的两倍,我们可以根据这个规律推理出下一个数字很有可能是80。
五年级奥数专题 图形规律(学生版)

学科培优数学“图形规律”学生姓名授课日期教师姓名授课时长知识定位找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.知识梳理一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:(1)图形数量的变化;(2)图形形状的变化;(3)图形大小的变化;(4)图形颜色的变化;(5)图形位置的变化;(6)图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.关于解决图形规律问题的常用方法:1、从图形数量、位置变化出发观察思考几何图形的规律2、从图形形状、大小变化发现寻找图形的变化规律3、掌握寻找复杂图形变化规律的方法图形规律问题的分类:1、从图形形状、大小、颜色变化发现寻找图形的变化规律2、从图形数量、位置变化出发观察思考几何图形的规律3、复杂图形变化规律竞赛考点挖掘1.从图形形状、大小、颜色变化发现寻找图形的变化规律题目2.从图形数量、位置变化出发观察思考几何图形的规律题目3.复杂图形变化规律题目例题精讲【试题来源】【题目】请找出下面哪个图形与其他图形不一样.【试题来源】【题目】根据左边图形的关系,画出右边图形的另一半.(1)(2)(3)【试题来源】【题目】在下面图形中找出一个与众不同的.【试题来源】【题目】按照下列图形的变化规律,空白处应是什么样的图形?【试题来源】【题目】如图,根据图中已知3个方格表中阴影的规律,在空白的方格表中也填上相应的阴影.【试题来源】【题目】观察图形变化规律,在右边补上一幅,使它成为一个完整系列【试题来源】【题目】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【试题来源】【题目】请观察下图中已有的几个图形,并按规律填出空白处的图形.【试题来源】【题目】下图中的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.?ihgfedcba【试题来源】【题目】观察下列各组图的变化规律,并在“?”处画出相关的图形. (1)(2)【试题来源】【题目】观察下图中的点群,请回答:(1)方框内的点群包含多少个点?(2)推测第10个点群中包含多少个点?(3)前10个点群中,所有点的总数是多少?【试题来源】【题目】仔细观察下图中图形的变化规律,并在“?”处填入合适的图形.abc【试题来源】【题目】将“猫”“狗”“兔”“鸡”“猴”“虎”六个动物名称分别写在六个正方体的六个面上,从下面三种不同摆法中,判断这个正方体上哪些动物名名称分别写在相对面上.【试题来源】【题目】图10—1是由9个小人排列的方阵,但有一个小人没有到位,请你从下面图10—2中的6个小人中,选一位小人放到问号的位置,你认为最合适的人选是几号?【试题来源】【题目】四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?习题演练【试题来源】【题目】顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形【试题来源】【题目】根据下列图形的变化规律,接着画下去.【试题来源】【题目】请找出下面哪个图形与其他图形不一样【试题来源】【题目】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【试题来源】【题目】仔细观察下列图形的变化,请先回答:(1)在方框(4)中应画出怎样的图形?(2)再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?。
小学奥数找规律填数

第一讲找规律填数课后巩固篇1.按规律填数。
(1)12345, 23451, 34512, (), 51234;【点评】根据前后数字出现的规律,都有1, 2, 3, 4, 5,并且数字的出现都是从小到大,然后循环的,首位数字分别是1,2, 3,所以第四个数字的首位应该出现4.【答案】:45123(2)109, 10099, 1000999, (), 10000099999;【点评】:给出的数首位都是1,第二位开始有变化,第一个是1个0, 第二个是2个0,第三个是3个0,那么第四个应该是4个0,后面的9出现的个数和0出现的个数是一样的。
【答案】:100009999(3)401, 4011, 40111, (), 4011111;【点评】本题和第3小题类似,首位都是4,第二位都是0,从0 后面开始有变化,后面一个数依次比前一个数多一个1.【答案】:401111(4)5, 55, 555, 5555,();【点评】:本题比较简单,后一个数依次比前一个数多一个5.【答案】: 55555(5)3, 8, 23, 68,();【点评】:观察每个数之间的关系,第二个数是第一个数的三倍少1, 第三个数是第二个数的三倍少1,第四个数是第三个数的三倍少1.【答案】:203(6)150, 135, 120, (), 90,(),();【点评】后面一个数分别比前面一个数少15.【答案】:(105),(75),(60)(7)1, 3, 6, 8, 16, 18,(),(), 76, 78;【点评】本数列两个两个分成一组,后面的数比前面的数多2,每组和每组数又是有关系的,每组第一个数是前一组后面一个数的两倍。
【答案】:(36)(38)(8)16, 48, 24, 72, 36,(),();【点评工本题的规律分别是第一个数乘以3得到第二个数,第二个数除以2得到第三个数,后面都是这样的规律.【答案】:(108),(54)(9)11, 12, 15, (), 27, 36;【点评】本题的规律后一个数与前一个数的差分别是1,3,5,7,9【答案】:(20)(10)3,2,6,4,9,16,12,128,(),();【点评】:本题是个双数列,奇数位上的数分别是3,6,9,12,都是3的倍数,并且后面的一个数比前一个数多3,偶数位上的数分别是2,4,16,128……,后面一个数是前一个数多2、4、8倍,倍数之间成等比的关系。
三年级奥数找规律填数题上下左右箭头方向

三年级奥数找规律填数题上下左右箭头方向(原创版)目录1.题目背景介绍2.奥数找规律填数题的解题思路3.上下左右箭头方向的规律应用4.结论正文1.题目背景介绍三年级的奥数题目中,找规律填数题一直是孩子们感到困扰的题型之一。
这种题型要求孩子们通过观察数字序列的规律,来推测下一个数字。
而在这类题目中,上下左右箭头方向的规律应用则是一个重要的解题技巧。
2.奥数找规律填数题的解题思路对于找规律填数题,首先要培养孩子的观察能力和逻辑思维能力。
观察数字序列的规律,可以从以下几个方面入手:- 数字的增减变化:观察数字序列是递增还是递减,或者是否存在周期性的变化。
- 数字的组合关系:观察数字序列中各个数字之间的关系,如是否存在加减乘除等运算关系。
- 数字的位置关系:观察数字序列中各个数字在序列中的位置关系,如是否与上下左右的箭头方向有关。
3.上下左右箭头方向的规律应用在解决找规律填数题时,上下左右箭头方向的规律应用是一个重要的解题技巧。
具体来说,可以从以下几个方面来应用:- 上下箭头方向:观察数字序列中每个数字与它上面的数字之间的关系,如是否相等、互换或者存在一定的比例关系。
- 左右箭头方向:观察数字序列中每个数字与它左边的数字之间的关系,如是否相等、互换或者存在一定的比例关系。
- 对角箭头方向:观察数字序列中每个数字与它对角线上的数字之间的关系,如是否相等、互换或者存在一定的比例关系。
通过应用上下左右箭头方向的规律,可以帮助孩子更好地理解和掌握数字序列的规律,从而解决找规律填数题。
4.结论总的来说,对于三年级的奥数找规律填数题,通过观察数字序列的规律以及应用上下左右箭头方向的规律,可以帮助孩子更好地理解和掌握解题技巧。
二年级奥数:《发现数列规律》

二年级奥数:《发现数列规律》(预热)前铺知识一、什么是数列按照一定顺序排列的一列数就是数列。
如最简单的:1,2,3,4,5,6 .........二、寻找数列变化规律1、变大【例1】2,4,6,8,10,答案:12解析:仔细观察,发现这列数是不断在增大的,让数增大我们学过的有两种方法——加法、乘法。
在这道题中我们可以先用加法试试看。
2, 4, 6, 8, 10,+2 +2 +2 +2发现从左往右每个数都依次+2,于是按照相同的规律得出下一个数是:10+2=12。
【例2】1,3,9,27,答案:81解析:仔细观察,发现这列数是不断在增大的,让数增大我们学过的有两种方法——加法、乘法。
在这道题中我们用加法的话:1, 3, 9, 27,+2 +6 +18发现找不到规律,所以可以试试乘法:1, 3, 9, 27,×3 ×3 ×3发现从左往右每个数都依次×3,于是按照相同的规律得出下一个数是:27×3=81.2、变小【例3】20,18,16,14,12,答案:10解析:通过观察,发现这列数是不断在减小的,让数减小我们学过的有两种方法——减法、除法。
在这道题中我们可以先用减法试试看。
20, 18, 16, 14, 12,-2 -2 -2 -2发现从左往右每个数都依次 -2,于是按照相同的规律得出下一个数是:12-2=10。
【例4】64,16,4, 答案:1解析:通过观察,发现这列数是不断在减小的,让数减小我们学过的有两种方法——减法、除法。
在这道题中我们用减法的话: 64, 16, 4,-48 -12发现找不到规律,所以可以试试除法: 64, 16, 4,÷4 ÷4发现从左往右每个数都依次 ÷4,于是按照相同的规律得出下一个数是: 4÷4=1。
三、数形结合【例5】填出?里的数: 答案:21解析:观察发现数都被放在了图形里,并且被分成一组一组的,这时候不妨一组一组的观察。
小学奥数图形找规律(四年级)

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化; ⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一 数量规律【例 1】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】 横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【解析】 (方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△. (方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出 “?”处应是三角形△.【例 2】 观察下面的图形,按规律在“?”处填上适当的图形.(4)(1)?图形找规律【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【例 4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:板块二旋转、轮换型规律【例5】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格,变成了下一排.(方法二)斜着看,每一斜列的图形是一样的.所以密码就是:□☆△○□☆△○【例 6】 观察下图的变化规律,画出丙图.DBA丙乙甲CB A【解析】ACD【总结】旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例 7】 下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.【解析】【例 8】 观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【解析】【例 9】 琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?图1987654321 图2B CA【解析】 从已摆好的第一行和第一列来看,无论横看或竖看,同一行中3只蝴蝶的翅膀形状各不相同,翅膀上的斑点的形状也各不相同.根据这个规律,剩下的3只蝴蝶图案的排列应该是:6号位置放图案C ;8号位置放图案B ;9号位置放图案A.【例 10】 观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)丁丙乙甲?【解析】 (1)这四个图形的变化规律是:每一个图形都是由其前一个图形顺时针旋转90°而得到的.见下面左图;(2)甲乙丙丁四个图形变化规律也类似,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点.丁图处的图形应是下面右图:丁【例 11】 请你认真仔细观察,按照下面图形的变化规律,在“?”处画出合适的图形。
四年级下册数学试题-奥数培优:在变化中找规律(含答案)全国通用

课题在变化中找规律教学内容事物的发展是有规律的,只有认真观察事物,找到事物发展变化的规律,才能深入地了解和掌握它,从而找到解决问题的方法和途径.在数学竞赛中,常常会出现一些数或者图形,它们的计算或者排列往往有一定的规律,我们要通过观察、思考去发现这些规律,也就是发现和总结数与数、图形与图形的内在联系和变化规律,然后就能分析和解决问题,根据下面四个算式,能否发现其中规律,然后在中,填人适当的数1×5+4 = 9-3×3,2×6+4=16=4×4;3×7+4=25=5×5;4×8+4=36-6×6;……10×+4= = ×;×+4= = ×102解四个算式中最重要的规律是被乘数与乘数相差4.10+4=14,就有10×14+4=144=12×12.又102×102= 10 404,10 404 - 4=10 400=100×104,于是得100×104+4=10404=102×102.请先计算下面一组算式的前三题,然后找出其中的规律,并根据规律直接写出后六题的得数1×8+1 =12×8+2 =123×8+3 =1234×8+4 =12 345×8+5 =123 456×8+6 =1234 567×8+7 =12 345 678×8+8 =123 456 789×8+9 =这组中的九个算式都是两个数的积加上一个数,数字的排列很有规律.通过计算,我们得出前三题的结果:1×8+1= 9,12×8+2=98:123×8+3 = 987.不难看出得数的变化规律:得数的位数与被乘数相同.最高位上的数是9.其余数位上的数依次是8,7,6,5,4,…解后六题的得数是:1234×8+4=9876:12 345×8+5 = 98 765;123 456×8+6 = 987 654;1234 567×8+7 = 9876 543,12 345 678×8+8 = 98 765 432;123 456 789×8+9 = 987 654 321.巩固练习1(1)找规律,在□里填上适当的数12 43 6 94 8 12 165 □□□□6 12 □□□□(2)找规律,填得数.12 345 679×9 = 111111111;12 345 679×18 =12 345 679×27 =12 345 679×36 =12 345 679×54 =12 345 679×45 =12 345 679×81=12 345 679×72 =12 345 679×63 =你做对了吗?答案:(1)10 15 20 25 18 24 30 36(2)222222222 333333333 444444444 666666666 555555555 999999999 888888888 777777777根据下列方框或等式中出现的数的规律,在括号内填上适当的数(1)(2) 22= 12+3;32= 22+5;42= 32+7;52= 42+9;…242=( ) 2+( ) 2(1)方框内上面两个数的差是3.且方框内下面第一个数是上面两个数的和,第二个数是方框内下面第二个数与下面第一个数的乘积,根据这一规律,括号内应填上:7,11和77.(2)从已给出的四个算式进行移项得到:22-12=3, 32-22=5,42-32=7,52- 42=9说明相邻自然数的平方相减的差等于这两个自然数的和,根据这一规律,括号内应该填上23和47.解(1)(2)242= (23) 2+(47).按规律填数(1){1,5,10},{2,10,20},{3,15,30}.{ }.(2)(1)观察已知三组数,发现:每组数中的第一个数是这个组的序号数,第二个数是第一个数的5倍,第三个数是第一个数的10倍(2) 前两组中,外围三个三角形内的三个数的乘积是中间三角形内的数的2倍,也就是中间三角形的数应是外围三个三角形内的=个数乘积的一半,解(1)第四组为{4,20,40},第五组为{5,25,50};(2)因为3×4×5÷2=30,所以应填30.巩固练习2(1)按规律填数,①2,3,5,8,13,21,( );②1,4,9,16,( ),( );③6,3,8,5,10,7,12,9,( ),( ).(2)找出规律后,直接填写出括号内的数.1999 998÷9 = 222 222;( )999 99( )÷9 = 333 333,( )999 99( )÷9= 444 444;( )999 99( )÷9 = 555 555;( )999 99( )÷9 = 666 666;( )999 99( )÷9 = 777 777;( )99999 ( )÷9= 888 888;( )999 99( )÷9 = 999 999.你做对了吗?答案:(1)○134 ○225 36 ○314 11(2)2,7 3,6 4,5 5,4 6,3 7,2 8,1如图5-l,一张黑白相间的方格纸,如果用记号(2,3)表示从上往下数第2行且从左往右数第3列的这一格,那么(18,7)这一格星黑色还是白色?解(1,1)是黑格,括号中一个数加1后就是白格,也就是两个数中,有一个数加l后,就改变一次颜色.(1,1)是(奇数,奇数),我们就知道(奇数,偶数)和(偶数,奇数)是白格;(奇数,奇数)和(偶数,偶数)是黑格.因此(18,7)是白色的格子想一想(99,102)和(200,198)这两格是黑色还是白色'如图5-2.在七色球下面,按照图示的规律,依次逐个写自然数.问:2012在什么颜色的球下面?解l到12算第一段,13到24算第二段,每12个数算一段,每段都是从赤色开始到紫色后再问到橙色结束,因此也可以看作是周期为12的循环,因为2012÷12=167……8.所以2012足在蓝色球的下面巩固练习3有249朵花,按照5朵红花、9朵黄花,13朵绿花的顺序循环排列,问:最后一朵花是什么颜色?这249朵花中,绿花有多少朵?你做对了吗?答案:最后一朵是黄色的,绿花有117朵“0”的故事小朋友,你们都知道,1,2,3,d,5.6,7,8,9,。
