螺栓计算
高强螺栓锚固长度计算

高强螺栓锚固长度计算一、高强螺栓概述高强螺栓,顾名思义,是一种具有高强度、高韧性的螺栓连接件。
它广泛应用于建筑、桥梁、机械等领域,起着固定和连接作用。
高强螺栓不仅具有较高的抗拉强度,还具有较好的抗震性能,因此在许多重要工程中发挥着重要作用。
二、锚固长度的计算方法1.基本公式高强螺栓的锚固长度计算公式为:L = (πD)^2 / 4πε其中,L表示锚固长度,D表示螺栓直径,ε表示混凝土的膨胀系数。
2.影响因素(1)混凝土强度:混凝土强度越高,允许的锚固长度越短。
(2)螺栓直径:螺栓直径越大,允许的锚固长度越长。
(3)锚固方式:不同锚固方式对锚固长度有不同要求。
例如,埋入式锚固的锚固长度相对较长,而粘结式锚固的锚固长度相对较短。
3.计算实例以一支直径为16mm的高强螺栓为例,根据公式计算:L = (π × 16mm)^2 / 4π × 1 × 10^-5 = 0.0001936m根据规范,16mm直径的高强螺栓允许的锚固长度为0.0001936m。
三、注意事项1.计算锚固长度时,应严格按照规范进行,以确保工程安全。
2.在实际施工中,锚固长度不得小于计算值,以确保螺栓的稳定性能。
3.不同工程结构、不同用途的高强螺栓,其锚固长度计算方法可能有所不同,需根据具体情况选用合适的计算公式。
四、总结高强螺栓的锚固长度计算是工程中一项十分重要的工作。
通过对高强螺栓的概述、锚固长度的计算方法、影响因素和注意事项的介绍,希望对大家在实际工程中计算高强螺栓锚固长度有所帮助。
在施工过程中,要严格按照规范操作,确保工程质量和安全。
m24带钩螺栓重量计算公式

m24带钩螺栓重量计算公式
要计算M24带钩螺栓的重量,我们可以使用以下公式:
重量(kg)= 钢材密度(kg/m³)× π × 半径²(m²)×
高度(m)× 螺栓数量。
首先,我们需要确定M24带钩螺栓的材料密度。
一般来说,碳
钢的密度约为7850千克/立方米,不锈钢的密度约为8000千克/立
方米。
假设我们使用碳钢,我们可以将密度设为7850千克/立方米。
接下来,我们需要确定螺栓的尺寸。
M24表示螺栓的直径为24
毫米。
带钩螺栓的重量取决于螺栓的长度和钢材的密度。
如果我们
知道螺栓的长度,我们可以计算出螺栓的体积。
假设螺栓的长度为L米,钢材的密度为7850千克/立方米,螺
栓数量为N个,那么螺栓的重量可以用以下公式表示:
重量(kg)= 7850 × π × (24/2000)² × L × N.
在这个公式中,24/1000将毫米转换为米,然后取平方得到螺
栓横截面的面积。
乘以π得到螺栓横截面的面积,再乘以长度L和螺栓数量N即可得到螺栓的重量。
需要注意的是,这个公式仅计算了螺栓本身的重量,不包括螺母、垫圈等附件的重量。
如果需要考虑这些附件的重量,还需要将其加入计算公式中。
希望这个回答能够帮助到你,如果你有其他问题,也欢迎继续提问。
标准 螺栓 计算

标准螺栓计算
计算螺栓的标准通常涉及以下几个方面:螺栓尺寸、螺栓强度等级、预紧力和螺栓的拧紧力。
1. 螺栓尺寸:螺栓的尺寸包括直径、长度和螺纹规格等。
根据具体的应用需求和设计标准,选择适当的螺栓尺寸。
2. 螺栓强度等级:螺栓的强度等级表示其抗拉强度和材料的硬度。
常见的螺栓强度等级包括4.8、8.8、10.9和12.9等。
根据需要,选择符合设计要求的螺栓强度等级。
3. 预紧力:预紧力是螺栓在拧紧前施加的力,用于保持连接件紧固并承受负荷。
预紧力的计算通常基于连接件的类型、材料和设计要求等因素。
可以通过使用紧固力计或根据工程经验来确定适当的预紧力。
4. 螺栓的拧紧力:螺栓的拧紧力是施加在螺栓上的力,使其产生摩擦力来保持连接件紧固。
拧紧力的计算通常基于摩擦力系数、螺纹的摩擦因数和预紧力等参数。
可以使用拧紧力计或根据标准拧紧规程来确定适当的拧紧力。
需要注意的是,具体的螺栓计算方法和标准可能因不同的应用和行业而有所不同。
在进行螺栓计算时,建议参考相应的设计规范、标准或咨询专业工程师,以确保螺栓的选择和设计满足安全和可靠性要求。
螺栓连接实用计算公式

螺栓连接实用计算公式螺栓连接是一种常见的机械连接方式,通常用于连接两个或多个零件。
在工程设计和计算中,我们需要根据实际情况来确定螺栓连接的尺寸和参数,以保证连接的可靠性和安全性。
本文将介绍一些常用的螺栓连接计算公式,以帮助读者更好地理解和应用。
一、螺栓拉力计算公式在螺栓连接中,螺栓的拉力是一个重要的参数。
拉力的大小决定了螺栓的紧固程度,直接影响连接的可靠性。
根据受力分析原理,我们可以使用以下公式计算螺栓的拉力:拉力(F)= 力矩(M)/ 杠杆臂(L)其中,力矩是指施加在螺栓上的力与螺栓中心轴线的垂直距离的乘积,杠杆臂则是指螺栓直径的一半。
通过测量力矩和杠杆臂的数值,我们可以计算出螺栓的拉力大小。
二、螺栓预紧力计算公式螺栓的预紧力是指在紧固过程中施加在螺栓上的力。
预紧力的大小直接影响螺栓连接的紧固程度和稳定性。
根据预紧力的计算公式,我们可以得到以下关系:预紧力(Fp)= 螺栓材料的屈服强度(σy)× 螺栓截面的面积(A)其中,螺栓材料的屈服强度是指螺栓材料在拉伸过程中发生塑性变形的临界应力值,螺栓截面的面积则是指螺栓剖面的有效面积。
通过测量螺栓材料的屈服强度和螺栓截面的面积,我们可以计算出螺栓的预紧力大小。
三、螺栓的剪切强度计算公式在螺栓连接中,除了拉力外,螺栓还要承受剪切力。
螺栓的剪切强度是指螺栓在剪切过程中能够承受的最大应力值。
根据剪切强度的计算公式,我们可以得到以下关系:剪切强度(τ)= 螺栓材料的抗剪强度(σs)× 螺栓剖面的面积(A)其中,螺栓材料的抗剪强度是指螺栓材料在剪切过程中能够承受的最大应力值,螺栓剖面的面积则是指螺栓剖面的有效面积。
通过测量螺栓材料的抗剪强度和螺栓剖面的面积,我们可以计算出螺栓的剪切强度大小。
螺栓连接的实用计算公式涉及到螺栓的拉力、预紧力和剪切强度等参数的计算。
根据这些公式,我们可以根据实际情况来确定螺栓连接的尺寸和参数,以保证连接的可靠性和安全性。
螺栓的有效底径计算公式

螺栓的有效底径计算公式
De = d 0.64952 P.
其中,De表示螺栓的有效底径,d表示螺栓的公称直径,P表示螺距。
这个公式是根据ISO标准推导出来的,适用于常见的螺纹类型,如普通螺纹和粗牙螺纹。
这个公式的推导过程涉及到螺纹的几何特性和力学原理,通过对螺纹的剖面和受力分析可以得出这个计算公式。
另外,对于特殊类型的螺纹,如细牙螺纹或特殊剖面的螺纹,可能需要使用其他的计算公式来计算有效底径。
在工程实践中,还需要考虑螺栓的材料特性、受力情况以及安全系数等因素,综合考虑来确定螺栓的合适尺寸。
总之,螺栓的有效底径计算公式是工程设计中重要的一部分,通过合适的公式可以准确计算螺栓的尺寸,保证螺栓在使用过程中能够承受设计要求的载荷,确保结构的安全可靠性。
螺栓的计算公式

螺栓的计算公式螺栓在机械领域中可是个相当重要的角色呢!咱们要搞清楚螺栓的计算公式,那得先从它的基本原理和用途说起。
螺栓,这小小的家伙,却有着大大的作用。
就说咱们常见的自行车吧,车把和车架的连接,脚踏板和轴的固定,都离不开螺栓。
我还记得有一次,我自己在家捣鼓修理自行车,结果不小心把一个螺栓给弄滑丝了。
这可把我急坏了,因为这意味着零件没法稳固连接,自行车骑起来会嘎吱嘎吱响,还可能存在安全隐患。
那螺栓的计算公式到底是咋回事呢?咱们先来说说螺栓的抗拉强度计算公式。
螺栓的抗拉强度可以通过材料的抗拉强度乘以螺栓的有效截面积来计算。
这就好比是一个大力士能举起的重量,取决于他本身的力气大小(材料强度)和他双手能抓住的面积(有效截面积)。
再来讲讲螺栓的预紧力计算公式。
预紧力就像是给螺栓提前施加的一个“压力”,让它在工作的时候能够紧紧地拉住两个零件,不让它们松动。
预紧力的计算要考虑到螺栓的材料、直径、摩擦系数等因素。
比如说,在一些需要高精度和高稳定性的机械装置中,预紧力的计算就显得尤为重要。
还有螺栓的屈服强度计算公式。
螺栓的屈服强度就像是它的“底线”,超过这个底线,螺栓就可能会发生永久性的变形,无法正常工作。
这个计算也得综合考虑各种材料和尺寸的参数。
在实际的工程应用中,螺栓的计算公式可不是随便算算就行的。
比如说在汽车制造厂里,工人们在组装发动机的时候,就得精确计算每个螺栓的参数,确保发动机在高速运转的时候,各个部件都能紧密连接,不出差错。
总之,螺栓的计算公式虽然看起来有点复杂,但只要咱们掌握了其中的原理和关键参数,就能让这些小小的螺栓发挥出大大的作用,保障各种机械装置的安全和稳定运行。
就像我那次修自行车,最后费了好大的劲,找了合适的螺栓替换,才让我的自行车重新欢快地跑起来。
所以啊,可别小看这螺栓的计算公式,它可是机械世界里的重要“密码”呢!。
螺栓计算方法

M20的螺栓一般性能等级为8.8,10.9 .性能等级小数点前的数字代表材料公称抗拉强度σb的1%,小数点后的数字代表材料的屈服强度σs与公称抗拉强度之比的10倍.M20螺栓8.8性能等级公称抗拉强度σb=800MPa,最小抗拉强度σb=830MPa.公称屈服强度σs=640 ,最小屈服强度σs=660 .
所以M20螺栓8.8性能等级最小抗拉力为188.41KN ,在这个数值上的螺栓为合格品.最大抗拉力就的试验了.
屈服强度
屈服强度是金属材料发生屈服现象时的屈服极限,亦即抵抗微量塑性生屈服现象时所承受的最大外力(N)
AO----试样原来的截面积(mm2)
三、计算方法
钢材受拉断裂前的最大应力值称为强度极限或抗拉强度。
F=σs*A,
其中F为拉力(许用载荷),σs为材料抗拉强度,A为有效面积,有效面积为螺栓有效长度上直径最小处的横截面积。
M20的有效直径为Φ17,M20的有效横截面积为227mm^2 。8.8级M20最小抗拉强度σb=830MPa
抗拉强度也叫强度极限指材料在拉断前承受最大应力值,当钢材屈服到一定程度后,由于内部晶粒重新排列,其抵抗变形能力又重新提高,此时变形虽然发展很快,但却只能随着应力的提高而提高,直至应力达最大值。此后,钢材抵抗变形的能力明显降低,并在最薄弱处发生较大的塑性变形,此处试件截面迅速缩小,出现颈缩现象,直至断裂破坏。
F=830*227=188410N=188.41KN
所以M20螺栓8.8性能等级最小抗拉力为188.41KN。
螺栓的承受最大的拉力=材料的屈服强度*螺栓的承载截面尺寸
物体由于外因(受力、湿度变化等)而变形时,在物体内各部分之间产生相互作用的内力,以抵抗这种外因的作用,并力图使物体从变形后的位置回复到变形前的位置。在所考察的截面某一点单位面积上的内力称为应力。同截面垂直的称为正应力或法向应力,同截面相切的称为剪应力或切应力。应力会随着外力的增加而增长,对于某一种材料,应力的增长是有限度的,超过这一限度,材料就要破坏。对某种材料来说,应力可能达到的这个限度称为该种材料的极限应力。极限应力值要通过材料的力学试验来测定。将测定的极限应力作适当降低,规定出材料能安全工作的应力最大值,这就是许用应力。材料要想安全使用,在使用时其内的应力应低于它的极限应力,否则材料就会在使用时发生破坏。
常用截面及螺栓长度计算

常用截面及螺栓长度计算在工程设计中,常常需要计算截面的尺寸和螺栓的长度。
以下是常用截面及螺栓长度计算的一些方法和公式。
1.矩形截面的计算:矩形截面的尺寸常用矩形包括长方形和正方形。
其计算方法如下:长方形截面:设矩形截面的宽度为b,高度为h,则截面面积A=b*h。
常见的应用是在梁和柱的计算,根据承载力计算截面的尺寸。
正方形截面:设正方形截面的边长为a,则截面面积A=a^22.圆形截面的计算:圆形截面常用于管道和轴类的计算。
圆形截面:设圆形截面的直径为d,则截面半径r=d/2截面面积A=π*r^23.T形截面的计算:T形截面常用于梁的计算。
T形截面:设T形截面的上翼板宽度为bt,下翼板宽度为bb,翼板厚度为t,腹板厚度为h,则截面面积A = bt * t + bb * t + h * t。
4.I形截面的计算:I形截面常用于梁的计算。
I形截面:设I形截面的上翼板宽度为bt,下翼板宽度为bb,翼板厚度为t,腹板厚度为h,则截面面积A = bt * t + bb * t + 2 * h * t。
5.椭圆截面的计算:椭圆截面常用于管道和轴类的计算。
椭圆截面:设椭圆截面的长半径为a,短半径为b,则截面面积A=π*a*b。
6.螺栓长度的计算:螺栓长度的计算通常需要根据相关标准和设计要求进行。
常见的计算方法包括以下几个步骤:-确定螺栓的标称直径d。
- 根据连接件的尺寸和要求,确定螺栓的贯穿长度lt和螺栓的松切面长度lf。
- 计算螺栓的有效长度le = lt - lf。
-根据设计要求和标准规定,确定螺栓的预紧力和间距。
-根据螺栓的材料和预紧力计算螺栓的系数。
-根据螺栓的系数和预紧力,计算螺栓的拉伸长度l。
- 最终的螺栓长度为lb = lt - l。
总结:截面和螺栓长度的计算在工程设计中是非常重要的一部分。
对于不同的截面形状和连接要求,需要采用相应的计算方法和公式。
通过合理的计算,可以确保截面的强度和稳定性,以及螺栓的安全连接。
螺栓计算——精选推荐
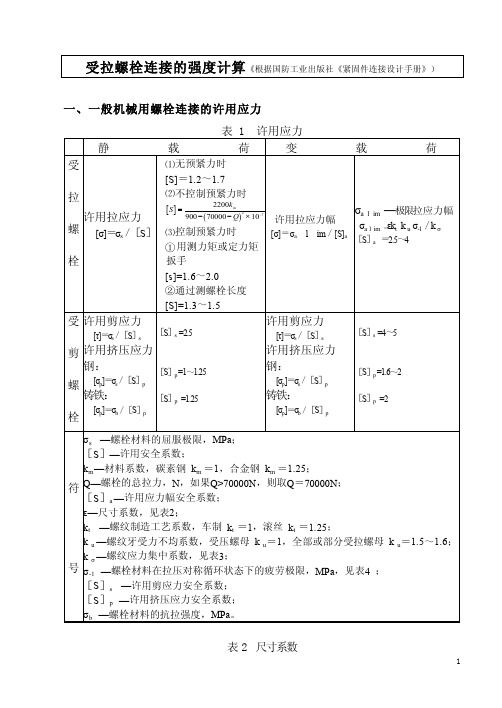
一、一般机械用螺栓连接的许用应力表2 尺寸系数二、松连接螺栓的强度计算一般机械用松连接螺栓,其螺纹部分的强度条件为:需要的计算直径为:式中: Q —螺栓的总拉力,此情况下是其工作拉力,N ;A c —螺栓螺纹部分的计算面积,(mm 2); d c —螺纹部分的计算直径(mm);d c =(d 2 + d 1 – H/6)/2≈d -0.94P ;其中: d 2和d 1 为螺纹的小径和大径,(mm ),H 为螺纹牙理论高度,(mm ), P 为螺纹螺距,(mm )。
[σ]—松连接螺栓的许用拉应力,MPa 。
三、紧连接螺栓的强度计算1、只受预紧力的螺栓一般结构形式的螺栓螺母连接,螺栓除受预紧力外还受拧紧力矩的作用,综合考虑拉应力σ和扭转剪应力τ=0.5σ,根据第四强度理论,可得螺纹部[]σπ≤=24c c d QA F[]σπQd c 4≥分的强度条件为:()[]στσσσσ2222330513+≈+≈≤..换算后得:[]4132⨯≤Q d cPπσ 螺栓需要的计算直径:[]d Q c P≥⨯413.πσ式中: Q P —螺栓的预紧力,N ;[σ]—静载紧连接螺栓的许用拉应力(按表1),MPa 。
当螺栓材料为低塑性材料时,如30CrMnSi 等,宜采用根据莫尔理论的强度条件:()()[]121121422-+++≤νσνστσ 式中:ν=σSL /σSY ,对于一般塑性材料,ν=1。
σSL 和σSY 分别是材料的拉伸、压缩屈服极限,MPa 。
2、受预紧力和静工作拉力的螺栓为保证连接的可靠性和充分发挥螺栓连接的潜力,螺栓的预紧应力σp 应在小于0.8σs 的条件下取较高值,对一般机械,σp =(0.5~0.7)σs 螺栓需要的预紧力:F C C C Q Q mb mP P ++'=螺栓总拉力:Q= Q p ’+F或表示为:Q Q C C C F P bb m=++ 式中: Q p —螺栓需要的预紧力,N ;Q p ’—被连接件中剩余预紧力( 承受工作拉力后,被连接 件中剩余预紧力 Q p ’的推荐值见表5),N ; F —螺栓的工作拉力,N ;C b 、C m ─分别为螺栓和被连接件的拉、压刚度,均为定值。
螺栓设计计算公式

尽管当Nt≤P时,栓杆的预拉力变化不大,但由 于μ随Nt的增大而减小,且随Nt的增大板件间的挤 压力减小,故连接的抗剪能力下降。规范规定在V 和N共同作用下应满足下式:
Nt N
b t
Nv N
b v
1
( 3 75)
N t、N v 外力作用下每个螺栓承 担的拉力和剪力设计值 ; N tb、N vb 单个高强度螺栓的抗拉 和抗剪承载力设计值。
2
2
N vb
b N min
(3 80)
( 3 81)
2 1Tx
三、高强度螺栓群的抗拉计算
1、轴心力作用 假定各螺栓均匀受力,故所 需螺栓数:
N M
N n b Nt
2、弯矩作用下
由于高强度螺栓的抗拉承载力一般总小于其预拉 力P,故在弯矩作用下,连接板件接触面始终处于紧 密接触状态,弹性性能较好,可认为是一个整体,所 以假定连接的中和轴与螺栓群形心轴重合,最外侧螺 栓受力最大。
y
F T
r1
1 N1Tx N1T
x
T
N1Ty
剪力F作用下每个螺栓受力:
N 1F
F n
扭矩T作用下:
N 1Tx T r1
2 2 x y i i i 1 i 1 n n
y1 r1 x1 r1
T y1
2 2 x y i i i 1 i 1 n n
B、承压型高强度螺栓的单栓抗拉承载力,因其破 坏准则为螺栓杆被拉断,故计算方法与普通螺栓 相同,即:
N tb Ae f tb
d e2
4
f tb
3 74
式中:Ae--螺栓杆的有效截面面积; de--螺栓杆的有效直径; ftb—高强度螺栓的抗拉强度设计值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Aim of Calculation
Determine bolt dimension allowing for: • Strength grade of the bolt • Reduction of preload by working load • Reduction of preload by embedding • Scatter of preload during tightening • Fatigue strength under an alternating load • Compressive stress on clamped parts
Beam Geometry, Ex. 2
• Axial force, FA • Transverse force, FQ • Moment of the plane of the beam, MZ
Rotation of Flanges
• Axial force, FA (pipe force) • Bending moment, MB • Internal pressure, p
Flanged Joint with Plane Bearing Face, Ex. 1
• Axial force, FA (pipe force) • Torsional moment, MT • Moment, MB
Flanged Joint with Plane Bearing Face, Ex. 2
Determining Bolt Dimensions
• Once working load conditions are known allow for:
– Loss of preload to embedding – Assembly preload reduced by proportion of
1. Range of Validity
• Steel Bolts • M4 to M39 • Room Temperature
2. Choice of Calculation Approach
• Dependent upon geometry
– Cylindrical single bolted joint – Beam connection – Circular plate – Rotation of flanges – Flanged joint with plane bearing face
axial bolt force – Necessary minimum clamp load in the joint – Preload scatter due to assembly method
Calculation Step R1
• Estimation of bolt diameter, d • Estimation of clamping length ratio, lK/d • Estimation of mean surface pressure under
Definitions
• Covers high-duty bolted joints with constant or alternating loads
• Bolted joints are separable joints between two or more components using one or more bolts
• Axial force, FA (pipe force) • Transverse force, FQ • Torsional moment, MT • Moment, MB
Flanged Joint with Plane Bearing Face, Ex. 3
• Axial force, FA (pipe force) • Transverse force, FQ • Torsional moment, MT • Moment, MB
3. Analysis of Force and Deformation
• Optimized by means of thorough and exact consideration of forces and deformations including:
– Elastic resilience of bolt and parts – Load and deformation ratio for parts in
Cylindrical Singl源自 Bolted Joint• Axial force, FA • Transverse force, FQ • Bending moment, MB
Beam Geometry, Ex. 1
• Axial force, FA • Transverse force, FQ • Moment of the plane of the beam, MZ
assembled state and operating state
4. Calculation Steps
• Begins with external working load, FB • Working load and elastic deformations may
cause:
– Axial force, FA – Transverse force, FQ – Bending Moment, MB – Torque moment, MT
Important Note
This summary of the VDI 2230 Standard is intended to provide a basic understanding of the method. Readers who wish to put the standard to use are urged to refer to the complete standard that contains all information, figures, etc.
