2016合肥二模理数试卷和答案
2016年合肥二模理科综合答案
高三理综试题答案第1页(共8页)合肥市2016年高三第二次教学质量检测理科综合试题参考答案及评分标准第Ⅰ卷题号1234567891011答案C A CB AC A DBBC题号12131415161718192021答案CDBBDCAA C DB CCD第Ⅱ卷22.(1)交流㊀㊀(2)乙;伸长量(或形变量㊁长度等)都相同;G K;D㊀㊀(3)伸长㊀(各1分)23.(1)149.5(1分)1500(1分)㊀ˑ10(1分)(2)14.5(2分)㊀㊀150(2分)㊀㊀100(2分)24.(12分)解:(1)假设开始时物块与木板会相对滑动,由牛顿第二定律:对木板:解得(1分)对物块:解得,故假设成立(1分)设F 作用t 秒后,小物块恰好从木板左端滑离,则,解得(1分)在此过程:木板位移,末速度(1分)物块位移,末速度(1分)在小物块从木板上滑落后的0.2s 内,由牛顿第二定律:对木板:解得(1分)高三理综试题答案第2页(共8页)木板发生的位移(1分)此时木板距平台边缘(1分)(2)小物块滑至平台后,做匀减速直线运动,由牛顿第二定律:对物块:㊀㊀解得(1分)若小物块在平台上速度减为0,则通过的位移(1分)要使木板最终不会从平台上掉下去需满足㊀㊀(1分)联立解得(1分)25.(20分)解:(1)由带电粒子在匀强磁场中运动可得:㊀㊀①(1分)解得:(1分)粒子进入匀强电场以后,做类平抛运动,设水平方向的位移为x ,竖直方向的位移为y ㊂水平方向:㊀㊀②(1分)竖直方向:㊀㊀③(1分)㊀㊀㊀㊀㊀㊀④(1分)㊀㊀⑤(1分)联立②③④⑤解得:,㊀㊀⑥(1分)由图示几何关系得:d =x +y +R =4m㊀㊀⑦(1分)高三理综试题答案第3页(共8页)(2)可使粒子无法运动到x 负半轴(a )设当匀强磁场磁感应强度为B ᶄ1时,粒子垂直打在y 轴上,粒子在磁场运动半径为r 1,由如图所示几何关系得:㊀㊀⑧(1分)解得:r 1=m 2v 0qB ᶄ1=22m㊀㊀⑨(1分)㊀㊀⑩(1分)故㊀㊀ʻ11(1分)(b )设当匀强磁场磁感应强度为B ᵡ1时,粒子从电场垂直边界进入匀强磁场后,轨迹与y 轴相切,此时粒子在磁场中运动半径为r 2,由如图所示几何关系得:㊀㊀ʻ12(1分)解得:r 2=m 2v 0qB ᵡ1=(4-22)m㊀㊀ʻ13(1分)㊀㊀㊀则㊀㊀ʻ14(各1分)(3)设粒子在B 2中运动时间为t 1,电场中运动时间为t 2,磁场B 1运动时间为t 3,㊀则:t =t 1+t 2+t 3=T 14+x v 0+T 22=14ˑ2πm q B 2+x v 0+12ˑ2πmq B ᵡ1=6.2ˑ10-5s ㊀㊀ʻ15(4分)26.(14分)(1)①球形干燥管㊀(1分)㊀碱石灰㊀(1分,其它合理答案均给分)②溶液由无色变为红色㊀(1分)㊀N H 3㊀㊀㊀(1分)(2)①D ㊁H ㊁E ㊁G ㊁F ㊀(2分)㊀赶走装置中的空气,防止对S O 3验证产生干扰㊀㊀(1分)②S O 3㊀(1分)㊀㊀㊀E 中无明显现象,G 中出现白色沉淀㊀㊀(2分)(3)①取固体样品少许,加入稀硫酸溶解,加入酸性KM n O 4溶液,不褪色ʌ或加入K 3F e (C N )6溶液,不产生蓝色沉淀ɔ㊀㊀(2分)②精确称量充分加热前后固体的质量,经过计算即可判定残留固体的成分是否全部为F e 2O 3(2分)27.(14分)(1)F e2O3+C u2O+8H C l=2C u C l2+2F e C l2+4H2O㊀㊀(2分)(2)①随着浸出时间(0~24h)的增加,铜的浸出率相应增加㊀②浸出时间超过24h后,铜的浸出率变化不明显㊀㊀㊀㊀(各1分,其它合理答案均给分)(3)5F e2++C l O2+4H+=5F e3++C l-+2H2O㊀(2分)㊀㊀㊀B㊁C㊀㊀(2分)(4)蒸发浓缩㊁冷却结晶㊁过滤㊀(2分)防止C u C l2㊃x H2O晶体溶解,乙醇易挥发㊀(1分)(5)80a-135b18b㊀㊀㊀(3分)28.(15分)(1)4㊀㊀(2分)㊀㊀㊀1.4ˑ10-15㊀(2分)(2)2ΔH2+ΔH3㊀㊀(2分)(3)>㊀㊀(1分)㊀㊀0.8c/tm o l㊃L-1㊃s-1㊀㊀(2分)㊀㊀4c/45m o l㊃L-1㊀㊀(2分)温度升高,反应速率加快,达到平衡所需的时间缩短(1分,其他合理答案均给分) (4)S2--2e-=Sˌ㊀㊀(1分)㊀㊀(n-1)S+S2-=S2-n㊀㊀(2分)ʌ或(n-2)S+2S2--2e-=S2-n㊀㊀(3分)ɔ29.(除注明外,其余每空1分,共9分)(1)生活㊀㊀(2)脂质㊀㊀细胞质基质㊀信息传递㊀㊀㊀(3)高尔基体㊀㊀催化(2分)㊀㊀B i p(2分)30.(11分)(除标明外,每空2分)(1)①无法得出结论(1分)㊀㊀②全为显性㊀㊀雌性为隐性雄性为显性(2)雌性㊀X a B X a b㊀Ⅱ-1产生配子时发生了交叉互换,产生X A b配子31.(每空2分,共10分)(1)电信号 化学信号 电信号㊀㊀(保持)正电位㊀㊀正电位 负电位 正电位(2)收缩和舒张㊀㊀㊀抑制32.(除注明外,其余每空1分,共9分)(1)R N A聚合酶㊀㊀㊀主动运输(2)神经 体液 免疫调节网络(2分)㊀㊀㊀激素调节(3)K值(或环境容纳量)㊀㊀物种多样性的增加和群落稳定性的提高(2分)㊀㊀间接高三理综试题答案第4页(共8页)33.(1)A B E(6分)(2)i.设左管中空气柱的长度增加h,由玻意耳定律:(2分)代入数据解得:h=0或h=17.5c m所以,左管中空气柱的长度为20c m或37.5c m(2分) i i.设左管水银面下降的高度为x,左㊁右管水银面的高度差为y,由几何关系:(1分)由玻意耳定律:(2分)联立两式解得:解方程得:x=10c m或x=-70c m(舍去)(2分)故左管水银面下降的高度为10c m34.ʌ物理 选修3-4ɔ(15分)(1)B C E(6分)(2)(9分)解答:ⅰ.设小球偏角为θ时离开平衡位置的位移为x,摆长为L ,,则: (1分)(1分)小球受到的回复力:(1分)联立解得:(1分)且因F与x方向相反,故小球做简谐运动㊂ⅱ.由图b可知摆球的振幅A=0.08m,周期T=2s(1分)以摆球为研究对象:由周期公式:(1分)高三理综试题答案第5页(共8页)高三理综试题答案第6页(共8页)由机械能守恒:(1分)由三角函数知识:由圆的知识:(1分)联立解得:(1分)说明:若用解答或对(m )求导得,也正确㊂35.(1)A B D(6分)(2)(i )B ㊁C碰撞动量守恒(1分)弹簧压缩至最短,此时弹性势能最大,由能量守恒定律可得:(1分)联立解得(1分)(i i )在弹簧恢复原长的过程中,系统机械能守恒㊂设弹簧恢复原长时,B C的速度为,有,则(1分)A 离开墙后,在弹簧的作用下速度逐渐增大,BC 的速度逐渐减小,当弹簧再次恢复原长时,A达到最大速度,B C的速度减小到最小值㊂在此过程中,系统动量守恒㊁机械能守恒,有㊀㊀㊀(2分)(2分)解得(1分)另一解不合题意舍去㊂高三理综试题答案第7页(共8页)36.ʌ化学 选修2:化学与技术ɔ(15分)(1)(氨)合成塔㊀㊀(1分)㊀㊀N 2+3H 2高温高压催化剂⥫⥬＝＝＝＝2N H 3㊀㊀(2分)此温度下催化剂效率最高㊀(1分)㊀㊀㊀㊀防止催化剂中毒㊀(1分)(2)冷却塔(或冷凝器)(1分)㊀利用余热,节约能源㊀(1分)㊀㊀b ㊀㊀(1分)(3)增大压强,加快反应速率,使平衡向生成NH 3的方向进行㊀(2分)(4)部分N O 转变成N 2㊀㊀(2分)(5)54㊀㊀(3分)37.ʌ化学 选修3:物质结构与性质ɔ(15分)(1)1s 22s 22p 63s 23p 63d 10㊀(1分)㊀㊀14㊀㊀(1分)(2)b ㊀(1分)(3)12㊀(1分)(4)原子晶体㊀(1分)㊀㊀G a N 晶体中,每1个G a 原子与4个N 原子结合,而G a 原子只有3个价电子,故需提供1个空轨道形成配位键㊂㊀㊀(2分)(5)s p3㊀㊀(1分)㊀㊀(6)G e O㊀㊀(2分)㊀㊀72.5㊀(3分)38.ʌ化学 选修5:有机化学基础ɔ(15分)(1)4-硝基甲苯(或对硝基甲苯)㊀(1分)㊀㊀ O H ㊁ C HO㊀(2分)(2)①㊁③㊁⑤㊀(全对给2分,漏选1个给1分,漏选2个或错选不给分)(3)高三理综试题答案第8页(共8页)(4)5㊀(2分)(5)(4分)39.ʌ生物 选修1:生物技术实践ɔ(15分)(除注明外,其余为2分)(1)碳源㊀㊀分解作用(或呼吸作用)㊀㊀无机物(或C O 2㊁无机盐)(2)无菌㊀㊀㊀㊀温度㊁湿度(有氧)㊀㊀(3分)(3)纤维素酶㊀㊀㊀稀释涂布平板法40.ʌ生物 选修3:现代生物科技专题ɔ(15分)(除注明外,其余的都为2分)(1)灭活的病毒㊀㊀选择性㊀㊀㊀克隆(2)动物细胞培养㊀㊀无菌㊁无毒的环境㊀(3分)(3)同期发情㊀㊀㊀免疫排斥反应。
2016高三上第二次段考数学理试卷定稿答案(原稿)
合肥八中2015---2016学年度高三第二次段考数学（理）试卷一、选择题:1．已知集合{}{}|1,|21x M x x N x =<=>，则M N = DA ．∅B ．{}|0x x <C ．{}|1x x <D ．{}|01x x <<2． “2a =” 是“函数()f x x a =-在区间[2,)+∞上为增函数”的（ A ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 3． 若b a b a ,,0,0>>的等差中项是21，且bb a a 1,1+=+=βα，则βα+的最小值为（ D ）A ．2B ．3C ．4D ．54. ABC ∆的三个内角C B A ,,的对边分别为c b a ,,，已知sin 1B =，向量p ()a b =，，q (12)=，. 若q p //，则C ∠角的大小为 B A.6πB.3π C.2π D.32π 5. 若函数)(2sin sin 22sin )(2R x x x x x f ∈⋅-=，则)(x f 是 DA.最小正周期为π的偶函数B. 最小正周期为π的奇函数C. 最小正周期为π2的偶函数D. 最小正周期为2π的奇函数 6．已知数列{}n a 为等差数列，且π=++1581a a a ，则)cos(124a a +的值为A A ．21-B23 C ．21D ．23±7. 设函数)0(1)6sin()(>-+=ωπωx x f 的导函数)(x f '的最大值为3，则)(x f 的图象的一条对称轴的方 程是（ A ） A ．9π=xB ．6π=xC ．3π=xD ．2π=x8. 已知等比数列{}n a 的公比0q <,其前n 项的和为n S ，则98a S 与89a S 的大小关系是( A)A ． 9889a S a S >B ．9889a S a S <C ．9889a S a S ≥D ．9889a S a S ≤9． 若定义在R 上的偶函数()x f 满足()()x f x f =+2，且当[]1,0∈x 时，(),x x f =，则函数()x x f y 3log -=的零点个数是BA ．6个B ．4个C ．2个D ．8个 10. 已知P N M ,,是单位圆上互不相同的三个点,PN PM =，则PM ⋅的最小值是（ B ）A ．41-B ．21-C ．43-D ．1-【答案】B11. 定义在0,2π⎛⎫⎪⎝⎭上的函数()f x ，其导函数)(x f '在0,2π⎛⎫⎪⎝⎭上总使得()'()tan f x f x x <⋅成立，则下列 各式中一定成立的是A ．363f f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭ B ．363f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭ C ．363f f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D ．363f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭【答案】D.12.已知等差数列{}n a 的前n 项和为n S ，向量),(n S n n =，),(1m S m m=，),(2k Sk OP k = ，且 21OP OP OP μλ+=，已知*∈N k n m ,,且互不相等，则用k n m ,,表示=μ（ C ）． A. m k n k --=μ B. k n m n --=μ C. m k m n --=μ D. nk mk --=μ【答案】C二、填空题:13. 如果复数)2)(1(i ai ++的实部和虚部相等，则实数a 等于 .31 14.设,0,()ln ,0,x e x f x x x ⎧≤=⎨>⎩则1(())3f f = 31 .15. 将函数)0)(3sin(2)(>+=ωπωx x f 的图象向右平移3πω个单位，得到函数()y g x =的图象，若()y g x =在[0,]4π上为增函数，则ω的最大值为 ．【答案】216. 设ABC ∆的内角,,A B C 所对的边,,a b c 成等比数列，则sin sin BA的取值范围是 ． 【答案】5151(,)-+ 【解析】试题分析：由条件得2b ac =，不妨设a b c ≤≤，则2b c a b a =<+，即2210b b a a --<，511b a +≤<；同理得当a b c ≥≥时，2b b c b a a +=+>，2210b b a a +->511ba-<≤．而sin sin B b A a =，∴sin sin B A 的取值范围是5151(-+．三、解答题：17.（本小题满分12分）已知函数2()21(),()()f x x ax a f x f x '=++∈R 是的导函数． （I ）解关于x 的不等式()()f x f x '>；（II ）若[2,1]x ∈--，不等式()()f x f x '≤恒成立，求a 的取值范围. 【解析】（I ）①当0a =时，原不等式的解集是(,1)(1,)-∞⋃+∞； ②当0a >时，原不等式的解集是(,12)(1,)a -∞-⋃+∞；③当0a <时，原不等式的解集是(,1)(12,)a -∞⋃-+∞； 6分（II ）因为()()f x f x '≤，所以2212(1)x x a x -+-≤，又因为21x --≤≤，所以2212(1)x x a x -+-≥在[2,1]x ∈--时恒成立，因为221132(1)22x x x x -+-=-≤，所以32a ≥． 12分18． （本小题满分12分）已知角C B A ,,为ABC ∆的三个内角，其对边分别为c b a ,,，若)2sin ,2cos(A A -=m ， )2sin ,2(cos A A =n ，32=a ，且21=⋅n m ．（I ）若ABC ∆的面积3=S ，求c b +的值； （II ）求c b +的取值范围．【解析】（I ）)2sin ,2cos (A A m -=，)2sin ,2(cos A A n =，且21=⋅n m .212sin 2cos 22=+-∴A A ，即21cos =-A ，又),0(π∈A ，32π=∴A 又由3sin 21=⋅=∆A bc S ABC ，4=∴bc由余弦定理得：bc c b bc c b a ++=⋅-+=2222232cos 2π2)(16c b +=∴，故4=+c b 6分（II ）由正弦定理得：432sin 32sin sin sin ====πA a C c B b ，又3ππ=-=+A C B ，)3sin(4)3sin(4sin 4sin 4sin 4ππ+=-+=+=+∴B B B C B c b30π<<B ，则3233πππ<+<B .则1)3sin(23≤+<πB ， 即c b +的取值范围是].4,32( 12分19. （本小题满分10分）已知数列{a n }的前n 项和为S n ，且满足S n ＋n ＝2a n (n ∈N *)． (I)求数列{a n }的通项公式；(II)若b n ＝(2n ＋1)a n ＋2n ＋1，数列{b n }的前n 项和为T n ，求满足不等式T n －22n －1>2 016的n 的最小值．【解析】（I ）21nn a =-； 6分（II ）10. 12分20. （本小题满分12分）已知函数)(ln 2)(),()(R b x xbx g R a ax x f ∈+=∈=，)()()(x g x f x G -=，且(1)0G =，()G x 在 1x =的切线斜率为0。
2016届高三第二次段考：数学(理科)参考答案(定稿)
合肥八中2015-2016学年上学期高三第二次段考数学（理科）参考答案一、选择题: DADBD AAABB DC 二、填空题:13. 如果复数)2)(1(i ai ++的实部和虚部相等，则实数a 等于 .31 14.设,0,()ln ,0,x e x f x x x ⎧≤=⎨>⎩则1(())3f f = 31 .15. 将函数)0)(3sin(2)(>+=ωπωx x f 的图象向右平移3πω个单位，得到函数()y g x =的图象，若()y g x =在[0,]4π上为增函数，则ω的最大值为 ．216. 设ABC ∆的内角,,A B C 所对的边,,a b c 成等比数列，则sin sin BA的取值范围是 ．【答案】 三、解答题：17.（本小题满分12分）已知函数2()21(),()()f x x ax a f x f x '=++∈R 是的导函数． （I ）解关于x 的不等式()()f x f x '>；（II ）若[2,1]x ∈--，不等式()()f x f x '≤恒成立，求a 的取值范围. 【解析】（I ）①当0a =时，原不等式的解集是(,1)(1,)-∞⋃+∞； ②当0a >时，原不等式的解集是(,12)(1,)a -∞-⋃+∞；③当0a <时，原不等式的解集是(,1)(12,)a -∞⋃-+∞； 6分 （II ）因为()()f x f x '≤，所以2212(1)x x a x -+-≤，又因为21x --≤≤， 所以2212(1)x x a x -+-≥在[2,1]x ∈--时恒成立，因为221132(1)22x x x x -+-=-≤，所以32a ≥． 12分 18． （本小题满分12分）已知角C B A ,,为ABC ∆的三个内角，其对边分别为c b a ,,，若)2sin ,2cos(A A -=m ， )2sin ,2(cos A A =n ，32=a ，且21=⋅n m ．（I ）若ABC ∆的面积3=S ，求c b +的值； （II ）求c b +的取值范围．【解析】（I ）)2sin ,2cos (A A m -=，)2sin ,2(cos A A n =，且21=⋅n m .212sin 2cos 22=+-∴A A ，即21cos =-A ，又),0(π∈A ，32π=∴A 又由3sin 21=⋅=∆A bc S ABC ，4=∴bc由余弦定理得：bc c b bc c b a ++=⋅-+=2222232cos 2π 2)(16c b +=∴，故4=+c b 6分（II ）由正弦定理得：432sin32sin sin sin ====πA a C c B b ，又3ππ=-=+A C B ，)3sin(4)3sin(4sin 4sin 4sin 4ππ+=-+=+=+∴B B B C B c b30π<<B ，则3233πππ<+<B .则1)3sin(23≤+<πB ， 即c b +的取值范围是].4,32(12分19. （本小题满分10分）已知数列{a n }的前n 项和为S n ，且满足S n ＋n ＝2a n (n ∈N *)． (I)求数列{a n }的通项公式；(II)若b n ＝(2n ＋1)a n ＋2n ＋1，数列{b n }的前n 项和为T n ，求满足不等式T n －22n －1>2 016的n的最小值．【解析】（I ）21n n a =-； 5分 （II ）10. 10分 20. （本小题满分12分）已知函数)(ln 2)(),()(R b x xbx g R a ax x f ∈+=∈=，)()()(x g x f x G -=，且 (1)0G =，()G x 在1x =处的切线斜率为0. （I ）求,a b ；（II ）设/1()2,n a G n n=+-求证：121111118n a a a +++< 【解析】（I ）()2ln (0)bG x ax x x x=-->，由(1)0G = 得：0a b -=/22()b G x a x x=+- 又/(1)0G =，则2a b += 1,1a b ∴==. ……5分（II ）/212()1(0)G x x x x=+->，/1()2,n a G n n =+- 21n a n n ∴=--2111n a n n ∴=--，易证：1n =时，111118a <；2n =时12111118a a +<；3n ≥时，221111111()12(2)(1)321n a n n n n n n n n =<==--------+ 121111*********(1)34253621n a a a n n ∴+++<-++-+-+-++--+ 11111111()361118n n n =---<-+. ……12分21. （本小题满分12分）已知数列{}n a 中，3,221==a a ，其前n 项和n S 满足),2(12*11N n n S S S n n n ∈≥+=+-+ （I ）求数列{}n a 的通项公式；（II ）设n a n n n b 2)1(41⋅-+=-λ(λ为非零整数，*N n ∈），试确定λ的值，使得对任意 *N n ∈，都有n n b b >+1成立．【解析】（I ）由已知，()()111n n n n S S S S +----=（2n ≥，*n ∈N ）， 即11n n a a +-=（2n ≥，*n ∈N ），且211a a -=．∴数列{}n a 是以12a =为首项，公差为1的等差数列．∴1n a n =+． …………5分（II ）∵1n a n =+，∴114(1)2n n n n b λ-+=+-⋅，要使n n b b >+1恒成立， ∴()()112114412120n n n n n n n n b b λλ-++++-=-+-⋅--⋅>恒成立，∴()11343120n n n λ-+⋅-⋅->恒成立，∴()1112n n λ---<恒成立．（ⅰ）当n 为奇数时，即12n λ-<恒成立，当且仅当1n =时，12n -有最小值为1，∴1λ<．（ⅱ）当n 为偶数时，即12n λ->-恒成立，当且仅当2n =时，12n --有最大值2-，∴2λ>-． 即21λ-<<，又λ为非零整数，则1λ=-．综上所述，存在1λ=-，使得对任意*n ∈N ，都有1n n b b +>． …………12分22. （本小题满分12分）已知a 为常数，R ∈a ，函数x ax x x f ln )(2-+=，x x g e )(=．（e 是自然对数的底数）（Ⅰ）过坐标原点O 作曲线)(x f y =的切线，设切点为),(00y x P ，试求0x 的值； （Ⅱ）令)()()(x g x f x F =，若函数)(x F 在区间]1,0(上是单调函数，求a 的取值范围． 【解析】（I ）xa x x f 12)(-+='（0>x ）． 所以切线的斜率0002000ln 12x x ax x x a x k -+=-+=，整理得01ln 020=-+x x .显然，10=x 是这个方程的解.…2分又因为1ln 2-+=x x y 在),0(+∞上是增函数， 所以方程01ln 2=-+x x 有唯一实数解．故10=x ．…4分（Ⅱ）xe xax x x g x f x F ln )()()(2-+==，x e x x a x a x x F ln 1)2()(2+-+-+-='．设x x a x a x x h ln 1)2()(2+-+-+-=，则a x xx x h -+++-='2112)(2．易知)(x h '在]1,0(上是减函数，从而a h x h -='≥'2)1()(． （1）当02≥-a ，即2≤a 时，0)(≥'x h ，)(x h 在区间)1,0(上是增函数． 0)1(=h ，0)(≤∴x h 在]1,0(上恒成立，即0)(≤'x F 在]1,0(上恒成立． )(x F ∴在区间]1,0(上是减函数．所以，2≤a 满足题意． …8分 （2）当02<-a ，即2>a 时，设函数)(x h '的唯一零点为1x ，则)(x h 在),0(1x 上递增，在)1,(1x 上递减. 又∵0)1(=h ，∴0)(1>x h ． 又∵0ln )2()(2<+-+-+-=----a a a a a e e a e a e e h ，∴)(x h 在)1,0(内有唯一一个零点x '，当),0(x x '∈时，0)(<x h ，当)1,(x x '∈时，0)(>x h .从而)(x F 在),0(x '递减，在)1,(x '递增，与在区间]1,0(上是单调函数矛盾． ∴2>a 不合题意． 综合（1）（2）得，2≤a ． …12分。
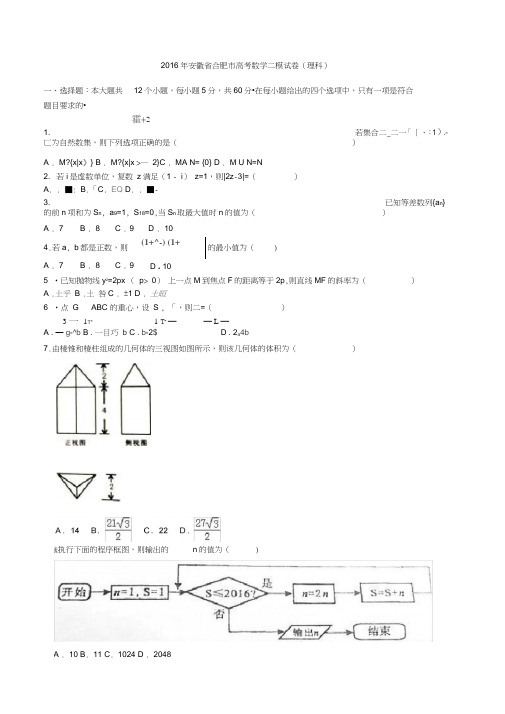
(完整word)2016年安徽省合肥市高考数学二模试卷(理科)(解析版)
2016年安徽省合肥市高考数学二模试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分•在每小题给出的四个选项中，只有一项是符合题目要求的•霍+21. 若集合二_二一「丨、：1）.-匸为自然数集，则下列选项正确的是（）A . M?{x|x》}B . M?{x|x >—2}C . MA N= {0}D . M U N=N2. 若i是虚数单位，复数z满足（1 - i）z=1，则|2z-3|=（）A. . ■:B.「C. EQD. . ■-3. 已知等差数列{a n}的前n项和为S n, a9=1, S18=0,当S n取最大值时n的值为（）A . 7B . 8C . 9D . 104.若a, b都是正数，则(1+^-) (1+的最小值为（)A . 7B . 8C . 9D . 105 •已知抛物线y2=2px （p> 0）上一点M到焦点F的距离等于2p,则直线MF的斜率为（）A .土乎B .土咎C . ±1D . 土晅6 •点G ABC 的重心，设S , 「，则二=（）3 一1T* 1 T-——L—A . —g-^bB . 一目巧bC . b-2$D . 2a4b7.由棱锥和棱柱组成的几何体的三视图如图所示，则该几何体的体积为（）&执行下面的程序框图，则输出的n的值为（)A . 10 B. 11 C. 1024 D . 20489.在三棱锥P - ABC 中，PA 丄平面ABC , _|■- - ■ '：J_'，则三棱锥P- ABC12. 定义在R 上的偶函数f (x )的导函数为f '(x ),若对任意的实数 x ，都有2f (x ) +xf '(x )v 2恒成 立，则使x 2f ( x )- f (1)v x 2- 1成立的实数x 的取值范围为()A . {x|x 工±}B . ( - s,- 1) U ( 1, + s)C . (- 1, 1)D . (- 1, 0) U (0, 1) 二、填空题(每题 5分，满分20分，将答案填在答题纸上)13. ________________________________________ 命题灯咒＞0,冥％＞1”的否定是 .214. 双曲线M: 的左，右焦点分别为 F 1, F 2，记|F 1F 2|=2C ,以坐标原点 O 为圆心，c 为半径的圆与双曲线 M 在第一象限的交点为 P ,若|PF 1|=C +2 ,贝V P 点的横坐标为 __________ .2 o15. ______________________________________________________________________________________ 已知各项均为正数的数列｛a n ｝前n 项和为S n ,若S ］二2・3片 一泊就1片二弘+1，则a n = _________________ 16. ____________________________________________________________________ 若函数f (x ) =x 2 (x - 2) 2- a|x -1|+a 有4个零点，贝V a 的取值范围为 ______________________________________ . 三、解答题(本大题共 5小题，共70分•解答应写出文字说明、证明过程或演算步骤 •) 17.在厶ABC 中，三个内角A, B , C 所对的边分别为 a, b,c,已知函数• ■ i - _ / - ■为偶函数，2F ( +) (1 )求 b ;(2 )若a=3，求△ ABC 的面积S.18. 某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间( 占有率(y% )的几组相关对应数据;的外接球的表面积为（）A . 20 nB . 24 nC . 28 nD . 32 nfx- y+l>010.已知实数x , y 满足{掘一3¥-1恋0,L<i若z=kx - y 的最小值为- 5，则实数k 的值为(A . - 3B . 3 或-5C . - 3 或-5D . ±311.某校组织由5名学生参加的演讲比赛， 采用抽签法决定演讲顺序, B 不是最后一个出场”的前提下，学生C 第一个出场的概率为(在学生A 和B 都不是第一个出场, )B .C .20x 个月)和市场(2)根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过 0.5% (精确到月)0.020.050.1(1)根据上表中的数据，用最小二乘法求出0.15 0.18y 关于x 的线性回归方程; 附:19. 如图，六面体ABCDHEFG 中，四边形ABCD为菱形，AE , BF , CG, DH都垂直于平面ABCD，若DA=DH=DB=4 , AE=CG=3(1)求证：EG丄DF;(2)求BE与平面EFGH所成角的正弦值.20. 已知椭圆Ei ~+~^l(a>b>0)经过点(2),且离心率为芈，F i, F2是椭圆E的左，右焦点(1)求椭圆E的方程；(2)若点A , B是椭圆E上关于y轴对称两点(A , B不是长轴的端点)，点P是椭圆E上异于A , B的一点，且直线PA, PB分别交y轴于点M, N，求证：直线MF i与直线NF2的交点G在定圆上.21 .已知函数g (x) =ax3+x2+x (a为实数)(1)试讨论函数g (x)的单调性；(2)若对？x € (0, +x)恒有二’•「：心,「-“；一^，求实数a的取值范围.请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分22.如图，PA为四边形ABCD外接圆的切线，CB的延长线交PA于点P, AC与BD相交于点M , PA// BD(1)求证：/ ACB= / ACD ；23.在直角坐标系xOy 中,曲线(a为参数)，在以0为极点, x轴的非负半轴为(2 )若PA=3, PC=6, AM=1，求AB 的长.24.已知函数f (x) =|x - 4|+|x-a| (a€ R)的最小值为a极轴的极坐标系中，直线I: p sin+p cos 0 =m(1 )若m=0，判断直线l与曲线C的位置关系；(2)若曲线C上存在点P到直线I的距离为-求实数m的取值范围.1)求实数a 的值；(2)解不等式f (x)有.2016年安徽省合肥市高考数学二模试卷（理科）答案与解析一、选择题1.若集合二丄匚「丨、：'匸为自然数集，则下列选项正确的是（）A . M?{x|x 羽}B . M?{x|x >— 2}C . MA N={0}D . M U N=N解：J'『J I"'：=[ - 2,1), N 为自然数集，故 M?{x|x > 1错误;M?{x|x >- 2}错误;Mn N={0}正确；M U N=N 错误；选C 2•若i 是虚数单位，复数 z 满足（1 - i ） z=1，则|2z -3|=（ A •二 B . 「 C. .， D . . 7z= (1 - i ) (a+bi ) =1, + (b - a ) i=1 , a - b=0, ，则 |2z - 3|=|2 (丄+〒i )- 3|=| -2+i|= _ ：选3.已知等差数列{a n }的前n 项和为S n , a 9=1, S 18=0,当S n 取最大值时n 的值为（）A . 7B . 8C . 9D . 10解：设等差数列{a n }的公差为d , T a 9=1, S 18=0 ,118X17…a 1+8d=1 , 18a 1+ d=0 ,可得：a 1=17 , d= - 2.•- a n =17 - 2 （n - 1） =19 - 2n , 出/111由a n >0解得:―二当S n 取最大值时n 的值为9 .选C4.若a , b 都是正数，则 ）的最小值为（ ）A . 7B . 8C . 9D . 10解：T a , b 都是正数，则寸牛）=5+号+辛》5+^^严，当且仅当b=2a >0时取等号 选C 5 .已知抛物线y 2=2px （ p > 0） 上一点M 到焦点F 的距离等于2p ,则直线MF 的斜率为（ ）A .土晳B . 土号C . ±1D . - V3解：设 z=a+bi , 则(1 - i ) ••• (a+b) ••• a+b=1, • a =b =-解：抛物线的焦点为 F (二-, T 点M 到焦点F 的距离等于y M = ± '；p .6 •点GABC 的重心，设 BG =刃,GC =卫，则忑=()A . 2苏B .C . b -萬D . 2且十b解：由题意知， F3+ -=「匚， 即丄—+7•由棱锥和棱柱组成的几何体的三视图如图所示，则该几何体的体积为(T \ I t A1A . 14C . 22 D.-解：由三视图可知：该几何体的体积0),准线方程为 2p , ••• M 到准线2p .1:.选 DV 〒—■ 二•： ■疋=14 .选 A不满足条件S <2016,退出循环，输出 n 的值为1024.选C 9.在三棱锥 P -ABC 中，PA 丄平面ABC, - »'■ ' = - ■：J ：,则三棱锥 P - ABC的外接球的表面积为（）A . 20 nB . 24 nC . 28 nD . 32 n解：•/ AB=AC=2 :, / BAC=60 , •••由余弦定理可得BC=2 .二,273 设厶ABC 外接圆的半径为r ,则2r= 一 =4 ,• r =2,设球心到平面 ABC 的距离为d ,则由勾股定理可得 R 2=d 2+22=22+ （ 2 -d ） 2 , •- d=1, R 2=5 ,•三棱锥P - ABC 的外接球的表面积为 4 nR =20 n 选ACx- y+l>010 .已知实数x , y 满足■:-厂% 'n=1， S=1满足条件S W 2016 n=2, 满足条件S W 2016 n=4, 满足条件S W 2016 n=8, 满足条件S W 2016 n=16, 满足条件S W 2016 n=32, 满足条件 S W 2016 n=64 , 满足条件 S W 2016 n=128 满足条件 S W 2016 n=256 满足条件 S W 2016 n=512S=1+2=3 S=3+4=7 S=7+8=15 S=15+16=31 S=31+32=63 S=63+64=127 ,S=127+128=255 ,S=255+256=511 ,S=511+512=1023满足条件S W 2016 n=1024, S=1023+1024=2047 若z=kx - y 的最小值为- 5,贝U 实数k 的值为（&执行下面的程序框图，则输出的 n 的值为（ )解：模拟执行程序框图，可得L<iA . - 3 B. 3 或-5 C. - 3 或-5D. ±3联立「孙“解得B 2,7, 化 z=kx - y 为 y=kx - z ,由图可知，当k v 0时，直线过A 时在y 轴上的截距最大，z 有最小值为k - 2= - 5,即k= - 3； 当k >0时，直线过B 时在y 轴上的截距最大，z 有最小值-2k+仁-5，即k=3. 综上，实数k 的值为±3 •选D11. 某校组织由5名学生参加的演讲比赛， 采用抽签法决定演讲顺序,B 不是最后一个出场”的前提下，学生C 第一个出场的概率为（ 1I 3g D. -20解：方法一： 学生A 和B 都不是第一个出场，B 不是最后一个出场”的出场顺序为：分为两类.第一类：A 最后一个出场，从除了 B 之外的3人选1人安排第一个，其它的任意排，故有 AjA 33=18种, 第二类：A 不是最后一个出场，从除了 A , B 之外的3人选2人安排在，第一个或最后一个，其余 3人 任意排，故有A 32A 33=36种，故学生A 和B 都不是第一个出场，B 不是最后一个出场的种数 18+36=54种，学生A 和B 都不是第一个出场，B 不是最后一个出场”的前提下，学生 C 第一个出场的”的出场顺序为: 分为两类 第一类：学生C 第一个出场，A 最后一个出场，故有 A 33=6种，第二类：学生C 第一个出场，A 不是最后一个出场，从除了 A , B 之外的2人选1人安排在最后一个， 其余3人任意排，故有 A 21A 33=12种，故在 学生A 和B 都不是第一个出场，B 不是最后一个出场 种，方法二： 先排B ，有A 31 （非第一与最后），再排A 有A 31 （非第一）种方法，其余三个自由排，共有A 31A 31A 33=54这是总结果；18 154 ：=3故学生C 第一个出场的概率为在学生A 和B 都不是第一个出场, ）C . 的前提下，学生C 第一个出场的种数 6+12=18学生C 第一个出场，先排 B ,有A 31 (非第一与最后)，再排A 有A 31, C 第一个出场，剩余 2人自由排， 故有 A 31A 31A 22=18 种，故学生C 第一个出场的概率为上二=丄，选A54 312. 定义在R 上的偶函数f ( x )的导函数为f '(x ),若对任意的实数 x ，都有2f (x ) +xf '(x )v 2恒成 立，则使x 2f ( x )- f (1)v x 2- 1成立的实数x 的取值范围为() A . {x|x 工土}B . ( - s,-1) U (1 ,+〜C . (- 1 ,1)D . (- 1 ,0) U (0, 1)解：当x ＞ 0时，由2f (x ) +xf ' (x )- 2v 0可知：两边同乘以 x 得： 2xf (x )- x 2f ( x )- 2x v 0 设：g (x ) =x 2f (x )- x 2则 g' (x ) =2xf (x ) +X 2f'(x )- 2x v 0,恒成立： ••• g (x )在(0, +s)单调递减， 由 x 2f (x )- f (1) v x 2- 1• x 2f (x )- x 2v f ( 1 )- 1 即 g (x )v g (1)即 x ＞ 1 ；当x v 0时，函数是偶函数，同理得：x v- 1综上可知：实数x 的取值范围为(-s,- 1) U (1, +s),选B 二、填空题 13.命题 灯艾＞0, _________________________ 買召■乂＞1”的否定是 .解：因为全称命题的否定是特称命题，所以，命题 W 工＞0, /匕＞ 1”的否定是：F 1, F 2，记|F 1F 2|=2C ,以坐标原点 O 为圆心，c 为半径的圆与双曲线 M 在第一象限的交点为P ,若|PF 1|=C +2 ,贝V P 点的横坐标为 ________ 解：坐标原点O 为圆心，C 为半径的圆的方程为 X 2+y 2=c 2,2,22丘-c--■，解得由 |PF 1|=C +2 ,由双曲线的定义可得|PF 2|=|PF 1|- 2a=c+2 - 2=C ,在直角三角形PF 1F 2中，可得C 2+ ( C +2) 2=4C 2, 解得c=1+ .二x 2=cW b 2-Kl14.双曲线的左，右焦点分别为由c2=a2+b2=1+b2,可得b2=3+2 二可得P的横坐标为」「•答案:5 g15. 已知各项均为正数的数列{a n}前n项和为S n,若厂,■.，则a n= 解：由S i=2，得a i=S i=2,由3叮- 2且血片二曰田勺得恋/二的口+齢1)2,又a n> 0,--2S n=S n+a n+1，即S n=a n+1 ,当n》2时，S n- i=a n,两式作差得：a n=a n+1 - a n,即卩----- Z又由3S n - ^a rrt-l S n=a n+l，求得a2=2，•••当n》2时，务二尹7.验证n=1时不成立，辽，iTl[产1. n>216. ______________________________________________________________________________ 若函数f (x) =x2(x - 2) 2- a|x- 1|+a有4个零点，贝V a的取值范围为_____________________________________ .解：函数 f (x) =x2(x- 2) 2- a|x- 1|+a 有 4 个零点，转化为：x2(x - 2) 2- a|x- 1|+a=0 由 4 个根,I »自宣問乞直二即y=x2(x - 2) 2; y=a|x- 1| - a= '..两个函数的图象有4个交点，[a(.x — 2 J ? 1/1在同一个直角坐标系中画出两个函数的图象，如图：当a v0时，如图中蓝色的折线，函数有4个零点，可得-1 v a v 0；当a>0时，如图中的红色折线，此时函数有4个零点•满足题意.综上：a€ (- 1, 0) U (0, +〜4/• A= 当A= —或一：:或兀 时，则C=n - 兀兀兀 362,△ ABC 的面积 S= ■ _ 一■= 一，.=,△△ ABC 的面积 S= ： •-'：=三、解答题17.在△ ABC 中，三个内角A,B ,C 所对的边分别为 a, b,c,已知函数，■ i -_ - ■为偶函数， （1 ）求 b ；（2 ）若a=3，求△ ABC 的面积S.解：（1）在厶ABC 中,7T 7C所以 f Ci)=2cos2s : b 二F ：—片五…asinBb2二由正弦定理得sinA=兀兀由f （X ）为偶函数可知■ ■，所以k 兀 » k £ Z又0 v B v n,故 当时，贝U C=n-(2) 根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该 款旗舰机型市场占有率能超过0.5% (精确到月)b 二斗;----------- ，a=y _ bxEL =1X (0.02+0.05+0.1+0.15+0.18 ) =0.1;i A i 1X0. 02+2X0. 05+3X0. 1+4X0.15+5X 0. 13- 5X3X0.=0.1 - 0.042 X = - 0.026,所以线性回归方程为I -・「：；…(2 )由上面的回归方程可知，上市时间与市场占有率正相关， 即上市时间每增加1个月，市场占有率都增加0.042个百分点;m I. -: 7：-- I.:-，解得 X 》13预计上市13个月时，市场占有率能超过0.5%.-18•某品牌手机厂商推出新款的旗舰机型， 占有率(y% )的几组相关对应数据；x 1 y0.02(1) 根据上表中的数据，用最小二乘法求出并在某地区跟踪调查得到这款手机上市时间( 2 3 4 0.05 0.10.15y 关于x 的线性回归方程； 5 0.18x 个月)和市场附: 解：(1)根据表中数据，计算4X (1+2+3+4+5)=3,12+22+32+4^52 YX 护=0.042,19. 如图，六面体ABCDHEFG 中，四边形ABCD为菱形，AE , BF , CG, DH都垂直于平面ABCD，若DA=DH=DB=4 , AE=CG=3(1) 求证：EG丄DF ；(2) 求BE与平面EFGH所成角的正弦值.解：（1）连接AC ,•••四边形ABCD 为菱形，••• AC 丄BD , •/ BF 丄平面 ABCD , AC?平面 ABCD , • AC 丄BF ,又 BD?平面 BDF , BF?平面 BDF , BD A BF=B , • AC 丄平面BDF , •/ AE // CG , AE=CG , •四边形AEGC 是平行四边形， • EG // AC ,• EG 丄平面BDF ,又DF?平面BDF , • EG 丄DF .(2)设 AS BD=O , EGH HF=P ,•/四边形ABCD 为菱形，AE 丄平面ABCD ，BF 丄平面ABCD , • AD // BC , AE // BF , •平面ADHE //平面BCGF ,• EH // FG , 同理可得：EH // HG ,•四边形EFGH 为平行四边形, 又 O 为 AC 的中点，• OP // AE , AE=OP ,• OP 丄平面ABCD ,又OA 丄OB ,所以OA , OB , OP 两两垂直,(BF+DH ) , • BF=2 .以O 为原点建立空间直角坐标系 O - xyz ,•••△ ABD 是等边三角形，AB=4 , • OA=2 :';.• E (2, 0 , 3), P ( 0 , 0 , 3), F ( 0 , 2 , 2), B( 0 , 2 , 0).•屈=(2 .「；, - 2 ,3),二 £= (2. ； , 0 , 0),平=(0 ,2 , - 1).,令 y=i ,得1 -二设BE 与平面EFGH 所成角为• P 为EG 的中点, 设平面EFGH 的一个法向量为4^520.已知椭圆B ： （&>b> 0）经过点（2近，2）,且离心率为- 右焦点 （1） 求椭圆E 的方程；（2）若点A , B 是椭圆E 上关于y 轴对称两点（A , B 不是长轴的端点），点P 是椭圆E 上异于A , B 的 一点，且直线PA , PB 分别交y 轴于点M , N ，求证：直线 MF i 与直线NF 2的交点G 在定圆上.2 2解: (1) T 椭圆 B J2=1 (r>b> Q)经过点(2^21 2),且离心率为a £亠解得 a=4, b=c=272, 2 2•椭圆C 的方程訂K 证明：(2)设 B (x o , y o ), P ( x i , y i )，则 A (- x o , y o )故灿Xiy n *卞仍同理可得J "■' ,Ki）-（-2^xi^x o2 2,F i , F 2是椭圆E 的左,直线PA 的方程为V y（乂 -垃］），令x=0，得尸K l +xO话（逅沁尹5硏（■碍迪亠,1 *0- 2 2 _ 2 2 工1厲 矶厂—_ L?4 X 1 y O•••由条件=巧坎呻-沽）r职欧卅肯〉--g-------------------------- ---------------- ------------- 空一=-E+8=0x i ~ K o•- F i M丄F2N，•直线F i M与直线F2N交于点G在以F1F2为直径的圆上.21 .已知函数g (x ) =ax 3+x 2+x (a 为实数)(1) 试讨论函数g (x )的单调性；(2) 若对？x €( 0, +〜 恒有百3£皿乜，求实数a 的取值范围.解：(1) g' (x ) =3ax 2+2x+1(i) 当 a=0时，g (x )在 (-0 —寺)单调减和(一 * 8 单调增;(ii) 当 a ^0寸，△ =4 - 12a , g (x )在R 单调增;当 Q<a<—时，由 g' (x ) =3ax 2+2x+ 仁0 得,J - 1 ■ 3a-[+寸1 - 3a 十3a ? - 3a g (乂)在(X1, X2)单调减，在(-汽X1)和(X2, +8)单调增；当a v 0时，g (乂)在(X2, X1)单调增，在(-8, X2)和(X1, +8)单调减；(2)令 f Cx)=lnx+-^，则 F 【工〕二：—■—J"K s x因此，f (X )在(0, 1)单调减，在(1 , +8)单调增fmin (X ) =f ( 1) =1当 a >- 1 时，g (1) =a+2> 仁f (1),显然，对？ x € (0, +8)不恒有 f (x ) >g (x )； 当a<- 1时，由(1)知，g (乂)在(0,禺)单调增，在(X1, +8)单调减，二1壬(衣]十1)尸⑹ 1]1 ? 1所以気做⑺十D ,即满足对?x € (0, +8)恒有f (X ) >g (x )综上，实数a € (- 8,- 1].22.如图，PA 为四边形ABCD 外接圆的切线，CB 的延长线交PA 于点P , AC 与BD 相交于点M , PA // BD(1)求证：/ ACB= / ACD ；(2 )若 PA=3, PC=6, AM=1，求 AB 的长.3日就[2-F2K 2+1=0，即所以，在(0, +8) 上, g' (x ) =3ax 2+2x+1亘成立，此时(1)证明：•/ PA 为切线，•••/PAB= / ACB .•/ PA / BD , PAB= / ABD= / ACD ,•••/ ACB= / ACD ・(2 )解：已知 PA=3, PC=6, AM=1，由切割线定理 PA 2=PB?PC 得：BC =—, •/ PA // BD ，得AB ACAM "AB所以 AB 2=AM?AC=4，所以 AB=2极轴的极坐标系中，直线（1 ）若m=0，判断直线 I : p sin+B p cos 0 =m I 与曲线C 的位置关系;解：（1）曲线匚 宴二寸©8岂口+1y=-/2sin CC +1|1+1 - TO |由已知可得：圆心 C 到直线Ix+y=m 的距离d — 解得-K m<524.已知函数f (x ) =|x - 4|+|x - a| (a € R )的最小值为 a(1)求实数a 的值；(2 )解不等式f (x )有.解：(1) f (x ) =|x - 4|+|x - a| 羽 | a|=a ,从而解得a=2…(2 )由(1)知，f ( x ) =|x - 4|+|x - 2|= .「 ,综合函数y=f (x )的图象知，解集为{訂寺©<*}23•在直角坐标系xOy 中，曲线C- （a 为参数），在以O 为极点，x 轴的非负半轴为（2）若曲线C 上存在点 P 到直线I 的距离为，求实数m 的取值范围. 曲线 直线 C 的直角坐标方程为：（x - 1） I : p sin 0 + p cos,0可得直线I 的直角坐标方程为: 2+ (y - 1) 2=2,是 「个圆；圆心（1, 1）,半径为：V2 x+y=0圆心 C 到直线I 的距离\ '，所以直线I 与圆C 相切 又知△ AMB 〜△ ABC ，所以 （a 为参数）， (2)。
安徽省合肥市届高三第二次教学质量检测数学理试题.docx
安徽省合肥市2016届高三第二次教学质量检测数学理试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.若集合20,1x M x R N x 禳+镲=危睚-镲铪为自然数集，则下列选项正确的是（ ）A ．{}1M x x统 B ．{}2M x x ?- C ．{}0MN = D ．MN N =2.若i 是虚数单位，复数z 满足()11i z -=，则23z -=（ ） A ．3 B ．5 C ．6 D ．73.已知等差数列{}n a 的前n 项和为n S ，9181,=0a S =，当n S 取最大值时n 的值为（ ） A ．7 B ．8 C ．9 D ．104.若,a b 都是正数，则411b a a b骣骣琪琪++琪琪桫桫的最小值为（ ） A ．7 B ．8 C ．9 D ．105.已知抛物线()220y px p =>上一点M 到焦点F 的距离等于2p ，则直线MF 的斜率为（ ）A ．3±B ．1±C ．34±D ．33±7.由棱锥和棱柱组成的几何体的三视图如图所示，则该几何体的体积为（ ）A ．14B ．2132C ．22D ．27328.执行下面的程序框图，则输出的n 的值为（ ）A ．10B ．11C ．1024D ．20489.在三棱锥P ABC -中，PA ABC ^平面，=60=23,2BAC AB AC PA ?=，，则三棱锥P ABC -的外接球的表面积为（ ）A ．20pB ．24pC ．28pD ．32p10.已知实数,x y 满足103101x y x y x ì-+?ïï--?íï£ïî，若z kx y =-的最小值为-5，则实数k 的值为（ ）A ．-3B ．3或-5C ．-3或-5D ．3±11.某校组织由5名学生参加的演讲比赛，采用抽签法决定演讲顺序，在“学生A 和B 都不是第一个出场，B 不是最后一个出场”的前提下，学生C 第一个出场的概率为（ ）A ．13 B ．15 C ．19 D ．32012.定义在R 上的偶函数()f x 的导函数为()f x ¢，若对任意的实数x ，都有()()22f x xf x ¢+<恒成立，则使()()2211x f x f x -<-成立的实数x 的取值范围为（ ） A ．{}1x x 贡 B ．()(),11,-?+? C ．()1,1- D ．()()1,00,1-第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.命题“20,1x x x ">+>”的否定是 ．14.双曲线222:1y M x b-=的左，右焦点分别为12,F F ，记12=2F F c ，以坐标原点O 为圆心，c 为半径的圆与双曲线M 在第一象限的交点为P ，若1=2PF c +，则P 点的横坐标为 ．15.已知各项均为正数的数列{}n a 前n 项和为n S ，若22111=2,32n n n n S S a S a ++-=，则n a = ．16.若函数()()2221f x xx a x a =---+有4个零点，则a 的取值范围为 ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.在ABC D 中，三个内角,,A B C 所对的边分别为,,a b c ，已知函数()()()sin 23cos 2f x x B x B =+++为偶函数，12b f p骣琪=琪桫（1）求b ；（2）若3a =，求ABC D 的面积S18.某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（x 个月）和市场占有率（%y ）的几组相关对应数据；x1 2 3 4 5 y0.020.050.10.150.18（1）根据上表中的数据，用最小二乘法求出y 关于x 的线性回归方程；（2）根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过0.5%（精确到月）附：1221ˆˆˆ,ni i i ni i x y nx y bay bx x nx==-?==--åå19.如图，六面体ABCDHEFG 中，四边形ABCD 为菱形，,,,AE BF CG DH 都垂直于平面ABCD ，若4,3DA DH DB AE CG =====（1）求证：EG DF ^；（2）求BE 与平面EFGH 所成角的正弦值20.已知椭圆()2222:10x y E a b a b+=>>经过点()222，，且离心率为22，12,F F 是椭圆E 的左，右焦点（1）求椭圆E 的方程；（2）若点,A B 是椭圆上E 关于y 轴对称两点（,A B 不是长轴的端点），点P 是椭圆E 上异于,A B 的一点，且直线,PA PB 分别交y 轴于点,N M ，求证：直线1MF 与直线2NF 的交点G 在定圆上 21.已知函数()32g x ax x x =++（a 为实数） （1）试讨论函数()g x 的单调性； （2）若对()0,x "??恒有()1ln g x xx?，求实数a 的取值范围 请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.如图，PA 为四边形ABCD 外接圆的切线，CB 的延长线交PA 于点P ，AC 与BD 相交于点M ，PA BD（1）求证：ACB ACD ??；（2）若3,6,1PA PC AM ===，求AB 的长23.在直角坐标系xOy 中，曲线2cos 1:2sin 1x C y a a ì=+ïíï=+î（a 为参数），在以O 为极点，x 轴的非负半轴为极轴的极坐标系中，直线:sin cos l m r q r q += （1）若0m =，判断直线l 与曲线C 的位置关系； （2）若曲线C 上存在点P 到直线l 的距离为22，求实数m 的取值范围 24.已知函数()4f x x x a =-+-（a R Î）的最小值为a （1）求实数a 的值； （2）解不等式()5f x £合肥市2016届高三第二次教学质量检测 数学试题（理）参考答案及评分标准一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CBBCADACADAB二、填空题13. 20000,1x x x $>+? 14.312+ 15. 12,12,2n n n a n -ì=ï=í³ïî 16. 3210027a a a a 禳镲=--<<>睚镲铪或或三、解答题17.解：（1）()()()sin 23cos 22sin 23f x x B x B x B p骣琪=+++=++琪桫由()f x 为偶函数可知,32B k k Z p p p +=+?，所以,6B k k Z pp =+? 又0B p <<，故6B p =所以()2sin 2=2cos 2,3212f x x x b f pp 骣骣琪琪=+==琪琪桫桫……………6分当23A p=时，ABC D 的面积334S =……………12分 18.解：（1）经计算ˆˆ0.042,0.026ba ==-，所以线性回归方程为ˆ=0.0420.026y x -；……………6分 （2）由上面的回归方程可知，上市时间与市场占有率正相关，即上市时间每增加1个月，市场占有率都增加0.042个百分点；由ˆ=0.0420.0260.5yx ->，解得13x ³ 预计上市13个月时，市场占有率能超过0.5% ……………12分19.解：（1）连接AC ，由,AE CG AE CG =可得AEGC 为平行四边形，所以EG AC ，而,AC BD AC BF ^^，所以,EG BD EG BF ^^，因为BD BF B =，所以EG BDHF ^平面，又DF BDHF Í平面，EG DF \^ ……………5分 （2）设,ACBD O EG HF P ==，由已知可得：ADHE BCGF 平面平面，所以EH FG ，同理可得：EH HG ，所以EFGH 为平行四边形，所以P 为EG 的中点，O 为AC 的中点，所以,OP AE AE OP =，从而OP ABCD ^平面，又OA OB ^，所以,,OA OB OP 两两垂直，由平几知识，得2BF =如图，建立空间直角坐标系O xyz -，则()()()()0,2,0,23,0,3,0,2,2,0,0,3B E F P()()()23,2,3,23,0,0,0,2,1BE PE PF \=-==-设平面EFGH 的一个法向量为(),,z n x y =，由00PE n PF n ì?ïíï?î可得：020x y z ì=ïí-=ïî，令1y =，则2z =()0,1,2n \=设BE 与平面EFGH 所成角为q ，则45sin 25BE nBE nq ×==× ……………12分20.解：（1）由条件得4,22a b c ===，所以椭圆C 的方程221168x y += ……………5分 （2）解设()()0011,,P ,B x y x y ，则()00,A x y - 直线PA 的方程为()101110y y y y x x x x --=-+，令0x =，得100110x y x y y x x +=+ 故1001100,x y x y M x x 骣+琪琪+桫，同理可得1001100,x y x yN x x 骣-琪琪-桫1001100112101022,,22,x y x y x y x y F M F N x x x x 骣骣+-琪琪==-琪琪+-桫桫所以，22221001100110011210101022,22,8x y x y x y x y x y x y F M F Nx x x x x x 骣骣+--琪琪??=-+琪琪+--桫桫222201102210818116168880x x x x x x 骣骣琪琪?-?琪琪桫桫=-+=-+=- 所以，12F M F N ^，所以直线1F M 与直线2F N 交于点G 在以12F F 为直径的圆上 ……………12分 21.解：（1）()2321g x ax x ¢=++1）当0a =时，()g x 在1,2骣琪-?琪桫单调减和1,2骣琪-+?琪桫单调增；2）当0a ¹时，=412a D -当13a ³时，()23210g x ax x ¢=++?恒成立，此时()g x 在R 单调增； 当103a <<时，由()2321=0g x ax x ¢=++得，12113113,33a a x x a a ----+-==， ()g x 在()12,x x 单调减，在()()12,,x x -??和单调增； 当0a <时，()g x 在()21,x x 单调增，在()()21,,x x -??和单调减， ……………5分（2）令()1ln f x x x =+，则()211f x x x¢=- 因此，()f x 在()0,1单调减，在()1,+?单调增()()min 11f x f \==当1a >-时，()()1211g a f =+>=，显然，对()0,x "?? 不恒有()()f x g x ³； 当1a ?时，由（1）知，()g x 在()10,x 单调增，在()1,x +?单调减211321=0ax x ++，即()2111213ax x =-+ 所以，在()0,+?上，()()()2322max 1111111121113333g x g x ax x x x x x ==++=+=+- 又(]111310,13131a x a a ---==?--所以()()()2max 1min 1111=33g x x f x =+-?，即满足对()0,x "?? 恒有()()f x g x ³综上，实数(],1a ?? ……………12分22.解：（1）PA 为切线，PAB ACB \??,PA BD PAB ABD ACD \???ACB ACD \?? ……………5分（2）已知3,6,1PA PC AM ===，由切割线定理2PA PB PC =?得：39,B ,22PB C PA BD ==，得,3AM PBMC MC BC=\= 又知AMB ABC D D ，所以AB ACAM AB= 所以24AB AM AC=?，所以2AB = ……………10分23.解：（1）曲线C 的直角坐标方程为：()()22112x y -+-=，是一个圆；直线l 的直角坐标方程为：0x y +=圆心C 到直线l 的距离2211211d r +===+，所以直线l 与圆C 相切 ……………5分（2）由已知可得：圆心C 到直线l 的距离221132211m d +-=?+ 解得15m-＃ ……………10分24.解：（1）()44f x x x a a a =-+-?=，从而解得2a = ……………5分（2）由（1）知，()()()()26242224264x x f x x x x x x ì-+?ïï=-+-=<?íïï->î 综合函数()y f x =的图象知，解集为11122x x禳镲＃睚镲铪……………10分。
(精品word版)2016年安徽省“合肥十校”联考中考二模数学
2016年安徽省“合肥十校”联考中考二模数学一、选择题(共10小题，每小题4分，满分40分.每小题只有一个选项符合题意)1.下列计算中，正确的是( )A.x3·x2=x6B.x3-x2=xC.(-x)2·(-x)=-x3D.x6÷x2=x3解析：利用同底数幂相乘，底数不变指数相加；同底数幂相除，底数不变指数相减，对各选项分析判断后利用排除法求解.A、应为x3·x2=x3+2=x5，故本选项错误；B、x3与x2没有同类项，不能合并，故本选项错误；C、(-x)2·(-x)=(-x)2+1=-x3，正确；D、应为x6÷x2=x4，故本选项错误.答案：C.2.如图是一个几何体的实物图，则其侧视图是( )A.B.C.D.解析：根据从左边看得到的图形是左视图，可得答案.从左边看下边是一个矩形，上边是一个梯形应该是.答案：C.3.据统计去年来国内旅游人数达到9.98亿人次，用科学记数法表示9.98亿正确的是( )A.9.98×107B.9.98×108C.0.998×109D.99.8×107解析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数.确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同.当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数.将9.98亿用科学记数法表示为：9.98×108.答案：B.4.如图，直线a∥b，AC丄AB，AC交直线b于点C，∠1=65°，则∠2的度数是( )A.65°B.50°C.35°D.25°解析：∵AC丄AB，∴∠BAC=90°，∴∠1+∠B=90°，∵∠1=65°，∴∠B=25°，∵a∥b，∴∠2=∠B=25°.答案：D.5.如图，AB 是⊙0的直径，点C 、D 在⊙0上，∠BOD=11O °，AD ∥OC ，则∠AOC=( )A.70°B.60°C.50°D.55°解析：∵∠BOD=110°， ∴∠OAD=12∠BOD=55°. ∵AD ∥OC ，∴∠AOC=∠OAD=55°. 答案：D.6.( ) A.6 B.12解析：如图，在Rt △AOG 中，AOG=30°，∴cos30°OGAO=， ∴OA=OG ÷cos 30°=2. 这个正六边形的周长=12. 答案：B.7.如图，反比例函数11k y x=和一次函数y 2=k 2x+b 的图象交于A 、B 两点.A 、B 两点的横坐标分别为2，-3.通过观察图象，若y 1＞y 2，则x 的取值范围是( )A.0＜x ＜2B.-3＜x ＜0或x ＞2C.0＜x ＜2或x ＜-3D.-3＜x ＜0解析：∵反比例函数11k y x=和一次函数y 2=k 2x+b 的图象交于A 、B 两点， A 、B 两点的横坐标分别为2，-3，∴通过观察图象，当y 1＞y 2时x 的取值范围是0＜x ＜2或x ＜-3. 答案：C.8.速录员小明打2500个字和小刚打3000个字所用的时间相同，已知小刚每分钟比小明多打50个字，求两人的打字速度.设小刚每分钟打x 个字，根据题意列方程，正确的是( )A.2500300050x x =- B.2500300050x x =+ C.2500300050x x =- D.2500300050x x=+解析：设每分钟打x 个字，则小刚每分钟比小明多打50个字，根据速录员小明打2500个字和小刚打3000个字所用的时间相同，列方程得：2500300050x x=-. 答案：C.9.如图，在△ABC 中，点D 、E 分别是边AB 、AC 的中点，∠B=50°，∠A=26°，将△ABC 沿DE 折叠，点A 的对应点是点A ′，则∠AEA ′的度数是( )A.145°B.152°C.158°D.160°解析：∵∠B=50°，∠A=26°，∴∠C=180°-∠B-∠A=104°，∵点D、E分别是边AB、AC的中点，∴DE∥BC，∴∠ADE=∠B=50°，∠AED=∠C=104°，∵将△ABC沿DE折叠，∴△AED≌△A′ED，∴∠DEA′=∠AED=104°，∴∠AEA′=360°-∠DEA′-∠AED=360°-104°-104°=152°.答案：B.10.如图，在矩形ABCD中，AB=2，BC=1，动点P从点B出发，沿路线B→C→D作匀速运动，那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( )A.B.C.D.解析：从点B到点C，△ABP的面积y与点P运动的路程x之间的函数关系是：y=x(0≤x≤1)；因为从点C到点D，△ABP的面积一定：2×1÷2=1，所以y与点P运动的路程x之间的函数关系是：y=1(1≤x≤3)，所以△ABP的面积y与点P运动的路程x之间的函数图象大致是：答案：B.二、填空题(本题共4小题，每小题5分，满分20分)11.把3x3-6x2y+3xy2分解因式的结果是 .解析：先提取公因式3x，再根据完全平方公式进行二次分解即可求得答案；完全平方公式：a2±2ab+b2=(a±b)2.3x3-6x2y+3xy2=3x(x2-2xy+y2)=3x(x-y)2.答案：3x(x-y)2.12.有六张正面分别标有数字-2，-1，0，1，2，3的不透明卡片，它们除数字不同外其余全部相同.现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，将该卡片上的数字加1记为b，则函数y=ax2+bx+2的图象过点(1，3)的概率为 .解析：∵函数y=ax2+bx+2的图象过点(1，3)，∴a×12+b×1+2=3即：a+b=1，根据题意列表得：共6种情况，其中只有(0，1)符合题意，故函数y=ax2+bx+2的图象过点(1，3)的概率为16.答案：16.13.如图，∠AOB=45°，过射线OA上到点O的距离分别为1，3，5，7，9，11，…的点作OA 的垂线与OB相交，得到并标出一组黑色梯形，它们的面积分别为S1，S2，S3，S4，….观察图中的规律，第n(n为正整数)个黑色梯形的面积是S n= .解析：∵∠AOB=45°，∴图形中三角形都是等腰直角三角形，从图中可以看出，黑色梯形的高都是2，第一个黑色梯形的上底为：1，下底为：3，第2个黑色梯形的上底为：5=1+4，下底为：7=1+4+2，第3个黑色梯形的上底为：9=1+2×4，下底为：11=1+2×4+2，则第n个黑色梯形的上底为：1+(n-1)×4，下底为：1+(n-1)×4+2，故第n个黑色梯形的面积为：12×2×[1+(n-1)×4+1+(n-1)×4+2]=8n-4.答案：8n-4.14.如图，在平行四边形ABCD中，AB＞AD，按以下步骤作图：以A为圆心，小于AD的长为半径画弧，分别交AB、CD于E、F；再分别以E、F为圆心，大于12EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论正确的有： .①AG平分∠DAB；②CH=12DH；③△ADH是等腰三角形；④S△ADH=12S四边形ABCH.解析：根据作图的方法可得AG平分∠DAB，故①正确；∵AG平分∠DAB，∴∠DAH=∠BAH，∵CD∥AB，∴∠DHA=∠BAH，∴∠DAH=∠DHA，∴AD=DH，∴△ADH是等腰三角形，故③正确；∴正确的有①③.答案：①③.三、(本题共两小题，每小题8分，满分16分)15.先化简，再求值：241132aa a⎛⎫⎪⎝----⎭，其中a=-3.解析：先把原式去括号，再化简，化为最简后，再把a的值代入求值.答案：241132 aa a⎛⎫⎪⎝----⎭()()222132a a a a a +---=--()()22332a a a a a +--=-- =a+2，当a=-3时，原式=-3+2=-1.16.小锦和小丽购买了价格不相同的中性笔和笔芯，小锦买了20支笔和2盒笔芯，用了56元；小丽买了2支笔和3盒笔芯，仅用了28元.求每支中性笔和每盒笔芯的价格.解析：设每支中性笔的价格为x 元，每盒笔芯的价格为y 元，根据单价×数量=总价建立方程组，求出其解即可.答案：设每支中性笔的价格为x 元，每盒笔芯的价格为y 元，由题意，得202562328x y x y +⎧⎨+⎩＝＝， 解得：28x y ⎧⎨⎩＝＝. 答：每支中性笔的价格为2元，每盒笔芯的价格为8元.四、(本题共两小题，每小题8分，满分16分)17.如图，在平面直角坐标系中，△ABC 的三个顶点坐标为A(1，-4)，B(3，-3)，C(1，-1).(每个小方格都是边长为一个单位长度的正方形)(1)将△ABC 沿y 轴方向向上平移5个单位，画出平移后得到的△A 1B 1C 1.解析：(1)根据网格结构找出点A 、B 、C 平移后的对应点A 1、B 1、C 1的位置，然后顺次连接即可.答案：(1)如图，△A 1B 1C 1即为所求.(2)将△ABC绕点O顺时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出点A旋转到点A2所经过的路径长.解析：(2)根据网格结构找出点A、B、C，A、B、C绕点O顺时针旋转90°后的对应点A2、B2、C2的位置，然后顺次连接即可，再利用勾股定理列式求出OA，然后利用弧长公式列式计算即可得解.答案：(2)如图，△A2B2C2即为所求；由勾股定理得，OA==点A旋转到点A2901717 180π=18.如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两地之间修建一条笔直的公路.(1)求改直的公路AB的长.解析：(1)作CH⊥AB于H.在Rt△ACH中，根据三角函数求得CH，AH，在Rt△BCH中，根据三角函数求得BH，再根据AB=AH+BH即可求解.答案：(1)作CH⊥AB于H.在Rt△ACH中，CH=AC·sin∠CAB=AC·sin25°≈10×0.42=4.2(千米)，AH=AC·cos∠CAB=AC·cos25°≈10×0.91=9.1(千米)，在Rt△BCH中，BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6(千米)，∴AB=AH+BH=9.1+5.6=14.7(千米).故改直的公路AB的长14.7千米.(2)问公路改直后比原来缩短了多少千米？(sin25°≈0.42，cos25°≈0.91，sin37°≈0.60，tan37°≈0.75)解析：(2)在Rt△BCH中，根据三角函数求得BC，再根据AC+BC-AB列式计算即可求解.答案：(2)在Rt△BCH中，BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7(千米)，则AC+BC-AB=10+7-14.7=2.3(千米).答：公路改直后比原来缩短了2.3千米.五、(本题共两小题，每小题10分，满分20分)19.某中学七(4)班一位学生针对七年级同学上学“出行方式”进行了一次调查.图(1)和图(2)是他根据采集的数据绘制的两幅不完整的统计图，请根据图中提供的信息解答以下问题：(1)补全条形统计图，并计算出“骑车”部分所对应的圆心角的度数.解析：(1)从两图中可以看出乘车的有25人，占了50%，所以共有学生50人；总人数减乘车的和骑车的就是步行的，根据数据画直方图就可；要求扇形的度数就要先求出骑车的占的百分比，然后再求度数.答案：(1)25×2=50人；50-25-15=10人；如图所示条形图，圆心角度数=30100×360°=108°.(2)如果全年级共800名同学，请估算全年级步行上学的学生人数.解析：(2)用这50人作为样本去估计该年级的步行人数.答案：(2)估计该年级步行人数：800×20%=160(人).(3)若由3名“乘车”的学生，1名“步行”的学生，2名“骑车”的学生组队参加一项活动，欲从中选出2人担任组长(不分正副)，列出所有可能的情况，并求出2人都是“乘车”的学生的概率.解析：(3)6人每2人担任班长，有15种情况，2人都是“喜欢乘车”的学生的情况有3种，然后根据概率公式即可求得.答案：(3)设3名“乘车”的学生表示为A、B、C，1名“步行”的学生表示为D，2名“骑车”的学生表示为E，F，则有：AB、AC、AD、AE、AF、BC、BD、BE、BF、CD、CE、CF、DE、DF、EF这15种等可能结果，而2人都是“乘车”的结果有AB、AC、AD这3种，故2人都是“乘车”的学生的概率31155P==.20.在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港.设甲、乙两船行驶x(h)后，与B港的距离分别为y1、y2(km)，y1、y2与x的函数关系如图所示.(1)填空：A、C两港口间的距离为 km，a= .解析：(1)由甲船行驶的函数图象可以看出，甲船从A港出发，0.5h后到达B港，ah后到达C港，又由于甲船行驶速度不变，则可以求出a的值.答案：(1)A、C两港口间距离s=30+90=120km，又由于甲船行驶速度不变，故30900.50.5a＝，则a=2(h).故答案为：120；2.(2)求图中点P的坐标，并解释该点坐标所表示的实际意义.解析：(2)分别求出0.5h后甲乙两船行驶的函数表达式，联立即可求解.答案：(2)由点(3，90)求得，y2=30x.当x＞0.5时，由点(0.5，0)，(2，90)求得，y1=60x-30.当y1=y2时，60x-30=30x，解得，x=1.此时y1=y2=30.所以点P的坐标为(1，30).该点坐标的意义为：两船出发1h后，甲船追上乙船，此时两船离B港的距离为30km.(3)若两船的距离不超过10km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围. 解析：(3)将该过程划分为0≤x≤0.5、0.5＜x≤1、1＜x三个范围进行讨论，得到能够相望时x的取值范围.答案：(3)①当x≤0.5时，由点(0，30)，(0.5，0)求得，y1=-60x+30依题意，(-60x+30)+30x≤10.解得，x≥23.不合题意.②当0.5＜x≤1时，依题意，30x-(60x-30)≤10解得，x≥23.所以23≤x≤1.③当x＞1时，依题意，(60x-30)-30x≤10解得，x≤43.所以1＜x≤43④当2≤x≤3时，甲船已经到了而乙船正在行驶，∵90-30x≤10，解得x≥83，所以，当83≤x≤3，甲、乙两船可以相互望见；综上所述，当23≤x≤43时或当83≤x≤3时，甲、乙两船可以相互望见.六、(本题满分12分)21.某生态农业园种植的青椒除了运往市区销售外，还可以让市民亲自去生态农业园购买.已知今年5月份该青椒在市区、园区的销售价格分别为6元/千克、4元/千克，今年5月份一共销售了3000千克，总销售额为16000元.(1)今年5月份该青椒在市区、园区各销售了多少千克？解析：(1)设在市区销售了x千克，则在园区销售了(3000-x)千克，根据等量关系：总销售额为16000元列出方程求解即可.答案：(1)设在市区销售了x千克，则在园区销售了(3000-x)千克，则6x+4(3000-x)=16000，解得x=2000，3000-x=1000.故今年5月份该青椒在市区销售了2000千克，在园区销售了1000千克.(2)6月份是青椒产出旺季.为了促销，生态农业园决定6月份将该青椒在市区、园区的销售价格均在今年5月份的基础上降低a%，预计这种青椒在市区、园区的销售量将在今年5月份的基础上分别增长30%、20%，要使6月份该青椒的总销售额不低于18360元，则a的最大值是多少？解析：(2)题目中的不等关系是：6月份该青椒的总销售额不低于18360元列出不等式求解即可.答案：(2)依题意有6(1-a%)×2000(1+30%)+4(1-a%)×1000(1+20%)≥18360，20400(1-a%)≥18360，1-a%≥0.9，a≤10.故a的最大值是10.七、(本题满分12分)22.在平面直角坐标系中，已知抛物线y=x2+bx+c与x轴交于点A(-1，0)和点B，与y轴交于点C(0，2).(1)求该抛物线的表达式，并写出其对称轴.解析：(1)把点B、C的坐标分别代入函数解析式，列出关于系数b、c的方程组，通过解方程组求得它们的值；然后由函数解析式和对称轴公式写出对称轴.答案：(1)∵抛物线y=x2+bx+c经过点A(-1，0)，点C(0，2)，∴102b cc-+⎧⎨⎩＝＝，解得12bc-⎧⎨⎩＝＝.故抛物线的表达式为：y=x2-x+2，对称轴为直线x=12.(2)点D为该抛物线的顶点，设点E(m，0)(m＞2)，如果△BDE和△CDE的面积相等，求E点坐标.解析：(2)由(1)中抛物线解析式求得点B、D的坐标，结合三角形的面积公式得到DE∥BC，所以结合直线上点的坐标特征进行解答即可.答案：(2)由(1)知，抛物线的表达式为：y=x2-x+2=(x-2)(x-1)=1924x⎛⎫--⎪⎝⎭，则点B(2，0)，点19()24D -，， 若△BDE 和△CDE 的面积相等，则DE ∥BC ，则直线BC 的解析式为y=x-2，∴直线DP 的解析式为114y x =-， 当y=0时，114m =， ∴0(114)E ，.八、(本题满分14分)23.在四边形ABCD 中，对角线AC 、BD 相交于点O ，将△COD 绕点O 按逆时针方向旋转得到△C 1OD 1，旋转角为θ(0°＜θ＜90°)，连接AC 1、BD 1，AC 1与BD 1交于点P.(1)如图1，若四边形ABCD 是正方形.①求证：△AOC 1≌△BOD 1.②请直接写出AC 1 与BD 1的位置关系.解析：(1)①如图1，根据正方形的性质得OC=OA=OD=OB ，AC ⊥BD ，则∠AOB=∠COD=90°，再根据旋转的性质得OC 1=OC ，OD 1=OD ，∠COC 1=∠DOD 1，则OC 1=OD 1，利用等角的补角相等得∠AOC 1=∠BOD 1，然后根据“SAS ”可证明△AOC 1≌△BOD 1.②由∠AOB=90°，则∠OAB+∠ABP+∠OBD 1=90°，所以∠OAB+∠ABP+∠OAC 1=90°，则∠APB=90°所以AC 1⊥BD 1.答案：(1)①证明：如图1，∵四边形ABCD 是正方形，∴OC=OA=OD=OB ，AC ⊥BD ，∴∠AOB=∠COD=90°，∵△COD 绕点O 按逆时针方向旋转得到△C 1OD 1，∴OC 1=OC ，OD 1=OD ，∠COC 1=∠DOD 1，∴OC 1=OD 1，∠AOC 1=∠BOD 1=90°+∠AOD 1，在△AOC 1和△BOD 1中1111OA OB AOC BOD OC OD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△AOC 1≌△BOD 1(SAS)；②AC 1⊥BD 1.(2)如图2，若四边形ABCD 是菱形，AC=5，BD=7，设AC 1=kBD 1.判断AC 1与BD 1的位置关系，说明理由，并求出k 的值.解析：(2)如图2，根据菱形的性质得OC=OA=12AC ，OD=OB=12BD ，AC ⊥BD ，则∠AOB=∠COD=90°，再根据旋转的性质得OC 1=OC ，OD 1=OD ，∠COC 1=∠DOD 1，则OC 1=OA ，OD 1=OB ，利用等角的补角相等得∠AOC 1=∠BOD 1，加上11OC OA OD OB＝，根据相似三角形的判定方法得到△AOC 1∽△BOD 1，得到∠OAC 1=∠OBD 1，由∠AOB=90°得∠OAB+∠ABP+∠OBD 1=90°，则∠OAB+∠ABP+∠OAC 1=90°，则∠APB=90°，所以AC 1⊥BD 1；然后根据相似比得到1157AC OA AC BD OB BD ===，所以k=57. 答案：(2)AC 1⊥BD 1.理由如下：如图2，∵四边形ABCD 是菱形，∴OC=OA=12AC ，OD=OB=12BD ，AC ⊥BD ， ∴∠AOB=∠COD=90°，∵△COD 绕点O 按逆时针方向旋转得到△C 1OD 1，∴OC 1=OC ，OD 1=OD ，∠COC 1=∠DOD 1，∴OC 1=OA ，OD 1=OB ，∠AOC 1=∠BOD 1， ∴11OC OA OD OB＝，∴△AOC 1∽△BOD 1，∴∠OAC 1=∠OBD 1，又∵∠AOB=90°，∴∠OAB+∠ABP+∠OBD 1=90°，∴∠OAB+∠ABP+∠OAC 1=90°，∴∠APB=90°∴AC 1⊥BD 1；∵△AOC 1∽△BOD 1， ∴11157212AC AC OA AC BD OB BD BD ====， ∴57k =.(3)如图3，若四边形ABCD 是平行四边形，AC=5，BD=10，连接DD1，设AC 1=kBD 1.请直接写出k 的值和AC 12+(kDD 1)2的值.解析：(3)与(2)一样可证明△AOC 1∽△BOD 1，则1112AC OA AC BD OB BD ===，所以k=12；根据旋转的性质得OD 1=OD ，根据平行四边形的性质得OD=OB ，则OD 1=OB=OD ，于是可判断△BDD 1为直角三角形，根据勾股定理得BD 12+DD 12=BD 2=100，所以(2AC 1)2+DD 12=100，于是有AC 12+(kDD 1)2=25.答案：(3)如图3，与(2)一样可证明△AOC 1∽△BOD 1， ∴1112AC OA AC BD OB BD ===， ∴12k =； ∵△COD 绕点O 按逆时针方向旋转得到△C 1OD 1，∴OD 1=OD ，而OD=OB ，∴OD 1=OB=OD ，∴△BDD 1为直角三角形，在Rt △BDD 1中，BD 12+DD 12=BD 2=100，∴(2AC 1)2+DD 12=100，∴AC 12+(kDD 1)2=25.。
安徽省示范高中2016届高三上学期第二次联考数学(理)试题 含解析
第I 卷（选择题共60分)一、选择题：本大题共12小题，每小题5分,共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． （1） 函数2lg(2)()x x f x x-++=的定义域为（）A （-1，0) (0，2）B ．(-1，0） (0，+∞)C ．(一∞，—1) （2,+∞） D ．（—1，2) 【答案】A 【解析】试题分析：()()2201,00,20x x x x ⎧-++>⇒∈-⎨≠⎩.故A 正确.考点：函数的定义域。
(2) 已知集合{}|2,*M x x a b a N ==+∈,对任意,x y M ∈，则下列说法错误的是（ ）A ．x y M +∈B ．2x M∈ C ．x y M ⋅∈ D ．x M y∈【答案】D考点：集合。
（3)已知225535232(),(),log ,,,555a b c a b c ===则的大小关系是（）A. a 〈c 〈b B 。
b 〈a<e C. c<a<b D 。
a<b<c 【答案】D 【解析】试题分析:因为2255352321,log 1555⎛⎫⎛⎫<<> ⎪⎪⎝⎭⎝⎭。
所以a b c <<，故D 正确.考点：指数函数,对数函数。
(4) 下列函数中，随x(x>0)的增大，增长速度最快的是（ ） A 。
y =1，x ∈Z B 。
y=x C 。
y= 2xD. y=xe【答案】D 【解析】试题分析:指数函数模型增长速度最快，并且e ＞2,因而y ＝e x 增长速度最快.考点：函数图像。
（5) 11(2)e x dx x+⎰等于（）A. e 2 -2 B 。
e 一1 C 。
e 2D.e+1 【答案】C 【解析】 试题分析:()221112ln eex dx x x e x ⎛⎫+=+= ⎪⎝⎭⎰。
故C 正确。
考点：定积分。
(6) 原命题为“三角形ABC 中,若cosA <0，则三角形ABC 为钝角三角形”，关于其逆命题，否命题，逆否命题真假性的判断依次如下,正确的是（ ）A ．真，真，真B 。
安徽省合肥市高考数学二模试卷(理科).docx
【考点】抛物线的简单性质．
【分析】根据抛物线的性质可求出M的横坐标，带诶抛物线方程解出M的纵坐标，代入斜率公式计算斜率．
【解答】解：抛物线的焦点为F（ ，0），准线方程为x=﹣ ．
∵点M到焦点F的距离等于2p，∴M到准线x=﹣ 的距离等于2p．
∴xM= ，代入抛物线方程解得yM=± p．
A．﹣3B．
【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，分k＞0和k＜0讨论得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．
【解答】解：由约束条件 作出可行域如图，
联立 ，解得A（1，2），
联立 ，解得B（﹣2，﹣1），
第一类：学生C第一个出场，A最后一个出场，故有A33=6种，
第二类：学生C第一个出场，A不是最后一个出场，从除了A，B之外的2人选1人安排在最后一个，其余3人任意排，故有A21A33=12种，
故在“学生A和B都不是第一个出场，B不是最后一个出场”的前提下，学生C第一个出场的种数6+12=18种，
故学生C第一个出场的概率为 = ，
【解答】解：模拟执行程序框图，可得
n=1，S=1
满足条件S≤2016，n=2，S=1+2=3
满足条件S≤2016，n=4，S=3+4=7
满足条件S≤2016，n=8，S=7+8=15
满足条件S≤2016，n=16，S=15+16=31
满足条件S≤2016，n=32，S=31+32=63
满足条件S≤2016，n=64，S=63+64=127
2016年安徽省合肥市高考数学二模试卷（理科）
一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
2016届高考模拟试题_安徽省示范高中2016届高三第二次联考 数学理附答案
安徽省示范高中2016届高三第二次联考数学（理科）第I 卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．(1)函数22()x x f x x-++=的定义域为A-(-1,0) (0,2) B ．（-1,0) (0,+∞) C ．（一∞，-1) (2,+∞) D ．（-1,2) (2)已知集合{}|,*M x x a a N ==∈，对任意,x y M ∈，则下列说法错误的是 A ．x y M +∈ B ．2x M ∈ C ．x y M ⋅∈ D ．xM y∈ (3)已知225535232(),(),log ,,,555a b c a b c ===则的大小关系是A. a<c<bB. b<a<eC. c<a<bD. a<b<c (4)下列函数中，随x(x>0)的增大，增长速度最快的是A. y =1，x ∈ZB. y=xC. y= 2xD. y=xe(5)11(2)ex dx x+⎰等于A. e 2 -2B. e 一1C. e 2D.e+1 (6)原命题为“三角形ABC 中，若cosA <0，则三角形ABC 为钝角三角形”，关于其遵命题，否命题，逆否命题真假性的判断依次如下，正确的是A ．真，真，真 B. 假，假，真 C ．真，真，假 D ．真，假，假(7)已知函数()ln f x x b x =+在区间(0，2)上不是单调函数，则b 的取值范围是 A ．（一∞，0) B ．（一∞，-2) C ．（-2,0) D ．（-2,+∞） (8)函数()sin ln ||f x x x =⋅的图象大致是(9)下列函数中，与函数()3x x e e f x --=的奇偶性、单调性均相同的是2.().().()tan .())x xx x e e A f x B f x x e eC f x xD f x x ---= =+= =--(10)已知函数()|1|x f x e =-满足()()()f a f b a b =≠，在区间[a ，2b]上的最大值为e-1，则b 为A. ln3B. 13C. 12D. l (11)已知定义在R上的函数()f x 满足：()2f x +∈①=2f(x);②当x [-1,1]时，()c os .2f x x π=记函数g (x)= f (x)-log 4(x+l)，则函数g(x)在区间[0，10]内零点个数是A ．12B ．11C ．10D ．9 (12)函数()f x 在R 上可导，下列说法正确的是A ．若()'()0f x f x +>对任意x ∈R 恒成立，则有(2)(1)ef f <B ．若()'()0f x f x -<对任意x ∈R 恒成立，则有3(1)(1)e f f ->C ．若()'()1f x f x +>对任意x ∈R 恒成立，则有(0)(1)1f e ef +>+D ．若()'()1f x f x -<对任意x ∈R 恒成立，则有(1)(0)1ef e f -+>+第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卡的相应位置． (13)命题“任意x ∈(0，+∞)，都有x 2 -2x >0”的否定是____。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(15) 三 、解 答 题 :
(16)
(17)解 :(Ⅰ )
,
由
为偶函数可知
,
所以
.
又
,
,
所以
,
. …………6分
(Ⅱ )因 为
,
,由 正 弦 定 理 可 得
,
所以
.
高 三 数 学 (理 )试 题 答 案 第 1 页 (共 6 页 )
当
时,
的面积
;
当
时,
的面积
.
… … … …12 分
(18)解 :(Ⅰ )经 计 算
,所 以 线 性 回 归 方 程 为
;
… … … …6 分 (Ⅱ)由上面的回归方程 可 知,上 市 时 间 与 市 场 占 有 率 正 相 关,即 上 市 时 间 每 增 加 1 个
月 ,市 场 占 有 率 都 增 加 0.042 个 百 分 点 ;
由
,解 得
,
预计上市13个月时,市场占有率能超过0.5% .
,即
,
所 以 ,在
上,
.
又
,
所以
,
即满足对
,恒 有
综 上 ,实 数
.
(22)解:(Ⅰ) 为切线
(Ⅱ )已 知
. ,
.
. ,
,由 切 割 线 定 理
… … … …12 分 … … … …5 分
得:
,
.∵PA ∥BD
,得AM MC
=BPCB
,∴MC=3.
又
知
△AMB∽
△ABC
,所 以AB AM
=AABC
… … … …12 分
(19)解:(Ⅰ )连 接 ,由
可得
为 平 行 四 边 形,所 以
,而
,
,所 以
所以
平面
,又Leabharlann (Ⅱ)设 以, ,同理可 得:
,
,因 为
,
平面
,
. …………5分
,由 已 知 可 得 :平 面
∥平面
,所
,所 以
为 平 行 四 边 形,所 以 为 的 中
点, 为 的 中 点,所 以
,从 而
在R 上单调增;
当
时 ,由
得,
,
在
和
当
时, 在
单 调 增 ,在
单调减;
和
单调减,在
单 调 增 .… … … …5 分
(Ⅱ)令
,则
,因 此
在
单 调 减 ,在
单调增,
.
当
时,
,显 然 ,对
不恒有
;
当
时 ,由 (Ⅰ )知 ,
在
单 调 增 ,在
单调减,
高 三 数 学 (理 )试 题 答 案 第 4 页 (共 6 页 )
高 三 数 学 (理 )试 题 答 案 第 6 页 (共 6 页 )
平面
,又
,所 以,
两两垂直.由平几知识,得 BF=2.
如 图 ,建 立 空 间 直 角 坐 标 系
,则
,
,
高 三 数 学 (理 )试 题 答 案 第 2 页 (共 6 页 )
设平面
的一个法向量为
由
可得:
,
令
,则
.
设 与平面
所成角为 ,则
,
z
H
G
P
E
F
D
C
x
A
O
B
y
.
… … … …12 分
(20)解 :(Ⅰ )由 条 件 得 故椭圆C 的方程为 (Ⅱ )解 设 直线 的方程为
,
所以
,所 以 ,
.
… … … …10 分
(23)解:(Ⅰ)曲线 的直角坐标方程为:
,是 一 个 圆 ;
直线 的直角坐标方程为:
,
圆心 C 到直线l 的距离为
,
所以直线l 与圆C 相切.
高 三 数 学 (理 )试 题 答 案 第 5 页 (共 6 页 )
… … … …5 分
(Ⅱ)由已知可得:圆心 C 到直线l 的距离为
,
解得
.
… … … …10 分
(24)解 :(Ⅰ )
,从 而 解 得
. …………5分
ì-2x+6 (x≤2)
(Ⅱ)由(Ⅰ)知,f(x)=|x-4|+|x-2|= í 2 î2x-6
(2<x≤4). (x>4)
结 合 函 数y=f(x)的 图 象 知 ,解 集 为 {x|1 2 ≤x≤121}.
… … … …10 分
合肥市2016年高三第二次教学质量检测
数学试题(理)参考答案及评分标准
一 、选 择 题 :每 小 题 5 分 . 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B B C A D A C A D A B
二 、填 空 题 :每 小 题 5 分 .
(13)
(14)
, .… …5 分 ,则
,
令
,得
故
同理可得
,
,
所以,
高 三 数 学 (理 )试 题 答 案 第 3 页 (共 6 页 )
所以, (21)解 :(Ⅰ )
,所 以 直 线
与直线
交于点G 在以
为直径的圆上.
… … … …12 分
.
(1)当
时, 在
单调减和
单调增;
(2)当
时,
.
当
时,
恒 成 立 ,此 时