加法器与减法器
减法器、加法器、倍乘器、反相器、积分器、微分器的运算特点

减法器、加法器、倍乘器、反相器、积分器、微分器的运算特点1. 引言1.1 概述减法器、加法器、倍乘器、反相器、积分器和微分器是数字电路中常用的基本运算单元。
它们在各种电子设备和系统中扮演着重要的角色。
这些运算特点的详细了解对于理解数字电路的工作原理以及设计和应用具有重要意义。
1.2 文章结构本文将从六个方面详细介绍减法器、加法器、倍乘器、反相器、积分器和微分器的运算特点。
首先,我们将介绍每个运算特点的原理,包括其工作原理和数学模型。
然后,我们将讨论它们各自的功能与用途,以及它们在不同领域中的实际应用案例。
最后,我们将进行对比分析,并展望未来关于这些运算特点的发展方向。
1.3 目的本文旨在全面介绍减法器、加法器、倍乘器、反相器、积分器和微分器的运算特点,并探讨它们在实际应用中起到的作用。
通过深入了解这些运算特点,读者可以更好地理解数字电路的基础知识,并能够灵活运用它们进行信息处理和信号处理。
此外,本文还将展望这些运算特点未来的发展方向,为读者提供了进一步研究和应用的参考依据。
2. 减法器的运算特点减法器是一种常见的数字电路,用于实现数字信号的减法运算。
本节将首先介绍减法器的基本原理,包括其电路结构和工作方式。
然后,我们将详细讨论减法器的功能与用途,以及在实际中广泛应用的案例。
2.1 原理介绍减法器是由数个逻辑门组成的电路,在输入端接收两个二进制数作为操作数,并输出它们的差值。
它采用补码运算进行计算,通过对被减数取反并加上减数进行补码相加来得到结果。
通常使用二进制加法器结构实现。
2.2 功能与用途减法器主要功能是进行数字信号的减法运算。
在数字电子领域中,大量应用了减法器来实现不同功能模块——如比较、编码、解码、数据处理和控制等,在计算机系统、通信设备、图像处理和音频处理等领域有着广泛应用。
2.3 实际应用案例减法器在很多领域中都有实际应用。
例如,在计算机的算术逻辑单元(ALU)中,减法器用于进行整数和浮点数的减法计算。
实验一四位加法器和减法器设计

实验一四位加法器和减法器设计一、实验背景在数字电路设计中,常常需要使用加法器和减法器来实现数字的加法和减法运算。
本实验的目的是设计一个四位加法器和一个四位减法器,将数字电路理论知识应用到实际电路设计中。
二、实验目的1.理解加法器和减法器的基本原理;2.掌握数字电路的设计方法;3.通过实验验证设计的正确性和可行性。
三、实验原理1.加法器原理加法器是一种能对两个二进制数进行相加运算的数字电路。
常用的加法器有半加法器、全加法器等。
其中,半加法器能够对两个1位二进制数进行相加运算,全加法器能对两个1位二进制数及一个进位进行相加运算。
2.减法器原理减法器是一种能对两个二进制数进行相减运算的数字电路。
减法器可以通过使用补码的方式进行实现。
四、实验设备和材料1.实验平台:数字电路实验箱;2.实验元件:逻辑门IC芯片、电路连接线等。
1.设计四位加法器电路:a.首先,设计并连接四个1位全加法器。
将输入端A、B和上一个全加法器的进位连线,将输出端S和进位连线,其中S为本全加法器的输出,进位作为下一个全加法器的输入。
b.最后一个全加法器的输出即为四位加法器的输出结果。
2.设计四位减法器电路:a.首先,将被减数输入端A和减数输入端B分别与减法器的输入端连接。
b.接下来,使用非门将减数B的每一位取反。
c.然后,将取反后的减数与被减数相加,得到相加结果。
d.最后,将相加结果输入到四位加法器电路中,即可得到减法结果。
六、实验验证2.搭建四位减法器电路,并输入A=1100、B=1010进行验证。
验证结果应为A-B=010。
七、误差分析及改进方法1.设计电路时要注意连接线的长度和接触的质量,以保证电路的正常运行。
2.如果电路不能正常工作,可以仔细检查电路连接是否正确,逐个排查错误并改正。
通过设计、搭建和验证的四位加法器和减法器电路,可以实现对二进制数的加法和减法运算。
九、实验心得通过本次实验,我深入了解了加法器和减法器的原理和实现方法。
加法器与减法器电路的设计与分析

加法器与减法器电路的设计与分析在数字电路设计中,加法器和减法器是最基本的运算器件之一。
它们能够对数字信号进行加法和减法运算,广泛应用于计算机及其他数字系统中。
本文将介绍加法器和减法器电路的设计原理和分析方法。
一、加法器电路的设计与分析加法器是实现数字信号加法运算的电路。
常见的加法器包括半加器、全加器和多位加法器。
这里我们介绍一种基于全加器的4位加法器电路设计。
1. 设计思路我们的目标是设计一个能够对4位二进制数进行加法运算的加法器电路。
首先,我们需要明确加法器的输入和输出。
对于4位加法器而言,它的输入包括两个4位的二进制数A和B,以及一个来自上一位的进位信号Cin。
输出则为一个4位的二进制数S,以及一个来自最高位的进位信号Cout。
2. 电路设计基于全加器的4位加法器电路可以通过级联多个全加器来实现。
我们首先设计一个全加器的电路,再将多个全加器连接起来。
全加器的电路如下:(图片)其中,输入信号为A、B和Cin,输出信号为S和Cout。
全加器的设计比较复杂,这里为了简化,我们采用了基于门电路的实现。
实际应用中,可以使用集成电路中已经实现好的全加器。
在连接多个全加器时,需要将进位信号Cout从低位传递到高位,以实现多位加法运算。
最高位的进位信号Cout则作为加法器的输出之一。
3. 电路分析通过对加法器电路的分析,我们可以得到以下结论:- 当输入的两个二进制数A和B的每一位都为0时,加法器的输出S为0,并且进位信号Cout为0。
- 当输入的两个二进制数A和B的每一位都为1时,加法器的输出S为0,并且进位信号Cout为1。
- 当输入的两个二进制数A和B的每一位有一个为1时,加法器的输出S为1,并且进位信号Cout为0。
- 当输入的两个二进制数A和B的每一位都为1,并且进位信号Cin 为1时,加法器的输出S为1,并且进位信号Cout为1。
二、减法器电路的设计与分析减法器是实现数字信号减法运算的电路。
常见的减法器包括半减器、全减器和多位减法器。
认识加法器减法器和放大器

认识加法器减法器和放大器1、加法器
加法器分为同相加法器和反相加法器。
a)同相加法器电路图如下所示:
其输出电压的计算公式:
b)反相加法器电路图如下所示:
其输出电压的计算公式:
2、减法器
减法器有两种:一种是先对输入信号实现反相,然后再做加法运算;另一种是直接利用差分电路实现a)输入信号实现反相实现减法器
b)差分电路实现减法器
其计算输出电压的公式如下:
3、放大器
放大器又分为同相放大器、反相放大器和差分放大器。
a)同相放大器
其电路图如下:
其输出计算公式如下:
b)反相放大器
其电路图如下:
其输出计算公式如下:
c)差分放大器
差分放大器又分为单运差分放大器和三运差分放大器。
1、单运差分放大器
其电路图如下:
其输出计算公式如下:
2、三运差分放大器
其电路图如下:
其输出计算公式如下:
备注:以上我们可以设置平衡电阻的阻值为10KΩ。
平衡电阻就是诸如加法器电路中的R3电阻。
cpu中用来对数据进行各种算术运算和逻辑运算的部件

cpu中用来对数据进行各种算术运算和逻辑运算的部件CPU是计算机的核心部件,它负责执行各种算术运算和逻辑运算,以处理和执行计算机程序中的指令。
CPU中的运算部件是实现这些功能的关键部分。
一、算术运算部件CPU中的算术运算部件主要负责执行加、减、乘、除等算术运算。
这些运算在计算机程序中非常常见,例如在处理数值数据、进行数学计算或执行科学计算时。
1. 加法器:加法器是CPU中最基本的算术运算部件,用于执行加法运算。
它接收两个操作数,并将它们相加,生成结果。
加法器在CPU中通常是多位的,可以处理不同长度的数据。
2. 减法器:减法器与加法器类似,用于执行减法运算。
它接收两个操作数,并将它们相减,生成结果。
3. 乘法器:乘法器用于执行乘法运算。
它接收两个操作数,并将它们相乘,生成结果。
乘法器在CPU中通常是多位的,可以处理不同长度的数据。
4. 除法器:除法器用于执行除法运算。
它接收两个操作数,其中一个作为被除数,另一个作为除数,生成商和余数。
除法器在CPU中通常是多位的,可以处理不同长度的数据。
二、逻辑运算部件CPU中的逻辑运算部件主要负责执行逻辑运算,如与、或、非等。
这些运算在计算机程序中也非常常见,例如在处理布尔逻辑、条件判断或控制流程时。
1. 逻辑与门:逻辑与门用于执行逻辑与运算。
它接收两个操作数,只有当两个操作数都为真时,结果才为真。
2. 逻辑或门:逻辑或门用于执行逻辑或运算。
它接收两个操作数,只要其中一个操作数为真,结果就为真。
3. 逻辑非门:逻辑非门用于执行逻辑非运算。
它接收一个操作数,并对其取反。
如果操作数为真,结果为假;如果操作数为假,结果为真。
除了以上介绍的算术运算和逻辑运算部件外,CPU中还可能包含其他类型的运算部件,如移位器、比较器等,以满足不同的计算需求。
三、总结CPU中的运算部件是实现计算机程序中各种算术和逻辑运算的关键部分。
这些部件通过精心的设计和优化,使得CPU能够高效地完成各种复杂的计算任务。
串行行波进位补码加减法电路

串行行波进位补码加减法电路串行行波进位补码加减法电路是一种常用于计算机中的数字逻辑电路,用于实现二进制数的加法和减法运算。
在计算机中,所有的数字都是以二进制形式进行表示的。
为了能够对二进制数进行加法和减法运算,需要使用补码表示法。
补码是一种将负数转化为二进制表示的方法,它可以简化数字的运算过程。
串行行波进位补码加减法电路主要由以下几个部分组成:1.输入端:用于输入待计算的两个二进制数。
2.补码生成器:用于将输入的负数转换为补码表示。
3.加法器/减法器:用于执行加法和减法运算。
4.进位生成器:用于生成进位信号。
5.输出端:用于输出计算结果。
补码生成器是串行行波进位补码加减法电路的核心部分,它用于将负数转换为补码表示。
补码生成器的基本原理是通过给定的数字的位数和进位信号将输入的负数进行转换。
具体的转换方式与计算机的架构有关,比较常用的有一补数和二补数。
在一补数表示法中,负数的补码是通过将其绝对值的二进制表示取反再加1得到的。
例如,-5的一补数表示为11111101。
在二补数表示法中,负数的补码是通过将其绝对值的二进制表示取反再加1得到的。
例如,-5的二补数表示为11111011。
加法器/减法器是串行行波进位补码加减法电路中的另一个重要组成部分,用于执行加法和减法运算。
加法器/减法器的原理是通过对两个输入数进行位运算,然后将结果相加或相减得到最终的运算结果。
进位生成器是串行行波进位补码加减法电路中的一个辅助部分,用于生成进位信号。
进位生成器通常使用逻辑门电路来实现,它根据输入的两个二进制数的位运算结果产生进位信号。
通过以上的各个部分的组合,串行行波进位补码加减法电路可以完成二进制数的加法和减法运算。
其基本原理是将输入的二进制数转化为补码表示,然后使用加法器/减法器执行运算,并通过进位生成器生成进位信号,最后将计算的结果输出。
串行行波进位补码加减法电路具有高速度和较低的成本等优点,因此在计算机中得到了广泛的应用。
加法器、减法器

加法器、减法器南京铁道职业技术学院创新电⼦培训项⽬:加法器⽼师:袁秀红姓名:⾼书杰⼆〇⼀三年三⽉⼆⼗五⽇⽬录⼀、实验⽬的 (3)⼆、实验设备 (3)三、实验原理 (3)1.加法电路 (3)(1) 反相加法电路 (3)(2) 同相加法电路 (5)2.差分放⼤电路 (6)四、实验过程 (7)1.双电源反相加法器电路 (7)(1) 双电源反相加法器直流测试电路 (7)(2) 双电源反相加法器交流测试电路 (16)(3) 双电源反相加法器动态范围测试 (22)2.单电源反相加法器电路 (29)3.双电源同相加法器电路 (29)(1) 双电源同相加法器直流测试电路 (29)(2) 双电源同相加法器交流测试电路 (37)4.单电源同相加法器电路 (42)5.双电源差分放⼤器电路 (43)(1)双电源差分放⼤器直流测试电路 (43)(2)双电源差分放⼤器交流测试电路 (50)6.单电源差分放⼤器电路 (56)五、实验结果 (57)六、实验⼼得 (57)加法器⼀、实验⽬的1.掌握运算放⼤器线性电路的设计⽅法。
2.熟悉掌握Multisim 软件对运算放⼤器进⾏仿真的⽤法及仿真分析的⽅法。
3.能正确判断和分析电路在仿真中的故障并正确解决。
4.理解运算放⼤器的⼯作原理。
⼆、实验设备表1序号设备、材料数量备注 1 计算机1台 2 Multisim 软件1套三、实验原理1.加法电路(1)反相加法电路反相加法器电路是根据“虚断”和“虚短”的概念,运⽤节点电流法推导⽽出。
由“虚断”可得n i f i i i i i +++== 21;再根据“虚短”可得111R u i i =,222R u i i =,…,nin n R u i =; )(2211nin i i f f f o R uR u R u R i R u +++-=-= 。
图1 反相加法运算电路R为平衡电阻,阻值为输⼊端所有电阻的反相加法电路亦可以由叠加原理进⾏推导,4并联值。
加法器 减法器电路结构

加法器减法器电路结构
加法器和减法器是数字电路中常见的两种基本算术运算器件,
用于执行加法和减法运算。
下面我将分别从加法器和减法器的电路
结构进行解释。
加法器的电路结构:
加法器是用来执行数字加法运算的电路。
最简单的加法器是半
加器,它可以对两个输入位进行相加并产生一个和位和一个进位位。
半加器的电路结构包括两个输入端(用来输入待相加的两个数字)、两个输出端(和位和进位位)以及逻辑门(一般是异或门和与门)
组成。
当需要对多位数进行加法运算时,可以使用全加器。
全加器
能够处理三个输入位(两个加数位和一个进位位)并产生一个和位
和一个进位位。
多个全加器可以通过级联的方式构成多位数加法器。
减法器的电路结构:
减法器是用来执行数字减法运算的电路。
最简单的减法器是通
过使用加法器和取反器(或者补码器)来实现的。
当需要对两个数
字进行减法运算时,可以将减法转化为加法,即将被减数与减数的
补码相加。
这样就可以利用加法器的电路结构来实现减法运算。
另外,也可以使用专门设计的减法器电路来执行减法运算,这种减法器包括多个输入端和输出端,并且内部结构复杂一些,可以直接对两个数字进行减法运算。
总结:
加法器和减法器是数字电路中常见的基本算术运算器件,它们的电路结构可以根据具体的需求和设计来进行不同的实现。
从最简单的半加器和全加器到复杂的多位数加法器和减法器,它们都在数字系统中扮演着重要的角色。
设计和实现高效的加法器和减法器电路对于数字系统的性能和功能至关重要。
头歌educoder计算机组成与结构实训作业运算器设计(hust)解答

头歌educoder计算机组成与结构实训作业运算器设
计(hust)解答
为了完成运算器的设计,我们需要考虑运算器的功能和结构。
运算器的主要功能是执行算术和逻辑运算,而其结构通常包括加法器、减法器、乘法器和除法器等基本单元。
首先,我们需要设计一个加法器。
加法器的作用是将两个二进制数相加,并产生它们的和。
在设计加法器时,我们需要考虑加法器的位数,因为加法器的位数决定了它可以处理的数字的大小。
例如,一个4位加法器可以处理最大为15的数字。
其次,我们需要设计一个减法器。
减法器的作用是将一个二进制数减去另一个二进制数,并产生它们的差。
与加法器类似,减法器的位数也决定了它可以处理的数字的大小。
此外,我们还可以设计乘法器和除法器。
乘法器的作用是将两个二进制数相乘,并产生它们的积。
而除法器的作用是将一个二进制数除以另一个二进制数,并产生商和余数。
最后,我们可以将上述基本单元组合在一起,形成一个完整的运算器。
运算器可以接收输入的算术和逻辑运算指令,并调用相应的基本单元来完成运算。
需要注意的是,在实际的计算机组成与结构中,运算器的设计需要考虑许多其他因素,例如功耗、速度、可靠性等。
因此,在实际应用中,需要根据具体需求和约束条件来选择合适的运算器设计方案。
计算机组成原理第二章 第7讲 基本的加减法

② 全加器(FA) 1位全加器真值表
输入
输出
Ai Bi Ci Si Ci+1 00000
00110
01010
01101
10010
10101
11001
11111
按照真值表可写出FA逻辑方程:
依照真值表,通过离散数学相关知识得到 描述其逻辑关系的1位全加器逻辑方程:
S A B C i
基本的加法/减法器
2.2.4基本的加法/减法器
基本的加法/减法器
• 半加器 Hi=Ai ⊕ Bi 不考虑进位
• 全加器 考虑低位进位Ci-1和向高位的进位Ci
各种逻辑门的图形符号
加法器
① 半加器——不考虑进位
YH
H n X n Yn X n Y n X n Yn
加法器
将若干个1位FA全加器串连即可实现N位行 波进位加法/减法器。
行(xing)波进位:
• 串行进位,高位的运算要等待低位的进位传到 才能执行,区别于并行进位或超前进位。
对行波进位加法/减法器的解读
1.行波进位加/减法器 n个1位的全加器(FA)可级联成一个n位
的行波进位加减器
2.M为方式控制输入线(控制进行加法,还 是减法运算):
4. n位行波进位加法器的延迟时间ta的计算 当前位全加和Si必须等低位进位Ci-1来到
后才能进行,加法时间与位数有关。
定义T:单级逻辑电路的单位门延迟 3T:异或门的延迟时间
FA逻辑电路和框图
11位位补补码码运运算算的的加加法法减减法法器器FA
加法器开启之后经过3T:
• 确定了是加运算还是减运算
当M=0时,作加法(A+B)运算; 当M=1时,作减法(A-B)运算;
224 基本的二进制加法减法器图22(a)示出了补码运算的二进(3)
B0y(v%s#oXlUiQfNbK8H5D2A+ x*u$qZnWkShPeMaJ7F4C 1z) w&t!pYmVj RgOcL9I6E3B0y( v% r#oXlTi QfNbK8G5D2A- x*u$qZnVkShPdMaJ7F4C 0z) w&s!pYmUjRfOc L9H6E3B+ y(u%r#oWlTiQeN bJ8G5D1A- x* t$qZnVkSgPdMaI7F4C0z) v&s!pXmUjRfOcK9H6E2B+ y( u%rZoWlThQeNbJ8G4D1A - w*t$qYnVjSgPdLaI7F3C0y) v&s#pXmUiRfOcK9H 5E2B+ x(u%r ZoWkT hQeMbJ8G4D 1z- w*t!qYnVjSgOdLaI6F3C0y) v%s #pXlUi RfNcK8H5E2A+ x(u$r ZnWkT hPeMbJ7G4C 1zw&t!qYmVjSgOdL9I6F3B0y)v% s#oXlU iQfNc K8H5D 2A+ x*u$rZnWkShPeMaJ7G4C1z) w&t!pYmVjRgOcL9I6E3B0y( v%r#oXl TiQfN bK8H5D2A- x* u$qZnWkShPdMaJ7F 4C1z) w&s!pYmUjRgOcL9H 6E3B+ y( v%r#oWlTi QeNbK8G5D1A- x*t$qZnVkSgPdMaI7F4C0z) w&s!pXmUj RfOcL9H6E2B+ y(u%r#oWl ThQeN bJ8G5D1A- w* t$qYnVkSg PdLaI7F3C0z) v&s#pXmUiRfOcK9H5E2B+ x( u%rZoW kThQeMbJ8G4D1A
模拟电子技术基础-第七章信号的运算和处理

在模拟电子技术中,信号的乘法运算是一种重要的运算方式。通过将一个信号 与另一个信号对应时间点的值相乘,可以得到一个新的信号。这种运算在信号 处理中常用于调制和解调、放大和衰减等操作。
除法运算
总结词
信号的除法运算是指将一个信号除以另一个信号,得到一个新的信号。
详细描述
在模拟电子技术中,信号的除法运算也是一种重要的运算方式。通过将一个信号除以另一个信号,可以得到一个 新的信号。这种运算在信号处理中常用于滤波器设计、频谱分析和控制系统等领域。需要注意的是,除法运算可 能会引入噪声和失真,因此在实际应用中需要谨慎使用。
减法运算
总结词
信号的减法运算是指将一个信号从另一个信号中减去,得到一个新的信号。
详细描述
信号的减法运算在模拟电子技术中也是常用的一种运算方式。通过将一个信号从 另一个信号中减去,可以得到一个新的信号。这种运算在信号处理中常用于消除 噪声、提取特定频率成分或者对信号进行滤波等操作。
乘法运算
总结词
信号的乘法运算是指将一个信号与另一个信号对应时间点的值相乘,得到大是指通过电子电路将输入的微弱信号放大到所需 的幅度和功率,以满足后续电路或设备的需要。
放大器的分类
根据工作频带的不同,放大器可以分为直流放大器和交流 放大器;根据用途的不同,放大器可以分为功率放大器、 电压放大器和电流放大器。
放大器的应用
在通信、音频、视频等领域,放大器是必不可少的电子器 件,例如在音响系统中,我们需要使用功率放大器来驱动 扬声器。
信号调制
信号调制的概念
信号调制是指将低频信息信号加载到 高频载波信号上,以便于传输和发送。
调制方式的分类
调制技术的应用
在无线通信中,调制技术是必不可少 的环节,通过调制可以将信息信号转 换为适合传输的载波信号,从而实现 信息的传输。
位可控加减法器设计32位算术逻辑运算单元

【位可控加减法器设计32位算术逻辑运算单元】1. 引言位可控加减法器是现代计算机中十分重要的组成部分,它可以在逻辑电路中实现对算术运算的功能。
其中,32位算术逻辑运算单元是计算机中非常常见的一个部件,它可以用来进行32位数据的加法、减法和逻辑运算。
本文将就位可控加减法器的设计和32位算术逻辑运算单元进行全面评估,并给出深度和广度兼具的解析。
2. 什么是位可控加减法器位可控加减法器是一种灵活的算术逻辑电路,它可以根据控制信号来选择进行加法运算或减法运算。
这种设计可以大大提高电路的灵活性和适用性,使得算术运算单元可以在不同的情况下实现不同的运算需求。
3. 32位算术逻辑运算单元的设计原理32位算术逻辑运算单元是计算机中进行32位数据运算的核心部件,它通常包括加法器、减法器、逻辑门等组件。
在设计中,需要考虑到加法器和减法器的位宽、进位和溢出等问题,同时还需要考虑逻辑门的多功能性和灵活性。
通过合理的组合和控制,可以实现对32位数据进行高效的算术逻辑运算。
4. 位可控加减法器设计在32位算术逻辑运算单元中的运用位可控加减法器的设计可以很好地应用在32位算术逻辑运算单元中,通过控制信号来选择进行加法或减法运算,从而满足不同情况下对数据的处理需求。
这种设计不仅能简化电路结构和控制逻辑,还能提高算术逻辑运算单元的灵活性和效率,使其更适用于不同的场景和运算需求。
5. 个人观点和理解从我个人的理解来看,位可控加减法器设计在32位算术逻辑运算单元中的应用,可以很好地提高计算机的运算效率和灵活性。
通过合理的设计和控制,可以使得算术逻辑运算单元在不同的情况下具有不同的功能,从而更好地满足计算机对于数据处理的需求。
这种设计也为计算机的设计和优化提供了很好的思路和方法。
6. 总结通过本文的评估和解析,我们对于位可控加减法器的设计以及在32位算术逻辑运算单元中的应用有了更深入的理解。
通过灵活的控制信号,可以实现算术逻辑运算单元在不同情况下对数据进行不同的处理,从而提高了计算机的运算效率和灵活性。
logisim加法器和减法器的原理

logisim加法器和减法器的原理Logisim加法器和减法器的原理一、引言Logisim是一款数字电路模拟软件,可以用于设计和模拟各种数字电路。
在数字电路中,加法器和减法器是最基本的运算电路,用于实现数字的加法和减法运算。
本文将介绍Logisim中加法器和减法器的原理及其实现方法。
二、Logisim加法器的原理加法器是一种用于实现数字加法运算的电路。
在Logisim中,常用的加法器电路是全加器电路。
全加器电路可以实现三个二进制数相加的功能,其中包括两个输入数和一个进位输入。
全加器电路的输出为相加结果和进位输出。
在Logisim中,全加器电路由三个半加器和一个或门组成。
半加器用于实现两个二进制位的相加,其中包括两个输入位和一个进位输入。
半加器的输出为相加结果和进位输出。
全加器电路的输入为两个二进制数和一个进位输入,输出为相加结果和进位输出。
三、Logisim减法器的原理减法器是一种用于实现数字减法运算的电路。
在Logisim中,常用的减法器电路是全减器电路。
全减器电路可以实现两个二进制数相减的功能,其中包括两个输入数和一个借位输入。
全减器电路的输出为相减结果和借位输出。
在Logisim中,全减器电路由三个半减器和一个与非门组成。
半减器用于实现两个二进制位的相减,其中包括两个输入位和一个借位输入。
半减器的输出为相减结果和借位输出。
全减器电路的输入为两个二进制数和一个借位输入,输出为相减结果和借位输出。
四、Logisim加法器和减法器的实现在Logisim中,可以通过将多个全加器或全减器电路连接起来实现多位数的加法和减法运算。
具体实现方法如下:1. 加法器的实现:将多个全加器电路按照位数连接起来,每个全加器的进位输出与下一个全加器的进位输入相连。
最低位的全加器的进位输入可以连接到一个常数输入,表示初始的进位。
最后,将每个全加器的相加结果输出连接到一个输出端口,即可实现多位数的加法运算。
2. 减法器的实现:将多个全减器电路按照位数连接起来,每个全减器的借位输出与下一个全减器的借位输入相连。
加法器减法器

加法器和减法器加法器加法器是为了实现加法的。
即是产生数的和的装置。
加数和被加数为输入,和数与进位为输出的装置为半加器。
若加数、被加数与低位的进位数为输入,而和数与进位为输出则为全加器。
常用作计算机算术逻辑部件,执行逻辑操作、移位与指令调用。
对于1位的二进制加法,相关的有五个的量:1,被加数A,2,被加数B,3,前一位的进位CIN,4,此位二数相加的和S,5,此位二数相加产生的进位COUT。
前三个量为输入量,后两个量为输出量,五个量均为1位。
对于32位的二进制加法,相关的也有五个量:1,被加数A(32位),2,被加数B(32位),3,前一位的进位CIN(1位),4,此位二数相加的和S(32位),5,此位二数相加产生的进位COUT(1位)。
要实现32位的二进制加法,一种自然的想法就是将1位的二进制加法重复32次(即逐位进位加法器)。
这样做无疑是可行且易行的,但由于每一位的CIN都是由前一位的COUT提供的,所以第2位必须在第1位计算出结果后,才能开始计算;第3位必须在第2位计算出结果后,才能开始计算,等等。
而最后的第32位必须在前31位全部计算出结果后,才能开始计算。
这样的方法,使得实现32位的二进制加法所需的时间是实现1位的二进制加法的时间的32倍。
基本方法可以看出,上法是将32位的加法1位1位串行进行的,要缩短进行的时间,就应设法使上叙进行过程并行化。
类型以单位元的加法器来说,有两种基本的类型:半加器和全加器。
半加器有两个输入和两个输出,输入可以标识为 A、B 或 X、Y,输出通常标识为合 S 和进制 C。
A 和 B 经 XOR 运算后即为 S,经 AND 运算后即为 C。
全加器引入了进制值的输入,以计算较大的数。
为区分全加器的两个进制线,在输入端的记作 Ci 或 Cin,在输出端的则记作 Co 或Cout。
半加器简写为 H.A.,全加器简写为 F.A.。
半加器:半加器的电路图半加器有两个二进制的输入,其将输入的值相加,并输出结果到和(Sum)和进制(Carry)。
算术运算电路

算术运算电路算术运算是数字系统的基本功能,更是计算机中不可缺少的组成单元。
本节介绍加法运算和减法运算的逻辑电路。
一、半加器和全加器1.半加器半加器和全加器是算术运算电路中的基本单元,它们是完成1位二进制数相加的一种组合逻辑电路。
两个1二进制的加法运算如下表所示,其中S表示和数C表示进位数。
由表中逻辑关系可见,这种加法运算只考虑了两个加数本身,而没有考虑由低位来的进位,所以称为半加。
半加器就是实现下面这个真值表关系的电路。
由真值表可得逻辑表达式运用逻辑代数,可将上式变换成与非形式根据这两个表达式可得由与非门组成的半加器:因为半加和是异或关系,所以半加器也可利用一个集成异或门和与门来实现:图中右边是半加器的代表符号。
2.全加器全加器能进行加数、被加数和低位来的进位信号相加,并根据求和结果给出该位的进位信号。
根据全加器的功能,可列出它的真值表:其中Ai和Bi分别是被加数及加数,Ci-1为相邻低位来的进位数,Si 为本位和数(称为全加和)。
以及Ci为向相邻高位的进位数。
为了求出Si和Ci的逻辑表达式,首先分别画出Si和Ci的卡诺图:为了比较方便地获得与-或-非的表达式,采用包围0的方法进行化简得:据此可以画出1位全加器的逻辑图:二、多位数加法器1.串行进位加法器若有多位数相加,则可采用并行相加串行进位的方式来完成。
例如,有两个4位二进制数A3A2A1A0和B3B2B1B0相加,可以采用两片内含两个全加器或1片内含4个全加器的集成电路组成,其原理图如下图所示:由图可以看出,每1位的进位信号送给下1位作为输入信号,因此,任1位的加法运算必须在低1位的运算完成之后才能进行,这种进位方式称为串行进位。
这种加法器的逻辑电路比较简单,但它的运算速度不高。
为克服这一缺点,可以采用超前进位等方式。
2.超前进位集成4位加法器74LS283由于串行进位加法器的速度受到进位信号的限制,人们又设计了一种多位数超前进位加法逻辑电路,使每位的进位只由加数和被加数决定,而与低位的进位无关。
224 基本的二进制加法减法器图22(a)示出了补码运算的二进

对一位全加器(FA)来说,Si的时间延迟 为6T(每级异或门延迟3T),Ci+1的时间 延迟为5T,其中T被定义为相应于单级 逻辑电路的单位门延迟。T通常采用 一个“与非”门或一个“或非”门的 图2.2(b) 行波进位的补码加法/减法器 时间延迟来作为度量单位。
现在我们计算一个n位的行波进位加法器的时间延迟。假如采用 图2.2(b)所示的一位全加器并考虑溢出检测,那么n位行波进位加 法器的延迟时间ta为 t a= n · 2T+9T=(2n+9)T (2.22)
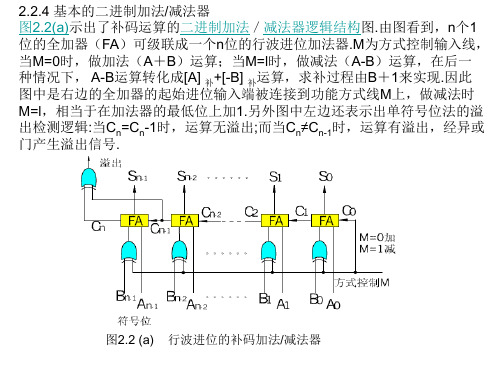
2.2.4 基本的二进制加法/减法器 图2.2(a)示出了补码运算的二进制加法/减法器逻辑结构图.由图看到,n个1 位的全加器(FA)可级联成一个n位的行波进位加法器.M为方式控制输入线, 当M=0时,做加法(A+B)运算;当M=l时,做减法(A-B)运算,在后一 种情况下, A-B运算转化成[A] 补+[-B] 补运算,求补过程由B+1来实现.因此 图中是右边的全加器的起始进位输入端被连接到功能方式线M上,做减法时 M=l,相当于在加法器的最低位上加1.另外图中左边还表示出单符号位法的溢 出检测逻辑:当Cn=Cn-1时,运算无溢出;而当Cn≠Cn-1时,运算有溢出,经异或 门产生溢出信号.
2.2.5 十进制加法器
十进制加法器可由BCD码(二-十进制码)来设计,它可以在 二进制加法器的基础上加上适当的“校正”逻辑来实现, 该校正逻辑可将二进制的“和”改变成所要求的十进制格 式。 n位BCD码行波式进位加法器的一般结构如图 2.3(a)所示,它由n级组成,每一级将一对4位的BCD数字相 加,并通过一位进位线与其相邻级连接。而每一位十进制 数字的BCD加法器单元的逻辑结构示于图2.3(b)。 在十进制运算时,当相加二数之和大于9时,便产生进位。可 是用BCD码完成十进制数运算时,当和数大于9时,必须对和 数进行加6修正。这是因为,采用BCD码后,在二数相加的和 数小于等于9时,十进制运算的结果是正确的;而当相加的 和数大于9时,结果不正确,必须加6修正后才能得出正确的 结果。因此,当第一次近似求值时,可将它看成每一级是一 个4位二进制加法器来执行,就好像xi和yi是普通4位二进 制数一样。
集成运放中的加法和减法运算电路

五、思考题
为了不损坏集现方式做保护处理对用户上传分享的文档内容本身不做任何修改或编辑并不能对任何下载内容负责
一、实验目的
1
研究由集成运算放大器组成的比例、加 法、减法和积分等基本运算电路的功能。 了解运算放大器在实际应用时应考虑的 一些问题。
2
二、实验原理
集成运算放大器是一种具有高电压放大倍数 的直接耦合多级放大电路。当外部接入不同的线 性或非线性元器件组成输入和负反馈电路时,可 以灵活地实现各种特定的函数关系。在线性应用
由于
V A VB
V V V i 1 A V A 0 i if 2 R R 1 f
VB V i2 Rf R 1 Rf
(已知 R ) 3 R f
所以
V 0
Rf R 1
V V i1 i2
3、积分器是指输出信号为输入信号积分后的结果, 用数学关系表示为:
y
方面,可组成比例、加法、减法、积分、微分、
对数等模拟运算电路。
基本运算电路 1.加法器是指输出信号为几个输入信号之和 的放大器。
用数学式子表示为:
yx x 1 x 2 n
i i i i i 1 2 3 n f
V i 1 V i 2 V i3 R R R V n i i f R
xdt
0
t
下图是最基本的积分器的结构图。
这里反馈网络的一个部分用电容来代替电阻, 则有:
Ii IC
i
而
I
V i R
,
IC
d V0 C dt
t 1 V V 0 idt 0 R C
上式表示了输出信号是输入信号积分的结果。
数字电路中加法器和减法器逻辑图分析

数字电路中加法器和减法器逻辑图分析1.加法器,减法器都是从一位的二进制数开始进行例题讲解,逐渐扩展到多位二进制位数之间的运算。
在设计逻辑电路的过程中,根据所描述的功能构建好真值表。
出题者喜欢要求读者用与或门,与或非门构建函数表达式。
它的原因在于依据真值表写函数表达式,最标准的就是最小项表达式。
以下小图的逻辑图来看与或门,我们的头脑中不能老是思维定势,认为输入就是两个,在实际生活中,输入应该非常多,远非两个,在逻辑符号中,要清楚地认识与非门的多输入的画法,将与门分成了好几格,每一格代表一个与门电路。
下小图可以写成AB+CD+EF(不认真考虑前面的输入),由细小的门集成为更大的门,将某一部分单独来看,它们就是一个整体,如(AB+CD+EF),体现在逻辑图中就是一个角。
如果从全图的角度看,在最后一级门电路中,每一个小整体代表着输出。
最后一级的与门中,有两个输入,有三个输入,这都是可以的,最多输入的个数是依照初始的输入的个数来定,不可能超过这个数,只可能少于这个数,因为对于某一输出而言,并非所有的输入对它都是有效的。
从最左边的所有输入,经过逻辑电路图,在最右边得到了所有的输出。
还有一点,这是与或表达式的逻辑图,如果在写逻辑表达式,包括化简变化函数式时,采用了不同于与或形式的表达式,那么最终得到的逻辑图就和下面的与或形式的逻辑图完全不一样。
2.一位的全减器是指,两个一位的二进制数之间进行减法运算。
全减器的特例就是半减器。
多位二进制减法器,是由加法电路构成的;在加法电路的基础上,减法与加法采用同一套电路,实现加减法共用。
3.这里的多位二进制数的减法,是指无符号数,为什么?将减法运算转换为加法运算,采用的是补数的方法完成的。
这就解释了为什么两者能共用一套电路,是不是减法在转换时,我们需要在加法电路的基础上进行一些小的扩展,来进行减法的补码转换?N反是每一位都取反,没有符号位,下式当中,A-B是减法,通过形式转化,将-B化为B反+1-2n,B是正数,A和B均为无符号数,通过补码的转变,我们成功的将-B变为了固定的-2n,但是这还是有减号,该怎么解决?仔细观察下面这张图,A和B是两个四位二进制数相减。
例:试用四位二进制加法器74283构成可控的加法、减法器(允许附加

实现加法 加法运算 X=0: 实现加法运算 实现减法 减法运算 X=1: 实现减法运算
S'0 S'1 S'2
0
Σ
A 0
S0 S1 S2
Σ 进位
B 3
S'2 S'3
S' =1 3 3
Σ 进位
3 B
3
0
1 0
CO CI
C' =1 C= C'
S3
S' 和 为 取 S’ 反 不 加 1 变
&
0 C'
3
CO CI
X 控制端X: 控制端 控制端X: 控制端
X=0: 实现加法运算 实现加法 加法运算 实现减法 减法运算 X=1: 实现减法运算
Σ
0
S'0 S'1 S'2
=A补+(-B)反+1 ( )
按位取反
B0 B1 B2 B3
1 1 1 1
Σ 进位
3
和S'
S'3
CO
1
C'
CIቤተ መጻሕፍቲ ባይዱ
借位C'为进位取反 借位 为进位取反
分析: 分析: A与B相减的结果 与采用补码相加的比较 与 相减的结果 1. A-B≥0时 时 求A-B A补 A=0101 补码相加 0101 B=0001 直接相减 A 0101 - B 0001 0100
加异或门求反
C'
CI
S' =(A+(-B))补 =(A+(-B))原 =A-B
C' =1, 实现加1 C' =0, 不实现加1
A0 A1 A2 A3 B0 B1 B2 B3 =1 =1 =1 =1 B0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子设计自动化大作业题目加法器与减法器学院泉城学院班级电气09Q2班姓名李文建学号 20093005034二O一一年十一月六日加法器和减法器一、设计要求:(1)构造一个四位二进制加法器和一个四位二进制减法器,完成各自的功能仿真。
(2)利用四个按键输入四位加数(或减数)和被加数(或被减数)。
(3)用七段数码管显示四位和(或差),用一只发光二极管指示进位(或借位)信号。
(4)利用个开关控制,确定是四位二进制加法器还是一个四位二进制减法器。
二、总体设计:1、总体结构图2、各模块功能(1)第一个4-16译码器实现输入四位加数(或减数)和被加数(或被减数)。
(2)开关模块:控制B0、B1、B2、B3,当M=0时,执行A+B,当M=1时,执行A-B。
(3)加法(减法)器模块:加法器:采用全加器的串行进位,本四位二进制加法器由四个一位二进制加法器组成,输入A i、B i、C i,输出S i、C i+1。
减法器:与加法器的区别仅仅在于最后的和数为两数相减。
(4)LED灯:加法器:灯亮表示有进位,灯灭表示无进位。
减法器:灯亮表示有借位,灯灭表示无进位。
(5)第二个4-16译码器:输入为四为加法器的和S0、S1、S2、S3,输出为Y0—Y6分别控制七段数码管的a1、b1、c1、d1、e1、f1、g1,输出Y9—Y15分别控制第二个七段数码管的a2、b2、c2、d2、e2、f2、g2。
(6)数码管:显示输出结果。
三、单元模块设计1、第一个4—16译码器(1)模块功能通过四个按键输入四位二进制数,由译码器得到四位加数(或减数)和被加数(或被减数)的所有组合,从而实现加法器(或减法器)的输入。
(2)端口定义输入端:X0、X1、X2、X3。
输出端:Y[0…15]。
Y[0…3]分别接到A[0…3],Y[4…6]分别接到B[0…3]。
(3)VHDL源程序library IEEE;use IEEE.STD_LOGIC_1164.ALL;entity Decoder isPort (DIN : in std_logic_vector(3 downto 0);DOUT : out std_logic_vector(15 downto 0) );end Decoder;architecture rtl of Decoder isbeginprocess (DIN) begincase(DIN) iswhen "0000" => DOUT <= "0111111111111111";when "0001" => DOUT <= "1011111111111111";when "0010" => DOUT <= "1101111111111111";when "0011" => DOUT <= "1110111111111111";when "0100" => DOUT <= "1111011111111111";when "0101" => DOUT <= "1111101111111111";when "0110" => DOUT <= "1111110111111111";when "0111" => DOUT <= "1111111011111111";when "1000" => DOUT <= "1111111101111111";when "1001" => DOUT <= "1111111110111111";when "1010" => DOUT <= "1111111111011111";when "1011" => DOUT <= "1111111111101111";when "1100" => DOUT <= "1111111111110111";when "1101" => DOUT <= "1111111111111011";when "1110" => DOUT <= "1111111111111101";when "1111" => DOUT <= "1111111111111110";when others => DOUT <= "1111111111111111";end case;end process;end rtl;2、开关模块(1)模块功能实现加法器和减法器的选择功能(2) VHDL源程序If(M=0)ENTITY adder isPORT(clk : in STD_LOGIC;Din1 :in signed (3downto 0);Din2 :in signed (3 downto 0);Dout:out signed (3 downto 0));END adder;If(M=1)ENTITY suber isPORT(clk : in STD_LOGIC;Din1 :in signed (13 downto 0);Din2 :in signed (15 downto 0);Dout :out signed(15 downto 0));END suber;3、加法(减法)器模块(1)模块功能实现两个二进制数字的相加(相减)运算。
当到达时钟上升沿时,将两数输入,运算,输出结果。
(2)端口定义输入端:A[0…3]B[0…3]C0输出端:S[0…3]C3(3)VHDL源程序一位全加器:library ieee;use ieee.std_logic_1164.all;entity edder1_VHDL isport(a,b,cin:in std_logic;sum,cout:out std_logic);end edder1_VHDL;architecture full1 of edder1_VHDL is beginsum<=(a xor b)xor cin;cout<=(a and b)or (cin and a)or (cin and b);end full1;一位减法器:library ieee;use ieee.std_logic_1164.all;entity suber1_VHDL isport(a,b,cin:in std_logic;sum,cout:out std_logic);end suber1_VHDL;architecture full2 of suber1_VHDL isbeginsum<=((a and (not b))or ((not a)and b));cout<=(not a)and b;end full2;(4)仿真结果加法器:减法器4、LED灯表示进位(或借位)5、第二个4-16译码器(1)模块功能将加法器(或减法器)得到的结果经译码器由七段数码管表示。
(2)端口定义输入端:S[0…3]输出端:Y[0…15](3) VHDL源程序library IEEE;use IEEE.STD_LOGIC_1164.ALL;entity Decoder isPort (DIN : in std_logic_vector(3 downto 0);DOUT : out std_logic_vector(15 downto 0) );end Decoder;architecture rtl of Decoder isbeginprocess (DIN) begincase(DIN) iswhen "0000" => DOUT <= "0111111111111111";when "0001" => DOUT <= "1011111111111111";when "0010" => DOUT <= "1101111111111111";when "0011" => DOUT <= "1110111111111111";when "0100" => DOUT <= "1111011111111111";when "0101" => DOUT <= "1111101111111111";when "0110" => DOUT <= "1111110111111111";when "0111" => DOUT <= "1111111011111111";when "1000" => DOUT <= "1111111101111111";when "1001" => DOUT <= "1111111110111111";when "1010" => DOUT <= "1111111111011111";when "1011" => DOUT <= "1111111111101111";when "1100" => DOUT <= "1111111111110111";when "1101" => DOUT <= "1111111111111011";when "1110" => DOUT <= "1111111111111101";when "1111" => DOUT <= "1111111111111110";when others => DOUT <= "1111111111111111";end case;end process;end rtl;(4) 仿真结果6、七段数码管(1)模块功能显示加法器与减法器输出的结果。
